ОПРЕДЕЛЕНИЕ УСЛОВНОГО ПРЕДЕЛА ТЕКУЧЕСТИ МЕТАЛЛА ПО КИНЕТИЧЕСКОЙ ДИАГРАММЕ ВДАВЛИВАНИЯ СФЕРИЧЕСКОГО ИНДЕНТОРА | Матюнин
1. Марковец М. П. Построение диаграммы истинных напряжений по твердости и технологической пробе / Журнал технической физики. 1949. Т. XIX. Вып. 3. С. 371 — 382.
2. Марковец М. П. Определение механических свойств металлов по твердости. — М.: Машиностроение, 1979. — 191 с.
3. Дегтярев В. И. Исследование диаграмм твердости и их связи с механическими свойствами металлов. Автореф. дис.. канд. техн. наук. — М., 1974. — 24 с.
4. Шабанов В. М. Разработка и внедрение метода определения комплекса физико-механических свойств материалов непрерывным вдавливанием.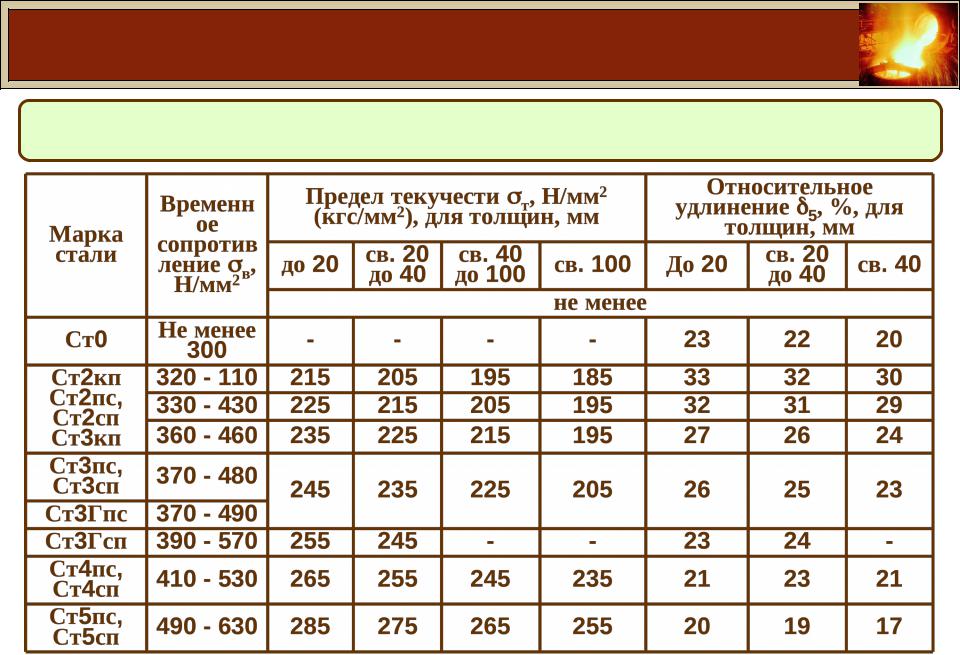
Автореф. дис.. канд. техн. наук. — М., 1988. — 18 с.
5. Бакиров М. Б. Разработка методов и средств контроля механических свойств металла корпуса ВВЭР в процессе эксплуатации по твердости. Автореф. дис.. канд. техн. наук. — М., 1990. — 28 с.
6. Бакиров М. Б., Потапов В. В. Феноменологическая методика определения механических свойств корпусных сталей ВВЭР по диаграмме вдавливания шарового индентора / Заводская лаборатория. Диагностика материалов. 2000. Т. 66. № 12. С. 35 — 44.
7. Матюнин В. М. Индентирование в диагностике механических свойств материалов. — М.: Издательский дом МЭИ, 2015. — 288 с.
8. Шабанов В. М. Сопротивление металлов начальной пластической деформации при вдавливании сферического индентора / Заводская лаборатория.
Диагностика материалов. 2008. Т. 74. № 6. С. 63 — 69.
9. Martens A., Heyn E. Vorrichtung zur vereinfachten Prüfung der kugeldruckharte / Z. VDI. 1908. Bd. 52. N43. S. 1719.
11. Дрозд М. С., Матлин М. М., Сидякин Ю. И. Инженерные расчеты упругопластической контактной деформации. — М.: Машиностроение, 1986. — 224 с.
12. Пилипчук Б. И. Обзор теорий твердости. — М. — Л.: Стандартгиз, 1962. — 112 с.
13. Матюнин В. М. Методика определения напряжения в области перехода упругой деформации в упругопластическую при растяжении образцов / Заводская лаборатория.
14. Матюнин В. М. Критические нагрузки и параметры отпечатка в начальной стадии пластического контакта шара с плоской поверхностью металла / Заводская лаборатория. Диагностика материалов. 2007. Т. 73. № 4. С. 62 — 65.
15. Матлин М. М. Методика оперативного контроля модуля нормальной упругости / Тезисы докладов Всероссийской научно-технической конференции «Физико-механические свойства материалов и их экспрессная оценка неразрушающим методом и портативными средствами». — Волгоград: ВГТУ, 1995. С. 27 — 29.
Кривая пластичности при расчете прочности МКЭ
Анализ конструкций при нагрузках, приводящих к пластическим деформациям – это то, с чем часто приходится сталкиваться инженерам при проведении расчетов прочности методом конечных элементов.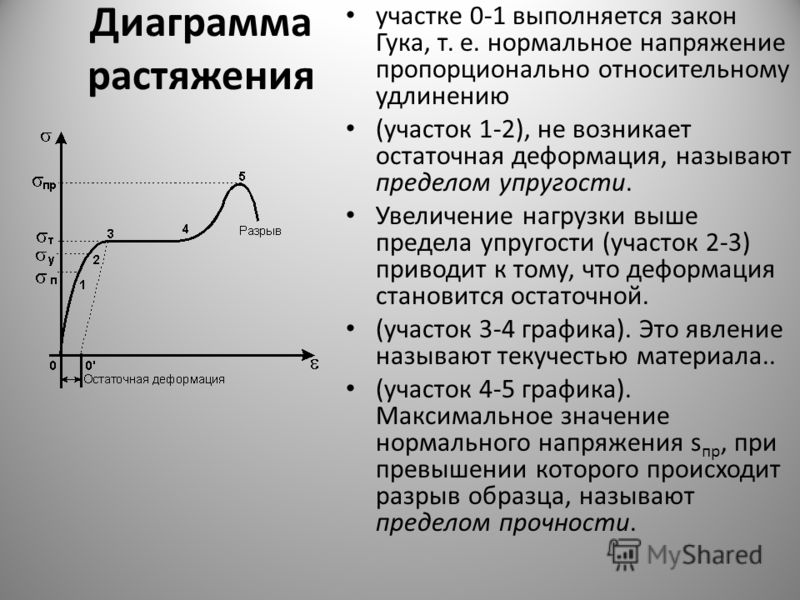
Для точного выполнения подобных расчетов необходимо правильно задавать механические свойства материалов за пределом текучести.
Кривую пластичности для металлов можно получить с помощью эксперимента на одноосное растяжение образца. Выходными данными экспериментальной установки является диаграмма «сила-удлинение». Как эта информация может быть использована для описания поведения материала? Приблизиться к ответу на этот вопрос можно, разделив значения нагрузки на площадь поперечного сечения образца (инженерные напряжения), а значения удлинения — на начальную длину образца (инженерные относительные деформации). На получившейся диаграмме напряжения-деформация можно выделить два характерных уровня напряжений: условный предел текучести (или просто предел текучести), а также предел временного сопротивления (или предел прочности).
Участок диаграммы от предела текучести до предела прочности называется зоной упрочнения. Напряжения будут продолжать увеличиваться с ростом деформаций до тех пор, пока упрочнение будет компенсировать уменьшение площади поперечного сечения образца.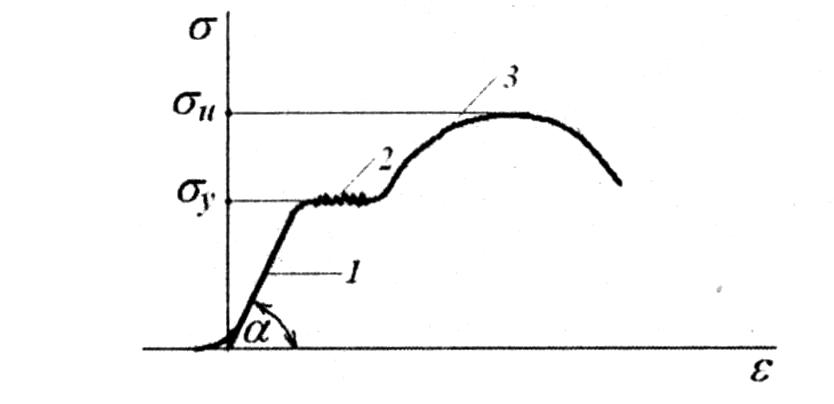
Если информация об актуальном напряженном состоянии важна, например, при моделировании методом конечных элементов, то для описания поведения материала потребуется уточненный подход. Рассмотрим, как конвертировать экспериментальные данные для их использования при конечно-элементном моделировании.
Уравнения, связывающие инженерные напряжения (engineering stress) и инженерные относительные деформации (engineering strain) с истинными напряжениями и истинные полными деформациями (true stress – true total strain) действительны вплоть до предела прочности.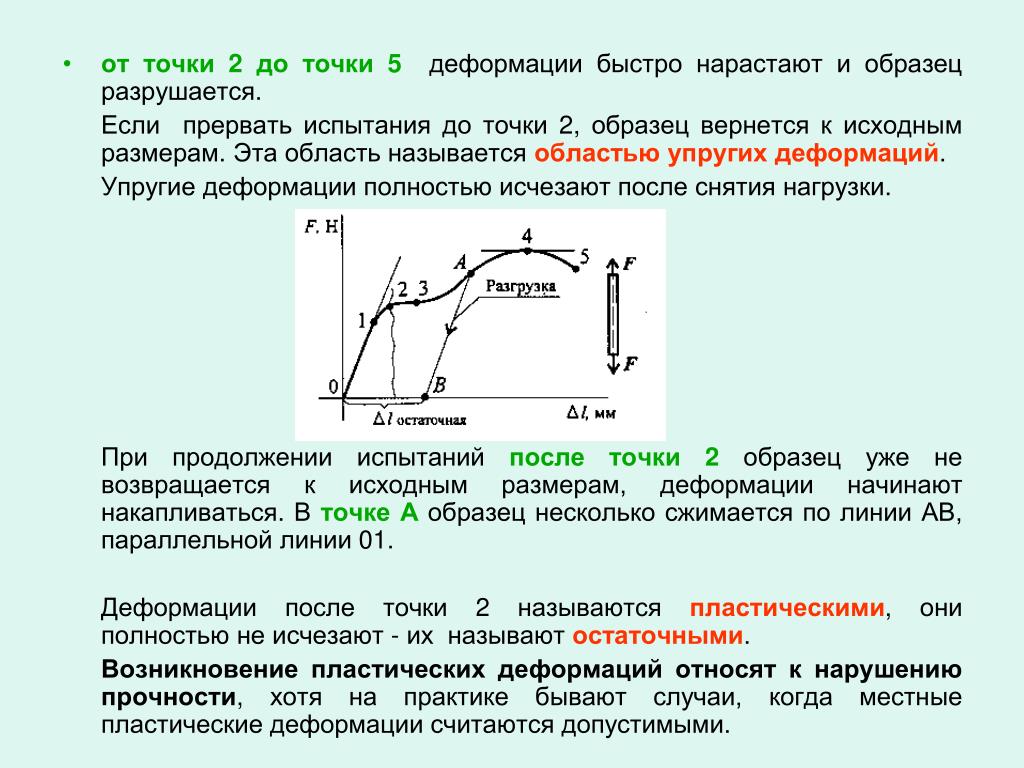
На рисунке ниже показано сравнение диаграмм инженерных и истинных напряжений:
Модуль упругости (Modulus) = истинные напряжения, в точке, соответствующей значению предела текучести (TrueStress)/истинные полные деформации в этой же точке (TrueStrain).
Далее, нужно перевести инженерные напряжения и инженерные относительные деформации в истинные напряжения и истинные полные деформации, используя формулы (1) и (2). Затем вычесть истинные упругие деформации из истинных полных деформаций в каждой точке, чтобы определить истинные пластические деформации (истинные пластические деформации (TruePlasticStrain) = истинные полные деформации (TrueTotalStrain) – истинные упругие деформации (TrueElasticStrain)).
Необходимо помнить следующее при анализе и обработке кривой деформации-напряжения:
- Прямолинейный участок кривой «истинные напряжения – истинные полные деформации» определяет наклон, или упругую характеристику материала (т.е. на этом участке справедлив закон Гука: Напряжение = Модуль упругости*Деформация)
- Истинная пластическая деформация находится путем вычитания из значения полной деформации упругой деформации (истинного напряжения, деленного на модуль упругости).
- Истинная полная деформация в точке, соответствующей значению предела текучести, эквивалентна истинной упругой деформации, а истинная пластическая деформация в этой точке равна нулю.
- Если программа для прочностного расчета позволяет задать входные данные в виде «истинные напряжения – истинные полные деформации», то первой точкой зависимости должны быть истинное напряжение, соответствующие пределу текучести и истинная полная деформация в этой же точке.
- Если программа требует ввода входных данных в виде «истинные напряжения- истинные пластические деформации», то первой точкой зависимости должны быть истинное напряжение, соответствующие пределу текучести и истинная пластическая деформация (равна нулю).
- Зависимость истинных напряжений от истинных деформаций вычисляется вплоть до предела прочности. При моделировании можно предполагать, что при достижении этой точки, материал является абсолютно пластичным (т.е. деформации продолжат увеличиваться без увеличения напряжений). Большинство кодов принимают это предположение по умолчанию.
справочник-сталь тонколистовая,
Краткие сведения
Марка 316 — улучшенная версия 304, с дополнением молибдена и немного более высоким никелевым содержанием.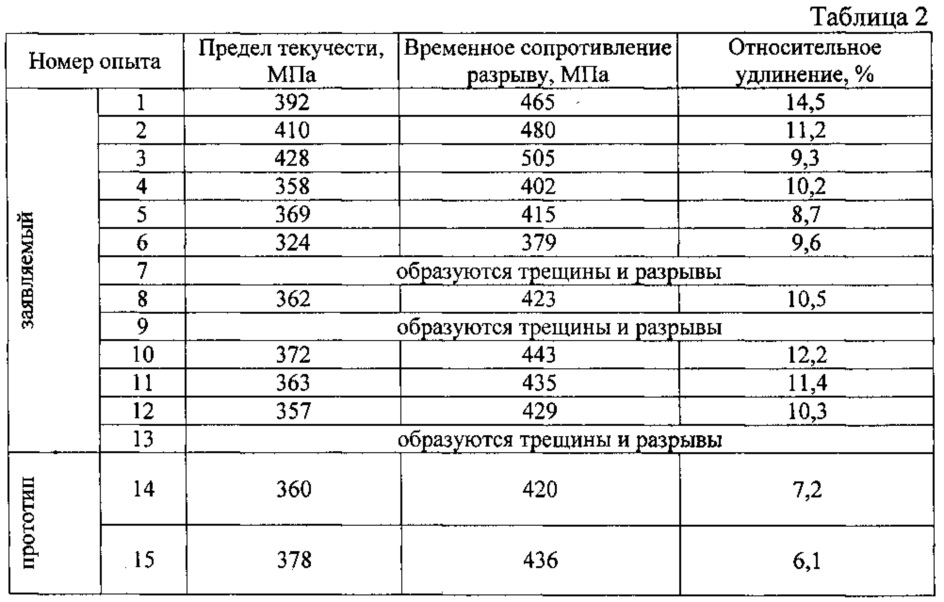
Данная композиция делает 316 значительно повышает коррозионное сопротивление в большинстве агрессивных средах. Молибден делает сталь более защищенной от питтинговой и щелевой коррозии в хлористой среде, морской воде и в парах уксусной кислоты. Более низкий показатель общей коррозии в слегка коррозионных средах дает хорошее коррозионное сопротивление в загрязненной и морской атмосфере.
316-я обладает более высокая прочностью и имеет лучшее сопротивление ползучести в более высоких температурах, чем 304. 316 ТАКЖЕ обладает отличными механическими и коррозионными свойствами в под-нулевых температурах. Когда есть опасность коррозии в околошовных сварных зонах , 316L должно быть использовано низко-углеродная марка — 316L. 316 Ti, стабилизированная титаном версия, используется для сопротивления сенсибилизации в течение продолжительного времени в температурном диапазоне 550oC -800oC.
Область применения
Из-за своего выдающегося сопротивления коррозии и окислению, хороших механических свойств и технологичности, 316 имеет приложения во многих секторах промышленности.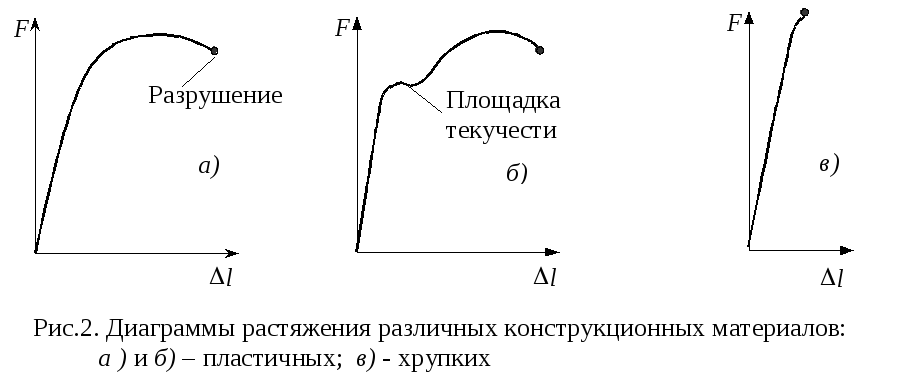
Некоторые из них включают:
Баки и судна для хранения коррозионных жидкостей.
Специализированное промышленное оборудование в химическом, продовольственном, бумажно-целюлозном, горнодобывающем, фармацевтическом и нефте-химическом секторах экономики..
Архитектурные приложения в очень коррозионных средах.
Химический Состав (ASTM A240)
|
| C
| Mn
| P
| S
| Si
| Cr
| Ni
| Mo
| Ti
|
| 316
316L 316Ti | 0.08 max
0.  03 max
0.08 max | 2.0
max | 0.045
max | 0.030
max | 1.0
max | 16.0
to 18.0 | 10.0
to 14.0 | 2.00
to 3.00 | —
0.5 max 5X%C |
Типичные Свойства в Отожженном Состоянии
Свойства, указанные в этой публикации типичны для производства одного из заводов и не должны быть расценены как гарантируемые минимальные значения для целой спецификации.
1. Механические Свойства при комнатной температуре
|
| 316
| 316L
| 316Ti
| |||
|
| Типичн
| Min
| Типичн
| Min
| Типичн
| Min
|
| Rp m
Предел прочности (при растяжении), N/mm2 | 580
| 515
| 570
| 485
| 600
| 515
|
| Rp0,2
Предел Упругости(текучесть), (0.  2 %), N/mm2
| 310
| 205
| 300
| 170
| 320
| 205
|
| удлинение (% in L = 5.65 So)
| 55
| 40
| 60
| 40
| 50
| 40
|
| Твердость по Бринеллю — НВ
| 165
| -
| 165
| -
| 165
| -
|
| Органолептическая проба Эриксена, мм
| 8 — 10
| -
| 10 — 11
| -
| -
| -
|
| Усталостная прочность, N/mm2
| 260
| -
| 260
| -
| 260
| -
|
2.
Свойства при высоких температурах
Все эти значения относятся только к 316 и 316 Ti .
Для 316L значения не приводятся, потому что её прочность заметно уменьшается выше 425oC.
Предел прочности при повышенных температурах
| Температура,oC
| 600
| 700
| 800
| 900
| 1000
|
| Rp m
Предел прочности (при растяжении), N/mm2 | 460
| 320
| 190
| 120
| 70
|
Минимальные величины Предела Упругости (Ползучесть) при высокой температуре (деформация в 1 % за 10 000 часов)
| Температура, oC
| 550
| 600
| 650
| 700
| 800
|
| Rp1,0
1.  0% пластичная деформация (текучесть) N/mm2
| 160
| 120
| 90
| 60
| 20
|
Максимум, рекомендованных Температур Обслуживания
(Условия окисления)
Непрерывное воздействие 925oC
прерывистые воздействия 870oC
3. Свойства в низких Температурах (316)
| Температура
| oC
| -78
| -161
| -196
|
| Rp m
Предел прочности (при растяжении), N/mm2 | N/mm2
| 400
| 460
| 580
|
| Rp0,2
Предел Упругости, (0.2 %), (условный предел текучести) N/mm2 | N/mm2
| 820
| 1150
| 1300
|
| Ударная вязкость
| J
| 180
| 165
| 155
|
4. Сопротивление Коррозии
4.1 Кислотные среды
примеры приводятся для некоторых кислот и их растворов (наиболее общие значения)
| Температура, oC
| 20
| 80
| ||||||||||
| Концентрация, % к массе
| 10
| 20
| 40
| 60
| 80
| 100
| 10
| 20
| 40
| 60
| 80
| 100
|
| Серная Кислота
| 0
| 1
| 2
| 2
| 1
| 0
| 2
| 2
| 2
| 2
| 2
| 2
|
| Азотная Кислота
| 0
| 0
| 0
| 0
| 0
| 1
| 0
| 0
| 0
| 0
| 1
| 2
|
| Фосфорная Кислота
| 0
| 0
| 0
| 0
| 1
| 2
| 0
| 0
| 1
| 2
| ||
| Муравьиная Кислота
| 0
| 0
| 0
| 1
| 1
| 2
| 0
| 0
| 1
| 1
| 1
| 0
|
Код:
0 = высокая степень защиты — Скорость коррозии менее чем 100 mm/год
1 = частичная защита — Скорость коррозии от 100m до 1000 mm/год
2 = non resistant — Скорость коррозии более чем 1000 mm/год
4.2 Атмосферные воздействия
Сравнение 304-й марки с другими металлами в различных окружающих средах (Скорость коррозии расчитана при 10-летнем подвергании).
| Окружающая среда
| Скорость коррозии (mm/год)
| ||
|
| 316
| Aлюминий -3S
| углеродистая сталь
|
| Сельская
| 0.0025
| 0.025
| 5.8
|
| Морская
| 0.0076
| 0.432
| 34.0
|
| Индустриальная Морская
| 0.0051
| 0.686
| 46.2
|
4.3 Тепловая Обработка
4.3.1 Отжиг.
Высокая температура от 1010oC до 1120 oC и быстрый отпуск (охлаждение) в воздухе или воде. Лучшее сопротивление коррозии получено, когда отжиг при 1070oC, и быстром охлаждении
4.3.2 Отпуск (Снятие напряжения).
Нагрев до 200-400oC с последующим воздушным охлаждением
4.3.3 Горячая обработка (интервал ковки)
Начальная температура: 1150 — 1200oC
Конечная температура: свыше 900oC
Для нарушения действия, ковка должна быть завершено между: 930 и 980oC
Любая горячая обработка должна сопровождаться отжигом.
Обратите внимание: Время для достижения однородности прогрева дольше для нерж. сталей чем для углеродистых сталей — приблизительно в 12 раз
5. Холодная Обработка
316 / 316L, 304 / 304L являясь чрезвычайно прочной, упругой и пластичной, с легкостью находит множество применений. Типичные действия включают изгиб, формовку растяжением, глубокую и ротационную вытяжку.
Механические свойства металлов. Механические свойства сталей. Механические свойства сплавов.
Основными механическими свойствами являются прочность, упругость, вязкость, твердость. Зная механические свойства, конструктор обоснованно выбирает соответствующий материал, обеспечивающий надежность и долговечность конструкций при их минимальной массе. Механические свойства определяют поведение материала при деформации и разрушении от действия внешних нагрузок.
В зависимости от условий нагружения механические свойства могут определяться при:
- Статическом нагружении – нагрузка на образец возрастает медленно и плавно.
- Динамическом нагружении – нагрузка возрастает с большой скоростью, имеет ударный характер.
- Повторно, переменном или циклическим нагружении – нагрузка в процессе испытания многократно изменяется по величине или по величине и направлению.
Для получения сопоставимых результатов образцы и методика проведения механических испытаний регламентированы ГОСТами.
Механические свойства металлов, сталей и сплавов. Прочность.
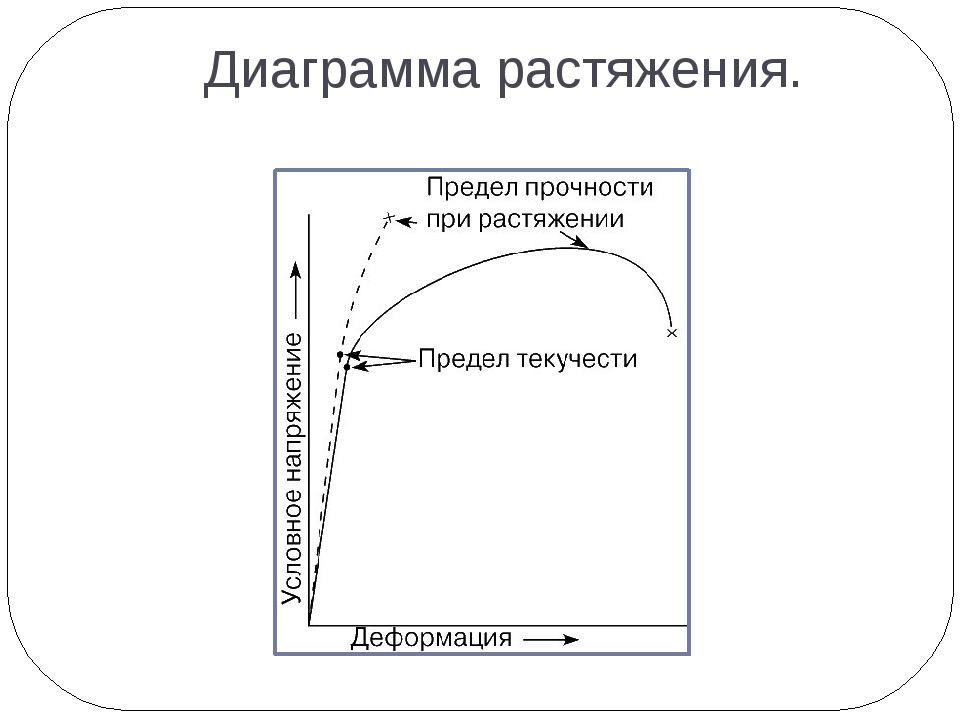
Прочность – способность материала сопротивляться деформациям и разрушению.
Испытания проводятся на специальных машинах, которые записывают диаграмму растяжения, выражающую зависимость удлинения образца Δl (мм) от действующей нагрузки Р, то есть Δl = f(P). Но для получения данных по механическим свойствам перестраивают: зависимость относительного удлинения Δl от напряжения δ.
Диаграмма растяжения материала
Рис 1: а – абсолютная, б – относительная; в – схема определения условного предела текучести
Проанализируем процессы, которые происходят в материале образца при увеличении нагрузки: участок оа на диаграмме соответствует упругой деформации материала, когда соблюдается закон Гука. Напряжение, соответствующее упругой предельной деформации в точке а, называется пределом пропорциональности.
Механические свойства металлов, сталей и сплавов. Предел пропорциональности.
Предел пропорциональности (σпц) – максимальное напряжение, до которого сохраняется линейная зависимость между деформацией и напряжением.
При напряжениях выше предела пропорциональности происходит равномерная пластическая деформация (удлинение или сужение сечения). Каждому напряжению соответствует остаточное удлинение, которое получаем проведением из соответствующей точки диаграммы растяжения линии параллельной оа.
Так как практически невозможно установить точку перехода в неупругое состояние, то устанавливают условный предел упругости, – максимальное напряжение, до которого образец получает только упругую деформацию. Считают напряжение, при котором остаточная деформация очень мала (0,005…0,05%). В обозначении указывается значение остаточной деформации (σ0.05).
Механические свойства металлов, сталей и сплавов. Предел текучести.
Предел текучести характеризует сопротивление материала небольшим пластическим деформациям. В зависимости от природы материала используют физический или условный предел текучести.
Физический предел текучести σm – это напряжение, при котором происходит увеличение деформации при постоянной нагрузке (наличие горизонтальной площадки на диаграмме растяжения). Используется для очень пластичных материалов.
Но основная часть металлов и сплавов не имеет площадки текучести.
Условный предел текучести σ0.2 – это напряжение вызывающее остаточную деформацию δ = 0.20%.
Физический или условный предел текучести являются важными расчетными характеристиками материала. Действующие в детали напряжения должны быть ниже предела текучести. Равномерная по всему объему пластическая деформация продолжается до значения предела прочности. В точке в в наиболее слабом месте начинает образовываться шейка – сильное местное утомление образца.
Механические свойства металлов, сталей и сплавов. Предел прочности.
Предел прочности σв – напряжение, соответствующее максимальной нагрузке, которую выдерживает образец до разрушения (временное сопротивление разрыву).
Образование шейки характерно для пластичных материалов, которые имеют диаграмму растяжения с максимумом. Предел прочности характеризует прочность как сопротивления значительной равномерной пластичной деформации. За точкой В, вследствие развития шейки, нагрузка падает и в точке С происходит разрушение.
Истинное сопротивление разрушению – это максимальное напряжение, которое выдерживает материал в момент, предшествующий разрушению образца (рисунок 2).
Истинное сопротивление разрушению значительно больше предела прочности, так как оно определяется относительно конечной площади поперечного сечения образца.
Истинная диаграмма растяжения
Рис. 2
Fк — конечная площадь поперечного сечения образца.
Истинные напряжения Si определяют как отношение нагрузки к площади поперечного сечения в данный момент времени.
При испытании на растяжение определяются и характеристики пластичности.
Механические свойства металлов, сталей и сплавов. Пластичность.
Пластичность – способность материала к пластической деформации, то есть способность получать остаточное изменение формы и размеров без нарушения сплошности. Это свойство используют при обработке металлов давлением.
Характеристики:
- относительное удлинение:
lо и lк – начальная и конечная длина образца;
Δlост – абсолютное удлинение образца, определяется измерением образца после разрыва.
- относительное сужение:
Fо – начальная площадь поперечного сечения;
Fк – площадь поперечного сечения в шейке после разрыва.
Относительное сужение более точно характеризует пластичность и служит технологической характеристикой при листовой штамповке.
Пластичные материалы более надежны в работе, так как для них меньше вероятность опасного хрупкого разрушения.
Текучести предел условный — Энциклопедия по машиностроению XXL
Для металлов, не имеющих площадки текучести, предел текучести определяют условно как напряжение, при котором остаточная деформация составляет величину, установленную ГОСТом или тех- [c.94]Предел текучести Оод (условный) — напряжение, при котором относительное остаточное удлинение образца равно 0,2 %. [c.39]
В тех случаях, когда на диаграмме напряжений отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация равна 0,2 %. [c.121]
Для металлов, не имеющих площадки текучести, предел текучести определяют условно как напряжение, при котором остаточная деформация составляет величину, установленную ГОСТом или техническими условиями. По гост 1497—84 величина остаточной деформации составляет 0,2 % от измеряемой длины образца. Условные пределы текучести отмечают нижним индексом в соответствии с заданной величиной деформации, например оо г. [c.103]
В 1.9 применительно к идеальному упругопластическому материалу, для реальных материалов можно говорить об условном пределе текучести. Предел прочности Ов определяют также ж для пластических материалов, однако значительное изменение формы образца в области больших деформаций, при которых происходит разрыв, делает эту величину еще более условной, чем предел текучести. [c.55]
Характеристики многих материалов не имеют плошадки текучести, поэтому для них за предел текучести принимается условное напряжение, при котором остаточная деформация равняется 0,2%. Условный предел текучести обозначается Сто 2, а его практическое определение показано на рис. 11.13. [c.44]
Следующей, более определенной характеристикой является предел текучести. Под пределом текучести ((Tj) понимается то напряжение, при котором происходит рост деформации без заметного увеличения нагрузки В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация е[c.69]
Высокоуглеродистые и другие стали большой прочности (как и другие материалы, кроме мягкой стали) не дают площадки текучести. Предел текучести для этих сталей принимается условно соответствующим напряжению, при котором остаточное удлинение образца составляет 0,2% или 0,5%-его длины обозначают его и Сто.б-После стадии текучести материал вновь начинает сопротивляться возрастающей нагрузке, наступает так называемая стадия упрочнения. [c.11]
Таким образом, при повышении скорости ударного деформирования возрастают характеристики прочности для всех исследованных материалов. Наиболее интенсивно растет сопротивление на начальном участке деформирования (верхний и нижний пределы текучести или условный предел текучести 00,2)- [c.126]
При ограниченных значениях температурных перепадов приспособляемость возможна и в условиях ползучести. Фактически существует некоторая область напряжений и температур, в которой при данной длительности нагружения ползучесть практи- чески не наблюдается. Таким образом, расчет на приспособляемость в условиях ползучести по существу состоит в замене нре- дела текучести некоторым условным пределом ползучести, т. е. напряжением, при котором деформация за данное время при известной температуре пе превысит некоторой малой величины, установленной допуском. [c.42]
Применительно к расчету турбинных дисков особого внимания заслуживает ползучесть. Как отмечалось, влияние ползучести может быть сведено к сужению области приспособляемости. Замена в расчетных формулах предыдущего параграфа предела текучести некоторым условным пределом ползучести (соответствующим заданным температурам и длительностям нахождения диска под нагрузкой) позволили бы приближенно оценить это влияние. [c.158]
Типичные для исследованного конструкционного материала температурные зависимости предела текучести и условного предела текучести приведены на рис. 4.50. [c.216]
Расчет сопротивления циклическому нагружению в соответствии СП. 1.8 производится с учетом асимметрии цикла по амплитудам максимальных условных упругих напряжений цикла, равным произведению местной упругой или упругопластической деформации, определяемой расчетом или экспериментально, на модуль упругости при расчетной температуре при деформациях, не превышающих деформаций предела текучести, значения условных и действительных напряжений совпадают. [c.220]
Расчеты на прочность деталей теплосиловых установок только по характеристикам статической и длительной статической прочности при высоких температурах являются недостаточными, поскольку ни предел текучести, ни условный предел длительной прочности не отражают в достаточной мере реальных условий нагружения материала в наиболее повреждаемых зонах. Так, например, применение сталей с повышенным пределом текучести для сосудов давления и других элементов с точки зрения сопротивления коррозионной усталости при высокой асимметрии цикла нагружения в ряде случаев не является достаточно технически оправданным [35]. [c.20]
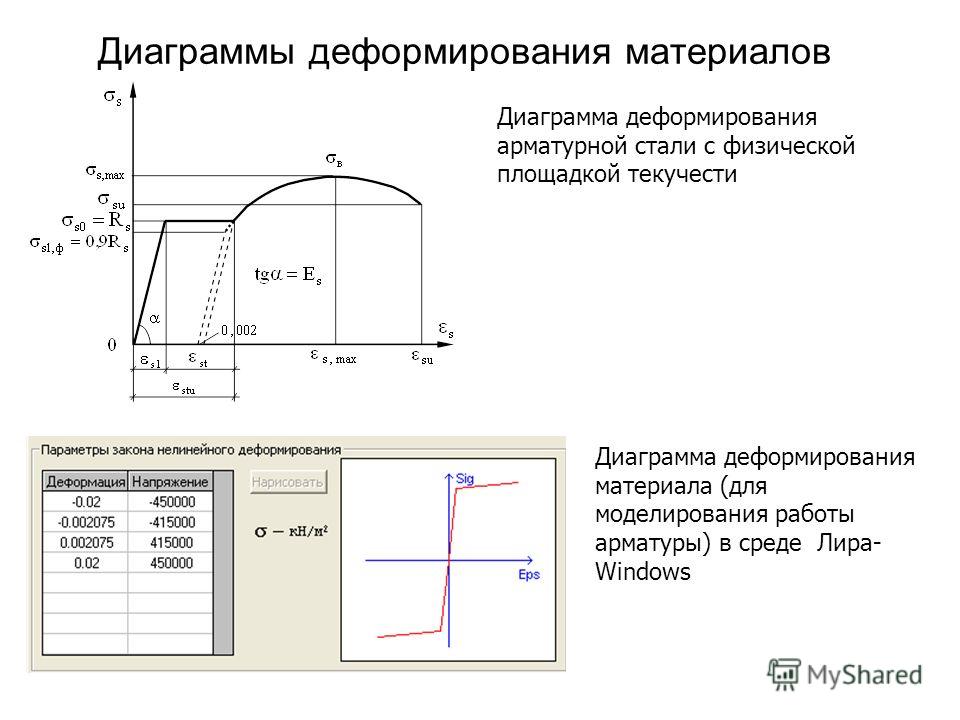
Различают два вида пределов текучести материалов (см. 2.3.1) — физический ст , соответствующий площадке текучести, и условный а 2. [c.54]
С повышением температуры малоуглеродистых сталей изменяется характер кривых растяжения. При комнатной температуре на кривой наблюдается отчетливо выраженная площадь текучести с повышением температуры она становится меньше и около 300° С исчезает. При отсутствии площадки текучести определяют условный предел текучести. [c.178]
Основные характеристики механических свойств (а — предел текучести, Оод — условный предел текучести, — временное сопротивление, 8 — сопротивление разрыву, )/, 5 — относительное сужение и удлинение соответственно, Е — модуль упругости и т — показатель деформационного упрочнения), определенные на укороченных образцах с диаметром рабочей части 6…10 мм указанных сплавов, приведены в табл. 7.1. Пределы текучести сплавов были в диапазоне от 9,4 до 41,4 кгс/мм , пределы прочности — от 20,5 до 49,0 кгс/мм , при этом отношение предела текучести к пределу прочности составляло о,46…о,94. На рис. 7.2 показаны начальные участки диаграмм статического растяжения в истинных координатах (а — е) для сплавов [c.181]
Кривая упрочнения проходит через три характерные точки точку Т (О, 0т), соответствующую началу текучести точку В (eSj, a ,), соответствующую началу образования шейки точку Gf ), соответствующую разрыву образца. Предел текучести равен либо физическому пределу текучести (если на индикаторной диаграмме есть площадка текучести), либо условному пределу текучести сГо,2- Определение е , и [c.169]
Предел текучести наплавленного металла по отечественному и международному стандартам не регламентируют, хотя знание его необходимо при расчете на прочность сварных соединений, поэтому значения пределов текучести представлены в табл. 4.21. Необходимо отметить, что по стандартам Англии, Германии и США предел текучести в условном обозначении электродов регламентируют. [c.119]
Произведение EF — называется жесткостью поперечного сечения стержня при растяжении или сжатии. Для материалов, у которых диаграмма напряжений не имеет площадки текучести (рис.5.11), предел текучести определяется условно как напряжение, при котором остаточная деформация составляет 0,2% и обозначается через ао 2 [c.68]
Физические и условные пределы текучести. Предел прочности. Построение кривой упрочнения [c.225]
Физический предел текучести = PJF — условное напряжение, соответствующее нагрузке на уровне площадки текучести, когда деформация образца происходит без увеличения нагрузки (рис. 3.8, а). Условный предел текучести з = -Ро.г/ о условное напряжение, при котором остаточная деформация достигает 0,2%. Последняя характеристика используется для материалов, не имеющих отчетливо выраженной площадки текучести (рис. 3.S, б, в). [c.81]
Для пластичного материала диаграмма зависимости между касательным напряжением и углом сдвига (характеристика материала при сдвиге), полученная путем соответствующей обработки результатов испытаний на кручение, показана на рис. 5.12. Площадка текучести на этой диаграмме отсутствует. В качестве предела текучести (Тт) условно принимают напряжение, при котором остаточный угол сдвига равен 0,003 радиана. [c.160]Большинство металлов не имеет ясно выраженной площадки текучести, тогда за предел текучести принимают условное напряжение, при котором образец получит остаточную деформацию 0,2% первоначальной длины образца, т. е. предел текучести (условный) [c.97]
При статической нагрузке и пластичных или хрупко-пластичных материалах предел текучести (или условный предел текучести (То,2 для пластичных материалов, диаграммы растяжения которых не имеют площадки текучести). [c.248]
Сопротивление текучести. Наиболее распространенной характеристикой сопротивления текучести является условный предел текучести при растяжении ао,2, причем ввиду малости изменения сечения оо,2 = 5о,г. Следует подчеркнуть, что при очень многих механических испытаниях, часто считающихся простыми, по существу измеряется не прочность элемента, а прочность тела. [c.256]
Предел текучести и условный предел текучести 0о,2 служат в качестве расчетных величин для определения размеров конструкций и деталей, подверженных преимущественно статическим нагрузкам. [c.48]
Если в задачу испытания входит определение условных пределов текучести, предела пропорциональности или модуля упругости, то тогда необходимо провести графическую обработку диаграммы напряжение — удлинение, для которой лучше всего выбрать следующие масштабы [20] [c.77]
Вслед за нахождением предела пропорциональности устанавливается и предел текучести. При отсутетвии площадки текучести предел текучести принимается условно как напряжение, соответствующее остаточному удлинению, равному 0,2% длины образца. [c.17]
В случае отсутствия явно выраженной площадки текучести определяют условный предел -екучести а 0,2 по формуле II, 4). Текучесть материала акже регистрируется тормо- ением стрелки силоизмери-я. Предел текучести соответствует опасному состоянию пластичного материала. [c.97]
Комплекс механических свойств стали Г13Л отличается высоким уровнем как прочностных характеристик, так и пластических. Это является результатом упрочнения стали в зонах повышенной деформации, вследствие чего растяжение образцов стали происходит практически без образования шейки, но с появлением большого количества надрывов и трещин. Диаграмма растяжения поэтому сильно отличается от таковой для углеродистых сталей. В частности, отсутствует площадка текучести и предел текучести рассчитывается условно по заданной деформации. [c.384]На рис. 3.46 приведены зависимость условного предела текучести предела длительной прочности за 100 ч и напряжения, соответствующего минимальной скорости ползучести 10 сплавов на основе никеля, дисперсионноупрочненных частицами ThOa при 1093 °С, от степени вытянутости зерен. Последняя определяется как отношение длины зерна в направлении оси напряжения к его ширине. Сплав TD-никель, подвергнутый волочению после литья и отжигу, является поликристаллическим сплавом, состоящим из тонких, вытянутых в одном направлении кристаллов. Из рис. 3.46 следует, что при увеличении степени вытянутости зерен прочность при высокотемпературном растяжении и сопротивление ползучести увеличиваются. Отсюда ясно, что в указанных сплавах интеркристаллитное разрушение, обусловленное зернограничным скольжением и механизмом диффузии, [c.87]
На рис. 53 схематически показана зависимость условных и истинных напряжений от степени деформации при растяжении образца. В упругой области до предела текучести кривые условных и истинных напряжений пргктически совпадают. После достижения предела текучести-металл начинает деформироваться пластячески и при этом он упрочняется. [c.123]
Пределы текучести являются условными, так как они определены по условному допуску, например 0,2% остаточного удлинения, независимо от того, каким образом подсчитывались напряжения. Давиденков Н. Н. Как определять предел текучести при изгибе и кручении.— Заводская лаборатория , 1948, № 10, с. 1233-—1236 см. также Кишкина-Ратнер С. И. Предел текучести условный и предел текучести физический (45, т. 3, с. 47—48). [c.47]
Метод продавливания может быть с успехом использован для испытания пластичных материалов толщиной от 0,1 до 20 мм как на специальных образцах, так и, на целых листах с возможностью косвенного определения условного предела текучести, предела прочности, сопротивления разрыву 5к, сужения шейки, условного и истинного сопротивления срезу и других характеристик [37, 38, 44]. Взаимосвязь между продавливанием и растяжением нарушается, если испытываемый материал дает при про-давливании разрушение путем среза, а при растяжении — путем отрыва. Наиболее распространенной пробой на продавливание является проба по Эриксену [37]. [c.53]
Основ1 ыми характеристиками при испытании материалов на растяжение являются условный предел пропорциональности о , условный предел упругости Оу, условный предел текучести ст,,, условный предел прочности Стд (или временное сопротивление), первоначальная площадь [c.138]
При отсутствии на диаграмме растяжения зуба и площадки текучести рассчитывают условный предел текучести — напряжение, при котором остаточное удлинение достигает заданной величины, обычно 0,2%, иногда 0,1 или 0,3% и более. Соответственно условный предел текучести обозначается (То,2, Оо,1 или 00,3. Как видно, эта характеристика отличается от условного предела упругости только величиной допуска. Предел теиучести характеризует напряжение, при котором происходит более полный переход к пластической деформации. [c.141]
Определяемый при кручении предел текучести обычно условный. Это касательное напряжение, вычисляемое по формуле (105), которому соответствует остаточный относительный сдвиг на 0,3% (то,з). Методика определения предела текучести с помощью тензометра аналогична рассмотренной для Тупр. Если масштаб диаграммы кручения таков, что 1 мм по оси деформаций соответствует Y 0,1%, а по оси Мкр —не более 1 кгс/мм касательного напряжения, то условный предел текучести то,з может быть найден графически по диаграмме, так же как Сто,2 при растяжении (см. рис. 91). [c.193]
Условный предел — текучесть — Большая Энциклопедия Нефти и Газа, статья, страница 1
Условный предел — текучесть
Cтраница 1
Условный предел текучести — это напряжение, которому соответствует пластическая деформация 0 2 %; его обозначают ( 70 2 — Физический предел текучести стт определяют по диаграмме растяжения, когда на ней имеется площадка текучести. [2]
Условный предел текучести — напряжение, при котором остаточное удлинение достигает 0 2 % длины участка образца, удлинение которого принимается в расчет при определении указанной характеристики. [3]
Условный предел текучести и временное сопротивление разрыву ( предел прочности) являются сдаточными характеристиками сталей. [5]
Условный предел текучести обозначается через а02 и а08 в зависимости от принятой величины допуска на остаточную деформацию. Индекс 0 2 обычно в обозначениях предела текучести опускается. Если необходимо отличить предел текучести на растяжение от предела текучести на сжатие, то в обозначение вводится дополнительный индекс р или с соответственно растяжению или сжатию. Таким образом, для предела текучести получаем обозначения отр и стс. [6]
Условный предел текучести cr0i2 кгс / мм2 ( н / м2) — напряжение, при котором остаточное удлинение достигает 0 2 % от расчетной длины образца. [7]
Условный предел текучести определяют также для легированной стали и для ковкого чугуна. С повышением содержания углерода прочность стали повышается, а ее пластичность падает. Это хорошо видно из представленных на рис. 2.46 диаграмм растяжения для качественной конструкционной углеродистой стали нескольких марок. [8]
Условный предел текучести a0i2 является напряжением, при котором остаточное удлинение образца составляет 0 2 % его начальной длины. [9]
Условный предел текучести — растягивающая нагрузка, при которой остаточное удлинение образца составляет 0 2 % его первоначальной расчетной длины. [10]
Условный предел текучести ст0 2 определяется графическим способом. Для этого значения полного и остаточного удлинений откладываются в прямоугольных координатах в зависимости от соответствующих ступеней нагружения. В результате получаются схематически показанные на рис. 27 кривые. На расстоянии 0 2 % остаточного удлинения проводится прямая, параллельная прямой Гука. [11]
Условный предел текучести определяют также для легированной стали и для ковкого чугуна. С повышением содержания углерода прочность стали повышается, а ее пластичность падает. Это хорошо видно из представленных на рис. 2.44 диаграмм растяжения для качественной конструкционной углеродистой стали нескольких марок. [12]
Условный предел текучести определяют также для легированной стали и ковкого чугуна. С повышением содержания углерода прочность стали повышается, а ее пластичность падает. Это хорошо видно из представленных на рис. 2.41 диаграмм растяжения, для качественной конструкционной углеродистой стали нескольких марок. [13]
Условный предел текучести а 2 широко применяют в расчетах на прочность. При дальнейшем нагружении пластическая деформация все больше увеличивает-ся, равномерно распределяясь по всему объему образца. В точке В нагрузка достигает максимального значения, в наиболее слабом месте образца начинается образование шейки — сужения попе — f речного сечения, деформация из равно — 54 диаграмма истинных мерной переходит в местную. [14]
Страницы: 1 2 3 4 5
Опыт проведения измерения механических характеристик металла
Продление срока службы металла энергетического оборудования осуществляется на основании анализа результатов неразрушающего и разрушающего контроля различными методами. Основные требования к методам и оценке результатов контроля полученных этими методами изложены в «Типовой инструкции по контролю металла и продлению срока службы основных элементов котлов, турбин и трубопроводов тепловых электростанций» (РД 10-577-03). Наиболее важные характеристики для оценки служебных свойств металла получаются на основании металлографического контроля и контроля механических характеристик при рабочей и комнатных температурах. Для оценки прочностных характеристик необходимо знать временное сопротивление разрыву, условный предел текучести, для оценки пластических свойств отношения предела текучести к временному сопротивлению разрыву, относительное конечное удлинение.
Была поставлена задача получить эти характеристики без вырезок непосредственно на объектах. Для этих целей был применён измеритель механических характеристик ПИМ-ДВ-1, который позволяет проводить прямые измерения механических характеристик металла оборудования.
Принцип работы прибора основан на регистрации в реальном масштабе времени процесса упругопластического контактного деформирования металла в виде диаграмм в координатах нагрузка-перемещение, нагрузка-время, перемещение-время при непрерывном вдавливании сферического индентора. Диаграмма вдавливания наиболее полно и объективно характеризует прочностные, упругие и пластические свойства материала при данном виде испытания и лежит в основе определения целого комплекса механических характеристик: условного предела текучести σ02 , временного сопротивления σв , твёрдости по шкалам Бринелля НВ и Виккерса HV, относительного конечного удлинения δ5 , поперечного сужения Ψк , равномерной деформации δрав, кривой упрочнения в координатах напряжение σi – деформация ɛi.
На рисунке 1 приведены результаты сравнительных неразрушающих испытаний образцов на ПИМ-ДВ-1 и разрушающих испытаний на испытательной машине ЦД 10/90. Значения механических характеристик полученных на ПИМ-ДВ-1 и на испытательной машине совпадают, и могут быть приняты для оценки прочностных свойств металла.
В процессе подготовки прибора к испытаниям на оборудовании было проведено сравнение результатов механических испытаний на одних и тех же образцах на разрывной машине и ПИМ-ДВ-1.
Сравнительному испытанию подвергались образцы из сталей: 34ХНЗМ, 30ХМА, Ст. 20, 15Х1М1Ф, 12Х13, 12Х1МФ, Ст. 35, 09Г2С, 38Х2МЮА, 20Х1М1Ф1ТР, 12Х13Ш, 30Х2НМФА, 20Х12ВНМФ, АМЦ 9-2 (бронза), титановый сплав ПТ-3ВМ, 34ХНЗМ, всего более 124 образцов. Условно результаты испытаний можно разделить на две группы. Первая группа результатов, где значения полученные на разрывной машине и ПИМ-ДВ-1 практически совпадают. Вторая группа результатов, где значение механических характеристик различаются. Отклонения по σ02достигают 27%, а в некоторых случаях и более. Образцы, которые вошли в первую группу по результатам испытаний, в основном были изготовлены из деталей полученных методом литья и поковки. Во второй группе оказались образцы из проката. Было сделано предположение, что разница в результатах аналогична разнице испытаний вдоль и поперек проката. После доработки образцов для ПИМ-ДВ-1 испытания проводились с таким расчетом, чтобы оси векторов нагрузки при испытании на разрывной машине и ПИМ-ДВ-1 совпадали. Результаты испытаний проведенные с этим учетом показали, что отклонения величин составили не более 5-7 %.
Далее на объектах с помощью ПИМ-ДВ-1 проводился контроль механических характеристик металла барабанов котлов, основного металла, зон термического влияния и наплавленного металла сварных соединений паропроводов, корпусов стопорных клапанов турбин.
На рис. 2-4 приведены фотографии иллюстрирующие применение ПИМ-ДВ-1 для контроля барабанов котлов из стали 22К и 16ГНМ и металла гибов паропроводов на электростанции, при работающем рядом оборудовании. Наиболее уязвимым блоком оказался Ноутбук. Для его нормальной работы пришлось организовывать обдув корпуса, клавиатуры сжатым воздухом. В Таблице-1 приведены результаты испытаний.
Таблица-1
|
Наименование оборудования |
Предел текучести σ02 МПа |
Предел прочности σв МПа |
Твердость, НВ |
Отношение σ02/ σв |
Относ. конечное удлинение δ5 % |
Пластическая деформация ɛi % |
|
Барабан из стали 22К (производ. 220 т/час) |
202 |
356 |
108 |
0,57 |
37 |
15,9 |
|
Барабан из стали 16 ГНМ |
270 |
427 |
134 |
0,63 |
32 |
10,6 |
|
Гиб паропровода из стали 12Х1МФ |
380 |
490 |
161 |
0,78 |
24 |
8,9 |
Полученные результаты послужили основанием для поверочного расчета элементов барабанов, а также оценить пластические свойства металла обечаек.
На рис. 2 приведено различное положение измерительной головки в барабанах (в нижнем положении и под углом 45 град. к вертикали). Разница в установке головки не сказалась на значениях результатов в нашем случае.
С помощью ПИМ-ДВ-1 проводились также испытания лопаток газовых турбин в лабораторных условиях. Результаты приведены в Таблице-2.
Механические характеристики лопаток, номера клейм – 1, 2, 3, 4, 5 оцениваются как удовлетворительные. Механические характеристики лопатки, номер клейма – 6, имеют низкое значение по пластичности. Это подтверждается наличием карбидов на микрошлифе этой лопатки (Рис. 5). Карбиды металлов расположены преимущественно цепочками по границам зерен. Отмечено наличие нитридов титана. Такое распределение карбидов объясняет и более высокую твердость металла этой лопатки. Это также объясняет и более низкие пластические свойства металла лопатки клейма – 6.
МЕХАНИЧЕСКИЕ СВОЙСТВА
Таблица 2
|
№ клейма |
Предел текучести, МПа |
Предел прочности, МПа |
Твердость НВ |
Твердость НV |
Относительное конечное удлинение, % |
Пластическая деформация, % |
|
1 |
696 |
830 |
253 |
255 |
18 |
2,4 |
|
2 |
751 |
881 |
267 |
270 |
17 |
2,1 |
|
3 |
713 |
846 |
257 |
259 |
18 |
2,3 |
|
4 |
736 |
868 |
263 |
266 |
18 |
2,2 |
|
5 |
622 |
762 |
236 |
237 |
20 |
3,0 |
|
6 |
1100 |
1218 |
358 |
371 |
13 |
1,0 |
-
Р.Л. ТВД т/а 83 I ступень, металл — ХН65ВМТЮ (ЭИ893) по ГОСТ5632-72 присвоено клеймо – 1;
-
т/а 22, металл — ХН65ВМТЮ (ЭИ893) по ГОСТ5632-72, присвоено клеймо – 2;
-
Р.Л. ТНД т/а 83 I ступень, металл — 16Х11Н2В2МФ (ЭИ962А) по ГОСТ5632-72, присвоено клеймо – 3;
-
Р.Л. ТВД т/а 22 III ступень, металл — 20Х12ВНМФ (ЭП428) по ГОСТ5632-72, присвоено клеймо – 4;
-
т/а 11, металл — 20Х12ВНМФ (ЭП428) по ГОСТ5632-72, присвоено клеймо – 5;
-
т/а 11, металл — ХН65ВМТЮ (ЭИ893) по ГОСТ5632-72, присвоено клеймо – 6.
Рис.1
Сравнительные неразрушающие испытания образцов на ПИМ-ДВ-1 и разрушающие испытания на испытательной машине ЦД 10/90
Рис.4 Проведение измерений механических характеристик металла на гибе паропровода.
Рис.6 Микроструктура металла барабана из стали 16 ГНМ (М:1500)
Рис.7 Микроструктура металла барабана из стали 22К (М:1500)
На рисунках 6 и 7 приведены микроструктуры металла барабанов котлов, изготовленных из стали 16ГНМ и 22К. Значения механических характеристик металла барабанов, измеренных с помощью ПИМ-ДВ-1 (Таблица-1) указывают на низкие прочностные свойства металла барабана изготовленного из стали 22К. Это подтверждается состоянием микроструктуры металла.
В результате длительной эксплуатации барабана (год изготовления барабана 1934 г.) произошла деградация металла с выделением отдельных глобулей структурно свободного графита и сфероидизацией перлита соответствующей 5 баллу по ОСТ 34-70-690-96 «Металл паросилового оборудования электростанций. Методы металлографического анализа в условиях эксплуатации». По состоянию металла барабана котла, котёл был выведен из эксплуатации и демонтирован.
В случае испытаний механических характеристик лопаток, сравнительные испытания на разрывной машине не проводились, из-за невозможности их проведения. Порядок значений величин механических свойств металла, при испытании лопаток подтверждался состоянием микроструктур металла. Так, например, низкие пластические свойства металла лопатки (клеймо №6) и высокое значение твердости, полученное при измерении на ПИМ-ДВ-1 подтверждается наличием карбидов металла и их распределением в микроструктуре приведенной на рис.5.
В лабораторных условиях проводился контроль механических характеристик при рабочей температуре вырезки паросборного коллектора из стали 12Х1МФ проработавшей 250 000 часов. Во всех случаях в зоне проведения контроля прибором ПИМ-ДВ-1 проводилась оценка состояния микроструктуры металла. По результатам анализа применения ПИМ-ДВ-1 сделан вывод о том, что прибор может быть применён для контроля механических характеристик на объектах энергетического оборудования.
Для контроля механических характеристик металла в диапазоне рабочих температур выше 300С требуется конструктивная доработка прибора с целью защиты измерительной головки от воздействия высокой температуры. В настоящее время разработчиками прибора решается эта проблема.
Выводы:
-
Измеритель механических характеристик ПИМ-ДВ-1 может применяться для оценки механических свойств металла элементов энергетического оборудования как в лабораторных условиях, так и в производственных.
-
Для проведения контроля механических свойств металла при рабочих температурах требуется доработка прибора с целью зашиты измерительной головки от воздействия высокой температуры.
ЛИТЕРАТУРА:
-
РД 10-577-03 «Типовая инструкция по контролю металла и продлению срока службы основных элементов котлов, турбин и трубопроводов тепловых электростанций».
-
ОСТ 34-70-690-96 «Металл паросилового оборудования электростанций. Методы металлографического анализа в условиях эксплуатации».
К списку
Предел пропорциональности — Instron
Предел пропорциональности — это точка на кривой напряжения-деформации, где область линейной упругой деформации переходит в область нелинейной пластической деформации. Другими словами, предел пропорциональности определяет наибольшее напряжение, которое прямо пропорционально деформации. Точку перехода можно рассчитать по заданному процентному изменению наклона. Поскольку пропорциональный предел не требуется многими стандартами тестирования, он часто используется в образовательных целях, а не на практике в индустрии тестирования материалов.
Чем предел пропорциональности отличается от предела эластичности?
Предел упругости — это наибольшее напряжение, которое может быть приложено к материалу, не вызывая пластической (остаточной) деформации. Для многих материалов предел упругости эквивалентен или почти эквивалентен пределу пропорциональности. Для других материалов, таких как эластомеры, зависимость напряжения от деформации является нелинейной, и материал все еще будет находиться в пределах своей упругой области еще долгое время после того, как он пройдет через свой предел пропорциональности.Предел упругости — это, по сути, теоретическое значение, которое трудно определить с помощью универсальной испытательной машины, и по этой причине оно используется в основном в образовательных целях, а не на практике в индустрии тестирования материалов.
Чем предел пропорциональности отличается от предела текучести?
Подобно пределу упругости, предел текучести материала также может выходить за пределы пропорционального предела материала. В отличие от предела упругости, предел текучести на кривой зависимости напряжения от деформации был определен стандартами испытаний ASTM и ISO.В зависимости от напряженно-деформационного поведения материала при текучести выбранный стандарт определяет предпочтительный расчет текучести. Например, стандарты испытаний металлов (ASTM E8 или ISO 6892) стандартизировали выход смещения 0,2%, что позволяет металлургической промышленности объективно оценивать различные металлы относительно друг друга. Кривая напряжения-деформации ниже отображает разницу между пределом пропорциональности (изменение наклона 4%) и пределом текучести смещения 0,2% при испытании металлов.
Прочность на разрыв — обзор
9.4.4 Прочность на растяжение
UTS — несколько устаревший, но хорошо описывающий эквивалент, кратко современный, экономичный, предел прочности на разрыв (TS). Это свойство композита, состоящее из (1) предела текучести плюс (2) дополнительного упрочнения от наклепа во время пластической деформации материала перед разрушением. Эти два компонента делают его поведение более сложным для понимания, чем поведение только предела текучести или пластичности.
TS равняется пределу текучести, или пределу прочности, когда (1) нет пластичности, как показано на рисунке 2.47 и рис. 9.20, и (2), когда деформационное упрочнение равно нулю. Условие нулевого наклепа встречается реже, но часто возникает при высоких температурах, когда скорость восстановления равна или превышает скорость упрочнения.
Проблема определения TS литого материала заключается в том, что результаты часто бывают разрозненными. Проблемы, связанные с этим разбросом, важны и подробно рассматриваются в Разделе 9.2 «Статистика отказов». Раздел 9.2 настоятельно рекомендуется прочитать.
Обычно для данного сплава в заданном состоянии термообработки предел текучести является фиксированным. Таким образом, по мере увеличения пластичности (например, за счет использования более чистого металла или более быстрого затвердевания) TS обычно увеличивается, потому что с дополнительным удлинением пластика деформационное упрочнение теперь имеет возможность накапливаться и, таким образом, повышать прочность. Эффект снова очевиден на рис. 2.47. Для литого алюминиевого сплава Hedjazi et al. (1975) показывают, что TS увеличивается за счет уменьшения количества дефектов, как показано на рисунке 9.28. Отклик TS в основном обусловлен увеличением пластичности, как видно из линейного отклика, и сдвигом свойств в основном вправо, а не просто вверх, для более чистого материала.
Рисунок 9.28. Механические свойства сплава Al-4.5Cu-1.5Mg в нефильтрованном и фильтрованном состояниях, демонстрирующие сильную реакцию пластичности.
Данные Hedjazi et al. (1975).Ожидается, что значительно большее влияние пористости слоя на пластичность будет дополнять меньшее влияние из-за потери площади на общий отклик TS.На рисунке 9.11 показано снижение TS и удлинение в системах сплавов Mg-Zn, где ухудшение свойств невелико. На рис. 7.34 TS сплава Al-11,5 Mg показывает более серьезные сокращения, особенно когда пористость имеет форму слоев, перпендикулярных приложенному напряжению. Даже в этом случае уменьшение не столь серьезное, как можно было бы ожидать, если бы слои были трещинами, что подчеркивает их природу как «сшитые» или «прихваточные» трещины, как описано в разделе 9.3.2.4.
Когда слои ориентированы параллельно направлению приложенного напряжения, тогда, как и можно было ожидать, Поллард (1965) показал, что пористость слоя даже до 3% по объему оказывает практически незаметное влияние на свойства.
Наконец, очевидно, что трещины или пленки, занимающие большую часть поперечного сечения отливки, будут очень вредными для TS, как и для пластичности. Само собой разумеющееся общее понимание того, что TS падает до нуля по мере того, как трещина занимает все большую часть исследуемой площади, количественно выражено Клайном и Дэвисом (1975) на Рисунке 9.12.
11.8: Условия текучести Tresca — Engineering LibreTexts
Напряженное состояние при одноосном растяжении стержня зависит от ориентации плоскости, в которой разрешаются напряжения.В главе 2 было показано, что напряжение сдвига \ (\ tau \) на плоскости, наклоненной к горизонтальной плоскости на угол \ (\ alpha \), составляет
\ [\ tau = \ frac {1} {2} \ sigma_ {11} \ sin 2 \ alpha \]
, где \ (\ sigma_ {11} \) — одноосное растягивающее напряжение, см. Рисунок (\ (\ PageIndex {1} \)).
Рисунок \ (\ PageIndex {1} \): касательные и нормальные напряжения при произвольном разрезе.Максимальный сдвиг возникает, когда \ (\ sin 2 \ alpha = 1 \) или \ (\ alpha = \ frac {\ pi} {4} \). Таким образом при одноосном растяжении
\ [\ tau _ {\ text {max}} = \ frac {\ sigma_ {11}} {2} \]
Распространяя анализ на трехмерный случай (см., Например, Fung), максимальные напряжения сдвига на трех плоскостях сдвига равны
\ [\ tau_1 = \ frac {| \ sigma_1 — \ sigma_2 |} {2}, \ quad \ tau_2 = \ frac {| \ sigma_2 — \ sigma_1 |} {2}, \ quad \ tau_3 = \ frac {| \ sigma_3 — \ sigma_1 |} {2} \]
, где \ (\ sigma_1 \), \ (\ sigma_2 \), \ (\ sigma_3 \) — главные напряжения.В 1860 году французский ученый и инженер Анри Треска выдвинул гипотезу о том, что пластичность материала происходит, когда максимальное напряжение сдвига достигает критического значения
.\ [\ tau_o = \ text {max} \ left \ {\ frac {| \ sigma_1 — \ sigma_2 |} {2}, \ frac {| \ sigma_2 — \ sigma_3 |} {2}, \ frac {| \ sigma_3 — \ sigma_1 |} {2} \ right \} \]
Неизвестная постоянная может быть откалибрована с помощью одноосного испытания, для которого справедливо уравнение (11.4.9). Следовательно, при yield \ (\ tau_o = \ sigma_y / 2 \) и условие доходности Tresca принимает вид
\ [\ text {max} \ {| \ sigma_1 — \ sigma_2 |, | \ sigma_2 — \ sigma_3 |, | \ sigma_3 — \ sigma_1 | \} = \ sigma_y \]
В пространстве главных напряжений условие текучести Трески представлено призматической трубкой с открытым концом, пересечение которой с октаэдрической плоскостью представляет собой правильный шестиугольник, см. Рисунок (\ (\ PageIndex {2} \)).
Рисунок \ (\ PageIndex {2} \): Представление условия текучести Трески в пространстве главных напряжений.Для плоского напряжения пересечение призматической трубы с плоскостью \ (\ sigma_3 = 0 \) образует знакомый шестиугольник Tresca, показанный на рисунке (\ (\ PageIndex {3} \)).
Рисунок \ (\ PageIndex {3} \): шестиугольник Трески, вписанный в эллипс фон Мизеса.Влияние гидростатического давления на текучесть можно легко оценить, учитывая \ (\ sigma_1 = \ sigma_2 = \ sigma_3 = p \).Тогда
\ [\ sigma_1 — \ sigma_2 = 0 \]
\ [\ sigma_2 — \ sigma_3 = 0 \]
\ [\ sigma_3 — \ sigma_1 = 0 \]
В этом напряженном состоянии и критерий текучести фон Мизеса (уравнение (–)), и критерий Трески (уравнение (–)) предсказывают отсутствие текучести.
Условное картирование идентифицированных локусов количественных признаков для концентрации белка в зерне, выражающихся независимо от урожайности зерна канадской твердой пшеницы
Front Plant Sci.2021; 12: 642955.
, 1, * † , 2, * † , 1 , 2 , 1, ‡ , 1 , 3 , 1, ‡ , 1 , 2, ‡ , 4 и 1Yuefeng Ruan
1 Swift Current Research and Development Center, Agriculture and Agri-Food Canada , Swift Current, SK, Canada
Bianyun Yu
2 Развитие водных и сельскохозяйственных ресурсов, Национальный исследовательский совет Канады, Саскатун, SK, Канада
Рон Э.Нокс
1 Центр исследований и разработок Свифт Каррент, Сельское хозяйство и агропродовольствие Канада, Свифт Каррент, Южная Каролина, Канада
Вентао Чжан
2 Развитие водных ресурсов и ресурсов сельскохозяйственных культур, Национальный исследовательский совет Канады, Саскатун, Южная Каролина, Канада
Ашиш К. Сингх
1 Центр исследований и разработок Swift Current, сельское хозяйство и агропродовольствие Canada, Swift Current, SK, Canada
Richard Cuthbert
1 Центр исследований и разработок Swift Current, сельское хозяйство и Agri-Food Canada, Swift Current, SK, Canada
Pierre Fobert
3 Aquatic and Crop Resource Development, National Research Council Canada, Ottawa, ON, Canada
Ron DePauw
1 Swift Current Research and Development Center, Agriculture and Agri-Food Canada, Swift Current, SK, Canada
Samia Berraies
1 Swift Current Resea rch and Development Center, Сельское хозяйство и агропродовольствие Canada, Swift Current, SK, Canada
Andrew Sharpe
2 Развитие водных и сельскохозяйственных ресурсов, Национальный исследовательский совет Канады, Саскатун, Южная Каролина, Канада
Бин Сяо Фу
4 Лаборатория исследований зерна, Канадская комиссия по зерну, Виннипег, МБ, Канада
Джатиндер Санга
1 Центр исследований и разработок Свифт Каррент, Сельское хозяйство и агропродовольствие Канада, Свифт Каррент, Южная Каролина, Канада
1 Центр исследований и разработок Свифт Каррент, Сельское хозяйство и агропродовольствие Канада, Свифт Каррент, СК, Канада
2 Развитие водных и сельскохозяйственных ресурсов, Национальный исследовательский совет Канады, Саскатун, СК, Канада
3 Водные ресурсы и ресурсы сельскохозяйственных культур Развитие, Национальный исследовательский совет Канады, Оттава, Онтарио, Канада
4 Лаборатория исследования зерна, Канадская комиссия по зерну, Виннипег, MB, Канада
Отредактировал: Луиджи Каттивелли, Совет сельскохозяйственных и экономических исследований, Италия
Рецензировал: Филиппо Мария Басси, Международный центр сельскохозяйственных исследований в засушливых регионах (ИКАРДА), Марокко; Сюэхуэй Ли, Государственный университет Северной Дакоты, США; Джакомо Манджини, Итальянский национальный исследовательский совет, Италия
Эта статья была отправлена в раздел «Селекция растений» журнала Frontiers in Plant Science
† Эти авторы внесли равный вклад в эту работу
‡ Текущий адрес: Ашиш К.Сингх, Департамент агрономии, Университет штата Айова, Эймс, Айова, США
Рон ДеПау, Advancing Wheat Technologies, Калгари, AB, Канада
Эндрю Шарп, Глобальный институт продовольственной безопасности, Саскатун, Южная Каролина, Канада
Получено 2020 Dec 17; Принято 2021 февраля 26.
Copyright © 2021 Руан, Ю, Нокс, Чжан, Сингх, Катберт, Фоберт, ДеПау, Беррейс, Шарп, Фу и Сангха.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (CC BY).Использование, распространение или воспроизведение на других форумах разрешено при условии указания автора (авторов) и правообладателя (ов) и ссылки на оригинальную публикацию в этом журнале в соответствии с принятой академической практикой. Запрещается использование, распространение или воспроизведение без соблюдения этих условий.
Реферат
Концентрация белка в зерне (GPC) является важным признаком в развитии твердых сортов, как главный определяющий фактор пищевой ценности зерна и качества конечного продукта.Однако сложно одновременно выбрать и GPC, и урожай зерна (GY) из-за отрицательной корреляции между ними. Чтобы охарактеризовать локусы количественных признаков (QTL) для GPC и понять генетическую связь между GPC и GY у твердой пшеницы Канады, мы выполнили как традиционное, так и условное картирование QTL с использованием популяции удвоенных гаплоидов (DH) из 162 линий, полученных из Pelissier × Strongfield. Популяция выращивалась в поле более 5 лет, и был измерен GPC. QTL, способствующий GPC, был обнаружен на хромосомах 1B, 2B, 3A, 5B, 7A и 7B с использованием традиционного картирования.Один основной QTL на 3A ( QGpc.spa-3A.3 ) последовательно выявлялся в течение 3 лет, составляя 9,4–18,1% фенотипической дисперсии, с благоприятным аллелем, происходящим от Пелисье. Другой основной QTL на 7A ( QGpc.spa-7A ), обнаруженный через 3 года, объясняет 6,9–14,8% фенотипической дисперсии с помощью полезного аллеля, полученного из Strongfield. Сравнение QTL, описанного здесь, с результатами, о которых сообщалось ранее, привело к идентификации одного нового основного QTL на 3A ( QGpc.spa-3A.3 ) и пять новых второстепенных QTL на 1B, 2B и 3A. Четыре QTL были общими для традиционного и условного сопоставления, причем QGpc.spa-3A.3 и QGpc.spa-7A были обнаружены в нескольких средах. QTL, идентифицированные условным картированием, были независимыми или частично независимыми от GY, что делало их очень важными для развития высоких GPC и высокоурожайных твердых сортов.
Ключевые слова: условное картирование , локусы количественных признаков, концентрация белка в зерне, твердая пшеница, урожай зерна
Введение
Твердая пшеница [ Triticum turgidum L.subsp. durum (Desf.) Husn.], Является экономически важной культурой из-за ее уникальных характеристик, которые способствуют производству манной крупы для производства макаронных изделий и других традиционных продуктов, таких как лепешки, кус-кус и булгур (Giraldo et al., 2016) . Концентрация белка в зерне (GPC) является важным признаком развития сорта твердой пшеницы. Это главный фактор, определяющий пищевую ценность зерна, реологические свойства теста для изготовления макаронных изделий, качество конечного продукта и, следовательно, экономическую ценность урожая.GPC — это сложный количественный признак, контролируемый множеством геномных локусов, которые взаимодействуют друг с другом (Nigro et al., 2019). Отбор твердых сортов пшеницы с высоким содержанием ГПХ также затруднен влиянием окружающей среды в той или иной степени. Следовательно, для скрининга GPC в программах разведения требуется несколько комбинаций генотипа и окружающей среды. Одновременный выбор GPC и урожайности зерна (GY) затруднен из-за отрицательной корреляции, часто наблюдаемой между этими двумя признаками в большинстве генетических фонов и условий выращивания (Blanco et al., 2002, 2006; Groos et al., 2003; Богард и др., 2011). Однако изменение отрицательной корреляции было продемонстрировано одновременным выбором для GPC и GY (DePauw et al., 2007).
Понимание генетической основы GPC у сортов в их целевой среде является ключом к внедрению селекции с помощью маркеров (MAS) в программах селекции твердых сортов для поддержания или улучшения качества зерна. Исследования, проведенные для анализа генетической основы GPC у твердых сортов пшеницы, выявили локусы количественных признаков (QTL) почти на всех хромосомах, как обобщено Kumar et al.(2018). Среди сообщенных QTL некоторые показали серьезные эффекты, в то время как многие вызвали незначительные эффекты. Кроме того, большинство идентифицированных QTL были экологически зависимыми и нестабильными в различных средах. Хорошо известным QTL для GPC является Gpc-B1 на хромосоме 6BS. Аллель с высоким GPC этого QTL был идентифицирован из дикого тетраплоидного ( Triticum turgidum L. ssp. dicoccoides ) образца FA-15-3, происходящего из Израиля (Avivi, 1978). Gpc-B1 был картирован на хромосоме 6BS, что составляет 66% дисперсии GPC (Joppa et al., 1997; Olmos et al., 2003). Предковый дикий аллель GPC-B1 кодирует фактор транскрипции NAC (NAM-B1) и связан с повышенной концентрацией белка зерна, Zn и Fe, а также ускоряет старение флаговых листьев у пшеницы (Uauy et al., 2006) . Современные сорта пшеницы несут нефункциональный аллель NAM-B1, а функциональный аллель Gpc-B1 интрогрессирован в элитные сорта твердой и мягкой пшеницы (Chee et al., 2001; Tabbita et al., 2017; Bokore et al. ., 2019). Однако аллель GPC-B1 дикого типа имеет большее отрицательное влияние на компоненты урожая твердой пшеницы в дополнение к нежелательному эффекту увеличения концентрации золы манной крупы (Tabbita et al., 2017).
Анализ картирования QTL GPC часто проводился без учета компонентов GY и урожайности. Однако некоторые недавние исследования, в которых одновременно учитывались компоненты GY и урожайности, привели к идентификации локусов GPC без отрицательного воздействия на признаки, связанные с урожайностью (Blanco et al., 2002, 2012; Супрайоги и др., 2009; Рапп и др., 2018; Нигро и др., 2019). Например, несколько исследований идентифицировали GPC QTL без отрицательного воздействия на GY путем картирования отклонения белка зерна (GPD), полученного из регрессии GPC, и урожайности в разнообразной панели твердых сортов (Rapp et al., 2018; Nigro et al., 2019) . Такие локусы полезны для одновременного генетического улучшения GPC и GY. Статистическая процедура, предложенная Чжу (1995), использовалась для анализа условных генетических эффектов для отдельных признаков развития, в которой применяется тот же статистический принцип, что и подход GPD (Rapp et al., 2018; Nigro et al., 2019) для анализа коррелированных признаков, включая белок зерна и урожайность. Этот условный анализ используется для оценки значений признаков на основе отсутствия вариаций в генетически коррелированных признаках, метод, который очень похож на оценку скорректированных значений в ковариационном анализе, исключающий влияние коррелированных признаков на генетические эффекты QTL для целевых черты (Zhao et al., 2006). Эта модель получила дальнейшее развитие для анализа вклада каждого составляющего признака в сложный признак, а также для анализа генетической взаимосвязи между близкородственными признаками.Условное картирование QTL успешно использовалось для оценки эффектов QTL на целевые признаки в зависимости от их составляющих признаков, таких как урожай зерна риса (Guo et al., 2005) и длина разрастания колоса на высоту растения у пшеницы (Li C. et al. , 2020). Генетическая взаимосвязь между родственными признаками на уровне QTL была исследована на предмет содержания масла в семенах рапса по отношению к содержанию белка (Zhao et al., 2006), увеличения объема разрастания кукурузы в зависимости от веса зерна на растение и веса 100 зерен (Li et al., 2008), GPC зависит от содержания крахмала в зерне пшеницы (Deng et al., 2015), а также содержания белка и масла в сое (Li X. et al., 2020). Кроме того, условное картирование QTL использовалось для выяснения влияния окружающей среды на экспрессию QTL на основе значений признаков, обусловленных различными средами (Xu et al., 2014; Fan et al., 2019). Был проведен условный анализ для изучения влияния удобрений азотом (N) и фосфором (P) на экспрессию QTL для урожайности и связанных с азотом признаков (Xu et al., 2014) и индуцированный низким N-стрессом QTL у пшеницы (Fan et al., 2019). Кроме того, условное отображение QTL может идентифицировать дополнительные QTL, которые не обнаруживаются при традиционном отображении.
Используя условное картирование, мы ожидали идентифицировать QTL для GPC, которые независимо экспрессируются от GY, что может облегчить одновременный отбор высокой концентрации белка и высокого GY при разведении твердых пород. Таким образом, цели этого исследования заключались в следующем: (1) определить QTL, лежащий в основе GPC у канадской твердой пшеницы, в частности тех, которые являются стабильными QTL в различных средах, (2) определить QTL для GPC без отрицательных коррелированных эффектов на GY с помощью условного анализа QTL. .
Материалы и методы
Популяция, полевые испытания и измерение признаков
В этом исследовании использовалась твердая популяция из 162 удвоенных гаплоидных (DH) линий, полученных от Pelissier × Strongfield. Strongfield — зарегистрированный сорт канадского западного янтаря Durum с высоким содержанием глютена, высоким содержанием GPC и низким содержанием кадмия, разработанный в Центре исследований и разработок Swift Current, Swift Current, SK (Clarke et al., 2005). Пелисье, отобранный из алжирского староместного сорта, завезенного из Соединенных Штатов Америки, является родителем-основателем генофонда канадской твердой пшеницы (Clarke et al., 2010). В нем высокое содержание кадмия и липоксигеназы. Линии DH вместе с двумя родительскими и контрольными линиями были испытаны в полевых испытаниях на южной ферме SCRDC (широта: 50 ° 17 ′ северной широты; долгота: 107 ° 41 ′ западной долготы; высота 825 м) на суглинке Суинтон (Orthic Brown Чернозем) на четырехрядных делянках (2,74 м 2 / делянка) в виде рандомизированной полной блочной схемы с двумя повторностями. Каждое испытание выращивалось при двух датах посева с интервалом в 1 неделю (ранний, E; поздний, L) каждый год с 2014 по 2016 год, и только ранняя дата посева в 2017 и 2018 годах.Каждая проба на дату посева выращивалась на разных участках. Заготовки собирали в индивидуальные мешки с помощью комбайна. GY каждого участка измеряли на весах и выражали в кг / га -1 . GPC манной крупы измеряли с помощью спектроскопии в ближнем инфракрасном диапазоне (NIR) (Foss NIR 6500) и выражали в процентах при влажности 13,5%. Для анализа фенотипических данных и картирования QTL каждую дату посева в каждый год рассматривали как одну среду, обеспечивающую в общей сложности восемь сред, обозначенных как E14, L14, E15, L15, E16, L16, E17 и E18.Ежегодно проводились предпосадочные испытания почвы для определения нормы внесения удобрений. Удобрения внесены на целевые 112 кг га -1 для азота, 70 кг га -1 для фосфора и 22,4 кг га -1 для серы. Почва богата калием и не требует дополнительного внесения.
Статистический анализ
Статистическая сводка и тест нормальности Шапиро-Уилка были проведены в R (R3.3.2, https://www.r-project.org/).Парные фенотипические корреляции между средами и между признаками были рассчитаны с использованием коэффициента корреляции Пирсона в R-пакете Hmisc (версия 4.2-0, http://cran.r-project.org/web/packages/Hmisc/index.html).
Дисперсионный анализ (ANOVA) и оценка наследуемости были выполнены с использованием процедуры PROC MIXED SAS 9.3 (Институт SAS, Кэри, Северная Каролина, США), как описано Ruan et al. (2020). В смешанной модели линии DH (генотипы, G) рассматривались как фиксированные эффекты, в то время как взаимодействия среды (E), генотип × среда (G × E) и репликации, вложенные в среду, рассматривались как случайные эффекты.Наследственность GPC рассчитывалась как отношение генетической дисперсии и фенотипической дисперсии по средам с использованием σg2 / (σg2 + σge2 / y + σε2 / год), где σg2, σge2 и σε2 были оценками генотипа (G), генотипа. × взаимодействие среды (G × E) и остаточная дисперсия (ошибка), соответственно, а y и r представляют собой числа среды и репликации. Наследственность GPC в каждой среде рассчитывалась с использованием σg2 / (σg2 + σε2 / r), где σg2 и σε2 были оценками генотипа и остаточной дисперсии, соответственно, а r представляло количество репликаций.Для оценки наследуемости все эффекты считались случайными.
Генетическая карта и картирование QTL
КартированиеQTL было выполнено с использованием генетической карты Pelissier × Strongfield, описанной Ruan et al. (2020). Для генотипирования использовали чип Infinium iSelect Wheat 90K SNP. В общей сложности 1212 полиморфных маркеров SNP с отсутствием данных <30% были использованы для построения генетической карты, что привело к идентификации 25 групп сцепления (LG). LG были отнесены к хромосомам на основании сравнения с существующей консенсусной картой твердой пшеницы на основе SNP с высокой плотностью (Maccaferri et al., 2019). Средние значения GPC из двух повторов в каждой среде использовали для обнаружения QTL. Выбросы значений признаков были обнаружены и удалены с помощью преобразования Z-оценки с порогом 3. Обнаружение QTL было выполнено с использованием составного интервального картирования (CIM) в программе WinQTL Cartographer v.2.5 (Wang S. et al., 2012) (http : //statgen.ncsu.edu/qtlcart/WQTLCart.htm). Те же параметры, что описаны Ruan et al. (2020) были использованы для CIM. QTL, обнаруженный в разных средах, считался одинаковым, если доверительные интервалы (ДИ) перекрывались и аддитивный эффект вносил один и тот же родитель.QTL, картированный по крайней мере в одной среде, объясняющий более 20% фенотипической дисперсии, или отображенный по крайней мере в двух средах с PVE ≥ 10%, считался основным QTL (Raihan et al., 2016; Zhao et al., 2016). QTL, обнаруженный в двух или более средах, считается стабильным QTL. Графическое представление групп сцепления и QTL на генетической карте было выполнено с использованием программного обеспечения MapChart 2.2 (Voorrips, 2002). Гаплотипы были присвоены с помощью пакета R Haplotyper.
Условные значения GPC [GPC | GY, GPC, обусловленные урожайностью зерна (GY)] для каждой среды были рассчитаны с использованием QGA Station 2.0 (Чжу, 1995) (http://ibi.zju.edu.cn/software/qga/v2.0/index.htm). Условные фенотипические значения (GPC | GY) представляют собой чистые значения признаков GPC независимо от вариации GY. Отображение QTL для условных значений GPC было выполнено с использованием того же метода, что и выше для традиционного отображения QTL. Идентифицированный QTL был определен как условный QTL. Когда QTL, идентифицированный двумя методами (традиционным и условным), имел перекрывающиеся КЭ, они считались идентичными. Все сообщенные QTL были обозначены в соответствии с Рекомендованными правилами для символизации генов в пшенице (http: // пшеница.pw.usda.gov/ggpages/wgc/98).
Лучший линейный несмещенный прогноз (BLUP) — популярный метод, используемый для анализа испытаний в различных средах (Xiao et al., 2016; Choudhury et al., 2019). Чтобы исключить влияние эффектов окружающей среды на фенотипические вариации, значение BLUP GPC для каждой линии во всех средах было оценено с использованием линейной модели в пакете R lme4 (Bates et al., 2015). Значения BLUP линий DH использовали в качестве данных признаков для картирования QTL во всех средах, как описано Xiao et al.(2016).
Результаты
Вариация GPC в популяции DH в нескольких средах
показывает частотное распределение GPC в популяции DH, полученное из Pelissier × Strongfield в восьми средах с 2014 по 2018 год. Сводная статистика, включая средние значения и стандартное отклонение (SD) среднее значение генеральной совокупности, минимальные и максимальные значения, диапазон и вероятность, связанные с тестом Стьюдента t для родительских средних значений в каждой среде, показаны в.Распределение GPC было нормальным во всех средах, кроме среды E16, на что указывает значение p теста нормальности Шапиро-Уилка. У родительской линии Strongfield GPC был значительно выше, чем у Pelissier во всех средах, кроме E16 (). Отдельные линии DH имели экстремальные значения GPC во всех средах и отображали двунаправленную трансгрессивную сегрегацию для GPC, как показано максимальными и минимальными значениями относительно родительских. Среднее значение GPC популяции DH было ближе к родительскому Strongfield, чем к родительскому Pelissier в большинстве сред.GPC популяции имел самое высокое среднее значение в среде E18 (среднее значение = 14,5%) и самое низкое среднее значение в E14 (среднее значение = 12,1%). Наибольший диапазон GPC наблюдался в среде E16, а наименьший — в E17. Умеренные коэффициенты корреляции Пирсона (0,3–0,67) наблюдались среди линий DH в разных средах (дополнительный рисунок 1). Значительные отрицательные корреляции от -0,16 до -0,84 наблюдались между GPC и GY во многих средах, за исключением E17 и E18 (). В целом, чем выше урожай зерна, тем сильнее отрицательная корреляция между GPC и GY.
Частотное распределение концентрации белка в зерне (GPC) в популяции Пелисье × Стронгфилд с 2014 по 2018 г. Полевые испытания с двумя датами посева в каждый год (ранний, E; поздний, L) в течение 2014–2016 гг. И только ранний срок посева в 2017 г. –2018. Синие сплошные линии представляют Пелисье; красные пунктирные линии обозначают Стронгфилд; серые пунктирные линии обозначают средние значения генеральной совокупности.
Таблица 1
Среднее значение, стандартное отклонение, минимум и максимум, коэффициент вариации, вероятность, связанная с тестом нормальности Шапиро-Уилка концентрации белка в зерне (GPC) в разных средах для популяции Пелисье × Стронгфилд, наследуемость в каждой среде, GPC среднее значение родителей и значение p- теста Стьюдента t- на значимость между двумя родителями.