ГОСТ 8509-93 Уголки стальные горячекатаные равнополочные. Сортамент
ГОСТ 8509-93
Группа В22
Сортамент
МКС 77.140.70
ОКП 09 3100, 09 3200, 09 3300
Дата введения 1997-01-01
1 РАЗРАБОТАН Украинским научно-исследовательским институтом металлов
ВНЕСЕН Госстандартом Украины
2 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол N 3 от 17 февраля 1993 г.)
За принятие проголосовали:
Наименование государства | Наименование национального органа по стандартизации |
Республика Армения | Армгосстандарт |
Республика Беларусь | Белстандарт |
Республика Казахстан | Госстандарт Республики Казахстан |
Республика Молдова | Молдовастандарт |
Российская Федерация | Госстандарт России |
Туркменистан | Туркменглавгосинспекция |
Республика Узбекистан | Узгосстандарт |
Украина | Госстандарт Украины |
3 Постановлением Комитета Российской Федерации по стандартизации, метрологии и сертификации от 20 февраля 1996 г.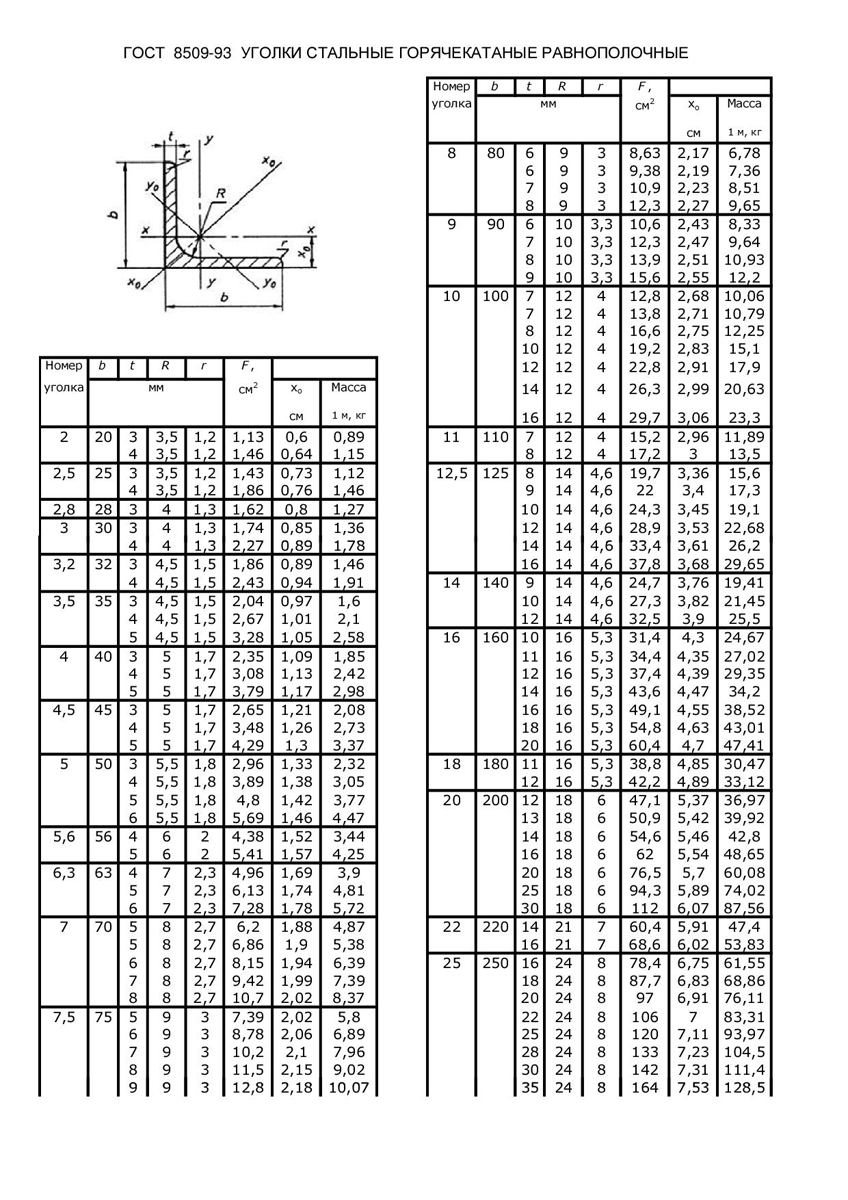
4 ВЗАМЕН ГОСТ 8509-86
5 ПЕРЕИЗДАНИЕ. Август 2012 г.
1 Настоящий стандарт распространяется на уголки стальные горячекатаные равнополочные.
Рисунок 1 Размеры уголков, площадь поперечного сечения, справочные величины для осей и масса 1 м уголков
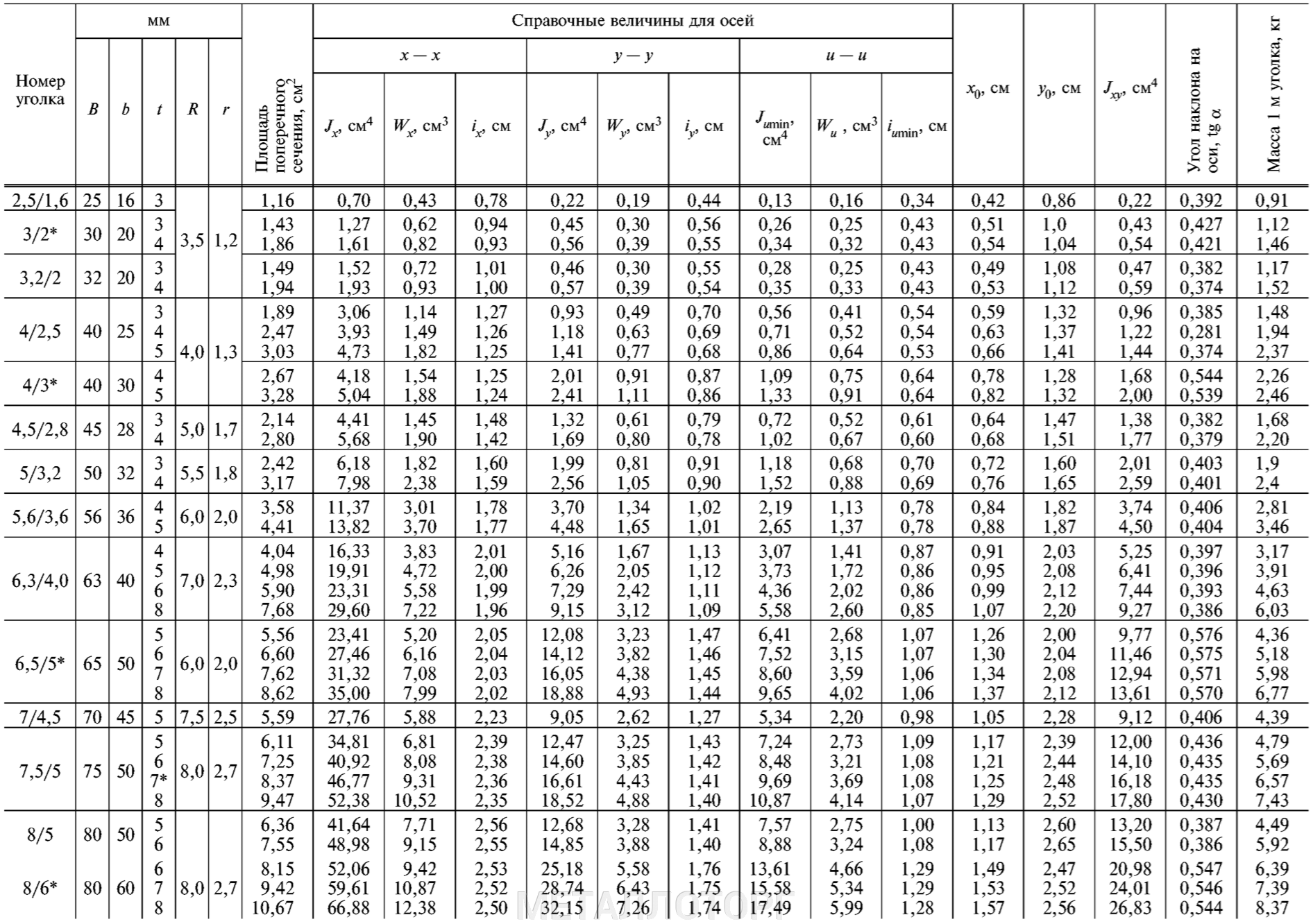
2 Размеры уголков, площадь поперечного сечения, справочные величины для осей и масса 1 м уголков должны соответствовать указанным на рисунке 1 и в таблице 1, а при поставках на экспорт — приложениям А и Б.
Рисунок 1
Таблица 1
Номер уголка | , см | Справочные значения величин для осей | Масса 1 м, кг | |||||||||||||
мм | , см | , см | ||||||||||||||
, см | , см | , см |
|
|
| , см |
| |||||||||
2 | 20 | 3 | 3,5 | 1,2 | 1,13 | 0,40 | 0,28 | 0,59 | 0,63 | 0,75 | 0,17 | 0,20 | 0,39 | 0,23 | 0,60 | 0,89 |
4 | 3,5 | 1,2 | 1,46 | 0,50 | 0,37 | 0,58 | 0,78 | 0,73 | 0,22 | 0,24 | 0,38 | 0,28 | 0,64 | 1,15 | ||
2,5 | 25 | 3 | 3,5 | 1,2 | 1,43 | 0,81 | 0,46 | 0,75 | 1,29 | 0,95 | 0,34 | 0,33 | 0,49 | 0,47 | 0,73 | 1,12 |
4 | 3,5 | 1,2 | 1,86 | 1,03 | 0,59 | 0,74 | 1,62 | 0,93 | 0,44 | 0,41 | 0,48 | 0,59 | 0,76 | 1,46 | ||
2,8 | 28 | 3 | 4,0 | 1,3 | 1,62 | 1,16 | 0,58 | 0,85 | 1,84 | 1,07 | 0,48 | 0,42 | 0,55 | 0,68 | 0,80 | 1,27 |
3 | 30 | 3 | 4,0 | 1,3 | 1,74 | 1,45 | 0,67 | 0,91 | 2,30 | 1,15 | 0,60 | 0,53 | 0,59 | 0,85 | 0,85 | 1,36 |
4 | 4,0 | 1,3 | 2,27 | 1,84 | 0,87 | 0,90 | 2,92 | 1,13 | 0,77 | 0,61 | 0,58 | 1,08 | 0,89 | 1,78 | ||
3,2 | 32 | 3 | 4,5 | 1,5 | 1,86 | 1,77 | 0,77 | 0,97 | 2,80 | 1,23 | 0,74 | 0,59 | 0,63 | 1,03 | 0,89 | 1,46 |
4 | 4,5 | 1,5 | 2,43 | 2,26 | 1,00 | 0,96 | 3,58 | 1,21 | 0,94 | 0,71 | 0,62 | 1,32 | 0,94 | 1,91 | ||
3,5 | 35 | 3 | 4,5 | 1,5 | 2,04 | 2,35 | 0,93 | 1,07 | 3,72 | 1,35 | 0,97 | 0,71 | 0,69 | 1,37 | 0,97 | 1,60 |
4 | 4,5 | |||||||||||||||
ГОСТ 8509-93
ГОСТ 8509-93
Группа В22
Сортамент
МКС 77.
ОКП 09 3100, 09 3200, 09 3300
Дата введения 1997-01-01
1 РАЗРАБОТАН Украинским научно-исследовательским институтом металлов
ВНЕСЕН Госстандартом Украины
2 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол N 3 от 17 февраля 1993 г.)
За принятие проголосовали:
Наименование государства | Наименование национального органа по стандартизации |
Республика Армения | Армгосстандарт |
Республика Беларусь | Белстандарт |
Республика Казахстан | Госстандарт Республики Казахстан |
Республика Молдова | Молдовастандарт |
Российская Федерация | Госстандарт России |
Туркменистан | Туркменглавгосинспекция |
Республика Узбекистан | Узгосстандарт |
Украина | Госстандарт Украины |
3 Постановлением Комитета Российской Федерации по стандартизации, метрологии и сертификации от 20 февраля 1996 г. N 85 межгосударственный стандарт ГОСТ 8509-93 введен в действие непосредственно в качестве государственного стандарта Российской Федерации с 1 января 1997 г.
N 85 межгосударственный стандарт ГОСТ 8509-93 введен в действие непосредственно в качестве государственного стандарта Российской Федерации с 1 января 1997 г.
4 ВЗАМЕН ГОСТ 8509-86
5 ПЕРЕИЗДАНИЕ. Август 2012 г.
1 Настоящий стандарт распространяется на уголки стальные горячекатаные равнополочные.
Рисунок 1 Размеры уголков, площадь поперечного сечения, справочные величины для осей и масса 1 м уголков
2 Размеры уголков, площадь поперечного сечения, справочные величины для осей и масса 1 м уголков должны соответствовать указанным на рисунке 1 и в таблице 1, а при поставках на экспорт — приложениям А и Б.
Рисунок 1
Таблица 1
Номер уголка | , см | Справочные значения величин для осей | Масса 1 м, кг | |||||||||||||
мм | , см | , см | ||||||||||||||
, см | , см | , см |
|
|
| , см |
| |||||||||
2 | 20 | 3 | 3,5 | 1,2 | 1,13 | 0,40 | 0,28 | 0,59 | 0,63 | 0,75 | 0,17 | 0,20 | 0,39 | 0,23 | 0,60 | 0,89 |
4 | 3,5 | 1,2 | 1,46 | 0,50 | 0,37 | 0,58 | 0,78 | 0,73 | 0,22 | 0,24 | 0,38 | 0,28 | 0,64 | 1,15 | ||
2,5 | 25 | 3 | 3,5 | 1,2 | 1,43 | 0,81 | 0,46 | 0,75 | 1,29 | 0,95 | 0,34 | 0,33 | 0,49 | 0,47 | 0,73 | 1,12 |
4 | 3,5 | 1,2 | 1,86 | 1,03 | 0,59 | 0,74 | 1,62 | 0,93 | 0,44 | 0,41 | 0,48 | 0,59 | 0,76 | 1,46 | ||
2,8 | 28 | 3 | 4,0 | 1,3 | 1,62 | 1,16 | 0,58 | 0,85 | 1,84 | 1,07 | 0,48 | 0,42 | 0,55 | 0,68 | 0,80 | 1,27 |
3 | 30 | 3 | 4,0 | 1,3 | 1,74 | 1,45 | 0,67 | 0,91 | 2,30 | 1,15 | 0,60 | 0,53 | 0,59 | 0,85 | 0,85 | 1,36 |
4 | 4,0 | 1,3 | 2,27 | 1,84 | 0,87 | 0,90 | 2,92 | 1,13 | 0,77 | 0,61 | 0,58 | 1,08 | 0,89 | 1,78 | ||
3,2 | 32 | 3 | 4,5 | 1,5 | 1,86 | 1,77 | 0,77 | 0,97 | 2,80 | 1,23 | 0,74 | 0,59 | 0,63 | 1,03 | 0,89 | 1,46 |
4 | 4,5 | 1,5 | 2,43 | 2,26 | 1,00 | 0,96 | 3,58 | 1,21 | 0,94 | 0,71 | 0,62 | 1,32 | 0,94 | 1,91 | ||
3,5 | 35 | 3 | 4,5 | 1,5 | 2,04 | 2,35 | 0,93 | 1,07 | 3,72 | 1,35 | 0,97 | 0,71 | 0,69 | 1,37 | 0,97 | 1,60 |
4 | 4,5 | |||||||||||||||
Сортамент уголков равнополочных | Нормативная база
Сортамент уголков равнополочных включает в себя много информации. Часть данных необходима только опытным инженерам-конструкторам, которые делают сложные расчеты. К таким характеристикам относится момент инерции и радиус инерции. Эти данные используются при выполнении расчетов.
Часть данных необходима только опытным инженерам-конструкторам, которые делают сложные расчеты. К таким характеристикам относится момент инерции и радиус инерции. Эти данные используются при выполнении расчетов.
Момент инерции вычисляется по сложной формуле, но гораздо проще использовать уже готовые данные, которые занесены в таблицу, чем каждый раз считать все заново. Сложные характеристики металлопроката иногда помогают подобрать нестандартное сечение и спрогнозировать его правильную работу в конструкции.
Основные параметры в сортаменте уголков равнополочных
В практическом строительстве сортамент уголков равнополочных позволяет подобрать необходимое сечение горячекатаного профиля. В частности, вентилируемые фасады зданий обычно крепятся с помощью уголков. Правильно подобрать уголок, распределить нагрузку позволяет сортамент.
С помощью сортамента можно узнать геометрические параметры равнополочного уголка, вес погонного метра, площадь поперечного сечения, геометрический центр масс, а также расположение отверстий в некоторых уголках.
Конструирование из уголка включает в себя определение размеров полки, которая подходит проектному решению, подсчет длины элементы и его общего веса в ведомости расхода стали. Исходя из конструктивных соображений, принимается длина уголка, которая умножается на вес погонного метра. В результате получается вес всего изделия.
Уголок сортамент ГОСТ
Все данные сортамента уголков равнополочных отображаются согласно ГОСТ 8509-93 «Уголки стальные горячекатаные равнополочные. Сортамент» или ДСТУ 2251-93 «Кутики сталеві гарячекатані рівнополичні. Сортамент».
Для того чтобы разобраться во всех данных таблицы, давайте разберем эскиз, на котором изображены условные обозначения, которые используются в сортаменте.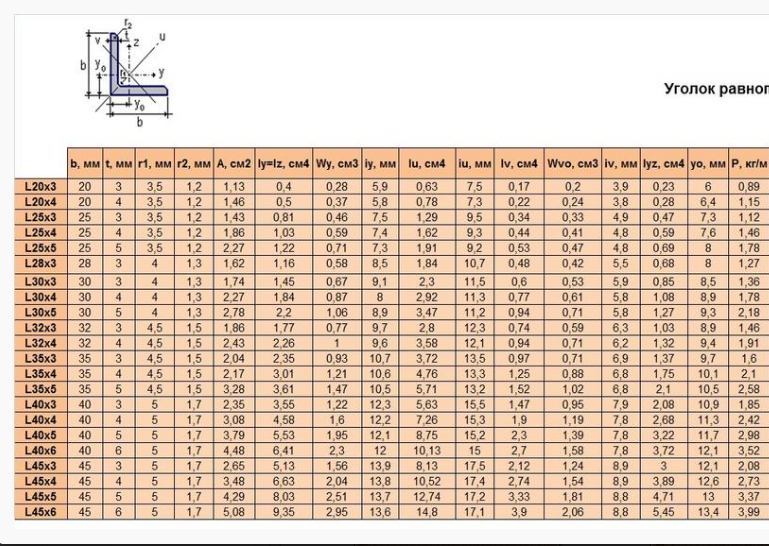
- b – ширина полки;
- t – толщина полки;
- R – радиус внутреннего закругления;
- r – радиус закругления полок;
- z0 – расстояние от центра тяжести до наружной грани полки;
- Ix – момент инерции по ос
Уголок равнополочный по ГОСТ 8509-93. Размеры и вес профиля.
Фильтровать выбранное
| Профиль | h, мм | b, мм | t, мм | R, мм | А, см2 | Ix, см4 | Wx, см3 | ix, см | Iy, см4 | Wy, см3 | iy, см | Iu, см4 | iu, см | Iv, см4 | Wv, см3 | Ixy, см4 | x0, см | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20x20x3 | 20. 0 0 | 20.0 | 3.0 | 3.5 | 1.13 | 0.89 | 0.4 | 0.28 | 5.9 | 0.4 | 0.28 | 5.9 | 0.63 | 7.5 | 0.17 | 0.2 | 3.9 | 0.23 | 6.0 | |
| 20x20x4 | 20.0 | 20.0 | 4.0 | 3.5 | 1.46 | 1.15 | 0.5 | 0.37 | 5.8 | 0.5 | 0.37 | 5.8 | 0.78 | 7.3 | 0.22 | 0.24 | 3.8 | 0.28 | 6.4 | |
| 25x25x3 | 25.0 | 25.0 | 3.0 | 3.5 | 1.43 | 1.12 | 0.81 | 0.46 | 7.5 | 0.81 | 0.46 | 7.5 | 1.29 | 9.5 | 0.34 | 0.33 | 4.9 | 0.47 | 7.3 | |
| 25x25x4 | 25.0 | 25.0 | 4.0 | 3.5 | 1.86 | 1.46 | 1.03 | 0.59 | 7.4 | 1.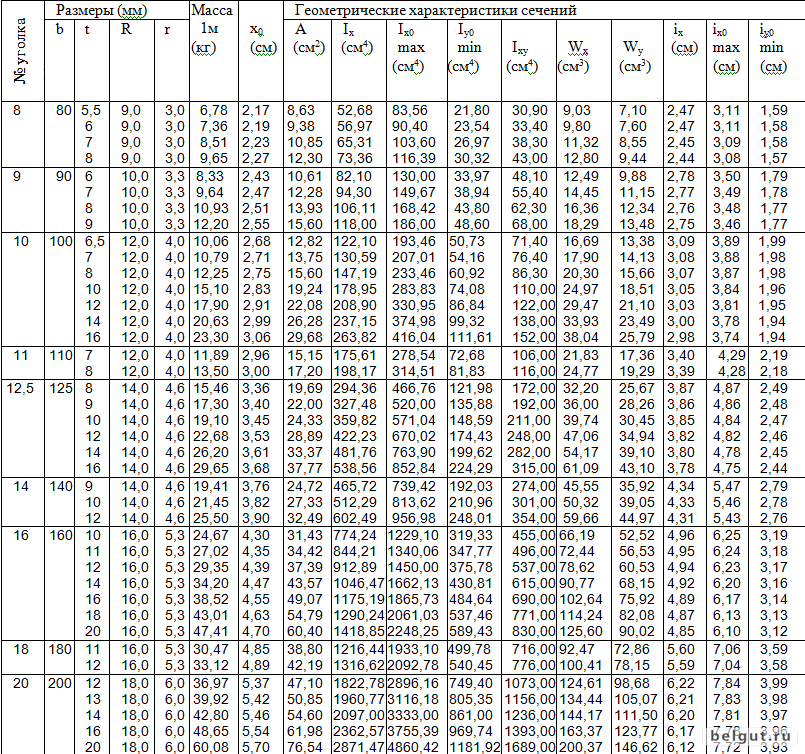 03 03 | 0.59 | 7.4 | 1.62 | 9.3 | 0.44 | 0.41 | 4.8 | 0.59 | 7.6 | |
| 25x25x5 | 25.0 | 25.0 | 5.0 | 3.5 | 2.27 | 1.78 | 1.22 | 0.71 | 7.3 | 1.22 | 0.71 | 7.3 | 1.91 | 9.2 | 0.53 | 0.47 | 4.8 | 0.69 | 8.0 | |
| 28x28x3 | 28.0 | 28.0 | 3.0 | 4.0 | 1.62 | 1.27 | 1.16 | 0.58 | 8.5 | 1.16 | 0.58 | 8.5 | 1.84 | 10.7 | 0.48 | 0.42 | 5.5 | 0.68 | 8.0 | |
| 30x30x3 | 30.0 | 30.0 | 3.0 | 4.0 | 1.74 | 1.36 | 1.45 | 0.67 | 9.1 | 1.45 | 0.67 | 9.1 | 2.3 | 11.5 | 0.6 | 0.53 | 5.9 | 0.85 | 8. 5 5 | |
| 30x30x4 | 30.0 | 30.0 | 4.0 | 4.0 | 2.27 | 1.78 | 1.84 | 0.87 | 8.0 | 1.84 | 0.87 | 8.0 | 2.92 | 11.3 | 0.77 | 0.61 | 5.8 | 1.08 | 8.9 | |
| 30x30x5 | 30.0 | 30.0 | 5.0 | 4.0 | 2.78 | 2.18 | 2.2 | 1.06 | 8.9 | 2.2 | 1.06 | 8.9 | 3.47 | 11.2 | 0.94 | 0.71 | 5.8 | 1.27 | 9.3 | |
| 32x32x3 | 32.0 | 32.0 | 3.0 | 4.5 | 1.86 | 1.46 | 1.77 | 0.77 | 9.7 | 1.77 | 0.77 | 9.7 | 2.8 | 12.3 | 0.74 | 0.59 | 6.3 | 1.03 | 8.9 | |
| 32x32x4 | 32.0 | 32.0 | 4.0 | 4.5 | 2.43 | 1.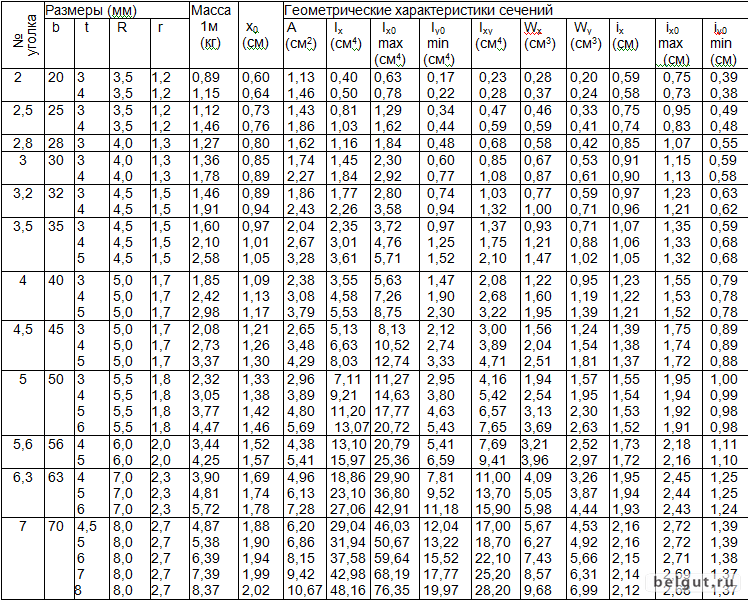 91 91 | 2.26 | 1.0 | 9.6 | 2.26 | 1.0 | 9.6 | 3.58 | 12.1 | 0.94 | 0.71 | 6.2 | 1.32 | 9.4 | |
| 35x35x3 | 35.0 | 35.0 | 3.0 | 4.5 | 2.04 | 1.6 | 2.35 | 0.93 | 10.7 | 2.35 | 0.93 | 10.7 | 3.72 | 13.5 | 0.97 | 0.71 | 6.9 | 1.37 | 9.7 | |
| 35x35x4 | 35.0 | 35.0 | 4.0 | 4.5 | 2.67 | 2.1 | 3.01 | 1.21 | 10.6 | 3.01 | 1.21 | 10.6 | 4.76 | 13.3 | 1.25 | 0.88 | 6.8 | 1.75 | 10.1 | |
| 35x35x5 | 35.0 | 35.0 | 5.0 | 4.5 | 3.28 | 2.58 | 3.61 | 1.47 | 10.5 | 3.61 | 1.47 | 10.5 | 5.71 | 13. 2 2 | 1.52 | 1.02 | 6.8 | 2.1 | 10.5 | |
| 40x40x3 | 40.0 | 40.0 | 3.0 | 5.0 | 2.35 | 1.85 | 3.55 | 1.22 | 12.3 | 3.55 | 1.22 | 12.3 | 5.63 | 15.5 | 1.47 | 0.95 | 7.9 | 2.08 | 10.9 | |
| 40x40x4 | 40.0 | 40.0 | 4.0 | 5.0 | 3.08 | 2.42 | 4.58 | 1.6 | 12.2 | 4.58 | 1.6 | 12.2 | 7.26 | 15.3 | 1.9 | 1.19 | 7.8 | 2.68 | 11.3 | |
| 40x40x5 | 40.0 | 40.0 | 5.0 | 5.0 | 3.79 | 2.98 | 5.53 | 1.95 | 12.1 | 5.53 | 1.95 | 12.1 | 8.75 | 15.2 | 2.3 | 1.39 | 7.8 | 3.22 | 11.7 | |
| 40x40x6 | 40. 0 0 | 40.0 | 6.0 | 5.0 | 4.48 | 3.52 | 6.41 | 2.3 | 12.0 | 6.41 | 2.3 | 12.0 | 10.13 | 15.0 | 2.7 | 1.58 | 7.8 | 3.72 | 12.1 | |
| 45x45x3 | 45.0 | 45.0 | 3.0 | 5.0 | 2.65 | 2.08 | 5.13 | 1.56 | 13.9 | 5.13 | 1.56 | 13.9 | 8.13 | 17.5 | 2.12 | 1.24 | 8.9 | 3.0 | 12.1 | |
| 45x45x4 | 45.0 | 45.0 | 4.0 | 5.0 | 3.48 | 2.73 | 6.63 | 2.04 | 13.8 | 6.63 | 2.04 | 13.8 | 10.52 | 17.4 | 2.74 | 1.54 | 8.9 | 3.89 | 12.6 | |
| 45x45x5 | 45.0 | 45.0 | 5.0 | 5.0 | 4.29 | 3.37 | 8.03 | 2.51 | 13. 7 7 | 8.03 | 2.51 | 13.7 | 12.74 | 17.2 | 3.33 | 1.81 | 8.8 | 4.71 | 13.0 | |
| 45x45x6 | 45.0 | 45.0 | 6.0 | 5.0 | 5.08 | 3.99 | 9.35 | 2.95 | 13.6 | 9.35 | 2.95 | 13.6 | 14.8 | 17.1 | 3.9 | 2.06 | 8.8 | 5.45 | 13.4 | |
| 50x50x3 | 50.0 | 50.0 | 3.0 | 5.5 | 2.96 | 2.32 | 7.11 | 1.94 | 15.5 | 7.11 | 1.94 | 15.5 | 11.27 | 19.5 | 2.95 | 1.57 | 10.0 | 4.16 | 13.3 | |
| 50x50x4 | 50.0 | 50.0 | 4.0 | 5.5 | 3.89 | 3.05 | 9.21 | 2.54 | 15.4 | 9.21 | 2.54 | 15.4 | 14.63 | 19.4 | 3.8 | 1.95 | 9. 9 9 | 5.42 | 13.8 | |
| 50x50x5 | 50.0 | 50.0 | 5.0 | 5.5 | 4.8 | 3.77 | 11.2 | 3.13 | 15.3 | 11.2 | 3.13 | 15.3 | 17.77 | 19.2 | 4.63 | 2.3 | 9.8 | 6.57 | 14.2 | |
| 50x50x6 | 50.0 | 50.0 | 6.0 | 5.5 | 5.69 | 4.47 | 13.07 | 3.69 | 15.2 | 13.07 | 3.69 | 15.2 | 20.72 | 19.1 | 5.43 | 2.63 | 9.8 | 7.65 | 14.6 | |
| 50x50x7 | 50.0 | 50.0 | 7.0 | 5.5 | 6.56 | 5.15 | 14.84 | 4.23 | 15.0 | 14.84 | 4.23 | 15.0 | 23.47 | 18.9 | 6.21 | 2.93 | 9.7 | 8.63 | 15.0 | |
| 50x50x8 | 50.0 | 50.0 | 8. 0 0 | 5.5 | 7.41 | 5.82 | 16.51 | 4.76 | 14.9 | 16.51 | 4.76 | 14.9 | 26.03 | 18.7 | 6.98 | 3.22 | 9.7 | 9.52 | 15.3 | |
| 56x56x4 | 56.0 | 56.0 | 4.0 | 6.0 | 4.38 | 3.44 | 13.1 | 3.21 | 17.3 | 13.1 | 3.21 | 17.3 | 20.79 | 21.8 | 5.41 | 2.52 | 11.1 | 7.69 | 15.2 | |
| 56x56x5 | 56.0 | 56.0 | 5.0 | 6.0 | 5.41 | 4.25 | 15.97 | 3.96 | 17.2 | 15.97 | 3.96 | 17.2 | 25.36 | 21.6 | 6.59 | 2.97 | 11.0 | 9.41 | 15.7 | |
| 60x60x4 | 60.0 | 60.0 | 4.0 | 7.0 | 4.72 | 3.71 | 16.21 | 3.7 | 18.5 | 16.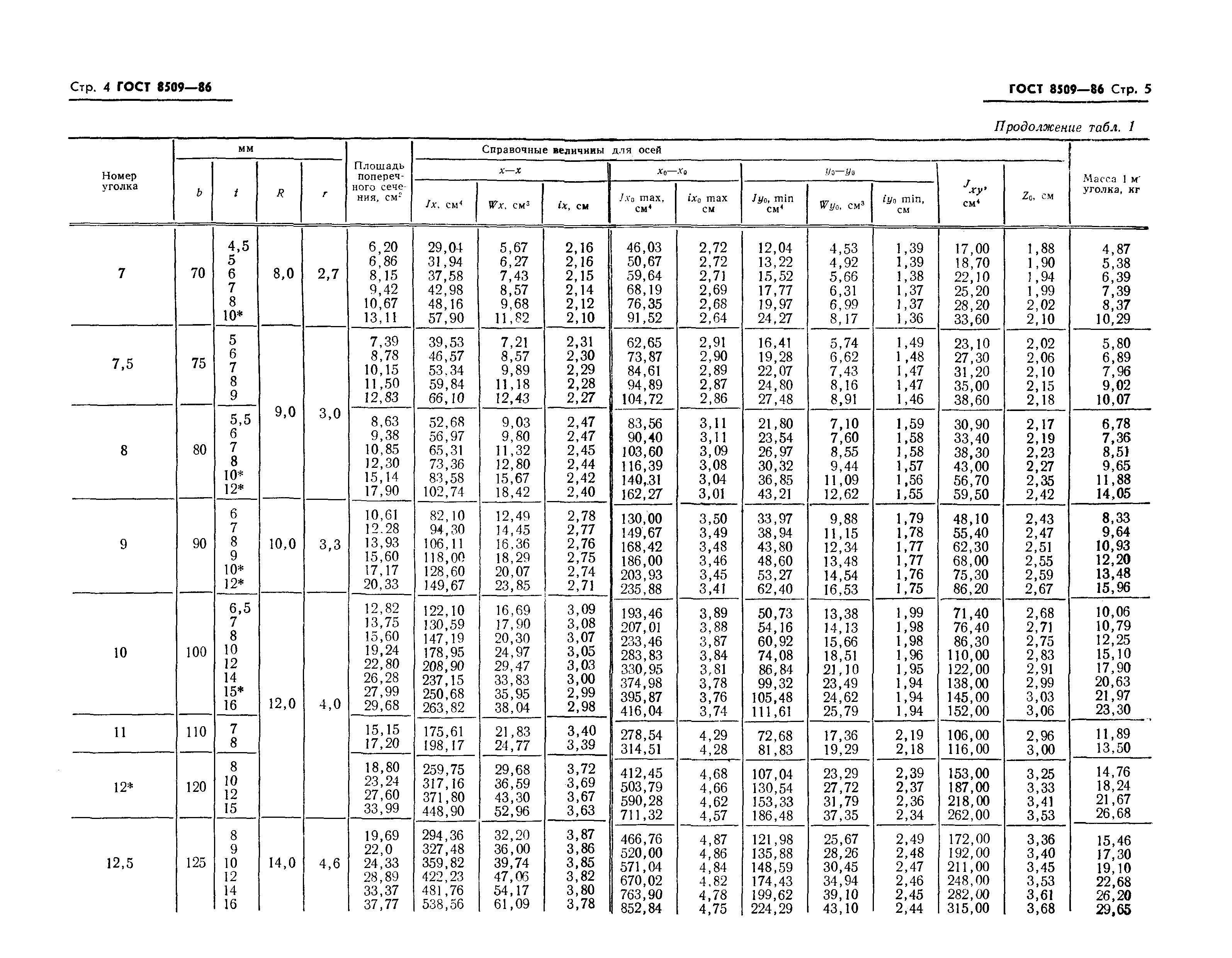 21 21 | 3.7 | 18.5 | 25.69 | 23.3 | 6.72 | 2.93 | 11.9 | 9.48 | 16.2 | |
| 60x60x5 | 60.0 | 60.0 | 5.0 | 7.0 | 5.83 | 4.58 | 19.79 | 4.56 | 18.4 | 19.79 | 4.56 | 18.4 | 31.4 | 23.2 | 8.18 | 3.49 | 11.8 | 11.61 | 16.6 | |
| 60x60x6 | 60.0 | 60.0 | 6.0 | 7.0 | 6.92 | 5.43 | 23.21 | 5.4 | 18.3 | 23.21 | 5.4 | 18.3 | 36.81 | 23.1 | 9.6 | 3.99 | 11.8 | 13.6 | 17.0 | |
| 60x60x8 | 60.0 | 60.0 | 8.0 | 7.0 | 9.04 | 7.1 | 29.55 | 7.0 | 18.1 | 29.55 | 7.0 | 18.1 | 46.77 | 22.7 | 12.34 | 4.9 | 11. 7 7 | 17.22 | 17.8 | |
| 60x60x10 | 60.0 | 60.0 | 10.0 | 7.0 | 11.08 | 8.7 | 35.32 | 8.52 | 17.9 | 35.32 | 8.52 | 17.9 | 55.64 | 22.4 | 15.0 | 5.7 | 11.6 | 20.32 | 18.5 | |
| 63x63x4 | 63.0 | 63.0 | 4.0 | 7.0 | 4.96 | 3.9 | 18.86 | 4.09 | 19.5 | 18.86 | 4.09 | 19.5 | 29.9 | 24.5 | 7.81 | 3.26 | 12.5 | 11.0 | 16.9 | |
| 63x63x5 | 63.0 | 63.0 | 5.0 | 7.0 | 6.13 | 4.81 | 23.1 | 5.05 | 19.4 | 23.1 | 5.05 | 19.4 | 36.8 | 24.4 | 9.52 | 3.87 | 12.5 | 13.7 | 17.4 | |
| 63x63x6 | 63.0 | 63.0 | 6. 0 0 | 7.0 | 7.28 | 5.72 | 27.06 | 5.98 | 19.3 | 27.06 | 5.98 | 19.3 | 42.91 | 24.3 | 11.18 | 4.44 | 12.4 | 15.9 | 17.8 | |
| 65x65x6 | 65.0 | 65.0 | 6.0 | 7.0 | 7.52 | 5.91 | 29.85 | 6.39 | 19.9 | 29.85 | 6.39 | 19.9 | 47.38 | 25.1 | 12.32 | 4.77 | 12.8 | 17.53 | 18.3 | |
| 65x65x8 | 65.0 | 65.0 | 8.0 | 7.0 | 9.84 | 7.73 | 38.13 | 8.3 | 19.7 | 38.13 | 8.3 | 19.7 | 60.42 | 12.7 | 15.85 | 13.15 | 24.8 | 22.29 | 19.0 | |
| 70x70x4 | 70.0 | 70.0 | 4.5 | 8.0 | 6.2 | 4.87 | 29.04 | 5.67 | 21.6 | 29.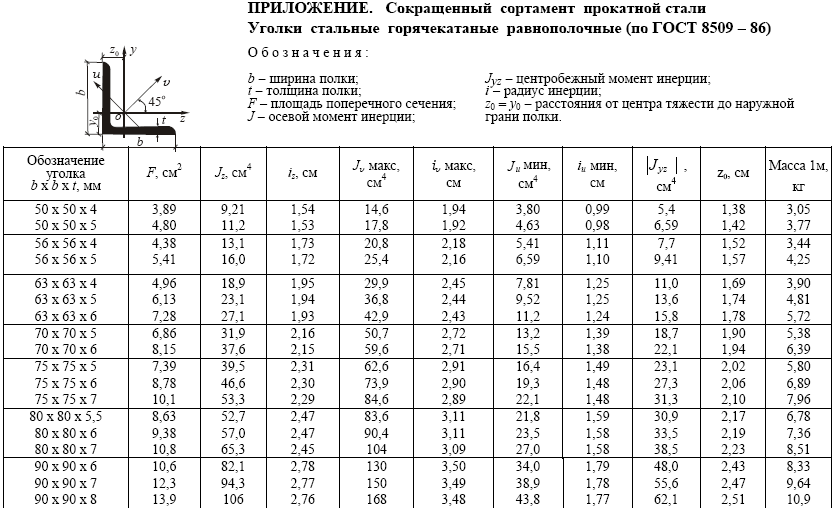 04 04 | 5.67 | 21.6 | 46.03 | 27.2 | 12.04 | 4.53 | 13.9 | 17.0 | 18.8 | |
| 70x70x5 | 70.0 | 70.0 | 5.0 | 8.0 | 6.86 | 5.38 | 31.94 | 6.27 | 21.6 | 31.94 | 6.27 | 21.6 | 50.67 | 27.2 | 13.22 | 4.92 | 13.9 | 18.7 | 19.0 | |
| 70x70x6 | 70.0 | 70.0 | 6.0 | 8.0 | 8.15 | 6.39 | 37.58 | 7.43 | 21.5 | 37.58 | 7.43 | 21.5 | 59.64 | 27.1 | 15.52 | 5.66 | 13.8 | 22.1 | 19.4 | |
| 70x70x7 | 70.0 | 70.0 | 7.0 | 8.0 | 9.42 | 7.39 | 42.98 | 8.57 | 21.4 | 42.98 | 8.57 | 21.4 | 68.19 | 26.9 | 17.77 | 6.31 | 13. 7 7 | 25.2 | 19.9 | |
| 70x70x8 | 70.0 | 70.0 | 8.0 | 8.0 | 10.67 | 8.37 | 48.16 | 9.68 | 21.2 | 48.16 | 9.68 | 21.2 | 76.35 | 26.8 | 19.97 | 6.99 | 13.7 | 28.2 | 20.2 | |
| 70x70x10 | 70.0 | 70.0 | 10.0 | 8.0 | 13.11 | 10.29 | 57.9 | 11.82 | 21.0 | 57.9 | 11.82 | 21.0 | 91.52 | 26.4 | 24.27 | 8.17 | 13.6 | 33.6 | 21.0 | |
Сортамент равнополочных уголков: виды, характеристики, ГОСТ
Довольно распространенным металлопрокатом можно назвать уголки равнополочные. При их изготовлении применяются стандарты, установленные в ГОСТ. За счет этого продукция представлена унифицированными видами. Рассматривая сортамент равнополочных уголков, следует учитывать тот момент, что вес и размеры имеют значение для проведения точных расчетов при разработке проектной или технической документации. Распространение материала можно связать с его исключительными эксплуатационными качествами, о чем далее поговорим подробнее.
Распространение материала можно связать с его исключительными эксплуатационными качествами, о чем далее поговорим подробнее.
Основные характеристики
В технической документации можно встретить самую различную информацию, которая может применяться при расчетах. Применяемая таблица позволяет определить нижеприведенные характеристики:
- Масса одного погонного метра. Вес уголка равнополочного учитывается при расчете того, какая будет оказываться нагрузка на создаваемую конструкцию. Вес стального уголка во многом зависит от размеров и типа применяемого материала при изготовлении. Плотность применяемого металла может варьироваться в достаточно большом диапазоне.
- Основные размеры. Уголок размеры может иметь самые различные. Они учитываются при расчетах. Размеры металлического уголка могут варьироваться в достаточно большом диапазоне, так как применяются при создании различных конструкций.
- Профиль металлического равнополочного материала может иметь самую различную площадь поперечного сечения.
 Этот параметр также указывает на то, какая будет оказываться нагрузка.
Этот параметр также указывает на то, какая будет оказываться нагрузка. - Чертеж и другая техническая информация также содержит информацию о том, какой радиус закругления у профиля. Этот показатель не является контролируемым параметром, но применяется для калибровки изделия. Сортамент уголков стальных горячекатаных равнополочных может быть представлен материалом, который имеет ровные или разные полки. Неравнополочные варианты исполнения также получили широкое распространение.
- В таблице указывается толщина стенок полок. При увеличении показателя толщины момент сопротивления увеличивается, изделие становится способным выдерживать большую нагрузку. Однако, за счет применения большего количества металла вес изделия существенно возрастает.
Характеристики уголков по ГОСТ 8509-93
Уголок равнополочный может классифицироваться по показателю точности. Примером назовем следующие группы изделий:
- Обычная точность, маркируемая буквой «В».
- Повышенной точности, маркировка представлена буквой «А».

Показатель толщины полки может иметь отклонение в соответствии с табличными данными.
В нормативной документации также указывает то, какой длины заготовки могут отправляться заказчику. Примером назовем то, что показатель длины должен составлять 3-12 м. При предварительной договоренности может отпускаться материал большей длины.
Виды равнополочных уголков
Равнополочные варианты исполнения на сегодняшний день получили весьма широкое распространение. Выпускаются они в различных вариантах исполнения. Рассматривая виды металлических уголков отметим, что геометрические размеры и классификация изделий регулируется двумя основными нормативными документами:
- Уголок горячекатаный равнополочный получается при применении технологии, которая предусматривает оказание воздействия высокой температуры. В качестве нормативной документации применяется ГОСТ 8509-93. За счет применения особой технологии производства получаемое изделие обладает весьма высокими эксплуатационными качествами.
 Однако, производственный процесс связан с достаточно большим количеством технологических сложностей.
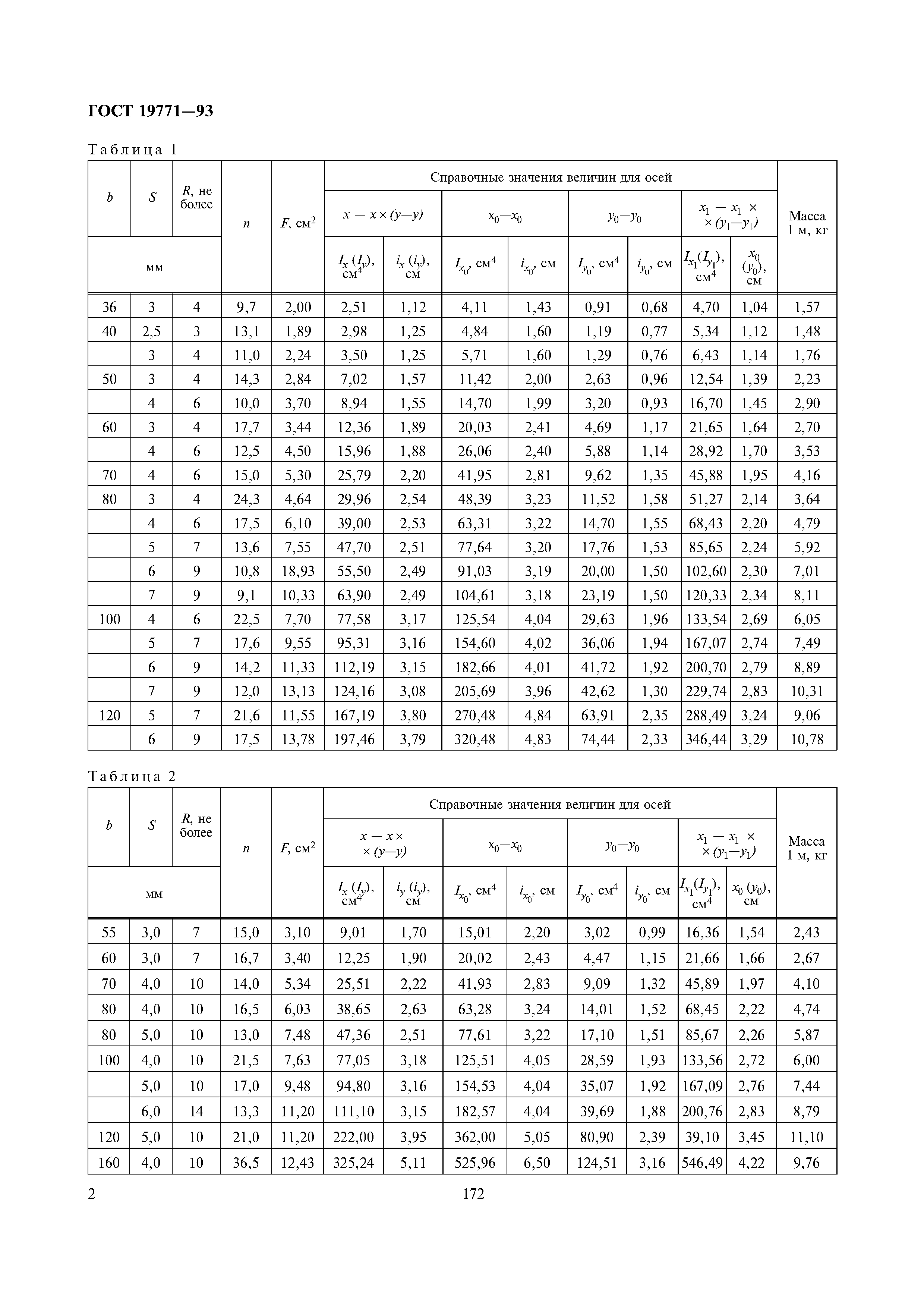
Однако, производственный процесс связан с достаточно большим количеством технологических сложностей. - Уголок стальной гнутый также получил широкое применение. Для стандартизации основных параметров в этом случае применяется ГОСТ 19771-93. За счет применения технологии холодной гибки существенно ускоряется производственный процесс.
Скачать ГОСТ 19771-93. Уголки стальные гнутые равнополочные. Сортамент.»
Отличительной особенностью равнополочных уголков назовем то, что полки у них имеют одинаковые геометрические размеры. Горячекатаные изделия производятся путем пропуска раскаленной заготовки через валики. При воздействии давления на размягченный сплав формируется геометрическая форма и определенные размеры.
При холодной гибке применяется специальное оборудование, которое способно оказывать существенно механическое воздействие. Стоит учитывать, что в данном случае в качестве заготовки может использоваться исключительно листовой прокат с относительно небольшой толщиной поперечного сечения.
- Уголок горячекатаный
- Уголок стальной гнутый
Горячекатаные изделия характеризуются следующими достоинствами:
- высокая прочность;
- более сложный профиль.
Гнутые обладают более точными геометрическими размерами, что также определило их распространение. Кроме этого, применение листового металла в качестве сырья позволило существенно снизить вес изделия и расширить сортамент.
Классификация проводится также по типу применяемого материала при изготовлении. От этого показателя зависят следующие моменты:
- Устойчивость материала к воздействию окружающей среды, к примеру, повышенной влажности.
- Прочность структуры и твердость поверхности.
- Плотность, которая определяет соотношение веса и геометрических размеров.
- Степень обрабатываемости.
При изготовлении равнополочного уголка могут применять следующие металлы:
- Стали повышенной прочности. Они обладают весьма большой прочностью, могут выдерживать существенное механическое воздействие.
 Стоит учитывать, что для достижения некоторых показателей проводится термическая обработка уже после получения требуемой формы и размеров.
Стоит учитывать, что для достижения некоторых показателей проводится термическая обработка уже после получения требуемой формы и размеров. - Легированные металлы с различной концентрацией примесей. За счет включения в состав различных веществ можно существенно изменить эксплуатационные качества изделия. К примеру, повышение концентрации хрома повышает коррозионную стойкость поверхности. При легировании металла учитывается, что получаемые равнополочные материалы должны обладать высокой прочностью.
- Сплавы, которые характеризуются высокой жаропрочностью, жаростойкостью или коррозионной устойчивостью. Некоторые равнополочные варианты исполнения строительных материалов могут применяться в особых эксплуатационных условиях. Для достижения требуемых качеств при их изготовлении могут применять высоколегированные сплавы.
Стальные уголки
Наиболее распространенным металлом, который применяется при производстве равнополочных уголков, является углеродистая сталь. Это связано с ее высокой прочностью и относительно низкой стоимостью, простотой получения.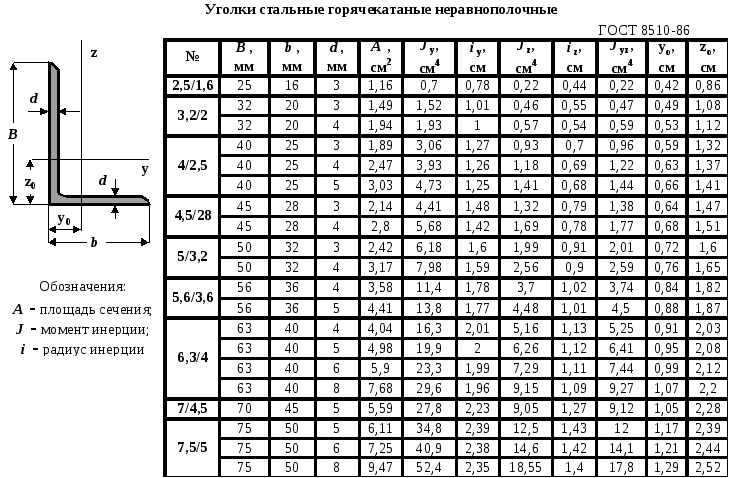
Размеры уголков
Вопрос размеров был затронут ранее при рассмотрении основных показателей, которые характеризуют уголок стальной. При этом также следует отметить нижеприведенные моменты:
- Указывается вес изделия. Металлический уголки применяются при изготовлении ответственных изделий. Именно поэтому при расчетах учитывается также вес самого материала.
- Основные размеры равнополочного уголка указываются также для разработки проектной документации и подбора наиболее подходящего изделия.
- Уголки стальные равнополочные также характеризуются площадью сечения профиля, шириной полки, радиусом закругления, толщиной стенок. Все эти показатели выдерживаются в качестве стандартов и не указываются производителями, при необходимости их можно найти в справочной документации.
Равнобокий уголок может иметь самые различные размеры. Широкой сортамент позволяет подобрать наиболее подходящий материал для применения в конкретном случае.
Широкой сортамент позволяет подобрать наиболее подходящий материал для применения в конкретном случае.
Применение стального уголка
Металлы сегодня встречаются практически на каждом шагу. При сочетании легкости и высокой прочности материал стал практически незаменим, применяется при строительстве различных сооружений и механизмов. Стальные уголки могут изготавливаться при применении различных металлов. За счет особой геометрии они могут воспринимать большую нагрузку, чем, к примеру, листовой материал. Прокат угловой или уголок стальной гнутый применяют:
- При строительстве несущих конструкций. Для того чтобы сооружение могло воспринимать большую нагрузку в качестве основного материала может применяться рассматриваемое изделие. Примером можно назвать возведение складских помещений, когда в качестве обшивки применяется легкий листовой металл, который покрывает устойчивый каркас. За счет этого существенно снижаются расходы и повышается прочность сооружения.
- В машиностроении и станкостроении.
 Особая форма определяет высокую жесткость и способность гашения вибрационной нагрузки. Именно поэтому рассматриваемый материал применяется для создания усиливающего каркаса, несущей рамы и других элементов.
Особая форма определяет высокую жесткость и способность гашения вибрационной нагрузки. Именно поэтому рассматриваемый материал применяется для создания усиливающего каркаса, несущей рамы и других элементов.
Angles — Mathematics GCSE Revision — Revision Maths
Углы измеряются в градусах, записываются в °. Максимальный угол 360 °. Это угол вокруг точки. Половина этого угла составляет 180 ° на прямой.
Видео ниже объясняет, как вычислить связанные углы, смежные углы, внутренние углы и дополнительные углы.
Связанные уголки
Линии AB и CD параллельны друг другу (отсюда »на линиях).
a и d известны как , вертикально противоположные углам . Вертикально противоположные углы равны. (b и c, e и h, f и g также противоположны по вертикали).
g и c — это соответствующих углов . Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
d и e — это альтернативных углов . Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют Z-образную форму и иногда называются Z-углами.
Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют Z-образную форму и иногда называются Z-углами.
a и b — это смежных углов . Смежные углы в сумме составляют 180 градусов. (d и c, c и a, d и b, f и e, e и g, h и g, h и f также смежны).
d и f — это внутренние углы . В сумме они составляют 180 градусов (е и с также являются внутренними).
Любые два угла, которые в сумме составляют 180 градусов, называются дополнительными углами .
Сумма углов треугольника
Используя некоторые из приведенных выше результатов, мы можем доказать, что сумма трех углов внутри любого треугольника всегда в сумме составляет 180 градусов.
Если у нас есть треугольник, вы всегда можете нарисовать две параллельные линии следующим образом:
Теперь мы знаем, что альтернативных углов равны. Следовательно, два угла, обозначенные x, равны. Кроме того, два угла, обозначенные буквой y, равны.
Мы знаем, что x, y и z вместе составляют 180 градусов, потому что вместе они представляют собой угол вокруг прямой. Таким образом, сумма трех углов треугольника должна составлять 180 градусов.
Сумма углов четырехугольника
Четырехугольник — это фигура с 4 сторонами.
Теперь, когда мы знаем сумму углов в треугольнике, мы можем вычислить сумму углов в четырехугольнике.
Для любого четырехугольника мы можем провести диагональную линию, чтобы разделить его на два треугольника. Каждый треугольник имеет сумму углов 180 градусов. Следовательно, общая сумма углов четырехугольника составляет 360 градусов.
Наружные углы
Внешние углы формы — это углы, которые вы получите, если удлинить стороны.Показаны внешние углы шестиугольника:
Многоугольник — это фигура с прямыми сторонами. Все внешние углы многоугольника составляют в сумме 360 °. потому что, если вы сложите их все вместе, они образуют угол вокруг точки:
Следовательно, если у вас есть правильный многоугольник (другими словами, где все стороны имеют одинаковую длину и все углы одинаковы), каждый из внешних углов будет иметь размер 360 ÷ количество сторон. Так, например, каждый из внешних углов шестиугольника составляет 360/6 = 60 °.
Так, например, каждый из внешних углов шестиугольника составляет 360/6 = 60 °.
Внутренние углы
Внутренние углы формы — это углы внутри нее. Если вы знаете размер внешнего угла, вы можете определить размер внутреннего угла рядом с ним, потому что в сумме они составляют 180 ° (поскольку вместе они составляют угол на прямой).
Внешний угол треугольника
Угол x — это внешний угол треугольника:
Внешний угол треугольника равен сумме внутренних углов в двух других вершинах.Другими словами, x = a + b на диаграмме.
Проба:
- Сумма углов в треугольнике составляет 180 градусов. Итак, a + b + y = 180.
- Сумма углов прямой линии составляет 180 градусов. Итак, x + y = 180.
- Следовательно, y = 180 — x. Помещение этого в первое уравнение дает нам: a + b + 180 — x = 180. Следовательно, a + b = x после перестановки. Это то, что мы хотели доказать.

Треугольники — равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или Нет равных сторон / углов:
Равносторонний треугольник Три равных сторон | |
Равнобедренный треугольник Две равные стороны | |
Чешуйчатый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : «равный» — боковой (боковой означает сторона), поэтому все стороны имеют равные стороны
- Равнобедренный : означает «равные ноги», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых «S ides», соединенных стороной « O dd».

- Scalene : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Правый треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Поиграй с ним. ..
..
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
Углы и параллельные прямые (Предварительная алгебра, Введение в геометрию) — Mathplanet
Когда две прямые пересекаются, они образуют две пары противоположных углов, A + C и B + D.Другое название противоположных углов — вертикальные углы.
Вертикальные углы всегда совпадают, что означает, что они равны.
Соседние углы — это углы, выходящие из одной вершины. Соседние углы имеют общий луч и не перекрываются.
Размер угла xzy на рисунке выше является суммой углов A и B.
Два угла считаются дополнительными, если сумма двух углов составляет 90 °.
Два угла считаются дополнительными, если сумма двух углов составляет 180 °.
Если у нас есть две параллельные линии и есть третья линия, которая их пересекает, как на картинке ниже — линия пересечения называется поперечной
Когда трансверсаль пересекается с двумя параллельными линиями, получается восемь углов.
Восемь углов вместе образуют четыре пары соответствующих углов. Углы 1 и 5 составляют одну из пар. Соответствующие углы равны. Все углы, которые имеют одинаковое положение относительно параллельных линий и трансверсали, представляют собой соответствующие пары e.грамм. 3 + 7, 4 + 8 и 2 + 6.
Углы, которые находятся в области между параллельными линиями, такими как угол 2 и 8 выше, называются внутренними углами, тогда как углы, которые находятся снаружи двух параллельных линий, таких как 1 и 6, называются внешними углами.
Углы, которые находятся на противоположных сторонах поперечной оси, называются альтернативными углами, например 1 + 8.
Все углы, которые являются либо внешними углами, либо внутренними углами, альтернативными углами или соответствующими углами, являются конгруэнтными.
Пример
На рисунке выше показаны две параллельные линии с трансверсалью. Угол 6 равен 65 °. Есть ли другой угол, который также составляет 65 °?
6 и 8 являются вертикальными углами и, таким образом, совпадают, что означает, что угол 8 также равен 65 °.
6 и 2 являются соответствующими углами и, таким образом, совпадают, что означает, что угол 2 составляет 65 °.
6 и 4 представляют собой чередующиеся внешние углы и, следовательно, совпадают, что означает, что угол 4 составляет 65 °.
Видеоурок
Найдите размеры всех углов на рисунке
равных углов — RFL
| Размер мм | кг / метр | Метры / тонна |
|---|---|---|
| 20 x 20 x 3 | 0.88 | 1136 |
| 20 х 20 х 4 | 1,14 | 877 |
| 25 х 25 х 3 | 1,12 | 893 |
| 25 х 25 х 4 | 1,47 | 680 |
| 25 х 25 х 5 | 1,78 | 562 |
| 25 х 25 х 6 | 2,22 | 450 |
| 30 х 30 х 3 | 1,36 | 735 |
| 30 х 30 х 4 | 1.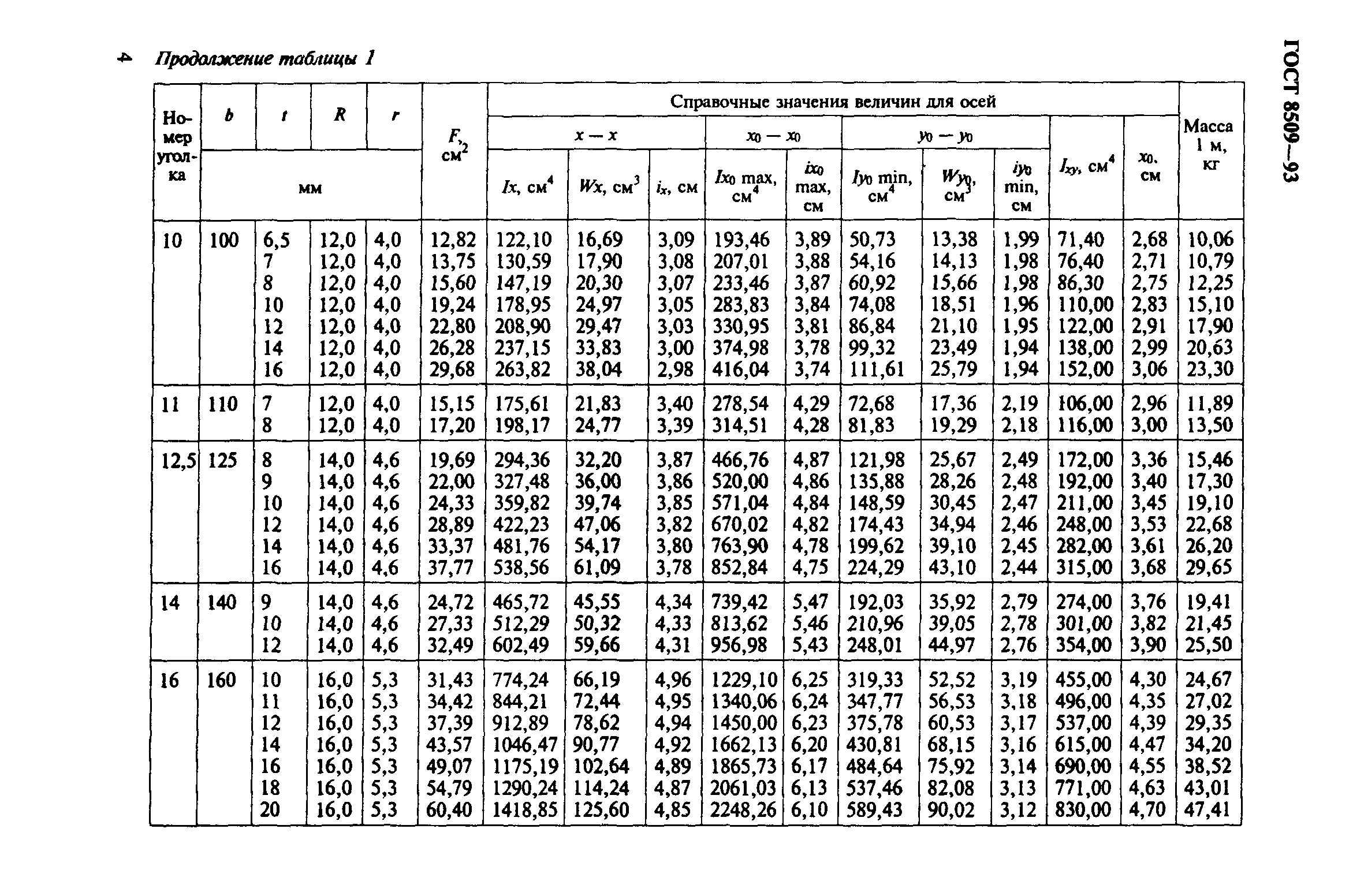 78 78 | 562 |
| 30 х 30 х 5 | 2,18 | 459 |
| 30 х 30 х 6 | 2,57 | 389 |
| 40 х 40 х 3 | 1,84 | 543 |
| 40 х 40 х 4 | 2,42 | 413 |
| 40 х 40 х 5 | 2,97 | 337 |
| 40 х 40 х 6 | 3,52 | 284 |
| 45 х 45 х 3 | 2.11 | 474 |
| 45 x 45 x 4,5 | 3,06 | 327 |
| 45 х 45 х 5 | 3,38 | 296 |
| 45 х 45 х 6 | 4,01 | 249 |
| 50 х 50 х 3 | 2,33 | 429 |
| 50 х 50 х 4 | 3,08 | 325 |
| 50 х 50 х 5 | 3,77 | 265 |
| 50 х 50 х 6 | 4.47 | 224 |
| 50 х 50 х 8 | 5,82 | 172 |
| 55 х 55 х 6 | 5,18 | 193 |
| 60 х 60 х 4 | 4,49 | 223 |
| 60 х 60 х 5 | 4,57 | 219 |
| 60 х 60 х 6 | 5,42 | 185 |
| 60 х 60 х 7 | 6,25 | 160 |
| 60 х 60 х 8 | 7. 09 09 | 141 |
| 60 х 60 х 10 | 8,69 | 115 |
| 65 х 65 х 6 | 6,15 | 163 |
| 65 х 65 х 7 | 7,15 | 140 |
| 65 х 65 х 8 | 8,16 | 123 |
| 65 х 65 х 9 | 9,19 | 109 |
| 70 х 70 х 5 | 5,15 | 194 |
| 70 х 70 х 6 | 6.38 | 157 |
| 70 х 70 х 7 | 7,69 | 130 |
| 70 х 70 х 8 | 8,36 | 120 |
| 70 х 70 х 10 | 10,31 | 97 |
| 75 х 75 х 6 | 6,87 | 146 |
| 75 х 75 х 7 | 8,25 | 121 |
| 75 х 75 х 8 | 9,01 | 111 |
| 75 х 75 х 10 | 11.11 | 90 |
| 75 х 75 х 12 | 13,07 | 77 |
| 80 x 80 x 5,5 | 6,91 | 145 |
| 80 х 80 х 6 | 7,34 | 136 |
| 80 x 80 x 6,5 | 8,17 | 122 |
| 80 х 80 х 8 | 9,63 | 104 |
| 80 х 80 х 10 | 11,9 | 84 |
| 80 х 80 х 12 | 14. 2 2 | 70 |
| 90 х 90 х 6 | 8,3 | 120 |
| 90 х 90 х 8 | 10,9 | 92 |
| 90 х 90 х 9 | 12,72 | 79 |
| 90 х 90 х 10 | 13,4 | 75 |
| 90 х 90 х 12 | 15,9 | 63 |
| 100 х 100 х 8 | 12,2 | 82 |
| 100 х 100 х 10 | 15 | 67 |
| 100 х 100 х 12 | 17.8 | 56 |
| 100 х 100 х 15 | 21,9 | 46 |
| 120 х 120 х 8 | 14,7 | 68 |
| 120 х 120 х 10 | 18,2 | 55 |
| 120 х 120 х 12 | 21,6 | 46 |
| 120 х 120 х 15 | 26,6 | 38 |
| 150 х 150 х 10 | 23 | 43 |
| 150 х 150 х 12 | 27.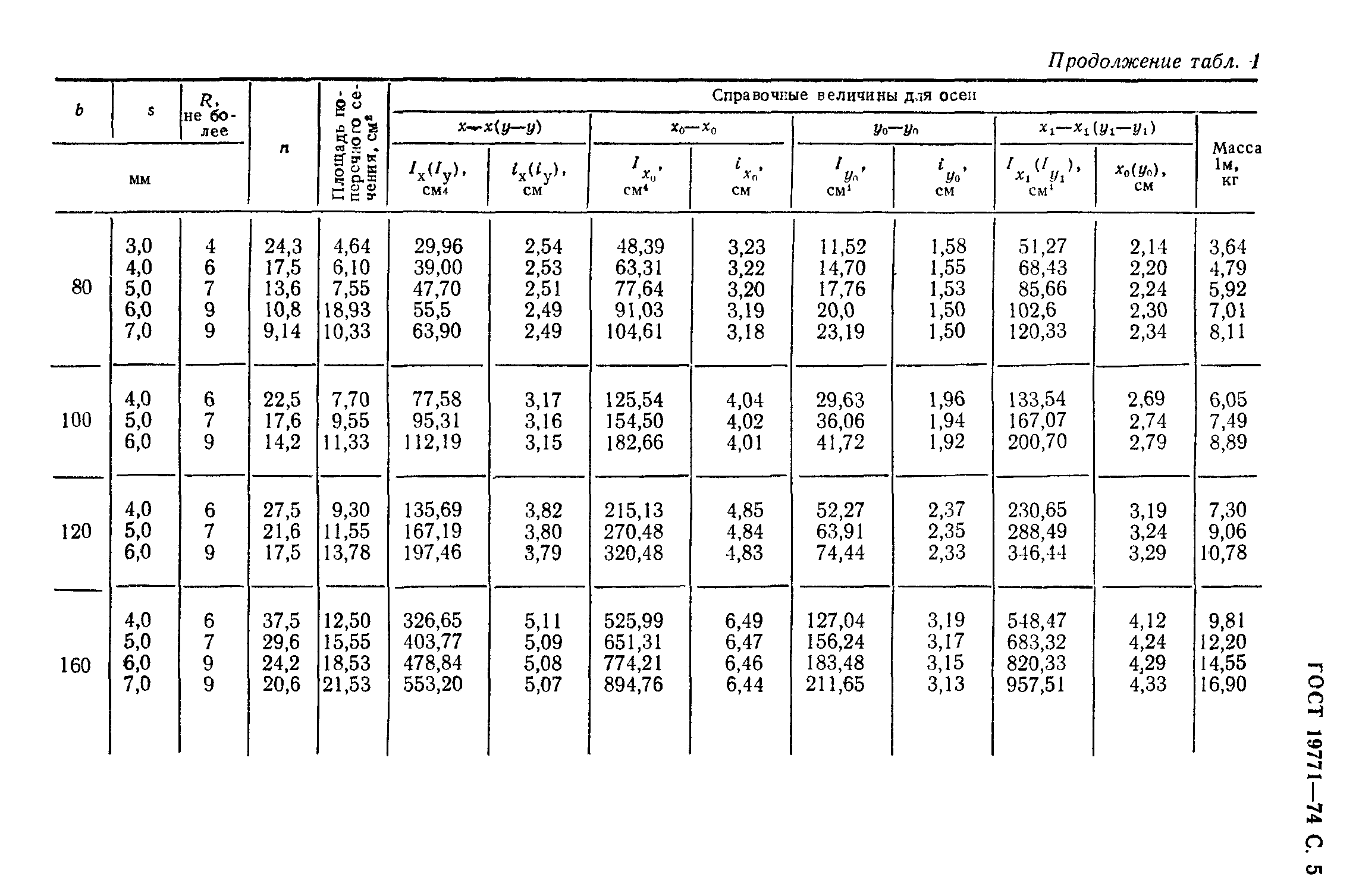 3 3 | 37 |
| 150 х 150 х 15 | 33,8 | 30 |
| 150 х 150 х 18 | 40,1 | 25 |
| 200 х 200 х 12 | 36,74 | 27 |
| 200 х 200 х 16 | 48,5 | 21 |
| 200 х 200 х 18 | 54,2 | 18 |
| 200 х 200 х 20 | 59,9 | 17 |
| 200 х 200 х 24 | 71.1 | 14 |
Классификация трех типов треугольников
- Образование
- Математика
- Геометрия
- Классификация трех типов треугольников
Марк Райан
Треугольники классифицируются в зависимости от длины их сторон или меры их углов. Эти классификации делятся на три, как и сами стороны и углы. То есть треугольник имеет три стороны, и три члена описывают треугольники на основе их сторон; у треугольника также есть три угла, и три классификации треугольников основаны на их углах.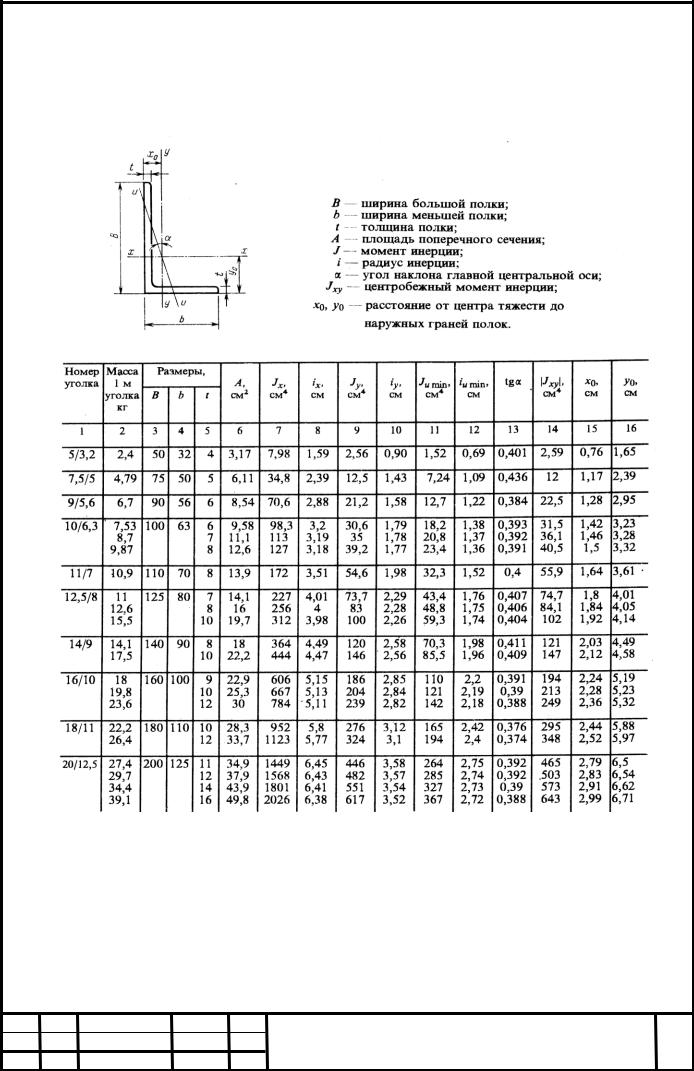 Ниже приведены классификации треугольников по сторонам:
Ниже приведены классификации треугольников по сторонам:
- Масштабный треугольник: Треугольник без совпадающих сторон
- Равнобедренный треугольник: Треугольник с как минимум двумя равными сторонами
- Равносторонний треугольник: Треугольник с тремя равными сторонами
Поскольку равносторонний треугольник также является равнобедренным, все треугольники либо равносторонние, либо равнобедренные. Но когда люди называют треугольник равнобедренным, они обычно имеют в виду треугольник, у которого только две равные стороны , потому что, если бы у треугольника было три равные стороны, они бы назвали его равносторонним.Однако вы не всегда можете предполагать это, когда делаете сложную домашнюю работу по геометрии.
Чешуйчатые треугольники
Помимо трех неравных сторон у разносторонних треугольников есть еще три неравных угла. Самая короткая сторона — поперек наименьшего угла, сторона средней длины — поперек среднего угла, и — сюрприз, сюрприз — самая длинная сторона поперек наибольшего угла.
Соотношение сторон не равно соотношению углов. Не думайте, что если одна сторона треугольника, скажем, вдвое длиннее другой, то углы, противоположные этим сторонам, также будут в соотношении 2: 1.Отношение сторон может быть близко к соотношению углов, но для разностороннего треугольника эти соотношения никогда не бывают точно равными.
Равнобедренные треугольники
Равнобедренный треугольник имеет две равные стороны и два равных угла. Равные стороны называются ножками , а третья сторона — основанием . Два угла, соприкасающиеся с основанием (которые совпадают или равны), называются углами основания . Угол между двумя ножками называется углом при вершине .
Равносторонние треугольники
Равносторонний треугольник имеет три равные стороны и три равных угла (каждый по 60 °). Равные углы делают его равноугольным и равносторонним. Однако вы не часто слышите выражение равносторонний треугольник , потому что единственный равносторонний треугольник — это равносторонний треугольник, и все называют этот треугольник равносторонним. (Однако для четырехугольников и других многоугольников вам понадобятся оба члена, потому что равносторонняя фигура, такая как прямоугольник, может иметь стороны разной длины, а равносторонняя фигура, такая как ромб, может иметь углы разных размеров.)
(Однако для четырехугольников и других многоугольников вам понадобятся оба члена, потому что равносторонняя фигура, такая как прямоугольник, может иметь стороны разной длины, а равносторонняя фигура, такая как ромб, может иметь углы разных размеров.)
Если вы разрежете равносторонний треугольник пополам прямо посередине, вы получите два прямоугольных треугольника 30 ° — 60 ° — 90 °, которые очень сильно влияют на геометрию и тригонометрию.
Углы Эйлера
Относительная ориентация между двумя ортогональными правыми трехмерными декартовыми системами координат, назовем их xyz и ABC, описывается реальной ортогональной матрицей вращения 3×3 R, которая обычно параметризуется тремя так называемыми углами Эйлера α, β и γ.
Углы Эйлера
Углы определяют относительную ориентацию между xyz и ABC. Углы описывают три последовательных поворота одной системы координат xyz, которая
выровняйте его с другим, ABC.
- Поверните xyz против часовой стрелки вокруг его оси z на α, чтобы получить x’y’z ‘.
- Поверните x’y’z ‘против часовой стрелки вокруг его оси y’ на β, чтобы получить x»y»z ».
- Поверните x»y»z » против часовой стрелки вокруг его оси z » на γ, чтобы получить окончательную ABC.
По понятным причинам это называется соглашением zyz или y. Он используется во многих учебниках:
- Теория углового момента: Роуз, Эдмондс.
- ЯМР: Ernst / Bodenhausen / Wokaun, Spiess, Mehring.
- EPR: Abragam / Bleaney, Schweiger / Jeschke, Atherton.
Ось z называется вертикальной , ось y ‘(так же, как ось y) называется линией узлов , а z » (то же самое, что и C) называется осью фигуры .
Матрица, описывающая это вращение, представляет собой произведение 3 матриц, каждая из которых описывает одно вращение по одной оси.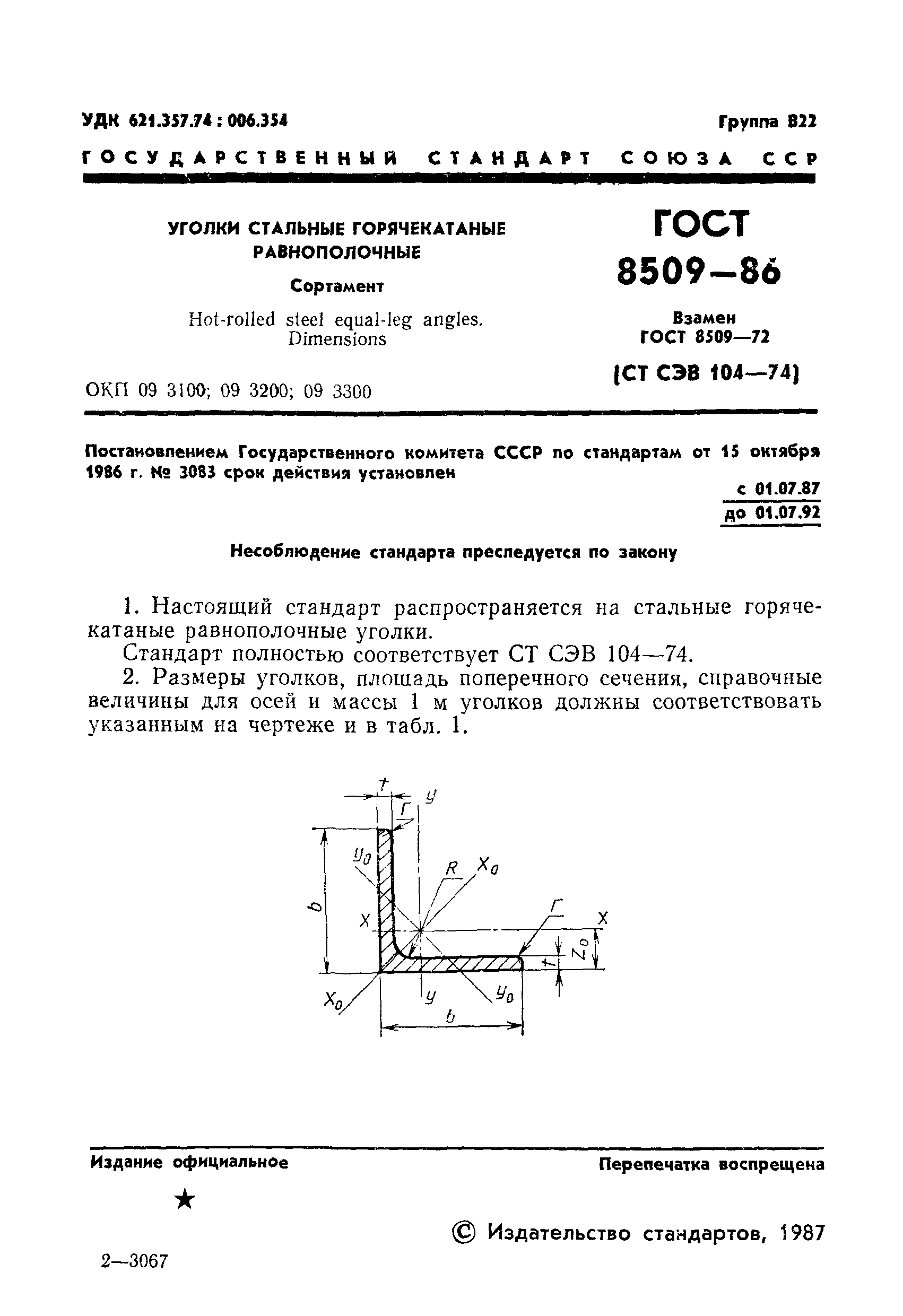
где c и s означают cos () и sin (). Матрицы вращения вещественные, симметричные и ортогональные, т.е. их инверсия равна их транспонированию. Определитель R равно +1.
Строки и столбцы R имеют простой геометрический смысл:
- Строки R являются представлениями A, B и C в xyz кадр.Например. первая строка R — векторное представление A в система координат xyz.
- Столбцы R содержат векторные представления x, y и z в системе ABC. Например, третий столбец R дает вектор z, представленный его координатами ABC.
Та же матрица вращения получается, если вращения выполняются в обратном порядке вокруг других осей: сначала на γ вокруг оси z ось, затем на β вокруг исходной оси y и, наконец, снова на α вокруг оси z на исходной .Другими словами
Чтобы получить углы Эйлера для поворота R 2 : ABC → xyz из Углы Эйлера поворота R 1 : xyz → ABC (описанный выше), использовать
т.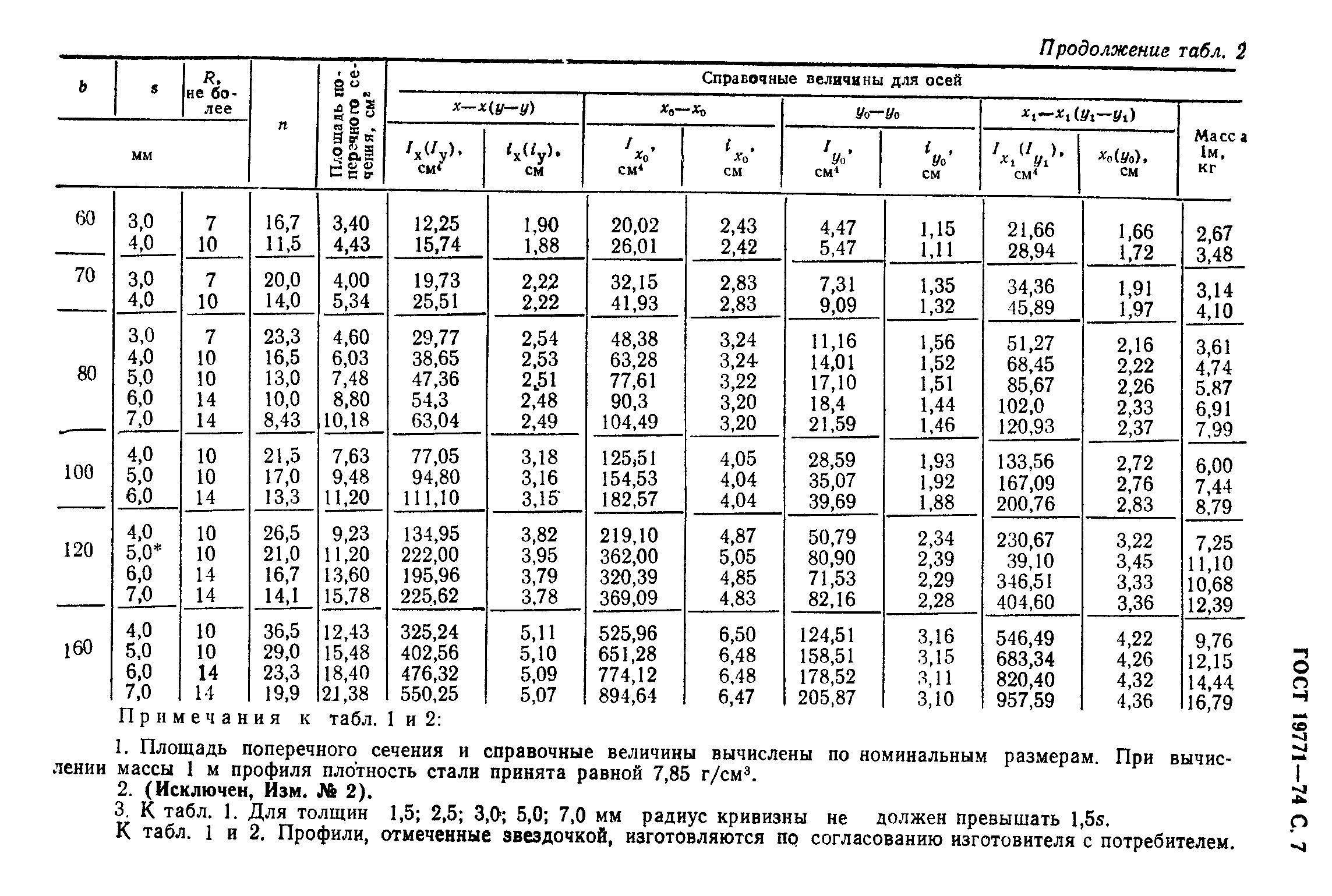 е. обмен и и
перевернуть все знаки.
е. обмен и и
перевернуть все знаки.
Эквивалентные наборы углов Эйлера
Конечно, прибавление к любому углу произвольного кратного 2 не влияет на матрицу вращения.
Однако существуют другие наборы углов Эйлера, которые дают ту же матрицу вращения
Итак, если вы перевернете знак β, вам придется добавить (или вычесть) как к α, так и к γ.
Как следствие, существует взаимно однозначное соответствие между углами Эйлера и матрицы вращения, только если области углов Эйлера ограничены, например к
Ось вращения и угол
Помимо набора из трех углов Эйлера и матрицы вращения, вращение также может быть представлено вектором, определяющим вращение ось и угол поворота вокруг этой оси.
Это представление редко используется в ЭПР, но визуально оно очень простое. понимать.
Выбор тензорных собственных кадров
Разметка главных осей тензора совершенно произвольна.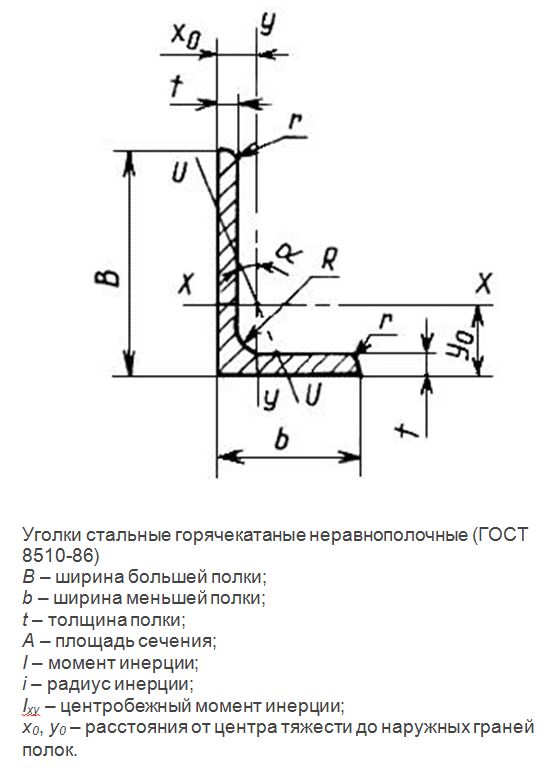 Всего существует 24 возможных расположения xyz, которые описывают основные
осей каркаса тензора. Соответственно, существует 24 различных набора Эйлера.
углы. Почему 24? Их легко перечислить: ось z может указывать на любой из шести
направление главной оси эллипсоида, а пара осей xy может иметь 4
возможных ориентаций для каждой ориентации z, всего 24.
Всего существует 24 возможных расположения xyz, которые описывают основные
осей каркаса тензора. Соответственно, существует 24 различных набора Эйлера.
углы. Почему 24? Их легко перечислить: ось z может указывать на любой из шести
направление главной оси эллипсоида, а пара осей xy может иметь 4
возможных ориентаций для каждой ориентации z, всего 24.
Если ось z требуется для точек вдоль осей с наибольшим собственным значением тензора, то он может иметь только 2 ориентации, а всего 8 различных системы координат и 8 наборов углов Эйлера.
Применение вращений
Вращения могут быть активными или пассивными. В активных («алиби») поворотах объект (вектор, тензор) поворачивается, а система координат остается неизменной. В пассивных («псевдонимах») ротациях объект остается неизменным, а система координатных осей вращается.
Вот как можно выполнить пассивное вращение, используя матрицу вращения R, как определено выше:
Для вектора v_xyz, определенного в кадре xyz, v_ABC = R * v_xyz является тем же вектором, что и v_xyz, но представлен в кадре ABC вместо кадра xyz.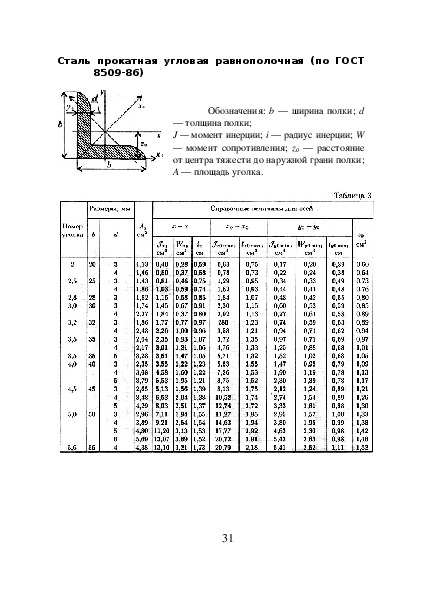

 Этот параметр также указывает на то, какая будет оказываться нагрузка.
Этот параметр также указывает на то, какая будет оказываться нагрузка.
 Однако, производственный процесс связан с достаточно большим количеством технологических сложностей.
Однако, производственный процесс связан с достаточно большим количеством технологических сложностей.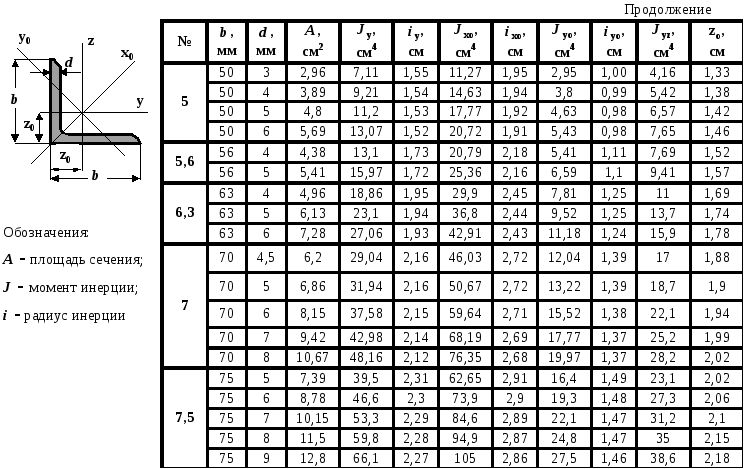 Стоит учитывать, что для достижения некоторых показателей проводится термическая обработка уже после получения требуемой формы и размеров.
Стоит учитывать, что для достижения некоторых показателей проводится термическая обработка уже после получения требуемой формы и размеров.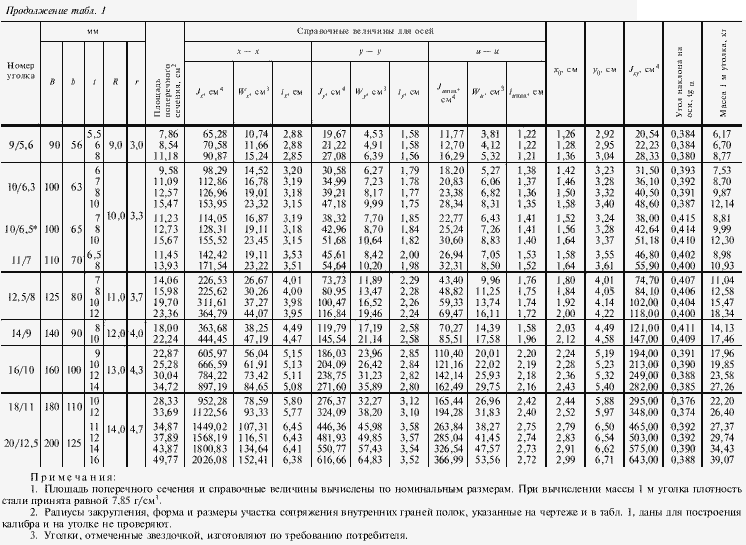 Особая форма определяет высокую жесткость и способность гашения вибрационной нагрузки. Именно поэтому рассматриваемый материал применяется для создания усиливающего каркаса, несущей рамы и других элементов.
Особая форма определяет высокую жесткость и способность гашения вибрационной нагрузки. Именно поэтому рассматриваемый материал применяется для создания усиливающего каркаса, несущей рамы и других элементов.

 ..
..