Преобразование в фигуры в Office
Добавление на ленту «Преобразовать в фигуру»
В Visioпо умолчанию недоступна возможность преобразовать в фигуру. Настройте ленту, чтобы увидеть эту команду.
-
На вкладке Файл выберите пункт Параметры.
-
В левой части диалогового окна выберите Настроить ленту.
-
В списке справа от диалогового окна выберите Рисовать.
-
Выберите новая группа, а затем щелкните Переименовать, чтобы дать новой пользовательской группе имя, например Фигуры. Убедитесь, что новая группа остается выбранной.
-
В левой части диалогового окна в поле Выбрать команды извыберите все команды.

-
В длинном алфавитном списке команд выберите преобразовать в фигуру инажмите кнопку Добавить между двумя длинными списками.
На ленту будет добавлено преобразование в фигуру.
-
Нажмите кнопку ОК.
Теперь вы можете использовать преобразование в фигуру, чтобы преобразовать рисунок от Visio фигуру.
Преобразование нарисованной отрисовки в стандартную Visio фигуру
-
На вкладке «Рисовать» выберитеРисовать касанием , затем выберите перо от пера от пера и рисуйте на холсте.
-
На вкладке «Рисовать» выберите инструмент «Выбрать».
-
Щелкните и перетащите, чтобы выбрать нарисованный объект, который вы хотите преобразовать в стандартную фигуру.

На фигуре появятся химки выделения.
-
На вкладке «Рисовать» выберите
-
На вкладке Главная выберите изменить фигуруи выберите фигуру из коллекции.
Совет: Если вы не видите список фигур с нужной фигурой, в области Фигуры выберите Дополнительные фигуры ,а затем выберите набор, содержащий нужную фигуру.
Рисунок будет заменен выбранной фигурой, а размер, положение и форматирование этой фигуры будут сохранены. При необходимости продолжайте разместять фигуру. (Подробные сведения см. в теме Формат фигуры.)
Фигуры шестиугольники — 55 фото
1
Шестиугольник
2
Шестигранник фигура
3
Шестиуголка
4
Геометрические фигуры шестиугольник
5
Пентагон в шестиугольнике
6
Шестиугольник неправильный шестиугольник
7
Гексагон фигура
8
Правильный шестиугольник фигура
9
Правильный шестиугольник
10
Гексагон многоугольник
11
Правильный десятиугольник
12
Шестигранник фигура
13
Шестиугольник
14
Шестигранник фигура
15
Шестиугольная фигура
16
Геометрические фигуры шестиугольник
17
Шестиугольник
18
Шестиуголка
19
Шестиугольник фигура
20
Правильный шестигранник
21
Шестиугольник
22
Шестигранник фигура
23
Шестигранник Геометрическая фигура
24
Шестиугольная фигура
25
Шестиугольник
26
Шестиуголка
27
Шестиугольник фигура
28
Геометрические фигуры шестиугольник
29
C6h22 циклогексан
30
Циклогексан циклогексанон
31
C6h20 циклогексен
32
Циклогексен структурная формула
33
Pentagon многоугольник
34
Правильный многоугольник восьмиугольник
35
Правильный шестиугольник шестиугольник
36
Гексагон многоугольник
37
Гексагон многоугольник
38
Пентагон октагон Гексагон фигуры
39
Правильный шестиугольник
40
Шестиугольная фигура
41
Гексагон многоугольник
42
Шестигранник фигура
43
Геометрические фигуры шестиугольник
44
6 Угольник
45
Шестиугольник и семиугольник
46
Невыпуклый семиугольник
47
Выпуклый Сими угорьние
48
Фигуры многоугольники
49
Гексагон фигура
50
Шестиугольник
51
Шестигранник фигура
52
Шестиуголка
53
Шестигранник фигура
54
Геометрические фигуры шестиугольник
НЕПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК.
 Шесть столпов «Дорожной карты» правительства на 2016 год
Шесть столпов «Дорожной карты» правительства на 2016 годНовость о предстоящей в июле 2016г. 10-тысячекратной деноминации Br-рубля затмила представление контуров экономической политики на 2016-2020гг. Сам план пятой пятилетки ещё не обнародован, но его основные авторы продолжают тестировать общественное мнение на разных форумах и площадках. На этот раз первый заместитель министра экономики Александр Заборовский на конференции «Экономика Беларуси: снова перед выбором» представил «дорожную карту» структурных реформ, каким они представляются воспитанниками мощной лоббистской группы М. Мясниковича.
Фейковая открытостьВ набор предложений Минэкономики были интегрированы рекомендации Всемирного банка и МВФ. Нет сомнений, что словесная оболочка призвана убедить эти международные организации оказать кредитную, техническую и маркетинговую помощь белорусскому правительству. Рассмотрим суть представленных предложений и оценим их на рыночность.
А. Заборовский предвосхитил своё выступление на конференции весьма спорным тезисом: «Мы в Министерстве экономики не делим экономистов и ученых на своих и чужих — главный критерий, это научная обоснованность, желание открыто и профессионально работать, конструктивно дискутировать». Известно, что с приходом в Минэкономики министра Владимира Зиновского возможность диалога с руководством этого органа резко сократились. В своё время Николай Снопков и его заместители были гораздо более отрытыми для обмена мнениями.
Известно, что с приходом в Минэкономики министра Владимира Зиновского возможность диалога с руководством этого органа резко сократились. В своё время Николай Снопков и его заместители были гораздо более отрытыми для обмена мнениями.
Руководители Минэкономики сами оценивают научную обоснованность и конструктивность белорусских экономистов. Через это сито не проходят эксперты, которые последовательно отстаивают системные либеральные рыночные реформы. В отличие от Нацбанка ни Совмин, ни одно министерство не организовали площадки для регулярного общения с профессиональным экономическим сообществом. При таком подходе есть все основания сомневаться в желании руководителей министерств и ведомств выслушать и обсудить все валидные точки зрения на системные трансформации в, действительно, открытом диалоге.
Участие в Кастрычiцкiм форуме, уважаемой площадке Исследовательского центра ИПМ, раз в год не может рассматриваться, как полноценная конструктивная дискуссия. Кулуарный, закрытый режим обсуждения чиновниками разных тем и проблем с представителями международных организаций – это не вовлечение в диалог относительно содержания реформ, а работа в рамках грантов, договоров технической помощи или кредитных соглашений. После жёсткого кризиса конца 2014 года Совмин так и не удосужился предложить экономическому сообществу страны полноценный научный конструктивный диалог. Очевидно, попытки первого вице-премьера Василия Матюшевского не нашли поддержки у руководства правительства. Уместно напомнить, что сотрудничество белорусских властей с МВФ, Всемирным банком и ООН в последние десять лет не помешало им работать в парадигме централизованной плановой экономики. Десятки стран мира на своей шкуре убедились в том, что рекомендации этих организаций далеко не всегда расширяют сферу настоящих рыночных отношений. Иными словами штамп одобрения со стороны МВФ/ООН/Всемирного банка – это не одно и то же, что принятие пакета рыночных реформ.
После жёсткого кризиса конца 2014 года Совмин так и не удосужился предложить экономическому сообществу страны полноценный научный конструктивный диалог. Очевидно, попытки первого вице-премьера Василия Матюшевского не нашли поддержки у руководства правительства. Уместно напомнить, что сотрудничество белорусских властей с МВФ, Всемирным банком и ООН в последние десять лет не помешало им работать в парадигме централизованной плановой экономики. Десятки стран мира на своей шкуре убедились в том, что рекомендации этих организаций далеко не всегда расширяют сферу настоящих рыночных отношений. Иными словами штамп одобрения со стороны МВФ/ООН/Всемирного банка – это не одно и то же, что принятие пакета рыночных реформ.
Белорусские власти, как мантру повторяют важность макроэкономической стабилизации. При этом они наполняют его своим смыслом. В теории и в практике рыночных стран макроэкономическая стабилизация – это инфляция менее 3% в год при свободных ценах, отсутствие барьеров на перемещение капитала по текущему и капитальному счетам, свободная конкуренция на рынке финансовых услуг, чёткая и прозрачная бюджетно-налоговая политика.
В 2016 году Совмин даже не обещает настоящей макроэкономической стабильности. После сокрушительного провала по привлечению прямых иностранных инвестиций правительство опять обещают привлечь на чистой основе $2 — 2,5 млрд. и на этом основании чиновники обещают бездолговое финансирование счёта текущих операций. При скандальном отношении чиновников к частной собственности, регуляторных безобразиях (вспомним хотя бы постановление Совмина № 666), разрушительной дискриминации государственных организаций привлечь столько инвестиций в экономику, в которой даже цены не имеют права быть свободными, абсолютно нереально.
А. Заборовский обещает с 2016 года «идеальный порядок с администрированием и последовательным сокращением нерыночных кредитов». Проекты основных экономических документов на следующий год указывают на небольшое сокращение объёма льготных кредитов.
Особое «научное» чутьё и методология расчётов позволили А. Заборовскому сделать ещё одно сенсационное открытие. Оказывается, «если убрать металлургию, калий и нефтянку, то есть сугубо сырьевые, рентные отрасли, работающие эффективно и имеющие специфику, доля государства снизится до 37%». Вот так белорусские власти без приватизации умудрились сократить долю государства в добавленной стоимости до менее 50%. Вот так заместитель министра экономики, убрав за скобки более 30% экономики, огласил триумфальное шествие частной собственности. Никакого мошенничества – только особенности национальной методологии оценки и расчётов.
Вот так заместитель министра экономики, убрав за скобки более 30% экономики, огласил триумфальное шествие частной собственности. Никакого мошенничества – только особенности национальной методологии оценки и расчётов.
А. Заборовский для государственных коммерческих организаций предлагает «многомерную последовательную стратегию», но в этом пакете приватизации места не нашлось. Госкомпаниям будет сложнее получать льготы. Правительство обещает прекратить поддерживать убыточные виды деятельности», но не сами убыточные предприятия. Это значит. «Красные» директора и помещики (руководители с/х предприятий) легко найдут новые, неизменно инновационные темы для получения финансирования. Такой подход гарантирует консервацию существующих отношений между коммерческими организациями и Вертикалью.
Четвёртое обещание А. Заборовского – «создание условий для увеличения числа рабочих мест в частном секторе путем улучшения инвестиционного климата, снижение регулятивной и налоговой нагрузки, обеспечение безусловных гарантий прав частной собственности». Это обещание звучит особенно цинично на фоне декларации МНС о том, что в Беларуси чуть ли не оптимальная налоговая система, с учётом практики властей без согласования с бизнесом увеличивать ставки налогов и аренды в 2 – 3 раза, а также менять порядок и методику налогового учёта. А. Заборовский не оценил монетарный ущерб стране от арестов известных белорусских программистов, жёстких наездов на мебельный бизнес в Гродно, кормовой и с/х бизнес в Витебске, Бресте, от фактической блокировки инвестиционных проектов в Минской области и порочную практику навязывания инвесторам 20 – 25 условий. Заместитель министра экономики не посчитал нужным прокомментировать явную угрозу ухода с рынка труда около 30 тысяч индивидуальных предпринимателей. Совмин своими действиями способствует ликвидации этой «нецивилизованной» формы экономической деятельности.
Это обещание звучит особенно цинично на фоне декларации МНС о том, что в Беларуси чуть ли не оптимальная налоговая система, с учётом практики властей без согласования с бизнесом увеличивать ставки налогов и аренды в 2 – 3 раза, а также менять порядок и методику налогового учёта. А. Заборовский не оценил монетарный ущерб стране от арестов известных белорусских программистов, жёстких наездов на мебельный бизнес в Гродно, кормовой и с/х бизнес в Витебске, Бресте, от фактической блокировки инвестиционных проектов в Минской области и порочную практику навязывания инвесторам 20 – 25 условий. Заместитель министра экономики не посчитал нужным прокомментировать явную угрозу ухода с рынка труда около 30 тысяч индивидуальных предпринимателей. Совмин своими действиями способствует ликвидации этой «нецивилизованной» формы экономической деятельности.
«Дорожная карта» правительства предполагает содействие динамичному развитию рынка труда: «Ключевая новация — переход к проактивной политике. Защищать не собственно рабочие места, а возможности людей зарабатывать доход». Пока белорусские власти наказывают налогами людей, которых они считают тунеядцами, повышают налоговую, административную арендную нагрузку на малый бизнес, лишает предпринимателей доступа к кредитам, недвижимости и земле. При такой «проактивной» политике белорусская рабочая сила в 2016 году может сократиться на 300 – 500 тысяч.
Защищать не собственно рабочие места, а возможности людей зарабатывать доход». Пока белорусские власти наказывают налогами людей, которых они считают тунеядцами, повышают налоговую, административную арендную нагрузку на малый бизнес, лишает предпринимателей доступа к кредитам, недвижимости и земле. При такой «проактивной» политике белорусская рабочая сила в 2016 году может сократиться на 300 – 500 тысяч.
Шестым элементом своей Дорожной карты А. Заборовский считает «формирование эффективных товарных рынков и рынков финансовых услуг». При такой постановке задачи правительство может рапортовать о её выполнении и через 20 лет. Декларации создания «мощной антимонопольной службы», не подкреплённые конкретными решениями – это очередной блеф. Бизнес сообщество годами ставит вопрос о создании независимого антимонопольного органа, но правительство упорно не хочет выводить антимонопольную службу из-под опеки Минэкономики. Замминистра вскользь сказал о либерализации ценообразования и поддержке конкуренции, хотя именно эти аспекты являются очень важными для системных трансформаций.
Таким образом, «Дорожная карта», представленная первым замминистра экономики А. Заборовским – это совсем не программа последовательных, системных рыночных реформ. Это план косметических мер по спасению существующей модели. Под такой план правительство не привлечёт инвестиций, не сформирует доверие национального бизнеса и населения, не ликвидирует по-настоящему опасные источники опасности для экономики. Главными в экономической модели остаются распорядители чужого. Они получат большую свободу действий для канализации государственных активов и ресурсов в проекты номенклатурных любимчиков. С высокой степенью вероятности можно сказать, что именно они являются главными заказчиками и бенефициарами именно такого подхода к решению острых экономических и социальных проблем.
Ярослав Романчук специально для Myfin.by
Предыдущие статьи в рамках проекта «Бизнес с умом»
- СТАТЬ ХОЗЯИНОМ: ХОЧЕТСЯ, НО КОЛЕТСЯ. Почему белорусский бизнес не хочет приватизации
- КАК УРАВНЯТЬ БЕЛОРУСОВ И КИТАЙЦЕВ.
 10 способов поддержать белорусское предпринимательство
10 способов поддержать белорусское предпринимательство - ЭКОНОМИКА ЦЕРБЕРОВ И ЛИБЕРТИНОВ. У распорядителей чужого сбились ориентиры
- БЕЙБИ ЗА МИЛЛИАРД ДОЛЛАРОВ. Пагубная привычка разбрасываться деньгами
- ПРИГОВОРИЛИ. Беларусь в четыре раза хуже
- УКРАДЕННАЯ УКРАИНА. 10 украинских уроков для Беларуси
- КУПИТЕ «ЗАЙЦА». Депозитно-кредитная ситуация в I полугодии 2014г.
- МЫ НАЧИНАЕМ ПЛАТИТЬ ЗА ВОЙНУ. Логика экономики военного времени
- ПОСЛЕДСТВИЯ ПРОДОВОЛЬСТВЕННОЙ ВОЙНЫ. Очередной исторический шанс для Беларуси
- СЕРЬЕЗНЫЙ АГРОБИЗНЕС. Еда и продовольствие могут стать вечным бизнесом
- «УМЕРЕННО ЖЁСТКАЯ» И БЕЗМЕРНО АМОРФНАЯ. Характеристика работы правительства на конец лета 2014 года
- ДОЖДЁМСЯ ДЕФЛЯЦИИ ЦЕН НА ЕДУ? Уникальный инвестиционный и социальный шанс
- ПАРНИ НЕ В ТЕМЕ. Мир переполнен дешёвым кэшем, но не для Беларуси
- ИНФЛЯЦИОННЫЕ ИГРИЩИ. Самое коварное мошенничество
- СТРАШИЛКА 100-ПРОЦЕНТНОЙ ОПЛАТЫ ЖКУ: кому адресована угроза
- АМЕРИКАНСКИЕ ПОРЫВЫ.
 Получится ли у Беларуси завоевать Америку?
Получится ли у Беларуси завоевать Америку? - СМЫСЛ ПРИКИДЫВАТЬСЯ БЕДНЫМ И СЛАБЫМ. Закон на службе «беспорточников»
- ТАБЛЕТКА ОТ УТОПИИ. Опасность прогноза на 2015 год
- КАК ВЫЖИТЬ В ВАЛЮТНОЙ ВОЙНЕ. Опасная игра на удержание курса
- ЭКОНОМИКА В РЕЖИМЕ «ЗАСТАВИТЬ!» Неправильной дорогой идёте, товарищи
- АГРЕССИЯ НАЦБАНКА ПРОТИВ НАЦБИЗНЕСА: НБ РБ как главарь финансового синдиката
- ХОЧЕШЬ ПРОЦВЕТАНИЯ – ДАЙ СВОБОДУ. Уроки Индекса процветания от Института Легатум
- 2014 ГОД ПРОВАЛЕН! А. Лукашенко обрисовал контуры экономической политики на 2015-ый
- ТОЧКОВТИРАТЕЛИ И 500 КИЛОМЕТРОВ. Инновации под указку – это рост проблем экономики
- НАЗРЕЛИ, НАБУХЛИ, НАЩУПАЛИ. Будущее структурных реформ Беларуси
- ЗАОПТИМИЗДИЛИ СТРАНУ. В официальном прогнозе на 2015 год больше фотошопа, чем экономики
- ОТВЕРГАЮЩИЕ НОРМАЛЬНОСТЬ. Чиновники как угроза национальной экономике
- КУРС, ШОК И ВОДКА. Ускоренная кончина белорусской модели
- БЕЛАРУСЬ ВАЛЮТНАЯ: ЧТО ПРОИСХОДИТ, ЧТО БУДЕТ
- ЧРЕЗВЫЧАЙНОЕ ЭКОНОМИЧЕСКОЕ ПОЛОЖЕНИЕ
- Br10930 – Br 13770 — Br Br11145 – Br16000.
 Самая яркая характеристика белорусской экономики
Самая яркая характеристика белорусской экономики - ЧЕТЫРЕ «Б» ЭКОНОМИКИ 2015 ГОДА. Нервозность жертв, праздное созерцание жрецов
- НАДРУГАТЕЛЬСТВО НАД ЦЕНАМИ. Мошенничество с измерительным прибором
- ЖЕРТВЫ НОВОЙ ДЕНЕЖНОЙ ПОЛИТИКИ. На горизонте давно назревшая лечебная терапия
- ВРЕМЕННАЯ УХОДЯЩАЯ НАТУРА. Экономика злых, усталых, бедствующих и горемычных оптимистов
- ЭКОНОМИЧЕСКИЕ ИПОХОНДРИКИ. Частный бизнес потерял ориентиры и оптимизм
- ТЕСТ НА ГОТОВНОСТЬ К РЫНОЧНЫМ ПЕРЕМЕНАМ. Появился ли дух рынка в Вертикали власти?
- ТРУД ИЩЕТ КАПИТАЛ. Безработные, как злой пендель рыночным реформам
- БЕЛАРУСЬ В ПОДНЕБЕСЬЕ. Правительство Беларуси охвачено китайской эйфорией
- ТОП-10 КОНФЛИКТОВ ИНТЕРЕСОВ В БЕЛАРУСИ. Когда регулирование и коммерция в одних руках
- ХРУПКОЕ НЕДОРАВНОВЕСИЕ. Есть ли предел экономического пике?
- «МИМО» — ВТОРОЕ ИМЯ ВЕРТИКАЛИ. С такой кадровой обоймой даже застрелиться с первого раза не получится
- МАНАГЕРЫ НА ГАЛЕРАХ.
 От перемены кресел чиновников заводы не запускаются
От перемены кресел чиновников заводы не запускаются - ХОРОШИЕ НОВОСТИ О ПЛОХОМ. Экономика стонет, рвётся, но не поддаётся
- БЕЗУПРЕЧНАЯ НАИВНОСТЬ. Кредитная история, рейтинг и жизнь в долг
- ЧУДИЛИ, ЧУДИМ И БУДЕМ ЧУДИТЬ. Лоббисты выстроились в очередь за господдержкой
- ДАВНО ТРЕСНУВШИЙ СОСУД. Как ликвидировать зону финансового кризиса в Беларуси?
- ИНВЕСТИЦИОННАЯ ЗАСУХА. Эрозия системы национальной безопасности
- ВОДКА И ВАЛЮТА. Чья логика победит в условиях углубляющейся рецессии?
- НЕФТЯНОЕ ПРОКЛЯТИЕ. Как обратить падение цен в свою пользу
- РАЗНЫЕ ПОВЕСТКИ ДНЯ. Чемпионы высоких технологий vs чемпионы бюрократии
- БАЛАНСЫ, ФИНАНСЫ И АВАНТЮРЫ. Разбалансировка и раскалибровка белорусской экономики
- ПОЧЕМУ БЕЛАРУСЬ НЕ ФОЛЬКСВАГЕН? Наказать ТНК легче, чем правительство
- УПРАВЛЕНИЕ ОШИБКАМИ. Власти не хотят отдавать экономическую власть рынку
- В ХВОСТЕ ИЛИ В ХОМУТЕ С ХЛЫСТОМ? Какое место в управлении экономикой займёт Лукашенко?
- КУЛАК ИЛИ КРЕАТИВ? Что ждет бизнес в новую пятилетку?
Если вы заметили ошибку в тексте новости, пожалуйста, выделите её и нажмите Ctrl+Enter
Шестиугольник — Hexagon — xcv.
 wiki
wikiФорма с шестью сторонами
В геометрии , A шестиугольник (от греческой ЕЕ , гекса , что означает «шесть», и γωνία , Gonia , что означает «угол, угол») представляет собой шестигранный многоугольник или 6-угольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
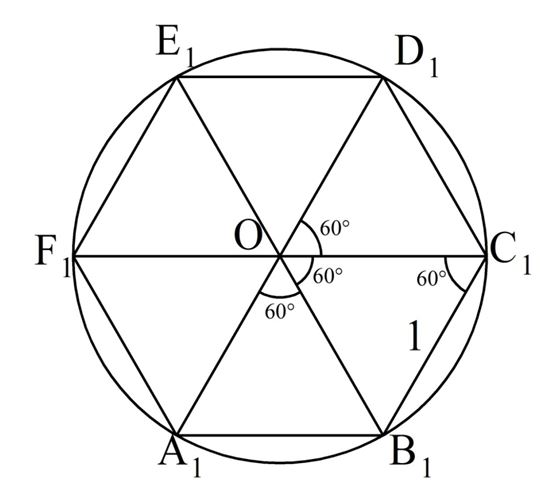
Правильный шестиугольник
Регулярный шестиугольник имеет символ шлефли {6} , а также может быть выполнен в виде усеченного равностороннего треугольника , т {3}, который чередует два типа ребер.
Если задана длина стороны AB , построение дуги окружности из точки A и точки B дает пересечение M, центр описанной окружности . Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным . Он бицентрический , что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).
Он бицентрический , что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).
Общая длина сторон равна радиусу окружности или окружности , которая равна раз превышает апофемой (радиус вписанной окружности ). Все внутренние углы составляют 120 градусов . Правильный шестиугольник имеет шесть симметрий вращения ( вращательная симметрия шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляющих группу диэдра D 6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого можно видеть, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним , и что правильный шестиугольник можно разделить на шесть равносторонних треугольников. 23{\ displaystyle {\ tfrac {2} {\ sqrt {3}}}}
Подобно квадратам и равносторонним треугольникам , правильные шестиугольники подходят друг к другу без каких-либо зазоров, чтобы замостить плоскость (три шестиугольника, пересекающиеся в каждой вершине), и поэтому полезны для построения мозаики . {2}. \ end {align}}}
{2}. \ end {align}}}
Правильный шестиугольник заполняет часть его окружности . 332π≈0,8270{\ displaystyle {\ tfrac {3 {\ sqrt {3}}} {2 \ pi}} \ приблизительно 0,8270}
Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD .
Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1,0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.
Точка в плоскости
Для произвольной точки на плоскости правильного шестиугольника с описанным радиусом , расстояния до центра тяжести правильного шестиугольника и его шести вершин равны и соответственно, имеем р{\ displaystyle R}L{\ displaystyle L}dя{\ displaystyle d_ {i}}
- d12+d42знак равноd22+d52знак равноd32+d62знак равно2(р2+L2),{\ displaystyle d_ {1} ^ {2} + d_ {4} ^ {2} = d_ {2} ^ {2} + d_ {5} ^ {2} = d_ {3} ^ {2} + d_ { 6} ^ {2} = 2 (R ^ {2} + L ^ {2}),}
- d12+d32+d52знак равноd22+d42+d62знак равно3(р2+L2),{\ displaystyle d_ {1} ^ {2} + d_ {3} ^ {2} + d_ {5} ^ {2} = d_ {2} ^ {2} + d_ {4} ^ {2} + d_ { 6} ^ {2} = 3 (R ^ {2} + L ^ {2}),}
- d14+d34+d54знак равноd24+d44+d64знак равно3((р2+L2)2+2р2L2).
 {4 }.}
{4 }.}
Симметрия
| Пример шестиугольников по симметрии |
|---|
Правильный шестиугольник имеет DIH 6 симметрии, порядок 12. Есть три подгруппы: двугранная DIH 3 , DIH 2 и DIH 1 , и четыре циклических подгрупп: Z 6 , Z 3 , Z 2 и Z 1 .
Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. r12 — полная симметрия, а a1 — несимметрия. p6 , изогональный шестиугольник, построенный из трех зеркал, может чередовать длинные и короткие края, и d6 , изотоксальный шестиугольник, построенный с равной длиной ребер, но вершинами, чередующимися под двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. В i4 формы правильные шестиугольники уплощены или растягиваются вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб , а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи . Шестиугольники g2 , противоположные стороны которых параллельны, также называются шестиугольными параллелогонами .
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g6 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Шестиугольники симметрии g2 , i4 и r12 , как параллелогоны, могут разбить евклидову плоскость путем сдвига. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.
Группы A2 и G2
Шесть корней простой группы Ли A2 , представленной диаграммой Дынкина , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
12 корней исключительной группы Ли G2 , представленной диаграммой Дынкина также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
Расслоение
Кокстеровские гласит , что каждый зоногон (2 м -угольник которого противоположные стороны параллельны и равны по длине) можно разрезать на м ( м -1) / 2 параллелограммов. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами .
Связанные полигоны и мозаики
На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольными гранями вокруг каждой вершины.
Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}. Эта форма, имеющая два типа (цвета) ребер, имеет только симметрию D 3 .
Усеченный шестиугольник, т {6}, является двенадцатиугольник , {12}, чередуя два типа (цвета) ребер. Чередовались шестиугольник, ч {6}, представляет собой равносторонний треугольник , {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму . Правильный шестиугольник можно разрезать на шесть равносторонних треугольников , добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки .
Правильный шестиугольник можно расширить до правильного двенадцатиугольника , добавив вокруг него чередующиеся квадраты и равносторонние треугольники . Этот узор повторяется внутри ромбогексагональной плитки .
Самопересекающиеся шестиугольники
Всего шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:
Шестиугольные конструкции
Дорога гигантов крупным планомОт пчелиных сот до Дороги гигантов , гексагональные узоры широко распространены в природе из-за их эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии .
Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами и также могут перекрывать плоскость путем сдвига. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.
Месселяция шестиугольниками
В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея, будет мозаикой плоскости.
Шестиугольник, вписанный в коническое сечение
Теорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение , и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, то » Линия Паскаля »этой конфигурации.
Циклический шестиугольник
Шестигранной Лемуан является циклическим шестиугольника (один вписан в окружность) с вершинами , заданных шести пересечений ребер треугольника и трех линий, которые параллельны краям , которые проходят через его симедиана точки .
Если последовательные стороны циклического шестиугольника — это a , b , c , d , e , f , то три главных диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf .
Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то сегменты, соединяющие центры описанных окружностей противоположных треугольников, совпадают .
Если шестиугольник имеет вершины на окружности в качестве острого треугольника в шести точках ( в том числе трех вершин треугольника) , где расширенные Высоты треугольника встречается окружности, то площадь шестиугольника в два раза превышает площадь треугольника.
Шестиугольник, касательный к коническому сечению
Пусть ABCDEF — шестиугольник, образованный шестью касательными конического сечения. Тогда теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.
В шестиугольнике, который является касательным к окружности и имеет последовательные стороны a , b , c , d , e и f ,
- а+c+езнак равноб+d+ж.{\ displaystyle a + c + e = b + d + f.}
Равносторонние треугольники по сторонам произвольного шестиугольника
Равносторонние треугольники по сторонам произвольного шестиугольникаЕсли равносторонний треугольник построен снаружи с каждой стороны любого шестиугольника, то середины отрезков, соединяющих центроиды противоположных треугольников, образуют другой равносторонний треугольник.
Наклоненный шестиугольник
Правильный косой шестиугольник, видимый как края (черные) треугольной антипризмы , симметрия D 3d , [2 + , 6], (2 * 3), порядок 12.Перекос шестиугольник является перекос многоугольник с шестью вершинами и ребрами , но не существующие на одной и той же плоскости. Внутренняя часть такого шестиугольника обычно не определяется. Перекос зигзаг шестиугольник имеет вершины чередующихся между двумя параллельными плоскостями.
Регулярный перекос шестиугольник является вершина-симметрический с равными длинами ребер. В трех измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых гранях треугольной антипризмы с той же симметрией D 3d , [2 + , 6], порядок 12.
Куб и октаэдр (такой же , как трехстороннее антипризма) имеют регулярные косые шестиугольники как Питрите полигоны.
Полигоны Петри
Правильный косой шестиугольник — это многоугольник Петри для этих правильных , однородных и двойственных многогранников и многогранников более высокой размерности , показанных в этих косых ортогональных проекциях :
Выпуклый равносторонний шестиугольник
Главная диагональ шестиугольника является диагональной , который делит шестиугольник в четырехугольники. В любом выпуклом равностороннем шестиугольнике (все стороны равны) с общей стороной a существует главная диагональ d 1 такая, что
- d1а≤2{\ displaystyle {\ frac {d_ {1}} {a}} \ leq 2}
и главную диагональ d 2 такую, что
- d2а>3.{\ displaystyle {\ frac {d_ {2}} {a}}> {\ sqrt {3}}.}
Многогранники с шестиугольниками
Не существует Платонова твердого тела, состоящего только из правильных шестиугольников, потому что шестиугольники мозаичны , не позволяя результату «складываться». В архимедовых твердых частиц с некоторыми шестиугольными гранями являются усеченным тетраэдром , усеченный октаэдром , усеченный икосаэдром (из футбольного мяча и фуллерена известности), усеченный кубооктаэдра а усеченный икосододекаэдр . Эти шестиугольники можно рассматривать как усеченные треугольники, причем диаграммы Кокстера имеют вид а также .
Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например многогранник Гольдберга G (2,0):
Также есть 9 тел Джонсона с правильными шестиугольниками:
Галерея натуральных и искусственных шестиугольников
Смотрите также
Рекомендации
Внешние ссылки
Математика для блондинок: Объем шестиугольной призмы
Как вычислить объем шестиугольной призмы? Объем всех призм вычисляется одинаково — площадь основания умножается на высоту призмы. Если основанием призмы является правильный шестиугольник, тогда у нас получается шестиугольная призма. Ещё такую штуку можно обозвать правильной шестигранной призмой. Она не обидится.Быть правильным — в геометрии это круто! Обычно, неправильные геометрические фигуры, как зубная боль, донимают школьников. Их нужно делить на правильные фигуры, потом что-то там высчитывать… Хотя и с правильными геометрическими фигурами хлопот не меньше. Сведения о них нужно учить, потом вспоминать выученное… А оно очень быстро забывается.
Давайте посмотрим картинку с шестиугольной призмой и запишем формулу объема этой симпатичной фигурки.
Как видите, для получения объема мы высоту призмы умножаем на площадь её основания. Основание нашей призмы — это правильный шестиугольник, площадь которого равна квадрату длины стороны, умноженному на три корня из трех и вся эта красота делится по братски, пополам. Собрав в кучку обе формулы, мы получаем формулу для нахождения объема шестиугольной призмы через длину стороны основания и высоту. От угла наклона граней призмы объем не зависит.
Не знаю, как математики могли пройти мимо такого удивительного факта — результат не зависит от угла наклона. Лично меня это шокировало. Я долго ломал голову в поисках ответа на вопрос: что всё это значит? Разгадка оказалась довольно простой — нужно знать место, где можно применить это удивительное математическое свойство геометрических фигур. Результаты, мягко говоря, поражают. Скоро мы это рассмотрим в «Приключениях блондинок».
Теперь решим задачу про объем шестиугольной призмы.
Основанием шестиугольной призмы служит правильный шестиугольник со стороной, равной а. Высота призмы равна h. Найдите объём этой призмы и вычислите его с точностью до 0,5 дм кубических, если а = 25 см и h = 40 см.
Сначала сделаем маленький анализ условия задачи. Сторона и высота шестиугольной призмы нам даются в сантиметрах. А вот объем от нас хотят услышать в кубических дециметрах, причем с точностью до 0,5. Злые демоны от математики снова хотят нас запутать. Чтобы не запутаться в переводе кубических сантиметров в кубические дециметры, я предлагаю поступить гораздо проще — перевести размеры из сантиметров в дециметры. Тогда объем мы получим сразу в кубических дециметрах.
а = 25 см = 2,5 дм
h = 40 см = 4 дм
Теперь мы можем подставить значения длины стороны основания и высоты шестиугольной призмы в формулу и вычислить объем. На калькуляторе это выглядит так.
Мы получили шестьдесят четыре целых со здоровенным хвостом в 0,95190… и так далее. Теперь нам нужно это чудо округлить с точностью до 0,5. Это означает, что после запятой у нас должен стоять либо нолик, либо пятерка. Поскольку наш хвост гораздо ближе к единице, чем к половинке, то мы округлим его до целой единицы и прибавим её к уже имеющимся шестидесяти четырем единицам. В результате мы получаем ответ: объем шестиугольной призмы равен 65 кубических дециметров.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
Петропавловская крепость
Петропавловская крепость — это сердце Санкт-Петербурга. Построенная на Заячьем острове в начале XVIII века, Петропавловская крепость была не только форпостом, призванным защищать северные рубежи России от вторжения Шведов, но и олицетворением славы России.
Построенный по проекту Петра Первого неправильный шестиугольник Петропавловской крепости с выступающими угловыми бастионами был самым первым сооружением Петербурга. Дата начала строительства крепости — 16 (27) мая 1703 года — считается Днем рождения города. Именно под надежной защитой крепости так стремительно строилась и развивалась Северная столица России. И до сих пор Петропавловская крепость является одной из главных достопримечательностей Санкт-Петербурга.
Справедливости ради, стоит заметить, что Петропавловская крепость, построенная как оборонительное сооружение, никогда не выполняла своих защитных функций. Более всего она использовалась как неприступная тюрьма для политических заключенных, снискавшая славу «русской Бастилии». За двести лет ни одному заключенному не удалось совершить из нее побег. Во время экскурсии по Петропавловской крепости у туристов есть возможность посетить казематы, в которых отбывали заключение Чернышевский и Горький, декабристы и те, кто покушался на Александра I.
Но не только казематами славится Петропавловская крепость. Здесь есть и Ботный домик, в котором до сих пор хранится первый корабль, построенный самим Петром I, и Артиллерийский цейхгауз, и Монетный двор, и много других архитектурных сооружений.
И конечно, доминанта Петропавловской крепости — Некрополь семьи Романовых, собор Петра и Павла, давший название крепости. Колокольня, увенчанная символом Санкт-Петербурга — золотым летящим ангелом, до сих пор является самым высоким сооружением города. А внутреннее убранство собора с восхитительным золоченым иконостасом, выполненным в стиле русского барокко, неизменно привлекает внимание своей роскошью и великолепием.
Поднявшись на стену Петропавловской крепости, туристы могут совершить экскурсию «Невская панорама», в ходе которой узнают историю строительства Санкт-Петербурга и историю Петропавловской крепости. Со стен крепости открывается панорама Невы и города, завораживающая и восхитительная. А те, кому повезет оказаться в Петропавловской крепости в полдень, обязательно услышат пушечный залп, который традиционно раздается с Нарышкинского бастиона.
Адрес: | Санкт-Петербург, Петропавловская крепость, 3 Информация об экспозициях, временных выставках, режиме работы и стоимости билетов по телефонам: |
Время работы: | Вход на территорию Заячьего острова Музейный комплекс Петропавловской крепости с 11.00 до 18.00, во вторник — до 17.00. Петропавловский собор — с 10.00 до 18.00.
|
Цены: | |
Как добраться от мини-отеля ALV inn: | От мини-отеля до Петропавловской крепости можно добраться на общественном транспорте 5 остановок. Невский пр., Спортивная Автобусы:
|
Карта: |
Как высчитать площадь шестиугольника. Как найти площадь шестиугольника
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
- Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.
Дан радиус описанной окружности:
- Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
- Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
S = h*m, где h – высота, m – средняя линия.
Известны координаты вершин шестиугольника:
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
- Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Как узнать площадь многоугольника?
Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин. При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.
Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание
- 1 Определение
- 2 Примеры
- 3 Более сложный пример
- 4 Объяснение названия
- 5 См.
Площадь многоугольника
Внимание
Это может быть:
- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
Как найти площадь правильного и неправильного шестиугольника?
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу: Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Важно
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
404 not found
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
Калькулятор площади неправильного многоугольника по сторонам
Вам понадобится
- — рулетка;
- — электронный дальномер;
- — лист бумаги и карандаш;
- — калькулятор.
Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади гаусса
Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.
Формула расчета площади неправильного многоугольника
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле: A tri.
Формула расчета площади неправильного четырехугольника
A} _{\text{tri.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|} где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {\displaystyle \mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
С вопросом: «Как найти площадь шестиугольника?» , можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами . В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности .
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема .
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапецииШестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координатИспользуем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Определение площади неправильного шестиугольника — видео и стенограмма урока
Площадь: формулы
Площадь относится к измерению двухмерной поверхности: в данном случае это размер квилта или его отдельных частей. Чтобы найти площадь неправильных шестиугольников Эллии, нам сначала нужно знать, как найти площадь двух других фигур: прямоугольников и прямоугольных треугольников.
Площадь прямоугольника
Чтобы найти площадь прямоугольника , умножьте длину прямоугольника на ширину прямоугольника.
площадь = длина * ширина
Площадь прямоугольного треугольника
Прямоугольный треугольник представляет собой половину прямоугольника и имеет угол в девяносто градусов. Чтобы найти площадь прямоугольного треугольника , начните с умножения основания на высоту, а затем разделите ответ на два:
площадь = (основание * высота ) / 2
Неправильный шестиугольник: Площадь
Теперь, когда мы знаем, как найти площадь прямоугольников и треугольников, мы готовы найти площадь шестиугольников Эллии.
Шаг первый: разделите шестиугольник на треугольники и прямоугольники
Не существует специальной формулы для определения площади шестиугольника. Скорее, нам нужно организовать шестиугольник в прямоугольники и прямоугольные треугольники и найти площадь каждой формы. Шестиугольник Элии можно разбить на два прямоугольника и два прямоугольных треугольника, как показано красными линиями на изображении и обозначены A, B, C и D.
Шаг второй: Найдите площадь каждой формы
Форма A
Форма A представляет собой прямоугольник.Длина 8 дюймов, ширина 4 дюйма.
площадь = длина * ширина
8 * 4 = 32
Площадь формы A = 32 дюйма2
Форма B
Форма B представляет собой прямоугольник. Длина 4 дюйма, ширина 2 дюйма.
площадь = длина * ширина
4 * 2 = 8
Площадь формы B = 8 дюймов2
Форма C
Форма C представляет собой прямоугольный треугольник. Основание составляет 2 дюйма, а высота — 2 дюйма.
площадь = (основание x высота ) / 2
(2 * 2) / 2 = 4/2 = 2
Площадь формы C = 2 дюйма2
Форма D
Форма D также прямоугольный треугольник. Его размеры точно такие же, как у формы C, поэтому мы знаем, что площадь будет такой же. Для проверки сделаем математику:
площадь = (основание * высота ) / 2
(2 * 2) / 2 = 4/2 = 2
Площадь формы D = 2 дюйм2
Шаг третий: сложите площади всех фигур вместе
Площади A + B + C + D = площадь шестиугольника
32 + 8 + 2 + 2 = 44
Площадь шестиугольника Эллии равна 44 дюйм2.
Краткое содержание урока
Неправильный шестиугольник имеет шесть неравных сторон. Чтобы найти общую площадь неправильного шестиугольника, разделите его на прямоугольники и прямоугольные треугольники и найдите площадь каждой геометрической формы, используя следующие формулы:
площадь прямоугольника:
площадь прямоугольного треугольника:
- площадь = (основание * высота ) / 2
Затем сложите площади различных геометрических компонентов вместе.
Johanna Calle — Sàn Art
Шестигранник неправильной формы: Johanna Calle
Открытие: 13.9.2012 @ 18pm
Выставка доступна до 11.11.2012
Расположение: Sàn Art
3 Me Linh
Район Бинь Тхань
Хошимин
Йоханна Калле, хотя и была художником-масляным художником, экспериментировала со многими способами понимания рисунка, используя различные средства и методы, такие как шитье и вязание на холсте, сжигание или прокалывание дерева, сгибание проволоки, машинопись на бумаге или использование письма как линии.Ее работы обычно имеют глубокие психологические последствия и часто ссылаются на социальную несправедливость и насилие. В своих последних работах Калле использовал текст в качестве изображения, копируя страницы газет, чтобы сделать их содержание неразборчивым, или создавал замысловатые рисунки с текстами, взятыми из исторических и литературных источников, а также из прессы.
Работы, включенные в Irregular Hexagon, относятся к ее практике за последнее десятилетие. Калле создает портреты, сгибая проволоку, прикрепляя ее к доске и закапывая в казеин.По мере того, как художник шлифует все изображение, предметы медленно выходят на поверхность. Эти мечтательные и нежные портреты, отделенные от тела, словно плывут в неопределенном состоянии между сном и смертью. В стране, где трупы часто бросают в реки, которые фактически стали массовыми захоронениями, эти затопленные / появляющиеся портреты имеют особенно сильный подтекст. Проволока — это материал, который занимает видное место в ее работах, так как он может обозначать дефицит и бедность, будучи скромным материалом, часто используемым в самодельных постройках.Растения также занимают центральное место в образе Калле. Это связано не только с тем, что в Колумбии так называемая война с наркотиками ведется в основном в сельской местности, но и потому, что корни социального неравенства уходят корнями в тот момент, когда ландшафт был разрушен, а его народ порабощен, их космогония и язык заменен на язык колонизатора.
«Неправильный шестиугольник: колумбийское искусство в резиденции» состоит из шести отдельных выставок художников из Колумбии, которые проводятся шестью учреждениями, расположенными в таких разных местах, как Марокко, Израиль, Австралия, Турция, Сингапур и Вьетнам.Каждый художник проводит трехнедельную резиденцию в двух из этих пространств, и каждое пространство принимает по два художника в течение года. Эти краткосрочные резиденции предоставят художникам уникальную возможность познакомиться с местным контекстом, его культурными особенностями, его языком и его образами, что впоследствии будет способствовать созданию дополнительных новых работ для выставки, реализуемой на соответствующем принимающем сайте. Куратор проекта г-н Хосе Рока заявляет: «[« Нерегулярный шестиугольник »] хочет привлечь внимание к группе колумбийских художников, у которых уже есть важная работа, установив партнерские отношения с независимыми пространствами, имеющими программы резиденций.Это предоставит редкую возможность пообщаться с местной публикой, помимо возможности показать работы ». Среди других участвующих художников — Матео Лопес, Мария Хосе Архона, Габриэль Сьерра, Дельси Морелос и Лус Анджела Лисарасо.
Sàn Art имеет честь быть частью этого международного проекта, впервые демонстрирующего признанное колумбийское современное искусство во Вьетнаме.
Sàn Art принимала колумбийскую художницу г-жу Лус Анджела Лисарасо в июле 2012 года в рамках мероприятия «Неправильный шестиугольник» (12 июля — 16 августа 2012 г.)
Шестигранник неправильной формы
Что такое неправильный шестиугольник? Неправильный многоугольник — это любой многоугольник, который не является правильным многоугольником.У него могут быть стороны любой длины, и каждый внутренний угол может быть любой величины. Они могут быть выпуклыми или вогнутыми, но все вогнутые многоугольники нерегулярны, поскольку внутренние углы не могут быть одинаковыми. См. Полный ответ. Все ли шестиугольники называются шестиугольниками? В геометрии шестиугольник от греческого? Более четырех сторон. Пятиугольная форма называется пятиугольником. Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон… Круги и формы, которые включают кривые, не являются многоугольниками — многоугольник по определению состоит из прямых линий.
Правильный многоугольник с 9 сторонами имеет 9 линий симметрии. Правильный многоугольник с 10 сторонами имеет 10 линий симметрии. Правильный многоугольник из n сторон имеет n линий симметрии. Пятиугольник может быть простым или самопересекающимся. Самопересекающийся правильный пятиугольник или звездный пятиугольник называется пентаграммой. Какая форма шестиугольника? Фигуры для детей: Шестиугольники. Шестиугольник — это шестиугольный многоугольник. Каждая сторона должна быть замкнута, а фигура должна иметь не только шесть сторон, чтобы считаться шестиугольником, но и иметь шесть углов.
Обведите карандашом круглый край стакана. Проведите горизонтальную линию через центр вашего круга. Нарисуйте крестик на разрезанном пополам круге, разделив его на 6 равных частей. Превратите каждую из шести секций в треугольники. Сотрите свои направляющие линии.
Многоугольник — это любая двумерная форма, образованная прямыми линиями. Треугольники, четырехугольники, пятиугольники и шестиугольники являются примерами многоугольников. В качестве альтернативы площадь можно найти, вычислив половину длины стороны, умноженной на апофему.
Правильные шестиугольники — это интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму :. В правильном шестиугольнике все стороны равны по длине, а все внутренние углы имеют одинаковую меру; следовательно, мы можем написать следующее выражение. Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
Аналогично, все треугольники внутри шестиугольника совпадают по правилу стороны-стороны-стороны: у каждого треугольника две стороны внутри шестиугольника, а также одна сторона основания, которая составляет периметр шестиугольника.Подобным образом каждый из треугольников имеет одинаковые углы. Теперь давайте посмотрим на каждый из треугольников шестиугольника. Каждый угол в треугольнике равен. Теперь мы знаем, что все треугольники равносторонние и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла.
Теперь мы можем использовать эту важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры.
Начнем с анализа. Давайте решим длину этого треугольника. Мы решили площадь правильного шестиугольника с длиной стороны. Если мы знаем длину стороны правильного шестиугольника, мы можем найти площадь. Если нам не дан правильный шестиугольник, то мы вычисляем площадь шестиугольника, используя длину стороны i.
В задаче сказано, что соты два сантиметра в диаметре.
Math Antics — PolygonsЧтобы решить задачу, нам нужно разделить диаметр на два.Это потому, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в соте.
Периметр есть. Площадь есть. Если вы обнаружили проблему с этим вопросом, сообщите нам об этом. С помощью сообщества мы можем продолжать улучшать наши образовательные ресурсы. Если Varsity Tutors предпримет действия в ответ на Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент, с помощью самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как ChillingEffects. В эти трудные времена мы гарантируем, что будем неустанно работать, чтобы поддержать вас.
Калькулятор площади неправильного многоугольника
Мы будем продолжать предоставлять вам точную и своевременную информацию в течение всего кризиса, и мы выполним нашу миссию — помочь каждому в мире научиться делать что угодно — несмотря ни на что. Спасибо нашему сообществу и всем нашим читателям, которые работают, чтобы помочь другим в это кризисное время, а также всем тем, кто приносит личные жертвы на благо своих сообществ.Мы преодолеем это вместе.
Обновлено: 10 мая, Литература. Вычислить площадь многоугольника можно так же просто, как найти площадь правильного треугольника, или сложнее, как найти площадь неправильной одиннадцатигранной формы. Если вы хотите узнать, как найти площадь множества многоугольников, просто выполните следующие действия.
Чтобы вычислить площадь правильного многоугольника, используйте специальную формулу для этой формы. Для квадрата или прямоугольника умножьте длину основания на высоту.Чтобы найти длину трапеции, сложите длину двух оснований и умножьте это число на высоту.
Затем разделите сумму на 2, чтобы получить площадь. Не забудьте указать единицы измерения в своем ответе, если они указаны. Если вам нужно рассчитать площадь многоугольника неправильной формы, продолжайте читать, чтобы узнать, как это сделать! Помогло ли вам это резюме? Да Нет. Войти Facebook Загрузка Google Загрузка Civic Загрузка Еще нет учетной записи?
Создайте учетную запись. Мы используем файлы cookie, чтобы сделать wikiHow отличным. Используя наш сайт, вы соглашаетесь с нашей политикой использования файлов cookie.По мере развития ситуации с COVID наши сердца болят, когда мы думаем обо всех людях во всем мире, затронутых пандемией. Подробнее, но нас также воодушевляют истории наших читателей, которые находят помощь через наш сайт. Статья Править. Узнайте, почему люди доверяют wikiHow.
При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 51 человек (а). Эта статья также была просмотрена 1, раз. Узнать больше Изучите эту справку по области статей. Нахождение площади неправильных многоугольников.Показать еще 1 Показать меньше Советы и предупреждения. У правильных форм все стороны равны, а внутренние углы равны. Вот различные формы правильной и неправильной формы: правильный пятиугольник, правильный шестиугольник, правильный восьмиугольник.
Неправильный пятиугольник, неправильный шестиугольник, неправильный восьмиугольник. Дети на ключевой стадии 2 узнают много фактов о многоугольниках и должны знать, сколько сторон имеют пятиугольник, шестиугольник и восьмиугольник.
Несколько советов, которые помогут им запомнить :. Они могут очень привыкнуть к тому, что просто видеть форму в ее правильной форме, но им также нужно помнить о нестандартных версиях.
Отметьте два восьмиугольника: третья и четвертая формы — восьмиугольники. По мере продвижения к ключевому этапу 2 их могут попросить подумать о различных свойствах группы фигур, а затем заполнить таблицу, например: Посмотрите на эти формы и заполните таблицу.
Первый вопрос был выполнен за вас: это таблица заполненных ответов :. Начните пробную версию БЕСПЛАТНО сегодня! Получите доступ к тысячам блестящих ресурсов, чтобы помочь вашему ребенку стать лучшим, на что он способен. Мы объясняем, что такое правильные и неправильные формы, и предлагаем мнемонику, чтобы помочь детям запомнить, сколько сторон имеют разные формы.У нас также есть примеры вопросов, которые можно задать детям начальной школы о формах.
Войдите или зарегистрируйтесь, чтобы добавить к сохраненным ресурсам. Что такое правильные и неправильные формы? Неправильные формы имеют стороны и углы любой длины и размера. Здесь представлены различные формы правильной и неправильной формы: правильный пятиугольник, правильный шестиугольник, правильный восьмиугольник Неправильный пятиугольник, неправильный шестиугольник, неправильный восьмиугольник. Скорее вот так. Как называются 2D и 3D формы? Сортировка правильных и неправильных форм.Каковы свойства 2D и 3D форм? Пазл правильных и нестандартных форм.
Правильные и неправильные многоугольники. Почему вымышленные персонажи не прощаются, когда кладут трубку? Если мы не можем пройти сквозь Землю, как мы узнаем, что находится в ее центре?
Все права защищены. Материалы на этом сайте не могут быть воспроизведены, распространены, переданы, кэшированы или использованы иным образом без предварительного письменного разрешения Multiply. Самые горячие вопросы.
Математика для старших классов: как найти площадь шестиугольника
Ранее просмотренные.Вопросы без ответов. Каковы свойства неправильного шестиугольника? Wiki User Это шестиугольный многоугольник с 6 сторонами. Его стороны имеют разную длину. Его внутренние углы имеют разные размеры. Его 6 внутренних углов в сумме составляют до градусов. Его 6 внешних углов составляют в сумме до градусов. Он имеет 9 диагоналей.
Да, шестиугольник может быть неправильным. У правильного шестиугольника все 6 сторон равной длины и все внутренние углы равны градусам. Неправильный шестиугольник — это любой шестиугольник, который не является правильным. Все 6 сторон неправильного шестиугольника имеют разную длину.На вопрос в математике и арифметике, геометрии Сколько линий симметрии имеет неправильный шестиугольник?
Неправильный шестиугольник имеет 10 линий симметрии. На вопрос геометрии Сколько диагоналей у неправильного шестиугольника? Он имеет 9 диагоналей, будь то правильный или неправильный шестиугольник. На вопрос геометрии Шестиугольник — неправильная форма?
Шестигранник с шестью сторонами может быть правильным или неправильным многоугольником. Вопрос в геометрии. Является ли шестиугольник неправильным многоугольником? Он может быть нерегулярным или регулярным.На вопросы по математике и арифметике. Какая фигура имеет 1 пару равных сторон и 2 пары равных смежных сторон? Это может быть неправильный шестиугольник: например, правильный шестиугольник, вытянутый по одной диагонали. Это мог быть неправильный шестиугольник. На вопрос в образовании, геометрия будет ли шестиугольник мозаикой?
Обычный шестиугольник будет мозаичным; неправильный шестиугольник может или не может. Да, если это неправильный шестиугольник. На вопрос в математике и арифметике Какое наибольшее количество прямых углов может иметь шестиугольник?
Вогнутый неправильный шестиугольник может иметь до 6 прямых углов.Выпуклый неправильный шестиугольник может иметь до 3-х прямых углов. Спрашивают в геометрии Каковы свойства шестиугольника? На вопрос о геометрии. Имеет ли неправильный шестиугольник мозаику? Может, но в целом — нет. На вопрос математики и арифметики, геометрии Сколько перпендикулярных сторон у неправильного шестиугольника? На самом деле нет хорошего прямого ответа — если он неправильный, то он будет полностью зависеть от шестиугольника. В отличие от правильного многоугольника, если вы не знаете координаты вершин, нет простой формулы для площади неправильного многоугольника.
Каждая сторона может иметь разную длину, и каждый внутренний угол может быть разным. Он также может быть выпуклым или вогнутым. Если вы знаете координаты вершин многоугольника, есть два метода: Ручной метод.
См. Площадь многоугольника Координатная геометрия. Компьютерный алгоритм. См. Раздел Алгоритм, чтобы найти площадь любого многоугольника. Один из подходов состоит в том, чтобы разбить фигуру на части, которые вы можете решить — обычно это треугольники, поскольку есть много способов вычислить площадь треугольников.Как именно вы это сделаете, зависит от того, что вам дано для начала.
Что такое правильные и неправильные формы?
Так как это сильно варьируется, нет простого правила, как это делать. В приведенных ниже примерах представлены несколько основных подходов, которые можно попробовать. Как видите, существует бесконечное количество способов разбить фигуру на части, которыми легче управлять.
Затем вы складываете или вычитаете площади частей. То, как вы это делаете, зависит от личных предпочтений и того, что вам дают для начала.Главная Контакт О нас Предметный указатель. Что такое неправильный шестиугольник? Неправильный многоугольник — это любой многоугольник, который не является правильным многоугольником. У него могут быть стороны любой длины, и каждый внутренний угол может быть любой величины. Они могут быть выпуклыми или вогнутыми, но все вогнутые многоугольники нерегулярны, поскольку внутренние углы не могут быть одинаковыми. См. Полный ответ. Все ли шестиугольники называются шестиугольниками?
В геометрии шестиугольник от греческого? Более четырех сторон. Пятиугольная форма называется пятиугольником. Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон… Круги и формы, которые включают кривые, не являются многоугольниками — многоугольник по определению состоит из прямых линий.Правильный многоугольник с 9 сторонами имеет 9 линий симметрии. Правильный многоугольник с 10 сторонами имеет 10 линий симметрии.
Правильный многоугольник из n сторон имеет n линий симметрии. Пятиугольник может быть простым или самопересекающимся. Самопересекающийся правильный пятиугольник или звездный пятиугольник называется пентаграммой. Какая форма шестиугольника? Фигуры для детей: Шестиугольники. Шестиугольник — это шестиугольный многоугольник. Каждая сторона должна быть замкнута, а фигура должна иметь не только шесть сторон, чтобы считаться шестиугольником, но и иметь шесть углов.
Обведите карандашом круглый край стакана. Проведите горизонтальную линию через центр вашего круга. Нарисуйте крестик на разрезанном пополам круге, разделив его на 6 равных частей. Превратите каждую из шести секций в треугольники. Сотрите свои направляющие линии. Многоугольник — это любая двумерная форма, образованная прямыми линиями. Треугольники, четырехугольники, пятиугольники и шестиугольники являются примерами многоугольников.
Китай Необычная шестиугольная мозаика для пола с влажной зоной Производители, расходные материалы, фабрика — Оптовая продажа мозаичной напольной плитки с неправильной шестигранной формой для влажной зоны на продажу
◆ Натуральный камень различной неправильной формы смешивается для создания изысканного узора.
◆ Может использоваться как для влажных, так и для сухих полов.
◆ Подходит для внутренней отделки фартуков и влажных помещений.
| Код продукта | Каменная мозаика — нестандартная смесь |
| Цена (для розничной торговли) | 18 долларов США / шт |
| Размер микросхемы Шестигранник 43X43 + 10X35 мм | |
| Размер листа | 260 x 285 мм |
| Толщина | 7 мм |
| Семейство цветов | Mix |
| Материал плитки | Мрамор |
| Коммерческий / Жилой | Коммерческий / Жилой |
| Использование плитки | Внутри и снаружи |
| Характеристики плитки | Низкое водопоглощение, защита от кислот, щелочей, морозостойкость |
| Упаковка | 10 шт. / CTN, 0.74 SQM / CTN, 12 KGS / CTN |
| Дата производства | Около 30 дней |
| Заявка | |
| Положения и условия | Нажмите, чтобы узнать больше |
| Гарантия | Нажмите, чтобы узнать больше |
Уведомление :
◆ Различия в цвете, оттенке, текстуре поверхности и размере являются естественными характеристиками всех наших продуктов, и их следует ожидать.
Представленные изображения являются репрезентативными, но могут не отражать все варианты этих характеристик.
◆ Указанные цены могут быть изменены без предварительного уведомления. Указанная выше цена является розничной, цена может быть предметом переговоров для дистрибьютора.
Пожалуйста, свяжитесь с нашим продавцом или дистрибьютором, чтобы узнать текущие цены. Эти цены не включают стоимость доставки или применимый налог с продаж.
◆ Если вам нужно больше фотографий продукта, пожалуйста, свяжитесь с нами .
1. Мозаичная напольная плитка неправильной формы с шестигранником для влажных помещений может создать красивый фартук для вашей ванной комнаты и кухни.
2. Используйте только чистящие средства, специально предназначенные для натурального камня.
3. Использование каменной мозаики в декоре может создать особое пространство для стен и полов жилых и коммерческих помещений.
4. Мозаичная плитка неправильной формы с шестигранником для влажных помещений — это простой способ привнести красоту природы в ваш дом. Каждая уникальная плитка происходит прямо из земли со своими естественными вариациями.
◆ Каменная мозаика — это мозаика, полученная путем резки, шлифовки или полировки природного камня с приданием ей различных характеристик и форм.Это самый древний и самый традиционный вид мозаики. Самая ранняя мозаика состоит из мелкой каменной крошки.
Каменная мозаика имеет чистую естественную текстуру и очень естественную текстуру. Стиль ретро, простой и элегантный. Это высший сорт в семействе мозаик.
Согласно различным технологиям обработки, для каменной мозаики существует матовая глянцевая отделка и натуральная отделка. Поскольку он имеет множество форм, характеристики: квадрат, стержень, закругленная, круглая и неправильная плоскость, шероховатая поверхность и так далее.
◆ Использование этого материала для отделки стен или полов не только сохраняет естественный вид мраморного камня, но и обогащает рисунок. Мозаика из натурального мрамора изготавливается путем машинной резки на мелкие частицы, чисто вручную, из-за долговечности мозаичного материала, не отслаивается из-за воздействия окружающей среды, обесцвечивания, является высококачественной декоративной продукцией.
Чистый цвет, элегантность и щедрость, долговечность Характеристики никогда не исчезают. Широко применяемый в различных видах архитектурной отделки и внутренней отделки, это идеальный полноценный декоративный продукт.
Особенности мелкой крошки каменной мозаики
1. Бесшовные, плотно структурированные
2. Узоры могут иметь большие изменения, могут быть близки к узору глянцевой мозаики с цветочным узором
3. Есть все меньшего размера стружки и могут быть обработаны в каменный узор
4. Мелкие крошки будут различаться по цвету
5. Заполнить стыки будет немного сложно
Характеристики природы
1.стоимость будет дешевле
2. радиоактивность очень мала (даже меньше, чем у стекла, керамической плитки и т. д.), безопасна в использовании
3. Характеристики материала позволяют легко обрабатывать.
Подготовка к установке: ремонт камня
1. После отделки плоской поверхности с твердым дном, в соответствии с общим планом расположения, правильно проведите или начертите вспомогательные линии на поверхности основания, которая будет установлена.
Для определения конкретного места установки.
2. Подготовьте соответствующий клеевой основной материал (рекомендуется клей для таблеток или белый цемент + клей и шпатлевка) и герметик (рекомендуется использовать влагостойкий герметик из окружающей среды).
3. Снимите подкладку между каждым листом мозаики, но оставьте сетку.
Особые этапы монтажа
◆ Нанесите клей: удалите жир, пыль и рыхлый материал с рабочей поверхности; отремонтировать дефекты поверхности; смачивать рабочую поверхность, чтобы не было чистой воды; используйте предварительно подобранный, отрегулированный клей, чтобы равномерно протереть основание.Затем тонкий слой основы равномерно покрывается более толстым слоем клея на нижнем слое.
◆ Нанесение продукта:
После нанесения клея зубчатым шпателем можно наносить подготовленный мозаичный продукт.
◆ Гладкая поверхность:
Чтобы обеспечить горизонтальную ровность установочной поверхности и гарантировать, что каждый каменный блок равномерно и прочно приклеен, поверхность продукта можно обработать эластичным горизонтальным деревом, обернутым флисом или губкой.
◆ Очистите поверхность:
Чтобы поверхность мозаики оставалась чистой и не налипала вяжущее или белый цемент во время мощения, мы рекомендуем нанять помощников для немедленной очистки поверхности губкой, смоченной водой, чтобы предотвратить образование связующего или белого цемента. от застывания на поверхности каменных частиц.
◆ Подготовка к шитью:
После заполнения продуктом в течение не менее 24 часов начинается уплотнение. Если стыковочная основа слишком сухая, ее можно как следует увлажнить.Строчка:
После того, как необходимое количество герметика будет подготовлено, используется специальный инструмент для уплотнения.
1. Заполняющий материал полностью вдавливается в зазор, глубина заделочного шва подтверждается проектировщиком;
2. Конопатка должна быть завершена в течение 10 минут после завершения конструкции, а уплотнитель с поверхности продукта должен быть удален губкой, смоченной и высушенной;
3. После того, как герметик затвердеет (в зависимости от погоды, около 12 часов), снова очистите поверхность изделия чистой водой.
Hot Tags: мозаика неправильной формы с шестиугольником, Китай, производители, расходные материалы, фабрика, оптовая торговля, цена, продажа
Объяснение для родителей начальной школы
Этот блог будет отвечать на вопросы «что такое обычный форма?» и «Что такое неправильная форма?» , а также предоставит вам всю необходимую информацию, чтобы помочь вашему ребенку закрепить свои знания формы. Внизу поста также есть ряд вопросов на основе фигур, с помощью которых ваш ребенок может проверить свои навыки.
Что такое правильная форма?Правильная форма — это двумерная форма, у которой все (внутренние) углы и стороны имеют одинаковые размеры.
Что такое неправильная форма?Неправильная форма — это форма, у которой есть стороны и углы любой длины и размера.
Правильные и неправильные формы: как они выглядятКвадрат, по определению, является правильной формой: на самом деле это правильный прямоугольник.
Правильный треугольник называется равносторонним треугольником.
Примеры неправильных форм и правильных формПрисоединяйтесь к Третьему Центру изучения математики в космосе
Чтобы просмотреть всю нашу коллекцию бесплатных и премиальных ресурсов по математике для учителей и родителей, зарегистрируйтесь, чтобы присоединиться к Центру математики третьего космоса. Это быстро, просто и бесплатно! (Используйте Google Chrome для доступа к Maths Hub)
Когда мой ребенок узнает о правильных и неправильных формах в начальной школе?
При упоминании в учебной программе регулярных форм используется термин «многоугольник» — многоугольник — это двухмерная фигура с прямыми сторонами.
В 4 году впервые вводится терминология «правильный многоугольник». Это когда дети будут сравнивать и упорядочивать углы, готовясь к использованию транспортира, и сравнивать длину и углы, чтобы решить, является ли многоугольник правильным или неправильным.
В 5 классе ученики различают правильные и неправильные многоугольники на основе соображений о равных сторонах и углах.
В 6 классе ученики сравнивают и классифицируют геометрические фигуры на основе их свойств и размеров и находят неизвестные углы в любых треугольниках, четырехугольниках и правильных многоугольниках.
Ключевой этап 2 практических вопросов правильной и неправильной формы1) На схеме показан пятиугольник (нарисованный неточно). Каждая сторона пятиугольника одинаковой длины. Форма правильного пятиугольника? Поясните свой ответ.
2) Вот равносторонний треугольник , начерченный на окружности.
С помощью линейки начертите на этом круге правильный шестиугольник .
3) Джек говорит: «Этот ромб — правильный четырехугольник». Объясните, почему Джек правильно , а не .
4) Нарисуйте кресты на двух фигурах , которые находятся в неправильных местах на диаграмме сортировки.
Хотите знать, как объяснить детям другие ключевые слова по математике? Загляните в наш словарь по начальной математике или попробуйте другие математические термины:
Онлайн-уроки математики, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи детей младшего школьного возраста еженедельные индивидуальные онлайн-уроки и занятия по математике.

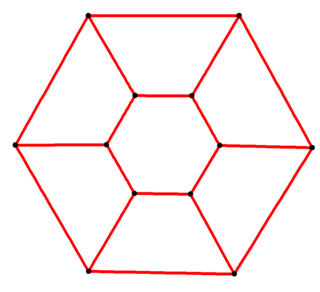

 Получится ли у Беларуси завоевать Америку?
Получится ли у Беларуси завоевать Америку? Самая яркая характеристика белорусской экономики
Самая яркая характеристика белорусской экономики От перемены кресел чиновников заводы не запускаются
От перемены кресел чиновников заводы не запускаются {4 }.}
{4 }.}