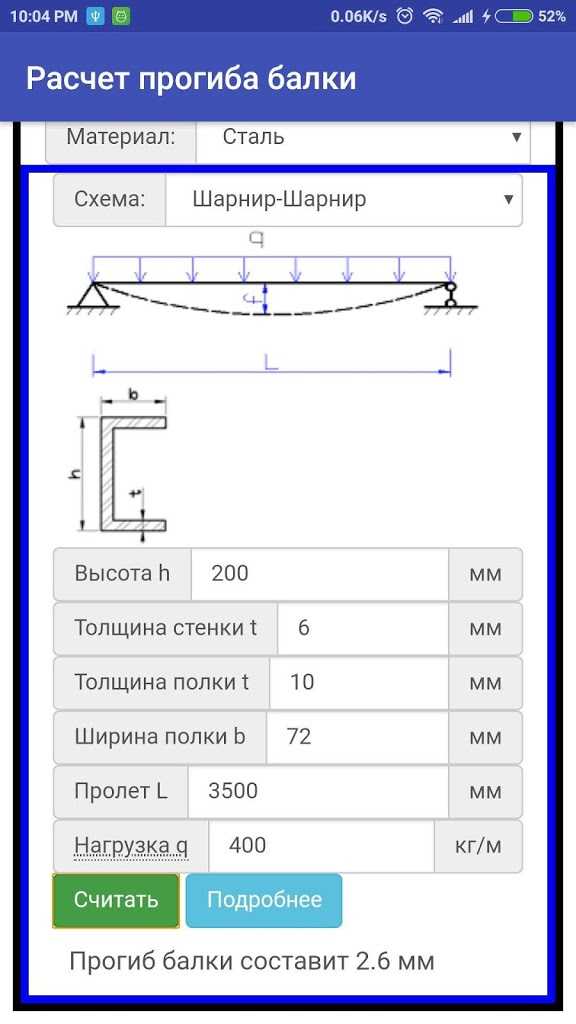
Расчет балки на прочность: онлайн-калькуляторы, пример, последовательность действий
Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение. В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.
- Как рассчитывать балки на прочность
- Последовательность действий
- Сравнение полученных напряжений с напряжением материалов
- Пример расчета
- Онлайн-калькуляторы
Как рассчитывать балки на прочность
Расчет балки на прогиб, калькулятор для которого можно найти в интернете, можно произвести следующими методами:
- Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
- Подобрать сечение;
- Проверочный перерасчет по максимальным значениям напряжения.
Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.
Последовательность действий
Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:
- Заделка — шарнир;
- Заделка — заделка;
- Шарнир — шарнир;
- Заделка — свободный конец.
Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.
Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.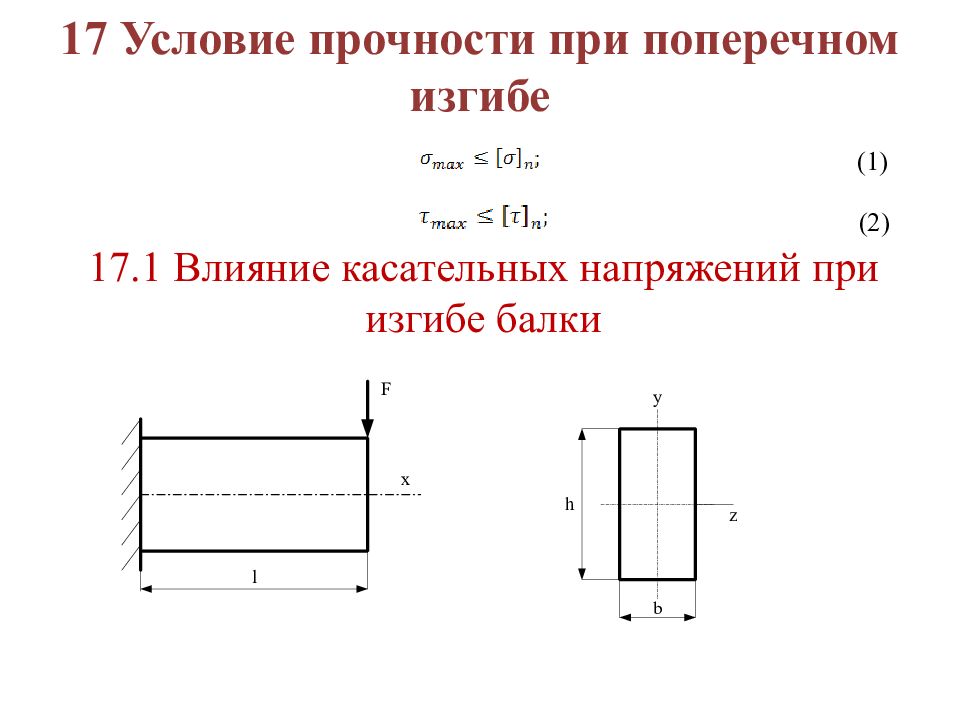
Сравнение полученных напряжений с напряжением материалов
Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.
Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности. Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.
Пример расчета
Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:
- Выбираем расчетную схему, в этом случае заделка — свободный конец;
- Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
- Находим по таблице сортаментов для данного двутавра момент сопротивления;
- Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0. 0000397 = 45,34 Мпа;
- Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.
Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.
Онлайн-калькуляторы
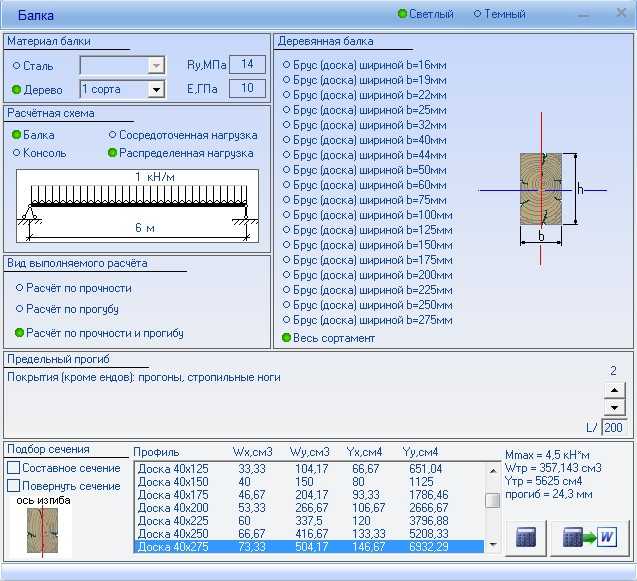
Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.
Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.
Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения. Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.
В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.
Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза.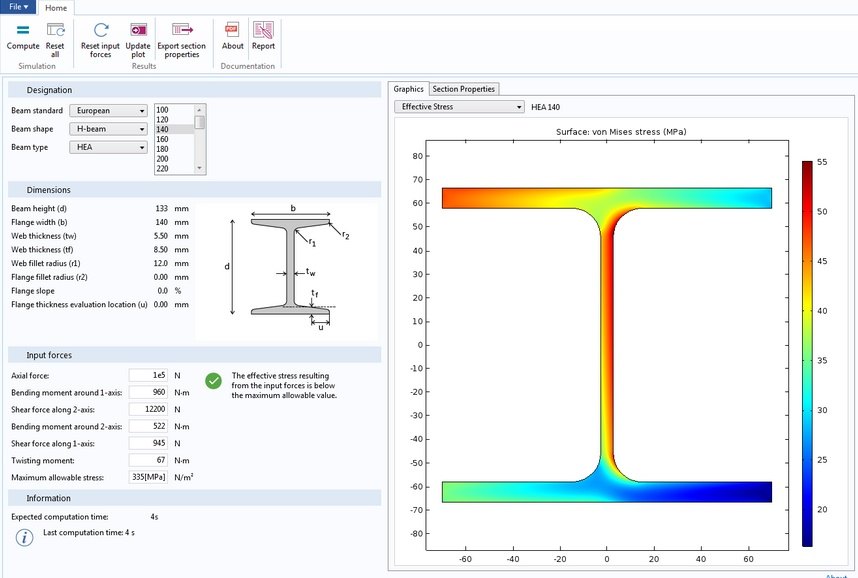
Удачных расчетов на прочность!
Онлайн калькулятор для расчета желебобетонных балок перекрытия дома
Габариты балки
Длина балки (l), м
Ширина балки (b), см
Высота балки (h), см
Расстояние центра поперечного сечения арматуры от низа балки (a), см
Характеристики бетона
Вид бетона ТяжелыйЛегкийЯчеистый
Класс бетона по прочности на сжатие
Призменная прочность, МПа кгс/см2
Сопротивление осевому растяжению, МПа кгс/см2
Характеристики арматуры
Класс арматуры
Сопротивление растяжению арматуры, МПа кгс/см2
Рассчетная нагрузка
Рассчетная распределенная нагрузка, кг*м2
Рассчеты
Требуемая площадь сечения арматуры, см
Относительная высота сжатой зоны бетона (E)
Максимальное значение поперечной силы (Qmax)
Рекомендуемые экономические показатели
Процент армирования, 1 < < 2
Относительная высота сжатой зоны бетона, 0.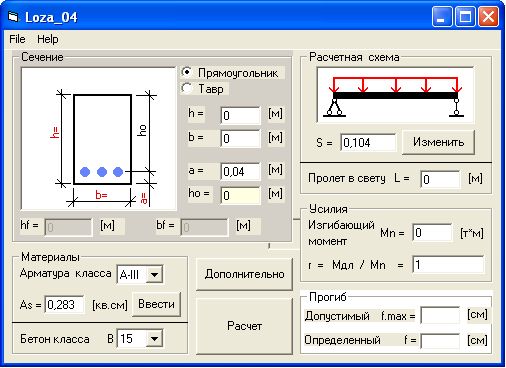
3 <
< 0.4
Максимальный изгиб, кг*м
A0
Характеристика сжатой зоны бетона (E0)
ita
Назначение калькулятора
Калькулятор для расчёта железобетонных балок перекрытий предназначен для определения габаритов, конкретного типа и марки бетона, количества и сечения арматуры, требующихся для достижения балкой максимального показателя выдерживаемой нагрузки.
Соответственно СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» габариты железобетонных балок перекрытия и их устройство подсчитываются по дальнейшим принципам:
- Минимальная высота балки перекрытия должна составлять не меньше 1/20 части длины перекрываемого проёма. К примеру при длине проёма в 5 м минимальная высота балок должна составлять 25 см;
- Ширина железобетонной балки устанавливается по соотношению высоты к ширине в коэффициентах 7:5;
- Армировка балки состоит минимум из 4 арматур – по два прута снизу и сверху.
- Железобетонные балки перекрытия бетонируются без перерывов заливки, одной порцией бетонной смеси, чтобы не было расслоения бетона.
Дистанцию между центрами укладываемых балок определяют длиной блоков и установленной шириной балок. К примеру, длина блока составляет 0,60 м, а ширина балки 0,15. Дистанция между центрами балок будет равна – 0,60+0,15=0,75 м.
Принцип работы
Согласно ГОСТ 26519-85 «Конструкции железобетонные заглублённых помещений с перекрытием балочного типа. Технические условия» формула расчёта полезной нагрузки железобетонных балок перекрытия складывается из следующих характеристик:
- Нормативно-эксплуатационная нагрузка на балки перекрытия с определённым коэффициентным запасом. Для жилых
зданий данный показатель нагрузки составляет 151 кг на м2, а коэффициентный запас равен 1,3. Получаемая
нагрузка – 151*1,3=196,3 кг/м2;
- Испытываемая нагрузка от массы армированного каркаса и последующей стяжки. Вес стяжки с толщиной слоя 5 см и показателем плотности 2000 кг на м3 будет образовывать следующую нагрузку – 2000*0,05=100 кг/м2 (масса армировки добавлена в плотность бетонной смеси).
Получаемая
нагрузка – 151*1,3=196,3 кг/м2;Показатель полезной нагрузки железобетонной балки перекрытия составляется из суммы всех трёх перечисленных показателей – 196,3+100+100=396,3 кг/м2.
Бесплатный онлайн-калькулятор луча | Civils.ai
Создание диаграмм изгибающих моментов, диаграмм поперечной силы и измерение прогиба для неопределенного пролета балки.
Рассчитайте изгибающий момент, поперечную силу, силы реакции и прогиб, используя свойства реального стального сечения.
Этот инструмент оптимизирован для настольного использования
Длина балки: 10,0 м
Второй момент площади: 473,0 см 4
Модуль Юнга: 210,0 ГПа
Загрузка…
Условия поддержки неудовлетворительны, добавьте другую поддержку.
Загрузка…
Макс. БМ: Мин. BM:
Макс. SF: Мин. SF:
Макс. отклонение:
Мин. отклонение:
Как работает этот анализ?
Введение
Балки бывают самых разных форм и размеров, понимание того, как рассчитать силы, действующие на конструкционную балку, может быть затруднено. Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжение балки .
youtube.com/embed/uNSmG1_3GAc» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Что такое напряжение балки и как рассчитать напряжение балки? Когда мы прикладываем силу где-то вдоль пролета балки, мы создаем внутренние напряжения. Существует два типа напряжений, которые создаются:
- Нормальное напряжение: Возникает из-за сил, действующих по длине балки при сжатии или растяжении.
- Напряжение сдвига: Возникает из-за сил, действующих параллельно направлению нагрузки.
Происхождение этих двух компонентов напряжения можно разделить на два компонента силы, которые мы называем Изгибающий момент и Сила сдвига .
Типы внешней нагрузкиПростейшие нагрузки, прикладываемые к балке, можно разделить на три категории:
- Точечные нагрузки: Это сила, приложенная к одной точке балки.
- Распределенные нагрузки: Эта сила распределяется по определенной длине и действует как форма давления.
- Сосредоточенный момент: Это чистый момент, действующий на балку в заданном положении.
Простейшие опоры для балки можно разделить на три категории:
- Штифтовая опора: Удерживает балку как в горизонтальном, так и в вертикальном направлениях, не ограничивая ее вращение.
- Роликовая опора: Опора балки только в одном направлении, без ограничения изгиба или вращения.
- Фиксированная опора: Эти опоры обеспечивают фиксацию балки во всех направлениях и препятствуют вращению.
Диаграмма сил свободного тела
Чтобы найти силы, действующие на балку, мы должны следовать процессу создания диаграммы сил свободного тела.
Как рассчитать силы реакции опор на пролет балки? Сначала мы рисуем балку в масштабе с указанием силовых составляющих приложенных нагрузок, а затем рассчитываем силы реакции опоры.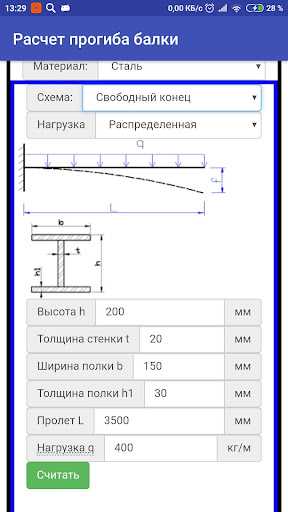
Для расчета реакций необходимо использовать уравнения равновесия для разрешения внешних сил:
- Σ Приложенные вертикальные силы = 0 кН
- Σ Приложенные горизонтальные силы = 0 кН
- Σ Прикладываемые моменты = 0 кНм
Существует два типа случаев при разрешении внешних условий балки:
- Статически определяемые: Где количество уравнений равно количеству неизвестных, и расчеты могут быть решены с помощью ручных вычислений в закрытой форме.
- Статически неопределимое: Когда количество неизвестных превышает количество уравнений и необходимо использовать более продвинутые методы, такие как теория сопротивления момента.
Чтобы создать диаграмму поперечной силы, вы работаете слева направо поперек балки, суммируя приложенные силы и реакции в каждой точке приложения.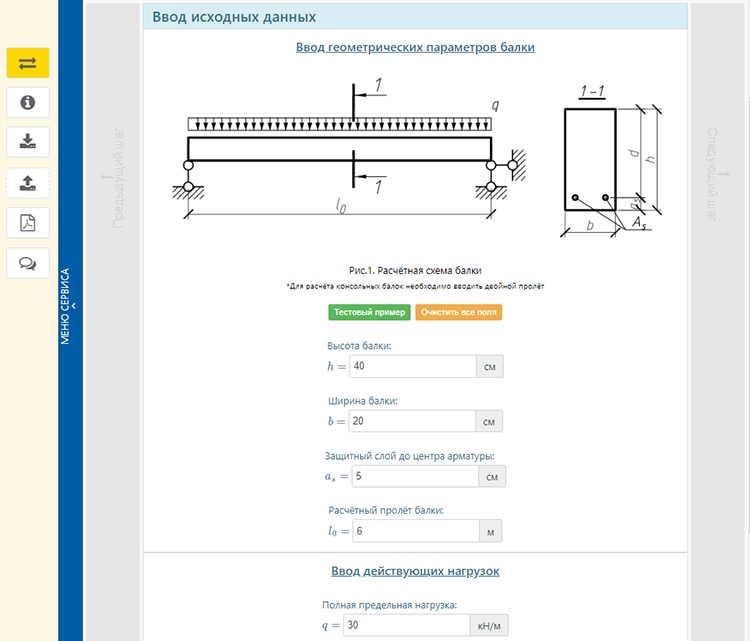
Консоли являются наиболее простым примером этого с единственной реакцией на одном конце пролета балки с нулевой силой сдвига на неподдерживаемом конце.
Чтобы создать диаграмму изгибающего момента, вы снова должны работать слева направо поперек балки и вычислять момент слева от каждой интересующей вас точки. наш расчет стальной балки для расчета в соответствии с Еврокодом 3.
Проектировщик стальных профилей
Расчет бетонной балки
Результаты этого анализа можно затем использовать в нашем расчете бетонной балки для расчета в соответствии с Еврокодом 2.
Конструктор бетонных секций
Внесите свой вклад в этот код
Этот код является открытым исходным кодом, и вы можете внести свой вклад в его разработку.
Вы можете найти исходный код на GitHub здесь:
IndeterminateBeamСпециальные кредиты: Джесси Бонанно
I Калькулятор прочности на напряжение балки
Калькулятор расчета прочности двутавровой балки для расчета
нормальное напряжение, напряжение сдвига и напряжение фон Мизеса в критических точках заданного
поперечное сечение двутавровой балки.
Поперечная нагрузка на двутавровую балку может привести к нормальным и касательным напряжениям. одновременно на любом поперечном сечении двутавра. Нормальное напряжение в данном поперечном сечении изменяется по отношению к расстояние y от нейтральной оси, и оно наибольшее в самой дальней точке от нервная ось. Нормальное напряжение также зависит от изгибающего момента в сечение и максимальное значение нормальных напряжений в двутавре возникает там, где изгибающий момент наибольший. Максимальное касательное напряжение возникает на нейтральной оси двутавровой балки, где поперечная сила максимальна.
Примечание. Для получения дополнительной информации о тему см. в разделах «Касательные напряжения в тонкостенных элементах» и «Расчетные балок и валов на прочность» главы механики материалов .
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота несущей балки [2c] | ||
| Ширина структурной балки [w] | ||
| I Толщина полки балки [t 1 ] | ||
| Толщина стенки двутавровой балки [t 2 ] | ||
| Сила сдвига [В] | кН фунт-сила | |
| Изгибающий момент [М] | Н*мкН*млфунт-сила*дюймфунт-сила*фут | |
| | ||
Примечание.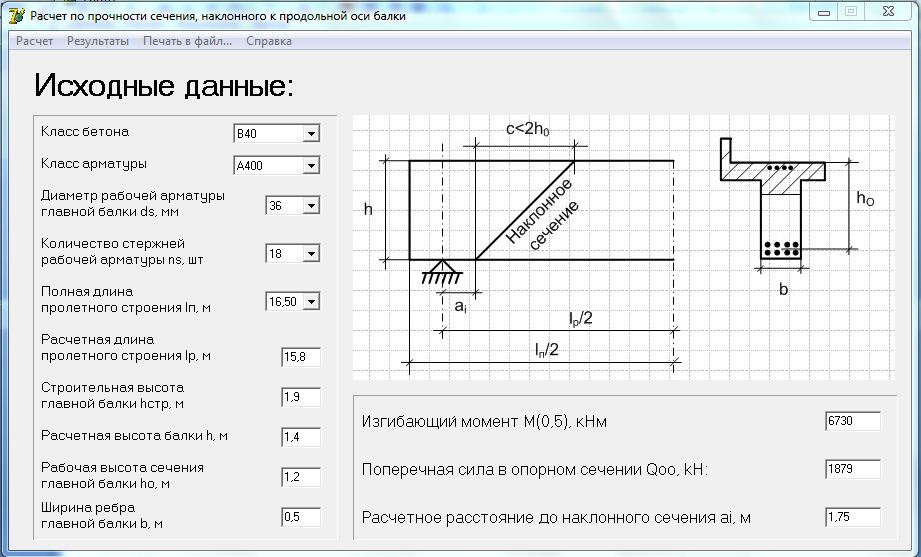
V и M — поперечная сила и изгибающий момент в сечении, как показано на рис.
рисунок.Посетить »
Калькуляторы прогиба и напряжения конструкционной балки». Для расчета поперечной силы и изгибающего момента.
Примечание. Предполагается, что конструкционная балка подвергается действию вертикальной поперечной силы в вертикальной плоскости симметрии.
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения [A] | 93||
| Первый момент площади для сечения B [Q B ] | — | |
| Первый момент площади сечения D [Q D ] | — | |
| Расчет напряжения на участке A | МПапсикси | |
| Нормальное напряжение [σ x_A ] | — | |
| Напряжение сдвига [τ ху_А ] | — | |
| Напряжение фон Мизеса при A [σ v_A ] | — | |
| Расчет напряжения на участке B | ||
| Нормальное напряжение в B [σ х_В ] | — | |
| Напряжение сдвига в B [τ xy_B ] | — | |
| Напряжение фон Мизеса в B [σ v_B ] | — | |
| Расчет напряжения на участке D | ||
| Нормальное напряжение в точке D [σ x_D ] | — | |
| Напряжение сдвига при D [τ xy_D ] | — | |
| Напряжение фон Мизеса в точке D [σ v_D ] | — | |
Примечание.