Как найти площадь сечения шара площадь сечения шара формула математика
Вопрос № 1: Как правильно задаются закрепления (связи) в системе SCAD Office?
Ответ: Связевые закрепления присваиваются узлам, перемещение или поворот, которых необходимо закрепить, опираясь исключительно на конструктивное решение рассматриваемого строения. При работе SCAD Office различают 6 видов связей: 3 перемещения и 3 поворота относительно 3-х глобальных осей. Закрепления X,Y,Z накалывают запрещение перемещений по соответствующим направлениям осей, а закрепления Ux, Uy, Uz – поворот вокруг глобальных осей.
Пример: Закрепление фермы при решении плоской задачи может выглядеть так: левый узел опирания закрепляется по направлению X и Z, правый край по направлению Z
Формула поперечного сечения проводника
Как правило, провода обладают круглым сечением, но допустимые токовые показатели должны рассчитываться согласно площади поперечного сечения
С целью самостоятельного определения площади сечения в одножильном или многожильном проводе осторожно вскрывается оболочка, представляющая собой изоляцию, после чего в одножильном проводнике замеряется диаметр
Площадь определяется в соответствии с хорошо известной даже школьникам физической формулой:
S = π х D²/4 или S = 0,8 х D², где:
- S является площадью сечения в мм2;
- π — число π, стандартная величина, равная 3,14;
- D является диаметром в мм.
Проводник
Замеры многожильного провода потребуют его предварительного распушения, а также последующего подсчета количества всех жилок внутри пучка. Затем измеряется диаметр одного составляющего элемента и вычисляется площадь сечения в соответствии со стандартной формулой, указанной выше. На заключительном этапе замеров суммируются площади жилок с целью определения показателей их общего сечения.
С целью определения диаметра проводной жилы используется микрометр или штангенциркуль, но при необходимости можно воспользоваться стандартной ученической линейкой или сантиметром.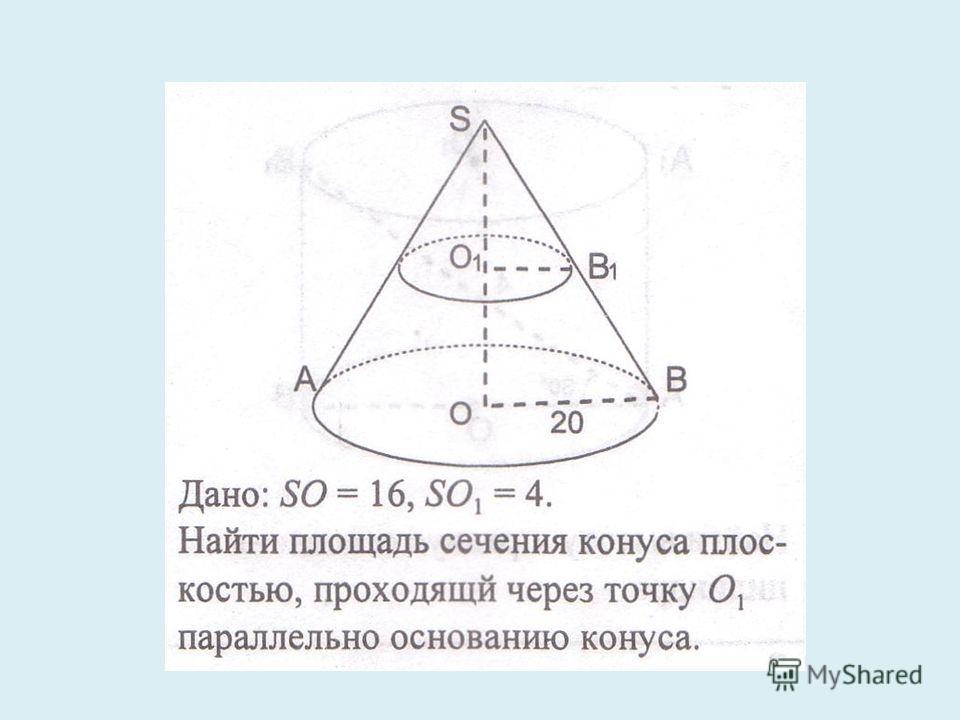
D = l/n,
Где:
- l представлено расстоянием намотки жилки в мм;
- n является числом витков.
Следует отметить, что большее сечение провода позволяет обеспечивать запас по показателям тока, в результате чего уровень нагрузки на электропроводку можно незначительно превышать.
Чтобы самостоятельно определить проводное сечение монолитной жилы, требуется посредством обычного штангенциркуля или микрометра выполнить замеры диаметра внутренней части кабеля без защитной изоляции.
Основные положения теории оболочек
Большинство
элементов инженерных конструкций в расчетной схеме, подлежащих расчету на
прочность, как это уже было отмечено, связаны с
расчетом бруса, пластинокили оболочек.
Предыдущие
разделы были достаточно подробно посвящены вопросам расчета стержней и
стержневых систем. Настоящий раздел книги посвящен различным вопросам расчета
пластинок и оболочек.
Под оболочкой
других. Геометрическое место точек, равноотстоящих от обеих поверхностей
оболочки, носит название срединной поверхности.
Если срединная
поверхность оболочки является плоскостью, то такую оболочку называют пластиной.
Геометрическая форма объектов, которые могут быть причислены к
оболочкам или пластинам, чрезвычайно разнообразна: в машиностроении — это
корпуса всевозможных машин; в гражданском и промышленном строительстве —
покрытия и перекрытия,навесы, карнизы;
в кораблестроении — корпуса судов, сухих и плавучих доков; в авиастроении —
фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта,
энергетике — защитная конструкция атомных станций, корпуса реакторов и т.
 д.
д.Если срединная
поверхность оболочки образует поверхность вращения в форме цилиндра, то
оболочку называют цилиндрической.
К схеме осесимметричной
цилиндрической оболочки сводится очень много инженерных конструкций, в том
числе: котлов, баков, нефтепроводов, газопроводов, деталей машин и др.
Задача о
расчете тонкостенных оболочек вращения наиболее просто решается в том случае,
толщине и, следовательно, изгиб оболочки отсутствует.
Теория
оболочек, построенная в этом предположении, называется безмоментной теорией оболочек.
Если оболочка
имеет резкий переход и жесткие защемления и, кроме того, нагружена
сосредоточенной силой и моментами, то в местах крепежа оболочки, резких
изменений формы, и в местах действия сосредоточенных сил и моментов возникают
интенсивные напряжения, обусловленные изгибным эффектом. Учет изгибных
эффектов можно получить в рамках моментной теории оболочек.
Следует
отметить, что чем меньше отношение толщины
оболочки к ее радиусу R, тем точнее выполняется
предположение о постоянстве напряжений по толщине и тем более
точнее выполняются расчеты по безмоментной
теории.
Отметим, что
оболочка считается тонкой, если h/R≤1/20.
Следовательно,
при расчете на прочность тонких оболочек в зависимости от характера
распределения внешних нагрузок, опорных закреплений, применяется или безмоментная или моментная теория. При этом предполагается
равномерное распределение напряжений по продольным и поперечным сечениям
оболочек (отсутствие в этих сечениях изгибающих, крутящих моментов и поперечных
сил).
При
осесимметричной нагрузке отсутствуют также сдвигающие силы. Определение усилий
на расстоянии, превышающем величину (3÷5)от мест скачкообразного изменения формы или
площади сечения, жестких контурных закреплений или от места приложения внешних
сосредоточенных сил и моментов.
 Вблизи указанных мест возникают дополнительные
Вблизи указанных мест возникают дополнительныенапряжения от изгибного эффекта.
В моментной и безмоментной теории тонких
оболочек или, так называемой технической теории оболочек,состоящей в резком различии их толщины и габаритных размеров, влечет за
собой возможность упрощения теории путем некоторой схематизации действительной
гипотезах, аналогичных гипотезам в теории стержней, т.е. гипотезам плоских
сечений и гипотезам “ненадавливания” слоев оболочки
друг на друга.
Эти гипотезы
позволяют свести трехмерную задачу механики сплошной среды к двумерной, подобно
тому как в теории стержней трехмерная задача сведена к
одномерной.
Далее в
технической теории тонких оболочек пренебрегают членами h/R по сравнению с
единицей.
Оболочки, к
которым применимы упомянутые выше гипотезы, называются тонкими, а те, к
которым эти гипотезы не применимы, называются
Граница между
тонкими и толстыми оболочками условны и определяются
отношением h/R≈1/20.
В тех случаях,
когда h/R≥1/20 для получения приемлемых результатов
по точности применяется аппарат механики сплошной среды, в частности теории
упругости или пластичности в зависимости от постановки задачи.
Про алюминиевый провод.
В отличие от меди, алюминий хуже пропускает электрический ток. Для алюминия (провод такого же сечения, что и медный), при токах до 32 А, максимальный ток будет меньше, чем для меди на 20 %. При токах до 80 А алюминий пропускает хуже ток на 30%.
Эмпирическое правило для алюминия:
Максимальный ток алюминиевого провода равен площади сечения, умножить на 6.
Имея знания, полученные в данной статье, можно выбрать провод по соотношениям «цена/толщина», «толщина/рабочая температура», а также «толщина/максимальный ток и мощность».
К максимально току в зависимости от площади сечения провода, немцы относятся несколько иначе. Рекомендация по выбору автоматического (защитного) выключателя, расположена в правом столбце.
Рекомендация по выбору автоматического (защитного) выключателя, расположена в правом столбце.
Таблица зависимости электрического тока защитного автомата (предохранителя) от сечения. Таблица 3.
Вопрос № 5: Можно ли скрыть не выделенные элементы или узлы в системе SCAD Office?
Ответ: Команда фрагментации выделенных узлов и элементов возможна с помощью соответствующих инструментов панели визуализации в программе SCAD. Команда «ножницы» позволяет выделить часть схемы, а команда «подтверждение фрагментации» оставит на экране только отмеченные элементы. В новой версии SCAD Office появилась возможность фрагментировать выделенные узлы и элементы с помощью одноименной команды (иконки находятся в правом нижнем углу). Преимущества второго метода в том, что фрагментации подвергаются элементы и узлы в разных частях схемы.
В следующей части статьи мы продолжим разбирать вопросы по работе в системе SCAD Office.
Конечные элементы и операции с ними
Прежде всего хотелось бы уделить внимание новым возможностям при работе с объемными элементами. Библиотека конечных элементов пополнилась такими высокоточными объемными элементами, как 10узловая пирамида (тип 38) и 20узловой изопараметрический конечный элемент (тип 37), рис
7.
Рис. 7. 20-узловой изопараметрический
конечный элемент (тип 37)
Появилась возможность выполнять дробление объемных элементов, что значительно облегчает задачу моделирования (рис. 8 и 9).
Рис. 8. Функция Дробление
объемных элементов
Рис. 9. Дробление объемных элементов
Появилась возможность учета преднапряжения для объемных конечных элементов (рис. 10).
Рис. 10. Функция Преднапряжение
Расширены возможности работы со стержневыми элементами: добавлены операции Дробление стержня полигоном (рис. 11) и Сопряжение стержней (рис. 12).
Рис. 11. Функция Дробление стержней полигоном
Рис. 12. Функция Сопряжение стержней
12. Функция Сопряжение стержней
При этом сопряжение стержней может быть выполнено под углом либо сопрягаться дугой окружности (рис. 13).
Рис. 13. Окно функции Сопряжение стержней
Операция Объединение стержневых элементов расширена возможностью объединения в один элемент нескольких стержней, лежащих на одной прямой и связанных между собой (рис. 14).
Рис. 14. Функция Объединение двух стержневых элементов
Реализованы новые функции и для работы с пластинчатыми элементами. Если ранее жесткие вставки можно было вводить только в стержневые элементы, то теперь добавлена возможность задавать смещение срединной плоскости (жесткой вставки) в пластинчатых элементах (рис. 15).
Рис. 15. Окно функции Смещение срединной плоскости пластин
Кроме того, добавлена операция дробления пластин с учетом промежуточных узлов, находящихся в границах пластин (рис. 16).
Рис. 16. Функция Дробление пластин с учетом промежуточных узлов
S=0,8D.
Небольшая поправка — является округленным коэффициентом. Точная расчетная формула:
В электропроводке и электромонтаже в 90 % случаях применяется медный провод. Медный провод по сравнению с алюминиевым проводом, имеет ряд преимуществ. Он более удобен в монтаже, при такой же силе токе имеет меньшую толщину, более долговечен. Но чем больше диаметр (площадь сечения), тем выше цена медного провода. Поэтому, несмотря на все преимущества, если сила тока превышает значение 50 Ампер, чаще всего используют алюминиевый провод. В конкретном случае используется провод, имеющий алюминиевую жилу 10 мм и более.
В квадратных миллиметрах измеряют площадь сечения проводов. Наиболее чаще всего на практике (в бытовой электрике), встречаются такие площади сечения: 0,75; 1,5; 2,5; 4 мм .
Существует иная система измерения площади сечения (толщины провода) — система AWG, которая используется, в основном в США. Ниже приведена таблица сечений проводов по системе AWG, а так же перевод из AWG в мм .
Выделяют, три основные принципа, при выборе сечения провода.
1. Для прохождения электрического тока, площадь сечения провода (толщина провода), должна быть достаточной. Понятие достаточно означает, что когда проходит максимально возможный, в данном случае, электрический ток, нагрев провода будет допустимый (не более 600С).
2. Достаточное сечение провода, что бы падение напряжения не превышало допустимого значения. В основном это относится к длинным кабельным линиям (десятки, сотни метров) и токам большой величины.
3. Поперечное сечение провода, а также его защитная изоляция, должна обеспечивать механическую прочность и надежность.
Для питания, например люстры, используют в основном лампочки с суммарной потребляемой мощностью 100 Вт (ток чуть более 0,5 А).
Выбирая толщину провода, необходимо ориентироваться на максимальную рабочую температуру. Если температура будет превышена, провод и изоляция на нем будут плавиться и соответственно это приведет к разрушению самого провода. Максимальный рабочий ток для провода с определенным сечением ограничивается только максимально его рабочей температурой. И временем, которое сможет проработать провод в таких условиях.
Далее приведена таблица сечения проводов, при помощи которой в зависимости от силы тока, можно подобрать площадь сечения медных проводов. Исходные данные – площадь сечения проводника.
Максимальный ток для разной толщины медных проводов. Таблица 1.
Сечение токопроводящей жилы, мм2 | Ток, А, для проводов, проложенных | ||
открыто | в одной трубе | ||
одного двух жильного | одного трех жильного | ||
0,5 | 11 | — | — |
0,75 | 15 | — | — |
1 | 17 | 15 | 14 |
1,2 | 20 | 16 | 14,5 |
1,5 | 23 | 18 | 15 |
2 | 26 | 23 | 19 |
2,5 | 30 | 25 | 21 |
3 | 34 | 28 | 24 |
4 | 41 | 32 | 27 |
5 | 46 | 37 | 31 |
6 | 50 | 40 | 34 |
8 | 62 | 48 | 43 |
10 | 80 | 55 | 50 |
16 | 100 | 80 | 70 |
25 | 140 | 100 | 85 |
35 | 170 | 125 | 100 |
50 | 215 | 160 | 135 |
70 | 270 | 195 | 175 |
95 | 330 | 245 | 215 |
120 | 385 | 295 | 250 |
Выделены номиналы проводов, которые используются в электрике. «Один двужильный» — провод, имеющий два провода. Один Фаза, второй – Ноль – это считается однофазное питание нагрузки. «Один трехжильный» — используется при трехфазном питании нагрузки.
«Один двужильный» — провод, имеющий два провода. Один Фаза, второй – Ноль – это считается однофазное питание нагрузки. «Один трехжильный» — используется при трехфазном питании нагрузки.
Таблица помогает определиться, при каких токах, а также в каких условиях эксплуатируется провод данного сечения.
Например, если на розетке написано «Мах 16А», то к одной розетке можно проложить провод сечением 1,5мм . Необходимо защитить розетку выключателем на ток не более чем 16А, лучше даже 13А, или 10 А. Эту тему раскрывает статья «Про замену и выбор защитного автомата».
Из данных таблицы видно, что одножильный провод – означает, что вблизи (на расстоянии менее 5 диаметров провода), не проходит более никаких проводов. Когда два провода рядом, как правило, в одной общей изоляции – провод двужильный. Здесь более тяжелый тепловой режим, поэтому меньше максимальный ток. Чем больше собрано в проводе или пучке проводов, тем меньше должен быть максимальный ток отдельно для каждого проводника, из-за возможности перегрева.
Однако, эта таблица не совсем удобна с практической стороны. Зачастую исходный параметр – это мощность потребителя электроэнергии, а не электрический ток. Следовательно, нужно выбирать провод.
Определяем ток, имея значение мощности. Для этого, мощность Р (Вт) делим на напряжение (В) – получаем ток (А):
Пример расчета элемента тонкостенной оболочки вращения
Рассчитать
коническую часть тонкостенной оболочки вращения (рис.8.13) с толщиной стенки
δ = 0,02 м. Давление внутри оболочки P= 0,2 МПа, удельный вес жидкости γ
= 1,5∙104 н/м3.
Рис.8.13
Решение:
Рассмотрим
отсеченную часть с действующими на нее силовыми факторами (см. рис.8.4).
Проводим через
точку А
первое сечение.
;
;
;
.
Второе сечение
проводим на расстоянии x= 0,15 м.
Высота столба
жидкости над сечением v= 10 —
0,15 = 9,85 м.
Давление .
В соответствии
с уравнением равновесия нижней отсеченной части оболочки (8.13) имеем
В соответствии
с уравнением Лапласаимеем,
Радиус
кривизны R2 для конуса равен ∞
Третье сечение
проведем через точку В(x=
0,25 м).
Высота столба
жидкости над сечением v= 10 —
0,25 = 9,75 м.
Давление .
Решая
уравнение равновесия (8.16) имеем
В соответствии
с уравнением Лапласа имеем,
Радиус
кривизны R2 для конуса равен ∞
Пример построения расчета МКИ в SCAD
Построение моделей расчета методом конечных элементов не обходится без приложения нагрузок, вычисленные вручную значения присваиваются в расчетных программах МКЭ на элемент. Помощь в сборе ветровых и снеговых нагрузках инженеру окажет программа ВЕСТ. Программа включает в себя несколько расчетных модулей, позволяющих по введенном району строительства и очертанием контура здания вычисляет ветровую и снеговую нагрузку (самые распространенные расчетные модули программы ВЕСТ). Так, при расчете навеса, конструктор должен указать высоту конька, угол наклона и ширину ската. По полученным эпюрам нагрузка вводится в расчетную программу, например, ПК ЛИРА 10.4.
В качестве вывода, могу сказать, что программный комплекс SCAD и его сателлиты позволяют пользователю существенно снизить трудозатраты при вычислении локальных задач, а также формировать точные расчетные модели, а также содержат справочные данные, необходимые в работе инженеров — строителей. Автономность программ позволяет конструкторам использовать их в сочетании с любыми расчетными комплексами, основанных на расчете методом конечных элементов.
Также рекомендую посмотреть вебинар по совместному использованию ПК ЛИРА 10 и программы ЗАПРОС (SCAD office) на примере расчета свайного основания.
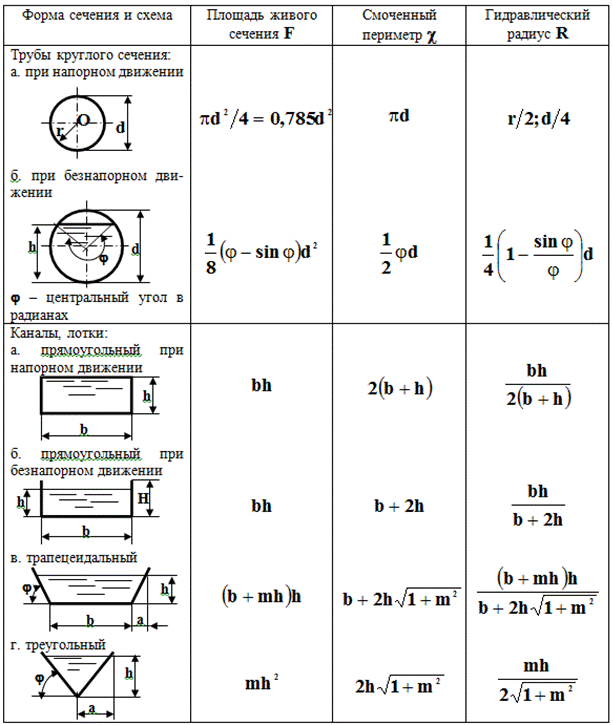
Пример расчета толстостенной стальной трубы
Для
толстостенной стальной трубы, имеющей внутренний диаметр d = 0,03 м и наружный диаметр D = 0,18 м, и изготовленной из пластичного материала
с σT = 250 МПа
и с коэффициентом Пуассона μ = 0,5,
требуется:
1. Определить
Определить
давление pT,
при котором в материале трубы начнется пластическое деформирование;
2. Определить
предельное внутреннее давление pПР, при котором весь материал будет находиться в
пластическом состоянии;
3. Построить
эпюры распределения напряжений σp, σφ,
σz по толщине стенки для двух
состояний трубы, рассмотрены в п. 1 и 2;
4. Определить
допускаемое значение давления pa = pДОП при коэффициенте
запаса прочности n = 1,5.
Решение.
1. По
формуле определяем давление, при котором на внутренней
поверхности трубы появятся пластические деформации:
2. С
учетом того, что pa = pT, из формул
определяем
напряжения, соответствующие началу пластического течения:
Данные для
числовых расчетов сводим в таблицу
1,5 | 148,5 | -140,5 |
3 | 40,1 | -32 |
6 | 13,0 | -5,0 |
9,5 | 8,0 |
Эпюры
напряжений σp, σφ, σz
для упругого состояния материала трубы приведены на рис. 1, а.
Рассмотрим
теперь предельное состояние трубы, когда весь материал трубы находится в
пластическом состоянии. Предельное давление в этом случае определяется по
формуле
Рис.1
3. Для
определения напряжений σp, σφ,
σz воспользуемся формулами
Данные для
числовых расчетов сводим в таблицу
1,5 | -517,8 | -228,9 | -373,4 |
3 | -317,6 | -28,6 | -173,1 |
6 | -117,5 | -171,7 | 27,2 |
9 | 289,0 | 144,5 |
Для более
точного построения эпюр и определим точки, в которых указанные
напряжения равны нулю:
для эпюры
для эпюры
4. Эпюры
Эпюры
напряжений σp, σφ, σz
приведены на рис. 1, б.
Допускаемое значение внутреннего давления определяется из условия pДОП = pПР/n pДОП = 517,8/1,5 = 345,2
МПа.
Пример 3.
Для стальной
составной трубы (рис. 1) заданы: внутренний радиус внутренней трубы а = 7см, внутреннее давление р = 100 МПа, расчетное сопротивление
стали Ry= 240 МПа, коэффициент Пуассона ν = 0,3; модуль продольной
упругости Е= 2∙105 МПа.
Требуется:
1) определить
внешний радиус внутренней трубы b,
внешний радиус наружной трубы с,
радиальный натяг δ;
2) проверить
прочность сплошной трубы с внутренним радиусом а и внешним радиусом с,
нагруженной внутренним давлением р, используя III теорию прочности;
3) проверить
прочность в опасных точках составнойтрубы, нагруженной внутренним давлением р, используя IIIтеорию
прочности;
4) определить
радиальные перемещения точек внутреннего канала.
Рис.1
Решение.
1) Определение
геометрических параметров b, c и δ.
Внешний радиус
с наружной трубы определяется на
основе условия прочности:
Внешний радиус
b внутренней трубы определяется по формуле:
Радиальный
натяг рассчитываем по формуле:
2) Проверка прочности сплошной трубы с внутренним радиусом а и внешним радиусом с, нагруженной давлением р.
Из теории
расчета толстостенных труб известно, что и при нагружении
внутренним давлением, и при нагружении внешним
давлением опасными являются точки на внутреннем канале трубы.
Рассчитываем
напряжения в точках 1 (рис. 1),
используя формулы
и полагая в
нихb = c, pa = p, pb = 0, r = a:
По аналогии
определяем в точках 2 и 3:
и в точке 4:
Эпюра
распределения напряжений по толщине сплошной трубы с внутренним радиусом a и внешним радиусом c показана на рис. 2.
2.
Рис.2
Условие
прочности по III теории
прочности имеет вид
В нашем случае
в точке 1 трубы будет
Таким образом,
получаем
Условие
прочности для сплошной трубы не выполняется.
3) Проверка
прочности в опасных точках составнойтрубы, нагруженной внутренним давлениемр.
Вначале
рассчитываем давление от натяга рк на поверхности контакта наружной и внутренней
трубы, используя формулу
Рассчитываем
напряжения и в точке 1
от действия натяга рк,
используя формулы
и полагая в
них pa = 0, pb = pk, r =a:
Рассчитаем
суммарные напряжения и в точке 1
от действия р
и pk:
Проверяем
прочность составной трубы в точке 1
по IIIтеории прочности:
Условие
прочности для составной трубы выполняется.
4) Определение
радиальных перемещений точек 1
составной трубы.
Воспользуемся
законом Гука для двухосного напряженного состояния
Особенности электрических проводов
Наиболее широкое применение находят марки проводов ПУHП и ПУГHП, а также ВПП, ПHCB и PKГM, которые обладают следующими, очень важными для получения безопасного подключения основными техническими характеристиками:
- ПУНП — плоское проводное изделие установочного или так называемого монтажного типа, с однопроволочными жилами из меди в ПВХ-изоляции. Такая разновидность отличается количеством жил, а также номинальным напряжением в пределах 250 В с частотой 50 Гц и температурным эксплуатационным режимом от минус 15 °C до плюс 50 °C;
- ПУГНП — гибкая разновидность с многопроволочными жилами. Основные показатели, которые представлены номинальным уровнем напряжения, частотой и температурным эксплуатационным режимом, не отличаются от аналогичных данных ПУHП;
- AПB — алюминиевая одножильная разновидность, круглый провод, имеющий защитную ПВХ-изоляцию и однопроволочную или многопроволочную жилу.
 Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C; - ПBC — многожильная медная разновидность с ПBX-изоляцией, придающей проводу высокие показатели плотности и традиционную округлую форму. Термоустойчивая жила рассчитана для номинального уровня 380 В при частоте 50 Гц;
- PKГM — силовая монтажная разновидность, представленная одножильным медным проводом с кремнийорганической резиновой или стекловолоконной изоляцией, пропитанной термостойким составом. Температурный эксплуатационный режим составляет от минус 60 °C до плюс 180 °C;
- ПHCB — нагревательная одножильная разновидность в виде однопроволочного провода на основе оцинкованной или вороненой стали. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 80 °C;
- ВПП — одножильная медная разновидность с многопроволочной жилой и изоляцией на основе ПBX или полиэтилена. Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
В условиях невысокой мощности применяется медный провод ШBBП с защитной внешней ПBX-изоляцией. Многопроволочного типа жила обладает прекрасными показателями гибкости, а само проводное изделие рассчитано максимум на 380 В, при частоте в пределах 50 Гц.
Проводные изделия самых распространенных типов реализуются в бухтах, и чаще всего имеют белое окрашивание изоляции.
Вопрос 22: Как следует анализировать результаты расчета здания на пульсационную составляющую ветрового воздействия?
Ответ:
Для начала необходимо проанализировать частоты полученных форм колебаний. Для этого смотрим в разделе «Перемещения — Частоты и периоды колебаний» значения полученных частот собственных колебаний здания. Согласно СП «Нагрузки и воздействия» необходимо учитывать формы колебаний, ниже предельного значения, указанного в нормах. Таким образом, Вы должны увидеть в появившемся окне форм колебаний, частоту выше предельного значения, если частота ниже, то необходимо увеличить количество форм колебаний. Дальнейший учет форм колебаний происходит автоматически: программа согласно требованиям норм суммирует полученные усилия по каждой форме колебаний и добавляет их в РСУ. Пользователь SCAD может анализировать отдельно усилия по пульсационной или средней составляющей ветрового воздействия. Выбрать нужный пункт можно в выпадающем окне текущего загружения.
Дальнейший учет форм колебаний происходит автоматически: программа согласно требованиям норм суммирует полученные усилия по каждой форме колебаний и добавляет их в РСУ. Пользователь SCAD может анализировать отдельно усилия по пульсационной или средней составляющей ветрового воздействия. Выбрать нужный пункт можно в выпадающем окне текущего загружения.
Вопрос 20: Как в SCAD создать объемные тела?
Ответ:
Создавать объемные тела в SCAD возможно способом выдавливание объемных тел из пластин. Необходимая для этой процедуры команда называется «Копирование схемы». Для начала выделяем ранее созданные пластины, и жмем команду «Копирование схемы». В появившемся окне задаем шаг и количество шагов копирования. Шаг выбирайте соизмеримый с шагом триангуляции плиты, так не получиться у Вас вытянутых объёмных элементов. Количество шагов выбирайте исходя из габаритных размеров создаваемого тела
Перед обращением к команде «Копирование схемы» пластинчатые элементы необходимо выделить! Это важно!
Нюансом здесь является то, что программа при использовании команды «Копирование схемы» работает и с невыделенными элементами, копируя их по указанным параметрам. В таком случае необходимо разделять конструкции на подсхему, соединив их потом в «Режиме сборки».
Список источников
- blog.infars.ru
- sapr.ru
- www.soprotmat.ru
- www.calc.ru
- proprovoda.ru
Поделитесь с друзьями!
Площадь поперечного сечения проводника: как найти площадь формулой
С необходимостью определения площади поперечного сечения проводника сталкивается каждый, кто хоть раз в жизни занимался ремонтом кабельной проводки в квартире, на даче, в гараже или офисе. Нехватка сечения может привести к пожару, так как провод будет сильно нагреваться. Если же сечение, наоборот, подобрано со значительным запасом, то стоимость проводки станет необоснованно высокой. В этой статье рассказывается, о различных методиках определения площади поперечного сечения проводника для круглых, одножильных, многожильных проводов и кабелей.
Если же сечение, наоборот, подобрано со значительным запасом, то стоимость проводки станет необоснованно высокой. В этой статье рассказывается, о различных методиках определения площади поперечного сечения проводника для круглых, одножильных, многожильных проводов и кабелей.
Что такое площадь поперечного сеченья
Если провод разрезать строго перпендикулярно его длине, чтобы металлические сердечники имели форму правильного круга, то несложно будет измерить диаметр этих жил и определить их площадь с использованием стандартной формулы.
Поперечное сечениеВажно! До недавнего времени опытные электрики могли определить этот параметр на глаз, но сегодня даже они вынуждены измерять провода, и проводить вычисления. Во времена Советского Союза все провода и кабели выпускались по единому ГОСТу, который и нормировал стандартные сечения. Если это 2.5 мм2, то электрик сразу мог отличить его от близких параметров 2 мм2 или 3 мм2. Сегодня производством кабельной продукции занимаются различные компании, которые могут сознательно уменьшать сечение провода и экономить на этом деньги. Вместо заявленных 2.5 мм2 в продажу может поступить провод 2,2 мм2, а это может иметь серьезные последствия и закончиться выгоранием проводки.
Чему равна площадь
Чему равна площадь поперечного сечения проводника – главный вопрос монтажника. Данный показатель является величиной, которая зависит от формы перпендикулярного среза геометрического тела. Проще всего определить площадь квадрата или прямоугольника, для чего достаточно перемножить между собой длину на ширину. Еще в Древней Греции научились рассчитывать площадь практически любой фигуры. Как правило, большинство проводов имеют круглую форму сечения, которую вычислить несложно по формуле или воспользовавшись справочной таблицей. Для этого нужно знать только диаметр или радиус жилы проводника.
Обратите внимание! Существуют кабели большого сечения, в составе которых расположены секторные провода. Но в конечном итоге, сердечники таких изделий рассчитываются исходя из общего приведённого диаметра всех металлических элементов в пучке. Для определения площади сечения каждой жилы необходимо общий показатель разделить на их количество в кабеле.
Но в конечном итоге, сердечники таких изделий рассчитываются исходя из общего приведённого диаметра всех металлических элементов в пучке. Для определения площади сечения каждой жилы необходимо общий показатель разделить на их количество в кабеле.
Чем измерять площадь
Для правильного измерения площади поперечного сечения важно сделать ровный перпендикулярный срез и измерить диаметр металла при помощи высокоточных приборов. В случае с многожильными проводами необходимо выполнить следующие шаги:
- Для точных расчетов нужна одиночная проволока. Из пучка проводов выделяют одну жилку и вычисляют площадь ее сечения.
- Пересчитывают количество жил в проводе.
- Перемножают площадь сечения жилки на их количество.
Полученный результат и будет искомой площадью многожильного проводника.
Многожильный проводДополнительная информация: Для вычисления площади сечения проводника необходимо, в первую очередь, измерить его диаметр, и сделать это лучше всего микрометром, штангенциркулем или, в крайнем случае, высокоточной инженерной линейкой. Так как микрометр – редкость в наборе инструментов электрика, то этот способ мы упустим и остановимся на штангенциркуле и линейке.
Штангенциркуль
Штангенциркуль — высокоточный измерительный инструмент, при помощи которого можно определить линейные размеры любого предмета, диаметры круглых изделий, а также глубину сквозных и глухих отверстий и выемок. Такой инструмент должен быть у каждого домашнего мастера, стоит он не дорого и при правильном обращении может прослужить не одно десятилетие.
ШтангенциркульШтангенциркули подразделяются на следующие виды:
- Нониусные — имеют классическую конструкцию и высокоточную измерительную шкалу, которая позволяет измерять предметы с точностью до 0.1 – 0.05 мм.
- Со стрелочным отображением результатов измерений — очень удобный для снятия точных показаний инструмент, но его главным недостатком является повышенная хрупкость.

- С электронной индикацией результатов — относительно новая разработка, предназначенная для получения максимальной точности и удобного снятия показаний измерений.
Рассмотрим самый распространенный вид штангенциркуля — нониусный. Из таких инструментов наибольшее распространение получили два вида:
- ШЦ-I с точностью измерений 0,1 мм, такой инструмент есть практически у каждого слесаря.
- ШЦ-II с точностью измерений 0,05 мм, этот штангенциркуль предпочтительнее, так как в результате работы он выдаёт меньшую погрешность.
Для правильного измерения диаметра достаточно оголить сердечник кабеля путём снятия изоляция, после чего прижать раздвижные губки инструмента к его поверхности. Риска на подвижной части штангенциркуля совпадёт с показателем на шкале, который и будет являться диаметром.
Карандаш + линейка
Если под рукой нет точных измерительных инструментов, а определить диаметр провода необходимо в настоящий момент, можно воспользоваться старым проверенным способом. Картинка 5. Метод карандаша.
Для данного способа понадобятся круглый карандаш и линейка. Суть метода состоит в следующем алгоритме:
- Прежде всего необходимо отрезать кусок провода и очистить его от изоляции.
- Далее проволока из металлического сердечника плотно наматывается на карандаш, причём, минимальное количество витков должно быть не меньше 15. Здесь все зависит от толщины провода, и чем он тоньше, тем больше витков необходимо намотать.
- Проводятся вычисления по формуле, приведённой на картинке 6.
Обратите внимание! Для получения точного результата следует наматывать провод на карандаш как можно плотнее. Для этого перед наматыванием его необходимо тщательно выровнять в местах перегибов и образования петель.
Как правильно найти площадь поперечного сечения (с помощью формулы)
Как найти площадь поперечного сечения проводника подскажет формула, известная из школьного курса геометрии – пr2. Когда известен диаметр провода, можно приступать к вычислению площади сечения. Сделать это несложно с помощью калькулятора по формуле, указанной на картинке 7.
Когда известен диаметр провода, можно приступать к вычислению площади сечения. Сделать это несложно с помощью калькулятора по формуле, указанной на картинке 7.
Таблица диаметров и сечения проводов
Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Таблица соотношений диаметров и площадей проводовТаким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.
Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.
Расчет стержня на прочность — Пример решения задачи
Задача
Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [σ]=160 МПа.
Полученные размеры принять согласно ГОСТ 6636.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций.
- Построение эпюр внутренних продольных сил.
Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.
где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня. 3-\frac34(1-\lambda)-\frac14=0,$$
откуда $%\lambda_1=\lambda_2=\frac32$%, $%\lambda_3=0$%.
3-\frac34(1-\lambda)-\frac14=0,$$
откуда $%\lambda_1=\lambda_2=\frac32$%, $%\lambda_3=0$%.
Если $%\lambda=\lambda_{1, 2}=\frac32$%, то получаем систему $$\left\{\begin{aligned} & -\frac12\alpha-\frac12\beta-\frac12\gamma=0,\\ & -\frac12\alpha-\frac12\beta-\frac12\gamma=0,\\ & -\frac12\alpha-\frac12\beta-\frac12\gamma=0, \end{aligned}\right.$$ которая фактически состоит из одного уравнения. Выберем в качестве базисной переменную $%\alpha$% и выразим ее через свободные переменные: $%\alpha=-\beta-\gamma$%. Запишем общее решение в столбец: $${\begin{pmatrix}-\beta-\gamma\\\beta\\\gamma\end{pmatrix}}.$$ Теперь найдем векторы фундаментальной системы. Для значений $%\beta=1$%, $%\gamma=0$% получаем: $$\vec{f}_1={\begin{pmatrix}-1\\1\\0\end{pmatrix}}$$ — первый вектор фундаментальной системы; и для $%\beta=0$%, $%\gamma=1$%: $$\vec{f}_2={\begin{pmatrix}-1\\0\\1\end{pmatrix}}$$ — второй вектор.
Вычислим их скалярное произведение: $%\vec{f}_1\cdot\vec{f}_2=1$%, значит, данные векторы не ортогональны, что нас не устраивает. Поэтому эту пару векторов следует ортогонализовать. Поскольку любая линейная комбинация векторов фундаментальной системы тоже является решением системы (уравнения $%\alpha=-\beta-\gamma$%), то рассмотрим вектор $%\vec{f}_1+k\vec{f}_2$%, где $%k$% — неизвестный числовой коэффициент, и составим следующее скалярное произведение, которое должно быть равно нулю: $%(\vec{f}_1+k\vec{f}_2)\vec{f}_2=0$%, откуда $$k=-\frac{\vec{f}_1\cdot\vec{f}_2}{\vec{f}_2\cdot\vec{f}_2}=-\frac12.$$ Таким образом, в качестве первого собственного вектора выбираем: $$ \vec{u}_1=\vec{f}_1+k\vec{f}_2={\begin{pmatrix}-\frac12\\1\\-\frac12\end{pmatrix}}$$ и в качестве второго: $$\vec{u}_2=\vec{f}_2={\begin{pmatrix}-1\\0\\1\end{pmatrix}}.$$
Если $%\lambda=\lambda_3=0$%, то получаем систему
$$\left\{\begin{aligned}
& \alpha-\frac12\beta-\frac12\gamma=0,\\
& -\frac12\alpha-\beta-\frac12\gamma=0,\\
& -\frac12\alpha-\frac12\beta-\gamma=0,
\end{aligned}\right. 2}3.$$
2}3.$$
отвечен 21 Дек ’19 12:30
Определяем площадь свечения
Зачем же все таки правильно определять сечение кабеля? Что случится, если произвести монтаж неподходящего кабеля? Предположим, вы рассчитали, что номинальная нагрузка данной линии 25 А, значит, для монтажа электропроводки вам нужен кабель диаметром 2,5 мм. кв. У вас имеется кабель без маркировки (маркировка могла стереться, смазаться) похожий на 2,5 мм кв., но на самом деле он меньше — 1,5 мм. кв. Кабель с сечением 1,5 мм не выдержит подобной нагрузки, так как он предназначен для линии с нагрузкой 10-12 А. В результате изоляция нагреется, оплавится, что грозит замыканием и как следствие — пожаром. Бывает, что приобретенный кабель на самом деле имеет сечение меньше указанного производителем. Допустим, вы приобрели провод сечением 4 мм, хотя на самом деле сечение составляет 3,5 мм. В результате чего нагрузочная способность также уменьшается, что влечет за собой негативные последствия. Почему сечение кабеля может быть меньше указанного? Так некоторые компании хотят сэкономить круглую сумму денег, вот и понижают сечение провода.Так что знать действительное сечение провода необходимо для безопасной и продолжительной эксплуатации.
Расчет сечения кабеля подручными средствами
Чтобы рассчитать площадь сечения жилы, для начала нужно узнать ее диаметр. В этом поможет микрометр — особый прибор, измеряющий диаметр жилы провода с высокой точностью. Для этой же задачи подойдет штангенциркуль. Профессиональному электрику приобретение микрометра необходимо в силу специфики работы. Для простого человека, которому понадобилось произвести замер 1 раз, нет смысла покупать микрометр. Но что делать, если даже штангенциркуль дома не нашелся? Есть вполне достойный, альтернативный метод. Вам понадобится линейка, простой карандаш или ручка. Только не пытайтесь измерить диаметр при помощи линейки! Такой метод даст большую погрешность. Линейка понадобится чуть позже. Берется кусок провода, предварительно зачищенный от изоляции примерно на 40 см, и наматывается на карандаш. Важно наматывать как можно плотнее! Если между витками останутся зазоры, измерения будут неверны. Считается, сколько витков вышло, а их длина измеряется линейкой. Например, на карандаше 21 виток, длина витков 37 мм. Длина витков делится на их количество и получается диаметр жилы (37/21=1,762).
Вам понадобится линейка, простой карандаш или ручка. Только не пытайтесь измерить диаметр при помощи линейки! Такой метод даст большую погрешность. Линейка понадобится чуть позже. Берется кусок провода, предварительно зачищенный от изоляции примерно на 40 см, и наматывается на карандаш. Важно наматывать как можно плотнее! Если между витками останутся зазоры, измерения будут неверны. Считается, сколько витков вышло, а их длина измеряется линейкой. Например, на карандаше 21 виток, длина витков 37 мм. Длина витков делится на их количество и получается диаметр жилы (37/21=1,762).
Далее нужно вспомнить курс школьной геометрии и применить формулу вычисления площади круга: (S=ПИ*D2/4), для облегчения расчетов можно преобразовать формулу (S=0,785*D2), где D — диаметр, а 0,785 — число ПИ разделенное на 4. Подставляем наши значения, результат округляем до сотых:(1,762*1,762)*0,785=2,44 мм. Точность полученных данных зависит от плотности намотки, и количества витков — чем их больше, тем точнее будет результат. Вот таким простым методом можно вычислить сечение одножильного кабеля.
Определяем сечение многожильного провода
Но если кабель многожильный? Потребуется значение сечения одной из жил, а высчитывается оно по вышеприведенной формуле. Далее умножается площадь одной жилы на их количество. Ну например: площадь жилы равна 0,2 мм, всего жил 15. Умножаем: 15*0,2=3мм. Но бывает, что жилы в кабеле не прилегают вплотную, и между ними образуется зазор, который нужно учесть. Если такой зазор имеется, результат умножается на 0,9. Возьмем наши значения: 3*0,9=2,7.
Заключение
Правда, у этого метода определения есть свои минусы — с его помощью можно узнать сечения только маленьких размеров. Разве реальным будет намотать на карандаш провод сечением 6 мм. кв.? Тут, конечно, без специального прибора никак не обойтись. Существуют специальные таблицы с номинальным значением сечения кабелей, как одножильных, так и многожильных, и соответствующие значения диаметров.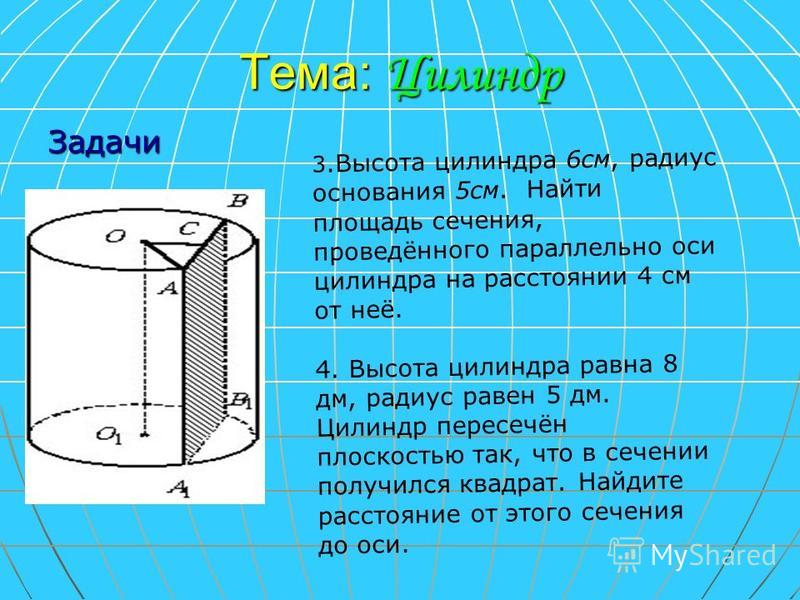 Но для того, чтобы проложить проводку у себя в квартире, способа с карандашом будет вполне будет достаточно.
Но для того, чтобы проложить проводку у себя в квартире, способа с карандашом будет вполне будет достаточно.
Торговая сеть «Планета Электрика» имеет большой ассортимент кабельно-проводниковой продукции, с которым можно ознакомиться в нашем каталоге.
Методы расчета площади сечения трубы
Параметры труб определяются согласно расчётам, сделанным при помощи специальных формул. Сегодня большинство вычислений производится посредством онлайн сервисов, однако в большинстве случаев требуется индивидуальный подход к вопросу, поэтому важно понимать, каким образом производится расчёт площади сечения трубы.
Как делаются вычисления?
Как известно, труба – это цилиндр. Следовательно, площадь её сечения рассчитывается по простым формулам, известным нам из курса геометрии. Основная задача – вычислить площадь круга, диаметр которого равен наружному диаметру изделия. При этом толщина стенок вычитается для получения истинного значения.
Как мы знаем из курса общеобразовательной школы, площадь круга равна произведению числа π на квадрат радиуса:
S = π • R2.
Здесь:
- R – радиус вычисляемой окружности. Он равен половине её диаметра;
- Π – постоянная равная 3,14;
- S – вычисляемая площадь поперечного сечения трубы.
Приступаем к расчёту
Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:
- S = π • (D/2 – N)2;
- В этой записи D – внешний диаметр окружности;
- N – толщина стенки трубы.
Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).
К примеру, требуется рассчитать сечение трубы, внешний диаметр которой 1 метр. Толщина её стенок 10 мм. (или 0,01 м.). Следовательно, нам известно:
D = 1 м.; N = 0,01 м.
Для упрощения возьмём π = 3,14. Подставляем значения в формулу:
Подставляем значения в формулу:
S = π • (D/2 – N)2 = 3,14 • (1/2 – 0,01)2 = 0,754 м2.
Некоторые физические особенности
От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.
При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.
О чём стоит помнить?
Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.
Как определить площадь сечения арматуры в жб балке
Тем кто самостоятельно считает строительные конструкции, интересует вопрос, как определить площадь сечения арматуры в жб балке? И если вам необходимо посчитать требуемую площадь сечения арматуры в железобетонном элементе, тогда воспользуйтесь данным примером.
Методика расчета принята согласно «Пособию по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003)»
Что бы определить требуемую площадь сечения арматуры в железобетонном элементе нам необходимо знать изгибающий момент (Му), марку бетона, класс арматуры, размер сечения.
Для определения изгибающего момента воспользуйтесь программой для расчета одно и многопролетных балок.
Также нам необходимо знать расчетное значение сопротивления бетона Rb в зависимости от класса бетона по прочности на сжатие и осевое растяжение. 2.
2.
Также не забудьте учесть привязку к центру арматуры: а=2,5 см (у вас будет свое значение)
После сбора всех данных, можно приступить к расчету.
Как определить площадь сечения арматуры в жб балке. Пример расчетаИли можете воспользоваться готовой программой написанной в Excel
Скачать программу для расчета площади сечения арматуры в жб балке:
После того как мы посчитали требуемую площадь сечения арматуры, необходимо подобрать количество стержней и их диаметр.
В программе реализован способ подбора армирования только одинакового диаметра, а если необходимо подобрать армирование балки с разными диаметрами тогда воспользуйтесь таблицей площади поперечного сечения арматуры:
Выполняя данные рекомендации, вы легко сможете посчитать требуемую площадь сечения арматуры в жб балке.
Поделиться ссылкой:
ПохожееКак рассчитать высоту по объему
Высота — это интегральный размер при определении объема объекта. Чтобы определить высоту объекта, вам необходимо знать его геометрическую форму, например куб, прямоугольник или пирамиду. Один из самых простых способов думать о высоте как о ее объеме — это думать о других размерах как о базовой области. Высота — это ровно столько базовых площадок, которые сложены друг на друга. Формулы объема отдельных объектов можно изменить для расчета высоты.Математики давно разработали формулы объема для всех известных геометрических фигур. В некоторых случаях, например, с кубом, вычислить высоту легко; в других случаях требуется немного простой алгебры.
Высота прямоугольных объектов
Формула объема сплошного прямоугольника: ширина x глубина x высота. Разделите объем на произведение длины и ширины, чтобы вычислить высоту прямоугольного объекта. В этом примере прямоугольный объект имеет длину 20, ширину 10 и объем 6000. Произведение 20 и 10 дает 200, а 6000 разделенных на 200 дает 30. Высота объекта равна 30.
Произведение 20 и 10 дает 200, а 6000 разделенных на 200 дает 30. Высота объекта равна 30.
Высота куба
Куб — это своего рода прямоугольник, у которого все стороны одинаковы. Итак, чтобы найти объем, возьмите в куб длину любой стороны. Чтобы найти высоту, вычислите кубический корень из объема куба. В этом примере куб имеет объем 27. Кубический корень из 27 равен 3. Высота куба равна 3.
Высота цилиндра
Цилиндр представляет собой прямой стержень или форму стержня с круглым крестом. сечение, имеющее одинаковый радиус сверху вниз.2) умноженное на высоту. Разделите объем цилиндра на квадрат радиуса, умноженный на число пи, чтобы вычислить его высоту. В этом примере объем цилиндра равен 300, а радиус равен 3. Возведение в квадрат 3 дает 9, а умножение 9 на пи дает 28,274. Разделив 300 на 28,274, получим 10,61. Высота цилиндра 10,61.
Высота пирамиды
Квадратная пирамида имеет плоское квадратное основание и четыре треугольные стороны, которые пересекаются в одной точке на вершине. Формула объема: длина x ширина x высота ÷ 3.Увеличьте объем пирамиды втрое, а затем разделите полученное количество на площадь основания, чтобы рассчитать ее высоту. В этом примере объем пирамиды равен 200, а площадь ее основания — 30. Умножение 200 на 3 дает 600, а деление 600 на 30 дает 20. Высота пирамиды равна 20.
Высота призмы
Геометрия описывает несколько различных видов призм: у некоторых есть прямоугольные основания, у некоторых основания треугольные. В любом случае поперечное сечение такое же на всем протяжении, как и у цилиндра.Объем призмы равен площади основания, умноженной на высоту. Итак, чтобы рассчитать высоту, разделите объем призмы на площадь ее основания. В этом примере объем призмы равен 500, а ее базовая площадь равна 50. Разделив 500 на 50, вы получите 10. Высота призмы равна 10.
Обучение расчету поперечного сечения
С технической точки зрения, поперечное сечение — это когда плоскость встречается с твердой формой. Вычисление очень похоже на вычисление площади фигуры; единственное отличие состоит в том, что поперечное сечение является частью трехмерной формы.Различные формы имеют разные формулы, и ниже приведены некоторые примеры того, как проводить вычисления.
Вычисление очень похоже на вычисление площади фигуры; единственное отличие состоит в том, что поперечное сечение является частью трехмерной формы.Различные формы имеют разные формулы, и ниже приведены некоторые примеры того, как проводить вычисления.
Прямоугольники Вы можете увидеть прямоугольное поперечное сечение прямоугольного здания, коробки с хлопьями или чего-то еще, что представляет собой прямоугольную призму. Это может быть самый простой способ вычисления площади поперечного сечения, так как это просто ширина x длина. Например, предположим, что одна сторона здания восьми футов в длину, а другая — шести футов в длину. Восемь, умноженная на шесть, дает 48, и вот вам поперечное сечение.
Квадраты Вы можете увидеть квадратное поперечное сечение в кости или в пирамиде с квадратным основанием, как в Египте. Поскольку все стороны квадрата имеют одинаковую длину, поперечное сечение — это просто длина, умноженная на себя. Например, если длина кости составляет два дюйма, площадь поперечного сечения составляет четыре дюйма в квадрате. Легкий способ запомнить это: поперечное сечение квадрата — это квадрат длины.
Треугольники Треугольное поперечное сечение может быть не таким распространенным, как другие формы, поскольку вы, вероятно, видели бы его только в пирамиде с треугольным основанием или треугольной призме.Самый простой способ найти эту площадь поперечного сечения — это умножить базовую длину на высоту и затем разделить на два. Однако эти длины может быть сложно найти, если они не указаны, и вам нужно будет полагаться на тригонометрию, чтобы найти любые недостающие цифры.
Кругов Площадь поперечного сечения круга довольно сложна, поскольку для получения точного числа обычно требуется калькулятор, так как оно включает число Пи. Формы с круглым поперечным сечением включают конусы, сферы и цилиндры.Площадь круга равна двум x пи x квадрату радиуса. Радиус равен половине диаметра, который равен длине реза по окружности. Если вам не нужно точное число, вы можете просто оставить результат с пи. Например, если радиус составляет пять дюймов, площадь поперечного сечения будет равна двум x пи x 25, что в конечном итоге будет равно 50 x pi без калькулятора.
Радиус равен половине диаметра, который равен длине реза по окружности. Если вам не нужно точное число, вы можете просто оставить результат с пи. Например, если радиус составляет пять дюймов, площадь поперечного сечения будет равна двум x пи x 25, что в конечном итоге будет равно 50 x pi без калькулятора.
Дополнительный шаг Хотя основное внимание здесь уделяется площади поперечного сечения формы, вы можете легко найти объем формы с помощью этой информации.Для большинства форм вы просто умножаете площадь поперечного сечения на длину объекта. Определенные формы, такие как сферы и конусы, имеют разные формулы, а это означает, что это не универсальное правило.
Это всего лишь простое руководство по расчету основных площадей поперечного сечения. Большинство форм можно разбить на эти четыре более простые формы. Самая сложная часть поперечных сечений — это возможность визуализировать, как выглядит форма, когда она разрезана. Зная форму поперечного сечения, вы можете легко применить одну из этих формул и провести математические вычисления.
Объем по площади поперечного сечения; Методы дисковых и шайб
Раздел 7.2 Объем по площади поперечного сечения; Дисковые и шайбовые методы
Объем правого цилиндра в целом, как показано на рисунке 7.2.1, равен
.Рисунок 7.2.1. Объем общего правого цилиндраПлощадь основания × высота.
Мы можем использовать этот факт в качестве строительного блока при нахождении объемов самых разных форм.
Рисунок 7.2.2. Видео-введение в Раздел 7.2.Для произвольного твердого тела мы можем аппроксимировать его объем, разрезав его на \ (n \) тонких срезов.Когда ломтики тонкие, каждый ломтик можно хорошо аппроксимировать обычным правым цилиндром. Таким образом, объем каждого среза приблизительно равен его площади поперечного сечения × толщине. (Эти срезы являются дифференциальными элементами.)
Ориентируя твердое тело по оси \ (x \), мы можем позволить \ (A (x_i) \) представлять площадь поперечного сечения \ (i \) -го среза, и пусть \ (\ dx_i \) представляют толщину этого среза (толщина — небольшое изменение в \ (x \)). n A (x_i) \ dx_i \ text {.б А (х) \, dx \ текст {.}
\ end {уравнение *}
n A (x_i) \ dx_i \ text {.б А (х) \, dx \ текст {.}
\ end {уравнение *}
Пример 7.2.4. Нахождение объема твердого тела.
Найдите объем пирамиды с квадратным основанием со стороной 10 дюймов и высотой 5 дюймов.
РешениеЕсть много способов «ориентировать» пирамиду по оси \ (x \); Рисунок 7.2.5 показывает один из таких способов, с заостренной вершиной пирамиды в начале координат и осью \ (x \), проходящей через центр основания.
Рисунок 7.2.5. Ориентация пирамиды по оси \ (x \) в примере 7.2 \ text {.} \)Если бы кто-то вырезал из пирамиды кусок в точке \ (x = 3 \ text {,} \), как показано на рисунке 7.2.6, у него была бы форма с квадратным низом и верхом с наклонными сторонами. Если бы срез был тонким, то и нижний, и верхний квадраты имели бы длину сторон около 6, и, таким образом, площадь поперечного сечения нижнего и верхнего квадрата была бы примерно 36 в 2 . Если обозначить \ (\ Delta x_i \) толщину среза, объем этого среза будет примерно \ (36 \ Delta x_i \) в 3 .3 \ текст {.} \ end {выровнять *}
Мы можем проверить нашу работу, посмотрев общее уравнение для объема пирамиды (см. Заднюю обложку в разделе «Объем общего конуса»):
\ (\ frac13 \ times \, \ text {область базы} \, \ times \, \ text {height} \ text {.} \)
Конечно, использование этой формулы из геометрии быстрее, чем наш новый метод, но метод, основанный на исчислении, может применяться не только к конусам.
Важным частным случаем теоремы 7.2.3 является случай, когда твердое тело представляет собой твердое тело вращения , то есть когда твердое тело формируется путем вращения формы вокруг оси.2 \ text {.} \) Применение теоремы 7.2.3 дает дисковый метод.
Пример 7.2.8. Нахождение тома дисковым методом.
Найдите объем твердого тела, образованного поворотом кривой \ (y = 1 / x \ text {,} \) от \ (x = 1 \) к \ (x = 2 \ text {,} \) вокруг \ (x \) — ось.
Решение Набросок может помочь нам разобраться в этой проблеме. На рис. 7.2.9. (A) изображена кривая \ (y = 1 / x \) вместе с дифференциальным элементом — диском — в точке \ (x \) с радиусом \ (R (x) = 1 / x \ text {.} \) На рисунке 7.2.9.3 \ текст {.}
\ end {выровнять *}
На рис. 7.2.9. (A) изображена кривая \ (y = 1 / x \) вместе с дифференциальным элементом — диском — в точке \ (x \) с радиусом \ (R (x) = 1 / x \ text {.} \) На рисунке 7.2.9.3 \ текст {.}
\ end {выровнять *}
Хотя ключевая идея 7.2.7 дана в терминах функций \ (x \ text {,} \), задействованный принцип может быть применен к функциям \ (y \), когда ось вращения вертикальна, а не горизонтальна. Продемонстрируем это на следующем примере.
Пример 7.2.10. Нахождение тома дисковым методом.
Найдите объем твердого тела, образованного поворотом кривой \ (y = 1 / x \ text {,} \) от \ (x = 1 \) к \ (x = 2 \ text {,} \) относительно \ (y \) — ось.
РешениеПоскольку ось вращения вертикальна, нам нужно преобразовать функцию в функцию от \ (y \) и преобразовать \ (x \) — границы в \ (y \) — границы.Поскольку \ (y = 1 / x \) определяет кривую, мы перепишем ее как \ (x = 1 / y \ text {.} \) Граница \ (x = 1 \) соответствует \ (y \) — граница \ (y = 1 \ text {,} \), а граница \ (x = 2 \) соответствует \ (y \) — границе \ (y = 1/2 \ text {.} \)
Таким образом, мы вращаем кривую \ (x = 1 / y \ text {,} \) от \ (y = 1/2 \) до \ (y = 1 \) вокруг оси \ (y \), чтобы сформировать твердый. Кривая и образец дифференциального элемента схематически показаны на рис. 7.2.11. (A), а полный эскиз твердого тела — на рис. 7.2.11. (B).
Рисунок 7.2.11. Построение эскиза твердого тела в примере 7.2 \ right) \, dx \ text {.} \ end {уравнение *} Рисунок 7.2.12. Установление метода промывки; см. также рисунок 7.2.13. Можно создать твердое тело вращения с отверстием в середине, вращая область вокруг оси. Рассмотрим рисунок 7.2.12. (A), на котором область нарисована вместе с пунктирной горизонтальной осью вращения. При вращении области вокруг оси образуется твердое тело, как показано на рис. 7.2.12. (B). Снаружи твердое тело имеет радиус \ (R (x) \ text {,} \), а внутреннее — радиус \ (r (x) \ text {.} \) Каждое поперечное сечение этого твердого тела представляет собой шайбу (диск с отверстием в центре), как показано на рис.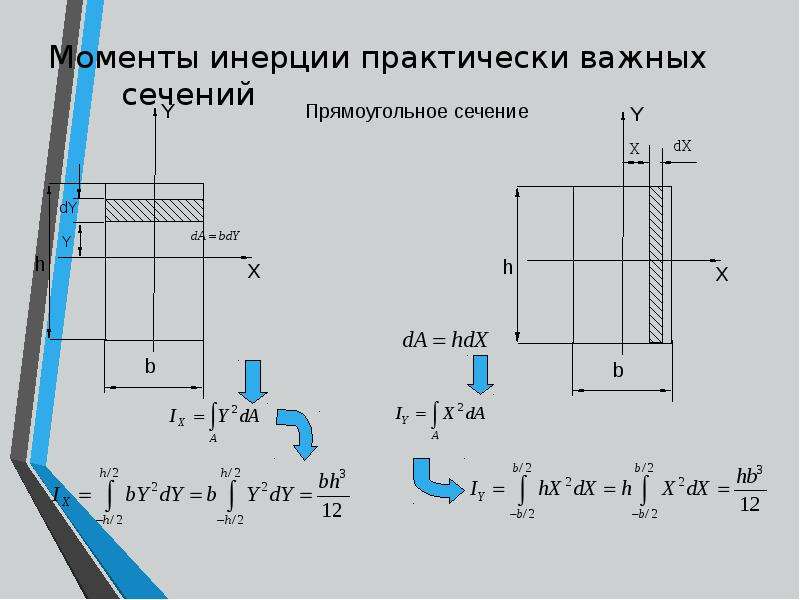 2-2x + 2 \) и \ (y = 2x-1 \), вокруг оси \ (x \) -.3 \ текст {.}
\ end {выровнять *}
2-2x + 2 \) и \ (y = 2x-1 \), вокруг оси \ (x \) -.3 \ текст {.}
\ end {выровнять *}
При вращении вокруг вертикальной оси функции внешнего и внутреннего радиуса должны быть функциями \ (y \ text {.} \)
Пример 7.2.17. Нахождение объема с помощью метода промывки.
Найдите объем твердого тела, образованного вращением треугольной области с вершинами в \ ((1,1) \ text {,} \) \ ((2,1) \) и \ ((2,3) \) относительно ось \ (y \).
РешениеТреугольная область показана на рисунке 7.2.18. (А); элемент дифференциала показан на рис. 7.2.18. (b), а сплошное тело — на рис. 7.2.18. (c). Они помогают нам установить внешний и внутренний радиус. Поскольку ось вращения вертикальна, каждый радиус является функцией \ (y \ text {.} \)
Внешний радиус \ (R (y) \) образован линией, соединяющей \ ((2,1) \) и \ ((2,3) \ text {;} \), это постоянная функция, поскольку независимо от значения \ (y \) — расстояние от линии до оси вращения равно 2. Таким образом, \ (R (y) = 2 \ text {.} \)
Рисунок 7.3 \ текст {.} \ end {выровнять *}В этом разделе представлено новое применение определенного интеграла. Наше стандартное представление об определенном интеграле таково, что он дает «площадь под кривой». Однако мы можем установить определенные интегралы, которые представляют другие величины; в этом разделе мы вычислили объем.
Конечная цель этого раздела — не вычислять объемы твердых тел. Это может быть полезно, но более полезным является понимание этого основного принципа интегрального исчисления, изложенного в ключевой идее 7.0.1: чтобы найти точное значение некоторой величины,
мы начинаем с аппроксимации (в этом разделе мы разрезаем твердое тело и аппроксимируем объем каждого среза),
затем сделайте приближение лучше, уточнив наше исходное приближение (т. Е. Используйте больше срезов),
затем используйте пределы, чтобы установить определенный интеграл, который дает точное значение.

Мы практикуем этот принцип в следующем разделе, где мы находим объемы, нарезая твердые частицы другим способом.3 \)
11.
В следующих упражнениях описывается область декартовой плоскости. Используйте метод диска / шайбы, чтобы найти объем твердого тела вращения, образованного вращением области вокруг каждой из заданных осей.
12.
Область, ограниченная: \ (y = \ sqrt {x} \ text {,} \) \ (y = 0 \) и \ (x = 1 \ text {.} \)
Повернуть примерно:
ось \ (x \)
\ (\ Displaystyle у = 1 \)
\ (y \) — ось
\ (\ Displaystyle х = 1 \)
\ (\ displaystyle \ pi / 2 \)
\ (\ Displaystyle 5 \ пи / 6 \)
\ (\ Displaystyle 4 \ пи / 5 \)
\ (\ Displaystyle 8 \ pi / 15 \)
13.2 \) и \ (y = 0 \ text {.} \)
Повернуть примерно:
ось \ (x \)
\ (\ Displaystyle у = 4 \)
\ (\ Displaystyle у = -1 \)
\ (\ Displaystyle х = 2 \)
\ (\ displaystyle 512 \ pi / 15 \)
\ (\ Displaystyle 256 \ pi / 5 \)
\ (\ Displaystyle 832 \ pi / 15 \)
\ (\ Displaystyle 128 \ pi / 3 \)
14.
Треугольник с вершинами \ ((1,1) \ text {,} \) \ ((1,2) \) и \ ((2,1) \ text {.} \)
Повернуть примерно:
ось \ (x \)
\ (\ Displaystyle у = 2 \)
\ (y \) — ось
\ (\ Displaystyle х = 1 \)
\ (\ displaystyle 4 \ pi / 3 \)
\ (\ Displaystyle 2 \ пи / 3 \)
\ (\ Displaystyle 4 \ pi / 3 \)
\ (\ Displaystyle \ пи / 3 \)
15.{-1} (1) \)
17,
Область, ограниченная \ (y = 2x \ text {,} \) \ (y = x \) и \ (x = 2 \ text {. } \)
} \)
Повернуть примерно:
ось \ (x \)
\ (\ Displaystyle у = 4 \)
\ (y \) — ось
\ (\ Displaystyle х = 2 \)
\ (\ displaystyle 8 \ pi \)
\ (\ Displaystyle 8 \ пи \)
\ (\ Displaystyle 16 \ pi / 3 \)
\ (\ Displaystyle 8 \ pi / 3 \)
В следующих упражнениях описывается твердое тело.3 \ text {.} \)
21.
Твердое тело длиной 10 с прямоугольным основанием и треугольной вершиной, в котором один конец представляет собой квадрат со стороной 5, а другой конец представляет собой треугольник с основанием и высотой 5.
Отвечать РешениеСориентируйте твердое тело так, чтобы ось \ (x \) была параллельна длинной стороне основания. Все поперечные сечения представляют собой трапеции (крайняя левая трапеция представляет собой квадрат; крайняя правая часть трапеции имеет верхнюю длину 0, что делает ее треугольником). Площадь трапеции в точке \ (x \) равна \ (A (x) = 1/2 (-1 / 2x + 5 + 5) (5) = -5 / 4x + 25 \ text {.3 \ text {.} \)
Объем твердого тела с известным поперечным сечением
В этом разделе мы узнаем, как найти объем твердого объекта, имеющего известные поперечные сечения.
Мы рассматриваем твердые тела, поперечные сечения которых имеют обычную форму, такую как треугольники, квадраты, прямоугольники, трапеции и полукруги.
Определение: Объем твердого тела с использованием интеграции
Пусть \ (S \) — твердое тело, и предположим, что площадь поперечного сечения в плоскости, перпендикулярной оси \ (x — \), равна \ (A \ left (x \ right) \) для \ (a \ ле х \ ле б.b {A \ left (x \ right) dx}. \]
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Твердое тело имеет основание, лежащее в первом квадранте плоскости \ (xy — \) и ограниченное прямыми \ (y = x, \) \ (x = 1, \) \ (y = 0.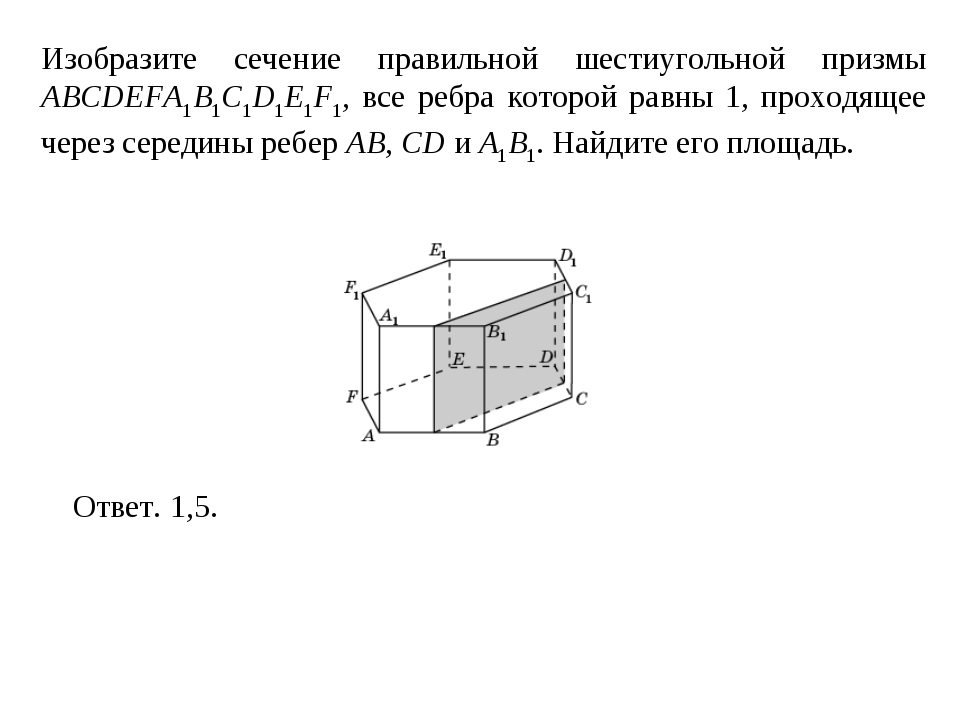 2}}}.H {A \ left (x \ right) dx}, \]
2}}}.H {A \ left (x \ right) dx}, \], где \ ({A \ left (x \ right)} \) — площадь поперечного сечения в точке \ (x. \)
Длины большой и малой осей линейно изменяются от \ (a, b \) до \ (A, B, \) и в точке \ (x \) определяются следующими выражениями:
\ [{\ text {большая ось:} \; \; a + \ left ({A — a} \ right) \ frac {x} {H} \; \;} \ kern0pt {\ text {малая ось: } \; \; b + \ left ({B — b} \ right) \ frac {x} {H}}. \]
Теперь посчитаем площадь поперечного сечения:
\ [{A \ left (x \ right) \ text {=}} \ kern0pt {\ pi \ left ({a + \ left ({A — a} \ right) \ frac {x} {H}} \ справа) \ left ({b + \ left ({B — b} \ right) \ frac {x} {H}} \ right)} = {\ pi \ left [{ab + b \ left ({A — a } \ right) \ frac {x} {H}} \ right.H {A \ left (x \ right) dx}} = {\ pi \ left [{abH + \ left ({bA + ab — 2ab} \ right) \ frac {H} {2}} \ right.} + {\ left. {\ left ({AB — aB — bA + ab} \ right) \ frac {H} {3}} \ right]} = {\ pi \ left [{\ cancel {abH} + \ frac { {bAH}} {2}} \ right.} + {\ left. {\ frac {{aBH}} {2} — \ cancel {abH}} \ right.} + {\ left. {\ frac {{ABH }} {3} — \ frac {{aBH}} {3}} \ right.} — {\ left. {\ Frac {{bAH}} {3} + \ frac {{abH}} {3}} \ right]} = {\ pi \ left [{\ frac {{bAH}} {6} + \ frac {{aBH}} {6}} \ right.} + {\ left. {\ frac {{ABH}}} {3} + \ frac {{abH}} {3}} \ right]} = {\ frac {{\ pi H}} {6} \ left [{bA + aB + 2AB + 2ab} \ right]} = {\ frac {{\ pi H}} {6} \ left [{\ left ({2A + a} \ right) B + \ left ({A + 2a} \ right) b} \ right].} \]
Пример 7.
Вычислите объем клина с учетом нижних сторон \ (a, b, \), верхней стороны \ (c, \) и высоты \ (H. \).Решение.
Рис. 8.Рассмотрим произвольное поперечное сечение на высоте \ (x. \). Это поперечное сечение представляет собой прямоугольник со сторонами \ (m \) и \ (n. \). Легко видеть, что
\ [{m = c + \ left ({a — c} \ right) \ frac {x} {h}, \; \;} \ kern0pt {n = \ frac {{bx}} {h}.} \]
Тогда площадь поперечного сечения \ (A \ left (x \ right) \) записывается как
\ [{A \ left (x \ right) = mn} = {\ left ({c + \ left ({a — c} \ right) \ frac {x} {h}} \ right) \ frac {{ bx}} {h}} = {\ frac {{bcx}} {h} + \ frac {{ab {x ^ 2}}} {{{h ^ 2}}} — \ frac {{bc {x ^ 2}}} {{{h ^ 2}}}} = {\ frac {{bcx}} {h} + \ frac {{b \ left ({a — c} \ right) {x ^ 2}}} {{{h ^ 2}}}. 2} H}} = \ frac {2} {{3 \ pi}} \ приблизительно 0,212 \]
2} H}} = \ frac {2} {{3 \ pi}} \ приблизительно 0,212 \]
от общего объема цилиндра. Результат не зависит от \ (R \) и \ (H! \)
Пример 10.
Оси двух круговых цилиндров одинакового радиуса \ (R \) пересекаются под прямым углом. Найдите объем твердого тела, общего для обоих этих цилиндров.Решение.
На рисунке ниже показано \ (\ large {\ frac {1} {8}} \ normalsize \) тела пересечения.
Рис. 11.Рассмотрим поперечное сечение \ (ABCD \), перпендикулярное оси \ (x — \) в произвольной точке \ (x \).3}}} {3}} \]
Расчет мышечной силы на единицу площади поперечного сечения мышцы человека посредством ультразвукового измерения
Посредством ультразвуковой фотографии поперечного сечения действующего мышечного пучка вместе с измерением мышечной силы, развиваемой испытуемым при максимальном усилии сила на единицу площади мышцы была рассчитана у 245 здоровых людей, включая 119 мужчин и 126 женщин.
Результат был резюмирован следующим образом:
- 1.
Ультразвуковой метод, использованный в этой работе, возможно, был признан лучшим способом расчета площади поперечного сечения мышцы.
- 2.
Сила руки была пропорциональна площади поперечного сечения сгибателя плеча независимо от возраста и пола.
- 3.
Сила на единицу площади поперечного сечения сгибателя плеча составила 6,3 кг / см. 2 в среднем, стандартное отклонение 0,81 кг / см. 2 . Когда площадь поперечного сечения мышцы измерялась при разгибании предплечья, рассчитанная сила на единицу площади составляла 4,7 кг / см 2 в согнутом положении предплечья.
- 4.
Что касается индивидуальных вариаций, сила на единицу площади была распределена в диапазоне от 4 кг / см 2 до 8 кг / см 2 .

- 5.
Сила на единицу площади поперечного сечения была почти одинаковой у мужчин и женщин независимо от возраста. Кроме того, не было обнаружено существенной разницы между обычным и тренированным взрослым.
Расчет площади поперечного сечения
Расчет площади поперечного сечения
- Детали
- Последнее обновление: 18 августа 2017 г., 06:31
Использование
Мы предлагаем здесь инструмент gromacs, который можно использовать для расчета площади поперечного сечения мембранного белка (или аналогичного включения) в мембране. Схематично показано на следующем рисунке:
Подробнее см. Документ (укажите его, если вы используете этот код):
Скомпилируйте его как любой инструмент, созданный с помощью шаблона gromacs.Затем просто запустите его как обычно:
g_de density3Darea -f traj.trr -s topol.tpr
Для этого расчета требуются две группы (2 — это ответ на вопрос « Сколько групп? »): первая включает все небелковые шарики, вторые — протеиновые шарики. С -sl вы можете изменить размер сетки 3D-плотности. В вашем каталоге должен быть файл electrons.dat, даже если он не используется (это глупо и должно быть исправлено!).
Профиль площади получается в области.xvg (три столбца имеют одинаковые номера по историческим причинам, это тоже следует исправить). Его можно визуализировать в 3D, открыв файл proteinformDENS.dat с помощью rasmol, выбрав «Цвета»> «Температура» и «Режим плиты».
Если вы хотите рассчитать изменение механической энергии бислоя из-за включения, как это сделано в публикации, вам необходимо рассчитать профиль давления вне включения. Это можно сделать с помощью скрипта, подобного этому:
паста протеинформДЭНС. |
Линия выше вычисляет профиль среднего бокового давления вне белка (эта идея должна быть описана в публикации).
proteinformDENS.dat и 3Dpp.dat (трехмерное поле давления, формат ascii) должны быть выходными данными из g_de density3Darea. Шаг сетки должен быть точно таким же.
За дополнительной информацией обращайтесь к Самули Оллила (Этот адрес электронной почты защищен от спам-ботов.У вас должен быть включен JavaScript для просмотра.).
Замечание
Код НЕ удаляет вращения или трансляции, и белок должен быть целиком внутри коробки во всех кадрах. Это можно сделать следующим образом (разумеется, для адаптации к каждой системе):
trjconv -pbc nojump |
Калькулятор калибра проволоки позволяет узнать диаметр диаметра и площадь поперечного сечения площади выбранного вами провода, а также электрическое сопротивление на единицу длины .Все это очень полезно, если вы подключаете динамики к системе домашнего кинотеатра и искали калькулятор калибра проводов динамика.
Используйте этот калькулятор размера проволоки вместо того, чтобы пробираться через утомительную таблицу размеров проволоки. Он поддерживает как стандарт American Wire Gauge (AWG) , так и систему Standard Wire Gauge (SWG). Читайте дальше, чтобы узнать больше об этих способах измерения сечения проводов.
Американский стандарт калибра проводов (AWG)
Американский калибр проволоки — это система калибра проволоки с логарифмическими ступенями, используемая в основном в Северной Америке с 1857 года. Это касается сплошного, круглого, цветного, электрического провода. AWG также обычно используется для указания размера ювелирных изделий , а именно пирсинга .
Это касается сплошного, круглого, цветного, электрического провода. AWG также обычно используется для указания размера ювелирных изделий , а именно пирсинга .
Для увеличивающихся номеров AWG диаметр и площадь поперечного сечения провода становятся на меньше. Шкала определяется в двух точках по диаметру проволоки. Номер 36 AWG проволока имеет диаметр 0,005 дюйма , а проволока 0000 (4/0) AWG имеет диаметр 0.46 дюймов . Отношение этих двух диаметров составляет 1:92 , и между ними 40 размеров , что дает 39 ступеней . Разница в диаметре каждого последующего калибра является постоянным соотношением 92 1/39 . Между двумя шагами номера шкалы разница в соотношении составляет 92 2/39 и так далее. Формула диаметра для любого номера AWG, n , выглядит так:
диаметр (дюйм) = 0,005 дюйма * 92 (36-n) / 39
диаметр (мм) = 0.127 мм * 92 (36-н) / 39
Для номеров датчиков AWG 00 , 000 и 0000 необходимо использовать отрицательное число для n . Итак, для датчика 00 используйте n = -1 ; 000, используйте n = -2 ; а для 0000 используйте n = -3 .
Как показывает опыт, если вы уменьшите AWG на шесть , диаметр проволоки увеличится на вдвое . Если хотите, проверьте это в калькуляторе калибра провода.
Площадь поперечного сечения по номеру AWG n можно найти, используя площадь круга:
площадь = (π / 4) * диаметр²
площадь (дюйм²) = 0.000019635 дюйм² * 92 (36-n) /19,5
площадь (мм²) = 0,012668 мм² * 92 (36-n) /19,5
Расчет сопротивления на единицу длины (обсуждается позже) требует вычисления площади поперечного сечения провода.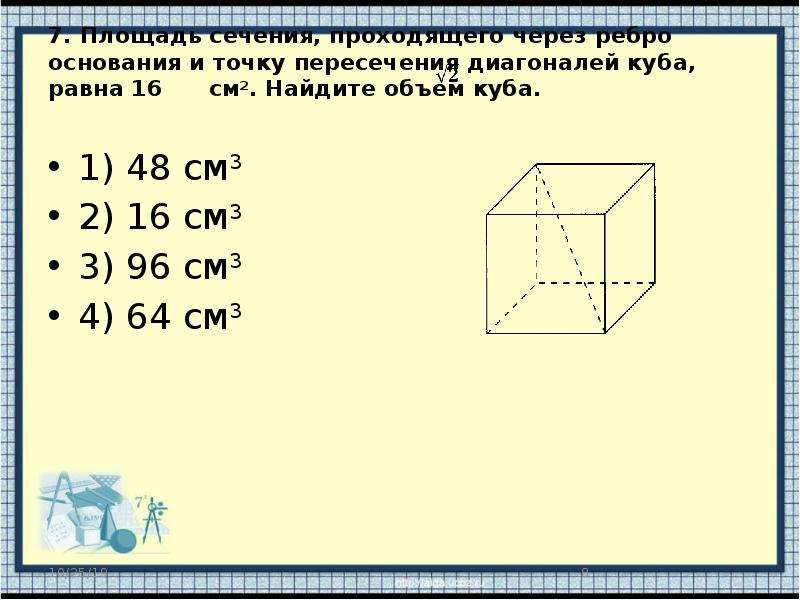
Стандартный калибр проводов (SWG)
Этот калькулятор калибра проволоки также поддерживает британский стандартный калибр проволоки (SWG) , также известный как имперский калибр проволоки или британский стандартный калибр. SWG не так популярен в наши дни, но он все еще используется для определения толщины гитарных струн , а также некоторых типов электропроводки.
SWG построен на базовой единице мил, которая составляет 0,001 дюйма , или тысячную долю дюйма. Номер калибра определяет диаметр провода и колеблется от самого большого, номер 7/0 при 500 мил (0,5 дюйма) , до самого маленького, номер 50 при 1 мил (0,001 дюйма) . Каждый шаг шкалы снижает вес на единицу длины примерно на 20 процентов . Вес на единицу длины провода пропорционален его площади поперечного сечения , которая, в свою очередь, связана с квадратным корнем из диаметра:
уменьшение диаметра за шаг = (1 - √ (1 - 0.2)) * 100 = 10,6%
К сожалению, шкала SWG не соответствует точно этому соотношению. Шаги между датчиками остаются постоянными в диапазоне датчиков, прежде чем перейти на новую постоянную для следующего диапазона. Эти изменения на этапах примерно следуют экспоненциальной кривой. Эта система означает, что для определения диаметра определенного калибра вам необходимо найти его в таблице размеров (показанной ниже).
| Калибр SWG | Диаметр (дюйм) | Диаметр (мм) | Шаг (дюйм) |
|---|---|---|---|
| 7/0 | 0.5 | 12,7 | 0,036 |
| 6/0 | 0,464 | 11,786 | 0,032 |
| 5/0 | 0,432 | 10,973 | |
| 4/0 | 0,4 | 10,16 | 0,028 |
| 3/0 | 0,372 | 9. 449 449 | 0,024 |
| 2/0 | 0,348 | 8,839 | |
| 0 | 0,324 | 8,23 | |
| 1 | 0,3 | 7,62 | |
| 2 | 0,276 | 7,01 | |
| 3 | 0,252 | 6.401 | 0,02 |
| 4 | 0,232 | 5,893 | |
| 5 | 0,212 | 5,385 | |
| 6 | 0,192 | 4,877 | 0,016 |
| 7 | 0,176 | 4,47 | |
| 8 | 0.16 | 4,064 | |
| 9 | 0,144 | 3.658 | |
| 10 | 0,128 | 3,251 | 0,012 |
| 11 | 0,116 | 2,946 | |
| 12 | 0,104 | 2,642 | |
| 13 | 0.092 | 2,337 | |
| 14 | 0,08 | 2,032 | 0,008 |
| 15 | 0,072 | 1,829 | |
| 16 | 0,064 | 1,626 | |
| 17 | 0,056 | 1,422 | |
| 18 | 0.048 | 1,219 | |
| 19 | 0,04 | 1,016 | 0,004 |
| 20 | 0,036 | 0,914 | |
| 21 | 0,032 | 0,813 | |
| 22 | 0,028 | 0,711 | |
| 23 | 0. 024 024 | 0,61 | 0,002 |
| 24 | 0,022 | 0,559 | |
| 25 | 0,02 | 0,508 | |
| 26 | 0,018 | 0,4572 | 0,0016 |
| 27 | 0,0164 | 0,4166 | |
| 28 | 0.0148 | 0,3759 | 0,0012 |
| 29 | 0,0136 | 0,3454 | |
| 30 | 0,0124 | 0,315 | 0,0008 |
| 31 | 0,0116 | 0,2946 | |
| 32 | 0,0108 | 0,2743 | |
| 33 | 0.01 | 0,254 | |
| 34 | 0,0092 | 0,2337 | |
| 35 | 0,0084 | 0,2134 | |
| 36 | 0,0076 | 0,193 | |
| 37 | 0,0068 | 0,1727 | |
| 38 | 0,006 | 0.1524 | |
| 39 | 0,0052 | 0,1321 | 0,0004 |
| 40 | 0,0048 | 0,1219 | |
| 41 | 0,0044 | 0,1118 | |
| 42 | 0,004 | 0,1016 | |
| 43 | 0,0036 | 0. 0914 0914 | |
| 44 | 0,0032 | 0,0813 | |
| 45 | 0,0028 | 0,0711 | |
| 46 | 0,0024 | 0,061 | |
| 47 | 0,002 | 0,0508 | |
| 48 | 0,0016 | 0,0406 | |
| 49 | 0.0012 | 0,0305 | 0,0002 |
| 50 | 0,001 | 0,0254 |
Электрическое сопротивление на единицу длины
Этот калькулятор калибра провода также рассчитывает электрическое сопротивление на единицу длины провода. Чтобы рассчитать это, нам нужно знать фундаментальное свойство материала электрического проводника, из которого состоит сердечник провода — удельное сопротивление .Вот его уравнение:
где:
-
R— электрическое сопротивление -
A— площадь поперечного сечения провода -
l— длина провода
Чтобы найти сопротивление на единицу длины провода , мы можем переписать уравнение удельного сопротивления в виде R / l :
Итак, это просто случай, когда делит удельное сопротивление на площадь поперечного сечения . Чтобы получить общее сопротивление конкретного провода, умножьте полученный выше результат на длину провода или воспользуйтесь нашим калькулятором сопротивления проводов.И если вам интересно узнать падение напряжения вдоль вашего провода, калькулятор падения напряжения — это то, что вам нужно.
Как пользоваться калькулятором калибра провода?
Давайте теперь шаг за шагом рассмотрим, как пользоваться калькулятором калибра провода. Это довольно просто.
Это довольно просто.
- Выберите стандарты калибра проводов AWG и SWG .
- Выберите требуемый калибр проволоки номер .
- Выберите материал сердечника провода .Для большинства проводов это медь . Расчет сопротивления предполагает, что провод имеет комнатную температуру. Расширенный режим : Если материала сердечника провода нет в списке, войдите в расширенный режим, и вы сможете ввести пользовательское значение для сопротивления материала .
- Время результатов! Затем появятся диаметр , площадь поперечного сечения и электрическое сопротивление на длину . От
- до измените любую из единиц этих величин, просто щелкните текущую единицу и выберите новую единицу из раскрывающегося меню.
Рабочий пример на американском калькуляторе калибра проволоки — проволока 12 калибра
В заключение, вот рабочий пример того, как рассчитать диаметр, площадь поперечного сечения и электрическое сопротивление на единицу длины провода 12 калибра . Сначала рассчитаем диаметр проволоки:
Диаметр = 0,005 дюйма * 92 (36-12) / 39 = 0,0808081 дюйма
Далее следует площадь поперечного сечения Расчет :
площадь = (π / 4) * диаметр² = 0.785398 * 0,08081² = 0,0051286 дюйма²
Если материал электрического проводника провода — , медь, , мы будем использовать значение удельного сопротивления для меди при комнатной температуре, которое составляет 1,68 * 10 -8 Ом · м в метрических единицах. Учитывая, что в метре 39,37 дюйма, это:
1,68 * 10 -8 * 39,37 = 6,6142 * 10 -7 Ом · дюйм
Тогда можно рассчитать сопротивление на единицу длины:
сопротивление на дюйм = 6.

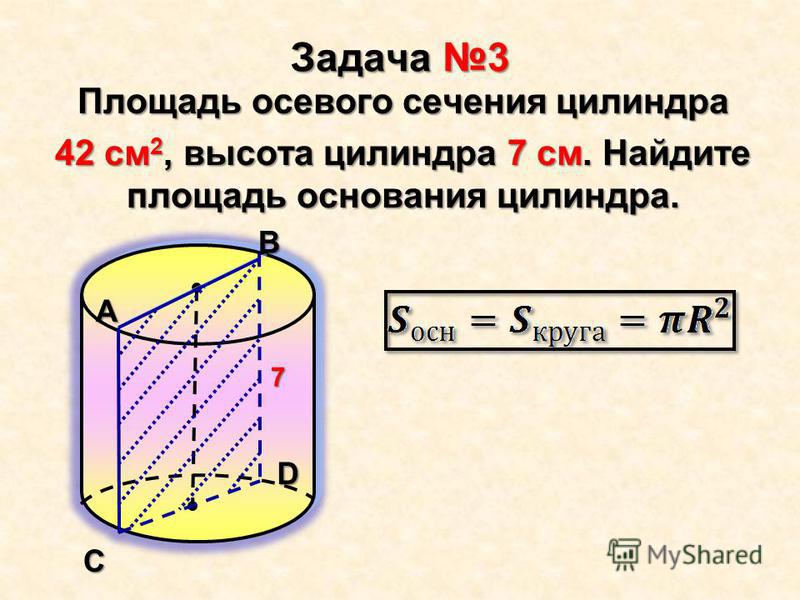 Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;


 dat 3Dpp.dat | awk ‘{если (10 $> 0) {pp [13 $] + = 14 $ + 18 $) / 2; sum [$ 13] ++;}} END {for (i = 0; i0) {print i «» pp [i] / sum [i]} else {print i «0»}}} ‘> test.dat
dat 3Dpp.dat | awk ‘{если (10 $> 0) {pp [13 $] + = 14 $ + 18 $) / 2; sum [$ 13] ++;}} END {for (i = 0; i0) {print i «» pp [i] / sum [i]} else {print i «0»}}} ‘> test.dat