Модуль упругости при сдвиге для стали — Moy-Instrument.Ru
Модуль упругости разных материалов, включая сталь
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
- Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.

- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам.
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы наход
Модуль (коэффициент) упругости бетона: формула для расчета
Определение упругости и единицы измерения
Изделия и конструкции из бетона подвергаются большим нагрузкам, причем этот процесс происходит постоянно.
Нормативные сведения также включают данные о:
- классе материала,
- его видах (тяжелый, мелкозернистый, легкий, пористый бетон и т. д:.),
В связи с этим модуль упругости бетона В30 может быть различным и определяться исходя из других характеристик. Если взять в качестве примера тяжелые и ячеистые бетоны одного и того же класса прочности, их модули будут иметь абсолютно разные значения. Таблица утверждена СНиП и составлена на основе результатов опытных исследований.
Таблица начальных модулей упругости E (МПа*10-3) при сжатии и растяжении бетонов с различными эксплуатационными характеристиками
|
Классы по прочности на сжатие |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
Характеристики бетона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тяжелые бетоны |
|||||||||||||||
|
Естественное твердение |
9,5 |
13 |
16 |
18 |
21 |
23 |
27 |
30 |
32,5 |
34,5 |
36 |
37,5 |
39 |
39,5 |
40 |
|
Тепловая обработка при атмосферном давлении |
8,5 |
11,5 |
14,5 |
16 |
19 |
20,5 |
24 |
27 |
29 |
31 |
32,5 |
34 |
35 |
35,5 |
36 |
|
Автоклавная обработка |
7 |
10 |
12 |
13,5 |
16 |
17 |
20 |
22,5 |
24,5 |
26 |
27 |
28 |
29 |
29,5 |
30 |
|
Мелкозернистые |
|||||||||||||||
|
Естественное твердение, А-группа |
7 |
10 |
13,5 |
15,5 |
17,5 |
19,5 |
22 |
24 |
26 |
27,5 |
28,5 |
— |
— |
— |
— |
|
Тепловая обработка при атмосферном давлении |
6,5 |
9 |
12,5 |
14 |
15,5 |
17 |
20 |
21,5 |
23 |
— |
— |
— |
— |
— |
— |
|
Естественное твердение, Б-группа |
6,5 |
9 |
12,5 |
14 |
15,5 |
17 |
20 |
21,5 |
23 |
— |
— |
— |
— |
— |
— |
|
Автоклавная теплообработка |
5,5 |
8 |
11,5 |
13 |
14,5 |
15,5 |
17,5 |
19 |
20,5 |
— |
— |
— |
— |
— |
— |
|
Автоклавное твердение, В-группа |
— |
— |
— |
— |
— |
16,5 |
18 |
19,5 |
21 |
21 |
22 |
23 |
24 |
24,5 |
25 |
|
Легкие и поризованные |
|||||||||||||||
|
Марка средней плотности, D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
800 |
4,5 |
5,0 |
5,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1000 |
5,5 |
6,3 |
7,2 |
8 |
8,4 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1200 |
6,7 |
7,6 |
8,7 |
9,5 |
10 |
10,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1400 |
7,8 |
8,8 |
10 |
11 |
11,7 |
12,5 |
13,5 |
14,5 |
15,5 |
— |
— |
— |
— |
— |
— |
|
1600 |
9 |
10 |
11,5 |
12,5 |
13,2 |
14 |
15,5 |
16,5 |
17,5 |
18 |
— |
— |
— |
— |
— |
|
1800 |
— |
11,2 |
13 |
14 |
14,7 |
15,5 |
17 |
18,5 |
19,5 |
20,5 |
21 |
— |
— |
— |
— |
|
2000 |
— |
— |
14,5 |
16 |
17 |
18 |
19,5 |
21 |
22 |
23 |
23,5 |
— |
— |
— |
— |
|
Ячеистые автоклавного твердения |
|||||||||||||||
|
Марка средней плотности, D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
700 |
2,9 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
800 |
3,4 |
4 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
900 |
3,8 |
4,5 |
5,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1000 |
— |
6 |
7 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1100 |
— |
6,8 |
7,9 |
8,3 |
8,6 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1200 |
— |
|
8,4 |
8,8 |
9,3 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
От чего зависит упругость бетона
1. Состав
Состав
Бетон с более высоким модулем упругости подвергается меньшей относительной деформации.
Значительную роль в этом играет качество цементного камня и наполнителя – двух компонентов, из которых и состоит бетон. И раствор, и заполнитель берут на себя всю нагрузку. При анализе зависимости модуля упругости бетона от модуля упругости его составляющих, исследователи выяснили, что прочность заполнителя не всегда задействуется для улучшения характеристик готового материала, а вот показатель упругости оказывает значительное влияние.
2. Класс
Начальный модуль упругости бетона при сжатии и расширении зависит от класса изделия по прочности на сжатие.
Эта зависимость устанавливается путем применения эмпирических формул, поэтому для практических целей проще всего получать информацию из готовой таблицы. Даже без сложных математических расчетов можно заметить, что модуль упругости увеличивается пропорционально прочности материала. Другими словами, чем выше класс, тем больше модуль упругости бетона, т.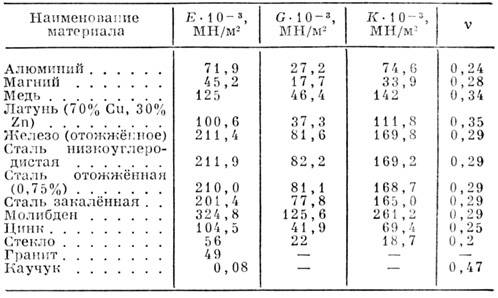 е. материал класса В25 является более устойчивым к относительным деформациям по сравнению с В20.
е. материал класса В25 является более устойчивым к относительным деформациям по сравнению с В20.
Расчет модуля упругости в лабораторных условиях
Когда речь идет о модуле упругости, принимают во внимание оба его варианта – динамический и статический. У первого значение выше и определяется в ходе вибрации образца. Статический модуль, помимо основной информации, предоставляет данные о такой характеристике, как ползучесть бетона – динамика образования деформаций при постоянной нагрузке.
При расчетах учитывают тождество модулей упругости материала как на растяжение, так и на сжатие. Замечено, что если напряжение составляет 0,2 и более максимальной прочности бетона, происходят остаточные деформации. Это приводит к тому, что при сцеплении раствора и наполнителей возникают микротрещины, а это становится причиной крошения и в конечном итоге разрушения.
Во время эксперимента образец подвергают непрерывной нагрузке, имеющей тенденцию к возрастанию, до полного разрушения. Для этого используют особое оборудование – нагружающие установки. В диаграмму вносят данные, показывающие влияние нагрузок на степень деформаций. На завершающем этапе производится расчет среднего модуля упругости всех образцов.
Для этого используют особое оборудование – нагружающие установки. В диаграмму вносят данные, показывающие влияние нагрузок на степень деформаций. На завершающем этапе производится расчет среднего модуля упругости всех образцов.
Справочные значения прочностных и деформационных характеристик грунтов
Для грунтов с промежуточными значениями е, не указанными в таблицах Б.1–Б.8, значения с, φ и Е определяют интерполяцией.
Если значения е, I L и Sr грунтов выходят за пределы, предусмотренные таблицами Б.1–Б.8, характеристики с, φ и Е следует определять по данным непосредственных испытаний этих грунтов. Допускается в запас надежности принимать характеристики с, φ и Е по соответствующим нижним пределам е, I L и Sr, если грунты имеют значения е, I L и Sr меньше этих предельных значений.
Для определения значений с, φ и Е по таблицам Б.1–Б.8 используют нормативные значения е, I L и Sr.
Таблица Б.1
| Пески | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости е, равном | |||
|---|---|---|---|---|---|
| 0,45 | 0,55 | 0,65 | 0,75 | ||
| Гравелистые и крупные | с φ Е | 2 43 50 | 1 40 40 | — 38 30 | — — — |
| Средней крупности | с φ Е | 3 40 50 | 2 38 40 | 1 35 30 | — — — |
| Мелкие | с φ Е | 6 38 48 | 4 36 38 | 2 32 28 | — 28 18 |
| Пылеватые | с φ Е | 8 36 39 | 6 34 28 | 4 30 18 | 2 26 11 |
 ), включая органическое вещество, независимо от степени влажности грунтов Sr.
), включая органическое вещество, независимо от степени влажности грунтов Sr.Таблица Б.2
| Наименование грунтов и пределы нормативных значений их показателя текучести I L | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости е, равном | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | 1,05 | |||
| Супеси | 0 ≤ I L ≤ 0,25 | с φ | 21 30 | 17 29 | 15 27 | 13 24 | — — | — — | — — |
| 0,25 < I L ≤ 0,75 | с φ | 19 28 | 15 26 | 13 24 | 11 21 | 9 18 | — — | — — | |
| Суглинки | 0 ≤ I L ≤ 0,25 | с φ | 47 26 | 37 25 | 31 24 | 25 23 | 22 22 | 19 20 | — — |
| 0,25 < I L ≤ 0,5 | с φ | 39 24 | 34 23 | 28 22 | 23 21 | 18 19 | 15 17 | — — | |
| 0,5 < I L ≤ 0,75 | с φ | — — | — — | 25 19 | 20 18 | 16 16 | 14 14 | 12 12 | |
| Глины | 0 ≤ I L ≤ 0,25 | с φ | — — | 81 21 | 68 20 | 54 19 | 47 18 | 41 16 | 36 14 |
| 0,25 < I L ≤ 0,5 | с φ | — — | — — | 57 18 | 50 17 | 43 16 | 37 14 | 32 11 | |
| 0,5 < I L ≤ 0,75 | с φ | — — | — — | 45 15 | 41 14 | 36 12 | 33 10 | 29 7 | |

Таблица Б.3
| Происхождение и возраст грунтов | Наименование грунтов и пределы нормативных значений их показателя текучести I L | Модуль деформации грунтов Е, МПа, при коэффициенте пористости е, равном | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,35 | 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | 1,05 | 1,2 | 1,4 | 1,6 | ||||
| Четвертичные отложения | Аллювиальные, делювиальные, озерные, озерно-аллювиальные | Супеси | 0 < I L ≤ 0,75 | — | 32 | 24 | 16 | 10 | 7 | — | — | — | — | — |
| Суглинки | 0 < I L ≤ 0,25 | — | 34 | 27 | 22 | 17 | 14 | 11 | — | — | — | — | ||
| 0,25 < I L ≤ 0,5 | — | 32 | 25 | 19 | 14 | 11 | 8 | — | — | — | — | |||
| 0,5 < I L ≤ 0,75 | — | — | — | 17 | 12 | 8 | 6 | 5 | — | — | — | |||
| Глины | 0 ≤ I L ≤ 0,25 | — | — | 28 | 24 | 21 | 18 | 15 | 12 | — | — | — | ||
| 0,25 < I L ≤ 0,5 | — | — | — | 21 | 18 | 15 | 12 | 9 | — | — | — | |||
| 0,5 < I L ≤ 0,75 | — | — | — | — | 15 | 12 | 9 | 7 | — | — | — | |||
| Флювиогляциальные | Супеси | 0 ≤ I L ≤ 0,75 | — | 33 | 24 | 17 | 11 | 7 | — | — | — | — | — | |
| Суглинки | 0 ≤ I L ≤ 0,25 | — | 40 | 33 | 27 | 21 | — | — | — | — | — | — | ||
| Суглинки | 0,25 < I L ≤ 0,5 | — | 35 | 28 | 22 | 17 | 14 | — | — | — | — | — | ||
| 0,5 < I L ≤ 0,75 | — | — | — | 17 | 13 | 10 | 7 | — | — | — | — | |||
| Мореные | Супеси Суглинки | I L ≤ 0,5 | 60 | 50 | 40 | — | — | — | — | — | — | — | — | |
| Юрские отложения оксфордского яруса | Глины | 0,25 ≤ I L ≤ 0 | — | — | — | — | — | — | 27 | 25 | 22 | — | — | |
| 0 < I L ≤ 0,25 | — | — | — | — | — | — | 24 | 22 | 19 | 15 | — | |||
| 0,25 < I L ≤ 0,5 | — | — | — | — | — | — | — | — | 16 | 12 | 10 | |||

Таблица Б.4
| Пределы нормативных значений показателя текучести I L | Обозначение характеристик грунтов | Характеристики глинистых грунтов при степени заторфованности Ir и коэффициенте пористости е, равных | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ir = 0,05–0,1 | Ir = 0,1–0,25 | ||||||||
| 0,65 | 0,75 | 0,85 | 0,95 | 1,05 | 1,15 | 1,25 | 1,35 | ||
| 0 ≤ I L ≤ 0,25 | Е | 13,0 | 12 | 11 | 10 | 8,5 | 8 | 7 | 5,0 |
| φ | 21 | 20 | 18 | 16 | 15 | — | — | — | |
| с | 29 | 33 | 37 | 45 | 48 | — | — | — | |
| 0,25 < I L ≤ 0,5 | Е | 11 | 10 | 8,5 | 7,5 | 7 | 6 | 5,5 | 5 |
| φ | 21 | 20 | 18 | 16 | 15 | 14 | 13 | 12 | |
| с | 21 | 22 | 24 | 31 | 33 | 36 | 39 | 42 | |
| 0,5 < I L ≤ 0,75 | Е | 8,0 | 7 | 6,0 | 5,5 | 5 | 5 | 4,5 | 4 |
| φ | 21 | 20 | 18 | 16 | 15 | 14 | 13 | 12 | |
| с | 18 | 19 | 20 | 21 | 23 | 24 | 26 | 28 | |
| 0,75 < I L ≤ 1 | Е | 6 | 5 | 4,5 | 4,0 | 3,5 | 3 | 2,5 | — |
| φ | — | — | — | 18 | 18 | 18 | 17 | — | |
| с | — | — | — | 15 | 16 | 17 | 18 | — | |
Таблица Б. 5
5
| Пески | Обозначение характеристик | Характеристики грунтов при коэффициенте пористости е, равном | ||||||
|---|---|---|---|---|---|---|---|---|
| 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 1,0 | 1,2 | ||
| Дресвянистые | с | 45 | 41 | 39 | 37 | 35 | 34 | — |
| φ | 34 | 31 | 28 | 25 | 23 | 21 | — | |
| Е | 44 | 33 | 24 | 18 | 15 | 14 | — | |
| Крупные и средней крупности | с | 41 | 35 | 29 | 23 | 19 | — | — |
| φ | 32 | 30 | 27 | 24 | 22 | — | — | |
| Е | 44 | 31 | 22 | 14 | 13 | — | — | |
| Пылеватые | с | 58 | 51 | 44 | 39 | 33 | 29 | 24 |
| φ | 32 | 30 | 27 | 24 | 22 | 20 | 18 | |
| Е | 48 | 38 | 29 | 21 | 16 | 12 | 10 | |

Таблица Б.6
| Наименование грунтов и пределы нормативных значений их показателя текучести I L | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости е, равном | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | 1,05 | 1,2 | |||
| Супеси | I L < 0 | с | 47 | 44 | 42 | 41 | 40 | 39 | — |
| φ | 34 | 31 | 28 | 26 | 25 | 24 | — | ||
| Е | 37 | 30 | 25 | 20 | 15 | 10 | — | ||
| 0 ≤ I L ≤ 0,75 | с | 42 | 41 | 40 | 39 | 38 | — | — | |
| φ | 31 | 28 | 26 | 25 | 24 | — | — | ||
| Е | 25 | 18 | 14 | 12 | 11 | — | — | ||
| Суглинки | 0 ≤ I L ≤ 0,25 | с | 57 | 55 | 54 | 53 | 52 | 51 | 50 |
| φ | 24 | 23 | 22 | 21 | 20 | 19 | 18 | ||
| Е | 27 | 25 | 23 | 21 | 19 | 17 | 14 | ||
| 0,25 < I L ≤ 0,5 | с | — | 48 | 46 | 44 | 42 | 40 | 37 | |
| φ | — | 22 | 21 | 20 | 19 | 18 | 17 | ||
| Е | — | 19 | 16 | 14 | 13 | 12 | 11 | ||
| 0,5 < I L ≤ 0,75 | с | — | — | 41 | 36 | 32 | 29 | 25 | |
| φ | — | — | 20 | 19 | 18 | 17 | 16 | ||
| Е | — | — | 15 | 13 | 11 | 10 | 9 | ||
| Глины | 0 I ≤ I L ≤ 0,25 | с | — | 62 | 60 | 58 | 57 | 56 | — |
| φ | — | 20 | 19 | 18 | 17 | 16 | — | ||
| Е | — | 19 | 18 | 17 | 16 | 15 | — | ||
| 0,25 < I L ≤ 0,5 | с | — | 54 | 50 | 47 | 44 | — | — | |
| φ | — | 17 | 15 | 13 | 12 | — | — | ||
| Е | — | 14 | 12 | 10 | 9 | — | — | ||
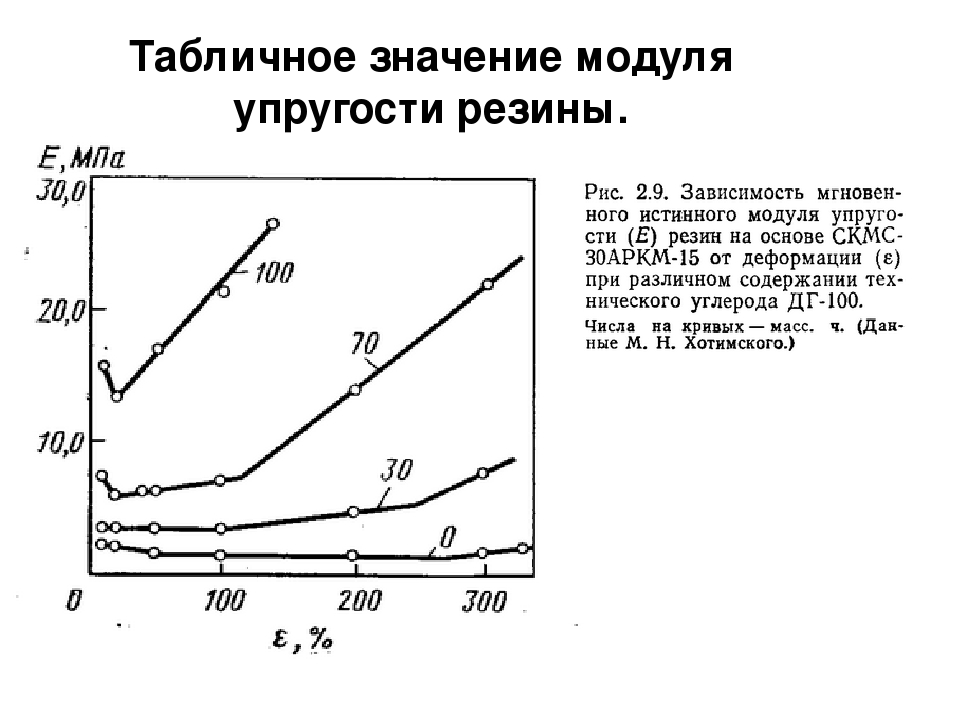
Таблица Б.7
| Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости е, равном | ||||
|---|---|---|---|---|---|
| 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | |
| с | 58 | 48 | 40 | 35 | 31 |
| φ | 29 | 24 | 21 | 19 | 17 |
| Е | 25 | 21 | 17 | 13 | 10 |
Таблица Б.8
| Пески | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости е, равном | |||||
|---|---|---|---|---|---|---|---|
| 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | ||
| Средней крупности | с | 8 | 4 | 3 | 2 | — | — |
| φ | 39 | 37 | 33 | 30 | — | — | |
| Е | 45 | 32 | 25 | 17 | — | — | |
| Мелкие | с | 10 | 6 | 4 | 3 | 1 | — |
| φ | 36 | 33 | 30 | 27 | 25 | — | |
| Е | 35 | 27 | 19 | 15 | 12 | — | |
| Пылеватые | с | — | 10 | 7 | 5 | 3 | 2 |
| φ | — | 33 | 29 | 25 | 23 | 20 | |
| Е | — | 20 | 16 | 10 | 8 | 5 | |
 Предыдущая статьяСоединения на винтах работающих на срезСледующая статьяНатягивание разметочного шнура
Предыдущая статьяСоединения на винтах работающих на срезСледующая статьяНатягивание разметочного шнураДеформация сдвига | MATHalino
Деформация сдвига
Сила сдвига вызывает деформацию сдвига. Элемент, подверженный сдвигу, не изменяется по длине, но претерпевает изменение формы.
Изменение угла в углу исходного прямоугольного элемента называется деформацией сдвига и выражается как
$ \ gamma = \ dfrac {\ delta_s} {L}
$ Отношение напряжения сдвига τ и деформации сдвига γ называется модулем упругости при сдвиге или модулем жесткости и обозначается как G в МПа.
$ G = \ dfrac {\ tau} {\ gamma}
$ Отношение между деформацией сдвига и приложенной силой сдвига составляет
$ \ delta_s = \ dfrac {VL} {A_s G} = \ dfrac {\ tau L} {G}
долларов США, где V — сила сдвига, действующая на площади A s .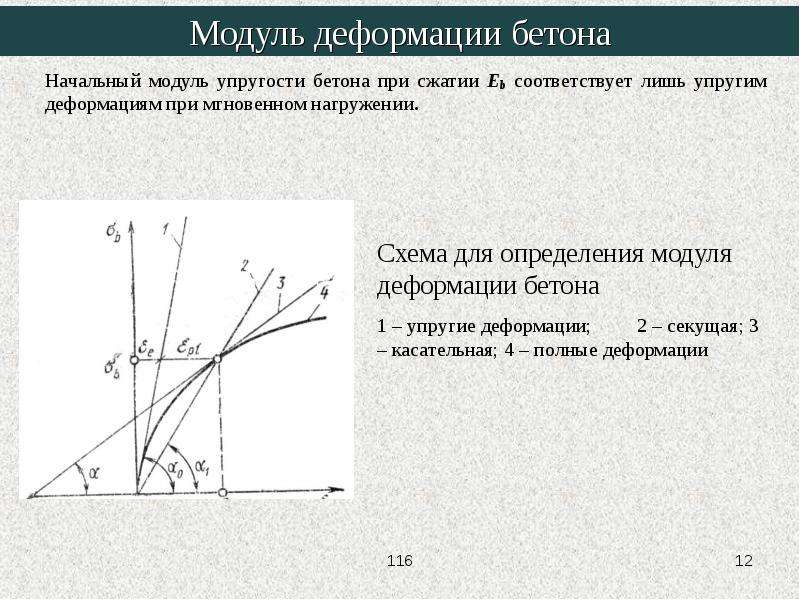
Коэффициент Пуассона
Когда стержень подвергается растягивающей нагрузке, длина стержня увеличивается в направлении приложенной нагрузки, но также уменьшается поперечный размер, перпендикулярный нагрузке.Отношение боковой деформации (или деформации) к продольной деформации (или деформации) называется коэффициентом Пуассона и обозначается ν. Для большинства сталей он находится в диапазоне от 0,25 до 0,3, а для бетона — 0,20.
$ \ nu = — \ dfrac {\ varepsilon_y} {\ varepsilon_x} = — \ dfrac {\ varepsilon_z} {\ varepsilon_x} $
, где ε x — деформация в направлении x, а ε y и ε z — деформации в перпендикулярном направлении.Отрицательный знак указывает на уменьшение поперечного размера, когда ε x положительно.
Двухосная деформация
Если элемент одновременно подвергается действию растягивающих напряжений, σ x и σ y , в направлениях x и y, деформация в направлении x составляет σ x / E, а деформация в направление y — σ y / E. Одновременно напряжение в направлении y вызовет поперечное сжатие в направлении x на величину -ν ε y или -ν σ y / E.2} $
Одновременно напряжение в направлении y вызовет поперечное сжатие в направлении x на величину -ν ε y или -ν σ y / E.2} $
Трехосная деформация
Если элемент одновременно подвергается воздействию трех взаимно перпендикулярных нормальных напряжений σ x , σ y и σ z , которые сопровождаются деформациями ε x , ε y и ε z соответственно
$ \ varepsilon_y = \ dfrac {1} {E} [\, \ sigma_y — \ nu (\ sigma_x + \ sigma_z) \,] $
$ \ varepsilon_z = \ dfrac {1} {E} [\, \ sigma_z — \ nu (\ sigma_x + \ sigma_y) \,] $
Растягивающие напряжения и относительное удлинение считаются положительными.Напряжения сжатия и сжатия считаются отрицательными.
Связь между E, G и ν
Связь между модулем упругости E, модулем сдвига G и коэффициентом Пуассона ν составляет:
$ G = \ dfrac {E} {2 (1 + \ nu)}
$ Объемный модуль упругости или модуль объемного расширения, K
Объемный модуль упругости K является мерой сопротивления материала изменению объема без изменения формы или формы. Дается как
Дается как
$ K = \ dfrac {E} {3 (1-2 \ nu)} = \ dfrac {\ sigma} {\ Delta V / V}
$ где V — объем, а ΔV — изменение объема. Отношение ΔV / V называется объемной деформацией и может быть выражено как
$ \ dfrac {\ Delta V} {V} = \ dfrac {\ sigma} {K} = \ dfrac {3 (1–2 \ nu)} {E}
долл. СШАБоковое продольное изгибание стальных балок при поперечной ударной нагрузке
В данном исследовании используются эксперименты и численное моделирование для анализа динамического отклика стальных балок при ударе огромной массы.Результаты показывают, что поперечное продольное изгибание при кручении (LTB) возникает для стальной балки с узким прямоугольным поперечным сечением при поперечном ударе. Эксперименты моделировались с помощью LS-DYNA. Численное моделирование хорошо согласуется с экспериментальными результатами, что указывает на то, что явление LTB является реальной тенденцией стальных балок при ударе. Между тем, исследование показывает, что LS-DYNA может легко прогнозировать LTB стальных балок.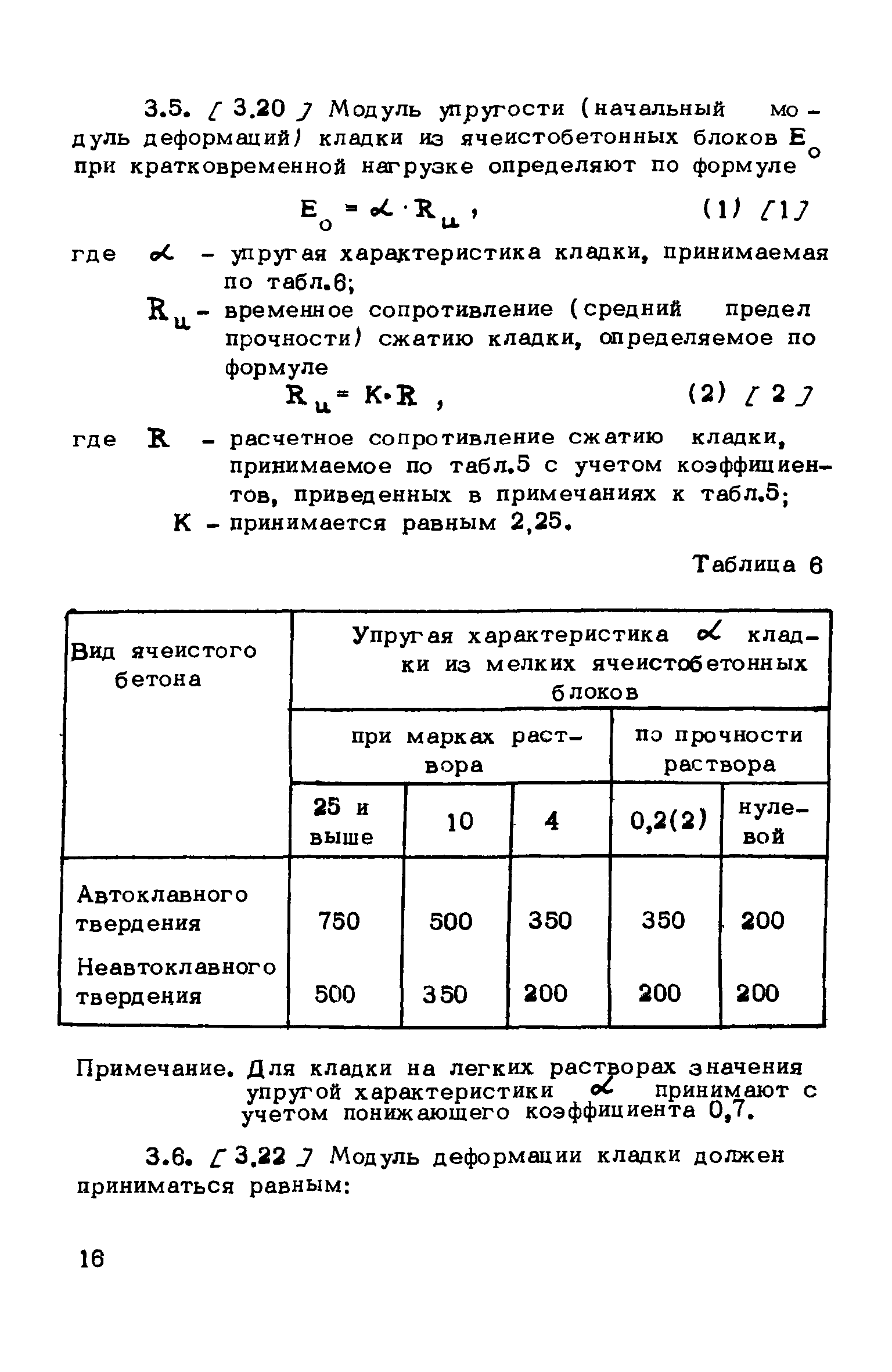 Для определения поведения LTB проводится численное моделирование динамического отклика стальных балок Н-образного поперечного сечения при ударе огромной массы.Явление динамического LTB иллюстрируется смещением, деформацией и деформацией H-образных стальных балок. После этого проводится параметрическое исследование для изучения влияния начальной скорости и импульса удара на LTB. LTB стальных балок H-образного поперечного сечения при поперечном ударе в первую очередь зависит от уровня кинетической энергии удара, тогда как импульс удара оказывает незначительное влияние на режим LTB.
Для определения поведения LTB проводится численное моделирование динамического отклика стальных балок Н-образного поперечного сечения при ударе огромной массы.Явление динамического LTB иллюстрируется смещением, деформацией и деформацией H-образных стальных балок. После этого проводится параметрическое исследование для изучения влияния начальной скорости и импульса удара на LTB. LTB стальных балок H-образного поперечного сечения при поперечном ударе в первую очередь зависит от уровня кинетической энергии удара, тогда как импульс удара оказывает незначительное влияние на режим LTB.
1. Введение
Балки и колонны специальных стальных каркасных конструкций должны выдерживать не только нормальную расчетную нагрузку, но также взрыв, удар, столкновение, пожар и другие экстремальные нагрузки в течение периода эксплуатации.Следовательно, необходимо изучить динамический отклик и поведение при разрушении стальных элементов при таких экстремальных нагрузках. Фактически, взрыв и сотрясение часто ассоциируются с огнем.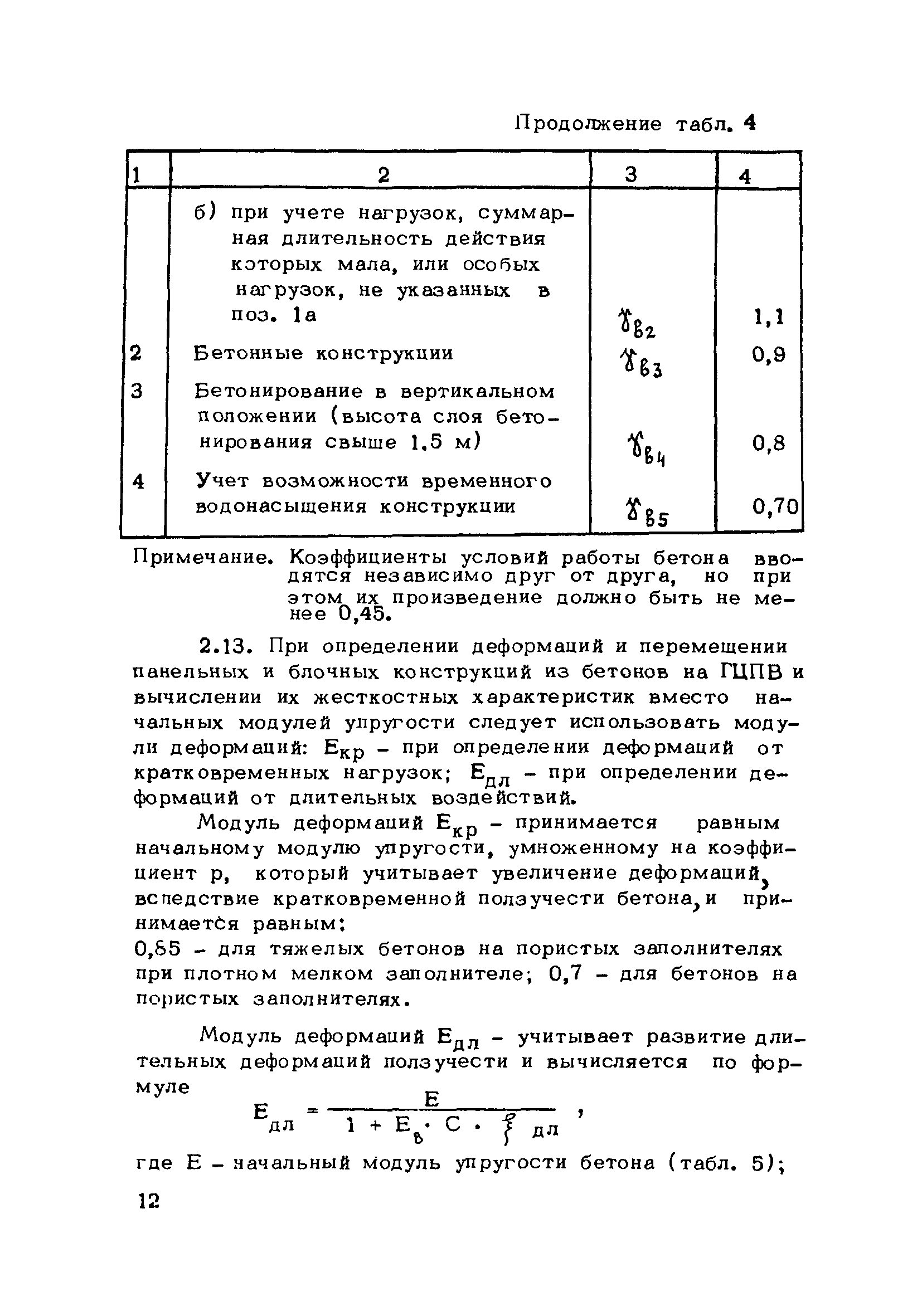 Следовательно, необходимо исследовать влияние взаимодействия конструкции под ударной нагрузкой и пожара.
Следовательно, необходимо исследовать влияние взаимодействия конструкции под ударной нагрузкой и пожара.
Устойчивость — серьезная проблема при проектировании стальных конструкций. Плохая стабильность стальных компонентов может привести к серьезному разрушению конструкции. Боковое изгибание компонента при кручении — очень распространенный тип неустойчивости, требующий дальнейшего изучения [1].Боковое продольное изгибание (общая неустойчивость) стальных балок под действием статических нагрузок можно описать следующим образом [2]: когда стальные балки без боковой опоры в чистом пролете подвергаются определенному значению поперечной нагрузки или момента относительно большой оси. , возникает большое боковое смещение и угол закручивания, как показано на рисунке 1. Затем балка теряет свою несущую способность. Очевидно, что анализ продольного изгиба сложнее, чем анализ продольного изгиба при изгибе в плоскости. Тем не менее, ряд исследований был проведен на основе теории упругого продольного изгиба, в частности экспериментальных исследований и теоретического анализа [3] бокового продольного изгиба стальных балок при статической нагрузке. Ян и др. провели экспериментальные испытания и численное моделирование продольного изгиба при кручении односимметричных двутавровых балок, изготовленных из стали Q460GJ [4, 5]. Их результаты показали, что стальные балки развивают поперечное продольное изгибание под действием сосредоточенных точечных нагрузок в середине пролета. Следовательно, местного коробления не наблюдалось. Кармазинова и др. [6] изучали поперечный изгиб-крутильный изгиб стальных балок сигма-сечения с отверстиями в стенке. Выводы их исследования легли в основу дополнений к указанным положениям по проектированию стальных конструкций.Кала и Валеш [7] исследовали горячекатаную стальную двутавровую балку, подверженную боковому изгибу при кручении (LTB) из-за изгибающего момента, и получили стохастические эффекты начального несовершенства и остаточного напряжения на сопротивление исследуемой стальной балки. Развитие численных методов, таких как метод конечных элементов (КЭ), облегчило исследования поперечного продольного изгиба стальных балок от экспериментальных исследований до численного анализа [8–10].
Ян и др. провели экспериментальные испытания и численное моделирование продольного изгиба при кручении односимметричных двутавровых балок, изготовленных из стали Q460GJ [4, 5]. Их результаты показали, что стальные балки развивают поперечное продольное изгибание под действием сосредоточенных точечных нагрузок в середине пролета. Следовательно, местного коробления не наблюдалось. Кармазинова и др. [6] изучали поперечный изгиб-крутильный изгиб стальных балок сигма-сечения с отверстиями в стенке. Выводы их исследования легли в основу дополнений к указанным положениям по проектированию стальных конструкций.Кала и Валеш [7] исследовали горячекатаную стальную двутавровую балку, подверженную боковому изгибу при кручении (LTB) из-за изгибающего момента, и получили стохастические эффекты начального несовершенства и остаточного напряжения на сопротивление исследуемой стальной балки. Развитие численных методов, таких как метод конечных элементов (КЭ), облегчило исследования поперечного продольного изгиба стальных балок от экспериментальных исследований до численного анализа [8–10]. Более того, исследования огнестойкости стальных конструкций достигли большого прогресса [11].Проблеме продольного изгиба при кручении стальных балок при пожаре уделяется значительное внимание [12–14]. Эта проблема связана со значительным количеством форм продольного изгиба стальной балки при пожаре. Стальная конструкция может очень долго выдерживать огонь. Следовательно, анализ конструкций при пожаре можно рассматривать как статическую задачу. Когда конструкции подвергаются огню, повышенная температура вызывает ухудшение свойств материала и вызывает пластическую деформацию конструкции.Таким образом, теория упругого изгиба больше не подходит. Таким образом, численное моделирование является эффективным методом исследования проблем неупругого изгиба. Например, Vila Real et al. [15, 16] провели численное исследование и предложили расчетную кривую для LTB стальных балок. Инь и Ван [17] численно исследовали влияние нескольких конструктивных факторов на сопротивление изгибающему моменту продольного изгиба при изгибе стальных двутавровых балок, подверженных неравномерному распределению температуры.
Более того, исследования огнестойкости стальных конструкций достигли большого прогресса [11].Проблеме продольного изгиба при кручении стальных балок при пожаре уделяется значительное внимание [12–14]. Эта проблема связана со значительным количеством форм продольного изгиба стальной балки при пожаре. Стальная конструкция может очень долго выдерживать огонь. Следовательно, анализ конструкций при пожаре можно рассматривать как статическую задачу. Когда конструкции подвергаются огню, повышенная температура вызывает ухудшение свойств материала и вызывает пластическую деформацию конструкции.Таким образом, теория упругого изгиба больше не подходит. Таким образом, численное моделирование является эффективным методом исследования проблем неупругого изгиба. Например, Vila Real et al. [15, 16] провели численное исследование и предложили расчетную кривую для LTB стальных балок. Инь и Ван [17] численно исследовали влияние нескольких конструктивных факторов на сопротивление изгибающему моменту продольного изгиба при изгибе стальных двутавровых балок, подверженных неравномерному распределению температуры. Couto et al.[18] изучали поперечное продольное изгибание балок с малым поперечным сечением в случае пожара с использованием численного метода.
Couto et al.[18] изучали поперечное продольное изгибание балок с малым поперечным сечением в случае пожара с использованием численного метода.
Возникает ли LTB, когда стальная балка подвергается комбинированному воздействию удара и пожарной нагрузки, трудно определить из-за сложности эффектов взаимодействия двух нагрузок. Кроме того, возникновение LTB на стальной балке, когда она подвергается только удару, трудно исследовать, поскольку ударная нагрузка влияет на пластическое изгибание балок, тогда как инерционный эффект может задержать пластическое изгибание или избежать его.С одной стороны, сталь является чувствительным к скорости материала, что означает, что предел текучести стали может быть улучшен за счет эффекта скорости деформации. Следовательно, влияние скорости деформации стали может привести к возникновению упругих LTB. Эти сложные факторы препятствуют полному пониманию поведения LTB стальных балок при ударе. В последние годы было проведено несколько исследований динамической реакции стальных элементов на удар.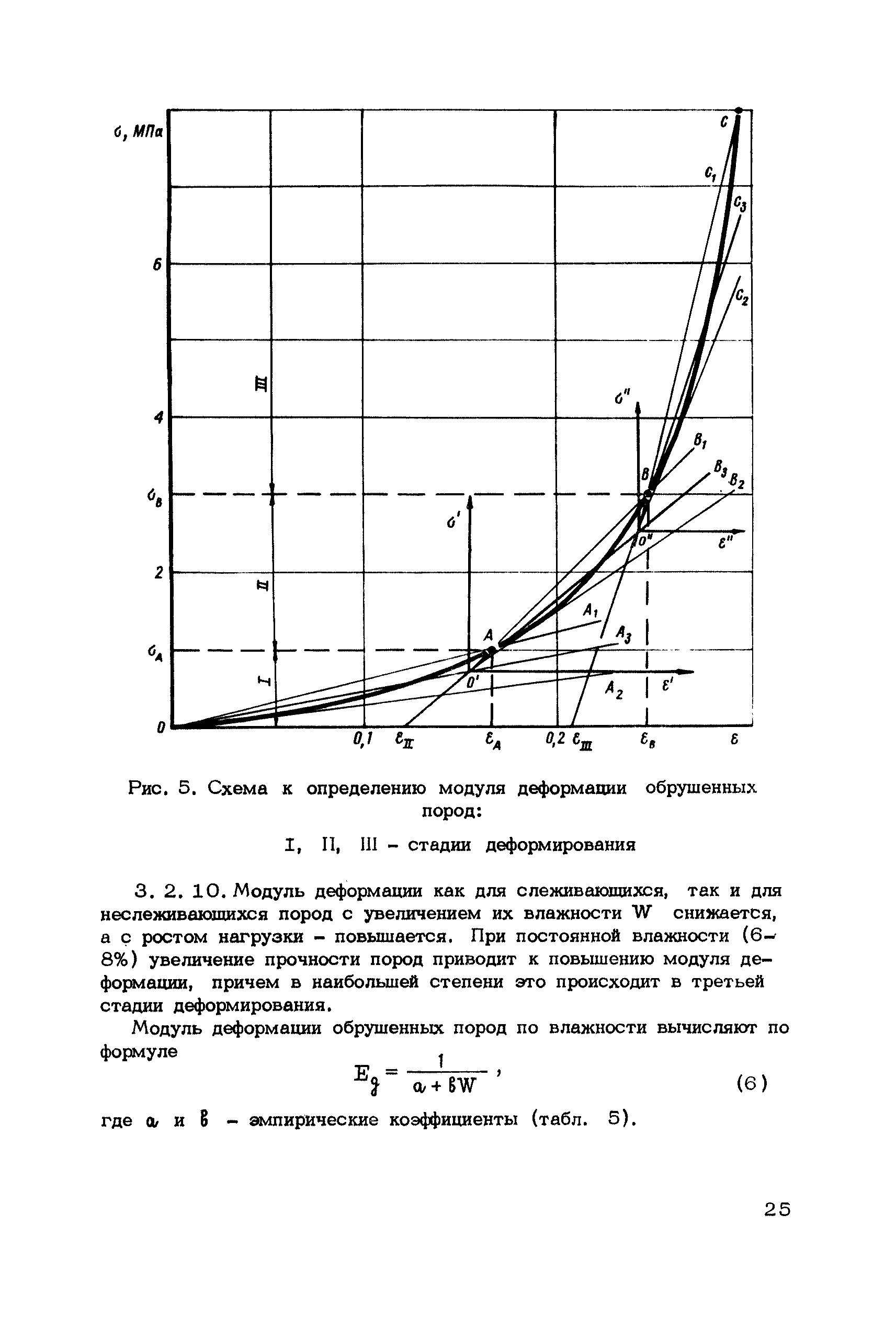 Вильявисенсио и Гедес Соареш [19] провели испытание на удар падающим грузом зажатых стальных балок, попавших поперек центра в центр с помощью массы с прямоугольным индентором, чтобы определить надлежащие граничные условия для балок, подвергшихся удару.Wang et al. [20] изучали динамическое поведение стальных балок с соединениями оребрения, подверженных ударным нагрузкам падающего пола. Результаты показывают, что стальные балки демонстрируют динамическое поведение при определенной энергии удара с различными массами и скоростями удара. Более высокая скорость удара может немного улучшить скорость рассеивания энергии. Стальные балки обладают разной стойкостью к ударам, в то время как ударные нагрузки применяются в разных местах. Аль-Тайри и Ван [21] исследовали поведение и режимы разрушения сжатых в осевом направлении стальных колонн, подверженных поперечному удару жесткой массой при различных скоростях и местах удара.Нин и Чжао [22, 23] завершили экспериментальное исследование устойчивости консольных балок из алюминиевого сплава при ударе ГБЦ.
Вильявисенсио и Гедес Соареш [19] провели испытание на удар падающим грузом зажатых стальных балок, попавших поперек центра в центр с помощью массы с прямоугольным индентором, чтобы определить надлежащие граничные условия для балок, подвергшихся удару.Wang et al. [20] изучали динамическое поведение стальных балок с соединениями оребрения, подверженных ударным нагрузкам падающего пола. Результаты показывают, что стальные балки демонстрируют динамическое поведение при определенной энергии удара с различными массами и скоростями удара. Более высокая скорость удара может немного улучшить скорость рассеивания энергии. Стальные балки обладают разной стойкостью к ударам, в то время как ударные нагрузки применяются в разных местах. Аль-Тайри и Ван [21] исследовали поведение и режимы разрушения сжатых в осевом направлении стальных колонн, подверженных поперечному удару жесткой массой при различных скоростях и местах удара.Нин и Чжао [22, 23] завершили экспериментальное исследование устойчивости консольных балок из алюминиевого сплава при ударе ГБЦ. Однако исследования LTB стальных балок под ударной нагрузкой отсутствуют.
Однако исследования LTB стальных балок под ударной нагрузкой отсутствуют.
Прежде всего, необходимы системные исследования LTB стальных балок при ударной нагрузке. Эта статья — предварительная попытка смежных исследований. В данной статье представлены экспериментальные результаты ЛТБ стальных балок прямоугольного сечения под действием ударного молота. Затем обсуждается LTB-поведение стальных балок прямоугольного сечения и Н-образных стальных балок при ударе.
2. Введение в экспериментальное испытание
Испытание стальных балок падающим весом проводилось с помощью установки для испытания ударным молотом DHR9401. Общая высота испытательной машины с ударным молотом DHR9401 составляет около 13,47 м над полом, а скорость удара — до 15,70 м / с. На рис. 2 показаны компоненты машины для испытания ударным молотком. Ударный молот состоит из нескольких основных компонентов. Первая деталь представляет собой упрочненную плоскую головку длиной 80 мм и толщиной 30 мм, изготовленную из высокопрочного хрома 15 (64HRC), как показано на рисунке 3. Вторая составляющая бойка — это весовой элемент. Этот компонент содержит основную массу ударника и обеспечивает различную массу ударника от 2 до 250 кг. Третья часть бойка — это датчики веса. Общий вес ударного молота составляет 57,8 кг, и его можно поднять на необходимую высоту для создания различных скоростей удара (до 15,7 м / с) и энергии [24].
Вторая составляющая бойка — это весовой элемент. Этот компонент содержит основную массу ударника и обеспечивает различную массу ударника от 2 до 250 кг. Третья часть бойка — это датчики веса. Общий вес ударного молота составляет 57,8 кг, и его можно поднять на необходимую высоту для создания различных скоростей удара (до 15,7 м / с) и энергии [24].
Листовой прокат из стали (Q235) был выбран для изготовления образцов. Образцы были классифицированы по толщине балки: #A: 3 мм, #B: 3 мм и #C: 3 мм.Эффективные пролеты стальных балок составляли 500, 750 и 1000 мм, как показано на Рисунке 4.
В таблице 1 показаны размеры стальных балок. Ограничения стальных балок были реализованы длиной зарезервированной. На обоих концах экспериментальных площадок закреплялись две опоры. Болты по бокам опоры для боковой фиксации. Ограничение вращения было зафиксировано стальной крышкой, как показано на рис. 5. Свойства материала образцов определялись стандартными испытаниями на статическое растяжение, которые проводились с помощью управляемой компьютером электронной машины для испытания на всемогущество CM5105A.Эксперимент повторяли 3 раза и усредняли данные. На рис. 6 представлена кривая деформации стали. Модуль упругости и предел текучести стальных балок составляют 185 ГПа и 315 МПа соответственно.
Свойства материала образцов определялись стандартными испытаниями на статическое растяжение, которые проводились с помощью управляемой компьютером электронной машины для испытания на всемогущество CM5105A.Эксперимент повторяли 3 раза и усредняли данные. На рис. 6 представлена кривая деформации стали. Модуль упругости и предел текучести стальных балок составляют 185 ГПа и 315 МПа соответственно.
| |||||||||||||||||||||||||||||||||||||||||
3. Результаты экспериментальных испытаний
Результаты экспериментальных испытаний
| Еще немного Особые случаи | |||||||||||||||||||||||||||||||
| В испытании на растяжение используется
одноосное напряжение; толкать или втягивать
только в одном направлении. Это особая ситуация; ссылка выше поможет вам
там. В реальной жизни всевозможные силы могут действовать со всех сторон на Образец всевозможных форм.Прежде чем я перейду к этому самому , вообще случай, мы дадим еще несколько особых случаев быстрый взгляд. | |||||||||||||||||||||||||||||||
На рисунке ниже показаны еще
весьма специфические стрессовые состояния; Вы наверняка можете сами приготовить еще немного. | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
То, что мы имеем слева направо:
| |||||||||||||||||||||||||||||||
Первые два у меня уже есть
иметь дело с. Основной материал
параметром, полученным в результате одноосных испытаний, был модуль Юнга Y и коэффициент Пуассона n . Основной материал
параметром, полученным в результате одноосных испытаний, был модуль Юнга Y и коэффициент Пуассона n . | |||||||||||||||||||||||||||||||
| чистый сдвиг и равномерное сжатие показаны ниже более научным образом. Чистый сдвиг означает, что приложенная сила не находится под прямым углом к поверхности. он действует, но лежит на поверхности. Напряжение сдвига, обычно сокращенно на t , а не s , по-прежнему сила, разделенная на площадь. | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Мы можем получить два новых материала
параметры, модуль сдвига G и модуль сжатия K, как показано. | |||||||||||||||||||||||||||||||
| Теперь у нас есть четыре числа, описывающих эластичный деформация некоторого материала Где это закончится? У меня для вас хорошие и плохие новости: | |||||||||||||||||||||||||||||||
| Итак, что такое изотропный материал, как в отличие от анизотропного? Просто: свойства изотропного материала не зависят от направления. Другими словами, если у вас есть группа материал, допустим, картофель, а теперь вырежьте из него образец для испытаний на растяжение (что-то вроде картофеля фри), результаты теста будут одинаковыми, как бы вы ни вырезать образец.Картофель — изотропный материал; вкус французского фри не зависит от того, как вы вырезали один из объема. | |||||||||||||||||||||||||||||||
Мясо другое. Резка
с или поперек волокна влияет на механические свойства и
текстура / вкус. Тот же принцип применим и к кристаллам. В принципе важно, как вы режете ваш экземпляр. Кристаллы имеют тенденцию быть анизотропными. Вы знаете это. Графит, для Например, очень легко поддается в одном направлении и чрезвычайно жестко в еще один.Вот почему вы можете использовать его, чтобы смазывать вещи или делать очень прочные композиты. | |||||||||||||||||||||||||||||||
Чтобы правильно описать, что происходит в
сложный кристалл, когда вы подвергаете его механическому воздействию, вам действительно нужно 21
номера затем назвали « эластичных
коэффициенты «. Извините. Но у меня еще раз хорошие новости:
| |||||||||||||||||||||||||||||||
Если это правда (это) логика
диктует, что если у меня есть два упругих параметров , я должен уметь вычислить все остальные . Вот что мы делаем, вот один результат, связывающий четыре обсуждаемых модуля так
далеко. Вот что мы делаем, вот один результат, связывающий четыре обсуждаемых модуля так
далеко. | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Модуль сдвига, кстати, равен
удобный модуль, когда мы идем на пластик вместо упругой деформации. | |||||||||||||||||||||||||||||||
| Общий случай деформации; Значение Нормальный и сдвиг Напряжение | |||||||||||||||||||||||||||||||
| В самом общем случае имеем
объект произвольной формы, который даже не однороден, но, возможно, состоит из
разные материалы — например, картошка с гнилыми пятнами, твоя машина, ты. На этот материал действуют всевозможные силы со всех сторон.Силы это вектора , показанные стрелками, а наши картофель, который вот-вот деформируется, можно проиллюстрировать так: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Нам нужно только , чтобы деформировать объект. Мы не хотим его перемещать, и мы
не хочу, чтобы он начал вращаться вокруг какой-то оси. Это означает, что вектор
сумма всех сил должна быть равна нулю, как и крутящие моменты. Мы не хотим его перемещать, и мы
не хочу, чтобы он начал вращаться вокруг какой-то оси. Это означает, что вектор
сумма всех сил должна быть равна нулю, как и крутящие моменты. Это несколько упрощает работу, но не совсем легкую. | |||||||||||||||||||||||||||||||
| Первое, что нужно понять, это то, что силам больше не нужно действовать исключительно перпендикулярно на какой-либо поверхности (как при испытании на растяжение), но может иметь любой произвольный угол. Это означает, что мы должны расширить определение стресса. | |||||||||||||||||||||||||||||||
Для этого мы смотрим на некоторую силу F действующий под некоторым углом на какую-либо поверхность A . Если
хотите, можете описать поверхность вектором A который
перпендикулярна описываемой поверхности и имеет величину (= длину)
что дает площади поверхности. Рисунок ниже дает представление об этом для некоторых
произвольная внутренняя область (синим цветом). Рисунок ниже дает представление об этом для некоторых
произвольная внутренняя область (синим цветом). | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Смотрим на какой-то самолет внутри
объект наклонен на некоторый угол Q к действующему
сила.Мы используем эту плоскость для виртуального реза через объект. Так как в разрезе предполагается оставить все ровно как
прежде, мы должны приложить силы с обеих сторон, которые выбраны таким образом
что ровно ничего не происходит. Поскольку внешние силы сдвинут два
части друг от друга, эти силы должны противодействовать внешним силам F ex . Это означает, что на нашей голубой плоскости отсчета мы
должен разложить F ex на компонент F по нормали по нормали к плоскости, и компонент a F сдвиг содержится в плоскости. Так как в разрезе предполагается оставить все ровно как
прежде, мы должны приложить силы с обеих сторон, которые выбраны таким образом
что ровно ничего не происходит. Поскольку внешние силы сдвинут два
части друг от друга, эти силы должны противодействовать внешним силам F ex . Это означает, что на нашей голубой плоскости отсчета мы
должен разложить F ex на компонент F по нормали по нормали к плоскости, и компонент a F сдвиг содержится в плоскости.Это довольно легко выразить уравнениями (если вы знаете основы векторная математика). | |||||||||||||||||||||||||||||||
Далее рассчитываем напряжения
действуя на выбранной плоскости. У нас есть напряжение, данное F нормальный делим на площадь плоскости, которую мы
называется нормальным стрессом и всегда сокращается до s , а стресс определяется как F сдвиг делится на площадь плоскости, которую мы называем
напряжение сдвига и всегда сокращайте до t . Площадь плоскости, находящейся внутри объекта, также легко вычислить. Для сил и площади А имеем | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| С с ex = номинальное напряжение, приложенное к объекту в целом, два напряжения выходят на | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Это было просто
геометрия. Однако результаты замечательные. Чтобы увидеть это, мы строим нормальный
и компоненты сдвига сил и вызываемых ими напряжений в зависимости от угла К . Однако результаты замечательные. Чтобы увидеть это, мы строим нормальный
и компоненты сдвига сил и вызываемых ими напряжений в зависимости от угла К . | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Пока сил и нормального напряжения просто
изменяется более или менее плавно между нулевым и максимальным значениями, сдвиг
напряжение имеет максимум для Q = 45 0 и равен нулю для Q = 0; 90 0 . Поскольку, забегая вперед, пластическая деформация зависит от сдвига. подчеркивает, мы уже здесь видим, почему так много происходит в самолетах примерно на 45 0 к направлению внешнего напряжения. Эти самолеты испытывают максимальное напряжение сдвига. | |||||||||||||||||||||||||||||||
Длинная и короткая части этого упражнения
было установить, что мы делаем в общем случае: некоторая сила действует на некоторую
самолет. Мы разлагаем эту силу на три основных компонента, а затем производим три напряжения:
| |||||||||||||||||||||||||||||||
| Общие Случай деформации; Тензор Состав | |||||||||||||||||||||||||||||||
Если мы оглянемся на общее
проблема, описанная выше, первое, что мы делаем
состоит в том, чтобы разделить картофель или что-то еще, что находится в стадии исследования, на партии
из (дифференциально) маленьких кубиков. Некоторые силы действуют на все шесть сторон всего этого.
кубики. Мы не знаем эти силы навскидку, но должны рассчитать их из
внешние силы, действующие на картофель снаружи. Это непросто, так что давайте
сначала посмотрите, что будет происходить в общих чертах. Некоторые силы действуют на все шесть сторон всего этого.
кубики. Мы не знаем эти силы навскидку, но должны рассчитать их из
внешние силы, действующие на картофель снаружи. Это непросто, так что давайте
сначала посмотрите, что будет происходить в общих чертах. | |||||||||||||||||||||||||||||||
| Вот полное представление о том, что можно найти за один из всех кубиков, которые мы сейчас рассматриваем. На других кубах направление и длина а всех стрелки могут быть разными, но в целом ситуация такая же. | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| На каждой из шести плоскостей у нас есть три действующих
стрессы; одно нормальное напряжение и два напряжения сдвига.Обратите внимание, что стрелки
указать направления действующей силы компоненты, поскольку напряжения , а не вектора —
они хуже — даже в этом случае они показаны стрелками. Система координат с x 1 , x 2 и x 3 — оси, как показано позволяет разобрать весь беспорядок; правила есть.
| |||||||||||||||||||||||||||||||
| Вот пример: t 2,3 — напряжение сдвига на плоскости перпендикулярно оси x 2 , вызванной силой компонент в направлении x 3 . | |||||||||||||||||||||||||||||||
| Теперь нужно написать все компоненты напряжения следующие: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| Девять чисел в этой матрице описывают все, что нужно знать о стрессовое состояние картофеля или любого другого объекта, который мы рассматриваем в точке, заданной координаты ( x 1 , x 2 , х 3 ) . | |||||||||||||||||||||||||||||||
| Это напоминает вам (я надеюсь) вектор , трехзначное число, которое описывает определенные
физические свойства, такие как скорости в некоторой точке пространства. Хорошая мысль. Приведенная выше девятикомпонентная матрица представляет собой своего рода обобщенный вектор назвал тензором второго ранга. Векторы просто тензоры первого ранга, скаляр или простое число описание некоторых физических свойств, таких как температура в какой-то момент, является тензор нулевого ранга.Прежде чем я углублюсь в тензорную математику, мы сделаем несколько упрощения. | |||||||||||||||||||||||||||||||
| Когда мы занимаемся наукой о деформации, мы обычно предполагают, что наш объект не движется и не вращается. Я отжимаю картошку или что бы то ни было таким образом, чтобы его центр тяжести оставался на месте, и он не начать вращаться. Это означает, что сумма всех сил и всех импульсов равно нулю. Если рассмотреть это подробно, то получится: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| Имеется некоторая симметрия элементов тензор напряжений.Это хорошо — это означает, что нам нужно знать только шесть чисел , а не девять, чтобы иметь возможность записать полный тензор напряжений в некоторых точка. Какое облегчение! | |||||||||||||||||||||||||||||||
| Во многих случаях, как показанные выше, тензор напряжений обладает некоторой симметрией, которая делает его проще. Вот примеры сверху плюс новенький. Одного числа хватит на четыре случая; только чистое кручение или сдвиг нужно два. | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| Так что же такое тензор ? Самый простой способ взглянуть на тензор должен понимать, что он соединяет два вектора в самом общем и простой способ. | |||||||||||||||||||||||||||||||
| Давайте еще раз посмотрим на определение стресса
чтобы увидеть, что это значит. Первоначально мы определили стресс как
«сила, деленная на площадь поперечного сечения» или с = F / A с использованием простого уравнения.В
слово «вектор» никогда не появлялось, и даже не сказав вам этого, я
предполагается, что сила всегда перпендикулярна плоскости, на которую она действует. Но здесь мы немного сложнее и понимаем, что оба F и A являются векторами, и нет необходимости в том, чтобы они всегда были параллельно. Поскольку вы не можете разделить вектор на вектор, простое определение напряжения в векторной записи становится. | |||||||||||||||||||||||||||||||
| Если s был бы простое число или скаляр, оба вектора будут иметь одинаковое направление, только длина была бы другой.Конечно, это слишком просто. В полной общности направление и длина могут быть разными, что означает, что каждый компонент одного вектор будет зависеть от всех трех компонентов другого вектора. Написано мы есть: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| Нам нужен девятизначный объект, чтобы соединить два векторов самым простым и общим способом.Мы называем это тензором (из второй ранг). | |||||||||||||||||||||||||||||||
| Теперь настанет ужасное предчувствие вверх. «Где это кончается?» — спросите вы. «Никогда» — это ответ вы получите от своего дружелюбного математика. Ученые-материаловеды будут быть более открытыми и заверить вас, что с тензорами четвертого ранга большинство все можно сделать. Физики склонны соглашаться, но часто ссылаются на четырехмерное для «эйнштейновского» пространства или даже11, если они заданы к теории струн. | |||||||||||||||||||||||||||||||
| Вы уже знаете тензор четвертого ранга. в основной текст, который я определил Модуль Юнга как «сколько напряжения нужно, чтобы удлинить материала на 0,01% «или как напряжение, деленное на деформацию. Поскольку полностью общность Y связывает два тензора второго ранга, это должен быть тензор четвертого ранга! В уравнениях (с компонентами Y записывается как c ijhk в соответствии с соглашением), что будет | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Когда я показал это своей дочери (той, что
изучает литературу), она отметила, что никогда не видела ничего более ужасного
за всю ее жизнь.Что ж, красота заключается в глазах смотрящего. Тем не менее, я
Предположим, вам будет приятно узнать, что 81 компонент Янга
собственно модуль упругости (затем называется упругой
коэффициенты ) сводятся к
| |||||||||||||||||||||||||||||||
| Длинное и короткое для железа и сталь, как и большинство других простых, потому что кубическая (и почти всегда поликристаллические) металлы, нам сойдет с рук всего два числа.Если мы назовем их коэффициенты упругости, или модуль Юнга плюс Коэффициент пумиссии, или модуль сдвига или что-то еще, не действительно важно. Вы всегда можете преобразовать один набор в другой — если знаете как это сделать. | |||||||||||||||||||||||||||||||
| Но не обманывайте себя. Что мы только что узнали
о модуле Юнга применяется ко многим другим свойствам материала, обычно
дано невиновным как простое число. Возьмем показатель преломления:
например, диэлектрическая «постоянная» или многие другие.Они на самом деле
тензоры разного ранга и не всегда распадаются на один-два
числа. Хуже того, компоненты этих тензоров могут быть комплексными числами, т.е. числами, которые содержат
квадратный корень из -1. Если вы когда-нибудь смотрели трехмерные фильмы, вам приходилось носить какие-то особенные очки. Когда вы носите эти очки, вы смотрите прямо сквозь них. сложные тензоры, если сказать так. Тензорные свойства материалов: становится все более важным, и Материаловедам необходимо знать о этот. | |||||||||||||||||||||||||||||||
| Хорошо — теперь, когда у нас есть решив самые простые вещи, мы можем, наконец, начать с расчета того, как картофель деформируется, если его сжать. | |||||||||||||||||||||||||||||||
| Ну, не будем. По крайней мере, не здесь. Не только бы
Мне трудно это сделать, это слишком сложно. Ответы на простые
повседневные вопросы о том, как что-то деформируется под действием силы,
заведомо труднодоступный, и область специалистов с большими компьютерами и огромной
и сложное программное обеспечение. Таким образом, мы рассмотрим только некоторые очень простые прочее чуть позже. | |||||||||||||||||||||||||||||||
Напряжение-деформация сталей | Протокол
Сталь — это общий термин для железа, легированного углеродом и другими элементами, такими как хром, марганец и никель.
Изменения в составе и методах обработки позволяют адаптировать его свойства для строительства автомобилей, мостов и небоскребов, и это лишь некоторые из почти бесконечных возможных применений.
Понимание реакции стали на нагрузку важно при проектировании безопасных зданий и сооружений. Одним из основных инструментов моделирования характеристик материала является кривая напряжения-деформации.
Мы будем использовать испытание на одноосное растяжение для изучения упругого и неупругого поведения мягкой горячекатаной стали и твердой холоднокатаной стали, которые представляют собой соответственно низкие и высокие пределы прочности на разрыв в приложениях гражданского строительства.
Напряжение определяется как сила, деленная на площадь, на которую она действует.Деформация — это изменение длины, деленное на исходную длину. Кривые напряжение-деформация описывают упругие и неупругие свойства материалов, показывая, как такой материал, как сталь, реагирует на приложенную силу.
Испытание на одноосное растяжение обычно используется для изучения напряжения и деформации. В этом испытании машина медленно вытягивает концы образца с все большей силой и измеряет полученное удлинение. Испытание на растяжение металла описано в стандарте ASTM E8, который определяет тип и размер образца, тип оборудования и данные, которые необходимо сообщить.
Кривая напряжения-деформации показывает многие свойства испытуемого материала. Среди них модуль упругости (наклон начальной линейной области, где деформация пропорциональна нагрузке), модуль упругости (область под линейной областью, которая измеряет способность материала поглощать энергию без остаточной деформации), пропорциональный предел ( напряжение в точке отклонения кривой от линейности), предельные значения текучести (где напряжение в зависимости от деформации внезапно уменьшается или изменяется) и плато текучести (где деформация быстро увеличивается без увеличения напряжения).
Сталь — пластичный материал. Пластичность определяется как изменение длины при разрыве, деленное на исходную длину. Прочность — это способность материала поглощать энергию до того, как он расколется.
Теперь, когда мы понимаем некоторые основные характеристики материалов, давайте рассмотрим метод измерения напряжения и деформации в лаборатории и исследуем взаимосвязь между этими двумя величинами.
Получите цилиндрические образцы для испытаний для двух типов стали: мягкой и горячекатаной, например, A36, и твердой и холоднокатаной, например, C1018.
Используйте штангенциркуль для измерения диаметра в нескольких точках около середины образца. Сделайте эти измерения с точностью до 2000-х дюйма.
Затем крепко удерживайте образец. Нарисуйте калибровочную длину примерно два дюйма. Сделайте отметку четкой, но очень мелкой, чтобы избежать концентрации напряжений, которая может привести к разрушению. Измерьте фактическую маркированную длину датчика с точностью до 2000-х дюйма.
Наконец, установите тензодатчик. Теперь образец готов к испытаниям.
Мы будем использовать универсальную испытательную машину, или UTM, для измерения свойств образцов при растяжении. Включите испытательную машину и инициализируйте программное обеспечение. Настройте соответствующие параметры построения графиков и сбора данных, затем выберите процедуру испытания, совместимую с протоколом ASTM E8.
Установите скорости деформации для низких деформаций от нуля до 5% и для диапазонов высоких деформаций более 5% соответственно. Они должны быть близки к 0,05 дюйма в минуту для начальной загрузки и 0.5 дюймов в минуту после 5% деформации. Затем установите любые дополнительные действия в программном обеспечении, такие как остановка машины при 5% деформации в экстензометре, чтобы удалить ее до разрушения образца.
Вручную поднимите траверсу так, чтобы образец по всей длине легко поместился между верхним и нижним захватами. Осторожно вставьте образец в верхний захват примерно на 80% глубины захвата. Выровняйте образец внутри верхней ручки и слегка затяните, чтобы образец не упал. Медленно опустите верхнюю траверсу.Как только образец окажется в пределах 80% глубины нижнего зажима, начните выравнивание образца в нижних зажимах. Образец должен плавать в центре полностью открытой нижней рукоятки. Приложите боковое давление к образцу через захваты, чтобы не допустить проскальзывания во время испытания. Обратите внимание на то, что процесс затяжки вызывает небольшое осевое усилие на образце.
Используйте программное обеспечение, чтобы наложить предварительную нагрузку, чтобы компенсировать эту силу, и запишите ее значение. Надежно прикрепите электронные экстензометры к образцу в соответствии с инструкциями производителя.Лезвия экстензометра должны быть примерно отцентрованы на образце. Если используется тензодатчик, подключите его.
Начните испытание с приложения растягивающей нагрузки к образцу. Наблюдайте за показаниями приложенной нагрузки в реальном времени на дисплее компьютера. Чтобы убедиться, что образец не проскальзывает через зажимы, убедитесь, что измеренная нагрузка увеличивается линейно. Незадолго до сбоя образца программное обеспечение автоматически приостановит тест. Оставьте образец в испытательной машине и снимите экстензометр.Продолжайте прикладывать растягивающую нагрузку до отказа. По достижении максимальной нагрузки измеренные нагрузки начинают уменьшаться. В этот момент образец начинает сгибаться. Окончательный перелом должен произойти в этой области шейки из-за пластичного разрыва.
По окончании испытания поднимите крейцкопф, ослабьте верхнюю рукоятку и извлеките из нее сломанный кусок образца. Ослабьте нижнюю ручку и удалите вторую половину образца. Запишите значение при максимальной растягивающей нагрузке. Сохраните записанные данные и кривую деформации.
Осторожно соедините концы сломанного образца вместе и измерьте расстояние между метками шкалы с точностью до 2000-х дюйма. Запишите окончательную калибровочную длину. Наконец, измерьте диаметр образца по наименьшему поперечному сечению с точностью до 2000-х дюйма.
Чтобы определить свойства материала, сначала взгляните на данные для мягкой горячекатаной стали A36 и данные для твердой холоднокатаной стали C1018 соответственно.
Теперь вычислите относительное удлинение для каждого образца, зная окончательный размер и начальную длину.Рассчитайте уменьшение площади для каждого образца, используя конечный диаметр и начальный диаметр образца. Запишите эти значения в таблицу результатов.
Затем рассчитайте другие параметры материала, используя экспериментальные кривые напряжения-деформации. Быстрое сравнение этих кривых для двух образцов показывает их очень разные упругие и неупругие свойства. Из-за гораздо большей деформации при более низких уровнях напряжения сталь A36 мягче и намного пластичнее, чем сталь C1018.
Для стали A36 напряжение при разрушении составляет около 58.6 кг на квадратный дюйм, что значительно превышает номинальное значение 36,0 кг на квадратный дюйм. Максимальное напряжение составляет около 86,6 фунтов на квадратный дюйм при деформации около 20%.
На этом увеличенном графике показан предел текучести вверх около 58,6 кг на квадратный дюйм и более низкий предел текучести около 56,8 кг на квадратный дюйм. Здесь также видно начало плато урожайности. Данные тензометра показывают линейную упругую область для стали A36 с наклоном, определенным как модуль Юнга, около 29 393 кг / кв. Дюйм.Этот результат очень близок к номинальной стоимости 29 000 килограмм на квадратный дюйм.
В точке, где данные отклоняются от линейности, мы можем определить, что предел пропорциональности составляет около 55,58 кг на квадратный дюйм. Для сравнения: из-за нелинейности кривой зависимости напряжения от деформации сталь C1018 имеет очень низкий предел пропорциональности.
Результаты экстензометра охватывают деформации до 5%. Данные для стали A36 показывают пластическое плато и начало деформационного упрочнения, где кривая снова поднимается при деформации около 2.7%. Напротив, у C1018 нет четкого плато урожайности.
Завершите анализ данных, суммируя результаты испытаний для двух стальных образцов в следующей таблице.
Относительное удлинение мягкой горячекатаной стали составляет от 25 до 40%. Напротив, удлинение твердой холоднокатаной стали составляет только половину этой величины. Удлинение в процентах — это среднее значение длины материала между отметками калибра, но почти вся деформация локализована в небольшой области вокруг точки разрушения.Следовательно, местная деформация может быть намного больше средней.
Физический осмотр двух образцов показывает большие различия в способах их разрушения, соответствующие различиям в их кривых напряжения-деформации.
Сталь A36 имеет поверхность разрушения с материалом, вытянутым на ободе во время постепенной окончательной деформации и большим удлинением при более низких напряжениях, что указывает на очень мягкий, но пластичный металл.
Напротив, сталь C1018 имеет плоскую поверхность разрушения, соответствующую внезапному разрушению и гораздо меньшее удлинение при гораздо более высоких напряжениях, характеристики высокой прочности, но низкой пластичности.
Давайте посмотрим на некоторые общие области применения стали с точки зрения взаимосвязи между напряжением и деформацией.
Инженеры-строители анализируют обрушения конструкций в мостах и зданиях, чтобы улучшить будущие конструктивные решения. Этот процесс привел к созданию стальных компонентов, таких как катаные двутавровые балки для многоэтажных зданий, сварные двутавровые балки из толстолистовой стали для мостов, а также высокопрочные болты и крепежные детали. Для каждого требуются разные типы стали с заданной прочностью и пластичностью, что часто сначала понимается путем изучения их кривых напряжения-деформации.
Инженеры используют механические характеристики материалов для создания более безопасных автомобилей. Зная прочность и пластичность рамы, а также то, как она деформируется в ответ на ударные нагрузки, инженеры могут спроектировать кузов автомобиля так, чтобы он поглощал энергию во время столкновения и увеличивал шанс выжить в аварии.
Вы только что посмотрели введение JoVE в характеристики напряжения-деформации стали.
Теперь вы должны знать, как выполнить испытание на одноосное растяжение для определения свойств при растяжении металлических материалов и как анализировать кривые напряжения-деформации для типичных сталей.
Спасибо за просмотр!
Примечания к редакции деформируемых тел и упругой деформации
(а) Твердое вещество: — это тип материи, имеющий определенную форму и определенный объем.
(b) Жидкость: — это вещество, которое имеет определенный объем, но не определенную форму.
(c) Газ: — это вещество, не имеющее определенной формы или определенного объема.
Эластичность: — Свойство, благодаря которому тело стремится восстанавливать свою первоначальную конфигурацию (форму и размер) при устранении деформирующих сил, является эластичность.
Пластиковые тела: — Пластмассовые тела, которые не проявляют тенденции к восстановлению своей первоначальной конфигурации после снятия деформирующих сил.
Напряжение: — Определяется как восстанавливающая сила на единицу площади.
Напряжение = F / A
(a) Нормальное напряжение: — Напряжение называется нормальным напряжением, если восстанавливающая сила действует под прямым углом к поверхности.
(напряжение) N = Fsinθ / A
(i) Напряжение сжатия: — Это напряжение приводит к уменьшению удельного веса тела на единицу объема.
(ii) Растягивающее напряжение: — это напряжение приводит к увеличению длины на единицу объема тела.
(b) Касательное напряжение: — Напряжение считается касательным, если оно действует в направлении, параллельном поверхности.
(c) Единица напряжения: — S.I- Н / м 2 , C.G.S-дин / см 2
(d) Размер напряжения: — Напряжение = F / A = [M 1 L -1 T -2 ]
- Деформация: — Относительное изменение конфигурации из-за приложения деформирующих сил называется деформацией.
(a) Продольная деформация: — Это отношение изменения длины к ее исходной длине.
Продольная деформация = l / L
(b) Поперечная деформация: — Поперечная деформация — это отношение изменения диаметра к исходному диаметру, когда на цилиндр действует сила, действующая вдоль его оси.
Боковое напряжение = изменение диаметра / исходный диаметр
(c) Объемная деформация: — Определяется как отношение изменения объема к его первоначальному объему.
Объемная деформация = об / об
(d) Деформация сдвига: — Деформация сдвига измеряется углом, повернутым линией, первоначально перпендикулярной фиксированной поверхности.
Деформация сдвига =?,
Для малых углов,
? = загар?
= DD 1 / AD
= смещение в плоскости CD / расстояние плоскости CD от фиксированной плоскости
Таким образом, деформация сдвига также определяется как отношение между перемещениями в одной плоскости к ее расстоянию от фиксированной плоскости. У него нет единицы.
(e) Единица деформации: — Нет единицы
(f) Размер деформации: — [M 0 L 0 T 0 ]
В нем говорится, что в пределах упругости напряжение пропорционально деформации.
В пределах упругости растяжение пропорционально растяжению.
Итак, Стресс ∝Strain
/ A∝l / L
(a) Для растяжения: напряжение = Y × деформация или Y = Fl / A (Δl)
(b) Для сдвига: напряжение = η × деформация или η = F / A?
(c) Для объемной эластичности: напряжение = B × деформация или B = — P / (ΔV / V)
Пластичность: — Это свойство тела, в силу которого оно теряет свойство упругости и приобретает остаточную деформацию при снятии деформирующей силы, называется пластичностью.
Коэффициент упругости: — Это соотношение между напряжением и деформацией.
Единица — S.I- Н / м 2 , C.G.S — дин / см 2
- Модуль упругости Юнга (Y): — Он определяется как отношение нормального напряжения к продольной деформации.
Y = нормальное напряжение / продольная деформация = (F / A) / (l / L) = (Mg × L) / (πr 2 × L)
- Объемный модуль упругости (B): — Он определяется как отношение нормального напряжения к объемной деформации.
B = нормальное напряжение / объемная деформация = (F / A) / (v / V) = pV / v
- Сжимаемость: — Сжимаемость материала определяется как величина, обратная его объемному модулю упругости.
Сжимаемость = 1 / B
- Модуль жесткости (η): — Он определяется как отношение тангенциальных напряжений к деформации сдвига.
η = касательное напряжение / деформация сдвига = (F / A) / θ = T / θ
Единица коэффициента упругости: — С.I- Н / м 2 , C.G.S — дин / см 2
Коэффициент упругости = напряжение / деформация = [M 1 L -1 T -2 ]
Влияние температуры на коэффициент эластичности: —
(a) Y t = Y 15 [1-α (t-15)]
(б) η t = η 15 [1-α ‘(t-15)]
Здесь Y 15 и η 15 — модуль Юнга и модуль жесткости при 15 ° C, тогда как Y t и η t — соответствующие значения при t ° C, α и α ‘- температурный коэффициент для Y и η .
- Выполненные работы на растяжке: —
(a) W = ½ × (напряжение) × (деформация) × (объем) = ½ Y (деформация) 2 × объем = ½ [(напряжение) 2 / Y] × объем
(b) Запасенная потенциальная энергия, U = W = ½ × (напряжение) × (деформация) × (объем)
(c) Потенциальная энергия, запасенная на единицу объема, U = ½ × (напряжение) × (деформация)
- Работа, проделанная во время вытяжки (плотность энергии): —
W = ½ F × l = ½ натяжения × удлинение
- Плотность энергии: — Количество энергии, хранящейся в проводе, на единицу объема называется его плотностью энергии.
Плотность энергии = проделанная работа / объем
= ½ [(Ш × Д) / (Д × Д)]
= ½ [напряжение × деформация]
- Сталь более эластична, чем резина: — Вещество, имеющее более высокий коэффициент эластичности, считается более эластичным.
Для стали, Y S = F L / al s
Для резины, Y R = F L / al R
Так, l с
Следовательно, сталь эластичнее резины.
Эластомер: — Вещество, в котором может возникать большая деформация из-за небольшого напряжения, называется эластомером.
Упругая усталость: — Явление, в результате которого вещество проявляет задержку в восстановлении своей первоначальной конфигурации, если оно подвергалось напряжению в течение более длительного времени, называется упругой усталостью.
Эластичность газа: —
(a) Изотермическое изменение: — Если температура газа остается постоянной, изменение называется изотермическим.
P = — (напряжение / объемная деформация) = B i
Здесь B i — объемный модуль упругости в изотермических условиях.
(b) Адиабатическое изменение: — Если температура газа не остается постоянной, изменение называется адиабатическим.
γ P = (напряжение / объемная деформация) = B a
Здесь B a — объемный модуль упругости в адиабатических условиях.
Поскольку γ всегда больше единицы, поэтому B a > B i .
Разрывное напряжение: — Разрывное напряжение = Разрушающий вес / πr 2
Коэффициент Пуассона (σ): — Коэффициент Пуассона материала проволоки определяется как отношение поперечной деформации на единицу напряжения к продольной деформации на единицу напряжения.
σ = поперечная деформация / продольная деформация = β / α = (ΔD / D) / (ΔL / L)
Значения σ лежат между -1 и 0.5.
- Соотношения между упругими постоянными: —
(а) B = Y / [3 (1-2σ)]
(б) η = Y / [2 (1+ σ)]
(в) 9 / Y = 3 / η + 1 / B
(d) σ = [3B-2η] / [6B + 2η]
(а) Депрессия, δ = Wl 3 / 4Ybd 3 (прямоугольная)
(б) Депрессия, δ = Wl 3 / 12Yπr 2 (цилиндрическая)
(а) rθ = l? (Где θ — угол закручивания, а? — угол сдвига)
(б) Восстанавливающий момент, = cθ
(c) Восстановление пары на единицу скрутки, c = πηr 4 / 2l (для цельного цилиндра)
(d) Восстановительная пара на единицу скрутки, c = πηr 2 4 -r 1 4 / 2l (для полого цилиндра)
- Объемный модуль идеального газа: —
(а) Бизотермический = P
(б) Бадиабатический = γ P
Здесь γ = C p / C v
- Удлинение проволоки от собственного веса: — Δl = ½ [Mgl / YA] = ½ [l 2 ρg / Y]
Особенности курса
- 728 Видео-лекции
- Примечания к редакции
- Документы за предыдущий год
- Интеллектуальная карта
- Планировщик исследования
- Решения NCERT
- Обсуждение Форум
- Тестовая бумага с видео-решением
Модуль Юнга — Infogalactic: ядро планетарных знаний
Каучук, материал с чрезвычайно низким модулем Юнга.Модуль Юнга , также известный как модуль упругости, представляет собой механическое свойство линейно-упругих твердых материалов.Он определяет соотношение между напряжением (силой на единицу площади) и деформацией (пропорциональной деформацией) в материале. Модуль Юнга назван в честь британского ученого XIX века Томаса Янга. Однако эта концепция была разработана в 1727 году Леонардом Эйлером, а первые эксперименты, в которых использовалась концепция модуля Юнга в его нынешней форме, были выполнены итальянским ученым Джордано Риккати в 1782 году, опередив работу Янга на 25 лет. [1] Термин модуль является уменьшительным от латинского термина modus , что означает , мера .
Твердое тело деформируется при приложении к нему нагрузки. Если материал эластичный, тело возвращается в исходную форму после снятия нагрузки. Материал является линейным, если отношение нагрузки к деформации остается постоянным в процессе нагружения. Не многие материалы являются линейными и эластичными за пределами небольшой деформации. Постоянный модуль Юнга применяется только к линейно-упругим материалам. Совершенно жесткий материал имеет бесконечный модуль Юнга, потому что для деформации такого материала требуется бесконечная сила.Материал с очень высоким модулем Юнга можно считать жестким. [2]
Жесткий материал требует большей силы для деформации по сравнению с мягким материалом. Следовательно, модуль Юнга является мерой жесткости твердого материала. Не путайте:
- жесткость и прочность: прочность материала — это сила, которую он может выдержать и при этом восстановить свою первоначальную форму;
- жесткость материала и геометрическая жесткость: геометрическая жесткость зависит от формы, например.грамм. жесткость двутавровой балки намного выше, чем у пружины из той же стали, и, следовательно, такой же жесткости;
- жесткость и твердость: твердость материала определяет относительное сопротивление, которое его поверхность оказывает на проникновение более твердого тела;
- жесткость и ударная вязкость: вязкость — это количество энергии, которое материал может поглотить перед разрушением.
Технический
Техническое определение: отношение напряжения (силы на единицу площади) вдоль оси к деформации (отношение деформации к начальной длине) вдоль этой оси в диапазоне напряжений, в котором выполняется закон Гука. [3]
Модуль Юнгаявляется наиболее распространенным модулем упругости , иногда называемым модулем упругости , но существуют и другие модули упругости, такие как объемный модуль и модуль сдвига.
Шт.
Модуль Юнга — это отношение напряжения (которое имеет единицы измерения давления) к деформации (которая безразмерна), поэтому модуль Юнга имеет единицы давления. Единицей СИ является паскаль (Па или Н / м 2 или м -1 · кг · с -2 ).Практически используются единицы измерения: мегапаскали (МПа или Н / мм 2 ) или гигапаскали (ГПа или кН / мм 2 ). В обычных единицах измерения США он выражается в фунтах (силах) на квадратный дюйм (psi). Аббревиатура ksi обозначает «kpsi» или тысячи фунтов на квадратный дюйм.
Использование
Модуль Юнга позволяет рассчитать изменение размеров стержня, сделанного из изотропного упругого материала, под действием растягивающих или сжимающих нагрузок. Например, он предсказывает, насколько образец материала расширяется при растяжении или укорачивается при сжатии.Модуль Юнга напрямую применим к случаям одноосного напряжения, то есть напряжения растяжения или сжатия в одном направлении и отсутствия напряжения в других направлениях. Модуль Юнга также используется для прогнозирования прогиба, который произойдет в статически определенной балке, когда нагрузка приложена в точке между опорами балки. Другие расчеты упругости обычно требуют использования одного дополнительного свойства упругости, такого как модуль сдвига, объемный модуль или коэффициент Пуассона. Любых двух из этих параметров достаточно, чтобы полностью описать эластичность изотропного материала.
Линейное и нелинейное
Модуль Юнга представляет собой коэффициент пропорциональности в законе Гука, который связывает напряжение и деформацию. Однако закон Гука действителен только при предположении, что упругий и линейный отклик . Любой настоящий материал со временем разрушится и сломается при растяжении на очень большом расстоянии или с очень большой силой; однако все твердые материалы демонстрируют почти гуковское поведение при достаточно малых деформациях или напряжениях.Если диапазон, в котором действует закон Гука, достаточно велик по сравнению с типичным напряжением, которое ожидается приложить к материалу, материал называется линейным. В противном случае (если типичное прикладываемое напряжение выходит за пределы линейного диапазона) материал называется нелинейным.
Сталь, углеродное волокно и стекло обычно считаются линейными материалами, в то время как другие материалы, такие как резина и грунт, являются нелинейными. Однако это не абсолютная классификация: если к нелинейному материалу приложены очень небольшие напряжения или деформации, отклик будет линейным, но если к линейному материалу будут приложены очень высокие напряжения или деформации, линейная теория не будет довольно.Например, поскольку линейная теория предполагает обратимость, было бы абсурдно использовать линейную теорию для описания разрушения стального моста под высокой нагрузкой; Хотя сталь является линейным материалом для большинства применений, в таких случаях катастрофический отказ не наблюдается.
В механике деформируемого твердого тела наклон кривой напряжения – деформации в любой точке называется касательным модулем. Его можно экспериментально определить по наклону кривой зависимости напряжения от деформации, полученной во время испытаний на растяжение, проведенных на образце материала.Касательный модуль начального линейного участка кривой напряжения-деформации называется модулем Юнга .
Направленные материалы
Модуль Юнга не всегда одинаков при всех ориентациях материала. Большинство металлов и керамики, наряду со многими другими материалами, изотропны, и их механические свойства одинаковы во всех ориентациях. Однако металлы и керамика можно обрабатывать определенными примесями, а металлы можно обрабатывать механически, чтобы сделать их зернистую структуру направленной.Затем эти материалы становятся анизотропными, и модуль Юнга будет изменяться в зависимости от направления вектора силы. Анизотропия также наблюдается во многих композитах. Например, углеродное волокно имеет гораздо более высокий модуль Юнга (намного жестче), когда сила прикладывается параллельно волокнам (вдоль волокон). К другим таким материалам относятся дерево и железобетон. Инженеры могут использовать это явление направленности в своих интересах при создании конструкций.
Расчет
Модуль Юнга при заданной деформации, E (ε) , может быть вычислен путем деления растягивающего напряжения на деформацию растяжения в упругой (начальной, линейной) части кривой физического напряжения-деформации:
где
- E — модуль Юнга (модуль упругости)
- F — сила, действующая на объект, находящийся под напряжением;
- A 0 — фактическая площадь поперечного сечения, через которую прикладывается сила;
- ΔL — величина, на которую изменяется длина объекта;
- L 0 — исходная длина объекта.
Сила, создаваемая растянутым или сжатым материалом
Модуль Юнга материала можно использовать для расчета силы, которую он оказывает при определенной деформации.
, где F — сила, прилагаемая материалом при сжатии или растяжении на ΔL .
Закон Гука можно вывести из этой формулы, которая описывает жесткость идеальной пружины:
, где насыщенность
- ,
- и
Упругая потенциальная энергия
Упругая потенциальная энергия, запасенная в линейно упругом материале, дается интегралом закона Гука:
теперь, объясняя интенсивные переменные:
Это означает, что плотность упругой потенциальной энергии (т.е.е., на единицу объема) определяется по формуле:
или, проще говоря, для линейно-упругого материала:, поскольку деформация определена.
В нелинейно-упругом материале модуль Юнга является функцией деформации, поэтому вторая эквивалентность больше не выполняется, и упругая энергия не является квадратичной функцией деформации:
Связь между упругими константами
Для однородных изотропных материалов существуют простые соотношения между упругими постоянными (модуль Юнга E , модуль сдвига G , объемный модуль K и коэффициент Пуассона ν ), которые позволяют вычислить их все, если известны два:
Приблизительные значения
Влияние добавок выбранных стеклянных компонентов на модуль Юнга определенного базового стеклаМодуль Юнга может несколько отличаться из-за различий в составе образцов и методах испытаний.Скорость деформации имеет наибольшее влияние на собираемые данные, особенно в полимерах. Значения здесь приблизительные и предназначены только для относительного сравнения.
См. Также
Список литературы
- ↑ Рациональная механика гибких или упругих тел, 1638–1788 : Введение в оперу Леонхарди Эйлера «Омния», т. X и XI, Seriei Secundae. Орелл Фуссли.
- ↑ В визуальных эффектах компьютерной графики термины линейный упругий материал и жесткий материал используются взаимозаменяемо, если модуль Юнга высокий.
- ↑ IUPAC, Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «Модуль упругости (модуль Юнга), E ».
- ↑ 4,00 4,01 4,02 4,03 4,04 4,05 4,06 4,07 4,08 4,09 4,08 4,19 4,10,11 4,1 4.16 4,17 4,18 4,19 «Упругие свойства и модуль упругости для некоторых материалов». Engineering ToolBox. Проверено 6 января 2012.
- ↑ «Обзор материалов для литого полиэтилена низкой плотности (LDPE)». Matweb. Проверено 7 февраля 2013 г.
- ↑ Субхаш Г., Яо С., Беллинджер Б., Гретц М.Р.(2005). «Исследование механических свойств панцирей диатомовых водорослей методом наноиндентирования». Дж. Наноси Нанотехнологии . 5 (1): 50–6. DOI: 10.1166 / jnn.2005.006. PMID 15762160. CS1 maint: несколько имен: список авторов (ссылка)
- ↑ Ивановска И.Л., де Пабло П.Дж., Сгалари Дж., МакКинтош ФК, Карраскоса Дж. Л., Шмидт К. Ф., Вуите Дж. Л. (2004). «Капсиды бактериофагов: прочные нанооболочки со сложными эластичными свойствами». Proc Nat Acad Sci USA . 101 (20): 7600–5. Bibcode: 2004PNAS..101.7600I. DOI: 10.1073 / pnas.0308198101. PMC 419652. PMID 15133147. CS1 maint: несколько имен: список авторов (ссылка)
- ↑ Данные о свойствах материала: Древесноволокнистая плита средней плотности (МДФ)
- ↑ Ро, JY (1993). «Модуль Юнга губчатого и кортикального костного материала: ультразвуковые и микротензионные измерения». Журнал биомеханики . 26 (2): 111–119. DOI: 10.1016 / 0021-9290 (93)
-д. - ↑ Полиэфирный матричный композит, армированный стекловолокном (стекловолокно). [SubsTech] (17 мая 2008 г.). Проверено 30 марта 2011.
- ↑ Кол, Н .; и другие. (8 июня 2005 г.). «Самособирающиеся пептидные нанотрубки представляют собой уникальные жесткие биоинспирированные супрамолекулярные структуры». Нано Письма . 5 (7): 1343–1346. Бибкод: 2005NanoL … 5.1343K. DOI: 10,1021 / NL0505896.
- ↑ Niu, L .; и другие. (6 июня 2007 г.). «Использование модели изгибающейся балки для оценки эластичности дифенилаланиновых нанотрубок». Ленгмюр . 23 (14): 7443–7446. DOI: 10.1021 / la7010106.
- ↑ Э-Г-ню.htm «Разработка и производство композитов (BEng) — MATS 324».
- ↑ Nabi Saheb, D .; Джог, JP. (1999). «Полимерные композиты из натуральных волокон: обзор». Достижения в полимерной технологии . 18 (4): 351–363. DOI: 10.1002 / (SICI) 1098-2329 (199924) 18: 4 <351 :: AID-ADV6> 3.0.CO; 2-X.
- ↑ Бодрос, Э.(2002). «Анализ поведения льняных волокон при растяжении и анализ увеличения жесткости при растяжении». Составная часть A . 33 (7): 939–948. DOI: 10.1016 / S1359-835X (02) 00040-4.
- ↑ А. П. Джексон, Дж. Ф. В. Винсент и Р. М. Тернер (1988). «Механический дизайн перламутра». Труды Королевского общества B . 234 (1277): 415–440. Bibcode: 1988RSPSB.234..415Дж. DOI: 10.1098 / rspb.1988.0056.
- ↑ DuPont (2001). «Техническое руководство по кевлару»: 9.
- ↑ М. Стейнс, У. Х. Робинсон и Дж. А. А. Худ (1981). «Сферическое вдавливание зубной эмали». Журнал материаловедения . 16 (9): 2551–2556. Bibcode: 1981JMatS..16.2551S. DOI: 10.1007 / bf01113595.
- ↑ Bodros, E .; Бейли, К. (15 мая 2008 г.). «Изучение свойств растяжения волокон крапивы двудомной (Urtica dioica)». Письма по материалам . 62 (14): 2143–2145. DOI: 10.1016 / j.matlet.2007.11.034.
- ↑ Эпоксидно-матричный композит, армированный 70% углеродными волокнами [SubsTech].Substech.com (2006-11-06). Проверено 30 марта 2011.
- ↑ Физические свойства кремния (Si). База данных Института Иоффе. Проверено 27 мая 2011.
- ↑ Э.Дж. Бойд; и другие. (Февраль 2012 г.). «Измерение анизотропии модуля Юнга в монокристаллическом кремнии». Журнал микроэлектромеханических систем . 21 (1): 243–249. DOI: 10.1109 / JMEMS.2011.2174415.
- ↑ Чоу, Х.М .; Кейс, Э. Д. (ноябрь 1988 г.). «Определение некоторых механических свойств поликристаллического железо-иттриевого граната (ЖИГ) неразрушающими методами». Журнал материаловедения . 7 (11): 1217–1220. DOI: 10.1007 / BF00722341.
- ↑ ЖИГ свойства
- ↑ [1]
- ↑ Адлер-Абрамович, Л .; и другие. (17 декабря 2010 г.). «Самособирающиеся органические наноструктуры с металлической жесткостью». Angewandte Chemie International Edition . 49 (51): 9939–9942. DOI: 10.1002 / anie.201002037.
- ↑ Фоли, Джеймс К .; и другие. (2010). «Обзор современных исследований и производственной практики порошковой металлургии». В Marquis, Фернан Д.С. (ред.). Порошковые материалы: современные исследования и производственная практика III . Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc.п. 263. DOI: 10.1002 / 9781118984239.ch42.
- ↑ . webelements http://www.webelements.com/molybdenum/physics.html. Получено 27 января 2015 г.
- ↑ (PDF). Glemco http://www2.glemco.com/pdf/NEW_MARTERIAL_LIST/Molybdenum.pdf. Получено 27 января 2014 г.
- ↑ Д. К. Пэнди; Singh, D .; Yadawa, P.K .; и другие. (2009). «Ультразвуковое исследование осмия и рутения» (PDF). Платиновые металлы Ред. . 53 (4): 91–97. DOI: 10.1595 / 147106709X430927. Проверено 4 ноября 2014 г.
- ↑ Л. Форро; и другие. «Электронные и механические свойства углеродных нанотрубок» (PDF).
- ↑ Ю. Х. Ян; Li, W. Z .; и другие. (2011). «Радиальная упругость однослойной углеродной нанотрубки, измеренная методом атомно-силовой микроскопии». Письма по прикладной физике . 98 (4): 041901. Bibcode: 2011ApPhL..98d1901Y. DOI: 10,1063 / 1,3546170.
- ↑ Фанг Лю, Пинбин Мин и Цзюй Ли. «Ab initio расчет идеальной прочности и фононной неустойчивости графена при растяжении» (PDF). CS1 maint: несколько имен: список авторов (ссылка)
- ↑ Spear and Dismukes (1994). Синтетический алмаз — Новые технологии CVD . Уайли, штат Нью-Йорк. п. 315. ISBN 978-0-471-53589-8 .
- ↑ Овано, Нэнси (20 августа 2013 г.). «Карбин прочнее любого известного материала». Phys.org .
- ↑ Минцзе Лю, Василий И. Артюхов, Хункён Ли, Фангбо Сю и Борис И. Якобсон (2 декабря 2013 г.). «Карбин из первых принципов: цепочка атомов углерода, наностержень или наноропа?» (PDF). arxiv.org . CS1 maint: несколько имен: список авторов (ссылка)
Дополнительная литература
- ASTM E 111, «Стандартный метод испытаний модуля Юнга, модуля упругости по касательной и модуля хорды», [2]
- Справочник ASM (различные тома) содержит модуль Юнга для различных материалов и информацию по расчетам.Онлайн-версия (требуется подписка)


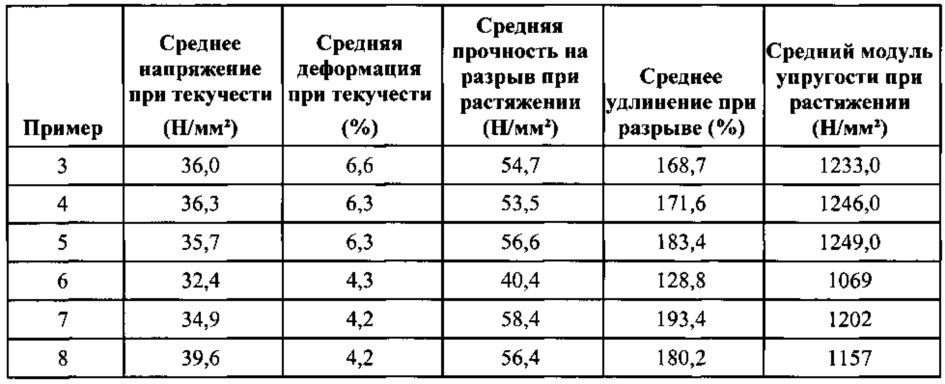 Результаты экспериментальных испытаний
Результаты экспериментальных испытаний