О вреде сотовых телефонов — SAR показатель
SAR (Specific absorption rate) — удельный коэффициент поглощения электромагнитного излучения.
Для того, чтоб как-то оценивать величину излучения сотового аппарата на организм человека, был придуман показатель «Удельный коэффициент поглощения электромагнитной энергии» — SAR.
SAR является мерой скорости, с которой энергия ВЧ излучения поглощается тканями организма, измеряется в Вт/кг.
Стоит отметить, что величины SAR указываемые в инструкциях для сотовых телефонов, подразумевают работу передатчика на полную мощность, к примеру когда вы находитесь в зоне не уверенного приема.
В Украине допустимый уровень SAR определяет стандарт ДСТУ EN 50360: 2007 и составляет он, как и в Европе, 2 Вт/кг для головы и 4 Вт/кг для других частей тела, а сертификацией устройств занимается Украинский государственный центр радиочастот. При этом показателе температура в тканях увеличивается не более чем на 0,3 градуса Цельсия, что не несет вреда организму. Тем не менее, уже при 0,3 градусах, обнаружено разрушение белковых цепочек, но ученые не связывают этот факт и воздействие на здоровье. Для сравнения,
Аналитическая компания Statista опубликовала рейтинг самых опасных смартфонов с точки зрения излучения, пагубно воздействующего на организм человека (изображение ниже), то Xiaomi Mi A1 с результатом 1,75 Вт/кг возглавил этот список.
Рейтинг самых безопасных телефонов по показателю SAR на рынке в целом:
Теперь в список безопасных телефонов можно добавить сети Xiaomi Mi A3. Как стало известно, удельный коэффициент поглощения электромагнитного излучения (Specific absorption rate, SAR) этой модели составляет всего 0,301 Вт/кг, что является достаточно низким показателем.
SAR показатель для популярных моделей XIAOMI:
удельный коэффициент — это… Что такое удельный коэффициент?
- удельный коэффициент
<opt.> relative trichromatic coordinate
Русско-английский технический словарь.
- удельный импульс
- удельный объем
Смотреть что такое «удельный коэффициент» в других словарях:
Удельный коэффициент поглощения электромагнитной энергии — Удельный коэффициент поглощения (англ. Specific Absorption Rate SAR) электромагнитной энергии показатель, определяющий энергию электромагнитного поля, выделяющуюся в тканях тела человека за одну секунду. Данным показателем, в… … Википедия
удельный коэффициент использования — удельная машинная постоянная — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы удельная машинная постоянная EN … Справочник технического переводчика
удельный коэффициент продуктивности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN specific productivity indexspecific productivity index … Справочник технического переводчика
удельный коэффициент пропускания — praleidimo koeficientas statusas T sritis fizika atitikmenys: angl. transmissivity vok. Transmissionskoeffizient, m rus. удельный коэффициент пропускания, m pranc. transmissivité, f … Fizikos terminų žodynas
Удельный коэффициент продуктивности скважины
Удельный расход — Расход турбины, отнесенный к 1 кВт×ч выработанной электроэнергии q м3/(кВт×ч) Источник: РД 153 34.
 0 09.161 97: Положение о нормативных энергетических характеристиках гидроагрегатов и гидроэлектростанций … Словарь-справочник терминов нормативно-технической документации
0 09.161 97: Положение о нормативных энергетических характеристиках гидроагрегатов и гидроэлектростанций … Словарь-справочник терминов нормативно-технической документацииудельный расход энергии криогенной установки (системы) — удельный расход энергии Ндп. коэффициент рефрижерации коэффициент энергозатрат коэффициент охлаждения Отношение энергии, затрачиваемой криогенной установкой (системой), к количеству получаемого продукта (продуктов) или мощности, затраченной… … Справочник технического переводчика
Удельный расход топлива — Удельный расход топлива единица измерения, используемая в грузопассажирских перевозках и обозначающая расход единицы топлива на единицу мощности на расстояние в один километр или в час (или секунду) например − 166 г/л.с.ч., «Удельный… … Википедия
КОЭФФИЦИЕНТ ФИНАНСОВОЙ УСТОЙЧИВОСТИ ПРЕДПРИЯТИЙ — коэффициент, который характеризует состояние и динамику финансовых ресурсов предприятий с точки зрения обеспечения ими производственного процесса и других сторон их деятельности. Для анализа финансовой устойчивости используются четыре основных… … Большой экономический словарь
коэффициент финансовой устойчивости предприятий — Коэффициенты, которые характеризуют состояние и динамику финансовых ресурсов предприятий с точки зрения обеспечения ими производственного процесса и другие сторон их деятельности. Для анализа финансовой устойчивости используются четыре основных… … Справочник технического переводчика
КОЭФФИЦИЕНТ МАТЕРИАЛОЕМКОСТИ — характеризует удельный вес затрат сырья, материалов, покупных полуфабрикатов и получаемых (по кооперации) изделий в стоимости валовой продукции. В экономико математических моделях показатель, выражающий количество материалов, затраченных на… … Большой Энциклопедический словарь
Определение удельного коэффициента поглощения электромагнитной энергии головой человека рядом с Wi-Fi антенной
Пользователи мобильных электронных устройств (телефонов и прочих беспроводных устройств) подвергаются в той или иной мере воздействию СВЧ-излучения. 2} {\rho}
2} {\rho}
где σ — электрическая проводимость материала, |E| — норма электрического поля (среднеквадратическая), а ρ — плотность живых тканей. Единицы измерения — ватт на килограмм (Вт/кг).
С помощью инструментов модуля Радиочастоты пакета COMSOL Multiphysics можно вычислить и проанализировать локальные значения коэффициента SAR в упрощенной модели головы и мозга человека, находящихся рядом с прямоугольной микрополосковой антенной, работающей в частотном диапазоне беспроводных сетей Wi-Fi. Такая модель позволит численно продемонстрировать процесс поглощения головой человека СВЧ-излучения, исходящего от антенны.
Визуализация распределения коэффициента SAR головы человека в приближенной модели головного мозга и напряженности электрического поля на поверзности прямоугольной микрополосковой антенны.
Моделирование облучения фантома человеческой головы СВЧ-излучением
В этой учебной модели используется CAD-геометрия человеческой головы, идентичная специальной антропометрической модели (specific anthropomorphic mannequin — SAM) головы человека, в соответствии со стандартной спецификацией IEEE, IEC и CENELEC по измерению удельного коэффициента поглощения электромагнитной энергии. Исходная геометрия была конвертирована во внутренний формат COMSOL Multiphysics с незначительными упрощениями, и для сокращения вычислительной сложности данной задачи она была уменьшена на 60%. За счет отрисовки эллипсоида была создана упрощенная форма мозга, а остальные части человеческой головы были определены как кортикальная костная ткань.
Антенна рядом с человеческой головой состоит из тонкого стоя металла, нанесенного на прямоугольную диэлектрическую подложку из FR4. На дне подложке также сделана металлизация для заземления. В интерфейсе  Возбуждение задается посредством граничного условия Lumped Port, являющегося упрощенной версией ГУ Port (для возбуждения TEM-мод). В данном случае питание антенны осуществляется при помощи сосредоточенного порта с сопротивлением 50 Ом.
Возбуждение задается посредством граничного условия Lumped Port, являющегося упрощенной версией ГУ Port (для возбуждения TEM-мод). В данном случае питание антенны осуществляется при помощи сосредоточенного порта с сопротивлением 50 Ом.
Для имитации испытания антенны в бесконечном свободном пространстве, фантом человеческой головы и антенна окружаются сферической воздушной областью с дополнительным слоем вдоль внешней границы, в котором используется условие Perfectly Matched Layer (PML). PML выступает в качестве «виртуальной» безэховой камеры, поглощая всю энергию волнового излучения и предотвращая ее нежелательное отражение.
Вид расчетной области: фантом человеческой головы и прямоугольная микрополосковая антенна Wi-Fi. Выделенная на втором изображении область — это PML, половина доменов скрыта с целью наглядного представления внутренней области.
И наконец, для расчета коэффициента SAR на область головы добавляется условие
Обратите внимание на то, что в этой модели применяется допущение об однородности всех материалов. Более реалистично вещество головного мозга описано в модели Specific Absorption Rate (SAR) in the Human Brain model, в которой свойства разных типов живых тканей головы характеризуются интерполяционными функциями, основанными на импортированных данных МРТ-исследований.
Выборка областей для условия Specific Absorption Rate .
Анализ воздействия СВЧ-излучения и расчет коэффициента SAR в области головы человека
Ниже приведены графики распределения коэффициента SAR в голове человека, расположенной рядом с Wi-Fi антенной. Наибольшее значение коэффициента SAR наблюдается на поверхности, обращенной к полю падающего СВЧ-излучения. Как правило, коэффициент SAR зависит от положения антенны и диэлектрических свойств. Человеческое тело имеет разные значения диэлектрических свойств (проницаемость и проводимость), которые к тому же являются частотнозависимыми и неоднородными в пространстве. И проводимость, и диэлектрическая проницаемость тканей человеческого тела влияют на количество поглощенного излучения. Значение коэффициента SAR возрастает при увеличении резистивных потерь.
Наибольшее значение коэффициента SAR наблюдается на поверхности, обращенной к полю падающего СВЧ-излучения. Как правило, коэффициент SAR зависит от положения антенны и диэлектрических свойств. Человеческое тело имеет разные значения диэлектрических свойств (проницаемость и проводимость), которые к тому же являются частотнозависимыми и неоднородными в пространстве. И проводимость, и диэлектрическая проницаемость тканей человеческого тела влияют на количество поглощенного излучения. Значение коэффициента SAR возрастает при увеличении резистивных потерь.
График распределения коэффициента SAR на частоте 2.45 ГГц.
В контексте данной модели также интересно оценить диаграмму направленности системы. Для многих привычно, что такая диаграмма для стандартной микрополосковой антенны должна показывать основное направление излучения сигнала — по нормали к поверхности подложки. Но ниже показаны результаты для излучаемого прямоугольной микрополосковой антенной поля (в дальней зоне), которое в данной системе искажено в силу отражения сигнала от человеческой головы.
Искаженные 2d-диаграмма направленности в плоскости xy (слева) и 3d-диаграмма направленности (справа) излучения в дальней зоне для прямоугольной микрополосковой антенны, расположенной рядом с головой человека, на частоте 2.45 ГГц. Для наглядной визуализации 3d-паттерна рядом с головой масштаб и положение на графике выше были изменены.
Таким образом, значение коэффициента SAR, которое представляет особый интерес для проектировщиков беспроводных устройств, легко получить с помощью COMSOL Multiphysics. После проведения моделирования коэффициент SAR можно также рассчитать для произвольного объема в любой части расчетной области. При создании электронных мобильных устройств, важно определить количество излучения, которое будет поглощаться человеческим телом. Пользователи программного пакета COMSOL Multiphysics и модуля Радиочастоты получают быстрый и наименее затратный метод разработки устройств в соответствии с требованиями безопасности.
Дальнейшие шаги
Для ознакомления с рассмотренной моделью по расчету SAR в человеческой голове, расположенной рядом с Wi-Fi антенной, нажмите кнопку ниже. При этом вы откроете страницу примера в Галерее моделей и приложений, в которой вы найдете подробную документацию с пошаговыми инструкциями по сборке и MPH-файл, который можно скачать при наличии действительной лицензии на программный пакет.
Удельный коэффициент — продуктивность — Большая Энциклопедия Нефти и Газа, статья, страница 1
Удельный коэффициент — продуктивность
Cтраница 1
Удельный коэффициент продуктивности определяется как суточный дебит нефтяной скважины, отнесенный к депрессии пластового давления н к эффективной мощности продуктивного горизонта. [1]
Удельный коэффициент продуктивности ( колонка 39) определяют по графикам рис. XXXII. [2]
Зная удельный коэффициент продуктивности скважины или его среднеарифметическое значение по какому-то участку залежи или площади, нетрудно по формуле ( 145) определить среднюю проницаемость. Коэффициент продуктивности скважины определяется одним из рассмотренных в гл. [3]
Зависимость удельного коэффициента продуктивности от проницаемости и геофизических параметров получена многочисленными исследователями по различным районам. [4]
Часто используется удельный коэффициент продуктивности, обозначающий коэффициент продуктивности, отнесенный на 1 м мощности продуктивного пласта. Когда используется термин удельный, это должно быть специально подчеркнуто. [5]
Продуктивность определяется удельным коэффициентом продуктивности. [6]
Различают: 1) удельный коэффициент продуктивности — К. [7]
[7]
Промежуточные результаты ( увеличение удельного коэффициента продуктивности в 2 раза) были получены вскрытием на глинистом растворе при положительном дифференциальном давлении и цементированием с селективной изоляцией продуктивного пласта. [8]
Приводятся графики корреляционной зависимости удельных коэффициентов продуктивности от проницаемости пластов, зависимости промыслово-геофизических показателей от пористости, проницаемости, нефтегазонасыщенности пластов. [9]
С учетом значений толщин продуктивного пласта приросты удельного коэффициента продуктивности по нефти ( коэффициент продуктивности, приходящийся на 1м толщины пласта) в скважинах 102 и 387 составили соответственно 0 105 и 0 120 м3 / ( сут МПа м), т.е. являются практически одинаковыми. [10]
С учетом значений толщин продуктивного пласта приросты удельного коэффициента продуктивности по нефти ( коэффициент продуктивности, приходящийся на 1м толщины пласта) в скважинах 102 и 387 составили соответственно 0 105 и 0 120 м3 / ( сут МПа м), т.е. являются практически одинаковыми. [11]
При малой относительной глинистости наблюдается большой азброс значений удельного коэффициента продуктивности. Это вязано с преобладающим по сравнению с глинистостью влияния гроения скелета неглинистых и слабоглинистых песчаников на х проницаемость, от которой удельный коэффициент продуктив-ости находится в прямой зависимости: Незначительные вариации ормы, размеров, степени от сортированности и плотности укладки грен скелета вызывают большие изменения коэффициента про-ицаемости. [12]
Нефтяные пласты различаются между собой по средней величине удельного коэффициента продуктивности скважины. [13]
[13]
Примем, что дебит скважины в основном определяется удельным коэффициентом продуктивности на единицу эффективной толщины и слабо зависит от эффективной толщины, поскольку последняя изменяется незначительно. Существует минимально допустимый дебит нефти, и, если фактический дебит добывающей скважины ниже минимального экономически допустимого, то ее следует выключать из работы вместе с ее балансовыми и подвижными запасами нефти. Доля таких скважин в общем числе скважин принимается равной их доле в общих балансовых и общих извлекаемых запасах нефти. Дебит нефти добывающей скважины принимается пропорциональным ее коэффициенту продуктивности. Зональная неоднородность нефтяной залежи по дебитам добывающих скважин равна зональной неоднородности по их коэффициентам продуктивности. При выключении из работы малодебитных скважин с дебитом ниже минимального экономически допустимого получается искусственное разрежение сетки скважин. Эмпирическая формула доли теряемых подвижных запасов была получена для ситуации, когда зональную неоднородность нефтяных пластов по продуктивности описывает функция гамма-распределения. [14]
При бурении с промывкой такими растворами сокращается время освоения, увеличиваются удельные коэффициенты продуктивности и удельные дебиты, а также увеличиваются механические скорости при бурении электробуром. [15]
Страницы: 1 2 3 4
Удельный вес дизельного топлива. расчет удельного веса дизтоплива.
Компания «Ренетоп» предлагает низкую цену на дизельное топливо с доставкой по Уралу.
Удельный вес рассчитывается путем умножения плотности на коэффициент ускорения свободного падения, который всегда составляет 9,81 м/с2. Например, 1 кг дизельного топлива плотностью 840 кг/м3 будет иметь удельный вес 8240 Н/м3.
Важную роль отыгрывает плотность дизельного топлива. Она меняется при перемене температуры топлива. При изменении температуры на 1 градус по Цельсию плотность изменяется коэффициент 0,0007. При снижении температуры на 1 градус плотность повышается, при повышении снижается.
Посмотрите наши цены:
Удельный вес дизтоплива летнего
Удельный вес летнего дизтоплива напрямую зависит от его температуры. Государственным стандартом установлен в пределах 8440 Н/м3.
Удельный вес дизтоплива зимнего
Удельный вес зимнего топлива зависит от его температуры. Государственным стандартом установлен в пределах 8240 Н/м3.
Формулы расчета плотности, веса и объема дизтоплива
Формула определения веса ДТ
Вес топлива определяется умножением плотности нефтепродукта на его объем. 1850 литров ДТ при плотности 0,840 кг/м3 будет весить 1554 кг. 1000 литров дизтоплива плотностью 0,860 кг/м3 будет весить 860 кг.
Формула определения объема ДТ
Актуальный при транспортировке, реализации и бухгалтерском учете вопрос: как перевести вес топлива в объем?
Чтобы узнать объем дизельного топлива необходимо его массу поделить на плотность. Если есть 1 тонна ДТ, а его плотность составляет 0,840 кг/м3 – объем составит 1 190 литров 476 грамм.
Формула определения плотности ДТ
Плотность дизельного топлива – это соотношение массы нефтепродукта к его объему. Если есть 860 кг дизтоплива объемом 1000 литров, то плотность составит 0,860 кг/м3.
Плотность дизельного топлива регламентируется ГОСТ 305-82. Стандарт фиксирует значение при 20 градусах по Цельсию. Плотность дизтоплива, в зависимости от его сезонного вида государственными стандартами установлена следующая:
- зимнего – 860 кг/м3;
- летнего — 840 кг/м3;
- арктического – 830кг/м3.
Для определения плотности дизельного топлива другим методом нужно:
- В паспортных данных нефтепродукта найти плотность нефтепродукта при 20 градусах по Цельсию.

- Замерять фактическую температуру дизельного топлива в емкости для транспортировки или хранения.
- Разность температуры умножаем на коэффициент 0,0007.
- Вносим поправку. Если температура выше – отнимаем значение от паспортной плотности, если ниже добавляем.
Коэффициент теплопроводности, удельная теплоемкость и удельный вес зависят от температуры и давления
Содержание:
Коэффициент теплопроводности, удельная теплоемкость и удельный вес зависят от температуры и давления
- Зависимость от давления. Для твердых тел эти величины очень мало зависят от давления. Однако, для всех твердых тел, которые имеют температуру внутри. Термин «температурное (тепловое) напряжение» известен как неравномерность, возникающая при напряжении. Эти напряжения такие же, как и связанные с ними остаточные напряжения при литье. Это потрясающе. Поэтому при таком высоком давлении никогда нельзя игнорировать мысль о том, что сказывается очень слабая зависимость от самого себя. Физические константы давления. Однако, с одной стороны, достоверной информации по этому вопросу нет, поскольку отсутствуют эмпирические данные о законе, подлежащем определению.
Такое явление называется эффектом Лейденфроста в связи с тем, что оно было доложено и объяснено Лейденфростом в 1756 г. Людмила Фирмаль
Эта зависимость и, с другой стороны, все расчеты становятся очень
сложными, как только учитываются флуктуации физических констант. б. Это
зависит от температуры. Сплав с Коэффициент теплового расширения равен
нулю. Это означает, что их плотность не зависит от температуры.
Аналогично, материал, теплопроводность или Его теплоемкость
не изменяется с температурой. Однако такие вещества встречаются редко
exceptions. In в общем случае X, c и p следует рассматривать как функцию
температуры. Отсюда следует дифференциальное уравнение(4)
Целесообразнее написать его в следующей форме: Способ, которым мы решали
исследуемую проблему, состоял в составлении общего решения
из конкретного решения.
- Однако эта техника разрешена только в том случае, если: Дифференциальные уравнения линейны. С другой стороны, уравнение с этим членом уже не является линейным、 Кроме того, способ суммирования конкретного решения отключен. Пути, которые необходимо выбирать в этих условиях-в большинстве случаев это математические методы аппроксимации*- Их аргументы настолько многочисленны и разнообразны, что выходят за рамки этой книги. В некоторых простых случаях возможны аналитические соображения(например, в случае линейной зависимости теплопроводности от температуры).
Низкая теплопроводность пленки пара, через которую должно проходить тепло, объясняет меньшие величины коэффициента теплообмена для этой области. Людмила Фирмаль
Тогда для пластинчатой плотности теплового потока толщиной X в установившихся условиях、 В этих условиях, естественно, возникает понятие среднего коэффициента теплопроводности Xh. Это и есть формула Очевидно, что в рассматриваемом случае величина kt будет равна среднему арифметическому значения X! А при температуре и или, в данном случае, это полностью эквивалентно, значение Х и Средняя температура=(O, 02) / 8.In простой расчет, это Зависимости также действительны для шариков и cylinders.
Смотрите также:
Плотность или удельный вес щебня фракций 5-20, 20-40 и 40-70. Таблица плотностей, насыпная плотность щебня.
Щебень – это строительный камень, получаемый в результате измельчения горных пород, а также из пемз, кирпичей, отходов металлургического производства. От технических характеристик щебня зависит качество получаемого бетона, его марка и др. параметры, при этом очень важную роль играют удельный вес или насыпная плотность щебня.
От чего зависит плотность гранитного щебня?
Что такое плотность вещества известно из школьного курса физики – это отношение массы вещества к его объёму. Плотность гранита составляет 2600 кг/м3, однако, представленная ниже таблица плотности щебня основных фракций даёт иные показатели;
Таблица 1. Плотность (удельный вес) различных фракций щебня
Плотность (удельный вес) различных фракций щебня
| Материал | фракция, мм | Удельный вес, т/ м3 |
| Отсев | 0-5 | 1,41 |
| Щебеночная смесь | 0-70 | 1,52 |
| Щебень | 5-10 | 1,38 |
| 5-20 | 1,35 | |
| 5-25 | 1,38 | |
| 20-40 | 1,35 | |
| 25-60 | 1,37 | |
| 40-70 | 1,35 |
Как видите, плотность щебня фракции 20-40 составляет 1,35 т/м3 или 1350 кг/м3 – почти в два раза меньше чем плотность гранита в недробленом состоянии. Столь большая разница образуется за счет воздушных прослоек, из-за чего собственно и введен показатель насыпной плотности. Большую роль играет фракция дробления – чем она мельче, чем выше показатель удельного веса. Поэтому плотность щебня 20-40, из-за меньшего количества воздушных прослоек выше, чем плотность щебня 40-70, крупнофракционного строительного камня. Также следует учитывать, что, плотность гранитного щебня указывается в сухом состоянии.
Что же касается термина «удельный вес» то, под ним часто подразумевается плотность вещества, хотя, с точки зрения физики это разные понятия. Удельный вес – это отношение веса к объёму вещества. Из-за того, что на поверхности Земли вес практически равен массе, то и удельный вес равен плотности. Соответственно удельный вес щебня 10-20 составляет 1,35 т/м3, т. е. 1350 кг в одном кубическом метре.
Есть и другие параметры, влияющие на насыпную плотность гранитного щебня:
- Вид и, соответственно, плотность породы из которого добывается щебень. Зависит от места добычи.
- Условия хранения щебня.
- Форма или лещадность щебня.
- Процент водопоглощения.
- Влажность материала.

К примеру, в сухом состоянии удельный вес щебня 20-40 по таблицам составляет 1,35 т/м3. При водопоглощении 0,5% его вес, соответственно, увеличится на данный показатель.
Значительно влияет и рельефность зерен щебня, его лещадность. Наиболее высокий показатель уплотнения имеют зерна кубовидной формы, содержащие до 15% игловатых и пластинчатых зерен. При большом содержании игольчатых и пластинчатых зерен плотность уменьшается. Такой щебень имеет наиболее высокую просадку и водопоглощение, требует особых условий при хранении и транспортировке.
Важность показателя насыпной плотности щебня
При производстве бетона существует зависимость – чем выше насыпная плотность или, к примеру, удельный вес щебня фракции 20-40, тем меньше используется цемента. Параметр насыпной плотности важен для транспортировки и хранения – определения грузоподъёмности транспорта и вместительности склада. От точности информации зависят параметры полученного бетона, характеристики строительных конструкций, транспортные расходы.
Для получения точного значения насыпной плотности проводятся лабораторные измерения. Так, например, чтобы определить удельный вес щебня 40-70 данным материалом заполняется определенная мера объёма, как правило, бочка объёмом до 50 литров. Взвешивание производится пустой и заполненной тары, разница показаний делится на объём. Полученный результат отражается в сертификатах сопровождающих материал.
Плотность определяет и после измельчения и высушивания единицы материала, что исключает наличие пустот. Так определяется реальная плотность щебня и его пористость. Например, если удельный вес щебня 5-20 составляет 1300 кг/м3, то полученный по данной методике результат будет составлять порядка 2500 кг/м3.
Можно и самостоятельно определить примерную насыпную плотность щебня, для чего необходима любая емкость, объём которой либо хорошо известен, либо легко определяется путем умножения длины на ширину и на высоту. Далее, как и в лаборатории, тара взвешивается пустой и заполненной материалом, полученная разница составляет чистый вес щебня. Полученный результат необходимо разделить на объем, и вы узнаете примерный удельный вес материала. Более точный результат дают только лабораторные исследования.
Полученный результат необходимо разделить на объем, и вы узнаете примерный удельный вес материала. Более точный результат дают только лабораторные исследования.
Удельный коэффициент поглощения и эффект пакета фитопланктона в озере Тайху, Китай
Алалли, К., А. Брико и Х. Клаустр, 1997. Пространственные вариации коэффициентов поглощения хлорофилла фитопланктоном и фотосинтетически активными пигментами в экваториальной зоне. Тихий океан. Журнал геофизических исследований 102: 12413–12423.
Артикул Google ученый
Андерсон Т. Р., 1993. Усредненная по спектру модель проникновения света и фотосинтеза.Лимнология и океанография 38: 1403–1419.
Google ученый
Бабин, М., А. Морель, Х. Клаустр, А. Брико, З. Колбер и П.Г. Фальковски, 1996. Вариации максимального квантового выхода фиксации углерода в эвтрофных, мезотрофных и олиготрофные морские системы. Deep Sea Research I 43: 1241–1272.
Артикул CAS Google ученый
Бабин, М., Stramski, D., Ferrari, GM, Claustre, H., Bricaud, A., Obloensky, G. & N. Hoepffner, 2003. Вариации коэффициентов поглощения света фитопланктоном, частицами, не содержащими водорослей, и растворенным органическим веществом в прибрежных водах. по Европе. Журнал геофизических исследований, 108 (C7): 3211.
Google ученый
Бидигар Р. Р., Ондрусек М. Э., Морроу Дж. Х. и др. 1990. Свойства поглощения пигментов водорослей in vivo. SPIE, Ocean Optical 1032: 290–302.
Э., Морроу Дж. Х. и др. 1990. Свойства поглощения пигментов водорослей in vivo. SPIE, Ocean Optical 1032: 290–302.
Артикул Google ученый
Браосио-Леон, Ó. А., Р. Миллан-Нунес и Э. Сантамарфа-дель-Анхель, 2006. Пространственная изменчивость коэффициентов поглощения фитопланктона и пигментов у побережья Нижней Калифорнии в ноябре 2002 г. Океанографический журнал 62: 873–885.
Артикул Google ученый
Брико, А., М. Бабин, А. Морель и Х. Клаустр, 1995. Анализ и параметризация изменчивости удельного коэффициента поглощения хлорофилла естественного фитопланктона.Журнал геофизических исследований 100 (C7): 13321–13332.
Артикул Google ученый
Брико, А., Х. Клаустр, Дж. Рас и К. Обелькхейр, 2004. Естественная изменчивость поглощения фитопланктона в океанических водах: влияние размерной структуры популяции водорослей. Журнал геофизических исследований 109: C11010.
Артикул CAS Google ученый
Cao, W.X., Y. Z. Yang, S. Liu, X. Q. Xu, D. T. Yang и J. L. Zhang, 2005. Спектральный коэффициент поглощения фитопланктона и его связь с хлорофиллом а и отражательная способность дистанционного зондирования в прибрежных водах южного Китая. Прогресс в естествознании 15 (4): 342–350.
Артикул Google ученый
Чен, Ю. В. , К. Л. Чен и Ю. Х. Ху, 2006. Обсуждение возможной ошибки при анализе концентрации хлорофилла А фитопланктона с использованием метода экстракции горячим этанолом (на китайском языке).Журнал озерной науки 18 (5): 550–552.
, К. Л. Чен и Ю. Х. Ху, 2006. Обсуждение возможной ошибки при анализе концентрации хлорофилла А фитопланктона с использованием метода экстракции горячим этанолом (на китайском языке).Журнал озерной науки 18 (5): 550–552.
CAS Google ученый
Чиотти, А. М., М. Р. Льюис и Дж. Дж. Каллен, 2002. Оценка взаимосвязи между размером доминирующих клеток в естественных сообществах фитопланктона и спектральной формой коэффициента поглощения. Лимнология и океанография 47 (2): 404–417.
CAS Google ученый
Кливленд, Дж.С. и А. Д. Вайдеманн, 1993. Количественная оценка поглощения водными частицами: поправка на многократное рассеяние для стекловолоконных фильтров. Лимнология и океанография 38: 1321–1327.
CAS Google ученый
Каллен, Дж. Дж., А. М. Чиотти, Р. Ф. Дэвис и М. Р. Льюис, 1997. Оптическое обнаружение и оценка цветения водорослей. Лимнология и океанография 42: 1223–1239.
CAS Статья Google ученый
Фальковски, П.G. & J. LaRoche, 1991. Акклимация водорослей к спектральному излучению. Журнал прикладной психологии 27: 8–14.
Артикул Google ученый
Фичек Д., С. Качмарек, Й. Стоу-Эгирт, Б. Возняк, Р. Майхровски и Дж. Дера, 2004. Спектры поглощения света пигментами фитопланктона в Балтийском море; выводы, которые следует сделать на основе гауссовского анализа эмпирических данных. Океанология 46 (4): 533–555.
Океанология 46 (4): 533–555.
Google ученый
Гордон, Х.Р., О. Б. Браун, Р. Х. Эванс, Дж. В. Браун, Р. С. Смит, К. С. Бейкер и Д. К. Кларк, 1988. Полуаналитическая модель яркости цвета океана. Журнал геофизических исследований 93: 10909–10924.
Артикул Google ученый
Харимото, Т., Дж. Исизака и Р. Цуда, 1999. Широтное и вертикальное распределение спектров поглощения фитопланктона в центральной части северной части Тихого океана весной 1994 года. Океанографический журнал 55: 667–679.
Артикул Google ученый
Hoepffner, N. & S. Sathyendranath, 1991. Влияние пигментного состава на абсорбционные свойства фитопланктона. Серия «Прогресс морской экологии» 73: 11–23.
Артикул CAS Google ученый
Халст, Х. К., 1981. Рассеяние света мелкими частицами. Dover Publ., Inc., Нью-Йорк: 470.
Google ученый
Кана, Т.М., П. М. Глиберт, Р. Герике и Н. А. Велшмевер, 1988. Зеаксантин и β-каротин в Synechococcus WH7803 по-разному реагируют на облучение. Лимнология и океанография 33: 1623–1627.
CAS Google ученый
Кифер, Д. А. и Б. Г. Митчелл, 1983. Простое стационарное описание роста фитопланктона, основанное на поперечном сечении поглощения и квантовой эффективности. Лимнология и океанография 28: 770–776.
Лимнология и океанография 28: 770–776.
Google ученый
Lazzara, L., A. Bricaud & H. Claustre, 1996. Свойства спектрального поглощения и возбуждения флуоресценции фитопланктонных популяций в мезотрофных и олиготрофных участках тропической Северной Атлантики (программа EUMELI). Deep Sea Research I 43: 1215–1240.
Артикул CAS Google ученый
Ли, З. П. и К. Л. Кардер, 2004 г.Спектр поглощения пигментов фитопланктона, полученный на основе гиперспектральной отражательной способности дистанционного зондирования. Дистанционное зондирование окружающей среды 89: 361–368.
Артикул Google ученый
Лоренц, С. Э., А. Д. Вайдеманн и М. Туэль, 2003. Спектральное поглощение фитопланктона под влиянием размерной структуры сообщества и состава пигмента. Журнал исследований планктона 25 (1): 35–61.
Артикул CAS Google ученый
Лоренцен, К.J., 1967. Определение хлорофилла и феопигментов: спектрофотометрические уравнения. Лимнология и океанография 12 (2): 343–346.
CAS Google ученый
Марра, Дж., К. К. Триз и Дж. Э. О’Рейли, 2007. Поглощение пигментов фитопланктоном: надежный предиктор первичной продуктивности на поверхности океана. Deep Sea Research 54: 155–163.
Артикул Google ученый
Mercado, J.М., Рамирес Т. и Д. Кортес, 2007. Изменения концентрации питательных веществ, вызванные гидрологической изменчивостью, и их влияние на поглощение света фитопланктоном в море Альборан (Западная часть Средиземного моря). Журнал морских систем. DOI: 10.1016 / j.jmarsys.2007.05.009
Милли, Д. Ф., О. М. Шофид, Г. Дж. Киркпатрик, Г. Джонсен, П. А. Тестер и Б. Т. Виньярд, 1997. Обнаружение вредоносного цветения водорослей с помощью фотопигмн и сигнатуры поглощения: исследование динофлагеллаты красного прилива Флориды, Gymnodinium breve .Лимнология и океанография 42: 1240–1251.
CAS Google ученый
Митчелл, Б. Г., 1990. Алгоритмы для определения коэффициента поглощения водных твердых частиц с использованием метода количественной фильтрации (QFT). Общество инженеров фотооптического приборостроения 1302: 137–148.
Google ученый
Моберг, Л., Б. Карлберг, К. Соренсен и Т. Келлквист, 2002.Оценка численности класса фитопланктона по спектрам поглощения и хемометрии. Таланта 56: 153–160.
PubMed Статья CAS Google ученый
Морель А., 1988. Оптическое моделирование верхнего слоя океана в зависимости от содержания в нем биогенного вещества (воды для случая I). Журнал геофизических исследований 93: 10749–10768.
Артикул Google ученый
Морель, А., 1991. Световой и морской фотосинтез: спектральная модель с геохимическими и климатологическими последствиями. Прогресс в океанографии 26: 263–306.
Артикул Google ученый
Морель, А. и А. Брико, 1981. Теоретические результаты, касающиеся поглощения света в дискретной среде, и их применение к удельному поглощению фитопланктоном. Deep Sea Research 28: 1375–1393.
Артикул Google ученый
Миллан-Нуньес, Э., М. Э. Серацки, Р. Миллан-Нуньес, Дж. Р. Лара-Лара, Г. Гаксиола-Кастро и К. К. Триес, 2004. Удельный коэффициент поглощения и биомасса фитопланктона в южной части Калифорнийского течения. Deep Sea Research 51: 817–826.
Google ученый
Мур, Л. Р., Р. Герике и С. В. Чизхолм, 1995. Сравнительная физиология Synechococcus и Prochlorococcus : влияние света и температуры на рост, пигменты, флуоресценцию и абсорбционные свойства.Серия «Прогресс морской экологии» 116: 259–275.
Артикул Google ученый
Stoń, J. & A. Kosakowska, 2000. Качественный и количественный анализ пигментов фитопланктона Балтии. Океанология 42 (4): 449–471.
Google ученый
Стюарт В., С. Сатиендранат, Т. Платт, Х. Маасс и Б. Д. Ирвин, 1998. Пигменты и видовой состав естественных популяций фитопланктона: влияние на спектры поглощения. Журнал исследований планктона 20: 187–217.
Журнал исследований планктона 20: 187–217.
Артикул CAS Google ученый
Сузуки, К., М. Кишино, К. Сасаока, С. Сайто и Т. Саино, 1998. Специфические для хлорофилла коэффициенты поглощения и пигменты фитопланктона у побережья Санрику, северо-западная часть северной части Тихого океана. Журнал океанографии 54: 517–526.
Артикул CAS Google ученый
Возняк, Б., Дж. Дера, Д. Фичек, Р. Майхровски, С. Качмарек, М. Островска и О. И. Кобленц-Мишке, 1999. Моделирование влияния акклиматизации на абсорбционные свойства морского фитопланктона. Океанология 41 (2): 187–210.
Google ученый
Йенч, С. С. и Д. А. Финни, 1989. Мост между оптикой океана и микробной экологией. Лимнология и океанография 34: 1694–1705.
Артикул Google ученый
Чжан, Ю.Л., Б. Чжан, X. Ван, Дж. С. Ли, С. Фэн, К. Х. Чжао, М. Л. Лю и Б. К. Цинь, 2007. Исследование характеристик поглощения хромофорных растворенных органических веществ и частиц в озере Тайху, Китай. Hydrobiologia 592: 105–120.
Артикул CAS Google ученый
Таблица коэффициентов для модели подходящей регрессии
Стандартная ошибка коэффициента оценивает изменчивость между оценками коэффициентов, которую вы получили бы, если бы вы снова и снова брали выборки из одной и той же совокупности.Расчет предполагает, что размер выборки и коэффициенты для оценки останутся прежними, если вы будете выполнять выборку снова и снова.
Интерпретация
Используйте стандартную ошибку коэффициента, чтобы измерить точность оценки коэффициента. Чем меньше стандартная ошибка, тем точнее оценка. Деление коэффициента на его стандартную ошибку дает значение t. Если p-значение, связанное с этой t-статистикой, меньше вашего уровня значимости, вы делаете вывод, что коэффициент статистически значим.
Например, технические специалисты оценивают модель инсоляции как часть теста солнечной тепловой энергии:Регрессионный анализ: инсоляция по сравнению с югом, севером, временем суток.
Коэффициенты Термин Coef SE Coef T-Value P-Value VIF Константа 809 377 2,14 0,042 Юг 20,81 8,65 2,41 0,024 2,24 Север -23,7 17,4 -1,36 0,186 2,17 Время суток -30,2 10,8 -2,79 0,010 3,86
В этой модели север и юг измеряют положение фокусной точки в дюймах.Коэффициенты для Севера и Юга похожи по величине. Стандартная ошибка коэффициента для юга меньше, чем стандартная ошибка коэффициента для севера. Таким образом, модель может оценить коэффициент для Юга с большей точностью.
Стандартная ошибка коэффициента Севера почти равна значению самого коэффициента. Полученное p-значение больше, чем обычные уровни уровня значимости, поэтому вы не можете сделать вывод, что коэффициент для Севера отличается от 0.
Хотя коэффициент для юга ближе к 0, чем коэффициент для севера, стандартная ошибка коэффициента для юга также меньше. Полученное p-значение меньше обычных уровней значимости. Поскольку оценка коэффициента для Юга более точна, можно сделать вывод, что коэффициент для Юга отличается от 0.
Статистическая значимость — это один из критериев, который вы можете использовать для сокращения модели в множественной регрессии. Для получения дополнительной информации перейдите к уменьшению модели.
% PDF-1.5
%
1 0 obj>
эндобдж
2 0 obj>
эндобдж
3 0 obj>
эндобдж
4 0 obj> поток конечный поток
эндобдж
xref
0 5
0000000000 65535 ф
0000000016 00000 н. 0000000075 00000 н.
0000000120 00000 н.
0000000210 00000 н.
трейлер
] >>
startxref
3378
%% EOF
1 0 obj>
эндобдж
2 0 obj>
эндобдж
3 0 obj>
эндобдж
5 0 obj null
эндобдж
6 0 obj> / ProcSet [/ PDF / Text] / ExtGState 7 0 R >> / StructParents 9 / LastModified (D: 200
0000000075 00000 н.
0000000120 00000 н.
0000000210 00000 н.
трейлер
] >>
startxref
3378
%% EOF
1 0 obj>
эндобдж
2 0 obj>
эндобдж
3 0 obj>
эндобдж
5 0 obj null
эндобдж
6 0 obj> / ProcSet [/ PDF / Text] / ExtGState 7 0 R >> / StructParents 9 / LastModified (D: 200
140828-05 ‘) >> эндобдж 7 0 obj> эндобдж 8 0 obj> эндобдж 9 0 obj> эндобдж 10 0 obj / По умолчанию эндобдж 11 0 obj / По умолчанию эндобдж 12 0 obj / по умолчанию эндобдж 13 0 obj> эндобдж 14 0 obj> эндобдж 15 0 obj> поток HViTTGn {- «nFVQ0 * FǸ ‘{DPTT1q} (QGl.qAmPGL9ў7L3 Os_zu ~ uH0ͩI} xȦΖ |
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с вашим системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Коэффициент детерминации: Обзор
Что такое коэффициент детерминации?
Коэффициент детерминации — это статистическое измерение, которое исследует, как различия в одной переменной могут быть объяснены разницей во второй переменной при прогнозировании исхода данного события. Другими словами, этот коэффициент, более известный как R-квадрат (или R 2 ), оценивает, насколько сильна линейная связь между двумя переменными, и на него сильно полагаются исследователи при проведении анализа тенденций.Приведем пример его применения: этот коэффициент может включать в себя следующий вопрос: если женщина забеременеет в определенный день, какова вероятность того, что она родит ребенка в определенный день в будущем? В этом сценарии этот показатель предназначен для расчета корреляции между двумя взаимосвязанными событиями: зачатием и рождением.
Ключевые выводы
- Коэффициент детерминации — это сложная идея, основанная на статистическом анализе моделей данных.
- Коэффициент детерминации используется для объяснения того, насколько изменчивость одного фактора может быть вызвана его отношением к другому фактору.

- Этот коэффициент обычно известен как R-квадрат (или R 2 ), и иногда его называют «степенью соответствия».
- Эта мера представлена как значение от 0,0 до 1,0, где значение 1,0 указывает на идеальное соответствие и, таким образом, является высоконадежной моделью для будущих прогнозов, а значение 0,0 указывает на то, что модель не может точно моделировать данные. вообще.
Понимание коэффициента детерминации
Коэффициент детерминации — это измерение, используемое для объяснения того, насколько изменчивость одного фактора может быть вызвана его взаимосвязью с другим связанным фактором. Эта корреляция, известная как «степень соответствия», представлена как значение от 0,0 до 1,0. Значение 1,0 указывает на идеальное соответствие и, таким образом, является высоконадежной моделью для будущих прогнозов, а значение 0,0 указывает на то, что расчет вообще не может точно смоделировать данные.Но значение 0,20, например, предполагает, что 20% зависимой переменной предсказывается независимой переменной, тогда как значение 0,50 предполагает, что 50% зависимой переменной предсказывается независимой переменной, и так далее.
График коэффициента детерминации
На графике степень соответствия измеряет расстояние между подогнанной линией и всеми точками данных, которые разбросаны по диаграмме. Плотный набор данных будет иметь линию регрессии, которая близка к точкам и будет иметь высокий уровень соответствия, что означает, что расстояние между линией и данными невелико.Хотя хорошее соответствие имеет R 2 , близкое к 1,0, само по себе это число не может определить, смещены ли точки данных или прогнозы. Он также не сообщает аналитикам, является ли значение коэффициента детерминации изначально хорошим или плохим. Пользователь по своему усмотрению может оценить значение этой корреляции и то, как ее можно применить в контексте анализа будущих тенденций.
Логит-модель случайных параметров (или смешанная)
Логит-модель случайных параметров оценивается путем предоставления аргумента rpar для mlogit .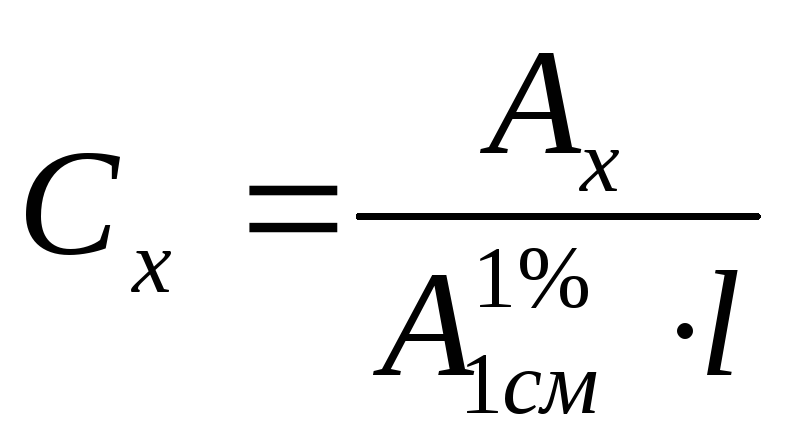 Этот аргумент представляет собой именованный вектор, имена которых являются случайными коэффициентами, а значения — именем закона распределения. В настоящее время нормальный (
Этот аргумент представляет собой именованный вектор, имена которых являются случайными коэффициентами, а значения — именем закона распределения. В настоящее время нормальный ( "n" ), логарифмически нормальный ( "ln" ), без цензуры нормальный ( "cn" ), равномерный ( "u" ) и треугольный ( "t" ) доступны дистрибутивы. Для этих распределений оцениваются два параметра, которые для нормальных связанных распределений являются средним значением и стандартным отклонением основного нормального распределения, а для равномерного и треугольного распределения — средним значением и половинным диапазоном распределения.Для этих двух последних дистрибутивов также предусмотрены варианты с нулевым ограничением ( «zbt» и «zbu» ). Эти два распределения определяются только одним параметром (средним), а их область определения варьируется от 0 до двойного среднего значения.
R — количество отрисовок, halton указывает, следует ли использовать отрисовки halton (см. Поезд 2009, глава 9) ( NA и NULL указывают, соответственно, что используются отрисовки halton по умолчанию и что псевдо- случайные числа), панель — логическое значение, которое указывает, следует ли использовать версию логарифмической вероятности панельных данных.
Корреляции между случайными параметрами могут быть введены только для распределенных случайных параметров, связанных с нормальным распределением, с использованием аргумента корреляции . Если ИСТИНА , все связанные с нормой случайные параметры коррелируются. Аргумент корреляции также может быть вектором символов, указывающим случайные параметры, которые считаются коррелированными.
Поезд
Мы используем набор данных Train , ранее приведенный к объекту dfidx с именем Tr .Сначала мы оценим полиномиальную модель: обе альтернативы — виртуальные поездки на поезде, уместно использовать только общие коэффициенты и удалить точку пересечения:
библиотека ("mlogit")
data ("Поезд", package = "mlogit")
Поезд $ choiceid <- 1: nrow (Поезд)
Tr <- dfidx (Поезд, choice = "choice", варьируясь = 4:11, sep = "_",
напротив = c ("цена", "комфорт", "время", "изменение"),
idx = list (c ("choiceid", "id")), idnames = c ("chid", "alt"))
Tr $ price <- Tr $ price / 100 * 2. 20371
Tr $ time <- Tr $ time / 60
Train.ml <- mlogit (выбор ~ цена + время + сдача + комфорт | - 1, Тр)
coef (сводка (Train.ml))
20371
Tr $ time <- Tr $ time / 60
Train.ml <- mlogit (выбор ~ цена + время + сдача + комфорт | - 1, Тр)
coef (сводка (Train.ml)) ## Estimate Std. Ошибка z-значения Pr (> | z |)
## цена 0,06735804 0,003393252 19,850585 0,000000e + 00
## время 1.72055142 0.160351702 10.729861 0.000000e + 00
## изменить 0,32634094 0,059489152 5,485722 4,117843e-08
## комфорт 0,94572555 0,064945464 14,561842 0,000000e + 00 Все коэффициенты высокозначимы и имеют прогнозируемый положительный знак (напомним, что увеличение переменной комфорт подразумевает использование менее комфортного класса).Коэффициенты нельзя интерпретировать напрямую, но разделив их на ценовой коэффициент, мы получим денежные значения:
coef (Train.ml) [- 1] / coef (Train.ml) [1] ## время переключения комфорт
## 25.54337 4.84487 14.04028 Мы получаем стоимость 26 евро за час путешествия, 5 евро за смену и 14 евро за поездку более комфортным классом. Затем мы оцениваем модель с тремя случайными параметрами: время , изменение и комфорт .Сначала оценим некоррелированную модель смешанного логита:
Train.mxlu <- mlogit (выбор ~ цена + время + изменение + комфорт | - 1, Tr,
панель = ИСТИНА, rpar = c (время = "n", изменение = "n", комфорт = "n"), R = 100,
correlation = FALSE, halton = NA, method = "bhhh")
имена (coef (Train.mxlu)) ## [1] «цена» «время» «изменить» «комфорт»
## [5] "sd.time" "sd.change" "sd.comfort" По сравнению с полиномиальной логит-моделью теперь есть еще три коэффициента, которые являются стандартными отклонениями распределения трех случайных параметров.Коррелированная модель получается путем установки аргумента корреляции на ИСТИНА .
Train.mxlc <- update (Train.mxlu, correlation = TRUE)
имена (coef (Train.mxlc)) ## [1] "цена" "время"
## [3] "изменение" "комфорт"
## [5] "chol. time: time" "chol.time: change"
## [7] "chol.change: change" "chol.time: comfort"
## [9] «чол.замена: комфорт» «чол.комфорт: комфорт»
time: time" "chol.time: change"
## [7] "chol.change: change" "chol.time: comfort"
## [9] «чол.замена: комфорт» «чол.комфорт: комфорт» Теперь существует 6 параметров, которые являются элементами разложения Холецкого ковариационной матрицы трех случайных параметров.2 \) и \ (\ sigma_ {ij} \) - это соответственно дисперсия случайного параметра \ (i \) и ковариация между двумя случайными параметрами \ (i \) и \ (j \). Следовательно, первый оцениваемый параметр можно просто интерпретировать как стандартное отклонение первого случайного параметра, но пять других не могут быть легко интерпретированы.
Случайные параметры могут быть извлечены с помощью функции rpar , которая принимает в качестве первого аргумента объект mlogit , а в качестве второго аргумента par - параметр (ы), который необходимо извлечь.Эта функция возвращает объект rpar , и для его описания предоставляется метод сводки :
marg.ut.time <- rpar (Train.mxlc, "время")
сводка (marg.ut.time) ## Мин. 1st Qu. Среднее значение 3-го кв. Максимум.
## -Inf 1.283749 4.893752 4.893752 8.503756 Inf Предполагаемый случайный параметр находится в «пространстве предпочтений», что означает, что это предельная полезность времени.
Обратите внимание, что сводка (марг.ut.time) отображает безусловное распределение предельной полезности времени.
Параметры в пространстве «готовность платить» (WTP) легче интерпретировать. Они могут быть оценены напрямую (функция, не поддерживаемая mlogit ) или могут быть получены из предельной полезности путем деления ее на коэффициент ковариаты, выраженный в денежном выражении (например, цена), взятый как неслучайный параметр. Затем соотношение можно интерпретировать как денежное выражение (или готовность платить).Чтобы получить распределение случайных параметров в пространстве WTP, можно использовать аргумент norm из rpar :
wtp. time <- rpar (Train.mxlc, "time", norm = "price")
сводка (wtp.time)
time <- rpar (Train.mxlc, "time", norm = "price")
сводка (wtp.time) ## Мин. 1st Qu. Среднее значение 3-го кв. Максимум.
## -Inf 8.753119 33.367588 33.367588 57.982056 Inf Среднее значение (и среднее значение, поскольку распределение симметрично) времени перевозки составляет около 33 евро.Предусмотрено несколько методов / функций для извлечения индивидуальных статистических данных ( среднее , среднее и стандартное отклонение соответственно для среднего, медианного и стандартного отклонения):
среднее (rpar (Train.mxlc, "time", norm = "price")) ## [1] 33.36759 med (rpar (Train.mxlc, "time", norm = "price")) ## [1] 33.36759 stdev (rpar (Train.mxlc, "time", norm = "price")) ## [1] 36.49347 В случае коррелированных случайных параметров, поскольку оцениваемые параметры не могут быть интерпретированы напрямую, предоставляется метод vcov для объектов mlogit . Он имеет аргумент what , значение по умолчанию - коэффициент . В этом случае возвращается обычная ковариационная матрица коэффициентов. Если what = "rpar" , ковариационная матрица коррелированных случайных параметров возвращается, если type = "cov" (по умолчанию), а корреляционная матрица (со стандартными отклонениями по диагонали) возвращается, если type = " cor ".Объект относится к классу vcov.mlogit , и для этого объекта предоставляется метод сводки , который вычисляет с помощью дельта-метода стандартные ошибки параметров ковариации или корреляционной матрицы.
vcov (Train.mxlc, what = "rpar") ## время переключения комфорт
## время 28.6460389 -0.2787999 5.557933
## изменить -0. 2787999 3.1047367 1.232467
## комфорт 5.5579334 1.2324667 7.895535
2787999 3.1047367 1.232467
## комфорт 5.5579334 1.2324667 7.895535 vcov (Поезд.mxlc, what = "rpar", type = "cor") ## время переключения комфорт
## время 5.35219945 -0.02956296 0.3695645
## изменить -0.02956296 1.76202630 0.2489270
## комфорт 0,36956453 0,24892701 2,8098994 сводка (vcov (Train.mxlc, what = "rpar", type = "cor")) ## Estimate Std. Ошибка z-значения Pr (> | z |)
## sd.time 5.352199 0.381135 14.0428 <2.2e-16 ***
## sd.change 1.762026 0,144592 12,1862 <2,2e-16 ***
## sd.comfort 2,809899 0,178295 15,7599 <2,2e-16 ***
## cor.time: изменить -0.029563 0.232414 -0.1272 0.898782
## cor.time: комфорт 0,369565 0,114068 3,2399 0,001196 **
## cor.change: комфорт 0,248927 0,110321 2,2564 0,024047 *
## ---
## Сигниф. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 дюйма 1 сводка (vcov (Train.mxlc, what = "rpar", type = "cov")) ## Estimate Std.Ошибка z-значения Pr (> | z |)
## var.time 28.64604 4.07982 7.0214 2.197e-12 ***
## var.change 3.10474 0.50955 6.0931 1.107e-09 ***
## var.comfort 7.89553 1.00198 7.8799 3.276e-15 ***
## cov.time: изменить -0,27880 0,51550 -0,5408 0,5886
## cov.time: comfort 5.55793 0.89161 6.2336 4.559e-10 ***
## cov.change: комфорт 1,23247 0,30131 4,0903 4,308e-05 ***
## ---
## Сигниф. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 дюйма 1 В случае коррелированных случайных параметров, поскольку оцененные параметры не поддаются прямой интерпретации, предоставляются дополнительные функции для анализа корреляции коэффициентов:
## время переключения комфорт
## время 1.00000000 -0,02956296 0,3695645
## изменить -0.02956296 1.00000000 0.2489270
## комфорт 0,36956453 0,24892701 1,0000000 ## время переключения комфорт
## время 28.6460389 -0.2787999 5.557933
## изменить -0.2787999 3.1047367 1.232467
## комфорт 5.5579334 1. 2324667 7.895535
2324667 7.895535 ## время переключения комфорт
## 5.352199 1.762026 2.809899 Корреляцию можно ограничить подмножеством случайных параметров, заполнив аргумент корреляции вектором символов, указывающим соответствующие ковариаты:
Поезд.mxlc2 <- update (Train.mxlc, correlation = c ("время", "комфорт"))
vcov (Train.mxlc2, what = "rpar", type = "cor") ## время комфорт
## время 5.5726158 0.3909467
## комфорт 0,3909467 3,0631462 Наличие случайных коэффициентов и их корреляция можно исследовать с помощью любого из трех тестов. Фактически, можно рассматривать три вложенные модели: модель без случайных эффектов, модель со случайными, но некоррелированными эффектами и модель со случайными и коррелированными эффектами.Сначала мы представляем три теста на отсутствие коррелированных случайных эффектов:
lr.mxc <- lrtest (Train.mxlc, Train.ml)
wd.mxc <- waldtest (Train.mxlc)
библиотека («машина»)
lh.mxc <- linearHypothesis (Train.mxlc, c ("chol.time: time = 0",
«chol.time: change = 0», «chol.time: comfort = 0», «chol.change: change = 0»,
"chol.change: comfort = 0", "chol.comfort: comfort = 0"))
sc.mxc <- scoretest (Train.ml, rpar = c (time = "n", change = "n",
комфорт = "n"), R = 100, корреляция = TRUE, halton = NA, панель = TRUE)
sapply (список (wald = wd.mxc, lh = lh.mxc, score = sc.mxc, lr = lr.mxc),
statpval) ## wald lh score lr
## stat 288.287 288.287 208.765 388.057
## p-значение 0,000 0,000 0,000 0,000 Гипотеза об отсутствии коррелированных случайных параметров категорически отвергается. Затем мы представляем три теста на отсутствие корреляции при сохранении существования случайных параметров.
lr.corr <- lrtest (Train.mxlc, Train.mxlu)
lh.corr <- linearHypothesis (Train.mxlc, c ("chol.time: change = 0",
«chol.time: comfort = 0», «chol.change: comfort = 0»))
wd. corr <- waldtest (Train.mxlc, correlation = FALSE)
#YC
sc.corr <- scoretest (Train.mxlu, correlation = TRUE)
sapply (список (wald = wd.corr, lh = lh.corr, score = sc.corr, lr = lr.corr),
statpval)
corr <- waldtest (Train.mxlc, correlation = FALSE)
#YC
sc.corr <- scoretest (Train.mxlu, correlation = TRUE)
sapply (список (wald = wd.corr, lh = lh.corr, score = sc.corr, lr = lr.corr),
statpval) ## wald lh score lr
## stat 103,195 103,195 10,483 42,621
## p-значение 0,000 0,000 0,015 0,000 Гипотеза об отсутствии корреляции категорически отвергается с помощью теста Вальда и критерия отношения правдоподобия, только на уровне 5% для теста оценки.
RiskyTransport
Второй пример - это исследование Леона и Мигеля (2017), которые рассматривают модель выбора режима для транзита из аэропорта Фритауна (Сьерра-Леоне) в центр города. Доступны четыре варианта: паром, вертолет, водное такси и судно на воздушной подушке. Поразительной особенностью их исследования является то, что все эти альтернативы в последние годы приводили к несчастным случаям со смертельным исходом, так что риск смертельного исхода не является незначительным и сильно отличается от альтернативы. Например, вероятность умереть при использовании водного такси и вертолета равна 2 соответственно.55 и 18,41 из 100 000 пассажиро-рейсов. Эта функция позволяет авторам оценить ценность статистической жизни. Для индивидуума \ (i \) полезность выбора альтернативы \ (j \) составляет:
\ [ U_ {ij} = \ beta_ {il} (1 - p_j) + \ beta_ {ic} (c_j + w_i t_j) + \ epsilon_ {ij}, \]
, где \ (p_j \) - вероятность смерти при использовании альтернативы \ (j \), \ (c_j \) и \ (t_j \), денежная стоимость и время транспортировки альтернативы \ (j \) и \ (w_i \) ставка заработной платы человека \ (i \) (которая должна быть его оценкой времени перевозки).\ (C_ {ij} = c_j + w_i t_j \), следовательно, является индивидуальной удельной обобщенной стоимостью для альтернативы \ (j \). \ (\ beta_ {il} \) и \ (\ beta_ {ic} \) - это (индивидуальная) предельная полезность выживания и затрат. Ценность статистической жизни (VSL) определяется следующим образом:
\ [
\ mbox {VSL} _i = - \ frac {\ beta_ {il}} {\ beta_ {îc}} = \ frac {\ Delta
C_ {ij}} {\ Delta (1-p_j)}. \]
\]
Две представляющие интерес ковариаты: стоимость , (обобщенная стоимость в долларах США по ППС) и риск , (смертность на 100 000 пассажироперевозок).Переменная риска является чисто альтернативной, поэтому точки пересечения альтернатив не могут быть оценены. Чтобы избежать проблем с эндогенностью, авторы вводят в качестве ковариат оценки, которые люди присвоили 5 атрибутам альтернатив: комфорт, уровень шума, многолюдность, удобство и местоположение трансфера, а также «качество» клиентуры. Сначала оценим полиномиальную логит-модель.
данных ("RiskyTransport", package = "mlogit")
RT <- dfidx (RiskyTransport, choice = "choice", idx = list (c ("chid", "id"), "mode"),
idnames = c ("chid", "alt"))
мл.rt <- mlogit (выбор ~ стоимость + риск + места + шум + скопление людей +
convloc + клиентура | 0, данные = RT, веса = вес) Обратите внимание на использование аргумента весов для установки весов для наблюдений, как это было сделано в исходном исследовании.
coef (ml.rt) [c («риск», «стоимость»)] ## стоимость риска
## -0.0930 -0.009540895 Соотношение коэффициентов риска и стоимости составляет р раунда (коэф (мл.rt) ['risk'] / coef (ml.rt) ['cost'], 2) (сотни тысяч долларов), что означает, что оценочная стоимость статистической жизни немного меньше одного миллиона долларов. Далее мы рассмотрим модель смешанного логита. Коэффициенты затрат и риска предполагаются случайными в соответствии с треугольным распределением, ограниченным нулем.
mx.rt <- mlogit (выбор ~ стоимость + риск + сиденья + шум + скопление людей +
convloc + клиентура | 0, данные = RT, веса = вес,
rpar = c (cost = 'zbt', risk = 'zbt'), R = 100, halton = NA, panel = TRUE) Результаты представлены в следующей таблице:
библиотека ("текрег")
htmlreg (list ('Multinomial logit' = ml. rt, 'Смешанный логит' = mx.rt),
digits = 3, float.pos = "hbt", label = "tab: risktr", single.row = TRUE,
caption = "Варианты транспорта.")
rt, 'Смешанный логит' = mx.rt),
digits = 3, float.pos = "hbt", label = "tab: risktr", single.row = TRUE,
caption = "Варианты транспорта.") | Полиномиальный логит | Смешанный логит | |
|---|---|---|
| Стоимость | -0,010 (0,001) *** | -0,019 (0,001) *** |
| риск | -0,094 (0,011) *** | -0.103 (0,016) *** |
| сиденья | 0,152 (0,244) | 0,108 (0,233) |
| шум | -0,029 (0,265) | 0,142 (0,229) |
| многолюдность | -0,919 (0,244) *** | -0,716 (0,223) ** |
| свернуть | -0,377 (0,202) | -0,150 (0,197) |
| клиентура | -0.257 (0,265) | -0,331 (0,254) |
| AIC | 3250,747 | 3177,250 |
| Журнал правдоподобия | -1618,374 | -1581,625 |
| Num. набл. | 1793 г. | 1793 г. |
| K | 4 | 4 |
| p <0,001; p <0,01; р <0.05 | ||
Не то, чтобы логарифм правдоподобия намного больше для логита смешанного эффекта. Параметры индивидуального уровня могут быть извлечены с помощью метода подгонки с параметром типа, установленным на параметров .
indpar <- fit (mx.rt, type = "parameters")
голова (индпар) ## id cost risk
## 1 8020605 -0.02096705 -0.10105817
## 2 8260102 -0.01666475 -0.11211057
## 3 8260104 -0.01728864 -0.08302831
## 4 8260106 -0.01494848 -0,07319789
## 5 8260108 -0. 01687051 -0.06501337
## 6 8260201 -0.02133116 -0.10285434
01687051 -0.06501337
## 6 8260201 -0.02133116 -0.10285434 Затем мы можем вычислить VSL для каждого человека и проанализировать их распределение, используя квантили и построив на рисунке 1 эмпирическую плотность VSL для африканских и неафриканских путешественников (как это сделано в León and Miguel 2017 Table 4, p. 219 и на рисунке 5, с.223).
indpar $ VSL <- с (indpar, риск / стоимость * 100)
квантиль (индпар $ VSL, c (0,025, 0,975)) ## 2.5% 97,5%
## 432.4199 1054.3428 ## [1] 608.94 Обратите внимание, что вычисление VSL как отношения двух случайных параметров, которые могут принимать нулевые значения, может привести к чрезвычайно высоким значениям, если отдельный параметр для стоимости близок к 0.
## [1] -0,002924437 ## [1] 3131.825 Это не тот случай, поскольку (абсолютное) минимальное значение стоимости равно \ (- 0,003 \), что приводит к максимальному значению VSL $ \ (3131 \).
Библиотека ("ggplot2")
RT $ id <- RT $ id
indpar <- слияние (уникальное (подмножество (as.data.frame (RT),
select = c ("id", "african"))),
indpar)
ggplot (indpar) + geom_de density (aes (x = VSL, linetype = african)) +
scale_x_continuous (пределы = c (200, 1200)) Получение коэффициента источника фосфора - Программа управления питательными веществами Пенсильвании - Расширение штата Пенсильвания
Тестирование навоза и твердых биологических веществ является ключом к минимизации потерь фосфора (P) из сельскохозяйственных почв, получающих эти материалы в качестве поправок.Большой объем работ теперь показывает, что потери P со сточными водами могут широко варьироваться в зависимости от различных видов навоза и твердых биологических веществ, вносимых в почву. Признавая эти различия, индекс P Пенсильвании включает фактор, коэффициент источника фосфора, который представляет относительную доступность фосфора в навозе и твердых биологических веществах для стока.
Получение коэффициента источника фосфора для навоза или твердых биологических веществ, подлежащих внесению в почву, может быть достигнуто путем обращения к общим значениям коэффициентов источника фосфора в таблице 1 индекса P Пенсильвании или путем отправки навоза и твердых биологических веществ в лабораторию для тестирование.В то время как тестирование влечет за собой оплату аналитического сбора, преимущество тестирования состоит в том, что достигается точный коэффициент источника фосфора, специфичный для конкретного навоза или твердых биологических веществ.
Отбор проб навоза и твердых биологических веществ
Образцы, представленные для тестирования, должны представлять навоз или твердые биологические вещества по мере их внесения в землю. Это означает, что отбор проб следует проводить незадолго до нанесения материалов. Со временем свойства этих материалов могут изменяться как при хранении, так и при последующем применении.Образцы следует отправлять на анализ как можно скорее после сбора и хранить в холодильнике, если это невозможно сделать немедленно. Конкретную информацию о соответствующих процедурах отбора проб можно получить на веб-сайте Лаборатории тестирования почвы Университета Висконсин-Мэдисон.
Тестирование
Пенсильвания недавно приняла протокол испытаний, который был принят лабораториями по всей Северной Америке. Протокол включает извлечение навоза деионизированной водой (раствор: твердые вещества = 100: 1) в течение одного часа и анализ экстракта с помощью атомно-эмиссионной спектроскопии с индуктивно связанной плазмой.Чтобы получить конкретную информацию об этом протоколе, лабораториям рекомендуется посетить веб-сайт лаборатории сельскохозяйственных аналитических служб штата Пенсильвания.
Получение коэффициента источника P
Следующий алгоритм используется для преобразования извлекаемого водой P (выраженного как % извлекаемого водой P в сухом веществе ) в коэффициент источника P:
Коэффициент источника P = 1,17 x% извлекаемой воды P.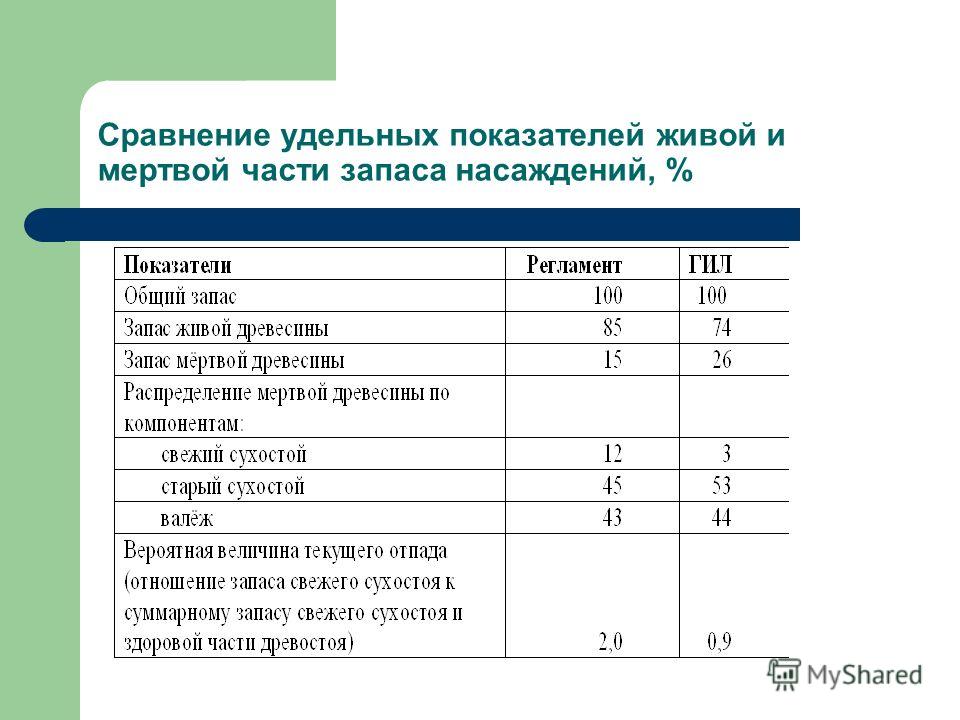

 0 09.161 97: Положение о нормативных энергетических характеристиках гидроагрегатов и гидроэлектростанций … Словарь-справочник терминов нормативно-технической документации
0 09.161 97: Положение о нормативных энергетических характеристиках гидроагрегатов и гидроэлектростанций … Словарь-справочник терминов нормативно-технической документации
 20371
Tr $ time <- Tr $ time / 60
Train.ml <- mlogit (выбор ~ цена + время + сдача + комфорт | - 1, Тр)
coef (сводка (Train.ml))
20371
Tr $ time <- Tr $ time / 60
Train.ml <- mlogit (выбор ~ цена + время + сдача + комфорт | - 1, Тр)
coef (сводка (Train.ml))  time: time" "chol.time: change"
## [7] "chol.change: change" "chol.time: comfort"
## [9] «чол.замена: комфорт» «чол.комфорт: комфорт»
time: time" "chol.time: change"
## [7] "chol.change: change" "chol.time: comfort"
## [9] «чол.замена: комфорт» «чол.комфорт: комфорт»  time <- rpar (Train.mxlc, "time", norm = "price")
сводка (wtp.time)
time <- rpar (Train.mxlc, "time", norm = "price")
сводка (wtp.time)  2787999 3.1047367 1.232467
## комфорт 5.5579334 1.2324667 7.895535
2787999 3.1047367 1.232467
## комфорт 5.5579334 1.2324667 7.895535  2324667 7.895535
2324667 7.895535  corr <- waldtest (Train.mxlc, correlation = FALSE)
#YC
sc.corr <- scoretest (Train.mxlu, correlation = TRUE)
sapply (список (wald = wd.corr, lh = lh.corr, score = sc.corr, lr = lr.corr),
statpval)
corr <- waldtest (Train.mxlc, correlation = FALSE)
#YC
sc.corr <- scoretest (Train.mxlu, correlation = TRUE)
sapply (список (wald = wd.corr, lh = lh.corr, score = sc.corr, lr = lr.corr),
statpval)  rt, 'Смешанный логит' = mx.rt),
digits = 3, float.pos = "hbt", label = "tab: risktr", single.row = TRUE,
caption = "Варианты транспорта.")
rt, 'Смешанный логит' = mx.rt),
digits = 3, float.pos = "hbt", label = "tab: risktr", single.row = TRUE,
caption = "Варианты транспорта.")  01687051 -0.06501337
## 6 8260201 -0.02133116 -0.10285434
01687051 -0.06501337
## 6 8260201 -0.02133116 -0.10285434