Как определить по формуле: Как найти область определения функции?

Как найти область определения функции — примеры и способы решения

В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).

Общие сведения

Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».

Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.

Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.

Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения.

Основные понятия

Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.

Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.

Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.

Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.

Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.

Типы функций

Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.

Рациональные целые — выражения полиномиального типа (линейные)

. Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.

Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.

К иррациональным функциям относят выражения, которые содержат переменную величину под корнем

. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.

Правильное обозначение

Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.

Следует руководствоваться такими правилами:

1. Использовать скобку «[» и/или «]», когда нужно указать принадлежность к множеству.
2. Круглые скобки используются в двух случаях: указывание границы бесконечности и значения, которое не входит в интервал.
3. Для объединения нескольких множеств нужно применять специальный символ «U».
4. Допускается использование круглых и квадратных скобок в одном множестве.

Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.

Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].

Алгоритмы определения

Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.

Если функция является дробной, то следует использовать следующий алгоритм:

1. Обратить внимание на знаменатель, который не должен быть равен 0.
2. Выписать выражение знаменателя и решить его, приравнивая к 0.
3. Записать интервал.

Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).

Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.

Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.

Другие методы

Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.

Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.

В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).

После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.

Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.

Примеры решения

Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.

С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.

Для линейного вида

Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:

1. Упростить выражение.
2. Определить D (f).

Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = — x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.

В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.

Дробные и иррациональные

Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).

Решается задача таким способом:

1. Приравнивается знаменатель к 0.
2. Решается уравнение.
3. Определяется интервал допустимых значений.

Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).

В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения.

Для решения квадратного уравнения следует применить такой алгоритм:

1. Записать неравенство: 4 * sqr (x) — 12 * x + 9 >= 0.
2. Дискриминант: D = [(- b)^2] — (4 * a * c) = [(-12)^2] — (4 * 4 * 9) = 144 — 144 = 0.
3. D = 0 — только одно решение.
4. x = (-b) / (2 * a) >= 12 / (2 * 4) >= 12 / 8 >= 6 / 4 >= 1,5.

Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).

Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.

Урок 6. Валентность – HIMI4KA

У нас вышел новый курс, где всё объясняется ещё проще. Подробннее по ссылке

В уроке 6 «Валентность» из курса «Химия для чайников» дадим определение валентности, научимся ее определять; рассмотрим элементы с постоянной и переменной валентностью, кроме того научимся составлять химические формулы по валентности. Напоминаю, что в прошлом уроке «Химическая формула» мы дали определение химическим формулам и их индексам, а также выяснили различия химических формул веществ молекулярного и немолекулярного строения.

Вы уже знаете, что в химических соединениях атомы разных элементов находятся в определенных числовых соотношениях. От чего зависят эти соотношения?

Рассмотрим химические формулы нескольких соединений водорода с атомами других элементов:

Нетрудно заметить, что атом хлора связан с одним атомом водорода, атом кислорода — с двумя, атом азота — с тремя, а атом углерода — с четырьмя атомами водорода. В то же время в молекуле углекислого газа СО₂ атом углерода связан с двумя атомами кислорода. Из этих примеров видно, что атомы обладают разной способностью соединяться с другими атомами. Такая способность атомов выражается с помощью численной характеристики, называемой валентностью.

Валентность — численная характеристика способности атомов данного элемента соединяться с другими атомами.

Поскольку один атом водорода может соединиться только с одним атомом другого элемента, валентность атома водорода принята равной единице. Иначе говорят, что атом водорода обладает одной единицей валентности, т. е. он одновалентен.

Валентность атома какого-либо другого элемента равна числу соединившихся с ним атомов водорода. Поэтому в молекуле HCl у атома хлора валентность равна единице, а в молекуле H₂O у атома кислорода валентность равна двум. По той же причине в молекуле NH₃ валентность атома азота равна трем, а в молекуле CH₄ валентность атома углерода равна четырем. Если условно обозначить единицу валентности черточкой |, вышесказанное можно изобразить схематически:

Следовательно, валентность атома любого элемента есть число, которое показывает, со сколькими атомами одновалентного элемента связан данный атом в химическом соединении.

Численные значения валентности обозначают римскими цифрами над символами химических элементов:

Определение валентности

Однако водород образует соединения далеко не со всеми элементами, а вот кислородные соединения есть почти у всех элементов. И во всех таких соединениях атомы кислорода проявляют валентность, равную двум. Зная это, можно определять валентности атомов других элементов в их бинарных соединениях с кислородом. (Бинарными называются соединения, состоящие из атомов двух химических элементов.)

Чтобы это сделать, необходимо соблюдать простое правило: в химической формуле вещества суммарные числа единиц валентности атомов каждого элемента должны быть одинаковыми.

Так, в молекуле воды H₂O общее число единиц валентности двух атомов водорода равно произведению валентности одного атома на соответствующий числовой индекс в формуле:

Так же определяют число единиц валентности атома кислорода:

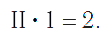
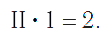
По величине валентности атомов одного элемента можно определить валентность атомов другого элемента. Например, определим валентность атома углерода в молекуле углекислого газа СО₂:

Согласно вышеприведенному правилу х·1 = II·2, откуда х = IV.

Существует и другое соединение углерода с кислородом — угарный газ СО, в молекуле которого атом углерода соединен только с одним атомом кислорода:

В этом веществе валентность углерода равна II, так как х·1 = II·1, откуда х = II:

Постоянная и переменная валентность

Как видим, углерод соединяется с разным числом атомов кислорода, т. е. имеет переменную валентность. У большинства элементов валентность — величина переменная. Только у водорода, кислорода и еще нескольких элементов она постоянна (см. таблицу).

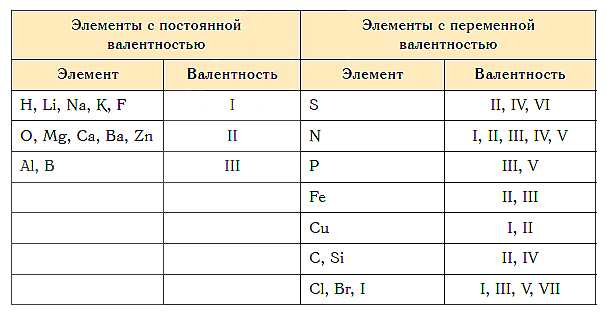
Составление химических формул по валентности

Зная валентность элементов, можно составлять формулы их бинарных соединений. Например, необходимо записать формулу кислородного соединения хлора, в котором валентность хлора равна семи. Порядок действий здесь таков.

Еще один пример. Составим формулу соединения кремния с азотом, если валентность кремния равна IV, а азота — III.

Записываем рядом символы элементов в следующем виде:

Затем находим НОК валентностей обоих элементов. Оно равно 12 (IV·III).

Определяем индексы каждого элемента:

Записываем формулу соединения: Si₃N₄.

В дальнейшем при составлении формул веществ не обязательно указывать цифрами значения валентностей, а необходимые несложные вычисления можно выполнять в уме.

Краткие выводы урока:

1. Численной характеристикой способности атомов данного элемента соединяться с другими атомами является валентность.
2. Валентность водорода постоянна и равна единице. Валентность кислорода также постоянна и равна двум.
3. Валентность большинства остальных элементов не является постоянной. Ее можно определить по формулам их бинарных соединений с водородом или кислородом.

Надеюсь урок 6 «Валентность» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии.

Хотите ещё проще? Мы создали новый курс, где максимум за 7 дней вы овладете химией с нуля. Подробннее по ссылке

Расчеты по формулам — Знаешь как

Состоящая из нескольких букв и цифр химическая формула вещества дает очень много важных для химика сведений.

Прежде всего она непосредственно пока­зывает, из каких элементов состоит данное вещество и сколько атомов каждого элемента содержит его молекула. Затем она позволяет рассчитать ряд величин, характеризующих данное вещество. Укажем важнейшие из этих расчетов.

1. Молекулярный вес вещества. Вычисляется по формуле как сумма весов атомов, входящих в состав молекулы вещества. О точности найденного таким образом молекулярного веса уже сказано в предыдущем статье.

2. Весовой состав сложного вещества. Состав всякого вещества может быть выражен отношением весовых количеств содержащихся в нем элементов. Это отношение прямо вытекает из формулы вещества.

Например, из формулы соды Na₂СО₃ видно, что в ней на два атома натрия приходится один атом углерода и три атома кислорода. Так как атомный вес натрия 23, углерода 12 и кислорода 16, то отношение между весовыми количествами этих элементов в любом количестве соды должно равняться:

23.2 : 12 : 16.3 = 46 : 12 : 48

Так же легко рассчитать по формуле и процентное содержание каждого элемента в данном веществе.

3. Плотность вещества в газообразном со­стоянии. Расчет производится по формуле

где D — плотность вещества, М — его молекулярный вес и M1 — молеку­лярный вес газа, по отношению к которому определяется плот­ность.

4. Вес 1 л газа при 0° и 760 мм давления. Граммо­лекула любого газа при нормальных условиях занимает объем 22,4 л, следовательно, вес (g) 1 л газа при тех же условиях бу­дет равняться грамм молекулярному весу (М), деленному на 22,4:

5. Объем, занимаемый любым количеством газа. Если газ взят при 0° и 760 мм давления, то расчет проще всего произвести, исходя из величины грамм молекулярного объема.
Если же газ находится при иных условиях давления и тем­пературы, то вычисление объема производится по уравнению:

По этому же уравнению легко рассчитать вес любого объема газа при данных условиях.

Статья на тему Расчеты по формулам

Формулы для решения задач по химии

Так как химия наука точная, она неразрывно связана с различного рода вычислениями. Чтобы решать задачи, нужно знать формулы и хорошо в них ориентироваться. Без этих базовых знаний и навыков изучение химии становится невозможным.
Мы собрали для вас основные химические формулы, изучаемые в школьном курсе. Они пригодятся каждому ученику, особенно тем, кто будет сдавать ОГЭ или ЕГЭ по этому непростому, но очень интересному предмету.

Нахождение количества вещества

Первое и основное понятие, которое необходимо усвоить – это количество вещества, измеряемое в молях и обозначающееся латинской буквой «n». Для его нахождения нужно основываться на условии задачи, так как вычислить количество вещества можно по трём формулам:

1) По массе. n=m/M — Массу вещества (в граммах) разделить на его молярную массу (в г/моль).

2) По объёму. n=V/V_m — Отношением объёма вещества к его молярному объёму (используется для газов).

3) По числу молекул. n=N/N_A – Число молекул вещества делённое на число Авогадро. Число Авогадро (N_A) – физическая величина, указывающая на число молекул, содержащихся в 1 моле вещества, и численно равная 6,0221 * 10²³ моль^-1.

Формулы для нахождения массы

Массу вещества можно найти несколькими способами:

1. Умножив количество вещества на молярную массу: m _(г) = n _(моль)×M _{(г/моль)}.

2. Произведением объёма раствора и его плотности: m = V _(л) ×ρ _(г/л).

3. Перемножив массовую долю с массой раствора: m = m_(р-ра) × ω.

Молярная масса (М) – это масса одного моля вещества. Вычисляется она следующим образом: посредством сложения атомных масс элементов, из которых состоит вещество, получаем относительную молекулярную массу. Молярная масса численно равна относительной молекулярной массе, но имеет размерность «г/моль». Также молярную массу можно найти с помощью отношения массы вещества к его количеству:

M = m/n

Формулы для нахождения объёма

Для вычисления объёма того или иного вещества можно воспользоваться одной из формул:

1. Объём раствора находится как отношение массы раствора к его плотности:

V_(р-ра) = m_(р-ра) / ρ

2. Объём газа равен отношению его количества вещества к молярному объёму:

V_(газа) = n/V_M

Молярный объём (V_M) – объём, который занимает 1 моль вещества при определённых показателях давления и температуры. Находится при делении молярной массы вещества на его плотность:

V_M = M/ρ

При нормальных условиях молярный объём газа равен 22,4 л/моль.

Формулы для нахождения плотности и относительной плотности

Плотность (ρ) – физическая величина, указывающая на массу определённого вещества, содержащуюся в единице объёма.
Следовательно, формула для её вычисления имеет вид:

ρ=m/V

Помимо основной, существует формула для нахождения плотности газа при нормальных условиях, где молярная масса делится на молярный объём газа при н.у.:

ρ=M/V_M

Относительная плотность (D) газов – величина, указывающая насколько одно вещество тяжелее или легче другого. Вычисляется она отношением молярных масс газов:

D = M₍₁₎ / M₍₂₎

Например, условием было найти плотность газа по водороду. Решение будет иметь вид: D = M_(газа)/M(H₂) = M_(газа)/2. Относительная плотность является безразмерной величиной.

Формулы для нахождения концентрации

Молярная концентрация (С) – отношение количества растворённого вещества к объёму раствора. Единица измерения – моль/л. Молярная концентрация вычисляется по формуле:

С = n/V

Массовая концентрация чаще всего называется титром (Т). Это отношение массы растворённого вещества к объёму раствора. Единица измерения — г/л.

T = m/V

Массовая доля (ω) – это один из вариантов выражения концентрации. С её помощью можно вычислить процентное содержание растворённого вещества в общей массе раствора:

ω = (m_р.в./m_р-ра) × 100%

По такому же принципу вычисляется массовая доля определённого компонента в смеси:

ω = (m_{компонента} / m_{системы}) × 100%

Если возникает необходимость найти массовую долю химического элемента в соединении, то нужно относительную атомную массу этого элемента умножить на число атомов в соединении и разделить на молекулярную массу вещества:

ω = (A_r × N) / M

Формулы для нахождения выхода продукта реакции

Под выходом продукта реакции (ᶯ) подразумевается отношение массы (объёма, количества) вещества, полученного на практике, к теоретически возможному (рассчитанному по уравнению реакции). Единица измерения – доля, а проценты — если результат умножить на 100 !
Для его вычисления, в зависимости от условия задачи, используются следующие формулы:

ᶯ=(m_практ./m_{теорет.}) × 100%
ᶯ=(V_практ./V_{теорет.}) × 100%
ᶯ=(n_практ./n_{теорет.}) × 100%

Попрактиковать решение задач и знание формул возможно в приложении «ХиШник». Оно содержит в себе каталог заданий, которые, в свою очередь, разделены по темам и уровням сложности. Если вы дали неверный ответ, то приложение не просто уведомит об этом, а предложит правильный алгоритм решения. Также в нём есть раздел для подготовки к ОГЭ и ЕГЭ, в котором собраны типовые задания.

Знание расчётных формул – это ключевой момент при решении задач. Главное, понимать их, а не бездумно заучивать. Так как они будут использоваться не только в школьных задачах, на ЕГЭ и ОГЭ, но и в дальнейшей жизни, даже если ваша профессиональная сфера будет далека от химии.

Валентность и степень окисления, подготовка к ЕГЭ по химии

Валентность

Валентность (лат. valere — иметь значение) — мера «соединительной способности» химического элемента, равная числу индивидуальных химических связей, которые может образовать один атом.

Определяют валентность по числу связей, которые один атом образует с другими. Для примера рассмотрим две молекулы

Для определения валентности нужно хорошо представлять графические формулы веществ. В этой статье вы увидите множество формул. Сообщаю вам также о химических элементах с постоянной валентностью, знать которые весьма полезно.

В электронной теории считается, что валентность связи определяется числом неспаренных (валентных) электронов в основном или возбужденном состоянии. Мы касались с вами темы валентных электронов и возбужденного состояния атома. На примере фосфора объединим эти две темы для полного понимания.

Подавляющее большинство химических элементов обладает непостоянным значением валентности. Переменная валентность характерна для меди, железа, фосфора, хрома, серы.

Ниже вы увидите элементы с переменной валентностью и их соединения. Заметьте, определить их непостоянную валентность нам помогают другие элементы — с постоянной валентностью.

Запомните, что у некоторых простых веществ валентность принимает значения: III — у азота, II — кислорода. Подведем итог полученным знаниям, написав графические формулы азота, кислорода, углекислого и угарного газов, карбоната натрия, фосфата лития, сульфата железа (II) и ацетата калия.

Как вы заметили, валентности обозначаются римскими цифрами: I, II, III и т.д. На представленных формулах валентности веществ равны:

• N — III
• O — II
• H, Na, K, Li — I
• S — VI
• C — II (в угарном газе CO), IV (в углекислом газе CO₂ и карбонате натрия Na₂CO₃
• Fe — II

Степень окисления

Степенью окисления (СО) называют условный показатель, который характеризует заряд атома в соединении и его поведение в ОВР (окислительно-восстановительной реакции). В простых веществах СО всегда равна нулю, в сложных — ее определяют исходя из постоянных степеней окисления у некоторых элементов.

Численно степень окисления равна условному заряду, который можно приписать атому, руководствуясь предположением, что все электроны, образующие связи, перешли к более электроотрицательному элементу.

Определяя степень окисления, одним элементам мы приписываем условный заряд «+», а другим «-«. Это связано с электроотрицательностью — способностью атома притягивать к себе электроны. Знак «+» означает недостаток электронов, а «-» — их избыток. Повторюсь, СО — условное понятие.

Сумма всех степеней окисления в молекуле равна нулю — это важно помнить для самопроверки.

Зная изменения электроотрицательности в периодах и группах периодической таблицы Д.И. Менделеева, можно сделать вывод о том какой элемент принимает «+», а какой минус. Помогают в этом вопросе и элементы с постоянной степенью окисления.

Кто более электроотрицательный, тот сильнее притягивает к себе электроны и «уходит в минус». Кто отдает свои электроны и испытывает их недостаток - получает знак «+».

Самостоятельно определите степени окисления атомов в следующих веществах: RbOH, NaCl, BaO, NaClO₃, SO₂Cl₂, KMnO₄, Li₂SO₃, O₂, NaH₂PO₄. Ниже вы найдете решение этой задачи.

Сравнивайте значение электроотрицательности по таблице Менделеева, и, конечно, пользуйтесь интуицией 🙂 Однако по мере изучения химии, точное знание степеней окисления должно заменить даже самую развитую интуицию ;-)

Особо хочу выделить тему ионов. Ион — атом, или группа атомов, которые за счет потери или приобретения одного или нескольких электронов приобрел(и) положительный или отрицательный заряд.

Определяя СО атомов в ионе, не следует стремиться привести общий заряд иона к «0», как в молекуле. Ионы даны в таблице растворимости, они имеют разные заряды — к такому заряду и нужно в сумме привести ион. Объясню на примере.

© Беллевич Юрий Сергеевич 2018-2020

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.

чему она равна и что это такое

В химических процессах главную роль играют атомы и молекулы, свойства которых определяют исход химических реакций. Одной из важных характеристик атома является окислительное число, которое упрощает метод учета переноса электронов в частице. Как определить степень окисления или формальный заряд частицы и какие правила необходимо знать для этого?

Определение

Любая химическая реакция обусловлена взаимодействием атомов различных веществ. От характеристик мельчайших частиц зависит процесс реакции и ее результат.

Термин окисление (оксидация) в химии означает реакцию, в ходе которой группа атомов или один из них теряют электроны или приобретают, в случае приобретения реакцию называют «восстановлением».

Степень окисления – это величина, которая измеряется количественно и характеризует перераспределяемые электроны в ходе реакции. Т.е. в процессе оксидации электроны в атоме уменьшаются или увеличиваются, перераспределяясь между другими взаимодействующими частицами, и уровень оксидации показывает, как именно они реорганизуются. Данное понятие тесно связано с электроотрицательностью частиц – их умением притягивать и отталкивать от себя свободные ионы.

Это интересно! Что такое алканы: строение и химические свойства

Определение уровня оксидации зависит от характеристик и свойств конкретного вещества, поэтому нельзя однозначно назвать процедуру вычисления легкой или сложной, но ее результаты помогают условно записать процессы окислительно-восстановительных реакций. Следует понимать, что полученный результат вычислений является результатом учета переноса электронов и не имеет физического смысла, а также не является истинным зарядом ядра.

Важно знать! Неорганическая химия часто использует термин валентности вместо степени окисления элементов, это не является ошибкой, но следует учитывать, что второе понятие более универсальное.

Понятия и правила вычислений движения электронов являются основой для классификации химических веществ (номенклатура), описания их свойств и составления формул связи. Но наиболее часто данное понятие используется для описания и работы с окислительно-восстановительными реакциями.

Правила определения степени окисления

Как узнать степень окисления? При работе с окислительно-восстановительными реакциями важно знать, что формальный заряд частицы всегда будет равен величине электрона, выраженного в числовом значении. Эта особенность связана с тем предположением, что электронные пары, образующие связь, всегда полностью смещаются в сторону более отрицательных частиц. Следует понимать, что речь идет об ионных связях, а в случае реакции при ковалентной связи электроны будут делиться поровну между одинаковыми частицами.

Окислительное число может иметь как положительные, так и отрицательные значения. Все дело в том, что в процессе реакции атом должен стать нейтральным, а для этого нужно либо присоединить к иону некое количество электронов, если он положительный, либо отнять их, если он отрицательный. Для обозначения данного понятия при записи формулы обычно прописывают над обозначением элемента арабскую цифру с соответствующим знаком. Например,

 или  и т.д.

Следует знать, что формальный заряд металлов всегда будет положительным, а в большинстве

случаев, чтобы определить его, можно воспользоваться таблицей Менделеева. Существует ряд особенностей, которые необходимо учитывать, чтобы определять показатели правильно.

Как определить степень окисления

Степень оксидации:

1. У простых элементов всегда равна нулю:  или .
2. У фтора всегда будет равна -1.
3. Как и у металлов, у элементов из групп IA, IIA и IIIA групп всегда одинаковая – это номер группы, в которой они расположены.
4. У кислорода в любой связи равна -2, кроме связей с пероксидами (Н2О2), когда значение равно -1 и оксидом фтора (O+2F2-1, O2+1F2-1), когда она равна +2.
5. У водорода всегда +1, кроме его взаимодействия с гидридами (Na+H- и связями по типу C+4h5-1).
6. У простого вещества без связей с другими элементами всегда равна нулю.
7. У простого иона с одним атомом равна числу его электрона (Na+, Ca+2).
8. Если рассматривается связь двух веществ различной природы (металл и неметалл), то отрицательное окислительное число будет наблюдаться у вещества, которое обладает большей электроотрицательностью (H+F-, Cu+Br-), а положительное, соответственно, у элемента с электроотрицательностью больше нуля.
9. У щелочных металлов, таких как литий, натрий, калий и прочих, всегда +1.
10. У металлов из главной подгруппы II (магний, барий, кальций и стронций) равна +2.
11. У алюминия всегда одинаковое значение — +3.

Запомнив эти особенности, достаточно просто будет определять окислительное число у элементов, независимо от сложности и количества уровней атомов.

Полезное видео: определение степени окисления

Как определить степень окисления

Периодическая таблица Менделеева содержит почти всю необходимую информацию для работы с химическими элементами. Например, школьники используют только ее для описания химических реакций. Так, чтобы определить максимальные положительные и отрицательные значения окислительного числа необходимо свериться с обозначением химического элемента в таблице:

1. Максимально положительное – это номер группы, в которой находится элемент.
2. Максимально отрицательная степень окисления – это разница между максимально положительной границей и числом 8.

Таким образом, достаточно просто узнать крайние границы формального заряда того или иного элемента. Такое действие можно совершить с помощью вычислений на основе таблицы Менделеева.

Важно знать! У одного элемента могут быть одновременно несколько различных показателей оксидации.

Различают два основных способа определения уровня оксидации, примеры которых представлены ниже. Первый из них – это способ, который требует знаний и умений применять законы химии. Как расставлять степени окисления с помощью этого способа?

Правило определения степеней окисления

Для этого необходимо:

1. Определить, является ли данное вещество элементарным и находится ли оно вне связи. Если да, то его окислительное число будет равно 0, независимо от состава вещества (отдельные атомы или многоуровневые атомные соединения).
2. Определить, состоит ли рассматриваемое вещество из ионов. Если да, то степень оксидации будет равна их заряду.
3. Если рассматриваемое вещество металл, то посмотреть на показатели других веществ в формуле и вычислить показания металла путем арифметических действий.
4. Если все соединение имеет один заряд (по сути это сумма всех частиц представленных элементов), то достаточно определить показатели простых веществ, затем вычесть их от общей суммы и получить данные металла.
5. Если связь нейтральная, то общая сумма должна быть равна нулю.

Это интересно! Уроки химии: что это такое галогены

Для примера можно рассмотреть объединение

 с ионом алюминия, чей общий заряд равен нулю. Правила химии подтверждают тот факт, что ион Cl имеет окислительное число -1, а в данном случае их три в соединении. Значит ион Al должен быть равен +3, чтобы все соединение было нейтральным.

Этот способ весьма хорош, поскольку правильность решения всегда можно проверить, если сложить все уровни оксидации вместе.

Второй метод можно применять без знания химических законов:

1. Найти данные частиц, по отношению к которым нет строгих правил и точное количество их электронов неизвестно (можно путем исключения).
2. Выяснить показатели всех прочих частиц и после из общей суммы путем вычитания найти нужную частицу.

Рассмотрим второй метод на примере вещества Na2SO4, в котором не определен атом серы S, известно лишь, что он отличен от нуля.

Это интересно! Уроки химии: катионы и анионы – что это такое

Чтобы найти, чему равны все степени окисления необходимо:

1. Найти известные элементы, помня о традиционных правилах и исключениях.
2. Ион Na = +1, а каждый кислород = -2.
3. Умножить количество частиц каждого вещества на их электроны и получить степени оксидации всех атомов, кроме одного.
4. В Na2SO4 состоят 2 натрия и 4 кислорода, при умножении получается: 2 X +1 = 2 – это окислительное число всех частиц натрия и 4 X -2 = -8 – кислородов.
5. Сложить полученные результаты 2+(-8) =-6 – это общий заряд соединения без частицы серы.
6. Представить химическую запись в виде уравнения: сумма известных данных + неизвестное число = общий заряд.
7. Na2SO4 представлено следующим образом: -6 + S = 0, S = 0 + 6, S = 6.

Таким образом, чтобы использовать второй метод, достаточно знать простые законы арифметики.

Таблица оксидации

Для простоты работы и вычисления показателей оксидации для каждого химического вещества используют специальные таблицы, где прописаны все данные.

Она выглядит следующим образом:

Полезное видео: учимся определять степень окисления по формулам

Вывод

Нахождение степени окисления для химического вещества – это простое действие, которое требует лишь внимательности и знания основных правил и исключений. Зная исключения и пользуясь специальными таблицами, это действие не будет занимать много времени.

Вконтакте

Одноклассники

Facebook

Мой мир

Twitter

Определение эмпирических и молекулярных формул

Когда новое химическое соединение, такое как потенциально новое лекарственное средство, синтезируется в лаборатории или выделяется из природного источника, химики определяют его элементный состав, его эмпирическую формулу и структуру, чтобы понять его свойства . В этом разделе мы сосредоточимся на том, как определить эмпирическую формулу соединения, а затем использовать ее для определения молекулярной формулы, если молярная масса соединения известна.

Расчет массовых процентов

Закон определенных пропорций гласит, что химическое соединение всегда содержит одинаковую пропорцию элементов по массе; то есть процентный состав — процентное содержание каждого элемента, присутствующего в чистом веществе.За некоторыми исключениями, процентный состав химического соединения постоянен (см. Закон определенных пропорций). Процент каждого элемента, присутствующего в чистом веществе, постоянен (хотя теперь мы знаем, что есть исключения из этого закона). Например, сахароза (тростниковый сахар) содержит 42,11% углерода, 6,48% водорода и 51,41% кислорода по массе. Это означает, что 100,00 г сахарозы всегда содержат 42,11 г углерода, 6,48 г водорода и 51,41 г кислорода. Сначала мы воспользуемся молекулярной формулой сахарозы (C ₁₂ H ₂₂ O ₁₁ ), чтобы рассчитать массовый процент составляющих элементов; затем мы покажем, как массовые проценты могут использоваться для определения эмпирической формулы.

Согласно молекулярной формуле каждая молекула сахарозы содержит 12 атомов углерода, 22 атома водорода и 11 атомов кислорода. Следовательно, моль молекул сахарозы содержит 12 моль атомов углерода, 22 моль атомов водорода и 11 моль атомов кислорода. Мы можем использовать эту информацию для расчета массы каждого элемента в 1 моль сахарозы, что даст нам молярную массу сахарозы. Затем мы можем использовать эти массы для расчета процентного состава сахарозы. С точностью до трех десятичных знаков вычисления следующие:

Уравнение 3.3

масса C / моль сахарозы = 12 моль C × 12,011 г C1 моль C = 144,132 г C Масса H / моль сахарозы = 22 моль H × 1,008 г h2 моль H = 22,176 г H Масса O / моль сахарозы = 11 моль O × 15,999 г O1 моль O = 175,989 г O

Таким образом, 1 моль сахарозы имеет массу 342,297 г; Обратите внимание, что более половины массы (175,989 г) составляет кислород, а почти половина массы (144,132 г) — углерод.

Массовый процент каждого элемента в сахарозе — это масса элемента, присутствующего в 1 моль сахарозы, деленная на молярную массу сахарозы, умноженную на 100 для получения процента.Результат отображается с двумя десятичными знаками:

% масс C в сахарозе = масса C / моль сахарозы Молярная масса сахарозы

Формулы Excel: Функции

/ ru / excelformulas / относительные-абсолютные-ссылки-ячейки / содержание /

Введение

Функция — это предопределенная формула , которая выполняет вычисления с использованием определенных значений в определенном порядке. Все программы для работы с электронными таблицами включают общие функции, которые можно использовать для быстрого поиска суммы , среднего , счетчика , максимального значения и минимального значения для диапазона ячеек.Чтобы правильно использовать функции, вам необходимо понимать различные части функции и то, как создавать аргументов для вычисления значений и ссылок на ячейки.

Посмотрите видео ниже, чтобы узнать больше об использовании функций в Excel.

Части функции

Для правильной работы функция должна быть написана особым способом, который называется синтаксисом . Базовый синтаксис функции — это знак равенства (=) , имя функции (например, SUM) и один или несколько аргументов .Аргументы содержат информацию, которую вы хотите вычислить. Функция в приведенном ниже примере добавит значения диапазона ячеек A1: A20.

Работа с аргументами

Аргументы могут относиться как к отдельным ячейкам , так и к диапазонам ячеек и должны быть заключены в скобки . Вы можете включить один аргумент или несколько аргументов, в зависимости от синтаксиса, необходимого для функции.

Например, функция = СРЕДНЕЕ (B1: B9) вычислит среднее значений в диапазоне ячеек B1: B9.Эта функция содержит только один аргумент.

Несколько аргументов должны быть разделены запятой . Например, функция = СУММ (A1: A3, C1: C2, E2) добавит значений всех ячеек в трех аргументах.

Использование функций

Есть множество функций. Вот некоторые из наиболее часто используемых функций:

• СУММ : эта функция добавляет всего va

Как определить, являются ли точки коллинеарными, используя формулу расстояния

Пусть A, B и C — три точки.

Нам нужно найти три длины AB, BC и AC среди данных трех точек A, B и C.

Три точки A, B и C коллинеарны, если сумма длин любых двух отрезков прямой между AB, BC и AC равна длине оставшегося отрезка.

То есть

AB + BC = AC

(или)

AB + AC = BC

(или)

AC + BC = AB

Пример:

Использование концепции расстояния между двумя точками, покажите, что точки A (5, -2), B (4, -1) и C (1, 2) лежат на одной прямой.

Решение:

Нам известно расстояние между двумя точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ) равно

d = √ [(x ₂ — x ₁ ) ² + (y ₂ — y ₁ ) ² ]

Давайте найдем длины AB, BC и AC, используя приведенную выше формулу расстояния.

AB = √ [(4-5) ² + (-1 + 2) ² ]

AB = √ [(- 1) ² + (1) ² ]

AB = √ [1 + 1]

AB = √2

BC = √ [(1 — 4) ² + (2 + 1) ² ]

BC = √ [(- 3) ² + (3) ² ]

BC = √ [9 + 9]

BC = √18

BC = 3√2

AC = √ [(1 — 5) ² + (2 + 2) ² ]

AC = √ [(-4) ² + (4) ² ]

AC = √ [16 + 16]

AC = √32

AC = 4√2

Следовательно, AB + BC = √2 + 3√2 = 4√2 = AC

Таким образом, AB + BC = AC

Следовательно, данные три точки A, B и C лежат на одной прямой.

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами при прямом и обратном изменении

Проблемы со словами по цене за единицу

Проблемы со словом при скорости единицы

задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование в метрические единицы в словесных задачах

Word задачи по простому проценту

Word по сложным процентам

Word по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами для разметки 9122 9122 задачи

задачи с десятичными числами

задачи со словами на дроби

задачи со словами на смешанные фракции

задачи со словами с одношаговым уравнением

задачи с линейным неравенством и соотношением слов

Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами из теоремы Пифагора

Процентное число проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций 9128 9122 функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

видение

Л.Метод CM для решения задач времени и работы

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Определитель матрицы

Определитель матрицы — это специальное число , которое может быть вычислено из квадратной матрицы.

Матрица — это массив чисел:

Матрица
(у нее 2 строки и 2 столбца)

Определитель этой матрицы (расчеты объяснены позже):

3 × 6 — 8 × 4 = 18 — 32 = −14

Для чего это нужно?

Определитель помогает нам найти обратную матрицу, говорит нам о матрице, которая полезна в системах линейных уравнений, исчислении и многом другом.

Символ

Символ для определителя представляет собой две вертикальные линии с каждой стороны.

Пример:

| A | означает определитель матрицы A

(точно такой же символ, что и абсолютное значение.)

Вычисление определителя

Прежде всего, матрица должна быть квадратной (т.е. иметь такое же количество строк, как и столбцов). Тогда это просто арифметика. Вот как:

Для матрицы 2 × 2

Для матрицы 2 × 2 (2 строки и 2 столбца):

Определитель:

| A | = ad — bc
«Определитель A равен a, умноженному на d минус b, умноженному на c»

Легко вспомнить, когда вы думаете о кресте: Синий положительный (+ объявление), Красный отрицательный (-bc)

Пример:

| B | = 4 × 8 — 6 × 3

= 32–18

= 14

Для матрицы 3 × 3

Для матрицы 3 × 3 (3 строки и 3 столбца):

Определитель:

| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
«Определитель A равен… etc »

Может показаться сложным, но есть шаблон :

Для определения определителя матрицы 3 × 3 :

• Умножьте на на определитель матрицы 2 × 2 , который равен не в строке или столбце .
• Аналогично для b и для c
• Суммируйте, но помните минус перед цифрой b

В виде формулы (вспомните, что вертикальные полосы || означают «определитель») :

«Определитель A равен умноженному на определитель… etc »

Пример:

| C | = 6 × (−2 × 7 — 5 × 8) — 1 × (4 × 7 — 5 × 2) + 1 × (4 × 8 — (−2 × 2))

= 6 × (−54) — 1 × (18) + 1 × (36)

= −306

Для матриц 4 × 4 и выше

Шаблон продолжается для матриц 4 × 4:

• плюс a , умноженное на определитель матрицы, которая равна , а не в строке или столбце a ,
• минус b , умноженное на определитель матрицы, которая равна , а не в строке или столбце b ,
• плюс c , умноженное на определитель матрицы, которая равна , а не в строке или столбце c ,
• минус d , умноженное на определитель матрицы, которая равна , а не в строке или столбце d ,

В виде формулы:

Обратите внимание на шаблон + — + — (+ a… −b … + c … −d …). Это важно помнить.

Шаблон продолжается для матриц 5 × 5 и выше. Обычно для этого лучше использовать Матричный калькулятор!

Не единственный путь

Этот метод расчета называется «разложением Лапласа», и мне он нравится, потому что его легко запомнить. Но есть и другие методы (чтобы вы знали).

Сводка

• Для матрицы 2 × 2 определитель равен ad — bc
• Для матрицы 3 × 3 умножьте a на определитель матрицы 2 × 2 , то есть , а не в строке или столбце a , аналогично для b и c , но помните, что b имеет отрицательный знак!
• Шаблон продолжается для более крупных матриц: умножьте a на определитель матрицы , которая равна , а не в строке или столбце , продолжайте таким же образом по всей строке, но помните + — + — шаблон.

Формулы стандартного отклонения

Отклонение просто означает, насколько далеко от нормы

Стандартное отклонение

Стандартное отклонение — это мера того, насколько разброс наши номера — .

Вы можете сначала прочитать эту более простую страницу о стандартном отклонении.

Но здесь мы объясняем формулы .

Символ стандартного отклонения: σ (греческая буква сигма).

Это формула для стандартного отклонения:

Сказать что? Объясните, пожалуйста!

ОК. Давайте объясним это шаг за шагом.

Допустим, у нас есть набор чисел вроде 9, 2, 5, 4, 12, 7, 8, 11.

Чтобы вычислить стандартное отклонение этих чисел:

• 1. Определите среднее (простое среднее номеров)
• 2. Затем для каждого числа: вычтите Среднее и возведите результат в квадрат
• 3.Затем вычислите среднее значение этих квадратов разностей .
• 4. Извлеките из этого квадратный корень и готово!

Формула действительно говорит обо всем этом, и я покажу вам, как это сделать.

Объяснение формулы

Во-первых, у нас есть несколько примеров значений для работы:

Пример: У Сэма 20 кустов роз.

Количество цветков на каждом кусте

9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4

Определите стандартное отклонение.

Шаг 1. Определите среднее значение

В приведенной выше формуле μ (греческая буква «мю») — это среднее всех наших значений …

Пример: 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4

Среднее значение:

9 + 2 + 5 + 4 + 12 + 7 + 8 + 11 + 9 + 3 + 7 + 4 + 12 + 5 + 4 + 10 + 9 + 6 + 9 + 4 20

= 140 20 = 7

Итак:

мк = 7

Шаг 2.Затем для каждого числа: вычтите Среднее и возведите результат в квадрат

Это часть формулы, которая гласит:

Так что же такое x ​​ _и ? Это отдельные значения x 9, 2, 5, 4, 12, 7 и т.д …

Другими словами x ​​ ₁ = 9, x ​​ ₂ = 2, x ​​ ₃ = 5 и т. Д.

Итак, здесь говорится: «для каждого значения вычтите среднее и возведите результат в квадрат», например,

Пример (продолжение):

(9-7) ² = (2) ² = 4

(2-7) ² = (-5) ² = 25

(5–7) ² = (-2) ² = 4

(4-7) ² = (-3) ² = 9

(12-7) ² = (5) ² = 25

(7-7) ² = (0) ² = 0

(8–7) ² = (1) ² = 1

… и т.д …

И получаем следующие результаты:

4, 25, 4, 9, 25, 0, 1, 16, 4, 16, 0, 9, 25, 4, 9, 9, 4, 1, 4, 9

Шаг 3. Затем вычислите среднее значение квадратов разностей.

Чтобы вычислить среднее значение, сложите все значения, , затем разделите на количество .

Сначала сложите все значения из предыдущего шага.

Но как сказать в математике «сложить все»? Используем «Сигму»: Σ

Удобная сигма-нотация позволяет суммировать столько терминов, сколько мы хотим:

Сигма-нотация

Мы хотим сложить все значения от 1 до N, где N = 20 в нашем случае, потому что есть 20 значений:

Пример (продолжение):

Это означает: суммировать все значения от (x ₁ -7) ² до (x _N -7) ²

Мы уже вычислили (x ₁ -7) ² = 4 и т. Д.на предыдущем шаге, поэтому просто суммируйте их:

= 4 + 25 + 4 + 9 + 25 + 0 + 1 + 16 + 4 + 16 + 0 + 9 + 25 + 4 + 9 + 9 + 4 + 1 + 4 + 9 = 178

Но это еще не среднее значение, нам нужно разделить на сколько , что делается на умножение на 1 / N (то же, что и деление на N):

Пример (продолжение):

Среднее значение квадратов разностей = (1/20) × 178 = 8,9

(Примечание: это значение называется «Дисперсия»)

Шаг 4.Извлеките квадратный корень из этого:

Пример (завершение):

σ = √ (8,9) = 2,983 …

СДЕЛАНО!

Стандартное отклонение выборки

Но подождите, это еще не все …

… иногда наши данные — это всего лишь выборка всего населения.

Пример: У Сэма 20 кустов роз , но посчитал цветов только на 6 из них !

«Население» — всего 20 кустов роз,

, а «образец» — это 6 кустов, цветы которых Сэм считал.

Скажем, у Сэма количество цветов:

9, 2, 5, 4, 12, 7

Мы все еще можем оценить стандартное отклонение.

Но когда мы используем выборку в качестве оценки для всей генеральной совокупности , формула стандартного отклонения меняется на это:

Формула для Стандартное отклонение выборки :

Важным изменением является «N-1» вместо «N» (что называется «поправкой Бесселя»).

Символы также меняются, чтобы отразить, что мы работаем с выборкой, а не со всей генеральной совокупностью:

• Среднее значение теперь x (для выборочного среднего) вместо μ (среднее для генеральной совокупности),
• И ответ: с (для стандартного отклонения выборки) вместо σ .

Но это не влияет на расчеты. Только N-1 вместо N меняет вычисления.

Хорошо, давайте теперь вычислим стандартное отклонение выборки :

Шаг 1.Найдите среднее значение

Пример 2: Использование значений выборки 9, 2, 5, 4, 12, 7

Среднее значение: (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39/6 = 6,5

Итак:

х = 6,5

Шаг 2. Затем для каждого числа: вычтите Среднее и возведите результат в квадрат

Пример 2 (продолжение):

(9 — 6,5) ² = (2,5) ² = 6,25

(2 — 6,5) ² = (-4,5) ² = 20,25

(5 — 6,5) ² = (-1.5) ² = 2,25

(4 — 6,5) ² = (-2,5) ² = 6,25

(12 — 6,5) ² = (5,5) ² = 30,25

(7 — 6,5) ² = (0,5) ² = 0,25

Шаг 3. Затем вычислите среднее значение квадратов разностей.

Чтобы вычислить среднее значение, сложите все значения, , затем разделите на количество .

Но подождите … мы вычисляем стандартное отклонение Sample , поэтому вместо деления на количество (N) мы разделим на N-1

Пример 2 (продолжение):

Сумма = 6.25 + 20,25 + 2,25 + 6,25 + 30,25 + 0,25 = 65,5

Разделить на N-1 : (1/5) × 65,5 = 13,1

(Это значение называется «Выборочная дисперсия»)

Шаг 4. Извлеките квадратный корень из этого:

Пример 2 (завершение):

с = √ (13,1) = 3,619 …

СДЕЛАНО!

Сравнение

Когда мы использовали всю популяцию , мы получили: Среднее = 7 , Стандартное отклонение = 2.983 …

Когда мы использовали образец , мы получили: среднее значение выборки = 6,5 , стандартное отклонение выборки = 3,619 …

Наше выборочное среднее было неверным на 7%, а стандартное отклонение нашей выборки было неверным на 21%.

Зачем нужно брать образец?

В основном потому, что так проще и дешевле.

Представьте, что вы хотите знать, что думает вся страна … вы не можете спрашивать миллионы людей, вместо этого вы спрашиваете, может быть, 1000 человек.

Есть хорошая цитата (возможно, Самуэль Джонсон):

«Не обязательно есть животное целиком, чтобы знать, что мясо жесткое.»

Это основная идея выборки. Чтобы получить информацию о совокупности (такую ​​как среднее значение и стандартное отклонение), нам не нужно рассматривать всех членов совокупности; нам нужен только образец.

Но когда мы берем образец, мы теряем некоторую точность.

Сводка

Население Стандартное отклонение:
Образец Стандартное отклонение:

Определение эмпирической формулы из элементного анализа

На другой странице мы обсуждаем, как получить эмпирическую формулу из заданного молекулярная формула.Здесь мы рассмотрим, как получить эмпирическую формулу на основе элементного анализа образца. Помните, что сравнение эмпирической формулы, полученной в результате элементного анализа, с формулой молекулярной формулы сообщает нам, соответствует ли образец молекулярной формуле.

Поиск эмпирического из текста фильма по элементному анализу

Допустим, у вас есть образец неизвестного вещества, и вы хотите получить его эмпирическую формулу.Вы отправляете почту образец для анализа, и они отправят вам отчет с указанием процентного содержания элементов в образце по массе. Наши цель — перейти от этого к эмпирической формуле.

Предположим, что результаты экспериментов говорят нам, что образец содержит 48,6% C, 8,16% H и 43,2% O по весу. Эти проценты скажите нам, что если бы у нас было 100 граммов образца, 48,6 грамма были бы углеродом, 8,16 грамма — водородом и 43,2 грамма будет кислородом.Чтобы получить эмпирическую формулу, нам нужно перевести из граммов углерода, водорода и кислорода к числу атомов углерода, атомов водорода и атомов кислорода. Мы можем преобразовать граммы в количество атомов (т. е. молей атомов), используя молекулярную массу. Сначала определим количество молей каждого из элементы в нашем 100-граммовом образце.

Мы начинаем с 48,6 грамма углерода на 100 граммов образца и умножаем на один моль углерода на каждые 12.011 граммов углерода, чтобы получить 4,05 моля углерода на 100 граммов образца. Аналогично для водорода мы начинаем с 8,16 грамма водорода, умножьте на один моль водорода на каждые 1,0079 грамма водорода, и получите 8,10 моль. водорода в 100 граммах образца. Наконец, для кислорода мы находим, что (43,2 грамма O) (1 моль O / 15,9994 г O) дает us 2,70 моль O на 100 г образца.

Теперь мы получили количество атомов C, H и O в 100 г образца.Это приближает нас к нашей цели вычисление эмпирической формулы. Однако эмпирическая формула связана с отношениями между величиной этих элементов, поэтому в следующий раз мы рассчитаем эти соотношения. Соотношение атомов C: атомов H: атомов O составляет 4,05: 8,10. : 2,70.

Чтобы получить эмпирическую формулу, нам нужно уменьшить эти отношения до их наименьших целых чисел. Для этого мы воспользоваться тем, что мы можем умножать или делить эти числа на все, что захотим, сохраняя соотношение такое же.Например, если мы разделим на два, разрезав все числа пополам, мы получим результаты, которые вы видите. на экране ниже, и мы не изменили отношения между количеством атомов.

Деление на 2 не особенно полезно, но предположим, что мы разделим каждое из этих чисел на 2,70, наименьшее из три числа. Тогда мы получим результаты, которые вы видите ниже. Теперь соотношение становится 1,50: 3,00: 1,00. Выбирая наименьшее из наших трех исходных чисел, мы сделали одно из чисел в соотношении a 1 и упростили другие числа.Сейчас мы очень близки к получению эмпирической формулы; мы знаем, что есть 1,50 атома углерода на каждые 3,00 атома водорода и 1,00 атом кислорода.

Эмпирическая формула должна представлять отношения между элементами в виде наименьших целых чисел. Чтобы добраться до наименьшее целочисленное отношение, мы можем умножить каждое из чисел на 2, чтобы получить 3,00: 6,00: 2,00. Умножение на 2 преобразовал 1,50 в целое число 3,00. Теперь это говорит нам о соотношении атомов каждого элемента в члены наименьших целочисленных соотношений, приводящие к эмпирической формуле C ₃ H ₆ O ₂ .

.

No related posts.