Как найти площадь сечения круга: определить площадь круга, если известна длина окружности — Лазерная резка металла от "ТМК" Ярославль (Тутаев)

Содержание

Как найти площадь круга 🚩 Школы

Кругом называется часть плоскости, ограниченная окружностью. Основным показателем и для окружности, и для круга является радиус. Если он задан, площадь круга можно вычислить по основной формуле S=πR2, где S – площадь круга, R – радиус окружности, ограничивающей круг, а π – константа, равная 3,14. В условиях задачи может быть дана длина окружности. Она равна L=2πR. В этом случае сначала необходимо вычислить радиус, разделив заданную величину L на 2π, то есть воспользоваться формулой R=L/2π.
В окружность, ограничивающую круг, может быть вписан четырехугольник, сумма противолежащих углов которого составляет 180°, то есть это квадрат или прямоугольник. В этом случае диаметр описанной вокруг четырехугольника окружности является одновременно диагональю. Если в условиях заданы размеры сторон четырехугольника, найти эту диагональ не составит особого труда, воспользовавшись теоремой Пифагора. Диагональ делит квадрат или прямоугольник на два прямоугольных треугольника, то есть является гипотенузой каждого из этих треугольников.

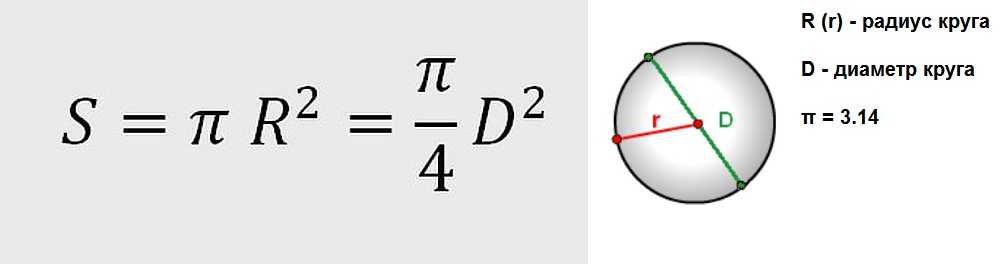Соответственно, найти ее можно, сложив квадраты сторон четырехугольника, то есть по формуле d2=a2+b2. Чтобы найти площадь круга, даже не нужно из полученного результата извлекать квадратный корень, поскольку R=d/2. Чтобы найти квадрат радиуса, достаточно квадрат диаметра разделить на 4.
Способ решения этого варианта задачи зависит от того, какой треугольник вписан и какие его параметры заданы. Если треугольник прямоугольны, алгоритм решения будет таким же, как для квадрата или прямоугольника, поскольку сторона, противолежащая прямому углу, всегда является диаметром описанной окружности. Если даны размеры катетов, возведите каждый из них в квадрат и найдите сумму, а затем полученный результат разделите на 4 и умножьте на число π. Если треугольник равносторонний, придется выполнить несколько дополнительных построений, чтобы в итоге получились прямоугольные треугольники, параметры которых вам известны. Например, в окружность с центром О вписан равносторонний треугольник АВС, сторона которого вам задана.

Проведите высоты AN, ВM и СQ. Рассмотрите, например, прямоугольный треугольник AQO. Вам известна его гипотенуза AQ, которая равна половине стороны исходного треугольника, а также все углы, так что найти длину отрезка AQ, который одновременно является радиусом круга, площадь которого вам надо найти, можно по теореме синусов или косинусов.

Площадь круга — Википедия

Материал из Википедии — свободной энциклопедии

Площадь круга с радиусом r равна πr². Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть ¹⁄₂ × 2πr × r).

История

Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов.^[1] Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге

Измерение круга^[en]. Длина окружности равна 2πr, а площадь треугольника равна половине основания на высоту, что даёт πr². До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек^[2] Однако он не установил константу пропорциональности.

Использование многоугольников

Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу.

Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус.^[3]

Доказательство Архимеда

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше

Круг с вписанными квадратом и восьмиугольником. Показан зазор

Предположим, что площадь круга C больше площади треугольника T = ¹⁄₂cr. Пусть E означает превышение площади. Впишем^[en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈.

Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

E=C−T>GnPn=C−Gn>C−EPn>T{\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из

n равных треугольников высоты h с основанием s, что даёт ¹⁄₂nhs. Но h < r и ns < c, так что площадь многоугольника должна быть меньше площади треугольника ¹⁄₂cr, получили противоречие.

Не меньше

Окружность с описанным квадратом и восьмиугольником. Показан зазор

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше

D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника P_n должна быть меньше T.

D=T−C>GnPn=C+Gn<C+DPn<T{\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&

Как найти площадь сечения

Множество задач в геометрии основаны на определении площади сечения геометрического тела. Одним из наиболее встречающихся геометрических тел является шар, и определение площади его сечения может подготовить к решению задач самых разных уровней сложности.

2). Эта формула будет верной и для граничных точек расположения площади, когда k = R или k = 0. При подстановке этих значений площадь сечения S равняется либо 0, либо площади круга с радиусом шара R.

Круговых формул в математике | Площадь, окружность, сектор, хорда, круговая дуга

Свойства круга в математике | Дуга, Периметр, Отрезок окружности

Окружность может быть определена как геометрическое место всех точек, равноудаленных от центральной точки. Здесь мы обсуждаем около свойств круга , формул круга , таких как площадь , периметр , длина дуги, длина сегмента, площадь сегмента .. . пр.

Терминология, связанная с кругами в математике:

Начало координат:

Это центральная (равноудаленная) точка круга.Здесь «O» — начало круга.

Радиус: Расстояние от центра круга до любой точки вокруг него окружности называется Радиус окружности. Обычно обозначается буквой «r».

Диаметр: Наибольшее расстояние от одного конца круга до другого конца круга называется диаметром круга. Обычно обозначается буквой «D». Диаметр круга = 2 x Радиус круга. я. е D = 2r.

Дуга окружности: Это часть окружности круга. Большая дуга называется большой, а меньшая — вспомогательной.

Сектор круга: Это часть площади круга между двумя радиусами (клин круга).

Хорда: Линия , отрезок внутри круга, который касается двух точек на окружности, называется хордой окружности.

Окружность: Расстояние по окружности называется окружностью или периметром окружности.

Пи (π ): Это число, равное 3,141592… или 22/7.

пи (π ) = (окружность) / (диаметр) любого круга.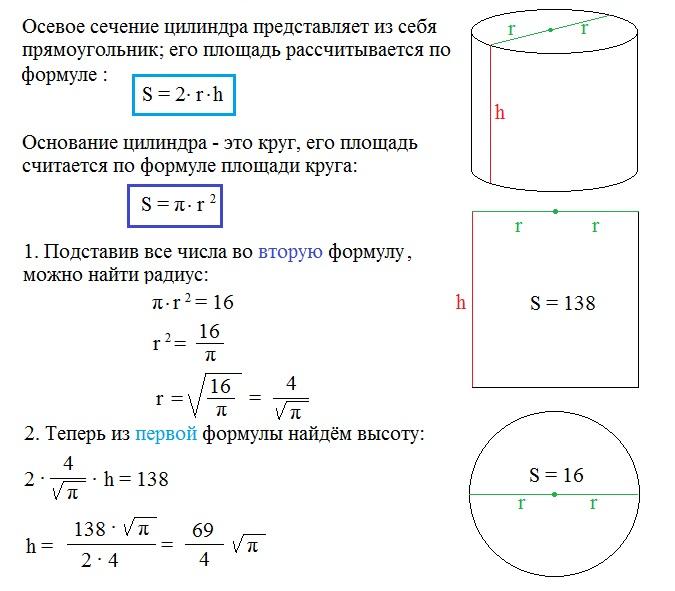

Касательная окружности: линия, перпендикулярная радиусу, которая касается ТОЛЬКО одной точки на окружности.

Секанс окружности : линия, пересекающая окружность в двух точках, называется Секанс окружности .

Свойства круга:

Конгруэнтность : две окружности могут быть конгруэнтными тогда и только тогда, когда они имеют равных радиусов.
Перпендикуляр от центра окружности к хорде делит хорду пополам. Обратное также верно.
Серединные перпендикуляры двух хорд окружности пересекаются в его центре.

Может быть одна и только одна окружность, проходящая через три или более неколлинеарных точек.
Если две окружности пересекаются в двух точках, то прямая, проходящая через центры, является серединным перпендикуляром к общей хорде.
Если две хорды окружности равны, то центр окружности лежит на биссектрисе двух хорд.
Равные хорды окружности или равные окружности равноудалены от центра.
Равноудаленные хорды от центра окружности равны друг другу по длине.
Градус дуги окружности равен удвоенному углу, который она образует в любой точке альтернативного сегмента окружности.

Равные хорды окружности (или конгруэнтных окружностей) имеют равные углы в центре (в соответствующих центрах). Верно и обратное.
Если сумма противоположных углов четырехугольника равна 180 °, то четырехугольник является вписанным.
Секущая означает линию, пересекающую окружность в двух точках. Касательная означает, что это линия, которая касается круга ровно в одной точке.
В двух концентрических окружностях хорда большего круга, касающаяся меньшего круга, делится пополам в точке контакта.

Круговые формулы в математике:

Площадь и длина окружности:

Здесь Начало круга = O, Диаметр = D и Радиус = r

Площадь круга (A) = π r ² = (π / 4) D ²

= 0,7854 D ²
Окружность круга (C) = 2 π r = π Д.

Площадь круга = (1/2) x окружность x радиус

A = (1/2) x C x r

Диаметр окружности (D) = √ (A / 0.7854).

Дуга и сектор круга:

Здесь угол между двумя радиусами равен ”θ” в градусах. . И сектор круга AOB.
Длина дуги окружности (l) (второстепенная) = (θ / 360) x 2 π r = θ π r / 180

Площадь сектора (второстепенная) =

(θ / 360) x π r ²

Если угол θ выражен в радианах, то

Площадь сектора = (θ / 2) r ²

Секторный угол окружности θ = (180 x l) / (π r).

Отрезок окружности и периметр отрезка:

Здесь радиус окружности = r, угол между двумя радиусами равен ”θ” в градусах.

Площадь сегмента круга = Площадь сектора — Площадь ΔOAB.

Площадь сегмента = (θ / 360) x π r ² — (1/2) x sinθ x r ²

Периметр отрезка = (θ π r / 180) + 2r sin (θ / 2).

Длина хорды окружности = 2 √ [h (2r — h)] = 2r sin (θ / 2).

Дуга Длина сегмента круга = l = 0,01745 x r x θ

Онлайн калькулятор для расчета площади сегмента круга

Площадь кругового кольца:

Здесь радиус большого круга = R и Dia = D,

Радиус малого круга = r и диаметр = d,

Площадь кругового кольца = 0,7854 (D ² — d ²) = (π / 4) (D ² — d ²)

Площадь кругового кольца = π (R ² — r ²).

Формула пересечения хорд в окружности:

Здесь AB и CD — две хорды в окружности, каждая из которых пересекается в точке E.

Тогда AE: EB = DE: EC.

Формула длины касательных окружностей:

Здесь Две окружности, начало O и O ’и радиус равны r1 и r2 соответственно.

Прямая общая касательная AB и поперечная общая касательная = CD

Длина прямой общей касательной AB = √ [(Расстояние между двумя исходными точками) ² — (r1 -r2) ²]

= √ [(OO ’) ² — (r1 -r2) ²]

Длина общей поперечной касательной AB = √ [(Расстояние между двумя исходными точками) ² — (r1 + r2) ²]

= √ [(OO ’) ² — (r1 + r2) ²]

Геометрия по математике

Формулы двухмерных фигур.

Четырехугольник Недвижимости | Трапеция, параллелограмм, Ромб

Типы треугольников с примерами | Свойства треугольника

Система счисления.

Категории номеров

Правила делимости чисел

Формулы суммы n последовательных чисел

Методы поиска HCF и LCM

Проблемы и решения GCD и LCM

Привет, друзья Спасибо за чтение. Надеюсь, вам понравилось. Оставляйте отзывы, комментарии и, пожалуйста, не забудьте поделиться ими.

Как найти центр круга

Образование
Математика
Тригонометрия
Как найти центр круга

Мэри Джейн Стерлинг

Один из способов описать середину круга — это для определения центроида . Эта средняя точка является центром тяжести, где вы можете уравновесить треугольник и повернуть его вокруг .

Когда вы строите круг, треугольник или линейный сегмент с использованием координатных осей, вы можете назвать эти средние точки парой координат x- и y- .Все, что вам нужно, чтобы найти эти коридоры, — это координаты некоторых других важных точек на соответствующих фигурах.

Если конечные точки одного диаметра окружности равны ( x ₁, y ₁) и ( x ₂, y ₂), то центр окружности имеет координаты

Вы, наверное, заметили, что центр круга совпадает с серединой диаметра. Центр круга разделяет диаметр на два равных сегмента, называемых радиусами (во множественном числе — радиус).

На рисунке показан круг диаметром с концами (7,4) и (–1, –2). Центр круга находится в точке (3,1). Координаты центра были найдены по формуле для средней точки сегмента:

Длину диаметра можно найти по формуле расстояния:

Диаметр показанного круга составляет 10 единиц.

Затем вы найдете длину одного из радиусов. Подойдет любой — они одинаковой длины.В этом примере изобразите длину радиуса от центра окружности (3,1) до конечной точки диаметра (7,4):

Радиус 5 единиц в длину. Но, конечно, вы ожидали такого ответа, потому что по определению радиус составляет половину длины диаметра.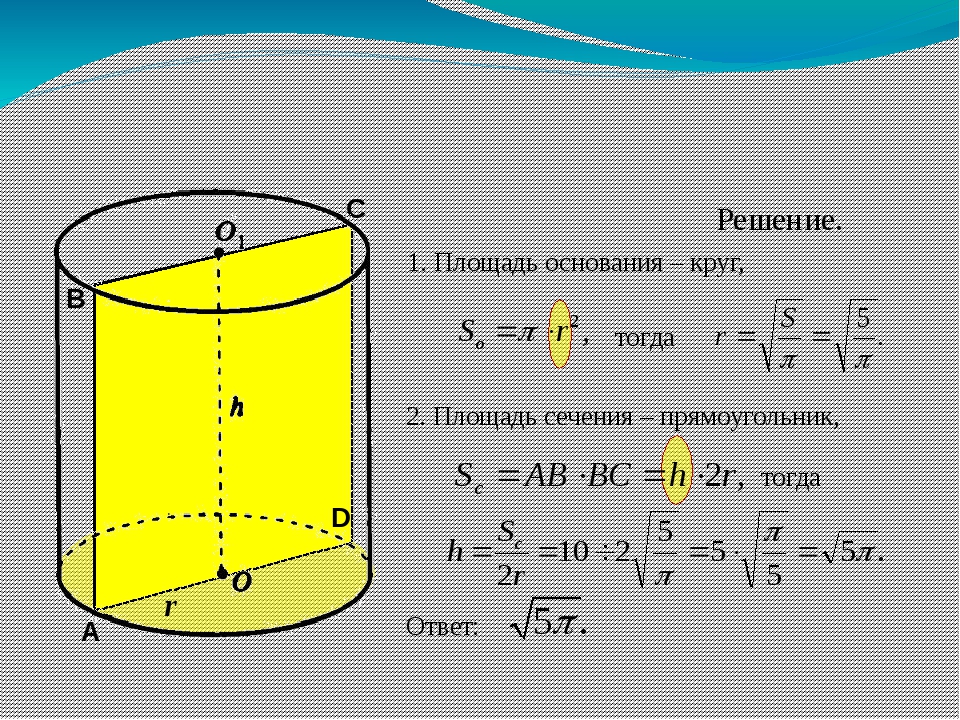

Об авторе книги

Мэри Джейн Стерлинг является автором Алгебра I для чайников и многих других книг для чайников .Она преподавала математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет и любила работать с будущими руководителями бизнеса, физиотерапевтами, учителями и многими другими.

Радиус круга для данной площади Калькулятор

Цель использования: Рассчитать радиус квадратного метра купола.

Цель использования: Определение площади пола башни площадью 100 кв.м в Dungeons and Dragons.

Цель использования: Рассчитайте размер пиццы, если вы превратили две 9-дюймовые пиццы в одну пиццу .

Цель использования: определение радиуса круга на основе площадь

Цель использования: edulastic…..
Комментарий / Запрос: что происходит

Цель используйте: Найдите радиус «локальной» территории на основе квадратного километра муниципального образования

Цель использования: Получение дополнительной информации о покрытии интернет-маршрутизатора

Цель использования: Назначение
Комментарий / Запрос: ничего

Цель использования: I я художник. Я использую этот сайт для исследования геометрических форм. Это ОЧЕНЬ полезно! Спасибо.

Цель использования: Чтобы получить знания и как найти радиус, когда дана только площадь круга
Комментарий / запрос: Пожалуйста, помогите мне рассчитать радиус с заданной площадью

Как найти площадь и окружность круга

Круги — это обычные формы.Вы можете увидеть их повсюду — колеса машин, компакт-диски с данными, летающие по воздуху летающие тарелки. Все это круги.

Круги — это двухмерные фигуры, такие же, как четырехугольники и многоугольники.

Однако круг измеряется иначе, чем все другие формы.

Нам даже нужно использовать несколько разных терминов для их описания. Давайте посмотрим на эти интересные формы.

Первый: Свойства кругов. Круги представляют собой наборы точек, которые находятся на одинаковом расстоянии от фиксированной центральной точки.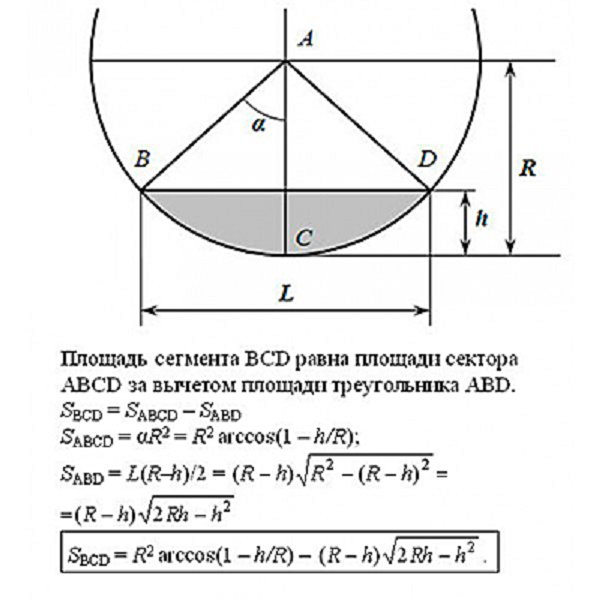

Мы называем эту фиксированную среднюю точку центром. А расстояние от центра круга до всех его точек — это то, что мы называем радиусом.

И когда мы складываем два радиуса (множественная форма радиуса) вместе и формируем один отрезок прямой через весь круг, мы получаем диаметр. Диаметры кругов проходят через центральную точку нашего круга и имеют свои концы на самом круге.

Итак, мы видим, что диаметр окружности в два (2) раза больше длины радиуса окружности.Мы можем представить это выражением «2r» или «в два раза больше его радиуса». Итак, если мы знаем радиус круга, мы умножаем его на два (2) и получаем его диаметр. Это также означает, что, если мы знаем диаметр круга, мы можем разделить его на 2 (два), чтобы определить его радиус.

Например:
Проблема: найти диаметр этого круга.

d = 2r Диаметр круга в 2 (два) раза больше его радиуса (или 2r).
d = 2 (7) Радиус этого круга равен семи (7) дюймам.