Колесо в зубчатой передаче — Энциклопедия по машиностроению XXL
Во фрикционной передаче вращение передается вследствие действия силы сцепления на поверхности соприкасающихся колес, в зубчатой передаче — от зацепления зубьев, [c.212]Перекосы (биение напрессованных на валы деталей) Взаимная непараллельность осей зубчатых колес в зубчатой передаче Неправильная сборка Технология [c.628]
Для проверочного расчета должны быть известны следующие параметры нарезаемого колеса и сопряженного колеса в зубчатой передаче профильный угол а и модуль по нормали т число зубьев г , толщина зуба по нормали на делительном цилиндре ад диаметр окружности головок Dei, диаметр окружности впадин Оц число зубьев сопряженного колеса г диаметр окружности головок и основного цилиндра doa сопряженного колеса межосевое расстояние Ai в зубчатой передаче. [c.592]
Независимо от степеней точности установлено четыре вида сопряжения колес в зубчатой передаче, определяемые величиной бокового зазора между зубьями.
При трении качения детали перекатываются одна по другой без скольжения и поверхности их касаются друг друга только по линии или в одной точке, причем по мере перекатывания деталей линия или точка касания все время сменяется новой, что наблюдается, например, при качении катков по рельсам, перекатывании (без скольжения) зубьев колес в зубчатой передаче и т. д. [c.27]
Меньшее колесо в зубчатой передаче, в большинстве случаев ведущее, часто называют шестерней. Во время работы зубья ведущего колеса входят во впадины ведомого и боковые поверхности зубьев вступают в соприкосновение, образуя высшую кинематическую пару IV класса. Соприкосновение зубьев колес, в результате которого осуществляется передача вращательного движения, носит название зацепления.
Вращательное движение колес в зубчатой передаче, как и во фрикционной, определяется передаточным отношением [c.87]
КОЛЕСО В ЗУБЧАТОЙ ПЕРЕДАЧЕ — зубчатое колесо передачи с боль-
[c. 160]
160]
ШЕСТЕРНЯ — зубчатое колесо с мень-щим числом зубьев по сравнению с другим зацепляющимся с ним зубчатым колесом (см. Колесо в зубчатой передаче).
Зубчатое колесо передачи с меньшим числом зубьев принято называть шестерней, а с большим числом зубьев — колесом. В зубчатых передачах при одинаковом числе зубьев колес шестерней называют ведущее зубчатое колесо, а колесом — ведомое. Термин зубчатое колесо относится как к шестерне, так и к колесу. По конструкции зубчатые колеса разделяют на насадные, т. е. насаживаемые на вал, и вал-шестерни, у которых зубья нарезаны непосредственно на валу. [c.7]
Погрешности изготовления деталей по осевым линейным размерам и погрешности сборки приводят к неточному осевому положению колес в зубчатых передачах, а также червячного колеса в червячных передачах.
Погрешности изготовления деталей по угловым и осевым линейным размерам, а также погрешности сборки приводят к неточному относительному положению колес в зубчатых передачах или червячного колеса и червяка в червячных передачах.
 [c.102]
[c.102]Угол зацепления нарезаемого и сопряженного с ним колеса в зубчатой передаче [c.608]
В зубчатой передаче зубчатое колесо с меньшим числом зубьев называют шестерней, а с большим — колесом.
В зубчатой передаче оси зубчатых колес могут быть параллельны (цилиндрические передачи, рис. 191, о) пересекаться (конические передачи, рис. 191, б) скрещиваться (червячные передачи, рис. 191, в). [c.205]
Передачи выполняют с постоянным или переменным (регулируемым) передаточным отношением. Как те, так и другие широко распространены. Регулирование передаточного отношения может быть ступенчатым или бесступенчатым. Ступенчатое регулирование выполняют в коробках скоростей с зубчатыми колесами, в ременных передачах со ступенчатыми шкивами и т. п. бесступенчатое регулирование — с помощью фрикционных или цепных вариаторов. Применение того или иного способа регулирования передаточного отношения зависит от конкретных условий работы машины, которую обслуживает передача.
При разборе этого примера необходимо вспомнить и написать наименования и суть всех показателей точности, приведенных в примере указать, при каких условиях работы и в зубчатых передачах каких машин может быть использовано данное зубчатое колесо.
В зубчатых передачах с промежуточном колесом расположение колеса очень влияет на величину нагрузки, действующей на опоры. [c.137]
В зубчатой передаче (рис, 417, а) нагрузка р1 на малое колесо от сил привода больше нагрузки Рг на большое колесо в отношении Пз/Рг 3. [c.577]
В зубчатых передачах целесообразно разгружать многооборотные валы от радиальных нагрузок посредством многопоточного привода (привод несколькими зубчатыми колесами, симметрично расположенными по окружности). [c.537]
[c.537]
В зубчатых передачах скорости скольжения перпендикулярны контактным линиям (прямозубые передачи) или близки к перпендикулярам (косозубые передачи). Между тем в червячных передачах в средней части зуба червячного колеса имеется зона, в которой скольжение происходит вдоль контактных линий (рис. 11.6). На рис. ] .6 цифрами J, 2, 3 отмечены контактные линии в их последовательном положении в процессе зацепления и скорости скольжения иск в некоторых точках (направление U K близко к направлению окружной скорости червяка У ). Зона, в которой направление U k почти совпадает с
Задача 758. В зубчатой передаче вращений, представленной на рис. 441, водило имеет угловую скорость (о,,, а колесо II обкатывается по неподвижному колесу V. Найти угловые скорости зубчатых колес / и IV. Радиусы колес соответственно равны i, г., г .
В зубчатых передачах вращение от одного колеса к другому передается за счет усилий в точках контакта поверхностей зубьев, образующих высшую кинематическую пару. Для обеспечения непрерывного зацепления зубьев и постоянного передаточного отношения, т. е. отношения угловых скоростей колес передачи, профили зубьев должны быть очерчены определенными кривыми. Чтобы установить, какими именно кривыми должны быть очерчены профили зубьев, рассмотрим передачу вращения от оси О, к оси посредством давления профиля / на профиль 2 (рис. 18.2, а). В точке К их соприкосновения линейные скорости точек обоих профилей будут
Для обеспечения непрерывного зацепления зубьев и постоянного передаточного отношения, т. е. отношения угловых скоростей колес передачи, профили зубьев должны быть очерчены определенными кривыми. Чтобы установить, какими именно кривыми должны быть очерчены профили зубьев, рассмотрим передачу вращения от оси О, к оси посредством давления профиля / на профиль 2 (рис. 18.2, а). В точке К их соприкосновения линейные скорости точек обоих профилей будут
Колеса винтовых зубчатых передач выполняются как цилиндрические косозубые. Касание зубьев происходит в точке, что, учитывая большое скольжение вдоль зубьев, обусловливает возможность передачи лишь небольших усилий. Поэтому винтовые передачи используют как кинематические. [c.242]
Регулирование передаточного отношения может быть ступенчатым или бесступенчатым. Ступенчатое регулирование выполняют в коробках передач с зубчатыми колесами, в ременных передачах со ступенчатыми шкивами и т.
В червячных передачах возможны все виды разрушений и повреждений, встречающихся в зубчатых передачах, т. е. усталостное выкрашивание, износ, заедание и поломка зубьев червячного колеса как менее прочных по сравнению с витками червяка, имеющего повышенную работоспособность по своим геометрическим параметрам и механическим характеристикам материала (сталь). [c.483]
Для проверочного и проектного расчетов должны быть известны следующие параметры нарезаемого колеса и сопряженного с ним колеса в зубчатой передаче профильный угол Од и модуль по нормали /и число аубьев 2i5 толщина зуба по нормали на делительном цилиндре 5д1 диаметр окружности головок Deli диаметр окружности впади 1 число зубьев сопряженного колеса Zg] диаметр окружности головок gj и основнбго. цилиндра d a сопряженного колеса межосевое расстояние в зубчатой передаче.
ТОЧКИ окунания зубьев, обычно превращается в пену, которая в состоянии отвести образующееся в зацеплении тепло только при небольших мощностях (не свыше 15 л. с. на 1 см ширины зацепления пары зубчатых колес в зубчатых передачах средних размеров). Зубчатые колеса должны погружаться в масляную ванну на глубину от 0,75й до 2к, где к — высота зуба, но не менее чем на 10 мм. Крупномодульные зубчатые колеса т Э 20 мм) прп очень высокой вяз-1 ости смазкп достаточно погружать на половину высоты зуба.
с. на 1 см ширины зацепления пары зубчатых колес в зубчатых передачах средних размеров). Зубчатые колеса должны погружаться в масляную ванну на глубину от 0,75й до 2к, где к — высота зуба, но не менее чем на 10 мм. Крупномодульные зубчатые колеса т Э 20 мм) прп очень высокой вяз-1 ости смазкп достаточно погружать на половину высоты зуба.
Рассмотрим вопрос о действии сил в зубчатой передаче с косыми зубьями. На зуб колеса 2 действует сила расположенная в нормальной к зубу плоскости, содержащей прямую 0 0 (рис. 22.49, а), и отклоненная на угол р (рис. 22.49, б) от торцового сечения. В ЭТОЙ плоскости силананравлена под углом зацепления к нормальной плоскости (рис. 22.49, е). Сила может быть представлена как сумма трех составляющих, лежащих в трех перпендикулярных плоскостях силы направленной по касательной к начальным цилиндрам, силы направленной [c.471]
ПО длине зуба шестерни. Более рациональным, с этой точки зрения, является неконсольное расположение шестерни. Однако такие конструкции сложнее. Дополнительную опору можно разместить в специально выполненной внутренней стенке редуктора (рис. 12.8, а, б). Так как зубья конической шестерни нарезают на валу, то посадочный диаметр под подшипник дополнительной опоры оказывается небольшим. Рядом расположенное колесо конической зубчатой передачи ограничивает радиальные размеры этой опоры.
[c.172]
Однако такие конструкции сложнее. Дополнительную опору можно разместить в специально выполненной внутренней стенке редуктора (рис. 12.8, а, б). Так как зубья конической шестерни нарезают на валу, то посадочный диаметр под подшипник дополнительной опоры оказывается небольшим. Рядом расположенное колесо конической зубчатой передачи ограничивает радиальные размеры этой опоры.
[c.172]
Чугун применяют главным образом для изготовления крупногабаритных, тихоходных колес и колес открытых зубчатых передач. Основной недостаток чугуна — пониженная прочность по напряжению изгиба. Однако чугун хорошо противостоит усталостному выкрап и-ванию и заеданию в условиях скудной смазки. Он не дорог и обладает хорошими литейными свойствами, хорошо обрабатывается. Разработанные новые сорта модифицированного чугуна позволяют чугунному литью конкурировать со стальным литьем также и в закрытых передачах. Для изготовления зубчатых колес применяют серый и модифицированный чугун, а также магниевый чугун с шаровидным графитом — см. ГОСТ 1412—79.
[c.144]
ГОСТ 1412—79.
[c.144]
Особое внимание уделяют нормам точности монтажа передачи, так как в червячной передаче ошибки положения колеса отггасительно червяка более вредны, чем в зубчатых передачах. Как было отмечено, в зубчатых передачах осевое смещение колес и небольшие изменения межосевого расстояния не влияют на распределение нагрузки по длине зуба. В червячных передачах это влияние весьма существенно. Поэтому здесь устанавливают более строгие допуски на межосевое расстояние и положение средней плоскости колеса относительно червяка. В конструкциях обычно предусматривают возможность регулировки положения средней плоскости колеса относительно червяка, а при монтаже это положение проверяют по пятну контакта (краске). [c.176]
У фрикционных передач контакт колес g и Ь осуществляется только в точках Л и Л (см. рис. 10.3). При этом используются только окруж пые скорости у,, так как в точках Л и Л радиальные скорости v равны нулю (см. выше). В зубчатых передачах контакт зубьев рас пространяется на участки, где обе скорости Vt и и, не равны нулю Со скоростью связана специфика преобразования движения в зуб чатой передаче.
[c.194]
В зубчатых передачах контакт зубьев рас пространяется на участки, где обе скорости Vt и и, не равны нулю Со скоростью связана специфика преобразования движения в зуб чатой передаче.
[c.194]
Способы натяжения рем ней. Выше показано, что значение натяжения fo ремня оказывает существенное влияние на долговечность, тяговую способность II к. п. д. передачи. Наиболее экономичными и долговечными являются передачи с малым запасом трепня (с малым запасом F ). На практике большинство передач работает с переменным режимом нагрузки, а расчет передачи выполняют по максимальной из-возможных нагрузок. При этом в передачах с постоянным предварительным натяжением в периоды недогрузок излишнее натяжение снижает долговечность и к. п. д. С этих позиций целесообразна конструкция передачи, у которой натяжение ремня автоматически изменяется с изменением нагрузки, т. е. отношение f(// onst. Пример такой передачи показан на рис. 12.12. Здесь ременная передача сочетается с зубчатой. Шкив / установлен на качающемся рычаге 2, который является одновременно осью ведомого колеса 3 зубчатой передачи. Натяжение 2Г ремпя равно окружной силе в зацеплении зубчатой передачи, т. е. пропорционально моменту нагрузки. Преимуществом передачи является также то, что центробежные силы не влияют на тяговую способность (передача может работать при больишх скоростях). Недостатки передачи сложность конструкции и потеря свойств само-предохранения от перегрузки.
[c.231]
Натяжение 2Г ремпя равно окружной силе в зацеплении зубчатой передачи, т. е. пропорционально моменту нагрузки. Преимуществом передачи является также то, что центробежные силы не влияют на тяговую способность (передача может работать при больишх скоростях). Недостатки передачи сложность конструкции и потеря свойств само-предохранения от перегрузки.
[c.231]
В зубчатых передачах роль радиусов с)зрикционных катков играют радиусы г, и Г2 так называемых начальных окружностей находящихся в зацеплении зубчатых колес. Точки касания этих окружностей имеют одинаковую скорость. Кроме того, можно показать, что числа зубьев г, и 2., указанных колес пропорциональны величинам г, и Гг- Поэтому [c.47]
Компенсация несоосности бывает необходима в связи с погрешностями изготовления или требованиями самоустановки. Примеры осевых перемеитений под нагрузкой — сверлильные шпиндели, карданные валы автомобилей без нагрузки — передвижные зубчатые колеса в коробках передач. [c.131]
[c.131]
В точках В и В» линия зацепления пересекается окружностями вершин зубьев колес в точке В сопряженные профили входят в зацепление, а в точке в»- -выходят из зацепления. Процесс взаимодействия главных поверхностей сопряженных зубьев проис-Щдйт на участке В В» линии зацепления эта часть линии зацеп-летгЯназывается активной линией зацепления. Зубчатая передача должна быть спроектирована так, чтобы участок В В» укладывался в пределах линии зацепления N N2- Ес и точки и В» вый. т за эти пределы, то в зубчатой передаче произойдет заклинивание. [c.374]
Основная теорема зацепления. В зубчатых передачах вращение от одного колеса другому передается силами в точках контакта боковых поверхностей зубьев. Поверхности взаимодействующих зубьев зубчатых колес, обеспечивающие постоянное передаточное число, называют сопряженными поверхностями зубьев. Для получения таких поверхностей профили зубьев нужно очертить кривыми, подчиняющимися определенным законам. Эти законы вытекают из основной теоремы зацепления общая нормаль пп к профилям зубьев, проведенная через точку их касания, в любой момент зацепления проходит через полюс зацепления П, делящий межосевую линию О1О2 на отрезки, обратно пропорциональные угловым скоростям.
[c.331]
Эти законы вытекают из основной теоремы зацепления общая нормаль пп к профилям зубьев, проведенная через точку их касания, в любой момент зацепления проходит через полюс зацепления П, делящий межосевую линию О1О2 на отрезки, обратно пропорциональные угловым скоростям.
[c.331]
Колесо 1 зубчатой передачи вращается по закону pi = 2f (ф1 —в радиаиах, —в секундах) и приводит [c.47]
| В Викисловаре есть статья «зубчатое колесо» |
Зубчатые передачи — Слесарно-механосборочные работы
Зубчатые передачи
Категория:
Слесарно-механосборочные работы
Зубчатые передачи
Зубчатые передачи имеются почти во всех сборочных единицах промышленного оборудования. С их помощью изменяют по величине и направлению скорости движущихся частей станков, передают от одного вала к другому усилия и крутящие моменты.
В зубчатой передаче движение передается с помощью пары зубчатых колес. В практике меньшее зубчатое колесо принято называть шестерней, а большее — колесом. Термин «зубчатое колесо» относится как к шестерне, так и к колесу.
Зубчатое колесо, сидящее на ведущем валу, называют ведущим, а сидящее на ведомом валу — ведомым. Число зубьев зубчатого колеса обозначается буквой z.
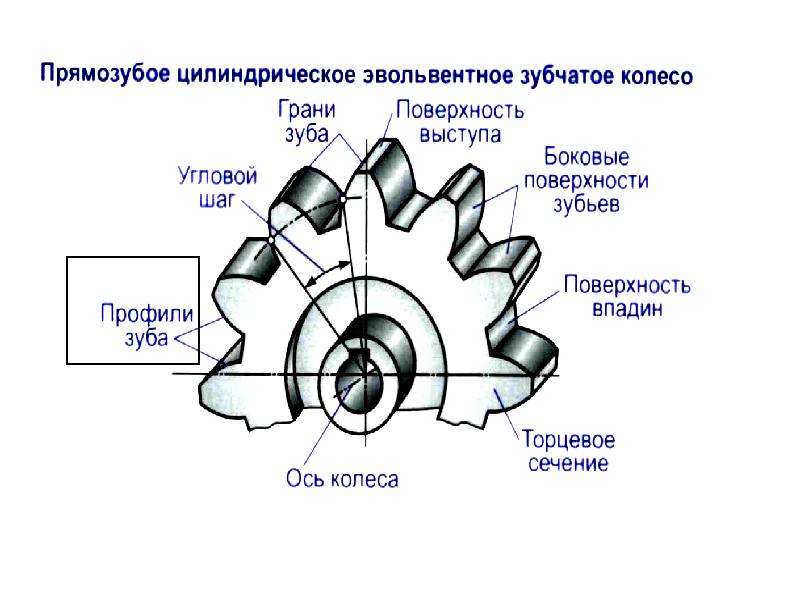
В зависимости от взаимного расположения геометрических осей валов зубчатые передачи бывают: цилиндрические, конические и винтовые. Зубчатые колеса для промышленного оборудования изготовляют с прямыми, косыми и угловыми (шевронными) зубьями.
По профилю зубьев зубчатые передачи различают: эволь-вентные и циклоидальные. Помимо зубчатых передач с эволь-вентным зацеплением в редукторах применяют передачу Новикова с круговым профилем зубьев. Передача Новикова позволяет применять колеса с малым числом зубьев, а значит, имеет большое передаточное число и может передавать значительные мощности. Циклоидальное зацепление используется в приборах и часах.
Циклоидальное зацепление используется в приборах и часах.
Цилиндрические зубчатые колеса с прямым зубом служат в передачах с параллельно расположенными осями валов и монтируются на последних неподвижно или подвижно.
Зубчатые колеса с косым зубом применяют для передачи движения между валами, оси которых пересекаются в пространстве, а в ряде случаев и между параллельными валами, например, когда в передаче должны сочетаться повышенная окружная скорость колес и бесшумность их работы при больших передаточных отношениях до 15:1.
Косозубые колеса монтируют на валах только неподвижно.
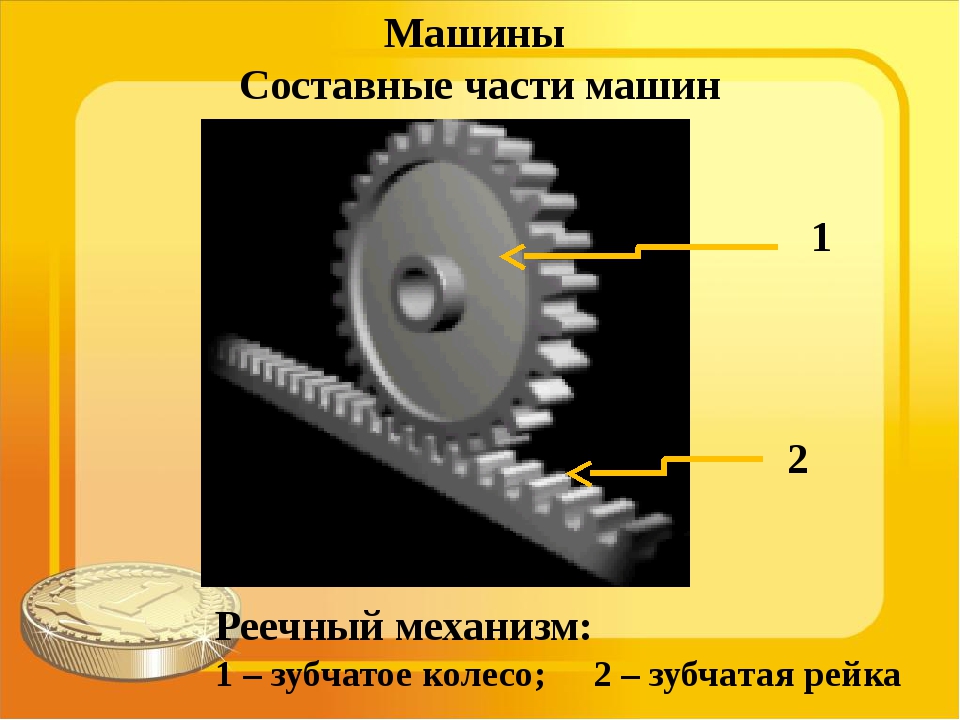
Рис. 1. Зубчатые зацепления: а — цилиндрическое с прямым зубом, б — то же, с косым зубом, в — с шевронным зубом, г — коническое, д — колесо — рейка, е — червячное, ж — с круговым зубом
Работа косозубых колес сопровождается осевым давлением. Осевое давление можно устранить, соединив два косозубых колеса с одинаковыми, но направленными в разные стороны зубьями. Так получают шевронное колесо (рис. 1, в), которое монтируют, обращая вершину угла зубьев в сторону вращения колеса. На специальных станках шевронные колеса изготовляют целыми из одной заготовки.
1, в), которое монтируют, обращая вершину угла зубьев в сторону вращения колеса. На специальных станках шевронные колеса изготовляют целыми из одной заготовки.
Конические зубчатые передачи различают по форме зубьев: прямозубые, косозубые и круговые.
На рис. 1, г показаны конические прямозубые, а на рис. 1, ж – круговые зубчатые колеса. Их назначение – передача вращения между валами, оси которых пересекаются. Для пересекающихся осей применяют также червячные передачи (рис. 1, е). Конические зубчатые колеса с круговым зубом применяются в передачах, где требуется особая плавность и бесшумность движения.
На рис. 1, д изображены зубчатое колесо и рейка. В этой передаче вращательное движение колеса преобразуется в прямолинейное движение рейки.
Элементы зубчатого колеса. В каждом зубчатом колесе (рис. 2) различают три окружности (делительную, окружность выступов, окружность впадин) и, следовательно, три соответствующих им диаметра.
Делительная, или начальная, окружность делит 3Уб по высоте на две неравные части: верхнюю, называемую головкой зуба, и нижнюю, называемую ножкой зуба.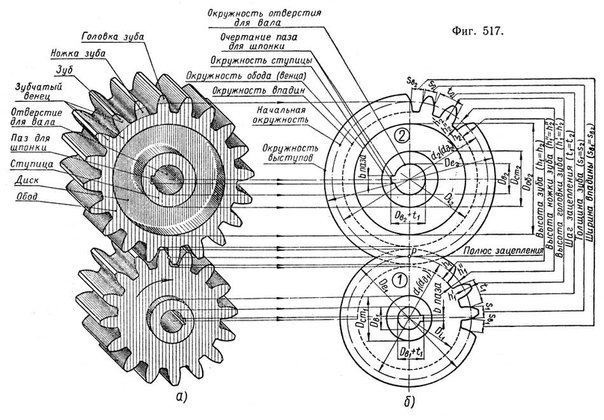 Высоту головки зуба принято обозначать ha, высоту ножки — hf, а диаметр окружности — d.
Высоту головки зуба принято обозначать ha, высоту ножки — hf, а диаметр окружности — d.
Окружность выступов – это окружность, ограничивающая сверху профили зубьев колеса. Обозначают ее da.
Окружность впадин проходит по основанию впадин зубьев. Диаметр этой окружности обозначают df.
Расстояние между серединами двух соседних зубьев, измеренное по дуге делительной окружности, называется шагом зубчатогозацепления. Шаг обозначают буквой Р. Если шаг, выраженный в миллиметрах, разделить на число л = 3,14, то получим величину, называемую модулем. Модуль выражают в миллиметрах и обозначают буквой т.
Дуга делительной окружности в пределах зуба называется толщиной зуба, дуга S1 — шириной впадины. Как правило, S = = Sx. Размер b зуба по линии, параллельной оси колес, называется длиной зуба.
Радиальный зазор — кратчайшее расстояние между вершиной зуба и основанием впадины сопряженного колеса.
Боковой зазор — кратчайшее расстояние между нерабочими профильными поверхностями смежных зубьев, когда их рабочие поверхности находятся в контакте.
С модулем связаны все элементы зубчатого колеса: высота головки зуба ha = т, высота ножки зуба hf= 1,2т, высота всего зуба h = 2,2 т.
Зная число зубьев z, с помощью модуля можно определить диаметр делительной окружности зубчатого колеса d = zm.
Рис. 2. Схема зацепления в передачах цилиндрическими зубчатыми колесами
Формулы, с помощью которых можно определить параметры цилиндрических зубчатых колес в зависимости от модуля и числа зубьев, приведены в табл. 5.
Тихоходные зубчатые колеса изготовляют из чугуна или углеродистой стали, быстроходные — из легированной стали. После нарезания зубьев на зуборезных станках зубчатые колеса подвергают термической обработке, чтобы увеличить их прочность и повысить стойкость против износа. У колес из углеро-
диетой CTa.‘irf поверхность зубьев улучшают химико-термическим способом — цементацией и потом закалкой. Зубья быстроходных колес после термической обработки шлифуют или притирают, Применяется также поверхностная закалка токами высокой частоты.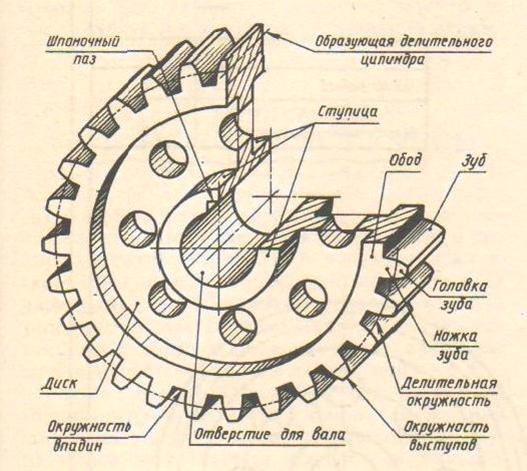
Чтобы зацепление было плавным и бесшумным, одно из двух колес в зубчатых парах в отдельных случаях, когда это позволяет нагрузка, выполняют из текстолита, древеснослои-стого пластика ДСП-Г или капрона. Для облегчения зацепления зубчатых колес при включении посредством перемещения по валу торцы зубьев со стороны включения закругляют.
Зубчатые передачи бывают открытые и закрытые. Открытые передачи, как правило, тихоходные. Они не имеют корпуса для масляной ванны и периодически смазываются густой смазкой. Закрытые передачи заключены в корпуса. Зубчатые колеса закрытых передач смазываются или в масляной ванне, или струйной смазкой под давлением.
По быстроходности зубчатые передачи разделяются на следующие виды (м/с): весьма тихоходные — v < 0,5, тихоходные — 0,5 < v < 3, среднескоростные — 3 < v < 15, скоростные — 15 < v < 40, высокоскоростные — v > 40.
Точность изготовления колес и сборка передач должны соответствовать государственному стандарту.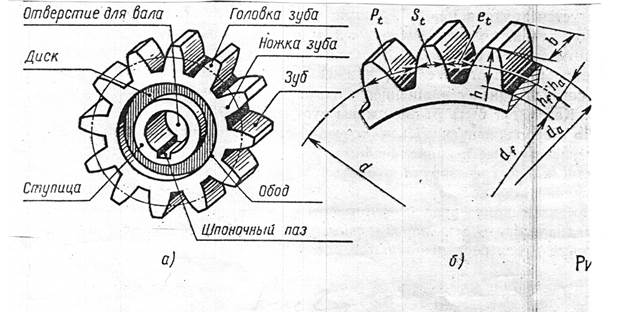 Для цилиндрических, конических и червячных зубчатых передач установлено 12 степеней точности, обозначаемых в порядке убывания точности степенями 1 —12.
Для цилиндрических, конических и червячных зубчатых передач установлено 12 степеней точности, обозначаемых в порядке убывания точности степенями 1 —12.
Наиболее точные 1-я и 2-я степени являются резервными, так как современные возможности производства и контроля не могут обеспечить изготовление точных колес. 12-я степень также резервная, так как согласно действующим ГОСТам зубчатые колеса пока не выполняются грубее 12-й степени точности.
Большое применение имеют зубчатые передачи 6, 7, 8 и 9-й степеней точности. Краткие характеристики наиболее распространенных зубчатых и червячных передач (6-й — 9-й степеней точности) приведены в табл. 6. Каждая степень точности зубчатой передачи соответствует нормали кинематической точности, установленной ГОСТом, а также плавности работы колеса и контакта зубьев.
Посадка зубчатых колес на валы ничем не отличается от посадки шкивов, поэтому ниже описана только проверка, регулирование зубчатых и червячных передач.
Основными техническими требованиями к зубчатым сборочным единицам являются следующие:
1. Зубья колес при проверке на краску должны иметь зону касания не менее 0,3 длины зуба, а по профилю — от 0,6 до 0,7 высоты зуба.
Зубья колес при проверке на краску должны иметь зону касания не менее 0,3 длины зуба, а по профилю — от 0,6 до 0,7 высоты зуба.
2. Радиальное торцовое биение колес не должно выходить за пределы, установленные техническими требованиями.
3. Оси валов сцепляющихся колес и оси гнезд корпусов должны лежать в одной плоскости и быть между собой параллельными. Допускаемые отклонения указаны в технических условиях.
4. Между зубьями сцепляющихся колес необходим зазор, величина которого зависит от степени точности передачи и определяется по таблице.
5. Собранная сборочная единица испытывается на холостом ходу или под нагрузкой. Она должна обеспечивать соответствующую прочность для передачи мощности, плавность хода и умеренный нагрев подшипниковых опор (не свыше 323 К, или 50 °С).
6. Передача должна работать плавно и почти бесшумно.
Ниже описан порядок сборки некоторых сборочных единиц составных зубчатых колес.
Зубчатый венец устанавливают на центрирующий бурт А ступицы и предварительно закрепляют тремя-четырьмя временными болтами, имеющими меньший диаметр.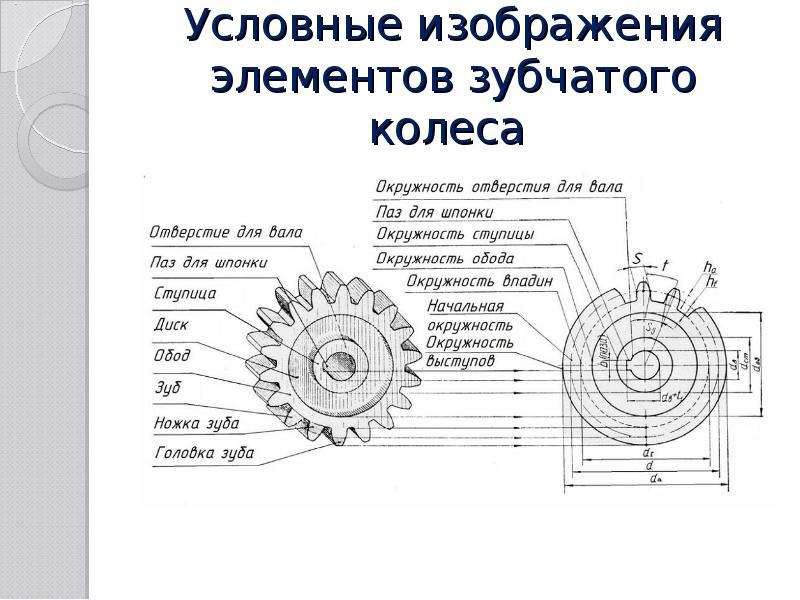 Сборочную единицу проверяют на оправке на радиальное биение и венец закрепляют временными болтами. Оставшиеся отверстия под болты в ступице и венце с помощью кондуктора совместно развертывают и зенкуют, а затем в эти отверстия вставляют нормальные болты, а временные болты снимают и освободившиеся отверстия обрабатывают так же, как и первые. После установки нормальных болтов во все отверстия зубчатое колесо окончательно проверяют на биение. В тяжелонагруженных передачах затягивать болты целесообразно динамометрическим ключом, чтобы на плоскостях фланцев создать силу трения, момент которой превосходил бы крутящий момент, передаваемый зубчатым колесом.
Сборочную единицу проверяют на оправке на радиальное биение и венец закрепляют временными болтами. Оставшиеся отверстия под болты в ступице и венце с помощью кондуктора совместно развертывают и зенкуют, а затем в эти отверстия вставляют нормальные болты, а временные болты снимают и освободившиеся отверстия обрабатывают так же, как и первые. После установки нормальных болтов во все отверстия зубчатое колесо окончательно проверяют на биение. В тяжелонагруженных передачах затягивать болты целесообразно динамометрическим ключом, чтобы на плоскостях фланцев создать силу трения, момент которой превосходил бы крутящий момент, передаваемый зубчатым колесом.
Зубчатый венец напрессовывают на диск ступицы с натя-том. Чтобы облегчить операцию и избежать возможных перекосов, венец предварительно нагревают в масляной ванне или специальном индукторе т. в. ч. до 393-423 К (120-150 °С). Затем сверлят отверстия под стопоры. Вместо стопоров нередко крепление осуществляют заклепками. В этом случае отверстия сверлят насквозь, устанавливают в них заклепки и расклепывают на прессах.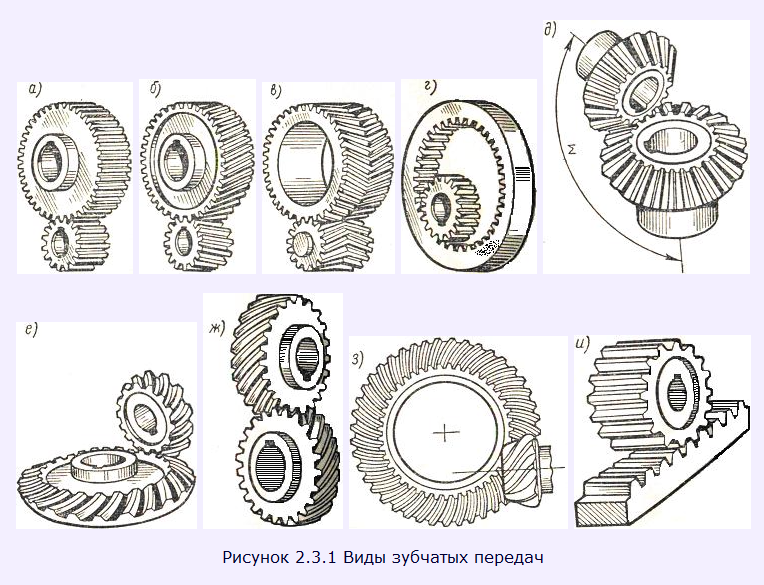
При установке зубчатых сборочных единиц на валах наиболее часто встречаются следующие погрешности: качание зубчатого колеса на шейке вала, радиальное биение по окружности выступов, торцовое биение и неплотное прилегание к упорному буртику вала.
На качание сборочную единицу проверяют обстукиванием напрессованного зубчатого колеса молотком из мягкого металла.
Проверку на радиальное и торцовое биение сборочной единицы — зубчатое колесо с валом производят на призмах или в центрах.
Рис. 3. Монтаж составных зубчатых колес и проверка на биение: а — составное зубчатое колесо, закрепленное болтами, б — закрепленное стопорами, в — схема проверка сборочной единицы вал — зубчатое колесо на радиальное и торцовое биение
Для этого вал укладывают на призмы, регулируют положение седла призмы винтами и устанавливают вал параллельно поверочной плите по индикатору. Во впадину колеса укладывают цилиндрический калибр, диаметр которого должен составлять 1,68 модуля зацепления колеса. Стойку с индикатором устанавливают так, чтобы ножка его вошла в соприкосновение с калибром и с натягом на один-два оборота стрелки. При этом замечают показание индикатора, затем, перекладывая калибр через 2-3 зуба и поворачивая колесо, подводят калибр к ножке индикатора. Отмечают показание стрелки и определяют величину диаметрального биения. Допустимое биение торца и диаметра венца зубчатого колеса зависит от степени точности колеса по ГОСТу. Торцовое биение проверяют индикатором.
Стойку с индикатором устанавливают так, чтобы ножка его вошла в соприкосновение с калибром и с натягом на один-два оборота стрелки. При этом замечают показание индикатора, затем, перекладывая калибр через 2-3 зуба и поворачивая колесо, подводят калибр к ножке индикатора. Отмечают показание стрелки и определяют величину диаметрального биения. Допустимое биение торца и диаметра венца зубчатого колеса зависит от степени точности колеса по ГОСТу. Торцовое биение проверяют индикатором.
Правильное зацепление зубьев происходит при параллельности осей колес, отсутствии их скрещивания и сохранении расстояния между осями валов, равного расчетной величине. Параллельность расположения осей подшипников корпуса зубчатой передачи (рис. 4) проверяют штихмассом, штангенциркулем и индикатором. Расстояние между осями подшипников проверяют контрольными оправками, устанавливаемыми в корпус. Расстояние измеряет или между оправками, или по их наружной поверхности.
Рис. 4. Схема проверки параллельности и перпендикулярности осей отверстий и валов контрольным валом и универсальным измерительным инструментом
Определив размеры или на обеих сторонах, устанавливают непараллельность осей отверстий подшипников. Чтобы добиться требуемого межосевого расстояния и параллельности, смещают корпуса подшипников. Непараллельность в вертикальной плоскости может быть определена при наложении уровня на каждый из валов. Величина непараллельности в этом случае будет равна разности показаний уровня в угловых делениях. Обычно цена деления уровней дается в долях миллиметра на 1 мм и для перевода показаний уровня в угловые секунды цену деления нужно умножить на число 200.
Чтобы добиться требуемого межосевого расстояния и параллельности, смещают корпуса подшипников. Непараллельность в вертикальной плоскости может быть определена при наложении уровня на каждый из валов. Величина непараллельности в этом случае будет равна разности показаний уровня в угловых делениях. Обычно цена деления уровней дается в долях миллиметра на 1 мм и для перевода показаний уровня в угловые секунды цену деления нужно умножить на число 200.
Например, цена деления уровня 0,1 мм на 1 м соответствует 20 угловым секундам (0,1-200/1 =20”).
От степени точности колес и передач устанавливают нормы бокового зазора. Основными являются нормы нормального гарантированного зазора (обозначаемого буквой X), компенсирующего уменьшение бокового зазора от нагрева передачи.
На рис. 5, а показана проверка бокового зазора, которую в цилиндрических зубчатых колесах выполняют щупом или индикатором. На валу одного из зубчатых колес крепят поводок, конец которого упирают в ножку индикатора, установленного на корпусе сборочной единицы.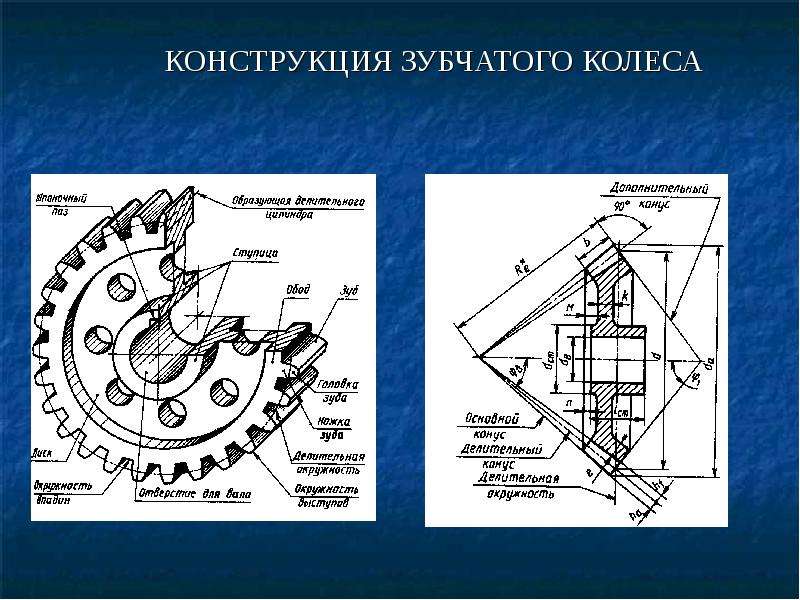 Другое зубчатое колесо удерживают от проворачивания фиксатором. Затем поводок вместе с валом и колесом слегка поворачивают то в одну, то в другую сторону, а это можно сделать только на величину зазора в зубьях. По показанию индикатора определяют боковой зазор. Наименьший боковой зазор С„ указывают в технических условиях на сборку сборочной единицы. При межосевом расстоянии 320 — 500 мм для передач средней точности зазор этот должен быть не менее 0,26 мм. Наиболее точно боковые зазоры измеряют с помощью индикаторных приспособлений так называемым выносным методом. Приспособления позволяют производить замеры зазора в глухих передачах.
Другое зубчатое колесо удерживают от проворачивания фиксатором. Затем поводок вместе с валом и колесом слегка поворачивают то в одну, то в другую сторону, а это можно сделать только на величину зазора в зубьях. По показанию индикатора определяют боковой зазор. Наименьший боковой зазор С„ указывают в технических условиях на сборку сборочной единицы. При межосевом расстоянии 320 — 500 мм для передач средней точности зазор этот должен быть не менее 0,26 мм. Наиболее точно боковые зазоры измеряют с помощью индикаторных приспособлений так называемым выносным методом. Приспособления позволяют производить замеры зазора в глухих передачах.
На рис. 5,б показано одно из таких приспособлений. Оно состоит из крестовины, закрепленной на валу редуктора рукоятками, и стойки с индикатором. Стойку с индикатором ввертывают в хомут, закрепляют винтом к крышке редуктора. При покачивании вала рукой до соприкосновения плоскости крестовины с ножкой индикатора, закрепленного на неподвижной крышке редуктора, определяют боковой зазор между зубьями. Малое колесо передачи должно быть неподвижным.
Малое колесо передачи должно быть неподвижным.
Рис. 5. Схема проверки бокового зазора индикатором: а — открытым способом, б — выносным
Замеренный зазор следует отнести к диаметру начальной окружности зубчатого колеса, на валу которого закреплена крестовина.
Таким же образом проверяют боковой зазор и для других пяти положений крестовины, при повороте ее вместе с валом на угол 60°. По результатам замеров определяют колебание величины боковых зазоров и судят о качестве собранной передачи. В зависимости от модуля и точности зубчатой передачи допустимая разность боковых зазоров составляет 0,08—0,15 мм.
Рис. 6. Расположение пятен контакта при проверке на краску:а — размеры контакта для оценки, б — одностороннее расположение пятна (перекос колеса на зуборезном станке или перекос отверстий в корпусе редуктора, в – большой зазор по всему венцу (мало или велико межосевое расстояние), г — недостаточный зазор по всему венцу (излишняя или недостаточная толщина зуба одного или обоих колес)
Неправильное пятно касания и неправильное место расположения на зубьях являются следствием погрешностей, возникших при обработке и сборке колес, валов, корпусов редукторов, подшипников. На рис. 6,б отпечаток краски расположен односторонне. Причиной неправильного пятна контакта может быть перекос колеса на зуборезном станке или перекос отверстий в корпусе редуктора.
На рис. 6,б отпечаток краски расположен односторонне. Причиной неправильного пятна контакта может быть перекос колеса на зуборезном станке или перекос отверстий в корпусе редуктора.
Если зуб колеса утоплен со стороны торца и при поворачивании на 180° положение не меняется, то, следовательно, перекошена ось отверстия в корпусе. Эту погрешность устраняют запрессовкой новой втулки и растачиванием ее или перепрессовкой пальца зубчатого колеса, если оно посажено на палец.
На рис. 6, в показан слишком большой зазор по всему венцу. Возможные причины: межосевое расстояние в корпусе недостаточное или слишком большое. Устраняют погрешность
перепрессовкой втулок в корпусе и их повторным растачиванием.
Недостаточный зазор по всему венцу показан на рис. 6, г. Возможные причины малой величины зазора: излишняя или недостаточная толщина зуба у одного или у обоих колес. В этом случае заменяют колеса или используют корпус с другим межосевым расстоянием.
Реклама:
Читать далее:
Винтовые механизмы
Статьи по теме:
Главная → Справочник → Статьи → Блог → Форум
Основные детали зубчатой передачи
Зубчатые колеса и шестерни применяют с наклонными зубцами, что обеспечивает плавность и бесшумность передачи. В косозубой передаче сопротивление зуба увеличивается пропорционально 1/sin ?, где ? — угол наклона зуба. Для компенсации осевых усилий зубчатые колеса и шестерни выполняются с двойным наклоном зубцов в разные стороны, т. е. шевронными.
В косозубой передаче сопротивление зуба увеличивается пропорционально 1/sin ?, где ? — угол наклона зуба. Для компенсации осевых усилий зубчатые колеса и шестерни выполняются с двойным наклоном зубцов в разные стороны, т. е. шевронными.
Зубчатые колеса состоят из вала, зубчатых венцов и средней части, соединяющей вал с венцами.
На современных судах среднюю часть колеса выполняют в виде стальных диафрагм, которые прикрепляют к валу и ободу болтами либо с помощью сварки. Такие колеса имеют небольшой вес и просты в изготовлении и для монтажа. На рис. 40 зубчатое колесо 4 второй ступени редуктора состоит из вала 11, двух внешних 14 и одного внутреннего 15 диска, соединенных с валом и зубчатым венцом болтами 12. Вал колеса изготовлен из стали 43Н, а ободы из стали 0ХН1М.
Шестерня 7 цельнокованая пустотелая изготовлена заодно свалом из материала с большей прочностью и твердостью, чем ободы, так как каждый зуб шестерни чаще находится в зацеплении. Поковка обода зубчатого колеса и шестерня подвергаются закалке до высокой степени твердости.
Поковка обода зубчатого колеса и шестерня подвергаются закалке до высокой степени твердости.
Торсионные, или гибкие, валики проходят через пустотелую шестерню и предназначены для передачи ей мощности от ротора турбины. Такое соединение шестерни и турбины обеспечивает защиту зубчатой передачи от ударных нагрузок, вызванных крутильными колебаниями, ударом лопастей о посторонние предметы и др.
Подшипники валов зубчатых колес и шестерен имеют разъемные вкладыши, залитые со стороны рабочей поверхности баббитом. Все вкладыши имеют отверстия для подвода масла и две продольные канавки для распределения масла вдоль шейки вала. Вкладыши закрывают литыми крышками подшипников, которые соединяются с корпусом редуктора шпильками и установочными штифтами. На крышках имеются отверстия для установки рымов, термометров и маслоуказателей и для заливки вкладышей консервирующим маслом.
Корпус зубчатой передачи воспринимает все усилия, возникающие в процессе работы редуктора, и крепится к судовому фундаменту.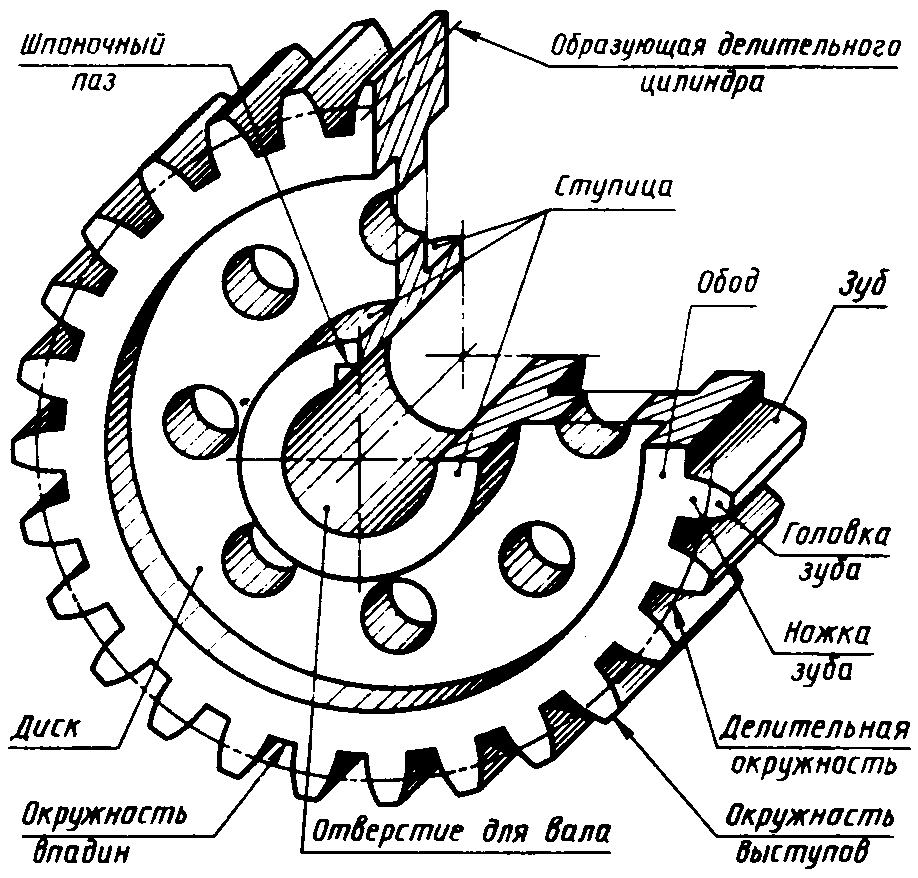 Корпус редуктора выполняется обычно сварно-литым. Его нижняя часть сварена из двух отливок и набора стальных листов, усиленных ребрами жесткости, а средняя часть — в виде трех сварных балок из отдельных стальных отливок, соединенных между собой продольными и поперечными стальными листами. В средней части расположены опорные подшипники зубчатых колес первой ступени и шестерен второй ступени, вспомогательные упорные подшипники и форсунки для смазки зацепления шестерен второй ступени и колеса. Средняя и нижняя части корпуса редуктора соединяются между собой болтами по горизонтальному разъему. Верхние части корпуса состоят из двух отливок и набора листов, усиленных ребрами жесткости. В отливках расположены опорные подшипники шестерен. Все детали, установленные в корпусе редуктора, и масляные полости закрыты сварными съемными кожухами. Поддон редуктора выполнен в виде легкой сварной конструкции из листов с ребрами жесткости и соединяется с нижней частью корпуса болтами. Собранное в поддоне масло отводится в цистерну, расположенную в междудонном пространстве.
Корпус редуктора выполняется обычно сварно-литым. Его нижняя часть сварена из двух отливок и набора стальных листов, усиленных ребрами жесткости, а средняя часть — в виде трех сварных балок из отдельных стальных отливок, соединенных между собой продольными и поперечными стальными листами. В средней части расположены опорные подшипники зубчатых колес первой ступени и шестерен второй ступени, вспомогательные упорные подшипники и форсунки для смазки зацепления шестерен второй ступени и колеса. Средняя и нижняя части корпуса редуктора соединяются между собой болтами по горизонтальному разъему. Верхние части корпуса состоят из двух отливок и набора листов, усиленных ребрами жесткости. В отливках расположены опорные подшипники шестерен. Все детали, установленные в корпусе редуктора, и масляные полости закрыты сварными съемными кожухами. Поддон редуктора выполнен в виде легкой сварной конструкции из листов с ребрами жесткости и соединяется с нижней частью корпуса болтами. Собранное в поддоне масло отводится в цистерну, расположенную в междудонном пространстве.
Форсунки предназначены для подвода масла к зубчатому зацеплению со стороны переднего и заднего ходов. Каждая форсунка состоит из распыливающей головки и трубки, изогнутой по месту. По длине шестерни устанавливается несколько форсунок с таким расчетом, чтобы конусы распыла масла перекрывали друг друга.
Смазка подшипников и зацепления осуществляется турбинным маслом под давлением 0,05—0,08 Мн/м2.
Валы зубчатых колес изготовляют коваными из стали с присадкой никеля (1,5—3%), венцы — из качественной углеродистой легированной стали (никелевой, хромоникельмолибденовой), а шестерни— из никелевой стали (3,5%). Корпуса и съемные крышки шестерней обычно сваривают из листовой стали, и для увеличения прочности к ним приваривают ребра жесткости из профильной стали и кованых или литых корпусов подшипников.
Зубчатая передача
Содержание:
Зубчатая передача
- А. Общие сведения Зубчатая передача осуществляется посредством пары колес с зубьями, расположенными на поверхностях круглых цилиндров. На фиг. 56 в поперечном сечении показано взаимное расположение зубьев сопряженной пары колес и проведены начальные окружности с центрами О. и О?. При вращении ведущего колеса зуб ведущего колеса, нажимая на зуб ведомого, увлекает ведомое колесо во вращение. До выхода из зацепления одной пары зубьев в зацеплениеЗубчатая передача 51 входит другая пара, поэтому вращение колес происходит непрерывно. В существующих
конструкциях одновременно могут находиться в зацеплении от одной до трех пар зубьев. На фиг. 56 показано взаимное расположение пары зубчатых колес с внешним зацеплением, при котором центры начальных окружностей Линия центров P полюс зацепления ТТ-линия зацепления А В-длина зацепления СВ-дуга зацепления t -шаг зацепления а угол зацепления h ’-высота головки зуда h -высота ножки зуба Фиг. 56. Окружность впадин Окружность основная Окружность начальная Окружность выступов расположены по разные стороны от точки их касания. Применяется также зубчатая передача с внутренним, зацеплением,
в которой центры начальных окружностей расположены по одну сторону от точки касания (фиг. Людмила Фирмаль
57). В передаче с внешним зацеплением зубья каждого из колес расположены на внешней стороне обода, в передаче с внутренним зацеплением зубья большего из колес располагаются на внутренней стороне обода. В передаче с внешним зацеплением колеса вращаются в разных направлениях, в передаче с внутренним зацеплением — в одном направлении. В дальнейшем мы будем иметь в виду только передачу с внешним зацеплением, так как передача с внутренним зацеплением применяется сравнительно редко. 452 Плоские механизмы для передачи вращательного движения С боков зубья
ограничиваются такими кривыми поверхностями, которые обеспечивают постоянное передаточное отношение в процессе зацепления пары зубьев. Кривая, по которой как по направляющей построена боковая поверхность зуба, называется профилем зуба.Для того чтобы при вращении колес зубья ведущего колеса попадали всегда в промежутки между зубьями ведомого, необходимо, чтобы расстояние между серединами смежных зубьев, измеряемое по начальной окружности, у одного из колес было равно такому же расстоянию у другого. Это расстояние называется ш а г о м зацепления и обозначается латинской буквой t. Шаг зацепления может быть измерен также по начальной окружности между одноименными профилями смежных зубьев, Обозначая число зубьев колеса через г, диаметр начальной окружности через d и выражая длину начальной окружности через диаметр с одной стороны и через число зубьев — с другой, получаем равенство • откуда тс-d — Z-t, d = Это
- равенство показывает, что нельзя диаметр и шаг выразить соизмеримыми числами. Для удобства изготовления зубчатых колес отношение — выбирается таким, чтобы оно выражалось или целым числом или целым числом с десятичной дробью с небольшим числом цифр после запятой. Отношение ~ называется м о д у л е м з а ц е п л е н и я и обозначается всегда строчной латинской буквой пг. Чтобы не иметь на машиностроительных заводах, изготовляющих зубчатые колеса, большие комплекты режущих инструментов, общесоюзным стандартом (ОСТ 1597) установлены следующие модули, до которых должны округляться модули, получаемые из расчета: от 0,3 до 0,8 мм — через 0,1 мм; от 1 до 5 мм — через 0,25 мм; от 5 до 7 мм — через 0,5 мм; от 7 до 15 мм — через 1 мм; от 16 до 30 мм — через 2 мм; от 30 до 45 мм — через 3 мм; от 45 мм — через 5 мм. Некоторые из
указанных модулей (2,75; 3,25; 3,75; 4,25 мм) допускаются стандартом, но не рекомендуются к применению без крайней необходимости. Ниже будет показано, что при правильно выполненных профилях зубьев межцентровое расстояние O J)2 (см. фиг. 56) может быть приЗубчатая передача 53 установке колес немного изменено без изменения передаточного отношения. При этом изменяются радиусы начальных окружностей. Следовательно, одну и ту же пару зубчатых колес можно устанавливать по-разному так, что колеса будут работать при разных диаметрах начальных окружностей и потому при разных отношениях . Очевидно, что с т а н д а р т н ы е м о д у л и могут относиться только к одной из возможных пар начальных окружностей.
Они относятся к так называемым делительным окружностям. Д е л и т е л ь н о й о к р у ж Людмила Фирмаль
н о с т ь ю называется воображаемая окружность с диаметром, равным ztn, где z — число зубьев колеса и ш — стандартный модуль. Из изложенного вытекает, что делительная окружность может совпадать с начальной (что часто и бывает), но может и отличаться от нее. Понятие о делительной окружности является необходимым не только потому, что именно ее диаметр приходится иметь в виду при изготовлении колеса, но и потому, что термин «начальная окружность» в приложении к одному колесу не имел бы смысла, так как начальные окружности появляются лишь при зацеплении двух колес Расчетным диаметром колеса считается диаметр делительной окружности. Делительной окружностью зуб делится на две части: часть зуба, лежащая вне делительной
окружности, в колесах с внешним зацеплением (и внутри делительной окружности в наружном колесе передачи с внутренним зацеплением) называется г о л о в к о й зуба Л’; часть зуба, лежащая между делительной окружностью и телом колеса, называется н о ж к о й зуба Л».При несовпадении начальной окружности с делительной зуб, в соответствии с ОСТ 8089, делится на головку и но)кку не делительной, а начальной окружностью. Размеры нормальных зубьев принимаются следующими: высота головки равна модулю, высота ножки равна 1,25 модуля. В некоторых случаях применяются колеса с укороченными зубьями, т. е. с высотой головки, равной 0,8 модуля, и высотой ножки, равной модулю. Толщина зуба, измеряемая по делительной окружности, принимается равной половине шага.
Модуль зацепления определяется в результате расчета на прочность и износ, излагаемого в курсе деталей машин. Окружность, описанная вокруг центра колеса и ограничивающая вершины зубьев, называется о к р у ж н о с т ь ю в ы с т у п о в . Промежуток между профилями смежных зубьев, ограниченный окружностью выступов и телом колеса, называется в п а д и н о й . Окружность, описанная вокруг центра колеса и ограничивающая впадины со стороны тела колеса, называется о к р у ж н о с т ь ю в п а д и н .54 Плоские механизмы для передачи вращательного движения Б. Сложные передачи В наиболее простом оформлении зубчатая передача представляет собой находящиеся в зацеплении ведущее и ведомое колеса, связанные каждое жестко со своим валом, вращающимся вокруг неподвижной оси. Необходимость в устройстве сложной передачи возникает тогда,
когда передаточное отношение выходит за предел, которьй практически представляется возможным осуществить при помощи одной пары колес. В таком случае прибегают к устройству многоступенчатой передачи: располагают между ведущим и ведомым валами один или несколько промежуточных валов (фиг. 58) и вращательное движение передают последовательно от одного вала к другому. В такой передаче на каждом промежуточном валу (валы В и С на фиг. 58) располагаются два колеса, из которых одно является ведомым, воспринимающим движение от предыдущего вала, а другое ведущим, передающим движение следующему валу. Такая передача может осуществить большое передаточное отношение. Обозначая угловые скорости вращения валов буквой <о с соответствующим индексом, передаточные числа — буквой i с двумя индексами, первым из которых отмечается ведущий, а вторым — ведомый вал, числа
зубьев колес — буквой z с индексами, указанными на фиг. 58 и считая вал А ведущим, а вал D ведомым, получаем: i _ <В _ . <»С *3 ’ 1вс *5 Перемножив эти равенства, получаем после сокращения 21‘ г 3’г 5 Следовательно, в передаче с промежуточными валами, на каждом из которых имеется и ведомое и ведущее колеса, общее передаточное число i равно произведению промежуточных передаточных чисел или отношению произведения чисел зубьев ведомых колес к произведению чисел зубьев ведущих колес (на фиг. 58 четными индексами отмечены числа зубьев ведомых, нечетными — ведущих колес).Зубчатая передача 55 На фиг. 58 изображены только два
промежуточных вала, но приведенное выше заключение будет верным и при любом числе промежуточных валов. При небольших передаточных числах, осуществимых при помощи одной пары колес, к устройству сложной передачи приходится при/ / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /7777777777777777777777777777777777777 Фиг. 60. бегать в том случае, когда передача вращательного движения должна быть выполнена без перемены направления вращения. Если требуется, чтобы ведущее и ведомое колеса вращались в одном направлении, то между ними располагают промежуточное (паразитное) колесо, сцепляющееся с ведущим и ведомым колесами (фиг. 59). Промежуточные колеса приходится устанавливать также и в том случае, когда расстояние между осями ведущего и ведомого колес должно быть большим, а колеса с большими диаметрами по
конструктивным соображениям не могут быть поставлены (фиг. 60). Считая колесо с числом зубьев (фиг. 60) ведущим колесом, а колесо с числом зубьев z4 — ведомым и определяя общее передаточное число, получим его равным — , т. е. z i таким же, каким оно получилось бы и в том случае, если бы передача осуществлялась без промежуточных колес. Следовательно, в передачах с промежуточными колесами ни число этих колес, ни количество зубьев их не оказывают влияния на величину общего передаточного числа. Число промежуточных колес выбирается нечетным, если ведомое колесо должно вращаться в одном направлении с ведущим, и четным — в противном случае. + 1 . В таком виде механизм часто применяется в аппаратах, реагирующие вещества в которых должны подвергаться энергичному размешиванию. В таких аппаратах рабочие органы (лопасти мешалок или пропеллеры), непосредственно воздействующие на обрабатываемые материалы, укрепляются на валах нескольких (обыкновенно трех) колес 77. При неподвижном колесе С изображенный на фиг. 61 механизм называется п л а н е т а р н ы м , колесо С называется солнечным, колесо 77 — планетным или сателлитом. Легко подсчитать, что этот механизм имеет одну степень подвижности (два подвижных звена В и 77, две вращательные и одна
высшая пары). При подвижном колесе С механизм обладает двумя степенями подвижности и называется д и ф ф ер ен ц и ал ьн ы м зубчатым механизмом. Фиг. 62. В. Теория зацепления Работа зубчатых колес в значительной сте. пени зависит от того, насколько тщательно выполнены профили зубьев. Прежде чем уяснить себе, по каким кривым следует очерчивать профили, выясним основное требование, которому эти кривые должны удовлетворять. Мы знаем, что при вращении находящихся в зацеплении зубчатых колес начальные окружности должны катиться одна по другой без скольжения. Это условие может быть выполнено только в том случае, если в процессе зацепления профиль зуба ведущего колеса будет находиться в постоянном соприкосновении с профилем зуба ведомого колеса.
Пусть точки Oi и О2 (фиг. 62) — центры начальных окружностей первого и второго колес соответственно; Р — точка касания начальных окружностей, называемая полюсом зацепления; pi — профиль зуба первого колеса; р2 — профиль зуба второго колеса; М — точка касания профилей в момент, соответствующий изображенному на чертеже взаимному расположению их. Рассмотрим движение одного колеса, например, второго относительно первого. При качении окружности с центром О2 по окружности с центром Oi окружность с центром 02 и жестко связанный с нею профиль р 2 в данный момент поворачиваются вокруг подноса Р,Зубчатая передача 57 являющегося мгновенным центром вращения. В точке М соприкасаются точка 7И1, связанная с профилем рх, и точка М 2, связанная с профилем р2. При повороте профиля ₽2 вокруг полюса Р скорость точки ТИ2
относительно точки 7И1 при правильной работе колес может быть направлена только по касательной к обоим профилям в точке М, иначе профиль ₽2 или отошел бы от профиля рх или вдавился бы в него. Вектор скорости точки ТИ2 относительно точки Mi9 направленный по касательной к обоим профилям, является перпендикуляром к линии РМ как к радиусу вращения. Из этого вытекает важное требование, которому должны удовлетворять профили находящихся в зацеплении зубьев: нормаль в точке касания профилей должна проходить через полюс зацепления. Профилей, удовлетворяющих этому требованию, для каждого заданного случая можно построить много, задаваясь почти произвольным профилем зуба одного колеса и строя сопряженный профиль для зуба другого колеса. Так как на практике при проектировании зубчатых передач никогда так не поступают, а очерчивают профили по математическим кривым, то способы построения сопряженных
профилей по заданным произвольным профилям мы рассматривать не будем. Исторически первыми математическими кривыми, по которым очерчивались профили зубьев, были кривые циклические (циклоида, эпициклоида, гипоциклоида, перициклоида). Теоретически циклические профили обладают большими достоинствами, но трудность точного изготовления циклических зубьев была причиной того, что от производства колес с циклическими зубьями пришлось вовсе отказаться. В настоящее время зубчатые колеса изготовляются только с эвольвентными
профилями. Чтобы правильно оценить достоинства эвольвентного профиля, необходимо предварительно выяснить свойства эвольвенты, которые используются в зубчатой передаче. Э в о л ь в е н т о й окружности называется кривая, описываемая точкой прямой линии, перекатываемой по окружности без скольжения. Окружность, по которой перекатывается прямая, описывающая одной из своих точек эвольвенту, называется о с н о в н о й о к р у ж н о с т ь ю ; перекатывающаяся по основной окружности прямая называется п р о и з в о д я щ е й п р я м о й . Одним из наиболее важных свойств эвольвенты является следующее: производящая прямая является нормалью к эвольвенте. Наиболее просто можно в этом убедиться,
рассматривая фиг. 63. Точка А производящей прямой АВ является мгновенным центром58 Плоские механизмы для передачи вращательного движения вращения, и отрезок АВ — мгновенным радиусом вращения для точки В, которая описывает эвольвенту; отрезок А В является нормалью к эвольвенте в этой точке, так как является перпендикуляром к вектору скорости этой точки, направленному по касательной к кривой. Представим себе (фиг. 64) эвольвенту С А В, связанную жестко с основной окружностью, и касательную Т Т к основной окружности, пересекающую эвольвенту в точке А. Отметим на эвольвенте точку В; отрезок В Bi является отрезком производящей прямой. Из определения эвольвенты следует
, что длина отрезка А А г равна длине дуги CAi, а длина отрезка ВВГ равна длине дуги CBi. Если оставить неподвижной линию ТТ, а основную окружность вместе с жестко связанной с ней эвольвентой повернуть в направлении против часовой стрелки на такой угол а, чтобы точка Bi совпала с точкой Дх, то эвольвента перейдет в положение СХВ2 , а отрезок ВВХ займет на линии Т Т положение В2Д1. окружности вместе с эвольвентой ТТ занимала положение линии ТТ, пробежав за ДВ2, пройденный точкой время поворота основной окруж-по которой переместилась точка До поворота основной пересечения эвольвенты с линией время поворота перемещалась по поворота расстояние Л В2 . Путь сечения эвольвенты с линией Т Т за ности, равен длине дуги B iA i, так как АВ2 = А1В2 — АА± = ВВг — ААХ = СВ1 — СА± = ВХЛГ точка А, во время переИз этого следует, что при вращении основной окружности вместе с эвольвентой вокруг центра основной окружности линейная скорость точки пересечения эвольвенты с любой касательной к основной окружности (по
скорости точек, лежащих на основной окружности. Это свойство эвольвенты дает возможность преобразовывать вращательное движение с равномерной угловой скоростью в поступательное движение с равномерной линейной скоростью, и наоборот. Для этого может быть использован простой кулачковый механизм с кулачком, очерченным по эвольвенте. Такой механизм схематически изображен на фиг. 65, где ₽ — эвольвентный профиль кулачка, вращающегося вокруг центра основной окружности; /С — основная окружность для эвольвенты р; Т — толкатель, направляемый втулкой В поЗубчатая передача 59 прямой линии касательной к основной окружности. При вращении кулачка с равномерной угловой скоростью против часовой стрелки эвольвентный профиль будет отжимать толкатель кверху с равномерной линейной скоростью и-, наоборот, при движении
толкателя вниз с равномерной линейной скоростью кулачок будет поворачиваться по часовой стрелке с равномерной угловой скоростью. На где v — линейная скорость толкателя, <о — угловая скорость вращения кулачка, г0 — радиус основной окружности. Представим себе (фиг. 66) два кулачка с соприкасающимися эвольвентными профилями и р2, которые вращаются вокруг неподвижных центров Oj. и О2. Общая касательная ТТ к основным окружностям является производящей прямой для обоих профилей, а поэтому она будет нормальна к каждому из профилей и должна проходить через точку их касания. Будем вращать с равномерной угловой скоростью 1, m = 2гх : z, где г — число зубьев меньшего колеса, Го2 = Г2 cos а = l r xcos ai> после сокращения всех членов на гх
и упрощений получаем (1 + 2/) sin2 а • z2 — 4/z — 4 = О, откуда _ о * + “И2 + 0 + 2) sin2 а (1 + 2Z) sin2 а На фиг. 69 приведены построенные, по этому уравнению кривые, выражающие зависимости возможных наименьших чисел зубьев от угла зацепления при разных постоянных передаточных отношениях. При i — оо вместо большего колеса получаем зубчатую рейку. Разделив числитель и знаменатель правой части полученного выше уравнения на i и положив затем i = со, зависимость наименьшего числа зубьев колеса в зацеплении колеса с рейкой получаем в виде 2 Z 30 sin2 а ’ 5 Зиновьев 61266 Плоские механизмы для передачи вращательного движения Выше (стр. 52) было сказано, что при правильно выполненных профилях зубьев межцентровое расстояние при установке колес может быть
немного изменено без нарушения передаточного отношения. Теперь мы знаем, что при этом имелись в виду эвольвентные профили. Так как при изменении межцентрового расстояния профили зубьев не измейяются, то, следовательно, остаются без изменения и диаметры основных окружностей, но направление общей касательной (т. е. линии зацепления) к основным окружностям изменяется, вследствие чего изменяется положение полюса зацепления на линии центров. Если до изменения межцентрового расстояния делительные окружности совпадали с начальными, то после перехода полюса зацепления в новую точку на линии центров и, следовательно, изменения диаметров начальных окружностей совпадение этих окружностей не будет иметь места. Изменение угла зацепления (вследствие изменения направления линии зацепления), а также изменение модуля зацепления (вследствие изменения диаметров начальных окружностей) не может не оказать влияния на условия
работы колес, в частности, на величину коэффициента перекрытия, но передача вращательного движения зубьями с эвольвентными профилями при несовпадении делительных окружностей с начальными будет происходить так же правильно и с таким же передаточным отношением, как и при совпадении этих окружностей. Г. Изготовление зубчатых колес Удовлетворительная работа зубчатых колес является возможной лишь при условии точного изготовления зубьев: при больших окружных скоростях (порядка 25 м/сек и более) неточность профилей порядка 0,005 мм уже заметно сказывается на работе передачи. Наилучшие результаты при нарезании зубьев
получаются при применении способа о б к а т к и . Для лучшего уяснения этого способа необходимо предварительно выяснить, как происходит зацепление зубчатого колеса с рейкой, представляющей собой зубчатое колесо с бесконечно большим радиусом и совершающей, следовательно, прямолинейное движение. Проведем (фиг. 70) начальную окружность колеса с центром О и радиусом ОР. Если Р — полюс зацепления, то прямая SS представляет собой начальную окружность рейки с бесконечно большим радиусом. Линия SS называется м о д у л ь н о й п р я м о й . Линия зацепления при любом взаимном расположении соприкасающихся профилей
должна, как это установлено выше, быть нормалью к обоим профилям в точке их соприкосновения. Чтобы это условие при движении сопряженных профилей зубьев колеса и рейки постоянно соблюдалось, профиль зуба колеса, вращающийся вокруг центра основной окружности, должен быть очерчен по эвольвенте; профиль же зуба рейки, движущийся прямолинейно, будет оставаться перпендикулярным к линии зацепления, если будетЗубчатая передача 67 очерчен по прямой, перпендикулярной к линии зацепления, так как при бесконечно большом радиусе основной окружности эвольвента переходит в прямую. Прямолинейность профиля зуба рейки для техники изготовления зубчатых колес имеет очень важное значение: зубья с прямолинейным профилем могут быть изготовлены с высокой степенью точности без особых
затруднений, а изготовленный точно режущий инструмент может быть использован для точной обработки зубьев с эвольвентным профилем независимо от того, с каким числом зубьев колесо будет изготовляться. Чтобы уяснить себе, как получается эвольвентный профиль зуба колеса посредством рейки (с зубьями трапецеидального сечения), представим себе сначала один зуб рейки, изготовленный из твердого материала, и цилиндрический диск, изготовленный из пластичного материала, могущего легко под давлением изменять свою форму. Расположим зуб рейки и диск так, как это показано на фиг. 71, ал левый нижний угол зуба касается наружной поверхности диска. Фиг. 71. Радиус диска равен г + т, где г — радиус делительной окружности колеса, т — модуль. При работе колеса и рейки начальная окружность колеса и модульная прямая катятся одна по другой без скольжения. Оставим зуб неподвижным и будем катить без скольжения делительную окружность диска по модульной прямой. В результате такого перекатывания зуб будет постепенно входить в
материал диска, образуя впадину между смежными зубьями. На фиг. 71, б показано взаимное расположение зуба рейки и диска в промежуточном положении, а на фиг. 71, в— зуб и получившаяся в результате перекатывания впадина, 568 Плоские механизмы для передачи вращательного движения ограниченная боковыми поверхностями смежных зубьев, с эвольвентj ными профилями. I Само собой разумеется, что такое практически невыполнимое ; получение зубчатого колеса из цилиндрической заготовки приведено лишь для иллюстрации принципа нарезания зубьев по способу i обкатки. При стальном зубе рейки и металлической заготовке вместо вдавливания рейки в заготовку производится постепенное срезывание материала заготовки зубом рейки, для чего рейка
выполняется в виде металлорежущего инструмента, в котором прямолинейные профили являются профилями режущих граней. Рейка при этом • совершает поступательно-возвратное движение в направлении, перпендикулярном к плоскости обрабатываемой заготовки, которая во время рабочего движения рейки остается неподвижной. Способ обкатки применяется в разных видоизменениях на отдельных зуборезных станках, на рассмотрении которых мы останавливаться не будем. При применении способа обкатки профили зубьев получаются эвольвентными на всем протяжении от окружности выступов до основной окружности только в том случае, если число нарезаемых зубьев не меньше того числа, какое получается при приведенной выше формуле для определения наименьшего возможного числа зубьев. Если число зубьев берется меньше
получаемого по формуле, то формула профиля искажается: головкой зуба рейки-инструмента часть эвольвентного участка профиля, начиная от основной окружности, подрезается, причем подрезается и корень зуба, т. е. часть зуба, расположенная между основной окружностью и окружностью впадин. В результате этого зуб получает форму, примерно изображенную на фиг. 72. Такие зубья называются подрезанными. Следует иметь в виду, что подрезка зуба, понижающая его сопротивление изгибу, получается заметной лишь при значительном уменьшении числа зубьев, вследствие чего наименьшее возможное число зубьев имеет условное значение.
Например, по формуле получается, что при а = 20°, / = оо, z = 17 зубья будут подрезаться, между тем как без особого ущерба для прочности число зубьев можно принимать равным 14, что часто и делается. Выше предполагалось, что при нарезании зубьев модульная прямая SS . (см. фиг. 70) направлена по касательной к делительной окружности. Так изготовляются нормальные или нулевые (некорригированные, т. е. не исправленные) колеса. Но при нарезании модульная прямая может быть сдвинута несколько дальше от оси заготовки (положительный сдвиг) или, наоборот, ближе к оси (отрицательный сдвиг). В таких случаях получаются так называемые ненулевые (корригированные) колеса. При сдвиге от оси заготовки зубья получаются неподрезанными и при числе зубьев, меньшем 17; зубья получаются при этом у оснований толще, а у вершин тоньше, чем у
нулевых колес. При сдвиге к оси заготовки подрезка зубьев получается большей, чем у нулевых колес, вследствиеЗубчатая передача 69 чего зубья получаются менее прочнымц; сдвиг в сторону оси заготовки применяется поэтому сравнительно редко, главным образом в тех случаях, когда не представляется возможным другим способом выдержать заданное межцентровое расстояние. Зубья колеса могут быть нарезаны и по так называемому способу к о п и р о в а н и я . Способ этот осуществляется при помощи режущего инструмента, режущие грани которого имеют форму впадины (фиг. 73, а). Расположив режущий инструмент относительно i Фиг. 73. т заготовки так, чтобы ось симметрии режущих граней инструмента была направлена по радиусу заготовки, можно образовать впадину, двигая инструмент в направлении, перпендикулярном к плоскости заготовки, и по мере удаления материала приближая заготовку к
инструменту в радиальном направлении. При осуществлении этого способа режущие грани располагаются на вращающемся инструменте, имеющем вид, изображенный на фиг. 73, б, и называемом фрезой. В соответствии с таким названием операция удаления материала из заготовки называется фрезерованием. Впадины фрезеруются по очереди после повертывания заготовки на угол — , где z — число зубьев. Так как форма эвольвентного профиля определяется углом зацепления, модулем и числом зубьев колеса, то при производстве зубчатых колес по способу копирования при стандартном угле зацепления необходимо иметь специальную фрезу для каждого модуля и каждого числа зубьев. Вследствие практической невозможности держать на заводах слишком большие комплекты фрез, приходится довольствоваться ограниченными
комплектами их, используя одну и ту же фрезу для изготовления колес с разными числами зубьев. Так, например, располагая комплектом из восьми фрез, приходится одной и той же фрезой пользоваться при изготовлении колес с 26—34 зубьями, другой — при изготовлении колес с 35—54 зубьями и т. д., получая при помощи каждой фрезы точные профили лишь при одном определенном числе зубьев и не вполне точные в остальных случаях.70 Плоские механизмы для передачи вращательного движения Поэтому способ копирования для изготовления зубчатых колес, предназначенных для работы с большими линейными скоростями на начальных окружностях, не применяется, так как зубья таких колес должны обрабатываться с
особенно большой точностью. между гой на Д. Косозубые и шевронные колеса Если разрезать зубчатое колесо плоскостью, перпендикулярной к его оси, на две равные части и затем жестко соединить эти части собой, раздвинув их одну относительно друо угол, меньшии — , и так же поступить с другим колесом, которое должно работать в зацеплении с первым, то получается два колеса со ступенчатыми зубьями. Выгода от такого усложнения колес будет состоять в том, что в каждый момент сдвинутые одна относительно другой части зуба будут работать разными участками профиля, вследствие чего колеса будут работать более плавно и с большим коэффициентом перекрытия: первая часть выйдет из зацепления, пройдет такую же дугу зацепления, какую
прошел бы и неразрезанный зуб, а вторая часть будет еще некоторое время находиться в зацеплении. Подобным же образом можно получить колеса с многоступенчатыми зубьями. Однако при указанных достоинствах ступенчатых колес они не получили распространения вследствие значительно большей сложности изготовления по сравнению с обыкновенными прямозубыми колесами. Увеличение коэффициента перекрытия и большую плавность работы можно получить, направляя боковые поверхности зубьев так, чтобы полюсные линии располагались на делительном цилиндре по винтовым линиям. Такого рода колеса называются к о с о з уб ы м и. На фиг. 74 изображен делительный цилиндр с линией АВ на нем, представляющей собой полюсную линию прямого зуба, и винтовой
линией А С — полюсной линией косого зуба. Если в колесе с прямыми зубьями, вращающемся по часовой стрелке, зуб выходит из зацепления в момент, когда линия А В занимает показанное на фиг. 74 положение, то в колесе с косыми зубьями в этот же момент зуб только начинает выходить из зацепления, а полностью зацепление заканчиваетсяпосле того, как точка В проходит дугу ВС. Развернув на плоскость часть поверхности делительного цилиндра, ограниченную линиями А В , А С и дугой В С, получаем треугольник А В С (фиг. 75), в котором р — угол наклона полюсной линииЗубчатая передача 71 к образующей, являющийся дополнительным к углу подъема полюсной винтовой линии, а ВС — дополнительная дуга зацепления. При длине прямого зуба АВ = Ь и коэффициенте в перекрытия прямозубых колес коэффициент перекрытия косозубых колес получается равным е + — = е + — tgp. часть отмена фиг. 76 изображена в развернутом на
плоскость виде делительного цилиндра с винтовыми полюсными линиями и чены: ts — торцовой шаг, т. е. расстояние по делительной окружности между обращенными в одну сторону профилями смежных зубьев в торцовом сечении; отношение ts : тс = ms называется торцовым модулем зацепления; tn — нормальный шаг, т. е. кратчайшее расстояние между обращенными в одну сторону профилями смежных зубьев по делительному цилиндру; отношение tn : tz = mn называется нормальным модулем зацепления; ta — осевой шаг, т. е. расстояние в параллельном оси колеса направлении между обращенными в одну сторону профилями смежных зубьев по делительному цилиндру. По сравнению с прямозубыми косозубые колеса обладают следующими достоинствами: 1) так как косые зубья
в каждый момент соприкасаются разными точками профиля, то они изнашиваются более равномерно, чем прямые зубья; 2) так как косые зубья в зацепление входят не сразу по всей длине, а постепенно, то они менее чувствительны к ударам, чем прямые; 3) при прочих равных условиях вследствие большего коэффициента перекрытия наименьшее возможное число зубьев у косозубого колеса получается меньшим, чем у прямого. Недостатком косозубых колес является то, что сила Р, с которой зуб одного колеса давит на зуб другого по общей нормали к винтовым линиям (см. фиг. 77, на которой винтовая линия показана в развернутом на плоскость положении), разлагается на силу Plf действующую в плоскости вращения колес, и силу Р2, которая направлена перпендикулярно к плоскости вращения колес. Сила Р 2 создает осевое давление на опоры. Это связано с дополнительными
потерями на трение в опорах, не говоря уже о необходимости усложнения конструкции опор. Избежать осевых давлений на опоры можно, располагая на одном валу два косозубых колеса с наклонами зубьев в разные стороны72 Плоские механизмы для передачи вращательного движения или, что проще, располагая на ободе колеса два ряда зубьев с наклонами в разные стороны. На фиг. 78 изображена в развернутом на плоскость виде часть поверхности делительного цилиндра такого колеса с лежащими на делительном цилиндре боковыми винтовыми линиями зубьев. Для удобства изготовления колес (для выхода режущего инструмента) между двумя рядами косых зубьев часто оставляется промежуточный желобок небольшой ширины. Фиг. 78. Такие колеса называются ш е в р о н н ы м и и обычно применяются при передаче больших мощностей и при больших линейных скоростях на начальных окружностях колес.
Смотрите также:
Предмет Теория Машин и Механизмов ТММ
Зубчатые передачи | Автомобильный справочник
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
СодержаниеТипы зубчатых передач
Эвольвентное зацепление
Эвольвентное зацепление — это зубчатая передача, которая нечувствительна к изменению межосевого расстояния. Его изготавливают методом обкатки.
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30\ 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
Коррегирование зубчатого зацепления
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчет зубчатой передачи
В таблице ниже приведены формулы для расчета зубчатой передачи:
Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модуль зубчатой передачи стартеров
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
Р = z/d = z/(z • m/25,4) =25,4/m
Для перевода стандарта США в европейский стандарт служит зависимость:
m = 25,4 мм / P
Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
CP = (25,4 мм / P) π.
Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
Обозначение (пример): Р 5 /7
Р = 7 для расчета головки зуба,
Р = 5 для расчета других параметров.
Система обозначений и преобразований
Диаметр окружности выступов: OD = da.
Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
Диаметр окружности впадин: RD = df
Начальный диаметр:
LD =(N+2x) / P (в дюймах)
или
LD= (N+2x)·m (в мм).
LD ≈ dw,
где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1. В случае зубчатого зацепления с z1< 20 следует принимать Sw ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления. Поскольку контактные давления равны по величине для обоих колес, значение kperm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n2, пользуясь помещаемой ниже таблицей.
Формулы для расчета наибольшего допустимого давления
Содержащиеся в таблице значения коэффициента &Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых колес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент kperm следует увеличить примерно в 1,8 раза. Для зубчатого зацепления лишь с одним поверхностно упрочненным колесом, коэффициент kperm для незакаленного колеса необходимо увеличить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы Lh = 5000 ч. При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ:
Зубчатая передача
Категория:
Крановщикам и стропальщикам
Публикация:
Зубчатая передача
Читать далее:
Зубчатая передача
Что называется зубчатой передачей?
Трехэвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару, называется зубчатой передачей. Как подразделяются зубчатые передачи в зависимости от расположения геометрических осей валов?
В зависимости от расположения геометрических осей валов зубчатые передачи подразделяются на передачи с параллельными, пересекающимися и со скрещивающимися геометрическими осями.
Какая зубчатая передача называется передачей с параллельными осями?
Передача, в которой, оси зубчатых колес параллельны, называется зубчатой передачей с параллельными осями (рис. 1).
Рекламные предложения на основе ваших интересов:
Какая зубчатая передача называется передачей с пересекающимися осями?
Рис. 1. Зубчатая передача с параллельными осями.
Передача, в которой оси зубчатых колес пересекаются, называется зубчатой передачей с пересекающимися осями (рис. 2).
Какая зубчатая передача называется передачей скрещивающимися осями?
Передача, в которой оси зубчатых колес скрещивав ются, называется зубчатой передачей со скрещивающимися осями.
Что называется передаточным числом зубчатой передачи?
Отношение числа зубьев колеса к числу зубьев шестерни называется передаточным числом зубчатой передачи.
Что называется передаточным отношением зубчатой передачи?
Отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса называется передаточным отношением.
Что называется зубчатым зацеплением?
Кинематическая пара, образованная зубчатыми колесами передачи, называется зубчатым зацеплением.
Что называется зубчатым колесом?
Зубчатое звено с замкнутой системой зубьев, обеспечивающее. непрерывное движение другого зубчатого колеса, называется зубчатым колесом.
Какое зубчатое колесо зубчатой передачи называется ведущим?
Зубчатое колесо передачи, торое сообщает движение пар му зубчатому колесу, называет ведущим.
Какое зубчатое колесо зубча- передачи называется ведомым?
Зубчатое колесо передачи, которому сообщает движение нов зубчатое колесо, называется ведомым.
Что называется шестерней?
Зубчатое колесо передачи е меньшим числом зубьев называется шестерней.
Какими зубчатые колеса могут быть по форме?
По форме зубчатые колеса могут быть цилиндрические, конические, эллиптические и фигурные, причем самое широкое применение имеют цилиндрические и конические зубчатые колеса.
Какими зубчатые колеса могут быть по форме зубьев?
По форме зубьев зубчатые колеса могут быть прямозубые, косозубые, шевронные и др.
Какие зубчатые колеса называются прямозубыми?
Прямозубыми называются такие зубчатые колеса, у которых зубья нарезаны адоль образующей цилиндра или конуса (зуб, делительная теоретическая линия которого лежит в плоскости, проходящей через ось зубчатого колеса).
Какие зубчатые колеса называются косозубьшн?
Косозубыми называются такие зубчатые колеса, у которых зубья нарезаны под углом к образующей цилиндра (винтовой зуб, теоретическая линия которого является частью винтовой линии постоянного шага на цилиндрической поверхности).
Какие зубчатые колеса называются шевронными?
Цилиндрические зубчатые колеса, венец которых по ширине состоит из участков с правыми и левыми, зубьями, называются шевронными.
Какое минимальное количество зубьев допускается на зубчатом колесе?
Не менее шести, иначе не будет соблюдено условие плавного и надежного зацепления. Даже самые маленькие зубчатые колеса имеют не менее шести зубьев.
Рис. 2. Зубчатая передача с пересекающимися осями
Отсюда и произошло слово «шестерня», которым часто в обиходе называют все зубчатые колеса. Максимальное количество зубьев не ограничено. Ведь длинная зубчатая рейка — это тоже своего рода зубчатое колесо с бесконечно большим диаметром.
Чем характеризуется зубчатое колесо?
Зубчатое колесо характеризуется: делительным диаметром (U), начальным диаметром (dw), диаметром вершин зубьев (da), диаметром впадин (df), числом зубьев (Z), модулем (т), шагом зацепления.
Что называется делительным диаметром зубчатого колеса (d)?
Диаметр делительной концентрической окружности зубчатого колеса называется делительным диаметром.
Что называется начальным диаметром зубчатого колеса (dw)?
Диаметр начальной концентрической окружности зубчатого колеса называется начальным диаметром.
Что называется диаметром вершин зубьев зубчатого колеса (da)?
Диаметр вершин зубьев концентрической окружности зубчатого колеса называется диаметром вершин зубьев.
Что называется диаметром впадин?
Диаметр впадин концентрических окружностей зубчатого колеса называется диаметром впадин.
Что называется нормальным шагом зубьев?
Кратчайшее расстояние по делительной, начальной или однотипной соосной поверхности зубчатого колеса между эквидистантными одноименными теоретическими линиями соседних зубьев называется нормальным шагом зубьев.
Что называется окружным шагом зубьев?
Расстояние между одноименными профилями соседних зубьев по дуге концентрической окружности зубчатого колеса называется окружным шагом зубьев.
Что называется угловым шагом зубьев?
Центральный угол концентрической окружности зубчатого колеса, равный 2я/Z, или 360°/Z, называется угловым шагом зубьев.
Что называется окружным модулем зубьев?
Линейная величина, в я раз меньшая окружного шага зубьев, называется окружным модулем зубьев.
Что называется нормальным модулем зубьев?
Рис. 3. Схема зубчатой передачи и ее параметры
Линейная величина, в я раз меньшая нормального шага зубьев, называется нормальным модулем (рис. 3).
В каких машинах и механизмах применяются зубчатые передачи?
Зубчатые передачи применяются почти во всех машинах, так как они весьма компактны, обслуживание их несложно, долговечны и надежны в работе, сохраняют постоянство передаточного числа. Поэтому из механических передач самое широкое распространение имеют зубчатые,
Рис. 4. Червячная передача: 1 — червяк; 2 —червячное колесо
Рекламные предложения:
Читать далее: Червячная передача
Категория: — Крановщикам и стропальщикам
Главная → Справочник → Статьи → Форум
Все, что вам нужно знать о шестеренках. Типы и детали
Шестерни являются фундаментальной частью любого механизма из-за их способности передавать движение, силу и крутящий момент между различными компонентами. Существует огромное количество различных типов шестерен, в зависимости от того, какую задачу они выполняют: изменение скорости или силы вращения, изменение оси вращения, передача мощности между двигателем и другими движущимися элементами…
Сегодня в Bitfab мы научим вас всему, что вам нужно знать о механизмах.
Что такое шестерня?
Шестерня определяется как колесо с зубьями на краю, обычно цилиндрическим, которое используется для передачи движения от элемента, генерирующего энергию, такого как двигатель, к месту, где мы хотим приложить силу, с преобразованиями в оси вращения. или скорость.
Какие части шестерни?
Зубчатая передача может быть очень сложной, но наиболее распространенные из них состоят из трех отдельных частей: зубчатой коронки, которая передает движение, подшипника, на котором соединяется вал (двигателя или другой части механизма), и перегородки. между ними, который иногда появляется в виде оружия.
Перегородка или рычаги шестерни
Это часть шестерни, которая соединяет заводную головку и подшипник для передачи движения. Существует множество вариантов этой детали, поскольку, в зависимости от технических требований, можно сделать очень прочную, но тяжелую прочную перегородку или тонкие радиальные рычаги, которые менее устойчивы, но легче. Весовой элемент может иметь решающее значение для того, чтобы не добавлять ненужную массу, поскольку, увеличивая вес движущегося элемента, мы увеличиваем инерцию нашей системы.
Из-за необходимости найти шестерни с подходящей перегородкой, существует множество промежуточных вариантов с тонкими, толстыми, прочными, перфорированными перегородками…
Подшипник шестерни
Подшипник — это часть, к которой прикреплена ось, передающая движение. Этот вал может быть от двигателя или от другой части механизма.
Заводная головка шестерни
Венец или обод шестерни — это место, где расположены зубья, и это часть шестерни, которая в значительной степени определяет поведение шестерни.И его форма, и форма и размер зубьев — вот что заставляет шестерню вести себя так или иначе.
Поскольку свойства самой шестерни тесно связаны с количеством зубьев и их расположением, давайте сначала рассмотрим детали зуба шестерни.
Части зуба
Как видите, зуб состоит из следующих частей:
- Top Land : Наружная часть зуба.
- Лицевая поверхность и боковая поверхность : верхняя и нижняя часть боковой поверхности зуба, которая является контактной поверхностью между двумя колесами, когда они входят в зацепление.
- Нижняя площадка : Нижняя часть зуба или промежуточная область между двумя зубьями.
Геометрия короны: определяющие ее окружности
Кроме того, геометрия заводной головки определяется серией окружностей, которые придают зубчатому колесу его форму:
- Корневой круг : отмечает нижнюю поверхность или основание зубов. Определяет внутренний диаметр шестерни.
- Промежуточная окружность : Обозначает разделение между двумя частями стороны зуба: лицевой стороной и боковой стороной.Это самая важная окружность, и все остальные определяются в соответствии с ней. Он делит зуб на две части: нижнюю часть и придаток.
- Внешний или дополнительный круг : отмечает верхнюю часть зубьев. Это внешний диаметр шестерни.
De esta manera nos quedaría el diente dividido en dos partes, el pie y la cabeza
- Dedendum : Нижняя часть зуба между корневой окружностью и делительной окружностью.
- Приложение : Верхняя часть зуба между делительной окружностью и внешней окружностью.
Возвращаясь к коронке и по отношению к зубам, основными параметрами коронки являются:
- Число зубцов : определяет передаточное число и является одним из наиболее важных параметров для определения поведения шестерни.
- Полная глубина : Общая высота, измеренная от Нижнего края до Верхнего края.
- Круговой шаг : расстояние между одной частью зуба и такой же частью следующего зуба.Он отмечает, насколько далеко друг от друга расположены зубы, и тесно связан с их количеством.
- Толщина круга : Толщина зуба.
Типы шестерен
В зависимости от того, что мы хотим сделать в нашем механизме, нам придется выбирать тот или иной тип шестерен, поскольку каждый из них предназначен для очень конкретной функции.
Шестерни прямозубые. прямая цилиндрическая шестерня
Самый распространенный тип передачи, используемый, когда необходимо уменьшить или увеличить силу или скорость в условиях, когда скорость не очень высока.
Цилиндрическая цилиндрическая шестерня
Чуть более усовершенствованная версия предыдущей. Более тихий и способный работать на более высоких скоростях. Они также двухзубые. Также доступны с двойными спиральными зубьями в противоположных направлениях, которые поддерживают даже более высокие скорости и выходную мощность.
Коническая шестерня с прямыми зубьями
Они используются для изменения направления вращения в механизме, обычно перпендикулярно, когда не требуются высокие скорости.
Коническая шестерня со спиральными зубьями
Как и предыдущие, они используются для изменения направления вращения, но в этом случае поддерживаемая скорость выше.
Внутренняя шестерня
Они работают так же, как традиционные внешние зубчатые передачи, но более компактны, чем внешние зубчатые колеса с такими же характеристиками.
Планетарные передачи
В этом типе шестеренок используется центральная шестерня, вокруг которой вращаются меньшие шестерни, отсюда и название, поскольку они напоминают нам о солнечной системе с Солнцем в центре и планетами, вращающимися вокруг нее.
Червячная передача
Эти шестерни широко используются, поскольку они обеспечивают очень постоянную выходную скорость и работают без вибрации и шума. К тому же эти механизмы обычно довольно компактны.
Зубчатая рейка и шестерня
Эти шестерни позволяют преобразовывать вращательное движение в линейное и наоборот, поэтому они чрезвычайно полезны.
Типы зубчатых колес и зубчатые передачи — Механические устройства — Edexcel — Редакция дизайна и технологии GCSE — Edexcel
Зубчатые колеса — это колеса с зубьями на внешней стороне.Когда несколько колес заблокированы, они могут передавать движение с одного места на другое, например, в некоторых ручных венчиках или на велосипедах.
Шестерни могут изменять направление или скорость движения. Поскольку по краю зубчатых колес есть зубья, они сцепляются друг с другом и поэтому могут выдерживать большую силу, что позволяет им перемещать большие предметы, такие как автомобили или велосипеды.
Зубчатые передачи
Зубчатые передачи — это когда две или более шестерни соединены вместе. В простой зубчатой передаче ведущая шестерня заставляет ведомую шестерню вращаться в противоположном направлении.
Мелкие шестерни с меньшим количеством зубьев вращаются быстрее, чем более крупные шестерни с большим количеством зубьев. Эта разница в скорости называется передаточным числом.
Передаточное число = количество зубьев ведомой шестерни ÷ количество зубьев ведущей шестерни
Пример
Ведомая шестерня имеет 60 зубьев, а ведущая шестерня — 15 зубцов.
Передаточное число = 60 ÷ 15
= 4
За каждый оборот ведущей шестерни ведомая шестерня будет вращаться четыре раза.
Передаточное число = 4: 1
Это называется повышением передачи.Если бы ведомая шестерня имела 15 зубьев, а ведущая шестерня — 60 зубцов, передаточное отношение было бы 4: 1, что называется понижающей передачей.
- Вопрос
Если велосипедист крутит педали с ведущей шестерней с 50 зубьями и ведомой шестерней с 25 зубьями, какое передаточное число?
- Показать ответ
Передаточное число = 50 ÷ 25
= 2
Передаточное число = 2: 1
Типы шестерен
Если ведущая шестерня и ведомая шестерня разделены другой шестерней, называется бездельник, они будут двигаться в том же направлении.
Коническая шестерня
Коническая шестерня — это специальная шестерня, которая может передавать вращение на 90 градусов. На схеме ниже показаны две шестерни одинакового размера — название, данное этой конструкции, — усеченная шестерня.
Однако две шестерни могут различаться по размеру для достижения разного передаточного числа. Примером этого является ручная дрель, у которой ведущая шестерня больше ведомой.
Ручная дрель с усеченной шестерней, где ведущая шестерня больше ведомой
Рейка и шестерня
Рейка и шестерня представляют собой конструкцию из зубчатого колеса и рейки, которая позволяет преобразовывать вращательное движение к линейному движению.Примером может служить буровая установка с колонной, когда станина стола перемещается вверх и вниз.
Буровая установка с зубчатой рейкой
Скорость вращения шестерни или колеса измеряется в оборотах в минуту (об / мин). Во многих автомобилях есть счетчик оборотов, который показывает водителю, насколько быстро вращается двигатель.
Счетчик оборотов автомобиля
Выходная скорость = входная скорость ÷ передаточное число
Пример
Ведущая шестерня, вращающаяся со скоростью 60 об / мин, соединена с зубчатой передачей с передаточным числом 60:20.
Рассчитайте выходную скорость.
Передаточное число = количество зубьев ведомой шестерни ÷ количество зубцов ведущей шестерни
= 60 ÷ 20 = 3
Выходная скорость = входная скорость ÷ передаточное число
= 60 (об / мин) ÷ 3 = 20 об / мин
В этой конфигурации выходная скорость в три раза медленнее по сравнению с входной скоростью.
- Вопрос
Ведущая шестерня, вращающаяся со скоростью 120 об / мин, соединена с зубчатой передачей с передаточным числом 6:12.Рассчитайте выходную скорость.
- Выявить ответ
Передаточное число = количество зубьев ведомой шестерни ÷ количество зубцов ведущей шестерни
= 6 ÷ 12 = 0,5
Выходная скорость = входная скорость ÷ передаточное число
= 120 ÷ 0,5 = 240 об / мин
В этой конфигурации выходная скорость в два раза выше по сравнению с входной скоростью.
Gear — Energy Education
Рисунок 1: Зубчатая передача [1]Шестерня (также называемая зубчатым колесом ) — это тип простого механизма, который используется для управления величиной или направлением силы.Шестерни используются в комбинации и связаны друг с другом своими зубьями, называемыми зубьями , для образования «зубчатой передачи» . Эти зубчатые передачи полезны для передачи энергии от одной части системы к другой. Системы, в которых используются шестерни и зубчатые передачи, включают велосипеды, автомобили, электрические отвертки и многие другие обычные машины. [2]
Как они работают
В зубчатых передачахиспользуется принцип механического преимущества, которое представляет собой отношение выходной силы к входной в системе.Для шестерен механическое преимущество обеспечивается передаточным числом , которое представляет собой отношение скорости последней шестерни к начальной скорости шестерни в зубчатой передаче. [3] Передаточное число определяется уравнением: [4]
Рисунок 2: Анимация зубчатой пары, видно, что меньшая шестерня вращается быстрее, чтобы успевать за большим количеством зубьев на большей шестерне. [5] [математика] MA = \ frac {\ omega_A} {\ omega_B} = \ frac {r_B} {r_A} = \ frac {N_B} {N_A} [/ math]где
- [math] N [/ math] — количество зубьев шестерни,
- [math] \ omega [/ math] — угловая скорость шестерни, а
- [math] r [/ math] — радиус шестерни.
Следовательно, если механическое преимущество зубчатой передачи равно 3, это означает, что последняя шестерня в передаче имеет радиус, в 3 раза превышающий радиус первой шестерни. При таком передаточном числе входная шестерня может вращаться с усилием в 3 раза меньшим, чем на выходе последней шестерни, но взамен она должна вращаться в 3 раза быстрее, чем последняя шестерня.
Это соотношение для зубчатых передач фундаментально зависит от закона сохранения энергии. При анализе зубчатых передач эту концепцию легче понять, если использовать анализ сохраненной мощности системы.Этот анализ связывает крутящие моменты шестерен с их угловыми скоростями. Полный анализ обмена можно посмотреть здесь BROKEN LINK .
использует
Шестернислужат двум основным целям: увеличение скорости или увеличение силы . Чтобы увеличить одно из них, я должен пойти на компромисс. Например, чтобы увеличить скорость колес велосипеда, необходимо увеличить силу, прилагаемую к педалям. Точно так же, чтобы увеличить усилие на колесах, педали нужно крутить быстрее.Этот прием используется, когда гонщик пытается подняться на холм на велосипеде. Все это связано с законами сохранения энергии и мощности.
Шестерни широко используются во многих системах, но их легче всего распознать в повседневной жизни в автомобилях, которые мы ведем. В автомобилях должны использоваться шестерни, чтобы эффективно и безопасно передавать энергию от двигателя к колесам. Двигатель на холостом ходу работает со скоростью около 1000 об / мин — если бы двигатель был подключен непосредственно к колесам, это означало бы, что автомобиль должен двигаться со скоростью около 120 км / ч.Это означает, что если двигатель автомобиля будет включен, он немедленно разгонится до этой скорости. Когда двигатель перешел в диапазон высоких оборотов — около 7000 — машина разгонится до 840 км / ч! Хотя это кажется очень забавным, это крайне непрактично. Это непрактично из-за того, что автомобилю требуется большое количество энергии для движения, поэтому двигатель, пытающийся набрать полную скорость при запуске, не будет генерировать достаточно силы для движения автомобиля. Поэтому в автомобиле используются передачи в трансмиссии или, альтернативно, «коробка передач», которая начинается с использования более низких передач, которые создают больше силы, чтобы заставить автомобиль двигаться, в конечном итоге переходя на более высокие передачи, ориентированные на скорость. [3]
Тот же принцип передач применяется к велосипедам; для подъема в гору требуются более низкие передачи, чтобы обеспечить большее усилие для противодействия силе тяжести, и как только гонщик возвращается на ровную землю, он может переключиться на более высокие передачи, чтобы увеличить скорость своего велосипеда.
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
зубчатая передача | Примеры предложений
gear train еще нет в Кембриджском словаре.Вы можете помочь!
Это было достигнуто путем размещения планетарной шестерни , цепи между осью и коронным колесом. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Зубчатая передача с приводом от двигателя приводит в движение нижнюю звездочку вертикальной звеньевой цепи (подобной велосипедной цепи) с подъемом около четырех футов.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Ведущая шестерня с делительным диаметром 50 мм установлена на валу шестерни передачи .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Назначение такой конструкции состояло в том, чтобы в случае поломки пружины разрушительные силы отдачи не применялись к уязвимой шестерне цепи .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Верхняя часть машины вращается на тележке с помощью «поворотного» гидравлического двигателя через шестерню , поезд .Нагрузка в планетарной передаче , цепи распределяется между несколькими планетами, поэтому крутящий момент значительно увеличивается. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Он двигался свободно, но близко к вращающемуся элементу, входящему в шестерню часов , поезд .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Это показывает, что если входная шестерня вращается быстрее, чем выходная шестерня, то шестерня передача усиливает входной крутящий момент.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Высокая вязкость обеспечивает передачу смазки по всей шестерне передаче .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Здесь термин относится к валу, передающему мощность от колес станка на шестерню , поезд , которая приводит в действие режущий механизм.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Вал двигателя соединен с малой шестерней и цепью посредством кулачковой муфты.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Каждая турбина была соединена с приводным валом через различную шестерню и цепь .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Ротор тягового двигателя соединен с шестерней и цепью через жесткую муфту (оболочку резинового корда).ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Передаточное число крутящего момента шестерни передачи , также известное как ее механическое преимущество, определяется передаточным числом.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Таким образом, передаточное число передачи , шестерни , , линии также определяет ее механическое преимущество.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Водяное колесо, приводимое в движение дорожкой мельницы, приводится в действие двумя рамными пилами через шестерню , поезд , режущую прямоугольные блоки.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Крутящий момент, прилагаемый радиально к шестерням планетарной шестерни , передачи , передается радиально шестерней без бокового давления на зубья шестерни. сообщение}}Выберите часть речи и введите свое предложение в поле «Определение».
{{/сообщение}} Часть речиВыберите существительное, глагол и т. Д. Прилагательноеприлагательноерекламабъявление существительноечислопрефикссуффиксглагол
Определение
Представлять на рассмотрение Отмена
Как работает трансмиссия | Как работает автомобиль
Проход через карданный вал
Двигатель передний — задний привод
Двигатель и коробка передач скреплены болтами, между ними находится муфта сцепления.Двигатель установлен жестко, но карданный вал должен быть гибким, чтобы задняя ось могла перемещаться.В автомобиле с передним расположением двигателя и задним приводом мощность передается от двигатель через сцепление и коробку передач сзади ось с помощью трубчатого карданного вала.
Задний мост должен иметь возможность перемещаться вверх и вниз на приостановка по вариациям дорожного покрытия.
Движение вызывает постоянное изменение угла карданного вала и расстояния между коробкой передач и задней осью.
Чтобы обеспечить постоянное движение, шлицы на переднем конце карданного вала выдвигается и выходит из коробки передач при изменении расстояния; вал также имеет универсальные шарниры на каждом конце, а иногда и посередине.
Универсальные шарниры позволяют карданному валу быть гибким, при этом постоянно передавая мощность.
Последняя часть коробка передач главная передача, которая включает в себя дифференциал и иногда его называют дифференциалом.
Главная передача
К карданному валу прикреплена шестерня, которая входит в корпус дифференциала в центре задней оси. Скошенные ведущие шестерни внутри дифференциала вращаются вместе с ведомым колесом и приводят полуоси к задним колесам, обычно с одинаковой скоростью. Во время поворота они позволяют одному опорному колесу вращаться быстрее, чем другому.Дифференциал выполняет три функции: поворачивать направление движения на 90 градусов к задним колесам; чтобы одно из задних колес поворачивалось быстрее другого при прохождении поворота; и произвести окончательный редуктор .
А шестерня внутри дифференциал приводится в движение карданным валом и имеет свой шестерни скошенный — срезанный под углом. Он входит в зацепление с зубчатым венцом со скошенной кромкой, так что две шестерни образуют угол 90 градусов.
Карданный шарнир
Самый распространенный тип универсального шарнира, шарнир крюка, использует крестообразную «крестовину» поперек оси приводного вала. «Крестовина» работает на игольчатых роликоподшипниках для минимизации трения.Ведущее колесо обычно имеет примерно в четыре раза больше зубьев, чем ведущая шестерня, поэтому колеса вращаются со скоростью, равной четверти скорости гребного вала.
Привод передается от дифференциала на задние колеса посредством полуосей, или приводные валы .
На конце дифференциала каждой полуоси коническая ведущая шестерня соединена с ведомой шестерней с помощью промежуточного набора конических шестерен.
Вождение через передние колеса
Поперечный двигатель
Коробка передач встроена в картер двигателя, а привод на передние колеса передается через универсальные шарнирные валы.Автомобили с передним приводом используют то же коробка передач принципы, как у автомобилей с задним приводом, но механические компоненты различаются по конструкции в зависимости от двигатель и компоновка коробки передач.
Двигатели с поперечным расположением двигателя обычно устанавливаются непосредственно над коробкой передач, и мощность передается через схватить к коробке передач цепочкой шестерен.
Рядный двигатель
В этой переднеприводной компоновке коробка передач находится в обычном положении в задней части двигателя.Рядные двигатели соединены непосредственно с коробкой передач, и привод проходит через сцепление обычным образом.
В обоих случаях привод переходит от коробки передач к бортовому редуктору.
В двигателе с поперечной установкой главная передача обычно находится в коробке передач. В рядном двигателе он обычно устанавливается между двигателем и коробкой передач.
Передача мощности от бортового редуктора к колесам осуществляется короткими ведущими валами. Чтобы справиться с подвеской и рулевое управление При движении в колесах в приводных валах используется высокоразвитый универсальный шарнир, называемый шарниром равных угловых скоростей (CV).
ШРУС
Шарнир предназначен для одновременного управления приводом и рулевым управлением на переднеприводных автомобилях.Шрус использует канавки со сталью шарикоподшипники в них вместо «паука», обнаруженного в карданном шарнире, передается мощность с постоянной скоростью, независимо от угла и расстояния между бортовым редуктором и колесами.
Некоторые автомобили, такие как более ранние модели Minis, также имеют муфты карданного вала, которые являются «крестовинами» и выполняют ту же работу, что и универсальные шарниры в автомобилях с задним приводом, обеспечивая перемещение подвески вверх и вниз.Обычно они сделаны из резины, приклеенной к металлу.
Задний двигатель ведущие задние колеса
Некоторые автомобили, такие как VW Beetles и меньшие Fiat, имеют расположенные сзади двигатели и коробки передач, приводящие в движение задние колеса.
Мощность передается через муфту на коробку передач, передаваясь на колеса через приводные валы.
Компоновка аналогична некоторым автомобилям с передним приводом, за исключением того, что не нужно делать поправки на поворот колес.
Иногда валы присоединяются к фланцы на коробке передач с помощью муфт типа «бублик».
Автомобильные дифференциалы
Зубчатая передача в автомобильном дифференциале — это обычное применение зубчатых передач, которое часто неправильно понимается широкой публикой. Здесь мы представляем упрощенное объяснение того, как и почему работает автомобильный дифференциал.
Автомобиль разворачивается по окружности с номинальным радиусом r n . (Для этого обсуждения мы предполагаем, что ось оси колеса для ведомых (задних) колес проходит через центр окружности поворота.Обычно это верно только для довольно большого радиуса поворота.)
Наружное колесо движется по дуге с радиусом r o , а внутреннее колесо проходит по дуге с радиусом r i . Как показано, длины пройденных дуг составляют s o , s n и s i . Внешняя дуга s o , очевидно, больше внутренней дуги s i для данного пройденного угла theta. Должен быть обеспечен некоторый способ обеспечения того, чтобы внешнее колесо могло вращаться немного быстрее, чем внутреннее колесо, чтобы предотвратить заедание и проскальзывание шин на дороге.Для неведущих колес, которые просто свободно вращаются независимо от других механизмов, это не проблема. Однако ведомые колеса, соединенные с двигателем через карданный вал, должны поворачиваться с помощью зубчатой передачи, и эта зубчатая передача должна допускать перемещение дифференциала левого колеса по отношению к правому колесу. Это сложная проблема, поскольку для каждого круга поворота дифференциальное вращение левого и правого колес различно. К счастью, автомобильный дифференциал решает эту проблему с помощью только одной трансмиссии и одного ведущего вала для обоих ведомых колес.
Так как s = r (THETA), длина дуги, пройденной для данного тета, пропорциональна радиусу. Поскольку r o больше r n на ту же величину, что r i меньше r n , центр правого колеса должен перемещаться дальше центра автомобиля на ту же величину, что и центр левого колеса. ехать меньше, чем до автоцентра. Как следует из названия, дифференциал позволяет левому и правому ведущим колесам по-разному поворачиваться относительно друг друга.Как можно увидеть, поворачивая ведущие колеса автомобиля на механическом подъемнике, поворот одного ведущего колеса приводит к тому, что противоположное колесо вращается с той же скоростью в противоположном направлении.
Как работает механический будильник
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Снятие заводных ручек и задней крышки часов показывает внутреннюю часть часов.& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Убрав подставку, руки, лицо и установочное кольцо, вы получите сам часовой механизм.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Вы увидите
основная пружина . Основная идея пружины — действовать как энергия
запоминающее устройство, чтобы часы могли работать без присмотра в течение длительного периода
время. «Потенциальная энергия» пружины обеспечивает движущую силу
запустить часы. Аналогичная пружина меньшего размера обеспечивает энергию для
будильник . Эти пружины имеют муфты для ограничения обратного вращения.
когда мы заводим основную пружину с помощью заводной головки.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Итак, предположим, что мы хотели использовать намотанную основную пружину для создания простейшего
возможные часы — часы, на которых есть только секундная стрелка. Нам нужна вторая рука
эти простые часы работают как обычная секундная стрелка на любых часах, что делает их полноценными
оборот каждые 60 секунд. Мы могли бы попытаться сделать это, просто прикрепив основную пружину
к колесу, а затем прикрепив вторую руку к колесу.Это, конечно,
не работает. Основная пружина всегда будет в напряжении, чтобы раскручиваться. Итак, в этом простом
механизм, отпускание пружины приведет к ее раскручиванию, и колесо будет вращаться
с очень высокой скоростью, пока основная пружина полностью не раскрутится.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Теперь, если мы наложим какое-то ограничение на пружину и позволим ей открыться
со временем — наша цель была бы достигнута.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Здесь показан спусковой механизм —-
| Этот анимированный GIF-изображение часового механизма спуска на самом деле всегда идёт против часовой стрелки, будучи заблокированным одним или другим зубцы маятника по очереди. Взято с http://www.howstuffworks.com. |
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Следует помнить, что поддон не будет раскачиваться вечно.
Следовательно, одна дополнительная задача спускового механизма — передать достаточно энергии.
в поддон, чтобы преодолеть трение и позволить ему продолжать качаться. Для этого
Задание, якорь и зубья на спусковом механизме имеют особую форму.Шестерни
зубы выходят правильно, и, кроме того, поддон толкается вправо
направление якоря каждый раз через качели. Толчок — это прилив энергии
что поддон должен преодолевать трение, поэтому он продолжает раскачиваться.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Итак, предположим, что мы создали такой спусковой механизм. Если бы мы дали
шестерня спуска 60 зубьев и прикрепила эту шестерню непосредственно к обсуждаемой нами пружине
выше, и если мы прикрепим к нему вторую стрелку, мы сделаем простые часы с
подержанный.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Хотя эти часы точны,
есть две проблемы, которые делают его бесполезным:
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp 1. Большинство людей обычно ожидают, что у часов также есть часовая и минутная стрелки, поэтому
в этом отношении эти часы будут считаться недостающими.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp 2.Через несколько минут вам придется заводить часы снова и снова. Так как
пружина через какое-то время раскрутится. Очевидно, этого никто не захочет.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Для решения этой проблемы используется зубчатая передача с большим передаточным числом. Это делает
основная пружина раскрутится через 35-45 часов. В этом можно убедиться, если отпустить спусковой механизм.
Сама шестерня приводит в движение другую зубчатую передачу с передаточным числом 60: 1, затем вы можете прикрепить
минутная стрелка к последней передаче в этом поезде.Финальный шлейф с соотношением 12: 1
будет обращаться с часовой стрелкой. У вас есть часы.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp Теперь давайте посмотрим, как
сигнализация работает? ». Здесь также есть пружина, которая накапливает в ней энергию.
А чтобы ограничить раскручивание пружины, есть сигнальный рычаг, который также
что-то вроде якоря . Этот рычаг управляется другим пружинным рычагом, который
всегда удерживается нажатой сигнализацией.Сигнальный механизм синхронизирован с
часовая передача. Теперь, когда часы бьют время, установленное на циферблате будильника, булавка в
циферблат попадает в паз, сделанный на сигнальном механизме. Это приводит к срабатыванию сигнализации.
подъем, который, в свою очередь, заставляет пружинный рычаг подниматься и отпускать рычаг аварийной сигнализации и т.
весна начинает раскручиваться. Есть шестерня со специальными зубьями, которая входит в зацепление с
Пружинная шестерня. Эта шестерня заставляет рычаг аварийной сигнализации вращаться взад и вперед, что ударяет
корпус и издает тревожный звук «Тррррррнннннннн».
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp. Вы можете видеть, что, хотя шестеренки в часах делают их сложными,
работа довольно проста, состоит из 5 основных частей:
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp 1. Пружина — это дает энергию для поворота стрелок часов.
& NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP 2.Весовая зубчатая передача — зубчатая передача с большим передаточным числом, передающая движение
пружина, чтобы не приходилось очень часто перематывать часы.
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp 3. Спусковой механизм — состоит из поддона, якоря и спускового механизма,
спусковой механизм точно регулирует скорость, с которой энергия пружины
выпущен.
& NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP 4.Механизм ручного переключения передач — понижает передачу, так что минутная и часовая стрелки поворачиваются.
по правильным ценам.
& NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP 5.

 Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось»)[3].
Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось»)[3].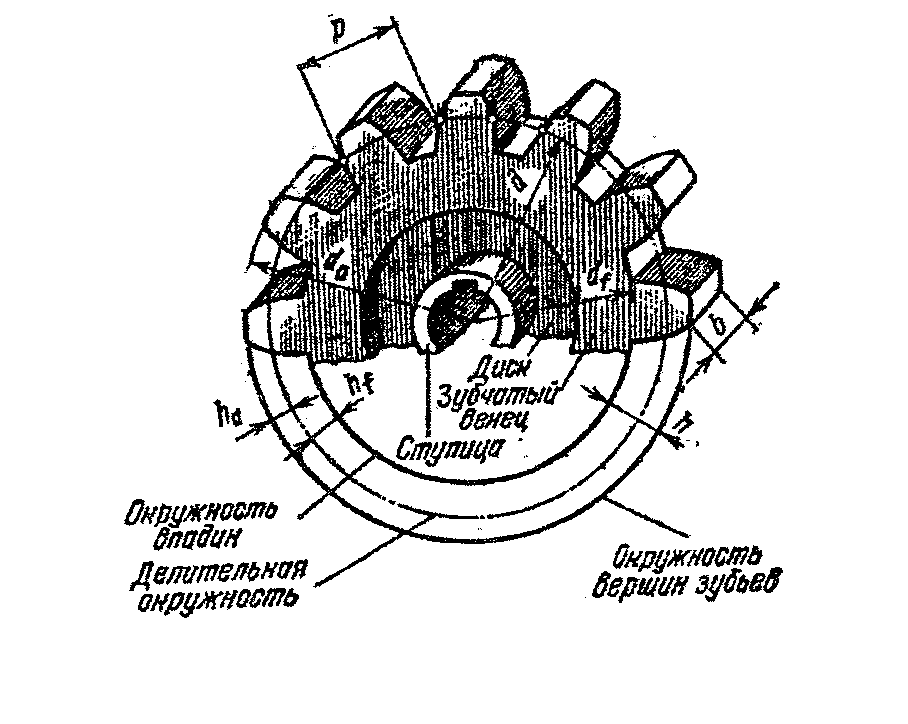 Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)
(подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули) Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:

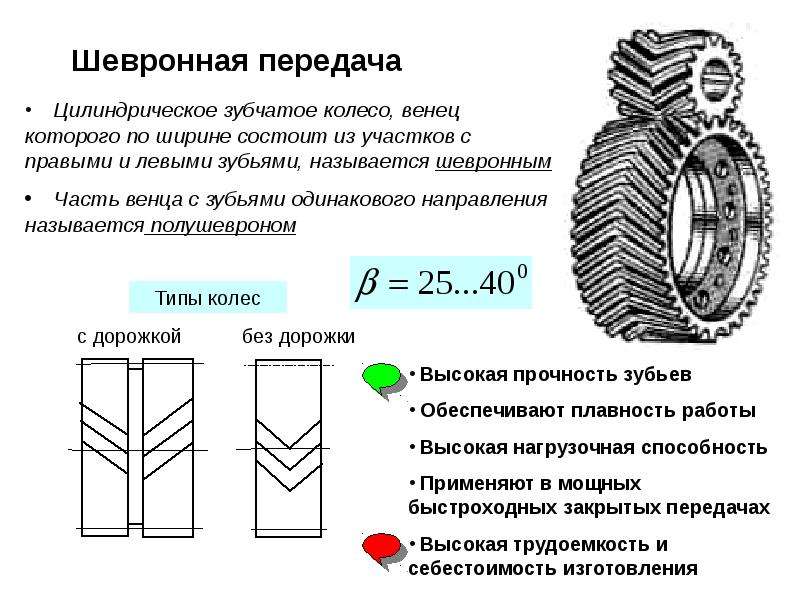 Вращение ведущего и ведомого колеса совершается в одну сторону. В такой передаче меньше потери на трение, то есть выше КПД.
Вращение ведущего и ведомого колеса совершается в одну сторону. В такой передаче меньше потери на трение, то есть выше КПД. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.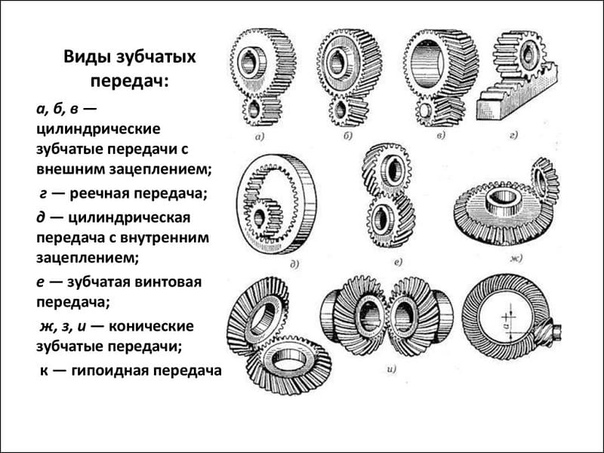
 При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.
При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.
 Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется.
Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется. Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.
Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.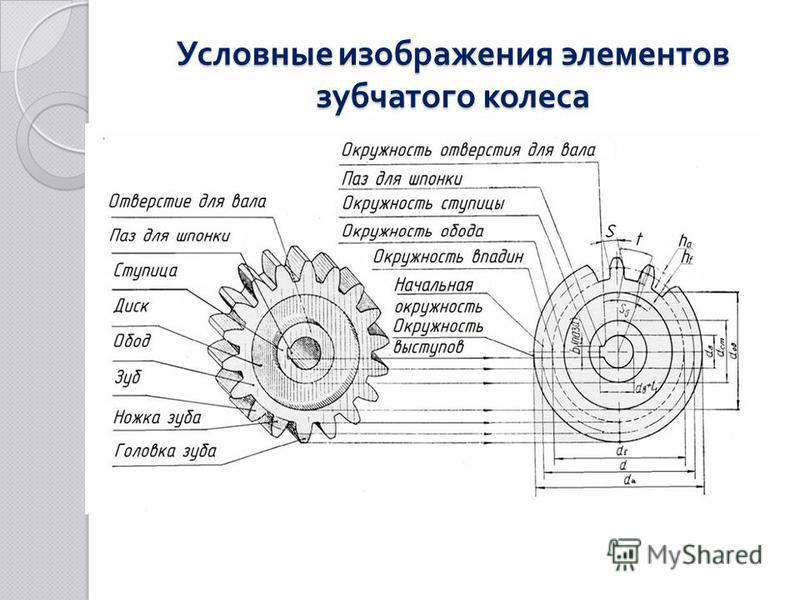 Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными.
Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными. Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится.
Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится. Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.
Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.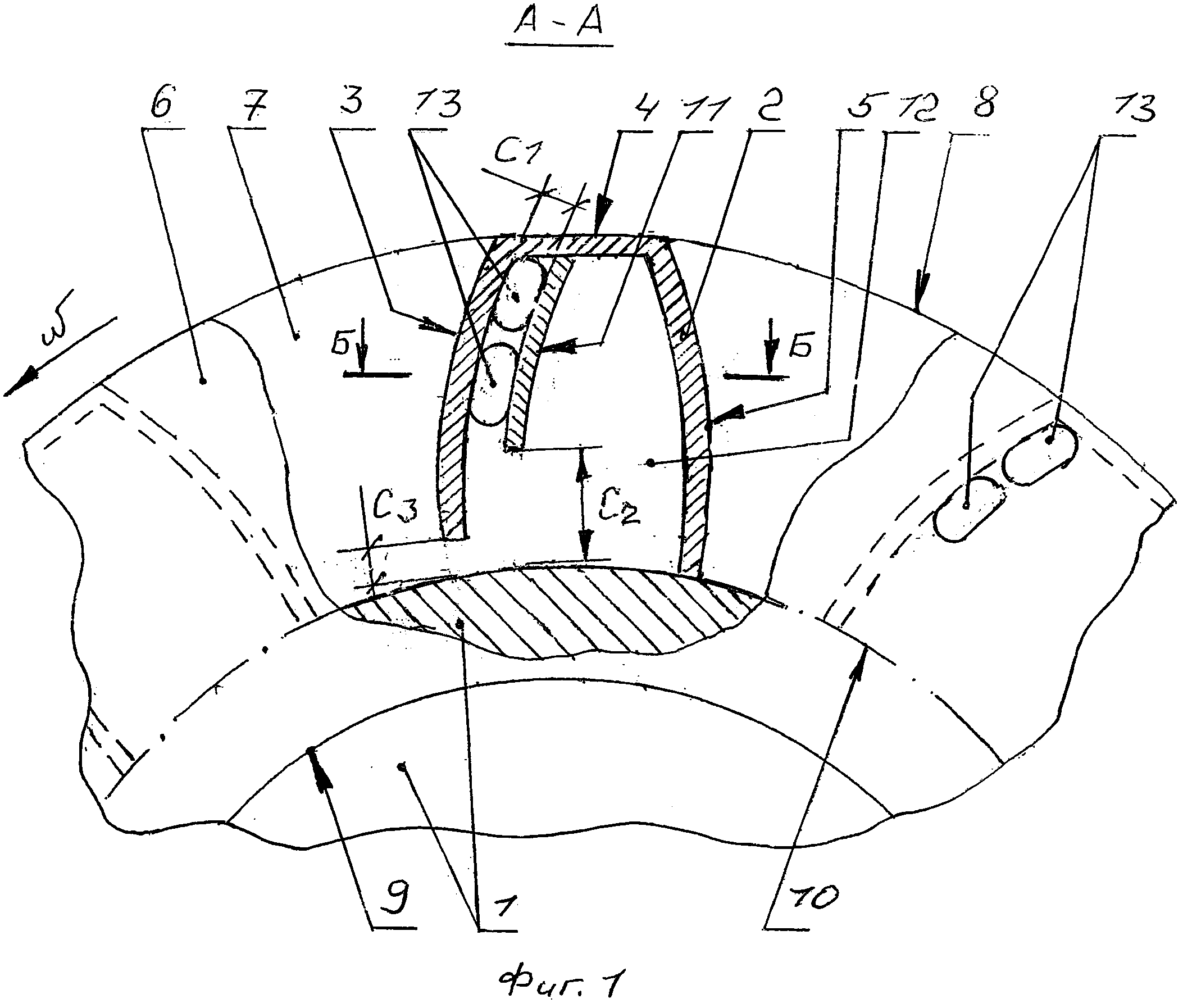 также
также — ISBN 5-217-02964-1 (5-217-02962-5), ББК 34.42я2, УДК 621.001.66 (035).
— ISBN 5-217-02964-1 (5-217-02962-5), ББК 34.42я2, УДК 621.001.66 (035).