Теория механизмов и машин | Зубчатые механизмы. Классификация зубчатых механизмов. Многозвенные механизмы с неподвижными осями колес и планетарные механизмы
Зубчатые механизмы, являющиеся составной частью привода, при выполнении одинаковых функций по сравнению с другими механизмами более экономичны в изготовлении, надежны в эксплуатации, имеют малые габаритные размеры и высокий КПД.
Зубчатые механизмы – передаточные механизмы, содержащие, по крайней мере, одно зубчатое зацепление. Они передают вращение от одного вала другому и изменяют модуль и направление угловой скорости. Их называют также зубчатыми передачами, где с изменениями угловой скорости одновременно меняется и вращающий момент на ведомых валах. В зубчатых передачах осуществляется контакт боковых поверхностей специально спрофилированных зубьев. Давление зубьев вращающегося ведущего колеса передается зубьям ведомого колеса, при этом осуществляется его вращение.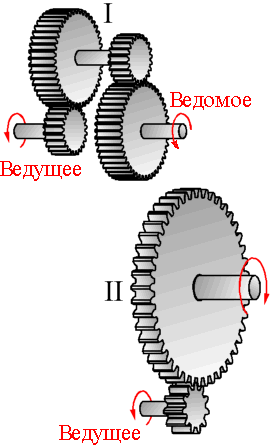
Зубчатые механизмы, в которых происходит уменьшение угловых скоростей при передаче движения от входного звена к выходному, называют понижающими передачами или редукторами. Зубчатые механизмы, в которых увеличиваются угловые скорости, называют повышающими передачамиилимультипликаторами. В машиностроении значительно чаще возникает необходимость понижения скорости, т.е. использования редуктора, поэтому расчету и проектированию редукторов уделяется особое внимание. Требования, которым должен удовлетворять зубчатый редуктор, заключаются в получении необходимых передаточных отношений (часто очень больших) при высоких показателях качества, каковыми являются КПД, кинематическая точность, крутильная жесткость, при возможно малых габаритных размерах, массе и высокой надежности редуктора.
Строение и классификация зубчатых механизмов
Зубчатые механизмы по геометрическому признаку подразделяют на плоские и пространственные. В плоских зубчатых механизмах оси вращения параллельны и все звенья вращаются в параллельных плоскостях. В пространственных зубчатых механизмах оси вращения звеньев пересекаются или перекрещиваются. В соответствии с признаком расположения осей вращения зубчатых колес простые трехзвенные механизмы можно разбить на следующие четыре группы.
В плоских зубчатых механизмах оси вращения параллельны и все звенья вращаются в параллельных плоскостях. В пространственных зубчатых механизмах оси вращения звеньев пересекаются или перекрещиваются. В соответствии с признаком расположения осей вращения зубчатых колес простые трехзвенные механизмы можно разбить на следующие четыре группы.
1. Реечные механизмы, в которых одно из зубчатых звеньев – зубчатая рейка.
2. Механизмы с параллельными осями вращения зубчатых колес, положение осей вращения которых определяется межосевым расстоянием aw.
3. Механизмы с пересекающимися осями вращения зубчатых колес, относительное положение осей вращения которых определяется межосевым углом Σ.
4. Механизмы со скрещивающимися осями вращения зубчатых колес, относительное поло-жение осей вращения которых определяется межосевым расстоянием aw и межосевым углом Σ.
Внутри каждой из этих групп, кроме первой, можно выделить две подгруппы, включающие схемы внешних и внутренних зацеплений.
Схемы зубчатых зацеплений простых трехзвенных механизмов с параллельными осями приведены на рис. 1.4. Варианты зацеплений (рис. 1.4, a) основаны на схеме с цилиндрическими колесами, имеющими линии зубьев в виде прямых, винтовых линий, дуг окружностей и двух винтовых линий правого и левого направлений. Для построения механизмов рассматриваемой группы можно использовать и более сложные геометрокинематические схемы зацепления (рис. 1.4, б, в). На рис. 1.4, б показана схема с коническими расчетными поверхностями и наклонными зубьями; на рис. 1.4,
Рис. 1.4. Схемы зубчатых зацеплений простых трехзвенных
механизмов с параллельными осями
Многообразие возможностей построения кинематических схем зацеплений с пересекающи-мися осями проиллюстрировано примерами на рис. 1.5, где Р – полюс зацепления.
1.5, где Р – полюс зацепления.
Рис.1.5. Схемы зубчатых зацеплений простых трехзвенных
механизмов с пересекающимися осями зацепления
Варианты а – г, е, к, л характеризуют подгруппу внешних конических зацеплений, а варианты д, ж, з, и – подгруппу внутренних зацеплений. Зацепление, изображенное на рис. 1.5, к, составлено из цилиндрического червяка и конического червячного колеса; зацепление, пока-занное на рис. 1.5, л, составлено из колес, имеющих конические расчетные, но тороидальные делительные поверхности.
Возможности построения простых трехзвенных механизмов со скрещивающимися осями показаны на рис. 1.6
Рис. 1.6. Схемы зубчатых зацеплений простых трехзвенных
механизмов со скрещивающимися осями
Варианты а – в характеризуют соответственно винтовое зацепление, гипоидное зацепление с коническими колесами и гипоидную передачу с цилиндрическим и плоским колесами. Варианты г – з иллюстрируют возможности построения червячных зацеплений с различными по форме делительных поверхностей червяками. На рис. 1.6, г, ж показаны схемы червячных зацеплений с цилиндрическим и глобоидным червяком, на рис. 1.6,
Варианты г – з иллюстрируют возможности построения червячных зацеплений с различными по форме делительных поверхностей червяками. На рис. 1.6, г, ж показаны схемы червячных зацеплений с цилиндрическим и глобоидным червяком, на рис. 1.6,
Передачу вращательного движения с заданным передаточным отношением осуществляют с помощью зубчатых, а иногда фрикционных механизмов. Представленные выше простейшие зубчатые механизмы имеют постоянное значение передаточного отношения u12= ω1 / ω2. Иногда в технике используются зубчатые механизмы с переменным передаточным отношением. В простейшем виде они состоят из некруглых зубчатых колес.
По кинематическому признаку различают зубчатыемеханизмы с неподвижными осями всех колес (рядовые передачи) и механизмы, оси отдельных колес которых перемещаются относительно стойки. Такие механизмы называют планетарнымии дифференциально-планетарными (зубчатыми дифференциалами). Они могут иметь несколько звеньев, которые соединяются с двигателями, другими механизмами, рабочими органами машины и неподвижными звеньями. Обычно механизм имеет одно ведущее звено, соединенное с двигателем непосредственно или через другой механизм, одно ведомое звено, соединенное с рабочим органом, и неподвижное звено. Такой механизм имеет одну степень подвижности.
Такие механизмы называют планетарнымии дифференциально-планетарными (зубчатыми дифференциалами). Они могут иметь несколько звеньев, которые соединяются с двигателями, другими механизмами, рабочими органами машины и неподвижными звеньями. Обычно механизм имеет одно ведущее звено, соединенное с двигателем непосредственно или через другой механизм, одно ведомое звено, соединенное с рабочим органом, и неподвижное звено. Такой механизм имеет одну степень подвижности.
Схемы планетарных механизмов с одной парой взаимодействующих колес показаны на рис. 1.7. Зубчатые передачи, в которых подвижны два звена, изображены на рис. 1.8. В дифференциальном механизме подвижным должно быть третье звено – корпус, в котором располагаются опоры. Можно сделать корпус (рис. 1.7, а) с геометрической осью вращения, совпадающей с осью вращения одного из колес, например колеса 2.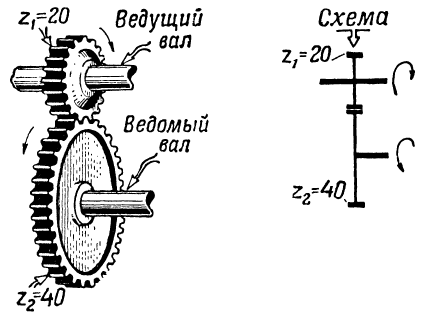
Намного проще придать подвижность третьему звену в передаче с внутренним зацеплением. Схема механизма с подвижным звеном 3 показана на рис. 1.7,  1.7, в) или так называемый механизм параллельных кривошипов 6 (рис. 1.7, г, д).
1.7, в) или так называемый механизм параллельных кривошипов 6 (рис. 1.7, г, д).
Механизм, показанный на рис. 1.7, б, может быть использован в качестве преобразователя вращательного движения в поступательное и наоборот. Для этого, например, к сателлиту присоединяют поступательно движущуюся штангу
Рис. 1.7. Схемы планетарных механизмов с одной парой взаимодействующих колес
Рис. 1.8. Зубчатые передачи с двумя подвижными звеньями
Колесо 1 с одним из выходных валов соединено при помощи гибкого тонкостенного стакана (рис. 1.7, е). Колесо выполнено также тонкостенным. Такую передачу называют волновой.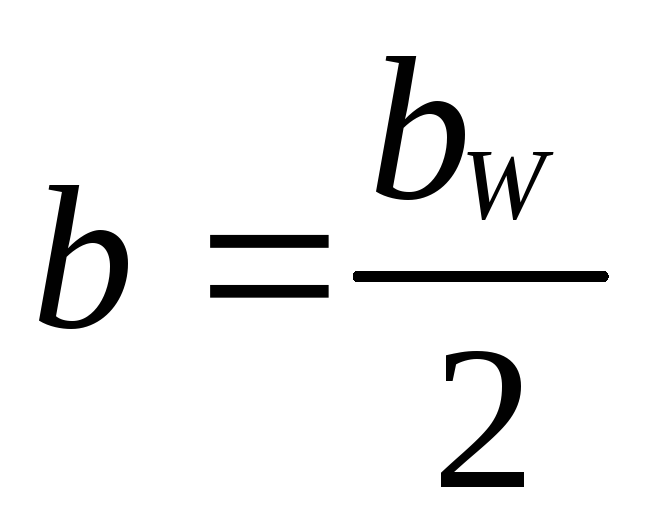
По аналогии с приведенными выше схемами может быть применена схема с подвижным третьим звеном, например, в реечном механизме (рис. 1.7, з) и конической передаче (рис. 1.7, и). Практически это можно осуществить, разместив один из двигателей на подвижном звене 3.
Наиболее просто можно осуществить связь звена 1 с валом при помощи пары зубчатых колес, установленных, как показано на рис. 1.8, а. Вращение колеса 1 в этом случае передается жестко связанному с ним колесу 4 и далее через зубчатое зацепление – на звено 5.
На рис. 1.8, б показана схема, полученная соединением колеса 1 (см. рис. 1.7, б) со звеном 5 при помощи зубчатой пары. Конструктивно эта схема может быть упрощена при выполнении колес 1 и 4 одинакового диаметра и с одинаковым числом зубьев (рис. 1.8, в).
В рассмотренных схемах содержатся три звена, которые могут быть соединены с двигателями, рабочими органами и звеньями других механизмов.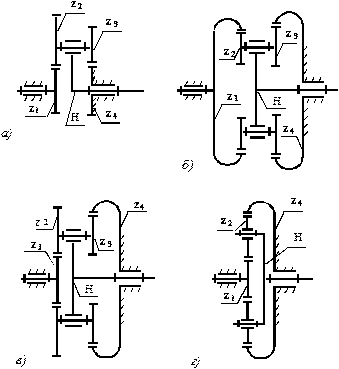 Эти звенья называют основными. По числу основных звеньев механизмы называют трехзвенными. Промежуточные зубчатые колеса называютсателлитами.
Эти звенья называют основными. По числу основных звеньев механизмы называют трехзвенными. Промежуточные зубчатые колеса называютсателлитами.
Многозвенные механизмы с неподвижными осями валов и механизмы со ступенчато изменяющимися передаточными отношениями
Зубчатые механизмы приводов машин выполняют не только в виде элементарных зубчатых механизмов (пары зубчатых колес) того или иного вида зацепления, но и в более сложных комбинациях, содержащих десятки, а иногда сотни зубчатых колес.
В случае, если передаточное отношение, которое требуется обеспечить механизмом привода, очень велико или очень мало, конструктивно удобно иметь между входными и выходными звеньями промежуточные оси с соответствующими зубчатыми колесами, вращающимися вокруг них. Передавая вращение с входного звена на промежуточные звенья и с них на выходное звено, можно последовательно отдельными ступенями изменять передаточные отношения, получая в результате требуемое передаточное отношение.
Таким образом, сложный зубчатый механизм привода можно разделить на отдельные ступени, каждая из которых представляет собой элементарный зубчатый механизм (см. рис. 1.4-1.6). В соответствии с указанным различают одно- и многоступенчатые зубчатые механизмы (передачи). Многоступенчатые механизмы, у которых оси вращения зубчатых колес неподвижны, называют многозвенными механизмами с неподвижными осями валовили рядовыми зубчатыми механизмами. Они могут быть соосными, когда оси входного и выходного звеньев располагаются на одной линии (рис. 1.9), либо несоосными (рис. 1.10).
Рис. 1.9. Рядовой зубчатый соосный механизм
Рис. 1.10. Рядовой зубчатый несоосный механизм
Рассмотрим соединение зубчатых колес, в котором имеется k параллельных валов; на каждом из k – 2 промежуточных валов закреплено по два зубчатых колеса, зацепляющихся: одно – с колесом, закрепленным на предыдущем валу, другое – с колесом, закрепленным на последующем валу (см. рис. 1.9). Такое рядовое зацепление зубчатых колес называют последовательным.
Отношение угловых скоростей первого и последнего валов сложной зубчатой передачи называют полным передаточным отношением механизма.
Полное передаточное отношение последовательного рядового зацепления равно произведению всех простых передаточных отношений каждой пары зубчатых колес. При ведущем вале 1 полное передаточное отношение равно отношению произведений чисел зубьев всех ведомых зубчатых колес к произведению чисел зубьев всех ведущих зубчатых колес.
Полному передаточному отношению можно присвоить определенный знак. Если в рядовом зацеплении т внешних и k– твнутренних зацеплений, то при переходе от одного вала передачи к другому происходит т раз изменение знака угловой скорости. Таким образом, об окончательном знаке угловой скорости можно судить по числу mвнешних зацеплений, т.е. по множителю (– l) m, вследствие чего полное передаточное отношение можно представить как
.(1.1)
Если при подсчете и1k окажется отрицательным, то знак минус покажет, что последнее колесо вращается противоположно первому.
Последовательное рядовое зацепление называют рядом с промежуточными колесами, если на каждом из валов закреплено по одному колесу, входящему одновременно в зацепление с колесами на предыдущем и последующем валах (см. рис. 1.10). Полное передаточное отношение такого ряда можно получить из (1.1), приняв и т.д.,
.(1.2)
Последнее выражение показывает, что промежуточные колеса не влияют на передаточное отношение, однако их включение может изменить знак передаточного отношения. Если число промежуточных колес четное, то знак передаточного отношения будет такой же, как если бы колеса z1и zkзацеплялись непосредственно. При нечетном числе таких колес знак передаточного отношения меняется на противоположный. Передаточное отношение таких зубчатых механизмов можно определить графически с использованием метода планов скоростей (см. рис.1.10).
Промежуточные зубчатые колеса применяют в тех случаях, когда расстояние между первым и последним валом велико и непосредственно зацепляющиеся колеса увеличивают габаритные размеры механизма, или же в тех случаях, когда нужно соответственно изменить направление вращения последнего вала. В качестве примера, иллюстрирующего последнее требование, можно указать на трензель (рис. 1.11), применяемый в токарных станках. Поворотом рукоятки а может быть включено одно (z2) или два (z2и z3) промежуточных колеса. В соответствии с этим направление вращения вала 4 будет совпадать или будет противоположным вращению вала 1. Пунктиром показано положение колес трензеля, при котором включено одно промежуточное колесо и направления вращения валов 1 и 4 совпадают.
Рис. 1.11. Трензель
Последовательное рядовое зацепление может быть построено не только из цилиндрических зубчатых колес, но и из конических или может представлять собой смешанную передачу, которую включены зубчатые колеса, передающие вращательное движение между параллельными и непараллельными валами.
Последовательное рядовое зацепление, составленное из конических зубчатых колес, показано на рис. 1.12.
Рис. 1.12. Последовательное рядовое коническое зацепление
Для рядового зацепления, включающего в себя конические зубчатые колеса, знак передаточного отношения не имеет смысла, если оси первого и последнего колес не параллельны. При наличии конических колес направление вращения последнего вала следует определять при помощи стрелок так, как это показано на рис. 1.12. Если первый и последний валы конической передачи параллельны, то при совпадении направлений стрелок для первого и последнего колес передаточное отношение положительно.
При совпадении направлений осей первого и последнего колес последовательного рядового зацепления ряд называют возвратным (рис. 1.13, а, б и в), а передачу – соосной. Возвратный ряд широко применяют в металлорежущих станках.
Возвратный ряд может быть составлен как из цилиндрических, так и из конических колес. Схема возвратного ряда из конических колес с одним промежуточным колесом показана на рис.1.13, в.
Возвратный ряд зубчатых колес применяют в редукторах, многоскоростных зубчатых передачах, планетарных и других механизмах. Если ведомый вал эпизодически требуется вращать с различными угловыми скоростями при неизменной угловой скорости ведущего вала, то применяют многоскоростные зубчатые механизмы с неподвижными осями колес, называемые коробками скоростей.
Рис. 1.13. Схемы возвратных рядов
Зубчатые передачи и планетарные механизмы применяют не только в качестве редукторов (мультипликаторов) с постоянным передаточным отношением, но и как многоскоростные зубчатые передачи (коробки скоростей), где осуществляется ступенчатое изменение передаточного отношения (рис. 1.14).
На практике применяется большое количество многоскоростных зубчатых передач, отличающихся одна от другой количеством валов, возможных передаточных отношений и некоторыми конструктивными особенностями. На рис. 1.14 приведены схемы двухвальных (1.14, а, б, в, д) и трехвальной (1.14, г) многоскоростных зубчатых передач.
Рис. 1.14. Многоскоростные зубчатые передачи (коробки скоростей)
Многоскоростная зубчатая передача (механизм) с неподвижными осями – зубчатая передача с несколькими (чаще двумя) валами, с помощью которой получают несколько передаточных отношений между ведомым и ведущим валами. Передаточные отношения рядовых зацеплений, включенных в такую передачу, определяются теми угловыми скоростями, которые должен иметь ведомый вал.
На валу 1 (см. рис. 1.14, а) установлены зубчатые колеса 5, которые могут свободно вращаться, а на валу 2 закреплены зубчатые колеса 3. При перемещении штока 4 защелка 6 зацепляется поочередно с колесами 5. Колесо, с которым зацепляется защелка, вращается вместе с валом 1, и в передаче движения участвует зубчатая пара 3 – 5. Перемещая шток 4, можно заставить вращаться с валом 1 другое зубчатое колесо и получить иное передаточное отношение.
На валу 2 (см. рис. 1.14, б) жестко установлено коническое колесо с несколькими зубчатыми венцами 7. Зубчатые венцы различаются числом зубьев. Шестерню 8 перемещают вдоль вала 1, вводя в зацепление с тем или иным венцом. Для удобства переключения с одного режима на другой предусмотрено перемещение шестерни 8 в положение, где зубья или впадины зубчатых венцов 7 совпадают.
В схеме на рис. 1.14, в оси валов 1 и 2 параллельны. Колесо 11 перемещают вдоль вала 1 и через промежуточную шестерню 9 вводят в зацепление с одним из колес, установленных на валу 2. Ось промежуточной шестерни 9 размещена в поворотной каретке 10. Путем поворота каретки получают требуемое расстояние между осью шестерни 9 и осью вала 2.
На каждом режиме (см. рис. 1.14, а – б) участвуют в зацеплении зубчатые колеса с разными числами зубьев, благодаря чему получаются различные передаточные отношения.
На рис. 1.14, г приведена кинематическая схема трехвальной многоскоростной передачи с двумя блоками а и б зубчатых колес, связанных с валами I и III при помощи скользящих шпонок. При различных положениях блоков на валах возможны следующие зацепления зубчатых колес: .
В зависимости от положения блоков а и б можно получить девять различных передаточных отношений, поэтому при одной и той же угловой скорости вала 1 вал 3 может иметь девять различных значений угловых скоростей, укладывающихся в ряд с заданной закономерностью.
В коробке скоростей (рис. 1.14, д) осуществляется связь между зубчатыми колесами, закрепленными на ведущем валу 0101 и зубчатыми колесами, закрепленными на шпоночном или шлицевом ведомом валу О2О2. Перемещая блок шестерен с зубчатыми колесами 4, 5, 6 с помощью механизма «заскакивающей шпонки» или винтовыми механизмами можно осуществить зацепление зубчатых колес 1 – 4, 2 – 5 или 3 – 6 и получить различные передаточные отношения и угловую скорость ведомого вала ω2.
Планетарные зубчатые механизмы
Планетарным называют зубчатый механизм для передачи и преобразования вращательного движения, составленный из цилиндрических или конических зубчатых колес, одно из которых (или группа) совершают сложное вращательное движение, состоящее из вращений вокруг собственной геометрической оси и вместе с осью – вокруг оси зацепляющихся с ним зубчатых колес. Планетарный механизм содержит центральные колеса, оси которых неподвижны, сателлиты– колеса с перемещаемыми осями, и водило– звено, в котором установлены сателлиты. Неподвижное центральное колесо называют опорным. Планетарные механизмы подразделяют на механизмы с одной степенью подвижности W = 1 (планетарные редукторы имультипликаторы) и имеющие опорное колесо и зубчатые дифференциальные механизмы, число степеней подвижности которых W ≥ 2. Планетарный механизм с одним водилом считается простым, а с числом водил более одного – сложным. Простые планетарные механизмы могут быть образованы сочетанием цилиндрических зубчатых колес с внешним и внутренним зацеплением, конических зубчатых колес, эллиптических колес, винтовых колес, червячных зацеплений, а также из фрикционных передач. Наиболее широко распространены планетарные механизмы с цилиндрическими зубчатыми колесами.
Типичный пример планетарного редуктора – соосный механизм с цилиндрическими колесами, конструкция которого представлена на рис. 1.15, а кинематическая схема изображена на рис. 1.16, а. Этот механизм состоит из центрального колеса 1 и водила Н, вращающихся вокруг неподвижных осей, трех сателлитов, составленных из двух жестко связанных в единый блок колес 2 и 3, опорного колеса 4 и стойки. При вращении колеса 1 сателлиты 2 – 3 поворачиваются как рычаг относительно мгновенного центра вращения В (колесо 4 неподвижно) и заставляют вращаться водило Н. При этом планетарные колеса (сателлиты) совершают сложное движение: вращаются вокруг собственной оси (относительно водила) с угловой скоростью ω2; и вместе с водилом обкатываются с угловой скоростью ωH вокруг оси О (переносное движение). Число степеней подвижности этого механизма равно единице. Обычно у реального механизма имеется несколько симметрично расположенных сателлитов k (колеса 2, 3 на рис. 1.16, а, в). Их вводят с целью уменьшения габаритных размеров механизма, снижения сил в зацеплении, разгрузки подшипников центральных колес, улучшения уравновешивания водила.
Рис.1.15. Планетарный редуктор
Рис. 1.16. Кинематическая схема планетарного редуктора
Если в рассмотренном механизме освободить от закрепления опорное колесо 4 (корпус редуктора) и сообщить ему вращение, то все центральные колеса станут подвижными и механизм превратится в дифференциальный (рис. 1.17), так как число степеней подвижности W его будет равно двум. Число степеней подвижности механизма показывает, скольким звеньям дифференциала необходимо сообщить независимые движения для получения заданного движения всех остальных звеньев. Здесь в зависимости от направления вращения наружных валов можно либо раскладывать движение (одного ведущего на два ведомых), либо суммировать. Ведущим считается такой вал, направление скорости вращения и момента сил которого совпадают. Планетарный редуктор (или мультипликатор), имеющий неподвижное колесо, можно преобразовать в дифференциал, если освободить неподвижное (опорное) колесо и сообщить ему вращение. Наоборот, любой дифференциал можно превратить в планетарный редуктор, если закрепить одно (при W = 2) или несколько из его центральных колес. Это так называемое свойство обратимости планетарных механизмов, которое позволяет применять одинаковые методы исследования и проектирования для редукторов и дифференциалов. При этом каждому элементарному дифференциалу будут соответствовать два планетарных механизма, получаемых при остановке одного из центральных колес. Планетарные механизмы применяются либо для воспроизведения заданной траектории (направляющие механизмы), либо для изменения скоростей вращения (воспроизведение заданного передаточного отношения).
Рис. 1.17. Схема дифференциального механизма
РАСЧЕТ ОТКРЫТОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ
Стр 1 из 2Следующая ⇒Студент: ( )
Группа: ЭП -10-1
Руководитель: ( Щеглов А.В.)
2012г.
Задание
АННОТАЦИЯ
47 с., 14 рис., 5табл., 5 библиограф. назв.
В курсовом проекте выполнен расчет электропривода, включающего в себя приводной двигатель, конический одноступенчатый редуктор и открытую зубчатую передачу. Выбран электродвигатель, выполнен расчет зубчатых передач, определены диаметры валов и сделан их прочностной расчет, подобраны подшипники, приведена технология сборки редуктора.
Графическая часть
1.Редуктор конический……………………………………
ОГЛАВЛЕНИЕ
С.
1. Назначение и краткое описание привода…………………………………..5
2. Выбор электродвигателя, кинематический и энергетический расчет…….6
3. Расчет открытой зубчатой передачи……………………………………………….11
4. Проектирование редуктора …………………………………………………15
4.1 Расчет зубчатой передачи редуктора……………………………………..15
4.2 Ориентировочный расчет валов редуктора……………………………….20
4.3 Определение конструктивных размеров зубчатых колес……………….22
4.4 Определение основных размеров корпуса редуктора …………………..23
4.5 Выбор подшипников, схемы их установки и условий смазки ………….25
4. 6 Первый этап компоновки редуктора….…………………………..……..28
4.7 Проверка долговечности подшипников …………………….……………29
4. 8 Проверка прочности шпоночных соединений.……………….………….34
4.9 Выбор уплотнений валов……………………………………….…….……36
4.10 Уточненный расчет валов……………………………………….……….37
4.11 Выбор крышек подшипников…………………………………………………………..42
4.12 Посадки основных деталей редуктора………………………………………………43
4.13 Сборка редуктора…………………………………………………………. 43
5 Выбор муфты……………………………………………………………..…..45
6. Правила безопасной эксплуатации привода. ………………………….…..46
Библиографический список……………………….…………….………….….47
1. НАЗНАЧЕНИЕ И КРАТКОЕ ОПИСАНИЕ ПРИВОДА
Привод включает в себя электродвигатель, соединительную упругую муфту, конический одноступенчатый редуктор, открытую зубчатую передачу.
Вращение от электродвигателя через упругую муфту передается на ведущий вал редуктора. Назначение редуктора – предварительное понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим.
На ведомом валу редуктора установлена ведущая шестерня открытой зубчатой передачи, а ведомое колесо передает движение выходному валу привода и звездочке цепи подвесного конвейера. Открытая зубчатая передача служит для дальнейшего понижения частоты вращения до требуемой.
Кинематическая схема привода приведена на рис.1.
Рис.1. Кинематическая схема привода
1 — Приводной электродвигатель
2 — Муфта упругая со звездочкой
3. — Цилиндрическая зубчатая передача
4 — Редуктор конический одноступенчатый
5 — Грузовая цепь
6 — Звездочка цепи
2. ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ, КИНЕМАТИЧЕСКИЙ И ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ
2.1 Определение требуемой мощности электродвигателя
Требуемая мощность электродвигателя определяется по формуле:
где Рвых – мощность на выходном валу привода, кВт;
Рвых = Ft/V,
где Ft –тяговая сила цепи; Ft =3,8кН;
V- скорость грузовой цепи; V=0,65 м/с;
Рвых =3,8.0,65=2,47кВт.
ηобщ – общий КПД привода.
ηобщ= η.м. ηз к.п.·. ηоц.п, η.п;
где η.м – КПД муфты; η.м =0,985;
ηз.п– КПД конической зубчатой передачи в закрытом корпусе, ηк.п=0,97;
ηоз.п -КПД открытой зубчатой передачи;
ηоз.п= 0,95; η.п— КПД пары подшипников; η.п=0,99 [1,табл. 1.1];
ηобщ=0,985.
Мощность на выходном валу привода Ртр= 2,47кВт, тогда требуемая мощность электродвигателя будет равна:
Ртр= 2,47/0,889 =2,78 кВт.
2.2. Определение требуемой частоты вращения и выбор электродвигателя
n дв.тр = nвых·iобщ, мин-1;
где nвых— частота вращения выходного вала привода, мин-1,
nвых= мин-1;
где z – число зубьев звездочки; z =8;
р – шаг грузовой цепи; р= 100мм;
nвых= мин-1;
iобщ— общее передаточное отношение привода:
iобщ= iз.к п.· iц.п.
где iзк.п.— передаточное отношение зубчатой конической передачи. Принимаем предварительно iзк.п.=3,15; iц.п.— передаточное отношение цилиндрической передачи, iц.п.=5,0 [2,c.7], тогда iобщ=3,15. 5=15,75;
n дв.тр = 48,75 . 15,75= 767,8 мин-1.
По полученным значениям Ртр и nдв.тр подбираем электродвигатель трехфазный асинхронный короткозамкнутый серии 4А (закрытый обдуваемый) по ГОСТ 19528-81 типа 4А112МВ8 [2,табл. 18.36]. мощностью Рдв=3,0 кВт, с частотой вращения nдв.= 700мин-1 (рис.2).
Рис.2 Эскиз электродвигателя 4А112МВ8 ГОСТ 19523-81
Таблица 1 Размеры электродвигателя 4А112МВ8
| Типоразмер | l1, мм | l2, мм | l3, мм | L1, мм | d1, мм | h, мм | b, мм | H, мм | D, мм |
| 4А112МВ8 |
По принятой частоте вращения вала электродвигателя при номинальной нагрузке nдв и частоте вращения выходного вала nвых определяется фактическое передаточное отношение привода по формуле:
Передаточное отношение открытой зубчатой передачи:
iобщ/ iз.п.=14,35 /3,15=4,56
2.3 Определение частот вращения и угловых скоростей валов привода
а) Частота вращения вала электродвигателя: nдв= 700 мин-1
угловая скорость вращения вала электродвигателя:
wДВ =pnдв/30= рад/с
б) Частота вращения ведомого вала редуктора:
n2= nдв/ iз.п.= 700/3,15=222,2 мин-1
угловая скорость вращения ведомого вала редуктора:
w2 =pn2/30= рад/с
в) частота вращения ведомого вала привода:
n3=n2/iзп= 222,2/4,56= 48,73 мин-1
угловая скорость вращения ведомого вала привода:
w3=w2/iзп= 23,2/4,56=5,1 рад/с
2.4 Определение вращающих моментов на валах привода.
а) Вращающий момент на валу электродвигателя:
ТДВ= T1=РТР ДВ/wДВ= Нм
б) Вращающий момент на ведущем валу редуктора :
T2=TДВ. η.м. hп =33,73.0,985.0,99=32,9Нм;
б) Вращающий момент на ведомом валу редуктора :
T2=TДВ. iзп. . hзп =32,9. 3,15.0,97.0,99=99,5Нм;
в) Вращающий момент на выходном валу привода :
Т3= Т1.iцп.hцп =99,5. 4,56.0,95 = 431 H.м.
2.5 Определение мощности на валах привода:
Мощность на валу электродвигателя: Р1=Ртр= 2,78 кВт
Мощность на ведомом валу редуктора:
Р2=Р1 ηм ηзп. ηп. =2,78.0,985.0,97.0,99=2,6 кВт
Мощность на ведомом валу привода:
Р3=Р1 ηцп. ηп. =2,6.0,95. 0,99=2,44кВт.
2.5. Определение мощности на валах привода:
Мощность на валу электродвигателя: Р1=Ртр= 2,78 кВт
Мощность на ведомом валу редуктора:
Р2=Р1 ηм ηзп. ηп. =2,78.0,985.0,97.0,99=2,62 кВт
Мощность на ведомом валу привода:
Р3=Р1 ηцп. ηп. =2,62.0,95. 0,99=2,47кВт
Проверка:
Рвых=Т3. 431. 5,1=2,3 кВт.
Величина ошибки: ΔР=(2,44 -2,3)/2,44.100%=5%.
Одноступенчатые конические редукторы с параметрами, аналогичными проектируемому, в настоящее время промышленность не выпускает.
В качестве аналога может быть использован редуктор цилиндрический одноступенчатый типа 1ЦУ-100=3,15 с крутящим моментом на выходном валу
Твых= 2000Нм (рис.3) [4, Т.3, с.485] и передаточным числом iз.п.= 3,15.
Рис.3 Редуктор цилиндрический одноступенчатый типа 1ЦУ-100=3,15
Таблица 2 Основные размеры редуктора, мм
| Типоразмер редуктора | Аw | В | В1 | L | L1 | L2 | L3 | L4 | L5 | L6 | H | H0 |
| 1ЦУ-100-3,15 |
Ширина зубчатого венца
Ширина зубчатого венца определяется по формуле:
b2=ψbd· d1=0, 5.64=32, мм,
aw— межосевое расстояние, мм. aw=( d1+ d2)/2=(64+292)/2=178 мм.
Ширина зубчатого венца шестерни определяется по формуле:
b1= b2+(5…10)мм,
b1= 32+5=37 мм.
ПРОЕКТИРОВАНИЕ РЕДУКТОРА
Сечение Б-Б.
В этом сечении концентратором напряжений является посадка подшипника опоры №1 с натягом (рис.9).
Коэффициент запаса прочности по напряжениям кручения:
,
где τ-1=238 МПа; β=0,95; kτ/ετ=2,56 [1, табл.8.7]. d=35 мм.
τυ = Т/Wк,
где Т1=32,9·103 Н·мм.
Момент сопротивления кручению определяется по формуле:
,
где — момент сопротивления изгибу:
,
τυ и τm – амплитуда и среднее напряжение:
τm=τυ = 32,9·103/2.12500= 1,31МПа,
Коэффициент запаса прочности по нормальным напряжениям:
,
где σ-1=410 МПа; kσ/εσ=3,6 [1, табл.8.7]; ψ=0,27 [1, c.166, 164];
Изгибающий момент в сечении Б-Б:
Ми= .Н·м (см. рис.9).
σ υ= Ми/Wи=38,1.103/25000=1,52МПа.
.
Результирующий коэффициент запаса прочности:
.
Сечение В-В. В этом сечении концентратором напряжений является посадка подшипника опоры №2 с натягом (рис.9).
τ-1=238 МПа; β=0,95; kτ/ετ=2,56 [1, табл.8.7]. d=35 мм.
τυ = Т1/Wк,
Т1=32,9·103 Н·мм.
Момент сопротивления кручению:
,
— момент сопротивления изгибу:
,
τυ и τm – амплитуда и среднее напряжение:
τm=τυ = 32,9·103/2.12500= 2,63 МПа,
где σ-1=410 МПа; kσ/εσ=3,6 [1, табл.8.7]; ψ=0,27 [1, c.166, 164];
Изгибающий момент в сечении В-В:
Ми= .Н·м (см. рис.9).
σ υ= Ми/Wи=77.103/12500=6,16МПа.
.
Результирующий коэффициент запаса прочности:
.
4.10.2. Ведомый вал:
Опасное сечение ведомого вала- сечение А-А( рис.10). Концентрацию напряжений вызывает наличие шпоночной канавки.
где β – коэффициент, учитывающий шероховатость поверхности, β=0,97;
ετ – масштабный фактор для касательных напряжений; ετ=0,83 [1, табл.8.8];
kτ – эффективный коэффициент концентрации касательных напряжений, kτ=1,9 [1, табл.8.5]; Т2=99,5·103 Н·мм.
Момент сопротивления кручению:
,
τυ = 99,5·103/3,06.103=32,5МПа,
S = >[S]=2,5
Другое опасное сечение –Б- Б-участок вала под подшипником, ослабленным посадкой с натягом (см. рис.10).
τ-1=238 МПа; β=0,95; kτ =1,9 [1, табл.8.7]; d=35 мм.
τυ = Т2/Wк,
Момент сопротивления кручению:
,
где — момент сопротивления изгибу.
,
τυ = 99,59·103/2.8,86.103= 5,628МПа.
.
где σ-1=410 МПа; kσσ=1,9 [1, табл.8.7]; ψ=0,27 [1, c.166, 164]; d=45 мм.
Изгибающий момент в сечении Б-Б:
Ми= Н·м (рис.10)
σ υ= Ми/Wи=276,4.103/4,13.103=56,9МПа.
Коэффициент запаса прочности по нормальным напряжениям:
.
Результирующий коэффициент запаса прочности:
.
Третье опасное сечение ведомого вала- сечение В-В (рис.10).
Концентрацию напряжений вызывает шпоночная канавка колеса.
Момент сопротивления кручению:
,
τυ = 99,5·103/2.17,36.103=2,86МПа,
— момент сопротивления изгибу.
,
Изгибающий момент в сечении В-В:
Ми= Н·м (рис.10).
σ υ= Ми/Wи=237,9/8,55=27,8МПа.
Коэффициент запаса прочности по нормальным напряжениям:
Результирующий коэффициент запаса прочности:
.
Полученные значения коэффициентов запаса прочности в наиболее опасных сечениях валов больше допускаемых , поэтому усталостная прочность валов в этих сечениях достаточна.
4.11 Выбор крышек редуктора
Выбираем привертные крышки подшипников (рис.13). Эти крышки крепятся к корпусу винтами. Для предотвращения вытекания масла из корпуса между крышками и корпусом устанавливаются уплотнительные прокладки из технического картона. Размеры крышек определяют в зависимости диаметра подшипника D [2, с.111].
Рис.13 Крышки подшипников привертные: глухая и сквозная
Для ведущего вала:
Крышка сквозная: — толщина крышки: =8 мм; d=90мм, Dф =125 мм; b=25 мм. Крышка глухая: — толщина крышки: =8 мм; d=900мм, Dф =125мм; b=25 мм. dм— диаметр под уплотнительную манжету. dм=52 мм.
Для ведомого вала:
Крышка сквозная: — толщина крышки: =8 мм; d=72мм, Dф =110 мм; b=25 мм. Крышка глухая: — толщина крышки: =8 мм; d=72мм, Dф =110мм; b=25 мм. dм— диаметр под уплотнительную манжету. dм=58 мм.
4.12 Посадки основных деталей редуктора
Посадки назначаем в соответствии с ГОСТ 25346-82
Посадка конического колеса на вал Н7/р6 по ГОСТ 25346-82 .
Посадка муфты на вал редуктора H8/h7.
Шейки валов под подшипники выполняем с отклонением к6.
Отклонения отверстий в корпусе под наружные кольца поН7.
Посадка крышек подшипников H7/h8.
4.13 Сборка редуктора
Перед сборкой внутреннюю полость корпуса редуктора тщательно обрабатывают, очищают и покрывают маслостойкой краской.
Сборку производят в соответствии со сборочным чертежом редуктора, начиная с узлов валов:
— на ведущий вал напрессовывают мазеудерживающее кольцо, затем подшипники, предварительно нагретые в масле до 80-100 градусов. Вал вставляют в стакан, предварительно установив регулировочные прокладки, а стакан устаналивают в корпус.
— в ведомый вал закладывают шпонку и напрессовывают зубчатое колесо до упора в бурт вала, затем надевают распорную втулку и устанавливают подшипники, предварительно нагретые в масле.
Собранный вал укладывают в основание корпуса редуктора и надевают крышку корпуса, покрывая предварительно поверхности стыка крышки и корпуса герметиком. Для центровки устанавливают крышку на корпус с помощью 2-х конических штифтов; затягивают болты, крепящие крышку к корпусу.
Проверяют проворачивание валов, отсутствие заклинивания подшипников , регулируют зазор в зацеплении конических колес и закрепляют крышки.
В паз ведомого вала в шпоночную канавку закладывают шпонку.
Затем ввертывают пробку маслоспускного отверстия с прокладкой и жезловый маслоуказатель, заливают в корпус масло и закрывают смотровое отверстие крышкой с прокладкой из технического картона, закрепляют крышку болтами.
Собранный редуктор обкатывают и подвергают испытанию на стенде по программе, устанавливаемой техническими условиями.
5. ВЫБОР МУФТЫ
Для соединения ведущего вала редуктора и вала электродвигателя выбираем муфту упругую со звездочкой по ГОСТ 14084-76, которую подбираем по величине момента и частоте вращения.
При dв.1 =28 мм предельный момент муфты [T]=125 Нм.
Максимальный момент на входном валу:
Т1max=Тдв·Кэ=33,73.1,5= 50,6 Нм<[T].
Кэ – коэффициент эксплуатации, принимаем Кэ=1,5 [1,табл.11.1]
Проверим муфту по частоте вращения:
n1=nдв=700 мин-1<[ nmax]= 2000 мин-1.
Муфта подходит частоте вращения. Принимаем муфту исполнения I с цилиндрическими расточками под валы.
Рис.15 Муфта упругая со звездочкой ГОСТ 14084-76.
Таблица 5 Размеры муфты, мм
| D, мм | d ,мм | dст,мм | L, мм | В, мм | D1, мм |
6. ПРАВИЛА БЕЗОПАСНОЙ ЭКСПЛУАТАЦИИ ПРИВОДА
1. Открытые вращающиеся части привода должны иметь ограждения в виде защитных кожухов для предотвращения производственных травм .
2. Следует систематически проверять уровень масла в редукторе; в случае недостатка доливать масло до уровня метки на маслоуказателе.
4. Систематически проверять и не допускать большого зазора в подшипниках и в зацеплении конических колес.
5. Следует систематически проверять надежность крепления редуктора и электродвигателя к раме .
6. Все регулировки и работы по техническому обслуживанию должны проводиться при выключенном электродвигателе.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Курсовое проектирование деталей машин/Под ред. С.А. Чернавского. М.-1988.
2. Конструирование узлов и деталей машин/ Дунаев П.Ф., Леликов О.П. М.: Высш. шк.- 1998.
3. Баранцов В.Я.,Зайцева Т.Г. Методические указания к расчету зубчатых передач в курсовом проектировании по деталям машин. Липецк. –2004.
4. Зайцева Т.Г., Баранцов В.Я. Метод. указ. Разработка и оформление курсовых проектов по деталям машин и ПТУ. Липецк. –1988.
5. Анурьев В.И. Справочник конструктора-машиностроителя. Т.3.,М.Машиностроение-1985г., 565с., ил.
Студент: ( )
Группа: ЭП -10-1
Руководитель: ( Щеглов А.В.)
2012г.
Задание
АННОТАЦИЯ
47 с., 14 рис., 5табл., 5 библиограф. назв.
В курсовом проекте выполнен расчет электропривода, включающего в себя приводной двигатель, конический одноступенчатый редуктор и открытую зубчатую передачу. Выбран электродвигатель, выполнен расчет зубчатых передач, определены диаметры валов и сделан их прочностной расчет, подобраны подшипники, приведена технология сборки редуктора.
Графическая часть
1.Редуктор конический……………………………………
ОГЛАВЛЕНИЕ
С.
1. Назначение и краткое описание привода…………………………………..5
2. Выбор электродвигателя, кинематический и энергетический расчет…….6
3. Расчет открытой зубчатой передачи……………………………………………….11
4. Проектирование редуктора …………………………………………………15
4.1 Расчет зубчатой передачи редуктора……………………………………..15
4.2 Ориентировочный расчет валов редуктора……………………………….20
4.3 Определение конструктивных размеров зубчатых колес……………….22
4.4 Определение основных размеров корпуса редуктора …………………..23
4.5 Выбор подшипников, схемы их установки и условий смазки ………….25
4. 6 Первый этап компоновки редуктора….…………………………..……..28
4.7 Проверка долговечности подшипников …………………….……………29
4. 8 Проверка прочности шпоночных соединений.……………….………….34
4.9 Выбор уплотнений валов……………………………………….…….……36
4.10 Уточненный расчет валов……………………………………….……….37
4.11 Выбор крышек подшипников…………………………………………………………..42
4.12 Посадки основных деталей редуктора………………………………………………43
4.13 Сборка редуктора…………………………………………………………. 43
5 Выбор муфты……………………………………………………………..…..45
6. Правила безопасной эксплуатации привода. ………………………….…..46
Библиографический список……………………….…………….………….….47
1. НАЗНАЧЕНИЕ И КРАТКОЕ ОПИСАНИЕ ПРИВОДА
Привод включает в себя электродвигатель, соединительную упругую муфту, конический одноступенчатый редуктор, открытую зубчатую передачу.
Вращение от электродвигателя через упругую муфту передается на ведущий вал редуктора. Назначение редуктора – предварительное понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим.
На ведомом валу редуктора установлена ведущая шестерня открытой зубчатой передачи, а ведомое колесо передает движение выходному валу привода и звездочке цепи подвесного конвейера. Открытая зубчатая передача служит для дальнейшего понижения частоты вращения до требуемой.
Кинематическая схема привода приведена на рис.1.
Рис.1. Кинематическая схема привода
1 — Приводной электродвигатель
2 — Муфта упругая со звездочкой
3. — Цилиндрическая зубчатая передача
4 — Редуктор конический одноступенчатый
5 — Грузовая цепь
6 — Звездочка цепи
2. ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ, КИНЕМАТИЧЕСКИЙ И ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ
2.1 Определение требуемой мощности электродвигателя
Требуемая мощность электродвигателя определяется по формуле:
где Рвых – мощность на выходном валу привода, кВт;
Рвых = Ft/V,
где Ft –тяговая сила цепи; Ft =3,8кН;
V- скорость грузовой цепи; V=0,65 м/с;
Рвых =3,8.0,65=2,47кВт.
ηобщ – общий КПД привода.
ηобщ= η.м. ηз к.п.·. ηоц.п, η.п;
где η.м – КПД муфты; η.м =0,985;
ηз.п– КПД конической зубчатой передачи в закрытом корпусе, ηк.п=0,97;
ηоз.п -КПД открытой зубчатой передачи;
ηоз.п= 0,95; η.п— КПД пары подшипников; η.п=0,99 [1,табл. 1.1];
ηобщ=0,985.
Мощность на выходном валу привода Ртр= 2,47кВт, тогда требуемая мощность электродвигателя будет равна:
Ртр= 2,47/0,889 =2,78 кВт.
2.2. Определение требуемой частоты вращения и выбор электродвигателя
n дв.тр = nвых·iобщ, мин-1;
где nвых— частота вращения выходного вала привода, мин-1,
nвых= мин-1;
где z – число зубьев звездочки; z =8;
р – шаг грузовой цепи; р= 100мм;
nвых= мин-1;
iобщ— общее передаточное отношение привода:
iобщ= iз.к п.· iц.п.
где iзк.п.— передаточное отношение зубчатой конической передачи. Принимаем предварительно iзк.п.=3,15; iц.п.— передаточное отношение цилиндрической передачи, iц.п.=5,0 [2,c.7], тогда iобщ=3,15. 5=15,75;
n дв.тр = 48,75 . 15,75= 767,8 мин-1.
По полученным значениям Ртр и nдв.тр подбираем электродвигатель трехфазный асинхронный короткозамкнутый серии 4А (закрытый обдуваемый) по ГОСТ 19528-81 типа 4А112МВ8 [2,табл. 18.36]. мощностью Рдв=3,0 кВт, с частотой вращения nдв.= 700мин-1 (рис.2).
Рис.2 Эскиз электродвигателя 4А112МВ8 ГОСТ 19523-81
Таблица 1 Размеры электродвигателя 4А112МВ8
| Типоразмер | l1, мм | l2, мм | l3, мм | L1, мм | d1, мм | h, мм | b, мм | H, мм | D, мм |
| 4А112МВ8 |
По принятой частоте вращения вала электродвигателя при номинальной нагрузке nдв и частоте вращения выходного вала nвых определяется фактическое передаточное отношение привода по формуле:
Передаточное отношение открытой зубчатой передачи:
iобщ/ iз.п.=14,35 /3,15=4,56
2.3 Определение частот вращения и угловых скоростей валов привода
а) Частота вращения вала электродвигателя: nдв= 700 мин-1
угловая скорость вращения вала электродвигателя:
wДВ =pnдв/30= рад/с
б) Частота вращения ведомого вала редуктора:
n2= nдв/ iз.п.= 700/3,15=222,2 мин-1
угловая скорость вращения ведомого вала редуктора:
w2 =pn2/30= рад/с
в) частота вращения ведомого вала привода:
n3=n2/iзп= 222,2/4,56= 48,73 мин-1
угловая скорость вращения ведомого вала привода:
w3=w2/iзп= 23,2/4,56=5,1 рад/с
2.4 Определение вращающих моментов на валах привода.
а) Вращающий момент на валу электродвигателя:
ТДВ= T1=РТР ДВ/wДВ= Нм
б) Вращающий момент на ведущем валу редуктора :
T2=TДВ. η.м. hп =33,73.0,985.0,99=32,9Нм;
б) Вращающий момент на ведомом валу редуктора :
T2=TДВ. iзп. . hзп =32,9. 3,15.0,97.0,99=99,5Нм;
в) Вращающий момент на выходном валу привода :
Т3= Т1.iцп.hцп =99,5. 4,56.0,95 = 431 H.м.
2.5 Определение мощности на валах привода:
Мощность на валу электродвигателя: Р1=Ртр= 2,78 кВт
Мощность на ведомом валу редуктора:
Р2=Р1 ηм ηзп. ηп. =2,78.0,985.0,97.0,99=2,6 кВт
Мощность на ведомом валу привода:
Р3=Р1 ηцп. ηп. =2,6.0,95. 0,99=2,44кВт.
2.5. Определение мощности на валах привода:
Мощность на валу электродвигателя: Р1=Ртр= 2,78 кВт
Мощность на ведомом валу редуктора:
Р2=Р1 ηм ηзп. ηп. =2,78.0,985.0,97.0,99=2,62 кВт
Мощность на ведомом валу привода:
Р3=Р1 ηцп. ηп. =2,62.0,95. 0,99=2,47кВт
Проверка:
Рвых=Т3. 431. 5,1=2,3 кВт.
Величина ошибки: ΔР=(2,44 -2,3)/2,44.100%=5%.
Одноступенчатые конические редукторы с параметрами, аналогичными проектируемому, в настоящее время промышленность не выпускает.
В качестве аналога может быть использован редуктор цилиндрический одноступенчатый типа 1ЦУ-100=3,15 с крутящим моментом на выходном валу
Твых= 2000Нм (рис.3) [4, Т.3, с.485] и передаточным числом iз.п.= 3,15.
Рис.3 Редуктор цилиндрический одноступенчатый типа 1ЦУ-100=3,15
Таблица 2 Основные размеры редуктора, мм
| Типоразмер редуктора | Аw | В | В1 | L | L1 | L2 | L3 | L4 | L5 | L6 | H | H0 |
| 1ЦУ-100-3,15 |
РАСЧЕТ ОТКРЫТОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ
Открытая зубчатая передача рассчитывается по изгибной прочности зубьев
Читайте также:
Тема «Геометрия зубчатых передач»
Тема «Геометрия зубчатых передач»Тема «Геометрия зубчатых передач»
I:
S: Какие передачи применяются для передачи движения между валами, оси которых параллельны?
+: Цилиндрические
-: Конические
-: Червячные
-: Гипоидные
I:
S: Какие передачи применяются для передачи движения между валами, оси которых пересекаются?
-: Цилиндрические
+: Конические
-: Червячные
-: Гипоидные
I:
S: Какие передачи применяются для передачи движения между валами, оси которых перекрещиваются?
-: Цилиндрические
-: Конические
+: Червячные
I:
S: Какие передачи работают на принципе зацепления?
-: Ременные
+: Зубчатые
-: Фрикционные
I:
S: Какие передачи работают на принципе трения?
-: Зубчатые
-: Червячные
+: Фрикционные
I:
S: Какой параметр может быть положительным, отрицательным?
-: Передаточное число
+: Передаточное отношение
-: Модуль зубьев
-: Шаг зацепления
Тема «Изготовление зубчатых колес»
I:
S: Какой способ изготовления зубчатых колес обеспечивает наибольшую точность?
-: Литье
-: Штамповка
-: Нарезание на станках
+: Накатка
I:
S: По какой прямой на рейке толщина зуба равна ширине впадины?
-: Граничной
+: Делительной (средней, модульной)
-: Вершин зубьев
-: Впадин
I:
S: Какие окружности не изменяются при нарезании колеса со смещением?
+: Делительные
-: Вершин зубьев
-: Впадин
I:
S: У какого колеса с внешними зубьями толщина зуба по делительной окружности больше ширины впадины?
-: Нормальное (нулевое) колесо
-: Отрицательное колесо
+: Положительное колесо
-: Такого колеса не существует
I:
S: Чему равна высота головки зуба инструментальной рейки?
+: h = m
-: h = 1,25·m
-: h = 2,25·m
-: h = 2,5·m
I:
S: Чему равен угол профиля зуба ИПК?
-: a = 15o
-: a = 25o
+: a = 20o
-: a = 30o
I:
S: В какой передаче межосевое расстояние сохраняет свое теоретическое значение (т.е. совпадает с делительным межосевым расстоянием)?
+: В нулевой
-: В неравносмещенной
-: В любой из перечисленных выше
I:
S: В какой передаче угол зацепления равен углу профиля ИПК?
+: В нулевой
-: В неравносмещенной
-: В любой из перечисленных выше
I:
S: Какой участок зуба инструментальной рейки формирует эвольвентный профиль зуба колеса?
-: Участок AC
+: Участок CD
-: Участок DE
-: Участок AE
I:
S: В какой передаче начальные окружности совпадают с делительными?
-: В равносмещенной
+: В нулевой
-: В неравносмещенной
-: Совпадают всегда
I:
S: Чему равно предельно минимальное число зубьев колеса при нарезании его инструментом реечного типа, у которого отсутствует подрез ножки зуба (ha*=1, a =20o)?
-: Z = 14
-: Z = 30
+: Z = 17
-: Z = 20
I:
S: При каком зацеплении суммарный коэффициент смещения равен нулю?
+: Нулевом
-: Неравносмещенном
-: Такого зацепления нет
I:
S: Чему равен суммарный коэффициент смещения в положительной передаче?
-: xS < 0
-: xS = 0
+: xS > 0
-: Суммарный коэффициент смещения у положительной передачи такой же как и у отрицательной передачи
I:
S: Какой параметр определяет основные геометрические размеры зуба и зубчатого колеса?
-: Шаг зубьев
+: Модуль зубьев
-: Передаточное отношение
-: Передаточное число
I:
S: По какой окружности нормального зубчатого колеса толщина зуба равна ширине впадины?
+: По делительной
-: По основной
-: По окружности вершин
-: По окружности впадин
I:
S: Что такое эвольвента?
-: Развертка делительной окружности
-: Развертка начальной окружности
+: Развертка основной окружности
-: Кривая, которую описывает любая точка прямой, перекатывающейся без скольжения по окружности
I:
S: При каком числе зубьев колеса, нарезанного инструментальной рейкой, будет наблюдаться подрез ножки зуба (ha* = 1, a = 20o)?
-: Z > 17
+: Z < 17
-: Z = 17
-: Z = 20
I:
S: Какой параметр зубчатого колеса обозначен буквой P? -: Толщина зуба
+: Шаг зубьев
-: Ширина впадины
-: Высота зуба
I:
S: Чему равно максимальное значение коэффициента перекрытия прямозубой цилиндрической передачи внешнего зацепления?
-: e = 1,5
-: e = 1,98
+: e = 2,0
-: e = 1,2
I:
S: Какой параметр зуба нормального зубчатого колеса численно равен модулю?
-: Толщина зуба S
-: Шаг зубьев P
+: Высота головки зуба ha
-: Высота ножки зуба hf
I:
S: Какой параметр зуба нормального зубчатого колеса численно равен 2,25 m?
-: Толщина зуба S
-: Шаг зубьев P
-: Высота головки зуба ha
+: Высота зуба h
I:
S: Чему равен модуль нормального зубчатого колеса, если Z = 20, d = 100 мм?
-: m = 6 мм
-: m = 4 мм
+: m = 5 мм
-: m = 3 мм
I:
S: При каком числе зубьев колеса, нарезанного инструментальной рейкой без смещения, будет наблюдаться подрез ножки зуба (ha* = 1, a = 20o)?
-: Z > 17
+: Z < 17
-: Z = 17
-: Z = 20
I:
S: При положительном смещении режущего инструмента толщина зуба у основания:
+: Увеличивается
-: Уменьшается
-: Не меняется
I:
S: Если делительная прямая режущего инструмента не касается делительной окружности нарезаемой заготовки, то такая установка инструмента называется:
-: Отрицательной
-: Нулевой
+: Положительной
I:
S: Чему равно (по модулю) передаточное отношение зубчатой пары, если угловая скорость ведущего колеса равна 1000 об/мин, а угловая скорость ведомого — 500 об/мин?
-: i = 0,5
+: i = 2,0
-: i = 5,0
-: i = 10,0
I:
S: При каком значении коэффициента смещения Х будет наблюдаться заострение головки зуба:
-: Х = Хmin
+: Х > Хmin
-: Х <Хmin
I:
S: Формула Герца при проверочном расчете зубчатых колес применяется для определения:
+: Контактных напряжений
-: Напряжений изгиба
-: Напряжений кручения
-: Допустимых напряжений
Тема «Многозвенные зубчатые передачи с неподвижными и подвижными осями вращения колёc
I:
S: Передаточное число данного редуктора вычисляется по формуле:
-:
1)
-:
-:
-:
+:
I:
S: Если Z1=20, Z2=10, Z3=40, то передаточное
отношение редуктора с точностью до десятых
равно…
-: 1
-: 2
+: 3
-: 4
-: 5
I:
S: На рисунке приведена структурная схема
многоступенчатой зубчатой передачи. Если
число зубьев зубчатого колеса 3 z3 увеличить
в два раза, то угловая скорость этого колеса
3…
-: Увеличится в два раза
-: Увеличится в четыре раза
+: Уменьшится в два раза
-: Не изменится
I:
S: Звено b планетарного механизма называется
+: Опорным колесом
-: Саттелитом
-:Водилом
-: Кривошипом
I:
S: Передаточное число данного редуктора вычисляется по формуле:
-:
+:
-:
-:
I:
S: Паразитными колёсами в данном редукторе являются…
-: 3 и 4
+: 4 и 5
-: 2 и 3
-: 1 и 6
I;
S: Передаточное число данного редуктора вычисляется по формуле…
-:
-:
+:
-:
-:
I:
S: Укажите схему планетарного зубчатого механизма
+:
-:
-:
-:
I:
S: Передаточное число данного редуктора вычисляется по формуле…
+:
-:
-:
I:
S: Дополнительное условие синтеза планетарно зубчатой передачи, выражающее необходимость расположения геометрических осей центральных зубчатых колес на одной прямой, называется…
-: Условие сборки
+: Условие соосности
-: Условием кинетостатической определенности
-: Условие соседства
I:
S: Зубчатые механизмы, повышающие угловую скорость вращения выходного вала по сравнению с входным, называются …
+: Мультипликаторами
-: Дифференциалами
-: Планетарными
I:
S: Зубчатые механизмы, понижающие угловую скорость вращения выходного вала по сравнению с входным, называются …
+:Редукторами
-: Планетарными
-: Дифференциалами
-: Мультипликаторами
I:
S: Параметрами зубчатого колеса, не зависящими от смещения инструмента Х при нарезке, являются:
+: Диаметр делительной окружности
-: Диаметр основной окружности
-: Толщина зуба по делительной окружности
-: Межосевое расстояние
-: Коэффициент торцевого перекрытия
I:
S: Степень подвижности планетарного многозвенного зубчатого механизма …
+: 1
-: >1
-: <1
-: 0
I:
S: Степень подвижности многозвенного дифференциального зубчатого механизма …
-: 1
+: 2
-: <1
-: 0
I:
S: Шаг зубчатого колеса по делительной окружности определяется уравнением:
+: р = π · m
-: р = π / m
-: р = m / π
-: р = 2 π m
I:
S: Диаметр делительной окружности зубчатого колеса определяется по формуле:
+: d = m Z
-: d = m (Z + 2ha)
-: d = m (Z + 2ha + 2X)
-: d = (m Z) / 2
Дата добавления: 2015-08-29; просмотров: 1658 | Нарушение авторских прав
mybiblioteka.su — 2015-2020 год. (0.065 сек.)
Все о редукторах. Справочная информация
Классификация, основные параметры редукторов
Цилиндрические редукторы
Червячные редукторы
Планетарные редукторы
Конические редукторы
Классификация редукторов в зависимости от вида передач и числа ступеней
Конструкция и назначение редуктора
Особенности редукторов по виду механических передач
Количество ступеней редуктора
Входные и выходные валы редукторов
Срок службы редуктора
Устройство редуктора
Монтажное исполнение
Как подобрать редуктор? Простые правила и примеры расчета
Передаточное отношение и как его определить?
Редукторы (латинского слова reductor) получили широкое распространение во всех отраслях промышленного и аграрного хозяйства, поэтому их производство с каждым годом увеличивается, появляются новые модификации, совершенствуются уже существующие модели.
Редуктор служит для снижения частоты вращения тихоходного вала и увеличения усилия на выходном валу. Редуктор может иметь одну или несколько ступеней, цель которых увеличение передаточного отношения. По типу механической передачи редукторы могут быть червячными, коническими, планетарными или цилиндрическими. Конструктивно редуктор выполнен как отдельное изделие, работающее в паре с электродвигателем и установленное с ним на одной раме.
Промышленностью сегодня выпускаются редукторы общего и специального назначения.
Редукторы общего назначения могут применяться во многих случаях и отвечают общим требованиям. Специальные же редукторы имеют нестандартные характеристики подходящие под определенные требования.
Классификация, основные параметры редукторов
В зависимости от типа зубчатой передачи редукторы бывают цилиндрические, конические, волновые, планетарные, глобоидные и червячные. Широко применяются комбинированные редукторы, состоящие из нескольких совмещенных в одном корпусе типов передач (цилиндро-конические, цилиндро-червячные и т.д.).
Конструктивно редукторы могут передавать вращение между перекрещивающимися, пересекающимися и параллельными валами.
Так, например цилиндрические редукторы позволяют передать вращение между параллельными валами, конические — между пересекающимися, а червячные — между пересекающимися валами.
Общее передаточное число может достигать до нескольких десятков тысяч, и зависит от количества ступеней в редукторе. Широкое применение нашли редукторы, состоящие из одной, двух или трех ступеней, при чем они могут, как описывалось выше, совмещать разные типы зубчатых передач.
Ниже представлены наиболее популярные виды редукторов, серийно выпускаемые промышленностью.
Цилиндрические редукторы
Цилиндрические редукторы являются самыми популярными в машиностроении. Они позволяют передавать достаточно большие мощности, при этом КПД достигает 95%. Вращение передается между параллельными или соосными валами. Передаваемая мощность зависит от типоразмера редуктора. В цилиндрических редукторах применяются передачи, состоящие из прямозубых, косозубых или шевронных зубчатых колес. Количество цилиндрических передач напрямую влияет на передаточное отношение. Например, одноступенчатый редуктор может иметь передаточное число 1,5 до 10, две ступени — от 10 до 60, а три ступени — от 60 до 400.
Кинематические схемы наиболее распространенных видов цилиндрических редукторов представлены на рисунке ниже:
А) — Простой одноступенчатый цилиндрический редуктор
Б) – Двухступенчатый редуктор цилиндрический с несимметричным расположением зубчатых колес
В) – Трехступенчатый цилиндрический редуктор, входной вал быстроходной передачи изготовлен с двумя шестернями
Г) – Соосный цилиндрический редуктор
Д) — Соосный цилиндрический редуктор с симметричным расположением опор относительно тихоходной передачи
Е) — Соосный цилиндрический редуктор с шевронной быстроходной передачей
Ж) — Соосный цилиндрический редуктор с раздвоенной передачей
З) — Соосный цилиндрический редуктор с посаженными на быстроходный вал двумя косозубыми шестернями с противоположенным наклоном зубьев
И) – Трехступенчатый цилиндрический редуктор с раздвоенной быстроходной и тихоходной передачей
Червячные редукторы
Червячные редукторы получили большую популярность в виду своей простоты и достаточно низкой стоимости. Из всех видов червячных редукторов наиболее распространены редукторы с цилиндрическими или глобоидными червяками. Как и многие другие типы редукторов червячные могут состоять из одной или нескольких ступеней. На одноступенчатом редукторе передаточное отношение может быть в пределах 5-100, а на двух ступенях может достигать 10000. Основными достоинствами редукторов червячного типа являются компактные размеры, плавность хода и самоторможение. Из недостатков можно отметить не очень высокий КПД и ограниченная нагружаемая способность. Основными элементами являются зубчатое колесо и цилиндрический червяк. Цилиндрический червяк представляет собой винт с нанесенной на его поверхности резьбой определенного профиля. Число заходов зависит от передаточного отношения, и может составлять от 1 до 4. Вторым основным элементом редуктора является червячное колесо. Оно представляет собой зубчатое колесо из сплава бронзы, количество зубьев также зависит от передаточного отношения и может составлять 26-100.
В ниже приведенной таблице представлена зависимость передаточного отношения от количества зубов колеса и заходов винта.
Передаточное отношение | Число заходов червяка | Число зубов колеса |
7-8 | 4 | 28-32 |
9-13 | 3-4 | 27-52 |
14-24 | 2-3 | 28-72 |
15-27 | 2-3 | 50-81 |
28-40 | 1-2 | 28-80 |
40 | 1 | 40 |
Кинематические схемы одноступенчатых червячных редукторов представлены ниже:
А) Редуктор с нижним расположением червяка
Б) Редуктор с верхним расположением червяка
В) Редуктор с боковым расположением червяка (ось червяка расположена горизонтально)
Г) Редуктор с боковым расположением червяка (ось червяка расположена вертикально)
Редукторы червячные двухступенчатые позволяют получить моменты в диапазоне 100 – 2800Нм. Конструкция представляет собой жесткую скрутку двух редукторов. Между собой редукторы соединены с помощью фланца. Цилиндрический вал первой ступени установлен в полый вал второй ступени.
Вариант расположения червячных пар представлен на рисунке ниже:
Расположение входного и выходного вала зависит от варианта сборки. Существуют следующие сборки: 11, 12, 13, 16, 21, 22, 23, 26.
Планетарные редукторы
Планетарные редукторы нашли широкое применение в тяжелом машиностроении, так как обладают рядом преимуществ перед редукторами другого типа. На редукторах планетарного типа можно получить достаточно большие передаточные числа, при этом габариты редуктора будут намного меньше чем у червячного или цилиндрического редуктора. Конструкция редуктора представляет собой планетарный механизм. Основными элементами редуктора являются сателлиты, солнечная шестерня, кольцевая шестерня и водило.
Внешний вид устройства планетарного редуктора представлен ниже:
А) сателлиты
Б) солнечная шестерня
В) водило
Г) кольцевая шестерня
Кольцевая шестерня планетарного редуктора находится в неподвижном состоянии, Вращение от входного вала передается на солнечную шестерню находящеюся в зацеплении со всеми сателлитами. Сателлиты вращаются внутри неподвижной кольцевой шестерни передавая энергию вращения на водило, а далее на выходной вал редуктора. Планетарный механизм может быть одно-, двух- и трехступенчатым, передаточное отношение зависит от количества зубьев на каждой шестерне.
Свое название планетарный редуктор получил благодаря тому, что зубчатые колеса вращаются подобно планетам солнечной системы. Планетарные редукторы могут быть одно-, двух- и трехступенчатыми. Передаточное отношение может быть в пределах 6 – 450. Редукторы планетарного типа обладают высоким КПД, и позволяют передавать большие мощности без потерь на нагрев. Для удобства монтажа планетарные редукторы выпускаются на лапах или на опорном фланце, а также возможен комбинированный вариант.
В настоящий момент на Российском рынке приводной техники пользуются популярностью редукторы серии 3МП и МПО.
Конические и цилиндро-конические редукторы
Конические и цилиндро-конические редукторы передают момент между пересекающимися или скрещивающимися валами. В редукторах применяются шестерни в виде конуса с прямыми или косыми зубами. Конические редукторы имеют большую плавность зацепления, что позволяет им выдерживать большие нагрузки. Редукторы могут быть одно-, двух- и трехступенчатыми. Большое распространение получили цилиндро-конические редукторы, где общее передаточное отношение может достигать 315. Быстроходный и тихоходный валы редуктора могут располагаться горизонтально и вертикально. По типу кинематической схемы конические и цилиндро-конические редукторы могут быть развернутые или соосные.
На рисунке ниже представлены кинематические схемы конических редукторов:
А) Реверсивный конический редуктор. Смена направления вращения достигается установкой зубчатого колеса с противоположенной стороны конической шестерни.
Б) Реверсивный конический редуктор. Конические шестерни вращаются в разных направлениях. Подключение тихоходного вала к одной из конических шестеренок происходит за счет кулачковой муфты.
В) Двухступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Г) Двухступенчатый коническо-цилиндрический редуктор. Входной и выходные валы перекрещиваются и лежат в разных плоскостях.
Д) Трехступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Е) Трехступенчатый коническо-цилиндрический редуктор. Промежуточная и тихоходная цилиндрическая передача собраны по соосной схеме.
Конические редукторы широко используются в изделиях, где требуются передать высокий момент под прямым углом. В отличие от червячных редукторов, конические редукторы не имеют быстро изнашиваемого бронзового колеса, что позволяет работать им в тяжелых условиях длительное время. Также важным отличием является обратимость, возможность передавать вращение от тихоходного вала к быстроходному валу. Обратимость позволяет разгрузить редукторный механизм в отличие от червячного редуктора, что позволяет использовать конический редуктор в установках с высокой инерцией.
Классификация редукторов в зависимости от вида передач и числа ступеней:
Тип редуктора | Количество ступеней | Тип механической передачи | Расположение тихоходного и быстроходного валов |
Цилиндрический | Одна ступень | Одна или несколько цилиндрических передач | Параллельное |
Две ступени; три ступени | Параллельное или соосное | ||
Четыре ступени | Параллельное | ||
Конический | Одна ступень | Одна коническая передача | Пересекающееся |
Коническо-цилиндрический | Две ступени; три ступени; четыре ступени | Одна коническая передача и одна или несколько цилиндрических передач | Пересекающееся или скрещивающееся |
Червячный | Одна ступень; две ступени | Одна или две червячные передачи | Скрещивающееся |
Параллельное | |||
Цилиндрическо-червячный или червячно-цилиндрический | Две ступени; три ступени | Одна или две цилиндрические передачи и одна червячная передача | Скрещивающееся |
Планетарный | Одна ступень; две ступени; три ступени | Каждая ступень состоит из двух центральных зубчатых колес и сателлитов | Соосное |
Цилиндрическо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной или нескольких цилиндрических и планетарных передач | Параллельное или соосное |
Коническо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Пересекающееся |
Червячно-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Скрещивающееся |
Волновой | Одна ступень | Одна волновая передача | Соосное |
Конструкция и назначение редуктора
Механизм, служащий для понижения угловой скорости и одновременно повышающий крутящий момент, принято называть редуктором. Энергия вращения подводится на входной вал редуктора, далее в зависимости от передаточного отношения на выходном валу получаем пониженную частоту и увеличенный момент.
В состав редуктора в зависимости от типа механической передачи обычно входят зубчатые или червячные пары, центрирующие подшипники, валы, различные уплотнения, сальники и т.д. Элементы редуктора помещаются в корпус, состоящий из двух частей – основания и крышки. Рабочие механизмы редуктора при работе непрерывно смазываются маслом путем разбрызгивания, а в отдельных случаях применяется принудительный насос, помещенный внутрь редуктора.
Существует огромное количество различных типов редукторов, но наибольшую популярность получили цилиндрические, планетарные, конические и червячные редукторы. Каждый тип редуктора имеет свои определенные преимущества и недостатки, которые следует учитывать при конструировании оборудования. Основными же критериями для подбора редуктора являются определение необходимой мощности или момента нагрузки, коэффициента редукции (передаточного отношения), а также монтажного расположения источника вращения и рабочего механизма.
Особенности редукторов по виду механических передач
Мировой промышленностью выпускается огромное количество редукторов и редукторных механизмов различающихся по типу передачи, вариантам сборки и т.д. Рассмотрим основные типы механических передач, их особенности и преимущества.
Цилиндрическая передача – является самой надежной и долговечной из всех видов зубчатых передач. Данная передача применяется в редукторах, где требуется высокая надежность и высокий КПД. Цилиндрические передачи обычно состоят из прямозубых, косозубых или шевронных зубчатых колёс.
а) Прямозубая цилиндрическая передача
б) Косозубая цилиндрическая передача
в) Шевронная цилиндрическая передача
г) Цилиндрическая передача с внутренним зацеплением
Конические передачи – обладают всеми преимуществами цилиндрических зубчатых передач и применяются в случае перекрещивания входного и выходного валов.
а) Коническая зубчатая передача с прямым зубом
б) Коническая зубчатая передача с косым зубом
в) Коническая зубчатая передача с криволинейным зубом
г) Коническая гипоидная передача
Червячная передача – позволяет передавать кинетическую энергию между пересекающимися в одной плоскости валами. Основными преимуществами данной передачи является высокий показатель передаточного отношения, самоторможение, компактные размеры. Недостатками являются низкий КПД, быстрый износ бронзового колеса, а также ограниченная способность передавать большие мощности.
Гипоидная передача – она же спироидная состоит из конического червяка и диска со спиральными зубьями. Ось червяка значительно смещена от оси конического колеса, благодаря чему число зубьев одновременно входящих в зацепление в несколько раз больше чем у червячных передач. В отличие от червячной пары в гипоидной передаче линия контакта перпендикулярна к направлению скорости скольжения, что обеспечивает масленый клин и уменьшает трение. Благодаря этому КПД гипоидной передачи выше, чем у червячной передачи на 25%.
а) Червячная передача с цилиндрическим червяком
б) Червячная передача с глобоидным червяком
в) Спироидная передача
г) Тороидно-дисковая передача
д) Тороидная передача внутреннего зацепления
Волновая передача – прототипом является планетарная передача с небольшой разницей количества зубов сателлита и неподвижного колеса. Волновая передача характеризуется высоким показателем передаточного отношения (до 350). Основными элементами волновой передачи являются гибкое колесо, жесткое колесо и волновой генератор. Под действием генератора гибкое колесо деформируется и происходит зацепление зубьев с жестким колесом. Волновые передачи широко применяются в точном машиностроении благодаря высокой плавности и отсутствия вибраций во время работы.
1) Зубчатое колесо с внутренними зубьями
2) Гибкое колесо с наружными зубьями соединенное с выходным валом редуктора
3) Генератор волн
Количество ступеней редуктора
Число ступеней редуктора напрямую влияет на передаточное отношение. В червячных редукторах наиболее распространены одноступенчатые пары. Цилиндрические же редукторы, состоящие из одной ступени, применяются реже, чем двух- или трехступенчатые редукторы. В производстве редукторов все чаще применяются комбинированные передачи, состоящие из разных типов передач, например коническо-цилиндрические редукторы.
Входные и выходные валы редукторов
В редукторах обычно применяются обычные прямые валы, имеющие форму тел вращения. На валы редукторов действуют внешние нагрузки, консольные нагрузки и усилия преодоления зацеплений. Крутящий момент на валу определяется рабочим крутящим моментом редуктора или реактивным крутящим моментом привода. Консольная нагрузка определяется способом соединения редуктора с двигателем, зависит от радиального или осевого усилия на вал. В ряде машин, к которым предъявляются особые требования в отношении габаритов или веса используются редукторы с полым валом. Полый вал редуктора позволяет располагать вал исполнительного механизма внутри редуктора, тем самым отпадает необходимость использовать переходные полумуфты и т.п.
Срок службы редуктора
Срок службы редуктора зависит от правильных расчетов параметров действующей нагрузки. Также на длительность работы влияет своевременное профилактическое обслуживание редуктора, замена масла и сальников. Регулярный профилактический осмотр позволит избежать незапланированного ремонта или замену редуктора. Уровень масла контролируется через смотровое окно в редукторе и при необходимости доливается до нужного уровня.
Ниже приведена таблица зависимости срока службы редуктора от типа передачи:
Тип передачи редуктора | Гарантированный ресурс в часах |
Цилиндрическая, планетарная, коническая, цилиндро-коническая | более 25000 |
Волновая, червячная, глобоидная | более 10000 |
Устройство редуктора
Основными элементами редуктора являются:
1. Прошедшие обработку зубчатые колеса с зубьями высокой твердости. Материалом обычно служит сталь марки (40Х, 40ХН ГОСТ 4543-71). В планетарных редукторах шестерни и сателлиты изготовлены из стали марки 25ХГМ ГОСТ 4543-71. Зубчатые венцы из стали 40Х. Червячные валы изготавливаются из стали марки ГОСТ 4543-71 – 18ХГТ, 20Х с последующей цементацией рабочих поверхностей. Венцы червячных редукторов изготавливают из бронзы Бр010Ф1 ГОСТ 613-79. Гибкое колесо волнового редуктора изготовлено из кованой стали 30ХГСА ГОСТ 4543-71.
2. Валы (оси) быстроходные, промежуточные и тихоходные. Материалом является — сталь марки (40Х, 40ХН ГОСТ 4543-71). В зависимости от варианта сборки выходные валы могут быть одно- и двухконцевыми, а также полыми со шпоночным пазом. Выходные валы планетарных редукторов изготовлены заодно с водилом последней ступени. Материалом служит чугун или сталь.
3. Подшипниковые узлы. Используются подшипники качения воспринимающие большие осевые и консольные нагрузки. Применяются обычно конические роликоподшипники.
4. Шлицевые, шпоночные соединения. Шлицевые соединения чаще применяются в червячных редукторах (выходной полый вал). Шпонки применяются для соединения валов с зубчатыми колесами, муфтами и другими деталями.
5. Корпуса редукторов. Корпуса и крышки редукторов выполняются методом литья. В качестве материалов используется чугун марки СЧ 15 ГОСТ 1412-79 или сплав алюминия АЛ11. Для улучшения отвода тепла корпуса редукторов снабжаются ребрами.
Монтажное исполнение
Соосный редуктор — входной и выходной вал находятся на одной оси
Червячный редуктор — входной и выходной вал находятся под прямым углом
Цилиндрический редуктор — входной и выходной вал находятся на параллельных осях
Коническо-цилиндрический редуктор — входной и выходной вал перекрещиваются
Монтажное положение соосных цилиндрических или планетарных редукторов
Монтажное положение и вариант сборки червячных одноступенчатых редукторов
Монтажное положение и вариант сборки червячных двухступенчатых редукторов
Монтажное положение и вариант сборки цилиндрических редукторов
Методика выбора редуктора в зависимости от нагрузки
Методика выбора редуктора заключается в грамотном расчете основных параметров нагрузки и условий эксплуатации.
Технические характеристики описаны в каталогах, а выбор редуктора делается в несколько этапов:
- выбор редуктора по типу механической передачи
- определение габарита (типоразмера) редуктора
- определение консольных и осевых нагрузок на входной и выходной валы
- определение температурного режима редуктора
На первом этапе конструктор определяет тип редуктора исходя из заданных задач и конструктивных особенностей будущего изделия. На этом же этапе закладываются такие параметры как: передаточное отношение, количество ступеней, расположение входного и выходного валов в пространстве.
На втором этапе следует определить межосевое расстояние. Исходные данные на каждый тип редуктора можно найти в каталоге. Следует помнить, что межосевое расстояние влияет на способность передать момент от двигателя к нагрузке.
Консольные и осевые нагрузки определяются уравнениями, а потом сравниваются со значениями в каталоге. В случае превышения расчетных нагрузок, на какой либо вал, редуктор выбирается на типоразмер выше.
Температурный режим определяется во время работы редуктора. Температура не должна превышать + 80° гр. при длительной работе редуктора с действующей нагрузкой.
Как выбрать редуктор?
Выбор редуктора должен производить квалифицированный сотрудник т.к. неправильные расчеты могут привести к поломке редуктора или сопутствующего оборудования. Грамотный выбор редуктора поможет избежать дальнейшие затраты на ремонт и покупку нового привода. Основными параметрами для выбора редуктора как было сказано выше, являются: тип редуктора, габарит или типоразмер, передаточное отношение, а также кинематическая схема.
Определить габарит редуктора можно с помощью каталога, где указаны максимальные значения крутящего момента для каждого типоразмера. Момент действующей нагрузки на редуктор определяется следующим выражением:
где:
M2 — выходной момент на валу редуктора (Н/М)
P1 — подводимая мощность на быстроходном валу редуктора (кВт)
Rd — динамический КПД редуктора (%)
n2 — частота вращения тихоходного вала (об/мин)
Частоту вращения тихоходного вала n2 можно определить, зная значения передаточного отношения редуктора i, а также значения скорости быстроходного вала n1.
где:
n1 — частота вращения быстроходного вала (об/мин)
n2 — частота вращения тихоходного вала (об/мин)
i — передаточное отношение редуктора
Еще одним важным фактором, который следует учитывать при подборе редуктора, является величина – сервис фактор (s/f). Сервис фактор sf – это отношение максимально допустимого момента M2 max указанного в каталоге к номинальному моменту M2 зависящего от мощности двигателя.
где:
M2 max — максимально допустимый момент (паспортное значение)
M2 — номинальный момент на валу редуктора (зависит от мощности двигателя)
Значение сервис фактора (s/f) напрямую связан с ресурсом редуктора и зависит от условий работы привода.
При работе редуктора с нормальной нагрузкой, где число стартов не превышает 60 пусков в час — сервис фактор может выбираться: sf = 1.
При средней нагрузке, где число стартов не превышает 150 пусков в час — сервис фактор выбирается: sf = 1,5.
При тяжелой ударной нагрузке с возможностью заклинивания вала редуктора сервис фактор выбирается: sf = 2 и более.
Передаточное отношение и как его определить?
Основное назначение любого редуктора понижение угловой скорости подводимой на его входной вал. Значения выходной скорости определятся передаточным отношением редуктора. Передаточное отношение редуктора — это отношение скорости входного вала к скорости выходного вала.
Все о редукторах. Справочная информация
Классификация, основные параметры редукторов
Цилиндрические редукторы
Червячные редукторы
Планетарные редукторы
Конические редукторы
Классификация редукторов в зависимости от вида передач и числа ступеней
Конструкция и назначение редуктора
Особенности редукторов по виду механических передач
Количество ступеней редуктора
Входные и выходные валы редукторов
Срок службы редуктора
Устройство редуктора
Монтажное исполнение
Как подобрать редуктор? Простые правила и примеры расчета
Передаточное отношение и как его определить?
Редукторы (латинского слова reductor) получили широкое распространение во всех отраслях промышленного и аграрного хозяйства, поэтому их производство с каждым годом увеличивается, появляются новые модификации, совершенствуются уже существующие модели.
Редуктор служит для снижения частоты вращения тихоходного вала и увеличения усилия на выходном валу. Редуктор может иметь одну или несколько ступеней, цель которых увеличение передаточного отношения. По типу механической передачи редукторы могут быть червячными, коническими, планетарными или цилиндрическими. Конструктивно редуктор выполнен как отдельное изделие, работающее в паре с электродвигателем и установленное с ним на одной раме.
Промышленностью сегодня выпускаются редукторы общего и специального назначения.
Редукторы общего назначения могут применяться во многих случаях и отвечают общим требованиям. Специальные же редукторы имеют нестандартные характеристики подходящие под определенные требования.
Классификация, основные параметры редукторов
В зависимости от типа зубчатой передачи редукторы бывают цилиндрические, конические, волновые, планетарные, глобоидные и червячные. Широко применяются комбинированные редукторы, состоящие из нескольких совмещенных в одном корпусе типов передач (цилиндро-конические, цилиндро-червячные и т.д.).
Конструктивно редукторы могут передавать вращение между перекрещивающимися, пересекающимися и параллельными валами.
Так, например цилиндрические редукторы позволяют передать вращение между параллельными валами, конические — между пересекающимися, а червячные — между пересекающимися валами.
Общее передаточное число может достигать до нескольких десятков тысяч, и зависит от количества ступеней в редукторе. Широкое применение нашли редукторы, состоящие из одной, двух или трех ступеней, при чем они могут, как описывалось выше, совмещать разные типы зубчатых передач.
Ниже представлены наиболее популярные виды редукторов, серийно выпускаемые промышленностью.
Цилиндрические редукторы
Цилиндрические редукторы являются самыми популярными в машиностроении. Они позволяют передавать достаточно большие мощности, при этом КПД достигает 95%. Вращение передается между параллельными или соосными валами. Передаваемая мощность зависит от типоразмера редуктора. В цилиндрических редукторах применяются передачи, состоящие из прямозубых, косозубых или шевронных зубчатых колес. Количество цилиндрических передач напрямую влияет на передаточное отношение. Например, одноступенчатый редуктор может иметь передаточное число 1,5 до 10, две ступени — от 10 до 60, а три ступени — от 60 до 400.
Кинематические схемы наиболее распространенных видов цилиндрических редукторов представлены на рисунке ниже:
А) — Простой одноступенчатый цилиндрический редуктор
Б) – Двухступенчатый редуктор цилиндрический с несимметричным расположением зубчатых колес
В) – Трехступенчатый цилиндрический редуктор, входной вал быстроходной передачи изготовлен с двумя шестернями
Г) – Соосный цилиндрический редуктор
Д) — Соосный цилиндрический редуктор с симметричным расположением опор относительно тихоходной передачи
Е) — Соосный цилиндрический редуктор с шевронной быстроходной передачей
Ж) — Соосный цилиндрический редуктор с раздвоенной передачей
З) — Соосный цилиндрический редуктор с посаженными на быстроходный вал двумя косозубыми шестернями с противоположенным наклоном зубьев
И) – Трехступенчатый цилиндрический редуктор с раздвоенной быстроходной и тихоходной передачей
Червячные редукторы
Червячные редукторы получили большую популярность в виду своей простоты и достаточно низкой стоимости. Из всех видов червячных редукторов наиболее распространены редукторы с цилиндрическими или глобоидными червяками. Как и многие другие типы редукторов червячные могут состоять из одной или нескольких ступеней. На одноступенчатом редукторе передаточное отношение может быть в пределах 5-100, а на двух ступенях может достигать 10000. Основными достоинствами редукторов червячного типа являются компактные размеры, плавность хода и самоторможение. Из недостатков можно отметить не очень высокий КПД и ограниченная нагружаемая способность. Основными элементами являются зубчатое колесо и цилиндрический червяк. Цилиндрический червяк представляет собой винт с нанесенной на его поверхности резьбой определенного профиля. Число заходов зависит от передаточного отношения, и может составлять от 1 до 4. Вторым основным элементом редуктора является червячное колесо. Оно представляет собой зубчатое колесо из сплава бронзы, количество зубьев также зависит от передаточного отношения и может составлять 26-100.
В ниже приведенной таблице представлена зависимость передаточного отношения от количества зубов колеса и заходов винта.
Передаточное отношение | Число заходов червяка | Число зубов колеса |
7-8 | 4 | 28-32 |
9-13 | 3-4 | 27-52 |
14-24 | 2-3 | 28-72 |
15-27 | 2-3 | 50-81 |
28-40 | 1-2 | 28-80 |
40 | 1 | 40 |
Кинематические схемы одноступенчатых червячных редукторов представлены ниже:
А) Редуктор с нижним расположением червяка
Б) Редуктор с верхним расположением червяка
В) Редуктор с боковым расположением червяка (ось червяка расположена горизонтально)
Г) Редуктор с боковым расположением червяка (ось червяка расположена вертикально)
Редукторы червячные двухступенчатые позволяют получить моменты в диапазоне 100 – 2800Нм. Конструкция представляет собой жесткую скрутку двух редукторов. Между собой редукторы соединены с помощью фланца. Цилиндрический вал первой ступени установлен в полый вал второй ступени.
Вариант расположения червячных пар представлен на рисунке ниже:
Расположение входного и выходного вала зависит от варианта сборки. Существуют следующие сборки: 11, 12, 13, 16, 21, 22, 23, 26.
Планетарные редукторы
Планетарные редукторы нашли широкое применение в тяжелом машиностроении, так как обладают рядом преимуществ перед редукторами другого типа. На редукторах планетарного типа можно получить достаточно большие передаточные числа, при этом габариты редуктора будут намного меньше чем у червячного или цилиндрического редуктора. Конструкция редуктора представляет собой планетарный механизм. Основными элементами редуктора являются сателлиты, солнечная шестерня, кольцевая шестерня и водило.
Внешний вид устройства планетарного редуктора представлен ниже:
А) сателлиты
Б) солнечная шестерня
В) водило
Г) кольцевая шестерня
Кольцевая шестерня планетарного редуктора находится в неподвижном состоянии, Вращение от входного вала передается на солнечную шестерню находящеюся в зацеплении со всеми сателлитами. Сателлиты вращаются внутри неподвижной кольцевой шестерни передавая энергию вращения на водило, а далее на выходной вал редуктора. Планетарный механизм может быть одно-, двух- и трехступенчатым, передаточное отношение зависит от количества зубьев на каждой шестерне.
Свое название планетарный редуктор получил благодаря тому, что зубчатые колеса вращаются подобно планетам солнечной системы. Планетарные редукторы могут быть одно-, двух- и трехступенчатыми. Передаточное отношение может быть в пределах 6 – 450. Редукторы планетарного типа обладают высоким КПД, и позволяют передавать большие мощности без потерь на нагрев. Для удобства монтажа планетарные редукторы выпускаются на лапах или на опорном фланце, а также возможен комбинированный вариант.
В настоящий момент на Российском рынке приводной техники пользуются популярностью редукторы серии 3МП и МПО.
Конические и цилиндро-конические редукторы
Конические и цилиндро-конические редукторы передают момент между пересекающимися или скрещивающимися валами. В редукторах применяются шестерни в виде конуса с прямыми или косыми зубами. Конические редукторы имеют большую плавность зацепления, что позволяет им выдерживать большие нагрузки. Редукторы могут быть одно-, двух- и трехступенчатыми. Большое распространение получили цилиндро-конические редукторы, где общее передаточное отношение может достигать 315. Быстроходный и тихоходный валы редуктора могут располагаться горизонтально и вертикально. По типу кинематической схемы конические и цилиндро-конические редукторы могут быть развернутые или соосные.
На рисунке ниже представлены кинематические схемы конических редукторов:
А) Реверсивный конический редуктор. Смена направления вращения достигается установкой зубчатого колеса с противоположенной стороны конической шестерни.
Б) Реверсивный конический редуктор. Конические шестерни вращаются в разных направлениях. Подключение тихоходного вала к одной из конических шестеренок происходит за счет кулачковой муфты.
В) Двухступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Г) Двухступенчатый коническо-цилиндрический редуктор. Входной и выходные валы перекрещиваются и лежат в разных плоскостях.
Д) Трехступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Е) Трехступенчатый коническо-цилиндрический редуктор. Промежуточная и тихоходная цилиндрическая передача собраны по соосной схеме.
Конические редукторы широко используются в изделиях, где требуются передать высокий момент под прямым углом. В отличие от червячных редукторов, конические редукторы не имеют быстро изнашиваемого бронзового колеса, что позволяет работать им в тяжелых условиях длительное время. Также важным отличием является обратимость, возможность передавать вращение от тихоходного вала к быстроходному валу. Обратимость позволяет разгрузить редукторный механизм в отличие от червячного редуктора, что позволяет использовать конический редуктор в установках с высокой инерцией.
Классификация редукторов в зависимости от вида передач и числа ступеней:
Тип редуктора | Количество ступеней | Тип механической передачи | Расположение тихоходного и быстроходного валов |
Цилиндрический | Одна ступень | Одна или несколько цилиндрических передач | Параллельное |
Две ступени; три ступени | Параллельное или соосное | ||
Четыре ступени | Параллельное | ||
Конический | Одна ступень | Одна коническая передача | Пересекающееся |
Коническо-цилиндрический | Две ступени; три ступени; четыре ступени | Одна коническая передача и одна или несколько цилиндрических передач | Пересекающееся или скрещивающееся |
Червячный | Одна ступень; две ступени | Одна или две червячные передачи | Скрещивающееся |
Параллельное | |||
Цилиндрическо-червячный или червячно-цилиндрический | Две ступени; три ступени | Одна или две цилиндрические передачи и одна червячная передача | Скрещивающееся |
Планетарный | Одна ступень; две ступени; три ступени | Каждая ступень состоит из двух центральных зубчатых колес и сателлитов | Соосное |
Цилиндрическо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной или нескольких цилиндрических и планетарных передач | Параллельное или соосное |
Коническо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Пересекающееся |
Червячно-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Скрещивающееся |
Волновой | Одна ступень | Одна волновая передача | Соосное |
Конструкция и назначение редуктора
Механизм, служащий для понижения угловой скорости и одновременно повышающий крутящий момент, принято называть редуктором. Энергия вращения подводится на входной вал редуктора, далее в зависимости от передаточного отношения на выходном валу получаем пониженную частоту и увеличенный момент.
В состав редуктора в зависимости от типа механической передачи обычно входят зубчатые или червячные пары, центрирующие подшипники, валы, различные уплотнения, сальники и т.д. Элементы редуктора помещаются в корпус, состоящий из двух частей – основания и крышки. Рабочие механизмы редуктора при работе непрерывно смазываются маслом путем разбрызгивания, а в отдельных случаях применяется принудительный насос, помещенный внутрь редуктора.
Существует огромное количество различных типов редукторов, но наибольшую популярность получили цилиндрические, планетарные, конические и червячные редукторы. Каждый тип редуктора имеет свои определенные преимущества и недостатки, которые следует учитывать при конструировании оборудования. Основными же критериями для подбора редуктора являются определение необходимой мощности или момента нагрузки, коэффициента редукции (передаточного отношения), а также монтажного расположения источника вращения и рабочего механизма.
Особенности редукторов по виду механических передач
Мировой промышленностью выпускается огромное количество редукторов и редукторных механизмов различающихся по типу передачи, вариантам сборки и т.д. Рассмотрим основные типы механических передач, их особенности и преимущества.
Цилиндрическая передача – является самой надежной и долговечной из всех видов зубчатых передач. Данная передача применяется в редукторах, где требуется высокая надежность и высокий КПД. Цилиндрические передачи обычно состоят из прямозубых, косозубых или шевронных зубчатых колёс.
а) Прямозубая цилиндрическая передача
б) Косозубая цилиндрическая передача
в) Шевронная цилиндрическая передача
г) Цилиндрическая передача с внутренним зацеплением
Конические передачи – обладают всеми преимуществами цилиндрических зубчатых передач и применяются в случае перекрещивания входного и выходного валов.
а) Коническая зубчатая передача с прямым зубом
б) Коническая зубчатая передача с косым зубом
в) Коническая зубчатая передача с криволинейным зубом
г) Коническая гипоидная передача
Червячная передача – позволяет передавать кинетическую энергию между пересекающимися в одной плоскости валами. Основными преимуществами данной передачи является высокий показатель передаточного отношения, самоторможение, компактные размеры. Недостатками являются низкий КПД, быстрый износ бронзового колеса, а также ограниченная способность передавать большие мощности.
Гипоидная передача – она же спироидная состоит из конического червяка и диска со спиральными зубьями. Ось червяка значительно смещена от оси конического колеса, благодаря чему число зубьев одновременно входящих в зацепление в несколько раз больше чем у червячных передач. В отличие от червячной пары в гипоидной передаче линия контакта перпендикулярна к направлению скорости скольжения, что обеспечивает масленый клин и уменьшает трение. Благодаря этому КПД гипоидной передачи выше, чем у червячной передачи на 25%.
а) Червячная передача с цилиндрическим червяком
б) Червячная передача с глобоидным червяком
в) Спироидная передача
г) Тороидно-дисковая передача
д) Тороидная передача внутреннего зацепления
Волновая передача – прототипом является планетарная передача с небольшой разницей количества зубов сателлита и неподвижного колеса. Волновая передача характеризуется высоким показателем передаточного отношения (до 350). Основными элементами волновой передачи являются гибкое колесо, жесткое колесо и волновой генератор. Под действием генератора гибкое колесо деформируется и происходит зацепление зубьев с жестким колесом. Волновые передачи широко применяются в точном машиностроении благодаря высокой плавности и отсутствия вибраций во время работы.
1) Зубчатое колесо с внутренними зубьями
2) Гибкое колесо с наружными зубьями соединенное с выходным валом редуктора
3) Генератор волн
Количество ступеней редуктора
Число ступеней редуктора напрямую влияет на передаточное отношение. В червячных редукторах наиболее распространены одноступенчатые пары. Цилиндрические же редукторы, состоящие из одной ступени, применяются реже, чем двух- или трехступенчатые редукторы. В производстве редукторов все чаще применяются комбинированные передачи, состоящие из разных типов передач, например коническо-цилиндрические редукторы.
Входные и выходные валы редукторов
В редукторах обычно применяются обычные прямые валы, имеющие форму тел вращения. На валы редукторов действуют внешние нагрузки, консольные нагрузки и усилия преодоления зацеплений. Крутящий момент на валу определяется рабочим крутящим моментом редуктора или реактивным крутящим моментом привода. Консольная нагрузка определяется способом соединения редуктора с двигателем, зависит от радиального или осевого усилия на вал. В ряде машин, к которым предъявляются особые требования в отношении габаритов или веса используются редукторы с полым валом. Полый вал редуктора позволяет располагать вал исполнительного механизма внутри редуктора, тем самым отпадает необходимость использовать переходные полумуфты и т.п.
Срок службы редуктора
Срок службы редуктора зависит от правильных расчетов параметров действующей нагрузки. Также на длительность работы влияет своевременное профилактическое обслуживание редуктора, замена масла и сальников. Регулярный профилактический осмотр позволит избежать незапланированного ремонта или замену редуктора. Уровень масла контролируется через смотровое окно в редукторе и при необходимости доливается до нужного уровня.
Ниже приведена таблица зависимости срока службы редуктора от типа передачи:
Тип передачи редуктора | Гарантированный ресурс в часах |
Цилиндрическая, планетарная, коническая, цилиндро-коническая | более 25000 |
Волновая, червячная, глобоидная | более 10000 |
Устройство редуктора
Основными элементами редуктора являются:
1. Прошедшие обработку зубчатые колеса с зубьями высокой твердости. Материалом обычно служит сталь марки (40Х, 40ХН ГОСТ 4543-71). В планетарных редукторах шестерни и сателлиты изготовлены из стали марки 25ХГМ ГОСТ 4543-71. Зубчатые венцы из стали 40Х. Червячные валы изготавливаются из стали марки ГОСТ 4543-71 – 18ХГТ, 20Х с последующей цементацией рабочих поверхностей. Венцы червячных редукторов изготавливают из бронзы Бр010Ф1 ГОСТ 613-79. Гибкое колесо волнового редуктора изготовлено из кованой стали 30ХГСА ГОСТ 4543-71.
2. Валы (оси) быстроходные, промежуточные и тихоходные. Материалом является — сталь марки (40Х, 40ХН ГОСТ 4543-71). В зависимости от варианта сборки выходные валы могут быть одно- и двухконцевыми, а также полыми со шпоночным пазом. Выходные валы планетарных редукторов изготовлены заодно с водилом последней ступени. Материалом служит чугун или сталь.
3. Подшипниковые узлы. Используются подшипники качения воспринимающие большие осевые и консольные нагрузки. Применяются обычно конические роликоподшипники.
4. Шлицевые, шпоночные соединения. Шлицевые соединения чаще применяются в червячных редукторах (выходной полый вал). Шпонки применяются для соединения валов с зубчатыми колесами, муфтами и другими деталями.
5. Корпуса редукторов. Корпуса и крышки редукторов выполняются методом литья. В качестве материалов используется чугун марки СЧ 15 ГОСТ 1412-79 или сплав алюминия АЛ11. Для улучшения отвода тепла корпуса редукторов снабжаются ребрами.
Монтажное исполнение
Соосный редуктор — входной и выходной вал находятся на одной оси
Червячный редуктор — входной и выходной вал находятся под прямым углом
Цилиндрический редуктор — входной и выходной вал находятся на параллельных осях
Коническо-цилиндрический редуктор — входной и выходной вал перекрещиваются
Монтажное положение соосных цилиндрических или планетарных редукторов
Монтажное положение и вариант сборки червячных одноступенчатых редукторов
Монтажное положение и вариант сборки червячных двухступенчатых редукторов
Монтажное положение и вариант сборки цилиндрических редукторов
Методика выбора редуктора в зависимости от нагрузки
Методика выбора редуктора заключается в грамотном расчете основных параметров нагрузки и условий эксплуатации.
Технические характеристики описаны в каталогах, а выбор редуктора делается в несколько этапов:
- выбор редуктора по типу механической передачи
- определение габарита (типоразмера) редуктора
- определение консольных и осевых нагрузок на входной и выходной валы
- определение температурного режима редуктора
На первом этапе конструктор определяет тип редуктора исходя из заданных задач и конструктивных особенностей будущего изделия. На этом же этапе закладываются такие параметры как: передаточное отношение, количество ступеней, расположение входного и выходного валов в пространстве.
На втором этапе следует определить межосевое расстояние. Исходные данные на каждый тип редуктора можно найти в каталоге. Следует помнить, что межосевое расстояние влияет на способность передать момент от двигателя к нагрузке.
Консольные и осевые нагрузки определяются уравнениями, а потом сравниваются со значениями в каталоге. В случае превышения расчетных нагрузок, на какой либо вал, редуктор выбирается на типоразмер выше.
Температурный режим определяется во время работы редуктора. Температура не должна превышать + 80° гр. при длительной работе редуктора с действующей нагрузкой.
Как выбрать редуктор?
Выбор редуктора должен производить квалифицированный сотрудник т.к. неправильные расчеты могут привести к поломке редуктора или сопутствующего оборудования. Грамотный выбор редуктора поможет избежать дальнейшие затраты на ремонт и покупку нового привода. Основными параметрами для выбора редуктора как было сказано выше, являются: тип редуктора, габарит или типоразмер, передаточное отношение, а также кинематическая схема.
Определить габарит редуктора можно с помощью каталога, где указаны максимальные значения крутящего момента для каждого типоразмера. Момент действующей нагрузки на редуктор определяется следующим выражением:
где:
M2 — выходной момент на валу редуктора (Н/М)
P1 — подводимая мощность на быстроходном валу редуктора (кВт)
Rd — динамический КПД редуктора (%)
n2 — частота вращения тихоходного вала (об/мин)
Частоту вращения тихоходного вала n2 можно определить, зная значения передаточного отношения редуктора i, а также значения скорости быстроходного вала n1.
где:
n1 — частота вращения быстроходного вала (об/мин)
n2 — частота вращения тихоходного вала (об/мин)
i — передаточное отношение редуктора
Еще одним важным фактором, который следует учитывать при подборе редуктора, является величина – сервис фактор (s/f). Сервис фактор sf – это отношение максимально допустимого момента M2 max указанного в каталоге к номинальному моменту M2 зависящего от мощности двигателя.
где:
M2 max — максимально допустимый момент (паспортное значение)
M2 — номинальный момент на валу редуктора (зависит от мощности двигателя)
Значение сервис фактора (s/f) напрямую связан с ресурсом редуктора и зависит от условий работы привода.
При работе редуктора с нормальной нагрузкой, где число стартов не превышает 60 пусков в час — сервис фактор может выбираться: sf = 1.
При средней нагрузке, где число стартов не превышает 150 пусков в час — сервис фактор выбирается: sf = 1,5.
При тяжелой ударной нагрузке с возможностью заклинивания вала редуктора сервис фактор выбирается: sf = 2 и более.
Передаточное отношение и как его определить?
Основное назначение любого редуктора понижение угловой скорости подводимой на его входной вал. Значения выходной скорости определятся передаточным отношением редуктора. Передаточное отношение редуктора — это отношение скорости входного вала к скорости выходного вала.
Все о редукторах. Справочная информация
Классификация, основные параметры редукторов
Цилиндрические редукторы
Червячные редукторы
Планетарные редукторы
Конические редукторы
Классификация редукторов в зависимости от вида передач и числа ступеней
Конструкция и назначение редуктора
Особенности редукторов по виду механических передач
Количество ступеней редуктора
Входные и выходные валы редукторов
Срок службы редуктора
Устройство редуктора
Монтажное исполнение
Как подобрать редуктор? Простые правила и примеры расчета
Передаточное отношение и как его определить?
Редукторы (латинского слова reductor) получили широкое распространение во всех отраслях промышленного и аграрного хозяйства, поэтому их производство с каждым годом увеличивается, появляются новые модификации, совершенствуются уже существующие модели.
Редуктор служит для снижения частоты вращения тихоходного вала и увеличения усилия на выходном валу. Редуктор может иметь одну или несколько ступеней, цель которых увеличение передаточного отношения. По типу механической передачи редукторы могут быть червячными, коническими, планетарными или цилиндрическими. Конструктивно редуктор выполнен как отдельное изделие, работающее в паре с электродвигателем и установленное с ним на одной раме.
Промышленностью сегодня выпускаются редукторы общего и специального назначения.
Редукторы общего назначения могут применяться во многих случаях и отвечают общим требованиям. Специальные же редукторы имеют нестандартные характеристики подходящие под определенные требования.
Классификация, основные параметры редукторов
В зависимости от типа зубчатой передачи редукторы бывают цилиндрические, конические, волновые, планетарные, глобоидные и червячные. Широко применяются комбинированные редукторы, состоящие из нескольких совмещенных в одном корпусе типов передач (цилиндро-конические, цилиндро-червячные и т.д.).
Конструктивно редукторы могут передавать вращение между перекрещивающимися, пересекающимися и параллельными валами.
Так, например цилиндрические редукторы позволяют передать вращение между параллельными валами, конические — между пересекающимися, а червячные — между пересекающимися валами.
Общее передаточное число может достигать до нескольких десятков тысяч, и зависит от количества ступеней в редукторе. Широкое применение нашли редукторы, состоящие из одной, двух или трех ступеней, при чем они могут, как описывалось выше, совмещать разные типы зубчатых передач.
Ниже представлены наиболее популярные виды редукторов, серийно выпускаемые промышленностью.
Цилиндрические редукторы
Цилиндрические редукторы являются самыми популярными в машиностроении. Они позволяют передавать достаточно большие мощности, при этом КПД достигает 95%. Вращение передается между параллельными или соосными валами. Передаваемая мощность зависит от типоразмера редуктора. В цилиндрических редукторах применяются передачи, состоящие из прямозубых, косозубых или шевронных зубчатых колес. Количество цилиндрических передач напрямую влияет на передаточное отношение. Например, одноступенчатый редуктор может иметь передаточное число 1,5 до 10, две ступени — от 10 до 60, а три ступени — от 60 до 400.
Кинематические схемы наиболее распространенных видов цилиндрических редукторов представлены на рисунке ниже:
А) — Простой одноступенчатый цилиндрический редуктор
Б) – Двухступенчатый редуктор цилиндрический с несимметричным расположением зубчатых колес
В) – Трехступенчатый цилиндрический редуктор, входной вал быстроходной передачи изготовлен с двумя шестернями
Г) – Соосный цилиндрический редуктор
Д) — Соосный цилиндрический редуктор с симметричным расположением опор относительно тихоходной передачи
Е) — Соосный цилиндрический редуктор с шевронной быстроходной передачей
Ж) — Соосный цилиндрический редуктор с раздвоенной передачей
З) — Соосный цилиндрический редуктор с посаженными на быстроходный вал двумя косозубыми шестернями с противоположенным наклоном зубьев
И) – Трехступенчатый цилиндрический редуктор с раздвоенной быстроходной и тихоходной передачей
Червячные редукторы
Червячные редукторы получили большую популярность в виду своей простоты и достаточно низкой стоимости. Из всех видов червячных редукторов наиболее распространены редукторы с цилиндрическими или глобоидными червяками. Как и многие другие типы редукторов червячные могут состоять из одной или нескольких ступеней. На одноступенчатом редукторе передаточное отношение может быть в пределах 5-100, а на двух ступенях может достигать 10000. Основными достоинствами редукторов червячного типа являются компактные размеры, плавность хода и самоторможение. Из недостатков можно отметить не очень высокий КПД и ограниченная нагружаемая способность. Основными элементами являются зубчатое колесо и цилиндрический червяк. Цилиндрический червяк представляет собой винт с нанесенной на его поверхности резьбой определенного профиля. Число заходов зависит от передаточного отношения, и может составлять от 1 до 4. Вторым основным элементом редуктора является червячное колесо. Оно представляет собой зубчатое колесо из сплава бронзы, количество зубьев также зависит от передаточного отношения и может составлять 26-100.
В ниже приведенной таблице представлена зависимость передаточного отношения от количества зубов колеса и заходов винта.
Передаточное отношение | Число заходов червяка | Число зубов колеса |
7-8 | 4 | 28-32 |
9-13 | 3-4 | 27-52 |
14-24 | 2-3 | 28-72 |
15-27 | 2-3 | 50-81 |
28-40 | 1-2 | 28-80 |
40 | 1 | 40 |
Кинематические схемы одноступенчатых червячных редукторов представлены ниже:
А) Редуктор с нижним расположением червяка
Б) Редуктор с верхним расположением червяка
В) Редуктор с боковым расположением червяка (ось червяка расположена горизонтально)
Г) Редуктор с боковым расположением червяка (ось червяка расположена вертикально)
Редукторы червячные двухступенчатые позволяют получить моменты в диапазоне 100 – 2800Нм. Конструкция представляет собой жесткую скрутку двух редукторов. Между собой редукторы соединены с помощью фланца. Цилиндрический вал первой ступени установлен в полый вал второй ступени.
Вариант расположения червячных пар представлен на рисунке ниже:
Расположение входного и выходного вала зависит от варианта сборки. Существуют следующие сборки: 11, 12, 13, 16, 21, 22, 23, 26.
Планетарные редукторы
Планетарные редукторы нашли широкое применение в тяжелом машиностроении, так как обладают рядом преимуществ перед редукторами другого типа. На редукторах планетарного типа можно получить достаточно большие передаточные числа, при этом габариты редуктора будут намного меньше чем у червячного или цилиндрического редуктора. Конструкция редуктора представляет собой планетарный механизм. Основными элементами редуктора являются сателлиты, солнечная шестерня, кольцевая шестерня и водило.
Внешний вид устройства планетарного редуктора представлен ниже:
А) сателлиты
Б) солнечная шестерня
В) водило
Г) кольцевая шестерня
Кольцевая шестерня планетарного редуктора находится в неподвижном состоянии, Вращение от входного вала передается на солнечную шестерню находящеюся в зацеплении со всеми сателлитами. Сателлиты вращаются внутри неподвижной кольцевой шестерни передавая энергию вращения на водило, а далее на выходной вал редуктора. Планетарный механизм может быть одно-, двух- и трехступенчатым, передаточное отношение зависит от количества зубьев на каждой шестерне.
Свое название планетарный редуктор получил благодаря тому, что зубчатые колеса вращаются подобно планетам солнечной системы. Планетарные редукторы могут быть одно-, двух- и трехступенчатыми. Передаточное отношение может быть в пределах 6 – 450. Редукторы планетарного типа обладают высоким КПД, и позволяют передавать большие мощности без потерь на нагрев. Для удобства монтажа планетарные редукторы выпускаются на лапах или на опорном фланце, а также возможен комбинированный вариант.
В настоящий момент на Российском рынке приводной техники пользуются популярностью редукторы серии 3МП и МПО.
Конические и цилиндро-конические редукторы
Конические и цилиндро-конические редукторы передают момент между пересекающимися или скрещивающимися валами. В редукторах применяются шестерни в виде конуса с прямыми или косыми зубами. Конические редукторы имеют большую плавность зацепления, что позволяет им выдерживать большие нагрузки. Редукторы могут быть одно-, двух- и трехступенчатыми. Большое распространение получили цилиндро-конические редукторы, где общее передаточное отношение может достигать 315. Быстроходный и тихоходный валы редуктора могут располагаться горизонтально и вертикально. По типу кинематической схемы конические и цилиндро-конические редукторы могут быть развернутые или соосные.
На рисунке ниже представлены кинематические схемы конических редукторов:
А) Реверсивный конический редуктор. Смена направления вращения достигается установкой зубчатого колеса с противоположенной стороны конической шестерни.
Б) Реверсивный конический редуктор. Конические шестерни вращаются в разных направлениях. Подключение тихоходного вала к одной из конических шестеренок происходит за счет кулачковой муфты.
В) Двухступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Г) Двухступенчатый коническо-цилиндрический редуктор. Входной и выходные валы перекрещиваются и лежат в разных плоскостях.
Д) Трехступенчатый коническо-цилиндрический редуктор. Быстроходный и тихоходный валы находятся под прямым углом в одной плоскости.
Е) Трехступенчатый коническо-цилиндрический редуктор. Промежуточная и тихоходная цилиндрическая передача собраны по соосной схеме.
Конические редукторы широко используются в изделиях, где требуются передать высокий момент под прямым углом. В отличие от червячных редукторов, конические редукторы не имеют быстро изнашиваемого бронзового колеса, что позволяет работать им в тяжелых условиях длительное время. Также важным отличием является обратимость, возможность передавать вращение от тихоходного вала к быстроходному валу. Обратимость позволяет разгрузить редукторный механизм в отличие от червячного редуктора, что позволяет использовать конический редуктор в установках с высокой инерцией.
Классификация редукторов в зависимости от вида передач и числа ступеней:
Тип редуктора | Количество ступеней | Тип механической передачи | Расположение тихоходного и быстроходного валов |
Цилиндрический | Одна ступень | Одна или несколько цилиндрических передач | Параллельное |
Две ступени; три ступени | Параллельное или соосное | ||
Четыре ступени | Параллельное | ||
Конический | Одна ступень | Одна коническая передача | Пересекающееся |
Коническо-цилиндрический | Две ступени; три ступени; четыре ступени | Одна коническая передача и одна или несколько цилиндрических передач | Пересекающееся или скрещивающееся |
Червячный | Одна ступень; две ступени | Одна или две червячные передачи | Скрещивающееся |
Параллельное | |||
Цилиндрическо-червячный или червячно-цилиндрический | Две ступени; три ступени | Одна или две цилиндрические передачи и одна червячная передача | Скрещивающееся |
Планетарный | Одна ступень; две ступени; три ступени | Каждая ступень состоит из двух центральных зубчатых колес и сателлитов | Соосное |
Цилиндрическо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной или нескольких цилиндрических и планетарных передач | Параллельное или соосное |
Коническо-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Пересекающееся |
Червячно-планетарный | Две ступени; три ступени; четыре ступени | Сборка из одной конической и планетарных передач | Скрещивающееся |
Волновой | Одна ступень | Одна волновая передача | Соосное |
Конструкция и назначение редуктора
Механизм, служащий для понижения угловой скорости и одновременно повышающий крутящий момент, принято называть редуктором. Энергия вращения подводится на входной вал редуктора, далее в зависимости от передаточного отношения на выходном валу получаем пониженную частоту и увеличенный момент.
В состав редуктора в зависимости от типа механической передачи обычно входят зубчатые или червячные пары, центрирующие подшипники, валы, различные уплотнения, сальники и т.д. Элементы редуктора помещаются в корпус, состоящий из двух частей – основания и крышки. Рабочие механизмы редуктора при работе непрерывно смазываются маслом путем разбрызгивания, а в отдельных случаях применяется принудительный насос, помещенный внутрь редуктора.
Существует огромное количество различных типов редукторов, но наибольшую популярность получили цилиндрические, планетарные, конические и червячные редукторы. Каждый тип редуктора имеет свои определенные преимущества и недостатки, которые следует учитывать при конструировании оборудования. Основными же критериями для подбора редуктора являются определение необходимой мощности или момента нагрузки, коэффициента редукции (передаточного отношения), а также монтажного расположения источника вращения и рабочего механизма.
Особенности редукторов по виду механических передач
Мировой промышленностью выпускается огромное количество редукторов и редукторных механизмов различающихся по типу передачи, вариантам сборки и т.д. Рассмотрим основные типы механических передач, их особенности и преимущества.
Цилиндрическая передача – является самой надежной и долговечной из всех видов зубчатых передач. Данная передача применяется в редукторах, где требуется высокая надежность и высокий КПД. Цилиндрические передачи обычно состоят из прямозубых, косозубых или шевронных зубчатых колёс.
а) Прямозубая цилиндрическая передача
б) Косозубая цилиндрическая передача
в) Шевронная цилиндрическая передача
г) Цилиндрическая передача с внутренним зацеплением
Конические передачи – обладают всеми преимуществами цилиндрических зубчатых передач и применяются в случае перекрещивания входного и выходного валов.
а) Коническая зубчатая передача с прямым зубом
б) Коническая зубчатая передача с косым зубом
в) Коническая зубчатая передача с криволинейным зубом
г) Коническая гипоидная передача
Червячная передача – позволяет передавать кинетическую энергию между пересекающимися в одной плоскости валами. Основными преимуществами данной передачи является высокий показатель передаточного отношения, самоторможение, компактные размеры. Недостатками являются низкий КПД, быстрый износ бронзового колеса, а также ограниченная способность передавать большие мощности.
Гипоидная передача – она же спироидная состоит из конического червяка и диска со спиральными зубьями. Ось червяка значительно смещена от оси конического колеса, благодаря чему число зубьев одновременно входящих в зацепление в несколько раз больше чем у червячных передач. В отличие от червячной пары в гипоидной передаче линия контакта перпендикулярна к направлению скорости скольжения, что обеспечивает масленый клин и уменьшает трение. Благодаря этому КПД гипоидной передачи выше, чем у червячной передачи на 25%.
а) Червячная передача с цилиндрическим червяком
б) Червячная передача с глобоидным червяком
в) Спироидная передача
г) Тороидно-дисковая передача
д) Тороидная передача внутреннего зацепления
Волновая передача – прототипом является планетарная передача с небольшой разницей количества зубов сателлита и неподвижного колеса. Волновая передача характеризуется высоким показателем передаточного отношения (до 350). Основными элементами волновой передачи являются гибкое колесо, жесткое колесо и волновой генератор. Под действием генератора гибкое колесо деформируется и происходит зацепление зубьев с жестким колесом. Волновые передачи широко применяются в точном машиностроении благодаря высокой плавности и отсутствия вибраций во время работы.
1) Зубчатое колесо с внутренними зубьями
2) Гибкое колесо с наружными зубьями соединенное с выходным валом редуктора
3) Генератор волн
Количество ступеней редуктора
Число ступеней редуктора напрямую влияет на передаточное отношение. В червячных редукторах наиболее распространены одноступенчатые пары. Цилиндрические же редукторы, состоящие из одной ступени, применяются реже, чем двух- или трехступенчатые редукторы. В производстве редукторов все чаще применяются комбинированные передачи, состоящие из разных типов передач, например коническо-цилиндрические редукторы.
Входные и выходные валы редукторов
В редукторах обычно применяются обычные прямые валы, имеющие форму тел вращения. На валы редукторов действуют внешние нагрузки, консольные нагрузки и усилия преодоления зацеплений. Крутящий момент на валу определяется рабочим крутящим моментом редуктора или реактивным крутящим моментом привода. Консольная нагрузка определяется способом соединения редуктора с двигателем, зависит от радиального или осевого усилия на вал. В ряде машин, к которым предъявляются особые требования в отношении габаритов или веса используются редукторы с полым валом. Полый вал редуктора позволяет располагать вал исполнительного механизма внутри редуктора, тем самым отпадает необходимость использовать переходные полумуфты и т.п.
Срок службы редуктора
Срок службы редуктора зависит от правильных расчетов параметров действующей нагрузки. Также на длительность работы влияет своевременное профилактическое обслуживание редуктора, замена масла и сальников. Регулярный профилактический осмотр позволит избежать незапланированного ремонта или замену редуктора. Уровень масла контролируется через смотровое окно в редукторе и при необходимости доливается до нужного уровня.
Ниже приведена таблица зависимости срока службы редуктора от типа передачи:
Тип передачи редуктора | Гарантированный ресурс в часах |
Цилиндрическая, планетарная, коническая, цилиндро-коническая | более 25000 |
Волновая, червячная, глобоидная | более 10000 |
Устройство редуктора
Основными элементами редуктора являются:
1. Прошедшие обработку зубчатые колеса с зубьями высокой твердости. Материалом обычно служит сталь марки (40Х, 40ХН ГОСТ 4543-71). В планетарных редукторах шестерни и сателлиты изготовлены из стали марки 25ХГМ ГОСТ 4543-71. Зубчатые венцы из стали 40Х. Червячные валы изготавливаются из стали марки ГОСТ 4543-71 – 18ХГТ, 20Х с последующей цементацией рабочих поверхностей. Венцы червячных редукторов изготавливают из бронзы Бр010Ф1 ГОСТ 613-79. Гибкое колесо волнового редуктора изготовлено из кованой стали 30ХГСА ГОСТ 4543-71.
2. Валы (оси) быстроходные, промежуточные и тихоходные. Материалом является — сталь марки (40Х, 40ХН ГОСТ 4543-71). В зависимости от варианта сборки выходные валы могут быть одно- и двухконцевыми, а также полыми со шпоночным пазом. Выходные валы планетарных редукторов изготовлены заодно с водилом последней ступени. Материалом служит чугун или сталь.
3. Подшипниковые узлы. Используются подшипники качения воспринимающие большие осевые и консольные нагрузки. Применяются обычно конические роликоподшипники.
4. Шлицевые, шпоночные соединения. Шлицевые соединения чаще применяются в червячных редукторах (выходной полый вал). Шпонки применяются для соединения валов с зубчатыми колесами, муфтами и другими деталями.
5. Корпуса редукторов. Корпуса и крышки редукторов выполняются методом литья. В качестве материалов используется чугун марки СЧ 15 ГОСТ 1412-79 или сплав алюминия АЛ11. Для улучшения отвода тепла корпуса редукторов снабжаются ребрами.
Монтажное исполнение
Соосный редуктор — входной и выходной вал находятся на одной оси
Червячный редуктор — входной и выходной вал находятся под прямым углом
Цилиндрический редуктор — входной и выходной вал находятся на параллельных осях
Коническо-цилиндрический редуктор — входной и выходной вал перекрещиваются
Монтажное положение соосных цилиндрических или планетарных редукторов
Монтажное положение и вариант сборки червячных одноступенчатых редукторов
Монтажное положение и вариант сборки червячных двухступенчатых редукторов
Монтажное положение и вариант сборки цилиндрических редукторов
Методика выбора редуктора в зависимости от нагрузки
Методика выбора редуктора заключается в грамотном расчете основных параметров нагрузки и условий эксплуатации.
Технические характеристики описаны в каталогах, а выбор редуктора делается в несколько этапов:
- выбор редуктора по типу механической передачи
- определение габарита (типоразмера) редуктора
- определение консольных и осевых нагрузок на входной и выходной валы
- определение температурного режима редуктора
На первом этапе конструктор определяет тип редуктора исходя из заданных задач и конструктивных особенностей будущего изделия. На этом же этапе закладываются такие параметры как: передаточное отношение, количество ступеней, расположение входного и выходного валов в пространстве.
На втором этапе следует определить межосевое расстояние. Исходные данные на каждый тип редуктора можно найти в каталоге. Следует помнить, что межосевое расстояние влияет на способность передать момент от двигателя к нагрузке.
Консольные и осевые нагрузки определяются уравнениями, а потом сравниваются со значениями в каталоге. В случае превышения расчетных нагрузок, на какой либо вал, редуктор выбирается на типоразмер выше.
Температурный режим определяется во время работы редуктора. Температура не должна превышать + 80° гр. при длительной работе редуктора с действующей нагрузкой.
Как выбрать редуктор?
Выбор редуктора должен производить квалифицированный сотрудник т.к. неправильные расчеты могут привести к поломке редуктора или сопутствующего оборудования. Грамотный выбор редуктора поможет избежать дальнейшие затраты на ремонт и покупку нового привода. Основными параметрами для выбора редуктора как было сказано выше, являются: тип редуктора, габарит или типоразмер, передаточное отношение, а также кинематическая схема.
Определить габарит редуктора можно с помощью каталога, где указаны максимальные значения крутящего момента для каждого типоразмера. Момент действующей нагрузки на редуктор определяется следующим выражением:
где:
M2 — выходной момент на валу редуктора (Н/М)
P1 — подводимая мощность на быстроходном валу редуктора (кВт)
Rd — динамический КПД редуктора (%)
n2 — частота вращения тихоходного вала (об/мин)
Частоту вращения тихоходного вала n2 можно определить, зная значения передаточного отношения редуктора i, а также значения скорости быстроходного вала n1.
где:
n1 — частота вращения быстроходного вала (об/мин)
n2 — частота вращения тихоходного вала (об/мин)
i — передаточное отношение редуктора
Еще одним важным фактором, который следует учитывать при подборе редуктора, является величина – сервис фактор (s/f). Сервис фактор sf – это отношение максимально допустимого момента M2 max указанного в каталоге к номинальному моменту M2 зависящего от мощности двигателя.
где:
M2 max — максимально допустимый момент (паспортное значение)
M2 — номинальный момент на валу редуктора (зависит от мощности двигателя)
Значение сервис фактора (s/f) напрямую связан с ресурсом редуктора и зависит от условий работы привода.
При работе редуктора с нормальной нагрузкой, где число стартов не превышает 60 пусков в час — сервис фактор может выбираться: sf = 1.
При средней нагрузке, где число стартов не превышает 150 пусков в час — сервис фактор выбирается: sf = 1,5.
При тяжелой ударной нагрузке с возможностью заклинивания вала редуктора сервис фактор выбирается: sf = 2 и более.
Передаточное отношение и как его определить?
Основное назначение любого редуктора понижение угловой скорости подводимой на его входной вал. Значения выходной скорости определятся передаточным отношением редуктора. Передаточное отношение редуктора — это отношение скорости входного вала к скорости выходного вала.
Знать о зубчатой передаче крутящего момента
1. Функции редуктора
Вот список функций передач для конструкций механизмов. (Таблица 3-1)
Таблица 3-1 Функции редуктора| Характерные функции шестерен | Объяснение |
| Изменить направление вращающегося вала | (уже объяснено) |
| Преобразование вращательного движения в линейное движение | (уже объяснено) |
| Изменить направление вращения (по часовой стрелке / против часовой стрелки) | (уже объяснено) |
| Изменение количества оборотов (увеличение / уменьшение скорости) | (уже объяснено) |
| Изменить усилие поворота (увеличить / уменьшить крутящий момент) | См. Эту главу |
Вы можете увеличивать или уменьшать крутящий момент шестерни (вращающее усилие), изменяя количество оборотов.
2. Определение крутящего момента (крутящего момента)
Крутящий момент — это сила поворота при приложении нагрузки F (Н) на расстоянии L (мм) от центра вращения. Крутящий момент T выражается следующей формулой в Н · мм (Ньютон-миллиметр). (Рисунок 3-1)
Рисунок 3-1 Крутящий момент
Крутящий момент T увеличивается по мере увеличения L (расстояния от центра вращения), даже если нагрузка F мала. С другой стороны, крутящий момент T увеличивается по мере увеличения нагрузки F, даже если L (расстояние от центра вращения) короткое.
Другими словами, крутящий момент T — это коэффициент, определяемый L (расстояние от центра вращения) и нагрузкой F.
3. Как определить передачу крутящего момента (без учета КПД машины)
Крутящий момент трансмиссии изменяется при увеличении или уменьшении скорости. Как правило, при уменьшении скорости небольшой крутящий момент на входной стороне передается как больший крутящий момент на выходной стороне. Расчет крутящего момента зависит от количества зубьев. Позвольте мне объяснить с помощью диаграммы, используя диаметры делительной окружности.
Крутящий момент рассчитывается следующим образом:
- Получите нагрузку F точки зацепления (на радиусе делительной окружности шестерни A) входного крутящего момента.
- Получите крутящий момент выходной стороны от нагрузки F точки зацепления зубьев (радиус делительной окружности шестерни B).
Состояние
Номинальный крутящий момент двигателя: TA = 600 Н · мм (0,6 Н · м)
Диаметр делительной окружности шестерни A φ20
Диаметр делительной окружности шестерни B φ40
Расчет передачи крутящего момента
Нагрузка точки зацепления шестерни A: F = TA / LA = 60 (Н)
Крутящий момент на выходной стороне: TB = F × LB = 60 (Н) × 20 (мм) = 1200 (Н · мм) )
Рисунок 3-2 Схема расчета передачи крутящего момента шестерни
Как видно из рисунка 3-2, при уменьшении скорости выходного вала от входного на 1/2 выходной крутящий момент увеличивается в 2 раза.
4. Учет эффективности машины
Как показано в предыдущей главе, вы можете рассчитать количество оборотов шестерни по количеству зубьев.
Однако вы не можете рассчитать крутящий момент трансмиссии просто, как показано ранее, по следующим причинам:
- При зацеплении зубьев выделяется тепло, и теряется энергия.
- Ударный звук из-за зацепления зубьев и потери энергии.
Следовательно, крутящий момент (сила поворота) уменьшается на столько же, сколько теряется энергия, как указано выше.
Отношение входных и выходных усилий шестерен называется «КПД машины», и его приблизительное значение известно в зависимости от типа шестерни. (Таблица 3-2)
| Взаимосвязь двух валов | Название шестерни | КПД машины η (%) |
|---|---|---|
| параллельный вал | цилиндрическое прямозубое колесо | 98.0 — 99,5 * КПД косозубой шестерни меньше, чем цилиндрической шестерни, так как зубья наклонены и сила создается в направлении тяги. |
| косозубая шестерня | ||
| двойная косозубая шестерня | ||
| внутренняя передача | ||
| стойка | ||
| винтовая стойка | ||
| пересекающийся вал | прямая коническая передача | 98.0–99,0 |
| спирально-коническая шестерня | ||
| косой вал | червячный редуктор | 30,0 — 90,0 |
| винтовая передача | 7 |
ПЕРЕДАЧИ ПЕРЕДАЧ. Приведение шестерен в действие Обратное направление вращения Увеличьте или уменьшите скорость вращения Переместите вращательное движение на другую ось.
Презентация на тему: «ПЕРЕДАЧИ.Приведение в действие шестерен Обратное направление вращения Увеличьте или уменьшите скорость вращения Переместите вращательное движение на другую ось »- стенограмма презентации:
1 ПЕРЕДАЧИ
2 Приведение в действие шестерен Обратное направление вращения Увеличьте или уменьшите скорость вращения Переместите вращательное движение на другую ось Поддерживайте синхронизацию вращения двух осей
3 Понимание передаточного числа Окружность круга — диаметр, умноженный на Пи –1.27 дюймов x 3,14 = 4,0 дюйма Окружность диаметром 0,635 дюйма имеет окружность 2 дюйма. Меньшая шестерня вращается дважды за каждый оборот более крупной шестерни, соотношение шестерен 2: 1.
4 Зубья шестерни Предотвращают проскальзывание шестерен — синхронизирует Подсчет зубьев на каждой шестерне определяет точное передаточное число — если у одного 60 зубьев, а у другого 20, то передаточное отношение составляет 3: 1 Небольшое несовершенство диаметра шестерни не имеет значения, передаточное отношение контролируется числом зубов
5 Зубчатые передачи Для создания больших передаточных чисел несколько шестерен соединяются вместе.
6 Червячная передача Создает очень высокое передаточное число Резьбовой вал входит в зацепление с зубьями шестерни За каждый оборот вала шестерня перемещает один зуб, если шестерня имеет 40 зубцов, достигается передаточное число 40: 1.
7 Планетарная зубчатая передача Допустим, вам нужно соотношение передач 6: 1 с входной и выходной шестернями, движущимися в одном направлении. Планетарные передачи очень компактны и производят тот же эффект.
8 Планетарная зубчатая передача. Различные передаточные числа могут быть достигнуты в зависимости от того, какая передача является входной и выходной, а какая остается неподвижной. Автоматическая коробка передач использует этот набор передач для достижения различных передаточных чисел для каждого диапазона передач.Использование муфт и тормозных лент для удержания различных частей редуктора в неподвижном состоянии и переключения входов и выходов
9 Синхронизация шестерен Чтобы две шестерни, находящиеся на большом расстоянии друг от друга, вращались в одном направлении, поместите между ними большую шестерню или используйте две маленькие шестерни между ними. Более практичным подходом является использование зубчатого ремня или цепи.
MECh2200 Несколько шестерен Скорость любой ведомой шестерни определяется путем расчета передаточного числа, используя ведомую шестерню в качестве выходной шестерни вместе с.
Презентация на тему: «МЭЧ2200 с несколькими шестернями. Скорость любой ведомой шестерни определяется путем расчета передаточного числа с использованием ведомой шестерни в качестве выходной шестерни вместе с.» — стенограмма презентации:
1 MECh2200 Несколько шестерен Скорость любой ведомой шестерни определяется путем расчета передаточного числа с использованием ведомой шестерни в качестве выходной шестерни вместе с входной шестерней и игнорирования всех других шестерен между ними. ременная или цепная передача.
2 MECh2200 Независимо от того, является ли дополнительная шестерня в зубчатой передаче холостым или приводит в движение дополнительный вал, метод определения скорости и крутящего момента остается прежним. Промежуточные шестерни не влияют на крутящий момент или скорость ведомого вала.Если вы рассчитываете передаточное число, умножая передаточные числа каждой пары соседних шестерен вместе, влияние холостых шестерен нивелируется.
3 MECh2200 Число зубьев обеих промежуточных шестерен используется в формуле дважды.Они нейтрализуют друг друга.
4 МЕЧ2200 Показанная шестерня имеет три ведомые шестерни, каждая из которых приводит в движение отдельный вал с отдельной нагрузкой. У него одна настоящая холостая передача.
5 MECh2200 Скорость каждого выходного вала теперь может быть рассчитана отдельно с использованием его собственного передаточного числа. Промежуточная шестерня не влияет на частоту вращения выходного вала.Скорость одного выходного вала не влияет на скорость других выходных валов, потому что они действуют как холостые передачи по отношению к другим валам.
Контроль угла поворота серводвигателя путем регулировки коэффициента ШИМ.
Презентация на тему: «Управление углом поворота серводвигателя путем регулировки коэффициента ШИМ.» — стенограмма презентации:
1 Контроль угла поворота серводвигателя путем регулировки коэффициента ШИМ.
УПРАВЛЕНИЕ СЕРВОДВИГАТЕЛЕМ Управление углом поворота серводвигателя путем регулировки коэффициента ШИМ.
2 Указатель Что такое серводвигатель? Как работают серводвигатели?
Информация о серводвигателе Hitec HS-311 Standard. Алгоритм управления двумя серводвигателями. Принципиальная схема и анализ работы схемы.
3 Что такое серводвигатель? Сервопривод — это небольшое устройство, которое включает трехпроводный двигатель постоянного тока, зубчатую передачу, потенциометр, интегральную схему и подшипник выходного вала (показано на рисунке).Из трех проводов, выходящих из корпуса двигателя, один предназначен для питания, один — для заземления и один — для линии управляющего входа. Вал сервопривода можно установить в определенные угловые положения, посылая кодированный сигнал. Пока кодированный сигнал существует на входной линии, сервопривод будет поддерживать угловое положение вала. При изменении кодированного сигнала изменяется угловое положение вала. Сервоприводы бывают разных размеров, но используют похожие схемы управления и чрезвычайно полезны в робототехнике.Моторы маленькие и чрезвычайно мощные для своего размера. Он также потребляет мощность, пропорциональную механической нагрузке. Таким образом, слегка загруженный сервопривод не потребляет много энергии. Очень часто сервоприводы используются в моделях с радиоуправлением, таких как автомобили, самолеты, роботы и марионетки. Они также используются в мощных парусных лодках большой грузоподъемности. Сервоприводы рассчитаны на скорость и крутящий момент. Обычно есть два сервопривода одного типа, один ориентирован на скорость (жертвуя крутящим моментом), а другой — крутящим моментом (жертвуя скоростью).
4 Сервоприводы состоят из трех основных частей; двигатель, потенциометр (переменный резистор), подключенный к выходному валу, и плата управления. Потенциометр позволяет схеме управления контролировать текущий угол серводвигателя. Двигатель через ряд шестерен одновременно вращает выходной вал и потенциометр. Потенциометр подается в схему сервоуправления, и когда схема управления определяет правильность положения, она останавливает двигатель.Если схема управления обнаруживает, что угол неправильный, она поворачивает двигатель в правильном направлении, пока угол не станет правильным. Обычно сервопривод используется для управления угловым перемещением от 0 до 180 градусов. Он не может механически (если не модифицирован) поворачиваться дальше из-за механического упора, установленного на главной выходной шестерне. Мощность, подаваемая на двигатель, пропорциональна расстоянию, которое ему необходимо преодолеть. Таким образом, если валу необходимо повернуться на большое расстояние, двигатель будет работать на полной скорости.Если нужно немного повернуть, двигатель будет работать с меньшей скоростью. Это называется пропорциональным управлением.
5 Как работают серводвигатели?
Сервоприводы управляются путем отправки им импульса переменной ширины. Управляющий провод используется для отправки этого импульса. Параметры этого импульса таковы, что он имеет минимальный импульс, максимальный импульс и частоту повторения. Учитывая ограничения вращения сервопривода, нейтраль определяется как положение, в котором сервопривод имеет точно такое же количество потенциального вращения в направлении по часовой стрелке, как и в направлении против часовой стрелки.Важно отметить, что разные сервоприводы будут иметь разные ограничения на их вращение, но все они имеют нейтральное положение, и это положение всегда составляет около 1,5 миллисекунд (мс). Угол определяется длительностью импульса, подаваемого на провод управления. Это называется широтно-импульсной модуляцией. Сервопривод ожидает увидеть импульс каждые 20 мс. Длина импульса определяет, как далеко вращается двигатель. Например, импульс 1,5 мс заставит двигатель повернуться в положение 90 градусов (нейтральное положение).Когда этим сервоприводам будет дана команда двигаться, они переместятся в положение и сохранят это положение. Если внешняя сила давит на сервопривод, когда сервопривод удерживает позицию, сервопривод будет сопротивляться выходу из этого положения. Максимальное количество силы, которое может оказать сервопривод, — это номинальный крутящий момент сервопривода. Однако сервоприводы не будут оставаться на своем месте вечно; импульс положения должен быть повторен, чтобы сервопривод оставался на месте.
6 Стандартные подробные технические характеристики Hitec HS-311 Система управления: + Регулировка ширины импульса 1500 мксек. Требуемая нейтраль Импульс: 3-5 вольт от пика до пика Рабочее напряжение прямоугольной формы: вольт Диапазон рабочих температур: от -20 до +60 градусов C Рабочая скорость (4.8 В): 0,19 с / 60 градусов без нагрузки Рабочая скорость (6,0 В): 0,15 с / 60 градусов без нагрузки Момент срыва (4,8 В): 42 унции / дюйм (3,0 кг / см) Момент срыва (6,0 В): унций / дюйм (4,5 кг / см) Потребление тока (4,8 В): 7,4 мА / холостой ход и 160 мА при работе без нагрузки Потребление тока (6,0 В): 7,7 мА / холостой ход и 180 мА при работе без нагрузки Ширина зоны нечувствительности: 5 мкс Рабочий угол: 40 Град. односторонний импульс 400 мс Направление: по часовой стрелке / импульсное перемещение от 1500 до 1900 мкс Тип двигателя: порошковая металлическая щетка Потенциометр Привод: 4 ползунка / прямой привод Тип подшипника: верхний / смоляная втулка Тип шестерни: нейлон 360 Возможность изменения: да Длина соединительного провода: 1181 дюйм (300 мм) Размеры: 1,57 дюйма x 0,79 дюйма x 1,44 дюйма (40 x 20 x 36,5 мм) Вес: 1,52 унции (43 г)
7 Когда импульс отправляется на HS-311, который меньше примерно 0
Когда импульс отправляется на HS-311, который меньше примерно 0,6 мс, сервопривод не вращается ни в какое положение и удерживает свой выходной вал в нулевая степень. Если импульс шире 0,6 мс, сервопривод вращается. Например, если ширина импульса равна 1,5 мс, HS-311 будет вращаться на 90 градусов, а если ширина импульса равна или больше 2 мс, HS-311 будет вращаться на 180 градусов.Минимальная ширина и максимальная ширина импульса, который заставит сервопривод повернуться в допустимое положение, являются функциями каждого сервопривода. Разные марки и даже разные сервомашинки одной марки будут иметь разные максимумы и минимумы. Обычно минимальный импульс имеет ширину около 1 мс, а максимальный — 2 мс.
9 Когда программа выполняется, данные начинают считываться из последовательного порта.
Когда программа выполняется, данные начинают считываться из последовательного порта.Алгоритм программы состоит из двух циклов, и после первого чтения данных из последовательной шины первый цикл программы ищет символы звездочки (*) и косой черты (/) для определения данных, которым принадлежит модуль ШИМ. На втором этапе программы данные записываются в соответствующий модуль ШИМ. Данные, поступающие из последовательного порта, сначала проверяются на наличие звездочки. Если данные закодированы в виде звездочки в двоичном формате, следующие данные будут записаны в модуль PWM1 PIC 16F877, затем программа перейдет к запуску для другой операции чтения.Если на этот раз первый символ данных, поступающих из USART, не является символом звездочки ASC II, тогда программа проверяет данные для первого символа, который может быть символом косой черты ASC II. Если символ косой черты, то следующие двоичные данные будут отправлены в модуль PWM2 в качестве информации о данных PWM, после чего программа снова запустит запуск. Если данные, поступающие из последовательного порта, не являются ни звездочкой, ни косой чертой, тогда программа начинает новую операцию чтения и следует по пути первого цикла, пока не будет удовлетворен один из этих двух критериев.Алгоритм Visual Basic части схемы рисовать не нужно. Если нам нужно что-то указать об этом; для одновременной работы двух серводвигателей сначала установите значение ШИМ для двигателя 2, затем установите ШИМ для двигателя 1 и удерживайте кнопку нажатой в течение требуемого времени работы. Пока кнопка мыши нажата, двигатели удерживают заданные позиции в сигналах ШИМ.
11 Период ШИМ = [(PR2) + 1] • 4 • TOSC • (Предварительное масштабное значение TMR2)
Режим ШИМ PIC16F877 В режиме широтно-импульсной модуляции вывод CCPx PIC16F877 выдает выходной сигнал ШИМ с разрешением до 10 бит.Поскольку вывод CCP1 мультиплексирован с защелкой данных PORTC, бит TRISC <2> должен быть очищен, чтобы вывод CCP1 стал выходом. При настройке модуля CCP для работы с ШИМ необходимо предпринять следующие шаги: 1. Установите период ШИМ, записав его в регистр PR2. 2. Установите рабочий цикл ШИМ, записав в регистр CCPR1L и биты CCP1CON <5: 4>. 3. Сделайте вывод CCP1 выходом, сбросив бит TRISC <2>. 4. Установите значение предварительного масштабирования TMR2 и включите Timer2, записав в T2CON. 5.Настройте модуль CCP1 для работы с ШИМ. Период ШИМ указывается записью в регистр PR2. Период ШИМ можно рассчитать по следующей формуле: Период ШИМ = [(PR2) + 1] • 4 • TOSC • (Предварительное масштабное значение TMR2)
Измерение угловой скорости пропеллера с помощью видеокамеры с использованием электронного рольставни
Бесконтактное измерение вращательного движения имеет преимущества перед традиционным методом измерения вращательного движения посредством установки на объекте некоторых устройств, таких как датчик угла поворота.Камеры могут использоваться в качестве датчиков дистанционного контроля или проверки для измерения угловой скорости воздушного винта из-за их обычной доступности, простоты и потенциально низкой стоимости. Недостатком измерения с помощью камер является обработка массивных данных, генерируемых камерами. Чтобы уменьшить количество данных, собираемых камерой, камера, использующая ERS (электронный скользящий затвор), применяется для измерения угловых скоростей, превышающих скорость камеры. Эффект рольставни может вызвать геометрическое искажение изображения, когда пропеллер вращается во время захвата изображения.Чтобы выявить взаимосвязь между угловой скоростью и искажением изображения, была создана модель вращения. Предлагаемый метод применен для измерения угловых скоростей двухлопастного и многолопастного винта. Результаты экспериментов показали, что этот метод позволяет обнаруживать угловые скорости, превышающие скорость камеры, и точность является приемлемой.
1. Введение
Вращение — это одно из основных движений, которое часто встречается в таких машинах, как двигатели, шестерни и другие колеса.Вращение должно находиться под контролем, чтобы машины оставались в исправном состоянии, и многие механические поломки вызваны вращательным движением. Поэтому важно измерить угловую скорость. Для измерения угловых скоростей широко используются датчики контактного типа, такие как механические тахометры, оптические тахометры, фотоэлектрические энкодеры и оптические энкодеры [1]. Эти методы обычно основаны на механическом контакте, и в результате на них легко влияет вращение цели или небольшая инерция цели.За последние двадцать лет были разработаны бесконтактные методы, такие как томография, ультразвук, лазер и компьютерное зрение [2]. Усовершенствованные датчики могут преодолеть недостатки датчиков контактного типа, и компьютерное зрение может быть более широко использовано по сравнению с другими бесконтактными датчиками.
За последнее десятилетие некоторые исследователи сосредоточились на угловых измерениях на основе компьютерного зрения. Wang et al. [3] измеряли угловые скорости двигателя с нечеткими изображениями, содержащими информацию о движении. Угловые скорости могут быть извлечены из этих размытых движущихся изображений в полярных координатах.Ait-Aider et al. [4, 5] получили позу и скорость объекта с помощью камеры с электронным скользящим затвором (ERS). Его метод был основан на предположении, что все линии в реальном мире прямые, а эти линии искажены на изображении, полученном камерой ERS. Magerand et al. [6] измерили позу и движение объекта на одном изображении ERS с автоматическим сопоставлением 2D-3D. Он и Вэй [7] измерили скорость вала с помощью камеры ERS. Чжу и Ю [2] измерили угловые скорости объекта с помощью преобразования Хафа.
Измерение угловой скорости с помощью компьютерного зрения также имеет некоторые недостатки, такие как качество воздуха в окружающей среде и трудоемкость процесса. Есть два способа повысить скорость обработки. Один из способов — уменьшить разрешение камеры, но этот способ не соответствует тенденции развития камер [8, 9]. Другой способ — снизить скорость камеры [10]. Другими словами, он измеряет высокоскоростное вращение с помощью низкоскоростной камеры. Но когда угловая скорость намного превышает скорость камеры, трудно определить угол неоднозначности или искажения изображения.Есть несколько исследований по измерению высокоскоростного вращения с помощью низкоскоростной камеры. Скорость ряда камеры ERS намного выше скорости камеры. Это специальное свойство поможет измерить высокоскоростное вращение некоторых объектов, таких как колеса или пропеллеры, которые имеют симметричную структуру. Эти объекты очень распространены в машинах, и их легко анализировать для определения угловых скоростей. Предыдущие исследования не пытались измерить высокоскоростное вращение камерой ERS [4–7].
В этом документе камера ERS работает как датчик для измерения угловой скорости пропеллера, который вращается быстрее, чем скорость камеры. Для измерения угловой скорости создается симуляция, демонстрирующая с помощью изображений, что пропеллер вращается с разными скоростями. По геометрическим особенностям изображений предлагается алгоритм расчета угловой скорости воздушного винта. Также демонстрируются эксперименты для проверки и проверки предложенного метода измерения угловой скорости.Оставшаяся часть теста организована следующим образом. В разделе 2 представлен принцип работы ERS, а также предложен алгоритм, проверенный на моделировании. В разделе 3 установлены два эксперимента для проверки предложенного метода в реальных условиях. Наконец, раздел 4 завершает статью.
2. Метод
В области цифровой обработки сигналов теорема Найквиста – Шеннона устанавливает достаточное условие для частоты дискретизации, которое позволяет дискретной последовательности выборок захватывать всю информацию из непрерывного сигнала конечной полосы пропускания. .Достаточная частота дискретизации как минимум вдвое превышает максимальную частоту дискретизации; более того, на практике частота дискретизации обычно четырехкратная. Чтобы измерить угловую скорость камерой, необходимо обработать большой объем данных. Чтобы уменьшить количество данных, генерируемых камерой, можно использовать низкоскоростную камеру с ERS. Камера ERS имеет специальную функцию, которая записывает изображения строка за строкой, и эта функция может некоторым образом увеличить скорость камеры.
2.1. Принцип работы ERS
Камера ERS — это тип CMOS-датчика изображения, который очень часто используется в мобильных телефонах.Количество сигнала, генерируемого датчиком изображения, зависит от количества света, попадающего на изображения, с точки зрения экспозиции.
Следовательно, для управления интенсивностью и продолжительностью экспонирования требуется встроенный электронный затвор. Затвор CMOS бывает двух типов: глобальный затвор и рольставни. С датчиками изображения с глобальным затвором каждая строка пикселей изображения экспонируется одновременно. Таким образом, в результирующем изображении нет артефактов движения. При использовании датчиков изображения с рольставнями, ряды изображения экспонируются последовательно, начиная сверху и постепенно снизу.Для каждой строки изображения время интегрирования и задержка строки фиксированы, что приводит к равномерному смещению времени по всему кадру. Когда направление движения объекта ортогонально направлению строки изображения, на захваченном изображении возникают визуальные артефакты. Принцип работы ERS показан на рисунке 1. Поскольку датчик изображения эффективно интегрирует каждую строку массива пикселей в разный момент времени, статический фонарный столб, расположенный вертикально по отношению к скоростной автомагистрали, становится наклонным, как показано на рисунке 1 (b ).С такими характеристиками камеры ERS низкоскоростная камера может записывать больше информации о быстро движущемся объекте. Хотя в некоторых работах это свойство применялось для измерения линейного движения или вибрации [7, 11], в большинстве работ пытались устранить этот эффект на изображении [12–14]. В данной статье это свойство используется для измерения угловой скорости пропеллера.
2.2. Фоновая сегментация
Перед вычислением скорости вращения воздушный винт должен быть сегментирован от фона.Модель гауссовой смеси (GMM) [15] используется в качестве неконтролируемого обнаружения изменения изображения для извлечения винта. Максимизация ожидания (EM) [16] — популярный метод, используемый для определения параметров смеси с заранее заданным числом компонентов. Алгоритм EM предоставляет особый способ, который реализует оценку максимального правдоподобия для параметра в GMM. Но M-шаг алгоритма EM не может оценить априорное распределение в закрытой форме из-за сложности оценки максимального правдоподобия.Следовательно, для каждой итерации в EM-алгоритме к M-шагу применяется корректирующий шаг [17] проекции с целью, чтобы априорные вероятности были положительными и в сумме равнялись единице.
Сегментация с помощью GMM имеет много дефектов, таких как дыры и шумы на изображении. Перед сегментацией изображения удаляются с помощью метода, предложенного Xu et al. [18]. Расчет вращения во многом зависит от геометрических характеристик винта, сегментированного от фона. Эти дефекты гребного винта могут привести к ошибкам в результатах расчетов.Отверстия должны быть заполнены, а небольшая изолированная область должна быть стерта.
2.3. Расчет угловой скорости
В качестве измеряемой величины выбран гребной винт, как показано на рисунке 2. Этот гребной винт имеет две изолированные лопасти, и его начальный угол определяется величиной. Для демонстрации закономерностей, записанных камерой ERS, моделирование показано на рисунке 3 (в этой статье все единицы угловой скорости — об / с). Пропеллер находится в центре одиночного изображения размером 1000 × 1000.Последовательность экспозиции камеры ERS — сверху вниз. Время задержки строки составляет 996 мкм с, а время экспонирования каждой строки составляет 4996 мкм с. Задержки кадра нет, поэтому время всего изображения составляет одну секунду. Пропеллер вращается по часовой стрелке с разными скоростями, как показано на рисунке 3. Начальный угол изображений первого ряда на рисунке 3 равен 0,25; начальный угол изображений второго ряда на рис. 3 равен 0,5. Чтобы извлечь угловую скорость из одного изображения, процедура состоит из двух частей: поиск центра винта и определение угла поворота.Все операции основаны на предположении, что двухлопастной винт имеет центральную симметрию.
Точки на разных кромках лезвия группируются в разные наборы:, где — количество изолированных лезвий. Точка выбирается на изображении случайным образом. Расстояние от до точки в
Пусть, где max () — математическая функция для нахождения максимальных значений входных данных. Если может удовлетворять условию в (2), центр есть.
Но этот метод вычисления центра чувствителен к шуму и в некоторых ситуациях неоднозначен, как показано на Рисунке 3 (iic, iid).Таким образом, этот метод нельзя использовать для поиска центра, но он может работать как быстрый поиск и сужение области вращающегося центра. Пусть
Угловая скорость и угловое ускорение ГЛАВА 9 ВРАЩЕНИЕ. Угловая скорость и угловое ускорение. ! уравнения вращательного движения
1 Угловая скорость и угловое ускорение ГЛАВА 9 ВРАЩЕНИЕ! r i ds i dθ θ i Угловая скорость и угловое ускорение! уравнения вращательного движения Крутящий момент и Момент инерции! Закон Ньютона для вращения Определение момента инерции Кинетическая энергия вращения! мощность Катящиеся объекты (без проскальзывания) Длина дуги, перемещаемая i-м элементом во вращающемся жестком недеформируемом диске, составляет: ds i = r i dθ, где dθ в радианах.Угловая скорость вращающегося диска определяется как: ω = dθ dt, поэтому линейная скорость i-го элемента (в направлении касательной) равна: v i = ds i dt = r iω.
2 Какая связь между угловой и линейной скоростью двух точек на одном диске? ОБСУЖДЕНИЕ ПРОБЛЕМА [9.1]: у вас есть друг, который живет в Миннесоте, а вы живете во Флориде. Когда Земля вращается, ваша линейная скорость принадлежит ей, а ваша угловая скорость — ее.RMM0VD.mov Угловая скорость ω одинакова для всех точек на диске, но линейная (или касательная) скорость — нет. Посмотрите, v = rω, так как r> r 1, то v> v 1. A: меньше; равно B: равно; больше, чем C: больше, чем; меньше D: меньше; больше, чем E: больше, чем; равно
3 Если угловая скорость изменяется, возникает угловое ускорение … Угловое ускорение диска: α = dω dt = d dt. dθ dt = d θ dt, а тангенциальное ускорение i-го элемента равно: a it = dv i dt = r i dω dt = r iα.Но поскольку i-й элемент движется по кругу, он испытывает радиальное (центростремительное) ускорение :! r i a ir (= a ic) = v i r i = r i ω. Результирующее линейное ускорение равно dθ Угловая скорость (ω) (вектор)! а! ds i a i it θ i! воздух! а ир а! Это! а я = а ир + а это. Размерность: ω 1 [T] (проверьте: v i = r i ω [L] 1 [T] = [L] [T]). Единицы: рад / с Угловое ускорение (α) (вектор) Размер: α 1 [T] Единицы: рад / с
4 СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМ И ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ Линейное движение a постоянное Вращательное движение α constant v = v! + при ω = ω! + αt (!) = v! t + 1 при (θ θ!) = ω! t + 1 αt v = v! + а (!) ω = ω! + α (θ θ!) Видите ли, они очень похожи на вопрос 9.1: Диск радиусом 1 см, первоначально находящийся в состоянии покоя, начинает вращаться вокруг своего носа с постоянным угловым ускорением 3,00 рад / с. Через 5 с, каковы (а) угловая скорость диска и (б) тангенциальное и центростремительное ускорение точки на периметре диска? (c) Сколько оборотов сделал диск за эти 5 с?
5 r r = 0,1 м: ω! = 0: θ! = 0: t = 5 с α = 3,00 рад / с. ω = ?: θ = ?: a t = ?: a c =? а) ω = ω! + αt = (3,00 рад / с) (5 с) = 15.0 рад / с. (б) v i = r i ω = (0,1 м) (15,0 рад / с) = 1,80 м / с (линейный). тангенциальное ускорение: a t = r i α = (0,1 м) (3,00 рад / с) = 0,36 м / с. центростремительное ускорение: ac = ri ω (Проверить … ac = vr = (0,1 м) (15,0 рад / с) = 7,0 м / с. = (1,80 м / с) 0,1 м = 7,0 м / с.) применения ремень или цепь натягивается или наматывается на шкив или шестерню … vtvtat R Когда струна (цепь или ремень) удаляется (или добавляется), ее мгновенная скорость совпадает с тангенциальной скоростью на ободе колесо, при условии отсутствия проскальзывания: i.е., v t = Rω. (в) (θ θ!) = ω! t + 1 αt = 1 (3,00 рад / с) (5 с) = 37,5 рад, n = 37,5 рад π = 5,97 об. Кроме того, при тех же условиях мгновенное ускорение струны такое же, как тангенциальное ускорение на ободе колеса: то есть a t = dv t dt = R dω dt = Rα.
6 Как мы видели в главе 4, сила вызывает изменение движения. Однако сила не всегда вызывает изменение вращательного движения. Именно крутящий момент вызывает изменение вращательного движения.Рассмотрим массу m, прикрепленную к безмассовому жесткому стержню, который вращается вокруг ais O. Показанная сила F заставит массу вращаться. O Величина крутящего момента, создаваемого силой F, действующей на m, равна: τ = lf = (r sin θ) f, где l называется плечом рычага. Плечо рычага — это перпендикулярное расстояние от оси вращения (O) до линии действия силы. ПРИМЕЧАНИЕ: если «F проходит через O, т. Е. L = 0, то τ = 0 и не будет изменений во вращательном движении. Lr θ m» F l = r sin θ Размер: τ [L] [M] [L ] [T] Единица: N m = [M] [L] [T] (вектор) Сформируйте радиальную и тангенциальную составляющие силы: O l Тогда τ = lf = (r sin θ) f = r (fsin θ) я.е., τ = rf t. Примечание: радиальная составляющая F r, проходящая через проход вращения, не создает крутящего момента и, следовательно, не вызывает вращения; только тангенциальная составляющая F t создает крутящий момент, который приводит к вращению. rm «FF t = F sin θ O lr θ m» FF r = F cosθ
7 F t = F sin θ O rl θ m «FF r = F cosθ Закон Ньютона s nd говорит нам, что тангенциальная составляющая силы F t создает тангенциальное ускорение при, т. Е. F t = ma t.τ = rf t = mra t. Но, как было сказано ранее, тангенциальное (линейное) ускорение связано с угловым ускорением α, а именно: a t = rα. τ = mra t = mr α. Таким образом, крутящий момент (τ) вызывает угловое ускорение (α). Сверху для каждого отдельного элемента массы имеем O r i Δm i τ i = (Δm i) r i α, где τ i — чистый крутящий момент на i-м элементе. Суммируя все элементы, общий чистый крутящий момент на объекте равен: τ net = i τ i = i (δm i) ri α = (Δm i) r (ii) α = Iα, где мы называем I = (Δm i) rii МОМЕНТ ИНЕРЦИИ.Это закон Ньютона для вращения, то есть τ net = Iα. Жесткий объект, который вращается вокруг аэродрома, можно представить как набор небольших отдельных элементов массы Δm i (), каждый из которых движется по круговой траектории с радиусом r i, где r i отсчитывается от аэродрома вращения. Чистый вечный крутящий момент, действующий на тело, вызывает угловое ускорение α этого тела, задаваемое Iα, где I — момент инерции. (а именно: F net = i F i = ma.)
8 Момент инерции… так о чем все это? Размерность: I [M] [L] Единицы: кг · м (скаляр) Каждый объект имеет момент инерции относительно оси вращения. Его значение зависит не только от массы, но и от того, как масса распределяется вокруг этого прохода. Для дискретного набора из n объектов момент инерции относительно вращения ais равен: Для непрерывного объекта: I = Предел Δm i 0 I = n I n = n m n r n. i (Δm i) r i = r dm, Вопрос 9: Найти момент инерции однородного тонкого стержня длины l и массы M, вращающегося вокруг оси, перпендикулярной стержню, и через его центр.y l, где m является функцией r.
9 ярдов [1] Убедитесь, что момент инерции стержня массы M и длины l относительно одного конца равен y. Стержень представляет собой сплошной объект, поэтому момент инерции равен I = r dm = = l dm. . = l Масса на единицу длины стержня равна M l, поэтому масса d 0 l I = 1 3 Ml. маленький элемент длины d равен dm = (M l) d. Подставляя вместо dm, интеграл принимает вид I = = l = M l () M l d = M l = l () l3 3 () 3 4 (l3) 4 = 1 1 Ml.l l [] Покажите себе, что момент инерции стержня массы M и длины l около a составляет одну треть расстояния от одного конца y d l 3 0 l 3 I = 1 9 Ml.
10 r Момент инерции определяется как I = r dm. Рассмотрим r 1 Вопрос 9.3: Найдите момент инерции круглого диска, показанного ниже, вращающегося вокруг оси, перпендикулярной плоскости, и через ее центр. Масса диска 1,50 кг. 10 см 0 см кольцо радиусом r и шириной dr.Если масса объекта равна M, масса кольца равна dm = M πrdr π r r 1 (), где r 1 и r — внутренний и внешний радиусы объекта. Затем, подставив вместо dm, r I = r M πrdr π rr 1 = r 1 M rr (1) r 4 4 r () = M rr (1) r = r1 rr 1 r 3 dr M rr (1) r 4 r 4 (1) = M rr (1) rr (1) r + r (1) = 1 M r + r (1).
11 I = 1 M r + r (1) = 1 (1,50 кг) ((0,0 м) + (0,10 м)) = кг · м. [1] Если r 1 = 0, то I disk = 1 MR, где R — радиус диска (= r).R Конечно, но каково значение «я»? Помните, из главы 4 … Массовая мера сопротивления изменению линейного движения, например, насколько сложно начать или остановить линейное движение. Момент инерции — мера сопротивления изменению вращательного движения, то есть насколько сложно начать или остановить вращательное движение. [] Для тонких обручей r 1 r = R, тогда I обруч = 1 M R () = MR. R При одинаковой толщине дисков моменты инерции не зависят от толщины. Таким образом, эти выемки также относятся к цилиндрам и трубкам.Одинаковые моменты инерции Различные моменты инерции RMM04VD1.MOV
12 Значения момента инерции для простых форм … Тонкий стержень I = 1 1 ML Плита I = 1 1 M (a + b) LL Тонкий стержень I = 1 3 ML Полый цилиндр I = 1 M (R + r) aba Плита I = 1 3 Ma b Полая сфера I = 3 MR Вопрос 9.4: Линейка длиной 1 м имеет массу 0,5 кг. К 100-сантиметровому концу линейки прикрепляется груз весом 5 кг. Каков его момент инерции относительно конца 0 см? Тонкостенный цилиндр I = MR Сплошной цилиндр I = 1 MR Твердая сфера I = 5 MR
13 b O O Комбинированный момент инерции равен I = I линейка + I масса, где I линейка и I масса рассчитываются относительно O O.Поскольку a >> b, мы предполагаем, что линейка метра представляет собой стержень (а именно: вопрос 9.) с I = 1 3 млн лет назад около 0 O. I линейка = 1 3 млн лет = 1 (0,5 кг) (1 м) 3 = кг · м . Момент инерции массы 5 кг относительно O O равен I mass = ma = (5,0 кг) (1 м) = 5,0 кг · м. Таким образом, суммарный момент инерции линейки и массы равен I линейке + I масса = кг · м. ПРОБЛЕМА ДЛЯ ОБСУЖДЕНИЯ 5 кг [9.]: Пара линейок для счетчиков размещается так, чтобы их нижний конец был прижат к стене. К верхнему концу одной из линейок прикреплена большая масса. Если одновременно отпустить линейки счетчиков и позволить упасть, какая из них упадет на пол первой? A: Измерительная линейка с массой.B: Измерительная линейка без массы. C: Они падают на пол одновременно.
14 Теорема о перпендикулярном ais: Теорема о параллельном ais: I cm I d Обычно момент инерции задается для ais, проходящего через центр масс (см) объекта. Что, если объект вращается вокруг прохода, для которого нам неизвестен момент инерции? Момент инерции относительно общего (параллельного) ais определяется как: I = I cm + Md, где I cm — момент инерции относительно центра масс, M — масса объекта, а d — расстояние между aes. .Примечание: два угла поворота должны быть параллельны. Рассмотрим плоский объект (например, тонкий диск или лист) в плоскости y. По определению, момент инерции относительно z-ais (перпендикулярно плоскости объекта) равен I z = imiri = mi (ii + yi) = miii + imiyi Но miii = I, т.е. момент инерции относительно, и imiyi = I y, т.е. момент инерции относительно y. Пример диска: z z y i r i m i y I z = I + I y. Примечание: объект должен быть плоским y I z = 1 MR. Но по симметрии I = I y.I = I y = 1 4 MR.
15 м 3 кг 4 кг м 3 м Вопрос 9.5: Четыре массы в углах квадрата в м см м с длиной стороны L = м соединены безмассовыми стержнями. Масса m 1 = m 3 = 3 кг и m = m 4 = 4 кг. 4 кг 3 кг D Найдите (а) момент инерции относительно оси z, (b) момент инерции zz относительно оси, которая перпендикулярна плоскости ансамбля и проходит через центр масс системы, (c) момент инерции относительно -ais, который проходит через м 3 и м 4.(a) Момент инерции относительно оси z: I z = mirii = (3 кг) (м) + (4 кг) (м) + (3 кг) (м) + (4 кг) (0) = 56 кг м. y L m 1 m L (b) По симметрии центр масс находится в центре квадрата. I см = m i r i i = (3 кг) (м) + (4 кг) (м) м 4 м 3 + (3 кг) (м) + (4 кг) (м) = 8 кг м. Проверьте, используя теорему о параллельности z I z = I cm + MD I cm = I z MD = (56 кг м) (14 кг) (м) = 8 кг м.
16 y м 3 кг 4 кг z м 4 кг 3 кг (c) Поскольку ансамбль является плоским и ограничен плоскостью y, мы можем использовать теорему о перпендикуляре ais, т.е.е., I z = I + I y. Но по симметрии I = I y. I = 1 I z = 1 (56 кг м) Проверить: I = m i r i i = 8 кг м. = (3 кг) (м) + (4 кг) (м) = 8 кг м. Вопрос 9.6: Четыре тонких стержня, каждая длиной l и массой M, расположены так, что образуют квадрат в плоскости y, как показано, с началом координат aes в центре квадрата. (a) Используя теорему о параллельности ais, покажите, что I z = 4 3 Ml. (b) Следовательно, найдите I и I y. z l l y
17 z l l y (a) Используя теорему о параллельности ais, для каждого стержня имеем I z = I cm + Md, где I cm — момент инерции, проходящий через центр масс каждого стержня, а d = l.I z (всего) = ml + m l = ml. (b) Поскольку объект плоский, мы можем использовать теорему о перпендикуляре ais, то есть I z = I + I y. Но в силу симметрии I = I y. I = I y = 1 I z = 3 мл. В главе 6 мы видели, что линейно движущийся объект имеет поступательную кинетическую энергию … объект, вращающийся вокруг ais, имеет кинетическую энергию вращения … ω O viri Δm i Если твердый объект вращается с угловой скоростью ω, кинетическая энергия i-й элемент: K i = 1 (Δm i) vi = 1 (Δm i) (ri ω), поскольку vi = ri ω.Итак, полная кинетическая энергия вращения равна: 1 K = i K i = i (Δm i) r i ω = 1 Iω. * K rot = 1 Iω является аналогом K trans = 1 mv.
18 Для вращения (или замедления) объекта требуется крутящий момент … но крутящий момент включает в себя силу … Когда сила прилагается на расстоянии, выполняется работа, определяемая выражением: O! r ds dθ! F dw =! F d! s = F.dscos γ = F cos γ.ds F t γ! F θ F r γ + θ = 90 «F t = F cos γ Вопрос 9.7: Двигатель развивает крутящий момент 400 Н · м при 3700 об / мин. Какую мощность развивает двигатель? = F t.ds = F t.rdθ = τ.dθ (Дж или Нм). Мощность — это скорость, с которой работает крутящий момент, то есть P = dw = τ dθ dt dt = τω (ватты). dw = τ.dθ является аналогом dw = F.ds. P = τω является аналогом P = Fv.
19 Крутящий момент τ = 400 Н · м. Угловая скорость ω = 3700 об / мин π (3700 об / мин) = = рад / с. 60 с / мин Изначально мощность P = τω = (400 Н · м) (387,5 рад / с) = Вт. Но 746 Вт = 1 л.с. P = Вт 746 Вт / л.с. = 08 л.с. Вопрос 9.8: Электродвигатель передает на вал точильного камня постоянный крутящий момент 10 Н · м.Если момент инерции точильного камня равен кг · м и система запускается из состояния покоя, найдите (а) кинетическую энергию вращения точильного камня через 8,0 с, (б) работу, выполненную двигателем за это время, и (в) средняя мощность, отдаваемая двигателем.
20 (a) Чтобы найти кинетическую энергию вращения, нам нужно знать угловую скорость ω. Поскольку τ = Iα, α = τ I = 10 Н · м · кг · м = 5,0 рад / с. Точильный камень запускается из состояния покоя (ω! = 0), поэтому ω = αt = (5,0 рад / с) (8.0 с) = 40 рад / с. K = 1 Iω = 1 (кг · м) (40 рад / с) = 1600 Дж. (B) Есть два способа определить работу, выполняемую двигателем. (i) По теореме о работе-кинетической энергии мы ожидаем, что двигатель отработал 1600 Дж работы. (ii) Мы можем использовать выемку W = τθ, но нам нужно найти θ, то есть угол, на который точильный камень повернулся за 8,0 с. (c) Средняя мощность — это общая проделанная работа, деленная на общий временной интервал, то есть P av = ΔW = 1600 Дж Δt 8,0 с = 00 Вт. Примечание: полученное нами ранее значение P = τω фактически является мгновенной мощностью.Мы не можем использовать это углубление здесь, поскольку ω не является постоянным. Обратите внимание, что мгновенная мощность увеличивается линейно от нуля при t = 0 до (10 Н · м) (40 рад / с) = 400 Вт при t = 8,0 с. θ = ω! t + 1 αt = 1 (5,0 рад / с) (8,0 с) = 160 рад (= 5,46 об). W = τθ = (10 Н · м) (160 рад) = 1600 Дж.
21 Если жесткий объект подвешен в произвольной точке O и может свободно вращаться вокруг этой точки, он будет поворачиваться до тех пор, пока центр масс не окажется вертикально. ниже точки подвеса.y r cm cm O cm Mg v cm ω v cm v = 0 Рассмотрим шар, цилиндр, колесо или диск), катящиеся по поверхности без скольжения. Точка контакта с поверхностью имеет нулевую мгновенную скорость относительно поверхности. Скорость см равна v см (= rω = v), скорость точки наверху равна v см (= v). Если направление y вертикально и точка подвеса не находится в центре масс, объект будет испытывать чистый крутящий момент, равный τ = Mg см, где см — составляющая центра масс. Следовательно, объект будет вращаться, пока cm = 0, т.е.Т. е. точка подвеса находится в направлении выше центра масс. Поскольку объект имеет ту же линейную скорость, что и cm, то есть v, общая кинетическая энергия равна: K tot = 1 mv + 1 Iω поступательное + вращательное, где ω = v r. Итак, когда мяч катится с холма … v, ω Гравитационная потенциальная энергия поступательная энергия + энергия вращения
22 Рассмотрим катание сферы, цилиндра и обруча по наклонной поверхности. У них одинаковая скорость внизу? h v Для каждого объекта закон сохранения энергии дает: mgh = 1 mv + 1 Iω, а без проскальзывания v = Rω, где R — радиус объекта.После манипуляции находим: v gh =. 1 + I mr Для максимальной скорости: I наименьшее значение. Итак, в гонке между объектами, катящимися по склону, порядок будет (1) сфера, () цилиндр, (3) обруч, и он полностью не зависит от m и R! v gh = 1 + I mr Для твердой сферы I = 5 mr. v = gh 1 +, т.е. v = 10gh 5 7. RMA07VD.MOV Поскольку это не зависит от m и R, шар для боулинга и шар для пула будут иметь одинаковые скорости в нижней части склона, несмотря на их разные массы и радиусы!
23 Вопрос 9.9: Однородный цельный шар массы M и радиуса R катится, не соскальзывая, по наклонной поверхности под углом θ к горизонту. Найдите (а) силу трения, действующую в точке контакта с поверхностью, и (б) ускорение центра масс мяча в терминах M, R, g и θ. ПРИМЕЧАНИЕ: в точке контакта должно быть трение, иначе мяч соскользнет вниз по склону! θ (a) Изобразите диаграмму свободного тела всех сил, действующих на мяч. Используйте закон Ньютона вниз по наклонной поверхности: f O R Mg N θ Mg sin θ f = Ma cm… (i) где см — ускорение центра масс. Чтобы получить вдавление на см, мы берем крутящий момент около O, центра шара. τ = fr = Iα, т.е. α = fr I, где I — момент инерции шара, а α — его угловое ускорение. (ПРИМЕЧАНИЕ: нормальная сила N и сила веса Mg не влияют на крутящий момент, поскольку их линии действия проходят через O.) Без проскальзывания a cm = Rα = fr I (ii) Подставляя cm в уравнение (i) , получаем Mg sin θ f = M fr I = MfR 5 MR = 5 f.
24 мг sin θ = 5 f + f = 7 f, т.е.е., f = Mg sin θ. 7 Обратите внимание, что это сила статического трения (потому что нет скольжения). (b) Подставляя f в уравнение (ii), мы получаем a cm = fr I = Mg sin θ 7 5 MR R = 5 gsin θ. 7 Вы можете показать себе, что если мы положим I = βmr, где β = 1 для обруча, β = 1 для диска и т. Д., То получится общее сжатие для силы статического трения, действующей на объект, катящийся по склону, с отсутствие скольжения, а ускорение центра масс составляет: Mg sin θ f = 1 + β 1 и a cm = gsin θ 1 + β. Вопрос 9.10: Предположим, вы можете выбрать колеса любого дизайна для гоночной машины в мыльном дерби. Если указан общий вес автомобиля, какую конструкцию колес вам следует выбрать, если вы хотите иметь больше шансов на победу в гонке?
25 Полная механическая энергия автомобиля составляет: поступательная кинетическая энергия + вращательная кинетическая энергия. Сохранение энергии дает: Mgh = K trans + K rot = 1 Mv + 1 Iω, где M — полная масса автомобиля, а I — момент инерции колес.С четырьмя колесами радиуса r, например, мы имеем, используя условие отсутствия проскальзывания, () vr K rot = 1 (4I) ω = 1 4 βmr Mgh = 1 Mv + βmv, т. Е. V = Mgh (M + 4βм). = βmv, Итак, для максимальной скорости (v) у подножия холма (и большей средней скорости) с M fied мы хотим, чтобы m и β были как можно меньше. Обратите внимание: результат не зависит от радиуса колес (r). Итак, цельнолитые колеса (β = 1) — хороший выбор с массой, сконцентрированной как можно ближе к элементу эля. F h R Вопрос 9.11: По битку нанесен удар горизонтальным кием на расстоянии h выше центра шара.Если биток должен катиться без скольжения, что такое h? Выразите свой ответ радиусом R шара. Вы можете предположить, что сила трения стола о шар незначительна по сравнению с приложенной силой F.
26 F h R f Чистый крутящий момент относительно центра равен τ = Fh fr. Как было сказано ранее, при наличии прилипания v cm = Rω, т.е. a cm = dv cm dt = R dω dt = Rα. Используя закон Ньютона F + f = ma cm. Если F >> f, то F ma cm и τ Fh = Iα.F m = a cm = Rα = R Fh I, т.е. h = Для твердой сферы I = 5 mr. h> 5 R h = 5 R. верхний отжим I mr. h <5 R обратное вращение SLIP m 30 кг 0 кг m 1 м Вопрос 9.1: 30-килограммовая гиря, показанная выше, высвобождается из состояния покоя с расстояния метров над землей. Моделируя шкив как однородный диск с радиусом 10 см и массой 5 кг, найдите (а) скорость массы 30 кг непосредственно перед тем, как она ударится о землю, (б) угловую скорость шкива в этот момент, ( c) натяжение двух струн и d) время, за которое 30-килограммовый блок достиг земли.Предположим, что подшипники в шкиве не имеют трения и между струной и шкивом нет проскальзывания.
27 ω ω 0 кг м 1 м 30 кг м v м 1 м v 0 кг м 1 м 30 кг м v м 1 м v У нас есть как поступательное, так и вращательное движение.
