Вершина — шестиугольник — Большая Энциклопедия Нефти и Газа, статья, страница 3
Вершина — шестиугольник
Cтраница 3
Три оси X, называемые электрическими, проходят через вершины шестиугольника в плоскости, перпендикулярной оси Z. Три оси У, проходящие перпендикулярно сторонам того же шестиугольника, называют механическими. [31]
Очевидно, что вид соотношений (1.10) не зависит от выбора вершины шестиугольника ( фиг. [32]
Заметьте, что у фенильного радикала одинаковы только пять из шести вершин шестиугольника, а в шестой вершине недостает атома водорода. [33]
Обозначим через А, В, С, D, E, F вершины шестиугольника, являющегося основанием данной пирамиды. [34]
Обозначим через А, В, С, D, Е, F вершины шестиугольника, являющегося основанием данной пирамиды.
Решить предыдущую задачу при условии, что все шесть зарядов, расположенных в вершинах шестиугольника, положительны. [36]
Решить предыдущую задачу при условии, что все шесть зарядов, расположенных в вершинах шестиугольника, положительны. [37]
Решить предыдущую задачу при условии, что все шесть зарядов, расположенных в
Полимер гидрида алюминия состоит из слоев, в которых атомы алюминия расположены в вершинах шестиугольников, причем каждый атом алюминия соединен со своими тремя соседями связью из двух атомов водорода, подобно связи в дибораие ( стр.
[39]
Докажите, что если неокрашенным останется один узел, то он не может быть вершиной исходного шестиугольника. [40]
При проявлении центральным ионом координационного числа 6 существование системы с шестью заместителями, расположенными в
Каждый атом углерода связан с одним атомом водорода, длина С — Н — связи 1 09 А от вершины шестиугольника. [42]
В процессе доказательства основной теоремы ( § 38) быдо обнаружено, что, как бы ни были выбраны вершины шестиугольника SiCSzADB на кривой второго порядка, три точки пересечения пар противоположных сторон Хь Х2 и М лежат на одной прямой. [43]
В справедливости последних утверждений можно непосредственно убедиться, заметив, что они получаются из теоремы Паскаля о шестиугольнике предельным переходом, когда некоторые вершины шестиугольника сливаются в одну точку, поскольку предельным положением секущей является касательная.
Однако такого рода соображения по непрерывности носят эвристический характер и не могут рассматриваться как доставляющие строгое доказательство.
[44]
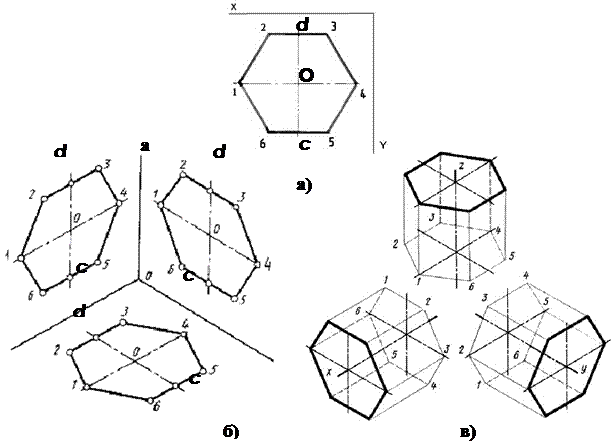
Построение шестиугольника, расположенного в плоскости W ( рис. 91, в), аналогично, только в этом случае сокращается в два раза расстояние между
Страницы: 1 2 3 4
Шестиугольники на решетке • Николай Авилов • Научно-популярные задачи на «Элементах» • Математика
а) Итак, рассмотрим правильный шестиугольник H со стороной n, нарисованный на треугольной сетке. Посчитаем, сколько в нем содержится правильных шестиугольников со сторонами, параллельными сторонам H.
Ясно, что шестиугольник со стороной n всего один — он совпадает с H. Шестиугольников со стороной \(n-1\) уже 7 штук: у одного центр совпадает с центром H, а остальные получаются из него сдвигами к каждой из вершин H. Если продолжить уменьшать размер шестиугольника, то после аккуратного разбора случаев можно получить, что со стороной \(n-2\) будет 19 шестиугольников, а со стороной \(n-3\) — уже 37. Как возникают эти числа и что их объединяет?
Зафиксируем натуральное \(k<n\) и посмотрим, какие положения может занимать, например, левая нижняя вершина шестиугольника со стороной k. Несложно понять, что она может находиться только внутри шестиугольника со стороной \(n-k\), «приклеенного» к левой нижней вершине шестиугольника
Поскольку у каждого шестиугольника ровно одна левая нижняя вершина, то получается, что всего таких шестиугольников будет столько же, сколько узлов сетки попадает внутрь и на стороны шестиугольника со стороной \(n-k\).
2.\]
Шестиугольный паркет — Википедия
Материал из Википедии — свободной энциклопедии
| Шестиугольная мозаика | |
|---|---|
| Тип | Правильная мозаика |
| Вершинная фигура | 6.6.6 (63) |
| Символ Шлефли | {6,3} t{3,6} |
| Символ Визоффа[en] | 3 | 6 2 2 6 | 3 3 3 3 | |
| Диаграмма Коксетера | |
| Группа симметрии | p6m[en], [6,3], (*632) |
| Вращательная симметрия | p6[en], [6,3]+, (632) |
| Двойственная мозаика | |
| Свойства | Вершинно транзитивна, рёберно транзитивна[en], транзитивна по граням[en] |
Шестиуго́льный парке́т (шестиугольный паркета́ж[1]) или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.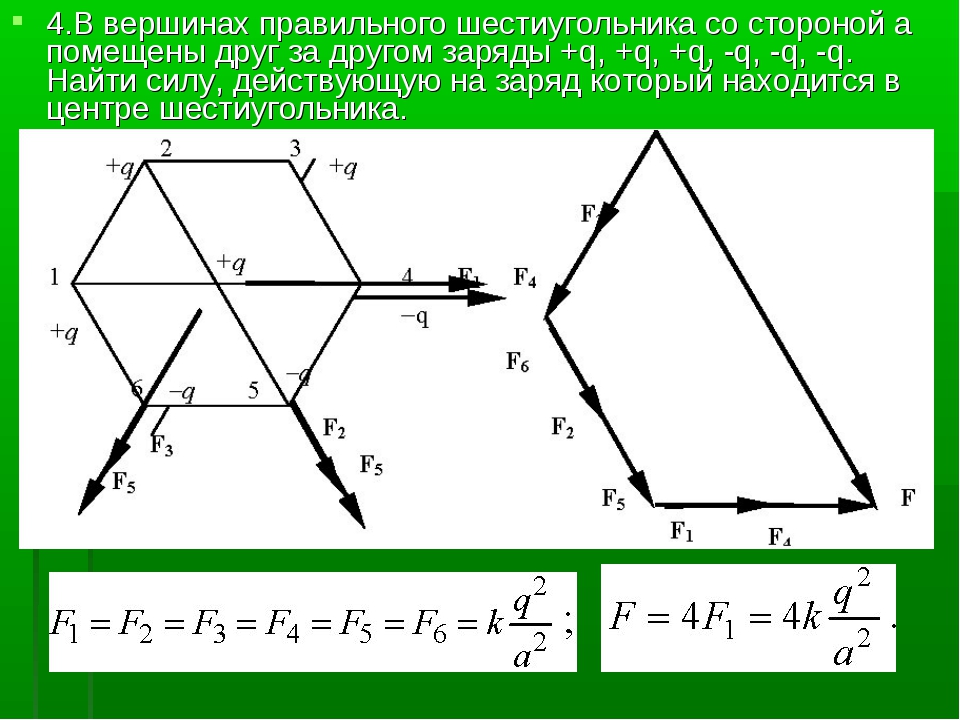
Шестиугольная мозаика является двойственной треугольной мозаике — если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольную мозаику[1][2]. Символ Шлефли шестиугольного паркета — {6,3} (что означает, что в каждой вершине паркета сходятся три шестиугольника), или
Английский математик Конвей называл мозаику hextille (шестипаркет).
Внутренний угол шестиугольника равен 120 градусов, так что три шестиугольника в одной вершине дают вместе 360 градусов. Это одна из трёх правильных мозаик плоскости. Другие две мозаики — треугольный паркет и квадратный паркет.
Приложения
Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.
Шестиугольная мозаика является наиболее плотным способом упаковки окружностей в двухмерном пространстве.
Гипотеза о сотах[en] утверждает, что шестиугольная мозаика является лучшим способом разбить поверхность на области равной площади с наименьшим суммарным периметром. Оптимальную трёхмерную структуру для сот (скорее, мыльных пузырей) исследовал лорд Кельвин, который верил, что структура Кельвина[en] (или объёмно-центрированная кубическая решётка) оптимальна. Однако менее правильная структура Уаеаире – Фелана[en] слегка лучше.
Эта структура существует в природе в виде графита, где каждый слой графена имеет сходство с проволочной сеткой, где роль проволоки играют сильные ковалентные связи. Были синтезированы трубчатые листы графена, они известны как углеродные нанотрубки. Они имеют много потенциальных приложений ввиду их высокой прочности на разрыв и электрических свойств. На графен похож силицен.
Шестиугольная мозаика появляется во многих кристаллах. В трёхмерном пространстве гранецентрированная кубическая структура и гексагональная плотноупакованная структура часто встречаются в кристаллах.
Они являются наиболее плотными сферами в трёхмерном пространстве. Структурно они состоят из параллельных слоёв шестиугольной мозаики подобно структуре графита. Отличаются они тем, как уровни смещены относительно друг друга, при этом гранецентрированная кубическая структура является более правильной. Чистая медь, среди прочих материалов, образует гранецентрированную кубическую решётку.
Однородные раскраски
Существуют три различные однородные раскраски[en] шестиугольной мозаики, все получаются из зеркальной симметрии построений Визоффа. Запись (h,k) представляет периодическое повторение цветной плитки с шестиугольными расстояниями h и k.
| k-однородные | 1- однородные | 2- однородные | 3- однородные | ||||
|---|---|---|---|---|---|---|---|
| Симметрия | p6m, (*632) | p3m1, (*333) | p6m, (*632) | p6, (632) | |||
| Рисунок | |||||||
| Цвета | 1 | 2 | 3 | 2 | 4 | 2 | 7 |
| (h,k) | (1,0) | (1,1) | (2,0) | (2,1) | |||
| Шлефли | {6,3} | t{3,6} | t{3[3]} | ||||
| Визофф[en] | 3 | 6 2 | 2 6 | 3 | 3 3 3 | | ||||
| Коксетер | |||||||
| Конвей[en] | H | tΔ | cH | ||||
3-цветная мозаика образуется
Hexagon — test2.
Википедия
Википедия Шаблон: правильный многоугольник db В геометрии шестиугольник (от греческого ἕξ hex , «шесть» и γωνία, gonía, «угол, угол») — это многоугольник с шестью ребрами и шестью вершинами. Сумма внутренних углов любого шестиугольника составляет 720 °.
Шестиугольные конструкции [править]
От пчелиных сот до Дороги гигантов — гексагональные узоры преобладают в природе из-за эффективности воздуха. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников.Это означает, что соты требуют меньше воска для изготовления и приобретают большую прочность при сжатии.
Правильный шестиугольник [править]
У правильного шестиугольника есть ряд подсимметрий, которые можно увидеть по раскраске или геометрическим вариациям. Правильный шестиугольник — это шестиугольник, который одновременно является равносторонним и равноугольным.
Он бицентрический, что означает, что он является одновременно циклическим (имеет описанную окружность) и касательным (имеет вписанную окружность).
Общая длина сторон равна радиусу описанной окружности, который равен 233 {\ displaystyle {\ tfrac {2 {\ sqrt {3}}} {3}}}, умноженным на апофему (радиус вписанной окружности). .Все внутренние углы составляют 120 градусов. Правильный шестиугольник имеет 6 симметрий вращения ( симметрии вращения шестого порядка ) и 6 симметрий отражения ( шесть линий симметрии ), составляя группу диэдра D 6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и одной стороной с шестиугольником является равносторонним, и что правильный шестиугольник можно разделить на шесть равносторонних треугольников.
Подобно квадратам и равносторонним треугольникам, правильные шестиугольники подходят друг к другу без каких-либо зазоров до мозаики плоскости (три шестиугольника, встречающиеся в каждой вершине), и поэтому полезны для построения мозаики.
Ячейки сотового улья имеют шестиугольную форму по этой причине и потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки — это сотовая мозаика шестиугольников. Обычно не считается триамбусом, хотя он равносторонний.{2}.}
Альтернативная формула площади:
- A = 32dt {\ displaystyle A = {\ frac {3} {2}} dt}
, где длина d — это расстояние между параллельными сторонами (также называемое расстоянием от плоскости до плоскости ), или высоту шестиугольника, когда он находится на одной стороне в качестве основания, или диаметр вписанного круга.
Другая альтернативная формула для площади, если известно только расстояние от плоскости до плоскости, d, определяется как
- А = 32d2≃0.{2},}
, где а — апофема, п — периметр.
Периметр правильного шестиугольника с длиной стороны т равен 6 т , его максимальный диаметр 2 т , а его минимальный диаметр d = t3 {\ displaystyle \ scriptstyle d \ = \ t {\ sqrt {3 }}}.
Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описывающей окружности между B и C, PE + PF = PA + PB + PC + PD.
Связанные полигоны и мозаики [править]
На правильном шестиугольнике есть символ Шлефли {6}.Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольниками вокруг каждой вершины.
Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}. Если смотреть с двумя типами (цветами) кромок, то эта форма имеет только симметрию D 3 .
Усеченный шестиугольник, t {6} — двенадцатигранник, {12}, чередующийся 2 типа (цвета) ребер. Переменный шестиугольник h {6} — это равносторонний треугольник {3}. Правильный шестиугольник может быть звездчатым с равносторонними треугольниками по краям, образующими гексаграмму.Правильный шестиугольник можно разрезать на 6 равносторонних треугольников, добавив центральную точку.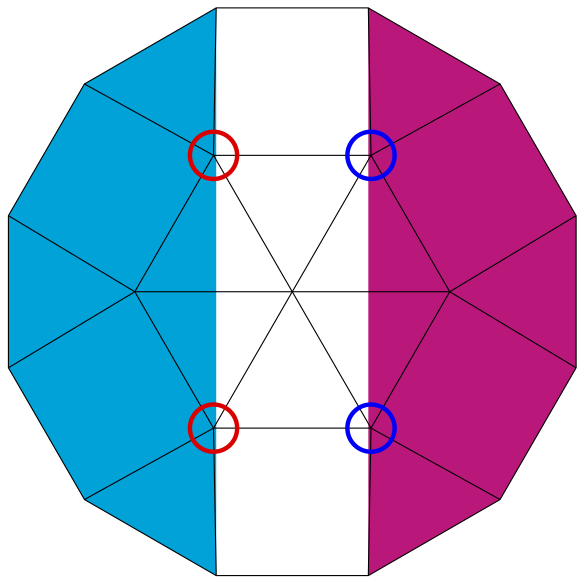
Этот узор повторяется внутри правильной треугольной плитки.
Правильный шестиугольник можно продолжить до правильного двенадцатиугольника, добавив чередующиеся квадраты и равносторонние треугольники вокруг него. Этот узор повторяется внутри ромбогексагональной плитки.
Связанные рисунки [править]
Мозаика по шестиугольникам [править]
В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея, будет мозаикой плоскости.
Шестиугольник, вписанный в коническое сечение [править]
Аорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, т.е. «Линия Паскаля» этой конфигурации.
Циклический шестиугольник [править]
Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку.
Если последовательные стороны циклического шестиугольника равны a , b , c , d , e , f , три главных диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf . [1]
Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до пересечения по воздуху, образуя треугольник, внешний по отношению к данной стороне, сегменты, соединяющие центры окружностей противоположных треугольников, совпадают. [2]
Если шестиугольник имеет вершины на описанной окружности остроугольного треугольника в шести точках (включая три вершины треугольника), где расширенные высоты треугольника пересекаются с описанной окружностью, площадь шестиугольника в два раза больше площади треугольника. [3] : стр. 179
Шестигранник по касательной к коническому сечению [править]
Пусть ABCDEF — шестиугольник, образованный шестью касательными к коническому сечению.
Затем аорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.
В касательном к окружности шестиугольнике с последовательными сторонами a , b , c , d , e и f , [4]
- a + c + e = b + d + f. {\ Displaystyle a + c + e = b + d + f.}
Выпуклый равносторонний шестиугольник [править]
Главная диагональ шестиугольника — это диагональ, которая делит шестиугольник на четырехугольники. В любом выпуклом равностороннем шестиугольнике (один со всеми равными сторонами) с общей стороной и существует [5] : p.184, # 286.3 главная диагональ d 1 такая, что
- d1a≤2 {\ displaystyle {\ frac {d_ {1}} {a}} \ leq 2}
и главная диагональ d 2 такая, что
- d2a> 3. {\ Displaystyle {\ frac {d_ {2}} {a}}> {\ sqrt {3}}.}
многоугольников Петри [править]
Правильный шестиугольник — это многоугольник Петри для правильных, однородных и двойственных многогранников и многогранников, показанных в косо-ортогональных проекциях:
Hexagon Ragasco — доверяют потребители и компании во всем мире
Наша деятельность зависит от непрерывности цепочки поставок, нашего собственного производства и логистических услуг.
Вирус короны (Covid-19) поражает всех нас. Как и большинство национальных властей, норвежские власти приняли строгие меры по сокращению распространения вируса.В Hexagon Ragasco мы реализовали следующие меры для обеспечения безопасной и непрерывной работы:
• Строгие правила гигиены рук и уборки в местах общего пользования.
• Столовая останется закрытой.
• Meetings : основные командные собрания перенесены на открытое пространство, чтобы участники не сидели ближе, чем в 1 метре друг от друга.Все остальные встречи, будь то внешние или внутренние, теперь проводятся онлайн через концепцию домашнего офиса.
• Внешние посетители : будет ограничение на количество внешних посетителей.
• Реализовано 1-метровое расстояние между теми, кто должен работать в группах или в непосредственной близости. Маски и очки являются обязательными, если работа требует нарушения правила 1 метра.
• Измерения температуры : Документированные измерения температуры для всех сотрудников и посетителей, которые входят в наши помещения.
Лица с температурой выше 37,5 C в наши помещения не допускаются.
• Избегайте общественного транспорта, группирования автомобилей и любых поездок, связанных с работой, если в этом нет необходимости.
По мере развития ситуации мы продолжим обновлять наши действия, чтобы лучше адаптировать их к новым требованиям.
С наилучшими пожеланиями,
Скьялг С. Ставхейм
Генеральный директор
Hexagon Ragasco — ведущий производитель композитных баллонов для сжиженного нефтяного газа с более чем 17 миллионами баллонов, используемых во всем мире и 20-летним опытом.
Используя новейшие технологии на своем производственном предприятии в Норвегии, продукция Hexagon Ragasco обеспечивает многочисленные преимущества по сравнению с традиционными стальными цилиндрами с точки зрения безопасности и удобства использования.
my-HEXAGON opp для экспериментального обучения и цифровых технологий
Lab03: что делает нас лучше?
Сейчас мы запускаем третью из трех лабораторий, это
время задуматься, и когда мы сомневаемся в себе, тогда
мы идем к истокам наших знаний, чтобы лучше понять
математика, вычисления и сложность обучения, оптимизировать,
обрабатывать сигналы и использовать другие языки, например визуальный.
Скачать презентацию,
уже 300 человек посетили наши лаборатории.
Забронируйте свое место.
Мы делаем учебные лаборатории.
Наша учебная лаборатория — интеллектуальная усилитель, который позволяет участникам понять главное — расставить приоритеты, исключить ненужное. Сортируйте, систематизируйте, обрабатывайте идеи, чтобы воплотить их артефакты. Наконец-то это шанс испытать новые идеи, инновационные методы, стимулирование творчества и веселитесь вместе.
Какой цели он служит?
Обучение означает многое, и среди них мы считаем необходимым быть активным для познания, поэтому не получать информацию пассивно но дайте ему форму. Вы можете думать о производство личных знаний как завоевание, требующее приключений и отваги. Также он служит для быстрой адаптации к изменениям, лучше понимать разнообразие и плюрализм, расширять собственные навыки в различных областях, таких как цифровой мир.Развивать рабочие и личные знания.
Для кого это?
Для тех, кто знает свои привычки,
например те, у кого есть
предрассудки и хотят удалить
их.