Как найти диагональ шестиугольника — Наука
Наука 2021
Шестиугольник — это шестигранный многоугольник. Правильный шестиугольник означает, что каждая сторона формы равна друг другу, в то время как неправильный шестиугольник имеет шесть неравных сторон. Фор
Содержание:
Шестиугольник — это шестигранный многоугольник. Правильный шестиугольник означает, что каждая сторона формы равна друг другу, в то время как неправильный шестиугольник имеет шесть неравных сторон. Форма имеет девять диагоналей, линии между внутренними углами. Хотя не существует стандартной формулы для нахождения диагоналей неправильных шестиугольников, для правильных шестиугольников девять диагоналей образуют шесть равносторонних треугольников, что позволяет легко определять длину каждой диагональной линии. Если известна одна сторона шестиугольника, то известны все стороны, и диагонали легко вычисляются.
Определите длину одной стороны шестиугольника. Для правильных шестиугольников все стороны равны: Таким образом, каждая сторона имеет одинаковую длину, и если одна сторона известна, то все равны.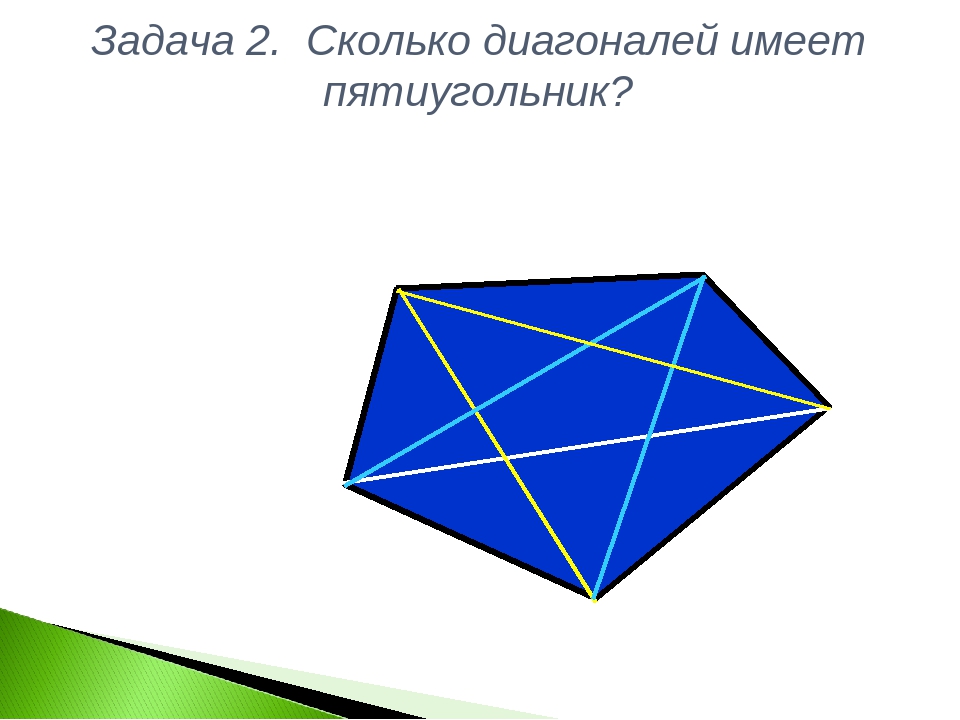
Выпишите уравнение для нахождения диагонали правильного шестиугольника: d (диагональ) = 2g (заданная сторона).
Умножьте известную или заданную сторону шестиугольника на 2. Произведение — это длина диагонали правильного шестиугольника.
Хотя вы можете рассчитать количество диагоналей в неправильном шестиугольнике, для нахождения диагонального измерения неправильного потребуется сначала разбить шестиугольник на четыре треугольника. Однако, если они не являются правильными треугольниками, каковыми они вряд ли являются, не существует формального определения длины внутренней стороны, которая была бы диагональю. Теорема Пифагора применима только к прямоугольным треугольникам. если бы каждая сторона и угол были указаны вместе с площадью, то можно было бы определить диагонали, но это много переменных, которые нужно принять.
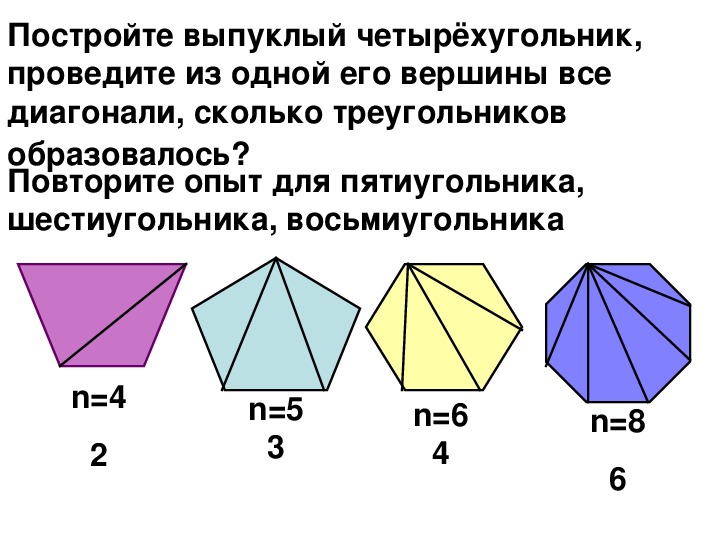
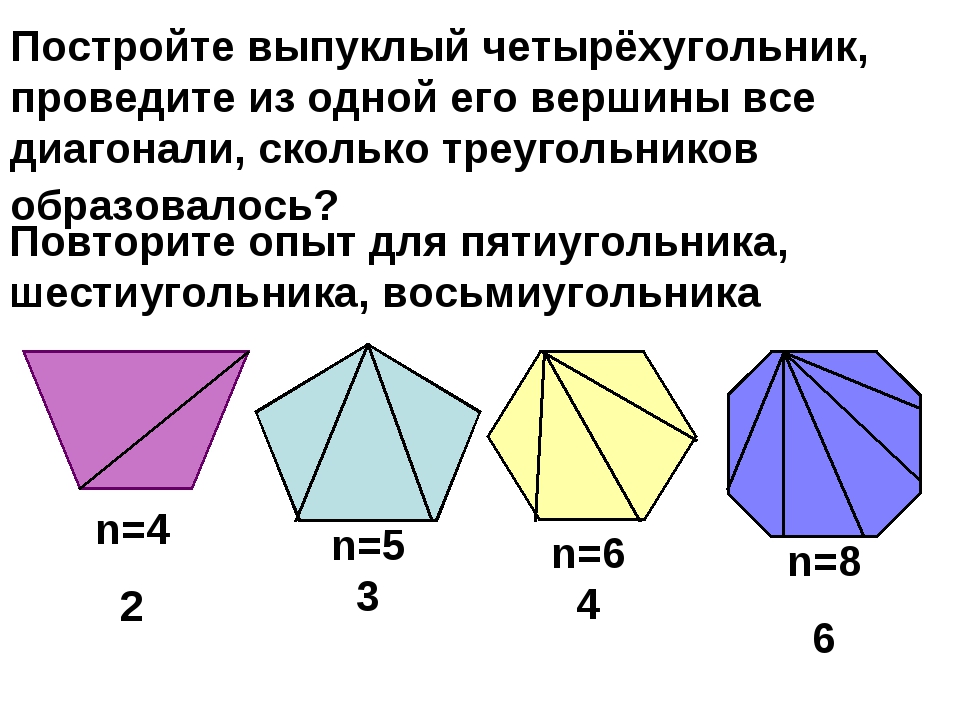
Сколько диагоналей у треугольника, четырехугольника, пятиугольника, шестиугольника, восьмиугольника? — Памятки по математике — Памятки ученикам
Диагональ в многоугольнике (многограннике) — отрезок, соединяющий любые две несмежные вершины, то есть, вершины, не принадлежащие одной стороне многоугольника (одному ребру многогранника).
У многогранников различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за пределы граней. У многогранников, имеющих треугольные грани есть только пространственные диагонали.
Подсчет диагоналей
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника легко вычислить по формуле:
N = n·(n – 3)/2,
где n — число вершин многоугольника. По этой формуле нетрудно найти, что
- у треугольника — 0 диагоналей
- у прямоугольника — 2 диагонали
- у пятиугольника — 5 диагоналей
- у шестиугольника — 9 диагоналей
- у восьмиугольника — 20 диагоналей
- у 12-угольника — 54 диагонали
- у 24-угольника — 252 диагонали
Количество диагоналей многогранника с числом вершин n легко подсчитать только для случая, когда в каждой вершине многогранника сходится одинаковое число ребер k. Тогда можно пользоваться формулой:
Тогда можно пользоваться формулой:
N = n·(n – k – 1)/2,
которая даем сумманое число пространственных и граневых диагоналей. Отсюда можно найти, что
- у октаэдра (n=6, k=4) — 3 диагонали (все пространственные)
- у куба (n=8, k=3) — 16 диагоналей (12 граневых и 4 пространственных)
- у икосаэдра (n=12, k=5) — 36 диагоналей (все пространственные)
- у додекаэдра (n=20, k=3) — 160 диагоналей (25 граневых и 135 пространственных)
Если в разных вершинах многогранника сходится разное число ребер, подсчет заметно усложняется и должен проводится индивидуально для каждого случая.
Фигуры с равными диагоналями
На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой. Этоквадрат и правильный пятиугольник. У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом.
Единственный правильный многогранник, у которого все диагонали равны между собой — правильный восьмигранник октаэдр. У него три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра — пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).
Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой. Это
Угол между сторонами правильного шестиугольника
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Правильный шестиугольник – это многоугольник, состоящий из шести равных сторон. Все соседние стороны образуют угол 120°.
Формулы
- P – периметр
- S – площадь
- R – радиус K
- r – радиус k
- S’ – центр
- a – сторона
- K – окружность описанная
- k – окружность вписанная
При предоставлении услуг веб-сайт «Calculat. org» использует файлы куки.
org» использует файлы куки.
Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
 circ) :
circ) :Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
5 класс.
 Математика. Никольский. Учебник. Ответы к стр. 128
Математика. Никольский. Учебник. Ответы к стр. 128Измерение величин
Многоугольники
Ответы к стр. 128570. а) Что называют многоугольником?
б) Что называют сторонами, углами, вершинами многоугольника?
в) Что называют периметром многоугольника?
г) Какой многоугольник называют выпуклым?
д) Какие многоугольники называют равными?а) Фигуру, образованную ломаной линией, конец которой совпадает с её началом (замкнутая ломаная), при условии, что никакие два звена ломаной не имеют общих точек, кроме концов соседних звеньев ломаной, называют многоугольником.
б) Звенья ломаной называют сторонами многоугольника, углы, составленные каждыми двумя соседними сторонами, – углами многоугольника, а эти вершины углов – вершинами многоугольника.
в) Сумму длин сторон многоугольника называют его периметром.
г) Многоугольник называют выпуклым, если он весь расположен по одну сторону от каждой прямой, содержащей его сторону.
д) Два многоугольника называют равными, если их можно совместить при наложении.571. Постройте пятиугольник ABCDE. Назовите все его стороны и вершины.
Стороны: AB, BC, CD, DE, EA.
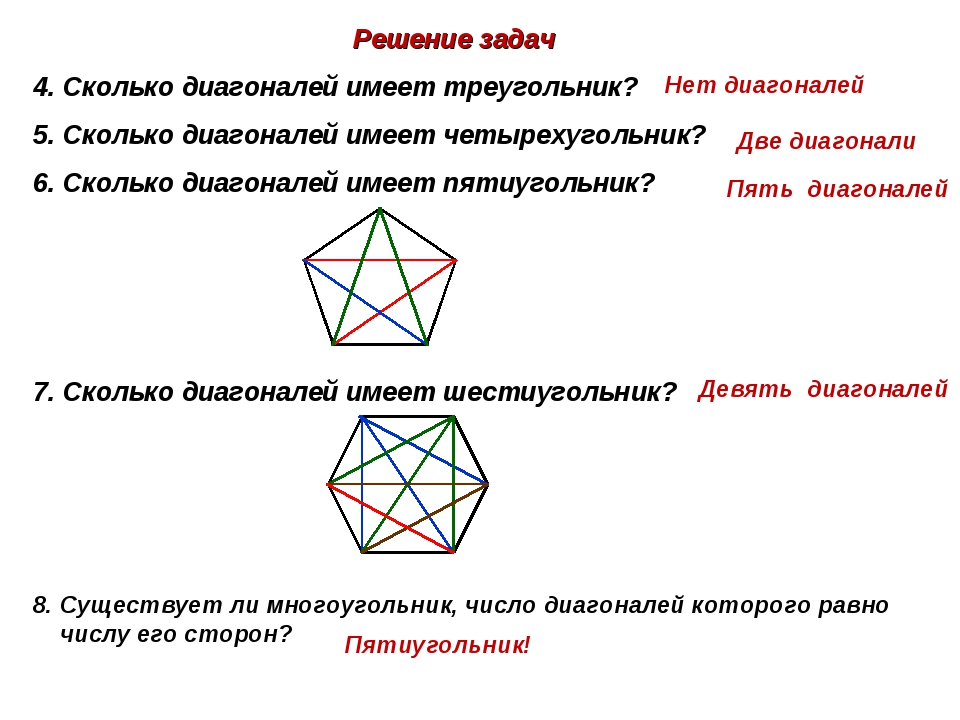
Вершины: A, B, C, D, E.572. Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. Например, в четырёхугольнике ABCD отрезка AC и BD – диагонали (рис. 119). Сколько диагоналей в выпуклом:
а) четырёхугольнике;
б) пятиугольнике;
в) шестиугольнике;
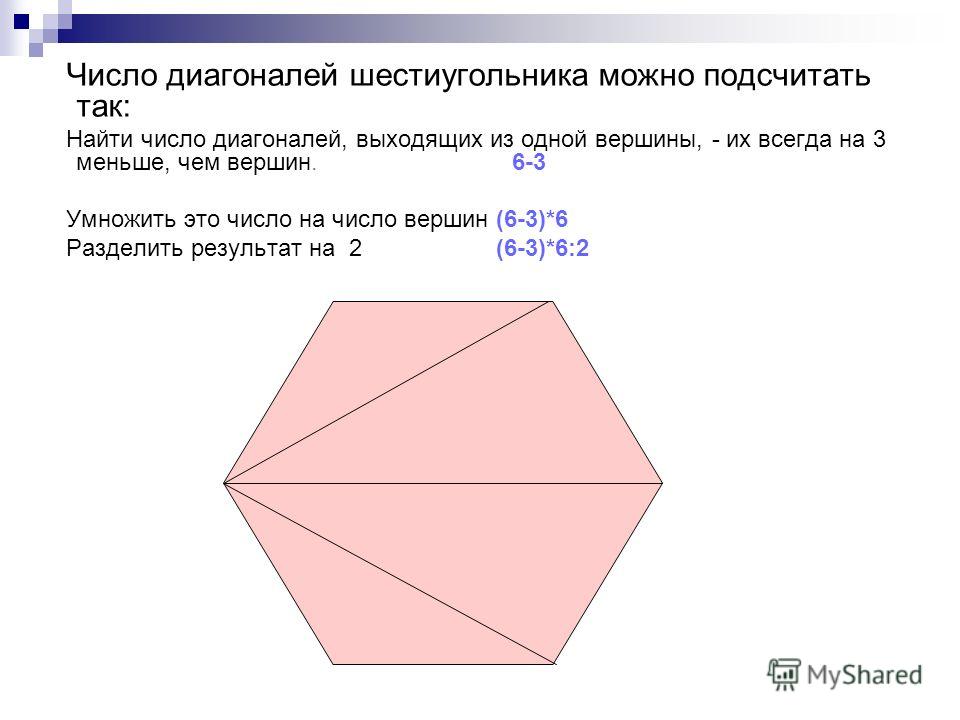
г) семиугольнике?Пусть многоугольник имеет n вершин. Тогда из каждой вершины выходит (n – 3) диагоналей: 1 – сама вершина и 2 – соседние вершины.
Так как диагональ соединяет 2 вершины, значит необходимо (n – 3) разделить пополам и умножить на количество вершин, тогда мы получим, что количество диагоналей n-угольника равняется n • (n – 3) : 2.
а) 4 • (4 – 3) : 2 = 4 • 1 : 2 = 2 (диагонали) – в выпуклом четырёхугольнике;
б) 5 • (5 – 3) : 2 = 5 • 2 : 2 = 10 : 2 = 5 (диагоналей) – в выпуклом пятиугольнике;
в) 6 • (6 – 3) : 2 = 6 • 3 : 2 = 18 : 2 = 9 (диагоналей) – в выпуклом шестиугольнике;
г) 7 • (7 – 3) : 2 = 7 • 4 : 2 = 28 : 2 = 14 (диагоналей) – в выпуклом семиугольнике.573. Сколько диагоналей в выпуклом: а) десятиугольнике; б) двадцатиугольнике?
а) 10 • (10 – 3) : 2 = 10 • 7 : 2 = 35 (диагоналей) – в выпуклом десятиугольнике;
б) 20 • (20 – 3) : 2 = 20 • 17 : 2 = 170 (диагоналей) – в выпуклом двадцатиугольнике.Исследуем
574. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника, выходящих из одной его вершины, от числа сторон этого многоугольника (n).
 Результаты занесите в таблицу.
Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.а) Зависимость: (число диагоналей выпуклого многоугольника, выходящих из одной его вершины, на 3 меньше, чем сторон этого многоугольника)
n 4 5 6 7 8 9 10 11 12 d 1 2 3 4 5 6 7 8 9 б) d = n – 3.
575. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника от числа его сторон (n). Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.
а) Зависимость:
n 4 5 6 7 8 9 10 11 12 d 2 5 9 14 20 27 35 44 54 б) d = n • (n – 3) : 2.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Как получить диагонали шестиугольника? — CodeRoad
Форма такая:
A,B,C D,E,F,G H,I,J,K,L M,N,O,P Q,R,Sи я хочу ограничить диагонали определенной суммой, т.
 е.:
е.:А+Д+Ч = Б+Е+Я+М = … = Л+П+С = CONST_SUM
Я подумал о том, чтобы сгладить список и попытаться разработать некоторые математические формулы для получения правильных элементов, вычисляя Прыжки на каждом уровне. Пока что у меня есть только это:
matrix([[1,2,3],[4,5,6,7][8,9,10,11,12],[13,14,15,16],[17,18,19]). check(M) :- matrix(M), flatten(M, L), check_sum(L, 1).Однако математический подход, похоже, не очень хорошо сочетается с идеями paper..Any?
EDIT :
Я не мог выработать математические правила (прыжки для каждой диагонали), может быть, есть другой подход, которому я должен следовать, а не уплощающий…
prolog geometry
Поделиться Источник gsamaras 26 ноября 2015 в 22:031 ответ
- Обрезать UIImage в форме шестиугольника?
Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные разделы? EDIT: если быть более точным, я надеюсь сохранить границы изображения одинаковыми, но сделать.
 2…
2…
3Одна вещь, которую вы можете сделать, это написать шестиугольник перекошенным вот так:
A,B,C . . D,E,F,G . H,I,J,K,L . M,N,O,P . . Q,R,SТогда один вид диагоналей будет иметь фиксированного элемента X (“columns”), еще одна запись фиксированного г (“rows”), а третий зафиксировал х − й разница (“нисходящей диагонали”). Если вы сгладите это, вы должны каким-то образом представить пустые ячейки, окружающие фигуру, и либо dkip их во время итерации, либо исключить их из итерации в первую очередь. Вы платите за более простую формулу дополнительными требованиями к памяти.
Поделиться MvG 26 ноября 2015 в 23:14
Похожие вопросы:
Как получить длину диагонали матрицы?Есть ли формула, которая дала бы мне длину диагонали матрицы в единицах? Например, если матрица имеет размер 3×3, то длина диагонали будет равна 3.

Граница необходима для программно созданных изображений шестиугольникаЯ создал шестиугольное изображение программно в виде прокрутки И я хочу черную рамку вокруг этих изображений шестиугольника, такую же форму, как у шестиугольника. Я взял изображение в форме…
Как создать форму шестиугольника в формате .xmlЯ хочу создать форму шестиугольника для своего проекта, поэтому я хочу создать эту форму в формате .xml, так как я могу ее создать.
Обрезать UIImage в форме шестиугольника?Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные…
Площадь шестиугольника вне окружностиПусть будет круг радиусом r. Я хочу узнать площадь шестиугольника, нарисованного вокруг круга. Дополнено образцовое изображение, за исключением того, что мне нужно, чтобы все были шестиугольника, а.
 ..
..
Рисование шестиугольникаИспользуя Firemonkey XE2, я смог использовать компонент TCube для создания кубической карты, но теперь мне нужна карта шестиугольника. Не было никакого варианта для формы шестиугольника 3d, которую…
Текст в углах шестиугольникаУ меня есть шестиугольник, и я хотел бы написать что-нибудь в каждом его углу. Чтобы быть точным, я хотел бы назвать каждый его угол, начиная с внешней области шестиугольника. Вы можете увидеть код…
Как сделать половину формы шестиугольника с помощью CSS с рамкой поверх прямоугольника с рамкой с изображением в середине половины шестиугольникаКак сделать половину шестиугольника с рамкой и сверху прямоугольник с рамкой и изображением внутри половины шестиугольника, используя CSS и HTML5 У меня нет кода для этого, как я уже пробовал, но не…
Чтобы получить диагонали матрицы в Matlab?Я хочу получить диагонали из Матрицы в Matlab.
 Например, дана следующая матрица M = [1 1 4 5 4 2 5 1 2 2 4 1 2 1 3 1 3 1 1 1 1 2 3 3 1] Я хочу получить список векторов, которые составляют верхние…
Например, дана следующая матрица M = [1 1 4 5 4 2 5 1 2 2 4 1 2 1 3 1 3 1 1 1 1 2 3 3 1] Я хочу получить список векторов, которые составляют верхние…
Просмотреть изображение шестиугольника в NSКак я могу создать такой компонент, как NS? Как придать форму шестиугольника ImageView Я хочу создать компонент изображения, который имеет вид шестиугольника, но я не могу понять, как правильно…
Как найти длину диагонали шестиугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Углы, площади и диагонали правильных многоугольников
Многоугольник — это часть плоскости, окруженная линейными сегментами, которые пересекаются в своих конечных точках.

Сегменты $ \ overline {A_1A_2} $, $ \ overline {A_2A_3}, \ overline {A_3A_4}, \ ldots, \ overline {A_ {n-1} A_n} $ называются сторонами многоугольника, а точки $ A_1, A_2, A_3, A_4, \ ldots, A_ {n-1}, A_n $ называются вершинами .
Многоугольник с $ n $ сторонами и $ n $ вершинами называется $ n $ -сторонним многоугольником .
Многоугольники могут быть выпуклым множеством, однако не каждый многоугольник является выпуклым множеством. Мы можем различать выпуклых и вогнутых многоугольников.{\ circ} $.
В этом уроке мы будем наблюдать только выпуклые многоугольники.
Диагонали
Диагональ многоугольника — это линия сегмента, концы которой не являются смежными вершинами многоугольника.
Сколько диагоналей у n-многоугольника? Посмотрим на несколько первых многоугольников.
Для $ n = 3 $ получается треугольник. Мы видим, что у треугольника нет диагоналей, потому что каждая вершина имеет только смежные вершины.
При $ n = 4 $ получаем четырехугольник.У него диагонали $ 2 $.
Для $ n = 5 $ у нас есть пятиугольник с диагоналями $ 5 $.
При $ n = 6 $ многоугольник $ n $ называется шестиугольником и имеет диагонали $ 9 $.
Поскольку $ n $ было меньшим числом, мы могли легко нарисовать диагонали $ n $ -полигонов, а затем посчитать их.
Как узнать количество диагоналей, не нарисовав их все? Попробуем логически придумать формулу для количества диагоналей любого выпуклого многоугольника.
Допустим, у многоугольника $ n $ вершин.Из любой вершины мы можем нарисовать $ n — 3 $ диагоналей и сделать это $ n $ раз (из любой вершины), поскольку мы не можем рисовать из этой вершины и двух соседних. Каждые две диагонали перекрываются, и поскольку мы не хотим считать каждую диагональ дважды, мы должны разделить это число на два. Окончательная формула:
$$ D_ {n} = \ frac {n (n — 3)} {2}. {\ circ} $.{\ circ}. $$
Полигоны также делятся на две специальные группы:
Правильный многоугольник — это многоугольник, у которого все стороны равны, а все внутренние углы равны.
Неправильный многоугольник — это многоугольник, у которого есть по крайней мере один набор неравных сторон.
Правильные многоугольники имеют как вписанный круг, (круг, который касается всех сторон правильного многоугольника), так и , описанный круг , , (круг, проходящий через все вершины правильного многоугольника).Их также называют вписанной окружности и вписанной окружности . Центр обоих этих кругов одинаковый и также называется центром многоугольника.
Центр правильного многоугольника
Центр многоугольника — это точка внутри правильного многоугольника, которая равноудалена от каждой вершины.
Как мы его находим?
В некоторых правильных многоугольниках центр многоугольника находится на пересечении диагоналей. Например в четырехугольниках и шестиугольниках.
Однако это не относится ко всем полигонам. Найдем универсальную стратегию поиска центра.
Давайте, например, возьмем пятиугольник.
Попробуем найти центр, разделив углы пополам. Таким образом мы получаем треугольников $ 5 $. Эти треугольники называются характеристическими треугольниками правильного многоугольника.
Эти трэнглы по 5 долларов совпадают. Поскольку это правильный многоугольник, все стороны имеют одинаковую длину и внутренние углы одинаковой меры.Следовательно, биссектрисы углов дают нам одинаковые углы в треугольниках.
Это означает, что $ | AS | = | BS | = | CS | = | DS | = | ES | $, а точка $ S $ — центр вписанной и описанной окружностей.
Площадь правильных многоугольников
Треугольники, которые мы получили, разделив наши $ n $ -сторонние правильные многоугольники, также будут полезны для определения его площади.
Так как мы уже знаем, как рассчитать площадь треугольника, мы просто умножаем эту площадь на $ n $, чтобы получить всю площадь обычного треугольника.Все эти треугольники — равные треугольники, углы которых нам известны. Тогда рассчитать площадь достаточно просто.
Еще раз возьмем для примера пятиугольник.
Мы знаем, что все треугольники, которые мы разделили на правильный пятиугольник, равнобедренные и равнобедренные. Это также означает, что их площади равны. Если $ | AB | = | BC | = | CD | = | DE | = | EA | = a $ и $ h_a $ — высота характеристического треугольника правильного пятиугольника, то площадь характеристического треугольника правильного пятиугольника равно $$ A_t = \ displaystyle {\ frac {a \ cdot h_a} {2}}.
$$ h_a $ также называется апофемой правильного многоугольника .
Используя площадь характеристического треугольника, мы можем получить площадь правильного пятиугольника. Это будет $ A_p = 5 \ cdot P_t $.
В общем случае площадь правильного многоугольника с $ n $ вершинами равна:
$$ A_t = п \ cdot \ displaystyle {\ frac {a \ cdot h_a} {2}}. $$
Четырехугольники
Четырехугольники — это многоугольники на плоскости с $ 4 $ сторонами и $ 4 $ вершинами.
Правильный четырехугольник — это квадрат , потому что квадрат — единственный четырехугольник, у которого все стороны равны по длине и все углы равны.{\ circ} $. Имеет две диагонали. Эти диагонали пересекаются в одной точке, которая является центром вписанной и описанной окружности.
Чтобы нарисовать описанную окружность квадрата, мы просто помещаем стрелку циркуля в точку пересечения диагоналей, продлеваем ее до одной вершины и рисуем. Описанный круг будет проходить через все вершины.
Чтобы нарисовать вписанный круг, мы должны сначала найти радиус. Чтобы найти радиус, мы должны провести перпендикулярную линию от центра в любую сторону. {\ circ} $$
Каков размер каждого угла правильного многоугольника?
Так как все правильные многоугольники имеют все углы одинаковой меры, чтобы получить меру каждого угла в многоугольнике с $ n $ вершинами, мы можем просто разделить сумму мер всех внутренних углов на $ n $.{\ circ} $.
Как мы уже заметили, диагонали правильного многоугольника не пересекаются в одной точке. Чтобы нарисовать вписанный и описанный круг, нам нужно найти их центр с помощью процесса, который мы описали ранее — путем деления углов пополам. В результате мы получили пять равных треугольников.
Это означает, что $ | AS | = | BS | = | CS | = | DS | = | ES | $, а точка $ S $ — центр вписанной и описанной окружностей. Чтобы нарисовать описанную окружность, просто поместим стрелку циркуля в точку $ S $ и продлим ее до любой вершины правильного пятиугольника.Чтобы получить радиус вписанной окружности, мы должны провести перпендикулярную линию в любую сторону от центра. {\ circ}.{\ circ} $. Для площади мы должны снова вычислить площадь одного треугольника и умножить ее на 6 долларов.
Те же правила и формулы применяются к другим правильным многоугольникам.
Листы с полигонами
Назовите многоугольник (72,8 KiB, 1097 обращений)
Обычные или нестандартные (122,5 KiB, 1018 просмотров)
Подобные полигоны (1.4 MiB, 792 обращений)
Вогнутая или выпуклая (132.3 KiB, 1027 просмотров)
Измерение углов (35,7 KiB, 1263 совпадений)
Правильные многоугольники — Площадь (256,4 KiB, 1159 просмотров)
Математическая задача: вращение шестиугольника — математическая задача (3739), сплошная геометрия
Правильный шестиугольник со стороной 6 см повернут на 60 ° по линии, проходящей через его самую длинную диагональ. Каков объем полученной таким образом фигуры?Правильный ответ:
Отображение 2 комментариев:
Укажите используемые переменные…использование фигуры будет отличным
Кузов состоит из 3-х частей: конус + цилиндр + конус.
Чтобы решить эту математическую задачу со словами, вам понадобятся следующие знания:
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2Сопутствующие математические задачи и вопросы:
- Cut and cone
Рассчитайте объем конуса вращения, боковая поверхность которого представляет собой дугу окружности с радиусом 15 см и центральной угол 63 градуса. - Четырехугольная пирамида
Вычислите площадь поверхности и объем правильной четырехугольной пирамиды: стороны оснований (низ, верх): a1 = 18 см, a2 = 6 см, угол α = 60 ° (угол α — это угол между боковой стенкой и базовая плоскость.) S =? , V =? - Угол диагонали
Угол между диагональю тела правильного четырехугольника и его основанием составляет 60 °. Край основания имеет длину 10 см. Рассчитайте объем тела. - Треугольная пирамида
Каков объем правильной треугольной пирамиды со стороной 3 см? - Тетраэдрическая пирамида
Вычислите объем и поверхность правильной тетраэдрической пирамиды, если площадь содержимого основания составляет 20 см 2 , а угол отклонения боковых граней от плоскости основания составляет 60 градусов. - Пирамида с шестигранной вырезкой
Рассчитайте объем обычной пирамиды с шестигранной вырезкой, если нижний край равен 30 см, верхний край — 12 см, а длина бокового края — 41 см. - Восьмиугольная пирамида
Найдите объем правильной восьмиугольной пирамиды с высотой v = 100 и углом бокового ребра к плоскости основания α = 60 °. - 4-сторонняя пирамида
Вычислите объем и поверхность 4-сторонней правильной пирамиды, длина основания которой составляет 4 см. Угол от плоскости боковины и плоскости основания составляет 60 градусов. - Конус
Объем вращающегося конуса 9,42 см 3 при высоте 10 см. Какой угол между стороной конуса и его основанием? - Периметр треугольника
В треугольнике угол ABC A равен 60 °, угол B равен 90 °, а размер стороны c равен 15 см. Рассчитайте длину окружности треугольника. - Квадратная пирамида
Вычислите объем пирамиды со стороной 5 см, с квадратным основанием и углом основания 60 градусов. - Шестиугольная пирамида
Основание пирамиды представляет собой правильный шестиугольник, который можно описать в круг с радиусом 1 метр.Рассчитайте объем пирамиды высотой 2,5 метра. - Поворотный конус
Объем вращения конуса составляет 472 см 3 , а угол между стороной конуса и углом основания составляет 70 °. Вычислите площадь боковой поверхности этого конуса. - Шестиугольная пирамида
Вычислите объем и поверхность правильной шестиугольной пирамиды с длиной ребра основания 3 см и высотой 5 см. - Шестиугольная пирамида
Вычислите высоту правильной шестиугольной пирамиды с краем основания 5 см и высотой стены w = 20 см.Пожалуйста, нарисуйте картинку. - Призма четырехугольная
Высота правильной четырехугольной призмы v = 10 см, отклонение диагонали тела от основания 60 °. Определите длину краев основания, поверхности и объем призмы. - Пирамида 8
Вычислите объем и площадь поверхности правильной четырехугольной пирамиды со стороной основания 9 см и боковой стенкой с основанием под углом 75 °.
Вопросы по CAT — Вопросы по геометрии: треугольники, онлайн-классы 2IIM CAT 2020, коучинг CAT в Ченнаи
Вопрос из правильного многоугольника.В нем говорится о правильном шестиугольнике, вписанном в круг. Вопросы по геометрии CAT тщательно проверяются на экзамене CAT. Убедитесь, что вы хорошо разбираетесь в задачах геометрии. Треугольники подвергаются серьезным испытаниям, замечательный многоугольник с бесконечными сторонами, которым является круг, также подвергается серьезным испытаниям. Между этими двумя находится масса правильных многоугольников.
Вопрос 13 : ABCDEF — правильный шестиугольник, вписанный в круг. Если самая короткая диагональ шестиугольника имеет длину 3 единицы, какова площадь заштрихованной области.
- 1/6 (3π — (9√3) / 2)
- 1/6 (2π — (6√3) / 2)
- 1/6 (3π — (8√3) / 2 )
- 1/6 (6π — (15√3) / 2)
🛠 Предложение ко Дню труда!
Сказочная скидка 4000 на онлайн-курсы CAT
Действительно до 2 мая2IIM: Лучший онлайн-коучинг CAT.
Описание видео
Лучший коучинг CAT в Ченнаи
Коучинг CAT в Ченнаи — CAT 2021
Онлайн-пакеты уже доступны!Пояснительный ответ
Метод решения этого вопроса CAT на основе правильного шестиугольника: Правильный шестиугольник — это всего лишь 6 равносторонних треугольников вокруг точки.
Пусть сторона правильного шестиугольника равна a.
Самая короткая диагональ будет иметь длину a√3. Почему?
Правильный шестиугольник — это всего лишь 6 равносторонних треугольников вокруг точки. Самая короткая диагональ — FD.
FD = FP + PD
△ FOE равносторонний, как и △ EOD.
Диагональ FD может быть разбита как FP + PD, оба из которых являются равносторонними по высоте.
FP = (√3a) / 2
FD = √3a = самая короткая диагональ
Вопрос говорит нам, что самая короткая диагональ составляет 3 см.
√3a = 3 => a = √3
Радиус круга = √3
Площадь шестиугольника = (√3a 2 ) / 4 * 6
Площадь круга — площадь шестиугольника = π (√3) 2 — √3 / 4 * (√3) 2 * 6
= 3π — (9√3) / 2
Площадь заштрихованной области = 1 / (6) (площадь (круг) — площадь (шестиугольник))
= 1 / ( 6) (3π — (9√3) / 2)Вопрос: «какова площадь заштрихованной области?»
Следовательно, ответ будет 1 / (6) (3π — (9√3) / 2)
Вариант А — правильный ответ.
Многоугольники вкратце
Мы долгое время уделяли внимание треугольникам и четырехугольникам. Но в этих геометрических джунглях существует гораздо больше форм, чем просто трех- и четырехгранные животные. Есть фигуры с пятью, шестью, семью и даже сорока двумя сторонами. И нам не пойдет на пользу держать головы под землей, как страусы, делая вид, что их не существует.
Если вы еще не догадались, полигонов — это замкнутые двумерные фигуры, состоящие только из отрезков прямых линий.Таким образом, треугольники и четырехугольники являются примерами многоугольников, но углы, кривые и окружности не обязательны.
Что касается именования полигонов, мы обычно называем их греческими префиксами (например, «три-» и «окто-»), которые соответствуют количеству их сторон. Конечно, после определенного момента это утомляет. Вот почему после 12 сторон мы просто называем их 13-угольными, 28-угольными и 146-угольными. Легче запоминать и легче писать. Нам это нравится.
905 905 905 905 905 905 905 905 905 905 905 905Стороны Название многоугольника 3 треугольник 4 четырехугольник 5 7 семиугольник 8 восьмиугольник 9 неугольник 10 десятиугольник 11c 905 905 n n -угольник
Как и четырехугольники, эти различные типы многоугольников также имеют диагонали.(За исключением треугольников, неважно, насколько сильно они или ). Но сколько именно диагоналей будет у этих многоугольников?Начнем с рисования непересекающихся диагоналей . У четырехугольника может быть только одна такая диагональ. Рисование в другом будет пересекаться с первым, и их не зря называют «непересекающимися».
Если мы возьмем пятиугольник, мы можем нарисовать две диагонали, которые не пересекаются. Ключ состоит в том, чтобы нарисовать ровно столько, чтобы разделить многоугольник на треугольники.
Когда мы смотрим на шестиугольники, мы можем разбить их на 4 различных треугольника, используя любые 3 непересекающиеся диагонали.
Когда мы переходим к семиугольникам, мы можем иметь 4 непересекающиеся диагонали. Это может быть какое-то странное математическое вуду … или это может быть особая связь между многоугольниками и треугольниками? По сути, это сводится к тому, что выпуклый многоугольник со сторонами n можно разделить на n — 2 различных треугольника, на n — 3 непересекающиеся диагонали.
Если мы вернемся к нашему шведскому столу многоугольников, мы знаем, что треугольник имеет внутренние углы, которые в сумме составляют 180 °. Четырехугольник имеет внутренние углы в сумме 360 °. Как оказалось, пятиугольники имеют внутренние углы 540 °, а шестиугольники имеют внутренние углы 720 °.
Больше математического вуду? Не так много. Многоугольник со сторонами n имеет внутренние углы, которые в сумме составляют ( n — 2) × 180 °.
Пример задачи
Используя треугольники, определите общую меру внутренних углов четырехугольника.
Нарисуем одну диагональ, соединяющую B и D через четырехугольник ABCD . Получаем два треугольника: Δ ABD и Δ BCD . Мера внутреннего ABC — это просто сумма мер ∠1 и ∠2. Измерение ADC является суммой измерений 3 и 4. Между тем, BAD и ∠ BCD являются общими для треугольников и четырехугольника.
Когда мы складываем углы обоих треугольников вместе, получаем 180 ° + 180 ° = 360 °.Это точно подтверждает то, что мы уже знали. Так держать, нам.
Если бы мы сделали то же самое для пятиугольника, мы бы разбили пятиугольник на три треугольника, каждый из которых дает 180 ° к сумме внутренних углов пятиугольника. Добавление каждого из этих вкладов дает нам 540 °. Это также согласуется с нашей формулой, поскольку ( n -2) × 180 °, когда n = 5, равно (5-2) × 180 ° = 3 × 180 ° = 540 °.
До сих пор мы придерживались треугольников и четырехугольников. Теперь, когда мы расширяем наш геометрический вкус, нам следует расширить наш словарный запас.
Правильный многоугольник — это многоугольник, стороны которого равны, а углы равны. Итак, правильный треугольник — это хорошо знакомый равносторонний треугольник. Правильный четырехугольник нам больше известен как квадрат. Это потому, что единственный четырехугольник, который одновременно является равносторонним и , является квадратом.
Мы можем считать стороны, мы можем считать углы и мы можем считать диагонали. (Вы знаете, кто любит считать? Счет.)
Количество непересекающихся диагоналей, как мы уже знаем, равно n — 3, где n — количество сторон многоугольника.Но как насчет общего количества диагоналей, даже если они и пересекаются? Что ж, каждая вершина может иметь те же самые диагонали n — 3, но мы будем считать каждую диагональ дважды (по одной для каждой вершины), поэтому мы должны разделить это число на 2. В итоге мы получим формулу для числа диагоналей в n -угольник.
Пример задачи
Сколько градусов в восьмиугольнике? Сколько может быть непересекающихся и пересекающихся диагоналей?
У восьмиугольников 8 сторон, поэтому n = 8.Теперь все, что нам нужно сделать, это применить наши формулы (и вспомнить, что означает каждая из них). Начнем с количества градусов.
( n -2) × 180 ° =
(8-2) × 180 ° =
6 × 180 ° =
1080 °Теперь о количестве непересекающихся и пересекающихся диагоналей. Мы просто должны помнить, какая формула есть какая.
n — 3 =
8 — 3 =
5=
=
4 × 5 =
20Не , что сложно, учитывая, что непересекающихся диагоналей всегда должно быть меньше, чем пересекающихся .Таким образом, восьмиугольник имеет в общей сложности 1080 ° внутренних углов, 5 непересекающихся диагоналей и 20 общих диагоналей.
И последний совет: не ешьте желтый снег.
Ладно, правда. И последний совет: если вы обнаружите, что имеете дело с массивным многоугольником с гораздо большим количеством сторон, чем вы можете обработать, попробуйте разбить его на те, с которыми вы можете справиться. По сути, если вы можете разбить многоугольник на треугольники и четырехугольники, доверяйте Nike, а просто сделайте это . Если серьезно. это сделает вашу жизнь проще.
Подсчет количества диагоналей N-стороннего многоугольника | Абрар Шариар | The Startup
Фото sutirta budiman на UnsplashМы начнем наше путешествие с четырехугольника, поскольку треугольники — самый неубедительный из всех многоугольников (конечно, в плане диагоналей!) Как хорошо преподают в классе, мы знаем, что у четырехугольника две диагонали. Теперь можем ли мы найти количество диагоналей N-стороннего многоугольника, где N = любое положительное целое число? На самом деле, кажется, есть изящный трюк, чтобы подсчитать — количество диагоналей любого многоугольника.Не пугайтесь, потому что мы не будем углубляться в какие-либо утомительные вычисления, а воспользуемся некоторыми простыми интуитивными шагами. Давайте посмотрим на несколько многоугольников в действии:
Прекрасный пятиугольник с 5 диагоналямиЗдесь у нас есть антагонист ABCDE p . Теперь, если мы начнем рисовать диагонали от вершины A, мы можем нарисовать 2 диагонали, соединяющие D и C, чтобы сформировать AD, и AC соответственно. Помните, что при рисовании диагоналей мы можем рассматривать только несмежные вершины. Опять же, взяв вершину B, соединяем E и D, образуя еще 2 диагонали: BE, и BD.
Теперь рассмотрим вершину C, какие вершины мы можем соединить? Мы можем соединиться с E, чтобы сформировать CE и с A, чтобы сформировать CA . Подожди секунду! Разве мы не рассматривали CA ранее при рисовании диагоналей из A? Действительно, так как CA = AC. Поскольку двойной счет будет блотом в нашем математическом смысле, мы рассматриваем только CE как жизнеспособного кандидата для рисования диагонали из C. Итак, мы можем провести только 1 уникальную диагональ из вершины C.
Переходя к вершинам D и E, мы можем применить вышеупомянутую логику и, к сожалению, обнаруживаем, что на самом деле мы не можем провести какую-либо уникальную диагональ из D и E. Неуклюжие маленькие D и E. рисуя еще несколько прямых линий! Так что вроде D и E.
Помните, последовательность диагоналей, которые мы расширили от каждой вершины: [ 2, 2, 1]
Теперь давайте проведем наш небольшой эксперимент по игре на шестиугольнике :
Уродливый шестиугольник с 9 диагоналямиПримените те же логические шаги, описанные выше, мы можем назначить количество диагоналей, которые будут расширены от каждой из вершин, за исключением F и E (нам просто нравятся уникальные диагонали).Итак, всего 3 + 3 + 2 + 1 = 9 диагоналей для шестиугольника . Соблюдайте последовательность здесь: [3,3,2,1].
Пришло время активировать наш режим сопоставления с образцом:
Количество уникальных диагоналей, вытянутых из вершинОбратите внимание, в пятиугольнике n = 5, у нас есть такая последовательность: (n-3) + (n-3 ) + (n-4)
И в шестиугольнике для n = 6, у нас есть такая последовательность: (n-3) + (n-3) + (n-4) + (n- 5)
Таким образом, последовательность начинается с (n-3) и заканчивается на 1.Это выглядит так: (n-3) + (n-3) +…. + 1
Теперь, рассматривая ведущий (n-3) постоянный член, мы замечаем, что остальное — это арифметическая последовательность с интервалом 1. Итак, мы можем найти сумму этих членов, используя этот изящный метод. Вкратце, метод использует:
Сумма = Среднее * Количество элементов
Где, Среднее = (Высокий + Низкий) / 2
и, Количество элементов = [(Высокий — Низкий) / приращение. ] + 1
Применим его к шестиугольнику:
Среднее = (3 + 1) / 2 = 2
Количество элементов = ((3-1) / 1) + 1 = 3
Следовательно, Sum = 3 * 2 = 6
Действительно, 3 + 2 + 1 = 6
Итак, количество диагоналей = (n-3) + 6 = (6–3) + 6 = 3 + 6 = 9
Теперь, Вы могли бы немного подразнить вас вопросом, почему такая сложность для такого простого суммирования? Подумайте, что произойдет, если мы рассмотрим 20-сторонний многоугольник или даже больше? Эти шаги спасут множество нейронов в вашем мозгу от слияния (!)
Пора срезать 20-сторонний многоугольник — lcosagon — с помощью нашей изящной маленькой уловки!
Мы знаем, что последовательность должна выглядеть так: (n-3) + (n-3) + (n-4) +….
- Обрезать UIImage в форме шестиугольника?

 circ) :
circ) : Математика. Никольский. Учебник. Ответы к стр. 128
Математика. Никольский. Учебник. Ответы к стр. 128
 Результаты занесите в таблицу.
Результаты занесите в таблицу.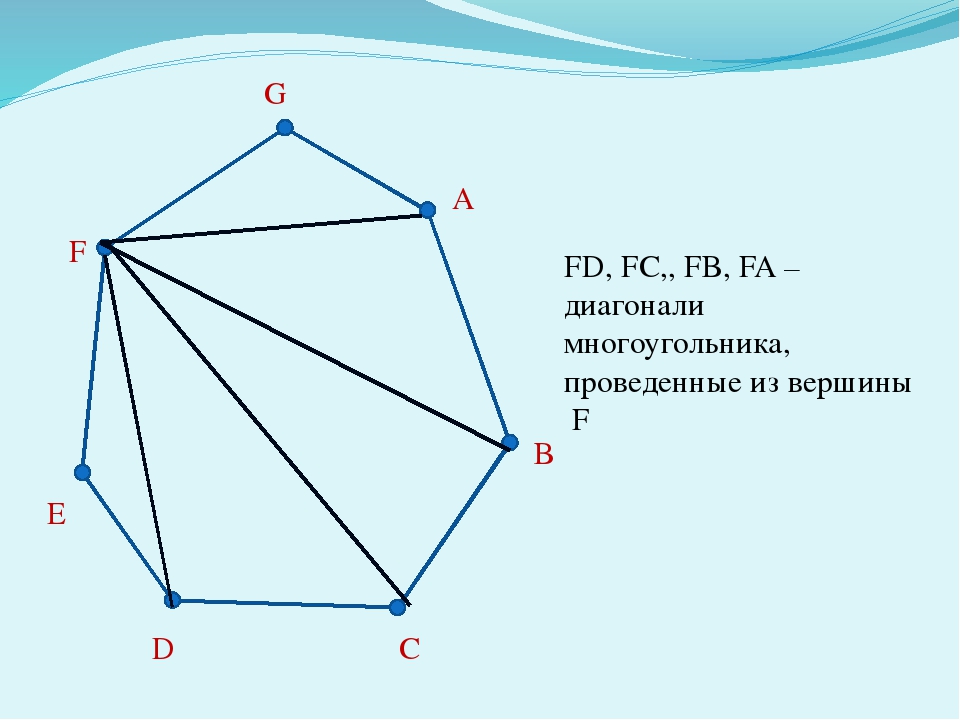
 е.:
е.: 2…
2…
 ..
.. Например, дана следующая матрица M = [1 1 4 5 4 2 5 1 2 2 4 1 2 1 3 1 3 1 1 1 1 2 3 3 1] Я хочу получить список векторов, которые составляют верхние…
Например, дана следующая матрица M = [1 1 4 5 4 2 5 1 2 2 4 1 2 1 3 1 3 1 1 1 1 2 3 3 1] Я хочу получить список векторов, которые составляют верхние…
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.