В правильном пятиугольнике угол: Пятиугольник — это… Что такое Пятиугольник?

Урок 6: Правильные многоугольники — 100urokov.ru

План урока:

Понятие правильного многоугольника

Описанная и вписанная окружности правильного многоугольника

Формулы для правильного многоугольника

Построение правильных многоугольников

 

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны.

Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

 

Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение.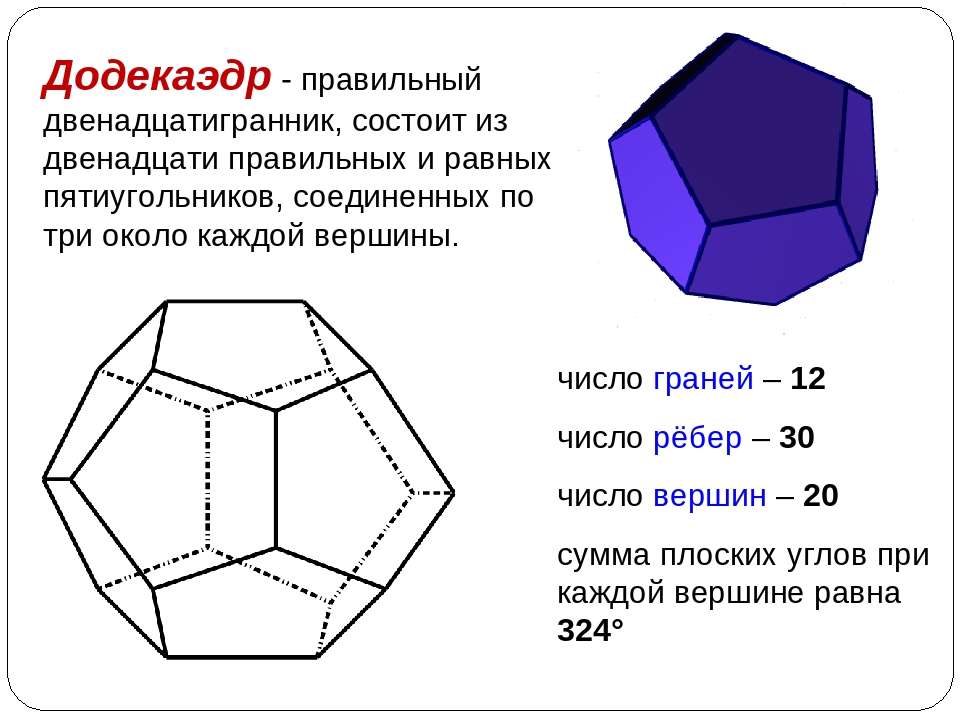 Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

 

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу 

 

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Ответ: не может.

 

Описанная и вписанная окружности правильного многоугольника

Докажем важную теорему о правильном многоуг-ке.

Для доказательства обозначим вершины произвольного правильного n-угольника буквами А₁, А₂, А₃…А_n. Далее проведем биссектрисы углов ∠А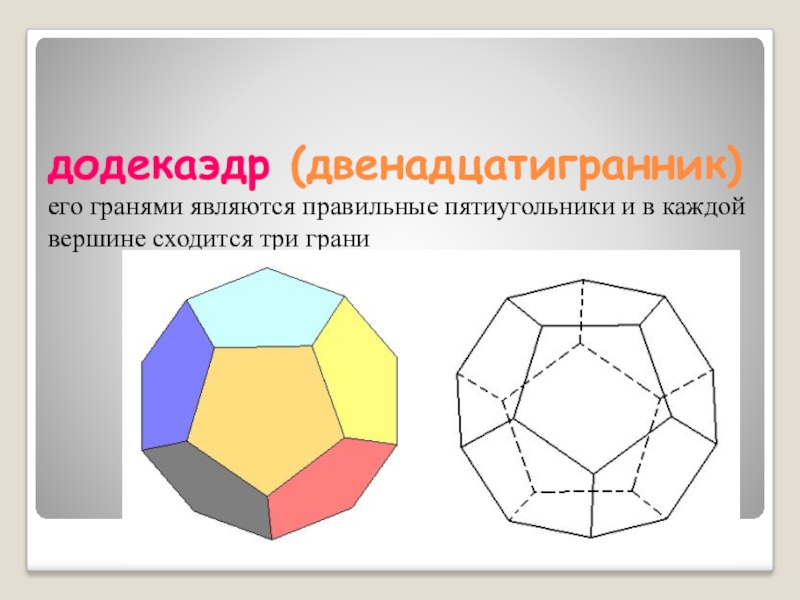

1 и ∠А₂. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА₃, ОА₄ и т. д.

∠А₁ и ∠А₂ одинаковы по определению правильного многоуг-ка:

Из этого факта вытекает два равенства:

Получается, что ОА₃ – это также биссектриса ∠А₃. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):

Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:

Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А₁, А₂ и А₃, можно провести только одну окружность, ч. т. д.

Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН₁, ОН₂, ОН₃… на стороны многоуг-ка.

Так как высоты проведены в равных треуг-ках, то и сами они равны:

Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН₁. Он должен будет пройти и через точки Н₂, Н₃, … Н_n. Причем отрезки ОН₁, ОН₂, ОН₃ окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:

Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А

1, ∠А₂, ∠А₃, то есть в точке О. Так как расстояние от О до А₁А₂ – это отрезок ОН₁, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.

Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.

Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН₁, ОН₂, ОН₃,… проведены в равнобедренных треуг-ках∆ОА

1А₂, ∆ОА₂А₃, ∆ОА₃А₄,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н₁, Н₂, Н₃,… – это середины сторон многоуг-ка.

 

Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?

Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют.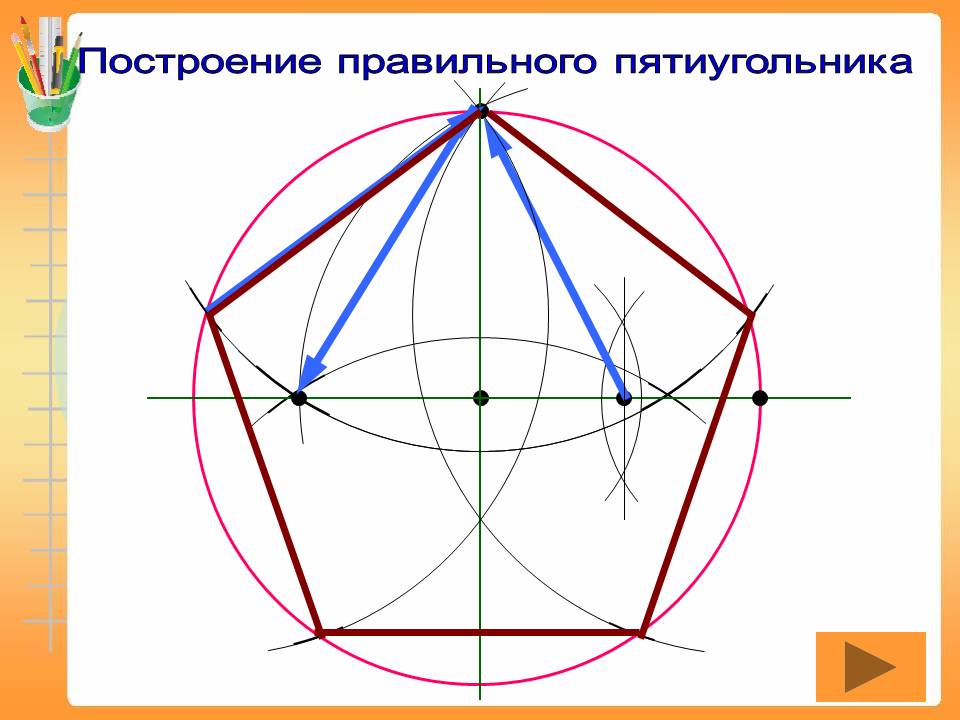 Получается, что биссектрисы не могут быть параллельными.

Ответ: не могут.

Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.

 

Формулы для правильного многоугольника

Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой a_n, где n– число сторон у многоуг-ка. Например a₄– это сторона квадрата, a₆– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой

R, а вписанной – маленькой буквой r.

Оказывается, все эти величины взаимосвязаны друг с другом.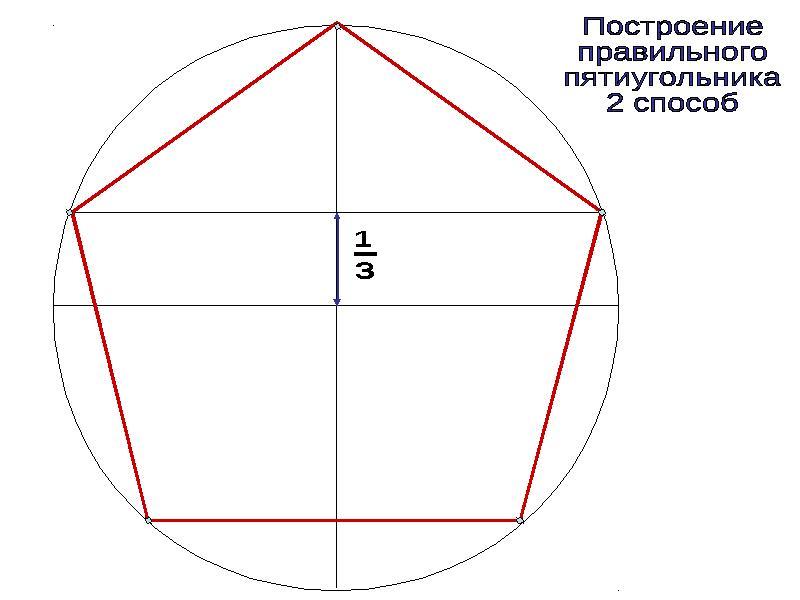 Ранее мы уже получили формулу

для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.

Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:

 

Теперь можно найти и ∠А₁ОН₁, рассмотрев ∆А₁ОН₁:

Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:

С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).

 

Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.

Решение. Запишем следующую формулу:

Это равенство как раз и надо было доказать в этом задании.

 

Задание. Около окружности описан квадрат.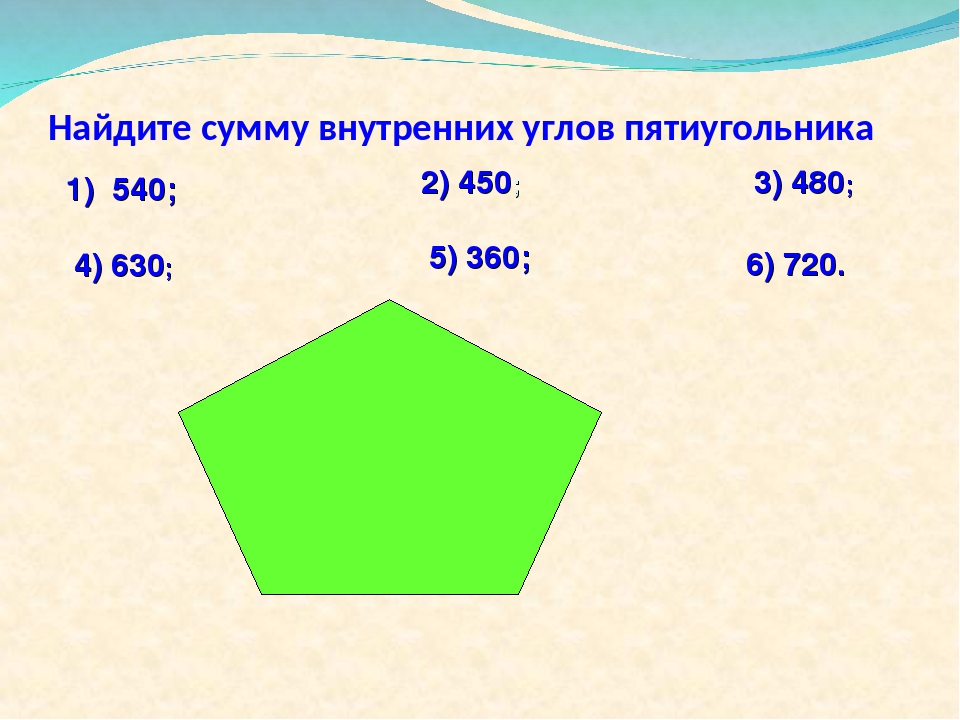 В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.

Решение. Запишем формулу:

 

Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.

Решение.

Найдем периметр шестиугольника:

 

Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?

Решение. Зная периметр треуг-ка, легко найдем и его сторону:

Далее вычисляется радиус описанной около треугольника окружности:

 

Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?

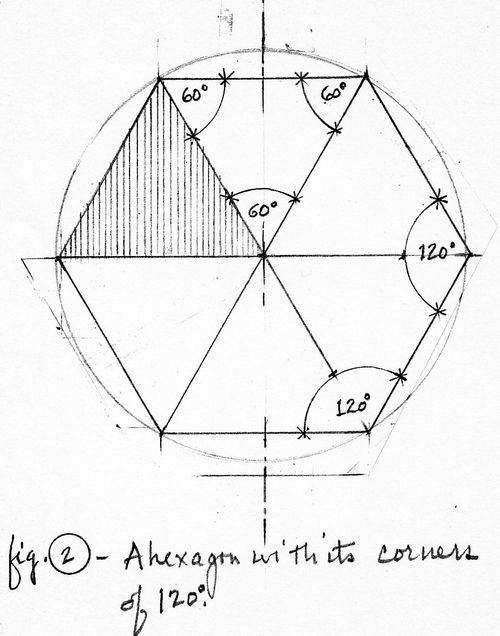
Решение.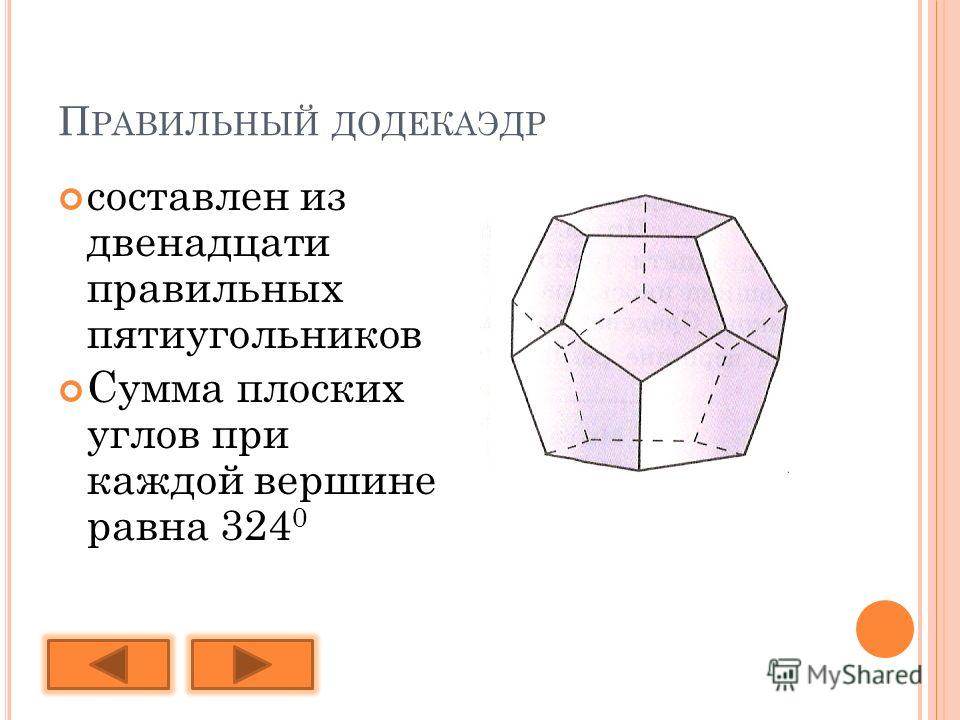 Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:

Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:

Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:

В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:

Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:

AC = 17 мм

∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:

AH = AC/2 = 17/2 = 8,5 мм

Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:

Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.

Ответ: 20 мм.

 

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника.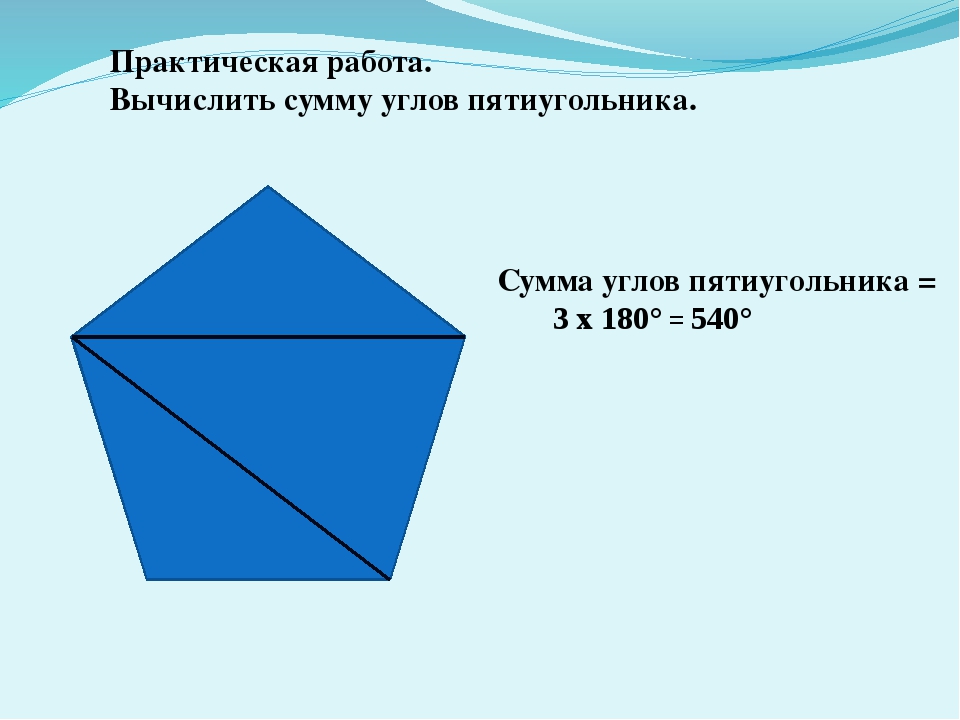 Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.

 

Правильный пятиугольник — Карта знаний

• Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Источник: Википедия

Связанные понятия

Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны. Пери́метр (др.-греч. περίμετρον — окружность, др.-греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина. Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r). Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Упоминания в литературе

Возможно, будущие чемпионаты мира отличатся более экзотическими Архимедовыми футбольными мячами. Мои предпочтения связаны с плосконосым додекаэдром, состоящим из 92 симметричных компонентов: 12 правильных пятиугольников и 80 равносторонних треугольников (рис. 2.08).

Связанные понятия (продолжение)

Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Простой многоугольник — это фигура, состоящая из непересекающихся отрезков («сторон»), соединённых попарно с образованием замкнутого пути. Если стороны пересекаются, многоугольник не является простым. Часто слово «простой» опускается из вышеприведённого определения. Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м (больше пяти) простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки (так, семи-, одиннадцати- и тринадцатиугольники построить циркулем и линейкой нельзя). Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет. Пятиугольник Роббинса — это вписанный пятиугольник, стороны которого и площадь являются рациональными числами. Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет. Пятиугольный паркет — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360°. Однако, ими можно замостить гиперболическую плоскость и сферу. Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой. В геометрии плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней. Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными… Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией. Гипотеза Тёплица, также известная как гипотеза о вписанном квадрате — нерешённая проблема геометрии. Формулировка гипотезы… Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника). Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис. Это биссектрисы двух внутренних углов противоположных углов четырёхугольника, биссектрисы внешних углов двух других вершин, и биссектрисы внешних углов в точках пересечения продолжений противоположных сторон (смотрите рисунок справа, указанные… Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон. Гиперокта́эдр — геометрическая фигура в n-мерном евклидовом пространстве: правильный политоп, двойственный n-мерному гиперкубу. Другие названия: кокуб, ортоплекс, кросс-политоп. Интегральное исчисление — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений. Окружности Мальфатти — три окружности внутри заданного треугольника, такие, что каждая окружность касается двух других и двух сторон треугольника. Окружности названы именем Джанфранческо Мальфатти, который начал исследовать задачу построения этих окружностей с ошибочным убеждением, что они в сумме дают максимальную возможную площадь трёх непересекающихся окружностей внутри треугольника. Задача Мальфатти относится к обеим задачам — как к построению окружностей Мальфатти, так и к задаче нахождения… В геометрии построение Витхоффа, или конструкция Витхоффа — это метод построения однородных многогранников или мозаик на плоскости.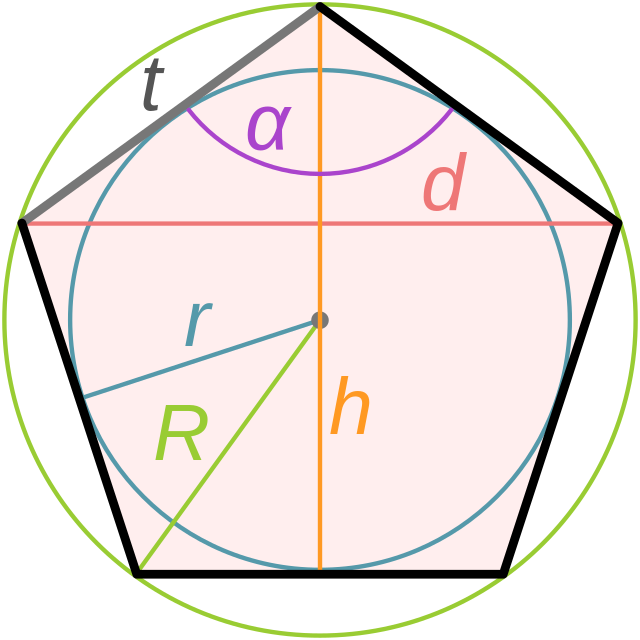 Метод назван по имени математика В. А. Витхоффа. Часто метод построения Витхоффа называют калейдоскопным построением. Сглаженный восьмиугольник — это область плоскости, предположительно, имеющая самую малую наибольшую плотность упаковки плоскости из всех центрально симметричных выпуклых фигур. Фигура получается заменой углов правильного восьмиугольника секцией гиперболы, которая касается двух сторон угла и асимптотически приближается к продолжениям сторон восьмиугольника, смежным сторонам угла. Многоугольник Петри для правильного многогранника в размерности n — это пространственный многоугольник, такой что любые (n-1) последовательных ребра (но не n) принадлежат одной (n-1)-мерной грани. Звёздчатый многоугольник — многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника. Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд, среди них пентаграмма, гексаграмма, две гептаграммы, октограмма, декаграмма, додекаграмма. Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их… Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая. В геометрии пространственный многоугольник — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется. Построение выпуклой оболочки методом «разделяй и властвуй» — алгоритм построения выпуклой оболочки.

Подробнее: Алгоритм Киркпатрика

В геометрии правильный косой многогранник — это обобщение множества правильных многогранников, которое включает возможность непланарных граней или вершинных фигур. Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани. В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников. В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство. Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади). Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины. Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).

Подробнее: Концентричные объекты

Круговой фрактал — класс геометрических (конструктивных) фракталов (см., например,), построенных многократным вписыванием в окружность других окружностей меньшего радиуса. (см. рис. 1a, 1b, 1c). Конфигурация вершины задаётся как последовательность чисел, представляющих число сторон граней, окружающих вершину. Обозначение «a.b.c» обозначает вершину с тремя гранями около неё и эти грани имеют a, b и c сторон (рёбер). Обобщённый многоугольник — это структура инцидентности, предложенная Жаком Титсом в 1959 году. Обобщённые n-угольники вмещают в качестве частных случаев проективные плоскости (обобщённые треугольники, n=3) и обобщённые четырёхугольники (n=4). Многие обобщённые многоугольники получаются из групп типа Ли, но существуют некоторые экзотические обобщённые многоугольники, которые таким способом не получаются. Обобщённые многоугольники, удовлетворяющие условию, известному как свойство Муфанга, полностью… Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников. Вписанно-описанный четырёхугольник — это выпуклый четырёхугольник, который имеет как вписанную окружность, так и описанную окружность. Из определения следует, что вписанно-описанные четырёхугольники имеют все свойства как описанных четырёхугольников, так и вписанных четырёхугольников. Другие названия этих четырёхугольников: хордо-касающийся четырёхугольник и бицентрический четырёхугольник. Их также называют двух-окружностными четырёхугольниками. Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло. Простая форма — совокупность граней, выводящихся друг из друга элементами симметрии точечной группы и удовлетворяющая закону Гаюи. Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения. Равносторонний многоугольник — многоугольник, у которого все стороны равны. Например, равносторонний треугольник — это треугольник, у которого все три стороны одинаковы; все равносторонние треугольники подобны и имеют внутренние углы 60 градусов. Равносторонний четырёхугольник — это ромб, и квадрат является частным случаем ромба. В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Подробнее: Барицентр

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Подробнее: Правильный четырёхмерный многогранник

Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.

Правильный пятиугольник: необходимый минимум информации

Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру, ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).

Чем интересен правильный пятиугольник?

Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!

Основные свойства и формулы

Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.

• Центральный угол α = 360 / n = 360/5 =72°.
• Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
• Отношение диагонали к боковой стороне равно (1+√5) /2, то есть «золотому сечению» (примерно 1,618).
• Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:

• если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
• в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
• бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.

• Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
• если имеется вписанная или описанная окружность, то используется одна из двух формул:

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R²*sin α)/2 ≈ 2,3776*R²;

• площадь можно также определить, зная лишь длину боковой стороны а:

S = (5*a²*tg54°)/4 ≈ 1,7205* a².

Правильный пятиугольник: построение

Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.

1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.

2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.

3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.

4. На середине расстояния между точками О и В постройте точку С.

5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.

6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.

7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить точкой G.

8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.

9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!

Площадь правильного пятиугольника — Циклопедия

Площадь правильного пятиугольника — это число, характеризующее правильный пятиугольник в единицах измерения площади.

Правильный пятиугольник (пентагон) — это пятиугольник, у которого все стороны и углы равны.

Введём обозначения:

a — длина стороны;

n — число сторон, n = 5;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α = π/5;

P₅ — периметр правильного пятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;

S₅ — площадь правильного пятиугольника.

Применима формула для площади правильного n-угольника при n=5:

[math]S_5=\frac{5a^2}{4}ctg\frac{\pi}{5} \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=5S_{\triangle}, \ S_{\triangle}=\frac{a^2}{4}ctg\frac{\pi}{5} \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=\frac{1}{2}P_5r, \ P_5=5a, \ r=\frac{a}{2}ctg\frac{\pi}{5} \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=5R^2\sin\frac{\pi}{5}\cos\frac{\pi}{5}, \ R=\frac{a}{2\sin\frac{\pi}{5}} \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=5r^2tg\frac{\pi}{5}, \ r=R\cos\frac{\pi}{5}[/math]

Используя значения тригонометрических функций углов для угла α=π/5:

[math]S_5=\frac{\sqrt{25+10\sqrt{5}}}{4}a^2 \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=5S_{\triangle}, \ S_{\triangle}=\frac{\sqrt{25+10\sqrt{5}}}{20}a^2 \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=\frac{1}{2}P_5r, \ P_5=5a, \ r=\frac{\sqrt{25+10\sqrt{5}}}{10}a \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=\frac{5\sqrt{10+2\sqrt{5}}}{8}R^2, \ R=\frac{\sqrt{50+10\sqrt{5}}}{10}a \Leftrightarrow[/math]

[math]\Leftrightarrow S_5=5\sqrt{5-2\sqrt{5}}r^2, \ r=\frac{\sqrt{5}+1}{4}R[/math]

где [math]\sin\frac{\pi}{5}=\frac{\sqrt{10-2\sqrt{5}}}{4}[/math], [math]\cos\frac{\pi}{5}=\frac{\sqrt{5}+1}{4}[/math], [math]tg\frac{\pi}{5}=\sqrt{5-2\sqrt{5}}[/math], [math]ctg\frac{\pi}{5}=\frac{\sqrt{25+10\sqrt{5}}}{5}[/math]

[править] Другие многоугольники

ⓘ Правильный пятиугольник. У правильного пятиугольника угол ра

Пользователи также искали:

как построить пятиугольник с заданной стороной, правильный пятиугольник диагонали, правильный пятиугольник по клеточкам, пятиугольник, Правильный, правильный, Правильный пятиугольник, правильный пятиугольник свойства, правильный пятиугольник диагонали, правильный пятиугольник площадь, неправильный пятиугольник, правильный пятиугольник по клеточкам, правильный пятиугольник углы, формулы, свойства, диагонали, площадь, неправильный, клеточкам, построить, заданной, стороной, углы, правильный пятиугольник формулы, как построить пятиугольник с заданной стороной, правильный пятиугольник, правильные многоугольники. правильный пятиугольник,

…

внутренних углов многоугольника — математическая открытая ссылка

внутренних углов многоугольника — математическая открытая ссылка

Попробуй это Отрегулируйте многоугольник ниже, перетащив любую оранжевую точку. Нажмите «сделать регулярным» и повторите. Обратите внимание на поведение внутренних углов и их сумму.

Внутренние углы многоугольника — это углы на каждом вершины, находящиеся внутри многоугольника. По одному на вершину. Итак, для многоугольника с N сторонами имеется N вершин и N внутренних углов.

Для правильного многоугольника по определению все внутренние углы одинаковы. На рисунке выше нажмите «Сделать регулярным», затем измените количество сторон и измените размер многоугольника, перетащив любую вершину. Обратите внимание, что для любого заданного количества сторон все внутренние углы одинаковы.

Для неправильного многоугольника каждый угол может быть разным. Нажмите «сделать нерегулярным» и посмотрите, что произойдет. при изменении количества сторон и перетаскивании вершины.

Сумма внутренних углов

Внутренние углы любого многоугольника всегда составляют постоянное значение, которое зависит только от количества сторон.Например, внутренние углы пятиугольник всегда составляет 540 ° независимо от того, регулярный он или нерегулярный, выпуклый или вогнутый или какого он размера и формы. Сумма внутренних углов многоугольника определяется по формуле: где
n — количество сторон

Так например:

А квадрат	Имеет 4 стороны, поэтому внутренние углы в сумме составляют 360 °
Пятиугольник	Имеет 5 сторон, поэтому внутренние углы в сумме составляют 540 °
Шестигранник	Имеет 6 сторон, поэтому внутренние углы в сумме составляют 720 °
… и т. д.

в правильных многоугольниках

Для правильного многоугольника сумма, описанная выше, равномерно распределяется между всеми внутренними углами, поскольку все они имеют одинаковые значения. Так например, внутренние углы пятиугольника всегда составляют в сумме 540 °, так что в правильном пятиугольнике (5 сторон) каждая из них составляет одну пятую от этого, или 108 °. Или, как формула, каждый внутренний угол правильного многоугольника определяется как: где
n — количество сторон

Прилегающие углы

Два внутренних угла, которые имеют общую сторону, называются «смежными внутренними углами» или просто «смежными углами».

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

правильный пятиугольник Википедия

пятисторонняя форма

Пентагон
Равносторонний пятиугольник, т.е.е. пятиугольник, пять сторон которого имеют одинаковую длину
Ребра и вершины	5
Внутренний угол (градусы)	108 ° (если равноугловой, включая правильный)

Геометрия пятиугольник (от греческих πέντε pente и γωνία gonia , что означает пять и угол ^[1] ) — любой пятиугольник или пятиугольник. Сумма внутренних углов в простом пятиугольнике составляет 540 °.

Пятиугольник может быть простым или самопересекающимся. Самопересекающийся правильный пятиугольник (или пятиугольник звезды ) называется пентаграммой.

Правильные пятиугольники []

Правильный пятиугольник имеет символ Шлефли {5}, а внутренние углы составляют 108 °.

Правильный пятиугольник имеет пять линий симметрии отражения и вращательную симметрию 5-го порядка (72 °, 144 °, 216 ° и 288 °). Диагонали выпуклого правильного пятиугольника находятся в золотой пропорции к его сторонам.Его высота (расстояние от одной стороны до противоположной вершины) и ширина (расстояние между двумя наиболее удаленными друг от друга точками, равное длине диагонали) задаются выражением

Высота = 5 + 252⋅ Сторона ≈ 1,539⋅ Сторона, {\ displaystyle {\ text {Высота}} = {\ frac {\ sqrt {5 + 2 {\ sqrt {5}}}} {2}} \ cdot {\ text {Side}} \ примерно 1,539 \ cdot {\ text {Side}},}

Ширина = Диагональ = 1 + 52⋅ Сторона ≈ 1,618⋅ Сторона, {\ displaystyle {\ text {Width}} = {\ text {Diagonal}} = {\ frac {1 + {\ sqrt {5}}} {2 }} \ cdot {\ text {Side}} \ приблизительно 1,618 \ cdot {\ text {Side}},}

Ширина = 2−25⋅Высота ≈1.{2}.}

Пентаграмма или пятиугольник — правильный пятиугольник в форме звезды. Его символ Шлефли — {5/2}. {\ circ})} {4}}}

с длиной стороны t .

Inradius []

Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет вписанную окружность. Апофема, которая представляет собой радиус r вписанной окружности, правильного пятиугольника связана с длиной стороны t соотношением

r = t2tan⁡ (π / 5) = t25−20≈0,6882⋅t. {\ Displaystyle r = {\ frac {t} {2 \ tan (\ pi / 5)}} = {\ frac {t} {2 {\ sqrt {5 — {\ sqrt {20}}}}}} \ приблизительно 0,6882 \ cdot t.}

Хорды ​​от описанной окружности до вершин []

Как любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет описанную окружность.Для правильного пятиугольника с последовательными вершинами A, B, C, D, E, если P — любая точка на описанной окружности между точками B и C, то PA + PD = PB + PC + PE.

Точка в плоскости []

Для произвольной точки на плоскости правильного пятиугольника с радиусом описанной окружности R {\ displaystyle R}, расстояние от которого до центроида правильного пятиугольника и его пяти вершин равно L {\ displaystyle L} и di {\ displaystyle d_ {i} } соответственно имеем ^[2]

∑i = 15di2 = 5 (R2 + L2), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {2} = 5 (R ^ {2} + L ^ {2}),}

∑i = 15di4 = 5 ((R2 + L2) 2 + 2R2L2), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ { 4} = 5 ((R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}),}

∑i = 15di6 = 5 ((R2 + L2) 3 + 6R2L2 (R2 + L2)), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {6} = 5 ((R ^ {2} + L ^ { 2}) ^ {3} + 6R ^ {2} L ^ {2} (R ^ {2} + L ^ {2})),}

∑i = 15di8 = 5 ((R2 + L2) 4 + 12R2L2 (R2 + L2) 2 + 6R4L4).{4}.}

Строительство правильного пятиугольника []

Правильный пятиугольник можно построить с помощью циркуля и линейки, так как 5 — простое число Ферма. Известно множество методов построения правильного пятиугольника. Некоторые обсуждаются ниже.

Метод Ричмонда []

Infogalactic: ядро ​​планетарного знания

В геометрии пятиугольник (от греческого πέντε pente и γωνία gonia , что означает пять и угол ^[1] ) — это любой пятиугольник или 5-угольник.Сумма внутренних углов в простом пятиугольнике составляет 540 °.

Пятиугольник может быть простым или самопересекающимся. Самопересекающийся правильный пятиугольник (или пятиугольник звезды ) называется пентаграммой.

Правильные пятиугольники

Правильный пятиугольник имеет символ Шлефли {5}, а внутренние углы составляют 108 °.

Правильный пятиугольник имеет пять линий симметрии отражения и вращательную симметрию 5-го порядка (72 °, 144 °, 216 ° и 288 °).Диагонали выпуклого правильного пятиугольника находятся в золотой пропорции к его сторонам. Его высота (расстояние от одной стороны до противоположной вершины) и ширина (расстояние между двумя наиболее удаленными друг от друга точками, равное длине диагонали) равны

.

, где R — радиус описанной окружности.

Площадь выпуклого правильного выпуклого пятиугольника с длиной стороны т. равна

.

Пентаграмма или пятиугольник — это правильный пятиугольник в форме звезды.Его символ Шлефли — {5/2}. Его стороны образуют диагонали правильного выпуклого пятиугольника — в этом расположении стороны двух пятиугольников находятся в золотом сечении.

Когда правильный пятиугольник вписан в круг радиусом R , длина его ребра t определяется выражением

, а его площадь

, поскольку площадь описанного круга представляет собой правильный пятиугольник, заполняет приблизительно 0.7568 его описанной окружности.

Вывод формулы площади

Площадь любого правильного многоугольника:

, где P — периметр многоугольника, а r — внутренний радиус (эквивалентно апофемой). Подстановка значений правильного пятиугольника на P и r дает формулу

с длиной стороны т .

Inradius

Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет вписанную окружность.Апофема, которая представляет собой радиус r вписанной окружности, правильного пятиугольника связана с длиной стороны t соотношением

.

Хорды ​​от описанной окружности до вершин

Как любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет описанную окружность. Для правильного пятиугольника с последовательными вершинами A, B, C, D, E, если P — любая точка на описанной окружности между точками B и C, то PA + PD = PB + PC + PE.

Построение правильного пятиугольника

Правильный пятиугольник можно построить с помощью циркуля и линейки, так как 5 — простое число Ферма.Известно множество методов построения правильного пятиугольника. Некоторые обсуждаются ниже.

Метод Ричмонда

Один из методов построения правильного пятиугольника в данной окружности описан Ричмондом ^[2] и далее обсуждается в «Многогранниках» Кромвеля. ^[3]

На верхней панели показана конструкция, использованная в методе Ричмонда для создания стороны вписанного пятиугольника. Окружность, определяющая пятиугольник, имеет единичный радиус. Его центр расположен в точке C , а средняя точка M отмечена на полпути по его радиусу.Эта точка присоединяется к периферии вертикально над центром в точке D . Угол CMD делится пополам, а биссектриса пересекает вертикальную ось в точке Q . Горизонтальная линия, проходящая через Q , пересекает окружность в точке P , а хорда PD является необходимой стороной вписанного пятиугольника.

Чтобы определить длину этой стороны, под кружком изображены два прямоугольных треугольника DCM и QCM .Используя теорему Пифагора и две стороны, гипотенуза большего треугольника находится как. Сторона h меньшего треугольника находится по формуле половинного угла:

, где косинус и синус ϕ известны из большего треугольника. Результат:

Когда эта сторона известна, внимание обращается на нижнюю диаграмму, чтобы найти сторону s правильного пятиугольника. Во-первых, сторона и правого треугольника снова находится с помощью теоремы Пифагора:

Тогда s находится с использованием теоремы Пифагора и левого треугольника как:

Сторона s следовательно:

хорошо зарекомендовавший себя результат. ^[4] Следовательно, эта конструкция пятиугольника верна.

Круги Карлайла

См. Основную статью : Carlyle Circle

Метод с использованием кругов Карлайла

Круг Карлайла был изобретен как геометрический метод нахождения корней квадратного уравнения. ^[5] Эта методика приводит к процедуре построения правильного пятиугольника. Шаги следующие: ^[6]

1. Нарисуйте круг, в который вписывается пятиугольник, и отметьте центральную точку O .
2. Проведите горизонтальную линию через центр круга. Отметьте одно пересечение с кругом как точку B .
3. Постройте вертикальную линию через центр. Отметьте одно пересечение с кругом как точку A .
4. Постройте точку M как среднюю точку O и B .
5. Нарисуйте круг с центром M через точку A . Отметьте его пересечение с горизонтальной линией (внутри исходного круга) как точку W и его пересечение за пределами круга как точку V .
6. Начертите окружность с радиусом OA и центром W . Он пересекает исходный круг в двух вершинах пятиугольника.
7. Начертите окружность с радиусом OA и центром V . Он пересекает исходный круг в двух вершинах пятиугольника.
8. Пятая вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.

Шаги 6-8 эквивалентны следующей версии, показанной на анимации:

6а.Постройте точку F как середину точек O и W.

7а. Постройте вертикальную линию через F. Она пересекает исходную окружность в двух вершинах пятиугольника. Третья вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.

8а. Постройте две другие вершины, используя циркуль и длину вершины, найденную на шаге 7a.

Использование тригонометрии и теоремы Пифагора

Использование тригонометрии и теоремы Пифагора для построения правильного пятиугольника.

Строительство

1. Сначала отметим, что правильный пятиугольник можно разделить на 10 конгруэнтных треугольников, как показано в наблюдении . Кроме того, cos 36 ° =. †
2. В Шаге 1 мы используем четыре единицы (показаны синим) и прямой угол, чтобы построить отрезок длиной 1 + √5, в частности, создав прямоугольный треугольник 1-2-√5 и затем расширив гипотенузу √ 5 на длину 1. Затем мы делим этот сегмент пополам, а затем снова делим пополам, чтобы создать отрезок длины (показан красным.)
3. На этапе 2 мы строим две концентрические окружности с центром в точке O с радиусом 1 и длиной. Затем мы помещаем P произвольно на меньший круг, как показано. Строя прямую, перпендикулярную OP, проходящую через P , мы строим первую сторону пятиугольника, используя точки, созданные на пересечении касательной и единичной окружности. Копирование этой длины четыре раза по внешнему краю единичных кругов дает нам правильный пятиугольник.

† Доказательство того, что cos 36 ° =

(с использованием формулы сложения углов для косинуса)

(используя формулы двойного и половинного угла)

Пусть u = cos 36. Сначала обратите внимание, что 0 < u <1 (что поможет нам упростить работу). Теперь

Полигоны — Основы работы с полигонами — Подробно

Слово многоугольник представляет собой сочетание двух греческих слов: «поли» означает «много» и «гон». означает угол.Помимо углов, у многоугольника есть стороны и вершины. «Три» означает «три», поэтому самый простой многоугольник называется треугольник, потому что у него три угла. Он также имеет три стороны и три вершины. Треугольник всегда компланарен, чего нельзя сказать о многих другие полигоны.

Правильный многоугольник — многоугольник, все углы и стороны которого совпадают или равны. Вот некоторые правильные многоугольники.

Мы можем использовать формула, чтобы найти сумму внутренних углов любого многоугольника.В этой формуле буква n обозначает количество сторон или углов многоугольника.

сум углов = (n — 2) 180 °

Давайте использовать формула, чтобы найти сумму внутренних углов треугольника. Запасной 3 для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить.

сум углов = (n — 2) 180 °
= (3 — 2) 180 ° = (1) 180 ° = 180 °

Чтобы найти Сумма внутренних углов четырехугольника, мы можем снова использовать формулу.На этот раз замените n на 4. Мы находим, что сумма внутренних углов четырехугольника 360 градусов.

сум углов = (n — 2) 180 °
= (4 — 2) 180 ° = (2) 180 ° = 360 °

Полигоны могут быть разделенными на треугольники, нарисовав все диагонали, которые можно нарисовать из одной единственной вершины. Давайте попробуем это с четырехугольником, показанным здесь. Из вершине A мы можем провести только одну диагональ, к вершине D.Четырехугольник может поэтому разделим на два треугольника.

Если вы посмотрите вернувшись к формуле, вы увидите, что n — 2 дает количество треугольников в многоугольнике, и это число умножается на 180, сумма мер всех внутренних углов в треугольнике. Вы видите, где «н — 2 «? Это дает нам количество треугольников в многоугольнике. Как Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника?

Вот пятиугольник, 5-сторонний многоугольник.Из вершины A можно провести две диагонали, разделяющие пятиугольник на три треугольника. Умножаем 3 раза на 180 градусов, чтобы найти сумма всех внутренних углов пятиугольника, составляющая 540 градусов.

сум углов = (n — 2) 180 °
= (5 — 2) 180 ° = (3) 180 ° = 540 °

Ссылки по теме:
Определения многоугольников, формулы полигонов (площадь, периметр) и имена полигонов (таблицы и формулы)

.