В чем выражается объем: Урок 11. понятие объема — Геометрия — 11 класс

Урок 11. понятие объема — Геометрия — 11 класс

Геометрия, 11 класс

Урок №11

Понятие объёма

Перечень вопросов, рассматриваемых на уроке:

Понятие объёма.

Свойства объёмов.

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Тезаурус

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

— равные тела имеют равные объёмы;

— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Основная литература:

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см³). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм

3), кубический метр (1 м³) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Пример:

Объём книги400 кубических сантиметров запишут: V = 400см³.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n³

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см³). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n³.

Объём прямоугольного параллелепипеда

Теорема

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Доказательство

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10ⁿ, b∙10ⁿ, c∙10ⁿ, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10ⁿ и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙10³ⁿ равных кубов с ребром 1/10ⁿ. Так как объём каждого куба равен 1/10³ⁿ, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.

Случай второй.

Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: a_n, b_n, c_n, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, a_n ≤ a ≤ a_n’, где a_n’ = a_n+1 : 10ⁿ. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение a_nb_nc_n ≤ abc ≤ a_n’b_n’c_n’, где b_n’= b_n+1 : 10ⁿ

, c_n’ = c_n+1 : 10ⁿ

По доказанному в первом случае, левая часть неравенства представляет собой объём V_n прямоугольного параллелепипеда P_n с измерениями a_n, b_n, c_n, а правая часть – это объём V_n’ прямоугольного параллелепипеда P_n’ с измерениями a_n’, b_n’, c_n’. Так как параллелепипед P содержит в себе параллелепипед P_n, а сам содержится в параллелепипеде P_n’, то объём V параллелепипеда P заключён между V_n, = a_nb_nc_n

и V_n’= a_n’b_n’c_n’. Будем неограниченно увеличивать n. Тогда 1/10ⁿ будет становиться сколь угодно малым, и поэтому произведение a_n’b_n’c_n’ будет сколь угодно мало отличаться от числа, выраженного произведением a_nb_nc_n. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением a_nb_nc_n, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Решение:

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см³

Ответ: V = 7500 см³.

№2.

Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см³, AB = 8 см, АА₁₌ 20 см.

Варианты ответов:

220 см²

100 см²

400 см²

200 см²

Решение.

Найдём длину АD:

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см².

Ответ: площадь закрашенной фигуры 200 см².

Верный ответ: 200 см².

Объем прямоугольного параллелепипеда / Геометрия / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Объем прямоугольного параллелепипеда

Каждое из рассматриваемых нами тел имеет объём, который можно измерить с помощью выбранной единицы измерения объёмов.

За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).

Единицы измерения объема:

Ребро куба	Название объема куба	Запись объема
1 мм	кубический миллиметр	1 мм3
1 см	кубический сантиметр	1 см3
1 дм	кубический дециметр	1 дм3
1 м	кубический метр	1 м3
1 км	кубический километр	1 км3

При измерении объемов жидкостей или газов 1 дм³ называют литром, и записывают так: 1 л = 1 дм³.

Обозначают объем буквой , т.е. если нам сказано, что объем фигуры равен 24 см³, то это можно записать так: = 24 см³.

Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.

Свойства объемов

1) Равные фигуры имеют равные объемы.

2) Объем фигуры равен сумме объемов фигур, из которых она состоит.

Формула для вычисления объема прямоугольного параллелепипеда

Если — длина параллелепипеда, — ширина параллелепипеда, — высота параллелепипеда, то объем такого параллелепипеда будет выражаться формулой: .

Пример:

Найдем объем параллелепипеда с ребрами 5 см, 2 см и 8 см:

= 528 = 80 (см³).

Связь объема параллелепипеда с площадью его основания

Если — длина прямоугольного параллелепипеда, — его ширина, то их произведение равно площади основания рассматриваемого параллелепипеда, т. к. основанием прямоугольного параллелепипеда является прямоугольник, т.е. (смотри рисунок ниже).

Если высоту данного прямоугольного параллелепипеда обозначить буквой , тогда объем данного параллелепипеда будет равен , откуда, учитывая то, что , получим: .

Пример:

Найдем объем прямоугольного параллелепипеда, площадь основания которого равна 20 см², а высота равна 7 см:

= 207 = 140 (см³).

Формула для вычисления объема куба

У куба все ребра равны, т.е. длина, ширина и высота совпадают, тогда, если ребро куба , его объем будет вычисляться по формуле: .

Пример:

Найдем объем куба с ребром 3 дм:

= 3³ = 333 = 27 (дм³).

Связь между метрическими единицами объема

1 м³ = 1 000 дм³ = 10³ дм³

1 дм³ = 1 000 см³ = 10³ см³

1 см³ = 1 000 мм³ = 10³ мм³

1 км³ = 1 000 м1 000 м1 000 = 10⁹ м³.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Измерение углов. Транспортир. Виды углов

Треугольник и его виды

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 823, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 955, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1068, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1099, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1794, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1804, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 606, Мерзляк, Полонский, Якир, Учебник

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 620, Мерзляк, Полонский, Якир, Учебник

Номер 1107, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 514, Мерзляк, Полонский, Якир, Учебник

Номер 539, Мерзляк, Полонский, Якир, Учебник

Номер 1, Мерзляк, Полонский, Якир, Учебник

Задание 156, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 476, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 519, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 739, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 782, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 991, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1041, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

---

© budu5. com, 2021

Пользовательское соглашение

Copyright

Единицы измерения оперативной памяти. Что такое бит, байт и килобайт?

Назад к результатам

В течение последних трех десятилетий объем компьютерной памяти увеличивался в геометрической прогрессии, и с каждым следующим поколением появляется новый уровень единиц памяти и новые условия для изучения. Давайте рассмотрим эти единицы измерения.

Структурные единицы

Биты и байты являются основными структурными единицами памяти. «Бит» обозначает двоичный символ. Бит — это единица или ноль, включение или выключение, так сохраняется вся информация в компьютере. Байт состоит из восьми бит. Исходный объем информации, необходимой для кодирования одного символа текста, был изначально равен восьми битам или одному байту. Позже, по мере развития компьютерного оборудования, это число было стандартизировано.

По техническим причинам емкость компьютерной памяти выражается в единицах кратных числу два. Затем к этим кратным единицам добавили приставки для образования кратных единиц, чтобы обеспечить простой способ выражения очень большого количества бит и байтов.

Приставки СИ

Для измерения компьютерной памяти используются некоторые приставки международной системы единиц (СИ) для образования производных единиц для байта. Однако эти приставки не являются метрическими, поскольку байт состоит из восьми бит, а килобайт равен 1024 байтам.

Приставка единицы измерения памяти	Объем
Кило- (килобайт, КБ)	1024 байт
Мега- (мегабайт, МБ)	1024 килобайт
Гига- (гигабайт, ГБ)	1024 мегабайт
Тера- (терабайт, ТБ)	1024 гигабайт
Пета- (петабайт, ПБ)	1024 терабайт

Единицы измерения памяти

Компьютеры используют память в оперативном запоминающем устройстве (ОЗУ), которое временно хранит информацию, и в накопителях, данные на которых хранятся постоянно.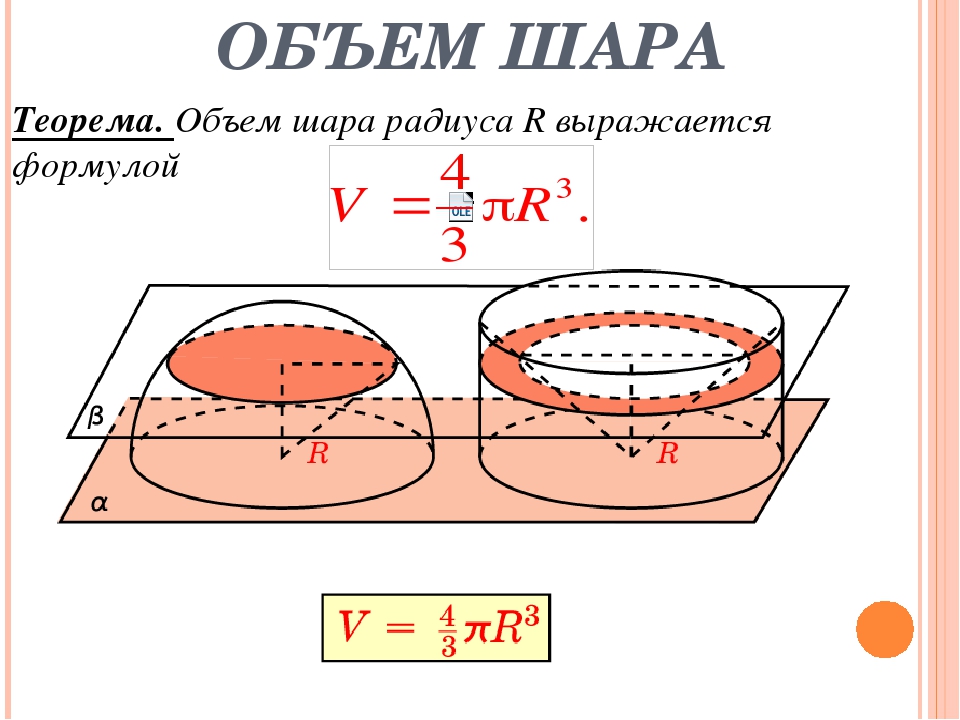 ОЗУ позволяет компьютеру переключаться между программами и иметь большие файлы наготове для просмотра.

В зависимости от того, для чего используется ваш компьютер, вам, как правило, понадобится установить максимально возможное количество памяти. Тип и объем памяти, установленной на вашем компьютере, а также максимальный объем и скорость, которые можно нарастить, зависят от производителя и модели компьютера. Воспользуйтесь инструментом Crucial® Advisor™ или системным сканером, чтобы найти память, совместимую с вашим компьютером. Подробнее о том, какой объем памяти необходим вашему компьютеру, читайте здесь.

Накопители: при описании емкости жестких дисков и твердотельных накопителей используются одни те же термины, относящиеся к памяти. По мере увеличения объема файлов  с видеороликами и очень большими фотографиями необходимо увеличение объема хранилищ.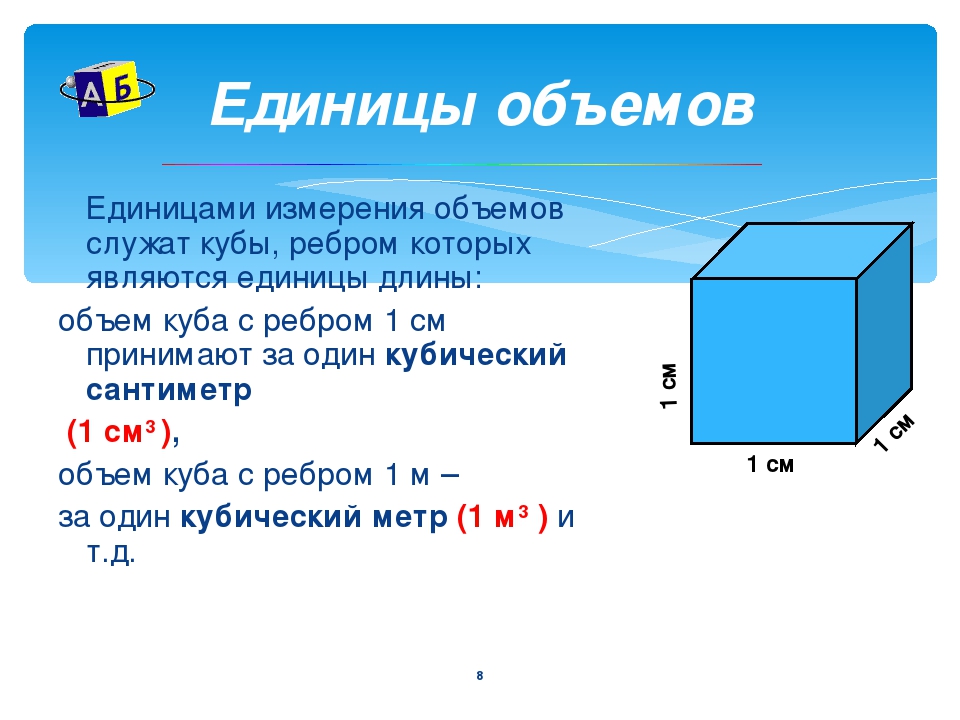 В настоящее время в продаже имеются твердотельные накопители разного объема, исчисляемого гигабайтами и терабайтами. Как и в случае с ОЗУ, вы можете использовать инструмент Crucial® Advisor™ или системный сканер для поиска твердотельного накопителя, совместимого с вашей системой.

Как найти Объем Параллелепипеда?

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.

Два свойства объёма У равных тел равные объёмы. Если два тела одинаковы, и имеют равное количество единиц измерения — их объёмы равны. Например, у двух одинаковых пакетов сока равные объемы. Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

Давайте вспомним, какие виды параллелепипедов бывают.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.

Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.

Какие бывают призмы:

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a * b * h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

a	длина параллелепипеда
b	ширина параллелепипеда
h	высота параллелепипеда
P (осн)	периметр основания
S (осн)	площадь основания
S (бок)	площадь боковой поверхности
S (п. п.)	площадь полной поверхности
V	объем

Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.

a = 9 см

b = 6 см

h = 3 см

V = a * b * h

V = 9 * 6 * 3 = 162 см3.

Ответ: объем прямоугольного параллелепипеда равен 162 см3.

Следствие 1 Объем параллелепипеда равен произведению площади основания на высоту. V = S осн * h

Из этого следствия выведем формулу нахождения площади основания параллелепипеда.

S осн = V : h

Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 82 см3, а высота 8 см.

V = 82 см3

h = 8 см

V = S осн * h

S осн = V : h

S осн = 82 см3: 8 см = 10,25 см2.

Ответ: площадь основания параллелепипеда равна 10,25 см2.

Следствие 2 Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. V = S осн * h

Пример 3. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 и 8 см. Боковое ребро равно 5. Найдем объем призмы.

V = S * h = 12* a * b * h

a = 6

b = 8

h = 5

V = 1/2 * 6 * 8 * 5 = 120 см3.

Ответ: объём прямой призмы, основанием которой является прямоугольный треугольник, равен 120 см3.

С каждым годом геометрия становится все более объемной. Формулы множатся, а задачки усложняются. В детской онлайн-школе Skysmart ваш ребенок сможет заполнить пробелы, разобрать сложные темы и научиться доказывать любые теоремы.

Записывайтесь на бесплатный вводный урок и знакомьтесь с устройством учебной платформы лично.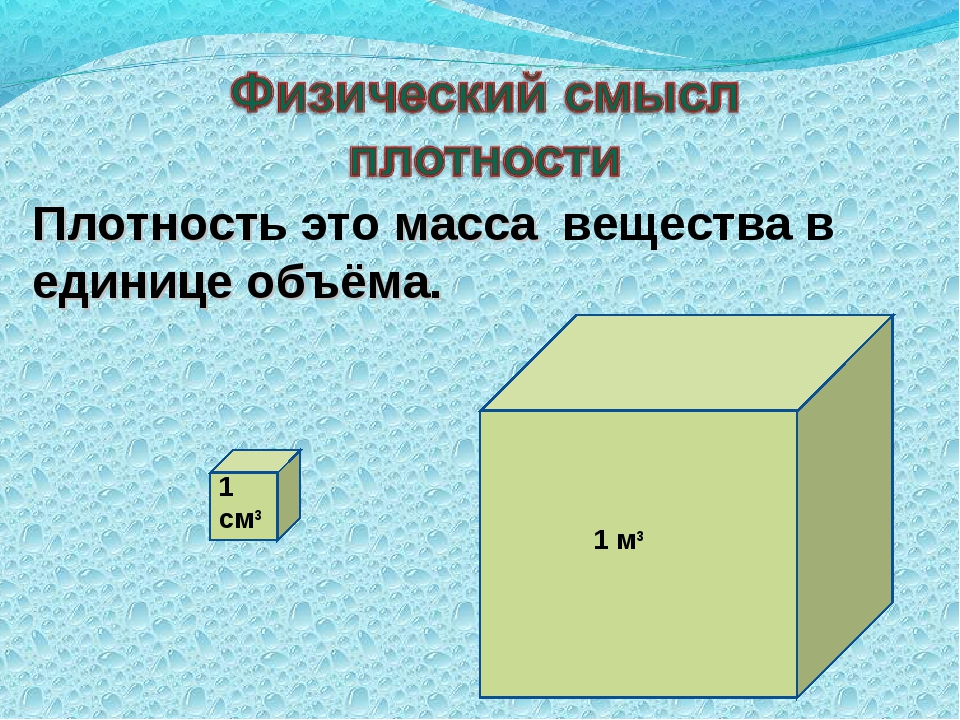

Вычисление площади

Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.

Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.

Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания.

• S п.п. = 2 (ab + ac + bc)

Пример 4. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.

S п.п. = 2 (ab + ac + bc)

S п.п. = 2(6 * 4 + 6 * 3 + 4 * 3) = 2 * (24 + 18 + 12) = 2 * 54 = 108 см2.

Ответ: площадь поверхности параллелепипеда — 108 см2.

Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно. В интернете есть много онлайн-калькуляторов, которые помогут вам быстро вычислить объем:

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.

Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a * b * h

Подставляем наши числа:

V = 18 * 10 * 7 = 1260 см3.

Ответ: объём параллелепипеда = 1260 см3.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём = 120 см3, а высота — 15 см.

Как решаем:

V = 120 см3

h = 15 см

V = S осн * h

S осн = V : h

S осн = 120 см3: 15 см = 8 см2.

Ответ: площадь основания параллелепипеда = 8 см2.

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания = 30 сантиметров, ширина = 12 см, а высота = 5 см.

Как решаем:

S п.п. = 2 (ab + ac + bc)

S п.п. = 2(30 * 12 + 30 *5 + 12 * 5) = 2 * (360 + 150 + 60) = 2 * 570 = 1140 см2.

Ответ: площадь полной поверхности параллелепипеда = 1140 см2.

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.

V параллелепипеда	V = a * b * h
	V = S осн * h
S боковой поверхности	S б.п. = 2(ac + bc)
S полной поверхности	S п.п. = 2 (ab + ac + bc)
Диагональ параллелепипеда	d2 = a2+ b2 + c2

На уроках математики в современной школе Skysmart нет скучных учебников, надоевших задачек и неинтересных тетрадей. Ученики занимаются по интерактивному учебнику, чертят на настоящей онлайн-доске и решают занимательные примеры.

Математика может быть по-настоящему увлекательной. Записывайтесь на бесплатный вводный урок, чтобы проверить, так ли это на самом деле.

Объем, единицы — Справочник химика 21

    Удельным объемом V называется объем единицы количества вещества (массы). Эта величина обратна плотности р, следовательно  [c.52]

    Удельный объем (и) тела представляет собой объем единицы его массы. [c.14]

    Удельным объемом газа называют объем единицы его массы. Определяют его как объем 1 кг газа, выраженный в кубических метрах. [c.21]

    Объем единицы теплообменника V [c.267]

    Таким образом, все величины, характеризующие кинетику массопереноса, связаны друг с другом коэффициент массопередачи, объемный коэффициент массопередачи, высота и объем единицы переноса. 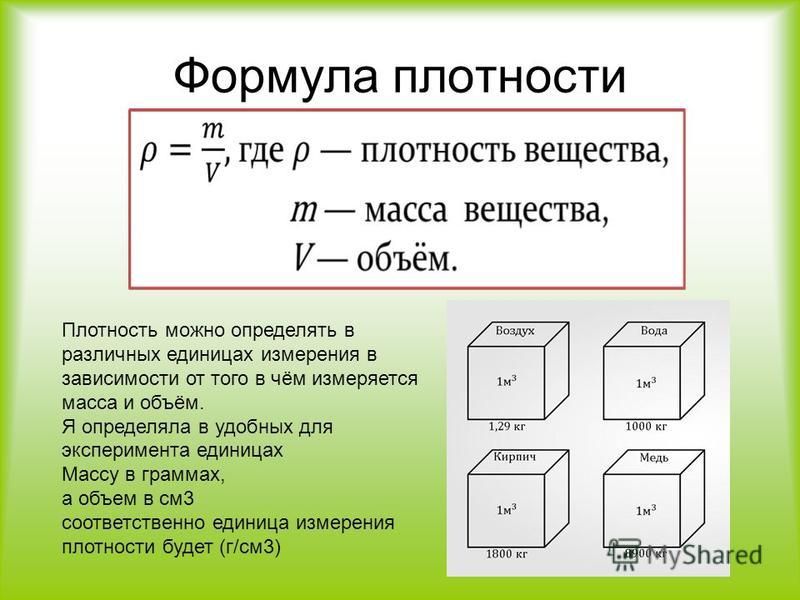Поэтому все методы расчета высоты массообменных аппаратов с помощью этих кинетических характеристик являются лишь разными математическими выражениями одного и того же процесса и в этом отношении равноценны. [c.33]

    Объем единицы массы теплообменника [c.267]

    Плотность —величина, определяемая как отношение массы вещества к занимаемому им объему. Единица плотности в Меж- [c.45]

    Объем характеризует макроскопическое свойство системы и, следовательно, также является параметром состояния. Свойства тел могут характеризоваться удельным (объем единицы массы) либо молярным (объем одного моля) объемом. [c.8]

    Здесь IIт — внутренняя энергия единицы массы 1/р = и — объем единицы массы — поток теплоты через единицу поверхности, замыкающей рассматриваемую систему. Тепловой поток связан с количеством теплоты йд/сИ, получаемым элементом массы вдоль линии его движения  [c.318]

    Плотность раствора — это отношение его массы к объему. Единицей плотности в Международной системе (СИ) является кг м . Эта единица слишком велика для лабораторной практики. В связи с этим применяют внесистемную единицу г см . Она с точностью до пятого знака совпадает с единицей системы СГС, так как 1 2= 1000,028 см , а 1 1,000028 лi  [c.92]

    Высота единицы переноса—характерная величина для аппаратов с непрерывным контактом (см. ниже). Более общей характеристикой, применимой для аппаратов с непрерывным и ступенчатым контактом (см. ниже), является объем единицы переноса йог, т. е. рабочий объем аппарата, соответствующий одной единице переноса. [c.195]

    Иными словами, критическая температура чистых веш,еств — это та максимальная температура, при которой жидкая и паровая фазы могут еш,е суи ествовать в равновесии. Давление паров лри этой температуре называется критическим давлением, а объем единицы массы вещества — критическим объемом. [c.21]

    Величина, обратная плотности, называется массовым, или удельным, объемом и представляет собой объем единицы массы газа, измеряемый в м кг.  [c.26]

    Удельный объем. Объем единицы массы вещества называется удельным объемом (обозначение у). Единица удельного объема в системе СИ — кубический метр на килограмм [c.13]

    Газ, образующийся при горении пороховой шашки, качественно отличается от газа, которым выдавливаются компоненты топлива при газобаллонной системе подачи. Горение пороха происходит при температуре примерно 2200° С. В топливный бак пороховые газы поступают с температурой 800—900° С. Известно, что объем единицы веса газа увеличивается с увеличением температуры газа. Поэтому для выдавливания одного и того же количе- [c.23]

    V — объем единицы массы  [c.303]

    Под плотностью газа понимают отношение массы газа к его объему. Единица плотности в СИ — килограмм на кубический метр (кг/м ). Плотность газа д, (в кг/м ) в нормальных физических условиях (при давлении 0,1013 МПа и температуре 273 К) можно определить по его молярной массе ц, [2]  [c. 146]

    Высота единицы переноса является кинетической характеристикой для аппаратов с непрерывным контактом фаз. Более общей характеристикой как для аппаратов с непрерывным контактом фаз, так и для аппаратов со ступенчатым контактом является объем единицы переноса Гд,,, т. е. рабочий объем массообменного аппарата, соответствующий по эффективности разделения одной единице переноса. [c.33]

    Свободный объем единицы массы полимера при температуре ниже Тс пропорционален температуре. [c.122]

    Объем единицы массы пульпы равен сумме объемов твердого и воды [c.792]

    Плотность пигмента имеет существенное значение при подсчете массы лакокрасочного покрытия, другой показатель — насыпную плотность — используют для расчета емкостей транспортирования и хранения пигмента Насыпная плотность (насыпнаЯ масса) — это масса единицы объема пигмента, занимаемая ил при свободном насыпании или при встряхивании Используют еще один показатель — насыпной объем, т е объем единицы массы пигмента при свободном насыпании или встряхивании Насыпная плотность, так же как и насыпной объем, зависит от формы частиц пигмента, их дисперсности и степени полидисперсности Эти свойства определяют плотность упаковки частиц пигмента Как правило, насыпная плотность пигмента меньше его физической плотности Например, плотность свинцовых кронов-5100—6100, а их насыпная плотность 700—1000 кг/м .  [c.241]

    Объем газа постоянного состава определяется давлением и температурой. Для данной температуры удельный объем газа (объем единицы веса) меняется от очень больших значений при низких давлениях до очень малых значений при высоких давлениях. При данном же давлении удельный объем газа с ростом температуры увеличивается, но не столь значительно, как при изменении давления. [c.18]

    Величина, обратная плотности, называется удельным объемом, что соответствует объему единицы массы жидкости или газа при данных температуре и давлении. С увеличением температуры удельный объем жидкости возрастает, а с увеличением давления уменьшается (табл. 15) [10]. [c.59]

    Удельным объемом газа v называется объем единицы веса газа [c.60]

    Размерность в общем случае обозначается квадратными скобками, например уд. вес [ у] = [вес/объем], единица уд. веса [кг/л ], единица уд. объема [л /кг]. [c.10]

    Объем единицы массы газа представляет собой удельный объем V — величину, обратную плотности пара р при тех же условиях. [c.77]

    Ниже будут использованы следующие определения удельный объем (объем единицы массы) [c.45]

    Объем единицы массы или моля вещества в системе СИ выражается в следующих единицах м /кг и м /кмоль. [c.749]

    Иное положение при крекинге тяжелого остаточпого сырья. В этом случае, как правило, сырье и продукты реакции паходятся в смешаниофазном состоянии (жидкость и пары). Чем выше температура, тем больше доля паровой фазы и тем, следовательно, больше удельный объем реакционной смеси (объем единицы массы, выраженный обычно в М 1кг). [c.38]

    Решение. Если для растворения справедливо уравнение (VIII, 51), то весовое количество растворенного газа увеличивается пропорционально давлению, но объем единицы массы его согласно уравнению (VI, 5) в той же степени уменьшается поэтому объем растворенного газа ие зависит от давления. Это положение справедливо, разумеется, лишь при небольших давлениях, когда растворяющийся газ можно считать идеальным. [c.251]

    Ген и»гаТоТо и в ная объему единицы течения, а по ющему значению напряжения смыслу—аналогичная понятию о сдвига. микронапряжении, введенном Ри [c.36]

    Плотность — это масса единицы объема (величина, опреденяемая как отношение массы вещества к занимаемому им объему). Единица плотности в Международной системе единиц (СИ) — килограмм на кубический метр (кг/м ). Относительная плотность — показывает, во сколько раз плотность вещества, определенная при 20 0 больше хшотности воды при 4 0. Нефтепродукты и вода имеют различные коэффициенты расширения, поэтому при определении относительной плоттюсти необходимо указывать температуры воды и нефтепродукта, при которых проводилось определение. [c.18]

    Рассмотрим, как это делается во фронтальном анализе [29] в случае непрерывной подачи в хроматографическую колонку с постоянной объемной скоростью потока газа-носителя, содержащего с молярных долей адсорбтива. В результате действия двух противоположных эффектов — диффузионного размывания и обостряющего действия криволи-нейности изотермы и изменения скорости потока в результате адсорбции через некоторое время устанавливается стационарный сорбционный фронт, перемещающийся с некоторой постоянной скоростью и . Скорость потока газа-носителя, выходящего из колонки Мвых, До появления фронта слагается из двух частей. Во-первых, из колонки выходит объем газа-носителя м (1 — с ). Кроме того, из колонки вытесняется движущимся фронтом объем ашп, где sx — свободный объем единицы длины колонки. Таким образом, объемная скорость газа, выходящего из колонки, связана со скоростью перемещения стационарного фронта следующим соотношением  [c.121]

---

Единица измерения объема жидкости – литр (1-й класс)

Цель: Ввести понятие литра как единицы измерения объема жидкости.

Задачи:

Образовательная:

• познакомить детей с единицей измерения объема жидкости – литром;
• формировать вычислительные навыки, умение решать задачи.

Развивающая:

• развивать логическое мышление, внимание, память;
• развивать коммуникативные навыки.

Воспитательная:

• воспитывать аккуратность, бережливость, любознательность.

Оборудование, обеспечение:

• учебник М. И. Моро и др. “МАТЕМАТИКА для 1 класса, часть 2”,
• емкости для воды (ведерко, две банки по 3 л, банки вместимостью 1 л, 0,5 л),
• карточки с дифференцированными заданиями для устного счета,
• карточки для работы по группам, индивидуальные наборные полотна,
• иллюстрации к познавательному материалу (изображение верблюда, страуса, ребенка, крана с вытекающей водой),
• изображение полянки, паровозика,
• музыкальный центр, диск с записью фонограммы песни из мультфильма “Паровозик из Ромашково”.

Ход урока

I. Организационный момент.

1) Вхождение в контакт.

– Здравствуйте, ребята! Я очень рада вас видеть! Тем более, что сегодня не совсем обычный урок. Мы отправимся в путешествие по стране Математике. А путешествовать мы будем вот на этом веселом паровозике.

Учитель демонстрирует изображение паровозика.

2) Чистописание.

– Откройте тетради. В ваших тетрадях карандашом нарисован паровозик с вагончиками. Обведите его ручкой.

– Сколько вагончиков везет паровозик? (2)

– Давайте пропишем цифру два. Посмотрите на доску. В каком порядке будем писать цифру? (Одна, через клеточку – три подряд, через клеточку – одна, и т.д.)

3) Сообщение темы и цели урока. Устный счет.

– Прежде чем отправиться в путь, ответьте на вопросы.

– Как называется единица измерения длины, с которой мы уже знакомы? (Сантиметр)

– С какой единицей массы мы познакомились на прошлом уроке? (Килограмм)

– Можно ли с помощью этих единиц измерить, сколько воды в нашем ведерке?

Учитель демонстрирует ведерко.

– Нам предстоит узнать, как называется единица, которой измеряется объем жидкости.

Учитель открывает часть темы: “Единица измерения объема жидкости”.

– Ну что же, все готовы к путешествию? Тогда закройте глазки и мы отправляемся.

Учитель включает музыку, открывает доску.

На доске – изображение полянки, паровозика, названия “станций”.

– Первая станция – “Считалкино”.

– Возьмите цветные карточки, решите примеры, найдите в таблице буквы, которые соответствуют ответам, составьте слово.

Карточка красного цвета:

Карточка желтого цвета:

Карточка зеленого цвета:

– Какое же слово у вас получилось? (Литр)

Полностью открывается название темы: “Единица измерения объема жидкости – литр”

– Прочитайте тему нашего урока хором.

II. Физкультминутка.

– Давайте представим себя паровозиками и отправимся к следующей станции.

– Загудел паровоз: Ту-ту!
– И вагончики повез: Ту-ту!
Чу, чу, чу, чу! Далеко я укачу!

Физкультминутка выполняется под мелодию “Песни Паровозика”.

III. Изучение новых знаний.

1) Фронтальная беседа с учащимися.

Учитель передвигает паровозик к следующей “станции”.

– Мы прибываем на следующую станцию. Давайте прочитаем, как она называется. (“Размышлялкино”)

– Что у нас в ведерке? (Вода)

– Что произойдет, если ведерко вдруг исчезнет, а вода останется? (Вода разольется, растечется по полу)

– Почему? (Вода – это жидкость)

– Какие еще жидкости бывают? (Молоко, сок, кефир, бензин и т.д.)

– Что нужно, чтобы жидкость не растекалась? (Емкость)

– Приведите примеры емкостей. (Банка, ведро, стакан, кастрюля, …)

– Ребята, посмотрите на эти банки. Как вы думаете, в них уместится одинаковое количество воды или разное? (На вид банки одинаковые)

– Как узнать, правы ли мы? (Измерить вместимость)

– Хорошо, тогда я попрошу вас помочь мне.

К доске выходят два ученика. Один получает банку 1л, другой – 0,5л.

– Ребята будут наливать воду в большие банки. Как надо наливать воду? (Аккуратно, чтобы не разлить ее, не разбить банки).

– Первый вариант считает, сколько баночек выльет 1-й ученик, а второй считает, сколько баночек выльет второй ученик.

2) Выполнение практического задания по измерению объема (вместимости) банок.

– Сколько банок насчитал первый вариант? (3 банки)

– Сколько банок насчитал второй вариант? (6 банок)

– Что же получается, банки на вид одинаковые, но в них умещается разное количество воды? Или мы допустили какую-то ошибку? (Ребята наливали воду банками разного размера, надо было взять одинаковые, для измерения величин надо пользоваться одинаковыми мерками)

– Правильно! Вот в такую банку вмещается 1 литр воды. Вспомните, сколько таких банок уместилось в большую банку ? (3)

– Значит, говорят, что она вмещает 3 литра. А если в емкости 4 таких банки, 5 банок? (Значит, в емкости 4 литра, 5 литров)

– Слово ЛИТР сокращенно пишут так: л.

Учитель вывешивает на доску карточку: ЛИТР – Л.

IV. Первичное закрепление нового материала.

1) Решение задачи.

а) Ознакомление с текстом задачи.

Учитель передвигает паровозик к следующей “станции”.

– Мы прибыли на станцию “Задачкино”.

– Откройте учебники на странице 36. Задача №3.

– Прочитайте задачу.

Текст задачи читает хорошо читающий ученик:

В банке 3 литра молока, а в бидоне на 4 литра больше. Сколько литров молока в бидоне? Сколько литров молока в банке и бидоне вместе?

б) Анализ текста задачи.

– О чем эта задача? (О молоке)

– Что такое молоко? (Жидкость)

– В каких емкостях находится молоко? (В банке и в бидоне)

– Сколько молока в банке? (3 л)

– Что известно про молоко в бидоне? (На 4 л больше, чем в банке)

– Что значит “на 4 больше”? (Столько же да еще 4)

– Ответим сначала на первый вопрос. Прочитайте его.

в) Поиск решения первой части задачи

– Посмотрите на схемы.

Рис. 1	Рис. 2
Рис. 3

– Выберите ту, которая иллюстрирует нашу задачу. Объясните свой выбор.

– Что неизвестно, целое или часть?

– Как найти целое? (Чтобы найти целое надо сложить части)

– Запишите решение первой части задачи.

г) Самостоятельная работа по решению первой части задачи. Оформление решения.

Один ученик работает за доской, затем дети проверяют решение.

Свое согласие или несогласие выражают с помощью сигнальных карточек.

На доске должна появиться запись: 3+4=7(л)

д) Анализ второй части задачи (в виде фронтальной беседы).

– Прочитайте второй вопрос задачи.

– Вспомним, сколько молока в банке? В бидоне?

– Дополните схему, чтобы она помогла нам ответить на второй вопрос задачи.

Рис. 4

– Посмотрите на эти выражения.

На доске: 7-3, 3+7, 4-3

– Какое из них вы выберите, чтобы ответить на второй вопрос? Почему? (Неизвестно целое; чтобы найти целое, надо сложить части)

е) Оформление решения второй части задачи. Формулировка ответа.

– Запишем решение второй части задачи.

Ученик комментирует с места, учитель записывает на доске: 3+7=10 (л)

– Сколько чисел будет в ответе? (2, потому что в задаче два вопроса)

– Запишем ответ.

Ученик комментирует с места, учитель записывает на доске: Ответ: 7 л, 10 л.

2) Физкультминутка.

– Отправляемся к следующей станции.

– Паровоз кричит: Ду-ду! Я иду, иду, иду!
– А колеса стучат, а колеса говорят: Так, так, так! Так, так, так! Так, так, так!

Физкультминутка выполняется под мелодию “Песни Паровозика”.

Учитель передвигает паровозик к следующей “станции”.

3) Составление неравенств.

– Мы добрались до станции “Ошибкино”. Здесь на каждом шагу нас подстерегают ошибки. В одиночку с ними справиться очень трудно, но если мы будем работать вместе, дружно, то ошибок вы не допустите. Объединимся в группы. Из карточек составьте два верных равенства.

Каждая группа получает карточки:

2 л + 5 л, 5 л + 2 л, 5 л, 7 л, 9 л, <, > – и индивидуальные наборные полотна.

– Проверяем задание по наборному полотну группы, которая выполнила задание первой.

– Какой знак можно поставить между выражениями 5 л + 2 л и 2 л + 5 л? (=)

– Почему? (От перестановки слагаемых сумма не меняется)

V. Подведение итогов урока.

1) Фронтальная беседа.

Учитель передвигает паровозик к следующей “станции”.

– Наше путешествие подходит к концу. Мы добрались до станции “Знайкино”. Что нового вы узнали на уроке? (Объем жидкости измеряется в литрах)

2) Игра “Верю – не верю”.

– А сейчас поиграем в игру “Верю – не верю”. Если вы согласны с моим утверждением, то “зажигаете” зеленый огонек, не согласны – “зажигаете” красный огонек.

• В эту банку (учитель демонстрирует банку в 1 литр) умещается 1 сантиметр жидкости.
• Массу арбуза нельзя измерить в литрах.
• Объем жидкости измеряется в килограммах.
• Единица измерения объема жидкости называется литр.

3) Беседа о значении измерений. Сообщения учащихся.

– Ребята, а для чего надо измерять объем жидкости, измерять длину, массу?

– Очень интересно иногда что-то измерить. Сейчас ребята расскажут вам о некоторых фактах.

К доске выходят ученики. У каждого рисунок, иллюстрирующий его сообщение.

• Тело человека на две трети состоит из жидкости, значит во мне примерно 14 литров жидкости.
• Страус, самая большая птица на земле, за один раз может выпить 70 литров воды.
• А верблюд выпивает 100 литров воды за один раз.
• Через струю воды шириной в иголку вытекает примерно 800 литров воды в сутки.

– Я знаю, что в пустыне Сахара за целый год выпадает всего 200 литров осадков на площадь равную площади нашего класса. Поэтому там не растут деревья, очень мало трав, живут только жуки и змеи.

– Кто запомнил, сколько литров воды может вытечь за сутки, если неплотно закрыть кран?

– Ребята, как вы думаете, что произойдет, если с нашей планеты исчезнет вся вода? (Все живое погибнет, потому что без воды жить нельзя, вода – это жизнь)

– Как вы думаете, что может привести к исчезновению воды? (Если мы будем оставлять открытыми краны с водой, не будем беречь воду)

– Как же мы должны относиться к воде? (Бережно, аккуратно, не забывать закрывать краны, заботиться о сохранении воды, ее чистоте)

– Я надеюсь, что вы будете аккуратными и бережливыми.

4) Оценка учебной деятельности.

– А наш урок подходит к концу. Вы активно и дружно работали сегодня. Как вы думаете, кто из ваших товарищей был самым активным, сообразительным, внимательным?

– Я бы отметила следующих учеников: …. .

Учитель отмечает сообразительность, внимательность, трудолюбие отдельных учащихся.

– Спасибо за работу!

Объем, масса, плотность, удельный объем. Приведение к нормальным и стандартным условиям и пересчет

Приведение к нормальным и стандартным условиям

Единицей измерения объема газа является кубический метр (м³). Измеренный объем приводится к нормальным физическим условиям.

Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 °С).

Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 °С).

В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относятся объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ приводится к 288,16 °К (+15 °С) и давлению 1 бар (105 Па).

Если известен объем газа при одних условиях, то пересчитать его в объемы при других условиях можно с помощью коэффициентов, приведенных следующей таблице.

Коэффициенты для пересчета объемов газа из одних условий в другие

Температура и даление газа	0 °С и 760 мм рт. ст.	15 °С и 760 мм рт. ст.	20 °С и 760 мм рт. ст.	15 °С (288,16 °К) и 1 бар
0 °С и 760 мм рт. ст. (норм. условия)	1	1,055	1,073	1,069
15 °С и 760 мм рт. ст. (в зар. литературе)	0,948	1	1,019	1,013
20 °С и 760 мм рт. ст. (ст. условия)	0,932	0,983	1	0,966
15 °С (288,16 °К) и 1 бар (СИ)	0,936	0,987	1,003	1

Для приведения объемов газа к 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²), а также к 20 °С (293,16 °К) и 760 мм рт. ст. (1,033 кгс/см²) могут быть применены следующие формулы:

где V_{0 °С и 760 мм рт. ст.}  — объем газа при 0 °С и 760 мм рт. ст., м³;
V_{20° С и 760 мм рт. ст.} — объем газа при 20 °С и 760 мм рт. ст., м³;
V_P — объем газа в рабочих условиях, м³;
р — абсолютное давление газа в рабочих условиях, мм рт. ст.;
Т — абсолютная температура газа в рабочих условиях, °К.

Пересчет объемов газа, приведенных к 0 °С и 760 мм рт. ст., а также к 20 °С и 760 мм рт. ст., в объемы при других (рабочих) условиях можно производить по формулам:

Любой газ способен расширяться. Следовательно, знание объема, который занимает газ, недостаточно для определения его массы, так как в любом объеме, целиком заполненном газом, его масса может быть различной.

Масса — это мера вещества какого-либо тела (жидкости, газа) в состоянии покоя; скалярная величина, характеризующая инерционные и гравитационные свойства тела. Единицы массы в СИ — килограмм (кг).

Плотность, или масса единицы объема, обозначаемая буквой p, — это отношение массы тела m, кг, к его объему, V, м³:

p = m/V

или с учетом химической формулы газа:

p = M/V_М = M/22,4,

где M — молекулярная масса,
V_М — молярный объем.

Единица плотности в СИ — килограмм на кубический метр (кг/м³).

Зная состав газовой смеси и плотность ее компонентов, определяем по правилу смешения среднюю плотность смеси:

p_см = (p₁V₁ + p₂V₂ + … + p_nV_n)/100,

где p₁, p₂, …, p_n — плотность компонентов газового топлива, кг/м³;
V₁, V₂, …, V_n — содержание компонента, об. %.

Величину, обратную плотности, называют удельным, или массовым, объемом (ν) и измеряют в кубических метрах на килограмм (м³/кг).

Как правило, на практике, чтобы показать, на сколько 1 м³ газа легче или тяжелее 1 м³ воздуха, используют понятие относительная плотность d, которая представляет собой отношение плотности газа к плотности воздуха:

d = p/1,293

и

d = M/(22,4×1,293).

Объем и плотность | Введение в химию

Цель обучения

• Опишите взаимосвязь между плотностью и объемом

---

Ключевые моменты

• Объем вещества связан с количеством вещества, присутствующего при определенной температуре и давлении.
• Объем вещества можно измерить в мерной посуде, такой как мерная колба и мерный цилиндр.
• Плотность указывает, сколько вещества занимает определенный объем при определенной температуре и давлении. Плотность вещества может использоваться для определения вещества.
• Вода необычна, потому что когда вода замерзает, ее твердая форма (лед) менее плотная, чем жидкая вода, и поэтому плавает поверх жидкой воды.

---

Условия

• Плотность — мера количества вещества, содержащегося в данном объеме.
• объем: Единица трехмерной меры пространства, которая включает длину, ширину и высоту.Он измеряется в кубических сантиметрах в метрических единицах.

---

Объем и плотность

Свойства материала можно описать разными способами. Любое количество любого вещества будет иметь объем. Если у вас есть две емкости с водой разного размера, каждая из них вмещает разное количество или объем воды. Единица измерения объема — это единица, производная от единицы длины в системе СИ, и не является основным измерением в системе СИ.

Если две пробы воды имеют разные объемы, они все равно имеют общее измерение: плотность.Плотность — это еще одно измерение, производное от основных единиц СИ. Плотность материала определяется как его масса на единицу объема. В этом примере каждый объем воды отличается и, следовательно, имеет определенную и уникальную массу. Масса воды выражается в граммах (г) или килограммах (кг), а объем измеряется в литрах (л), кубических сантиметрах (см ³ ) или миллилитрах (мл). Плотность рассчитывается путем деления массы на объем, поэтому плотность измеряется в единицах массы / объема, часто г / мл.Если обе пробы воды имеют одинаковую температуру, их плотности должны быть одинаковыми, независимо от объема пробы.

Измерительные инструменты

Мерная чашка Мерная чашка — это обычная домашняя утварь, используемая для измерения объемов жидкостей.

Если вы когда-либо готовили на кухне, вы, вероятно, видели какую-то мерную чашку, которая позволяет пользователю измерять объемы жидкости с разумной точностью. Мерная чашка показывает объем жидкости в стандартных единицах СИ — литрах и миллилитрах.Большинство американских мерных стаканчиков также измеряют жидкость в более старой системе, состоящей из стаканов и унций.

Объемная посуда

Ученые, работающие в лаборатории, должны быть знакомы с типичной лабораторной посудой, которую часто называют мерной посудой. Это могут быть химические стаканы, мерная колба, колба Эрленмейера и градуированный цилиндр. Каждый из этих контейнеров используется в лабораторных условиях для измерения объемов жидкости в различных целях.

Лабораторная мерная посуда Стеклянная посуда, такая как эти мензурки, обычно используется в лабораторных условиях для удобного измерения и разделения различных объемов жидкостей.

Плотность воды

Различные вещества имеют разную плотность, поэтому плотность часто используется как метод идентификации материала. Сравнение плотностей двух материалов также может предсказать, как вещества будут взаимодействовать. Вода используется в качестве общего стандарта для веществ, и ее плотность составляет 1000 кг / м. ³ при стандартной температуре и давлении (называемых STP).

Использование воды для сравнения плотности

Когда объект помещается в воду, его относительная плотность определяет, плавает он или тонет. Если объект имеет меньшую плотность, чем вода, он всплывет на поверхность воды. Объект с большей плотностью утонет. Например, пробка имеет плотность 240 кг / м ³ , поэтому она будет плавать. Плотность воздуха составляет примерно 1,2 кг / м. ³ , поэтому он сразу поднимается к вершине водяного столба. Металлы натрий (970 кг / м ³ ) и калий (860 кг / м ³ ) будут плавать на воде, а свинец (11340 кг / м ³ ) тонуть.

Плотность: история Архимеда и золотой короны Корона сделана из чистого золота? Древнегреческий король должен знать, обманул ли его ювелир.Он вызывает Архимеда, который решает использовать плотность для определения металла. Но как он может определить объем короны?

Жидкости имеют тенденцию образовывать слои при добавлении в воду. Глицерин сахарного спирта (1 261 кг / м ³ ) погрузится в воду и образует отдельный слой, пока он не будет тщательно перемешан (глицерин растворим в воде). Растительное масло (прибл. 900 кг / м ³ ) будет плавать в воде и, независимо от того, насколько сильно перемешано, всегда будет возвращаться в виде слоя на поверхность воды (масло не растворяется в воде).

Переменная плотность воды

Вода — сложная и уникальная молекула. Даже при постоянном давлении плотность воды будет меняться в зависимости от температуры. Напомним, что тремя основными формами материи являются твердое тело, жидкость и газ (пока не будем рассматривать плазму). Как показывает практика, почти все материалы в твердой или кристаллической форме более плотны, чем в жидкой форме; поместите твердую форму практически любого материала на поверхность его жидкой формы, и она утонет.С другой стороны, вода делает нечто особенное: лед (твердая форма воды) плавает на жидкой воде.

Внимательно посмотрите на соотношение между температурой воды и ее плотностью. Начиная с 100 ° C, плотность воды неуклонно увеличивается до 4 ° C. В этот момент тенденция плотности меняется на противоположную. При 0 ° C вода замерзает до льда и плавает.

Плотность воды при постоянном давлении В этой таблице перечислены плотности воды при различных температурах и постоянном давлении.

Последствия этого простого факта огромны: когда озеро замерзает, ледяная корка на поверхности изолирует жидкость внизу от замерзания, в то же время позволяя более холодной воде (с температурой около 4 ° C и высокой плотность) опуститься на дно. Если бы лед не плавал, он бы опустился на дно, позволяя образоваться и утонуть большему количеству льда, пока озеро не замерзнет! Аквалангисты и пловцы часто сталкиваются с этими градиентами температуры воды, и они могут даже столкнуться со слоем воды на самом дне озера с температурой примерно 4 ° C.Это примерно так же холодно, как и на дне озера; как только вода становится холоднее, жидкая вода становится менее плотной и поднимается вверх.

Слои воды в зимнем озере В зимние месяцы с сезонным климатом самая теплая вода в большинстве озер и рек составляет всего 4 ° C. Эта вода с температурой 4 ° C имеет самую высокую плотность и опускается на дно озера. По мере того, как вода становится холоднее (<4 ° C), она становится менее плотной и поднимается, образуя лед на поверхности озера. В результате в зимние месяцы в озерах и реках всегда присутствует жидкая вода.Это уникальное свойство воды позволяет животным и растениям выживать под замерзшим озером или зимой, гарантируя, что всю пресноводную жизнь не вымирают каждую зиму. Показать источники

Boundless проверяет и курирует высококачественный контент с открытой лицензией из Интернета. Этот конкретный ресурс использовал следующие источники:

SI Единицы длины и объема

Цели обучения

• Определите длину.
• Определите объем.
• Опишите стандартную меру длины и объема.

Как моряки могли измерять глубины моря?

Еще до того, как появились все электронные устройства для измерения глубины и определения местоположения подводных объектов, «сажень» была единицей измерения глубины.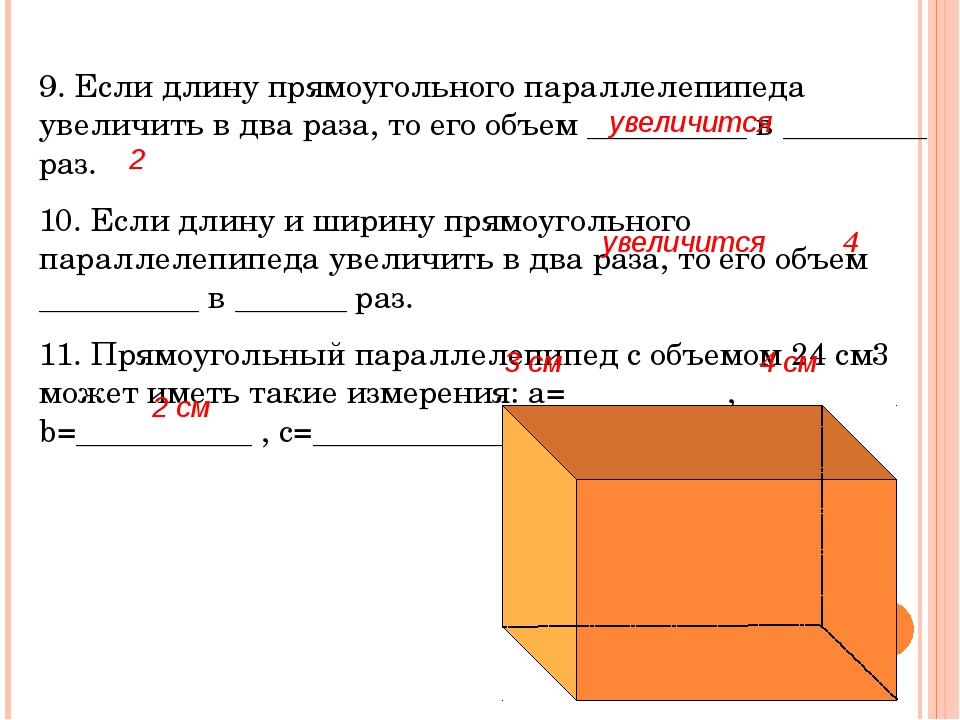 Через каждые шесть футов завязывалась веревка, и конец ее сбрасывали за борт корабля. Вы могли определить, насколько глубока была вода, по тому, сколько узлов прошло под водой, прежде чем веревка коснулась дна.Сегодня мы просто включаем прибор и считываем глубину с высокой точностью.

Длина — это измерение протяженности чего-либо по его наибольшему измерению. Базовая единица измерения длины в системе СИ, или линейная мера, — это метр (м). Все измерения длины могут производиться в метрах, хотя префиксы, перечисленные в различных таблицах, часто бывают более удобными. Ширина комнаты может быть выражена примерно как 5 метров (м), тогда как большое расстояние, такое как расстояние между Нью-Йорком и Чикаго, лучше выразить как 1150 километров (км).Очень маленькие расстояния могут быть выражены в таких единицах, как миллиметр или микрометр. Ширина типичного человеческого волоса составляет около 20 микрометров (мкм).

Объем — это объем пространства, занимаемого образцом материи. Объем обычного объекта можно рассчитать, умножив его длину на ширину и высоту. Поскольку каждое из них является линейным измерением, мы говорим, что единицы объема производятся от единиц длины. Единицей объема в системе СИ является кубический метр (м ³ ), который представляет собой объем, занимаемый кубом размером 1 м с каждой стороны.Этот очень большой объем не очень удобен для обычного использования в химической лаборатории. Литр (L) — это объем куба размером 10 см (1 дм) с каждой стороны. Таким образом, литр равен как 1000 см ³ (10 см × 10 см × 10 см), так и 1 дм ³ . Меньшей единицей объема, которая обычно используется, является миллилитр (мл — обратите внимание на заглавную букву L, которая является стандартной практикой). Миллилитр — это объем куба размером 1 см с каждой стороны. Следовательно, миллилитр равен кубическому сантиметру ( ³ см).В 1 л 1000 мл, что равносильно утверждению, что в 1 дм 1000 см ³ .

Рис. 1. (a) Типичная бутылка для воды имеет объем 1 литр; б) кубик Рубика; (c) Градуированный цилиндр

Кубик Рубика имеет длину 5,7 см с каждой стороны и объем 185,2 см. ³ или 185,2 мл. Объем в лаборатории часто измеряется с помощью градуированного цилиндра, который бывает разных размеров (см. Рисунок 1).

Сводка

• Длина — это мера протяженности чего-либо по его наибольшему измерению.
• Объем — это объем пространства, занимаемого образцом материи.
• Объем можно определить, зная длину каждой стороны предмета.

Практика

Прочтите раздел длины и объема по ссылке ниже и ответьте на следующие вопросы:

http://www.montgomerycollege.edu/Departments/biotp/Metric.html

1. Какие единицы длины в метрической системе?
2. Сделайте первые три преобразования длины.
3. Где на мениске вы измеряете объем в градуированном цилиндре?
4. Сделайте первые два примера преобразования объема.

Обзор

1. Определите длину.
2. Определите объем.
3. Объект измерения. Какое значение равно длине объекта?
4. Насколько велик мл?

Глоссарий

• длина: Измерение протяженности чего-либо по его наибольшему измерению
• метр: Основная единица измерения длины в системе СИ или линейная мера
• volume: Объем пространства, занимаемого образцом материи.Объем обычного объекта можно рассчитать, умножив его длину на ширину и высоту. Поскольку каждое из них является линейным измерением, мы говорим, что единицы объема производятся от единиц длины
.

Объем

| Единицы измерения Wiki

Мерную чашку можно использовать для измерения объемов жидкостей. Эта чашка измеряет объем в стаканах, жидких унциях и миллилитрах.

Объем — это объем трехмерного пространства, ограниченного некоторой замкнутой границей, например, пространством, которое занимает или содержит вещество (твердое тело, жидкость, газ или плазма) или форма. ^[1] Объем часто определяется численно с использованием производной единицы СИ — кубического метра. Под объемом контейнера обычно понимают вместимость контейнера, т.е. е. количество жидкости (газа или жидкости), которое может вместить контейнер, а не количество пространства, которое сам контейнер не смещает.

Трехмерным математическим формам также приписываются объемы. Объемы некоторых простых форм, таких как правильные, прямые и круглые, можно легко вычислить с помощью арифметических формул.Объемы более сложных форм можно вычислить с помощью интегрального исчисления, если существует формула для границы формы. Одномерные фигуры (например, линии) и двухмерные фигуры (например, квадраты) получают нулевой объем в трехмерном пространстве.

Объем твердого тела (правильной или неправильной формы) можно определить по вытеснению жидкости. Вытеснение жидкости также можно использовать для определения объема газа. Общий объем двух веществ обычно больше, чем объем одного из веществ. Однако иногда одно вещество растворяется в другом, и общий объем не складывается. ^[2]

В дифференциальной геометрии объем выражается с помощью формы объема и является важным глобальным римановым инвариантом. В термодинамике объем является фундаментальным параметром и является переменной, сопряженной с давлением.

Файл: Измерения объема из Справочной работы нового студента.svg

Измерения объема из Справочной работы нового студента 1914 года.
Приблизительное преобразование в миллилитры: ^[3] {

Любая единица длины дает соответствующую единицу объема, а именно объем куба, сторона которого имеет заданную длину. Например, кубический сантиметр ( ³ см) будет объемом куба, длина сторон которого составляет один сантиметр (1 см).

В Международной системе единиц (СИ) стандартной единицей объема является кубический метр (м ³ ). Метрическая система также включает литр (L) как единицу объема, где один литр — это объем 10-сантиметрового куба. Таким образом

1 литр = (10 см) ³ = 1000 кубических сантиметров = 0,001 кубических метров,

так

1 кубический метр = 100000 литров.

Небольшие количества жидкости часто измеряются в миллилитрах, где

1 миллилитр = 0,0011 литра = 19 кубических сантиметров.

Также используются различные другие традиционные единицы объема, включая кубический дюйм, кубический фут, кубическую милю, чайную ложку, столовую ложку, жидкую унцию, жидкий драм, жабры, пинту, кварту, галлон, минимум, бочка, шнур, пек, бушель и бочка.

Объем и вместимость Иногда различают , при этом емкость используется для определения того, сколько контейнер может вместить (при этом содержимое обычно измеряется в литрах или производных единицах), а объем — это сколько места перемещает объект (обычно измеряется в кубических метрах или его производные единицы).

Объем и емкость также различаются в управлении емкостью, где емкость определяется как vo. Плотность объекта определяется как масса на единицу объема.Плотность, обратная величине, равна удельному объему .

Форма	Формула объема	Переменные
Curcle		a = длина любой стороны (или края)
Цилиндр		r = радиус круглой грани, h = высота
Призма		B = площадь основания, h = высота
Прямоугольная призма		l = длина, w = ширина, h = высота
Сфера		r = радиус сферы , который является интегралом площади поверхности сферы
Эллипсоид		a , b , c = полуоси эллипсоида
Пирамида		B = площадь основания, h = высота пирамиды
Конус		r = радиус окружности в основании, h = расстояние от основания до вершины
Тетраэдр [4]		длина кромки
параллелепипед		a , b и c — длины ребер параллелепипеда, а α, β и γ — внутренние углы между ребрами.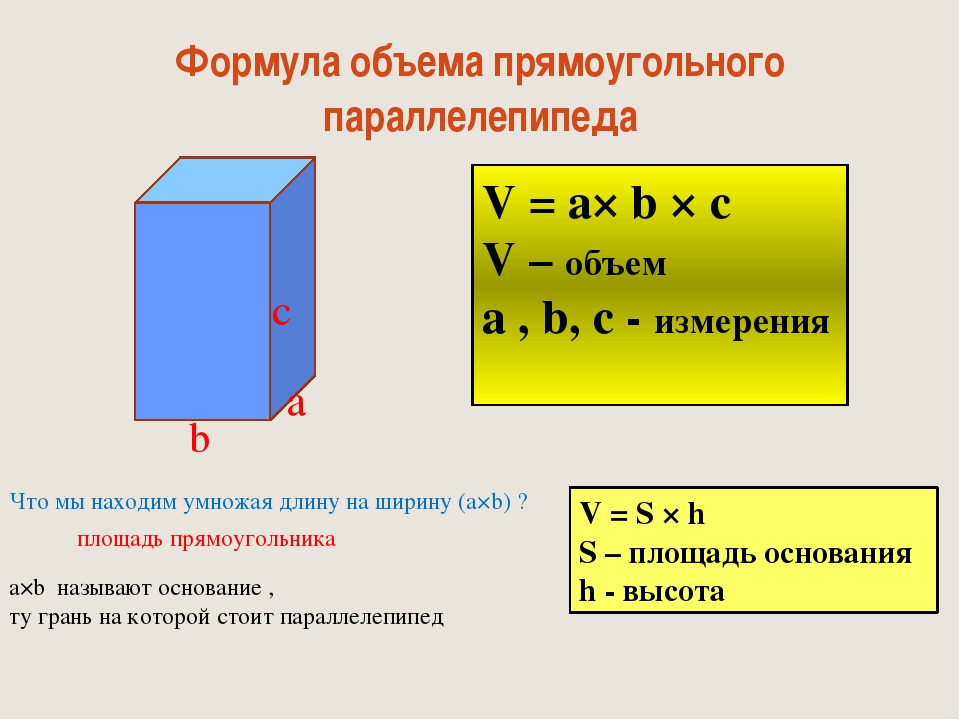
Любая развертка по объему (требуется расчет)		h = любой размер фигуры, A ( h ) = площадь поперечных сечений, перпендикулярных к h , описанная как функция положения вдоль h . a и b — это пределы интегрирования для объемной развертки. (Это будет работать для любой фигуры, если ее площадь поперечного сечения можно определить по h).
Любая повернутая фигура (метод шайбы) (требуется исчисление)		и — функции, выражающие внешний и внутренний радиусы функции соответственно.
бутылка Клейна		Нет объема — нет внутри.

Соотношение объемов конуса, сферы и цилиндра одинакового радиуса и высоты [править | править источник]

Файл: Вписанный конический сферический цилиндр.svg

Конус, сфера и цилиндр с радиусом r и высотой h

Приведенные выше формулы можно использовать, чтобы показать, что объемы конуса, сферы и цилиндра одинакового радиуса и высоты находятся в соотношении 1 : 2: 3 следующим образом.

Пусть радиус r и высота h (что составляет 2 r для сферы), тогда объем конуса равен

объем сферы равен

при этом объем цилиндра равен

Архимеду принадлежит открытие соотношения объемов сферы и цилиндра 2: 3 . ^[5]

Вывод формулы объема [править | править источник]

Сфера [править | править источник]

Объем сферы — это интеграл бесконечно малых круглых плит толщиной dx . Расчет объема сферы с центром 0 и радиусом r выглядит следующим образом.

Площадь круглой плиты составляет.

Радиус круглых плит, определенный таким образом, что ось x проходит через них перпендикулярно, составляет;

или

где y или z могут быть взяты для представления радиуса плиты при конкретном значении x.

Используя y в качестве радиуса плиты, объем сферы можно рассчитать как

Теперь

Объединение урожайности дает

Эту формулу можно получить быстрее, используя формулу для площади поверхности сферы, которая равна. Объем сферы состоит из слоев бесконечно малых сферических пластин, а объем сферы равен

=

Конус [править | править источник]

Конус представляет собой разновидность пирамидальной формы. Основное уравнение для пирамид, в три раза превышающее высоту основания, умноженную на высоту, также применяет конусы.Но для объяснения с использованием исчисления:

Объем конуса представляет собой интеграл бесконечно малых круглых плит толщиной dx . Расчет объема конуса высотой h с центром в точке (0,0,0) с радиусом r выполняется следующим образом.

Радиус каждой круглой плиты равен r , если x = 0 и 0, если x = h , и линейно изменяется между ними, то есть

Площадь поверхности круглой плиты тогда составляет

Объем конуса затем может быть рассчитан как

и после извлечения констант:

Интегрирование дает нам

Шаблон: Викиучебники Шаблон: Викиучебники

*

единиц СИ — Объем | NIST

Объем — это мера трехмерного пространства, занимаемого материей или ограниченного поверхностью, измеряемая в кубических единицах. Единицей объема в системе СИ является кубический метр (м ³ ), который является производной единицей.

• Литр (L) — специальное название кубического дециметра (дм ³ ). Символ литра — это прописная буква «элл» (L), поэтому предпочтительнее избегать риска путаницы между строчной буквой «элл» (l) и цифрой один (1). Буква l (l) не является утвержденным обозначением литра.
• Миллилитр (мл) — это особое название кубического сантиметра (см ³ ).

Единицы измерения объема
1000 кубических миллиметров (мм 3 )	= 1 кубический сантиметр (см 3 )
1 см 3	= 1 миллилитр (мл)
10 мл	= 1 сантилитр (с)
10 мл	= 1 децилитр (дл)
1 дл	= 100 миллилитров (мл)
1000 см 3	= 1 кубический дециметр (дм 3 )
1 дм 3	= 1 литр (л)
10 дл	= 1 л
1000 мл	= 1 л
10 л	= 1 декалитр (дал)
10 дал	= 1 гектолитр (гл)
1 гл	= 100 л
1000 дм 3	= 1 кубический метр (м 3 )
1000 л	= 1 м 3
1000 л	= 1 кл
1 кл	= 10 гл

Визуализируйте один литр (1 л) в виде куба, каждая сторона которого:

• 1000 мм;
• 10 см;
• 1 дм; или
• 0. 1 мес.

Визуализируйте один литр (1 л) как:

Ежедневные объемы
15 мл	Флакон для глазных капель
80 мл	Пустой человеческий желудок
200 мл	Коробка для сока
355 мл	Банка содовой
4L	Полный желудок человека
5 л	Кровь в теле человека
235 л	Ванна
1 мл	Олимпийский бассейн

Водоемы	Континент	Объем воды (расчетный)
Каспийское море	Азия	78700 км 3
Озеро Байкал	Азия	23600 км 3
Озеро Верхнее	Северная Америка	12100 км 3
Озеро Мичиган	Северная Америка	4920 км 3
Озеро Гурон	Северная Америка	3 540 км 3
Озеро Виктория	Африка	2700 км 3
Озеро Онтарио	Северная Америка	1 700 км 3
Лодожское озеро	Европа	908 км 3
Озеро Эри	Северная Америка	484 км 3
Озеро Маракайбо	Южная Америка	280 км 3
Озеро Тахо	Северная Америка	151 км 3
Лейк-Мид	Северная Америка	35 км 3

Ресурсы:

Перейдите к дополнительной информации о базовом блоке SI:

Что такое определение объема в науке?

Объем — это объем трехмерного пространства, занимаемого жидкостью, твердым телом или газом. Общие единицы измерения объема включают литры, кубические метры, галлоны, миллилитры, чайные ложки и унции, хотя существует множество других единиц.

Ключевые выводы: определение объема

• Объем — это трехмерное пространство, занятое веществом или ограниченное поверхностью.
• В Международной системе единиц (СИ) стандартной единицей объема является кубический метр (м ³ ).
• В метрической системе в качестве единицы объема используется литр (L). Один литр равен объему 10-сантиметрового куба.

Примеры объема

• В качестве примера объема студент может использовать мерный цилиндр для измерения объема химического раствора в миллилитрах.
• Можно купить литр молока.
• Газы обычно продаются в единицах объема, таких как кубические сантиметры, см. ³ или кубические литры.

Измерение объема жидкостей, твердых веществ и газов

Поскольку газы заполняют их контейнеры, их объем такой же, как внутренний объем контейнера. Жидкости обычно измеряются с помощью контейнеров, где указывается объем или внутренняя форма контейнера. Примеры инструментов, используемых для измерения объема жидкости, включают мерные стаканы, градуированные цилиндры, колбы и химические стаканы. Есть формулы для расчета объема правильных твердых форм. Другой метод определения объема твердого тела — это измерение количества вытесняемой им жидкости.

Объем относительно массы

Объем — это объем пространства, занимаемый веществом, а масса — это количество вещества, которое оно содержит.Количество массы на единицу объема — это плотность образца.

Вместимость относительно объема

Вместимость — это мера содержимого емкости, в которой содержатся жидкости, зерна или другие материалы, принимающие форму емкости. Емкость не обязательно совпадает с объемом. Это всегда внутренний объем сосуда. Единицы вместимости включают литр, пинту и галлон, а единица объема (СИ) является производной от единицы длины.

Объем твердых веществ — пояснения и примеры

Как найти объем твердого тела?

Объем твердого тела — это мера того, сколько места занимает объект.В этой статье будет показано, как рассчитать объем твердого тела, а также объем твердых тел правильной и неправильной формы.

Метод определения объема твердого тела зависит от его формы. Объем твердого тела измеряется в кубических единицах, т. Е. В кубических сантиметрах, кубических метрах, кубических футах и ​​т. Д.

Формула объема твердого тела

Вот формулы объема для различных твердых тел:

Объем прямоугольная призма равна произведению площади основания (длина, умноженная на ширину) и высоты призмы:

Объем твердой прямоугольной призмы = lxwxh

Поскольку мы знаем, что все стороны или края куба равны по длине, тогда объем куба равен любой стороне или кубу ребра.

Объем куба = a³

Объем призмы равен произведению площади основания и высоте призмы.

Объем призмы = Площадь основания x высота

= B x h

Объем цилиндра равен площади его круглого основания и высоте цилиндра.

Объем цилиндра = πr²h

Объем пирамиды равен одной трети произведения площади основания и высоты.

Объем пирамиды = 1 / 3Bh

Для квадратной пирамиды объем задается как:

Объем = 1 / 3s²h

Где s — длина стороны основания, а h — высота пирамиды.

Объем прямоугольной пирамиды = 1/3 л / ч

Для сферы объем задается как:

Объем сферы = 4/3 πr³

Поскольку конус представляет собой пирамиду с круглым основанием, следовательно объем конуса равен:

Объем = 1/3 πr²h

Объем твердых тел неправильной формы

Поскольку не все твердые тела имеют правильную форму , их объем не может быть определен с помощью формулы объема.

В этом случае объем твердых тел неправильной формы может быть определен методом вытеснения воды :

Твердое тело неправильной формы сбрасывается в градуированный цилиндр, заполненный водой.

Затем определяется объем твердого вещества путем определения разницы между начальным и конечным показаниями градуированного цилиндра.

Метод вытеснения воды для определения объема твердых тел неправильной формы подходит только в том случае, если: твердое вещество не поглощает воду, а также если твердое вещество не реагирует с водой.

В качестве альтернативы вы можете определить объем объекта неправильной формы, выполнив следующие действия:

• Сначала разбейте твердое тело неправильной формы на правильные формы, объем которых можно рассчитать.
• Вычислить частичные объемы малых форм
• Сложить частичные объемы, чтобы получить общий объем твердого тела неправильной формы.

Рабочие примеры:

Пример 1

Сравните объем твердой сферы радиусом 2 см и сплошной квадратной пирамиды с длиной основания 2,5 см и высотой 10 см.

Раствор

По формуле объем шара = 4/3 πr³

= 4/3 x 3. 14 x 2 x 2 x 2

= 33,49 см ³

А объем квадратной пирамиды = 1 / 3s²h

= 1/3 x 2,5 x 2,5 x 10

= 20,83 см ³

Следовательно, сфера по объему больше пирамиды.

Пример 2

Цилиндрический резервуар радиусом 3 м и высотой 10 имеет полусферическую крышку радиусом 3 м наверху. Найдите объем бака.

Раствор

Сначала рассчитайте объем цилиндрической части резервуара.

Объем цилиндра = π r² ч

= 3,14 x 3 x 3 x 10

= 282,6 м ³

Объем полусферы = 2/3 πr³

= 2/3 x 3,14 x 3 x 3 x 3

= 56,52 м ³

Общий объем резервуара = объем цилиндра + объем полусферы

= 282,6 м ³ + 56,52 м ³

= 339,12 м ³

Пример 3

Усеченная квадратная пирамида имеет высоту 15 см.Предположим, что длина основания и вершины усеченной пирамиды составляет 8 см и 4 см соответственно. Найдите объем усеченной пирамиды.

Решение

Усеченная пирамида является примером усеченной пирамиды.

Пусть начальная высота пирамиды = x

Подобными треугольниками

x / x — 15 = 8/4

4x = 8x — 120

–4x = –120

x = 30

Следовательно, высота пирамиды до усечения составляла 30 см

Теперь найдите объем полной пирамиды

Объем = 1/3 x 8 x 8 x 30

= 640 см ³

Объем отрубленной части пирамиды = 1/3 x 4 x 4 x (30-15)

= 1/3 x 16 x 15

= 80 см ³

Итак, объем усеченной пирамиды = (640-80 ) см ³

= 560 см ³ .

Практические задачи

1. Размер коробки для сока: 5 единиц на 4 единицы на 3 единицы. Какой объем коробки?
2. Петр сделал твердую фигуру из 12 блоков, из которых 8 — маленькие, а 4 — большие. Если маленький блок состоит из 3-дюймового куба, а большой — из 5-дюймового куба, каков общий объем твердой формы?
3. Два куба размером 0,5 фута на 1,5 фута на 3 фута каждый соединены третьим кубом размером 0. 25 футов на 0,75 на 1,25 фута. Найдите общий объем сформированной формы.

Предыдущий урок | Главная страница | Следующий урок

11.8: Закон Бойля — давление и объем

Цели обучения

• Узнайте, что подразумевается под термином законы о газе .
• Изучите и применяйте закон Бойля.

Когда ученые семнадцатого века начали изучать физические свойства газов, они заметили некоторые простые отношения между некоторыми измеряемыми свойствами газа.Возьмем, например, давление ( P ) и объем ( V ). Ученые отметили, что для данного количества газа (обычно выраженного в молях [ n ]), если температура ( T ) газа поддерживалась постоянной, давление и объем были связаны: при увеличении другие снижаются. По мере того, как одно уменьшается, другое увеличивается. Это означает, что давление и объем обратно пропорциональны .

Но это еще не все: давление и объем данного количества газа при постоянной температуре численно связаны с .Если вы возьмете значение давления и умножите его на значение объема, произведение будет постоянным для данного количества газа при постоянной температуре:

\ [P × V = \ text {постоянная при постоянных n и T} \]

Если объем или давление изменяются, а количество и температура остаются неизменными, то другое свойство должно измениться, чтобы произведение этих двух свойств по-прежнему равнялось той же константе. То есть, если исходные условия обозначены \ (P_1 \) и \ (V_1 \), а новые условия обозначены \ (P_2 \) и \ (V_2 \), мы имеем

\ [P_1V_1 = \ text {constant} = P_2V_2 \]

, где предполагается, что свойства перемножаются.Не считая средней части, мы имеем просто

\ [P_1V_1 = P_2V_2 \ text {при постоянных n и T} \]

Это уравнение является примером закона газа. Газовый закон — это простая математическая формула, которая позволяет моделировать или предсказывать поведение газа. Этот конкретный газовый закон называется законом Бойля в честь английского ученого Роберта Бойля, который впервые объявил о нем в 1662 году. На рисунке \ (\ PageIndex {1} \) показаны два представления того, как работает закон Бойля.

Рисунок \ (\ PageIndex {1} \): закон Бойля.Поршень с определенным давлением и объемом (левый поршень) будет иметь половину объема, когда его давление в два раза больше (правый поршень). Можно также построить график P в сравнении с V для данного количества газа при определенной температуре; такой график будет выглядеть как график справа.

Закон Бойля — это пример второго типа математических задач, которые мы видим в химии, основанных на математической формуле. Тактика работы с математическими формулами отличается от тактики работы с коэффициентами пересчета.Во-первых, большинство вопросов, на которые вам придется ответить с помощью формул, представляют собой вопросы словесного типа, поэтому первый шаг — определить, какие величины известны, и присвоить их переменным. Во-вторых, в большинстве формул необходимо выполнить некоторые математические преобразования (например, алгебру), чтобы найти неизвестную переменную. Правило состоит в том, что для нахождения значения неизвестной переменной вы должны математически изолировать неизвестную переменную отдельно от себя и в числителе одной стороны уравнения. Наконец, единицы должны быть последовательными.Например, в законе Бойля есть две переменные давления; у них должен быть один и тот же блок. Также есть две переменные объема; у них также должен быть один и тот же блок. В большинстве случаев не имеет значения, что такое единица измерения , но единица измерения должна быть той же в обеих частях уравнения.

Пример \ (\ PageIndex {1} \)

Образец газа имеет начальное давление 2,44 атм и начальный объем 4,01 л. Его давление изменяется до 1,93 атм. Какой будет новый объем, если температура и количество остаются постоянными?

Решение

Этапы решения проблем
Определите «данную» информацию и то, что проблема просит вас «найти».«	Дано: P 1 = 2,44 атм и V 1 = 4,01 л P 2 = 1,93 атм Найти: V 2 =? L
Перечислите другие известные количества.	нет
Спланируйте проблему.	Сначала измените уравнение алгебраически, чтобы найти \ (V_2 \). \ [V_2 = \ frac {P_1 \ times V_1} {P_2} \]
Отменить единицы и рассчитать.	Теперь подставьте известные величины в уравнение и решите. \ [V_2 = \ frac {2.44 \: \ cancel {\ text {atm}} \ times 4.01 \: \ text {L}} {1.93 \: \ cancel {atm}} = 5.07 \: \ text {L} \]
Подумайте о своем результате.	Мы знаем, что давление и объем обратно пропорциональны; по мере того, как одно уменьшается, другое увеличивается. Давление снижается (с 2,44 атм до 1,93 атм), поэтому объем должен увеличиваться для компенсации, и он есть (с 4,01 л до 5,07 л). Итак, ответ имеет смысл на основе закона Бойля.

Упражнение \ (\ PageIndex {1} \)

Если P ₁ = 334 торр, V ₁ = 37.8 мл и P ₂ = 102 торр, что такое V ₂ ?

Ответ

124 мл

Как уже упоминалось, вы можете использовать любые единицы для давления и объема, но оба давления должны быть выражены в одних и тех же единицах, и оба объема должны быть выражены в одних и тех же единицах.

Пример \ (\ PageIndex {2} \):

Проба газа имеет начальное давление 722 торр и начальный объем 88.8 мл. Его объем изменится до 0,663 л. Что такое новое давление?

Решение

Этапы решения проблем
Определите «данную» информацию и то, что проблема просит вас «найти».	Дано: P 1 = 722 торр и V 1 = 88.8 мл В 2 = 0,633 л Найти: P 2 =? торр
Перечислите другие известные количества.	1 л = 1000 мл, чтобы иметь те же единицы измерения объема.
Спланируйте проблему.	1. Выполните преобразование второй единицы объема с л в мл. 2. Переставьте уравнение алгебраически, чтобы найти \ (P_2 \). \ [P_2 = \ frac {P_1 \ times V_1} {V_2} \]
Отменить единицы и рассчитать.	1. \ [0.663 \, \ cancel {L} \ times \ frac {1000 \, ml} {1 \, \ cancel {L}} = 663 \, ml \] 2. Подставьте известные величины в уравнение и решите. \ [P_2 = \ frac {722 \: \ text {torr} \ times 88.8 \: \ cancel {\ text {mL}}} {663 \: \ cancel {\ text {mL}}} = 96.7 \: \ text {torr} \]
Подумайте о своем результате.	Когда объем увеличивался, давление уменьшалось, что соответствует закону Бойля.

Упражнение \ (\ PageIndex {2} \)

Если V ₁ = 456 мл, P ₁ = 308 торр и P ₂ = 1,55 атм, что будет V ₂ ?

Ответ

119 мл

Сводка

• Поведение газов можно смоделировать с помощью газовых законов.
• Закон Бойля связывает давление и объем газа при постоянной температуре и количестве.

Материалы и авторство

Эта страница была создана на основе содержимого следующими участниками и отредактирована (тематически или широко) командой разработчиков LibreTexts в соответствии со стилем, представлением и качеством платформы:

.