Предел текучести — механическая характеристика материала, характеризующая напряжение, при котором деформации продолжают расти без увеличения нагрузки. С помощью
Пользователи также искали:
предел текучести — это,
предел текучести формула,
предел текучести сопромат,
предел текучести стали 45,
предел текучести стали таблица,
предел текучести таблица,
предел текучести и предел прочности,
условный предел текучести,
Предел,
текучести,
предел,
Предел текучести,
таблица,
стали,
условный,
формула,
сопромат,
предел текучести стали,
предел текучести сопромат,
предел текучести таблица,
текучести и предел прочности,
условный предел текучести,
прочности,
предел текучести — это,
предел текучести формула,
предел текучести стали таблица,
предел текучести стали 45,
предел текучести,
cтатьи по механике.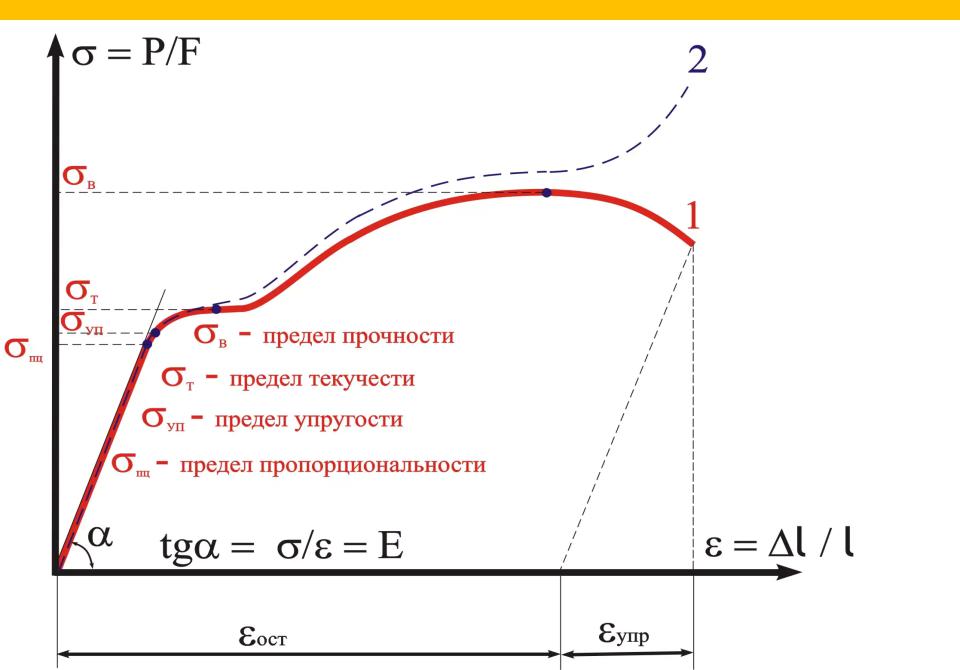
Tensile tests may also be carried out on the base metal and weld […]metal to determine the mechanical properties for these instron.com |
Испытания на растяжение можно также проводить на основном металле или сварном соединении для […]определения механических свойств данных […] материалов. Результаты могут включать предел прочности на растяжение, условный предел текучести, точку текучести, полное удлинение и относительное [. сужение. instron.ru |
ASTM E 21 covers tension testing methods […] to determine yield strength, tensile strength, elongation and […]reduction of area of metals at elevated temperatures. instron.us |
ASTM E 21 описывает методы испытаний на растяжение металлов при повышенной […]температуре для определения условного […] предела текучести, предела прочности на разрыв, удлинения и относительного […]instron.ru |
At temperatures lower than the NDT that […] same piece of steel will fail in a brittle manner when loaded to its yield strength (roughly half of its ultimate tensile strength).instron.com |
При температурах [.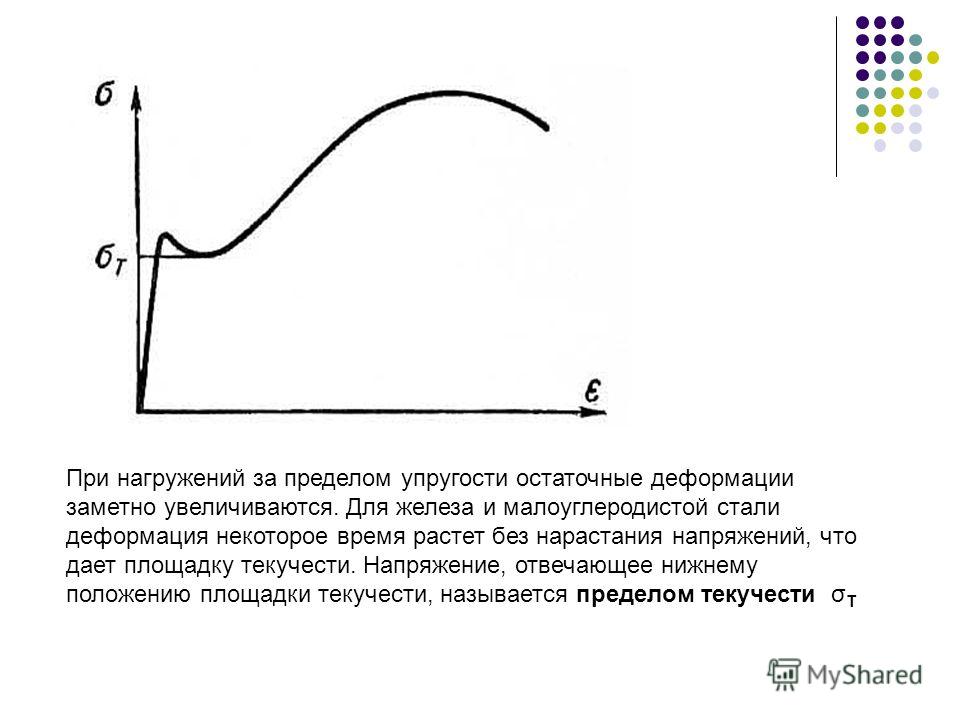 ..] ..]ниже ТНП тот же самый образец […] стали подвергается разрушению в хрупком состоянии при достижении предела текучести (грубо половина предела прочностиinstron.ru |
| The shaft material should have a yield point of at least 320 N/mm2. download.sew-eurodrive.com |
Минимальный предел текучести материала ведомого вала должен составлять 320 Н/мм2. download.sew-eurodrive.com |
The Register of the Russian […] Federation stipulates application of standard-strength shipbuilding steel of categories A, B, D, E (yield point 235 MPa), high—strength stee mir-forum.ru |
Правилами Регистра Российской Федерации для изготовления корпусных […] конструкций морских судов предусматривается использование судостроительной стали нормальноmir-forum.ru |
AS 1391 specifies methods for calculating […]various material properties […] of rebar including: the lower and up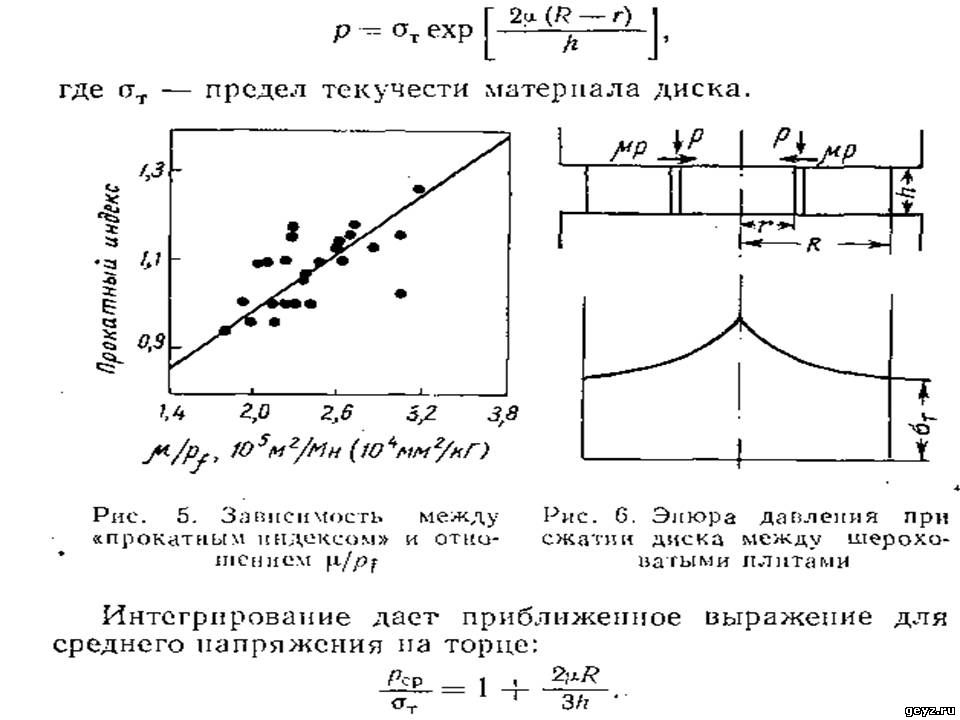 ..] ..]force (Ag), total extension […]at maximum force (Agt), and total elongation after fracture (A). instron.us |
Стандарт AS 1391 устанавливает методы определения […]таких свойств […] арматурного стержня, как например: нижний и верхний предел текучести ( ReL и ReH ), условный предел текучести (Rp и Rtпластическое удлинение […]при максимальном усилии (Ag), общее относительное удлинение при максимальном усилии (Agt) и общее относительное удлинение после разрыва (А). instron.ru |
Depending on the direction of the load and the type of the […] load carrying point on site, the reaction force either results in tensile force or pressure [.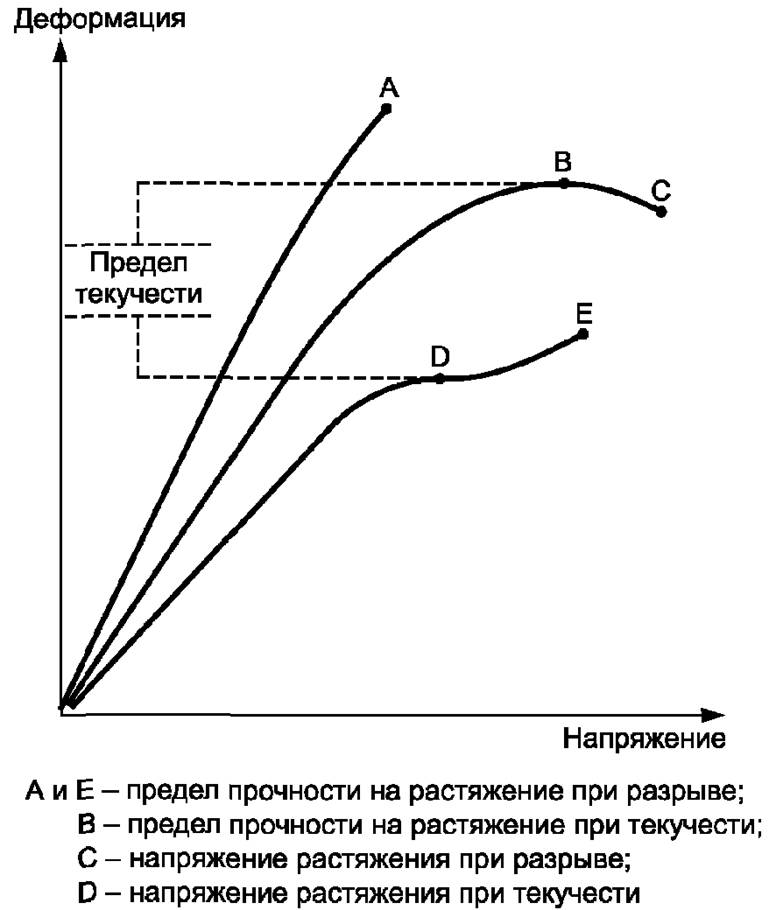 ..] ..]force depending on the reaction torque. download.sew-eurodrive.com | В зависимости от направления нагрузки и условий ее […] восприятия на месте эксплуатации реакция опоры может работать на растяжение или на сжатие.download.sew-eurodrive.com |
Modern ASTM A746 tests need to be run at specific stress rates […]under servo control and require an extensometer […] for accurate calculation of 0.2% Offset Yield and Ultimate Tensile Strength.instron.us |
Современные испытания согласно ASTM A746 нужно проводить при определенных скоростях изменения напряжения с помощью сервоуправления и экстензометра для точных […] расчетов (0,2%) условного предела текучести и предельной прочности при растяжении.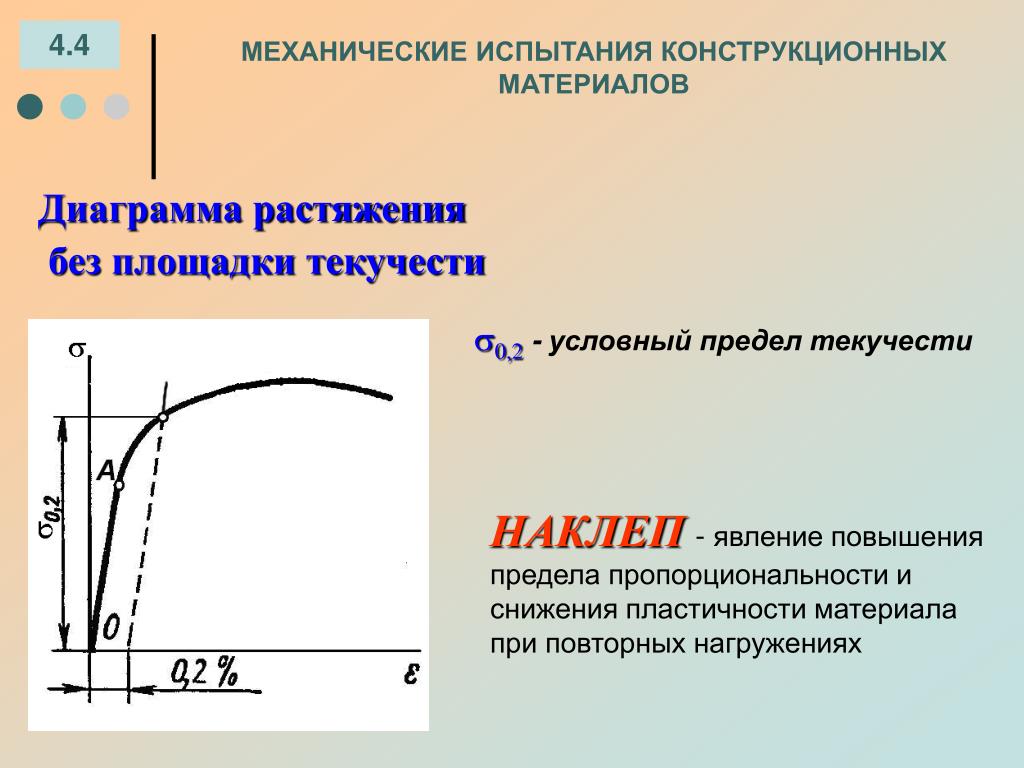 instron.ru |
| Thus, while the yield strength* may be similar to that of the ferritic grades, the tensile strength and ductility […] are much greater. nornickel.ru |
Таким образом, хотя условный […]предел текучести […] может быть аналогичным по сравнению с ферритными сталями, предел прочности на разрыв и эластичность гораздо выше.nornickel.ru |
| This is the point of intersection of the thread related seam strength and the leather tensile strength depending on which cutting point is used. groz-beckert.pl |
На графике это пересечение прочности нити по шву с прочностью кожи на разрыв в зависимости от выбора острия.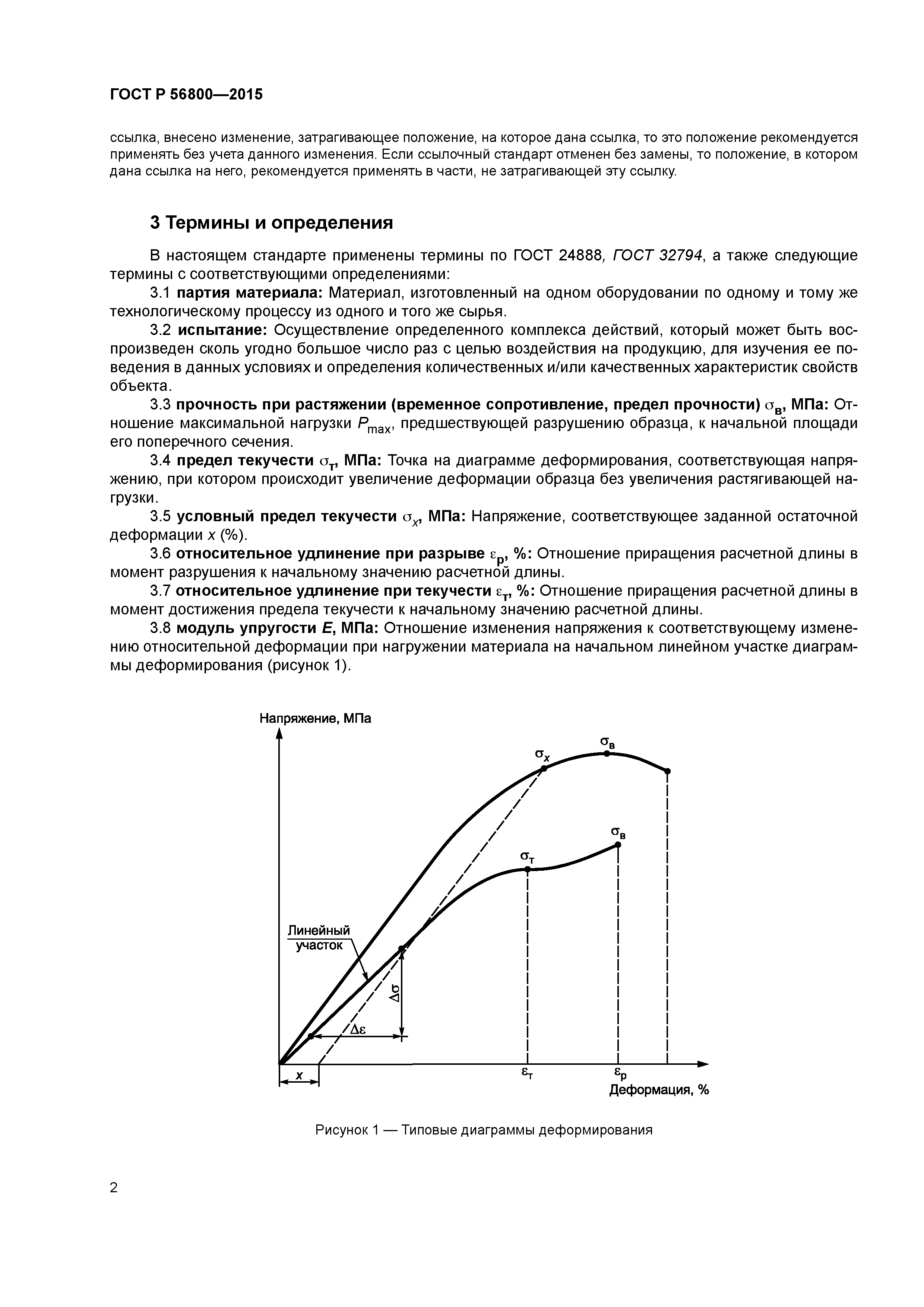 groz-beckert.pl |
Furthermore, vitamys® is the first and only highly cross-linked polyethylene used in total hip replacement that is equivalent to the best PE type 1 […]classification (according to ISO 5834-2), meeting the […] highest requirements for yield strength, ultimate tensile strength and elongation at break.mathysmedical.com |
Кроме того, vitamys® является первым и единственным какой смысл в слове полиэтиленом для заменителей тазобедренных суставов, что соответствует лучшему РЕ-Типу 1 […](согласно ISO 5834-2) и, таким образом, […] соответствует всем требованиям по напряжению текучести, пределу прочности при растяжении […]и растяжимости. mathysmedical.com |
These grades have low yield strength in comparison with the tensile strength, but the yield strength increases substantially [.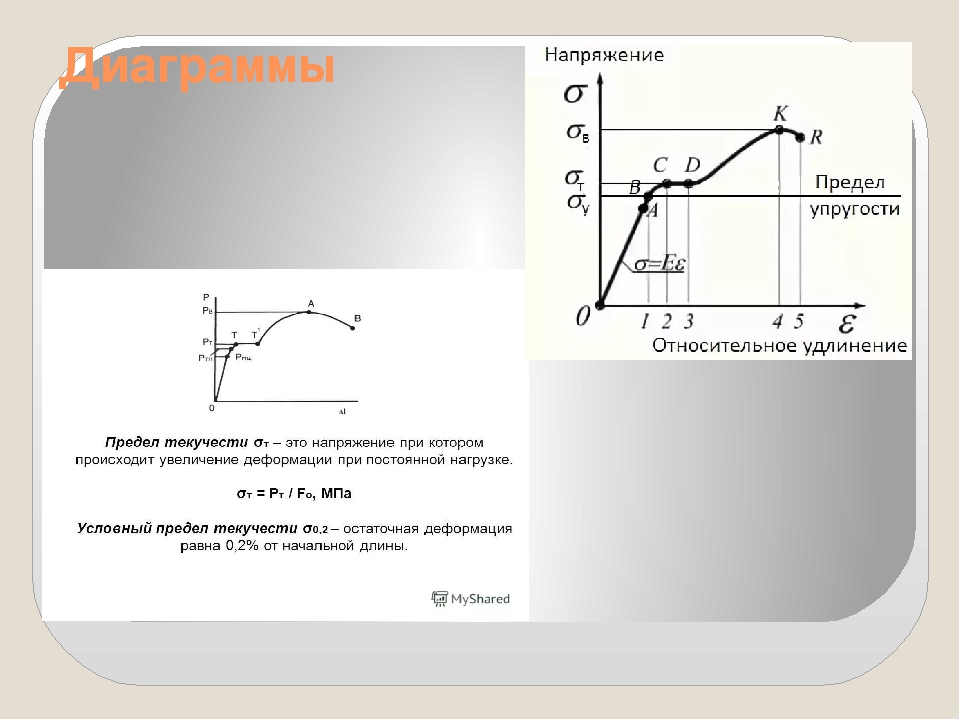 ..] ..]with both strain-hardening and bake-hardening. ssab.com |
Эти марки имеют низкий предел текучести по сравнению с пределом прочности, но предел текучести существенно […] увеличивается при деформационном упрочнении и упрочнении обжигом. ssab.com |
Derived on the basis of review and analysis of original data and those taken from literature are equations for […]description of yield point as a function of temperature, for […] calculation of increment in yield point and ultimate strength as well as for reduction […]of critical strains as a function of neutron fluency and […]irradiation/test temperature for type X18H9 austenitic steels. crism-prometey.ru |
На основе анализа и обобщения литературных и [. ..] ..]оригинальных данных разработаны уравнения для описания температурной зависимости […] предела текучести, расчета приращения предела текучести и предела прочности, а также снижения […]критической деформации в зависимости […]от флюенса нейтронов, температуры облучения и испытания аустенитных сталей типа Х18Н9. crism-prometey.ru |
| This process is approaching a point where it must yield results. daccess-ods.un.org |
Этот процесс в […] скором времени достигнет этапа, когда он должен начать приносить результаты.daccess-ods.un.org |
This way, 2-year Spanish […] securities currently at 2.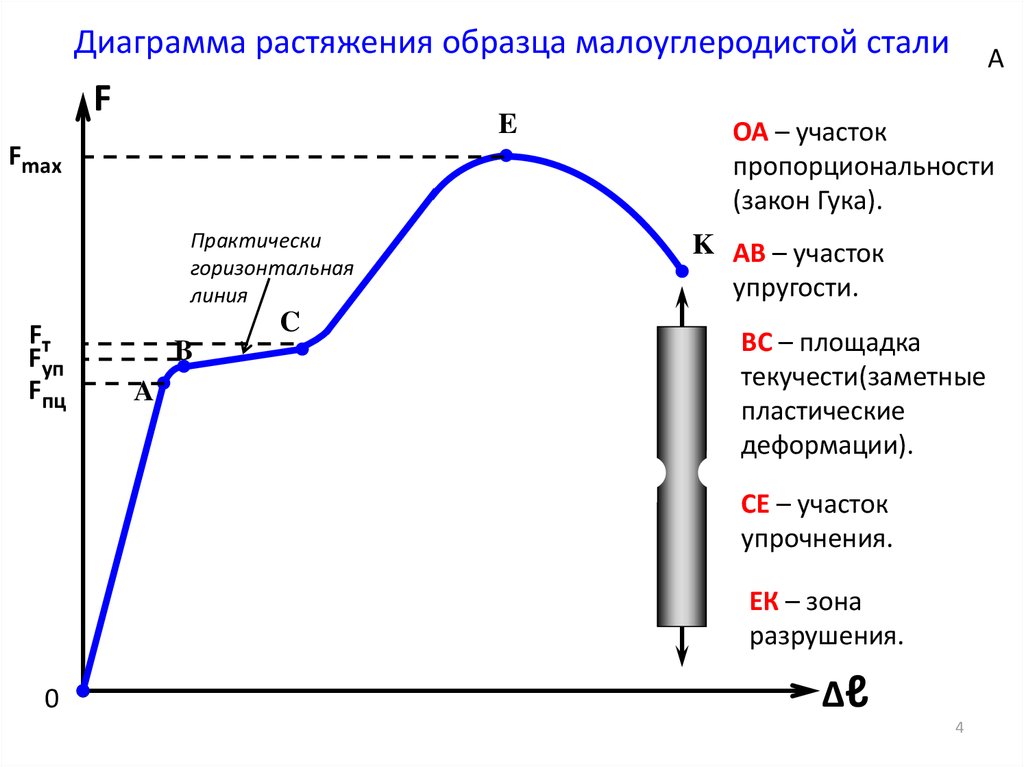 50% currently yield more than 1% point over Irish bonds with the same […] 50% currently yield more than 1% point over Irish bonds with the same […]remaining term which represents […]an attractive pick-up in our opinion, not least against the background that this maturity sector is potentially covered by the OMT programme of ECB. valartisbank.li |
Так, 2-летние испанские государственные […] ценные бумаги при 2,50% приносят доход, свыше 1% пункта превышающий доходность по ирландским […]облигациям с тем же сроком погашения, […]что, по нашему мнению, не в последнюю очередь по причине того, что бумаги с таким сроком погашения потенциально покрываются программой ОМТ, инициируемой ЕЦБ, обуславливает эффектный рост доходности. valartisbank.li |
Thermoprofiles are made of hot zinc-coated thin sheet steel with [. ..]
specified minimum yield strength of 350 N/mm2 and tensile strength of 420 N/mm. ..]
specified minimum yield strength of 350 N/mm2 and tensile strength of 420 N/mm.arkada-rus.com |
Изготавливаются термопрофили из […]горячеоцинкованной тонколистовой стали с […] нормативным пределом текучести 350 Н/мм2 и прочностью на растяжение 420 Н/мм2 .arkada-rus.com |
Very strict and rigid requirements are imposed for castings: manufacture in accordance […]with European norms […] and standards; mechanical properties occurred: tensile strength of 490 — 690 N/mm2, yield strength ≥ 315 N/mm2; impact strength ≥ 27 J; visual […]inspection of all […]exterior and interior surfaces; magnetic particle flaw detection (MPI) of 100%; ultrasonic testing (UT) 100% of the volume, X-ray inspection of locations specified in the drawings, etc. emss.ua |
К отливкам предъявляются очень жесткие и высокие […]требования: изготовление в […] соответствии с европейскими нормами и стандартами; механические свойства стали: предел прочности 490 — 690 Н/мм2; предел текучести ≥ 315 Н/мм2; […]ударная вязкость […]≥ 27 Дж; визуальный контроль всех наружных и внутренних поверхностей; магнитопорошковая дефектоскопия (МПД) 100% объема; ультразвуковой контроль (УЗК) 100% объема; рентгенографический контроль мест указанных в чертежах и т. д. Изготавливаются отливки из марки стали G17GrMo55. emss.ua |
| Considering its high yield and tensile strength Docol 1400 MZE still provides you […] with a balanced set of technical properties [. ..] ..]that can be used in conventional production equipment, while supplying the advantages you are looking for. ssab.com |
Учитывая высокие пределы текучести и прочности, сталь Docol 1400 MZE обеспечивает […] сбалансированный набор технических свойств, […]позволяющих использовать ее в обычном производственном оборудовании и в то же время получать дополнительные преимущества. ssab.com |
Enhanced proof […] strength levels from 350 to 1300 MPa and tensile strength levels from 700 to 1500 MPa are listed […]in EN 10088-2:2005. nornickel.ru |
Увеличение уровня прочности с 350 до 1300 МПа и предела прочности с 700 до 1500 МПа представлены […] в EN 10088-2:2005. nornickel.ru |
We offer a complete line of flat, wedge, and countersunk test washers and short bolt adapters, as [. ..] ..]well as a nutproof loading […] mandrel for proof, tensile, and head strength testing in accordance […]with ASTM F606, NASM 1312 […]and ISO 898-1 fastener standards. instron.us |
Мы предлагаем полный ассортимент плоских, клиновых и потайных испытатльных шайб и удинителей для коротких болтовых соединений, а также […]стандартную гаечную оправку […] для испытаний крепежных деталей на предел прочности, растяжение […]и прочность головки, проводимых […]в соответствии со стандартами ASTM F 606, NASM 1312 и ISO 898-1. instron.ru |
Leather tensile seam strength also depends on which point style is chosen. groz-beckert.pl |
При одинаковой толщине иглы уровень прореза и тем самым уровень прочности на разрыв зависит в том числе и от выбора острия. groz-beckert.pl |
| The high tensile strength of the film ensures precise positioning. orafol.com |
Высокая прочность на растяжение материала пленки обеспечивает возможность […] точного позиционирования. orafol.com |
This module allows for measurements of six different types of modulus, […]outer fiber stress and […] strain, four types of yield, break, pre-set point detection, peak […]values, and creep/relaxation (total and delta). instron.us |
Он позволяет измерять 6 различных типов модулей, напряжение и […]деформацию наружных волокон, 4 типа […] текучести, разрушение, заданные точки обнаружения, пиковые […]значения и ползучесть/релаксацию (общую и дельта). instron.ru |
A comparison of the scattering of slow and swift […] β-rays should yield important information on this point.web.ihep.su |
С этой точки зрения важная информация должна быть получена […] от сравнения рассеяния быстрых и медленных β-лучей. web.ihep.su |
Used for […] sintered carbide, cast iron and low tensile strength material.chris-marine. |
Используется для твёрдых сплавов на основе […] карбида, чугуна и материалов с низким пределом прочности на разрыв.chris-marine.com |
| The impact of a shift up or down of up to 200 basis point in the yield curve is shown (100 basis points equals 1 per cent). daccess-ods.un.org |
В таблице, отражающей кривую […] доходов, показано воздействие уменьшения/увеличения доходности на 200 базовых пунктов (100 базовых пунктов равны 1 проценту).daccess-ods.un.org |
One of these tests is the tensile strength perpendicular to surface test, also known as the internal bond strength test, and is also commonly used as a fundamental measure of the adhesive performance in [.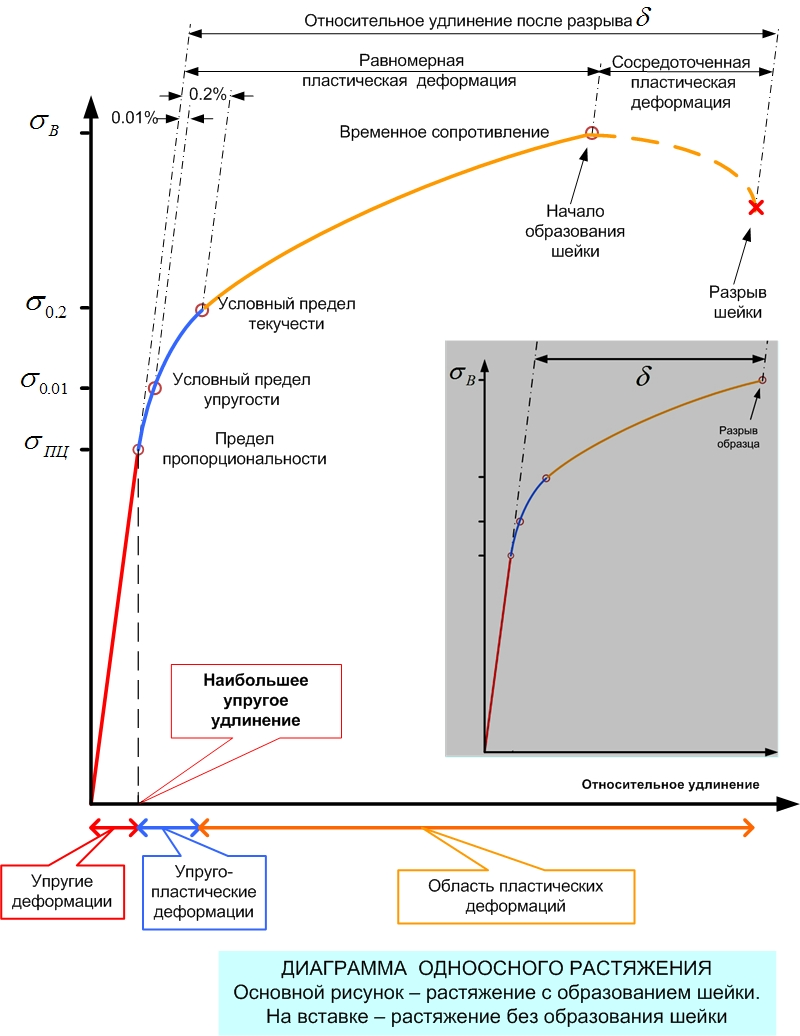 ..] ..]wood composites. instron.us |
Одно из таких испытаний — испытание на прочность при растяжении перпендикулярно поверхности, также известное, как испытание на прочность внутренней связи между волокнами, которое часто используется в качестве […] основной меры определения клеящих свойств […]полимера в древесных композитах. instron.ru |
Since film strength is so important, many […]companies have used the single column […] machines with pneumatic grips for tensile testing of thin films to investigate film tensile strength performance.instron.com |
Поскольку важна прочность пленки, многие компании используют […]машину с одной колонной и пневматическими […] захватами для испытаний на растяжение тонких пленок для исследования прочностных свойств пленок при растяжении. instron.ru |
| Maraging steels having an ultimate tensile strength equal to or greater than 1.5 […] GPa, measured at 20o C, in the form of sheet, […]plate or tubing with a wall or plate thickness equal to or less than 5.0 mm usable in systems specified in 1. daccess-ods.un.org |
Мартенситностареющие стали, которые […] характеризуются пределом прочности при растяжении, равным или более 1,5 ГПа […](определенным при температуре […]20ºC), в виде листов или плит толщиной 5 мм или менее, или труб с толщиной стенки, равной 5 мм или менее, используемые в системах, указанных в позиции 1. daccess-ods.un.org |
Череповецкий государственный университет — ведущий вуз Вологодчины
Колледж – вуз – предприятие
В прямом эфире расскажем о поступлении в Череповецкий государственный университет после колледжа; как будет строиться обучение вузе, сократится ли его срок; какие кадры сейчас ценны для предприятий. Свои вопросы можно задать прямо сейчас, перейдя по ссылке.
Наука в лицах: доктор политических наук Евгений Марков
С 2003 года Евгений Алфеевич преподает в Череповецком государственном университете. В 2003 году защитил диссертацию на соискание ученой степени кандидата политических наук, в 2012 году – защитил докторскую диссертацию.
Подведены итоги по организации деятельности педагогических классов
На встрече присутствовали – заместитель начальника Управления образования Череповца О.В. Иванова, первый проректор ЧГУ А.Н. Стрижов, директор ИПиП Н.В. Иванова и заведующие кафедрами, администрация СОШ 4, 9, 25, 31, ОЦ № 23, преподаватели Череповецкого государственного университета, которые принимали участие в организации учебных модулей в педагогических классах.
Студенты ЧГУ могут стать участниками «Российской студенческой весны»
Представители опорного вуза Вологодской области, входящие в состав музыкальных коллективов «Friends band» и «Бриз», завоевали Гран-при областного фестиваля. Ребята также стали победителями направлений «Театр», «Музыка» и «Хореография».
Космос сегодня: лекция профессора ЧГУ для школьников города
Лекцию на тему «Российский космос сегодня» для школьников провел Борис Валентинович Петелин, доктор исторических наук, профессор кафедры истории и философии Череповецкого государственного университета.
Магистранты ЧГУ испытали себя в роли педагогических дизайнеров
Они получили возможность узнать об основных направлениях деятельности Центра и испытали себя в роли специалистов по проектированию программ дополнительного профессионального образования педагогов.
Общегородское Родительское собрание: видеозапись прямого эфира
Гостями в студии стали: ответственный секретарь приемной комиссии ЧГУ Дарья Васильевна Спирина, начальник отдела общего и дополнительного образования мэрии Светлана Валериевна Клейнер. В прямом эфире ответили на актуальные вопросы о сдаче ЕГЭ и поступлении в Череповецкий государственный университет.
Конференция «Молодые исследователи – регионам»: успех студентов ЧГУ
Студенты Череповецкого государственного университета получили дипломы I степени на международной научной конференции «Молодые исследователи – регионам», проводимой в рамках одноименного молодежного форума.
Студенты напишут рецензию на спектакль «Кошкин дом»
В рамках посещения Череповецкого Камерного театра, будущие педагоги дошкольного и дополнительного образования получили возможность понаблюдать, как воспитанники детских садов воспринимают утренний спектакль «Кошкин дом» [0+] по пьесе-сказке С.Я. Маршака.
Наука в лицах: доктор философских наук Светлана Касаткина
Светлана Сергеевна – автор многочисленных научных публикаций в высокорейтинговых изданиях, нескольких учебных пособий по философии и философским дисциплинам, ряда монографий по вопросам исследования городов, городской жизни.
Определение предела текучести стали — Токарь Мастер
Определение предела текучести стали, чугуна: измерение напряжений
Прокатное производство включает изготовление различных марок конструкционных сталей, каждая из которых обладает индивидуальными механическими характеристиками.
В процессе эксплуатации стальные сооружения подвергаются в разной степени нагрузкам на изгиб и сжатие, растяжение и удары и только от механических свойств металлов зависит степень их прочность и стойкость.
Чтобы сделать правильные расчеты, применяется специальная расчетная формула.
Виды деформации стали
Тяжелым конструкциям необходимо придать дополнительную прочность и надежность, в связи с чем к свойствам используемых для изготовления металлов предъявляются особые требования.
При расчете размеров конструкции важную роль играет снижение массы сооружения без потери его несущих способностей. Используемые для изготовления металлических сооружений конструкционные металлы должны иметь достаточно высокие показатели прочности и хорошую пластичность.
Сопротивляемость деформации и разрушению под воздействием внешней нагрузки во многом зависит от того, какими свойствами наделен металл. В производстве стали деформация встречается в двух видах: упругой и пластической.
Описываются они разными характеристиками. Сегодня для испытания образцов металлов применяют несколько методик, которые определяют значения пропорциональности, упругости, текучести и других важных характеристик.
Современное определение стали звучит как твердый сплав железа с углеродом, процентным содержанием которого и обусловлены основные свойства стали.
Чем выше содержание углерода, тем металл прочнее и тверже, но ниже вязкость и пластичность.
Поэтому так важно правильно рассчитать соотношение этих показателей для производства тех или иных изделий из стали. Маркировать стали принято каждую группу по-разному.
Конструкционная углеродистая сталь маркируется буквами Ст и цифровыми обозначениями от 1 до 9, а также двумя буквами в зависимости от способа раскисления металла (ст.3кп):
- кп — кипящая;
- пс — полуспокойная;
- сп — спокойная.
Качественная — цифрами двузначными: 05,08,10,… 45…, что указывает на среднее количество углерода в составе стали.
Предел текучести стали
Граничный предел пропорциональности стали определяет напряжение, при котором действует закон Гука, согласно с которым деформация, возникшая в упругом теле, пропорциональна приложенной к нему силе. Если напряжение меняется, этот закон теряет актуальность.
Немаловажной физической величиной, участвующей в формуле при расчете прочности конструкции, является предел текучести металла.
Когда металлом достигается физический предел, даже самое малое поднятие напряжения способно удлинить образец, который начинает как бы течь, откуда и произошло его обозначение.
В связи с этим граница текучести стали показывает критическое напряжение, когда материал деформируется уже без увеличения нагрузки.
Единица, в которой производится измерение предела текучести будет называться Паскаль (Па) либо МегаПаскаль (МПа). Преодолевший этот предел образец получает необратимые изменения — разные степени деформации, нарушение структурного строения кристаллической решетки, различные пластические преобразования.
Если при увеличении растягивающего значения силы пройдена площадка текучести, деформация металла усиливается. На диаграмме это представляется в виде горизонтально расположенной прямой, на которой может измеряться напряжение, максимально получаемое после остановки усиления нагрузки. Так называемый предел текучести Ст 3 составляет 2450 кг/кв.см.
Этот показатель отличается у различных марок стали и может меняться от применения разных температурных режимов и типов термообработки. Чтобы иметь возможность точно определить предел текучести стали таблица используется, где в зависимости от марок сталей приведены величины пределов текучести. Как пример, по данным таблицы сталь 20 предел текучести имеет 250 МПа, а сталь 45 — 360.
При проведении испытаний некоторые металлы на диаграмме имеют слабо выраженную площадку тягучести либо она вовсе отсутствует, поэтому к ним применяется условный предел тягучести.
Материалы, на которые распространяется применение условного предела текучести, это в основном представители высокоуглеродистых и легированных сталей, дюралюминий, чугун, бронза и многие другие.
Предел упругости
Весьма важной составляющей механического состояния металлов является предел упругости стали. С его помощью устанавливается предельно допустимый уровень нагрузок при эксплуатации металла, когда им испытываются незначительные деформации в допустимых значениях.
Конструкционные материалы в себе должны сочетать высокие пределы тягучести, при которых они смогут выдерживать серьезные нагрузки, и иметь достаточную упругость, которая обеспечит необходимую жесткость изготовляемой конструкции. Сам модуль упругости обладает одинаковой величиной при растяжении и сжатии, но иметь совершенно отличные пределы упругости — так что одинаково жесткие конструкции диапазоны упругости могут иметь абсолютно разные.
При этом металл в упругом состоянии макропластических деформаций не получает, хотя в его отдельных микроскопических объемах локальные деформации вполне могут иметь место. Благодаря им происходят неупругие явления, серьезно воздействующие на поведение отдельных металлов в состоянии упругости.
При этом нагрузки статические приводят к возникновению гистерезисных явлений, релаксации и упругого последействия, в то время как нагрузки динамические провоцируют появление внутреннего трения.
В процессе релаксации происходит несанкционированное снижение напряжения. Это приводит к проявлению остаточной деформации, когда активная нагрузка уже не действует. При наступлении внутреннего трения происходит потеря энергии. Это вызывает необратимые последствия, которые характеризуются декрементом затухания и коэффициентом внутреннего трения.
Такие металлы активно гасят вибрацию и сдерживают звук, например, серый чугун, или свободно распространяют колебания, как это делает колокольная бронза. С повышением температурного воздействия упругость металлов снижается.
Предел прочности
Предел прочности стали, который возникает после прохождения его границы текучести и позволяет образцу вновь начать сопротивление к растяжению, отображается на графике линией, которая поднимается уже более полого.
Наступает фаза временного сопротивления действующей постоянной нагрузке. При применении максимума напряжения в точке предела прочности возникает участок, где площадь сечения уменьшается, а шейка значительно сужается.
При этом испытываемый образец разрывается в наиболее узком месте, его напряжение снижается и значение величины силы уменьшается. Предел прочности для ст. 3 составляет 4000−5000 кГ/кв.см.
Источник: https://remoskop.ru/opredelenie-predela-tekuchesti-stali-vspomogatelnyie-tablitsyi.html
Способ определения предела текучести материала
Изобретение относится к области испытания физико-механических свойств материалов, в частности к способам определения предела текучести металлов.
Известен способ определения предела текучести материала по твердости на пределе текучести, заключающийся в получении на образцах определенного материала зависимости между твердостью, измеренной с созданием в лунке деформации, равной 0,2%, и пределом текучести образцов, измерении твердости на пределе текучести и определении предела текучести с помощью полученной зависимости (см. Марковец М.П. Определение механических свойств металлов по твердости. – М.: Машиностроение, 1979. – С.61-64).
Недостатком известного способа является сложность определения точной величины степени деформации в лунке вследствие неравномерности распределения напряжений и деформаций на ее поверхности.
Известен способ определения предела текучести в процессе статических испытаний на растяжение, заключающийся в отборе фрагментов материала из изделия, изготовлении из них образцов, нагружении образцов в разрывной испытательной машине, измерении деформации образца в процессе нагружения и определении напряжения, считающегося пределом текучести, при достижении площадки текучести, характеризуемой ростом деформации без заметного увеличения нагрузки (см. Феодосьев В.И. Сопротивление материалов. – М.: Наука. Главная редакция физико-математической литературы, 1979. – С.53).
Недостатками известного способа являются:
1. Низкая точность определения предела текучести при отсутствии площадки текучести у материала (например, при испытании малоуглеродистых конструкционных сталей). При этом определяют условный предел текучести при относительной деформации образца 0,2% с применением тензометров или по диаграмме растяжения графическим способом.
2. Невозможность оценки стабильности свойств материала изделия, для чего требуется проведение испытаний серии образцов, так как в ходе однократного испытания определяется среднее значение предела текучести в наименее прочном сечении данного образца.
Известен способ определения предела текучести материала, взятый нами за прототип, заключающийся в подготовке гладкой поверхности образца материала, ступенчатом нагружении образца внешней растягивающей силой, выявлении полос скольжения, регистрации того значения силы, при котором наблюдается появление полос скольжения [см. Феодосьев В.И. Сопротивление материалов. – М.: Наука. Главная редакция физико-математической литературы, 1979. – С.57].
Недостатками прототипа являются:
1. Необходимость наличия сложного оптического оборудования.
2. Невозможность наблюдения за процессом в динамике его развития, так как для выявления полос скольжения требуется химическое травление поверхности.
В качестве разъяснения сути предлагаемого способа приводим следующее.
Известно, что начало пластического течения, характеризуемое пределом текучести, связано со сложными процессами изменения дислокационной структуры материала при увеличивающихся напряжениях.
В силу того, что структура конструкционных сталей разнородна (гетерогенна), разные участки образца имеют различные характеристики механических свойств, разную сопротивляемость деформациям, то есть различные величины предела текучести.
Поэтому, в ходе нагружения образец деформируется неоднородно. Это приводит к тому, что при поэтапном приращении нагрузки в каком-то наиболее слабом месте образца появляются первичные системы (линии) скольжения, соответствующие начальным пластическим деформациям.
В других местах образца при данной нагрузке линий скольжения пока нет.
С увеличением нагрузки первичные линии скольжения появляются и в других местах образца, а в месте первого появления линии скольжения прогрессируют, число дислокаций увеличивается, появляются развитые нарушения, дефекты сплошности, соответствующие развитым пластическим деформациям.
Таким образом, величина нагрузки (или механические напряжения), при которой появляются линии скольжения в конкретном месте образца, характеризует предел текучести материала определенного конкретного места на образце.
При этом в месте с наибольшей концентрацией дислокации материал разупрочняется, что приводит к уменьшению микротвердости.
В другом месте материал может несколько упрочняться за счет блокирования дислокации примесными атомами, что приводит к увеличению микротвердости.
Происходит увеличение вариации микротвердости относительно первоначального (исходного – до нагружения) среднего значения, что можно выявить по увеличению дисперсии выборки измеренных значений.
Технической задачей изобретения является установление предела текучести материала путем измерения твердости взамен выявления линий скольжения оптическим способом.
Цель изобретения – оценка стабильности механических свойств материала по пределу текучести в ходе испытаний одного образца.
Поставленная задача решается тем, что в известном способе определения предела текучести материала, включающем подготовку гладкой поверхности образца, ступенчатое нагружение образца внешней растягивающей силой, согласно изобретению, перед нагружением на поверхности образца размечают не менее трех областей измерения микротвердости, которую измеряют на каждой ступени нагружения, вычисляют дисперсию результатов измерений в каждой области и определяют предел текучести материала образца по увеличению дисперсии на величину не менее 20% от значения, полученного на предыдущем этапе нагружения.
Способ поясняется чертежом. На чертеже представлен эскиз образца 1, на котором изображены участки зажима 2 в захватах разрывной машины (на чертеже не показана), области измерения твердости 3 (№1, №2, №3, №4) и место разрушения образца 4.
Способ реализуется следующим образом.
Из фрагмента материала вырезают образец 1. Шлифованием готовят поверхность образца до гладкого состояния.
На подготовленной поверхности в пределах рабочей части образца длиной 2/3 от длины всего образца, размещенной по центру образца, отмечают не менее трех областей для измерения твердости. Зажимают участки зажима 2 образца 1 в захватах разрывной машины. Ступенчато нагружают образец.
При этом на каждом шаге нагружения в каждой из областей измеряют микротвердость поверхности не менее 50 раз. Замеры твердости делают произвольно по всей поверхности области, преимущественно в разных точках.
Считают дисперсию результатов измерения на каждом шаге нагружения в каждой области. При увеличении дисперсии на величину более чем 20% от значения, полученного на предыдущем шаге нагружения, считают, что в данной области металла достигнут предел текучести.
Пример
Необходимо определить предел текучести материала труб газопроводов, изготовленных из стали марки 17Г1С, не имеющей выраженной площадки текучести. Из трубы вырезают фрагмент металла и фрезерованием доводят его до формы параллелепипеда длиной 280 мм, шириной 50 мм, толщиной 5 мм.
Среднюю часть одной из сторон образца на длину около 200 мм шлифуют мелкозернистой наждачной бумагой до шероховатости поверхности не более Rz=10. С помощью маркера отмечают на шлифованной поверхности образца четыре области измерения твердости размерами 45×45 мм. Зажимают участки зажима 2 образца в захватах разрывной машины МР-100.
Ступенчато нагружают образец растягивающей нагрузкой с шагом 1,25 кН, при этом напряжения в образце ступенчато увеличиваются на 5,0 МПа. На каждом шаге нагружения измеряют микротвердость шлифованной поверхности в каждой из областей не менее 50 раз. С помощью программы Microsoft Excel определяют дисперсию результатов измерения твердости на каждом шаге нагружения в каждой области (см.
таблицу). Устанавливают, что при увеличении напряжения в образце с 330 до 335 МПа в области №2 дисперсия показаний микротвердости увеличивается с 59,236 до 75,822, т.е. изменение составляет более 28%. При этом считают, что в области №2 образца при напряжении 335 МПа достигнут предел текучести. Далее по полученным данным (см.
таблицу) определяют, что предел текучести металла в области №3 – 340 МПа, области №1 – 345 МПа, области №4 – 350 МПа. Таким образом, установлено, что предел текучести для данного материала может изменяться в пределах 335-350 МПа.
Дальнейшее увеличение нагрузки привело к разрушению образца. Место разрушения 4 проходит через область №2, в которой и зафиксирован минимальный предел текучести для данного образца материала. Графическим способом по величине относительной деформации 0,2% определили условный предел текучести всего образца, равный 370 МПа.
| Результаты вычислений дисперсии чисел твердости, измеренных на различных ступенях нагружения в четырех областях образца. | ||||
| Напряжения в образце, МПа | Дисперсия измеренных значений твердости | |||
| Область №1 | Область №2 | Область №3 | Область №4 | |
| 300 | 46,751 | 46,458 | 44,528 | 43,574 |
| 305 | 48,589 | 49,568 | 44,489 | 45,442 |
| 310 | 49,569 | 50,104 | 47,552 | 44,648 |
| 315 | 52,630 | 53,189 | 51,307 | 46,081 |
| 320 | 52,126 | 54,468 | 54,421 | 48,266 |
| 325 | 57,454 | 58,744 | 55,454 | 54,639 |
| 330 | 60,256 | 59,236 | 58,260 | 55,790 |
| 335 | 62,542 | 75,822 | 59,867 | 64,111 |
| 340 | 63,145 | 77,569 | 59,236 | 78,024 |
| 345 | 79,832 | 79,124 | 63,781 | 81,903 |
| 350 | 82,541 | 84,589 | 77,308 | 86,667 |
Эффект изобретения проявляется в том, что в ходе испытания одного образца с помощью статической растягивающей нагрузки возможно определить предел текучести для конструкционных материалов, к которым относятся трубные стали, не имеющие площадки текучести, оценить стабильность свойств испытываемого материала по расхождению установленных пределов текучести в пределах одного образца, упростить реализацию способа за счет применения не сложного измерительного оборудования.
Способ определения предела текучести материала, включающий подготовку гладкой поверхности образца и ступенчатое нагружение образца внешней растягивающей силой, отличающийся тем, что перед нагруженнием на поверхности образца размечают не менее трех областей измерения микротвердости, которую измеряют на каждой ступени нагружения, вычисляют дисперсию результатов измерений в каждой области и определяют предел текучести материала образца по увеличению дисперсии на величину не менее 20% от значения, полученного на предыдущем этапе нагружения.
Источник: http://www.FindPatent.ru/patent/233/2339017.html
Взаимосвязь напряжения текучести с твердостью и пределом прочности
Связь между напряжением текучести и пределом прочности устанавливается по зависимости между экстраполированным пределом текучести и σB. Поскольку по экстраполированному пределу текучести можно достаточно точно определить напряжение текучести для большинства материалов, начиная со степени деформации , то такое допущение можно считать оправданным.
Ниже рассмотрены зависимости между пределом прочности и экстраполированным пределом текучести кривых упрочнения при растяжении первого рода и при сжатии второго рода.
Экстраполированный предел текучести у кривых упрочнения первого рода при растяжениинаходится по пересечению касательной к кривой упрочнения в точке начала образования шейки с осью ординат.
У кривых упрочнения второго рода при сжатии экстраполированный предел текучести S0 (см. рис.
1) представляет собой напряжение, соответствующее по величине отрезку ординаты, отсекаемому прямой, являющейся продолжением участка III кривой упрочнения.
Согласно теоретическим выкладкам М. П. Марковца для материалов, у которых равномерное относительное поперечное сужение ΨB не более 0,15, разница между экстраполированным пределом текучести определеннымпо кривым упрочнения при растяжении, и пределом прочности σB не превышает 3%, а при ΨB до 0,2 — не более 7%. При этомвсегда должно быть меньше величины σB.
Теоретически установленную зависимость междуи σB М.П. Марковец подтвердил экспериментально.
Было показано, что независимо от рода материала (цветные и черные металлы), вида предшествующей термической обработки (отжиг, нормализация, закалка, закалка + отпуск) и прочности ( изучаемых материалов составлял 20-180 кГ/мм2) отношениедля материалов с до 15% близко к единице (рис. 1). Только для латуни и аустенитной стали ЭИ69, у которых величина ΨB доходит до 30%, это соотношение составляет 1,2-1,3.
П. Марковцем также была проведена большая работа по сопоставлениюи σB по экспериментальным данным других исследователей — Н. Н. Давиденкова, Кербера и Роланда.
Было установлено, что данные различных авторов, полученные экспериментально в разных лабораториях над огромным количеством металлов н сплавов (алюминии, меди и их сплавах, углеродистых и легированных сталях) при комнатных и повышенных температурах (от 20 до 300°С), подтверждают теоретически установленную закономерность для металлов и сплавов, у которых ΨB не превышает 15%.
Экспериментально определим взаимосвязь между экстраполированным пределом текучести при сжатии S0 и σB. В качестве исследуемого материала служили углеродистые и легированные горячекатаные и термически обработанные стали (табл. 1).
Кривые упрочнения строили по результатам осадки образцов с торцовыми цилиндрическими выточками. Результаты сравнения графически изображены на рис. 1, из которого видно, что между величинами S0 и σB независимо от марки изделия и вида, и режима предварительной обработки имеется линейная зависимость.
Математическая обработка экспериментальных данных показывает, что S0 в среднем меньше σB примерно на 6%, т. е.
Полученные экспериментальные данные согласуются с экспериментальными и теоретическими данными М. П. Марковца о зависимости между экстраполированным пределом текучести при растяжениии σB в том смысле, что S0 меньше σB примерно на ту же величину.
Таблица 1
Химический состав и вид предшествующей обработки сталей, для которых устанавливали зависимость между экстраполированным пределом текучести при сжатии S0 и пределом прочности σB
| 10 | Горячая прокатка | 0,11 | 0,45 | 0,21 | – | – | – |
| 15 | То же | 0,15 | 0,43 | 0,27 | – | – | – |
| 20 | » | 0,19 | 0,37 | 0,37 | – | – | – |
| 15Х | » | 0,13 | 0,42 | 0,32 | 0,90 | – | – |
| 20Х | » | 0,24 | 0,67 | 0,25 | 0,91 | – | – |
| 45Х | » | 0,44 | 0,61 | 0,19 | 0,90 | – | – |
| 12ХНЗА | » | 0,13 | 0,26 | 0,64 | 2,95 | – | |
| 12ХНЗА | Отжиг, нормализация | 0,16 | 0,40 | 0,36 | 0,66 | 2,81 | – |
| 40ХНМА | Отжиг, нормализация, улучшение (t0 mn=600°С) | 0,37 | 0,60 | 0,24 | 0,66 | 1,39 | 0,15-0,25 |
Зависимость между напряжением текучести и твердостью
На основании обработки экспериментальных данных установлены закономерности взаимосвязи:
- а) между S0 и твердостью исходного металла НВ;
- б) между S и твердостью сформированных образцов НВ’.
Напряжение текучести и экстраполированный предел текучести определяем по кривым упрочнения при сжатии, построенным по результатам осадки образцов с торцовыми цилиндрическими выточками. Твердость определяем обычным методом на твердомере типа ИТР с замером ее на торцах и по образующей.
Для определения зависимости между величинами S и НВ’ испытанию подвергали армко-железо, углеродистые и легированные стали, предварительно горячекатаные или термически обработанные (отжиг,
нормализация или улучшение). Вид предшествующей обработки и химический состав сталей, используемых при этих исследованиях, приведены в табл. 2.
Таблица 2
Химический состав и вид предшествующей обработки материала, исследуемого для установления зависимости между S и НВ’
| Армко-железо | Горячая прокатка | 0,057 | 0,10 | 0,17 | – | – |
| Сталь 30 | Нормализация | 0,29 | 0,61 | 0,30 | – | – |
| » 40 | Нормализация, улучшение | 0,41 | 0,59 | 0,30 | – | – |
| » 50 | Горячая прокатка | 0,50 | 0,70 | 0,27 | – | – |
| 12ХНЗА | » » | 0,13 | – | 0,26 | 0,64 | 2,95 |
| 12ХНЗА | Отжиг, нормализация | 0,11 | 0,42 | 0,23 | 0,64 | 2,79 |
Результаты экспериментальных данных приведены на рис.
3, из которого видно, что для всех исследуемых материалов независимо от вида предшествующей обработки и всего диапазона степеней деформации между напряжением текучести и соответствующей твердостью сформированных образцов имеется линейная зависимость. При обработке опытных данных установлено, что эта зависимость может быть представлена в следующем виде:
Влияние исходной твердости на величину экстраполированного предела текучести при сжатии изучали на примере углеродистых и легированных термически обработанных (отжиг, нормализация, улучшение) и горячекатаных сталей (табл. 3). Экспериментальные данные графически изображены на рис. 4.
Таблица 3
Химический состав и вид предшествующей обработки материала, исследуемого для определения зависимости между экстраполированным пределом текучести при сжатии S0 и исходной твердостью НВ
| Сталь 40 | Отжиг, нормализация, улучшение (tотп=500, 600°С) | 0,41 | 0,59 | 0,30 | – | – | – |
| Сталь 45 | Отжиг, нормализация, улучшение (tотп=700, 600, 540°С) | 0,43 | 0,58 | 0,30 | – | – | – |
| Сталь 50 | Горячая прокатка | 0,50 | 0,70 | 0,27 | – | – | – |
| 15Х | Горячая прокатка | 0,13 | 0,42 | 0,32 | 0,90 | – | – |
| 20Х | Отжиг, нормализация, улучшение (tотп=600, 500, 400°С) | 0,19 | 0,59 | 0,30 | 0,88 | – | – |
| 40Х | Отжиг, нормализация, улучшение (tотп=500, 600°С) | 0,38 | 0,62 | 0,32 | 1,03 | – | – |
| 12ХНЗА | Улучшение (tотп=600°С) | 0,16 | 0,40 | 0,36 | 0,66 | 2,81 | – |
| 30ХГСА | Отжиг, улучшение (tотп=550°С) | 0,34 | 0,98 | 1,13 | 1,08 | – | – |
| 40ХНМА | Отжиг, нормализация, улучшение (tотп=600°С) | 0,37 | 0,60 | 0,24 | 0,66 | 1,39 | 0,25 |
На основании экспериментальных данных установлено, что с увеличением твердости исходных образцов экстраполированный предел текучести возрастает по следующей зависимости:
Следует учесть, что в реальных металлических телах твердость в разных точках тела может отличаться на несколько единиц, а точность измерения составляет 3% при испытании на твердомере Бринелля, поэтому зависимости (2) и (3) носят несколько приближенный характер.
Источник: https://metrotest.ru/article/vzaimosvyaz-napryazheniya-tekuchesti-s-tverdostyu-i-predelom-prochnosti
3.1 Методы определения механических свойств
Металлам присущи высокая пластичность, тепло- и электропроводность. Они имеют характерный металлический блеск.
Свойствами металлов обладают около 80 элементов периодической системы Д.И. Менделеева. Для металлов, а также для металлических сплавов, особенно конструкционных, большое значение имеют механические свойства, основными из которых являются прочность, пластичность, твердость и ударная вязкость.
Под действием внешней нагрузки в твердом теле возникают напряжение и деформация. Напряжение это нагрузка (сила),отнесенная к первоначальной площади поперечного сечения образца.
Деформация – это изменение формы и размеров твердого тела под действием внешних сил или в результате физических процессов, возникающих в теле при фазовых превращениях, усадке и т.п.
Деформация может быть упругая (исчезает после снятия нагрузки) и пластическая (сохраняется после снятия нагрузки).
При все возрастающей нагрузке упругая деформация, как правило, переходит в пластическую, и далее образец разрушается.
В зависимости от способа приложения нагрузки методы испытания механических свойств металлов, сплавов и других материалов делятся на статические, динамические и знакопеременные.
Прочность – способность металлов оказывать сопротивление деформации или разрушению статическим, динамическим или знакопеременным нагрузкам.
Прочность металлов при статических нагрузках испытывают на растяжение, сжатие, изгиб и кручение. Испытание на разрыв является обязательным.
Прочность при динамических нагрузках оценивают удельной ударной вязкостью, а при знакопеременных нагрузках – усталостной прочностью.
Для определения прочности, упругости и пластичности металлы в виде образцов круглой или плоской формы испытывают на статическое растяжение. Испытания проводят на разрывных машинах. В результате испытаний получают диаграмму растяжения (рис. 3.1). По оси абсцисс этой диаграммы откладывают значения деформации, а по оси ординат – значения напряжения, приложенного к образцу.
Из графика видно, что сколь бы ни было мало приложенное напряжение, оно вызывает деформацию, причем начальные деформации являются всегда упругими и величина их находится в прямой зависимости от напряжения. На кривой, приведенной на диаграмме (рис. 3.1), упругая деформация характеризуется линией ОА и ее продолжением.
Рис. 3.1. Кривая деформации
Выше точки А нарушается пропорциональность между напряжением и деформацией. Напряжение вызывает уже не только упругую, но и остаточную, пластическую деформацию. Величина ее равна горизонтальному отрезку от штриховой линии до сплошной кривой.
При упругом деформировании под действием внешней силы изменяется расстояние между атомами в кристаллической решетке. Снятие нагрузки устраняет причину, вызвавшую изменение межатомного расстояния, атомы становятся на прежние места и деформация исчезает.
Пластическое деформирование представляет собой совершенно другой, значительно более сложный процесс. При пластическом деформировании одна часть кристалла перемещается по отношению к другой. Если нагрузку снять, то перемещенная часть кристалла не возвратится на старое место; деформация сохранится.
Эти сдвиги обнаруживаются при микроструктурном исследовании.
Кроме того, пластическое деформирование сопровождается дроблением блоков мозаики внутри зерен, а при значительных степенях деформации наблюдается также заметное изменение форм зерен и их расположения в пространстве, причем между зернами (иногда и внутри зерен) возникают пустоты (поры).
Представленная зависимость ОАВ (см. рис. 3.1) между приложенным извне напряжением (σ) и вызванной им относительной деформацией (ε) характеризует механические свойства металлов.
· наклон прямой ОА показывает жесткость металла, или характеристику того, как нагрузка, приложенная извне, изменяет межатомные расстояния, что в первом приближении характеризует силы межатомного притяжения;
· тангенс угла наклона прямой ОА пропорционален модулю упругости(Е), который численно равен частному от деления напряжения на относительную упругую деформацию:
· напряжение, которое называется пределом пропорциональности (σпц), соответствует моменту появления пластической деформации. Чем точнее метод измерения деформации, тем ниже лежит точка А;
· в технических измерениях принята характеристика, именуемая пределом текучести (σ0,2). Это напряжение, вызывающее остаточную деформацию, равную 0,2 % от длины или другого размера образца, изделия;
· максимальное напряжение (σв) соответствует максимальному напряжению, достигнутому при растяжении, и называется временным сопротивлением или пределом прочности.
Еще одной характеристикой материала является величина пластической деформации, предшествующая разрушению и определяемая как относительное изменение длины (или поперечного сечения) – так называемое относительное удлинение (δ) или относительное сужение(ψ), они характеризуют пластичность металла. Площадь под кривой ОАВ пропорциональна работе, которую надо затратить, чтобы разрушить металл. Этот показатель, определяемый различными способами (главным образом путем удара по надрезанному образцу), характеризует вязкость металла.
При растяжении образца до разрушения фиксируются графически (рис. 3.2) зависимости между приложенным усилием и удлинением образца, в результате этого получают так называемые диаграммы деформации.
Рис. 3.2. Диаграмма «усилие (напряжение) – удлинение»
Деформация образца при нагружении сплава сначала является макроупругой, а затем постепенно и в разных зернах при неодинаковой нагрузке переходит в пластическую, происходящую путем сдвигов по дислокационному механизму.
Накопление дислокаций в результате деформации ведет к упрочнению металла, но при значительной их плотности, особенно в отдельных участках, возникают очаги разрушения, приводящие, в конечном счете, к полному разрушению образца в целом.
Прочность при испытании на растяжение оценивают следующими характеристиками:
1) пределом прочности на разрыв;
2) пределом пропорциональности;
3) пределом текучести;
4) пределом упругости;
5) модулем упругости;
6) пределом текучести;
7) относительным удлинением;
8) относительным равномерным удлинением;
9) относительным сужением после разрыва.
Предел прочности на разрыв(предел прочности или временное сопротивление разрыву) σв, – это напряжение, отвечающее наибольшей нагрузке РВ предшествующей разрушению образца:
σв = Рв/F0,
Эта характеристика является обязательной для металлов.
Предел пропорциональности(σпц)– это условное напряжение Рпц, при котором начинается отклонение от пропорциональной зависимости мости между деформацией и нагрузкой. Он равен:
σпц = Рпц/F0.
Значения σпц измеряют в кгс/мм2 или в МПа.
Предел текучести(σт) – это напряжение (Рт)при котором образец деформируется (течет) без заметного увеличения нагрузки. Вычисляется по формуле:
σт = Рт/F0.
Предел упругости (σ0,05) – напряжение, при котором остаточное удлинение достигает 0,05 % длины участка рабочей части образца, равного базе тензометра. Предел упругости σ0,05 вычисляют по формуле:
σ0,05 = Р0,05/F0.
Модуль упругости (Е) – отношение приращения напряжения к соответствующему приращению удлинения в пределах упругой деформации. Он равен:
Е = Рl/lсрF0,
где ∆Р – приращение нагрузки; l0 – начальная расчетная длина образца; lср – среднее приращение удлинения; F – начальная площадь поперечного сечения.
Предел текучести (условный) – напряжение при котором остаточное удлинение достигает 0,2 % длины участка образца на его рабочей части, удлинение которого принимается в расчет при определении указанной характеристики.
Вычисляется по формуле:
σ 0,2 = Р0,2/F0.
Условный предел текучести определяют только при отсутствии на диаграмме растяжения площадки текучести.
Относительное удлинение (после разрыва) – одна из характеристик пластичности материалов, равная отношению приращения расчетной длины образца после разрушения (lк) к начальной расчетной длине (l0) в процентах:
.
Относительное равномерное удлинение (δр) – отношение приращения длины участков в рабочей части образца после разрыва к длине до испытания, выраженное в процентах.
Относительное сужение после разрыва (ψ), как и относительное удлинение – характеристика пластичности материала. Определяется как отношение разности F0 и минимальной (Fк)площади поперечного сечения образца после разрушения к начальной площади поперечного сечения (F0), выраженное в процентах:
.
Упругость–свойство металлов восстанавливать свою прежнюю форму после снятия внешних сил, вызывающих деформацию. Упругость – свойство, обратное пластичности.
Очень часто для определения прочности пользуются простым, не разрушающим изделие (образец), упрощенным методом – измерением твердости.
Под твердостью материала понимается сопротивление проникновению в него постороннего тела, т.е., по сути дела, твердость тоже характеризует сопротивление деформации. Существует много методов определения твердости.
Наиболее распространенным является метод Бринелля (рис. 3.3, а), когда в испытуемое тело под действием силы Р внедряется шарик диаметром D.
Число твердости по Бринеллю (НВ) есть нагрузка (Р), деленная на площадь сферической поверхности отпечатка (диаметром d).
Рис. 3.3. Испытание на твердость:
а – по Бринеллю; б – по Роквеллу; в – по Виккерсу
При измерении твердости методом Виккерса (рис. 3.3, б) вдавливается алмазная пирамида. Измерив диагональ отпечатка (d), судят о твердости (HV) материала.
При измерении твердости методом Роквелла (рис. 3.3, в) индентором служит алмазный конус (иногда маленький стальной шарик). Число твердости – это значение, обратное глубине вдавливания (h). Имеются три шкалы: А, В, С (табл. 3.1).
Методы Бринелля и Роквелла по шкале B применяют для мягких материалов, а метод Роквелла по шкале C – для твердых, а метод Роквелла по шкале A и метод Виккерса – для тонких слоев (листов). Описанные методы измерения твердости характеризуют среднюю твердость сплава.
Для того чтобы определить твердость отдельных структурных составляющих сплава, надо резко локализовать деформацию, вдавливать алмазную пирамиду на определенное место, найденное на шлифе при увеличении в 100 – 400 раз под очень небольшой нагрузкой (от 1 до 100 гс) с последующим измерением под микроскопом диагонали отпечатка.
Полученная характеристика (Н) называется микротвердостью, и характеризует твердость определенной структурной составляющей.
Таблица 3.1 Условия испытания при измерении твердости методом Роквелла
| Условия испытания | Шкала | Обозначение твердости |
| При испытании алмазным конусом и нагрузке Р = 150 кгс | С | HRC |
| При испытании алмазным конусом и нагрузке Р = 60 кгс | А | HRA |
| При вдавливании стального шарика и нагрузке Р = 100 кгс | В | HRB |
Значение НВ измеряют в кгс/мм2 (в этом случае единицы часто не указываются) или в СИ – в МПа (1 кгс/мм2 = 10 МПа).
Вязкость – способность металлов оказывать сопротивление ударным нагрузкам. Вязкость – свойство, обратное хрупкости. Многие детали в процессе работы испытывают не только статические нагрузки, но подвергаются также ударным (динамическим) нагрузкам. Например, такие нагрузки испытывают колеса локомотивов и вагонов на стыках рельсов.
Основной вид динамических испытаний – ударное нагружение надрезанных образцов в условиях изгиба. Динамическое нагружение ударом осуществляется на маятниковых копрах (рис. 3.4), а также падающим грузом. При этом определяют работу, затраченную на деформацию и разрушение образца.
Обычно в этих испытаниях, определяют удельную работу, затраченную на деформацию и разрушение образца. Ее рассчитывают по формуле:
КС = K/S,
где КС – удельная работа; К – полная работа деформации и разрушения образца, Дж; S0 – поперечное сечение образца в месте надреза, м2 или см2.
Рис. 3.4. Испытания на ударную вязкость с помощью маятникового копра
Ширина образцов всех типов измеряется до испытаний. Высоту образцов с U- и V-образным надрезом измеряют до испытаний, а с Т-образным надрезом уже после испытаний. Соответственно удельная работа деформации разрушения обозначается KCU, KCV и КСТ.
Хрупкостьметаллов в условиях низких температур называют хладоломкостью. Значение ударной вязкости при этом существенно ниже, чем при комнатной температуре.
Ещё одной характеристикой механических свойств материалов является усталостная прочность. Некоторые детали (валы, шатуны, рессоры, пружины, рельсы и т.п.) в процессе эксплуатации испытывают нагрузки, изменяющиеся по величине или одновременно по величине и направлению (знаку).
Под действием таких знакопеременных (вибрационных) нагрузок металл как бы устает, прочность его понижается и деталь разрушается. Это явление называют усталостью металла, а образовавшиеся изломы – усталостными. Для таких деталей необходимо знать предел выносливости,т.е.
величину наибольшего напряжения, которое металл может выдержать без разрушения при заданном числе перемен нагрузки (циклов) (N).
Износостойкость – сопротивление металлов изнашиванию вследствие процессов трения.
Это важная характеристика, например, для контактных материалов и, в частности, для контактного провода и токосъемных элементов токоприемника электрифицированного транспорта.
Износ заключается в отрыве с трущейся поверхности отдельных ее частиц и определяется по изменению геометрических размеров или массы детали.
Усталостная прочность и износостойкость дают наиболее полное представление о долговечности деталей в конструкциях, а вязкость характеризует надежность этих деталей.
Источник: http://libraryno.ru/3-1-metody-opredeleniya-mehanicheskih-svoystv-material_bashkov_2010/
Определение характеристик прочности
⇐ ПредыдущаяСтр 3 из 34Следующая ⇒
Модуль упругости первого рода (Е) – физическая константа материала, определяемая путем эксперимента и являющаяся коэффициентом пропорциональности между напряжениями и деформациями:
σ = εЕ.
Модуль упругости можно определять измерением образца тензометром (расчетный способ) или графическим способом по начальному участку диаграммы растяжения.
Расчетный способ. Нагружают образец равными ступенями до нагрузки, соответствующей напряжению, равному 70-80% от предполагаемого σпц. Величина ступени нагружения должна составлять 5-10% от предполагаемого σпц. По результатам испытаний определяют среднюю величину приращения удлинения образца ∆lcp на ступень нагружения ∆Р.
Графический способ. Записывают диаграмму нагружения образца в координатах “нагрузка (ордината) – деформация (абсцисса)”. ∆Р и ∆lcp определяют по диаграмме на участке от нагрузки Р0 до нагрузки, соответствующей напряжению равному 70-80% от предполагаемого σпц.
Модуль упругости вычисляют по формуле
МПа
Стандарты регламентируют также определение относительного равномерного удлинения δР, конечной расчетной длины образца lK, относительного удлинения образца после разрыва δ, относительного сужения ψ.
Предел пропорциональности σпц – наибольшее напряжение, до которого материал следует закону Гука, можно определять расчетным или графическим способами.
Расчетным способомопределяют или с помощью зеркального прибора при последовательном нагружении образца. Нагружение ведут сначала крупными ступенями, а затем при напряжении 0,65-0,8 от определяемого σпц – малыми ступенями. Рпц определяют при установленном отклонении деформации от закона пропорциональности, фиксируемом показаниями тензометра.
Графическим способомРпц определяют по машинной диаграмме растяжения.
От начала координат (рис.2.7) проводят прямую, совпадающую с начальным линейным участком диаграммы растяжения.
На произвольном уровне нагрузки проводят прямую АВ, параллельную оси абсцисс, и на этой прямой откладывают отрезок kn, равный половине отрезка mk. Через точку n и начала координат проводят прямую On и параллельно ей проводят касательную CD к диаграмме растяжения. Точка касания определяет искомую нагрузку Рпц.
Рис.2.7. Графические способы определения предела пропорциональности по диаграмме растяжения
Предел пропорциональности вычисляют по формуле
, МПа
Предел упругости σ 0,05 – наибольшее напряжение, до которого материал не получает остаточных деформаций. Так как пластические деформации в отдельных кристаллах появляются уже в самой ранней стадии нагружения, величина предела упругости (как и σпц) зависит от требований точности, которые налагаются на производимые измерения.
Расчетный способ. Образец нагружают до величины в два раза больше начальной Р0, и после выдержки в течение 5-7 с разгружают до Р0. Затем образец нагружают до величины, соответствующей 70-80% от предполагаемого σ0,05.
Дальнейшее нагружение проводят ступенями с выдержкой на каждой ступени 5-7 с и последующей разгрузкой до Р0 с измерением остаточного удлинения. Испытания прекращают, если остаточное удлинение превысит установленный допуск.
По результатам испытаний определяют нагрузку Р0,05
Графический способ, σ0,05 определяют по начальному участку диаграммы “нагрузка-деформация” (рис.2.8). Удлинения определяют на участке, равном базе измерителя деформации.
Для определения Р0,05 вычисляют соответствующую величину остаточного удлинения с учетом базы измерителя деформации.
Найденную величину увеличивают пропорционально масштабу диаграммы по оси деформаций; отрезок полученной длины 0Е откладывают по оси абсцисс вправо от начала координат 0.
Из точки Е проводят прямую ЕР, параллельную прямой 0А. Точка пересечения Р с диаграммой растяжения определяют нагрузку Р0,05.
Предел упругости вычисляет по формуле
.
Рис.2.8. Определение предела упругости
Предел текучести физическийσт, верхний предел текучести σтв и нижний предел текучести σтн определяют по диаграмме растяжения.
Скорость относительной деформации на площадке текучести устанавливают в пределах 0,00025- 0,0025 с-1. Если такая скорость на площадке текучести не может быть установлена, то до начала текучести устанавливают скорость нагружения от 1 до 30 МПа/с.
Допускается определять нагрузку Рт по явно выраженной остановке стрелки силоизмерителя машины, обусловленной удлинением образца без заметного увеличения нагрузки.
Пределы текучести вычисляют по формуле
.
В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести (или явно выраженный начальный переходный эффект), за предел текучести принимается условно величина напряжения, при котором остаточная деформация σост = 0,002 или 0,2%.
Предел текучести условныйσ0,2 можно определить расчетным или графическим способом.
Расчетный способ.σ0,2 определяют аналогично расчетному способу определения предела упругости σ 0,05.
Графический способ. σ0,2- определяют аналогично графическому способу определения σ0,05, по точке пересечения с кривой растяжения прямой KL, параллельной начальному участку кривой и отстоящей от него по горизонтали на расстоянии 0К=0,2(1о/100) в соответствии с принятым допуском (рис.2.9).
Рис. 2.9. Определение предела текучести σ0,2 по диаграмме растяжения
Условный предел текучести можно определять графически по диаграмме, записанной на машине в масштабе, если масштаб ее диаграммного аппарата по оси деформаций не менее 50:1.
При определении σ0,2 скорость нагружения должна быть от от 1 до 30 МПа/с. Предел текучести условный вычисляют по формуле
.
Временное сопротивление σв (предел прочности). Для определения σв образец растягивают под действием плавно возрастающей нагрузки до разрушения. Наибольшая нагрузка, предшествующая разрушению образца, Рmах соответствует временному сопротивлению.
Временное сопротивление вычисляется по формуле
.
Для пластичных материалов характеристикой сопротивления разрушению гладкого образца при растяжении служит истинное сопротивление разрушению – истинный предел прочности Sk
,
где Fk- площадь сечения в месте разрушения; Pk-усилие в момент разрушения;
Характер разрушения определяют по виду излома образца (рис.2.10).
Источник: https://lektsia.com/2×5882.html
Механические характеристики конструкционных материалов (Лекция №9)
Механические характеристики определяются следующими факторами:
- веществом, его структурой и свойствами;
- конструктивными особенностями элемента, т. е, размерами, формой, наличием концетраторов, состоянием поверхности;
- условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др.
Конструкционные материалы в процессе деформирования вплоть до разрушения ведут себя по разному. Пластичное поведение характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки. Такие материалы называют пластичными. При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими. Однако одни и те же конструкционные материалы, находящиеся в различных условиях деформирования, ведут себя по разному: при одних условиях проявляют себя как пластичные материалы, при другихкак хрупкие. В связи с этим, основные макромеханические характеристики материалов упругость, пластичность, вязкость и др. правильнее относить не к их свойствам, а к состояниям материала.
МЕХАНИЧЕСКИЕ СОСТОЯНИЯ ДЕФОРМИРУЕМЫХ ТЕЛ
В упругом состоянии деформации обратимы, и вся энергия, затраченная на деформирование, при разгрузке возвращается (диссипация энергии отсутствует). Для любого твердого тела процесс деформирования начинается с упругой деформации. Изотропное тело имеет две константы упругости модуль упругости Е и коэффициент Пуассона . Для анизотропных тел число упругих констант в общем случае равно 21. Из основных констант упругости можно получить их производныемодуль сдвига G, модуль объемной реформации К и постоянную Ламе .
Вязкое сопротивление в некотором смысле противоположно упругому работа внешних сил, уравновешенных силами вязкого сопротивления, полностью рассеивается в виде тепла. Вязкое сопротивление определяется величиной касательной силы, необходимой для поддержания ламинарного скольжения слоев, или течения с определенной скоростью. Таким образом вязкость можно определить как сопротивление течению.
Представление о вязкоупругой деформации дает поведение моделей, сочетающих свойства вязкости и упругости в такой последовательности: при нагружении тела в нем возникает мгновенная упругая деформация, подчиняющаяся закону Гука; далее при том же максимальном напряжении наблюдается вязкая деформация, подчиняющаяся закону Ньютона.
Наиболее распространенными в теории линейной вязко-упругости являются реологические модели Максвелла и Фойгта, дающие связь между напряжениями и деформациями и скоростями их изменения:
модель Максвелла,
модель Фойгта,
тде коэффициент вязкости.
Пластическое состояниехарактеризуется наличием остаточных деформаций, фиксируемых после снятия внешних нагрузок. Объем тела при пластической деформации не изменяется; условие постоянства объема записывается в виде , (эксперименты показывают, что изменение объема не превышает 0,5%).
В случае, когда все напряжения изменяются пропорционально одной из составляющих, в процессе пластической деформации направления главных деформаций совпадают с направлениями главных нормальных напряжений, направления максимальных сдвигов с направлениями максимальных касательных напряжений, а главные направления девиатора напряжений с главными направлениями девиатора деформаций.
Одной из распространенных моделей поведения материала при упруго-пластических деформациях является модель пластичности, основанная на деформационной теории ГенкиИльюшина, описываемая уравнениями:
Здесь средняя деформация,
среднее напряжение,
безразмерный коэффициент, называемый параметром пластичности (с точностью до множителя он совпадает с интенсивностью касательных напряжений). При эта модель описывает поведение упругого материала.
Высокоэластическое состояние наиболее характерно для полимеров; особенностями этого состояния являются большая изменяемость формы и деформирование без изменения объема. Для материалов, находящихся в высокоэластическом состоянии, наблюдается существенная зависимость их свойств от длительности и скорости нагружения, температуры и т. д.
Состояние разрушения состояние, при котором за счет интенсивного развития трещин в материале тела начинается нарушение его сплошности и непрерывности. Физический процесс разрушения материала представляется в виде двух основных стадий стадии рассеянных разрушений (зарождение и развитие микроскопических трещин) и стадии развития магистральной трещины. Очаги зарождения микротрещин распределены по всему объему материала, находящегося в однородном напряженном состоянии, достаточно равномерно. Относительная длительность первой и второй стадии разрушения зависит от свойств материала, характера напряженного состояния и условий нагружения.
ДИАГРАММЫ УПРУГО-ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
Основным опытом для определения механических характеристик конструкционных материалов является опыт на растяжение призматического образца центрально приложенной силой, направленной по продольной оси; при этом в средней части образца реализуется однородное напряженное состояние. Форма, размеры образца и методика проведения испытаний определяются соответствующими стандартами, например, ГОСТ 3464381, ГОСТ 1497-73. По результатам испытаний строится зависимость между напряжениями и деформациями , которая называется диаграммой деформирования. Опыты на растяжение образцов выявляют некоторые общие свойства конструкционных материаловсвойства упругости и пластичности. На рис. 1 показаны типичные кривые деформирования при растяжении образцов из материала сталь 30 и сталь 40Х.
Если напряжения не превышают предела пропорциональности (точка / на диаграмме), и зависимость между напряжениями и деформациями линейна, то она описывается законом Гука , где Емодуль продольной упругости материала. Размерность модуля упругостиН/м2 (Паскаль). Значение модуля упругости Е на кривой деформирования численно равно тангенсу угла наклона линейного участка: . Таким образом, величину Е можно рассматривать как характеристику упругого сопротивления или как характеристику интенсивности- нарастания напряжения с увеличением деформации. Физический смысл коэффициента Е определяется как напряжение, необходимое для увеличения длины образца в два раза. Такое толкование довольно искусственно, поскольку величина упругого удлинения у большинства твердых тел редко достигает даже 1%.
Рис.1. Характерные диаграммы растяжения
Напряжения, являющиеся верхней границей проявления чисто упругих деформаций, соответствуют точке 2 диаграммы и называются пределом упругости .
Точка 3 диаграммы характерна тем, что при достижении напряжениями величины ( предел текучести), дальнейшее удлинение образца (для малоуглеродистых сталей) происходит практически без увеличения нагрузки. Это явление носит название текучести, а участок диаграммы, расположенный непосредственно правее точки 3, называется площадкой текучести. При этом полированная поверхность образца мутнеет, докрывается ортогональной сеткой линий (линии ЧерноваЛюдерса), расположенных под углом 45o к продольной оси образцапо направлению плоскостей действия максимальных касательных напряжений.
У многих конструкционных материалов площадка текучести не выражена столь явно, как у малоуглеродистых сталей. Для таких материалов вводится понятие условного предела текучести ; это напряжение, которому соответствует остаточная (пластическая) деформация, равная s %. Обычно принимается s = 0,2%.
После площадки текучести для дальнейшего увеличения деформации необходимо увеличение растягивающей силы. Материал снова проявляет способность сопротивляться деформации; участок за площадкой текучести (до точки 4) называется участком упрочнения. Точка 4 соответствует максимальной нагрузке, выдерживаемой образцом. Соответствующее напряжение называется временным сопротивлением (или пределом прочности ). Дальнейшая деформация образца происходит без увеличения или даже с уменьшением нагрузки вплоть до разрушения (точка 5). Точке 4 на диаграмме соответствует начало локального уменьшения размеров поперечного сечения образца, где, в основном, сосредоточивается вся последующая пластическая деформация.
Диаграмма, приведенная на рис.1, является диаграммой условных напряжений, условность состоит в том, что все силы относились к F0 первоначальной площади поперечного сечения образца; в действительности же при растяжении площадь поперечного сечения образца уменьшается. Если учитывать текущее значение площади поперечного сечения при определении напряжений, то получим диаграмму истинных напряжений (рис. 2).
Рис.2. Диаграмма истинных напряжений
Если в некоторый момент нагружения (точка А на рис. 1) прекратить нагружение и снять нагрузку, то разгрузка образца пойдет по линии АВ, параллельной линейному участку диаграммы 0 1. При этом полная деформация в точке А равна:
где упругая деформация, пластическая (остаточная деформация). Уравнение это справедливо для любой точки диаграммы.
После того как материал испытал воздействие осевого усилия одного знака (например, растяжение) в области пластических деформаций сопротивляемость этого материала пластической деформации при действии сил другого знака (сжатие) понижается. Это явление носит название эффекта Баушингера.
При растяжении образца происходит не только увеличение его длины, но и уменьшение размеров поперечного сечения, т. е. в упругой области деформация в поперечном направлении , где деформация в продольном направлении, коэффициент Пуассона. Для изотропных материалов значения коэффициента Пуассона находятся в пределах .
Таблица 1. Механические характеристики некоторых материалов
Примечание. В знаменателе указана соответствующая характеристика при сжатии».
Для сталей различных марок Е = 195-206 ГПа, G = 79-89 ГПа, = 0,23-0,31, для сплавов алюминия Е = 69-71 ГПа, G = 26-27 ГПа, = 0,30-0,33. Упругие свойства некоторых материалов даны в табл. 3.1.
Характеристиками пластичности материала являются относительное удлинение и относительное сужение при разрыве:
где l0, F0 длина рабочей части образца и площадь поперечного сечения до деформации; lк длина рабочей части образца после разрыва; F0 конечная площадь поперечного сечения в шейке образца после разрыва.
По величине относительного удлинения при разрыве проводится разделение состояния материалов на пластичное и хрупкое. Материалы, имеющие к моменту разрушения достаточно большие значения , относят к пластическим материалам; к хрупким относят материалы с относительным удлинением .
Оценка пластических свойств материала может быть проведена по такой характеристике, как ударная вязкость
KC=A/F,
где А работа, затрачиваемая на ударное разрушение образца, Дж (или ), F площадь поперечного сечения образца в месте концентратора, м2 (или см2),
Работа А деформации при разрушении образца может быть определена по диаграмме растяжения . Так, если первоначальная длина образца l0, то работа деформации, совершаемая силой Р на перемещении и:
где uк перемещение в момент, предшествующий разрушению. Тогда по зависимости и , находим
,
где площадь диаграммы деформирования (работа деформации на единицу объема материала). Для сталей КС=50100 Н м/см2. Материалы с ударной вязкостью КС < 30 Н м/см2 относят к числу хрупких.
Некоторые пластичные материалы в районе площадки текучести обнаруживают особенность (например титан), называемую «зубом текучести»; для таких материалов вводится понятие верхнего и нижнего предела текучести .
Экспериментальное изучение свойств материалов при сжатии проводится на коротких образцах с тем, чтобы исключить возможность искривления образца. Для пластичных материалов характер диаграммы при сжатии примерно до возникновения текучести такой же, как и при растяжении. В процессе деформации сжатия образец укорачивается; при этом размеры поперечного сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так.как образец сплющивается.
Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем деформациям растяжения; для них разрушающее напряжение при сжатии превышает предел прочности при растяжении в несколько раз. Разрушение хрупких материалов при сжатии происходит за счет образования трещин.
Дальше…MYsopromat.ru: Механические характеристики материалов
Под механическими характеристиками подразумеваются значения напряжений и деформаций, соответствующие определенным точкам на диаграмме условных напряжений.
Пределом пропорциональности σпц называется наибольшее напряжение, до которого деформации прямо пропорциональны напряжениям.
Пределом упругости σу называется напряжение, до которого материал не получает остаточных деформаций.
Пределом текучести σт называется напряжение, при котором деформации растут без заметного увеличения нагрузки.
Пределом прочности, или временным сопротивлением σв называется максимальное напряжение (подсчитанное по первоначальной площади сечения образца), выдерживаемое материалом при растяжении. Его величина определяется ординатой точки C условной диаграммы (см. Рис. 4.6).
При экспериментальном определении величин пределов пропорциональности и упругости вносится определенный элемент условности. Объясняется это тем, что начало отклонения от линейной зависимости, как и начало образования остаточных деформаций, будет отмечено тем раньше, чем выше точность измерения деформаций.
Поэтому под пределом пропорциональности σпц понимается напряжение, при котором отступление от линейной зависимости достигает определенной величины, устанавливаемой техническими условиями.
Пределом упругости считается напряжение, при котором остаточные деформации достигают заранее установленной величины в пределах 0.001-0.005%. Условный предел упругости при остаточной деформации 0.005% обозначается σ0,005.
Для материалов, не имеющих площадки текучести, в качестве предела текучести условно принимается напряжение, при котором остаточные деформации составляют 0.2 или 0.3% от первоначальной длины образца. Условный или, иначе, технический предел текучести в соответствии с допуском на остаточную деформацию обозначается σ0,2 или σ0,3.
В теоретических исследованиях индексы 0.2 и 0.3 обычно опускаются и условный предел текучести обозначается символом σт. Предел текучести является одной из основных характеристик материала. Пластические свойства материала, то есть способность к образованию остаточных деформаций, характеризуются величиной остаточного удлинения образца при разрыве
|
, |
(4.7) |
а также относительным уменьшением площади сечения образца в шейке
|
, |
(4.8) |
где l1, F1 — длина рабочей части образца и площадь наименьшего сечения шейки разорванного образца, соответственно; lo, Fo — их величины до нагружения.
Основные механические характеристики применяемых в технике материалов приводятся в справочной литературе.
Зависимости условного предела текучести (σ 0,2) ВТ1-0 …
Context 1
… от условного предела текучести σ 0,2 для образцов с разным размером зерен определяли с использованием кривых деформации для квазизучения. статическое напряжение, которое мы получили как в этом исследовании (рис. 1 и таблица I), так и в нашей ранее опубликованной статье. 23 Для выявления эффекта упрочнения ГЗ полученные значения σ 0,2 были нанесены в координаты σ 0. Рис. 2) с использованием соотношения Холла-Петча…
Context 2
… с другой стороны, в интервале температур T ≲ 180 K экспериментальные значения σ 0.2 на зависимостях σ 0.2 (d −1/2) отклоняются от линейной классическое соотношение Холла-Петча для увеличения предела текучести (рис. 2) при переходе от структурного состояния с микронными / субмикронными размерами зерен к NC-состоянию. Более того, в области размеров зерен меньше критической (d ≤ d cr), в окрестности которой происходит этот переход, зависимость предела текучести от размера зерна также может быть представлена в координатах σ 0.2 -d −1/2. Однако это …
Context 3
… размеры зерен (d ≥ d cr) в довольно широком диапазоне температур. Весьма вероятно, что при низких температурах (T ≲ 200 K) механизм, лежащий в основе уравнения (1) связано исключительно с активностью дислокационных источников ГБ. Когда температура поднимется до комнатной, источники дислокаций IG начнут конкурировать с источниками GB. Как видно из рис. 2, увеличение активности источников ИГ и переход к смешанным источникам дислокаций не нарушают согласия экспериментальных данных с величиной σ 0.2 -d −1/2 зависимость. Этот результат является экспериментальным подтверждением данных моделирования дискретной дислокации62, согласно которому активность внутризеренной дислокации …
Контекст 4
… механизма может приводить к уменьшению наклона Холла-Петча с размер зерна менее ∼30 нм. [63] [64] [65] [66] Экспериментальные зависимости предела текучести от размера зерна при температурах 293 и 395 K могут быть достаточно хорошо аппроксимированы соотношением Холла-Петча в координатах σ 0.2 -d −1/2 до наноразмеров (d = 35-80 нм) (рис. 2). Краткий обзор 35 основных механизмов, ответственных за пластическую деформацию НК-металлов, указывает на то, что, согласно результатам молекулярно-динамического моделирования и аналитического описания, 66-70 зарождение / аннигиляция дислокаций на границах зерен и проскальзывание ГЗ являются доминирующими, когда размеры зерен от 20 до 50 нм. …
Context 5
… обнаружено, что при низких температурах, в случае наноразмерного титана, экспериментальное значение σ 0.2 значения отклоняются от линейного соотношения Холла-Петча, наблюдаемого для образцов КЗ / УМЗ (рис. 2). В титане CG диаметр дислокационной петли [см. Ее передний сегмент на рис. 5 (a)], создаваемой источником GB, практически не зависит от …
Предел текучести — обзор
8.3 Зависимость от температуры и скорости деформации предела текучести
Предел текучести стали увеличивается с понижением температуры при комнатной температуре и ниже (см. рис. 8.3). При пластической деформации при низкой температуре барьер Пайерлса (ближнее препятствие) является основным препятствием для движения дислокаций.Дислокации преодолевают препятствие с помощью тепловых колебаний атомов и приложенного напряжения. Поскольку тепловая энергия уменьшается с понижением температуры, предел текучести увеличивается при низкой температуре.
8.3. Температурная зависимость предела текучести σ y , нормированная на модуль Юнга E , и влияние скорости деформации на кривую. σ a — атермический предел текучести, не зависящий от температуры и скорости деформации.
При промежуточных температурах в диапазоне от 100 до 450 ° C для стали энергия тепловых колебаний становится достаточно большой для того, чтобы дислокации преодолели барьер Пайерлса, и основное препятствие для движения дислокаций переходит в другое препятствие на большие расстояния, такое как другие дислокации и частицы.Поскольку эти препятствия слишком велики, чтобы дислокации могли преодолеть их с помощью тепловой энергии, дислокации могут преодолевать препятствия только с помощью приложенного напряжения. Следовательно, предел текучести при промежуточной температуре практически не зависит от температуры и скорости деформации. Такой предел текучести называется атермическим пределом текучести a . Предел текучести связан с плотностью дислокаций ρ и расстоянием между частицами λ следующими уравнениями:
[8.3] σa = αMGbρ
[8.4] σa = βMGb / λ
, где α — константа около 0,4, M — коэффициент Тейлора (= 3), G — модуль сдвига, b — длина вектора Бюргерса, а β — постоянная около 0,8. Пределы текучести слабо зависят от температуры испытания из-за температурной зависимости G . Они действительно не зависят от температуры, если их нормализовать с помощью постоянной упругости, такой как G или модуль Юнга E . Динамическое деформационное старение, вызванное атомами углерода и азота, может привести к появлению пика на кривой «предел текучести – температура» при промежуточной температуре, но пик несущественен при 0.В качестве предела текучести используется 02 или 0,2% условного предела текучести.
При повышенной температуре диффузия атомов и вакансий помогает дислокациям проходить через атермические препятствия, что приводит к другой пластической деформации, зависящей от температуры и скорости деформации, а именно ползучести. Этот температурный диапазон называется режимом ползучести. Предел текучести при высокой температуре выражается как:
[8,5] σy = Eε˙ / ε˙01 / nexpQD / nRT
, где ε˙ — скорость деформации, ε˙0 — постоянная материала, n — напряжение. экспонента, которая обычно больше 3, Q D — это энергия активации решеточной диффузии, R — универсальная газовая постоянная, а T — абсолютная температура.Следовательно, предел текучести высокотемпературной деформации уменьшается с увеличением температуры или уменьшением скорости деформации.
При низкотемпературной деформации тепловая энергия помогает дислокациям преодолеть барьер Пайерлса. Помощь тепловой энергии увеличивается с уменьшением скорости деформации ε˙, что приводит к уменьшению предела текучести. Однако σ a является нижним пределом предела текучести при низкой температуре, поскольку приложенное напряжение ниже σ a не позволяет дислокациям проходить через препятствия на большом расстоянии.При высокой температуре предел текучести увеличивается с увеличением скорости деформации, как и ожидалось из уравнения [8.5]. Однако предел текучести не может превышать атермический предел текучести σ a , поскольку выше σ a дислокации могут проходить через атермические препятствия без помощи диффузии. Атермический предел текучести является важным значением даже при высокотемпературной деформации, поскольку это верхний предел предела текучести.
python — Неожиданное поведение с условным выражением генератора
Выражения генератора Python являются поздним связыванием (см. PEP 289 — Выражения генератора) (то, что другие ответы называют «ленивым»):
Раннее связывание по сравнению с поздним связыванием
После долгого обсуждения было решено, что первое (самое внешнее) выражение for [выражения генератора] должно оцениваться немедленно, а остальные выражения оцениваться при выполнении генератора.
[…] Python использует подход позднего связывания к лямбда-выражениям и не имеет прецедента для автоматического раннего связывания. Было сочтено, что введение новой парадигмы излишне усложняет ситуацию.
После изучения многих возможностей пришел к консенсусу, что проблемы связывания трудно понять и что пользователям следует настоятельно рекомендовать использовать выражения генератора внутри функций, которые немедленно потребляют их аргументы. Для более сложных приложений полные определения генераторов всегда лучше с точки зрения наглядности в отношении области действия, времени жизни и привязки.
Это означает, что только оценивает самый внешний для при создании выражения генератора. Таким образом, на самом деле связывает значение с именем array в «подвыражении» в массиве (на самом деле в этот момент он связывает эквивалент iter (array) ). Но когда вы перебираете генератор, вызов if array.count фактически относится к тому, что в настоящее время называется array .
Поскольку на самом деле это список , а не массив , я изменил имена переменных в оставшейся части ответа, чтобы они были более точными.
В вашем первом случае список , который вы перебираете, и список , в котором вы учитываете, будут разными. Как будто вы использовали:
list1 = [1, 2, 2, 4, 5]
list2 = [5, 6, 1, 2, 9]
f = (x для x в list1, если list2.count (x) == 2)
Таким образом, вы проверяете для каждого элемента в list1 , если его счетчик в list2 равен двум.
В этом легко убедиться, изменив второй список:
>>> lst = [1, 2, 2]
>>> f = (x вместо x в lst, если lst.count (x) == 2)
>>> lst = [1, 1, 2]
>>> список (е)
[1]
Если бы он прошел по первому списку и посчитал в первом, то вернул бы [2, 2] (потому что первый список содержит два 2 ). Если он повторяется и учитывается во втором списке, на выходе должно быть [1, 1] . Но поскольку он выполняет итерацию по первому списку (содержащий один 1 ), но проверяет второй список (который содержит два 1 с), на выходе получается всего один 1 .
Решение с использованием функции генератора
Есть несколько возможных решений. Обычно я предпочитаю не использовать «выражения генератора», если они не повторяются немедленно. Для правильной работы достаточно простой функции генератора:
def keep_only_duplicated_items (lst):
для элемента в lst:
если lst.count (item) == 2:
доходный пункт
А потом используйте это так:
lst = [1, 2, 2, 4, 5]
f = keep_only_duplicated_items (lst)
lst = [5, 6, 1, 2, 9]
>>> список (е)
[2, 2]
Обратите внимание, что в PEP (см. Ссылку выше) также указано, что для чего-либо более сложного предпочтительнее полное определение генератора.
Лучшее решение с использованием функции генератора со счетчиком
Лучшим решением (избегая квадратичного поведения во время выполнения, потому что вы перебираете весь массив для каждого элемента в массиве) было бы подсчитать ( collection.Counter ) элементы один раз, а затем выполнить поиск за постоянное время (что приведет к линейному время):
из коллекций Счетчик импорта
def keep_only_duplicated_items (lst):
cnts = Счетчик (lst)
для элемента в lst:
если cnts [item] == 2:
доходный пункт
Приложение: Использование подкласса для «визуализации» того, что происходит и когда это происходит
Довольно легко создать подкласс list , который будет печатать при вызове определенных методов, так что можно убедиться, что он действительно так работает.
В этом случае я просто переопределяю методы __iter__ и count , потому что меня интересует, в каком списке выполняется итерация выражения генератора и в каком списке оно учитывается. Тела методов фактически просто делегируют суперклассу и что-то печатают (поскольку он использует super без аргументов и f-строк, для него требуется Python 3.6, но его должно быть легко адаптировать для других версий Python):
класс MyList (список):
def __iter __ (сам):
print (f '__ iter __ () вызвал {self! r}')
вернуть super ().__iter __ ()
def count (self, item):
cnt = super (). count (элемент)
print (f'count ({item! r}) вызвал {self! r}, результат: {cnt} ')
вернуть cnt
Это простой подкласс, который просто печатает, когда вызываются методы __iter__ и count :
>>> lst = MyList ([1, 2, 2, 4, 5])
>>> f = (x вместо x в lst, если lst.count (x) == 2)
__iter __ () вызвал [1, 2, 2, 4, 5]
>>> lst = MyList ([5, 6, 1, 2, 9])
>>> print (list (f))
count (1) вызвал [5, 6, 1, 2, 9], результат: 1
count (2) вызвал [5, 6, 1, 2, 9], результат: 1
count (2) вызвал [5, 6, 1, 2, 9], результат: 1
count (4) вызвал [5, 6, 1, 2, 9], результат: 0
count (5) вызвал [5, 6, 1, 2, 9], результат: 1
[]
границ | Условное картирование выявило локусы количественных признаков для концентрации белка в зерне, независимо от урожайности зерна канадской твердой пшеницы
Введение
Твердая пшеница [ Triticum turgidum L.subsp. durum (Desf.) Husn.], Является экономически важной культурой из-за ее уникальных характеристик, которые способствуют производству манной крупы для производства макаронных изделий и других традиционных продуктов питания, таких как лепешки, кус-кус и булгур (Giraldo et al., 2016) . Концентрация белка в зерне (GPC) является важным признаком развития сорта твердой пшеницы. Это главный фактор, определяющий пищевую ценность зерна, реологические свойства теста для изготовления макаронных изделий, качество конечного продукта и, следовательно, экономическую ценность урожая.GPC — это сложный количественный признак, контролируемый множеством геномных локусов, которые взаимодействуют друг с другом (Nigro et al., 2019). Отбор твердых сортов пшеницы с высоким содержанием ГПХ также затруднен влиянием окружающей среды в той или иной степени. Следовательно, для скрининга GPC в программах разведения требуется несколько комбинаций генотипа и окружающей среды. Одновременный выбор GPC и урожайности зерна (GY) затруднен из-за отрицательной корреляции, часто наблюдаемой между этими двумя признаками в большинстве генетических фонов и условий выращивания (Blanco et al., 2002, 2006; Groos et al., 2003; Богард и др., 2011). Однако изменение отрицательной корреляции было продемонстрировано путем одновременного выбора как для GPC, так и для GY (DePauw et al., 2007).
Понимание генетической основы GPC у сортов в их целевой среде является ключом к внедрению селекции с помощью маркеров (MAS) в программах селекции твердых сортов для поддержания или улучшения качества зерна. Исследования, проведенные для анализа генетической основы GPC у твердой пшеницы, выявили локусы количественных признаков (QTL) почти на всех хромосомах, как обобщено Kumar et al.(2018). Среди сообщенных QTL некоторые показали серьезные эффекты, в то время как многие вызвали незначительные эффекты. Кроме того, большинство идентифицированных QTL были экологически зависимыми и нестабильными в различных средах. Хорошо известным QTL для GPC является Gpc-B1 на хромосоме 6BS. Аллель высокого GPC этого QTL был идентифицирован из дикого тетраплоидного ( Triticum turgidum L. ssp. dicoccoides ) образца FA-15-3, происходящего из Израиля (Avivi, 1978). Gpc-B1 был картирован на хромосоме 6BS, что составляет 66% дисперсии GPC (Joppa et al., 1997; Olmos et al., 2003). Предковый дикий аллель GPC-B1 кодирует фактор транскрипции NAC (NAM-B1) и связан с повышенной концентрацией белка зерна, Zn и Fe, а также ускоряет старение флаговых листьев у пшеницы (Uauy et al., 2006) . Современные сорта пшеницы несут нефункциональный аллель NAM-B1, а функциональный аллель Gpc-B1 интрогрессирован в элитные сорта твердой и мягкой пшеницы (Chee et al., 2001; Tabbita et al., 2017; Bokore et al. ., 2019). Однако аллель GPC-B1 дикого типа имеет большее отрицательное влияние на компоненты урожая твердой пшеницы, помимо нежелательного эффекта увеличения концентрации золы манной крупы (Tabbita et al., 2017).
Анализ картированияQTL GPC часто проводился без учета компонентов GY и урожайности. Однако некоторые недавние исследования, в которых одновременно учитывались компоненты GY и урожайности, привели к идентификации локусов GPC без отрицательного воздействия на признаки, связанные с урожайностью (Blanco et al., 2002, 2012; Супрайоги и др., 2009; Рапп и др., 2018; Нигро и др., 2019). Например, несколько исследований идентифицировали GPC QTL без отрицательного воздействия на GY путем картирования отклонения белка зерна (GPD), полученного из регрессии GPC, и урожайности в разнообразной панели твердых сортов (Rapp et al., 2018; Nigro et al., 2019) . Такие локусы полезны для одновременного генетического улучшения GPC и GY. Статистическая процедура, предложенная Чжу (1995), использовалась для анализа условных генетических эффектов для отдельных признаков развития, в которой применяется тот же статистический принцип, что и подход GPD (Rapp et al., 2018; Nigro et al., 2019) для анализа коррелированных признаков, включая белок зерна и урожайность. Этот условный анализ используется для оценки значений признаков, основанных на отсутствии изменений в генетически коррелированных признаках, метод, который очень похож на оценку скорректированных значений в ковариационном анализе, исключающий влияние коррелированных признаков на генетические эффекты QTL для целевых черты (Zhao et al., 2006). Эта модель получила дальнейшее развитие для анализа вклада каждого компонента в сложный признак, а также для анализа генетической взаимосвязи между близкородственными признаками.Условное картирование QTL успешно использовалось для оценки эффектов QTL на целевые признаки в зависимости от их составляющих признаков, таких как урожайность зерна риса (Guo et al., 2005) и длина разрастания колоса на высоту растения у пшеницы (Li C. et al. , 2020). Генетическая взаимосвязь между родственными признаками на уровне QTL была исследована на предмет содержания масла в семенах рапса по отношению к содержанию белка (Zhao et al., 2006), увеличения объема разрастания кукурузы в зависимости от веса зерна на растение и веса 100 зерен (Li et al., 2008), GPC зависит от содержания крахмала в зерне пшеницы (Deng et al., 2015), а также содержания белка и масла в сое (Li X. et al., 2020). Кроме того, условное картирование QTL использовалось для выяснения влияния окружающей среды на экспрессию QTL на основе значений признаков, обусловленных различными средами (Xu et al., 2014; Fan et al., 2019). Был проведен условный анализ для изучения влияния удобрений азотом (N) и фосфором (P) на экспрессию QTL для урожайности и связанных с азотом признаков (Xu et al., 2014) и индуцированный низким N-стрессом QTL у пшеницы (Fan et al., 2019). Кроме того, условное отображение QTL может идентифицировать дополнительные QTL, которые не обнаруживаются при традиционном отображении.
Используя условное картирование, мы ожидали идентифицировать QTL для GPC, которые независимо экспрессируются от GY, что может облегчить одновременный отбор высокой концентрации белка и высокого GY при разведении твердых пород. Таким образом, цели этого исследования заключались в следующем: (1) определить QTL, лежащий в основе GPC в канадской твердой пшенице, в частности тех, которые являются стабильными QTL в различных средах, (2) определить QTL для GPC без отрицательных коррелированных эффектов на GY с помощью условного анализа QTL. .
Материалы и методы
Население, полевые испытания и определение признаков
В этом исследовании использовалась популяция твердых сортов из 162 линий двойных гаплоидов (DH), полученных от Pelissier × Strongfield. Strongfield — это зарегистрированный в Канаде сорт янтарной твердой древесины с высоким содержанием глютена, высоким содержанием GPC и низким содержанием кадмия, разработанный в Центре исследований и разработок Swift Current, Swift Current, SK (Clarke et al., 2005). Пелисье, отобранный из алжирского староместного сорта, завезенного из Соединенных Штатов Америки, является родителем-основателем генофонда канадской твердой пшеницы (Clarke et al., 2010). В нем высокое содержание кадмия и липоксигеназы. Линии DH вместе с двумя родительскими и контрольными линиями были испытаны в полевых испытаниях на южной ферме SCRDC (широта: 50 ° 17 ′ северной широты; долгота: 107 ° 41 ′ западной долготы; высота 825 м) на суглинке Суинтон (Orthic Brown Чернозем) на четырехрядных делянках (2,74 м 2 / делянка) в виде рандомизированной полной блочной схемы с двумя повторностями. Каждое испытание выращивалось при двух датах посева с интервалом в 1 неделю (ранний, E; поздний, L) каждый год с 2014 по 2016 год, и только ранняя дата посева в 2017 и 2018 годах.Каждая проба на дату посева выращивалась на разных участках. Заготовки собирали в индивидуальные мешки с помощью комбайна. GY каждого участка измеряли на весах и выражали в кг га -1 . GPC манной крупы измеряли с помощью спектроскопии в ближнем инфракрасном диапазоне (NIR) (Foss NIR 6500) и выражали в процентах при влажности 13,5%. Для анализа фенотипических данных и картирования QTL каждая дата посева в каждый год рассматривалась как одна среда, обеспечивающая в общей сложности восемь сред, обозначенных как E14, L14, E15, L15, E16, L16, E17 и E18.Ежегодно проводились предпосадочные испытания почвы для определения нормы внесения удобрений. Удобрения внесены на целевые 112 кг га -1 по азоту, 70 кг га -1 по фосфору и 22,4 кг га -1 по сере. Почва богата калием и не требует дополнительного внесения.
Статистический анализ
Статистическая сводка и тест нормальности Шапиро-Уилка были проведены в R (R3.3.2, https://www.r-project.org/).Парные фенотипические корреляции между средами и между признаками были рассчитаны с использованием коэффициента корреляции Пирсона в R-пакете Hmisc (версия 4.2-0, http://cran.r-project.org/web/packages/Hmisc/index.html).
Дисперсионный анализ (ANOVA) и оценка наследуемости были выполнены с использованием процедуры PROC MIXED SAS 9.3 (Институт SAS, Кэри, Северная Каролина, США), как описано Ruan et al. (2020). В смешанной модели линии DH (генотипы, G) рассматривались как фиксированные эффекты, в то время как взаимодействия среды (E), генотип × среда (G × E) и репликации, вложенные в среду, рассматривались как случайные эффекты.Наследственность GPC рассчитывалась как отношение генетической дисперсии и фенотипической дисперсии в разных средах с использованием σg2 / (σg2 + σge2 / y + σε2 / год), где σg2, σge2 и σε2 были оценками генотипа (G), генотипа. × взаимодействие среды (G × E) и остаточная дисперсия (ошибка), соответственно, а y и r представляют собой числа среды и репликации. Наследственность GPC в каждой среде рассчитывалась с использованием σg2 / (σg2 + σε2 / r), где σg2 и σε2 были оценками генотипа и остаточной дисперсии, соответственно, а r представляло количество репликаций.Для оценки наследуемости все эффекты считались случайными.
Генетическая карта и сопоставление QTL
КартированиеQTL было выполнено с использованием генетической карты Pelissier × Strongfield, представленной Ruan et al. (2020). Для генотипирования использовали чип Infinium iSelect Wheat 90K SNP. В общей сложности 1212 полиморфных маркеров SNP с отсутствием данных <30% были использованы для построения генетической карты, что привело к идентификации 25 групп сцепления (LG). LG были отнесены к хромосомам на основании сравнения с существующей согласованной картой твердой пшеницы на основе SNP с высокой плотностью (Maccaferri et al., 2019). Средние значения GPC из двух повторов в каждой среде использовали для обнаружения QTL. Выбросы значений признаков были обнаружены и удалены с помощью преобразования Z-оценки с порогом 3. Обнаружение QTL было выполнено с использованием составного интервального картирования (CIM) в программе WinQTL Cartographer v.2.5 (Wang S. et al., 2012) (http : //statgen.ncsu.edu/qtlcart/WQTLCart.htm). Те же параметры, что описаны Ruan et al. (2020) были использованы для CIM. QTL, обнаруженный в разных средах, считался одинаковым, если доверительные интервалы (ДИ) перекрывались и аддитивный эффект вносил один и тот же родитель.QTL, картированный по крайней мере в одной среде, объясняющий более 20% фенотипической дисперсии, или отображенный по крайней мере в двух средах с PVE ≥ 10%, считался основным QTL (Raihan et al., 2016; Zhao et al., 2016). QTL, обнаруженный в двух или более средах, считается стабильным QTL. Графическое представление групп сцепления и QTL на генетической карте было выполнено с использованием программного обеспечения MapChart 2.2 (Voorrips, 2002). Гаплотипы были присвоены с помощью пакета R Haplotyper.
Условные значения GPC [GPC | GY, GPC, обусловленные урожайностью зерна (GY)] для каждой среды были рассчитаны с использованием QGA Station 2.0 (Чжу, 1995) (http://ibi.zju.edu.cn/software/qga/v2.0/index.htm). Условные фенотипические значения (GPC | GY) представляют собой чистые значения признаков GPC независимо от вариации GY. Отображение QTL для условных значений GPC было выполнено с использованием того же метода, что и выше для традиционного отображения QTL. Идентифицированный QTL был определен как условный QTL. Когда QTL, идентифицированный двумя методами (традиционным и условным), имел перекрывающиеся КЭ, они считались идентичными. Все указанные QTL были обозначены в соответствии с Рекомендованными правилами для символизации генов в пшенице (http: // пшеница.pw.usda.gov/ggpages/wgc/98).
Лучший линейный несмещенный прогноз (BLUP) — популярный метод, используемый для анализа испытаний в нескольких средах (Xiao et al., 2016; Choudhury et al., 2019). Чтобы исключить влияние эффектов окружающей среды на фенотипические вариации, значение BLUP GPC для каждой линии во всех средах было оценено с использованием линейной модели в пакете R lme4 (Bates et al., 2015). Значения BLUP линий DH использовали в качестве данных признаков для картирования QTL во всех средах, как описано Xiao et al.(2016).
Сравнение с ранее сообщенным QTL
Последовательности из 90К SNP были загружены из базы данных маркеров SNP Канзасского университета (http://wheatgenomics.plantpath.ksu.edu/snp/). Последовательности маркеров SSR были получены из базы данных GrainGenes (https://wheat.pw.usda.gov/GG3/). Последовательности маркеров DArT были загружены с веб-сайта DArT P / L (https://www.diversityarrays.com/technology-and-resources/sequences). Положения на физической карте маркеров SNP, SSR и DArT в геноме твердой пшеницы сорта.Svevo (Maccaferri et al., 2019) были согласованы с использованием BLASTn на портале Svevo (https://d-data.interomics.eu). QTL, описанные в литературе и идентифицированные в этом исследовании, были спроецированы на геном durum cv. Svevo путем проецирования единственного маркера, ближайшего к положению пика QTL. Маркеры QTL на физической карте Свево были нарисованы с использованием программного обеспечения PhenoGram (http://visualization.ritchielab.org/phenograms/plot).
Результаты
Изменения GPC в популяции ЦТ в различных средах
На Рисунке 1 показано частотное распределение GPC в популяции DH, полученное с помощью Pelissier × Strongfield, в восьми средах с 2014 по 2018 год.Сводная статистика, включая средние значения и стандартное отклонение (SD) среднего, минимального и максимального значений, диапазон и вероятность, связанные с тестом Стьюдента t для родительских средних значений в каждой среде, показаны в таблице 1. Распределение GPC был нормальным во всех средах, кроме среды E16, на что указывает значение p теста нормальности Шапиро-Уилка. Родительская линия Strongfield имела значительно более высокий GPC, чем Pelissier, во всех средах, кроме E16 (Таблица 1).Отдельные линии DH имели экстремальные значения GPC во всех средах и отображали двунаправленную трансгрессивную сегрегацию для GPC, как показано максимальными и минимальными значениями относительно родителей. Среднее значение GPC популяции DH было ближе к родительскому Strongfield, чем к родительскому Pelissier в большинстве сред. GPC популяции имел самое высокое среднее значение в среде E18 (среднее значение = 14,5%) и самое низкое среднее значение в E14 (среднее значение = 12,1%). Наибольший диапазон GPC наблюдался в среде E16, а наименьший — в E17.Умеренные коэффициенты корреляции Пирсона (0,3–0,67) наблюдались среди линий DH в разных средах (дополнительный рисунок 1). Значительные отрицательные корреляции от -0,16 до -0,84 наблюдались между GPC и GY во многих средах, за исключением E17 и E18 (рис. 2). В целом, чем выше урожай зерна, тем сильнее отрицательная корреляция между GPC и GY.
Рисунок 1 . Частотное распределение концентрации белка в зерне (GPC) в популяции Пелисье × Стронгфилд с 2014 по 2018 г. Полевые испытания с двумя датами посева в каждый год (ранний, E; поздний, L) в течение 2014–2016 гг. И только ранний срок посева в 2017–2018 гг. .Синие сплошные линии представляют Пелисье; красные пунктирные линии обозначают Стронгфилд; серые пунктирные линии обозначают средние значения генеральной совокупности.
Таблица 1 . Среднее значение, стандартное отклонение, минимум и максимум, коэффициент вариации, вероятность, связанная с тестом нормальности Шапиро-Уилка концентрации белка зерна (GPC) в разных средах для популяции Пелисье × Стронгфилд, наследуемость в каждой среде, среднее значение GPC для родителей и p- значение теста Стьюдента t- на значимость между двумя родителями.
Рисунок 2 . Диаграмма рассеяния и коэффициент корреляции Пирсона между концентрацией белка в зерне (GPC) и урожайностью зерна (GY) популяции Пелисье × Стронгфилд в восьми средах. Символ * указывает на значимость p <0,05 и *** p <0,001.
Традиционное сопоставление QTL с использованием фенотипических данных из отдельных сред и значений BLUP в разных средах
Хотя высокая наследуемость в широком смысле 0,87 наблюдалась для GPC, взаимодействия генотип × среда были значительными, как показал ANOVA (таблица 2).Таким образом, QTL-анализ был сначала выполнен для GPC в каждой среде. В каждой среде было обнаружено от двух до трех QTL (Таблица 3 и Рисунок 3). Всего было обнаружено 11 QTL в восьми средах, семь из которых были специфичными для одной среды. Обе родительские линии внесли благоприятные аллели в разные QTL (три по Strongfield и восемь по Пелисье). Два QTL были обнаружены по крайней мере в четырех средах с небольшими сдвигами в положении пика. Самый стабильный QTL, QGpc.spa-3A.3 , расположенный на хромосоме 3A, был обнаружен в пяти средах с диапазоном баллов LOD 5,5–10,7 и объясняет 9,4–18,1% фенотипической дисперсии ( R 2 ) в каждой индивидуальной среде. Пелисье внес более высокий аллель GPC в QGpc.spa-3A.3 . Другой стабильный QTL, QGpc.spa-7A , был обнаружен на хромосоме 7A в четырех средах, что объясняет до 14,8% фенотипической дисперсии с более высоким аллелем GPC, полученным из Strongfield.Два QTL на хромосоме 2B, QGpc.spa-2B.1 и QGpc.spa-2B.2 , были обнаружены в двух из восьми сред. QGpc.spa-2B.1 объяснил 15–16% фенотипической дисперсии, а QGpc.spa-2B.2 объяснил 9–13% фенотипической дисперсии с более высоким аллелем GPC от Пелисье в обоих QTL. Кроме того, семь QTL на 1B ( QGpc.spa-1B.1 ), 2B ( QGpc.spa-2B.3 ), 3A ( QGpc.spa-3A.1, QGpc.spa-3A. 2 и QGpc.spa-3A.4 ), 5B ( QGpc.spa-5B ) и 7B ( QGpc.spa-7B ) были обнаружены в одной среде со значениями R 2 в диапазоне от 4,9 до 6,9%. Пелисье и Стронгфилд внесли аллели, увеличивающие признаки, в пять и два QTL, обнаруженных в одной среде.
Таблица 2 . Дисперсионный анализ (ANOVA) концентрации белка зерна (GPC) в разных средах.
Таблица 3 . Локусы количественных признаков (QTL), идентифицированные для концентрации белка зерна (GPC) в популяции Пелисье × Стронгфилд в каждой среде с использованием значений GPC и условного картирования, а также с использованием значений наилучшего линейного несмещенного предсказания (BLUP) для восьми сред, маркера на пике LOD , пиковое значение LOD, аддитивный эффект, R 2 , и интервал, в котором оценка LOD упала на 2 пункта от максимального значения LOD.
Рисунок 3 . Распределение локусов количественных признаков (QTL) для концентрации белка зерна (GPC), обнаруженных в каждой среде, с использованием значений наилучшего линейного несмещенного предсказания (BLUP) и условного картирования.
Когда было проведено картирование QTL с использованием значений BLUP во всех средах, всего пять QTL были обнаружены на хромосомах 1B, 2B, 3A, 5B и 7A. Фенотипическая дисперсия, объясняемая каждым QTL, составляла от 4,6 до 20,7% (таблица 3). Примечательно, что четыре ( QGpc.spa-2B.1, QGpc.spa-3A.3, QGpc.spa-5B и QGpc.spa-7A ) из пяти QTL также были обнаружены с помощью картирования QTL в отдельных средах. QTL на 1B, 2B, 3A и 7B, которые отображены только в одной среде с использованием значений GPC, не были обнаружены с использованием значений BLUP. Один дополнительный QTL, QGpc.spa-1B.2 , был картирован на хромосоме 1B с использованием значений BLUP с аллелем, увеличивающим признак, приписываемым Strongfield.
Условный анализ QTL
Девять QTL были обнаружены на семи хромосомах с использованием условного картирования QTL (Таблица 3).Эти QTL объясняют 5,7–13,3% фенотипической дисперсии со значениями LOD 3,2–6,9. Шесть из девяти QTL имели аллели увеличения признака от Strongfield, тогда как другие три QTL имели благоприятные аллели от Pelissier. Среди идентифицированных условных QTL четыре ( QGpc.spa-1B.2, QGpc.spa-3A.2, QGpc.spa-3A.3 и QGpc.spa-7A ) также были обнаружены с помощью традиционного картирования QTL. . Особенно важно, что QGpc.spa-7A был обнаружен в тех же четырех средах как условным, так и традиционным картированием QTL. QGpc.spa-3A.2 был обнаружен в двух средах (E17 и E18), тогда как он был обнаружен только в E17 с помощью традиционного картирования. Напротив, QGpc.spa-3A.3 был обнаружен в двух средах (E15 и L15), но в этих двух, а также трех дополнительных средах с помощью традиционного картирования. QTL, обнаруженный на хромосомах 2B, 5B и 7B традиционным анализом, не был идентифицирован условным картированием. Однако пять дополнительных QTL на хромосомах 1B ( QGpc.spa-1B.3 ), 2A ( QGpc.spa-2A ), 5A ( QGpc.spa-5A ), 6A ( QGpc.spa-6A ) и 6B ( QGpc.spa-6B ) были идентифицированы только с использованием условного сопоставления.
Анализ гаплотипов в нескольких QTL
Для исследования накопленных эффектов в нескольких QTL благоприятных аллелей на GPC, комбинированный анализ гаплотипов, проведенный для QTL, обнаруженного с использованием значений BLUP и идентифицированного в двух или более средах с использованием традиционного и условного картирования, был ограничен QGpc.spa-3A.3 и QGpc.spa-7A . SNP в интервале 2 LOD каждого QTL использовались для анализа гаплотипов. Четыре разных гаплотипа (от Hap1 до Hap4) были идентифицированы с разными частотами, причем каждый гаплотип представлен в 23–41 линиях DH (рис. 4A). Линии DH с Hap2 имели наилучшую комбинацию всех благоприятных аллелей в каждом QTL, о чем свидетельствует самый высокий GPC во всех средах, хотя не было значительных различий между Hap 2 и Hap3 в E14, L14, E16 и L16.Линии с Hap4 имели наименее благоприятное сочетание аллелей. Значительные различия наблюдались для GPC в линиях с этими двумя группами гаплотипов Hap2 и Hap4 во всех средах. Значительные различия между линиями с Hap1 и Hap4 для GPC также наблюдались во всех средах. За исключением E14 и E17, GPC значительно отличался между линиями, несущими Hap3 и Hap4 (Рисунок 4B). Мы провели предварительную оценку эффективности MAS с использованием маркера пика Ku_c70534_1215 ( IWB39901 ) в QTL QGpc.spa-3A.3 и маркер пика BobWhite_c6193_298 ( IWB4104 ) в QTL QGpc.spa-7A в общей сложности 131 элитная линия твердой древесины, которые были фенотипированы для GPC и генотипированы тем же чипом SNP, что и использованный для линий DH в данном исследовании. Основываясь на генотипах маркера пика в области QTL, элитные линии были разделены на две группы со значительно разными средними значениями GPC (тест t- , p <0,01) (рис. 4C). Отрицательная корреляция между GPC и GY в разных группах гаплотипов была обозначена линиями регрессии (дополнительный рисунок 2).Линия регрессии GPC на GY от Hap4 имела наибольший наклон, пересечение и R 2 , в то время как линия регрессии Hap3, несущая благоприятный аллель, полученный от Пелисье на QGpc.spa-3A.3 , показала наименьший наклон, пересечение и R 2 . Линия регрессии Hap 1, несущая благоприятный аллель, внесенный Strongfield на QGpc.spa-7A , имела уменьшенный наклон, пересечение и R 2 по сравнению с линией регрессии Hap4.
Рисунок 4 . Анализ гаплотипов двух локусов количественных признаков (QTL) в интервале 2 LOD, которые были обнаружены с использованием значений наилучшего линейного несмещенного предсказания (BLUP) и идентифицированы в двух или более средах с использованием традиционного и условного картирования. (A) Блок гаплотипа на основе маркеров SNP в каждой области QTL. (B) Коробчатые диаграммы фенотипических значений, соответствующих четырем различным группам гаплотипов в каждой среде. Гаплотипы, содержащие <3 линий DH, не были включены в таблицу.Линии DH с неопределенным гаплотипом не показаны. (C) Коробчатые диаграммы значений GPC в двух группах элитных линий твердых сортов ( n = 131), разделенных по генотипу маркера пика Ku_c70534_1215 в QTL QGpc.spa-3A.3 и маркера пика BobWhite_c6193_298 в QTL QGpc.spa-7A . ГПХ, концентрация зернового белка. * p <0,05; ** p <0,01; *** p <0,001 теста t- .
Проекция QTL на эталонный геном твердой пшеницы cv.Свево
Когда мы спроецировали QTL для GPC, идентифицированного в этом исследовании, и те, о которых сообщалось в литературе, на эталонный геном сорта твердой пшеницы. Свево, мы смогли сравнить близость каждого из них (дополнительная таблица 1 и рисунок 5). QTL QGpc.spa-1B.1 (M3, IWB12562 ) был спроектирован на коротком плече хромосомы 1B физической карты твердых сортов пшеницы, на расстоянии ~ 34,4 МБ от QTL (M2, wPt-0655 ). Автор: Giraldo et al. (2016) и 35,3 МБ из SSR-маркера barc18 (M4), связанного с GPC, о котором сообщили Suprayogi et al.(2009). QTL QGpc.spa-1B.2 (M8, IWB72499 ) на длинном плече хромосомы 1B находится на расстоянии 29,7 МБ от QTL (M7, D1112546 ), идентифицированного Rapp et al. (2018) и 30,9 МБ из QTL (M9, IWB60663 ), о котором сообщают Фатюха и др. (2020) в твердой пшенице.
Рисунок 5 . Проекция локусов количественных признаков (QTL) для концентрации белка зерна (GPC), представленных в литературе, и QTL, идентифицированного в двух или более средах с использованием традиционного и условного картирования и с использованием значений наилучшего линейного несмещенного прогноза (BLUP) в этом исследовании на эталоне. геном твердой пшеницы сорта.Свево.
В настоящем исследовании QGpc.spa-2B.1 был идентифицирован на коротком плече, а QGpc.spa-2B.2 — на длинном плече хромосомы 2B. Среди QTL, о которых сообщалось в предыдущих исследованиях, ближайшим к QTL QGpc.spa-2B.1 является тот (M18, IWB72906 ) с расстоянием 22 Мб, о котором сообщают Giancaspro et al. (2019). QGpc.spa-2B.2 (M20, IWB38099 ) — это 27,7 МБ из QTL (M19, gwm1249 ), о котором сообщил Peleg et al.(2009) и 22,6 МБ из QTL (M21, , IWA544 ), о которых сообщил Marcotuli et al. (2017). На коротком плече 3A Giancaspro et al. (2019) сообщили о QTL (M27, IWB72484 ), связанном с GPC, который составляет 187,6 МБ за исключением пикового маркера QGpc.spa-3A.1 (M26, IWB6837 ), обнаруженного в этом исследовании. QTL QGpc.spa-3A.3 (M32, IWB39901 ) на длинном плече хромосомы 3A, обнаруженный в этом исследовании, и QTL (M31, IWB28341 ), сообщенный Fatiukha et al.(2020) разделены физическим расстоянием 59,5 Мб. QGpc.spa-3A.4 (M33, IWB58656 ) находится на расстоянии ~ 7,8 МБ от SNP (M34, IWB35484 ), который, по сообщениям Nigro et al., Связан с GPC у твердой пшеницы. (2019). QGpc.spa-5B (M36, IWB10851 ) (M35, D1118885 ) на 5B находится в непосредственной близости примерно на 3,15 МБ от QTL, о чем сообщил Rapp et al. (2018). QGpc.spa-7A (M49, IWB4104 ) на хромосоме 7A находится на расстоянии 2.24 Мбайт в QTL (M48, D1382367 ), о котором сообщили Rapp et al. (2018) и 2,94 МБ в QTL (M50, IWB65659 ), о которых сообщил Nigro et al. (2019).
Обсуждение
Стабильный QTL
В настоящем исследовании наблюдалась высокая наследуемость в широком смысле для GPC, которая аналогична ранее опубликованному исследованию (Conti et al., 2011), что указывает на то, что GPC в основном контролируется генетическими факторами. Умеренные корреляции, наблюдаемые между различными средами, снова указывают на существенный генетический компонент изменчивости GPC.11 QTL, обнаруженный для GPC с использованием традиционного картирования, указывает на сложное количественное наследование многих QTL с малым и средним эффектом. Четыре QTL, QGpc.spa-2B.1, QGpc.spa-2B.2, QGpc.spa-3A.3 и QGpc.spa-7A , неоднократно обнаруживались в двух или более средах, несмотря на аддитивные эффекты из этих QTL различались по величине в разных средах. Сходным образом, взаимодействие QTL × среда было описано для GPC у твердой пшеницы (Conti et al., 2011). Дело в том, что два из этих QTL, QGpc.spa-3A.3 и QGpc.spa-7A , также были картированы с использованием значений BLUP, что позволяет предположить, что они стабильно экспрессируются во всех средах. Учитывая, что взаимодействие генотип × среда имеет большое влияние на GPC твердой пшеницы, QTL, который стабильно экспрессируется в разных средах, должен быть ценным для поддержания GPC в отборе для усиления зародышевой плазмы.
Сравнение с предыдущими исследованиями
Физическое расстояние QGpc.spa-1B.1 (M3, IWB12562 ) составляет ~ 34.4 мб от маркера пика QTL, wPt-0655 (M2), сообщенный Giraldo et al. (2016) и 35,3 МБ от маркера SSR, barc18 (M4), сообщается Suprayogi et al. (2009) предположили, что это разные локусы. Но из-за плохого разрешения картирования нельзя исключать возможность того, что один и тот же ген функционирует во всех исследованиях. Близость QTL QGpc.spa-1B.2 (M8, IWB72499 ) на расстоянии 29,7 Mb от QTL (M7, D1112546 ), идентифицированная Rapp et al.(2018) и 30,9 МБ из QTL (M9, IWB60663 ), о котором сообщают Фатюха и др. (2020) снова предложили бы разные контролирующие локусы. Физическое сопоставление предполагает, что QGpc.spa-1B.1 отличается от QGpc.spa-1B.2 . TRITD2Bv1G082940 , вероятно, кодирующий NAM-B2 — паралогическую копию NAM-B1, находится в интервале QGpc.spa-2B.1 (156,604,237–231,697,558 п.н.). TRITD2Bv1G082940 имеет четыре транскрипта сплайсинга и кодирует белок с помощью 95.3–99,2% идентичности с NAM-B2 из Triticum turgidum L. subsp. durum (Desf.) Husn. (GenBank ABI94355.1) (дополнительный рисунок 3).
Физическое расстояние 187,6 Мб между QGpc.spa-3A.1 (M26, IWB6837 ) и QTL, указанное Giancaspro et al. (2019) (M27, IWB72484 ) указывает, что эти два QTL отличаются. Поскольку QGpc.spa-3A.2 находится всего в 3,21 мб от маркера пика QTL, IWB14495 (M29), по данным Nigro et al.(2019), скорее всего, это один и тот же QTL. SNP, связанный с метаболизмом азота IWB71028 (M30) (Nigro et al., 2019) находится на расстоянии 5,33 Mb до QGpc.spa-3A.2 . Маркер пика QGpc.spa-3A.3 , IWB39901 (M32), был отделен физическим расстоянием 59,5 Мб от маркера пика IWB28341 (M31), о котором сообщают Fatiukha et al. (2020), поэтому QGpc.spa-3A.3 , вероятно, является новым QTL. Учитывая близость QGpc.spa-3A.4 , маркер пика IWB58656 (M33), обнаруженных в этом исследовании ~ 7.8 Mb из SNP IWB35484 (M34), по сообщениям Nigro et al., Он связан с GPC у твердой пшеницы. (2019), скорее всего, это один и тот же QTL.
QGpc.spa-5B (M36, IWB10851 ) на коротком плече хромосомы 5B, идентифицированный в нашем исследовании, вероятно, тот же QTL, что и тот, о котором сообщалось в предыдущем исследовании Rapp et al. (2018) из-за их близкого физического расстояния. Очень непосредственная близость (2,724 kb) QGpc.spa-7A (M49, IWB4104 ) к SNP (M50, IWB65659 ), связанному с GPC (Nigro et al., 2019) указывает, что эти два QTL одинаковы. Аналогично, QGpc.spa-7A может быть тем же QTL, что и QTL (M48, D1382367 ), идентифицированный Rapp et al. (2018), поскольку расстояние между маркерами пиков этих двух QTL составляет 3,0 Мб. Кроме того, на длинном плече хромосомы 7B QGpc.spa-7B (M67, IWB32614 ), вероятно, совпадает с QTL, описанным Zhang et al. (2008) и Conti et al. (2011) из-за близости 2,24 МБ и 2,94 МБ к этим двум сообщенным QTL.Некоторые гены, такие как аспарагиновые протеиназы, участвующие в метаболизме аминокислот и белков, находятся в непосредственной близости от QGpc.spa-2B.1 и QGpc.spa-3A.3 . Сообщалось, что аспарагиновые протеиназы участвуют в протеолитическом процессинге и созревании запасных белков (Simões and Faro, 2004).
Условный QTL
Отрицательная корреляция между GY, компонентами урожайности и GPC у твердой и мягкой пшеницы хорошо задокументирована (DePauw et al., 2007; Suprayogi et al., 2009; Blanco et al., 2012; Богард и др., 2013). Точно так же в настоящем исследовании умеренная отрицательная корреляция между этими двумя признаками наблюдалась в большинстве сред. Большинство предыдущих исследований было сосредоточено только на фенотипической корреляции этих признаков. Сравнивая традиционный и условный QTL, мы попытались выяснить генетические отношения в индивидуальном QTL между этими двумя коррелированными признаками, чтобы идентифицировать QTL для GPC независимо от GY.
Когда значения GPC, условные для GY, использовались для отображения QTL, восемь из одиннадцати первоначально отображали QTL для GPC на 1B ( QGpc.spa-1B.1 ), 2B ( QGpc.spa-2B.1, QGpc.spa-2B.2, QGpc.spa-2B.3 ), 3A ( QGpc.spa-3A.1, QGpc. spa-3A.4 ), 5B ( QGpc.spa-5B ) и 7B ( QGpc.spa-7B ) не обнаружены. Это указывает на то, что экспрессия этих QTL, вероятно, зависит от GY. Между GPC и GY может существовать генетическая или физиологическая ассоциация, такая как эффект разбавления белка углеводами. Об аналогичном наблюдении сообщили Blanco et al. (2012). Некоторые из их первоначально обнаруженных QTL для GPC не показали значительных эффектов, когда значения GPC были скорректированы с учетом компонентов урожая (масса тысячи зерен, урожай зерна на колос, количество ядер на колос), а затем были использованы для картирования.Предполагается, что такие QTL представляют гены, участвующие в биосинтезе углеводов и, таким образом, вносящие вклад в общую массу зерна, однако с косвенным влиянием на GPC (Blanco et al., 2012).
Результаты условного картирования в этом исследовании показали, что несколько QTL GPC не имеют плейотропного эффекта на GY, что указывает на то, что эти QTL независимы или частично независимы от GY и будут иметь незначительное или нулевое отрицательное влияние на GY при выборе для высокого GPC. Три QTL, QGpc.spa-3A.2 и QGpc.spa-3A.3 на хромосоме 3A и QGpc.spa-7A на 7A, были обнаружены при условном картировании, но со сниженными или слегка уменьшенными эффектами. Это говорит о том, что они функционируют, по крайней мере, до некоторой степени, независимо от GY. Частичная независимость экспрессии QGpc.spa-3A.3 и QGpc.spa-7A также отражалась меньшим наклоном линий регрессии GPC на GY, наблюдаемым для Hap1 и Hap3 по сравнению с Hap4. Стоит отметить, что QGpc.spa-7A был обнаружен в тех же средах как традиционным, так и условным отображением с небольшим уменьшением эффектов, что указывает на то, что этот QTL контролирует GPC более независимо от GY.И QGpc.spa-3A.2 , и QGpc.spa-3A.3 были обнаружены только в средах, где не наблюдалась значимая (E17 и E18) или слабая / умеренная (E15 и L15) корреляция между GPC и GY. . Относительно более низкий GY также наблюдался в этих средах, отражая частичную зависимость от GY для экспрессии этих GPC QTL. Эти QTL, обнаруженные при условном картировании, имеют большое значение для селекции твердых сортов пшеницы, поскольку их включение позволит улучшить GPC без значительного ущерба для GY.
Пять дополнительных QTL для GPC были обнаружены при условном отображении, в то время как они не были обнаружены при традиционном отображении. Экспрессия этих QTL могла быть замаскирована GY и была ниже порога обнаружения при традиционном картировании GPC; следовательно, их эффекты могут быть обнаружены только после устранения мешающего эффекта GY. О аналогичном наблюдении сообщалось в предыдущем исследовании, что два дополнительных QTL были обнаружены, когда значения GPC были скорректированы для получения компонентов урожая твердой пшеницы (Blanco et al., 2012). Точно так же у мягкой пшеницы были идентифицированы еще три QTL для GPC с использованием условных значений GPC для GY и его компонентов (Wang L. et al., 2012).
Выводы
Результаты этого исследования обеспечивают дальнейшее понимание генетического контроля GPC в канадской твердой пшенице и генетической взаимосвязи между GPC и GY. Сравнение описанного здесь QTL с ранее сообщенными результатами привело к идентификации одного нового основного QTL на 3A ( QGpc.spa-3A.3 ) и пяти новых второстепенных QTL на 1B, 2B и 3A.На условный и стабильный QTL ( QGpc.spa-3A.3 и QGpc.spa-7A ), идентифицированный для GPC, частично влиял или независимо экспрессировался GY. Эти QTL имеют большое значение, и их тесно связанные маркеры полезны для MAS при высоком GPC без сопутствующего компромисса с GY.
Заявление о доступности данныхВсе наборы данных, созданные для этого исследования, были включены в статью / дополнительные материалы, дальнейшие запросы можно направлять соответствующим авторам.
Взносы авторов
г.Р. и РК концептуализировали это исследование. YR, RK, AKS, RD и RC сформировали популяцию и внесли свой вклад в прирост этой популяции. YR, RD, RC, SB и JS реализовали полевые испытания и фенотипирование популяции. WZ, AS и PF предоставили платформу для генотипирования. BY и YR проанализировали данные, интерпретировали результаты и внесли свой вклад в управление данными и их визуализацию. RK, RD, BXF и JS внесли свой вклад в интерпретацию результата. BY и YR написали оригинал рукописи.BY, YR, RK, RD, AKS, BXF и PF внесли свой вклад в рецензирование и редактирование рукописи. YR был главным исследователем и руководил проектом. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Финансовая поддержка была получена от Национальной программы улучшения пшеницы и Канадского сельскохозяйственного партнерства при поддержке Министерства сельского хозяйства и агропродовольствия Канады, Западного фонда исследований зерна, Комиссии по пшенице Альберты, Комиссии по развитию пшеницы Саскачевана и Альянса сельскохозяйственных культур Манитобы.Работа также была поддержана канадской флагманской программой по улучшению пшеницы, которая была вкладом Национального исследовательского совета Канады в Канадский пшеничный альянс, и Фондом развития сельского хозяйства Саскачевана.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Управляющий редактор и рецензент FB заявил о прошлом соавторстве с несколькими авторами RK и AKS.
Благодарности
Мы с благодарностью отмечаем поддержку Министерства сельского хозяйства и агропродовольствия Канады (AAFC), Национального исследовательского совета Канады (NRC), Western Grain Research Foundation (WGRF), Комиссии по пшенице Альберты, Комиссии по развитию пшеницы Саскачевана, Альянса сельскохозяйственных культур Манитобы и Развития сельского хозяйства Саскачевана. Финансирование проведения этого исследования. Мы благодарим Кристин Сайдботтом и Джанет Конди из NRC за техническую помощь в выделении ДНК и генотипировании с использованием чипа Infinium iSelect Wheat 90K SNP.Искренне признательны за техническую поддержку группы по селекции пшеницы в Центре исследований и разработок Swift Current.
Дополнительные материалы
Дополнительные материалы к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fpls.2021.642955/full#supplementary-material
Список литературы
Авиви, Л. (1978). «Высокое содержание зернового протеина в дикой тетраплоидной пшенице Triticum dicoccoides Korn», в Proc. 5-й Int.Пшеница Генет. Symp (Нью-Дели), 372–380.
Бейтс Д., Мехлер М., Болкер Б. М. и Уокер С. С. (2015). Подгонка линейных моделей смешанных эффектов с использованием lme4. J. Stat. Софтв. 67, 1–48. DOI: 10.18637 / jss.v067.i01
CrossRef Полный текст | Google Scholar
Blanco, A., Mangini, G., Giancaspro, A., Giove, S., Colasuonno, P., Simeone, R., et al. (2012). Взаимосвязь между содержанием белка в зерне и компонентами урожайности зерна посредством количественного анализа локусов признаков в популяции рекомбинантных инбредных линий, полученных от двух элитных сортов твердой пшеницы. Мол. Порода. 30, 79–92. DOI: 10.1007 / s11032-011-9600-z
CrossRef Полный текст | Google Scholar
Бланко А., Паскуалоне А., Трокколи А., Ди Фонцо Н. и Симеоне Р. (2002). Определение QTL содержания белка в зерне по средам у тетраплоидной пшеницы. Plant Mol. Биол. 48, 615–623. DOI: 10.1023 / A: 1014864230933
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Богард, М., Аллард, В., Мартр, П., Хоймес, Э., Снейп, Дж. У., Орфорд, С. и др. (2013). Выявление геномных регионов пшеницы для повышения концентрации белка в зерне независимо от урожайности зерна с использованием нескольких взаимосвязанных популяций. Мол. Порода. 31, 587–599. DOI: 10.1007 / s11032-012-9817-5
CrossRef Полный текст | Google Scholar
Богард М., Журдан М., Аллард В., Мартр П., Перретант М. Р., Равель К. и др. (2011). Дата антезиса в основном объясняла корреляцию между старением листьев после цветения, урожайностью зерна и концентрацией белка в зерне в популяции озимой пшеницы, сегрегированной по QTL времени цветения. J. Exp. Бот. 62, 3621–3636. DOI: 10.1093 / jxb / err061
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бокор Ф. Э., Нокс Р. Э., ДеПау Р. М., Катберт Р. Д., Валерио И. П., Кларк Ф. Р. и др. (2019). Подтверждение эффектов локуса с высокой концентрацией белка в зерне Gpc-B1 из твердой красной яровой пшеницы Lillian (Triticum aestivum L.) с использованием маркеров, специфичных для локуса. Euphytica 215: 2. DOI: 10.1007 / s10681-018-2322-0
CrossRef Полный текст | Google Scholar
Чи, П.В., Элиас, Э. М., Андерсон, Дж. А., и Кианиан, С. Ф. (2001). Оценка QTL с высоким содержанием белка зерна Triticum turgidum L. var. dicoccoides на адаптированном фоне твердых сортов пшеницы. Crop Sci. 41, 295–301. DOI: 10.2135 / cropci2001.412295x
CrossRef Полный текст | Google Scholar
Чоудхури С., Ларкин П., Сюй Р., Хайден М., Форрест К., Мейнке Х. и др. (2019). Полногеномное ассоциативное исследование выявило новый QTL устойчивости пшеницы к вирусу желтой карликовости ячменя. BMC Genomics 20: 891. DOI: 10.1186 / s12864-019-6249-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кларк, Дж. М., Кларк, Ф. Р., и Позняк, К. Дж. (2010). 46 лет генетического улучшения канадских сортов твердой пшеницы. Банка. J. Plant Sci. 90, 791–801. DOI: 10.4141 / cjps10091
CrossRef Полный текст | Google Scholar
Кларк, Дж. М., Маккейг, Т. Н., ДеПау, Р. М., Нокс, Р. Э., Кларк, Ф. Р., Фернандес, М.R., et al. (2005). Твердая пшеница Strongfield. Банка. J. Plant Sci. 85, 651–654. DOI: 10.4141 / P04-119
CrossRef Полный текст | Google Scholar
Конти В., Ронкалло П. Ф., Бофорт В., Червиньи Г. Л., Миранда Р., Йенсен К. А. и др. (2011). Картирование QTL основного и эпистатического эффекта, связанных с зерновым белком и прочностью глютена, с использованием популяции RIL твердой пшеницы. J. Appl. Genet. 52, 287–298. DOI: 10.1007 / s13353-011-0045-1
CrossRef Полный текст | Google Scholar
Дэн, З., Hu, S., Chen, F., Li, W., Chen, J., Sun, C., et al. (2015). Генетическое вскрытие взаимодействия между белком пшеницы и крахмалом с использованием трех картированных популяций. Мол. Порода. 35:12. DOI: 10.1007 / s11032-015-0216-6
CrossRef Полный текст | Google Scholar
Депау, Р. М., Нокс, Р. Э., Кларк, Ф. Р., Ван, Х., Фернандес, М. Р., Кларк, Дж. М. и др. (2007). Сдвиг нежелательных корреляций. Euphytica 157, 409–415. DOI: 10.1007 / s10681-007-9379-5
CrossRef Полный текст | Google Scholar
Вентилятор, X., Цуй, Ф., Цзи, Дж., Чжан, В., Чжао, X., Лю, Дж. Дж. И др. (2019). Рассечение плейотропных областей QTL, контролирующих характеристики колосьев пшеницы при различных обработках азотом, с использованием традиционного и условного картирования QTL. Фронт. Plant Sci. 10, 1–13. DOI: 10.3389 / fpls.2019.00187
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фатюха А., Филлер Н., Лупо И., Лидзбарский Г., Климиюк В., Король А. Б. и др. (2020). Содержание белка в зерне и QTL с массой тысяч зерен, идентифицированные в картированной популяции твердой × дикой пшеницы emmer, испытанной в пяти средах. Теор. Прил. Genet. 133, 119–131. DOI: 10.1007 / s00122-019-03444-8
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джанкаспро А., Джове С. Л., Зачео С. А., Бланко А. и Гадалета А. (2019). Генетическая изменчивость содержания белка и связанных с урожайностью признаков в популяции твердых сортов пшеницы, полученных от межвидового скрещивания гексаплоидных и тетраплоидных сортов пшеницы. Фронт. Plant Sci. 10: 1509. DOI: 10.3389 / fpls.2019.01509
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хиральдо, П., Ройо, К., Гонсалес, М., Каррильо, Дж. М., и Руис, М. (2016). Генетическое разнообразие и сопоставление агроморфологических признаков и признаков качества зерна структурированной коллекции староместных сортов твердой пшеницы, включая subsp. durum, turgidum и diccocon. PLoS ONE 11: e0166577. DOI: 10.1371 / journal.pone.0166577
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Groos, C., Robert, N., Bervas, E., and Charmet, G. (2003). Генетический анализ содержания белка в зерне, урожайности зерна и массы тысячи зерен мягкой пшеницы. Теор. Прил. Genet. 106, 1032–1040. DOI: 10.1007 / s00122-002-1111-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Го, Л. Б., Син, Ю. З., Мэй, Х. У., Сюй, К. Г., Ши, К. Х., Ву, П. и др. (2005). Рассечение экспрессии компонента QTL при формировании урожая риса. Растительная порода. 124, 127–132. DOI: 10.1111 / j.1439-0523.2005.01093.x
CrossRef Полный текст | Google Scholar
Joppa, L.R., Du, C., Hart, G.E., and Hareland, G.А. (1997). Картирование гена (ов) белка зерна в тетраплоидной пшенице (Triticum turgidum L.) с использованием популяции рекомбинантных инбредных хромосомных линий. Crop Sci. 37, 1586–1589. DOI: 10.2135 / cropci1997.0011183X003700050030x
CrossRef Полный текст | Google Scholar
Кумар А., Джайн С., Элиас Э. М., Ибрагим М. и Шарма Л. К. (2018). «Обзор идентификации QTL и селекции с помощью маркеров для определения содержания белка в пшенице BT — экологически чистые агробиологические методы повышения урожайности сельскохозяйственных культур», под ред.Р. С. Сенгар и А. Сингх (Сингапур: Springer Singapore), 245–274. DOI: 10.1007 / 978-981-10-6934-5_11
CrossRef Полный текст | Google Scholar
Ли, К., Тан, Х., Ло, В., Чжан, X., Му, Ю., Дэн, М., и др. (2020). Новый, подтвержденный и не зависящий от высоты растения QTL для длины удлинения колоса связан с признаками, связанными с урожайностью у пшеницы. Теор. Прил. Genet. 133, 3381–3393. DOI: 10.1007 / s00122-020-03675-0
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ли, Х., Xue, H., Zhang, K., Li, W., Fang, Y., Qi, Z., et al. (2020). Картирование QTL для содержания белка и масла в сое путем устранения влияния родственных признаков в популяции четырехкомпонентной рекомбинантной инбредной линии. J. Agric. Sci. 158: 254. DOI: 10.1017 / S0021859620000519
CrossRef Полный текст | Google Scholar
Ли Ю. Л., Донг Ю. Б., Цуй Д. К., Ван Ю. З., Лю Ю. Ю., Вэй М. Г. и др. (2008). Генетическая взаимосвязь между объемом всплывающего расширения и двумя компонентами урожайности в попкорне с использованием безусловного и условного анализа QTL. Euphytica 162, 345–351. DOI: 10.1007 / s10681-007-9513-4
CrossRef Полный текст | Google Scholar
Маккаферри М., Харрис Н. С., Твардиок С. О., Пасам Р. К., Гундлах Х., Спаннагл М. и др. (2019). Геном твердой пшеницы подчеркивает прошлые признаки одомашнивания и будущие цели по улучшению. Нат. Genet. 51, 885–895. DOI: 10.1038 / s41588-019-0381-3
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Маркотули, И., Гадалета, А., Мангини, Г., Синьориль, А. М., Зачео, С. А., Бланко, А. и др. (2017). Разработка карты сцепления на основе SNP с высокой плотностью и определение QTL для β-глюканов, содержания белка, урожайности зерна с колоса и времени колошения у твердой пшеницы. Внутр. J. Mol. Sci. 18: 1329. DOI: 10.3390 / ijms18061329
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нигро Д., Гадалета А., Мангини Г., Коласуонно П., Маркотули И., Джанкаспро А. и др. (2019). Гены-кандидаты и полногеномное ассоциативное исследование содержания белка в зерне и отклонений белка в твердой пшенице. Planta 249, 1157–1175. DOI: 10.1007 / s00425-018-03075-1
CrossRef Полный текст | Google Scholar
Olmos, S., Distelfeld, A., Chicaiza, O., Schlatter, A.R., Fahima, T., Echenique, V., et al. (2003). Точное картирование локуса, влияющего на содержание белка в зерне твердой пшеницы. Теор. Прил. Genet. 107, 1243–1251. DOI: 10.1007 / s00122-003-1377-y
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Пелег З., Чакмак И., Ozturk, L., Yazici, A., Jun, Y., Budak, H., et al. (2009). Локусы количественных признаков, определяющие концентрацию минеральных питательных веществ в зерне в популяции RIL твердой пшеницы × дикой пшеницы emmer Теор. Прил. Genet. 119, 353–369. DOI: 10.1007 / s00122-009-1044-z
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Райхан, М.С., Лю, Дж., Хуан, Дж., Го, Х., Пан, К., и Янь, Дж. (2016). QTL-анализ морфологии зерна в нескольких средах и точное картирование QTL ширины ядра в популяции кукурузы Zheng58 × SK. Теор. Прил. Genet. 129, 1465–1477. DOI: 10.1007 / s00122-016-2717-z
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Рапп, М., Лейн, В., Лакудр, Ф., Лафферти, Дж., Мюллер, Э., Вида, Г. и др. (2018). Одновременное повышение урожайности зерна и содержания протеина у твердых сортов пшеницы по разным фенотипическим показателям и геномной селекции. Теор. Прил. Genet. 131, 1315–1329. DOI: 10.1007 / s00122-018-3080-z
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Руань, Ю., Ю, Б., Нокс, Р. Э., Синг, А. К., ДеПау, Р., Катберт, Р. и др. (2020). Картирование с высокой плотностью локусов количественных признаков, определяющих силу глютена в канадской твердой пшенице. Фронт. Plant Sci. 11: 170. DOI: 10.3389 / fpls.2020.00170
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Супрайоги Ю., Позняк, К. Дж., Кларк, Ф. Р., Кларк, Дж. М., Нокс, Р. Е., и Сингх, А. К. (2009). Идентификация и проверка локусов количественных признаков для концентрации белка зерна в адаптированных популяциях твердой пшеницы Канады. Теор. Прил. Genet. 119, 437–448. DOI: 10.1007 / s00122-009-1050-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Таббита, Ф., Пирс, С., и Барнекс, А. Дж. (2017). Селекция на повышенное содержание зернового протеина и микронутриентов в пшенице: десять лет гена GPC-B1. J. Cereal Sci. 73, 183–191. DOI: 10.1016 / j.jcs.2017.01.003
CrossRef Полный текст | Google Scholar
Uauy, C., Distelfeld, A., Fahima, T., Blechl, A.и Дубцовский Дж. (2006). Ген NAC, регулирующий старение, улучшает содержание белка в зерне, цинка и железа в пшенице. Наука 314, 1298–1301. DOI: 10.1126 / science.1133649
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Wang, L., Cui, F., Wang, J., Jun, L., Ding, A., Zhao, C., et al. (2012). Условное QTL-картирование содержания белка в пшенице в зависимости от урожайности зерна и его компонентов. J. Genet. 91, 303–312. DOI: 10.1007 / s12041-012-0190-2
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сяо, Ю., Тонг, Х., Ян, X., Сюй, С., Пан, К., Цяо, Ф., и др. (2016). Полногеномное вскрытие генетической архитектуры початка кукурузы с использованием нескольких популяций. New Phytol. 210, 1095–1106. DOI: 10.1111 / nph.13814
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Xu, Y., Wang, R., Tong, Y., Zhao, H., Xie, Q., Liu, D., et al. (2014). Картирование QTL для урожайности и связанных с азотом признаков у пшеницы: влияние азотных и фосфорных удобрений на экспрессию QTL. Теор. Прил. Genet. 127, 59–72. DOI: 10.1007 / s00122-013-2201-y
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Zhang, W., Chao, S., Manthey, F., Chicaiza, O., Brevis, J.C., Echenique, V., et al. (2008). QTL-анализ качества макаронных изделий с использованием композитной микросателлитной и SNP-карты твердой пшеницы. Теор. Прил. Genet. 117, 1361–1377. DOI: 10.1007 / s00122-008-0869-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чжао, Дж., Беккер, Х. К., Чжан, Д., Чжан, Ю., и Экке, В. (2006). Условное QTL-картирование содержания масла в семенах рапса в отношении содержания белка и признаков, связанных с развитием растений и урожайностью зерна. Теор. Прил. Genet. 113, 33–38. DOI: 10.1007 / s00122-006-0267-5
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Zhao, W., Wang, X., Wang, H., Tian, J., Li, B., Chen, L., et al. (2016). Полногеномная идентификация QTL для урожайности семян и признаков, связанных с урожайностью, и построение согласованной карты с высокой плотностью для сравнения QTL в Brassica napus. Фронт. Plant Sci. 7, 1–14. DOI: 10.3389 / fpls.2016.00017
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Условная приватизация публичного сидерофора позволяет Pseudomonas aeruginosa противостоять вторжению мошенников
Бактериальные штаммы и условия роста
Бактериальные штаммы и плазмиды, использованные в этом исследовании, перечислены в дополнительной таблице 1. Штаммы выращивали на чашках с агаром LB при 37 ° C для 12 ч. Моноклональные колонии инокулировали и культивировали с минимальной средой (SSM) при 37 ° C в аэробных условиях, в которых среда имела следующий состав на литр: K 2 HPO 4 · 3H 2 O, 7.86 г; KH 2 PO 4 , 3,00 г; (NH 4 ) 2 SO 4 , 1,00 г; MgSO 4 · 7H 2 O, 0,20 г; к среде добавляли янтарную кислоту, 4,00 г NaOH для доведения pH до 7,0 перед стерилизацией. {- 1} \)) или гентамицина (2.{- 1} \)) были добавлены в среду для регулирования антимикробного стресса. Мы обнаружили, что бактерии P. aeruginosa дикого типа медленно растут в среде CAA +20 мМ апотрансферрина в течение первых 12 часов, что отражает ограничение по железу. Однако рост стал быстрым после 20 часов культивирования, и бактериальная культура в конечном итоге достигла высокой плотности (OD = 1,0, 44 часа), что позволяет предположить, что содержание железа больше не ограничено. Предположительно это связано с тем, что P. aeruginosa может постепенно секретировать протеазы, которые могут расщеплять апотрансферрин 46 , высвобождая, таким образом, эти хелатирующие утюги на более поздней стадии.Наиболее важно то, что мы обнаружили, что PVDI не может защитить клетки от стресса ROS на более поздней стадии культивирования (24 часа) (дополнительный рис. 3g, h) в среде CAA +20 мМ апотрансферрин, что в дальнейшем приведет к отличительному эволюционному результату (дополнительный рис. Рис. 13), в котором непродуцент PVDI превосходит штамм-продуцент в присутствии антимикробного стресса 47 . Наши результаты показали, что среда CAA + 20 мМ апотрансферрина ненадежна для создания состояния, ограниченного железом.Поэтому в наших эволюционных экспериментах использовалась среда SSM.
Конструирование мутантов P. aeruginosa
Делеционные мутанты \ (\ Delta \ mathrm {\ it {pvdA}} \), \ (\ Delta \ mathrm {\ it {pvdA}} \ Delta \ mathrm {\ it {fpvA}} \), \ (\ Delta \ mathrm {\ it {pvdRT}} — \ mathrm {\ it {opmQ}} \) были сконструированы путем аллельного обмена с использованием модифицированных процедур для P. aeruginosa . Мы сконструировали немаркированные делеционные мутанты с помощью Flp-опосредованного иссечения маркера устойчивости к антибиотикам 48 .Во-первых, два фрагмента ДНК, каждый из которых был получен выше и ниже целевых генов делеции с помощью ПЦР, были клонированы в вектор замены гена pEX18Ap с помощью трехкомпонентного лигирования. Затем сконструированную плазмиду вставляли в устойчивый к гентамицину / тетрациклину кусок между вышестоящим и нижележащим фрагментами. Конечную плазмиду электропорировали в PAO1, и соответствующий рекомбинантный штамм идентифицировали путем скрининга на чашках с агаром LB, содержащих 5% ( мас. / Об. ) сахарозы в пределах 30.{- 1} \) гентамицин. Затем штаммы подвергали электропорации с плазмидой pFLP2 и выделяли на чашках с агаром LB, содержащим 5% ( мас. / Об. ) сахарозы, для удаления маркера устойчивости. Окончательно мутации были проверены с помощью ПЦР и секвенирования. Сконструированные плазмиды перечислены в дополнительной таблице 1. Штаммы PAO1 psfGFP, PAO1 pmCherry, PAO1 \ (\ Delta \ mathrm {\ it {pvdA}} \) psfGFP были сконструированы путем специфической вставки в геном PAO1 с плазмидой pUC18T-mini- Тн7Т-ГМ 49 .{- 1} \) гентамицин.
Экстракция и очистка пиовердина
Экстракция и очистка пиовердина точно выполнялись в соответствии с ранее описанным протоколом 50 . Вкратце, конические колбы объемом 1 л, содержащие 200 мл SSM, инокулировали PAO1. Бактерии выращивали до экспоненциальной фазы в аэробных условиях при 37 ° C. После этого бактериальные культуры центрифугировали при 10000 × g в течение 10 мин при 4 ° C. Супернатант дополнительно фильтровали через фильтр 0.{- 1} \)), где колонка была предварительно насыщена CuSO 4 и уравновешена 20 мМ буфером HEPES (pH = 7,0), содержащим 100 мМ NaCl. Затем колонку промывали 20 мМ буфером HEPES и элюировали 20 мМ ацетатным буфером (pH = 5,0), содержащим 100 мМ NaCl. Фракции (5 мл) собирали и оптическую плотность при 400 нм (A 400 ) определяли с помощью спектрофотометра (NanoDrop 2000, Thermo SCIENTIFIC). Фракции, содержащие пиовердин, отдельно объединяли и лиофилизировали.{- 1} \) и 2 ‘, 7’-дихлорфлуоресцина диацетат (H 2 DCFDA, Thermo Fisher Scientific) с конечной концентрацией 20 \ (\ mu \ mathrm {M} \) были предварительно добавлены в среду. . Пиовердин H 2 DCFDA или PI возбуждали с использованием лазера с длиной волны 405, 488 или 561 нм, соответственно, и отображали изображение с помощью трех различных каналов излучения (450, 524 или 607 нм). Конфокальные изображения с разными каналами были дополнительно проанализированы для количественной оценки интенсивности флуоресценции отдельных клеток с использованием стандартного алгоритма, закодированного в Matlab, в котором для каждого состояния обычно подсчитывалось ≥2000 клеток.{- 1} \)) среда SSM в присутствии 50,0 \ (\ mu \ mathrm {M} \) очищенного PVDI. Затем флэш-среду SSM в отсутствие PVDI использовали для промывки прикрепленных к поверхности клеток в течение 30 минут для удаления PVDI, присутствующего в окружающей среде. После этого для генерации различных фотонных напряжений использовалось освещение 405 нм лазера с разной мощностью и временем экспозиции. Между тем, конфокальный микроскоп с вращающимся диском (Revolution Andor), оснащенный 100-кратным масляным объективом и EMCCD (iXon 897i Andor), применялся для непрерывной записи яркопольных и конфокальных изображений, в которых PVDI возбуждали с использованием 405 нм и изображение с каналом излучения 450 нм.Конфокальные изображения или изображения в светлом поле были дополнительно проанализированы для количественной оценки снижения интенсивности флуоресценции PVDI, обнаруженного в бактериальной периплазме, или скорости роста отдельных клеток, соответственно, в присутствии различных фотонных стрессов.
Прямая эволюция пятен кооператора и читера
Штаммы кооператора (PAO1 pmCherry) и читера (PAO1 \ (\ Delta \ mathrm {\ it {pvdA}} \) psfGFP) инокулировали в среды SSM в соотношении 1: 1. в присутствии различных количеств \ ({\ mathrm {FeCl}} _ 3 \) (10 −5 , 0.{- 1} \)). Контрольную группу устанавливали путем инокуляции штаммов PAO1 pmCherry и PAO1 psfGFP в соотношении 1: 1 в среде SSM в отсутствие \ ({\ mathrm {FeCl}} _ 3 \) и тобрамицина. Каждое условие было повторено трижды. Полученные смешанные бактериальные культуры дополнительно культивировали в шейкере при 37 ° C в течение 24 часов. После этого бактериальные культуры разводили ( об / об 1: 1000) в свежих средах SSM, содержащих соответствующие количества \ ({\ mathrm {FeCl}} _ 3 \) и тобрамицин для следующего цикла культивирования.Всего было проведено 30 циклов культивирования. В конце каждого цикла был тщательно подготовлен образец для подсчета бактерий, помещая 2,0 \ (\ mu \ mathrm {L} \) бактериальной культуры между покровным стеклом и агарозным гелем толщиной 2,0 мм. {b_2}}} + b_3} \ right], $$
(4)
$$ \ mathrm {Верный} \, \ mathrm {сотрудничество} \ frac {{\ gamma _1}} {{\ mu _1}} = \ frac {{\ gamma _2}} {{\ mu _2}} \ gg 1, $$
(5)
$$ \ mathrm {Эгоизм} \ frac {{\ gamma _1}} {{\ mu _1}} = \ frac {{\ gamma _2}} {{\ mu _2}} \ ll 1, $$
(6)
где \ (\ gamma _1 / \ mu _1 \) или \ (\ gamma _2 / \ mu _2 \) нелинейно (в виде холма) относится к величине стресса окружающей среды (Ens), если бактерии следуют условной приватизации, а \ (\ gamma _1 / \ mu _1 \) и \ (\ gamma _2 / \ mu _2 \) не зависят от Ens, если бактерии следуют за лояльным сотрудничеством или эгоизмом.Ens нормализуется путем деления на уровень стресса (\ (E_ {50} \)), который приводит к гибели 50% клеток. После нормализации коэффициенты \ (b_1 \), \ (b_2 \), \ (b_3 \) и \ (b_4 \) могут быть получены путем подгонки экспериментальных данных (рис. {3 +} \) будет способствовать образованию гидроксильных радикалов посредством реакции Фентона, \ (\ Delta t \) = 1 мин.o, $$
(10)
$$ \ frac {{\ mathrm {d} \ phi _1}} {{\ mathrm {d} t}} = \ phi _1 (\ mu _1 — p_1 — \ delta), $$
(11)
$$ \ frac {{\ mathrm {d} \ phi _2}} {{\ mathrm {d} t}} = \ phi _2 (\ mu _2 — p_2 — \ delta), $$
(12)
где \ (\ phi _1 \) и \ (\ phi _2 \) — объемные доли \ (\ left ({\ phi \ эквив vN / V} \ right) \) штаммов-продуцентов и штаммов, не являющихся продуцентами, соответственно. , \ (v \) и \ (V \) — объемы бактерий и системы, соответственно, \ (N \) — количество бактерий, а \ (\ delta \) — глобальная скорость разбавления в нашем эволюционном эксперименте.о \ влево (0 \ вправо) = 0 \; \ му М \). Параметры, используемые в нашей модели, перечислены в Таблице 1.
Таблица 1 Параметры, используемые для теоретического моделированияДля улучшения эволюционного анализа мы оценили общий размер популяции \ (\ left ({N \ left (t \ right) } \ right) \) вторгающегося штамма во время соревнования. Обратите внимание, что \ (N \ left (t \ right) \ Equiv \ phi (t) V / v \). Чтобы гарантировать, что \ (N \ left (t \ right) \) (или \ (\ phi \ left (t \ right) \)) не зависит от δ , мы нормализовали \ (N \ left (t \ right) \) by \ (N \ left (t \ right) / N_r \ left (t \ right) \) для расчета относительной доходности, определенной ниже:
$$ {\ mathrm {Relative}} \, {\ mathrm { yield}} \, \ overset {\ mathrm {def}} {=} \, \ mathrm {log} _ {10} [N \ left (t \ right) / N_r \ left (t \ right)], $$
(13)
, где \ (N_r \ left (t \ right) \) представляет собой общее количество бактерий эталонного штамма (штамм дикого типа, используемый для эталона), выращенного в условиях, идентичных тем, которые использовались в конкурентном анализе (т.е.е. идентичное содержание железа, стресс для АФК и исходное количество бактерий). В результате относительный выход можно использовать для оценки того, может ли тестируемый штамм проникать в штамм дикого типа; т.е. положительный или отрицательный относительный доход (\ (\ mathrm {log} _ {10} [N \ left (t \ right) / N_r \ left (t \ right)] \)> 0 или \ (\ mathrm {log} \, _ {10} [N \ left (t \ right) / N_r \ left (t \ right)] \) <0) означает, что тестируемый штамм может или не может проникнуть, соответственно.
Доступность данных
Все данные, полученные или проанализированные в ходе этого исследования, доступны у авторов по разумному запросу.
Напряжение фон Мизеса
Введение
Напряжение по Мизесу часто используется для определения того, является ли изотропным и пластичный металл будет деформироваться при сложных условиях нагружения. Это достигается путем вычисления напряжения фон Мизеса и сравнения его с предел текучести материала, составляющий критерий текучести по Мизесу .Цель — разработать критерий текучести пластичных металлов. который работает для любых сложных условий трехмерного нагружения, независимо от смесь нормальных и касательных напряжений.Напряжение фон Мизеса делает это путем кипячения сложное напряженное состояние до одного скалярного числа, которое сравнивается с предел текучести металла , также определяется одно скалярное числовое значение из испытания материала на одноосное растяжение (потому что это самый простой способ) в лаборатории.
Следует отметить, что это не точная наука, например, \ (F = m \, a \). Это эмпирический процесс с присущими ему ошибками и отклонениями. По факту, не существует жесткого правила, согласно которому металлы должны уступать критерии уступаемости фон Мизеса.Это такое же совпадение, как и все остальное. Тем не менее, он действительно работает очень хорошо и остается методом выбора спустя целое столетие после него было впервые предложено.
История
Определяющее уравнение для напряжения фон Мизеса было впервые предложено Хубером [1] в 1904 г., но, по-видимому, не получил особого внимания пока фон Мизес [2] не предложил его снова в 1913 году. Однако определение Хубера и фон Мизеса было не более чем математическим уравнением без физическая интерпретация до 1924 года, когда Хенки [3] Было признано, что это фактически связано с девиаторной энергией деформации .В 1931 году Тейлор и Куинни [4] опубликовали результаты испытаний на медь, алюминий и низкоуглеродистую сталь, демонстрирующих, что стресс фон Мизеса является более точным предиктором начала податливость металла, чем максимальное напряжение сдвига критерий , предложенный Треска [5] в 1864 г. и на сегодняшний день является лучшим предсказателем текучести металлов. Сегодня стресс фон Мизеса иногда называют стрессом Хубера-Мизеса в признание вклада Хубера в его развитие.Его также называют эффективное напряжение Мизеса и просто эффективное напряжение .
Техническая информация
Полное понимание стресса фон Мизеса требует понимания гидростатическая и девиаторная составляющие стресс и тензоры деформации, Закон Гука и плотность энергии деформации. Гидростатические и девиаторные напряжения и деформации уже были рассмотрены. И закон Гука уже затрагивался. здесь и здесь, но нужно будет можно обсудить более подробно на этой странице.Здесь также будет введена плотность энергии деформации.Гидростатические и девиаторные компоненты
Напомним, что любой тензор напряжений можно разложить на сумму гидростатические и девиаторные напряжения следующим образом \ [
\ sigma_ {ij} = {1 \ over 3} \ delta_ {ij} \ sigma_ {kk} + \ sigma ‘\! _ {ij}
\]
где \ ({1 \ over 3} \ delta_ {ij} \ sigma_ {kk} \) — гидростатический член
а \ (\ sigma ‘\) — девиаторное напряжение.
То же самое и для штамма.
\ [
\ epsilon_ {ij} = {1 \ over 3} \ delta_ {ij} \ epsilon_ {kk} + \ epsilon ‘\! _ {ij}
\]
где \ ({1 \ over 3} \ delta_ {ij} \ epsilon_ {kk} \) — гидростатический член
и \ (\ epsilon ‘\) — девиаторная деформация.
Эти два будут перемножены дальше вниз по странице.
Закон Гука
Мы видели, что закон Гука можно записать как \ [
\ epsilon_ {ij} = {1 \ over E} \ left [(1 + \ nu) \ sigma_ {ij} —
\ nu \, \ delta_ {ij} \ sigma_ {kk} \ right]
\]
, что является сокращением для
\ [
\оставил [
\ matrix {
\ epsilon_ {xx} & \ epsilon_ {xy} & \ epsilon_ {xz} \\
\ epsilon_ {xy} & \ epsilon_ {yy} & \ epsilon_ {yz} \\
\ epsilon_ {xz} & \ epsilon_ {yz} & \ epsilon_ {zz}
}
\верно ]
= {1 \ над E}
\оставил \{
(1 + \ ню)
\оставил [
\ matrix {
\ sigma_ {xx} & \ sigma_ {xy} & \ sigma_ {xz} \\
\ sigma_ {xy} & \ sigma_ {yy} & \ sigma_ {yz} \\
\ sigma_ {xz} & \ sigma_ {yz} & \ sigma_ {zz}
}
\верно ]
— 3 \; \ nu
\оставил [
\ matrix {
\ sigma_ {hyd} & 0 & 0 \\
0 & \ sigma_ {hyd} & 0 \\
0 & 0 & \ sigma_ {hyd}
}
\верно ]
\верно \}
\]
, который, в свою очередь, представляет собой матричную запись для следующей системы уравнений
\ [
\ epsilon_ {xx} = {1 \ over E} \ big [\ sigma_ {xx} — \ nu \, (\ sigma_ {yy} + \ sigma_ {zz}) \ big]
\]
\ [
\ epsilon_ {yy} = {1 \ over E} \ big [\ sigma_ {yy} — \ nu \, (\ sigma_ {xx} + \ sigma_ {zz}) \ big]
\]
\ [
\ epsilon_ {zz} = {1 \ over E} \ big [\ sigma_ {zz} — \ nu \, (\ sigma_ {xx} + \ sigma_ {yy}) \ big]
\]
для обычных условий и
\ [
\ epsilon_ {xy} = {1 + \ nu \ over E} \ sigma_ {xy} \ qquad
\ epsilon_ {yz} = {1 + \ nu \ over E} \ sigma_ {yz} \ qquad
\ epsilon_ {xz} = {1 + \ nu \ over E} \ sigma_ {xz}
\]
для условий сдвига.Условия сдвига чаще записываются как
\ [
\ gamma_ {xy} = {\ tau_ {xy} \ над G} \ qquad \ quad
\ gamma_ {yz} = {\ tau_ {yz} \ над G} \ qquad \ quad
\ gamma_ {xz} = {\ tau_ {xz} \ над G}
\]
где
\ [
\ gamma_ {xy} = 2 \ epsilon_ {xy} \ qquad
\ gamma_ {yz} = 2 \ epsilon_ {yz} \ qquad
\ gamma_ {xz} = 2 \ epsilon_ {xz} \ qquad
{\ rm и} \ qquad
G = {E \ более 2 (1 + \ nu)}
\]
Теперь вернемся к закону Гука в тензорной форме
\ [
\ epsilon_ {ij} = {1 \ over E} \ left [(1 + \ nu) \ sigma_ {ij} —
\ nu \, \ delta_ {ij} \ sigma_ {kk} \ right]
\]
и умножьте обе стороны на \ (\ delta_ {ij} \).
\ [
\ delta_ {ij} \ epsilon_ {ij} = {1 \ over E} \ left [(1 + \ nu) \ sigma_ {ij} —
\ nu \, \ delta_ {ij} \ sigma_ {kk} \ right] \ delta_ {ij}
\]
Это упрощает
\ [
\ epsilon_ {kk} = {(1-2 \ nu) \ over E} \ sigma_ {kk}
\]
А затем снова умножьте обе стороны на \ ({1 \ over 3} \ delta_ {ij} \), чтобы получить
\ [
{1 \ over 3} \ delta_ {ij} \ epsilon_ {kk} = {(1-2 \ nu) \ over 3 E} \ delta_ {ij} \ sigma_ {kk}
\]
Это приводит к уравнению, связывающему гидростатическое напряжение
и значения деформации.
Теперь вычтите указанное выше уравнение из исходного уравнения закона Гука, чтобы получить
\ [
\ begin {eqnarray}
\ epsilon_ {ij} — {1 \ over 3} \ delta_ {ij} \ epsilon_ {kk}
знак равно
{(1 + \ nu) \ over E} \ sigma_ {ij} —
{\ nu \ over E} \, \ delta_ {ij} \ sigma_ {kk} —
{(1-2 \ nu) \ over 3 E} \ delta_ {ij} \ sigma_ {kk} \\
\\
\\
\\
\\
знак равно
{(1 + \ nu) \ over E} \ sigma_ {ij} —
{1 \ over E} \ left (\ nu + {1-2 \ nu \ over 3} \ right)
\ delta_ {ij} \ sigma_ {kk} \\
\\
\\
\\
\\
знак равно
{(1 + \ nu) \ over E} \ sigma_ {ij} —
{1 \ over 3} {(1 + \ nu) \ over E}
\ delta_ {ij} \ sigma_ {kk} \\
\\
\\
\\
\\
знак равно
{(1 + \ nu) \ over E} \ big (\ sigma_ {ij} —
{1 \ over 3} \ delta_ {ij} \ sigma_ {kk} \ big) \\
\ end {eqnarray}
\]
Замечательный результат состоит в том, что обе части уравнения содержат
девиаторный тензорный результат.Уравнение можно резюмировать как
\ [
\ epsilon ‘\! _ {ij} = {(1 + \ nu) \ over E} \ sigma’ \! _ {ij}
\]
\ [
\ epsilon ‘\! _ {ij} = {1 \ более 2 гигабайт} \ sigma’ \! _ {ij}
\]
Итак, девиаторное напряжение и деформация
прямо пропорциональны друг другу.
Самое замечательное здесь то, что это всегда верно для закона Гука, всегда,
даже для компонентов нормальной деформации.
Как бы то ни было, уравнение также можно записать как
\ [ \ sigma ‘\! _ {ij} = 2 \, G \, \ epsilon’ \! _ {ij} \]
Девиаторный пример с законом Гука
Предположим, у вас есть материал с коэффициентом Пуассона, \ (\ nu = 0.5 \) и модуль упругости \ (E = 15 \; МПа \).Для тензора напряжений, приведенного ниже, используйте закон Гука, чтобы вычислить деформированное состояние. Затем получить девиаторные тензоры напряжений и деформаций и покажем, что они пропорциональны друг другу множителем \ (2G \).
\ [
\ boldsymbol {\ sigma} \; знак равно
\ left [\ matrix {
8 и 2 и 4 \\
2 и 6 и 6 \\
4, 6 и 4}
\верно]
\]
Обратите внимание, что этот тензор напряжения явно имеет значительную
гидростатическое напряжение. это
\ [
\ boldsymbol {\ sigma} _ \ text {Hyd} \; знак равно
\ left [\ matrix {
6 & 0 & 0 \\
0 и 6 и 0 \\
0 & 0 & 6}
\верно]
\]
Закон Гука
\ [
\ begin {eqnarray}
\ left [\ matrix {
\ epsilon_ {xx} & \ epsilon_ {xy} & \ epsilon_ {xz} \\
\ epsilon_ {xy} & \ epsilon_ {yy} & \ epsilon_ {yz} \\
\ epsilon_ {xz} & \ epsilon_ {yz} & \ epsilon_ {zz}}
\верно]
знак равно
{1 \ более 15}
\оставил\{
(1 + 0.5)
\ left [\ matrix {
8 и 2 и 4 \\
2 и 6 и 6 \\
4, 6 и 4}
\верно]
— 3 \; (0,5)
\оставил[
\ matrix {
6 & 0 & 0 \\
0 и 6 и 0 \\
0 & 0 & 6}
\верно]
\верно\} \\
\\
\\
\\
\\
знак равно
{1 \ более 15}
\оставил\{
\ left [\ matrix {
12 и 3 и 6 \\
3 и 9 и 9 \\
6, 9 и 6}
\верно]
—
\оставил[
\ matrix {
9 & 0 & 0 \\
0 и 9 и 0 \\
0 & 0 & 9}
\верно]
\верно\} \\
\\
\\
\\
\\
знак равно
\ left [\ matrix {
0.2 & \; 0,2 & \; 0,4 \\
0,2 & \; 0,0 & \; 0,6 \\
0,4 & \; 0,6 & \ text {-} 0,2}
\верно]
\ end {eqnarray}
\]
Обратите внимание, что этот тензор деформации уже девиаторный. Это потому что
мы использовали \ (\ nu = 0.5 \) для коэффициента Пуассона, который является используемым значением
для несжимаемых материалов. Так мы получили несжимаемую,
негидростатический тензор деформации.
Таким образом, возникает вопрос: «Будет ли (\ (2 \, G \, \ boldsymbol {\ epsilon} ‘\)») дать \ (\ boldsymbol {\ sigma} ‘\)? »
Чтобы ответить на этот вопрос, сначала вычислите \ (G \).
\ [
\ begin {eqnarray}
грамм
знак равно
{E \ over 2 (1 + \ nu)}
знак равно
{15 \ text {МПа} \ over 2 (1 + 0,5)} \\
\\
\\
\\
\\
знак равно
5 \ text {МПа}
\ end {eqnarray}
\]
Итак, \ (2 \, G \, \ boldsymbol {\ epsilon} ‘\) равно
\ [
2 \, G \, \ boldsymbol {\ epsilon} ‘=
\ left [\ matrix {
2 & \; 2 & \; 4 \\
2 & \; 0 & \; 6 \\
4 & \; 6 & \ text {-} 2}
\верно]
\]
И сравните это с \ (\ boldsymbol {\ sigma} — \ boldsymbol {\ sigma} _ \ text {Hyd} \)
\ [
\ boldsymbol {\ sigma} — \ boldsymbol {\ sigma} _ \ text {Hyd}
\; знак равно
\ left [\ matrix {
8 и 2 и 4 \\
2 и 6 и 6 \\
4, 6 и 4}
\верно]
—
\оставил[
\ matrix {
6 & 0 & 0 \\
0 и 6 и 0 \\
0 & 0 & 6}
\верно]
знак равно
\оставил[
\ matrix {
2 & \; 2 & \; 4 \\
2 & \; 0 & \; 6 \\
4 & \; 6 & \ text {-} 2}
\верно]
\]
Так что это действительно удовлетворяет
\ (\ boldsymbol {\ sigma} ‘= 2 \, G \, \ boldsymbol {\ epsilon}’ \).Хотя это был пример с несжимаемым материалом,
\ (\ nu = 0.5 \), он также работает для сжимаемых материалов
а также всегда.
Плотность энергии деформации
Плотность энергии деформации, Вт, имеет единицы Энергия / объем и составляет \ [
W = \ int \ boldsymbol {\ sigma}: d \ boldsymbol {\ epsilon}
\]
Для линейно-упругих материалов это равно
\ [
W = {1 \ более 2} \ boldsymbol {\ sigma}: \ boldsymbol {\ epsilon}
\]
, который расширяется, чтобы дать
\ [
{1 \ over 2} \ boldsymbol {\ sigma}: \ boldsymbol {\ epsilon} = {1 \ over 2} [
\ sigma_ {xx} \ epsilon_ {xx} + \ sigma_ {yy} \ epsilon_ {yy} + \ sigma_ {zz} \ epsilon_ {zz} +
2 (\ sigma_ {xy} \ epsilon_ {xy} + \ sigma_ {yz} \ epsilon_ {yz} + \ sigma_ {xz} \ epsilon_ {xz})]
\]
Но поскольку \ (\ boldsymbol {\ sigma} = \ boldsymbol {\ sigma} _ \ text {Hyd} + \ boldsymbol {\ sigma} ‘\)
и \ (\ boldsymbol {\ epsilon} = \ boldsymbol {\ epsilon} _ \ text {Hyd} + \ boldsymbol {\ epsilon} ‘\),
эти тождества можно подставить в уравнение, чтобы получить
\ [
W = {1 \ более 2} \ boldsymbol {\ sigma}: \ boldsymbol {\ epsilon} =
{1 \ более 2}
(\ boldsymbol {\ sigma} _ \ text {Hyd} + \ boldsymbol {\ sigma} ‘):
(\ boldsymbol {\ epsilon} _ \ text {Hyd} + \ boldsymbol {\ epsilon} ‘)
\]
и расширение умножения дает
\ [
W = {1 \ более 2} \ boldsymbol {\ sigma}: \ boldsymbol {\ epsilon} =
{1 \ более 2}
\ boldsymbol {\ sigma} _ \ text {Hyd}: \ boldsymbol {\ epsilon} _ \ text {Hyd}
+ {1 \ более 2}
\ boldsymbol {\ sigma} _ \ text {Hyd}: \ boldsymbol {\ epsilon} ‘
+ {1 \ более 2}
\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ epsilon} _ \ text {Hyd}
+ {1 \ более 2}
\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ epsilon}’
\]
Но (\ (\ boldsymbol {\ sigma} _ \ text {Hyd}: \ boldsymbol {\ epsilon} ‘\))
и (\ (\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ epsilon} _ \ text {Hyd} \))
равны нулю! Это потому, что произведение любой гидростатической
тензор с девиаторным тензором всегда равен нулю.Таким образом, уравнение сводится к
\ [
W = {1 \ более 2} \ boldsymbol {\ sigma}: \ boldsymbol {\ epsilon} =
\ underbrace {
{1 \ более 2} \ boldsymbol {\ sigma} _ \ text {Hyd}: \ boldsymbol {\ epsilon} _ \ text {Hyd}
} _ {гидростатический}
+
\ underbrace {
{1 \ более 2} \ boldsymbol {\ sigma} ‘: \ boldsymbol {\ epsilon}’
} _ {deviatoric}
\]
Это показывает, что энергия деформации может быть разделена на
гидростатические и девиаторные компоненты.
Напряжение фон Мизеса
Напряжение фон Мизеса напрямую связано с девиаторной энергией деформации. в приведенном выше уравнении.\ [ W ‘= {1 \ over 2} \ boldsymbol {\ sigma}’: \ boldsymbol {\ epsilon} ‘ \]Вспомните из раздела о законе Гука, что
\ [
\ boldsymbol {\ epsilon} ‘= {1 \ over 2 \, G} \ boldsymbol {\ sigma}’
\]
Объединение двух дает
\ [
W ‘= {1 \ over 4 \, G} \ boldsymbol {\ sigma}’: \ boldsymbol {\ sigma} ‘
\]
Итак, девиаторная часть плотности энергии деформации
напрямую связано с
двойное точечное произведение девиаторного напряжения
с собой. 2 \) и любые
другая форма, о которой можно подумать.2 =
{1 \ over 4 \, G} \ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’
\]
Ясно \ (\ sigma_ {Rep} \)
представляет собой скалярное значение напряжения, которое дает такую же девиаторную энергию деформации
как фактический трехмерный тензор напряжений. Сокращение \ (4 \, G \) с обеих сторон дает
\ [
\ sigma_ {Rep} = \ sqrt {\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’}
\]
Последний шаг — простое удобство. Это мотивировано простейшими
прямолинейный случай одноосного растяжения. Чтобы увидеть это, вычислите \ (\ sigma_ \ text {Rep} \)
для этого случая.Напряженное состояние при одноосном растяжении равно
\ [
\ boldsymbol {\ sigma} =
\ left [\ matrix {
\ sigma & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0}
\верно]
\]
Гидростатическое напряжение равно \ ({1 \ over 3} \ sigma \), а тензор девиаторного напряжения равен
\ [
\ boldsymbol {\ sigma} ‘=
\ left [\ matrix {
{2 \ sigma \ over 3} & 0 & 0 \\
0 & {- \ sigma \ over 3} & 0 \\
0 & 0 & {- \ sigma \ over 3}}
\верно]
\]
Итак, \ (\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’ \) равно \ (2 \ sigma ^ 2/3 \).И поэтому
\ [
\ sigma_ \ text {Rep} = \ sqrt {\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’} = \ sqrt {2 \ over 3} \; \сигма
\]
И в этом заключается разочарование. Типичное напряжение для одноосного растяжения не равно
напряжение одноосного растяжения, \ (\ sigma \), но вместо этого составляет около 82% от него. Это ужасно
неудобно, но исправить несложно. Просто увеличивайте репрезентативное напряжение до тех пор, пока оно
равняется напряжению одноосного растяжения. Это делается простым умножением \ (\ sigma_ \ text {Ref} \)
Автор: \ (\ sqrt {3/2} \).
Это приемлемо, потому что все пропорционально \ (\ sqrt {\ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’} \) по-прежнему будет отражать отношение к девиаторной энергии деформации. Он просто будет немного увеличен. Конечный результат — это напряжение фон Мизеса.
\ [
\ sigma_ \ text {VM} = \ sqrt {{3 \ over 2} \ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’}
\]
И это определяющее уравнение.
Альтернативные формы
Алгебраические манипуляции с вышеупомянутым уравнением дают много других эквивалентных форм.2_ {xy}} \]Тензорное манипулирование уравнением фон Мизеса
Можно (относительно) легко получить другие уравнения для напряжения фон Мизеса с помощью тензорных манипуляций с уравнением на основе девиаторных значений. Начиная с \ [
\ sigma_ \ text {VM} = \ sqrt {{3 \ over 2} \ sigma ‘\! _ {ij} \ sigma’ \! _ {ij}}
\]
и выразив \ (\ sigma ‘\! _ {Ij} \) через полный тензор напряжений как
\ [
\ sigma ‘\! _ {ij} = \ sigma_ {ij} — {1 \ over 3} \ delta_ {ij} \ sigma_ {kk}
\]
дает следующую форму.2}
\]
Остальные формы, перечисленные выше, можно получить, указав это
явно в терминах \ (\ sigma_ {xx} \), \ (\ sigma_ {xy} \), \ (\ sigma_ {xz} \),
и т.п.
Ящики для особых нагрузок
Во время вышеприведенного вывода мы уже видели, что для одноосного растяжения Напряжение по Мизесу равно напряжению одноосного растяжения. Но это тоже (почти) верно и для сжатия. Единственная проблема заключается в том, что для сжатия числовое значение сжимающего напряжения будет отрицательным, но фон Мизеса напряжение всегда положительно, потому что это квадратный корень из суммы значений напряжения в квадрате.Поэтому, когда кто-то читает напряжение по Мизесу, скажем, 10 МПа, оно Только на основании этого невозможно узнать, подвергается ли объект растяжению или сжатию. Чтобы определить это, можно посмотреть на значения главных напряжений.На самом деле, некоторые постпроцессоры FEA делают контуры цветового напряжения звоните подписанный фон Мизес стресс . Он имеет то же абсолютное значение, что и обычное напряжение фон Мизеса, но знак +/- определяется проверкой признак гидростатического напряжения. Если он отрицательный, то напряжение по Мизесу со знаком также отрицательно.
Случай чистого напряжения сдвига наиболее интересен. Из уравнений видно выше, чем для чистого напряжения сдвига, \ (\ tau_ {xy} \), напряжение фон Мизеса равно
\ [
\ sigma_ \ text {VM} = \ sqrt {3} \, \ tau
\]
Итак, если металл поддается одноосному растяжению (или сжатию) при
\ (\ sigma = \ pm 500 \ text {MPa} \), тогда он также уступит
сдвиг при напряжении, составляющем только 58% от этого, или
\ (\ tau = \ pm 290 \ text {МПа} \).
Графические представления
Это снова набросок вверху страницы.Он показывает ограничивающую поверхность в трехмерной системе координат главного напряжения, где напряжение фон Мизеса является постоянным значение. (Это так называемое пространство High-Westerguard ). Оно основано на фактах. что любое напряженное состояние можно преобразовать в его основные значения и сравнить к этому эскизу. Если результирующая точка главного напряжения в системе координат находится внутри цилиндра, значит, материал не поддается. Если он на поверхности, затем материал уступил место. А если он находится вне цилиндра, значит, вы провели эластичный анализ ситуации, которая на самом деле не может быть правильной, потому что уступки давно бы имели место.Замечательный результат состоит в том, что если вы посмотрите вниз на \ (\ sigma_1 = \ sigma_2 = \ sigma_3 \) По оси поперечное сечение цилиндра представляет собой идеальный круг. Обратите внимание, что гидростатическое напряжение в этой ситуации вообще не проявляется.
Экспериментальные данные
На рисунке представлены экспериментальные данные, подтверждающие, что пластичные металлы дают гораздо более стабильный результат при предписанных уровнях напряжения по Мизесу, независимо от состояния нагрузки, чем при любых других критериях.График представляет собой срез плоскости \ (\ sigma_1 — \ sigma_2 \) с \ (\ sigma_3 = 0 \).Поскольку цилиндр срезан под углом, кажется, что быть эллипсом в этой ситуации. На самом деле это все еще круг. Мы просто смотрим на это под углом.
Напомним, что критерий напряжения сдвига был впервые предложен Треска в 1864 году, и этот акт считается рождением поля исследования пластичности металлов.
Единственным исключением является чугун. Он уступает, фактически трещит при критерий постоянного максимального главного напряжения. Это означает, что железо хрупкое и ведет себя больше как стекло, чем пластичный металл.
Ссылка: Даулинг, Н.Э., Механическое поведение материалов , Прентис Холл, 1993.
Обратите внимание, что корреляция здесь не идеальна. Это следствие тот факт, что так называемый критерий доходности фон Мизеса НЕ является законом природа. Это скорее удобное совпадение. Это следствие перемещение дислокаций на миллионы и миллиарды плоскостей атомов, скользящих друг по другу в атомном масштабе. Эти самолеты все атомы ориентированы случайным образом, и результирующий отклик в макромасштабе есть…. критерий уступчивости фон Мизеса.
Противопоставление напряжения и деформации
Мы видели, что стресс фон Мизеса является «стрессом» при беспокойстве о податливость и пластичность металла. Напомним, что это \ [
\ sigma_ \ text {VM} = \ sqrt {{3 \ over 2} \ boldsymbol {\ sigma} ‘: \ boldsymbol {\ sigma}’}
\]
Следующий вопрос: «Существует ли деформация, аналогичная напряжению фон Мизеса?»
Ответ положительный. Это эффективный штамм , а иногда и Эффективный штамм Мизеса .это
\ [
\ epsilon_ \ text {eff} = \ sqrt {{2 \ over 3} \ boldsymbol {\ epsilon} ‘: \ boldsymbol {\ epsilon}’}
\]
Обратите внимание, что это \ (2/3 \), а не \ (3/2 \). 2/2 \).Поэтому необходимо умножить на \ (2/3 \), чтобы получить
\ (\ boldsymbol {\ epsilon} _ \ text {eff} \) равно деформации одноосного растяжения.
Это позволяет более объективно сравнивать напряженное и деформированное состояние
два разных режима деформации, скажем, растяжение по сравнению с сдвигом. Фактически, в идеальном
изотропного металла, графики зависимости эффективного напряжения от эффективной деформации будут
неразличимы в пластической области независимо от режима деформации.
Хотя на самом деле металлы обычно становятся все более анизотропными после текучести.
Список литературы
- Huber, M.T. (1904) Czasopismo Techniczne , Лемберг, Австрия, Vol. 22. С. 181.
- Фон Мизес, Р. (1913) «Mechanik der Festen Korper im Plastisch Deformablen Zustand», Nachr. Ges. Wiss. Gottingen , стр. 582.
- Хенки, Х.З. (1924) «Zur Theorie Plasticher Deformationen und der Hierdurch im Material Hervorgerufenen Nachspannungen», Z. Angerw. Математика. Мех. , т. 4, стр.323.
- Тейлор Г.И., Куинни Х. (1931) «Пластическая деформация металлов», Phil. Пер. R. Soc., Лондон, , Vol. A230, стр. 323.
- Треска, Х. (1864) «Sur l’Ecoulement des Corps Solides Soumis a de Fortes Pressions», C. R. Acad. Sci., Paris , Vol. 59, с. 754.
- Dowling, N.E. (1993) Механическое поведение материалов , Прентис Холл.
11.4: Условие текучести — Engineering LibreTexts
Из предыдущего раздела условие одноосной текучести при растяжении / сжатии в направлении x равно
\ [\ sigma_ {11} = \ pm \ sigma_y \]
В общей трехмерной модели все шесть компонентов тензора напряжений способствуют деформации материала.2_г \]
, где \ (\ sigma_ {1} \), \ (\ sigma_ {2} \) \ (\ sigma_ {3} \) — главные напряжения. Графическое представление уравнения ( ?? ) представляет собой цилиндр с открытым концом, нормальный к октаэдрической плоскости, рисунок (\ (\ PageIndex {1} \)).
Уравнение прямой, нормальной к плоскости октаэдра и проходящей через начало координат, равно
\ [\ sigma_1 + \ sigma_2 + \ sigma_3 = 3p \]
где \ (p \) — гидростатическое давление. Поскольку гидростатическое давление не влияет на текучесть, поверхность текучести представляет собой открытый цилиндр.2_г \]
Рисунок \ (\ PageIndex {2} \): Эллипс фон Мизеса в главной системе координат.Графическое представление уравнения ( ?? ) представляет собой эллипс, показанный на рисунке (\ (\ PageIndex {2} \)). На рисунке (\ (\ PageIndex {2} \)) можно выделить несколько важных напряженных состояний.
- Точки 1 и 2: одноосное растяжение, \ (\ sigma_ {1} = \ sigma_ {2} = \ sigma_ {y} \)
- Точки 7 и 11: одноосное сжатие, \ (\ sigma_ {1} = \ sigma_ {2} = — \ sigma_ {y} \)
- Точка 3: Равно-двухосное растяжение, \ (\ sigma_ {1} = \ sigma_ {2} \)
- Точка 9: Равно-двухосное сжатие, \ (- \ sigma_ {1} = — \ sigma_ {2} \)
- Точки 2, 4, 8 и 10: обычная деформация, \ (\ sigma_ {1} = \ frac {2} {\ sqrt {3}} \ sigma_ {y} \)
- Пункты 6 и 12: чистый сдвиг, \ (\ sigma_ {1} = — \ sigma_ {2} \)
Концепция плоской деформации будет объяснена в разделе, посвященном правилу потока.

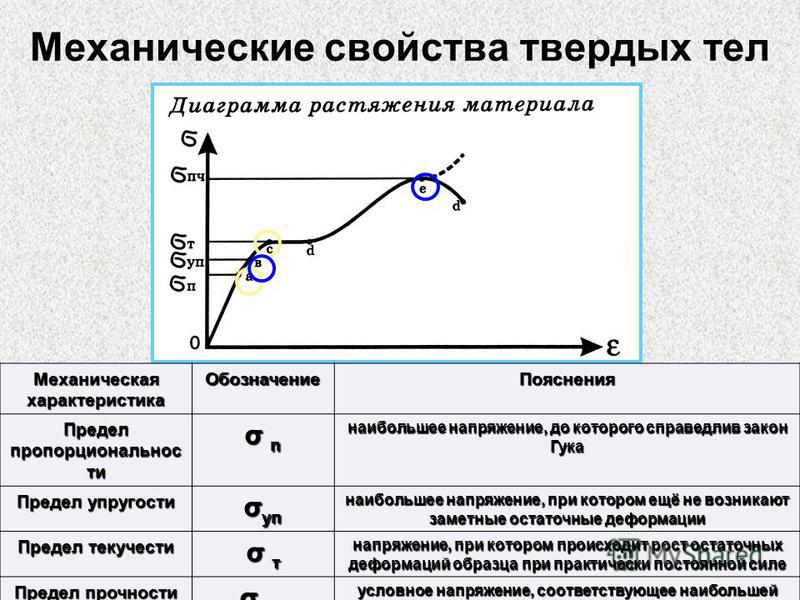 They are made of cast steel of grade G17GrMo55.
They are made of cast steel of grade G17GrMo55.
 com
com