Что такое Угол? Определение, виды, как обозначают? Примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре.
Иногда можно встретить обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Что такое вершина и стороны угла:
- Стороны угла — лучи, из которых состоит угол.
- Вершина угла — общее начало сторон угла.
Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Определение смежных и вертикальных углов
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол.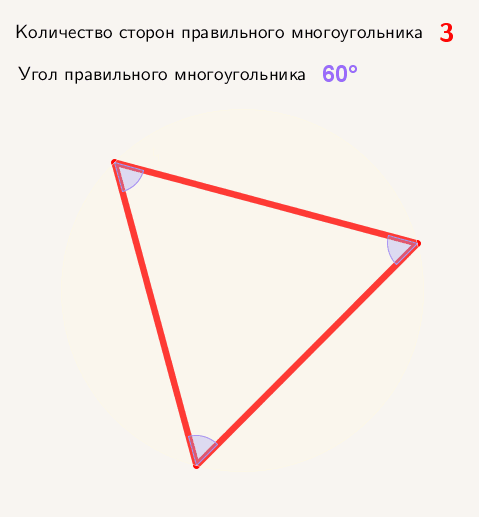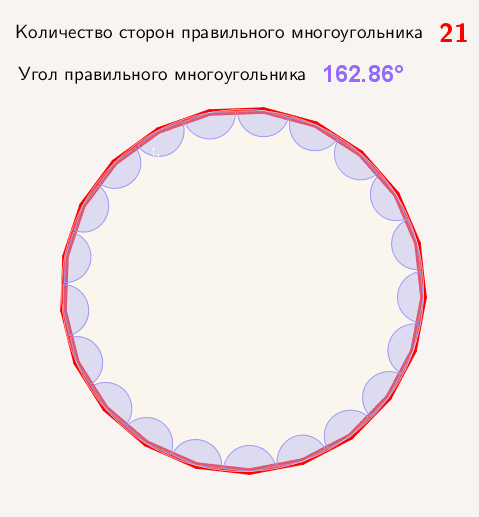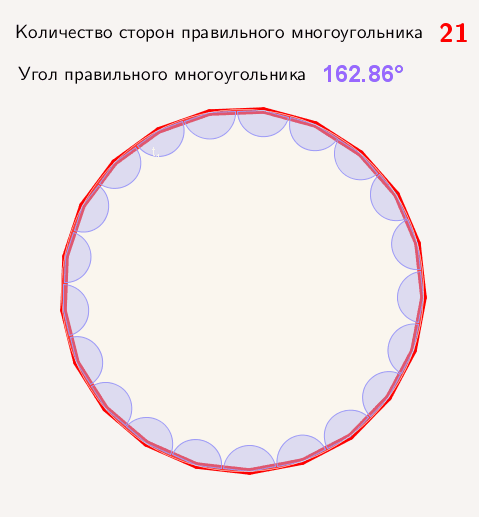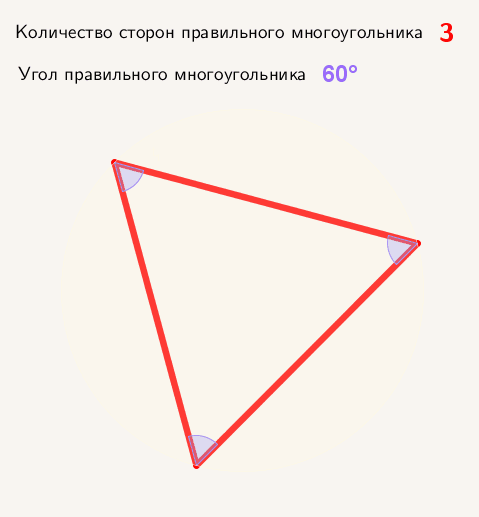 Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Вертикальные углы
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.
Если два смежных угла равны между собой, то каждый из них является прямым.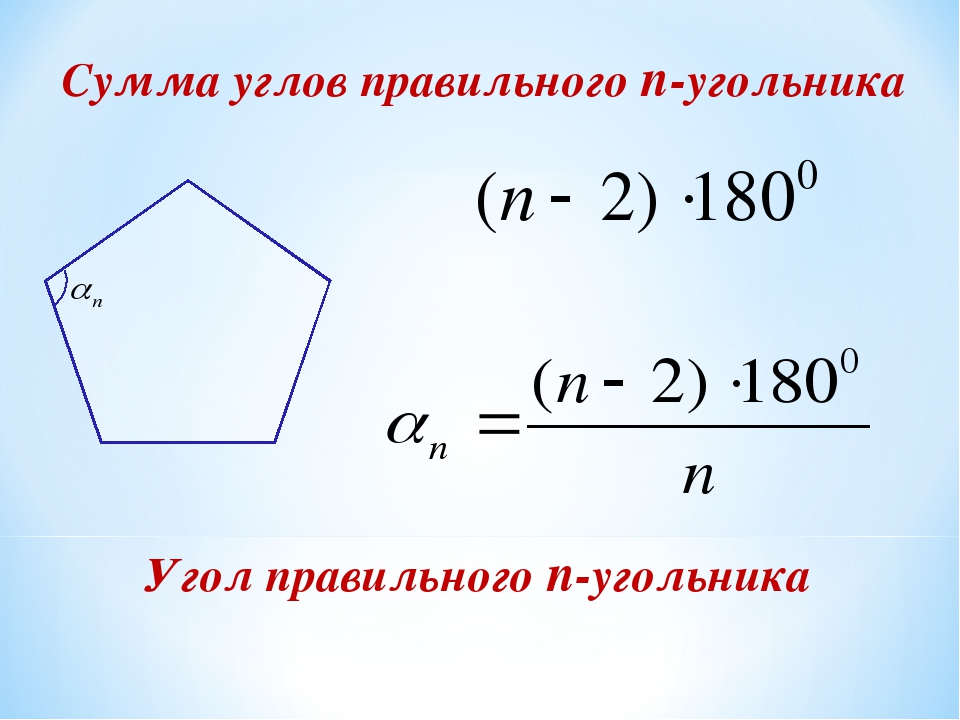 Для удобства прямой угол обозначается уголком. Вот так:
Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.
Неразвернутый угол
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB — ∠COB,
- ∠COB = ∠AOB — ∠AOC.
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.

- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается — ´.
Секунда — 1/60 часть минуты. Обозначается — ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.
Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.
Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее.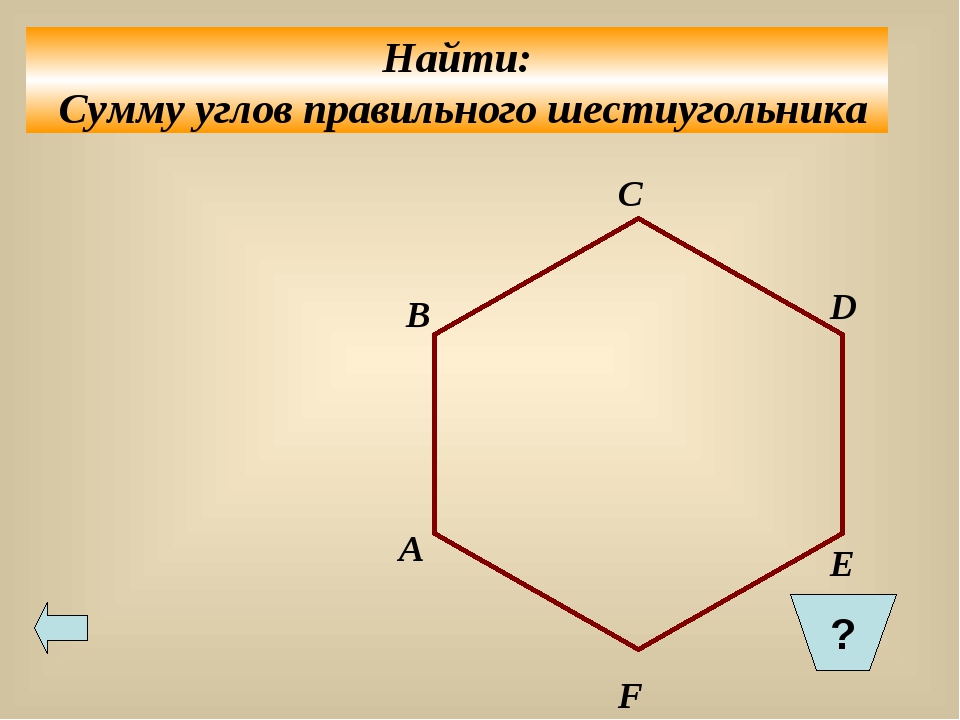 Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
- Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
На чертеже отмечены острые, равные и неравные углы.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие.
| Найди правильный угол, и эта малышка могла снести твою голову. | |
| Еще у него есть ножка сзади, которая раскладывается, чтобы поставить его под правильным углом. С точки зрения эргономики, правильный угол использования — 11 градусов. | |
| Эффект заключается в том, что, когда выливаешь это, если у меня получится правильный угол, оно вытягивает само себя из ёмкости. | |
| Нужно просто поймать правильный угол. | |
| Практика необходима, чтобы найти правильный угол. | |
| Горизонтальное боковое движение ручки управляет скоростью крена, и самолет поддерживает правильный угол тангажа после того, как поворот был установлен, до 33° крена. | |
Вращение с правильной скоростью, известной как VR, и на правильный угол важно из соображений безопасности и для уменьшения взлетной дистанции. | |
| Это требует точности, так как вращение шара, его скорость и расположение влияют на правильный угол наклона блока. | |
| Редактировать это можно, регулируя уровень увеличения в игре и получая правильный угол обзора камеры. | |
| Другие результаты | |
| Я могу направить ее на задний ряд или, как вы правильно заметили, за угол. | |
| Надо только найти правильтный угол. | |
| Здесь главное — правильно рассчитать угол броска. | |
| Ну, найти нужный угол, правильно подсоединить, и отключить звук, поскольку у нас есть ордер только на микрофон в туфле. | |
| Как правило, он похожи на лисиц, загнанных в угол, диких и смущенных. | |
| Однако угол крена 120 ° делает двигатель довольно широким, поэтому серийный V6, как правило, использует угол 60° с кривошипным штифтом, который смещен на 60° для противоположных цилиндров. | |
Опытный образец испытательного самолета, Messerschmitt Me P. 1101, был построен для исследования компромиссов конструкции и разработки общих правил о том, какой угол стреловидности использовать. 1101, был построен для исследования компромиссов конструкции и разработки общих правил о том, какой угол стреловидности использовать. | |
| Как правило, угол обзора составляет около 45°, и этот угол должен согласовываться с последовательностью, предусмотренной мастером. | |
| Современные системы управления полетом, Как правило, ограничивают угол атаки истребителя значительно ниже его максимального аэродинамического предела. | |
| У прыгунов, как правило, более короткий круп и более тупой угол в скакательном суставе. | |
| Как правило, режущие оси имеют неглубокий угол Клина, в то время как расщепляющие оси имеют более глубокий угол. | |
| Ошибка, которая влияет на k битов, перемещает сообщение в угол, который является k шагов, удаленными от его правильного угла. | |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.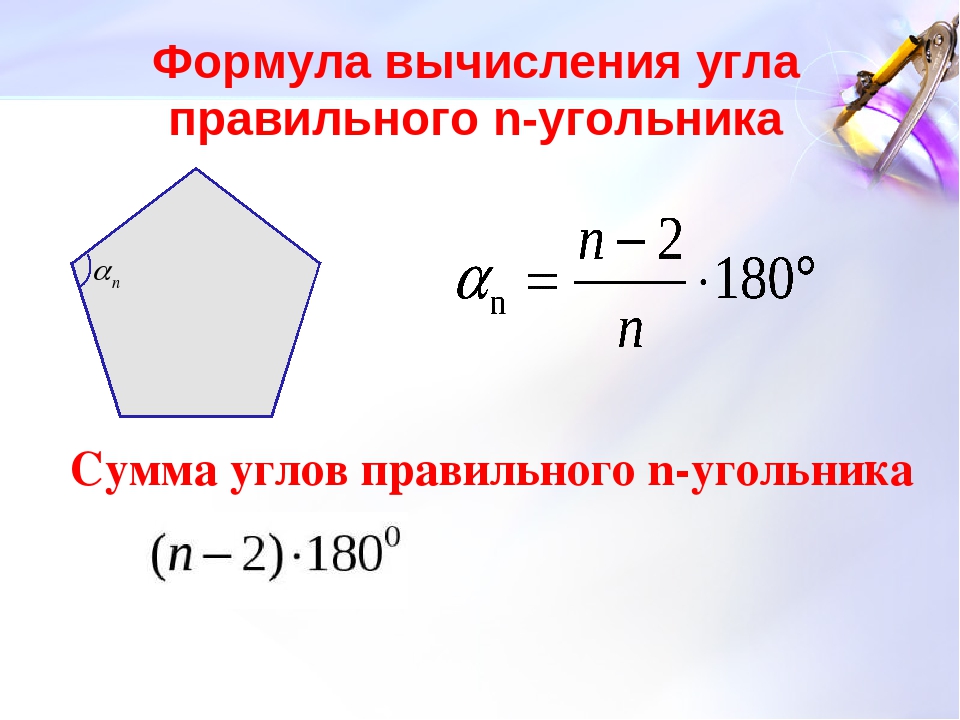 1).
1).
Рис. 1
Определение 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U …
… U [An An +1]
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
Рис. 2
Определение 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Рис. 3
Определение 3. Многоугольник называют n – угольником, если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |
| Диагонали n – угольника, выходящие из одной вершины | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |
| Все диагонали n – угольника | Число диагоналей n – угольника равно |
| Диагональ многоугольника |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
Свойства углов многоугольника
Свойства углов правильного n – угольника
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные. Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов n – угольника равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
- Остроугольный треугольник — все углы треугольника острые.
- Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
- Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).

По числу равных сторон
- Разносторонний треугольник — все три стороны не равны.
- Равнобедренный треугольник — две стороны равны.
- Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке.
 (Точка пересечения медиан называется центроидом)
(Точка пересечения медиан называется центроидом)В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2. Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника.
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
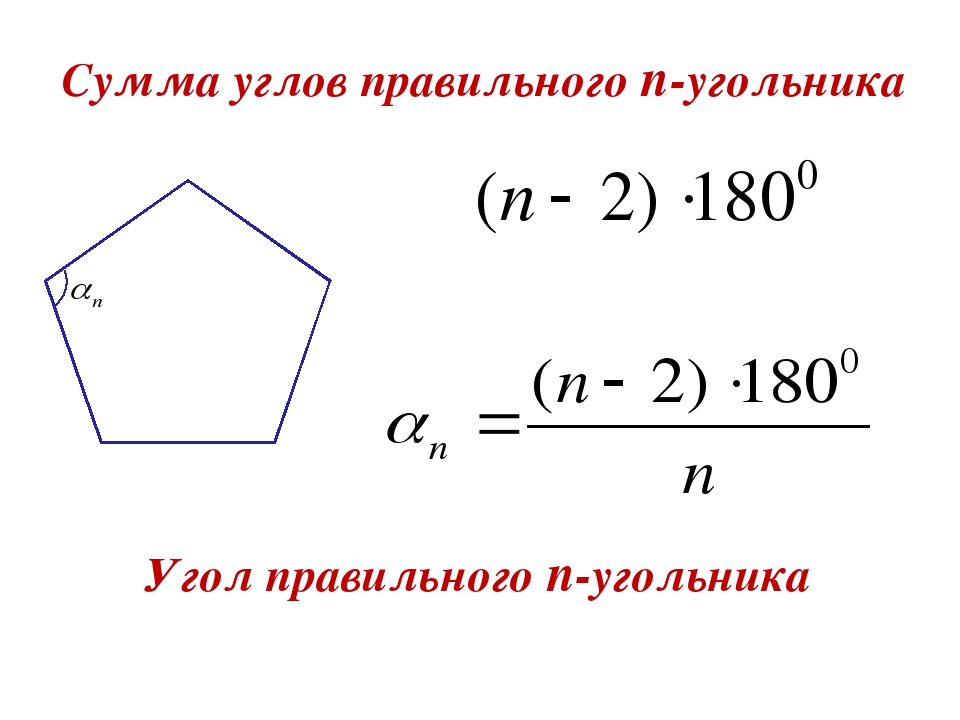
Расчет углов правильного многоугольника онлайн
- Главная
- Калькуляторы
- Математика
- Геометрия
- Правильный многоугольник. Расчет углов правильного многоугольника
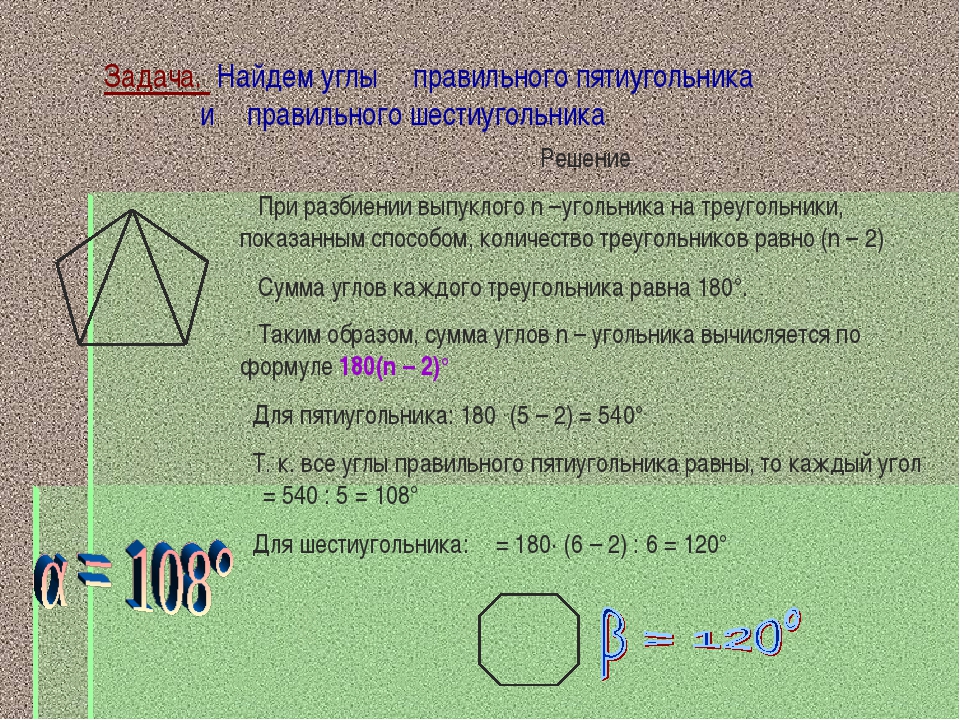
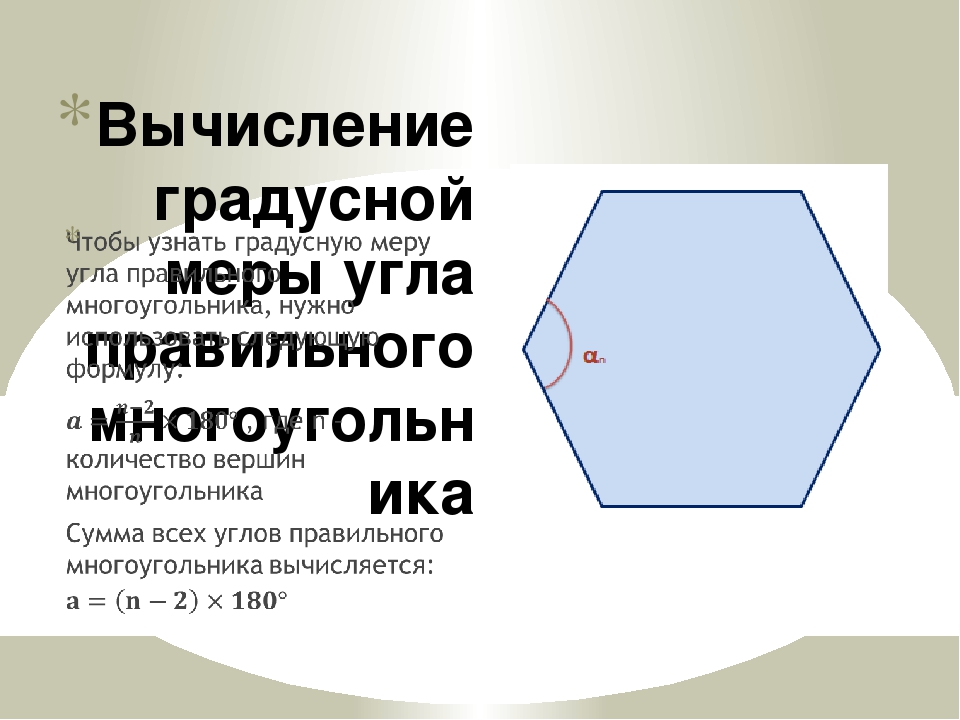
Многоугольник представляет плоскую замкнутую геометрическую фигуру, у которой может быть три, четыре и более сторон, пересекающихся в трех, четырех и более точках, называющихся вершинами. Называются они в соответствии с количеством сторон или вершин. Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с равными углами и сторонами. Например, квадрат.
Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с равными углами и сторонами. Например, квадрат.
(n — 2) · 180°
а сумма всех его сторон будет равна:
P = n · a
P — периметр;
а — сторона;
n — количество сторон.
Определяем угол правильного n-угольника:
А = (n — 2) / n · х · 180°
Если в задании имеется радиус вписанной окружности ®, тогда сторону (а) правильного n-угольника определяет по формуле:
a = 2r · tg · 180° / n
a = 2r · tg · π / n
Если задан радиус ® описанной окружности, то находим сторону по формуле:
a = 2 R · sin · 180° / n
a = 2 R · sin · π / n
Соответственно, если известна сторона правильного n-угольника, находим r вписанной окружности:
r = a / (2 tg · 180° / n)
r = a / (2 tg · π / n)
и R описанной окружности n-угольника по его стороне:
R = a / (2 sin · 180° / n)
R = a / (2 sin · π / n)
Онлайн калькулятор поможет вам быстро и правильно определить число и величину сторон правильного многоугольника, размер его внешнего и внутреннего углов, а также другие показатели.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Угол— перевод на испанский — примеры английский
Эти примеры могут содержать грубые слова на основании вашего поиска.
Эти примеры могут содержать разговорные слова, основанные на вашем поиске.
Его лезвие было под правильным углом .
Процесс не требует усилий. Это происходит почти автоматически, учитывая правильный угол .
El processso es sin esfuerzo y se производит casi automáticamente dado el ángulo correctiveo .
Выбор правильного угла для измерения блеска
Во время полета пропеллеры удерживаются под правильным углом за счет гидравлического давления.
Durante el vuelo las hélices se mantienen en el ángulorecto por presión hidráulica.Ознакомьтесь с инструкциями производителя вашего сиденья, чтобы определить правильный угол .
Ознакомьтесь с инструкциями по изготовлению азиатских материалов для определения правильного значения .Какой правильный угол для лестницы?
Пясти: Сильная, сухая резинка с правильным углом .
Если нанести резкий удар под правильным углом , камень может полностью расколоться.
Устройство для установки и поддержки машин под правильным углом при установке наклонных болтов.
Dispositivo para situar y mantener las máquinas en el ángulo righto cuando están introduciendo bulones inclinados.Многие сиденья имеют индикатор угла наклона или могут быть отрегулированы до правильного угла .
Muchos asientos tienen un indicador de ángulo o se pueden ajustar al ángulo righto .С помощью силы я узнал, что если ударить старика по голове с правильного угла , его череп превратится в порошок.
Aprendí en la Fuerza que si le pegas a un . .. anciano en la cabeza en el ángulo righto … su cráneo se convierte en polvo.
.. anciano en la cabeza en el ángulo righto … su cráneo se convierte en polvo.Если капсула находится не под правильным углом … тупым концом и теплозащитным экраном вниз, она сгорит.
Si la cápsula no está en el ángulo righto , con la parte roma y el escudo térmico hacia abajo, se quemará.С двойной гироскопической системой устраняется нестабильность на поворотах, и транспортное средство будет крениться под правильным углом , так что на борту не будет ощущаться чистая боковая сила.
Con el sistema de doble giróscopo, se elimina la inestabilidad en las curvas y el vehículo se alinea con el ángulo correo , de modo que no se Experimente ninguna fuerza lateral neta a bordo. Система передает информацию в реальном времени в систему ЧПУ, которая настраивается для обеспечения правильного угла .
Следующим шагом в изготовлении хорошей детали с зазором заподлицо является обрезка края фанеры и несущей задней конструкции под правильным углом .
El siguiente paso para hacer una buena pieza de hueco a juego es cortar el borde de la madera contrachapada y la estructura posterior de apoyo en el ángulo correctiveo .При резке древесина может образовывать нечеткую или шерстяную поверхность, поэтому важно использовать острые лезвия, установленные под правильным углом , чтобы избежать этой проблемы.
La madera puede producir una superficie replosa o lanuda cuando se corta, por lo que es esencial utilizar cuchillas afiladas en el ángulo correctiveo para evitar este проблема.
Уловить момент, изолировать картинку, найти правильный угол — вот задачи, на которые я раньше не обращал особого внимания.
Capturar momentos, aislar imágenes, encontrar el ángulo righto eran cosas a las cuales no había prestado mucha atención en el pasado.Отталкивающее поле, конечно, должно лежать в абсолютном правильном угле к поверхности Земли.
El campo de rechazo por supuesto debe hallarse en el ángulo righto absoluto con la superficie de la Tierra.правильный угол кола, когда он входит в мое сердце?
Чувствительные устройства передают информацию в реальном времени в блок управления ЧПУ, который обрабатывает ее и впоследствии повторно вычисляет правильную регулировку глубины для получения правильного угла .
введите адрес электронной почты: |
Мысленное вычисление угла поправки на ветер
| Мысленное вычисление угла поправки на ветер Луис Роберто Монтейро де Оливейра © 2010 Луис Роберто Монтейру де Оливейра |
I — Введение
Навык, который дает огромное преимущество пилоту по приборам, — это способность мысленно оценивать в полете угол поправки на ветер (WCA), также известный как угол краба. В следующем разделе показано, как это сделать.
В следующем разделе показано, как это сделать.
Рис.1 Визуализация угла поправки на ветер (WCA)
Рис.1 — СОКРАЩЕНИЯ: CRS * : курс | Рис. 1 — УСЛОВИЯ: острый угол: угол меньше 90 o |
Угол поправки на ветер (WCA) — это угол между курсом (CRS) и курсом (HDG), который требуется воздушному судну для отслеживания этого курса при ветре (см. Рисунок 1).WCA в основном добавляется (когда ветер правый) или вычитается (когда ветер левый) к курсу. Результатом этого сложения или вычитания является курс, по которому пилот должен лететь, чтобы сохранить этот курс.
На рисунке 1 обратите внимание на следующее:
- Угол поправки на ветер (WCA) всегда находится на той же стороне линии CRS, что и направление ветра (WD).
- Курс (HDG) для отслеживания курса (CRS) всегда будет находиться где-то между CRS и направлением ветра (WD).
| * | При расчете WCA для желаемого трека (TRK) просто замените TRK вместо конечно (CRS) и используйте метод, описанный в этой статье. Тогда формула для заголовка будет следующей. Тогда формула для заголовка будет следующей. | |
II — Метод оценки угла поправки на ветер (WCA)
Шаг 1: Большинство самолетов имеют типичную крейсерскую скорость.Определите наиболее частую истинную воздушную скорость, на которой вы летите.
Шаг 2: Определите ваш максимальный угол поправки на ветер (WCA max ) для скорости ветра (WS) 10 узлов, используя приведенную ниже формулу при истинной воздушной скорости (TAS), которую вы только что получили выше (шаг 1) . Это будет WCA, когда направление ветра (WD) составляет 90 o по отношению к линии CRS. Точный максимальный угол поправки на ветер определяется по формуле:
где WS — скорость ветра, а TAS — истинная воздушная скорость самолета. Убедитесь, что ваш калькулятор находится в режиме DEG (градусов). В этом примере WS составляет 10 узлов, а TAS — 110 узлов. Следовательно, у нас будет:
Убедитесь, что ваш калькулятор находится в режиме DEG (градусов). В этом примере WS составляет 10 узлов, а TAS — 110 узлов. Следовательно, у нас будет:
, что означает, что в худшем случае, когда ветер составляет 90 o по отношению к желаемому курсу (так же, как AWA = 90 o ), угол поправки на ветер (WCA) составляет 5 o для ветер 10 узлов при нашей истинной скорости 110 узлов. Вы должны запомнить этот результат 5 o для вашего WCA max .
Шаг 3: Запомните несколько простых правил:
- Если скорость ветра удвоится, утроится и т. Д., Ваш угол поправки на ветер (WCA) будет приблизительно удвоен, утроен и т. Д. Соответственно. Это работает при скорости ветра до 50% от истинной воздушной скорости (TAS).
- Если скорость ветра уменьшится вдвое, на треть и т.
 Д., Ваш угол коррекции (WCA) будет примерно наполовину, одна треть и т. Д. Соответственно.
Д., Ваш угол коррекции (WCA) будет примерно наполовину, одна треть и т. Д. Соответственно. - Если истинная воздушная скорость вашего самолета (TAS) увеличивается вдвое, втрое и т. Д.поправка на ветер составит примерно половину, одну треть и т.д. соответственно от того, что было.
- , если истинная воздушная скорость (TAS) вашего самолета уменьшена вдвое, составляет одну треть и т. Д., Поправка на ветер будет приблизительно вдвое, утроена и т. Д. Соответственно по сравнению с тем, что было.
Причина, по которой мы использовали 10 узлов для скорости ветра (WS) при вычислении WCA max , заключается в том, что с этим числом легко работать позже, когда у нас будут другие скорости ветра. Например, если скорость ветра составляет 20 узлов, мы легко знаем, что 20 узлов в два раза больше, чем 10 узлов, поэтому угол поправки на ветер будет вдвое больше.
Шаг 4: Поправочный коэффициент основан на остром угле ветра (AWA).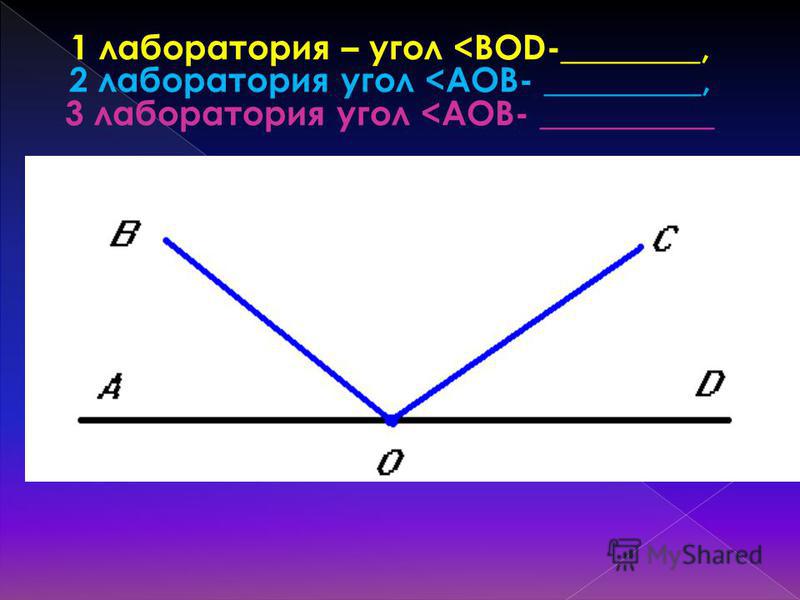 Это один из двух углов, в зависимости от того, какой из них составляет 90 o или меньше, образованных направлением ветра и линией CRS. Запомните поправочные коэффициенты для WCA, когда ветер дует с направления, отличного от 90 o по отношению к нашему курсу (AWA не равно 90 o ). В следующей таблице перечислены эти поправочные коэффициенты. Помните, что вы просто получаете очень приблизительное число, чтобы вы могли оценить свой начальный WCA (угол краба) при перехвате или отслеживании курса.
Это один из двух углов, в зависимости от того, какой из них составляет 90 o или меньше, образованных направлением ветра и линией CRS. Запомните поправочные коэффициенты для WCA, когда ветер дует с направления, отличного от 90 o по отношению к нашему курсу (AWA не равно 90 o ). В следующей таблице перечислены эти поправочные коэффициенты. Помните, что вы просто получаете очень приблизительное число, чтобы вы могли оценить свой начальный WCA (угол краба) при перехвате или отслеживании курса.
| или |
| ||||||||||||||||||||||||||||||||
| (а) | б) |
Рис.2 Поправочные коэффициенты для максимального угла поправки на ветер
Выше две таблицы, первая (слева) более полная и точная.Мы будем использовать менее точную таблицу справа для наших примеров. Вы увидите, что даже с этой более упрощенной таблицей мы получим довольно хорошую оценку.
Чтобы определить угол поправки на ветер (WCA), просто умножьте максимальный угол поправки на ветер на соответствующий коэффициент. Если скорость ветра такая же **, как при расчете WCA max ***, мы имеем:
| ** | Позже в тексте мы также обсудим, как регулировать скорость ветра, отличную от 10 узлов, которые мы использовали для нашего WCA max .Мы будем применять правила на шаге 3. Я также покажу вам, как визуализировать AWA с помощью инструментов вашего самолета. |
| *** | Примечание: точка (.) В приведенной выше формуле означает умножение. |
В таблице используйте AWA, наиболее близкое к имеющемуся у вас значению. Например: для AWA 33 o используйте поправочный коэффициент 30 o , который равен 1/2 или 0,5 (см. Рисунок 2b). Если вы рассчитали WCA max как 5 o , ваша WCA будет 5 o x 0.5 или 5/2 = 2,5 o . Округлите это до ближайшего градуса и получите расчетный угол коррекции 3 o .
Например: для AWA 33 o используйте поправочный коэффициент 30 o , который равен 1/2 или 0,5 (см. Рисунок 2b). Если вы рассчитали WCA max как 5 o , ваша WCA будет 5 o x 0.5 или 5/2 = 2,5 o . Округлите это до ближайшего градуса и получите расчетный угол коррекции 3 o .
Вы можете сравнить свой расчетный угол поправки на ветер (WCA) с приведенной ниже формулой (эта формула является точной), чтобы определить, как далеко вы находитесь. Помните, что ваша цель, используя описанную выше технику, — просто получить приблизительное представление о том, каков угол поправки на ветер, он не обязательно должен быть точным.
III — Применение метода
Пример:
Если ваша типичная крейсерская истинная скорость вашего самолета составляет 130 узлов. Оцените угол поправки на ветер (WCA) для следующих условий:
Оцените угол поправки на ветер (WCA) для следующих условий:
а) WS = 10 узлов; AWA = 40 o
б) WS = 20 узлов; AWA = 40 o
в) WS = 5 узлов; AWA = 40 o
г) WS = 10 узлов; AWA = 70 o
д) WS = 30 узлов; AWA = 90 o
е) WS = 20 узлов; AWA = 10 o
ж) WS = 27 узлов; AWA = 60 o
з) WS = 3 узла; AWA = 45 o
i) WS = 12 узлов; AWA = 20 o
к) WS = 48 узлов; AWA = 70 o
л) WS = 63 узла; AWA = 25 o
Раствор:
| Шаг 1: Мы знаем, что типичная крейсерская скорость составляет 130 узлов TAS. | |||
| Шаг 2: Рассчитайте максимальный угол поправки на ветер, используя формулу ниже для скорости ветра (WS) 10 узлов: заменяя 130 узлов на TAS и 10 узлов на WS, получаем: Результат максимального угла поправки (WCA max ), равный 4 o , будет основой для всех наших оценок углов поправки на ветер (WCA), когда истинная скорость самолета составляет около 130 узлов. |
Оценка каждой части с помощью метода вычисления в уме:
а) WS = 10 узлов; AWA = 40 o
| Шаг 3: Поскольку WS в 10 узлов совпадает с 10 узлами, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет таким же : 4 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 40 o . Если использовать таблицу справа, 40 o находится прямо посередине между 30 o и 50 o . Если он посередине, выберите значение для следующего по величине, которое будет от 50 до . Коэффициент равен 3/4 или 0,75. Следовательно, наша оценка поправки на ветер будет 4 o x 0.75 = 3 o . Следовательно, наша оценка поправки на ветер будет 4 o x 0.75 = 3 o . |
б) WS = 20 узлов; AWA = 40 o
| Шаг 3: Поскольку WS 20 узлов вдвое больше, чем 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет удвоен: 4 o x 2 = 8 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 40 o .Если использовать таблицу справа, 40 o находится прямо посередине между 30 o и 50 o . Если он посередине, выберите значение для следующего по величине, которое будет от 50 до . Коэффициент равен 3/4 или 0,75. Следовательно, наша расчетная поправка на ветер будет 8 o x 0,75 = 6 o . Коэффициент равен 3/4 или 0,75. Следовательно, наша расчетная поправка на ветер будет 8 o x 0,75 = 6 o . |
в) WS = 5 узлов; AWA = 40 o
| Шаг 3: Поскольку WS, равная 5 узлам, составляет половину от 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет уменьшен вдвое: 4 o /2 = 2 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 40 o . Если использовать таблицу справа, 40 o находится прямо посередине между 30 o и 50 o . Если он посередине, выберите значение для следующего по величине, которое будет от 50 до .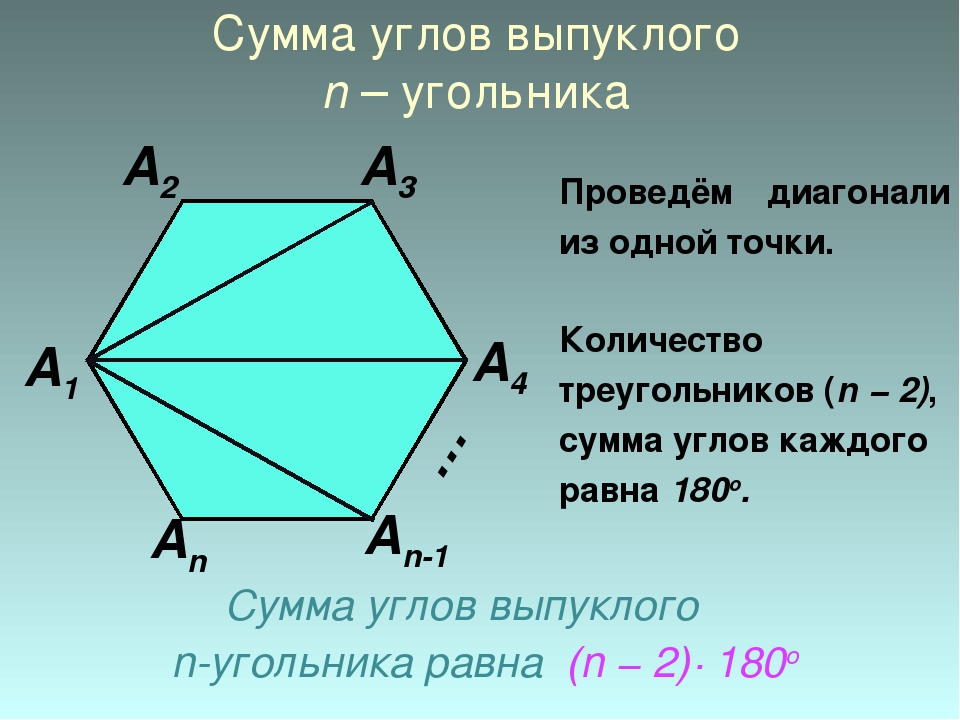 Коэффициент равен 3/4 или 0,75. Следовательно, наша расчетная поправка на ветер будет 2 o x 0.75 = 1,5 o . Вы можете округлить это до 2 или . Коэффициент равен 3/4 или 0,75. Следовательно, наша расчетная поправка на ветер будет 2 o x 0.75 = 1,5 o . Вы можете округлить это до 2 или . |
г) WS = 10 узлов; AWA = 70 o
| Шаг 3: Поскольку WS в 10 узлов совпадает с 10 узлами, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет таким же : 4 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 70 o .Если мы воспользуемся таблицей справа, 70 o будет множителем 1. Следовательно, наша расчетная поправка на ветер будет 4 o x 1 = 4 o . |
д) WS = 30 узлов; AWA = 90 o
| Шаг 3: Поскольку WS 30 узлов в три раза больше 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет утроен: 4 o x 3 = 12 o . | |
| Шаг 4: Поскольку направление ветра составляет 90 o по отношению к нашему курсу, угол поправки на ветер будет максимальным. Следовательно, WCA = 12 o . |
е) WS = 20 узлов; AWA = 10 o
Шаг 3: Поскольку WS 20 узлов вдвое больше, чем 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет удвоен: 4 o x 2 = 8 o . | |
| Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 10 o . В этом случае это будет 0 o . Коэффициент равен 0. Следовательно, наша оценка поправки на ветер будет 0 o . |
г) WS = 27 узлов; AWA = 63 o
| Шаг 3: Округлите WS до ближайшего кратного 5, поэтому для WS 27 узлов мы будем рассчитывать, как если бы WS составляла 25 узлов.Так как WS 25 узлов в 2,5 или 2 1/2 раза больше 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет 2 1/2 умноженное на: 4 o x (2 + 1/2) = 8 o + 2 o = 10 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 63 o . Если мы воспользуемся таблицей справа, 60 o будет множителем 1. Следовательно, наша расчетная поправка на ветер будет 10 o x 1 = 10 o . Если мы воспользуемся таблицей справа, 60 o будет множителем 1. Следовательно, наша расчетная поправка на ветер будет 10 o x 1 = 10 o . |
ч) WS = 3 узла; AWA = 45
| Шаг 3: Для скорости ветра меньше 5 узлов я бы, вероятно, просто проигнорировал их и предположил, что WCA составляет 0 o . Однако мы должны были использовать этот метод, округляя WS до ближайшего кратного 5, поэтому для WS, равного 3 узлам, мы будем рассчитывать, как если бы WS составляла 5 узлов.Поскольку WS 5 узлов составляет половину от 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет уменьшен вдвое: 4 o /2 = 2 или . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 45 o . Если мы воспользуемся таблицей справа, 50 o будет множителем 3/4 или 0.75. Следовательно, наша расчетная поправка на ветер будет 2 o x 0,75 = 1,5 o . Вы можете округлить это до 2 или . Если мы воспользуемся таблицей справа, 50 o будет множителем 3/4 или 0.75. Следовательно, наша расчетная поправка на ветер будет 2 o x 0,75 = 1,5 o . Вы можете округлить это до 2 или . |
i) WS = 12 узлов; AWA = 20 o
| Шаг 3: Округлите WS до ближайшего кратного 5, поэтому для WS, равного 12 узлам, мы рассчитаем, как если бы WS составляла 10 узлов. Поскольку WS в 10 узлов совпадает с 10 узлами, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет таким же: 4 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 20 o . Если мы воспользуемся таблицей справа, 30 o будет множителем 1/2 или 0,5. Следовательно, наша расчетная поправка на ветер будет 4 o x 1/2 = 2 o . Если мы воспользуемся таблицей справа, 30 o будет множителем 1/2 или 0,5. Следовательно, наша расчетная поправка на ветер будет 4 o x 1/2 = 2 o . |
j) WS = 48 узлов; AWA = 70 o
| Шаг 3: Округлите WS до ближайшего кратного 5, поэтому для WS 48 узлов мы будем рассчитывать, как если бы WS составляла 50 узлов.Поскольку WS 50 узлов в пять раз больше 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет в пять раз больше: 4 o x 5 = 20 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 70 o . Если мы воспользуемся таблицей справа, 60 o будет множителем 1.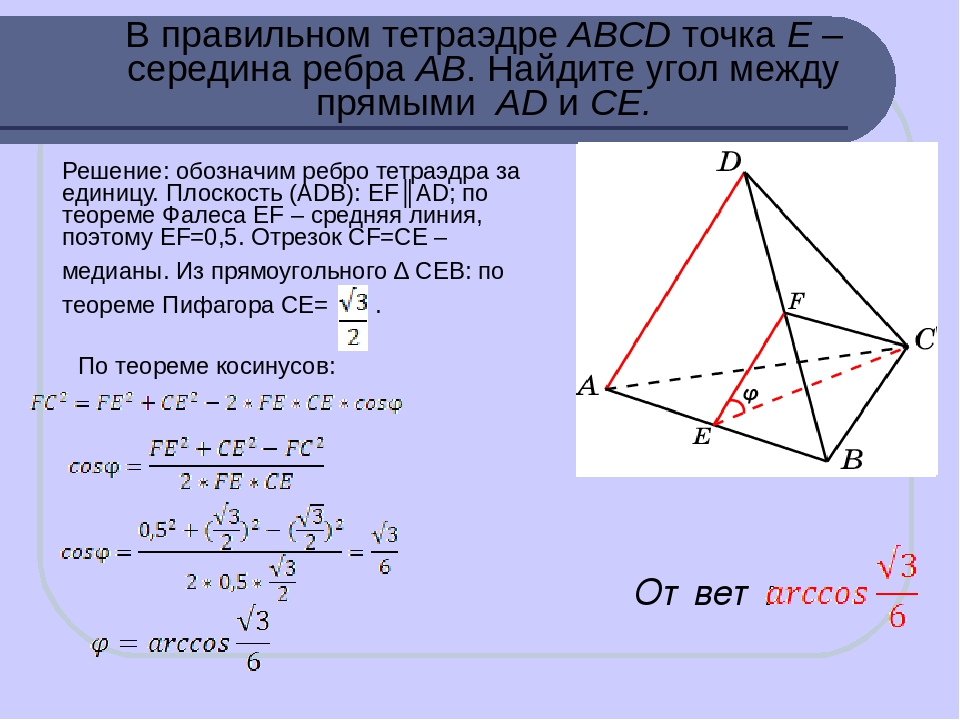 Следовательно, наша расчетная поправка на ветер будет составлять 20 o x 1 = 20 o . Следовательно, наша расчетная поправка на ветер будет составлять 20 o x 1 = 20 o . |
л) WS = 63 узла; AWA = 25 o
| Шаг 3: Округлите WS до ближайшего значения, кратного 5, поэтому для WS, равного 63 узлам, мы будем рассчитывать, как если бы WS составляла 65 узлов. Поскольку WS 65 узлов в 6 с половиной раз больше, чем 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет 6 и 1/2. больше: 4 o x (6 + 1/2) = 24 o +2 o = 26 o . | |
Шаг 4: Затем мы смотрим на таблицу на рисунке 2b и видим, какое значение ближе всего к 25 o . Если мы воспользуемся таблицей справа, 30 o будет множителем 1/2 или 0,5. Следовательно, наша расчетная поправка на ветер будет 26 o x 1/2 = 13 o . Если мы воспользуемся таблицей справа, 30 o будет множителем 1/2 или 0,5. Следовательно, наша расчетная поправка на ветер будет 26 o x 1/2 = 13 o . |
IV — Сравнение метода мысленной оценки с точной формулой
Хотя использование точной формулы для расчета WCA лишит смысла выполнение мысленной оценки, мы можем использовать ее здесь, чтобы сравнить и увидеть, насколько близки были наши оценки.Следующая формула дает точный результат:
а) WS = 10 узлов; AWA = 40 o .
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 3 o . Это тот же результат, который мы получили при мысленной оценке.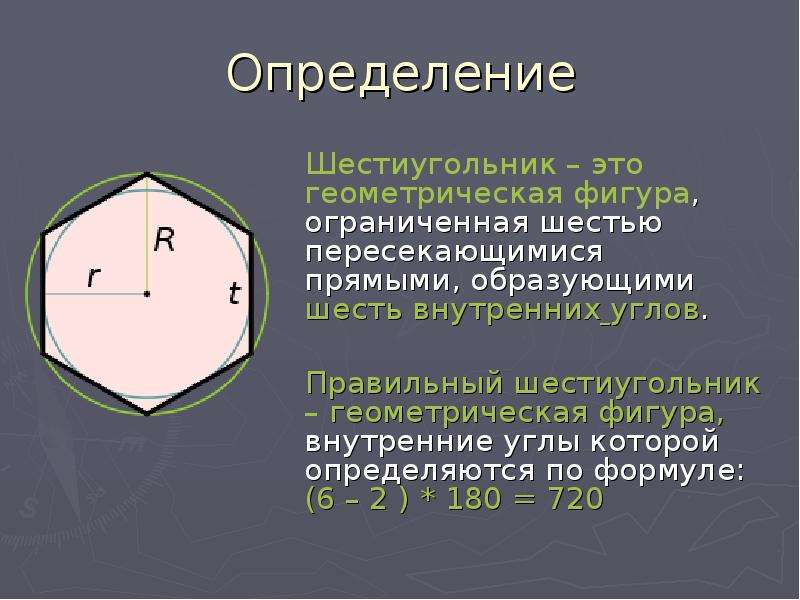
б) WS = 20 узлов; AWA = 40 o .
WCA, рассчитанная по формуле, составляет 6 o . Это тот же результат, который мы получили при мысленной оценке.
в) WS = 5 узлов; AWA = 40 o .
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 1 o . Этот результат, который мы получили, используя мысленную оценку, был 2 o , поэтому мы отклонились на 1 o .
г) WS = 10 узлов; AWA = 70 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 4 o . Это тот же результат, который мы получили при мысленной оценке.
Это тот же результат, который мы получили при мысленной оценке.
д) WS = 30 узлов; AWA = 90 o .
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 13 o .Этот результат, который мы получили, используя мысленную оценку, был 12 o , поэтому мы отклонились на 1 o .
е) WS = 20 узлов; AWA = 10 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 0 o . Этот результат, который мы получили, используя мысленную оценку, был 2 o , поэтому мы отклонились на 2 o .
ж) WS = 27 узлов; AWA = 63 o .
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 11 o . Этот результат, который мы получили, используя мысленную оценку, был 10 o , поэтому мы отклонились на 1 o .
з) WS = 3 узла; AWA = 45 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 1 o .Этот результат, который мы получили, используя мысленную оценку, был 2 o , поэтому мы отклонились на 1 o .
и) 12 узлов; AWA = 20 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 2 o .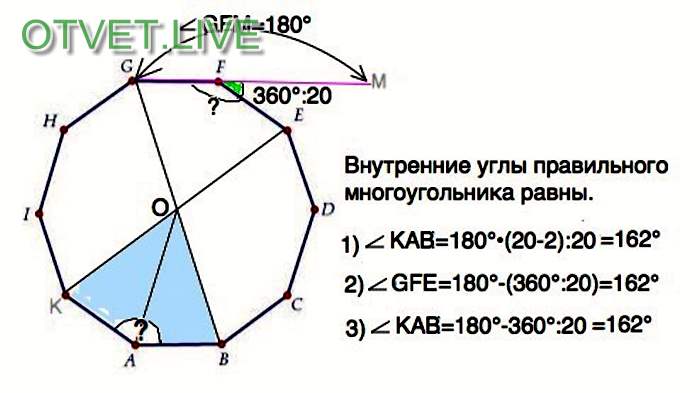 Это тот же результат, который мы получили при мысленной оценке.
Это тот же результат, который мы получили при мысленной оценке.
к) WS = 48 узлов; AWA = 70 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 20 o .Это тот же результат, который мы получили при мысленной оценке.
л) WS = 63 узла; AWA = 25 o
Подставляя значения в уравнение:
WCA, рассчитанная по формуле, составляет 12 o . Этот результат, который мы получили, используя мысленную оценку, был 13 o , поэтому мы отклонились на 1 o .
Обратите внимание, насколько близки были наши оценки, даже с использованием более простой таблицы справа для поправки AWA!
V — Техника визуализации ветра во время полета
Во время полета пилот должен будет визуализировать направление ветра по отношению к курсу и курсу самолета. Ниже приведены несколько советов, как это сделать и выяснить, что такое AWA.
Ниже приведены несколько советов, как это сделать и выяснить, что такое AWA.
Ошибка заголовка
Рис. 3 Ошибка направления на индикаторе направления (a), аналоговом HSI (b) и цифровом HSI (c).
Если ошибка курса (рис. 3) не используется автопилотом или по другим причинам, ошибка курса может быть настроена так, чтобы напоминать пилоту, где дует ветер.
Визуализация AWA перед перехватом курса (CRS)
Рис. 4 Визуализация AWA с использованием указателя курса для правого встречного ветра.
На рис. 4 показано, как ошибку курса можно использовать на указателе курса, чтобы напомнить пилоту, откуда дует ветер. В этом случае направление ветра (WD) от 090. Если, например, курс (CRS), по которому будет осуществляться навигация, равен 040, пилот может визуализировать отметку 040 на указателе курса, которая соответствует этому курсу.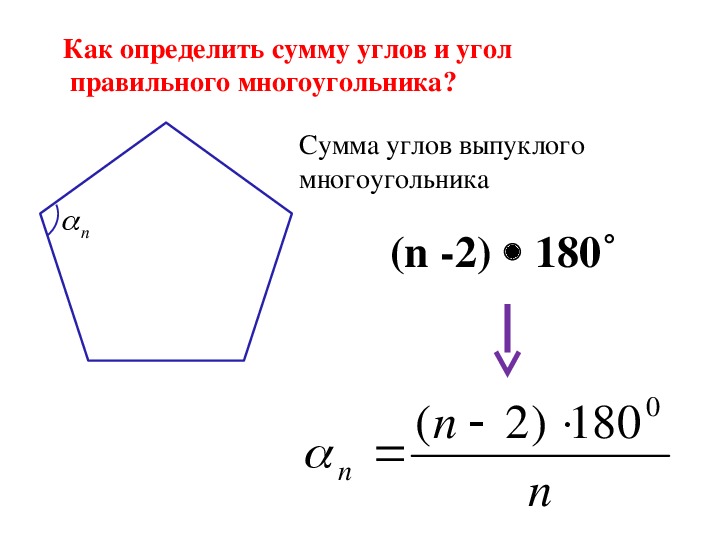 В этом случае ветер дует спереди (встречный), поэтому угол между курсом (CRS) и ветром (WD) будет острым углом ветра (AWA).Если бы ветер был попутным, AWA было бы углом между обратной величиной курса (CRS + 180) и направлением ветра (WD).
В этом случае ветер дует спереди (встречный), поэтому угол между курсом (CRS) и ветром (WD) будет острым углом ветра (AWA).Если бы ветер был попутным, AWA было бы углом между обратной величиной курса (CRS + 180) и направлением ветра (WD).
Знание AWA позволяет рассчитать, используя методы, описанные в предыдущих параграфах, угол поправки на ветер (WCA). После того, как пилот перехватил курс (CRS), WCA может быть добавлен или вычтен из CRS для определения курса (HDG), необходимого для сохранения этого курса и компенсации ветра. В этом конкретном примере, поскольку CRS — 040, а WD — 090, AWA составляет 90-40 = 50 o .
| (а) | б) |
Рис. 5 Визуализация AWA с использованием аналогового (a) и цифрового (b) HSI для правого встречного ветра.
На рис. 5 показано, как визуализировать AWA вышеуказанного сценария на аналоговом и цифровом HSI.Если по какой-то причине ошибка курса используется для чего-то еще, пилот может вместо этого мысленно отметить, где дует ветер. Общее представление о ветре имеет решающее значение для плавной и точной навигации.
Если скорость ветра (WS) в этом примере составляет 40 узлов, а истинная воздушная скорость (TAS) составляет 110 узлов. Рассчитайте угол поправки на ветер (WCA).
Сначала подведем итоги информации, которая у нас есть и которой нет:
CRS = 040
WD = 090
WS = 40 узлов
AWA = 50 o
TAS =
110 узлов
WCA max для ветра 10 узлов =?
WCA =?
Чтобы использовать наш метод мысленного вычисления угла поправки на ветер (WCA), мы должны сначала вычислить и запомнить максимальную поправку на ветер (WCA max ) для ветра 10 узлов при нашей типичной истинной воздушной скорости (TAS) 110 узлов.
Максимальный угол поправки на ветер определяется по формуле:
где WS — скорость ветра, а TAS — истинная воздушная скорость самолета. Убедитесь, что ваш калькулятор находится в режиме DEG (градусов). В том случае, если фактическая WS составляет 40 узлов, мы будем использовать 10 узлов для расчета нашей базы (WCA max ). Помните, что нам нужно будет сделать это только один раз, и тогда он будет служить основой для любого расчета WCA для нашей типичной истинной воздушной скорости.
Это означает, что в худшем случае для ветра 10 узлов, когда направление ветра составляет 90 o относительно нашего желаемого курса, угол поправки на ветер (WCA) составляет 5 o . Следовательно, WCA max для ветра 10 узлов = 5 o .
Давайте теперь посчитаем WCA: WS = 40 узлов; AWA = 50 o . Начните с округления WS до ближайшего числа, кратного 5, так что для WS, равного 40 узлам, мы уже имеем его кратное 5.Поскольку WS 40 узлов в четыре раза больше 10 узлов, которые мы использовали для расчета максимального угла поправки на ветер (WCA max ), наш максимальный угол поправки на ветер для этой скорости ветра будет увеличен в четыре раза: 5 o x 4 = 20 или . Затем мы смотрим на таблицу на рисунке 2 (b) и видим, какое значение ближе всего к 50 o . Если мы воспользуемся таблицей справа, 50 o будет множителем 3/4 или 0,75. Поэтому наша расчетная поправка на ветер: WCA = 20 o x 3/4 = 15 o .
Визуализация угла поправки на ветер (WCA) однажды установленный на курсе (CRS)
Рис. 6 Визуализация WCA, установленной на курсе (CRS).
Стрелка прибора VOR один раз центрируется по курсу (рисунок 6). Если в этот момент самолет движется по правильному курсу для сохранения курса (держите стрелку в центре), разница между курсом и этим курсом будет равна углу поправки на ветер (WCA).На практике пилот, который мысленно рассчитал угол поправки на ветер, сможет оценить, что это за курс, добавив или вычтя WCA из CRS. В этом случае ветер дует справа от курса, поэтому WCA будет добавлена к CRS для получения курса (HDG). В частности, в приведенном выше примере CRS равен 040, а мысленно рассчитанный WCA равен 15 o , следовательно: HDG = 040 + 15 o = 055.
Ранее при перехвате курса 040 пилот будет маневрировать таким образом, чтобы самолет находился на курсе 055, когда стрелка прибора VOR находится в центре.Находясь на курсе, пилоту, возможно, придется внести незначительные поправки в курс самолета, чтобы стрелка оставалась в центре. Это сделано для исправления фактического ветра, который может отличаться от прогнозируемого ветра, или для ошибки в мысленном вычислении АВП. В этом примере точное значение WCA составляет 16 или . Эта разница в 1 o — это небольшая корректировка, которую должен был сделать пилот. Следовательно, пилот сейчас летит с HDG: 040 + 16 o = 056.
| (а) | б) |
Рис. 7 Визуализация WVA и AWA с использованием аналогового (a) и цифрового (b) HSI.
На рисунке 7 показано, как визуализировать WCA и AWA вышеуказанного сценария на аналоговом и цифровом HSI.
Другие примеры ветров с других направлений
Ниже приведены несколько других примеров того, как визуализировать угол поправки на ветер (WCA) и острый угол ветра относительно линии курса (AWA) для ветров, дующих с других направлений. Примеры намеренно имеют одинаковый AWA 50 o , чтобы мы могли использовать тот же WCA 16 o , который уже был рассчитан.
Пример 2
Рис. 8 Визуализация правого попутного ветра с помощью прибора VOR и указателя курса.
| (а) | б) |
Рис. 9 Визуализация правого попутного ветра с помощью аналогового (a) и цифрового (b) прибора HSI.
На рисунках 8 и 9 мы имеем следующую конфигурацию:
CRS = 040
WD = 170 (правый попутный ветер)
Ответный курс (CRS + 180) = 220
AWA = 50 o
WCA = 16 o
HDG = 040 + 16 o = 056
Пример 3
Рис. 10 Визуализация встречного ветра влево с помощью прибора VOR и указателя направления.
| (а) | б) |
Рис. 11 Визуализация левого встречного ветра с помощью аналогового (a) и цифрового (b) прибора HSI.
На рисунках 10 и 11 мы имеем следующую конфигурацию:
CRS = 040
WD = 350 (левый встречный ветер)
AWA = 50 o
WCA = 16 o
HDG = 040 — 16 o = 024
Пример 4
Рис. 12 Визуализация левого попутного ветра с помощью прибора VOR и указателя курса.
| (а) | б) |
Рис.


 (Точка пересечения медиан называется центроидом)
(Точка пересечения медиан называется центроидом)
 Д., Ваш угол коррекции (WCA) будет примерно наполовину, одна треть и т. Д. Соответственно.
Д., Ваш угол коррекции (WCA) будет примерно наполовину, одна треть и т. Д. Соответственно. 5
5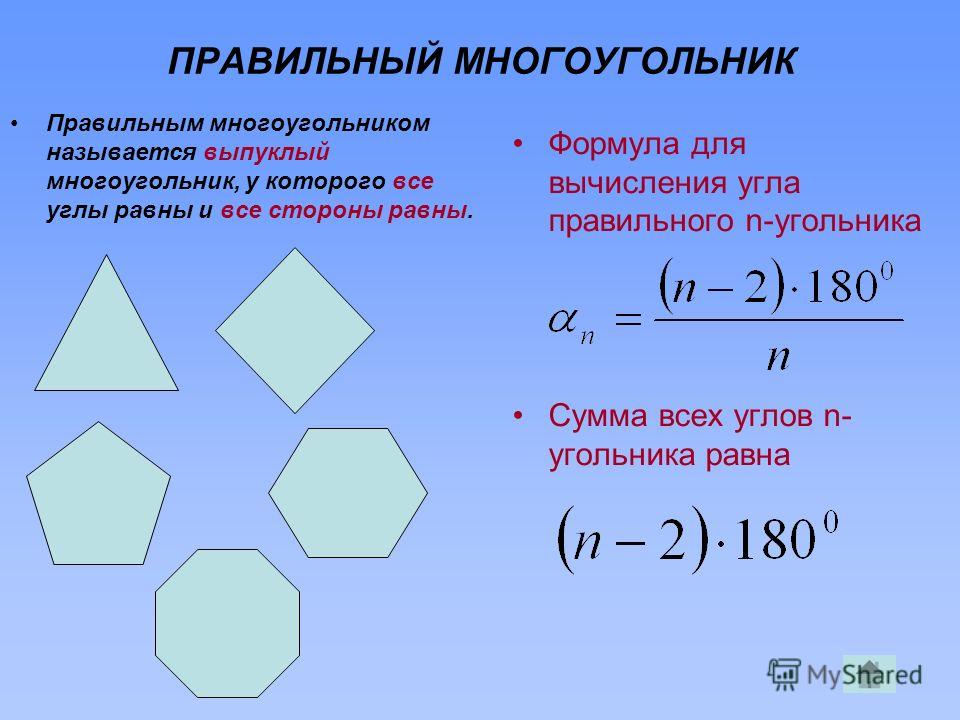 5
5