Правильный шестиугольник — Карта знаний
- Правильный шестиугольник (гексагон) — правильный многоугольник с шестью сторонами.
Источник: Википедия
Связанные понятия
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами. Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Упоминания в литературе
Действительно, семь из 13 Архимедовых тел могут быть получены отрезанием кусочков от Платоновых тел – среди этих многогранников и классический футбольный мяч из пятиугольников и шестиугольников.
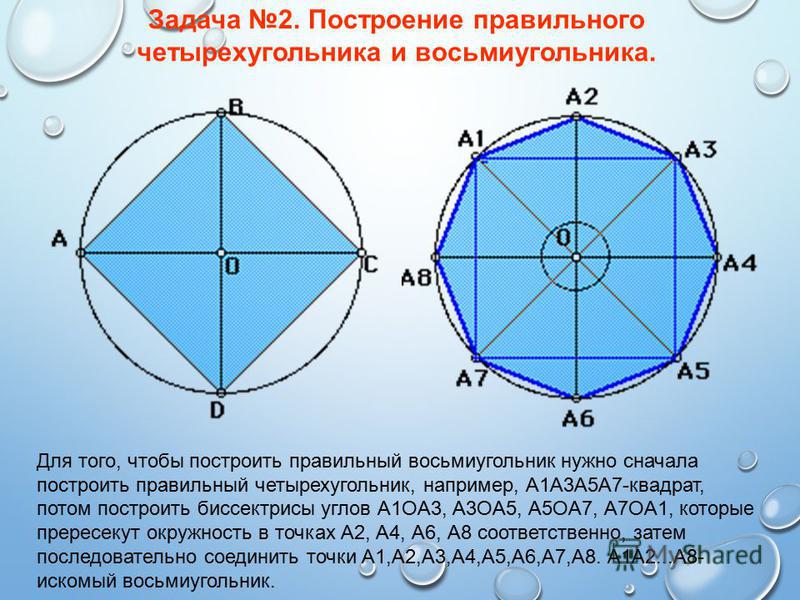
Связанные понятия (продолжение)
В геометрии пространственный многоугольник — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется. Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны. Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность.
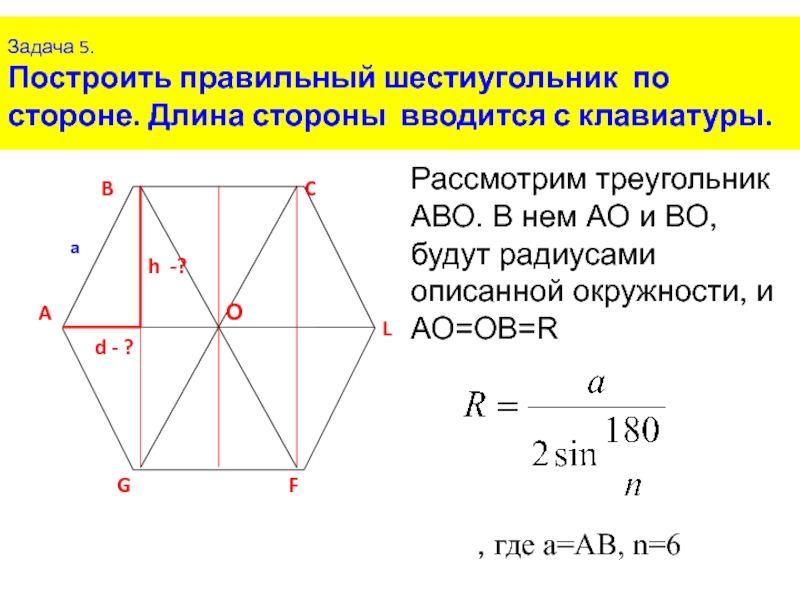Формулировка гипотезы…
Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.
Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.
В геометрии семиугольная мозаика — это правильная мозаика на гиперболической плоскости. Она представляется cимволом Шлефли {7,3} и имеет три правильных семиугольника в каждой вершине.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.
-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
Квадратная антипризма — это второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Квадратная антипризма известна также как антикуб.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
Звёздчатый многогра́нник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).
Многогранник, двойственный (или дуальный) к заданному многограннику — многогранник, у которого каждой грани исходного многогранника соответствует вершина двойственного, каждой вершине исходного — грань двойственного и каждому ребру исходного — ребро двойственного.
Многогранник, двойственный двойственному, гомотетичен исходному.
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник (архимедово тело) с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию (что эквивалентно повороту на 180°), усечённый кубооктаэдр является зоноэдром.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5). Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум.
..
Шестиуго́льный парке́т (шестиугольный паркета́ж) или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой.
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.
Лемма о трезубце или теорема трилистника, или лемма Мансиона (жарг. лемма о куриной лапке) — теорема в геометрии треугольника.
При́зма (лат. prisma от др.-греч. πρίσμα «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Обобщённый многоугольник — это структура инцидентности, предложенная Жаком Титсом в 1959 году. Обобщённые n-угольники вмещают в качестве частных случаев проективные плоскости (обобщённые треугольники, n=3) и обобщённые четырёхугольники (n=4). Многие обобщённые многоугольники получаются из групп типа Ли, но существуют некоторые экзотические обобщённые многоугольники, которые таким способом не получаются. Обобщённые многоугольники, удовлетворяющие условию, известному как свойство Муфанга, полностью…
Растянутый многоугольник серединных точек вписанного многоугольника P — это другой вписанный в ту же самую окружность многоугольник, вершины которого являются серединами дуг между вершинами многоугольника P. Многоугольник может быть получен из серединного многоугольника (многоугольника, вершины которого лежат в серединах сторон), если провести радиусы из центра окружности через вершины серединного многоугольника.
В геометрии трёхскатный купол представляет собой один из многогранников Джонсона (J3 = (по Залгаллеру) М4). Купол можно рассматривать как половину кубооктаэдра.
В геометрии n-угольный осоэдр — это такая мозаика из двуугольников на сферической поверхности, что каждый такой двуугольник имеет две общие вершины (противоположные точки сферы) с другими двуугольниками.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.Подробнее: Правильный четырёхмерный многогранник
Правильная шестиугольная призма
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.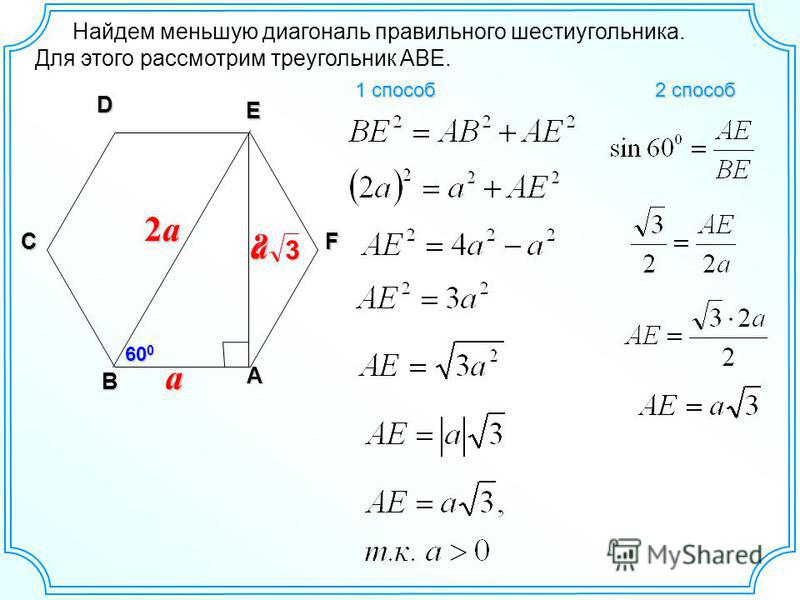
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник. Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов. Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6). Ещё вам пригодится навык извлечения квадратного корня их большого числа.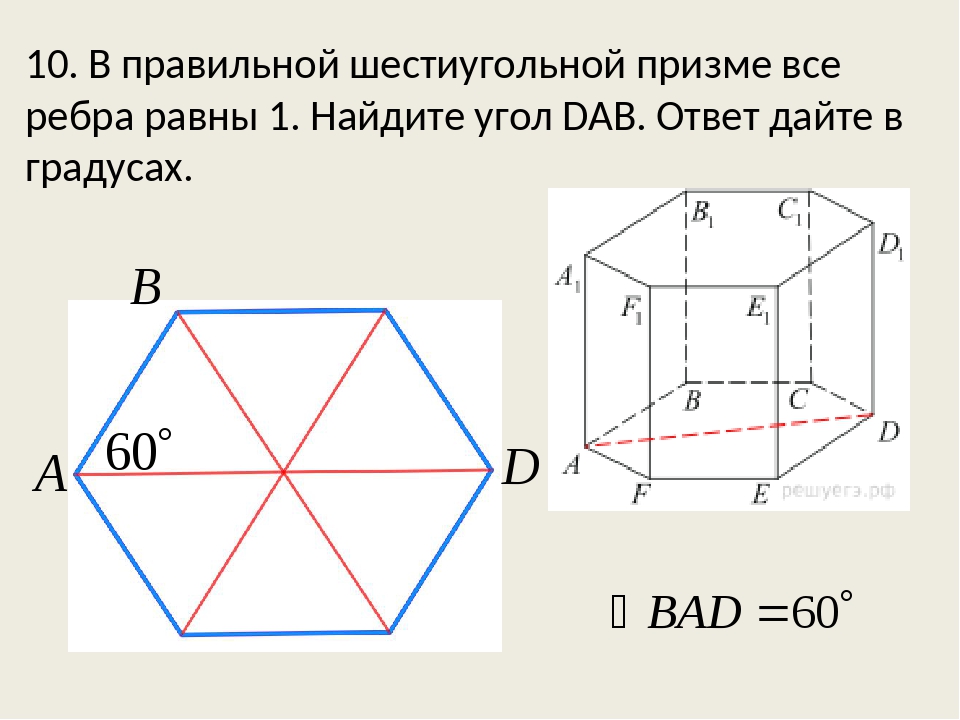
Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны.
*Противолежащие стороны параллельны.
Дополнительная информация
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 600 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
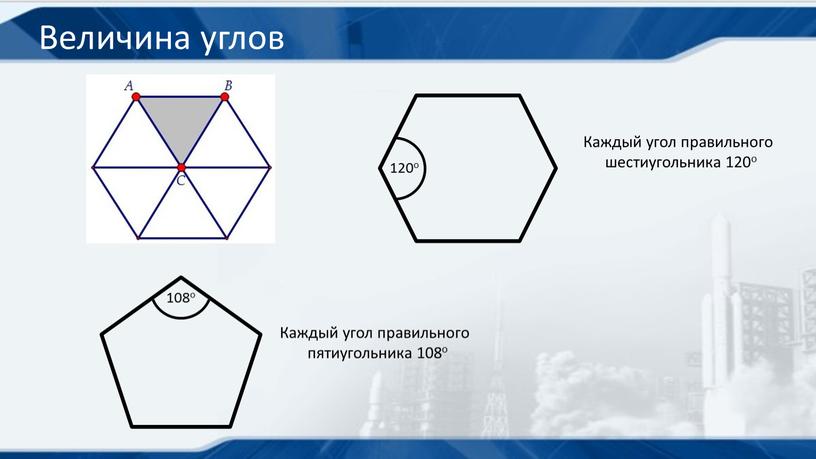
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
Рассмотрим задачи:
272533. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA1E1. По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ1 является гипотенузой, АА1 и А1Е1 катеты. Ребро АА1 нам известно. Катет А1Е1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно
По теореме Пифагора:
Ответ: 96
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
Таким образом,
Ответ: 70
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB1E1. По теореме Пифагора:
Отрезок B1E1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
Таким образом,
Ответ: 200
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Таким образом,
Ответ: 2
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
Ответ: 60
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC. В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Таким образом,
Значит, угол AC1C равен 60 градусам.
Ответ: 60
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС1С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
Следовательно
Таким образом:
Ответ: 60
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
Посмотреть решение
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
Посмотреть решение
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
Посмотреть решение
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
Посмотреть решение
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Посмотреть решение
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Посмотреть решение
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Построить правильный 6 угольник по его апофеме
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
n=6 число сторон и вершин правильного шестиугольника, шт α центральный угол правильного шестиугольника, радианы, ° β половина внутреннего угла правильного шестиугольника, радианы, ° γ внутренний угол правильного шестиугольника, радианы, ° a сторона правильного шестиугольника, м R радиусы правильного шестиугольника, м p полупериметр правильного шестиугольника, м L периметр правильного шестиугольника, м h апофемы правильного шестиугольника, м Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Растянутый шестиугольник — Калькулятор геометрии
1D линия 2D правильных многоугольников:
равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, многоугольник кольцодругие многоугольники:
треугольник, прямоугольный треугольник, равнобедренный треугольник ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, воздушный змей, воздушный змей, правая трапеция, равнобедренная трапеция, треугольная равносторонняя трапеция, трапеция, циклический четырехугольник, тангенциальный четырехугольник, стрелка, вогнутый четырехугольник, крест Антипараллелограмм, Форма дома, Симметричный пятиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Параллелогон, Вытянутый шестиугольник, Вогнутый шестиугольник, Стрелка-шестиугольник, Прямоугольный шестиугольник, L-образная форма, Острый перегиб, T-образная форма, Усеченный квадрат, Рамка, Открытая рамка, сетка, крест, форма X, форма H, тройная звезда, четыре звезды, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, двойная звезда, многоугольник, многоугольник, многоугольник90 004 Круглые формы:
3D Платоновых тел:
Круг, Полукруг, Круговой сектор, Круговой сегмент, Круговой слой, Круговой центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Остроконечный овал, Ланцетная арка, Бугорок, Кольцо, Кольцевой сектор , Изогнутый прямоугольник, закругленный многоугольник, закругленный прямоугольник, эллипс, полуэллипс, эллиптический сегмент, эллиптический сектор, эллиптическое кольцо, стадион, спираль, бревно.Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круговой квадрат, Дигон, Сферический треугольник
тетраэдр, куб, октаэдр, додекаэдр, икосаэдрархимедова Solids:
усеченный тетраэдр, кубооктаэдр, усеченный куб, усеченный октаэдр, ромбокубооктаэдр, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, Snub куб, ромбоикосододекаэдр , Усеченный икосододекаэдр, Snub ДодекаэдрКаталонских Сухой остаток:
триакистетраэдр, ромбический додекаэдр, триакисоктаэдр, тетракисгексаэдр, дельтоидальный икоситетраэдр, гексакис октаэдр, ромбический триаконтаэдр, триакисикосаэдр, пентакисдодекаэдр, Пятиугольные Icositetrahedron, дельтоидальный гексеконтаэдр, гексакис Икосаэдр, Пятиугольный гексеконтаэдрТвердые тела Джонсона:
Пирамиды, купола, ротонда, удлиненные пирамиды, гиро-продолговатые пирамиды, бипирамиды, удлиненные бипирамиды, гиро-продолговатая квадратная дипирамида, гиробифастигениум, дисфагениум Sphenocorona, DisphenocingulumДругие многогранники:
Кубоид, квадратный столб, треугольная пирамида, квадратная пирамида, правильная пирамида, пирамида, правильная пирамида, конус, правильная бипирамида, бипирамида, бифрустум, клин-фрустум, клин-фрустум Полутетраэдр, ромбоэдр, параллелепипед, правильная призма, призма, наклонная призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клин-кубоид, полукубоид, скошенный кубоид, слиток, скошенная трехгранная призма , Усеченный кубоид, Кубоид с тупыми краями, Удлиненный додекаэдр, Усеченный ромбоэдр,Правильный шестиугольник — определение правильного шестиугольника в The Free Dictionary
«Вместо того, чтобы использовать квадрат или прямоугольник, как это делалось до сих пор, вы предположите, что ваше место заключено в правильный шестиугольник, причем преимущество этого многоугольника состоит в том, что он предлагает больше углов, чем четырехугольник.Мы с ле Виконт де Шаньи были заключены в правильный шестиугольник, полностью выровненный с зеркалами. Тем не менее, мы встречаем правильный шестиугольник, выровненный по песку. Ясно [6,1] и [6,5] образуют правильный шестиугольник, но [6, 2], [6,3] и [6,4] не образуют правильных звездообразных многоугольников. Таблица 1 Пример таблицы наблюдения многоугольника Многоугольник Нечетный или четный # Степень симметрии вращения вершин Равносторонний треугольник Нечетный 3 Квадратный Четный 4 Правильный пятиугольник Нечетный 5 Обычный шестиугольник Четный 6 Правильный семиугольник Нечетный 7 Правильный восьмиугольник Четный 8 Градусов многоугольника на Наборы параллельных сторон поворота Равносторонний треугольник 120 0 Квадрат 90 2 Правильный пятиугольник 72 0 Правильный шестиугольник 60 3 Правильный семиугольник [приблизительно равен] 51.4 0 Правильный восьмиугольник 45 4 Многоугольника Наборы параллельных диагоналей? Следовательно, мы должны расширить каждую точку дефекта до модели правильной поверхности шестиугольника, как показано на рисунке 6. Таким образом, метрически корона произвольной вершины x выглядит следующим образом (см. Рисунок 4) : правильный шестиугольник, два равных параллелограмма, которые касаются x под разными углами (или равны, если и только если они являются прямоугольниками), и правильный треугольник. В этой статье мы предлагаем алгоритм локализации с помощью мобильного якоря, основанный на правильном шестиугольнике (MAALRH) с целью максимального увеличения коэффициента локализации и точности локализации.Первый — это фаза обнаружения, когда датчик в центре правильного шестиугольника пытается обнаружить событие. Давайте соединим смежные концы этих сегментов так, чтобы с каждой стороны икосаэдра образовался аффинный правильный шестиугольник, а аффинный правильный пятиугольник появляется в окрестности каждой вершины икосаэдра (рис. 3). Чтобы подтвердить эту точку зрения, были выбраны и исследованы два дополнительных СШП PMA с типичными формами участков скошенного прямоугольника и правильного шестиугольника, как показано на рис.Теоретически, если плоская область разделена на несколько правильных многоугольников без зазоров, есть только три способа: правильный треугольник, квадрат и правильный шестиугольник. По соотношению площади и периметра правильный треугольник 0,144, квадрат 0,25, правильный шестиугольник составляет максимум 0,433.Язык регулярных выражений — Краткий справочник
- 10 минут на чтение
В этой статье
Регулярное выражение — это шаблон, которому обработчик регулярных выражений пытается сопоставить входной текст.Шаблон состоит из одного или нескольких символьных литералов, операторов или конструкций. Краткое введение см. В разделе Регулярные выражения .NET.
В каждом разделе этого краткого справочника перечислены определенные категории символов, операторов и конструкций, которые можно использовать для определения регулярных выражений.
Мы также предоставили эту информацию в двух форматах, которые вы можете скачать и распечатать для удобства:
Персонаж сбегает
Символ обратной косой черты (\) в регулярном выражении означает, что следующий за ним символ либо является специальным символом (как показано в следующей таблице), либо должен интерпретироваться буквально.Для получения дополнительной информации см. Побеги персонажей.
Экранированный символ Описание Узор Матчи \ аСоответствует символу колокольчика, \ u0007. \ а"\ u0007"в"Ошибка!" + '\ u0007'\ бВ классе символов соответствует символу возврата \ u0008. [\ b] {3,}"\ b \ b \ b \ b"дюйм"\ b \ b \ b \ b"\ тСоответствует табуляции, \ u0009. (\ ш +) \ т"item1 \ t","item2 \ t"в"item1 \ titem2 \ t"\ rСоответствует возврату каретки, \ u000D. ( \ rне эквивалентно символу новой строки,\ n.)\ г \ п (\ ш +)"\ r \ nЭто"в"\ r \ nЭто \ nдве строки."\ вСоответствует вертикальной табуляции, \ u000B. [\ v] {2,}"\ v \ v \ v"дюйм"\ v \ v \ v"\ fСоответствует подаче страницы, \ u000C. [\ f] {2,}"\ f \ f \ f"дюйм"\ f \ f \ f"\ пСоответствует новой строке, \ u000A. \ г \ п (\ ш +)"\ r \ nЭто"в"\ r \ nЭто \ nдве строки."\ eСоответствует побегу, \ u001B. \ e"\ x001B"дюйм"\ x001B"\nnnИспользует восьмеричное представление для указания символа ( nnn состоит из двух или трех цифр). \ w \ 040 \ w"a b","c d"in"a bc d"\ xnnИспользует шестнадцатеричное представление для указания символа ( nn состоит ровно из двух цифр). \ ш \ х20 \ ш"a b","c d"in"a bc d"\ cX\ cxСоответствует управляющему символу ASCII, заданному как X или x , где X или x — это буква управляющего символа. \ куб.см"\ x0003"дюйм"\ x0003"(Ctrl-C)\ unnnnСоответствует символу Юникода с использованием шестнадцатеричного представления (ровно четыре цифры, как представлено nnnn ). \ w \ u0020 \ w"a b","c d"in"a bc d"\Если за ним следует символ, который не распознается как экранированный символ в этой и других таблицах этого раздела, соответствует этому символу. Например, \ *совпадает с\ x2Aи\.совпадает с\ x2E. Это позволяет механизму регулярных выражений устранять неоднозначность языковых элементов (например, * или?) И символьных литералов (представленных\ *или\?).\ d + [\ + - x \ *] \ d +"2 + 2"и"3 * 9"дюйм"(2 + 2) * 3 * 9"Классы символов
Класс символов соответствует любому из набора символов. Классы символов включают языковые элементы, перечисленные в следующей таблице. Для получения дополнительной информации см. Классы символов.
Класс символов Описание Узор Матчи [группа_знаков]Соответствует любому одиночному символу в группе символов .aei] "r","g","n"в"царствование"[первый-последний]Диапазон символов: соответствует любому одиночному символу в диапазоне от первых до последних . [А-Я]"A","B"дюйм"AB123".Подстановочный знак: соответствует любому одиночному символу, кроме \ n. Чтобы соответствовать буквальному символу точки (. Или
\ u002E), вы должны предшествовать ему escape-символом (\.).а.е.«аве»в«неф»«съел»в«вода»\ p {название}Соответствует любому одиночному символу в общей категории Unicode или именованному блоку, указанному в name . \ p {Lu}\ p {IsCyrillic}«C»,«L»в«City Lights»«Д»,«Ж»в«ДЖem»\ P {название}Соответствует любому одиночному символу, который не входит в общую категорию Unicode или именованный блок, указанный в name . \ P {Lu}\ P {IsCyrillic}"i","t","y"в"Город""e","m"в"ДЖem"\ wСоответствует любому символу слова. \ w"I","D","A","1","3"дюйм"ID A1.3"\ ВтСоответствует любому символу, не являющемуся словом. \ Вт"","."дюйм"ID A1.3"\ сСоответствует любому символу пробела. \ Вт \ с"D"дюйм"ID A1.3"\ SСоответствует любому символу, отличному от пробела. \ с \ с"_"в"int __ctr"\ dСоответствует любой десятичной цифре. \ д"4"дюйм"4 = IV"\ DСоответствует любому символу, кроме десятичной цифры. \ D"","=","","I","V"в"4 = IV"Анкеры
Якоря, или атомарные утверждения нулевой ширины, приводят к успешному или неудачному совпадению в зависимости от текущей позиции в строке, но они не заставляют движок продвигаться по строке или потреблять символы.\ d {3}
"901"дюйм"901-333-"$По умолчанию совпадение должно происходить в конце строки или до \ nв конце строки; в многострочном режиме он должен находиться до конца строки или до\ nв конце строки.- \ d {3}"-333"дюйм"-901-333"\ AСоответствие должно происходить в начале строки. \ A \ d {3}"901"дюйм"901-333-"\ ZСоответствие должно происходить в конце строки или до \ nв конце строки.- \ d {3} \ Z"-333"дюйм"-901-333"\ zСоответствие должно произойти в конце строки. - \ d {3} \ z"-333"дюйм"-901-333"\ GМатч должен произойти в точке, где закончился предыдущий матч. \ G \ (\ d \)"(1)","(3)","(5)"дюйм"(1) (3) (5) [7] (9)"\ бСоответствие должно происходить на границе между \ w(буквенно-цифровым) и\ W(не буквенно-цифровым) символом.\ б \ ш + \ с \ ш + \ б"их тема","они их"в"их тема их"\ BСоответствие не должно происходить на границе \ b.\ Изгиб \ ш * \ б"конец","конец"в"конец отправляет долгосрочный кредитор"Группирование конструкций
Группирующие конструкции очерчивают подвыражения регулярного выражения и обычно захватывают подстроки входной строки. Группирующие конструкции включают языковые элементы, перечисленные в следующей таблице. Для получения дополнительной информации см. Группирующие конструкции.
Построение группировки Описание Узор Матчи (подвыражение)Захватывает совпавшую часть выражения и присваивает ей порядковый номер, отсчитываемый от единицы. (\ ш) \ 1"ee"дюйм"глубина"(? <имя>часть выражения)
или
(? 'имя'часть выражения)Захватывает совпадающее подвыражение в именованную группу. (? <Двойной> \ w) \ k <двойной>"ee"дюйм"глубина"(? <name1-name2>подвыражение)
или
(? 'name1-name2'подвыражение )Определяет определение балансирующей группы.((1-3) * (3-1)) « (?:подвыражение)Определяет группу без захвата. Запись (?: Строка)?"WriteLine"в"Console.WriteLine ()""Запись"в"Console.Write (значение)"(? Imnsx-imnsx:подвыражение)Применяет или отключает указанные параметры в подвыражении .Для получения дополнительной информации см. Параметры регулярного выражения. A \ d {2} (? I: \ w +) \ b"A12xl","A12XL"дюйм"A12xl A12XL a12xl"(? =подвыражение)Утверждение положительного просмотра вперед нулевой ширины. \ ш + (? = \.)"это","побежал"и"вышел"в"Он есть. Собака побежала. Солнце вышло."(?!подвыражение)Утверждение отрицательного просмотра вперед нулевой ширины. \ b (?! Un) \ w + \ b"уверен","использован"в"не уверен, что используется единство"(? <=часть выражения)Утверждение положительного просмотра назад нулевой ширины. (? <= 19) \ d {2} \ b"99","50","05"дюйм"1851 1999 1950 1905 2003"(? часть выражения)Утверждение отрицательного просмотра назад нулевой ширины. (?"51","03"дюйм"1851 1999 1950 1905 2003"(?>подвыражение)Атомная группа. [13579] (?> A + B +)"1ABB","3ABB"и"5AB"в"1ABB 3ABBC 5AB 5AC"Кванторы
Квантификатор указывает, сколько экземпляров предыдущего элемента (который может быть символом, группой или классом символов) должно присутствовать во входной строке, чтобы совпадение произошло.Квантификаторы включают языковые элементы, перечисленные в следующей таблице. Для получения дополнительной информации см. Квантификаторы.
Квантификатор Описание Узор Матчи *Соответствует предыдущему элементу ноль или более раз. \ д * \. \ Д".0","19.9","219.9"+Один или несколько раз соответствует предыдущему элементу. "be +""пчела"в"было","было"в"изогнуто"?Соответствует предыдущему элементу ноль или один раз. "Район"«пробежал»,«дождь»{n}Точно соответствует предыдущему элементу n раз. ", \ d {3}"", 043"дюйм"1043.6 ",", 876 ",", 543 "и", 210 "дюймов" 9 876 543 210 "{n,}Соответствует предыдущему элементу не менее n раз. "\ d {2,}""166","29","1930"{n,m}Соответствует предыдущему элементу не менее n раз, но не более m раз. "\ d {3,5}""166","17668""19302"дюйм"193024"*?Соответствует предыдущему элементу ноль или больше раз, но как можно меньше раз. \ д *? \. \ Д".0","19.9","219.9"+?Соответствует предыдущему элементу один или несколько раз, но как можно меньше раз. "быть +?""быть"в"было","быть"в"изогнуто??Соответствует предыдущему элементу ноль или один раз, но как можно меньше раз. "Район"«пробежал»,«дождь»{n}?Точно соответствует предыдущему элементу n раз. ", \ d {3}?"", 043"дюйм"1043,6",", 876",", 543"и", 210"дюйм"9 876 543 210"{n,}?Соответствует предыдущему элементу как минимум n раз, но как можно меньше раз. "\ d {2,}?""166","29","1930"{n,m}?Соответствует предыдущему элементу между n и m раз, но как можно меньше раз. "\ d {3,5}?""166","17668""193","024"дюйм"193024"Конструкции обратных ссылок
Обратная ссылка позволяет идентифицировать ранее сопоставленное подвыражение в том же регулярном выражении. В следующей таблице перечислены конструкции обратной ссылки, поддерживаемые регулярными выражениями в .NET. Для получения дополнительной информации см. Конструкции обратных ссылок.
Конструкция обратной ссылки Описание Узор Матчи \номерОбратная ссылка. Соответствует значению пронумерованной части выражения. (\ ш) \ 1"ee"в"seek"\ k <название>Именованная обратная ссылка. Соответствует значению именованного выражения. (?\ w) \ k "ee"в"seek"Конструкции чередования
Конструкции чередования модифицируют регулярное выражение, чтобы включить или / или сопоставление. Эти конструкции включают языковые элементы, перечисленные в следующей таблице. Для получения дополнительной информации см. Альтернативные конструкции.
Чередование конструкции Описание Узор Матчи |Соответствует любому элементу, разделенному вертикальной чертой ( |).-е (e | is | at)"," это "в" это день ".(? (выражение)да|нет)Соответствует да , если соответствует шаблон регулярного выражения, обозначенный выражением выражение ; в противном случае соответствует необязательной части № . Выражение интерпретируется как утверждение нулевой ширины. (? (A) A \ d {2} \ b | \ b \ d {3} \ b)"A10","910"дюйм"A10 C103 910"(? (имя)да|нет)Соответствует да , если имя , именованная или пронумерованная группа захвата, имеет совпадение; в противном случае соответствует необязательному № . (? <Кавычки> ")? (? (Цитируется).+? "| \ S + \ s)"Dogs.jpg","\" Yiska plays.jpg \ ""in"Dogs.jpg \" Yiska plays.jpg \ ""Замены
Замены - это элементы языка регулярных выражений, которые поддерживаются в шаблонах замены. Для получения дополнительной информации см. Замены. Метасимволы, перечисленные в следующей таблице, являются атомарными утверждениями нулевой ширины.
Персонаж Описание Узор Схема замены Входная строка Строка результата $номерЗаменяет подстроку, соответствующую номеру группы . \ b (\ w +) (\ s) (\ w +) \ b$ 3 $ 2 $ 1"один два""два на один"$ {название}Заменяет подстроку, соответствующую названной группе name . \ b (?\ w +) (\ s) (? \ w +) \ b $ {word2} $ {word1}"один два""два на один"$$Заменяет буквальный символ "$". \ b (\ d +) \ s?$$$ 1"103 долл.""103 доллара"$ иЗаменяет копию всего матча. \ $? \ D * \.? \ D +** $ и **"1,30 $""** 1,30 доллара США **"$Заменяет весь текст входной строки перед совпадением. Б +$"AABBCC""AAAACC"$Заменяет весь текст входной строки после совпадения. Б +$"AABBCC""AACCCC"$ +Заменяет последнюю захваченную группу. В + (К +)$ +"AABBCCDD""AACCDD"$ _Заменяет всю входную строку. Б +$ _"AABBCC""AAAABBCCCC"Параметры регулярного выражения
Можно указать параметры, управляющие тем, как обработчик регулярных выражений интерпретирует шаблон регулярного выражения. Многие из этих параметров могут быть указаны либо встроенными (в шаблоне регулярного выражения), либо как одна или несколько констант RegexOptions. В этом кратком справочнике перечислены только встроенные параметры.Дополнительные сведения о параметрах inline и RegexOptions см. В статье Параметры регулярного выражения.
Вы можете указать встроенный параметр двумя способами:
- При использовании разной конструкции
(? Imnsx-imnsx), где знак минус (-) перед параметром или набором параметров отключает эти параметры. Например,(? I-mn)включает сопоставление без учета регистра (i), выключает многострочный режим (m) и отключает захват безымянных групп (n).Параметр применяется к шаблону регулярного выражения с точки, в которой параметр определен, и действует либо до конца шаблона, либо до точки, где другая конструкция отменяет параметр. - Используя конструкцию группирования
(? Imnsx-imnsx:подвыражение), которая определяет параметры только для указанной группы.
Механизм регулярных выражений .NET поддерживает следующие встроенные параметры:
Опция Описание Узор Матчи яИспользуйте сопоставление без учета регистра. и $соответствуют началу и концу строки, а не началу и концу строки.Для примера см. Раздел «Многострочный режим» в параметрах регулярных выражений. нНе захватывайте безымянные группы. Для примера см. Раздел «Только явные захваты» в параметрах регулярного выражения. сИспользовать однострочный режим. Для примера см. Раздел «Однострочный режим» в параметрах регулярных выражений. хИгнорировать неэкранированные пробелы в шаблоне регулярного выражения. \ b (? X) \ d + \ s \ w +"1 трубкозуб","2 кошки"в"1 трубкозуб 2 кошки IV центурионы"Разные конструкции
Разные конструкции либо изменяют шаблон регулярного выражения, либо предоставляют информацию о нем. В следующей таблице перечислены различные конструкции, поддерживаемые.СЕТЬ. Для получения дополнительной информации см. Разные конструкции.