| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Электрическое сопротивление и проводимость. / / Удельное электрическое сопротивление обычных электроизоляционных материалов при 20 ° C. Ом*м. Таблица.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
Зависимость удельного сопротивления чистого металла от температуры
Зависимость удельного сопротивления чистого металла от температуры [c.193]На рис. 7.6, а схематически показана кривая зависимости удельного сопротивления чистых металлов от температуры, достаточно хорошо подтверждаемая экспериментально (рис. 7.6, б). [c.188]
Зависимость удельного сопротивления чистых металлов от температуры не может быть удовлетворительно объяснена в рамках классической электронной теории электропроводности.
Никель и железо. Никель и железо обладают значительно более высоким температурным коэфициентом сопротивления, чем все прочие металлы 6,28 10″1 град и л= 6,4-10 . град). Кроме того, эти металлы обладают довольно высоким удельным сопротивлением, равным приблизительно 0,1—0,13 ом-мм /м. Однако возможность использования никеля и железа для изготовления термометров сопротивления ограничена в силу присущих этим металлам существенных недостатков. Получение никеля и железа в чистом виде затруднительно, а поэтому низка воспроизводимость их свойств. Далее, зависимость сопротивления этих металлов от температуры выражается к,ривыми, которые не могут быть записаны в виде простых эмпирических формул.
Электросопротивление алюминия высокой чистоты (99,99 %) при температуре 20 °С составляет 2,6548-10 Ом-м (0,0265 МКОМ М). В интервале температур 273—300 К температурная зависимость электрического сопротивления чистого алюминия почти линейна при постоянном коэффициенте 1,15-10 Ом-м-К . Электрическая проводимость алюминия в значительной степени зависит от чистоты металла, причем влияние различных примесей на электрическое сопротивление зависит не только от концентрации данной примеси, но и от ее нахождения в твердом растворе или вне его. Наиболее сильно повышают сопротивление алюминия примеси хрома, лития, марганца, магния, титана и ванадия [5]. Удельное электросопротивление р (мкОм м) отожженной алюминиевой проволоки в зависимости от содержания примесей (%) можно приближенно определить по следующей формуле [9]
12]
Для определения результирующих потоков излучения необходимо располагать данными по коэффициентам излучения. Коэффициент излучения является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности, а для металлов — от степени окисления этой поверхности. Для чистых металлов с полированными поверхностями коэффициент излучения имеет низкие значения. Так, при температуре 100 °С коэффициент излучения по отношению к его величине для абсолютно черного тела не превышает 0,1. Металлы характеризуются высокой отражательной способностью, так как из-за большой электропроводности луч проникает лишь на небольшую глубину. Для чистых металлов коэффициент излучения может быть найден теоретическим путем. Относительный коэффициент (степень черноты) полного нормального излучения для них связан с удельным электрическим сопротивлением рэ зависимостью
Наряду с малым удельным сопротивлением чистые металлы обладают хорошей пластичностью, т.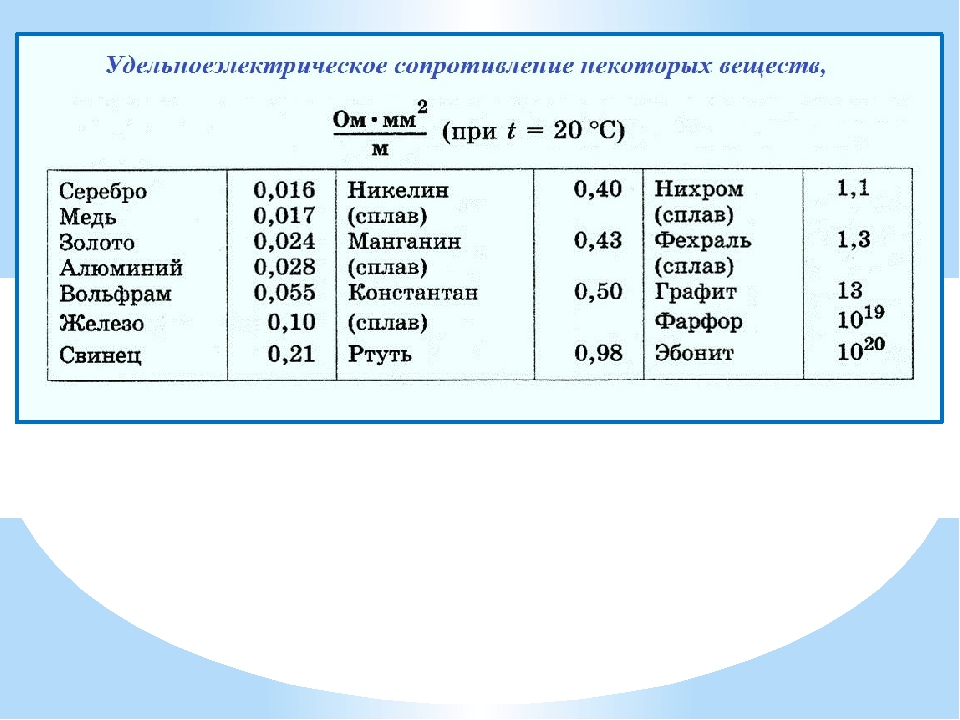
е. могут вытягиваться в тонкую проволоку (до диаметра 0,01 мм), ленты (до толщины 0,01 мм) и прокатываться в фольгу толщиной менее 0,01 мм. Сплавы металлов обладают меньшей пластичностью по сравнению с чистыми металлами, они более упруги и имеют большую механическую прочность. Характерной особенностью всех металлических проводниковых, материалов является их электронная электропроводность. Удельное сопротивление всех металлических проводников увеличивается с ростом температуры и в зависимости от температурного коэффициента сопротивления, а также в результате механической обработки, вызывающей остаточную деформацию в металле. К холодной обработке (прокатка, волочение) приходится прибегать для получения проводниковых изделий с повышенным пределом прочности при разрыве, например при изготовлении проводов воздушных линий, троллейных проводов и т. д. Чтобы вернуть деформированным металлическ , проводникам прежнюю величину удельного сопротивления, их подвергают термической обработке — отжигу без доступа кислорода.
[c.225]
Прежде чем перейти к подробному обсуждению зависимости удельного сопротивления металлов и полупроводников от температуры, коснемся особенностей поведения концентрированных сплавов. Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави- [c.191]
Теоретические соображения. Интересно обсудить возможный механизм частичной сверхпроводимости проволоки из фосфористой бронзы. Кеезом [25] и Бэббит и Мендельсон [45] предположили, что явление частичной сверхпроводимости обусловливается наличием большого количества сверхпроводящих включений в виде чистого металла или сверхпроводящего сплава, растворенного в фосфористой бронзе.
Кроме того, они предположили, что эти включения имеют форму тонких игл, образовавшихся при протяжке и расположенных параллельно оси проволоки. Однако эти авторы дают различную интерпретацию линейной зависимости удельного сопротивления от температуры. Кеезом полагал, что благодаря очень малым и случайно распределенным размерам игл сверхпроводящие переходы в них беспорядочно распределены по всему температурному интервалу. По мере понижения температуры все большее и большее число игл становится сверхпроводящим и, таким образом, уменьшается сопротивление проволоки. Бэббит и Мендельсон, напротив, предположили, что иглы образуют цепи, и так как один и тот же ток проходит через все иглы, составляющие одну цепь, то более тонкие иглы становятся сверхпроводниками при более низких температурах, чем более толстые. Этим можно объяснить незначительный наклон кривой зависимости удельного электросопротивления от температуры.
[c.205]
Простая модель электронного газа, созданная Друде в 1900 г.
, успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ . В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]ЛР №1
Лабараторная работа № 1
Изучение зависимости сопротивления реальных проводников от их геометрических параметров и удельных сопротивлений материалов.
Цель: определить удельное сопротивление проводника и сравнить его с табличным значением.
1. Краткое теоретическое описание
Немецкий физик Георг Ом (1787-1854) в 1826 году обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I в цепи есть величина постоянная:
(1)
Эту величину R называют электрическим сопротивлением проводника. Электрическое сопротивление измеряется в Омах. Электрическим сопротивлением 1 Ом обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
Опыт показывает, что электрическое сопротивление проводника прямо пропорционально его длине L и обратно пропорционально площади S поперечного сечения проводника:
(2)
Постоянный для
данного вещества параметр
называется удельным электрическим
сопротивлением вещества.
Удельное
сопротивление измеряется в Ом
м.
2. Порядок выполнения работы
2.1. Соберите на монтажном столе электрическую схему, показанную на рисунке:
Рис.1.
2.2. Выберите материал проводника – никель, установите значения длины и площади поперечного сечения:
L = 100 м; S = 0.1 мм2;
2.3. Определите экспериментально с помощью мультиметра напряжение на проводнике.
Для этого необходимо подключить параллельно проводнику мультиметр в режиме измерения постоянного напряжения, соблюдая полярность.
Запишите показания мультиметра.
2.4. Определите экспериментально с помощью мультиметра силу тока в цепи.
Включите мультиметр в режиме измерения постоянного тока последовательно в цепь, соблюдая полярность.
Запишите показания мультиметра.
2.5. Рассчитайте сопротивление проводника по формуле (1).
2.6. Определите
удельное сопротивление никеля по формуле
(2).
2.7. Проделайте пункты 2.3 – 2.6. изменяя длину, но, не меняя площадь поперечного сечения и материал проводника.
2.8. Результаты измерений занесите в таблицу:
№ опыта | Длина, м | Напряжение, В | Сила тока, А | Сопротивление, Ом | Удельное сопротивление, Ом м |
1 | 100 | 1,44 | 0,198 | 0,7272 | 0,07272 |
2 | 100 | 1,493 | 0,2 | 72,475 | 0,07247 |
3 | 100 | 1,496 | 0,01 | 149,6 | 0,07262 |
4 | 100 | 1,498 | 0,0041 | 365,3 | 0,07307 |
5 | 100 | 1,499 | 0,002 |
| 0,07495 |
2.
9. Найдите среднее
значение удельного сопротивления и
сравните его с табличным значением.
2.10. Измерьте сопротивление проводника непосредственно с помощью омметра. Сравните полученные результаты.
Выводы:
Научился определять удельное сопротивление проводника и сравнивать его с табличным значением.
3. Контрольные вопросы.
3.1. Что называют удельным сопротивление проводника?
3.2. Как зависит сопротивление проводника от его длины?
3.3. По какой формуле можно рассчитать удельное сопротивление проводника?
3.4. В каких единицах измеряется удельное сопротивление проводника?
Ответы:
3.1 Постоянный параметр для определенного вещества, определяющийся произведением сопротивления на длину и деленным на площадь поперечного сечения проводника
3.2 Сопротивление прямо пропорционально его длине
3.3
3.
4 Ом
на метр
Удельное электрическое сопротивление никеля — Яхт клуб Ост-Вест
Удельное электрическое сопротивление является физической величиной, которая показывает, в какой степени материал может сопротивляться прохождению через него электрического тока. Некоторые люди могут перепутать данную характеристику с обыкновенным электрическим сопротивлением. Несмотря на схожесть понятий, разница между ними заключается в том, что удельное касается веществ, а второй термин относится исключительно к проводникам и зависит от материала их изготовления.
Обратной величиной данного материала является удельная электрическая проводимость. Чем выше этот параметр, тем лучше проходит ток по веществу. Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Формула расчета и величина измерения
Рассматривая, в чем измеряется удельное электрическое сопротивление, также можно проследить связь с не удельным, так как для обозначения параметра используются единицы Ом·м.
Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм 2 /м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм 2 /м равняется 10 -6 Ом·м.
Формула удельного электрического сопротивления выглядит следующим образом:
R= (ρ·l)/S, где:
- R – сопротивление проводника;
- Ρ – удельное сопротивление материал;
- l – длина проводника;
- S – сечение проводника.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия.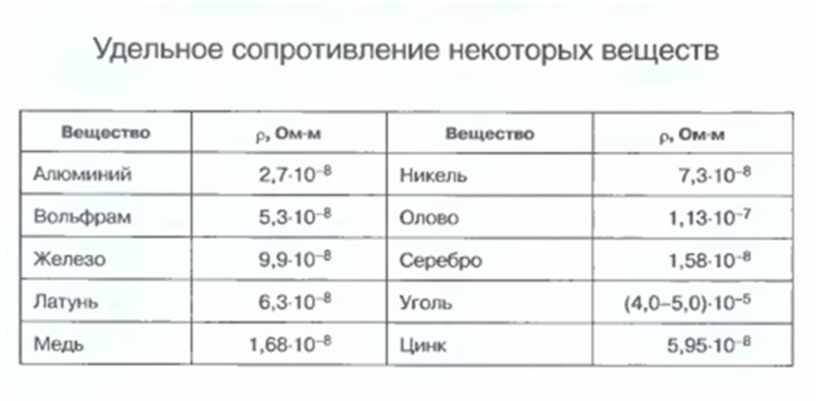
Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 10 16 |
| Бензол | 10 15 . 10 16 |
| Бумага | 10 15 |
| Вода дистиллированная | 10 4 |
| Вода морская | 0.3 |
| Дерево сухое | 10 12 |
| Земля влажная | 10 2 |
| Кварцевое стекло | 10 16 |
| Керосин | 10 1 1 |
| Мрамор | 10 8 |
| Парафин | 10 1 5 |
| Парафиновое масло | 10 14 |
| Плексиглас | 10 13 |
| Полистирол | 10 16 |
| Полихлорвинил | 10 13 |
| Полиэтилен | 10 12 |
| Силиконовое масло | 10 13 |
| Слюда | 10 14 |
| Стекло | 10 11 |
| Трансформаторное масло | 10 10 |
| Фарфор | 10 14 |
| Шифер | 10 14 |
| Эбонит | 10 16 |
| Янтарь | 10 18 |
Более активно в электротехнике применяются вещества с низкими показателями.
Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10 -8 |
| Вольфрам | 5.5·10 -8 |
| Графит | 8.0·10 -6 |
| Железо | 1.0·10 -7 |
| Золото | 2.2·10 -8 |
| Иридий | 4.74·10 -8 |
| Константан | 5.0·10 -7 |
| Литая сталь | 1.3·10 -7 |
| Магний | 4.4·10 -8 |
| Манганин | 4.3·10 -7 |
| Медь | 1.72·10 -8 |
| Молибден | 5.4·10 -8 |
| Нейзильбер | 3.3·10 -7 |
| Никель | 8.7·10 -8 |
| Нихром | 1. 12·10 -6 |
| Олово | 1.2·10 -7 |
| Платина | 1.07·10 -7 |
| Ртуть | 9.6·10 -7 |
| Свинец | 2.08·10 -7 |
| Серебро | 1.6·10 -8 |
| Серый чугун | 1.0·10 -6 |
| Угольные щетки | 4.0·10 -5 |
| Цинк | 5.9·10 -8 |
| Никелин | 0,4·10 -6 |
Удельное объемное электрическое сопротивление
Данный параметр характеризует возможность пропускать ток через объем вещества. Для измерения необходимо приложить потенциал напряжения с разных сторон материала, изделие из которого будет включено в электрическую цепь. На него подается ток с номинальными параметрами. После прохождения измеряются данные на выходе.
Формула удельного сопротивления
Сопротивление проводника
Удельное сопротивление
И вот мы плавно переходим к другому вопросу, что такое сопротивление проводника? Как я уже говорил выше, чем больше свободных электронов в веществе, тем лучше такое вещество проводит электрический ток.
Следовательно, сопротивление проводника зависит от того, сколько свободных электронов содержит такой проводник. Поэтому, в физике есть такое понятие, как удельное сопротивление вещества.
Еще раз. Если в каком-либо веществе полно свободных электронов, то такое вещество будет хорошо проводить электрический ток. Если электронов еще меньше, то такое вещество будет плохо проводить электрический ток. А если свободных электронов почти нет, то такое вещество совсем не будет проводить ток. Поэтому, удельное сопротивление вещества показывает способность этого вещества препятствовать электрическому току, проходящему через него.
Удельное сопротивление выражается в единицах Ом × м.
Формула удельного сопротивления проводника
где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Площадь поперечного сечения проводника – это что-то типа этого:
площадь поперечного сечения проводника
Формула сопротивления проводника
Итак, мы теперь знаем такую физическую величину, как удельное сопротивление.
Теперь мы с легкостью можем найти сопротивление проводника.
где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом.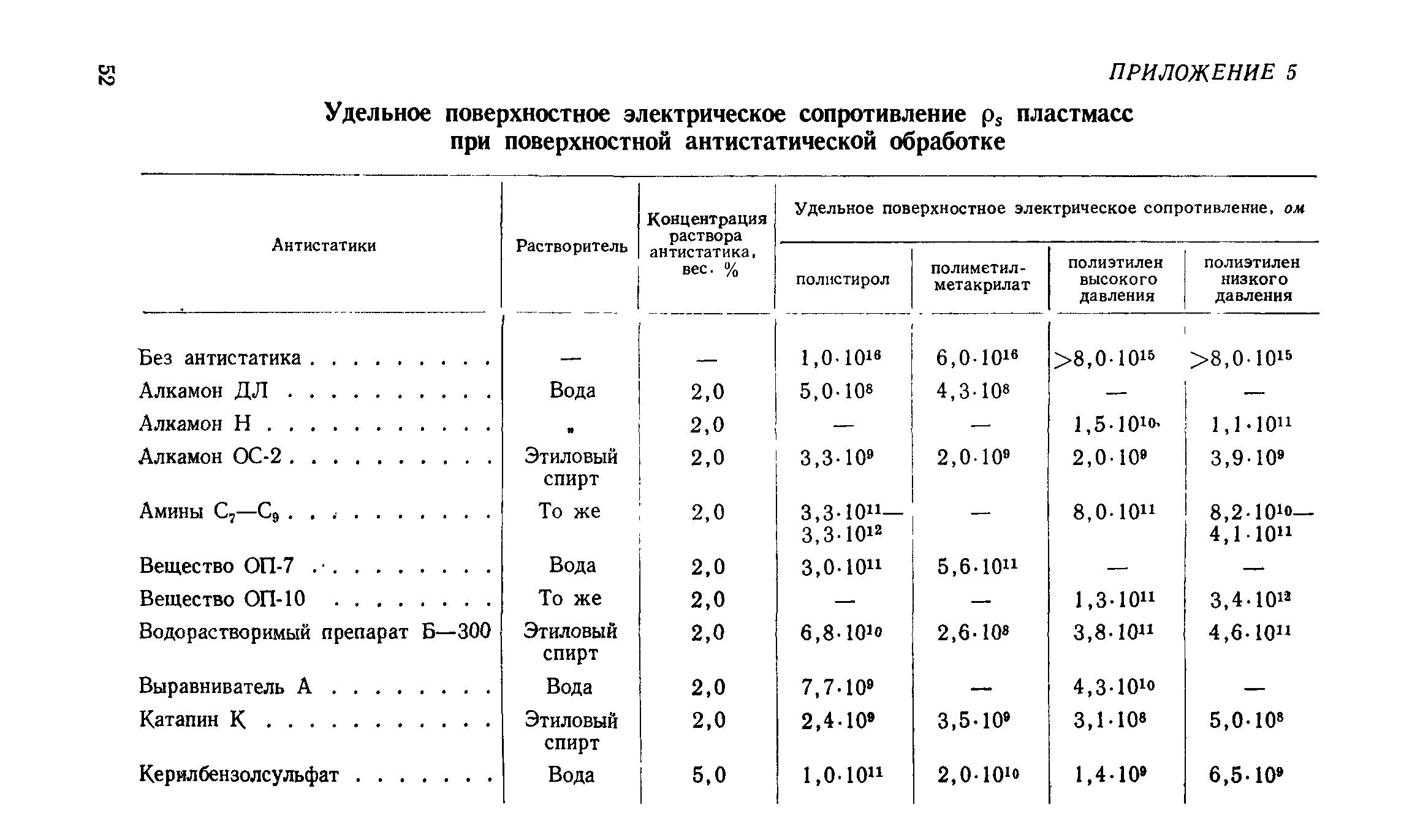
Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2.
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2.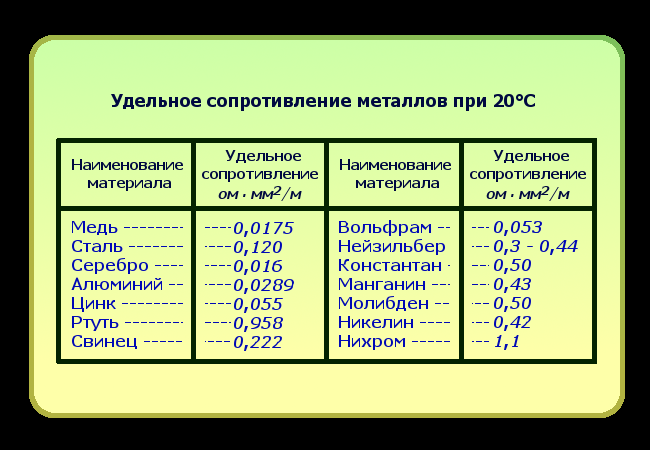
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2.
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться.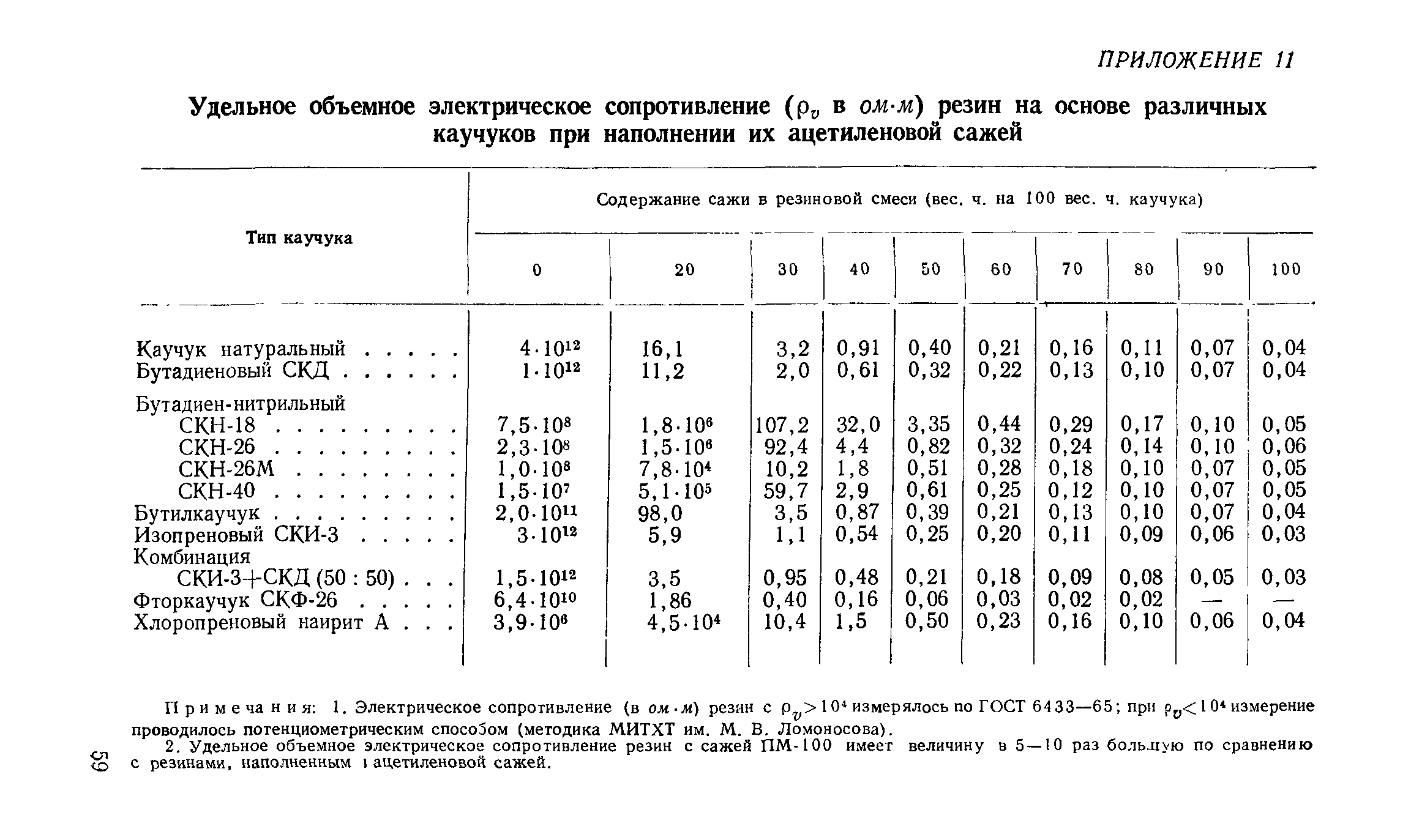
Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
температурный коэффициент сопротивления — это изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, обозначается буквой α.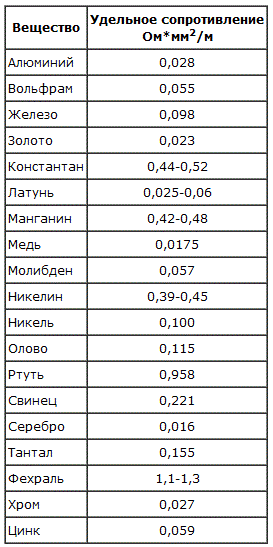
Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Удельное электрическое сопротивление
Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.
Эта функциональная связь хорошо описывается следующей формулой:
$ R = ρ *{ L\over S} $ (4)
Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества.
Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:
$ ρ = R*{ S\over L } $ (5)
Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.
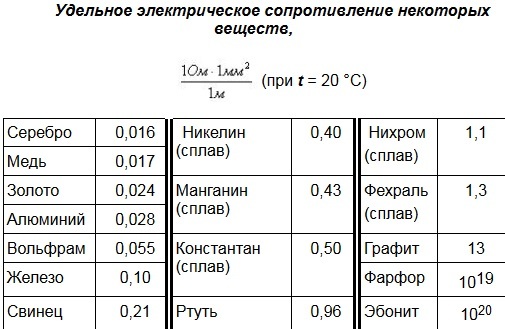
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 20С)
Серебро | 0,016 | Бронза (сплав) | 0,1 |
Медь | 0,017 | Олово | 0,12 |
Золото | 0,024 | Сталь (сплав) | 0,12 |
Алюминий | 0,028 | Свинец | 0,21 |
Иридий | 0,047 | Никелин (сплав) | 0,42 |
Молибден | 0,054 | Манганин (сплав) | 0,45 |
Вольфрам | 0,055 | Константан (сплав) | 0,48 |
Цинк | 0,06 | Титан | 0,58 |
Латунь (сплав) | 0,071 | Ртуть | 0,958 |
Никель | 0,087 | Нихром (сплав) | 1,1 |
Платина | 0,1 | Висмут | 1,2 |
Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается.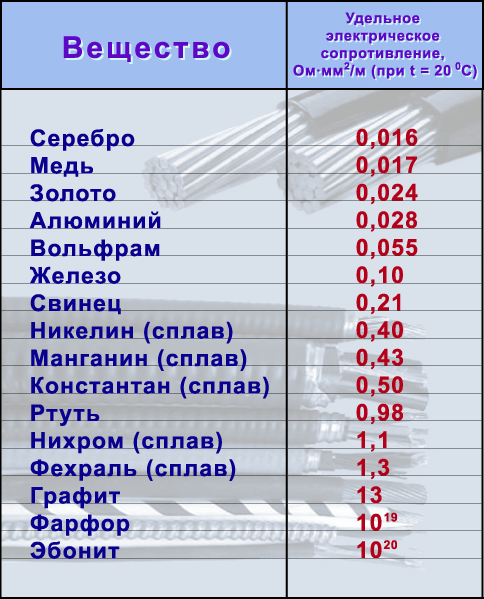
При приближении к температуре абсолютного нуля, которая равна -273С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.
Что мы узнали?
Итак, мы узнали, что способность проводника ограничивать величину электрического тока называется сопротивлением. Величину сопротивления проводника можно определить с помощью закона Ома, измерив напряжение и ток. Если известно удельное сопротивление проводника, его длина и поперечное сечение, то сопротивление можно вычислить с помощью формулы (4), не измеряя ток и напряжение.
Обобщение понятия удельного сопротивления
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}.
{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρij{\displaystyle \rho _{ij}}симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.
Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать
ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую
- Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается :
- E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}.
{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρij{\displaystyle \rho _{ij}}симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.
Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую
- Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Единица измерения электрического сопротивления
Единицу измерения сопротивления назвали в честь Георга Ома. В Международной интернациональной системе единиц СИ электрическое сопротивление 1 Ом имеет участок цепи, на котором падает напряжение равное 1 В при силе тока 1 А:
$ 1 Ом = { 1 В\over 1 A} $ (3)
Для определения сопротивления с помощью закона Ома требуется измерить предварительно напряжение и ток. Двух измерений можно избежать с помощью прибора, разработанного для непосредственного измерения сопротивления. Прибор называется омметром.
Рис. 3. Приборы для измерения сопротивления – омметры.
На практике большинство используемых в электрических схемах и приборах сопротивлений гораздо больше, чем 1 Ом. Поэтому чаще применяются кратные единицы измерений : килоом и мегом:
- 1 кОм = 1000 Ом;
- 1 МОм = 1000 000 Ом.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке.
Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.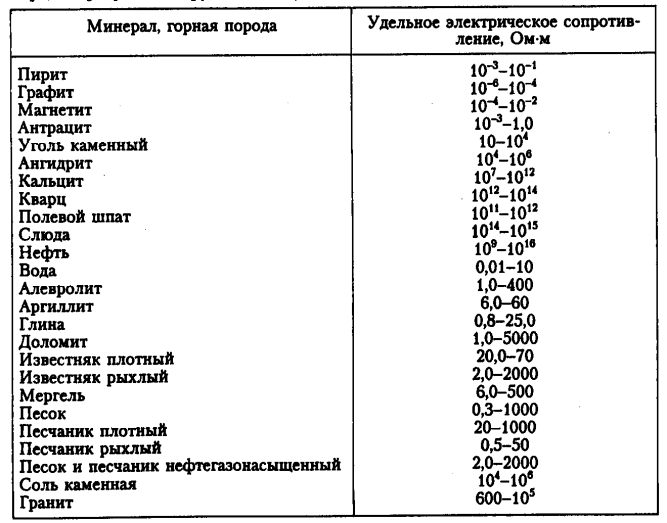
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе.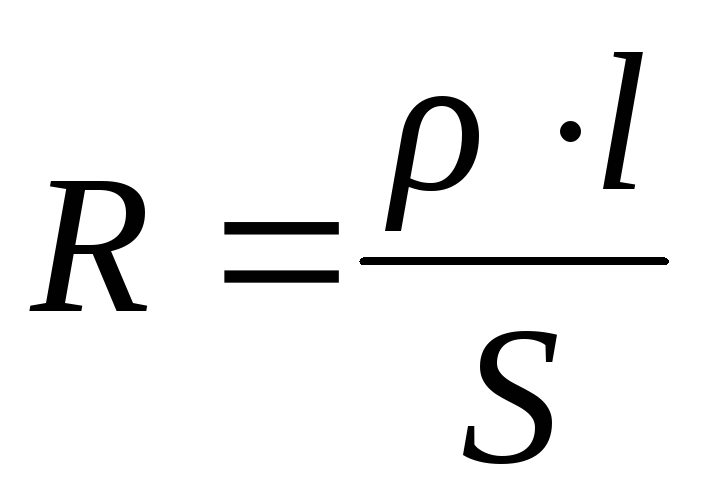
Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное.
Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Оцените статью:удельное сопротивление, применение, состав, температура плавления
Манганин – сплав красного цвета, производящийся на основе меди. Он относится к категории металлов с высоким электрическим сопротивлением. В состав сплава может входить небольшое количество меди, марганца и никеля, что повышает его прочность и термостойкость. Манганин был открыт в 1880-х гг. и активно используется в современной промышленности.
Свойства манганина
Основные свойства манганин приобретает во время термообработки. Изначально сплав не подвержен внутренней деформации. По этой причине его кристаллическая решетка с течением времени практически не изменяется.
При термической обработке фиксируется величина электрического сопротивления. Среднее значение этого параметра составляет 450 Ом/м. Плотность равняется 8000 кг/см3. Предельная рабочая температура сплава достигает 200 °C. При превышении этих значений его характеристики ухудшаются на 10 – 20%.
На механические, химические и физические параметры металла влияет его химический состав. Для этого материала характерно высокое процентное содержание меди (84%). Также в нем присутствует большое количество различных смесей из марганца (12%) и никеля (4%). При таком соотношении веществ металл становится наиболее термостойким. Температура плавления сплава составляет 960 °C. В данном случае сопротивление изменяется на 0,05% в год. Многие производители при изготовлении сплава, вместо никеля, добавляют в него кобальт. Это позволяет уменьшить стоимость материала без изменения его основных характеристик. Если вместо меди использовать серебро, то металл приобретет белый окрас.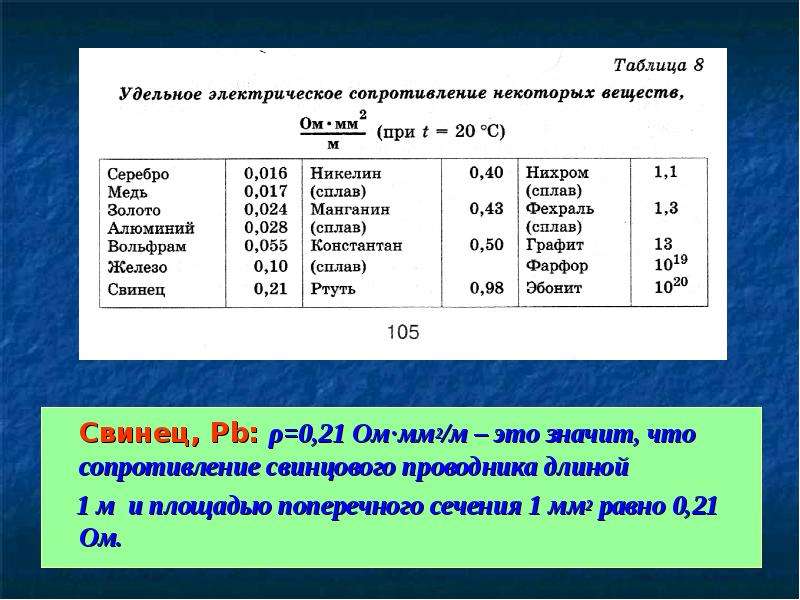
При этом его химические свойства сохранятся.
В отличие от остальных термостойких сплавов, манганин обладает низкой термической ЭДС (0,9 мВ — 1 мВ/°C). Но он уступает по показателям удельного сопротивления и предельной рабочей температуры. Сравнительная характеристика термостойких сплавов представлена в следующей таблице:
| Наименование материала | Удельное сопротивление, Ом/м | Термическая ЭДС, мВ/°C | Максимальная рабочая температура, °C | Температура плавления, °C |
| Манганин | 450 | 2 | 100 – 200 | 960 |
| Константан | 480 | 50 | 450 – 500 | 1260 |
| Нихром | 1000 | 110 | 1000 | 1100 |
Манганин отличается от константана и нихрома следующими свойствами:
- низкая устойчивость к коррозии в атмосфере с повышенным содержанием кислот из аммиака;
- высокая чувствительность к влажности воздуха;
- устойчивость к физическим деформациям с течением времени.
Технология производства данного прецизионного материала была разработана в 1889 г. на территории Германии. В России он производится в соответствии с ГОСТ 492-2006.
Металл производится в виде пластин, листов, полос и проволочных механизмов небольшого размера. Для получения этого материала используют хлористые слои железа и марганца. Полученный раствор промывается, высушивается и нагревается. После этого вещество сплавляется с медью в магнезиальных тиглях или электрических печах. При производстве важно, чтобы в него не попали частицы углерода, снижающие величину сопротивления манганина.
Применение сплава
Манганин нашел широкое применение в электронике. Он используется при создании высокоточных резисторов, мостовых схем и шунтов. Благодаря высокому удельному сопротивлению, материал применяется при изготовлении комплектующих для электроизмерительных приборов: гальванометров, амперметров, вольтметров и ваттметров. Он позволяет устройству точнее фиксировать изменения электротока.
Манганиновая проволока
Также манганин применяется при изготовлении проволочных механизмов. С помощью этого металла можно производить проволоки и металлические ленты разной длины и толщины. Он используется при производстве обмоточных проводов с изоляцией от натурального шелка, покрытых специальной эмалью.В зависимости от химического состава сырья меняются свойства проволок. При наличии алюминиевых примесей улучшаются механические характеристики, что позволяет использовать проволочные механизмы в кабельной промышленности. Твердый манганин, обладающий большой прочностью, используют для изготовления каркасов и внешних оболочек, мягкий – для внутреннего наполнения.
Благодаря наличию электрических свойств, сплав применяется при производстве прецизионных резисторов, являющихся главными компонентами электрометров. Изготовленные приспособления обладают устойчивым коэффициентом удельного сопротивления, что позволяет избежать появления термоэлектрических токов.
Электрическое сопротивление латуни. Сопротивление проводников. Удельное сопротивление
Удельное электрическое сопротивление является физической величиной, которая показывает, в какой степени материал может сопротивляться прохождению через него электрического тока. Некоторые люди могут перепутать данную характеристику с обыкновенным электрическим сопротивлением. Несмотря на схожесть понятий, разница между ними заключается в том, что удельное касается веществ, а второй термин относится исключительно к проводникам и зависит от материала их изготовления.
Обратной величиной данного материала является удельная электрическая проводимость. Чем выше этот параметр, тем лучше проходит ток по веществу. Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Формула расчета и величина измерения
Рассматривая, в чем измеряется удельное электрическое сопротивление, также можно проследить связь с не удельным, так как для обозначения параметра используются единицы Ом·м. Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм 2 /м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм 2 /м равняется 10 -6 Ом·м.
Формула удельного электрического сопротивления выглядит следующим образом:
R= (ρ·l)/S, где:
- R – сопротивление проводника;
- Ρ – удельное сопротивление материал;
- l – длина проводника;
- S – сечение проводника.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 10 16 |
| Бензол | 10 15 …10 16 |
| Бумага | 10 15 |
| Вода дистиллированная | 10 4 |
| Вода морская | 0.3 |
| Дерево сухое | 10 12 |
| Земля влажная | 10 2 |
| Кварцевое стекло | 10 16 |
| Керосин | 10 1 1 |
| Мрамор | 10 8 |
| Парафин | 10 1 5 |
| Парафиновое масло | 10 14 |
| Плексиглас | 10 13 |
| Полистирол | 10 16 |
| Полихлорвинил | 10 13 |
| Полиэтилен | 10 12 |
| Силиконовое масло | 10 13 |
| Слюда | 10 14 |
| Стекло | 10 11 |
| Трансформаторное масло | 10 10 |
| Фарфор | 10 14 |
| Шифер | 10 14 |
| Эбонит | 10 16 |
| Янтарь | 10 18 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10 -8 |
| Вольфрам | 5.5·10 -8 |
| Графит | 8.0·10 -6 |
| Железо | 1.0·10 -7 |
| Золото | 2.2·10 -8 |
| Иридий | 4.74·10 -8 |
| Константан | 5.0·10 -7 |
| Литая сталь | 1.3·10 -7 |
| Магний | 4.4·10 -8 |
| Манганин | 4.3·10 -7 |
| Медь | 1.72·10 -8 |
| Молибден | 5.4·10 -8 |
| Нейзильбер | 3.3·10 -7 |
| Никель | 8.7·10 -8 |
| Нихром | 1.12·10 -6 |
| Олово | 1.2·10 -7 |
| Платина | 1.07·10 -7 |
| Ртуть | 9.6·10 -7 |
| Свинец | 2.08·10 -7 |
| Серебро | 1.6·10 -8 |
| Серый чугун | 1.0·10 -6 |
| Угольные щетки | 4.0·10 -5 |
| Цинк | 5.9·10 -8 |
| Никелин | 0,4·10 -6 |
Удельное объемное электрическое сопротивление
Данный параметр характеризует возможность пропускать ток через объем вещества. Для измерения необходимо приложить потенциал напряжения с разных сторон материала, изделие из которого будет включено в электрическую цепь. На него подается ток с номинальными параметрами. После прохождения измеряются данные на выходе.
Использование в электротехнике
Изменение параметра при разных температурах широко применяется в электротехнике. Наиболее простым примером является лампа накаливания, где используется нихромовая нить. При нагревании она начинает светиться. При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
Широкое применение коснулось и благородных металлов, которые обладают подходящими характеристиками для электротехники. Для ответственных схем, которым требуется быстродействие, подбираются серебряные контакты. Они обладают высокой стоимостью, но с учетом относительно небольшого количества материалов их применение вполне оправданно. Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
В условиях, где можно использовать предельно низкие температуры, применяются сверхпроводники. Для комнатной температуры и уличной эксплуатации они не всегда уместны, так как при повышении температуры их проводимость начнет падать, поэтому для таких условий лидерами остаются алюминий, медь и серебро.
На практике учитывается много параметров и этот является одним из наиболее важных. Все расчеты проводятся еще на стадии проектирования, для чего и используются справочные материалы.
Уде?льное электри?ческое сопротивле?ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока .
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м .
Из соотношения следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом . Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи , выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10 −6 от 1 Ом·м . Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом . Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянногоили переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура .
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре ЭДС будет равна:
где — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого? источника равна нулю.
Каждое вещество способно проводить ток в разной степени, на эту величину влияет сопротивление материала. Обозначается удельное сопротивление меди, алюминия, стали и любого другого элемента буквой греческого алфавита ρ. Эта величина не зависит от таких характеристик проводника, как размеры, форма и физическое состояние, обычное же электросопротивление учитывает эти параметры. Измеряется удельное сопротивление в Омах, умноженных на мм² и разделенных на метр.
Категории и их описание
Любой материал способен проявлять два типа сопротивления в зависимости от подаваемого на него электричества. Ток бывает переменным или постоянным, что значительно влияет на технические показатели вещества. Так, существуют такие сопротивления:
- Омическое. Проявляется под воздействием постоянного тока. Характеризует трение, которое создается движением электрически заряженных частиц в проводнике.
- Активное. Определяется по такому же принципу, но создается уже под действием переменного тока.
В связи с этим определений удельной величины тоже два. Для постоянного тока она равна сопротивлению, которое оказывает единица длины проводящего материала единичной фиксированной площади сечения. Потенциальное электрополе воздействует на все проводники, а также полупроводники и растворы, способные проводить ионы. Эта величина определяет проводящие свойства самого материала. Форма проводника и его размеры не учитываются, поэтому ее можно назвать базовой в электротехнике и материаловедении.
При условии прохождения переменного тока удельная величина рассчитывается с учетом толщины проводящего материала. Здесь уже происходит воздействие не только потенциального, но и вихревого тока, кроме того, принимается во внимание частота электрических полей. Удельное сопротивление этого типа больше, чем при постоянном токе, поскольку здесь идет учет положительной величины сопротивления вихревому полю. Также эта величина зависит от формы и размеров самого проводника. Именно эти параметры и определяют характер вихревого движения заряженных частиц.
Переменный ток вызывает в проводниках определенные электромагнитные явления. Они очень важны для электротехнических характеристик проводящего материала:
- Скин-эффект характеризуется ослаблением электромагнитного поля тем больше, чем дальше оно проникает в среду проводника. Это явление также носит название поверхностного эффекта.
- Эффект близости снижает плотность тока благодаря близости соседних проводов и их влиянию.
Эти эффекты являются очень важными при расчете оптимальной толщины проводника, так как при использовании провода, у которого радиус больше глубины проникновения тока в материал, остальная его масса останется незадействованной, а следовательно, такой подход будет неэффективным. В соответствии с проведенными расчетами эффективный диаметр проводящего материала в некоторых ситуациях будет следующим:
- для тока в 50 Гц — 2,8 мм;
- 400 Гц — 1 мм;
- 40 кГц — 0,1 мм.
Ввиду этого для высокочастотных токов активно применяется использование плоских многожильных кабелей, состоящих из множества тонких проводов.
Характеристики металлов
Удельные показатели металлических проводников содержатся в специальных таблицах. По этим данным можно производить необходимые дальнейшие расчеты. Пример такой таблицы удельных сопротивлений можно увидеть на изображении.
На таблице видно, что наибольшей проводимостью обладает серебро — это идеальный проводник среди всех существующих металлов и сплавов. Если рассчитать, сколько потребуется провода из этого материала для получения сопротивления в 1 Ом, то выйдет 62,5 м. Проволоки из железа для такой же величины понадобится целых 7,7 м.
Какими бы замечательными свойствами ни обладало серебро, оно является слишком дорогим материалом для массового использования в электросетях, поэтому широкое применение в быту и промышленности нашла медь. По величине удельного показателя она стоит на втором месте после серебра, а по распространенности и простоте добычи намного лучше его. Медь обладает и другими преимуществами, позволившими ей стать самым распространенным проводником. К ним относятся:
Для применения в электротехнике используют рафинированную медь, которая после плавки из сульфидной руды проходит процессы обжигания и дутья, а далее обязательно подвергается электролитической очистке. После такой обработки можно получить материал очень высокого качества (марки М1 и М0), который будет содержать от 0,1 до 0,05% примесей. Важным нюансом является присутствие кислорода в крайне малых количествах, так как он негативно влияет на механические характеристики меди.
Часто этот металл заменяют более дешевыми материалами — алюминием и железом, а также различными бронзами (сплавами с кремнием, бериллием, магнием, оловом, кадмием, хромом и фосфором). Такие составы обладают более высокой прочностью по сравнению с чистой медью, хотя и меньшей проводимостью.
Преимущества алюминия
Хоть алюминий обладает большим сопротивлением и более хрупок, его широкое использование объясняется тем, что он не настолько дефицитен, как медь, а следовательно, стоит дешевле. Удельное сопротивление алюминия составляет 0,028, а его низкая плотность обеспечивает ему вес в 3,5 раза меньше, чем медь.
Для электрических работ применяют очищенный алюминий марки А1, содержащий не более 0,5% примесей. Более высокую марку АВ00 используют для изготовления электролитических конденсаторов, электродов и алюминиевой фольги. Содержание примесей в этом алюминии составляет не более 0,03%. Существует и чистый металл АВ0000 , включающий не более 0,004% добавок. Имеют значение и сами примеси: никель, кремний и цинк незначительно влияют на проводимость алюминия, а содержание в этом металле меди, серебра и магния дает ощутимый эффект. Наиболее сильно уменьшают проводимость таллий и марганец.
Алюминий отличается хорошими антикоррозийными свойствами. При контакте с воздухом он покрывается тонкой пленкой окиси, которая и защищает его от дальнейшего разрушения. Для улучшения механических характеристик металл сплавляют с другими элементами.
Показатели стали и железа
Удельное сопротивление железа по сравнению с медью и алюминием имеет очень высокие показатели, однако благодаря доступности, прочности и устойчивости к деформациям материал широко используют в электротехническом производстве.
Хоть железо и сталь, удельное сопротивление которой еще выше, имеют существенные недостатки, изготовители проводникового материала нашли методы их компенсирования. В частности, низкую стойкость к коррозии преодолевают путем покрытия стальной проволоки цинком или медью.
Свойства натрия
Металлический натрий также очень перспективен в проводниковом производстве. По показателям сопротивления он значительно превышает медь, однако имеет плотность в 9 раз меньше, чем у неё. Это позволяет использовать материал в изготовлении сверхлёгких проводов.
Металлический натрий очень мягкий и совершенно неустойчив к любого рода деформационным воздействиям, что делает его использование проблемным — провод из этого металла должен быть покрыт очень прочной оболочкой с крайне малой гибкостью. Оболочка должна быть герметичной, так как натрий проявляет сильную химическую активность в самых нейтральных условиях. Он моментально окисляется на воздухе и демонстрирует бурную реакцию с водой, в том числе и с содержащейся в воздухе.
Еще одним плюсом использования натрия является его доступность. Его можно получить в процессе электролиза расплавленного хлористого натрия, которого в мире существует неограниченное количество. Другие металлы в этом плане явно проигрывают.
Чтобы рассчитать показатели конкретного проводника, необходимо произведение удельного числа и длины проволоки разделить на площадь ее сечения. В результате получится значение сопротивления в Омах. Например, чтобы определить, чему равно сопротивление 200 м проволоки из железа с номинальным сечением 5 мм², нужно 0,13 умножить на 200 и разделить полученный результат на 5. Ответ — 5,2 Ом.
Правила и особенности вычисления
Для измерения сопротивления металлических сред пользуются микроомметрами. Сегодня их выпускают в цифровом варианте, поэтому проведенные с их помощью измерения отличаются точностью. Объяснить ее можно тем, что металлы обладают высоким уровнем проводимости и имеют крайне маленькое сопротивление. Для примера, нижний порог измерительных приборов имеет значение 10 -7 Ом.
С помощью микроомметров можно быстро определить, насколько качественен контакт и какое сопротивление проявляют обмотки генераторов, электродвигателей и трансформаторов, а также электрические шины. Можно вычислить присутствие включений другого металла в слитке. Например, вольфрамовый кусок, покрытый позолотой, показывает вдвое меньшую проводимость, чем полностью золотой. Тем же способом можно определить внутренние дефекты и полости в проводнике.
Формула удельного сопротивления выглядит следующим образом: ρ = Ом · мм 2 /м . Словами ее можно описать как сопротивление 1 метра проводника , имеющего площадь сечения 1 мм². Температура подразумевается стандартная — 20 °C.
Влияние температуры на измерение
Нагревание или охлаждение некоторых проводников оказывает значительное влияние на показатели измерительных приборов. В качестве примера можно привести следующий опыт: необходимо подключить к аккумулятору спирально намотанную проволоку и подключить в цепь амперметр.
Чем сильнее нагревается проводник, тем меньше становятся показания прибора. Сила тока имеет обратно пропорциональную зависимость от сопротивления. Следовательно, можно сделать вывод, что в результате нагрева проводимость металла уменьшается. В большей или меньшей степени так ведут себя все металлы, однако изменения проводимости у некоторых сплавов практически не наблюдается.
Примечательно, что жидкие проводники и некоторые твердые неметаллы имеют тенденцию уменьшать свое сопротивление с повышением температуры. Но и эту способность металлов ученые обратили себе на пользу. Зная температурный коэффициент сопротивления (α) при нагреве некоторых материалов, можно определять внешнюю температуру. Например, проволоку из платины, размещенную на каркасе из слюды, помещают в печь, после чего проводят измерение сопротивления. В зависимости от того, насколько оно изменилось, делают вывод о температуре в печи. Такая конструкция называется термометром сопротивления.
Если при температуре t 0 сопротивление проводника равно r 0, а при температуре t равно rt , то температурный коэффициент сопротивления равен
Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200 °C).
Содержание:
В электротехнике одними из главных элементов электрических цепей являются провода. Их задача состоит в том, чтобы с минимальными потерями пропустить электрический ток. Экспериментальным путем уже давно определено, что для минимизации потерь электроэнергии провода лучше всего изготавливать из серебра. Именно этот металл обеспечивает свойства проводника с минимальным сопротивлением в омах. Но поскольку этот благородный металл дорог, в промышленности его применение весьма ограничено.
А главными металлами для проводов стали алюминий и медь. К сожалению, сопротивление железа как проводника электричества слишком велико для того, чтобы из него получился хороший провод. Несмотря на более низкую стоимость, оно применяется только как несущая основа проводов линий электропередачи.
Такие разные сопротивления
Сопротивление измеряется в омах. Но для проводов эта величина получается очень маленькой. Если попытаться провести замер тестером в режиме измерения сопротивления, получить правильный результат будет сложно. Причем, какой бы провод мы ни взяли, результат на табло прибора будет мало отличаться. Но это не значит, что на самом деле электросопротивление этих проводов будет одинаково влиять на потери электроэнергии. Чтобы в этом убедиться, надо проанализировать формулу, по которой делается расчет сопротивления:
В этой формуле используются такие величины, как:
Получается, что сопротивление определяет сопротивление. Существует сопротивление, вычисляемое по формуле с использованием другого сопротивления. Это удельное электрическое сопротивление ρ (греческая буква ро) как раз и обуславливает преимущество того или иного металла как электрического проводника:
Поэтому, если применить медь, железо, серебро или какой-либо иной материал для изготовления одинаковых проводов или проводников специальной конструкции, главную роль в его электротехнических свойствах будет играть именно материал.
Но на самом деле ситуация с сопротивлением сложнее, чем просто вычисления по формулам, приведенным выше. Эти формулы не учитывают температуру и форму поперечника проводника. А при увеличении температуры удельное сопротивление меди, как и любого другого металла, становится больше. Весьма наглядным примером этого может быть лампочка накаливания. Можно замерить тестером сопротивление ее спирали. Затем, измерив силу тока в цепи с этой лампой, по закону Ома вычислить ее сопротивление в состоянии свечения. Результат получится значительно больше, нежели при измерении сопротивления тестером.
Так же и медь не даст ожидаемой эффективности при токе большой силы, если пренебречь формой поперечного сечения проводника. Скин-эффект, который проявляется прямо пропорционально увеличению силы тока, делает неэффективными проводники с круглым поперечным сечением, даже если используется серебро или медь. По этой причине сопротивление круглого медного провода при токе большой силы может оказаться более высоким, чем у плоского провода из алюминия.
Причем, даже если их площади поперечников одинаковы. При переменном токе скин-эффект также проявляется, увеличиваясь по мере роста частоты тока. Скин-эффект означает стремление тока течь ближе к поверхности проводника. По этой причине в некоторых случаях выгоднее использовать покрытие проводов серебром. Даже незначительное уменьшение удельного сопротивления поверхности посеребренного медного проводника существенно уменьшает потери сигнала.
Обобщение представления об удельном сопротивлении
Как и в любом другом случае, который связан с отображением размерностей, удельное сопротивление выражается в разных системах единиц. В СИ (Международная система единиц) используется ом м, но допустимо использование также и Ом*кВ мм/м (это внесистемная единица измерения удельного сопротивления). Но в реальном проводнике величина удельного сопротивления непостоянна. Поскольку все материалы характеризуются определенной чистотой, которая может изменяться от точки к точке, необходимо было создать соответствующее представление о сопротивлении в реальном материале. Таким проявлением стал закон Ома в дифференциальной форме:
Этот закон, скорее всего, не будет применяться для расчетов в быту. Но в ходе проектирования различных электронных компонентов, например, резисторов, кристаллических элементов он непременно используется. Поскольку позволяет выполнить расчеты, исходя из данной точки, для которой существует плотность тока и напряженность электрического поля. И соответствующее удельное сопротивление. Формула применяется для неоднородных изотропных, а также анизотропных веществ (кристаллов, разряда в газе и т.п.).
Как получают чистую медь
Для того чтобы максимально уменьшить потери в проводах и жилах кабелей из меди, она должна быть особо чистой. Это достигается специальными технологическими процессами:
- на основе электронно-лучевой, а так же зонной плавки;
- многократной электролизной очисткой.
Как нам известно из закона Ома, ток на участке цепи находится в следующей зависимости: I=U/R . Закон был выведен в результате серии экспериментов немецким физиком Георгом Омом в XIX веке. Он заметил закономерность: сила тока на каком-либо участке цепи прямо зависит от напряжения, которое к этому участку приложено, и обратно — от его сопротивления.
Позже было установлено, что сопротивление участка зависит от его геометрических характеристик следующим образом: R=ρl/S ,
где l- длина проводника, S — площадь его поперечного сечения, а ρ — некий коэффициент пропорциональности.
Таким образом, сопротивление определяется геометрией проводника, а также таким параметром, как удельное сопротивление (далее — у. с.) — так назвали этот коэффициент. Если взять два проводника с одинаковым сечением и длиной и поставить их в цепь по очереди, то, измеряя силу тока и сопротивление, можно увидеть, что в двух случаях эти показатели будут разными. Таким образом, удельное электрическое сопротивление — это характеристика материала, из которого сделан проводник, а если быть еще более точным, то вещества.
Проводимость и сопротивление
У.с. показывает способность вещества препятствовать прохождению тока. Но в физике есть и обратная величина — проводимость. Она показывает способность проводить электрический ток. Выглядит она так:
σ=1/ρ, где ρ — это и есть удельное сопротивление вещества.
Если говорить о проводимости, то она определяется характеристиками носителей зарядов в этом веществе. Так, в металлах есть свободные электроны. На внешней оболочке их не больше трех, и атому выгоднее их «отдать», что и происходит при химических реакциях с веществами из правой части таблицы Менделеева. В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В растворах носителями заряда являются ионы.
Если говорить о таких веществах, как кремний, то по своим свойствам он является полупроводником и работает несколько по иному принципу, но об этом позже. А пока разберемся, чем же отличаются такие классы веществ, как:
- Проводники;
- Полупроводники;
- Диэлектрики.
Проводники и диэлектрики
Есть вещества, которые ток почти не проводят. Они называются диэлектриками. Такие вещества способны поляризоваться в электрическом поле, то есть их молекулы могут поворачиваться в этом поле в зависимости от того, как распределены в них электроны . Но поскольку электроны эти не являются свободными, а служат для связи между атомами, ток они не проводят.
Проводимость диэлектриков почти нулевая, хотя идеальных среди них нет (это такая же абстракция, как абсолютно черное тело или идеальный газ).
Условной границей понятия «проводник» является ρ
Между этими двумя классами существуют вещества, называемые полупроводниками. Но выделение их в отдельную группу веществ связано не столько с их промежуточным состоянием в линейке «проводимость — сопротивление», сколько с особенностями этой проводимости в различных условиях.
Зависимость от факторов внешней среды
Проводимость — не совсем постоянная величина. Данные в таблицах, откуда берут ρ для расчетов, существуют для нормальных условий среды, то есть для температуры 20 градусов. В реальности для работы цепи сложно подобрать такие идеальные условия; фактически у.с. (а стало быть, и проводимость) зависят от следующих факторов:
- температура;
- давление;
- наличие магнитных полей;
- свет;
- агрегатное состояние.
Разные вещества имеют свой график изменения этого параметра в разных условиях. Так, ферромагнетики (железо и никель) увеличивают его при совпадении направления тока с направлением силовых линий магнитного поля. Что касается температуры, то зависимость здесь почти линейная (существует даже понятие температурного коэффициента сопротивления, и это тоже табличная величина). Но направление этой зависимости различно: у металлов оно повышается с повышением температуры, а у редкоземельных элементов и растворов электролитов увеличивается — и это в пределах одного агрегатного состояния.
У полупроводников зависимость от температуры не линейная, а гиперболическая и обратная: при повышении температуры их проводимость увеличивается. Это качественно отличает проводники от полупроводников. Вот так выглядит зависимость ρ от температуры у проводников:
Здесь представлены удельное сопротивление меди, платины и железа. Немного другой график у некоторых металлов, например, ртути — при понижении температуры до 4 К она теряет его почти полностью (такое явление называется сверхпроводимостью).
А для полупроводников эта зависимость будет примерно такая:
При переходе в жидкое состояние ρ металла увеличивается, а вот дальше все они ведут себя по-разному. Например, у расплавленного висмута оно ниже, чем при комнатной температуре, а у меди — в 10 раз выше нормального. Никель выходит из линейного графика еще при 400 градусах, после чего ρ падает.
Зато у вольфрама температурная зависимость настолько высока, что это становится причиной перегорания ламп накаливания. При включении ток нагревает спираль, и ее сопротивление увеличивается в несколько раз.
Также у. с. сплавов зависит от технологии их производства. Так, если мы имеем дело с простой механической смесью, то сопротивление такого вещества можно посчитать по среднему, а вот оно же у сплава замещения (это когда два и более элемента складываются в одну кристаллическую решетку) будет иным, как правило, куда большим. Например, нихром, из которого делают спирали для электроплиток, имеет такую цифру этого параметра, что этот проводник при включении в цепь греется до красноты (из-за чего, собственно, и используется).
Вот характеристика ρ углеродистых сталей:
Как видно, при приближении к температуре плавления оно стабилизируется.
Удельное сопротивление различных проводников
Как бы то ни было, а при расчетах используется ρ именно в нормальных условиях. Приведем таблицу, по которой можно сравнить эту характеристику у разных металлов:
Как видно из таблицы, лучший проводник — это серебро.-7 Ом · м.
Разница между у. с. различных проводников определяет и их применение. Так, медь и алюминий массово применяются при производстве кабеля, а золото и серебро — в качестве контактов в ряде радиотехнических изделий. Высокоомные проводники нашли свое место среди производителей электроприборов (точнее, они и создавались для этого).
Изменчивость этого параметра в зависимости от условий внешней среды легла в основу таких приборов, как датчики магнитного поля, терморезисторы, тензодатчики, фоторезисторы.
* Удельное сопротивление полупроводников сильно зависит от наличия примесей в материале, что делает их полезными в твердотельной электронике. Ссылки: 1. Джанколи, Дуглас К., Физика, 4-е изд., Прентис Холл, (1995). 2. Справочник CRC по химии и физике, 64-е изд. 3. Википедия, Удельное электрическое сопротивление и проводимость. | Индекс Таблицы Ссылка | |||||||||||
Тепловая и электрическая
Техническая информация, включая механические и электрические свойства, спецификации материалов, а также данные теплового коэффициента и проводимости, представлена на вкладках выше.Никто не предлагает более широкий ассортимент металлов и сплавов, чем HPM. С любыми вопросами обращайтесь к представителю службы технической поддержки HPM.
Коэффициент теплового расширения (TEC)
Коэффициент теплового расширения для данного материала является мерой относительного изменения длины на градус изменения температуры. Сам коэффициент незначительно изменяется с температурой и чаще всего указывается как среднее значение для интересующего температурного диапазона, обычно от комнатной температуры до 100 ° C.Ниже приводится рейтинг группы материалов, доступных от Hamilton Precision Metals.
| Металлический сплав | TEC 10 6 / ° C | Диапазон температур |
| Шунт Манганин | 18,7 | от 20 ° до 100 ° C |
| Фосфорная бронза A | 17,8 | от 20 до 300 ° C |
| Бериллий Медь 25 | 17.5 | от 20 ° до 200 ° C |
| нерж. Сталь 302/304 / 304L | 17,3 | от 0 ° до 100 ° C |
| SS 305 | 17,3 | от 0 ° до 100 ° C |
| Медь 102 | 17,0 | от 20 ° до 100 ° C |
| СС 301 | 16,9 | от 0 ° до 100 ° C |
| Нейзильбер 55-18 | 16.7 | от 20 до 300 ° C |
| Cu-Ni 715 | 16,2 | от 20 до 300 ° C |
| Нерж. Сталь 316 / 316L | 16,0 | от 0 ° до 100 ° C |
| Balco | 15,0 | от 20 ° до 100 ° C |
| Константан | 14,9 | от 20 ° до 100 ° C |
| Бериллиевый никель HPM | 14.4 | от 20 ° до 550 ° C |
| л.с.M 600 | 14,2 | от 20 ° до 315 ° C |
| л.с.M 400 | 13,9 | от 20 ° до 100 ° C |
| HPM 80/20 A — 80 / 20AL | 13,4 | от 20 ° до 100 ° C |
| Никель HPM 200/201/270 | 13,3 | от 0 ° до 100 ° C |
| Evanohm ® R / S | 13.0 | от 20 ° до 100 ° C |
| молибденовый пермаллой | 12,7 | от 25 ° до 200 ° C |
| HPM X 750 | 12,6 | от 20 ° до 100 ° C |
| Гавар | 12,5 | от 0 ° до 50 ° C |
| HPM C-276 | 11,2 | от 25 ° до 100 ° C |
| SS 410 | 11.0 | от 0 ° до 100 ° C |
| SS 17-4 PH (HT) | 10,8 | от 21 ° до 93 ° C |
| л.с. / мин 455 | 10,6 | от 22 ° до 93 ° C |
| SS 430 | 10,5 | от 0 ° до 100 ° C |
| SS 420 | 10,3 | от 0 ° до 100 ° C |
| SS 17-7 PH | 10.3 | от 21 ° до 93 ° C |
| Точность C | 10,1 | от 30 ° до 200 ° C |
| HPM Ni 52 | 10,0 | от 30 ° до 500 ° C |
| CP Титан | 8,6 | от 0 ° до 100 ° C |
| Точность C | 8,1 | от -45 ° до 65 ° C |
| HPM Ni 42 | 6.0 | от 30 ° до 400 ° C |
| Родар | 4,9 | от 30 ° до 400 ° C |
| HPM Ni 36 | 1,05 | от 20 ° до 200 ° C |
Удельное электрическое сопротивление
Удельное сопротивление характеризует присущую металлу способность поддерживать прохождение электрического тока. Измеренное удельное сопротивление является обратной величиной удельной электропроводности и выражается в мкОм • см.Преобразование в другие общепринятые единицы удельного сопротивления выглядит следующим образом:
- 1 мкОм • см = 6,015 Ом CMF (Ом, круговые милы на фут)
- 1 мкОм • см = 4,724 Ом SMF (Ом, квадратный мил на фут)
| Металл / сплав | Удельное сопротивление @ R.T. Микромм • см |
| Медь 102 | 1.71 |
| Никель HPM 270 | 7,5 |
| Бериллий Медь 25 | 7,8 |
| Никель HPM 201 | 8,5 |
| Никель HPM 200 | 9,5 |
| Фосфорная бронза A | 11,5 |
| Balco | 19,9 |
| Бериллиевый никель HPM | 28.7 |
| Нейзильбер 55-18 | 31,4 |
| Шунт Манганин | 38,1 |
| Cu-Ni 715 | 39,5 |
| HPM Ni 52 | 43,0 |
| Родар | 49,0 |
| Константан | 50,8 |
| л.с.M 400 | 51.0 |
| SS 420 | 55,0 |
| CP Титан | 56,0 |
| SS 410 | 57,0 |
| молибденовый пермаллой | 59,0 |
| SS 430 | 60,0 |
| HPM Ni 42 | 70,0 |
| СС 301 | 72.0 |
| нерж. Сталь 302/304 / 304L | 72,0 |
| SS 305 | 74,0 |
| Нерж. Сталь 316 / 316L | 74,0 |
| л.с. / мин 455 | 79,0 |
| SS 17-4 PH (HT) | 80,0 |
| HPM Ni 36 | 82,0 |
| SS 17-7 PH | 83.0 |
| Гавар | 92,0 |
| Точность C | 102,0 |
| л.с.M 600 | 103,0 |
| HPM 80/20 A — 80/20 AL | 108,0 |
| HPM X 750 | 119,0 |
| HPM C-276 | 130,0 |
| Evanohm ® R | 133.0 |
| Evanohm ® S | 137,0 |
Теплопроводность
Теплопроводность описывает присущую металлу способность поддерживать поток тепловой энергии. Теплопроводность выражается в Вт / м • К (ватт на метр градус Кельвина). Преобразование в другие общепринятые единицы теплопроводности выглядит следующим образом:
- 1 Вт / м • K = 0,5782 BTU • FT / HR • FT2 • ° F
- 1 Вт / м • K =.0024 кал / см. С. ° С
| Металл / сплав | Вт / м • K @ R.T. |
| Медь 102 | 390,0 |
| Бериллий Медь 25 | 105,0 |
| Никель HPM 270 | 79,0 |
| Никель HPM 201 | 74.0 |
| Фосфорная бронза A | 69,2 |
| Никель HPM 200 | 67,0 |
| Бериллиевый никель HPM | 48,4 |
| молибденовый пермаллой | 34,6 |
| Cu Ni 715 | 29,4 |
| Нейзильбер 55-18 | 29.3 |
| Balco | 28,9 |
| SS 430 | 26,1 |
| SS 410/420 | 24,9 |
| л.с.M 400 | 21,8 |
| Константан | 21,2 |
| Шунт Манганин | 19,8 |
| л.с. / мин 455 | 18.0 |
| SS 17-4 PH (HT) | 17,9 |
| Родар | 16,7 |
| SS 17-7 PH | 16,7 |
| СС 301 | 16,3 |
| нерж. Сталь 302/304 / 304L | 16,3 |
| Нерж. Сталь 316 / 316L | 16,3 |
| SS 305 | 16.2 |
| CP Титан | 16,0 |
| HPM 80/20 A — 80/20 AL | 15,0 |
| л.с.M 600 | 14,8 |
| Evanohm ® R / S | 14,6 |
| HPM Ni 52 | 14,0 |
| Точность C | 13,0 |
| Гавар | 13.0 |
| HPM X 750 | 12,0 |
| HPM Ni 42 | 10,7 |
| HPM Ni 36 | 10,5 |
| HPM C-276 | 9,4 |
Удельное сопротивление обычных материалов
Заявление об отказе от ответственности: Хотя я пытался убедиться, что данные о свойствах материалов, содержащиеся здесь, являются точными, Я не могу гарантировать его точность.Ни в коем случае поставщик этой информации несет ответственность в случае ошибки в заявленных значениях. |
| Предел прочности на разрыв — США / английский | ||
| Фунт на квадратный дюйм (ksi) | 0,7031 | Килограмм на квадратный миллиметр (кг / мм²) |
| Ом-квадрат миллиметр на метр (Ом-мм² / м) | 6,8948 | мегапаскалей (МПа) или ньютонов на квадратный миллиметр (Н / мм²) |
| Предел прочности — метрическая система | ||
| Килограмм на квадратный миллиметр (кг / мм²) | 1422.3 | фунтов на квадратный дюйм (psi) |
| мегапаскалей (MPA) | 0,145 | Фунтов на квадратный дюйм (ksi) |
| Force — США / английский | ||
| Фунт-сила (фунт) | 4,4482 | Ньютон (Н) |
| Force –Metric | ||
| Ньютон (Н) | 0,22481 | Фунт-сила (фунт) |
| Сопротивление — США / английский | ||
| Ом на 1000 футов (Ω / mft) | 3.2808 | Ом на километр (Ом / км) |
| Ом на милю (Ом / милю) | 0,62137 | Ом на километр (Ом / км) |
| Сопротивление — метрическая система | ||
| Ом на километр (Ом / км) | 0,3048 | Ом на 1000 футов (Ω / mft) |
| Ом на километр (Ом / км) | 1,6093 | Ом на милю (Ом / милю) |
| Удельное сопротивление — США / английский | ||
| Ом-круговой мил на фут (Ом-смил / фут) | 0.16624 | Микроом-сантиметр (мОм-см) |
| Ом-круговой мил на фут (Ом-смил / фут) | 0,0016624 | Ом-квадрат миллиметр на метр (Ом-мм² / м) |
| Ом-круговой мил на фут (Ом-смил / фут) | 0,065450 | Микроом-дюйм (мОм-дюйм) |
| Микроом-дюйм (мОм-дюйм) | 15 279 | Ом-круговой мил на фут (Ом-смил / фут) |
| % IACS | 1037.1 ÷% IACS | Ом-круговой мил на фут (Ом-смил / фут) |
| Удельное сопротивление — метрическая система | ||
| Микроом-сантиметр (мОм-см) | 6.0153 | Ом-круговой мил на фут (Ом-смил / фут) |
| Микроом-сантиметр (мОм-см) | 0,39370 | Микроом-дюйм (мОм-дюйм) |
| Микроом-сантиметр (мОм-см) | 0,0100 | Ом-квадрат миллиметр на метр (Ом-мм² / м) |
| Ом-квадрат миллиметр на метр (Ом-мм² / м) | 601.54 | Ом-круговой мил на фут (Ом-смил / фут) |
| % IACS | 172,41 ÷% МАКО | Микроом-сантиметр (мОм-см) |
| Вес — США / английский | ||
| фунтов на 1000 футов (фунт / фут) | 1.4882 | Килограмм на километр (кг / км) |
| Вес — метрическая система | ||
| Килограмм на километр (кг / км) | 0,67197 | фунтов на 1000 футов (фунт / фут) |
| Плотность — США / английский | ||
| Фунтов на кубический дюйм (фунт / дюйм³) | 27.68 | Грамм на кубический сантиметр (г / см³) |
| Плотность — метрическая система | ||
| Грамм на кубический сантиметр (г / см³) | 0,03613 | фунтов на кубический дюйм (фунт / дюйм³) |
| Площадь поперечного сечения — США / английский | ||
| Круглые милы (CMA или cmil) | 0,0005067 | Квадратный миллиметр (мм²) |
| Квадратные дюймы (дюйм²) | 645,16 | Квадратный миллиметр (мм²) |
| Круглые милы (CMA или cmil) | 0.0000007854 | Квадратные дюймы (дюйм²) |
| Квадратные дюймы (дюйм²) | 1273240 | Круглые милы (CMA или cmil) |
| Площадь поперечного сечения — метрическая система | ||
| Квадратный миллиметр (мм²) | 1973,6 | Круглые милы (CMA или cmil) |
| Квадратный миллиметр (мм²) | 0,00155 | Квадратные дюймы (дюйм²) |
Коммерчески чистый никель — свойства, изготовление и применение коммерчески чистого никеля
Химическая формула
Ni
Охваченные темы
Предпосылки
Коммерчески чистый или низколегированный никель находит свое основное применение в химической обработке и электронике.
Коррозионная стойкость
Из-за коррозионной стойкости чистого никеля, в частности, к различным восстанавливающим химическим веществам и особенно к едким щелочам, никель используется для поддержания качества продукта во многих химических реакциях, особенно при обработке пищевых продуктов и производстве синтетического волокна.
Свойства технически чистого никеля
По сравнению с никелевыми сплавами, технически чистый никель обладает высокой электропроводностью, высокой температурой Кюри и хорошими магнитострикционными свойствами.Никель используется для изготовления электронных выводных проводов, компонентов батарей, тиратронов и искровых электродов.
Никель также обладает хорошей теплопроводностью. Это означает, что его можно использовать для теплообменников в агрессивных средах.
Таблица 1. Свойства никеля 200, технически чистого сорта (99,6% Ni).
| Свойство | Значение | |
| Предел прочности при отжиге при 20 ° C | 450 МПа | |
| Отожженный 0.2% Устойчивое напряжение при 20 ° C | 150 МПа | |
| Удлинение (%) | 47 | |
| Плотность | 8,89 г / см 3 | |
| Диапазон плавления | 1435 | |
| Удельная теплоемкость | 456 Дж / кг. ° C | |
| Температура Кюри | 360 ° C | |
| Относительная проницаемость | Начальная | 110 |
| Максимум | 600 | |
| Коэффициент расширения, если ) | 13.3×10 -6 м / м. ° C | |
| Теплопроводность | 70 Вт / м. ° C | |
| Удельное электрическое сопротивление | 0,096×10 -6 Ом.м | |
Изготовление никеля
Никель отожженный имеет низкую твердость и хорошую пластичность. Никель, как золото, серебро и медь, имеет относительно низкую скорость деформационного упрочнения, то есть он не имеет тенденции становиться таким твердым и хрупким, когда он изгибается или иным образом деформируется, как большинство других металлов.Эти свойства в сочетании с хорошей свариваемостью позволяют легко производить из металла готовые изделия.
Никель в хромировании
Никель также часто используется в качестве грунтовочного покрытия при декоративном хромировании. Необработанный продукт, такой как отливка из латуни или цинка или прессование листовой стали, сначала покрывается слоем никеля толщиной примерно 20 мкм. Это придает ему устойчивость к коррозии. Последний слой представляет собой очень тонкий слой хрома (1-2 мкм) для придания ему цвета и устойчивости к потускнению, которые обычно считаются более желательными для посуды с покрытием.Сам по себе хром имел бы неприемлемую коррозионную стойкость из-за в целом пористой природы хромовой гальванической пластины.
Таблица свойств
| Материал | Никель — свойства, изготовление и применение технически чистого никеля |
|---|---|
| Состав: | > 99% Ni или лучше |
80314
| Минимальное значение (SI) | Максимальное значение (S.I.) | Единицы (SI) | Минимальное значение (Imp.) | Максимальное значение (Imp.) | Единицы (Imp.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Атомный объем (средний) | 0,0065 | 0,0067 | м 3 / кмоль | 396,654 | 408,859 | дюйм 3 / кмоль | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Плотность | 8,83 | 8,95 | мг / м | 550001.239 | 558,731 | фунт / фут 3 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Энергосодержание | 230 | 690 | МДж / кг | 24917,9 | 74753,7 | 000 | ккал / фунт000 ккал / фунт200 | ГПа | 23,4961 | 29,0075 | 10 6 psi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прочность на сжатие | 70 | 935 | МПа | 10.1526 | 135,61 | тысяч фунтов на кв. Дюйм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пластичность | 0,02 | 0,6 | 0,02 | 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| тысяч фунтов / кв. Дюйм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Предел выносливости | 135 | 500 | МПа | 19.5801 | 72,5188 | тысяч фунтов / кв. Дюйм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вязкость разрушения | 100 | 150 | МПа · м 1/2 | 91.0047 | 136.507 | 3 1/2800 | 3000 | МПа | 116,03 | 435,113 | тысяч фунтов / кв. Дюйм | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент потерь | 0.0002 | 0,0032 | 0,0002 | 0,0032 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Модуль разрыва | 70 | 935 | МПа | 10.1526 | 0,315 | 0,305 | 0,315 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Модуль сдвига | 72 | 86 | ГПа | 10.4427 | 12,4732 | 10 6 psi | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прочность на разрыв | 345 | 1000 | МПа | 50.038 | 145.038 | 0003 ksi | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27,5572 | 31,9083 | 10 6 фунтов на кв. Дюйм | ||||||||||
| Температура стекла | K | ° F | 2803 Fusion | кДж / кг | 120.378 | 133,275 | БТЕ / фунт | |||||
| Максимальная рабочая температура | 510 | 640 | K | 458,33 | 692,33 | ° F 1707 | 2614,73 | 2670,53 | ° F | |||
| Минимальная рабочая температура | 0 | 0 | K | -459.67 | -459,67 | ° F | ||||||
| Удельная теплоемкость | 452 | 460 | Дж / кг · К | 0,349784 | 0,355975 | БТЕ / 9000 | фунтов 9000 Тепловая теплопроводность | 91 | Вт / м · К | 125,426 | 170,355 | BTU.ft / h.ft 2 .F |
| Тепловое расширение | 12 | 13.5 | 10 -6 / K | 21,6 | 24,3 | 10 -6 / ° F | ||||||
| Потенциал пробоя | МВ / м | |||||||||||
| Диэлектрическая постоянная | ||||||||||||
| Удельное сопротивление | 8 | 10 | 10 -8 Ом.м | 8 | 10 | 10 -8 Ом · м |
| Экологические свойства | |
|---|---|
| Коэффициенты сопротивления | 70 = Плохо 91 |
| Воспламеняемость | 5 |
| Пресная вода | 5 |
| Органические растворители | 5 |
| Окисление при 500C | 5 |
| 4 | |
| Сильные щелочи | 5 |
| UV | 5 |
| Износ | 4 |
| Слабая кислота | 5 |
| Слабые щелочи | 5 |
Источник: Выдержано из Справочника по инженерным материалам, 5 -е издание .
Для получения дополнительной информации об этом источнике посетите Австралазийский институт материаловедения.
Приведены свойства технически чистого никеля. Также объясняются приложения, к которым они приводят. Также описывается его использование для хромирования. Также предоставляются примечания к изготовлению.Сопротивление листа и расчет удельного сопротивления или толщины по отношению к полупроводниковым приложениям напряжение между двумя внутренними точками.
Если расстояние между точками зонда постоянное, а толщина проводящей пленки менее 40% расстояния, а края пленки более чем в 4 раза превышают расстояние между точками измерения, среднее сопротивление пленки или сопротивление листа определяется по формуле:
Rs = 4,53 x V / I
Толщина пленки (в см) и ее удельное сопротивление (в Ом · см) связаны с Rs соотношением:
Rs = удельное сопротивление / толщина
Следовательно, можно вычислить удельное сопротивление, если известна толщина пленки, или можно вычислить толщину, если известно удельное сопротивление.
Словарь терминов
Ом на квадрат: Единица измерения при измерении сопротивления тонкой пленки материала с использованием метода четырехточечного зонда. Он равен сопротивлению между двумя электродами на противоположных сторонах теоретического квадрата. Размер квадрата не имеет значения.
Подробнее читайте здесь, в Википедии: http://en.wikipedia.org/wiki/Sheet_resistance
Ом-сантиметр (Ом-см): Единица измерения при измерении объемного или объемного удельного сопротивления толстых или однородных материалов, таких как голые кремниевые пластины или кремниевые слитки, с использованием метода четырехточечного зонда.
В. Является ли сопротивление листа «неотъемлемым» свойством материала или оно зависит от толщины?
СОПРОТИВЛЕНИЕ — это неотъемлемое свойство материала, которое придает ему электрическое сопротивление. Иногда его называют удельным сопротивлением. Сопротивление листа — это сопротивление тонкого листа материала, которое при умножении на толщину (в см) дает значение удельного сопротивления.
В. Как преобразовать из омов на квадрат в ом-сантиметр?
Термин Ом-см (Ом-сантиметр) относится к измерению «объемного» или «объемного» удельного сопротивления полупроводящего материала.Ом-см используется для измерения проводимости трехмерного материала, такого как слиток кремния или толстый слой материала. Термин «Ом на квадрат» используется при измерении сопротивления листа, то есть значения сопротивления тонкого слоя полупроводящего материала.
Чтобы рассчитать Ом-см с помощью четырехточечного зонда, необходимо знать толщину пластины (если это однородная пластина) или толщину измеряемого верхнего слоя, чтобы иметь возможность рассчитать Ом-см.Метод четырехточечного зонда используется для измерения одного слоя или одного однородного материала. При измерении образца с двумя или более проводящими слоями результатом будет какое-то бессмысленное среднее всех подключенных проводников.
Как упоминалось выше, поскольку метод четырехточечного зонда не позволяет напрямую измерять толщину тонких пленок, если известны две из следующих трех характеристик для данного образца, четырехточечный зонд можно использовать для определения третьей характеристики: 1) объемное сопротивление в Ом-см, 2) сопротивление листа в Ом-квадрат, 3) толщина образца.Подробнее об этом можно узнать здесь: http://www.fourpointprobes.com/understanding-volume-resistivity-measurements/
Уравнения для расчета объемного сопротивления отличаются от тех, которые используются для расчета сопротивления листа, однако, если сопротивление листа уже известно, объемное сопротивление можно рассчитать, умножив сопротивление листа в Ом на квадрат на толщину материала в сантиметры.
В. В какой момент вы перестаете умножать сопротивление листа на толщину в сантиметрах, чтобы получить Ом-см?
Когда толщина превышает 0.1 расстояния между двумя иглами — после которого сопротивление листа не применяется. Итак, 0,1 мм для головки зонда с расстоянием между иглами 1 мм. Однако из-за исправлений подойдет до 0,3 мм.
Если толщина равна или превышает пятикратное расстояние между датчиками, поправочный коэффициент, применяемый к формуле удельного сопротивления (rho) = 2 x pi x s x V / I, составляет менее 0,1%. С точки зрения удельного сопротивления листа, таблицы поправочных коэффициентов, которые у нас есть, начинаются с отношения толщины к расстоянию между зондами, равного 0.3, где поправочный коэффициент равен единице, до отношения 2, где поправочный коэффициент равен x0,6337.
Я ожидаю, что эти таблицы могут быть расширены до большего соотношения, но ясно, что от толщины в 2 раза до 5-кратного расстояния — это немного нейтральная зона, но если предположить, что ситуация « объемная », есть поправочные коэффициенты, охватывающие отношение толщины к расстоянию от 10 до 0,4, где поправочный коэффициент равен x0,288.
Дополнительная информация: Взаимосвязь между сопротивлением листа (Ом на квадрат), толщиной пленки и объемным сопротивлением (Ом-см)
Подробнее читайте здесь, в Википедии: http: // en.wikipedia.org/wiki/Resistivity
Четырехточечные зонды — это подразделение компании Bridge Technology. Чтобы запросить дополнительную информацию, позвоните в Bridge Technology по телефону (480) 988-2256 или отправьте электронное письмо Ларри Бриджу по адресу: [email protected]