характеристики, свойства и сферы применения
Одним из самых востребованных металлов в отраслях промышленности является медь. Наиболее широкое распространение она получила в электрике и электронике. Чаще всего ее применяют при изготовлении обмоток для электродвигателей и трансформаторов. Основная причина использования именно этого материала заключается в том, что медь обладает самым низким из существующих в настоящий момент материалов удельным электрическим сопротивлением. Пока не появится новый материал с более низкой величиной этого показателя, можно с уверенностью говорить о том, что замены у меди не будет.Общая характеристика меди
Говоря про медь, необходимо сказать, что еще на заре электрической эры она стала использоваться в производстве электротехники. Применять ее стали во многом по причине уникальных свойств, которыми обладает этот сплав. Сам по себе он представляет материал, отличающийся высокими свойствами в плане пластичности и обладающий хорошей ковкостью.
Наряду с теплопроводностью меди, одним из самых главных ее достоинств является высокая электропроводность. Именно благодаря этому свойству медь и получила широкое распространение в энергетических установках, в которых она выступает в качестве универсального проводника. Наиболее ценным материалом является электролитическая медь, обладающая высокой степенью чистоты -99,95%. Благодаря этому материалу появляется возможность для производства кабелей.
Плюсы использования электролитической меди
Применение электролитической меди позволяет добиться следующего:- Обеспечить высокую электропроводность;
- Добиться отличной способности к уложению;
- Обеспечить высокую степень пластичности.
Сферы применения
Кабельная продукция, изготавливаемая из электролитической меди, получила широкое распространение в различных отраслях. Чаще всего она применяется в следующих сферах:
Чаще всего она применяется в следующих сферах:- электроиндустрия;
- электроприборы;
- автомобилестроение;
- производство компьютерной техники.
Чему равно удельное сопротивление?
Чтобы понимать, что собой представляет медь и его характеристики, необходимо разобраться с основным параметром этого металла — удельным сопротивлением. Его следует знать и использовать при выполнении расчетов.Под удельным сопротивлением принято понимать физическую величину, которая характеризуется как способность металла проводить электрический ток.
Знать эту величину необходимо еще и для того, чтобы правильно произвести расчет электрического сопротивления проводника. При расчетах также ориентируются на его геометрические размеры. При проведении расчетов используют следующую формулу:
R = р l / S
Это формула многим хорошо знакома.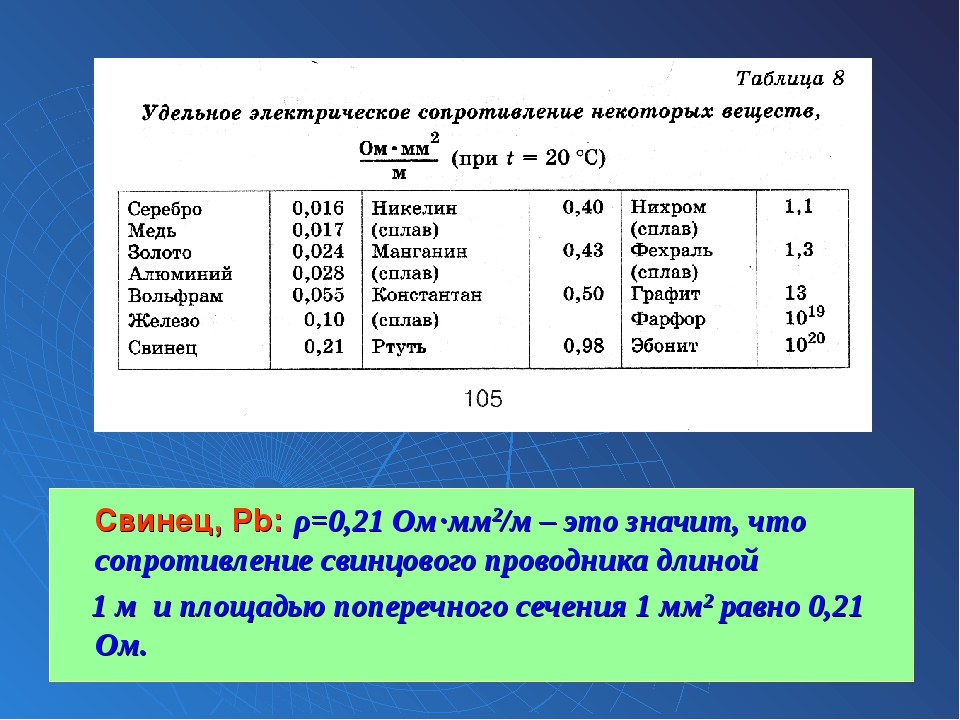 Пользуясь ею, можно легко рассчитать сопротивление медного кабеля, ориентируясь только на характеристики электрической сети. Она позволяет вычислить мощность, которая неэффективно расходуется на нагрев сердечника кабеля. Кроме этого, подобная формула позволяет выполнить расчеты сопротивления любого кабеля. При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
Пользуясь ею, можно легко рассчитать сопротивление медного кабеля, ориентируясь только на характеристики электрической сети. Она позволяет вычислить мощность, которая неэффективно расходуется на нагрев сердечника кабеля. Кроме этого, подобная формула позволяет выполнить расчеты сопротивления любого кабеля. При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
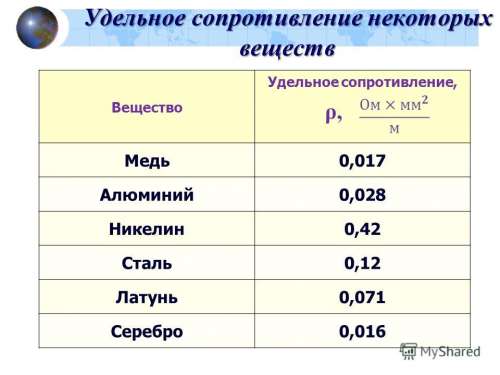
Сименс = 1/ Ом.
У меди любого веса этот параметр состав равен 58 100 000 См/м. Что касается серебра, то величина обратной проводимости у нее равна 62 500 000 См/м.
В нашем мире высоких технологий, когда в каждом доме имеется большое количество электротехнических устройств и установок, значение такого материала, как медь просто неоценимо. Этот материал используют для изготовления проводки, без которой не обходится ни одно помещение. Если бы меди не существовало, тогда человеку пришлось использовать провода из других доступных материалов, например, из алюминия. Однако в этом случае пришлось бы столкнуться с одной проблемой. Все дело в том, что у этого материала удельная проводимость гораздо меньше, чем у медных проводников.
Удельное сопротивление
Использование материалов с низкой электро- и теплопроводностью любого веса ведет к большим потерям электроэнергии.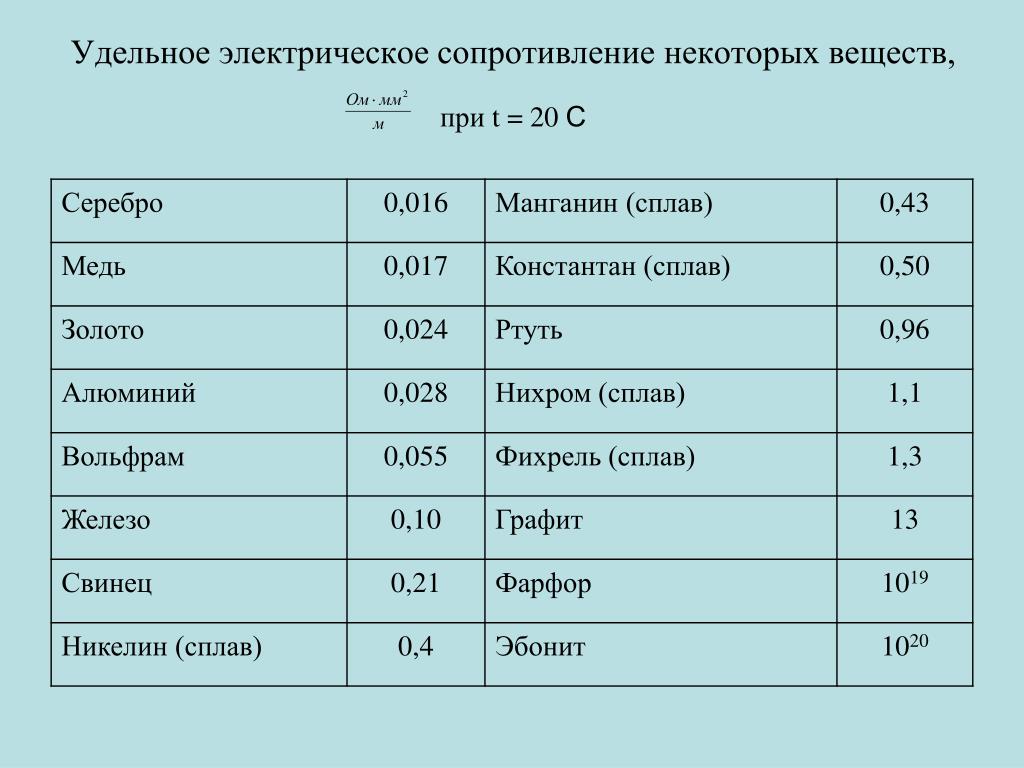 А это влияет на потерю мощности у используемого оборудования. Большинство специалистов в качестве основного материала для изготовления проводов с изоляцией называют медь. Она является главным материалом, из которого изготавливаются отдельные элементы оборудования, работающего от электрического тока.
А это влияет на потерю мощности у используемого оборудования. Большинство специалистов в качестве основного материала для изготовления проводов с изоляцией называют медь. Она является главным материалом, из которого изготавливаются отдельные элементы оборудования, работающего от электрического тока.- Платы, устанавливаемые в компьютерах, оснащаются протравленными медными дорожками.
- Медь также используется для изготовления самых разных элементов, применяемых в электронных устройствах.
- В трансформаторах и электродвигателях она представлена обмоткой, которая изготавливается из этого материала.
Можно не сомневаться, что расширение сфер применения этого материала будет происходить с дальнейшим развитием технического прогресса. Хотя, кроме меди, существуют и другие материалы, но все же конструктора при создании оборудования и различных установок используют медь. Главная причина востребованности этого материала заключается в хорошей электрической и теплопроводности этого металла, которую он обеспечивает в условиях комнатной температуры.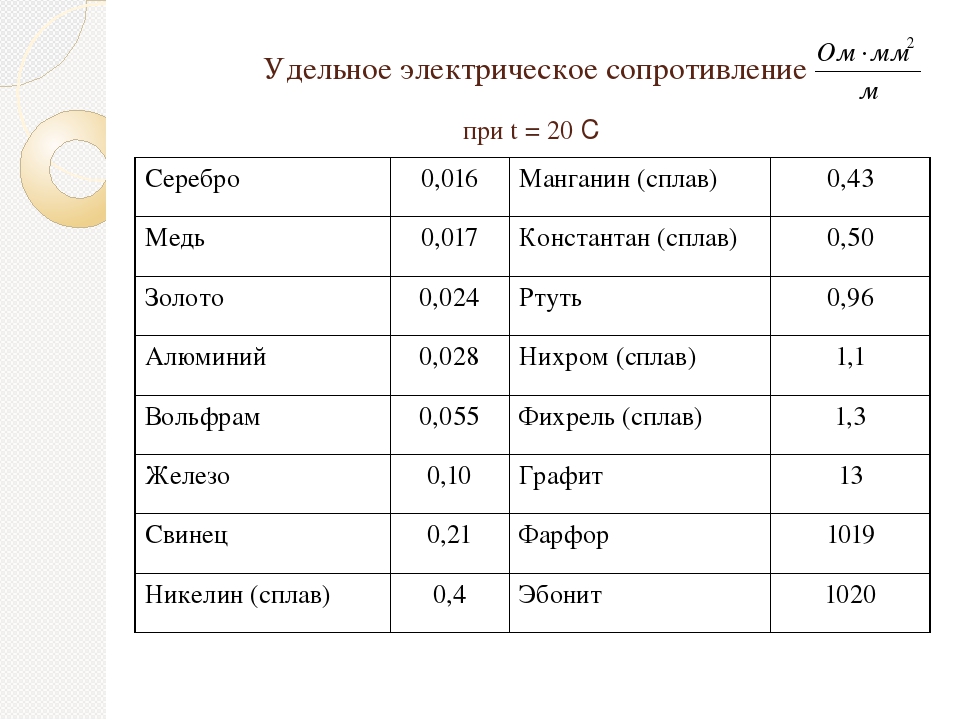
Температурный коэффициент сопротивления
Свойством уменьшения проводимости с повышением температуры обладают все металлы с любой теплопроводностью. При понижении температуры проводимость возрастает. Особенно интересным специалисты называют свойство уменьшения сопротивления с понижением температуры. Ведь в этом случае, когда в комнате температура снижается до определенной величины, у проводника может исчезнуть электрическое сопротивление и он перейдет в класс сверхпроводников.Для того чтобы определить показатель сопротивления конкретного проводника определенного веса в условиях комнатной температуры, существует коэффициент критического сопротивления. Он представляет собой величину, которая показывает изменение сопротивления участка цепи при изменении температуры на один Кельвин. Для выполнения расчета электрического сопротивления медного проводника в определенном временном промежутке используют следующую формулу:
ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления.
Заключение
Медь — материал, который широко применяют в электронике. Его используют не только в обмотке и схемах, но и в качестве металла для изготовления кабельной продукции. Чтобы техника и оборудование работали эффективно, необходимо правильно рассчитать удельное сопротивление проводки, прокладываемой в квартире. Для этого существует определенная формула. Зная её, можно произвести расчет, который позволяет узнать оптимальную величину сечения кабеля. В этом случае можно избежать потери мощности оборудования и обеспечить эффективность его использования.
Оцените статью: Поделитесь с друзьями!Удельное сопротивление железо медь — Морской флот
В связи с тем, что существует два типа электрических сопротивлений –
В связи с электромагнитными явлениями, возникающими в проводниках при прохождении через него переменного тока в них возникает два важных для их электротехнических свойств физических явления.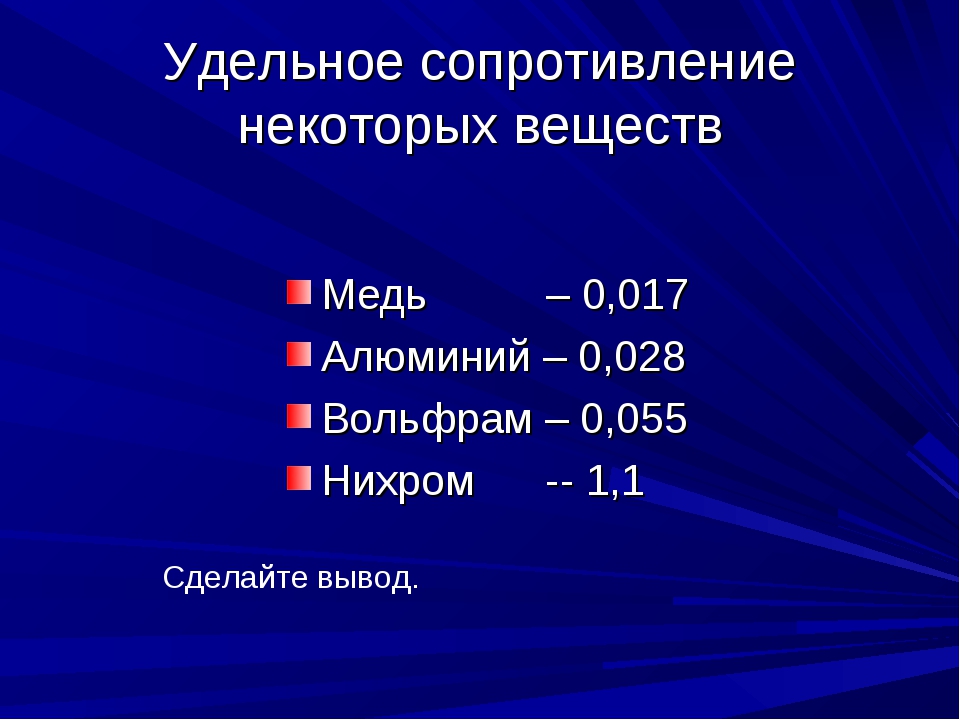
Два последних явления делают неэффективным применение проводников радиусом больше характерной глубины проникновения электрического тока в проводник. Эффективный диаметр проводников (2RБхар): 50Гц -7 Ом. Используя микроомметры, можно определить качество электрических контактов, сопротивление электрических шин, обмоток трансформаторов, электродвигателей и генераторов, наличие дефектов и инородного металла в слитках (например, сопротивление слитка чистого золота вдвое ниже позолоченного слитка вольфрама).
Для расчета длины провода, его диаметра и необходимого электрического сопротивления, необходимо знать удельное сопротивление проводников ρ.
В международной системе единиц удельное сопротивление ρ выражается формулой:
Оно означает: электрическое сопротивление 1 метра провода (в Омах), сечением 1 мм 2 , при температуре 20 градусов по Цельсию.
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025.  0,108 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095. 0,1 0,1 0,103. 0,137 0,12 0,22 0,42 0,43. 0,51 0,5 0,6 0,94 1,05. 1,4 1,15. 1,35 1,2 1,3. 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм 2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм 2 . Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм 2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм 2 .
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм 2 .
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм 2 .
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм 2 . Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм 2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Если при температуре t сопротивление проводника равно r, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Значения температурного коэффициента для некоторых металлов
| Металл | α | ||
| Серебро Медь Железо Вольфрам Платина | 0,0035 0,0040 0,0066 0,0045 0,0032 | Ртуть Никелин Константан Нихром Манганин | 0,0090 0,0003 0,000005 0,00016 0,00005 |
Из формулы температурного коэффициента сопротивления определим rt:
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику.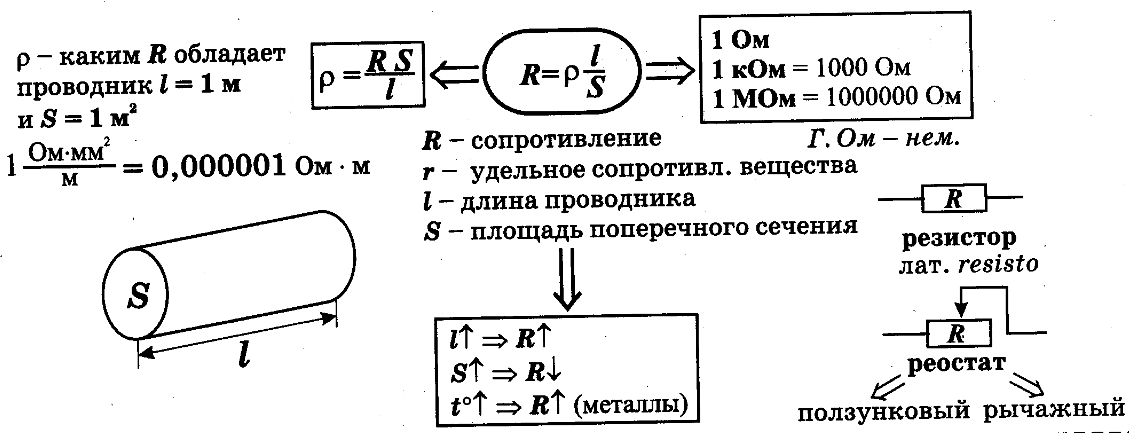 Поэтому сопротивление и проводимость проводника есть величины обратные.
Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10 -20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).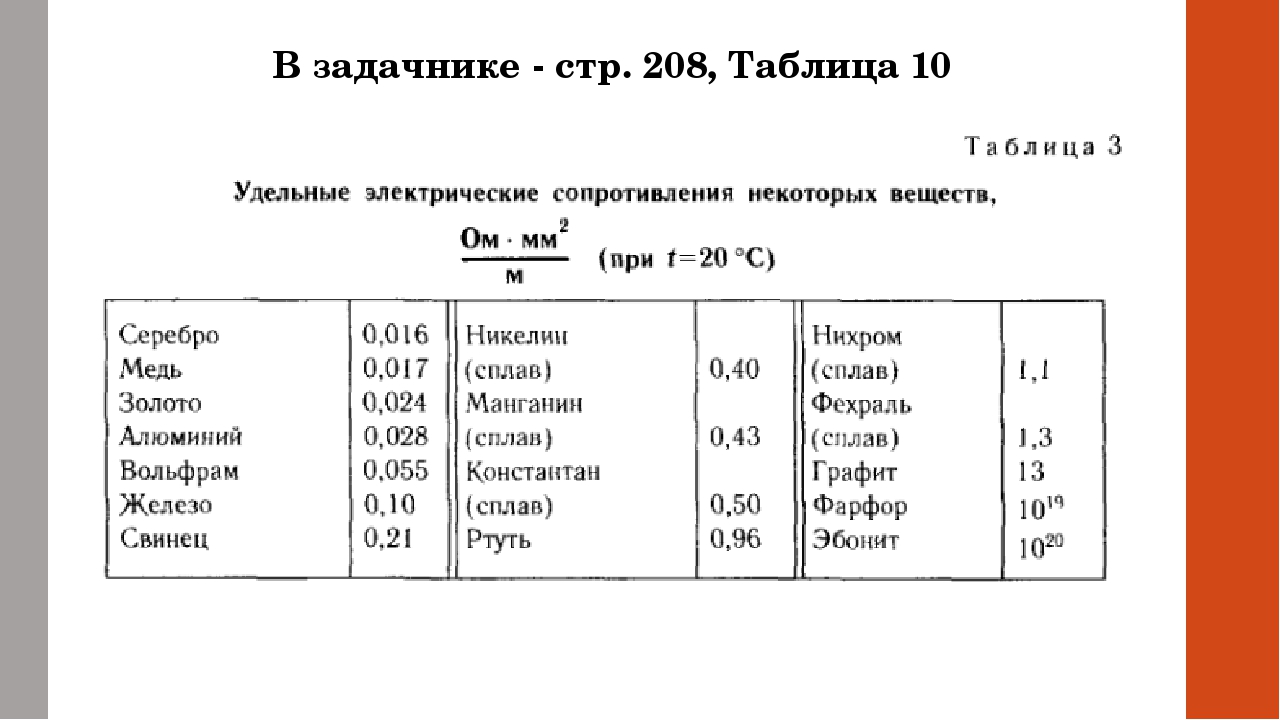
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0. 05% примесей, в том числе не свыше 0.02% кислорода.
05% примесей, в том числе не свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного – 2.7 Мг/м 3 . Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами – как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением.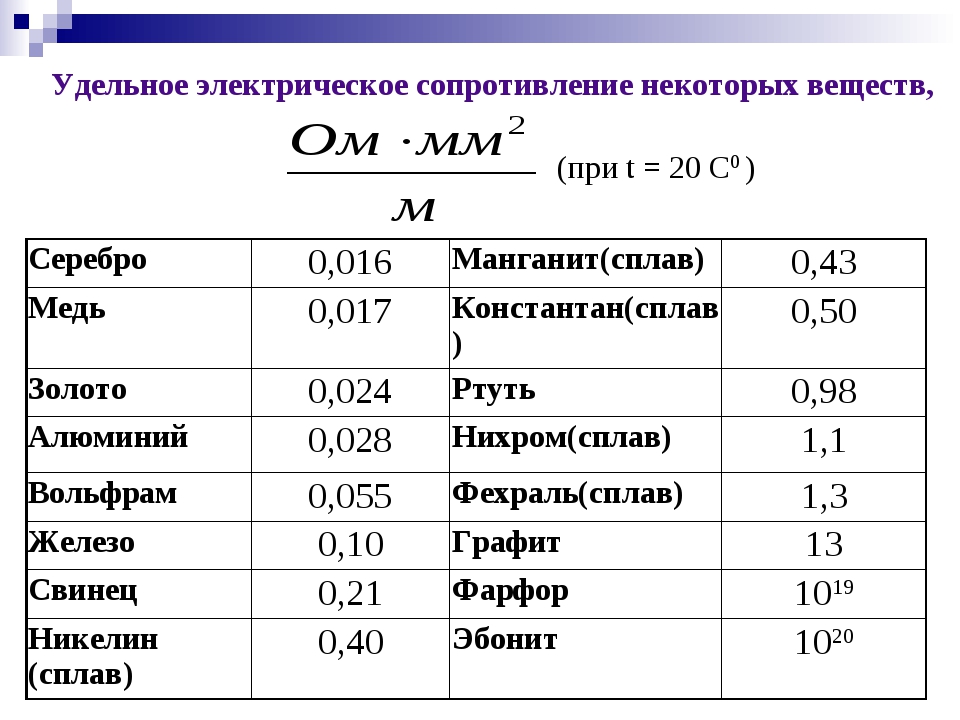 Эта пленка предохраняет металл от дальнейшей коррозии.
Эта пленка предохраняет металл от дальнейшей коррозии.
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Литература по удельному сопротивлению проводников
- Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
- Бачелис Д. С., Белоруссов Н. И., Саакян А. Е. Электрические кабели, провода и шнуры. Справочник. — М.: Энергия, 1971.
- Гершун А. Л. Кабель // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Р. Лакерник, Д. Шарле. От меди к стеклу // Наука и жизнь. — 1986. — Вып. 08. — С. 50—54, 2-3 стр. цветной вкладки.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.
Удельное сопротивление
Удельное электрическое сопротивление определяется как отношение между напряженностью электрического поля внутри металла к плотности тока в нем:
где:
ρ — удельное сопротивление металла (Ом⋅м),
Е — напряженность электрического поля (В/м),
J — величина плотности электрического тока в металле (А/м2)
Если напряженность электрического поля (Е) в металле очень большая, а плотность тока (J) очень маленькая, это означает, что металл имеет высокое удельное сопротивление.
Обратной величиной удельного сопротивления является удельная электропроводность, указывающая, насколько хорошо материал проводит электрический ток:
σ — проводимость материала, выраженная в сименс на метр (См/м).
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
Формула для расчета сопротивления провода:
где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
Поверхностное сопротивление
Величина поверхностного сопротивления рассчитывается таким же образом, как и сопротивление провода. В данном случае площадь сечения можно представить в виде произведения w и t:
Для некоторых материалов, таких как тонкие пленки, соотношение между удельным сопротивлением и толщиной пленки называется поверхностное сопротивление слоя RS:
где RS измеряется в омах. При данном расчете толщина пленки должна быть постоянной.
При данном расчете толщина пленки должна быть постоянной.
Часто производители резисторов для увеличения сопротивления вырезают в пленке дорожки, чтобы увеличить путь для электрического тока.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.
Описание
Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.
Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.
С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.
Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.
Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.
Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.
Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.
Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.
Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.
Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.
Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.
Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).
Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A. Таким образом, мы можем правильно сказать, что сопротивление это:
Таким образом, мы можем правильно сказать, что сопротивление это:
Пропорциональность сопротивления
Но помимо длины и площади проводника, мы также ожидаем, что электрическое сопротивление проводника будет зависеть от фактического материала, из которого он изготовлен, потому что разные проводящие материалы, медь, серебро, алюминий и т.д., имеют разные физические и электрические свойства. Таким образом, мы можем преобразовать знак пропорциональности (∝) вышеприведенного уравнения в знак равенства, просто добавив «пропорциональную константу» в вышеприведенное уравнение, давая:
Уравнение удельного электрического сопротивления
Где: R — сопротивление в омах (Ω), L — длина в метрах (м), A — площадь в квадратных метрах (м 2 ), и где известна пропорциональная постоянная ρ (греческая буква «rho») — удельное сопротивление .
Удельное электрическое сопротивление
Удельное электрическое сопротивление конкретного материала проводника является мерой того, насколько сильно материал противостоит потоку электрического тока через него. Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.
Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.
Например, удельное сопротивление хорошего проводника, такого как медь, составляет порядка 1,72 х 10 -8 Ом (или 17,2 нОм), тогда как удельное сопротивление плохого проводника (изолятора), такого как воздух, может быть значительно выше 1,5 х 10 14 или 150 трлн.
Такие материалы, как медь и алюминий, известны низким уровнем удельного сопротивления, благодаря чему электрический ток легко проходит через них, что делает эти материалы идеальными для изготовления электрических проводов и кабелей. Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.
Тогда факторы, которые влияют на сопротивление (R) проводника в омах, могут быть перечислены как:
- Удельное сопротивление (ρ) материала, из которого сделан проводник.
- Общая длина (L) проводника.
- Площадь поперечного сечения (А) проводника.
- Температура проводника.
Пример удельного сопротивления № 1
Рассчитайте общее сопротивление постоянному току 100-метрового рулона медного провода 2,5 мм 2 , если удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 Ом метр.
Приведенные данные: удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 , длина катушки L = 100 м, площадь поперечного сечения проводника составляет 2,5 мм 2 , что дает площадь: A = 2,5 x 10 -6 м 2 .
Ответ: 688 МОм или 0,688 Ом.
Удельное электрическое сопротивление материала
Ранее мы говорили, что удельное сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения проводника, таким образом, показывая, что удельное сопротивление ρ имеет размеры в Ом-метрах или Ом · м, как это обычно пишется. Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.
Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.
Электрическая проводимость
Хотя как электрическое сопротивление (R), так и удельное сопротивление ρ, являются функцией физической природы используемого материала, а также его физической формы и размера, выраженных его длиной (L) и площадью его сечения ( А), Проводимость или удельная проводимость относится к легкости, с которой электрический ток проходит через материал.
Проводимость (G) является обратной величиной сопротивления (1 / R) с единицей проводимости, являющейся сименсом (S), и ей дается перевернутый символ омов mho, ℧. Таким образом, когда проводник имеет проводимость 1 сименс (1S), он имеет сопротивление 1 Ом (1 Ом). Таким образом, если его сопротивление удваивается, проводимость уменьшается вдвое, и наоборот, как: Сименс = 1 / Ом, или Ом = 1 / Ом.
В то время как сопротивление проводников дает степень сопротивления потоку электрического тока, проводимость проводника указывает на легкость, с которой он пропускает электрический ток. Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Проводимость, σ (греческая буква сигма), является обратной величиной удельного сопротивления. Это 1 / ρ и измеряется в сименах на метр (S / m). Поскольку электропроводность σ = 1 / ρ, предыдущее выражение для электрического сопротивления R можно переписать в виде:
Электрическое сопротивление как функция проводимости
Тогда мы можем сказать, что проводимость — это эффективность, посредством которой проводник пропускает электрический ток или сигнал без потери сопротивления. Поэтому материал или проводник, который имеет высокую проводимость, будет иметь низкое удельное сопротивление, и наоборот, поскольку 1 сименс (S) равен 1 Ом -1 . Таким образом, медь, которая является хорошим проводником электрического тока, имеет проводимость 58,14 x 10 6 Симен на метр.
Пример удельного сопротивления №2
Кабель длиной 20 метров имеет площадь поперечного сечения 1 мм 2 и сопротивление 5 Ом. Рассчитать проводимость кабеля.
Приведенные данные: сопротивление постоянному току, R = 5 Ом, длина кабеля, L = 20 м, а площадь поперечного сечения проводника составляет 1 мм 2, что дает площадь: A = 1 x 10 -6 м 2 .
Ответ: 4 мега-симена на метр длины.
Таблица удельных сопротивлений проводников
| Проводник | Удельное сопротивление ρ | Температурный коэффициент α |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан | 0,5 | 0,05 |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин | 0,43 — 0,51 | 0,01 |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.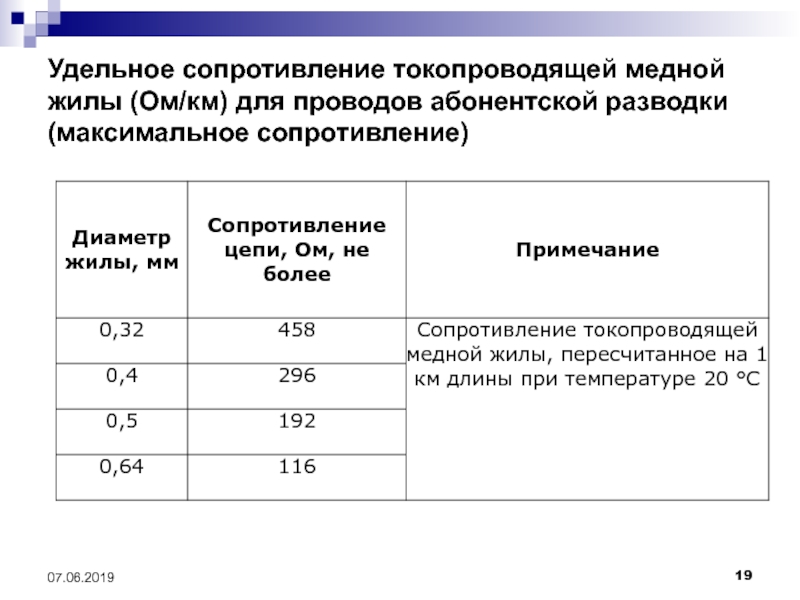 107 107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Где: удельное сопротивление ρ измеряется в Ом*мм 2 /м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 -3 *C -1 (или K -1 ) .
Краткое описание удельного сопротивления
Мы поговорили в этой статье об удельном сопротивлении, что удельное сопротивление — это свойство материала или проводника, которое указывает, насколько хорошо материал проводит электрический ток. Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Сопротивление проводника прямо пропорционально его длине (L) как R ∝ L. Таким образом, удвоение его длины удвоит его сопротивление, в то время как последовательное удвоение проводника уменьшит вдвое его сопротивление. Также сопротивление проводника обратно пропорционально его площади поперечного сечения (A) как R ∝ 1 / A. Таким образом, удвоение его площади поперечного сечения уменьшило бы его сопротивление вдвое, тогда как удвоение его площади поперечного сечения удвоило бы его сопротивление.
Мы также узнали, что удельное сопротивление (символ: ρ) проводника (или материала) связано с физическим свойством, из которого он изготовлен, и варьируется от материала к материалу. Например, удельное сопротивление меди обычно дается как: 1,72 х 10 -8 Ом · м. Удельное сопротивление конкретного материала измеряется в единицах Ом-метров (Ом), которое также зависит от температуры.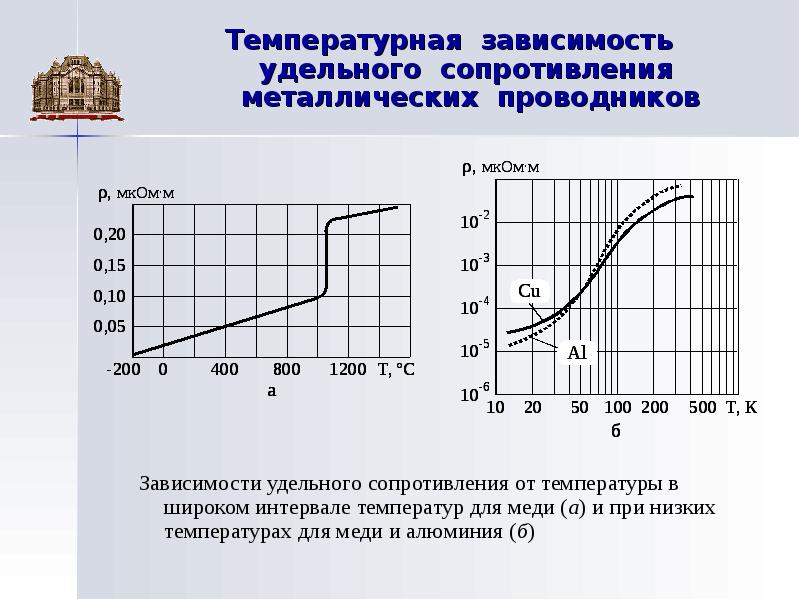
В зависимости от значения удельного электрического сопротивления конкретного материала его можно классифицировать как «проводник», «изолятор» или «полупроводник». Обратите внимание, что полупроводники — это материалы, в которых их проводимость зависит от примесей, добавляемых в материал.
Удельное сопротивление также важно в системах распределения электроэнергии, так как эффективность системы заземления для системы электропитания и распределения сильно зависит от удельного сопротивления земли и материала почвы в месте расположения системы.
Проводимость — это имя, данное движению свободных электронов в форме электрического тока. Проводимость, σ является обратной величиной удельного сопротивления. Это 1 / ρ и имеет единицу измерения сименс на метр, S / m. Проводимость варьируется от нуля (для идеального изолятора) до бесконечности (для идеального проводника). Таким образом, сверхпроводник имеет бесконечную проводимость и практически нулевое омическое сопротивление.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Сопротивление меди — Энциклопедия по машиностроению XXL
В том, что электрическое сопротивление металлов обусловлено взаимодействиями электронов проводимости с различными дефектами решетки, убеждает и тот факт, что удельное сопротивление кристаллов металлов сильно зависит от наличия в них примесей. Например, введение 1% примеси марганца увеличивает удельное сопротивление меди в три раза. [c.152]Рис, 4.5. Зависимость удельного сопротивления меди от температуры [c.116]
При достижении температуры плавления (для меди она составляет 1083 °С) увеличивается объем металла, т. е. уменьшается его плотность, а вместе с ней и концентрация носителей. В результате сопротивление меди возрастет примерно в 2,4 раза. Для металлов, уменьшающих свой объем при плавлении (галлий, висмут, сурьма), значение удельного сопротивления имеет тенденцию к уменьшению.
Для металлов, уменьшающих свой объем при плавлении (галлий, висмут, сурьма), значение удельного сопротивления имеет тенденцию к уменьшению.
Заметное влияние на указа -ные характеристики меди оказывает и температура. При нагревании (особенно выше 200 °С) в результате процесса рекристаллизации (рис. 4.7) механические характеристики и удельное сопротивление меди резко изменяются. [c.120]
ОКОЛО 800° С и, следовательно, Ра 10 ОМ.-М., р= 1. Удельное сопротивление меди принято равным 2-10 ом-м. [c.174]
В диапазоне температур от —50 до 180 °С сопротивление меди находится в линейной зависимости от температуры [c.455]
Коэффициент подсчитан по литературным значениям удельных сопротивлений меди [2] и натрия [3]. Расчеты показали, что в стенке трубы выделяется около 97(% тепла и эта доля практически не меняется с температурой. Некоторая возможная неточность в величинах удельных сопротивлений влияет на коэффициент К слабо, и нет необходимости учитывать разность температур между стенкой и жидкостью для выбора соответствующих значений удельных сопротивлений.
Медь — металл красного, в изломе розового цвета. Температура плавления 1083 °С. Кристаллическая решетка ГЦК с периодом а = 0,31607 нм. Плотность меди 8,94 г/см . Медь обладает высокими электропроводимостью и теплопроводностью Удельное электрическое сопротивление меди 0,0175 мкОм.м. В зависимости от чистоты медь изготовляют следующих марок МОО (99,99 % Си), МО (99,97 % Си), М1 (99,9 % Си), М2 (99,7 % Си), М3 (99,50 % Си). Присутствующие в меди примеси оказывают большое влияние на ее свойства.
Сопротивление меди, как и других металлов зависит от температуры и определяется температурным коэффициентом сопротивления. Для определения коэффициента изменения сопротивления можно воспользоваться табл. 1.7. В таблице вертикальный столбец соответствует температуре в десятках градусов, а верхняя горизонтальная строка — в единицах градусов. Изменение сопротивление меди при 15 °С принято за единицу. Коэффициент для произвольной температуры соответствует пересечению соответствующих строки и столбца.
Д. Мп-бронзы. Содержат 25 % Мп. Высокая жаропрочность и электрическое сопротивление. Медь в твердом состоянии растворяет до 30 % Мп поэтому структура этих бронз — гомогенные а-твердые растворы.
ТКС определяется по сопротивлениям Rf и Rt чувствительного элемента медного ТС, измеренных соответственно при точке таяния льда и кипения воды. В диапазоне температур от —50 до 200 °С зависимость сопротивления меди от температуры носит линейный характер R = Ro (1 + ai). [c.138]
Стальная оцинкованная проволока. Сталь наиболее дешевый из проводниковых материалов, который в отдельных случаях может быть использован в качестве проводника тока. Сталь обладает высокой механической прочностью. Удельное электрическое сопротивление стали значительно выше удельного электрического сопротивления меди и алюминия. Для проводников тока обычно применяется мягкая сталь, содержащая 0,10-0,15% углерода. Основные характеристики мягкой стали
Удельное электрическое сопротивление стали значительно выше удельного электрического сопротивления меди и алюминия. Для проводников тока обычно применяется мягкая сталь, содержащая 0,10-0,15% углерода. Основные характеристики мягкой стали
Удельное сопротивление меди при температуре г, С (( = 30 -f 60 =С) [c.509]
Реле и контакторы, работающие на постоянном токе, конструктивно ничем не отличаются от рассмотренных. Различие их заключается в том, что магнитопровод изготавливается сплошным из специальной электротехнической стали с высокой магнитной проницаемостью. Катушка электроаппарата, работающего на постоянном токе, имеет в несколько раз большее число витков, чем катушка электроаппарата, работающего на переменном токе. Это объясняется тем, что полное сопротивление катушки электроаппарата, работающего на переменном токе, слагается из двух составляющих — активного и индуктивного сопротивлений. В начальный момент после подачи напряжения пусковой ток в катушке превышает номинальный в несколько раз и созданный им магнитный поток достаточен для притягивания якоря.
Лучшими проводниками электрического тока являются металлы с наименьшим сопротивлением — медь, алюминий и т. д. [c.286]
В табл. 1 приведены величины удельного электрического сопротивления некоторых технических металлов. Лучшими проводниками электрического тока являются металлы с наименьшим электрическим сопротивлением — медь, алюминий и т. д.
 39]
39]
Для постоянного тока сопротивление реактора (если пренебречь небольшим сопротивлением меди его катушки) почти равно нулю, и ток силовой цепи свободно пройдет через него. Для токов же высокой частоты, например / = 0,16 МГц (160 000 Гц), сопротивление реактора У . = 2.3,14-160 000-0,63 = 633 024 Ом. [c.249]
Жесткие излучения могут влиять и на другие, помимо электроизоляционных, электротехнические материалы так, под их действием может возрастать удельное электрическое сопротивление меди и других проводников, нарушаться работоспособность полупроводниковых приборов и др.
С возрастанием содержания примесей удельное сопротивление меди возрастает в следующем порядке [c.257]
СТИ сопротивления меди от температуры в интервале от —50 до 200 . Эта зависимость выражается уравнением [c.77]
Мендоза и Томас [92, 298] исследовали также несколько других металлов.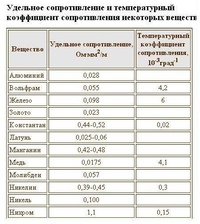
С соответственно. Угол между направлением потока воздуха и осью трубы ср =60°. Вычислить допустимую силу тока в электрическом проводе, если температура резиновой изоляции не должна превышать 70° С. Определить критический диаметр тепловой изоляции. Удельное электрическое сопротивление меди р =0,0175 Om-mmVm теплопроводность резиновой изоляции Хр = 0,15 Вт/(м-К)-
Медь. Вторым после серебра металлом с низким сопротивлением является медь. Для проводников используется электролитическая медь с содержанием Си 99,9% и кислорода 0,08%. Высокой вязкостью и пластичностью обладает бескислородная медь, содержащая кислорода не более 0,02%.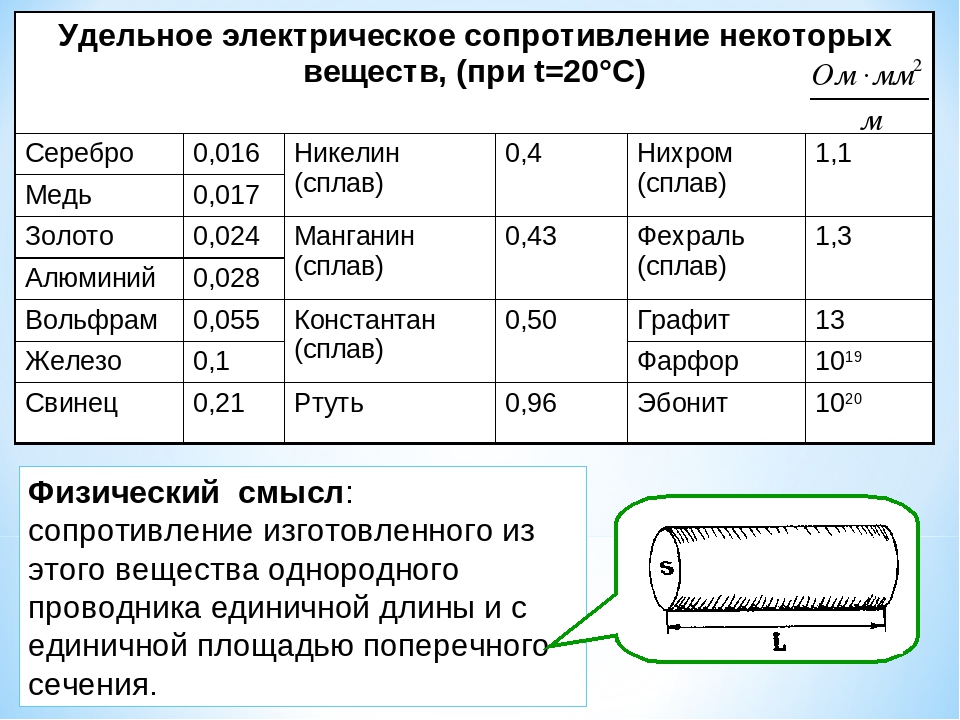 Температура плавления меди 1084° С, температура рекристаллизации — около 270° С. При нагревании выше этой температуры резко снижается прочность и возрастает пластичность. На воздухе поверхность медного проводника быстро покрывается слоем закиси — окиси меди с высоким удельным сопротивлением. Высокочастотные медные токоведущие элементы защищают от окисления покрытием из серебра. Для обмоток маслонаполненных трансформаторов используют луженую медную проволоку. Техническая медная проволока диаметром от 0,1 до 12 мм выпускается твердая и мягкая, подвергаемая отжигу в печах без доступа воздуха. Мягкая проволока диаметром до 3 мм имеет временное сопротивление в среднем 0р = 27 /сГ/лл для твердой проволоки больше (Ор = 39 кГ мм% удельное сопротивление для твердой проволоки р = 0,018 ом -мм 1м, а для мягкой р = 0,0175 ом-мм м. Температурный коэффициент сопротивления меди TKR =4-45-10″ Ijapad. Твердую медь применяют для контактных проводэв, коллекторов и т. п. Во всех этих
Температура плавления меди 1084° С, температура рекристаллизации — около 270° С. При нагревании выше этой температуры резко снижается прочность и возрастает пластичность. На воздухе поверхность медного проводника быстро покрывается слоем закиси — окиси меди с высоким удельным сопротивлением. Высокочастотные медные токоведущие элементы защищают от окисления покрытием из серебра. Для обмоток маслонаполненных трансформаторов используют луженую медную проволоку. Техническая медная проволока диаметром от 0,1 до 12 мм выпускается твердая и мягкая, подвергаемая отжигу в печах без доступа воздуха. Мягкая проволока диаметром до 3 мм имеет временное сопротивление в среднем 0р = 27 /сГ/лл для твердой проволоки больше (Ор = 39 кГ мм% удельное сопротивление для твердой проволоки р = 0,018 ом -мм 1м, а для мягкой р = 0,0175 ом-мм м. Температурный коэффициент сопротивления меди TKR =4-45-10″ Ijapad. Твердую медь применяют для контактных проводэв, коллекторов и т. п. Во всех этих
Для компенсацпи температурной погрешности из-за изменения Яя сопротивление 1R3 сделано из медной ироволоки. Практически полная темиературная компенсация нроисходит при давлении газа, соответствующем равенству сопротивлений Rn=давления газа от указанного возникает дополнительная погрешность, равная (считая температурные коэффициенты сопротивления меди и молибдена равными и пренебрегая малыми составляющими погрешности)
[c.43]
Практически полная темиературная компенсация нроисходит при давлении газа, соответствующем равенству сопротивлений Rn=давления газа от указанного возникает дополнительная погрешность, равная (считая температурные коэффициенты сопротивления меди и молибдена равными и пренебрегая малыми составляющими погрешности)
[c.43]
Повышение температуры приводит к увеличению сопротивления меди обмотки дросселя, т.е. к повышению сопротивления правого плеча делителя. Поэтому напряжение генератора, при котором напряжение на стабилитроне достигает стабилизации, увеличрггся, т.е. величина регулируемого напряжения в горячем состоянии возрастает. Повышение уровня регулируемого напряжения при нагреве способствует и некоторому изменению характеристик стабилитрона, так как напряжение стабилизации с увеличением температуры несколько возрастает. [c.10]
Температура плавления меди 1083 °С, плотность 8,94 Mг/м Она обла- 1ает Г1ЦС решеткой, диамагнитна и не имеет полиморфизма. Удельное электрическое сопротивление меди равно 0,0178 мкОм м. Нашей промышленностью производится И марок меди с различным содержанием примесей. В электронике применяют бескислородную (б) медь марок МООб (99,99% Си) и МОб (99,97% Си), в электротехнике и металлургии МО (99,95% Си), М1 (99,9% Си) М2 (99,7% Си) и др.
[c.199]
Удельное электрическое сопротивление меди равно 0,0178 мкОм м. Нашей промышленностью производится И марок меди с различным содержанием примесей. В электронике применяют бескислородную (б) медь марок МООб (99,99% Си) и МОб (99,97% Си), в электротехнике и металлургии МО (99,95% Си), М1 (99,9% Си) М2 (99,7% Си) и др.
[c.199]
Медь — металл красного цвета, розовый в изломе, обладает лучшей после серебра электропроводностью. Плотность меди 8890…8940кг/м , предел прочности при растяжении 256…409 МПа, температура плавления 1083 °С. Удельное электрическое сопротивление меди при 20 °С находится в пределах 0,01724…0,0180 мкОм м, удельная проводимость при 20 С в пределах 58…55,5 МСм/м. [c.10]
Ряд металлов и сплавов и иных материалов при весьма низких температурах, близких к абсолютному нулю, резко снижают свое удельное сопротивление, которое может принимать SHaneHHfr порядка 10 Ом-м, что в 10 раз- меньше, чем сопротивление меди, а плотность тока более 10 А/м-.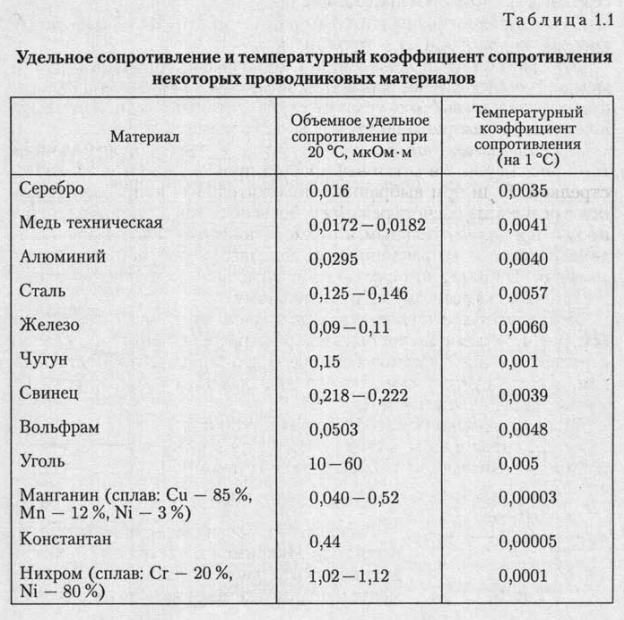 Свойство материалов, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охла15кдении ниже определенной критической температуры КР > характерной для данного материала, называют сверхпроводимостью. На состояние сверхпроводимости влияет тгкже величина магнитной индукции, наибольшее допустимое значение которой также называют критической.
[c.341]
Свойство материалов, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охла15кдении ниже определенной критической температуры КР > характерной для данного материала, называют сверхпроводимостью. На состояние сверхпроводимости влияет тгкже величина магнитной индукции, наибольшее допустимое значение которой также называют критической.
[c.341]
Чем вызваны столь характерные изменения постоянной кристаллической решетки металлов при трении в поверхностно-ак-тивных смазочных средах Совершенно очевидно, что при трении в инактивных смазочных средах, когда роль смазки проявляется в том, что действующие нагрузки воспринимаются металлом распределенными через слой смазки, равномерное по глубине зоны деформации уменьшение периода решетки определяют макронапряжения в поверхностных слоях. Остаточные напряжения I рода ст = Eh) tg 0 А0, где А0 = MId) tg О,, здесь Е — модуль упругости V — коэффициент Пуассона, Adid — относительное изменение межплоскостного расстояния. Оценка остаточных напряжений по этой формуле дает величину о 1300 МПа, что в несколько раз превышает временное сопротивление меди. Эти результаты хорошо согласуются с данными работы [15], где показано, что в процессе трения могут возникать напряжения, намного большие, чем в условиях статического или динамического деформирования. Оценка о для никеля и железа также указывает на превышение временного сопротивления.
[c.127]
Оценка остаточных напряжений по этой формуле дает величину о 1300 МПа, что в несколько раз превышает временное сопротивление меди. Эти результаты хорошо согласуются с данными работы [15], где показано, что в процессе трения могут возникать напряжения, намного большие, чем в условиях статического или динамического деформирования. Оценка о для никеля и железа также указывает на превышение временного сопротивления.
[c.127]
Из оксидированного алюминия изготовляют различные катушки, работающие при высокой температуре возможность нагрузки провода большей плотностью тока при малой толщине изоляции позволяет во многих случаях заменять медь алюминием, несмотря на, его более высокое удельное сопротивление (медь — 0,0172, алюминий — 0,028 ом мм 1м). Для получения медного провода с весьма высокой пагревостойкостью изоляции иногда покрывают медь алюминием, а затем поверхность алюминия оксидируют. [c.548]
На кранах применяют резисторы из фехралевой или, реже, констан-тановой проволоки или из фехралевой ленты. Константан и фехраль — это сплавы, обладающие большим удельным сопротивлением у кон-стантана более чем в 25 раз, а у фехраля, в 75 раз превышающим удельное сопротивление меди. Величина сопротивления этих сплавов почти не изменяется от температуры. Они рассчитаны на работу при высоких температурах так, для константана предельная температура равна 300, а для фехраля — 350°С.
[c.351]
Константан и фехраль — это сплавы, обладающие большим удельным сопротивлением у кон-стантана более чем в 25 раз, а у фехраля, в 75 раз превышающим удельное сопротивление меди. Величина сопротивления этих сплавов почти не изменяется от температуры. Они рассчитаны на работу при высоких температурах так, для константана предельная температура равна 300, а для фехраля — 350°С.
[c.351]
Удельное электрическое сопротивление меди при разных температурах. Электрическое сопротивление металлов. Сверхпроводимость
2.1. Общие сведения о проводниках
В качестве проводников электрического тока могут быть использованы как твердые тела, так и жидкости, а при соответствующих условиях (в состоянии ионизации) и газы.
Из
металлических проводниковых материалов могут быть выделены металлы
высокой проводимости , имеющие удельное сопротивление при нормальной
температуре не более 0.05 мкОм·м, и сплавы высокого сопротивления с удельным сопротивлением не менее 0. 3 мкОм·м.
3 мкОм·м.
Особый интерес представляют обладающие чрезвычайно малым удельным сопротивлением при весьма низких температурах материалы сверхпроводники и криопроводники .
К жидким проводникам относятся расплавленные металлы и электролиты. Для большинства металлов температура плавления высока, только ртуть, имеющая температуру плавления минус 39°С, может быть использована в качестве жидкого металлического проводника при нормальной температуре. Другие металлы являются жидкими проводниками только при повышенных температурах.
Механизм
прохождения тока в металлах – как в твердом, так и в жидком состоянии
– обусловлен движением свободных электронов под воздействием электрического
поля; поэтому металлы называют проводниками с электронной электропроводностью
или проводниками первого рода . Проводниками второго рода, или электролитами, являются растворы, в частности,
водные, кислот, щелочей и солей. Прохождение тока через эти вещества связано
с переносом вместе с электрическими зарядами ионов в соответствии с законами
Фарадея, вследствие чего состав электролита постепенно изменяется, а
на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном
состоянии также являются проводниками второго рода. Пример – соляные закалочные
ванны с электронагревом.
Прохождение тока через эти вещества связано
с переносом вместе с электрическими зарядами ионов в соответствии с законами
Фарадея, вследствие чего состав электролита постепенно изменяется, а
на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном
состоянии также являются проводниками второго рода. Пример – соляные закалочные
ванны с электронагревом.
Все газы и пары, в том числе и пары металлов, при низких напряженностях электрического поля не являются проводниками. Однако, если напряженность поля превзойдет некоторое критическое значение, обеспечивающее начало ударной и фотоионизации, то газ может стать проводником с электронной и ионной проводимостью. Сильно ионизированный газ при равенстве числа электронов числу положительно заряженных ионов в единице объема представляет собой особую проводящую среду, называемую плазмой .
2.2. Электропроводность металлов
Классическая
электронная теория металлов представляет проводник в виде системы, состоящей
из узлов ионной кристаллической решетки, внутри которой находится электронный
газ из свободных электронов. В свободное состояние от каждого атома переходит
от одного до двух электронов. К электронному газу применялись представления
и законы статистики обычных газов. Рассматривая тепловое и направленное
под действием электрического поля движение электронов, получили выражение
закона Ома. При столкновениях электронов с узлами кристаллической решетки
энергия, накопленная при ускорении электронов в электрическом поле, передается
металлической основе проводника, вследствие чего он нагревается. Рассмотрение
этого роцесса привело к выводу закона Джоуля-Ленца. Т.о., электронная
теория металлов дала возможность теоретически описать и объяснить найденные
ранее экспериментальным путем основные законы электропроводности и потерь
электрической энергии в металлах. Оказалось возможным также объяснить
связь между электро- и теплопроводностью металлов.
В свободное состояние от каждого атома переходит
от одного до двух электронов. К электронному газу применялись представления
и законы статистики обычных газов. Рассматривая тепловое и направленное
под действием электрического поля движение электронов, получили выражение
закона Ома. При столкновениях электронов с узлами кристаллической решетки
энергия, накопленная при ускорении электронов в электрическом поле, передается
металлической основе проводника, вследствие чего он нагревается. Рассмотрение
этого роцесса привело к выводу закона Джоуля-Ленца. Т.о., электронная
теория металлов дала возможность теоретически описать и объяснить найденные
ранее экспериментальным путем основные законы электропроводности и потерь
электрической энергии в металлах. Оказалось возможным также объяснить
связь между электро- и теплопроводностью металлов.
Однако
появились и противоречия некоторых выводов теории с опытными данными.
Они состояли в расхождении кривых температурной зависимости удельного
сопротивления, в несоответствии теоретически полученных значений теплоемкости
металлов опытным данным.
Эти трудности удалось преодолеть, встав на позиции квантовой механики. В отличие от классической электронной теории квантовая механика полагает, что электронный газ в металлах при обычных температурах находится в состоянии вырождения. В этом состоянии энергия электронного газа почти не зависит от температуры, т.е. тепловое движение почти не изменяет энергию электронов. Поэтому теплота не затрачивается на нагрев электронного газа, что и обнаруживается при измерениях теплоемкости металлов. В состояние, аналогичное обычным газам, электронный газ приходит при температурах порядка тысяч Кельвинов. Представляя металл как систему, в которой положительные ионы скрепляются посредством свободно движущихся электронов, легко понять природу всех основных свойств металлов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.
2.3. Свойства проводников
К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
- удельная проводимость g или обратная ей величина – удельное сопротивление r,
- температурный коэффициент удельного сопротивления ТКr или a r ,
- теплопроводность g т,
- контактная
разность потенциалов и термо-э.
 д.с.,
д.с., - работа выхода электронов из металла,
- предел прочности при растяжении s r и относительное удлинение при разрыве Dl/l.
2.3.1. Удельная проводимость и удельное сопротивление проводников
Связь плотности тока J, А/м 2 , и напряженности электрического поля Е, В/м, в проводнике дается известной формулой:
Здесь g, См/м – параметр проводникового материала, называемый его удельной проводимостью ; в соответствии с законом Ома g не зависит от напряженности электрического поля при изменении последней в весьма широких пределах. Величина r=1/g, oбратная удельной проводимости и называемая удельным сопротивлением , для имеющего сопротивление R проводника длиной l с постоянным поперечным сечением S вычисляется по формуле
ρ = R·S/l. (2.2)
Единица
СИ для удельного сопротивления — Ом·м. Диапазон значений удельного сопротивления
ρ металлических проводников при нормальной температуре довольно узок:
от 0. 016 для серебра и до примерно 10 мкОм·м для железохромоалюминиевых
сплавов, т.е. он занимает всего три порядка. Значение удельной проводимости
γ в основном зависит от средней длины свободного пробега электронов
в данном проводнике, которая, в свою очередь, определяется структурой
проводникового материала. Все чистые металлы с наиболее правильной кристаллической
решеткой характеризуются наименьшими значениями удельного сопротивления;
примеси, искажая решетку, приводят к увеличению ρ. И с точки зрения
волновой теории, рассеяние электронных волн происходит на дефектах кристаллической
решетки, которые соизмеримы с расстоянием порядка четверти длины электронной
волны. Нарушения меньших размеров не вызывают заметного рассеяния волн.
016 для серебра и до примерно 10 мкОм·м для железохромоалюминиевых
сплавов, т.е. он занимает всего три порядка. Значение удельной проводимости
γ в основном зависит от средней длины свободного пробега электронов
в данном проводнике, которая, в свою очередь, определяется структурой
проводникового материала. Все чистые металлы с наиболее правильной кристаллической
решеткой характеризуются наименьшими значениями удельного сопротивления;
примеси, искажая решетку, приводят к увеличению ρ. И с точки зрения
волновой теории, рассеяние электронных волн происходит на дефектах кристаллической
решетки, которые соизмеримы с расстоянием порядка четверти длины электронной
волны. Нарушения меньших размеров не вызывают заметного рассеяния волн.
2.3.2. Температурный коэффициент удельного сопротивления металлов
Число
носителей заряда в металлическом проводнике при повышении температуры
остается практически неизменным. Однако вследствие колебаний узлов кристаллической
решетки с ростом температуры появляется все больше и больше препятствий
на пути направленного под действием электрического поля движения свободных
электронов, т. е. уменьшается средняя длина свободного пробега электрона,
уменьшается подвижность электронов и, как следствие, уменьшается удельная
проводимость металлов, и увеличивается удельное сопротивление. Иными словами,
температурный коэффициент удельного сопротивления металлов положителен.
е. уменьшается средняя длина свободного пробега электрона,
уменьшается подвижность электронов и, как следствие, уменьшается удельная
проводимость металлов, и увеличивается удельное сопротивление. Иными словами,
температурный коэффициент удельного сопротивления металлов положителен.
2.3.3. Изменение удельного сопротивления металлов при плавлении
При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления, как это видно из рис.2.1; однако некоторые металлы при плавлении повышают ρ.
Скачок соответствует температуре плавления меди 1083°С
Удельное сопротивление увеличивается при плавлении у тех металлов, которые при плавлении увеличивают объем, т.е. уменьшают плотность; у металлов с противоположным характером изменения объема при плавлении (аналогичным фазовому переходу лед-вода) ρ уменьшается.
2.3.4. Изменение удельного сопротивления металлов при деформациях
Изменение удельного сопротивления при растяжении или сжатии приближенно может оцениваться формулой
ρ
= ρ 0 (1± σ ·s) , (2. 3)
3)
где ρ — удельное сопротивление металла при механическом напряжении σ, ρ 0 – удельное сопротивление металла, не подверженного механическому воздействию, s – коэффициент механического напряжения, характеризующий данный металл; знак плюс в формуле соответствует растяжению, минус – сжатию.
Изменение ρ при упругих деформациях объясняется изменением амплитуды колебаний узлов кристаллической решетки металла. При растяжении эти амплитуды увеличиваются, при сжатии – уменьшаются. Увеличение амплитуды колебаний узлов кристаллической решетки приводит к уменьшению подвижности носителей зарядов и, как следствие, к возрастанию ρ. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем отжига удельное сопротивление может быть вновь снижено до первоначального значения.
2.3.5. Удельное сопротивление сплавов
Значительное
возрастание ρ наблюдается при сплавлении двух металлов в том случае,
если они образуют друг с другом твердый раствор , т.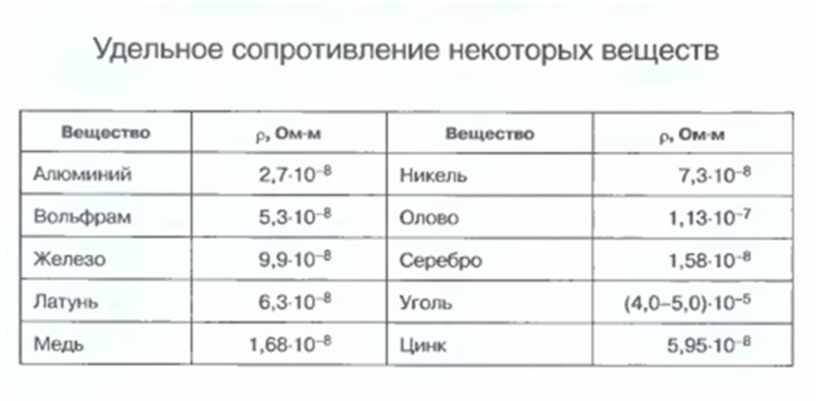 е. создают
при отвердевании совместную кристаллизацию, и атомы одного металла входят
в кристаллическую решетку другого. ρ имеет максимум, соответствующий
некоторому определенному соотношению между содержанием компонентов в сплаве.
Так, Н.С.Курнаков открыл, что в тех случаях, когда при определенном соотношении
между компонентами они образуют друг с другом явно выраженные химические
соединения (интерметаллиды ), на кривых ρ в функции
состава наблюдаются изломы (рис.2.2).
е. создают
при отвердевании совместную кристаллизацию, и атомы одного металла входят
в кристаллическую решетку другого. ρ имеет максимум, соответствующий
некоторому определенному соотношению между содержанием компонентов в сплаве.
Так, Н.С.Курнаков открыл, что в тех случаях, когда при определенном соотношении
между компонентами они образуют друг с другом явно выраженные химические
соединения (интерметаллиды ), на кривых ρ в функции
состава наблюдаются изломы (рис.2.2).
Рис. 2.2. Зависимость удельного сопротивления
сплавов цинк
– магний от состава.
Точка 1 соответствует
чистому Mg, 2 – соединению
MgZn, 3 — Mg 2 Zn 3 ,
., 4 – MgZn 4 5 – MgZn 6 , 6
– чистому Zn.
Исследования А.Ф.Иоффе показали, что многие интерметаллиды являются не веществами с металлическим характером электропроводности, а электронными полупроводниками.
Если
же сплав двух металлов создает раздельную кристаллизацию, и структура
застывшего сплава представляет собой смесь кристаллов каждого из компонентов
(т. е. искажение кристаллической решетки каждого компонента не имеет места),
то удельная проводимость γ сплава меняется с изменением состава приблизительно
линейно, т.е. определяется арифметическим правилом смешения (рис.2.3).
е. искажение кристаллической решетки каждого компонента не имеет места),
то удельная проводимость γ сплава меняется с изменением состава приблизительно
линейно, т.е. определяется арифметическим правилом смешения (рис.2.3).
Рис.2.3. Зависимость
удельной проводимости сплавов медь – вольфрам от
состава (в процентах по массе)
2.3.6. Теплопроводность металлов
За
передачу тепла через металл в основном ответственны те же свободные электроны,
которые определяют и электропроводность металлов, и количество которых
в единице объема весьма велико. Поэтому, как правило, теплопроводность
γ т металлов намного больше, чем теплопроводность диэлектриков.
Очевидно, что при прочих равных условиях, чем больше удельная электрическая
проводимость γ металла, тем больше должна быть и его теплопроводность.
Легко также видеть, что при повышении температуры, когда подвижность электронов
в металле и соответственно его удельная проводимость уменьшаются, отношение
γ т /γ δ должно возрастать.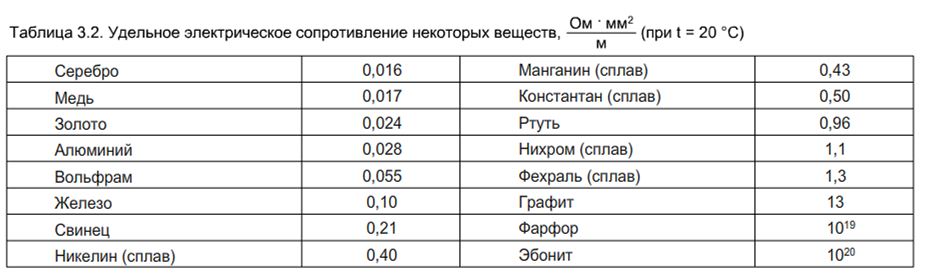
Чистота и характер механической обработки металла могут заметно сказываться на его теплопроводности, в особенности при низких температурах.
2.3.7. Термоэлектродвижущая сила
При соприкосновении двух металлических проводников между ними возникает контактная разность потенциалов . Причина ее появления заключается в различии значений работы выхода электронов из различных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной теории металлов следует, что контактная разность потенциалов между металлами А и В равна:
(2.4)
где U А и U В – потенциалы соприкасающихся металлов; n А и n В – концентрации электронов в металлах А и В.
Если температуры «спаев» одинаковы, то сумма разностей потенциалов равны нулю. Иначе обстоит дело, когда один металл имеет температуру Т 1 , а другой – Т 2 .
В
этом случае между «спаями» возникает термо-э. д.с., равная
д.с., равная
что можно записать в виде
Где с – постоянный для данной пары проводников коэффициент термо-э.д.с., т.е. термо-э.д.с. должна быть пропорциональна разности температур металлов.
Провод, составленный из двух изолированных друг от друга проволок из различных металлов или сплавов (термопара ), может быть использован для измерения температур.
2.3.8. Механические свойства проводников
Они характеризуются пределом прочности при растяжении σ р и относительным удлинением при разрыве Δl/l, а так же хрупкостью, твердостью и тому подобными свойствами. Механические свойства металлических проводников в большой степени зависят от механической и термической обработки, от наличия легирующих примесей и т.п. Влияние отжига приводит к существенному уменьшению σ р и увеличению Δl/l. Такие параметры проводниковых материалов, как температуры кипения и плавления, удельная теплоемкость и др., не требуют особых пояснений.
2.
 4.
Материалы высокой проводимости
4.
Материалы высокой проводимостиК наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий.
2.4.1. Медь
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В
качестве проводникового материала чаще всего используется медь марок М1
и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%)
кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает
ее механические свойства. Лучшими механическими свойствами обладает медь
марки М0, в которой содержится не более 0.05% примесей, в том числе не
свыше 0.02% кислорода.
Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%)
кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает
ее механические свойства. Лучшими механическими свойствами обладает медь
марки М0, в которой содержится не более 0.05% примесей, в том числе не
свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
2.4.2. Алюминий
Алюминий
является вторым по значению после меди проводниковым материалом. Это важнейший
представитель так называемых легких металлов: плотность литого алюминия
около 2.6, а прокатанного – 2.7 Мг/м 3 . Т.о., алюминий примерно
в 3.5 раза легче меди. Температурный коэффициент расширения, удельная
теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие
высоких значений удельной теплоемкости и теплоты плавления для нагрева
алюминия до температуры плавления и перевода в расплавленное состояние
требуется большая затрата тепла, чем для нагрева и расплавления такого
же количества меди, хотя температура плавления алюминия ниже, чем меди.
Температурный коэффициент расширения, удельная
теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие
высоких значений удельной теплоемкости и теплоты плавления для нагрева
алюминия до температуры плавления и перевода в расплавленное состояние
требуется большая затрата тепла, чем для нагрева и расплавления такого
же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами – как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для
электротехнических целей используют алюминий, содержащий не более 0.5%
примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03%
примесей) применяют для изготовления алюминиевой фольги, электродов и
корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000
имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при
содержании их 0.5% снижают γ отожженного алюминия не более, чем на
2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же
массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают
электропроводность алюминия Ti и Mn.
Добавки Ni, Si, Zn или Fe при
содержании их 0.5% снижают γ отожженного алюминия не более, чем на
2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же
массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают
электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей , содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg 2 Si, которое сообщает высокие механические свойства сплаву.
2.4.3. Железо
Железо
(сталь) как наиболее дешевый и доступный металл, обладающий к тому же
высокой механической прочностью, представляет большой интерес для использования
в качестве проводникового материала. Однако даже чистое железо имеет значительно
более высокое сравнительно с медью и алюминием удельное сопротивление;
ρ стали, т.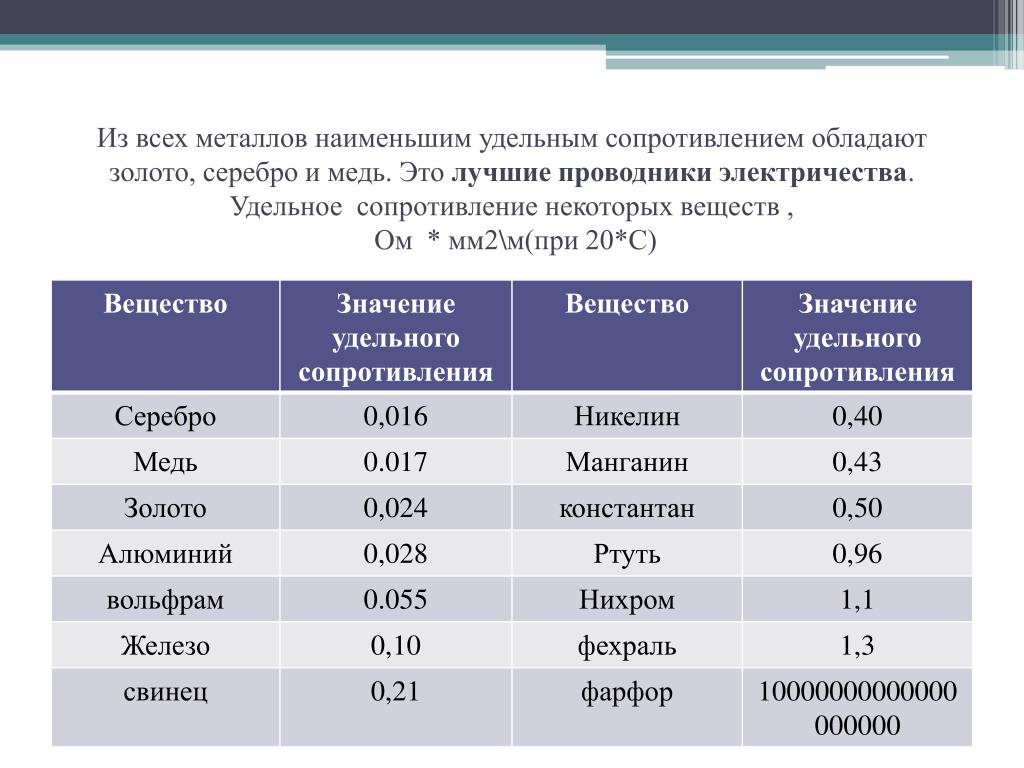 е. железа с примесью углерода и других элементов, еще
выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной
температуре, особенно в условиях повышенной влажности, она быстро ржавеет;
при повышении температуры скорость коррозии резко возрастает. Поэтому
поверхность стальных проводов должна быть защищена слоем более стойкого
материала. Обычно для этой цели применяют покрытие цинком.
е. железа с примесью углерода и других элементов, еще
выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной
температуре, особенно в условиях повышенной влажности, она быстро ржавеет;
при повышении температуры скорость коррозии резко возрастает. Поэтому
поверхность стальных проводов должна быть защищена слоем более стойкого
материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл . Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
2.4.4. Натрий
Весьма
перспективным проводниковым материалом является металлический натрий.
Натрий может быть получен электролизом расплавленного хлористого натрия
NaCl в практически неограниченных количествах. Из сравнения свойств натрия
со свойствами других проводниковых металлов видно, что удельное сопротивление
натрия примерно в 2.8 раза больше ρ меди и в 1. 7 раз больше ρ
алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его
почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости
на единицу длины должен быть значительно легче, чем провод из любого другого
металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется
на воздухе, бурно реагирует с водой), почему натриевый провод должен быть
защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую
механическую прочность, так как натрий весьма мягок и имеет малый предел
прочности при деформациях.
7 раз больше ρ
алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его
почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости
на единицу длины должен быть значительно легче, чем провод из любого другого
металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется
на воздухе, бурно реагирует с водой), почему натриевый провод должен быть
защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую
механическую прочность, так как натрий весьма мягок и имеет малый предел
прочности при деформациях.
2.5. Сверхпроводники и криопроводники
Как
уже отмечалось, при понижении температуры удельное сопротивление металлов
падает. Представляет особый интерес вопрос об электропроводности металлов
при весьма низких температурах, приближающихся к абсолютному нулю. Исчезновение
электрического сопротивления, т.е. появление практически бесконечной электрической
проводимости материала, называется сверхпроводимостью , а
температура, при охлаждении до которой совершается переход вещества в
сверхпроводящее состояние – температурой сверхпроводникового перехода Т с. Переход в сверхпроводящее состояние является обратимым:
при повышении температуры до Т с сверхпроводимость разрушается
и материал переходит в нормальное состояние, приобретая конечное значение
удельной проводимости γ. В настоящее время известно 27 простых (чистых
металлов) и более тысячи сложных (сплавов и химических соединений).
Переход в сверхпроводящее состояние является обратимым:
при повышении температуры до Т с сверхпроводимость разрушается
и материал переходит в нормальное состояние, приобретая конечное значение
удельной проводимости γ. В настоящее время известно 27 простых (чистых
металлов) и более тысячи сложных (сплавов и химических соединений).
В то же время некоторые вещества, в том числе такие наилучшие проводниковые материалы, как серебро и медь, при наиболее низких, достигнутых в настоящее время температурах (порядка тысячных долей Кельвина; согласно третьему закону термодинамики, абсолютный нуль температуры принципиально недостижим) перевести в сверхпроводящее состояние не удалось. Интересно отметить, что сверхпроводниками могут быть не только соединения и сплавы металлов, обладающих сверхпроводимостью, но и соединения таких элементов с несверхпроводящими и даже соединения, в состав молекул которых входят исключительно атомы элементов, не являющихся сверхпроводящими.
Помимо
сверхпроводящих электромагнитов можно отметить возможности использования
сверхпроводников для создания электрических машин, трансформаторов и тому
подобных устройств малой массы и габаритов, но с высокими к. п.д.; линий
электропередачи весьма больших мощностей на дальние расстояния; волноводов
с особо малым затуханием; накопителей энергии и пр.
п.д.; линий
электропередачи весьма больших мощностей на дальние расстояния; волноводов
с особо малым затуханием; накопителей энергии и пр.
Помимо явления сверхпроводимости в современной электротехнике все шире используется явление криопроводимости , т.е. достижение некоторыми металлами весьма малой удельной проводимости при криогенных температурах (но более высоких, чем температура сверхпроводникового перехода, если данный металл вообще принадлежит к сверхпроводникам. Материалы, обладающие особо благоприятными свойствами для применения в качестве проводников в условиях криогеннных температур, называются криопроводниками или гиперпроводниками .
Весьма
малое, но все же конечное значение удельного сопротивления криопроводника
при его рабочей температуре ограничивает допустимую плотность тока в нем,
хотя эта плотность может быть намного выше, чем в обычных проводниках.
Криопроводники, у которых при изменении температуры в широких пределах
удельное сопротивление изменяется плавно, без скачков, не могут использоваться
в ряде устройств, действие которых основано на триггерном эффекте появления
и разрушения сверхпроводимости. Однако применение криопроводников в электрических
машинах, аппаратах, кабелях и т.п. имеет и свои преимущества, притом весьма
существенные. Так, если в сверхпроводниковых устройствах в качестве охлаждающего
агента применяется жидкий гелий, рабочая температура криопроводников достигается
применением более высококипящих и дешевых хладоагентов: жидкого водорода
или даже жидкого азота. Это значительно упрощает и удешевляет выполнение
и эксплуатацию устройства. Кроме того, в сверхпроводниковом устройстве,
например электромагните, по обмотке которого проходит сильный ток, накапливается
большая энергия магнитного поля. Если из-за случайного повышения температуры
или магнитной индукции хотя бы на малом участке сверхпроводящего контура
сверхпроводимость будет разрушена, внезапно освободится большое количество
энергии, что может вызвать серьезную аварию. В случае же криопроводниковой
цепи повышение температуры вызовет лишь постепенное возрастание сопротивления
этой цепи без эффекта взрыва.
Однако применение криопроводников в электрических
машинах, аппаратах, кабелях и т.п. имеет и свои преимущества, притом весьма
существенные. Так, если в сверхпроводниковых устройствах в качестве охлаждающего
агента применяется жидкий гелий, рабочая температура криопроводников достигается
применением более высококипящих и дешевых хладоагентов: жидкого водорода
или даже жидкого азота. Это значительно упрощает и удешевляет выполнение
и эксплуатацию устройства. Кроме того, в сверхпроводниковом устройстве,
например электромагните, по обмотке которого проходит сильный ток, накапливается
большая энергия магнитного поля. Если из-за случайного повышения температуры
или магнитной индукции хотя бы на малом участке сверхпроводящего контура
сверхпроводимость будет разрушена, внезапно освободится большое количество
энергии, что может вызвать серьезную аварию. В случае же криопроводниковой
цепи повышение температуры вызовет лишь постепенное возрастание сопротивления
этой цепи без эффекта взрыва.
Во всех случаях для получения криопроводниковых материалов требуется высокая чистота металла и отсутствие наклепа. Вредное влияние примесей и наклепа на ρ металлов при криогенных температурах сказывается намного сильнее, чем при нормальных. Криопроводники могут с успехом использоваться для обмоток электрических машин и трансформаторов, для токопроводящих жил кабелей и т.п.
2.6. Сплавы высокого сопротивления
Помимо высокого сопротивления от таких материалов требуются высокая стабильность ρ во времени, малый ТКρ и малый коэффициент термо-э.д.с. в паре данного сплава с медью. Желательно, чтобы такие сплавы были дешевыми и по возможности не содержали дефицитных компонентов.
2.6.1. Манганин
Это
наиболее типичный и широко применяемый для образцовых резисторов сплав.
Примерный его состав: Cu- 85%, Mn- 12% и Ni- 3%; название происходит от
наличия в нем марганца; желтоватый цвет объясняется большим содержанием
меди. ρ манганина 0.42-0.48 мкОм∙м, коэффициент термо-э. д.с.
в паре с медью всего 1-2 мкВ/К, α ρ весьма мал. Предельная
длительно допустимая рабочая температура не более 200°С.
д.с.
в паре с медью всего 1-2 мкВ/К, α ρ весьма мал. Предельная
длительно допустимая рабочая температура не более 200°С.
2.6.2. Константан
Сплав, содержащий около 60% меди и 40% никеля; этот состав отвечает минимуму α ρ в системе Cu-Ni при довольно высоком значении ρ. Название константан объясняется значительным постоянством ρ при изменении температуры. Нагревостойкость константана выше, чем манганина, а механические свойства близки. Существенным отличием последнего является высокая термо-э.д.с. в паре с медью и с железом. Широкому применению константана препятствует большое содержание дорогого и дефицитного никеля.
2.6.3. Сплавы на основе железа
Сплавы
системы Fe – Ni – Cr называются нихромами или (при повышенном
содержании железа) ферронихромами ; сплавы системы Fe – Cr
– Al называются фехралями и хромалями . Нихромы
весьма технологичны: их можно легко протягивать в тонкую проволоку или
ленту, они имеют высокую рабочую температуру. Однако, как и в костантане,
в них велико содержание никеля. Нихромы применяются в качестве электронагревательных
элементов.
Однако, как и в костантане,
в них велико содержание никеля. Нихромы применяются в качестве электронагревательных
элементов.
Хромо-алюминиевые сплавы намного дешевле нихромов, однако эти сплавы менее технологичны, более тверды и хрупки. Они в основном используются для электронагревательных устройств большой мощности.
2.7. Тугоплавкие металлы
К тугоплавким относятся металлы с температурой плавления, превышающей 1700°С. Как правило, они химически устойчивы при низких температурах, но становятся активными при повышенных. Эксплуатация их при высоких температурах может быть обеспечена в атмосфере инертных газов или в вакууме. В плотном виде чаще всего эти металлы получают методами порошковой металлургии – прессовкой и спеканием. В электронной технике начинают распространяться плавка электронным или лазерным лучом, зонная очистка, плазменная обработка и т.д. Механическая обработка этих материалов трудна и часто требует подогрева.
2.7.1. Вольфрам
Чрезвычайно
тяжелый, твердый металл серого цвета. Из всех металлов вольфрам обладает наиболее
высокой температурой плавления (3380°С). Его извлекают из руд различного состава,
наиболее известными среди которых являются вольфрамит (FeWO 4 + MnWO 4)
и шеелит (CaWO 4) путем сложной химической обработки. Для вольфрама
характерна слабая механическая связанность кристаллов, поэтому при зернистом
строении сравнительно толстые вольфрамовые изделия весьма хрупки и легко ломаются.
В результате механической обработки ковкой и волочением вольфрам приобретает
волокнистую структуру и излом его весьма затруднен. Этим объясняется гибкость
тонких вольфрамовых нитей.
Из всех металлов вольфрам обладает наиболее
высокой температурой плавления (3380°С). Его извлекают из руд различного состава,
наиболее известными среди которых являются вольфрамит (FeWO 4 + MnWO 4)
и шеелит (CaWO 4) путем сложной химической обработки. Для вольфрама
характерна слабая механическая связанность кристаллов, поэтому при зернистом
строении сравнительно толстые вольфрамовые изделия весьма хрупки и легко ломаются.
В результате механической обработки ковкой и волочением вольфрам приобретает
волокнистую структуру и излом его весьма затруднен. Этим объясняется гибкость
тонких вольфрамовых нитей.
Из вольфрама
изготавливают нити ламп накаливания, а также электроды, подогреватели, пружины
и крючки в электронных лампах, рентгеновских трубках и т.п. Вследствие тугоплавкости
и большой механической прочности, вольфрам может работать при высоких температурах
(более 2000°С), но лишь в глубоком вакууме или в атмосфере инертного газа, т.к.
при нагревании до температуры в несколько сот градусов в присутствии кислорода
он сильно окисляется.
2.7.2. Молибден
Этот металл по внешнему виду, а также по технологии обработки близкий к вольфраму. Важнейшей промышленной рудой молибдена является молибденит MoS 2 . Молибден применяют в электровакуумной технике при менее высоких температурах, чем вольфрам; накаливаемые детали из молибдена должны работать в вакууме или восстановительной атмосфере.
2.7.3. Тантал
Его получают из мало распространенной руды – танталита Fe(TaO 3) 2 методами порошковой металлургии, подобно вольфраму и молибдену. Основное отличие его заключается лишь в том, что процесс спекания его осуществляют в вакуумных печах, т.к. тантал склонен к поглощению газов, в результате чего он становится хрупким. Тантал характеризуется высокой пластичностью даже при комнатной температуре. Тантал относят к сверхпроводникам, применяют при изготовлении анодов и сеток генераторных ламп и др.
2.7.4. Титан
Относительно
легкий металл, применяющийся в электровакуумной технике благодаря своим хорошим
механическим свойствам. Основными минералами, содержащими титан, являются рутил
и ильмений. Получают титан методами порошковой металлургии. Его используют не
только в качестве конструкционного материала, но и для порошкообразных покрытий
молибденовых и вольфрамовых анодов и сеток генераторных ламп. Из него также
получают резисторы интегральных микросхем.
Основными минералами, содержащими титан, являются рутил
и ильмений. Получают титан методами порошковой металлургии. Его используют не
только в качестве конструкционного материала, но и для порошкообразных покрытий
молибденовых и вольфрамовых анодов и сеток генераторных ламп. Из него также
получают резисторы интегральных микросхем.
2.7.5. Рений
Один из редких очень тяжелых металлов, с температурой плавления, близкой к вольфраму. Рений отличается редким сочетанием свойств, удовлетворяющих большинству требований электровакуумной техники. В атмосфере водорода и во влажной среде он испаряется в меньшей степени, чем вольфрам. Ценной особенностью рения является его меньшая, по сравнению с вольфрамом, степень взаимодействия при высоких температурах с окисью алюминия, из которой изготовляют изоляционные трубки подогревных катодов прямого накала и сеток некоторых типов ламп.
2.8. Благородные металлы
К благородным
металлам относят золото, серебро, платину и металлы платиновой группы (рутений
Ru, родий Rh, палладий Pd, осмий Os и иридий Ir). Эти металлы названы благородными
за их красивый внешний вид и высокую химическую стойкость. Они применяются в
качестве проводников и контактов для коррозионно-устойчивых покрытий, электродов
фотоэлементов. Серебро применяют также для непосредственного нанесения на диэлектрики
в качестве обкладок в производстве керамических и слюдяных конденсаторов.
Эти металлы названы благородными
за их красивый внешний вид и высокую химическую стойкость. Они применяются в
качестве проводников и контактов для коррозионно-устойчивых покрытий, электродов
фотоэлементов. Серебро применяют также для непосредственного нанесения на диэлектрики
в качестве обкладок в производстве керамических и слюдяных конденсаторов.
2.9. Неметаллические проводники
Из числа твердых неметаллических проводниковых материалов наибольшее значение имеют материалы на основе углерода. Из угля изготавливают щетки электрических машин, электроды для прожекторов, электроды для дуговых электрических печей и электролитических ванн, аноды гальванических элементов. Угольные порошки используют в микрофонах, из угля делают высокоомные резисторы, разрядники для телефонных сетей.
В качестве
сырья для производства электроугольных изделий можно использовать сажу, графит
и антрацит. Природный графит – одна из модификаций чистого углерода слоистой
структуры с большой анизотропией как электрических, так и механических свойств. Сажи представляют собой мелкодисперсный углерод с примесями слоистых веществ.
Лаки, в состав которых в качестве пигмента добавлена сажа, обладают малым удельным
сопротивлением и могут быть использованы для выравнивания электрического поля
в электрических машинах высокого напряжения.
Сажи представляют собой мелкодисперсный углерод с примесями слоистых веществ.
Лаки, в состав которых в качестве пигмента добавлена сажа, обладают малым удельным
сопротивлением и могут быть использованы для выравнивания электрического поля
в электрических машинах высокого напряжения.
Наиболее существенный вклад в остаточное сопротивление вносит рассеяние на примесях, которые всегда присутствуют в реальном проводнике или в виде загрязнения, или в виде легирующего (т. Е Намеренно вводится) элемента. Любая примесная добавка приводит к повышению г., даже если она обладает повышенной проводимостью по сравнению с основным металлом. Так, введение в медный проводник 0, 01 ат. доли примеси серебра вызывает увеличение удельного сопротивления меди на 0,002 мкОм м. Экспериментально установлено, что при малом содержании примесей удельное сопротивление возрастает пропорционально концентрации примесных атомов. Различные примеси по-разному влияют на остаточное сопротивление проводников. Кроме примесей некоторый вклад в остаточное сопротивление, вносят собственные дефекты структуры — вакансии, атомы внедрения, дислокации, границы зерен.
Причинами рассеяния электронных волн в металле является не только тепловые колебания узлов решетки, но и статические дефекты структуры, которые также нарушают правильность кристаллической решетки. Рассеяния на статических дефектах структуры не зависит от температуры. Поэтому по мере приближения температуры к абсолютному нулю сопротивление реальных металлов стремится к некоторому постоянному значению, называемом остаточным сопротивлением.
Удельное сопротивление вещества зависит от температуры. Как правило, сопротивление металлов растет с температурой. Этому не следует удивляться: с повышением температуры атомы движутся быстрее, их расположение становится менее упорядоченным, и можно ожидать, что они будут сильнее мешать движению потока электронов. В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
При очень низких температурах удельное сопротивление некоторых металлов, а также сплавов и соединений падает в пределах точности современных измерений к нулю.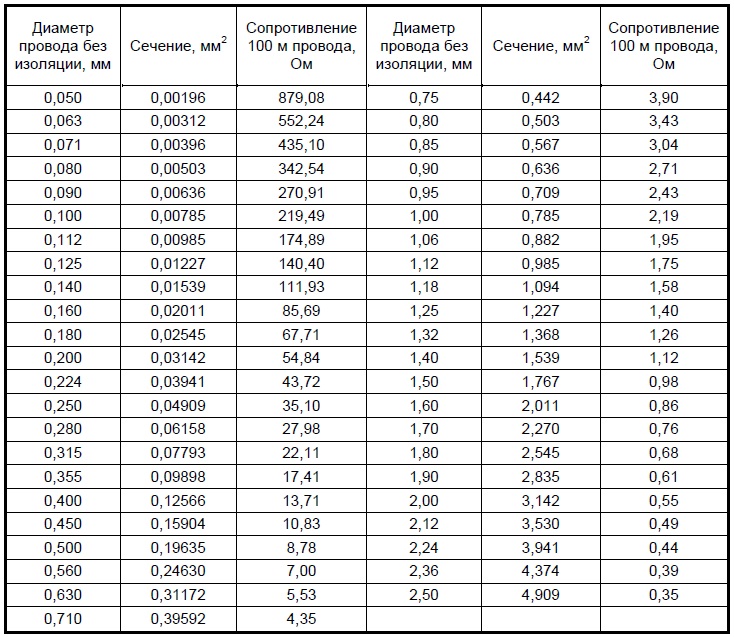 Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейко Камер- Линг — Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейко Камер- Линг — Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Стоит отметить, что среди хороших проводников, которыми являются металлы, наиболее предпочтительны драгоценные металлы, при этом серебро считается лучшим проводником, т. К У него наименьшую малый удельное сопротивление. Этим объясняется использование драгоценных металлов при пайке особо важных элементов в электротехнике. Из значений удельных сопротивлений веществ можно судить об их практическом применении — вещества с большим удельным сопротивлением подойдут для изготовления изоляционных материалов, а с небольшим — для проводников.
Для получения зависимости силы тока в цепи от сопротивления Ому пришлось провести огромное количество экспериментов, в которых необходимо было менять сопротивление проводника. В связи с этим он столкнулся с проблемой изучения сопротивления проводника в зависимости от его отдельно взятых параметров. В первую очередь, Георг Ом обратил внимание на зависимость сопротивления проводника от его длины, о которой уже бегло говорилось на предыдущих уроках. Он сделал вывод, что при увеличении длины проводника прямо пропорционально увеличивается и его сопротивление. Кроме того, было установлено, что на сопротивление влияет еще и сечение проводника, т. Е Площадь фигуры, которая получается при поперечном разрезе. При этом, чем площадь сечения больше, тем сопротивление меньше. Из этого можно сделать вывод, что чем провод толще, тем его сопротивление меньше. Все эти факты были получены опытным путем.
В первую очередь, Георг Ом обратил внимание на зависимость сопротивления проводника от его длины, о которой уже бегло говорилось на предыдущих уроках. Он сделал вывод, что при увеличении длины проводника прямо пропорционально увеличивается и его сопротивление. Кроме того, было установлено, что на сопротивление влияет еще и сечение проводника, т. Е Площадь фигуры, которая получается при поперечном разрезе. При этом, чем площадь сечения больше, тем сопротивление меньше. Из этого можно сделать вывод, что чем провод толще, тем его сопротивление меньше. Все эти факты были получены опытным путем.
Если обратить внимание на эту формулу, то можно сделать вывод, что с ней выражается удельное сопротивление проводника, т. Е., Определив силу тока и напряжение на проводнике и измерив его длину с площадью поперечного сечения, можно с помощью закона Ома и указанной формулы вычислить удельное сопротивление. Затем, его значение можно сверить с данными таблицы и определить, из какого вещества изготовлен проводник.
Число носителей заряда в металлическом проводнике при повышении температуры практически остается неизменным. Однако вследствие усиления колебаний узлов кристаллической решетки с ростом температуры появляется все больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т. Е. Уменьшается средняя длина свободного пробега электрона? , Уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рисунок 2.1)
Как уже указывалось, примеси и нарушения правильной структуры металлов увеличивают их удельное сопротивление. Значительный рост? наблюдается при сплава двух металлов в том случае, если они образуют друг с другом твердый раствор, т. Е. При утверждении совместно кристаллизуются, и атомы одного металла входят в кристаллическую решетку другого.
Этот коэффициент, интересен не только при рассмотрении работы различных сопряженных материалов в той или иной конструкции (возможность растрескивания или нарушения вакуум плотного соединения со стеклами, керамикой при изменении температуры). Он необходим также и для расчета температурного коэффициента сопротивления провода
Он необходим также и для расчета температурного коэффициента сопротивления провода
При столкновении двух разных металлических проводниковмежду них возникает контактная разность потенциалов. Причина появления этой разности потенциалов заключается в различии значений работы выхода электронов из разных металлов, а также в том, что концентрация электронов, а, следовательно, и давление электронного газа в различных металлов и сплавов могут быть неодинаковыми. С электронной теории металлов следует, что контактная разность потенциалов между металлами А и В равна
Етитрудности удалось преодолеть, встав на позиции квантовой механики. В отличиеот классической электронной теории квантовая механика считает, что електроннийгаз в металлах при обычных температурах находится в состоянии вирождения.В этом состоянии энергия электронного газа почти не зависит от температуры, т.е. тепловое движение почти не изменяет энергию электронов. Поэтому теплотане затрачивается на нагрев электронного газа, и оказывается приизмерениях теплоемкости металлов.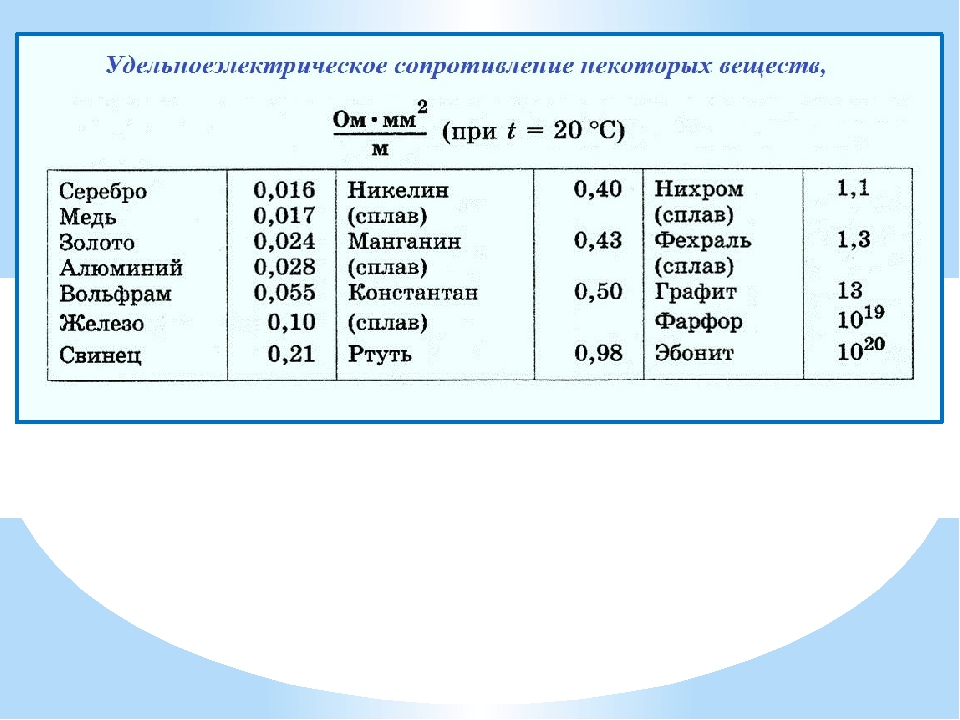 В состояние, аналогичное обычным газам, электронный газ приходит при температурах порядка тысяч кельвинов. Представляяметалл как систему, в которой положительные ионы скрепляются посредствомсвободно подвижных электронов, легко понять природу всех основных свойствметаллов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.
В состояние, аналогичное обычным газам, электронный газ приходит при температурах порядка тысяч кельвинов. Представляяметалл как систему, в которой положительные ионы скрепляются посредствомсвободно подвижных электронов, легко понять природу всех основных свойствметаллов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.
Достаточно перспективным проводниковому материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше? меди и в 1.7 раз больше? алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод с натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из другого металла. Однако натрий чрезвычайно активный химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), чем натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна предоставлять провода необходимую механическую прочность, так как натрий весьма мягкий и имеет малый предел прочности при деформациях.
Оболочка должна предоставлять провода необходимую механическую прочность, так как натрий весьма мягкий и имеет малый предел прочности при деформациях.
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокую по сравнению с медью и алюминием удельное сопротивление; ? стали, то есть железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытия цинком.
Это электрическое сопротивление единицы длины проводника единичной площади сечения [ Ohm · m ], оказываемое движения носителей заряда в проводнике, а также полупроводников проводят ионы растворах, под действием потенциального электрического поля. Удельное электрическое сопротивление постоянному току с одной строны является производным понятием от электрического сопротивления проводника, а с другой -Базовый понятием электротехнического материаловедения, поскольку определяет свойства материала проводника независимо от его длины и формы вообще.
Удельное электрическое сопротивление постоянному току с одной строны является производным понятием от электрического сопротивления проводника, а с другой -Базовый понятием электротехнического материаловедения, поскольку определяет свойства материала проводника независимо от его длины и формы вообще.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Поместив термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
В металлах уровень Ферми лежит в зоне проводимости, заполненной лишь частично. Электроны, находящиеся в зоне проводимости, получив сколь угодно малуюенергетическую добавку (например, за счет теплового движения или електрическогополя), могут перейти на более высокий (свободный) энергетический уровень той же зоне, тоесть стать свободными электронами и участвовать в проводимости. Сростом температуры сопротивление будет расти, поскольку увеличивается рассеяниеелектронов проводимости на тепловых колебаниях решетки, и средняя длинасвободного пробега электрона уменьшается.
Сростом температуры сопротивление будет расти, поскольку увеличивается рассеяниеелектронов проводимости на тепловых колебаниях решетки, и средняя длинасвободного пробега электрона уменьшается.
(везде ниже под сопротивлением понимается активное (резистивное) сопротивление, в котором происходит диссипация (рассеяние) електрическойенергии и необратимый переход ее в другие виды энергии, например, тепловую)
При абсолютном нуле в идеально совершенном кристалле атомы расположены строго периодически и электромагнитные волны беспрепятственно проходят сквозь кристаллическую решетку, не испытывая при этом сопротивления. В реальных условиях металлы — проводники имеют искаженную решетку и используются при температурах, отличных от абсолютного нуля.
При увеличении температуры атомы металла совершают колебания около узлов решетки, вызывает рассеяние электронных волн, приводит к увеличению электрического сопротивления. Это увеличение может быть выражено зависимостью
При очень малых деформациях иногда наблюдается уменьшение сопротивления, что должно быть приписано побочных явлений: уплотнению металла, разрушение изолирующих межкристаллитных пленок и т.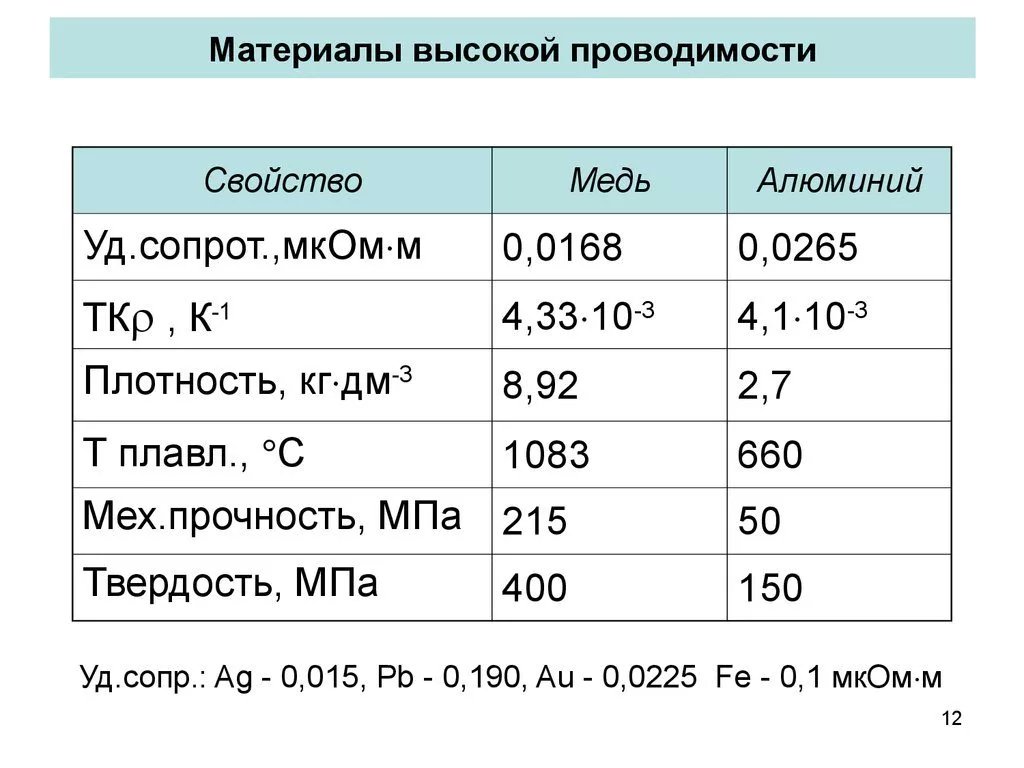 П.
П.
Возникновение упорядочения в твердых растворах — это результат усиления химического взаимодействия компонентов, в результате чего электроны связываются сильнее, чем в неурегулированных твердом растворе. Усиление химического взаимодействия компонентов уменьшает число электронов проводимости и увеличивает остаточное электрическое сопротивление. Однако при составлении электрическое поле ионного остова решетки становится более симметричным, а это, естественно, приводит к снижению остаточного сопротивления. Последнее обстоятельство оказывается превалирующим, и при составлении электрическое сопротивление снижается.
1. Электрическое сопротивление металлов. Квантовая теория электропроводности металлов сводится к следующему:
а. В идеальной кристаллической решетке электроны проводимости при своем движении не должны испытывать сопротивления. Сопротивление возникает тогда, когда в решетке появляются дефекты структуры , то есть нарушается периодичность решетки.
б. В реальных кристаллах есть два механизма нарушения структуры: примесный и тепловой. Соответственно различают примесное удельное сопротивление r n и тепловое (колебательное ) r Т . Согласно правилу аддитивности сопротивлений полное сопротивление металла r равно их сумме, r = r n + r Т . (13.1)
в. Примесное сопротивление r n обусловлено наличием инородных атомов в решетке (атомов примеси). Если металл достаточно чистый и концентрация атомов примеси невелика, то примесное сопротивление практически не зависит от температуры и становиться заметным лишь вблизи абсолютного нуля. Благодаря примеси удельное сопротивление металла не должно обращаться в нуль даже при Т = 0 К.
г. Тепловое сопротивление r Т возникает благодаря рассеянию электронов проводимости на флуктуациях плотности узлов кристаллической решетки, возникающих при тепловом колебательном движении узлов. В квантовой теории тепловое колебательное движение атомов решетки трактуется как система стоячих звуковых волн в кристалле — фононов . Поэтому говорят о рассеянии электронов проводимости на фононах .
В квантовой теории тепловое колебательное движение атомов решетки трактуется как система стоячих звуковых волн в кристалле — фононов . Поэтому говорят о рассеянии электронов проводимости на фононах .
В отличие от классической теории электропроводности металлов Друде — Лоренца , прогнозирующей зависимость сопротивления от температуры вида r ~ , квантовая теория дает правильный прогноз линейной зависимости r ~Т . При температурах металла Т ³ 50 К r = r 0 aТ , что соответствует эмпирической формуле r = r 0 (1 + a t ). В квантовой теории получается, что при Т ® 0 полное удельное сопротивление металла r должно стремиться к примесному r n . На рис.90 показана опытная зависимость удельного сопротивления чистого натрия от температуры.
При Т ® 0 К r ® r n = 4·10 -11 Ом·м, что составляет примерно 0,4% от сопротивления при Т = 273 К. Уже при температурах Т ³ 20 К зависимость r (Т ) становится практически линейной.
Уже при температурах Т ³ 20 К зависимость r (Т ) становится практически линейной.
д. Электрический ток толкуется в квантовой теории как дрейф электронов в периодическом поле кристалла. Этот дрейф происходит под действием постоянной электрической силы еЕ , где Е — напряженность электрического поля, создающего ток. Оказалось, что скорость дрейфа электронов зависит от глубины их положения в зоне проводимости. Эта зависимость выражается через эффективную массу m эф электрона. В отличие от массы покоя m е свободного электрона эффективная масса электрона в зоне проводимости металла – величина переменная, зависящая от ширины зоны.
Вблизи дна зоны эффективная масса электронов положительна. Направление дрейфа соответствует вектору плотности тока. По мере подъема к верхней границе зоны эффективная масса принимает бесконечно большое значение m эф = ¥, а затем становится отрицательной. Соответственно и скорость дрейфа электронов, имея “правильное” направление у дна зоны, постепенно проходит через нуль и принимает отрицательные (“неправильные”) значения у верхней границы зоны.
Соотношения, полученные в приближении свободных электронов в теории Друде – Лоренца , оказываются справедливыми для электронов, движущихся в периодическом поле решетки, если в них заменить массу покоя электрона m е на эффективную m эф .
2. Сверхпроводимость. В 1911 году Камерлинг – Оннес , измеряя сопротивление ртути в области низких температур, обнаружил, что при Т = 4,2 К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью . На рис.91 показаны опытные кривые зависимости удельного сопротивления некоторых чистых металлов от температуры вблизи абсолютного нуля. Очевидно, что явление не сводится к нормальному падению удельного сопротивления бездефектного кристалла, когда r n = 0, и r Т . Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Т кр , которую называют критической температурой перехода. Сейчас известно около 30 сверхпроводящих химических элементов и свыше 500 сверхпроводящих материалов.
3. Эффекты сверхпроводимости.
а. Электрический ток , возбужденный в сверхпроводящем кольце, может циркулировать в нем годами.
б. Эффект Мейснера . В 1933 году Вальтер Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле (рис.92 слева), при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема (рис. 92 справа). Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m = 0.
Из того, что магнитное поле не проникает в сверхпроводник, следует, что электрический ток может течь лишь по поверхности сверхпроводника. Ведь если бы ток мог протекать в толще сверхпроводника, то вокруг него в толще сверхпроводника было бы магнитное поле. И действительно, опыт показывает, что электрический ток течет в сверхпроводнике в поверхностном слое толщиной l = 10 ¸ 100 нм. На эту глубину в сверхпроводник проникает и магнитное поле, убывая с расстоянием x от поверхности по экспоненциальному закону
В = В 0 exp(-xçl ). (13.2)
Вещество в сверхпроводящем состоянии приобретает два не связанных друг с другом фундаментальных свойства: идеальную проводимость и идеальный диамагнетизм .
Эффект Мейснера позволяет устойчиво подвешивать сверхпроводящие тела в магнитном поле (рис.93). При пререходе шара в сверхпроводящее состояние 1-го рода магнитное поле из него вытесняется. В результате в поверхностном слое шара индуцируется ток такого направления, при котором шар выталкивается из поля.
в. Эффект критического магнитного поля . Он состоит в том, что при достижении магнитным полем, в котором находится сверхпроводник, некоторого предельного значенияиндукции В кр »10 -2 ¸ 10 1 Тл, сверхпроводимость исчезает.
На рис.94 показана зависимость В кр от температуры для свинца (верхняя кривая) и для олова (нижняя кривая). При критической температуре Т = Т кр критическое поле равно нулю, В кр = 0, а с понижением температуры В кр увеличивается.
Если усиливать ток, идущий по сверхпроводнику, то при некотором его критическом значении I кр сверхпроводящее состояние разрушается. Поскольку магнитное поле В пропорционально току I , то зависимость I кр от температуры аналогична зависимости В кр (Т ). Эффект критического магнитного поля усложняет технику получения сверхсильных магнитных полей с помощью сверхпроводящих контуров. Расчет критического тока должен учитывать, что ток течет в приповерхностном слое. Например, у проводника диаметром 1 мм при l = 35 нм сечение приповерхностного слоя, по которому течет ток, около 10 -4 мм 2 . Это составляет около 0,01% всего сечения проводника.
г. Эффект Джозефсона . В 1962 году Брайан Джозефсон теоретически предсказал два эффекта, суть которых в следующем.
Подсоединим к сверхпроводнику (на рис.95-а он изображен в виде бруска) амперметр А с источником постоянного тока, ЭДС которого E , и вольтметр V . В цепи идёт постоянный ток, регистрируемый амперметром. Так как сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль.
Разрежем сверхпроводник на две части и раздвинем их, чтобы между ними возник зазор толщиной d » 1 нм. Как предсказал Джозефсон , при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов.
Стационарный эффект Джозефсона. Через сверхпроводник по-прежнему идёт постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка (рис.95-б).
Нестационарный эффект Джозефсона . На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов . В этом случае из щели излучается высокочастотная электромагнитная волна (рис.95-в). Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток.
В настоящее время эффекты Джозефсона не только подтверждены экспериментально, но и используются в микроэлектронике.
4. Теорию сверхпроводимости построили в 1957г Джон Бардин, Леон Купер и Джон Шриффер . По первым буквам их фамилий ее назвали БКШ – теорией . В основе БКШ- теории лежит представление, что между электронами проводимости металла могут действовать силы притяжения , возникающие вследствие поляризации ими кристаллической решетки.
Электрон, движущийся в решетке, притягивает к себе положительно заряженные ионы, несколько сближая их, и тем самым создает вдоль пути своего следования избыточный положительный заряд поляризованной решетки, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, только действующей не непосредственно, а через поляризованную решетку.
Можно предположить, что сверхпроводимость следует ожидать прежде всего у тех металлов, у которых имеет место сильное взаимодействие электронного газа с решеткой, приводящее в обычных условиях к высокому удельному сопротивлению. И действительно, из чистых металлов лучшими сверхпроводниками оказались наиболее высокоомные — свинец Рb, ниобий Nb, олово Sn, ртуть Hg. В то же время у таких низкоомных металлов, как медь Cuи сереброAg, у которых электронный газ имеет высокую подвижность, сверхпроводимость не наблюдается.
Как показал Леон Купер, при Т Т кр , самые верхние электроны,расположенные на уровне Ферми, могут спариваться . При этом их суммарная энергия оказывается меньше суммы энергий отдельных электронов . Выделяющаяся энергия должна отводиться от кристалла охлаждением. Понижение энергии куперовских пар приводит к понижению верхнего занятого электронами уровня. В результате между уровнями куперовских пар и ближайшими свободными уровнями возникает запрещенная зона шириной 2D (рис.96 слева). Эта возникшая энергетическая щель не позволяет куперовским парам электронов принимать малую энергию. Они могут принять лишь энергию не менее 2D, которая позволит электронам перепрыгнуть через эту щель. Поэтому при Т Т кр куперовские пары оказываются весьма устойчивыми.
При Т Т кр спариваются не все электроны. При каждой температуре устанавливается некоторое равновесное соотношение между концентрациями нормальных и спаренных электронов. Оказывается, что ширина 2D энергетической щели в сверхпроводнике зависит от количества неспаренных электронов. Их концентрация понижается с уменьшением температуры и соответственно растет ширина щели (рис.96 справа).
Электроны, образующие куперовские пары, имеют противоположные спины. Поэтому спин пары равен нулю, и она представляет собой бозон . Бозоны могут накапливаться в основном энергетическом состоянии, из которого их трудно перевести в возбужденное состояние. Поэтому куперовские пары в состоянии согласованного движения могут оставаться неопределенно долго. Такое согласованное движение пар и есть ток сверхпроводимости.
Расстояние между электронами пары велико. Оно составляет примерно 1000 нм, что около 5000 поперечников атомов. Примерно 1000 пар перекрываются, занимая общий объем.
5. Объяснение БКШ – теорией эффекта критического тока. У известных сверхпроводников величина энергетической щели составляет в среднем 2D = 3 мэВ » 5·10 -22 Дж. Для разрушения куперовской пары один из электронов пары должен уменьшить энергию своего движения, по крайней мере, на величину 2D.
Предположим, что электрон отдает эту энергию при лобовом столкновении с узлом решетки так, что после столкновения он отскакивает с той же скоростью дрейфа v д в обратном направлении. Энергия электрона до соударения Е к1 = m e (v ф + v д ) 2 ç 2, энергия после соударения Е к2 = m e (v ф — v д ) 2 ç 2. Здесь v ф – тепловая скорость электронов на уровне Ферми (»10 6 мç с), v д – скорость дрейфа электронов в электрическом поле, она не превышает 1 мç с.
Убыль кинетической энергии электрона должна быть по крайней мере равной 2D. Так что DЕ к = = 2m e v ф v д = 2D. (13.3)
Отсюда, минимальная скорость дрейфа v д , необходимая для разрушения куперовской пары, есть v д = Dçm e v ф . (13.4)
Плотность электронного тока проводимости естьj = env д , (13.5)
где n – концентрация электронов проводимости в металле. Подставив критическую скорость дрейфа из (13.4), получаем критическую плотность тока j кр .
j кр = env д = en Dçm e v ф . (13.6)
У типичных сверхпроводников n = 3·10 28 м -3 , v ф = 10 6 мç с, 2D = 3 мэВ. Подставляем.
j кр = =10 12 . Это соответствует току 10 6 А через проводник сечением 1 мм 2 . Но в реальном сверхпроводнике ток течет лишь в тонком приповерхностном слое толщиной около 35 нм, что соответствует сечению S = 10 -4 мм 2 . Поэтому критический ток в сверхпроводнике толщиной около 1 мм составляет всего лишь i кр = j кр S = 10 6 Аç мм 2 ·10 — 4 мм 2 = 100 А. Это вполне соответствует эксперименту.
6. Объяснение БКШ-теорией критического магнитного поля. При помещении сверхпроводника в магнитное поле В в поверхностном слое сверхпроводника наводится незатухающий ток. Этот незатухающий ток имеет такие величину и направление, что его магнитное поле внутри сверхпроводника полностью компенсирует внешнее поле В . При увеличении поля В плотность компенсирующего тока в сверхпроводнике растет. Если внешнее поле В будет настолько большим, что плотность наведенного им индукционного тока достигнет критического значения, сверхпроводимость разрушается.
Все выше сказанное относится к сверхпроводникам 1-го рода , в которых электрический ток существует только в приповерхностном слое. Несколько позже были открыты и изучены сверхпроводники 2-го рода . В них возникающие во внешнем магнитном поле В сверхпроводящие токи текут не только по поверхности, но и проникают в толщу проводника. У сверхпроводников 1-го рода критическое магнитное поле В кр не превышает 0,1 Тл, а у сверхпроводников 2-го рода достигает величины В кр » 20 Тл.
7. Эффекты Джозефсона объясняются БКШ — теорией как результат туннелирования куперовских пар через узкую щель между сверхпроводниками. Согласно теории, частота n переменного сверхпроводящего тока определяется выражением: n = . (13.7)
При напряжении на щели U = 1 мВ частота n = 485 ГГц, что соответствует длине волны ЭМ излучения l = сçn = 0,6 мм.
8. Реактивное сопротивление сверхпроводника . При любой температуре Т Т кр сверхпроводник практически всегда содержит как сверхпроводящие электроны концентрацией n c , так и нормальные (n н ) электроны. Если поместить сверхпроводник в высокочастотное поле, то в этом переменном электрическом поле ускоряются не только куперовские пары, но и нормальные электроны. Поэтому ток имеет как сверхпроводящую, так и нормальную составляющую.
Те и другие электроны обладают массой, вследствие их инерции ток отстает по фазе от напряженности ВЧ – поля. Куперовские пары движутся в проводнике как бы без трения. Согласно классической механике, скорость частиц в этом случае отстает по фазе от действующей на них периодической силы на pç 2. Поэтому сверхпроводящая составляющая высокочастотного тока отстает от напряженности поля на pç 2. Это значит, что куперовские пары создают чисто реактивное сопротивление.
Нормальные электроны движутся как бы с трением. Поэтому они создают как реактивное, так и активное сопротивление.
Сплавы для проводников и элементов сопротивления :: Технология металлов
Проводниковые материалы должны изготовляться из возможно чистых металлов, а материалы высокого сопротивления — из сплавов, структура которых представляет твердый раствор.
Основными проводниковыми материалами являются медь и алюминий. Понятие «чистого» металла условно, так как чистота получаемых металлов повышается из года в год по мере роста технических средств в производстве и в лабораториях. С другой стороны, электрическое сопротивление чистых металлов резко возрастает при наличии малых количеств растворенных примесей. Из рис. видно, как значительно падает проводимость меди при введении в ее состав таких примесей, как кремний, железо, мышьяк, бериллий в количествах <0,2%. Для проводниковой техники разработан интернациональный стандарт технически чистой отожженной меди (1913 г.), удельное сопротивление которой при 20° С равно 1,7241 мкОм-см. С тех пор добились дальнейшего очищения меди и повышения ее проводимости.
Для повышения прочности медного провода в его состав вводят примеси Cd, Sn, Αl, Ρ, Cr, Be. Электропроводность при этом, естественно, понижается.
Рис. 1. Влияние примесей на электропроводность меди
Наиболее распространенной является так называемая кадмиевая бронза (0,9% Cd, остальное медь), которая в твердотянутом состоянии обладает проводимостью до 90% от проводимости меди при временном сопротивлении при растяжении, в 2—2,5 раза большем, чем у меди. В табл. 25 приведены составы и свойства медных проводниковых материалов.
Проводниковый алюминий имеет электропроводность, равную 65% от проводимости меди. Однако ввиду малой плотности алюминия его проводимость, рассчитанная на 1 кг проводника, составляет 214% от таковой для меди. Это позволяет облегчить конструкцию опор на линиях передач с алюминиевыми проводами. Для повышения прочности алюминиевых проводов в их состав вводят магний и кремний (совместно), которые образуют соединение Mg2Si, очень мало растворимое в алюминии при комнатной температуре (меньше 0,25%). Путем закалки и старения удается повысить временное сопротивление такого сплава в 2 раза при электропроводности 90% от проводимости чистого алюминия. Сплавы такого типа (альдрей и альмелек) содержат 0,4 и 0,7% Mg, 0,5—0,6% Si и до 0,3% Fe. Альдрей (0,4% Mg, 0,6% Si и 0,3% Fe) имеет температурный коэффициент электрического спротивления, равный 3,6 * 10-4, т. е. весьма близкий к температурному коэффициенту чистого алюминия (4,0 * 10-4). Это еще раз свидетельствует о том, что при обработке путем дисперсионного твердения Mg2Si выделяется из раствора почти нацело.
Для реостатов в нагревательных приборах, а также там, где необходимо высокое электрическое сопротивление и малый температурный коэффициент, применяют сплавы железа с примесями, образующими твердые растворы. В табл. 2 приводятся типичные железные сплавы, а также для сравнения сплавы на никелевой основе.
Эти сплавы являются не только сплавами высокого сопротивления, но и жаростойкими. Для придания жаростойкости в железные сплавы вводятся хром и алюминий. Железные сплавы дешевле никелевых, однако они не только не являются заменителями, но имеют также и более высокую рабочую температуру.
В качестве элементов сопротивления применяются медноникелевые сплавы— константан и никелин. Рабочая температура константана до 400° С, никелина — до 200° С.
Таблица 1
Медные проводниковые сплавы
Сплав | Состояние | Электропроводность, % | Временное сопротивление при растяжении, МПа | Удлинение, % |
Чистая медь | Отожженная | 101 | 220—270 | 50 |
Твердотянутая | 98 | До 480 | 4 | |
Кадмиевая бронза (0,9% Cd) | Отожженная | 95 | 310—380 | 50 |
Твердотянутая | 83—90 | До 730 | 4 | |
Бронза (0,75% Sn или 0,8% Cd и 0,6% Sn) | Отожженная | 55—60 | 290 . | 55 |
Твердотянутая | 50—55 | До 730 | 4 | |
Бронза (2,5% А1, 2% Sn) | Отожженная | 15—18 | 370 | 45 |
Твердотянутая | 15—18 | До 970 | 4 | |
Фосфористая бронза (7% Sn, 0,1% Ρ) | Отожженная | 10—15 | 400 | 60 |
Твердотянутая | 10—15 | 1050 | 3 |
Таблица 2
Сплавы для реостатов и нагревательных приборов
Сплав | Состав (средний), % | Удельное электросопротивление, мкОм · см | Температурный коэффициент α | Наивысшая рабочая температура, °С |
Х13Ю4 (фехраль) | 13,5 Сr; 4,5 Аl; остальное Fe | 126 | 0,00005 | 1000 |
0Х23Ю5 | 23 Сr; 5 Аl; остальное Fe | 137 | — | 1200 |
0Х27Ю5А | 27 Сr; 5,5 Аl; остальное Fe | 142 | 0,00002 | 1300 |
Сверхмегапир | 37 Сr; 7,5 Аl; остальное Fe | 180 | 0,00012 | 1350 |
Х15Н60 (нихром) | 16,5 Сr: 58 Ni: остальное Fe | 110 | 0,00017 | 1000 |
Х20Н80 | 21,5 Сr; остальное Ni | 100 | — | 1100 |
Таблица 3.
Влияние различных элементов на удельное электросопротивление железа
Элемент
| Пределы концентрации и температуры | Средние значения возрастания удельного сопротивления, мкОм.см | ||
% (по массе) | °с | на 1 % (по массе) | на 1 % (ат.) | |
Аl | 0—2,0 | 18—23 | 11,1—14,4 | 6,0—7,7 |
As | 0—2,6 | — | 6,8 | 9,10 |
Au | — | — | 1.1 | 5,80 |
В | 0—0,45 | — | 6,2 | 1,25 |
С | 0—0,9 | 20 | 34,0 | 7,6 |
Со | 0,5 | 18—30 | 1,0—3,0 | 1,1—3,2 |
Сг | 0,3 | 12 | 2,5—5,4 | 2,3—5,0 |
Сu | 0—1 | — | 3,0—4,0 | 3,4—4,6 |
Μn | 0—2 | 18—30 | 5,0—10,5 | 4,9—10,3 |
Mo | 0—1 | 17 | 3,4 | 5,8 |
Ν | 0—0,1 | 20 | 14,6 | 3,8 |
Ni | 0—5 | 18—30 | 1,55—4,45 | 1,7-4,7 |
Ρ | 0—0,3 | — | 11,4 | 6,1 |
S | 0—0,1 | 20 | 12,0 | 6,9 |
Si | 0—1 | 20 | 13—15,8 | 6,5—8,0 |
Ti | — | — | 1,0 | 0,9 |
V | 0—1 | — | 6,7 | 6,1 |
W | 0—2 | 15—20 | 2,0—3,6 | 6,5—11,8 |
Источник:
Лившиц Б.Г., Крапошин В.С, Липецкий Я.Л. «Физические свойства металлов и сплавов». М. «Металлургия», 1980.
Удельное сопротивление проводников — основные электрические таблицы
Удельное сопротивление проводников
Базовая электроэнергия
Вопрос 1
Учитывая две длины металлической проволоки, которая будет иметь наименьшее электрическое сопротивление: короткое или длинное «# 1»> Показать ответ Скрыть ответ
Короткая проводка будет иметь меньшее электрическое сопротивление, чем длинный провод.
Заметки:
Существует много аналогий, выражающих это понятие: вода через трубу, сжатый воздух через шланг и т. Д. Какая труба или шланг менее ограничительная: короткая или длинная?
вопрос 2
Учитывая две длины сплошной металлической проволоки с круглыми поперечными сечениями, которая будет иметь наименьшее электрическое сопротивление: одно из которых имеет малый диаметр или большой диаметр? Предположим, что все остальные факторы равны (один и тот же тип металла, одна и та же длина провода и т. Д.).
Показать ответ
Провод большого диаметра будет иметь меньшее электрическое сопротивление, чем проволока малого диаметра.
Заметки:
Существует много аналогий, выражающих это понятие: вода через трубу, сжатый воздух через шланг и т. Д. Какая труба или шланг менее ограничительны: тощий или толстый?
Вопрос 3
Какое конкретное сопротивление, обозначенное греческой буквой «rho» (ρ)?
Показать ответ
Удельное сопротивление — это показатель того, насколько резистивным является какое-либо конкретное вещество по отношению к его длине и площади поперечного сечения.
Заметки:
Спросите своих учеников: «Почему важно иметь количество, называемое конкретным сопротивлением? Почему бы нам просто не сравнить «удельное сопротивление» различных веществ в обычных единицах ома?
Вопрос 4
Напишите одно уравнение, связывающее сопротивление, удельное сопротивление, длину и площадь поперечного сечения электрического проводника вместе.
Показать ответ
Где,
R = сопротивление, измеренное вдоль длины проводника
ρ = удельное сопротивление вещества
l = длина проводника
A = площадь поперечного сечения проводника
Последующий вопрос: алгебраически манипулировать этим уравнением для решения длины (1) вместо решения для сопротивления (R), как показано.
Заметки:
Благоприятное упражнение, связанное с вашими учениками, состоит в том, чтобы анализировать это уравнение (и фактически любое уравнение) качественно, а не просто количественно . Спросите учащихся, что произойдет с R, если ρ увеличится, или если l уменьшится, или если A уменьшится. Многие студенты считают эту проблему более сложной задачей, чем работу с реальными числами, потому что они не могут использовать свои калькуляторы, чтобы дать им качественные ответы (если они не вводят случайные числа в уравнение, а затем меняют одно из этих чисел и пересчитывают), но это дважды работа решения уравнения с одним набором чисел, один раз!).
Вопрос 5
Изучите следующую таблицу удельного сопротивления для различных металлов:
Металлический тип ρ в Ω · cmil / ft @ 32 o F ρ в Ω · cmil / ft при 75 o F Цинк (очень чистый) 34, 595 37, 957 Олово (чистый) 78, 489 86, 748 Медь (чистый отжиг) 9, 390 10, 351 Медь (жестко нарисованная) 9, 810 10, 745 Медь (отожженная) 9, 590 10, 505 Платиновый (чистый) 65, 670 71, 418 Серебро (чистый отжиг) 8, 831 9, 674 никель 74, 128 85, 138 Стальная проволока) 81, 179 90, 150 Железо (приблизительно чистый) 54, 529 62, 643 Золото (чистота 99, 9%) 13, 216 14, 404 Алюминий (чистота 99, 5%) 15, 219 16, 758
Из показанных металлов, который является лучшим проводником электричества? Что хуже всего? Что вы замечаете в отношении удельного сопротивления этих металлов при увеличении температуры от 32 o F до 75 o F?
Показать ответ
Вот та же таблица, порядок переориентирован, чтобы показать удельное сопротивление от наименьшего к наибольшему:
Металлический тип ρ в Ω · cmil / ft @ 32 o F ρ в Ω · cmil / ft при 75 o F Серебро (чистый отжиг) 8, 831 9, 674 Медь (чистый отжиг) 9, 390 10, 351 Медь (отожженная) 9, 590 10, 505 Медь (жестко нарисованная) 9, 810 10, 745 Золото (чистота 99, 9%) 13, 216 14, 404 Алюминий (чистота 99, 5%) 15, 219 16, 758 Цинк (очень чистый) 34, 595 37, 957 Железо (приблизительно чистый) 54, 529 62, 643 Платиновый (чистый) 65, 670 71, 418 никель 74, 128 85, 138 Олово (чистый) 78, 489 86, 748 Стальная проволока) 81, 179 90, 150
Заметки:
Данные для этой таблицы были взяты из таблицы 1-97 «Справочника американского электрика» (одиннадцатое издание) Террелла Крофта и Уилфорда Саммерса.
Некоторые ученики могут удивить, что золото действительно хуже проводника электричества, чем меди, но данные не лежат! Серебро на самом деле самое лучшее, но золото выбрано для многих микроэлектронных приложений из-за его стойкости к окислению.
Вопрос 6
Каково электрическое сопротивление медной проволоки диаметром 12 мм, длиной 500 футов, при комнатной температуре?
Показать ответ
Сопротивление провода = 0.7726 Ом
Заметки:
Попросите своих учеников поделиться своими источниками данных: значения ρ, площадь поперечного сечения и т. Д.
Вопрос 7
Катушка имеет неизвестную длину алюминиевой проволоки. Размер провода составляет 4 AWG. К счастью, оба конца провода доступны для контакта с омметром, чтобы измерить сопротивление всей катушки. При измерении общее сопротивление провода составляет 0, 135 Ом. Сколько проволоки на катушке (при условии, что катушка находится при комнатной температуре)?
Показать ответ
353, 51 футов
Заметки:
Этот вопрос иллюстрирует другое практическое применение конкретных расчетов сопротивления: как определить длину провода на катушке. Количество сопротивления в этом примере довольно низкое, составляя лишь небольшую долю ома. Спросите своих учеников, какие проблемы они могут столкнуться, пытаясь точно измерить такое низкое сопротивление. Будут ли типичные ошибки, возникающие при таком измерении с низким сопротивлением, сделать их расчет длины чрезмерными или слишком низкими? Зачем?
Вопрос 8
Размеры поперечного сечения медной «сборной шины» составляют 8 см на 2, 5 см. Сколько сопротивления будет иметь эта шина, измеренная от конца до конца, если ее длина составляет 10 метров? Предположим, что температура составляет 20 o Цельсия.
Показать ответ83, 9 мкОм
Заметки:
Этот вопрос является хорошим обзором метрической системы, касающейся сантиметров до метров и т. Д. Это также может быть хорошим обзором конверсий единиц, если ученики предпочтут выполнить расчеты сопротивления, используя английские единицы (cmils или квадратные дюймы), а не метрические.
Студенты могут быть удивлены фигурой с низким сопротивлением, но напоминают им, что они имеют дело с сплошным стержнем из меди, размером более 3 квадратных дюймов в поперечном сечении. Это один большой дирижер!
Вопрос 9
Рассчитайте сквозное сопротивление 20-метровой длины медной проволоки диаметром 0, 05 см. Для удельного сопротивления меди используйте 1, 678 × 10 -6 Ом · см.
Показать ответ
1, 709 Ом
Заметки:
Здесь нечего комментировать — просто прямолинейный расчет сопротивления. Тем не менее, студенты должны быть осторожны с сантиметровым измерением!
Вопрос 10
Рассчитайте количество мощности, подаваемой на нагрузочный резистор в этой схеме:
Также вычислите величину мощности, которая будет передаваться нагрузочному резистору, если провода были сверхпроводящими (R- провод = 0, 0 Ом).
Показать ответ
P- нагрузка ≈ 170 Вт (с резистивным проводом)
P load = 180 Вт (со сверхпроводящим проводом)
Последующий вопрос: Сравните направление тока через все компоненты этой схемы с полярностями их соответствующих падений напряжения. Что вы замечаете относительно взаимосвязи между текущим направлением и полярностью напряжения для батареи, а также для всех «замеченных» резисторов »Примечания:
Этот вопрос не только является хорошей практикой для серийных вычислений (законы Ома и Джоуля), но также вводит сверхпроводники в практическом контексте.
Вопрос 11
Предположим, что энергосистема подавала мощность переменного тока на резистивную нагрузку, составляющую 150 ампер:
Рассчитайте напряжение нагрузки, рассеивание мощности нагрузки, мощность, рассеиваемую сопротивлением провода ( провод R), и общую эффективность мощности, обозначенную греческой буквой «eta» (η = ((P load ) / ( источник P))),
- E load =
- P load =
- P строк =
- η =
Теперь предположим, что мы должны перепроектировать как генератор, так и нагрузку для работы на 2400 вольт вместо 240 вольт. Это десятикратное увеличение напряжения позволяет всего лишь на одну десятую ток передавать такое же количество энергии. Вместо того, чтобы заменить весь провод на другой провод, мы решили использовать тот же самый провод, что и раньше, с таким же сопротивлением (0, 1 Ом на длину), как и раньше. Перераспределите напряжение нагрузки, мощность нагрузки, потраченную мощность и общий КПД этой системы (более высокого напряжения):
- E load =
- P load =
- P строк =
- η =
Система 240 вольт:
- E load = 210 вольт
- П нагрузки = 31, 5 кВт
- P- линии = 4, 5 кВт
- η = 87, 5%
Система 2400 вольт:
- E load = 2397 вольт
- П нагрузки = 35, 96 кВт
- P строк = 45 Вт
- η = 99, 88%
Заметки:
Пример, подобный этому, обычно делает хорошую работу, разъясняя преимущества использования высокого напряжения при низком напряжении для передачи больших объемов электроэнергии на значительные расстояния.
Вопрос 12
Эффективность (η) простой силовой системы с потерями, возникающими по проводам, зависит от тока цепи, сопротивления провода и общей мощности источника:
Здесь дается простая формула для расчета эффективности:
|
Где,
P = выходная мощность источника напряжения, Вт (Вт)
I = ток цепи, в амперах (A)
R = общее сопротивление провода (R- провод 1 + R- провод2 ), в омах (Ω)
Алгебраически манипулировать этим уравнением для решения проблемы сопротивления провода (R) по всем другим переменным, а затем рассчитать максимальный допустимый уровень сопротивления провода для энергосистемы, где источник, подающий 200 кВт, работает при токе цепи 48 ампер, при минимальный КПД — 90%.
Показать ответ
|
Максимально допустимое (общее) сопротивление провода составляет 8, 681 Ом.
Заметки:
Обычная ошибка для студентов, чтобы сделать здесь, составляет 90%, как «90», а не «0, 9» в своих калькуляторах.
Вопрос 13
Какой размер (калибр) медного провода необходим в этой цепи, чтобы обеспечить загрузку нагрузки не менее 110 вольт »// www.beautycrew.com.au//sub.allaboutcircuits.com/images/quiz/00166×01.png»>
Показать ответМедная проволока № 6 приближается, но недостаточно велика. № 5 калибра или больше будет достаточно.
Заметки:
Для решения этой проблемы необходимы несколько шагов: Закон Ома, алгебраическое манипулирование конкретным уравнением сопротивления и исследование размеров проводов. Обязательно проводите достаточное время, обсуждая эту проблему со своими учениками!
Концепция общей «нагрузки» представляет собой любой компонент или устройство, которое рассеивает электроэнергию в цепи. Часто общие нагрузки символизируются символом резистора (зигзагообразная линия), даже если они не могут быть резистором.
Вопрос 14
Тензодатчик — это тип чувствительного устройства, широко используемого в аэрокосмической промышленности, для испытания транспортных средств и механических компонентов. Объясните, что делает тензодатчик, и как он функционирует.
Показать ответТензодатчик преобразует микромеханические движения («деформация») в электрические изменения сопротивления. Как правило, тензодатчики используются для измерения растяжения, сжатия и скручивания металлических компонентов под напряжением.
Заметки:
Попросите ваших учеников рассказать о своих ответах на иллюстрации, показанные в вопросе. Как это странно выглядящее устройство на самом деле измеряет деформацию «панели панелей панелей панелей по умолчанию» itemscope>
Вопрос 15
Как проводимость (G) проводника связана с его длиной? Другими словами, чем дольше проводник, тем (
) его проводимость равна, при прочих равных условиях.
Показать ответ
Проводимость уменьшается по мере увеличения длины, при прочих равных условиях.
Последующий вопрос: как «проводимость» (G) математически относится к сопротивлению (R), и какова единица измерения проводимости?
Заметки:
Есть две единицы измерения для проводимости: старая единица (которая имеет прекрасный смысл, даже если ваши ученики могут сначала рассмеяться над ней) и новый блок (названный в честь известного электрического исследователя). Убедитесь, что ваши ученики знакомы с обоими.
← Предыдущая работа
Индекс рабочих листов
Следующая рабочая таблица →
Удельное сопротивление никеля ом м. Удельное сопротивление меди
Содержание:
В электротехнике одними из главных элементов электрических цепей являются провода. Их задача состоит в том, чтобы с минимальными потерями пропустить электрический ток. Экспериментальным путем уже давно определено, что для минимизации потерь электроэнергии провода лучше всего изготавливать из серебра. Именно этот металл обеспечивает свойства проводника с минимальным сопротивлением в омах. Но поскольку этот благородный металл дорог, в промышленности его применение весьма ограничено.
А главными металлами для проводов стали алюминий и медь. К сожалению, сопротивление железа как проводника электричества слишком велико для того, чтобы из него получился хороший провод. Несмотря на более низкую стоимость, оно применяется только как несущая основа проводов линий электропередачи.
Такие разные сопротивления
Сопротивление измеряется в омах. Но для проводов эта величина получается очень маленькой. Если попытаться провести замер тестером в режиме измерения сопротивления, получить правильный результат будет сложно. Причем, какой бы провод мы ни взяли, результат на табло прибора будет мало отличаться. Но это не значит, что на самом деле электросопротивление этих проводов будет одинаково влиять на потери электроэнергии. Чтобы в этом убедиться, надо проанализировать формулу, по которой делается расчет сопротивления:
В этой формуле используются такие величины, как:
Получается, что сопротивление определяет сопротивление. Существует сопротивление, вычисляемое по формуле с использованием другого сопротивления. Это удельное электрическое сопротивление ρ (греческая буква ро) как раз и обуславливает преимущество того или иного металла как электрического проводника:
Поэтому, если применить медь, железо, серебро или какой-либо иной материал для изготовления одинаковых проводов или проводников специальной конструкции, главную роль в его электротехнических свойствах будет играть именно материал.
Но на самом деле ситуация с сопротивлением сложнее, чем просто вычисления по формулам, приведенным выше. Эти формулы не учитывают температуру и форму поперечника проводника. А при увеличении температуры удельное сопротивление меди, как и любого другого металла, становится больше. Весьма наглядным примером этого может быть лампочка накаливания. Можно замерить тестером сопротивление ее спирали. Затем, измерив силу тока в цепи с этой лампой, по закону Ома вычислить ее сопротивление в состоянии свечения. Результат получится значительно больше, нежели при измерении сопротивления тестером.
Так же и медь не даст ожидаемой эффективности при токе большой силы, если пренебречь формой поперечного сечения проводника. Скин-эффект, который проявляется прямо пропорционально увеличению силы тока, делает неэффективными проводники с круглым поперечным сечением, даже если используется серебро или медь. По этой причине сопротивление круглого медного провода при токе большой силы может оказаться более высоким, чем у плоского провода из алюминия.
Причем, даже если их площади поперечников одинаковы. При переменном токе скин-эффект также проявляется, увеличиваясь по мере роста частоты тока. Скин-эффект означает стремление тока течь ближе к поверхности проводника. По этой причине в некоторых случаях выгоднее использовать покрытие проводов серебром. Даже незначительное уменьшение удельного сопротивления поверхности посеребренного медного проводника существенно уменьшает потери сигнала.
Обобщение представления об удельном сопротивлении
Как и в любом другом случае, который связан с отображением размерностей, удельное сопротивление выражается в разных системах единиц. В СИ (Международная система единиц) используется ом м, но допустимо использование также и Ом*кВ мм/м (это внесистемная единица измерения удельного сопротивления). Но в реальном проводнике величина удельного сопротивления непостоянна. Поскольку все материалы характеризуются определенной чистотой, которая может изменяться от точки к точке, необходимо было создать соответствующее представление о сопротивлении в реальном материале. Таким проявлением стал закон Ома в дифференциальной форме:
Этот закон, скорее всего, не будет применяться для расчетов в быту. Но в ходе проектирования различных электронных компонентов, например, резисторов, кристаллических элементов он непременно используется. Поскольку позволяет выполнить расчеты, исходя из данной точки, для которой существует плотность тока и напряженность электрического поля. И соответствующее удельное сопротивление. Формула применяется для неоднородных изотропных, а также анизотропных веществ (кристаллов, разряда в газе и т.п.).
Как получают чистую медь
Для того чтобы максимально уменьшить потери в проводах и жилах кабелей из меди, она должна быть особо чистой. Это достигается специальными технологическими процессами:
- на основе электронно-лучевой, а так же зонной плавки;
- многократной электролизной очисткой.
При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Скорость движения электронов непрерывно изменяется: при столкновении электронов с атомами, молекулами и другими электронами она уменьшается, потом под действием электрического поля увеличивается и снова уменьшается при новом столкновении. В результате этого в проводнике устанавливается равномерное движение потока электронов со скоростью нескольких долей сантиметра в секунду. Следовательно, электроны, проходя по проводнику, всегда встречают с его стороны сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.
Электрическое сопротивление
Электрическим сопротивлением проводника, которое обозначается латинской буквой r , называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
На схемах электрическое сопротивление обозначается так, как показано на рисунке 1, а .
Переменное электрическое сопротивление, служащее для изменения тока в цепи, называется реостатом . На схемах реостаты обозначаются как показано на рисунке 1, б . В общем виде реостат изготовляется из проволоки того или иного сопротивления, намотанной на изолирующем основании. Ползунок или рычаг реостата ставится в определенное положение, в результате чего в цепь вводится нужное сопротивление.
Длинный проводник малого поперечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.
Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.
Температура проводника также оказывает влияние на его сопротивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, констаитан, никелин и другие) с увеличением температуры своего сопротивления почти не меняют.
Итак, мы видим, что электрическое сопротивление проводника зависит от: 1) длины проводника, 2) поперечного сечения проводника, 3) материала проводника, 4) температуры проводника.
За единицу сопротивления принят один Ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому вместо того чтобы писать «Сопротивление проводника равно 15 Ом», можно написать просто: r = 15 Ω.
1 000 Ом называется 1 килоом (1кОм, или 1кΩ),
1 000 000 Ом называется 1 мегаом (1мгОм, или 1МΩ).
При сравнении сопротивления проводников из различных материалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Видео 1. Сопротивление проводников
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм².
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления и обозначается буквой α.
Если при температуре t 0 сопротивление проводника равно r 0 , а при температуре t равно r t , то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t :
r t = r 0 .
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t = r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r , то проводимость определяется как 1/r . Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Электрический ток I в любом веществе создается движением заряженных частиц в определенном направлении за счет приложения внешней энергии (разности потенциалов U). Каждое вещество обладает индивидуальными свойствами, по-разному влияющими на прохождение тока в нем. Эти свойства оцениваются электрическим сопротивлением R.
Георг Ом эмпирическим путем определил факторы, влияющие на величину электрического сопротивления вещества, вывел от напряжения и тока, которая названа его именем. Единица измерения сопротивления в международной системе СИ названа его именем. 1 Ом — это величина сопротивления, замеренного при температуре 0 О С у однородного ртутного столба длиной 106,3 см с площадью поперечного сечения в 1 мм 2 .
Определение
Чтобы оценить и применять на практике материалы для изготовления электротехнических устройств, введен термин «удельное сопротивление проводника» . Добавленное прилагательное «удельное» указывает на фактор использования эталонной величины объема, принятой для рассматриваемого вещества. Это позволяет оценивать электрические параметры разных материалов.
При этом учитывают, что сопротивление проводника возрастает при увеличении его длины и уменьшении поперечного сечения. В системе СИ используется объем однородного проводника с длиной 1 метр и поперечным сечением 1м 2 . В технических расчетах применяется устаревшая, но удобная внесистемная единица объема, состоящая из длины 1 метр и площади 1мм 2 . Формула удельного сопротивления ρ представлена на рисунке.
Для определения электрических свойств веществ, введена еще одна характеристика — удельная проводимость б. Она обратно пропорциональна значению удельного сопротивления, определяет способность материала проводить электрический ток: б =1/ρ.
Как удельное сопротивление зависит от температуры
На величину проводимости материала влияет его температура. Разные группы веществ ведут себя не одинаково при нагреве или охлаждении. Это свойство учитывают в электрических проводах, работающих на открытом воздухе в жару и холод.
Материал и удельное сопротивление провода подбираются с учетом условий его эксплуатации.
Возрастание сопротивления проводников прохождению тока при нагреве объясняется тем, что с повышением температуры металла в нем увеличивается интенсивность передвижения атомов и носителей электрических зарядов во всех направлениях, что создает лишние препятствия для движения заряженных частиц в одну сторону, снижает величину их потока.
Если уменьшать температуру металла, то условия для прохождения тока улучшаются. При охлаждении до критической температуры во многих металлах проявляется явление сверхпроводимости, когда их электрическое сопротивление практически равно нулю. Это свойство широко используется в мощных электромагнитах.
Влияние температуры на проводимость металла используется электротехнической промышленностью при изготовлении обыкновенных ламп накаливания. Их при прохождении тока нагревается до такого состояния, что излучает световой поток. В обычных условиях удельное сопротивление нихрома составляет около 1,05÷1,4 (ом ∙мм 2)/м.
При включении лампочки под напряжение через нить проходит большой ток, который очень быстро разогревает металл. Одновременно возрастает сопротивление электрической цепи, ограничивающее первоначальный ток до номинального значения, необходимого для получения освещения. Таким способом осуществляется простое регулирование силы тока через нихромовую спираль, отпадает необходимость применения сложной пускорегулирующей аппаратуры, используемой в светодиодных и люминесцентных источниках.
Как используется удельное сопротивление материалов в технике
Цветные благородные металлы обладают лучшими свойствами электрической проводимости. Поэтому ответственные контакты в электротехнических устройствах выполняют из серебра. Но это увеличивает конечную стоимость всего изделия. Наиболее приемлемый вариант — использование более дешевых металлов. Например, удельное сопротивление меди, равное 0,0175 (ом ∙мм 2)/м, вполне подходит для таких целей.
Благородные металлы — золото, серебро, платина, палладий, иридий, родий, рутений и осмий, получившие название главным образом благодаря высокой химической стойкости и красивому внешнему виду в ювелирных изделиях. Кроме того, золото, серебро и платина обладают высокой пластичностью, а металлы платиновой группы — тугоплавкостью и, как и золото, химической инертностью. Эти достоинства благородных металлов сочетаются.
Медные сплавы, обладающие хорошей проводимостью, используются для изготовления шунтов, ограничивающих протекание больших токов через измерительную головку мощных амперметров.
Удельное сопротивление алюминия 0,026÷0,029 (ом ∙мм 2)/м чуть выше, чем у меди, но производство и стоимость этого металла ниже. К тому он же легче. Это объясняет его широкое применение в энергетике для изготовления проводов, работающих на открытом воздухе, и жил кабелей.
Удельное сопротивление железа 0,13 (ом ∙мм 2)/м также допускает его применение для передачи электрического тока, но при этом возникают бо́льшие потери мощности. Стальные сплавы обладают повышенной прочностью. Поэтому в алюминиевые воздушные провода высоковольтных линий электропередач вплетают стальные нити, которые предназначены для противостояния нагрузкам, действующим на разрыв.
Особенно актуально это при образовании наледи на проводах или сильных порывах ветра.
Часть сплавов, например, константин и никелин обладают термостабильными резистивными характеристиками в определенном диапазоне. У никелина удельное электрическое сопротивление практически не меняется от 0 до 100 градусов по Цельсию. Поэтому спирали для реостатов изготавливают из никелина.
В измерительных приборах широко применяется свойство строгого изменения значений удельного сопротивления платины от ее температуры. Если через платиновый проводник пропускать электрический ток от стабилизированного источника напряжения и вычислять значение сопротивления, то оно будет указывать температуру платины. Это позволяет градуировать шкалу в градусах, соответствующих значениям Омам. Этот способ позволяет измерять температуру с точностью до долей градусов.
Иногда для решения практических задач требуется узнать полное или удельное сопротивление кабеля . Для этого в справочниках на кабельную продукцию приводятся значения индуктивного и активного сопротивления одной жилы для каждого значения поперечного сечения. С их помощью рассчитываются допустимые нагрузки, выделяемая теплота, определяются допустимые условия эксплуатации и подбираются эффективные защиты.
На удельную проводимость металлов оказывает влияние способ их обработки. Использование давления для пластической деформации нарушает структуру кристаллической решетки, увеличивает число дефектов и повышает сопротивление. Для его уменьшения применяют рекристаллизационный отжиг.
Растяжения или сжатия металлов вызывают в них упругую деформацию, от которой уменьшаются амплитуды тепловых колебаний электронов, а сопротивление несколько снижается.
При проектировании систем заземления необходимо учитывать . Оно имеет отличия в определении от вышеперечисленного метода и измеряется в единицах системы СИ — Ом∙метр. С его помощью оценивают качество растекания электрического тока внутри земли.
На удельную проводимость грунта влияют многие факторы, включая влажность почвы, плотность, размеры ее частиц, температуру, концентрацию солей, кислот и щелочей.
Поэтому важно знать параметры всех используемых элементов и материалов. И не только электрические, но и механические. И иметь в распоряжении какие-то удобные справочные материалы, позволяющие сравнивать характеристики разных материалов и выбирать для проектирования и работы именно то, что будет оптимальным в конкретной ситуации.
В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
Для сравнения данные обычно приводятся к единому, сопоставимому виду. Зачастую к таким характеристикам добавляется эпитет «удельный», а сами значения рассматриваются на неких унифицированных по физическим параметрам эталонах. Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Виды удельного сопротивления
Так как сопротивление бывает:
- активное — или омическое, резистивное, — происходящее от затрат электроэнергии на нагревание проводника (металла) при прохождении в нем электрического тока, и
- реактивное — емкостное или индуктивное, — которое происходит от неизбежных потерь на создание всякими изменениями тока, проходящего через проводник электрических полей, то и удельное сопротивление проводника бывает двух разновидностей:
- Удельное электрическое сопротивление постоянному току (имеющее резистивный характер) и
- Удельное электрическое сопротивление переменному току (имеющее реактивный характер).
Здесь удельное сопротивление 2 типа является величиной комплексной, оно состоит из двух компонент ТП — активной и реактивной, так как резистивное сопротивление существует всегда при прохождении тока, независимо от его характера, а реактивное бывает только при любом изменении тока в цепях. В цепях постоянного тока реактивное сопротивление возникает только при переходных процессах, которые связаны с включением тока (изменение тока от 0 до номинала) или выключением (перепад от номинала до 0). И их учитывают обычно только при проектировании защиты от перегрузок.
В цепях же переменного тока явления, связанные с реактивными сопротивлениями, гораздо более многообразны. Они зависят не только от собственно прохождения тока через некоторое сечение, но и от формы проводника, причем зависимость не является линейной.
Дело в том, что переменный ток наводит электрическое поле как вокруг проводника, по которому протекает, так и в самом проводнике. И от этого поля возникают вихревые токи, которые дают эффект «выталкивания» собственно основного движения зарядов, из глубины всего сечения проводника на его поверхность, так называемый «скин-эффект» (от skin — кожа). Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Разумеется, уменьшением толщины круглых в сечении проводов не исчерпывается эффективное проведение переменного тока. Проводник можно утончить, но при этом сделать его плоским в виде ленты, тогда сечение будет выше, чем у круглого провода, соответственно, и сопротивление ниже. Кроме того, простое увеличение площади поверхности даст эффект увеличения эффективного сечения. Того же можно добиться, используя многожильный провод вместо одножильного, к тому же, многожилка по гибкости превосходит одножилку, что часто тоже бывает ценно. С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
Кроме скин-эффекта на протекание переменного тока в проводниках влияет возбуждение вихревых токов в окружающих проводниках. Такие токи называются токами наводки, и они наводятся как в металлах, не играющих роль проводки (несущие элементы конструкций), так и в проводах всего проводящего комплекса — играющих роль проводов других фаз, нулевых, заземляющих.
Все перечисленные явления встречаются во всех конструкциях, связанных с электричеством, это еще более усиливает важность иметь в своем распоряжении сводные справочные сведения по самым разным материалам.
Удельное сопротивление для проводников измеряется очень чувствительными и точными приборами, так как для проводки и выбираются металлы, имеющие самое низкое сопротивление -порядка ом *10 -6 на метр длины и кв. мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
Таблица
Таблица удельных сопротивлений проводников (металлов и сплавов) | ||||
Материал провод-ника | Состав (для сплавов) | Удельное сопротивление ρ мом × мм 2 / м | ||
медь, цинк, олово, никель, свинец, марганец, железо и др. | ||||
Алюминий | ||||
Вольфрам | ||||
Молибден | ||||
медь, олово, алюминий, кремний, бериллий, свинец и др. (кроме цинка) | ||||
железо, углерод | ||||
медь, никель, цинк | ||||
Манганин | медь, никель, марганец | |||
Константан | медь, никель, алюминий | |||
никель, хром, железо, марганец | ||||
железо, хром, алюминий, кремний, марганец | ||||
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
Где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
Будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм 2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10 -6 . Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм 2 .
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Скорость движения электронов непрерывно изменяется: при столкновении электронов с атомами, молекулами и другими электронами она уменьшается, потом под действием электрического поля увеличивается и снова уменьшается при новом столкновении. В результате этого в проводнике устанавливается равномерное движение потока электронов со скоростью нескольких долей сантиметра в секунду. Следовательно, электроны, проходя по проводнику, всегда встречают с его стороны сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.
Электрическое сопротивление
Электрическим сопротивлением проводника, которое обозначается латинской буквой r , называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
На схемах электрическое сопротивление обозначается так, как показано на рисунке 1, а .
Переменное электрическое сопротивление, служащее для изменения тока в цепи, называется реостатом . На схемах реостаты обозначаются как показано на рисунке 1, б . В общем виде реостат изготовляется из проволоки того или иного сопротивления, намотанной на изолирующем основании. Ползунок или рычаг реостата ставится в определенное положение, в результате чего в цепь вводится нужное сопротивление.
Длинный проводник малого поперечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.
Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.
Температура проводника также оказывает влияние на его сопротивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, констаитан, никелин и другие) с увеличением температуры своего сопротивления почти не меняют.
Итак, мы видим, что электрическое сопротивление проводника зависит от: 1) длины проводника, 2) поперечного сечения проводника, 3) материала проводника, 4) температуры проводника.
За единицу сопротивления принят один Ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому вместо того чтобы писать «Сопротивление проводника равно 15 Ом», можно написать просто: r = 15 Ω.
1 000 Ом называется 1 килоом (1кОм, или 1кΩ),
1 000 000 Ом называется 1 мегаом (1мгОм, или 1МΩ).
При сравнении сопротивления проводников из различных материалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Видео 1. Сопротивление проводников
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм².
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления и обозначается буквой α.
Если при температуре t 0 сопротивление проводника равно r 0 , а при температуре t равно r t , то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t :
r t = r 0 .
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t = r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r , то проводимость определяется как 1/r . Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Медь
Расчет сопротивления
Сопротивление проводника (например, медного)
Сопротивление R медного провода длиной l можно рассчитать по следующей формуле:
где
R — сопротивление проводника в Ом
l — длина проводника в метрах
ρ — удельное электрическое сопротивление (также известное как удельное электрическое сопротивление) проводника.
A — площадь поперечного сечения, измеренная в квадратных миллиметрах
π — математическая константа
d — номинальный диаметр проволоки в миллиметрах
Удельное сопротивление ρ
Удельное электрическое сопротивление (также известное как удельное электрическое сопротивление) — это мера того, насколько сильно провод сопротивляется электрическому току. Низкое удельное сопротивление указывает на провод, который легко допускает движение электрического заряда. Медь имеет удельное сопротивление 0.0171 Ом · мм² / м и поэтому является одним из лучших проводников для электрического тока (немного уступая чистому серебру).
Проводимость γ
Электропроводность или удельная проводимость — это мера способности материала проводить электрический ток. Это обратное (обратное) значение удельного электрического сопротивления. Отожженная медная проволока имеет минимальную проводимость 58 См * м / мм², что эквивалентно 100% IACS (Международный стандарт отожженной меди), фактические значения обычно достигают 58,5-59 См * м / мм².
Термический коэффициент электрического сопротивления
Электрическое сопротивление зависит от температуры, которой подвергается провод.Эта взаимосвязь между сопротивлением и температурой выражается термическим коэффициентом сопротивления α . Для расчета сопротивления катушки или провода при температуре Тл можно использовать следующую формулу:
где
α — термический коэффициент сопротивления
R T — сопротивление катушки при температуре T
R 20 — сопротивление катушки при 20 ° С
IACS
Международный стандарт отожженной меди
Международный стандарт отожженной меди (IACS) устанавливает стандарт проводимости технически чистой отожженной меди.Стандарт был установлен в 1913 году Международной электротехнической комиссией. Комиссия установила, что при 20 ° C технически чистая отожженная медь имеет удельное сопротивление 1,7241×10 -8 Ом-метр или 5,8001×10 7 Сименс / метр, если выразить в терминах проводимости.
Для удобства проводимость часто выражается в процентах IACS. Электропроводность 5,8001×10 7 См / м может быть выражена как 100% IACS при 20 ° C. Все остальные значения проводимости относятся к этому стандартному значению проводимости для отожженной меди.Следовательно, железо со значением проводимости 1,04 x 10 7 См / м имеет проводимость примерно 18% от проводимости отожженной меди, и это составляет 18% IACS. Интересно отметить, что коммерчески чистая медная продукция теперь часто имеет значения проводимости IACS, превышающие 100% IACS, поскольку методы обработки улучшились с момента принятия стандарта в 1913 году, и теперь из металла можно удалить больше примесей. Был произведен провод высокой чистоты с проводимостью чуть более 103% IACS, что очень близко к значению, ожидаемому для меди без каких-либо примесей.
Краткая история МАКО
До создания стандарта IASC в 1913 году не было единообразия в значениях для отожженной меди, принятых в разных странах. Эти условия побудили Комитет по стандартам Американского института инженеров-электриков обратиться в Бюро стандартов США с просьбой провести расследование по данному вопросу. Это было сделано, и в результате были установлены стандартные значения на основе измерений большого количества репрезентативных образцов меди из 14 важных переработчиков меди.Измерения удельного сопротивления проводились на образцах медной проволоки длиной один метр и поперечным сечением один квадратный миллиметр. Это расследование привело к принятию МАКО Международной электротехнической комиссией. Стандарт IACS был задокументирован в Публикации 28 Международной электротехнической комиссии в марте 1914 года. Публикация 28, озаглавленная «Международный стандарт сопротивления для меди», гласит:
В качестве нормальных значений для стандартной отожженной меди следует принять следующие значения:
При температуре 20 ° C сопротивление провода из стандартной отожженной меди длиной один метр и однородного сечения в один квадратный миллиметр составляет 1/58 Ом, что в десятичном выражении равно 0.017241ohm (метр, мм 2 ).
При температуре 20 ° C плотность стандартной отожженной меди составляет 8,89 грамма на кубический сантиметр.
При температуре 20 ° C постоянный массовый температурный коэффициент сопротивления стандартной отожженной меди, измеренный между двумя потенциальными точками, жестко прикрепленными к проводу, равен 0.00393 на градус Цельсия.
Как следствие, из (1) и (2) следует, что при температуре 20 ° C сопротивление проволоки из стандартной отожженной меди однородного сечения длиной один метр и массой одного грамма составляет 1/58 x 8,89, что равно 0,15328 Ом (метр, грамм).
Обратите внимание, что единица измерения удельного сопротивления была выражена как 0,017241 Ом (метр, 2 мм), что отражает единицы длины и поперечного сечения стандартного провода.Чтобы избежать путаницы, единицы поперечного сечения миллиметры преобразуются в единицы длины, измеряемые метрами, а удельное сопротивление IACS теперь обычно выражается как 1,7241×10 -8 Ом-метр. Также обратите внимание, что единицы объемного сопротивления и массового сопротивления взаимосвязаны через плотность, которая была принята Международной электротехнической комиссией равной 8,89 грамма на см 3 при 20 ° C.
Для получения дополнительной информации см. Циркуляр Национального бюро стандартов №31 (издание 1914 г.), который доступен на сайте openlibrary.org. Примечание. Публикация № 28 Международной электротехнической комиссии «Международный стандарт сопротивления меди (март 1914 г.)» включена в Приложение V к настоящему документу.
Удельное электрическое сопротивление чистой меди, обработанной с помощью аддитивного процесса плавления в порошковом слое лазера средней мощности для использования в электромагнитных приложениях
Основные характеристики
- •
Машины LPBF средней мощности могут обрабатывать чистую Cu до приемлемого уровня.
- •
Удельное сопротивление готовой меди увеличивается на 33% в зависимости от ориентации сборки.
- •
Удельное сопротивление может быть снижено более чем на 50% по сравнению с исходными условиями путем термообработки.
- •
Значения удельного электрического сопротивления после термообработки ниже значений AlSi10Mg.
Реферат
Чистая медь является прекрасным проводником тепла и электричества, однако попытки обработать ее с помощью технологий аддитивного производства (AM) имели различные уровни успеха.В то время как электронно-лучевая плавка (EBM) успешно обработала чистую медь до высоких плотностей, сплавление в лазерном порошковом слое (LPBF) столкнулось с трудностями при достижении тех же результатов без использования лазеров очень высокой мощности. Это требование препятствовало исследованию использования LPBF с чистой медью, поскольку большинство машин оснащено лазерами с низкой и средней плотностью мощности лазера. В этой работе были проведены эксперименты по обработке чистой меди на установке LPBF мощностью 200 Вт с малым диаметром лазерного пятна, в результате чего удельная мощность лазера была выше средней, чтобы максимизировать плотность и достичь низкого удельного электрического сопротивления.Эффекты первоначальной ориентации сборки и последующей термообработки были также исследованы, чтобы изучить их влияние на электрическое сопротивление. Было обнаружено, что, несмотря на проблемы с высокой пористостью, термически обработанные образцы имели более низкое удельное электрическое сопротивление, чем другие распространенные материалы AM, такие как алюминиевый сплав AlSi10Mg. Проведя эти испытания, было обнаружено, что, несмотря на то, что удельное сопротивление примерно вдвое больше, чем у коммерчески чистой меди, удельное сопротивление было достаточно низким, чтобы продемонстрировать возможность использования AM для обработки меди, пригодной для электрических применений.
Ключевые слова
Лазерное наплавление в порошковой среде
Медь
Аддитивное производство
3D-печать
Удельное электрическое сопротивление
Электропроводность
Рекомендуемые статьи Цитирующие статьи (0)
Полный текст© 2019 Elsevier B.V. Все права защищены.
Рекомендуемые статьи
Цитирующие статьи
Электрическое сопротивление — гипертекст по физике
Обсуждение
введение
Йех! Что за беспорядок.
Проводимость: С. Грей, 1729 г. — Сопротивление: Георг Симон Ом, 1827 г.
Обычная версия…
I ∝ В
| Я = | В | ⇒ | .В = ИК | ⇒ | .R = | В |
| R | я |
Variableogy…
- количество: сопротивление R
единица: Ом [Ом] Георг Ом (1787–1854) Германия
Причудливая версия (магнитогидродинамическая версия?)…
Дж ∝ E
| J = σ E | ⇐ | ⇒ | .E = ρ J |
Добро пожаловать в ад символов…
| количество | символ | шт. | символ | собственности… |
|---|---|---|---|---|
| сопротивление | R | Ом | Ом | объектов |
| проводимость | г | siemens | S | |
| удельное сопротивление | ρ | омметр | Ом · м | материалов |
| проводимость | σ | siemens | См / м |
Закон Ома не является серьезным законом.Это непростая физика. Разумные материалы и устройства подчиняются ему, но есть много мошенников, которые этого не делают.
резисторы
Плохая выпивка портит наши молодые кишки, но водка идет хорошо.
Лучше постройте крышу над гаражом, пока фургон не намок.
| цвет | цифра | множитель | допуск | tcr (10 −6 / К) | |
|---|---|---|---|---|---|
| нет | ± 20% | ||||
| розовый | 10 −3 | ||||
| серебристый | 10 -2 | ± 10% | |||
| золото | 10 -1 | ± 5% | |||
| черный | 0 | 10 0+ | ± 250 | ||
| коричневый | 1 | 10 1+ | ± 1% | ± 100 | |
| красный | 2 | 10 2+ | ± 2% | ± 50 | |
| оранжевый | 3 | 10 3+ | ± 0.05% | ± 15 | |
| желтый | 4 | 10 4+ | ± 0,02% | ± 25 | |
| зеленый | 5 | 10 5+ | ± 0,50% | ± 20 | |
| синий | 6 | 10 6+ | ± 0,25% | ± 10 | |
| фиолетовый | 7 | ± 0.10% | ± 5 | ||
| серый | 8 | ± 0,01% | ± 1 | ||
| белый | 9 | ||||
материалы
Сопротивление и удельное сопротивление. Факторы, влияющие на сопротивление в проводящем проводе.
Проводники и изоляторы
Лучшие электрические проводники: серебро, медь, золото, алюминий, кальций, бериллий, вольфрам
Удельное сопротивление и проводимость взаимны.
Электропроводность металлов — это статистическая / термодинамическая величина.
Удельное сопротивление определяется рассеянием электронов. Чем больше рассеяние, тем выше сопротивление.
где…
| σ = | Электропроводность [См / м] |
| n = | плотность свободных электронов [э / м 3 ] |
| e = | заряд электрона (1.60 × 10 −19 С) |
| м e = | масса электрона (9,11 × 10 −31 кг) |
| v среднеквадратичное значение = | Среднеквадратичная скорость электронов [м / с] |
| ℓ = | средняя длина свободного пробега [м] |
Графит
Кому принадлежит эта идея? Нихром был изобретен в 1906 году, что сделало возможными электрические тостеры.
Полимеры электропроводящие.
| металлы | ρ (нОм м) | неметаллы | ρ (Ом м) |
|---|---|---|---|
| алюминий | 26,5 | оксид алюминия (14 ° C) | 1 × 10 14 |
| латунь | 64 | оксид алюминия (300 ° C) | 3 × 10 11 |
| хром | 126 | оксид алюминия (800 ° C) | 4 × 10 6 |
| медь | 17.1 | углерод аморфный | 0,35 |
| золото | 22,1 | карбон, алмаз | 2,7 |
| утюг | 96,1 | уголь, графит | 650 × 10 −9 |
| свинец | 208 | оксид индия и олова, тонкая пленка | 2000 × 10 −9 |
| литий | 92.8 | германий | 0,46 |
| ртуть (0 ° C) | 941 | пирекс 7740 | 40 000 |
| марганец | 1440 | кварц | 75 × 10 16 |
| нихром | 1500 | кремний | 640 |
| никель | 69,3 | диоксид кремния (20 ° C) | 1 × 10 13 |
| палладий | 105.4 | диоксид кремния (600 ° C) | 70 000 |
| платина | 105 | диоксид кремния (1300 ° C) | 0,004 |
| плутоний | 1414 | вода, жидкость (0 ° C) | 861 900 |
| серебристый | 15,9 | вода, жидкость (25 ° C) | 181 800 |
| припой | 150 | вода, жидкость (100 ° C) | 12 740 |
| сталь гладкая | 180 | ||
| сталь, нержавеющая | 720 | ||
| тантал | 131 | ||
| банка (0 ° C) | 115 | ||
| титан (0 ° C) | 390 | ||
| вольфрам | 52.8 | ||
| уран (0 ° C) | 280 | ||
| цинк | 59 |
температура
Общее правило — удельное сопротивление увеличивается с увеличением температуры в проводниках и уменьшается с увеличением температуры в изоляторах. К сожалению, не существует простой математической функции для описания этих отношений.
Температурную зависимость удельного сопротивления (или обратной ему проводимости) можно понять только с помощью квантовой механики. Точно так же, как материя представляет собой совокупность микроскопических частиц, называемых атомами, а луч света — это поток микроскопических частиц, называемых фотонами, тепловые колебания в твердом теле представляют собой рой микроскопических частиц, называемых фононами . Электроны пытаются дрейфовать к положительному полюсу батареи, но фононы продолжают врезаться в них.Случайное направление этих столкновений нарушает попытку организованного движения электронов против электрического поля. Отклонение или рассеяние электронов на фононах — один из источников сопротивления. С повышением температуры количество фононов увеличивается, а вместе с ним и вероятность столкновения электронов и фононов. Таким образом, когда температура повышается, сопротивление повышается.
Для некоторых материалов удельное сопротивление линейно зависит от температуры.
ρ = ρ 0 (1 + α ( T — T 0 ))
Удельное сопротивление проводника увеличивается с температурой.В случае меди зависимость между удельным сопротивлением и температурой примерно линейна в широком диапазоне температур.
Для других материалов лучше работает соотношение сил.
ρ = ρ 0 ( T / T 0 ) μ
Удельное сопротивление проводника увеличивается с температурой. В случае вольфрама зависимость между удельным сопротивлением и температурой лучше всего описывается соотношением мощности.
см. Также: сверхпроводимость
разное
магнитосопротивление
фотопроводимость
жидкости
электролиты
газы
пробой диэлектрика
плазма
микрофоны
Угольный микрофон — ничто задом наперед
| тип | звука производят изменений в… | , что вызывает изменения в… | , что приводит к изменению … |
|---|---|---|---|
| углерод | Плотность гранул | сопротивление | напряжение |
| конденсатор | разделительная пластина | емкость | напряжение |
| динамический | расположение катушки | флюс | напряжение |
| пьезоэлектрический | компрессия | поляризация | напряжение |
Медно-никель (CuNi) | Катушки, проволока сопротивления, печи, резка пеной | Провод сопротивления
Сопротивление медно-никелевым сплавам
Медно-никелевые (CuNi) сплавы — это материалы со средним и низким сопротивлением, которые обычно используются в приложениях с максимальными рабочими температурами до 400 ° C (750 ° F).
С низкими температурными коэффициентами электрического сопротивления, сопротивления и, следовательно, производительности, независимо от температуры. Сплавы медно-никелевые механически обладают хорошей пластичностью, легко паяются и свариваются, а также обладают выдающейся коррозионной стойкостью. Эти сплавы обычно используются в сильноточных устройствах, требующих высокого уровня точности.
Hyndman Industrial Products предлагает широкий выбор медно-никелевых сплавов и хранит самые распространенные в наличии.
294: Общее название: Alloy 294, Cuprothal 294, Nico, MWS-294, Cupron, Copel, Alloy 45, Cu-Ni 102, Cu-Ni 44
Управление двигателем, нагревательные провода и кабели; прецизионные и стекловидные резисторы, потенциометры.
Лист данных
A30: Общее название: Alloy 30, MWS-30, Cu-Ni 23, Cuprothal 5, Cu-Ni 23, Alloy 260
Сплав обладает низким удельным сопротивлением и высоким температурным коэффициентом сопротивления. Типичные применения включают регуляторы напряжения, устройства синхронизации, термочувствительные резисторы, устройства компенсации температуры, управление двигателем, нагревательные провода и кабели, прецизионные и стекловидные резисторы, потенциометры и приложения для низкотемпературного нагрева.
Лист данных
A90: Общее название: Alloy 95, 90 Alloy, MWS-90, Cu-Ni 10, Cuprothal 15, Cu-Ni 10, Alloy 320
Сплав демонстрирует низкое удельное сопротивление и высокий температурный коэффициент сопротивления. Типичные применения включают регуляторы напряжения, устройства синхронизации, термочувствительные резисторы, устройства компенсации температуры, управление двигателем, нагревательные провода и кабели, прецизионные и стекловидные резисторы, потенциометры и приложения для низкотемпературного нагрева.
Лист данных
A180: Общее название: Alloy 180, 180 Alloy, MWS-180, Cuprothal 30, Midohm, Cu-Ni 23, Nickel Alloy 180
Сплав демонстрирует низкое удельное сопротивление и высокий температурный коэффициент сопротивления. Типичные применения включают регуляторы напряжения, устройства синхронизации, термочувствительные резисторы, устройства компенсации температуры, управление двигателем, нагревательные провода и кабели, прецизионные и стекловидные резисторы, потенциометры и приложения для низкотемпературного нагрева.
Лист данных
Все названия сплавов и компаний являются товарными знаками соответствующих владельцев. Их использование не означает аффилированности или одобрения.
Удельное сопротивление и проводимость: определение, причины, формула и единицы (с диаграммой)
Удельное сопротивление и проводимость — две стороны одной медали, но оба являются ключевыми понятиями, которые нужно понять, когда вы изучаете электронику. По сути, это два разных способа описания одного и того же фундаментального физического свойства: насколько хорошо электрический ток течет через материал.
Удельное электрическое сопротивление — это свойство материала, которое показывает, насколько он сопротивляется прохождению электрического тока, а проводимость количественно определяет, насколько легко ток течет. Они очень тесно связаны между собой: электропроводность является обратной величине удельного сопротивления, но детальное понимание того и другого важно для решения проблем физики электроники.
Удельное электрическое сопротивление
Удельное сопротивление материала является ключевым фактором при определении электрического сопротивления проводника, и это часть уравнения для сопротивления, которая учитывает различные характеристики различных материалов.
Само электрическое сопротивление можно понять с помощью простой аналогии. Представьте, что поток электронов (носителей электрического тока) по проводу представлен шариками, стекающими по пандусу: вы получите сопротивление, если поместите препятствия на пути пандуса. Когда шарики натыкаются на преграды, они теряют часть своей энергии из-за препятствий, и общий поток шариков по рампе замедляется.
Другая аналогия, которая может помочь вам понять, как сопротивление влияет на ток, — это влияние, которое прохождение через гребное колесо оказывает на скорость потока воды.Опять же, энергия передается лопастному колесу, и в результате вода движется медленнее.
Реальность протекания тока через проводник ближе к примеру с мрамором, потому что электроны протекают через материал, но решетчатая структура ядер атомов препятствует этому потоку, который замедляет электроны.
Электрическое сопротивление проводника определяется как:
R = \ frac {ρL} {A}
Где ρ (rho) — удельное сопротивление материала (которое зависит от его состава), длина L — длина проводника, а A — площадь поперечного сечения материала (в квадратных метрах).Уравнение показывает, что более длинный проводник имеет более высокое электрическое сопротивление, а провод с большей площадью поперечного сечения имеет меньшее сопротивление.
Единицей измерения сопротивления в системе СИ является ом (Ом), где 1 Ом = 1 кг · м 2 с -3 A -2 , а единицей измерения удельного сопротивления в системе СИ является ом-метр (Ом · м). . У разных материалов разное удельное сопротивление, и вы можете посмотреть значения удельного сопротивления материала, который вы используете в расчетах, в таблице (см. Ресурсы).
Электропроводность
Электропроводность определяется просто как величина, обратная удельному сопротивлению, поэтому высокое удельное сопротивление означает низкую проводимость, а низкое удельное сопротивление означает высокую проводимость. Математически проводимость материала представлена как:
σ = \ frac {1} {ρ}
, где σ — проводимость, а ρ — удельное сопротивление, как и раньше. Конечно, вы можете перестроить уравнение для сопротивления в предыдущем разделе, чтобы выразить это через сопротивление, R , площадь поперечного сечения A проводника и длину L . , В зависимости от того, какую проблему вы решаете.
Единицы измерения проводимости в системе СИ являются обратными единицам удельного сопротивления, что делает их Ω −1 м −1 ; однако обычно оно выражается в сименсах на метр (См / м), где 1 S = 1 Ом -1 .
Расчет удельного сопротивления и проводимости
Учитывая определения удельного электрического сопротивления и проводимости, просмотр примера расчета поможет закрепить идеи, представленные до сих пор. Для медного провода длиной L = 0.1 м и площадью поперечного сечения A = 5,31 × 10 −6 м 2 и сопротивлением R = 3,16 × 10 −4 Ом, что такое удельное сопротивление ρ меди? Во-первых, вам нужно перестроить уравнение для сопротивления, чтобы получить выражение для удельного сопротивления ρ следующим образом:
R = \ frac {ρL} {A}
ρ = \ frac {RA} {L }
Теперь вы можете вставить значения, чтобы найти результат:
\ begin {align} ρ & = \ frac {3.7 \ text {s / m} \ end {align}
Очень низкое сопротивление и высокая проводимость объясняют, почему именно такой медный провод, вероятно, используется в вашем доме для подачи электричества.
Температурная зависимость
Значения, которые вы найдете в таблице для удельного сопротивления различных материалов, будут значениями при определенной температуре (обычно выбираемой равной комнатной температуре), поскольку удельное сопротивление увеличивается с увеличением температуры для большинства материалов.
Хотя для некоторых материалов (например, полупроводников, таких как кремний) удельное сопротивление уменьшается с повышением температуры, повышение с температурой является общим правилом.Это легко понять, если вернуться к аналогии с мрамором: когда барьеры вибрируют вокруг (в результате повышенной температуры и, следовательно, внутренней энергии), они с большей вероятностью заблокируют мрамор, чем если бы они были полностью неподвижны. .
Удельное сопротивление при температуре T определяется соотношением:
ρ (T) = ρ_0 (1 + α (T — T_0))
Где альфа ( α ) — температурный коэффициент удельного сопротивления, T — это температура, при которой вы рассчитываете удельное сопротивление, T 0 — эталонная температура (обычно принимаемая как 293 K, примерно комнатная температура) и ρ 0 — удельное сопротивление при эталонной температуре.Все температуры в этом уравнении выражены в кельвинах (K), а единицей СИ для температурного коэффициента является 1 / K. Температурный коэффициент удельного сопротивления обычно имеет то же значение, что и температурный коэффициент сопротивления, и имеет тенденцию быть порядка 10 -3 или ниже.
Если вам нужно рассчитать температурную зависимость для различных материалов, вам просто нужно найти значение соответствующего температурного коэффициента и обработать уравнение с эталонной температурой T 0 = 293 K (пока поскольку она соответствует температуре, используемой для эталонного значения удельного сопротивления).
Из формы уравнения видно, что это всегда будет увеличение удельного сопротивления при повышении температуры. В следующей таблице приведены некоторые ключевые данные по удельному электрическому сопротивлению, проводимости и температурным коэффициентам для различных материалов:
\ def \ arraystretch {1.5} \ begin {array} {c: c: c: c} \ text {Material} & \ text {Удельное сопротивление,} ρ \ text {(при 293 К) / Ом · м} & \ text {Проводимость,} σ \ text {(при 293 К) / См / м} & \ text {Температурный коэффициент,} α \ text {/ K} ^ {- 1} \\ \ hline \ text {Silver} & 1.{-23} & \\ \ hdashline \ end {array}
Обратите внимание, что изоляторы в списке не имеют установленных значений для их температурных коэффициентов, но они включены для отображения полного диапазона значений удельного сопротивления и проводимости.
Расчет удельного сопротивления при разных температурах
Хотя теория о том, что удельное сопротивление увеличивается при повышении температуры, имеет смысл, стоит взглянуть на расчет, чтобы подчеркнуть влияние, которое повышение температуры может оказать на проводимость и удельное сопротивление материала.В качестве примера расчета рассмотрим, что происходит с удельным сопротивлением и проводимостью никеля при нагревании от 293 K до 343 K. Еще раз взглянув на уравнение:
ρ (T) = ρ_0 (1 + α (T — T_0))
Вы можете видеть, что значения, необходимые для расчета нового удельного сопротивления, приведены в таблице выше, где удельное сопротивление ρ 0 = 6,99 × 10 −8 Ом · м, а температурный коэффициент α = 0,006. Вставка этих значений в приведенное выше уравнение позволяет легко вычислить новое удельное сопротивление:
\ begin {align} ρ (T) & = 6.{−8} \ text {Ω m} \ end {align}
Расчет показывает, что довольно существенное повышение температуры на 50 K приводит только к 30-процентному увеличению значения удельного сопротивления и, следовательно, к 30-процентному увеличению в сопротивлении данного количества материала. Конечно, затем вы можете продолжить и вычислить новое значение проводимости на основе этого результата.
Влияние повышения температуры на удельное сопротивление и проводимость определяется размером температурного коэффициента, при этом более высокие значения означают большее изменение температуры, а более низкие значения — меньшее изменение.
Сверхпроводники
Голландский физик Хайке Камерлинг-Оннес исследовал свойства различных материалов при очень низких температурах в 1911 году и обнаружил, что ниже 4,2 К (т. Е. -268,95 ° C) ртуть полностью теряет свое сопротивление воздействию электрический ток, поэтому его удельное сопротивление становится равным нулю.
В результате этого (и зависимости между удельным сопротивлением и проводимостью) их проводимость становится бесконечной, и они могут проводить ток неограниченное время без потери энергии.Позже ученые обнаружили, что многие другие элементы демонстрируют такое поведение при охлаждении ниже определенной «критической температуры» и называются «сверхпроводниками».
В течение долгого времени физика не предлагала реального объяснения сверхпроводников, но в 1957 году Джон Бардин, Леон Купер и Джон Шриффер разработали теорию сверхпроводимости «БКШ». Это утверждает, что электроны в материале группируются в «куперовские пары» в результате взаимодействий с положительными ионами, составляющими решеточную структуру материала, и эти пары могут перемещаться через материал без каких-либо препятствий.
Когда электрон движется через охлаждаемый материал, положительные ионы, образующие решетку, притягиваются к ним и немного меняют свое положение. Однако это движение создает в материале положительно заряженную область, которая притягивает другой электрон, и процесс начинается снова.
Сверхпроводники обладают многими потенциальными и уже реализованными применениями благодаря их способности проводить ток без сопротивления. Одно из наиболее распространенных применений, с которым вы, скорее всего, знакомы, — это магнитно-резонансная томография (МРТ) в медицинских учреждениях.
Тем не менее, сверхпроводимость также используется для таких вещей, как поезда на маглеве, которые работают за счет магнитной левитации и нацелены на устранение трения между поездом и рельсом, и ускорители частиц, такие как Большой адронный коллайдер в ЦЕРНе, где сверхпроводящие магниты используются для ускорять частицы со скоростью, приближающейся к скорости света. В будущем сверхпроводники могут быть использованы для повышения эффективности производства электроэнергии и увеличения скорости компьютеров.
Учебное пособие по физике: электрическое сопротивление
Электрон, движущийся по проводам и нагрузкам внешней цепи, встречает сопротивление. Сопротивление — это помеха течению заряда. Для электрона путешествие от терминала к терминалу не является прямым маршрутом. Скорее, это зигзагообразный путь, возникающий в результате бесчисленных столкновений с неподвижными атомами в проводящем материале. Электроны сталкиваются с сопротивлением — препятствием для их движения. В то время как разность электрических потенциалов, установленная между двумя выводами , способствует перемещению заряда , — это сопротивление, которое препятствует ему.Скорость, с которой заряд перетекает от терминала к терминалу, является результатом совместного действия этих двух величин.
Переменные, влияющие на электрическое сопротивлениеПоток заряда по проводам часто сравнивают с потоком воды по трубам. Сопротивление потоку заряда в электрической цепи аналогично эффектам трения между водой и поверхностями трубы, а также сопротивлению, создаваемому препятствиями на ее пути.Именно это сопротивление препятствует потоку воды и снижает как скорость потока, так и скорость дрейфа . Подобно сопротивлению потоку воды, общее сопротивление потоку заряда в проводе электрической цепи зависит от некоторых четко идентифицируемых переменных.
Во-первых, общая длина проводов влияет на величину сопротивления. Чем длиннее провод, тем большее сопротивление будет. Существует прямая зависимость между величиной сопротивления, с которым сталкивается заряд, и длиной провода, который он должен пройти.В конце концов, если сопротивление возникает в результате столкновений между носителями заряда и атомами провода, то, вероятно, столкновений будет больше в более длинном проводе. Больше столкновений означает большее сопротивление.
Во-вторых, на величину сопротивления влияет площадь поперечного сечения проводов. Более широкие провода имеют большую площадь поперечного сечения. Вода будет течь по более широкой трубе с большей скоростью, чем по узкой. Это можно объяснить меньшим сопротивлением, которое присутствует в более широкой трубе.Таким же образом, чем шире провод, тем меньше будет сопротивление прохождению электрического заряда. Когда все другие переменные одинаковы, заряд будет течь с большей скоростью через более широкие провода с большей площадью поперечного сечения, чем через более тонкие провода.
Третья переменная, которая, как известно, влияет на сопротивление потоку заряда, — это материал, из которого сделан провод. Не все материалы одинаковы с точки зрения их проводящей способности. Некоторые материалы являются лучшими проводниками, чем другие, и обладают меньшим сопротивлением потоку заряда.Серебро — один из лучших проводников, но никогда не используется в проводах бытовых цепей из-за своей стоимости. Медь и алюминий являются одними из наименее дорогих материалов с подходящей проводящей способностью, позволяющей использовать их в проводах бытовых цепей. На проводящую способность материала часто указывает его удельное сопротивление . Удельное сопротивление материала зависит от электронной структуры материала и его температуры. Для большинства (но не для всех) материалов удельное сопротивление увеличивается с повышением температуры.В таблице ниже приведены значения удельного сопротивления для различных материалов при температуре 20 градусов Цельсия.
Материал | Удельное сопротивление (Ом • метр) |
Серебро | 1,59 х 10 -8 |
Медь | 1.7 х 10 -8 |
Золото | 2,2 х 10 -8 |
Алюминий | 2,8 х 10 -8 |
Вольфрам | 5,6 х 10 -8 |
Утюг | 10 х 10 -8 |
Платина | 11 х 10 -8 |
Свинец | 22 х 10 -8 |
Нихром | 150 х 10 -8 |
Углерод | 3.5 х 10 -5 |
Полистирол | 10 7 — 10 11 |
Полиэтилен | 10 8 — 10 9 |
Стекло | 10 10 — 10 14 |
Твердая резина | 10 13 |
Как видно из таблицы, существует широкий диапазон значений удельного сопротивления для различных материалов.Материалы с более низким сопротивлением обладают меньшим сопротивлением потоку заряда; они лучшие дирижеры. Материалы, показанные в последних четырех строках приведенной выше таблицы, обладают таким высоким удельным сопротивлением, что их даже нельзя рассматривать как проводники.
Посмотри! Используйте виджет Resistivity of a Material , чтобы найти удельное сопротивление данного материала. Введите название материала и нажмите кнопку Отправить , чтобы узнать его удельное сопротивление. Математическая природа сопротивленияСопротивление — это числовая величина, которую можно измерить и выразить математически. Стандартной метрической единицей измерения сопротивления является ом, представленный греческой буквой омега -. Электрическое устройство с сопротивлением 5 Ом будет представлено как R = 5 . Уравнение, представляющее зависимость сопротивления ( R ) проводника цилиндрической формы (например,, провод) от влияющих на него переменных —
, где L представляет длину провода (в метрах), A представляет площадь поперечного сечения провода (в метрах 2 ) и представляет удельное сопротивление материала (в Ом • метр). В соответствии с вышеизложенным, это уравнение показывает, что сопротивление провода прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения провода.Как показывает уравнение, знание длины, площади поперечного сечения и материала, из которого сделан провод (и, следовательно, его удельного сопротивления), позволяет определить сопротивление провода.
Расследовать! Резисторы — один из наиболее распространенных компонентов в электрических цепях. На большинстве резисторов нанесены цветные полосы или полосы. Цвета отображают информацию о значении сопротивления.Возможно, вы работаете в лаборатории и вам нужно знать сопротивление резистора, используемого в лаборатории. Используйте виджет ниже, чтобы определить значение сопротивления по цветным полосам.
1. В бытовых цепях часто используются провода двух разной ширины: калибра 12 и калибра 14. Проволока 12-го калибра имеет диаметр 1/12 дюйма, а проволока 14-го калибра — 1/14 дюйма.Таким образом, провод 12-го калибра имеет более широкое сечение, чем провод 14-го калибра. Цепь на 20 А, используемая для настенных розеток, должна быть подключена с использованием провода 12-го калибра, а цепь на 15 А, используемая для цепей освещения и вентилятора, должна быть подключена с помощью провода 14-го калибра. Объясните физику, лежащую в основе такого электрического кода.
2. Основываясь на информации, указанной в вопросе выше, объясните риск, связанный с использованием провода 14-го калибра в цепи, которая будет использоваться для питания 16-амперной пилы.
3. Определите сопротивление медного провода 12-го калибра длиной 1 милю. Дано: 1 миля = 1609 метров и диаметр = 0,2117 см.
4. Два провода — A и B — круглого сечения имеют одинаковую длину и изготовлены из одного материала. Тем не менее, сопротивление провода A в четыре раза больше, чем у провода B.Во сколько раз диаметр проволоки B больше диаметра проволоки A?
.
 д.с.,
д.с.,