Сторона восьмиугольника через радиус: Правильный восьмиугольник — Википедия — Лазерная резка металла от "ТМК" Ярославль (Тутаев)

Содержание

Правильный восьмиугольник — Википедия

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8} ^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt{\displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

S=2aA.{\displaystyle \ S=2aA.}

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

Симметрия

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄

, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8

, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника

m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника
На 6 ромбов	Тессеракт

Применение восьмиугольников

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии

[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования

Производные фигуры

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

См. также

Примечания

Литература

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.


Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Восьмиугольник, виды, свойства и формулы

Восьмиугольник, виды, свойства и формулы.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник, выпуклый и невыпуклый восьмиугольник

Правильный восьмиугольник (понятие и определение)

Свойства правильного восьмиугольника

Формулы правильного восьмиугольника

Правильный восьмиугольник в природе, технике и культуре

Шестиугольник

Восьмиугольник, выпуклый и невыпуклый восьмиугольник:

Восьмиугольник – это многоугольник с восемью углами.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник

Рис. 2. Невыпуклый восьмиугольник

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Свойства правильного восьмиугольника:

1. Все стороны правильного восьмиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇ = a₈.

2. Все углы равны между собой и составляют 135°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = α₈ = 135°.

Рис. 4. Правильный восьмиугольник

3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник

5. Количество диагоналей правильного восьмиугольника равно 20.

Рис. 6. Правильный восьмиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный восьмиугольник

Формулы правильного восьмиугольника:

Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.

Формула константы правильного восьмиугольника:

Формула периметра правильного восьмиугольника:

Формулы площади правильного восьмиугольника:

Формулы радиуса окружности, вписанной в правильный восьмиугольник:

Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:

Формулы стороны правильного восьмиугольника:

Правильный восьмиугольник в природе, технике и культуре:

Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Найти что-нибудь еще?

Правильный восьмиугольник — Википедия

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

S=2aA.{\displaystyle \ S=2aA.}

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

Симметрия

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Разрезание правильного восьмиугольника

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника
На 6 ромбов	Тессеракт

Применение восьмиугольников

Восьмиугольный план Купола Скалы

Другие использования

Производные фигуры

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

См. также

Примечания

Литература

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.


Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Правильный восьмиугольник — Википедия

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

S=2aA.{\displaystyle \ S=2aA.}

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

Симметрия

Разрезание правильного восьмиугольника

Разрезание правильного восьмиугольника
На 6 ромбов	Тессеракт

Применение восьмиугольников

Восьмиугольный план Купола Скалы

Другие использования

Производные фигуры

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

См. также

Примечания

Литература

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.


Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Правильный восьмиугольник — Википедия

Построение правильного восьмиугольника

Построение правильного 8-угольника путем складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет

Формулы расчёта параметров правильного восьмиугольника[править]

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

Радиус описанной окружности правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Площадь через квадрат[править]

Площадь можно также вычислить как усечение квадрата

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A (ширину восьмиугольника)

Ещё одна простая формула площади:

Два катета углового треугольника можно получить по формуле

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный^[en] восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Разрезание правильного восьмиугольника[править]

Разрезание правильного восьмиугольника
На 6 ромбов	Тессеракт

Применение восьмиугольников[править]

Российский дорожный знак «STOP» Восьмиугольный план Купола Скалы.

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «STOP» имеет вид красного восьмиугольника.

В мультфильме Приключения Джеки Чана магические талисманы имеют форму правильного восьмиугольника.

Другие использования[править]

Производные фигуры[править]

Связанные многогранники[править]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого^[en] квадрата является первым в последовательности растянутых гиперкубов:

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press. — ISBN 9780521098595. Есть перевод на русский Веннинджер, Модели многогранников, но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278.

Символ Шлефли
Многоугольники	{1} · {2} · {3} · {4} · {5} · {6} · {7} · {8} · {9} · {10} · {11} · {12} · {17} · {257} · {65537} · {∞}
Звёздчатые многоугольники	{5/2} · {6/2} · {7/2} · {7/3} · {8/2} · {8/3} · {9/2} · {9/3} · {9/4}
Паркеты на плоскости	{3,6} · {4,4} · {6,3}
Правильные многогранники и сферические паркеты	{2,n} · {3,3} · {4,3} · {3,4} · {5,3} · {3,5} · {n,2}
Многогранники Кеплера — Пуансо	{5/2,5} · {5,5/2} · {5/2,3} · {3,5/2}
Соты	{4,3,4}
Четырёхмерные многогранники	{3,3,3} · {4,3,3} · {3,3,4} · {3,4,3} · {5,3,3} · {3,3,5}

Правильный восьмиугольник — Википедия. Что такое Правильный восьмиугольник

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

S=2aA.{\displaystyle \ S=2aA.}

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

Симметрия

Разрезание правильного восьмиугольника

Разрезание правильного восьмиугольника
На 6 ромбов	Тессеракт

Применение восьмиугольников

Восьмиугольный план Купола Скалы

Другие использования

Производные фигуры

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

См. также

Примечания

Литература

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.


Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Wikizero — Правильный восьмиугольник

Из Википедии, бесплатной энциклопедии

Правильный восьмиугольник имеет символ Шлефли {8}^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника[править | править код]

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружност

Радиус восьмиугольника от длины стороны

Калькулятор Радиус восьмиугольника вычисляет радиус окружности ( r ), которая огибает правильный восьмиугольник со сторонами длиной ( s ).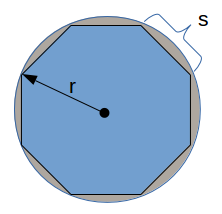

ИНСТРУКЦИИ: Выберите единицы и введите следующее:

( с ) Это длина одной стороны восьмиугольника

Радиус восьмиугольника (r): Калькулятор возвращает радиус ( r ) в метрах.Однако их можно автоматически преобразовать в другие единицы длины (например, футы) через раскрывающееся меню.

Математика / Наука

Правильный восьмиугольник — это восьмиугольный многоугольник, у которого все длины сторон и внутренние углы одинаковы. Формы восьмиугольника используются во многих приложениях и даже в природе. Формы восьмиугольника обеспечивают удобство прямых сторон с общим видом более круглого многоугольника.

Формула для вычисления радиуса основания восьмиугольника на длину сторон:

`r = s * sqrt (1 + 1 / sqrt (2))`

где:

r — внешний радиус восьмиугольник
s — длина стороны

Калькуляторы восьмиугольника

Калькуляторы связанной геометрии

Общая информация

Правильный восьмиугольник — это восьмиугольный многоугольник, у которого все длины сторон и внутренние углы одинаковы.Формы восьмиугольника используются во многих приложениях и даже в природе. Формы восьмиугольника обеспечивают удобство прямых сторон с общим видом более круглого многоугольника. Повышенный сад восьмиугольника

Сад восьмиугольника

Как расположить стороны сада восьмиугольника:

Найдите центр сада и вбейте кол в землю. Вам понадобится это место.
Разрежьте 9 кольев. Один для центра сада восьмиугольника и по одному для каждого внешнего угла.
Выберите длину сторон восьмиугольника. Типичный пример — обработанная под давлением ландшафтная древесина высотой восемь футов. Для восьмиугольного сада вам понадобится 8 штук.
Вычислите радиус круга вокруг восьмиугольника вокруг кола с помощью этого калькулятора.
Обвяжите веревку вокруг центрального стержня и разрежьте или завяжите узел или отметьте на дальнем конце радиус (r)
Возьмите один из садовых бревен и поместите один из его концов в точку на конце веревка.
Не перемещая этот конец бруса, возьмите веревку или бечевку и другой конец бруса, протяните их оба до точки, где веревка натянута, и закрепите второй конец бруса в точке земля, которая также находится на конце веревки. Цель состоит в том, чтобы оба конца бруса находились на одинаковом расстоянии (r) от центра.
Поместите конец следующего бруса в конец первого и повторите седьмой шаг. У этого агрегата все восемь частей уложены на свои места, и у вас получится восьмиугольник.

Конструкция и формулы восьмиугольника

1. Постройте правильный восьмиугольник, задав длину a одной из его сторон.

Построить, а не измерить.
Совет: Постройте прямой угол на каждом конце сегмента длиной a. Разделите пополам каждый прямой угол вне сегмента. Обозначьте длину еще двух сторон восьмиугольника.Продолжать . . . При этом используется то свойство, что внешние углы обычного восьмиугольника составляют 45 градусов каждый.
2. Постройте правильный восьмиугольник из квадрата со стороной s.
Конструируйте, а не измеряйте. Расстояние от каждой вершины равно a + x, где a — длина стороны восьмиугольника, а x — длина катета равнобедренного прямоугольного треугольника, который «отрезан» от каждого угла квадрата, но x + а — половина диагонали квадрата.
3. Постройте правильный восьмиугольник, учитывая расстояние от центра до вершины восьмиугольника (т.е. радиус описанной окружности ).
Строить, а не измерять. Диагонали восьмиугольника будут разделены (конструктивными) углами в 45 градусов. И т. Д.
4.Постройте правильный восьмиугольник, учитывая расстояние по перпендикуляру от одной стороны восьмиугольника до противоположной (то есть в два раза больше радиуса вписанного круга ).
Постройте квадрат вокруг круга и постройте из него восьмиугольник.
5. Какова длина Apothem правильного восьмиугольника со стороной a .
Перпендикулярное расстояние от центра многоугольника до одной из его сторон — это Апофема. «Срез» одной восьмой восьмиугольника представляет собой равнобедренный треугольник с длиной основания а и высотой апофемы. Центральный угол 45 градусов. Создайте прямоугольный треугольник и используйте функцию касательной.
6. Какова площадь правильного восьмиугольника со стороной a?
Найдите хотя бы два разных подхода —
а.Площадь разрезана на квадрат, прямоугольники и равнобедренные треугольники
г. Площадь, образованная суммой восьми равнобедренных треугольников с общим центральным углом в центре восьмиугольника.
7. Какова длина R радиуса описанной окружности?
8. Сравните площади
Восьмиугольник
Вписанный круг
Описанная окружность
9.Предположим, вы планировали построить беседку на фундаменте из обычного восьмиугольника. Планы восьмиугольных беседок бывают размером от 6 до 30 футов. Обычно веб-сайт, посвященный планам беседок, не дает никаких указаний относительно их размеров. ПРИНЯТЬ, что это радиус вписанной окружности ; другими словами, это ширина от одной стороны восьмиугольника до его противоположной стороны.
а. Для беседки размером N футов найдите ее площадь пола A кв. Футов, и длину стороны s футов.
г. Какой размер беседки выбрать, чтобы иметь площадь пола не менее 120 квадратных футов? Какой стороны у него будет длина?
г. Предположим, вам нужна беседка площадью 200 квадратных футов. Какой будет длина каждой стороны?
Примечание. Ссылка Gazebo ведет на GazeboCreations.com. На фото НЕ одна из их беседок. Фотография является общественным достоянием из государственных архивов США.

Возврат

Octagon — определение математического слова

Octagon — определение математического слова — Math Open Reference Попробуй это Отрегулируйте восьмиугольник ниже, перетащив любую оранжевую точку. Нажав на верхнюю левую командную строку, вы можете переключать его между регулярные и неправильный восьмиугольник.

Поскольку у восьмиугольника четное число сторон, в правильный восьмиугольник, противоположные стороны параллельно.

Свойства правильных восьмиугольников

Внутренний угол	135 °	Как и любой правильный многоугольник, чтобы найти внутренний угол, мы используем формулу (180н – 360) / л.Для восьмиугольника n = 8. См. Внутренние углы многоугольника
Внешний угол	45 °	Чтобы найти внешний угол правильного восьмиугольника, мы используем тот факт, что внешний угол образует линейная пара с внутренним углом, поэтому в целом он определяется формулой 180-внутренний угол. См. Внешние углы многоугольника
Площадь	4,828 с ² прибл.	Где S — длина стороны.Чтобы определить точную площадь восьмиугольника или любого многоугольника различными методами, см. Площадь правильного многоугольника и Площадь неправильного многоугольника

Свойства всех восьмиугольников

Количество диагоналей	20	Количество различных диагоналей, возможных для всех вершин. (Обычно ½n (n – 3)). На рисунке выше нажмите «показать диагонали», чтобы увидеть их. См. Диагонали многоугольника
Количество треугольников	6	Количество треугольников, созданных путем рисования диагоналей из заданной вершины.(В общем n – 2). На рисунке выше нажмите «показать треугольники», чтобы увидеть их. Увидеть треугольники многоугольника
Сумма внутренних углов	1080 °	Обычно 180 (n – 2) градусов. См. Внутренние углы многоугольника

Дома восьмиугольника

Дома и комнаты иногда имеют восьмиугольную форму (произносится: «ок-ТАГ-на-все»), возможно потому, что они они напоминают круглое пространство, но состоят из прямых стеновых секций, которые легче построить.

Хотя это уже не так популярно, есть примеры, которые сохранились как исторические здания. Тот, что выше, Октагон-хаус Лорена Андруса в Вашингтоне, штат Мичиган, США, построен в 1860 году.

Поскольку они основаны на правильном восьмиугольнике, противоположные стены параллельны, а комнаты имеют приятную симметрию.

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

Как рассчитать площадь правильного восьмиугольника

Образование
Математика
Геометрия
Как рассчитать площадь правильного восьмиугольника

Марк Райан

Вы можете рассчитать площадь правильного восьмиугольника со стандартным методом правильного многоугольника, но есть отличный альтернативный метод, основанный на том факте, что правильный восьмиугольник — это квадрат с обрезанными четырьмя углами. Например, вот как вы найдете площадь EIGHTPLU на рисунке ниже, учитывая, что это правильный восьмиугольник со сторонами длиной 6.

Четыре угла (как треугольник SUE на рисунке), которые вы отрезаете от квадрата, чтобы превратить его в восьмиугольник, представляют собой треугольники 45 ° — 45 ° — 90 ° (вы можете доказать это себе, если захотите). Итак, все, что вам нужно сделать, чтобы получить площадь восьмиугольника, — это вычислить площадь квадрата, а затем вычесть четыре угловых треугольника. Кусок торта.

Но сначала вот два отличных совета для решения этой и других проблем.

Для задач, связанных с правильными восьмиугольниками, могут пригодиться треугольники 45 ° — 45 ° — 90 °.Добавьте сегменты на диаграмму, чтобы получить один или несколько треугольников 45 ° — 45 ° — 90 °, а также несколько квадратов и прямоугольников, которые помогут решить проблему.
Мыслите нестандартно. Легко выработать привычку смотреть только внутрь фигуры, потому что этого достаточно для подавляющего большинства задач. Но иногда (как в этой задаче) вам нужно вырваться из этой колеи и посмотреть за пределы периметра фигуры.

Хорошо, вот что вы делаете.Вам дано, что стороны восьмиугольника имеют длину 6. Рассмотрим сторону EU .

Не просто вычислить площадь квадрата, а площадь единственного углового треугольника:

Чтобы закончить, вычтите общую площадь четырех угловых треугольников из площади квадрата: