Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Базовый курс лекций по сопромату, теория, практика, задачи.::Оглавление:: 1.1. Статический момент сечения Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей. Рассмотрим изменение статических моментов при параллельном переносе осей (рис.
или Sx1 = Sx — bF; Sy1 = Sy — aF; (1.1) Оси x1, y1 можно выбрать таким образом, чтобы выполнились условия: Sx1 = 0, Sy1 = 0. Оси, относительно которых статические моменты сечения равны нулю, называются центральнми. Точка пересечения центральных осей называется центром тяжести сечения. Принимая Sx1 = 0 и Sy1 = 0, из выражения (1.1) координаты центра площади сечения относительно вспомогательных осей x, y определяются по формулам (обозначим x
Соответственно, если площадь F и положение центра площади сечения (координаты xc, yc) в системе координат 0xy известны, то статические моменты сечения относительно осей x, y можно определить из выражений (1.2): Sx = F yc; Sy = F xc. (1.3) Можно показать, что статический момент относительно любой оси, проходящей через центр площади сечения, равен нулю. При определении центра площади сложного сечения применяется следующая процедура: 1) сечение разбивается на n частей, площади (Fi) и положение центров (Ci) площади которых известны; 2) задается вспомогательная система координат, в которой определяются координаты центров площадей (xci, yci) этих частей; 3) вычисляются координаты составного сечения по формулам:
Примеры Пример 1. ::Старый вариант этой лекции:: ::Оглавление:: |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
Подбор сечения балки (сопромат)
Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.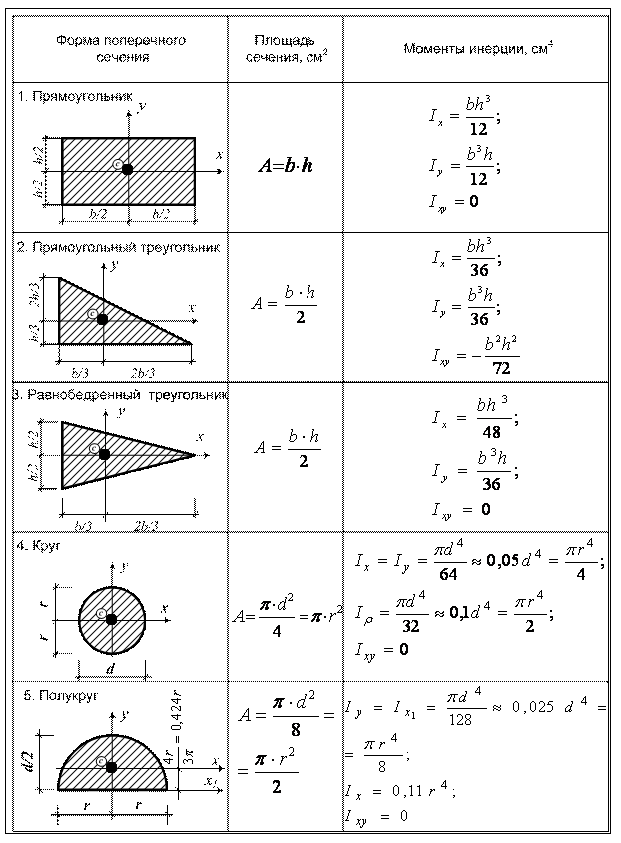
Условие прочности при изгибе по нормальным напряжениям: ,
где допускаемое напряжение принимается, как и при растяжении (сжатии) стержня из такого же материала.
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: .
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон , расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на , в три раза, так как . В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
Проверка прочности двутавров
Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:
в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле ;
в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.
в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям:
Расчет на растяжение стержня — Доктор Лом
где N — продольная растягивающая сила, действующая на стержень;
F — площадь поперечного сечения стержня;
σ — нормальные напряжения, возникающие в рассматриваемом поперечном сечении стержня в ответ на действие растягивающей продольной силы;
Rр — расчетное сопротивление материала стержня растяжению (для некоторых материалов расчетные сопротивления растяжению, сжатию, изгибу и т.
Визуально это может выглядеть так:
Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
На рисунке 525.1.а) мы видим прямолинейный стержень длиной l, показанный серым цветом, к которому приложена растягивающая сила N. При этом точка приложения силы находится на нейтральной оси стержня, совпадающей с осью х, показанной пунктирной линией.
Для упрощения расчетов заменяем опору А соответствующей опорной реакцией А (рис.525.1.б). Исходя из условий статического равновесия:
∑х = А + N = 0 (149.5.2)
А = — N (525.2)
Это означает, что опорная реакция A равна по значению растягивающей силе N, но направлена в противоположную сторону.
Если взглянуть на эту ситуацию под некоторым углом, то она будет выглядеть так, как показано на рисунке 525. 1.в). На этом рисунке мы видим, что нормальные напряжения — это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения — направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие — как отрицательные.
1.в). На этом рисунке мы видим, что нормальные напряжения — это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения — направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие — как отрицательные.
Сечение стержня, показанное на рисунке 525.1.в) розовым цветом, является перпендикулярным нейтральной оси стержня и называется поперечным сечением.
Как следует из формулы (525.1) и из приведенного рисунка, длина стержня l на значение нормальных напряжений никак не влияет. А вот параметры поперечного сечения стержня: ширина сечения b и высота сечения h, если сечение прямоугольное, очень даже влияют, так как от этих параметров зависит площадь
Примечание: конечно же поперечное сечение стержня далеко не всегда имеет прямоугольную форму, как показано на рисунке 525.1.в). Поперечное сечение может быть и круглым, и овальным, и ромбическим, и вообще иметь любую сколь угодно сложную форму, тем не менее форма поперечного сечения никак на значение нормальных напряжений не влияет (во всяком случае такое допущение принимается в теории сопротивления материалов), а влияет только площадь сечения, определить которую тем сложнее, чем более сложной является форма поперечного сечения.
Проверить данные постулаты теории сопротивления материалов очень легко и просто.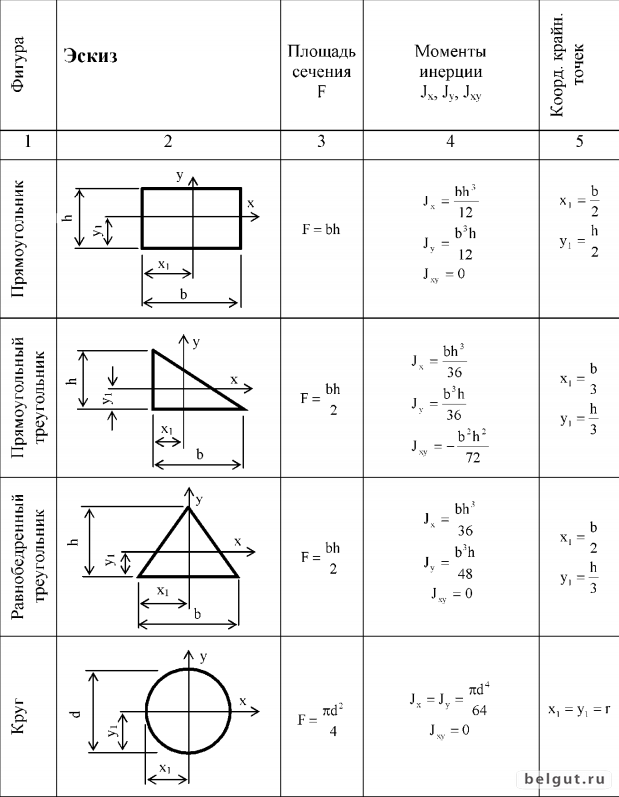
Но если одну из ниток сложить вдвое и попробовать разорвать, то усилие, необходимое для разрыва нитки, увеличится в 2 раза. Все потому, что условная площадь сечения стержня, работающего на растяжение, увеличится при складывании нитки в 2 раза.
Таким образом известная пословица: «где тонко, там и рвется» в переводе на язык теории сопротивления материалов будет звучать примерно так: «при действии растягивающих нормальных напряжений разрушение материала, обладающего постоянным сопротивлением растяжению по всей длине, будет происходить в сечении с минимальной площадью». Это особенно актуально для стержней с изменяющейся по длине площадью сечения.
С учетом различных факторов формула (525. 1) может иметь другой вид:
1) может иметь другой вид:
Nγn/Fn = σ ≤ Rрγs (512.1.2)
где γn — коэффициент надежности по нагрузке (как правило больше единицы), Fn — минимальная площадь сечения (с учетом возможных ослаблений отверстиями, пазами и т.п.), γs — коэффициент условий работы (как правило меньше единицы).
Т.е. теория сопротивления материалов допускает, что нормальные напряжения в стержне могут быть равны расчетному сопротивлению материала на растяжение, умноженному на коэффициент условий работы.
Пример расчета стержня на растяжение
Дано: На стальной стержень (см. рис.525.1.а)) с расчетным сопротивлением Rp = 2250 кг/см2 действует продольная растягивающая сила N = 30 тонн. Коэффициент надежности по нагрузке γn = 1.05, коэффициент условий работы γs = 0. 9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
Требуется: Подобрать диаметр стержня.
Решение:
1. Определяем требуемую площадь сечения стержня, преобразовав формулу (525.1.2)
F = Nγn/Rpγs = 30000·1.05/(2250·0.9) = 15.56 см2.
2. Определяем диаметр стержня
d = √4F/п = √4·15.56/3.14 = 4.45 см
Как видим сам расчет занимает гораздо меньше времени, чем описание физических характеристик используемых данных и даже формулировка условия задачи.
| | Навигация по справочнику TehTab. ru: главная страница / / Техническая информация / / Материалы — свойства, обозначения / / Сопротивление материалов. Сопромат. / / Таблица. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур. ru: главная страница / / Техническая информация / / Материалы — свойства, обозначения / / Сопротивление материалов. Сопромат. / / Таблица. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.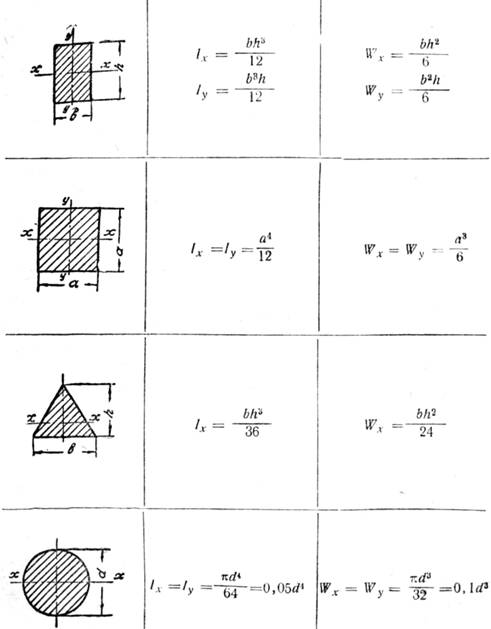 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Геометрические характеристики сплошных сечений 017
Внимание! Размер «с» игнорируется!
Внимание! Размер «a» игнорируется!
Ошибка! Проверьте правильность построения треугольника и формат ввода данных.
Площадь треугольника:
Центр тяжести треугольника:
Размеры треугольника:
Моменты инерции треугольника:
Полярные моменты инерции треугольника:
Радиусы инерции треугольника:
Моменты сопротивления треугольника:
Верхние волокна:
Нижние волокна:
Левые волокна:
Правые волокна:
Практические работы: Сопротивление материалов
государственное автономное учреждение
Калининградской области
профессиональная образовательная организация
Колледж сервиса и туризма
Методические рекомендации
по выполнению практических работ
«Сопротивление материалов»
по дисциплине Техническая механика
для студентов 3 курса
специальности 20. 02.04 Пожарная безопасность
02.04 Пожарная безопасность
Калининград
УТВЕРЖДАЮ
Заместитель директора по УР ГАУ КО ПОО КСТ Н.Н. Мясникова
ОДОБРЕНО
Методическим советом ГАУ КО ПОО КСТ
РАССМОТРЕНО
На заседании ПЦК технологических дисциплин
Редакционная коллегия:
Колганова А.А., методист
Фалалеева А.Б., преподаватель русского языка и литературы
Цветаева Л.В.., председатель ПЦК общематематических и естественнонаучных дисциплин
Составитель:
Незванова И.В. преподаватель ГАУ КО ПОО КСТ
Содержание
Практическое занятие 6: Расчёты на прочность и жёсткость при растяжении и сжатии
4
Практическая работа 7: Геометрические характеристики плоских сечений
9
Практическая работа 8: Кручение. Расчёты на прочность и жесткость при кручении
11
Практическая работа 9: Расчёты на прочность при изгибе
14
Практическая работа 10: Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.
17
Приложение
19
Список литературы
23
Практическое занятие 6
Расчёты на прочность и жёсткость при растяжении и сжатии
Необходимые формулы
Нормально напряжение
где N- продольная сила; А- площадь поперечного сечения.
Удлинение (укорочение) бруса
Е-модуль упругости; l- начальная длина стержня.
Допускаемое напряжение
[s]-допускаемые запасы прочности.
Условие прочности при растяжении и сжатии:
Примеры расчётов на прочность и сжатие
Пример 1: Груз закреплён на стержнях и находится в равновесии (рисунок 6. 1). Материал стержней – сталь, допускаемое напряжение 160 МПа. Вес груза 100кН. Длина стержней: первого – 2м, второго – 1м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения – круг.
1). Материал стержней – сталь, допускаемое напряжение 160 МПа. Вес груза 100кН. Длина стержней: первого – 2м, второго – 1м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения – круг.
Рисунок 6.1
Решение:
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статики (закон действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей. (рисунок 6.1)
Выбираем систему координат так, чтобы одна из осей координат совпадала с неизвестной силой. (рисунок 6.1. б)
Составим систему уравнений равновесия для точки В:
Решим систему уравнений и определяем реакции стержней.
Направление реакций выбрано верно.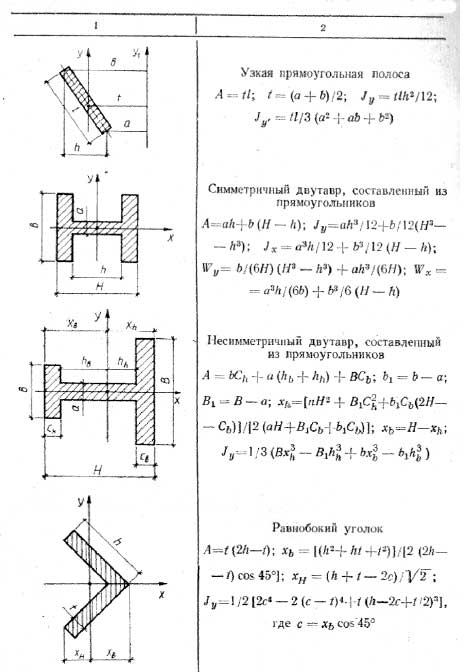 Оба стержня сжаты. Нагрузки на стержни: F1=57,4kH; F2=115,5kH.
Оба стержня сжаты. Нагрузки на стержни: F1=57,4kH; F2=115,5kH.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие:
откуда
Стержень 1 (N1=F1)
Для круга
Стержень 2 (N2=F2)
Полученные диаметры округляем: d1=25мм, d2=32мм.
3. Определяем удлинение стержней
Укорочение стержня 1:
Укорочение стержня 2:
Пример 2: Однородная жесткая плита с силой тяжести 10кН, нагруженная силой F=4,5кН и моментом m=3 кН*м, оперта в точке А и подвешена на стержень ВС (рисунок 6. 2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1м, материал – сталь, предел текучести 570 МПа, запас прочности для материала 1,5.
2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1м, материал – сталь, предел текучести 570 МПа, запас прочности для материала 1,5.
Решение:
1. Определить усилие в стержне под действием внешних сил.
Система находится в равновессии, можно использовать уравнение равновессия для плиты:
RB – реакция стержня, реакции шарнира А не рассматриваем.
Откуда
По третьему закону динамики реакция в стержне равна силе, действующей от стержня на плиту. Усилие в стержне равно 14 кН.
Рисунок 6.2
2. По условию прочности определяем потребную величину площади поперечного сечения:, откуда
Допускаемое напряжение для материала стержня:
Следовательно
3. Подберём сечение стержня по ГОСТ (Приложение 1)
Подберём сечение стержня по ГОСТ (Приложение 1)
Минимальная площадь швелера 6,16см2
Целесообразнее оспользовать равнополочный уголок №2 (d=3мм), площадь поперечного сечения которого 1,13 см2.
4. Определить удлинение стержня
Расчётно-графическая работа
Задание 1: Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брос нагружен силами F1, F2,F3.Площадь поперечного сечения А1 и А2.
Принять
Рисунок 6.3
Задание 2: Балка АВ, на которую действуют указанные нагрузки, удерживается в равновесии тягой ВС. Определить размеры поперечного сечения тяги для двух случаев: 1) сечение – круг; 2)сечение – уголок равнополочный. Принять . Собственный вес конструкции не учитывать.
Принять . Собственный вес конструкции не учитывать.
Рисунок 6.4
Практическая работа 7
Геометрические характеристики плоских сечений
Моменты инерции простейших сечений
Прямоугольник и квадрат (Рисунок 7.1)
Осевые:
Jx-относительно оси хх
Jy-относительно оси yy
Полярный: Jp=Jx+Jy
Рисунок 7.1
Круг и кольцо (рисунок 7.2)Осевые: — круг;
—кольцо
Полярные — круг;
— кольцо.
Рисунок 7.2
Моменты инерции относительно параллельных прямых (рисунок 7.3),
где Jx — момент инерции относительно оси хх;
Jx0 — момент инерции относительно оси х0х0;
Рисунок 7. 3
3
Рекомендации для решения задач расчетно–графической работы.
1. Момент инерции сложной фигуры является суммой моментов инерции частей, на которые ее разбивают. Разбить заданную фигуру на простейшие части, для каждой определить главные центральные моменты инерции по известным формулам.
2. Моменты инерции вырезов и отверстий можно представить отрицательными величинами.
3. Заданные сечения симметричны, главные центральные оси совпадают с осями симметрии составного сечения.
4. Моменты инерции частей, чьи главные центральные оси не совпадают с главными центральными осями сечения в целом, пересчитывают с помощью формулы для моментов инерции относительно параллельных осей. Расстояние между параллельными осями определить по чертежу.
5. При выполнении задания 2 главные центральные моменты инерции отдельных стандартных профилей определить по таблицам ГОСТ (Приложение 1).
Для использованных в составных сечениях полос моменты инерции определить по известной формуле для прямоугольника.
Расчетно-графическая работа
Геометрические характеристики плоских сечений
Задание 1: Вычислить главные центральные моменты инерции сечений, представленных на схемах (рисунок 7.4). При расчётах воспользоваться данными таблицы, выбрав необходимые значения.
Рисунок 7.4
Практическая работа 8
Кручение. Расчёты на прочность и жёсткость при кручении.
Основные положения расчётов при кручении
Распределение касательных напряжений по сечению при кручении (рисунок 8.1).
Касательное напряжение в точке А:
, где ρА—расстояние от точки А до центра сечения.
Условие прочности при кручении
Рисунок 8.1
Мк — крутящий момент в сечении, Н*м
Wp – момент сопротивления при кручении, м3
— допускаемое напряжение при кручении, Н/м2
Проектировочный расчёт, определение размеров поперечного сечения
Сечение-круг:
Сечение – кольцо:
где d – наружный диаметр круглого сечения;
dвн— внутренний диаметр кольцевого сечения; с= dвн/ d
Определение рационального расположения колёс на валу
Рациональное расположение колес – расположение, при котором максимальное значение крутящего момента на валу – наименьшее из возможных.
Для экономии металла сечение бруса рекомендуется выполнять кольцевым.
Условие жесткости при кручении
G – модуль упругости при сдвиге, Н/м2
E – модуль упругости при растяжении, Н/м2
– допускаемый угол закручивания,
— полярный момент инерции в сечении, м4
Проектировочный расчёт, определение наружного диаметра сечения
Рекомендации по выполнению расчетно-графической работы
1. Построить эпюру крутящих моментов по длине вала для предложенной в задании схемы.
Построить эпюру крутящих моментов по длине вала для предложенной в задании схемы.
2. Выбрать рациональное расположение колес на валу и дальнейшие расчеты проводить для вала с рационально расположенными шкивами.
3. Определить потребные диаметры вала круглого сечения из расчета на прочность и жесткость и выбрать наибольшее из полученных значений, округлив величину диаметра. 4. Сравнить затраты металла для случая круглого и кольцевого сечений. Сравнение провести по площадям поперечных сечений валов.
Площади валов рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).
Расчетно-графическая работа
Для стального вала круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного или оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью 25 рад/ с; материал вала — сталь, допускаемое напряжение кручения 30 МПа, модуль упругости при сдвиге 8-104 МПа; допускаемый угол закручивания = 0, 02 рад/ м.
Провести расчет для вала кольцевого сечения, приняв с = 0,9.
Сделать выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив площади поперечных сечений.
Рисунок 8.2
Практическая работа 9
Расчёты на прочность при изгибе
Основные положения и расчётные формулы при изгибе
Распределение нормальных и касательных напряжений при изгибе
где Ми – изгибающий момент в сечении;
Q-поперечная сила в сечении;
Рисунок 9.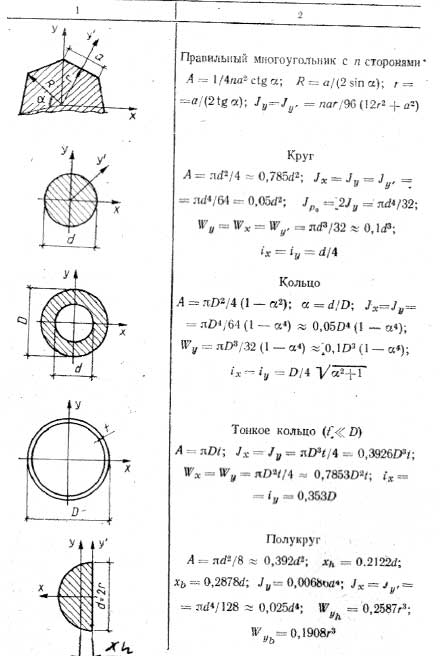 1
1
Jx— осевой момент инерции сечения (рисунок 9.1)
Wx – осевой момент сопротивления сечения; А-площадь сечения\
Условие прочности при изгибе
где – допускаемое напряжение\
Знаки изгибающих моментов и поперечных сил (рисунок 9.2)
Рисунок 9.2
Расчётно-графическая работа
Задание 1: Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавра и прямоугольника с отношением сторон h=2b. Материал – сталь, допускаемое напряжение 160 МПа. Рассчитать площади поперечных сечений и сделать вывод о целесообразности применения сечения.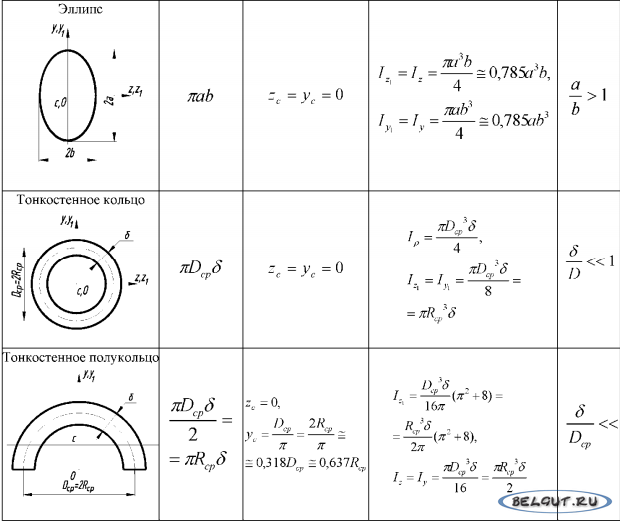 Для выбора профелей балок использовать приложение 1.
Для выбора профелей балок использовать приложение 1.
Рисунок 9.3
Задание 2: Для двухопорной балки, нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах. Найти максимальный изгибающий момент и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 Мпа. Сечение – швелер.
Рисунок 9.4
Практическая работа 10
Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.
Основные положения и расчётные формулы
Геометрические характеристики круга и кольца
Круг (рисунок 10.1)
— круг;
Рисунок 10.1
Кольцо (рисунок 10. 2)
2)
Рисунок 10.2
Моменты сопротивления:
Площади сечения
Условие прочности при совместном действии изгиба и кручения.
Эквивалентные моменты
Расчетно-графическая работа
Для промежуточного вала редуктора, передающего мощность Р при угловой скорости ω, определить вертикальную и горизонтальную составляющие реакции подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметры вала по сечениям, приняв [σ] – 60 МПа и полагая FT— 0,364 Ft. Расчёт произвести по гипотезе максимальных касательных напряжений.
Рисунок 10.3
Указание: Окружную силу определить по формуле
Приложение № 1
Сталь горячекатная. Швеллеры.
Швеллеры.
Обозначение:
h- высота швеллера; b- ширина швеллера
d- толщина стенки; t-средняя толщина полки
А- площадь швеллера
J- момент инерции
W- момент сопротивления
i – радиус инерции
S – статический момент полусечения
Z0— расстояние от оси у до наружной грани стенки
Таблица 1
Сталь горячекатная. Балки двутавровые.
Обозначение:
h- высота балки ;b- ширина балки
d- толщина стенки; t-средняя толщина полки
А- площадь сечения; J- момент инерции
W- момент сопротивления
i – радиус инерции
S – статический момент полусечения
Таблица 2
Сталь прокатная угловая равнополочная.
Обозначение:
b- ширина полки;
d- толщина полки;
А- площадь уголка;
W- момент сопротивления
i – радиус инерции
Z0— расстояние от оси у до наружной грани полки
J- момент инерции
Таблица 3
Продолжение таблицы 3
Список литературы
Олофинская В.
 П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.
П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.
Площадь сечения брутто нетто — Энциклопедия по машиностроению XXL
Сечение т —п . Площадь сечения брутто и нетто [c.78]Площадки чистого сдвига 126 Площадь сечения брутто 26, 569 —нетто 26, -271 [c.727]
Площадь сечения брутто и нетто. В предшествующих параграфах не принималось во внимание, что поперечные сечения могут меняться по длине стержня часто в стержнях имеются отверстия, врубки, -выемки, выточки, уменьшающие рабочую площадь сечения и носящие название местных ослаблений. Например, стержни клепаной фермы имеют отверстия для постановки заклепок, которыми их прикрепляют к узловым фасонным листам. Полную площадь поперечного сечения стержня называют площадью брутто — [c.44]
Ап, А— площадь сечения соответственно нетто (за вычетом площади отверстий) и брутто [c.
 5]
5]Почему при расчете сжатых стержней используются понятия площадь сечения брутто и площадь сечения нетто (Р ) [c.203]
Здесь т — параметр, равный отношению характерных площадей сечения стержня т = где и — площади соответственно нетто и брутто сечения. [c.119]
При определении напряжений принято различать площадь нетто/ и площадь брутто / вр, причем / —площадь сечения стержня за вычетом отверстия и — полная площадь сечения. Если бы напряжения распределялись равномерно, то мы получили бы напряжения по сечению с отверстием или выточкой, разделив действующую силу на Однако, проведя такую операцию, мы получим какую-то величину средних напряжений [c.54]
Под / нетто подразумевается фактическая площадь поперечного сечения, т. е. разность между площадью поперечного сечення стержня без учета ослабления, называемой / брутто, и площадью ослабления [c.98]
Отсюда можно найти величину Ь, задавшись толщиной листа t. Площадь Ь—md)t ослабленного сечения называется площадью нетто, площадь же полного сечения листа bt называется площадью брутто. [c.152]
Необходимая полная площадь / брутто поперечного сечения уголка больше / нетто па площадь ослабления уголка в сечении [c.138]
В формулы (32) — (33) подставляют площадь брутто (всю плошадь сечения без учета местных ослаблений). При наличии значительных местных, ослаблений производят дополнительную проверку на прочность по площади нетто / н, учитывающей эти ослабления, по формуле [c.408]
Полученный диаметр определён по дну нарезки для наименьшей площади поперечного сечения. В тех случаях, когда площадь отдельных сечений стержня меньше других, например из-за наличия отверстий для болтов или заклёпок, наружных выкружек или канавок (нарезки), определяется эта наименьшая площадь сечения, называемая площадью нетто и обозначаемая Рнетто или Р . Площадь поперечных сечений, не имеющих ослаблений, называется площадью брутто и обозначается / брутто или бр Определив расчётом сечение Р , размеры др получаем уже из конструктивных соображений. [c.31]
Подбор надлежащих размеров поперечного сечения колонны обычно производится путем последовательных попыток. Зная нагрузку Р, действующую на колонну, мы принимаем некоторые размеры поперечного сечения и вычисляем и для этих размеров. Тогда значение безопасного сжимающего напряжения по%поперечное сечение является удовлетворительным. В противном случае вычисления нужно псдаторить. В случае колонн с заделанными концами при вычислении принимается плоЩадь поперечного сечения брутто, так как заклепочные отверстия не оказывают заметного влияния на величину критической нагрузки. Однако при вычислении безопасной нагрузки на колонну допускаемое напряжение умножается на площадь поперечного сечения нетто для того, чтобы застраховать от чрезмерных напряжений в колонне. [c.231]
При пользовании приведенными формулами необходимо иметь в виду, что в реальных конструкциях стержни не всегда имеют постоянное по длине поперечное сечение. Необходимость соединения стержней, между собой ведет к местным ослаблениям сечении. Так, для прпсоеди 1Лння стальной полосы к листу (рис. 35) при помощи заклепок или болтов в полосе просверливаются или продавливаются отверстия разрушение полосы вероятнее может произойти по сечению тт., ослабленному отверстиями. Поэтому в условие прочности в таких случаях следует вводить наименьшую по длине стержня площадь поперечного сечения с наибольшим ослаблением. Такая площадь называется рабочей площадью, или площадью нетто, в отличие от площади брутто в неослабленном сечении. Если и продольная сила, и поперечные сечения стержня по длине переменны, то следует найти сечение, в котором возникают наибольшие напряжевдя (это сечение называется опасным), и составить для него условие прочности. [c.57]
Принимаем шесть болтов в два вертикальных ряда по три болта в каждом. Проверяем несущую способность листов по ослабленному сечению площадь поверхности сечения одного листа брутто А==2-30=60 см то же, нетто /4 =2(30—3 2,3) =46,2 см отношение площадей Л /Л=46,2/60=0,77[c.81]
Расчет диаметра провода и площади поперечного сечения
В этом блоге мы рассмотрим концепцию сопротивления, удельного сопротивления и шаги для расчета минимальной площади поперечного сечения и диаметра любого желаемого проводника.
Что такое сопротивление?
Свойство устройства или цепи, которое препятствует прохождению тока через нее. Сопротивление измеряется в Ом (Ом). Прочность любого материала с равномерной площадью поперечного сечения определяется следующими четырьмя факторами:
- Вид материала
- Длина
- Площадь поперечного сечения
- Температура
Что такое удельное сопротивление?
Удельное сопротивление — это мера того, насколько данный размер конкретного материала сопротивляется току.Хотя материалы сопротивляются прохождению электрического тока, некоторые из них проводят его лучше, чем другие. Удельное сопротивление используется для сравнения характеристик внутреннего сопротивления различных материалов. Материалы, которые легко проводят ток, называются проводниками. Проводники обладают низким удельным сопротивлением. В то время как материалы, которые плохо проводят ток, называются изоляторами. Изоляторы обладают высоким сопротивлением. Удельное сопротивление материала играет важную роль при выборе материалов, используемых для электрического провода.
Теперь, когда мы ясно понимаем концепции сопротивления и удельного сопротивления, давайте рассмотрим общую взаимосвязь между основным сопротивлением проводника, которая предполагает, что сопротивление данного проводника равно удельному сопротивлению материала, умноженному на отношение его длины к площади его поперечного сечения. . Это может помочь нам рассчитать минимальную площадь поперечного сечения и диаметр любого желаемого проводника.
Давайте рассмотрим пример, чтобы понять, как рассчитать минимальную площадь поперечного сечения и диаметр любого желаемого проводника.
Пример: Каковы минимальная площадь поперечного сечения и диаметр жилы для медного провода длиной 750 метров с максимальным сопротивлением 0,2 Ом?
Минимальная площадь поперечного сечения:
Чтобы решить эту проблему, мы будем использовать общее соотношение для расчета сопротивления проводника по следующей формуле:
Сопротивление = Удельное сопротивление * (Длина / Площадь)
R =
R = Сопротивление материала, Ом
Ρ = Удельное сопротивление материала, Ом на метр
L = Длина проводника, в метрах
A = Площадь поперечного сечения, в квадратных метрах
Чтобы использовать это общее соотношение для решения нашей примерной задачи, нам требуется удельное сопротивление или удельное сопротивление меди.Обратите внимание, что мы получаем удельное сопротивление материалов проводников из таблицы удельных сопротивлений проводников, и теперь мы знаем, что удельное сопротивление меди составляет 1,72 x 10e-8 Ом на метр.
При вычислении сопротивления проводника не забудьте выразить сопротивление в омах, удельное сопротивление материала в омах на метр, длину проводника в метрах и площадь поперечного сечения в квадратных метрах, чтобы это соотношение было действительным. Затем мы можем перейти к вычислению площади поперечного сечения провода, подставив известные величины в примере.
A = Ур. (1)
Диаметр жилы:
Площадь круга может быть представлена с помощью формулы ниже. Чтобы найти диаметр, нам придется изменить формулу.
А =
4 * А =
=
г =
Теперь мы можем заменить наше полученное значение площади поперечного сечения из уравнения. (1) в это соотношение и рассчитайте диаметр медной проволоки, чтобы получить диаметр 0.2 и диаметром не менее 9,062 мм.
Калькулятор площади поперечного сечения
Калькулятор площади поперечного сечения определяет площадь для различных типов балок. Балка — очень ответственный элемент в строительстве. Несущие элементы мостов, крыш и перекрытий в зданиях доступны в различных сечениях. Прочтите, чтобы понять, как рассчитать площадь поперечного сечения профиля I , профиля T , балки C , балки L , круглого стержня, трубы и балок с прямоугольным и треугольным поперечным сечением.
Что такое поперечное сечение и как рассчитать площадь поперечного сечения?
Поперечное сечение определяется как общая область, полученная от пересечения плоскости с трехмерным объектом. Например, рассмотрим разрез (пересечение) длинной круглой трубы с плоскостью. Вы увидите пару концентрических кругов. Концентрические круги — это поперечное сечение трубы. Точно так же балки — L , I , C и T — называются в зависимости от формы поперечного сечения.
Вид трубы в разрезе Чтобы вычислить площадь поперечного сечения, вам нужно рассматривать их как базовые формы. Например, трубка представляет собой концентрический круг. Следовательно, для трубы с внутренним и внешним диаметром ( d и D ) толщиной t площадь поперечного сечения может быть записана как:
A C = π * (D 2 - d 2 ) / 4 Мы также знаем, что внутренний диаметр d связан с толщиной t и внешним диаметром D как:
d = D - 2 * t Следовательно, площадь поперечного сечения становится:
A C = π * (D 2 - (D - 2 * t) 2 ) / 4 Аналогичным образом, площади поперечного сечения для всех других форм, имеющих ширину W , высоту H и толщину t 1 и t 2 , приведены в таблице ниже.
| Раздел | Площадь |
|---|---|
| полый прямоугольник | (В * Ш) — ((Ш — 2 т 1 ) * (Ш — 2 т 2 )) |
| прямоугольник | Ш * В |
| Я | 2 * W * t 1 + (H — 2 * t 1 ) * t 2 |
| С | 2 * W * t 1 + (H — 2 * t 1 ) * t 2 |
| т | Вт * т 1 + (В — т 1 ) * т 2 |
| л | Вт * т + (В — т) * т |
| Равнобедренный треугольник | 0.5 * Ш * В |
| Равносторонний треугольник | 0,4330 * длина 2 |
| Круг | 0,25 * π * D 2 |
| Трубка | 0,25 * π * (D 2 — (D — 2 * t) 2 ) |
Как найти площадь поперечного сечения?
Чтобы найти площадь поперечного сечения, выполните следующие действия.
- Шаг 1. Выберите форму поперечного сечения из списка, скажем, Полый прямоугольник .Теперь будет видна иллюстрация поперечного сечения и связанных полей.
- Шаг 2: Введите ширину полого прямоугольника,
W. - Шаг 3: Заполните высоту поперечного сечения,
H. - Шаг 4: Вставьте толщиной полого прямоугольника,
t. - Шаг 5: Калькулятор вернет площадь поперечного сечения .
Пример: Использование калькулятора площади поперечного сечения.
Найдите площадь поперечного сечения трубы, имеющей внешний диаметр 10 мм и толщину 1 мм .
- Шаг 1: Выберите форму поперечного сечения из списка, то есть Tube .
- Шаг 2: Введите внешний диаметр трубы,
D = 10 мм. - Шаг 3: Вставьте толщину трубы,
t = 1 мм. - Шаг 4: Площадь поперечного сечения:
A C = π * (D 2 - (D - 2 * t) 2 ) / 4 A C = π * (10 2 - (10-2 * 1) 2 ) / 4 = 28.274 мм 2 Как рассчитать площадь поперечного сечения трубы?
Для расчета поперечного сечения трубы:
- Вычтем квадратов внутреннего диаметра из внешнего диаметра.
- Умножьте число на π.
- Разделите произведение на 4.
Как рассчитать площадь двутаврового сечения?
Площадь I секции общей шириной W , высотой H и толщиной t может быть рассчитана как:
Площадь = 2 × W × t + (H - 2 × t) × t Как рассчитать площадь Т-образного сечения?
Площадь Т-образного профиля общей шириной W , высотой H и толщиной t может быть рассчитана как:
Площадь = W × t + (H - 2 × t) × t Каково поперечное сечение куба?
Поперечное сечение куба — квадратов .Точно так же для кубоида это либо квадрат, либо прямоугольник.
Пример для «определения наименьшего допустимого поперечного сечения проводников цепи».
Из доступных входов;
позволяет нам узнать, как определить «наименьшую допустимую площадь поперечного сечения» проводников цепи.
Доступные входы;
Ток нагрузки | 200 А |
THDi | 48% |
Изоляция проводника * | XLPE |
Тип проводника | Многожильный кабель |
Материал проводника * | Медь |
Установка | Непосредственно в земле |
Удельное сопротивление грунта * | 2 км / ш |
Температура почвы * | 40 * С |
* Предполагается, что в этом примере некоторые из входов обеспечивают; и они не были получены ни от пользователя, ни из среды.
Процедура:
- Определитель проводника : нейтраль
Поскольку THDi составляет> 33% (то есть THDI = 48%). Таким образом, токоведущий провод, определяющий размер, — нейтраль
.- Ток нейтрали : 3 × 0,48 × 200 = 288 А
- Поправочный коэффициент K3 : Фактор, основанный на устройстве защиты от перегрузки.
Предполагается, что эта цепь защищена автоматическим выключателем.
Так что K3 = 1.0
- F1 Температура: Таблица B.52.15
Для 40 ° C и с изоляцией из сшитого полиэтилена. F1 = 0,85
- Метод установки: 72 (Одножильные или многожильные кабели в оболочке, прямо в землю — без дополнительной механической защиты) Метод сравнения: D2
- Группа F2: Таблица B.52,18
Нет дополнительных цепей прикосновения, т.е. схем 1
F2группа = 1.00
- Поправочный коэффициент F3: Таблица (E.52.1)
THDI> 45% = THDI = 48% à f3 Нейтральный THDI = 1,00
- F3RSoil : Таблица B.52.16
Способ установки = в земле -> Rth = 2.0 Км / Вт
f3RthSoil = 1,12
Поправочный коэффициент f
f = 0,85 × 1,00 × 1,00 × 1,05 × 1,00 = 0,952
Общий поправочный коэффициент определяется путем умножения всех имеющихся поправочных коэффициентов ».
Теоретический Iz ’ = (K3 x IB) / (F x N в реальном времени) = (1,0 x 288) / (0,952 x1) = 302,52 A = 303 A
Выбор проводника осуществляется из данной Таблицы B.52,5 Колонка 8
185 мм2 сможет выдержать 324 А
240 мм2 сможет выдержать 375 А
С учетом допуска + 5% рекомендуется принять размер 185 мм²
K3 (поправочный коэффициент на основе устройства защиты) | 1 |
F1 (поправочный коэффициент в зависимости от температуры) | 0.85 |
F2 (поправочный коэффициент для группы проводников) | 1 |
F3 (поправочный коэффициент на основе THDi) | 1 |
F3 (поправочный коэффициент, основанный на удельном сопротивлении почвы) | 1,05 |
K пользователь (поправочный коэффициент определяется пользователем) | 1 |
Изъ (А) Теоретическая | 303 А |
Из (А) считается из таблицы | 324 А |
Теоретическая площадь поперечного сечения Ph (мм²) | 1 x 185 мм² |
Теоретическая площадь поперечного сечения нейтрали (мм²) | 1 x 185 мм² |
Теоретическая площадь поперечного сечения PE (мм²) | 1 x 95 мм² |
Площадь поперечного сечения нижней артерии сонных и позвоночных артерий и более высокая частота вторичных сосудов шеи связаны с рассеянным склерозом исследованы.Таким образом, целью этого исследования было изучить частоту появления сосудов шеи и их площади поперечного сечения (в квадратных миллиметрах) между пациентами с РС и здоровыми людьми из контрольной группы.
МАТЕРИАЛЫ И МЕТОДЫ: В этом исследовании 193 пациентам с РС и 193 здоровым пациентам из контрольной группы того же возраста и пола проведена 2D TOF-венография при 3Т. Основные артериальные (сонная и позвоночная), венозные (внутренняя яремная) и вторичные шейные сосуды были исследованы на 4 отдельных шейных уровнях (C2 / 3, C4, C5 / 6 и C7 / T1).ANCOVA с поправкой на возраст, индекс массы тела, статус курения, гипертонию и сердечные заболевания использовался для сравнения различий между пациентами с РС и здоровыми людьми из контрольной группы.
РЕЗУЛЬТАТЫ: После учета всех влияющих факторов пациенты с РС имели значительно более низкие площади поперечного сечения сонных артерий на уровне C2 / 3 ( P = 0,03), C5 / 6 ( P =. 026) и C7 / T1 ( P, = 0,005), а также позвоночных артерий на уровне C2 / 3 ( P =.02), C4 ( P, = 0,012) и C7 / T1 ( P, = 0,006) по сравнению со здоровым контролем. Более высокая частота вторичных сосудов шеи была обнаружена на всех 4 уровнях у пациентов с МС: C2 / 3 (12,9 против 10, P <0,001), C4 (9,1 против 7,5, P <0,001), C5 / 6 (7,8 против 6,8, P = 0,012) и C7 / T1 (8,8 против 6, P <0,001). Общая площадь поперечного сечения вторичных сосудов шеи также была значительно выше на всех 4 уровнях ( P <.03). Не было обнаружено значительных различий в площади поперечного сечения яремных вен между пациентами с РС и здоровыми людьми из контрольной группы.
ВЫВОДЫ: Пациенты с рассеянным склерозом показали меньшую площадь поперечного сечения сонных и позвоночных артерий и более высокую частоту вторичных шейных сосудов и их площади поперечного сечения по сравнению со здоровой контрольной группой.
СОКРАЩЕНИЯ:
- ИМТ
- индекс массы тела
- CCA
- общая сонная артерия
- CSA
- площадь поперечного сечения
- ECA
- внешняя здоровая сонная артерия8 9018 908 HCA 908 внутренняя яремная вена
- VA
- позвоночная артерия
Рассеянный склероз — наиболее частое неврологическое заболевание, вызывающее инвалидность среди активного работающего населения.Перекрывающиеся механизмы хронической аутоиммунной демиелинизации и прогрессирующей нейродегенерации являются отличительными признаками патофизиологии заболевания, которое сильно варьирует в зависимости от спектра течения рассеянного склероза. 1 Из-за огромной неоднородности представлений о болезни, в исследованиях использовались разные пути для понимания потенциального многофакторного взаимодействия аутоиммунных, дегенеративных, экологических, генетических и сердечно-сосудистых факторов. 2
Появляется все больше свидетельств того, что повышенная распространенность РС и тяжесть заболевания связаны с более частыми сердечно-сосудистыми факторами риска, такими как ожирение и гипертония. 3 Сидячий образ жизни, отсутствие физических упражнений, 4 гипертония, 5,6 статус курения, 7 измененный липидный обмен, 8 и особенно ожирение на ранних стадиях развития 9 — все они были неизменно связаны с более раннее начало заболевания рассеянным склерозом, ускоренное прогрессирование инвалидности и худшие исходы воспалительных и нейродегенеративных заболеваний. Недавнее общенациональное исследование в Дании, в котором участвовали 8947 пациентов с РС и 44 735 здоровых людей из контрольной группы (ХК), показало более низкую частоту сопутствующих цереброваскулярных заболеваний до начала рассеянного склероза, а затем более высокую частоту после начала заболевания. 10 Следовательно, растет интерес к пониманию патофизиологических механизмов, с помощью которых сердечно-сосудистые факторы могут влиять на течение и тяжесть заболевания РС.
Исследование сосудистого кровообращения головы и шеи является важнейшей общей основой для лучшего понимания связи между сердечно-сосудистыми сопутствующими заболеваниями и рассеянным склерозом. Поскольку эта система является конституциональным членом гематоэнцефалического барьера, любое изменение ее целостности может иметь пагубные последствия для обеих систем.Следовательно, изучение информации о площади поперечного сечения сосудов шеи (ППС) имеет решающее значение для дальнейшего понимания взаимосвязей между экстракраниальными и внутричерепными сосудистыми изменениями, наблюдаемыми при РС. Однако комплексный комплексный подход к изучению CSA артериальной и венозной систем сосудов шеи, как правило, отсутствует. Кроме того, насколько нам известно, степень нормальных сосудистых изменений в зависимости от возраста, пола и индекса массы тела (ИМТ) не была полностью исследована.
Предыдущие исследования изучали важность некоторых сосудистых аспектов рассеянного склероза с использованием перфузионной визуализации. 11 Как позитронно-эмиссионная томография 12 , так и исследования перфузионной МР-визуализации с контрастированием динамической восприимчивости показали широко распространенное снижение церебрального кровотока, влияющее как на белое, так и на серое вещество. 11 Сообщения о нарушении цереброваскулярной связи и реактивности 13 могут дополнительно объяснить причину нейродегенеративных процессов при РС. Пациенты с РС также продемонстрировали нарушение цереброваскулярной реактивности в различных сетях мозга, особенно в сетях режима по умолчанию. 14 Хотя патогенез этих изменений внутримозговой перфузии неизвестен, это может быть связано с сердечно-сосудистыми сопутствующими заболеваниями или хроническими высокими уровнями оксида азота, связанными с патологией заболевания. 15
На этом фоне мы стремились изучить частоту сосудов шеи и их CSA (в квадратных миллиметрах) между пациентами с MS и HC. Кроме того, мы исследовали возможные смешивающие факторы, такие как возраст, сопутствующие сосудистые заболевания и ИМТ, при сравнении сосудистой системы шеи у пациентов с РС и ГК.
Материалы и методы
Участники исследования
Участники исследования, включенные в это исследование, являются частью продолжающегося проспективного исследования сердечно-сосудистых, экологических и генетических факторов риска при РС, в котором приняли участие> 1000 субъектов с РС и HC. 16 Критерии включения в это подисследование, изучающее характеристики сосудов шеи при РС, были следующими: 1) МР-венографическое исследование, проведенное в течение 30 дней после клинического обследования, 2) возрастной диапазон от 18 до 80 лет, 3) РС, определенный Пересмотренные критерии Макдональда 2010 г., 17 или 4) здоровый контроль без известного в анамнезе неврологического заболевания.Критериями исключения были следующие: 1) известные морфологические сосудистые аномалии в анамнезе (синдромы Клиппеля-Тренауна-Вебера, Паркса Вебера, Сервелля-Марторелла или Бадда-Киари), 2) вторично-прогрессирующий или первично-прогрессирующий РС и 3) беременность. или кормящие матери.
Сто девяносто три пациента с РС и 193 HC соответствующего пола и возраста прошли медицинский скрининг, а также физические, неврологические и МРТ обследования. Истории курения, сердечных заболеваний и гипертонии также были собраны с использованием структурированных вопросников в соответствии с перекрестным исследованием больничных медицинских карт для всех субъектов.Испытуемые были разделены на курильщиков, никогда и никогда не куривших. Активные курильщики были классифицированы как люди, которые выкуривали> 10 сигарет в день в течение 3 месяцев до начала исследования. Субъекты были классифицированы как курильщики в прошлом, если они курили последовательно в течение как минимум 6 месяцев в какой-то момент в прошлом. 7 Заболевание сердца включало диагноз застойной сердечной недостаточности, сердечного приступа, аритмии, клапанных нарушений, сердечных шумов или операции на сердце. Диагностика артериальной гипертензии проводилась в соответствии с седьмым отчетом Объединенного национального комитета по профилактике, выявлению, оценке и лечению высокого кровяного давления. 18 Пациенты со стадией 1 (систолическое артериальное давление 140–159 мм рт. Ст. Или диастолическое артериальное давление 90–99 мм рт. Ст.) И стадией 2 (систолическое артериальное давление ≥160 мм рт. классифицируется как гипертензия. ИМТ оценивался у всех испытуемых. Пациентов с РС обследовал опытный невролог с использованием расширенной шкалы инвалидности.
Исследование было одобрено наблюдательным советом государственного университета Нью-Йорка в Буффало, и все субъекты подписали письменную форму информированного согласия.
Получение и анализ МР-изображений
Все сканы были получены на сканере 3T Signa Excite HD 12.0 Twin Speed (GE Healthcare, Милуоки, Висконсин) с использованием 8-канальной катушки для головы и шеи. Как частота сосудов шеи, так и CSA сосудов были измерены с использованием последовательности 2D-MRV, которая состояла из 150 срезов (толщиной 1,5 мм) с использованием матрицы 320 × 192 и поля зрения 22,0 см. Фазовое поле обзора составило 75% для разрешения 0,69 × 1,15 × 1,5 мм 3 . Параметры изображения: TE / TR / угол переворота 4.3 мс / 14 мс / 70 ° и общее время сбора данных 5 минут 19 секунд.
Сосуды шеи были исследованы на 4 отдельных шейных уровнях, включая C2 / C3, C4, C5 / C6 и C7 / T1. Сначала 2 обученных оператора (PB и CM, каждый с опытом работы не менее 5 лет) определили CSA общей сонной артерии (CCA), внутренней сонной артерии, наружной сонной артерии (ECA) и позвоночных артерий (VA), а также внутренних яремные вены (IJVs). В шейных отделах выше бифуркации ОСА (C4 или C2 / C3) CSA как ICA, так и ECA были добавлены вместе.Общий CSA каждого сосуда был рассчитан путем суммирования значений соответствующих левосторонних и правосторонних измерений. Поскольку позвоночная вена обычно присутствует не у всех пациентов, 19 она была классифицирована как дополнительный дренажный путь и включена в сегментацию вторичных сосудов. Из-за возможного наличия медленного и извилистого потока, который может создать насыщение сигнала в очень маленьких сосудах, порог включения вторичного сосуда был установлен на 2,0 мм 2 .Были отмечены все видимые сосуды шеи на 4 шейных уровнях, их частота подсчитывалась вручную и оценивались их CSA. Дополнительными критериями исключения сосудов были следующие: 1) сосуды, которые создавали петли в рострокаудальном направлении, и 2) оператор не мог проследить обнаруженный сигнал на срезах выше и ниже заданного уровня.
CSA всех сосудов шеи определяли с помощью инструмента обработки изображений Java (JIM), версия 7.0 (http://www.xinapse.com) инструментария ROI.Для наилучшего выбора краев использовался инструмент Contour ROI Tool, часть автоматизированного набора инструментов Preview Contours. При необходимости оператор вручную скорректировал границу ROI. Ручная регулировка в основном использовалась в следующем: 1) сканирование MRV со значительным шумом изображения на заданном контрасте, 2) разделение 2 близко расположенных, но разных сосудов, когда инструмент автоматического контурирования выделил оба, и 3) исключить возникновение сигнала. ответвления сосудов. Максимальный контраст был установлен на уровне яркости 900.Общее правило определения идеального контраста анализа основывалось на стабильности границ сигнала. Была проведена тщательная сегментация основных артериальных, венозных и вторичных сосудов на 4 шейных уровнях с высокой воспроизводимостью (межклассовая корреляция> 0,818; P <0,001) (онлайн-таблица 1). 20 На интерактивном рисунке показан пример выбора соответствующего сосуда и репрезентативных измерений CSA в здоровом контроле.
Статистический анализ
Статистический анализ проводился с использованием SPSS, версия 24.0 (IBM, Армонк, Нью-Йорк). Для клинических и демографических сравнений между группами использовались перекрестные таблицы χ 2 и тест Стьюдента t соответственно. Чтобы определить связь между количеством сосудов шеи и их площадью поперечного сечения с возрастом и ИМТ, мы использовали ранговую корреляцию Спирмена.
Порядковые переменные, относящиеся к частоте вторичных судов, были преобразованы в тип ранжированного порядка. Различия в частоте и размере сосудов шеи (CSA) между группами MS и HC оценивались с помощью анализа ковариации с поправкой на возраст, ИМТ, историю курения, болезни сердца и гипертонию.Радиолокационные графики использовались для комплексной визуализации данных (рис. 1). Все анализы были дополнительно повторены в подгруппах субъектов без наличия сопутствующих сердечно-сосудистых заболеваний (ожирение, болезни сердца, гипертония, сахарный диабет 1 типа), чтобы дополнительно контролировать, связаны ли результаты с сопутствующими сердечно-сосудистыми заболеваниями. Чтобы изучить влияние курения на показатели CSA, мы провели дополнительный дополнительный анализ у пациентов с РС, которые были курильщиками и некурящими.
Рис 1.Радиолокационное изображение различий сосудов шеи между пациентами с рассеянным склерозом и здоровыми людьми из контрольной группы. Значимые корреляции выделены жирным шрифтом.
Во всех анализах минимальный уровень значимости P ≤ 0,05 на основе двустороннего критерия считался статистически значимым.
Результаты
Демографические и клинические характеристики
У всех 193 пациентов с РС был ремиттирующий РС. Демографические и клинические данные представлены в таблице 1.Соотношение женщин в обеих группах составляло 130/193 (67,4%). Возраст пациентов с МС составлял 42,2 ± 13,9 года, средний ИМТ — 26,8 ± 5,8, средняя продолжительность заболевания — 12 ± 9,4 года, а средний балл по расширенной шкале статуса инвалидности — 2,0. Группа HC составляла 42,9 ± 17,5 лет и имела средний ИМТ 26,8 ± 5,7. Не было значительных различий между обеими группами относительно возраста ( P, = 0,676), пола ( P, = 1.000) и ИМТ ( P, = 0,940). Только 2 пациента с РС и 1 здоровый контроль имели диагноз сахарного диабета 1 типа.Однако сердечно-сосудистая нагрузка была выше в группе MS по сравнению с HC, включая анамнез курения ( P = 0,005) и гипертонию ( P = 0,001), и наблюдалась тенденция к увеличению распространенности сердечных заболеваний ( P = 0,053). Демографические и клинические данные о подгруппе субъектов без гипертонии и сердечных заболеваний обобщены в интерактивной таблице 2.
Таблица 1:Демографические и клинические характеристики пациентов с рассеянным склерозом ( n = 193) и здоровых людей ( человек). n = 193) a
Связь возраста и ИМТ с размером и количеством вторичных сосудов шеи
Взаимосвязь между возрастом и сосудами шеи представлена в таблице 2.Возраст показал значительную обратную корреляцию с количеством вторичных сосудов шеи при HC. У более старшего поколения HC было меньше сосудов, измеренных в точках C2 / 3 ( P = 0,039), C4 ( P = 0,003), C5 / 6 ( P = 0,05) и C7 / T1 ( P = 0,031) уровней. Напротив, у пациентов с РС не было обнаружено значимой связи возраста и частоты вторичных сосудов шеи. Возраст не был связан с общим CSA вторичных сосудов ни у пациентов с MS, ни у пациентов с HC. Как показано для вторичных сосудов, был проведен такой же анализ корреляций между артериальной CSA и возрастом.Не было обнаружено связи между возрастом и артериальной CSA на любом уровне шейки матки, за исключением уровня C2 / 3 в когортах MS и HC ( P = 0,031 и P = 0,023, соответственно). Напротив, у обоих пациентов с РС и ГК наблюдалась значительная связь возраста и увеличения ППС IJV.
Таблица 2:Корреляция частоты артериальных, венозных и вторичных сосудов шеи и площади поперечного сечения с возрастом и ИМТ в исследуемых группах a
ИМТ показал еще более сильную обратную связь с частотой вторичных сосудов шеи. у пациентов с ХК и МС (таблица 2).У HC с более низким ИМТ была более высокая частота вторичных сосудов, измеренных на C2 / 3 ( P = 0,05), C4 ( P <0,001), C5 / 6 l ( P = 0,001) и Уровни C7 / T1 ( P = 0,025). Точно так же более низкий ИМТ у пациентов с РС был связан с более высокой частотой вторичных сосудов шеи на уровне C2 / 3 ( P = 0,007), уровне C4 ( P <0,001), уровне C5 / 6 ( P <0,001) и уровень C7 / T1 ( P = 0,017). CSA вторичных сосудов шеи показал обратную связь с ИМТ у пациентов с МС на уровнях C2 / 3, C4 и C5 / 6 ( P <.01).
Различия между когортами MS и HC по частоте и площади поперечного сечения артериальных, венозных и вторичных сосудов шеи
Частота и размер артериальных, венозных и вторичных сосудов шеи в группах MS и HC суммированы в таблицах 3 и 4 и Рис. 1. Из-за зависимости от возраста и ИМТ, проявляемой размером и количеством вторичных сосудов у пациентов с РС и ГК, а также различий в факторах риска сердечно-сосудистых заболеваний между двумя группами, все сравнения были скорректированы по возрасту, ИМТ. , история курения, болезни сердца и гипертония.
Таблица 3:Частота и площадь поперечного сечения артериальных, венозных и вторичных сосудов шеи в исследуемых группах a
Таблица 4:Частота вторичных сосудов шеи и площадь поперечного сечения в исследуемых группах a
После того, как мы учли эти смешивающие факторы, пациенты с РС имели значительно более низкую CSA сонных артерий на уровне C2 / 3 (55,1 ± 16,4 по сравнению с 60,9 ± 17,9, P = 0,03), C5 / 6 ( 50,1 ± 10.1 против 53,9 ± 12,5, P = 0,026) и C7 / T1 (47,6 ± 9,8 против 52 ± 9,9, P = 0,005), а также позвоночных артерий на уровне C2 / 3 (20,1 ± 4,4 против 21,8 ± 5,8, P = 0,02), C4 (18,6 ± 4,2 против 20,3 ± 5, P = 0,012) и C7 / T1 (16,3 ± 4,5 против 18,4 ± 5,9, P = .006) по сравнению с HC. Более высокая частота вторичных сосудов шеи была обнаружена на всех 4 уровнях у пациентов с МС: C2 / 3 (12,9 против 10, P <.001), C4 (9,1 против 7,5, P <0,001), C5 / 6 (7,8 против 6,8, P = 0,012) и C7 / T1 (8,8 против 6, P <0,001). Общий CSA вторичных сосудов также был значительно выше на всех 4 уровнях у пациентов с MS ( P <0,03). Разница была наиболее значимой на уровне C7 / T1, где CSA пациентов с МС составлял 71,1 ± 40,5 мм 2 по сравнению с 56,7 ± 32,5 мм 2 в HC ( P <0,001). Не было обнаружено значительных различий в CSA IJV между когортами MS и HC.На рис. 2 показан пример различий в количестве сосудов и CSA, наблюдаемых у пациентов с РС и ГК соответствующего возраста и пола.
Рис. 2.Сравнение количества основных и вторичных сосудов и площади поперечного сечения на последовательности 2D-MRV на 4 шейных уровнях у пациентов с рассеянным склерозом (4 соответствующие панели слева) и здоровых контрольных лиц соответствующего возраста и пола ( 4 соответствующие панели справа). VV указывает на позвоночную вену; L, слева; Р, верно. Зеленый цвет представляет вторичные сосуды, красный цвет представляет CCA, ICA, EAC и VA, а синий цвет представляет IJV.
В подгруппе субъектов без факторов риска сердечно-сосудистых заболеваний сравнение пациентов с РС ( n = 135) и HC ( n = 142) дало результаты, аналогичные результатам основного анализа для артериальных, венозных и вторичных сосудов. частота и их CSA (интерактивные таблицы 3 и 4). За исключением количества вторичных сосудов на уровне C5 / C6 (7,0 против 8,3, P = 0,034), курильщики с РС не показали значительных различий по сравнению с некурящими (онлайн-таблицы 5 и 6).
Обсуждение
В этом исследовании были выявлены два основных вывода. Во-первых, даже после корректировки всех сердечно-сосудистых факторов, включая ИМТ, гипертензию, сердечные заболевания, историю курения и возраст, когорта с рассеянным склерозом показала более высокую частоту вторичных сосудов шеи и большие CSA по сравнению с HC. Этот результат был согласован на всех исследованных уровнях шейки матки. Самое интересное, что у пациентов с РС также была меньшая ППС основных и вторичных артериальных сосудов (ОСА, ВСА, НСА и ПА, соответственно).Кроме того, эти данные были подтверждены в подгруппе пациентов (70%) без наличия сопутствующих сердечно-сосудистых заболеваний. Кроме того, мы показали, что демографические факторы, такие как возраст и ИМТ, являются существенными препятствиями между пациентами с РС и HC при рассмотрении морфологии сосудов шеи и должны учитываться в будущих исследованиях.
Обнаружение того, что пациенты с РС демонстрируют разные паттерны морфологии сосудов шейки сосудов в отношении старения по сравнению с ХК, предполагает, что у РС и сердечно-сосудистых заболеваний взаимосвязаны пути. 10 Известно, что факторы риска сердечно-сосудистых заболеваний влияют на тяжесть заболевания рассеянным склерозом. Например, курение было связано с более высокой нагрузкой на поражение и более тяжелой атрофией головного мозга у пациентов с рассеянным склерозом. 7 Когда сочетаются несколько сопутствующих сердечно-сосудистых заболеваний, эта взаимосвязь становится еще более устойчивой. 6 Два независимых эпидемиологических исследования показали интересное несоответствие между снижением распространенности ишемической болезни сердца и увеличением распространенности инсульта у пациентов с РС по сравнению с ГК. 21,22 Это открытие предполагает, что артериальные сосуды, снабжающие центральную нервную систему, возможно, подвержены особым атеросклеротическим повреждениям. 23 Фактически, одно исследование показало, что пациенты с РС имеют более низкую податливость сонных артерий по сравнению с ГК. 23 Хотя уменьшение просвета сонных и позвоночных артерий, обнаруженное у пациентов с РС, может указывать на то, что воспалительные механизмы способствуют раннему атеросклерозу у пациентов с РС, 24 мы обнаружили аналогичные результаты в подгруппе пациентов с РС без наличия сердечно-сосудистых заболеваний.Другие авторы также показали более низкие значения CCA у пациентов с MS по сравнению с HC (65 против 78 мм 2 ). 25 Другое исследование MS, в котором использовалась методика MRV с фазовым контрастом, показало несколько более высокую площадь CSA CCA по сравнению с нашими измерениями с использованием MRV времени пролета (65 против 48,9 мм 2 , соответственно). 26 Неоднородность популяции пациентов с РС между двумя исследованиями также может способствовать объяснению этих результатов. Поэтому в будущих исследованиях следует более подробно изучить этот вопрос в начале заболевания, когда наличие сердечно-сосудистых рисков минимально.
Гипоперфузия нормального белого вещества, обычно обнаруживаемая у пациентов с РС, может быть частично связана с анатомическими различиями артериальной системы шеи, наблюдаемыми в настоящем исследовании. 27 Ранее сообщалось о снижении мозгового кровотока как в нормальном белом, так и в сером веществе. 11 Отчетливые перфузионные кластеры у пациентов с РС показали ассоциации локальной гипоперфузии и образования Т1-гипоинтенсивных поражений, что подчеркивает необходимость улучшения перфузии при восстановлении поражений. 28 Наиболее важно то, что наблюдаемая при ГМ гипоперфузия в отсутствие потери объема указывает на то, что снижение перфузии головного мозга может быть временным предшественником развития атрофии головного мозга при РС. 29 Несмотря на то, что появляется все больше свидетельств сосуществующей сосудистой патологии при РС, текущие исследования перфузии, как правило, включают небольшой размер выборки и ограниченный размер эффекта. Следовательно, при любой интерпретации прямой причинно-следственной связи следует проявлять осторожность.
Нейроваскулярное соединение — это физиологический механизм, ответственный за увеличение коркового кровотока из-за активации клеток. 30 У здоровых людей это приводит к расширению сосудов головного мозга, которое компенсирует повышенную потребность в глюкозе и кислороде. 31 Гипокапническое исследование показало, что пациенты с РС не могут физиологически увеличивать церебральный кровоток, что, в свою очередь, приводит к глобальной диффузной гипоперфузии. 13 Эта аномалия ранее была связана как триггерный фактор для формирования поражения РС и может до некоторой степени объяснять нейродегенеративный аспект процесса болезни РС. 32 В целом, морфологические изменения шейных артерий, кровоснабжающих мозг, которые наблюдались в этом исследовании, могут быть следствием длительной гипоперфузии белого вещества / ГМ с нормальным внешним видом и нарушения цереброваскулярной реактивности, что приводит к ускоренной нейродегенерации при РС.
Альтернативное обратное объяснение уменьшения артериальной CSA, наблюдаемого в этом исследовании, может быть связано с увеличением инвалидности, что вызывает снижение физической активности у пациентов с MS. 4 Поскольку ухудшение инвалидности приводит к малоподвижному образу жизни, это в конечном итоге приведет к увеличению нагрузки на сердечно-сосудистую систему и сосудистым осложнениям. 4 Кроме того, меры по улучшению деятельности, связанной с резервами, и поддержанию напряженной деятельности привели к лучшим клиническим результатам и результатам РС, полученным с помощью МРТ. Хотя настоящее исследование не может ответить на вопрос, являются ли наблюдаемые морфологические изменения шейных артерий вторичными или первичными по отношению к процессу заболевания РС, будущие исследования должны расширить наши предварительные результаты на ранних и более поздних стадиях заболевания с использованием продольного дизайна исследования.
При сравнении размеров IJV между когортами MS и HC не было обнаружено различий между двумя группами на любом уровне шейки матки. Таким образом, наши результаты согласуются с несколькими недавними исследованиями MRV, показывающими отсутствие анатомических различий IJV между пациентами с MS и HC, 33,34 , но в отличие от некоторых других исследований, показывающих противоположные результаты. 26,35,36 Несколько недавних исследований показали, что CSA IJV имеет заметную изменчивость в своем течении через шею и усиливается сужением с возрастом. 20,37
В нескольких исследованиях MRV использовалась для изучения распространенности и протяженности вторичных сосудов в шее у пациентов с рассеянным склерозом. Одно исследование показало повышенную частоту возникновения задних параспинальных коллатералей у пациентов с рассеянным склерозом. 36 В другом исследовании наблюдалась тенденция к увеличению числа залогов, не связанных с IJV. 35 Еще одно исследование показало отсутствие различий между пациентами с РС и HC во вторичных сосудах шеи с использованием 5 мм 2 в качестве порогового значения для идентификации. 33 Напротив, используя 2 мм 2 в качестве отсечки в настоящем исследовании, мы показали, что пациенты с РС имели значительно повышенную частоту вторичных сосудов шеи и их CSA. В настоящем исследовании не использовалась фазово-контрастная визуализация, что не позволило нам охарактеризовать вторичные сосуды шеи по отношению к их артериальным или венозным компонентам; следовательно, повышенная частота вторичных сосудов шеи может свидетельствовать об артериальной или венозной коллатерализации. С другой стороны, большое исследование MRV с фазовым контрастом показало, что пациенты с РС имели более низкий IJV и более высокий параспинальный венозный кровоток по сравнению с HC. 38 Хотя наше исследование не может ответить на этот вопрос, одна из возможных гипотез может заключаться в том, что уменьшенный размер сонной и позвоночной артерии, поступающей в ЦНС, может привести к вторичным механизмам артериальной компенсации.
Возраст — важный фактор в развитии изменений венозной гемодинамики шеи. В этом исследовании увеличение возраста показало связь с меньшим количеством вторичных сосудов в шейке HC. Кроме того, увеличение ИМТ показало связь со снижением частоты шейных сосудов, измеренных на всех уровнях как в группах MS, так и в HC.Влияние возраста и ИМТ на морфологические изменения IJV у здорового стареющего населения было описано ранее. 20,39 Даже когда мы скорректировали вышеупомянутые факторы риска, когорта РС показала повышенную частоту вторичных сосудов шеи и ППС вторичных сосудов по сравнению с HC. Различия были наиболее значительными как на уровне C2 / C3, представляющем сосуды у основания черепа, так и на уровне C7 / T1, представляющем уровень верхнего грудного выхода.Следовательно, в то время как при HC мы обнаружили уменьшение количества вторичных сосудов с возрастом, эта связь отсутствовала у пациентов с MS; это открытие предполагает возможное влияние болезни на рекрутирование сосудов.
Дополнительная васкуляризация может быть вызвана либо повторяющейся гипоперфузией головного мозга, либо воспалительными факторами, участвующими в сложном ремоделировании уже существующих каналов, идущих вдоль основных артерий. 40,41 Например, субпопуляция Т-хелперов 17 и интерлейкин 17 были связаны как важные факторы тяжести рассеянного склероза и как важный фактор неоваскуляризации. 41
Динамическое количественное определение потока вторичной сосудистой сети могло бы дополнительно помочь в понимании анатомических различий потока вторичных сосудов шеи, наблюдаемых в этом исследовании, предоставляя данные о потоке, а не чисто структурные измерения. Кроме того, текущая методика MRV времени пролета позволяет сегментировать только просвет сосуда, но не анатомическую CSA. Любые области двунаправленного потока, отсутствия потока и неоднородности потока могут привести к частично неточной оценке размера сосуда.Что касается гемодинамических свойств, измерение просвета CSA может быть лучшим анатомическим представителем, чем включение толщины стенки сосуда. Кроме того, исследования, связывающие морфологию сосудистой сети шеи с динамической перфузией мозга, дадут важный ответ на анатомическую и динамическую сосудистую роль этих сосудов в сложном патогенезе рассеянного склероза. Основным преимуществом исследования является использование большой сопоставимой выборки 1: 1 HC и пациентов с MS, что уменьшило потенциальную систематическую ошибку сравнения между двумя исследуемыми популяциями.Дополнительное продольное исследование с использованием фазового контраста и изучения атеросклеротической нагрузки должно дополнительно устранить ограничения текущего дизайна исследования. Поскольку это было обсервационное исследование, мы не делали поправок на множественные сравнения в нашем статистическом анализе. Таким образом, более масштабные продольные исследования должны подтвердить наши предварительные выводы.
Выводы
Пациенты с РС показали более низкую ППС сонных и позвоночных артерий и более высокую частоту вторичных сосудов шеи и их ППС по сравнению с ГК.Эти данные могут свидетельствовать о том, что воспалительные механизмы, которые присутствуют у пациентов с РС с самого начала, могут способствовать ускорению атеросклероза у пациентов с РС. Более высокая частота вторичных сосудов шеи может указывать на то, что уменьшенный размер сонной и позвоночной артерии, поступающей в ЦНС, может привести к формированию вторичных механизмов артериальной компенсации. Однако, прежде чем можно будет сделать окончательные выводы, необходимы дальнейшее воспроизведение и продолжение исследования.
Сноски
Раскрытие информации: Кристофер Маньяно — НЕ СВЯЗАННО : Занятость : General Electric, Комментарии : независимо от работы, представленной в этой статье. Бьянка Вайншток-Гуттман — БЕЗ СВЯЗИ : Консультации : Biogen Idec, Teva Neuroscience, EMD Serono, Novartis, Genzyme & Sanofi, Genetech *; Гранты / ожидающие гранты : Biogen Idec, Teva Neuroscience, EMD Serono, Novartis, Genzyme & Sanofi *; Оплата лекций, включая услуги бюро докладчиков : Biogen Idec, Teva Neuroscience, EMD Serono, Novartis, Genzyme & Sanofi, Genentech.Роберт Зивадинов — ОТНОСИТЕЛЬНО : Консультации : Genzyme-Sanofi, Novartis; Гранты / ожидающие гранты : Genzyme-Sanofi, Intekrin-Coherus, Novartis, IMS Health *; Оплата лекций, включая услуги бюро докладчиков : Genzyme-Sanofi, Novartis *. * Деньги, выплаченные учреждению.
Это исследование частично финансировалось Исследовательским фондом неврологических заболеваний Аннетт Фуничелло и внутренними ресурсами Аналитического центра нейровизуализации Буффало.Кроме того, мы получили поддержку от Фонда семьи Жакмен. Исследования, представленные в этой публикации, также частично финансировались Национальным центром развития трансляционных наук Национальных институтов здравоохранения в рамках гранта № UL1TR001412. Авторы несут полную ответственность за содержание, которое не обязательно отражает официальную точку зрения Национальных институтов здравоохранения.
- Поступила 23 мая 2017 г.
- Принята после доработки 17 августа 2017 г.
- © 2018 Американский журнал нейрорадиологии
Диаграммы площади поперечных сечений, Транспортная инженерия (TE), Engineering
Площадь поперечного сечения кабелепровода разного диаметра
Площадь в квадратных миллиметрах (1 дюйм = 25,381 мм)
| ТОРГОВЫЙ РАЗМЕР ТРУБОПРОВОДА | ЖЕСТКИЙ МЕТАЛЛИК | ЖЕСТКИЙ НЕМЕТАЛЛИЧЕСКИЙ (ПРИЛОЖЕНИЕ 40) | ||
|---|---|---|---|---|
| ПЛОЩАДЬ 100% | ПЛОЩАДЬ 40% | ПЛОЩАДЬ 100% | ПЛОЩАДЬ 40% | |
| 41 | 1334.380 | 533,752 | 1279.091 | 511,637 |
| 53 | 2195.260 | 878.104 | 2120.035 | 848.014 |
| 63 | 3134.420 | 1253.768 | 3024,580 | 1209.832 |
| 78 | 4830,858 | 1932,343 | 4681.939 | 1872,776 |
Приведенные выше значения кабелепровода взяты из таблицы 4, глава 9 Национального электротехнического кодекса (NEC).
Сечения проводов различных типов и размеров
Единицы измерения площади указаны в квадратных миллиметрах (1 IN = 25.381 ММ)
| КОЛИЧЕСТВО ПРОВОДНИКОВ | ДЕТЕКТОР КОНТУРА XHHW | СИГНАЛЬНЫЙ КАБЕЛЬ ТИПА XHHW | ||
|---|---|---|---|---|
| 2 / C # 14 | 2 / C # 14 | 5 / C # 14 | 10 / C # 14 | |
| 1 | 73.059 | 67,405 | 107.059 | 207.237 |
| 2 | 146.118 | 134,810 | 214.118 | 414,474 |
| 3 | 219.177 | 202,215 | 321.177 | 621.711 |
| 4 | 292,237 | 269.621 | 428,236 | 828,948 |
| 5 | 365,296 | 337.026 | 535,295 | 1036.185 |
| 6 | 438,355 | 404,431 | 642,354 | 1243.422 |
| 7 | 511.414 | 471,836 | 749,413 | 1450.659 |
| 8 | 584,473 | 539,241 | 856,472 | 1657,896 |
| 9 | 657,532 | 606.646 | 963,531 | 1865.133 |
| 10 | 730.591 | 674,051 | 1070,590 | 2072.370 |
Указанные выше значения петлевого детектора и кабеля светофора являются фактические размеры кабеля из материала, утвержденного NJDOT в соответствии с примечанием 5, глава 9 НИК.
| КОЛИЧЕСТВО ПРОВОДНИКОВ | НЕСКОЛЬКО ПРОВОДОВ ДЛЯ ОСВЕЩЕНИЯ, ТИП RHW | ТИП ЗАЗЕМЛЕНИЯ THW | |||||
|---|---|---|---|---|---|---|---|
| # 2 AWG | # 4 AWG | # 6 AWG | # 8 AWG | # 10 AWG | # 8 AWG (голый) | # 8 AWG (ИЗОЛИРОВАННЫЙ) | |
| 1 | 112.717 | 85,882 | 67,036 | 53,770 | 28,179 | 10,785 | 35,799 |
| 2 | 225.435 | 171,764 | 134.073 | 107,541 | 56,359 | 21,570 | 71.598 |
| 3 | 338,152 | 257,646 | 201.109 | 161,311 | 84,538 | 32,354 | 107,397 |
| 4 | 450,870 | 343,528 | 268.145 | 215.081 | 112.717 | 43,139 | 143,196 |
| 5 | 563,587 | 429,410 | 335,182 | 268,852 | 140,897 | 53,924 | 178,995 |
| 6 | 676.305 | 515,292 | 402.218 | 322,622 | 169.076 | 64,709 | 214.794 |
| 7 | 789.022 | 601.173 | 469,254 | 376,392 | 197,256 | 75,494 | 250,593 |
| 8 | 901.740 | 687.055 | 536,290 | 430.162 | 225.435 | 86,279 | 286,392 |
| 9 | 1014,457 | 772,937 | 603,327 | 483,933 | 253,614 | 97.063 | 322.191 |
| 10 | 1127.175 | 858,819 | 670,363 | 537,703 | 281,794 | 107,848 | 357.990 |
Вышеуказанные значения нескольких проводов освещения и заземления взяты из таблицы 5 и таблицы 8 главы 9 NEC. (NEC)
жидкостей в движении | Безграничная физика
Расход и уравнение непрерывности
Расход жидкости — это то, сколько жидкости проходит через область за заданное время.
Цели обучения
Определение расхода на основе скорости и площади или прошедшего времени и обоснование использования непрерывности при выражении свойств жидкости и ее движения
Основные выводы
Ключевые точки
- Расход можно выразить либо через площадь поперечного сечения и скорость, либо через объем и время.
- Так как жидкости несжимаемы, скорость потока в область должна равняться скорости потока из области.Это известно как уравнение неразрывности.
- Уравнение неразрывности может показать, насколько увеличивается скорость жидкости, если она вынуждена течь через меньшую площадь. Например, если площадь трубы уменьшится вдвое, скорость жидкости увеличится вдвое.
- Хотя газы часто ведут себя как жидкости, они не несжимаемы, как жидкости, и поэтому уравнение неразрывности не применяется.
Ключевые термины
- несжимаемый : Невозможно сжимать или конденсировать.
- непрерывность : отсутствие прерывания или отключения; качество непрерывности в пространстве или времени.
Расход жидкости — это объем жидкости, который проходит через поверхность в заданную единицу времени. Обычно обозначается символом Q.
.
Уравнение непрерывности для жидкостей : Краткое введение в уравнение непрерывности для жидкостей.
Расход
Объемный расход определяется как
[латекс] \ text {Q} = \ text {v} * \ text {a} [/ latex],
, где Q — скорость потока, v — скорость жидкости, а a — площадь поперечного сечения пространства, через которое движется жидкость.Объемный расход также можно найти с помощью
.[латекс] \ text {Q} = \ frac {\ text {V}} {\ text {t}} [/ latex]
где Q — расход, V — объем жидкости, а t — прошедшее время.
Непрерывность
Уравнение неразрывности работает в предположении, что входящий поток равен выходному. Это может быть полезно для решения многих свойств жидкости и ее движения:
Входящий поток = Выходящий : Используя известные свойства жидкости при одном условии, мы можем использовать уравнение неразрывности для определения свойств той же жидкости при других условиях.
[латекс] \ text {Q} _1 = \ text {Q} _2 [/ латекс]
Это может быть выражено разными способами, например: [латекс] \ text {A} _1 * \ text {v} _1 = \ text {A} _2 * \ text {v} _2 [/ latex]. Уравнение неразрывности применимо к любой несжимаемой жидкости. Поскольку жидкость не может быть сжата, количество жидкости, которая втекает на поверхность, должно равняться количеству, вытекающему с поверхности.
Применение уравнения непрерывности
Вы можете наблюдать действие уравнения неразрывности в садовом шланге.Вода течет по шлангу, и когда она достигает более узкого сопла, скорость воды увеличивается. Скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения. Это следствие уравнения неразрывности. Если поток Q остается постоянным, когда площадь A уменьшается, скорость v должна увеличиваться пропорционально. Например, если сопло шланга составляет половину площади шланга, скорость должна удвоиться, чтобы поддерживать непрерывный поток.
5.1 Поток потока | Мониторинг и оценка
Что такое сток и почему он важен?Поток или расход воды — это объем воды, который движется над заданной точкой за фиксированный период времени. Часто выражается в кубических футах в секунду (фут 3 / сек).
Расход ручья напрямую зависит от количества воды, уходящей с водораздела в русло ручья. На нее влияет погода, она увеличивается во время ливней и уменьшается в засушливые периоды.Он также меняется в разные сезоны года, снижаясь в летние месяцы, когда интенсивность испарения высока и прибрежная растительность активно растет и удаляет воду с земли. Август и сентябрь — обычно месяцы самого низкого стока для большинства ручьев и рек на большей части страны.
Забор воды для целей орошения может серьезно истощить сток воды, как и промышленный забор воды. Плотины, используемые для выработки электроэнергии, особенно сооружения, предназначенные для выработки электроэнергии в периоды пиковой потребности, часто блокируют течение потока, а затем выпускают его в виде скачка.
Расход зависит от объема и скорости воды. Это важно из-за своего воздействия на качество воды, а также на живые организмы и среду обитания в ручье. Крупные реки с быстрым течением могут получать сбросы загрязняющих веществ и подвергаться незначительному воздействию, в то время как небольшие реки обладают меньшей способностью разбавлять и разлагать отходы.
Скорость потока, которая увеличивается по мере увеличения объема воды в ручье, определяет виды организмов, которые могут жить в ручье (некоторым нужны участки с быстрым течением, другим нужны тихие бассейны).Это также влияет на количество ила и наносов, переносимых ручьем. Осадок, внесенный в тихие, медленно текущие потоки, быстро оседает на дно ручья. Быстро движущиеся потоки дольше удерживают осадок во взвешенном состоянии в толще воды. Наконец, быстро движущиеся потоки обычно имеют более высокий уровень растворенного кислорода, чем медленные потоки, потому что они лучше аэрируются.
В этом разделе описан один метод оценки потока в определенной области или на участке реки. Он адаптирован из методов, используемых несколькими программами мониторинга добровольцев, и использует поплавок (такой объект, как апельсин, мяч для пинг-понга, сосновая шишка и т. Д.) для измерения скорости потока. Расчет расхода включает решение уравнения, которое исследует взаимосвязь между несколькими переменными, включая площадь поперечного сечения потока, длину потока и скорость воды. Один из способов измерения расхода — решить следующее уравнение:
| Расход = ALC / T | ||
| Где: | ||
| А | = | Средняя площадь поперечного сечения ручья (ширина ручья, умноженная на среднюю глубину воды). |
| л | = | Измеренная длина участка ручья (обычно 20 футов) |
| С | = | Коэффициент или поправочный коэффициент (0,8 для потоков с каменистым дном или 0,9 для потоков с илистым дном). Это позволяет вам скорректировать тот факт, что вода на поверхности движется быстрее, чем у дна ручья из-за сопротивления гравия, булыжника и т. Д. Умножение скорости на поверхности на поправочный коэффициент уменьшает значение и дает более точную оценку общей протяженности потока. скорость. |
| Т | = | Время в секундах, за которое поплавок проходит длину L |
Задача 1 Подготовиться перед выездом на место отбора проб
См. Раздел 2.3 — Меры безопасности для получения подробной информации о подтверждении даты и времени отбора проб, соображениях безопасности, проверке расходных материалов, а также проверке погоды и направления. В дополнение к стандартному оборудованию для отбора проб и одежде, при измерении и расчете расхода, необходимо включать следующее оборудование:
- Шар из прочной струны, четыре колья и молоток для забивания кольев в землю.Трос будет натянут по ширине ручья перпендикулярно берегу в двух местах. Ставки заключаются в том, чтобы закрепить веревку на каждом берегу, чтобы сформировать линию разреза.
- Рулетка (минимум 20 футов)
- Водонепроницаемая линейка или другой прибор для измерения глубины воды
- Завязки-закрутки (для обозначения интервалов на нити линии трансекты)
- Апельсин и рыболовная сеть (чтобы вычерпать апельсин из ручья)
- Секундомер (или часы с секундной стрелкой)
- Калькулятор (опционально)
Задача 2 Выберите участок потока
| Рисунок 5.4 Схема трансекты 20 футов |
Участок ручья, выбранный для измерения расхода, должен быть прямым (без изгибов), глубиной не менее 6 дюймов и не должен содержать области с медленной водой, например бассейн. Идеальны беспрепятственные перекаты или беговые дорожки. Выбранная длина будет равна L при решении уравнения потока. Двадцать футов — стандартная длина, используемая во многих программах. Измерьте свою длину и отметьте верхний и нижний конец, проведя линию разреза поперек ручья перпендикулярно берегу, используя веревку и колья (рис.5.4). Трос должен быть натянут и находиться у поверхности воды. Трансект выше по течению — это разрез №1, а нижний по течению — разрез №2.
Задача 3 Рассчитать среднюю площадь поперечного сечения
Площадь поперечного сечения (A в формуле) — произведение ширины ручья на среднюю глубину воды. Чтобы рассчитать среднюю площадь поперечного сечения для охвата исследуемого ручья, добровольцы должны определить площадь поперечного сечения для каждой трансекты, сложить результаты вместе, а затем разделить на 2, чтобы определить среднюю площадь поперечного сечения для участка протока.
Для измерения площади поперечного сечения:
Рисунок 5.5
Поперечный разрез для измерения ширины и глубины потока- Определите среднюю глубину вдоль трансекты, отметив равные интервалы вдоль струны с помощью скрученных стяжек. Интервалы могут составлять одну четвертую, половину или три четверти расстояния через ручей.Измерьте глубину воды в каждой точке интервала (рис. 5.5). Чтобы рассчитать среднюю глубину для каждого разреза, разделите сумму трех измерений глубины на 4. (Вы делите на 4 вместо 3, потому что вам нужно учитывать нулевые глубины, которые встречаются на берегу). В примере, показанном на Рисунке 5.6. , средняя глубина трансекты № 1 составляет 0,575 футов, а средняя глубина трансекты № 2 составляет 0,625 футов.
- Определите ширину каждой трансекты, измерив расстояние от береговой линии до береговой линии.Просто сложите все интервалы ширины для каждого разреза, чтобы определить его ширину. В примере на Рисунке 5.6 ширина трансекты № 1 составляет 8 футов, а ширина трансекты № 2 — 10 футов.
- Рассчитайте площадь поперечного сечения каждой трансекты, умножив ширину на среднюю глубину. Пример, приведенный на Рисунке 5.6, показывает, что средняя площадь поперечного сечения трансекты № 1 составляет 4,60 квадратных футов, а средняя площадь поперечного сечения трансекты № 2 составляет 6,25 квадратных футов.
- Чтобы определить среднюю площадь поперечного сечения всего участка ручья (A в формуле), сложите среднюю площадь поперечного сечения каждой трансекты и затем разделите на 2.Средняя площадь поперечного сечения ручья на Рисунке 5.6 составляет 5,42 квадратных фута.
Задача 4 Измерение времени в пути
Добровольцы должны отсчитывать с помощью секундомера, сколько времени требуется апельсину (или другому объекту), чтобы проплыть от верхнего к нижнему разрезу. Апельсин — хороший объект для использования, потому что он обладает достаточной плавучестью, чтобы плавать чуть ниже поверхности воды. Именно в этом положении обычно возникает максимальная скорость.
Доброволец, позволяющий апельсину пройти на разрезе выше по течению, должен расположить его так, чтобы он протекал по самому быстрому течению.Часы останавливаются, когда оранжевый полностью проходит под линией разреза вниз по течению. Оказавшись под линией трансекты, апельсин можно вычерпать из воды с помощью рыболовной сети. Это измерение «времени в пути» должно быть проведено не менее трех раз, а результаты усреднены — чем больше испытаний вы сделаете, тем точнее будут ваши результаты. Усредненные результаты равны T в формуле. Рекомендуется размещать апельсин на разных расстояниях от берега, чтобы получить различные оценки скорости.Вам следует отказаться от любых попыток поплавка, если объект застрял в потоке (булыжниками, корнями, обломками и т. Д.).
Задача 5 Рассчитать расход
Напомним, что расход можно рассчитать по формуле:
Продолжая пример на рис. 5.6. скажем, среднее время путешествия оранжевого между трансектом №1 и №2 составляет 15 секунд, а дно ручья было каменистым. Расчет расхода:
| Где: | ||
| А | = | 5.42 фут2 |
| л | = | 20 футов |
| С | = | 0,8 (коэффициент для каменистого течения) |
| Т | = | 15 секунд |
| Расход = 15 секунд (5,42 футов 2 ) (20 футов) (0,8) / 15 секунд. | ||
| Расход = 86,72 фута 3 /15 сек. | ||
| Расход = 5,78 фут3 / сек. |
Задача 6 Записать поток в форме данных
На следующей странице волонтеры могут использовать форму для расчета расхода ручья.
Список литературыФонд Adopt-A-Stream.


 1.1). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты Sx1, Sy1 относительно новых осей x1, y1.
1.1). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты Sx1, Sy1 относительно новых осей x1, y1. 2)
2)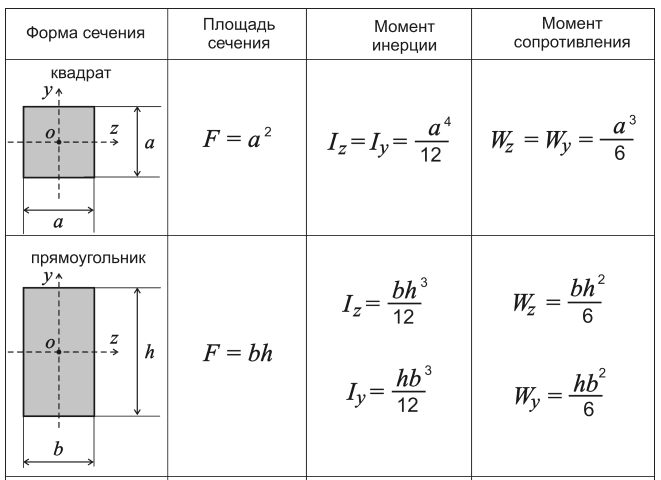 Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет»)
Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет») П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.
П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.