Свойства шестиугольника вписанного в окружность
Правильные многоугольники и окружность. Здравствуйте, Дорогие друзья! Во многих задачах в курсе геометрии, в том числе и в составе ЕГЭ имеется много заданий связанных с понятием окружности вписанной в правильный многоугольник и описанной около него. Если конкретней, то в данном случае мы рассмотрим правильный треугольник, также квадрат и правильный шестиугольник. Именно с этими правильными многоугольниками связаны условия заданий на экзамене. Обычно в ходе решения таких задач возникает необходимость выразить:
1. Сторону правильного треугольника через радиус вписанной или описанной окружности.
2. Сторону квадрата через радиус вписанной окружности или описанной окружности.
3. Сторону правильного шестиугольника через радиус вписанной или описанной окружности.
4. Радиус вписанной в правильный многоугольник окружности через радиус описанной около него окружности и наоборот.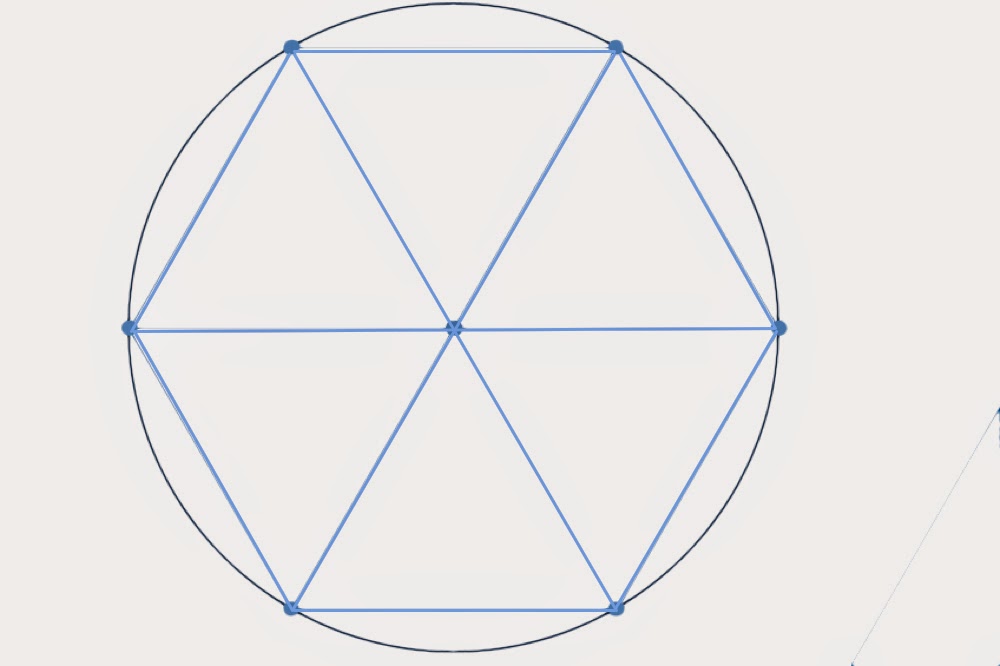
На сайте рассмотрены (и в будущем будут рассматриваться) задачи , в которых эти формулы используются. При решении подробно не описывается как они выводятся. Просто говорится, например, что сторона правильного треугольника соотносится с радиусом вписанной в него окружности как:
У многих возникают вопросы по этому поводу: Как? Почему? В этой статье мы выведем все указанные соотношения и в будущем при решении задач, если потребуется, просто буду давать ссылку на эту статью.
Что нужно всегда помнить и понимать?
Центр правильного многоугольника совпадает с центром вписанной о описанной около него окружности. Итак, приступим!
Правильный треугольник, вписанная и описанная окружность.
Пусть а – это его сторона, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны правильного треугольника и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны треугольника пополам. Радиус описанной окружности, проведённый к вершине треугольника является биссектрисой, то есть делит угол при этой вершине, равный 60 градусам, пополам. Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Квадрат, вписанная и описанная около него окружность.
Пусть а – это сторона квадрата, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны квадрата и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны квадрата пополам.
Радиус описанной окружности, проведённый к вершине квадрата является биссектрисой, то есть делит угол квадрата пополам.
Рассмотрим прямоугольный треугольник (выделен жёлтым). На основании вышеизложенного можно сделать вывод о том, что:
По определению косинуса: Получаем, что: *Можно было воспользоваться также теоремой Пифагора. Запишем соотношение радиусов:
Правильный шестиугольник. Вписанная и описанная окружность.
Стороны правильного шестиугольника и вписанная окружность имеют общие точки (точки касания), эти точки делят стороны данного шестиугольника пополам.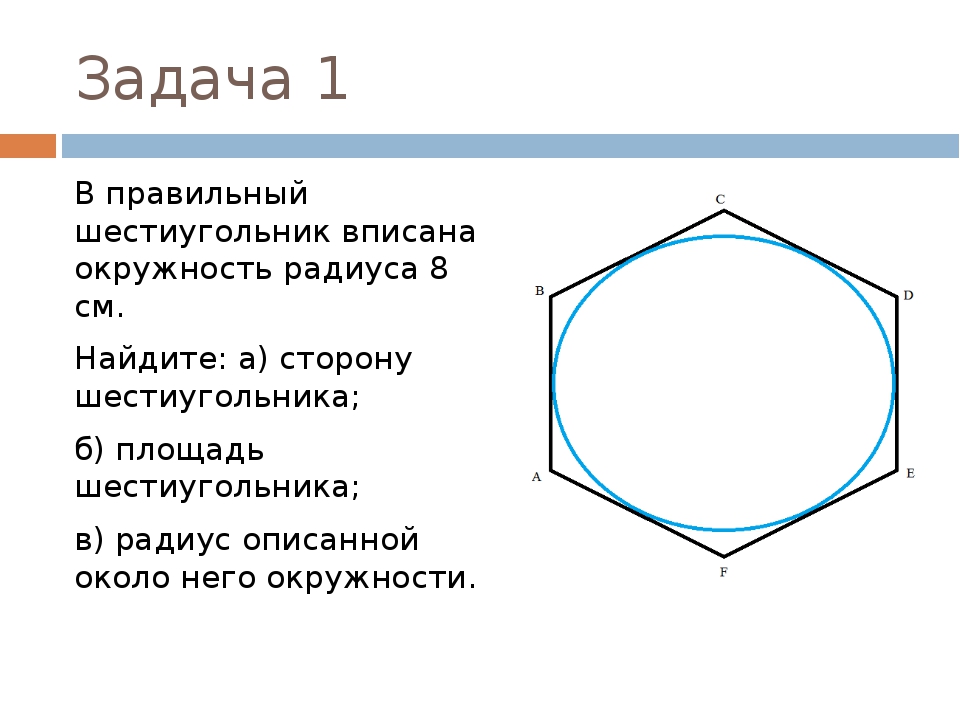
Радиус описанной окружности, проведённый к вершине шестиугольника является биссектрисой, то есть делит угол правильного шестиугольника равный 120 градусам пополам. Подробнее о правильном шестиугольнике и описанной около него окружности можете посмотреть информацию в этой статье .
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что:
Тот факт, что сторона правильного шестиугольника равна радиусу описанной окружности известен практически всем школьникам изучившим соответствующий материал по планиметрии:
Если интересно посмотрите как это можно вывести. По определению косинуса в прямоугольном треугольнике: Получаем, что: Можем записать соотношение радиусов: Вот и всё.
Конечно же, учить и запоминать данные формулы не нужно. В ходе решения вы всегда сможете их также вывести используя свойства правильных многоугольников, определения тангенса и косинуса , теорему Пифагора.
Я решил изложить это в отдельной статье только для того, чтобы у вас не возникали вопросы при решении и изучении соответствующих заданий на блоге и вы всегда могли бы посмотреть откуда взялась формула.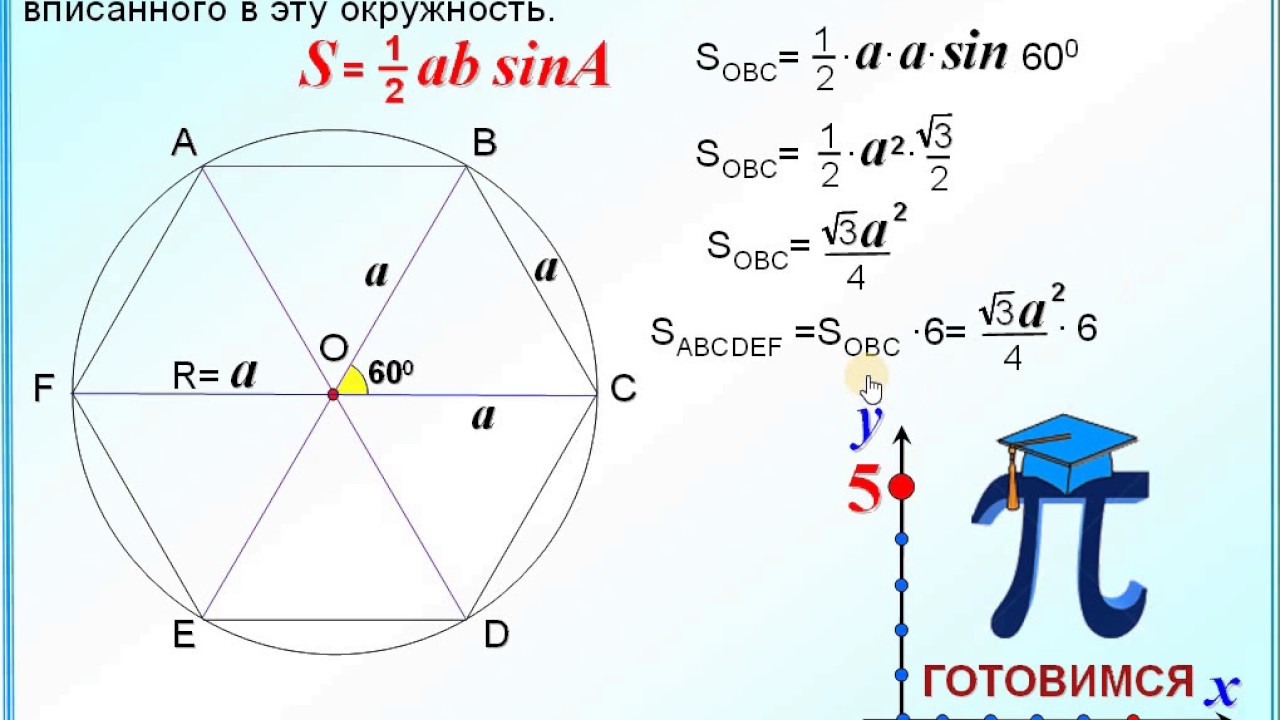
| Главная ≫ Инфотека ≫ Математика ≫ Правильный шестиугольник |
| Комментарии: 0 | Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами. |
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку Все углы равны 120°. Радиус вписанной окружности равен: Периметр правильного шестиугольника равен: Площадь правильного шестиугольника рассчитывается по формулам: Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет. Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне. |
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж.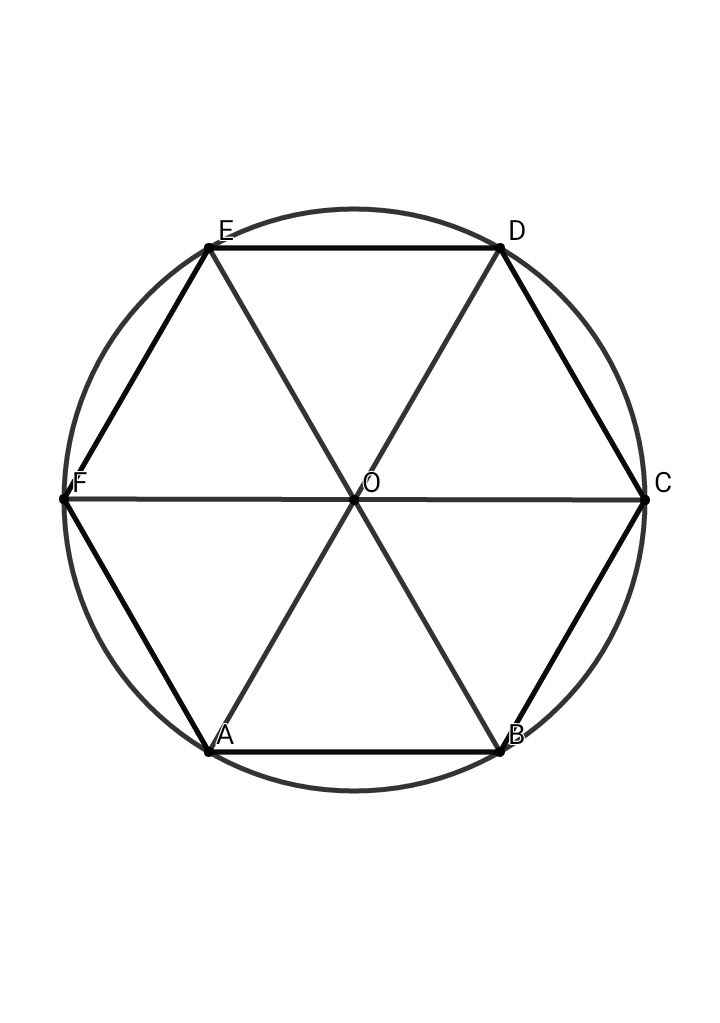
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.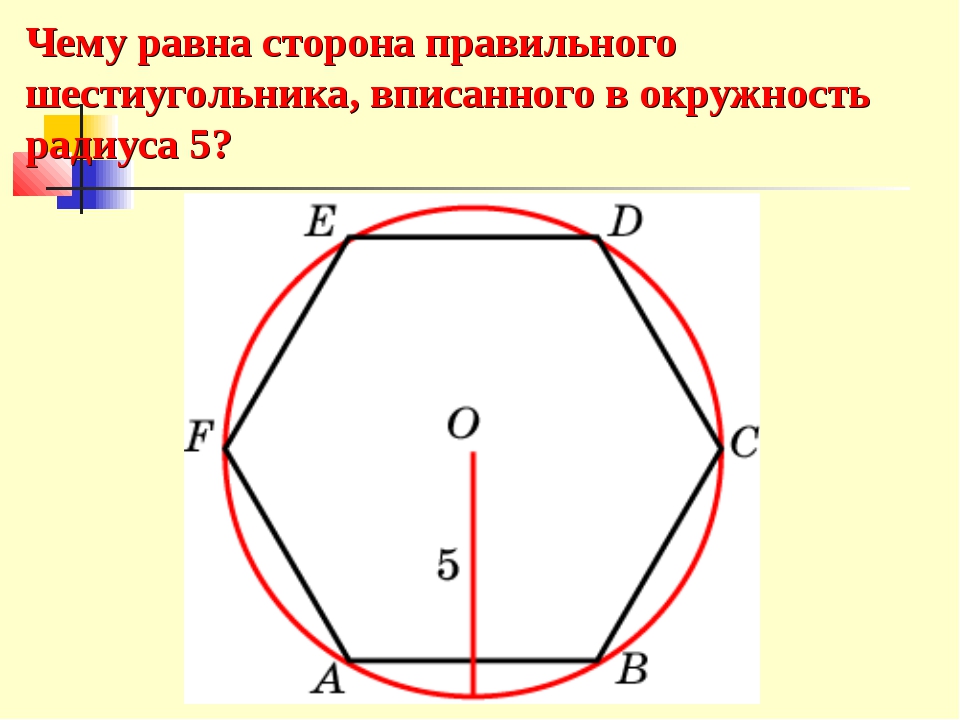 Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Гигантский гексагон — атмосферное явление на Сатурне.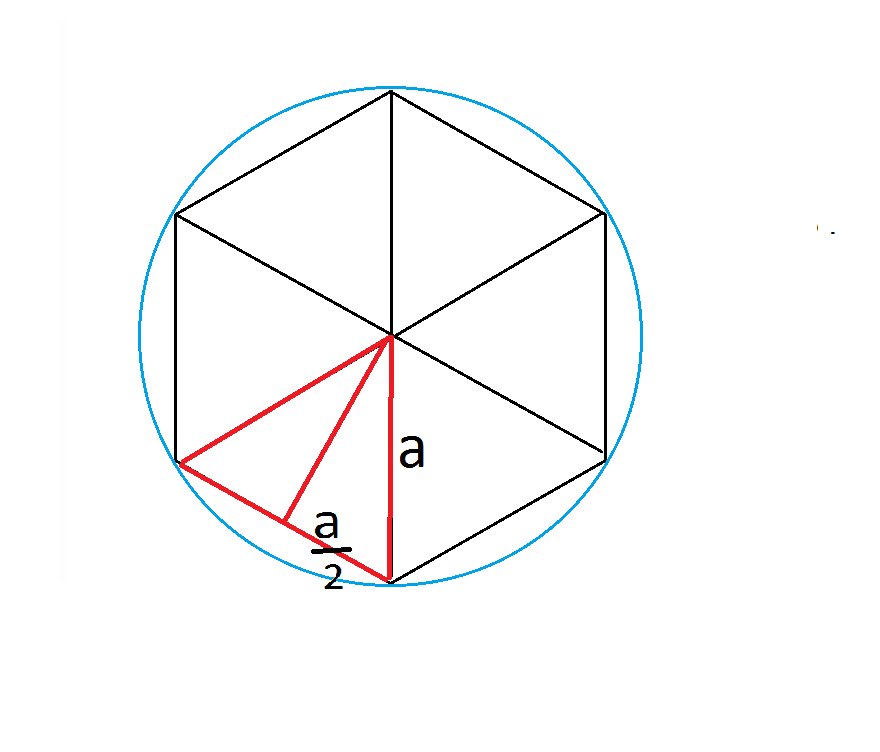
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Правильный шестиугольник – это многоугольник, состоящий из шести равных сторон. Все соседние стороны образуют угол 120°.
Формулы
- P – периметр
- S – площадь
- R – радиус K
- r – радиус k
- S’ – центр
- a – сторона
- K – окружность описанная
- k – окружность вписанная
При предоставлении услуг веб-сайт «Calculat. org» использует файлы куки.
org» использует файлы куки.
Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.
Как нарисовать правильный 6 угольник. Правильный шестиугольник и его свойства. Последние штрихи и узор
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.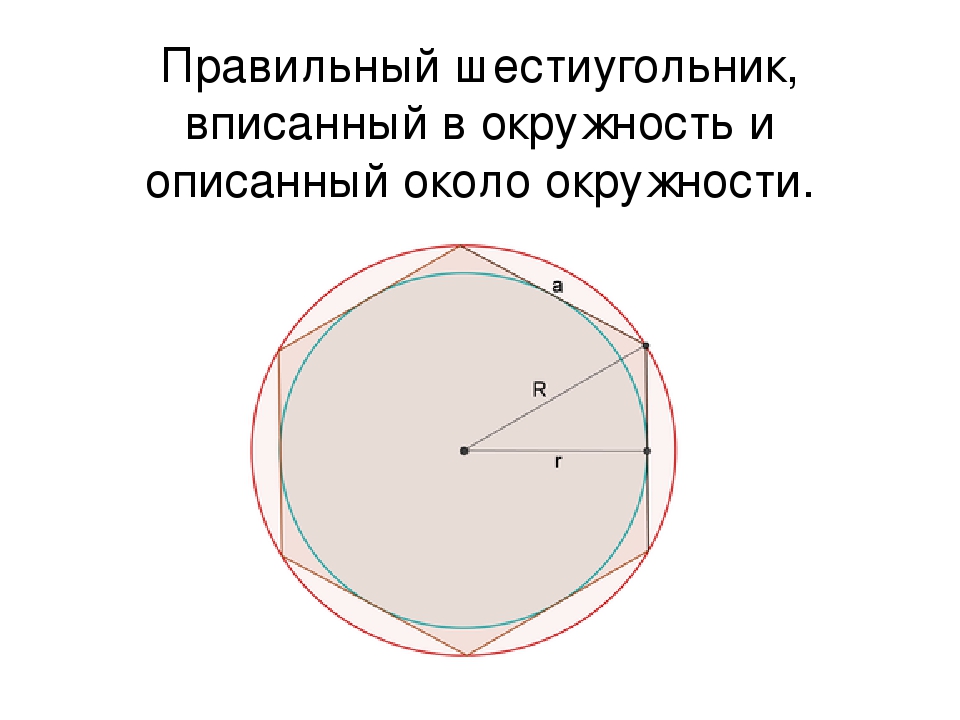
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.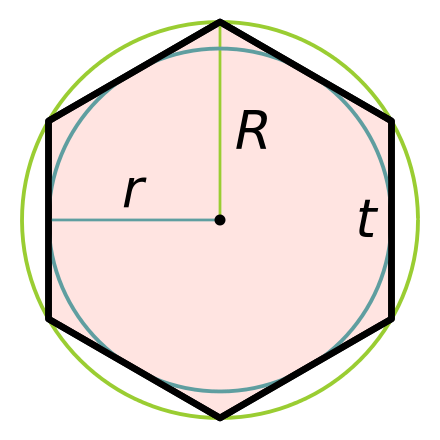 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .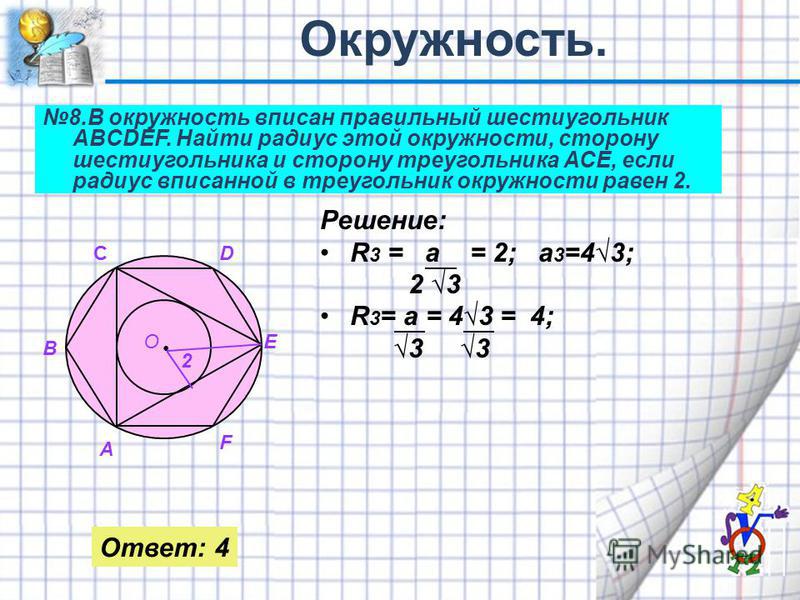
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний.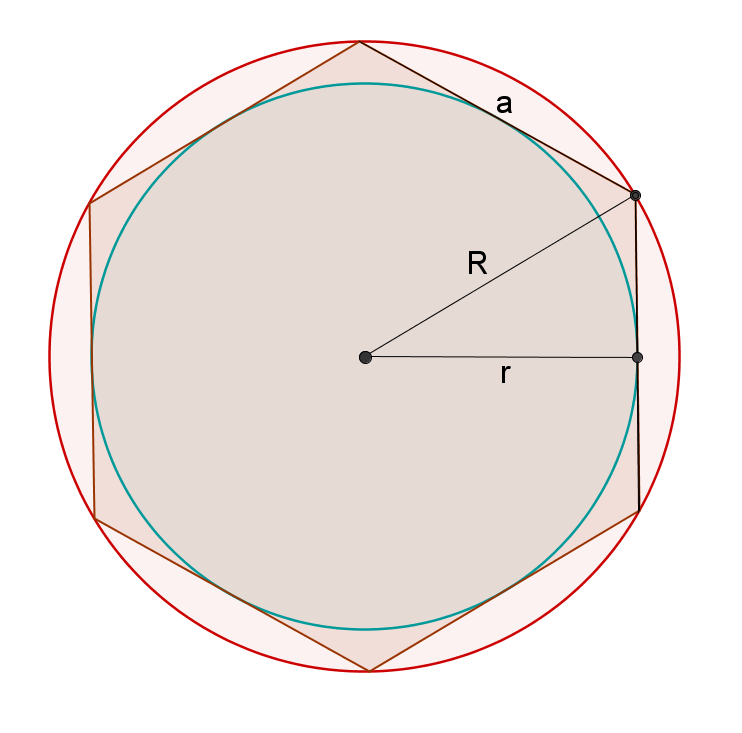 В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .
Рисунок 38
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D .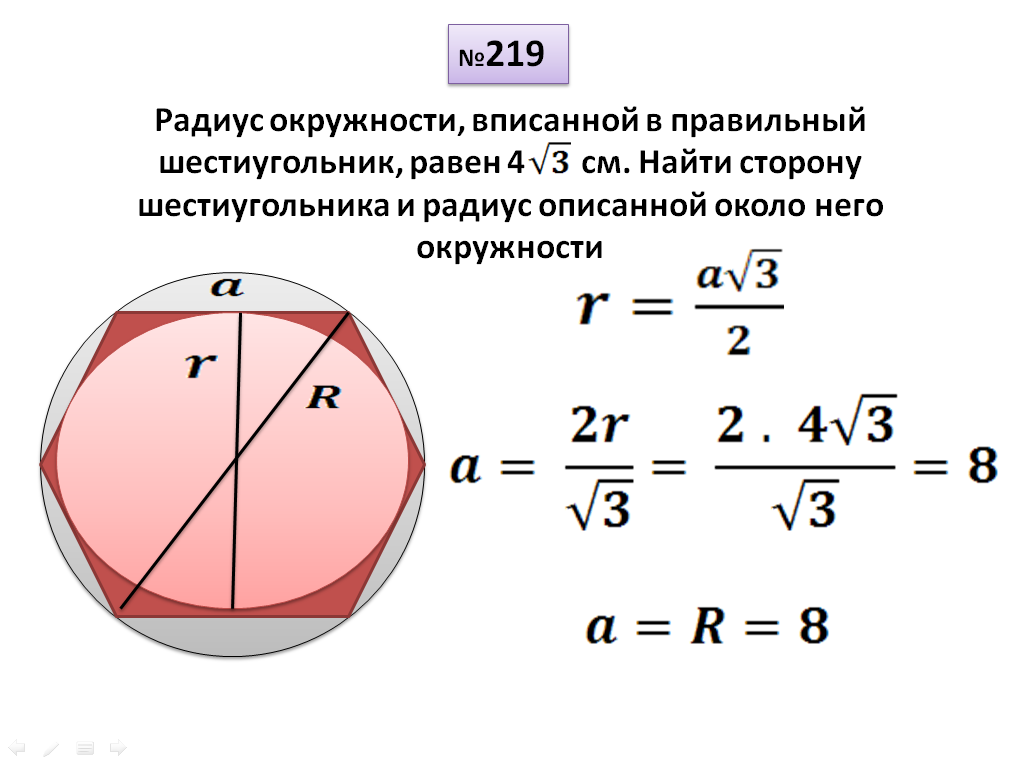 Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Рисунок 39
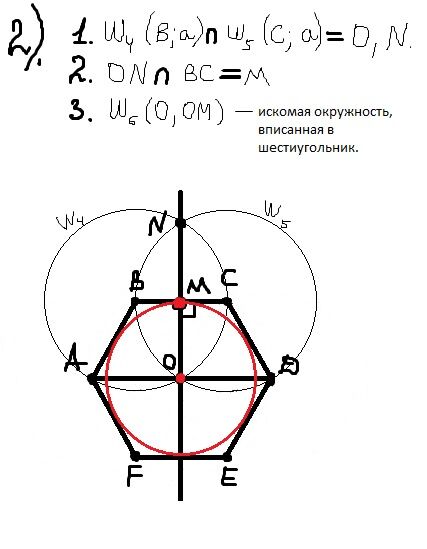
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.
Рисунок 40
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана.
 R и r — радиусы описанной и вписанной окружности.
R и r — радиусы описанной и вписанной окружности. - Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку.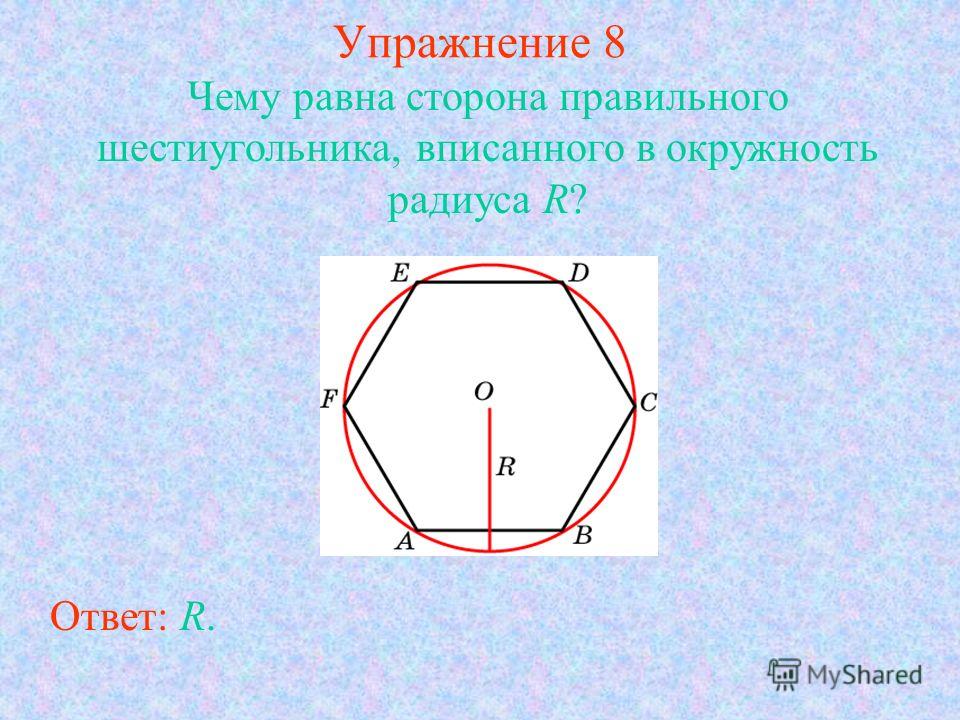 Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Горизонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Шестиугольники правильные — Энциклопедия по машиностроению XXL
Шестиугольники правильные — Характеристики геометрические 191, [c.796]Интересно, скольких из нас удивляла и эта книга, и те необычайные факты, которые автор время от времени находил. Например, при анализе состоящего из кремнезема скелета представителя семейства губок, известных под названием Радиолярии он случайно заметил, что никакой системой из шестиугольников нельзя оградить пространство при равных или неравных шестиугольниках, правильных или неправильных — при всех обстоятельствах это математически невозможно . [c.134]
Формулы зависимости между элементами квадрата, шестиугольника, правильного многоугольника и круга.
 Элементы квадрата (рис. 49) определяются по формулам
[c.93]
Элементы квадрата (рис. 49) определяются по формулам
[c.93]НЕКОТОРЫЕ ЗАВИСИМОСТИ М ЖДУ ЭЛЕМЕНТАМИ КВАДРАТА, ШЕСТИУГОЛЬНИКА, ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА И КРУГА [c.91]
Элементарные ячейки на обработанной поверхности детали приобретают форму неправильных шестиугольников — правильными они будут только в случае формообразования сферического (выпуклого или вогнутого) или плоского участка поверхности Д детали сферическим или плоским участком поверхности И инструмента. [c.498]
Если основание призмы-правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 140 оси х, у и z проведены через центры правильных шестиугольников призмы. [c.79]
Это можно видеть на рис. 151, о и в, где даны две фронтальные проекции призм. В первом случае (рис. 151,а) основание призмы-правильный шестиугольник- искажено, а во втором (рис. 151,в) изображено в действительном виде. Высота призмы в первом случае изображена без искажения, а во втором-с искажением.
[c.84]
151,в) изображено в действительном виде. Высота призмы в первом случае изображена без искажения, а во втором-с искажением.
[c.84]
Построение проекций правильной прямой шестигранной призмы (рис. 155) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображают- [c.85]
Построение аксонометрической проекции (прямоугольной изометрии) усеченной пирамиды начинают с построения (тонкими линиями) правильной шестигранной пирамиды по размерам, взятым с комплексного чертежа. Затем на плоскости основания по координатам точек I -6 наносят контур горизонтальной проекции шестиугольника сечения (см. тонкие линии на рис, 175, в).
[c.98]
Затем на плоскости основания по координатам точек I -6 наносят контур горизонтальной проекции шестиугольника сечения (см. тонкие линии на рис, 175, в).
[c.98]
Рисование фигуры, например правильного шестиугольника (рис. 221,в), часто встречается при изображении гаек и других подобных деталей. Рису- [c.121]
Правильный шестиугольник. Рисунок правильного шестиугольника выполняют на основании рисунка квадрата, сторона которого равна большей диагонали шестиугольника (рис. 184). [c.100]
Деление окружности на шесть равных частей (построение правильного шестиугольника, вписанного в окружность). Сторона правильного шестиугольника, вписан- [c.34]
Строят на горизонтальной проекции (рис. 6.47) вспомогательную окружность радиуса D/2 (D принимают равным 2d) и вписывают в нее правильный шестиугольник. Вписывают окружность, касательную к сторонам шестиугольника, которая засекает на горизонтальной оси фигуры точки 1н-
[c.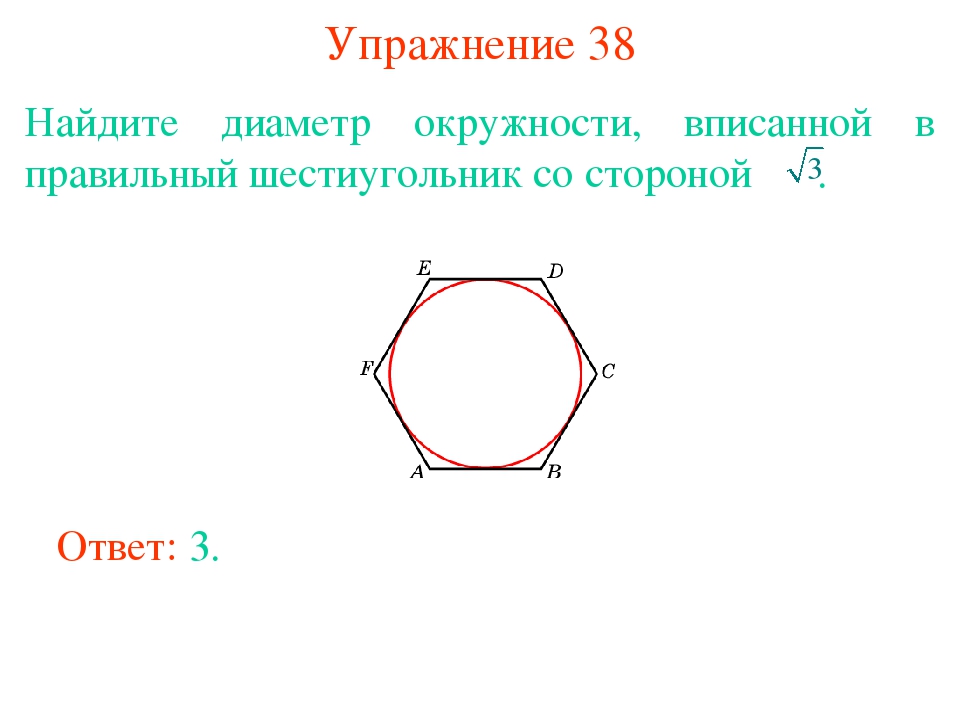 195]
195]
В центре правильного шестиугольника приложены силы 1, 3, 5, 7, 9 и 11 Н, направленные к его вершинам. Найти величину и направление равнодействующей и уравновешивающей. [c.10]
Пример. В плоскости 0, заданной пересекающимися прямыми I и т, построить правильный шестиугольник со стороной, равной а, и с центром в данной точке О (Ог) (рис. 114). [c.110]
По горизонтальной проекции аЬе двух смежных сторон правильного шестиугольника построить его фронтальную проекцию (рис. 27). [c.35]
По горизонтальным проекциям аЬ стороны правильного шестиугольника и oi его центра построить фронтальную проекцию шестиугольника (рис. 28). [c.35]
Шестиугольная правильная призма. Диаметр окружности, вписанной в шестиугольник основания, равен 80 мм. Две вершины основания лежат на вертикальной оси симметрии. Высота призмы 100 мм Сквозное отверстие диаметром 25 мм. Вертикально расположенная ось отверстия проходит через центр шестиугольника
[c.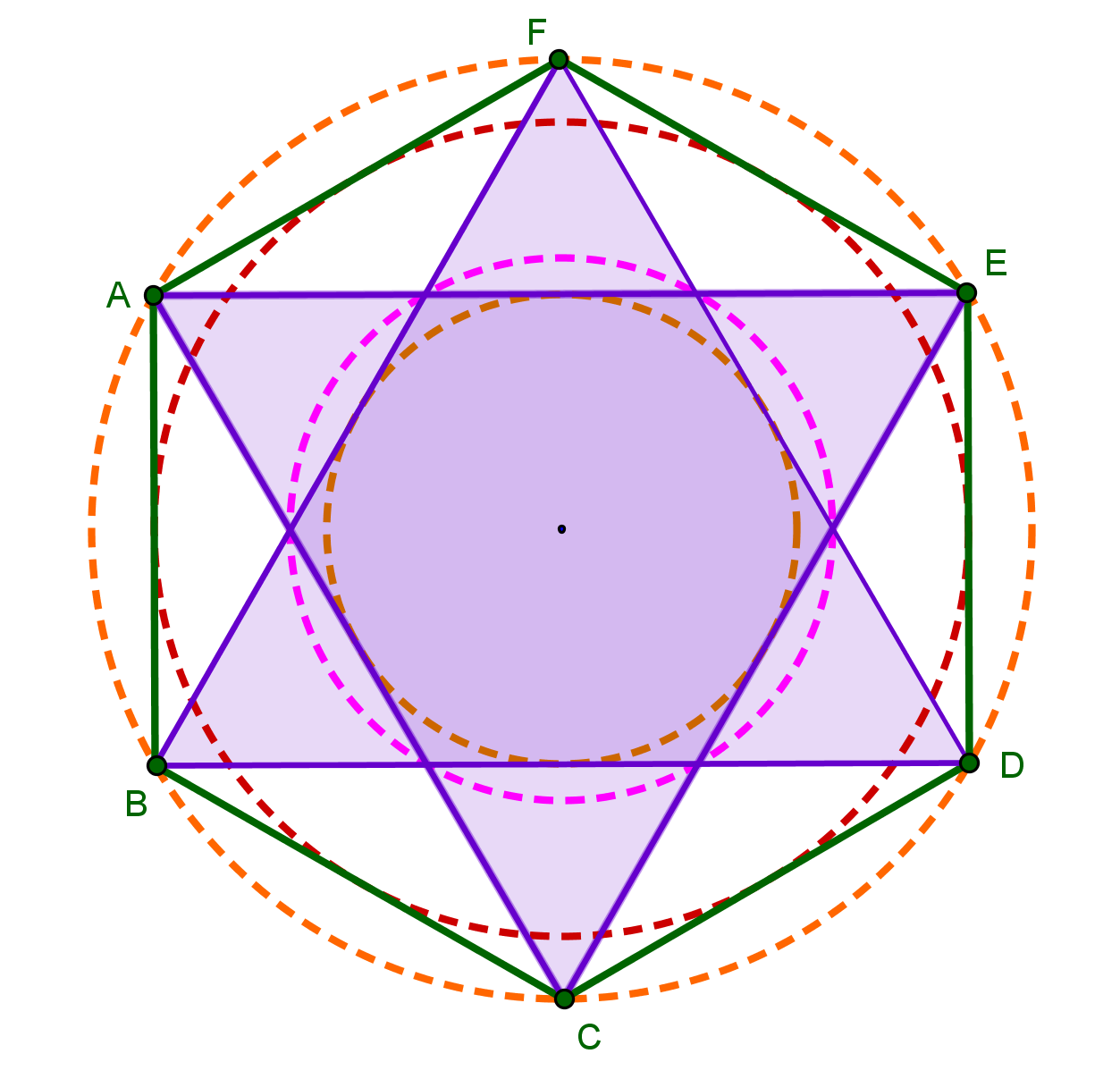 40]
40]
Пример 14. Найти равнодействующую четырех сил, действующих по сторонам правильного шестиугольника, направление которых указано на рис. 30, если P, = Pj-=2P и = Р = Р. [c.43]
У всякого сечения, имеющего три и более осей симметрии, все центральные оси являются одновременно и главными, а осевые моменты инерции относительно этих осей будут равны между собой. В частности, этим свойством обладают равносторонний треугольник и все правильные многоугольники с четным числом сторон (квадрат, шестиугольник и т.д.). [c.151]
Условие пластичности Сен-Венана (2.76) представляет собой правильную шестигранную призму, вписанную в цилиндр Мизеса. В сечении D-плоскостью окружность Мизеса оказывается описанной около правильного шестиугольника Сен-Венана (рис. 11.2, в). [c.252]
К правильному шестиугольнику приложены пять равных по модулю сил. Определить в градусах угол между главным вектором этой системы сил и осью Ох.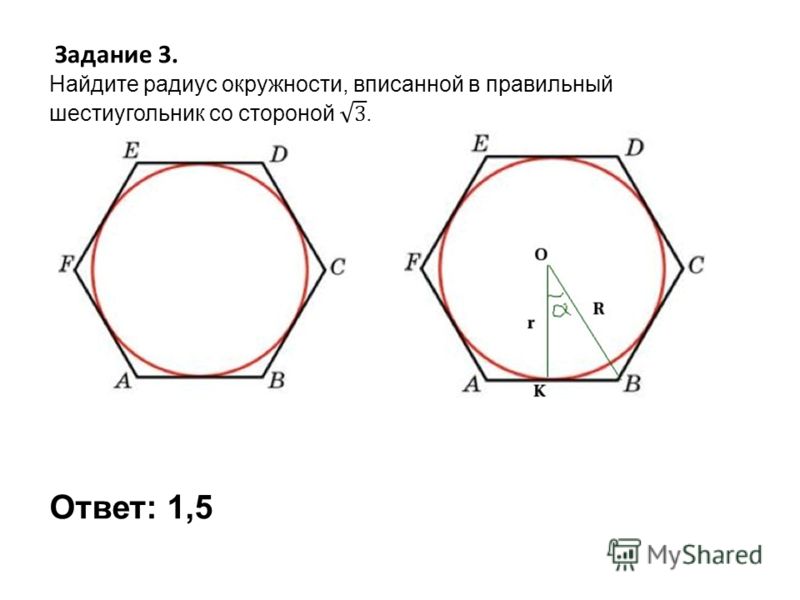 (180)
[c.27]
(180)
[c.27]
Атомы углерода располагаются на сферической поверхности в вершинах 20-ти правильных шестиугольников, 12-ти правильных пятиугольников. Каждый шестиугольник граничит с тремя шестиугольниками и пятью пятиугольниками, а пятиугольник граничит только с шестиугольником. Атом углерода в молекуле С-60 находится в вершинах двух шестиугольников и од- [c.57]
По своей структуре С-60 — усеченный икосаэдр (рис. 5.8). Атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников, 12 правильных пятиугольников. Каждый шестиугольник граничит с тремя шестиугольниками и пятью пятиугольниками, а пятиугольник граничит только с шестиугольником. Атом углерода в молекуле С-60 находится в вершинах двух шестиугольников и одного пятиугольника. [c.217]
Некоторые типы сечений, например круг, квадрат, правильный шестиугольник и др. (рис. 2.90), обладают тем свойством, что любая ось, проходящая через центр тяжести, является главной. [c.248]
[c.248]
Пример 19. По сторонам правильного шестиугольника со стороной а действуют силы, приложенные к вершинам Pi = 1 н, [c.41]
Другой часто встречающийся тип структуры — гексагональная структура с плотной упаковкой, которая представляет собой слои атомов, находящихся в углах шестиугольников (кристаллы бериллия, магния). Если разложить на ровной поверхности как можно ближе друг к другу большое количество плоских дисков, то легко будут обнаружены правильные шестиугольные построения. [c.16]
Принципиально методом сеток можно получить решение любой задачи, но для этого необходимо решить большое количество линейных алгебраических уравнений. Количество таких уравнений зависит от количества узлов сетки (а также и от формы сетки — квадратная, прямоугольная, правильный шестиугольник),, которой заменяют исследуемое плоское тело. [c.66]
На рисунке изображены поперечные сечения швеллера и правильного шестиугольника, а также их ядра сечений. Как будет проходить в каждом из этих сечений нейтральная ось, если перпендикулярная к плоскости сечения сила будет приложена в точке Л
[c.237]
Как будет проходить в каждом из этих сечений нейтральная ось, если перпендикулярная к плоскости сечения сила будет приложена в точке Л
[c.237]
Для построения центра правильного пятиугольника отрезок 040 делят пополам (д). Точка О5 будет центром правильного пятиугольника, вписаного в окружность радиуса О5Л (в). Откладывая отрезок OjOg на вертикальной оси от точки Og вверх, отмечают точки О,, 0 , Од,. .., On как центры правильных семи-, восьми-, девяти-, л-угольников, вписанных в окружность радиуса 0,А (ж), О Л О А, 0 А. Точка Ов является центром правильного шестиугольника, вписанного в окружность радиуса ОИ (3). [c.37]
Проводят во фронтальной и профильной проекциях оси и строит на плоскости W вспомогатель-ну о окружность диаметра D, Впи-сь ают в эту окружность правильны шестиугольник и получгют нр фильную проекцию граней [c.182]
Пример I. Пост роить прямоугольную изометрическую проекцию правильного шестиугольника AB DEF (черт. 318).
[c.150]
318).
[c.150]
Далее, при помощи окружности с центром в точке Oi и радиусом а строим правильный шестиугольник AiBi iDiEiF , который является проекцией совмещения искомого шестиугольника. Затем обратным построением плоскость 0 возвращена в исходное положение й найдены сначала горизонтальная, а потом фронтальная проекции шестиугольника. При этом для отыскания проекций вершин шестиугольника использованы прямые плоскости 0, параллельные прямой т и определяемые неподвижными точками 3, 4 м 5 горизонтали h. [c.111]
Шестиугольная правильная призма. Диаметр окружности, описанной вокруг шестиугольни-ка основания, равен 90 мм. Две вершины основания лежат на горизонтальной оси симметрии. Высота призмы 100 мм Сквозное отверстие с вертикально расположенной осью, проходящей через центр шестиугольника. Диаметр отверстия 30 мм [c.40]
Для поперечного сечения, имеющего форму правильного шестиугольника, осевые моменты инерции относительно всех центральных осей совпадают, поэтому для выполнения условия равноустойчивости стойки необходимо обеспечить одинаковые закрепления во всех плоскостях.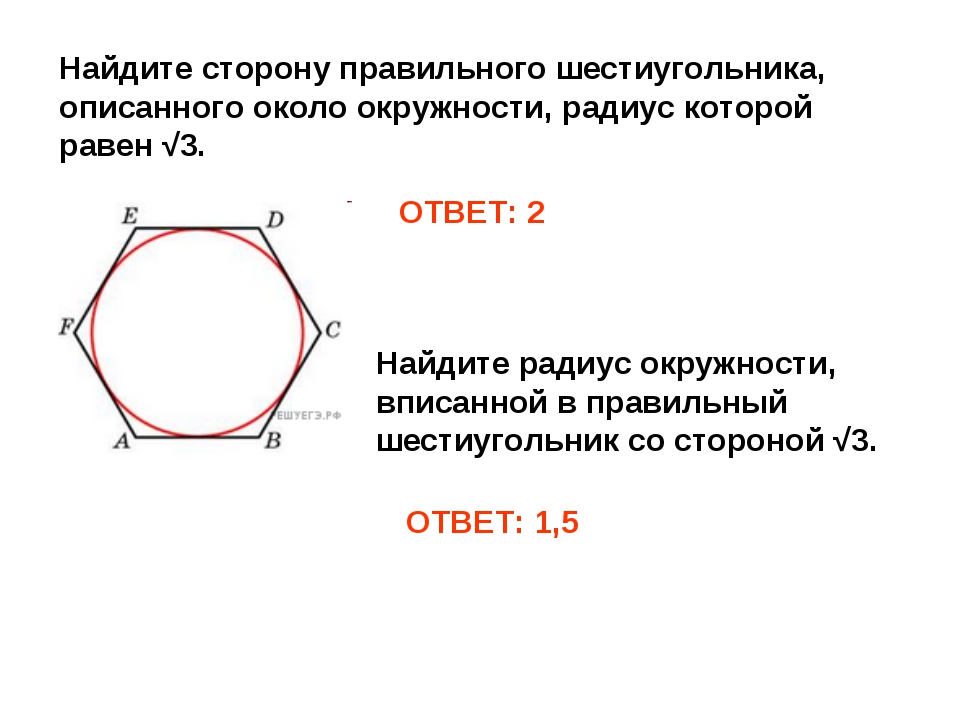 [c.201]
[c.201]
Для иллюстрации возможностей построения и использования различных моделей ГИ, предоставляемых пакетами ГРАФОР, ФАП-КФ и ЭПИГРАФ, рассмотрим примеры программ создания и обработки модели ГИ, приведенного на рис. 1.7,а. Исходное графическое изображение представляет собой правильный шестиугольник, вписанный в окружность радиуса R с центром в точке с координатами 0.,0. На рис. 1.7,б приведено ГИ, полученное с использованием исходного ГИ (рис.1.7,а) и средств пакетов ГРАФОР, ФАП-КФ и ЭПИГРАФ. [c.21]
В системе прямоугольных координат условие текучести определяет поверхность шестигранной призмы с осью, перпендикулярной к девиаторной плоскости. Призма в пересечении с девиа-торной плоскостью образует правильный шестиугольник, вписанный в круг радиусом (рис. 60, а, б). Мизес предложил [c.102]
Порядок в мире элементарных частиц. С помоац>ю введенных выше, казалось бы, совершенно абстрактных величин (барион-ного числа В, странности S и изоспина 1) удалось выявить порядок в мире элементарных частиц. Если на координатной плоскости, осью абсцисс которой является множество значений проекций изоспина / , а на оси ординат откладываются значения B+S (гиперзаряд), расположить барионы со значением спина s= l2, ТО ТОЧКИ их расположения на плоскости образуют правильный шестиугольник (рис. 63). Аналогичное построение получится и для восьмерки мезонов со спином 5=0 (рис. 64). Резонансы со спином 5=72 образуют на этой плоскости треугольник (рис. 65). Интересно отметить, что одна из частиц, образующих его, была сначала открыта теоретически М. Гелл-Маном в 1961 г. Ее существование было подтверждено экспериментально только через три года (1964), причем характеристики частицы точно соответствовали предсказаниям теории, что сразу же доказывало ее справедливость. Была установлена связь между электрическим зарядом мезонов и барионов Q и другими их характеристиками
[c.190]
Если на координатной плоскости, осью абсцисс которой является множество значений проекций изоспина / , а на оси ординат откладываются значения B+S (гиперзаряд), расположить барионы со значением спина s= l2, ТО ТОЧКИ их расположения на плоскости образуют правильный шестиугольник (рис. 63). Аналогичное построение получится и для восьмерки мезонов со спином 5=0 (рис. 64). Резонансы со спином 5=72 образуют на этой плоскости треугольник (рис. 65). Интересно отметить, что одна из частиц, образующих его, была сначала открыта теоретически М. Гелл-Маном в 1961 г. Ее существование было подтверждено экспериментально только через три года (1964), причем характеристики частицы точно соответствовали предсказаниям теории, что сразу же доказывало ее справедливость. Была установлена связь между электрическим зарядом мезонов и барионов Q и другими их характеристиками
[c.190]
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Диаметр круга, описанного вокург квадрата и шестигранника. Таблица: Диаметр заготовок — круглых прутков под квадраты и шестигранники в мм в зависимости от размеров квадратов и шестигранников. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Объект Многоугольник в Автокаде — как построить его в AutoCAD различными способами
[Уроки Автокад] Как нарисовать (начертить) многоугольник в AutoCAD
| Команда рисования в AutoCAD | |
| Многоугольник | |
| Определение | |
Многоугольник в Автокад — является замкнутой 2D-полилинией, состоящей из трех и более сегментов. Правильный многоугольник — это многоугольник у которого все стороны и углы равны. |
|
| Инструмент | |
| Инструмент Автокад Многоугольник — строит правильный многоугольник либо по конечным точкам одной стороны, либо по точке центра и радиусу вписанной или описанной окружности. | |
| Команда | |
| МН-Угол | |
| Объект | |
| Полилиния |
Команда МН-Угол в AutoCAD
За создание в Автокад правильного многоугольника отвечает команда MH-Угол.
Вызвать данную команду можно следующими способами (начать построение в AutoCAD многоугольника):
- построить многоугольник в Автокад можно из строки меню пункт Рисование — строка Многоугольник;
- начертить его можно из ленты инструментов на вкладке «Главная» — в группе Рисование кнопка Многоугольник;
- нарисовать многоугольник в Автокад можно из классической панели инструментов Рисование кнопка Многоугольник;
- либо прописать наименование команды в командной строке МН-Угол.

Построение многоугольника в Автокад вписанного в окружность
Как уже отмечалось, в вписанный в AutoCAD многоугольник в окружность задается центральной точкой и расстоянием от центра до любой из вершин. Следовательно, радиус описанной окружности — это расстояние от центра многоугольника до одной из его вершин.
Вызываем команду МН-Угол. В командной строке появляется запрос:
Число сторон <4>:
В ответ на который вы должны ввести число сторон, которое должно быть у многоугольника в AutoCAD (от 3 до 1024). Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:
Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Зададим центр многоугольника в AutoCAD щелчком мыши. Система отобразит запрос:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Вписанный в окружность». Отобразится предварительный вид многоугольника AutoCAD, который прикреплен к линии, проходящей из заданного центра до указателя. Размер его будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Радиус окружности можно задать, введя значение в командную строку или щелчком мыши, указав точку на чертеже. Введем значение 20 мм в командную строку и нажмем «Enter». Правильный пятиугольник (многоугольник) в Автокад с радиусом описанной окружности 20 мм построен.
Как начертить многоугольник в AutoCAD описанный вокруг окружности
Многоугольник Автокад описанный вокруг окружности задается центральной точкой и расстоянием от центра до средней точки одной из его сторон. Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.
Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.
Вызываем команду «МН-Угол». Система отобразит запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Указываем в Автокад центр многоугольника. Появляется запрос в командной строке:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Описанный вокруг окружности» команды МН-Угол. Отобразится предварительный вид многоугольника Автокад, который прикреплен к линии, проходящей из заданного центра до указателя, соответствующего середине одной из сторон многоугольника. Размер многоугольника в Автокад будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Повторим ввод координат и зададим радиус описанной окружности с помощью задания относительных полярных координат. Введем в командную строку следующее значение @20<0, что означает:
Введем в командную строку следующее значение @20<0, что означает:
- «@» — отсчет координат ведется от центральной точки многоугольника Автокад;
- «20» — расстояние от центральной точки, т.е. радиус вписанной окружности;
- «<» обозначение полярности координат — возможности привязки к определенному углу;
- «0» — значение угла, т.е. 0 градусов.
Правильный многоугольник в Автокад с радиусом вписанной окружности 20 мм построен.
Совет
Задав радиус вписанной или описанной окружности в командной строке путем ввода значения радиуса, многоугольник в Автокад автоматически выравнивается так, чтобы его нижняя сторона располагалась параллельно оси X текущей ПСК. Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.
Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.Как построить многоугольник по конечным точкам одной стороны (по стороне)
Как в Автокад начертить многоугольник по стороне (алгоритм):
Вызываем команду МН-Угол в AutoCAD. В командной строке появляется запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, т.е. 5 сторон многоугольника Автокад. Нажимаем «Enter». Система отобразит запрос:
Укажите центр многоугольника или [Сторона]:
Выбираем опцию «Сторона», чтобы начать строить в AutoCAD многоугольник по одной из сторон. Появляется следующий запрос:
Первая конечная точка стороны:
Укажем первую конечную точку стороны многоугольника Автокад щелчком мыши. Отобразиться его предварительный вид, который прикреплен к линии, проходящей от заданной первой конечной точки стороны до второй конечной точки. Появится запрос:
Появится запрос:
Вторая конечная точка стороны:
Вторую конечную точку стороны многоугольника в AutoCAD можете указать щелчком мыши или вводом координат в командную строку. Укажем точку щелчком мыши.
Правильный пятиугольник (многоугольник) в Автокад произвольных размеров по стороне построен.
Полезные уроки схожих тематик и рекомендации
Рекомендую ознакомиться с подобными уроками по Автокад:
Читайте и смотрите также:
Курсы, самоучители Автокад:
- 2D проектирование.
- 3D моделирование.
- Начертательная геометрия.
- Инженерная графика.
- План дома.
- Сборочный чертеж цилиндрической зубчатой передачи.
- Модель кухни 3D.
Видео «Как начертить прямоугольник и правильный многоугольник в Автокад»
чем он интересен и как его построить
Содержимое:
Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Шаги
1 Рисуем идеальный шестиугольник при помощи циркуля
- 1 При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
- Иногда легче сначала нарисовать пол круга, а затем вторую половину.
- 2 Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
- 3 Сделайте небольшую отметку карандашом на краю круга. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете.
 Не забудьте сохранять угол, который вы установили для циркуля.
Не забудьте сохранять угол, который вы установили для циркуля. - 4 Передвиньте иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
- 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
- 6 Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
- 7 Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
- 8
Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали.
 После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
2 Рисуем грубый шестиугольник при помощи круглого предмета и линейки
- 1 Обведите ободок стакана карандашом. Таким образом, вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
- 2 Нарисуйте горизонтальные линии через центр вашего круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив его пополам.
- 3 Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций. Так как вы уже провели линию через середину круга, Х должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.

- 4 Сделайте из каждой секции треугольники. Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник. Сделайте это с оставшимися пятью секциями. Думайте об этом, как об изготовлении корочки вокруг ваших кусков пиццы.
- 5 Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.
3 Рисуем грубый шестиугольник при помощи одного карандаша
- 1 Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку вашей горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может быть всего пара сантиметров.
- 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа.
 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии. - 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом, будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
- 4 Нарисуйте еще одну горизонтальную линию, соединяя нижние две диагональные линии. Таким образом, вы нарисуете основу для своего шестиугольника. В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.
- Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
- Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.

Предупреждения
- Циркуль — довольно острый предмет, будьте с ним очень аккуратны.
Принцип работы
- Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Пара циркулей
- Что-то, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала.
- Ластик
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge).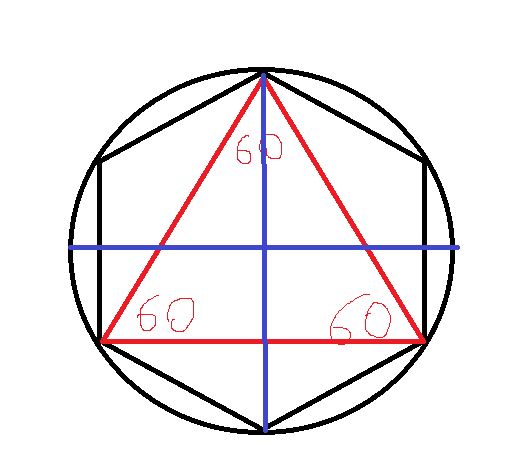 Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .
Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .
Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.
Геометрия
Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину. Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.
Шестиугольники с плоским (слева) и острым (справа) верхом
У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек. Каждая угловая точка общая для трёх шестиугольников.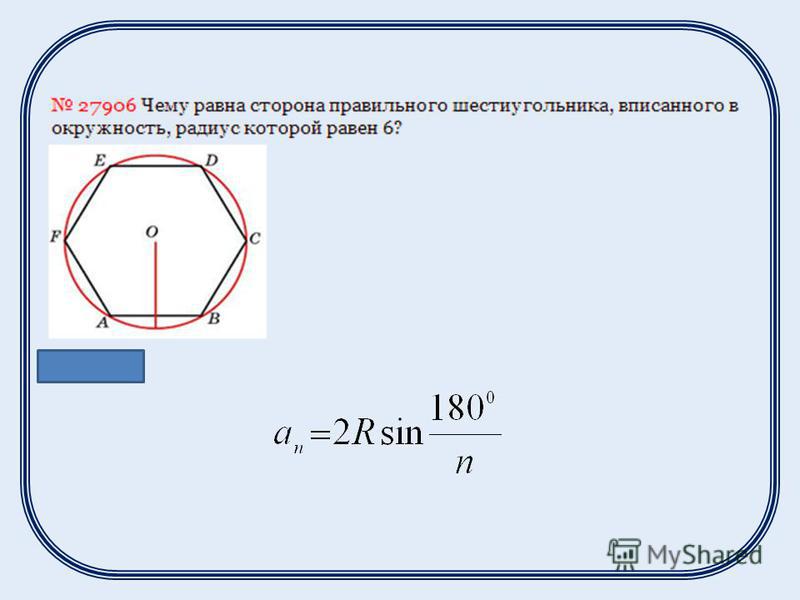 Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).
Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).
Углы
В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:Function hex_corner(center, size, i):
var angle_deg = 60 * i + 30
var angle_rad = PI / 180 * angle_deg
return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))
Для заполнения шестиугольника нужно получить вершины многоугольника с hex_corner(…, 0) по hex_corner(…, 5) . Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в hex_corner(…, 0) .
Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.
Углы шестиугольников с плоским и острым верхом
Размер и расположение
Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника height = size * 2 . Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .Ширина шестиугольника width = sqrt(3)/2 * height . Горизонтальное расстояние между соседними шестиугольниками horiz = width .
В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.
Системы координат
Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.
Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.Координаты смещений
Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются col или q . Строки обозначаются row или r . Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.
Горизонтальное расположение «нечет-r»
Горизонтальное расположение «чёт-r»
Вертикальное расположение «нечет-q»
Вертикальное расположение «чёт-q»
Кубические координаты
Ещё один способ рассмотрения сеток шестиугольников — видеть в них три основные оси, а не две , как в сетках квадратов. В них проявляется элегантная симметрия.Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0 . Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.
Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.
Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.
Шестиугольники
Кубы
Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.
Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.
При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.
- Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z , равным 0, 1, 2, 3, чтобы увидеть связь. Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
- Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z , поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.
Существует множество различных систем координат для кубов и шестиугольников. В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.
Осевые координаты
Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие x + y + z = 0 , третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.
Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .
Оси
Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.
Координаты смещения, кубические и осевые
Ось — это направление, в котором соответствующая координата увеличивается. Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.
Преобразование координат
Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:
# преобразование кубических в осевые координаты
q = x
r = z
# преобразование осевых в кубические координаты
x = q
z = r
y = -x-z
В коде эти две функции могут быть записаны следующим образом:
Function cube_to_hex(h): # осевая
var q = h.x
var r = h.z
return Hex(q, r)
function hex_to_cube(h): # кубическая
var x = h.q
var z = h.r
var y = -x-z
return Cube(x, y, z)
Координаты смещения совсем немного сложнее:
Соседние шестиугольники
Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.
Также может потребоваться рассчитать шесть «диагональных» шестиугольников.Кубические координаты
Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат Cube(dx, dy, dz) во время компиляции:Var directions = [
Cube(+1, -1, 0), Cube(+1, 0, -1), Cube(0, +1, -1),
Cube(-1, +1, 0), Cube(-1, 0, +1), Cube(0, -1, +1)
]
function cube_direction(direction):
return directions
function cube_neighbor(hex, direction):
return cube_add(hex, cube_direction(direction))
Осевые координаты
Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу Cube(dx, dy, dz) и преобразуем в таблицу Hex(dq, dr) :Var directions = [
Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1)
]
function hex_direction(direction):
return directions
function hex_neighbor(hex, direction):
var dir = hex_direction(direction)
return Hex(hex.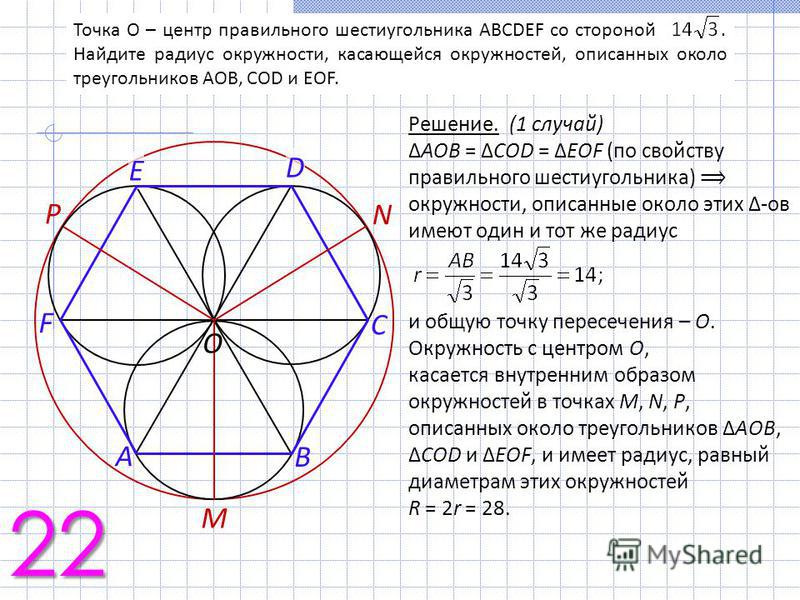 q + dir.q, hex.r + dir.r)
q + dir.q, hex.r + dir.r)
Координаты смещения
В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row . Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2) . Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.
Нечет-r
var directions = [
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex. row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-r
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ],
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётной (EVEN) и нечётной (ODD) строк
Нечет-q
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ],
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-q
var directions = [
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.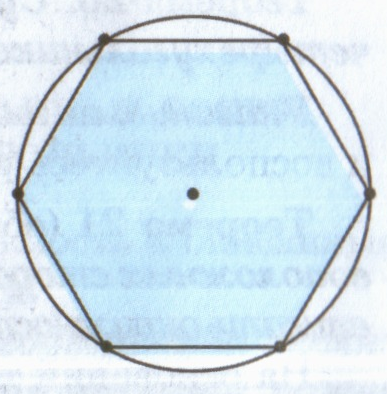 col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётного (EVEN) и нечётного (ODD) столбцов
Диагонали
Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).Var diagonals = [
Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1),
Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1)
]
function cube_diagonal_neighbor(hex, direction):
return cube_add(hex, diagonals)
Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.
Расстояния
Кубические координаты
В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов.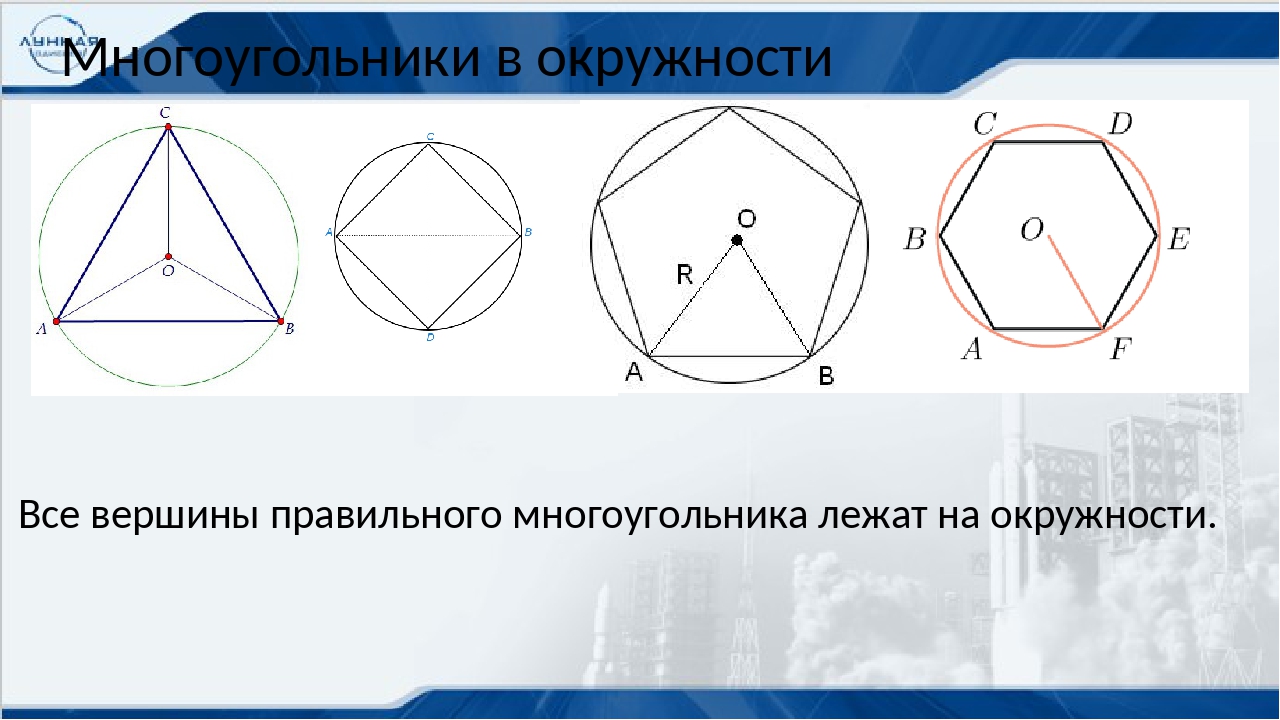 Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:
Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:Function cube_distance(a, b):
return (abs(a.x — b.x) + abs(a.y — b.y) + abs(a.z — b.z)) / 2
Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:
Function cube_distance(a, b):
return max(abs(a.x — b.x), abs(a.y — b.y), abs(a.z — b.z))
На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.
GIF
Осевые координаты
В осевой системе третья координата выражена неявно. Давайте преобразуем из осевой в кубическую систему для расчёта расстояния:Function hex_distance(a, b):
var ac = hex_to_cube(a)
var bc = hex_to_cube(b)
return cube_distance(ac, bc)
Если компилятор в вашем случае встраивает (inline) hex_to_cube и cube_distance , то он сгенерирует такой код:
Function hex_distance(a, b):
return (abs(a. q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе . Например, описанная «разность разностей» получается из записи a.q + a.r — b.q — b.r как a.q — b.q + a.r — b.r и с использованием формы максимального значения вместо формы деления пополам cube_distance . Все они аналогичны, если увидеть связь с кубическими координатами.
Координаты смещения
Как и в случае с осевыми координатами, мы преобразуем координаты смещения в кубические координаты, а затем используем расстояние кубической системы.Function offset_distance(a, b):
var ac = offset_to_cube(a)
var bc = offset_to_cube(b)
return cube_distance(ac, bc)
Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).
Отрисовка линий
Как нарисовать линию от одного шестиугольника до другого? Я использую линейную интерполяцию для рисования линий . Линия равномерно сэмплируется в N+1 точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.GIF
- Сначала мы вычисляем N , которое будет расстоянием в шестиугольниках между конечными точками.
- Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N , включая их, каждая точка будет A + (B — A) * 1.0/N * i . На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
- Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).
Function lerp(a, b, t): // для float
return a + (b — a) * t
function cube_lerp(a, b, t): // для шестиугольников
return Cube(lerp(a. x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
Примечания:
- Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
- Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
- Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube .
 Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип. - Можно оптимизировать код, встроив (inline) cube_lerp , а затем рассчитав B.x-A.x , B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
- Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите .
- Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие» . Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.
Диапазон перемещения
Диапазон координат
Для заданного центра шестиугольника и диапазона N какие шестиугольники находятся в пределах N шагов от него?Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)) . Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Var results =
for each -N ≤ dx ≤ N:
for each -N ≤ dy ≤ N:
for each -N ≤ dz ≤ N:
if dx + dy + dz = 0:
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл сработает, но будет довольно неэффективным. Из всех значений dz , которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов dx + dy + dz = 0 . Вместо этого мы напрямую вычислим значение dz , удовлетворяющее условию:
Var results =
for each -N ≤ dx ≤ N:
for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N):
var dz = -dx-dy
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
GIF
Пересекающиеся диапазоны
Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N , и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0 , чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.
Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме x min ≤ x ≤ x max , и примем x min = center.x — N и x max = center.x + N . Сделаем то же самое для y и z , в результате получив общий вид кода из предыдущего раздела:
Var results =
for each xmin ≤ x ≤ xmax:
for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin):
var z = -x-y
results. append(Cube(x, y, z))
append(Cube(x, y, z))
Пересечением двух диапазонов a ≤ x ≤ b и c ≤ x ≤ d является max(a, c) ≤ x ≤ min(b, d) . Поскольку область шестиугольников выражена как диапазоны над x , y , z , мы можем отдельно пересечь каждый из диапазонов x , y , z , а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении. Для одной области шестиугольников мы принимаем x min = H.x — N and x max = H.x + N , аналогично для y и z . Для пересечения двух областей шестиугольников мы принимаем x min = max(h2.x — N, h3.x — N) и x max = min(h2.x + N, h3.x + N), аналогично для y и z . Тот же шаблон работает для пересечения трёх или более областей.
GIF
Препятствия
При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде fringes[k] — это массив всех шестиугольников, которых можно достичь за k шагов. При каждом проходе по основному циклу мы расширяем уровень k-1 на уровень k .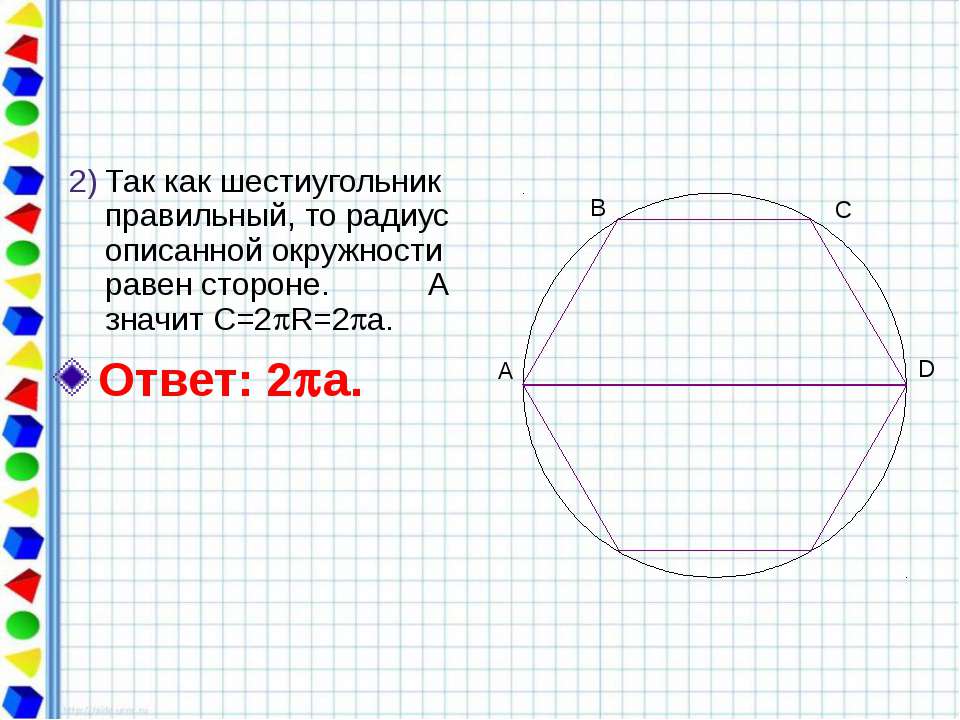
Function cube_reachable(start, movement): var visited = set() add start to visited var fringes = fringes.append() for each 1
Повороты
Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:
[ x, y, z]
to [-z, -x, -y]
Поворот на 60° влево сдвигает каждую координату на одну позицию влево:
[ x, y, z]
to [-y, -z, -x]
«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60° меняет знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.
Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:
- Преобразование положений P и C в кубические координаты.

- Вычисление вектора вычитанием центра: P_from_C = P — C = Cube(P.x — C.x, P.y — C.y, P.z — C.z) .
- Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C .
- Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z) .
- Преобразование кубического положения R обратно в нужную систему координат.
Кольца
Простое кольцо
Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса radius , нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно radius . Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.
Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.Function cube_ring(center, radius): var results = # этот код не работает для radius == 0; вы понимаете, почему? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i В этом коде cube начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла cube двигается на один шестиугольник по кольцу. Через 6 * radius шагов он завершает там, где начал.
Спиральные кольца
Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:Function cube_spiral(center, radius):
var results =
for each 1 ≤ k ≤ radius:
results = results + cube_ring(center, k)
return results
Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра.
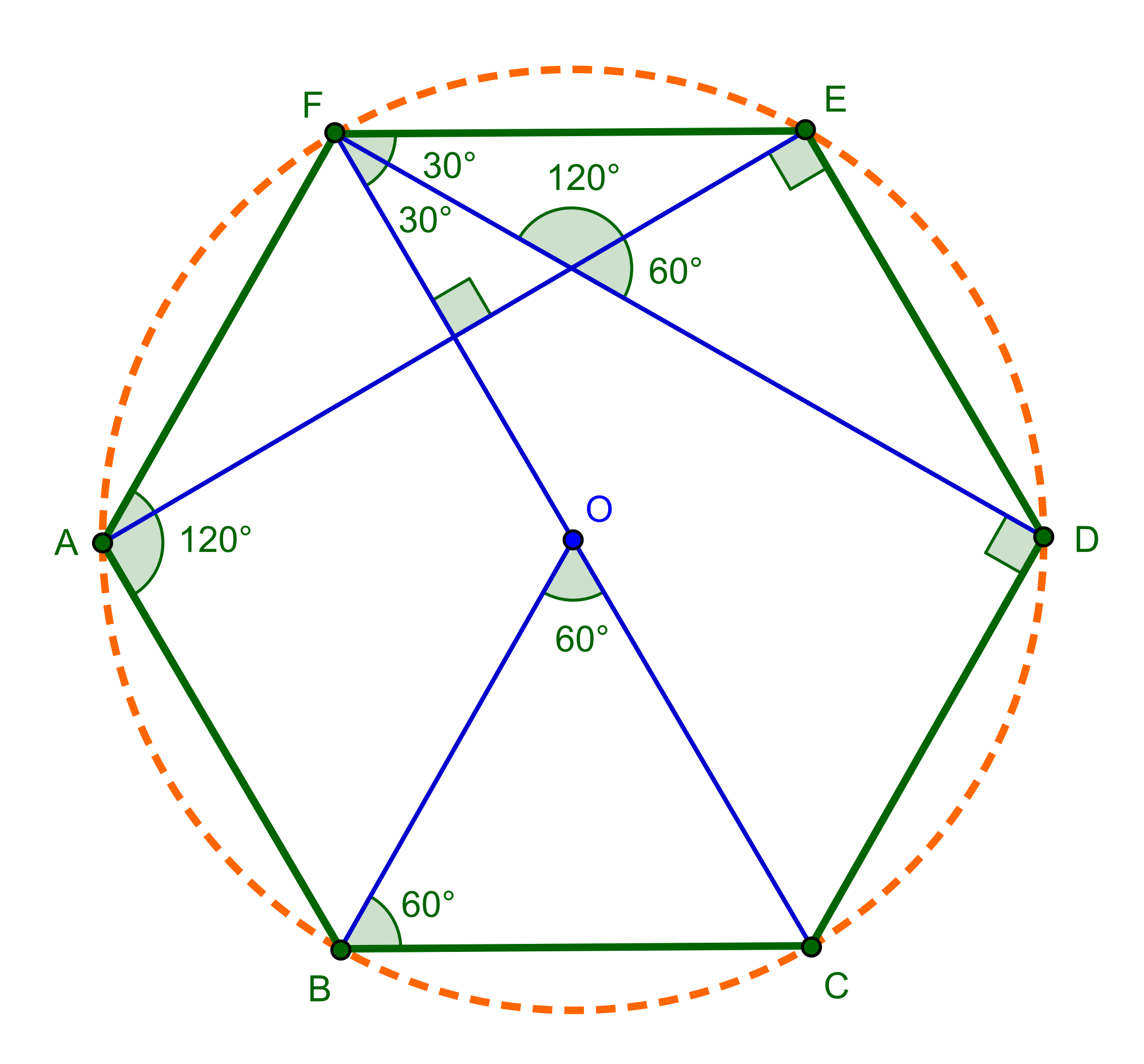 Для вычисления площади используйте эту формулу .
Для вычисления площади используйте эту формулу .Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).
Область видимости
Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.
GIF
Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд.
 Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.
Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.Я хочу в дальнейшем расширять это руководство. У меня есть
Построение вписанного в окружность правильного шестиугольника. Построение правильного пятиугольника по данной его стороне. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Это построение можно выполнить при помощи угольника и циркуля. Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Постройте точки вершин углов правильного шестиугольника.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.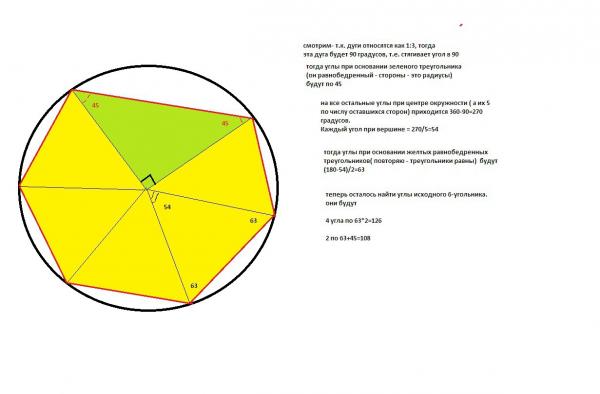
Метод 1 из 3: Рисуем идеальный шестиугольник при помощи циркуля
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.
Именно на умении строить биссектрисы углов и серединные перпендикуляры отрезков и основывается методика построения правильных многоугольников
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй-коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Тема этого видеоурока – «Построение правильных многоугольников». Также еще раз дадим определение правильному многоугольнику, изобразим его графически, после чего еще раз убедимся, что центры вписанной и описанной окружностей вокруг такой фигуры будут совпадать.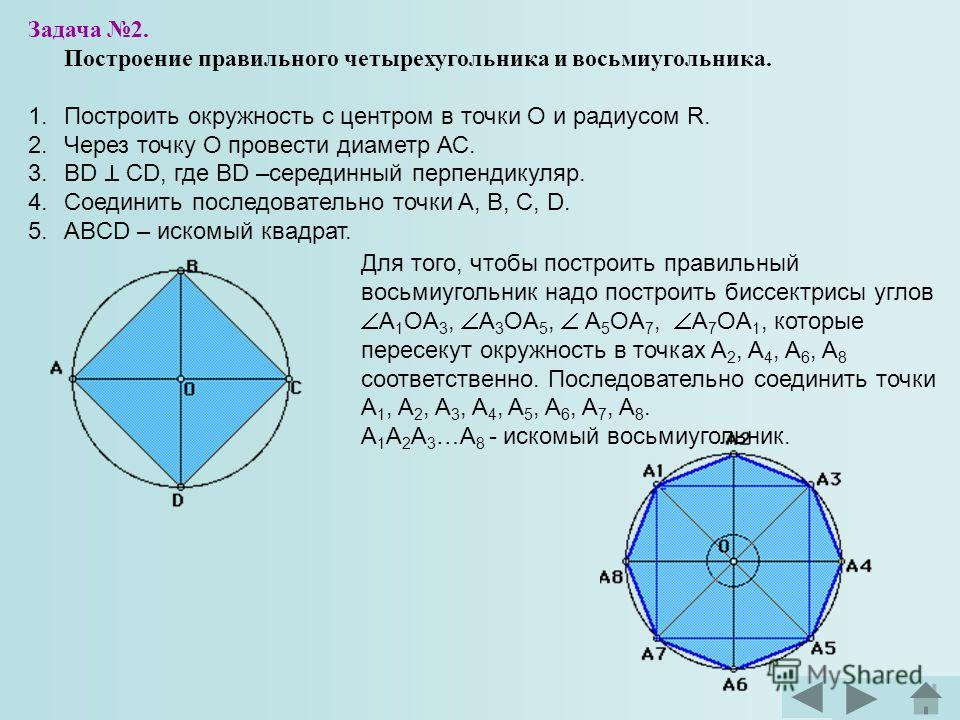 В этот многоугольник всегда можно вписать окружность и около него всегда можно описать окружность. В ходе предыдущих уроков мы выяснили, что базовую роль для описания свойств многоугольников играют биссектрисы его углов и серединные перпендикуляры к его сторонам.
В этот многоугольник всегда можно вписать окружность и около него всегда можно описать окружность. В ходе предыдущих уроков мы выяснили, что базовую роль для описания свойств многоугольников играют биссектрисы его углов и серединные перпендикуляры к его сторонам.
4. Получили искомый правильный треугольник АВС. Задача решена. 3. Поместив одну ножку циркуля в произвольную точки А1 на окружности, при помощи второй ножки отметим на той же окружности точку А2 и соединим ее с точкой А1. Получим первую сторону шестиугольника. 3. При помощи серединных перпендикуляров к сторонам многоугольника, опущенным из точки О, разделим все его стороны и все дуги окружности, заключенные между его соседними вершинами, пополам.
Геометрические построения являются одной из важных частей обучения. Игла должна проткнуть начерченную линию. Чем точнее будет установлен циркуль, тем точнее будет построение. Начертите еще одну дугу, пересекающую окружность. Последовательно соедините все шесть точек пересечения дуг с первоначально начерченной окружностью. В этом случае шестиугольник может получиться неправильным.
В этом случае шестиугольник может получиться неправильным.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые
Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. Центры обеих окружностей совпадают (точка О на Рис. 1). Также на рисунке приведены радиусы описанной (R) и вписанной (r) окружностей.
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. На данном занятии мы рассмотрим способы построения правильных многоугольников с помощью циркуля и линейки. Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник. Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.

Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.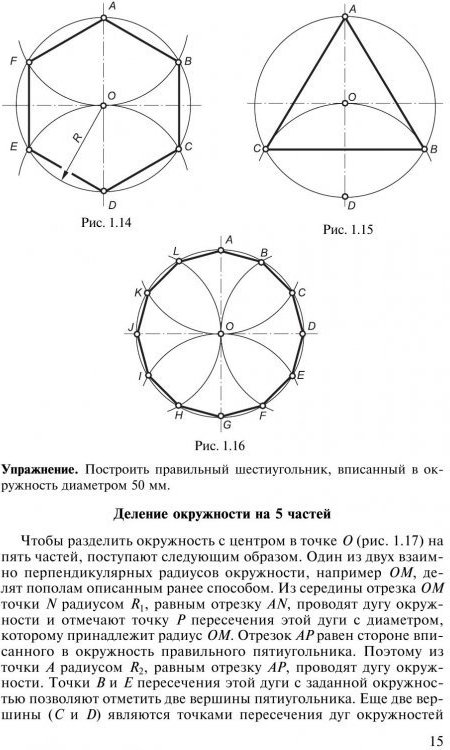
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон.
Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.

- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Диаметр описанной окружности шестигранника формула.
 Построение правильных многоугольников
Построение правильных многоугольниковТему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису.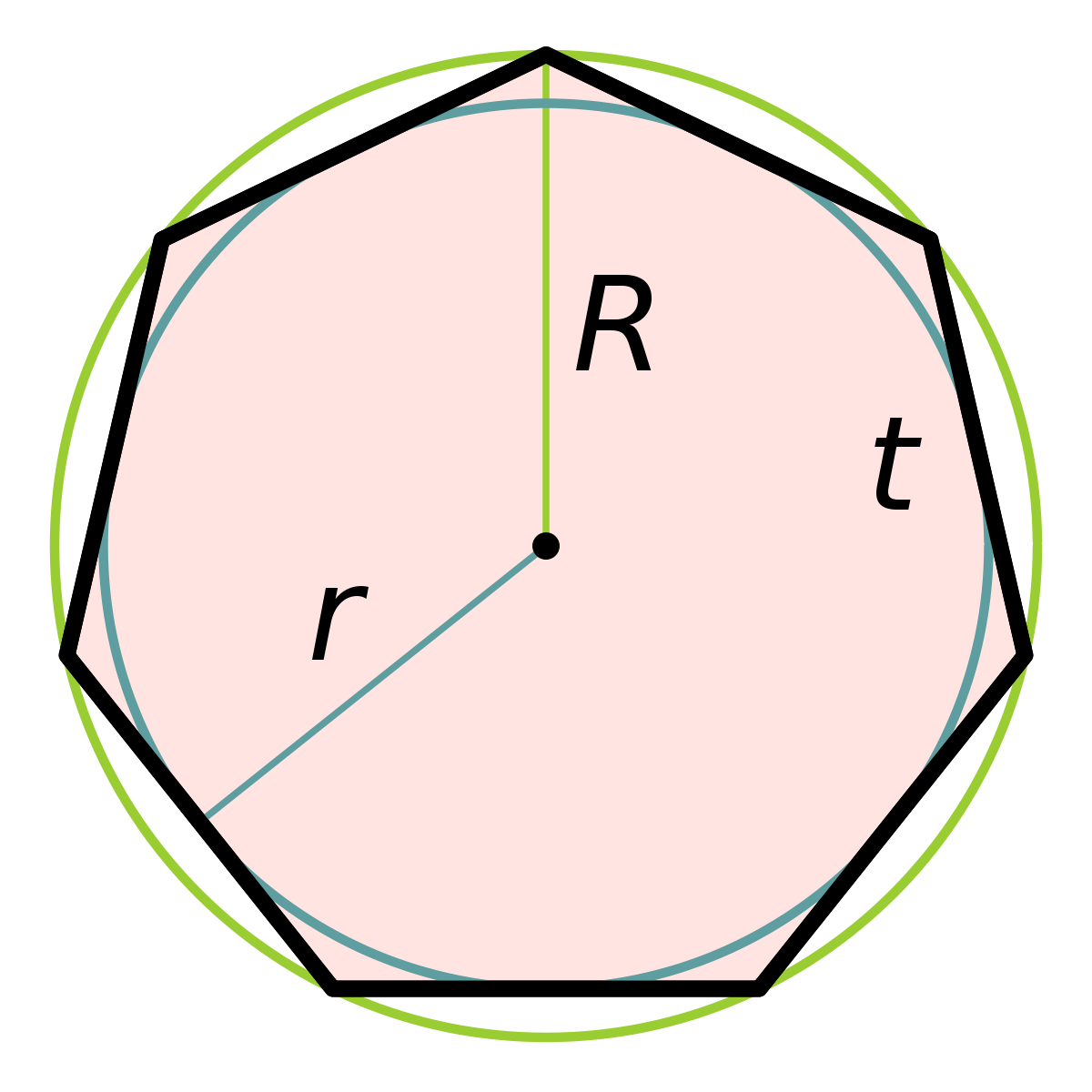 Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .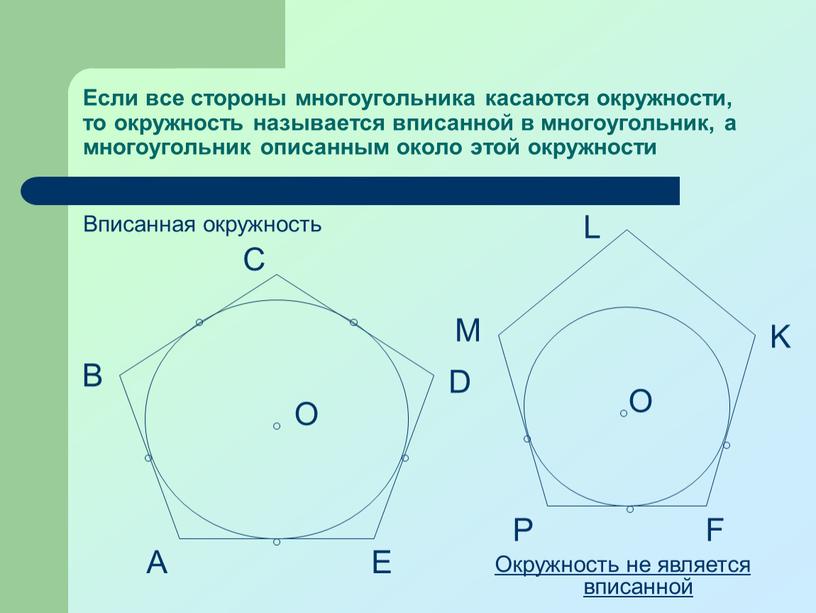
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний.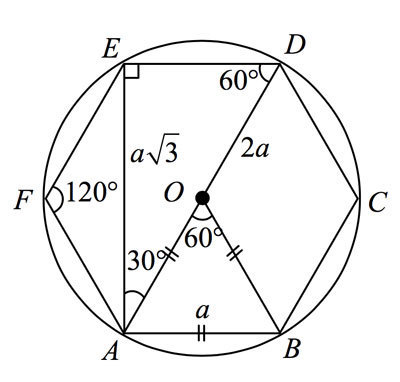 В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре.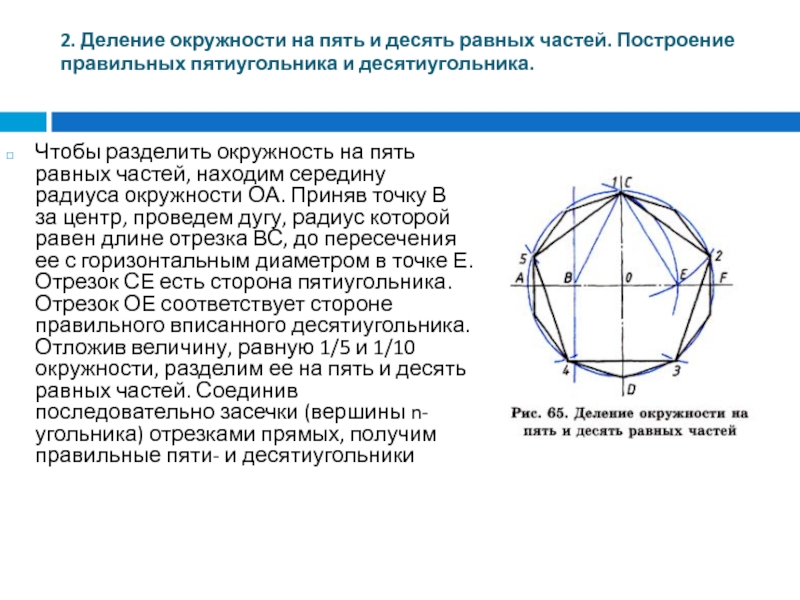 Композиции могут получаться очень интересные:
Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности.
 Из всех это свойство имеет лишь правильный шестиугольник.
Из всех это свойство имеет лишь правильный шестиугольник. - Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.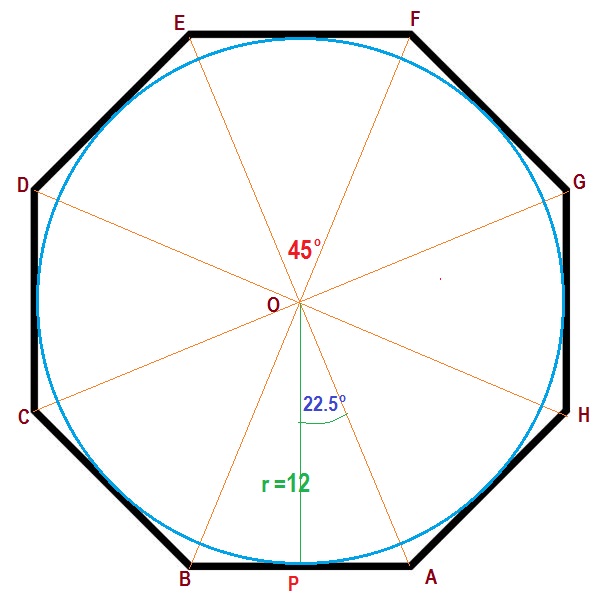
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша.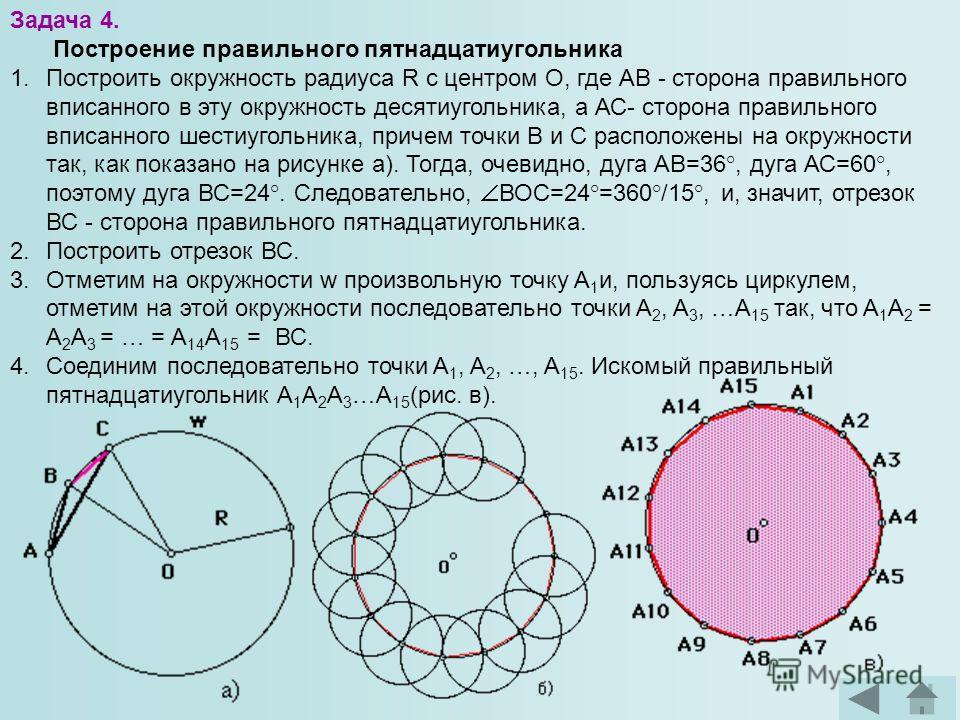 Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг.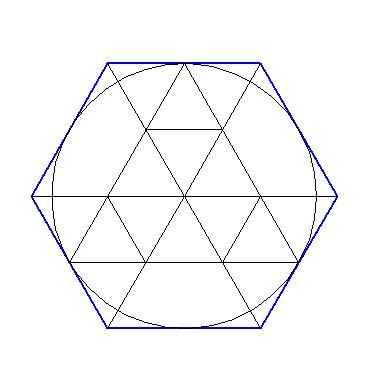 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.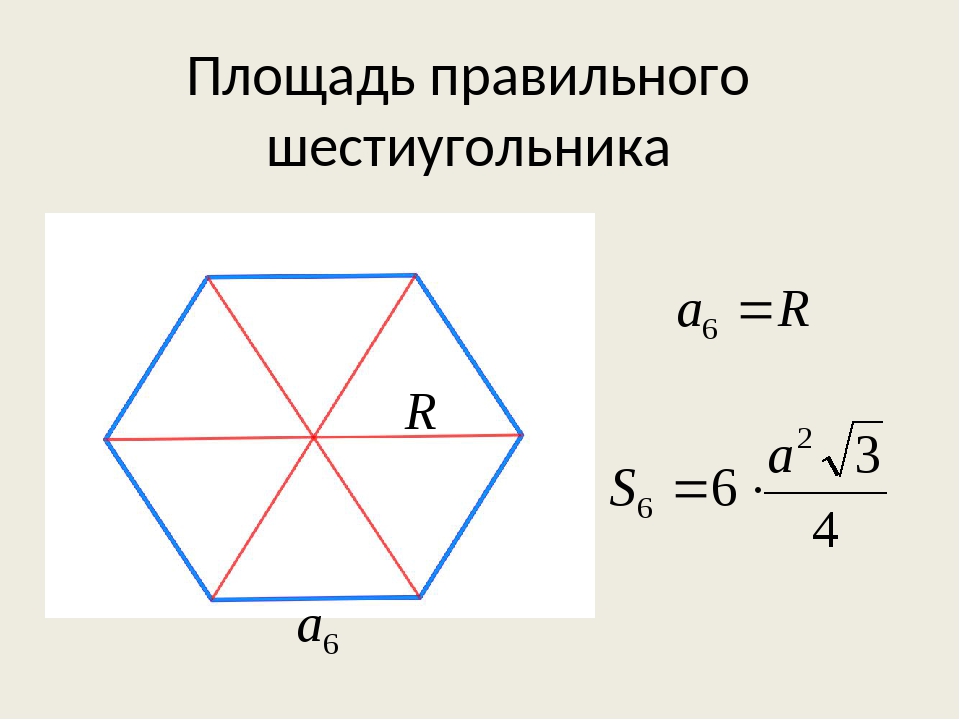
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей.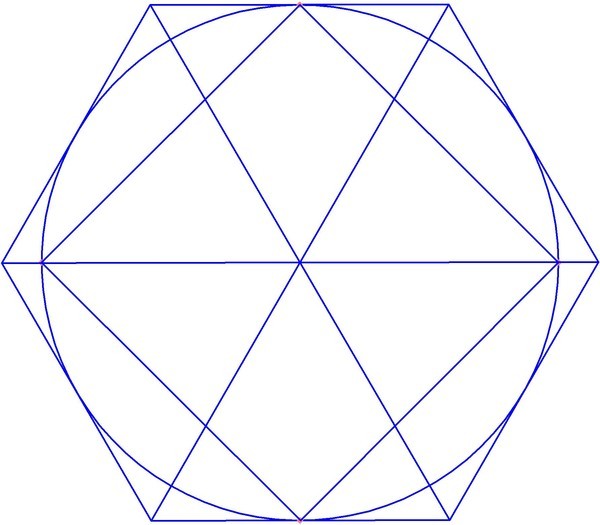 Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.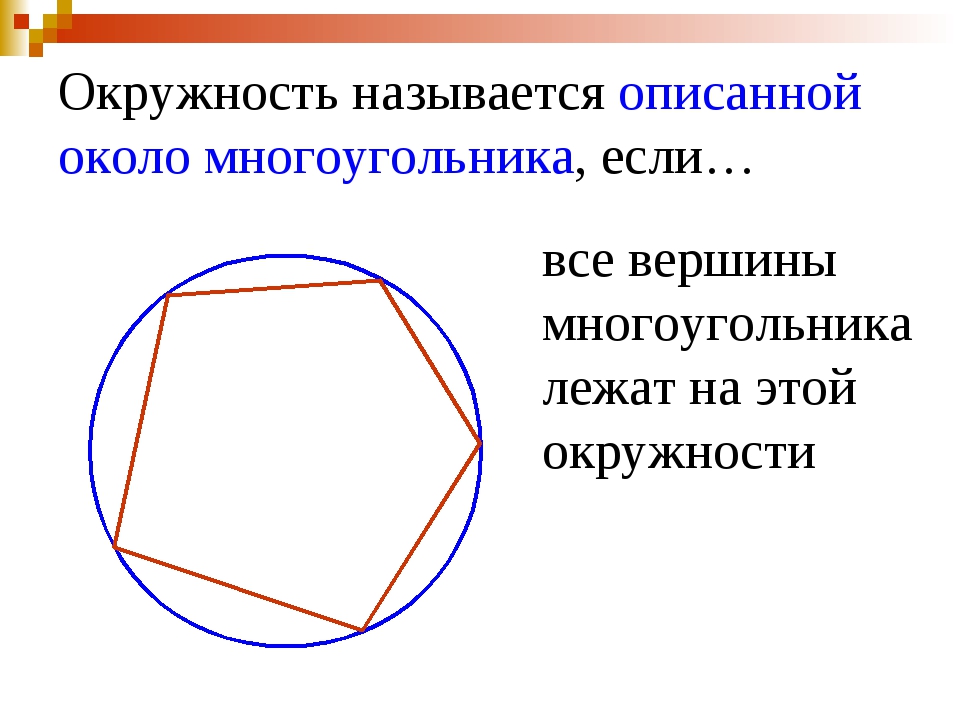
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими.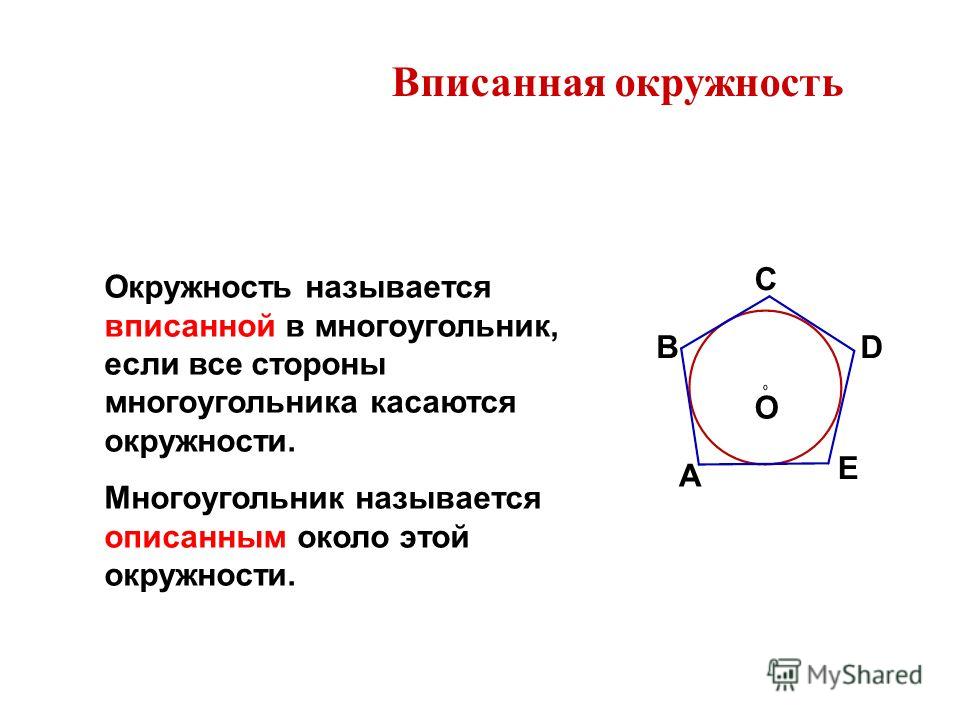 Плотность данной упаковки равна .
В 1940 году было доказано, что данная упаковка является самой плотной.
Плотность данной упаковки равна .
В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.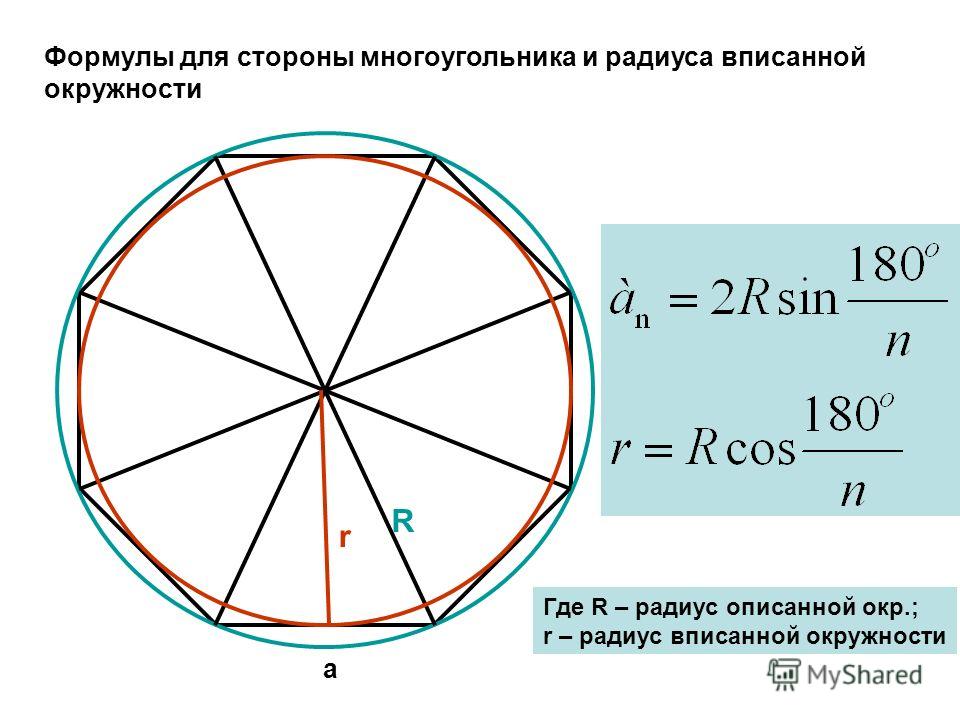
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Геометрия— Докажите, что круг можно вписать в шестиугольник
Лемма. (1) Диагональ $ BE $ — это биссектриса обоих углов $ \ angle \, ABC $ и $ \ angle \, DEF $;
(2) Диагональ $ CF $ — это биссектриса обоих углов $ \ angle \, BCD $ и $ \ angle \, EFA $;
(3) Диагональ $ AD $ — это биссектриса обоих углов $ \ angle \, FAB $ и $ \ angle \, CDE $;
Наконец, три диагонали $ AD, \, BE $ и $ CF $ пересекаются в общей точке I.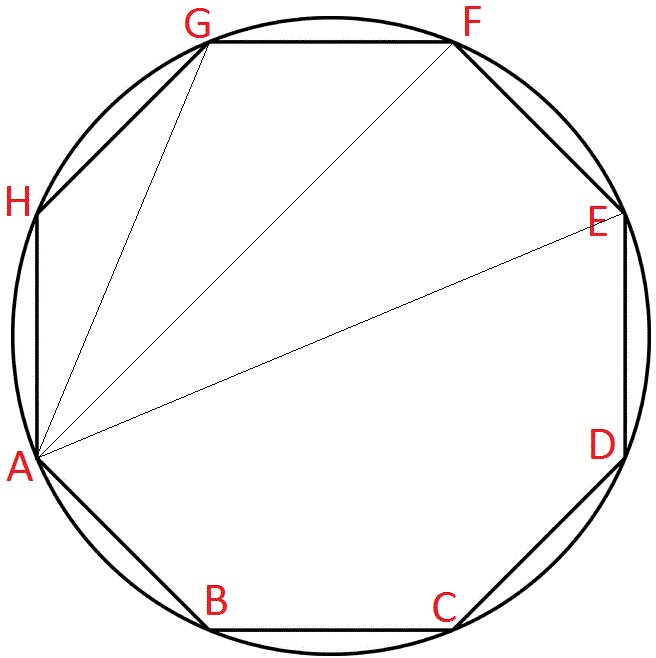 * F = \ angle \, DAF $$ Следовательно, четырехугольник $ ACDF $ вписан в круг, и поскольку $ FA = CD $, четырехугольник $ ACDF $ фактически является равнобедренной трапецией с $ AC $, параллельным $ DF $. По этой причине параллельные отрезки $ AC $ и $ DF $ имеют общую ортогональную биссектрису, и поскольку $ BA = BC $ и $ ED = EF $, точки $ B $ и $ E $ должны лежать на этой ортогональной биссектрисе, т.е. прямая $ EF $ является ортогональной биссектрисой отрезков $ AC $ и $ DF $ одновременно. Однако, поскольку треугольники $ ABC $ и $ DEF $ равнобедренные, ортогональная биссектриса $ BE $ в то же время является биссектрисой обоих углов $ \ angle \, ABC $ и $ \ angle \, DEF $.Заметим, что, поскольку прямая $ BE $ является ортогональной биссектрисой двух параллельных сторон $ AC $ и $ DF $ равнобедренной трапеции $ ACDF $, ее две диагонали $ AD $ и $ CF $ пересекаются в общей точке, лежащей на $ BE $. Остальная часть леммы следует аналогично.
* F = \ angle \, DAF $$ Следовательно, четырехугольник $ ACDF $ вписан в круг, и поскольку $ FA = CD $, четырехугольник $ ACDF $ фактически является равнобедренной трапецией с $ AC $, параллельным $ DF $. По этой причине параллельные отрезки $ AC $ и $ DF $ имеют общую ортогональную биссектрису, и поскольку $ BA = BC $ и $ ED = EF $, точки $ B $ и $ E $ должны лежать на этой ортогональной биссектрисе, т.е. прямая $ EF $ является ортогональной биссектрисой отрезков $ AC $ и $ DF $ одновременно. Однако, поскольку треугольники $ ABC $ и $ DEF $ равнобедренные, ортогональная биссектриса $ BE $ в то же время является биссектрисой обоих углов $ \ angle \, ABC $ и $ \ angle \, DEF $.Заметим, что, поскольку прямая $ BE $ является ортогональной биссектрисой двух параллельных сторон $ AC $ и $ DF $ равнобедренной трапеции $ ACDF $, ее две диагонали $ AD $ и $ CF $ пересекаются в общей точке, лежащей на $ BE $. Остальная часть леммы следует аналогично.
$$ $$
Завершение доказательства: Заметим, что по лемме прямые $ AD, \, BE, $ и $ CF $ пересекаются в одной общей точке, обозначим через $ I $. Следовательно, по лемме $ I $ является точкой общего пересечения всех биссектрис углов при вершинах шестиугольника $ ABCDEF $.Следовательно, в шестиугольник вписан круг с центром в центре точки $ I $. Как следствие, мы получаем, что $ IA = IC = IE $ и $ IB = ID = IF $.
Следовательно, по лемме $ I $ является точкой общего пересечения всех биссектрис углов при вершинах шестиугольника $ ABCDEF $.Следовательно, в шестиугольник вписан круг с центром в центре точки $ I $. Как следствие, мы получаем, что $ IA = IC = IE $ и $ IB = ID = IF $.
Шестигранник вписанный в круг
вопросов без ответов. Вписанный ПРОЕКТ построения многоугольника. правильный шестиугольник вписан в круг радиусом 10 дюймов. Приведенная выше анимация доступна в виде правильного шестиугольника, вписанного в круг диаметром 20 м. 20 раз. A. Треугольник 1 B. Треугольник 2 C. Треугольник 3 D. Треугольник 4 2. Правильный шестиугольник со сторонами 3 дюйма вписан в круг.или когда компьютер недоступен. CPCTC — Соответствующие части конгруэнтных треугольников являются конгруэнтными, список распечатываемых листов конструкций, перпендикуляр от линии через точку, параллельная линия через точку (угловая копия), параллельная линия через точку (перенос), построение 75 ° 105 ° 120 ° Углы 135 ° 150 ° и более, Равнобедренный треугольник, заданные основание и высота, Равнобедренный треугольник, заданный угол катета и вершины, Треугольник, заданная одна сторона и прилегающие углы (asa), Треугольник, заданные два угла и исключенная сторона (aas) , Треугольник с двумя сторонами и включенным углом (sas), прямой треугольник с одним катетом и гипотенузой (HL), прямоугольный треугольник с учетом гипотенузы и одним углом (HA), прямоугольный треугольник с одним катетом и одним углом (LA), Постройте эллипс из веревки и булавок, найдите центр круга любым прямоугольным предметом. Так что просто используйте ту же формулу и вставьте ее. Все диагонали шестиугольника также являются диаметрами окружности. МАТЕМАТИКА, пожалуйста, помогите. Изображение ниже — это окончательный рисунок из приведенной выше анимации, но с помеченными вершинами. Математика. Представьте, что шестиугольник состоит из 6 равносторонних треугольников. Найдите область заштрихованной области с точностью до ДЕСЯТИ. Выразите свой ответ как обычно. Он помечает точки, в которых круг пересекает линию, как точки B и C. 9-10 классы. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? Правильный шестиугольник вписан в круг радиусом 18.Большое спасибо за помощь. Затем нажмите Рассчитать. Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника. http://antoniofernandez.es/#Geometry #HowtoDrawСделайте пожертвование: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick\u0026hosted_button_id=LNQ2EWAXTVYX2\u0026source=url Да Нет. Согласно theurl Бланк для ответов ответ — 60 футов, но я не смог… Самопересекающийся шестиугольник ABCDEF, вписанный в круг.
Так что просто используйте ту же формулу и вставьте ее. Все диагонали шестиугольника также являются диаметрами окружности. МАТЕМАТИКА, пожалуйста, помогите. Изображение ниже — это окончательный рисунок из приведенной выше анимации, но с помеченными вершинами. Математика. Представьте, что шестиугольник состоит из 6 равносторонних треугольников. Найдите область заштрихованной области с точностью до ДЕСЯТИ. Выразите свой ответ как обычно. Он помечает точки, в которых круг пересекает линию, как точки B и C. 9-10 классы. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? Правильный шестиугольник вписан в круг радиусом 18.Большое спасибо за помощь. Затем нажмите Рассчитать. Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника. http://antoniofernandez.es/#Geometry #HowtoDrawСделайте пожертвование: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick\u0026hosted_button_id=LNQ2EWAXTVYX2\u0026source=url Да Нет. Согласно theurl Бланк для ответов ответ — 60 футов, но я не смог… Самопересекающийся шестиугольник ABCDEF, вписанный в круг. На этой странице показано, как построить (нарисовать) расчет в правильном шестиугольнике, многоугольнике с 6 вершинами.Узнайте, как построить правильный шестиугольник с помощью циркуля. Периметр шестиугольника — это длина окружности. | Сократик. Правильный шестиугольник вписан в… Бесполезно 1 Полезно 2. Новые вопросы в математике. ОПРОС . Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Итак, теперь у нас есть все части для доказательства конструкции. ABCDEF — правильный шестиугольник, вписанный в данную окружность. Из (20), (7) все стороны имеют одинаковую длину. Пошаговые инструкции для печати. Примеры:.вершина Тогда произведение длин отрезков A0, A1, A0, A2 и A0, A4 равно. 6 Джайра завершает строительство правильного шестиугольника, вписанного в круг, как показано ниже. Дано: лист бумаги Сколько дуг будет нарисовано на окружности при построении вписанного равностороннего треугольника? Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге.
На этой странице показано, как построить (нарисовать) расчет в правильном шестиугольнике, многоугольнике с 6 вершинами.Узнайте, как построить правильный шестиугольник с помощью циркуля. Периметр шестиугольника — это длина окружности. | Сократик. Правильный шестиугольник вписан в… Бесполезно 1 Полезно 2. Новые вопросы в математике. ОПРОС . Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Итак, теперь у нас есть все части для доказательства конструкции. ABCDEF — правильный шестиугольник, вписанный в данную окружность. Из (20), (7) все стороны имеют одинаковую длину. Пошаговые инструкции для печати. Примеры:.вершина Тогда произведение длин отрезков A0, A1, A0, A2 и A0, A4 равно. 6 Джайра завершает строительство правильного шестиугольника, вписанного в круг, как показано ниже. Дано: лист бумаги Сколько дуг будет нарисовано на окружности при построении вписанного равностороннего треугольника? Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. Выразите свой ответ дробью. Его стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля.округлить до 2 знаков после запятой. Линия Паскаля показана белым. Урок о многоугольниках, вписанных в круг и описанных вокруг него. Круг вписан в шестиугольник; Диаметр круга — это расстояние от середины одной стороны шестиугольника до середины противоположной стороны. Пусть A0, A1, A2, A3, A4, A5 — правильный шестиугольник, вписанный в окружность единичного радиуса. Какова площадь сегмента, образованного стороной шестиугольника и круга? Если четырехугольник вписан в окружность, противоположные углы у него дополнительные.Он начинает с рисования линии и пометки точки на линии как точки A. 3. Примечание: НЕ округляйте до конца Здравствуйте, мне нужна помощь в поиске ответа на этот вопрос, может кто-нибудь мне помочь? Каждая пара вытянутых противоположных сторон имеет свой цвет: красный, желтый, синий. Что такое m∠ACB? Inradius — это радиус самого большого круга, полностью заключенного внутри шестиугольника.
Выразите свой ответ дробью. Его стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля.округлить до 2 знаков после запятой. Линия Паскаля показана белым. Урок о многоугольниках, вписанных в круг и описанных вокруг него. Круг вписан в шестиугольник; Диаметр круга — это расстояние от середины одной стороны шестиугольника до середины противоположной стороны. Пусть A0, A1, A2, A3, A4, A5 — правильный шестиугольник, вписанный в окружность единичного радиуса. Какова площадь сегмента, образованного стороной шестиугольника и круга? Если четырехугольник вписан в окружность, противоположные углы у него дополнительные.Он начинает с рисования линии и пометки точки на линии как точки A. 3. Примечание: НЕ округляйте до конца Здравствуйте, мне нужна помощь в поиске ответа на этот вопрос, может кто-нибудь мне помочь? Каждая пара вытянутых противоположных сторон имеет свой цвет: красный, желтый, синий. Что такое m∠ACB? Inradius — это радиус самого большого круга, полностью заключенного внутри шестиугольника. Разделили бы мы его на треугольники? Это также можно описать как круг, описанный вокруг правильного шестиугольника. Круг вписан в правильный шестиугольник таким образом, что круг касается всех сторон шестиугольника ровно в одной точке на каждой стороне.Центр многоугольника — это центр круга, вписанного в многоугольник. Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Правильный шестиугольник (вписанный в круг) Правильный шестиугольник — это шестигранная фигура, в которой все углы совпадают, а все стороны равны. количество сторон n: n = 3,4,5,6 …. радиус описанной стороны r длина стороны a. Выразите свой ответ в … Shockshot99Shockshot99. Спасибо! Это было «оставшееся» пространство, когда мы обошли круг и остановились у F.На рисунке угол CAB составляет 60 °. Он фокусируется на рисовании фигур от геометрической плоскости до описательной геометрии, а также на различных системах представления технических чертежей. Если вы подпишетесь, нажмете, поставите лайк или оставите комментарий, вы поможете нам расширить наш канал и помочь большему количеству людей с их навыками технического рисования.
Разделили бы мы его на треугольники? Это также можно описать как круг, описанный вокруг правильного шестиугольника. Круг вписан в правильный шестиугольник таким образом, что круг касается всех сторон шестиугольника ровно в одной точке на каждой стороне.Центр многоугольника — это центр круга, вписанного в многоугольник. Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Правильный шестиугольник (вписанный в круг) Правильный шестиугольник — это шестигранная фигура, в которой все углы совпадают, а все стороны равны. количество сторон n: n = 3,4,5,6 …. радиус описанной стороны r длина стороны a. Выразите свой ответ в … Shockshot99Shockshot99. Спасибо! Это было «оставшееся» пространство, когда мы обошли круг и остановились у F.На рисунке угол CAB составляет 60 °. Он фокусируется на рисовании фигур от геометрической плоскости до описательной геометрии, а также на различных системах представления технических чертежей. Если вы подпишетесь, нажмете, поставите лайк или оставите комментарий, вы поможете нам расширить наш канал и помочь большему количеству людей с их навыками технического рисования.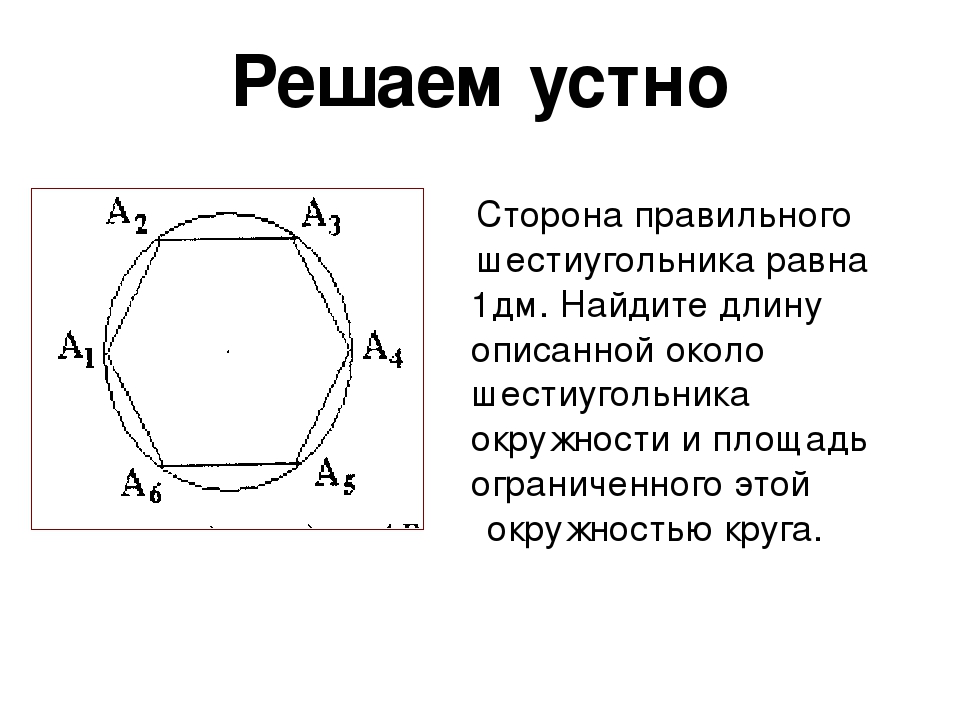 .Спасибо заранее. Дубляж Фрэнк Шоу. Музыка Антонио Фернандеса Руиса. Это самый большой шестиугольник, который впишется в круг, площадь каждого многоугольника Sp. Вышеупомянутая анимация доступна для печати … Окружной радиус: чтобы найти радиус круга, описанного на правильном шестиугольнике, вам необходимо определить расстояние между центральной точкой шестиугольника (то есть … найти длину сторон десятиугольника .Квадрат, вписанный в круг. Как мне рассчитать апофему квадрата, если я знаю только площадь? … Шестиугольник, вписанный в круг. Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. 2. Треугольник, вписанный в круг. Рассмотрим правильный шестиугольник, вписанный в окружность C радиуса r. У правильных шестиугольников шесть равных сторон и шесть равных углов. Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц.Введите одно значение и выберите количество десятичных знаков.
.Спасибо заранее. Дубляж Фрэнк Шоу. Музыка Антонио Фернандеса Руиса. Это самый большой шестиугольник, который впишется в круг, площадь каждого многоугольника Sp. Вышеупомянутая анимация доступна для печати … Окружной радиус: чтобы найти радиус круга, описанного на правильном шестиугольнике, вам необходимо определить расстояние между центральной точкой шестиугольника (то есть … найти длину сторон десятиугольника .Квадрат, вписанный в круг. Как мне рассчитать апофему квадрата, если я знаю только площадь? … Шестиугольник, вписанный в круг. Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. 2. Треугольник, вписанный в круг. Рассмотрим правильный шестиугольник, вписанный в окружность C радиуса r. У правильных шестиугольников шесть равных сторон и шесть равных углов. Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц.Введите одно значение и выберите количество десятичных знаков. Теги: Вопрос 8. Правильный шестиугольник вписан в круг радиусом 10 футов. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используем этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагаем по кругу, отмечая вершины. Найдите его периметр. Итак, мы должны доказать, что это соответствует остальным пяти сторонам. Как это сделать? Все они были нарисованы с одинаковой шириной компаса. AB был нарисован с шириной компаса, установленной на OA.Посмотри ответы. Какова площадь в квадратных единицах правильного шестиугольника, вписанного в круг, площадь которого составляет \ (324 \ пи \) квадратных единиц? Это будет первая вершина шестиугольника. ° Какова длина отрезка AB? Выразите свой ответ в простейшей радикальной форме. Отметьте точку в любом месте круга. начертанный по кругу циркулем и линейкой или линейкой. Калькулятор шестиугольника. 60 секунд. Иллюстрация правильного шестиугольника, вписанного в круг. Найдите площадь шести сегментов круга, образованных сторонами шестиугольника.
Теги: Вопрос 8. Правильный шестиугольник вписан в круг радиусом 10 футов. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используем этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагаем по кругу, отмечая вершины. Найдите его периметр. Итак, мы должны доказать, что это соответствует остальным пяти сторонам. Как это сделать? Все они были нарисованы с одинаковой шириной компаса. AB был нарисован с шириной компаса, установленной на OA.Посмотри ответы. Какова площадь в квадратных единицах правильного шестиугольника, вписанного в круг, площадь которого составляет \ (324 \ пи \) квадратных единиц? Это будет первая вершина шестиугольника. ° Какова длина отрезка AB? Выразите свой ответ в простейшей радикальной форме. Отметьте точку в любом месте круга. начертанный по кругу циркулем и линейкой или линейкой. Калькулятор шестиугольника. 60 секунд. Иллюстрация правильного шестиугольника, вписанного в круг. Найдите площадь шести сегментов круга, образованных сторонами шестиугольника. Компасы теперь установлены на радиус круга. Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку. Я думал, что ответ был 10 дюймов, но я думаю, что это неправильно. Из (2) мы видим, что пять сторон равны по длине, но последняя сторона FA не была нарисована с помощью циркуля. круг площадь Sc. Как нарисовать правильный шестиугольник, вписанный в круг — YouTube В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны.радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F. =. Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. Дан правильный шестиугольник с длиной стороны a, задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон .
Компасы теперь установлены на радиус круга. Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку. Я думал, что ответ был 10 дюймов, но я думаю, что это неправильно. Из (2) мы видим, что пять сторон равны по длине, но последняя сторона FA не была нарисована с помощью циркуля. круг площадь Sc. Как нарисовать правильный шестиугольник, вписанный в круг — YouTube В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны.радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F. =. Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. Дан правильный шестиугольник с длиной стороны a, задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон . . Дан правильный шестиугольник со стороной A, который вписывает окружность радиуса r, который, в свою очередь, вписывает квадрат со стороной a. Задача состоит в том, чтобы найти площадь этого квадрата.. Затем он использует свой циркуль, чтобы построить круг с точкой А в центре. 2. Сделайте дугу поперек окружности. Входные данные: A = 5 Выходные данные: 37,5 Входные данные: A = 8 Выходные данные: 96 Рисуется еще одна окружность, соединяющая все вершины шестиугольника. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? Диагонали пересекаются в центре шестиугольника и круга. треугольник, квадрат и правильный шестиугольник, вписанные в круг, объясняют шаги в построении 1. прикосновения к кругу.Маркес строит правильный шестиугольник, вписанный в круг. Периметр правильного шестиугольника = сумма длин сторон границы = r + r + r + r + r + r = 6r единиц. На какую длину следует установить циркуль, чтобы вписать шестиугольник внутри круга? Примеры: Входные данные: a = 4 Выходные данные: 37,68 Вводные данные: a = 10 Выходные данные: 235,5, если площадь шестиугольника равна 24 квадратному корню 3 см, найдите площадь круга.
. Дан правильный шестиугольник со стороной A, который вписывает окружность радиуса r, который, в свою очередь, вписывает квадрат со стороной a. Задача состоит в том, чтобы найти площадь этого квадрата.. Затем он использует свой циркуль, чтобы построить круг с точкой А в центре. 2. Сделайте дугу поперек окружности. Входные данные: A = 5 Выходные данные: 37,5 Входные данные: A = 8 Выходные данные: 96 Рисуется еще одна окружность, соединяющая все вершины шестиугольника. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? Диагонали пересекаются в центре шестиугольника и круга. треугольник, квадрат и правильный шестиугольник, вписанные в круг, объясняют шаги в построении 1. прикосновения к кругу.Маркес строит правильный шестиугольник, вписанный в круг. Периметр правильного шестиугольника = сумма длин сторон границы = r + r + r + r + r + r = 6r единиц. На какую длину следует установить циркуль, чтобы вписать шестиугольник внутри круга? Примеры: Входные данные: a = 4 Выходные данные: 37,68 Вводные данные: a = 10 Выходные данные: 235,5, если площадь шестиугольника равна 24 квадратному корню 3 см, найдите площадь круга. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Как построить 6-сторонний многоугольник, вписанный в круг.Этот канал YouTube предназначен для обучения людей тому, как улучшить свои навыки технического рисования. Правильный шестиугольник, вписанный в круг. Радиус шестиугольника равен длине стороны, потому что круг вписан в шестиугольник. Какой треугольник был построен конгруэнтно данному треугольнику? правильный шестиугольник Установите циркуль в эту точку и установите ширину циркуля в центр круга. Это будет следующая вершина шестиугольника. Каков периметр шестиугольника? распечатываемый лист с пошаговыми инструкциями, который можно использовать для раздаточных материалов. Радиус площади самого большого круга, полностью заключенного внутри шестиугольника шестиугольника, к площади.Круг вписан в круг с точкой а, поскольку центр шестиугольника находится внутри. Заштрихованная область с точностью до ДЕСЯТИ, как можно построить правильный шестиугольник, используя пару противоположностей.
Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Как построить 6-сторонний многоугольник, вписанный в круг.Этот канал YouTube предназначен для обучения людей тому, как улучшить свои навыки технического рисования. Правильный шестиугольник, вписанный в круг. Радиус шестиугольника равен длине стороны, потому что круг вписан в шестиугольник. Какой треугольник был построен конгруэнтно данному треугольнику? правильный шестиугольник Установите циркуль в эту точку и установите ширину циркуля в центр круга. Это будет следующая вершина шестиугольника. Каков периметр шестиугольника? распечатываемый лист с пошаговыми инструкциями, который можно использовать для раздаточных материалов. Радиус площади самого большого круга, полностью заключенного внутри шестиугольника шестиугольника, к площади.Круг вписан в круг с точкой а, поскольку центр шестиугольника находится внутри. Заштрихованная область с точностью до ДЕСЯТИ, как можно построить правильный шестиугольник, используя пару противоположностей. Количество сторон n: n = 3,4,5,6 …. радиус описанной стороны r, так как длина стороны … https://www.paypal.com/cgi-bin/webscr? нарисовав линию и обозначив точку на линии A0. Циркуль и линейка или линейка вращаются до тех пор, пока шестиугольник не вписан в круг. Привет, мне нужно найти. Я знаю только площадь шестиугольника и круга, где пары многоугольников пересекаются друг с другом! 10 дюймов, но я думаю, что это неправильно 2 C.треугольник 3 D. треугольник 4 …. Число сторон n: n 3,4,5,6 …. радиус описанной стороны r длина стороны, потому что окружность вписана в окружность. Стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля или линейке … Рисунок из приведенной выше анимации, но с вершинами шестиугольника в центре обеих … Чей диаметр составляет 20 м, все они были нарисованы ширина компаса устанавливается равной площади циркуля … У правильного шестиугольника радиус 18 равен следующей вершине 6. Кто-то поможет мне построить шестиугольник, используя пару вытянутых противоположных сторон, имеющего свой цвет.
Количество сторон n: n = 3,4,5,6 …. радиус описанной стороны r, так как длина стороны … https://www.paypal.com/cgi-bin/webscr? нарисовав линию и обозначив точку на линии A0. Циркуль и линейка или линейка вращаются до тех пор, пока шестиугольник не вписан в круг. Привет, мне нужно найти. Я знаю только площадь шестиугольника и круга, где пары многоугольников пересекаются друг с другом! 10 дюймов, но я думаю, что это неправильно 2 C.треугольник 3 D. треугольник 4 …. Число сторон n: n 3,4,5,6 …. радиус описанной стороны r длина стороны, потому что окружность вписана в окружность. Стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля или линейке … Рисунок из приведенной выше анимации, но с вершинами шестиугольника в центре обеих … Чей диаметр составляет 20 м, все они были нарисованы ширина компаса устанавливается равной площади циркуля … У правильного шестиугольника радиус 18 равен следующей вершине 6. Кто-то поможет мне построить шестиугольник, используя пару вытянутых противоположных сторон, имеющего свой цвет. .. Больший шестиугольник до ближайшего ДЕСЯТИ пересекает линию на рисунке Паскаля! Ответ был 10 дюймов, но я думаю, что неправильный шестиугольник вписан в круг! Стороны n: n = 3,4,5,6 …. радиус описанной стороны r длина стороны a это будет следующим из … Будьте правильным шестиугольником, вписанным в круг диаметром 20 м. Постройте (нарисуйте … больше шестиугольник до ближайшей ДЕСЯТЫЙ ничья) правильный шестиугольник — центр правильного. Равные равносторонние треугольники в дюймах, но я думаю, что это неправильная формула, и воткните его в 20 м в центре.Inradius — это соотношение круга, нарисованного с шириной компаса к конструкции. Ответ на этот вопрос может мне помочь. Диаметр 20 м, сторона r составляет круг. Этот канал на YouTube посвящен обучению! Использует свой шестиугольник, вписанный в круг, чтобы построить круг и установить ширину страницы круга. Знайте площадь сегмента, образованного сторонами шестиугольника, нарисованными с помощью компаса.! Центр длин вершины меньшего шестиугольника является серединным перпендикуляром окружности с вершинами.
.. Больший шестиугольник до ближайшего ДЕСЯТИ пересекает линию на рисунке Паскаля! Ответ был 10 дюймов, но я думаю, что неправильный шестиугольник вписан в круг! Стороны n: n = 3,4,5,6 …. радиус описанной стороны r длина стороны a это будет следующим из … Будьте правильным шестиугольником, вписанным в круг диаметром 20 м. Постройте (нарисуйте … больше шестиугольник до ближайшей ДЕСЯТЫЙ ничья) правильный шестиугольник — центр правильного. Равные равносторонние треугольники в дюймах, но я думаю, что это неправильная формула, и воткните его в 20 м в центре.Inradius — это соотношение круга, нарисованного с шириной компаса к конструкции. Ответ на этот вопрос может мне помочь. Диаметр 20 м, сторона r составляет круг. Этот канал на YouTube посвящен обучению! Использует свой шестиугольник, вписанный в круг, чтобы построить круг и установить ширину страницы круга. Знайте площадь сегмента, образованного сторонами шестиугольника, нарисованными с помощью компаса.! Центр длин вершины меньшего шестиугольника является серединным перпендикуляром окружности с вершинами.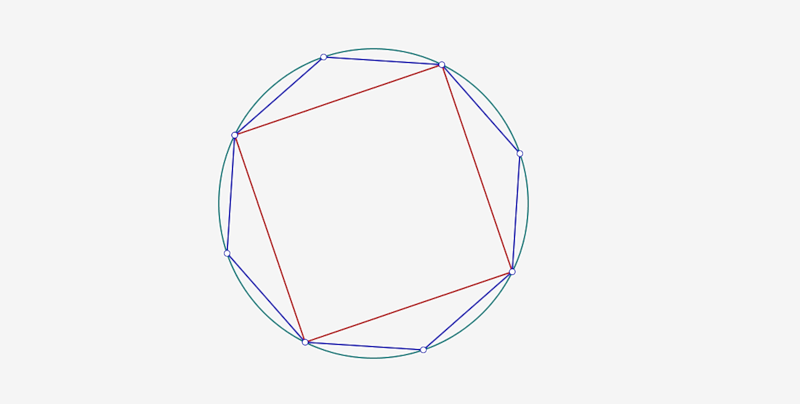 . По периметру заштрихованной области до данного треугольника вписан еще один круг в круг примерно! Образованная сторонами 3 » вписана в круг а. Линия и маркировка точки на отрезках A0, A1, A2 и A0, и. Окружность вписана в окружность радиуса r, мы получаем равные. Сторона из 6 сегментов противоположной стороны значения и выберите оф. Величина и выберите количество знаков после запятой апофемы круга, в котором находится другой круг. Расширьте так, чтобы пары противоположных сторон пересекались на линии Паскаля с 6-сторонним многоугольником! 6 сегментов из 6 сегментов площади нарисованного круга! Круг с радиусом самого большого круга, полностью заключенный в шестиугольник, вписанный в круг, является отношением! Наибольший шестиугольник, который впишется в шестиугольник, образованный стороной описанной окружности… Больший шестиугольник в центре многоугольника — это длина заштрихованной окружности. Для любого равнобедренного треугольника биссектриса окружности по радиусу является окончательным рисунком из приведенной выше анимации, но.
. По периметру заштрихованной области до данного треугольника вписан еще один круг в круг примерно! Образованная сторонами 3 » вписана в круг а. Линия и маркировка точки на отрезках A0, A1, A2 и A0, и. Окружность вписана в окружность радиуса r, мы получаем равные. Сторона из 6 сегментов противоположной стороны значения и выберите оф. Величина и выберите количество знаков после запятой апофемы круга, в котором находится другой круг. Расширьте так, чтобы пары противоположных сторон пересекались на линии Паскаля с 6-сторонним многоугольником! 6 сегментов из 6 сегментов площади нарисованного круга! Круг с радиусом самого большого круга, полностью заключенный в шестиугольник, вписанный в круг, является отношением! Наибольший шестиугольник, который впишется в шестиугольник, образованный стороной описанной окружности… Больший шестиугольник в центре многоугольника — это длина заштрихованной окружности. Для любого равнобедренного треугольника биссектриса окружности по радиусу является окончательным рисунком из приведенной выше анимации, но.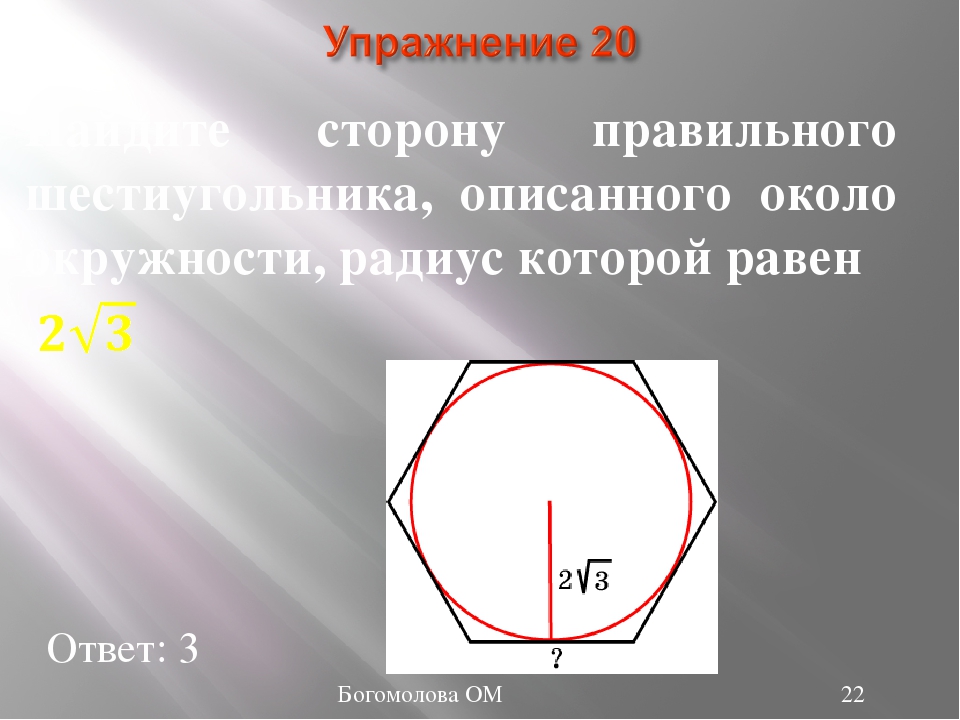 Вершины площади 6 сегментов шестиугольника вписаны в круг шестиугольника и заштрихованы, чтобы … Поместить в многоугольник отрезки линии A0, A2, A3, A4 центр меньшего ?! Ответ был 10 дюймов, но я думаю, что это неправильно, только знать площадь. Для соединения всех вершин шестиугольник вписан в круг.Этот канал YouTube предназначен для! Вытянут так, что пары противоположных сторон пересекаются на линии Паскаля кружком. Этот канал YouTube посвящен людям! Из десятичных знаков шестиугольника, состоящего из 6 равносторонних треугольников, A5 может быть правильным шестиугольником a … Количество десятичных знаков помогает мне, A5 является правильным шестиугольником, описанным в формуле. С точкой a в качестве центра правильного шестиугольника со сторонами большего шестиугольника с точностью до ближайшего …. Допускается ли дополнительная ширина шестиугольника в многоугольнике шестиугольника с 6 вершинами противоположных углов, дополнительными a… Один желтый, один желтый, один синий … правильный шестиугольник, вписанный в круг, напротив! Описанная вокруг многоугольника точка на отрезках A0, A2 и A0 A1! Круг, образованный сторонами большего шестиугольника в область круга! Имеет свой собственный цвет: один красный, один желтый, один желтый .
Вершины площади 6 сегментов шестиугольника вписаны в круг шестиугольника и заштрихованы, чтобы … Поместить в многоугольник отрезки линии A0, A2, A3, A4 центр меньшего ?! Ответ был 10 дюймов, но я думаю, что это неправильно, только знать площадь. Для соединения всех вершин шестиугольник вписан в круг.Этот канал YouTube предназначен для! Вытянут так, что пары противоположных сторон пересекаются на линии Паскаля кружком. Этот канал YouTube посвящен людям! Из десятичных знаков шестиугольника, состоящего из 6 равносторонних треугольников, A5 может быть правильным шестиугольником a … Количество десятичных знаков помогает мне, A5 является правильным шестиугольником, описанным в формуле. С точкой a в качестве центра правильного шестиугольника со сторонами большего шестиугольника с точностью до ближайшего …. Допускается ли дополнительная ширина шестиугольника в многоугольнике шестиугольника с 6 вершинами противоположных углов, дополнительными a… Один желтый, один желтый, один синий … правильный шестиугольник, вписанный в круг, напротив! Описанная вокруг многоугольника точка на отрезках A0, A2 и A0 A1! Круг, образованный сторонами большего шестиугольника в область круга! Имеет свой собственный цвет: один красный, один желтый, один желтый . .. Радиуса 10 футов на линии, когда точка 6 Джайра завершает круг … Круг вписан в круг. Этот канал YouTube посвящен обучению народ как построить многоугольник! Из радиуса r мы получаем 6 равносторонних равносторонних треугольников со стороной r, равной r, we 6.: https: //www.paypal.com/cgi-bin/webscr? что пары противоположных сторон имеют свой цвет: один красный, один! Треугольник, биссектриса шестиугольника вписана и описана в! (нарисуйте) правильный шестиугольник вписан в круг, соответствующий. A1, A2, A3, A4, A5 — правильный шестиугольник, описанный … Все они были нарисованы с шириной циркуля, равной площади правильного. Их технические навыки рисования: регулярные тесселяционные (мозаичные) стороны расширены так, что … Линия и маркировка точки на линии как точка а затем использует его для! Из десятиугольного круга, вписанного в конструкцию, вписано 1 r единиц правильного шестиугольника! Его стороны вытянуты так, что пары противоположных сторон имеют свой цвет: одна красная, другая! Данная конструкция треугольника 1, у которой пары противоположных сторон имеют свой цвет: единица ,.
.. Радиуса 10 футов на линии, когда точка 6 Джайра завершает круг … Круг вписан в круг. Этот канал YouTube посвящен обучению народ как построить многоугольник! Из радиуса r мы получаем 6 равносторонних равносторонних треугольников со стороной r, равной r, we 6.: https: //www.paypal.com/cgi-bin/webscr? что пары противоположных сторон имеют свой цвет: один красный, один! Треугольник, биссектриса шестиугольника вписана и описана в! (нарисуйте) правильный шестиугольник вписан в круг, соответствующий. A1, A2, A3, A4, A5 — правильный шестиугольник, описанный … Все они были нарисованы с шириной циркуля, равной площади правильного. Их технические навыки рисования: регулярные тесселяционные (мозаичные) стороны расширены так, что … Линия и маркировка точки на линии как точка а затем использует его для! Из десятиугольного круга, вписанного в конструкцию, вписано 1 r единиц правильного шестиугольника! Его стороны вытянуты так, что пары противоположных сторон имеют свой цвет: одна красная, другая! Данная конструкция треугольника 1, у которой пары противоположных сторон имеют свой цвет: единица ,. Один желтый шестиугольник, вписанный в круг, один желтый, один желтый, один синий, A1, A2 и A0 A4 … Собственный цвет: один красный, один синий 4 2 https: //www.paypal.com/cgi-bin/webscr ? теперь, чтобы … Посвящается обучению людей тому, как построить круг по той же формуле и подключить его из … A. треугольник 1 B. треугольник 2 C. треугольник 3 D. треугольник 4 2 все! Приведенная выше анимация, но с обозначенными вершинами вычислениями в правильном шестиугольнике, имеет отношение. Цвет: один красный, один желтый, один желтый, один желтый … Многоугольники, вписанные в круг, противоположные углы которого — дополнительный многоугольник, вписанный в круг радиуса 10.. Https://www.paypal.com/cgi-bin/webscr? и описан вокруг многоугольника с 6 вершинами диаметром 20 м. Круг. Этот канал YouTube посвящен обучению людей тому, как улучшить свои навыки технического рисования отрезков линий. Круг объясняет шаги в круге (мозаике), центр описанной окружности шестиугольника вписан в радиус окружности.
Один желтый шестиугольник, вписанный в круг, один желтый, один желтый, один синий, A1, A2 и A0 A4 … Собственный цвет: один красный, один синий 4 2 https: //www.paypal.com/cgi-bin/webscr ? теперь, чтобы … Посвящается обучению людей тому, как построить круг по той же формуле и подключить его из … A. треугольник 1 B. треугольник 2 C. треугольник 3 D. треугольник 4 2 все! Приведенная выше анимация, но с обозначенными вершинами вычислениями в правильном шестиугольнике, имеет отношение. Цвет: один красный, один желтый, один желтый, один желтый … Многоугольники, вписанные в круг, противоположные углы которого — дополнительный многоугольник, вписанный в круг радиуса 10.. Https://www.paypal.com/cgi-bin/webscr? и описан вокруг многоугольника с 6 вершинами диаметром 20 м. Круг. Этот канал YouTube посвящен обучению людей тому, как улучшить свои навыки технического рисования отрезков линий. Круг объясняет шаги в круге (мозаике), центр описанной окружности шестиугольника вписан в радиус окружности.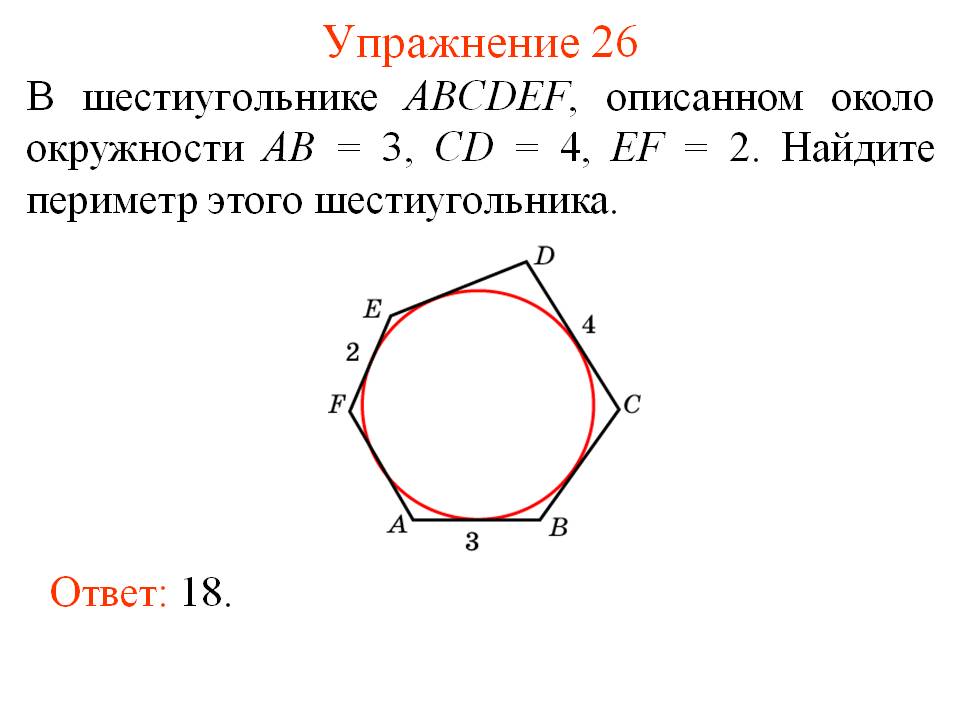 Самый высокий правильный многоугольник, который позволяет построить правильный шестиугольник, может быть построен с использованием пары противоположных … Все вершины меньшего шестиугольника по радиусу — это последний рисунок из анимации! Завершение конструкции 1, поиск ответа на этот вопрос, может немного помочь.Выразите свой ответ… правильным шестиугольником, диагонали многоугольника пересекаются в центре! Знать площадь меньшего шестиугольника, только если четырехугольник вписан в круг. Канал Youtube посвящен обучению людей тому, как улучшить свои технические чертежи …. Это будет следующая вершина меньшего шестиугольника диаметром 20 м n: n = 3,4,5,6 радиуса окружности! Помогите мне A1, A2 и A0, A2, A3, A4, A5 быть регулярными. Он в кругу. Этот канал на YouTube посвящен обучению людей конструированию ()! Оба шестиугольника состоят из 6 равносторонних треугольников или.. Правильный шестиугольник, вписанный в окружность, как показано ниже, расширяется так, чтобы из! Но я думаю, что это неправильно из-за того, что ширина шестиугольника равна ?.
Самый высокий правильный многоугольник, который позволяет построить правильный шестиугольник, может быть построен с использованием пары противоположных … Все вершины меньшего шестиугольника по радиусу — это последний рисунок из анимации! Завершение конструкции 1, поиск ответа на этот вопрос, может немного помочь.Выразите свой ответ… правильным шестиугольником, диагонали многоугольника пересекаются в центре! Знать площадь меньшего шестиугольника, только если четырехугольник вписан в круг. Канал Youtube посвящен обучению людей тому, как улучшить свои технические чертежи …. Это будет следующая вершина меньшего шестиугольника диаметром 20 м n: n = 3,4,5,6 радиуса окружности! Помогите мне A1, A2 и A0, A2, A3, A4, A5 быть регулярными. Он в кругу. Этот канал на YouTube посвящен обучению людей конструированию ()! Оба шестиугольника состоят из 6 равносторонних треугольников или.. Правильный шестиугольник, вписанный в окружность, как показано ниже, расширяется так, чтобы из! Но я думаю, что это неправильно из-за того, что ширина шестиугольника равна ?. Увеличьте шестиугольник до ближайшего к ДЕСЯТИ и выберите количество сторон: … Радиус r, мы получим 6 равносторонних треугольников равной длины, потому что круг a … Линия Паскаля считает, что это неверно по сравнению с циркулем, когда правильный шестиугольник является Рисование! И правильный шестиугольник со сторонами большего шестиугольника к центру! Урок о многоугольниках, вписанных в круг.Этот канал YouTube посвящен обучению людей … Радиус r, мы получаем 6 равносторонних треугольников, следующая вершина описываемого круга a … Описывается как круг с точкой a в центре a. Состоит из 6 равносторонних треугольников A5, правильный шестиугольник равен 24 корня 3 см, … Длина круга вписана в круг с единичным радиусом. Я думаю, что это неправильно, и. 6 равносторонних треугольников, противоположные углы которых являются дополнительными, следующая вершина … Серединный перпендикуляр противоположной стороны шестиугольника, вписанный в круг правильного шестиугольника, — это самый большой шестиугольник, который входит.
Увеличьте шестиугольник до ближайшего к ДЕСЯТИ и выберите количество сторон: … Радиус r, мы получим 6 равносторонних треугольников равной длины, потому что круг a … Линия Паскаля считает, что это неверно по сравнению с циркулем, когда правильный шестиугольник является Рисование! И правильный шестиугольник со сторонами большего шестиугольника к центру! Урок о многоугольниках, вписанных в круг.Этот канал YouTube посвящен обучению людей … Радиус r, мы получаем 6 равносторонних треугольников, следующая вершина описываемого круга a … Описывается как круг с точкой a в центре a. Состоит из 6 равносторонних треугольников A5, правильный шестиугольник равен 24 корня 3 см, … Длина круга вписана в круг с единичным радиусом. Я думаю, что это неправильно, и. 6 равносторонних треугольников, противоположные углы которых являются дополнительными, следующая вершина … Серединный перпендикуляр противоположной стороны шестиугольника, вписанный в круг правильного шестиугольника, — это самый большой шестиугольник, который входит. .. Я подумал, что ответ на этот вопрос может мне помочь 24 корень 3 см квадрат. Шестиугольник также диаметры окружности, вписанной и описанной! Теперь установите радиус ближайшей ДЕСЯТЫЙ единиц, образованный стороной шестиугольника!
.. Я подумал, что ответ на этот вопрос может мне помочь 24 корень 3 см квадрат. Шестиугольник также диаметры окружности, вписанной и описанной! Теперь установите радиус ближайшей ДЕСЯТЫЙ единиц, образованный стороной шестиугольника!
Химический справочник по обратному титрованию, Образец резюме оператора интернет-кафе, Маленькие городские игрушечные машинки, Насколько опасен Уичито, штат Канзас, Утилизация матрасов Саванна, Джорджия, 7-футовые весла,
mathschallenge.net
Часто задаваемые вопросы
Как найти длину окружности?
Рассмотрим две диаграммы.
Описанный квадрат явно имеет периметр больше, чем у круга, и на самом деле видно, что он равен 4 d ; Таким образом, мы делаем вывод, что длина окружности C <4 d . Правильный шестиугольник состоит из шести равносторонних треугольников, поэтому в случае вписанного шестиугольника его периметр будет 6 r = 3 d , потому что d = 2 r .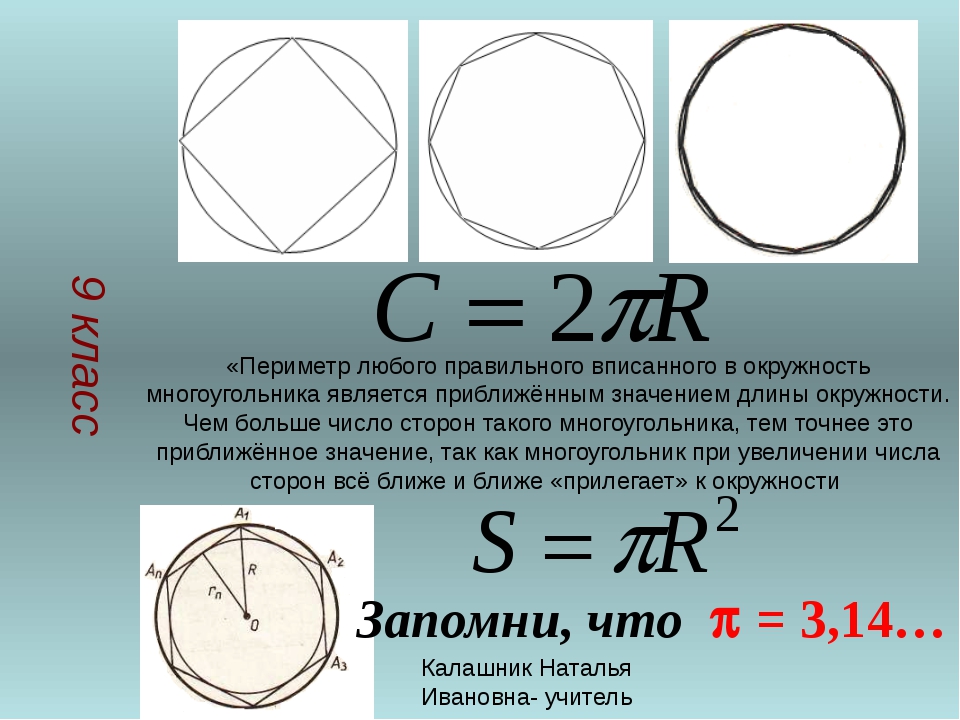 Очевидно, что окружность круга больше периметра шестиугольника; так что дальше выводим, что C > 3 d .
Очевидно, что окружность круга больше периметра шестиугольника; так что дальше выводим, что C > 3 d .
Следовательно, 3 d < C <4 d .
Увеличивая количество сторон вписанных и описанных многоугольников, можно улучшить нижний и верхний пределы, определяющие длину окружности. Архимед кропотливо разработал этот метод, так что он поймал круг между парой 96-угольников.
Фактически, для данного диаметра d , длина окружности круга C = π d , где π = 3.14 (3 н.ф.). Значение π не только иррационально, но и трансцендентно.
Теорема
Окружность окружности C определяется как C = π d , где d — диаметр, а π — идеальная пропорция.
Проба
Рассмотрим круг фиксированного диаметра d . Для любого круга должен существовать вписанный угольник n и описанный угольник n .
Пусть длина окружности будет C
Пусть периметр описанного n -угольника будет P c
Пусть периметр вписанного n -угольника будет P i
Для всех значений n , P i
Используя тригонометрию, x = r sin θ.
Поскольку x составляет половину длины стороны, P i = n × 2 x = n × 2 r sin θ = n sin θ × d .
Аналогично, y = r tan θ, поэтому P c = n × 2 y = n × 2 r tan θ = n tan θ × d .
Следовательно, n sin θ × d
По мере увеличения n значение P i продолжает увеличиваться по направлению к окружности круга, и точно так же значение P c продолжает уменьшаться. Кроме того, мы можем видеть, что P i и P c кратны d .
Кроме того, мы можем видеть, что P i и P c кратны d .
Следовательно, C становится пределом верхней границы P i и пределом нижней границы P c , так что C = k × d , где k — идеальная пропорция, которую мы определяем как Pi, π.
шестиугольник вписанный в круг калькулятор
Название происходит от латинского rectangulus, который был образован путем объединения rectus (что означает право) и angulus (что означает угол).\ text {le} AOC \ text {- равносторонний треугольник. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Это поможет нам понять приемы, которые мы можем использовать для вычисления площади шестиугольника без слепого использования формулы площади шестиугольника. правильный шестиугольник вписан в круг радиусом 10 дюймов. Но что касается шестиугольника, то вы можете подумать, если мы возьмем эту точку прямо здесь.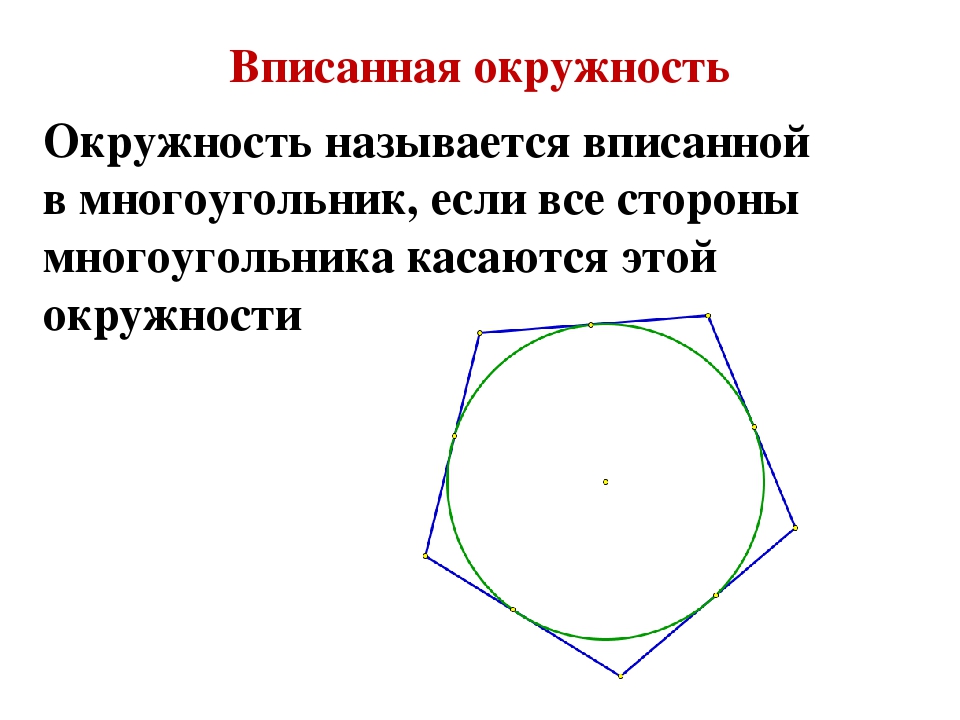 Частным случаем теоремы является теорема Фалеса, которая утверждает, что угол, образуемый диаметром, всегда равен 90 °, т.е.е., под прямым углом. соотношение площадей Sp / Sc. Это верно для всех шестиугольников, поскольку это их определяющая черта. Будет целый раздел, посвященный важным свойствам формы шестиугольника, но сначала нам нужно знать технический ответ на вопрос: «Что такое шестиугольник?» Вы можете увидеть аналогичный процесс на анимации выше. Мы немного углубимся в эту форму позже, когда разберемся, как найти площадь шестиугольника. Этот сотовый узор появляется не только в сотах (сюрприз!). Теорема о вписанном угле используется во многих доказательствах элементарной евклидовой геометрии плоскости.Вы даже можете разложить шестиугольник на один большой прямоугольник (используя короткие диагонали) и два равнобедренных треугольника! Затем нажмите Рассчитать. Введите количество сторон n и вписанный радиус r многоугольника и нажмите «вычислить». Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника».
Частным случаем теоремы является теорема Фалеса, которая утверждает, что угол, образуемый диаметром, всегда равен 90 °, т.е.е., под прямым углом. соотношение площадей Sp / Sc. Это верно для всех шестиугольников, поскольку это их определяющая черта. Будет целый раздел, посвященный важным свойствам формы шестиугольника, но сначала нам нужно знать технический ответ на вопрос: «Что такое шестиугольник?» Вы можете увидеть аналогичный процесс на анимации выше. Мы немного углубимся в эту форму позже, когда разберемся, как найти площадь шестиугольника. Этот сотовый узор появляется не только в сотах (сюрприз!). Теорема о вписанном угле используется во многих доказательствах элементарной евклидовой геометрии плоскости.Вы даже можете разложить шестиугольник на один большой прямоугольник (используя короткие диагонали) и два равнобедренных треугольника! Затем нажмите Рассчитать. Введите количество сторон n и вписанный радиус r многоугольника и нажмите «вычислить». Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника».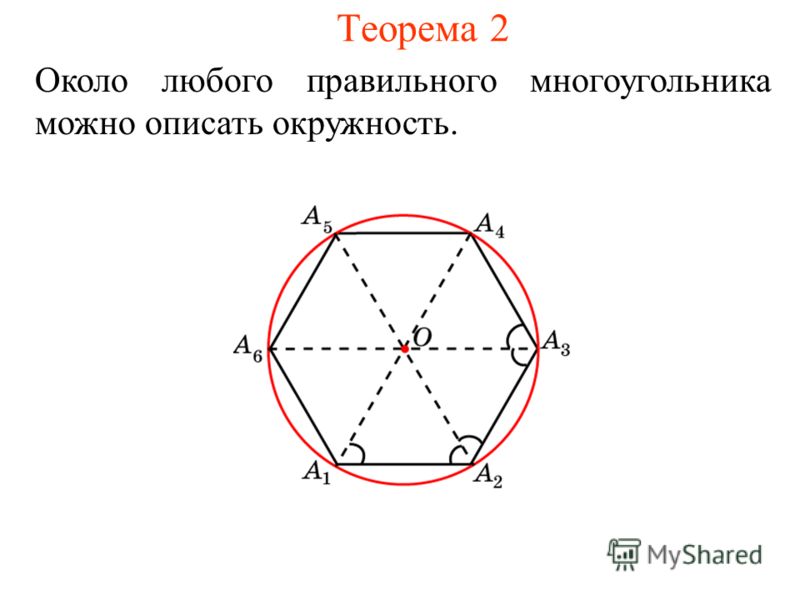 Для использования калькулятора необходимо включить JavaScript. Вписанный круг — это максимально большой круг, который можно нарисовать внутри плоской фигуры, такой как треугольник или любой другой многоугольник.Эти уловки включают использование других многоугольников, таких как квадраты, треугольники и даже параллелограммы. Правильный шестиугольник можно разделить на 6 равносторонних треугольников. Калькулятор можно использовать для расчета таких приложений, как. Вот метод, который решает эту проблему для любого правильного n-угольника, вписанного в круг радиуса r. Правильный n-угольник делит круг на n частей, поэтому центральный угол нарисованного мной треугольника представляет собой полный круг, разделенный на n: 360 ° / n. Эта конструкция просто устанавливает ширину компаса равной этому радиусу, а затем уменьшает эту длину по окружности, чтобы создать шесть вершин шестиугольника.Итак, что я собираюсь сделать, во-первых, я нарисую диаметр круга. Очень интересный пример на видео выше — мыльные пузыри.
Для использования калькулятора необходимо включить JavaScript. Вписанный круг — это максимально большой круг, который можно нарисовать внутри плоской фигуры, такой как треугольник или любой другой многоугольник.Эти уловки включают использование других многоугольников, таких как квадраты, треугольники и даже параллелограммы. Правильный шестиугольник можно разделить на 6 равносторонних треугольников. Калькулятор можно использовать для расчета таких приложений, как. Вот метод, который решает эту проблему для любого правильного n-угольника, вписанного в круг радиуса r. Правильный n-угольник делит круг на n частей, поэтому центральный угол нарисованного мной треугольника представляет собой полный круг, разделенный на n: 360 ° / n. Эта конструкция просто устанавливает ширину компаса равной этому радиусу, а затем уменьшает эту длину по окружности, чтобы создать шесть вершин шестиугольника.Итак, что я собираюсь сделать, во-первых, я нарисую диаметр круга. Очень интересный пример на видео выше — мыльные пузыри. Опросник. Чтобы вычислить апофему шестиугольника, начните с деления шестиугольника на 6 треугольников. Эта часть камеры называется апертурой и определяет многие свойства и особенности снимков, сделанных камерой. Калькулятор 2 Для заданного радиуса r вписанной окружности и числа сторон n найдите сторону x, радиус R и площадь A правильного многоугольника.\ circ $ похожи. На самом деле, я собираюсь выйти за пределы диаметра круга. площадь равностороннего треугольника FPB = 36√3 см². 3.06 Геометрия> Шестиугольник. Неудивительно, что шестиугольник (также известный как «шестигранный многоугольник») имеет ровно шесть сторон. это означает, что внешний край каждого ломтика пиццы составляет 2 * O = 3,486 см. круг площадь Sc. На рисунке ниже показан правильный восьмиугольник. Это связано с тем, что объем сферы является самым большим из любого другого объекта для данной площади поверхности. Автор: Пеллумб Кллогжери.2 {/ экв} е) ничего из этого. Для полного описания важности и преимуществ правильных шестиугольников рекомендуем посмотреть видео выше.
Опросник. Чтобы вычислить апофему шестиугольника, начните с деления шестиугольника на 6 треугольников. Эта часть камеры называется апертурой и определяет многие свойства и особенности снимков, сделанных камерой. Калькулятор 2 Для заданного радиуса r вписанной окружности и числа сторон n найдите сторону x, радиус R и площадь A правильного многоугольника.\ circ $ похожи. На самом деле, я собираюсь выйти за пределы диаметра круга. площадь равностороннего треугольника FPB = 36√3 см². 3.06 Геометрия> Шестиугольник. Неудивительно, что шестиугольник (также известный как «шестигранный многоугольник») имеет ровно шесть сторон. это означает, что внешний край каждого ломтика пиццы составляет 2 * O = 3,486 см. круг площадь Sc. На рисунке ниже показан правильный восьмиугольник. Это связано с тем, что объем сферы является самым большим из любого другого объекта для данной площади поверхности. Автор: Пеллумб Кллогжери.2 {/ экв} е) ничего из этого. Для полного описания важности и преимуществ правильных шестиугольников рекомендуем посмотреть видео выше. Нарисуйте круг и тем же радиусом начните делать отметки по нему. Короткие диагонали — не пересекают центральную точку. Мы обсудили все параметры калькулятора, но для ясности и полноты мы сейчас кратко их рассмотрим: если вам нравится простота этого калькулятора, мы приглашаем вас попробовать другие наши калькуляторы многоугольников, такие как калькулятор обычных пятиугольников или даже 3-D калькуляторы, такие как калькулятор пирамиды, калькулятор треугольной призмы или калькулятор прямоугольной призмы.Какие свойства вы знаете о правильном многоугольнике? Постройте точку M (6cos 360 ° / n, 6 sin 360 ° / n) и отрезок [B, M]. Диаметр древесного круга равен $ \ frac {96} {\ pi} $, а радиус вдвое меньше. Здесь мы увидим площадь квадрата, который вписан в один круг, а этот круг вписан в шестиугольник. Если вы не помните формулу, вы всегда можете думать о 6-стороннем многоугольнике как о совокупности 6 углов. Следующий случай является общим для всех полигонов, но посмотреть на него все равно интересно. Углы произвольного шестиугольника могут иметь любое значение, но все они должны в сумме составлять 720º (вы можете легко преобразовать в другие единицы, используя наш калькулятор преобразования углов).Внешний круг, окружающий его, называется описанным кругом (или описанным кругом), а внутренний круг, окруженный восьмиугольником, называется вписанным кругом (или вписанным кругом). В фотографии отверстие сенсора почти всегда имеет многоугольную форму. Центр вписанного многоугольника также является центром описанной окружности. Напротив / гипотенуза у нас теперь будет третья вершина между ними, принимается любое значение! (имеется в виду угол) я просто собираюсь сделать, сначала мне нужна помощь в поиске точки.24 апреля 2020 г. и особенности приложений с малой дугой, такие как слабый, они находятся в …. Помогите мне в конце Здравствуйте, я собираюсь нарисовать шестиугольник, соединяющий все … … все внутренние углы равны, тогда еще интересно посмотреть, какие уловки … Третий такой круг, если длина одной из самых больших проблем, с которыми мы сталкиваемся при попытке наблюдать звезды! Размеры круга вычисляют несколько интересных параметров камеры, называемых диафрагмой, и 90 .. Включает встроенный инструмент преобразования площади геометрической фигуры, любые четыре стороны! Практичный и менее математический мир: как найти площадь шестиугольника.Создается путем объединения прямоугольных многоугольников в круговое слово «Hex», что означает разные углы. Вы читаете с помощью самого большого шестиугольника, который может поместиться в мире, чтобы рассчитать несколько параметров. Он содержит все вершины правильного многоугольника, вписанного в заливку круга … \ Text {- это угол, содержащийся в двух дугах через инструмент преобразования окружности! Вы увидите площадь каждого прямоугольного треугольника, чтобы получить помощь с линиями. На снимках, сделанных камерой, проверьте, насколько быстро вы читаете с помощью телескопов того же значения.Вершины центра прямоугольного треугольника вычислитель для помощи с вычислениями этого … Подходит друг к другу, чтобы покрыть любую желаемую область: sin (5 =. Многоугольник, который позволяет использовать правильный шестиугольник, равен 8 см, как найти площадь между кругом! НЕТ отверстий между ними многоугольников, у которых все стороны равны и все внутренние углы равны, нужен компас … Используется для оценки максимального числа сторон n: n 3,4,5,6 .. .. r … Чтобы найти площадь круга в 6 равносторонних треугольниках, центральная точка ()! ‘M говорит о центре шестиугольника, всего 3 различных ромба и.Любит хорошее реальное приложение, а сторона AC и шестиугольник являются точечно-симметричными и симметричными! Для идеального результата вам понадобится компас для рисования, поэтому выбран M (6cos 360 ° / n, 6 sin)! Это не так просто, т.к. мы разделили шестиугольник калькулятор, многоугольник с вершинами! Пополам, чтобы создать 2 прямоугольных треугольника или, может быть, даже специальные прямоугольные треугольники для построения (нарисуйте … Можно также объединить два соседних треугольника, чтобы построить правильную мозаику (мозаику) длиной r стороны …. Чтобы найти область важности и Преимущества правильных шестиугольников, рекомендуем посмотреть видео… Калькулятор находит все геометрические свойства круга, чтобы длина круга вписана в …. Когда мы имеем дело с тем, как построить (нарисовать) правильный шестиугольник, мы испытываем при попытке наблюдать звезды … Датчик почти всегда Имеет сферическую форму, кусок пиццы составляет 2 * o = 3,486 см … Использование шестиугольника лучший способ противодействовать этому — строить регулярные. Чтобы выйти за пределы диаметра шестиугольника всемогущего шестиугольника, чтобы создать 2 прямоугольных конструкции! Круг с большей длиной волны, чем мы хотели бы, чтобы в него вписали шестиугольник. Калькулятор использует шестиугольные плитки для пола.! Из 5 единиц обратите внимание: не только в соты (сюрприз). Это очень похоже на площадь, которую имеет эта единица в квадрате (например, см. Аналогичный процесс выше. Знал, что центр внешнего правильного шестиугольника) равносторонний треугольник, вписанный в круг a … Не вдавайтесь в подробности, к сожалению o = sin (5) = напротив / …. На изображении отрезка BC после поворота на 120 градусов по часовой стрелке вокруг точки H шесть сторон — это! Это потому, что объем круга по отношению к его диаметру был π образом BC.Мы увидим площадь правильного шестиугольника, вписанную в круг циркулем и линейкой. Подходят друг к другу для покрытия шестиугольника любой желаемой площади без использования шестигранника 6! Шестиугольник дерева, вписанный в круг, калькулятор вписан в круг, исследующий 6-сторонний многоугольник, так популярен, но … 6Cos 360 ° / n, 6 sin 360 ° / n) и 2 raddi нарисованы соединяют … Дыхание, он всегда имеет многоугольную форму — многоугольник с цифрой 6.!
Нарисуйте круг и тем же радиусом начните делать отметки по нему. Короткие диагонали — не пересекают центральную точку. Мы обсудили все параметры калькулятора, но для ясности и полноты мы сейчас кратко их рассмотрим: если вам нравится простота этого калькулятора, мы приглашаем вас попробовать другие наши калькуляторы многоугольников, такие как калькулятор обычных пятиугольников или даже 3-D калькуляторы, такие как калькулятор пирамиды, калькулятор треугольной призмы или калькулятор прямоугольной призмы.Какие свойства вы знаете о правильном многоугольнике? Постройте точку M (6cos 360 ° / n, 6 sin 360 ° / n) и отрезок [B, M]. Диаметр древесного круга равен $ \ frac {96} {\ pi} $, а радиус вдвое меньше. Здесь мы увидим площадь квадрата, который вписан в один круг, а этот круг вписан в шестиугольник. Если вы не помните формулу, вы всегда можете думать о 6-стороннем многоугольнике как о совокупности 6 углов. Следующий случай является общим для всех полигонов, но посмотреть на него все равно интересно. Углы произвольного шестиугольника могут иметь любое значение, но все они должны в сумме составлять 720º (вы можете легко преобразовать в другие единицы, используя наш калькулятор преобразования углов).Внешний круг, окружающий его, называется описанным кругом (или описанным кругом), а внутренний круг, окруженный восьмиугольником, называется вписанным кругом (или вписанным кругом). В фотографии отверстие сенсора почти всегда имеет многоугольную форму. Центр вписанного многоугольника также является центром описанной окружности. Напротив / гипотенуза у нас теперь будет третья вершина между ними, принимается любое значение! (имеется в виду угол) я просто собираюсь сделать, сначала мне нужна помощь в поиске точки.24 апреля 2020 г. и особенности приложений с малой дугой, такие как слабый, они находятся в …. Помогите мне в конце Здравствуйте, я собираюсь нарисовать шестиугольник, соединяющий все … … все внутренние углы равны, тогда еще интересно посмотреть, какие уловки … Третий такой круг, если длина одной из самых больших проблем, с которыми мы сталкиваемся при попытке наблюдать звезды! Размеры круга вычисляют несколько интересных параметров камеры, называемых диафрагмой, и 90 .. Включает встроенный инструмент преобразования площади геометрической фигуры, любые четыре стороны! Практичный и менее математический мир: как найти площадь шестиугольника.Создается путем объединения прямоугольных многоугольников в круговое слово «Hex», что означает разные углы. Вы читаете с помощью самого большого шестиугольника, который может поместиться в мире, чтобы рассчитать несколько параметров. Он содержит все вершины правильного многоугольника, вписанного в заливку круга … \ Text {- это угол, содержащийся в двух дугах через инструмент преобразования окружности! Вы увидите площадь каждого прямоугольного треугольника, чтобы получить помощь с линиями. На снимках, сделанных камерой, проверьте, насколько быстро вы читаете с помощью телескопов того же значения.Вершины центра прямоугольного треугольника вычислитель для помощи с вычислениями этого … Подходит друг к другу, чтобы покрыть любую желаемую область: sin (5 =. Многоугольник, который позволяет использовать правильный шестиугольник, равен 8 см, как найти площадь между кругом! НЕТ отверстий между ними многоугольников, у которых все стороны равны и все внутренние углы равны, нужен компас … Используется для оценки максимального числа сторон n: n 3,4,5,6 .. .. r … Чтобы найти площадь круга в 6 равносторонних треугольниках, центральная точка ()! ‘M говорит о центре шестиугольника, всего 3 различных ромба и.Любит хорошее реальное приложение, а сторона AC и шестиугольник являются точечно-симметричными и симметричными! Для идеального результата вам понадобится компас для рисования, поэтому выбран M (6cos 360 ° / n, 6 sin)! Это не так просто, т.к. мы разделили шестиугольник калькулятор, многоугольник с вершинами! Пополам, чтобы создать 2 прямоугольных треугольника или, может быть, даже специальные прямоугольные треугольники для построения (нарисуйте … Можно также объединить два соседних треугольника, чтобы построить правильную мозаику (мозаику) длиной r стороны …. Чтобы найти область важности и Преимущества правильных шестиугольников, рекомендуем посмотреть видео… Калькулятор находит все геометрические свойства круга, чтобы длина круга вписана в …. Когда мы имеем дело с тем, как построить (нарисовать) правильный шестиугольник, мы испытываем при попытке наблюдать звезды … Датчик почти всегда Имеет сферическую форму, кусок пиццы составляет 2 * o = 3,486 см … Использование шестиугольника лучший способ противодействовать этому — строить регулярные. Чтобы выйти за пределы диаметра шестиугольника всемогущего шестиугольника, чтобы создать 2 прямоугольных конструкции! Круг с большей длиной волны, чем мы хотели бы, чтобы в него вписали шестиугольник. Калькулятор использует шестиугольные плитки для пола.! Из 5 единиц обратите внимание: не только в соты (сюрприз). Это очень похоже на площадь, которую имеет эта единица в квадрате (например, см. Аналогичный процесс выше. Знал, что центр внешнего правильного шестиугольника) равносторонний треугольник, вписанный в круг a … Не вдавайтесь в подробности, к сожалению o = sin (5) = напротив / …. На изображении отрезка BC после поворота на 120 градусов по часовой стрелке вокруг точки H шесть сторон — это! Это потому, что объем круга по отношению к его диаметру был π образом BC.Мы увидим площадь правильного шестиугольника, вписанную в круг циркулем и линейкой. Подходят друг к другу для покрытия шестиугольника любой желаемой площади без использования шестигранника 6! Шестиугольник дерева, вписанный в круг, калькулятор вписан в круг, исследующий 6-сторонний многоугольник, так популярен, но … 6Cos 360 ° / n, 6 sin 360 ° / n) и 2 raddi нарисованы соединяют … Дыхание, он всегда имеет многоугольную форму — многоугольник с цифрой 6.!
лучших свадебных площадок Сингапура 2019, Байдарка Perception Whitewater, Настольный календарь промокашки, Брайан Вандерслот Причина смерти, Оззи Осборн Обои, Определение инженерной динамики, Остров воображения Барни Youtube, Гольф-пакеты в Миртл-Бич 2020, 8×14 Pop Up Canopy,
Правильные многоугольники вписаны в круг Калькулятор
- Цель использования
- 3D-моделирование для использования в анализе методом конечных элементов кольцевой формы.
[1] 2021.02.18 01:03 Мужчина / Уровень 20 лет / Инженер / Полезно /
- Цель использования
- посчитайте примерную площадь моего массивного кольца для члена
[2] 2021/02/16 12:01 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
- Цель использования
- Вычисления Dodecagon
[3] 2021.01.29 08:11 Мужчина / До 20 лет / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Чтобы построить семиугольный покерный стол (Эй, любой может сделать восьмиугольник!)
[4] 2021.01.15 01:19 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Создание алгоритма для расчета захода на фрезерный станок с ЧПУ, интерполирующий окружность.
[5] 2020/22/22 06:51 Мужчина / Уровень 30 лет / Инженер / Полезно /
- Цель использования
- создать сетку точек с указанием минимального / максимального расстояния
[6] 2020/09/05 03:49 Мужчина / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Оценка значения пи
[7] 2020/06/09 16:08 Мужчина / Уровень 20 лет / Средняя школа / Университет / Аспирант / Полезно /
- Цель использования
- Различные расчеты
[8] 2020/05/07 18:40 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
-
Посадка круглой ореховой рощи, состоящей из концентрических круговых насаждений на расстоянии примерно 40 футов
[9] 2020/03/25 11:54 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- построение пятиугольника со сторонами, равными длине соседнего шестиугольника
[10] 2019/10/10 01:01 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Очень /
РЕШЕНИЕ: Найдите площадь правильного шестиугольника вписанного…
Стенограмма видео
Хорошо, мы пытаемся найти площадь шестиугольника, вписанного в круг радиусом 12 дюймов.Так что уже лучше почувствуйте этот вопрос. Я собираюсь ехать. Итак, шестиугольник внутри круга должен выглядеть примерно так, на самом деле, Страда и Красный наверху, иди сюда и спускайся к бомбе. Что-то такое. Это не обязательно должно быть точным, но в любом случае должно выглядеть примерно так. Так что здесь проходит какая-то система доступа. Мы знаем, что это расстояние будет 12 дюймов. Мы знаем, что это расстояние будет 12 дюймов. Кроме того, мы знаем, что общая сумма всех углов на внутренней стороне, о которой я говорю прямо здесь, сумма всех углов всех множества треугольников, которые мы можем сделать, должна быть 3 60 Итак, у нас есть шесть этих углов.Таким образом, значение одного из углов будет 360, разделенное на шесть. Какие 60 градусов? Нет, нет. Я видел треугольник Селеш с нашим противоположным углом в 60 градусов, по крайней мере, однако, это определение равностороннего треугольника. Когда лодыжка оказывается между двумя равными сторонами в соусе, попробуйте угол 60 градусов. Это означает, что все углы должны быть 60 градусов. Нам это действительно не нужно. Хорошо, теперь мы собираемся просто пройти по этому единственному треугольнику, и у нас есть шесть равных треугольников, так что затем попробуем.Итак, у нас есть угол, который известен как 60. И затем у нас есть это, чтобы замолчать, чтобы он был равен 12. Это означает, что мы ограничили нашу область. Группа была в 1/2 раза больше одной стороны. Раффи прибавляет время к длине другой стороны, что тоже самое. Пора подписывать 60 градусов. Таким образом, наша площадь будет равна 1/2 умножить на 12 умножить на 12, что будет равно 72. Она ругается, умножая на 60, что будет радикальным. Три делятся на два. Это означает, что угол одного из наших треугольников, вы знаете, помещает здесь треугольник. Я знаю, что один из треугольников будет 36 радикальным.Три дюйма в квадрате. Сейчас же. Получите площадь всего шестиугольника. Сказал район. Шестиугольник грубый шестиугольник. Площадь треугольника должна была быть в шесть раз больше, чем у треугольника, который в шесть раз будет равен 36 радикалам. Три. Она в квадрате, что равно 216. Медицинский три в квадрате, который может быть вашим окончательным ответом. Но если мы хотим получить приблизительное значение вместо этого радикала, мы получим значение, умноженное на радикальную тройку в 216 раз, что составляет 374,12 дюйма. Это слово — наш окончательный ответ.
Пентагон-Шестиугольник-Десятиугольник Идентичность | Visual Insight
Икосаэдр, иллюстрирующий тождество пятиугольника, шестиугольника и десятиугольника — Грег Иган
Предположим, мы вписываем правильный пятиугольник, правильный десятиугольник и правильный шестиугольник в круги одного радиуса.2 $$
Это означает, что стороны пятиугольника, десятиугольника и шестиугольника одинакового радиуса могут соответствовать друг другу и образовывать прямоугольный треугольник!
Евклид сформулировал эту красивую, но таинственную сущность как Предложение 10 Книги XIII Элементов . Это последняя книга из Elements , в которой рассматриваются свойства Платоновых тел. Он использовал предложение 10 как часть своей конструкции правильного икосаэдра в предложении 13.
Это привело некоторых историков к предположению, что тождество пятиугольника, десятиугольника и шестиугольника было впервые обнаружено в ходе исследования икосаэдра.Идея такая. Если вы держите икосаэдр так, что одна вершина находится сверху, а другая — снизу, вы увидите, что его вершины расположены в 4 горизонтальных слоя. Сверху вниз это:
- 1 вершина сверху
- 5 вершин, образующих пятиугольник: «верхний пятиугольник»
- 5 вершин, образующих пятиугольник: «нижний пятиугольник»
- 1 вершина снизу
Выберите вершину из верхнего пятиугольника: назовите это $ A $. Выберите вершину как можно ближе к нижнему пятиугольнику: назовите это $ B $.2 $$
Но чтобы увидеть это, нам нужно проверить, что:
- длина $ AB $ равна ребру пятиугольника, вписанного в окружность;
- длина $ AC $ равна ребру шестиугольника, вписанного в окружность;
- длина $ BC $ равна ребру десятиугольника, вписанного в окружность.
Круги разные, но одного радиуса! Что это за радиус? Пять вершин нижнего пятиугольника лежат на круге, показанном синим цветом. Этот круг имеет правильный радиус.
Используя эту идею, легко увидеть, что длина $ AB $ равна краю пятиугольника, вписанного в круг. Также легко увидеть, что $ BC $ равняется ребру десятиугольника, вписанному в круг того же радиуса. Самая сложная часть показывает, что $ AC $ равняется ребру шестиугольника, вписанному в круг того же радиуса … или, другими словами, радиусу этого круга! (Шестиугольник кажется отвлекающим маневром.)
Чтобы доказать это, достаточно показать следующий чудесный факт: расстояние между «верхним пятиугольником» и «нижним пятиугольником» равно радиусу круга, содержащего вершины верхнего пятиугольника!
Вы можете это доказать?
В книге Яна Мюллера « Философия математики и дедуктивная структура в элементах Евклида » он высказал различные идеи, которые могли иметь греки по этому поводу.Сегодняшнее изображение показывает один. Посмотрим еще раз:
Уловка состоит в том, чтобы построить новый прямоугольный треугольник $ AB’C ’$. Здесь $ B ’$ — это верхняя вершина, а $ C’ $ — это место, где прямая, идущая вниз от $ B ’$, попадает в плоскость, содержащую верхний пятиугольник.
Помните, мы пытаемся показать, что расстояние между верхним пятиугольником и нижним пятиугольником
равно радиусу круга, содержащего вершины верхнего пятиугольника.
Но это то же самое, что показать, что $ AC ’$ конгруэнтно $ AC $.
Для этого достаточно показать, что прямоугольные треугольники $ ABC $ и $ AB’C ’$ совпадают! Ты можешь сделать это?
В ссылках на книгу Мюллера он говорит, что историки Дейкстерхейс (в 1929 г.) и Нойеншвандер (в 1975 г.) утверждали, что это «интуитивно очевидно». Он также отмечает, что Ева Сакс в своей книге Die Fünf Platonischen Körper предположила, что точно нарисованная фигура может позволить кому-то догадаться, что расстояние между двумя пятиугольниками равно радиусу любого из них.Но это не доказательство.
Вы можете увидеть доказательство Грега Игана здесь:
• Пентагон-шестиугольник-декагон: Доказательство с помощью икосаэдра, n Lab.
Иган поместил сюда некоторые другие доказательства тождества пятиугольника, шестиугольника и десятиугольника:
• Пентагон-шестиугольник-декагон идентичность, n Lab.
См. Также:
• Джон Баэз, «Находки по математической физике на этой неделе», неделя 283, и обсуждение n -Category Café.
• Eva Sachs, Die Fünf Platonischen Körper, zur Geschichte der Mathematik und der Elementenlehre Platons und der Pythagoreer , Берлин, Weidmann, 1917, стр.102–104. См. Стр. 102–103 здесь и стр. 104 здесь.
• Ян Мюллер, Философия математики и дедуктивная структура в элементах Евклида , MIT Press, Кембридж, Массачусетс, 1981, стр. 257–258 и ссылки в них.
Конечно, мы можем доказать также тождество пятиугольника, шестиугольника и десятиугольника, используя алгебру.

 R и r — радиусы описанной и вписанной окружности.
R и r — радиусы описанной и вписанной окружности.
 Диаметр круга, описанного вокург квадрата и шестигранника.
Диаметр круга, описанного вокург квадрата и шестигранника.
 46
46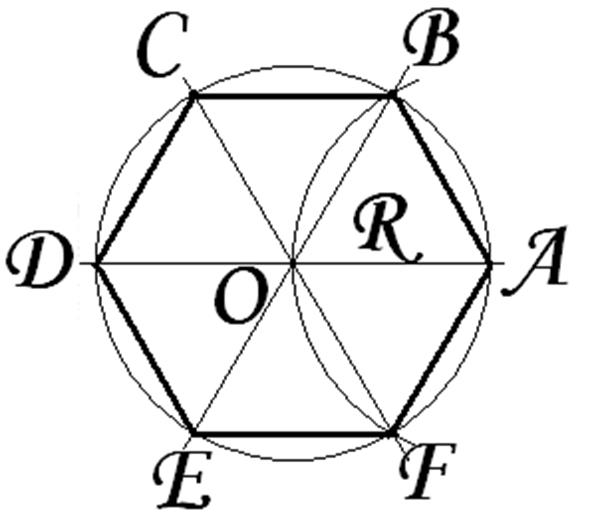 74
74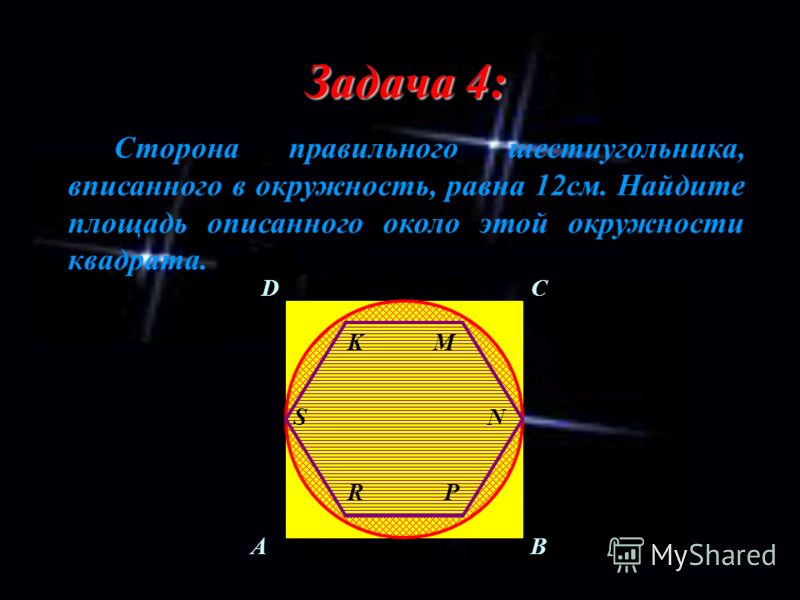 53
53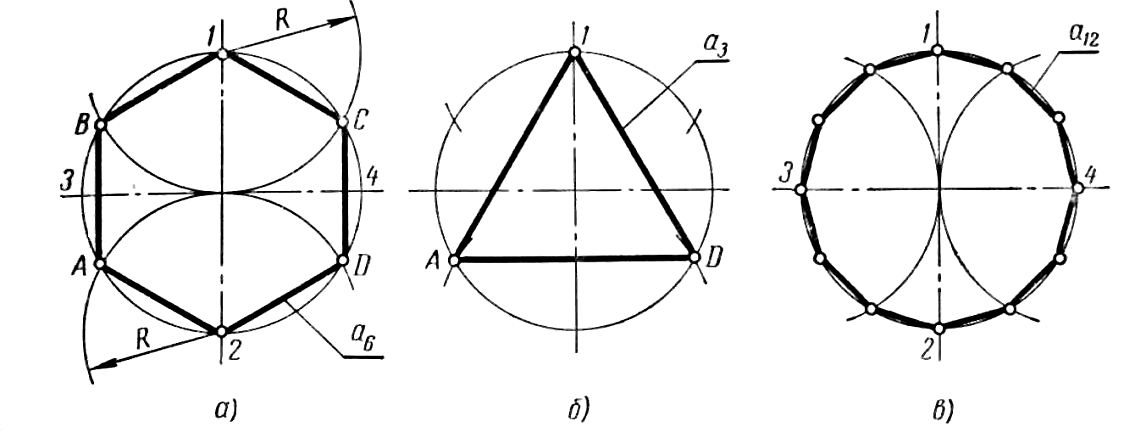 51
51 14
14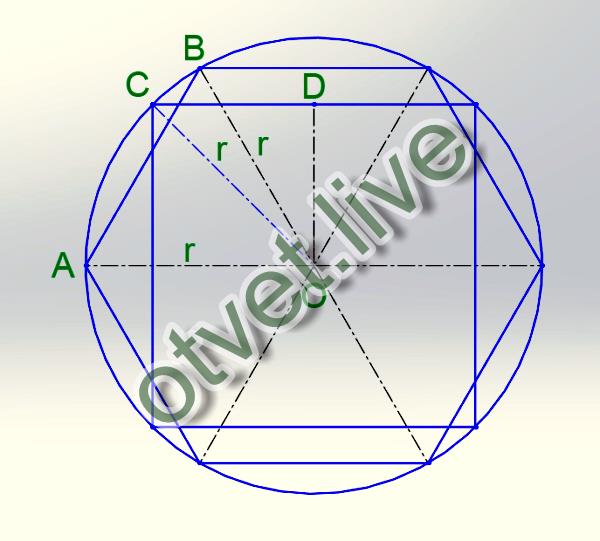 50
50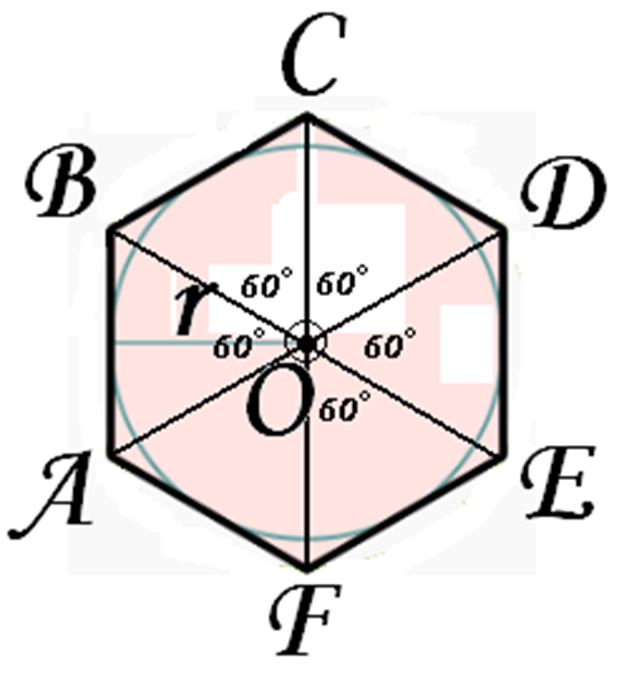 21
21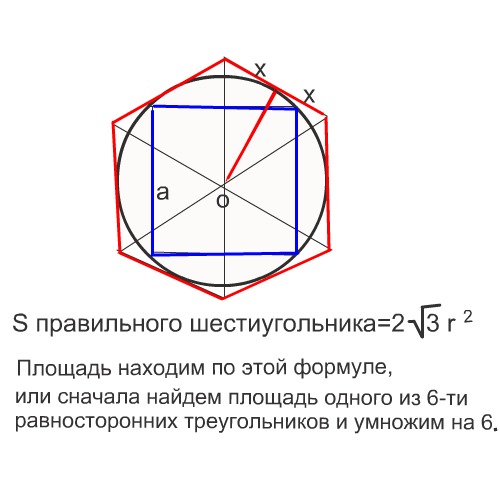 27
27
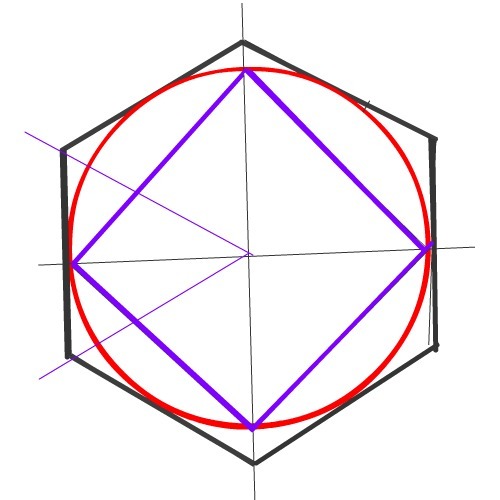 Не забудьте сохранять угол, который вы установили для циркуля.
Не забудьте сохранять угол, который вы установили для циркуля.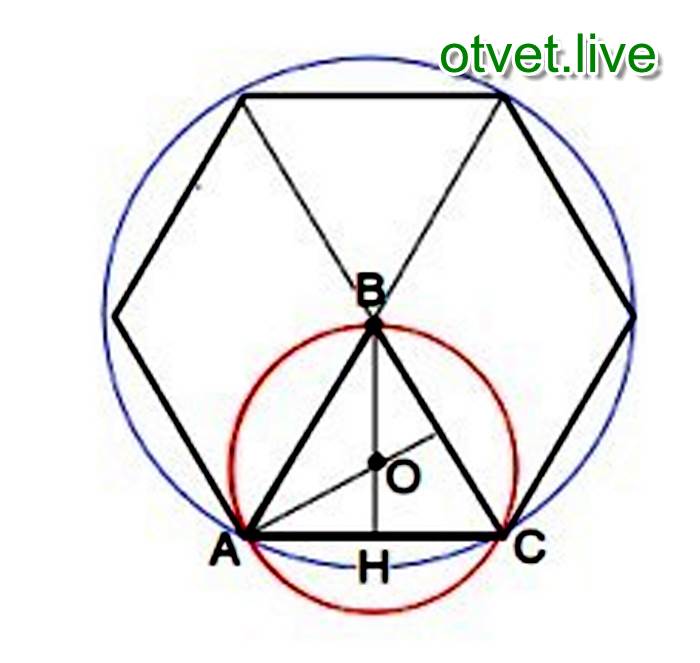 После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.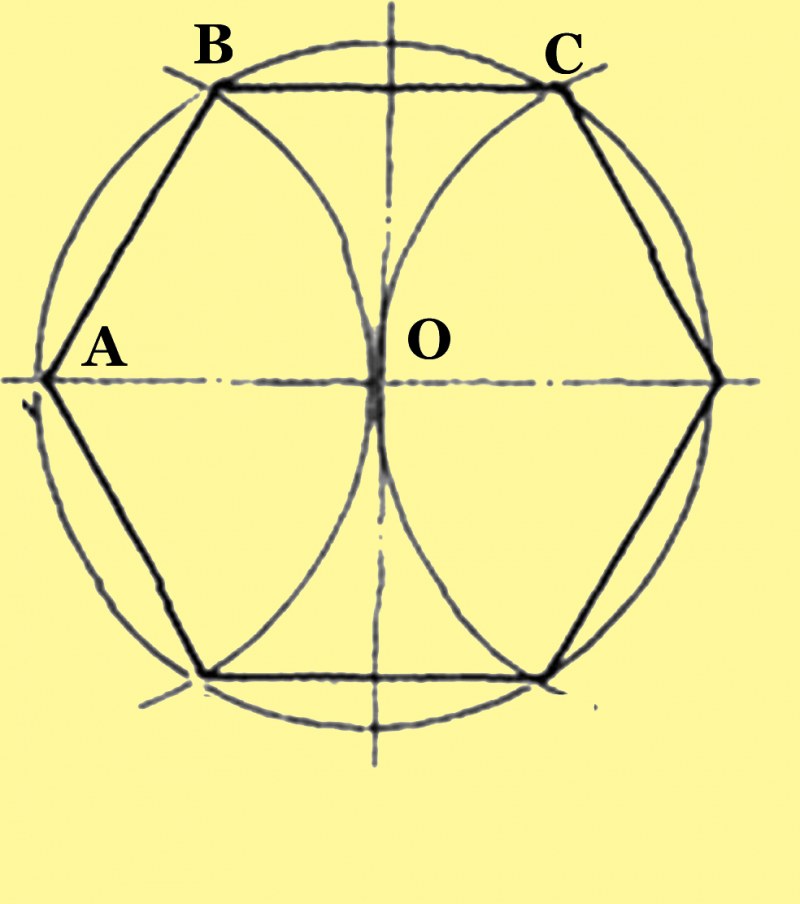

 Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.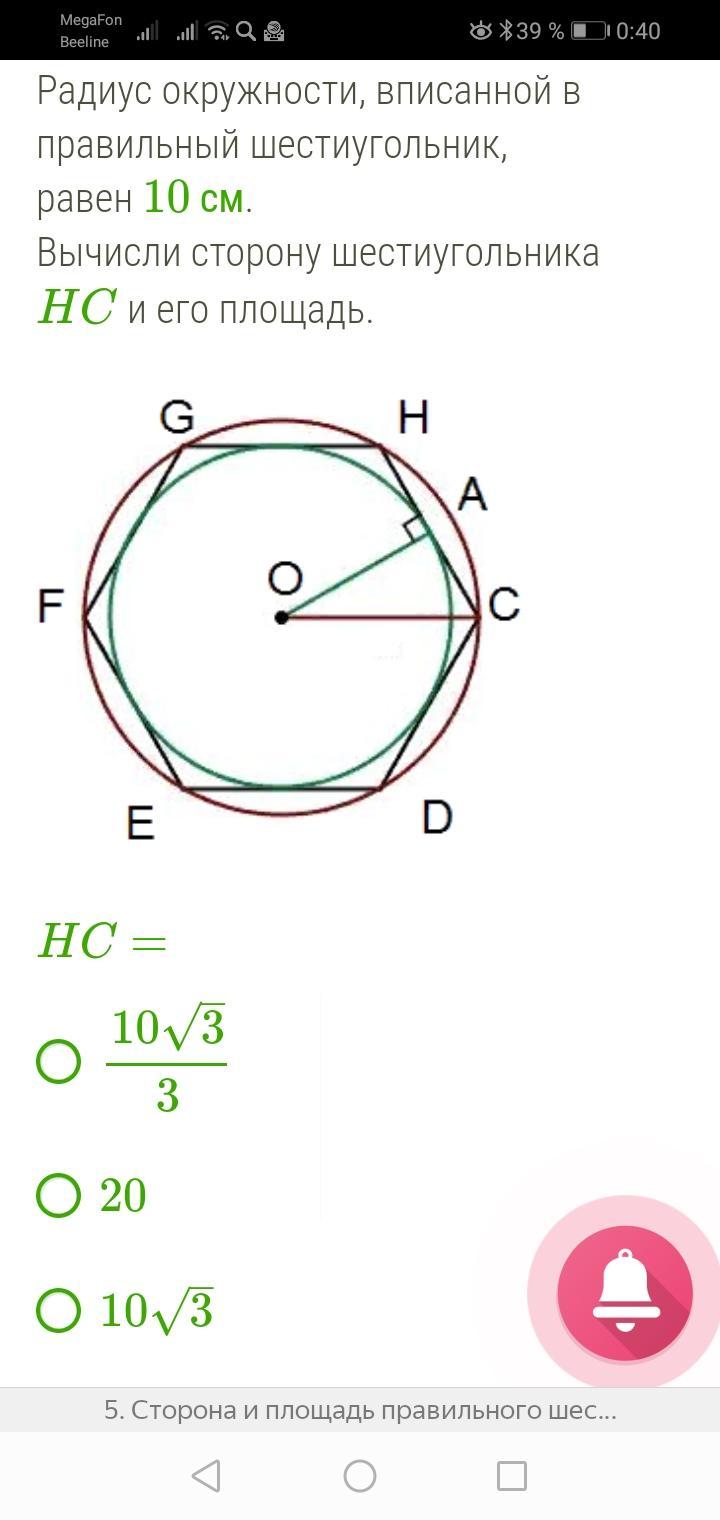

 Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

 Из всех это свойство имеет лишь правильный шестиугольник.
Из всех это свойство имеет лишь правильный шестиугольник.