Расчет металлической балки
Двутавp колонный (К) по ГОСТ 26020-83
20К1
20К2
23К1
23К2
26К1
26К2
26К3
30К1
30К2
30К3
35К1
35К2
35К3
40К1
40К2
40К3
40К4
Двутавp с уклоном полок по ГОСТ 8239-89
10
12
14
16
18
20
22
24
27
30
33
36
40
45
50
55
60
Двутавp дополнительной серии (Д) по ГОСТ 26020-83
24ДБ1
27ДБ1
36ДБ1
35ДБ1
40ДБ1
45ДБ1
30ДШ1
40ДШ1
50ДШ1
Двутавp нормальный (Б) по ГОСТ 26020-83
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
23Б1
26Б1
26Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б2
55Б1
55Б2
60Б1
60Б2
70Б1
70Б2
80Б1
80Б2
90Б1
90Б2
100Б1
100Б2
100Б3
100Б4
Двутавp широкополочный по ГОСТ 26020-83
20Ш1
23Ш1
26Ш1
26Ш2
30Ш1
30Ш2
30Ш3
35Ш1
35Ш2
35Ш3
40Ш1
40Ш3
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
70Ш5
Двутавp нормальный (Б) по СТО АСЧМ 20-93
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
25Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
50Б3
55Б1
55Б2
60Б1
60Б2
70Б0
70Б1
70Б2
Двутавp широкополочный (Ш) по СТО АСЧМ 20-93
20Ш1
25Ш1
30Ш1
30Ш2
35Ш1
35Ш2
40Ш2
45Ш1
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
80Ш1
80Ш2
90Ш1
90Ш2
100Ш1
100Ш2
100Ш3
100Ш4
Двутавp колонный (К) по СТО АСЧМ 20-93
20К1
20К2
25К1
25К3
30К1
30К2
30К3
30К4
35К1
35К2
40К1
40К2
40К3
40К4
40К5
Расчеты металлической балки перекрытия на прочность и прогиб, онлайн-калькулятор
Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.
При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.
- Описание ↓
- Область применения ↓
- Расчет ↓
- Онлайн ↓
- Пример расчета ↓
Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.
Описание
Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.
Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.
Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.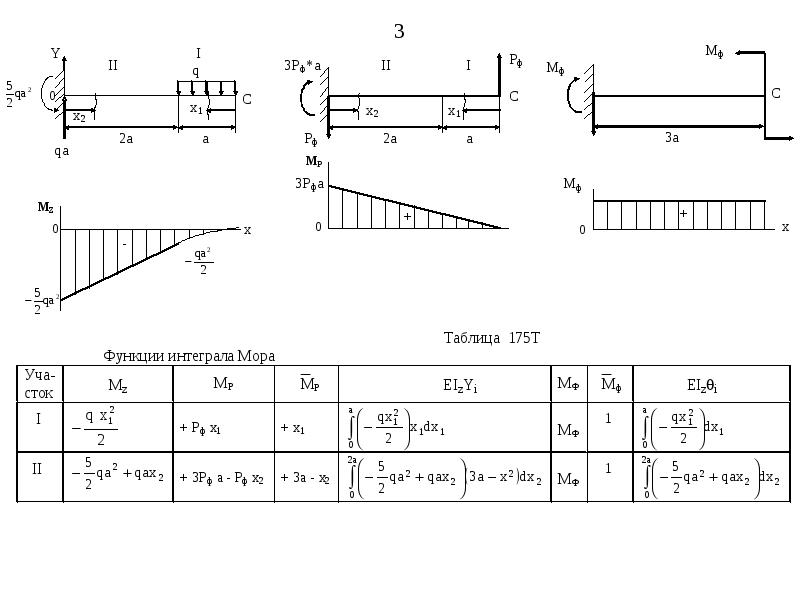
Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.
Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.
Для большей экономии использования металла и для облегчения всей конструкции существует сортамент балок двутаврового и швеллерного поперечного сечения. Площадь сечения изменяется от минимальной равной 12 кв. см до максимальной 234 кв. см, соответственно, для номеров профиля 10 и 70б.
Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь. Точная методика представлена ниже.
Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.
Область применения
Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.
Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.
В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах. После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.
Расчет
Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.
Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.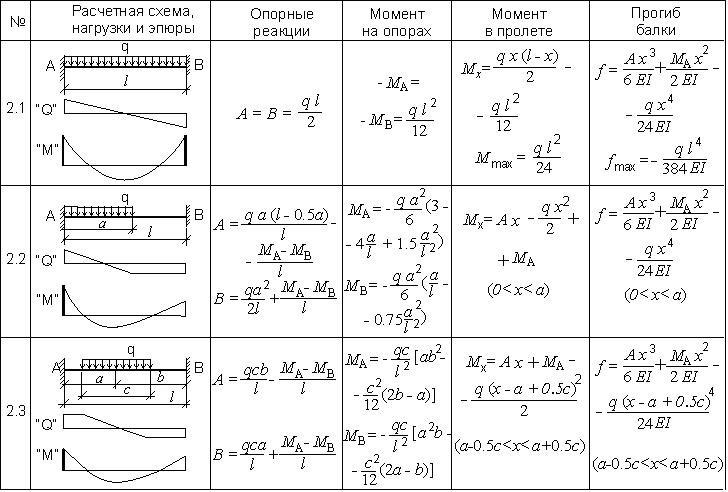
Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.
Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.
Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:
Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.
После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок.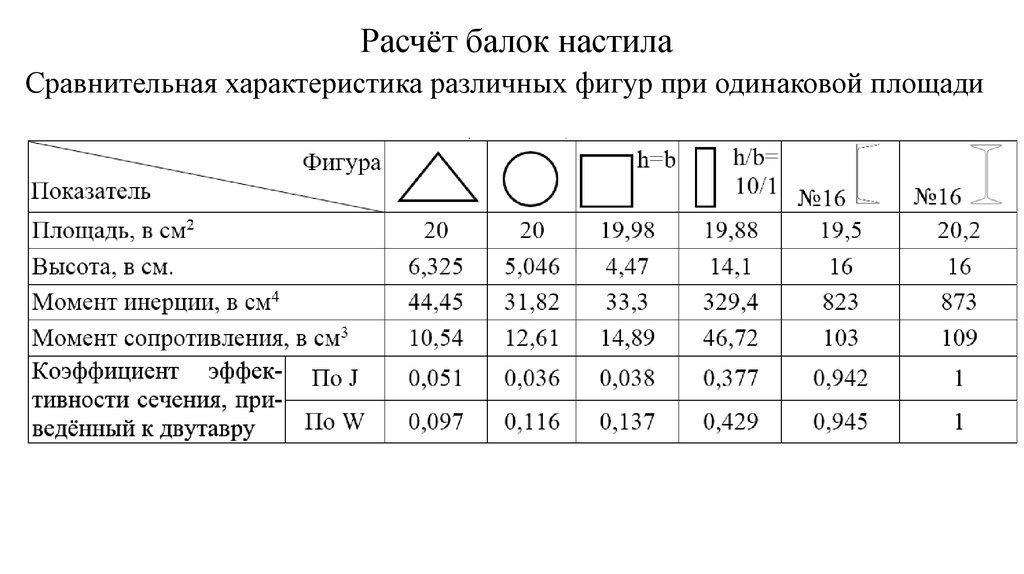 Далее, вычисляется осевой момент сопротивления сечения:
Далее, вычисляется осевой момент сопротивления сечения:
По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.
Онлайн
Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку. Поэтому, стоит довериться расчётам профессионалов.
Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.
Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.
Данный калькулятор требует введения следующих исходных данных:
- Сначала нужно ввести условия эксплуатации металлической балки.

- После этого характеристики предварительно выбранной металлической балки.
- Указать нормативную и расчётную нагрузку на балку и произвести расчёт.
В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.
Так же определяется минимально допустимый момент инерции, по которому можно выбрать номер профиля из сортамента. Если для строительства в первую очередь важно не допустить прогиб балки, тогда стоит выбирать балку исходя из полученного момента инерции.
Пример расчета
Металлической балки перекрытия:
Расчет несущей способности:
- Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
- Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.

Расчет сечения металлических балок:
- Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
- После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.
При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.
Статья была полезна?
0,00 (оценок: 0)
Просто поддерживаемый калькулятор балки | Calcresource
Прыжки до
-калькулятор
-Фон
Соглашение
-Калькулятор
-Фон
-Введение
-Aspuction
-Соглашение
-Символы
-Com равномерная распределенная нагрузка
— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном месте
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапециевидной нагрузкой
— Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
— Свободно опертая балка с частично распределенной равномерной нагрузкой load
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Поделиться
См. также
также
Калькулятор балки с простой опорой
— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 11 мая 2022 г.
Главная > Статика > Балка с простой опорой
Этот инструмент вычисляет статическую реакцию балки с простой опорой при различных сценариях нагрузки. Инструмент рассчитывает и строит диаграммы для следующих величин:
- реакции
- изгибающие моменты
- поперечные сдвигающие силы
- прогибы
- уклоны
Обратите внимание, что приняты предположения теории балок Эйлера-Бернуля. является упругим, а поперечное сечение постоянным на всем пролете балки (призматическая балка).
- Вместо этого переходите к теории и формулам!
Units: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Структура | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L = | mcmmmydftin | 94|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT |
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Imposed loading: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uniform distributed loadUniform распр. нагрузка (суммарная)Точечная нагрузка (по центру)Точечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reactions: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R A = | KNNKGTLBFKIP | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R B = | KNNKGGIP | KNNKGGIP | KNNKGPKIP | . 0079 0079 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bending Moment: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M u = | kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x m = | McMmmyDftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поперечное сдвиг0081 | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deflection: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d u = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x d = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Slopes : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ A = | DEGRADMRAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = | 9999 B = | 9919 B = 9003 | 9002 B = | θ0086 degradmrad | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Request results at a specific point: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X = | MCMMMYDFTIN | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M (X) = | KNMNMKG. MT.MLBF.FTLB.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP. MT.MLBF.FTLB.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP. | .0081 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V(x) = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d(x) = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ(x) = | degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .0003 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kN/mN/mkg/mt/mlbf /ftlbf/inkip/ft | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Реклама
Верхние страницы
Поделитесь этим
Фон
Таблица
-ВВЕДЕНИЕ
-Предложения
-Стои0003
— Обозначения
— Свободно опертая балка с равномерно распределенной нагрузкой
— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном положении
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапециевидной нагрузкой
— Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
— Свободно опертая балка с частично распределенной равномерной нагрузкой
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Введение
Свободно опертая балка является одной из самых простых конструкций.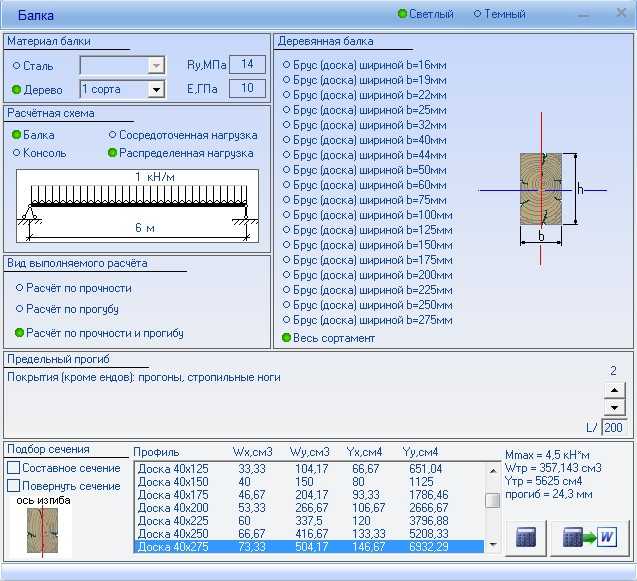 Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Удаление любой из опор или вставка внутреннего шарнира превратит свободно опертую балку в механизм, который будет перемещаться без ограничений в одном или нескольких направлениях. Очевидно, что это нежелательно для несущей конструкции. Таким образом, свободно опертая балка не предлагает избыточности опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными 9.0574 конструкций. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией.
РЕКЛАМА
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для свободно опертой балки, которая воспринимает только поперечные нагрузки, осевая сила всегда ноль, поэтому им часто пренебрегают. Расчетные результаты на странице основаны на следующих предположениях:
- Материал однородный и изотропный (другими словами, его характеристики одинаковы во всех точках и направлениях)
- Материал линейно-упругий
- Нагрузки действуют статически (не меняются со временем) )
- Сечение одинаковое по всей длине балки
- Прогибы малы
- Каждое поперечное сечение, изначально плоское и перпендикулярное к продольной оси, остается плоским и нормальным также к отклоненной оси. Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).

Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принимается здесь.
Правила знаков
Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:
- Осевая сила считается положительной, если она вызывает растяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.
Обозначения
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опорная реакция
- d: прогиб
- M: изгибающий момент
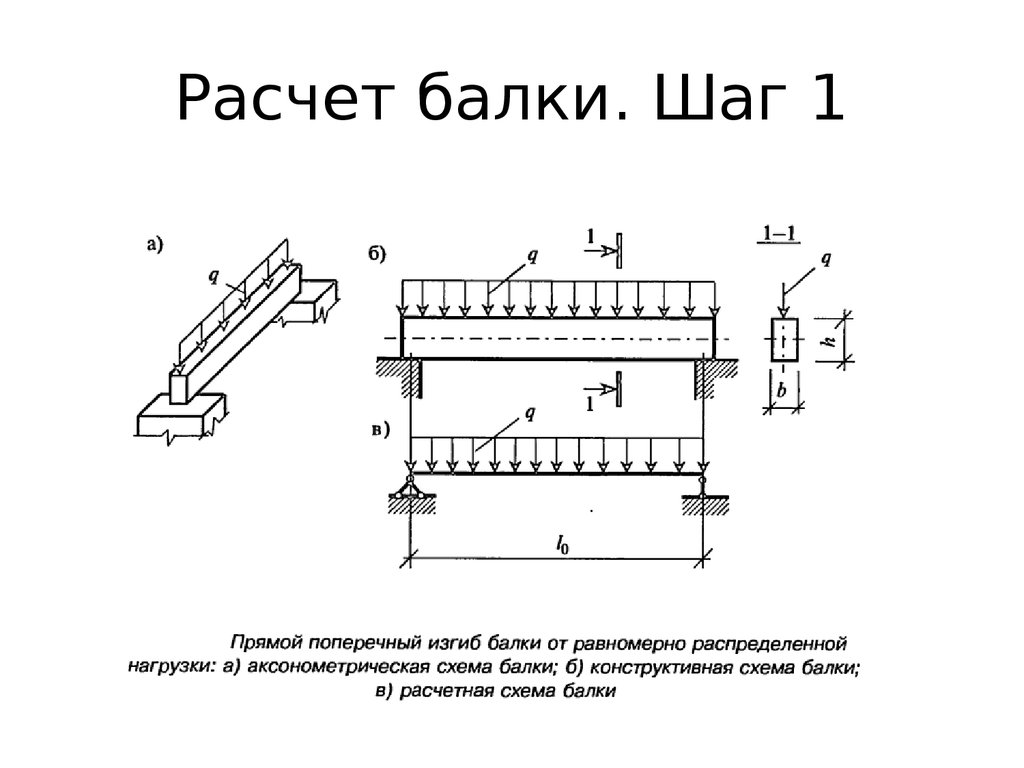
- V: поперечная поперечная сила Нагрузка w распределяется по всему пролету балки, имея постоянную величину и направление.
 Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}РЕКЛАМА
Свободно опертая балка с точечной силой посередине
Сила сосредоточена в одной точке, расположенной в середине балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана. 92)}{16 E I} &, x>L/2 \end{выровнено}\right.
где:
\acute{x}=L-x
Свободно поддерживаемая балка с точечной силой в произвольном месте
Сила сосредоточена в одной точке, в любом месте поперек балки.
 Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенную точечную силу P, приложенную на случайном расстоянии a от левого конца.
Просто поддерживаемый луч с точечной нагрузкой в случайном положении
Количество Формула Реакции: 9 2 2 2 2 2 2 2 2 2 2 2 .  3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.где:
b=L-a
\acute{x}=L-x
Свободно опертая балка с точечным моментом
, в любом месте на пролете балки. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину балки, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения предсказанные результаты с помощью классической теории балок, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), по мере удаления предсказанные результаты совершенно достоверны, как заявил Святой — Принцип Венана.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенный точечный момент M, приложенный на расстоянии a от левого конца.

просто поддержанный луч с точечным моментом
Количество Формула Реакции: 9 9 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_ r_29000 2
. } Концевые уклоны: 92}{2 E I} &, x>a\end{выровнено} \right. где:
b=L-a
\acute{x}=L-x
Просто опертая балка с треугольной нагрузкой, однако, ее величина не распределена по пролету
постоянна, но изменяется линейно, начиная с нуля на левом конце и заканчивая пиковым значением w_1 на правом конце. Размеры w_1 — это сила на длину. Суммарная сила, приложенная к балке, равна W={1\over2}w L, где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на линейно изменяющуюся (треугольную) распределенную нагрузку, возрастающую слева направо.

Просто поддерживаемый луч с линейной разной распределенной нагрузкой (треугольная)
. 1\over3}w_1L 94} {24EIL} где:
C=\sqrt{15-\sqrt{120}}\left(\sqrt{15}+\sqrt{50}\right)\приблизительно 22,01237
Свободно опертая балка с трапециевидной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и до w_2 на правом конце. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки трапециевидной формы на переменную распределенную нагрузку.
Просто поддерживаемый луч с линейно изменяющейся распределенной нагрузкой (трапециевидная)
. 
R_B={(w_1+2w_2)L\over6}
где:
w_x=w_1+{(w_2-w_1)x\over L}
Опорная балка с трапециевидным распределением нагрузки характерны для балок по периметру плиты. Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах она становится равной нулю. Размеры (\w\) представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L — длина пролета, а a, b — длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Свободно опертая балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет не нагружен. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=\left(L-a-b\right)w, где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.

В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную равномерную нагрузку. 92}{2 E I} &,x\ge L-b \end{выровнено}\right.
Где:
\ Острый {x} = L-X
x_a = x-a
L_W = L-A-B
просто поддержанный. пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок могут быть получены путем соответствующей установки значений w_1 и w_2. Кроме того, соответствующие случаи для полностью загруженного пролета могут быть получены путем установки a и b равными нулю.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную трапециевидную нагрузку.

Свободно опертая балка с частично распределенной линейно-переменной нагрузкой (трапециевидная) 93
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Реклама
См. Также
Beams — Поддерживается на обоих концах
. Напряжение в изгибающей луче может быть выражена как
σ = Y M / I (1)
, где
9000 2 43434343434343939 . напряжение (Па (Н/м 2 ), Н/мм 2 , psi)y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = bending moment (Nm, lb in)
I = moment of Inertia (m 4 , mm 4 , in 4 )
- Beams — Supported at Both Ends — Непрерывные и точечные нагрузки
- Балки — фиксированные с одного конца и поддерживаемые с другого — непрерывные и точечные нагрузки
- Балки — закрепленные с обоих концов — непрерывные и точечные нагрузки
Для расчета можно использовать приведенный ниже калькулятор максимальные напряжения и прогибы балок при однократной или равномерно распределенной нагрузке.

Балка с опорой на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой на обоих концах в положении x может быть выражен как
M x = q x (L — x) / 2 (2)
, где
M x = момент в положении x (нм, фунт в)
x = расстояние от конца (мм, мм, в)
.0573 Момент находится в центре луча на расстоянии L / 2 и может быть выражен какM MAX = Q L 2 /8 (2A)
Скуда
3 439439439439439439439439439439439439439439439439439439439439439439439439439439439439439439439439439939939939939939939.. max = максимальный момент ( Нм, фунт·дюйм)
q = равномерная нагрузка на единицу длины балки (Н/м, Н/мм, фунт/дюйм)
6 9 154346 9 L = длина балки (м, мм, дюйм)Максимальное напряжение
Уравнение 1 и 2A можно объединить для выражения максимума напряжения в луче с однородной нагрузкой, поддерживаемыми на обоих концах на расстоянии L/2, как
6434343434343434343434343434343434343434343434343434343434343434343434343443434343434343н.
 = Y MAX Q L 2 /(8 I) (2B)
= Y MAX Q L 2 /(8 I) (2B) , где
σ MAX = максимальный стресс (PA (N/M 9144 2 = максимальный стресс (N/M 9144 2 = Maximum (N/M 9144 2 =. 2 , PSI)
Y MAX = Расстояние до экстремальной точки от нейтральной оси (м, мм, в)
- 1 N/M 2
444444444444444444414944444444444444444444444444449
- 1 N/M 2
44444444444444449
- . /mm 2 = 1 Pa = 1.4504×10 -4 psi
- 1 psi (lb/in 2 ) = 144 psf (lb f /ft 2 ) = 6,894.8 Pa (N/ м 2 ) = 6,895×10 -3 Н/мм 2
- 1 N/M 2
- Максимальная прочность на растяжение для некоторых распространенных материалов
Максимум отклонение :
Δ MAX = 5 Q L 4 / (384 E I) (2C)
, где
, где
, где9000 2 9000 2
. , in)
, in) E = Modulus of Elasticity (Pa (N/m 2 ), N/mm 2 , psi)
Deflection in position x:
δ х = Q x ( L 3 — 2 L x 2 + x 3 ) / (24 E I) (2d)
Примечание! — прогиб часто является ограничивающим фактором в конструкции балки. В некоторых случаях балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимых прогибов.
Силы, действующие на концах:
R 1 = R 2
= q L / 2 1435
где
R = сила реакции (Н, фунты)
Пример — балка с равномерной нагрузкой, метрические единицы из
6 Н/мм . Момент инерции балки равен 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, равен 200 ГПа (200000 Н/мм 2 9)1435 . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).Максимальное напряжение в балке может быть рассчитано = 34,3 Н/мм 2
= 34,3 10 6 Н/м 2 (Па)
3 МПа
3
6 0 =
6.0002 The maximum deflection in the beam can be calculated
δ max = 5 (6 N/mm) (5000 mm) 4 / (( 200000 N/mm 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Uniform Beam Calculator — Matic Anits units
Uniform Beam Beagulator — Matic Units
Unired Beam BEALUTOL — MTIC
. — Длина балки (мм)
I — Момент инерции (мм 4 )
E — Модуль эластичности (N/мм 2 )
Y — Расстояние от экстра экстрамки Экстральны Экстральны.

- 1 mm 4 = 10 -4 cm 4 = 10 -12 m 4
- 1 cm 4 = 10 -8 m = 10 4 мм
- 1 из 4 = 4,16×10 5 мм 4 = 41,6 см 4
- 1 N/MM 2 = 10 444444443 2 = 10 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444 Калькулятор балки — британские единицы
q — нагрузка (фунты/дюймы)
L — длина балки (дюймы)
I — момент инерции (в модулях 4
9
4
9
7 0 упругости (psi)г — Расстояние от крайней точки до нейтральной оси (дюймы)
Пример — балка с равномерной нагрузкой, британские единицы inertia
285 in 4 , modulus of elasticity 200 psi
, with uniform load 100 lb/in can be calculated asσ max = y max q L 2 / (8 я)
= (6.
 25 in) (100 lb/in) (100 in) 2 / (8 (285 in 4 ))
25 in) (100 lb/in) (100 in) 2 / (8 (285 in 4 )) = 2741 (lb/in 2 , psi)
Максимальное отклонение может быть рассчитано как
Δ MAX = 5 Q L 4 / (E I 384)
= 5 (100 фунтов/ дюйм) (100 дюймов) 4 6 = 5 (100 фунтов/ дюймов) (100 дюймов) 4 / (2
0000 (100 ° C00 дюймов)
436 = 5 (100 фунтов/ дюймов) (100 дюймов) 40002. фунт/дюйм 2 ) (285 дюймов 4 ) 384)
= 0,016 дюйма
Луч, поддерживаемый на обоих концах — нагрузка в центре
Максимум Момент в луче с центральной нагрузкой, поддерживаемой на обоих концах:
M MAX = F L / 4 (3A)
844 = F L / 4 (3A)
88344 = F L / 4 (3A)
883844 = F L / 4 (3A)
(3b)1537, где
F = нагрузка (N, LB)
Максимум отклонение может быть выражено как
Δ Max = F L 344444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н.

Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
ОДНОГО ЦЕНТРОВА0539
F — Load (N)
L — Length of Beam (mm)
I — Moment of Inertia (mm 4 )
E — Modulus of Elasticity (N/mm 2 )
y — Расстояние от крайней точки до нейтральной оси (мм)
Калькулятор одноцентровой нагрузки на балку — британские единицы
F — нагрузка (фунты) — длина балки
(в)I — Момент инерции (в 4 )
E — Модуль упругости (psi)
y — Расстояние от крайней точки до нейтральной оси a Одноцентровая нагрузка
Максимальное напряжение в стальной широкополочной балке размером «W 12 x 35», длина 100 дюймов , момент инерции 285 дюймов 4 , модуль упругости 2
00 psi
, с центром загрузить 10000 фунтов можно рассчитать какσ макс.
 = y макс. F L / (4 I)
= y макс. F L / (4 I) 4 ))
= 5482 (фунт / в 2 , PSI)
Максимальное отклонение может быть рассчитано как
Δ MAX = F L 344444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. (10000 фунтов/дюйм) (100 дюймов) 3 / ((2
00 фунтов/дюйм
2 ) (285 в 4 ) 48)= 0,025 в
. пролёт/180
- деревянные балки перекрытий: пролёт/330 (макс. 14 мм)
- хрупкие элементы: пролёт/500
- крановые балки: пролёт/600
Балка, опирающаяся на оба конца – внецентренная нагрузка
0003
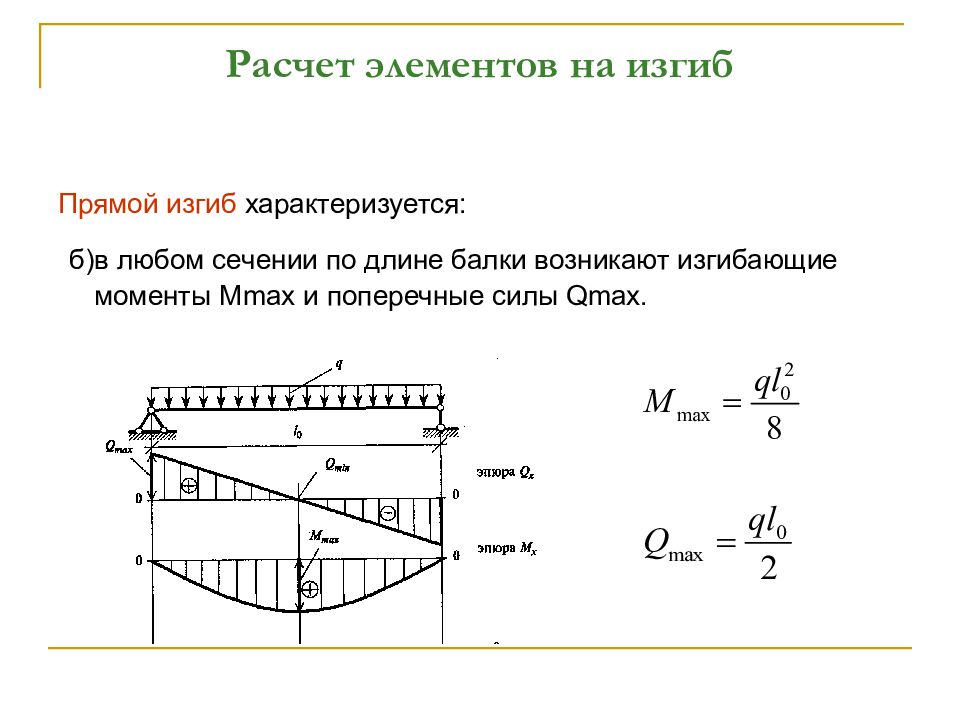
Максимум Момент в луче с одной эксцентрической нагрузкой в точке нагрузки:
M MAX = F A B / L (4A)
Максимальный напряжение
Максимум напряжение в сингл -стрессе с синглом с синглом с синглом с синглом с синглом с синглом
.




 Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}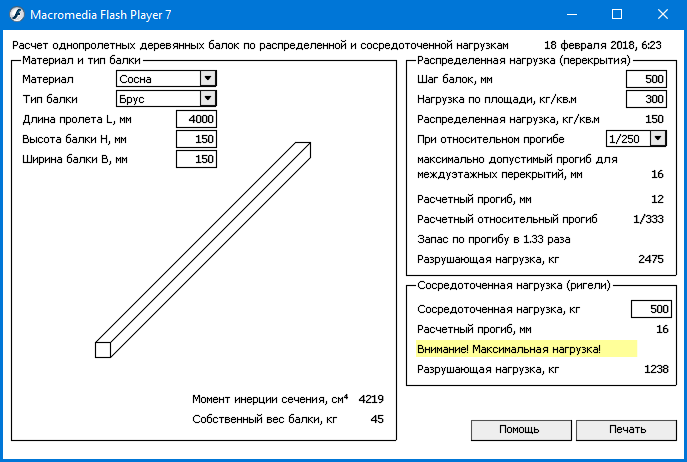 Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным. 3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.


 = Y MAX Q L 2 /(8 I) (2B)
= Y MAX Q L 2 /(8 I) (2B)  , in)
, in)  Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
 25 in) (100 lb/in) (100 in) 2 / (8 (285 in 4 ))
25 in) (100 lb/in) (100 in) 2 / (8 (285 in 4 )) 
 = y макс. F L / (4 I)
= y макс. F L / (4 I)