Расчет на прогиб балки онлайн: Расчет балки на прогиб и прочность

Расчет прогиба балки методом начальных параметров: учимся составлять формулы

В этой статье будем рассматривать универсальный метод расчёта прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера возьмём металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. А также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Кроме того, сечения поворачиваются на определенный угол. Эти две величины, для любого сечения, можно определить с помощью метода начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Расчет прогибов необходим для выполнения расчета на жесткость. Балка может считаться жесткой, только если расчётные значения прогибов не превышают допустимых значений. Если же условие жесткости не выполняется, то принимаются меры по ее повышению. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод, можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине).

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти свойства, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

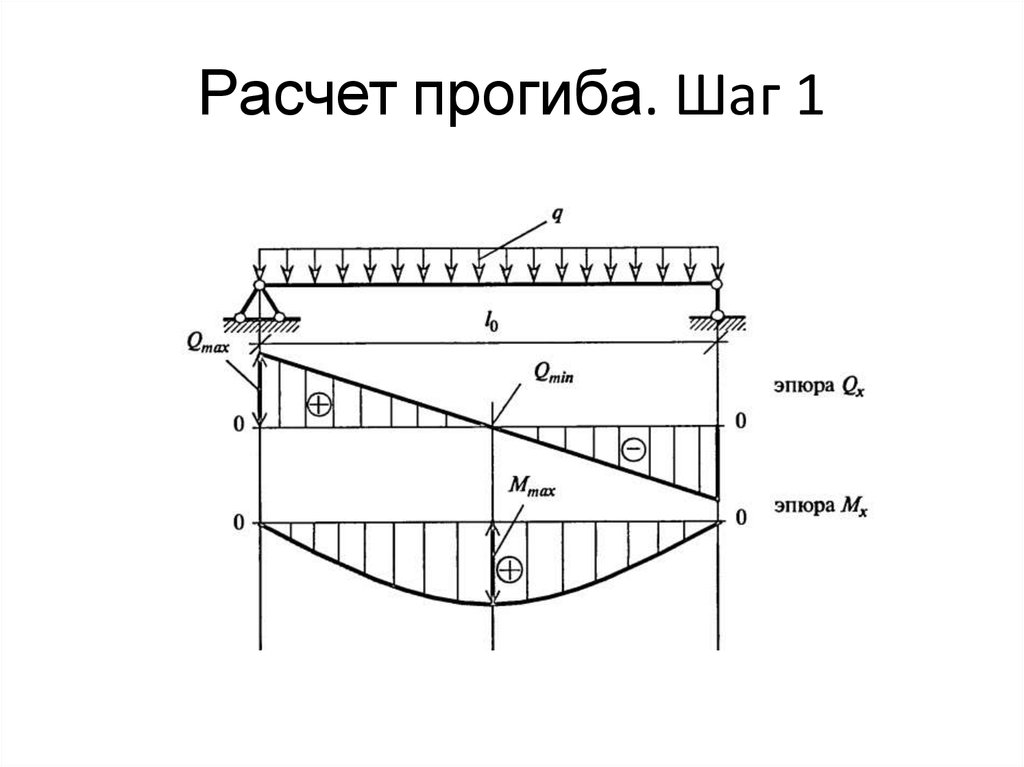
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой же балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат.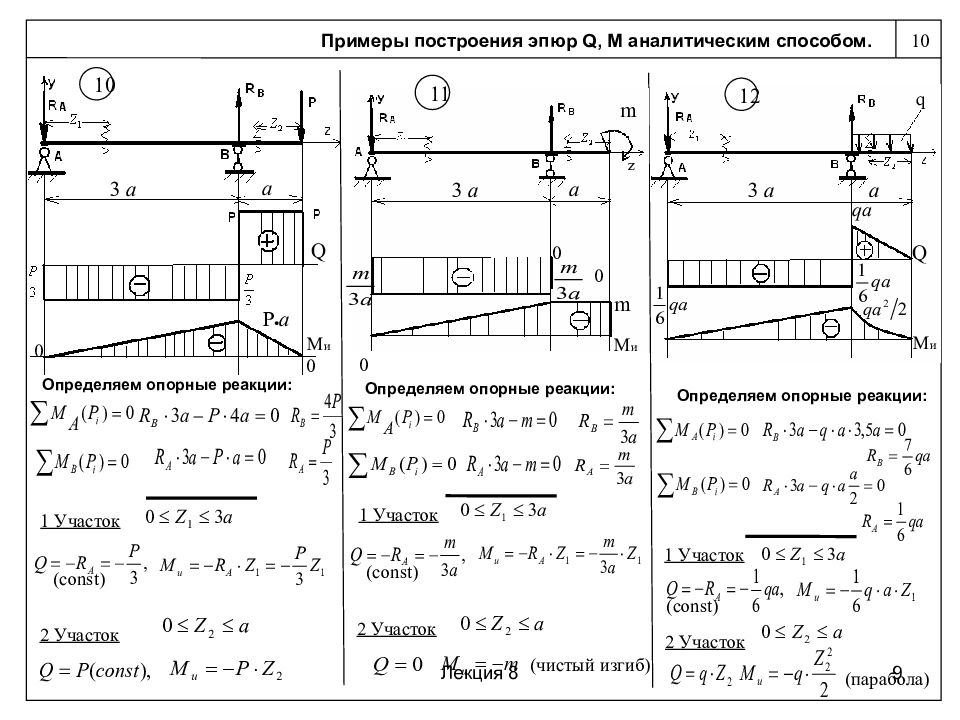

Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим сечение в середине пролета – сечение C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала, из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. { 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

Другие уроки

Расчет балки на изгиб, прогиб и прочность, включая калькулятор © Геостарт

Рубрика: Строительные материалы

Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение.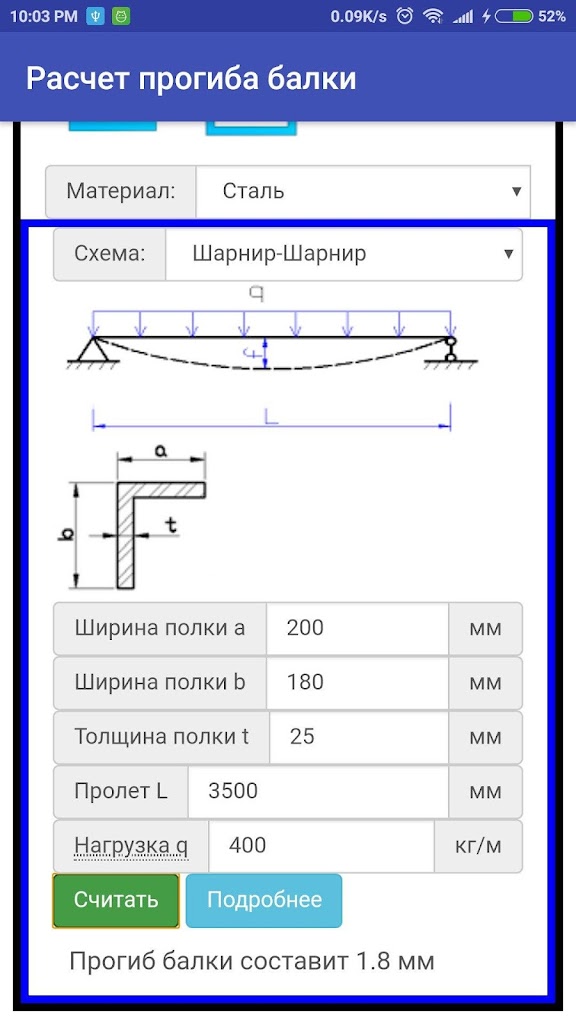

В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.

Как рассчитывать балки на прочность

Расчет балки на прогиб , калькулятор для которого можно найти в интернете, можно произвести следующими методами:

• Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
• Подобрать сечение;
• Проверочный перерасчет по максимальным значениям напряжения.

Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.

Последовательность действий

Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:

1. Заделка — шарнир;
2. Заделка — заделка;
3. Шарнир — шарнир;
4. Заделка — свободный конец.

Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.

Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.

Сравнение полученных напряжений с напряжением материалов

Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.

Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности. Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.

Пример расчета

Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:

• Выбираем расчетную схему, в этом случае заделка — свободный конец;
• Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
• Находим по таблице сортаментов для данного двутавра момент сопротивления;
• Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0. 0000397 = 45,34 Мпа;
• Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.

Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.

Онлайн-калькуляторы

Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.

Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.

Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения.

Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.

В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.

Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза. Удачных расчетов на прочность!

автор Олейников Константин

Геодезические измерения: виды, классификация и характеристики.

Пример заполнения страницы журнала измерения направлений

Геодезические сети, классификация и способы их развития

Калькулятор расчета
цен на кадастровые
работы

Расчитать

Электропроводка в доме своими руками: пошаговая схема

Подготовка к производству монтажных работ

Проектирование грунтовой заделки трубчатой моноопоры

Калькулятор фиксированного отклонения балки — Бесплатно

Танвеш

Магистр строительных конструкций | Научный интерес — искусственный интеллект и машинное обучение в гражданском строительстве | Ютубер | Учитель | В настоящее время работает научным сотрудником в NIT Goa

. Содержание

Свяжитесь с нами:

Если вы обнаружите какую-либо ошибку в этом калькуляторе, мы будем очень признательны за ваши отзывы.

Пожалуйста, напишите по адресу support@dcbaonline. com

Калькулятор прогиба фиксированной балки для точечной нагрузки, udl, uvl, трапециевидной нагрузки, треугольной нагрузки для прогиба, наклона, изгибающего момента, фиксированного конечного момента и сдвига.

Калькулятор с фиксированной балкой

Другие калькуляторы

Что такое фиксированная балка

Когда оба конца балки удерживаются от вертикального перемещения, горизонтального перемещения или вращения, такая балка называется фиксированной балкой.

Неподвижная балка также называется балкой Encaster или встроенной балкой, так как в обычной конструкции концы балок, встроенных за одно целое с колоннами или другими конструкциями, способны создавать моменты и развивать вертикальную и горизонтальную реакции.

Фиксированная балка имеет 6 степеней закрепления на обоих концах. в трехмерном случае и 3 ограничения на каждом конце в двумерном случае.

Как пользоваться калькулятором​

Калькулятор 1 : – Это калькулятор фиксированной балки, который может найти прогиб, наклон, момент и сдвиг для равномерно распределенной нагрузки (udl), равномерно изменяющейся нагрузки (uvl), треугольной нагрузки и трапециевидной нагрузки.

Калькулятор 2 :-  Это калькулятор фиксированной балки, который может найти прогиб, наклон, момент и сдвиг для точечной нагрузки и нагрузки сосредоточенного момента.

Шаг 1 — выбрать единицы измерения: метрические или британские.

Пользователю предоставляется возможность назначать все единицы входных величин отдельно. Единицы для каждой величины взяты из метрической системы единиц и имперской системы единиц.

Необходимое количество:

• Длина балки (L)
• Модуль Юнга материала (E) —> для расчета прогиба и уклона.
• Момент инерции площади (I) для расчета наклона и прогиба.
• Жесткость при изгибе рассчитывается автоматически, однако пользователю предоставляется возможность ввести пользовательскую жесткость при изгибе. Также могут быть изменены единицы изгибной жесткости.
• Интенсивность нагрузки 1 и/или интенсивность нагрузки 2.
• Расстояние интенсивности нагрузки 1 от левой опоры и/или расстояние интенсивности нагрузки 2 от левой опоры.

Входные данные для интенсивности нагрузки и расстояния можно увидеть на самой верхней диаграмме, изменяющейся в реальном времени.

Условные обозначения:

• Нагрузки, направленные вниз, считаются положительными.
• Момент против часовой стрелки и реакция против часовой стрелки положительны.
• Восходящая реакция положительная, нисходящая реакция отрицательная.
• Отклонение вниз считается отрицательным.
• Отрицательный наклон представляет собой вращение по часовой стрелке и измеряется в радианах. Положительный наклон — это вращение против часовой стрелки, измеряемое в радианах.

Предположения:

• Материал однородный и изотропный.
• Поперечное сечение остается одинаковым по всей длине.
• Нагрузка применяется постепенно.

Неподвижная балка с трапециевидной нагрузкой Формула

Неподвижная балка с трапециевидной нагрузкой может использоваться для анализа неподвижной балки с любым типом непрерывной распределенной нагрузки. В Калькуляторе 1 пользователь может выбрать тип нагрузки «Трапеция»

Многократное использование трапециевидной нагрузки:

• При одинаковой интенсивности нагрузки 1 и 2 и расстоянии «b» = расстоянию «a» и расстоянию «d» = расстоянию «c», трапецеидальная нагрузка может быть преобразована в UDL.
• При сохранении интенсивности нагрузки w1=0 и сохранении расстояния «b» = расстоянию «a» и расстоянию «d» = расстоянию «c», трапециевидную нагрузку можно преобразовать в левосторонний прямоугольный треугольник.
• Сохраняя w2=0 и другие настройки из предыдущего пункта, трапециевидную нагрузку можно преобразовать в прямоугольный треугольник.

Неподвижная балка с трапециевидной нагрузкой

Найдите формулу прогиба неподвижной балки, уравнение наклона, момент, реакции концевых опор и уравнение сдвига в следующей таблице:-

Обратите внимание: Нагрузка вниз положительна, реакции вверх положительны, момент против часовой стрелки положителен. {2}} {5} 9{4}}{24 * L}

Калькулятор неподвижной балки с формулой UDL

Калькулятор неподвижной балки с udl запрограммирован для определения прогиба, поворота или наклона, момента и сдвига неподвижной балки с UDL. Пользователь должен выбрать тип нагрузки «UDL» для расчета равномерно распределенной нагрузки.

Неподвижная балка с нагрузкой udl может рассматриваться как непрерывная нагрузка на балку от стены или непрерывная нагрузка на балку.

Неподвижная балка с udl, охватывающим всю длину, будет иметь расстояние a, равное нулю, и расстояние b, равное длине балки.

Фиксированная балка, несущая половину udl, будет иметь расстояние a=0 или a= L/2 и расстояние b=L/2 или b=L соответственно для двух случаев.

Фиксированный луч с udl в любом другом положении необходимо вводить с соответствующими расстояниями.

Уравнения для неподвижной балки, несущей UDL для всего пролета, приведены в следующей таблице:- 

Пожалуйста, обратите внимание: Нагрузка вниз положительна, реакции вверх положительны, момент против часовой стрелки положителен.

Формула фиксированного отклонения балки для UDL​ 9{3}}{6}

Фиксированная балка с треугольной нагрузкой

Фиксированная балка с треугольной нагрузкой Калькулятор можно использовать, выбрав тип нагрузки «Треугольный» в калькуляторе 1

Обратите внимание, что расстояние a<=b и b<=c для треугольной нагрузка

Для фиксированной балки с uvl левостороннего прямоугольного треугольника, расстояние b=расстоянию c. Для фиксированной балки с uvl прямостороннего прямоугольного треугольника расстояние a = расстояние b.

Фиксированная балка с треугольной формулой нагрузки​ 9{4}}{24 * L}

Неподвижная балка с точечной нагрузкой

Неподвижная балка с точечной нагрузкой анализируется с помощью «Калькулятора 2».

Необходимые параметры для расчета: информация о геометрии балки, интенсивность нагрузки (w) и расстояние, на котором действует нагрузка (a). Обратите внимание, что a < = L

Неподвижная балка, несущая центральную точечную нагрузку, может быть найдена путем сохранения a=L/2. {2}} 9{2}}{2}

Неподвижная балка с моментной нагрузкой

Неподвижная балка с вычислителем момента анализируется с помощью «Калькулятора 2» путем выбора типа нагрузки «Момент»

Для неподвижной балки с моментом в центре расстояние «а» должно быть равно половине длины пучка.

Фиксированная балка с моментом в центре формула

Калькулятор отклонения фиксированной балки сосредоточенный момент

Для фиксированной балки с моментом в центре подставьте a=L/2 в следующих уравнениях. 9{2}}{2} -M_{A} * x-M(x-a)

Последние сообщения

Калькулятор консольной балки

| Calcresource

Прыжки до

-Калькулятор

-Теоретический фон

Соглашение о Таблице

-Калькулятор

-Теоретический фон

-Введение

-Запуск

-Соглашение. с равномерно распределенной нагрузкой

— Консольная балка с сосредоточенной силой на конце

— Консольная балка с точечной силой в произвольном положении

— Консольная балка с точечным моментом

— Консольная балка с переменной распределенной нагрузкой

— Консольная балка с трапециевидным распределением нагрузки плитного типа

— Консольная балка с частично распределенной равномерной нагрузкой load

—  Консольная балка с частично распределенной трапециевидной нагрузкой

—  Статьи по теме

Поделиться

См. также

Калькулятор консольной балки

— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 27 июня 2020 г.

Главная > Статика > Консольная балка

Этот инструмент рассчитывает статическую реакцию консольных балок при различных сценариях нагрузки. Инструмент рассчитывает и строит диаграммы для следующих величин:

• реакции
• изгибающие моменты
• поперечные силы сдвига
• прогибы
• уклоны

Пожалуйста, имейте в виду, что приняты предположения теории балок Эйлера-Бернуля. является упругим, а поперечное сечение постоянным на всем пролете балки (призматическая балка).

• Вместо этого переходите к теории и формулам!

Units:
	Imperial Metric

94

1	2	3	4
Структура
L =		mcmmmydftin
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов.

ADVERTISEMENT

1	2	3	4
Imposed loading:
Uniform distributed loadUniform распр. нагрузка (суммарная)Точечная нагрузка на остриеТочечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка
Calculate

1	2	3	4
Results:
Reactions:
R A =		kNNkgtlbfkip
M A =		kNmNmkg. mt.mlbf.ftlbf.inkip.ftkip.in
Bending Moment:
M u =		kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
x m =		mcmmmydftin
Transverse Shear Force:
V u =		kNNkgtlbfkip
x v =		mcmmmydftin
Deflection:
d u =		mcmmmydftin
x d =		mcmmmydftin
Slopes:
θ A =		degradmrad
θ B =		degradmrad

1	2	3	4
Request results at a specific point:
X =		MCMMMYDFTIN
м (x) =		м. 0484
V(x) =		kNNkgtlbfkip
d(x) =		mcmmmydftin
θ(x) =		degradmrad

ADVERTISEMENT

1	2
Diagrams
kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
kNNkgtlbfkip
mcmmmydftin
degradmrad
kN/mN/mkg/mt /mlbf/ftlbf/inkip/ft

РЕКЛАМА

Лучшие страницы

Поделитесь этим

Теоретическая основа

Содержание 9 —

 Введение0003

— Условные знаки

— Условные обозначения

— Консольная балка с равномерно распределенной нагрузкой

— Консольная балка с точечной силой на конце

— Консольная балка с точечной силой в произвольном положении

— Консольная балка с точечным моментом3

— Консольная балка с переменной распределенной нагрузкой

— Консольная балка с плитным трапециевидным распределением нагрузки

— Консольная балка с частично распределенной равномерной нагрузкой

—  Консольная балка с частично распределенной трапециевидной нагрузкой

—  Статьи по теме

Введение

Консольная балка является одной из самых простых конструкций. Он имеет только одну опору на одном из концов. Опора представляет собой так называемую неподвижную опору , которая препятствует любому перемещению, включая вертикальные или горизонтальные смещения, а также любые повороты. Другой конец не поддерживается, поэтому он может свободно перемещаться или вращаться. Этот свободный конец часто называют 9.0009 наконечник кантилевера.

Консоль имеет только одну фиксированную опору

Удаление единственной опоры или вставка внутреннего шарнира превратили бы консольную балку в механизм: тело движется без ограничений в одном или нескольких направлениях. Это нежелательная ситуация для несущей конструкции. В результате консольная балка не имеет избыточности в плане опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются 9.0009 критическая или определительная структур. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией.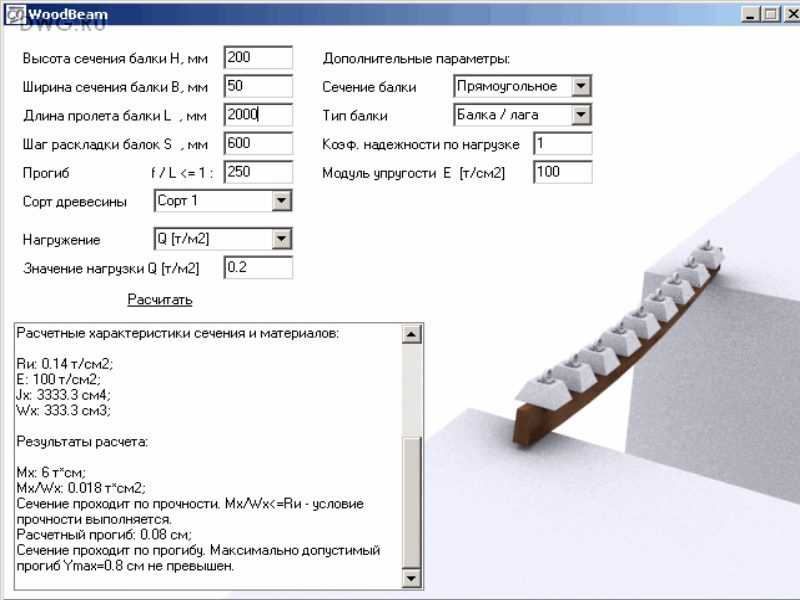 Консольная балка является определяющей конструкцией.

РЕКЛАМА

Допущения

Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для консольной балки, которая воспринимает только поперечные нагрузки, осевая сила всегда равна нулю. , при условии, что прогибы малы. Поэтому довольно часто пренебрегают осевыми силами.

Результаты расчетов на этой странице основаны на следующих предположениях:

• Материал однородный и изотропный (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
• Материал линейно-упругий
• Нагрузки приложены статически (не меняются со временем)
• Поперечное сечение одинаково по всей длине балки
• Прогибы малы
• Каждое поперечное сечение, изначально плоское, а также нормальное к продольному ось, остается плоской и нормальной к отклоненной оси. Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).

Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принята здесь.

Правила знаков

Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:

1. Осевая сила считается положительной, если она вызывает растяжение детали.
2. Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
3. Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.

Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.

Условные обозначения положительного знака для внутренней осевой силы, Н, поперечной силы, В, и изгибающего момента, М

Символы

• E: модуль упругости материала (модуль Юнга)
• I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
• L: общая длина балки
• R: опорная реакция
• d: прогиб
• M: изгибающий момент
• V: поперечный сдвиг усилие
• \тета: наклон

Консольная балка с равномерно распределенной нагрузкой

Нагрузка w распределена по всему консольному пролету, имеет постоянную величину и направление. Его размеры представляют собой силу на длину. Суммарная сила, приложенная к консольной балке, равна W=w L, где L — длина балки. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 92)}{6 E I}

РЕКЛАМА

Консольная балка с точечной силой на конце

Сила сосредоточена в одной точке, расположенной на свободном конце балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины кантилевера. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана.

В следующей таблице приведены формулы, описывающие статическую реакцию консольной балки на сосредоточенную точечную силу P, приложенную к концу.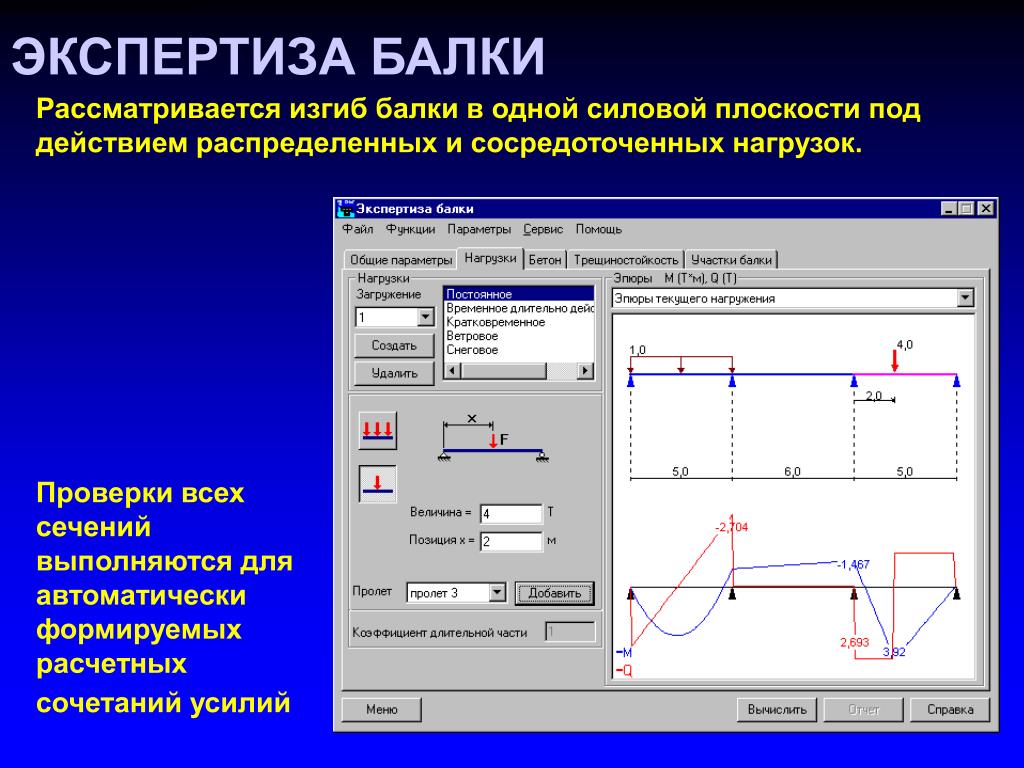 2}{2EI} 92(3L-x)}{6EI} Уклон в точке x: \theta(x)=-\frac{Px(2L — x)}{2EI}

Консольная балка с сосредоточенной силой в произвольном положении

Сила сосредоточена в одной точке в любом месте по длине кантилевера. Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.

Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на сосредоточенную точечную силу P, приложенную на произвольном расстоянии a от неподвижной опоры.

Cantilever beam with point load at random position
Quantity	Formula
Reactions:	R_A=P M_A=-Pa
End slopes : 92(3x — a)\over 6EI} &, x>a\end{выровнено} \right.
Наклон в точке x:	\theta(x)=\left\{\begin{align} -& {Px(2a — x)\over 2EI} &, x\le a \\& \theta_B & , x>a\end{выровнено} \right.

Консольная балка с точечным моментом

В этом случае момент создается в одной точке балки в любом месте по пролету. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.

В любом случае область приложения момента должна распространяться на небольшую длину кантилевера, чтобы его можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения результаты, предсказанные классической теорией балки, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), предсказанные результаты становятся полностью достоверными, когда мы удаляемся, как заявил Святой — Принцип Венана.

Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на сосредоточенный точечный момент M, приложенный на расстоянии a от неподвижной опоры.

_u=9049 2 _ u=9049 22}{2 E I} &, x\le a \\& -\theta_B \left(x-{a\over2}\right) &, x>a\end{aligned} \right.

Cantilever beam with point moment
Quantity	Formula
Reactions:	R_A=0 M_A=M
End slopes:	\theta_A =0 \theta_B =\frac{M a}{E I }
Предельный изгибающий момент:	M_u=M
Предельная сила сдвига:
Наклон в точке x:	\theta(x)=\left\{\begin{align}& \frac{M x}{E I} &, x\le a \\& \theta_B &, x> a\end{выровнено} \right.

Консольная балка с переменной распределенной нагрузкой

Нагрузка распределяется по всей длине консоли с линейно изменяющейся величиной, начиная с w_1 на неподвижной опоре до w_2 на свободном конце. Размеры w_1 и w_2 являются силой на длину.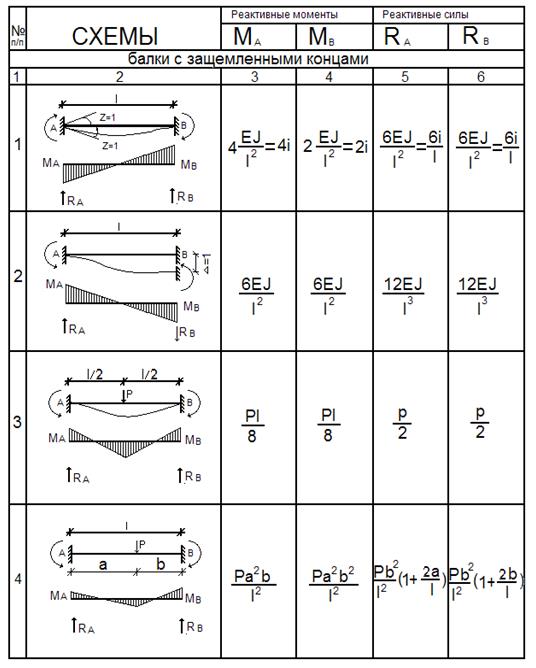 Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина кантилевера.

Если w_1=0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с возрастающей величиной (пик на вершине).

Если w_2=0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с уменьшающейся величиной (пик на неподвижной опоре).

В следующей таблице приведены формулы, описывающие статическую реакцию консольной балки трапециевидной формы на переменную распределенную нагрузку.

93}{24EI}

где: w_x=w_1+{(w_2-w_1)\over L}x

Распределение нагрузки трапециевидной формы на консольной балке является типичным 9

для консольных балок, поддерживающих плиту. Распределение имеет вид прямой трапеции с возрастающей частью вблизи неподвижной опоры и постоянной частью с величиной, равной w, на оставшейся длине до вершины. Размеры w представляют собой силу на длину. 2\right) 93}{6EI} &,x> a \end{align}\right.

Консольная балка с частично распределенной равномерной нагрузкой

Нагрузка распределяется на часть длины консоли с постоянной величиной w, а остальная часть не нагружена. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w\left(L-a-b\right), где L — длина консоли, а a, b — ненагруженные длины левой и правой сторон балки соответственно.

Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на частично распределенную равномерную нагрузку.

93}{6EI}&, a{<}x{<}L-b\\ &\theta_B &,x\ge L-b \end{выровнено}\right.

Кантилеверный луч с частично распределенной однородной нагрузкой
Количество	Формула
Реакции:
:
:
. 2}\справа)
Концевые откосы: