Калькулятор расчета деревянных балок перекрытия и стропильной системы!
Как пользоваться онлайн калькулятором расчета балок перекрытия и стропил
Чтобы правильно произвести прочностной расчет балки перекрытия и подобрать необходимый тип двутавровой балки, вы можете воспользоваться онлайн-калькулятором. На основе полученных вычислений можно точно рассчитать количество, необходимое для устройства стропильной системы или укладки лаг. Расчет деревянных балок перекрытия возможен только после того, как будет известно расстояние между стенами (расчетная длина балки). Кроме того, необходимо знание величины предполагаемой нагрузки на всю конструкцию.
Для межэтажных перекрытий, в том числе цокольного, используйте значение 400 кг/м2; для чердачного — 200 кг/м2 (или 250 кг/м2, если нагрузка от стропильной системы передается непосредственно на чердачное перекрытие). Для стропильной системы 220 кг/м2 для Московского региона, для других регионов принимайте значения в зависимости от снегового района.
Заказать бесплатный расчет балок по проекту или проконсультироваться у специалистов нашей компании можно по телефону
+7(495)105-91-63
+7(812)425-65-03
+7(843)207-04-92
+7(4722)77-73-16
+7(800)333-79-86
+7(421)240-08-29
+7(818)246-42-27
+7(861)212-30-63
+7(800)333-37-59
Онлайн калькулятор расчета деревянных балок перекрытия и стропил
Где используются балки
ПерекрытиеСтропила
Вам необходимо выбрать конструкцию, для которой вы будете использовать балки: будет ли это расчет перекрытий (применяются в качестве лаг) или стропильной системы (используются в качестве стропил).
Расчетная длина балки (м)
Длина при расчете перекрытия – это наибольший пролет, т.е. наибольшее расстояние между соседними стенами «в свету», на которые опирается балка.
 Например, в двускатной кровле расчетной длиной будет считаться расстояние по скату от конька до мауэрлата (опоры на стену).
Например, в двускатной кровле расчетной длиной будет считаться расстояние по скату от конька до мауэрлата (опоры на стену).Измеряется в метрах (пример: 7.8 м).
Шаг балки (0.2 м – 1.2 м)
Шаг (понятие, используемое при расчете) – это межцентровое расстояние между балками. В перекрытии дома с черновым полом (настилом) из плитных материалов, таких как OSB-3, ЦСП, мы рекомендуем использовать шаг в 0.4 м (40 см). Это связано с прогибом самого плитного материала при большем шаге балок. При более сложном «пироге» перекрытия можно использовать любой другой шаг.
Расчетная нагрузка (кг/м2)
Расчетной нагрузкой называется сумма временной и постоянной нагрузок. В СНиПе «Нагрузки и воздействия» расчетная нагрузка на перекрытие равна 400 кг/м2, на стропильную систему — 220 кг/м2. В частных случаях можно использовать другие значения.
Измеряется в килограммах на квадратный метр (пример: 400 кг/м2).
Отправить чертежи на бесплатный расчет
Узнать
цены на балки
Заказать
обратный звонок
Компания «ИнтерСити» производит износоустойчивые деревянные двутавры. Благодаря отличным эксплуатационным свойствам, изделия могут использоваться в различных конструкциях. Однако нужно помнить, что самостоятельно производить расчет балки перекрытия «на глаз» не следует. Ошибка может привести к прогибу конструкции под нагрузкой и, как следствие, потере возможности дальнейшей эксплуатации. Последующий ремонт или замена балок — очень трудоемкий и дорогой процесс. Отнеситесь серьезно к подбору и расчету конструкции перекрытий и стропил; излишняя экономия и подбор без расчета по принципу «всегда так строили» может привести к серьезным проблемам.
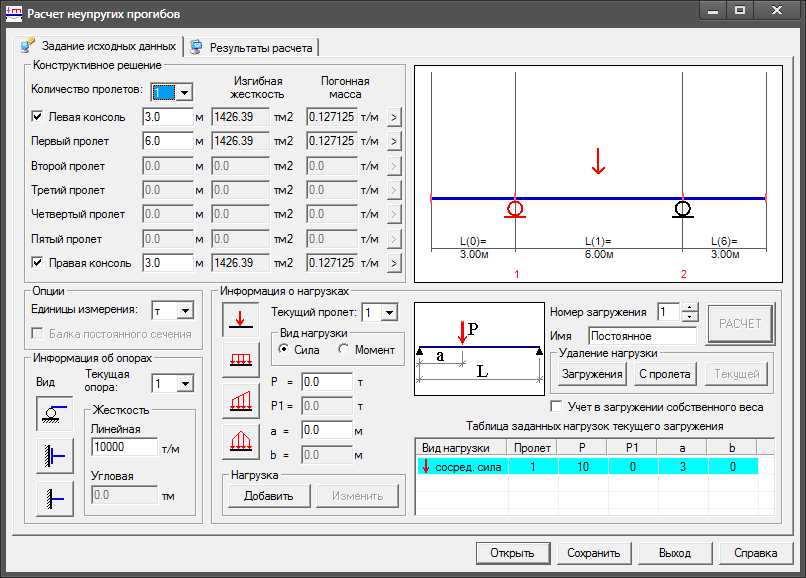
Расчет балок на изгиб и прогиб, крутящие моменты и выбор двутавра для монтажа
Главная / Статьи / Расчет балок
Расчет нагрузки двутавровой балки – определяем нагрузку на изгиб
Расчет нагрузки двутавровой балки осуществляется с целью вычисления номера из реестра металлопроката при составлении проекта основных конструкций и сооружений, а так же производства по ГОСТ или СТО АСЧМ. Он выполняется точно по формулам и таблицам, а вычисленные значения оказывают влияние на проектировку и ход строительных работ, также на рабочую функциональность и технические характеристики при эксплуатации.
Он выполняется точно по формулам и таблицам, а вычисленные значения оказывают влияние на проектировку и ход строительных работ, также на рабочую функциональность и технические характеристики при эксплуатации.
Сфера применения и параметры металлических двутавров
Главное предназначение двутавра во время проектировки любого типа сооружения заключается в изготовлении безопасной и крепкой несущей конструкции. В отличие от железобетонных опорных оснований, применение двутавровой балки дает возможность наиболее увеличить площадь пролетов частных либо коммерческих строений и снизить предельный вес важных опорных элементов. Благодаря этому, значительно увеличивается прибыльность строительства и решается ряд важных инженерных задач.
Двутавровая балка подбирается из расчета длины и массы. Балочная продукция бывает обычного горячего проката либо специализированного, и иметь параллельные и с наклоном полочные грани. Они производятся из углеродистой или из низколегированной стали и применяются во всех строительных отраслях.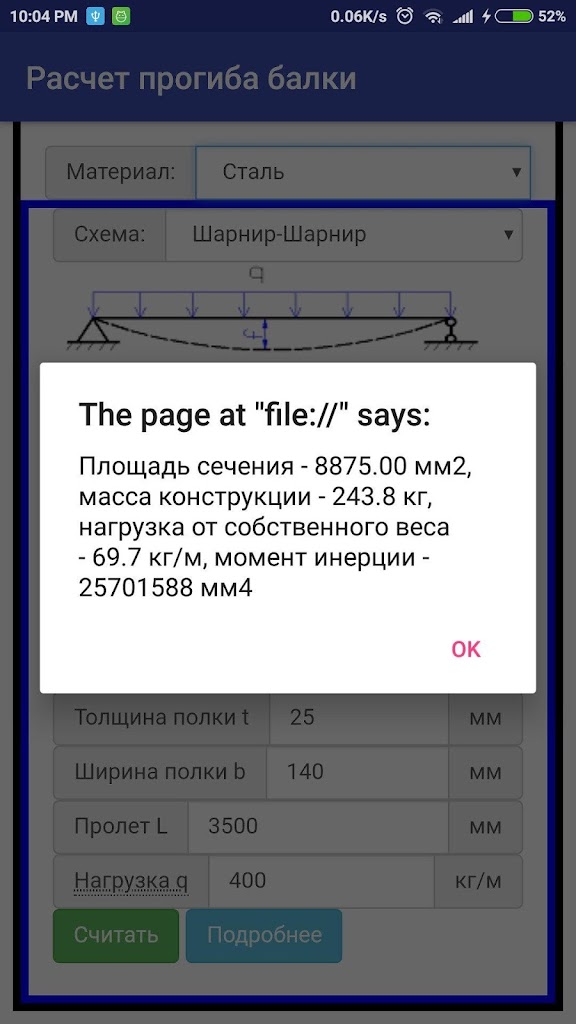
Согласно требованиям стандартизации 8239-89, размер металлического двутавра варьируется от трех до двенадцати метров. По способу применения данные элементы являются балочными, колонными, широко — полочными либо монорельсными, использующиеся при возведении подвесных элементов подкрановых путей и мостов. Определяется категория балки по специальному маркированию в таблице металлопроката, а точнее в ГОСТе и СТО АСЧМ, а правила применения и монтажа регламентированы документацией СНиП (Строительных норм и правил).
Масса двутавра определяется по утвержденному графику, в котором четко указан определенный числовой символ и обозначение балки, а еще немало важные параметры (ширина, высота, объемность полок и оптимальная толщина граней). Таким образом, для вычисления массы, по реестру требуется учесть установленный нетто погонного метра. К примеру, изделие под номером 46, при массе 65,5 кг, обладает длинной 15,5 метров.
Кроме расчетов массы, которые выполняются при помощи обычного калькулятора, во время проектирования важно вычислить наибольшую и наименьшую совокупность сил на предмет повреждения.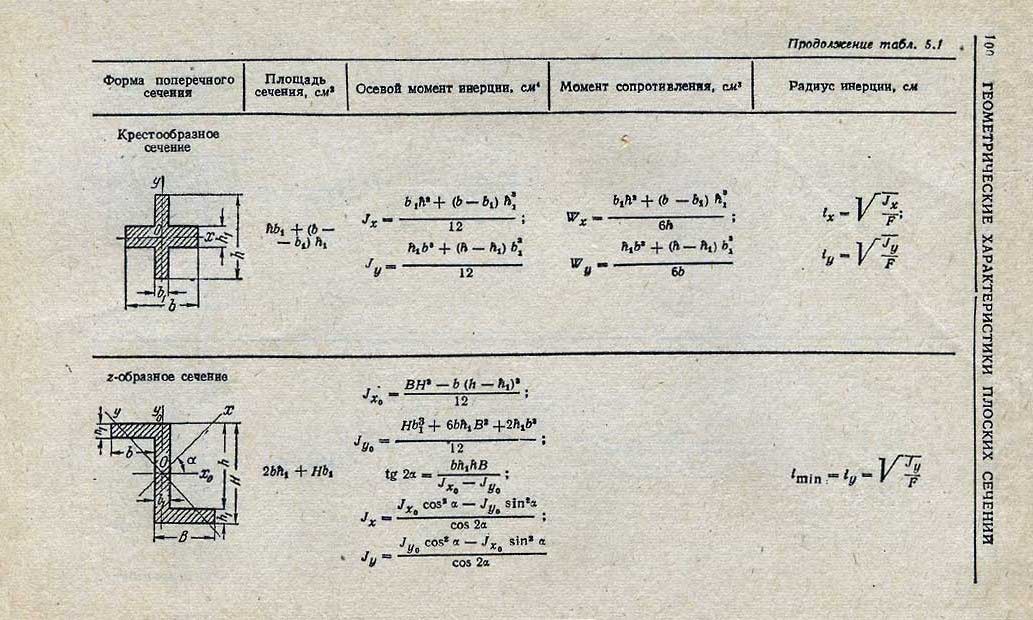
Расчеты основываются на следующих характеристиках металлопрофиля:
- Минимальная и максимальная дистанция между полками, беря во внимание их размеры.
- Наибольшая нагрузочная величина на проектируемое сооружение.
- Тип и геометрические формы изделий, способ фиксирования.
- Плоскость поперечного диаметра.
- Возникают ситуации, когда для вычислений требуется укладочный шаг (промежуток укладывания балок относительно друг друга).
Расчет двутавровой балки зачастую производится по критериям безопасности и просчета изгиба. Для достижения наиболее высокоточных значений в таблице металлопроката и основных требованиях указываются все дополнительные значения (момент сопротивления, делящийся на осевой и статический). Кроме этого нужно учитывать нагрузку на двутавр, зависящую от разновидностей металла, из которого изготавливается двутавр, и метод производства (сварка либо прокат). При сварном производстве во время расчетов добавляется около 30% к опорной нагрузке металлопрофиля.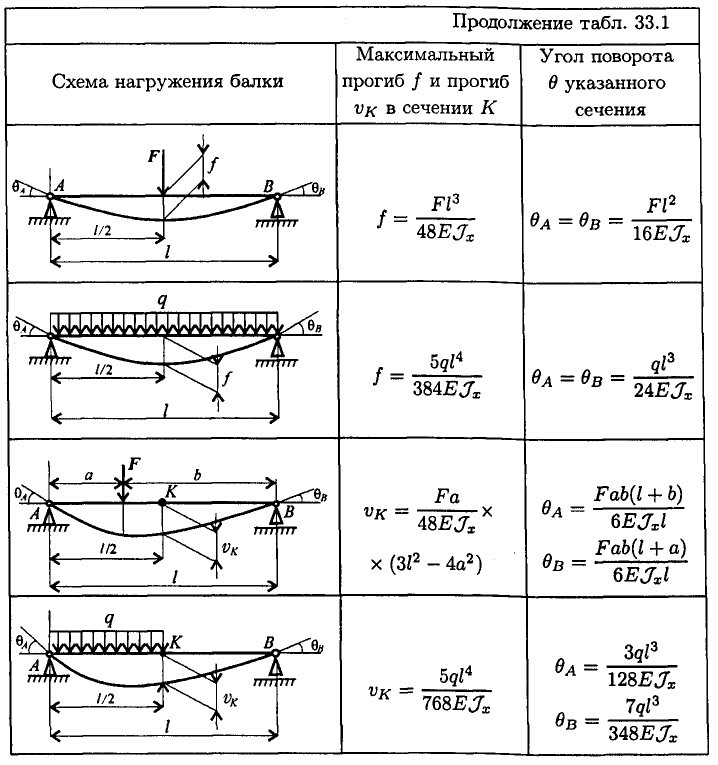
Выбор металлической балки по номеру и примеры расчета
В реестре металлопроката все номера двутавровых швеллеров указаны по всем требованиям ГОСТ стандарта. Таким образом, подбор номера обязан производиться, учитывая рабочую нагрузку, расстояние пролетов и вес продукции. К примеру, если наибольшая нагрузка на двутавр равняется 300 кг/м.п, из таблицы берется двутавровая балка под цифрой 16, при этом промежуточная дистанция равняется шести метрам при укладочном шаге от 1 до 1,2 метров. При подборе 20 металлопрофиля нагрузка на двутавр сильнее – до 500 кг/ м.п, а шаг соответственно до 1,5 метра. Изделие с порядковой нумерацией 10 либо 12 обозначает предельно установленную нагрузку до 300 кг/м.п и уменьшение пролета.
Таким образом, расчетные действия, какую нагрузку может выдержать металлическое изделие, осуществляются так:
- Высчитывается единица нагрузки на двутавр, давящая на опорное основание с учетом массы металлопрофиля, которая рассматривается на один погонный метр изделия.

- Полученная величина, согласно нормативным документам, перемножается на коэффициент прочности стали, указанным в ГОСТ.
- Пользуясь данными расчетных величин, требуется вычислить значение сопротивляющегося момента.
- Далее из полученного результата, выбираем нужный элемент из реестра металлопроката.
- Делая расчеты опорной физической нагрузки при определении профиля, советуем подбирать числа на пару строк больше имеющегося значения. Несущая особенность металлопрофиля определяется при вычислении двутавра на сгибание.
Как марки стали воздействуют на предстоящее проектирование?
При вычислении прочности опорной балки следует учитывать марку металла, использующегося в технологическом процессе, и категорию металлопроката. Для сложнейших металлоконструкций и строений, перекрытий многоэтажных коттеджей, индустриальных комплексах, требуется подбирать элементы из наиболее крепкого металла высшего качества. Продукция с наивысшей прочностью отличается небольшими габаритами, но при этом могут выдерживать существенные нагрузки. Поэтому вычисления на прочность рекомендуется выполнять несколькими методами, а информацию всегда требуется сравнивать для получения наиболее правильных математических расчетов. При определении пределов надежности и безопасности требуется учитывать существующие величины давления и не забывать немаловажные факторы, такие как, поперечные и продольные силы, крутящий момент. Можно применять разные способы калькуляции, при помощи которой можно определить разрешенные пределы надежности.
Поэтому вычисления на прочность рекомендуется выполнять несколькими методами, а информацию всегда требуется сравнивать для получения наиболее правильных математических расчетов. При определении пределов надежности и безопасности требуется учитывать существующие величины давления и не забывать немаловажные факторы, такие как, поперечные и продольные силы, крутящий момент. Можно применять разные способы калькуляции, при помощи которой можно определить разрешенные пределы надежности.
Как подсчитать предстоящую нагрузку?
С целью определения нагрузочных параметров на деформирование требуется четко придерживаться нижеперечисленных моментов:
- Прогнозируемая и существующая нагрузка.
- Размеры и масса предполагаемой конструкции.
- Нормативная сопротивляемость.
Для многих видов балок нет возможности произвести определение нагрузки на сгибание, ввиду их конфигурации и разновидности установки при возведении сооружений. Деформирование балки (прогиб) образуется в поворотных углах. Поэтому оно очень зависит от общих параметров сооружения, ее предназначения, марки стали и иных функциональных факторов.
Поэтому оно очень зависит от общих параметров сооружения, ее предназначения, марки стали и иных функциональных факторов.
Существуют различные варианты уравнений и способов для расчета балки на прогиб, их использование характеризуется расчетом деформирования обоих оснований. Наиболее чаще для проведения любых вычислений максимального нагрузочного давления на прогиб, профессионалы применяют специальную математическую формулу. Величину нагрузки проектируемой опоры следует перемножить на промежуток пролета в кубе. Итоговый результат делится на общую сумму модуля гибкости и величины момента инерции.
Модуль гибкости можно вычислить по марке стали, момент инерции обозначен в правилах стандартизации по цифровому коду исходного материала. Исходные цифры требуется удвоить на коэффициент, который равен 0,013. Если уже имеющийся относительный коэффициент деформирование выше либо ниже, чем обозначено в существующих правилах, то в будущей конструкции следует брать изделия большего либо меньшего диаметра.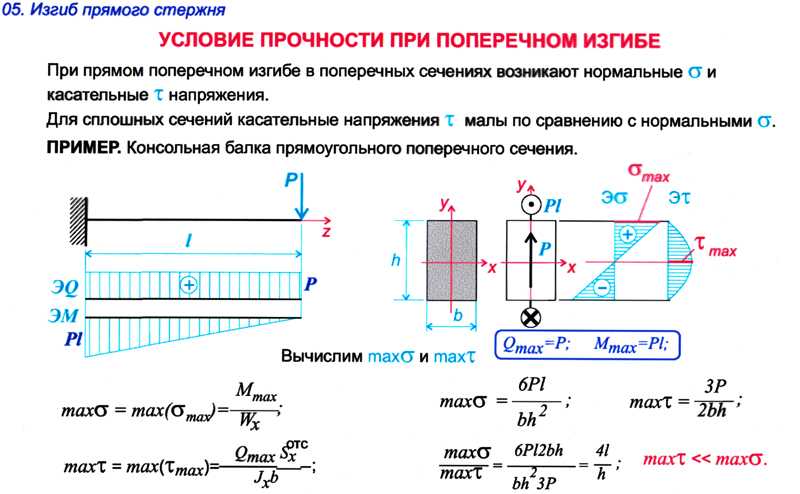
Требуется понимание того, что двутавровая балка, из — за своей конфигурации и массы, не очень часто находит применение при строительстве частных одноэтажных сооружений. Зачастую вместо них применяются облегченные швеллеры либо металлические углы. Но если вы все же планируете приобретение балок для постройки маленького домика, то не нужно решать сложнейшие математические задачи по всем критериям деформационных нагрузок. Хватит и элементарных расчетов допустимых пределов.
- Двутавровая балка
- Балка Б1
- Балка Б2
- Балка К1
- Балка К2
- Балка Ш1
- Балка Ш2
- Балка М
- Балка 09г2с
WebStructural — Расчет балки
Экстремальные значения


 калькулятор балки использует эти уравнения для расчета изгибающего момента, поперечной силы, наклона и прогиба.
диаграммы.
калькулятор балки использует эти уравнения для расчета изгибающего момента, поперечной силы, наклона и прогиба.
диаграммы.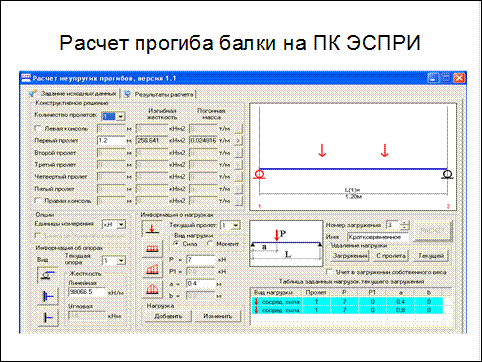 Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для проектирования стальных или деревянных балок
и вы хотите спроектировать следующую балку за считанные минуты, вам могут понравиться наши
Инструмент «Конструктор балок».
Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для проектирования стальных или деревянных балок
и вы хотите спроектировать следующую балку за считанные минуты, вам могут понравиться наши
Инструмент «Конструктор балок». чтобы получить к ним доступ.
чтобы получить к ним доступ.

 Например, если балка закреплена в направлении y в определенной точке, то в этой точке может возникнуть поперечная (y) внешняя сила реакции. Точно так же, если балку зафиксировать от вращения в определенной точке, то в этой точке может возникнуть внешний реактивный момент.
Например, если балка закреплена в направлении y в определенной точке, то в этой точке может возникнуть поперечная (y) внешняя сила реакции. Точно так же, если балку зафиксировать от вращения в определенной точке, то в этой точке может возникнуть внешний реактивный момент.
 Выбранная сторона отображается в виде синего участка луча, а участок, показанный серым цветом, игнорируется. Внутренние реакции на разрезе показаны синими стрелками. Реакции рассчитываются таким образом, чтобы рассматриваемое сечение балки находилось в статическом равновесии.
Выбранная сторона отображается в виде синего участка луча, а участок, показанный серым цветом, игнорируется. Внутренние реакции на разрезе показаны синими стрелками. Реакции рассчитываются таким образом, чтобы рассматриваемое сечение балки находилось в статическом равновесии.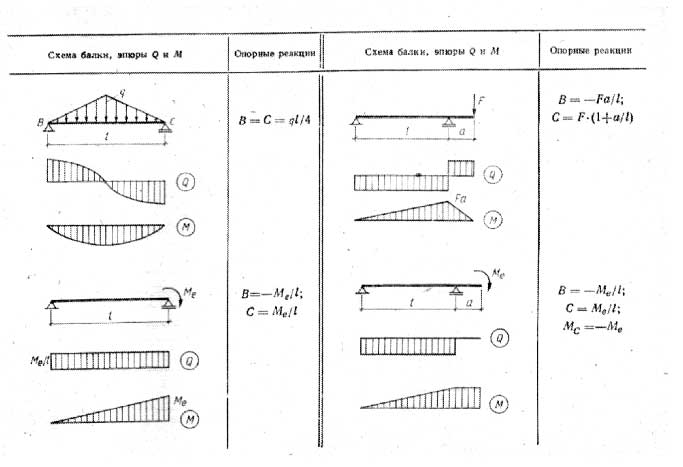 Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет верхнюю (т. е. заставляет балку «нахмуриться»).
Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет верхнюю (т. е. заставляет балку «нахмуриться»). Пример диаграммы поперечного момента показан на следующем рисунке:
Пример диаграммы поперечного момента показан на следующем рисунке: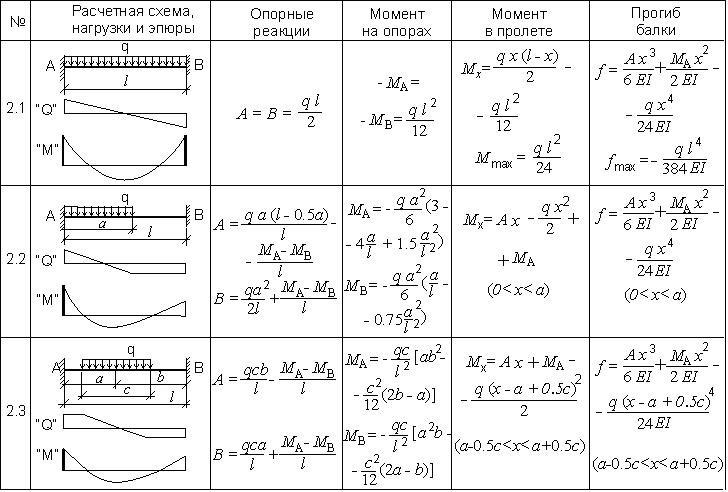
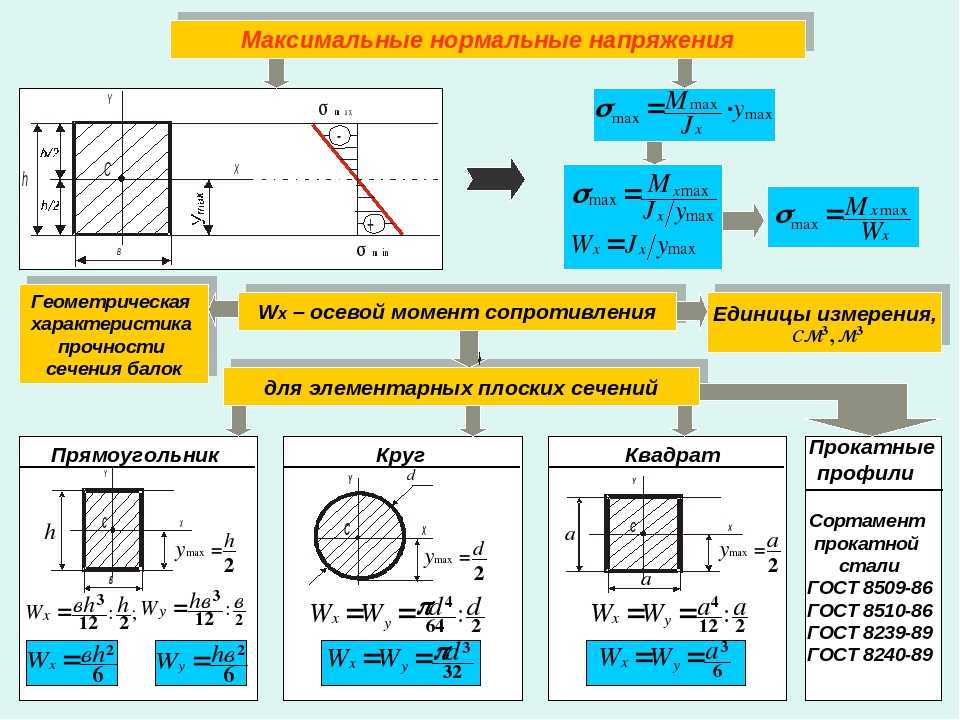
 Напряжение изгиба увеличивается линейно от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Напряжение изгиба увеличивается линейно от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.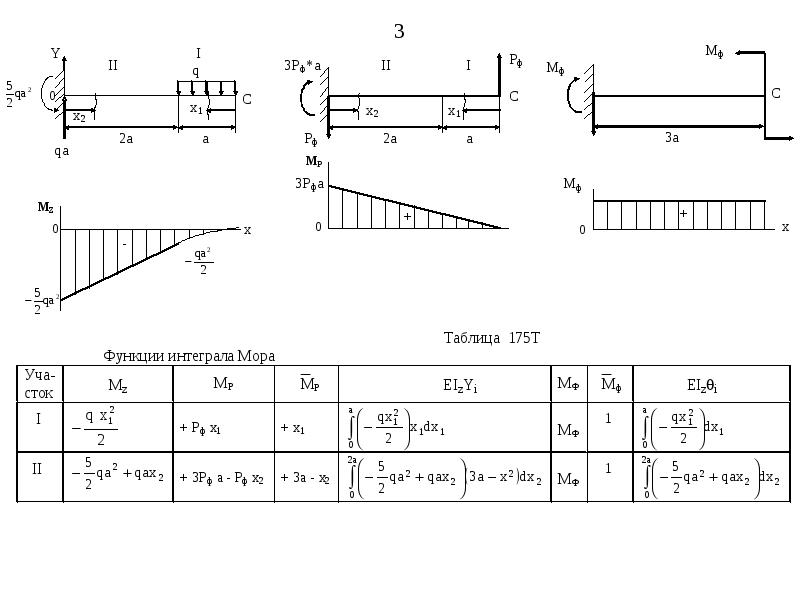 Все эти термины являются константами. Член Q — это первый момент площади, ограниченной точкой интереса и крайним слоем поперечного сечения:
Все эти термины являются константами. Член Q — это первый момент площади, ограниченной точкой интереса и крайним слоем поперечного сечения:

 Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.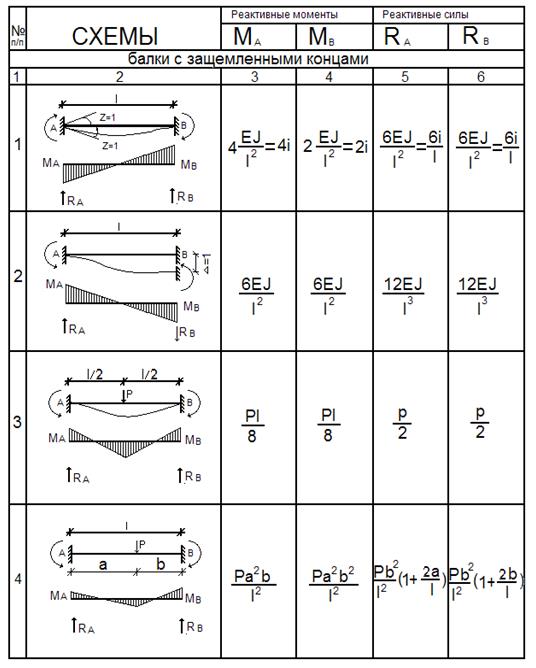 = +wL
= +wL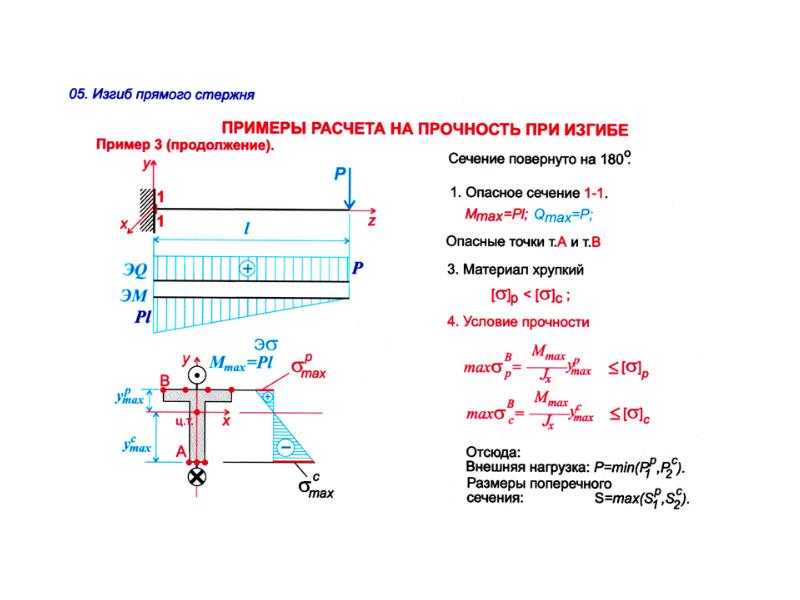 = FL / 4
= FL / 4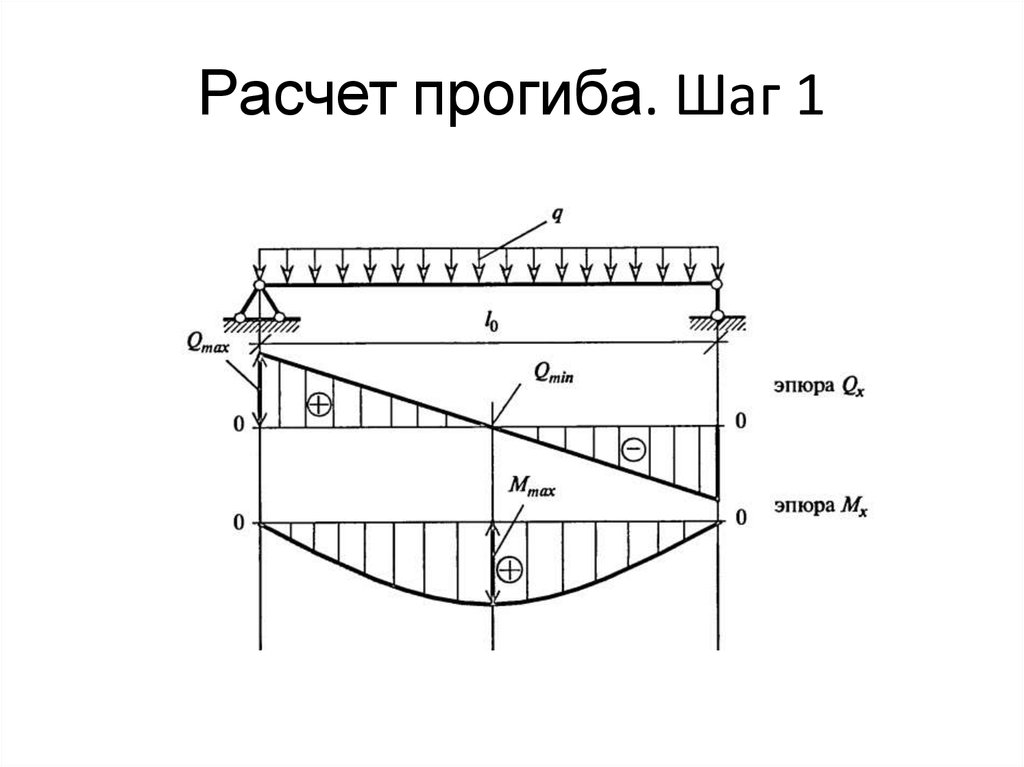 = wL 2 / 8
= wL 2 / 8