Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность. • AST3D
Skip to content
 Главная › Инфо › Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.
Расчет прогиба балки онлайн
Профиль
Материал
СтальЧугунАлюминийДеревоФанераМедьФторопластАкрилПоликарбонат
Способ фиксации
Шарнир-Шарнир (распределенная) Шарнир-Шарнир (точечная) Заделка-Шарнир (распределенная) Заделка-Шарнир (точечная) Заделка-Заделка (распределенная) Заделка-Заделка (точечная) Свободный конец (распределенная) Свободный конец (точечная)Схема фиксации
Значения
Выберите профиль
Результаты расчетов
Площадь поперечного сечения профиля:
—
Расчетный вес профиля (балки):
—
Прогиб балки F
—
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр».
Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Сделать расчет вала ЧПУ на прогиб также можно произвести на данном калькуляторе. Следовательно Вы будете знать предварительные прочностные показатели перед сборкой ЧПУ станка.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Ключевые слова: расчет балки на прогиб, расчет балки на прочность, расчет балки на двух опорах, расчет балки на изгиб, расчет балки онлайн бесплатно, расчет балки перекрытия, расчет балки на прогиб пример, расчет балки онлайн, расчет прогиба деревянной балки, расчет прогиба балки, расчет прогиба профильной трубы онлайн, расчет прогиба балки на двух опорах, расчет прогиба плиты перекрытия, расчет прогиба швеллера, beam deflection calculator, free, calculator online, Free Online Beam Calculator, Elastic beam deflection calculator, расчет прогиба металлической балки, расчет прогиба листа, расчет прогиба фанеры, расчет на прочность онлайн, расчет на прочность при изгибе, расчет на прогиб деревянной балки, расчет на прогиб металлической балки, расчет на прогиб, расчет на прогиб уголка
Редакция AST3D 17.
09.2018 11:11
Расчет балки
построение эпюр в балках
Расчетная схема №1841248
Для более удобной и быстрой оплаты Вы можете зарегистрироваться, пополнить счет на сайте и оплачивать со своего счета
Почему не бесплатно? — Сайт создан исключительно на энтузиазме автора и дабы этот энтузиазм не угас, хотелось бы его подкрепить хоть каким-нибудь материальным поощрением. Кроме того, возросшее количество пользователей вынудило перейти на платный хостинг.
Условия оплаты? — Взнос денег считаем спонсорским взносом, поэтому ни о каком возврате речь идти не может, тем более суммы мизерные — практически не о чем спорить.
Но! Если Вы оплатили взнос, но недовольны результатом, Вы всегда можете обратиться за помощью к автору —
Telegram: sopromat_xyz
WhatsApp
А Ваш сайт не сворует мой номер карты, пароли и т.
Слева Справа
Расстояние от левого края балки, м
Шарнирно неподвижная опора
Расстояние от левого края балки, м
Расстояние от левого края балки, м
плюс — вверх
минус — вниз
Расстояние от левого края балки
Значение, кНм
плюс — по часовой
минус — против
Координата начала, м
Координата конца, м
Значение в начале, кН/м
Значение в конце, кН/м
Название схемы
Общая длина балки, м
Эпюра М на сжатых волокнах (для механиков)
Подбор сечения и прогибы
подобрать двутавр [σ] = МПа
подобрать круг [σ] = МПа
подобрать квадратное сечение [σ] = МПа
подобрать трубчатое сечение [σ] = МПа при d/D=
подобрать прямоугольное сечение [σ] = МПа при h/b=
записать уравнения начальных параметров для каждого участка и посчитать прогибы и углы поворота в промежуточных точках
Какие балки можно здесь расчитать?
Как поставить треугольную нагрузку?
Добавить нагрузки / опоры
Заменим распределенную нагрузку равнодействующей
Q1 = 6·2 = 12кН
Составим уравнения равновесия для определения реакций опор
Σ MA = + P · 2 + M + Q1 · 3 — RE · 6= + 12 · 2 + 8 + 12 · 3 — RE · 6=0
Σ ME = — P · 4 + M — Q1 · 3 + RA · 6= — 12 · 4 + 8 — 12 · 3 + RA · 6=0
Из этих уравнений находим реакции опор
RA = 12.
RE = 11.33кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 12.67 = 12.667 кН
M(z1) = + RA · z = + 12.67 · z
M(0) = 0 кНм
M(2) = 25.333 кНм
На участке BC: (2 ≤ z2 ≤ 4 м )
Q(z2) = + RA — P — q1·(z — 2) = + 12.67 — 12 — 6·(z — 2)
Q(2) = 0.667 кН
Q(4) = -11.333 кН
M(z2) = + RA · z — P·(z — 2) — q
M(2) = 25.333 кНм
M(4) = 14.667 кНм
Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M
M(2.11) = 25.4 кНм
На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA — P — Q1 = + 12.
67 — 12 — 12 = -11.333 кН
M(z3) = + RA · z — P·(z — 2) — Q1·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)
M(4) = 14.667 кНм
M(5) = 3.333 кНм
На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA — P — Q1 = + 12.67 — 12 — 12 = -11.333 кН
M(z4) = + RA · z — P·(z — 2) + M — Q1·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)
M(5) = 11.333 кНм
M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 25.4 кНм. По этому значению подбираем сечение балки.
Условие прочности при изгибе σ = Mmax / W ≤ [σ]
Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
Посмотреть примеры
Не получается решить задачу? Есть вопросы? Нужна помощь? Обратитесь к авторам сайта через ВКонтакте Telegram: sopromat_xyz WhatsApp: +380936422175
Калькулятор балки онлайн (расчет реакции, изгибающий момент, поперечная сила, осевая сила)
- Расчеты
- Период
Выберите необходимое количество расчетов:
2 расчета 5 расчетов 10 расчетов
Цена: 4.
99$
Выбранный тариф позволяет сделать 2 расчета балок, рам или ферм. Бессрочно.
Выберите нужный период:
Цена: 39 $
Непродлеваемая подписка. Выбранный тариф позволяет произвести расчет балки, каркаса или фермы за 1 месяц без ограничений по количеству расчетов.
Количество пользователей: 1 (3 IP-адреса в день)
Узнать больше
Куда отправить код доступа ?
Согласитесь с условиями, чтобы продолжить.
Предварительно заполните данные о местоположении в платежной форме по IP-адресу.
Куда был отправлен код доступа ?
Для получения числовых значений диаграмм и подробного текста расчета необходимо Получить код доступа
(пример подробного отчета)
Конструкция рассчитывается с использованием математического аппарата метода конечных элементов. Для получения числовых значений диаграмм и опорных реакций необходимо Получить код доступа
Требуется длина балки!
Бесплатный калькулятор луча | ClearCalcs
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и нагрузку балки для анализа за несколько простых шагов.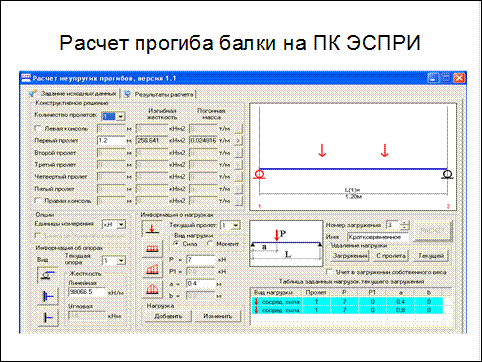
Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет доступ к дополнительным расширенным функциям для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет выполнять проектирование из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Основные свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно вводить распределенные, точечные и моментные нагрузки,
- «Сводка», в которой отображаются основные выходные данные и диаграммы.
Также имеется раздел «Комментарии», в котором пользователь может оставить любые примечания к дизайну. Щелчок по любой из меток ввода/свойства дает описательное справочное объяснение.
1. Свойства ключа ввода
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.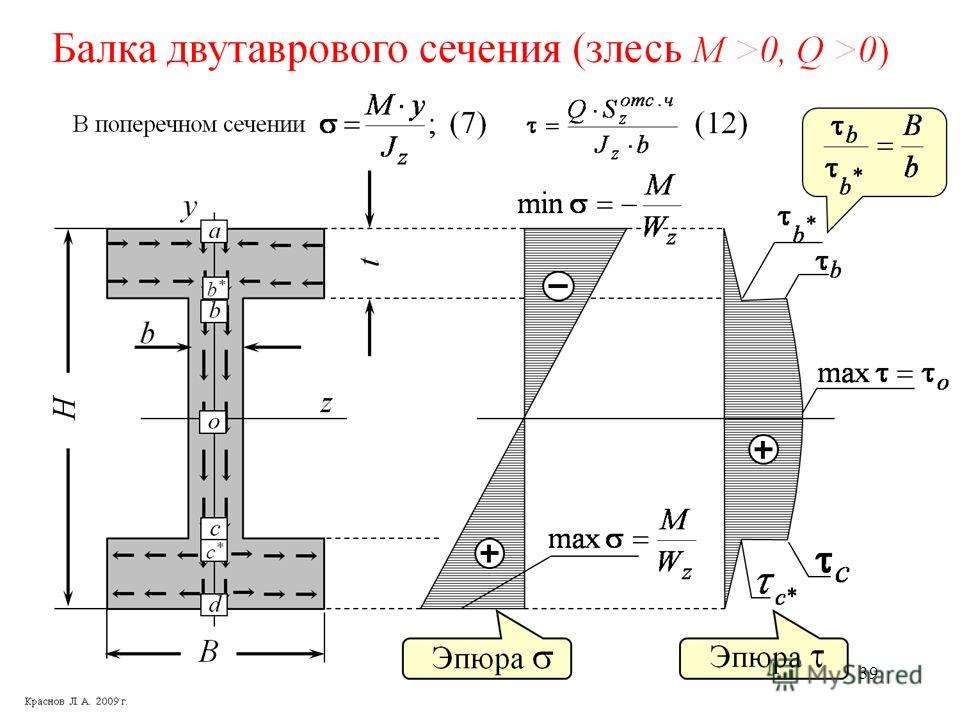
Длина балки – это общая сумма, включая все пролеты балки, в мм или футах.
Для модуля Юнга установлено значение по умолчанию 200 000 МПа или 29 000 тысяч фунтов на квадратный дюйм для конструкционной стали, но пользователь может изменить его.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также относится к выбранному сечению балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других сечений балки можно получить из библиотеки свойств сечений ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю ввести любое количество опор и указать их положение по длине балки. Тип опоры может быть фиксированным (фиксированным при перемещении, свободным при вращении) или фиксированным (фиксированным как при перемещении, так и при вращении) и выбирается из раскрывающегося меню.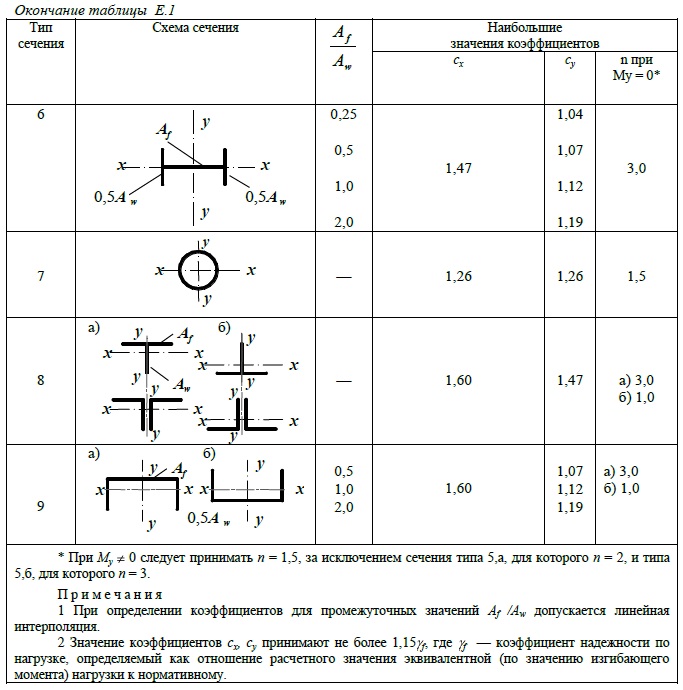
Требуется как минимум одна фиксированная опора или две опоры на штифтах.
Калькулятор балки также позволяет использовать консольные пролеты на каждом конце, так как положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются при добавлении, изменении или удалении опор в зависимости от заданной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждая загрузка может быть названа пользователем.
Для нагрузки используются следующие знаки (показаны положительные значения):
Распределенные нагрузки указаны в единицах силы на единицу длины, кН/м или pf, вдоль балки и могут быть приложены между любыми двумя точками. В калькуляторе можно применять два разных типа:
Равномерные нагрузки имеют постоянную величину по длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны совпадать.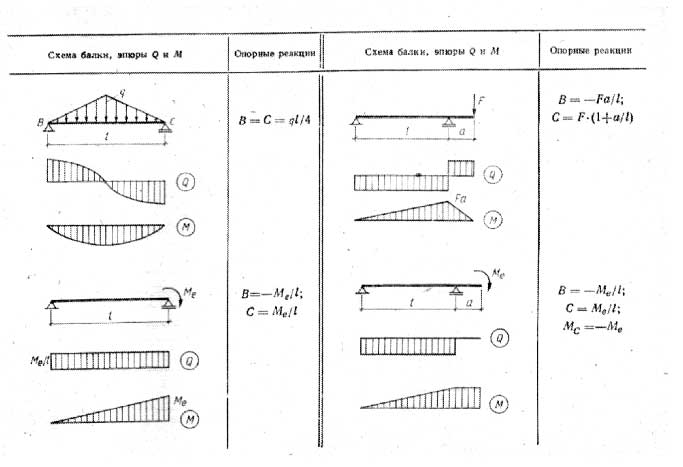
Линейные нагрузки имеют различную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и их можно использовать для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указаны в единицах силы, кН или тысяч фунтов, и площади, приложенной в отдельных точках вдоль балки. Например, они могут представлять реакции других элементов, соединяющихся с балкой. Пользователь вводит имя, величину и местоположение слева от луча.
На диаграмме ниже в качестве примера из сводного раздела показана двухпролетная неразрезная балка с линейной распределенной патч-нагрузкой и точечной нагрузкой.
3. Итоговые результаты расчетов
После задания нагрузки и геометрии калькулятор автоматически использует механизм анализа методом конечных элементов ClearCalcs для определения моментов, поперечных сил и прогибов. Максимальные значения каждого из них выводятся как
