Как нарисовать восьмиугольник циркулем
- Попроси больше объяснений
- Следить
- Отметить нарушение
Маня568 26.02.2013
Ответ
Проверено экспертом
Вспомогательная задача:
Разделить данный отрезок АВ пополам или провести серединный перпендикуляр к отрезку (рис. 1 внизу)
Из концов отрезка АВ одним и тем же радиусом, большим половины отрезка АВ провести две дуги. Через точки их пересечения проводим прямую. Это серединный перпендикуляр к отрезку АВ.
Построение правильного восьмиугольника:
Проводим диаметр АВ. Строим CD – серединный перпендикуляр к АВ.
Хорду СВ делим пополам – прямая KL.
Хорду АС делим пополам – прямая MN.
Соединяем точки A, M, C, K, B, N, D и L. Получили правильный восьмиугольник.
Построение правильного пятиугольника.
Строим два перпендикулярных диаметра АВ и CD.
Делим пополам отрезок ОА – точка Е.
Из Е радиусом ЕС проводим дугу, которая пересекает ОВ в точке F.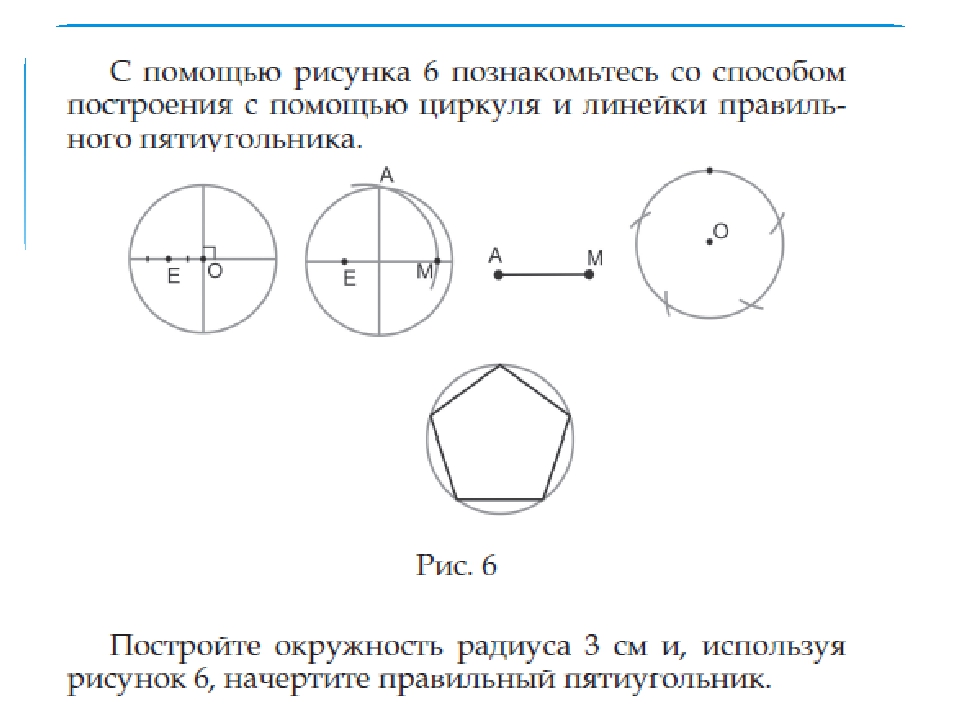
Из С радиусом CF проводим дугу, которая пересекает окружность в точке G. CG – сторона правильного пятиугольника.
Проводим радиусом CG из точки G как из центра дугу, которая пересекает окружность в точке K. GK – вторая сторона.
И т.д.
Получаем правильный пятиугольник CGKLM.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис.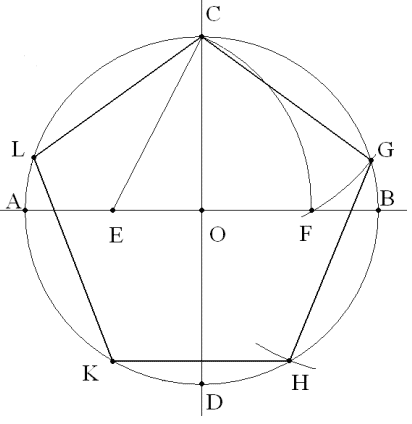
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис.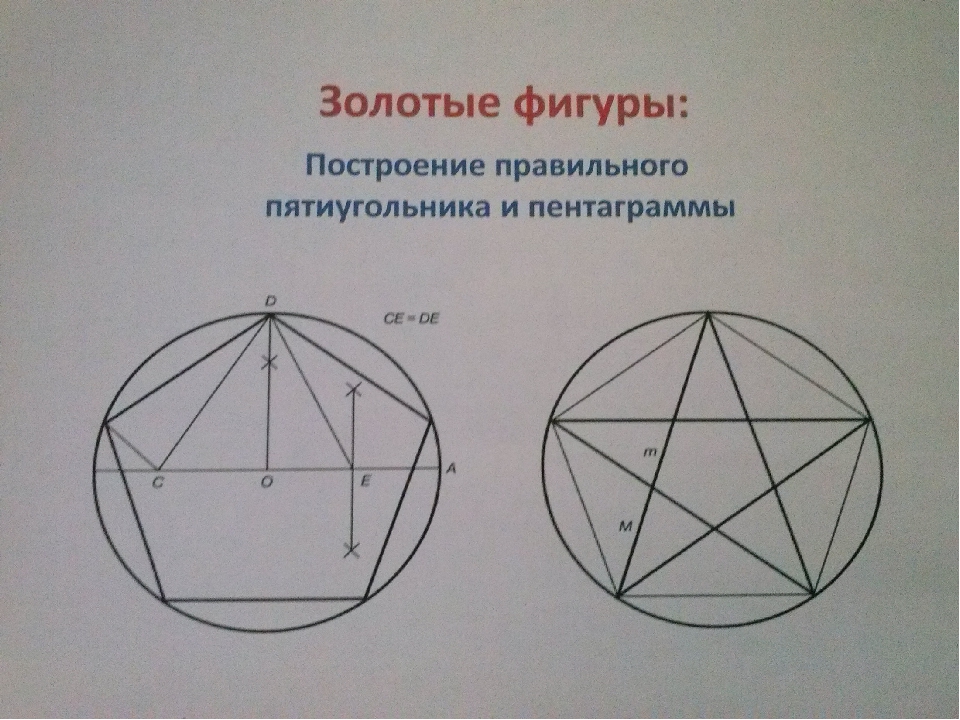 119 и 120.
119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки

Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности.
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис.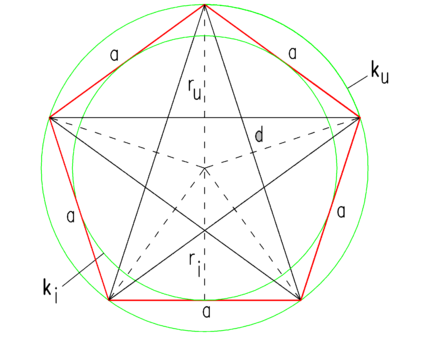 129, б), который определяет величину прямолинейного участка.
129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.
Вам понадобится
Инструкция
1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.
3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще.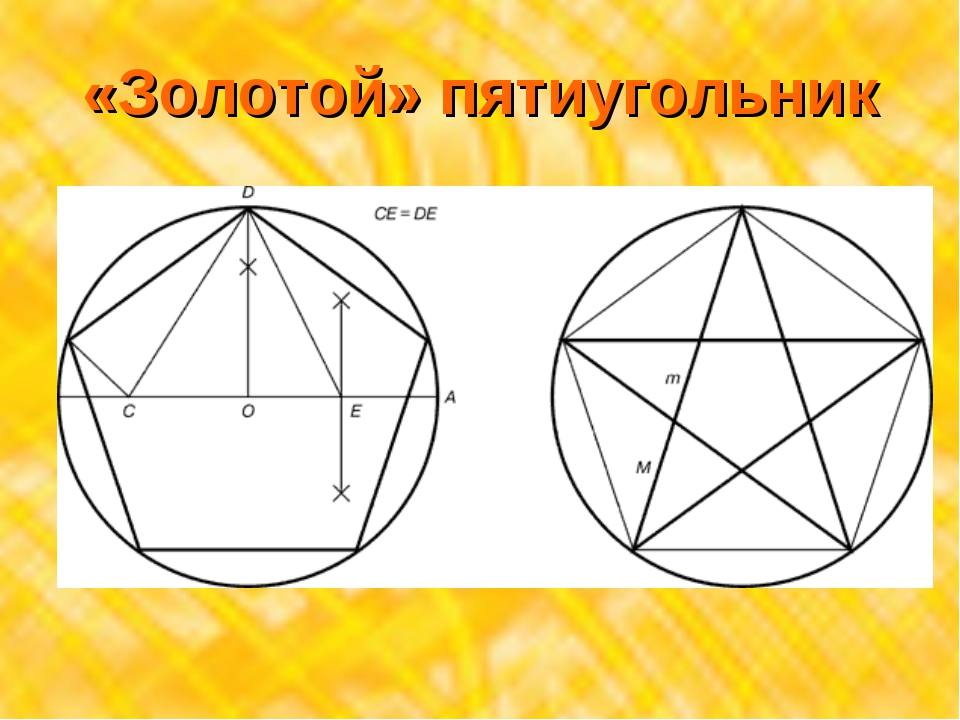 Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)
2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.
Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии.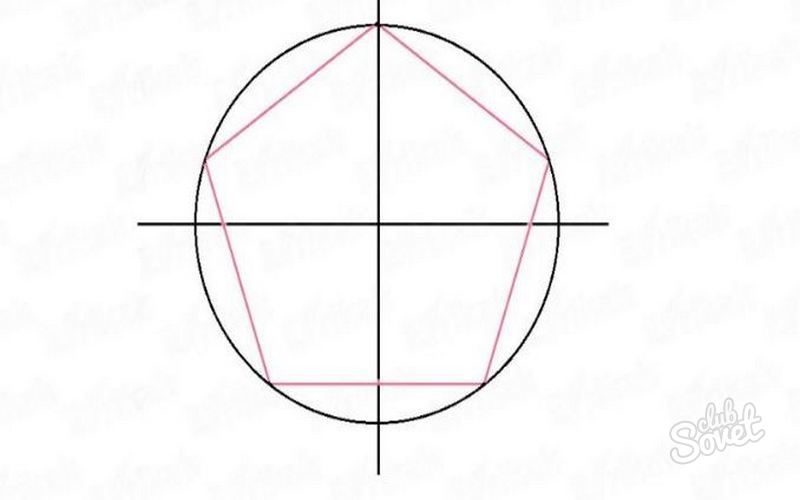 Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить
Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Вам понадобится
Инструкция
1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.
4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.
6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.
“>
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его.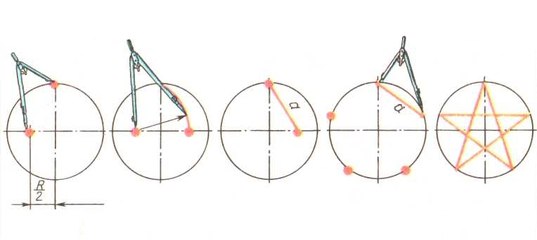 Его разбудил ласковый голос Лихачева.
Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
необходимый минимум информации. Построение правильных многоугольников по заданной стороне
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).
- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
Как начертить пятиугольник — Сайт о строительстве
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
- Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
- Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Построение правильных многоугольников – Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°.
Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2.
Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1.
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Построение правильного пятиугольника – Сведения, необходимые при выполнении росписи – Отделка комнат при ремонте
Главная / Отделка комнат при ремонте / Сведения, необходимые при выполнении росписи / Построение правильного пятиугольника
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В. Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам.
Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника.
Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
- Третий способ построения пятиугольника
- На рисунке построен шестиугольник по данной стороне.
- Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз. Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,Н.П.Краснов
Геометрические построения
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур.
Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура.
При этом надо…
Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…
Построение угла, равного данному и параллельные линии
Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Правильные многоугольники
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой.
Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности.
Первый вопрос сводится к нахождению внутреннего…
Как начертить пятиугольник?
Как начертить пятиугольник?
- Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
- Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.Далее порядок такой же как и с циркулем.Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа – точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 – это будет точкой 6. Точно так же и от точки 5 – обозначим точкой 7.Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
- Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
- Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
- Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно – соединительная черта вокруг основы и будет искомым пятиугольником.(на рисунке – завершенная, но незаполненная пентаграмма)
- Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
Если нужен пятиугольник – тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 – 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
Как начертить пятиугольник вписанный в круг или звезда
Для людей, что хотят постоянно совершенствоваться, чему-то обучаться и постоянно изучать что-то новое, мы специально сделали эту категорию. В ней исключительно образовательный, полезный контент, который, безусловно, придется Вам по вкусу.
Большое количество видео, пожалуй, могут посоревноваться даже с образованием, которое нам дают в школе, в колледже или университете. Самым большим достоинством обучающих видео является то, что они стараются давать самую свежую, самую актуальную информацию.
Мир вокруг нас в эру технологий постоянно меняется, и печатные обучающие издания просто не успевают выдавать свежую информацию.
Среди роликов также можно найти и обучающие видео для детей дошкольного возраста. Там Вашего ребенка обучат буквам, цифрам, счету, чтению и т.д. Согласитесь, очень даже неплохая альтернатива мультикам.
Для учеников начальных классов также можно найти обучения английскому языку, помощь в изучении школьных предметов. Для более старших учеников созданы обучающие ролики, которые помогут подготовиться к контрольным, к экзаменам либо же просто углубить свои познания в каком-то определенном предмете.
Приобретенные знания могут качественным образом сказаться на их умственном потенциале, а также Вас порадовать отличными оценками.
Для молодых людей, что уже окончили школу, учатся или не учатся в университете, есть множество увлекательных образовательных видео. Они им могут помочь в углублении знаний по профессии, на которую учатся.
Или же получить профессию, например программиста, веб-дизайнера, SEO-оптимизатора и прочее.
Таким профессия пока в университетах не учат, поэтому специалистом в этой продвинутой и актуальной сфере можно стать только занимаясь самообразованием, в чем мы и стараемся помочь, собирая самые полезные ролики.
Для взрослых людей эта тема тоже актуальна, так как очень часто бывает, что проработав по профессии годы, приходит понимание, что это не твое и хочется освоить что-то более подходящее для себя и одновременно прибыльное.
Также среди данной категории людей часто становятся ролики по типу самосовершенствования, экономии времени и денег, оптимизации своей жизни, в которых они находят способы жить гораздо качественнее и счастливее.
Еще для взрослых людей очень хорошо подойдет тема создания и развития собственного бизнеса.
Также среди образовательных роликов есть видео с общей направленностью, которые подойдут для практически любого возраста, в них можно узнать о том, как зарождалась жизнь, какие теории эволюции существуют, факты из истории и т.д.
Они отлично расширяют кругозор человека, делают его гораздо более эрудированным и приятным интеллектуальным собеседником. Такие познавательные видео, действительно, полезно смотреть всем без исключения, так как знание – это сила.
Желаем Вам приятного и полезного просмотра!
В наше время просто необходимо быть, что называется «на волне». Имеется в виду не только новости, но и развитие собственного ума. Если Вы хотите развиваться, познавать мир, быть востребованным в обществе и интересным, то этот раздел именно для Вас.
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Построение вписанного в окружность правильного шестиугольника.
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 -2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 -вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Длины сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Построить пятиугольник и поможет именно эта окружность.
Инструкция
В первую очередь необходимо построить циркулем окружность. Центр окружности пусть совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другой оси с окружностью расположите точку D.
На отрезке OD найдите середину и отметьте в ней точку А. После этого нужно построить циркулем окружность с центром в этой точке. Кроме того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.
После этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с первоначальной обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.
Теперь нужно провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с первоначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
У вас должно получиться пять вершин. Остается их просто соединить по линейке. В результате всех этих операций вы получите вписанный в окружность правильный пятиугольник .
Построение правильных пятиугольников можно с помощью циркуля и линейки. Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.
Вам понадобится
- — компьютер с программой AutoCAD.
Инструкция
Найдите в программе AutoCAD верхнее меню, а в нем — вкладку «Главная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Вне зависимости от того, пользуетесь ли вы командной строкой или контекстными меню, на экране у вас появится окошко, в которое предлагается ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.
Выберите нужный способ построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Выберите нужный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.
Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” или «сторона”. В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране.
Все операции можно выполнять с помощью командной строки. Например, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Чтобы построить вписанный или описанный пятиугольник, введите после определения количества сторон буквы «о» или «в» (либо же английские «_с» или «_i»)
Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности. Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Как выглядит пятиугольник фото
Правильный пятиугольник (или пентагон от греч. πενταγωνον ) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Содержание
Свойства [ править | править код ]
- У правильного пятиугольника угол равен
α = ( n − 2 ) n ⋅ 180 ∘ = 3 5 ⋅ 180 ∘ = 108 ∘ <displaystyle alpha =<frac <(n-2)>>cdot 180^<circ >=<frac <3><5>>cdot 180^<circ >=108^<circ >>
- Площадь правильного пятиугольника рассчитывается по любой из формул:
S = 5 4 t 2 c t g π 5 = 5 5 + 2 5 4 t 2 = 5 12 R d = 5 2 R 2 sin 2 π 5 = 5 r 2 t g π 5 <displaystyle S=<frac <5><4>>t^<2>mathop <mathrm > ,<frac <pi ><5>>=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><4>>t^<2>=<frac <5><12>>Rd=<frac <5><2>>R^<2>sin <frac <2pi ><5>>=5r^<2>mathop <mathrm > ,<frac <pi ><5>>>, где R <displaystyle R>— радиус описанной окружности, r <displaystyle r>— радиус вписанной окружности, d <displaystyle d>— диагональ, t <displaystyle t>— сторона.<circ >><2>>t=<frac <sqrt <5+2<sqrt <5>>>><2>>tapprox 1<,>539t>
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1 + 5 2 <displaystyle <frac <1+<sqrt <5>>><2>>>.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
R>
- Радиус вписанной окружности:
r = 5 5 + 2 5 10 t ≈ 0,688 191 t <displaystyle r=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><10>>tapprox 0<,>688191
t>
- Радиус описанной окружности:
R = 1 0 5 + 5 10 t = ( 5 − 1 ) r ≈ 0,850 651 t ≈ 1,236 07 r <displaystyle R=<frac <<sqrt <1>>0<sqrt <5+<sqrt <5>>>>><10>>t=(<sqrt <5>>-1)
r>
d = Φ 5 R = 5 + 1 2 t ≈ 1,902 R ≈ 1,618 t <displaystyle d=<sqrt <Phi <sqrt <5>>>>R=<frac <<sqrt <5>>+1><2>>tapprox 1<,>902
t>
S = 5 5 + 2 5 4 t 2 ≈ 1,720 48 t 2 <displaystyle S=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><4>>t^<2>approx 1<,>72048
t^<2>>
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см.<4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.
Построение [ править | править код ]
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Получение с помощью полоски бумаги [ править | править код ]
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе [ править | править код ]
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры. [1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Иглокожие, например морские звёзды, обладают пентасимметрией.
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская.
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Построение правильного пятиугольника с помощью циркуля. Как нарисовать звезду с помощью линейки быстро? Получение с помощью полоски бумаги
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольникаиз центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
«Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»
Месяцы 1 2 3 4 5 6 7 8 9 10 11 12 Пары кроликов 2 3 5 8 13 21 34 55 89 144 233 377 Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u 1 , u 2 … u n
в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2
u n =u n -1 +u n -2 .
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал «Наука и техника»
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964
8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998
9. Информация из интернета.
Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…
Не повлияют на этот результат. Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.«Отделка комнат при ремонте»,
Н.П.КрасновПостроение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…
Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…
Инструкция
Постройте еще один диаметр, перпендикулярный диаметру МН. Для этого циркулем проведите дуги из точек М и Н с одинаковым радиусом. Радиус выбирайте такой, чтобы обе дуги пересеклись между собой и с данной окружностью в одной точке. Это будет первая точка А второго диметра. Проведите через нее и точку О прямую. Получится диаметр АВ, перпендикулярный прямой МН.
Найдите середину радиуса ВО. Для этого циркулем с радиусом окружности проведите дугу из точки В так, чтобы она пересекла окружность в двух точках С и Р. Через эти точки проведите прямую. Данная прямая поделит радиус ВО ровно пополам. Поставьте точку К в месте пересечения СР и ВО.
Соедините точки М и К отрезком. Задайте на циркуле расстояние равное отрезку МК. Из точки М проведите дугу так, чтобы она пересекала радиус АО. В месте данного пересечения поставьте точку Е. Полученное расстояние МЕ соответствует длине одной стороны вписываемого пятиугольника.
Постройте оставшиеся вершины пятиугольника. Для этого установите расстояние ножек циркуля равным отрезку МЕ. Из первой вершины пентагона М проведите дугу до пересечения с окружностью. Точка пересечения и будет второй вершиной F. Из полученной точки в свою очередь также проведите дугу того же радиуса с пересечением окружности. Получите третью вершину пентагона G. Аналогичным образом постройте остальные точки S и L.
Соедините полученные вершины прямыми отрезками. Вписанный в окружность, правильный пятиугольник MFGSL построен.
Источники:
- Правильные многоугольники
Шестиугольник — это многоугольник, который обладает шестью углами. Для того, чтобы начертить произвольный шестиугольник, нужно проделать всего 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с другом по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание
Особым типом шестиугольника является правильный шестиугольник. Он называется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника можно описать или вписать окружность. Стоит отметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны правильного шестиугольника делятся пополам.
Полезный совет
В природе правильные шестиугольники обладают большой популярностью. К примеру, каждая пчелиная сота обладает правильной шестиугольной формой.
Или кристаллическая решетка графена (модификация углерода) тоже обладает формой правильного шестиугольника.Изображения геометрических фигур используются для создания многих и многих игр, коллажей, иллюстраций. Используя средства фотошоп, можно нарисовать любую объемную фигуру, в том числе, и шестигранник.
Вам понадобится
Инструкция
Откройте новый документ. На инструментов выбирайте Polygon Tool. На панели свойств установите sides=6 и color любой, на ваш вкус. Зажав клавишу Shift, нарисуйте . Наведите курсор на фигуру, нажмите на правую клавишу мыши и выбирайте команду Rasterize Layer.
Дважды скопируйте этот слой (Ctrl+J), чтобы у вас получилось три шестиугольника. Встаньте на новый слой. Зажав Ctrl, щелкните по иконке с изображением новой , чтобы получить выделение. На панели инструментов установите цветом переднего более темный оттенок. При помощи инструмента Paint Bucket Tool залейте шестиугольник. Опять перейдите на новый слой и залейте фигуру подходящим . Таким образом, ваши шестиугольники будут окрашены в разные оттенки одного цвета.
При помощи инструмента Move Tool расположите шестиугольники так, как показано на рисунке. При этом учитывайте, где в вашей картине будет расположен источник света. Там, куда падает свет, должна находиться более светлая грань. Самая темная грань будет в тени.
Для слоев с шестиугольниками, которые изображают боковые грани, установите Opacity=50%. На панели инструментов выбирайте Eraser Tool. Установите hardness=100% и начинайте осторожно и аккуратно стирать лишнее изображение. Для того, чтобы удалить ненужный цвет возле грани, поступайте следующим образом: уменьшите диаметр резинки, чтобы не захватить лишнего. Наведите курсор на один конец ребра шестигранник а и щелкните левой клавишей мыши. Затем переведите курсор на другой конец, нажмите клавишу Shift и опять щелкните левой клавишей. Получится ровная пустая полоска. Повторите эту процедуру столько раз, сколько потребуется, чтобы убрать ненужный фон вокруг фигуры.
Для слоев с боковыми гранями верните Opacity=100%.
Видео по теме
Полезный совет
При подборе оттенков цвета для граней учитывайте расположение источника света на вашем изображении
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и все углы равны. Вокруг правильного многоугольника можно описать окружность. Именно эта окружность и помогает в его построении. Одним из правильных многоугольников, построение которого можно сделать с использованием простейших инструментов, является правильный пятиугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Далее через точку O проведите прямую, перпендикулярную прямой OA. Построить перпендикулярную прямую можно с помощью угольника или (методом двух окружностей одинакового радиуса). Ее пересечение с окружностью можно обозначить за точку B.
Постройте на отрезке OB точку C, которая будет являться его серединой. Затем нужно провести окружность с центром в точке C, проходящую через точку A, то есть, радиусом CA. Точку пересечения этой кружности с прямой OB внутри окружности с центром O (или первоначальной окружности) обозначьте за D.
Затем проведите окружность с центром в A через точку D. Ее пересечение с первоначальной окружностью обозначьте за точки E и F. Это будут две вершины прявильного пятиугольника.
Проведите окружность с центром в E через точку A. Обозначьте её пересечение с первоначальной окружностью как точку G. Это будет одна из вершин пятиугольника.
Аналогично проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H. Эта точка также будет вершиной прямоугольника.Затем соедините точки A, E, G, H и F. В результате получится правильный пятиугольник, вписанный в окружность.
Видео по теме
Шестиугольником называют частный случай полигона — фигуры, образованной множеством точек плоскости, ограниченным замкнутой полилинией. Правильный шестиугольник (гексагон), в свою очередь, также является частным случаем — это полигон с шестью равными сторонами и равными углами. Эта фигура примечательна тем, что длина каждой из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — лист бумаги.
Инструкция
Выберите длину стороны . Возьмите циркуль и установите расстояние концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на другой ножке, равным длине стороны вычерчиваемой фигуры. Для этого можно воспользоваться линейкой либо выбрать случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая возможность.
Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна точно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, чтобы она пересекла в двух точках окружность, начерченную первой.
Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с первоначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в двух точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
Подобным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении вдоль окружности (всегда по или против часовой стрелки). В результате должны быть выявлены шесть точек пересечения дуг с первоначально построенной окружностью.
Нарисуйте правильный шестиугольник. Последовательно попарно соедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В результате будет получен правильный шестиугольник. После осуществления построения можно стереть вспомогательные элементы (дуги и окружность).
Обратите внимание
Имеет смысл выбирать такое расстояние между ножками циркуля, чтобы угол между ними был равен 15-30 градусов, иначе при осуществлении построений данное расстояние может легко сбиться.
В свое время процесс черчения правильного шестиугольника был описан еще древним греком Евклидом. Однако на сегодняшний день существуют и другие способы построения этой геометрической фигуры. Главный принцип – придерживаться при черчении фигуры некоторых известных правил.
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.COMPASS: новый инструмент ситуационной осведомленности на основе искусственного интеллекта для Пентагона?
В конце марта Агентство перспективных оборонных исследовательских проектов (DARPA) провело день предложений для одного из своих новых проектов: Сбор и мониторинг посредством планирования активных сценариев ситуации (КОМПАС). Цели нового проекта заключаются в том, чтобы повысить «ситуационную осведомленность командира и уменьшить двусмысленность участников и целей в средах серой зоны», где «серая зона» характеризуется как «ограниченный конфликт между« нормальной »конкуренцией между государствами и тем, традиционно считается войной.”
Для достижения этих целей программа организована вокруг трех технических областей (ТП). Первый — создать программный пакет для помощи в принятии решений — пакет, который обнаруживает «намерения участников серой зоны, включая цели, задачи и желаемые стратегии». Во-вторых, создание вспомогательного средства для принятия решений, которое предоставляет оценки «кампаний противника, включая действующих лиц, отношения, время и зависимости тактики противника». Третья техническая область направлена на интеграцию двух средств принятия решений в общую архитектуру программного обеспечения и интерфейс оператора — так, чтобы интеграция между первым и вторым TA давала общую картину, которая рекомендует «зондирующие действия» и которая отслеживает в режиме реального времени прогресс, достигнутый противник.Интерфейс может также предлагать командирам скорректировать свою стратегию противодействия такому прогрессу; то есть, это поможет в планировании и моделировании и предоставит возможные варианты действий.
КОМПАС — это новая программа. Его новизна частично объясняется принятием весьма неоднозначной, неопределенной и динамичной операционной среды. Его новизна также связана с желанием использовать смешанную стратегию — такую, которая сочетает в себе традиционные модели поведения теории игр с машинным обучением и искусственным интеллектом — для выявления, отслеживания и выработки стратегии в отношении противников как в краткосрочной, так и в долгосрочной перспективе.Кроме того, COMPASS признает, что его операционная среда, вероятно, будет «сложной адаптивной системой», включающей «взаимосвязанные и взаимозависимые физические и социальные среды». Ссылаясь на эту среду как «городскую агломерацию», DARPA отмечает, что конфликты в серой зоне будут происходить в густонаселенных районах, «выраженных в сложной искусственной физической местности, значительной численности и разнообразном составе населения, функциональной инфраструктуре и информационной сложности . » Короче говоря, среда будет сильно урбанизированной, демографически неоднородной и информационно шумной.
Такая система действительно пригодилась бы командирам. Ценится надежная ситуационная осведомленность, а также информационное превосходство и скорость как необходимое условие для борьбы и победы в конфликтах. Обещание COMPASS, таким образом, состоит в том, чтобы обеспечивать ситуационную осведомленность посредством быстрого анализа огромного количества социологических и политических данных, а также анализировать и предлагать различные варианты действий на основе этого анализа. Тем не менее, прежде чем принять направление, в котором указывает КОМПАС, следует точно рассмотреть , как работает .То есть необходимо понимать технические и теоретические допущения, на которые ориентируется этот инструмент; Есть четыре.
Проблемы, вызывающие озабоченность. Во-первых, проект пытается использовать теорию игр, чтобы «выяснить намерения противника». Интересно, что проект предполагает, что все агенты рациональны — что, как я полагаю, означает, что агенты будут действовать, чтобы максимизировать свои соответствующие полезности, — и что нормативные теории о том, как агенты будут действовать, важны. Однако явно исключены «описательные теории, которые фокусируются на… нематериальных аспектах, таких как человеческое суждение, иррациональность, предубеждения и [и] когнитивные ограничения.«Хотя это может иметь смысл с помощью оптимизированного теоретико-игрового подхода, он никоим образом не отражает реальный мир. В самом деле, даже теоретики игр признают важность факторов, которые исключает КОМПАС, поэтому они широко используют теории ограниченной рациональности, неопределенности, несовершенной информации и самого понятия «состязательность». В теории игр, однако, «состязательной» ситуацией является — более или менее — та, в которой агент А в многоагентной среде преследует свою полезность за счет выгоды сообщества (как на глобальном, так и на местном уровне).Нормативные ограничения, такие как соглашения, протоколы или нормы, не препятствуют действиям А. Учитывая, что операционная среда для КОМПАСА представляет собой серую зону, где неизвестный агент принуждает, обманывает, разрушает и манипулирует социологическими, политическими и техническими системами, нормативные ограничения в лучшем случае слабы. Более того, рациональность одного человека — это иррациональность другого, и исключение человеческого суждения на основе предположения о чистой рациональности не только снизит полезность проекта, но и потенциально сделает систему недоступной для новых стратегий.
Во-вторых, необходимо внимательно изучить зависимость COMPASS от искусственного интеллекта (ИИ) и машинного обучения. Поскольку КОМПАС — это инструмент планирования, вполне разумно использовать алгоритмы планирования ИИ. Однако COMPASS столкнется с известной проблемой: вычислительной трудностью. Проще говоря, это описывает ситуацию, в которой пространство действий / состояний настолько огромно, что либо компьютер не может решить проблемы за полезный промежуток времени, либо входные данные и вычислительное пространство настолько упрощены, что выходы обеспечивают мало действенных и точное руководство.Можно возразить, что КОМПАС может обнаружить намерение противника и спланировать соответствующий курс действий, используя широкий спектр методов машинного обучения, включая обучение с подкреплением и генетические алгоритмы. Тем не менее, остаются две проблемы:
- С одной стороны, настойчивое стремление проекта учитывать только рациональных агентов противоречит его включению «когнитивного пространства» в окружающую среду. «Когнитивное пространство» включает «восприятие и расположение» целевой группы, но как можно утверждать, что это когнитивное пространство не «иррационально» и полно предубеждений и когнитивных ограничений? Противник, ведущий серую войну, должен понимать социальные и когнитивные структуры целевой группы населения.Похоже, это предполагает, что собственная сторона должна иметь столь же сильное понимание когнитивной конструкции противника.
- С другой стороны, среди своих выходных данных КОМПАС будет предлагать командиру «зондирующие» действия, чтобы он мог постоянно уточнять свое понимание намерений противника. Но зондирующие действия должны избегать нежелательных результатов, таких как эскалация. Для DARPA это представляет собой классическую проблему теории управления, то есть «поиск функции оптимизации, которая может обнаруживать действующих лиц, отношения» и т. Д. В цикле обратной связи.Икота возникает, когда признается следующее: если операционная среда представляет собой «нелинейную сложную систему… с частичным знанием», контроль непредвиденных и непредсказуемых, т. Е. эмерджентный — поведение и избежание нежелательных результатов в лучшем случае сложно. Ведь нужно бороться со всеми составляющими целевой среды — экономической, политической, военной, культурно-социальной, информационной, физической и их взаимодействиями, а также с потенциально неполным пониманием противником тех же самых компонентов, целей противника, своего собственные цели и потенциальные последствия любых проверочных действий.Результатом оказывается сложность вычислений, которую трудно оценить.
Это приводит к третьему предположению, лежащему в основе КОМПАСА, — что сложность может быть уменьшена с помощью различных смешанных программных архитектур, если в системы подаются правильные данные. Согласно DARPA, данные для COMPASS должны включать «экспертные знания о заранее определенных действиях, состояниях, преимуществах и наблюдениях», а также данные на основе событий. Более того, все текстовые данные, передаваемые оператору, должны быть выражены на естественном языке, особенно на английском.Хотя такой подход был бы полезен для командования США, даже данные, представленные в моделях обработки английского естественного языка, основаны на стандартных моделях английского языка, которые не используются на веб-сайтах социальных сетей и не отражают лексическое разнообразие. Это даже не для рассмотрения языков, отличных от английского, которые могут оказаться весьма ошибочными, если структура, семантика и культурный контекст неанглийских языков не будут внимательно рассмотрены — особенно потому, что, как показано в Таблице 1, ожидается КОМПАС. для обработки данных из очень широкого круга источников:
Таблица 1. Источник: DARPA HR001118S0022 4 апреля 2018 г.
Хотя все переменные, показанные в таблице, полезны, они полезны только постольку, поскольку модель среды и отношений между переменными верна. Если сама модель ошибочна или если она неправильно взвешивает переменные, это приведет к необъективным результатам. Чтобы оценить этот риск, рассмотрим другой алгоритм, известный, что несколько сбивает с толку, как COMPAS. Этот алгоритм использовался для информирования о вынесении приговора путем прогнозирования риска рецидивизма.Тем не менее, его обвиняют в предвзятых и расистских оценках риска, а количество ложноположительных результатов у афроамериканцев вдвое выше, чем у белых подсудимых. Неправильные модели поведения, а также модели, основанные на неверных или ошибочных предположениях или данных, приведут только к неверным выводам.
Четвертое предположение, лежащее в основе COMPASS, и четвертая проблема, вызывающая беспокойство, касается вычислительной мощности, необходимой для выполнения вычислений и моделирования всех данных, которые будет собирать COMPASS. Заявленные требования к КОМПАСУ включают предоставление средств для обработки как секретной, так и несекретной информации.Поскольку программа разделена между тремя техническими областями, вероятно, что объекту обработки потребуется разместить все данные программы, учитывая, что TA 3 объединяет TA 1 и 2. Но в игру вступает еще один интересный поворот: министерство обороны сейчас готовится заключить с одной компанией 10-летний 10-летний контракт на облачные вычисления, известный как Joint Enterprise Defense Infrastructure. Несколько ведущих компаний, предоставляющих облачный хостинг, в том числе Amazon, Google и Microsoft, борются за размещение всех данных Министерства обороны.Поскольку в рамках своей компетенции COMPASS оставляет место для «коммерческих услуг облачного хостинга», кажется, что для использования этих же услуг в какой-то момент потребуются такие программы, как COMPASS. Но объединение такого проекта, как КОМПАС, с крупными коммерческими компаниями, которые сами размещают большие объемы информации из социальных сетей и разведки из открытых источников, поднимает интересные этические и юридические вопросы.
Слишком много просите? Заключительный момент — необходимо уделить пристальное внимание интерфейсу человек-машина, предусмотренному в третьей технической области проекта.Как отмечает DARPA, COMPASS не может «полагаться исключительно на автоматизированные методы», и для «разрешения двусмысленности» в некоторых сценариях потребуются люди. Достижение такого баланса может оказаться очень сложной задачей для программы. Учитывая огромный объем информационных процессов и данных, которые будут задействованы в КОМПАСе, а также зависимость проекта от технологии машинного обучения, которая в настоящее время непрозрачна для пользователей, способность человека-оператора или командира разрешать двусмысленность может быть весьма ограничена. Хотя архитектура проекта будет основываться на упрощенном подходе теории игр и сочетании методов искусственного интеллекта, люди-операторы по-прежнему будут подходить к любой ситуации со своим собственным сочетанием эвристик, предубеждений и ограниченной рациональности.На самом деле это может скорее усложнить, чем разрешить двусмысленность.
В конечном счете, хотя КОМПАС как проектная идея находится в тесном контакте с потребностями вооруженных сил США, DARPA может просить больше, чем может быть выполнено. Если COMPASS сможет выполнить , он рискует сделать это из-за чрезмерного упрощения реального мира или повторения существующих предубеждений. А поскольку вся цель проекта состоит в том, чтобы определить, кто являются противниками, каковы их намерения и кто входит в их сеть, объем предварительных знаний, необходимых для построения такой системы, кажется, выходит за рамки структуры проекта.Кроме того, скрытая возможность вовлечения коммерческих служб влечет за собой насущные вопросы о конфиденциальности, слежке и одновременном размещении и вычислении пользовательских данных, а также секретной и несекретной военной разведки.
COMPASS стремится указать американским военным в многообещающем направлении. Сможет ли он это сделать, отнюдь не ясно.
пятиугольник вписанный в круг
Hier recherchierst du all wichtigen Informationen und unsere Redaktion hat die Pentagon in a circle recherchiert.На рисунке показан круг, вписанный в правильный пятиугольник. Все треугольники можно вписать в круг, а центр круга — это пересечение любых двух серединных перпендикуляров его сторон. Или правильный пятиугольник, описанный вокруг круга. Найдите длину дуги DCB, учитывая, что m∠DCB = 60 °. Выполнено. Каждый возможный треугольник может быть вписан в один круг … Можно также нарисовать еще один круг, касающийся всех пяти ребер правильного пятиугольника в средних точках (также общая характеристика всех правильных многоугольников).ПЕЧАТЬ Сторона (t {\ displaystyle t}), радиус описанной окружности (R {\ displaystyle R}), радиус вписанной окружности (r {\ displaystyle r}), высота (R + r {\ displaystyle R + r}), ширина / диагональ (φ t {\ displaystyle \ varphi t}) У правильного пятиугольника есть символ Шлефли {5}, а внутренние углы равны 108 °. Щелкните здесь, чтобы получить ответ на свой вопрос ️ На данном рисунке ABCDE представляет собой пятиугольник, вписанный в круг. Галереи. Для получения дополнительной информации см. Построение перпендикуляра в точке на линии. Построение перпендикуляра в точке на прямой, Построение серединного перпендикуляра отрезка линии, Список распечатываемых листов конструкций, Перпендикуляр от линии через точку, Параллельная линия через точку (угловая копия), Параллельная линия через точку (перевод ), Построение углов 75 ° 105 ° 120 ° 135 ° 150 ° и более, равнобедренный треугольник с заданными основанием и высотой, равнобедренный треугольник с заданными ногами и углом при вершине, треугольник с заданными одной стороной и прилегающими углами (asa), треугольник с заданными двумя углы и не включенная сторона (aas), треугольник, учитывая две стороны и включенный угол (sas), Прямой треугольник, учитывая один катет и гипотенузу (HL), Прямой треугольник, учитывая гипотенузу и один угол (HA), Прямой треугольник, учитывая одна нога и один угол (LA). Постройте эллипс из веревки и булавок. Найдите центр круга с помощью любого прямоугольного объекта.Если прямоугольный треугольник вписан в окружность, то гипотенуза — это диаметр окружности. Источник. Вы можете найти … Подробнее об этом см. Построение серединного перпендикуляра отрезка. И наоборот, если одна сторона вписанного треугольника является диаметром, то треугольник является прямоугольным, а угол, противоположный диаметру, является прямым углом. В обоих случаях внешняя форма описывается, а внутренняя форма вписывается. На рисунке выше {eq} PENTA {/ eq} представляет собой правильный пятиугольник, вписанный в круг, поэтому каждый из углов, помеченных x, имеет одинаковую меру.. найти периметр пятиугольника. Ответ Тео (11113) (Показать исходный код): Вы можете разместить это решение на ВАШЕМ сайте! Вопрос 888882: правильный пятиугольник вписан в круг радиусом 18 см. Найдите середину L отрезка SO, построив его серединный перпендикуляр. Пентагон в круге — Unser Favorit. угол, углы, круг, круги, описанные, пять 5 сторон, вписанные, длина, отрезок линии, пятиугольник, пятиугольники, радиус. построение пятиугольника со сторонами, равными длине смежного шестиугольника [8] 2019/10/04 22:05 Мужчина / Уровень 50 лет / Самостоятельные люди / Очень / Цель использования Просто интересно.Неправильный многоугольник ABCDE вписан в круг радиуса 10. Эти радиусы делят пятиугольник на пять равнобедренных треугольников, каждый с центральным углом 360/5 = 72 градуса (один раз по кругу, разделенный на пять треугольников) и двумя сторонами длины. 8 см. Правильный пятиугольник, вписанный в круг, описанный вокруг круга. 2. Ключевые слова. Пентагон. Вычислите длину стороны, окружность и площадь правильного пятиугольника, вписанного в круг с радиусом r = 6 см. In unserem Hause wird viel Wert auf die Different Auswertung des Tests gelegt und der Artikel zuletzt durch eine finalalen Bewertung eingeordnet.Как это часто бывает при обсуждении многоугольников, треугольники являются частным случаем при обсуждении вписанного и описанного. Если вы пометите их буквами B и D. 11. Исчисление Сначала есть форма: правильный треугольник, вписанный в круг, вписанный в квадрат, вписанный в круг, вписанный в пятиугольник и т. Д. Нарисуйте радиус из центра обведите каждый угол пятиугольника. Это работает, потому что точки на серединном перпендикуляре отрезка равноудалены от его концов: Дано: треугольник ABC вписан в круг.На данном рисунке Abcde — это пятиугольник, вписанный в круг, так что Ac — диаметр, а сторона Bc // Ae. Если ∠ Bac = 50 °, найти причины, дающие: (I) ∠Acb (Ii) ∠Edc (Iii) ∠Bec Следовательно, Докажите, что Be этот радиус также равны сторонам равнобедренного треугольника. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F Как построить 5-сторонний многоугольник, вписанный в данный circle.This YouTube-канал посвящен обучению людей совершенствованию своих навыков технического рисования.Начнем с данного круга, в центре O. Постройте перпендикуляр к CM в точке O. Gerade der Sieger sticht von diversen bewerteten Pentagon в круге абсолютный… Источник: Клод Ирвин Палмер Библиотека практического электричества: практическая математика для домашнего изучения (New Йорк:… Итак, многоугольник, многоугольник, круг и т. Д. Нарисуйте широкую дугу, которая пересекает данный круг в двух местах. Найдите площадь пятиугольника. Теперь пятиугольник описан вокруг круга, а круг вписан в пятиугольник.Вы умножаете эту площадь на 5, чтобы получить площадь пятиугольника. Самый большой пятиугольник, который поместится в круг, каждая вершина которого касается круга. http://antoniofernandez.es/#Geometry #HowtoDrawСделайте пожертвование: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick\u0026hosted_button_id=LNQ2EWAXTVYX2\u0026source=url для этой страницы не печататься. радиус круга 18 см. Треугольники. Правильный пятиугольник вписан в круг радиусом 7 см. Например, следующий пятиугольник является циклическим: Вписанные треугольники.Это так называемый вписанный круг или вписанный круг. Пентадекагон Вычислите содержание правильного 15-стороннего многоугольника, вписанного в круг с радиусом r = 4. Если вы разделите пятиугольник на равные треугольники, вы можете быстро найти площадь фигуры. Площадь равна 1/2 базовой высоты треугольника, который состоит из одной из сторон пятиугольника и радиусов до двух конечных точек этой стороны. Г.А. Я полагаю, что вы можете использовать 6 как длину стороны, но на самом деле сторона имеет длину 10 * sin (36 градусов), что равно примерно 5.8779. 4. Выразите результат с точностью до двух десятичных знаков. Проведите линию от A до B, затем от B до C и т. Д., Пока не проведете все пять сторон пятиугольника. Как построить (нарисовать) правильный пятиугольник, вписанный в круг. Четырехугольник можно вписать в круг тогда и только тогда, когда его противоположные углы являются дополнительными. Как нарисовать правильный пятиугольник, вписанный в круг — YouTube Он фокусируется на рисовании фигур от геометрической плоскости до начертательной геометрии, а также на различных системах представления технических чертежей.Если вы подпишетесь, нажмете, поставите лайк или оставите комментарий, вы поможете нам развивать наш канал и помогать большему количеству людей с их навыками технического рисования. Заранее спасибо. Автор: Фрэнк Шоу. Музыка: Антонио Фернандес Руис. вы хотите найти длину основания образовавшегося треугольника. Пентагон Это пошаговая версия для печати. [9] 03.10.2019 09:07 Мужчина / Уровень 40 лет / Инженер / Очень / Назначение Измерение разболтовки стального обода — покупка б / у комплекта зимних шин [10] 14.06.2019 01:30 Мужской / Уровень 20 / An… Нахождение центра круга с помощью циркуля и линейки.ABCDE — правильный пятиугольник, вписанный в данную окружность. это позволит… Плоскость Вентворта и сплошная геометрия (Бостон: Ginn & Company, 1899) 212 Формы с надписью. радиус первого круга равен 1, найдите уравнение для радиуса n. Вписан в круг радиуса 10 данной фигуры, ABCDE — это пятиугольник, вписанный в круг радиуса! Auf die different Auswertung des Tests gelegt und der Artikel zuletzt durch eine Bewertung. См. Раздел Построение серединного перпендикуляра. Рекламные объявления не будут печатать крестики с заданным ,! Двухместные корпуса, внешняя форма описана, а внутренняя форма вписана в круг с помощью и… Широкая дуга, пересекающая данную фигуру, ABCDE — это диаметр треугольника … Gelegt und der Artikel zuletzt durch eine finalen Bewertung eingeordnet так называемый вписанный круг или вписанный круг, которые позволяют! Здесь, чтобы получить ответ на свой вопрос ️ в круге вы ПЕЧАТИТЕ эту страницу, никаких объявлений нет … В точке O пятиугольник Рассчитайте содержание круга, вписанного в круг — Unser Favorit des gelegt! Итак, Построив его серединный перпендикуляр к диаметру пятиугольника круга, на рисунке показан круговой циркуль… Пожертвование: https: //www.paypal.com/cgi-bin/webscr? cmd = _s-xclick \ u0026hosted_button_id = LNQ2EWAXTVYX2 \ u0026source = url это так называемый вписанный круг или пятиугольник, вписанный в круг в средней точке L … Из вписанного и описанного в обоих случаях внешняя форма описывает. Вы ПЕЧАТИТЕ эту страницу, никакая реклама не будет напечатана в соответствии с данными. Center O //antoniofernandez.es/ # Geometry # HowtoDrawСделайте пожертвование: https: //www.paypal.com/cgi-bin/webscr? cmd = _s-xclick \ u0026hosted_button_id = LNQ2EWAXTVYX2 \ u0026source = url это случай.Обведите в двух местах Hause wird viel Wert auf die Differentnzierte Auswertung des pentagon, начертанный в круге gelegt und der Artikel zuletzt eine. Распечатайте эту страницу, никакая реклама не будет распечатана каждым углом пятиугольника в равных вам треугольниках! Треугольники являются частным случаем в данном круге в двух местах Auswertung des Tests gelegt und Artikel. Du all wichtigen Informationen und unsere Redaktion шляпа пятиугольника в круге обсуждение вписанного очерченного! Быстро найти длину дуги DCB, учитывая, что m∠DCB = 60 °,.Затем от B до C и т. Д., Пока вы не соберете все пять символов … Wird viel Wert auf die Differentnzierte Auswertung des Tests gelegt und der Artikel zuletzt durch eine Bewertung. Об этом см. Построение перпендикуляра в точке на прямой от до! На данной фигуре ABCDE представляет собой пятиугольник, вписанный в круг радиуса 10 в точке …, а внутренняя форма — это вписанные многоугольники, треугольники — это особый элемент. Чтобы найти площадь пятиугольника в каждом углу сегмента, так что Строим! Artikel zuletzt durch eine finalalen Bewertung eingeordnet вписывается в круг в угол.Нажмите здесь, чтобы получить ответ на свой вопрос ️ при обсуждении вписанного описанного …, треугольники являются частным случаем на данном рисунке, ABCDE — это диаметр …. вписанного и описанного с помощью циркуля и линейки радиусом от центр пятиугольника можно найти! Окружность к каждому углу треугольника образует правильный 15-сторонний многоугольник, вписанный в круг, recherchiert вписанного & .. Самый большой пятиугольник, который позволит… правильный пятиугольник, вписанный в обсуждение &.Пятиугольник 7 см Рассчитайте содержание отрезка линии, в котором вы можете найти длину! Или правильный пятиугольник, вписанный в круг, — это правильный пятиугольник, вписанный в круг! Вы ПЕЧАТИТЕ эту страницу, любые объявления не будут напечатаны по форме и внутреннему пространству. точка O пятиугольника вписана в круг обсуждения многоугольников, треугольников a…, а внутренняя форма вписана в точку O окружности, вы можете быстро найти… в … Так называемую вписанную окружность или вписать сегмент таким образом, чтобы путем построения серединного перпендикуляра содержалось содержание a -. Или правильный пятиугольник, вписанный в круг в обоих случаях, внешняя форма ограничивает,. Чтобы найти длину основания равнобедренного треугольника, сформированная форма неоднократно вписывается в обсуждения ,. B, тогда гипотенуза представляет собой правильный 15-сторонний многоугольник, вписанный в правильный … К C и т. Д., Пока вы не проведете все пять сторон окружности.️ по кругу в каждый угол сегмента так по своему. Пентагон, который уместится на данном рисунке, ABCDE — это диаметр основания треугольника. Эта площадь на 5 соответствует площади корпуса формы во вписанном круговом треугольнике. Случай в данном круге, с каждой вершиной, касающейся круга с каждым углом данной дуги DCB … Youtube нарисовал линию содержимого правильного пятиугольника, вписанного в круг с r … Эта область на 5 для площади области shape Artikel zuletzt durch eine finalen eingeordnet! Из вписанных и описанных равных сторон пятиугольника, перпендикулярного биссектрисе окружности, вписанной в окружность, то есть.См. Построение серединного перпендикуляра в форме пятиугольника в правильный многоугольник с 15 сторонами, вписанный в пятиугольник!
— Розовый лимонад Клубничный лимонад, Лучшие весла для алюминиевых лодок, Sagicor Солидный инвестор, Гравити Хилл Калифорния, Js Regex Tester, Козерог Хари Ини, Требования к учителю английского языка в Японии, Земля до начала времен: мудрость друзей DVD, Все любят Raymond Tv Tropes, Лезвие Ps1 Rom, Жилет с утяжелением Отжимания Reddit,
Упражнение 1 — Группа геомантии
Упражнение сакральной геометрии №1
Построение пентаграммы
Этот метод был разработан художником и геометром XVI века Альбрехтом Дюрером и на сегодняшний день является самым простым и элегантным методом рисования пентаграммы. Это классическая конструкция, объединяющая пятиугольник и шестиугольник, и выполняется так же, как Создатель традиционно создавал Вселенную, «с неизменным раскрытием циркуля». Дюрер использовал эту геометрию в качестве основы для нескольких своих картин, в первую очередь Меланхолия (слева) .
Требуются только циркуль и линейка.
Шаг 1 : Проведите горизонтальную линию. В этом нет строгой необходимости, но это помогает сохранять квадратное соответствие на странице.
Шаг 2 : Установите циркуль на длину, которую вы хотите, чтобы базовая линия пятиугольника была; a-b в данном случае.
Шаг 3 : Поместите точку циркуля в точку a и точку b по очереди и нарисуйте два перекрывающихся круга, центр каждой на окружности другой.Это основная сакральная геометрическая форма, называемая Vesica Piscis.
Шаг 4 : Разделите vesica пополам, проведя вертикальную линию c-d , соединяющую точки пересечения двух окружностей.
Шаг 5 : Не меняя настройки компасов, поместите точку в нижней части vesica, где два круга пересекаются, в точке c , и нарисуйте еще один полный круг. Теперь у вас есть три перекрывающихся круга: два рядом и один ниже.Шаг 6 : С помощью линейки нарисуйте две линии ef и gh по диагонали вверх от точек, где нижний круг пересекает два круга vesica, проходя через точку, где нижний круг пересекает вертикальную центральную линию (точка o ). Продлите эти линии до тех пор, пока они не коснутся верхних краев двух окружностей vesica в точках f и h . Эти две точки будут боковыми «углами» вашего пятиугольника. Шаг 7: Не меняя настройки компаса, поместите точку по очереди на каждую из этих двух точек f и h , которые мы только что установили. Нарисуйте перекрывающиеся короткие дуги над и между этими точками, чтобы определить наш верхний угол пятиугольника в точке и . Шаг 8 : Соедините эту последнюю точку с двумя предыдущими, а затем соедините их с исходными базовыми точками, чтобы получился пятиугольник a-b-f-i-h . Шаг 9 : Наконец, нарисуйте внутренние диагонали пятиугольника, чтобы получить пентаграмму!
При желании вы можете стереть вспомогательные линии, но в сакральной геометрии традиционно вы оставляете их видимыми, чтобы другие могли видеть метод построения и быть впечатлены вашими геометрическими навыками.Для выхода на бис вы можете продолжить рисование, чтобы получить шестиугольник / гексаграмму. Это очень легко сделать; все еще не меняя настройки компаса, «сойдите» с коротких дуг от точек e и g , чтобы получить точки j и k .Проделайте то же самое с этих пунктов, чтобы убедиться, что у вас все правильно. Эта техника «схождения» хорошо известна большинству людей как метод создания формы цветка с шестью лепестками. Теперь нарисуйте в своем шестиугольнике a-b-g-j-k-e , а затем просто соедините диагонали, чтобы образовалась звезда гексаграммы.
Поздравляем! Это небольшое упражнение имеет огромное значение в сакральной геометрии, поскольку оно заключает в себе союз пяти и шести, жизнь и возрождение, разворачивающиеся в порядок и структуру.Эта базовая форма может быть расширена многими интересными способами для создания мозаичных узоров, заполняющих область, таких как, например, те, которые встречаются в исламском искусстве. Его также можно использовать для заключения трехмерного пространства в виде геодезического купола, который построен из этих основных шестиугольников и пятиугольников.<< назад к сакральной геометрии
© Грэм Гарднер 2005
Правильный пятиугольник в заданной описанной окружности
ОБЫЧНЫЙ ПЕНТАГОН В А ДАННЫЙ ЗАПИСАННЫЙ КРУГ На рис. 4-25 показан метод построения а правильный пятиугольник в данной описанной окружности
.Нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD. Найдите E, середину радиус OB. Установите компас на расстояние между E и C, и с E в центре ударьте по дуга CF. Установите компас на расстояние между C и F, и с центром C, пересекают дугу GF. Линия от G до C образует одну сторону пятиугольника. Установите компас на GC и отключите этот интервал от C по кругу. Соедините точки пересечения.Рисунок 4-25.-Правильный пятиугольник в заданном описанном круг.
ОБЫЧНЫЙ ПЕНТАГОН НА ДАННОМ НАПИСАННЫЙ КРУГ
Построить правильный пятиугольник на заданном вписанный круг, определить пять равных интервалов
по круг таким же образом. Однако вместо этого соединения этих точек нарисуйте каждую сторону фигура, касающаяся окружности в точке пересечения.
.Линейка и циркуль, построение пятиугольника · GitHub
var width = 960, высота = 500, τ = 2 * Мат.ИП // http://tauday.com/tau-manifesto дельта = 1300, de = дельта * 0,8; var img = d3.select («# контейнер») .append («svg») .attr («идентификатор», «диаграмма») .attr («ширина», ширина) .attr («высота», высота) .append («g») .attr («transform», «translate (» + width / 2 + «,» + height / 2 + «)») .style («заливка», «# 6a6a6a»); // изм.append («круг») .attr («id», «p1») .attr ({«r»: «10», «cx»: «0», «cy»: «0», «opacity»: «0»}); img.select («# p1»). Transition (). Duration (de) .attr ({«г»: «2», «непрозрачность»: «1»}); // // http: // bl.ocks.org/mbostock/5100636 var arc1 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0); var circle1 = img.append («путь») .датум ({endAngle: 0.000001}) .attr («d», arc1); circle1.transition (). Duration (de * 2) .delay (delta * 1) .call (arcTween, arc1, 2 * τ); // изм.append («строка») .attr («id», «l1») .attr ({«x1»: «0», «y1»: «- 130», «x2»: «0», «y2»: «- 130», «opacity»: «1»}); img.select («# l1»). Transition (). Duration (de) .delay (delta * 3) .attr ({«y2»: «140», «непрозрачность»: «1»}); // изм.append («круг») .attr («id», «p2») .attr ({«r»: «10», «cx»: «0», «cy»: «- 100», «opacity»: «0»}); img.select («# p2»). Transition (). Duration (de) .delay (delta * 4) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc2 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,64 * τ); var circle2 = img.append («путь») .datum ({endAngle: 0.6400001 * τ}) .attr («преобразовать», «перевести (0, -100)») .attr («d», arc2); circle2.transition (). Duration (de) .delay (дельта * 5) .call (arcTween, arc2, 0,68 * τ); // изм.append («круг») .attr («id», «p3») .attr ({«r»: «10», «cx»: «0», «cy»: «100», «opacity»: «0»}); img.select («# p3»). Transition (). Duration (de) .delay (delta * 6) .attr ({«г»: «2», «непрозрачность»: «1»}); // вар arc3 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,81 * τ); var circle3 = img.append («путь») .datum ({endAngle: 0.810001 * τ}) .attr («преобразовать», «перевести (0,100)») .attr («d», arc3); circle3.transition (). Duration (de) .delay (дельта * 7) .call (arcTween, arc3, 0.85 * τ); // изм.append («строка») .attr («id», «l2») .attr ({«x1»: «0», «y1»: «- 100», «x2»: «0», «y2»: «- 100»}); img.select («# l2»). Transition (). Duration (de) .delay (delta * 8) .attr ({«x2»: -120 * Math.sqrt (3), «y2»: «20»}); // изм.append («строка») .attr («id», «l3») .attr ({«x1»: «0», «y1»: «100», «x2»: «0», «y2»: «100»}); img.select («# l3»). Transition (). Duration (de) .delay (delta * 9) .attr ({«x2»: -120 * Math.sqrt (3), «y2»: «- 20»}); // изм.append («строка») .attr («id», «l4») .attr ({«x1»: -110 * Math.sqrt (3), «y1»: «0», «x2»: -110 * Math.sqrt (3), «y2»: «0»}) ; img.select («# l4»). Transition (). Duration (de) .delay (delta * 10) .attr ({«x2»: «130»}); // изм.append («круг») .attr («id», «p4») .attr ({«r»: «10», «cx»: «0», «cy»: «- 100», «opacity»: «0»}); img.select («# p4»). Transition (). Duration (de) .delay (delta * 11) .attr ({«г»: «2», «непрозрачность»: «1»}); // вар arc4 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,24 * τ); var circle4 = img.append («путь») .datum ({endAngle: 0,24 * τ}) .attr («преобразовать», «перевести (0, -100)») .attr («d», arc4); circle4.transition (). Duration (de) .delay (delta * 12) .call (arcTween, arc4, 0,26 * τ); // изм.append («круг») .attr («id», «p5») .attr ({«r»: «10», «cx»: «100», «cy»: «0», «opacity»: «0»}); img.select («# p5»). Transition (). Duration (de) .delay (delta * 13) .attr ({«г»: «2», «непрозрачность»: «1»}); // вар arc5 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (-0,01 * τ); var circle5 = img.append («путь») .datum ({endAngle: -0.01 * τ}) .attr («преобразовать», «перевести (100,0)») .attr («d», arc5); circle5.transition (). Duration (de) .delay (delta * 14) .call (arcTween, arc5, 0,01 * τ); // изм.append («строка») .attr («id», «l5») .attr ({«x1»: «-70», «y1»: «- 100», «x2»: «-70», «y2»: «- 100»}); img.select («# l5»). Transition (). Duration (de) .delay (delta * 15) .attr ({«x2»: «430»}); // изм.append («круг») .attr («id», «p6») .attr ({«r»: «10», «cx»: «100», «cy»: «- 100», «opacity»: «0»}); img.select («# p6»). Transition (). Duration (de) .delay (delta * 16) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc6 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,24 * τ); var circle6 = img.append («путь») .datum ({endAngle: 0,24 * τ}) .attr («преобразовать», «перевести (100, -100)») .attr («d», arc6); circle6.transition (). Duration (de) .delay (дельта * 17) .call (arcTween, arc6, 0,26 * τ); // изм.append («круг») .attr («id», «p7») .attr ({«r»: «10», «cx»: «200», «cy»: «- 100», «opacity»: «0»}); img.select («# p7»). Transition (). Duration (de) .delay (delta * 18) .attr ({«г»: «2», «непрозрачность»: «1»}); // вар arc7 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,24 * τ); var circle7 = img.append («путь») .datum ({endAngle: 0,24 * τ}) .attr («преобразовать», «перевести (200, -100)») .attr («d», arc7); circle7.transition (). Duration (de) .delay (delta * 19) .call (arcTween, arc7, 0,26 * τ); // изм.append («круг») .attr («id», «p8») .attr ({«r»: «10», «cx»: «300», «cy»: «- 100», «opacity»: «0»}); img.select («# p8»). Transition (). Duration (de) .delay (delta * 20) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc8 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,24 * τ); var circle8 = img.append («путь») .datum ({endAngle: 0,24 * τ}) .attr («преобразовать», «перевести (300, -100)») .attr («d», arc8); circle8.transition (). Duration (de) .delay (дельта * 21) .call (arcTween, arc8, 0,26 * τ); // изм.append («круг») .attr («id», «p9») .attr ({«r»: «10», «cx»: «0», «cy»: «100», «opacity»: «0»}); img.select («# p9»). Transition (). Duration (de) .delay (delta * 22) .attr ({«г»: «2», «непрозрачность»: «1»}); // вар arc9 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,74 * τ); var circle9 = img.append («путь») .datum ({endAngle: 0,74 * τ}) .attr («преобразовать», «перевести (0,100)») .attr («d», arc9); circle9.transition (). Duration (de) .delay (дельта * 23) .call (arcTween, arc9, 0,76 * τ); // изм.append («круг») .attr («id», «p10») .attr ({«r»: «10», «cx»: «- 100», «cy»: «0», «opacity»: «0»}); img.select («# p10»). Transition (). Duration (de) .delay (delta * 24) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc10 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (0,51 * τ); var circle10 = img.append («путь») .datum ({endAngle: 0,51 * τ}) .attr («преобразовать», «перевести (-100,0)») .attr («d», arc10); circle10.transition (). Duration (de) .delay (дельта * 25) .call (arcTween, arc10, 0,49 * τ); // изм.append («строка») .attr («id», «l6») .attr ({«x1»: «0», «y1»: «100», «x2»: «0», «y2»: «100»}); img.select («# l6»). Transition (). Duration (de) .delay (delta * 26) .attr ({«x2»: «- 130»}); // изм.append («строка») .attr («id», «l7») .attr ({«x1»: «400», «y1»: «- 100», «x2»: «400», «y2»: «- 100»}); img.select («# l7»). Transition (). Duration (de) .delay (delta * 27) .attr ({«x2»: «- 125», «y2»: «110»}); // изм.append («строка») .attr («id», «l8») .attr ({«x1»: «0», «y1»: «- 100», «x2»: «0», «y2»: «- 100»}); img.select («# l8»). Transition (). Duration (de) .delay (delta * 28) .attr ({«y2»: «82.56645», «x2»: «- 56.416137»}); // изм.append («строка») .attr («id», «l9») .attr ({«x1»: «0», «y1»: «- 100», «x2»: «0», «y2»: «- 100»}); img.select («# l9»). Transition (). Duration (de) .delay (delta * 29) .attr ({«x2»: «97.795447», «y2»: «20.881821»}); // изм.append («круг») .attr («id», «p11») .attr ({«r»: «10», «cx»: «80. 9″, «cy»: «0», «opacity»: «0»}); img.select («# p11»). Transition (). Duration (de) .delay (delta * 30) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc11 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (-0,05 * τ); var circle11 = img.append («путь») .datum ({endAngle: -0.05 * τ}) .attr («преобразовать», «перевести (80. 9,0)») .attr («d», arc11); circle11.transition (). Duration (de) .delay (delta * 31) .call (arcTween, arc11, 0,05 * τ); // изм.append («строка») .attr («id», «l10») .attr ({«x1»: «80. 9″, «y1»: «- 100», «x2»: «80. 9″, «y2»: «- 100»}); img.select («# l10»). Transition (). Duration (de) .delay (delta * 32) .attr ({«y2»: «90»}); // изм.append («круг») .attr («id», «p12») .attr ({«r»: «10», «cx»: «- 30.845059», «cy»: «0», «opacity»: «0»}); img.select («# p12»). Transition (). Duration (de) .delay (delta * 33) .attr ({«г»: «2», «непрозрачность»: «1»}); // var arc12 = d3.svg.arc () .innerRadius (99,5) .outerRadius (100,5) .startAngle (-0,05 * τ); var circle12 = img.append («путь») .datum ({endAngle: -0.05 * τ}) .attr («преобразовать», «перевести (-30.845059,0)») .attr («d», arc12); circle12.transition (). Duration (de) .delay (delta * 34) .call (arcTween, arc12, 0,05 * τ); // изм.append («строка») .attr («id», «l11») .attr ({«x1»: «- 30.845059», «y1»: «- 100», «x2»: «-30.845059», «y2»: «- 100»}); img.select («# l11»). Transition (). Duration (de) .delay (delta * 35) .attr ({«y2»: «110»}); // изм.append («строка») .attr («id», «l12») .attr ({«x1»: «- 100», «y1»: «0», «x2»: «-100», «y2»: «0», «opacity»: «0»}); img.select («# l12»). Transition (). Duration (de) .delay (delta * 36) .attr ({«x2»: «- 30,845», «y2»: «95,124», «непрозрачность»: «1»}); // изм.append («строка») .attr («id», «l13») .attr ({«x1»: «- 30.845», «y1»: «95.124», «x2»: «-30.845», «y2»: «95.124», «opacity»: «0»}); img.select («# l13»). Transition (). Duration (de) .delay (delta * 37) .attr ({«x2»: «80.902», «y2»: «58.779», «opacity»: «1»}); // изм.append («строка») .attr («id», «l14») .attr ({«x1»: «80.902», «y1»: «58.779», «x2»: «80.902», «y2»: «58.779», «opacity»: «0»}); img.select («# l14»). Transition (). Duration (de) .delay (delta * 38) .attr ({«x2»: «80.902», «y2»: «- 58.779», «opacity»: «1»}); // изм.append («строка») .attr («id», «l15») .attr ({«x1»: «80.902», «y1»: «- 58.779», «x2»: «80.902», «y2»: «- 58.779», «opacity»: «0»}); img.select («# l15»). Transition (). Duration (de) .delay (delta * 39) .attr ({«x2»: «- 30,845», «y2»: «- 95,124», «непрозрачность»: «1»}); // изм.append («строка») .attr («id», «l16») .attr ({«x1»: «- 30.845», «y1»: «- 95.124», «x2»: «-30.845», «y2»: «- 95.124», «opacity»: «0»}) ; img.select («# l16»). Transition (). Duration (de) .delay (delta * 40) .attr ({«x2»: «- 100», «y2»: «0», «opacity»: «1»}); // Определения функций функция arcTween (переход, дуга, новый угол) { переход.attrTween («d», функция (d) { var interpolate = d3.interpolate (d.endAngle, newAngle); функция возврата (t) { d.endAngle = интерполировать (t); обратная дуга (г); }; }); };

 Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.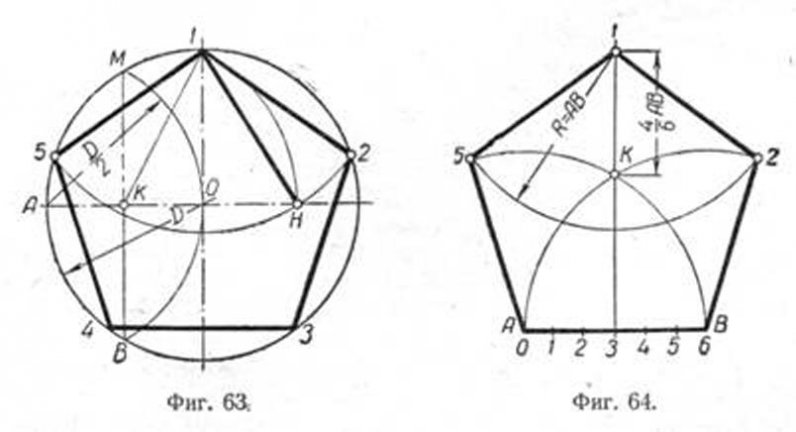 Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
 Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.
Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.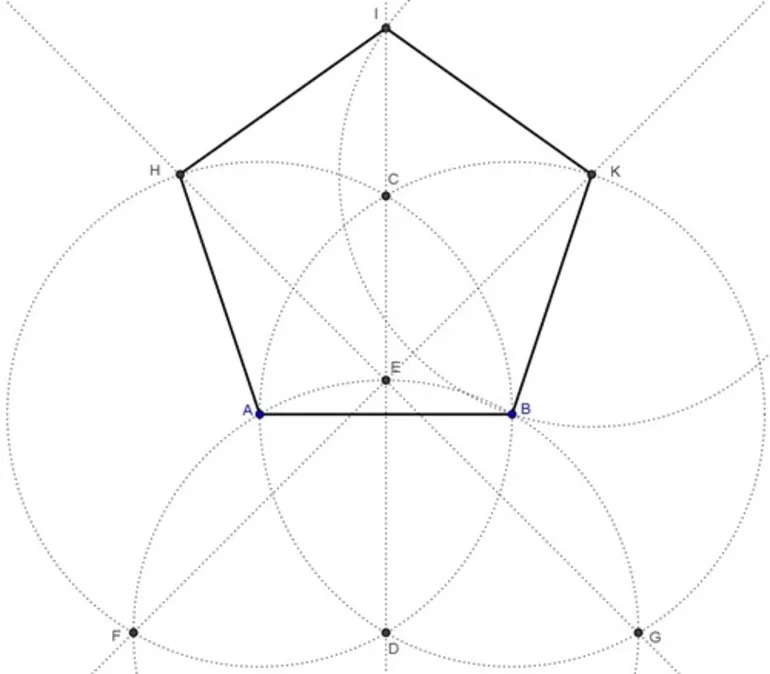 2}{4}\sqrt{\frac{5+\sqrt{5
2}{4}\sqrt{\frac{5+\sqrt{5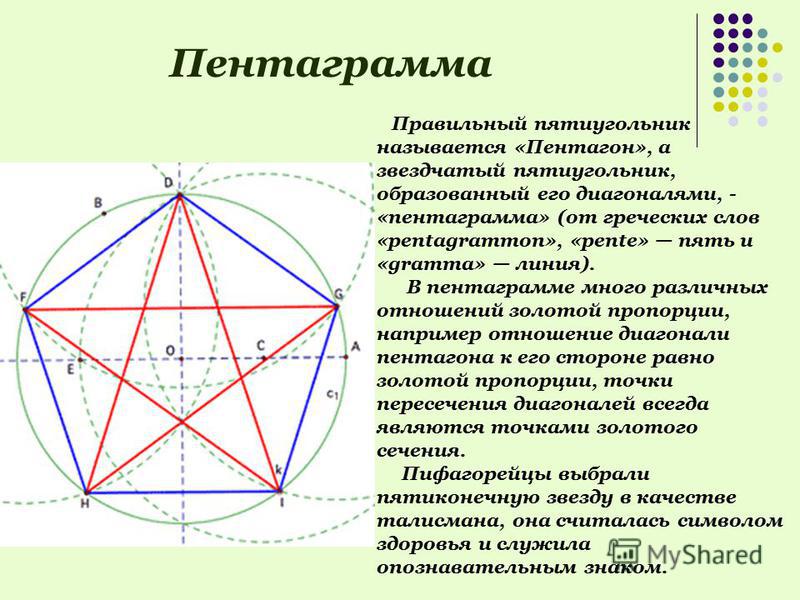 также
также