Построение правильного шестиугольника без циркуля: Как нарисовать шестиугольник с помощью линейки

Как начертить правильный шестиугольник без циркуля

Шаг 1

Построение правильного шестиугольника. Шаг 1

Шаг 2

На окружности выбрать произвольную точку, которая и будет вершиной шестиугольника.

Построение правильного шестиугольника. Шаг 2

Шаг 3

Так как сторона шестиугольника равна радиусу окружности, описанной около него, то от выбранной точки построить отрезок, равный радиусу нарисованной окружности. Причем конец отрезка должен лежать на окружности (т.е. строим хорду, равную радиусу).

Как построить правильный шестиугольник. Шаг 3

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты.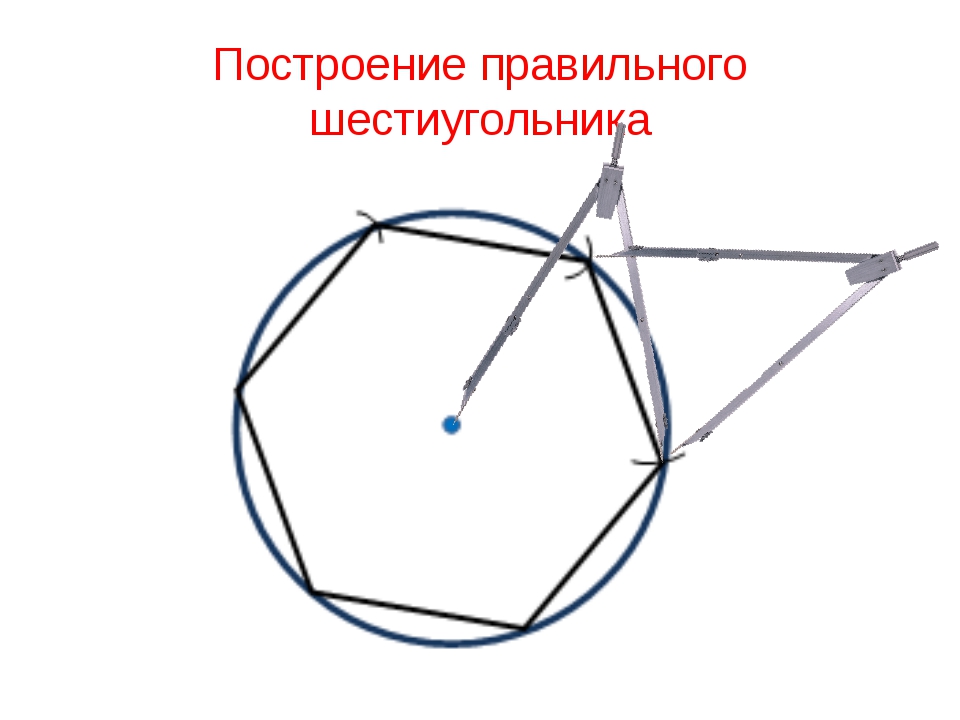

Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника.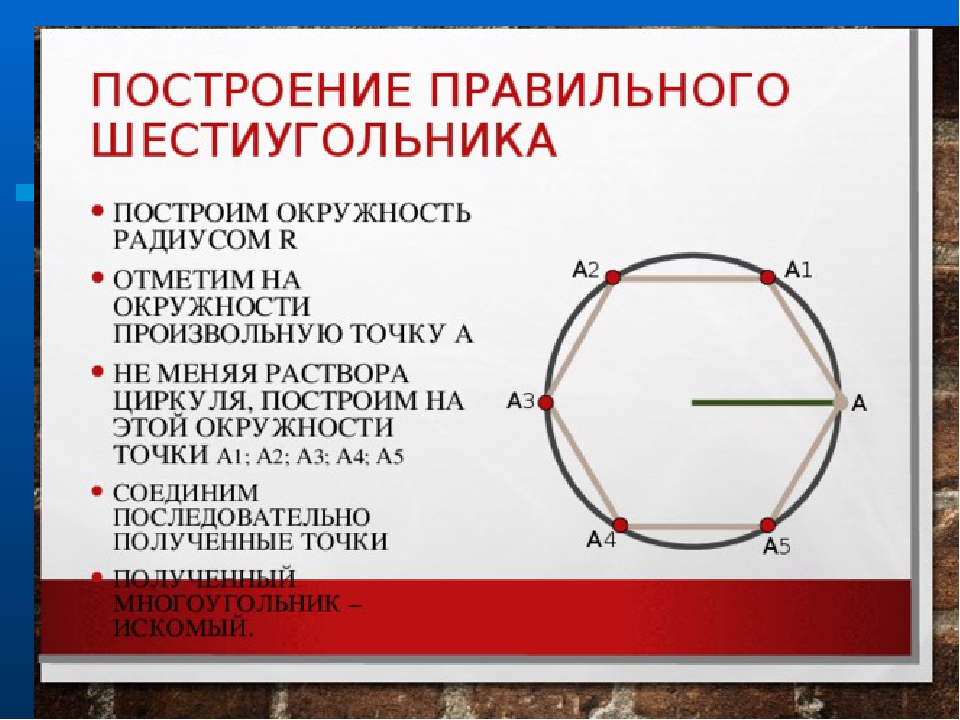 Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Построение правильных многоугольников — презентация онлайн

Геометрия, 9 класс
Устные упражнения
Построение правильных многоугольников
с помощью циркуля и линейки
Построение правильных многоугольников
с помощью компьютера
Практическая работа
Тестирование
Какие из утверждений верны?
1
Ромб является правильным
четырехугольником.
2
Квадрат является правильным
четырехугольником.
3
Любой четырехугольник с
равными сторонами
является правильным.
4
Прямоугольник является
правильным четырехугольником
ВЕРНО!
ПОДУМАЙ
!
ПОДУМАЙ!
Установить соответствие между элементами
1 и 2 столбцов
R
R 3
R 2
№ 1091 Поперечное сечение деревянного бруска является
квадратом со стороной 6 см. Найдите наибольший диаметр
круглого стержня , который можно выточить из этого бруска
6см

6. № 1090 Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3 см. Каким должен быть минимальный диа

Проверка домашнего задания
№ 1090
Сечение головки газового вентиля имеет форму правильного
треугольника, сторона которого равна 3 см. Каким должен быть минимальный
диаметр круглого железного стержня, из которого изготовляют вентиль?
В геометрии выделяют задачи на построение, которые
можно решить только с помощью двух инструментов:
циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Пифагор
Еще в глубокой древности
была поставлена практическая
задача
построения
правильного многоугольника с помощью циркуля и
линейки.
Решение этой задачи можно
найти в трудах древнегреческих ученых Архимеда,
Евклида, Пифагора, математиков XYII — XIX веков

Карла Гаусса…
К.Ф.Гаусс (1777-1855)
(365-300 гг-IVв до
н.э. )
Основоположник
геометрии, описал
построение циркулем и линейкой 3, 4,
5, 6, 15 — угольников
ЕВКЛИД
Деление окружности на 5 равных частей
А1
А1
А1
А5
С
С
в
А1 А2
А1
А2
в
А4
А3
сторона
пятиугольника
К. Ф.Гаусс (1777-1855)-великий
немецкий математик. Открыл способ
построения правильного 17-угольника
и указал все значения n, при которых
возможно построение правильного nугольника с помощью циркуля и
линейки. Этими многоугольниками
оказались лишь многоугольники, у
которых количество сторон является
простым числом вида
где k -натуральное
или нуль
а также те, которые получаются из них
удвоением числа сторон.
3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40 … — угольники можно
построить!
7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28… – угольники невозможно
построить.

18. Моделирование в среде графического редактора.

• Модель – это упрощённое подобие предмета
или процесса. Она повторяет какие-то
свойства оригинала и заменяет его в
некоторых случаях.
• Модель — способ замещения реального
объекта, используемый для его изучения.
• Моделирование – процесс создания модели
предмета.

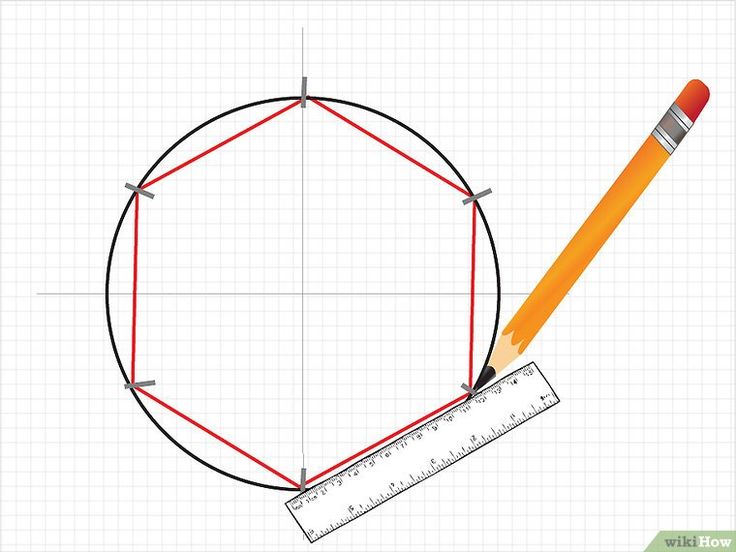
19. Алгоритм построения правильного четырехугольника

1. Нарисовать сторону прямоугольника.
2. Копировать сторону четырехугольника и вставить.
Рис. 1.
3. Копировать сторону и вставить. Рисунок повернуть
на 90 градусов, перенести и получить рис. 2.
4. Копировать рис. 2 и вставить. Повернуть на 180
градусов Перенести. И получить рисунок 3.
5. Полученный рисунок сохраните как «многоугольник»
в папке «Мои рисунки»

20. Алгоритм построения правильного шестиугольника

1. Нарисовать сторону шестиугольника.
2. Копировать сторону шестиугольника и вставить. Рис 1.
3. Копировать сторону и вставить. Рисунок повернуть на
60 градусов, перенести 2 раза с помощью кнопки Ctrl
на клавиатуре и получить рис 2.
4. Копировать рис.2 и вставить. Рисунок отразить слева
направо, перенести и получить рис 3.
5. Получить рисунок 4.
6. Копировать половину правильного шестиугольника,
вставить. Повернуть на 180 градусов и совместить с
рисунком 4. Получить рисунок 5.
7. Стереть вспомогательные линии и получить
правильный шестиугольник.
8. Полученный рисунок сохраните как «многоугольник» в
папке «Мои рисунки»
• GstarCAD — полноценная,
самостоятельная система,
обладающая всем необходимым
функционалом для работы с графикой.
• GstarCAD — это программа для
создания чертежей в формате
DWG/DXF,

22. Пчелиные соты покрыты без просветов и перекрытий «правильными шестиугольниками»

23. Алгоритм покрытия плоскости без просветов и перекрытий:

• 1. Выделить выбранный многоугольник.
• 2. Одновременно с нажатием кнопки Ctrl
передвигать многоугольник с помощью
мышки, вставляя так, чтобы исходный
многоугольник и его копия
соприкасались сторонами.
• 3. Сохранить работу.
n=3
P=
S=
n=4
P=
S=
n=6
P=
S=
Задание на дом:
1. Построить правильный пятиугольник.
2.№1095.
Расстояние между параллельными гранями шестигранной головки
болта, верхнее основание которого имеет форму правильного
шестиугольника, равно 1,5 см.

Найдите площадь верхнего
основания
1,5см
Мир геометрических знаний богат и
разнообразен. На самом деле
«геометрические хлеба» не являются
легкими. Геометрия требует не
меньшего трудолюбия, чем
крестьянские поля от их владельцев.
Счастливых вам геометрических
исканий!

Урок по геометрии «Построение правильных многоугольников» (9 класс)

Урок-практикум по геометрии на тему:

«Решение задач на построение правильных многоугольников»

9 класс

Цель урока.

        Дать представления о задачах на построение правильных многоугольников, рассмотреть наиболее простые задачи на построение и научить учащихся их решать. Привить интерес к таким задачам, обращая внимание учащихся на необычность и оригинальность их решения, а также точность и красоту геометрических фигур, получающихся в процессе построения. Для расширения кугозора дать представление о месте многоугольников в живой и неживой природе, использовании в архитектуре, быту и искусстве.

Тип урока: изучение нового материала

Вид урока: урок – практикум

Форма обучения: коллективная и индивидуальная

Приборы и материалы:

Циркуль, линейка, карандаш, ручка и альбомный лист.

Ход урока:

Учитель:

        Сегодня на уроке мы познакомимся с геометрическими задачами на построение. Вы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, строили углы, треугольники и другие фигуры. При этом вы пользовались чертежными инструментами: масштабной линейкой, циркулем, транспортиром, чертежным угольником.  (Видео 0.0-1.13)

        В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов:

1) циркуля, с помощью которого можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку;

2) линейки без масштабных делений, которая позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.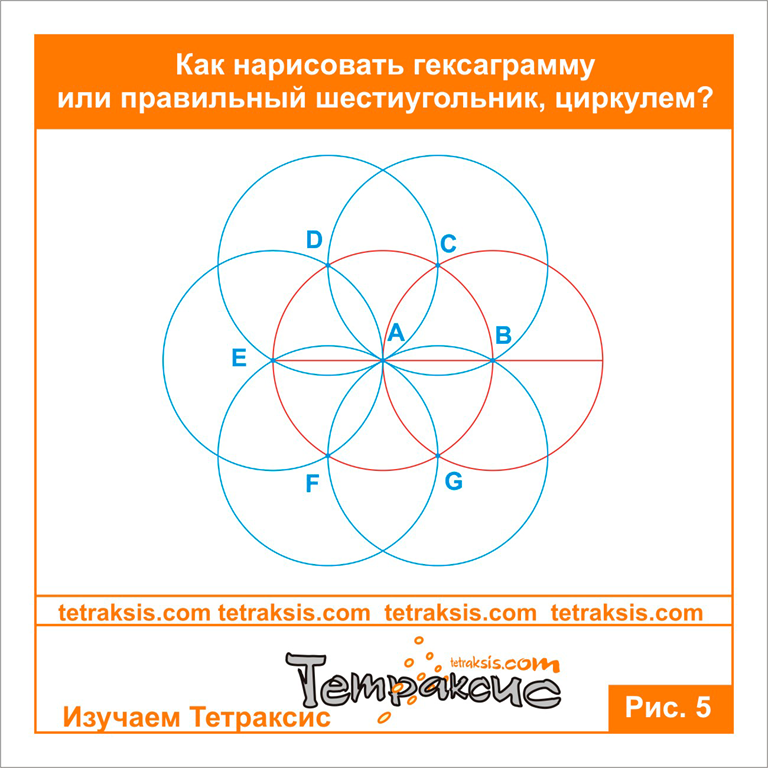

Сегодня на уроке вы научитесь решать наиболее простые задачи на построение. Они являются основой для решения более сложных геометрических задач на построение, которые вы будете решать в дальнейшем.  (Видео 0.0-1.13)

        Простейшими задачами на построение считаются следующие задачи:

1. Построение середины отрезка.

2. Построение угла, равного данному углу.

3. Построение биссектрисы угла.

4. Построение перпендикуляра к прямой, проходящего через точку, лежащую на этой прямой.

5. Построение перпендикуляра к прямой, проходящего через точку, не лежащую на этой прямой.

        Задача 1. Построить серединный перпендикуляр к отрезку.

            Задача 2. Рассчитать  величину угла правильного треугольника и построить треугольник с заданной стороной с помощью транспортира и линейки. Величина угла: 1800 : 3 = 600  

        Задача 3.  Рассчитать  величину угла правильного шестиугольника и построить его с заданной стороной с помощью транспортира и линейки.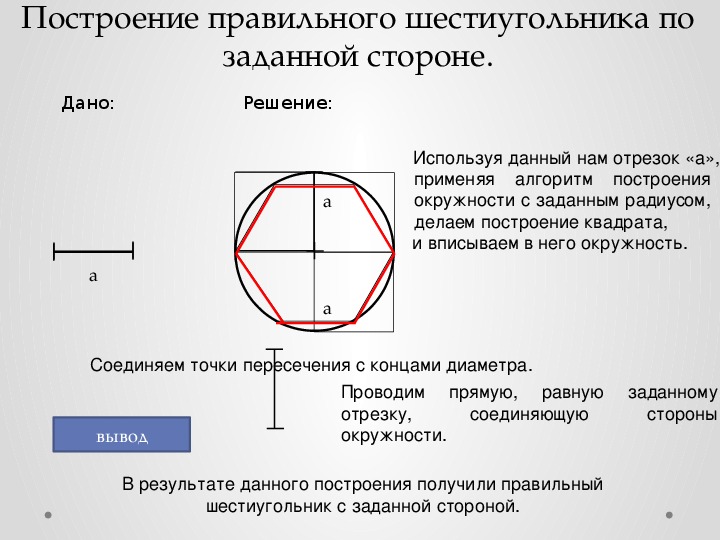  

Алгоритм № 1.  (Слайд 2)

        Для построения правильного n –  угольника   произведём расчёт величины его углов.  

        Так как сумма всех углов правильного  n – угольника  равна (n – 2)∙180º  и  все его углы равны, то угол правильного многоугольника будет вычисляться по формуле:

        Вычислив  величину угла правильного n – угольника и зная длину его стороны, мы можем построить при помощи транспортира и линейки любой правильный многоугольник.

Например: Построить правильный шестиугольник с заданной стороной а.

Дано: a

Решение:

Построение выполняем последующему алгоритму.

1.Вычисляем по формуле угол правильного шестиугольника,

2.Проводим при помощи линейки прямую линию.

3.Откладываем при помощи циркуля на прямой отрезок длиной равной а.

4. Строим при помощи транспортира углы величиной 120º с вершинами на

концах отрезка  а.

5. Откладываем при помощи циркуля на полученных лучах отрезки длинной равной а.

6. Строим при помощи транспортира углы величиной 120º с вершинами на

концах полученных отрезков.  

7. Откладываем при помощи циркуля на полученных лучах отрезки длинной равной а.

8. Соединяем концы полученных отрезков.

        Алгоритм построения правильного многоугольника можно изобразить

в следующей последовательности чертежей. (Слайд 3)

        Полученный многоугольник является правильным шестиугольником. Аналогично можно построить любой правильный n – угольник.

Алгоритм № 2. (Слайд 4)

        Этот алгоритм очень прост, поэтому особого внимания математики ему не уделяют.

Центральный угол окружности составляет 360º.

1. Делим 360º на n равных частей.

2. Проводим лучи до пересечения с окружностью.

3. Соединяем точки пересечения.

Полученный многоугольник является правильным n –угольником.

 

Алгоритм №3.

построения правильных многоугольников с помощью циркуля и линейки.

Следующий алгоритм построения правильных многоугольников основан на свойствах  описанной окружности около правильного многоугольника и  вписанной в правильный многоугольник.

                                                   

Теорема 1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

Теорема 2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствие 1. Окружность, вписанная в правильный многоугольник, касается

сторон многоугольника в их серединах.

Следствие 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот многоугольник  

Для построения правильных n – угольников при n › 4 обычно используется окружность, описанная около многоугольника.

Задача 1. Построить правильный шестиугольник, сторона которого равна данному отрезку. (Видео 5.02-6.05. Слайд 5)

 Дано: a=5 см

Построить: правильный 6-угольник

Решение:

Для решения задачи воспользуемся формулой  а 6 = R

(Доказать по формуле:  a = 2 R sin )

Пусть а – данный отрезок.

Алгоритм построения.  (видео 5.02-6.05)

1.Построим окружность радиуса а.

2. Отметим на ней произвольную точку А1.

3. Не меняя раствора циркуля, построим на этой окружности точки А2 ,  А3 , А4 , А5 , А6 так, чтобы выполнялись равенства

А1 А2 =  А2 А3 = А3 А4  = А4 А5 = А5 А6 

4.Соединим последовательно построенные точки отрезками, получим искомый правильный шестиугольник

А1 А2 А3 А4 А5 А6

Задача 4. Построить правильный треугольник

Алгоритм. Соединить через одну  3 точки на окружности. (Слайд 6-7)

Задача 5. Построить правильный четырехугольник. (видео 3.14-3.50)

Алгоритм.

        Провести диаметр окружности. Провести к нему диаметр, перпендикулярный данному. Соединить четыре точки окружности.

Задача 6. Построить правильный 8-угольник

Алгоритм.

        Построить серединные перпендикуляры к сторонам  4-угольника и соединить 8 точек окружности.

Задача 7. Дан правильный n – угольник. Построить правильный

                2n – угольник.

Решение. Пусть А1 А2 … А n  — данный правильный n – угольник. Опишем около него окружность. Для этого построим биссектрисы углов А1 и А2 и обозначим буквой О точку их пересечения. Затем проведём окружность с центром О радиуса О А1.

Для решения задачи достаточно разделить дуги А1 А2 , А2 А3, …, А n А1 пополам и каждую из точек деления В1,В2 ,… ,В n  соединить отрезками с концами соответствующей дуги. Для построения точек В1,В2 ,… ,В n  можно воспользоваться серединными перпендикулярами к сторонам данного

n – угольника. По такому алгоритму построим правильный двенадцатиугольник  А1В1 А2В2  А3В3  А4В4 А5В5  А6В6

Применяя указанный алгоритм, можно построить целый ряд правильных n – угольников, если построен один из них. Например, построив правильный  шестиугольник, можно построить правильный двенадцатииугольник, построив правильный четырёхугольник, т. е. квадрат, можно построить правильный восьмиугольник, затем правильный шестнадцатиугольник и вообще правильный 2 К – угольник, где к – любое целое число.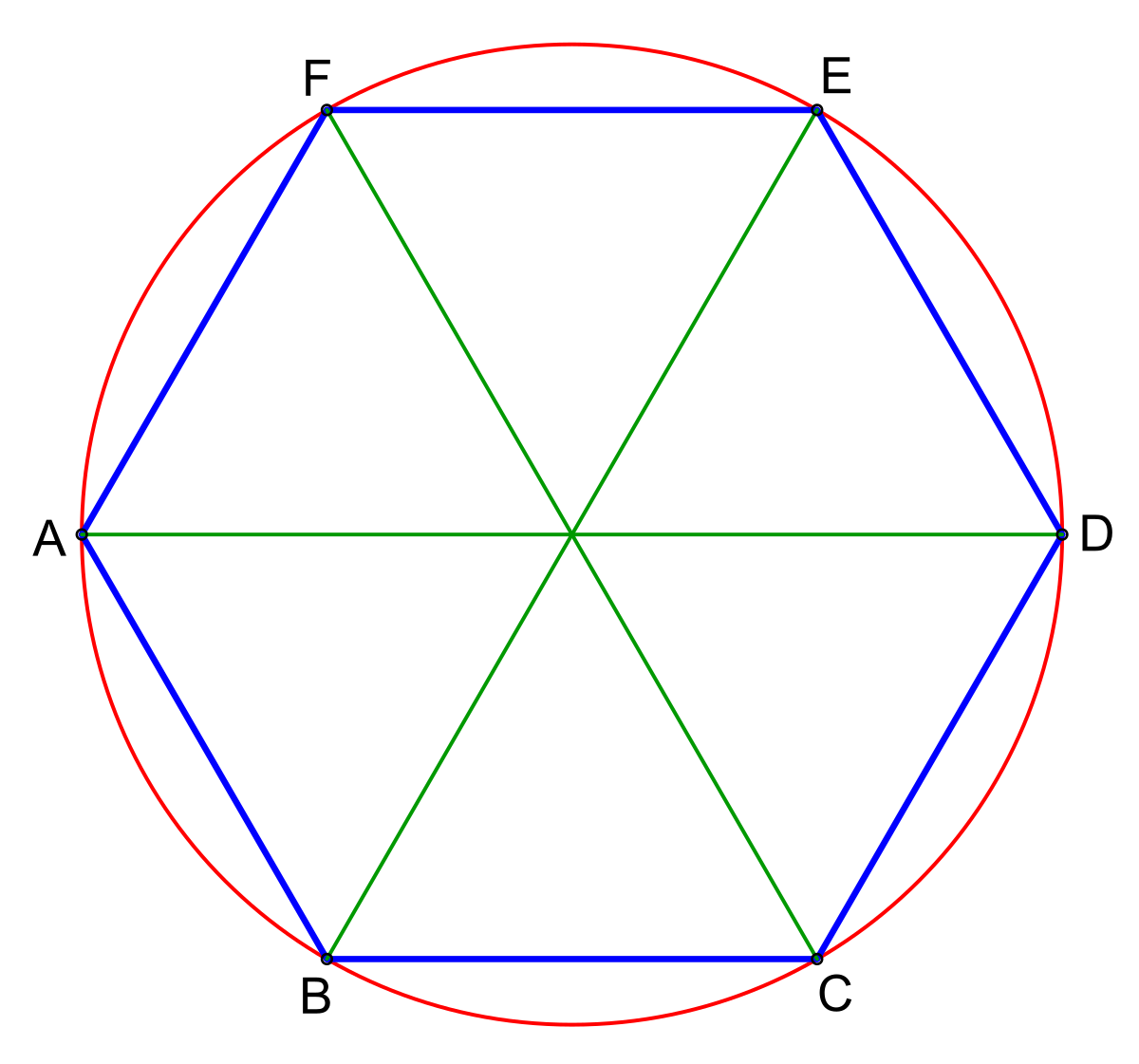  

Историческая справка и подведение итогов (видео 8.24-10.09)

 Из истории построения правильных многоугольников

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Примерами правильных  многоугольников являются равносторонний треугольник, квадрат, правильный шестиугольник  и другие правильные многоугольники.

Построение правильного многоугольника с n сторонами оставалась проблемой для математиков вплоть до ХIХ века. Построение правильного многоугольника с n сторонами идентично разделению окружности на n равных частей, так как соединив между собой точки делящие окружность на части, можно получить искомый многоугольник.

Древнегреческий математик Архимед  использовал правильные  многоугольники для вычисления числа π. Он вычислял площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон. Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решал задачу для

n = 3, 4, 5, 15. Древнегреческие математики умели строить правильные многоугольники.

Средневековая математика почти никак не продвинулась в вопросе построения правильных многоугольников.

Лишь в1796 году Карл Фридрих Гаусс доказал, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить с помощью циркуля и линейки. На сегодняшний день известны следующие числа Ферма: 3, 5, 17, 257, 65537. Вопрос о наличии или отсутствия других таких чисел остаётся открытым.Интересно, что поиски простых чисел Ферма  на современных компьютерах не дали результатов, все проверенные числа оказывались составными. Поскольку число 7 не является простым числом Ферма, то построить правильный семиугольник с помощью циркуля и линейки невозможно, как невозможно построить одиннадцатиугольник, тринадцати- и четырнадцатиугольники, невозможно построить правильный девятиугольник. Пока известна возможность построения лишь 31 правильного многоугольника с нечётным числом вершин.

В 1894 году была поставлена точка в деле построения правильных многоугольников, когда были построены правильные 17-257-и 65537-угольника.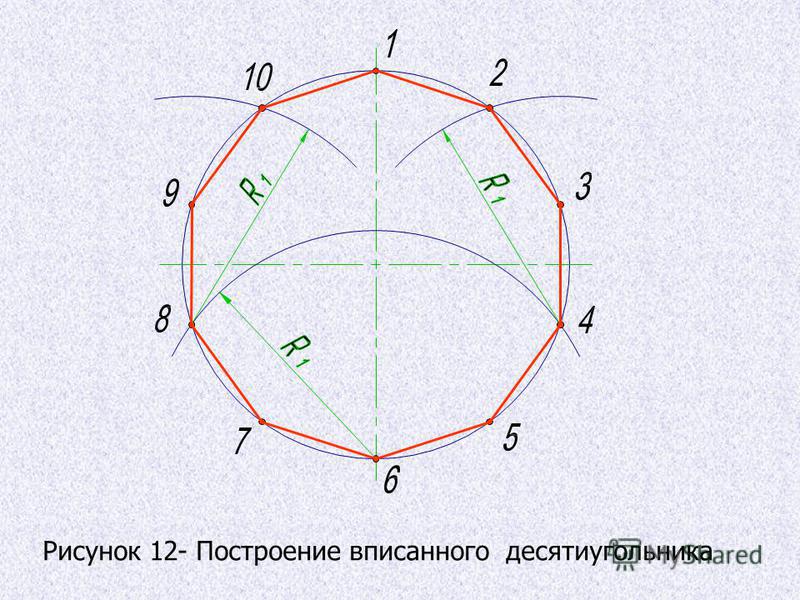

        Для расширения кугозора дать представление о месте многоугольников в живой и неживой природе, использовании в архитектуре, быту и искусстве.

 (Презентация . Слайд)

Как построить шестигранник

Один из первых способов построения правильного шестиугольника описал древнегреческий ученый Евклид в своем известном труде «Начала». Предложенный Евклидом способ не единственно возможный.Вам понадобится

Рассматриваемые здесь способы построения правильного шестиугольника основаны на следующих известных утверждениях. Около всякого правильного многоугольника можно описать окружность. Сторона правильного шестиугольника равна радиусу описанной около него окружности.

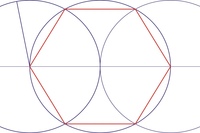
Способ первый. Чтобы построить правильный шестиугольник с заданной стороной а, необходимо с помощью циркуля провести окружность с центром в точке О и радиусом R, равным стороне а. Из центра окружности в точке О проведите луч в любую точку, лежащую на окружности. На пересечении окружности и луча вы получите некоторую точку А. С помощью циркуля из точки А радиусом R, равным стороне а, сделайте на окружности засечку и получите точку В. Из точки В раствором циркуля, равным радиусу R=a, сделайте следующую засечку и получите точку С. Делая аналогичным образом на окружности последовательные засечки радиусом R, равным заданной стороне а, вы получите в общей сложности шесть точек — A, B, C, D, E, F, которые будут являться вершинами шестиугольника. Соединив их с помощью линейки, получите правильный шестиугольник со стороной, равной а.

Способ второй. Через некоторую точку А проведите отрезок KB так, что KA=AB=a. На отрезке BK, равном 2а, как на диаметре постройте полукруг с центром в точке А и радиусом, равным а. Этот полукруг поделите на шесть равных частей. Получите точки C, D, E, F, G. Центр А соедините лучами со всеми полученными точками, кроме последних двух точек — K и G. Из точки В радиусом АВ проведите дугу, делая засечку на луче АС. Получите точку L. Из точки L тем же радиусом проведите дугу, делая засечку на луче AD. Получите точку М. Аналогичным способом проводите дуги и делайте засечки для остальных точек. Точки B, L, M, N, F, A последовательно соедините прямыми линиями. Получите ABLMNF – правильный шестиугольник со стороной, равной а.

Построение правильного многоугольника с помощью циркуля и линейки » Аналитическая геометрия f(x)dx.Ru

п.7. Исторический экскурс к вопросу о построении правильного многоугольника с помощью циркуля и линейки.

   Геометрические задачи на построение с помощью циркуля и линейки зародились еще в древней Греции во времена Евклида и Платона. Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты.

   Более того, они умели с помощью циркуля и линейки делить угол пополам, поэтому они умели строить и правильные 6-ти, 10-ти и 15-ти угольники и все правильные n-угольники, где, ,  и , . Очень важно, что с помощью линейки проводятся только отрезки прямых, а длины отрезков измеряются с помощью циркуля, а не делений на линейке.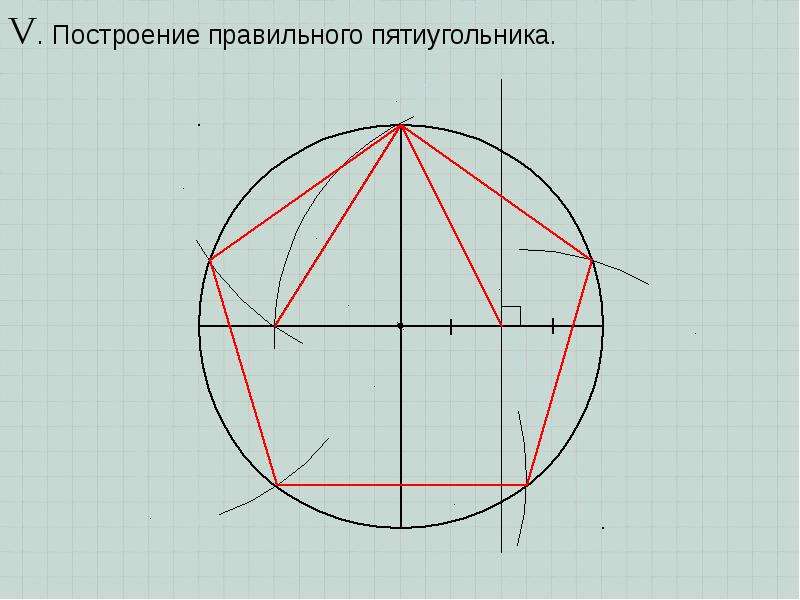 Так, используя эти инструменты можно построить отрезок, длина которого выражается числом, полученным из 1 с помощью четырех арифметических действий (сложения, вычитания, умножения, деления) и извлечением квадратного корня. Т.е. вначале есть только отрезок, длина которого принимается за 1. Тогда можно построить отрезок, длина которого равна рациональному числу или квадратному корню из рационального числа. Далее, если отрезок длины а уже построен с помощью циркуля и линейки, то можно построить с помощью этих инструментов отрезок  длины b, если число b выражается через а с помощью арифметических действий и квадратного корня. Говорят, что такое число выражается в квадратных радикалах.

   Таким образом, с помощью циркуля и линейки можно построить отрезок, длина которого выражается в квадратных радикалах. Все это знали еще математики древней Греции. Задачу построения других правильных многоугольников (или доказательство невозможности таких построений) не могли решить в течение двух последующих тысячелетий, а решена она была немецким студентом филологического факультета Гёттингенского университета  Карлом Фридрихом Гауссом в 1796 году. В то время Гауссу было 18 лет и он разрывался между занятиями филологией и математикой и не мог сделать окончательного выбора. Решение древней задачи помогло ему сделать окончательный выбор в пользу (и на пользу) математики. Страшно даже подумать на сколько бы затормозилось развитие математики останься Гаусс филологом! До сих пор математики всего мира называют Гаусса королем математики.

   Однако, вернемся к обсуждаемой задаче. Сначала Гаусс доказал, что с помощью циркуля и линейки можно построить только такие отрезки, длины которых выражаются в квадратных радикалах и только они. Гаусс использовал для решения задачи комплексные числа, в частности, корни из единицы. Так как корни из 1 делят окружность на равные дуги, то задача построения правильного n-угольника сводится к вопросу: при каких n корни n-й степени из 1 выражаются в квадратных радикалах. Здесь имеется ввиду их действительные и мнимые части. Таким образом, геометрическая задача была сведена к чисто алгебраической.

   Обозначим через  длину стороны правильного n-угольника. Гаусс нашел способ, с помощью которого ему удалось выразить число  в квадратных радикалах и тем самым доказать, что с помощью циркуля и линейки можно построить правильный n-угольник.

   Но Гаусс не был бы Гауссом, если бы он остановился на этом. Позднее он решил задачу полностью, выяснив при каких n задача построения правильного n-угольника может быть решена, а при каких нет. Чтобы понять этот результат нам понадобится одно определение.

Определение. Числа вида

                            ,

где  или , называются числами Ферма.

При , получаем . Далее,

, , , .

   Первые пять чисел Ферма являются простыми числами, т.е. не имеют натуральных делителей, кроме 1 и самого себя. Однако, до сего момента не известно более ни одного простого числа Ферма. Более того, неизвестно, существует ли еще хотя бы одно простое число Ферма и эта проблема еще ждет своего юного гения.

   Гаусс доказал следующую теорему.

Теорема. С помощью циркуля и линейки построить правильный n-угольник можно тогда и только тогда, когда

                                ,

где  или , а  – различные между собой простые числа Ферма.

Замечание. Теорема утверждает только принципиальную возможность построения правильного n-угольника. Поэтому оставалась задача выразить сторону р-угольника в квадратных радикалах для оставшихся известных простых чисел Ферма  и . Для числа 257 эту задачу решил немецкий математик Фридрих Ришелло. Решение занимает 80 страниц текста. Случай числа 65537 был выполнен О.Гермесом, который потратил на вычисления 10 лет, а сама работа не опубликована ввиду ее необъятных размеров и хранится в архивах Гёттингенсного университета. Интересно, можно ли составить программу для компьютера для решения этой задачи?

   Гаусс очень ценил эту свою первую математическую работу и перед смертью просил высечь на своей могильной плите правильный 17-ти угольник. Увы, это не было сделано. Но в городе Брауншвейге стоит на 17-ти угольном постаменте памятник Карлу Фридриху Гауссу – королю математики.

   Прошло всего 10 дней, а юный Карл Гаусс получил свой самый выдающийся результат, доказав квадратичный закон взаимности.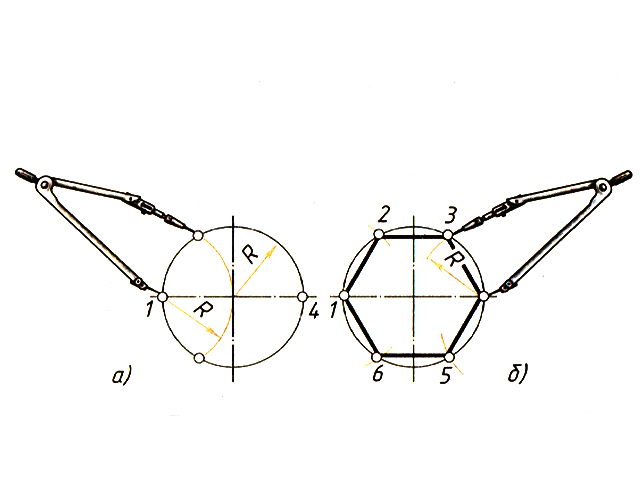 Эту теорему многие математики считают одной из самых красивейших теорем математики.

Теорема. Для любых двух нечетных простых чисел р и q верно равенство

                        ,

где  и  символы Лежандра.

Возможно найдутся ответы здесь:

Построение правильных многоугольников

Оглавление
Деление окружности на шесть, три, двенадцать равных частей.
Деление окружности на четыре, восемь, шестнадцать и т.д. частей.
Деление окружности на произвольное количество частей.

1) На ШЕСТЬ ЧАСТЕЙ. Чтобы разделить окружность на шесть равных частей, от любой ее точки (1) отложим отрезки, равные радиусу окружности (R).

От одной из полученных точек (в нашем случае 2) отложим с помощью того же раствора циркуля еще один отрезок, получим точку  3, от нее отложим еще один такой же отрезок, получим точку  4, и т.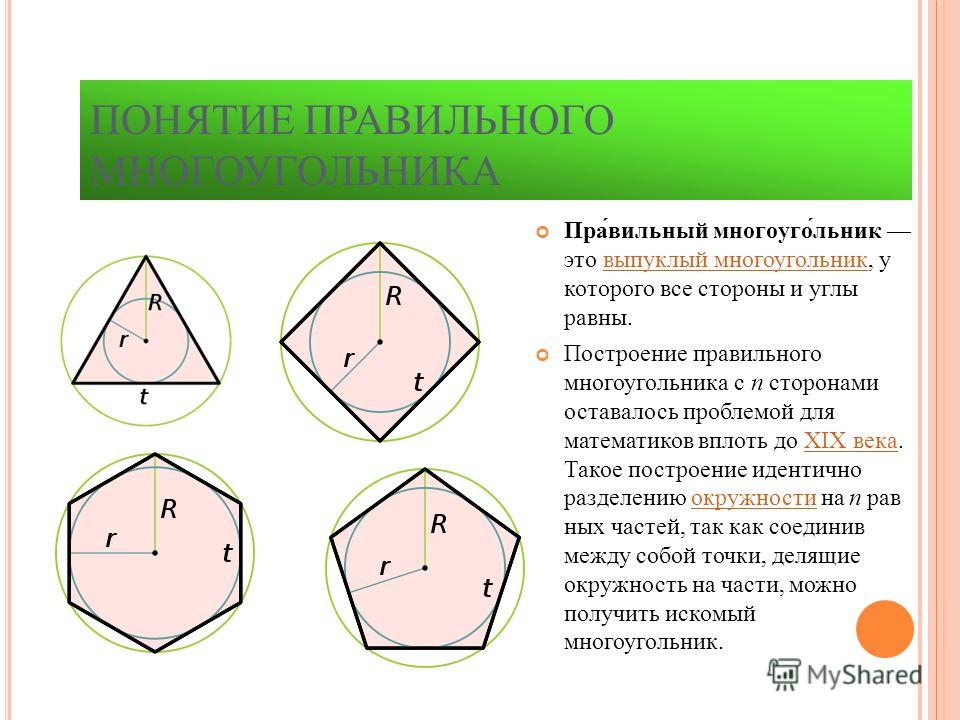 д.

Полученные дуги делят окружность на шесть равных частей. Приняв точки 1, 2, 3, 4, 5, 6 за вершины шестиугольника, соединим их отрезками прямых, таким образом построим   правильный шестиугольник.

2) На ТРИ ЧАСТИ. Полученные после построения шестиугольника точки соединим через одну получим правильный (равносторонний) треугольник.

3) На ДВЕНАДЦАТЬ ЧАСТЕЙ.  Одну из сторон полученного при первом построении шестиугольника разделим пополам (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) вместе с соответствующей дугой. Измерим циркулем полученную половину дуги, отложим данное расстояние по окружности от вершин 6-уголька. Новые точки на дуге вместе с вершинами шестиугольника – вершины двенадцатиугольника.

4) На 24 части, 48 частей и т.д.  Выполнив  алгоритм пункта 3 для сторон двенадцатиугольника – получим 24-угольник, выполнив этот же алгоритм со сторонами 24-угольника, получим 48-угольник и т. д.

1) На ЧЕТЫРЕ ЧАСТИ.  Проведем в окружности диаметр. Построим второй диаметр, перпендикулярный первому. (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) Полученные четыре точки и будут являться вершинами правильного четырехугольника (квадрата).

2) На ВОСЕМЬ ЧАСТЕЙ.  Одну из сторон полученного при первом построении квадрата  разделим пополам (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) вместе с соответствующей дугой. Измерим циркулем полученную половину дуги, отложим данное расстояние по окружности от вершин квадрата. Новые точки на дуге вместе с вершинами квадрата – вершины 8-угольника.

3) На 16, 32 и т.д. частей. Выполнив  алгоритм пункта  для сторон 8-угольника – получим 16-угольник, выполнив этот же алгоритм со сторонами 16-угольника, получим 32-угольник и т.д.

Вспомним о том, что величина дуги  всей окружности – 360 ⁰ .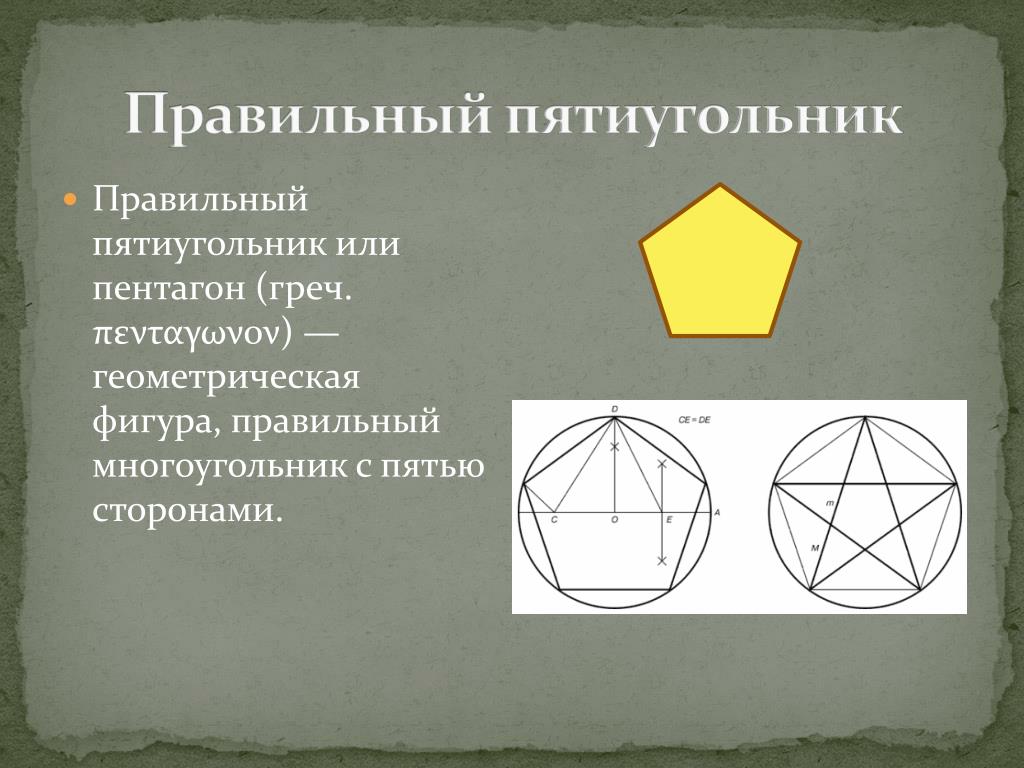 Тогда дуги, стянутые сторонами правильного многоугольника как хордами  равны 360/n, где n – количество сторон многоугольника.

количество сторон, n	3	4	5	6	7	8	9	10	11	12	13
величина угла между радиусами, соединяющими соседние вершины многоугольника, в градусах	120	90	72	60	51,4	45	40	36	32,7	30	27,7

Для построения многоугольника провести произвольно радиус, отложить от него с помощью транспортира центральный угол, соответствующий значениям таблицы или вычислениям, измерить получившуюся дугу циркулем, отложить с помощью полученного раствора циркуля дуги, равные первой. ВНИМАНИЕ! На точность построения зависит точность транспортира и количество сторон многоугольника.

ДЕЛЕНИЕ ОТРЕЗКА ПОПОЛАМ

Из концов отрезка проведем две дуги одинакового радиуса (R – больше половины отрезка). Через точки пересечения этих дуг проведем прямую, которая разделит отрезок (а в нашем случае и соответствующую дугу) пополам.

 

 

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА К ОТРЕЗКУ

Из концов отрезка проведем две дуги одинакового радиуса (R – больше половины отрезка). Через точки пересечения этих дуг проведем прямую, которая и буде перпендикуляром к данному отрезку.

Как построить правильный 6 ти угольник. Построение правильных многоугольников

Построение вписанного в окружность правильного шестиуголь­ника. Построение правильного пятиугольника по данной его стороне. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Это построение можно выполнить при помощи угольника и циркуля. Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Постройте точки вершин углов правильного шестиугольника.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Метод 1 из 3: Рисуем идеальный шестиугольник при помощи циркуля

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.

Именно на умении строить биссектрисы углов и серединные перпендикуляры отрезков и основывается методика построения правильных многоугольников

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй-коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Тема этого видеоурока – «Построение правильных многоугольников». Также еще раз дадим определение правильному многоугольнику, изобразим его графически, после чего еще раз убедимся, что центры вписанной и описанной окружностей вокруг такой фигуры будут совпадать. В этот многоугольник всегда можно вписать окружность и около него всегда можно описать окружность. В ходе предыдущих уроков мы выяснили, что базовую роль для описания свойств многоугольников играют биссектрисы его углов и серединные перпендикуляры к его сторонам.

4. Получили искомый правильный треугольник АВС. Задача решена. 3. Поместив одну ножку циркуля в произвольную точки А1 на окружности, при помощи второй ножки отметим на той же окружности точку А2 и соединим ее с точкой А1. Получим первую сторону шестиугольника. 3. При помощи серединных перпендикуляров к сторонам многоугольника, опущенным из точки О, разделим все его стороны и все дуги окружности, заключенные между его соседними вершинами, пополам.

Геометрические построения являются одной из важных частей обучения. Игла должна проткнуть начерченную линию. Чем точнее будет установлен циркуль, тем точнее будет построение. Начертите еще одну дугу, пересекающую окружность. Последовательно соедините все шесть точек пересечения дуг с первоначально начерченной окружностью. В этом случае шестиугольник может получиться неправильным.

Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые

Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра. Центры обеих окружностей совпадают (точка О на Рис. 1). Также на рисунке приведены радиусы описанной (R) и вписанной (r) окружностей.

Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. На данном занятии мы рассмотрим способы построения правильных многоугольников с помощью циркуля и линейки. Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник. Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности.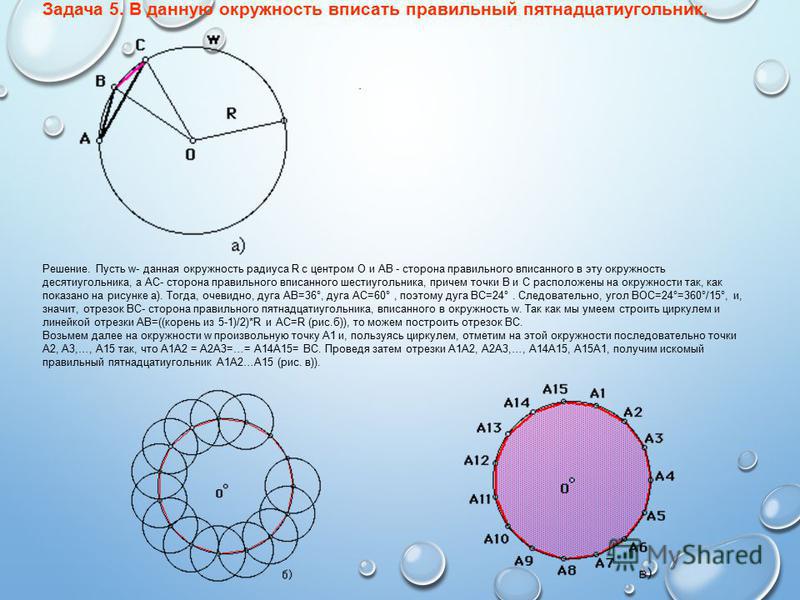 Каждого должно получиться шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.

Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкция

1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.

2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.

Видео по теме

Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.

Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)

2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.

Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.

Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.

Вам понадобится

• транспортир, угольник, циркуль, линейка

Инструкция

1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.

2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.

3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.

4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.

5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.

6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.

Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.

Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

• – циркуль;
• – линейка;
• – карандаш;
• – лист бумаги.

Инструкция

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.

2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.

4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.

5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).

Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.

При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.

Инструкция

1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.

2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.

3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.

4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.

5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.

6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.

Видео по теме

Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.

Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.

Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:

• Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.

Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.

Результат

Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .

2. Переход между шестиугольниками

Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.

3. Делим на секции

Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.

4. Закрашиваем секции

Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:

• Синий: C 65 M 23 Y 35 K 0
• Бежевый: C 13 M 13 Y 30 K 0
• Персиковый: C 0 M 32 Y 54 K 0
• Светло-розовый: C 0 M 64 Y 42 K 0
• Темно-розовый: C 30 M 79 Y 36 K 4

В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.

5. Последние штрихи и узор

Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.

Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).

Содержимое:

Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.

Шаги

1 Рисуем идеальный шестиугольник при помощи циркуля

1. 1 При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
   • Иногда легче сначала нарисовать пол круга, а затем вторую половину.
2. 2 Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
3. 3 Сделайте небольшую отметку карандашом на краю круга. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете. Не забудьте сохранять угол, который вы установили для циркуля.
4. 4 Передвиньте иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
5. 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
6. 6 Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
7. 7 Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
8. 8 Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали. После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.

2 Рисуем грубый шестиугольник при помощи круглого предмета и линейки

1. 1 Обведите ободок стакана карандашом. Таким образом, вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
2. 2 Нарисуйте горизонтальные линии через центр вашего круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив его пополам.
3. 3 Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций. Так как вы уже провели линию через середину круга, Х должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.
4. 4 Сделайте из каждой секции треугольники. Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник. Сделайте это с оставшимися пятью секциями. Думайте об этом, как об изготовлении корочки вокруг ваших кусков пиццы.
5. 5 Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.

3 Рисуем грубый шестиугольник при помощи одного карандаша

1. 1 Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку вашей горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может быть всего пара сантиметров.
2. 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа. Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
3. 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом, будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
4. 4 Нарисуйте еще одну горизонтальную линию, соединяя нижние две диагональные линии. Таким образом, вы нарисуете основу для своего шестиугольника. В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.

• Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
• Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.

Предупреждения

• Циркуль — довольно острый предмет, будьте с ним очень аккуратны.

Принцип работы

• Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.

Что вам понадобится

• Бумага
• Карандаш
• Линейка
• Пара циркулей
• Что-то, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала.
• Ластик

Шестиугольник | Лучшая вики по поп-культуре

В геометрии шестиугольник (от греческого ἕξ hex , «шестерка» и γωνία, gonía , «угол, угол») представляет собой шестиугольник или шестиугольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.

Правильный шестиугольник имеет символ Шлефли {6} ^[1] , а также может быть построен как усеченный равносторонний треугольник t {3}, в котором чередуются два типа ребер.

Правильный шестиугольник — это шестиугольник, который одновременно является равносторонним и равноугольным. Он бицентрический, что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).

Общая длина сторон равна радиусу описанной окружности или описанной окружности, что равно апофемой (радиус вписанной окружности).Все внутренние углы составляют 120 градусов. Правильный шестиугольник имеет 6 симметрий вращения ( симметрии вращения шестого порядка ) и 6 симметрий отражения ( шесть линий симметрии ), составляя группу диэдра D ₆ . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним, и что правильный шестиугольник можно разделить на шесть равносторонних треугольников.

Подобно квадратам и равносторонним треугольникам, правильные шестиугольники подходят друг к другу без каких-либо зазоров до мозаики плоскости (три шестиугольника, пересекающихся в каждой вершине), и поэтому полезны для построения мозаики. Ячейки сотового улья имеют шестиугольную форму по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки представляет собой сотовую мозаику шестиугольников. Обычно не считается триамбусом, хотя он равносторонний.

Параметры

[править | править источник]

Файл: Правильный шестиугольник 1.svg

Максимальный диаметр (который соответствует длинной диагонали шестиугольника), D , в два раза больше максимального радиуса или окружного радиуса, R , что равняется длине стороны, t . Минимальный диаметр или диаметр вписанного круга (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d , в два раза больше минимального радиуса или внутреннего радиуса, r .Максимумы и минимумы связаны одним и тем же фактором:

и аналогично

Площадь правильного шестиугольника

Для любого правильного многоугольника площадь также может быть выражена через апофему a и периметр p . Для правильного шестиугольника они равны , = r и p , поэтому

Правильный шестиугольник заполняет часть описанной окружности.

Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD.

Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1,0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.

Файл: Hexagon Reflection.svg

Шесть линий отражения правильного шестиугольника с симметрией Dih ₆ или r12 , порядок 12.

Файл: Regular hexagon Simries.svg

Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров) Циклические симметрии в среднем столбце обозначены как g для их приказы центрального вращения. Полная симметрия правильной формы — r12 , а отсутствие симметрии — a1 .

Правильный шестигранник имеет симметрию Dih ₆ , порядок 12.Существует 3 двугранных подгруппы: Dih ₃ , Dih ₂ и Dih ₁ и 4 циклические подгруппы: Z ₆ , Z ₃ , Z ₂ и Z ₁ .

Эти симметрии выражают 9 различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. ^[2] r12 — полная симметрия, а a1 — несимметрия. p6 ​​, изогональный шестиугольник, образованный тремя зеркалами, может чередовать длинные и короткие края, и d6 , изотоксический шестиугольник, построенный с равной длиной ребер, но вершинами с чередующимися двумя разными внутренними углами.Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. Формы i4 представляют собой правильные шестиугольники, сплющенные или вытянутые вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб, а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи. g2 шестиугольников с параллельными противоположными сторонами также называют шестиугольными параллелогонами.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм.Только подгруппа g6 не имеет степеней свободы, но может рассматриваться как направленные ребра.

Пример шестиугольника по симметрии

Шестиугольники симметрии g2 , i4 и r12 , поскольку параллелогоны могут разбивать евклидову плоскость путем преобразования. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.

группы A2 и G2 [править | править источник]

Шесть корней простой группы Ли A2, представленной диаграммой Дынкина Шаблон: Дынкин, образуют правильный шестиугольный узор.Угол между двумя простыми корнями составляет 120 °.

12 корней исключительной группы Ли G2, представленные диаграммой Дынкина Шаблон: Дынкин2, также находятся в гексагональной структуре. Два простых корня двух длин имеют угол между собой 150 °.

Коксетер утверждает, что каждый зоногон (2 угона м , противоположные стороны которого параллельны и равной длины) может быть разрезан на м ( м -1) / 2 параллелограмма. ^[3] В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими.Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами.

Связанные многоугольники и мозаики [править | править источник]

На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольниками вокруг каждой вершины.

Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}.Если смотреть с двумя типами (цветами) кромок, то эта форма имеет только симметрию D ₃ .

Усеченный шестиугольник t {6} представляет собой двенадцатиугольник {12}, чередующиеся 2 типа (цвета) ребер. Переменный шестиугольник h {6} — это равносторонний треугольник {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму. Правильный шестиугольник можно разрезать на 6 равносторонних треугольников, добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки.

Правильный шестиугольник можно расширить до правильного двенадцатиугольника, добавив чередующиеся квадраты и равносторонние треугольники вокруг него.Этот узор повторяется внутри ромбогексагональной плитки.

Есть 6 самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:

«Дорога гигантов» крупным планом

От пчелиных сот до «Дороги гигантов» гексагональные узоры широко распространены в природе благодаря своей эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии.

Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами, они также могут перекрывать плоскость путем перемещения. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.

В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея, будет мозаикой плоскости.

Шестиугольник вписан в коническое сечение [править | править источник]

Теорема Паскаля (также известная как «Hexagrammum Mysticum Theorem») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, «Линия Паскаля» этой конфигурации.

Циклический шестиугольник [править | править источник]

Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку.

Если последовательные стороны циклического шестиугольника равны a , b , c , d , e , f , то три главные диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf . ^[4]

Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то сегменты, соединяющие центры окружностей противоположных треугольников, совпадают. ^[5]

Если шестиугольник имеет вершины на описанной окружности острого треугольника в шести точках (включая три вершины треугольника), где увеличенные высоты треугольника пересекаются с описанной окружностью, то площадь шестиугольника в два раза больше площади треугольника. ^{[6] : стр. 179}

Шестиугольник, касательный к коническому сечению [править | править источник]

Пусть ABCDEF — шестиугольник, образованный шестью касательными конического сечения. Тогда теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.

В касательном к окружности шестиугольнике с последовательными сторонами a , b , c , d , e и f , ^[7]

Равносторонние треугольники по сторонам произвольного шестиугольника [править | править источник]

Файл: Равносторонний в шестиугольнике.svg

Равносторонние треугольники по сторонам произвольного шестиугольника

Если равносторонний треугольник построен снаружи с каждой стороны любого шестиугольника, то середины отрезков, соединяющих центроиды противоположных треугольников, образуют другой равносторонний треугольник. ^{[8] : Thm. 1}

Файл: Skew polygon in triangular antiprism.png

Правильный наклонный шестиугольник, видимый как края (черные) треугольной антипризмы, симметрия D _3d , [2 ⁺ , 6], (2 * 3), порядок 12.

Наклоненный шестиугольник — это косой многоугольник с 6 вершинами и ребрами, который не находится в одной плоскости. Внутренняя часть такого шестиугольника обычно не определяется. Наклонный зигзагообразный шестиугольник имеет вершины, чередующиеся между двумя параллельными плоскостями.

Правильный косой шестиугольник является вершинно-транзитивным с равными длинами ребер. В 3-х измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых гранях треугольной антипризмы с той же симметрией D _3d , [2 ⁺ , 6], порядок 12.

Куб и октаэдр (такие же, как треугольная антипризма) имеют правильные скошенные шестиугольники как многоугольники Петри.

полигонов Петри [править | править источник]

Правильный косой шестиугольник — это многоугольник Петри для этих правильных, однородных и двойственных многогранников и многогранников более высоких измерений, показанных в этих косых ортогональных проекциях:

Выпуклый равносторонний шестиугольник [править | править источник]

Главная диагональ шестиугольника — это диагональ, которая делит шестиугольник на четырехугольники.В любом выпуклом равностороннем шестиугольнике (один со всеми равными сторонами) с общей стороной a существует ^{[9] : p.184, # 286.3} главная диагональ d ₁ такая, что

и главной диагональю d ₂ такой, что

Многогранники с шестиугольниками [править | править источник]

Не существует Платонового тела, состоящего только из правильных шестиугольников, потому что шестиугольники мозаичны, не позволяя результату «складываться».Архимедовы тела с несколькими шестиугольными гранями — это усеченный тетраэдр, усеченный октаэдр, усеченный икосаэдр (футбольного мяча и фуллеренов), усеченный кубооктаэдр и усеченный икосододекаэдр. Эти шестиугольники можно рассматривать как усеченные треугольники, с диаграммами Кокстера вида Ошибка скрипта: Нет такого модуля «Диаграмма Кокстера – Дынкина». и Ошибка скрипта: нет такого модуля «Диаграмма Кокстера – Дынкина». .

Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например многогранник Гольдберга G (2,0):

Есть также 9 тел Джонсона с правильными шестиугольниками:

Галерея естественных и искусственных шестиугольников [редактировать | править источник]

Идеальная кристаллическая структура графена представляет собой гексагональную сетку.Собранные сегменты зеркала E-ELT

Микрофотография снежинки

Шестиугольный порядок пузырьков в пене.

Метрополия Франции имеет неопределенно шестиугольную форму. На французском языке l’Hexagone относится к континентальной части Европы, Франции. Павильон в ботаническом саду Тайваня
Добавить фото в эту галерею

1. ↑ Веннингер, Магнус Дж. (1974), Модели многогранников , Cambridge University Press, стр. 9, ISBN 9780521098595, https://books.google.com/books?id=N8lX2T-4njIC&pg=PA9.
2. ↑ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275 -278)
3. ↑ Кокстер, Математические развлечения и эссе, тринадцатое издание, стр.141.
4. ↑ Картенсен, Йенс, «О шестиугольниках», Mathematical Spectrum 33 (2) (2000–2001), 37–40.
5. ↑ Дергиадес, Николаос (2014). «Теорема Дао о шести центрах окружности, связанных с циклическим шестиугольником». Forum Geometricorum 14 : 243–246. http://forumgeom.fau.edu/FG2014volume14/FG201424index.html.
6. ↑ Джонсон, Роджер А., Advanced Euclidean Geometry , Dover Publications, 2007 (ориг. 1960).
7. ↑ Gutierrez, Antonio, «Hexagon, Inscribed Circle, Tangent, Semiperimeter», [1], доступ 2012-04-17.
8. ↑ Дао Тхань Оай (2015). «Равносторонние треугольники и перспективы Киперта в комплексных числах». Forum Geometricorum 15 : 105–114.http://forumgeom.fau.edu/FG2015volume15/FG201509index.html.
9. ↑ Неравенства, предложенные в “Crux Mathematicorum” , [2].

Шаблон: внешние ссылки

Шаблон: Полигоны Шаблон: Многогранники

Как построить правильный шестиугольник с помощью циркуля. Как построить правильный шестиугольник. Определение и конструкция

В последнее время очень популярны геометрические узоры. В сегодняшнем уроке мы узнаем, как создать один из этих шаблонов.Используя переходы, типографику и модные цвета, мы создадим узор, который вы сможете использовать в веб-дизайне и полиграфическом дизайне.

Результат

Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньшего размера — выберите радиус в 20pt .

2. Переход между шестиугольниками

Шаг 1
Выберите оба шестиугольника и выровняйте их по центру (по вертикали и горизонтали). Используя инструмент Blend (W) , выделите оба шестиугольника и придайте им переход к 6 шагов (Steps) … Чтобы было удобнее видеть, измените цвет фигур перед переходом.

3. Разделить на части

Шаг 1
Инструмент Сегмент линии (\\) нарисуйте линию, пересекающую шестиугольники в центре от крайнего левого угла до крайнего правого угла. Нарисуйте еще две линии, пересекающие шестиугольники в центре с противоположных углов.

4. Закрасить секции

Шаг 1
Прежде чем мы начнем закрашивать секции, давайте определимся с палитрой.Вот палитра из примера:

• Синий: C 65 M 23 Y 35 K 0
• Бежевый: C 13 M 13 Y 30 K 0
• Персик: C 0 M 32 Y 54 K 0
• Светло-розовый: C 0 M 64 Y 42 K 0
• Темно-розовый: C 30 M 79 Y 36 K 4

В примере сразу использовался режим CMYK, так что узор можно было напечатать без изменений.

5. Последние штрихи и узор

Шаг 1
Group (Control-G) все секции и шестиугольники после того, как вы закончите их раскрашивать. Скопируйте (Control-C) и Вставьте (Control-V) группу шестиугольников. Назовем исходную группу Hexagon A, и ее копию Hexagon B … Выровняйте группы.

Шаг 2
Примените Linear Gradient к группе Hexagon B. В палитре Gradient укажите заливку от фиолетового ( C60 M86 Y45 K42 ) до кремового цвета ( C0 M13 Y57 K0 ).

Правильный описанный треугольник имеет вид (рисунок 38). Из центра данного круга радиусом R 1 начертить окружность радиусом R 2 = 2R 1 и разделите на три равные части. Пункты деления A, B, C — вершины правильного треугольника, описанного вокруг окружности радиуса R 1 .

Рисунок 38

Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рис. 39).В данном круге нарисованы два взаимно перпендикулярных диаметра. Принимая точки пересечения диаметров с окружностью за центры, радиус окружности R описывают дуги до их взаимного пересечения в точках A, B, C, D … Очки A , Б , К , D и являются вершинами квадрата, описанного вокруг данной окружности.

Рисунок 39

Для построения правильного описанного шестиугольника необходимо сначала построить вершины описанного квадрата указанным выше способом (рис. 40, а).Одновременно с определением вершин квадрата заданная окружность радиуса R делится на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и нарисуйте вертикальные стороны квадрата. Проведение через точки раздела окружности 2–5 и 3–6 прямых до пересечения с вертикальными сторонами квадрата (рисунок 40, б), получаем вершины A, B, D, E описал правильный шестиугольник.

Рисунок 40

Оставшиеся пики C и F определяются с помощью дуги окружности радиусом OA , которая проводится до пересечения с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЕ

Есть ли рядом карандаш? Взгляните на его поперечное сечение — это правильный шестиугольник или, как его еще называют, шестиугольник. Такую же форму имеют поперечное сечение гайки, поле в виде шестиугольных шахмат, некоторых сложных молекул углерода (например, графита), снежинки, соты и других объектов.Недавно был обнаружен гигантский правильный шестиугольник. Не кажется ли странным, что природа часто использует структуры именно этой формы для своих творений? Рассмотрим подробнее.

Правильный шестиугольник — это многоугольник с шестью равными сторонами и равными углами. Из школьного курса мы знаем, что он имеет следующие свойства:

• Длина его сторон соответствует радиусу описанной окружности. Этим свойством обладает только правильный шестиугольник.
• Углы равны друг другу, а величина каждого равна 120 °.
• Периметр шестиугольника можно найти по формуле P = 6 * R, если известен радиус описанной окружности вокруг него, или P = 4 * √ (3) * r, если окружность вписана в этом. R и r — радиусы описанной и вписанной окружностей.
• Площадь, занимаемая правильным шестиугольником, определяется следующим образом: S = (3 * √ (3) * R 2) / 2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, которая делает его настолько широко распространенным в природе — он способен заполнять любую поверхность плоскости без перекрытий и зазоров. Есть даже так называемая лемма Пала, согласно которой правильный шестиугольник со стороной, равной 1 / √ (3), является универсальной крышкой, то есть может покрывать любое множество диаметром в одну единицу.

Теперь давайте посмотрим, как построить правильный шестиугольник. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки.Сначала нарисуйте циркулем произвольный круг, затем нарисуйте точку в произвольном месте на этом круге. Не меняя решения циркуля, кладем наконечник в эту точку, отмечаем следующую выемку на круге, продолжаем так, пока не получим все 6 точек. Теперь осталось только соединить их между собой прямыми отрезками, и у вас получится желаемая фигура.

На практике бывают случаи, когда вам нужно нарисовать большой шестиугольник. Например, на двухуровневом потолке из гипсокартона вокруг точки крепления центральной люстры нужно установить шесть фонариков на нижнем уровне.Найти компас такого размера будет очень и очень сложно. Как действовать в этом случае? Как нарисовать большой круг? Очень простой. Нужно взять прочную нить необходимой длины и связать один из ее концов напротив карандаша. Теперь осталось только найти помощника, который прижал бы второй конец нити к потолку в нужной точке. Конечно, в этом случае возможны мелкие ошибки, но вряд ли они вообще будут заметны постороннему.

Содержание:

Правильный шестиугольник, также называемый совершенным шестиугольником, имеет шесть равных сторон и шесть равных углов.Вы можете нарисовать шестиугольник с помощью рулетки и транспортира, грубый шестиугольник с круглым предметом и линейкой или даже более грубый шестиугольник с помощью простого карандаша и небольшой интуиции. Если вы хотите узнать, как нарисовать шестиугольник по-разному, просто читайте дальше.

Ступеньки

1 Нарисуйте идеальный шестиугольник с помощью циркуля

1. 1 Нарисуйте круг с помощью циркуля. Вставьте карандаш в циркуль. Расширьте циркуль до желаемой ширины для радиуса вашего круга.Радиус может быть от пары до десяти сантиметров в ширину. Затем поместите циркуль с карандашом на бумагу и нарисуйте круг.
   • Иногда проще нарисовать сначала половину круга, а затем вторую половину.
2. 2 Переместите стрелку циркуля к краю круга. Поместите его поверх круга. Не меняйте угол и положение компаса.
3. 3 Сделайте маленькую отметку карандашом на краю круга. Сделайте это четким, но не слишком темным, так как позже вы его сотрете.Не забудьте сохранить угол, установленный для компаса.
4. 4 Переместите стрелку циркуля к только что сделанной отметке. Поставьте иглу прямо на метку.
5. 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенном расстоянии от первой отметки. Продолжайте двигаться в одном направлении.
6. 6 Таким же образом сделайте еще четыре отметки. Вы должны вернуться к исходной отметке. Если нет, то, скорее всего, угол, под которым вы держали компас и наносили отметки, изменился.Возможно, это произошло из-за того, что вы его слишком сильно сжали или наоборот немного ослабили.
7. 7 Соедините отметки линейкой. Шесть мест, где ваши метки пересекаются с краем круга, — это шесть вершин шестиугольника. С помощью линейки и карандаша нарисуйте прямые линии, соединяющие соседние отметки.
8. 8 Сотрите круг, отметки по краям круга и любые другие отметки, которые вы оставили. После того, как вы стерли все линии построения, ваш идеальный шестиугольник должен быть готов.

2 Нарисуйте грубый шестиугольник с помощью круглого предмета и линейки

1. 1 Обведите карандашом край стакана. Таким образом вы нарисуете круг. Очень важно рисовать карандашом, так как в дальнейшем вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-нибудь еще с круглым основанием.
2. 2 Нарисуйте горизонтальные линии через центр вашего круга. Вы можете использовать линейку, книгу, все, что угодно с прямым краем.Если у вас есть линейка, вы можете отметить середину, вычислив длину круга по вертикали и разделив его пополам.
3. 3 Нарисуйте крестик на половине круга, разделив его на шесть равных частей. Так как вы уже провели линию через середину круга, X должен быть шире, чем высота, чтобы части были равны. Представьте, что вы разрезаете пиццу на шесть частей.
4. 4 Сделайте треугольники из каждой секции. Для этого с помощью линейки проведите прямую линию под изогнутой частью каждой секции, соединив ее с двумя другими линиями, чтобы сформировать треугольник.Проделайте это с оставшимися пятью разделами. Думайте об этом как о корке вокруг ломтиков пиццы.
5. 5 Сотрите все вспомогательные линии. Вспомогательные линии включают ваш круг, три линии, разделяющие ваш круг на секции, и другие отметки, сделанные вами по пути.

3 Нарисуйте грубый шестиугольник одним карандашом

1. 1 Проведите горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точки горизонтальной линии.Затем поместите карандаш в начальную точку и продлите линию к концу. Длина этой строчки может составлять всего пару сантиметров.
2. 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия на левой стороне должна быть обращена наружу так же, как диагональная линия на правой стороне. Вы можете представить, что эти линии образуют угол в 120 градусов к горизонтальной линии.
3. 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных линий, проведенных внутрь. Это создаст зеркальное отображение первых двух диагональных линий. Левая нижняя линия должна быть отражением верхней левой линии, а нижняя правая линия должна быть отражением верхней правой линии. Верхние горизонтальные линии должны смотреть наружу, а нижние — внутрь основания.
4. 4 Нарисуйте еще одну горизонтальную линию, соединяющую две нижние диагональные линии. Таким образом вы нарисуете основу для вашего шестиугольника. В идеале эта линия должна быть параллельна верхней горизонтальной линии.Теперь вы завершили свой шестиугольник.

• Карандаш и циркуль должны быть острыми, чтобы свести к минимуму ошибки из-за слишком широких отметок.
• Если при использовании метода компаса вы соединили каждую метку вместо всех шести, вы получите равносторонний треугольник.

Предупреждения

• Компас — довольно острый объект, будьте с ним очень осторожны.

Принцип действия

• Каждый метод поможет вам нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон.Шесть нарисованных радиусов имеют одинаковую длину, и все линии, образующие шестиугольник, также имеют одинаковую длину, поскольку ширина циркуля не изменилась. Из-за того, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусам.

Что вам понадобится

• Бумага
• Карандаш
• Линейка
• Циркуль
• Что-нибудь, что можно положить под бумагу, чтобы стрелка компаса не соскользнула.
• Ластик

Геометрическое построение — одна из основных частей обучения. Они формируют пространственное и логическое мышление, а также позволяют понять примитивные и естественные геометрические рассуждения. Конструкции выполняются на плоскости с помощью циркуля и линейки. Эти инструменты позволяют создавать большое количество геометрических фигур. В то же время многие фигуры, которые кажутся довольно сложными, строятся по простейшим правилам. Допустим, как построить правильный шестиугольник, можно в нескольких словах описать каждый.

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкции

1. Нарисуйте круг. Установите некоторое расстояние между ножками компаса. Это расстояние будет радиусом круга. Радиус выбирайте таким образом, чтобы рисовать круг было достаточно удобно. Круг должен полностью уместиться на листе бумаги. Слишком большое или слишком маленькое расстояние между ножками циркуля может привести к его изменению во время рисования.Оптимальным будет расстояние, при котором угол между ножками циркуля составляет 15-30 градусов.

2. Постройте вершины углов правильного шестиугольника. Поместите ножку циркуля, в которой закреплена стрелка, в любой точке круга. Игла должна проткнуть нарисованную линию. Чем правильнее выставлен компас, тем правильнее будет конструкция. Нарисуйте дугу окружности так, чтобы она пересекала нарисованный ранее круг. Переместите стрелку циркуля на точку пересечения только что нарисованной дуги с кругом.Нарисуйте еще одну дугу, пересекающую круг. Снова переместите стрелку циркуля в точку пересечения дуги и круга и заново проведите дугу. Выполните это действие еще три раза, двигаясь в одном направлении по кругу. У каждого должно быть шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Соедините все шесть точек пересечения дуг с первоначально нарисованной окружностью пошагово. Соедините точки прямыми линиями, проведенными линейкой и карандашом.Позже выполненные действия получат правильный шестиугольник, вписанный в круг.

Hexagon рассматривается многоугольник с шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые; для вогнутого — один или несколько углов острые. Шестиугольник построить довольно просто. Это делается за пару шагов.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкции

1. Берется лист бумаги и на нем отмечается 6 точек примерно так, как показано на рис. 1.

2. Позже, после того, как точки были размечены, берутся линейка, карандаш и с их помощью ступенчато соединяются точки одна за другой, как показано на рис. 2.

Видео по теме

Примечание!
Сумма всех внутренних углов шестиугольника составляет 720 градусов.

Шестиугольник Многоугольник с шестью углами.Чтобы нарисовать произвольный шестиугольник, нужно проделывать каждые 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкции

1. Нужно взять в руку карандаш и отметить на листе 6 произвольных точек. В будущем эти точки будут играть роль углов в шестиугольнике. (рис.1)

2. Возьмите линейку и по этим точкам нарисуйте 6 отрезков, которые будут соединены друг с другом согласно ранее начерченным точкам (рис.2)

Видео по теме

Примечание!
Особый тип шестигранника — положительный шестиугольник. Он называется таковым, потому что все его стороны и углы равны между собой. Вокруг такого шестиугольника можно описать или начертать круг. Стоит отметить, что в точках, которые получаются прикосновением к вписанной окружности и сторонам шестиугольника, стороны положительного шестиугольника делятся пополам.

Полезный совет
В природе очень популярны положительные шестиугольники.Например, вся сотовая структура имеет положительную шестиугольную форму. Или кристаллическая решетка графена (модификация углерода) также имеет форму положительного шестиугольника.

Как построить тот или иной угол Большой вопрос. Но для некоторых ракурсов задача незаметно упрощается. Один из этих углов равен , угол составляет 30 градусов. Это равно? / 6, то есть число 30 является делителем 180. Плюс известен его синус. Это помогает в его построении.

Вам понадобится

• транспортир квадратный циркуль линейка

Инструкции

1. Для начала давайте посмотрим на особенно примитивную среду, когда у вас в руках транспортир. Тогда прямую под углом 30 градусов к этой можно легко отложить, опираясь на нее.

2. Кроме транспортира имеется угловых зарубок, зарубок, один из углов которых равен 30 градусам. Тогда еще один угол угол будет равен 60 градусам, то есть вам понадобится визуально меньший угол , чтобы построить нужную прямую.

3. А теперь перейдем к нетривиальным способам построения угла в 30 градусов. Как известно, синус угла 30 градусов равен 1/2. Чтобы его построить, нам нужно построить прямо угол ны tre угол ник. Возможно, мы сможем построить две перпендикулярные линии. Но тангенс 30 градусов — это иррациональное число, поэтому мы можем рассчитать соотношение между ногами только приблизительно (исключительно, если нет калькулятора), и, следовательно, построить угол примерно с 30 градусами.

4. В этом случае допускается изготовление аккуратной конструкции. Снова возведем две перпендикулярные прямые, на которых будут располагаться ноги непосредственно угол новый tre угол ник. Отложите одну прямую ногу BC некоторой длины с опорой на циркуль (B — прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Рисуя круг с центром в точке C и радиусом этой длины, мы находим точку пересечения круга с другой прямой линией.Эта точка будет точкой A прямой угол новый tre угол прозвище ABC, а угол A будет равен 30 градусам.

5. Возведение под углом под углом 30 градусов допускается и с опорой на окружность, применяя, что он равен? / 6. Построим окружность радиуса OB. Рассмотрим в теории угол ника, где OA = OB = R — радиус окружности, где угол OAB = 30 градусов.Пусть OE будет высотой этого равнобедренного тре угла ника, и, следовательно, его биссектрисой и серединой. Тогда угол AOE = 15 градусов, и, используя формулу половинного угла, sin (15o) = (sqrt (3) -1) / (2 * sqrt (2)). Следовательно, AE = R * sin (15o). Отсюда AB = 2AE = 2R * sin (15o). Построив окружность радиуса BA с центром в точке B, находим точку A пересечения этой окружности с начальной. AOB будет 30 градусов.

6. Если мы можем каким-то образом определить длину дуг, то, отложив дугу длины? * R / 6, тоже получаем угол при 30 градусах.

Примечание!
Следует помнить, что в пункте 5 мы можем построить угол только приблизительно, потому что в расчетах появятся иррациональные числа.

Шестиугольник называется частный случай многоугольника — фигура, образованная большинством точек плоскости, ограниченная замкнутой ломаной линией. Положительный шестиугольник (шестиугольник), в свою очередь, также является частным случаем — это многоугольник с шестью равными сторонами и равными углами.Эта фигура значима тем, что длина всех ее сторон равна радиусу окружности, описанной вокруг фигуры.

Вам понадобится

• — компасы;
• — линейка;
• — карандаш;
• — бумага.

Инструкции

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенным на одной из его ножек, и концом иглы, расположенным на другой ножке, равным длине стороны нарисованной фигуры.Для этого разрешается использовать линейку или отдавать предпочтение случайному расстоянию, если момент незначителен. По возможности закрепите ножки компаса винтом.

2. Нарисуйте круг с помощью циркуля. Выбранное расстояние между ногами будет радиусом круга.

3. Разделите круг с точками на шесть равных частей. Эти точки будут вершинами углов шестиугольника и, соответственно, концами отрезков прямых, представляющих его стороны.

4. Установите ножку циркуля со стрелкой в ​​произвольную точку, расположенную на линии очерченного круга. Игла должна правильно прокалывать леску. Точность построений напрямую зависит от точности компаса. С помощью циркуля нарисуйте дугу так, чтобы она пересекалась в 2 точках с первым нарисованным кругом.

5. Переместите ножку циркуля со стрелкой в ​​одну из точек пересечения начерченной дуги с исходной окружностью.Нарисуйте еще одну дугу, также пересекающую круг в 2 точках (одна из них будет совпадать с точкой предыдущего положения стрелки компаса).

6. Аналогичным образом переставьте стрелку циркуля и проведите дуги еще четыре раза. Переместите ножку циркуля с иглой в одном направлении по окружности (всегда по или против часовой стрелки). В результате необходимо выделить шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Пошагово попарно соедините шесть точек, полученных на предыдущем шаге. Нарисуйте отрезки линий карандашом и линейкой. В результате у вас получится правильный шестиугольник. Позже в конструкции разрешается стирать вспомогательные элементы (дуги и окружности).

Примечание!
Расстояние между ножками компаса хорошо выбрать, чтобы угол между ними был равен 15-30 градусам, наоборот, при построении это расстояние легко может потеряться.

При построении или разработке планов дизайна дома часто требуется построить угол , равный более доступному. На помощь приходят образцы и школьные навыки геометрии.

Инструкции

1. Угол образован двумя прямыми линиями, начинающимися из одной точки. Эта точка будет называться вершиной угла, а линии — сторонами угла.

2. Используйте три буквы для обозначения углов: одна вверху, две по бокам.Называется угол , начиная с буквы, стоящей на одной стороне, затем называется буква, стоящая наверху, а затем буква на другой стороне. Используйте другие методы для обозначения углов, если вам удобнее обратное. Иногда называют только одну букву, стоящую наверху. А углы можно обозначать греческими буквами, скажем, α, β, γ.

3. Бывают ситуации, когда нужно провести угол так, чтобы он был ближе к заданному углу.Если нет вероятности использовать транспортир при построении чертежа, то можно делать только линейкой и циркулем. Возможно, на прямой, обозначенной на чертеже буквами MN, необходимо построить в точке K угол , чтобы он был равен углу B. То есть из точки K нужно провести начертите прямую, образующую с линией MN угол , тот, который будет равен углу B.

4. Вначале проведите по точке на всей стороне этого угла, скажем, по точкам A и C, затем объедините точки C и A прямой линией.Получить tre angle Nick ABC.

5. Теперь постройте на прямой MN те же три угла а, так, чтобы его вершина B оказалась на прямой в точке K. Воспользуйтесь правилом построения дерева угла ника с трех сторон. Отложите отрезок KL от точки K. Он должен быть равен отрезку BC. Получить точку L.

6. Из точки K начертите окружность с радиусом, равным отрезку BA. Нарисуйте окружность радиуса CA из L. Объедините полученную точку (P) пересечения двух окружностей с K. угол ник KPL, тот, который будет равен трем углу ник ABC. Таким образом, вы получите угол K. Он будет равен углу B. Для того, чтобы сделать эту конструкцию более удобной и быстрой, отложите равные отрезки от вершины B одним компасом, не двигая ногами, опишите круг. с таким же радиусом от точки K.

Видео по теме

Примечание!
Избегайте случайного изменения расстояния между ножками компаса.В этом случае шестиугольник может оказаться неправильным.

Полезный совет
Он умеет строить конструкции с помощью циркуля с идеально заточенным грифелем. Это сделает конструкцию особенно аккуратной.

открытых учебников | Сиявула

Математика

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 7A

      • Марка 7Б

      • 7 класс (A и B вместе)

    • Африкаанс

      • Граад 7А

      • Граад 7Б

      • Граад 7 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 8A

      • Сорт 8Б

      • 8 класс (A и B вместе)

    • Африкаанс

      • Граад 8А

      • Граад 8Б

      • Граад 8 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 9А

      • Марка 9Б

      • 9 класс (A и B вместе)

    • Африкаанс

      • Граад 9А

      • Граад 9Б

      • Граад 9 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 4A

      • Класс 4Б

      • Класс 4 (вместе A и B)

    • Африкаанс

      • Граад 4А

      • Граад 4Б

      • Граад 4 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 5A

      • Марка 5Б

      • Оценка 5 (вместе A и B)

    • Африкаанс

      • Граад 5А

      • Граад 5Б

      • Граад 5 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 6А

      • Марка 6Б

      • 6 класс (A и B вместе)

    • Африкаанс

      • Граад 6А

      • Граад 6Б

      • Граад 6 (A en B saam)

  • Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (безымянные версии)

Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Шестиугольник — HandWiki

В геометрии шестиугольник (от греческого ἕξ hex , «шестерка» и γωνία, gonía , «угол, угол») представляет собой шестиугольник или шестиугольник.Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.

Шестигранник правильный

Правильный шестиугольник имеет символ Шлефли {6} ^[1] , а также может быть построен как усеченный равносторонний треугольник t {3}, в котором чередуются два типа ребер.

Пошаговая анимация построения правильного шестиугольника с помощью циркуля и линейки, представленная Евклидом Elements , Книга IV, Предложение 15: это возможно как 6 [math] \ displaystyle {=} [/ math] 2 × 3, произведение степени двух и различных простых чисел Ферма.Когда задана длина стороны AB, вы рисуете вокруг точки A, а вокруг точки B — дугу окружности. Пересечение M — центр описанной окружности. Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.

Правильный шестиугольник — это шестиугольник, который одновременно является равносторонним и равноугольным. Он бицентрический, что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).

Общая длина сторон равна радиусу описанной окружности или описанной окружности, который равен [math] \ displaystyle {\ tfrac {2} {\ sqrt {3}}} [/ math], умноженному на апофему (радиус вписанный круг).Все внутренние углы составляют 120 градусов. Правильный шестиугольник имеет шесть симметрий вращения ( симметрии вращения шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляя группу диэдра D ₆ . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним, и что правильный шестиугольник можно разделить на шесть равносторонних треугольников.

Подобно квадратам и равносторонним треугольникам, правильные шестиугольники подходят друг к другу без каких-либо зазоров до мозаики плоскости (три шестиугольника, пересекающихся в каждой вершине), и поэтому полезны для построения мозаики. Ячейки сотового улья имеют шестиугольную форму по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки представляет собой сотовую мозаику шестиугольников. Обычно не считается триамбусом, хотя он равносторонний.

Параметры

Максимальный диаметр (который соответствует длинной диагонали шестиугольника), D , в два раза больше максимального радиуса или радиуса описанной окружности, R , что равняется длине стороны, t . Минимальный диаметр или диаметр вписанного круга (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d , в два раза больше минимального радиуса или внутреннего радиуса, r . \ circ) R = \ frac {\ sqrt {3}} {2} R = \ frac {\ sqrt { 3}} {2} t} [/ math] и аналогично [math] \ displaystyle {d = \ frac {\ sqrt {3}} {2} D.2. \ end {align}} [/ math]

Правильный шестиугольник заполняет часть [math] \ displaystyle {\ tfrac {3 \ sqrt {3}} {2 \ pi} \ приблизительно 0,8270} [/ math] своего описанный круг.

Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD.

Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1.0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.

Симметрия

Шесть линий отражения правильного шестиугольника с симметрией Dih ₆ или r12 , порядок 12. Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g для их центральных порядков вращения. Полная симметрия правильной формы — r12 , а отсутствие симметрии — a1 .

Правильный шестиугольник имеет симметрию Dih ₆ , порядок 12. Есть три двугранные подгруппы: Dih ₃ , Dih ₂ и Dih ₁ , и четыре циклические подгруппы: Z ₆ , Z ₃ , Z ₂ и Z ₁ .

Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. ^[2] r12 — полная симметрия, а a1 — несимметрия. p6 ​​, изогональный шестиугольник, образованный тремя зеркалами, может чередовать длинные и короткие края, и d6 , изотоксический шестиугольник, построенный с равной длиной ребер, но вершинами с чередующимися двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. Формы i4 представляют собой правильные шестиугольники, сплющенные или вытянутые вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб, а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи. g2 шестиугольников с параллельными противоположными сторонами также называют шестиугольными параллелогонами.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g6 не имеет степеней свободы, но может рассматриваться как направленные ребра.

Пример шестиугольника по симметрии

Шестиугольники симметрии g2 , i4 и r12 , поскольку параллелогоны могут разбивать евклидову плоскость путем преобразования.Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.

Группы A2 и G2

Шесть корней простой группы Ли A2, представленной диаграммой Дынкина Ошибка сценария: Нет такого модуля «Дынкин». , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.

12 корней исключительной группы Ли G2, представленные диаграммой Дынкина, также имеют гексагональный узор. Два простых корня двух длин имеют угол между собой 150 °.

Рассечение

6-кубический выступ	Рассечение 12 ромбов

Коксетер утверждает, что каждый зоногон (2 м -угольника, противоположные стороны которого параллельны и равной длины) может быть разрезан на м ( м -1) / 2 параллелограмма. ^[3] В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими.Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами.

Связанные многоугольники и мозаики

На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольниками вокруг каждой вершины.

Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}.Если смотреть с двумя типами (цветами) кромок, то эта форма имеет только симметрию D ₃ .

Усеченный шестиугольник t {6} представляет собой двенадцатиугольник {12}, чередующиеся два типа (цвета) ребер. Переменный шестиугольник h {6} — это равносторонний треугольник {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму. Правильный шестиугольник можно разрезать на шесть равносторонних треугольников, добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки.

Правильный шестиугольник можно расширить до правильного двенадцатиугольника, добавив чередующиеся квадраты и равносторонние треугольники вокруг него.Этот узор повторяется внутри ромбогексагональной плитки.

Есть шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:

Гексагональные конструкции

От пчелиных сот до Дороги гигантов, гексагональные узоры широко распространены в природе из-за их эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии.

Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами, они также могут перекрывать плоскость путем перемещения. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.

Мозаика с шестигранной призмой

Форма	Шестиугольная черепица	Гексагональные призматические соты
Обычный
Параллелогональный

Мозаика по шестиугольникам

Основная страница: Гексагональная мозаика

В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея, будет мозаикой плоскости.

Шестиугольник, вписанный в коническое сечение

Теорема Паскаля (также известная как «Hexagrammum Mysticum Theorem») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, «Линия Паскаля» этой конфигурации.

Циклический шестигранник

Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку.

Если последовательные стороны циклического шестиугольника равны a , b , c , d , e , f , то три главные диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf . ^[4]

Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то сегменты, соединяющие центры окружностей противоположных треугольников, совпадают. ^[5]

Если шестиугольник имеет вершины на описанной окружности острого треугольника в шести точках (включая три вершины треугольника), где увеличенные высоты треугольника пересекаются с описанной окружностью, то площадь шестиугольника в два раза больше площади треугольника. ^{[6] : стр. 179}

Шестигранник по касательной к коническому сечению

Пусть ABCDEF — шестиугольник, образованный шестью касательными конического сечения. Тогда теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.

В касательном к окружности шестиугольнике с последовательными сторонами a , b , c , d , e и f , ^[7]

[математика] \ displaystyle {a + c + e = b + d + f. } [/ math]

Равносторонние треугольники по сторонам произвольного шестиугольника

Равносторонние треугольники по сторонам произвольного шестиугольника

Если равносторонний треугольник построен снаружи с каждой стороны любого шестиугольника, то середины отрезков, соединяющих центроиды противоположных треугольников, образуют другой равносторонний треугольник. ^{[8] : Thm. 1}

Шестигранник с перекосом

Правильный наклонный шестиугольник, видимый как края (черные) треугольной антипризмы, симметрия D _3d , [2 ⁺ , 6], (2 * 3), порядок 12.

Наклонный шестиугольник — это косой многоугольник с шестью вершинами и ребрами, который не находится в одной плоскости. Внутренняя часть такого шестиугольника обычно не определяется. Наклонный зигзагообразный шестиугольник имеет вершины, чередующиеся между двумя параллельными плоскостями.

Правильный косой шестиугольник является вершинно-транзитивным с равными длинами ребер.В трех измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых гранях треугольной антипризмы с той же симметрией D _3d , [2 ⁺ , 6], порядок 12.

Куб и октаэдр (такие же, как треугольная антипризма) имеют правильные скошенные шестиугольники как многоугольники Петри.

Полигоны Петри

Правильный косой шестиугольник — это многоугольник Петри для этих правильных, однородных и двойственных многогранников и многогранников более высоких измерений, показанных в этих косых ортогональных проекциях:

Шестигранник выпуклый равносторонний

Главная диагональ шестиугольника — это диагональ, которая делит шестиугольник на четырехугольники.В любом выпуклом равностороннем шестиугольнике (один со всеми равными сторонами) с общей стороной a существует ^{[9] : p.184, # 286.3} главная диагональ d ₁ такая, что

[math] \ displaystyle {\ frac {d_1} {a} \ leq 2} [/ math]

и главная диагональ d ₂ такая, что

[математика] \ displaystyle {\ frac {d_2} {a} \ gt \ sqrt {3}. } [/ math]

Многогранники с шестиугольниками

Не существует Платонового тела, состоящего только из правильных шестиугольников, потому что шестиугольники мозаичны, не позволяя результату «складываться».Архимедовы тела с несколькими шестиугольными гранями — это усеченный тетраэдр, усеченный октаэдр, усеченный икосаэдр (футбольного мяча и фуллеренов), усеченный кубооктаэдр и усеченный икосододекаэдр. Эти шестиугольники можно рассматривать как усеченные треугольники, причем диаграммы Кокстера имеют вид и.

Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например многогранник Гольдберга G (2,0):

Есть также 9 тел Джонсона с правильными шестиугольниками:

Галерея натуральных и искусственных шестиугольников

• Идеальная кристаллическая структура графена представляет собой гексагональную сетку.

• Собранные сегменты зеркала E-ELT

• Микрофотография снежинки

• Бензол, простейшее ароматическое соединение гексагональной формы.

• Шестиугольный порядок пузырьков в пене.

• Кристаллическая структура молекулярного шестиугольника, состоящего из гексагональных ароматических колец.

• Естественно сформированные базальтовые колонны с Дороги гигантов в Северной Ирландии; большие массы должны медленно остывать, чтобы образовался полигональный узор изломов

• Вид с воздуха на Форт Джефферсон в национальном парке Драй Тортугас

• Метрополитен Франция имеет неопределенно шестиугольную форму. На французском языке l’Hexagone относится к континентальной части Европы, Франции.

• Шестиугольник, шестиугольный театр в Рединге, Беркшир

• Шестиугольные шахматы Владислава Глинского

• Павильон в Тайваньском ботаническом саду

См. Также

Список литературы

1. ↑ Веннингер, Магнус Дж.(1974), Модели многогранников , Cambridge University Press, стр. 9, ISBN 9780521098595, https://books.google.com/books?id=N8lX2T-4njIC&pg=PA9, получено 06.11.2015.
2. ↑ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN: 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
3. ↑ Кокстер, Математические развлечения и эссе, тринадцатое издание, стр.141.
4. ↑ Картенсен, Йенс, «О шестиугольниках», Mathematical Spectrum 33 (2) (2000–2001), 37–40.
5. ↑ Дергиадес, Николаос (2014). «Теорема Дао о шести центрах окружности, связанных с циклическим шестиугольником». Forum Geometricorum 14 : 243–246. http://forumgeom.fau.edu/FG2014volume14/FG201424index.html. Проверено 17 ноября 2014.
6. ↑ Джонсон, Роджер А., Advanced Euclidean Geometry , Dover Publications, 2007 (ориг. 1960).
7. ↑ Gutierrez, Antonio, «Hexagon, Inscribed Circle, Tangent, Semiperimeter», [1], доступ 2012-04-17.
8. ↑ Дао Тхань Оай (2015).«Равносторонние треугольники и перспективы Киперта в комплексных числах». Forum Geometricorum 15 : 105–114. http://forumgeom.fau.edu/FG2015volume15/FG201509index.html. Проверено 12 апреля 2015.
9. ↑ Неравенства, предложенные в “Crux Mathematicorum” , [2].

Внешние ссылки

Home — eCabs — Вместе в путешествие

Место получения:

Дополнительная остановка:

Место возврата:

Тип транспортного средства:

Номер рейса:

---

Имя:

Фамилия:

Электронная почта:

Телефон:

Способ оплаты:

---

На счету Утверждено:

Запросить кабину за € AT Назад

Цены указаны с учетом НДС
НДС №MT 2158-3611 | Торговый № 39/898

Вы получите подтверждение по электронной почте и SMS

Вы бы хотели заказать
поездку туда и обратно?

да

Вы получите подтверждение по электронной почте и SMS

Чтобы отслеживать такси, загрузите наше приложение с:

Что-то пошло не так.Звоните +356 21 38 38 38

Попробуй еще раз

Цены указаны с учетом НДС.
№ НДС MT 2158-3611 | Торговый № 39/898

Забронируйте обратную поездку

На счету Утверждено:

Пожалуйста, заберите меня по номеру

Номер рейса

от до

Расчетное время прибытия:

Неверный номер рейса или рейса не работает в выбранную дату

Возврат книги

Место получения:

Место возврата:

Тип транспортного средства:

Номер рейса:

---

Имя:

Фамилия:

Электронная почта:

Телефон:

Способ оплаты:

Изменить детали

Цены указаны с учетом НДС
НДС №MT 2158-3611 | Торговый № 39/898

Построение сеток с помощью линейки и циркуля

В сентябре 2018 года я сделал презентацию о моделях, построенных с использованием сеток, на 4-м международном семинаре по геометрическим образцам в исламском искусстве в Стамбуле. Для презентации я подготовил эти видеоролики с замедленной съемкой, демонстрирующие различные методы построения сеток с использованием линейки и компаса, и разместил их здесь, чтобы они были полезны более широкой аудитории.

Квадратные и изометрические (треугольные) сетки обеспечивают богатую и обширную основу для исследования геометрических узоров.Они возникли из простейших регулярных делений 2D-плоскости. Треугольник и квадрат — это два из трех правильных многоугольников, которые сами по себе могут замостить 2D-плоскость. Шестиугольник является третьим, но его можно рассматривать как комбинацию из 6 треугольников, что напрямую соответствует изометрической сетке. Эти первые два видеоролика показывают базовое построение шестиугольника и квадрата из круга, фундаментальные конструкции в изучении геометрического искусства.

Чтобы исследовать закономерности, мы должны сначала построить более широкие сетки.Рисование этих сеток с использованием традиционных геометрических инструментов, таких как линейка и циркуль, помогает понять роль круга (и, следовательно, компаса) в их построении. Обе сетки широко использовались в качестве основы для дизайна узоров во многих культурах мира и на протяжении всей истории.

Изометрическая сетка — метод 1

Как мы видели выше, круг легко делится на шесть равных сегментов. Этот первый метод основан на структуре, которую часто называют Цветком Жизни.Профессор Кейт Кричлоу описывает это как диаграмму творения.

Мы начинаем с маленького кружка в центре, и узор растет наружу от этой начальной точки, теоретически бесконечно, с дальнейшими кругами, центрированными на новых пересечениях, созданных предыдущими кругами. Очень приятно видеть, как эта красивая конструкция разворачивается, когда вы ее рисуете. Однако с практической точки зрения неточности могут усугубиться, если начать с малого и развить внешнюю сторону. Также сложно создать окончательную сетку определенного размера.

Изометрическая сетка — метод 2

Второй метод начинается с большого круга, и область внутри подразделяется (опять же, теоретически бесконечно) на все более мелкие треугольники. Работа снаружи внутрь более точна и имеет дополнительное преимущество, позволяя вам работать в пределах исходного круга (и, следовательно, шестиугольника) фиксированных размеров.

Квадратная сетка — метод 1

Квадратную сетку можно создать двумя аналогичными способами.Сначала начните с четырех кругов вокруг центрального, а затем расширьте его наружу, используя пересечения, создаваемые каждым дополнительным кругом.

Квадратная сетка — метод 2

Опять же, начиная с большого квадрата и деления более точно. Взаимодействие статических и динамических (горизонтальных и диагональных) сеток может привести к очень интересным проектам, в которых исследуется пропорциональная зависимость √2 между длиной края квадрата и его диагональю.

Также возможно деление нечетных чисел, но это уже другая история.

Другой метод (здесь не показан) — использовать заданный квадрат для построения любой сетки. Заданный квадрат 30-60-90 основан на углах треугольника, поэтому его можно использовать для построения изометрической сетки, а заданный квадрат 45-45-90 можно использовать для квадратной сетки.

После того, как сетка будет построена с желаемым размером, ее пересечения можно использовать для создания повторяющихся узоров.

Поделиться:

• Нажмите, чтобы поделиться в Facebook (Открывается в новом окне)
• Нажмите, чтобы поделиться в LinkedIn (Открывается в новом окне)
• Нажмите, чтобы поделиться в Pinterest (Открывается в новом окне)
• Подробнее

• Нажмите, чтобы поделиться в Pocket (Открывается в новом окне)
• Нажмите, чтобы поделиться на Reddit (Открывается в новом окне)
• Нажмите, чтобы отправить это другу по электронной почте (Открывается в новом окне)

Как это:

Нравится Загрузка…

Правильные шестиугольники в Adobe Illustrator: алгоритмы для масс

Правильные шестиугольники в Adobe Illustrator

12 лет назад

Вчера вечером мне пришлось нарисовать правильный шестиугольник в Adobe Illustrator, а теперь я помню со школьных лет, как рисовать его с помощью циркуля и линейки (нарисуйте круг с помощью циркуля, а затем выберите точку на окружности и отметьте радиусов с помощью циркуля, обходя круг; вы отметите шесть пересечений, а затем соедините их прямыми линиями: voilà !), но у меня нет циркуля в Illustrator.

(ОБНОВЛЕНИЕ. это. да ладно.)

Мгновенное размышление дало мне ответ.

• Проведите горизонтальную линию
  
• Скопируйте эту строку в буфер обмена
• Вставьте копию строки
• Поверните его на 60 °, переместите так, чтобы он касался горизонтальной линии слева
  
• Вставьте копию строки
• Поверните на -60 °, переместите так, чтобы он касался горизонтальной линии справа
  

Теперь у вас есть половина шестиугольника.

• Используя инструмент лассо, наложите лассо на левый угол и соедините отрезки линии (используйте метод «Угол»)
  
• Лассо правый угол и делаем то же
  

Теперь линии образуют путь.

• Скопируйте половину шестиугольника в буфер обмена
• Вставить копию
• Отразите копию по горизонтали
• Переместите копию так, чтобы она касалась другой половины
• Соедините две половинки с помощью инструмента лассо
  

Теперь у вас есть правильный шестиугольник.Линии образуют замкнутый контур, поэтому вы можете раскрасить периметр и интерьер по своему желанию.

Магический угол поворота — это внешний угол для сторон правильного шестиугольника. Если вам нужен еще один правильный многоугольник, вычислите соответствующий внешний угол (360, разделенные на количество сторон) и продолжайте, как прежде. Если количество сторон не четное, вы не сможете использовать трюк с отражением для экономии времени, но вам придется вставлять / вращать каждую сторону по мере необходимости. Например, вот правильный пятиугольник (внешний угол = 72 °):

Очевидно, что если количество сторон не делится на 360 ° точно, в углах будут какие-то искажения, чтобы все было правильно.

Сейчас играет:
Псевдоним — шестерок последний
(из Приглушенный )

Загрузка ссылок на сообщения на похожие темы … .

No related posts.