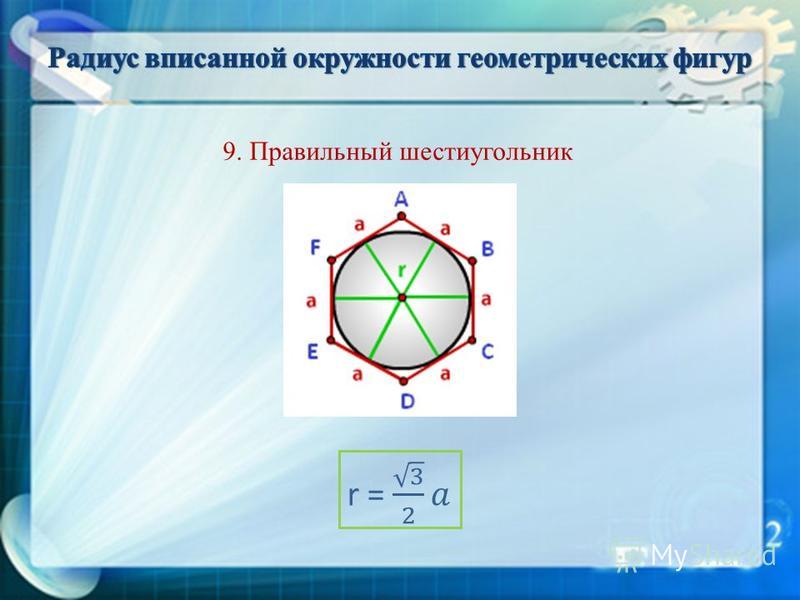
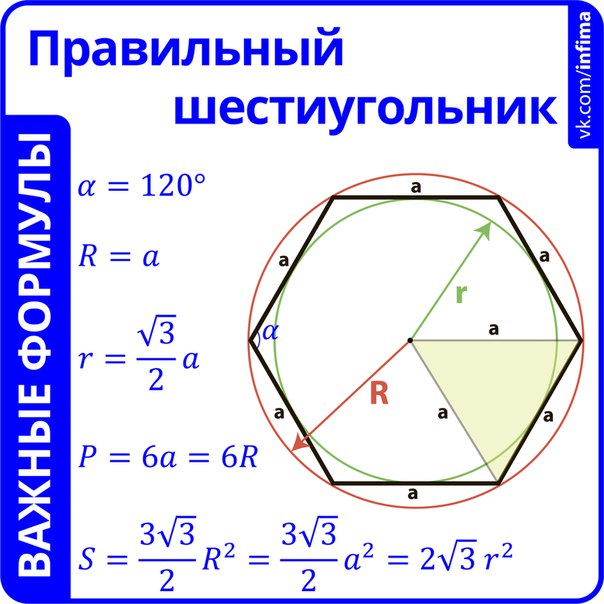
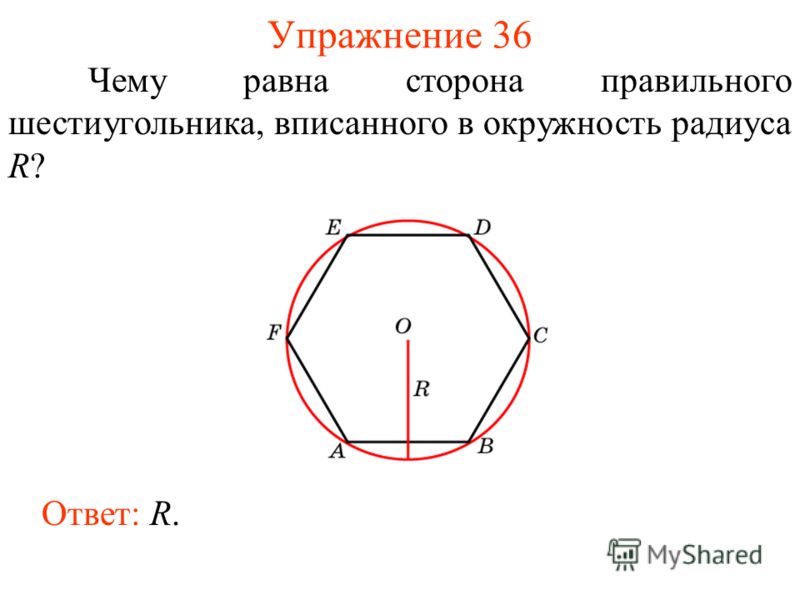
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac<<sqrt 3 >><2>
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.
Если внимательно посмотреть на правильный шестиугольник, то можно увидеть, что он состоит из шести равносторонних треугольников со стороной a .
Площадь правильного шестиугольника равна площади равностороннего треугольника умноженной на шесть.
Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов.
Выпуклый шестиугольник
Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:
S = 2,59 R 2 = 2,59 a 2 .
Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:
Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.
Гексаграмма
Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды.
Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Шестиугольные числа
В теории чисел существуют фигурные числа, связанные с определенными геометрическими фигурами. Наибольшее применение находят треугольные и квадратные, а также тетраэдрические и пирамидальные числа, используя которые легко выкладывать геометрические фигуры при помощи реальных предметов. Например, пирамидальные числа подскажут вам, как сложить пушечные ядра в устойчивую пирамиду. Существуют также и шестиугольные числа, которые определяют число точек, необходимое для построения гексагона.
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений.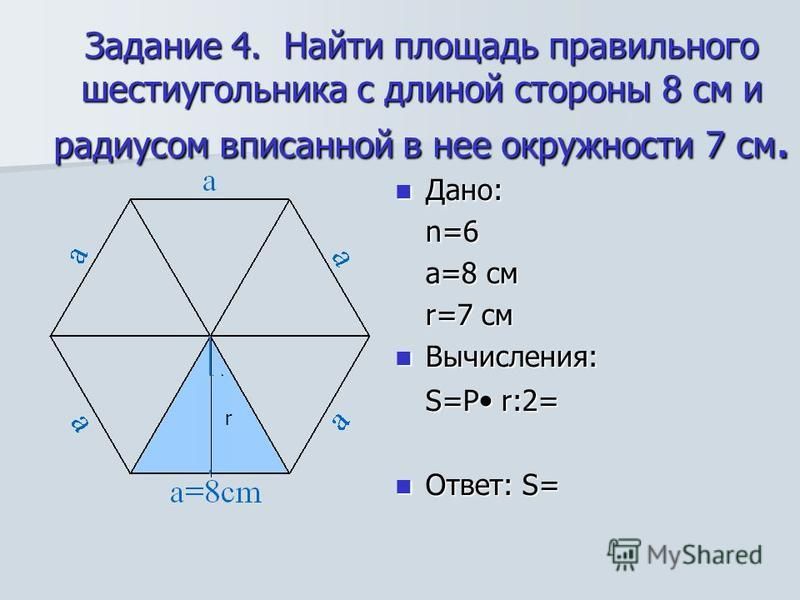
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Упаковка кругов на плоскости
И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно.
Гескагон — решение данной проблемы.
Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника. Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров.
Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Заключение
Шестиугольник часто встречается в реальности, хотя мы и не замечаем этого. Используйте наш онлайн-калькулятор для расчета площадей гексагонов при решении повседневных или школьных задач.
Найдите длину окружности, если площадь вписанного в окружность правильного шестиугольника равна 72√3 см2.
избегайте прогулок в одиночестве в малолюдных местах;
откажитесь, по возможности, от ночных передвижений, в крайнем случае, воспользуйтесь такси;
если к вам грубо обращаются по поводу якобы допущенной ошибки или делают вас объектом насмешек, не отвечайте и не поддавайтесь на провокации;
старайтесь предвидеть и избегать неприятных ситуаций;
не останавливайте, по возможности, машины автостопом и не соглашайтесь на то, чтобы вас подвозили незнакомые люди;
никогда не показывайте деньги или драгоценности, их надо держать во внутреннем кармане, в дипломате или в другом надежном месте;
не нагружайте себя свертками и пакетами, лучше всегда иметь свободу движений на тот случай, если возникнет необходимость защищаться;
если кто-либо мешает вам передвигаться, и вы не можете освободиться, обратитесь к милиционеру, позвоните в звонок на любой входной двери;
в незнакомом городе передвигайтесь с картой, которая позволит время; по той же причине побольше обращайтесь к разным людям, когда вы ищите какой-нибудь адрес, потому что единственный ответ может быть неправильным;
не показывайте слишком ясно, что вы турист; прогуливайтесь с местной газетой под мышкой, смешивайтесь с местными жителями;
будьте внимательны к подворотням и плохо освещенным углам, стараясь по возможности их избегать;
если какой-нибудь автомобилист спрашивает совета, дайте его быстро и четко или извинитесь, что вы не знаете этого места, но не вызывайтесь сопровождать незнакомого человека;
избегайте садиться в пустой автобус, а если вам все-таки приходится делать это, садитесь ближе к водителю;
когда вы передвигаетесь в городе, всегда удобно иметь в распоряжении несколько мелких монет и билетов на городской транспорт.
избегайте мест большого скопления людей: рынки, толпы, очереди и т.д. именно в толпе легко столкнуться с тем, кто крадет сумки и бумажники. сами вы этого даже не заметите из-за нехватки времени. вот еще несколько советов, которые, хотя они и очевидны, полезно не забывать:
обращайтесь в учреждения для оплаты какой-либо квитанции или для продления срока действия какого-либо документа не в час пик и не в последние дни перед окончанием срока действия документа;
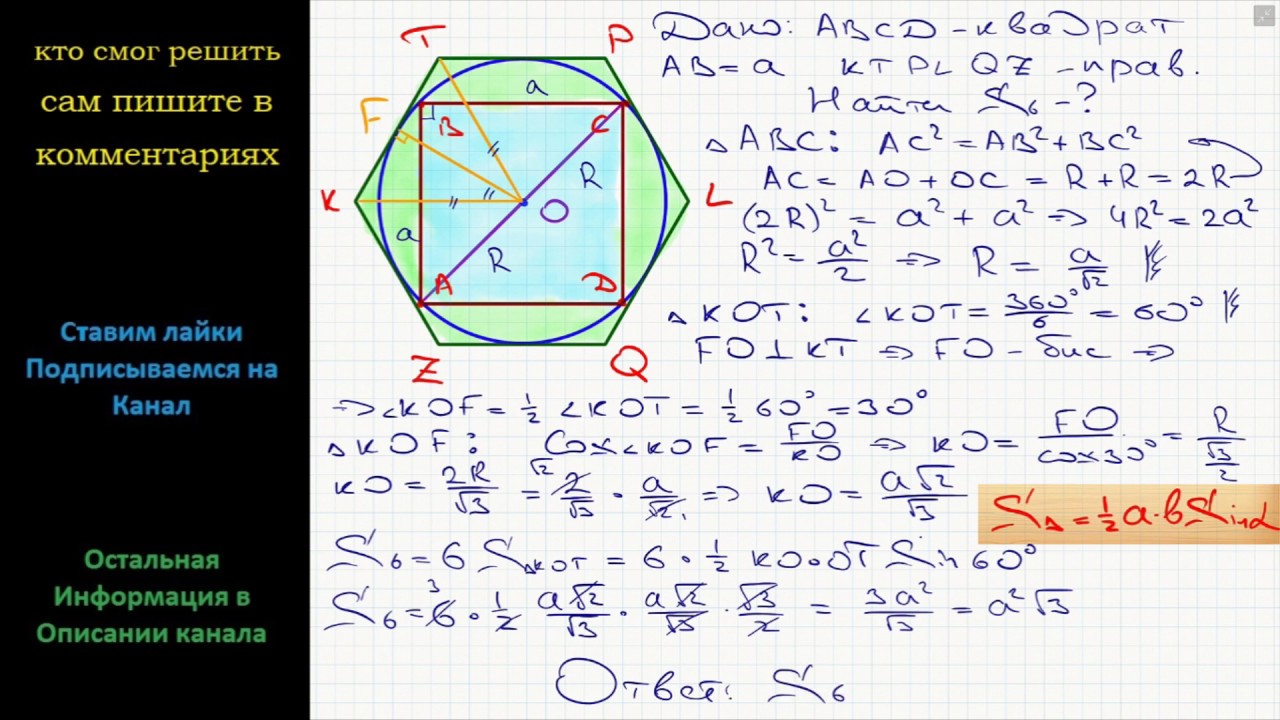
Урок 22. формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности — Геометрия — 9 класс
Обозначим S площадь правильного n-угольника, an его сторону, Р периметр, r и R – радиусы соответственно вписанной и описанной окружностей.
Рассмотрим сначала доказательство, что площадь данного многоугольника будет равна: S = 1/2 P r
Выполним следующее построение
Проведем линии из центра многоугольника к его вершинам.
Многоугольник разбили на несколько треугольников. Применяя формулу площади треугольника запишем следующее равенство. Площадь каждого треугольника будет равна: S = 1/2 anr, где an – сторона многоугольника; r – радиус вписанной окружности, является высотой каждого рассматриваемого треугольника.Так как все треугольники равны, то умножим количество треугольников на площадь треугольника:
S = n ∙ 1/2 anr, где
После преобразований получим формулу: S = 1/2 (n ∙ an)r
Произведение в скобках отражает периметр рассматриваемого многоугольника. Таким образом, формула расчёта площади многоугольника выглядит следующим образом: S = 1/2 Pr
Выведем формулы для вычисления стороны правильного многоугольника и радиуса вписанной окружности.
Рассмотрим прямоугольный треугольник А1Н1О.
Угол А1 рассматриваемого треугольника будет равен половине угла αn многоугольника (отмечен красным), т.к. сторона треугольника По формуле вычисления угла α правильного многоугольника αn = (n — 2)/n ∙ 180° применяя простые преобразования получим равенство для угла А1 рассматриваемого треугольника: ∠A1 = αn/2 = (n — 2)/2n ∙ 180° = 90° — (180°)/n
Полагая, что сторона правильного многоугольника an будет равна an = 2A1H1 и, учитывая, что треугольник А1Н1О является прямоугольным, воспользуемся соотношениями между сторонами и углами прямоугольного треугольника.
Итак, сторона правильного многоугольника an = 2 R sin (180°)/n
радиус вписанной окружности r = R cos (180°)/n
Формулы расчета сторон для правильного треугольника, квадрата и правильного шестиугольника.
Треугольник: a3 = 2 R sin(180°)/3 = 2 R sin60° = 2 R ∙ √3/2 = R√3
Шестиугольник: a6 = 2 R sin(180°)/6 = 2 R sin30° = 2 R ∙ 1/2 = R
Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 корней из 3 см2.
По теореме Пифагора найдем второй катет:
29*29=21*21+х*х
х*х=841-441
х*х=400
х=20
Площадь равна катет1*катет2
тогда 21*20=420
Ответ 420
1.
Построить треугольник с двумя заданными углами2. Разделить третий угол пополам
Построение треугольника по по двум углам и биссектрисе третьего
3. Построить отрезок = данному — биссектриса третьего угла
4. Отложить от начала отрезка (биссектрисы) по половинке третьего угла в разные полуплоскости
5. На одной из сторон угла, построить угол = одному из данных, с вершиной в ЛЮБОЙ точке.
6. Построим прямую походящую через второй конец биссектрисы и параллельной стороне построенного угла в п.5. (через точку НЕ лежащую на данной прямой можно провести прямую параллельную данной и притом только одну.
7. Параллельная прямая п.6, пересекает стороны ПЕРВОГО угла п.4, в вершинах треугольника.
ПОСТРОЕННЫЙ треугольник — искомый.
Камера 2Мп.
…………………………
Я нарисовала треугольник ABCD AB=BC=13. AC основание, BD- высота. В треугольнике ABD по т. Пифагора- AB в квадрате = BD в квадрате + AD в квадрате. Подставляешь стороны и получаешь, что AD=12, 12+12=14 это AC. Дальше 13 умножить на 14, и это будет площадь.
Задания для самостоятельного решения. 1. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
1. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
2.
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
3. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
4. Радиус окружности, вписанной в правильный треугольник, равен . Найдите сторону этого треугольника.
5. Найдите радиус окружности, вписанной в квадрат со стороной 4.
6. Найдите сторону квадрата, описанного около окружности радиуса 4.
7. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
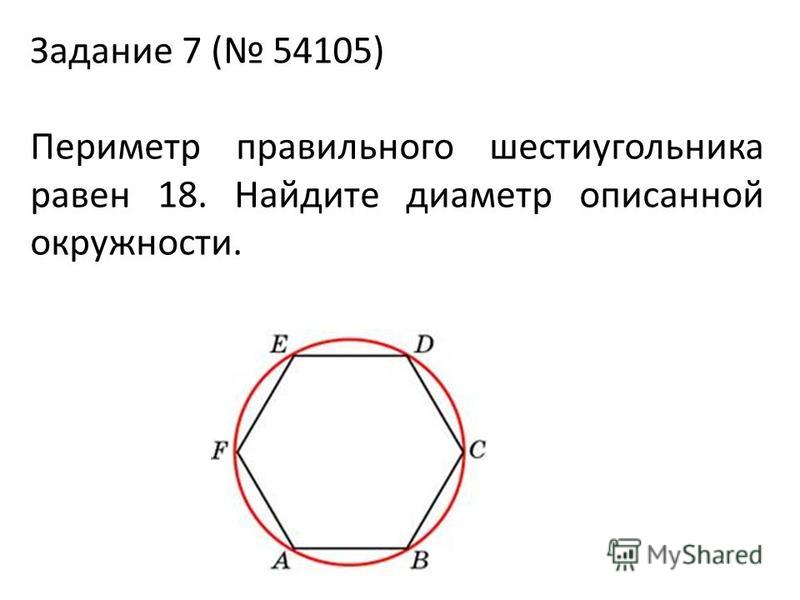
8. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
9. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
10. Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.
11.
Найдите радиус окружности, вписанной в четырехугольник ABCD. В ответе укажите .
12. Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
13. Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
14. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .
15. В окружность вписаны правильный треугольник и правильный шестиугольник. Найти площадь треугольника, если периметр шестиугольника равен 36.
16. В окружность вписаны квадрат и правильный шестиугольник. Найти площадь квадрата, если периметр шестиугольника равен 24.
17. В окружность вписаны правильный треугольник и квадрат. Найти площадь квадрата , если площадь треугольника равна 9
18. В круг вписан правильный треугольник. Найти площадь треугольника и площадь круга, если длина окружности данного круга равна 20 .
19. В квадрат, площадь которого равна 16 вписан круг. Найти его площадь и длину окружности
20. В круг, площадь которого равна 100 , вписан правильный шестиугольник. Найти его площадь..
21. В правильный треугольник, периметр которого равен 6, вписан круг. Найти его площадь и длину окружности
22. В круг, у которого длина окружности равна 10 , вписан правильный шестиугольник. Найти его площадь.
23. Найти площадь круга, описанного около правильного треугольника со стороной 8.
24. Найти радиус круга, описанного около правильного треугольника, высота которого равна 18.
25. Медиана правильного треугольника равна 24.Найти площадь круга, вписанного в этот треугольник.
26. Меньшая диагональ правильного шестиугольника равна .Найти длину окружности, описанной около этого шестиугольника.
27. Сторона правильного шестиугольника равна .Найти сторону правильного треугольника, равновеликого данному шестиугольнику.
28. Радиус окружности, описанной около правильного шестиугольника равна12.
Найти длину меньшей диагонали шестиугольника
29. Точка О является центром правильного девятиугольника ABCDEFGHK. Площадь треугольника OAD равна . Найти длину перпендикуляра ОМ, опущенного на диагональ AD.
30. В круге радиусом 12 проведены по одну сторону от центра две параллельные хорды, из которых одна стягивает дугу в 120º, а другая в 60º. Найти площадь части круга, заключенную между хордами.
31. Из точки, лежащей на окружности проведены две хорды, длина каждой из которых равна радиусу. Найти угол между этими хордами.
32. Площадь квадрата, описанного около окружности , равна 16.Найти площадь правильного треугольника, вписанного в ту же окружность.
33. Сумма площадей правильного четырехугольника, описанного около окружности и правильного треугольника , вписанного в эту окружность, равна Найти длину окружности
34. Сторона правильного восьмиугольника ABCDEFGH равна . Найти радиус окружности, вписанной в четырёхугольник MNPK, если точки M, N, P, K — середины сторон AB, CD, EF и GH соответственно
9 класс
Вариант 1.
1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в эту окружность.
2. Найдите площадь круга, если площадь вписанного в окружность квадрата равна 72 дм.
3. Радиус окружности равен 8 см, а градусная мера дуги равна 150 . Найдите длину этой дуги.
4. Определите площадь кругового сектора, если он образован центральным углом в 120 градусов и стягивает дугу длиною в 0,6 π дм.
Вариант 2.
1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в эту же окружность.
2. Найдите длину окружности, если площадь вписанного в окружность правильного шестиугольника равна 72 м.
3. Радиус круга равен 12 дм, а градусная мера дуги равна 120. Найдите площадь ограниченного этой дугой сектора.
4. Определите
площадь кругового сектора, если радиус
круга равен 2 метра, а длина дуги кругового
сектора составляет 0,2 π см.
Вариант 1.
1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в эту окружность.
2. Найдите площадь круга, если площадь вписанного в окружность квадрата равна72 дм.
3. Радиус окружности равен 8 см, а градусная мера дуги равна 150 . Найдите длину этой дуги.
4. Определите площадь кругового сектора, если он образован центральным углом в 120 градусов и стягивает дугу длиною в 0,6 π дм.
Вариант 2.
1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в эту же окружность.
2. Найдите длину окружности, если площадь вписанного в окружность правильного шестиугольника равна 72 м.
3. Радиус круга равен 12 дм, а градусная мера дуги равна 120. Найдите площадь ограниченного этой дугой сектора.
4. Определите
площадь кругового сектора, если радиус
круга равен 2 метра, а длина дуги кругового
сектора составляет 0,2 π см.
Как найти площадь шестиугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы
искажать информацию о том, что продукт или действие нарушает ваши авторские права.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
вопросов о кругах, вписанных в многоугольники
На прошлой неделе мы рассмотрели вопросы о многоугольниках, вписанных в круг. На этой неделе давайте рассмотрим вопросы о кругах, вписанных в правильные многоугольники.
Как отмечалось ранее, важно помнить, что правильные многоугольники — это симметричные фигуры. Вам нужно очень мало информации, чтобы найти что-либо в симметричной фигуре.
Вопрос 1 : Круг вписан в правильный шестиугольник. В этот круг вписан правильный шестиугольник. Другой круг вписывается во внутренний правильный шестиугольник и так далее. Какова площадь десятого такого круга?
Положение I. Длина стороны крайнего правильного шестиугольника составляет 6 см.
Положение II: Длина диагонали внешнего правильного шестиугольника составляет 12 см.
Решение : К счастью, в вопросах DS нам не нужно вычислять ответ. Нам просто нужно установить достаточность предоставленных данных. Обратите внимание, что мы обнаружили, что существует определенная связь между сторонами правильного шестиугольника и радиусом вписанной окружности, а также существует определенная связь между радиусом окружности и стороной вписанного правильного шестиугольника.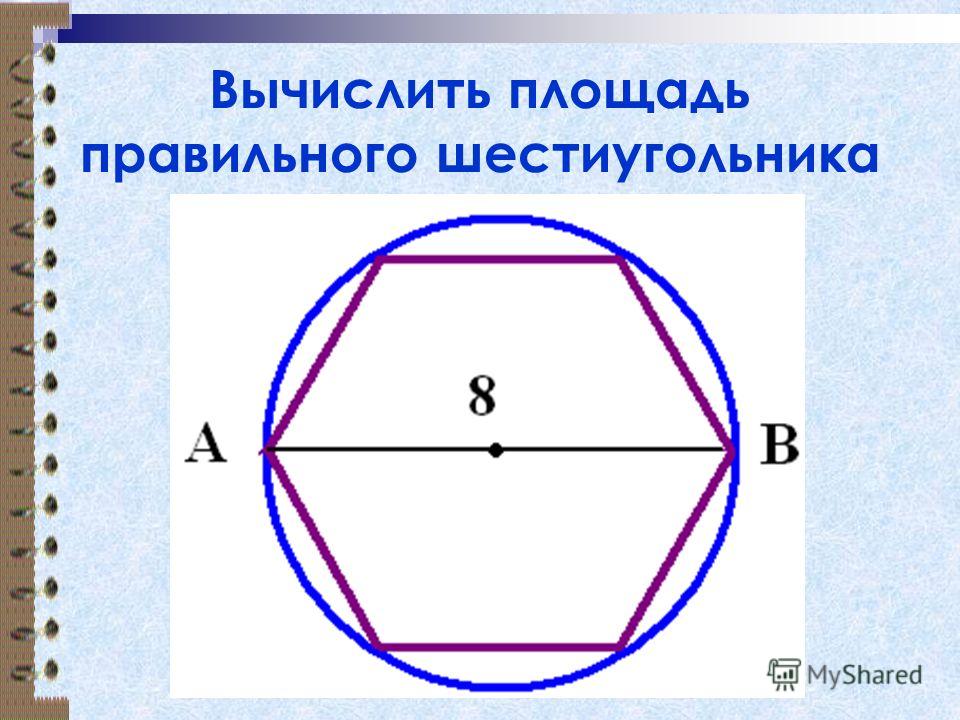
Когда круг вписан в правильный шестиугольник,
Радиус вписанной окружности = (? 3/2) * Сторона шестиугольника
Когда правильный шестиугольник вписан в круг,
Сторона вписанного правильного шестиугольника = Радиус окружности
Итак, все, что нам нужно, это сторона любого правильного шестиугольника или радиус любого одного круга, и мы будем знать длину сторон всех шестиугольников и радиусы всех кругов.
Положение I. Длина стороны крайнего правильного шестиугольника составляет 6 см.
Если длина стороны крайнего правильного шестиугольника равна 6 см, радиус вписанной окружности равен (? 3/2) * 6 = 3? 3 см
В этом случае сторона правильного шестиугольника, вписанного в этот круг, также составляет 3 × 3 см. Теперь мы можем получить радиус круга, вписанного во второй шестиугольник, и идти по тем же линиям, пока не дойдем до десятого круга. Одного этого утверждения достаточно.
Положение II: Длина диагонали внешнего правильного шестиугольника составляет 12 см.
Обратите внимание, что шестиугольник имеет диагонали двух разной длины.Диагонали, соединяющие вершины с одной вершиной между ними, меньше диагоналей, соединяющих вершины с двумя вершинами между ними. Длина AC будет меньше длины AD. Учитывая длину диагонали, мы не знаем, какая это диагональ. AC = 12 или AD = 12? Длина стороны будет разной в двух случаях. Так что одного этого утверждения недостаточно.
Ответ (A)
Имейте в виду, что на самом деле вам не нужно решать, чтобы получить ответ DS; на самом деле, в некоторых вопросах вы не сможете найти ответ при заданных временных ограничениях.Все, что вам нужно сделать, это убедиться, что через неограниченное время вы получите уникальный ответ.
Вопрос 2 : Четыре идентичных круга нарисованы в квадрате, так что каждый круг касается двух сторон квадрата и двух других кругов (как показано на рисунке ниже). Если сторона квадрата имеет длину 20 см, какова площадь заштрихованной области?
(А) 400 — 100?
(В) 200 — 50?
(С) 100 — 25?
(Д) 8?
(E) 4?
Решение : сначала давайте вспомним, что квадраты и круги — это симметричные фигуры.
Данная фигура симметрична.
Мы не знаем никакой формулы, которая поможет нам получить площадь изогнутой заштрихованной серой формы в центре. В таких случаях очень часто вам нужно найти площадь одного региона и вычесть из нее площадь другого. Здесь, если мы вычтем площадь четырех кругов из площади квадрата, оставшаяся область включает заштрихованную область, но также включает другие области (вокруг углов и т. Д.). Здесь нам помогает симметрия.
Обратите внимание, что мы можем разделить фигуру на четыре равные области, чтобы получить четыре меньших квадрата.2 = 100 — 25?
Ответ (C)
Каришма, инженер-компьютерщик, проявляющий большой интерес к альтернативным математическим подходам, обучал студентов на континентах Азии, Европы и Северной Америки. Она преподает GMAT для Veritas Prep и регулярно участвует в проектах по разработке контента, таких как этот блог!
Что из нижеперечисленного показывает равносторонний треугольник, вписанный в круг мозгом?
5.
Пусть 4ABC — прямоугольный треугольник с прямым углом в C. Пусть D и E — основания биссектрис угла от A и B до BC и CA соответственно. Предположим, что AD и BE пересекаются в точке F. Найдите \ AFB. 6. [AHSME 1990] Острый равнобедренный треугольник ABC вписан в круг. Через точки B и C проводятся касательные к окружности, пересекающиеся в точке D. Длина стороны равностороннего треугольника составляет 20 см. В него вписывается второй равносторонний треугольник, соединяющий середины сторон первого треугольника.спросил 20 февраля 2018 г. в классе XI по математике nikita74 (-1 017 баллов)
В главе 4 вы узнали, что равносторонний треугольник — это треугольник с тремя равными сторонами. Вы также узнали, что равносторонний треугольник является равноугольным, что означает, что все его углы совпадают. В этой лабораторной работе вы будете строить равносторонние и равноугольные многоугольники, вписывая их в круги. Задание 1 1 Построение круга … Введите сторону, периметр, площадь или высоту равностороннего треугольника, затем выберите недостающее значение, и калькулятор покажет вам пошаговое объяснение, как найти это значение.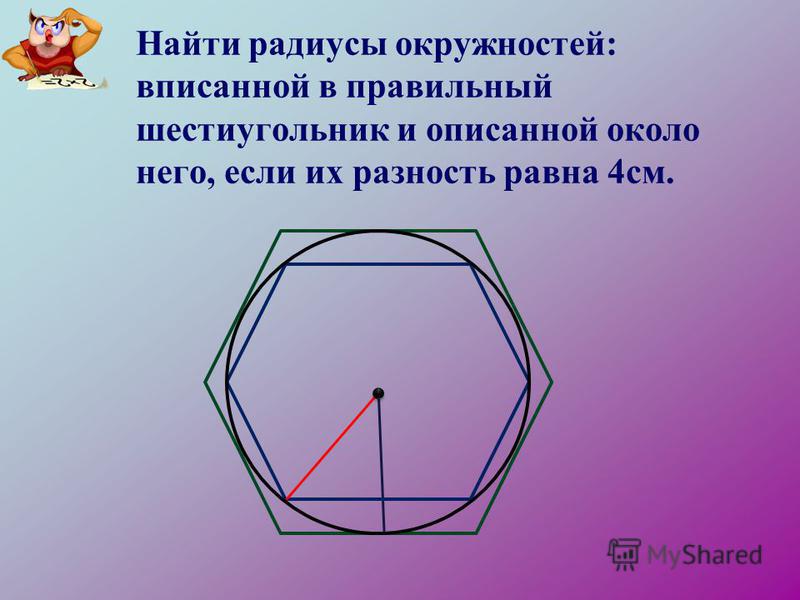
Обратите внимание, что это половина квадрата, разрезанного по диагонали квадрата, а также равнобедренный треугольник (обе ножки имеют одинаковую длину). На следующем рисунке показан пример треугольника 45 ° — 45 ° — 90 °. Попробуй пару задач. Найдите длины неизвестных сторон в треугольниках BAT и BOY, показанных на следующем рисунке. 01.03 MC) Лейла с помощью циркуля и линейки завершает построение многоугольника, вписанного в круг. Какой многоугольник она строит? (1 балл) Нарисовывается круг с двумя отметками дуги над и под диаметром.Равносторонний треугольник Квадрат Правильный пятиугольник Правильный шестиугольник Равносторонний треугольник и правильный шестиугольник имеют равные периметры длины. Какое соотношение их площадей? Наш учитель попросил нас сделать это … Я думаю, я могу найти одно решение, поскольку шестиугольник будет составлен из 6 равносторонних треугольников, и если шестиугольник и треугольник имеют равные периметры, тогда треугольники в шестиугольнике будут иметь 1/2 длины площадь большего треугольника.