Площадь шестиугольника неправильного формула: Как найти площадь правильного и неправильного шестиугольника? — журнал «Рутвет»

Как найти площадь правильного и неправильного шестиугольника? — журнал «Рутвет»

Оглавление:

1. Площадь правильного шестиугольника
2. Площадь неправильного шестиугольника
3. Площадь равностороннего шестиугольника

Умение определять площадь различных фигур играет немалую роль в жизни каждого человека. Рано или поздно приходится иметь дело с этими знаниями. К примеру, в процессе ремонта помещения для определения необходимого количества рулонов обоев, линолеума, паркета, плитки в ванную или на кухню нужно уметь рассчитывать необходимую площадь.

Знаниями в области геометрии пользовались еще в древнем Вавилоне и других странах. На первых шагах к культуре всегда возникала необходимость измерить участок, расстояние. При строительстве первых значительных сооружений требовались умения выдерживать вертикаль, спроектировать план.

Роль эстетических потребностей людей также имела немалое значение. Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение.

Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту.

Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника. Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести.

Площадь правильного шестиугольника

Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.

В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейки пчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняются плоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, как плитка укладывается одна возле другой, не оставляя пустых мест.

Свойства правильного шестиугольника

• Правильный шестиугольник всегда будет иметь равные углы, каждый из которых составляет 120˚.
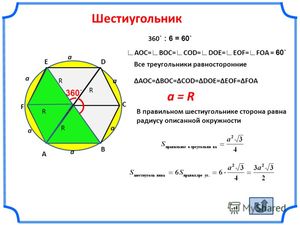
• Сторона фигуры равняется радиусу описанной окружности.
• Все стороны в правильном шестиугольнике равны.
• Правильный шестиугольник плотно заполняет плоскость.

Как посчитать площадь правильного шестиугольника?

Площадь правильного шестиугольника можно рассчитать, разбив его на шесть треугольников, каждый из которых будет иметь равные стороны.

Для расчета площади правильного треугольника используется следующая формула:

Зная площадь одного из треугольников, можно легко рассчитать площадь шестиугольника. Формула для ее расчета проста: поскольку правильный шестиугольник — это шесть равных треугольников, следует площадь нашего треугольника умножить на 6.

Если провести от центра фигуры к любой из ее сторон перпендикуляр, получим отрезок, который называется апофема. Рассмотрим, как найти площадь шестиугольника при известной апофеме:

1. Площадь = 1/2*периметр*апофему.
2. Предположим, наша апофема равняется 5√3 см.

3. Используя апофему, находим периметр: Поскольку апофема расположена перпендикулярно к стороне шестиугольника, то углы треугольника, созданного при помощи апофемы, будут равняться 30˚—60˚—90˚. Каждая сторона полученного треугольника будет соответствовать: x-x√3-2x, где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона, расположенная напротив угла в 60˚ — это x√3, а гипотенуза — 2x.
4. Поскольку апофема представлена, как x√3, можно подставить ее в формулу a = x√3 и решить. Если, к примеру, апофема = 5√3, тогда подставим эту величину в формулу и получим: 5√3 см = x√3, или x = 5 см.
5. Итак, короткая сторона треугольника равняется 5 см. поскольку эта величина является половиной длины стороны шестиугольника, умножаем 5 на 2 и получим 10 см, которая является длиной стороны.
6. Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
7. Подставим полученные результаты в нашу формулу:

  Площадь = 1/2*периметр*апофему

  Площадь = ½*60см*5√3

Решаем:

Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах:

½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см²

Видео о том, как найти площадь правильного шестиугольника

Площадь неправильного шестиугольника

Существует несколько вариантов определения площади неправильного шестиугольника:

• Метод трапеции.
• Метод расчета площади неправильных многоугольников при помощи оси координат.
• Метод разбивания шестиугольника на другие фигуры.

В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.

Метод трапеции

Площадь шестиугольника, имеющего произвольную (неправильную) форму, рассчитывается методом трапеции, суть которого состоит в разделении шестиугольника на отдельные трапеции и последующим вычислением площади каждой из них.

Метод с осями координат

Кроме этого, площадь неправильного шестиугольника можно рассчитать при помощи метода расчета площади неправильных многоугольников. Рассмотрим его на следующем примере:

Вычисление будем выполнять методом использования координат вершин многоугольника:

1. На этом этапе следует сделать таблицу и записать координаты вершин x и y. Выбираем вершины в последовательном порядке по направлению против часовой стрелки, завершив конец списка повторной записью координаты первой вершины:

2. Теперь следует умножить значения координаты х 1-й вершины на y 2-й вершины и продолжить таким образом умножение далее. Затем необходимо сложить полученные результаты. В нашем случае получилось 82:

3. Последовательно умножаем значения координат y1-й вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В нашем случае получилось 38:

4. Вычитаем сумму, которую получили на четвертом этапе из суммы, которая получилась на третьем этапе: 82 – (-38) = 120

5. Теперь необходимо разделить результат, который был получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60 см²

Метод разбивания шестиугольника на другие фигуры

Каждый многоугольник можно разделить на несколько других фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из известных данных, пользуясь формулами определения площадей перечисленных фигур, последовательно вычисляются их площади и затем суммируются.

Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади.

Видео о том, как найти площадь многоугольника

Площадь равностороннего шестиугольника

Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.

Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура.

Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника.

Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.

А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в комментариях.

По какой формуле следует определять площадь правильного шестиугольника

С вопросом: «Как найти площадь шестиугольника?», можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.

Немного фактов из истории

Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.

Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.

Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.

Площадь правильного 6-угольника

Итак, у нас шестиугольная фигура с равными сторонами и углами. В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.

К примеру:

• гайка;
• пчелиные соты;
• снежинка.

Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.

Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности

.

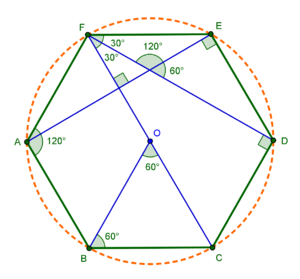
Расчет

Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.

Чтоб рассчитать S , пользуются следующей формулой:

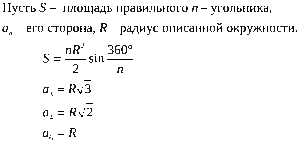
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.

Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.

Посмотрим, как находить S шестиугольника, если апофема известна:

1. S =1/2×периметр×апофема.
2. Возьмем апофему равную 5√3 см.

1. Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
2. Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
3. Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
4. Полученную величину умножим на 6 и получим значение периметра – 60см.

Подставляем полученные результаты в формулу: S=1/2×периметр×апофема

S=½×60 см× 5√3

Считаем:

Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².

Как находить площадь неправильного шестиугольника

Есть несколько вариантов:

• Разбивка 6-угольника на другие фигуры.
• Метод трапеции.
• Расчет S неправильных многоугольников с помощью осей координат.

Выбор способа диктуется исходными данными.

Метод трапеции

Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.

Использование осей координат

Используем координаты вершин многоугольника:

• В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
• Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
• Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
• Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
• Делим результат, полученный на предыдущем этапе, и находим, что искали.

Разбивка шестиугольника на другие фигуры

Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.

Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.

Площадь равностороннего шестиугольника

У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.

Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.

Площадь шестиугольника: онлайн калькулятор, формулы, примеры решений

Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов. Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.

Выпуклый шестиугольник

Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:

S = 2,59 R² = 2,59 a².

Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:

r = 3,46 a.

Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.

Гексаграмма

Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды. Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.

Шестиугольные числа

В теории чисел существуют фигурные числа, связанные с определенными геометрическими фигурами. Наибольшее применение находят треугольные и квадратные, а также тетраэдрические и пирамидальные числа, используя которые легко выкладывать геометрические фигуры при помощи реальных предметов. Например, пирамидальные числа подскажут вам, как сложить пушечные ядра в устойчивую пирамиду. Существуют также и шестиугольные числа, которые определяют число точек, необходимое для построения гексагона.

Шестиугольник в реальности

Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.

Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.

Упаковка кругов на плоскости

И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.

Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.

При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.

Примеры из реальной жизни

Гигантский гексагон

Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника. Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:

S = 494 777 633

Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров. Поистине впечатляет.

Гексагональные шахматы

Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:

S = 10,39

Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.

Заключение

Шестиугольник часто встречается в реальности, хотя мы и не замечаем этого. Используйте наш онлайн-калькулятор для расчета площадей гексагонов при решении повседневных или школьных задач.

Как найти площадь правильного и неправильного шестиугольника? — журнал «Рутвет»

В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму – от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры. В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму – от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры.

Площадь многоугольника

Внимание Это может быть:

• треугольник;
• четырехугольник;
• пяти- или шестиугольник и так далее.

Такая фигура непременно будет характеризоваться двумя положениями:

1. Смежные стороны не принадлежат одной прямой.
2. У несмежных отсутствуют общие точки, то есть они не пересекаются.

Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.

Немного теории о многоугольниках

Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет. Они дают название получившейся фигуре. Это может быть:

• треугольник;
• четырехугольник;
• пяти- или шестиугольник и так далее.

Такая фигура непременно будет характеризоваться двумя положениями:

1. Смежные стороны не принадлежат одной прямой.
2. У несмежных отсутствуют общие точки, то есть они не пересекаются.

Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.

Ситуация с неправильной фигурой

Выходом для того, как узнать площадь многоугольника, если он не является правильным и его нельзя отнести ни к одной из известных ранее фигур, является алгоритм:

• разбить его на простые фигуры, например, треугольники, чтобы они не пересекались;
• вычислить их площади по любой формуле;
• сложить все результаты.

Как поступить, если фигура имеет три или четыре вершины?

В первом случае он окажется треугольником, и можно воспользоваться одной из формул:

• S = 1/2 * а * н, где а — сторона, н — высота к ней;
• S = 1/2 * а * в * sin (А), где а, в — сторон\ы треугольника, А — угол между известными сторонами;
• S = √(p * (p — а) * (p — в) * (p — с)), где с — сторона треугольника, к уже обозначенным двум, р — полупериметр, то есть сумма всех трех сторон, разделенная на два.

Фигура с четырьмя вершинами может оказаться параллелограммом:

• S = а * н;
• S = 1/2 * d1 * d2 * sin(α), где d1 и d2 — диагонали, α — угол между ними;
• S = a * в * sin(α).

Формула для площади трапеции: S = н * (a + в) / 2, где а и в — длины оснований.

Какие их виды существуют?

Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника. В выпуклом всегда все вершины лежат с одной стороны от такой прямой.

В школьном курсе геометрии большая часть времени уделяется именно выпуклым фигурам. Поэтому в задачах требуется узнать площадь выпуклого многоугольника. Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.

Формула площади гаусса

Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.

5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.

Как найти площадь правильного и неправильного шестиугольника?

• Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
• Подставим полученные результаты в нашу формулу:
• Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:

• Метод трапеции.
• Метод расчета площади неправильных многоугольников при помощи оси координат.
• Метод разбивания шестиугольника на другие фигуры.

В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Важно Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.

Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.

Калькулятор площади неправильного многоу

Как найти площадь правильного шестиугольника вписанного в окружность: формула

Правильный шестиугольник – это геометрическая фигура; правильный многоугольник с 6 равными углами и сторонами.

Общая формула вычисления площади

Площадь (S) правильного шестиугольника вычисляется по формуле ниже, где a – длина его стороны:

Формула получена следующим образом:

Правильный шестиугольник состоит из шести равных равносторонних треугольников. Площадь каждого рассчитывается так:

Следовательно, площадь правильного шестиугольника равна:

Площадь правильного шестиугольника, вписанного в окружность

Сторона правильного шестиугольника равняется радиусу окружности, описанной вокруг него (a=r).

Это значит, что формула площади может быть представлена в таком виде (а заменяем на r):

Примеры задач

Задание 1
Сторона правильного шестиугольника равна 8 см. Найдите его площадь.

Решение:
Используем первую формулу, в которой задействована длина стороны:

Задание 2
Вычислите площадь правильного шестиугольника, ели радиус описанной вокруг нее окружности равен 15 см.

Решение:
Воспользуемся второй формулой (через радиус окружности):

Как вычислить площадь шестиугольника. Как находится площадь шестиугольника формула

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.

Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:

• Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.

Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.

Как найти площадь правильного шестиугольника

Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.

Дана длина стороны:

• Формула площади: S = (3√3*a²)/2
• Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
• В противном случае длину стороны можно найти через периметр и апофему.
• Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
• Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.

Дана апофема:

• Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
• Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.

Как найти площадь неправильного многоугольника формула

Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника

• Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.

Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.

Как узнать площадь многоугольника?

Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин. При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.

Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание

• 1 Определение
• 2 Примеры
• 3 Более сложный пример
• 4 Объяснение названия
• 5 См.

Площадь многоугольника

• треугольник;
• четырехугольник;
• пяти- или шестиугольник и так далее.

Такая фигура непременно будет характеризоваться двумя положениями:

1. Смежные стороны не принадлежат одной прямой.
2. У несмежных отсутствуют общие точки, то есть они не пересекаются.

Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.

Как найти площадь правильного и неправильного шестиугольника?

• Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
• Подставим полученные результаты в нашу формулу:
• Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:

• Метод трапеции.
• Метод расчета площади неправильных многоугольников при помощи оси координат.
• Метод разбивания шестиугольника на другие фигуры.

В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.

Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.

404 not found

Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.

Калькулятор площади неправильного многоугольника по сторонам

• — рулетка;
• — электронный дальномер;
• — лист бумаги и карандаш;
• — калькулятор.

Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.

Формула площади гаусса

Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.

5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.

Формула расчета площади неправильного многоугольника

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.

Для примера возьмём треугольник с координатами <(2, 1), (4, 5), (7, 8)>. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле:[3] A tri.

Формула расчета площади неправильного четырехугольника

A> _< ext>=<1 over 2>|x_<1>y_<2>+x_<2>y_<3>+x_<3>y_<1>-x_<2>y_<1>-x_<3>y_<2>-x_<1>y_<3>|> где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | <displaystyle mathbf _< ext>=<1 over 2>|x_<1>y_<2>+x_<2>y_<3>+x_<3>y_<4>+x_<4>y_<5>+x_<5>y_<1>-x_<2>y_<1>-x_<3>y_<2>-x_<4>y_<3>-x_<5>y_<4>-x_<1>y_<5>|> A для четырехугольника — переменные до x4 и y4: A quad.

Цели:

• обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
• многоугольнике, графические и измерительные навыки;
• развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
• воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
• методическая: создание условий для проявления познавательной активности учащихся.

Оснащение урока:

1. Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
2. Листок “К исследованию”.
3. Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).

Метод урока:

• По взаимодействию учителя и учащихся – диалог-общение;
• По способу решения задач – частично-поисковый;
• По способу умственной деятельности — (СУД) развивающее обучение.

Форма урока — фронтальная, в парах, индивидуальная.

Тип урока — урок усвоения новых знаний, умений и навыков.

Структура урока — постепенное углубление в тему, гибкая, диалогическая.

Ход урока

Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.

Рассмотрите фигуры (на доске многоугольники).

Они все вместе. Почему? Какой у них общий признак? (Многоугольники).

Назовите этот многоугольник (5-угольник, 6-угольник…)

Может быть, вы знаете, что такое площадь многоугольника?

Тогда покажите на одной из фигур.

(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)

В русском языке это слово имеет несколько значений.

(Ученик по словарю знакомит со значениями.)

1. Часть плоскости внутри замкнутой геометрической фигуры.
2. Большое незастроенное и ровное место.
3. Помещение для какой-либо цели.

Какое из значений используется в математике?

В математике используется первое значение.

(На доске фигура).

Это многоугольник? Да.

Назовите фигуру по-другому. Прямоугольник.

Покажи длину, ширину.

Как найти площадь многоугольника?

Запишите при помощи букв и знаков формулу.

Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?

Площадь равна 200 см 2

Подумайте, как приложить линейку, чтобы фигура разделилась на:

1. Два треугольника
2. Два четырехугольника
3. Треугольник и четырехугольник
4. Треугольник и пятиугольник

Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.

( Части фигуры лежат на партах. Дети собирают из них прямоугольник ).

Сделайте вывод по наблюдениям.

Целую фигуру можно разделить на части и из частей составить целую.

Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.

(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).

Какие фигуры использовал? У тебя получился сложный многоугольник.

Постановка учебной задачи.

На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?

Для чего человеку нужно находить площадь?

(Ответы детей и обобщение учителем).

Задача определения площади возникла из практики.

(Показывается план школьного участка).

Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.

Решение учебной задачи.

(Раздаются листы для исследования).

Перед вами фигура. Назовите ее.

Найдем площадь многоугольника. Что для этого надо делать?

Разделить на прямоугольники.

(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).

Из двух прямоугольников.

С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.

Найдем площадь первой фигуры.

(Учащиеся предлагают следующие варианты решений и записывают их на доске).

1способ:

• S₁ = 5 ? 2 = 10 см 2
• S₂ = 5 ? 1 = 5 см 2

Зная площадь частей, как найти площадь целой фигуры?

S = 10 + 5 = 15 см 2

2 способ:

• S₁ = 6 ? 2 = 12 см 2
• S₂ = 3 ? 1 = 3 см 2
• S = 12 + 3 = 15 см 2 .

Сравните результаты и сделайте вывод.

Проследим наши действия

Как находили площадь многоугольника?

Составляется и записывается на плакате алгоритм:?

1. Делим фигуру на части

2. Находим площади частей этих многоугольников ( S₁, S₂ ).

3. Находим площадь целого многоугольника ( S₁ + S ₂ ).

( Несколько учащихся проговаривают алгоритм).

Мы нашли два способа, а может, есть еще?

А можно фигуру достроить.

Сколько прямоугольников получилось?

Обозначим части 1 и 2. Проведем измерения.

Найдите площадь каждой части многоугольника.

• S₁₌6? 5=30см 2
• S₂= 5 ? 3 = 15 см 2

Как найти площадь нашего шестиугольника?

S = 30 – 15 = 15 см 2

Достроили фигуру до прямоугольника

Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?

Закройте глазки, опустите головки. Мысленно повторите алгоритм.

Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.

Перед вами многоугольники.

Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.

Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.

Что можно сказать о форме? ( Форма разная)

А какова площадь этих многоугольников? ( Площади этих многоугольников равны)

У кого правильно – поставь “+”.

У кого сомнения, затруднения – “?”

Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.

Составить свои листки исследования, вычислить площадь многоугольника разными способами.

Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.

Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см (^2) , мм (^2) соответственно.

Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.

Свойства площади

1. Площадь любого многоугольника — величина положительная.

2. Равные многоугольники имеют равные площади.

3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

4. Площадь квадрата со стороной (a) равна (a^2) .

Теорема: площадь прямоугольника

Площадь прямоугольника со сторонами (a) и (b) равна (S=ab) .

Доказательство

Достроим прямоугольник (ABCD) до квадрата со стороной (a+b) , как показано на рисунке:

Данный квадрат состоит из прямоугольника (ABCD) , еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b) . Таким образом,

Определение

Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD) , а высота (BH) — на продолжение стороны (CD) :

Теорема: площадь параллелограмма

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.

Доказательство

Проведем перпендикуляры (AB’) и (DC’) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD) .

Тогда (AB’C’D) – прямоугольник, следовательно, (S_=AB’cdot AD) .

Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,

Определение

Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.

Теорема

Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

Доказательство

Пусть (S) – площадь треугольника (ABC) . Примем сторону (AB) за основание треугольника и проведём высоту (CH) . Докажем, что [S = dfrac<1><2>ABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:

Треугольники (ABC) и (DCB) равны по трем сторонам ( (BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC) ), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC) , то есть (S = dfrac<1><2>ABcdot CH) .

Теорема

Если два треугольника ( riangle ABC) и ( riangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.

Следствие

Медиана треугольника делит его на два треугольника, равных по площади.

Теорема

Если два треугольника ( riangle ABC) и ( riangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.

Доказательство

Пусть (angle A=angle A_2) . Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2) ):

Проведем высоты (BH) и (C_2K) .

Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K) , следовательно: [dfrac>>=dfrac]

Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH) , следовательно: [dfrac>>=dfrac]

Теорема Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.

Теорема

Площадь прямоугольного треугольника равна половине произведения катетов.

Теорема: формула Герона

Пусть (p) – полупериметр треугольника, (a) , (b) , (c) – длины его сторон, тогда его площадь равна [S_< riangle>=sqrt]

Замечание

Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.

Теорема

Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.

Доказательство

Рассмотрим четырехугольник (ABCD) . Обозначим (AO=a, CO=b, BO=x, DO=y) :

Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:

(egin S_=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\ frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end)

Следствие: площадь ромба

Площадь ромба равна половине произведения его диагоналей: [S_< ext<ромб>>=dfrac12 d_1cdot d_2]

Определение

Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.

Теорема: площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Доказательство

Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD) . Проведем (CD’parallel AB) , как показано на рисунке:

Тогда (ABCD’) – параллелограмм.

Проведем также (BH’perp AD, CHperp AD) ( (BH’=CH) – высоты трапеции).

Тогда (S_

Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:

[S_=S_=BH’cdot BC+dfrac12CHcdot D’D=dfrac12CHleft(2BC+D’D
ight)=] [=dfrac12 CHleft(BC+AD’+D’D
ight)=dfrac12 CHleft(BC+AD
ight)]

Шестиугольник | Площадь шестиугольника | Обычный шестиугольник

• • БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
  • КОНКУРСНЫЕ ЭКЗАМЕНА
    • BNAT
    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 110003 CBSE
        • Книги NCERT
          • Книги NCERT для класса 5
          • Книги NCERT, класс 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • NCERT Книги для класса 11
          • NCERT Книги для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11
          9plar
          • RS Aggarwal
            • RS Aggarwal Решения класса 12
            • RS Aggarwal Class 11 Solutions
            • RS Aggarwal Решения класса 10
            • Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • RD Sharma
            • RD Sharma Class 6 Решения
            • RD Sharma Class 7 Решения
            • Решения RD Sharma класса 8
            • Решения RD Sharma класса 9
            • Решения RD Sharma класса 10
            • Решения RD Sharma класса 11
            • Решения RD Sharma Class 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика
            • Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Статистика
            • 9000 Pro Числа
            • Числа
            • 9000 Pro Числа Тр Игонометрические функции
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убытки
            • Полиномиальные уравнения
            • Деление фракций
          • Microology
          0003000
        • FORMULAS
          • Математические формулы
          • Алгебраные формулы
          • Тригонометрические формулы
          • Геометрические формулы
        • КАЛЬКУЛЯТОРЫ
          • Математические калькуляторы
          0003000
          • 000 CALCULATORS
          • 000
          • 000 Калькуляторы по химии 900 Образцы документов для класса 6
          • Образцы документов CBSE для класса 7
          • Образцы документов CBSE для класса 8
          • Образцы документов CBSE для класса 9
          • Образцы документов CBSE для класса 10
          • Образцы документов CBSE для класса 1 1
          • Образцы документов CBSE для класса 12
        • Вопросники предыдущего года CBSE
          • Вопросники предыдущего года CBSE, класс 10
          • Вопросники предыдущего года CBSE, класс 12
        • HC Verma Solutions
          • HC Verma Solutions Класс 11 Физика
          • HC Verma Solutions Класс 12 Физика
        • Решения Лакмира Сингха
          • Решения Лахмира Сингха класса 9
          • Решения Лахмира Сингха класса 10
          • Решения Лакмира Сингха класса 8
        9000 Класс
        9000BSE 9000 Примечания3 2 6 Примечания CBSE
      • Примечания CBSE класса 7
      Примечания
      • Примечания CBSE класса 8
      • Примечания CBSE класса 9
      • Примечания CBSE класса 10
      • Примечания CBSE класса 11
      • Класс 12 Примечания CBSE
    • Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
    • CBSE Примечания к редакции класса 10
    • CBSE Примечания к редакции класса 11
    • Примечания к редакции класса 12 CBSE
  • Дополнительные вопросы CBSE
    • Дополнительные вопросы по математике класса 8 CBSE
    • Дополнительные вопросы по науке 8 класса CBSE
    • Дополнительные вопросы по математике класса 9 CBSE
    • Дополнительные вопросы по науке
    • CBSE Class 9 Вопросы
    • CBSE Class 10 Дополнительные вопросы по математике
    • CBSE Class 10 Science Extra questions
  • CBSE Class
    • Class 3
    • Class 4
    • Class 5
    • Class 6
    • Class 7
    • Class 8 Класс 9
    • Класс 10
    • Класс 11
    • Класс 12
  • Учебные решения
• Решения NCERT
  • Решения NCERT для класса 11
    • Решения NCERT для класса 11 по физике
    • Решения NCERT для класса 11 Химия
    • Решения NCERT для биологии класса 11
    • Решение NCERT s Для класса 11 по математике
    • NCERT Solutions Class 11 Accountancy
    • NCERT Solutions Class 11 Business Studies
    • NCERT Solutions Class 11 Economics
    • NCERT Solutions Class 11 Statistics
    • NCERT Solutions Class 11 Commerce
  • NCERT Solutions for Class 12
    • Решения NCERT для физики класса 12
    • Решения NCERT для химии класса 12
    • Решения NCERT для биологии класса 12
    • Решения NCERT для математики класса 12
    • Решения NCERT, класс 12, бухгалтерия
    • Решения NCERT, класс 12, бизнес-исследования
    • NCERT Solutions Class 12 Economics
    • NCERT Solutions Class 12 Accountancy Part 1
    • NCERT Solutions Class 12 Accountancy Part 2
    • NCERT Solutions Class 12 Micro-Economics
    • NCERT Solutions Class 12 Commerce
    • NCERT Solutions Class 12 Macro-Economics
  • NCERT Solut Ионы Для класса 4
    • Решения NCERT для математики класса 4
    • Решения NCERT для класса 4 EVS
  • Решения NCERT для класса 5
    • Решения NCERT для математики класса 5
    • Решения NCERT для класса 5 EVS
  • Решения NCERT для класса 6
    • Решения NCERT для математики класса 6
    • Решения NCERT для науки класса 6
    • Решения NCERT для класса 6 по социальным наукам
    • Решения NCERT для класса 6 Английский язык
  • Решения NCERT для класса 7
    • Решения NCERT для математики класса 7
    • Решения NCERT для науки класса 7
    • Решения NCERT для социальных наук класса 7
    • Решения NCERT для класса 7 Английский язык
  • Решения NCERT для класса 8
    • Решения NCERT для математики класса 8
    • Решения NCERT для науки 8 класса
    • Решения NCERT для социальных наук 8 класса ce
    • Решения NCERT для класса 8 Английский
  • Решения NCERT для класса 9
    • Решения NCERT для класса 9 по социальным наукам
  • Решения NCERT для математики класса 9
    • Решения NCERT для математики класса 9 Глава 1
    • Решения NCERT для математики класса 9, глава 2
    Решения NCERT
    • для математики класса 9, глава 3
    • Решения NCERT для математики класса 9, глава 4
    • Решения NCERT для математики класса 9, глава 5
    Решения NCERT
    • для математики класса 9, глава 6
    • Решения NCERT для математики класса 9, глава 7
    Решения NCERT
    • для математики класса 9, глава 8
    • Решения NCERT для математики класса 9, глава 9
    • Решения NCERT для математики класса 9, глава 10
    Решения NCERT
    • для математики класса 9, глава 11
    Решения
    • NCERT для математики класса 9 Глава 12
    Решения NCERT
    • для математики класса 9 Глава 13
    • NCER Решения T для математики класса 9 Глава 14
    • Решения NCERT для математики класса 9 Глава 15
  • Решения NCERT для науки класса 9
    • Решения NCERT для науки класса 9 Глава 1
    • Решения NCERT для науки класса 9 Глава 2
    • Решения NCERT для науки класса 9 Глава 3
    • Решения NCERT для науки класса 9 Глава 4
    • Решения NCERT для науки класса 9 Глава 5
    • Решения NCERT для науки класса 9 Глава 6
    • Решения NCERT для науки класса 9 Глава 7
    • Решения NCERT для науки класса 9 Глава 8
    • Решения NCERT для науки класса 9 Глава 9
    • Решения NCERT для науки класса 9 Глава 10
    • Решения NCERT для науки класса 9 Глава 12
    • Решения NCERT для науки класса 9 Глава 11
    • Решения NCERT для науки класса 9 Глава 13
    Решения NCERT
    • для науки класса 9 Глава 14
    • Решения NCERT для класса 9 по науке Глава 15
  • Решения NCERT для класса 10
    • Решения NCERT для класса 10 по социальным наукам
  • Решения NCERT для математики класса 10
    • Решения NCERT для математики класса 10 Глава 1
    • Решения NCERT для математики класса 10, глава 2
    • Решения NCERT для математики класса 10, глава 3
    • Решения NCERT для математики класса 10, глава 4
    • Решения NCERT для математики класса 10, глава 5
    • Решения NCERT для математики класса 10, глава 6
    • Решения NCERT для математики класса 10 Глава 7
    • Решения NCERT для математики класса 10 Глава 8
    • Решения NCERT для математики класса 10 Глава 9
    • Решения NCERT для математики класса 10 Глава 10
    • Решения NCERT для математики класса 10 Глава 11
    • Решения NCERT для математики класса 10 Глава 12
    • Решения NCERT для математики класса 10 Глава ter 13
    • Решения NCERT для математики класса 10 Глава 14
    • Решения NCERT для математики класса 10 Глава 15
  • Решения NCERT для науки класса 10
    • Решения NCERT для класса 10 науки Глава 1
    • Решения NCERT для класса 10 Наука, глава 2
    • Решения NCERT для класса 10, глава 3
    • Решения NCERT для класса 10, глава 4
    • Решения NCERT для класса 10, глава 5
    • Решения NCERT для класса 10, глава 6
    • Решения NCERT для класса 10 Наука, глава 7
    • Решения NCERT для класса 10, глава 8,
    • Решения NCERT для класса 10, глава 9
    • Решения NCERT для класса 10, глава 10
    • Решения NCERT для класса 10, глава 11
    • Решения NCERT для класса 10 Наука Глава 12
    • Решения NCERT для класса 10 Наука Глава 13
    • NCERT S Решения для класса 10 по науке Глава 14
    • Решения NCERT для класса 10 по науке Глава 15
    • Решения NCERT для класса 10 по науке Глава 16
  • Программа NCERT
  • NCERT
• Commerce
  • Class 11 Commerce Syllabus
    • Учебный план класса 11
    • Учебный план бизнес-класса 11 класса
    • Учебный план экономического факультета 11
  • Учебный план по коммерции 12 класса
    • Учебный план класса 12
    • Учебный план бизнес-класса 12
    Учебный план
    • Класс 12 Образцы документов для коммерции
      • Образцы документов для коммерции класса 11
      • Образцы документов для коммерции класса 12
    • TS Grewal Solutions
      • TS Grewal Solutions Class 12 Accountancy
      • TS Grewal Solutions Class 11 Accountancy
    • Отчет о движении денежных средств 9 0004
    • Что такое предпринимательство
    • Защита потребителей
    • Что такое основные средства
    • Что такое баланс
    • Что такое фискальный дефицит
    • Что такое акции
    • Разница между продажами и маркетингом
  03
  • Образцы документов ICSE
  • Вопросы ICSE
  • ML Aggarwal Solutions
    • ML Aggarwal Solutions Class 10 Maths
    • ML Aggarwal Solutions Class 9 Maths
    • ML Aggarwal Solutions Class 8 Maths
    • ML Aggarwal Solutions Class 7 Maths Решения Математика класса 6
  • Решения Селины
    • Решения Селины для класса 8
    • Решения Селины для класса 10
    • Решение Селины для класса 9
  • Решения Фрэнка
    • Решения Фрэнка для математики класса 10
    • Франк Решения для математики 9 класса
    9000 4
  • ICSE Class
    • ICSE Class 6
    • ICSE Class 7
    • ICSE Class 8
    • ICSE Class 9
    • ICSE Class 10
    • ISC Class 11
    • ISC Class 12
• IC
• 900 Экзамен по IAS
  • Экзамен по государственной службе
  • Программа UPSC
  • Бесплатная подготовка к IAS
  • Текущие события
  • Список статей IAS
  • Мок-тест IAS 2019
    • Мок-тест IAS 2019 1
    • Мок-тест IAS4
    2
  • Комиссия по государственным услугам
    • Экзамен KPSC KAS
    • Экзамен UPPSC PCS
    • Экзамен MPSC
    • Экзамен RPSC RAS ​​
    • TNPSC Group 1
    • APPSC Group 1
    • Экзамен BPSC
    • Экзамен WPSC
    • Экзамен JPSC
    • Экзамен GPSC
  • Вопросник UPSC 2019
    • Ответный ключ UPSC 2019
  • 900 10 Коучинг IAS
    • Коучинг IAS Бангалор
    • Коучинг IAS Дели
    • Коучинг IAS Ченнаи
    • Коучинг IAS Хайдарабад
    • Коучинг IAS Мумбаи
• JEE4
9000 JEE 9000 JEE 9000 Advanced
• Образец статьи JEE
• Вопросник JEE
• Биномиальная теорема
• Статьи JEE
• Квадратное уравнение

NEET

• Программа BYJU NEET
• NEET 2020
• NEET Eligibility
• NEET Eligibility
• NEET Eligibility 2020 Подготовка
• NEET Syllabus
• Support
  • Разрешение жалоб
  • Служба поддержки
  • Центр поддержки

Государственные советы

• GSEB
  • GSEB Syllabus
  GSEB Образец статьи 003 GSEB Books
• MSBSHSE
  • MSBSHSE Syllabus
  • MSBSHSE Учебники
  • MSBSHSE Образцы статей
  • MSBSHSE Вопросники
• AP Board
• AP Board
• AP Board
  9000
  • AP 2 Year Syllabus
• MP Board
  • MP Board Syllabus
  • MP Board Образцы документов
  • MP Board Учебники
• Assam Board
  • Assam Board Syllabus
  • Assam Board
  • Assam Board
  • Assam Board Документы
• BSEB
  • Bihar Board Syllabus
  • Bihar Board Учебники
  • Bihar Board Question Papers
  • Bihar Board Model Papers
• BSE Odisha
  • Odisha Board
  • Odisha Board
    • Odisha Board 9000
    • ПСЕБ 9 0002
    • PSEB Syllabus
    • PSEB Учебники
    • PSEB Вопросы и ответы
  • RBSE
    • Rajasthan Board Syllabus
    • RBSE Учебники
    • RBSE
    • RBSE
    000 HPOSE
    • 000 HPOSE
    • 000
    000 HPOSE
    • 000
    000 HPOSE
    • 000
    0000003 Контрольные документы
  • JKBOSE
    • JKBOSE Syllabus
    • JKBOSE Образцы документов
    • JKBOSE Образец экзамена
  • TN Board
    • TN Board Syllabus
    9000 Papers 9000 TN Board Syllabus 9000 Книги
  • JAC
    • Программа JAC
    • Учебники JAC
    • Вопросы JAC
  • Telangana Board
    • Telangana Board Syllabus

    0325

    25 25

    .

    Площадь неправильного шестиугольника

    Привет, Ашиш.

    Это В предыдущем вопросе объясняется, почему просто указать длины сторон неправильного многоугольника недостаточно для определения площади. Вам нужно будет указать дополнительные измерения, например длину не менее трех диагоналей или нескольких углов.

    Стивен Ла Рок.>

    Ашиш ответил

    Уважаемый господин / госпожа,

    Я хочу узнать площадь неправильного ШЕСТИУГОЛЬНИКА в квадратных футах,
    чьи стороны следующие,
    Сторона 1 = 60.6 футов
    Сторона 2 = 44 фута
    Сторона 3 = 41 фут
    Сторона 4 = 14 футов
    Сторона 5 = 21 фут
    Сторона 6 = 27,6 футов
    Диагональ между (Сторона 1, Сторона 2) и (Сторона 3, Сторона 4) составляет 64,6 футов
    Диагональ между (Сторона 1, Сторона 2) и (Сторона 4, Сторона 5) составляет 72 фута
    Диагональ между (Сторона 1, Сторона 2) и (Сторона 5, Сторона 6) составляет 68 футов

    Буду вам благодарен, если вы мне поможете.

    С уважением,

    Ашиш

    Спасибо Ашиш,

    Я нарисовал диаграмму (не в масштабе) неправильного шестиугольника и сложил ваши длины в футах.

    Суть диаграммы состоит в том, чтобы увидеть, что диагонали делят шестиугольник на четыре треугольника, которые я обозначил A, B, C и D. Тогда площадь шестиугольника является суммой площадей четырех треугольников.

    Площадь каждого из треугольников можно найти по формуле Герона. Для треугольника со сторонами длиной a, b и c положим s = (a + b + c) / 2. Тогда формула Герона равна

    .

    Площадь треугольника

    = sqrt (s (s — a) (s — b) (s — c)), где sqrt — квадратный корень.

    Для треугольника A на диаграмме я получил

    с = (44 + 41 + 64.6) / 2 = 74,8 футов
    площадь треугольника A
    = sqrt (74,8 (74,8 — 44) (74,8 — 41) (74,8 — 64,6))
    = sqrt (794271,88) = 891,22 квадратных футов

    Используя ту же технику, я нашел

    треугольник	площадь
    А	891.22 кв. Футов
    B	403.72 кв. Футов
    С	713.38 кв. Футов
    D	834.93 кв. Футов
    всего	2843.25 кв. Футов

    Таким образом, площадь шестиугольника составляет 2843,3 квадратных футов

    Пенни

    .

    Площадь неправильного многоугольника

    Площадь неправильного многоугольника — Math Open Reference

    В отличие от обычного многоугольника, если вы не знаете координаты вершин, не существует простой формулы для площади неправильного многоугольника. Каждая сторона могла быть разной длины, и каждый внутренний угол мог быть другим. Он также может быть выпуклым или вогнутым.

    Если вы знаете координаты вершин многоугольника, есть два метода:

    1. Ручной метод.См. Площадь многоугольника (Координатная геометрия).
    2. Компьютер алгоритм. См. Алгоритм, чтобы найти площадь любого многоугольника

    Итак, как это сделать?

    Один из подходов — разбить фигуру на части, которые может решить — обычно треугольники, так как есть много способов вычислить площадь треугольников. Как именно вы это сделаете, зависит от того, что вам дано для начала. Поскольку это очень вариативно, нет простого правила, как это сделать. В приведенных ниже примерах представлены некоторые основные подходы, которые можно попробовать.

    1. Разбейте на треугольники и сложите

    . На рисунке выше многоугольник можно разбить на треугольники, нарисовав все диагонали. от одной из вершин. Если вы знаете достаточно сторон и углов, чтобы найти площадь каждого из них, вы можете просто сложить их, чтобы найти общую. Не бойтесь рисовать где-нибудь лишние линии, если они помогут найти фигуры, которые вы сможете решить.

    Здесь неправильный шестиугольник разделен на 4 треугольника добавлением красных линий. (См. Площадь треугольника)

    2.Найдите «недостающие» треугольники, затем вычтите

    На рисунке выше общая форма представляет собой правильный шестиугольник, но отсутствует треугольная деталь.

    Мы знаем, как найти площадь правильного многоугольника, поэтому мы просто вычитаем площадь «недостающего» треугольника, созданного путем рисования красной линии. (См. Площадь правильного многоугольника и Площадь треугольника.)

    3. Рассмотрим другие формы

    На рисунке выше фигура представляет собой неправильный шестиугольник, но его симметрия позволяет разбить его на два параллелограмма. нарисовав красную пунктирную линию.(при условии, конечно, что параллельные линии действительно таковы!)

    Мы знаем, как найти площадь параллелограмма, поэтому мы просто находим площадь каждого из них и складываем их вместе. (См. Площадь параллелограмма).

    Как видите, существует бесконечное количество способов разбить фигуру на части, которыми легче управлять. Затем вы складываете или вычитаете площади частей. То, как вы это делаете, зависит от личных предпочтений и того, что вам дают для начала.

    4.Если известны координаты вершин

    Если вам известны координаты x, y вершин (углов) фигуры, существует метод прямого поиска области. См. Площадь многоугольника (Координатная геометрия). Это работает для всех типов многоугольников (правильных, неправильных, выпуклых, вогнутых). Также есть компьютер алгоритм это делает то же самое. См. Алгоритм, чтобы найти площадь любого многоугольника

    Другие темы полигонов

    Общие

    Типы многоугольника

    Площадь различных типов полигонов

    Периметр различных типов полигонов

    Углы, связанные с многоугольниками

    Именованные полигоны

    (C) Открытый справочник по математике, 2011 г.
    Все права защищены.

    .

    Как рассчитать площадь правильного шестиугольника

    2. Образование
    3. Математика
    4. Геометрия
    5. Как рассчитать площадь правильного шестиугольника

    Марк Райан

    Один из способов найти площадь правильного шестиугольника Шестиугольник получается, предварительно разделив его на равносторонние треугольники. Вам также необходимо использовать апофему — сегмент, который соединяет центр правильного многоугольника со средней точкой любой стороны и который перпендикулярен этой стороне.

    Вы поймете, что все это означает, когда решите следующую задачу:

    Сначала нарисуйте шестиугольник с тремя диагоналями, образуя шесть равносторонних треугольников. Затем нарисуйте апофему, идущую от центра к середине стороны. На следующем рисунке показан шестиугольник EXAGON с его диагоналями и апофемой.

    
    

    Теперь вы можете закончить, используя формулу правильного многоугольника или формулу равностороннего треугольника (умноженную на 6).Они одинаково просты. Сделайте ваш выбор. Вот как это выглядит с формулой правильного многоугольника:

    А вот как это сделать с помощью удобной формулы равностороннего треугольника:

    Для задач с шестигранником часто пригодятся треугольники 30 ° — 60 ° — 90 ° и равносторонние треугольники. Правильный шестиугольник можно разрезать на шесть равносторонних треугольников, а равносторонний треугольник можно разделить на два треугольника 30 ° — 60 ° — 90 °. Итак, если вы решаете задачу с шестиугольником, вы можете разрезать фигуру и использовать равносторонние треугольники или треугольники 30 ° — 60 ° — 90 °, чтобы помочь вам найти апофему, периметр или площадь.

    .

    No related posts.