Площадь сечения трубы формула: площади поверхности, толщины стенки, массы

alexxlab

Содержание

площади поверхности, толщины стенки, массы

При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов. Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих. В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления. 

Содержание статьи

Для чего нужны расчеты параметров труб

В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ,  полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка. Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна. Вес металлических труб еще важнее — доставку считают по тоннажу.

Так что этот параметр желательно контролировать.

То, что нельзя измерить, можно рассчитать

Знать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред. Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.

При сооружении системы водоснабжения частного дома или дачи, трубы прокладывают от источника воды (колодца или скважины) до дома — под землей. И все равно, чтобы они не замерзли, требуется утепление. Рассчитать количество утеплителя можно зная площадь наружной поверхности трубопровода. Только в этом случае надо брать материал с солидным запасом — стыки должны перекрываться с солидным запасом.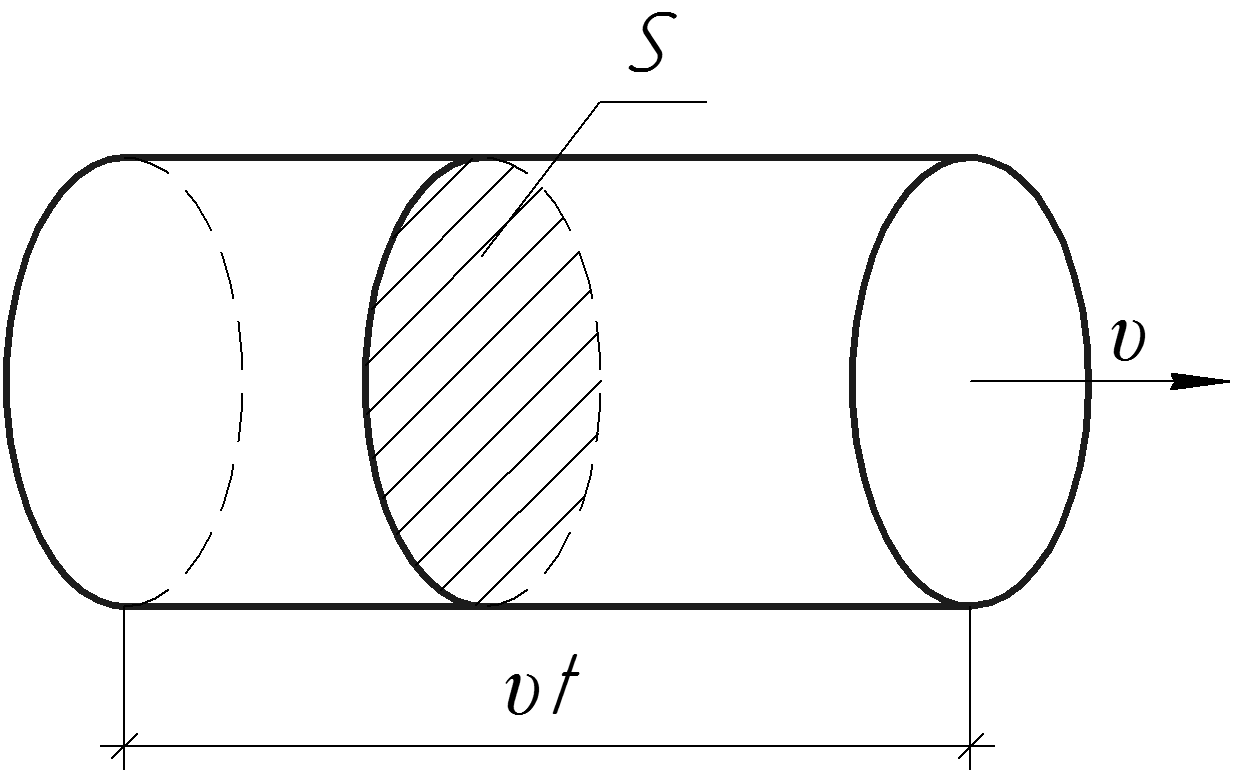

Сечение трубы необходимо для определения пропускной способности — сможет ли данное изделие провести требуемое количество жидкости или газа. Этот же параметр часто нужен при выборе диаметра труб для отопления и водопровода, расчета производительности насоса и т.д.

Внутренний и наружный диаметр, толщина стенки, радиус

Трубы — специфический продукт. Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.

Внутренний и наружный диаметр трубы, толщина стенки

Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.

Если же наоборот, имеется внутренний диаметр и толщина стенки, а нужен наружный — к имеющемуся значению добавляем удвоенную толщину стеки.

С радиусами (обозначаются буквой R) еще проще — это половина от диаметра: R = 1/2 D. Например, найдем радиус трубы диаметром 32 мм. Просто 32 делим на два, получаем 16 мм.

Измерения штангенциркулем более точные

Что делать, если технических данных трубы нет? Измерять. Если особая точность не нужна, подойдет и обычная линейка, для более точных измерений лучше использовать штангенциркуль.

Расчет площади поверхности трубы

Труба представляет собой очень длинный цилиндр, и площадь поверхность трубы рассчитывается как площадь цилиндра. Для вычислений потребуется радиус (внутренний или наружный — зависит от того, какую поверхность вам надо рассчитать) и длина отрезка, который вам необходим.

Формула расчета боковой поверхности трубы

Чтобы найти боковую площадь цилиндра, перемножаем радиус и длину, полученное значение умножаем на два, а потом — на число «Пи», получаем искомую величину. При желании можно рассчитать поверхность одного метра, ее потом можно умножать на нужную длину.

Для примера рассчитаем наружную поверхность куска трубы длиной 5 метров, с диаметром 12 см. Для начала высчитаем диаметр: делим диаметр на 2, получаем 6 см. Теперь все величины надо привести к одним единицам измерения. Так как площадь считается в квадратных метрах, то сантиметры переводим в метры. 6 см = 0,06 м. Дальше подставляем все в формулу: S = 2 * 3,14 * 0,06 * 5 = 1,884 м2. Если округлить, получится 1,9 м2.

Расчет веса

С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах. Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки. Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.

Таблица веса круглых стальных труб

В таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.

Таблица веса профилированной трубы квадратного сечения

Как высчитать площадь поперечного сечения

Формула нахождения площади сечения круглой трубы

Если труба круглая, площадь сечения считать надо по формуле площади круга: S = π*R2. Где R — радиус (внутренний), π — 3,14. Итого, надо возвести радиус в квадрат и умножить его на 3,14.

Например, площадь сечения трубы диаметром 90 мм. Находим радиус — 90 мм / 2 = 45 мм. В сантиметрах это 4,5 см. Возводим в квадрат: 4,5 * 4,5 = 2,025 см2, подставляем в формулу S = 2 * 20,25 см2

= 40,5 см2.

Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где  a и b — длины сторон прямоугольника. Если считать сечение профиля 40 х 50 мм, получим S = 40 мм * 50 мм = 2000 мм2 или 20 см2 или 0,002 м2.

Как рассчитать объем воды в трубопроводе

При организации системы отопления бывает нужен такой параметр, как объем воды, которая поместится в трубе. Это необходимо при расчете количества теплоносителя в системе. Для данного случая нужна формула объема цилиндра.

Формула расчета объема воды в трубе

Тут есть два пути: сначала высчитать площадь сечения (описано выше) и ее умножить на длину трубопровода. Если считать все по формуле, нужен будет внутренний радиус и общая длинна трубопровода. Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров.

Сначала переведем миллиметры в метры: 32 мм = 0,032 м, находим радиус (делим пополам) — 0,016 м. Подставляем в формулу V = 3,14 * 0,0162 * 30 м = 0,0241 м3. Получилось = чуть больше двух сотых кубометра. Но мы привыкли объем системы измерять литрами. Чтобы кубометры перевести в литры, надо умножить полученную цифру на 1000. Получается 24,1 литра.

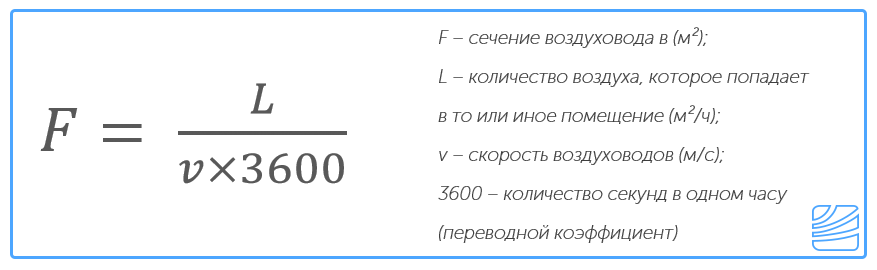
как посчитать окраску поверхности, формула расчета живого сечения

С самыми разными целями зачастую приходится рассчитывать площадь поверхности трубы или ее сечение.

Разумеется, чтобы узнать площадь трубы — формула должна опираться на ее диаметр и протяженность.

Нужны ли какие-то еще параметры? Зачем все эти расчеты могут быть нужны? Как рассчитать площадь и сечение? Все это мы узнаем из этой статьи.

С точки зрения геометрии труба представляет собой цилиндр. Отсюда и простые формулы расчета

Зачем это нужно?

Начнем все же с того, что еще раз перечислим основные ситуации, когда нам нужен расчет площади трубы — ее поверхности или сечения.

  • Формула площади трубы будет полезна, если нам нужно рассчитать теплоотдачу регистра или теплого пола
    .
    Оба значения выводятся именно из суммарной площади, отдающей воздуху в помещении тепло от теплоносителя.

От площади поверхности регистра линейно зависит его теплоотдача

  • Часто встречается обратная ситуация — когда нужно подсчитать потери тепла по пути к отопительному прибору.
    Для того, чтобы можно было принять решение о количестве и размере радиаторов, конвекторов или других приборов — нужно знать, каким количеством калорий мы располагаем. Оно выводится опять-таки с учетом площади поверхности  трубы, которая транспортирует воду от элеваторного узла.
  • Расчет площади поверхности трубы нужен для того, чтобы закупить необходимое количество теплоизолирующего материала.
    Если протяженность теплотрассы исчисляется километрами — а это именно так и бывает — точный расчет может сэкономить предприятию огромные суммы.

Здесь теплоотдачу нужно сократить до минимума. Чтобы посчитать количество необходимого теплоизолирующего материала — нужно узнать площадь поверхности, которую предстоит защитить от потери тепла

  • Затраты на антикоррозионное покрытие или краску — из той же категории. Площадь окраски трубы стальной вместе с расходом краски на квадратный метр дадут нам точный объем необходимых закупок.
    Заодно в этом случае будет очень хорошо видно, скажем вежливо, нецелевое использование материала: если краски или битумного лака уходит в полтора раза больше расчетного количества — предприятию следует пресекать воровство.

Производители краски указывают ее расход в граммах на квадратный метр поверхности

  • Расчет площади сечения трубы необходим для того, чтобы узнать ее максимальную проходимость.
    Да, можно просто поставить трубу заведомо больше необходимой;  но при составлении типового проекта, по которому будет строиться много домов, перерасход средств в этом случае будет большим.

Важно: в случае частного дома перерасход бюджета, если вы просто возьмете трубу на шаг больше, невелик. А вот потери тепла вырастут заметно. Непонятно? Вспомните: больше поверхность трубы — больше тепла на ней рассеивается.

Кроме того, между моментами, когда открывается кран горячей воды, весь объем в соответствующем водопроводе бесцельно остывает.

Чем больше диаметр трубы — тем больше воды в ней будет стоять, тем больше тепла вы потратите на бесцельный нагрев помещения.

Чем толще трубы — тем больше горячей воды бесцельно остывает после каждого открытия крана

Методики расчета

Расчет сечения

Собственно, задача-то из геометрии средних классов. 2=0,754296 м2.

Важно: в напорных водопроводах вода всегда заполняет весь объем трубы.

В самотечной канализации же это не так: большую часть времени поток смачивает лишь часть стенок и, соответственно, труба оказывает ему меньшее сопротивление по сравнению  с полностью заполненной.

Именно для гидравлических расчетов самотечной канализации введено такое понятие, как площадь живого сечения трубы.

Это площадь поперечного сечение потока в ней, перпендикулярного направлению движения потока.

От точного подбора сечения трубы порой очень многое зависит

Площадь внешней поверхности трубы

И это тоже задача сугубо геометрическая. Как посчитать площадь поверхности трубы снаружи?

А как найти в общем случае площадь стенок цилиндра?

Поверхность цилиндра — это, в сущности, прямоугольник, одна сторона которого — длина окружности цилиндра, а вторая —  длина самого цилиндра. Так?

Длина окружности, как мы помним, равна Pi*D, где Pi — число Пи, а D — диаметр трубы.

Как рассчитать площадь прямоугольника? Необходимо его длину умножить на ширину.

Площадь заветного прямоугольника будет такой: S=Pi*D*L, где Pi — старое доброе число Пи, D — диаметр трубы, а L — ее длина.

Для теплотрассы диаметром в один метр при ее длине в десять километров площадь окраски труб будет равной:  3,14159265*1*10000=31415,9265 м2. Теплоизоляции понадобится чуть больше: она имеет толщину, отличную от нуля, к тому же труба заворачивается в минеральную вату с перехлестом полотен.

И здесь точный расчет площади поверхности был необходим

Площадь внутренней поверхности трубы

Зачем внутренняя поверхность? Неужели трубы красят изнутри?

Нет, площадь внутренней поверхности может пригодиться при гидродинамических расчетах. Это площадь поверхности, с которой контактирует вода при движении по трубам.

Есть несколько связанных с этой площадью нюансов:

  • Чем больше диаметр трубы для водопровода — тем меньше влияние шероховатости ее стенок на скорость потока в ней.
    Для трубопроводов большого диаметра при небольшой протяженности сопротивлением трубы можно полностью пренебречь;
  • Для гидродинамических расчетов шероховатость поверхности имеет не меньшее значение, чем ее площадь.
    Ржавая внутри стальная водопроводная труба и идеально гладкая полипропиленовая очень по разному влияют на скорость потока;
  • Трубы из неоцинкованной стали имеют, так сказать, непостоянную площадь внутренней поверхности.
    Они со временем зарастают ржавчиной и минеральными отложениями, в результате чего просвет сужается.
    Если вам придет в голову странная фантазия изготовить из стали водопровод холодного водоснабжения — этим фактом нельзя пренебрегать, поскольку проходимость водопроводной трубы может упасть вдвое уже за десять лет.

Зарастание стальной неоцинкованной трубы приходиться учитывать при расчете водопровода

Ну а что с формулой? Она проста. Диаметр цилиндра в этом случае, как легко догадаться, равен разности диаметра и удвоенной толщины стенок трубы.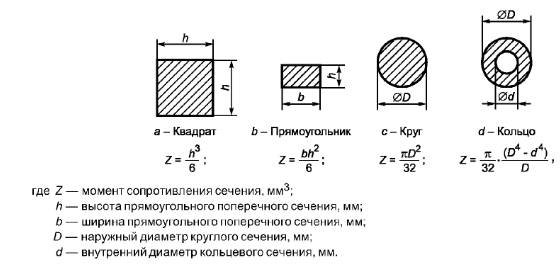

Раз так — площадь стенок цилиндра приобретает вид S=Pi*(D-2N)*L, где D — по-прежнему диаметр трубы, N-толщина ее стенок, а L — протяженность.

Для теплотрассы длиной в 10 километров из трубы диаметром 1 метр со стенками толщиной 10 мм площадь внутренней поверхности окажется равной: 3,14159265*(1-2*0,01)*10000 = 30787,60797 м2.

Заключение

Подводя итоги — в сущности, мы с вами заново прошли курс геометрии средних классов, вспомнив школу и знания, забытые за годы скучной взрослой жизни. Будем надеяться, что эти простые формулы пригодятся вам не раз. Удачи в строительстве!

площадь трубы для воды, формула в м³, калькулятор онлайн, сечение и поверхность

При монтаже труб важно знать их объем

Расчет объема необходим для определения вместимости какой-либо емкости, также отражает размеры определенного объекта. Для упрощения всех расчетов, можно использовать онлайн-калькулятор, но не всегда есть возможность им пользоваться. Проще сделать несколько замеров, и умножить между собой получившиеся цифры.

Измерения для расчета объема труб

Некоторые для этого пользуются онлайн-калькуляторами, а другие, пользуясь формулами, рассчитывают объем трубы вручную. Есть и другие, несколько иные, способы расчета объема труб, например, с использованием таблиц. В строительстве, причем не только в промышленных масштабах, но и в домашних условиях, иногда рассчитывается объем.

Так, иногда возникает необходимость расчета объема труб, например, при обустройстве:

  • Водопровода;
  • Канализации;
  • И иных нужд, где используются трубы.

Для правильного определения объема какой-либо трубы в м3, например, ВГП трубы, следует проделать определенные манипуляции. Измерить внутренний радиус трубы, или же определить внутренний, а также внешний диаметр трубы и записать полученные результаты. Измерить длину трубы, и также записать полученные значения. Для расчета, какой объем воды может вместить труба, необходимо перевести миллиметры в метры, далее необходимо радиус возвести в квадрат и умножить его на число Пи, таким образом, будет определено сечение.

Пи равно значению 3,14.

Далее длину трубы следует умножить на площадь ее сечения, таким достаточно нехитрым способом можно найти объем. Таблица представляет собой несколько столбцов, в которых прописаны внутренний и внешний диаметр труб, указана погонная длина (как правило, это 10 м) и объем 1 м в литрах. Достаточно найти в таблице подходящую по размеру трубу для того, чтобы определить ее объем.

Расчет площади труб

Помимо определения объема труб, требуется иногда рассчитать и площадь, например, для того, чтобы знать, сколько потребуется краски для окрашивания или покрытия каким-либо иным материалом. Расчет площади также производиться либо с помощью онлайн калькуляторов, либо с использованием формулы.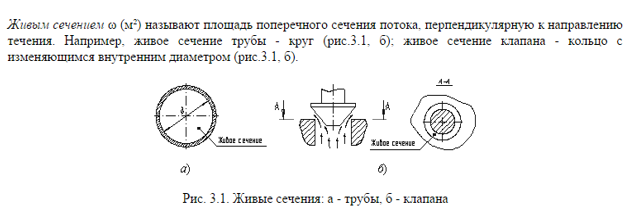

Таким образом, можно заранее вычислить, какой объем материала потребуется для:

  • Покраски;
  • Покрытия изоляцией;
  • Обезжиривания поверхности трубы.

Формула для расчета площади используется не сложная. Сначала требуется измерить длину трубы, а также определить ее внешний радиус, все полученные сантиметры (если труба небольшого размера) переводятся в метры. Пи, равное 3,14, нужно умножить на 2, далее получившееся число умножается на длину и радиус трубы.

В результате всех расчетов можно узнать, чему равна площадь трубы.

Для определения площади квадратной трубы, нужно сначала вычислить ее периметр, а уже получившееся число умножить на длину. Тоже самое касается и трубы в форме прямоугольника – расчет производится точно также. Но, так считать просто, если трубы имеют прямую форму, а если они изогнутые, то необходимо к полученным цифрам добавлять определенные допуски. Такую информацию можно отыскать в специальных строительных нормах.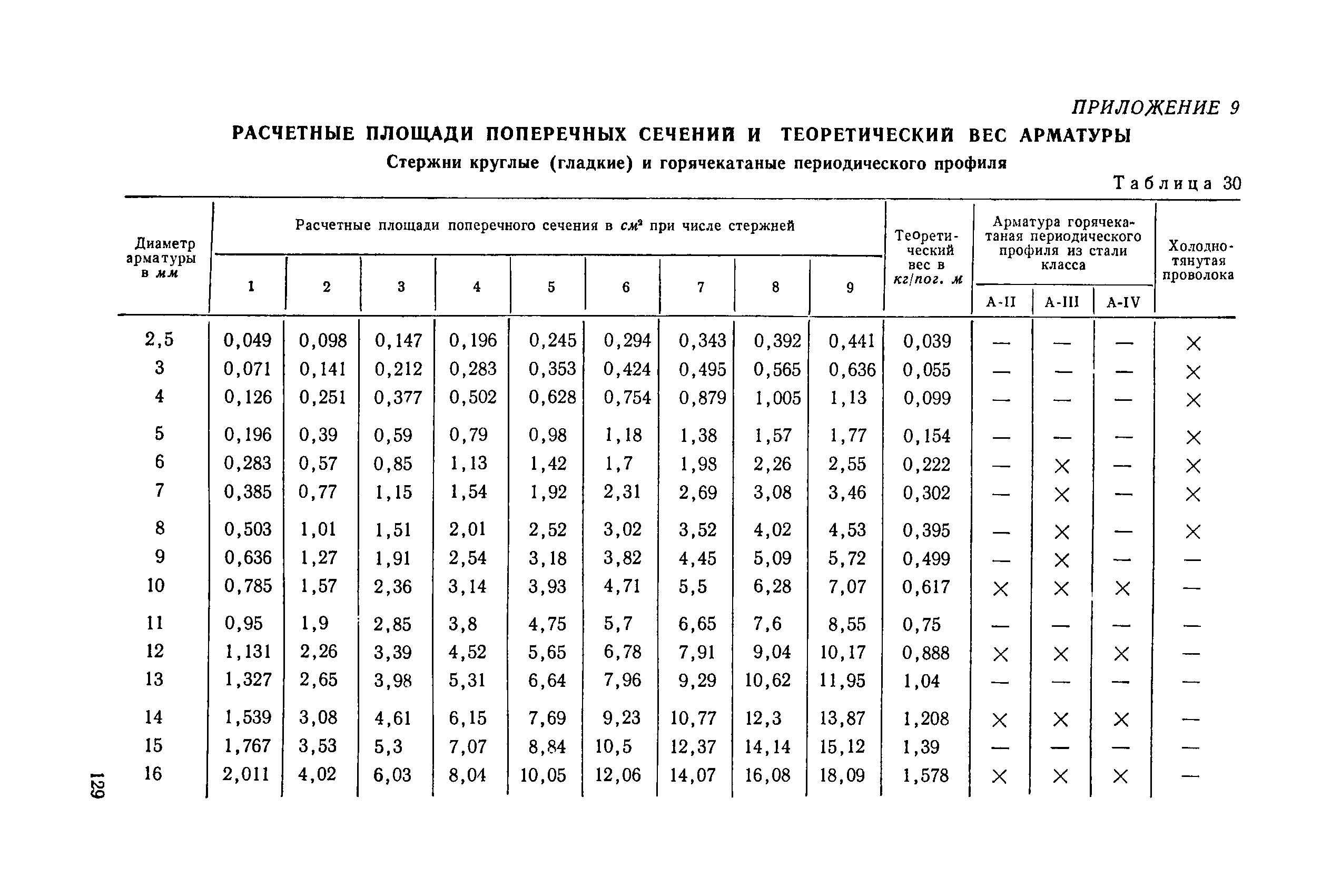

Подробный расчет площади трубы

Для самых разных целей требуется знать, какая площадь будет у какой-либо трубы. Посчитать ее можно с помощью онлайн-калькулятора или же с помощью простых формул. Для расчета площади трубы, например, стальной, необходимо воспользоваться алгоритмом.

Алгоритм:

  1. Сначала следует определить диаметр трубы, полученный результат необходимо умножить на число Пи.
  2. Полученную цифру следует умножить на длину трубы, в результате чего будет известна внешняя площадь.
  3. Если требуется высчитать внутреннюю площадь трубы, формула несколько изменяется, сначала также определяется диаметр, после измеряется толщина ее стенок.
  4. Из диаметра вычитают толщину стенок трубы, и полученный результат снова умножается на длину.

Расчет наружной площади необходим для того, чтобы знать, какое количество краски или укрывного материала понадобится для трубы. Также это знание поможет при проектировании систем теплоснабжения с тем, чтобы знать, какие теплопотери могут быть.

Расчет внутренней площади необходим для определения объема кубатуры жидкости, которая может проходить через трубу.

Помимо расчета площади труб, предназначенных для жидкости, есть воздуховодные варианты, для круглой расчет примерно такой же. А вот для расчета площади овала или овальной трубы, следует определить 2 радиуса, после чего их следует перемножить между собой, и получившийся результат умножить на число Пи.

Вычисление площади сечения трубы

Большинство вычислений для разных нужд в современном мире производится с помощью онлайн-расчетов. Зная необходимые параметры, их следует подставить в соответствующие поля с тем, чтобы узнать результат. Но не всегда есть возможность воспользоваться такими «помощниками». В этом случае считать, например, площадь сечения трубы, приходится вручную.

Расчет:

  1. Труба чаще всего имеет форму круга и реже встречается в форме квадрата или овала.
  2. Для расчета круглой трубы, необходимо определить ее диаметр, поучившееся значение следует умножить на число Пи.
  3. Для определения внутреннего сечения трубы, из получившегося числа следует прибавить к стенке, для удобства все расчеты лучше всего производить в метрах.

Расчет площади сечения необходим для того, чтобы знать скорость движения жидкости или газов, и для этого необходимо выбрать наиболее оптимальный диаметр круглого трубопровода. Также при расчете следует учитывать температуру газа или жидкости, с которой они двигаются по трубам.

Для более качественного расчета площади сечения какой-либо металлической трубы, следует пользоваться дополнительно специальными строительными таблицами и справочниками.

Но, если производится расчет сечения самотечных трубопроводов, следует принимать во внимание не полное сечение трубы, а так называемое живое или фактическое. Сечение живого потока обычно равно половине фактического сечения трубы.

Математическая формула расчета объема

Для расчета объема какой-либо трубы, следует воспользоваться формулой расчета объема цилиндра, так как труба по сути своей представляет цилиндр.

Алгоритм расчета:

  • Сначала следует определить размер поперечного сечения трубы;
  • Из полученной цифры следует вычесть толщину стенок трубы;
  • Полученную цифру разделить на 2, чтобы определить радиус трубы.

Если нет возможности определить радиус, то в этом случае следует ориентироваться на размер окружности трубы, получившийся результат следует разделить на число Пи в квадрате (примерно 9,85). Следует также определить площадь сечения, для этого снова следует воспользоваться числом Пи, которое умножают на квадрат радиуса. Причем квадрат радиуса может быть рассчитан, как в метрах, так и сантиметрах, все зависит от диаметра самой трубы.

Для определения объема воды или иной жидкости, в выше приведенные расчеты следует подставить размеры внутреннего диаметра трубы.

Если нет большого желания что-либо рассчитывать по формуле, можно воспользоваться специальными таблицами для расчета погонного метра какой-либо трубы в литрах. В таких таблицах указано, сколько воды или иной жидкости может через себя пропустить погонный метр в литрах или же кубах. Расчет такого параметра важен при проектировании систем отопления. Также следует учитывать такую особенность – трубы, изготовленные из стали, пропускают объема воды меньше из-за шероховатостей и отложений внутри, чем, например, пропиленовые, при расчете следует это учитывать.

Определение площади поверхности трубы

Важно определять площадь поверхности, так как это позволяет рассчитать, какое количество грунта, краски или укрывного материала потребуется для той или иной трубы с учетом ее формы, материала и веса. Масса труб, изготовленных из ПВХ или пропилена, значительно меньше, чем стальных, хотя площадь их одинакова.

Для вычисления площади трубы, потребуется выполнить следующие действия:

  • Определить радиус трубы сначала в сантиметрах;
  • После перевести полученный результат в метры;
  • После следует высчитать длину трубы также в метрах;
  • Умножить полученный результат на известный радиус, в результате чего можно узнать внешнюю площадь трубы.

Можно вычислить площадь и прямоугольной трубы с учетом веса, достаточно знать, сколько весит погонный метр, тоннаж можно определить по специальным таблицам, применяемым в строительстве. Данную величину следует умножить на длину трубы в метрах. Такие расчеты позволяют определить количество краски, грунта и теплоизоляционного материала, а также потери тепла при передаче последнего от такого теплового узла, как котельная.

Определение внутренней площади трубы необходимо и для расчета ее максимальной проходимости.

Водопроводные трубы: как рассчитать объем (видео)

Практически каждому человеку доступны расчеты, достаточно знать все необходимые параметры, квадратуру, овальность и плотность потока жидкости в трубе. Если возникают трудности при расчете, то лучше всего обратиться к специалистам. Благодаря данной информации, каждый человек, используя необходимые данные, может вычислить необходимые параметры, в том числе по длине, площадь.

Площади сечений круглых труб — Энциклопедия по машиностроению XXL

В (10.9), справедливой для наиболее распространенного турбулентного течения при Re = 10 Ч-5 1 О и Рг = 0,6- 2500, определяющим размером является внутренний диаметр трубы d. Если это не круглая труба, а канал произвольного сечения, то формула (10.9) тоже применима, только определяющим размером будет эквивалентный диаметр канала d KB = 4F/n, где F — площадь поперечного сечения П — внутренний периметр этого сечения.  [c.85]
Сравнить ее с потерей в круглой трубе, имеющей равновеликую площадь сечения.  [c.211]

Иногда в качестве гидравлического радиуса принимают отношение площади поперечного сечения трубы к полупериметру. Тогда при переходе к круглой трубе гидравлический радиус совпадает с ее радиусом.  [c.283]

ХОДЯЩИМИ через отверстие расходом и перепадом давления [см. формулу (7.21)] может быть использована для измерения расхода жидкости с помощью измерительной диафрагмы (рис. 7.5). Измерительная диафрагма обычно выполняется в виде плоской перегородки с круглым отверстием в центре и устанавливается между фланцами трубопровода. Края отверстия имеют острые входные кромки под углом 45° или же закругляются примерно по форме втекающей в отверстие струи жидкости. Для измерения перепада давления до и после диафрагмы служат два пьезометра а и б или дифференциальный манометр. Коэффициент расхода можно определить по формуле (7.22), положив в ней т=п (так как площади сечения трубы до и после диафрагмы одинаковы), в результате чего формула получит вид  [c.307]

Задача IX-36. Сравнить потери напора на трение в круглой и квадратной трубах равной длины и равной площади сечения при одинаковом расходе данной жидкости, предполагая, что в трубах имеют место 1) ламинарный режим 2) турбулентный режим (квадратичная область сопротивления), причем шероховатость труб одинакова.  [c.259]

Лабораторная установка состоит (см. рис. 2.14) из напорного бачка и круглой трубы, составленной из труб различного сечения с диаметрами ь 2 я з я площадями 5], 5а и 5з. Из каждого сечения выведены по две трубки пьезометрическая и Пито (см. 2.4). Выводы от всех пьезометрических трубок и трубок Пито смонтированы над трубой на общем щите с миллиметровой шкалой  [c.307]

При обобщении опытных данных важным также является вопрос о выборе определяющего размера. Хотя с точки зрения теории подобия в подобных геометрических системах любой размер может быть принят в качестве определяющего, в качестве такого целесообразно выбирать тот размер, которым определяется развитие процесса. При этом обобщенные зависимости для однотипных, но геометрически не подобных систем, оказываются близкими или даже одинаковыми, что представляет большое удобство для практических расчетов. Например, при конвективном теплообмене в круглых трубах в качестве определяющего размера обычно берется диаметр. Для каналов неправильного и сложного сечения целесообразно брать эквивалентный диаметр, равный учетверенной площади поперечного сечения канала, деленной на полный смоченный периметр сечения (независимо от того, какая часть этого периметра участвует в теплообмене). При поперечном обтекании трубы и пучка труб в качестве определяющего размера берется диаметр  [c.66]


Анализ структуры числа Рейнольдса позволяет найти решение этой задачи. Рассмотрим круглую трубу с периметром рис площадью поперечного сечения А . Для этой трубы  [c.221]

Если обозначить через Qq расход через круглую трубу с такой же площадью поперечного сечения, как и у трубы с квадратным сечением, то при помощи (2.5.8) находим  [c.56]

Для приближенной оценки сопротивления цилиндрических или призматических труб сложного фигурного профиля применяют прием сравнения сопротивлений этих труб с эквивалентной им по сопротивлению трубой круглого сечения, у которой за радиус (или диаметр) принимается так называемый гидравлический радиус Гр (или диаметр др = 2гр), равный отношению площади нормального сечения 8 трубы (рис. 154) к периметру Р сечения  [c.386]

Преимуществами ламельного теплообменника являются увеличение коэффициента теплопередачи в 1,4-2 раза за счет уменьшения толщины слоя жидкости и общего повышения скоростей потоков, а также увеличение площади теплообмена, так как при равном поперечном сечении плоские трубы имеют большую поверхность, чем круглые.  [c.386]

Часто к стенкам канала прикрепляют ребра для увеличения площади поверхности, за счет чего улучшается теплообмен. Присутствие ребер приводит также и к увеличению перепада давления по длине канала при том же расходе через его сечение. Рассмотрим круглую трубу с ребрами, показанную на рис. 10.2. При вычислении темпера-  [c.200]

В задаче о наивыгоднейшей форме балки прямоугольного сечения, вырезанной из заданного кругового цилиндра, Юнг находит самой жесткой балкой будет та, высота которой относится к ширине, как ]ЛЗ 1, самой прочной—та, у которой это отношение равно / 1, но наибольшей упругостью будет обладать та, у которой высота и ширина равны . Это следует из того, что при данном пролете жесткость балки определяется величиной момента инерции ее поперечного сечения, прочность— моментом сопротивления, а упругость—площадью поперечного сечения. Аналогично он решает задачу и для тонкостенных круглых труб. Юнг утверждает Положим, что труба весьма малой  [c.119]

Формулы для определения 5, %, / г и 1)г для потоков различной формы приведены в табл. 3.1, значения относительных глубин наполнения и площадей живых сечений при частичном заполнении круглой трубы радиусом г — в табл. 3.2 (см. и. б табл. 3.1).  [c.45]

Эта величина относится к расходу жидкости в круглой трубе с такой же площадью поперечного сечения, как 2ай (а + Ь )- Для небольших значений эксцентриситета е эта дробь отличается от единиц на величину порядка е. Поэтому поперечные сечения могут иметь довольно разнообразную форму без того, чтобы расход менялся значительно, если только площадь поперечного сечения остается неизменной. Даже если о 6 = 8 7, то н тогда расход уменьшается меньше, чем на 1%.  [c.735]

Следовательно, идеальной формой сжатого стержня будет труба круглого сечения, так как она обладает одинаковой жесткостью по всем направлениям и наибольшим для данной площади сечения моментом инерции. При этом стенка трубы не должна быть слишком тонкой, иначе сама стенка может при сжатии потерять устойчивость и измяться в складки. Во избежание этого следует усиливать стенки трубы продольными ребрами.  [c.363]

В формуле (2-4) в качестве характерного геометрического размера русла принят диаметр й, а в формуле (2-5) — гидравлический радиус Р, равный отношению площади живого сечения круглой трубы при напорном движении R = (1  [c.78]


Определение критических чисел Рейнольдса, при которых происходит переход одного режима течения в другой, имеет исключительно важное значение. При указанном переходе резко меняется структура потока, распределение скоростей, гидравлическое сопротивление, способность к переносу тепла и др. Хотя проблема перехода изучается уже много лет, однако она еще далека от разрешения. Наиболее полно изучен переход для случая течения в трубах постоянной по длине площади сечения (особенно в круглых). Поэтому остановимся подробнее на рассмотрении перехода режимов применительно к указанным случаям.  [c.37]

Трубы некруглого сечения рассчитываются, как круглые, с введением коэффициента формы и заменой диаметра трубопровода учетверенным гидравлическим радиусом, равным отношению площади сечения к периметру [92], [67].  [c.30]

Сравнить прочность и жесткость прямоугольной трубы (см. предыдущую задачу) и круглой трубы с равновеликой площадью сечения и той же толщиной стенок.  [c.70]

Ответ. Перегружена на 4,83%. ф = 23,4-10 рад = Г 20. 3. 56. Сравнить прочность и жесткость прямоугольной трубы (см. предыдущую задачу) и круглой трубы с равновеликой площадью сечения и той же толщиной стенок.  [c.82]

Испытание на растяжение производится на нормальных круглых образцах или на пропорциональных обр цах, длина которых рассчитывается по формулам I = Для длинного образца и / = 5,65 для короткого образца, где Р — площадь сечения образца. Пропорциональный образец представляет собой планку, вырезанную вдоль трубы. Он употребляется в случаях, когда толщина стенки трубы не позволяет изготовить круглый образец.  [c.7]

В случае трубы э.члиитического сечения напряжение трения ма сгенке меняется по периметру сечения, так как поток не симметричен. Интересно отметить, что среднее значение иапряжения трения но периметру эллипса меньше, чем напряжение трении н круглой грубе той же площадн сечеиня. Аналогичный результат имеет место и по отношению к объемному расходу при том же перепаде давления расход сквозь трубу эллиптического сечения меньше, чем чepe равновеликое ему по площади сечение круглой трубы.  [c.494]

Площадь, осевой момент инерции, осевой момент сопротивле кил и радиус инерции аинеречных сечений круглых труб  [c.43]

Живым сечением называют час ь поперечного сечения канала (трубы), заполненную жидкостью. Так, в круглой трубе диаметром d (рис. П1.4,а) живое сечеиие потока меньще площади круга, если не все сечение трубы заполнено жидкостью, тогда как для случая, когда все поперечное сечение занято жидкостью, живым сечением является площадь круга nd l4 (рис. 111.4,6).  [c.67]

Указ я и и е. По заданно] относительной глубине наполнения (см. таблицы приложет-1я 1 или 2) находим . Определяя из условий задачи площадь живого сечения, устанавливаем глубину протекания потока, необходимый параметр. При опре-деле1и1и уклона для круглой трубы или тоннеля скоростная характеристика берется с соответствующим коэфс()ициентом уменьшения.  [c.117]

Требуется выявить влияние на течение реагирующего газа притока теплоты за счет химической реакции. Интересно рассмотреть вопрос о переходе через критическую скорость звука в газовом потоке и выяснить условия, при которых этот переход возможен. Известно, что в сопле Лаваля переход через скорость звука достигается за счет геометрии сопла. Поток сначала разгоняется за счет сужения сопла, а затем, после достижения звуковой скорости, за счет расширения сопла достигается сверхзвуковая скорость. Таксе сопло называют геометрическим, а достижение скорости звука в критическом сечении — аэродинамическим кризисом. Выясним, как влияет приток энергии за счет химических реакций на газовый поток в круглой трубе с постоянней площадью поперечного сечения, когда геометрия сопла ге играет никакой роли, и как меняются основные с )изическг е величины, характеризующие поток, при переходе через скорость звука.  [c.359]

Итак, при заданной площади сечения и данном расходе жидкости (а ледрвательно, и при, заданной средней скорости) сила трения пропорциональна периметру сечения. Наименьщим периметром при заданной площади обладает круглое сечение, которое поэтому является наивыгод-нейщим с точки зрения получения минимальных потерь энергии (напора) на трение в трубе.  [c.59]

Л—.площадь, площадь поверхности Ас — площадь полеречного сечения потока Лт — см. уравнение (8-39) а — коэффициент температурмтроводности В— движущая сила массоп реноса Сп — см. уравнение i(8-33) с— удельная теплоемкость при лостоянном давлении Си — удельная теплоемкость при постоянном объеме j — удельная теплоемкость при постоянном давлении /-компонента смеси D — внутренний диаметр круглой трубы Dr — гидравлический диаметр  [c.11]

При течении в круглой трубе эквивалентный диаметр равен внутреннему. При течении в некруглой трубе или в кольцевом канале с1д — =4Р1и, м, где Р — площадь живого сечения канала, м и—омываемый периметр, м. Для прямоугольного сечения, заполненного трубами ширм или конвективных пучков,  [c.206]

Диафрагма. Диафрагма представляет собой установленный перпендикулярно направлению течения диск с отверстием (рис. 9.13). Диафрагмы применяются для измерения расхода жидкости в трубах. Коэффициент сопротивления диафрагхмы д, установленной в трубе круглого постоянного сечения со1 при круглом концентрическом отверстии площадью соо, зависит от отношения площади отверстия о и площади сечения мь  [c.195]


Задвижка. Для простой плоской односторонней задвижки, установленной на трубе круглого поперечного сечения, коэффициент потерь зависит от степени перекрытия сечения трубы, которая характеризуется отношением aid (рис. 9.14). При обтекании такой задвижки такн е происходят сужение, а затем расширение потока, отрыв потока от стенок и образование водоворотной области. На границе транзитной струи происходят интенсивное вихреоб-разованне и пульсации скорости. Отношение площади ип, перекрытой такой задвижкой, к площади сечения трубы определяется по формуле  [c.196]

Пример 3.4. Определить расходы воды в трубе прямоугильного поперечного сечения с отношением сторон а 6=0,25 и в круглой трубе при той же площади поперечного сечения со=2-10 м , если потери давления в этих трубах одинаковы к равны Дрд=100 Па, а длина каждой трубы /=10 м. Температура воды 20°С.  [c.68]

Таким образом, в условиях ламина,рного движения при одной и той же площади живого сечення и одинаковых потерях давления круглая труба пропускает расход, в 2у5 раза ббльший, чем труба прямоугольного сечешя.  [c.68]

Как посчитать объем трубы при выборе расширительного мембранного бака.

Как посчитать объем трубы.

Данные вычисления требуются для определения объёма системы отопления, при выборе расширительного мембранного бака.
Объём расширительного мембранного бака подбирается из расчета не менее 10% от всего литража системы.

Определите радиус трубы R. Если необходимо рассчитать внутренний объем трубы, то надо найти внутренний радиус. Если необходимо рассчитать объем, занимаемый трубой, следует рассчитать радиус внешний. Путем измерений можно легко получить диаметр (как внутренний, так и внешний) и длину окружности сечения трубы. Если известен диаметр трубы, поделите его на два. Так, R=D/2, где D — диаметр. Если известна длина окружности сечения трубы, поделите его на 2*Пи, где Пи=3.14159265. Так, R=L/6,28318530, где L — длина окружности.

Найдите площадь сечения трубы. Возведите значение радиуса в квадрат и помножьте его на число Пи. Так, S=Пи*R*R, где R — радиус трубы. Площадь сечения будет найдена в той же системе единиц, в которой было взято значение радиуса. Например, если значение радиуса представлено в сантиметрах, то площадь сечения будет вычислена в квадратных сантиметрах.

Вычислите объем трубы. Помножьте площадь сечения трубы на нее длину. Объем трубы V=S*L, где S — площадь сечения, а L — длина трубы.

Программа расчета объема воды в трубе и радиаторах

Внутренний диаметр трубы, мм. = объём секции радиатора, литров =
Длина трубы, м = количество секций радиатора, шт. =
Объем воды в трубе, м³ = объём воды в радиаторе, м³ =
Объем воды в трубе, литров = объём воды в радиаторе, литров =
 
Объем воды в системе, м³ =
Объем воды в системе, литров =

 


Таблица объёма жидкости в одном метре трубы:  

Внутренний диаметр,
мм

Внутренний объем 1 м погонного трубы,
литров

  

Внутренний диаметр,
мм

Внутренний объем 1 м погонного трубы,
литров

4

0,0126

105

8,6590

5

0,0196

110

9,5033

6

0,0283

115

10,3869

7

0,0385

120

11,3097

8

0,0503

125

12,2718

9

0,0636

130

13,2732

10

0,0785

135

14,3139

11

0,0950

140

15,3938

12

0,1131

145

16,5130

13

0,1327

150

17,6715

14

0,1539

160

20,1062

15

0,1767

170

22,6980

16

0,2011

180

25,4469

17

0,2270

190

28,3529

18

0,2545

200

31,4159

19

0,2835

210

34,6361

20

0,3142

220

38,0133

21

0,3464

230

41,5476

22

0,3801

240

45,2389

23

0,4155

250

49,0874

24

0,4524

260

53,0929

26

0,5309

270

57,2555

28

0,6158

280

61,5752

30

0,7069

290

66,0520

32

0,8042

300

70,6858

34

0,9079

320

80,4248

36

1,0179

340

90,7920

38

1,1341

360

101,7876

40

1,2566

380

113,4115

42

1,3854

400

125,6637

44

1,5205

420

138,5442

46

1,6619

440

152,0531

48

1,8096

460

166,1903

50

1,9635

480

180,9557

52

2,1237

500

196,3495

54

2,2902

520

212,3717

56

2,4630

540

229,0221

58

2,6421

560

246,3009

60

2,8274

580

264,2079

62

3,0191

600

282,7433

64

3,2170

620

301,9071

66

3,4212

640

321,6991

68

3,6317

660

342,1194

70

3,8485

680

363,1681

72

4,0715

700

384,8451

74

4,3008

720

407,1504

76

4,5365

740

430,0840

78

4,7784

760

453,6460

80

5,0265

780

477,8362

82

5,2810

800

502,6548

84

5,5418

820

528,1017

86

5,8088

840

554,1769

88

6,0821

860

580,8805

90

6,3617

880

608,2123

92

6,6476

900

636,1725

94

6,9398

920

664,7610

96

7,2382

940

693,9778

98

7,5430

960

723,8229

100

7,8540

980

754,2964

—

—

1000

785,3982

 

Момент инерции и момент сопротивления

05-12-2012: Адольф Сталин

Было бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно

05-12-2012: Доктор Лом

В принципе, что такое момент инерции и откуда он взялся, достаточно подробно объяснено в статье «Основы сопромата, расчетные формулы», здесь лишь повторюсь: «W — это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы». Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям. Момент инерции необходимо знать для определения углов поворота поперечного сечения и прогиба (смещения) центра тяжести поперечного сечения, так как максимальные деформации возникают в самом верхнем и в самом нижнем слое изгибаемой конструкции, то определить момент инерции можно, умножив момент сопротивления на расстояние от центра тяжести сечения до верхнего или нижнего слоя, поэтому для прямоугольных сечений I=Wh/2. При определении момента инерции сечений сложных геометрических форм сначала сложная фигура разбивается на простейшие, затем определяются площади сечения этих фигур и моменты инерции простейших фигур, затем площади простейших фигур умножаются на квадрат расстояния от общего центра тяжести сечения до центра тяжести простейшей фигуры. Момент инерции простейшей фигуры в составе сложного сечения равен моменту инерции фигуры + квадрат расстояния умноженный на площадь. Затем полученные моменты инерции суммируются и получается момент инерции сложного сечения. Но это максимально упрощенные формулировки (хотя, соглашусь, все равно выглядит достаточно мудрено). Со временем напишу отдельную статью.

05-12-2012: Гиви

В принципе все предельно ясно, но здесь проще www.kataltim.ru

20-04-2013: Petr

Не нужно полностью доверять поданной в сайтах информации. Её никто по-хорошему не проверяет. И ссылки на неё не даются. Так в Таблице 1. «Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм» для тонкостенной трубы дается определение, что отношение диаметра к толщине оболочки должно быть больше 10. По другим источникам — должно быть больше 20!!! (Н.М. Беляев. Сопротивление материалов. М.1996. стр.160. или Н.И.Безухов. Основы теории упругости, пластичности и ползучести.М.1961.стр.390)

21-04-2013: Доктор Лом

Верно. Доверять нельзя. Но логическое мышление пока никто не отменял. Самый правильный вариант — рассчитывать момент инерции или момент сопротивления для любой трубы по формулам, приведенным для обычной трубы (на 1 пункт выше). Формулы, приводимые для тонкостенной трубы, в любом случае будут приближенными и годятся только для первичного расчета и об этом забывать нельзя.
Впрочем параметры максимально допустимой толщины стенки исправил.

25-06-2013: Саня

требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву «Ш». не получается найти какую либо информацию. буду признателен за какую нибудь информацию

25-06-2013: Доктор Лом

Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона» (http://doctorlom.com/item249.html)
там в частности определяется момент инерции тоже не совсем простого сечения.

03-11-2014: Радик

Вот здесь http://otvet.mail.ru/question/33111076
дана другая формула для момента сопротивления трубы, а именно: W=(D^3-d^3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).

04-11-2014: Доктор Лом

Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.

04-11-2014: Радик

Спасибо, док!

11-11-2014: Ильгам

Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.

11-11-2014: Доктор Лом

Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).

04-01-2015: Valerij

Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).

05-01-2015: Доктор Лом

Для определения момента инерции вам нужно вычесть из момента инерции трубы момент инерции вашего отверстия. Для этого нужно определить площадь сечения отверстия и затем умножить ее на квадрат расстояния до центра трубы плюс собственный момент инерции отверстия. Больше подробностей в статье «Моменты инерции поперечных сечений».
Если расчет не требует особой точности и диаметр отверстия в 5 и более раз меньше диаметра трубы (вроде ваш случай, если 32.39 — это наружный диаметр), то сегмент отверстия можно привести к прямоугольнику. Если отверстие не сквозное, то следует дополнительно определить положение центра тяжести трубы с отверстием для того, чтобы потом вычислить новое значение момента сопротивления.
Но и это еще не все. Вам следует учесть, что возле отверстий возникают значительные локальные напряжения.

09-10-2015: Борис

Неравноплечий уголок.При вычислении Wy не y,а H-y

09-10-2015: Доктор Лом

Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.

09-10-2015: Борс

Для треугольников при вычислении Wzп h в квадрате.

09-10-2015: Борис

Пардон,Wz

09-10-2015: Доктор Лом

Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.

28-04-2016: Jama

Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!

28-04-2016: Доктор Лом

Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).

29-08-2016: Максим

Здравствуйте ! Имеется швеллер № 12. В верхний пояс будут вкручиваться саморезы и винты для крепления кровли. Как учесть ослабление швеллера, т.е как определить W ослабленного сечения.

29-08-2016: Доктор Лом

Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.

21-03-2017: игорь

здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.

21-03-2017: Доктор Лом

Игорь, я отправил вам письмо.

30-08-2017: Али

Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.

31-08-2017: Доктор Лом

Посмотрите статью «Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял

Площадь сечения трубы расчет поперечного сечения, как рассчитать, как найти проходное сечение — Строительный проект

Как высчитать площадь сечения трубы – обыкновенные и выверенные способы

Произвести расчет сечения трубы очень просто, ведь для этого есть ряд типовых формул, и также бесчисленные калькуляторы и сервисы во всемирной сети, которые могут выполнить ряд несложных манипуляций. В этом материале мы поговорим про то, как высчитать площадь сечения трубы собственными силами, ведь в большинстве случаев необходимо брать во внимание ряд особенностей конструкции трубопровода.

Формулы вычислений

При проведении вычислений необходимо брать во внимание, что по сути трубы имеют цилиндрическую форму. Благодаря этому для нахождения площади их сечения воспользуйтесь геометрической формулой площади окружности. Зная внешний размер трубы и значение толщины его стенок, можно найти критерий диаметра внутри, который пригодится для вычислений.

Классическая формула площади окружности такая:

? – постоянное число, равное 3,14;

R – величина радиуса;

S – площадь сечения трубы, вычисленная для диаметра внутри.

Порядок расчета

Потому как важная задача – это отыскать площадь проходного сечения трубы, главная формула будет несколько видоизменена.

В результате вычисления производятся так:

D – значение внешнего сечения трубы;

N – толщина стенок.

Примите во внимание, что, чем больше знаков в числе ? вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число ? равным 3,14.

Итак, расчеты смотрятся так:

S=??(D/2-N) 2 =3,14?(1/2-0,01) 2 =0,754 м 2 .

Физические характеристики труб

Нужно знать, что критерии площади поперечного сечения трубы прямо влияют на скорость транспортировки газообразных и жидких веществ. Благодаря этому очень и очень важно заложить в проект трубы с правильным сечением. Также, на выбор трубного диаметра будет влиять еще и рабочее водопроводное давление. Читайте также: «Как сосчитать площадь трубы – способы и формулы расчета».

Также в процессе проектирования трубо-проводов необходимо учесть химические свойства среды работы, и также ее показатели температуры. если вы даже знакомы с формулами, как отыскать площадь сечения трубы, необходимо выучить дополнительный теоретический материал. Так, информация относительно требований к диаметрам трубо-проводов под горячее и холодное обеспечение водой, отопительные коммуникации или перевозку газов, содержатся в специализированной справочной литературе. Имеет значение также именно материал, из которого сделаны трубы.

Выводы

Аналогичным образом, обозначение площади сечения трубы считается довольно существенным, но, в процессе проектировки необходимо смотреть на характеристики и характерности системы, материалы трубных изделий и их показатели прочности.

Tagged : площадь / поперечный / проходной / сечение / труба

Раздел Калькулятор — Труба Раздел

Сталь Раздел — CISC

W1100X499W1100X433W1100X390W1100X343W1000X883W1000X748W1000X642W1000X591W1000X554W1000X539W1000X483W1000X443W1000X412W1000X371W1000X321W1000X296W1000X584W1000X494W1000X486W1000X438W1000X415W1000X393W1000X350W1000X314W1000X272W1000X249W1000X222W920X1191W920X970W920X787W920X725W920X656W920X588W920X537W920X491W920X449W920X420W920X390W920X368W920X344W920X381W920X345W920X313W920X289W920X271W920X253W920X238W920X223W920X201W840X576W840X527W840X473W840X433W840X392W840X359W840X329W840X299W840X251W840X226W840X210W840X193W840X176W760X582W760X531W760X484W760X434W760X389W760X350W760X314W760X284W760X257W760X220W760X196W760X185W760X173W760X161W760X147W760X134W690X802W690X548W690X500W690X457W690X419W690X384W690X350W690X323W690X289W690X265W690X240W690X217W690X192W690X170W690X152W690X140W690X125W610X551W610X498W610X455W610X415W610X372W610X341W610X307W610X285W610X262W610X241W610X217W610X195W610X174W610X155W610X153W6 10X140W610X125W610X113W610X101W610X91W610X84W610X92W610X82W530X300W530X272W530X248W530X219W530X196W530X182W530X165W530X150W530X138W530X123W530X109W530X101W530X92W530X82W530X72W530X85W530X74W530X66W460X464W460X421W460X384W460X349W460X315W460X286W460X260W460X235W460X213W460X193W460X177W460X158W460X144W460X128W460X113W460X106W460X97W460X89W460X82W460X74W460X67W460X61W460X68W460X60W460X52W410X149W410X132W410X114W410X100W410X85W410X74W410X67W410X60W410X54W410X46W410X39W360X1086W360X990W360X900W360X818W360X744W360X677W360X634W360X592W360X551W360X509W360X463W360X421W360X382W360X347W360X314W360X287W360X262W360X237W360X216W360X196W360X179W360X162W360X147W360X134W360X122W360X110W360X101W360X91W360X79W360X72W360X64W360X57W360X51W360X45W360X39W360X33W310X500W310X454W310X415W310X375W310X342W310X313W310X283W310X253W310X226W310X202W310X179W310X158W310X143W310X129W310X118W310X107W310X97W310X86W310X79W310X74W310X67W310X60W310X52W310X45W310X39W310X31W310X33W310X28W310X24W310X21W250X167W250X149W250X131W2 50X115W250X101W250X89W250X80W250X73W250X67W250X58W250X49W250X45W250X39W250X33W250X24W250X28W250X25W250X22W250X18W200X100W200X86W200X71W200X59W200X52W200X46W200X42W200X36W200X31W200X27W200X21W200X22W200X19W200X15W150X37W150X30W150X22W150X24W150X18W150X14W150X13W130X28W130X24W100X19S610X180S610X158S610X149S610X134S610X119S510X143S510X128S510X112S510X98-2S460X104S460X81-4S380X74S380X64S310X74S310X60-7S310X52S310X47S250X52S250X38S200X34S200X27S150X26S150X19S130X15S100X14-1S100X11S75X11S75X8M310X17-6M310X16-1M310X14-9M250X13-4M250X11-9M250X11-2M200X9-7M200X9-2M150X6-6M150X5-5M130X28-1M100X8-9HP360X174HP360X152HP360X132HP360X108HP310X125HP310X110HP310X94HP310X79HP250X85HP250X62HP200X54WWF2000X732WWF2000X648WWF2000X607WWF2000X542WWF1800X700WWF1800X659WWF1800X617WWF1800X575WWF1800X510WWF1600X622WWF1600X580WWF1600X538WWF1600X496WWF1600X431WWF1400X597WWF1400X513WWF1400X471WWF1400X405WWF1400X358WWF1200X487WWF1200X418WWF1200X380WWF1200X333WWF1200X302WWF1200X263WWF1100X458WWF1100X388WWF1100X351WWF1 100X304WWF1100X273WWF1100X234WWF1000X447WWF1000X377WWF1000X340WWF1000X293WWF1000X262WWF1000X223WWF1000X200WWF900X417WWF900X347WWF900X309WWF900X262WWF900X231WWF900X192WWF900X169WWF800X339WWF800X300WWF800X253WWF800X223WWF800X184WWF800X161WWF700X245WWF700X214WWF700X196WWF700X175WWF700X152WWF650X864WWF650X739WWF650X598WWF650X499WWF650X400WWF600X793WWF600X680WWF600X551WWF600X460WWF600X369WWF550X721WWF550X620WWF550X503WWF550X420WWF550X280WWF500X651WWF500X561WWF500X456WWF500X381WWF500X343WWF500X306WWF500X276WWF500X254WWF500X223WWF500X197WWF450X503WWF450X409WWF450X342WWF450X308WWF450X274WWF450X248WWF450X228WWF450X201WWF450X177WWF400X444WWF400X362WWF400X303WWF400X273WWF400X243WWF400X220WWF400X202WWF400X178WWF400X157WWF350X315WWF350X263WWF350X238WWF350X212WWF350X192WWF350X176WWF350X155WWF350X137C380X74C380X60C380X50C310X45C310X37C310X31C250X45C250X37C250X30C250X23C230X30C230X22C230X20C200X28C200X21C200X17C180X22C180X18C180X15C150X19C150X16C150X12C130X13C130X10C100X11C100X9C100X8C100X7C75X9C75X7C 75X6C75X5MC460X86MC460X77-2MC460X68-2MC460X63-5MC330X74MC330X60MC330X52MC330X47-3MC310X74MC310X67MC310X60MC310X52MC310X46MC310X15-8MC250X61-2MC250X50MC250X42-4MC250X37MC250X33MC250X12-5MC230X37-8MC230X35-6MC200X33-9MC200X31-8MC200X29-8MC200X27-8MC200X12-6MC180X33-8MC180X28-4MC150X26-8MC150X22-8MC150X24-3MC150X22-5MC150X17-9L203X203X29L203X203X25L203X203X22L203X203X19L203X203X16L203X203X14L203X203X13L203X152X25L203X152X22L203X152X19L203X152X16L203X152X14L203X152X13L203X102X25L203X102X19L203X102X13L178X102X19L178X102X16L178X102X13L178X102X11L178X102X9-5L152X152X25L152X152X22L152X152X19L152X152X16L152X152X14L152X152X13L152X152X11L152X152X9-5L152X152X7- 9L152X152X6-4L152X102X22L152X102X19L152X102X16L152X102X14L152X102X13L152X102X11L152X102X9-5L152X102X7-9L152X89X16L152X89X13L152X89X9-5L152X89X7-9L127X127X22L127X127X19L127X127X16L127X127X13L127X127X11L127X127X9-5L127X127X7-9L127X127X6-4L127X89X19L127X89X16L127X89X13L127X89X9-5L127X89X7-9L127X89X6-4L127X76X13L127X76X11L127X76X9-5L127X76X7-9L1 27X76X6-4L102X102X19L102X102X16L102X102X13L102X102X11L102X102X9-5L102X102X7-9L102X102X6-4L102X89X13L102X89X11L102X89X9-5L102X89X7-9L102X89X6-4L102X76X16L102X76X13L102X76X11L102X76X9-5L102X76X7-9L102X76X6-4L89X89X13L89X89X11L89X89X9-5L89X89X7-9L89X89X6-4L89X76X13L89X76X9-5L89X76X7-9L89X76X6-4L89X64X13L89X64X9-5L89X64X7-9L89X64X6-4L76X76X13L76X76X11L76X76X9-5L76X76X7-9L76X76X6-4L76X76X4-8L76X64X13L76X64X9-5L76X64X7- 9L76X64X6-4L76X64X4-8L76X51X13L76X51X9-5L76X51X7-9L76X51X6-4L76X51X4-8L64X64X13L64X64X9-5L64X64X7-9L64X64X6-4L64X64X4-8L64X51X9-5L64X51X7-9L64X51X6-4L64X51X4-8L51X51X9-5L51X51X7-9L51X51X6-4L51X51X4-8L51X51X3-2L51X38X6-4L51X38X4-8L51X38X3-2L44X44X6-4L44X44X4-8L44X44X3- 2L38X38X6-4L38X38X4-8L38X38X3-2L32X32X6-4L32X32X4-8L32X32X3-2L25X25X6-4L25X25X4-8L25X25X3-2L19X19X3-2WT460X223WT460X208-5WT460X193-5WT460X182-5WT460X171WT460X156-5WT460X144-5WT460X135-5WT460X126-5WT460X119WT460X111-5WT460X100-5WT420X179-5WT420X164-5WT420X149-5WT420X113WT420X105WT420X96-5WT420X88WT380X157WT380X142W T380X128-5WT380X98WT380X92-5WT380X86-5WT380X80-5WT380X73-5WT345X132-5WT345X120WT345X108-5WT345X85WT345X76WT345X70WT345X62-5WT305X120-5WT305X108-5WT305X97-5WT305X87WT305X77-5WT305X70WT305X62-5WT305X56-5WT305X50-5WT305X46WT305X41WT265X109-5WT265X98WT265X91WT265X82-5WT265X75WT265X69WT265X61-5WT265X54-5WT265X50-5WT265X46WT265X41WT265X42-5WT265X37WT265X33WT230X88-5WT230X79WT230X72WT230X64WT230X56-5WT230X53WT230X48-5WT230X44- 5WT230X41WT230X37WT230X34WT230X30WT230X26WT205X74-5WT205X66WT205X57WT205X50WT205X42-5WT205X37WT205X33-5WT205X30WT205X27WT205X23WT205X19-5WT180X543WT180X495WT180X450WT180X409WT180X372WT180X338-5WT180X317WT180X296WT180X275-5WT180X254-5WT180X231-5WT180X210-5WT180X191WT180X173-5WT180X157WT180X143-5WT180X131WT180X118-5WT180X108WT180X98WT180X89-5WT180X81WT180X73-5WT180X67WT180X61WT180X55WT180X50-5WT180X45-5WT180X39-5WT180X36WT180X32WT180X28-5WT180X25-5WT180X22-5WT180X19-5WT180X16-5WT155X250WT155X227WT155X207-5WT155X187-5WT155X171WT155X156- 5WT155X141-5WT155X126-5WT155X113WT155X 101WT155X89-5WT155X79WT155X71-5WT155X64-5WT155X59WT155X53-5WT155X48-5WT155X43WT155X39-5WT155X37WT155X33-5WT155X30WT155X26WT155X22-5WT155X19-5WT155X16-5WT155X14WT155X12WT155X10-5WT125X83-5WT125X74-5WT125X65-5WT125X57-5WT125X50-5WT125X44-5WT125X40WT125X36-5WT125X33-5WT125X29WT125X24-5WT125X22-5WT125X19-5WT125X16-5WT125X14WT125X12-5WT125X11WT125X9WT100X50WT100X43WT100X35- 5WT100X29-5WT100X26WT100X23WT100X21WT100X18WT100X15-5WT100X13-5WT100X11WT100X9-5WT100X7-5WT75X18-5WT75X15WT75X11WT75X12WT75X9WT75X7WT65X14WT65X12WT50X9-5WWT275X360-5WWT275X310WWT275X251-5WWT275X210WWT275X140WWT250X325-5WWT250X280-5WWT250X228WWT250X190-5WWT250X171-5WWT250X153WWT250X138WWT250X127WWT250X111-5WWT250X98-5WWT225X251-5WWT225X204-5WWT225X171WWT225X154WWT225X137WWT225X124WWT225X114WWT225X100-5WWT225X88-5WWT200X222WWT200X181WWT200X151-5WWT200X136-5WWT200X121-5WWT200X110WWT200X101WWT200X89WWT200X78-5WWT175X157-5WWT175X131- 5WWT175X119WWT175X106WWT175X96WWT175X88WWT175X77-5WWT175X68-52L203X152X252L203X152X222L203X152X 192L203X152X162L203X152X142L203X152X132L203X102X252L203X102X192L203X102X132L178X102X192L178X102X162L178X102X132L178X102X112L178X102X9-52L152X102X222L152X102X192L152X102X162L152X102X142L152X102X132L152X102X112L152X102X9-52L152X102X7-92L152X89X162L152X89X132L152X89X9-52L152X89X7-92L127X89X192L127X89X162L127X89X132L127X89X9-52L127X89X7-92L127X89X6-42L127X76X132L127X76X112L127X76X9-52L127X76X7-92L127X76X6-42L102X89X132L102X89X112L102X89X9-52L102X89X7-92L102X89X6-42L102X76X162L102X76X132L102X76X112L102X76X9-52L102X76X7-92L102X76X6-42L89X76X132L89X76X9-52L89X76X7-92L89X76X6-42L89X64X132L89X64X9-52L89X64X7-92L89X64X6-42L76X64X132L76X64X9-52L76X64X7- 92L76X64X6-42L76X64X4-82L76X51X132L76X51X9-52L203X203X292L203X203X252L203X203X222L203X203X192L203X203X162L203X203X142L203X203X132L76X51X7-92L76X51X6-42L76X51X4-82L64X51X9-52L64X51X7-92L64X51X6-42L64X51X4-82L51X38X6-42L51X38X4-82L51X38X3-22L152X152X252L152X152X222L152X152X192L152X152X162L152X152X142L152X152X132L152X152X112L152X152X9-52L152X152X7-92L 152X152X6-42L127X127X222L127X127X192L127X127X162L127X127X132L127X127X112L127X127X9-52L127X127X7-92L127X127X6-42L102X102X192L102X102X162L102X102X132L102X102X112L102X102X9-52L102X102X7-92L102X102X6-42L89X89X132L89X89X112L89X89X9-52L89X89X7-92L89X89X6-42L76X76X132L76X76X112L76X76X9-52L76X76X7-92L76X76X6-42L76X76X4-82L64X64X132L64X64X9-52L64X64X7-92L64X64X6-42L64X64X4-82L51X51X9-52L51X51X7-92L51X51X6-42L51X51X4-82L51X51X3-22L44X44X6-42L44X44X4- 82L44X44X3-22L38X38X6-42L38X38X4-82L38X38X3-22L32X32X6-42L32X32X4-82L32X32X3-22L25X25X6-42L25X25X4-82L25X25X3-22L19X19X3-2HS305X305X16HS305X305X13HS305X305X9-5HS305X305X8-0HS305X305X6-4HS254X254X16HS254X254X13HS254X254X9-5HS254X254X8-0HS254X254X6-4HS203X203X16HS203X203X13HS203X203X9-5HS203X203X8-0HS203X203X6-4HS178X178X16HS178X178X13HS178X178X9-5HS178X178X8-0HS178X178X6-4HS178X178X4-8HS152X152X13HS152X152X9- 5HS152X152X8-0HS152X152X6-4HS152X152X4-8HS127X127X13HS127X127X9-5HS127X127X8-0HS127X127X6-4HS127X127X4-8HS114X114X13HS114X114X9-5HS8-0HS1HS1X114X 14X114X6-4HS114X114X4-8HS114X114X3-2HS102X102X13HS102X102X9-5HS102X102X8-0HS102X102X6-4HS102X102X4-8HS102X102X3-2HS89X89X9-5HS89X89X8-0HS89X89X6-4HS89X89X4-8HS89X89X3-2HS76X76X9-5HS76X76X8-0HS76X76X6-4HS76X76X4-8HS76X76X3-2HS64X64X8-0HS64X64X6-4HS64X64X4-8HS64X64X3-2HS51X51X6-4HS51X51X4-8HS51X51X3- 2HS38X38X4-8HS38X38X3-2HS356X254X16HS356X254X13HS356X254X9-5HS305X203X16HS305X203X13HS305X203X9-5HS305X203X8-0HS305X203X6-4HS254X152X16HS254X152X13HS254X152X9-5HS254X152X8-0HS254X152X6-4HS203X152X13HS203X152X9-5HS203X152X8-0HS203X152X6-4HS203X152X4-8HS203X102X13HS203X102X9-5HS203X102X8-0HS203X102X6-4HS203X102X4-8HS178X127X13HS178X127X9-5HS178X127X8-0HS178X127X6-4HS178X127X4-8HS152X102X13HS152X102X9-5HS152X102X8-0HS152X102X6-4HS152X102X4- 8HS152X76X13HS152X76X9-5HS152X76X8-0HS152X76X6-4HS152X76X4-8HS127X76X9-5HS127X76X8-0HS127X76X6-4HS127X76X4-8HS102X76X9-5HS102X76X8-0HS102X76X6-4HS102X76X4-8HS102X76X3-2HS102X51X9-5HS102X51X8-0HS102X51X6-4HS102X51X4-8HS102X51X3-2HS89X64X8-0HS89X64X6-4HS89X64X4- 8HS89X64X3-2HS76X51X8-0HS76X51X6-4HS76X51X4-8HS76X51X3-2HS51X25X4-8HS51X25X3-2HS406X13HS406X9-5HS406X6-4HS356X16HS356X13HS356X9-5HS356X6-4HS324X13HS324X9-5HS324X6-4HS273X13HS273X6-4HS273X4-8HS219X16HS219X13HS219X9-5HS219X6-4HS219X4-8HS178X13HS178X9-5HS178X8-0HS178X6-4HS178X4-8HS168X13HS168X9-5HS168X8-0HS168X6- 4HS168X4-8HS168X3-2HS152X9-5HS152X8-0HS152X6-4HS152X4-8HS152X3-2HS141X9-5HS141X6-4HS141X4-8HS127X13HS127X9-5HS127X8-0HS127X6-4HS127X4-8HS127X3-2HS114X9-5HS114X4-8HS114X3-2HS102X8-0HS102X6-4HS102X4-8HS102X3-2HS89X8-0HS89X6-4HS89X4- 8HS89X3-2HS76X6-4HS76X4-8HS73X6-4HS73X4-8HS73X3-2HS64X6-4HS64X4-8HS64X3-2HS60X6-4HS60X4-8HS60X3-2HS48X4-8HS48X3-2

Расход и его отношение к скорости

Цели обучения

К концу этого раздела вы сможете:

  • Рассчитать расход.
  • Определите единицы объема.
  • Описывать несжимаемые жидкости.
  • Объясните последствия уравнения неразрывности.

Расход Q определяется как объем жидкости, проходящей через некоторое место через область в течение определенного периода времени, как показано на рисунке 1. В символах это может быть записано как

[латекс] Q = \ frac {V} {t} \\ [/ latex],

, где V — объем, а t — прошедшее время.Единица измерения скорости потока в системе СИ — 3 / с, но обычно используются другие единицы измерения для Q . Например, сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5 литров в минуту (л / мин). Обратите внимание, что литровый (L) составляет 1/1000 кубического метра или 1000 кубических сантиметров (10 -3 м 3 или 10 3 см 3 ). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рисунок 1.Скорость потока — это объем жидкости в единицу времени, проходящий мимо точки через область A, . Здесь заштрихованный цилиндр жидкости проходит через точку P по однородной трубе за время t . Объем цилиндра составляет Ad , а средняя скорость составляет [латекс] \ overline {v} = d / t \\ [/ latex], так что скорость потока составляет [латекс] Q = \ text {Ad} / t. = A \ overline {v} \\ [/ latex].

Пример 1. Расчет объема по скорости потока: сердце накачивает много крови за всю жизнь

Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если средняя скорость потока равна 5.00 л / мин?

Стратегия

Время и расход Q даны, поэтому объем V можно рассчитать из определения расхода.

Решение

Решение Q = V / т для объема дает

В = Qt.

Подстановка известных значений дает

[латекс] \ begin {array} {lll} V & = & \ left (\ frac {5. {3} \ text {L}} \ right) \ left (5.{3} \ end {array} \\ [/ latex].

Обсуждение

Это количество около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 6-полосном 50-метровом бассейне с дорожками.

Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, подумайте о скорости течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера реки.Быстрый горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом Q и скоростью [латекс] \ bar {v} \\ [/ latex] составляет

[латекс] Q = A \ overline {v} \\ [/ latex],

, где A — это площадь поперечного сечения, а [latex] \ bar {v} \\ [/ latex] — средняя скорость. Это уравнение кажется достаточно логичным. Это соотношение говорит нам, что скорость потока прямо пропорциональна величине средней скорости (далее называемой скоростью) и размеру реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. На рисунке 1 показано, как получается это соотношение. Заштрихованный цилиндр имеет объем

V = Ad,

, который проходит мимо точки P за время t . Разделив обе стороны этого отношения на т , получим

[латекс] \ frac {V} {t} = \ frac {Ad} {t} \\ [/ latex].

Отметим, что Q = V / t и средняя скорость [latex] \ overline {v} = d / t \\ [/ latex].Таким образом, уравнение принимает вид [латекс] Q = A \ overline {v} \\ [/ latex]. На рис. 2 показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для точек 1 и 2,

[латекс] \ begin {case} Q_ {1} & = & Q_ {2} \\ A_ {1} v_ {1} & = & A_ {2} v_ {2} \ end {cases} \\ [/ latex ]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости.Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — это и есть назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.

Рисунок 2.Когда трубка сужается, тот же объем занимает большую длину. Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим. Если жидкость течет в обратном направлении, ее скорость будет уменьшаться при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не масштабированы.)

Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей.Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 2. Расчет скорости жидкости: скорость увеличивается, когда труба сужается

Насадка радиусом 0,250 см крепится к садовому шлангу радиусом 0,900 см. Расход через шланг и форсунку составляет 0,500 л / с. Рассчитайте скорость воды (а) в шланге и (б) в форсунке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости.{2}} = 1,96 \ text {m / s} \\ [/ latex].

Решение для (b)

Мы могли бы повторить этот расчет, чтобы найти скорость в сопле [латекс] \ bar {v} _ {2} \\ [/ latex], но мы воспользуемся уравнением непрерывности, чтобы получить несколько иное представление. {2}} \ bar {v} _ {1} \\ [/ latex].{2}} 1,96 \ text {m / s} = 25,5 \ text {m / s} \\ [/ latex].

Обсуждение

Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга без сопла. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма скоростей потока в каждом из ответвлений в любой части вдоль трубы. Уравнение неразрывности в более общем виде принимает вид

[латекс] {n} _ {1} {A} _ {1} {\ overline {v}} _ {1} = {n} _ {2} {A} _ {2} {\ overline {v} } _ {2} \\ [/ latex],

, где n 1 и n 2 — количество ответвлений в каждой из секций вдоль трубы.

Пример 3. Расчет скорости потока и диаметра сосуда: разветвление сердечно-сосудистой системы

Аорта — это главный кровеносный сосуд, по которому кровь покидает сердце и циркулирует по всему телу. (а) Рассчитайте среднюю скорость кровотока в аорте, если скорость потока составляет 5,0 л / мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. Когда скорость кровотока в аорте составляет 5,0 л / мин, скорость кровотока в капиллярах составляет около 0.33 мм / с. Учитывая, что средний диаметр капилляра составляет 8,0 мкм м, рассчитайте количество капилляров в системе кровообращения.

Стратегия

Мы можем использовать [latex] Q = A \ overline {v} \\ [/ latex] для расчета скорости потока в аорте, а затем использовать общую форму уравнения непрерывности для расчета количества капилляров как всех другие переменные известны. {2} \ left (0.{9} \ text {capillaries} \\ [/ latex].

Обсуждение

Обратите внимание, что скорость потока в капиллярах значительно снижена по сравнению со скоростью в аорте из-за значительного увеличения общей площади поперечного сечения капилляров. Эта низкая скорость предназначена для того, чтобы дать достаточно времени для эффективного обмена, хотя не менее важно, чтобы поток не становился стационарным, чтобы избежать возможности свертывания. Кажется ли разумным такое большое количество капилляров в организме? В активной мышце обнаруживается около 200 капилляров на мм 3 , или около 200 × 10 6 на 1 кг мышцы.На 20 кг мышц это составляет примерно 4 × 10 9 капилляров.

Сводка раздела

  • Расход Q определяется как объем V , протекающий через момент времени t , или [латекс] Q = \ frac {V} {t} \\ [/ latex], где V объем и т время.
  • Единица объема в системе СИ — м 3 .
  • Другой распространенной единицей измерения является литр (л), который составляет 10 -3 м 3 .
  • Расход и скорость связаны соотношением [латекс] Q = A \ overline {v} \\ [/ latex], где A — площадь поперечного сечения потока, а [латекс] \ overline {v} \\ [ / латекс] — его средняя скорость.
  • Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть

[латекс] \ begin {case} Q_ {1} & = & Q_ {2} \\ A_ {1} v_ {1} & = & A_ {2} v_ {2} \\ n_ {1} A_ {1 } \ bar {v} _ {1} & = & n_ {2} A_ {2} \ bar {v} _ {2} \ end {case} \\ [/ latex].

Концептуальные вопросы

1. В чем разница между расходом и скоростью жидкости? Как они связаны?

2. На многих рисунках в тексте показаны линии тока. Объясните, почему скорость жидкости максимальна там, где линии тока находятся ближе всего друг к другу.(Подсказка: рассмотрите связь между скоростью жидкости и площадью поперечного сечения, через которую она протекает.)

3. Определите, какие вещества несжимаемы, а какие нет.

Задачи и упражнения

1. Каков средний расход бензина в см 3 / с на двигатель автомобиля, движущегося со скоростью 100 км / ч, если он составляет в среднем 10,0 км / л?

2. Сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5,00 л / мин. (a) Преобразуйте это в см 3 / с.(b) Какова эта скорость в м 3 / с?

3. Кровь перекачивается из сердца со скоростью 5,0 л / мин в аорту (радиусом 1,0 см). Определите скорость кровотока по аорте.

4. Кровь течет по артерии радиусом 2 мм со скоростью 40 см / с. Определите скорость потока и объем, который проходит через артерию за 30 с.

5. Водопад Хука на реке Вайкато — одна из самых посещаемых природных достопримечательностей Новой Зеландии (см. Рис. 3).В среднем река имеет скорость потока около 300 000 л / с. В ущелье река сужается до 20 м в ширину и в среднем 20 м в глубину. а) Какова средняя скорость реки в ущелье? b) Какова средняя скорость воды в реке ниже водопада, когда она расширяется до 60 м, а глубина увеличивается в среднем до 40 м?

Рис. 3. Водопад Хука в Таупо, Новая Зеландия, демонстрирует скорость потока. (Источник: RaviGogna, Flickr)

6. Основная артерия с площадью поперечного сечения 1.00 см 2 разветвляется на 18 артерий меньшего размера, каждая со средней площадью поперечного сечения 0,400 см 2 . Во сколько раз снижается средняя скорость крови при переходе в эти ветви?

7. (a) Когда кровь проходит через капиллярное русло в органе, капилляры соединяются, образуя венулы (маленькие вены). Если скорость кровотока увеличивается в 4 раза, а общая площадь поперечного сечения венул составляет 10,0 см 2 , какова общая площадь поперечного сечения капилляров, питающих эти венулы? (б) Сколько вовлечено капилляров, если их средний диаметр равен 10.0 мкм м?

8. Система кровообращения человека насчитывает примерно 1 × 10 9 капиллярных сосудов. Каждый сосуд имеет диаметр около 8 мкм м. Предполагая, что сердечный выброс составляет 5 л / мин, определите среднюю скорость кровотока через каждый капиллярный сосуд.

9. (a) Оцените время, которое потребуется для наполнения частного бассейна емкостью 80 000 л с использованием садового шланга со скоростью 60 л / мин. (b) Сколько времени потребуется для заполнения, если вы сможете перенаправить в него реку среднего размера, текущую на высоте 5000 м 3 / с?

10.Скорость потока крови через капилляр с радиусом 2,00 × 10 -6 составляет 3,80 × 10 9 . а) Какова скорость кровотока? (Эта малая скорость дает время для диффузии материалов в кровь и из нее.) (B) Если предположить, что вся кровь в организме проходит через капилляры, сколько их должно быть, чтобы нести общий поток 90,0 см 3 / с? (Полученное большое количество является завышенной оценкой, но все же разумно.)

11. (a) Какова скорость жидкости в пожарном шланге с 9.Диаметр 00 см, пропускающий 80,0 л воды в секунду? б) Какая скорость потока в кубических метрах в секунду? (c) Вы бы ответили иначе, если бы соленая вода заменила пресную воду в пожарном шланге?

12. Диаметр главного всасывающего воздуховода воздухонагревателя составляет 0,300 м. Какова средняя скорость воздуха в воздуховоде, если его объем равен объему внутреннего пространства дома каждые 15 минут? Внутренний объем дома эквивалентен массивному прямоугольному массиву шириной 13,0 м на 20.0 м в длину на 2,75 м в высоту.

13. Вода движется со скоростью 2,00 м / с по шлангу с внутренним диаметром 1,60 см. а) Какая скорость потока в литрах в секунду? (b) Скорость жидкости в сопле этого шланга составляет 15,0 м / с. Каков внутренний диаметр сопла?

14. Докажите, что скорость несжимаемой жидкости через сужение, например, в трубке Вентури, увеличивается на коэффициент, равный квадрату коэффициента уменьшения диаметра. (Обратное применимо к потоку из сужения в область большего диаметра.)

15. Вода выходит прямо из крана диаметром 1,80 см со скоростью 0,500 м / с. (Из-за конструкции крана скорость потока не меняется.) (A) Какова скорость потока в см 3 / с? (b) Каков диаметр ручья на 0,200 м ниже крана? Пренебрегайте эффектами поверхностного натяжения.

16. Необоснованные результаты Горный ручей имеет ширину 10,0 м и среднюю глубину 2,00 м. Во время весеннего стока сток в ручье достигает 100 000 м 3 / с.а) Какова средняя скорость потока в этих условиях? б) Что неразумного в этой скорости? (c) Что неразумно или непоследовательно в помещениях?

Глоссарий

расход:
сокращенно Q , это объем V , который проходит мимо определенной точки в течение времени t , или Q = V / t
литр:
единица объема, равная 10 −3 м 3

Избранные решения проблем и упражнения

1.2,78 см 3 / с

3. 27 см / с

5. (а) 0,75 м / с (б) 0,13 м / с

7. (а) 40.0 см 2 (б) 5.09 × 10 7

9. (а) 22 ч (б) 0,016 с

11. (а) 12,6 м / с (б) 0,0800 м 3 / с (в) Нет, не зависит от плотности.

13. (а) 0,402 л / с (б) 0,584 см

15. (а) 128 см 3 / с (б) 0,890 см

онлайн-курсов PDH. PDH для профессиональных инженеров. ПДХ Инжиниринг.

«Мне нравится широта ваших курсов по HVAC; не только экологичность или экономия энергии

курсов.

Russell Bailey, P.E.

Нью-Йорк

«Это укрепило мои текущие знания и научило меня еще нескольким новым вещам.

, чтобы познакомить меня с новыми источниками

информации.

Стивен Дедак, П.E.

Нью-Джерси

«Материал был очень информативным и организованным. Я многому научился, и они были

.

очень быстро отвечает на вопросы.

Это было на высшем уровне. Будет использовать

снова. Спасибо. «

Blair Hayward, P.E.

Альберта, Канада

«Простой в использовании веб-сайт. Хорошо организованный. Я действительно буду снова пользоваться вашими услугами.

проеду по вашей компании

имя другим на работе. «

Roy Pfleiderer, P.E.

Нью-Йорк

«Справочные материалы были превосходными, и курс был очень информативным, особенно потому, что я думал, что уже знаком с

с деталями Канзас

Городская авария Хаятт »

Майкл Морган, П.E.

Техас

«Мне очень нравится ваша бизнес-модель. Мне нравится просматривать текст перед покупкой. Я нашел класс

.

информативно и полезно

на моей работе »

Вильям Сенкевич, П.Е.

Флорида

«У вас большой выбор курсов, а статьи очень информативны. You

— лучшее, что я нашел.»

Russell Smith, P.E.

Пенсильвания

«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, давая время на просмотр

материал. «

Хесус Сьерра, П.Е.

Калифорния

«Спасибо, что позволили мне просмотреть неправильные ответы. На самом деле

человек узнает больше

от сбоев.»

John Scondras, P.E.

Пенсильвания

«Курс составлен хорошо, и использование тематических исследований является эффективным.

способ обучения »

Джек Лундберг, P.E.

Висконсин

«Я очень впечатлен тем, как вы представляете курсы, т. Е. Разрешение

студент для ознакомления с курсом

материала до оплаты и

получает викторину.»

Арвин Свангер, П.Е.

Вирджиния

«Спасибо за то, что вы предложили все эти замечательные курсы. Я определенно выучил и

получил огромное удовольствие «.

Мехди Рахими, П.Е.

Нью-Йорк

«Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска.

на связи

курса.»

Уильям Валериоти, P.E.

Техас

«Этот материал в значительной степени оправдал мои ожидания. По курсу было легко следовать. Фотографии в основном обеспечивали хорошее наглядное представление о

.

обсуждаемых тем ».

Майкл Райан, P.E.

Пенсильвания

«Именно то, что я искал. Потребовался 1 балл по этике, и я нашел его здесь.»

Джеральд Нотт, П.Е.

Нью-Джерси

«Это был мой первый онлайн-опыт получения необходимых мне кредитов PDH. Это было

информативно, выгодно и экономично.

Я очень рекомендую

всем инженерам. »

Джеймс Шурелл, П.Е.

Огайо

«Я понимаю, что вопросы относятся к« реальному миру »и имеют отношение к моей практике, и

не на основании какой-то непонятной раздел

законов, которые не применяются

по «нормальная» практика.»

Марк Каноник, П.Е.

Нью-Йорк

«Отличный опыт! Я многому научился, чтобы перенести его на свой медицинский прибор.

организация «

Иван Харлан, П.Е.

Теннесси

«Материалы курса имели хорошее содержание, не слишком математическое, с хорошим акцентом на практическое применение технологий».

Юджин Бойл, П.E.

Калифорния

«Это был очень приятный опыт. Тема была интересной и хорошо изложенной,

а онлайн-формат был очень

Доступно и просто

использовать. Большое спасибо. «

Патрисия Адамс, P.E.

Канзас

«Отличный способ добиться соответствия требованиям PE Continuing Education в рамках ограничений по времени лицензиата.»

Джозеф Фриссора, P.E.

Нью-Джерси

«Должен признаться, я действительно многому научился. Помогает иметь распечатанный тест во время

обзор текстового материала. Я

также оценил просмотр

предоставлено фактических случаев «

Жаклин Брукс, П.Е.

Флорида

«Документ» Общие ошибки ADA при проектировании объектов «очень полезен.

испытание действительно потребовало исследования в

документ но ответы были

в наличии. «

Гарольд Катлер, П.Е.

Массачусетс

«Я эффективно использовал свое время. Спасибо за широкий выбор вариантов.

в транспортной инженерии, что мне нужно

для выполнения требований

Сертификат ВОМ.»

Джозеф Гилрой, П.Е.

Иллинойс

«Очень удобный и доступный способ заработать CEU для моих требований PG в Делавэре».

Ричард Роудс, P.E.

Мэриленд

«Я многому научился с защитным заземлением. До сих пор все курсы, которые я прошел, были отличными.

Надеюсь увидеть больше 40%

курса со скидкой.»

Кристина Николас, П.Е.

Нью-Йорк

«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду возможности сдать дополнительный

курса. Процесс прост, и

намного эффективнее, чем

придется путешествовать. «

Деннис Мейер, P.E.

Айдахо

«Услуги, предоставляемые CEDengineering, очень полезны для Professional

Инженеры получат блоки PDH

в любое время.Очень удобно »

Пол Абелла, P.E.

Аризона

«Пока все отлично! Поскольку я постоянно работаю матерью двоих детей, у меня мало

время искать где

получить мои кредиты от. «

Кристен Фаррелл, P.E.

Висконсин

«Это было очень познавательно и познавательно.Легко для понимания с иллюстрациями

и графики; определенно делает это

легче поглотить все

теории »

Виктор Окампо, P.Eng.

Альберта, Канада

«Хороший обзор принципов работы с полупроводниками. Мне понравилось пройти курс по

.

мой собственный темп во время моего утром

метро проезд

на работу.»

Клиффорд Гринблатт, П.Е.

Мэриленд

«Просто найти интересные курсы, скачать документы и взять

викторина. Я бы очень рекомендовал

вам на любой PE, требующий

CE единиц. «

Марк Хардкасл, П.Е.

Миссури

«Очень хороший выбор тем из многих областей техники.»

Randall Dreiling, P.E.

Миссури

«Я заново узнал то, что забыл. Я также рад оказать финансовую помощь

по ваш промо-адрес электронной почты который

сниженная цена

на 40%. «

Конрадо Казем, П.E.

Теннесси

«Отличный курс по разумной цене. Воспользуюсь вашими услугами в будущем».

Charles Fleischer, P.E.

Нью-Йорк

«Это был хороший тест и фактически подтвердил, что я прочитал профессиональную этику

кодов и Нью-Мексико

правила. «

Брун Гильберт, П.E.

Калифорния

«Мне очень понравились занятия. Они стоили потраченного времени и усилий».

Дэвид Рейнольдс, P.E.

Канзас

«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng

.

при необходимости дополнительно

аттестат. «

Томас Каппеллин, П.E.

Иллинойс

«У меня истек срок действия курса, но вы все же выполнили свое обязательство и дали

мне то, за что я заплатил — много

оценено! «

Джефф Ханслик, P.E.

Оклахома

«CEDengineering предлагает удобные, экономичные и актуальные курсы.

для инженера »

Майк Зайдл, П.E.

Небраска

«Курс был по разумной цене, материал был кратким, а

хорошо организовано. «

Глен Шварц, П.Е.

Нью-Джерси

«Вопросы подходили для уроков, а материал урока —

.

хороший справочный материал

для деревянного дизайна. «

Брайан Адамс, П.E.

Миннесота

«Отлично, я смог получить полезные рекомендации по простому телефонному звонку.»

Роберт Велнер, П.Е.

Нью-Йорк

«У меня был большой опыт работы в прибрежном строительстве — проектирование

Building курс и

очень рекомендую .»

Денис Солано, P.E.

Флорида

«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики Нью-Джерси были очень хорошими.

хорошо подготовлены. »

Юджин Брэкбилл, P.E.

Коннектикут

«Очень хороший опыт. Мне нравится возможность загружать учебные материалы на

.

обзор везде и

всякий раз, когда.»

Тим Чиддикс, P.E.

Колорадо

«Отлично! Поддерживаю широкий выбор тем на выбор».

Уильям Бараттино, P.E.

Вирджиния

«Процесс прямой, никакой ерунды. Хороший опыт».

Тайрон Бааш, П.E.

Иллинойс

«Вопросы на экзамене были зондирующими и демонстрировали понимание

материала. Полная

и комплексное ».

Майкл Тобин, P.E.

Аризона

«Это мой второй курс, и мне понравилось то, что мне предлагали курс

поможет по моей линии

работ.»

Рики Хефлин, П.Е.

Оклахома

«Очень быстро и легко ориентироваться. Я определенно буду использовать этот сайт снова».

Анджела Уотсон, П.Е.

Монтана

«Легко выполнить. Никакой путаницы при подходе к сдаче теста или записи сертификата».

Кеннет Пейдж, П.E.

Мэриленд

«Это был отличный источник информации о солнечном нагреве воды. Информативный

и отличный освежитель ».

Луан Мане, П.Е.

Conneticut

«Мне нравится подход, когда я могу зарегистрироваться и читать материалы в автономном режиме, а затем

Вернуться, чтобы пройти викторину «

Алекс Млсна, П.E.

Индиана

«Я оценил объем информации, предоставленной для класса. Я знаю

это вся информация, которую я могу

использование в реальных жизненных ситуациях »

Натали Дерингер, P.E.

Южная Дакота

«Обзорные материалы и образец теста были достаточно подробными, чтобы позволить мне

успешно завершено

курс.»

Ира Бродский, П.Е.

Нью-Джерси

«Веб-сайт прост в использовании, вы можете скачать материал для изучения, а потом возвращаться

и пройдите викторину. Очень

удобно а на моем

собственный график «

Майкл Глэдд, P.E.

Грузия

«Спасибо за хорошие курсы на протяжении многих лет.»

Деннис Фундзак, П.Е.

Огайо

«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH

сертификат. Спасибо за создание

процесс простой. »

Фред Шейбе, P.E.

Висконсин

«Положительный опыт.Быстро нашел курс, который соответствовал моим потребностям, и закончил

один час PDH в

один час. «

Стив Торкильдсон, P.E.

Южная Каролина

«Мне понравилась возможность скачать документы для проверки содержания

и пригодность, до

имея платить за

материал .»

Ричард Вимеленберг, P.E.

Мэриленд

«Это хорошее напоминание об ЭЭ для инженеров, не занимающихся электричеством».

Дуглас Стаффорд, П.Е.

Техас

«Всегда есть возможности для улучшения, но я ничего не могу придумать в вашем

.

процесс, которому требуется

улучшение.»

Thomas Stalcup, P.E.

Арканзас

«Мне очень нравится удобство участия в викторине онлайн и получение сразу

сертификат. «

Марлен Делани, П.Е.

Иллинойс

«Учебные модули CEDengineering — это очень удобный способ доступа к информации по номеру

.

много разные технические зоны за пределами

своя специализация без

надо ехать.»

Гектор Герреро, П.Е.

Грузия

Программное обеспечение для расчета падения давления в трубах


Pipe Flow Software также имеет веб-сайт по адресу www.pipeflow.com (на котором в настоящее время имеется дополнительная информация)

Программа Pipe Flow Expert: Расчет расхода и падения давления в трубе Попробуйте Pipe Flow Expert прямо сейчас!
Pipe Flow Software Отзывы: «Отличное программное обеспечение», «Отличная поддержка» Купить и лицензировать в
Загрузите программное обеспечение Pipe Flow Expert для бесплатной пробной версии: узнайте, почему оно используется более чем в 100 странах мира


 Pipe Flow Expert ™
Рассчитайте потерю давления и расход в трубопроводных системах.Программное обеспечение моделирует открытые / замкнутые контуры, компоненты и кривые насосов. Включает базу данных по жидкостям и трубам.

Расширенные вычисления
Улучшенный интерфейс

Решить трубопроводные сети
  • До 1000 труб
  • Расчет расхода
  • Падение давления в трубе
  • Системы рециркуляции
  • Характеристики насоса и NPSHa
  • Регулирование расхода и требования

    • Интерактивные результаты
    Изометрический 3D-чертеж
    Новые примеры систем



    Цены указаны в британских фунтах стерлингов: 1 фунт стерлингов.00 фунтов стерлингов составляет примерно 1,40 доллара США или примерно 1,19 евро.



    		 Программа Pipe Flow Wizard ™
    для «Что если?» расчеты расхода жидкости и газа в трубе. Найдите перепад давления в трубе, расход, диаметр или длину трубы. База данных жидкостей включена.    		 Калькулятор потери давления
  • Жидкости и газы
  • Вкл.Сжатый воздух
  • Расчет расхода в трубе
  • Расчет падения давления
  • Расчет длины трубы
  • Расчет диаметра трубы



    • Программа Pipe Flow Advisor ™
    Flow Advisor рассчитывает время опорожнения резервуара и расход воды в каналах с помощью уравнения укомплектования персоналом.
    Расход в каналах …
    		Для каналов и резервуаров
  • Трубы с частичным заполнением
  • Открытый канал потока
  • Расход воды
  • Резервуар пустой раз
  • Объем и вместимость
  • Масса и расширение

    • Бесплатное программное обеспечение ИЛИ
    Купить фирменную версию

    		 Конвертировать 123
    Преобразование между множеством различных единиц и измерений, включая площадь, плотность, энергию, расход, силу, длину, массу и т. Д.
    Преобразование единиц …
    		Продвигайте свое имя
    Получите фирменную версию
  • Наш логотип удален
  • Ваше имя добавлено
  • Ваш логотип добавлен
  • Ссылки на ваш веб-сайт
  • Отдайте свою версию
  • One Fee. Неограниченное использование.
    • Рекламное программное обеспечение

    Give-Away с вашим именем. Единовременная плата за брендирование и неограниченное использование.


    Все цены указаны без НДС.

    USA : НДС НЕ ОБЯЗАН при покупке в США.

    За пределами Европейского Союза : НДС НЕ ВЗИМАЕТСЯ при покупках за пределами ЕС. (Европейский Союз).

    Европейский Союз : НДС НЕ ОБЯЗЫВАЕТСЯ при покупках, совершаемых предприятиями в Европейском Союзе.
    Необходимо предоставить VRN компании (регистрационный номер плательщика НДС) (или другое подтверждение хозяйственной деятельности).

    Великобритания : НДС взимается со всех покупок в Великобритании.

    Лицензии сайта : Если вам требуется несколько копий определенной программы, мы можем предоставить
    значительных скидок на дополнительные экземпляры. Свяжитесь с нами по электронной почте нам с вашими требованиями, чтобы получить цитату.

    Pipe Flow Software для профессиональных инженеров используется более чем в 100 странах мира, более чем 3000 компаниями и консультантами, где бы ни возникла необходимость в расчетах.


    Калькулятор скорости воды — Дюймовый калькулятор

    Введите расход и диаметр трубы, чтобы рассчитать скорость проходящей через нее воды.

    Как рассчитать скорость воды

    Скорость воды — это мера скорости воды, протекающей по замкнутой системе трубопроводов. [1] Скорость воды можно найти по простой формуле:

    v = QA

    Таким образом, скорость v равна расходу Q , деленному на площадь A поперечного сечения.

    При использовании этой формулы все единицы должны быть в одной форме. Если скорость потока измеряется в кубических метрах в секунду, тогда площадь должна быть в квадратных метрах, а если скорость потока измеряется в кубических футах в секунду, тогда площадь должна быть в квадратных футах.

    Площадь поперечного сечения трубы можно найти по формуле:

    A = πr²

    Площадь A равна π, умноженному на квадрат радиуса r .

    Например, , давайте найдем скорость воды при скорости потока 35 кубических футов в секунду и трубе диаметром 1 дюйм.

    Начните с определения площади поперечного сечения трубы.

    Диаметр в футах = 1 ″ ÷ 12 = 0,0833333333 ′
    Радиус = 0,0833333333 ′ ÷ 2 = 0,0416666667 ′
    Площадь = π × 0,0416666667²
    A = π × 0,001736111111111
    A = 0,005454152777778 кв. Футов

    Затем рассчитайте скорость.

    v = 350,005454152777778
    v = 6417,1 фут3 / с

    Альтернативная формула

    Приведенная выше формула отлично работает, когда расход измеряется в кубической форме стандартной единицы длины.Но когда расход измеряется в галлонах в минуту или литрах в минуту, все становится немного сложнее.

    В этом случае начните с преобразования скорости потока в кубические футы в секунду или кубические метры в секунду.

    В качестве альтернативы, если скорость потока измеряется в галлонах в минуту, для расчета скорости воды можно использовать следующую формулу.

    v = 0,408 × QD²

    Таким образом, скорость v в футах в секунду равна 0,408 скорости потока Q в галлонах в минуту, деленной на диаметр трубы D в дюймах в квадрате. [2]

    Например, , давайте найдем скорость воды при скорости потока 15 галлонов в минуту и ​​трубе диаметром 0,75 дюйма.

    Начните с определения площади поперечного сечения трубы.

    v = 0,408 × 150,75²
    v = 0,408 × 150,5625
    v = 6,120,5625
    v = 10,88

    Таким образом, скорость воды внутри трубы диаметром 0,75 дюйма при расходе 15 галлонов в минуту равна 10,88 фут / с.

    Непрерывность для жидкостей

    Когда жидкости движутся по полной трубе, объем жидкости, поступающей в трубу, должен равняться объему жидкости, покидающей трубу, даже если диаметр трубы изменяется.Это повторение закона сохранения массы жидкостей.

    Объем жидкости, движущейся по трубе в любой точке, можно количественно выразить с помощью объемного расхода, который равен площади трубы в этой точке, умноженной на скорость жидкости. Этот объемный расход должен быть постоянным по всей трубе, поэтому вы можете записать уравнение неразрывности для жидкостей (также известное как уравнение неразрывности жидкости) как:

    Это уравнение говорит, что по мере уменьшения поперечного сечения трубы скорость жидкости увеличивается, а по мере увеличения поперечного сечения скорость жидкости уменьшается.Возможно, вы сами применили это, поливая цветы из садового шланга. Если вы хотите увеличить скорость воды, выходящей из конца шланга, вы кладете большой палец на часть отверстия шланга, эффективно уменьшая площадь поперечного сечения конца шланга и увеличивая скорость выходящей воды!

    Вопрос: Вода течет по водоводу сечением 0,4 м 2 со скоростью 6 м / с.Рассчитайте скорость воды в трубе, когда труба сужается до площади поперечного сечения 0,3 м. 2 .

    Ответ:

    Вопрос: Вода поступает в обычный садовый шланг диаметром 1,6 см со скоростью 3 м / с. Рассчитайте скорость выхода воды из садового шланга, когда к концу шланга прикреплена насадка диаметром 0,5 см.

    Ответ: Сначала определите площади поперечного сечения входной (A 1 ) и выходной (A 2 ) сторон шланга.

    Затем примените уравнение неразрывности для жидкостей, чтобы найти скорость воды на выходе из шланга (v 2 ).

    Калькулятор расхода трубы

    | Уравнение Хейзена – Вильямса

    Используйте этот калькулятор расхода в трубе для анализа свойств воды , текущей в системе с гравитационной подачей. Вам нужно знать только диаметр трубы, материал, из которого она сделана, ее длину и перепад высоты.Затем мы применяем для вас уравнение Хазена-Вильямса , которое вычисляет результирующую скорость и расход. Заинтересованы? Читайте дальше, чтобы узнать, какие формулы мы используем, и увидеть простой пример расчета.

    Что такое гравитационный поток?

    Самотечный поток воды — это когда поток воды в трубе вызван силой тяжести. Течение будет происходить до тех пор, пока существует разница высот между источником воды (выше по течению) и точкой сброса.Также не должно быть никакой внешней энергии (например, от насоса), используемой для перемещения воды вперед.

    Наш калькулятор расхода воды учитывает частный случай гравитационного потока, когда вода течет в закрытой трубе. На его скорость влияют не только наклон и размер трубы, но и материал, из которого сделана труба — его шероховатость вызывает трение между сторонами трубы и водой, уменьшая скорость воды.

    Уравнение Хазена-Вильямса

    Уравнение Хазена-Вильямса — это эмпирически выведенная формула, описывающая скорость воды в гравитационном потоке.Помните, что уравнение Хазена-Вильямса действительно только для воды — его применение для любой другой жидкости даст вам неточные результаты. Он также не учитывает температуру воды и является точным только для диапазона 40–75 ° F (4–25 ° C).

    Вы можете записать эту формулу как:

    v = k * C * R 0,63 * S 0,54

    где:

    • v обозначает скорость воды, текущей в трубе (в м / с для метрической системы и фут / с для британской системы мер)
    • C — коэффициент шероховатости
    • R означает гидравлический радиус (в метрах или футах в зависимости от системы единиц)
    • S — наклон энергетической линии (потеря напора на трение на длину трубы).Он безразмерный, но иногда выражается в м / м.
    • k — коэффициент преобразования, зависящий от системы единиц (k = 0,849 для метрической системы и k = 1,318 для британской системы)

    Вам не нужно знать значения C , R или S , чтобы использовать наш калькулятор расхода трубы — мы рассчитаем их для вас!

    Коэффициент шероховатости C зависит от материала трубы. Вы можете выбрать материал из раскрывающегося списка или ввести значение C вручную, если вам известен коэффициент шероховатости вашей проточной системы.Мы используем следующие значения:

    Материал Коэффициент шероховатости
    Чугун 100
    Бетон 110
    Медь 140
    Пластик 150
    Сталь 120

    Гидравлический радиус , R, — это пропорция между площадью и периметром вашей трубы.Если труба круглая, вы найдете ее в соответствии со следующим уравнением:

    R = A / P = πr² / 2πr = r / 2 = d / 4

    , где r — радиус трубы, а d — диаметр трубы. Вы можете просмотреть и изменить все эти параметры (площадь, периметр, гидравлический радиус) в расширенном режиме этого калькулятора расхода трубы.

    Чтобы рассчитать уклон , S, , необходимо разделить длину трубы на перепад (разница высот между начальной и конечной точками).Помните, что если наклон трубы непостоянен, а постоянно меняется, реальная скорость потока воды будет отличаться от полученного результата.

    Если вы знаете скорость гравитационного потока, вы также можете найти расход , Q, , умножив площадь поперечного сечения трубы на скорость потока:

    Q = A * v

    Обязательно используйте наш калькулятор расхода для преобразования расхода (объемного расхода) и массового расхода.

    Скорость потока воды в трубе: пример

    Давайте воспользуемся калькулятором расхода в трубе, чтобы определить скорость и расход пластиковой трубы диаметром 0,5 фута. Длина трубы составляет 12 футов, а разница в высоте между начальной и конечной точками трубы равна 3 футам.

    1. Разделите диаметр на 2, чтобы найти радиус трубы.

      r = d / 2 = 0,5 / 2 = 0,25 фута

    2. Найдите площадь поперечного сечения трубы.

      A = πr² = π * 0,25² ≈ 0,1963 фут²

    3. Определите периметр трубы.

      P = 2πr = 2π * 0,25 ≈ 1,57 фута

    4. Разделите площадь на периметр, чтобы найти гидравлический радиус трубы.

      R = A / P = 0,1963 / 1,57 ≈ 0,125 фута

    5. Выберите «пластик» из выпадающего списка и запишите его коэффициент шероховатости.

      С = 150

    6. Разделите падение на длину трубы, чтобы рассчитать уклон.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *