Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона a
Высота h
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
Сторона a
Сторона b
Угол α° между сторонами a и b
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника по стороне и двум прилежащим углам
Сторона a
Угол β°
Угол
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию
Сторона a (a = b)
Сторона c
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
Боковая сторона a (a = b)
Угол α° между боковыми сторонами
9
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними
Боковая сторона a (a = b)
Основание треугольника c
Угол
10
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника по стороне
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанной окружности
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам
Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника через катет и угол
Сечения. Основные определения (ЕГЭ — 2021)
Основные определения (ЕГЭ — 2021)
P.S. Последний бесценный совет 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Площадь сечения треугольника формула — Морской флот
Открытый банк заданий по теме площадь сечения. Задания C2 из ЕГЭ по математике (профильный уровень)
Задание №1186
Условие
В правильном тетраэдре DABC с ребром 5 на рёбрах AD , BD и AC выбраны точки K , L и M соответственно так, что KD=MC=2, LD=4.
а) Постройте сечение тетраэдра плоскостью KLM .
б) Найдите площадь этого сечения.
Решение
а) Так как AK=AM=5-2=3, то riangle AKM равнобедренный.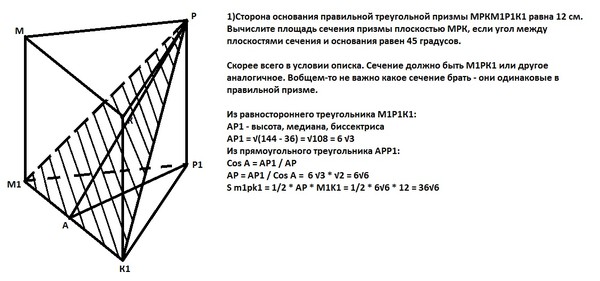 2-2cdot 2cdot 4cdot frac12= 12.
2-2cdot 2cdot 4cdot frac12= 12.
4. По теореме Пифагора LH= sqrt = sqrt <12-1>= sqrt <11>.
5. S_= frac12(KM+LN)cdot LH= frac12(3+1)cdot sqrt <11>= 2sqrt <11>.
Ответ
Задание №1185
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 сторона основания равна 9 , боковое ребро равно 14 . Точка K принадлежит ребру A_1B_1 и делит его в отношении 2:7, считая от вершины A_1.
а) Докажите, что сечение призмы плоскостью, проходящей через точки A , C и K , является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Решение
а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL parallel AC. Следовательно, искомым сечением будет трапеция AKLC .
KB_1parallel AB, B_1Lparallel BC, KLparallel AC. 2>= 10sqrt 2.
2>= 10sqrt 2.
AC=ABsqrt 2=9sqrt 2; KL =frac79AC=frac79cdot 9sqrt 2=7sqrt 2.
Так как трапеция AKLC — равнобедренная, имеем
Из riangle AKH,, KH= sqrt = sqrt <200-2>= sqrt <198>.
S_=frac2cdot KH,= 8sqrt 2cdot sqrt <198>=48sqrt <11>.
Ответ
Задание №1180
Условие
В правильной четырёхугольной призме ABCDA_1 B_1C_1 D_1 сторона основания равна 7 , а боковое ребро — 12 . На рёбрах A_1D_1, C_1D_1 и CB взяты точки F, К, L соответственно так, что A_1F=C_1K=CL=3.
а) Пусть P — точка пересечения плоскости FKL с ребром AB . Докажите, что FKLP — прямоугольник.
б) Найдите площадь сечения призмы плоскостью FKL.
Решение
а) Найдём положение точки P . Эта точка пересечения плоскости FKL и ребра AB, лежащего в плоскости ABCD.
Плоскость ABCD параллельна плоскости A_1B_1C_1D_1, в которой лежит отрезок KF. Плоскость FKL пересекает параллельные плоскости ABCD и A_1B_1C_1D_1 по параллельным прямым, отсюда KF parallel LP. 2>= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
2>= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
б) Пусть Q и R — точки пересечения прямой KF и прямых B_1C_1 и A_1B_1. Проведём прямые RL и QP , они пересекут рёбра CC_1 и AA_1 в точках M и N соответственно. Тогда RC_1=KC_1=CL, поэтому можно доказать, что равны треугольники RC_1M и MCL. Прямая RL , а значит, и плоскость FKL пересекают ребро CC_1 в его середине — точке M . Аналогично плоскость FKL пересекает ребро AA_1 в его середине —точке N .
В диагональном сечении CC_1A_1A, которое является прямоугольником, отрезок MN — средняя линия. В прямоугольнике MCAN противоположные стороны равны: MN=CA=7sqrt 2.
Сечение FKMLPN состоит из двух равных трапеций MKFN и MLPN , причём
мы доказали, что LK perp KF и LK perp LP. Высота каждой из этих трапеций равна frac2=frac<9sqrt 2>2.
S_< ext<сечения>>= 2S_= 2cdot frac2cdot frac2= (4sqrt 2+7sqrt 2)cdot frac<9sqrt 2>2= 99.
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на вы
Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади.
Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.
Справочно: число пи
Пример 1
Прямоугольный поднос имеет длину 900 мм и ширину 350 мм.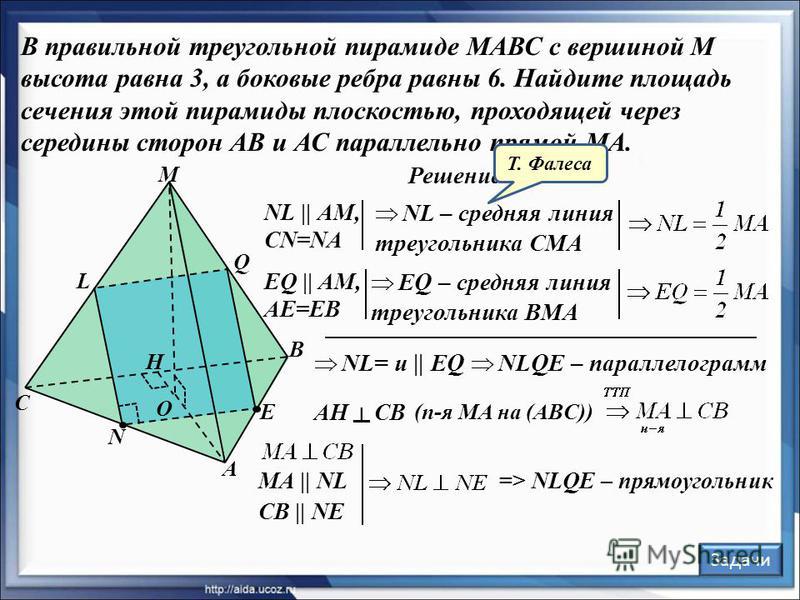 Определить его площадь в а) мм2, б) в см2, в) в м2
Определить его площадь в а) мм2, б) в см2, в) в м2
Решение:
а) Площадь =длина*ширина=900*350=315000 мм2
б) 1 см2=100 мм2, следовательно,
315000 мм2=315000/100=3150 см2
1 м2=10000 см2, следовательно,
3150 см2=3150/10000=0.315 м2
Пример 2
Определить площадь поперечного сечения балки, изображенной на рисунке.
Сечение балки можно разделить на три отдельных прямоугольника, как показано на рисунке
Sa=3*50=150 мм2
Sb=(65-5-3)*4=228 мм2
Sc=60*5=300 мм2
Общая площадь балки 150+228+300=678 мм2=6.78 см2.
Пример 3
Определить площадь дорожки, показанной на рисунке.
Решение:
Площадь дорожки = площадь большого прямоугольника — площадь малого прямоугольника
S=35*15-29*11=206 м2
Пример 4
Определить площадь параллелограмма, показанного на рисунке (размеры приведены в миллиметрах).
Площадь параллелограмма = основание * высота. Высота h определяется по теореме Пифагора BC2=CE2+h2
Тогда
202=(36-30)2+h2
h2=202-62=164
h=14,3 (приблизительно)
Следовательно, Sabcd=30*14.3=429 мм2
Пример 5
Показана боковая сторона здания. Определить площадь кирпичной кладки на боковой стороне.
Боковая сторона состоит из прямоугольника и треугольника.
Sпрям.=6*10=60 м2
S треуг. =1/2*основание*высота
CD=5 м, AD=6 м, следовательно, AC=3 м (по т. Пифагора). Следовательно,
S треуг. =1/2*10*3=15 м2.
Общая площадь кирпичной кладки есть 60+15=75 м2
Пример 6
Определить площади кругов, имеющих а) радиус 3 см, б) диаметр 10 мм, в) длину окружности 60 мм.
S=πr2 или πd2/4.
а) S=πr2=π(3)2=9π=28.26 см2
б) S=πd2/4=π(10)2/4=100π/4=78.5 мм2
в) Длина окружности с=2πr, следовательно,
r=c/2π=60/2π=30/π
S=πr2=π(30/π)2=286.62 мм2
Пример 7
Вычислить площадь правильного восьмиугольника со стороной 5 см и поперечником 10 см.
Восьмиугольник — это многоугольник с 8 сторонами. Если из центра многоугольника провести лучи к вершинам, получится восемь одинаковых треугольников.
S треуг. =1/2*основание*высота=1/2*5*10/2=12.5 см2
Площадь восьмиугольника есть 8*12.5=100 см2
Пример 8
Определить площадь правильного шестиугольника со стороной 10 см.
Шестиугольник — это многоугольник с шестью сторонами, который может быть разбит на шесть равных треугольников, как показано на рис. сходящиеся в центре многоугольника углы треугольника равны 360о/6=60о
Другие два угла каждого треугольника составляют в сумме 120о и равны между собой.
Следовательно, все треугольники являются равносторонними с углами 60о и стороной 10 см
S треуг. =1/2*основание*высота
Высоту h находим по теореме Пифагора:
102=h2+52
Отсюда h2=100-25=75
h=8.66 см
Следовательно, S треуг. =1/2*10*8.66=43.3 см 2
Площадь шестиугольника равна 6*43.3=259.8 см2
Построение сечений
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию.
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая \(a\), не лежащая в плоскости \(\pi\), параллельна некоторой прямой \(p\), лежащей в плоскости \(\pi\), то она параллельна данной плоскости.
2. Пусть прямая \(p\) параллельна плоскости \(\mu\). Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\), то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\).
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4.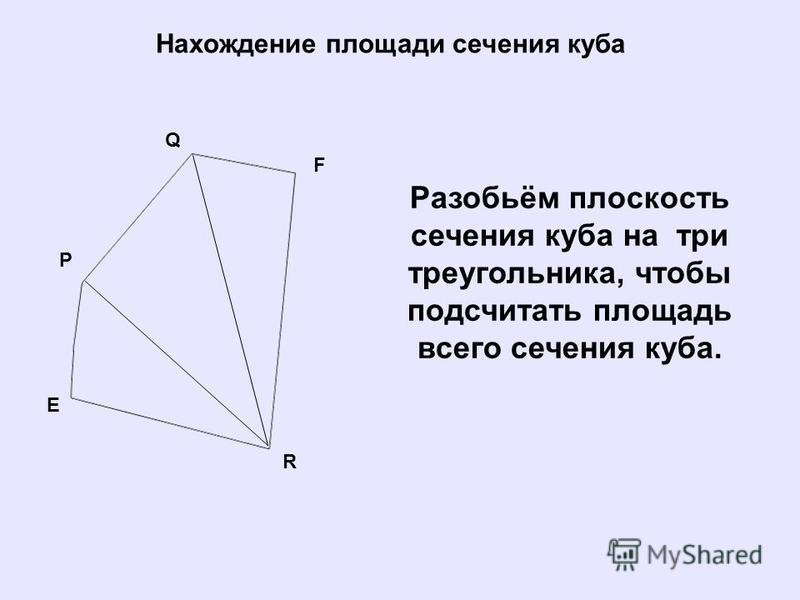 Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]
5. Пусть прямая \(l\) лежит в плоскости \(\lambda\). Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\), не лежащей на прямой \(l\), то прямые \(l\) и \(s\) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
7. Теорема о трех перпендикулярах.
Пусть \(AH\) – перпендикуляр к плоскости \(\beta\). Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\). Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.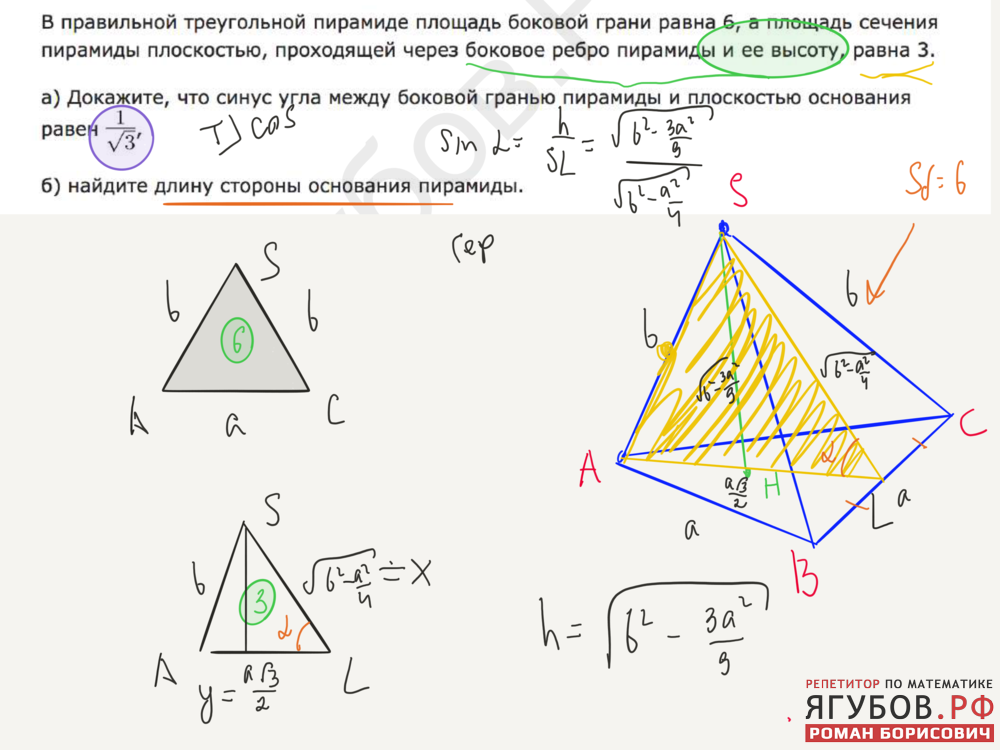
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA’\) и \(BB’\) (точки \(A’, B’\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A’B’\) – проекция прямой \(a\) на плоскость \(\mu\). Точка \(M=a\cap A’B’\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\).
Причем заметим, что все точки \(A, B, A’, B’, M\) лежат в одной плоскости.
Пример 1.
Дан куб \(ABCDA’B’C’D’\). \(A’P=\dfrac 14AA’, \ KC=\dfrac15 CC’\). Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\).
Решение
1) Т.к. ребра куба \(AA’, CC’\) перпендикулярны \((ABC)\), то точки \(A\) и \(C\) — проекции точек \(P\) и \(K\).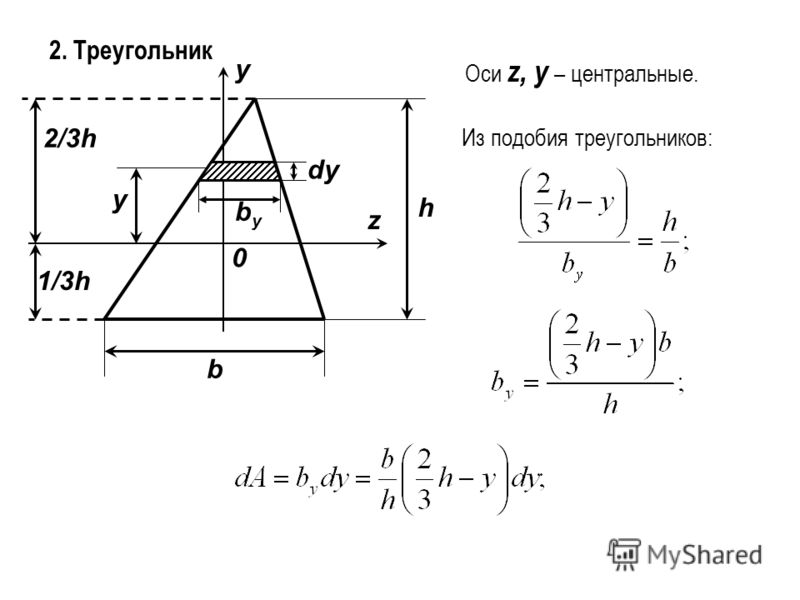 \circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
\circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
Если обозначить ребро куба за \(a\), то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\). Тогда:
\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]
Пример 2.
Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\), высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\), считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\), считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\).
Решение
1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\) пересечения медиан основания. Найдем проекцию прямой \(MN\) на плоскость \(ABC\). Т.к. \(DO\perp (ABC)\), то и \(NO\perp (ABC)\). Значит, \(O\) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\). Точка \(Q\) будет лежать на медиане \(AK\).
Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\). Точка \(Q\) будет лежать на медиане \(AK\).
Действительно, т.к. \(MQ\) и \(NO\) перпендикулярны \((ABC)\), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\) лежат в одной плоскости \(ADK\), то и точка \(Q\) будет лежать в этой плоскости. Но еще (по построению) точка \(Q\) должна лежать в плоскости \(ABC\), следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\).
Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\). \(L\) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\). \circ, \ \angle L\) – общий). Значит,
\circ, \ \angle L\) – общий). Значит,
\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]
Следовательно, \(OL>OK\), значит, точка \(L\) действительно лежит вне отрезка \(AK\).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\)).
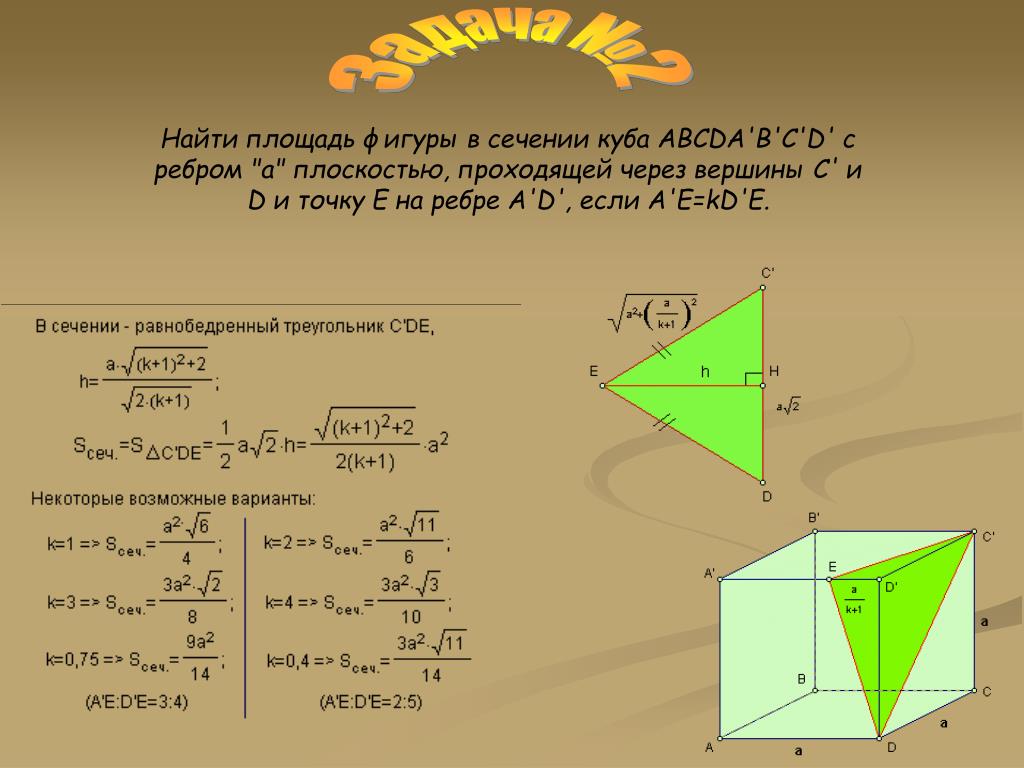
Пример 3
Дана правильная четырехугольная пирамида \(SABCD\). Найдите сечение пирамиды плоскостью \(\alpha\), проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\).
Решение
1) Обозначим середину ребра \(SA\) за \(M\).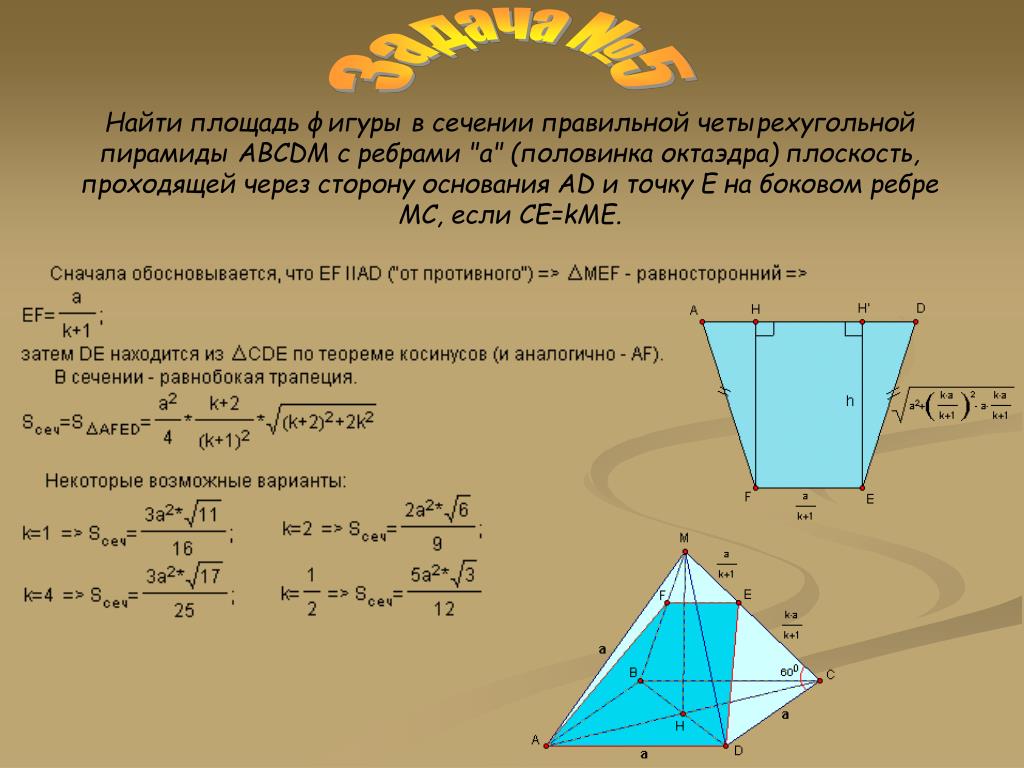 Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\). Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\).
Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\). Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\).
Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\), она должна содержать некоторую прямую, параллельную \(BD\). Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\). Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) (\(K\in SB, P\in SD\)). Тогда, соединив точки \(C, P, M, K\), получим сечение пирамиды плоскостью \(\alpha\).
2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\). Таким образом мы полностью определим построенное сечение.
Заметим, что так как \(KP\parallel BD\), то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\). Но \(SB=SD\), значит и \(SK=SP\). Таким образом, можно найти только \(SP:PD\).
Рассмотрим \(\triangle ASC\). \circ\), то \(\triangle
ABD=\triangle CBD\), следовательно, \(AD=CD\), следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\).
\circ\), то \(\triangle
ABD=\triangle CBD\), следовательно, \(AD=CD\), следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\).
Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\); наклонная \(BK\perp AC\), значит и проекция \(HK\perp AC\). Но мы уже определили, что \(DK\perp AC\). Таким образом, точка \(H\) лежит на отрезке \(DK\).
Соединив точки \(A\) и \(H\), получим отрезок \(AN\), по которому плоскость \(\alpha\) пересекается с гранью \(DAC\). Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\).
2) Определим точное положение точки \(N\) на ребре \(DC\).
Обозначим \(AB=CB=DB=x\). Тогда \(BK\), как медиана, опущенная из вершины прямого угла в \(\triangle ABC\), равна \(\frac12 AC\), следовательно, \(BK=\frac12 \cdot \sqrt2 x\).
Рассмотрим \(\triangle BKD\). Найдем отношение \(DH:HK\).
Заметим, что т.к. \(BH\perp (DAC)\), то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\). Тогда \(\triangle DBH\sim \triangle DBK\), следовательно
Тогда \(\triangle DBH\sim \triangle DBK\), следовательно
\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]
Рассмотрим теперь \(\triangle ADC\). Медианы треугольника точной пересечения делятся в отношении \(2:1\), считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\).
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора
Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = w × h
w = ширина
h = высота
Мы знаем, что w = 5 и h = 3 , поэтому:
Площадь = 5 × 3 = 15
Пример: Какова площадь этого круга?
Радиус = r = 3
| Площадь | = π × r 2 | |
| = π × 3 2 | ||
| = π × (3 × 3) | ||
| = 3.14159 … × 9 | ||
| = 28,27 (до 2 знаков после запятой) |
Пример: Какова площадь этого треугольника?
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Более сложный пример:
Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр
Сколько зарабатывает Сэм, обрабатывая эту область:
Разобьем область на две части:
Часть A — квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.
При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итого общая площадь:
Площадь = Площадь A + Площадь B = 400 м 2 + 140 м 2 = 540 м 2
Сэм зарабатывает 0,10 доллара за квадратный метр
Сэм зарабатывает = 0,10 доллара × 540 млн 2 = 54 доллара
Площадь треугольника (формула Герона) Калькулятор
- Цель использования
- ответов
- Комментарий / запрос
- вариант отображения результата в виде квадратного корня, кратного
[1] 2020/09/10 03:08 Мужской / До 20 лет / Высшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Проверка ответов
[2] 2020/08/11 18:10 Женский / До 20 лет / Начальная школа / Ученица неполной средней школы / Полезно /
- Цель использования
- Проверить результат
- Комментарий / запрос
- Отсутствует пошаговая визуализация
[3] 2020/08/10 20:00 Мужчина / 20-летний уровень / Средняя школа / Университет / аспирант / Немного /
- Цель использования
- Перекрестная проверка
[4] 2020/07/21 00:30 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Очень /
- 9 0002 [5] 2020/07/08 13:31 Мужчина / Моложе 20 лет / Средняя школа / Университет / Высшее образование / Очень /
- Цель использования
- Проверить работу
- Цель использования
- Проверка ответов
- Комментарий / запрос
- Отображение ответов в виде корней вместо длинных чисел
[6] 2020/07/ 07 00:56 Мужчина / До 20 лет / Начальная школа / Неполный средний класс / Полезно /
- Цель использования
- Проверка ответов
[7] 2020/07/05 13:03 Мужской / До 20 лет / Средняя школа / Университет / Аспирант / Полезно /
- Цель использования
- для землеустройства
[8] 2020/06/ 21 20:12 Мужчина / До 20 лет / Инженер / Очень /
- Назначение
- Перекрестная проверка.

- Комментарий / запрос
- Дайте окончательный ответ, используя корни, а не десятичные дроби …
[9] 2020/06/04 21:01 Мужчина / До 20 лет / Начальная школа / Младший школьник / Полезное /
- Комментарий / Запрос
- Вы можете улучшить, преобразовав в корневой формат
[10] 21.04.2020 15:58 Мужчина / До 20 лет / Средняя школа / Университет / Выпускник студент / Очень /
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Неравенства и отношения в треугольнике
Много информации можно получить даже из самых простых характеристик
треугольников. В этом разделе мы узнаем о
неравенства и отношения внутри треугольника, раскрывающего информацию
о сторонах и углах треугольника. Во-первых, давайте взглянем на два существенных неравенства.
которые характеризуют треугольники.
В этом разделе мы узнаем о
неравенства и отношения внутри треугольника, раскрывающего информацию
о сторонах и углах треугольника. Во-первых, давайте взглянем на два существенных неравенства.
которые характеризуют треугольники.
Неравенства треугольника
Напомним, что неравенство — это математическое выражение относительного размера или заказ двух предметов.В геометрии мы видим использование неравенств, когда говорим о длине сторон треугольника, или мера углов треугольника. Начнем изучение неравенств треугольника, рассмотрев теорему о неравенстве треугольника.
Теорема о неравенстве треугольника
Сумма длин двух сторон треугольника всегда должна быть больше, чем длина третьей стороны.
Давайте посмотрим, что означает эта теорема в терминах треугольника, который мы имеем ниже.
Теорема о неравенстве треугольника дает три неравенства:
Поскольку на рисунке выполнены все неравенства, мы знаем эти три длины сторон могут образовывать треугольник.
Важно понимать, что каждое неравенство должно выполняться. Если для некоторых причина, треугольник должен был иметь одну сторону, длина которой была больше, чем сумма две другие стороны, у нас будет треугольник с отрезком, который либо слишком короткий (чтобы треугольник не был замкнут) или слишком длинный (чтобы сторона треугольник выходит слишком далеко).
Не все наши неравенства на диаграмме выше. Начало координат
Начало координат
Поперечные сечения куба
Когда плоскость пересекает куб, получается множество форм поперечного сечения.
Последние пять из них (невырожденные случаи) проиллюстрированы ниже и на http://cococubed.asu.edu/images/raybox/five_shapes_800.png. Некоторые из них также показаны на видео ниже.
Можно использовать [1] для интерактивных экспериментов с поперечными сечениями, заданными точками на краях или гранях, в то время как [2] показывает, как завершить поперечное сечение геометрически, если заданы три точки на краях.
Давайте будем систематическими в определении свойств приведенных выше сечений. Во-первых, если плоскость параллельна ребру (любому из четырех параллельных ребер), поперечное сечение можно рассматривать как линию или прямоугольник с большим размером длины, чаще всего другим. Этот прямоугольник становится квадратом, если плоскость параллельна грани.
Этот прямоугольник становится квадратом, если плоскость параллельна грани.
Если плоскость не параллельна грани, мы можем установить систему координат, в которой единичный куб помещается в первый октант, выровненный с осями координат, а нормаль к плоскости имеет положительные координаты x, y и z.Другими словами, мы можем предположить, что плоскость имеет уравнение и пересекает точки и, где положительные.
Сечение удовлетворяет и неравенствам, и. Это можно считать пересечением двух регионов
, каждый из которых представляет собой остроугольный треугольник в той же плоскости (острый, потому что можно показать, что сумма квадратов любых двух сторон строго больше, чем квадрат третьей стороны). Обратите внимание, что треугольники имеют параллельные стороны, ограниченные парами параллельных граней куба.Следовательно, два треугольника противоположно подобны с центром подобия.
На следующей диаграмме показаны координаты вершин двух треугольников, которые в данном случае пересекаются в шестиугольнике.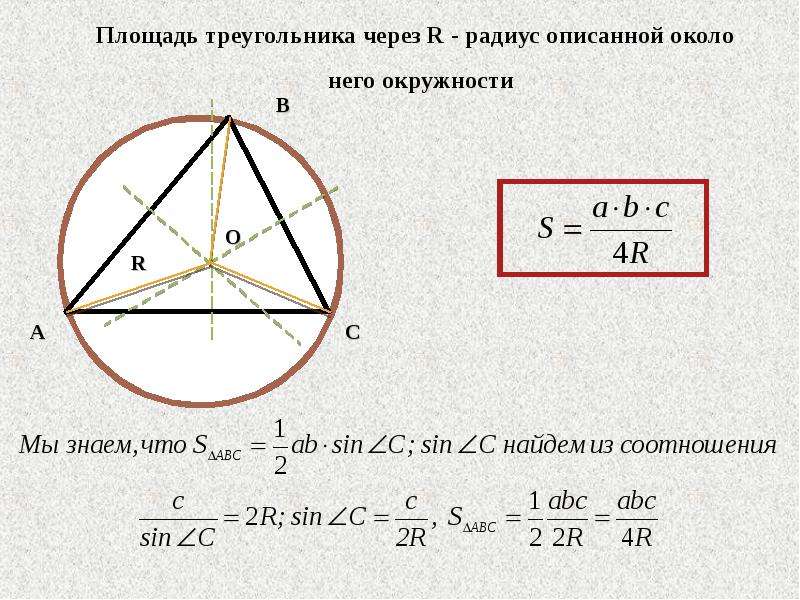
Центр подобия двух треугольников — это пересечение двух линий, соединяющих соответствующие стороны — это может быть точка, которая является пересечением диагонали единичного куба от начала координат (до) и плоскости.
Длины сторон треугольников и расстояния между соответствующими параллельными сторонами могут быть найдены с помощью теоремы Пифагора и показаны ниже для одной пары соответствующих сторон (остальные длины могут быть найдены путем циклической перестановки).
Подводя итог, можно сказать, что все возможные поперечные сечения куба, где плоскость не параллельна ребру, могут быть описаны пересечением двух противоположно подобных треугольников с соответствующими параллельными сторонами.
Тип полученного многоугольника зависит от того, какие вершины на рисунке ниже выбраны, что определяется значениями.
На этом рисунке выбрана вершина многоугольника поперечного сечения, если соблюдается связанное с ней ограничение.Красная вершина имеет конфликтующее ограничение с двумя соседними синими вершинами, поэтому можно выбрать либо красную точку, либо одну или несколько синих точек в этой области.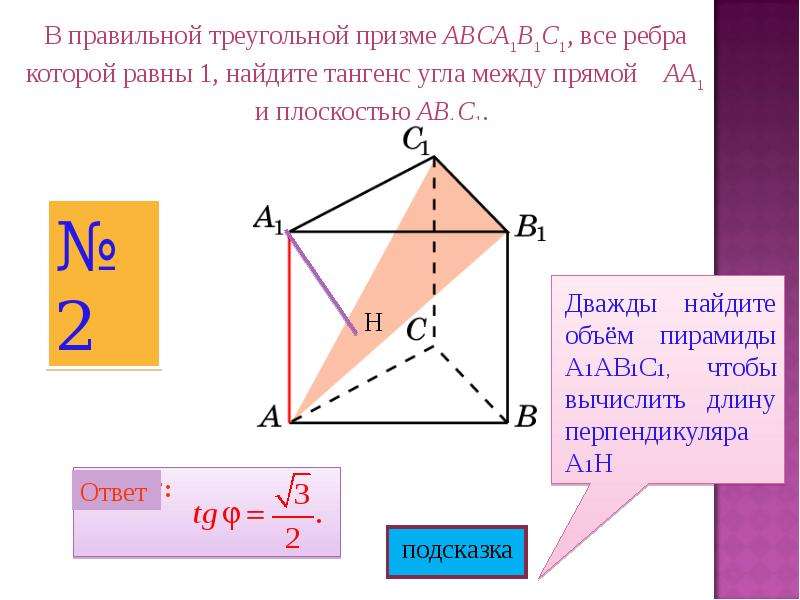 Обратите внимание, что для того, чтобы плоскость вообще пересекала куб, нам нужно находиться на другой стороне плоскости от начала координат, или, другими словами,.
Обратите внимание, что для того, чтобы плоскость вообще пересекала куб, нам нужно находиться на другой стороне плоскости от начала координат, или, другими словами,.
Давайте рассмотрим несколько примеров. Во-первых, если все больше 1, мы выбираем следующий треугольник.
Аналогичным образом, если все меньше 1, будет выбран противоположно подобный треугольник на красных вершинах.
Далее, если мы получим следующий параллелограмм.
Если мы получим либо пятиугольник (параллелограмм, усеченный в вершине), либо трапецию, в зависимости от того, или соответственно.
:
:
Наконец, если меньше 1 и больше 1, мы получаем шестиугольник.
Для получения подробной информации о вычислении площадей таких многоугольников обратитесь к [3], особенно к методу, применяющему принцип косинуса площадей, который связывает площадь фигуры с ее проекцией.Для расчета объемов, относящихся к областям, полученным по поперечному сечению, см.

 Основные определения (ЕГЭ — 2021)
Основные определения (ЕГЭ — 2021)