особенности величины, как найти её для круга
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой.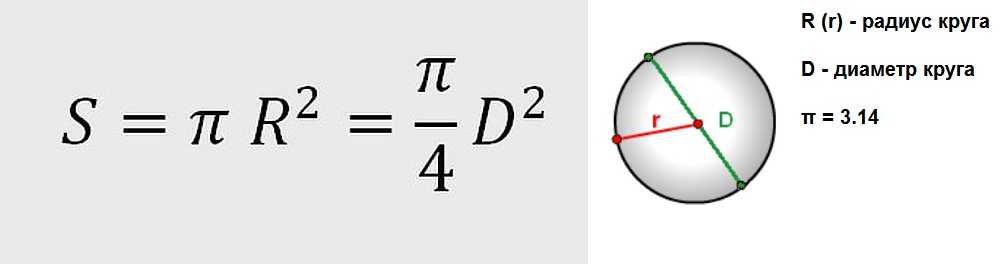
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга.
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью.
Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
Способов определения того, чему равна площадь круга, достаточно много.
Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».Площадь круга все формулы и примеры расчета
Площадь круга часто требуется рассчитать в различных задачах и это не только задачи по геометрии, иногда знать как рассчитывается площадь круга важно знать и в некоторых текстовых задачах алгебры. Итак, давайте разбираться.
Что такое площадь круга
Площадь круга — это мера заполненности области внутри окружности, являющейся границей круга, выраженная в квадратных единицах (м2, см2, кв.ед.). В математике эти единицы могут разными, в физике же если вы определяете площадь круга — вы должны указать единицы в системе СИ, а это м2.
Визуально, площадь круга это величина закрашенной области на рисунке:
Как можно найти площадь круга
Если дан радиус круга
Здесь все зависит от того, какие вам величины даны в самом начале.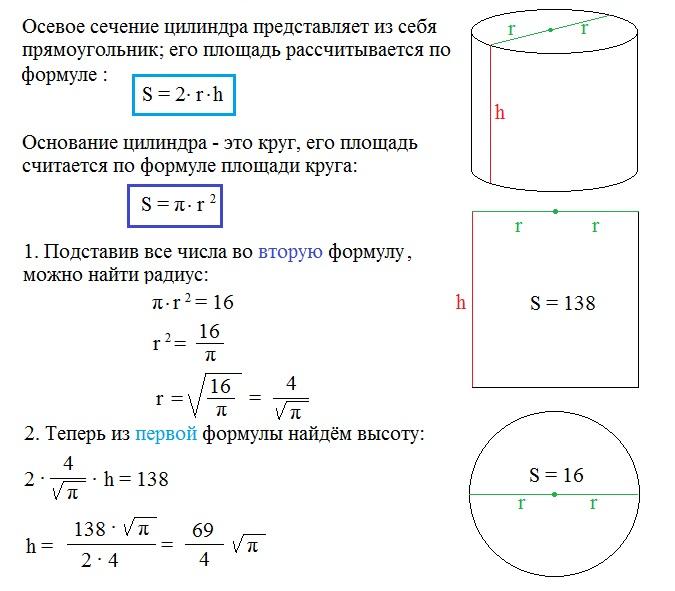
, (1)
— число . Число пи является одним из наиболее важных констант в математике, определяется как постоянное отношение длины окружности к ее диаметру в евклидовой плоскости. Другими словами:
π = длина окружности круга/диаметр этого круга.
Таким образом, приблизительное значение , наиболее известное, как: 3,14.
Это приблизительное значение, потому что число π — это то, что мы называем иррациональным числом. Оно не может быть записано как отношение двух целых чисел. Сегодня мы знаем более 12 000 миллиардов знаков после запятой. Однако до сих пор нет определенной модели, которая давала бы все эти значения.
Если дан диаметр круга
Если известен диаметр круга, то площадь круга можно найти по формуле:
. (2)
Если дана длина окружности
Так как длина окружности определяется по формуле: , то можно выразить радиус круга: . Тогда площадь: . (3)
Примеры расчета
Пример 1.
Рассчитать площадь круга, если известен радиус круга .
Решение: По формуле (1) находим .
Пример 2.
Найдите площадь, если дан диаметр круга .
Решение: По формуле (2) находим .
Вы видите, что находить площадь круга совсем не сложно, если известны все формулы и даны все необходимые для расчета величины.
Площадь круга — формулы, примеры расчетов
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π.
представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности.
Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Площадь круга — Википедия
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
История
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов.[1] Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге Измерение круга[en]. Длина окружности равна 2πr, а площадь треугольника равна половине основания на высоту, что даёт πr2. До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек[2] Однако он не установил константу пропорциональности.
Использование многоугольников
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту).
При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус.[3]
Доказательство Архимеда
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше
Круг с вписанными квадратом и восьмиугольником. Показан зазорПредположим, что площадь круга C больше площади треугольника T = 1⁄2cr. Пусть E означает превышение площади. Впишем[en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента.
Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
- E=C−T>GnPn=C−Gn>C−EPn>T{\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1⁄2nhs.
Но h < r и ns < c, так что площадь многоугольника должна быть меньше площади треугольника 1⁄2cr, получили противоречие.
Не меньше
Окружность с описанным квадратом и восьмиугольником. Показан зазорПредположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
- D=T−C>GnPn=C+Gn<C+DPn<T{\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}}
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.
е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Доказательство перегруппировкой
Площадь круга после перегруппировки Анимация перегруппировкиСледуя Сато Мошуну [4] и Леонардо да Винчи [5], мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда).
Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной πr и высотой r.
Приближения площади круга единичного радиуса перегруппировкой треугольников. многоугольник параллелограмм n сторона основание высота площадь 4 1,4142136 2,8284271 0,7071068 2,0000000 6 1,0000000 3,0000000 0,8660254 2,5980762 8 0,7653669 3,0614675 0,9238795 2,8284271 10 0,6180340 3,0901699 0,9510565 2,9389263 12 0,5176381 3,1058285 0,9659258 3,0000000 14 0,4450419 3,1152931 0,9749279 3,0371862 16 0,3901806 3,1214452 0,9807853 3,0614675 96 0,0654382 3,1410320 0,9994646 3,1393502 ∞ 1/∞ π 1 π
Интегрирование
Площадь круга путём интегрированияИспользуя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице.
{2}.\end{aligned}}}
Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:
- Area(r)=∫02πr
Формула площади круга
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность, а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
Формула расчёта площади круга
При необходимости площадь круга можно вычислить по формуле:
r – радиус круга
D – диаметр круга
S – площадь круга
π – 3.
14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг. К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг. Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга, а впервые они стали строиться еще во времена античности.
Само слово «circus» в переводе с латинского языка означает «круг». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна.
Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол», которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Площадь сечения сферы формула
Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия.
Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.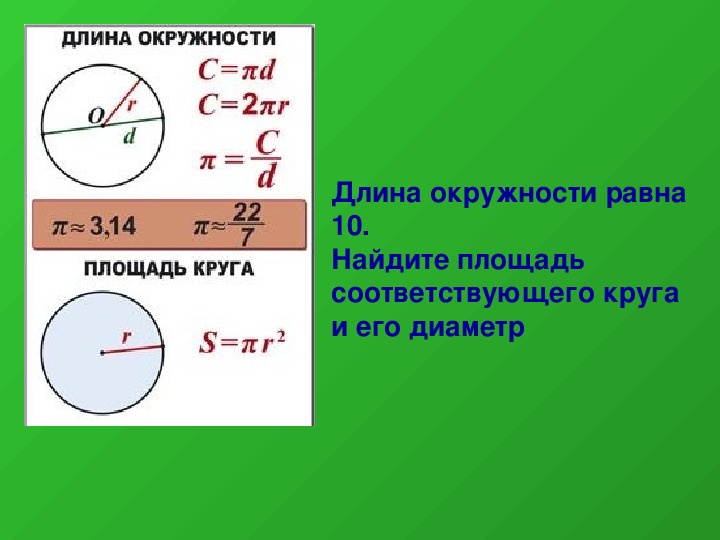
Сфера
Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.
Объем шара
Формула для вычисления объема шара имеет вид:
где R — радиус шара.
Если нужно найти объем шарового сегмента — воспользуйтесь формулой:
V сег=πh 2 (R-h/3), h — высота шарового сегмента.
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
где R — радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»
Сфера – это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Сечение сферы – это изображение фигуры, образованной рассечением сферы плоскостью в поперечном или продольном направлении.
Формула для расчета площади осевого сечения сферы:
S = π * d 2 / 4, где
d – осевой диаметр сферы.
Формула для расчета площади сечения сферы плоскостью:
S = π * d 2 / 4, где
d – диаметр окружности сферы в этой плоскости.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади сечения сферы, если известен диаметр сферы. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения сферы через любую плоскость сечения (площадь осевого сечения сферы и площадь сечения сферы плоскостью).
| Шар, сфера и их части |
| Площади сферы и ее частей. Объемы шара и его частей |
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1.
Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.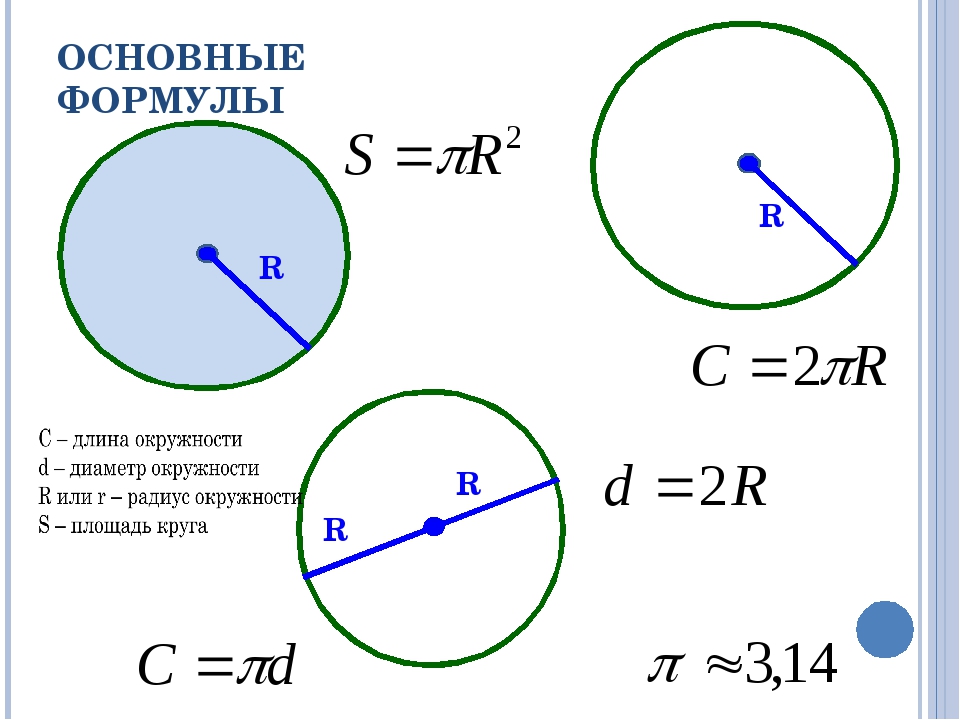
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера | Площадь сферы | ||
| Шар | Объем шара | ||
| Сферический пояс | Площадь сферического пояса | ||
| Шаровой слой | Объем шарового слоя | ||
| Сферический сегмент | Площадь сферического сегмента | ||
| Шаровой сегмент | Объем шарового сегмента | ||
| Шаровой сектор | Объем шарового сектора |
| Сфера |
где
r – радиус сферы.
где
r – радиус шара.
Площадь сферического пояса:
Площадь сферического пояса не зависит от радиусов r1 и r2 !
Объем шарового слоя:
Площадь сферического сегмента:
Объем шарового сегмента:
Объем шарового сектора:
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике , позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными».
Запись по телефону (495) 509-28-10
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
Площадь поперечного сечения в диаметре пересечение круга пересечение диаметр поперечного сечения электрический кабель формула проводника диаметр провода и расчетное сечение проводки и расчетное сечение AGW American Wire Gauge Толщина площади сплошного провода формула удельное сопротивление многожильный провод литц длина ток
Площадь поперечного сечения к диаметру преобразование круг пересечение поперечное сечение диаметр электрический кабель формула проводника диаметр провода и сечение проводки и расчетное сечение AGW American Wire Gauge толстая площадь сплошного провода формула удельное сопротивление многожильный провод длина литц ток — sengpielaudio Sengpiel BerlinПреобразование и расчет — поперечное сечение <> диаметр
● Диаметр кабеля по окружности площадь поперечного сечения и наоборот
электрический кабель , провод , провод , шнур , строка , проводка и веревка
Поперечное сечение — это просто двухмерный вид среза через объект. Часто задаваемый вопрос: как преобразовать диаметр круглого провода d = 2 × r в площадь поперечного сечения круга или площадь поперечного сечения A (плоскость среза) в кабель диаметр d ? Почему значение диаметра больше, чем значение площади? Потому что это не то же самое. Сопротивление обратно пропорционально площади поперечного сечения провода. Требуемое поперечное сечение электрической линии зависит от следующих факторов: 1) Номинальное напряжение.Чистая форма. (Трехфазный (DS) / AC (WS)) 2) Предохранитель — резервный восходящий поток = Максимально допустимый ток (А) 3) По расписанию передаваемая мощность (кВА) 4) Длина кабеля в метрах (м) 5) Допустимое падение напряжения (% от номинального напряжения) 6) Материал линии. Медь (Cu) или алюминий (Al) |
| Используемый браузер не поддерживает JavaScript. Вы увидите программу, но функция работать не будет.  |
«Единицей» обычно являются миллиметры, но также могут быть дюймы, футы, ярды, метры (метры),
или сантиметры, если за площадь принять квадрат этой меры.
Литц-провод (многожильный провод), состоящий из множества тонких проводов, требует на 14% большего диаметра по сравнению со сплошным проводом.
| Площадь поперечного сечения не диаметр. |
| Поперечное сечение — это площадь. Диаметр — это линейная мера. Это не может быть то же самое. Диаметр кабеля в миллиметрах — это не поперечное сечение кабеля в квадратных миллиметрах. |
Поперечное сечение или площадь поперечного сечения — это площадь такого разреза. Это не обязательно должен быть круг. Имеющийся в продаже размер провода (кабеля) как площадь поперечного сечения: 0,75 мм 2 , 1,5 мм 2 , 2,5 мм 2 , 4 мм 2 , 6 мм 2 , 10 мм 2 , 16 мм 2 . |
r = радиус провода или кабеля
d = 2 r = диаметр провод или кабель
Расчет диаметра d = 2 r , вход в сечение A :
Жила (электрокабель)
| Есть четыре фактора, которые влияют на сопротивление проводника: 1) площадь поперечного сечения проводника A , рассчитанная по диаметру d 2) длина проводника 3) температура в проводнике 4) материал, составляющий проводник |
Нет точной формулы для минимального сечения провода из максимального тока . Это зависит от многих обстоятельств, таких как, например, если расчет выполняется для постоянного, переменного тока или даже для трехфазного тока, свободно ли отпускается кабель или проложен под землей . Кроме того, это зависит от температуры окружающей среды, допустимой плотности тока и допустимого падения напряжения , а также от наличия одножильного или гибкого провода. И всегда есть хороший, но неудовлетворительный совет использовать по соображениям безопасности более толстый и, следовательно, более дорогой кабель .Общие вопросы касаются падения напряжения на проводах. |
Падение напряжения Δ В
Формула падения напряжения с удельным сопротивлением (удельным сопротивлением) ρ (rho):
I = Ток в амперах l = Длина провода (кабеля) в метрах (умноженная на 2, потому что всегда есть обратный провод) ρ = rho, удельное электрическое сопротивление (также известное как удельное электрическое сопротивление или объемное удельное сопротивление) меди = 0.  01724 Ом × мм 2 / м (также Ом × м) (Ом для l = длина 1 м и A = 1 мм 2 площадь поперечного сечения провода) ρ = 1/ σ A = Площадь поперечного сечения в мм 2 σ = сигма, электрическая проводимость (электропроводность) меди = 58 S · м / мм 2 |
|
Производная единица удельного электрического сопротивления в системе СИ ρ — Ом × м, сокращенная от
прозрачный Ω × мм / м.
Электропроводность, обратная величине удельного электрического сопротивления.
Электропроводность и электрическое сопротивление ρ = 1/ κ = 1/ σ
Разница между удельным электрическим сопротивлением и электропроводностью
| Проводимость в сименсах обратно пропорциональна сопротивлению в омах. |
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
| Значение электропроводности (проводимости) и удельного электрического сопротивления (удельное сопротивление) зависит от температуры материала постоянной.  В основном его дают при 20 или 25 ° C. |
Сопротивление = удельное сопротивление x длина / площадь
| Удельное сопротивление проводников изменяется с температурой. В ограниченном температурном диапазоне это примерно линейно: , где α — температурный коэффициент, T — температура и T 0 — любая температура, , например T 0 = 293,15 K = 20 ° C, при котором известно удельное электрическое сопротивление ρ ( T 0 ). |
Преобразование сопротивления в электрическую проводимость
Преобразование обратного сименса в ом
1 Ом [Ом] = 1 / сименс [1 / S]
1 сименс [S] = 1 / Ом [1 / Ом]
Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
1 миллисименс = 0,001 МО = 1000 Ом
| Математически проводимость является обратной или обратной величине сопротивления: Символ проводимости — заглавная буква «G», а единица измерения — мхо, что означает «ом», записанное наоборот. Позже блок MHO был заменен блоком на блок Siemens — сокращенно буквой «S». |
Калькулятор: закон Ома
Таблица типовых кабелей для громкоговорителей
| Диаметр кабеля d | 0.798 мм | 0,977 мм | 1,128 мм | 1,382 мм | 1.784 мм | 2,257 мм | 2.764 мм | 3.568 мм |
| Номинальное сечение кабеля A | 0,5 мм 2 | 0,75 мм 2 | 1,0 мм 2 | 1,5 мм 2 | 2,5 мм 2 | 4,0 мм 2 | 6,0 мм 2 | 10.0 мм 2 |
| Максимальный электрический ток | 3 А | 7,6 А | 10,4 А | 13,5 А | 18,3 А | 25 А | 32 А | – |
Всегда учитывайте, что поперечное сечение должно быть больше при большей мощности и большей длине кабеля
, но также и с меньшим сопротивлением. Вот таблица, в которой указаны возможные потери мощности.
| Длина кабеля в м | Сечение в мм 2 | Сопротивление Ом | Потеря мощности при | Коэффициент демпфирования при | ||
| Импеданс 8 Ом | Импеданс 4 Ом | Импеданс 8 Ом | Импеданс 4 Ом | |||
| 1 | 0.75 | 0,042 | 0,53% | 1,05% | 98 | 49 |
| 1,50 | 0,021 | 0,31% | 0,63% | 123 | 62 | |
| 2,50 | 0,013 | 0,16% | 0,33% | 151 | 75 | |
| 4,00 | 0,008 | 0,10% | 0,20% | 167 | 83 | |
| 2 | 0.75 | 0,084 | 1,06% | 2,10% | 65 | 33 |
| 1,50 | 0,042 | 0,62% | 1,26% | 85 | 43 | |
| 2,50 | 0,026 | 0,32% | 0,66% | 113 | 56 | |
| 4,00 | 0,016 | 0,20% | 0,40% | 133 | 66 | |
| 5 | 0.75 | 0,210 | 2,63% | 5,25% | 32 | 16 |
| 1,50 | 0,125 | 1,56% | 3,13% | 48 | 24 | |
| 2,50 | 0,065 | 0,81% | 1,63% | 76 | 38 | |
| 4,00 | 0,040 | 0,50% | 1,00% | 100 | 50 | |
| 10 | 0.75 | 0,420 | 5,25% | 10,50% | 17 | 9 |
| 1,50 | 0,250 | 3,13% | 6,25% | 28 | 14 | |
| 2,50 | 0,130 | 1,63% | 3,25% | 47 | 24 | |
| 4,00 | 0,080 | 1,00% | 2,00% | 67 | 33 | |
| 20 | 0.75 | 0,840 | 10,50% | 21,00% | 9 | 5 |
| 1,50 | 0,500 | 6,25% | 12,50% | 15 | 7 | |
| 2,50 | 0,260 | 3,25% | 6,50% | 27 | 13 | |
| 4,00 | 0,160 | 2,00% | 4,00% | 40 | 20 | |
Значения коэффициента демпфирования показывают, что осталось от принятого коэффициента демпфирования 200
в зависимости от длины кабеля, сечения и импеданса громкоговорителя.
Преобразование и расчет диаметра кабеля в AWG
и AWG в диаметр кабеля в мм — American Wire Gauge
| Чаще всего мы используем четные числа, например 18, 16, 14 и т. Д. Если вы получили нечетный ответ, например 17, 19 и т. Д., Используйте следующее меньшее четное число. AWG означает American Wire Gauge и указывает на прочность проводов. Эти номера AWG обозначают диаметр и, соответственно, поперечное сечение в виде кода. Используются только в США. Иногда номера AWG можно найти также в каталогах и технических данных в Европе. |
Американский калибр проводов — диаграмма AWG
| AWG номер | 46 | 45 | 44 | 43 | 42 | 41 | 40 | 39 | 38 | 37 | 36 | 35 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Диаметр дюйм | 0.0016 | 0,0018 | 0,0020 | 0,0022 | 0,0024 | 0,0027 | 0,0031 | 0,0035 | 0,0040 | 0,0045 | 0,0050 | 0,0056 | 0,0063 |
| Диаметр (Ø) в мм | 0,04 | 0,05 | 0,05 | 0,06 | 0,06 | 0,07 | 0,08 | 0,09 | 0,10 | 0,11 | 0.13 | 0,14 | 0,16 |
| Поперечное сечение в мм 2 | 0,0013 | 0,0016 | 0,0020 | 0,0025 | 0,0029 | 0,0037 | 0,0049 | 0,0062 | 0,0081 | 0,010 | 0,013 | 0,016 | 0,020 |
| | |||||||||||||
| AWG номер | 33 | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 |
| Диаметр дюйм | 0.0071 | 0,0079 | 0,0089 | 0,0100 | 0,0113 | 0,0126 | 0,0142 | 0,0159 | 0,0179 | 0,0201 | 0,0226 | 0,0253 | 0,0285 |
| Диаметр (Ø) в мм | 0,18 | 0,20 | 0,23 | 0,25 | 0,29 | 0,32 | 0,36 | 0,40 | 0,45 | 0,51 | 0.57 | 0,64 | 0,72 |
| Поперечное сечение в мм 2 | 0,026 | 0,032 | 0,040 | 0,051 | 0,065 | 0,080 | 0,10 | 0,13 | 0,16 | 0,20 | 0,26 | 0,32 | 0,41 |
| | |||||||||||||
| AWG номер | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 |
| Диаметр дюйм | 0.0319 | 0,0359 | 0,0403 | 0,0453 | 0,0508 | 0,0571 | 0,0641 | 0,0719 | 0,0808 | 0,0907 | 0,1019 | 0,1144 | 0,1285 |
| Диаметр (Ø) в мм | 0,81 | 0,91 | 1.02 | 1,15 | 1,29 | 1,45 | 1,63 | 1,83 | 2,05 | 2.30 | 2.59 | 2,91 | 3,26 |
| Поперечное сечение в мм 2 | 0,52 | 0,65 | 0,82 | 1,0 | 1,3 | 1,7 | 2,1 | 2,6 | 3,3 | 4,2 | 5,3 | 6,6 | 8,4 |
| | |||||||||||||
| AWG номер | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 (1/0) (0) | 00 (2/0) (-1) | 000 (3/0) (-2) | 0000 (4/0) (-3) | 00000 (5/0) (-4) | 000000 (6/0) (-5) |
| Диаметр дюйм | 0.1443 | 0,1620 | 0,1819 | 0,2043 | 0,2294 | 0,2576 | 0,2893 | 0,3249 | 0,3648 | 0,4096 | 0,4600 | 0,5165 | 0,5800 |
| Диаметр (Ø) в мм | 3,67 | 4,11 | 4,62 | 5,19 | 5,83 | 6.54 | 7,35 | 8,25 | 9,27 | 10,40 | 11.68 | 13,13 | 14,73 |
| Поперечное сечение в мм 2 | 10,6 | 13,3 | 16,8 | 21,1 | 26,7 | 33,6 | 42,4 | 53,5 | 67,4 | 85,0 | 107,2 | 135,2 | 170,5 |
Как высокие частоты демпфируются длиной кабеля?
Площадь круга — формула и примеры
Площадь круга можно представить как количество квадратных единиц пространства, которое занимает круг.Это можно найти, используя радиус или диаметр, которые мы рассмотрим в примерах ниже. Мы также рассмотрим несколько примеров словесных задач, касающихся области, с которой вы можете столкнуться во время учебы.
объявление
Примеры нахождения площади круга
Мы будем использовать следующую формулу, чтобы найти площадь любого круга. Обратите внимание, что в этой формуле используется радиус, поэтому нам придется преобразовать, если вместо этого нам будет задан диаметр. Давайте посмотрим на оба случая.2 \). Кроме того, окончательный ответ можно записать в единицах \ (\ pi \) (\ (25 \ pi \) квадратных метров) или в десятичном приближении (75,5 квадратных метров). Какой из них вы используете, зависит от приложения и проблемы, над которой вы работаете.
Пример (заданный диаметр)
Найдите площадь круга диаметром 6 футов.
Решение
Радиус любого круга всегда равен половине диаметра. Поскольку диаметр круга 6 футов, радиус должен быть 3 фута (радиус всегда равен половине диаметра).2} \ end {align} \)
Как видите, важно обращать внимание на то, даны ли вам радиус или диаметр круга. Однако в некоторых задачах со словами это не всегда так ясно.
Задачи со словом, связанные с областью круга
Не каждая проблема, с которой вы столкнетесь, просто скажет «найдите место». В следующих двух примерах вы увидите другие типы вопросов, которые вам могут задать.
Пример
Джейсон рисует большой круг на стене своей новой квартиры.Наибольшее расстояние по кругу будет 8 футов. Примерно сколько квадратных футов стены покроет круг?
Решение
Всякий раз, когда вас просят определить количество квадратных футов, покрытых чем-либо, вы находите область. Чтобы найти площадь круга Джейсона, нам сначала нужно выяснить, был ли нам дан радиус или диаметр. По определению, диаметр круга — это наибольшее расстояние по кругу, поэтому мы знаем, что диаметр составляет 8 футов.2 \\ & = 16 \ pi \\ & \ ок \ bbox [граница: сплошной черный 1 пиксель; отступ: 2px] {50.2 \ text {квадратные футы}} \ end {align} \)
Итак, круг Джейсона будет покрывать около 50,2 квадратных футов его стены.
Пример
Площадь круга составляет \ (81 \ pi \) квадратных единиц. Каков радиус этого круга?
Решение
Чтобы ответить на этот вопрос, вам нужно немного запомнить алгебру. Воспользуйтесь формулой и подставьте известные вам значения. Затем найдите радиус \ (r \).2 = 81 \)
Извлеките квадратный корень, чтобы найти \ (r \). Поскольку это радиус, значение \ (r \) должно быть положительным.
\ (\ begin {align} r & = \ sqrt {81} \\ & = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {9} \ end {align} \)
Следовательно, радиус должен быть 9.
объявление
Сводка
Чтобы найти площадь круга, нужно применить формулу. Но будь осторожен! Вы всегда должны обращать внимание на информацию, которую вам дают, особенно в прикладных задачах.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
Площадь круга
ПЛОЩАДЬ КРУГА
Площадь круга означает поверхность, занимаемую кругом.
В приведенной выше форме часть, залитая красным цветом, называется областью круга.
Формула:
Площадь круга = π r 2
Здесь значение π приблизительно равно 22/7 или 3,14, а буква r известна как радиус круга.
Пример 1:
Найдите площадь круга, имеющего радиус 21 см.
Решение:
Формула для площади круга:
= πr 2
Заменить π = 22/7 и r = 21.
≈ (22/7) x 21 2
= (22/7) x 21 x 21
= 22 x 3 x 21
= 1386
Итак, площадь данного круга составляет около 1386 квадратных см.
Пример 2:
Найдите площадь круга диаметром 28 см.
Решение:
Дано: Диаметр = 28 см
Тогда радиус
= диаметр / 2
= 28/2
= 14 см
Формула площади круга
= Πr 2
Заменить π = 22/7 и r = 14.
≈ (22/7) x 14 2
= (22/7) x 14 x 14
= 22 x 2 x 14
= 616
Итак, площадь данного круга составляет около 616 кв. См.
Пример 3:
Если площадь круглой области составляет 3850 см 2 , найдите ее диаметр.
Решение:
Площадь круглой области = 616 см 2
πr 2 = 616
(22/7) r 2 = 616
Умножьте каждую сторону на 7/22.
r 2 = 616 x 7/22
r 2 = 28 x 7
r 2 = 196
r = 14 см
Тогда диаметр равен
= 2 x радиус
= 2 x 14
= 28 см
Пример 4:
Найдите площадь круга с окружностью 28π футов.
Решение:
Окружность круга = 28π футов
2πr = 28π
Разделите каждую сторону на 2π.
r = 14
Формула для площади круга:
= πr 2
Замените π = 22/7 и r = 14.
≈ (22/7) x 14 2
= (22/7) x 14 x 14
= 22 x 2 x 14
= 616
Итак, площадь данного круга составляет около 616 квадратных футов.
Пример 5:
Найдите длина веревки, за которую должна быть привязана коза, чтобы она могла пасти площадь 9856 квадратных метров.
Решение:
Область, на которой пасется коза, будет иметь форму круга. Тогда длина веревки, на которой привязана коза, будет радиусом.
Принято, что площадь выпаса козы составляет 9856 квадратных метров.
Тогда
πr 2 = 9856
Заменим π = 22/7.
(22/7) x r 2 = 9856
Умножьте каждую сторону на 7/22.
r 2 = 9856 x 7/22
r 2 = 448 x 7
r 2 = 3136
r = 56
Итак, длина веревки, на которой козел должен быть привязан 56 метров.
Помимо вышеперечисленного, если вам нужно что-то еще, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
v4formath@gmail.