Площадь круга в чем измеряется: Площадь параллелограмма

Площадь параллелограмма

Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.

Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Таблица с формулами площади параллелограмма (в конце страницы)

— Вычисления   (показано)   (скрыто)

— примечания   (показано)   (скрыто)

1

Площадь параллелограмма по основанию и высоте параллелограмма

.

.. подготовка …

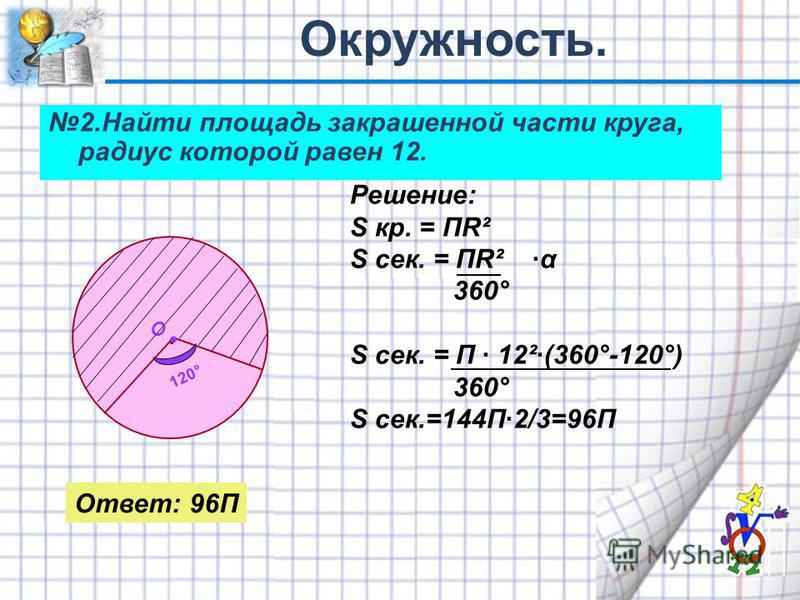
a — сторона

h — высота

---

2

Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

… подготовка …

b — сторона

h_b — высота

---

3

Площадь параллелограмма по двум сторонам и углу между ними

… подготовка …

a — сторона

b — сторона

α° — угол между сторонами

---

4

Площадь параллелограмма по двум диагоналям и углу между этими диагоналями

… подготовка …

d₁ — диагональ

d₂ — диагональ

α° — угол между диагоналями

---

5

Площадь параллелограмма по вписанной окружности и стороне

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

… подготовка …

a — сторона

r — радиус вписанной окружности

---

6

Площадь параллелограмма по вписанной окружности и углу между сторонами

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

… подготовка …

r — радиус вписанной окружности

α° — угол между сторонами

---

Примечание:

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

---

Таблица с формулами площади параллелограмма

---

Определения

Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.

Некоторые свойства параллелограмма:

• Сумма углов параллелограмма равна 360 градусов
• Сумма углов, прилегающих к любой из сторон равна 180 градусов
• Противоположные стороны параллельны и имеют одинаковую длину
• Противолежащие углы равны

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Радиус окружности — что такое, формула, как найти ⚪

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a² + b², где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Вместо скучных учебников ученики проходят интерактивные задания с автоматической проверкой, рисуют вместе с учителем на онлайн-доске и задают вопросы, которые бывает неловко спросить перед всем классом.

 

Как находить площадь круга

Большое количество точек расположенных на равном расстоянии от центра и находящиеся на одном расстоянии — образуют круг, плоскую фигуру. Радиус круга — это прямая которая соединяет середину круга с любой из точек находящейся в его окружности. При этом в одной окружности, какая бы точка не была, радиус будет одинаков. Диаметр круга — это отрезок исходящий от любой точки окружности, проходящий через середину круга и заканчивающийся в параллельной точке той же окружности.

Как находить площадь круга? Площадь круга находится с помощью формулы в которой участвует число ?.

Интересный факт: Числом ? представляется отношение между длиной окружности и длиной диаметра этой же окружности. При этом имеет постоянную величину. А как нам известно ?= 3,1415926 и стало применяться с 1737 года.

Заметка: Ни как не можете определиться, какую машину выбрать? В автосалоне москва автомобили с пробегом (http://center-carauto.ru/), вы сможете в комфортных условиях подобрать наилучший вариант и при этом сэкономить. Согласитесь, заманчивое предложение!

Как рассчитать площадь круга? Как и говорилось выше благодаря формуле, в которой участвует число ? и радиус, записывается так:

S = ?R²

Разберем для наглядности
Найдем площадь круга с помощью его радиуса который равен 4 см.
Площадь круга равна:
Решение
S= 3,14 * 4² = 3,14 * 16 = 50,24 кв/см

Так же площадь круга через диаметр находиться по формуле

S = (?/4)d²

Разберем для наглядности
Найдем площадь круга с помощью его диагонали. Возьмем радиус равный 4 см.
Решение
1) Вычислим диаметр, который больше радиуса в два раза.

d=2R
d = 2 * 4 =8
2) Подставляем значения в формулу
S =(3,14/4) * 8² = 0,785 * 64 = 50,24
Если сверить полученный ответ с предыдущим, то они равны.

Когда мы ищем площадь сегмента круга или сектора, очень помогает знание основных формул. С их помощью них можно узнавать не известные значения.
Сегментом — называется ограниченная часть круга, которую ограничивают хорда и дуга данного круга.
Как нам уже известно расчет площади круга вычисляется с использованием числа ? умноженного на радиус в квадрате. Используя длину окружности, мы сможем найти радиус.

R = (l/2)?

Если подставить эту формулу в формулу расчета площади., у нас получится:

S = ? ((l/2)?)² = l²/4?

Разберем для наглядности
Найти площадь круга с окружностью равной 8 см.
Решение
Используем формулу S= 8²/4*3,14 = 64 / 12,56 = 5 см

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Урок 76. длина окружности. площадь круга — Математика — 6 класс

Математика

6 класс

Урок № 76

Длина окружности. Площадь круга

Перечень рассматриваемых вопросов:

• окружность, круг и их элементы: радиус, диаметр, хорда;
• понятие длины окружности, площади круга;
• задачи на вычисление длины окружности и площади круга.

Тезаурус

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которую называют центром окружности.

Круг – это часть плоскости, ограниченная окружностью.

Радиус – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Хорда – это отрезок, соединяющий две точки окружности.

Диаметр – это хорда, проходящая через центр окружности.

Длина окружности вычисляется по формулам: С = πd или С = 2πR, где π ≈ 3, 14 – иррациональное число.

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Окружность

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которая называется центром окружности.

Элементы окружности: центр, радиус, диаметр.

Отрезок, соединяющий две точки окружности, называется хордой.

Диаметр – это хорда, проходящая через центр окружности.

Ещё в древности было установлено, что какой бы ни была окружность, отношение её длины к её диаметру является постоянным числом. Сейчас это число обозначают греческой буквой π. (читается – «пи»)

Как измерить дину окружности?

Можно взять сантиметровую ленту (если нет ленты, можно воспользоваться нитью или полоской бумаги).

Можно прокатить кольцо по ровной поверхности, сделав полный оборот.

Проверьте, верно ли, что отношение длины окружности к диаметру ≈ 3?

Возьмите несколько круглых предметов (тарелка, стакан, игрушечное колесо и др.).

Результаты измерений можно записать в таблицу в тетради.

Закон для более точного вычисления числа π очень сложен. В настоящее время значение π для точных расчётов в строительстве, авиационной или космической промышленности находят при помощи компьютера.

Вспомните, что π – это иррациональное число, которое выражается бесконечной непериодической дробью.

π = 3,141592653589793238…

При решении обычных задач используют приближенное значение

π ≈ 3,14

иногда используют π ≈ 3

Обозначим длину окружности буквой С, а её диаметр – буквой d, и запишем формулу:

Следовательно, справедливы формулы:

С = πd или С = 2πR

Круг – это часть плоскости, ограниченная окружностью.

С помощью числа π вычисляют площадь круга.

S = πR²

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

Впишите верный ответ.

Радиус круга равен 5 см. Найдите длину окружности С, площадь круга S.

Решение

С = 2πR = 2 ∙ 3,14 ∙ 5 = 31,4 (см).

S = πR² = 3,14 ∙ 5² = 3,14 ∙ 25 = 78,5 (см²).

Ответ: 31,4 см; 78,5 см.

Тип 2. Множественный выбор

Вычислите площади заштрихованных фигур (размер 1 клетки равен 1 см²).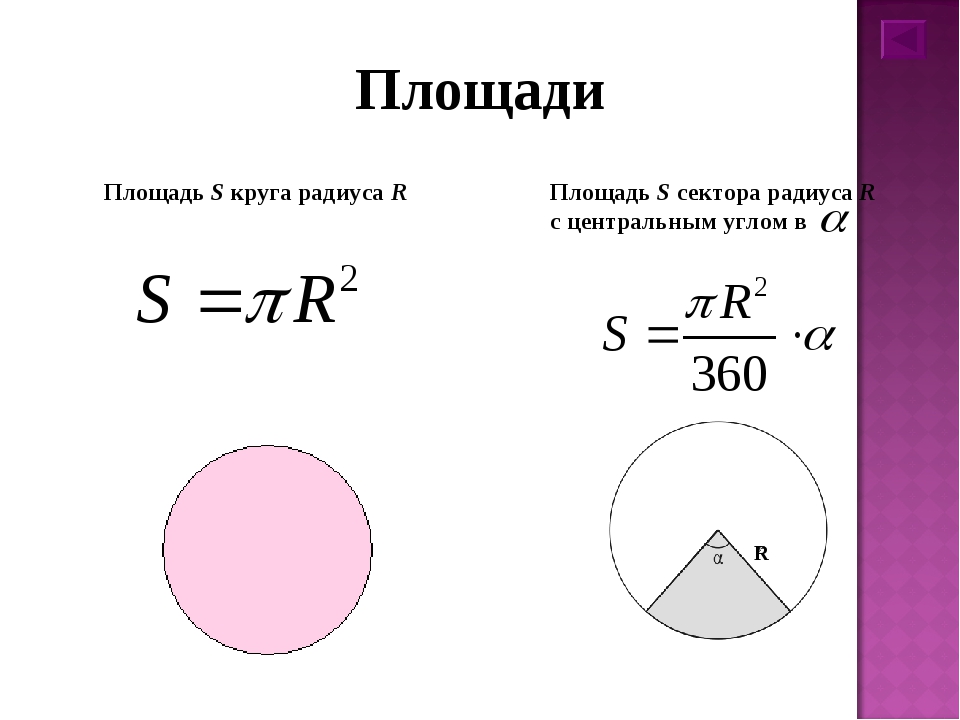

Варианты ответов

34,24 см²

84,78 см²

50,24 см²

113,04 см²

Фигура 1

Из круга вырезали квадрат.

S_круга = πR² = 3,14 ∙ 4² = 3,14 ∙ 16 = 50,24 (см²).

S_{квадрата} = а² = 4² = 16 (см²).

S_{заштрих} = 50,24 – 16 = 34,24 (см²).

Фигура 2

Из круга вырезали круг.

S₁ = πR² = 3,14 ∙ 6² = 3,14 ∙ 36 = 113,04 (см²).

S₂ = πR² = 3,14 ∙ 3² = 3,14 ∙ 9 = 28,26 (см²).

S_{заштрих} = 113,04 – 28,26 = 84,78 (см²).

Выбираем ответы: 34,24 см² и 84,78 см².

Что такое площадь в математике? Единицы площади :: SYL.ru

Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.

Что такое площадь в математике?

Площадь — это мера того, сколько пространства есть на плоской поверхности. Например, есть два одинаковых куска бумаги, чья суммарная площадь, очевидно, больше чем у каждого из них по отдельности.

Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.

Имеем ответ: 2 × 4 = 8 см². Задача решена.

Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.

Единица измерения площади в математике

Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см²«. Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.

Допустим имеем 9000 м². Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м². Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.

Пример

Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.

Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

S_квад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см².

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

S_круг = ∏ × 3 × 3 ≈ 28,26 см².

По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.

S_круг — S_квад = 28,26 — 9 = 19,26 см².

Ответ найден.

Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.

Площадь сектора круга

Содержание

1. Сектор круга
2. Как найти площадь сектора
3. Найдите радиус круга
4. Площадь сектора Формула
5. Площадь сектора Радианы
6. Площадь сектора круга Примеры
7. Длина дуги и площадь сектора

Сектор круга

Каждый раз, когда вы отрезаете кусок тыквенного пирога, круглого праздничного торта или круглой пиццы, вы удаляете сектор.Сектор образован центральным углом, образованным двумя радиусами, и включает в себя область внутри круга от этой центральной точки до самой окружности. Часть окружности окружности, ограниченная радиусами, дуга , является частью сектора.

Дуги окружности

Острые центральные углы всегда будут давать малые дуги и небольшие сектора. Когда центральный угол, образованный двумя радиусами, равен 90 °, сектор называется квадрантом (поскольку полный круг включает четыре квадранта, или четверти).Когда два радиуса образуют 180 ° или половину окружности, сектор называется полукругом и имеет большую дугу .

В отличие от треугольников, границы секторов , а не , установленные отрезками линий. Действительно, у вас есть два радиуса, образующие центральный угол, но часть окружности, которая составляет третью «сторону», изогнута, поэтому найти площадь сектора немного сложнее, чем найти площадь треугольника. Расстояние вдоль этой изогнутой «стороны» составляет длины дуги .

Как найти площадь сектора

Вы не можете найти площадь сектора, если не знаете радиус круга. Однако будьте осторожны; вы можете найти радиус, если у вас есть диаметр или окружность. Возможно, вам придется проделать небольшую предварительную математику, чтобы добраться до радиуса.

Найдите радиус окружности

Учитывая диаметр d окружности, радиус r равен:

г = d2

Учитывая длину окружности,

Измерительный круг ▷ Французский перевод

Измерительный круг ▷ Французский перевод — Примеры использования Измерительного круга в предложении на английском языке де мезюр месурер évaluer de mesurage мезурант

3D-геометрия — Площадь и объем поверхности. Вопросы и ответы.

Q.1. Если площадь круга равна объему сферы с одинаковыми радиусами, найдите радиус.

1. √3

2. √3 / 2

3. 1/2

4. 3/4

5. 1

Ответ и объяснение

Sol: Option 4
Пусть r будет радиусом, у нас есть
πr ² = 4/3 πr ³
⇒ r = 3/4

Q.2. Длина сада втрое больше его ширины. Детская площадка 180 кв.м занимает 1/15 общей площади сада.Длина сада составляет

1. 60 м

2. 30 м

3. 40 м

4. 50 м

5. 90 м

Ответ и объяснение

Sol: Option 5
Пусть L — длина, а B — ширина сада. Имеем L = 3B.
Общая площадь сада = 180 х 15 = 2700 кв.м. ⇒ LB = 2700
⇒ 3B ² = 2700 ⇒ B ² = 900 ⇒ B = 30 м
Следовательно, длина сада = 30 × 3 = 90 м

В.3. Периметр равностороннего треугольника 96√3 см. Найдите его высоту.

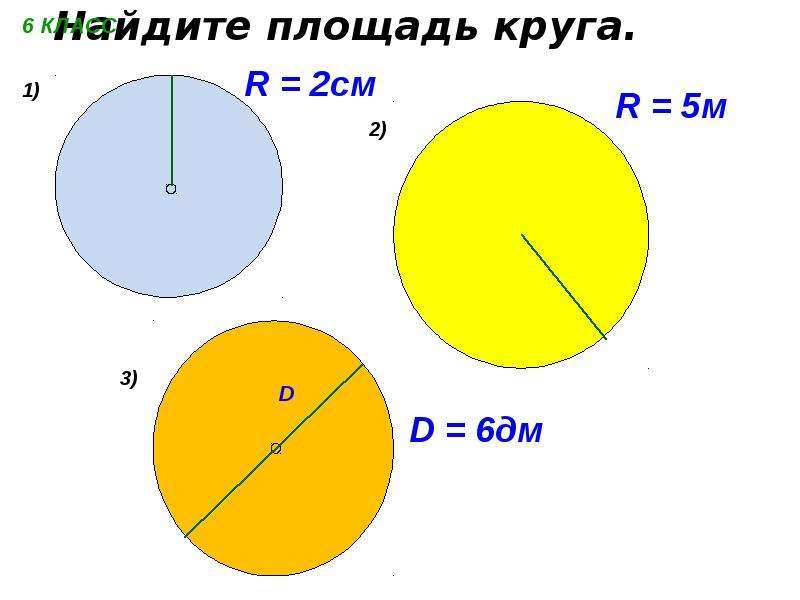
1. 32 см

2. 48 см

3. 16 см

4. 64 см

5. 24 см

Ответ и объяснение

Sol: Вариант 2
Периметр равностороннего треугольника 96√3 см.
Каждая сторона равностороннего треугольника равна 96√3 / 3 = 32√3 см.
Высота равностороннего треугольника будет = (√3 / 2) x 32√3 = 48см

В.4. Если соотношение радиусов двух сфер равно 4: 7, то соотношение их объемов равно

1. 4: 7

2. 64: 343

3. 49: 16

4. 16:49

5. Ни один из этих

Ответ и объяснение

Sol: Опция 2
Соотношение радиусов двух сфер 4: 7.
∴Отношение их объема = 4 ³ : 7 ³ = 64: 343

Q.5. Диаметр (в метрах) сферы объемом 268 (4/21) м ³ равен

1.6

2. 12

3. 8

4. 24

5. 16

Ответ и объяснение

Sol: опция 3
Объем сферы = 268 (4/21) = 5632/21 м ³ . Теперь 4/3 π ³ = 5632/21 ⇒ r ³ = (5632/21) x (3/4) x (7/22) = 64 ⇒ r = 4 м Следовательно, диаметр = 8 м

Обязательно прочтите статьи о трехмерной геометрии

Q.6. Наклонная высота правого кругового конуса 13 м, высота 5 м.Найдите площадь изогнутой поверхности.

1. 490,28 м ²

2. 288,28 м ²

3. 450м ²

4. 200 м ²

5. Ни один из этих

Ответ и объяснение

Sol: опция 1
Площадь криволинейной поверхности = πrl
Теперь r = √ (13 ² — 5 ² ) = √169 — 25 = √144 = 12 м
Требуемая площадь = (22/7 ) x 13 x 12 = 490,28 м ²

В.7. Соотношение объемов куба и сферы 6 / π. Найдите отношение стороны куба к радиусу сферы.

1. 2: 1

2. 3: 1

3. 4: 1

4. 5: 1

5. 1: 2

Ответ и объяснение

Sol: Option 1
Пусть сторона куба равна «a», а радиус сферы равен «r».
Теперь Объем куба = a ³
Объем сферы = 4 / 3π xr ³
a ³ / (4/3) π r ³ = 6 / π
a / r = 2/1
Следовательно, ответ 2: 1.

Q8. Каков радиус круга, если его длина численно равна четырехкратной площади?

1. 1/2

2. 3

3. 1

4. 4

5. 5

Ответ и объяснение

Sol: Option 1
Пусть ‘r’ будет радиусом окружности. Имеем 2πr = 4πr ² ⇒ r = 1/2

Q9. Найдите площадь равнобедренного треугольника со сторонами 10 см, 6 см и 6 см.

1. 25√11 кв. См.

2. √11 кв. См.

3. 5 кв. См.

4. 11 кв. См.

5. 5√11 кв. См.

Ответ и объяснение

Sol: опция 5
Полупериметр треугольника s = (10 + 6 + 6) / 2 = 11.
Площадь треугольника = √11 x (11-10) x (11-6) x (11 -6) = √11 x 5 x 5 = 5√11 см ²

Q10. Площадь поверхности сферы 616см ² . Найдите его радиус.

1. 8 см

2. 10 см

3. 9 см

4. 11 см

5. 7 см

Ответ и объяснение

Sol: Option 5
Пусть r будет радиусом сферы. Имеем
4πr ² = 616
4 × 22/7 × r ² = 616
r = 7

.