Единицы измерения объёма — Карта знаний
- Единицы измерения объёма — единицы измерения размера пространства, занимаемого твёрдым, сыпучим или жидким. В СИ объём измеряется в кубических метрах]] (м³, метр в кубе). Применяются также кратные и дольные приставки, увеличивающие или уменьшающие размер стандартной единицы — кубический сантиметр (10-6 м3), кубический дециметр(10-3 м3) и т. д.
Источник: Википедия
Связанные понятия
Дециметр (от деци- и метр) — дольная единица измерения расстояния в Международной системе единиц (СИ), равная ⅒ доле метра. Обозначения: русское «дм», международное «dm». Сантиме́тр (русское обозначение: см; международное: cm; устар. стм.) — единица длины в различных метрических системах мер, равная 0,01 метра.



Подробнее: Порядок величины (площадь)
Градуиро́вка (нем. graduiren «градуировать» от лат. gradus «шаг, ступень, степень») средств измерений, иногда тари́рование — метрологическая операция, при помощи которой средство измерений (меру или измерительный прибор) снабжают шкалой или градуировочной таблицей (кривой). Отметки шкалы должны с требуемой точностью соответствовать значениям измеряемой величины, а таблица (кривая) с требуемой точностью отражать связь эффекта на выходе прибора с величиной, подводимой ко входу (например, зависимость… Радлю́кс (обозначения: рлк, rlx) — единица светимости, равная люмену на квадратный метр (лм/м2).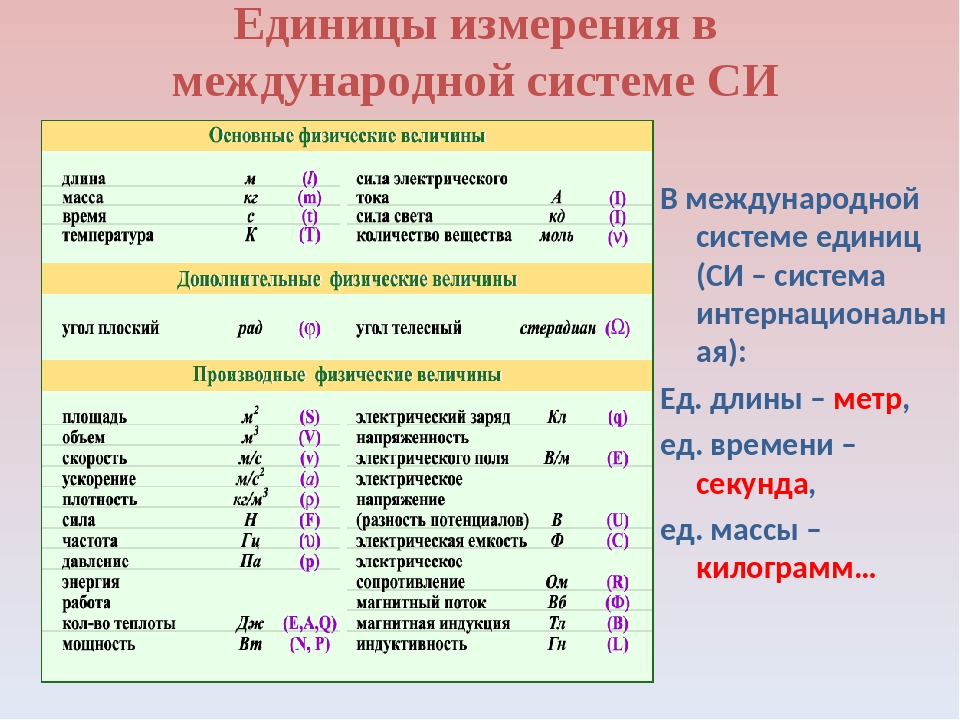



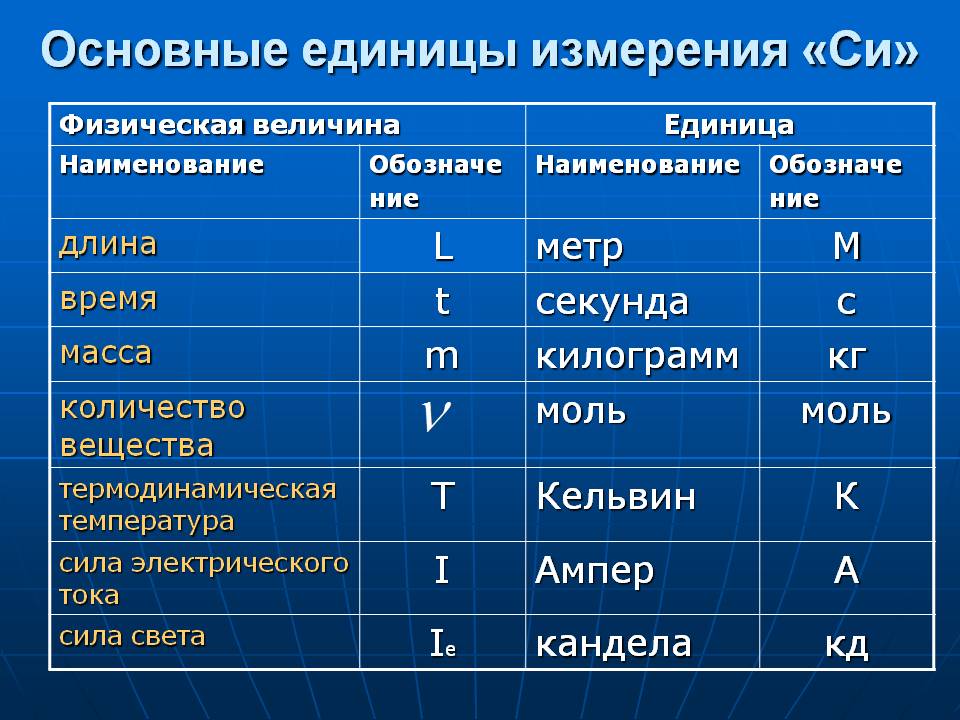 Физические величины имеют род, размер, единицу(измерения) и значение.
Стокс (русское обозначение: Ст; международное: St) — единица кинематической вязкости, входящая в систему единиц СГС. Названа в честь Дж. Г. Стокса. В Российской Федерации стокс допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность». Международная организация законодательной метрологии (МОЗМ) относит стокс к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться…
Пикоме́тр (русское обозначение: пм; международное: pm) — дольная единица измерения длины в Международной системе единиц (СИ), равная одной триллионной (то есть 1/1.000.000.000.000) части метра, основной единицы СИ. В экспоненциальной записи представляется как 10−12 метров.
Оборо́т в мину́ту (обозначение об/мин, 1/мин, мин−1, также часто используется английское обозначение rpm ) — единица измерения частоты вращения: количество полных оборотов, совершенных вокруг фиксированной оси.
Физические величины имеют род, размер, единицу(измерения) и значение.
Стокс (русское обозначение: Ст; международное: St) — единица кинематической вязкости, входящая в систему единиц СГС. Названа в честь Дж. Г. Стокса. В Российской Федерации стокс допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность». Международная организация законодательной метрологии (МОЗМ) относит стокс к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться…
Пикоме́тр (русское обозначение: пм; международное: pm) — дольная единица измерения длины в Международной системе единиц (СИ), равная одной триллионной (то есть 1/1.000.000.000.000) части метра, основной единицы СИ. В экспоненциальной записи представляется как 10−12 метров.
Оборо́т в мину́ту (обозначение об/мин, 1/мин, мин−1, также часто используется английское обозначение rpm ) — единица измерения частоты вращения: количество полных оборотов, совершенных вокруг фиксированной оси. Используется для измерения скорости вращения механических компонентов.
Вискозиметр (от лат. viscosus — вязкий) — прибор для определения динамической или кинематической вязкости вещества. В системе единиц СГС и в СИ динамическая вязкость измеряется соответственно в пуазах (П) и паскаль-секундах (Па·с), кинематическая — соответственно в стоксах (Ст) и квадратных метрах на секунду (м²/с).
Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Преобразова́ние едини́ц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта.
Люкс (от лат.
Используется для измерения скорости вращения механических компонентов.
Вискозиметр (от лат. viscosus — вязкий) — прибор для определения динамической или кинематической вязкости вещества. В системе единиц СГС и в СИ динамическая вязкость измеряется соответственно в пуазах (П) и паскаль-секундах (Па·с), кинематическая — соответственно в стоксах (Ст) и квадратных метрах на секунду (м²/с).
Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Преобразова́ние едини́ц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта.
Люкс (от лат.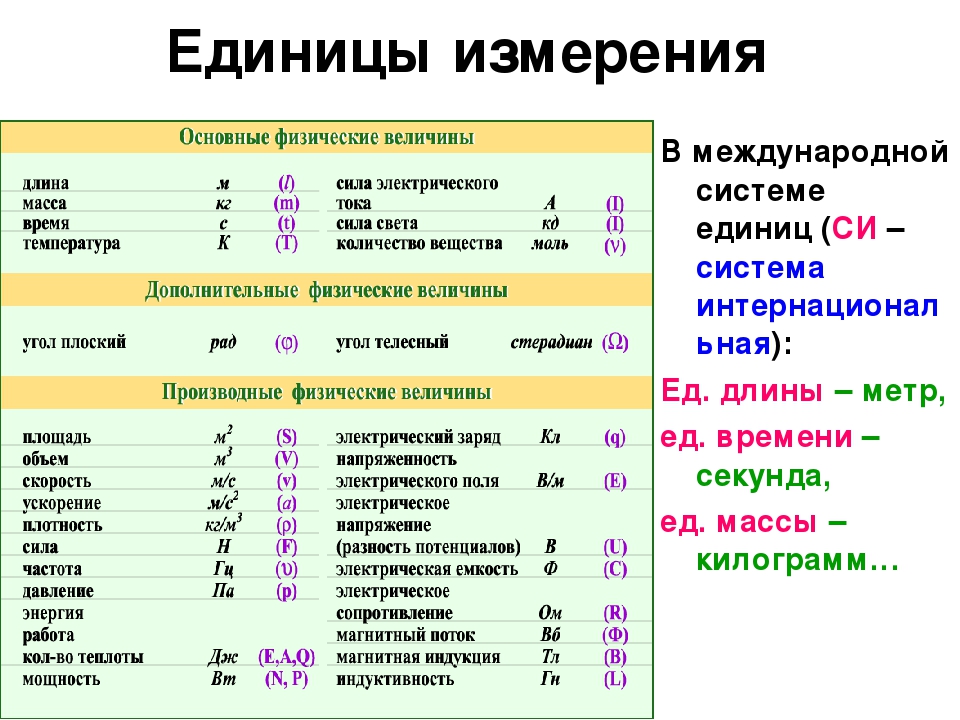 lux — свет; русское обозначение: лк, международное обозначение: lx) — единица измерения освещённости в Международной системе единиц (СИ). Люкс равен освещённости поверхности площадью 1 м² при световом потоке падающего на неё излучения, равном 1 лм. Соответственно, выполнятся: 1 лк = 1 лм/м2. С другой стороны, люкс равен освещённости поверхности сферы радиусом 1 м, создаваемой точечным источником света, находящимся в её центре, сила света которого составляет 1 кд. Таким образом, с основными…
Гидродинамический радиус (англ. hydrodynamic radius или Stokes radius, Stokes-Einstein radius) — размер объекта, который рассчитывается, исходя из предположения о его сферической форме, по величине коэффициента диффузии в жидкости.
Постоя́нная решётки, или, что то же самое, параметр решётки — размеры элементарной кристаллической ячейки кристалла. В общем случае элементарная ячейка представляет собой параллелепипед с различными длинами рёбер, обычно эти длины обозначают как a, b, c.
lux — свет; русское обозначение: лк, международное обозначение: lx) — единица измерения освещённости в Международной системе единиц (СИ). Люкс равен освещённости поверхности площадью 1 м² при световом потоке падающего на неё излучения, равном 1 лм. Соответственно, выполнятся: 1 лк = 1 лм/м2. С другой стороны, люкс равен освещённости поверхности сферы радиусом 1 м, создаваемой точечным источником света, находящимся в её центре, сила света которого составляет 1 кд. Таким образом, с основными…
Гидродинамический радиус (англ. hydrodynamic radius или Stokes radius, Stokes-Einstein radius) — размер объекта, который рассчитывается, исходя из предположения о его сферической форме, по величине коэффициента диффузии в жидкости.
Постоя́нная решётки, или, что то же самое, параметр решётки — размеры элементарной кристаллической ячейки кристалла. В общем случае элементарная ячейка представляет собой параллелепипед с различными длинами рёбер, обычно эти длины обозначают как a, b, c.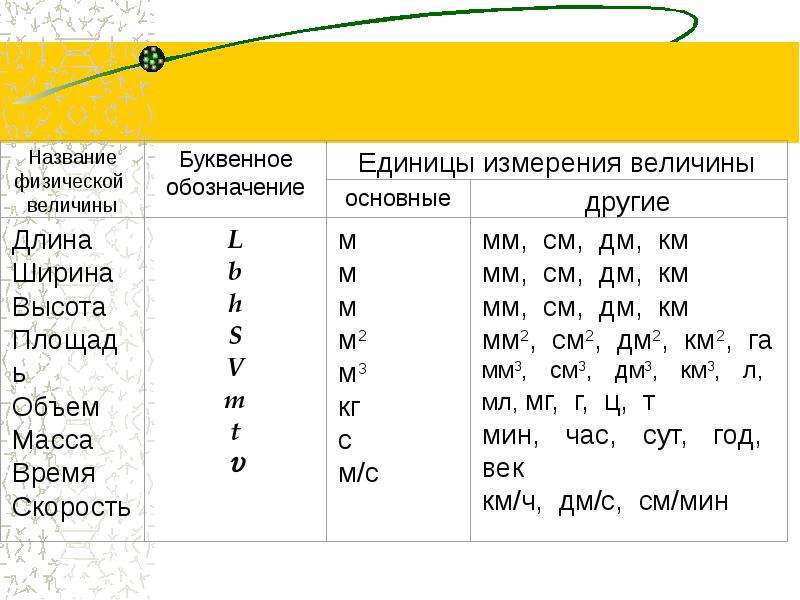 Но в некоторых частных случаях кристаллической структуры дли́ны этих рёбер совпадают. Если к тому же выходящие из одной вершины рёбра равны и взаимно перпендикулярны, то такую структуру называют кубической. Структуру с двумя равными рёбрами, находящимися…
Воздухопроница́емость — способность материалов и конструкций пропускать воздух под влиянием перепада давления воздуха. Во многих областях материального производства воздухопроницаемость материала является одним из важнейших параметров, т.к определяет свойства конечного продукта (например, при производстве одежды, обуви, упаковочных и строительных материалов).
Двадцатифу́товый эквивале́нт (TEU или teu от англ. twenty-foot equivalent unit) — условная единица измерения вместимости грузовых транспортных средств. Часто используется при описании вместимости контейнеровозов и контейнерных терминалов. Основана на объёме 20-футового (6,1 метров) интермодального ISO-контейнера — металлической коробки стандартного размера, которая может транспортироваться различными видами транспорта: автомобильным, железнодорожным и морским.
Но в некоторых частных случаях кристаллической структуры дли́ны этих рёбер совпадают. Если к тому же выходящие из одной вершины рёбра равны и взаимно перпендикулярны, то такую структуру называют кубической. Структуру с двумя равными рёбрами, находящимися…
Воздухопроница́емость — способность материалов и конструкций пропускать воздух под влиянием перепада давления воздуха. Во многих областях материального производства воздухопроницаемость материала является одним из важнейших параметров, т.к определяет свойства конечного продукта (например, при производстве одежды, обуви, упаковочных и строительных материалов).
Двадцатифу́товый эквивале́нт (TEU или teu от англ. twenty-foot equivalent unit) — условная единица измерения вместимости грузовых транспортных средств. Часто используется при описании вместимости контейнеровозов и контейнерных терминалов. Основана на объёме 20-футового (6,1 метров) интермодального ISO-контейнера — металлической коробки стандартного размера, которая может транспортироваться различными видами транспорта: автомобильным, железнодорожным и морским.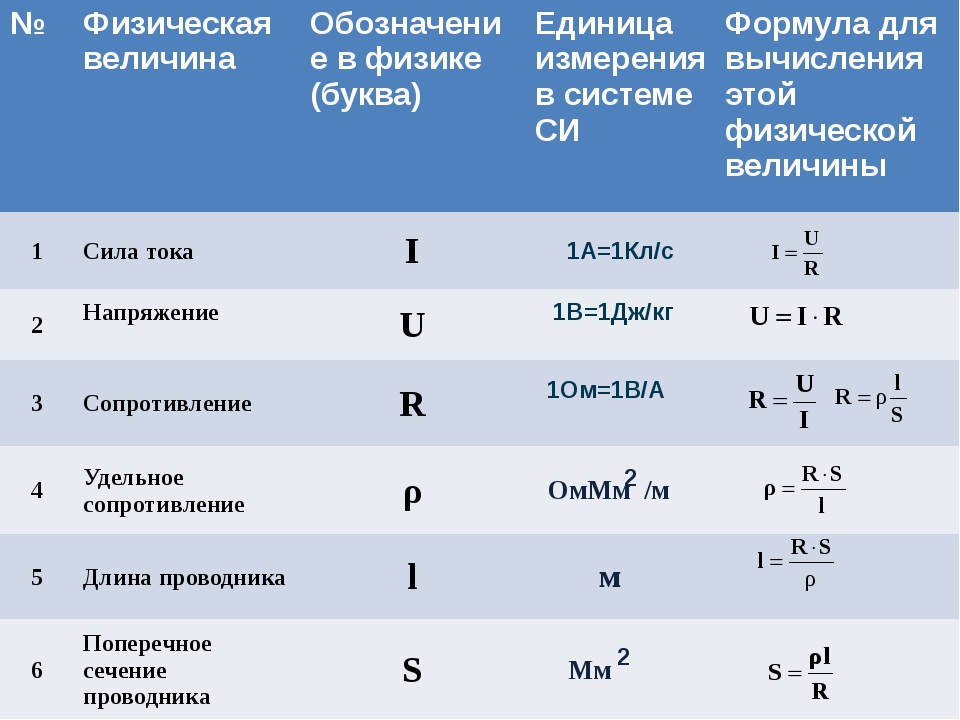 Цилиндр Фарадея — устройство для определения полного электрического заряда и интенсивности пучка частиц. Назван в честь известного английского физика Майкла Фарадея.
Миллиме́тр рту́тного столба́ (русское обозначение: мм рт.ст.; международное: mm Hg) — внесистемная единица измерения давления, равная 101 325 / 760 ≈ 133,322 368 4 Па; иногда называется «торр» (русское обозначение — торр, международное — Torr) в честь Эванджелисты Торричелли.
Разме́рность физической величины — выражение, показывающее связь этой величины с основными величинами данной системы физических величин; записывается в виде произведения степеней сомножителей, соответствующих основным величинам, в котором численные коэффициенты опущены.
Французская шкала диаметра катетеров (часто сокращаются как Fr или F) обычно используется для измерения наружного диаметра цилиндрических медицинских инструментов включая катетеры.
Цилиндр Фарадея — устройство для определения полного электрического заряда и интенсивности пучка частиц. Назван в честь известного английского физика Майкла Фарадея.
Миллиме́тр рту́тного столба́ (русское обозначение: мм рт.ст.; международное: mm Hg) — внесистемная единица измерения давления, равная 101 325 / 760 ≈ 133,322 368 4 Па; иногда называется «торр» (русское обозначение — торр, международное — Torr) в честь Эванджелисты Торричелли.
Разме́рность физической величины — выражение, показывающее связь этой величины с основными величинами данной системы физических величин; записывается в виде произведения степеней сомножителей, соответствующих основным величинам, в котором численные коэффициенты опущены.
Французская шкала диаметра катетеров (часто сокращаются как Fr или F) обычно используется для измерения наружного диаметра цилиндрических медицинских инструментов включая катетеры.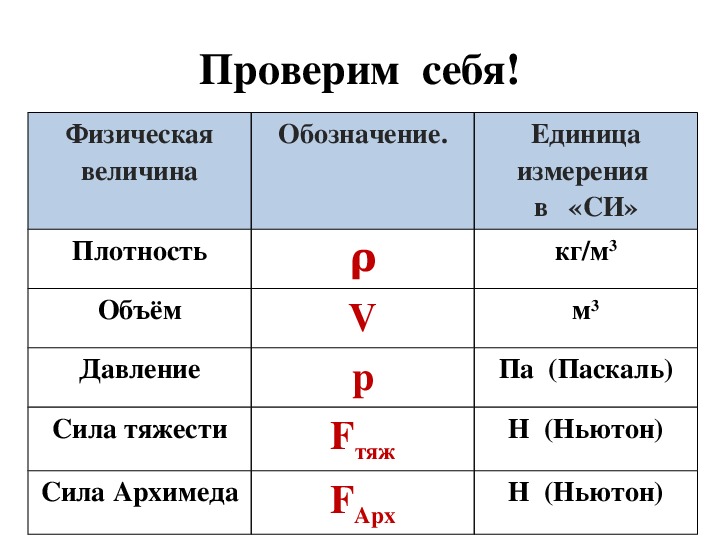 Во французской шкале диаметр в миллиметрах определяется делением числа на 3, таким образом увеличение числа во французской шкале соответствует большему диаметру катетера. Это можно представить с помощью следующего уравнения…
Твип (англ. twip) — типографская единица измерения, равная одной двадцатой пункта (point, отсюда и название: Twentieth of a Point).
Дюйм рту́тного столба́, дюйм рт. ст., in Hg, inHg — внесистемная единица измерения давления, равная 3386,389 Па при 0 °C (32 °F).
Шкала́ (лат. scala — лестница) — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией или техническая отметка на шкале измерительного прибора. Шкалы могут располагаться по окружности, дуге или прямой линии. Показания отсчитываются невооружённым глазом при расстояниях между делениями до 0,7 мм, при меньших — при помощи лупы или микроскопа, для долевой оценки делений применяют дополнительные шкалы — нониусы.
Во французской шкале диаметр в миллиметрах определяется делением числа на 3, таким образом увеличение числа во французской шкале соответствует большему диаметру катетера. Это можно представить с помощью следующего уравнения…
Твип (англ. twip) — типографская единица измерения, равная одной двадцатой пункта (point, отсюда и название: Twentieth of a Point).
Дюйм рту́тного столба́, дюйм рт. ст., in Hg, inHg — внесистемная единица измерения давления, равная 3386,389 Па при 0 °C (32 °F).
Шкала́ (лат. scala — лестница) — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией или техническая отметка на шкале измерительного прибора. Шкалы могут располагаться по окружности, дуге или прямой линии. Показания отсчитываются невооружённым глазом при расстояниях между делениями до 0,7 мм, при меньших — при помощи лупы или микроскопа, для долевой оценки делений применяют дополнительные шкалы — нониусы.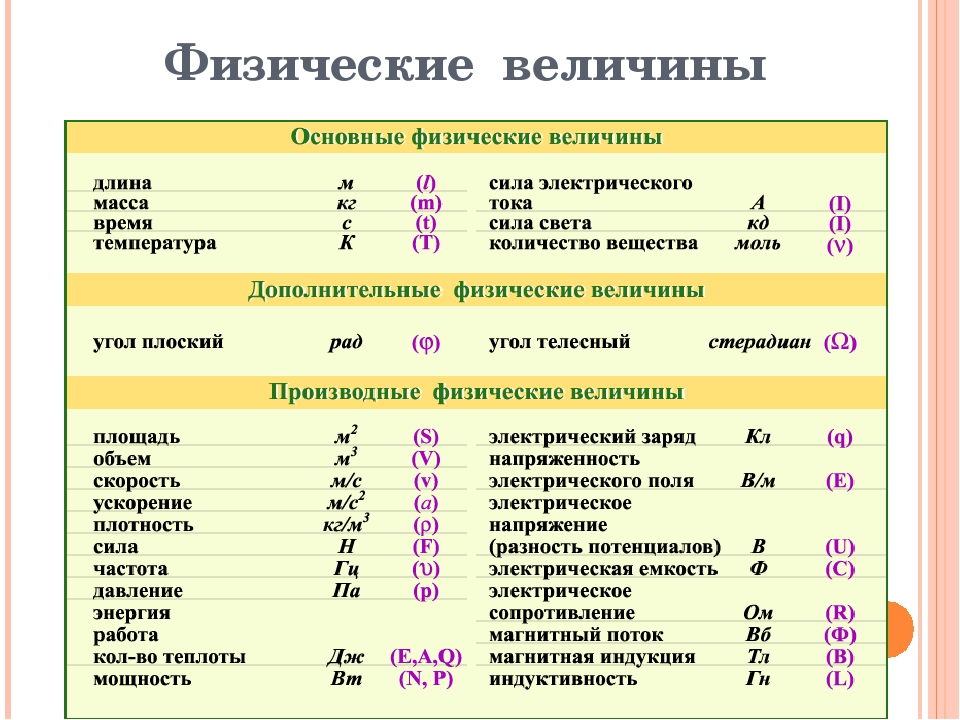 Внесистемная единица — единица физической величины, не входящая ни в одну из систем единиц, или, в более широком смысле, единица, не входящая в систему единиц, применяемую в конкретном случае. В качестве примеров внесистемных единиц можно привести миллиметр ртутного столба, лошадиную силу и т. п.Продолжающееся существование единиц, не входящих в систему СИ, частично связано с тем, что некоторые внесистемные единицы по своей величине весьма удобны для специализированных отраслей науки и техники или…
Относительное отверстие объектива — оптическая мера светопропускания объектива. Различают геометрическое и эффективное относительные отверстия. Геометрическим отверстием считается отношение диаметра входного зрачка объектива к его заднему фокусному расстоянию. Эффективное относительное отверстие всегда меньше, чем геометрическое, поскольку учитывает потери света при его прохождении через стекло и рассеянии на границах с воздухом и деталях оправы.
Внесистемная единица — единица физической величины, не входящая ни в одну из систем единиц, или, в более широком смысле, единица, не входящая в систему единиц, применяемую в конкретном случае. В качестве примеров внесистемных единиц можно привести миллиметр ртутного столба, лошадиную силу и т. п.Продолжающееся существование единиц, не входящих в систему СИ, частично связано с тем, что некоторые внесистемные единицы по своей величине весьма удобны для специализированных отраслей науки и техники или…
Относительное отверстие объектива — оптическая мера светопропускания объектива. Различают геометрическое и эффективное относительные отверстия. Геометрическим отверстием считается отношение диаметра входного зрачка объектива к его заднему фокусному расстоянию. Эффективное относительное отверстие всегда меньше, чем геометрическое, поскольку учитывает потери света при его прохождении через стекло и рассеянии на границах с воздухом и деталях оправы. Те́сла (русское обозначение: Тл; международное обозначение: T) — единица измерения индукции магнитного поля в Международной системе единиц (СИ), равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.
Твёрдость по Шору — метод определения твёрдости очень твёрдых материалов, преимущественно металлов, по высоте, на которую после удара отскакивает специальный боёк (основная часть склероскопа Шора), свободно и вертикально падающий с определённой высоты. Твердость по этому методу Шора оценивается в условных единицах, пропорциональных высоте отскакивания бойка.
Те́сла (русское обозначение: Тл; международное обозначение: T) — единица измерения индукции магнитного поля в Международной системе единиц (СИ), равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.
Твёрдость по Шору — метод определения твёрдости очень твёрдых материалов, преимущественно металлов, по высоте, на которую после удара отскакивает специальный боёк (основная часть склероскопа Шора), свободно и вертикально падающий с определённой высоты. Твердость по этому методу Шора оценивается в условных единицах, пропорциональных высоте отскакивания бойка.Физическая величина — Карта знаний
- Физи́ческая величина́ — измеряемое качество, признак или свойство материального объекта или явления, общее в качественном отношении для класса материальных объектов или процессов, явлений, но в количественном отношении индивидуальное для каждого из них.
 Физические величины имеют род, размер, единицу(измерения) и значение.
Физические величины имеют род, размер, единицу(измерения) и значение.Для обозначения физических величин применяются прописные и строчные буквы латинского или греческого алфавита. Часто к обозначениям добавляют верхние или нижние индексы, указывающие, к чему относится величина, например Eп часто обозначает потенциальную энергию, а cp — теплоёмкость при постоянном давлении.
Устойчивые, повторяющиеся во множестве опытов связи между физическими величинами, присущие самой природе, называются физическими законами.
Источник: Википедия
Связанные понятия
Разме́рность физической величины — выражение, показывающее связь этой величины с основными величинами данной системы физических величин; записывается в виде произведения степеней сомножителей, соответствующих основным величинам, в котором численные коэффициенты опущены. Виды измерений — области измерений, выделяемые по одному из классифицирующих признаков. Рассматриваются в метрологии.
Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).
Анализ размерности (чаще говорят «соображения размерности» или «метрические соображения») — инструмент, используемый в физике, химии, технике и нескольких направлениях экономики для построения обоснованных гипотез о взаимосвязи различных параметров сложной системы. Неоднократно применялся физиками на интуитивном уровне не позже XIX века.
Пара́метр (от др.-греч. παραμετρέω — «отмеривающий»; где παρά: «рядом», «второстепенный», «вспомогательный», «подчинённый»; и μέτρον: «измерение») — величина, значения которой служат для различения элементов некоторого множества между собой.
Рассматриваются в метрологии.
Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).
Анализ размерности (чаще говорят «соображения размерности» или «метрические соображения») — инструмент, используемый в физике, химии, технике и нескольких направлениях экономики для построения обоснованных гипотез о взаимосвязи различных параметров сложной системы. Неоднократно применялся физиками на интуитивном уровне не позже XIX века.
Пара́метр (от др.-греч. παραμετρέω — «отмеривающий»; где παρά: «рядом», «второстепенный», «вспомогательный», «подчинённый»; и μέτρον: «измерение») — величина, значения которой служат для различения элементов некоторого множества между собой.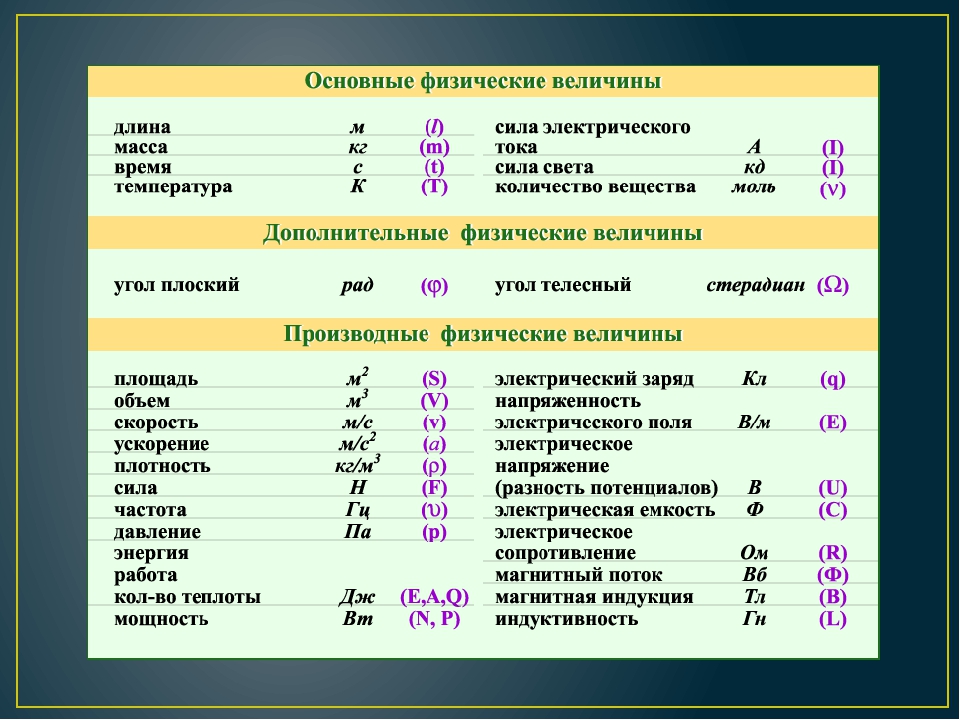 . Параметр — величина, постоянная в пределах данного явления или задачи, но при переходе к другому явлению или задаче могущая изменить своё значение. Иногда параметрами называют также величины, очень медленно изменяющиеся по сравнению с другими величинами (переменными…
. Параметр — величина, постоянная в пределах данного явления или задачи, но при переходе к другому явлению или задаче могущая изменить своё значение. Иногда параметрами называют также величины, очень медленно изменяющиеся по сравнению с другими величинами (переменными…Упоминания в литературе
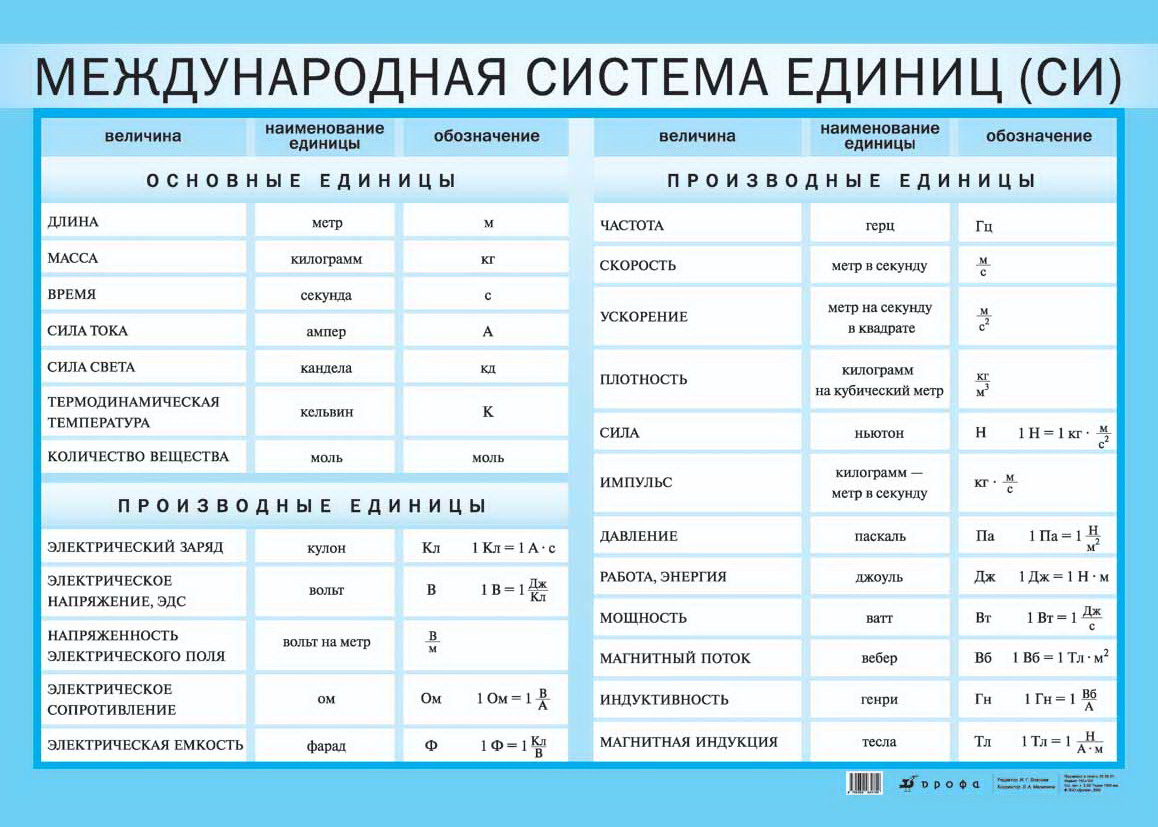
Объектом измерения для метрологии, как правило, являются физические величины. Физические величины используется для характеристики различных объектов, явлений и процессов. Разделяют основные и производные от основных величины. Семь основных и две дополнительных физических величины установлены в Международной системе единиц. Это длина, масса, время, термодинамическая температура, количество вещества, сила света и сила электрического тока, дополнительные единицы – это радиан и стерадиан. У физических величин есть качественные и количественные характеристики. Метрологией называют науку об измерениях, методах и средствах обеспечения их единства, способах достижения требуемой точности. Измерением называют нахождение значения физической величины опытным путем с помощью технических средств. Измерения позволяют установить закономерности природы и являются элементом познания окружающего нас мира. Различают измерения прямые, при которых результат получается непосредственно из измерения самой величины (например, измерение температуры тела медицинским термометром, измерение длины предмета линейкой), и косвенные, при которых искомое значение величины находят по известной зависимости между ней и непосредственно измеряемыми величинами (например, определение массы тела при взвешивании с учетом выталкивающей силы, определенной вязкостью жидкости по скорости падения в ней шарика). Технические средства для производства измерений могут быть разных типов. Наиболее известными являются приборы, в которых измерительная информация представляется в форме, доступной для непосредственного восприятия (например, температура представлена в термометре длиной столбика ртути, сила тока – показанием стрелки амперметра или цифровым значением).
Измерением называют нахождение значения физической величины опытным путем с помощью технических средств. Измерения позволяют установить закономерности природы и являются элементом познания окружающего нас мира. Различают измерения прямые, при которых результат получается непосредственно из измерения самой величины (например, измерение температуры тела медицинским термометром, измерение длины предмета линейкой), и косвенные, при которых искомое значение величины находят по известной зависимости между ней и непосредственно измеряемыми величинами (например, определение массы тела при взвешивании с учетом выталкивающей силы, определенной вязкостью жидкости по скорости падения в ней шарика). Технические средства для производства измерений могут быть разных типов. Наиболее известными являются приборы, в которых измерительная информация представляется в форме, доступной для непосредственного восприятия (например, температура представлена в термометре длиной столбика ртути, сила тока – показанием стрелки амперметра или цифровым значением).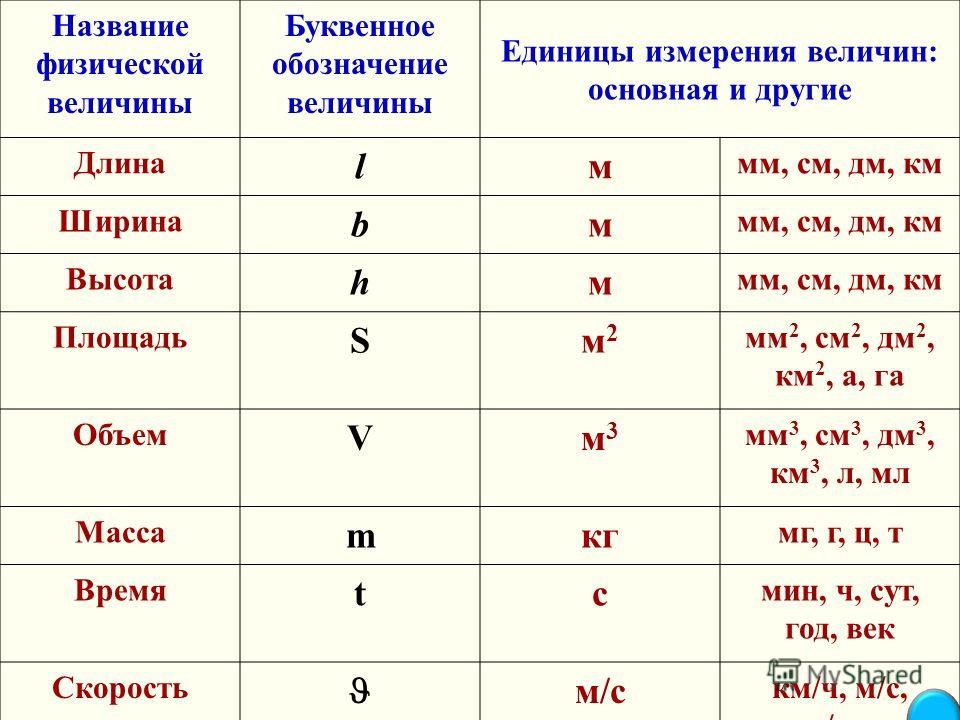 Косвенное измерение – измерение, при котором значение физической величины получают на основании известной зависимости между этой величиной и величиной (величинами), подвергаемыми прямым измерениям:
1) определение физических величин путем указания на совокупность операций, посредством которых измеряется (определяется) та или иная физическая величина;
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности [111]. Метрология изучает и имеет дело только с измерениями физических величин, т.е. величин, для которых может существовать физически реализуемая и воспроизводимая единица величины.
Косвенное измерение – измерение, при котором значение физической величины получают на основании известной зависимости между этой величиной и величиной (величинами), подвергаемыми прямым измерениям:
1) определение физических величин путем указания на совокупность операций, посредством которых измеряется (определяется) та или иная физическая величина;
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности [111]. Метрология изучает и имеет дело только с измерениями физических величин, т.е. величин, для которых может существовать физически реализуемая и воспроизводимая единица величины.Связанные понятия (продолжение)
Величина́ — математическое понятие, описывающее объекты, для которых может быть определено отношение неравенства и смысл операции сложения, а также выполняется ряд свойств, включая аксиомы Архимеда и непрерывности.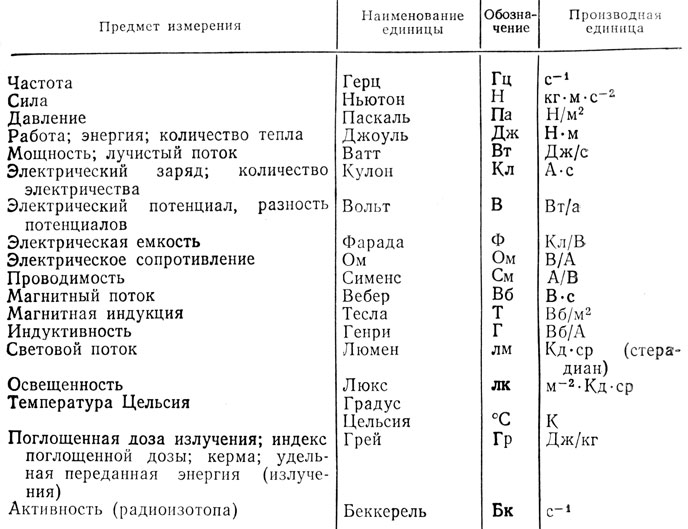 Величина является одним из основных понятий математики.
Система физических величин (далее СФВ) — совокупность взаимосвязанных физических величин, образованная по принципу, когда одни физические величины являются независимыми (основными физическими величинами), а другие являются их функциями (производными физическими величинами). СФВ представляет собой структурную схему связей или алгебраическую диаграмму операторов физических величин. Эти связи описываются математическими выражениями, называемыми определяющими уравнениями.
В метрологии различают понятия размерность физической величины и единица физической величины. Размерность физической величины определяется используемой системой физических величин, которая представляет собой совокупность физических величин, связанных между собой зависимостями, и в которой несколько величин выбраны в качестве основных. Единица физической величины — это такая физическая величина, которой по соглашению присвоено числовое значение, равное единице.
Величина является одним из основных понятий математики.
Система физических величин (далее СФВ) — совокупность взаимосвязанных физических величин, образованная по принципу, когда одни физические величины являются независимыми (основными физическими величинами), а другие являются их функциями (производными физическими величинами). СФВ представляет собой структурную схему связей или алгебраическую диаграмму операторов физических величин. Эти связи описываются математическими выражениями, называемыми определяющими уравнениями.
В метрологии различают понятия размерность физической величины и единица физической величины. Размерность физической величины определяется используемой системой физических величин, которая представляет собой совокупность физических величин, связанных между собой зависимостями, и в которой несколько величин выбраны в качестве основных. Единица физической величины — это такая физическая величина, которой по соглашению присвоено числовое значение, равное единице. Системой единиц физических величин называют…
Системой единиц физических величин называют…Подробнее: Список физических величин
Преобразова́ние едини́ц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта. Не́пер (русское обозначение: Нп; международное: Np) — единица логарифмического отношения физической величины к одноимённой физической величине, принимаемой за исходную. В основе единицы лежит натуральный логарифм. Единица названа в честь шотландского математика Джона Непера. Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие их физического подобия. Параметр — это обобщенное название определенного физического, геометрического или иного свойства устройства (процесса).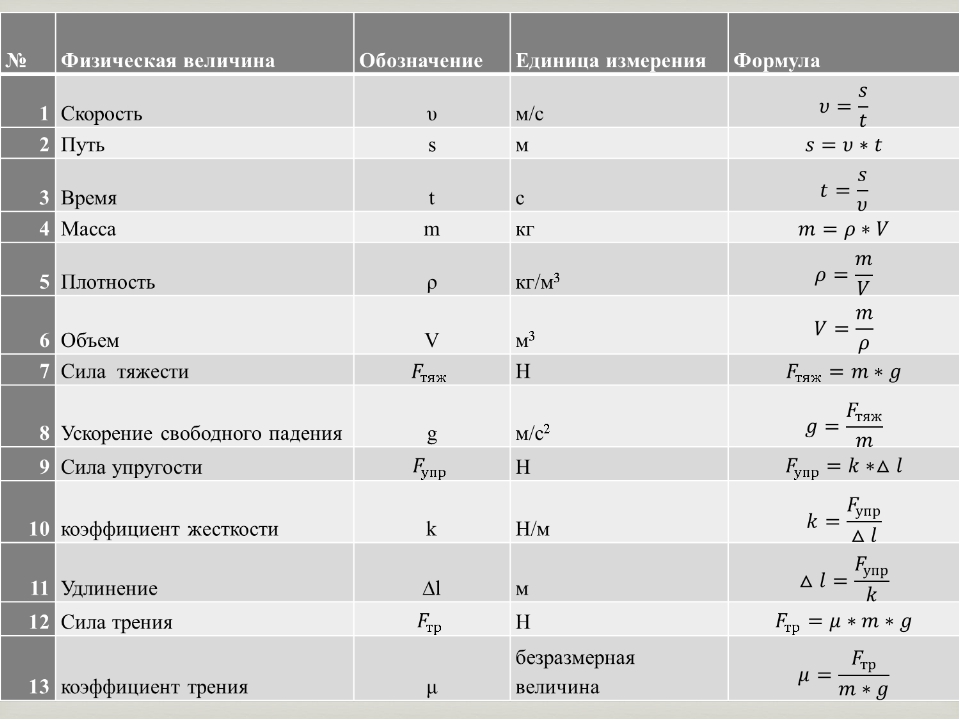 Это могут быть, например, размер, скорость, напряжение и т. д.
Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Математически распределение частот является функцией, которая в первую очередь определяет для каждого показателя идеальное значение, так как эта величина обычно уже измерена. Такое распределение можно представить в виде таблицы или графика, моделируя функциональные уравнения. В описательной статистике частота распределения имеет ряд математических функций, которые используются для выравнивания…
Имено́ванные чи́сла — действительные числа (на практике всегда заданные с конечной точностью), являющиеся значением какой-нибудь физической величины, и сопровождающиеся названием единицы измерения, например 2 кг; 3,4 м, 220 В, 1,75 А,
Чётность — свойство физической величины сохранять свой знак (или изменять на противоположный) при некоторых дискретных преобразованиях.
Это могут быть, например, размер, скорость, напряжение и т. д.
Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Математически распределение частот является функцией, которая в первую очередь определяет для каждого показателя идеальное значение, так как эта величина обычно уже измерена. Такое распределение можно представить в виде таблицы или графика, моделируя функциональные уравнения. В описательной статистике частота распределения имеет ряд математических функций, которые используются для выравнивания…
Имено́ванные чи́сла — действительные числа (на практике всегда заданные с конечной точностью), являющиеся значением какой-нибудь физической величины, и сопровождающиеся названием единицы измерения, например 2 кг; 3,4 м, 220 В, 1,75 А,
Чётность — свойство физической величины сохранять свой знак (или изменять на противоположный) при некоторых дискретных преобразованиях.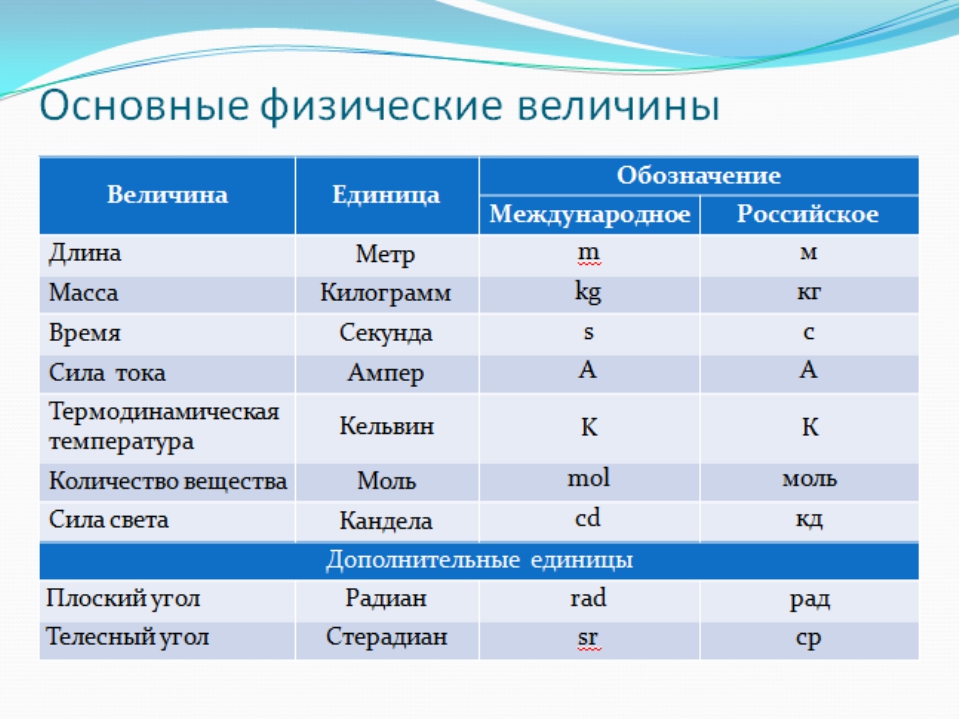 Она выражается числом, принимающим два значения: +1 и −1.
Крива́я титрова́ния — графическое изображение зависимости определяемой в ходе титрования величины от объёма добавленного стандартного раствора титранта. Построение кривых проводится в инструментальных методах аналитической химии, где отсутствует возможность визуального определения точки эквивалентности (например, по индикатору).
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Канде́ла (от лат. candela — свеча; русское обозначение: кд; международное: cd) — единица силы света, одна из семи основных единиц Международной системы единиц (СИ). Определена как «сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540⋅1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср».
Она выражается числом, принимающим два значения: +1 и −1.
Крива́я титрова́ния — графическое изображение зависимости определяемой в ходе титрования величины от объёма добавленного стандартного раствора титранта. Построение кривых проводится в инструментальных методах аналитической химии, где отсутствует возможность визуального определения точки эквивалентности (например, по индикатору).
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Канде́ла (от лат. candela — свеча; русское обозначение: кд; международное: cd) — единица силы света, одна из семи основных единиц Международной системы единиц (СИ). Определена как «сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540⋅1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср». Принята в качестве единицы СИ в 1979 году XVI Генеральной конференцией по мерам и весам.
Интенсивная величина — физическая величина значение которой не зависит от размера системы (например, температура, давление).
Смещение Малмквиста (сдвиг Малмквиста) — эффект в наблюдательной астрономии, приводящий к преимущественному обнаружению объектов с высокой светимостью. Впервые данный эффект описал в 1922 году шведский астроном Гуннар Малмквист (1893–1982), подробно исследовавший данное явление в 1925 году. В статистике данное смещение является систематической ошибкой и влияет на результаты обзоров в выборках, ограниченных по видимой звёздной величине, в которые не попадают звёзды, видимые звёздные величины которых…
Соотноше́ния Кра́мерса — Кро́нига — интегральная связь между действительной и мнимой частями любой комплексной функции, аналитичной в верхней полуплоскости.
Принята в качестве единицы СИ в 1979 году XVI Генеральной конференцией по мерам и весам.
Интенсивная величина — физическая величина значение которой не зависит от размера системы (например, температура, давление).
Смещение Малмквиста (сдвиг Малмквиста) — эффект в наблюдательной астрономии, приводящий к преимущественному обнаружению объектов с высокой светимостью. Впервые данный эффект описал в 1922 году шведский астроном Гуннар Малмквист (1893–1982), подробно исследовавший данное явление в 1925 году. В статистике данное смещение является систематической ошибкой и влияет на результаты обзоров в выборках, ограниченных по видимой звёздной величине, в которые не попадают звёзды, видимые звёздные величины которых…
Соотноше́ния Кра́мерса — Кро́нига — интегральная связь между действительной и мнимой частями любой комплексной функции, аналитичной в верхней полуплоскости. Часто используются в физике для описания связи действительной и мнимой частей функции отклика физической системы, поскольку аналитичность функции отклика подразумевает, что система удовлетворяет принципу причинности, и наоборот . В частности, соотношения Крамерса — Кронига выражают связь между действительной и мнимой частями диэлектрической проницаемости…
Показа́тель рассе́яния — величина, обратная расстоянию, на котором поток монохроматического излучения, распространяющегося в среде в виде параллельного пучка, уменьшается вследствие рассеяния в среде в некоторое заранее оговоренное число раз. В принципиальном плане степень уменьшения потока излучения в данном определении можно выбирать любой, однако в научно-технической, справочной и нормативной литературе и в целом на практике используются два значения степени уменьшения: одно, равное 10 (десятичный…
Весовая функция — математическая конструкция, используемая при проведении суммирования, интегрирования или усреднения с целью придания некоторым элементам большего веса в результирующем значении по сравнению с другими элементами.
Часто используются в физике для описания связи действительной и мнимой частей функции отклика физической системы, поскольку аналитичность функции отклика подразумевает, что система удовлетворяет принципу причинности, и наоборот . В частности, соотношения Крамерса — Кронига выражают связь между действительной и мнимой частями диэлектрической проницаемости…
Показа́тель рассе́яния — величина, обратная расстоянию, на котором поток монохроматического излучения, распространяющегося в среде в виде параллельного пучка, уменьшается вследствие рассеяния в среде в некоторое заранее оговоренное число раз. В принципиальном плане степень уменьшения потока излучения в данном определении можно выбирать любой, однако в научно-технической, справочной и нормативной литературе и в целом на практике используются два значения степени уменьшения: одно, равное 10 (десятичный…
Весовая функция — математическая конструкция, используемая при проведении суммирования, интегрирования или усреднения с целью придания некоторым элементам большего веса в результирующем значении по сравнению с другими элементами. Задача часто возникает в статистике и математическом анализе, тесно связана с теорией меры. Весовые функции могут быть использованы как для дискретных, так и для непрерывных величин.
Показа́тель ослабле́ния (показатель экстинкции) — величина, обратная расстоянию, на котором поток излучения, образующего параллельный пучок, уменьшается за счет поглощения и рассеяния в среде в некоторое заранее оговоренное число раз.
Уравне́ние состоя́ния — соотношение, отражающее для конкретного класса термодинамических систем связь между характеризующими её макроскопическими физическими величинами, такими как температура, давление, объём, химический потенциал, энтропия, внутренняя энергия, энтальпия и др. Уравнения состояния необходимы для получения с помощью математического аппарата термодинамики конкретных результатов, касающихся рассматриваемой системы. Эти уравнения не содержатся в постулатах термодинамики, так что для.
Задача часто возникает в статистике и математическом анализе, тесно связана с теорией меры. Весовые функции могут быть использованы как для дискретных, так и для непрерывных величин.
Показа́тель ослабле́ния (показатель экстинкции) — величина, обратная расстоянию, на котором поток излучения, образующего параллельный пучок, уменьшается за счет поглощения и рассеяния в среде в некоторое заранее оговоренное число раз.
Уравне́ние состоя́ния — соотношение, отражающее для конкретного класса термодинамических систем связь между характеризующими её макроскопическими физическими величинами, такими как температура, давление, объём, химический потенциал, энтропия, внутренняя энергия, энтальпия и др. Уравнения состояния необходимы для получения с помощью математического аппарата термодинамики конкретных результатов, касающихся рассматриваемой системы. Эти уравнения не содержатся в постулатах термодинамики, так что для. ..
Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.
..
Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.Подробнее: Пропорциональность
Число Штреля (англ. Strehl ratio) — величина, характеризующая качество оптического изображения, впервые предложенная Карлом Штрелем и названная в честь него. Используется в ситуациях, когда оптическое разрешение ухудшается из-за аберраций в линзе или из-за искажений при прохождении через турбулентную атмосферу.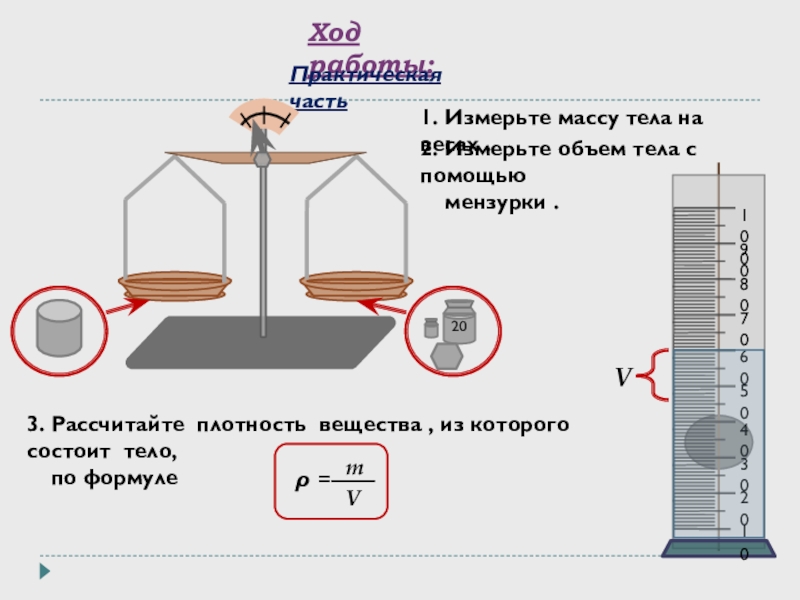 Имеет значение от 0 до 1, при этом в гипотетической идеальной оптической системе число Штреля равно 1.
Система одновременных уравнений — совокупность эконометрических уравнений (часто линейных), определяющих взаимозависимость экономических переменных. Важным отличительным признаком системы «одновременных» уравнений от прочих систем уравнений является наличие одних и тех же переменных в правых и левых частях разных уравнений системы (речь идет о так называемой структурной форме модели, см. ниже).
Распределение по размерам пор (частиц) (англ. size (pore, particle) distribution) — зависимость количества (объема, массы) частиц или пор от их размеров в исследуемом материале и кривая (гистограмма), описывающая эту зависимость.
В статистике степенной закон (англ. power law) — это такая функциональная зависимость между двумя величинами, при которой относительное изменение одной величины приводит к пропорциональному относительному изменению другой величины, независимо от исходных значений этих величин: зависимость одной величины от другой представляет собой степенную функцию. Например, рассмотрим зависимость площади квадрата от длины его стороны. Если длина будет увеличена вдвое, то площадь увеличится вчетверо.
Микроканонический ансамбль — статистический ансамбль макроскопической изолированной системы с постоянными значениями объёма V, числа частиц N и энергии E. Понятие микроканонического ансамбля является идеализацией, так как в действительности полностью изолированных систем не существует. В микроканоническом распределении Гиббса все микроскопические состояния, отвечающие данной энергии, равновероятны согласно эргодической гипотезе. Теорема Гиббса, доказанная автором, утверждает, что малую часть микроканонического…
Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистское сокращение длины движущегося тела или масштаба — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя, движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.
Нат — одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Нат равен log2e ≈ 1,443 бит.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых…
Имеет значение от 0 до 1, при этом в гипотетической идеальной оптической системе число Штреля равно 1.
Система одновременных уравнений — совокупность эконометрических уравнений (часто линейных), определяющих взаимозависимость экономических переменных. Важным отличительным признаком системы «одновременных» уравнений от прочих систем уравнений является наличие одних и тех же переменных в правых и левых частях разных уравнений системы (речь идет о так называемой структурной форме модели, см. ниже).
Распределение по размерам пор (частиц) (англ. size (pore, particle) distribution) — зависимость количества (объема, массы) частиц или пор от их размеров в исследуемом материале и кривая (гистограмма), описывающая эту зависимость.
В статистике степенной закон (англ. power law) — это такая функциональная зависимость между двумя величинами, при которой относительное изменение одной величины приводит к пропорциональному относительному изменению другой величины, независимо от исходных значений этих величин: зависимость одной величины от другой представляет собой степенную функцию. Например, рассмотрим зависимость площади квадрата от длины его стороны. Если длина будет увеличена вдвое, то площадь увеличится вчетверо.
Микроканонический ансамбль — статистический ансамбль макроскопической изолированной системы с постоянными значениями объёма V, числа частиц N и энергии E. Понятие микроканонического ансамбля является идеализацией, так как в действительности полностью изолированных систем не существует. В микроканоническом распределении Гиббса все микроскопические состояния, отвечающие данной энергии, равновероятны согласно эргодической гипотезе. Теорема Гиббса, доказанная автором, утверждает, что малую часть микроканонического…
Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистское сокращение длины движущегося тела или масштаба — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя, движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.
Нат — одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Нат равен log2e ≈ 1,443 бит.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых…Подробнее: Критерий Уилкоксона
Твёрдость — свойство материала сопротивляться внедрению более твёрдого тела — индентора. Дисперсионный анализ — метод в математической статистике, направленный на поиск зависимостей в экспериментальных данных путём исследования значимости различий в средних значениях. В отличие от t-критерия, позволяет сравнивать средние значения трёх и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований. В литературе также встречается обозначение ANOVA (от англ. ANalysis Of VAriance). Вариа́ция — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений. Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Если вероятность задана в процентах, то квантиль называется процентилем или перцентилем (см. ниже). Килогра́мм-си́ла (русское обозначение: кгс или кГ; международное: kgf или kgF) — единица силы в системе единиц МКГСС; наряду с метром и секундой является основной единицей этой системы. III Генеральная конференция по мерам и весам (1901) дала этой единице следующее определение: «килограмм-сила равен силе, которая сообщает покоящейся массе, равной массе международного прототипа килограмма, ускорение, равное нормальному ускорению свободного падения (9,80665 м/с2)». Метод конечных объёмов (в русскоязычной литературе метод контрольных объёмов) — численный метод интегрирования систем дифференциальных уравнений в частных производных. Постоя́нная Ха́ббла (конста́нта Ха́ббла) — коэффициент, входящий в закон Хаббла, который связывает расстояние до внегалактического объекта (галактики, квазара) со скоростью его удаления. Обычно обозначается буквой H. Имеет размерность, обратную времени (H ≈ 2,2⋅10−18 с−1), но выражается обычно в км/с на мегапарсек. Ме́ра физи́ческой величины́ (мера величины, мера) — средство измерений в виде какого-либо тела, вещества или устройства, предназначенное для воспроизведения и хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью. Коэффицие́нт (от лат. co(cum) «совместно» + efficients «производящий») — числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине. До́пуск — разность между наибольшим и наименьшим предельными значениями параметров (размеров, массовой доли, массы), задаётся на геометрические размеры деталей, механические, физические и химические свойства. Назначается (выбирается) исходя из технологической точности или требований к изделию (продукту). Любое значение параметра, оказывающееся в заданном интервале, является допустимым. Коэффициент формы — это отношение среднеквадратичного значения какой-то величины к среднему модулю (среднему абсолютному значению) той же величины. Если зависимость этой величины от другой переменной изобразить в виде графика, то коэффициент формы покажет, насколько форма этой линии отличается от горизонтальной прямой. Коэффициент формы постоянной функции равен единице. Ядерная оценка плотности (ЯОП, англ. Kernel Density Estimation, KDE) — это непараметрический способ оценки плотности случайной величины. Ядерная оценка плотности является задачей сглаживания данных, когда делается заключение о совокупности, основываясь на конечных выборках данных. В некоторых областях, таких как обработка сигналов и математическая экономика, метод называется также методом окна Парзена-Розенблатта. Как считается, Эммануэль Парзен и Мюррей Розенблатт независимо создали метод в существующем… Радиационное трение, реакция излучения, лучистое трение, торможение излучением — сила, действующая на заряженную точечную частицу (например, электрон), со стороны её собственного электромагнитного излучения, вызываемого неравномерностью движения этой частицы. Фундамента́льные физи́ческие постоя́нные — постоянные величины, входящие в уравнения, описывающие фундаментальные законы природы и свойства материи. Фундаментальные физические постоянные возникают в теоретических моделях наблюдаемых явлений в виде универсальных коэффициентов в соответствующих математических выражениях.Упоминания в литературе (продолжение)
Обозначения единиц счета и единиц физических величин применяют в таблицах, пояснениях символов и числовых коэффициентов, входящих в формулы, и в тексте только при числовых значениях и записывают без точки. Такие физические величины, как протяженность, время и масса, в теории относительности утратили свой статус абсолютности. Эйнштейн в качестве величины, которая имеет статус постоянной, оставил лишь силу (например, сила тяготения). Общая теория относительности содержит геометрическое толкование явления тяготения. Объектами технического нормирования и стандартизации являются продукция, услуги, процессы, работы, информация (условные обозначения, термины, определения, единицы физических величин, пиктограммы и пр.). Задача состоит в том, чтобы подобрать научно обоснованные правила построения алгоритма и в результате получить компактно изложенные основы построения вероятностных моделей, охватывающие все возможное многообразие конкретных алгоритмов, вместо рассмотрения конкретного алгоритма для построения конкретной характеристики. При этом необходимо осуществлять как синтез искомого алгоритма, так и его анализ. Поскольку алгоритм состоит из системы последовательно выполняемых действий от измерения физических величин до выдачи готового результата статистических измерений, расчленение алгоритма на составные элементы начинается с декомпозиции синтезированного алгоритма. В настоящее время общепринято разделение ледовой нагрузки на локальную и глобальную. Однако в нормативной документации, как в отечественной, так и в зарубежной, не приводятся определения этих физических величин, поэтому авторы предлагают следующие формулировки.Объём — Википедия. Что такое Объём
Примеры вычисления объёмов:Куба с помощью перемножения трех сторон[1] Пирамиды с помощью умножения площади основания пирамиды на её высоту и делению на три[1] Конуса с помощью умножения площади основания на треть высоты[1] Цилиндра с помощью перемножения площади на высоту[1] Шара с помощью перемножения четырёх третьих числа Пи на радиус шара в кубе[1] Тетраэдра с помощью произведения длины его ребра в кубе на корень из двух и деления полученного на двенадцать[1] Видеоурок: объём
Объём — количественная характеристика пространства, занимаемого телом или веществом.
Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п..
Единица измерения объёма в СИ — кубический метр; от неё образуются производные единицы, такие как кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель.
В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить погрузив это тело в жидкость.{3}}.
Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Через плотность
Зная массу (m) и плотность (ρ) тела объём рассчитывается по формуле: V=mρ{\displaystyle V={\frac {m}{\rho }}}
Единицы объёма жидкости
- 1 л = 1,76 пинты = 0,23 галлона
Английские
Античные
Древнееврейские[2]
- Эйфа = 24,9 литра
- Гин = 1/6 эйфы = 4,15 литра
- Омер = 1/10 эйфы = 2,49 литра
- Кав = 1/3 гина = 1,38 литра
Русские[3]
Единицы объёма сыпучих веществ
Английские
Русские
Прочие единицы
- 1 унция (англ.) = 2,841·10−5 м³
- 1 унция (амер.) = 2,957·10−5 м³
- 1 кубический дюйм = 1,64·10−5 м³
- 1 кубический фут = 2,83·10−2 м³
- 1 кубический ярд = 0,765 м³
- 1 кубическая астрономическая единица =3,348·1024 км³
- 1 кубический световой год = 8,466·1038 км³
- 1 кубический парсек = 2,938·1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938·1049 км³
Примечания
Литература
Ссылки
Единицы измерения объёма — Википедия. Что такое Единицы измерения объёма
Материал из Википедии — свободной энциклопедии
Единицы измерения объёма — единицы измерения размера пространства, занимаемого твёрдым, сыпучим, жидким или газообразным телом. В СИ объём измеряется в кубических метрах (м³, кубометр). Применяются также кратные и дольные приставки, увеличивающие или уменьшающие размер стандартной единицы — кубический сантиметр (10-6 м3), кубический дециметр(10-3 м3) и т. д.
Внесистемные единицы измерения объёма жидкостей, газов и сыпучих тел
- литр — внесистемная единица объёма жидких и газообразных тел, допускаемая к применению наравне с единицами СИ во всех областях применения. Равна одному кубическому дециметру (10-3 м3)[1][2][3]. Используются также миллилитры (1 мл = 10-3 л = 1 см3 ).
- аам — старинная мера ёмкости в Нидерландах, Бельгии и Прибалтике, применялась преимущественно для измерения объёма вина и спирта (140-220 литров)
- анкер — старинная мера объёма, использовавшаяся в разных странах для вина, коньяка и масла.
- ка — вавилонская мера ёмкости (=0,84 л, иногда 0,42 л)
- арбата
- бочка виленская — мера объёма в Великом княжестве Литовском
- шоппен — старинная мера жидкостей (в том числе напитков) и сыпучих тел сначала в Южной Германии, затем в ряде других германских, швейцарских и французских регионов.
Английская система мер
- баррель — единица английской системы мер, применяется для измерения объёма нефти (= 158,983 л)
- галлон — единица английской системы мер, применяется для измерения объёма жидкостей (редко твёрдых тел). Примерно равен 4 литрам, размер зависит от страны и разновидности галлона[4].
- пинта — единица английской системы мер, 1/8 галлона, примерно 1/2 литра.
- кварта — единица английской системы мер, 1/4 галлона, примерно литр.
- кубический дюйм — единица английской системы мер, 1,64·10−5 м³
- кубический фут[5]
Примечания
Ссылки
Объём — это… Что такое Объём?
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.
Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма
Математически
В общем случае математически объём тела вычисляется по следующей интегральной формуле:
- ,
где — характеристическая функция геометрического образа тела.
Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен .
Через плотность
Объём находится по формуле:
Единицы объёма жидкости
- 1 л = 1,76 пинты = 0,23 галлона
Английские внесистемные
Американские внесистемные
- 1 американский галлон = 3,785 л (Распространён в США)
Античные внесистемные
Древнееврейские
- Эйфа = 24 883 см³ (Эйфа́)
- Омер = 1/10 эйфы
- Гин = 4147 см³ [1]
- Кав = 1382 см³
Русские внесистемные
Единицы сыпучих веществ
Английские внесистемные
Русские внесистемные
Молярный объём
Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:
- Vm = V/n
Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль
- Единица: м³/mol; м³/моль
Прочие единицы измерения
- 1 дюйм кубический = 1,63871·10−5 м³
- 1 литр = 1·10−3 м³
- Лямбда 1 λ = 1·10−9 м³
- 1 унция = 2,841·10−5 м³ (анг.)
- 1 унция = 2,957·10−5 м³ (амер.)
- 1 фут кубический = 2,83168·10−2 м³
- 1 ярд кубический = 0,76455 м³
- 1 стер = 1 м³
- 1 ае кубическая =3,348071936e+40 км³
- 1 км кубический = 1 000 000 000 м³
- 1 световой год кубический = 8,46590536e+38 км³
- 1 пк кубический = 2,9379989989648103256576e+40 км³
- 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³
Примечания
Литература
Единицы измерения объёма — Википедия
Материал из Википедии — свободной энциклопедии
Единицы измерения объёма — единицы измерения размера пространства, занимаемого твёрдым, сыпучим, жидким или газообразным телом. В СИ объём измеряется в кубических метрах (м³, кубометр). Применяются также кратные и дольные приставки, увеличивающие или уменьшающие размер стандартной единицы — кубический сантиметр (10-6 м3), кубический дециметр(10-3 м3) и т. д.
Внесистемные единицы измерения объёма жидкостей, газов и сыпучих тел
- литр — внесистемная единица объёма жидких и газообразных тел, допускаемая к применению наравне с единицами СИ во всех областях применения. Равна одному кубическому дециметру (10-3 м3)[1][2][3]. Используются также миллилитры (1 мл = 10-3 л = 1 см3 ).
- аам — старинная мера ёмкости в Нидерландах, Бельгии и Прибалтике, применялась преимущественно для измерения объёма вина и спирта (140-220 литров)
- анкер — старинная мера объёма, использовавшаяся в разных странах для вина, коньяка и масла.
- ка — вавилонская мера ёмкости (=0,84 л, иногда 0,42 л)
- арбата
- бочка виленская — мера объёма в Великом княжестве Литовском
- шоппен — старинная мера жидкостей (в том числе напитков) и сыпучих тел сначала в Южной Германии, затем в ряде других германских, швейцарских и французских регионов.
Английская система мер
- баррель — единица английской системы мер, применяется для измерения объёма нефти (= 158,983 л)
- галлон — единица английской системы мер, применяется для измерения объёма жидкостей (редко твёрдых тел). Примерно равен 4 литрам, размер зависит от страны и разновидности галлона[4].
- пинта — единица английской системы мер, 1/8 галлона, примерно 1/2 литра.
- кварта — единица английской системы мер, 1/4 галлона, примерно литр.
- кубический дюйм — единица английской системы мер, 1,64·10−5 м³
- кубический фут[5]
Примечания
Ссылки
Simple English Wikipedia, бесплатная энциклопедия
- Эта статья о физическом объекте; для значения из звукового поля см. громкость.
Объем объекта является мерой объема пространства, занимаемого этим объектом, и его не следует путать с массой. Объем горы, например, намного больше, чем объем камня.
По соглашению слово «объем» подразумевает трехмерный контекст, где:
- Длина — это наибольшее расстояние между конечностями объекта.
- Ширина (или ширина) относится к размеру объекта в направлении, перпендикулярном его длине.
- Высота (или глубина) обозначает размер этого объекта в направлении, перпендикулярном длине и ширине.
Для объектов, находящихся на поверхности Земли или около нее, высота или глубина часто относятся к размеру объекта по местной вертикали. Все физические объекты занимают объем, даже если некоторые из них настолько тонкие, что кажутся двумерными, как лист бумаги.
Единицей объема в Международной системе единиц является кубический метр, который обозначается символом m 3 .
В некоторых областях или приложениях часто используются разные единицы, чтобы упростить обсуждения или записи. Например:
- Ежедневное количество жидкости часто измеряется в литрах, которые записываются как L, что означает объем, занимаемый кубическим дециметром.
- Большие количества жидкостей, таких как нефть, а иногда и другие материалы, могут измеряться и продаваться в баррелях.Есть много разных справочных объемов, называемых бочками, в зависимости от характера содержимого.
Традиционные единицы все еще встречаются в некоторых странах: Имперские единицы, такие как галлон или жидкая унция, широко использовались в Британской империи. Некоторые из них до сих пор популярны в Соединенных Штатах, где также используются такие единицы, как бушель, литр, чашка и чайная ложка (например, в рецептах приготовления). Дополнительные примеры см. В стандартных единицах США.
Объем объекта не является фундаментальным свойством этого объекта: он может меняться в зависимости от условий окружающей среды, таких как давление и температура, особенно если объект сильно сжимается.
Объем смеси флюидов (жидкости, газы) может быть равен или не равен сумме их объемов до их смешивания.
В математике объем простых геометрических объектов, записанный V {\ displaystyle V}, [1] , часто можно вычислить на основе их формы и размеров:
- Объем идеального куба со стороной c равен c 3 . [2]
- Объем прямоугольной коробки — это произведение трех линейных размеров: длины, ширины и длины. [2] [3]
- Объем параллелепипеда со сторонами a , b и c равен a × b × c.
- Объем шара радиусом r равен (4/3) π r 3 . [2]
Объем газа обычно равен объему его контейнера, но он может быть плохо определен, как в случае атмосферы, у которой нет четкого верхнего предела. Объем жидкости часто измеряют, переливая ее в мерную емкость.Объем небольшого твердого вещества можно оценить, погрузив его в градуированный контейнер, частично заполненный известным количеством жидкости, при условии, что твердое вещество не растворяется в жидкости.
- ↑ «Список символов геометрии и тригонометрии». Математическое хранилище . 2020-04-17. Проверено 25 сентября 2020.
- ↑ 2,0 2,1 2,2 Вайсштейн, Эрик В. «Объем». mathworld.wolfram.com . Проверено 25 сентября 2020.
- ↑ «Длина, площадь и объем | геометрия». Британская энциклопедия . Проверено 25 сентября 2020.
Единица измерения — Простая английская Википедия, бесплатная энциклопедия
Единицы измерения предоставляют стандартов , так что числа из наших измерений относятся к одному и тому же. Измерение — это процесс, который использует числа для описания физической величины. Мы можем измерить, насколько большие вещи, насколько они теплые, насколько они тяжелые, а также множество других функций.
Например, метр — это стандартная единица измерения длины.До 1982 года оно определялось как расстояние между двумя маркерами на специальной рейке. Теперь ученые определяют метр, используя скорость света. Сказать, что что-то имеет длину два метра, означает, что это ровно в два раза больше, чем длина стержня, используемого для определения метра.
В прошлые века в разных странах использовалось много разных единиц измерения. Сегодня большинство единиц измерения относятся к одной из трех систем:
Две старые, британская имперская система и тесно связанная с ней обычная система США, используют стопу как меру длины, фунт как меру веса, а второй как меру времени.Они также используют другие единицы. Количество меньших единиц, из которых состоят большие единицы в этих двух системах, различается: например, 12 дюймов в футе и 16 унций в фунте.
Самая новая и наиболее используемая из трех систем — это метрическая система или система СИ, в которой используется 10, 100 или 1000 единиц меньшего размера для создания большей. Например, в одном метре 100 сантиметров или в килограмме 1000 граммов. Эта система использует метр для длины и килограмм для массы.
Обычное неметрическое измерение времени не следует этому шаблону.Второй является основой для измерения времени, и он основан на шестидесятеричной системе счисления: 60 секунд составляют одну минуту, а 60 минут составляют один час.
Свойство измеряемой вещи выражается в количестве единиц измерения. Число имеет смысл только тогда, когда указана единица измерения.
Например, Эйфелева башня в Париже, Франция, имеет высоту 300 метров (980 футов). [1] То есть расстояние от верха до низа Эйфелевой башни составляет 300 метров.Свойство измеряемой Эйфелевой башни — это расстояние. Было измерено 300. 300 из которых? Единица измерения — метр.
Стандарты — это специальные объекты, которые используются для проведения измерений. Метр — пример стандарта. Когда вы измеряете что-либо с помощью измерительной линейки, вы можете сравнить это измерение с чем-либо еще, что также измеряется с помощью измерительной линейки. Это упрощает измерения и упрощает сравнение результатов измерений.
В науке, медицине и технике используются меньшие единицы измерения для измерения мелких вещей с меньшими ошибками.Большие предметы легко измерить, используя большие единицы измерения. В астрономических измерениях, таких как ширина галактики, используются световые годы и парсеки.
Для малых измерений, таких как масса атома, используются специальные единицы измерения.
Во всем мире используется множество различных стандартов и единиц измерения. Некоторые стали меньше использоваться в 19 и 20 веках.
Метрическая система [изменить | изменить источник]
Метрическая система — это система измерения, используемая в большинстве стран мира.Ее также называют Международной системой единиц или СИ.
Единицы измерения в метрической системе включают:
- Единица измерения — литр. Он используется для измерения количества жидкости. Миллилитр (сокращенно мл ) — это количество жидкости, которое может заполнить куб размером 1 сантиметр с каждой стороны. Один литр жидкости заполнит куб размером 10 см с каждой стороны.
- Единицей массы является килограмм. Килограмм ( кг, ) — это масса 1 литра воды (при температуре 4 ° C или 39 ° F и 1,013.Давление 25 кПа или 146,959 фунтов на квадратный дюйм). 1 грамм ( г ) — это масса 1 миллилитра воды при 4 ° C (39 ° F). Метрическая тонна составляет 1000 килограммов или миллион граммов.
Британские единицы [изменить | изменить источник]
Имперские единицы были определены в Соединенном Королевстве в 1824 году. Эти единицы были основаны на аналогичных единицах, которые использовались до 1824 года. Имперские единицы использовались в странах, которые были частью Британской империи. Хотя многие из этих стран, включая Соединенное Королевство, официально приняли СИ, старая система единиц все еще используется.
единиц измерения в США [изменить | изменить источник]
обычных единиц США — официальные единицы, используемые в США. Они похожи на британские имперские единицы, а также основаны на единицах, используемых в Соединенном Королевстве до независимости США. Некоторые подразделения отличаются от британских. Например, в имперской пинте 20 имперских жидких унций, а в американской пинте — 16 американских жидких унций. Кроме того, жидкая унция США немного больше имперской жидкой унции.В результате пинты и галлоны США меньше английских пинт и галлонов. В Соединенных Штатах метрическая система является законной для торговли с 1866 года, но другие измерения, такие как галлон, дюйм и фунт, все еще широко используются.
Имперские и американские единицы измерения включают:
- Длина — дюйм ( дюйм ), фут ( футов ), ярд ( ярда ) и миля.
- 1 фут = 12 дюймов
- 1 ярд = 3 фута (во множественном числе футов) = 36 дюймов
- 1 миля = 1760 ярдов = 5280 футов
- Объем США — жидкая унция США ( жидких унций ), чашка США ( cp ), пинта США ( pt ), кварта США ( qt ) ) и галлон США ( галлона ).
- 1 чашка США = 8 жидких унций США
- 1 пинта США = 2 чашки США = 16 жидких унций США
- 1 кварта США = 2 пинты США = 4 чашки США = 32 унции США
- 1 галлон США = 4 кварты США = 8 пинт США = 16 чашек США
- Вес и масса — унции ( унции ), фунт ( фунта ) и стоун ( st ).
- 1 фунт = 16 унций
- 1 камень = 14 фунтов
Унции для веса и объема различаются.Даже при измерении воды количество унций веса не совпадает с количеством жидких унций.
Преобразование между системами [изменить | изменить источник]
- Метрическая система США
- 1 метр = 1,09 ярда = 39,37 дюйма.
- 1 литр = 33,3 жидких унций = 1,76 пинты = 0,26 галлона США.
- 1 килограмм = 35,32 унции = 2,2 фунта
- США в метрических единицах
- Длина
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30.48 см
- 1 ярд = 0,9144 метра
- 1 миля = 1,609344 километра
- Объем
- 1 жидкая унция = 29,6 миллилитра
- 1 пинта = 473,1 миллилитра
- 1 галлон = 3,79 литра
- 1 чашка = 236,55 миллилитра
- Масса
- 1 унция = 28,35 грамма
- 1 фунт = 0,45359237 килограмма
Единица времени — секунда. Минута (60 секунд) и час (60 минут или 3600 секунд) — большие единицы.День определяется как 24 часа, но вращение Земли замедлилось. Разница корректируется в конце нескольких лет с помощью так называемой дополнительной секунды. Неделя (7 дней) и месяц также являются стандартными единицами.
Единица измерения, применяемая к деньгам, называется расчетной единицей. Обычно это валюта, выпущенная страной. Например, в США используются доллары. Каждый доллар составляет 100 центов. Соединенное Королевство использует фунты. Каждый фунт равен 100 пенни или пенсу. Европейский Союз использует евро.В евро 100 центов.
Единицы измерения электричества, магнетизма и излучения в основном были изобретены в 19 веке, когда ученые научились их измерять. Большинству из них изначально были присвоены имперские системы, но сегодня для них обычно используются метрические системы.
- ↑ Можно также сказать: «Высота Эйфелевой башни 300 метров».
Новый подход к ICSE Physics Part 1 Class 9 Solutions Измерения и эксперименты
Новый подход к ICSE Physics Part 1 Class 9 Solutions Измерения и эксперименты
Эти решения являются частью нового подхода к ICSE Physics Part 1 Class 9 Solutions.Здесь мы представили новый подход к ICSE Physics Part 1 Class 9 Solutions Измерения и эксперименты
Unit 1
Exercise 1
(A) Объективные вопросы
I. Вопросы с несколькими вариантами ответов.
Выберите правильный вариант:
1. Что из следующего не является основным элементом?
(а) Второй
(б) Ампер
(в) Кандела
(г) Ньютон
Отв. (d) Ньютон
Пояснение: Секунда, Ампер и Кандела — основные единицы измерения, а Ньютон — производная единица.
2. Что из следующего является основным элементом?
(а) м / с 2
(б) Джоуль
(в) Ньютон
(г) метр
Отв. (d) метр
Пояснение: м / с 2 , Джоуль и Ньютон — производные единицы, а метр — основная единица.
3. Что не является единицей расстояния?
(а) метр
(б) миллиметр
(в) високосный год
(г) километр
Отв. (c) Високосный год
Пояснение: Високосный год — это единица времени, а метр, миллиметр и километр — единицы расстояния.
II Заполните пропуски
- Единица, в которой мы измеряем количество, называется постоянным количеством.
- Один световой год равен 9,46 × 10 15 м.
- Один средний солнечный день = 86400 сек
- Один год = 3,1536 × 10 7 сек
- Один микрометр = 10 -6 м.
(B) Субъективные вопросы
Вопрос 1.
Что вы понимаете под термином «измерение»?
Ответ:
«Измерение подразумевает сравнение физической величины со стандартной единицей, чтобы узнать, сколько раз данный стандарт содержится в физической величине».
Физика, как и другие отрасли науки, требует экспериментальных исследований, включающих измерения.
Вопрос 2.
Что вы понимаете под термином
- единица
- величина применительно к физической величине?
Ответ:
(i) Единица: Единица «это стандартная величина того же типа, с которой сравнивается физическая величина для ее измерения.«Чтобы измерить физическую величину, необходим стандарт (который является международным). Эталоном должна быть некоторая удобная, определенная и легко воспроизводимая величина того же типа, через которую выражается физическая величина в целом. Этот стандарт называется единицей
(ii) Величина физической величины: Количество раз, когда стандартная величина присутствует в данной физической величине, называется величиной физической величины.
Физическая величина = Величина × Единица
Вопрос 3.
Размер кузова 25 м. Укажите единицу измерения и ее величину в заявлении.
Ответ:
Здесь была использована единица измерения длины S.I, т.е. метр (м). Величина данной величины = 25
Метр: Она определяется как длина волны указанной оранжево-красной спектральной линии в 1,650,763,73 раза больше длины волны спектра излучения Криптона-86 или в 1,553,164,1 раза больше длины волны красной линии в спектре излучения кадмия.
или один метр определяется как расстояние, проходимое светом за 1/299 792 458 секунды в воздухе / вакууме.
Вопрос 4.
Укажите четыре характеристики стандартного устройства.
Ответ:
Характеристики стандартного блока:
- Должен быть удобного размера.
- Не должно меняться по месту и времени.
- Это должно быть четко определено.
- Его легко воспроизвести.
Вопрос 5.
Определите термин фундаментальная единица. Назовите основные единицы массы; длина; время; ток и температура.
Ответ:
Фундаментальная единица: Фундаментальная или базовая единица — это единица, которая не зависит от какой-либо другой единицы или которую нельзя изменить или связать с какой-либо другой фундаментальной единицей. например единицы массы, длины, времени и температуры.
Вопрос 6.
Что вы понимаете под термином производная единица? Приведите три примера.
Ответ:
Производные единицы. «Производные единицы — это единицы, которые могут быть выражены в основных единицах.”
Пример.
2. S.I. единица площади, т. Е. М 2 — производная единица.
Площадь = длина × ширина
Теперь метр — это единица длины и ширины, поэтому единица площади S.I. получается путем умножения основной единицы «м» на себя. Итак, м 2 — производная единица площади.
3. Плотность = масса / объем
S.I. единица плотности, т.е. кг / м. 3 — производная единица плотности, потому что ее можно получить, объединив две основные единицы — килограмм и метр.
Вопрос 7.
(a) Определите счетчик в соответствии со старым определением.
(b) Определите измеритель с точки зрения длины волны света.
(c) Почему метр длины волны света считается более точным?
Ответ:
(a) Метр: Один метр определяется как одна десятимиллионная часть расстояния от полюса до экватора.
(b) Счетчик: Один метр определяется как 1 650 763.В 73 раза больше длины волны указанной оранжево-красной спектральной линии в спектре излучения криптона = 86.
OR
Один метр определяется как 1,553,164,1 длины волны красной линии в спектре излучения кадмия.
(c) Длина метра с точки зрения длины волны света считается более точной, потому что
- Длина волны света не меняется со временем, температурой, давлением и т. Д.
- Ее можно воспроизвести где угодно в любое время, потому что криптон является доступен везде.
Вопрос 8.
Назовите удобную единицу измерения, которую вы будете использовать для измерения:
(a) длина холла
(b) ширина книги
(c) диаметр волос
(d) расстояние между двумя городами.
Ответ:
(a) Фут (фут)
(b) Сантиметр (см)
(c) Микрометр (мкм)
(d) Километр (км)
Вопрос 9.
(a) Определите массу.
(b) Укажите единицы измерения массы в (1) C.GS. система (2) Система S.I.
(c) Назовите наиболее удобную единицу массы, которую вы будете использовать для измерения:
- Масса небольшого количества лекарства.
- Зерновой выход состояния
- Мешок сахара
- Масса крикетного мяча.
Ответ:
(a) Масса: количество вещества, содержащегося в теле, называется его массой.
(b) В C.GS. системы, масса измеряется в граммах. В системе S.I. масса измеряется в килограммах.
Вопрос 10.
(a) Определите время.
(b) Укажите или определите следующие термины:
- Солнечный день
- Средний солнечный день
- Час
- Минуту
- Второй
- Год.
Ответ:
(a) Время: Определяется как временной интервал между двумя событиями
(b)
(i) Солнечный день: Время, затрачиваемое Землей на один оборот вокруг собственной оси называется солнечным днем.
(ii) Средний солнечный день: Среднее значение различных солнечных дней, когда Земля совершает один оборот вокруг Солнца, называется средним солнечным днем.
(iii) Час: Он определяется как 1/24 часть среднего солнечного дня.
(iv) Минута: Она определяется как 1/1440 часть среднего солнечного дня.
(v) Секунда: «Секунда определяется как 1/86400-я часть среднего солнечного дня».
OR
Второй также может быть определен как «равный длительности 9 192 631 770 колебаний, соответствующих переходу между двумя сверхтонкими уровнями атома цезия-133 в основном состоянии.
(vi) Год: Один год определяется как время, за которое Земля совершает один полный оборот вокруг Солнца.
Раздел II
Практические задачи 1
Вопрос 1.
Студент экспериментально вычисляет значение плотности железа как 7,4 драгоценного камня -3 . Если фактическая плотность железа составляет 7,6 г · см -3 , рассчитайте процентную ошибку в эксперименте.
Ответ:
Вопрос 2.
Ученик обнаруживает, что температура кипения воды в конкретном эксперименте составляет 97,8 ° C. Если фактическая температура кипения воды составляет 99,4 ° C, рассчитайте погрешность в процентах.
Ответ:
Экспериментальное значение точки кипения воды = B.P 1 = 97,8 ° C
Фактическое значение точки кипения воды = B.P 2 = 99,4 ° C
Абсолютная погрешность = B.P. 2 — B.P 1 = 99,4 — 97,8 = 1,6 ° C
Вопрос 3.
Ученик определяет скорость звука как 320 мс -1 .Если фактическая скорость звука составляет 332 мс -1 , вычислите ошибку в процентах.
Ответ:
Скорость звука определяется зрачком = V 1 = 320 мс -1
Фактическое значение скорости звука = V 2 = 332 мс -1
Абсолютная погрешность = V 2 — V 1 = 332 — 320 = 12 мс -1
Упражнение 2
Вопрос 1.
(a) Что вы понимаете под термином «порядок величины» количество?
(b) Почему физические величины выражаются по порядку величины? Подтвердите свой ответ примером.
Ответ:
(a) Порядок величины величины: Показательная часть конкретного измерения называется порядком величины.
OR
Порядок величины данной числовой величины — это ближайшая степень десяти, в которой может быть записано ее значение. (B) Измерения определенных физических величин либо слишком велики, либо слишком малы, чтобы их нельзя было удобно выразить. Их сложно написать или запомнить. Таким образом, такие количества можно выразить по порядку величины.
Например: Диаметр Солнца составляет 1 390 000 000 м. Такое измерение сложно записать или запомнить. Таким образом, это выражается как 1,39 × 109 м.
Здесь степень десяти, т. Е. 9 (то есть экспоненциальная часть измерения) дает порядок величины данной величины.
Итак, диаметр Солнца по порядку величины равен 10 9 м.
Вопрос 2.
Выразите порядок величины следующих величин:
- 12578935 м
- 222444888 кг
- 0.000,000,127 с
- 0,000,000,000,00027 м
Ответ:
Вопрос 3.
(a) Что вы понимаете под термином «степень точности»?
(b) Среди различных физических измерений, зарегистрированных в ходе эксперимента, какое физическое измерение определяет степень точности?
Ответ:
(a) Степень точности: Это означает, что мы можем измерить количество без какой-либо ошибки в оценке.
В любом эксперименте все наблюдения должны проводиться с одинаковой степенью точности.
(b) Среди различных физических измерений, зарегистрированных в ходе эксперимента, наименее точное наблюдение определяет степень точности.
Вопрос 4.
(a) Сформулируйте формулу для вычисления процентной погрешности
(b) Можно ли увеличить степень точности математическими манипуляциями? Подтвердите свой ответ примером.
Ответ:
(а) Процентную погрешность можно рассчитать по формуле:
(б) Повысить точность математическими манипуляциями невозможно.
Например: Когда несколько значений добавляются или вычитаются, результат не может быть более точным, чем наименее точное значение.
В приведенном выше добавлении 72,5 имеет наименьшую точность. Когда мы . скажем, 72,5, это означает, что значение находится между 72,45 и 72,55, и 72,5 является наиболее вероятным значением. Таким образом, ошибка 72,5 составляет +0,05. Поскольку конечный результат не может быть более точным, чем наименее точное наблюдение, правильный и самый надежный ответ в приведенном выше дополнении — 72,9.
Вопрос 5.
Укажите коэффициенты, определяющие количество значащих цифр для расчета окончательного результата эксперимента.
Ответ:
Факторами, определяющими количество значащих цифр для расчета окончательного результата эксперимента, являются:
- Характер эксперимента.
- Точность выполнения различных измерений.
Вопрос 6.
Окончательный результат расчетов в эксперименте 125 347 200.Выразите число через значащие разряды, когда точность
- составляет от 1 до 10
- точность составляет от 1 до 100
- точность составляет от 1 до 1000
Ответ:
Окончательный результат расчетов в эксперименте = 125,347,200
- Когда точность находится между 1 и 10, окончательный результат может быть записан как 1,2 × 10 8 .
- Когда точность находится между 1 и 100, окончательный результат может быть записан как 1.25 × 10 8 .
- Когда точность находится между 1 и 1000, окончательный результат может быть записан как 1,253 × 10 8 .
Unit 3
Практические задачи 1
Вопрос 1.
Основная шкала штангенциркуля имеет 10 делений в сантиметре, и 10 делений нониусной шкалы совпадают с 9 основными делениями шкалы. Рассчитать
- шаг
- L.C. штангенциркуля.
Ответ:
Деление основной шкалы штангенциркуля в один сантиметр = 10
Вопрос 2.
В штангенциркулях 19 основных делений шкалы совпадают с 20 делениями нониусной шкалы. Если основная шкала имеет 20 делений в сантиметре, рассчитайте шаг
- L.C. штангенциркуля.
Ответ:
Основные деления шкалы штангенциркуля в один сантиметр = 20 единиц
Практические задачи 2
Вопрос 1.
На рисунке показано положение нониусной шкалы при измерении внешней длины деревянный цилиндр.
- Какую длину фиксирует основная шкала?
- Какое значение нониусной шкалы совпадает с основной шкалой?
- Рассчитайте длину.
Ответ:
Деление главной шкалы штангенциркуля в одном сантиметре = 10
Вопрос 2.
На рисунке для штангенциркуля рассчитайте записанную длину.
Ответ:
Основные деления шкалы штангенциркуля в один сантиметр = 10
Практические задачи 3
Вопрос 1.
(a) Нониусная шкала имеет 10 делений. Он скользит по основной шкале с шагом 1,0 мм. Если количество делений слева от нуля нониусной шкалы на основной шкале равно 56 и 8-е деление нониусной шкалы совпадает с основной шкалой, рассчитайте длину в сантиметрах.
(b) Если указанный выше инструмент имеет отрицательную ошибку 0,07 см, рассчитайте скорректированную длину.
Ответ:
Число делений на нониусной шкале = 10
Шаг = 1.0 мм
Вопрос 2.
(a) Нониусная шкала имеет 20 делений. Он скользит по основной шкале с шагом 0,5 мм. Если количество делений слева от нуля нониусной шкалы на основной шкале равно 38, а 18-е деление нониусной шкалы совпадает с основной шкалой, вычислите диаметр сферы, удерживаемой в губках штангенциркуля.
(b) Если нониус имеет отрицательную ошибку 0,04 см, вычислите скорректированный радиус сферы.
Ответ:
Количество делений на нониусной шкале = 20
Шаг 0,5 мм
Практические задачи 4
Вопрос 1.
Наименьшее количество штангенциркуля составляет 0,0025 см, и он имеет погрешность + 0,0125 см. При измерении длины цилиндра показание на основной шкале составляет 7,55 см, а 12-е деление нониусной шкалы совпадает с основной шкалой. Рассчитайте исправленную длину.
Ответ:
Наименьшее количество (L.C.) = 0,0025 см
Погрешность = +0,0125 см
Поправка = — (Ошибка) = — (+0,0125) = — 0,0125 см
Показание основной шкалы = 7,55 см
Деление нониусной шкалы (VSD), совпадающее с основной шкалой = 12-я
Зарегистрированная длина = показание основной шкалы + LC × В.С.Д.
= 7,55 + 0,0025 × 12
= 7,55+ 0,0300 = 7,58 см
Правильная длина = записанная длина + поправка
= 7,58+ (-0,0125)
= 7,58 — 0,0125 = 7,5675 см = 7,567 см
Вопрос 2.
Наименьшее количество штангенциркулей — 0.01 см и имеет погрешность + 0,07 см. При измерении радиуса сферы основное показание шкалы составляет 2,90 см, а 5-е деление шкалы нониуса совпадает с основной шкалой. Рассчитайте правильный радиус.
Ответ:
Наименьшее количество (LC) = 0,01 см
Погрешность = + 0,07 см
Поправка = (Ошибка) = — (+ 0,07) = — 0,07 см
Показание основной шкалы = 2,90 см
Деление на нониусной шкале (VSD) совпадает с основной шкалой = 5-й Наблюдаемый диаметр сферы = Показание основной шкалы + L.C. × V.S.D.
= 2,90 + 0,01 x 5 = 2,90 + 0,0 = 2,95 см
Скорректированный диаметр = наблюдаемый диаметр + поправка
= 2,95 + (-0,07) = 2,95 — 0,07 = 2,88 см
∴ Скорректированный радиус = 2,88 / 2 = 1,44 см
Упражнение 3
Вопрос 1.
Кто изобрел штангенциркуль?
Ответ:
Штангенциркуль нониус изобрел Пьер Вернье.
Вопрос 2.
Зачем нужно измерение длины штангенциркулем?
Ответ:
Для измерения точной длины с большей точностью, особенно когда мы измеряем очень маленькую длину, мы используем штангенциркуль с нониусом.Штангенциркуль может измерять с точностью до 1/100 доли сантиметра.
Вопрос 3.
С точностью до десяти знаков после запятой можно измерить длину в см обычным штангенциркулем?
Ответ:
Обычный штангенциркуль может измерять длину с точностью до двух десятичных знаков, если длина измеряется в сантиметрах
, т.е. до 1/100 части сантиметра.
Вопрос 4.
Определите термины:
- шаг
- наименьший счет применительно к штангенциркулям.
Ответ:
- Шаг: «Шаг винта — это расстояние, на которое винт перемещается за один полный оборот его головки».
OR
Шаг можно также определить как «расстояние между двумя последовательными витками резьбы винта, измеренное вдоль оси винта». - Наименьшее количество нониусных штангенциркулей: Наименьшее количество нониусных штангенциркулей — это разница между одним делением основной шкалы (M.S.D.) и одним делением нониусной шкалы (V.S.D.)
Вопрос 5.
Сформулируйте формулу для определения:
- шаг
- наименьшее количество для штангенциркуля.
Ответ:
Вопрос 6.
Укажите формулу для расчета длины, если:
- Число делений нониусной шкалы, совпадающее с основной шкалой, и число делений основной шкалы слева от нуля нониусной шкалы.
- Показание основной шкалы известно, и известно количество делений нониусной шкалы, совпадающих с основной шкалой.
Ответ:
- Если мы знаем количество делений нониусной шкалы (VSD), совпадающее с основной шкалой, и количество главных делений шкалы (MSD) слева от нуля нониусной шкалы, то записанная длина = основная шкала чтение + LC × В.С.Д.
- То же, что и в части (i).
Вопрос 7.
(a) Что вы понимаете под термином «ошибка нуля»?
(b) Когда штангенциркуль имеет
- положительную ошибку
- отрицательную ошибку?
(c) Укажите исправление, если
- положительная ошибка составляет 7 делений
- отрицательная ошибка составляет 7 делений, когда наименьший счет равен 0.01 см.
Ответ:
(a) Ошибка нуля: Считается, что штангенциркуль имеет нулевую ошибку, если ноль основной шкалы не совпадает с нулем нониусной шкалы.
(b) Положительная ошибка: Если ноль нониусной шкалы находится справа от нуля основной шкалы, то ошибка считается положительной, а коррекция — отрицательной.
Погрешности измерения
| Ошибка? №.. ты не измерил неправильно … это примерно точность . |
Измерительные приборы не точны!
Степень точности
Точность зависит от прибора, которым вы проводите измерения. Но как правило:
Степень точности составляет половину единицы с каждой стороны единицы измерения
Примеры:
| Когда ваш прибор измеряет в «1» с , тогда любое значение от 6½ до 7½ измеряется как «7» | |
| Когда ваш прибор измеряет в «2» с , тогда любое значение от 7 до 9 измеряется как «8» |
Обратите внимание, что стрелка указывает на одно и то же место, но измеренные значения отличаются!
Плюс или Минус
| Мы можем показать ошибку с помощью знака «плюс» или «минус»: | ± |
Когда значение может быть между 6½ и 7½ : 7 ± 0.5 Погрешность ± 0,5 | |
Когда значение может быть от 7 до 9 : 8 ± 1 Погрешность ± 1 |
Пример: длина забора составляет 12,5 метра с точностью до 0,1 метра
С точностью до 0,1 м означает, что это может быть до 0,05 м в любую сторону:
Длина = 12.5 ± 0,05 м
Так что это действительно может быть от 12,45 м до 12,55 м в длину.
Абсолютная, относительная и процентная ошибка
Абсолютная ошибка — это разница между фактическим и измеренным значением .Но … при измерении мы не знаем действительного значения! Итак, мы используем максимально возможную ошибку.
В приведенном выше примере абсолютная ошибка составляет 0,05 м.
Что случилось с ±…? Ну, нам просто нужен размер (абсолютное значение) разницы.
Относительная ошибка — это абсолютная ошибка, деленная на фактическое измерение.Мы не знаем фактического измерения, поэтому лучшее, что мы можем сделать, это использовать измеренное значение :
Относительная ошибка = Абсолютная ошибка Измеренное значение
Ошибка в процентах — это относительная ошибка, отображаемая в процентах (см. Ошибка в процентах).Давайте посмотрим на них на примере:
Пример: забор (продолжение)
Длина = 12.5 ± 0,05 м
Итак:
Абсолютная ошибка = 0,05 м
А:
Относительная погрешность = 0,05 м 12,5 м = 0,004
А:
Ошибка в процентах = 0,4%
Другие примеры:
Пример: термометр измеряет с точностью до 2 градусов. Температура составила 38 ° C
Температура может составлять до 1 ° в любую сторону от 38 ° (т. Е. От 37 ° до 39 °).
Температура = 38 ± 1 °
Итак:
Абсолютная ошибка = 1 °
А:
Относительная погрешность = 1 ° 38 ° = 0.0263 …
А:
Ошибка в процентах = 2,63 …%
Пример: вы измеряете высоту растения 80 см (с точностью до см)
Это означает, что вы можете ошибиться на 0,5 см (высота растения может быть от 79,5 до 80,5 см).
Высота = 80 ± 0,5 см
Итак:
Абсолютная ошибка = 0,5 см
А:
Относительная ошибка = 0,5 см 80 см = 0.00625
А:
Ошибка в процентах = 0,625%
Площадь
При проработке областей вы должны думать как о ширине , так и о длине … они могут быть как наименьшей мерой, так и обеими наибольшими.
Пример: Алекс измерил поле с точностью до метра и получил ширину 6 м и длину 8 м.
Измерение с точностью до метра означает, что истинное значение может быть до полметра меньше или больше.
Ширина (w) может составлять от 5,5 м до 6,5 м:
5,5 ≤ ширина <6,5
Длина (l) может быть от 7,5 м до 8,5 м:
7,5 ≤ л <8,5
Площадка ширина × длина:
A = ш × д
Наименьшая возможная площадь: 5,5 м × 7,5 м = 41,25 м 2
Измеренная площадь: 6 м × 8 м = 48 м 2
И максимально возможная площадь: 6,5 м × 8.5 м = 55,25 м 2
41,25 ≤ A <55,25
Абсолютная, относительная и процентная ошибка
Единственная хитрость здесь … какой является абсолютной ошибкой?
- От 41,25 до 48 = 6,75
- От 48 до 55,25 = 7,25
Ответ: выбирайте самый большой! Итак:
Абсолютная ошибка = 7,25 м 2
Относительная ошибка = 7.25 м 2 48 м 2 = 0,151 …
Ошибка в процентах = 15,1%
(что не очень точно, правда?)
Том
А объем имеет три измерения: ширины, длины и высоты!
Каждое измерение могло быть самым маленьким или самым большим.
Пример: Сэм измерил коробку с точностью до 2 см и получил 24 см × 24 см × 20 см
Измерение с точностью до 2 см означает, что истинное значение может быть до на 1 см меньше или больше.
Три размера:
- 24 ± 1 см
- 24 ± 1 см
- 20 ± 1 см
Объем: ширина × длина × высота:
В = ш × д × в
Наименьший возможный объем: 23 см × 23 см × 19 см = 10051 см 3
Измеренный объем: 24 см × 24 см × 20 см = 11520 см 3
Максимально возможный объем: 25 см × 25 см × 21 см = 13125 см 3
И так получаем:
10051 ≤ В <13125
Абсолютная, относительная и процентная ошибка
Абсолютная ошибка:
- От 10051 до 11520 = 1469
- От 11520 до 13125 = 1605
Выберите самый большой:
Абсолютная ошибка = 1605 см 3
Относительная погрешность = 1605 см 3 11520 см 3 = 0.139 …
Ошибка в процентах = 13,9%
Frontiers | Измерение абсолютного объема клеток с помощью количественно-фазовой цифровой голографической микроскопии и недорогой проточной камеры с открытым исходным кодом и 3D-печати
Введение
Мембраны клеток животных очень водопроницаемы. Движение воды через мембраны в значительной степени определяется градиентами осмотического давления. Следовательно, даже при постоянной внеклеточной осмолярности постоянство объема любой клетки млекопитающего постоянно подвергается сомнению из-за ее собственной активности, включая, например, перемещения различных видов ионов через клеточную мембрану или транспорт осмотически активных веществ, участвующих в метаболизме клетки, все из которых индуцируют осмотические водные движения [1, 2].С другой стороны, множество жизненно важных функций клетки, включая активность ферментов, механизмы экспрессии генов, каскады вторичных мессенджеров и высвобождение гормонов, в значительной степени зависят от гомеостатического внутриклеточного ионного окружения [3, 4]. Следовательно, объем клетки является одним из критических параметров клетки и строго регулируется. Соответственно, клетки разработали множество эффективных механизмов регулирования объема, включающих множественные процессы переноса ионов, включая каналы, котранспортеры и обменники, которые работают для поддержания постоянного ионного баланса и градиента гидростатического давления.Для этого осмотически активные растворенные вещества (в основном неорганические ионы, такие как Na + , K + , Cl — или органические осмолиты) приобретаются или теряются, чтобы регулировать объем клетки [5].
В настоящее время надежные и неинвазивные измерения абсолютного объема клеток V c являются труднодостижимыми [6]. Хотя современные и распространенные методы проточной цитометрии предлагают огромную производительность и могут рассматриваться как золотой стандарт, они предназначены для измерения V c с использованием больших образцов изолированных клеток в суспензии [7].Тем не менее, изучение объемного гомеостаза и его регуляторных механизмов требует способности измерять V c в условиях окружающей среды, в которых клетки растут, мигрируют и связываются друг с другом. В этом случае не существует методологического консенсуса для достижения таких V c измерений. Среди немногих подходящих методов микроскопия для исключения красителей, основанная на абсорбции [8] или флуоресценции [9], использует эквивалентное вытеснение окрашенной жидкости, создаваемое клеткой, для измерения ее толщины, но для этого требуются внеклеточные метки.Это измерение толщины используется вместе с проецируемой поверхностью клетки (в данном случае, измеренной на соответствующем микроскопическом изображении) для вычисления V c .
В качестве альтернативы, количественно-фазовая визуализация (QPI) состоит из набора методов микроскопии, предлагающих возможность получения изображений без меток, неинвазивных методов с высоким разрешением и в реальном времени прозрачных микроскопических образцов, таких как живые клетки в культуре [ 10, 11].QPI измеряет незначительный фазовый сдвиг, а именно количественно-фазовый сигнал (QPS), который прозрачные образцы создают на дифрагированном волновом фронте, если наблюдаемый образец является слабо рассеивающим объектом, т. Е. Отличается от окружающей среды только на небольшая разница показателя преломления [12–17]. Таким образом, QPS, пропорциональный длине оптического пути (OPL), зависит как от внутриклеточного показателя преломления (IRI), так и от толщины клетки. Согласно основополагающей работе Barer [18], эта зависимость IRI позволила разработать QPI как эффективный метод количественного мониторинга динамики сухой массы клеток, особенно в связи с циклом роста клеток [19–22].Различные подходы QPI, основанные на интерферометрических принципах, также позволили обнаружить флуктуации клеточных мембран в нанометрическом масштабе, особенно в отношении красных кровяных телец [23-25].
Несмотря на эти плодотворные применения в простых случаях, информация о внутреннем сочетании клеточного содержимого и морфологии, QPS и его вариациях остается в целом трудной для интерпретации в клеточной биологии [26]. Измерение IRI и толщины клетки по отдельности представляет собой ключевой научный шаг, ведущий к расчету различных количественных биофизических параметров клетки, включая V c [27, 28], водопроницаемость осмотической мембраны [29], показатель преломления трансмембранной воды и потока растворенных веществ [29], позволяющий изучать специфические физиологические и патофизиологические клеточные процессы [30–33].В частности, V c рассчитывается как из толщины клетки, так и из проекции поверхности клетки, как в случае микроскопии исключения красителя.
Оптическая дифракционная томография позволяет получить также с помощью QPS как распределение показателя преломления, так и морфологию живых клеток в 3D [34, 35]. Однако за эту уникальную возможность 3D приходится расплачиваться сложными схемами построения изображений и в значительной степени полагаться на приближения, используемые в алгоритмах процесса реконструкции, что требует значительного опыта.
Однако были разработаны менее сложные экспериментальные процедуры для извлечения как IRI, так и соответствующей толщины ячеек из QPS [26, 36–42], что значительно способствует их применению. Концептуально существует два основных класса таких процедур. Первый включает извлечение IRI путем оценки толщины клеток либо путем аппроксимации формы с использованием геометрических моделей, прямого измерения с дополнительными модальностями визуализации или физического ограничения в осевом направлении с использованием микроструктур с известной априори геометрией.Хотя аппроксимация формы и физическое ограничение больше подходят для взвешенных, чем прикрепленных клеток, прямое измерение с дополнительным методом визуализации обычно проводится отдельно, что затрудняет наблюдение динамических биологических процессов. Вторая группа процедур решает IRI и проблему связи толщины ячейки путем достижения двух разных измерений QPS, что приводит к системе независимых линейных уравнений с двумя неизвестными, имеющими единственное решение.Среди этих методов — двухжидкостная развязка, которая особенно привлекательна для адгезивных клеток, поскольку не требует никаких предположений о морфологии клеток или осевого ограничения, что обычно приводит к лучшим физиологическим условиям окружающей среды, чем в процедурах первого класса. Используемый в сочетании с количественно-фазовой цифровой голографической микроскопией (QP-DHM), он обеспечивает точные измерения среднего показателя преломления n¯c и средней толщины h¯c клеточного тела [26].Однако этот метод имеет несколько недостатков, связанных с процессом вымывания, возникающим из-за необходимости последовательной перфузии двух различных эквиосмолярных физиологических растворов с разными, но a priori , известными показателями преломления.
Последние разработки доступных и точных 3D-принтеров, а также доступность программного обеспечения для автоматизированного проектирования (САПР) посредством аддитивного производства открывают прекрасные возможности для создания нестандартных и инновационных устройств, отвечающих потребностям конкретного приложения.Для исследователей 3D-печать — это универсальный и недорогой метод, который позволяет быстро создавать прототипы и значительно улучшать предыдущие версии и варианты дизайна [43]. Таким образом, в контексте визуализации живых клеток 3D-печать идеальна для создания аксессуаров микроскопов, адаптированных к точным потребностям QP-DHM, и с QPI в более общем виде.
Насколько нам известно, авторы создали первую недорогую проточную камеру с открытым исходным кодом и напечатанную на 3D-принтере проточную камеру с индивидуализированными характеристиками поля потока, которая обеспечивает эффективный процесс вымывания.В рамках подхода двухжидкостной развязки такой процесс вымывания характеризуется ранней стадией, во время которой QPS является временно нестабильной, за которым следует период стабилизации QPS, соответствующий состоянию, в котором показатель преломления второго раствора распределен равномерно по всей проточной камере. С точки зрения механики жидкости в этой ситуации может быть полезным использование стационарного и полностью развитого ламинарного потока (который уменьшает поперечное перемешивание).
Конструкция и научные особенности этой 3D-печатной проточной камеры будут представлены в этой статье. Сначала представлена механическая конструкция проточной камеры, сделанной своими руками. Во-вторых, будет объяснена оптимизация геометрии проточной камеры для получения такого потока жидкости (в результате численного моделирования). Кроме того, наличие стационарного и полностью развитого ламинарного потока было подтверждено экспериментально для геометрии проточной камеры. В такой ситуации время вымывания, необходимое для чередования двух жидкостей, было тщательно экспериментально охарактеризовано.Оценивалась скорость, с которой стабилизируется QPS (показатель однородности показателя преломления перфузионной среды). В качестве подтверждения для демонстрации того, как работает эта предлагаемая напечатанная на 3D-принтере проточная камера, она использовалась для проведения экспериментов по разделению в состоянии покоя трех распространенных типов клеток в культуре, а именно первичных нейронов, клеток HEK293T и NIh4T3. В частности, как n¯c, так и h¯c, а также их соответствующие V c систематически рассчитывались для каждого типа ячеек.Кроме того, уровень жизнеспособности клеток внутри проточной камеры сравнивался с контрольным условием, чтобы определить его совместимость с визуализацией живых клеток. Наконец, изменения этих биофизических параметров были количественно оценены во время гипоосмотической и гиперосмотической нагрузки.
Теория и принципы
Сигнал фазы ячейки каждого ( x, y ) -пикселя количественно-фазового изображения QP-DHM можно выразить как:
ϕc (x, y) = 2πλ0 (∫0hc (x, y) nc (x, y, z) dz + nm (H-hc (x, y))) (1) ϕc (x, y) = 2πλ0 ((n¯c (x, y) -nm) hc (x, y) + nmH) (2), где λ 0 — длина волны источника света в свободном пространстве, z — осевая координата, h c ( x, y ) — толщина ячейки, соответствующая OPL каждого пиксель, n c ( x, y, z ) — трехмерное распределение IRI, n¯c (x, y) = 1hc (x, y) ∫0hc (x, y) nc (x, y, z) dz — среднее значение IRI вдоль h c ( x, y ) (иначе известное как интегральный IRI), n m — это показатель преломления перфузионной среды, а H — толщина проточной камеры.Точно так же фазовый сигнал, соответствующий фону количественно-фазового изображения, можно сформулировать как:
ϕbkgd = 2πλ0nmH (3)Мониторинг и последующее повторное использование этого фонового значения важны, потому что это компенсирует механическую и термическую нестабильность установки во время эксперимента. Кроме того, учитывая ограниченные фоновые области вокруг исследуемой ячейки, эффективные изменения высоты камеры не являются проблемой [44]. Вычитая Уравнение (3) из Уравнения (2), QPS каждого ( x, y ) -пикселя [12] можно выразить как:
Δϕc (x, y) = ϕc (x, y) -ϕbkgd = 2πλ0 (n¯c (x, y) -nm) hc (x, y) (4)Хотя временная зависимость явно не указана в уравнении (4), она остается действительной для каждого количественно-фазового изображения покадровой съемки.Двойная зависимость, выраженная уравнением (4) (известная как проблема связи показателя преломления и толщины [45]), приводит к противоречивой и сложной интерпретации QPS.
Чтобы получить эти два вклада независимо, была проведена двухжидкостная процедура развязки [26]. В этом методе используются две изоосмотические и изотонические перфузионные среды, имеющие два разных, но априори известных показателей преломления (а именно n m 1 и n m 2 ) были последовательно перфузированы.Внеклеточный показатель преломления перфузионной среды варьировал от n м 1 до n м 2 с переходным периодом, в течение которого QPS не определяется, с последующим периодом стабилизации . Между тем, была записана покадровая съемка количественно-фазовых изображений. Этот подход разделения двух жидкостей создает систему двух уравнений с двумя неизвестными, которые могут быть решены как:
n¯c (x, y) = Δϕc2 (x, y) nm1-Δϕc1 (x, y) nm2Δϕc2 (x, y) -Δϕc1 (x, y) (5) hc (x, y) = λ02πΔϕc2 (x, y) -Δϕc1 (x, y) nm1-nm2 (6), где индексы 1 и 2 относятся к двум различным состояниям стабилизации QPS, соответствующим двум разным перфузионным средам [26].Отсюда вычисление n¯c и h¯c может быть выполнено путем усреднения для каждого состояния i = 1, 2, Δϕ c i ( x, y ) по всем сегментированные пиксели, содержащиеся в одноклеточном теле, а именно Δϕ¯ci = Δϕci (x¯, y¯). Следовательно, получаем:
n¯c = Δϕ¯c2nm1-Δϕ¯c1nm2Δϕ¯c2-Δϕ¯c1 (7) h¯c = λ02πΔϕ¯c2-Δϕ¯c1nm1-nm2 (8)С помощью автоматизированной сегментации получается проекционная поверхность ячейки, S c , что позволяет рассчитать абсолютный объем ячейки [29], V c , как показано ниже:
Vc = ∫Schc (x, y) ds = h¯cSc≅h¯cApNc (9), где A p — это площадь увеличенного пикселя, а N c — количество пикселей, соответствующих телу ячейки.Однако для получения точных результатов необходимо выполнить следующие рабочие предположения. Предполагается, что n¯c и h¯c не претерпевают значительных изменений во время задержки, вызванной процессом вымывания. Это, в частности, требует использования двух равноосмолярных перфузионных сред, чтобы избежать любых осмотических проблем. Кроме того, чтобы минимизировать эффект изменений клеток, которые происходят с течением времени и влияют либо на n¯c, либо на h¯c (или на то и другое), процесс вымывания позволяет вернуть внеклеточные показатели преломления по всей щели изображения в сторону известные значения n м 1 или n м 2 , должны быть как можно короче.
Материалы и методы
Изготовление проточной камеры
Механический дизайн проточной камеры был разработан с помощью SolidWorks (2016, Dassault Systèmes). Проточная камера была напечатана на 3D-принтере из высокопрочного пластика PETG (Guideline, Taulman3D) на принтере Ultimaker 2 Extended +. Основание и крышка были напечатаны соплом 0,4 мм (Micro Swiss) с легким заполнением. И в основании, и в крышке есть по четыре круглых отверстия, предназначенных для вставки редкоземельных магнитов (5862K961, McMaster-Carr).Эти магниты склеены быстросохнущим клеем (5551T72, McMaster-Carr). Прокладка из парафильма, содержащаяся в основе, была вырезана ножницами из листа парафильма (M, BEMIS). На держателе образца напечатали сопло 0,25 мм (Micro Swiss) с перекрытием 100 и 30% заполнения. 30% -ное перекрытие центрального элемента при заполнении обычно предотвращает внутренние утечки; однако его необходимо обработать ацетоном для обеспечения полной водонепроницаемости с учетом уровня давления во время протекания жидкости [46]. Только верхняя часть (самая грубая поверхность) держателя образца должна подвергаться воздействию паров ацетона (270725, Sigma-Aldrich) в течение рекомендованных 15 минут.После этой обработки чистое покровное стекло толщиной 18 мм вдавливается в паз, сделанный для этой цели, что приводит к его герметизации и фиксации. Прикладывали давление на покровное стекло и удерживали его около 1 мин, причем первые 10 с были решающими. С каждой стороны центрального элемента частично вставлены микропробирки из нержавеющей стали (304F10125X006SL, MicroGroup) и приклеены быстрым клеем. Нарезка трубок — деликатный процесс, так как неправильная техника приведет к их разрушению. Острое лезвие (LB, OLFA) используется для катания микропробирки с приложением некоторого давления.После нескольких циклов назад и вперед микропробирки можно разрезать без изменения их полости. Подробный пошаговый протокол изготовления проточной камеры можно найти в Приложении A.
Монтаж проточной камеры
Камера предназначена для сокращения времени обработки и обеспечения благополучия исследуемых клеток в соответствии с реальностью клеточной визуализации. Сначала на основу накладывается парапленочная прокладка. Затем небольшое количество перфузионной жидкости вводится с помощью подсоединенного шприца в перевернутый держатель образца, который имеет окно с фиксированной верхней частью.Покровное стекло диаметром 18 мм, содержащее культуру клеток (нижнее покровное стекло), затем помещается вертикально прямо на нижнее крепление и смачивается каплей умеренной среды. Затем заполненный центральный элемент поворачивается назад и устанавливается на основание. Затем камера закрывается за счет давления только крышки и магнитов. Наконец, любые пузырьки воздуха быстро удаляются путем осторожного введения среды через шприц, закрепленный на держателе образца.
Вычислительная гидродинамика
Моделирование проводилось с помощью модуля вычислительной гидродинамики (CFD) COMSOL Multiphysics (5.3а, COMSOL) и поиск стационарных решений. Поперечное сечение на виде сверху использовалось для определения геометрии для моделирования и в предположении, что 2D-представление является удовлетворительным приближением. Для обеспечения большего сходства с экспериментальной установкой в геометрию были включены микротрубки с использованием их внутреннего диаметра в качестве входного размера. Чтобы ввести ламинарный поток на входе в проточную камеру, длина входа была рассчитана для каждого расхода с выражением для числа Рейнольдса в круглой трубе, в результате чего были получены значения от 1 до 2 мм.Скорость ламинарного потока на входе варьировалась от 0,2 до 5,1 мл / мин. Граничное условие прилипания использовалось для краев, а также условие отсутствия давления на выходе из проточной камеры. Во всех симуляциях жидкость течет справа налево.
Измерение скорости изображения микрочастиц
Экспериментальный поток внутри щели для визуализации контролировался с помощью установки для измерения скорости изображения микрочастиц (μPIV), состоящей из камеры машинного зрения (Grasshopper3, FLIR) и системы линз с переменным увеличением (MVL-7000, NAVITAR).Камера была оснащена монохромным 2,3-мегапиксельным CMOS-сенсором Sony IMX174 с размером пикселя 5,86 мкм и максимальной скоростью съемки 163 кадра в секунду. Зумом служил макрообъектив с переменным фокусным расстоянием от 18 до 108 мм. Максимальное увеличение составляет ~ 1,1 раза при минимальном рабочем расстоянии 130 мм. Объем 200 мкл был взят из 1% (вес. / Об.) Исходного раствора полистирольных микросфер со средним диаметром 104 мкм (PPB-1000-5, Spherotech). Затем микросферы суспендировали в 10 мл раствора 1X PBS, содержащего BSA в концентрации 1 мг / мл.Раствор суспендированных микросфер вводили перфузионным насосом (PPS-1100, Scientifica) при эквивалентных непрерывных скоростях потока от 0,2 до 5,1 мл / мин. В общей сложности для всех четырех держателей образцов было записано примерно три видеоролика на скорость потока, каждое продолжительностью 3 с. Подключаемый модуль TrackMate ImageJ [47] использовался для отслеживания траектории шариков в данных μPIV для получения экспериментальных линий тока внутри щели для визуализации.
Культура клеток
Первичные нейроны крыс получали из рассеченного гиппокампа головного мозга новорожденных крыс (P0-P1), как описано ранее [44, 48], затем наносили на 18-миллиметровый покрытый боросиликатным покровным стеклом поли-D-лизин (GG-18-1.5, Neuvitro) и культивировали в течение 2 недель в нейробазальной среде с добавлением B27 (LS21103049, Gibco ™) для получения зрелых нейронов, образующих эффективные сети. В этом исследовании также использовались две клеточные линии, эмбриональные мышиные фибробластные клетки NIh4T3 (ATCC ® CRL-1658 ™) и эмбриональные клетки человека HEK293T (ATCC ® CRL-11268 ™). Вкратце, клетки NIh4T3 и HEK293T высевали за 12–24 ч перед визуализацией на 18-миллиметровом покровном стекле, покрытом матригелем (C354277, Corning ™) при плотности 25 000 клеток или 50 000 клеток на лунку соответственно.Обе клеточные линии содержались в среде DMEM с высоким содержанием глюкозы (10-017-CV, Corning ™) с добавлением 10% бычьей телячьей сыворотки (97068-085, VWR) или 5% фетальной бычьей сыворотки высшего сорта (10158-358, VWR). соответственно.
Анализ жизнеспособности нейронов
Всего в двух экспериментальных группах было приготовлено 10 культур клеток первичных нейронов крыс. Пять культур контрольной группы содержали в чашке Петри (08-772B, Fisher Scientific) и погружали в физиологический раствор на основе маннита без перфузии на 30 мин при комнатной температуре.Пять культур клеток тестовой группы помещали в проточную камеру и перфузировали со скоростью 2 мл / мин тем же физиологическим раствором при комнатной температуре в течение 30 минут. Затем все покровные стекла окрашивали в течение 3 минут 0,04% раствором трипанового синего (MT25900CI, Fisher Scientific). С помощью микроскопа проходящего света (EVOS FL, Invitrogen) было записано четырнадцать изображений с 20-кратным увеличением, случайным образом расположенных вдоль центральной линии визуализирующей щели, и два с 4-кратным увеличением, центрированных в визуальной щели.Отрицательно- и положительно окрашенные клетки на каждом изображении идентифицировали и вручную подсчитывали с помощью ImageJ (v1.52p, NIH) для оценки количества живых и мертвых клеток. Общие показатели жизнеспособности клеток были рассчитаны на случайно расположенных изображениях с 20-кратным увеличением, поскольку они представляют всю культуру клеток, тогда как изображения с 4-кратным увеличением предназначались для количественной оценки жизнеспособности клеток в зависимости от положения, поскольку края щели для визуализации являются видимый. В этом случае изображения были разделены на четыре сегмента, параллельных длине прорези для визуализации, а затем живые и мертвые клетки были затем отдельно подсчитаны в каждом сегменте.
Количественно-фазовая цифровая голографическая микроскопия
Использовался цифровой голографический микроскоп (T-1003, Lyncée Tec) на основе интерферометра Маха-Цендера. В микроскопе луч, создаваемый лазерным диодом с длиной волны 666 нм, разделяется на два, образуя объектную волну и опорную волну. Объектная волна, рассеянный образец, препятствует опорной волне, производя внеосевую голограмму, записанную с помощью цифровой камеры. Увеличение объектива микроскопа составляет 20X, рабочее расстояние 590 мкм и числовая апертура 0.70 (HC PL APO, Leica). Камера оснащена монохромным 2,3-мегапиксельным CMOS-сенсором Sony IMX174 с размером пикселя 5,86 мкм и возможностью записи со скоростью 164 кадра в секунду (acA1920-155um, Basler). Цифровые голограммы интегрировались за период ~ 100 мкс и регистрировались с частотой 4 Гц. Время интеграции тщательно регулировали в начале каждого сеанса визуализации, чтобы избежать насыщения голограмм. Геометрия внеосевой (это означает, что голограммы записываются с объектом и опорной волн, имеющих малый угол между их направлениями распространения) позволяет реконструировать количественно-фазовых изображений из одной записанной голограммы [49].Реконструкция количественно-фазового изображения из голограммы численно вычисляется с использованием проприетарного программного обеспечения (Koala, Lyncée Tec), и результирующее поле зрения составляет 215 мкм на 215 мкм. Алгоритм реконструкции состоит из моделирования освещения записанной голограммы с помощью цифровой опорной волны [50]. После этого проводится численная коррекция аберрации волнового фронта, вызванной оптическими компонентами, объективом и внеосевой геометрией микроскопа, с использованием сопряженной с эталоном голограммы [51].Что касается выравнивания фона, то оно было выполнено с помощью полиномов [52].
Метод двухжидкостной развязки
Подход с разделением на две жидкости требует последовательной перфузии двух разных физиологических растворов с одинаковой осмолярностью и разными, но априори известными показателями преломления. В частности, небольшое количество NaCl (25 мМ) изоосмотической и изотонической среды с осмолярностью, подходящей для исследуемой клетки (то есть 220 мОсм / кг для нейронов или 340 мОсм / кг для клеток HEK293T и NIh4T3) было заменено либо 50 мМ маннита, либо 50 мМ Nycodenz для получения двух различных перфузионных сред [26].На практике показатель преломления и осмолярность каждого физиологического раствора измеряли с помощью рефрактометра Аббе (Abbemat MW, Anton Paar) при 666 нм и осмометра точки замерзания (Micro-Sample модель 3320, Advanced Instruments), соответственно, до сеанс QP-DHM. Показатель преломления перфузионной среды на основе маннита составляет ~ 1,3335, тогда как для физиологического раствора на основе Никоденца он составляет 1,3380. Наконец, последовательная перфузия этих физиологических растворов с использованием перфузионной гравитационной системы, связанной с 8-портовым ручным распределительным клапаном [44], выполнялась либо последовательно три раза, либо до и после того, как клетки подвергались осмотической проверке.Для всех физиологических растворов скорость перфузии составляла 2 мл / мин.
Осмотические испытания
Три разных типа клеток, первичные нейроны гиппокампа, клетки NIh4T3 и клетки HEK293T, установленные по крайней мере в четырех разных держателях образцов, подвергались гипоосмотической или гиперосмотической проверке. В этих экспериментах первичные нейроны перфузировали физиологическим раствором, забуференным HEPES, с осмолярностью, аналогичной среде Neurobasal + B27 ® , содержащей (в мМ) 75 NaCl, 5.4 KCl, 1,8 CaCl 2 , 0,8 MgCl 2 , 0,9 NaH 2 PO 4 , 10 HEPES, 5 декстроза (D-глюкоза), 50 маннитол или никоденз (pH 7,4; 225-230 мОсм) . Другие культуры клеток (HEK293T и NIh4T3) поддерживали в среде DMEM, которая имеет более высокую осмолярность (330 мОсм), и, таким образом, перфузировали подходящим изоосмотическим раствором (в мМ) 135 NaCl, 3 KCl, 5 декстрозой, 10 HEPES, 3 CaCl 2 и 1,8 MgCl 2 , 50 маннитол или никоденз (pH 7,4; 330–335 мОсм).Гипоосмотические среды были приготовлены путем удаления 25 мМ NaCl из изоосмотических растворов, а гиперосмотические среды — путем добавления 25 мМ NaCl к изоосмотическим растворам, что привело к изменениям показателя преломления на -0,0003 и 0,0003. соответственно, от их изоосмотического аналога. Все клетки перфузировали соответствующей изоосмотической средой с маннитом, и запись QP-DHM начиналась, когда QPS был стабильным, обычно через 2 мин. Обычно базовая линия записывалась в течение ~ 1 мин, а затем заменялась изоосмотическим раствором Найкоденца, необходимым для отделения клеток от состояния покоя на ~ 30 с.Затем клетки подвергали осмотической стимуляции путем перфузии в течение ~ 5 мин либо гипоосмотическим, либо гиперосмотическим раствором, содержащим Nycodenz. Наконец, после того, как осмотическая контрольная проба была завершена, была выполнена вторая последовательность разделения путем изменения среды для раствора на основе маннита, но имеющей ту же осмолярность, что и использованная для контрольной проба, в течение ~ 1 мин.
Постобработка количественных фазовых изображений
Ректификации обычно применяются при численной реконструкции голограмм для исправления фазовых аберраций и искажений изображения.Однако на изображениях с количественной фазой все же могут сохраняться некоторые неровности. Сопряженная с эталоном голограмма и многочлены (оба определены в начале эксперимента) постепенно ухудшаются и теряют часть своей эффективности с течением времени. Поэтому метод сплайн-сглаживания использовался для итеративного определения функции освещения, которая при вычитании из количественно-фазового изображения эффективно компенсирует фоновые флуктуации. Эта поправка применялась индивидуально к каждому количественно-фазовому изображению во временном ряду, как показано в ссылке [44].После этого глобальная стратегия сегментации на основе порогов, реализующая алгоритм минимальной кросс-энтропии, использовалась для классификации каждого пикселя количественно-фазового изображения как принадлежащего либо фону, либо переднему плану. Кроме того, был использован метод, основанный на интенсивности, чтобы различать отдельные объекты на переднем плане, которые касаются друг друга и, следовательно, не были должным образом выделены как два объекта только посредством сегментации. Наконец, сегментированные клетки были численно помечены в течение промежутка времени количественно-фазовых изображений для выполнения анализа клеток.
Результаты и обсуждение
Как упоминалось ранее, эффективный и точный подход разделения двух жидкостей необходим для получения быстрого и однородного возврата внеклеточного показателя преломления к известным значениям n m 1 или n м 2 по всей щели изображения проточной камеры. Соответственно, в механике жидкости хорошо известно, что проточная система, в которой диаметр трубы резко меняется от одного размера к другому, дает начало тому, что называется вена контракта .Коэффициент потерь для внезапного изменения размера является функцией геометрии, при резком изменении размера потери больше. Соответственно, говорят, что поток отделяется от острого угла. В этом случае в отделенном месте потока возникает завихрение, которое захватывает жидкость и создает противоток или завихрение. Размер такого завихрения зависит от скорости потока; при более быстром течении он охватывает большую зону. В контексте подхода с разделением двух жидкостей (где два разных физиологических раствора последовательно перфузируются), эти мертвые объемы и неперемешиваемые слои вредны для получения быстрого однородного возврата внеклеточного показателя преломления к n m 1 или n m 2 .Большинство доступных перфузионных камер имеют резкое увеличение размера, например, вход и выход с квадратными краями. Конкретным примером являются соединения между микропробирками для перфузии и щелью для визуализации. В этих местах возникают значительные потери, вызывающие разделенные потоки, содержащие завихрения даже при очень низких скоростях потока, что подтверждается моделированием CFD, показанным на рисунке 1. Это моделирование соответствует скорости потока 2 мл / мин на входе в прямоугольную щель изображения с вход и выход с квадратными краями того же размера, что и разработанный и описанный ниже.Таким образом, прямоугольная щель для визуализации с квадратными краями на входе и выходе не обеспечивает быстрого и однородного размывания. Однако с точки зрения механики жидкости ожидается получение устойчивого и полностью развитого ламинарного потока. Следовательно, геометрия проточной камеры была оптимизирована для обеспечения такого поля потока.
Рисунок 1 . Разделенный поток и водовороты. Моделирование потока при скорости потока 2 мл / мин через прямоугольную щель для визуализации без диффузоров.Линии тока показаны черным цветом и накладываются на поле скорости со значениями, указанными на цветной полосе. Формирование вены контракта и завихрений становится очевидным при разделении потока. Направление потока указано черной стрелкой.
Механическая конструкция
Покомпонентное изображение предлагаемой проточной камеры показано на рисунке 2A. Проточная камера была напечатана на 3D-принтере с пластиковой нитью, предназначенной для медицинских и клинических применений, поскольку само сырье является биосовместимым.Сырье зарегистрировано Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов и прошло специальные тесты на биосовместимость, а именно ISO 10993, включая клеточную цитотоксичность [43]. Держатель образца содержит канал для потока и закрыт двумя покровными стеклами диаметром 18 мм. Верхнее покровное стекло действует как смотровое окно, а нижнее покровное стекло служит для фиксации культуры клеток. Прокладка из парафильма помещается под нижнее покровное стекло для обеспечения водонепроницаемости. Микропробирки из нержавеющей стали с внутренним диаметром 0,4 мм и 0.Внешний диаметр 8 мм, частично вставляются до входа в канал в центральном элементе для транспортировки перфузионной среды. Базовая пластина удерживает держатель образца. Вся камера закрывается крышкой и четырьмя редкоземельными магнитами. Для определения размеров смонтированная проточная камера (вверху) и держатель образца (внизу) показаны на рисунке 2В.
Рисунок 2 . Механический дизайн. (A) Разобранный вид CAD-модели, представляющий проточную камеру и детально описывающий ее составляющие. (B) Фотография, показывающая собранную проточную камеру (вверху) и держателя образца (внизу), а также линейку для определения размеров. (C, D) CAD-модели держателя образца, показывающие, соответственно, вертикальное и горизонтальное поперечное сечение канала, выделяющего диффузоры, где выход микропробирок из нержавеющей стали будет прикреплен к щели для визуализации.
Центральный элемент, показанный на рисунках 2C, D и являющийся, соответственно, вертикальным и горизонтальным поперечным сечением канала, является ключевым компонентом проточной камеры и более подробно описывается в этом параграфе.Канал плавно изменяется от круглого поперечного сечения диаметром 0,4 мм (на выходе из микропробирок из нержавеющей стали) до прямоугольного поперечного сечения высотой 1,2 мм и шириной 2,0 мм на уровне щели изображения с использованием пирамидальной формы. диффузоры. Углы открытия и закрытия этих пирамидальных диффузоров, показанные на рисунках 2C, D, были оптимизированы, и этот аспект будет обсуждаться в разделе «Устойчивый и полностью развитый ламинарный поток». Щель изображения длиной 9,0 мм имеет площадь 18.0 мм 2 и внутренним объемом 28,8 мкл. Внутренний объем был добровольно сведен к минимуму, чтобы обеспечить быструю промывку. В частности, площадь прорези изображения в ~ 400 раз больше, чем у типичного поля зрения для объектива микроскопа с 20-кратным увеличением. Толщина держателя образца не может быть дополнительно уменьшена, потому что микропробирки вставлены в него. Исходя из ежедневного использования в лаборатории, срок службы центрального элемента составляет ~ 3 месяца, после чего могут произойти утечки или может наблюдаться ухудшение рабочих характеристик жидкости.Хотя крышка и основание служат дольше держателя образца, прокладка предназначена для одноразового использования. Стоимость изготовления всей проточной камеры составляет 12 долларов США, из которых 0,86 долларов США — на сам пластик. Печать всех деталей проточной камеры занимает ~ 4 ч. Приклеивание пробирок к держателю образца и магнитов к держателям занимает 15 мин. Обработка ацетоном занимает ~ 30 мин. После обработки рекомендуется подождать не менее 2 часов, чтобы проверить ее водонепроницаемость. Весь процесс занимает ~ 7 часов, 6 из которых тратятся на ожидание.Файлы проекта самодельной проточной камеры будут переданы научному сообществу через модель с открытым исходным кодом для быстрого распространения и максимального воздействия. Технические чертежи будут доступны на веб-странице исследовательской группы авторов после публикации.
Стационарный и полностью развитый ламинарный поток
Простой способ уменьшить упомянутые выше потери — скруглить входную и выходную области щели формирования изображения, которая соединяет ее с каналами.Такая геометрия, форма которой замедляет скорость жидкости, называется диффузором. Существует оптимальный угол, при котором коэффициент потерь минимален, обычно он составляет около 10 °. Относительно небольшое значение этого угла для минимальных потерь приводит к получению длинного диффузора и свидетельствует о том, что трудно эффективно замедлить жидкость [53]. Таким образом, пирамидальные диффузоры длиной 6,5 мм с общим углом открытия и закрытия 11,45 ° были добавлены на концах щели для визуализации, как показано на рисунках 2C, D.Такой угол, близкий к оптимальному, был выбран, чтобы иметь как минимальные потери, так и размер щели для изображения, совместимый с разрешением 3D-принтера. Чтобы оценить предложенный дизайн, моделирование CFD было рассчитано для 16 значений расхода в диапазоне от 0,2 до 5,1 мл / мин. В качестве указания, результаты, показанные на рисунках 3A – C, увеличены на щели изображения, и жидкость течет справа налево. Для целей синтеза показаны только 3 из 16 скоростей потока. Поле линий тока (черные сплошные линии) для 1.0, 2,0 и 2,8 мл / мин, наложенные на соответствующие распределения скорости и обозначенные цветом, показаны на рисунках 3A – C (вверху). Моделирование показывает, что жидкость течет в параллельных слоях с постоянной скоростью по пути, параллельному стенке прорези для изображения. Соседние слои показывают немного разные скорости в зависимости от градиента скорости, перпендикулярного линиям тока. Такое поведение типично для стационарного и полностью развитого ламинарного потока. Однако при относительно высокой скорости потока 2,8 мл / мин на входе есть небольшая область, где появляется отрывной поток.Для конкретного приложения, представленного здесь, было отмечено, что число Рейнольдса не является достаточно чувствительной метрикой для прогнозирования наличия вихрей и обратных потоков. Например, при скорости потока 5,1 мл / мин проточная камера полностью заполнена завихрениями, что видно по линиям тока. Но максимальное соответствующее число Рейнольдса равно 12, что значительно ниже порогового значения 2100, после которого поток якобы перестает быть ламинарным, и это примерно в 200 раз (данные не показаны).Поэтому нецелесообразно оптимизировать геометрию и размер проточной камеры на основе этой меры.
Объем цилиндровПомните! Объем измеряется в кубических единицах.
Презентация на тему: «Помните, объем цилиндров! Объем измеряется в кубических единицах» — стенограмма презентации:
1 Объем цилиндров Помните! Объем измеряется в кубических единицах.
Курс 3 Объем цилиндров Объем измеряется в кубических единицах. Помнить!
2 Курс 3 Объем цилиндров Найдите объем фигуры с точностью до десятых. Используйте 3,14 для . B = (42) = 16 дюйм2 Площадь основания 4 дюйма V = Bh Объем цилиндра 12 дюймов = 16 • 12 = 192 дюйма3
3 Объем цилиндров Пример 2:
Ход 3 Объем цилиндров Пример 2: Барабанная компания рекламирует малый барабан высотой 4 дюйма и диаметром 12 дюймов.Оцените объем барабана. d = 12, h = 4 d 2 r = = = 6 V = (r2) h Объем цилиндра. = (3.14) (6) 2 • 4 Используйте 3.14 для p. = (3,14) (36) (4) = ≈ 452 Объем барабана составляет примерно 452 дюйма 2.
4 Объем цилиндров, пример 3
Ряд 3 Объем цилиндров, пример 3 Цилиндр имеет высоту 3 см и радиус 2 см. Объясните, приведет ли утроение радиуса или высоты цилиндра к увеличению объема в три раза.Исходный цилиндр имеет объем 4 • 3 = 12 см3. V = 36 • 3 = 108 см3. Увеличив радиус втрое, вы увеличите объем в девять раз.
5 Объем цилиндров, продолжение примера 3
Ряд 3 Объем цилиндров, пример 3 (продолжение) Исходный цилиндр имеет объем 4 • 3 = 12 см3. V = 4 • 9 = 36 см3. Увеличение высоты втрое увеличит объем.
6 Курс 3 Объем цилиндров Банка для сока имеет радиус 2 дюйма.и высотой 5 дюймов. Объясните, повлияет ли утроение высоты банки на объем так же, как утроение радиуса. Увеличив высоту втрое, вы утроите объем. Увеличив радиус в три раза, вы увеличите громкость в девять раз по сравнению с исходной.
7 Объем цилиндров Урок Викторина
Курс 3 Объем цилиндров Урок Викторина Найдите объем каждой цифры с точностью до десятых.

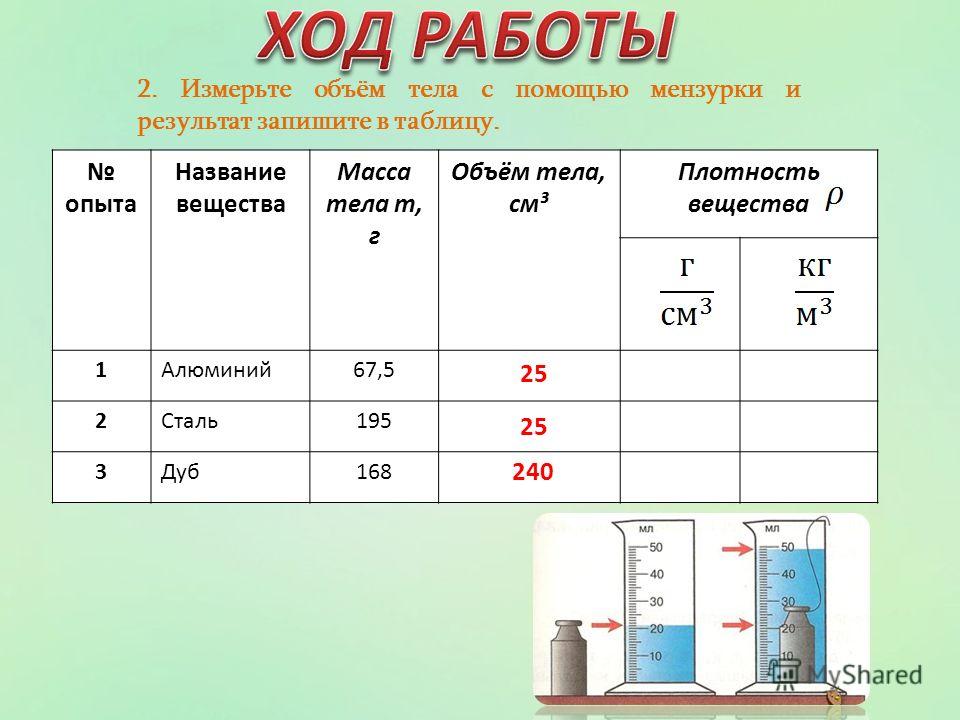 Физические величины имеют род, размер, единицу(измерения) и значение.
Физические величины имеют род, размер, единицу(измерения) и значение.