Модуль Юнга
Модуль ЮнгаВ системе единиц СИ за единицу напряжения принимается 1 Па=1 Н/м2, как и для давления Модуль упругости (модуль Юнга) различных материалов:
| Материал | E, 109 Па | E, 103 МПа | E, 103 кг/см2 |
| Сталь | 200,0-220,0 | 200,0-220,0 | 2000-2200 |
| Чугун серый, белый | 115,0-160,0 | 115,0-160,0 | |
| Бетон | 14,6-23,2 | 14,6-23,2 | 146-232 |
| Медь | 118 | 118 | 1180 |
| ПВХ | 2,758 | 2,758 | 27,58 |
| 2,898 | 2,898 | 28,98 |
При вводе параметров в базу данных, чтобы не писать много нулей, используется
размерность МПа.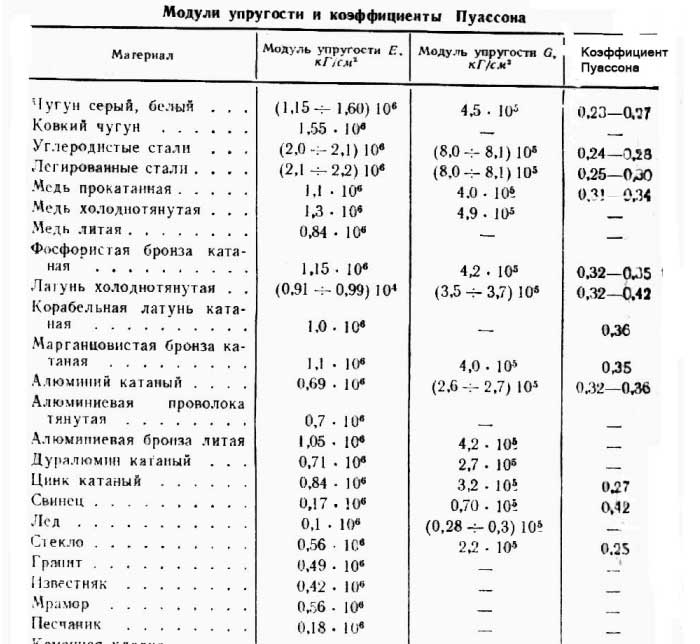
Упругость модуль Юнга — Справочник химика 21
Модуль упругости (модуль Юнга) для различных материалов, кг/мм [c.372]Модуль упругости, сдвига, коэффициент Пуассона. Модуль упругости (модуль Юнга) Е = [c.499]
Самым прочным металлом является 1г, если оценивать его прочность по модулю нормальной упругости (модуль Юнга).
ГУКА ЗАКОН, устанавливает линейную зависимость между упругой деформацией твердого тела и приложенным мех напряжением Напр, если стержень длиной I и поперечным сечением S растянуть продольной силой F, то удлинение стержня Д/ = FI/ES, где -модуль упругости (модуль Юнга), зависящий от материала стержня Для деформации сдвига (см рис) Г з имеет вид т = Gy, где [c.618]
Модуль продольной упругости (модуль Юнга) Сосредоточенная сила воздействие вообще Модуль упругости при сдвиге постоянная нагрузка (вес)
375]Величина О однозначно связана с модулем упругости (модулем Юнга) Е по формуле [c.77]
В работе [228] исследовали эволюцию структуры и упругие свойства Си, подвергнутой интенсивной деформации РКУ-прессованием при комнатной температуре и последующему отжигу при температурах до 500° С. Упругие модули Юнга Е и сдвига О вычисляли из величин скоростей VI и VI соответственно продольных и поперечных ультразвуковых волн по известным соотношениям [c.169]
Упругие характеристики изотропных твердых тел определяются двумя независимыми параметрами постоянной Ламе Л и модулем упругости при сдвиге Сили жесткостью) ц. При практических исследованиях механических свойств твердых полимеров, кроме того, измеряют другие независимые упругие постоянные модуль продольной упругости (модуль Юнга) Е, коэффициент Пуассона V и объемный модуль упругости (модуль упругости при всестороннем сжатии) В -
Начальной стадией деформации металла является упругая деформация (участок АВ рис.
2.8). С точки зрения кристаллического строения, упругая деформация проявляется в некотором увеличении расстояния между атомами в кристаллической решетке. После снятия нафузки атомы возвращаются в прежнее положение и деформация исчезает. Другими словами, упругая деформация не вызывает никаких последствий в металле. Чем меньщую деформацию вызывают напряжения, тем более жесткий и более упругий металл. Характеристикой упругости металла являются дна вида модуля упругости модуль нормальной упругости (модуль Юнга) — характеризует силы, стремящиеся оторвать атомы друг от друга, и модуль касательной упругости (модуль Гука) — характеризует силы, стремящиеся сдвинуть атомы относительно друг друга. Значения модулей упругости являются константами материала и зависят от сил межатомного взаимодействия. Все конструкции и изделия из металлов эксплуатируются, как правило, в упругой области. Таким образом, упругость — это свойство твердого тела восстанавливать свою первоначальнуто фор.му и объем после прекращения действия внешней нафузки.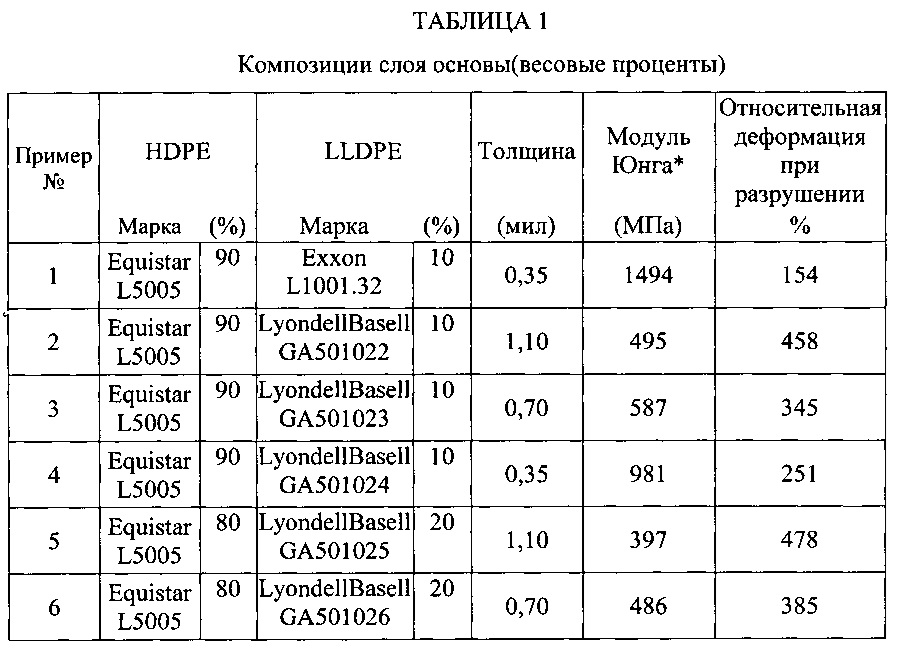
X — степень кристалличности полимера У — модуль упругости (модуль Юнга) [c.6]
Термостойкость стекла зависит от цел ого ряда его свойств, важнейшими и з которых являются коэффициент термического расширения, прочность на разрыв и модуль упругости (модуль Юнга).
Модуль продольной упругости (модуль Юнга) Е и [c.37]
Модуль упругости (модуль Юнга) — одна из существенных характеристик эластомеров. Этот параметр коррелирует с молекулярной массой между узлами поперечной сшивки [76, с. 165] по кинетике изменения с наибольшей достоверностью можно судить о степени завершенности процесса структурирования. Значение модуля упругости является определяющим при расчете конструкций ряда изделий из эластомеров, например шин, акустических устройств и т.
Пластич. деформация твердого тола всегда сопровождается его упрочнением, т. е. ростом напряжения по мере роста пластич. деформации. У п р о ч н е-н и е в процессе пластич. деформации характеризуется коэфф. упрочнения к = йР1модулем нормальной пластичности. Его величина на 2—3 порядка меньше модуля нормальной упругости (модуля Юнга). [c.34]
Кристаллические твердые вещества обладают модулем продольной упругости (модулем Юнга) порядка 10 —10 дин1см и очень малым конечным удлинением. Если такое тело растянуто до постоянной длины и температура понижается при сохранении той же длины тела, то напряжение непрерывно возрастает. По ур. (XVII, 3) это означает, что изменение внутренней энергии, связан-
Если течение не является типичным свойством твердообразных систем, что особенно характерно для конденсационно-кристаллизационных структур, то реологические зависимости строят по отношению к деформации, а не к ее скорости.
Типичная кривая зависимости деформации от напряжения для твердых тел показана на рис. VII. 15. Прямолинейный участок кривой ОА отвечает пропорциональности деформации напряжению сдвига в соответствии с законом Гука (VII. 3). До напряжения Ри отвечающего точке А, размер и форма тела восстанавливаются после снятия нагрузки. Важными параметрами такой системы являются модуль упругости (модуль Юнга) и модуль эластической деформации. Считают, что в суспензиях с коагуляционной структурой модуль упругости (модуль быстрой эластической деформации) характеризует твердую фазу дисперсий, а модуль медленной эластической деформации — пространственную сетку с прослойками дисперсионной среды (возможно скольжение частиц относительно друг друга без разрыва связей). Напряжение Р соответствует пределу текучести (правильнее — пределу упругости). С увеличением напряжения проявляется пластичность, а после его снятия — остаточные деформации. При напряжении Рг (точка ) происходит течение твердообразной системы. При дальнейшем увеличении напряжения до величины Рз (точка В), соответствующей пределу прочности, обычно наблюдается негупрочнение тела, затем наступает разрушение системы.
Удобным методом определения модуля упругости жестких материало в со слабым поглощением является возбуждение свободных колебаний и определение собственных частот, которые завмодуля упругости (модуля Юнга Е) материала. При динамических измерениях модуль Юнга заменяется модулем накопления при растяжении Е. [c.148]
Обозначения основных величин, принятые ниже, следующие р — плотность (объемная масса) Ею — модуль упругости (модуль Юнга) 8 — диэлектрическая проницаемость tg б— тангенс угла диэлектрических потерь Q — добротность / — частота А///о — уход резонансной частоты в указанном интервале температур Сзв — скорость звука d — пьезоэлектрический модуль 33 — пьезоэлектрический модуль продольных колебаний 31 — пьезоэлектрический модуль радиальных колебаний d/e, d/Y — характеристика эффективности в режиме приема iotgS. ro/etg6 — характеристики эффективности в режиме излучения
Кристаллические твердые вещества обладают модулем продольной упругости (модулем Юнга) порядка 10 —дин/см и очень малым конечным удлинением.
Если такое тело растянуто до постоянной длины и температура понижается при сохранении той же длины тела, то напряжение непрерывно возрастает. По ур. (XVII, 3) это означает, что изменение внутренней энергии, связанное с этим напряжением dUldl)T,v, значительно по величине и положительно по знаку, т. е. внутренняя энергия тела возрастает. [c.568]
С коэфф. т.ер.чического расширения 8,28 10 град коэфф. теплопроводности 0,0218 кал см X X сек град теплоемкость 6,56 кал г-атом — град электрическое сопротивление 140,5 мком см. Отличается самым высоким поперечным сечением захвата тепловых нейтронов — 460С0 барн. Работа выхода электронов — 3,07 эв. Кюри точка 17° С (290 К). Модуль норм, упругости (модуль Юнга) 5730 кгс мм предел прочности 18,6 кгс мм НВ = = 60. Легко поддается мех. обработке. Химически активен. При высоких т-рах активно взаимодействует с кислородом, галогенами, серой, азотом, углеродом и др. неметаллами. Во время длительного хранения на воздухе при наличии водяных паров подвергается коррозии (см.
Коррозия металлов). Г. сплавляется [c.240]
Характеристики основных физико-механических и физико-химических свойств, температуры литья и горячей обработки меди
Атомное строение меди
Медь в Периодической системе имееет атомный номер 29 является первым элементом 1B группы или первым элементом одиннадцатой группы. Электроннная конфигурация свободного атома в нормальном состоянии (OK) ls22s22p63s23p63d104s1.
Медь изоморфна и кристаллизуется с образованием гранецентрированной кубической решетки типа A1. Период решетки меди при 18°С равен 0,36074нм; с повышением температуры он возрастает.
Элементы, находящиеся в твердом растворе, изменяют период решетки меди. Чем больше разница в размерах атомов меди и растворенного элемента, тем больше эти изменения.
| T, °K | 0 | 291 | 573 | 773 | 944 | 1044 | 1144 |
| Период решетки, нм | 0,35957 | 0,36074 | 0,36260 | 0,36308 | 0,36526 | 0,36603 | 0,36683 |
Атомный радиус по Гольдшмидту для координационного числа 12 составляет 0,12773нм, межатомное расстояние 0,25546нм.
Большинство физических свойств зависит от чистоты и состояния меди.
Атомный номер |
29 |
Относительная атомная масса |
63,54 |
Решетка |
Кубическая гранецентрированная ( α = 3,6080 Å) |
Плотность г/см2 |
8,94 |
|
Температура плавления, °С |
1083 |
Скрытая теплота плавления, кал/г |
50,6 |
Температура кипения, °С |
2595 |
Скрытая теплота испарения, кал/г |
1290 |
|
Теплопроводность, кал / (см·с·°С), при: |
0,941 |
100° С |
0,900 |
700°С |
0,840 |
Удельная теплоемкость, кал/(г·°С), при: |
0,092 |
600° С |
0,103 |
1000° С |
0,112 |
Коэффициент линейного расширения α · 10-6, 1/° С, при: |
16,7 |
25—300° С |
17,7 |
0 — 600° С |
18,6 |
0—900° С |
19,3 |
Отражательная способность, %, при λ= 5500 Å |
61 |
Излучательная способность, % (λ = 6650 Å), при: |
9,6 |
1080° С |
11,7 |
1100° С |
15,0 |
Удельное электросопротивление, Ом·мм2/м, при:
|
0,0178 |
500° С |
0,053 |
Электропроводность, м/(Om·мм2) при 20°С |
57 |
Температурный коэффициент электросопротивления,1/°С, при 20°С |
3,93·10-3 |
Мощность излучаемой энергии, Вт/см2, при: |
0,05 |
227°С |
0,11 |
1227°С |
4,26 |
Работа выхода, э·В |
4,46 |
Сжатие объема при затвердевании, % |
4,05-4,2 |
Вязкость при 1145° С, г/(см·с) |
0,0341 |
Поверхностное натяжение, дин/см |
1178 |
Нормальный потенциал по отношению к водородному электроду, В |
+0,34 |
Предел прочности, кгс/мм2: |
20-25 |
твердой меди |
40-49 |
Относительное удлинение, %: |
60 |
твердой меди |
6 |
Твердость по Бринелю, кгс/мм2: |
45 |
твердой меди |
110 |
Предел текучести, кгс/мм2: |
|
мягкой меди |
9-15 |
твердой меди |
30-45 |
Ударная вязкость, кгс·м/см2 |
10-18 |
Сопротивление сжатию, кгс/мм2 |
55-65 |
Предел прочности на срез, кгс/мм2: |
15 |
твердой меди |
21 |
Предел ползучести кгс/мм2, при: |
7 |
200° С |
5 |
400° С |
1,4 |
Модуль сдвига, кгс/мм2 |
4240 |
Модуль упругости, кгс/мм2: |
11700—12600 |
твердой меди |
12200—13500 |
Температура рекристаллизации,° С |
180-300 |
Температура горячей деформации ° С |
1050—750 |
Температура литья ° С |
1150 — 1250 |
Линейная усадка, % |
2,1 |
Травитель после отжига на воздухе |
10%-ная серная кислота |
Характеристики упругости
Упругие свойства меди характеризуется модулем нормальной упругости Е (модуль Юнга), сдвига G и объемного сжатия Есж, а также величиной отношения поперечной и продольной упругой деформации, т.
е. коэффициентом Пуассона μ. Эти характеристики упругих свойств связаны между собой. Для большинства металлов абсолютное значение коэффициента Пуассона мало отличается от 1/3. Для меди оно составляет :
μ = 0,33 Есж = E G ≅ 3/8E
Статистически усредненные значения характеристик упругости меди при 20°С по данным многочисленных исследований представлены с указанием стандартных отклонений:
Е= 123,5 ± 0,7 ГПа
Есж = 140,2 ± 3,9 ГПа
G = 45,4 ± 1,2 ГПа;
μ = 0,33 ± 0,09
Константы упругости монокристаллов меди зависят от кристаллографических направлений. У поликристаллов квазиизотропной меди вследствие произвольной ориентации зерен эти константы усредняются.
| Состояние | Направление кристаллической решетки |
Е, ГПа | G, ГПа | Есж, ГПа | м |
| <111> | 159 | 33,8 | — | — | |
| Монокристаллическое | <100> | 77,5 | 61,0 | — | — |
| <110> | 126 | 38,0 | — | — | |
| Поликристаллическое | — | 115—125 | 42—46 | 139 | 0,32—0,34 |
Значения модулей Е и G в интервале температур 300—1300°К уменьшаются по линейному закону.
Лишь в области низких температур наблюдается отклонение от равномерного изменения модулей.
| Т. к | 4,2 | 100 | 200 | 300 | 500 | 700 | 900 | 1100 | 1300 |
| Е, ГПа | 141 | 139 | 134 | 128 | 115 | 103 | 89,7 | 76,8 | 63,7 |
| G, ГПа | 50 | 49,5 | 47,3 | 44,7 | 37,8 | 31,0 | 24,1 | 18,5 | 11,5 |
Плотность
В качестве международного стандарта (IACS) плотность меди равна 8890кг/м3, при температуре 20°С.
Плотность меди различных марок при температуре 20°С имеет небольшие различия:
| Марка | Плотность, кг/м3 |
| Медь бескислородная М00б | 8963 ± 3 |
| Медь бескислородная М00б | 8950 |
| Медь, раскисленная фосфором М2р (0,04%Р) | 8930 |
Литая медь имеет плотность 8920кг/м3. Холодная деформация отожженной меди уменьшает ее плотность вследствие увеличения концентрации вакансий, дислоцированных атомов, дислокаций и других дефектов тонкой структуры. Возврат и рекристаллизация при нагреве наклепанного металла повышают плотность меди до исходного значения.
При нагреве плотность меди уменьшается вследствие расширения решетки, при плавлении она снижается на 5%.
| T, °C | 20 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 |
| Плотность, кг/м3 | 8890 | 8680 | 8610 | 8550 | 8470 | 8400 | 7960 | 7860 | 7770 | 7700 |
Медь Модуль сдвига — Энциклопедия по машиностроению XXL
Подвижность дислокаций.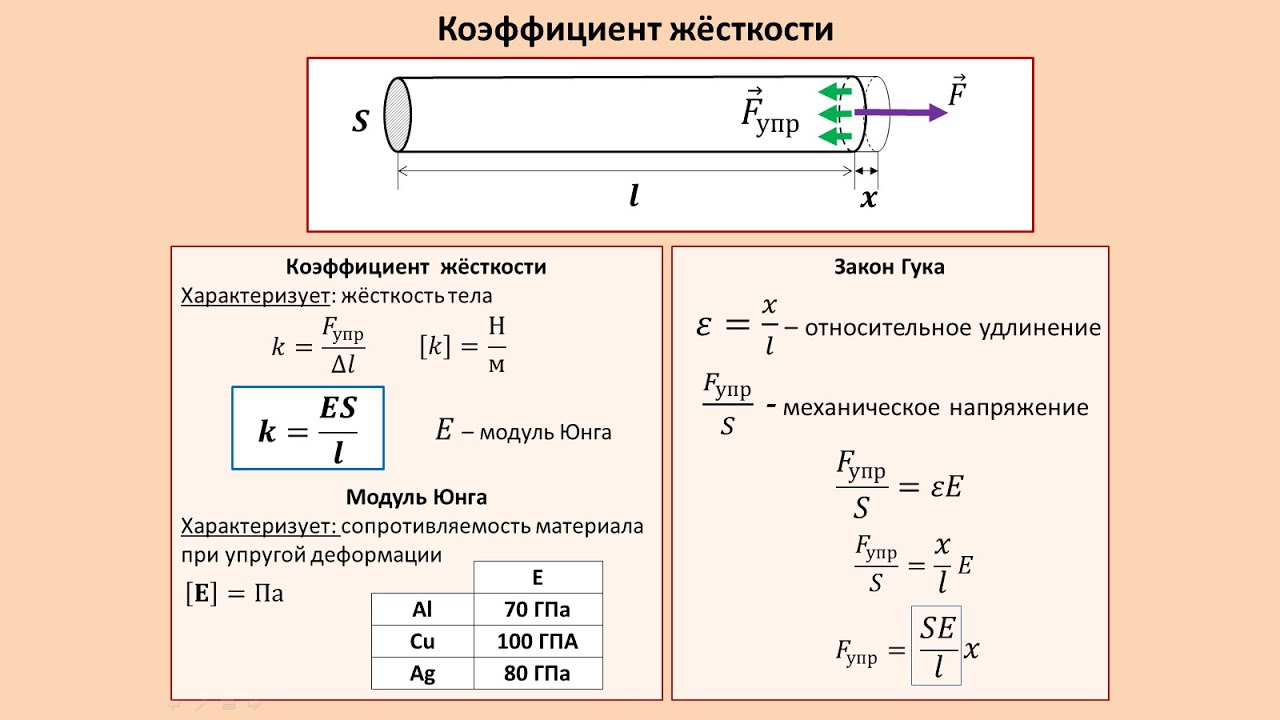
Было показано, что присутствие окалины или покрытия с хорошей адгезией упрочняет материал, затрудняя выход из поверхности краевых дислокаций [122] и движение пересекающих поверхность винтовых дислокаций [114]. Простой анализ сил реакции показывает, что препятствующее движению дислокаций напряжение, связанное с наличием поверхностной окалины, пропорционально величине (ца—РА)/(ца+р.л) [130], где ца и Ца — модули сдвига окалины и сплава соответственно. Можно было бы ожидать, что напряжение будет притягивающим, если модуль упругости окалины меньше, чем подложки. Однако это обычно не имеет места для окалины, состоящей из оксидов или других коррозионных продуктов. Возможность существования уменьшающих деформацию напряжения подтверждается, например, данными по пластической деформации при комнатной температуре, полученными при исследовании покрытых медью кристаллов цинка [122], окисленных кристаллов алюминия [121], а также окисленных кристаллов [125] и поликристаллов [126] кадмия. Несмотря на отсутствие экспериментальных данных, можно ожидать, что этот эффект распространяется также и на скольжение границ зерен, поскольку такое скольжение (или вращение зерен) связано с образованием поверхностных ступенек.
[c.28]
Проведенные исследования в этой области дали положительные результаты для определения упругих постоянных латуни, сплавов железа и алюминия, монокристаллов германия и кремния, никеля, твердых растворов меди и поликристаллического сплава магний— кадмий. Ультразвуковые методы позволяют определять модули Юнга и сдвига на одном и том же образце, что открывает большие возможности для исследования упругих постоянных экспериментальных сплавов и установления для них взаимосвязей модулей с другими характеристиками межатомного взаимодействия. Так же как и при контроле жидкостей, скорость распространения ультразвука в жидких металлах в основном определяется величиной коэффициента адиабатической сжимаемости, а последний -относится к числу физических величин, которые в значительной степени зависят от строения жидких металлов. Поэтому, зная скорость, распространения ультразвуковых колебаний в данном металле, можно рассчитать величину модуля Юнга, модуля Пуассона и модуля сдвига.
Для точного измерения интервала между ультразвуковыми импульсами достаточно иметь длину образца, равную 25 мм.
[c.223]Модуль сдвига какого композита выше медь-окись кремния (волокно), никель-окись кремния (волокно) Доля волокна одинакова (0,2). [c.181]
В соответствии с изложенным в металлических г. ц. к. кристаллах (алюминий, свинец, медь) напряжения старта дислокаций малы 10 — G G — модуль сдвига), в ковалентных что отвечает сопротивлению движения дислокаций со стороны самой решетки. Действительно, в монокристаллах кремния после тщательной обработки поверхности образца с целью удаления [c.287]
Технически чистая медь имеет невысокие прочностные свойства. При снижении температуры от 293 до 20 К прочность и твердость меди повышаются почти в два раза, пластичность сохраняется на том же уровне. Ударная вязкость даже увеличивается, сохраняя при 20 К столь высокие значения, что надрезанные образцы не разбиваются копром, а протягиваются между его опорами.
Усталостная прочность меди и ее сплавов с понижением температуры растет так же, как модуль упругости и модуль сдвига.
[c.622]
ГПа для ма ксимального значения Уд. Максимальное значение модуля сдвига в ударно сжатом состоянии примерно в 3 раза превышает значение С при нормальных условиях, что много меньше упрочнения меди в ударных волнах. В работе [5] считается, 1 (ОУ /ас [c.207]
Введение золота снижает модуль нормальной упругости Е и модуль сдвига О меди и повышает коэффициент Пуассона ,1 [259], как показывают приведенные ниже данные [c.98]
Модуль сдвига меди, содержащей незначительные количества (3,3-10 — 10-10 ат.%) золота, и изменение его в результате холодной деформации [c.98]
Расчет отношения Ар/О (где О—модуль сдвига) для рассматриваемых металлов при фиксированной деформации е = = 0,24 показал, что для золота оно равно 74 7 Ом м (Дж/м ), для меди 49 и для серебра 94.
Значения модуля сдвига взя-30
[c.30]
Показано, что при одинаковой деформации. меди, золота и серебра отношение Ap/G, где G —. модуль сдвига, тем больше, чем меньше энергия дефектов упаковки. [c.131]
Механич. свойства Ц. сильно зависят от степени его чистоты, свойства чистого Ц. близки к меди. Коэфф. сжимаемости 1,097 1Q- см /кг (30°). Модуль упругости 7522 кг/мм , модуль сдвига 3330 кг/мм . Твердость по Бринеллю 64—67 кг/мм , предел прочности 25,3 кг/мм , относит, удлинение 26%. [c.400]
Модули упругости металлов находятся в указанных ниже пределах для стали разных марок модуль нормальной упругости (модуль Юнга) — = (2,0-4-2,2) МПа модуль сдвига (модуль касательной упругости) G = (8,0 -ь 8,5) 10 МПа. Для алюминиевых сплавов 0 = (7,0 -f- 7,5) 10 МПа G = 2,7-10 МПа. Для титановых сплавов 0 = (1,10-i-1,20) 10 МПа G — = (4,0 4-4,5)-104 МПа. Для меди ю= (1.13 1,32) 10 МПа 0 = = 4,24-10 МПа. Для никеля (чистого) =2,20-10 МПа. [c.226]
Модуль упругости стали при сдвиге. … Температурный коэффициент линейного расширения стали Температурный коэффициент линейного расширения меди Коэффициент поперечной деформации стали…… [c.8]
Модули упругости и сдвига представляют собой важнейшие характеристики металлов, предопределяющие так называемую жесткость металлических конструкций и деталей. Значение модуля упругости можно видеть из следующего примера. Если одна и та же деталь изготовлена из вольфрама, стали и сплава на основе меди, то одинаковые напряжения вызовут в ней различные упругие деформации, величины которых будут относиться (по закону Гука) обратно пропорционально модулям упругости материалов, т. е. как 1 2 3. [c.39] Электрохимический экви-. валент для двухвалентной меди в Г/а-ч. … Модуль нормальной упругости в кГ/мм . … Модуль сдвига в кГ1мм . Предел упругости в [c.162]Согласно высказанным выше предпосылкам генерированные источником дислокации в стальном образце будут притягиваться поверхностью раздела, так как значение модуля сдвига для стали больше, чем для меди. Для бронзы имеет место условие Gi кристаллическую решетку. В этом случае приповерхностные объемы бронзового образца будут наклепываться ввиду того, что дислокации отталкиваются от поверхности. Однако если учесть исследования структуры медной пленки при ИП [45], где высказано предположение о сильной разрыхленности ее в процессе трения, то наклеп приповерхностных объемов бронзы будет значительно меньшим. [c.29]
Данные табл. 1 свидетельствуют о повышении удельного модуля упругости композиционного материала вследствие упрочнения волокнами. Удельный модуль упругости борного волокна примерно в 6 раз выше, чем у любых стандартных конструкционных металлов, включая стали, алюминий, молибден, медь, магний, что является следствием более жесткой ковалентной связи по сравнению с металлической. Жесткость металлической связи, в свою очередь, более высокая, чем жесткость в органических смолах. В то время как материалы с металлической связью имеют удельный модуль упругости 2500 км, наиболее типичный уровень этой характеристики для материалов на основе органической смолы составляет около 250 км. Из-за низкой жесткости смол композиционные материалы на их основе имеют низкий модуль упругости в направлении, перпендикулярном направлению укладки Болох на, и малый модуль сдвига. Преимущество однонаправленного боралюминиевого композиционного материала в отношении жесткости распространяется и на материал с волокнами, уложенными в различных направлениях, поскольку волокна, не ориентированные в направлении действия главных напряжений, вносят значительный вклад в величину модуля упругости материала в этом направлении. [c.422]
Для сравнения на рис. 2.26 линией с крестиками отмечена кривая пластического деформирования поликристалла, состоящего из анизотропных зерен. Их упругие свойства приняты соответствующими характеристикам монокристаллов меди при Т = 300 К (см. табл. 2.3). 1 роме того, принято G = 0,01Gq, причем модуль сдвига поликристалла Gq определялся из решения кубического уравнения (2.38). Такой поликристалл в целом оказался более жестким и его кривая пластического деформирования лежит несколько выше, чем для поликристалла, состоящего из упругоизотропных зерен. [c.105]
Для таких металлов, как алюминий, медь, железо, упругая и объемная скорости звука измерены в широком диапазоне напряжений О], что позволяет проследить ход зависимостей Е, К, С VI л вдоль ударной адиабаты. Модуль всестороннего сжатия К и коэффициент Пуассона р в области твердого состояния монотонно растут с повышением амплитуды ударной ролны, а модуль сдвига 6 вначале возрастает с ростом 01, а затем начиная с некоторого [c.179]
Концы трубок жестко скреплены между собой, и в месте скрепления приложены пары сил с крутящими моментами по 100 кгм. Длина трубок 3 м. Модуль упругости меди при сдвиге равен 4-10 Kzf M . [c.95]
Джоуль изготавливал спиральные пружины из медной и стальной проволок и определял изменение их длины при изменении температуры. На основании результатов измерений он вычислил, что изменение модуля сдвига составляло 0,00041 на градус по Цельсию для стали и 0,00047 на градус для меди 2. В дополнительной заметке от 1 августа (статья была передана 18 июня) Джоуль отметил, что он не был осведомлен о предшествовавшей работе Куп-фера ) (Kupfer [1856, 1[), который в 1856 г. получил близкие зна- [c.369]
Отношение напряжения т к сдвигу у на линейном участке зависимости между т и Y называется модулем сдвига и обозначается через G. Для стали G—S-IO h zl M , для холоднокатаной меди G = 4- 0 f zj M y для алюминия G = 2J- 0 h zI m . [c.111]
Измерение скоростей продольных и поперечных ультразвуковых колебаний в СМК-Си в зависимости от температуры отжига позволило оценить величину модуля упругости Е и модуля сдвига G [45]. Размер зерен СМК-Си до отжига составлял 200-400 нм. Отжиг проводили в интервале температур 373-623 К с шагом 25-50 К с выдержкой в течение 1 часа при каждой температуре. Значения Е и G исходной СМК-Си были на 10-15 % меньше в сравнении с крупнозернистой медью. Ранее пониженная на 30 % величина упругих модулей была обнаружена в на-нокристаллическом n -Pd [11, 46]. При температуре отжига 423-456 К наблюдалось скачкообразное увеличение Е и G (рис. 5.6). Наблюдаемые изменения упругих модулей авторы [45] объяснили изменением структурного состояния границ зерен в образцах СМК-Си с размером зерен 200 нм границы зерен были неравновесными и обладали избыточной энергией. Отжиг при Г 423 К привел к релаксации границ зерен. В [47, 48] на основе данных [45] были оценены упругие модули границ зерен. Для границы толгциной 1 нм в равновесном состоянии E l = 0,1QE [c.157]
Определить коэффициенты запаса прочности для валика и трубки, если для стали предел текучести = 210 н/мм , а для меди = 120 н/мм . Модуль сдвига для стали 0 = 8 — 10 н ам и для меди = 4 10 н1мм . [c.186]
Модуль продольной упругости меди =1,0-10 н/мм =, Ь2- 0 кГ1слА Модуль сдвига стали 0=8,0-10 /лл =8,16 — 10 кГ/см [c.6]
Неоднократно предпринимались попытки связать эффекты упрочнения, рассчитанные по пределу текучести Кт, с параметрами размерного несоответствия емодулей сдвига ес- Флейшер и Хиббард [62] установили, что упрочнение твердых растворов на основе меди обусловлено совместпылг влиянием несоответствия атомных диаметров растворяемого элемента и [c.78]
Если известные опытные значения модуля сдвига для холодного металла считать достоверными, например, для процесса сварки взрывом, то получаются значения ударной энергии сдвига, при которых пластическое (вязкожидкостное) течение металла переходит в хрупкое разрушение. Согласно (3.52), эти значения таковы для алюминия 13 500, для меди 22 ООО, для железа 42 ООО Дж/см . Большие энергии уже могут вызывать хрупкое поведение твердого металла, так как время действия ударного сдвига меньше времени релаксации. [c.154]
Постоянные, определяющие упругие свойства меди, можно рассчитать теоретически. Рассчитывая изменение энергии, сопровождающее сдвиг, происходящий без изменения объёма, можно вычислить модуль сдвига. Приближённый расчёт можно [c.248]
Рассмотрим сначала действие гетерогенных источников в объеме кристалла. В работе [344] подвергали гидростатическому сжатию медь, содержащую частицы S1O2 или Alj О3, образованные в результате внутреннего окисления. При давлении свыше 25 кбар вокруг частиц возникали дислокации, которые наблюдали методом электронной микроскопии. Была определена зависимость критического давления начала образования дислокаций от размера частиц. Как видно из рис. 59,а, величина критического давления повышается по мере уменьшения размера частиц. Зная модули матрицы и частицы, оценивали также критический уровень сдвиговых напряжений Тщах и параметра несоответствия на межфазной поверхности раздела матрица-включение . Из полученных данных (рис. 59,а) следуют два важных вывода. Во-первых, величины критического давления, напряжения сдвига и параметра несоответствия, необходимые для начала пластического течения, зависят от размера частиц. Во-вторых, максимальное локальное напряжение, необходимое для начала дефор.мации (см. рис. 59,а), находится между 0,001 и 0,008 Gy , что гораздо меньше теоретической СДВИ10В0Й проадости матрицы, равной 0,04 при комнатной температуре [345]. Полученные экспериментальные данные приведены на рис. 59,0 в сравнении с расчетными критериями начала пластической деформации [c.91]
Кольрауш указал, что при сравнении поведения модуля упругости при сдвиге железа с поведением модуля меди и латуни не было обнаружено ничего специфического. Он не мог полностью отбросить идею, что различие между результатами его собственных экспериментов и экспериментов Вертгейма объяснялось изменением объема, которое имеет место в одноосных опытах. Как отмечал Кольрауш в начале своей статьи, Вертгейм действительно не претендовал на высокую точность в своих исследованиях изменения Е с температурой Вертгейм был удовлетворен тем, что впервые продемонстрировал сам факт изменения модулей упругости с температурой. В заключение Кольрауш не использовал возможность сравнить свои экспериментальные значения для железа, меди и латуни с результатами измерений Купфера (Kupffer [1852, 1]), которые тот проделал восемнадцатью годами раньше, на том основании, что экспериментальные исследования Купфера, по его мнению, были проведены недостаточно глубоко, чтобы такое сравнение могло быть сделано ). [c.466]
Пример 3.14. Составной стержень круглого поперечного сечения (рис.3.13) представляет собой стальную трубу, внутри которой помещен жестко соединенный с ней медный стержень. К торцам составного сечения приложены пары сил М р = 2000 кГсм. Определить максимальные касательные напряжения в стальной и медной частях стержня, если г = г, =2 см, Гс= Г2 =4 см, модули упругости при сдвиге для стали и меди соответственно С. =8-10 к-Г/слг и С =АЛ0 кГ1см . [c.103]
Модуль упругости, коэффициент Пуассона, модуль Юнга. Таблицы
Модуль Юнга — характеристика вещества, описывающая упругие свойства материала при деформации растяжения/сжатия. Чаще всего указывается в ГПа (гигапаскалях).
При деформации растяжения/сжатия вдоль одной оси, в теле наблюдается изменение размеров тела вдоль оставшихся. Так, цилиндрическое тело, которое деформируют растягивая вдоль осевой линии, уменьшает диаметр основания (по сути, при неизменной массе и плотности объекта должен оставаться неизменным и его объём).
Введём:
В результате деформации растяжения, площадь основания уменьшается, также введём:
(2)Коэффициентом Пуассона (коэффициентом поперечной деформации) называется модуль отношения относительной поперечной деформации к относительной продольной:
(3)Модуль сдвига — характеристика вещества, описывающая упругие свойства материала при деформации сдвига. Чаще всего указывается в ГПа (гигапаскалях).
Для быстрого поиска нажмите «ctrl+F» и в открывшейся строке поиска введите интересующее вещество.
| Наименование материала | Модуль Юнга, ГПа | Модуль сдвига, ГПа | Коэффициент Пуассона |
| Алюминиевая бронза, литьё | 102,97 | 41,19 | — |
| Алюминиевая проволока тянутая | 68,65 | — | — |
| Алюминий катаный | 67,67 | 25,50-26,48 | 0,32-0,36 |
| Бекелит | 1,96-2,94 | — | — |
| Винипласт | 2,94 | — | — |
| Гетинакс | 9,81-16,67 | — | — |
| Гранит | 48,05 | — | — |
| Дерево | 3,92-17,65 | — | — |
| Дюралюминий катаный | 69,63 | 26,48 | — |
| Известняк | 41,19 | — | — |
| Инвар | 137,29 | 54,92 | — |
| Каучук | 0,00786 | — | 0,47 |
| Константан | 162,79 | 60,80 | 0,33 |
| Латунь корабельная катаная | 98,07 | — | 0,36 |
| Латунь холоднотянутая | 89,24-97,09 | 34,32-36,29 | 0,32-0,42 |
| Лёд | 9,81 | 2,75-2,94 | — |
| Манганин | 123,56 | 46,09 | 0,33 |
| Медь, литьё | 82,38 | — | — |
| Медь прокатная | 107,87 | 39,23 | 0,31-0,34 |
| Медь холоднотянутая | 107,87 | 39,23 | 0,31-0,34 |
| Мрамор | 54,92 | — | — |
| Плексиглас | 5,25 | 1,48 | 0,35 |
| Свинец | 16,67 | 6,86 | 0,42 |
| Сталь легированная | 205,94 | 79,43 | 0,25-0,30 |
| Сталь углеродистая | 196,13-205,94 | 79,43 | 0,24-0,28 |
| Стальное литьё | 171,62 | — | — |
| Стекло | 49,03-78,45 | 17,65-29,49 | 0,2-0,3 |
| Текстолит | 5,89-9,81 | — | — |
| Форсфористая бронза катаная | 112,78 | 41,19 | 0,32-0,35 |
| Целлулоид | 0,017-0,019 | — | 0,39 |
| Цинк катаный | 82,38 | 31,38 | 0,27 |
| Чугун белый, серый | 112,78-156,91 | 44,13 | 0,23-0,27 |
| Чугун кованый | 152,00 | — | — |
Поделиться ссылкой:
Механические свойства крепежа
В этом разделе представлено краткое описание механических характеристик болтов, винтов, шпилек.
Когда на металлический образец действует сила или система сил он реагирует на это, изменяя свою форму (деформируется). Различные характеристики, которыми определяются поведение и конечное состояние металлического образца в зависимости от вида и интенсивности сил, называется механическими свойствами металла.
Интенсивность силы, действующей на образец, называется напряжением и измеряется как полная сила, отнесенная к площади, на которую она действует. Под деформацией понимается относительное изменение размеров образца, вызванное приложенными усилиями. Деформации бывают упругие и пластические. При упругой деформации образец после снятия нагрузки возвращается к исходным размерам (деформация исчезает, как только исчезает её причина). Упругая деформация металлического образца пропорциональна силе или сумме сил, действующих на него. Это выражается законом Гука, согласно которому напряжение равно упругой деформации, умноженной на постоянный коэффициент пропорциональности, называемый модулем упругости: s =ε хY, где s – напряжение, ε – упругая деформация, а Y – модуль упругости (модуль Юнга). Модули упругости ряда металлов представлены в табл. 1.
Таблица 1
|
Металл |
Вольфрам |
Железо (сталь) |
Медь |
Алюминий |
Магний |
Свинец |
|
Модуль Юнга, |
3,5 |
2,0 |
1,1 |
0,70 |
0,45 |
0,18 |
Пользуясь данными этой таблицы, можно вычислить, например, силу, необходимую для того, чтобы растянуть стальной стержень квадратного поперечного сечения со стороной 1 см на 0,1% его длины:
F = Y х A х ΔL/L = 200 000 МПа х 1 см2 х 001 = 20 000 Н (= 20 кН)
Когда к металлическому образцу прикладываются напряжения, превышающие его предел упругости, они вызывают пластическую (необратимую) деформацию, приводящую к необратимому изменению его формы. Более высокие напряжения могут вызвать разрушение материала.
Определение модуля Юнга
Дальневосточный государственный технический университет
(ДВПИ им. В.В. Куйбышева)
Методические указания и отчет по лабораторной работе
ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПРИ РАСТЯЖЕНИИ
ЦЕЛЬ РАБОТЫ. Экспериментальное определение величины модуля упругости при растяжении Е (модуля Юнга) и сопоставление его со справочным значением.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Многолетняя практика возведения инженерных сооружений, опыт их эксплуатации и наблюдение за поведением при различных типах внешних воздействий, в том числе и разрушающих, показал, что их перемещения в определенных пределах пропорциональны действующим нагрузкам.
Впервые указанная закономерность была высказана в 1678г. Робертом Гуком в книге «О восстановительной способности или об упругости» — первой печатной работе по упругим свойствам материалов, в виде формулировки: «каково перемещение, такова и сила», которая носит название закона Гука. Такая трактовка устанавливает соотношение между перемещением (угловым или линейным) произвольной точки А системы от внешней нагрузки в виде
UA = Δ P, (1)
где Δ – коэффициент, зависящий от типа внешней нагрузки, района ее приложения, положения точки А, вида перемещения и рассматриваемого направления, геометрических особенностей системы и физико-механических свойств материала.
В общем случае, множество возможных сочетаний упомянутых факторов определяет и множество конкретных значений Δ. Таким образом, выражение (1) следует рассматривать как закон Гука для системы не очень удобный для конкретных расчетов.
Геометрические изменения системы являются проявлением деформации ее материала, интенсивность которых определяет прочность системы в целом. Современная трактовка закона Гука принадлежит Огюстену Коши, который свел его в точку, установив для материала в ней соотношение
σ = Ε ε, (2)
где σ – нормальное напряжение,
ε – относительная линейная деформация,
Е – модуль упругости при растяжении (модуль Юнга).
Соотношение (2) уже не связано с конкретными особенностями системы и отражает свойства только самого материала. Тем самым прочность системы в целом стала определяться прочностью ее материала в точке.
Линейные соотношения типа (1) между внешней нагрузкой и перемещениями для конкретных систем, которые обычно используются в инженерной практике расчетов, могут быть получены на основании выражения (2).
В общем случае закон Гука является линейной идеализацией начального участка зависимости σ = f(ε). Для некоторых материалов, таких, например, как сталь, эта идеализация обладает высокой степенью точности, однако, для таких, как чугун, строительные материалы, композиты она является довольно грубым приближением.
Наиболее наглядно закон
Гука проявляется при растяжении прямых стержней постоянного поперечного сечения, на которых и проводится определение основных механических характеристик материалов.Впервые понятие о модуле упругости ввел в 1820г Томас Юнг, который вычислил его для стали, определяя частоту колебаний камертона.
Для наиболее распространенных материалов Е имеет следующие значения (МПа)
Сталь…………………………………………(2,0-2,1) 105
Медь.…………………………………………1,2 105
Алюминиево-магниевые сплавы…………..(0,7-0,8) 105
Дерево (вдоль волокон)…………………….(0,08-0,12) 105
Известняк, гранит……………………………(0,4-0,5) 105
ОПИСАНИЕ НАЛАДКИ
Схема наладки для проведения лабораторной работы приведена на рис.1.
На силовой плите (1) лабораторного стола установлены две опорные стойки (2) и (3), закрепленные болтами в Т-образном пазе силовой плиты. В отверстии опорной стойки (3) зафиксирована неподвижная шарнирная ось (4), на конце которой закреплен датчик усилий ДУ (5) до 5,0кН с соединительной вилкой (6).
Рис.1 Схема наладки для лабораторной работы
В отверстии опорной стойки (2) установлена подвижная шарнирная ось (7), продольное перемещение которой создается нагрузочным штурвалом (8). Испытываемый образец (9)закреплен в вилке (6) и на оси (7) специальными штифтами.
На поверхности испытуемого образца наклеены четыре тензорезистора (рис.2), из которых №1 и №2 измеряют продольные деформации, а №3 и №4 — поперечные.
Нагружение образца производится вращением штурвала (8). Величина растягивающей силы контролируется блоком измерителя силы (ИС), а показания тензорезисторов – блоком измерителя деформаций (ИД).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Для устранения зазоров в собранной наладке произвести предварительное нагружение испытываемого образца. Снять начальные (no) показания ИД для тензорезисторов №1 и №2 и занести их в журнал измерений.
2. Произвести последовательное нагружение образца дополнительными усилиями в 1кН, 2кН и 3кН, контролируя их значение по показаниям ИС. Показания тензорезисторов регистрировать по ИД для каждого этапа нагружения, занося их в журнал измерений.
3. Для каждого тензорезистора построить график Pi – ni и аппроксимировать его прямой линией.
4. Определить среднее приращение показаний ИД для ступени нагружения (ΔP = 1кН) для каждого тензорезистора в отдельности Δni и среднее ΔnСР для обоих вместе.
5. Определить среднее приращение относительной линейной деформации для ступени нагружения (ΔР = 1кН) по формуле
Δεпрод = KИД ΔnСР,
где KИД = 10-6 — цена единицы измерения ИД в единицах относительной деформации.
6. Определить модуль нормальной упругости по формуле
Е = ΔP / F Δεпрод,
где F – площадь поперечного сечения образца (ширина 30мм, толщина 2мм).
7. Сравнить полученный результат со справочными значениями модуля Юнга.
8. Составить отчет по лабораторной работе.
9. Защитить лабораторную работу.
Журнал экспериментальных измерений и их обработки
Растягивающее усилие, кН | Показания ИД | |
Резистор №1 | Резистор №2 | |
n1 | n2 | |
0 1 2 3 | ||
Среднее приращение показаний ИД на ступень нагружения, Δni | ||
Среднее приращение показаний ИД на ступень нагружения для обоих тензорезисторов ΔnСР | ||
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое нормальные напряжения?
2. По какой формуле нормальные напряжения рассчитываются для поперечного сечения растянутого образца?
3. В каких единицах измеряются нормальные напряжения в системе СИ?
4. Что такое относительная линейная деформация?
5. По какой формуле относительная линейная деформация рассчитывается для растянутого образца?
6. В каких единицах измеряются относительные линейные деформации?
7. Напишите закон Гука «для точки».
8. В чем разница закона Гука «для точки» и системы?
9. Какой ученый свел закон Гука в точку?
10. Почему прочность системы определяется прочностью «в точке»?
11. Что такое модуль упругости при растяжении?
12. В каких единицах измеряется модуль Юнга
13. Чему модуль Е равен для стали (меди, алюминиево-магниевых сплавов, гранита, дерева)?
14. Почему закон Гука считается условно линейным?
15. Для каких материалов закон Гука имеет наименьшее отклонение от линейности, для каких наибольшее и почему?
16. Что такое тензорезистор и в чем принцип его работы?
БИОГРАФИЧЕСКАЯ СПРАВКА
Гук Роберт (1635-1703) английский физик, секретарь Лондонского королевского общества, профессор Лондонского университета, куратор экспериментаторов Лондонского королевского общества. Научные работы относятся к теплоте, оптике, небесной механике.
Коши Огюстен Луи (1789-1857) французский математик, член Парижской академии наук. Научные работы относятся к математике, математической физике, теории упругости, оптике.
Юнг Томас (1773-1829) английский физик, астроном и врач, профессор Королевского института (Лондон). Научные работы относятся к физике, химии, астрономии, геофизике, механике, оптике, философии и медицине.
Выполнил студент группы
Принял Е. Борисов
3CRC химии и физики (2003-2004)
Модуль Юнга
130 ГПа
Л.Б. Фройнд, С. Суреш. Тонкопленочные материалы: напряжение, дефект Формирование и эволюция поверхности (2003)
Коэффициент Пуассона
0.34
Л.Б. Фройнд, С. Суреш. Тонкопленочные материалы: напряжение, дефект Формирование и эволюция поверхности (2003)
Константы жесткости
C11 = 168,3 ГПа,
C12 = 1,221 ГПа,
C44 = 0,757 ГПа
CRC химии и физики (2003-2004)
Прочность на растяжение или излом
193 МПа [1] 262 МПа [2]
[1] Дж.W. Dini, Электроосаждение Материаловедение покрытий и подложек
[2] Д. Рид, Дж. Далли, Mechanical Поведение тонких пленок алюминия и меди. В Механика и материалы для электронной упаковки: Vol. 2 (1994), ASME
Остаточное напряжение кремния
0400 МПа
Х. Чой, С.К. Choi et.al. Влияние плотности пленки от остаточного напряжения и удельного сопротивления для тонких пленок Cu, нанесенных методом распыления под смещением. Тонкие твердые пленки 358 (2000) 202-205.
Удельная теплоемкость
385 Дж / кг * К (при 300 К)
CRC химии и физики (2003-2004)
Теплопроводность
401 Вт / м * К (при 300 К)
CRC химии и физики (2003-2004)
Диэлектрическая проницаемость
Показатель преломления
0.-1
Х. Чой, С.К. Choi et. al. Влияние плотности пленки от остаточного напряжения и удельного сопротивления для тонких пленок Cu, нанесенных методом распыления под смещением. Тонкие твердые пленки 358 (2000) 202-205.
Магнитная проницаемость
~ 1 Диамагнитный
ASM Speciality Handbook: Медь и медные сплавы (2001)
Пьезорезистивность
п. 11 = 5.-1
К. Ху, Ю. Гао, З. Шэн. Пьезосопротивление коэффициенты для меди и медно-никелевых сплавов. Журнал материаловедения 35 (2000) 381-386
Пьезоэлектричество
Метод мокрого травления
Серная кислота / перекись водорода
Обмен MEMS (http: // www.mems-exchange.org/)
Метод плазменного травления
Cl2, HCl и плазменное травление HBr
Я. Куо, С. Ли. Медь комнатной температуры травление на основе реакции плазма-медь. Applied Physics Letters, 78 (7) февраль 2001 г.
Адгезия к диоксиду кремния
Вариант (1.2). Обычно слабый и улучшенный за счет легирования, использование адгезионного слоя или подготовка поверхности
[1] К. Нагао, Дж. Нитон, Н. Эшкрофт. Ab initio исследование адгезии на границе раздела Cu / SiO2. (CornellUniv. И RutgersUniv. — Презентация)
[2] П.Дж. Динг, В.А. Ланфорд, С. Хаймс, С.П. Мурарка. Устойчив к окислению, высокая проводимость фильмы Письма о прикладной физике 64 (21) Май 1994
www.ccmr.Cornell.edu/IRG-Glass/nagao.ppt
Биосовместимость
ДА, если покрытие должным образом (например, силикон)
Э. Пина, Э. Burgos, et. al. Магнитоэластичный датчик как датчик мышечной активности, эксперимент in vivo. Датчики и приводы A 91 (2001) 99-102
Гидрофобность
5 градусов с водой (полированная медь)
Покрытие смазываемых поверхностей Бумага VITEK Research Corporation (www.vitekres.com)
| Значения модуля Юнга для медных сплавов | ||
| Материал | Модуль упругости (модуль Юнга) | |
| ГПа | ksi | |
| C10200 (бескислородная медь) | 117 | 17000 |
| C11000 (медь с твердой электролитической смолой) | 117 | 17000 |
| C17200 (бериллий — медь) | 128 | 18 500 |
| C22000 (техническая бронза, 90%) | 115 | 16700 |
| C23000 (красная латунь, 85%) | 117 | 17000 |
| C26000 (патрон латунь) | 110 | 16000 |
| C27000 (желтая латунь) | 103.4 | 15000 |
| C36000 (латунная резка) | 96,5 | 14000 |
| C60800 (алюминиевая бронза, 5%) | 121 | 17500 |
| C71500 (медь — никель, 30%) | 152 | 22000 |
| C86300 (марганцевая латунь) | 97.9 | 14200 |
| C93200 (подшипник бронза) | 100 | 14500 |
| C95500 (алюминиевая бронза) | 110 | 16000 |
Промышленное: Руководство по проектированию — Модуль упругости
Фото © 1998 AMP INC.
Существует множество сплавов с заметно разными диапазонами прочности. Таким образом, прочность является важным фактором в процессе выбора, который определяет медный сплав, который будет использоваться для пружины соединителя. Как описано в теме «Контактная сила», важность силы заключается в ее соотношении с контактной силой. Модуль упругости Юнга — это мера жесткости пружинного элемента. Жесткость — важный фактор в конструкции пружины, потому что она также влияет на силу контакта. Это легко увидеть из уравнений, связывающих прогиб с контактной силой.Например, в конструкции с консольной балкой (закрепленной на одном конце, нагрузка на противоположном конце) контактная сила прямо пропорциональна модулю. Ясно, что это важное соображение при проектировании соединительной пружины.
Модуль упругости медных сплавов составляет от 16 до 20 миллионов фунтов на квадратный дюйм (примерно от 110 до 138 кМпа). Этот диапазон представляет практически все медные сплавы, используемые для соединительных пружин. Хотя это изменение намного меньше, чем изменение прочности и проводимости, его не следует игнорировать.Значения для каждого сплава приведены в таблицах в различных справочниках и таблицах данных.
Модуль упругости Юнга определяется как отношение между напряжением и деформацией для напряжений ниже предела пропорциональности. При высоких расчетных напряжениях использование этого модуля в уравнениях, которые связывают контактное усилие и прогиб, не может точно предсказать фактическое поведение. Температурный режим, ориентация и режим напряжения влияют на модуль упругости, но незначительно. О таких подробных измерениях этой характеристики подробно не сообщалось, и обычно с каждым медным сплавом связано одно значение модуля Юнга.Это еще раз подтверждает важность прототипов.
Еще одно связанное свойство — коэффициент Пуассона. Это число представляет собой свойство материала, которое связывает деформацию в поперечном направлении при испытании на растяжение с деформацией в продольном направлении. Это почти постоянная величина для большинства медных сплавов, и значение 0,3 может быть присвоено всем сплавам соединителей без ущерба для любого важного параметра конструкции.
Измерение модуля Юнга для свободного от меди Эссе, пример
Цель:
Для изучения поведения напряжения / деформации медной проволоки и аппроксимации модуля Юнга меди
Аппарат:
Медный провод s.w.g. 32 около 4 мес.
G-зажим? 1.
Деревянный блок? 2.
Правило счетчика? 4.
Колесо на зажиме? 1.
Калибр для микрометра? 1.
Вешалка (0,01 кг)? 1.
Масса с прорезями (0,05 кг)? 8.
Масса с прорезями (0,1 кг)? 6.
Масса с прорезями (0,2 кг)? 4.
Масса с прорезями (0,5 кг)? 1.
Белая этикетка-наклейка? 1.
Защитные очки? 1.
Резиновая плитка? 1.
Теория :.
Когда сила F приложена к концу провода с площадью поперечного сечения A по его длине, растягивающее напряжение =.
Не теряйте время
Обратитесь к проверенному писателю, который поможет вам с измерением модуля Юнга меди
Нанять проверенного писателя$ 35,80 за 2-страничную статью
Если удлинение провода есть? l, а его исходная длина — lo, растягивающее напряжение =.
В условиях упругости модуль упругости проволоки, называемый модулем Юнга E, определяется как отношение растягивающего напряжения, применяемого к телу, к создаваемому растягивающему давлению.где E выражается в Н · м-2 или Паскалях (Па).
E является непрерывным, когда? l мало в соответствии с законом Гука, в котором упоминается, что напряжение, применяемое к любому твердому телу, пропорционально давлению, которое оно создает при небольшом напряжении.
По этой причине, когда продукт имеет большую ценность E, он сильно выдерживает гибкое искривление, и для создания небольшого напряжения требуется большое напряжение. Таким образом, E — это процедура эластичной герметичности материала.
Тем не менее, когда растяжение (деформация) проволоки слишком велико, сверх пропорционального предела, сила больше не будет подчиняться закону Гука i.е. E больше не является последовательным.
По мере дополнительного увеличения натяжения, превышающего предел гибкости, проволока имеет длительное удлинение, так что проволока перестает быть эластичной и претерпевает пластическую деформацию.
Удлинение быстро увеличивается, поскольку усилие на тросе еще больше. Проволока удлиняется и рвется. Напряжение непосредственно перед разрывом проволоки называется разрывным напряжением.
Обработки :.
Настройка устройства.
1. Устройство было установлено на столе, как показано ниже.
— Трос был надежно закреплен с помощью G-зажима, чтобы он не скользил.
— На медный провод был отремонтирован ярлык с белой этикеткой, который действует как маркер, так что он должен находиться на расстоянии 50 см от шкива.
— Отремонтирована линия метра рядом с проводом с изготовителем для определения удлинения.
Проведение эксперимента
1. Вешалка была привязана к концу проволоки так, чтобы расправить изгибы проволоки, и была измерена нерастянутая длина (lo) проволоки от краев деревянных брусков до маркера.
2. Для измерения диаметра проволоки под разными углами для каждого из 8 участков вдоль проволоки использовали микрометрический калибр.
3. Проволока была загружена с пазами массой m в
Было зарегистрированошага по 0,10 кг, а затем по 0,05 кг и удлинения? L после каждой нагрузки до тех пор, пока провод не порвался.
Таблица данных:
Исходная длина провода lo = (3.000 ï1½ 0,001) м
Ошибка в процентах в lo =
Диаметр проволоки (мм)
0.255
0,250
0,225
0,230
0,225
0,255
0,225
0,255
Средний диаметр проволоки = (0,240 ± 0,005) мм
Ошибка в процентах в d =
Показаний для графика:
Нагрузка м / кг
0,10
0,20
0,30
0,40
0,50
0,60
0,65
Удлинитель? Л / мм
0,5
1.0
1,5
2,0
2,5
3,0
3,5
Нагрузка м / кг
0,70
0,75
0,8
0,85
0,90
0,95
1,00
Удлинитель? Л / мм
3,5
4,0
5,0
6,0
6,5
7,5
Сломался
Анализ данных:
Модуль Юнга,
, где F — натяжение проволоки, A — площадь поперечного сечения
.С и
На графике наклон линии наилучшего соответствия, проходящей через точки прямой части графика,
Предположим, что площадь поперечного сечения не изменилась при увеличении напряжения.
Ошибки и точность:
По графику,
наклон наиболее подходящей линии:
максимальный уклон:
минимальный уклон:
Отклонения: m + — m = 12,1
Отклонения: m — m- = 26,0
Максимальная погрешность наклона = большее из отклонений = 26,0
Наклон графика нагрузки-расширения = (192,7 ± 26,0)
Ошибка уклона в процентах:
Ошибка в процентах в E
=% ошибки в наклоне +% ошибки в lo + 2? % ошибка в d
Модуль Юнга меди, E = (125 ± 22) ГПа
Вывод:
— Напряжение, приложенное к медному проводу (см.w.g. 32) прямо пропорциональна деформации, которую он производит до того, как удлинение станет 3,5 мм.
— Отношение напряжения к деформации станет меньше и не будет постоянным, когда удлинение превышает 3,5 мм (предел пропорциональности), то есть после того, как удлинение достигнет 3,5 мм, небольшое увеличение напряжения может привести к значительному увеличению деформации.
— Медь подчиняется закону Гука.
— Модуль Юнга меди составляет (125 ± 22) ГПа
Источники ошибок:
1. Медный провод не имел постоянной площади поперечного сечения по длине.
2. Из-за приложения шкива к проволоке возникла незначительная сила.
3. Ошибка считывания при измерении удлинения и нерастянутой длины.
4. Колебания комнатной температуры могут изменить диаметр проволоки во время эксперимента.
5. Проволока в экспериментальной установке была не совсем горизонтальной, что сделало наши измерения удлинения неточными.
6. Площадь поперечного сечения проволоки под нагрузкой стала тоньше, так что ожидаемое напряжение будет меньше фактически приложенного напряжения.
Улучшение эксперимента:
1. Закрепите линейку счетчика другим зажимом G, чтобы измерение удлинения было более точным.
2. Чтобы измерить чрезвычайно малое удлинение с высокой точностью, можно использовать «оптический рычаг» (зеркало, установленное на небольшой шарнирной опоре) вместо простой измерительной линейки.
3. Повторите эксперимент несколько раз и возьмите среднее значение расширений, чтобы получить более точный результат.
4.Эксперимент можно повторить, как показано ниже, чтобы можно было точно измерить небольшое удлинение провода по нониусной шкале; кроме того, не будет дополнительной дробной форсы из-за наличия шкива.
5. Повторите эксперимент, используя медную проволоку с другой удельной массой, и возьмите среднее значение полученного модуля Юнга, чтобы мы могли более точно оценить значение модуля Юнга для меди.
Меры предосторожности:
1. Во время эксперимента надевайте защитные очки, чтобы защитить глаза, когда в конечном итоге обрывается провод
2.Груз не должен быть слишком высоким от пола, и должна быть подходящая мягкая площадка для приземления, например бегунок, прямо под грузом.
3. Длина нерастянутого провода должна быть не менее 3 м, чтобы провод можно было удлинить.
Что такое прочность медных сплавов — определение
Медные сплавы — это сплавы на основе меди, в которых основными легирующими элементами являются Zn, Sn, Si, Al, Ni. Сплавы на основе меди представляют собой в основном твердые растворы замещения, в которых растворенные или примесные атомы заменяют или замещают основные атомы.Некоторые особенности атомов растворенного вещества и растворителя определяют степень, в которой первые растворяются во втором. Они выражаются в виде правил Юма – Ротери . Существует до 400 различных составов меди и медных сплавов свободно сгруппированных по категориям: медь, сплав с высоким содержанием меди, латунь, бронза, медно-никелевый сплав, медь-никель-цинк (нейзильбер), свинцованная медь и специальные сплавы. Кроме того, ограниченное количество медных сплавов можно упрочнить термической обработкой.; следовательно, для улучшения этих механических свойств необходимо использовать холодную обработку и / или легирование твердым раствором.
Виды медных сплавов
Как было написано, существует около 400 различных составов меди и медных сплавов, которые свободно сгруппированы по категориям: медь, высокосортный медный сплав, латунь, бронза, медь-никель, медь-никель-цинк (нейзильбер), свинцовая медь и специальные сплавы. В следующих пунктах мы суммируем ключевые свойства выбранных материалов на основе меди.
- Электролитическая смола (ЭТП) медь . Электролитическая вязкая пековая медь UNS C11000 — это чистая медь (с максимальным содержанием примесей 0,0355%), очищенная методом электролитического рафинирования, и это наиболее широко используемый сорт меди во всем мире. ETP имеет минимальный рейтинг проводимости 100% IACS и должен иметь чистоту 99,9%. Он содержит от 0,02% до 0,04% кислорода (типичное). Электропроводка — самый важный рынок для медной промышленности.Сюда входят структурная силовая проводка, силовой распределительный кабель, приборный провод, коммуникационный кабель, автомобильный провод и кабель, а также магнитный провод. Примерно половина всей добываемой меди используется для изготовления электрических проводов и кабельных жил. Чистая медь имеет лучшую электрическую и теплопроводность из всех промышленных металлов. Электропроводность меди составляет 97% от проводимости серебра. Из-за своей гораздо более низкой стоимости и большего количества медь традиционно была стандартным материалом, используемым для передачи электроэнергии.
- Латунь . Латунь — это общий термин для диапазона медно-цинковых сплавов . Латунь может быть легирована цинком в различных пропорциях, что приводит к получению материала с различными механическими, коррозионными и термическими свойствами. Повышенное количество цинка придает материалу повышенную прочность и пластичность. Латуни с содержанием меди более 63% являются наиболее пластичными из всех медных сплавов и формуются с помощью сложных операций холодной штамповки. Латунь имеет более высокую пластичность, чем бронза или цинк.Относительно низкая температура плавления латуни и ее текучесть делают ее относительно легким в литье материалом. Цвет поверхности латуни может варьироваться от красного до желтого в зависимости от содержания цинка. Некоторые из распространенных применений латунных сплавов включают бижутерию, замки, петли, шестерни, подшипники, шланговые соединения, гильзы для боеприпасов, автомобильные радиаторы, музыкальные инструменты, электронную упаковку и монеты. Латунь и бронза являются общими инженерными материалами в современной архитектуре и в основном используются для кровли и облицовки фасадов из-за их внешнего вида.
- Бронза . Бронзы представляют собой семейство сплавов на основе меди, традиционно легированных оловом, но могут относиться к сплавам меди и других элементов (например, алюминия, кремния и никеля). Бронза несколько прочнее латуни, но при этом обладает высокой степенью коррозионной стойкости. Обычно они используются, когда помимо коррозионной стойкости требуются хорошие свойства при растяжении. Например, бериллиевая медь обладает наибольшей прочностью (до 1400 МПа) из всех сплавов на основе меди.
- Медно-никелевый сплав . Мельхиор — это медно-никелевый сплав, который обычно содержит от 60 до 90 процентов меди и никеля в качестве основного легирующего элемента. Два основных сплава — 90/10 и 70/30. Также могут содержаться другие упрочняющие элементы, такие как марганец и железо. Мельхиор обладают отличной устойчивостью к коррозии, вызываемой морской водой. Несмотря на высокое содержание меди, мельхиор имеет серебристый цвет. Добавление никеля к меди также улучшает прочность и коррозионную стойкость, но сохраняет хорошую пластичность.
- Нейзильбер . Нейзильбер, известный также как немецкое серебро, никелевая латунь или альпакка, представляет собой сплав меди с никелем и часто цинком. Например, медный сплав UNS C75700 Нейзильбер 65-12 имеет хорошую коррозионную стойкость и устойчивость к потускнению, а также высокую формуемость. Нейзильбер назван из-за его серебристого цвета, но он не содержит элементарного серебра, если не покрыт металлическим покрытием.
Прочность медных сплавов
В механике материалов сила материала — это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации. Прочность материалов в основном учитывает взаимосвязь между внешними нагрузками , приложенными к материалу, и результирующей деформацией или изменением размеров материала. Прочность материала — это его способность выдерживать эту приложенную нагрузку без разрушения или пластической деформации.
Предел прочности на разрыв
Предел прочности на разрыв электролитической смолы (ЭТП) меди составляет около 250 МПа.
Предел прочности на разрыв патронной латуни — UNS C26000 составляет около 315 МПа.
Предел прочности на разрыв алюминиевой бронзы — UNS C95400 составляет около 550 МПа.
Предел прочности на разрыв оловянной бронзы — UNS C Предел прочности на разрыв меди бериллия — UNS C17200 составляет около 1380 МПа. Предел прочности на разрыв для мельхиора — UNS C70600 составляет около 275 МПа. Предел прочности на разрыв для нейзильбера — UNS C75700 составляет около 400 МПа. Предел прочности на растяжение является максимальным на инженерной кривой зависимости напряжения от деформации. Это соответствует максимальному напряжению , которое может выдержать конструкция при растяжении. Предел прочности на разрыв часто сокращают до «прочности на разрыв» или даже до «предела». Если это напряжение приложить и поддерживать, в результате произойдет разрушение. Часто это значение значительно превышает предел текучести (на 50–60 процентов больше, чем предел текучести для некоторых типов металлов).Когда пластичный материал достигает предела прочности, он испытывает образование шейки, где площадь поперечного сечения локально уменьшается. Кривая «напряжение-деформация» не содержит напряжения, превышающего предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца. Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов и температура температуры испытательной среды и материала. Предел прочности на разрыв варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочных сталей. Доказательная прочность электролитической смолы (ЭТП) меди составляет 60-300 МПа. Предел текучести алюминиевой бронзы — UNS C95400 составляет около 250 МПа. Предел текучести оловянной бронзы — UNS C Предел текучести бериллиевой меди — UNS C17200 составляет около 1100 МПа. Предел текучести мельхиора — UNS C70600 составляет около 105 МПа. Предел текучести нейзильбера — UNS C75700 составляет около 170 МПа. Предел текучести — это точка на кривой зависимости напряжения от деформации, которая указывает предел упругого поведения и начало пластического поведения. Предел текучести или предел текучести — это свойство материала, определяемое как напряжение, при котором материал начинает пластически деформироваться, тогда как предел текучести — это точка, в которой начинается нелинейная (упругая + пластическая) деформация.До достижения предела текучести материал будет упруго деформироваться и вернется к своей исходной форме, когда приложенное напряжение будет снято. После достижения предела текучести некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют поведение, называемое явлением предела текучести. Предел текучести варьируется от 35 МПа для алюминия с низкой прочностью до более 1400 МПа для высокопрочных сталей. Модуль упругости Юнга для электролитической смолы (ЭТП), меди составляет около 120 ГПа. Модуль упругости Юнга патронной латуни — UNS C26000 составляет около 95 ГПа. Модуль упругости алюминиевой бронзы — UNS C95400 составляет около 110 ГПа. Модуль упругости оловянной бронзы — UNS C Модуль упругости Юнга меди бериллия — UNS C17200 составляет около 131 ГПа. Модуль упругости Юнга мельхиора — UNS C70600 составляет около 135 ГПа. Модуль упругости Юнга для нейзильбера — UNS C75700 составляет около 117 ГПа. Модуль упругости Юнга представляет собой модуль упругости для растягивающего и сжимающего напряжения в режиме линейной упругости при одноосной деформации и обычно оценивается с помощью испытаний на растяжение. С точностью до предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из положения равновесия.Все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и остаточная деформация не происходит. Согласно закону Гука , напряжение пропорционально деформации (в упругой области), а наклон равен модулю Юнга . Модуль Юнга равен продольному напряжению, деленному на деформацию. Алерс Дж. Б. Сукамто, П. Войтовиц, X Лу, С. Кайласам и Дж. Рейд (2005) «Миграция напряжений и механические свойства меди.”В 2005 г. Международный симпозиум IEEE по физике надежности, 2005 г. Труды. 43rd Annual., 36–40. IEEE. DOI: 10.1109 / RELPHY.2005.1493058. Бакланов, Михаил Р., Пол Шо и Эренфрид Зшех, ред. (2012) Advanced Interconnects for ULSI Technology. Джон Вили и сыновья. доступно по адресу http://www.wiley.com/WileyCDA/WileyTitle/productCd-0470662549,subjectCd-PH62.html Brien BB O (2013) Текстура боковых стенок и микроструктура медных семян iPVD в узких траншеях дамасского периода.СТАТЬЯ 160 (12): D3139. DOI: 10.1680 / udap.2010.163 Артикул
Google Scholar Бурцева Л., Вернер Ф., Валд Б., Пестряков А., Ромеро Р. и Петрановский В. (2015) «Методы мозаики для моделирования структуры материала». Прикладная механика и материалы 756: 426-435. https://www.scientific.net/AMM.756.426 Цао Линьцзюнь, К.Дж. Ганеш, Лиджуан Чжан, Оливер Обель, Кристиан Хеннесталь, Мейке Хаушильдт, Пауло Дж. Феррейра и Пол Шо (2013) «Анализ зеренной структуры и влияние на надежность электромиграции в наноразмерных соединениях Cu.Письма по прикладной физике 102 (13). DOI: 10.1063 / 1.4799484. Цао Линьцзюнь, Лицзюань Чжан, Пол Шо, Патрик Джастисон и Мейке Хаушильдт (2014) «Влияние масштабирования на микроструктуру и надежность электромиграции для соединений Cu и Cu (Mn)». Труды международного симпозиума по физике надежности IEEE 3–7. DOI: 10.1109 / IRPS.2014.6860660. Ceric H, Selberherr S (2011) Электромиграция в субмикронных межсоединениях интегральных схем. Mat Sci Eng R Rep 71 (5–6): 53–86.DOI: 10.1016 / j.mser.2010.09.001, Elsevier B.V Статья
Google Scholar Чен Л. (2015) «Влияние соотношения сторон и межстрочного интервала на микроструктуру в межсоединениях из дамасской меди». В 2015 г. 22-й Международный симпозиум IEEE по физическому анализу и анализу отказов интегральных схем, 451–54. IEEE. DOI: 10.1109 / IPFA.2015.7224430. Choi ZS, Mönig R, Thompson CV (2007) Зависимость потока электромиграции от кристаллографической ориентации различных зерен в межсоединениях поликристаллической меди.Appl Phys Lett 90 (24): 2005–8. DOI: 10.1063 / 1.2742285 Google Scholar Choi ZS, Mönig R, Thompson CV (2008) Влияние микроструктуры на формирование, форму и движение пустот во время электромиграции в пассивированных медных межсоединениях. J Mater Res 23 (2): 383–91. DOI: 10.1557 / JMR.2008.0054, Cambridge University Press Статья
Google Scholar Фишер А.Х., Абель А., Леппер М., Зицельсбергер А.Е. и фон Гласов А.Э. (2000) «Экспериментальные данные и статистические модели для бимодальных электромагнитных отказов.”В материалах международного симпозиума по физике надежности IEEE 2000 г. 38-й Ежегодник (Кат. № 00Ч47059), 359–63. IEEE. DOI: 10.1109 / RELPHY.2000.843940. Fischer AH, Abel A, Lepper M, Zitzelsberger AE, Von Glasow A (2001) Моделирование бимодальных распределений отказов электромиграции. Microelectron Reliab 41 (3): 445–53. DOI: 10.1016 / S0026-2714 (00) 00246-8 Артикул
Google Scholar Ганеш К.Дж., С. Раджасекхара, Дж.П. Чжоу и П.Дж. Феррейра (2010 г.) «Анализ текстуры и напряжений медных межсоединений 120 Нм.”Scripta Materialia 62 (11). Acta Materialia Inc .: 843–46. DOI: 10.1016 / j.scriptamat.2010.02.016. Ганеш К.Дж., Дарбал А.Д., Раджасекхара С., Рорер Г.С., Бармак К., Феррейра П.Дж. (2012) Влияние масштабирования нано-медных межсоединений на микроструктуру, выявленное с помощью TEM-ориентационного картирования с высоким разрешением. Нанотехнологии 23 (13): 135702. DOI: 10.1088 / 0957-4484 / 23/13/135702 Артикул
Google Scholar Гао Го Цзе Дж, Юн Цзян В., Шигенобу О (2013) Изучение упругих свойств нанокристаллической меди с использованием модели случайно упакованных однородных зерен.Comput Mater Sci 79: 56–62. doi: 10.1016 / j.commatsci.2013.05.053, Elsevier B.V Статья
Google Scholar Gianola DS, Van Petegem S, Legros M, Brandstetter S, Van Swygenhoven H, Hemker KJ (2006) Прерывистый рост зерна под действием напряжения и его влияние на деформационное поведение тонких пленок нанокристаллического алюминия. Acta Mater 54 (8): 2253–63. DOI: 10.1016 / j.actamat.2006.01.023 Артикул
Google Scholar Hau-Riege CS, Thompson CV (2001) Электромиграция в межсоединениях меди с очень разными зернистыми структурами.Appl Phys Lett 78 (22): 3451–53. DOI: 10.1063 / 1.1355304 Артикул
Google Scholar Герцберг Ричард В., Ричард Пол Винчи и Джейсон Л. Герцберг (1983) Механика деформации и разрушения технических материалов. Джон Вили и сыновья. доступно по адресу http://www.wiley.com/WileyCDA/WileyTitle/productCd-EHEP002042.html Heryanto A, Pey KL, Lim YK, Liu W, Raghavan N, Wei J, Gan CL, Lim MK, Tan JB (2011) Влияние миграции напряжения на электромиграцию в двойных дамасских медных межсоединениях.Журнал прикладной физики 109 (1): 1–10. DOI: 10.1063 / 1.3531393 Артикул
Google Scholar Hommel M, AH Fischer, A Glasow и A.E Zitzelsberger (2002) «Вызванное напряжением пустотное пространство в алюминиевых и медных межсоединениях». Материалы конференции AIP 612, 157–168. http://aip.scitation.org/doi/abs/10.1063/1.1469900 Итакура М., Х. Кабураки и К. Аракава (2005) «Механизм ветвления межкристаллитного распространения трещин в трех измерениях.Физический обзор E 71 (5). Американское физическое общество: 55102. DOI: 10.1103 / PhysRevE.71.055102. Кауаш Б., Лабат С., Томас О., Майтреджан С., Карро В. (2008) Текстура и деформация в узких соединительных линиях из дамасского меди: анализ дифракции рентгеновских лучей. Microelectron Eng 85 (10): 2175–78. DOI: 10.1016 / j.mee.2008.06.017 Артикул
Google Scholar Karmarkar AP, Xu X, Yeap KB, Zschech E (2012) Эффекты анизотропии меди в трехмерных интегральных схемах с использованием сквозных кремниевых переходных отверстий.IEEE Trans Device Mater Reliab 12 (2): 225–32. DOI: 10.1109 / TDMR.2012.2189401 Артикул
Google Scholar КИМ ДЖИ ЙОНГ (2006) Исследование механизма межфазной электромиграции в тонких пленках меди, Диссертация. Техасский университет в Арлингтоне. DOI: 10.1017 / CBO9781107415324.004 Google Scholar Кокс У.Ф., К. Н. Томе и Х. Р. Венк (2000) «Текстура и анизотропия: предпочтительные ориентации в поликристаллах и их влияние на свойства материалов.Издательство Кембриджского университета. доступно по адресу http://www.cambridge.org/catalogue/catalogue.asp? isbn = 9780521794206 Li JCM (2006) Механический рост зерен в нанокристаллической меди. Phys Rev Lett 96 (21): 2–5. DOI: 10.1103 / PhysRevLett.96.215506 Google Scholar Li B, Cathryn C, Dinesh B, Chih Chao Y (2014) Проблемы электромиграции для продвинутых межкомпонентных соединений на кристалле.Microelectron Reliab 54 (4): 712–24. DOI: 10.1016 / j.microrel.2014.01.005, Elsevier Ltd Артикул
Google Scholar Lin CC, HM Hsu, YH Chen, T Shih, SM Jang, CH Yu и MS Liang (2001) «Процесс металлизации полностью Cu Damascene для высокодобротного индуктора RF CMOS SoC с суб-0,18 / spl Mu / m. и применение конденсатора MIM на частотах 2,4 и 5,3 ГГц ». В материалах Международной конференции по технологиям межсоединений IEEE 2001 (кат. № 01EX461), 113–15.IEEE. DOI: 10.1109 / IITC.2001.930033. Lloyd JR (1999) Электромиграция в проводниках интегральных схем. J. Phys. D. Appl. Phys. 32 (17): R109–18. DOI: 10.1088 / 0022-3727 / 32/17/201 Артикул
Google Scholar Ллойд Дж. Р., Клемент Дж. Дж. (1995) Электромиграция в медных проводниках. Тонкие твердые пленки 262 (1-2): 135–41. DOI: 10.1016 / 0040-6090 (94) 05806-7 Артикул
Google Scholar Lloyd JR, Murray CE, Shaw TM, Lane MW, Liu XH, Liniger EG (2006) Теория электромиграционного разрушения в медных проводниках.AIP Conf Proc 817 (2006): 23–33. DOI: 10.1063 / 1.2173528 Артикул
Google Scholar Маркус М.А., У.Ф. Флад, Р.А. Чирелли, Р.К. Кистлер, Н.А. Чампа, В.М. Мэнсфилд, Д.Л. Барр, К.А. Волкерт и К.Г. Штайнер (1994) «Измерения деформации рентгеновскими лучами в пленках AL-CU с тонкими узорами». MRS Proceedings 338 (январь). Издательство Кембриджского университета: 203. DOI: 10.1557 / PROC-338-203. Meyer MA, Zienert I, Zschech E (2005) Дифракция обратного рассеяния электронов: применение к межсоединениям из Cu на виде сверху и в поперечном сечении.В кн .: Материалы для информационных технологий. Springer, London, стр. 485–95. DOI: 10.1007 / 1-84628-235-7_39 Google Scholar Muppidi T, Field DP, Sanchez JE, Woo C (2005) Барьерный слой, геометрия и эффекты легирования на микроструктуру и текстуру гальванических тонких пленок меди и линий дамасского покрытия. Тонкие твердые пленки 471 (1-2): 63–70. DOI: 10.1016 / j.tsf.2004.04.057 Артикул
Google Scholar Musienko A, Tatschl A, Schmidegg K, Kolednik O, Pippan R, Cailletaud G (2007) Трехмерное конечно-элементное моделирование образца поликристаллической меди.Acta Mater 55 (12): 4121–36. DOI: 10.1016 / j.actamat.2007.01.053 Артикул
Google Scholar Nabiollahi N, Nele M, Mario G, Joke De M, Wilson CJ, Kristof C, Eric B, Ingrid De W (2015) Моделирование микроструктуры роста зерен в Cu через кремниевые переходные отверстия с использованием моделирования фазового поля. Microelectron Reliab 55 (5): 765–70. DOI: 10.1016 / j.microrel.2015.02.009, Elsevier Ltd Артикул
Google Scholar Nucci JA, Keller RR, Field DP, Shacham-Diamand Y (1997) Углы разориентации границ зерен и вызванные напряжением пустоты в пассивированных оксидом медных межсоединениях.Appl Phys Lett 70 (10): 1242. DOI: 10.1063 / 1.118942 Артикул
Google Scholar Ogawa ET, Lee KD, Blaschke VA, Paul SH (2002) Проблемы надежности электромиграции в соединениях с двойным дамасцем из меди. IEEE Trans Reliab 51 (4): 403–19. DOI: 10.1109 / TR.2002.804737 Артикул
Google Scholar Oh Yong-Seog, Hyerim Lee, Ibrahim Avci, Sora Park, Jongsung Jeon, Jinseok Kim и Windu Sari (2013) «Численная модель, использующая метод фазового поля для вызванного напряжением пустот в металлической линии во время термической обжига. .»Международная конференция по моделированию полупроводниковых процессов и устройств, 2013 г. (SISPAD), No. 1: 13–16. DOI: 10.1109 / SISPAD.2013.6650562. Paik JM, Park H, Joo YC (2004) Влияние низкокалорийного диэлектрика на напряжение и вызванное напряжением повреждение в медных межсоединениях. Microelectron Eng 71 (3-4): 348-57. DOI: 10.1016 / j.mee.2004.02.094 Артикул
Google Scholar Piekoś K, Tarasiuk J, Wierzbanowski K, Bacroix B (2008) Обобщенная вертексная модель рекристаллизации — приложение к поликристаллической меди.Comput Mater Sci 42 (4): 584–94. DOI: 10.1016 / j.commatsci.2007.09.014 Артикул
Google Scholar Rhee SH, Yong D, Paul SH (2003) Характеристики термического напряжения субмикронных межсоединительных структур Cu / оксид и Cu / low-K. J Appl Phys 93 (7): 3926–33. DOI: 10.1063 / 1.1560851 Артикул
Google Scholar Рикман Дж. М. и К. Бармак (2013) «Моделирование электропроводности в тонких поликристаллических металлических пленках: влияние микроструктуры.Журнал прикладной физики 114 (13). DOI: 10,1063 / 1,4823985. Риццоло Майкл (2014) «Влияние примесей и металлических покрывающих слоев на микроструктуру медных межсоединений». Университет Олбани, Государственный университет Нью-Йорка. доступно по адресу http://search.proquest.com/openview/35783cb6674ab29255ebc6a98a43273f/1 Rudd RE, Belak JF (2002) Зарождение пустот и связанная с ними пластичность при динамическом разрушении поликристаллической меди: атомистическое моделирование.Comput Mater Sci 24 (1-2): 148-53. DOI: 10.1016 / S0927-0256 (02) 00181-7 Артикул
Google Scholar Ryu Changsup, ALS Loke, T. Nogami и SS Wong (1997) «Влияние текстуры на электромиграцию CVD-меди». IEEE International Reliability Physics Symposium, 35th Annual Proceedings, 201–5. DOI: 10.1109 / RELPHY.1997.584260. Ryu C, Kee Won K, Loke ALS, Haebum L, Takeshi N, Dubin VM, Kavari RA, Ray GW, Simon Wong S (1999) Микроструктура и надежность медных межсоединений.IEEE Trans Electron Devices 46 (6): 1113–20. DOI: 10.1109 / 16.766872 Артикул
Google Scholar Сухарев В., Зшеч Э. (2004) Модель механизмов деградации, вызванной электромиграцией, в медных межсоединениях с двойной инкрустацией: влияние прочности межфазного соединения. J Appl Phys 96 (11): 6337–43. DOI: 10.1063 / 1.1805188 Артикул
Google Scholar Сухарев В., Ктеян А., Зшеч Э., Никс В.Д. (2009) Влияние микроструктуры на ЭМ-индуцированную деградацию в соединителях с двойной инкрустацией из меди.IEEE Trans Device Mater Reliab 9 (1): 87–97. DOI: 10.1109 / TDMR.2008.2011642 Артикул
Google Scholar Suo Z (2003) Надежность межсоединительных конструкций. Aerosp Eng 8: 265–324 Google Scholar Synopsys (2015) Руководства пользователя и справочные руководства TCAD sentaurus. Synopsys, Mountain View, http://www.synopsys.com/ Thompson CV (2000) Эволюция структуры при обработке поликристаллических пленок.Annu Rev Mater Sci 30 (1): 159–90. DOI: 10.1146 / annurev.matsci.30.1.159 Артикул
Google Scholar Timma A, Caubet P, Chenevier B, Thomas O, Kaouache B, Dumas L, Normandon P, Giraudin JC (2010) Зарождение бугорков Si (C) N в микроэлектронике и рост в линиях меди IC, контролируемых диффузной ползучестью . Microelectron Eng 87 (3): 361–64. DOI: 10.1016 / j.mee.2009.08.003, Elsevier B.V Статья
Google Scholar Винчи Р.П., Зилински Э.М. и Бравман Дж. К. (1994) «Термические напряжения в пассивированных медных межсоединениях, определенные с помощью рентгеновского анализа и моделирования методом конечных элементов.MRS Proceedings 338 (январь). Издательство Кембриджского университета: 289. DOI: 10.1557 / PROC-338-289. Ван Ф., Дж. Чжао, П Хуанг, А. С. Шнайдер, Т. Дж. Лу и К. В. Сюй (2013) «Влияние свободной поверхности и неоднородного остаточного внутреннего напряжения на рост зерна в нанокристаллических металлах». J Nanomaterials 2013. DOI: 10.1155 / 2013/934986. Weide-zaage K (2012) Анализ методом конечных элементов слабых мест в межкомпонентных соединениях и корпусах Книга
Google Scholar Wu Zhen Y, Yin Tang Y, Chang Chun C, Yue Jin L, Jia You W, Bin L, Jing L (2010) Структурно-зависимое поведение вызванного стрессом пустот в медных соединениях.Тонкие твердые пленки 518 (14): 3778–81. DOI: 10.1016 / j.tsf.2009.12.093, Elsevier B.V Статья
Google Scholar Ян C-C, Витт C, Wang P-C, Edelstein D, Rosenberg R (2011) Контроль напряжения во время термического отжига медных межсоединений. Appl Phys Lett 98 (5): 51911. DOI: 10.1063 / 1.3551627 Артикул
Google Scholar Yeap KB, Zschech E, Hangen UD, Wyrobek T, Kong LW, Karmakar A, Xu X, Panchenko I (2011) Упругая анизотропия Cu и ее влияние на управление напряжением для 3D IC: исследование наноиндентирования и моделирования TCAD.J Mater Res 27 (1): 339–48. DOI: 10.1557 / jmr.2011.323 Артикул
Google Scholar Чжан К., Вертман Дж. Р., Истман Дж. А. (2005) Быстрое укрупнение зерна под действием напряжения в нанокристаллической меди при температуре окружающей среды и криогенных температурах. Appl Phys Lett 87 (6): 6–9. DOI: 10.1063 / 1.2008377 Google Scholar Zhang L, Im J, Paul SH (2009) Эффект масштабирования линии на зернистую структуру для межсоединений из меди.AIP Conf Proc 1143 (2009): 151–55. DOI: 10.1063 / 1.3169254 Артикул
Google Scholar Зелински Е.М., Винчи Р.П., Бравман Дж. К. (1995) Влияние энергии деформации на аномальный рост зерен в тонких пленках меди. Appl Phys Lett 67 (июнь 1995 г.): 1078–80, http://scitation.aip.org/content/aip/journal/apl/67/8/10.1063/1.114455 Артикул
Google Scholar Zschech E, Huebner R, Chumakov D, Aubel O, Friedrich D, Guttmann P, Heim S, Schneider G (2009) Явления, вызванные напряжением в наноразмерных медных межсоединительных структурах, изучены с помощью рентгеновской и электронной микроскопии.Журнал прикладной физики 106 (9): 1–6. DOI: 10.1063 / 1.3254166 Артикул
Google Scholar Вопрос 9 Модуль Юнга
сталь вдвое больше меди. Длина 50 см.
медная проволока диаметром 2,0 мм соединяется с отрезком стальной проволоки диаметром 50 см.
1,0 мм, сделав комбинированный провод длиной 1,0 м, как показано. Комбинированная проволока
растягивается грузом, добавленным к его концу. И медная, и стальная проволока
подчиняться закону Гука. Какое соотношение удлинитель стальной проволоки ? удлинение медной проволоки А 4 В 2 С 1 D 0.5 Ссылка: Отчет о прошедшем экзамене — Отчет за март 2016 г. 12 Q19 Решение: Ответ:
Б. Модуль Юнга E = Напряжение /
Штамм E = FL / Ae Длина L как
медная проволока и стальная проволока — по 50 см. Вес прикреплен на
конец комбинированной проволоки. Это вызывает силу F на каждом проводе. Площадь поперечного сечения A = πd 2 /4 Площадь поперечного сечения
пропорциональна квадрату диаметра (d 2 ).С молодых
модуля E = FL / Ae, можно сказать, что модуль Юнга пропорционален 1 / d 2 (так как π / 4 в области — постоянная величина). Модуль Юнга стали
вдвое больше меди. E сталь = 2 × E медь F × 50 / (d сталь 2 × e сталь ) = 2 × F × 50 / (d медь 2 × e медь ) 1 / (d сталь 2 × e сталь )
= 2 / (d медь 2 × e медь ) e сталь / e медь = d медь 2 /2 × d сталь 2 = 2.0 2 / (2 × 1.0 2 ) e сталь / e медь = 4/2 = 2 — оружейного металла составляет около 310 МПа. Предел текучести
— оружейного металла составляет около 150 МПа. Модуль упругости Юнга
— оружейного металла составляет около 103 ГПа. Моделирование микроструктуры меди и упругой анизотропии и изучение ее влияния на надежность в межсоединениях в наноразмерном масштабе | Механика перспективных материалов и современные процессы
Модуль Юнга стали в два раза больше, чем у меди. Медная проволока длиной 50 см и диаметром 2,0 мм соединяется с 50-сантиметровой стальной проволокой диаметром 1,0 мм, образуя комбинированную проволоку длиной 1,0 м, как показано.