Модуль сдвига стали: Величина модуля сдвига зависит от. Определение модуля сдвига стали. Сталь и несколько разных её марок

Величина модуля сдвига зависит от. Определение модуля сдвига стали. Сталь и несколько разных её марок

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Предел прочности при растяжении — это максимальное растягивающее напряжение, достигаемое при растяжении образца. Удлинение: деформация или конечное удлинение — это величина растяжения в момент разрыва. Модуль: также называется ПМод 100, У — это напряжение, необходимое для получения данного удлинения. В случае ПМод 100, У модуль будет напряжением, необходимым для удлинения образца 100%. В эластомерах напряжение не является линейным с деформацией. Поэтому модуль не является ни отношением, ни постоянным наклоном, а скорее обозначает точку на кривой деформации напряжений.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин , которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Испытания на растяжение используются для контроля качества продукции и для определения влияния химического или термического воздействия или эластомера. В последнем случае существенным является сохранение этих физических свойств, а не абсолютных значений растягивающего напряжения, удлинения или модуля.

Эластомеры часто рассматриваются как несжимаемые материалы для аналитической консистенции. Однако во многих случаях сжимающий ответ эластомеров очень важен. Объемный модуль является свойством материала, который определяет его сопротивление изменению объема при сжатии.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали , рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа .

На практике положительная объемная деформация определяется как уменьшение объема. Измерение реакции деформации материала на приложенное давление является простым испытанием на объемный модуль. Объемный модуль можно выразить как производную кривой давления-деформации.

Когда молот маятника воздействует на образец резины с определенного расстояния или угла, степень или расстояние, которое маятник не возвращается, является указанием на потерю энергии во время деформации. Комплект компрессии представляет собой измерение отношения упругих и вязких компонентов реакции эластомера к заданной деформации. Более длинные полимерные цепи, как правило, дают лучшую устойчивость к питсу, поскольку улучшенная способность хранить энергию. Стандарты измерения компрессионного набора требуют сжатия 25% для заданного времени и температуры.

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

Поперечное сечение измеряется после снятия нагрузки. Набор компрессии — это процент исходного сжатия, который не восстанавливается. Этот тест может проводиться на цилиндрических дисках или уплотнительных кольцах. По окончании испытания образцы удаляют и дают возможность остыть при комнатной температуре в течение 30 минут перед измерением. После выгрузки нагрузки из эластомера разница между конечными размерами и исходными размерами считается комплектом сжатия.

Использование измерений компрессионного набора наиболее выгодно для контроля качества продукции, что указывает на степень отверждения. Эластомеры с высокими значениями сжатия могут потребовать особых соображений для дизайна и обработки сальника. Набор компрессии является относительно простым тестом для выполнения и, как таковой, может не дать тип прогнозирующей информации, необходимой для пользовательских приложений уплотнения.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

2 .

И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Когда постоянная нагрузка помещается на эластомер, деформация не является постоянной, а скорее постепенно возрастает со временем. Термины, используемые для описания этого поведения, — это расслабление или ползучесть. Эти свойства, включая компрессионный набор, являются результатом физических и химических изменений эластомера.

Испытательный стенд. Эластомеры являются вязкоупругими по своей природе. При деформировании хранение энергии всегда сопровождается некоторой диссипацией энергии. Заглушки длинных эластомерных цепей действуют как препятствия для перемещения полимерных цепей. Эти препятствия позволяют эластомеру сохранять энергию эластичным свойством. Перегруппировки полимерных цепей зависят от конкретной химической структуры, времени, температуры и скорости деформации. Поскольку эластомеры являются вязкоупругими, накопленная энергия уменьшается с течением времени.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга , так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей , которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Это уменьшение накопленной энергии во времени известно как релаксация напряжений. Другими словами, релаксация напряжений — это изменение напряжения во времени, когда эластомер удерживается под постоянным напряжением.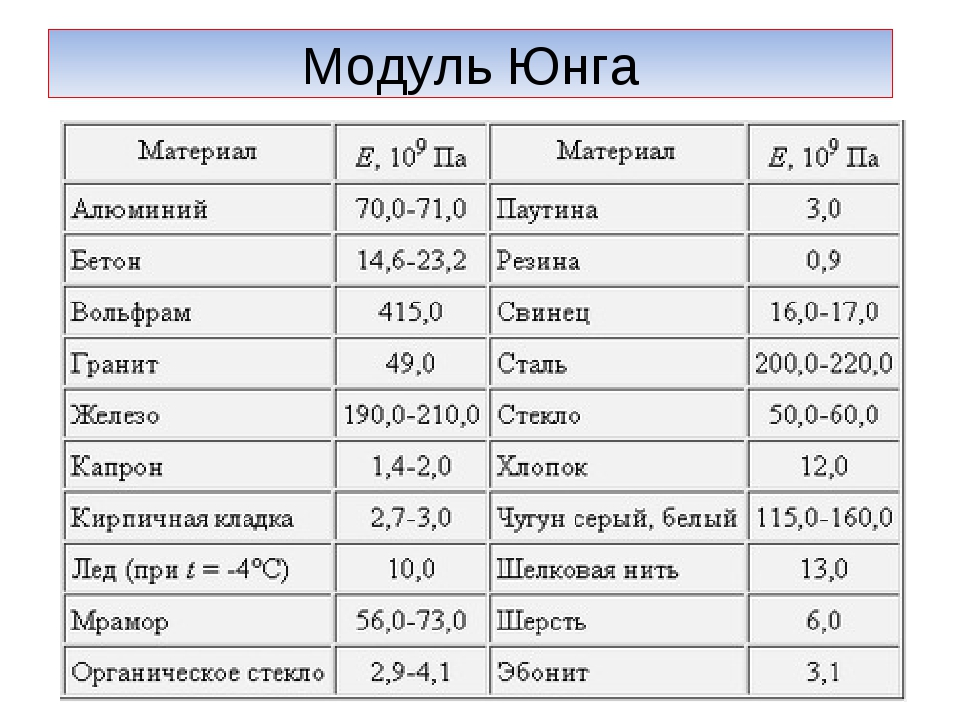 2 .

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Прочность на разрыв: для соображений удаления формованной детали из производственной формы или для определения легкости, с которой может начинаться разрастание и пропагация в применении, прочность на разрыв является важным свойством. Различные методы испытаний используют разные формы и методы применения силы разрыва.

Динамический стресс-деформация: в циклических или динамических применениях вязкоупругие свойства эластомеров очень важны. Потеря энергии в виде тепла возникает из-за молекулярного трения в результате приложенной нагрузки. Процент потери энергии за цикл известен как Писсерез. У Когда цикл погрузки и разгрузки продолжается, меняется форма и положение кривой гистерезиса.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения.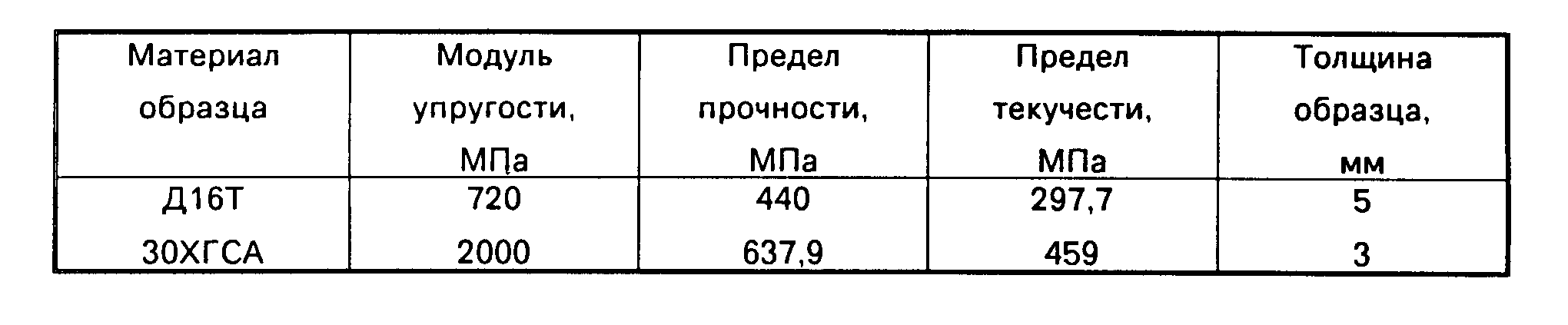

Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Реакция образца на синусоидальную деформацию может наилучшим образом проявлять динамические свойства эластомера. Эластичный компонент эластомера отвечает за синфазное напряжение, в то время как вязкая составляющая отвечает за постфазное напряжение. Чем более вязкий эластомер, тем больше угол фазы или потери.

Тангенсом этого угла Пт п, У в простейших терминах является отношение вязкого модуля к модулю упругости. Динамические свойства для различных уплотнительных эластомеров. Сейсмология — это геофизика, которая занимается распространением и измерением упругих волн в земном теле. Причиной таких упругих волн могут быть землетрясения или крупные взрывы. Волны измеряются с помощью сейсмографов, которые покрывают большую часть всей планеты в узкой сети.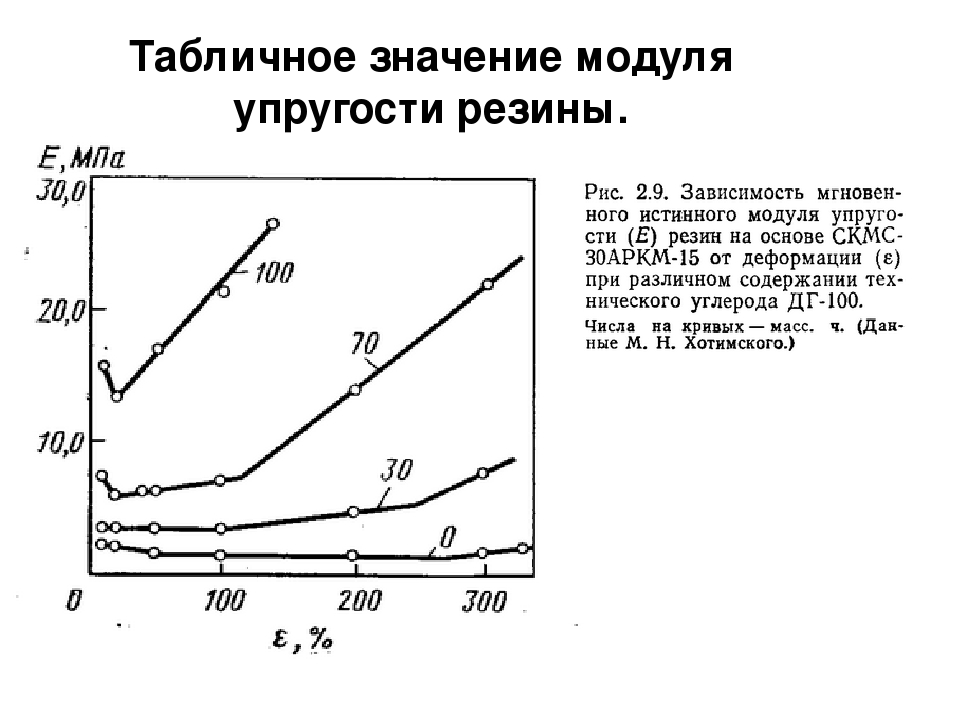

Глава 11

ТАЙНЫ СДВИГА И КРУЧЕНИЯ,
или
«Поларис» и вечерние туалеты

Помнится, одно из книжных обозрений Дороти Паркер начиналось словами: «Эта книга рассказала мне о принципах бухгалтерского учета больше, чем мне хотелось бы знать». Осмелюсь предположить, что поведение материалов и конструкций при сдвиге многие из нас склонны оставить специалистам. Кажется, что с растяжением и сжатием можно еще справиться, но относительно сдвига уверенности такой нет. Вдобавок к этому, если в учебниках по сопротивлению материалов говорится о сдвиге, то непременно в связи с какими-нибудь коленчатыми валами или балками особенно хитрых типов. После этих учебников, несмотря на их несомненную пользу, предмет нередко теряет всякую привлекательность и вдобавок при этом как-то ускользает от внимания тот простой факт, что напряжения сдвига и деформации сдвига возникают не только в балках и коленчатых валах, а практически во всех предметах, с которыми нам приходится иметь дело, и иногда это приводит к неожиданным последствиям. Именно из-за них дают течь суда, шатаются столы, в неожиданных местах вытягивается одежда. Если бы не напряжения сдвига, жить было бы легче и приятней не только инженерам, но и биологам, хирургам, плотникам-любителям и даже тем, кто выпускает болтающиеся чехлы для мебели.

Землетрясения землетрясения происходят там, где большие наземные массы толкнуты друг против друга или друг против друга. Во время спуска одной плиты она трется о вершину. Это создает огромную напряженность, которая сбрасывается в форме землетрясений. Однако землетрясения также возникают, когда пластины стремятся по-разному и, таким образом, часто проскальзывают друг мимо друга.

Однако землетрясения вблизи поверхности гораздо более распространены, чем землетрясения. Вертикальная проекция гипоцентра на земную поверхность называется эпицентром. Энергия, выделяемая во время землетрясения, частично принимает форму упругих волн, движущихся по Земле.

Если растяжение — это когда тянут, сжатие — когда сдавливают, то сдвиг — это когда происходит взаимное проскальзыванне. Другими словами, напряжение сдвига служит мерой тенденции к скольжению одной части твердого тела относительно другой. (Обратите внимание на скольжение карт в брошенной на стол колоде или ковра, когда его выдергивают у вас из-под ног.) Почти всегда сдвиг возникает и при скручивании, например в лодыжке, рулевой колонке или любой другой детали механизма. В условиях сдвига или кручения материалы обычно ведут себя довольно просто. Но прежде чем перейти к обсуждению особенностей этого поведения, нам необходимо договориться о терминологии. Поэтому мы начнем с нескольких определений.

Физическое описание таких волн происходит здесь с помощью волнового уравнения. Волны землетрясения можно разделить на космические волны и поверхностные волны. Оптические волны снова различаются продольными волнами и поперечными волнами. В случае поперечной волны материал осциллирует перпендикулярно направлению распространения. Соответствующие скорости валов теперь могут быть указаны следующим образом. Модуль сжатия определяется формулой.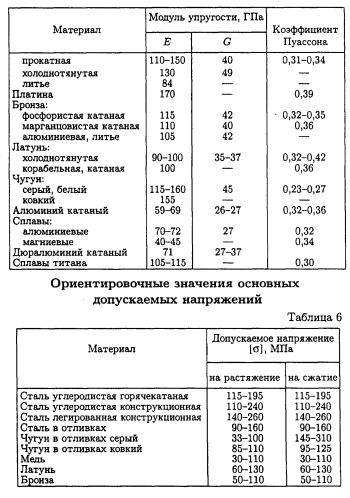 Которая является сжимаемостью. Понятно, что модуль сжатия представляет собой константу пропорциональности, используемую для указания того, какое изменение давления приводит к определенному изменению объема.

Терминология

Упругие свойства вещества при сдвиге очень похожи на его свойства при сжатии и растяжении, а такие понятия, как напряжение сдвига и деформация сдвига, аналогичны и не сложнее соответствующих понятий в случае растяжения.

Напряжение сдвига, или касательное напряжение, — t . Как мы уже говорили, касательное напряжение служит мерой тенденции одной части твердого тела скользить относительно другой его части, как это схематически показано на рис. 118, а . Следовательно, если на поперечное сечение материала, имеющее площадь А , действует сдвигающая сила Р , то напряжение сдвига в некоторой точке материала будет (Это среднее значение касательного напряжения. — Прим. ред. ) :

Скорости волн были указаны выше. Выведем теперь формулу для продольных волн. Начнем с упрощенной модели, в которой поперечное сжатие не учитывается. В этом случае относительное изменение длины как вариации отклонения было упрощено. Теперь разница в напряжении. Разность сил от этой разности потенциалов такова.

Из уравнения движения Ньютона. Теперь можно увидеть волновое уравнение, которое показывает скорость. Найденная скорость может быть использована в качестве приблизительной оценки. Однако поперечное сжатие все еще впадает в вышеупомянутую точную формулу для скорости продольных волн. Чтобы принять это во внимание, число Пуассона определено.

касательное напряжение = (перерезывающая сила / площадь) = Р / А = t .

Касательное напряжение t имеет туже размерность, что и растягивающее напряжение, например МН/м 2 (кгс/мм 2).

Деформация сдвига — g . Все твердые тела при действии напряжения сдвига деформируются аналогично тому, как это происходит и при растяжении. Однако в этом случае деформация представляет собой искажение углов и измеряется поэтому, как все углы, в градусах или радианах, чаще в радианах (рис. 118, б ). Радиан, конечно, не имеет размерности, будучи просто числом или отношением двух длин. Мы будем обозначать деформацию сдвига буквой g : подобно относительной деформации растяжения, обозначаемой е , g — безразмерное число.

Это материально-зависимое число. Два модуля упругости связаны следующим образом. Скорость вала, проходящего через цилиндр с поперечным сжатием, теперь. Эта скорость обычно относится к однородной и изотропной среде. В качестве добавления отметим, что модуль сдвига представляет собой соотношение между растягивающим напряжением, приложенным к блоку, и углом сдвига, вызванным сдвигом.

Для жидкостей модуль тяги — это тот факт, что жидкости не могут быть повреждены, поэтому в жидкостях нет упругих поперечных волн. С помощью этой реализации можно лучше понять историческое открытие строительства земли.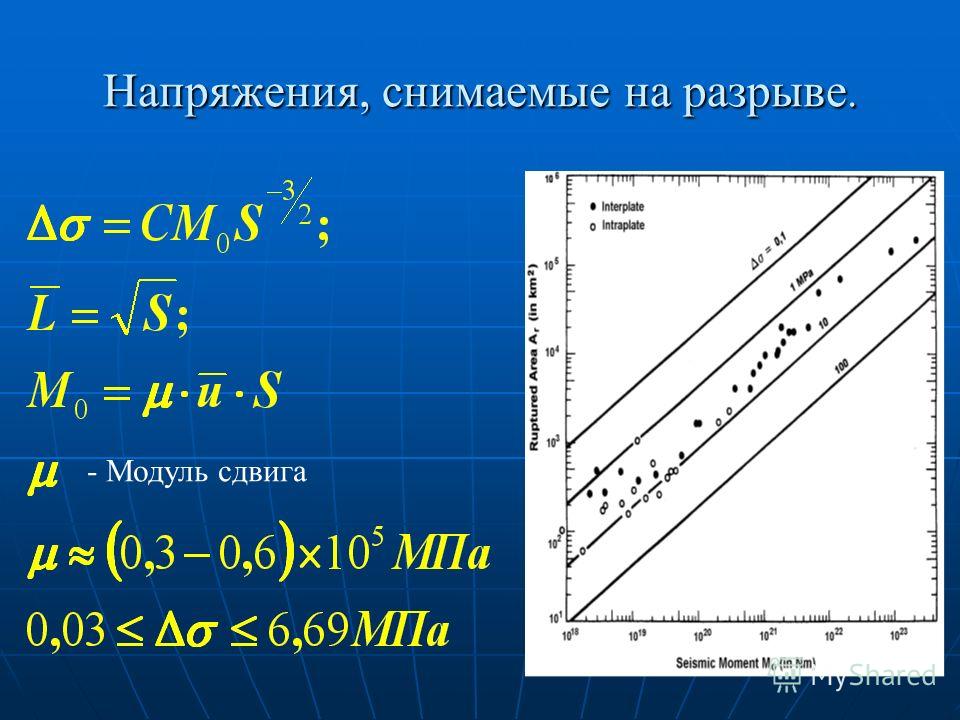 Гутенберг определяет существование основного ядра с использованием сейсмологии. Это можно объяснить только внутренним ядром, которое должно отражать входящие волны. В дополнение к вышеупомянутым космическим волнам также важны поверхностные волны. Плотность энергии космических волн также уменьшается, а плотность энергии поверхностных волн также уменьшается.

Рис. 118. Напряжение сдвига, или касательное напряжение, и деформация сдвига.

а — касательное напряжение = (перерезывающая сила / площадь) = Р / А = t .
б — деформация сдвига — это угол g , на который искажается прямой угол в результате действия касательного напряжения t .

Рис. 119. Кривая деформирования при сдвиге похожа
на соответствующую зависимость при растяжении.
Тангенс угла наклона прямолинейной части равен модулю сдвига: G = t /g .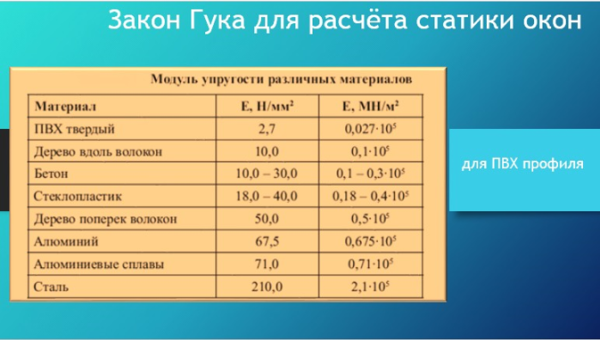

На поверхностные волны в основном влияют волны Любви и волны Рэлея. Волны любви — это более быстрые поверхностные волны, земное движение которых перпендикулярно направлению распространения в земле. Рэлеевские волны колеблются как параллельно, так и перпендикулярно направлению распространения. В дополнение к горизонтальному движению можно наблюдать вертикальные движения. Эти движения вызывают наибольшее разрушение во время землетрясения, поскольку волны Рэлея имеют наибольшие амплитуды. Из-за того, что волны Рэлея являются самыми медленными волнами, время предварительного предупреждения часто возникает после измерения Р-волны.

Для таких твердых тел, как металл, бетон или кость, упругая деформация сдвига обычно меньше 1° (1/57 радиана). При больших деформациях материалы этого типа либо разрушаются, либо испытывают необратимые пластические деформации — текут подобно сливочному маслу.

Однако такие материалы, как резина, текстильные ткани или мягкие биологические ткани, могут испытывать гораздо большие упругие и обратимые деформации сдвига — примерно до 30-40°. Для жидкостей и вязких материалов вроде патоки, крема или пластилина деформации сдвига не ограничены, но они и необратимы.

Мы теперь видели, что космические волны менее разрушительны, чем поверхностные. Но как точно определяется энергия землетрясения? Гутенберг — масштаб великолепия. Он посмотрел на выражения сейсмограмм и использовал логарифмы амплитуд А в зависимости от расстояния до печи, чтобы определить энергию. Кроме того, был введен поправочный коэффициент, который выводит наименьшие возможные землетрясения. Масштаб масштаба для поверхностных волн был закончен.

Для больших величин высвобождаемая энергия очень велика, однако количество землетрясений в год очень мало. Обильные землетрясения с малой величиной происходят чаще. Эмпирически было найдено следующее соотношение между энергией и величиной. Материалов.

Модуль сдвига — G . Как и при растяжении, при малых и умеренных напряжениях большинство твердых тел следуют закону Гука при сдвиге. Так, построив график зависимости напряжения сдвига t от деформации g , мы получим кривую, которая по крайней мере на ее начальном участке близка к прямой линии (рис.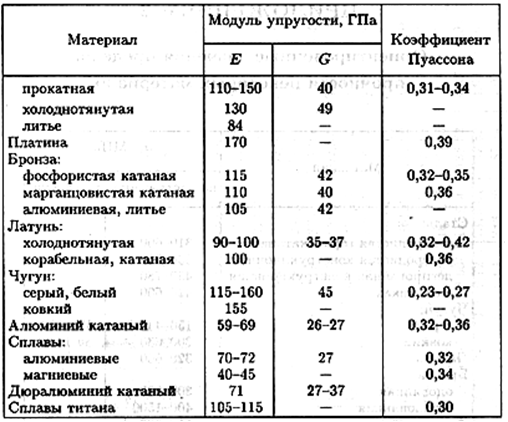 119). Наклон этой прямой характеризует сдвиговую жесткость материала; тангенс угла наклона называется модулем сдвига. Он обозначается G . Таким образом,

модуль сдвига = (касательное напряжение / деформация сдвига) = t /g =G

Модуль сдвига G аналогичен по смыслу модулю Юнга Е и, подобно последнему, имеет размерность единиц напряжения, например МН/м 2 (кгс/мм 2) *.

* Отметим, что между величинами G и Е существует связь. Для изотропных материалов, например для большинства металлов, G = E / 2(1 + n ) , где n — коэффициент Пуассона.

Стенка балки в условиях сдвига — изотропные и анизотропные материалы

Как мы уже видели в предыдущей главе, хотя в верхней и нижней полках балки (или верхних и нижних стержнях фермы) возникают большие растягивающие или сжимающие напряжения (или усилия в стяжках), которые уравновешивают направленную вниз нагрузку и позволяют балке выполнять возложенную на нее миссию, — это напряжения сдвига, возникающие в стенке балки, соединяющей верхнюю и нижнюю ее полки.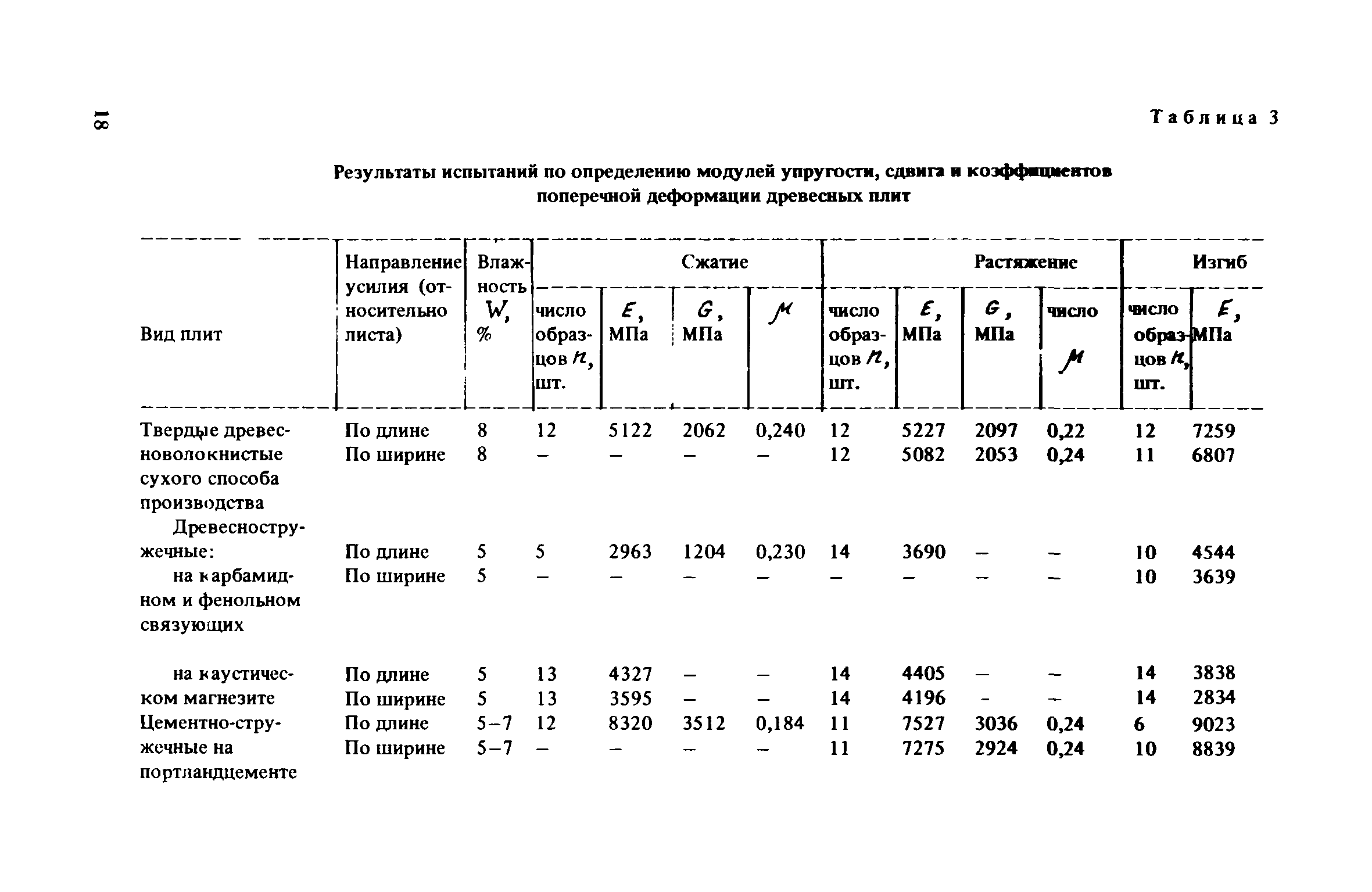 Стенка балки обычно представляет собой сплошную металлическую пластину, в ферме те же самые функции выполняет какая-либо решетчатая структура.

Так как между материалом и конструкцией нельзя провести четкой грани, то и здесь не очень важно, чем воспринимается перерезывающая сила в балке, сплошной ли стенкой или же решеткой, которая может быть из стержней, проволоки, деревянных брусьев или чего-либо другого. Правда, одно важное отличие здесь есть. Если стенка сделана, скажем, из металлической пластины, то не имеет никакого значения, под каким углом она была вырезана из большого листа, так как свойства металла по всем направлениям одинаковы. Такие материалы, а к ним относятся металлы, кирпич, бетон, стекло и большинство видов камня, называются изотропными, что по-гречески означает «одинаковые во всех направлениях», Тот факт, что металл изотропен (или почти изотропен) и имеет одинаковые по всем направлениям свойства, упрощает жизнь инженеров и объясняет их особое пристрастие к металлам.

Рассмотрим теперь стенку в виде решетки. Очевидно, что ее стержни должны располагаться под углом около ±45° к оси балки. В противном случае стенка не будет иметь достаточной сдвиговой жесткости (рис. 120 и 121), под нагрузкой решетка сложится, и ферма скорее всего разрушится. Материалы, поведение которых напоминает поведение нашей решетки, называются анизотропными (или иногда аллотропными), что по-гречески означает «различные в различных направлениях».

Дерево, ткани и почти все биологические материалы анизотропны, причем каждый по-своему; это обстоятельство весьма усложняет жизнь, и не только инженерам. Ткань для одежды является самым распространенным рукотворным материалом, и она в высшей степени анизотропна. Как мы уже не раз говорили, различия между материалом и конструкцией довольно туманны, и ткань, хотя портные и называют ее материалом, на самом деле представляет собой конструкцию, состоящую из отдельных нитей, перекрещивающихся под прямым углом, и ведет себя при действии нагрузкой почти так же, как и решетчатая стенка балки или фермы.

Взяв в руки квадратный кусок обыкновенной ткани — это может быть носовой платок, — вы увидите, что в зависимости от направления приложенной растягивающей силы она деформируется совершенно по-разному. Если вы тянете строго вдоль нитей основы или утка *, ткань почти не растягивается; другими словами, ее жесткость на растяжение в этих направлениях велика. Более того, внимательно присмотревшись, вы заметите, что при этом сужение ткани в поперечном направлении тоже невелико (рис. 122), так что коэффициент Пуассона (о котором мы говорили в гл. 7 в связи с артериями) мал.

* Нити основы идут параллельно длине рулона ткани, а нити утка переплетают их в перпендикулярном направлении.

Рис. 122. При растяжении ткани параллельно нитям основы или утка материал оказывается жестким и его поперечное сокращение незначительно.

Но если вы теперь потянете ткань под углом 45° к направлению нити, то есть по диагонали, или, как говорят портные, «по косой», то она растянется гораздо больше; можно сказать, что в этом случае модуль Юнга весьма невелик. Одновременно произойдет большое поперечное сокращение, так что в этом направлении величина коэффициента Пуассона станет гораздо больше, а он может достигать величин порядка 1 (рис. 123). В целом же, чем более свободно соткана ткань, тем больше будет различие между ее поведением в диагональном и продольно-поперечном направлениях.

Думаю, что немногие слышали слово «анизотропия», но такое поведение тканей на протяжении веков, должно быть, было известно почти каждому. Довольно удивительно, однако, что анизотропные свойства тканей до недавнего времени не только не использовались в технике и обыденной жизни, но даже не были осознаны.

Оставим пока в стороне существо анизотропии и обратимся к ее проявлениям. Первое, что нам совершенно ясно, это то, что мы можем свести к минимуму искажения формы текстильных изделий, если нам удастся направить главные напряжения по возможности вдоль нитей основы и утка. Обычно это приводит к продольно-поперечному раскрою материала. Если обстоятельства таковы, что ткань тянется под углом 45°, по косой, возникают гораздо большие искажения первоначальной формы, но они симметричны. А вот если мы окажемся настолько непредусмотрительными, что рабочие нагрузки будут приложены не в продольном или поперечном и не в диагональном, а в некотором промежуточном направлении, тогда возникнут не только большие, но и совершенно не симметричные искажения. Одежда в этом случае растянется и примет странный и почти наверняка непривлекательный вид *.

* Понимание этого принципа очень важно при изготовлении таких предметов, как воздушные шары и надувные лодки из прорезиненной ткани. При сдвиговых формоизменениях резиновое покрытие деформируется и ткань дает течь.

Изготовление парусов почти во все времена было важной отраслью хозяйства, и тем не менее европейские мастера никогда до конца не понимали сути поведения парусины. Столетиями они делали паруса таким образом, что их материал растягивался в косом по отношению к нитям основы и утка направлении. Такие паруса быстро делались мешковатыми и плохо работали при встречном ветре. Свою лепту внесло здесь европейское пристрастие к льняной парусине, которая особенно легко деформировалась из-за неплотного переплетения нитей.

Изготовление парусов на современном уровне относится к началу XIX в. Приоритет здесь принадлежит американским мастерам, которые использовали туго сотканную парусину из хлопка и так располагали швы, чтобы направление нитей более или менее соответствовало направлению возникающих напряжений. Вследствие этого американские корабли могли плавать быстрее и круче к ветру, чем британские. Потребовалась, однако, основательная встряска, прежде чем все эти простые факты дошли до сознания английских мастеров. Это произошло благодаря шуму вокруг яхты «Америка», которая в 1851 г. пришла из Нью-Йорка в Ковец для участия в гонках с быстроходнейшими английскими яхтами.

Гонки происходили вокруг острова Уайт. В качестве приза победителю предназначался довольно безобразный предмет из серебра, подаренный королевой Викторией. (Эта кувшиноподобная штука впоследствии получила известность как «Кубок Америки».) Когда королеве доложили, что первой пересекла финишную черту «Америка», она спросила:

А второй?

И услышала в ответ:

Второй еще не видно, ваше величество.

После этого английские мастера пересмотрели свою технологию и подтянулись настолько, что через несколько лет американские яхтсмены уже покупали паруса у Ратсея из Ковеца. Урок, преподанный американцами, запомнился надолго, и, хотя современные паруса в большинстве своем делаются из терилена, кроятся они таким образом, чтобы нити утка, насколько это возможно, были параллельны свободным краям паруса, в направлении которых обычно действуют наибольшие напряжения (рис. 124).

Задачи, связанные с приданием ткани желаемой трехмерной формы, не сильно различаются, шьем ли мы паруса или одежду. Однако портные и модельеры оказались здесь более сведущими, чем строители судов. Всегда, когда это было практически возможно, они резали ткань лишь вдоль и поперёк, чтобы наибольшие окружные напряжения действовали в направлении нитей. Если же требовалось, чтобы одежда тесно прилегала к телу, то это достигалось с помощью системы сосредоточенных нагрузок, иными словами, с помощью шнуровки. Молодая леди викторианских времен порой имела не меньшую оснастку, чем парусный корабль. В годы, последовавшие за правлением короля Эдуарда, от системы шнуровок стали отказываться (возможно, в связи с недостатком горничных), так что над женщинами нависла угроза «бесформенности».

Но вот в 1922 г. мадемуазель Вионе, открывшая магазин в Париже, изобрела «диагональный крой». Вряд ли мадемуазель Вионе слышала о своем знаменитом соотечественнике Пуассоне и тем более о коэффициенте его имени, но она интуитивно поняла, что добиться нужного облегания можно не только с помощью шнурков, крючков и кнопок. В материале платья действуют вертикальные растягивающие напряжения, связанные как с весом самой ткани, так и с движениями его владельца. И если ткань расположить так, чтобы ее нити составляли угол 45° с этими вертикальными нагрузками, то можно использовать большое поперечное сокращение и добиться эффектного облегания фигуры. Такого рода наряды были, несомненно, дешевле и удобней, чем решения времен Эдуарда, но тем не менее тоже могли разорить (рис. 125 и 126).

Аналогичные проблемы возникают и при конструировании больших ракет. Существуют ракеты на жидком топливе, например на керосине, для сжигания которого требуется жидкий кислород. Но жидкостные ракетные двигатели имеют сложную систему подачи топлива и окислителя, которая работает не всегда надежно. Поэтому лучше, наверное, использовать двигатели на твердом топливе (на полимерной основе). Оно горит очень хорошо, но относительно медленно, выделяя огромное количество горячих газов, которые со страшным шумом вылетают из сопла двигателя, толкая ракету вперед.

Как топливо, так и производимые им газы находятся в прочном цилиндрическом корпусе или сосуде давления, стенки которого не следует подвергать действию пламени и высоких температур. По этой причине заряду топлива придается форма толстостенной полой трубы, которая плотно прилегает к корпусу ракеты. Когда ракету запускают, горение начинается с внутренней поверхности трубы и распространяется затем в направлении корпуса. В результате благодаря наличию еще не сгоревшего топлива материал корпуса оказывается защищенным от воздействия пламени вплоть до последнего момента.

Твердое топливо на полимерной основе и выглядит, и ведет себя подобно пластилину и, как и пластилин, склонно к растрескиванию, особенно при низких температурах. При запуске ракеты ее корпус, естественно, стремится расшириться вследствие давления газа, так же как расширяются артерии от давления крови; но вместе с корпусом должно расширяться и твердое топливо. Если заряд еще не нагрелся, в нем могут возникнуть трещины, когда окружная деформация корпуса достигнет примерно 1%, после чего пламя проникнет через трещины и разрушит корпус. Это приводит иногда к сенсационным взрывам, подобным тому, когда развалилась одна из ракет Поларис.

Примерно около 1950 г. кому-то пришло в голову, что корпус ракеты лучше делать не из металла, а в виде цилиндрической трубы, полученной геликоидной намоткой двух семейств прочных стекловолокон, связанных между собой смолой. Если правильно рассчитать углы намотки, то можно добиться того, чтобы изменение диаметра трубы под давлением было мало. Правда, при этом осевая деформация такого корпуса будет больше, чем металлического (как и талин в платьях мадемуазель Вионе). Однако по ряду причин продольное удлинение менее опасно для топлива. Если не ошибаюсь, эта идея берет свое начало от диагонального кроя вечерних туалетов, популярных в то время.

Допустимые деформации корпуса ракеты отнюдь не допустимы для кровеносных сосудов. Как мы видели в гл. 7, при колебаниях давления крови артерия должна при значительных изменениях ее диаметра сохранять более или менее постоянную длину. Оба эти требования может удовлетворить конструкция трубы с соответствующей геликоидной намоткой волокон, С такого рода проблемами, как ни странно, постоянно сталкиваются биологи. Примечательно, что Стив Вейнрайт, профессор университета Дюка, изучающий червей, совершенно независимо провел те же самые расчеты, которыми мы занимались лет 20 назад в области ракетной техники *. Заинтересовавшись этим обстоятельством, я выяснил через профессора Биггса, что и в этом случае толчком послужил крой по косой.

* Кожица многих червей и других мягкотелых армирована системой геликоидно расположенных коллагеновых волокон (см. гл. 7.), При «создании» червя возникали те же проблемы, что и при создании туалета, но для червя они решились успешнее: «одежда» на нем не мнется.

Изобретение косого кроя принесло мадемуазель Вионе. славу в мире модельеров. Она дожила до глубокой старости и умерла недавно в возрасте 98 лет, так, по-видимому, и не узнав о своем весьма значительном вкладе в космическую и военную технику и биомеханику червей.

Касательное напряжение — это растяжение и сжатие,
действующие под углом ±45°, и наоборот

Если еще немного подумать о стенках балок, решетчатых стенках ферм и о вечерних туалетах косого кроя, то становится очевидным, что касательное напряжение представляет собой просто комбинацию напряжений растяжения и сжатия, действующих под углом ±45° (рис. 120). Более того, любое напряжение сжатия и растяжения * приводит к появлению под углом 45° касательного напряжения.

* В отличие от касательного напряжения растягивающее и сжимающее напряжения называют нормальными, поскольку они действуют по нормали к некоторой площадке. — Прим. ред.

Действительно, твердые тела, особенно металлы, очень часто при растяжении разрушаются вследствие касательных напряжении под углом 45° к направлению растяжения. Именно эти напряжения приводят к появлению «шеек» в металлических стержнях и пластинах при растяжении и к пластичности металлов (рис. 127 и гл. 4). Как мы увидим в следующей главе, почти то же самое может происходить и при сжатии. Многие твердые вещества при сжатии разрушаются путем скольжения, вызванного касательными напряжениями.

Рис. 127. В пластичных металлах наблюдается тенденция к разрушению путем сдвига.

Складкообразование

Толстая пластина или просто кусок металла способны хорошо сопротивляться сжатию, так что если их нагрузить сдвигом, то возникающие под углом ±45° напряжения сжатия и растяжения будут для них неопасны. Тонкие панели, мембраны, пленки и ткани плохо сопротивляются сжатию в их плоскости, поэтому при сдвиге на этих элементах образуются складки. Это весьма обычно для тонких металлических панелей, широко используемых в конструкциях самолетов, образование таких складок часто можно наблюдать на поверхности их крыла и фюзеляжа (рис. 128). Инженеры называют это «вагнеровским полем».

Еще чаще такие складки можно видеть на одежде, просторных чехлах, скатертях и плохо скроенных парусах. Вряд ли портные так уж часто говорят о вагнеровском поле, но иногда они упоминают о некоем довольно таинственном качестве, известном в текстильном товароведении как сминаемость. Сминаемость ткани зависит главным образом от ее модуля сдвига, и хотя немногие из модельеров могут указать с системе СИ или других единицах величину модуля сдвига G для используемых ими шелковых или хлопчатобумажных тканей, но, чем меньше модуль сдвига материала, тем меньше у него тенденция к образованию нежелательных складок, или сминаемость.

Причина того, что мы не можем использовать для одежды бумагу или целлофан, не показавшись при этом смешными, заключается главным образом в слишком большой жесткости на сдвиг, которой обладают эти материалы, именно поэтому они не могут принимать нужные формы. А вот трикотажные ткани, наоборот, имеют как малый модуль Юнга, так и малый модуль сдвига, поэтому при их использовании легко добиться плотного облегания фигуры. Девушки быстро открыли это качество в вязаных свитерах. Точно так же у молодых людей кожа имеет малый модуль Юнга и модуль сдвига и поэтому легко «подстраивается» под форму тела *. В старости кожа становится более жесткой на сдвиг, печальные результаты чего бывают, к сожалению, слишком очевидными. Недавно профессор М. Кенеди из Стрэтклайдского университета провел широкие исследования упругих свойств кожи человека. В результате старческие морщины, кажется, впервые получили количественное описание.

* Отметим, что для того, чтобы пленка, плоская в исходном состоянии, легко облегала поверхность двойной кривизны, необходимо, чтобы у пленки были малы как модуль Юнга, так и модуль сдвига, — обстоятельство, существенное при картографировании (с ним столкнулся Меркатор в середине XVI в.).

Кручение

Самолет превратился из чего-то, чего «вообще не может быть», в грозное военное оружие за каких-нибудь 10 лет. Это случилось почти без помощи науки. Пионеры авиации зачастую были талантливыми любителями и заядлыми спортсменами, но лишь немногие из них имели какую-то теоретическую подготовку. Как и современных автомобилистов, их скорее интересовали шумные и ненадежные двигатели, чем несущая конструкция, о которой они мало что знали и еще меньше заботились. Естественно, выжав из двигателя достаточную мощность, вы можете поднять в воздух почти любой самолет. А вот что с ним будет дальше, зависит от управления, устойчивости в полете и прочности конструкции, существо которых весьма сложно.

На заре авиации слишком многие храбрецы, такие, как К. С. Ролле и С. Ф. Коди, поплатились жизнью за столь легкомысленный подход. Теоретические основы аэродинамики были разработаны Ф. В. Ланчестером еще в 90-х годах прошлого столетия, но очень немногие из инженеров-практиков представляли себе, о чем там вообще идет речь *. Катастрофы того времени часто происходили из-за срыва потока и штопора, но почти столь же часто виной тому было разрушение конструкций, а так как первые пилоты редко использовали парашюты, катастрофы эти почти всегда заканчивались трагически.

* То же касается большинства профессиональных инженеров. Даже в 1936 г. фундаментальная теория Ланчестера — Прандтля (теория вихрей) в курс гидродинамики не включалась даже на судостроительном факультете университета в Глазго; больше того, ею даже не разрешалось пользоваться. Тем, кто может не поверить этому, добавлю, что я сам был студентом этого факультета в то время, а сейчас такое же отношение наблюдается на инженерных факультетах к теории механики разрушения (см. гл. 4).

Требование к инженерной конструкции быть одновременно и надежной, и.легкой было тогда внове. На крыло самолета действуют изгибающие нагрузки, весьма напоминающие нагрузки на мост. Предшествующий опыт позволял с этими нагрузками управиться без особых опасений за надежность. Но что было совершенно новым, так это действующие на крыло самолета крутящие моменты. Если не принять должных конструктивных мер, крыло самолета будет скручено.

Применение самолетов с началом первой мировой войны возросло — резко увеличилось и число аварий. К счастью, в Англии в Фарнборо этими вопросами занималась небольшая группа блестящих молодых инженеров, чьи имена впоследствии стали широко известны, — это лорд Черуелл, Джеффри Тейлор, Генри Тизард и «Иегова» Грин. Благодаря их усилиям к 1918 г. традиционный биплан сделался самой надежной из всех конструкций, так что его считали почти неразрушающимся. Немцам в этом отношении повезло меньше. Их технические авиационные эксперты не могли похвастать репутацией людей с широким кругозором. Во всяком случае, у них долгое время одна за другой следовали катастрофы, причина которых крылась главным образом в непонимании действия на крыло самолета крутящего момента.

К началу 1917 г. благодаря высоким техническим данным своих истребителей страны Антанты достигли на западном фронте явного превосходства в воздухе.

Однако тем временем немецкий конструктор Антони Фоккер работал над созданием нового истребителя — моноплана «Фоккер Д-8», который по своим качествам превосходил не только то, что было у союзников, но и то, чего они ждали в перспективе. Из-за критической ситуации на фронтах производство Д-8 было ускорено. Они поступили на вооружение нескольких немецких эскадрилий без проведения достаточной программы летных испытаний. И вскоре после того, как эти самолеты начали полеты в боевых условиях, обнаружилось, что в воздушных боях при выводе машины из пике у него ломалось крыло. Было много жертв, в том числе среди опытнейших летчиков-истребителей. Все это заставило проанализировать причины неудач.

В те дни большинство самолетов были бипланами, ибо конструкция этого типа считалась самой легкой и надежной. Однако при двигателе той же мощности моноплан развивает большую скорость, так как не испытывает дополнительного сопротивления воздуха из-за аэродинамического взаимодействия двух близко расположенных крыльев. Это настойчиво побуждало к разработке истребителей-монопланов. Но, хотя и без понимания действительных причин, монопланы считались конструктивно ненадежными уже с 1903 г., когда в США над Потомаком отвалилось крыло знаменитого самолета Сэмюеля Ленгли.

Крыло Д-8, как и большинства монопланов того времени, было обшито тканью с целью придания ему желаемой аэродинамической формы. Ткань была просто натянута на силовой каркас и сама не должна была нести основных изгибающих нагрузок. Эти нагрузки воспринимались двумя параллельными деревянными лонжеронами — консольными балками, идущими в сторону от фюзеляжа. Они были соединены через каждые несколько дюймов рядом легких деревянных нервюр определенной формы, на которые и натягивалась проклеенная ткань (рис. 129).

Когда стало известно о катастрофах с Д-8, командование немецких военно-воздушных сил отдало приказ провести испытания конструкции. Как это обычно делалось в те времена, готовый самолет перевернули вверх ногами и установили на испытательный стенд, нагружая мешками с дробью, расположенными так, чтобы имитировать возникающие в полете аэродинамические нагрузки. Испытанное таким образом крыло не обнаружило признаков слабости, оно разрушалось лишь при нагрузке, эквивалентной шестикратному весу самолета. Правда, в настоящее время требуется, чтобы истребители выдерживали двенадцатикратные перегрузки, но в 1917 г. шестикратной перегрузки считалось вполне достаточно, и она определенно превышала те перегрузки, которые могли возникнуть в тогдашних боевых условиях. Другими словами, самолет, казалось бы, был вполне надежен.

Однако при стендовых испытаниях Д-8 обратили внимание на то, что разрушение самолета начиналось в зад» нем лонжероне. Решили перестраховаться, и задние лонжероны на всех самолетах Д-8 заменили более толстыми и прочными. Но и после замены число аварий не сократилось, а, напротив, увеличилось. Командование немецких военно-воздушных сил оказалось перед фактом, что «усиление» крыла путем добавления конструкционного материала на самом деле приводит к его ослаблению.

К тому времени Фоккеру стало ясно, что на помощь от официальных умов рассчитывать не приходится, и он сам подверг Д-8 испытаниям на своем заводе. На этот раз догадались измерить перемещения крыла под нагрузкой. Оказалось, что приложенная нагрузка не только изгибает (при выводе самолета из пике концы крыла поднимаются относительно фюзеляжа), но и скручивает крылья, хотя к ним явным образом не приложено никаких крутящих нагрузок. И, что особенно важно, направление скручивания было таким, что значительно увеличивался угол атаки крыла, то есть его подъемная сила.

Обдумав эти результаты, Фоккер внезапно понял, что именно здесь лежит причина не только загадочных аварий с Д-8, но и большинства неприятностей со многими другими монопланами. Когда пилот берет ручку на себя, нос самолета поднимается и нагрузка на крыло растет. Но одновременно крыло закручивается, и это приводит к дальнейшему увеличению подъемной силы крыла, то есть нагрузки на крыло; оно закручивается еще больше, еще больше растет нагрузка и так до тех пор, пока пилот полностью не теряет контроль над ситуацией и крыло не отваливается. Фоккер обнаружил здесь ту форму неустойчивости, которая часто приводит к «летальному» исходу.

Что же в действительности происходит с крылом с точки зрения теории упругости?

Центр изгиба и центр давления

Рассмотрим пару одинаковых параллельных консольных балок, или лонжеронов, соединенных через определенные интервалы горизонтальными нервюрами (рис. 129). Пусть к одной из этих нервюр у кончика крыла приложена сосредоточенная сила, направленная вверх. Если эта сила не приложена точно посередине между лонжеронами (рис. 130), нагрузка не распределится поровну между ними и сила, действующая на один из лонжеронов, будет больше.силы, действующей на другой. Если это произойдет, то один из двух лонжеронов (тот, который более нагружен) отклонится вверх больше другого (рис. 131). В таком случае нервюры, соединяющие лонжероны, отклонятся от горизонтального положения, а все крыло окажется закрученным. В любом сечении балки можно указать точку, называемую центром изгиба. Если линия действия силы проходит через эту точку, то сила не вызывает кручения балки.

Рис. 130. Взаимосвязанные изгиб и кручение возникают в случае, если равнодействующая подъемных сил в каждом поперечном сечении крыла проходит через точку, называемую центром изгиба (в данном случае посередине между двумя лонжеронами), тогда крыло будет изгибаться без кручения.	Рис. 131. Если равнодействующие подъемных сил не проходят через центр изгиба, а смещены, например, в направлении передней кромки крыла, то крыло (или любая другая балка) будет скручиваться при изгибе.

Естественно, когда в сечении крыла больше двух лонжеронов или если пара лонжеронов имеет разную жесткость, то центр изгиба будет находиться не посередине, а где-то между передней и задней кромкой крыла. Однако в каждой балке любого типа центр изгиба всегда существует. Сила, линия действия которой проходит через эту точку, не вызывает закручивания балки или крыла, тогда как любая иная нагрузка обязательно приводит не только к перемещениям крыла вследствие изгиба, но и к закручиванию крыла на некоторый угол.

До сих пор мы рассматривали случай сосредоточенной силы, приложенной к балке или крылу. Естественно, что аэродинамическая подъемная сила, которая в полете направлена вверх и удерживает машину в воздухе, представляет собой нагрузку, распределенную по всей поверхности крыла. Однако, чтобы упростить расчеты, всю эту нагрузку можно заменить одной равнодействующей, приложенной в точке, которую называют центром давления (ЦД) крыла.

Несведущему человеку может показаться, что ЦД подъемной силы, действующей на крыло в полете, лежит где-то посередине между передней и задней кромкой крыла, скажем, возле середины хорды крыла. На самом же деле, как хорошо известно из аэродинамической практики, это совсем не так. Как правило, центр давлений подъемной силы расположен недалеко от передней кромки крыла — обычно на расстоянии примерно в четверть длины хорды *.

* По этой причине опавший лист или лист копирки падает именно так, как мы это привыкли видеть.

Следовательно, пока крыло не спроектировано таким образом, чтобы центр изгиба был расположен примерно на расстоянии одной четвертой длины хорды от передней кромки, оно обязательно будет закручиваться. Угол поворота крыла при этом будет, конечно, зависеть от крутильной жесткости крыла (жесткости на кручение). Но, вообще говоря, всякое закручивание крыла — вещь вредная и опасная, так что конструкторы стремятся свести его к минимуму. Именно поэтому и стержень пера в крыле птицы расположен обычно на расстоянии в четверть хорды от его передней кромки (рис. 132).

В простом крыле моноплана с тканевой обшивкой как положение центра изгиба, так и его крутильная жесткость почти целиком зависят от относительной жесткости лонжеронов на изгиб. В самолете Д-8 центр изгиба находился значительно дальше центра давлений, где-то около середины хорды. Крыло не имело достаточной жесткости, чтобы сопротивляться закручиванию, в результате чего оно разрушалось. После модификации крыла, когда задний лонжерон был сделан более жестким и прочным, центр изгиба передвинулся еще дальше назад, что еще больше ухудшило ситуацию.

Осмыслив все это, Фоккер предпринял теперь уже очевидный шаг: уменьшил толщину и жесткость заднего лонжерона и передвинул тем самым центр изгиба вперед, ближе к центру давления. После этого Д-8 превратился в сравнительно надежную машину, опасную для британских и французских военно-воздушных сил.

По законам аэродинамики центр давления подъемной силы, действующей на крыло самолета, должен всегда находиться примерно на расстоянии четверти хорды от передней кромки крыла. Для уменьшения крутящего момента, действующего на крыло, его необходимо сконструировать таким образом, чтобы передвинуть центр изгиба вперед, как можно ближе к центру давления. Однако элероны, с помощью которых самолет получает крен и выполняет виражи, действуют на конец крыла большими вертикальными силами, приложенными вверх или вниз вблизи задней кромки, то есть далеко сзади от центра изгиба. Тем самым элероны неизбежно вызывают большие крутящие нагрузки на крыло всякий раз, когда летчик закладывает вираж.

Рис. 133. Элерон действует с большой направленной вниз силой на заднюю кромку крыла. Эта сила приложена довольно далеко от центра изгиба, она стремится закрутить крыло таким образом, что возникающие аэродинамические силы будут противоположны тем, к которым стремился летчик, отклоняя элерон.

Из рис. 133 видно, что направление закрутки изменяет величину подъемной силы в направлении, противоположном действию элеронов, уменьшая производимый ими эффект. Если крыло имеет недостаточную крутильную жесткость, его элероны могут оказать на самолет обратное действие: выполнив операции, необходимые для крена вправо, летчик может вдруг обнаружить, что самолет делает крен влево. Этот не только неожиданный, но и весьма опасный эффект носит название «обратные элероны». С ним связаны серьезные трудности при проектировании современных скоростных самолетов. Профилактической мерой здесь является достаточная крутильная жесткость конструкции крыла.

В ранних обшитых тканью монопланах, таких, как Д-8, крутильная жесткость крыла почти целиком определялась относительной жесткостью на изгиб двух главных лонжеронов и их расположением. Однако это не очень эффективное средство, и величина крутильной жесткости, достигаемая в таких конструкциях даже с помощью системы проволочных растяжек, довольно ограничена. По этой причине такие самолеты были довольно опасны, и правительственные органы почти каждой страны были настроены против монопланов, а кое-где они даже были запрещены.

Предпочтение, отдаваемое бипланам, не было следствием консерватизма некоторой части чиновников соответствующих ведомств; скорее оно явилось следствием характерных для биплана больших прочности и жесткости, особенно на кручение. На практике бипланы были и легче, и безопасней монопланов в течение многих лет, а разница в скоростях поначалу у них была не так уж велика. Конструкция крыла биплана с растяжками и распорками представляет собой, по существу, некоторую коробчатую, или кессонную, балку, которая обеспечивает большую прочность и жесткость не только на изгиб, но и на кручение. Из рис. 134 видно, что четыре главных лонжерона (по два в каждом крыле) идут вдоль ребер короба, а расположенные между ними элементы образуют решетчатую ферму. На самолете диагональные распорки на верхнем и нижнем крыле, конечно, не видны, так как скрыты обшивкой. Однако на самом деле эти горизонтально расположенные элементы имеются, и их назначение состоит в том, чтобы воспринимать сдвиг, возникающий при кручении крыла.

Рис. 134. Схематическая конструкция пары крыльев биплана с проволочными растяжками, на которую действуют крутящие моменты, возникающие, например, от элеронов.

На рис. 134 схематически показано, как такая конструкция работает на кручение. Видно, что каждая сторона короба нагружена сдвигом подобно решетчатой стенке при изгибе фермы. Заметим, что сдвиг всех четырех сторон короба происходит совместно и взаимозависимо. Если разрезать или убрать одну из четырех сторон, конструкция вовсе не сможет сопротивляться кручению. В биплане эти работающие на сдвиг панели по необходимости делаются из стержней и тросов. Но если конструкция призвана не летать, а работать на земле, то решетка из стержней и тросов может быть заменена сплошными металлическими панелями или листами фанеры. С чисто конструктивной точки зрения работать она будет точно так же, как и рассмотренные нами выше фермы.

Кручению может противостоять короб или трубы любого типа как со сплошными стенками, так и со стенками решетчатой конструкции. И в том и в другом случае в стенках действуют касательные напряжения. Если же сравнивать прочность и жесткость с весом, то крыло биплана с точки зрения крутильных характеристик гораздо более эффективно, чем конструкция, в которой все зависит от пары соединенных между собой балок.

Формулы для прочности и жесткости на кручение стержней и труб различных типов приведены в приложении 3. Следует отметить, что жесткость на кручение трубы или короба определяется квадратом площади поперечного сечения. Поэтому короб большого поперечного сечения (такой, как в старомодных бипланах) требует мало материала и имеет очень небольшой вес. Когда мы строим современный моноплан, то, по существу, заставляем работать всю конструкцию крыла вместе с ее обшивкой, будь она металлической или фанерной. Хотя мы вынуждены делать крыло гораздо толще, чем крылья бипланов, все же площадь его поперечного сечения гораздо меньше, чем у крыла биплана. Поэтому, чтобы добиться необходимой жесткости и прочности, мы вынуждены применять относительно толстую и тяжелую обшивку. Таким образом, довольно большая доля веса всей конструкции современного самолета предназначена для того, чтобы сопротивляться кручению.

Недостаток крутильной жесткости для автомобиля не так опасен, как для самолета, хотя качество подвески автомобиля и его способность «держать дорогу» также определяются жесткостью корпуса. Автомобили довоенного времени были порой великолепны, но, как и самолеты прошлого, страдали от того, что их создатели гораздо больше внимания уделяли двигателю и трансмиссии, чем кузову или шасси. Действительно, крутильная жесткость их кузова целиком зависела от разницы изгибов двух длинных довольно гибких балок, как и в старом Д-8. Именно малая крутильная жесткость кузова приводила к тому, что автомобиль так плохо «держал дорогу», и управление им было трудным и утомительным делом.

Чтобы удержать колеса от потери контакта с дорогой, рессоры и амортизаторы спортивных автомобилей тех времен делались все более жесткими, пока не превратились в практически недеформируемые элементы. В результате, конечно, езда сделалась почти невыносимой из-за резких толчков и подпрыгиваний. Как и громкий выхлоп, все это, без сомнения, производило впечатление на тогдашних пассажирок, но в действительности не очень-то помогало удерживать автомобиль на дороге. Решение, принятое большинством конструкторов современных автомобилей, состоит в том, что они выбросили не выдерживавшее кручения шасси, а изгибающие и крутящие нагрузки переложили на стальной штампованный кузов. Вместе с крышей он образует коробку, которая в принципе не очень сильно отличается от крыльев старых бипланов. Имея в своем распоряжении такую жесткую конструкцию, инженер может сосредоточить свои усилия на разработке научно обоснованной системы подвески, которая одновременно была бы и безопасной, и комфортабельной.

Как мы уже говорили, крутильная жесткость конструкции пропорциональна квадрату ее поперечного сечения. В этом отношении с такими крупными предметами, как крыло самолета, корпус корабля или кузов автомобиля, все обстоит более или менее неплохо. А вот вращающиеся валы двигателей или других механизмов часто имеют совершенно недостаточную прочность, хотя и делаются обычно из сплошной стали, так как площадь поперечного сечения у них обычно жестко ограничена. В этом одна из причин огромного веса таких машин. Как скажет вам всякий опытный конструктор, именно требования к жесткости и прочности на кручение, когда они становятся определяющими, являются бичом их создателей. Сразу возрастают вес и стоимость, и все это вместе приводит к непропорциональному росту трудностей и забот инженера.

Природа, кажется, не заботится об экономии времени и своих усилий, а тем более о деньгах, но она очень чувствительна к «метаболической стоимости», то есть стоимости конструкции в терминах пищи и энергии, кроме того, она вообще довольно тонко «чувствует» вес конструкции. Не удивительно поэтому, что она избегает кручения как яда. Действительно, ей почти всегда удается увернуться от любой серьезной необходимости обеспечить большую жесткость и прочность на кручение. Животные, как правило, пока на них не действуют «нерасчетные» нагрузки, могут позволить себе быть «слабыми» на кручение. Никто из нас не любит, когда ему выкручивают руки, а крутящие нагрузки на ноги обычно достаточно малы. Однако, когда мы крепим к своим ногам длинные рычаги, называемые лыжами, то при неважной езде легко возникают действующие на ноги большие крутящие моменты. Поскольку в этом причина большинства переломов ног, для горнолыжников были разработаны современные безопасные крепления, автоматически освобождающие ногу при кручении.

Не только ноги, но и практически все кости удивительно слабы на кручение. При надобности убить курицу или другую домашнюю птицу проще всего, как хорошо известно, свернуть ей шею. Но не все знают, как слаб на кручение позвоночник, а сей малоприятный прием очень наглядно демонстрирует это. Но сворачивание голов, как и катание на лыжах, — это опасности, совершенно не предусмотренные природой. В отличие от инженеров она никогда не проявляла интереса к вращательному движению и (подобно африканцам) даже не позаботилась об изобретении колеса.

Сталь Модуль сдвига — Энциклопедия по машиностроению XXL

Сталь Модуль сдвига в кг/мм Рекомендуемая для расчёта величина модуля сдвига в кг мм  [c.201]

Для стали модуль сдвига равен  [c.75]

Структуру и свойства металлических сплавов, как уже известно, можно изменять в широких пределах с помощью термической обработки особенно эффективна термическая обработка для стали. Однако не все свойства изменяются при такой обработке. Одни (структурно чувствительные свойства) зависят от структуры металла (это большинство свойств), и, следовательно, изменяются при термической обработке, другие (структурно нечувствительные свойства) практически не зависят от структуры. К последним относятся характеристики жесткости (модуль нормальной упругости Е, модуль сдвига С).  [c.180]

Модуль сдвига G, Н/мм Для пружинной стали G = 8-10  [c.103]

Модуль упругости стали при сдвиге. … Температурный коэффициент линейного расширения стали Температурный коэффициент линейного расширения меди Коэффициент поперечной деформации стали……  [c.8]

В табл. 2 приведены основные материалы, применяемые дая изготовления пружин, и их механические свойства после термообработки. Модуль упругости пружинных сталей Е = (2,1 — 2,2) 10 кгс/мм модуль сдвига G = (7,6 8,2) 10 кгс/мм .  [c.156]

Модуль сдвига пружинной стали зависит от её химического состава и термообработки. С повышением в стали содержания углерода и кремния модуль сдвига понижается, а с увеличением содержания хрома и марганца он возрастает (в среднем величина модуля сдвига примерно равна 8000 кг мм ). С повышением  [c.651]

В табл. 41 и 42 приведены величины модуля сдвига для горячекатанной стали и проволоки, применяемых при изготовлении пружин [7].  [c.201]

Модуль сдвига горячекатанной стали  [c.201]

Сравнительные данные изменений модуля упругости и модуля сдвига при различных температурах для ковкого, серого высокопрочного чугуна, стали и армко-железа приведены в табл. 18, из которой видно, что  [c.124]

Модуль сдвига, кгс/мм G Для пружинной стали 0=8-10  [c.561]

Найти модуль продольной упругости Е для стали, модуль сдвига которой равен 6=75-10 пПсм и коэффициент Пуассона (i =0,3.  [c.95]

Принимая для стали модуль сдвига С = 8-10° кг см и плотность р = == 8-10 кгсек — см , получим при круглом сечении витка то = 356уо и при квадратном сечении то = 455 0, где то выражено в кг см , а а, — в м1сск.  [c.514]

Задача 3.2.15. Для вала, показанного на рис.32.3, сплошного 1фуглого поперечного сеченИя найти необходимые диаметры по участкам. Материал вала — сталь, модуль сдвига С = 8-10 МПа, расчетное сопротивление на  [c.89]

Здесь (3 — модуль сдвига, упругая постоянная материала, характеризующая его жесткость при деформации сдвига. Для стали 8,0-10 кПсм . Произведение называют жесткостью  [c.59]

Следует иметь в виду, что примеси в малых количествах, например примеси углерода в сталях, легирующие добавки в сплавах, пластическая и термическая обработка мало влияют на упругие и термодинамические свойства металлов и сплавов, характеризуемые зависимостями для давления />(р°, Т), впут-ренпей энергии и = и(р°, Т) и модулем сдвига G, но в это же время могут существенно изменить предел текучести т .  [c.148]

При испытании паровой машины вал диаметром d=l50 мм при л=60 об1мин закручивается на ЗГ на длине 1=3 м. Определить мощность испытываемой машины, если модуль сдвига G стали, из которой сделан вал, равен 0,8-10 кГ/см .  [c.59]

Коэффициент Пуассона ц для различных мaтep a-лов имеет значение от нуля до 0,5 и, следователью, на основании формулы (4.7) модуль сдвига С составляет от 0,33 до 0,5 модуля упругости Е. Дня больншнства материалов можно приближенно при и-мать С = 0,4Е, т. е. для стали, для которой = = 2-10 МПа, можно принимать С = 0,8-10 МПа.  [c.128]

Располагая данными о функциях напряжений и температуры, а также зависимостью модуля сдвига от температуры, можно рассчитать различные процессы неизотермического нагружения. Расчет проводился применительно к аустенитной нержавеющей стали Х18Н10Т для уже использованных в предшествующем разделе двух режимов пропорционального изменения нагрузок и температур, а также других контрастных режимов. Одновременно велось сопоставление результатов расчета путей неизотермического нагружения с использованием теории пластического течения и деформационной теории.  [c.123]

Обобщим эти закономерности для случая контакта поверхностей в условиях ИП. В случае контакта пары сталь — бронза дислокации, появившиеся в стали даже в период приработки, всегда будут притягиваться к поверхности раздела фаз, ввиду того что модуль сдвига стали значительно больше модуля сдвига бронзы. В результате приповерхностный слой стального образца будет слабо наклепываться. СЗднако полностью наклеп в стали исключить невозможно ввиду того, что кристаллы с решеткой объемно-центрированного куба имеют 48 равноценных систем скольжения, в результате чего движение дефектов сразу приобретает характер множественного скольжения, сопровождающегося упругим взаимодействием дислокаций и образованием сеток, скоплений.  [c.29]

Согласно высказанным выше предпосылкам генерированные источником дислокации в стальном образце будут притягиваться поверхностью раздела, так как значение модуля сдвига для стали больше, чем для меди. Для бронзы имеет место условие Gi кристаллическую решетку. В этом случае приповерхностные объемы бронзового образца будут наклепываться ввиду того, что дислокации отталкиваются от поверхности. Однако если учесть исследования структуры медной пленки при ИП [45], где высказано предположение о сильной разрыхленности ее в процессе трения, то наклеп приповерхностных объемов бронзы будет значительно меньшим.  [c.29]

Модуль норм, упругости Е в кг1мм Ориентировочные значения см, сталь 15 19 Модуль сдвига G в кг-мм 1 1 1  [c.673]

Резиновые изделия, несущие нагрузку-Амортизаторы [11] — разнообразные конструктивные элементы — обычно состоят из металлических (плоских, трубчатых или фасонных) оснований, между которыми прочно закреплена резина. Амортизаторы применяются в качестве подвесок, опор, буферов и тому подобных деталей, поглощающих вибрации и толчки. Они используются при деформациях сдвига, кручения, сжатия и их комбинациях. Прочность крепления резины к металлу (стали, алюминию, бронзе, латуни) зависит от принятого способа крепления, состава резины и условий работы конструкции и достигает при отрыве (от стали и латуни) 40 кГ/см и выше. Модуль сдвига резины для амортизаторов 5—7 кПсм .  [c.402]

---

1.11. Определите модуль сдвига для стали, если модуль Юнга для нее равен 198,00 гПа, а коэффициент Пуассона равен 0,31.

1.12. Определите модуль Юнга для стали, если модуль сдвига для нее равен 79, 00 ГПа, а коэффициент Пуассона равен 0,35.

1.13. Цилиндрический образец с начальной длиной 10,00 мм изготовленный из сплава золота 900-й пробы подвергался испытаниям на растяжение. При этом его длина увеличилась до 10,70 мм, а диаметр уменьшился с 7,00 мм до 6,80 мм. Определите коэффициент Пуассона сплава.

1.14. Сосредоточенная сила действует на пломбу при надкусывании. Действие силы вызывает продольное сжатие и поперечные деформации в тканях зуба со сформированной полостью под пломбу. Поперечные деформации будут наименьшими, когда коэффициент Пуассона материала пломбы

1.равен 0,5.	3. больше, чем коэффициент Пуассона тканей зуба.
2. равен 0.	4. меньше, чем коэффициент Пуассона тканей зуба.
	5. равен коэффициенту Пуассона тканей зуба.

1.15. Известны методы определения твердости материалов по:

1. Бринеллю; 2. Виккерсу; 3. Роквеллу; 4. Шору; 5. Давиденкову.

Выберите номер, под которым указан метод, при котором в испытываемый образец вдавливают индентор в виде стального шарика.

1.16. Для образца золотого желтого литьевого зуботехнического сплава I типа при стандартных испытаниях на твердость по Бринеллю получено число твердости HB = 474 МПа. Определите площадь шаровой поверхности отпечатка индентора в исследуемом образце. К индентору прикладывалась нагрузка 30 кН.

1.17. Для образца серебряно-палладиевого литьевого зуботехнического сплава Пд-150 при испытаниях на твердость по Виккерсу с нагрузкой 1000 Н было получено число твердости HV = 641 МПа. Определите величину диагонали отпечатка индентора, оставшегося на поверхности исследованного образца, в миллиметрах.

1.18. На рисунке представлены зависимости предела хрупкой прочности — линия “а” и предела текучести — линия “б” от абсолютной температуры для литьевого зуботехнического сплава.

Определите характер разрушения, которое претерпит образец сплава при температуре 350^оК.

1.19. На рисунке представлена зависимость условного напряжения от относительной деформации, полученная при растяжении образца из желтого золотого литьевого зуботехнического сплава.

Оцените предел текучести сплава в МПа.

1.20. В конструкции мостовидного протеза определено ‘опасное’ сечение. Мостовидный протез необходимо изготовить из желтого золотого сплава, предел текучести которого равен 196 МПа. Определите допустимое напряжение в ‘опасном’ сечении протеза в МПа, если коэффициент запаса прочности для такого рода изделий должен быть равен 3.

1.21. На рисунке представлены температурные зависимости долговечности образцов материала для базисов протезов – “акрела” при трех приложенных напряжениях: 0,2 ГПа, 0,4 ГПа и 0,6 ГПа. Определите время, прошедшее до разрушения образца, находящегося под напряжением 0,2 ГПа и температуре 49,6 градуса по Цельсию. По оси ординат отложен десятичный логарифм частного от деления времени в секундах на одну секунду.

1.22. На рисунке представлен график зависимости долговечности от напряжения при постоянной температуре для образца поливинилхлорида, применяемого при изготовлении эластичных прокладок базисов зубных протезов. Образец разрушился через 10 с. Определите напряжение σ, при котором разрушился образец.

(τ = 1с, t – в секундах).

1.23. Опираясь на идеи Гриффитса, оцените теоретическую прочность кристаллического материала, у которого слои атомов в кристаллах находятся на расстоянии один от другого. Удельная поверхностная энергия разрушения материала (поверхностное натяжение, у А. Гриффитса – the surface tension of the material) , модуль Юнга .

1.24. Опираясь на идеи Гриффитса, оцените отношение модуля Юнга к теоретической прочности для кристаллического материала, у которого слои атомов в кристаллах находятся на расстоянии один от другого. Удельная поверхностная энергия разрушения материала (поверхностное натяжение, у А. Гриффитса – the surface tension of the material) , модуль Юнга Па.

1.25. Определите критическую глубину () поверхностного дефекта (трещины Гриффитса) для стеклянной пластинки, находящейся под действием одноосного растягивающего напряжения . Удельная поверхностная энергия разрушения материала (поверхностное натяжение, у А. Гриффитса – the surface tension of the material), модуль Юнга Па. При решении не учитывайте концентрацию напряжения.

1.26. Критическая глубина поверхностного дефекта (трещины Гриффитса) для стеклянного волокна, находящегося под действием одноосного растягивающего напряжения составила 5,4 мкм. Определите критическую глубину трещины при напряжении . Удельная поверхностная энергия стекла (поверхностное натяжение) , модуль Юнга Па. При решении не учитывайте концентрацию напряжения.

1.27. Постойте график зависимости изменения потенциальной энергии упругой деформации в кубике с ребром a от глубины трещины Гриффитса L. Кубик изготовлен из хрупкого материала и находится под действием одноосного растягивающего напряжения . Удельная поверхностная энергия материала (поверхностное натяжение) , модуль Юнга E. (a = 0,1 м, Па, , E = 0,56 Па)

1.28. Постойте график зависимости убыли потенциальной энергии упругой деформации в кубике с ребром a от глубины трещины Гриффитса L. Кубик изготовлен из хрупкого материала и находится под действием одноосного растягивающего напряжения . Удельная поверхностная энергия материала (поверхностное натяжение) , модуль Юнга E. (a = 0,1 м, Па, , E = 0,56 Па)

1.29. Постойте график зависимости роста поверхностной энергии в кубике с ребром a от глубины трещины Гриффитса L. Кубик изготовлен из хрупкого материала и находится под действием одноосного растягивающего напряжения . Удельная поверхностная энергия материала (поверхностное натяжение) , Юнга E. (a = 0,1 м, Па, , E = 0,56 Па)

Механические свойства конструкционных и нержавеющих сталей :: HighExpert.RU

Используемые в машиностроении стали делятся на конструкционные (углеродистые и легированные) и высоколегированные нержавеющие. Марка конструкционной углеродистой стали содержит двузначное число, обозначающее среднее содержание углерода в сотых долях процента. В обозначении марок конструкционной легированной стали (ГОСТ 4543) первые две цифры указывают среднее содержание углерода в сотых долях процента, а буквы за цифрами обозначают: Р — бор, Ю — алюминий, С — кремний, Т — титан, Ф — ванадий, Х — хром, Г — марганец, Н — никель, М — молибден, В — вольфрам. Цифры после буквы указывают примерное процентное содержание легирующего элемента в целых единицах процента; отсутствие цифр означает, что в стали содержится до 1,5% этого легирующего элемента. В конце наименования марки высококачественной стали ставится буква А. У особо высококачественной стали в конце обозначения марки стоит через три тире буква Ш. В марках нержавеющих высоколегированный сталей (ГОСТ 5632) химические элементы обозначаются следующими буквами: А — азот, В — вольфрам, Д — медь, М — молибден, Р — бор, Т — титан, Ю — алюминий, Х — хром, Б — ниобий, Г- марганец, Е — селен, Н — никель, С — кремний, Ф — ванадий, К — кобальт, Ц — цирконий. Цифры, стоящие в наименовании марки после букв, указывают, так же как и в наименовании марок конструкционных сталей, процентное содержание легирующего элемента.

Основные характеристики механических свойств сталей:

• E — модуль упругости — коэффициент пропорциональности между нормальным напряжением и относительным удлинением;
• G — модуль сдвига (модуль касательной упругусти) — коэффициент пропорциональности между касательным напряжением и относительным сдвигом;
• μ — коэффициент Пуассона — абсолютное значение отношения поперечной деформации к продолной в упругой области;
• σ_т — предел текучести (условный) — напряжение при котором остаточная деформация после снятия нагрузки составляет 0,2%;
• σ_в — временное сопротивление (предел прочности) — прочность на разрыв;
• δ — относительное удлинение — отношение абсолютного остаточного удлинения образца после разрыва к начальной расчётной длине;
• твёрдость (HB, HRC, HV).

Механические свойства сталей

E = 200…210 ГПа, G = 77…81 ГПа, коэффициент Пуассона μ = 0,28…0,31.

Наименование	ГОСТ	Параметры термической обработки	Предел прочности σв, МПа	Предел текучести σт, МПа	Твердость
Сталь 10	1050-74	Сталь калиброванная после отжига и отпуска.	315-410	—	HB 143
Сталь 20	1050-74	Сталь калиброванная после отжига и отпуска.	390-490	—	HB 163
Сталь 40	1050-74	После отжига и отпуска.	590	—	HB 197
Сталь 40Х	4543-71	Пруток. Закалка 860 оС , отпуск 500 оС вода или масло.	590	345	HB 174-217
Сталь 20Х13	5949-75	Пруток. Закалка 1000-1050 оС, отпуск 600-700 оС воздух или масло.	830	635	HRC 29
Сталь 08Х18Н10Т	5945-75	Пруток. Закалка и отпуск.	420-520	180-200	—
Сталь 12Х18Н10Т	5945-75	Пруток. Закалка 1020-1100 оС, воздух, масло или вода.	510	196	—

Сталь 12Х13 (СТ12Х13) — характеристики, состав

Характеристика стали 12Х13 (СТ12Х13)

Материал Документ Заменитель 1 Заменитель 2 Заменитель 3 Сталь 12х13 ГОСТ 5632-72 Сталь 20Х13

 

Плотность	7720 кг/м.куб.
Назначение	клапаны гидравлических прессов
Модуль упругости	E=217000 МПа
Модуль сдвига	G=85000 МПа
Свариваемость	ограниченно свариваемая. Способы сварки: РДС, АДС под флюсом, АрДС и КТС. Подогрев и термообработка применяются в зависимости от метода сварки, вида и назначения конструкции.
Температура ковки	Начала 1230, конца 850. Сечения до 100 мм охлаждаются на воздухе, 101-350 мм — в ямах.
Химический состав	Кремний:0.8, Марганец:0.8, Медь:0.30, Никель:0.6, Сера:0.025, Углерод:0.09-0.15, Фосфор:0.030, Хром:12.0-14.0, Титан:0.2,
Склонность к отпускной способности	склонна [82]

Механические характеристики стали 12Х13 (СТ12Х13)

Состояние	Сигма-В, МПа	Сигма-Т, МПа	Кси, %	Дельта, %	НВ
закалка 1030гр (возд/масло), отпуск 750гр (возд/масло/вода)	590	410	60	20
закалка 960гр (возд), отпуск 250гр (возд)	1270	930	60	15	370
	500	350		21
	400			21
	600	420	60	20
	400			21
	500			14
	400			17
	400	220		н/д
Закалка 1000 — 1050 C, воздух, Отпуск 700 — 790 C, воздух	600	420	60	20

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА СТАЛИ ДИНАМИЧЕСКИМ МЕТОДОМ — Мегаобучалка

КРАТКАЯ ТЕОРИЯ. Под влиянием внешних сил всякое тело изменяет свою форму и размеры, т.е. деформируется. Упругой называется деформация, исчезающая с прекращением действия силы. Существуют различные типы деформации: растяжение (сжатие), сдвиг, кручение.

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1).

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде:

(1)

где СС₁=ΔX- абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению F/S, где S — площадь поверхности грани ВС, т.е.

, (2)

где N — модуль сдвига:

. (3)

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном единице (при условии, что закон Гука выполняется).

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ — угол кручения. По закону Гука:

. (4)

Модуль кручения f показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем

(5)

Поэтому расчет деформации кручения может быть сведен к расчету деформации сдвига. Приведем без вывода соотношение, существующее между модулем кручения f и модулем сдвига N материала проволоки

(6)

где r, l — соответственно радиус и длина проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки. Из формулы (6) имеем

(7)

Таким образом, модуль сдвига материала можно найти, зная модуль кручения, радиус и длину проволоки.

Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной L,радиусом r (см. рис. 3).

Если колеблющиеся тела совершают вращательное движение, то к ним может быть применен основной закон динамики вращательного движения:

(8)

где М — вращающий момент относительно оси АВ, J — момент инерции тела относительно той же оси, — угловое ускорение.

Учитывая (4) и (8) можно переписать в виде:

(9)

Знак минус говорит о том, что вращающий момент сдвига направлен так, чтобы уменьшить угловое отклонение.

Таким образом, тело совершает гармонические колебания, периоды которых можно найти из условия, что множитель пропорциональности между и φ в уравнении (9) в данном случае f/J должен быть равен:

, т.е. .

Откуда

, (10)

где Т — период колебания маятника.

Чтобы найти f, необходимо исключить неизвестный момент инерции J. Для этого в задаче определяются два периода колебаний маятника. Используя возможность передвижения груза Р на рейке установки, меняем расстояние от оси вращения. В соответствии с l₁ и l₂ получаем моменты инерции J₁ и J₂.

, , (11)

где J₀ — момент инерции рейки крутильного маятника. Периоды колебаний будут соответственно равны:

, Þ . (12)

Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника:

. (13)

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА изображена на рис. 4. Крутильный маятник представляет собой стальной цилиндр Ц с двумя рейками С, подвешенный с помощью двух стальных проволок к неподвижному кронштейну К. Момент инерции маятника J можно изменять перемещая вдоль реек одинаковые стальные цилиндры m.

ЗАДАНИЕ

1. Измерить L₁, L₂ и радиус проволоки r.

2. Снять зависимость периода Т полного колебания крутильного маятника от момента инерции , измеряя время t пятидесяти полных колебаний.

3. Результаты эксперимента занести в таблицу.

i, j
, мм
t, с
T, с

4. Используя соотношения:

, кг/м³, m=0,64 кг, =3,4, =1.2, вычислить N_ji. Оценить погрешность измерения модуля сдвига стали.

5.Результаты вычислений занести в таблицу.

j,i	N,1010Н/м2	Nср,1010 Н/м2	ΔN,1010 Н/м2	ΔNср,1010Н/м2
3, 1
3, 2
4, 1
4, 2

6.Результат эксперимента представить в виде

Н/м².

 

Сталь 10 конструкционная углеродистая качественная

• Заменители
• Иностранные аналоги
• Расшифровка
• Вид поставки
• Характеристики и описание
• Назначение
• Температура критических точек, °С
• Химический состав, % (ГОСТ 1050-88)
• Химический состав, % (ГОСТ 1050-2013)
• Износостойкость цементованной стали 10
• Механические свойства
• Механические свойства при повышенных температурах
• Предел выносливости
• Ударная вязкость KCU
• Технологические свойства
• Прокаливаемость
• Твердость HB (по Бринеллю) для металлопродукции из стали 10 (ГОСТ 1050-2013)
• Применение стали 10 для трубопроводов в зависимости от параметров транспортируемой среды (ГОСТ 32569-2013)
• Пределы применения, виды обязательных испытаний и контроля прокладок из стали 10 для давления свыше 10 МПа (100 кгс/см²) (ГОСТ 32569-2013)
• Применение стали 10 для изготовления крепежных деталей (ГОСТ 32569-2013)
• Минимальное значение предела текучести, МПа (кгс/мм²) при расчетной температуре (ПНАЭ Г-7-002-86)
• Минимальное значение предела прочности (временного сопротивления), МПа (кгс/мм²) при расчетной температуре (ПНАЭ Г-7-002-86)
• Плотность ρ_п кг/см³ при температуре испытаний, °С
• Коэффициент линейного расширения α*10⁶, К^-1
• Модуль нормальной упругости (Модуль Юнга) Е, ГПа
• Коэффициент теплопроводности λ Вт/(м*К)
• Удельная теплоемкость c, Дж/(кг*К)
• Модуль упругости при сдвиге на кручение G, ГПа
• Удельное электросопротивление ρ нОм*м
• Узнать еще

Заменители

Стали 08, 15, 08кп.

Иностранные аналоги

Европа	Ck10(2), С 10(2)
США (AISI, ASTM)	1010, M1010, M1012, 1110, 1012
Япония JIS	S10C, S09CK

Расшифровка

Цифра 10 обозначает, что среднее содержание углерода в стали составляет 0,10%.

Вид поставки

• Сортовой прокат, в том числе фасонный: ГОСТ 1050-88, ГОСТ 2590-88, ГОСТ 2591-88, ГОСТ 2879-88, ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 8240-89, ГОСТ 8239-89.
• Калиброванный пруток ГОСТ 10702-78, ГОСТ 7417-75, ГОСТ 8559-75, ГОСТ 8560-78.
• Шлифованный пруток и серебрянка ГОСТ 10702-78, ГОСТ 14955-77.
• Лист толстый ГОСТ 1577-93, ГОСТ 19903-74.
• Лист тонкий ГОСТ 16523-89.
• Лента ГОСТ 6009-74. ГОСТ 10234-77.
• Полоса ГОСТ 1577-93, ГОСТ 103-76, ГОСТ 82-70.
• Проволока ГОСТ 17305-91, ГОСТ 5663-79.
• Трубы ГОСТ 8731-74, ГОСТ 8732-78, ГОСТ 8733-74, ГОСТ 8734-75, ГОСТ 10705-80, ГОСТ 10704-91, ГОСТ 1060-83, ГОСТ 5654-76, ГОСТ 550-75.

к содержанию ↑

Характеристики и описание

Сталь 10 относится к конструкционным малоуглеродистым нелегированным качественным сталям и характеризуется высокими пластическими свойствами и применяется преимущественно для изготовления изделий холодной штамповкой, высадкой и волочением.
Для повышения прочности и улучшения обрабатываемости низкоуглеродистая сталь марок 10 подвергается нормализации с температуры 930-950° С.

Назначение

Детали, работающие при температуре от -40 до 450 °С, к которым предъявляются требования высокой пластичности. После ХТО — детали с высокой поверхностной твердостью при невысокой прочности сердцевины.

Температура критических точек, °С

Ас1	Ас3	Аr3	Ar1
732	870	854	680

Химический состав, % (ГОСТ 1050-88)

C	Si	Mn	Cr	S	Р	Cu	Ni	As
			не более
0,07-0,14	0,17-0,37	0,35-0,65	0,15	0,04	0,035	0,25	0,25	0,08

Химический состав, % (ГОСТ 1050-2013)

Марка стали	Массовая доля элементов, %
	C	Si	Mn	P	S	Cr	Ni	Cu
				не более
10	0,07-0,14	0,17-0,37	0,35-0,65	0,030	0,035	0,15	0,30	0,30

к содержанию ↑

Износостойкость цементованной стали 10

Характеристика термической обработки	Твердость по Виккерсу HV	Износ, мг
		образца	бронзового вкладыша
Цементация на глубину 1,5 мм, закалка при 780°С, отпуск при 170°С	782	4,0	3,0

Механические свойства

ГОСТ	Состояние поставки	σ0,2, МПа	δ5(δ4), %	Ψ, %	Твердость HB, не более
		не менее
ГОСТ 1050-88	Сталь горячекатаная кованая, калиброванная и серебрянка 2-й категории после нормализации	335	31	55	—
ГОСТ 10702-78	Сталь калиброванная и калиброванная со специальной отделкой:
	после отжига или отпуска	335-450	—	55	143
	после сфероидизирующего отжига	315-410	—	55	143
	нагартованная без термообработки	390	8	50	187
ГОСТ 1577-93	Полоса нормализованная или горячекатаная	335	31	55	—
ГОСТ 16523-89 (образцы поперечные)	Лист горячекатаный	295-410	(24)	—	—
	Лист холоднокатаный	295-410	(25)	—	—
ГОСТ 4041-71 (образцы поперечные)	Лист термически обработанный 1 и 2-й категорий	295-420	32	—	117
ГОСТ 8731-74	Труба горячедеформированная термообработанная	355	24	—	137
ГОСТ 8733-74	Труба холодно- и теплодеформированная термообработанная	345	24	—	137
—	Цементация при 920-950 °С [81]; закалка с 790-810 °С в воде; отпуск при 180-200 °С, охл. на воздухе	390	25	55	Св. HRCs 137*1; 63*2

• *1 Сердцевины.
• *2 Поверхности.

к содержанию ↑

Механические свойства при повышенных температурах

tисп., °С	σ0,2, МПа	σв, МПа	δ5, %	Ψ, %	KCU, Дж/см2
20	260	420	32	69	221
200	220	485	20	55	176
300	175	515	23	55	142
400	170	355	24	70	98
500	160	255	19	63	78

ПРИМЕЧАНИЕ. Нормализация при 900-920 °С, охл. на воздухе.

к содержанию ↑

Предел выносливости

Термообработка	σ-1, МПа	τ-1, МПа	n
Нормализация при 900-920°С	157-216	51	108

ПРИМЕЧАНИЕ. σ⁴⁰⁰_1/1000 = 108 МПа, σ⁴⁰⁰_1/100000 = 78 МПа, σ⁴⁵⁰_1/10000 = 69 МПа, σ⁴⁵⁰_1/100000 = 44 МПа

Ударная вязкость KCU

Термообработка	KCU, Дж/см2, при температуре, °С
	+20	-20 (-30)	-40 (-50)	-60
Отсутствует	235	196	157	78
Нормализация [81]	73-265	(203-216)	(179)	—
Отжиг [28]	59-245	49-174	45-83	19-42

ПРИМЕЧАНИЕ. Пруток диаметром 35 мм.

Технологические свойства

Температура ковки, °С: начала 1300, конца 700. Охлаждение на воздухе.
Свариваемость — сваривается без ограничений, кроме деталей после химикотермической обработки. Способы сварки: РДС, АДС под флюсом и газовой защитой, КТС.
Обрабатываемость резанием — K_{v тв.спл} = 2,1 и K_{v б.ст.} = 1,6 в горячекатаном состоянии при НВ 99-107 и σ_в = 450 МПа.
Флокеночувствительность — не чувствительна.
Склонность к отпускной хрупкости — не склонна.

к содержанию ↑

Прокаливаемость

Твердость HRCэ на расстоянии от торца, мм
1,5	3	4,5	6
31	29	26	20,5

Твердость HB (по Бринеллю) для металлопродукции из стали 10 (ГОСТ 1050-2013)

Марка стали	Твердость HB, не более, для металлопродукции
	горячекатаной и кованой		калиброванной и со специальной отделкой поверхности
	без термической обработки	после отжига или высокого отпуска	нагартованной	после отжига или высокого отпуска
10	143	—	187	143

к содержанию ↑

Применение стали 10 для трубопроводов в зависимости от параметров транспортируемой среды (ГОСТ 32569-2013)

Марка стали, класс прочности, стандарт или ТУ	Технические требования на трубы (стандарт или ТУ)	Номинальный диаметр, мм	Виды испытаний и требований (стандарт или ТУ)	Транспортируемая среда (см. ГОСТ 32569-2013 обозначения таблицы 5.1)	Расчетные параметры трубопровода
					Максимальное давление, МПа	Максимальная температура, °С	Толщина стенки трубы, мм	Минимальная температура в зависимости от толщины стенки трубы при наряжении в стенке от внутреннего давления [σ], °C
								более 0,35[σ]	не более 0,35[σ]
Бесшовные трубы
Сталь 10 ГОСТ 1050	ГОСТ 550 группы А, Б	10-300	ГОСТ 550	Все среды	≤32	475	≤12 >12	минус 40 минус 30	минус 40
	ГОСТ 8731, ГОСТ Р 53383 группа В, кроме изготовленных из слитка	50-400	ГОСТ 8731, ГОСТ Р 53383 с гарантией гидроиспытания		≤5		≤12 >12	минус 40 минус 30
				Среды группы В, кроме пара и горячей воды	≤5		≤12 >12	минус 40 минус 30
	ГОСТ 8733, ГОСТ Р 54157 группа В	10-150	ГОСТ 8733, ГОСТ Р 54157	Все среды с гарантией гидроиспытания	32		≤6	минус30
	ТУ 14-3-826-79	20-50	ТУ 14-3-826-79	Все среды			≤12	минус 30
	ТУ 14-3-1486-87	300, 350, 400	ТУ 14-3-1486-87				—	минус 40
	ТУ 14-3-587-77	500	ТУ 14-3-587-77				≤12 >12	минус 40 минус 30
	ТУ 14-ЗР-55-2001	50-400	ТУ 14-ЗР-55-2001				—	минус 30
	ТУ 14-3-1577-88		ТУ 14-3-1577-88				—	минус 40
	ТУ 14-3-1128-2000 ТУ 14-ЗР-1128-2007		ТУ 14-3-1128-2000 ТУ 14-ЗР-1128-2007				≤12 >12	минус 40 минус 30	минус 60 минус 40
Электросварные трубы спиральношовные
Сталь 10 ГОСТ 1050	ГОСТ 3262	6-150	ГОСТ 3262	Среды группы В, кроме пара и горячей воды	≤1,6	200	≤5	минус 20	минус 20

к содержанию ↑

Пределы применения, виды обязательных испытаний и контроля прокладок из стали 10 для давления свыше 10 МПа (100 кгс/см

²) (ГОСТ 32569-2013)

Марка стали, стандарт или ТУ		10 ГОСТ 1050
Технические требования		ОСТ 26-01-49-82
Наименование детали		Прокладки металлические
Предельные параметры	Температура стенки, °С, не более	От -40 до +250
	Давление номинальное, МПа (кгс/см2) не более	32 (320)
Обязательные испытания	σ0,2	+
	σв	+
	σ	+
	f	—
	KCU	+
	HB	+
Контроль	Дефектоскопия	+
	Неметаллические включения	—

к содержанию ↑

Применение стали 10 для изготовления крепежных деталей (ГОСТ 32569-2013)

Марка стали	Технические требования	Допустимые параметры эксплуатации		Назначение
		Температура стенки, °С	Давление среды, МПа (кгс/см2), не более
Сталь 10 ГОСТ 1050	СТП 26.260.2043	От 0 до +300	2,5 (25)	Гайки
		От -40 до +450	10 (100)	Шайбы

к содержанию ↑

Минимальное значение предела текучести, МПа (кгс/мм

²) при расчетной температуре (ПНАЭ Г-7-002-86)

Марка стали	Сортамент	Температура, К (°С)
		293 (20)	323 (50)	373 (100)	423 (150)	473 (200)	523 (250)	573 (300)	623 (350)
10	Трубы холодно и теплодефор- мированные бесшовные наружным диаметром от 5 до 250 мм, с толщиной стенки от 0,3 до 20 мм; наружным диаметром от 6 до 250 мм, с толщиной стенки от 1,6 до 24 мм; наружным диаметром от 6 до 160 мм, с толщиной стенки от 2 до 22 мм	206 (21)	196 (20)	195 (19)	181 (18,5)	176 (18)	157 (16)	137 (14)	118 (12)
	Сортовая горячекатаная и кованая сталь толщиной или диаметром до 80 мм	186 (19)	186 (19)	186 (19)	177 (18)	177 (18)	157 (16)	137 (14)	118 (12)

ПРИМЕЧАНИЕ. В предел «от» и «до» включаются обе значащие цифры.

к содержанию ↑

Минимальное значение предела прочности (временного сопротивления), МПа (кгс/мм

²) при расчетной температуре (ПНАЭ Г-7-002-86)

Марка стали	Сортамент	Температура, К (°С)
		293 (20)	323 (50)	373 (100)	423 (150)	473 (200)	523 (250)	573 (300)	623 (350)
10	Трубы холодно и теплодефор- мированные бесшовные наружным диаметром от 5 до 250 мм, с толщиной стенки от 0,3 до 20 мм; наружным диаметром от 6 до 250 мм, с толщиной стенки от 1,6 до 24 мм; наружным диаметром от 6 до 160 мм, с толщиной стенки от 2 до 22 мм	343 (35)	333 (34)	333 (34)	333 (34)	333 (34)	323 (33)	314 (32)	294 (30)
	Сортовая горячекатаная и кованая сталь толщиной или диаметром до 80 мм	333 (34)	333 (34)	333 (34)	333 (34)	333 (34)	323 (33)	314 (32)	294 (30)

ПРИМЕЧАНИЕ. В предел «от» и «до» включаются обе значащие цифры.

к содержанию ↑

Плотность ρ

_п кг/см³ при температуре испытаний, °С

Сталь 10	20	100	200	300	400	500	600	700	800	900
	7856	7832	7800	7765	7730	7692	7653	7613	7582	7594

Коэффициент линейного расширения

α*10⁶, К^-1

Марка стали	α*106, К-1 при температуре испытаний, °С
	20-100	20-200	20-300	20-400	20-500	20-600	20-700	20-800	20-900	20-1000
10	12,4	13,2	13,9	14,5	14,9	15,1	15,3	12,1	14,8	12,6

Модуль нормальной упругости (Модуль Юнга) Е, ГПа

Марка Стали	При температуре испытаний, °С
	20	100	200	300	400	500	600	700	800	900
10	206	199	195	186	178	169	157	—	—	—

Коэффициент теплопроводности λ Вт/(м*К)

Марка Стали	λ Вт/(м*К), при температуре испытаний, °С
	20	100	200	300	400	500	600	700	800	900
10	—	58	54	49	45	40	36	32	29	27

Удельная теплоемкость

c, Дж/(кг*К)

Марка стали	c, Дж/(кг*К), при температуре испытаний, °С
	20-100	20-200	20-300	20-400	20-500	20-600	20-700	20-800	20-900	20-1000
10	466	479	—	512	—	567	—	—	—	—

Модуль упругости при сдвиге на кручение G, ГПа

Марка стали	При температуре испытаний, °С
	20	100	200	300	400	500	600	700	800	900
10	78	77	76	73	69	66	59	—	—	—

Удельное электросопротивление ρ нОм*м

марка стали	ρ нОм*м, пРи темпеРатуРе испытаний, °С
	20	100	200	300	400	500	600	700	800	900
10	—	190	263	352	458	584	734	905	1081	1130

Что такое модуль сдвига? Определение и примеры

Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига. Он также известен как модуль жесткости и может обозначаться G или, реже, S или μ . Единицей измерения модуля сдвига в системе СИ является паскаль (Па), но значения обычно выражаются в гигапаскалях (ГПа). В английских единицах измерения модуль сдвига выражается в фунтах на квадратный дюйм (PSI) или в килограммах (тысячах) фунтов на квадратный дюйм (ksi).

• Большое значение модуля сдвига указывает на высокую жесткость твердого тела. Другими словами, для создания деформации требуется большая сила.
• Небольшое значение модуля сдвига указывает на то, что твердое тело является мягким или гибким. Чтобы его деформировать, требуется небольшое усилие.
• Одно определение жидкости — это вещество с нулевым модулем сдвига. Любая сила деформирует его поверхность.

Уравнение модуля сдвига

Модуль сдвига определяется путем измерения деформации твердого тела от приложения силы, параллельной одной поверхности твердого тела, в то время как противоположная сила действует на ее противоположную поверхность и удерживает твердое тело на месте.Думайте о сдвиге как о толкании одной стороны блока с трением как противодействующей силе. Другой пример — попытка отрезать проволоку или волосы тупыми ножницами.

Уравнение для модуля сдвига:

G = τ _xy / γ _xy = F / A / Δx / l = Fl / AΔx

Где:

• G — модуль сдвига или модуль жесткости
• τ _xy — напряжение сдвига
• γ _xy — деформация сдвига
• A — площадь, на которую действует сила
• Δx — поперечное смещение
• л — начальная длина

Деформация сдвига равна Δx / l = tan θ или иногда = θ, где θ — угол, образованный деформацией, вызванной приложенной силой.

Пример расчета

Например, найдите модуль сдвига образца при напряжении 4×10 ⁴ Н / м ² , испытывающем деформацию 5×10 ^-2 .

G = τ / γ = (4×10 ⁴ Н / м ² ) / (5×10 ^-2 ) = 8×10 ⁵ Н / м ² или 8×10 ⁵ Па = 800 кПа

Изотропные и анизотропные материалы

Некоторые материалы изотропны по отношению к сдвигу, что означает, что деформация в ответ на силу одинакова независимо от ориентации.Другие материалы анизотропны и по-разному реагируют на напряжение или деформацию в зависимости от ориентации. Анизотропные материалы гораздо более восприимчивы к сдвигу по одной оси, чем по другой. Например, рассмотрим поведение деревянного блока и то, как он может реагировать на силу, приложенную параллельно волокну древесины, по сравнению с его реакцией на силу, приложенную перпендикулярно волокну. Рассмотрим, как алмаз реагирует на приложенную силу. Насколько легко кристалл сдвигается, зависит от ориентации силы по отношению к кристаллической решетке.

Влияние температуры и давления

Как и следовало ожидать, реакция материала на приложенную силу изменяется в зависимости от температуры и давления. В металлах модуль сдвига обычно уменьшается с повышением температуры. Жесткость уменьшается с увеличением давления. Для прогнозирования влияния температуры и давления на модуль сдвига используются три модели: модель напряжения пластического течения при механическом пороговом напряжении (MTS), модель модуля сдвига Надаля и Лепоака (NP) и модуль сдвига Стейнберга-Кохрана-Гинана (SCG). модель.Для металлов обычно существует область температуры и давления, в которой изменение модуля сдвига является линейным. Вне этого диапазона моделировать поведение сложнее.

Таблица значений модуля сдвига

Это таблица значений модуля сдвига образца при комнатной температуре. Мягкие, гибкие материалы обычно имеют низкие значения модуля сдвига. Щелочноземельные и основные металлы имеют промежуточные значения. Переходные металлы и сплавы имеют высокие значения. Алмаз, твердое и жесткое вещество, имеет чрезвычайно высокий модуль сдвига.

Материал	Модуль сдвига (ГПа)
Резина	0,0006
Полиэтилен	0,117
Фанера	0,62
Нейлон	4,1
Свинец (Pb)	13,1
Магний (Mg)	16,5
Кадмий (Cd)	19
Кевлар	19
Бетон	21
Алюминий (Al)	25.5
Стекло	26,2
Латунь	40
Титан (Ti)	41,1
Медь (Cu)	44,7
Железо (Fe)	52,5
Сталь	79,3
Алмаз (C)	478,0

Обратите внимание, что значения модуля Юнга следуют аналогичной тенденции. Модуль Юнга — это мера жесткости твердого тела или линейного сопротивления деформации.Модуль сдвига, модуль Юнга и объемный модуль — это модули упругости, все они основаны на законе Гука и связаны друг с другом уравнениями.

Источники

• Crandall, Dahl, Lardner (1959). Введение в механику твердого тела . Бостон: Макгроу-Хилл. ISBN 0-07-013441-3.
• Guinan, M; Стейнберг, Д. (1974). «Производные по давлению и температуре модуля изотропного поликристаллического сдвига для 65 элементов». Журнал физики и химии твердого тела .35 (11): 1501. DOI: 10.1016 / S0022-3697 (74) 80278-7
• Ландау Л.Д., Питаевский Л.П., Косевич А.М., Лифшиц Е.М. (1970). Теория упругости , т. 7. (Теоретическая физика). 3-е изд. Пергамон: Оксфорд. ISBN: 978-0750626330
• Варшни Ю. (1981). «Температурная зависимость упругих постоянных». Физический обзор B . 2 (10): 3952.

Характеристика стальных пен для конструкционных элементов

% PDF-1.5 % 2 0 obj > эндобдж 5 0 obj > поток application / pdf

Brooks H. Smith 1

Стефан Шинишевский 2

*

Джером Ф. Хаджар 3

Бенджамин В. Шафер 2 и Санджай Р. Арвад 1

Характеристики пенополистирола для конструктивных элементов

Экспериментально измеренные механические свойства стального пенопласта с полыми сферами являются предметом данной статьи. Характеристики пенопласта с полыми сферами включают в себя предел текучести при сжатии и деформацию уплотнения, коэффициент Пуассона при пластическом сжатии и модуль разгрузки при сжатии, а также модуль упругости при растяжении, модуль упругости при растяжении и разгрузке, предел текучести при растяжении и деформацию разрушения при растяжении.Также включены свойства сдвига. Эти тесты предоставляют достаточно информации для калибровки макроскопической модели континуума. В таблице приведены калиброванные параметры пенопласта и объяснены его уникальные особенности. Также сообщается о первоначальной разработке мезомасштабных моделей, которые явно моделируют пустоты и спеченные полые сферы. Эта работа является частью более масштабных усилий, направленных на развитие вспененной стали как материала, пригодного для применения в гражданском строительстве.

стальная пена

металлическая полая сфера

эксперимент

напряжение

перелом

коэффициент Пуассона

панель

2012-11-01T15: 04: 20 + 08: 00PScript5.dll Версия 5.2.22012-11-01T15: 04: 52 + 08: 00 Acrobat Distiller 9.0.0 (Windows) стальная пена; металлический полый шар; эксперимент; напряжение; перелом; коэффициент Пуассона; панель uuid: 64fa25bf-bf0d-4c75-a693-7cef13f05ca9uuid: 6a19936c-d9bc-4b6e-9406-cdf136123c1f конечный поток эндобдж 22 0 объект > поток h | YvJ} W # Hm; KdOfiF- VϘ / 嬳 V ޵ kWNfyq \ zi E qip񂹮GwhIr’e & 0f {!,? 7 & ‘3 {״ +2 O $ qDӥ)! Fq8Cz8Kb_4d

Разница между модулем Юнга, модулем объемной упругости и модулем сдвига

Основное различие между модулем Юнга, модулем объемной упругости и модулем сдвига заключается в том, что модуль Юнга — это отношение растягивающего напряжения к деформации растяжения, объемный модуль — это отношение объемного напряжения к объемной деформации, а модуль сдвига — это отношение напряжения сдвига к деформации. деформация сдвига.

Модуль Юнга

Отношение растягивающего напряжения к растягивающей деформации называется модулем Юнга.

Формула модуля Юнга

См. Также : Разница между напряжением и деформацией

Объемный модуль

Для трехмерной деформации, когда задействован объем, отношение приложенного напряжения к объемной деформации называется объемным модулем. Математически это выражается как:

Формула объемного модуля

Где ΔV — изменение исходного объема V.

Модуль сдвига

Отношение напряжения сдвига и деформации сдвига называется модулем сдвига. Математически это выражается как:

Формула модуля сдвига

Константы упругости для некоторых материалов приведены в таблице:

Материал	Модуль Юнга 10 9 Нм -2	Объемный модуль 10 9 Нм -2	Модуль сдвига 10 9 Нм -2
Алюминий	70	70	30
Кость	15	–	80
Медь	110	140	44
Алмаз	1120	540	450
Стекло	55	31	23
Сталь	200	160	84
Вольфрам	390	200	150
Вода	0	2.2	0
Свинец	15	7,7	5,6

Посетите нашу страницу по соответствующим темам: Механика

Механика материалов: деформация »Механика тонких конструкций

---

Штамм

До сих пор мы сосредоточились на напряжении внутри структурных элементов. Когда вы прикладываете напряжение к объекту, он деформирует .Представьте себе резинку: вы тянете за нее, и она становится длиннее — она ​​ тянется . Деформация — это мера того, насколько объект растянут, а деформация — это соотношение между деформацией и исходной длиной. Думайте о деформации как о -процентном удлинении — насколько больше (или меньше) объект при его нагрузке.

Как и напряжение, конструкция может испытывать два типа деформации: 1. Нормальная деформация и 2. Деформация сдвига .Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она вызывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим стержень при одноосном растяжении. Стержень удлиняется под этим натяжением до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к исходной длине стержня.

Деформация — это безразмерная мера того, насколько объект становится больше или меньше из-за приложенной нагрузки. Нормальная деформация возникает, когда удлинение объекта происходит в ответ на нормальное напряжение (то есть перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует деформации при растяжении , а отрицательное — при сжатии . Деформация сдвига возникает, когда деформация объекта является ответом на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой , гамма .

Механическое поведение материалов

Ясно, что напряжение и напряжение связаны.Напряжение и деформация связаны согласно основному закону , и мы можем определить их взаимосвязь экспериментально, измерив, сколько напряжения требуется для растяжения материала. Это измерение может быть выполнено с помощью испытания на растяжение . В простейшем случае, чем сильнее вы тянете за объект, тем сильнее он деформируется, а при малых значениях деформации это соотношение является линейным. Эта линейная упругая связь между напряжением и деформацией известна как Закон Гука . Если вы построите график зависимости напряжения от деформации, для малых деформаций этот график будет линейным, а наклон линии будет свойством материала, известного как модуль упругости .Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали. Для большинства конструкционных материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-упругими (т.е. они следуют закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простое соотношение для деформации материала.

Интуитивно этот экзамен имеет некоторый смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или более толстому материалу, получите меньшую деформацию. Если конструкция меняет форму или материал, или по-разному нагружается в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип наложения .

Обобщенный закон Гука

На последнем уроке мы начали узнавать о том, как связаны стресс и напряжение — через закон Гука.Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили о напряжении или деформации только в одном направлении. В этом уроке мы собираемся рассмотреть обобщенный закон Гука для однородных, изотропных и упругих материалов, подвергающихся воздействию сил по более чем одной оси.

Перво-наперво, даже простое вытягивание (или толкание) большинства материалов в в одном направлении на самом деле вызывает деформацию в во всех трех ортогональных направлениях .Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что при натяжении объекта в осевом направлении он сжимает в поперечном направлении в поперечных направлениях:

Таким образом, если потянуть за него в направлении x , он сожмется в направлениях y и z . Это свойство материала известно как коэффициент Пуассона и обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это в виде уравнения:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона — это свойство материала . Коэффициент Пуассона может находиться в диапазоне от -1 до 0,5. Для большинства конструкционных материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а у каучуков коэффициент Пуассона составляет около 0,5, которые называются «несжимаемыми». Несжимаемый просто означает, что любая сумма, которую вы сжимаете в одном направлении, будет расширяться на такую ​​же величину в других направлениях — следовательно, его объем не изменится.

За последнее десятилетие было проведено несколько очень интересных исследований по созданию структурированных материалов , которые используют геометрию и упругую нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона.Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип может быть применен в 3D для создания расширяемых / складных оболочек:

Благодаря коэффициенту Пуассона у нас теперь есть уравнение, которое связывает деформацию в направлении y или z с деформацией в направлении z. Мы, в свою очередь, можем связать это со стрессом с помощью закона Гука.Это важное замечание: при натяжении объекта в одном направлении возникает напряжение только в этом направлении , а при — во всех трех направлениях . Итак, сигма _y = сигма _z = 0. Давайте запишем деформации в направлении y и z через напряжение в направлении x .

Помните, что до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях.Полезный способ понять это — представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжений , которые по нормали к каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях .Итак, теперь мы включили эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Что ж, если объект меняет форму во всех трех направлениях, это означает, что он изменит свой объем на .Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:

Теперь, когда у нас есть уравнение для изменения объема, или расширения , в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, вызывающий расширение, известен как гидростатический стресс. Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Итак, в случае гидростатического давления мы можем свести наше окончательное уравнение для расширения к следующему:

Это последнее соотношение важно, потому что оно является определяющим соотношением того, как объем материала изменяется под действием гидростатического давления.Префактор p можно переписать как модуль объемной упругости материала , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой изменения объема материала при заданном давлении — если коэффициент Пуассона для материала равен 0,5?

Закон Гука при сдвиге

В предыдущем разделе мы разработали взаимосвязь между нормальным напряжением и нормальной деформацией.Теперь поговорим о сдвиге. Вернемся к этому воображаемому кубу материала. Помимо внешних сил, вызывающих напряжения, нормальные к каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, напряжения, параллельные поперечному сечению, составляют напряжения сдвига

Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж и плохо. На каждой поверхности есть два напряжения сдвига, а нижние индексы говорят вам, в каком направлении они указывают и какой поверхности параллельны.Например, возьмем правую грань куба. Напряжения, нормальные к этой грани, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно направлено в направлении y (обозначено tau _xy ), а другое направлено в направлении z (обозначено tau _xz ). Чтобы куб находился в равновесии, tau _xy = tau _yx (в противном случае куб вращался бы). Таким образом, теперь существует шести напряжений (сигма _x , сигма, сигма, тау _xy, тау _yz, тау _xz ), которые характеризуют состояние напряжения в однородном, изотропном, упругом материале.

Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука для сдвига очень похож на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорциональность между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала. Это уравнение в его общей форме, но мы можем переписать его более явно в терминах его компонентов: x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, эластичных материалов.

В нашем обобщенном законе Гука есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это соотношение задается следующим уравнением:

Сводка

В этой лекции мы представили понятие напряжения. Деформация — это деформация материала под действием напряжения. Это просто отношение изменения длины к исходной длине.Деформации, приложенные перпендикулярно поперечному сечению, составляют нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, составляют деформации сдвига . Для линейных упругих материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под воздействием внешней нагрузки.

Кроме того, в этом разделе мы узнали о многоосном нагружении .В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона — соотношение между поперечной и осевой деформациями. Деформации, возникающие в трех ортогональных направлениях, могут дать нам меру расширения материала в ответ на многоосную нагрузку. В частности, материал обычно может изменять объем в ответ на изменение внешнего давления или гидростатического напряжения .Это привело к определению сопротивления материалов изменению объема под действием гидростатического напряжения — модуля объемной упругости . Изучив воображаемый кубический элемент в произвольном материале, мы смогли представить себе напряжения, возникающие нормально и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы связали друг с другом, используя обобщенный закон Гука для однородных материалов , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости , модулем сдвига и коэффициентом Пуассона .

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.

Модуль сдвига

— объяснение, пример проблемы и часто задаваемые вопросы

Модуль сдвига также известен как модуль жесткости, это постоянное число, которое описывает упругие свойства твердого тела при использовании возникающих поперечных внутренних сил. Например, при кручении скручивание металла вокруг собственной оси известно как модуль сдвига. В материалах этих типов любой из небольших объемов материала искажается таким образом, что обе грани материала скользят параллельно друг другу на небольшое расстояние, а две другие грани меняют форму с квадрата на ромбовидную.

Определение модуля жесткости — это мера жесткости тела, представленная как отношение напряжения сдвига к деформации сдвига.

[Изображение будет загружено в ближайшее время]

Модуль сдвига измеряет прочность объекта, чтобы выдерживать гибкие деформации, и является достоверным индикатором поведения, которое распространяется только на небольшую деформацию, после которой объект может вернуться к своему исходному состоянию. конфигурация. Чрезмерное усилие сдвига приводит к необратимой деформации и вращению или разрушению материала.

Математически

В физическом материаловедении модуль сдвига или модуль жесткости обозначается буквой «G», а иногда также обозначается как «S» или «μ». Модуль сдвига — это мера упругой жесткости материала на сдвиг, а определение модуля сдвига — это отношение напряжения сдвига к деформации сдвига:

G = \ [\ frac {\ tau_ {xy}} {\ gamma_ {xy} } \] = \ [\ frac {F / A} {\ frac {\ Delta x} {l}} \] = \ [\ frac {Fl} {A \ Delta x} \]

где,

\ [\ tau \] \ [_ {xy} \] = F / A = напряжение сдвига.

«F» — это действующая сила.

«А» — это площадь материала, на которую будет действовать сила.

\ [\ gamma \] \ [_ {xy} \] = деформация сдвига. В инженерии \ [\ frac {\ Delta x} {l} \] = tanθ,

в другом месте будет ‘θ’

\ [\ Delta \] x ’- поперечное смещение.

‘l’ — начальная длина области.

Единицей измерения модуля сдвига в системе СИ является паскаль (Па), но обычно он выражается в гигапаскалях (ГПа) или иногда также выражается в тысячах на квадратный дюйм (KSI).И размерная формула модуля сдвига задается как M1L − 1T − 2, заменяя силу на массу, умноженную на ускорение.

Пояснение

Модуль сдвига — это одна из различных величин, используемых для измерения жесткости материалов, причем все они возникают в соответствии с законом Гука в целом.

• Модуль Юнга, обозначенный буквой «E», описывает реакцию деформации материала (изменение длины до исходной длины) на одноосное напряжение в направлении этого напряжения (например, вытягивание концов проволоки с помощью проволоки. становится длиннее).

• Коэффициент Пуассона, обозначенный «ν», представляет собой отношение, которое описывает реакцию в ортогональных направлениях на это одноосное напряжение (проволока становится тоньше по сравнению с предыдущей толщиной).

• Объемный модуль «k» материала описывает реакцию на гидростатическое (равномерное) давление (например, давление на дне бассейна).

• Модуль сдвига G материала описывает реакцию на напряжение сдвига, эти модули не являются независимыми, и для изотропных материалов они связаны уравнениями 2G (1 + v) = E = 3K (1-2v )

Модуль сдвига связан с преобразованием твердого тела, когда он сталкивается с той же силой, что и одна из его поверхностей.В то время как его противостоящая грань встречает противодействующие силы (например, трение). В случае прямоугольного призматического объекта он будет отключен как параллелепипед. Анизотропные материалы, такие как дерево, бумага и практически все монокристаллы, демонстрируют различную реакцию веществ на стресс или затруднения при испытании в разных направлениях. В этом случае может потребоваться использовать полный акцент упругой постоянной, а не одно скалярное значение материала.

Значение модуля сдвига для различных материалов

Материал	Типичные значения модуля сдвига (ГПа) (при комнатной температуре)
Алмаз 900 478.0
Сталь	79,3
Железо	52,5
Медь	44,7
Титан
Стекло	26,2
Алюминий	25,5
Полиэтилен	0.117
Резина	0,0006
Гранит	24
Сланец	1,6
Известняк
Мел	3,2
Песчаник	0,4
Дерево	4

Из приведенного выше чтобы узнать значение модуля сдвига различных материалов, например, модуль сдвига стали / модуль жесткости стали равен 79.3 ГПа.

Пример Задача

1. Представьте, что блок неизвестного материала, хранящийся на столе (квадратная грань материала помещается на стол), находится под действием силы сдвига. Некоторые данные приведены ниже для расчета модуля сдвига материала, размеры = 60 мм x 60 мм x 20 мм, усилие сдвига = 0,245 Н, смещение = 5 мм.

Решение:

Подставляя значения в формулу, мы получаем-

Напряжение сдвига = \ [\ frac {F} {A} \] = \ [\ frac {0.{-6}} \] = \ [\ frac {2450} {50} \] Н / м2

Деформация сдвига = \ [\ frac {\ Delta x} {l} \] = \ [\ frac {5} {60} \] = \ [\ frac {1} {12} \]

Таким образом,

Модуль сдвига, G = \ [\ frac {\ text {напряжение сдвига}} {\ text {деформация сдвига}} \ ] = \ [\ frac {2450 \ times 12} {12} \]

= 2450 Н / м2.

Знаете ли вы?

Какая связь между упругими константами?

Модули упругости материала, такие как модуль Юнга, объемный модуль, модуль сдвига, являются специфическими формами закона Гука, который гласит, что для упругого материала деформация, испытываемая соответствующим приложенным напряжением, пропорциональна этому напряжению.Таким образом, мы можем записать связь между упругими постоянными следующим уравнением: 2G (1 + v) = E = 3K (1-2v)

Где,

Различия между жесткостью и прочностью в металле

Рисунок 1
На кривой зависимости деформации от напряжения, созданной во время испытания на растяжение, наклон линейного участка в начале определяет модуль Юнга. Первое отклонение от линейности — это предел текучести.

Термины «прочность» и «жесткость» часто используются как синонимы, но они имеют разное значение и значение.

Прочность

Прочность — это мера напряжения, которое может быть приложено к материалу до того, как он необратимо деформируется (предел текучести) или разрушается (предел прочности). Если приложенное напряжение меньше предела текучести, материал возвращается к своей исходной форме, когда напряжение снимается. Если приложенное напряжение превышает предел текучести, происходит пластическая или остаточная деформация, и материал больше не может вернуться к своей исходной форме после снятия нагрузки.

Имейте в виду, что эта остаточная деформация является целью штамповки. Исходной формой является плоский листовой металл, а формованные компоненты должны постоянно сохранять свою форму. Если выбранный листовой металл не может быть сформирован в желаемую форму при выбранных условиях обработки, приложенные напряжения превышают предел прочности листового металла на растяжение, что вызывает образование трещин в детали.

Прочность материала зависит от его химического состава, способа термомеханической обработки (например, преобразование толстого сляба в тонкий лист) и последующей термообработки.Эти переменные не позволяют утверждать, что один материал всегда прочнее другого. Например, многие марки алюминия прочнее марок стали, но редко предназначены для одного и того же применения.

Жесткость

Жесткость относится к тому, как компонент изгибается под нагрузкой, но при этом возвращается к своей исходной форме после снятия нагрузки. Поскольку размеры компонентов не изменяются после снятия нагрузки, жесткость связана с упругой деформацией.

С одной стороны, резиновая лента является примером материала с низкой жесткостью — она ​​может выдерживать большую деформацию и все еще возвращаться к своим первоначальным размерам при снятии нагрузки.С другой стороны, материал с высокой жесткостью, такой как алмаз, будет упруго деформироваться лишь на небольшую величину при приложении нагрузки.

Жесткость компонента зависит как от материала, так и от геометрии. Что касается материала, жесткость зависит от модуля упругости, также известного как модуль Юнга и сокращенно Е. Модуль Юнга — это отношение напряжения к деформации при очень малых деформациях. На кривой напряжение-деформация, созданной во время испытания на растяжение, наклон на линейном участке в начале — это место, где определяется модуль.Первое отклонение от линейности — это предел текучести (см. , рис. 1, ).

В отличие от прочности, которая может варьироваться от марки к марке или даже от рулона к рулону, модуль Юнга постоянен для данного металла и не зависит от термической обработки, обработки или холодной обработки. Модуль Юнга для стали (29 миллионов фунтов на квадратный дюйм) в три раза больше, чем у алюминия (10 миллионов фунтов на квадратный дюйм). Это означает, что при фиксированной геометрии деталь, сделанная из стали, будет в три раза жестче, чем если бы она была сделана из алюминия.Другими словами, алюминиевая деталь под нагрузкой будет прогибаться в три раза больше, чем стальная деталь, нагруженная аналогичным образом.

Толщина и форма формованной детали также влияют на ее жесткость. Жесткость пропорциональна кубу толщины. Чтобы нейтрализовать алюминий, который составляет одну треть жесткости стали, алюминиевая деталь должна быть на 44 процента толще, чем стальная. Даже при такой увеличенной толщине есть потенциал для снижения веса, поскольку плотность алюминия составляет одну треть от плотности стали.

Большая форма детали также увеличивает жесткость. Лист бумаги непрочный, но складка в центре делает его более жестким. Вытачки, бусинки и ребра — это формы, которые можно добавлять к деталям, чтобы ограничить изгиб. На частях поверхности, видимых потребителю, они называются характерными линиями или символьными линиями, выделенными из-за их эстетических преимуществ.

Рисунок 2
Ребра добавлены к конструкциям кузова грузовика, чтобы повысить общую жесткость.(Источник: www.tfltruck.com/2014/11/2015-ford-f-150-2-7l-v6-ecoboost-first-impressions-w-video)

Например, панели, которые составляют платформу пикапа (см. , рис. 2 ), являются одними из самых плоских на грузовике. Тем не менее, на рынке нет грузовика, который был бы разработан без этих ребер, которые помогли бы увеличить общую жесткость.

Однако листовой металл должен быть достаточно податливым, чтобы приспособиться к дополнительным формам. Ребра в панели кузова грузовика могут быть не очень глубокими, но металл необходимо растягивать на короткие расстояния.Также необходим штамповочный пресс большей мощности, чтобы создавать необходимые силы по всей панели.

Алюминий против стали в автомобилях

Для панелей обшивки, таких как капоты, двери и подъемные двери, автопроизводители предпочитают использовать листовой металл с максимально высокой прочностью, чтобы панель имела достаточную стойкость к вмятинам. Толщина также влияет на сопротивление вмятинам, ограничивая степень уменьшения толщины панели для уменьшения веса.

Ограничения жесткости дополнительно ограничивают толщину панелей обшивки.Если панели слишком тонкие, они могут начать раскачиваться и трепетать при движении автомобиля по дороге — если только линии символов не добавлены для дополнительного стиля.

Хотя это может показаться очевидным, автопроизводителям также необходимо указать продукт из листового металла, который может быть произведен в соответствии со стандартами поверхности класса А. Современные технологии ограничивают это листовой сталью или алюминием с прочностью менее 45 000 фунтов на квадратный дюйм. Соединение не является серьезным препятствием, поскольку существует несколько экономичных методов соединения внешней панели с внутренней.

При одинаковой верхней прочности, доступной для любого материала, и нескольких марок от нескольких поставщиков любого металла, которые могут быть произведены достаточно тонкими, тот, который предлагает наилучшее сочетание стоимости и экономии веса, станет оптимальным выбором для приложений навесных панелей. .

Применение

в конструкции кузова связано с различными проблемами. Жесткость важна для обработки, а также шума, вибрации и резкости (NVH). В дополнение к внутренней жесткости, связанной с материалом и геометрией детали, характеристики NVH можно улучшить с помощью легких вспененных полимеров.С другой стороны, сопротивление столкновению более тесно связано с силой. Для той же конструкции сталь имеет значительное преимущество в доступных вариантах. Если поверхность класса A не требуется, в продаже имеются марки стали с пределом прочности на разрыв, превышающим 230000 фунтов на квадратный дюйм.

Это не означает, что алюминиевые конструкции кузова невозможны. На рынке есть много примеров, хотя они склоняются к более дорогим автомобилям, в которых облегчение для повышения экономии топлива не является основной проблемой, а стоимость листового металла составляет меньший процент от цены сделки.

Улучшенная ударопрочность будет обеспечиваться за счет более высокой прочности, а также компонентов, которые имеют ударопрочную конструкцию, например, закрытые секции, фланцы большего размера или более высокую форму — все это может потребовать большей пластичности от более прочных марок алюминия.

Кроме того, эти части должны соединяться прочно, быстро и экономично. Ford потратил почти 1 миллиард долларов на реконструкцию завода F150 для штамповки и сборки алюминиевой кабины и кровати и соединения их со стальной рамой.Это финансовое препятствие может ограничить количество автопроизводителей, готовых пойти ва-банк и создать кузов с высоким содержанием алюминия.

Дэниел Шеффлер — президент Engineering Quality Solutions Inc., P.O. Box 187, Southfield, MI 48037, 248-667-8335, [email protected], www.eqsgroup.com, и главный контент-директор 4M Partners LLC, P.O. Box 71191, Rochester Hills, MI 48307, www.learning4m.com.

Лист материала углеродистой стали A36

Углеродистая сталь A36 Технические характеристики Углерод 0.29 макс Утюг Баланс Марганец 0,85 — 1,2 фосфор 0,04 макс Кремний 0.15 — 0,4 Сера 0,05 макс Плотность 0,284 фунта / дюйм Прочность на разрыв 58000 — 79800 фунтов на кв. Дюйм Предел прочности при растяжении 36300 фунтов на кв. Дюйм Удлинение при разрыве 20% Удлинение при разрыве 23% Модуль упругости 29000 тысяч фунтов / кв. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт