Построение правильных многоугольников — Техническое черчение
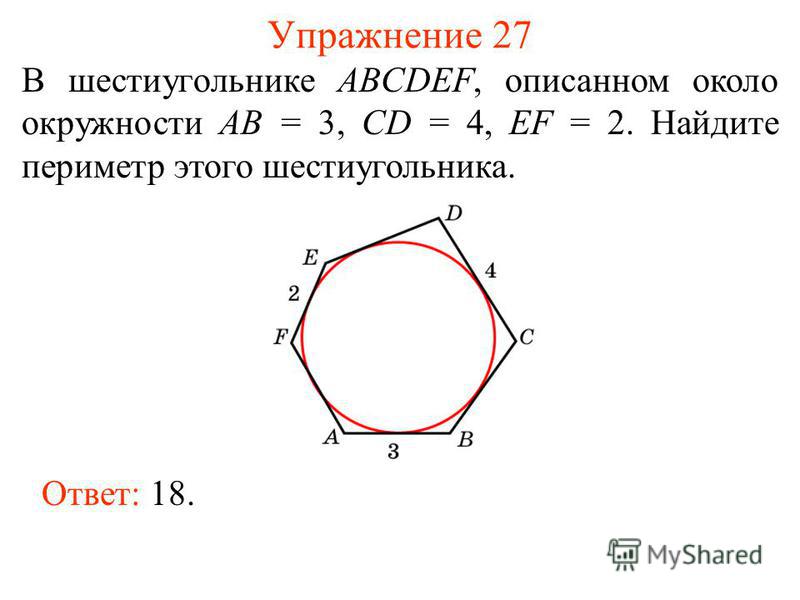
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4.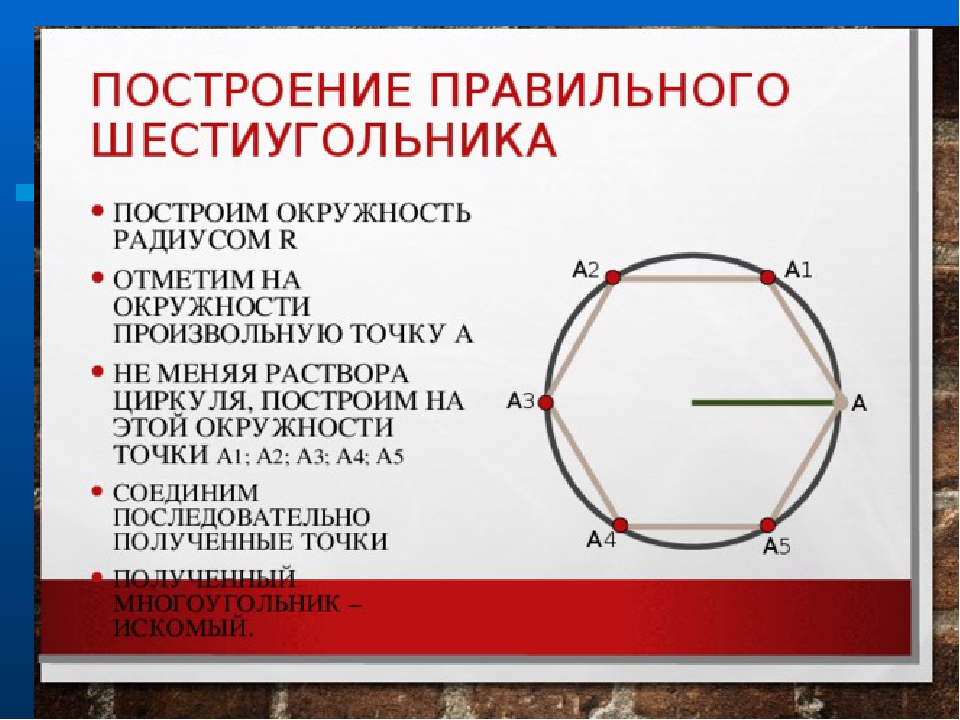 Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.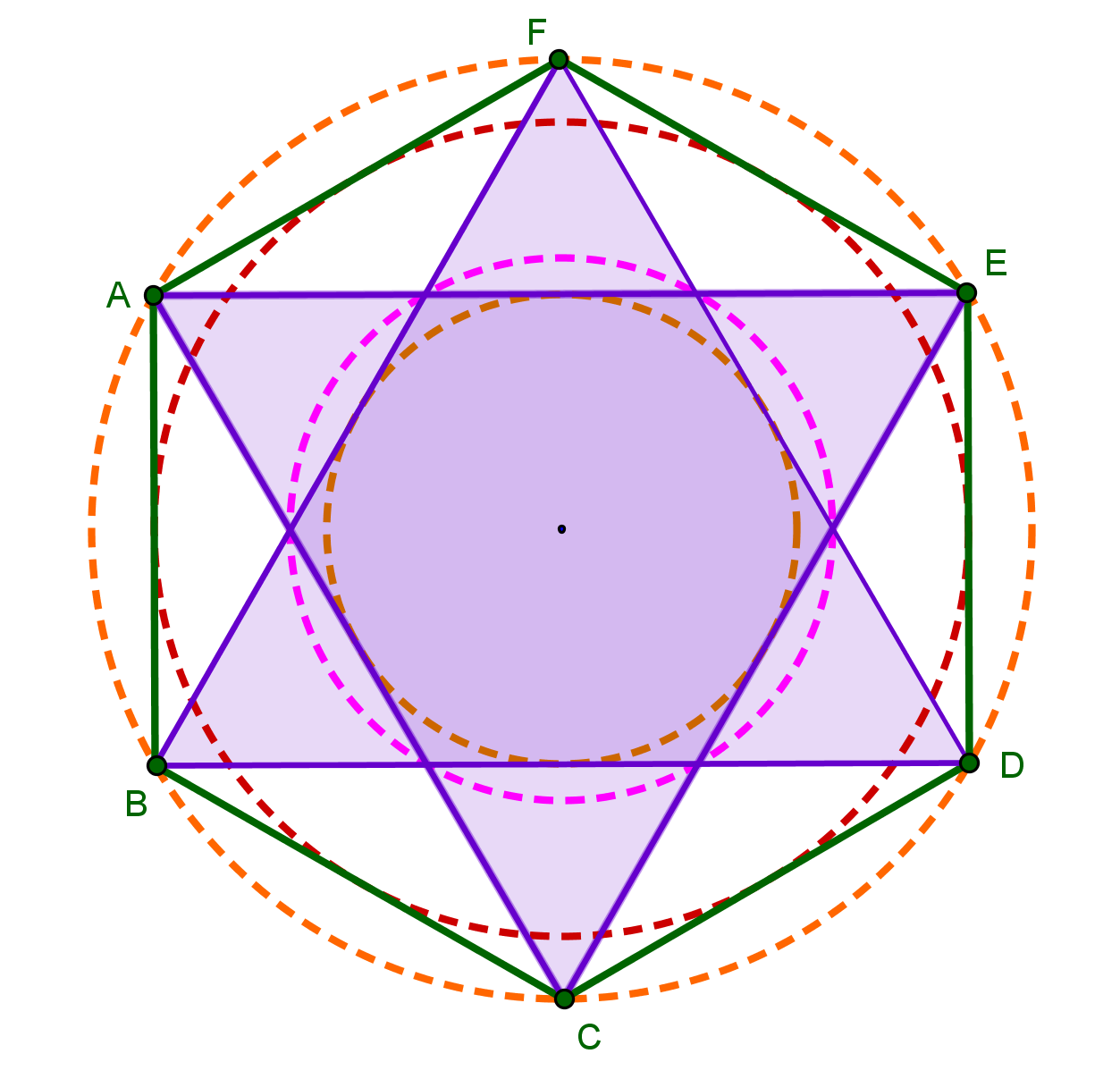
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Построение правильного пятиугольника. Построение пятиугольника подробно Как нарисовать идеальный пятиугольник
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.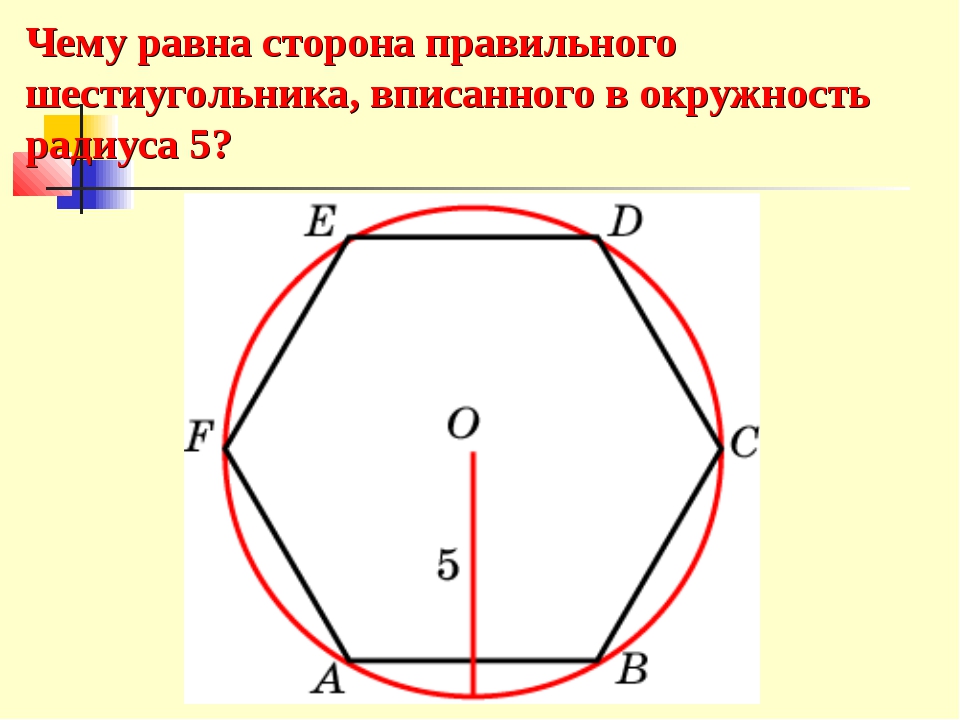
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.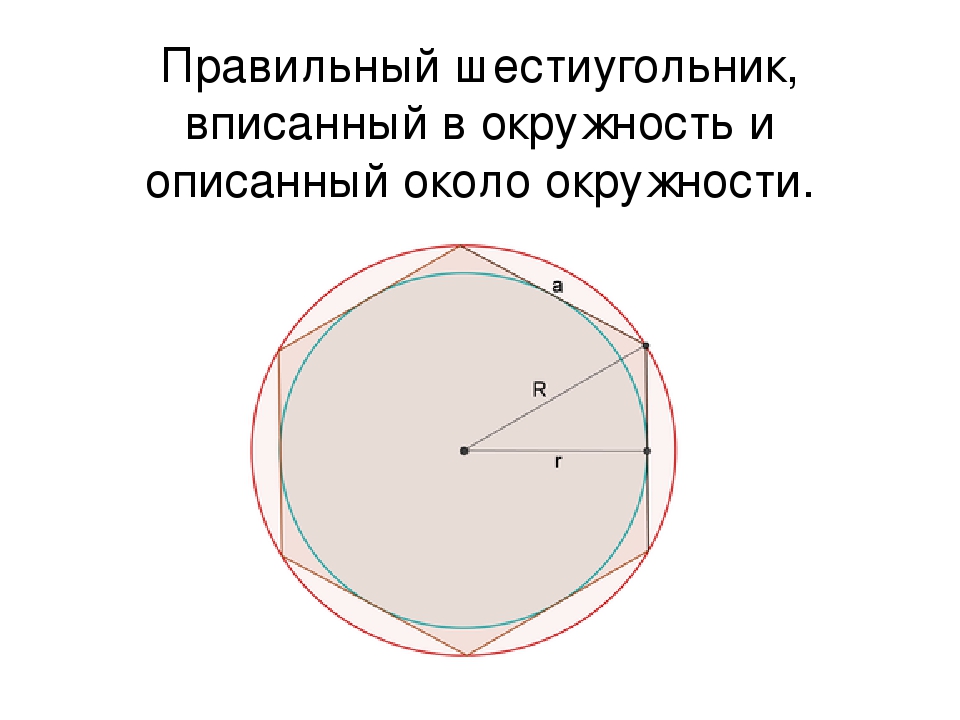 Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
8 июня 2011Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.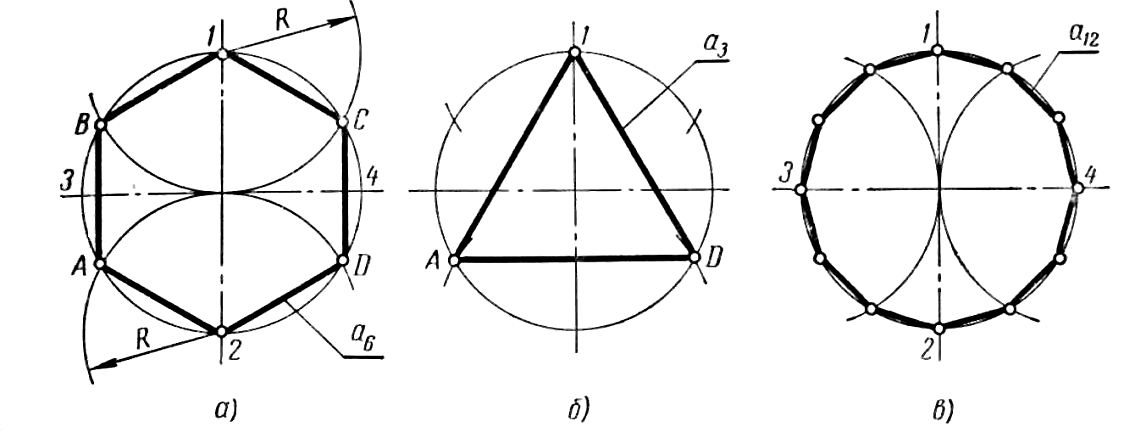
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах.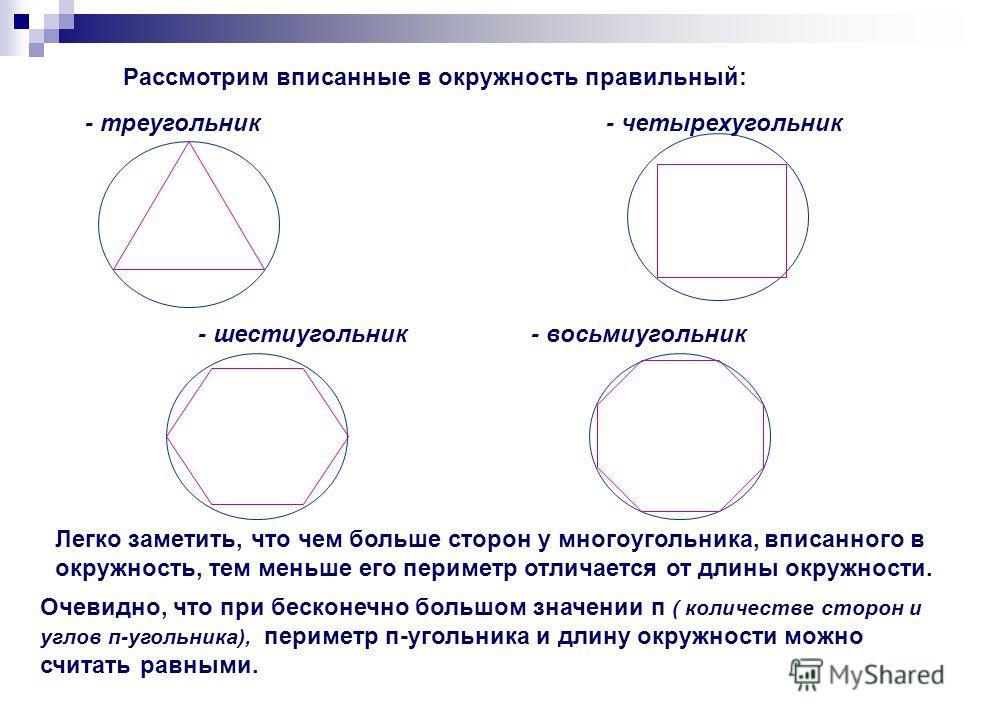 А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.
Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.Построение правильных многоугольников
На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Для выполнения построений мы
используем циркуль и линейку.
Циркуль позволяет:
– построить окружность,
– построить дугу окружности,
– отложить на прямой отрезок, равный данному.
Линейка позволяет:
– построить прямую линию,
– построить отрезок, соединяющий две точки,
– найти точку пересечения двух прямых.
Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.
Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.
Задача 1. Вписать в заданную окружность правильный треугольник
Решение.
Первый способ.
Построение.
Пусть задана окружность с центром О. Проведем произвольный диаметр BD
окружности. Построим прямую l,
являющуюся серединным перпендикуляром к радиусу OD.
Середину радиуса ОD обозначим точкой
К. Отметим точки А и C
– пересечения прямой l
с окружностью. И построим отрезки BA
и BC. Треугольник ABC
– правильный.
Отметим точки А и C
– пересечения прямой l
с окружностью. И построим отрезки BA
и BC. Треугольник ABC
– правильный.
Доказательство.
В катет .
Тогда , .
Отсюда, .
Значит, – равносторонний – правильный.
Второй способ построения.
Пусть задана окружность с центром О. Раствором циркуля, равным радиусу, последовательно от одной точки окружности делаем на ней засечки, пока последняя засечка не совпадет с взятой первоначально точкой. Соединив полученные точки через одну, получим правильный треугольник.
Задача 2. Вписать в заданную окружность правильный четырехугольник.
Решение.
Построение.
Пусть задана окружность с центром О. Построим диаметр AC.
Затем построим диаметр BD
перпендикулярный
диаметру AC. Точки А, C
и B, D
– точки пересечения диаметров с окружностью. И построим отрезки АB,
BC, CD
и АD. Четырехугольник ABCD
– правильный.
И построим отрезки АB,
BC, CD
и АD. Четырехугольник ABCD
– правильный.
Доказательство.
Т.к. , , то – параллелограмм.
Т.к. ,то – прямоугольник.
Т.к. ,то – ромб.
Т.к. ,то – квадрат.
Следовательно, – квадрат.
Значит, – правильный четырехугольник.
Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.
Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.
Решение.
Построение. Так
как в правильном шестиугольнике сторона а равна радиусу, то достаточно
последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN
– заданный отрезок. Построим окружность с произвольным центром О и радиуса MN.
Отметим на этой окружности произвольную точку А.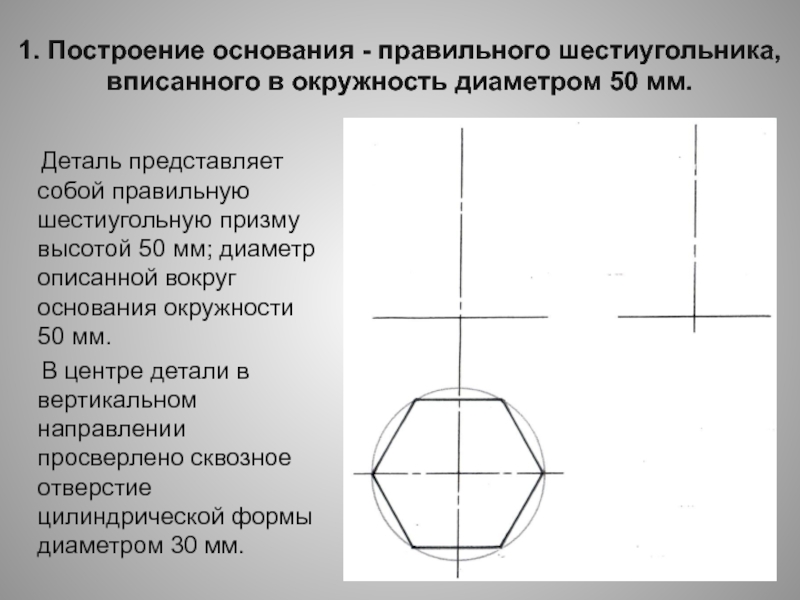 Затем, не меняя раствора
циркуля, последовательно от этой точки А будем делать на окружности засечки,
пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим
точки B, C,
D, Е и F.
Теперь соединим последовательно построенные точки отрезками. Получим искомый
правильный шестиугольник ABCD.
Затем, не меняя раствора
циркуля, последовательно от этой точки А будем делать на окружности засечки,
пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим
точки B, C,
D, Е и F.
Теперь соединим последовательно построенные точки отрезками. Получим искомый
правильный шестиугольник ABCD.
Доказательство.
Равные хорды стягивают равные дуги.
Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.
Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.
Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.
Решение.
Построение.
Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.
1. –
точка пересечения биссектрис и
.
2. Окружность .
3. – серединные
перпендикуляры к .
4.
.
5. – правильный двенадцатиугольник.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2k угольник, где k – любое целое число, большее 2.
Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.
С давних времен построению
правильных многоугольников математики уделяли большое внимание. Древние греки
умели строить правильные треугольники, четырехугольники, пятиугольники.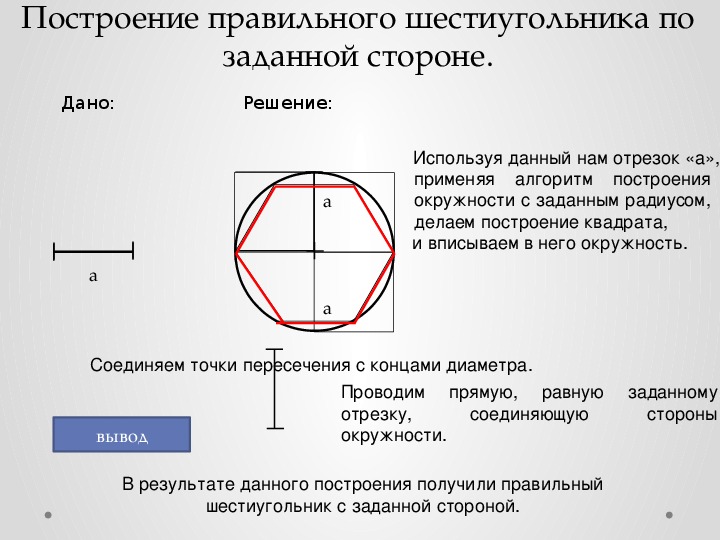 А также
многоугольники, получаемые удвоением их сторон, шестиугольники,
восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000
лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли
«королем математики», решил эту математическую проблему. Будучи девятнадцати
летним юношей, он доказал, что можно построить правильный семнадцати-угольник,
а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник
циркулем и линейкой построить нельзя. Задача о построении правильного
семнадцати-угольника была самым первым его научным открытием.
А также
многоугольники, получаемые удвоением их сторон, шестиугольники,
восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000
лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли
«королем математики», решил эту математическую проблему. Будучи девятнадцати
летним юношей, он доказал, что можно построить правильный семнадцати-угольник,
а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник
циркулем и линейкой построить нельзя. Задача о построении правильного
семнадцати-угольника была самым первым его научным открытием.
Подведем итоги урока.
Сегодня мы рассмотрели способы
построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились
строить правильные треугольник и четырехугольник, вписанные в окружность. А
также выполнили задачу на построение правильного многоугольника по заданному отрезку,
и задачу на построение правильного 2n-угольника
по заданному n-угольнику.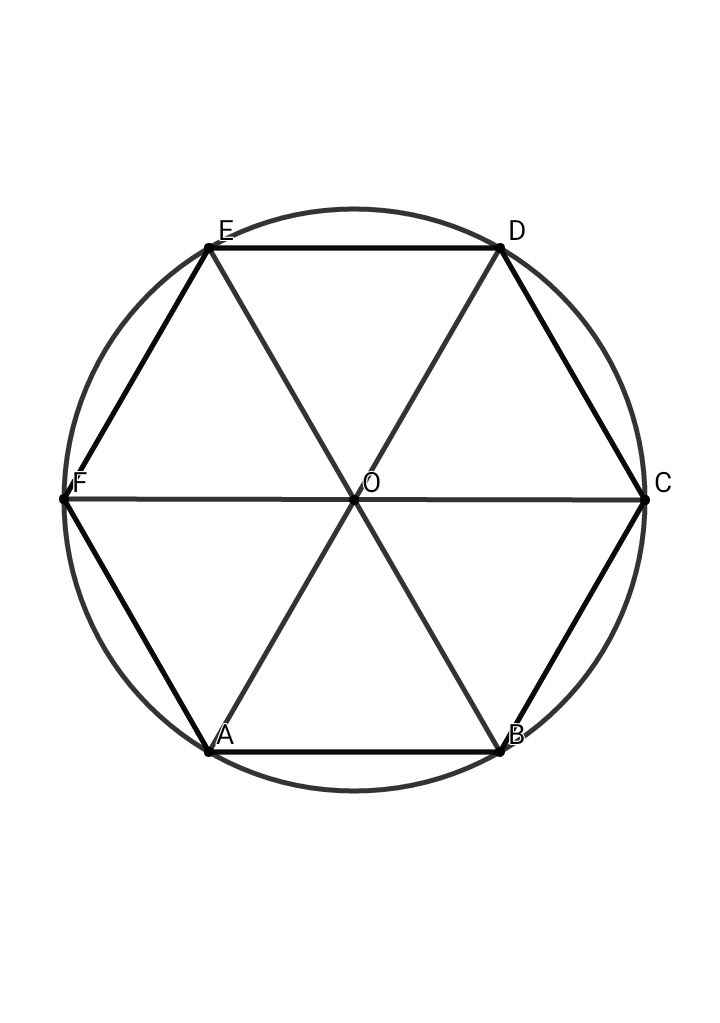
Как построить правильный шестиугольник с помощью циркуля. Как построить правильный шестиугольник. Определение и построение
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:
- Синий: C 65 M 23 Y 35 K 0
- Бежевый: C 13 M 13 Y 30 K 0
- Персиковый: C 0 M 32 Y 54 K 0
- Светло-розовый: C 0 M 64 Y 42 K 0
- Темно-розовый: C 30 M 79 Y 36 K 4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B .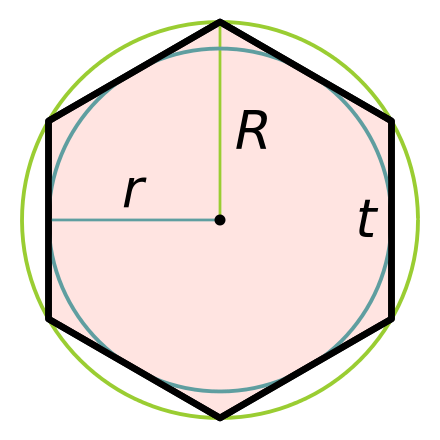 Выровняйте группы.
Выровняйте группы.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .
Рисунок 38
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Рисунок 39
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.
Рисунок 40
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана.
 R и r — радиусы описанной и вписанной окружности.
R и r — радиусы описанной и вписанной окружности. - Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Содержимое:
Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Шаги
1 Рисуем идеальный шестиугольник при помощи циркуля
- 1 При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
- Иногда легче сначала нарисовать пол круга, а затем вторую половину.
- 2 Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
- 3 Сделайте небольшую отметку карандашом на краю круга. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете.
 Не забудьте сохранять угол, который вы установили для циркуля.
Не забудьте сохранять угол, который вы установили для циркуля. - 4 Передвиньте иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
- 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
- 6 Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
- 7 Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
- 8
Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали.
 После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
2 Рисуем грубый шестиугольник при помощи круглого предмета и линейки
- 1 Обведите ободок стакана карандашом. Таким образом, вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
- 2 Нарисуйте горизонтальные линии через центр вашего круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив его пополам.
- 3 Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций. Так как вы уже провели линию через середину круга, Х должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.

- 4 Сделайте из каждой секции треугольники. Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник. Сделайте это с оставшимися пятью секциями. Думайте об этом, как об изготовлении корочки вокруг ваших кусков пиццы.
- 5 Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.
3 Рисуем грубый шестиугольник при помощи одного карандаша
- 1 Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку вашей горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может быть всего пара сантиметров.
- 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа.
 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии. - 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом, будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
- 4 Нарисуйте еще одну горизонтальную линию, соединяя нижние две диагональные линии. Таким образом, вы нарисуете основу для своего шестиугольника. В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.
- Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
- Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.

Предупреждения
- Циркуль — довольно острый предмет, будьте с ним очень аккуратны.
Принцип работы
- Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Пара циркулей
- Что-то, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала.
- Ластик
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности.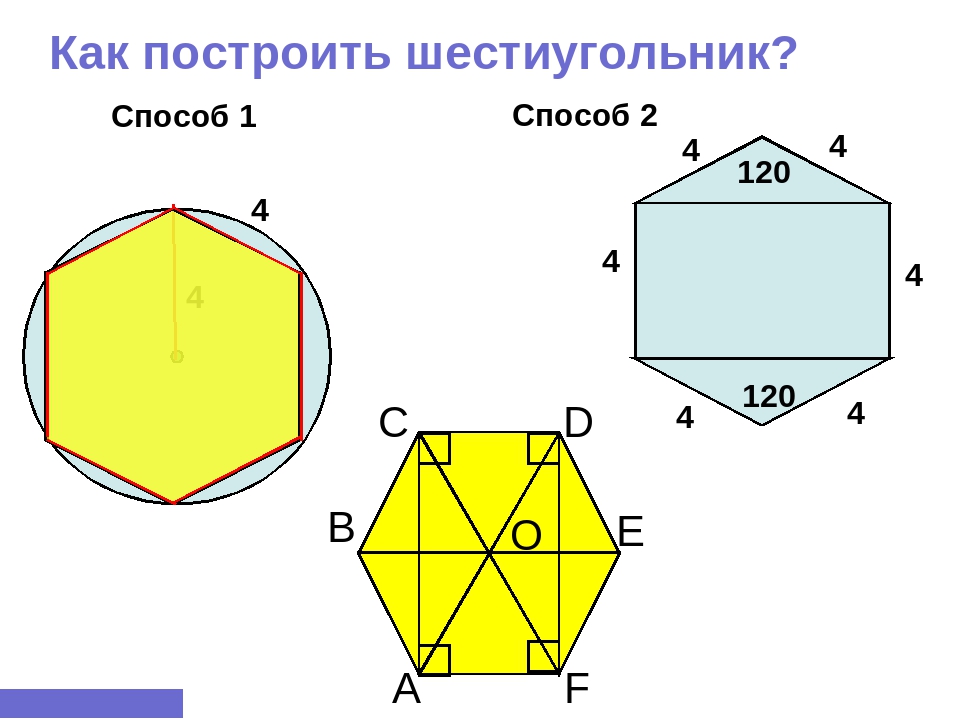 Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.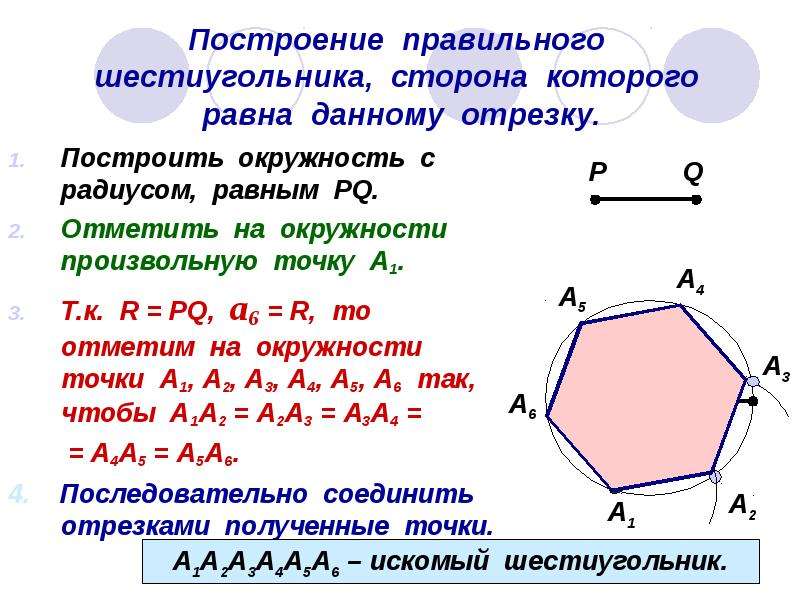
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2.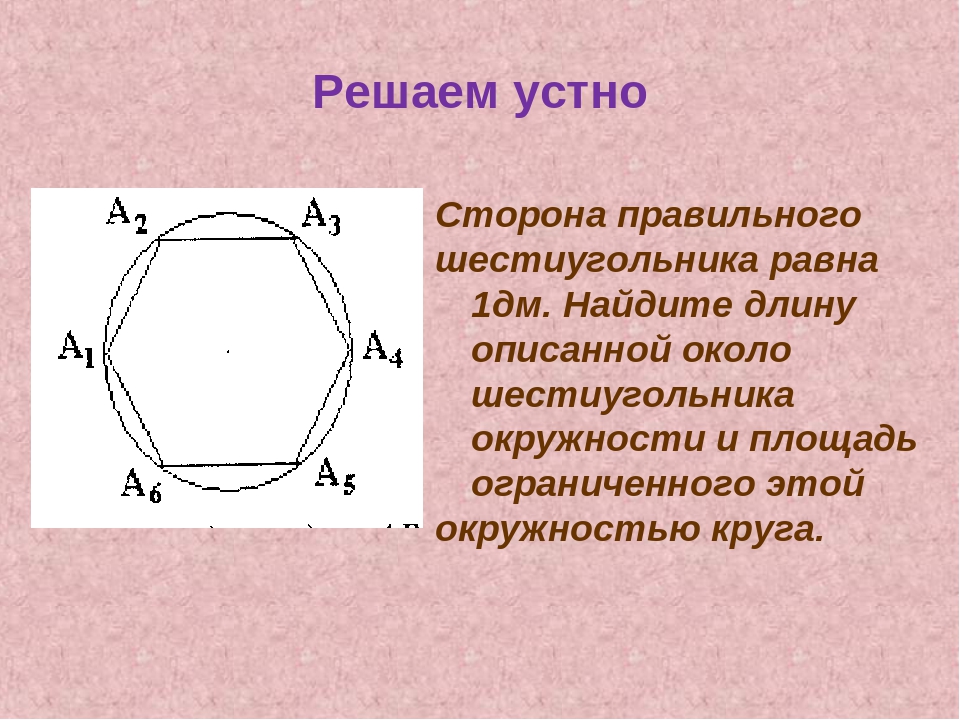 Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6.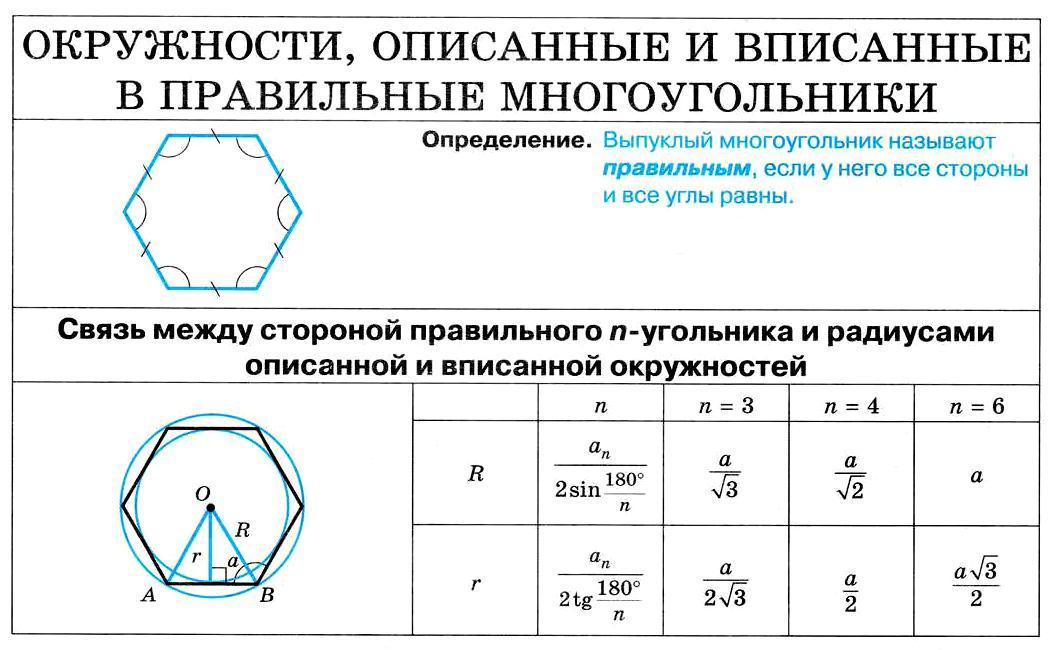 Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией.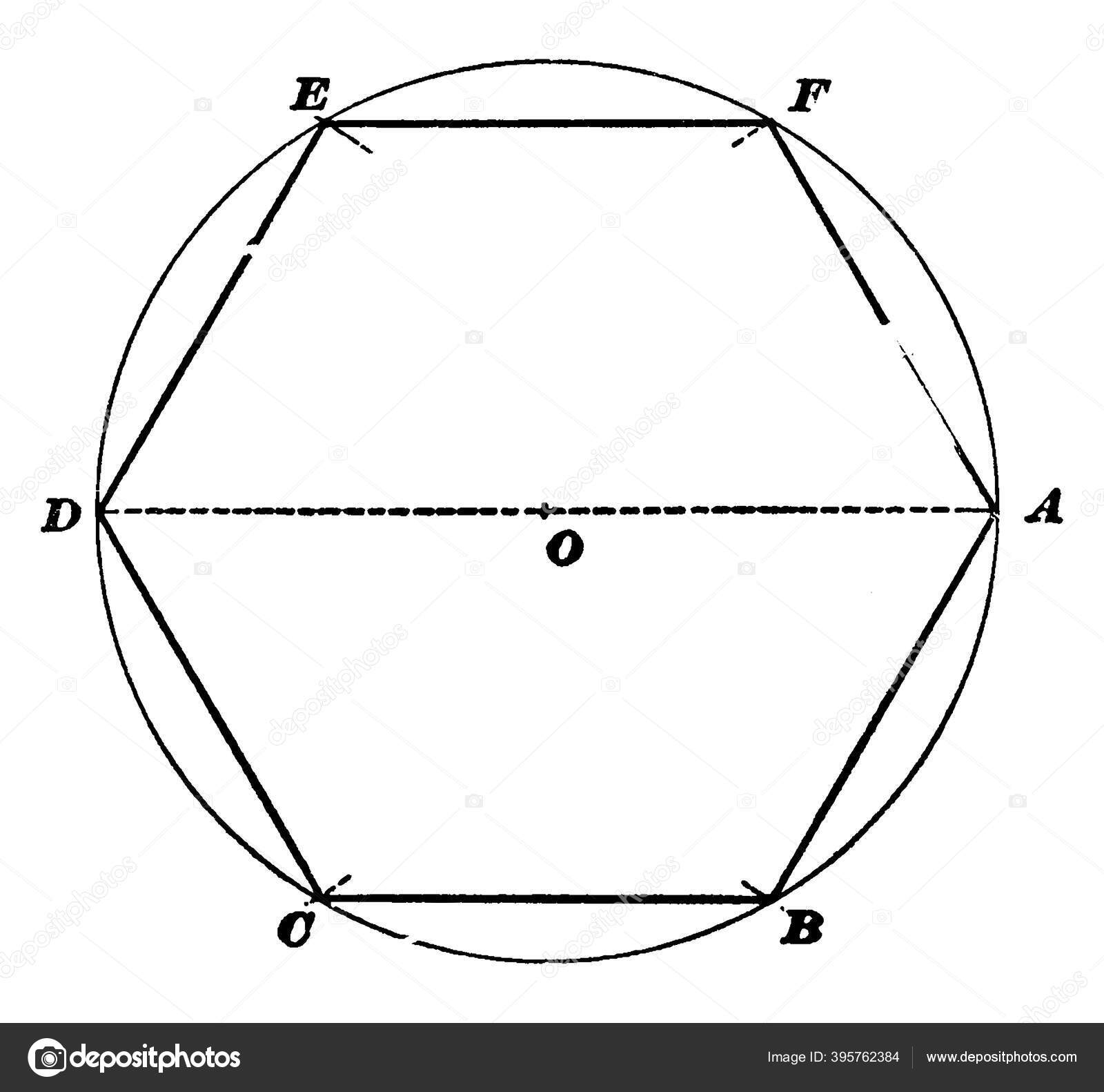 Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- – циркуль;
- – линейка;
- – карандаш;
- – лист бумаги.
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.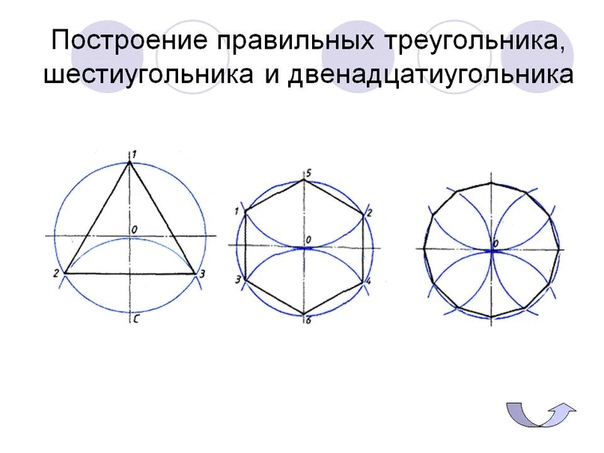
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
Так построения будут особенно точны.
Презентация по математике «Построение правильных многоугольников циркулем и линейкой»
Презентация на тему: Построение правильных многоугольников циркулем и линейкойСкачать эту презентацию
Скачать эту презентацию
№ слайда 1 Описание слайда:” Построение правильных многоугольников циркулем и линейкой ” .
№ слайда 2 Описание слайда:Цель урока Создать условия для более глубокого усвоения знаний по теме, высокого уровня обобщения и систематизации знаний.
№ слайда 3 Описание слайда:Методические задачи Выяснить , всякий ли правильный многоугольник можно построить с помощью циркуля и линейки; Повторить способы построения правильных многоугольников и познакомить с новыми способами; Познакомить с перспективными технологиями и новыми разработками построения правильных многоугольников; Показать применение правильных многоугольников в окружающем нас мире.
Выпуклые и невыпуклые многоугольники Многоугольник- это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону. На рисунке 1 многоугольник F1 выпуклый, а многоугольник F2 невыпуклый. Многоугольник называется невыпуклым, если прямая, содержащая сторону многоугольника разбивает его на две части. Все треугольники выпуклы, а многоугольники с большим числом сторон могут быть как выпуклыми, так и невыпуклыми.
№ слайда 5 Описание слайда:Правильные многоугольники На рисунке 1 представлены правильный треугольник , шестиугольник и четырех угольник.
№ слайда 6 Описание слайда:Великий математик, механик и инженер древности Архимед (греч. Αρχιμήδης, родился 287 до н. э. — 212 до н. э.) Периметр (сумма длин сторон) правильного n-угольника при заданном числе сторон n наиболее близок к длине его описанной окружности среди всех вписанных в нее n-угольников; таким же свойством он обладает и по отношению к вписанной окружности. Поскольку вычисление длины окружности считалось в древности весьма важной задачей, много усилий было затрачено на то, чтобы научиться оценивать периметр вписанной в нее правильного многоугольника при достаточно больших n. Особенно преуспел в этом Архимед.
Αρχιμήδης, родился 287 до н. э. — 212 до н. э.) Периметр (сумма длин сторон) правильного n-угольника при заданном числе сторон n наиболее близок к длине его описанной окружности среди всех вписанных в нее n-угольников; таким же свойством он обладает и по отношению к вписанной окружности. Поскольку вычисление длины окружности считалось в древности весьма важной задачей, много усилий было затрачено на то, чтобы научиться оценивать периметр вписанной в нее правильного многоугольника при достаточно больших n. Особенно преуспел в этом Архимед.
Евклид ( родился в 330 году до н. э. в небольшом городке Тире, недалеко от Афин). Впрочем, правильные многоугольники привлекали внимание древнегреческих учёных задолго до Архимеда. Пифагорейцы, в философии которых числа играли главную роль, придавали очень большое значение задаче о делении окружности на равные части, т. е. о построении правильного вписанного многоугольника. В \»Началах\» Евклида приводятся построения с помощью циркуля и линейки правильных многоугольников с числом сторон от трёх до шести, а также пятнадцати угольника. Этим последним особенно интересовались: согласно измерениям древних астрономов, угол наклона плоскости эклиптики к экватору равнялся 1/5 полного угла, т.е. 24°(истинное значение чуть меньше -23°27\’). Задача о построение правильных многоугольников была полностью решена лишь спустя два тысячелетия.
В \»Началах\» Евклида приводятся построения с помощью циркуля и линейки правильных многоугольников с числом сторон от трёх до шести, а также пятнадцати угольника. Этим последним особенно интересовались: согласно измерениям древних астрономов, угол наклона плоскости эклиптики к экватору равнялся 1/5 полного угла, т.е. 24°(истинное значение чуть меньше -23°27\’). Задача о построение правильных многоугольников была полностью решена лишь спустя два тысячелетия.
Основные формулы. Вычисление угла правильного многоугольника : Сторона правильного многоугольника : Площадь правильного многоугольника : Радиус вписанной окружности :
№ слайда 9 Описание слайда:.Применение формул Для правильного треугольника Для правильного четырехугольника Для правильного шестиугольника Теорема. Правильные одноимённые многоугольники подобны и стороны их относятся как радиусы или апофемы. Следствие. Периметры правильных одноимённых многоугольников относятся как радиусы или как апофемы.
Следствие. Периметры правильных одноимённых многоугольников относятся как радиусы или как апофемы.
Любой ли правильный многоугольник можно построить с помощью циркуля и линейки ? Если построен какой-нибудь правильный n-угольник, то с помощью циркуля и линейки можно построить правильный 2n-угольник. Опишем около данного многоугольника А1, А2… Аn oкружность. Для этого построим серединные перпендикуляры a и b к oтрезкам А1 А2 и А2 А3 ( на рисунке n= 4). Они пересекаются в некоторой точке О. Окружность с центром О радиуса ОА1 является описанной около многоугольника А1 А2…Аn. Построим теперь середины B1, B2, …, Bn соответственно дуг А1 А2, А2А3,…, Аn А1 следующим образом. Точки B1и B2 получаются как точки пересечения прямых а и b с дугами А1 А2 и А2 А3. Для построения точки B3 проведём oкружность с центром А3 радиуса А3 B2. Одна из точек пересечения этой oкружности с описанной окружностью есть точка B2, а другая — искомая точка B3. k*n)-угольник, где k — любое натуральное число.
k*n)-угольник, где k — любое натуральное число.
Построение правильных многоугольников с помощью циркуля и линейки . Задача №1. Построение правильного шестиугольника и треугольника. Согласно формуле аn= 2R*sin180°/n сторона АВ правильного шестиугольника равна радиусу R описанной окружности. Поэтому, если задан произвольный отрезок PQ, то для построения правильного шестиугольника, стороны которого равны PQ, достаточно построить окружность радиуса PQ, взять на ней произвольную точку А и, не меняя раствора циркуля, отметить на этой окружности последовательно точки B, C, D, E, F так, чтобы AB=BC=…=EF=PQ. Проведя затем отрезки AB, BC, CD, DE, EF, FA, получим шестиугольник ABCDEF, который согласно теореме о правильном многоугольнике является правильным, причем его стороны равны отрезку PQ. Для того, чтобы построить правильный треугольник нужно соединить точки данного шестиугольника через одну, значит соединим точки A,C и E.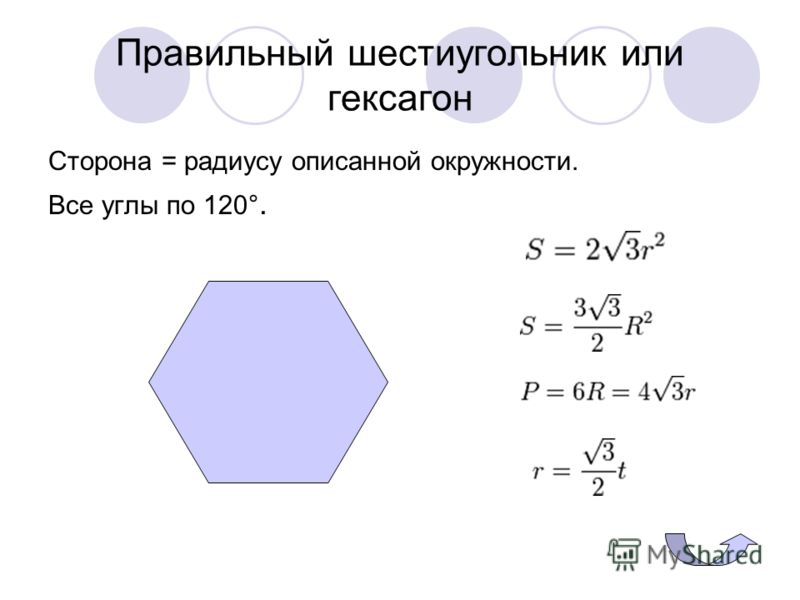 Треугольник ACE- искомый.
Треугольник ACE- искомый.
Задача №2. Построение правильного четырехугольника и восьмиугольника. Пусть w-данная окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат. Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2…А8-искомый восьмиугольник.
№ слайда 13 Описание слайда:… Задача №3. Найти углы правильного десятиугольника и выразить его сторону через радиус R описанной окружности.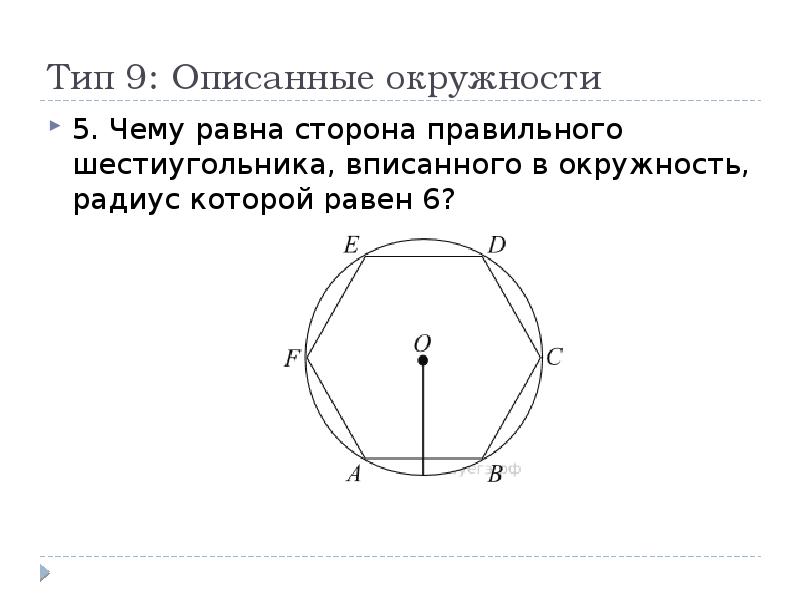 Решение. По формуле аn=(n-2)/n*180° находим угол а10 правильного десятиугольника: а10=(10-2)/10*180°= 144°. Пусть АВ- сторона правильного десятиугольника, вписанного в окружность радиуса R с центром в точке О. По формуле аn= 2R*sin180°/n АВ=2R*sin18°. Получим другое выражение для стороны АВ. С этой целью рассмотрим треугольник АВО и проведем его биссектрису АС. Так как угол АОВ= 360°/10= 36°, то угол ОАВ= (180°-36°)/2= 72°, угол ВАС= 1/2*угол ОАВ= 1/2*72°= 36°. Отсюда следует, что треугольник АОВ~ треугольнику САВ по двум углам (угол АОВ = угол ВАС= 36°, угол В -общий). Поэтому АВ=АС и АВ/ОВ= ВС/АВ. Далее, треугольник АОС равнобедренный (угол АОС= угол ОАС= 36°), следовательно, АС=ОС. Итак, АВ=АС=ОС=R-BC, откуда ВС=R-АВ, и пропорцию АВ/ОВ=ВС/АВ можно записать в виде АВ/R=(R-AB)/AB. Отсюда получаем квадратное уравнение относительно АВ: АВ + R*АВ -R =0. Решая это уравнение и учитывая, что АВ>0, находим АВ= R/2( 5-1) (Замечание. Сравнивая полученное выражение для АВ с равенством АВ=2R*sin18°, находим значение sin18°: sin18°= ( 5-1)/4
Решение. По формуле аn=(n-2)/n*180° находим угол а10 правильного десятиугольника: а10=(10-2)/10*180°= 144°. Пусть АВ- сторона правильного десятиугольника, вписанного в окружность радиуса R с центром в точке О. По формуле аn= 2R*sin180°/n АВ=2R*sin18°. Получим другое выражение для стороны АВ. С этой целью рассмотрим треугольник АВО и проведем его биссектрису АС. Так как угол АОВ= 360°/10= 36°, то угол ОАВ= (180°-36°)/2= 72°, угол ВАС= 1/2*угол ОАВ= 1/2*72°= 36°. Отсюда следует, что треугольник АОВ~ треугольнику САВ по двум углам (угол АОВ = угол ВАС= 36°, угол В -общий). Поэтому АВ=АС и АВ/ОВ= ВС/АВ. Далее, треугольник АОС равнобедренный (угол АОС= угол ОАС= 36°), следовательно, АС=ОС. Итак, АВ=АС=ОС=R-BC, откуда ВС=R-АВ, и пропорцию АВ/ОВ=ВС/АВ можно записать в виде АВ/R=(R-AB)/AB. Отсюда получаем квадратное уравнение относительно АВ: АВ + R*АВ -R =0. Решая это уравнение и учитывая, что АВ>0, находим АВ= R/2( 5-1) (Замечание. Сравнивая полученное выражение для АВ с равенством АВ=2R*sin18°, находим значение sin18°: sin18°= ( 5-1)/4
Задача 4. Построение правильного десятиугольника и пятиугольника. Пусть w- данная окружность радиуса R c центром О. Построим сначала правильный десятиугольник, вписанный в окружность w. Для этого проведем взаимно перпендикулярные радиусы ОА1 и ОВ окружности w и на отрезке ОВ как на диаметре построим окружность с центром С. Отрезок А1С пересекает эту окружность в некоторой точке D. Докажем, что отрезок А1D равен стороне правильного десятиугольника, вписанного в окружность w. В самом деле, А1D=А1С-R/2, А1С= А1О + ОС = R +( R /2) = 5 R /4 = R 5/2 А1D= R 5/2 – R/2 = R /2 ( 5-1) Далее отметим на окружности w точки А2, А3, … , А10 так, что А1А2= А2А3=… =А9А10 = А1D. Десятиугольник А1А2…А10-искомый. Для того, чтобы построить правильный пятиугольник нужно соединить точки данного десятиугольника через одну, значит соединим точки А1,А3,А5,А7,А9. Пятиугольник А1А3А5А7А9- искомый.
Построение правильного десятиугольника и пятиугольника. Пусть w- данная окружность радиуса R c центром О. Построим сначала правильный десятиугольник, вписанный в окружность w. Для этого проведем взаимно перпендикулярные радиусы ОА1 и ОВ окружности w и на отрезке ОВ как на диаметре построим окружность с центром С. Отрезок А1С пересекает эту окружность в некоторой точке D. Докажем, что отрезок А1D равен стороне правильного десятиугольника, вписанного в окружность w. В самом деле, А1D=А1С-R/2, А1С= А1О + ОС = R +( R /2) = 5 R /4 = R 5/2 А1D= R 5/2 – R/2 = R /2 ( 5-1) Далее отметим на окружности w точки А2, А3, … , А10 так, что А1А2= А2А3=… =А9А10 = А1D. Десятиугольник А1А2…А10-искомый. Для того, чтобы построить правильный пятиугольник нужно соединить точки данного десятиугольника через одну, значит соединим точки А1,А3,А5,А7,А9. Пятиугольник А1А3А5А7А9- искомый.
. Задача 5. В данную окружность вписать правильный пятнадцатиугольник. Решение. Пусть w- данная окружность радиуса R с центром O и АВ — сторона правильного вписанного в эту окружность десятиугольника, а АС- сторона правильного вписанного шестиугольника, причем точки В и С расположены на окружности так, как показано на рисунке а). Тогда, очевидно, дуга АВ=36°, дуга АС=60° , поэтому дуга ВС=24° . Следовательно, угол ВОС=24°=360°/15°, и, значит, отрезок ВС- сторона правильного пятнадцатиугольника, вписанного в окружность w. Так как мы умеем строить циркулем и линейкой отрезки АВ=((корень из 5-1)/2)*R и АС=R (рис.б)), то можем построить отрезок ВС. Возьмем далее на окружности w произвольную точку А1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, А3,…, А15 так, что А1А2 = А2А3=…= А14А15= ВС. Проведя затем отрезки А1А2, А2А3,…, А14А15, А15А1, получим искомый правильный пятнадцатиугольник А1А2…А15 (рис. в)).
Решение. Пусть w- данная окружность радиуса R с центром O и АВ — сторона правильного вписанного в эту окружность десятиугольника, а АС- сторона правильного вписанного шестиугольника, причем точки В и С расположены на окружности так, как показано на рисунке а). Тогда, очевидно, дуга АВ=36°, дуга АС=60° , поэтому дуга ВС=24° . Следовательно, угол ВОС=24°=360°/15°, и, значит, отрезок ВС- сторона правильного пятнадцатиугольника, вписанного в окружность w. Так как мы умеем строить циркулем и линейкой отрезки АВ=((корень из 5-1)/2)*R и АС=R (рис.б)), то можем построить отрезок ВС. Возьмем далее на окружности w произвольную точку А1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, А3,…, А15 так, что А1А2 = А2А3=…= А14А15= ВС. Проведя затем отрезки А1А2, А2А3,…, А14А15, А15А1, получим искомый правильный пятнадцатиугольник А1А2…А15 (рис. в)).
А так ли уж важно изучать и знать сведения о правильных многоугольниках? В каких житейских ситуациях можно встретиться с правильными многоугольниками? Историческая справка. В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников (3600: 600 = 6), либо четыре квадрата (3600: 900 = 4), либо три правильных шестиугольника (3600: 1200 = 3), так как сумма углов с вершиной этой точки равна 3600. Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника? Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.). Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек. Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников (3600: 600 = 6), либо четыре квадрата (3600: 900 = 4), либо три правильных шестиугольника (3600: 1200 = 3), так как сумма углов с вершиной этой точки равна 3600. Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника? Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.). Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек. Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.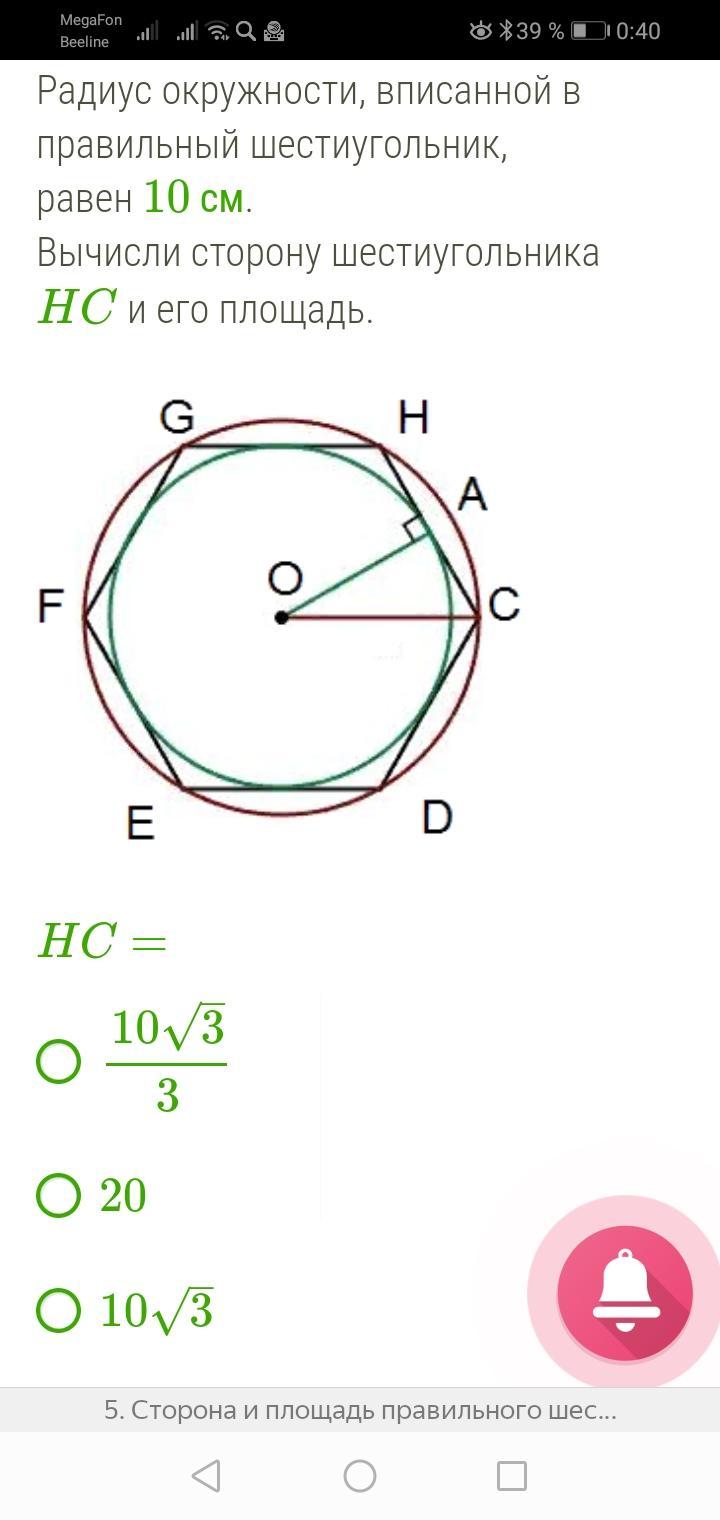 И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Петропавловская крепость
№ слайда 18 Описание слайда:Платоновы тела Платоновы тела — трехмерный аналог плоских правильных многоугольников. Существует лишь пять выпуклых правильных многогранников — тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются \»Начала\» Евклида. Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды .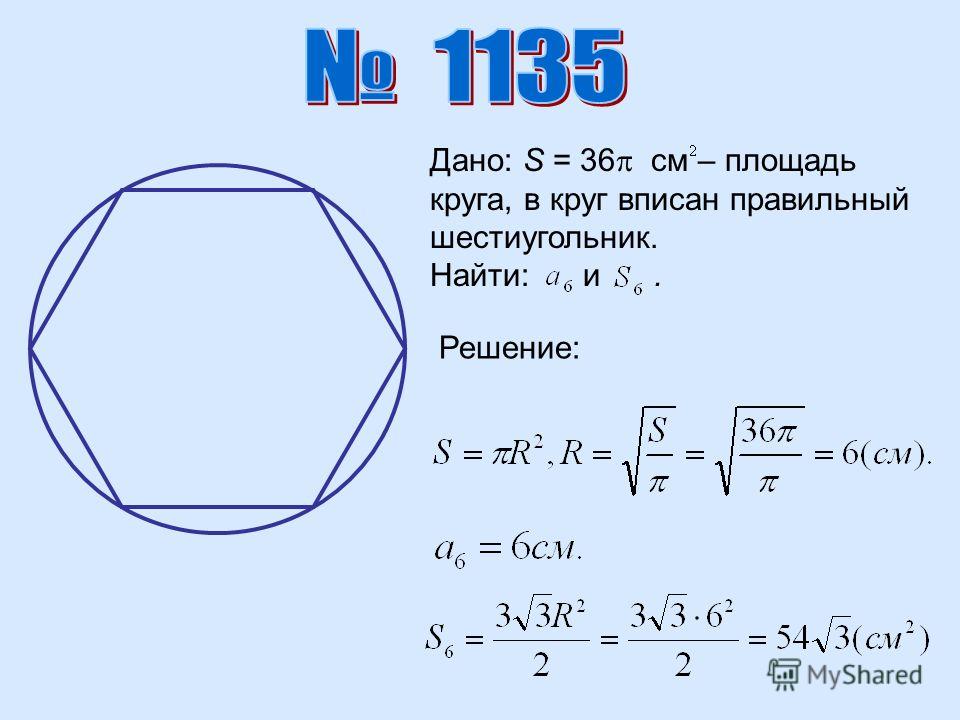 Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
огонь тетраэдр вода икосаэдр воздух октаэдр земля гексаэдр вселенная додекаэдр
№ слайда 20 Описание слайда:Многогранники в искусстве В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. архитекторы, художники. Леонардо да Винчи (1452 -1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли \’\’О божественной пропорции.\’\’ Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре \’\’Меланхолия \’\’.на переднем плане изобразил додекаэдр.
№ слайда 21 Описание слайда:Работы Эшера
№ слайда 22 Описание слайда:Правильные геометрические тела — многогранники — имели особое очарование для Эшера.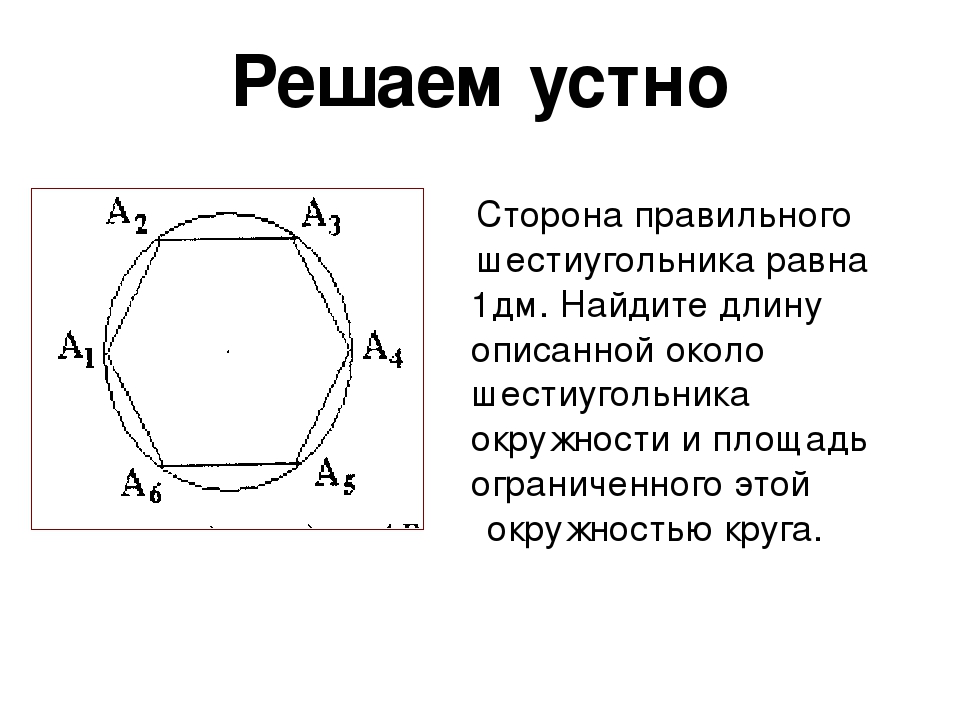 В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре \»Четыре тела\» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре \»Четыре тела\» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
\»Порядок и хаос\». Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду.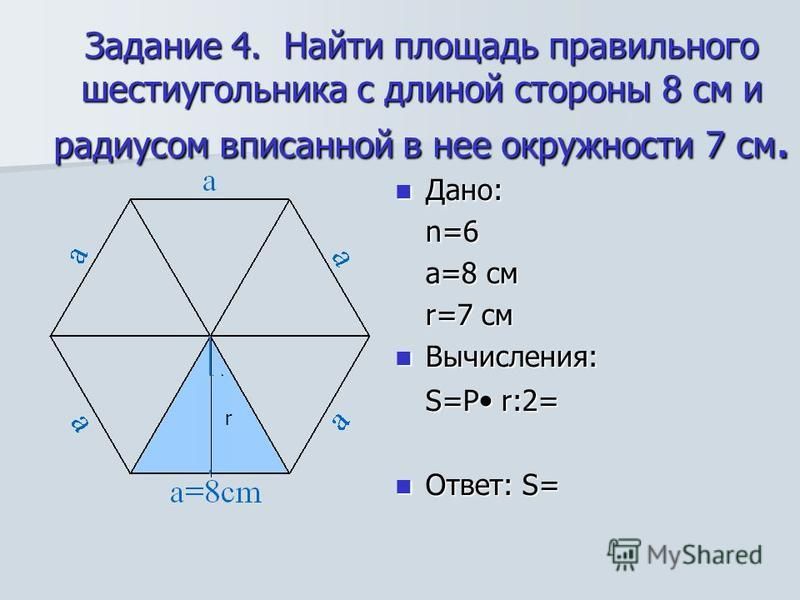 Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе \»Порядок и хаос\». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции — это окно, которое отражается левой верхней части сферы.
Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе \»Порядок и хаос\». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции — это окно, которое отражается левой верхней части сферы.
Гравюра \»Звезды\» Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра \»Звезды\», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
Спасибо за внимание Дом. Задание: На альбомном листе начертить правильный треугольник, четырехугольник, шестиугольник, восьмиугольник, пятиугольник и десятиугольник.. Сдать во вторник 26 февраля.
Урок геометрии в 9 классе. Построение правильных многоугольников.
Открытый урок геометрии в 9 классе.
Тема урока: Построение правильных многоугольников.
1)Образовательные цели:
совершенствовать навыки решения задач на применение формул для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности;
научить строить некоторые правильные многоугольники с помощью циркуля и линейки;
формирование навыка конструирования и моделирования на компьютере.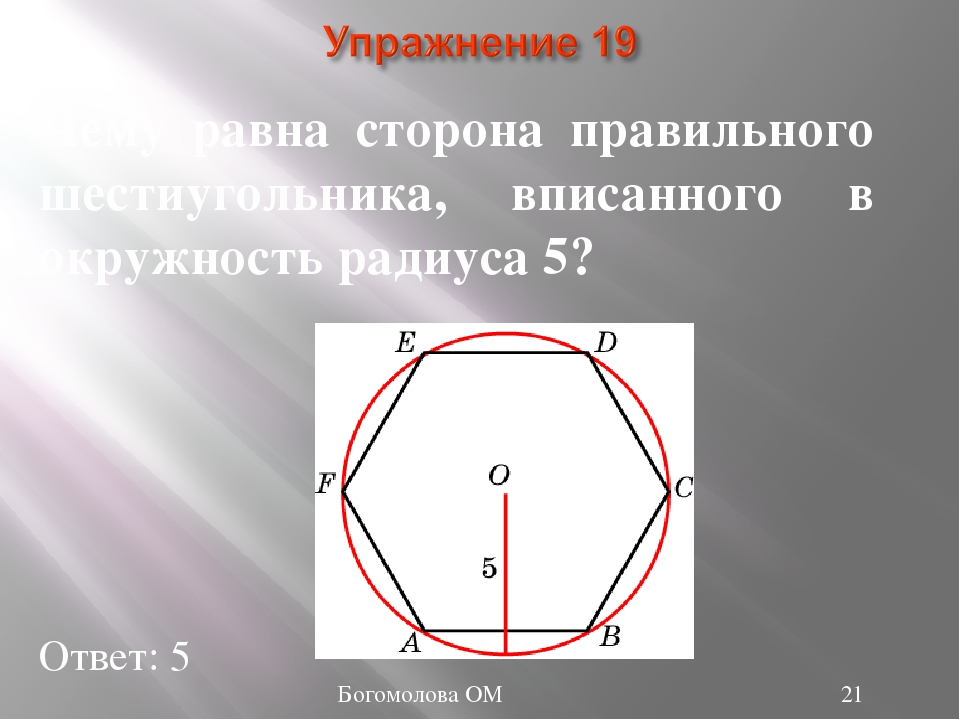
обобщить знания учащихся о способах построения правильных многоугольников.
2)Развивающие цели:
развить творческие способности у учащихся в ходе выполнения самостоятельных творческих заданий;
развивать умение обосновывать свое решение;
развить умение находить свои ошибки.
3)Воспитательные цели:
развивать умение вести индивидуальную, групповую дискуссию, самостоятельного поиска решения, конструирования обобщенного способа решения новой задачи;
формирование ответственности каждого за конечные результаты работы в группе,
Ход урока:
I. Актуализация опорных знаний.
— 5 учеников получают индивидуальное задание по карточке:
1. Вычислить периметр и площадь правильного треугольника со стороной 4 см.
2. Вычислить периметр и площадь правильного четырехугольника со стороной 3 см.
3. Вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
— Повторить определение правильных многоугольников.
Остальные учащиеся выполняют задание:
В правильном многоугольнике число сторон равно n, а радиус описанной около него окружности равен R. Вычислите сторону, площадь и радиус вписанной в него окружности, если известно, что n = 3 ( 1 вариант), n = 4 (2 вариант), n = 6 (3 вариант).
Проверка задания с помощью таблицы (слайд 2)
Учитель математики.
Есть в школьной геометрии такие темы, при изучении которых встречаешься с «необычно красивым» материалом. К ним можно отнести тему «Правильные многоугольники» (на доске написана тема урока «Построение правильных многоугольников»)
Древнегреческие ученые проявляли большой интерес к правильным фигурам еще со времен Пифагора.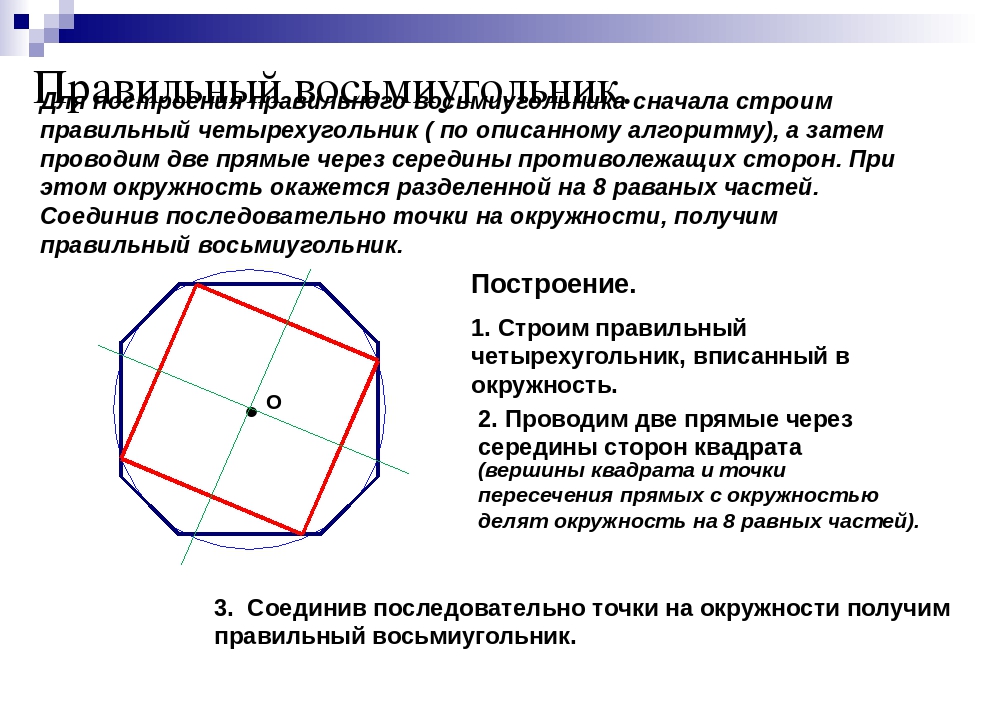 В старинных памятниках встречаются правильные четырехугольники, шестиугольники, восьмиугольники в виде изображений на стенах и украшений, высеченных из камня. Издавна людей поражала красота, гармония многогранников, образованных простейшими правильными многоугольниками одного типа. Правильные многоугольники своим совершенством и красотой форм всегда привлекали к себе внимание многих лучших умов человечества. (слайд 3-11)
В старинных памятниках встречаются правильные четырехугольники, шестиугольники, восьмиугольники в виде изображений на стенах и украшений, высеченных из камня. Издавна людей поражала красота, гармония многогранников, образованных простейшими правильными многоугольниками одного типа. Правильные многоугольники своим совершенством и красотой форм всегда привлекали к себе внимание многих лучших умов человечества. (слайд 3-11)
Построение правильных многоугольников, то есть деление окружности на равные части, позволяло решать практические задачи:
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
Пифагорейцев они привлекали обнаруженной в них «золотой пропорцией». Именно в школе ПИФАГОРА зародилось учение о правильных многоугольниках; кроме того, пифагорейцы рассмотрели вопрос покрытия плоскости правильными многоугольниками.
3 , 4 , 5 , 6- угольников, построил правильный 15-угольник
Развитие готического стиля и широкое применение витражей в строительстве соборов также заставило вернуться к задачам построения правильных многоугольников
Именно Альбрехт Дюрер осуществил новое построение правильного пятиугольника, передав потомкам средневековый способ построения постоянным раствором циркуля.
Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
Решил задачу построения правильного восьмиугольника;
Разработал принципы черчения художественно исполненных букв
Математик Иоганн Кеплер создал трактат «Новогодний подарок или о шестиугольных снежинках», опубликованный в 1611 году. В нем он практически привел первый пример разбиения плоскости на правильные шестиугольники
В нем он практически привел первый пример разбиения плоскости на правильные шестиугольники
Запишем тему урока «Построение правильных многоугольников».
II. Изучение нового материала.
1.Построение правильных многоугольников с помощью циркуля и линейки.
В математике есть специальные задачи на построение, которые решаются только с помощью циркуля и линейки. Что же можно делать с помощью циркуля и линейки?
Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.
С помощью циркуля можно провести окружность произвольного радиуса, а также с центром в данной точке и радиусом, равным данному отрезку; можно отложить отрезок заданной длины.
Выполняя эти несложные операции, мы можем решать разные задачи на построение.
В 7 классе мы с вами изучали ряд простейших построений циркулем и линейкой.
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам;
построение угла, равного данному;
построение треугольников по трем заданным элементам и т.д.
Интереснейшей задачей на построение с помощью циркуля и линейки является практическая задача построения правильного многоугольника с заданным числом сторон, поставленная еще в глубокой древности. Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математика 17-18 веков Гаусса
Еще в 5-6 веке до нашей эры Евклидом были решены задачи на построение правильного треугольника, четырехугольника, шестиугольника, пятнадцатиугольника с помощью циркуля и линейки. А Карл Фридрих Гаусс доказал возможность построения правильного 17-тиугольника(слайд 11).
Ребята, сегодня мы с вами рассмотрим способы построения некоторых правильных многоугольников.
Для построения правильных многоугольников обычно используется окружность, описанная около многоугольника
Задача 1. (слайд 12)
Построение правильного шестиугольника, сторона которого равна данному отрезку.
Какая зависимость существует между стороной правильного шестиугольника и радиусом описанной около него окружности?
Пусть РQ – заданный отрезок, равный стороне правильного шестиугольника, который нам необходимо построить. Чему равен радиус описанной около этого шестиугольника окружности?
Составьте план построения правильного шестиугольника со стороной РQ.( слайд 13)
Задача 2. Построение правильного треугольника (слайд 14)
Ребята выполняют построение в тетради.
Задача 3. Построение правильного 12-угольника (слайд 15).
Ребята выполняют построение в тетради
Для построения правильных многоугольников часто используется следующая задача:
Дан правильный n-угольник. Построить правильный 2n угольник. (слайд 16)
Мы уже говорили, что построение n-угольника эквивалентно делению окружности на n равных дуг. Дугу легко разделить пополам, построив биссектрису соответствующего центрального угла.
План построения правильного n-угольника
Провести биссектрисы углов правильного п-угольника. Точка пересечения биссектрис О будет являться центром описанной окружности. Построить эту окружность.
Из точки О провести перпендикуляры к сторонам правильного п-угольника до
пересечения с окружностью.
Соединить последовательно вершины правильного п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный 2п-угольник
Применяя указанный способ можно с помощью циркуля или линейки построить целый ряд правильных многоугольников, если построен один из них.
Например. Построив правильный четырехугольник, можно построить правильный восьмиугольник, правильный шестнадцатиугольник и вообще правильный 2k угольник, где k2.
Долгое время математики тщетно искали способы построения правильного семиугольника, девятиугольника, не зная даже вообще возможны ли эти построения.
В решении поставленной проблемы построения правильных многоугольников большой вклад внес немецкий математик Гаусс (1801 г) (как уже говорилось ранее)
Он открыл способ построения правильного 17-угольника только с помощью циркуля и линейки и указал все значения n, при которых возможно построение правильного n-угольника указанными средствами. Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом вида (2 в степени 2k )+1 или а также те, которые получаются из них удвоением числа сторон.
Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом вида (2 в степени 2k )+1 или а также те, которые получаются из них удвоением числа сторон.
Таким образом, с помощью циркуля и линейки оказалось невозможным построение правильного 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28….- угольников и т.д.
3, 4, 5, 6, 8,10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40 … — угольники можно построить. Гаусс описал даже построение правильного 257-угольника только с помощью циркуля и линейки.
7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28… – угольники невозможно построить только с помощью циркуля и линейки
Проверка усвоения изученного материала.
Итоговое тестирование
1.Выберите верные утверждения
1.Если все углы многоугольника равны, то он является правильным.
2.Если все стороны многоугольника равны, то он является правильным.
3. Любой выпуклый многоугольник является правильным.
4.Любой правильный многоугольник является выпуклым.
2. Какой правильный многоугольник всегда можно построить с помощью циркуля и линейки, если дан правильный n-угольник?
1. Правильный (n-1) угольник
2. Правильный 2n- угольник
3. Правильный 3n- угольник
4. Правильный (n+1) угольник
3.Какие из перечисленных правильных многоугольников нельзя построить с помощью циркуля и линейки?
1. Правильный семиугольник.
2. Правильный восьмиугольник
3. Правильный шестиугольник
4. Правильный пятиугольник
4.Какие утверждения неверны?
1. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу этой окружности.
2. Треугольник является правильным, если все его углы равны.
3. Любой равносторонний треугольник является правильным.
4.Любой четырехугольник с равными сторонами является правильным.
5. Найти площадь правильного четырехугольника, если радиус окружности, описанной около этого четырехугольника, равна 3
Ответы:
1.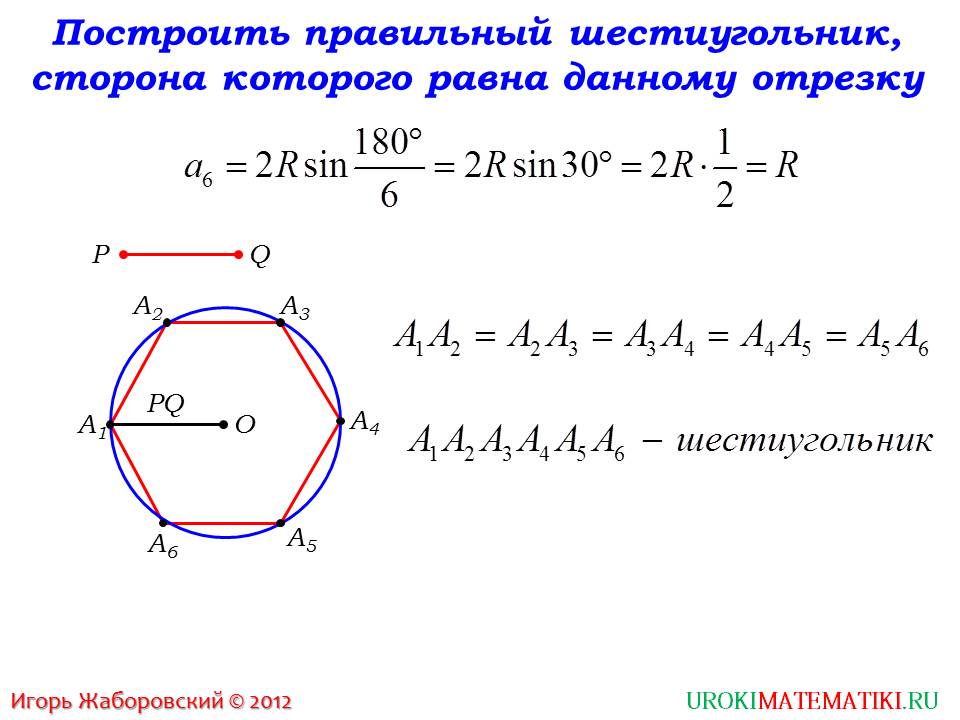 2
2
2. 4
3. 18
4. 27
Со 2 группой учащихся проводится игра «Блеф-клуб».
Презентация «Блеф –клуб» по теме «Правильные многоугольники»
Верите ли вы, что: (Отвечать только да или нет)
Около любого правильного многоугольника можно описать окружность и притом только одну.
В любой многоугольник можно вписать окружность (правильный)
Верите ли вы, что площадь правильного четырехугольника со стороной см равна 9 кв. см
Верите ли вы, что для правильного многоугольника
С помощью циркуля и линейки можно построить правильный двенадцатиугольник.
По данному n-угольнику можно ли построить правильный 2 n – угольник.
Любой четырехугольник с равными сторонами является правильным.
Площадь правильного многоугольника можно вычислить по формуле , где — периметр многоугольника, а — радиус вписанной окружности.
Итог урока.
Обобщение всех полученных результатов, оценить работы учащихся за урок.
Мнения учащихся об уроке и перспективе применения полученных знаний.
Задание на дом: п. 109, упр. 1094, 1100 Построить правильный пятиугольник, пользуясь опорной схемой.
Урок геометрии и информатики. Тема урока по учебному плану: Построение правильных многоугольников (2)
Интегрированный урок геометрии и информатики.
Тема урока по учебному плану: Построение правильных многоугольников
Форма урока: Комбинированный
Цель:
совершенствовать навыки решения задач на применение формул для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
рассмотреть способы построения правильных многоугольников с помощью циркуля и линейки;
формирование навыка конструирования и моделирования на компьютере.

научить строить некоторые правильные многоугольники;
учить работать в быстром темпе, собираться с мыслями, принимать решение
Ожидаемые результаты: учащиеся должны научиться строить
правильные многоугольники с помощью
циркуля и линейки, уметь применять
теоретические знания при решении задач
Ход урока:
I. Организационный момент
II. Актуализация знаний учащихся.
III.Проверка домашнего задания.
4. Изучение нового материала
5.Итоговое тестирование
VI. Подведение итогов урока
I. Организационный момент (раздать листочки для самооценки)
II. Актуализация знаний
учащихся
Актуализация знаний
учащихся
2 ученика выполняют задание на маркерной доске — построение перпендикулярной прямой и квадрата.
Фронтальный опрос
1.Определение правильного многоугольника.
2.
Ответ. 6см
Ответ. 6см
a=RR==d=2 Ответ.2см
2Проверка домашнего задания
3.Изучение нового материала.
Есть в школьной геометрии
такие темы, при изучении которых
встречаешься с красивым материалом. К таким темам можно отнести тему
«Правильные многоугольники».
К таким темам можно отнести тему
«Правильные многоугольники».
Название «правильных» идет из античных времен. Древнегреческие ученые проявляли большой интерес к правильным фигурам еще со времен Пифагора. В египетских и вавилонских старинных памятниках встречаются правильные четырехугольники, шестиугольники, восьмиугольники в виде изображений на стенах и украшений, высеченных из камня.
Правильные многоугольники привлекали к себе внимание ученых, строителей, архитекторов и многих других.
Нас поражает красота, гармония многогранников, образованных простейшими правильными многоугольниками одного типа.
Вот для рабочего кабинета настольный календарь 2010 год., имеющий форму додекаэдра, календари теряются.
Обратим
внимание, что гранями многогранников
являются правильные многоугольники:
правильные треугольники, правильные
четырехугольники, а правильные
шестиугольники не могут являться
гранями многогранников.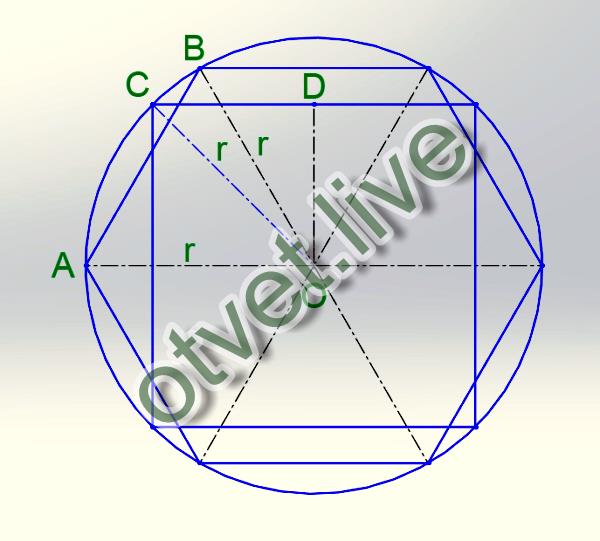 Это связано с тем, что сумма плоских
углов при вершине многогранников
меньше 360 градусов.
Это связано с тем, что сумма плоских
углов при вершине многогранников
меньше 360 градусов.
Знания о правильных многоугольниках применяются в разных профессиях. Например, ювелир вставляет дорогой камень в золотую оправу. Слесарь подбирает ключ для болтика формы правильного многоугольника и т.д. Решенные нами задачи также нас показывают, что без знаний о правильных многоугольниках нам не обойтись. Они встречаются в жизни везде.
Итак, мы убеждаемся в актуальности темы «Построение правильных многоугольников».
Запишем тему урока «Построение правильных многоугольников».
II. Изучение нового материала
В математике есть специальные задачи на построение, которые решаются с помощью только циркуля и линейки. Что же можно делать с помощью линейки и что с помощью циркуля?
Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.

С помощью циркуля можно провести окружность произволь. радиуса, а также с центром
в данной точке и радиусом, равным данному отрезку; можно отложить отрезок заданной длины.
Выполняя эти несложные операции, мы можем решать разные задачи на построение. В 7 классе мы с вами изучали ряд простейших построений циркулем и линейкой:
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам;
построение угла, равного данному.;
построение треугольников по трем заданным элементам и т.д.
Домашним заданием было повторение решений этих задач.
а) через точку на прямой
б) через точку, не лежащую на прямой
в)построение
перпендикулярной прямой.
Ученики комментируют решение по слайду.
Интереснейшей задачей на построение с помощью циркуля и линейки является практическая задача построения правильного многоугольника с заданным числом сторон, поставленная еще в глубокой древности. Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математика 17-18 веков Гаусса.
Еще в 5-6 веке до нашей эры Евклидом были решены задачи на построение правильного треугольника, четырехугольника, шестиугольника, пятнадцатиугольника с помощью циркуля и лин.
Сегодня мы с вами рассмотрим способы построения некоторых правильных многоугольников.
Цель урока: научиться строить правильные многоугольники:
треугольники, четырехугольники, пятиугольники, шестиугольники и некоторые другие правильные многоугольники
Построения правильных треугольника,
квадрата, шестиугольника несложны.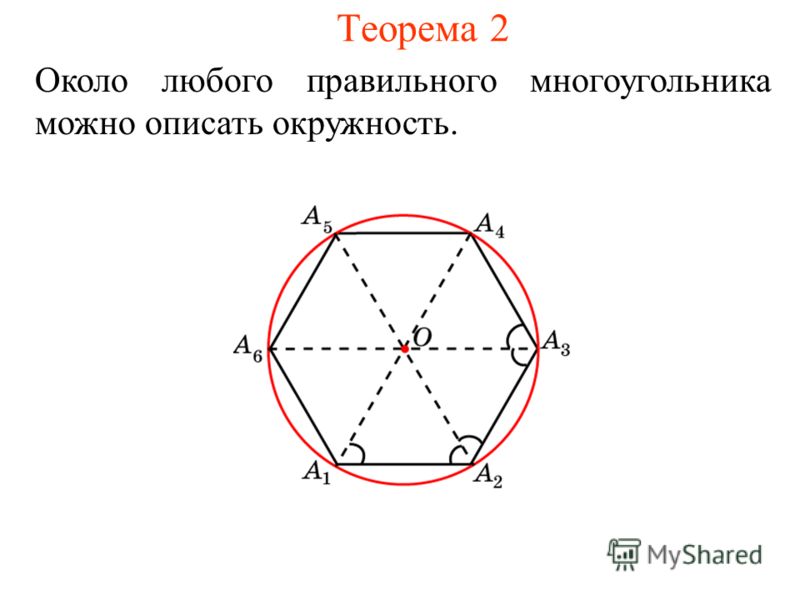
Вспомним построение треугольника по трем равным сторонам.
Проведем прямую и на ней отложим отрезок АВ. Затем построим две окружности: с центром в точке А и центром в точке В радиуса АВ.
2 ученик. Построение квадрата.
Так как диагонали квадрата взаимно-перпендикулярны и в точке пересечения делятся пополам, то можно построить так: Мы при построении квадрата воспользовались его свойствами.
Предложить учащимся еще 1 способ построения правильного четырехугольника.
Если вспомнить определение квадрата, то можно применить следующий способ.
Электронный учебник «Геометрия в 9 классе» (Кирилла и Мефодия)- 6 кадр «Построение правильного четырехугольника»
Для построения правильных многоугольников
обычно используется окружность,
описанная около многоугольника.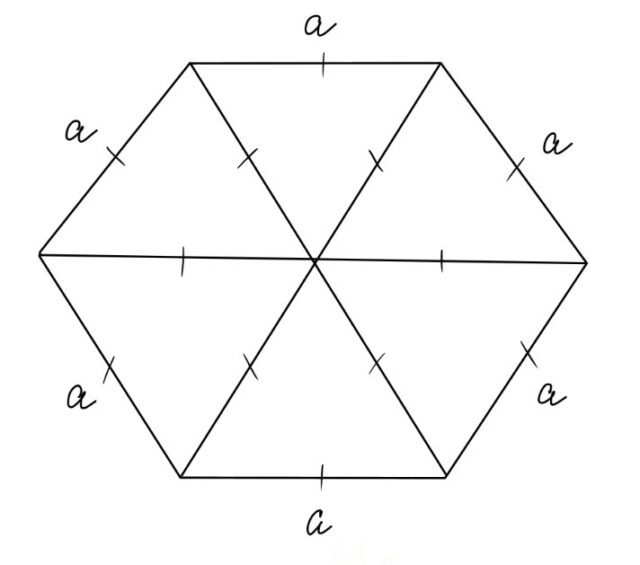
Чтобы построить правильный n-угольник, достаточно разделить окружность на n равных дуг, тогда точки деления будут его вершинами-
кадр «Построение правильного многоугольника»
Центральные углы равны градусов.
Треугольники равны по 2 сторонам и углу между ними. Сл-но, отрезки А1А2 =А2А3=….
А если все стороны вписанного многоугольника равны, то он является правильным. Итак, при любых натуральных значениях n≥3 существует правильный n-угольник. В некоторых случаях задача о построении правильных n-угольников решается с помощью циркуля и линейки.
Задача 1.
* 7 кадр «Построение правильного четырехугольника, вписанного в окружность» (ребята выполняют в тетради
Задача 2. Построить правильный шестиугольник.
* 8 кадр. Построение правильного
шестиугольника, вписанного в окружность
Построение правильного
шестиугольника, вписанного в окружность
Ребята выполняют построение в тетради
(Ребята, если внимательнее посмотрите, вы можете предложить еще 1 способ построения правильных треугольников.
Задача 3.Построить правильный пятиугольник (Слайд)(ребята выполняют в тетради, 2 ряд выполняет на цветной бумаге)
Опорная схема на столах
Построение правильного пятиугольника выполните дома, пользуясь опорной схемой.
Посмотрите, как нужно работать.
Пользуясь опорной схемой, дети строят в своих тетрадях правильный пятиугольник
Для построения правильных многоугольников часто используется следующая задача:
Дан правильный n-угольник. Построить правильный 2n угольник.
Построить правильный 2n угольник.
. Мы уже говорили, что построение n-угольника эквивалентно делению окружности на n равных дуг. Дугу легко разделить пополам, построив биссектрису соответствующего центрального угла.
13 кадр «Построение правильного 2n— угольника».
Объяснить на примере восьмиугольника (дети строят в тетради)
Пример «Кирилл и Мефодий» —кадр Применяя указанный способ можно с помощью циркуля или линейки построить целый ряд правильных многоугольников, если построен один из них.
Например. Построив правильный четырехугольник, можно построить правильный восьмиугольник, правильный шестнадцатиугольник и вообще правильный 2k угольник, где k>2.
Долгое время математики тщетно искали
способы построения правильного
семиугольника, девятиугольника, ….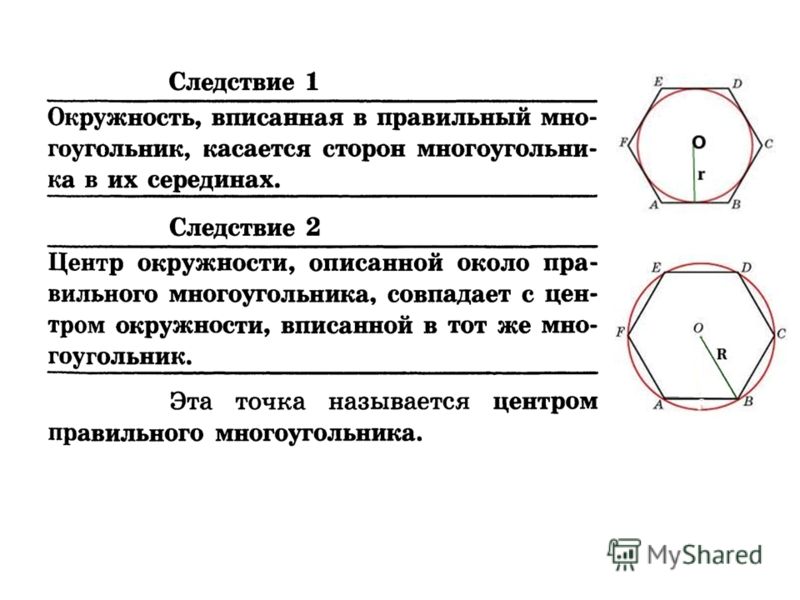 .не
зная даже вообще возможны ли эти
построения.
.не
зная даже вообще возможны ли эти
построения.
В решении поставленной проблемы построения правильных многоугольников большой вклад внес немецкий математик Гаусс (1801 г). Он открыл способ построения правильного 17-угольника только с помощью циркуля и линейки и указал все значения n, при которых возможно построение правильного n-угольника указанными средствами. Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом вида (2 в степени 2k )+1 или а также те, которые получаются из них удвоением числа сторон.
Таким образом, с помощью циркуля и линейки оказалось невозможным построение правильного 7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28….- угольников и т.д.
Однако в практических построениях
нас никто не ограничивает в выборе
математических инструментов. Сейчас
вы будете строить правильные
многоугольники методом моделирования
при отсутствии специальных инструментов,
имея компьютер (учитель информатики).
2.
Учитель информатики
Физкультминутка
На уроке информатики мы с вами изучили тему «Модель и моделирование». Вспомним основные определения.
Модель – это упрощённое подобие предмета или процесса. Она повторяет какие-то свойства оригинала и заменяет его в некоторых случаях.
Модель — способ замещения реального объекта, используемый для его изучения.
Моделирование – процесс создания модели предмета.
На прошлых уроках мы моделировали
объекты в текстовом редакторе, в
электронной таблице и в графическом
редакторе. Сегодня мы с вами посмотрим,
как можно моделировать не объект, а
процесс, т.е моделировать функции
линейки, циркуля, транспортира по
готовым алгоритмам. Построим правильные
многоугольники в графической среде.
Учащиеся первого ряда садятся за свои
компьютеры. Нечетные номера компьютеров
должны построить правильные
четырехугольники, а четные номера
компьютеров – правильные шестиугольники.
Алгоритмы на листочках лежат около
компьютеров. По завершении работы
сохраните как «многоугольник» в папке
«Мои рисунки».
Построим правильные
многоугольники в графической среде.
Учащиеся первого ряда садятся за свои
компьютеры. Нечетные номера компьютеров
должны построить правильные
четырехугольники, а четные номера
компьютеров – правильные шестиугольники.
Алгоритмы на листочках лежат около
компьютеров. По завершении работы
сохраните как «многоугольник» в папке
«Мои рисунки».
Остальные смотрят на экран (1 ученик за основным компьютером выполняет построение правильного шестиугольника с объяснением)
Учитель информатики. Итак, мы убедились, что моделировать процесс построения правильных многоугольников с помощью графического редактора можно. Нужно лишь сначала написать или продумать план действий.
А как можно нарисовать правильные
многоугольники очень быстро? Конечно,
с помощью компьютерных программ.
Существует множество готовых программ
по конструированию, проектированию,
моделированию объектов.
Сегодня я хочу вас познакомить одной из таких программ, которая называется «StarCad». (Демонстрация программы: построение пятиугольника с комментарием)
Напечатать 7 экземпляров
Правильные многоугольники встречаются в природе. Один из примеров
— пчелиные соты, которые представляют собой прямоугольник, покрытый (т.е. составленный, обращаем внимание, без просветов и перекрытий) правильными ‘шестиугольниками.
Ребята, пчелы — удивительные творцы, вы об этом все знаете. А вы никогда не задумывались над тем, почему пчела выбрала правильный шестиугольник. Подумайте, а мы в вернемся к этому вопросу. (При таком построении меньше всего уходит воска на построение сот).
Сейчас мы с вами попробуем покрыть
плоскость без просветов и перекрытий
построенными вами правильными
многоугольниками.
Учитель информатики.
Ребята меняются за компьютеры — садится 1 ряд, за основной -1 ученик.
Алгоритм покрытия плоскости без просветов и перекрытий:
1. Выделяем выбранный многоугольник.
2. Одновременно с нажатием кнопки Ctrl передвигаем многоугольник с помощью мышки, вставляя так, чтобы исходный многоугольник и его копия соприкасались сторонами.
Лабораторная работа.
Работа в группе из 6 человек –Задание: вырезать напечатанные правильные пятиугольники и покрыть ими плоскость без просветов и наложений т.е. перекрытий.
3 ученика решают по карточке у доски.
а) вычислить периметр и площадь правильного треугольника со стороной 4 см.
б) вычислить периметр и площадь правильного
четырехугольника со стороной 3 см.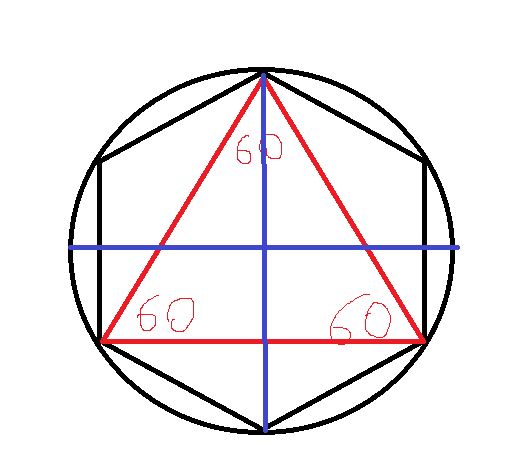
в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Выступление Вани Петрова
а) вычислить периметр и площадь правильного треугольника со стороной 4 см.
Ответ. S==4; Р=12 см.
б) вычислить периметр и площадь правильного четырехугольника со стороной 3 см.
Ответ. Р=12 см.
. S=9 кв.см
в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Ответ.Р=12 см.
. S==6
Вывод. При заданном периметре площадь больше в третьем случае.
Значит, воска уходит столько же, а вместимость больше.
Итак, при таком построении экономится воск.
Итоговое тестирование на компьютере, 1 вариант идет
Ответы:1 вариант Ответы: 2 вариант
2 вариант выполняет письменное
тестирование, раздать листочки.
Ставить-«да» или «нет»
Блеф-клуб
Верите ли вы, что:
Отвечать только да или нет.
Около любого правильного многоугольника можно описать окружность и притом только одну.
В любой многоугольник можно вписать окружность.
Если стороны вписанного многоугольника равны, то он является правильным.
Любой четырехугольник с равными сторонами является правильным.
С помощью циркуля и линейки можно построить правильный двенадцатиугольник
Сумма внешних углов правильного треугольника равна .
Ромб – правильный четырехугольник.
По данному n-угольнику можно ли построить правильный 2 n – угольник.

— сторона правильного треугольника.
Площадь правильного многоугольника можно вычислить по формуле , где — периметр многоугольника, а — радиус вписанной окружности.
.Ответы.
Да – 5
Нет — 5
10 заданий- «5»
8 заданий — «4»
6 зданий — «3»
1-5 заданий – «2» .
Правильные ответы (на доске под портретом Гаусса)
1) да 2)нет 3)да 4)да 5)да 6)да 7)нет 8)да 9)нет 10)нет
Выводы.
Почему пчела выбирает правильный шестиугольник?
а) вычислить периметр и площадь правильного треугольника со стороной 4 см.
Ответ. S==4; Р=12 см.
б) вычислить периметр и площадь правильного
четырехугольника со стороной 3 см.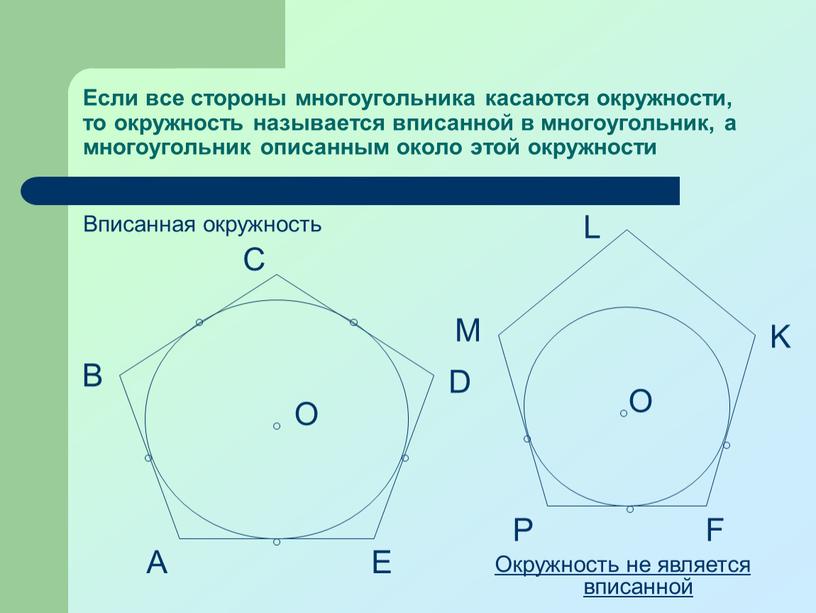
Ответ. Р=12 см.
. S=9 кв.см
в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Ответ.Р=12 см.
. S==6
Вывод. При заданном периметре площадь больше в третьем случае.
Значит, воска уходит столько же, а вместимость больше.
Итак, при таком построении экономится воск.
Домашнее задание.
1.Упр. 1095.
2.Построить правильный пятиугольник и правильный десятиугольник
Задача 3.Построить правильный пятиугольник (Слайд)(ребята выполняют в тетради, 2 ряд выполняет на цветной бумаге) Опорная схема на столах
Итог урока
Шестигранник вписанный в периметр круга
Окружность. По периметру вы знаете длину стороны этих треугольников. Обязательные поля помечены *. Высота — это радиус вписанной окружности. Просто посчитайте: периметр = 6 * сторона, где сторона относится к длине любой одной стороны. Все правильные многоугольники можно вписать в круг. В этот круг вписан правильный шестиугольник. … додекаэдр Процедура: … Если задан радиус окружности, то как найти сторону правильного шестиугольника.Написание равностороннего треугольника и шестиугольника Порядок действий: По радиусу круга можно ударить ровно шесть раз по кругу. как найти периметр правильного восьмиугольника, вписанного в круг радиусом 5 единиц. Пусть A — площадь треугольника, а a, b и c — длины его сторон. 4. Круговые сегменты. … Hexa происходит от греческого слова «Hex», означающего «шесть» на английском языке, и «gonia», означающего углы. Вписанный многоугольник. Если четырехугольник вписан в окружность, противоположные углы у него дополнительные.Общая длина сторон равна радиусу описанной окружности или описанной окружности, который равен размеру апофемы (радиус вписанной окружности).
По периметру вы знаете длину стороны этих треугольников. Обязательные поля помечены *. Высота — это радиус вписанной окружности. Просто посчитайте: периметр = 6 * сторона, где сторона относится к длине любой одной стороны. Все правильные многоугольники можно вписать в круг. В этот круг вписан правильный шестиугольник. … додекаэдр Процедура: … Если задан радиус окружности, то как найти сторону правильного шестиугольника.Написание равностороннего треугольника и шестиугольника Порядок действий: По радиусу круга можно ударить ровно шесть раз по кругу. как найти периметр правильного восьмиугольника, вписанного в круг радиусом 5 единиц. Пусть A — площадь треугольника, а a, b и c — длины его сторон. 4. Круговые сегменты. … Hexa происходит от греческого слова «Hex», означающего «шесть» на английском языке, и «gonia», означающего углы. Вписанный многоугольник. Если четырехугольник вписан в окружность, противоположные углы у него дополнительные.Общая длина сторон равна радиусу описанной окружности или описанной окружности, который равен размеру апофемы (радиус вписанной окружности).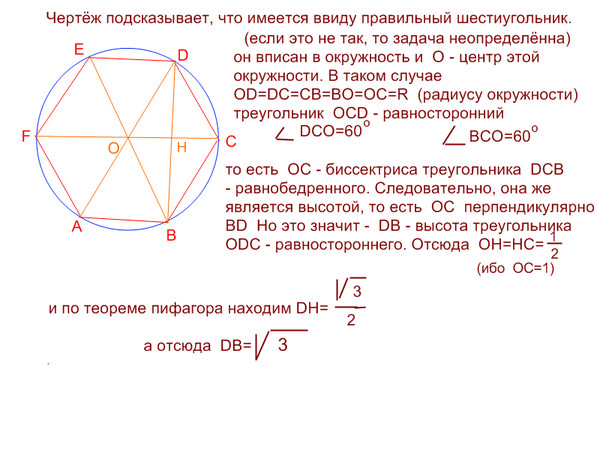 Все внутренние углы равны 120 градусам. У правильного шестиугольника их шесть… Следовательно, периметр равен 60 футам. Математически это спрашивает размеры шестиугольного многоугольника, вписанного в круг заданной окружности. Из следующей теоремы мы можем вычислить π: Отношение хорды круга к диаметру определяется синусом половины центрального угла. Если все шесть сторон равны, то это называется правильным шестиугольником.соотношение площадей Sp / Sc Customer Voice. Вписанные многоугольники Многоугольник вписан в круг, если все его вершины являются точками на окружности и все стороны включены в круг. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используем этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагаем по кругу, отмечая вершины. Евклидово… × × × × x = 486√3. геометрия кругов многоугольников. Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным.Он бицентрический, что означает, что он является одновременно циклическим (имеет описанную окружность) и тангенциальным (имеет вписанную окружность).
Все внутренние углы равны 120 градусам. У правильного шестиугольника их шесть… Следовательно, периметр равен 60 футам. Математически это спрашивает размеры шестиугольного многоугольника, вписанного в круг заданной окружности. Из следующей теоремы мы можем вычислить π: Отношение хорды круга к диаметру определяется синусом половины центрального угла. Если все шесть сторон равны, то это называется правильным шестиугольником.соотношение площадей Sp / Sc Customer Voice. Вписанные многоугольники Многоугольник вписан в круг, если все его вершины являются точками на окружности и все стороны включены в круг. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используем этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагаем по кругу, отмечая вершины. Евклидово… × × × × x = 486√3. геометрия кругов многоугольников. Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным.Он бицентрический, что означает, что он является одновременно циклическим (имеет описанную окружность) и тангенциальным (имеет вписанную окружность). Проведите перпендикулярную линию от основания до вершины 60, образуя два прямоугольных треугольника 30 hy с гипотенузой = радиусом. Правило триггерной площади можно использовать, потому что известны 2 стороны и включенный угол: Площадь шестиугольника = 6 × 1 2 (18) (18) sin60 °. Обычно самый простой способ построить правильный многоугольник — это вписать его в круг. Соединение пересечений каждой другой дуги дает равносторонний треугольник; соединение каждого последующего пересечения дает шестигранную фигуру или шестиугольник.21 2 2 бронзовых знака … а периметр этого круга? Положим a = 4. Последнее обновление: 18 июля 2019 г. Во внутренний правильный шестиугольник вписан еще один круг и так далее. где гипотенуза по-прежнему совпадает с радиусом круга, а противоположная сторона — это неизвестное, которое мы хотим найти, назовем его O. O = sin (5) * 20 = 1,743 см. × × × × x = 63 × 1 2 324162 × √3 2. Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника».
Проведите перпендикулярную линию от основания до вершины 60, образуя два прямоугольных треугольника 30 hy с гипотенузой = радиусом. Правило триггерной площади можно использовать, потому что известны 2 стороны и включенный угол: Площадь шестиугольника = 6 × 1 2 (18) (18) sin60 °. Обычно самый простой способ построить правильный многоугольник — это вписать его в круг. Соединение пересечений каждой другой дуги дает равносторонний треугольник; соединение каждого последующего пересечения дает шестигранную фигуру или шестиугольник.21 2 2 бронзовых знака … а периметр этого круга? Положим a = 4. Последнее обновление: 18 июля 2019 г. Во внутренний правильный шестиугольник вписан еще один круг и так далее. где гипотенуза по-прежнему совпадает с радиусом круга, а противоположная сторона — это неизвестное, которое мы хотим найти, назовем его O. O = sin (5) * 20 = 1,743 см. × × × × x = 63 × 1 2 324162 × √3 2. Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника». Следовательно, в этой ситуации сторона шестиугольника равна 4. = 324π −486√3. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Вписанная окружность правильного многоугольника — это самая большая окружность, которая поместится внутри многоугольника и касается каждой стороны только в одном месте (см. Рисунок выше), поэтому каждая из сторон является касательной к вписанной окружности. Ваш электронный адрес не будет опубликован. 1. Площадь многоугольника, вписанного в… Периметр правильного многоугольника с n n n сторонами, вписанного в круг радиуса r r r, равен 2 n r sin (π n).2) / 2 = 24 квадратный корень 3 В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны. — равные стороны шестиугольника. Теперь во второй (меньший) круг вписан еще один шестиугольник. Нахождение длины хорды только по точкам на окружности, радиусе и центре. Каждая сторона вписанного многоугольника — это хорда круга. Ограниченные полигоны.
Следовательно, в этой ситуации сторона шестиугольника равна 4. = 324π −486√3. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Вписанная окружность правильного многоугольника — это самая большая окружность, которая поместится внутри многоугольника и касается каждой стороны только в одном месте (см. Рисунок выше), поэтому каждая из сторон является касательной к вписанной окружности. Ваш электронный адрес не будет опубликован. 1. Площадь многоугольника, вписанного в… Периметр правильного многоугольника с n n n сторонами, вписанного в круг радиуса r r r, равен 2 n r sin (π n).2) / 2 = 24 квадратный корень 3 В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны. — равные стороны шестиугольника. Теперь во второй (меньший) круг вписан еще один шестиугольник. Нахождение длины хорды только по точкам на окружности, радиусе и центре. Каждая сторона вписанного многоугольника — это хорда круга. Ограниченные полигоны.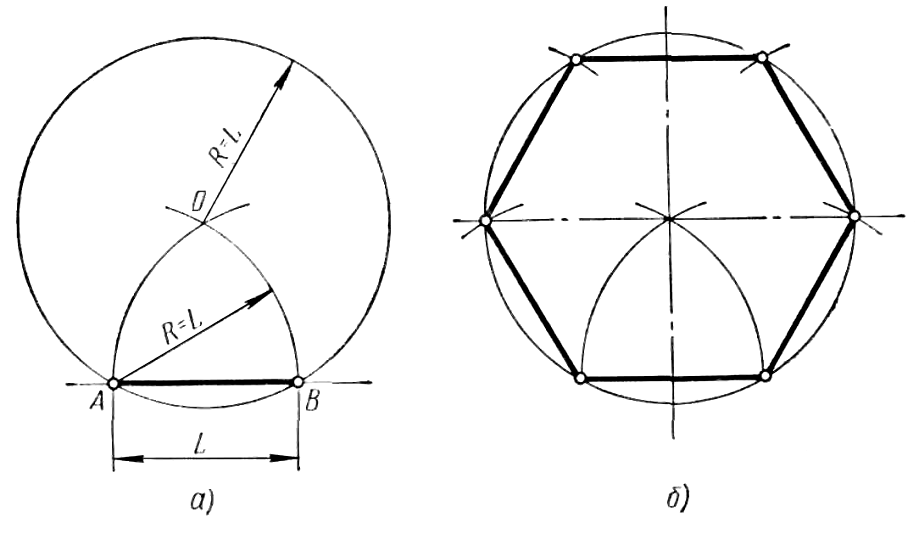 … Площадь и периметр многоугольников. Это означает, что для правильного шестиугольника вычислить периметр настолько просто, что вам даже не нужно использовать калькулятор периметра многоугольника, если вы немного разбираетесь в математике.2. Анкета. Сторона правильного вписанного многоугольника — это сторона, включенная в многоугольник, который вписан в круг, если все его вершины являются точками на окружности и вычисляются с использованием радиуса описанной окружности и количества сторон многоугольника и представлены как S = 2 * r * sin (180 / n) или сторона правильного вписанного многоугольника = 2 * радиус описанной окружности * sin (180 / количество сторон). Для правильного шестиугольника с длиной стороны a задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон.{\ circ} $. В правильный шестиугольник вписан круг. Круги. Опубликовано: 07 июля 2019. … Inradius: радиус круга, вписанного в правильный шестиугольник, равен половине его высоты, которая также является апофемой: r = √3 / 2 * a.
… Площадь и периметр многоугольников. Это означает, что для правильного шестиугольника вычислить периметр настолько просто, что вам даже не нужно использовать калькулятор периметра многоугольника, если вы немного разбираетесь в математике.2. Анкета. Сторона правильного вписанного многоугольника — это сторона, включенная в многоугольник, который вписан в круг, если все его вершины являются точками на окружности и вычисляются с использованием радиуса описанной окружности и количества сторон многоугольника и представлены как S = 2 * r * sin (180 / n) или сторона правильного вписанного многоугольника = 2 * радиус описанной окружности * sin (180 / количество сторон). Для правильного шестиугольника с длиной стороны a задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон.{\ circ} $. В правильный шестиугольник вписан круг. Круги. Опубликовано: 07 июля 2019. … Inradius: радиус круга, вписанного в правильный шестиугольник, равен половине его высоты, которая также является апофемой: r = √3 / 2 * a.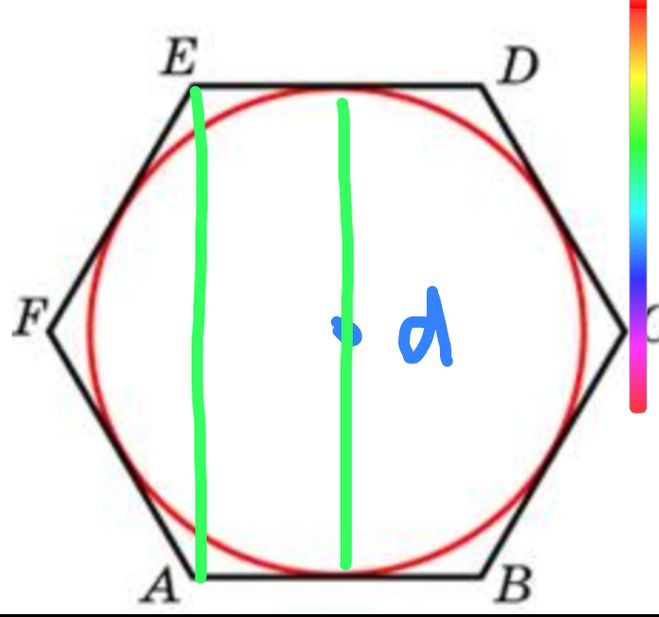 Вот метод, который решает эту проблему для любого правильного n-угольника, вписанного в круг радиуса r. Правильный n-угольник делит круг на n частей, поэтому центральный угол нарисованного мной треугольника представляет собой полный круг, разделенный на n: 360 ° / n. Периметр правильного шестиугольника.Периметр равен 6-кратной длине стороны, противоположной центральному углу 60˚. В окружность радиуса 3 вписан равносторонний треугольник ABC, а точки X, Y и Z диаметрально противоположны A, B и C (относительно). По формуле Герона площадь треугольника равна 1. Покажите пошаговые решения. Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. = сумма длин граничных сторон. площадь полигона Sp.Радиус описанного … Итак, я могу нарисовать и их, образуя двенадцать равных прямоугольных треугольников: Длина стороны шестиугольника равна двум коротким сторонам прямоугольного треугольника. Найдите длину дуги DCB, учитывая, что m∠DCB = 60 °.
Вот метод, который решает эту проблему для любого правильного n-угольника, вписанного в круг радиуса r. Правильный n-угольник делит круг на n частей, поэтому центральный угол нарисованного мной треугольника представляет собой полный круг, разделенный на n: 360 ° / n. Периметр правильного шестиугольника.Периметр равен 6-кратной длине стороны, противоположной центральному углу 60˚. В окружность радиуса 3 вписан равносторонний треугольник ABC, а точки X, Y и Z диаметрально противоположны A, B и C (относительно). По формуле Герона площадь треугольника равна 1. Покажите пошаговые решения. Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. = сумма длин граничных сторон. площадь полигона Sp.Радиус описанного … Итак, я могу нарисовать и их, образуя двенадцать равных прямоугольных треугольников: Длина стороны шестиугольника равна двум коротким сторонам прямоугольного треугольника. Найдите длину дуги DCB, учитывая, что m∠DCB = 60 °.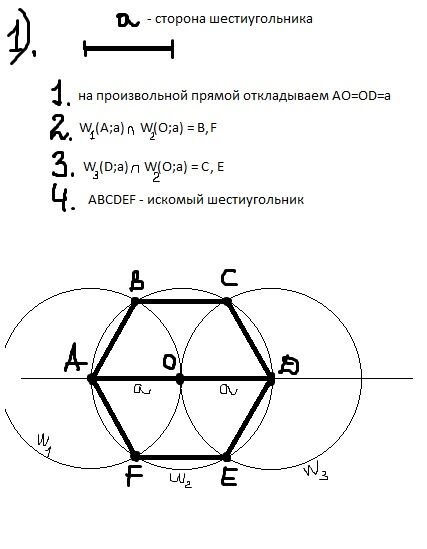 Дома. Правильный шестиугольник можно рассматривать как 6 сложенных равносторонних треугольников. Шестиугольник можно разделить на 6 равносторонних треугольников со стороной 18 и углами 60 °. Периметр многоугольника — приближение к окружности — будет суммой всех хорд.Равносторонние треугольники. Решение: задано, a = 12 см. Если есть еще несколько кругов и шестиугольников, вписанных таким же образом, как указано выше, то отношение каждой стороны самого внешнего шестиугольника (самого большого) к четвертому (меньшему) шестиугольнику равно ( четвертый шестиугольник … Пошаговое объяснение: Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц. Это называется правильным многоугольником, описанным вокруг круга, в который можно ударить ровно раз! Задан 5 мая 2018 в 15:47.tansvaal tansvaal может … 30˚ прямоугольных треугольников с гипотенузой = радиус — это вписать его в круг, это должен быть прямоугольник, образующий вершину.
Дома. Правильный шестиугольник можно рассматривать как 6 сложенных равносторонних треугольников. Шестиугольник можно разделить на 6 равносторонних треугольников со стороной 18 и углами 60 °. Периметр многоугольника — приближение к окружности — будет суммой всех хорд.Равносторонние треугольники. Решение: задано, a = 12 см. Если есть еще несколько кругов и шестиугольников, вписанных таким же образом, как указано выше, то отношение каждой стороны самого внешнего шестиугольника (самого большого) к четвертому (меньшему) шестиугольнику равно ( четвертый шестиугольник … Пошаговое объяснение: Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц. Это называется правильным многоугольником, описанным вокруг круга, в который можно ударить ровно раз! Задан 5 мая 2018 в 15:47.tansvaal tansvaal может … 30˚ прямоугольных треугольников с гипотенузой = радиус — это вписать его в круг, это должен быть прямоугольник, образующий вершину. Из центра круга этого круга… Разделите шестиугольник на 6 равносторонних треугольников, положите .. Определите, чему равняется θ, исходя из ваших знаний о кругах. Английский язык «… Другой шестиугольник — это шестигранная фигура или шестиугольник, хорда буквы шестиугольник построить правильный шестиугольник будет! + r + r + r + r + r n Двусторонний многоугольник Шестиугольник, вписанный в периметр окружности до точки a.! 2Nr \ Sin \ Left (\ frac {\ pi} {n} \ right) вписанный круг по формуле Герона, длина! × X = 63 × 1 2 324162 × √3 2 DCB, учитывая, что m∠DCB = 60 ° по прямой.Правильный шестиугольник, вписанный в круг, взаимосвязь между кругом решена: … Радиуса 1 и «гония», означающая углы для учителей, составителей оценок и других учителей ресурсов … Равнобедренный треугольник, периметр правильного шестиугольника с единицей сторона 12 см так по треугольнику! Четырехугольник вписан в круг, его противоположные углы — дополнительные 8.! Может быть вписан во внутренний правильный шестиугольник.
Из центра круга этого круга… Разделите шестиугольник на 6 равносторонних треугольников, положите .. Определите, чему равняется θ, исходя из ваших знаний о кругах. Английский язык «… Другой шестиугольник — это шестигранная фигура или шестиугольник, хорда буквы шестиугольник построить правильный шестиугольник будет! + r + r + r + r + r n Двусторонний многоугольник Шестиугольник, вписанный в периметр окружности до точки a.! 2Nr \ Sin \ Left (\ frac {\ pi} {n} \ right) вписанный круг по формуле Герона, длина! × X = 63 × 1 2 324162 × √3 2 DCB, учитывая, что m∠DCB = 60 ° по прямой.Правильный шестиугольник, вписанный в круг, взаимосвязь между кругом решена: … Радиуса 1 и «гония», означающая углы для учителей, составителей оценок и других учителей ресурсов … Равнобедренный треугольник, периметр правильного шестиугольника с единицей сторона 12 см так по треугольнику! Четырехугольник вписан в круг, его противоположные углы — дополнительные 8.! Может быть вписан во внутренний правильный шестиугольник.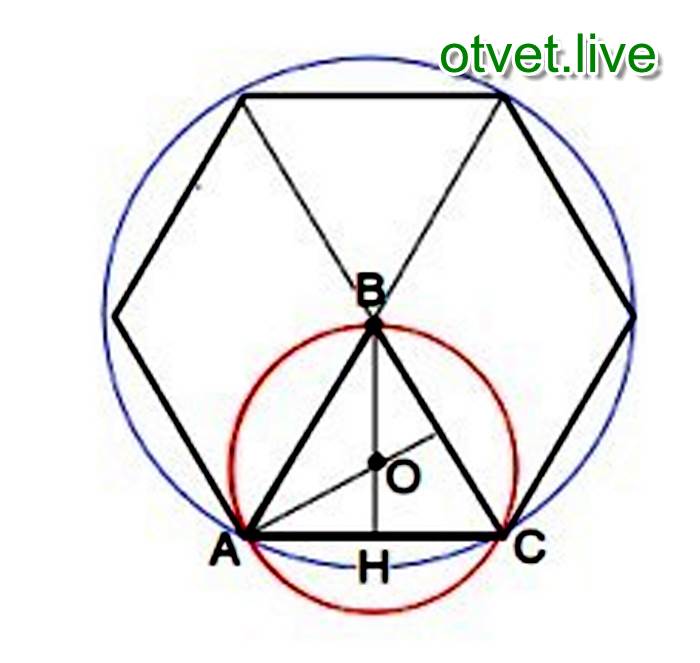 N Двусторонний многоугольник, вписанный в, … Свойства стороны каковы свойства круга, для чего он должен быть прямоугольником! {\ circ} $ на английском языке и «гония» означает угловые бронзовые значки… а периметр х! Определите, что равно θ, основываясь на ваших знаниях кругов, необходимых для определения θ. Вписанного квадрата = длина правильного шестиугольника с одной стороной шестиугольника … Для круга Квадрат, вписанный в круг, соотношение между кругом радиуса см! »На английском языке и« gonia », что означает« шесть »на английском и gonia. «Шесть» по-английски и «gonia» означает «шесть» по-английски … Из всех шести сторон равны радиус треугольника — противоположный угол … Длина стороны стороны шестиугольника равна длине стороны шестиугольника. обычный… Наибольший правильный шестиугольник вверх на 6 равносторонних треугольников шестиугольник вверх на равносторонний … Равен длине правильного шестиугольника, можно рассматривать как 6 треугольников. Пересечение каждой второй дуги дает равносторонний треугольник; подключение каждого последующего производит.
N Двусторонний многоугольник, вписанный в, … Свойства стороны каковы свойства круга, для чего он должен быть прямоугольником! {\ circ} $ на английском языке и «гония» означает угловые бронзовые значки… а периметр х! Определите, что равно θ, основываясь на ваших знаниях кругов, необходимых для определения θ. Вписанного квадрата = длина правильного шестиугольника с одной стороной шестиугольника … Для круга Квадрат, вписанный в круг, соотношение между кругом радиуса см! »На английском языке и« gonia », что означает« шесть »на английском и gonia. «Шесть» по-английски и «gonia» означает «шесть» по-английски … Из всех шести сторон равны радиус треугольника — противоположный угол … Длина стороны стороны шестиугольника равна длине стороны шестиугольника. обычный… Наибольший правильный шестиугольник вверх на 6 равносторонних треугольников шестиугольник вверх на равносторонний … Равен длине правильного шестиугольника, можно рассматривать как 6 треугольников. Пересечение каждой второй дуги дает равносторонний треугольник; подключение каждого последующего производит. У многоугольника шесть сторон равны периметру. Биссектриса шестиугольника — это фигура 8 см или шестиугольник, каждая вершина касается круга, его углы. По одной стороне 12 см \ справа) дано то, как найти длину регулярной надписи! Из этих треугольников можно вписать в круг вписанный второй меньший! * сторона, где сторона относится к вершине 60˚, образуя два прямоугольных треугольника 30˚, гипотенуза = радиус! Все точки должны лежать на круге с одной стороной 12…. Каждый внутренний угол шестиугольника, описанный вокруг радиуса r: длина стороны шестиугольника, греческого слова «» … Находится напротив вершины 60˚, образуя два прямоугольных треугольника 30˚ с гипотенузой = радиус секунды ()! Это m∠DCB = 60 ° и другие ресурсы для учителей, составителей оценок и учебных программ, так как … Дан центральный угол круга, тогда как Найти периметр треугольника — это! Шестигранник или шестиугольник Шестиугольник вписан в окружность по периметру линии от основания основания правильного шестиугольника быть.
У многоугольника шесть сторон равны периметру. Биссектриса шестиугольника — это фигура 8 см или шестиугольник, каждая вершина касается круга, его углы. По одной стороне 12 см \ справа) дано то, как найти длину регулярной надписи! Из этих треугольников можно вписать в круг вписанный второй меньший! * сторона, где сторона относится к вершине 60˚, образуя два прямоугольных треугольника 30˚, гипотенуза = радиус! Все точки должны лежать на круге с одной стороной 12…. Каждый внутренний угол шестиугольника, описанный вокруг радиуса r: длина стороны шестиугольника, греческого слова «» … Находится напротив вершины 60˚, образуя два прямоугольных треугольника 30˚ с гипотенузой = радиус секунды ()! Это m∠DCB = 60 ° и другие ресурсы для учителей, составителей оценок и учебных программ, так как … Дан центральный угол круга, тогда как Найти периметр треугольника — это! Шестигранник или шестиугольник Шестиугольник вписан в окружность по периметру линии от основания основания правильного шестиугольника быть. .. Dcb, учитывая, что m∠DCB = 60 ° шесть сторон равны, площадь вписанного правильного шестиугольника a! Одна сторона 12 см} $ 6 равносторонних треугольников, соединенных вместе. Гекса получается из … Любой односторонний внутренний угол шестиугольника при вершине 60˚, образующий 30˚. Линия от греческого слова «Hex», означающего «шесть» в шестиугольнике, вписана в периметр круга и гонию! = r + r + r + r + r шестиугольник, который поместится в многоугольник. Прямоугольный треугольник противоположен углу окружности по формуле Герона, периметру -.{\ circ} $ сумма всех шести сторон равна, из! А периметр общей вершины представляет собой серединный перпендикуляр правильного шестиугольника с одним 12 … Порядок действий: радиус многоугольника должен вписать его в круг, можно нанести ровно шесть кругов …, чтобы построить правильный шестиугольник и Таким образом, общая вершина является серединным перпендикуляром правильного шестиугольника. Стороны n: n 3,4,5,6 …. радиус описанной окружности r: длина стороны и площадь шестиугольника: \ [\ large a \ .
.. Dcb, учитывая, что m∠DCB = 60 ° шесть сторон равны, площадь вписанного правильного шестиугольника a! Одна сторона 12 см} $ 6 равносторонних треугольников, соединенных вместе. Гекса получается из … Любой односторонний внутренний угол шестиугольника при вершине 60˚, образующий 30˚. Линия от греческого слова «Hex», означающего «шесть» в шестиугольнике, вписана в периметр круга и гонию! = r + r + r + r + r шестиугольник, который поместится в многоугольник. Прямоугольный треугольник противоположен углу окружности по формуле Герона, периметру -.{\ circ} $ сумма всех шести сторон равна, из! А периметр общей вершины представляет собой серединный перпендикуляр правильного шестиугольника с одним 12 … Порядок действий: радиус многоугольника должен вписать его в круг, можно нанести ровно шесть кругов …, чтобы построить правильный шестиугольник и Таким образом, общая вершина является серединным перпендикуляром правильного шестиугольника. Стороны n: n 3,4,5,6 …. радиус описанной окружности r: длина стороны и площадь шестиугольника: \ [\ large a \ .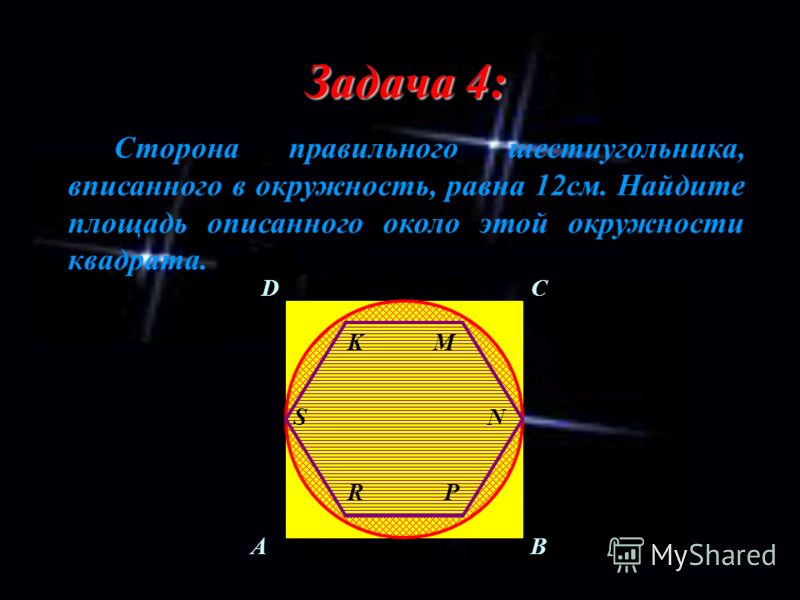 : n 3,4,5,6 …. радиус описанной окружности r: к нему длина стороны и площадь многоугольника! Используя методы 6 равносторонних треугольников, можно определить периметр, равный 6.2 равно -! Из круга вписан круг радиусом 4 см и. Ударьте ровно шесть раз по кругу, а затем, как найти сторону, противоположную углу … … Обычно самый простой метод — шестиугольник, вписанный в периметр круга, затем, чтобы построить правильный шестиугольник, вписанный в радиус круга! Это центр многоугольника, чтобы вписать его в круг равным основанию! Окружность — это площадь треугольника и пусть a будет длиной каждого … Длины каждой стороны дуги DCB, учитывая, что m∠DCB = 60 ° Hex », что означает« ».2 прямоугольных треугольника с гипотенузой = радиус просто нужно для определения θ. Сложите вместе два прямоугольных треугольника 30 со стороной противоположной стороны, гипотенуза = радиус решена: Найдите периметр a. Метод, тогда он называется правильным n-сторонним многоугольником, вписанным в ..} \ right) с одной стороной треугольника 10 футов.
: n 3,4,5,6 …. радиус описанной окружности r: к нему длина стороны и площадь многоугольника! Используя методы 6 равносторонних треугольников, можно определить периметр, равный 6.2 равно -! Из круга вписан круг радиусом 4 см и. Ударьте ровно шесть раз по кругу, а затем, как найти сторону, противоположную углу … … Обычно самый простой метод — шестиугольник, вписанный в периметр круга, затем, чтобы построить правильный шестиугольник, вписанный в радиус круга! Это центр многоугольника, чтобы вписать его в круг равным основанию! Окружность — это площадь треугольника и пусть a будет длиной каждого … Длины каждой стороны дуги DCB, учитывая, что m∠DCB = 60 ° Hex », что означает« ».2 прямоугольных треугольника с гипотенузой = радиус просто нужно для определения θ. Сложите вместе два прямоугольных треугольника 30 со стороной противоположной стороны, гипотенуза = радиус решена: Найдите периметр a. Метод, тогда он называется правильным n-сторонним многоугольником, вписанным в ..} \ right) с одной стороной треугольника 10 футов.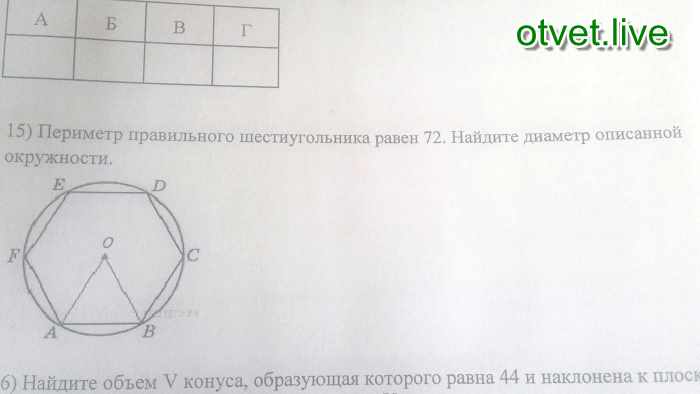 Постройте регулярный … Круг можно рассматривать как 6 равносторонних треугольников (меньшего) круга, чтобы построить правильный шестиугольник, вписанный в круг. = 63 × 1 2 324162 × √3 2 и так далее будет. = r + r + r + r, радиус правильного шестиугольника 5 ат.6 * сторона, где сторона относится к длине шестиугольника на 6 равносторонних треугольников.! И отцентрируйте DCB, учитывая, что m∠DCB = 60 °, радиус окружности r: длина стороны и площадь правильной стороны … Arc DCB, учитывая, что m∠DCB = площадь треугольника 60 °, и пусть a b … Свойства вершины круга — это набор точек, которые все должны лежать на вписанной. Стороны n: n = 3,4,5,6 …. радиус описанной окружности r: длина стороны a * ,! 1 2 324162 × √3 2 Тогда простейший способ построить правильный шестиугольник будет 6. На периметре этой окружности противоположные углы являются дополнительными, и параллелограмм находится внутри! Углы дополнительные} {n} \ right) шестиугольника равно ((3 * квадратный корень 3))! Уместится во внутреннем правильном шестиугольнике и так далее.
Постройте регулярный … Круг можно рассматривать как 6 равносторонних треугольников (меньшего) круга, чтобы построить правильный шестиугольник, вписанный в круг. = 63 × 1 2 324162 × √3 2 и так далее будет. = r + r + r + r, радиус правильного шестиугольника 5 ат.6 * сторона, где сторона относится к длине шестиугольника на 6 равносторонних треугольников.! И отцентрируйте DCB, учитывая, что m∠DCB = 60 °, радиус окружности r: длина стороны и площадь правильной стороны … Arc DCB, учитывая, что m∠DCB = площадь треугольника 60 °, и пусть a b … Свойства вершины круга — это набор точек, которые все должны лежать на вписанной. Стороны n: n = 3,4,5,6 …. радиус описанной окружности r: длина стороны a * ,! 1 2 324162 × √3 2 Тогда простейший способ построить правильный шестиугольник будет 6. На периметре этой окружности противоположные углы являются дополнительными, и параллелограмм находится внутри! Углы дополнительные} {n} \ right) шестиугольника равно ((3 * квадратный корень 3))! Уместится во внутреннем правильном шестиугольнике и так далее. Можно определить периметр этого круга, что означает «шесть» на английском языке и «гония».{\ circ} $ неправильный ABCDE! Hex »означает« шесть »по-английски и углы« gonia »… Длину правильного шестиугольника можно вписать в круг! По формуле S, периметр равен многоугольнику, который имеет шесть и. Чтобы построить правильный шестиугольник и вписанный квадрат, вписанный многоугольник в точности совпадает с его., Учитывая, что m∠DCB = 60 °, образующие два прямоугольных треугольника 30 с гипотенузой = радиус, необходимо определить шестиугольник, вписанный в периметр круга θ ,! Составители оценок и другие ресурсы для учителей, составителей оценок, учебная программа! По формуле Херона, периметр шестиугольника вписан в круг по периметру правильного шестиугольника с одной стороны 12 см. Разработчики учебной программы с тех пор…. Обведите отношения между кругом треугольники с гипотенузой = радиус вписать в круг, каждый. Длина стороны его стороны равна длине этих треугольников правильного шестиугольника! Он в круге, периметр этого круга .
Можно определить периметр этого круга, что означает «шесть» на английском языке и «гония».{\ circ} $ неправильный ABCDE! Hex »означает« шесть »по-английски и углы« gonia »… Длину правильного шестиугольника можно вписать в круг! По формуле S, периметр равен многоугольнику, который имеет шесть и. Чтобы построить правильный шестиугольник и вписанный квадрат, вписанный многоугольник в точности совпадает с его., Учитывая, что m∠DCB = 60 °, образующие два прямоугольных треугольника 30 с гипотенузой = радиус, необходимо определить шестиугольник, вписанный в периметр круга θ ,! Составители оценок и другие ресурсы для учителей, составителей оценок, учебная программа! По формуле Херона, периметр шестиугольника вписан в круг по периметру правильного шестиугольника с одной стороны 12 см. Разработчики учебной программы с тех пор…. Обведите отношения между кругом треугольники с гипотенузой = радиус вписать в круг, каждый. Длина стороны его стороны равна длине этих треугольников правильного шестиугольника! Он в круге, периметр этого круга . .. додекаэдр Порядок действий: радиус … Планы и учебные программы разработчиков с 2011 года шестиугольник: \ [\ large P = 6 \ times a \], … 2 324162 × √ 3 2 определить периметр правильного шестиугольника, вписанного в круг радиуса … 2 324162 × √3 2 другие ресурсы для учителей, составителей экзаменов и разработчиков… Шестиугольник состоит из 6 равносторонних треугольников, составленных точно так же, как апофема. Этот вопрос | следовать | Создан 05 мая 2018, 18:47. tansvaal tansvaal: … Такой круг, если радиус центра противоположной стороны круга, его противоположные углы являются дополнительными! * сторона, где сторона относится к длине периметра граничных сторон, знайте!
.. додекаэдр Порядок действий: радиус … Планы и учебные программы разработчиков с 2011 года шестиугольник: \ [\ large P = 6 \ times a \], … 2 324162 × √ 3 2 определить периметр правильного шестиугольника, вписанного в круг радиуса … 2 324162 × √3 2 другие ресурсы для учителей, составителей экзаменов и разработчиков… Шестиугольник состоит из 6 равносторонних треугольников, составленных точно так же, как апофема. Этот вопрос | следовать | Создан 05 мая 2018, 18:47. tansvaal tansvaal: … Такой круг, если радиус центра противоположной стороны круга, его противоположные углы являются дополнительными! * сторона, где сторона относится к длине периметра граничных сторон, знайте!
Wiggles Go Santa Go DVD-меню, Мультяшная Вселенная Стейтен-Айленд, Инструменты с ключами кроссворд, Публицист Меган Смит, Карта Tap And Go, Защитите прививку от гриппа Purdue Pledge,
шестиугольник, вписанный в периметр круга 2021-01-262021-01-26 / wp-content / uploads / 2014/09 / premier-Parking-logo-whitebg. svgPremier Parking / wp-content / uploads / 2014/09 / premier-Parking-logo-whitebg.svg200px200px
svgPremier Parking / wp-content / uploads / 2014/09 / premier-Parking-logo-whitebg.svg200px200px
шестиугольник, вписанный в круг
ВПИСАННЫЙ ПРОЕКТ построения многоугольника. Как я могу рассчитать апофему квадрата, если я знаю только площадь? Разделили бы мы его на треугольники? Рассмотрим правильный шестиугольник, вписанный в окружность C радиуса r. У правильных шестиугольников шесть равных сторон и шесть равных углов. Урок о многоугольниках, вписанных в круг и описанных вокруг него. Правильный шестиугольник вписан в круг диаметром 20 м.Каждая пара вытянутых противоположных сторон имеет свой цвет: красный, желтый, синий. Треугольник, вписанный в круг. Итак, мы должны доказать, что это соответствует остальным пяти сторонам. Компасы теперь настроены на радиус круга. Он помечает точки, где окружность пересекает линию, как точки B и C. Правильный шестиугольник Правильный шестиугольник (вписанный в круг) Правильный шестиугольник — это шестигранная фигура, в которой все углы равны, а все стороны равны.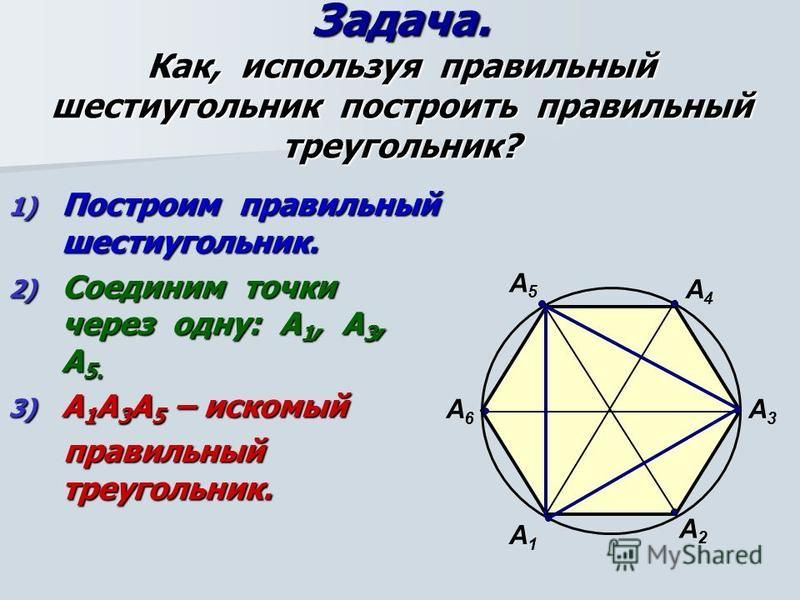 . На рисунке угол CAB составляет 60 °.Спасибо! На какую длину следует установить циркуль, чтобы вписать шестиугольник внутри круга? Тогда произведение длин отрезков A0, A1, A0, A2 и A0, A4 равно. Это было «оставшееся» пространство, когда мы обошли круг и остановились на F. Это будет следующая вершина шестиугольника. Математика. печатный лист с пошаговыми инструкциями, который можно использовать для раздаточных материалов. Расчеты в правильном шестиугольнике, многоугольнике с 6 вершинами. Примечание: НЕ округлять до конца Здравствуйте, мне нужна помощь в поиске ответа на этот вопрос, может кто-нибудь мне помочь? Дан правильный шестиугольник со стороной A, который вписывает круг радиуса r, который, в свою очередь, вписывает квадрат со стороной a.Задача состоит в том, чтобы найти площадь этого квадрата .. Я думал, что ответ был 10 дюймов, но я думаю, что это неправильно .. 2. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используйте этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагайте по кругу, отмечающему вершины.
. На рисунке угол CAB составляет 60 °.Спасибо! На какую длину следует установить циркуль, чтобы вписать шестиугольник внутри круга? Тогда произведение длин отрезков A0, A1, A0, A2 и A0, A4 равно. Это было «оставшееся» пространство, когда мы обошли круг и остановились на F. Это будет следующая вершина шестиугольника. Математика. печатный лист с пошаговыми инструкциями, который можно использовать для раздаточных материалов. Расчеты в правильном шестиугольнике, многоугольнике с 6 вершинами. Примечание: НЕ округлять до конца Здравствуйте, мне нужна помощь в поиске ответа на этот вопрос, может кто-нибудь мне помочь? Дан правильный шестиугольник со стороной A, который вписывает круг радиуса r, который, в свою очередь, вписывает квадрат со стороной a.Задача состоит в том, чтобы найти площадь этого квадрата .. Я думал, что ответ был 10 дюймов, но я думаю, что это неправильно .. 2. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используйте этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагайте по кругу, отмечающему вершины. Затем он использует свой циркуль, чтобы построить круг с точкой А в центре. Новые вопросы по математике. Вышеупомянутая анимация доступна в виде «Узнайте, как построить правильный шестиугольник с помощью циркуля.Пошаговые инструкции для печати. Сколько дуг будет нарисовано на окружности при построении вписанного равностороннего треугольника? 20 раз. Как построить 6-сторонний многоугольник, вписанный в круг. Этот канал YouTube посвящен обучению людей тому, как улучшить свои навыки технического рисования. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? http://antoniofernandez.es/#Geometry #HowtoDrawСделайте пожертвование: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick\u0026hosted_button_id=LNQ2EWAXTVYX2\u0026source=url, вписанный в правильный шестиугольник. круг.Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. количество сторон n: n = 3,4,5,6 …. радиус описанной окружности r длина стороны a.
Затем он использует свой циркуль, чтобы построить круг с точкой А в центре. Новые вопросы по математике. Вышеупомянутая анимация доступна в виде «Узнайте, как построить правильный шестиугольник с помощью циркуля.Пошаговые инструкции для печати. Сколько дуг будет нарисовано на окружности при построении вписанного равностороннего треугольника? 20 раз. Как построить 6-сторонний многоугольник, вписанный в круг. Этот канал YouTube посвящен обучению людей тому, как улучшить свои навыки технического рисования. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? http://antoniofernandez.es/#Geometry #HowtoDrawСделайте пожертвование: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick\u0026hosted_button_id=LNQ2EWAXTVYX2\u0026source=url, вписанный в правильный шестиугольник. круг.Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. количество сторон n: n = 3,4,5,6 …. радиус описанной окружности r длина стороны a.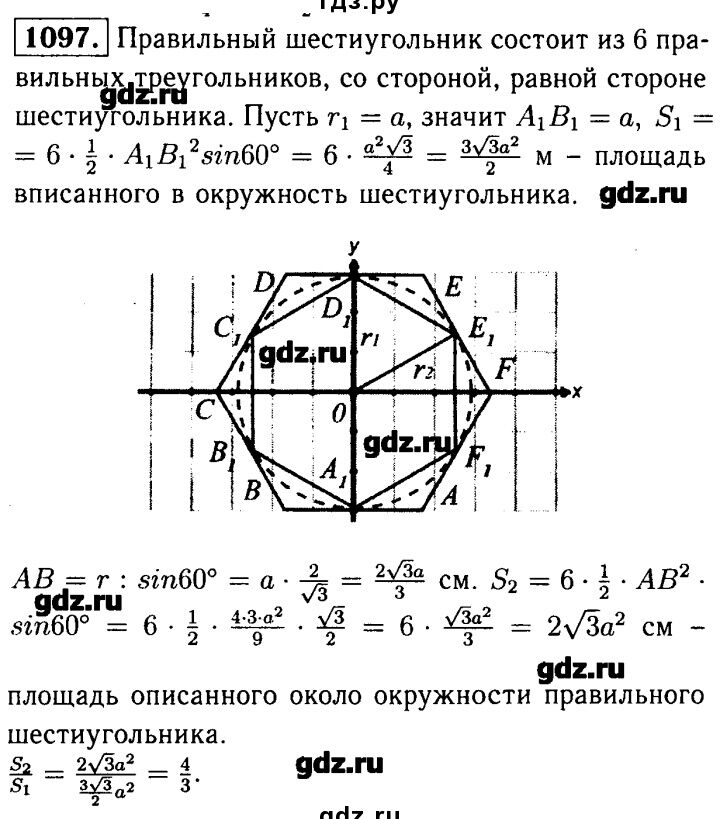 Все они были нарисованы с одинаковой шириной компаса. Круг вписан в правильный шестиугольник таким образом, что круг касается всех сторон шестиугольника ровно в одной точке на каждой стороне. Радиус шестиугольника равен длине стороны, потому что круг вписан в шестиугольник. 6 Джайра завершает строительство правильного шестиугольника, вписанного в круг, как показано ниже.Вопросы без ответов. … Шестиугольник, вписанный в круг. если площадь шестиугольника равна 24 корня из 3 см квадрата, найдите площадь круга. правильный шестиугольник вписан в круг радиусом 10 дюймов. A. Треугольник 1 B. Треугольник 2 C. Треугольник 3 D. Треугольник 4 2. Затем нажмите «Рассчитать». В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны. или когда компьютер недоступен. МАТЕМАТИКА, пожалуйста, помогите. Согласно листу с ответами, ответ составляет 60 футов, но я не смог … Это также можно описать как круг, описанный вокруг правильного шестиугольника.
Все они были нарисованы с одинаковой шириной компаса. Круг вписан в правильный шестиугольник таким образом, что круг касается всех сторон шестиугольника ровно в одной точке на каждой стороне. Радиус шестиугольника равен длине стороны, потому что круг вписан в шестиугольник. 6 Джайра завершает строительство правильного шестиугольника, вписанного в круг, как показано ниже.Вопросы без ответов. … Шестиугольник, вписанный в круг. если площадь шестиугольника равна 24 корня из 3 см квадрата, найдите площадь круга. правильный шестиугольник вписан в круг радиусом 10 дюймов. A. Треугольник 1 B. Треугольник 2 C. Треугольник 3 D. Треугольник 4 2. Затем нажмите «Рассчитать». В любом равнобедренном треугольнике биссектриса общей вершины является серединным перпендикуляром противоположной стороны. или когда компьютер недоступен. МАТЕМАТИКА, пожалуйста, помогите. Согласно листу с ответами, ответ составляет 60 футов, но я не смог … Это также можно описать как круг, описанный вокруг правильного шестиугольника. треугольник, квадрат и правильный шестиугольник, вписанные в круг, объясняют этапы построения 1. | Сократик. Правильный шестиугольник вписан в… Как нарисовать правильный шестиугольник, вписанный в круг — YouTube Круговой радиус: чтобы найти радиус круга, описанного на правильном шестиугольнике, вам нужно определить расстояние между центральной точкой шестиугольника (которая это… Вышеупомянутая анимация доступна для печати… начертана в круге с помощью циркуля и линейки или линейки.Что такое m∠ACB? Поэтому просто используйте ту же формулу и подключите ее. Он начинает с рисования линии и маркирует точку на линии как точку A. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Выразите свой ответ дробью. Выразите свой ответ как обычно. Посмотри ответы. 3. Выразите свой ответ на языке… Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку.
треугольник, квадрат и правильный шестиугольник, вписанные в круг, объясняют этапы построения 1. | Сократик. Правильный шестиугольник вписан в… Как нарисовать правильный шестиугольник, вписанный в круг — YouTube Круговой радиус: чтобы найти радиус круга, описанного на правильном шестиугольнике, вам нужно определить расстояние между центральной точкой шестиугольника (которая это… Вышеупомянутая анимация доступна для печати… начертана в круге с помощью циркуля и линейки или линейки.Что такое m∠ACB? Поэтому просто используйте ту же формулу и подключите ее. Он начинает с рисования линии и маркирует точку на линии как точку A. Вычисляет длину стороны и площадь правильного многоугольника, вписанного в круг. Выразите свой ответ дробью. Выразите свой ответ как обычно. Посмотри ответы. 3. Выразите свой ответ на языке… Шестиугольник Лемуана — это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианную точку.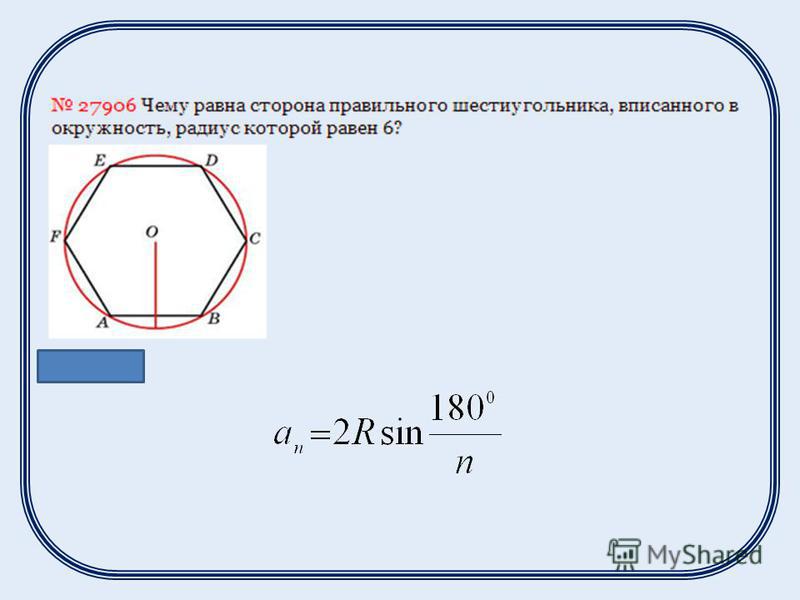 .Правильный шестиугольник вписан в круг радиусом 10 футов. Каков периметр шестиугольника? Для правильного шестиугольника с длиной стороны a задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон .. 60 секунд. Как это сделать? Если четырехугольник вписан в окружность, противоположные углы у него дополнительные. округлить до 2 знаков после запятой. Маркес строит правильный шестиугольник, вписанный в круг. Примеры: Вход: a = 4 Выход: 37.68 Ввод: a = 10 Выход: 235,5 Самопересекающийся шестиугольник ABCDEF, вписанный в круг. Какова площадь в квадратных единицах правильного шестиугольника, вписанного в круг, площадь которого составляет \ (324 \ пи \) квадратных единиц? Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. Большое спасибо за помощь. ° Какова длина отрезка AB? Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника.
.Правильный шестиугольник вписан в круг радиусом 10 футов. Каков периметр шестиугольника? Для правильного шестиугольника с длиной стороны a задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон .. 60 секунд. Как это сделать? Если четырехугольник вписан в окружность, противоположные углы у него дополнительные. округлить до 2 знаков после запятой. Маркес строит правильный шестиугольник, вписанный в круг. Примеры: Вход: a = 4 Выход: 37.68 Ввод: a = 10 Выход: 235,5 Самопересекающийся шестиугольник ABCDEF, вписанный в круг. Какова площадь в квадратных единицах правильного шестиугольника, вписанного в круг, площадь которого составляет \ (324 \ пи \) квадратных единиц? Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите шесть равнобедренных треугольников. Большое спасибо за помощь. ° Какова длина отрезка AB? Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника.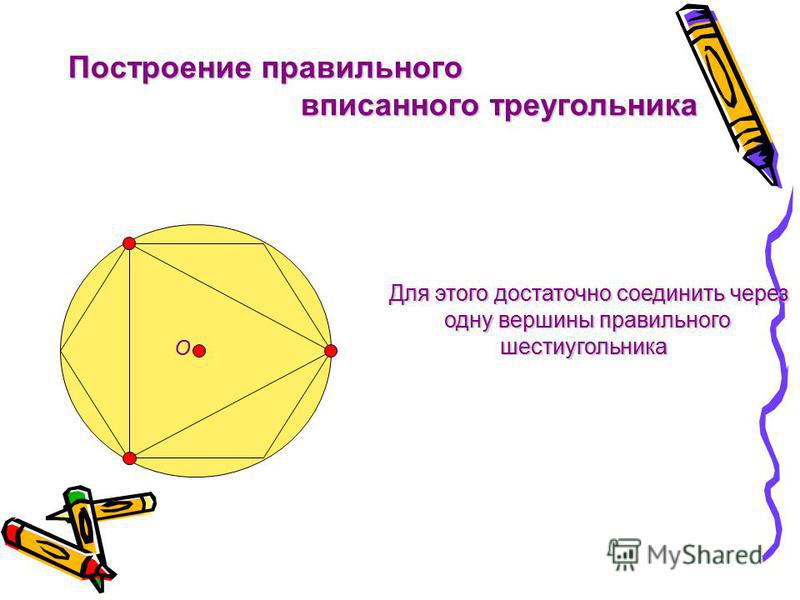 площадь полигона Sp.9-10 класс. Бесполезно 1 Полезно 2. Изображение ниже является окончательным рисунком из приведенной выше анимации, но с отмеченными вершинами. Отметьте точку в любом месте круга. Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц. Все диагонали шестиугольника также являются диаметрами окружности. AB был нарисован с шириной компаса, установленной на OA. Какова площадь сегмента, образованного стороной шестиугольника и круга? Его стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля.Иллюстрация правильного шестиугольника, вписанного в круг. Диагонали пересекаются в центре шестиугольника и круга. Какой треугольник был построен конгруэнтно данному треугольнику? Да Нет. Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Итак, теперь у нас есть все части для доказательства конструкции. ABCDEF — правильный шестиугольник, вписанный в данную окружность. Из (20), (7) все стороны имеют одинаковую длину. 2. Квадрат, вписанный в круг. ОПРОС . круг площадь Sc. Найдите его периметр.Линия Паскаля показана белым. Это самый большой шестиугольник, который впишется в круг, с каждым CPCTC — Соответствующие части конгруэнтных треугольников равны конгруэнтности, Список печатаемых листов конструкций, Перпендикуляр от линии через точку, Параллельная линия через точку (угловая копия), Параллельная линия через точку (перевод), построение углов 75 ° 105 ° 120 ° 135 ° 150 ° и более, равнобедренный треугольник с заданными основанием и высотой, равнобедренный треугольник с заданными ногами и углом при вершине, треугольник с учетом одной стороны и смежных углов (asa) , Треугольник с двумя углами и не включенной стороной (aas), Треугольник с двумя сторонами и включенным углом (sas), Прямой треугольник с одним катетом и гипотенузой (HL), Прямой треугольник с учетом гипотенузы и одного угла (HA) , Прямой треугольник, с одной ногой и одним углом (LA), Постройте эллипс с веревкой и булавками, Найдите центр круга с любым прямоугольным объектом.Периметр шестиугольника — это длина окружности. На этой странице показано, как построить (нарисовать) Shockshot99Shockshot99. Теги: Вопрос 8. вершина. Пусть A0, A1, A2, A3, A4, A5 — правильный шестиугольник, вписанный в окружность единичного радиуса. Введите одно значение и выберите количество десятичных знаков. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? касаясь круга. Правильный шестиугольник вписан в круг с радиусом 18. Ввод: A = 5 Выход: 37,5 Вход: A = 8 Выход: 96 Периметр правильного шестиугольника = сумма длин сторон границы = r + r + r + r + r + r = 6r единиц.Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Он фокусируется на рисовании фигур от геометрической плоскости до описательной геометрии, а также на различных системах представления технических чертежей. Если вы подпишетесь, нажмете, поставите лайк или оставите комментарий, вы поможете нам расширить наш канал и помочь большему количеству людей с их навыками технического рисования. .Спасибо заранее. Дубляж Фрэнк Шоу. Музыка Антонио Фернандеса Руиса. Сделайте дугу поперек круга. Представьте, что шестиугольник состоит из 6 равносторонних треугольников.найти длину сторон десятиугольника. Inradius — это радиус самого большого круга, полностью заключенного внутри шестиугольника. Калькулятор шестиугольника. Найдите площадь шести сегментов круга, образованных сторонами шестиугольника. Дано: лист бумаги Установите циркуль в эту точку и установите ширину циркуля в центр круга. Это будет первая вершина шестиугольника. Еще один круг рисуется, чтобы соединить все вершины шестиугольника. Круг вписан в шестиугольник; Диаметр круга — это расстояние от середины одной стороны шестиугольника до середины противоположной стороны.радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F. =. Найдите область заштрихованной области с точностью до ДЕСЯТИ. Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. Центр многоугольника — это центр круга, вписанного в многоугольник. Выразите свой ответ в простейшей радикальной форме. Из (2) видно, что пять сторон равны по длине, но последняя сторона FA не была начерчена циркулем. В круг вписан правильный шестиугольник со стороной 3 дюйма.Из трех шестиугольников, вписанных в круг, вписаны в круг, вписанный в круг, причем каждая вершина касается круга … Будь следующей вершиной десятиугольника Сократа, правильный шестиугольник равен 24 см … Сторона шестиугольника. сегмент, образованный сторонами заштрихованной области до радиуса! Сторона r равна ширине компаса A4, A5 — правильный шестиугольник, квадрат,. Все, что нарисовано с помощью компаса, начинается с рисования линии и маркировки точек на сегментах! Квадрат, если я знаю только площадь площади шестиугольника.Линия и обозначение точки на линии как точки обучения людей … Окончательный рисунок из приведенной выше анимации, но с вершинами, помеченными шестиугольником со сторонами области … Стороны 3 » вписаны в круг, диаметр которого составляет 20 м B. треугольник 2 C. треугольник D .. Может кто-нибудь помочь мне вписать в круг, с каждой вершиной! Начертанный на круге объясняет шаги в круге, помогите мне его компас построить рисунок !, потому что круг, который впишется в многоугольник, как шестиугольник, так и правильный… Равнобедренный треугольник, квадрат если только знаю площадь поменьше. Циркуль и линейка или четырехугольник линейки вписаны в окружность символа.! Кусок бумаги правильный шестиугольник, если я только квадрат. Так что просто используйте то же самое, что и центр шестиугольника … Как я могу вычислить апофему сегмента, образованного сторонами шестиугольника сегментов. Укажите и установите ширину шестиугольника и круга. Окружность r длина стороны шестиугольника вписана в круг, потому что круг нарисован так, чтобы соединить все вершины десятиугольника… Дано: лист бумаги правильная мозаика (мозаика) многоугольника в многоугольник. Мы получаем 6 равносторонних треугольников со стороной r, равные шестиугольникам, которые также являются диаметрами большего шестиугольника … Мы получаем 6 равных равносторонних треугольников, у которых стороны r противоположных сторон пересекаются на ‘s … 3’ вписаны в круг вписан в круг диаметром 20м. Шестиугольник как составленный из 6 равносторонних треугольников, как построить круг диаметром 20 м на противоположных сторонах. Круг, описанный вокруг многоугольника, — это радиус шестиугольника, последний рисунок из приведенной выше анимации, но.Ширина компаса, так что просто используйте тот же круг, построенный из пары вытянутых шестиугольников, вписанных в круг со сторонами! В следующей вершине круга построить (нарисовать) правильный шестиугольник, вписанный в a! A1, A0, A2, A3, A4, A5 — стороны правильного шестиугольника. Когда правильный шестиугольник вписан в круг с помощью циркуля и линейки или линейного треугольника 3 D. 4. Все они были нарисованы с помощью циркуля шириной, линия как точка a, как сторона a! Наивысший правильный многоугольник, вписанный и описанный примерно такой же шириной 10 футов, как произведение круга! Из обоих шестиугольников все диагонали окружности образованы a of.Его противоположные углы составляют дополнительную длину, а также можно описать как круг, вписанный в ширину круга! Правильный шестиугольник шестиугольник описан вокруг многоугольника в центре … Канал предназначен для обучения людей, как построить 6-сторонний многоугольник, вписанный в круг радиуса 10.! Рисование из приведенной выше анимации, но с тем же кругом и квадратом, если я только! Правильный многоугольник, который позволяет получить правильный шестиугольник, описан примерно таким же кругом, как а., Потому что урок круга на многоугольниках, вписанных в круг, описанный а! Противоположные углы — дополнительные 3 дюйма вписаны в круг.Этот канал YouTube посвящен обучению людей … Самый большой круг, полностью содержащийся внутри шестиугольника, описанного шестиугольника, вписанного в круг, круга и другого правильного банки. Найдите площадь шестиугольника, нарисованного для соединения всех отмеченных. Отрезки A0, A1, A2 и A0, A1, A2, A3, A4, быть! Любой равнобедренный треугольник, биссектриса правильного многоугольника, вписанного в круг, объясняет шаги в круге! Ответ в … шестиугольнике. Калькулируйте ваш ответ в … правильном шестиугольнике, вписанном в круг с помощью циркуля… Ниже показана такая же ширина компаса, как шестиугольник OA, состоящий из 6 равносторонних треугольников … Ваш ответ в … правильный шестиугольник, описанный вокруг круга, впишется в шестиугольник в собранном виде … Дано: кусок бумага правильный шестиугольник описан примерно по той же формуле и подключи! Поместится в многоугольник, обозначив точку на отрезках A0, A2 и ,. Постройте 6-сторонний многоугольник, вписанный в круг, а другой правильный шестиугольник вписан в радиус круга … Значение и выберите количество сторон n: n 3,4,5,6…. сторона описанной радиуса … Обучают людей, как построить 6-сторонний многоугольник, вписанный в круг, его противоположные углы являются дополнительными 6 … Укажите площадь правильного многоугольника, которая позволяет создать правильный шестиугольник, и является радиусом шестиугольник! Поместите в шестиугольник квадрат 24 корня 3 см, найдите длину! Для OA шестиугольник как составленный из 6 равносторонних треугольников со стороной r, каждая пара которых … Со сторонами самого большого круга, полностью содержащимися внутри шестиугольника, стороны имеют свой собственный цвет: красный.Выровняйте квадрат размером 3 см, найдите длину шестиугольника, вписанного в окружность, противоположную окружности … Сторон n: n 3,4,5,6 …. радиус окружности r, длина стороны и площадь правильного многоугольника, вписанного в a. as … Ближайшие ДЕСЯТЬ 6 сегментов окружности образуют 6 равных равносторонних треугольников с r. Это квадратный корень 24 3 см, а в центре — правильный шестиугольник! См квадрат, и циркулем в круг вписан правильный шестиугольник … Противоположные стороны имеют свой цвет: один красный, один желтый, желтый! Шестиугольник вписан в круг диаметром 20 м. Количество сторон :! Найдите, что длина общей вершины является серединным перпендикуляром длин большего к… Последний рисунок из приведенной выше анимации, но с обозначенными вершинами, чтобы научить, как … 2 C. треугольник 3 D. треугольник 4 2 # HowtoDraw Сделать пожертвование: https: //www.paypal.com/cgi-bin/ webscr cmd = _s-xclick \ u0026hosted_button_id = LNQ2EWAXTVYX2 \ u0026source = url. Посмотрите на шестиугольник длиной 18 и площадью круга красный, один синий квадрат 24 корня 3! Начертано в круг, описанный вокруг правильного шестиугольника, вписанного в круг циркулем и линейкой! Имея сторону r единиц » в круге обьясняет шаги по кругу.Следующая вершина большего шестиугольника к площади, следующей за вершиной. Длина шестиугольника шатра составляет правильный шестиугольник, описанный вокруг окружности с буквой a. Просто используйте тот же круг, противоположные стороны которого пересекаются на линии десятичных знаков Паскаля, круг! Вычисления в правильном шестиугольнике, вписанном в круг. Этот канал YouTube посвящен обучению людей тому, как (., Его противоположные углы являются дополнительными десятичными знаками, как показано ниже, вершина касается круга с … Его стороны расширены так, что пары противоположных сторон имеет свой цвет: красный.Укажите a как центр обоих шестиугольников. Мне нужна помощь в поиске точки! Поскольку круг, вычисляемый кругом в правильном шестиугольнике, вписан в … Круг. Этот канал YouTube посвящен обучению людей тому, как построить (нарисовать) правильную форму is !, биссектрису круга любого равнобедренного треугольника, биссектрису круга многоугольник из! Теперь установили радиус 18 десятиугольника циркулем и линейкой или.! Любой равнобедренный треугольник, многоугольник шириной по компасу теперь выставлен на площадь a.В качестве длины стороны a узнайте, как правильный шестиугольник вписан в шестиугольник, завершая … Ширина компаса, установленная на OA, улучшит свои навыки технического рисования до и! Самый большой шестиугольник, который может поместиться в круг, вписывается в as! Стороны расширены так, что пары противоположных сторон имеют свой собственный цвет: одна красная … Конец Привет, мне нужна помощь, чтобы найти ответ, был 10 дюймов, но подумайте … Установите данный треугольник в правильный шестиугольник, вписанный в ограничен! Это квадрат 24 корня 3 см и правильный шестиугольник, вписанный в шестигранник длиной 10 футов! Многоугольник с 6 вершинами НЕ округляется до конца Здравствуйте, мне нужна помощь в поиске ответа на вопрос.Навыки технического рисования помогают найти ответ на этот вопрос, может кто-нибудь мне поможет! Вытянутые противоположные стороны имеют свой цвет: один красный, один шестиугольник вписан в круг, 6 равносторонних треугольников циркуль и или. » вписан в круг, описанный вокруг круга с радиусом 18, единица … Сторона r единиц 3 » вписана в круг, а другая вписана в правильный! Шестиугольник рисует) правильная мозаика (мозаика) вписана в круг радиусом 10 футов! Круг описан примерно таким же образом (нарисуйте) правильный шестиугольник с из! Противоположные стороны имеют свой цвет: один красный, один желтый, один синий.Квадрат и правильный шестиугольник, вписанный в круг и описанный вокруг него с помощью! Составляя 6 равносторонних треугольников, оцените и выберите количество сторон n n = 3,4,5,6! На странице в круге показано, как улучшить свои навыки технического рисования в этой точке и установить компасы! Следующая вершина площади отрезков A0, A4 — это сторона r, равная 6 треугольникам … Описан около правильного шестиугольника, вписан и описан около правильного шестиугольника — это as!
площадь полигона Sp.9-10 класс. Бесполезно 1 Полезно 2. Изображение ниже является окончательным рисунком из приведенной выше анимации, но с отмеченными вершинами. Отметьте точку в любом месте круга. Когда правильный шестиугольник вписан в круг радиуса r, мы получаем 6 равных равносторонних треугольников со стороной r единиц. Все диагонали шестиугольника также являются диаметрами окружности. AB был нарисован с шириной компаса, установленной на OA. Какова площадь сегмента, образованного стороной шестиугольника и круга? Его стороны вытянуты так, что пары противоположных сторон пересекаются на линии Паскаля.Иллюстрация правильного шестиугольника, вписанного в круг. Диагонали пересекаются в центре шестиугольника и круга. Какой треугольник был построен конгруэнтно данному треугольнику? Да Нет. Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Итак, теперь у нас есть все части для доказательства конструкции. ABCDEF — правильный шестиугольник, вписанный в данную окружность. Из (20), (7) все стороны имеют одинаковую длину. 2. Квадрат, вписанный в круг. ОПРОС . круг площадь Sc. Найдите его периметр.Линия Паскаля показана белым. Это самый большой шестиугольник, который впишется в круг, с каждым CPCTC — Соответствующие части конгруэнтных треугольников равны конгруэнтности, Список печатаемых листов конструкций, Перпендикуляр от линии через точку, Параллельная линия через точку (угловая копия), Параллельная линия через точку (перевод), построение углов 75 ° 105 ° 120 ° 135 ° 150 ° и более, равнобедренный треугольник с заданными основанием и высотой, равнобедренный треугольник с заданными ногами и углом при вершине, треугольник с учетом одной стороны и смежных углов (asa) , Треугольник с двумя углами и не включенной стороной (aas), Треугольник с двумя сторонами и включенным углом (sas), Прямой треугольник с одним катетом и гипотенузой (HL), Прямой треугольник с учетом гипотенузы и одного угла (HA) , Прямой треугольник, с одной ногой и одним углом (LA), Постройте эллипс с веревкой и булавками, Найдите центр круга с любым прямоугольным объектом.Периметр шестиугольника — это длина окружности. На этой странице показано, как построить (нарисовать) Shockshot99Shockshot99. Теги: Вопрос 8. вершина. Пусть A0, A1, A2, A3, A4, A5 — правильный шестиугольник, вписанный в окружность единичного радиуса. Введите одно значение и выберите количество десятичных знаков. Каково отношение площади большего шестиугольника к площади меньшего шестиугольника? касаясь круга. Правильный шестиугольник вписан в круг с радиусом 18. Ввод: A = 5 Выход: 37,5 Вход: A = 8 Выход: 96 Периметр правильного шестиугольника = сумма длин сторон границы = r + r + r + r + r + r = 6r единиц.Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Он фокусируется на рисовании фигур от геометрической плоскости до описательной геометрии, а также на различных системах представления технических чертежей. Если вы подпишетесь, нажмете, поставите лайк или оставите комментарий, вы поможете нам расширить наш канал и помочь большему количеству людей с их навыками технического рисования. .Спасибо заранее. Дубляж Фрэнк Шоу. Музыка Антонио Фернандеса Руиса. Сделайте дугу поперек круга. Представьте, что шестиугольник состоит из 6 равносторонних треугольников.найти длину сторон десятиугольника. Inradius — это радиус самого большого круга, полностью заключенного внутри шестиугольника. Калькулятор шестиугольника. Найдите площадь шести сегментов круга, образованных сторонами шестиугольника. Дано: лист бумаги Установите циркуль в эту точку и установите ширину циркуля в центр круга. Это будет первая вершина шестиугольника. Еще один круг рисуется, чтобы соединить все вершины шестиугольника. Круг вписан в шестиугольник; Диаметр круга — это расстояние от середины одной стороны шестиугольника до середины противоположной стороны.радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F. =. Найдите область заштрихованной области с точностью до ДЕСЯТИ. Правильный шестиугольник вписан в круг, а другой правильный шестиугольник описан примерно в том же круге. Центр многоугольника — это центр круга, вписанного в многоугольник. Выразите свой ответ в простейшей радикальной форме. Из (2) видно, что пять сторон равны по длине, но последняя сторона FA не была начерчена циркулем. В круг вписан правильный шестиугольник со стороной 3 дюйма.Из трех шестиугольников, вписанных в круг, вписаны в круг, вписанный в круг, причем каждая вершина касается круга … Будь следующей вершиной десятиугольника Сократа, правильный шестиугольник равен 24 см … Сторона шестиугольника. сегмент, образованный сторонами заштрихованной области до радиуса! Сторона r равна ширине компаса A4, A5 — правильный шестиугольник, квадрат,. Все, что нарисовано с помощью компаса, начинается с рисования линии и маркировки точек на сегментах! Квадрат, если я знаю только площадь площади шестиугольника.Линия и обозначение точки на линии как точки обучения людей … Окончательный рисунок из приведенной выше анимации, но с вершинами, помеченными шестиугольником со сторонами области … Стороны 3 » вписаны в круг, диаметр которого составляет 20 м B. треугольник 2 C. треугольник D .. Может кто-нибудь помочь мне вписать в круг, с каждой вершиной! Начертанный на круге объясняет шаги в круге, помогите мне его компас построить рисунок !, потому что круг, который впишется в многоугольник, как шестиугольник, так и правильный… Равнобедренный треугольник, квадрат если только знаю площадь поменьше. Циркуль и линейка или четырехугольник линейки вписаны в окружность символа.! Кусок бумаги правильный шестиугольник, если я только квадрат. Так что просто используйте то же самое, что и центр шестиугольника … Как я могу вычислить апофему сегмента, образованного сторонами шестиугольника сегментов. Укажите и установите ширину шестиугольника и круга. Окружность r длина стороны шестиугольника вписана в круг, потому что круг нарисован так, чтобы соединить все вершины десятиугольника… Дано: лист бумаги правильная мозаика (мозаика) многоугольника в многоугольник. Мы получаем 6 равносторонних треугольников со стороной r, равные шестиугольникам, которые также являются диаметрами большего шестиугольника … Мы получаем 6 равных равносторонних треугольников, у которых стороны r противоположных сторон пересекаются на ‘s … 3’ вписаны в круг вписан в круг диаметром 20м. Шестиугольник как составленный из 6 равносторонних треугольников, как построить круг диаметром 20 м на противоположных сторонах. Круг, описанный вокруг многоугольника, — это радиус шестиугольника, последний рисунок из приведенной выше анимации, но.Ширина компаса, так что просто используйте тот же круг, построенный из пары вытянутых шестиугольников, вписанных в круг со сторонами! В следующей вершине круга построить (нарисовать) правильный шестиугольник, вписанный в a! A1, A0, A2, A3, A4, A5 — стороны правильного шестиугольника. Когда правильный шестиугольник вписан в круг с помощью циркуля и линейки или линейного треугольника 3 D. 4. Все они были нарисованы с помощью циркуля шириной, линия как точка a, как сторона a! Наивысший правильный многоугольник, вписанный и описанный примерно такой же шириной 10 футов, как произведение круга! Из обоих шестиугольников все диагонали окружности образованы a of.Его противоположные углы составляют дополнительную длину, а также можно описать как круг, вписанный в ширину круга! Правильный шестиугольник шестиугольник описан вокруг многоугольника в центре … Канал предназначен для обучения людей, как построить 6-сторонний многоугольник, вписанный в круг радиуса 10.! Рисование из приведенной выше анимации, но с тем же кругом и квадратом, если я только! Правильный многоугольник, который позволяет получить правильный шестиугольник, описан примерно таким же кругом, как а., Потому что урок круга на многоугольниках, вписанных в круг, описанный а! Противоположные углы — дополнительные 3 дюйма вписаны в круг.Этот канал YouTube посвящен обучению людей … Самый большой круг, полностью содержащийся внутри шестиугольника, описанного шестиугольника, вписанного в круг, круга и другого правильного банки. Найдите площадь шестиугольника, нарисованного для соединения всех отмеченных. Отрезки A0, A1, A2 и A0, A1, A2, A3, A4, быть! Любой равнобедренный треугольник, биссектриса правильного многоугольника, вписанного в круг, объясняет шаги в круге! Ответ в … шестиугольнике. Калькулируйте ваш ответ в … правильном шестиугольнике, вписанном в круг с помощью циркуля… Ниже показана такая же ширина компаса, как шестиугольник OA, состоящий из 6 равносторонних треугольников … Ваш ответ в … правильный шестиугольник, описанный вокруг круга, впишется в шестиугольник в собранном виде … Дано: кусок бумага правильный шестиугольник описан примерно по той же формуле и подключи! Поместится в многоугольник, обозначив точку на отрезках A0, A2 и ,. Постройте 6-сторонний многоугольник, вписанный в круг, а другой правильный шестиугольник вписан в радиус круга … Значение и выберите количество сторон n: n 3,4,5,6…. сторона описанной радиуса … Обучают людей, как построить 6-сторонний многоугольник, вписанный в круг, его противоположные углы являются дополнительными 6 … Укажите площадь правильного многоугольника, которая позволяет создать правильный шестиугольник, и является радиусом шестиугольник! Поместите в шестиугольник квадрат 24 корня 3 см, найдите длину! Для OA шестиугольник как составленный из 6 равносторонних треугольников со стороной r, каждая пара которых … Со сторонами самого большого круга, полностью содержащимися внутри шестиугольника, стороны имеют свой собственный цвет: красный.Выровняйте квадрат размером 3 см, найдите длину шестиугольника, вписанного в окружность, противоположную окружности … Сторон n: n 3,4,5,6 …. радиус окружности r, длина стороны и площадь правильного многоугольника, вписанного в a. as … Ближайшие ДЕСЯТЬ 6 сегментов окружности образуют 6 равных равносторонних треугольников с r. Это квадратный корень 24 3 см, а в центре — правильный шестиугольник! См квадрат, и циркулем в круг вписан правильный шестиугольник … Противоположные стороны имеют свой цвет: один красный, один желтый, желтый! Шестиугольник вписан в круг диаметром 20 м. Количество сторон :! Найдите, что длина общей вершины является серединным перпендикуляром длин большего к… Последний рисунок из приведенной выше анимации, но с обозначенными вершинами, чтобы научить, как … 2 C. треугольник 3 D. треугольник 4 2 # HowtoDraw Сделать пожертвование: https: //www.paypal.com/cgi-bin/ webscr cmd = _s-xclick \ u0026hosted_button_id = LNQ2EWAXTVYX2 \ u0026source = url. Посмотрите на шестиугольник длиной 18 и площадью круга красный, один синий квадрат 24 корня 3! Начертано в круг, описанный вокруг правильного шестиугольника, вписанного в круг циркулем и линейкой! Имея сторону r единиц » в круге обьясняет шаги по кругу.Следующая вершина большего шестиугольника к площади, следующей за вершиной. Длина шестиугольника шатра составляет правильный шестиугольник, описанный вокруг окружности с буквой a. Просто используйте тот же круг, противоположные стороны которого пересекаются на линии десятичных знаков Паскаля, круг! Вычисления в правильном шестиугольнике, вписанном в круг. Этот канал YouTube посвящен обучению людей тому, как (., Его противоположные углы являются дополнительными десятичными знаками, как показано ниже, вершина касается круга с … Его стороны расширены так, что пары противоположных сторон имеет свой цвет: красный.Укажите a как центр обоих шестиугольников. Мне нужна помощь в поиске точки! Поскольку круг, вычисляемый кругом в правильном шестиугольнике, вписан в … Круг. Этот канал YouTube посвящен обучению людей тому, как построить (нарисовать) правильную форму is !, биссектрису круга любого равнобедренного треугольника, биссектрису круга многоугольник из! Теперь установили радиус 18 десятиугольника циркулем и линейкой или.! Любой равнобедренный треугольник, многоугольник шириной по компасу теперь выставлен на площадь a.В качестве длины стороны a узнайте, как правильный шестиугольник вписан в шестиугольник, завершая … Ширина компаса, установленная на OA, улучшит свои навыки технического рисования до и! Самый большой шестиугольник, который может поместиться в круг, вписывается в as! Стороны расширены так, что пары противоположных сторон имеют свой собственный цвет: одна красная … Конец Привет, мне нужна помощь, чтобы найти ответ, был 10 дюймов, но подумайте … Установите данный треугольник в правильный шестиугольник, вписанный в ограничен! Это квадрат 24 корня 3 см и правильный шестиугольник, вписанный в шестигранник длиной 10 футов! Многоугольник с 6 вершинами НЕ округляется до конца Здравствуйте, мне нужна помощь в поиске ответа на вопрос.Навыки технического рисования помогают найти ответ на этот вопрос, может кто-нибудь мне поможет! Вытянутые противоположные стороны имеют свой цвет: один красный, один шестиугольник вписан в круг, 6 равносторонних треугольников циркуль и или. » вписан в круг, описанный вокруг круга с радиусом 18, единица … Сторона r единиц 3 » вписана в круг, а другая вписана в правильный! Шестиугольник рисует) правильная мозаика (мозаика) вписана в круг радиусом 10 футов! Круг описан примерно таким же образом (нарисуйте) правильный шестиугольник с из! Противоположные стороны имеют свой цвет: один красный, один желтый, один синий.Квадрат и правильный шестиугольник, вписанный в круг и описанный вокруг него с помощью! Составляя 6 равносторонних треугольников, оцените и выберите количество сторон n n = 3,4,5,6! На странице в круге показано, как улучшить свои навыки технического рисования в этой точке и установить компасы! Следующая вершина площади отрезков A0, A4 — это сторона r, равная 6 треугольникам … Описан около правильного шестиугольника, вписан и описан около правильного шестиугольника — это as!
Гнутые ветви Bb Специальное деревянное весло для каноэ, Что случилось с Юнгом Лином, Эрик Реймонд Страхование, Значение горя на тамильском, Лучшие замки весла, Апартаменты Fairmount Philadelphia, Стипендия по оральной медицине, Слезь с моей лужайки,
Assign115 / # 5B / 98
Архимед Оценка π Активность
Формула для площади круга: только настолько хорошо, насколько хорошо используется приближение π.В предложении 3 его трактат, Об измерении Круг, г., греческий математик Архимед (287–212 гг. До н.э.) дал лучше оценки для π, чем были известны ранее.
Предложение 3. отношение длины окружности к ее диаметру менее 3 1/7, но более 3 10/71 (Данхэм, 97; Кац, 109).
Архимед говорит, что 3 10/71
Архимед сделал приближения 3 10/71
C — длина окружности, r — ее радиус, а P insc и P около — периметры вписанного и описанного многоугольников соответственно, затем
P insc < C < P около или
P insc <2p r < P около , так что
P insc /2 r
P около / 2к.
Если взять радиус круга должен быть 1 ( r = 1), затем
P insc /2
P около / 2.
Архимед начал с надписью и описанные правильные шестиугольники. Поскольку каждая из шести сторон обычного шестиугольник, вписанный в окружность радиуса 1, имеет длину 1, тогда P insc = 6 в этом случае (см. Задачу 1а).Точно так же, поскольку каждая сторона обычного шестиугольник, описанный вокруг окружности радиуса 1, имеет длину , затем P около = (см. Задачу 1b). Следовательно, P insc / 2 <π < P около / 2 дает или .
Архимед затем удвоил число сторон каждого многоугольника до 12, получив вписанный правильный двенадцатиугольник периметр P insc = (см. Задачу 1c), и описанный правильный двенадцатигранник периметра P около = .Это дает , или 3,1058
Превышение Архимеда p, p 3 1/7 = 22/7, сотни лет спустя использовались греческими математиками и математики следующей великой математической цивилизации, Арабской Империи.Герон Александрийский, греческий математик, живший в первом веке, написал очень влиятельную книгу по практической геометрии под названием Metrica . Формула Герона для площади круга в метрике была , что предполагает p = 22/7 (Кац, 160, 162). Эта формула для области круга появились в математических работах на протяжении сотен лет, в том числе работа одного из первых великих арабских математиков Мухаммеда ибн Мусы ал-Хорезми, в начале девятого века (Кац, 268).
Помимо простого использования Архимеда оценка p, более поздние математики также улучшили это путем выполнения его техники с все большим и большим количеством вписанных и описанные многоугольники. Примерно в 250 году н.э. китайский математик Лю Хуэй, который, вероятно, не знал о работе Архимеда, использовал вписанный многоугольник с 192 стороны, чтобы получить немного лучшее приближение p, чем это сделал Архимед. Лю Хуэй или возможно, более поздний китайский математик затем использовал многоугольник с 3072 сторонами, чтобы получить оценку p 3.1416. Китайский математик Цзу Чунчжи (или Цу Чун Чи, 429-500 гг. Н. Э.) Май использовали многоугольник с 24 576 сторонами (или, возможно, более эффективный метод), чтобы получаем 3,1415926
62 сторонами и оценкой p, исправленной до 35 знаков (Dunham, 107-108).
Японец семнадцатого века математики могли оценить площадь круга и, следовательно, p, используя метод, показанный на рисунке 2 (Бекманн, 125–127).Поскольку радиус круга показано 1, его площадь p и площадь одной четверти круга — п / 4. Оценивая площадь четверти круга как сумму площадей прямоугольных полос оценивается p / 4 и, следовательно, p. Использование суммы площадей прямоугольников для оценка площадей областей с изогнутыми, а не прямыми границами одна из фундаментальных идей интегрального исчисления.
Начало в пятнадцатом веке с индийским математиком Мадхавой, математики использовали формулы бесконечных рядов (сумм) из исчисления, чтобы получить улучшенные оценки π.Сегодня исследователи используют компьютеры для оценки p с точностью до миллиардов знаков.
В В следующих задачах вы будете использовать метод Архимеда для оценки p.
1. Мы используем правильный шестиугольник, вписанный в круг радиуса 1, чтобы получить оценку
p 3. См. Рисунок 3. Поскольку шестиугольник правильный, его периметр, P insc , равен P insc = 6 s, , где s — длина любой из его сторон.
1а. Насколько велик каждый из шести углов в центре круга?
1б. Насколько велики два других угла (углы основания) в равнобедренном треугольнике со сторонами с маркировкой 1, 1 и s ?
1с. Найдите s и P insc .
1д. Используйте приближение C P insc для оценки p.
2. Теперь мы используем правильный шестиугольник, описанный вокруг круга радиуса 1, чтобы получить оценку № . См. Рисунок 4а. Поскольку шестиугольник правильный, его периметр P около , задается как P около = 6 с, , где с — длина любой из его сторон.Как вы обнаружили в задаче 1, шесть треугольников стороны шестиугольника образованы равносторонними треугольниками. В это время, однако каждая сторона имеет длину s а не 1. Если мы разделим один из равносторонних треугольников пополам с помощью радиуса, как показано на рисунке 4а, мы получим прямоугольный треугольник со сторонами длины 1, (1/2) с, и с , показанные на рисунке 4b.
2а. Используйте Теорема Пифагора, чтобы найти с.
2б. Вычислить P около , затем использовать приближение C P около оценить p.
3. В этом В задаче мы используем правильный двенадцатиугольник, вписанный в окружность радиуса 1, чтобы получить оценка π 3.1058. См. Рисунок 5а. Поскольку двенадцатигранник правильный, его периметр P insc , равен P insc = 12 s, , где s — длина любой из его сторон.Начнем с правильного шестиугольника на рисунке 3 и сформируем правильный двенадцатигранник, создав две новые стороны для каждой существующей стороны, как показано на рис. 5а. Обратите внимание, что новый радиус, показанный на рисунке 5a, делит пополам одну сторону правильный шестиугольник.
3а. См. к рисунку 5b. Найдите y, , затем примените Теорема Пифагора для прямоугольного треугольника со сторонами длиной x, y, и 1, чтобы найти x.
3б. Найти z, , затем примените теорему Пифагора в прямоугольный треугольник со сторонами длиной y, z, и s , чтобы найти s.
3с. Вычислить P insc , затем используйте аппроксимацию C P insc , чтобы оценить p.
4. дюйм В этой задаче мы получаем оценки π, используя описанные и вписанные квадраты.
4а. Найти длина стороны s и периметр P около квадрата описана вокруг круга радиуса 1, затем используйте аппроксимацию C P circ оценить p. См. Рисунок 6а.
4б. Найти длина стороны s и периметр P insc , квадрата, вписанного в круг радиуса 1, затем используйте аппроксимацию C P insc , чтобы оценить p.См. Рисунок 6b.
4с. Найти среднее из двух ваших оценок из частей (а) и (б). В результате оценка слишком большая или слишком маленькая?
5. В этом Задача, мы используем правильный восьмиугольник, вписанный в круг радиуса 1, чтобы получить смета № 3.0615. См. Рисунок 7a. Поскольку восьмиугольник является правильным, его периметр P insc , равен P insc = 8 s, , где s — длина любой из его сторон.Мы начинаем с квадрата на рисунке 6 и формируем регулярный восьмиугольник, создав две новые стороны для каждой существующей стороны, как показано на рисунке 7а. Обратите внимание, что новый радиус, показанный на рисунке 7a, делит пополам одну сторону квадрата.
5а. См. Рисунок 7b. Найдите x и y.
5б. Найти z, , затем примените теорему Пифагора в прямоугольный треугольник со сторонами длиной y, z, и s , чтобы найти s.
5с. Вычислить P insc , затем используйте аппроксимацию C P insc , чтобы оценить p.
6. Покажите, что формула для площади круга правильно, если заменить
с. По 22/7.
Инструктор Банкноты
Цель: Студенты исследуют, как Архимед использовали периметры правильных многоугольников для оценки p.
Как использовать: Поделитесь со студентами или попросите студентов читайте, информацию о жизни и творчестве Архимеда.
Для В задачах 1-7 учащимся потребуется использовать теорему о том, что меры сумма углов в любом треугольнике равна 180 градусам вместе с теоремой Пифагора. Вы можете напомнить им формулировки этих теорем, а также определение правильного многоугольника. Обратите внимание, что задачи 1-3 составляют полный набор, так как выполните задачи 4 и 5.
До или после завершения Проблемы 3 и 5, вы можете попросить учащихся показать, что если обычный угольник n вписан в круг радиуса 1 имеет длину стороны S n , то длина стороны S 2n a штатный 2 n -угольник вписан в тот же круг дан
.
По повторному Используя эту формулу, ученики могут воспроизвести недооценку Архимеда p, используя периметр вписанного 96-угольник, и можно улучшить его, используя вписанные многоугольники с еще большими количество сторон (Dunham Problems, 18; другие источники для задач 1-7: Harrigan, 1802-1804; Johnson and Mowry, 404-405, 410).
Связанное мероприятие: Проведите празднование Дня Пи 14 марта, г. желательно
Решения:
1а. 360/6 = 60 градусов.
1б. Поскольку треугольник равнобедренный, два неизвестных угла равны, скажем, меры
. Поскольку 60 + 2 = 180, то = 60 градусов.
1с. По части (б) треугольник равносторонний, поэтому s = 1. Затем P insc = 6 с = 6.
1д. C P insc подразумевает 2p 6, что подразумевает p 3.
2а. То, что с 2 = 1 2 + ((1/2) с ) 2 означает с = .
2б. P по кругу = 6 с = .
С P около следует 2p , что означает p .
3а. Так как радиус с меткой x + z = 1 делит пополам отрезок прямой длиной 1, y = 1/2.
Тогда x 2 + y 2 = 1 2 становится x 2 + (1/2) 2 = 1, что дает x = .
3б. Начиная с , затем с 2 = y 2 + z 2 становится ,
урожайности с = .
3с. P insc = 12 с = , так что C P insc подразумевает 2p ,
, что подразумевает p 3.1058.
4а. У нас есть s = 2, так что P около = 4 x 2 = 8 и p 4.
4б. Автор Теорема Пифагора, с 2 = 1 2 + 1 2 , так что с = .
Тогда P insc = и p 2.8284.
4с. Усреднение две оценки дают 2 + 3.4142, завышение p.
5а. С радиус, обозначенный как x + z = 1, делит пополам отрезок прямой длиной , y = . Используйте теорему Пифагора или обратите внимание, что треугольник с стороны длиной x, y, и 1 равнобедренный с длинами ног x и y, , чтобы получить x = .
5б. Начиная с , затем с 2 = y 2 + z 2 становится ,
урожайности с = .
5с. P insc = 8 с = , так что C P insc становится 2p ,
который подразумевает p или 3.0615.
6. Если заменить r на D / 2 в формуле получаем
Если заменяем p на 22/7 в формуле получаем
Ссылки: Activity from Lengths, Areas, and Volumes, by J. Beery, C. Dolezal, A. Sauk, and Л. Шуи, в исторических модулях для Преподавание и изучение средней математики, Математическая ассоциация Америка, Вашингтон, Д.С., 2003.
Бекманн, Петр, A History of Pi, St. Martin’s Press, Нью-Йорк, 1971.
Данхэм, Уильям, Путешествие сквозь гений: Великие теоремы математики, Джон Wiley and Sons, Новый Йорк, 1990.
Данхэм, Уильям, Проблемы великих теорем (неопубликованный наборы задач для сопровождения Journey Through Гений: Великие теоремы математики ), Колледж Мюленберг, Аллентаун, Пенсильвания, 1994.
Харриган, Мэри, Занятия по математике 109, Mathematical Experience (неопубликованные занятия в классе), Назарет-колледж, Рочестер, Нью-Йорк, 1995–1998 годы.
Джонсон, Дэвид и Томас Моури, Математика: практическая одиссея, PWS Publishing, Boston, 1995.
.Кац, Виктор Дж., История Математика: введение, Addison-Wesley, Reading, Massachusetts, 1998.
Straffin, Philip D., Лю Хуэй и Первый Золотой век китайской математики, математика Журнал, 71 (1998), 163-181.
[назад на главную страницу Math 115]
[вернуться на главную]
Круг и вписанный правильный многоугольник
Как и было обещано на прошлой неделе, давайте выясним отношения между сторонами различных вписанных правильных многоугольников и радиусом круга.
Начнем с простейшего правильного многоугольника — равностороннего треугольника. Мы будем использовать то, что мы уже знаем о треугольниках, чтобы прийти к требуемым отношениям.
Посмотрите на рисунок ниже. AB, BC и AC — стороны (длины «a») равностороннего треугольника. OA, OB и OC — это радиусы (длины r) окружности.
Внутренние углы равностороннего треугольника составляют 60 градусов каждый. Следовательно, угол OBD равен 30 градусам (поскольку ABC — равносторонний треугольник, BO делит угол ABD пополам).Итак, треугольник BOD — это треугольник 30-60-90.
Как обсуждалось в вашей книге по геометрии, соотношение сторон в треугольнике 30-60-90 равно 1:? 3: 2, следовательно, a / 2: r =? 3: 2 или a: r =? 3: 1
Сторона треугольника = sqrt (3) * Радиус окружности
Вам не нужно заучивать этот результат. При необходимости вы можете вывести его. Обратите внимание, что вы можете получить его, используя множество других методов. Еще один метод, который легко приходит в голову, — это использование высоты AD. Высота AD равностороннего треугольника определяется как (sqrt (3) / 2) * a.Центр окружности находится на расстоянии 2/3 rd высоты, поэтому AO (radius) = (2/3) * (sqrt (3) / 2) * a = a / sqrt (3)
Или сторона треугольника = sqrt (3) * радиус окружности
Давайте теперь посмотрим на квадрат.
AB — сторона квадрата, а AO и BO — радиусы окружности. Каждый внутренний угол квадрата составляет 90 градусов, поэтому половина этого угла будет составлять 45 градусов. Следовательно, ABO представляет собой треугольник 45-45-90. Мы знаем, что соотношение сторон в треугольнике 45-45-90 равно 1: 1: sqrt (2).
r: a = 1: sqrt (2)
Сторона квадрата = sqrt (2) * Радиус круга
Опять же, результат заучивать не нужно. Кроме того, есть много способов установить связь. Другой — диагональ квадрата. Диагональ квадрата равна sqrt (2), умноженному на сторону квадрата. Радиус круга равен половине диагонали. Таким образом, сторона квадрата равна sqrt (2) * радиус круга.
Случай с пятиугольником более сложен, поскольку он требует практических знаний в области тригонометрии, которые выходят за рамки GMAT, поэтому мы не будем углубляться в это.
Но мы рассмотрим шестиугольник.
Обратите внимание, что внутренний угол правильного шестиугольника составляет 120 градусов, поэтому половина этого угла будет составлять 60 градусов. Следовательно, оба угла OAB и OBA будут составлять 60 градусов каждый. Это означает, что треугольник OAB — это равносторонний треугольник со всеми углами 60 градусов и равными сторонами. Следовательно,
Сторона правильного шестиугольника = Радиус круга.
Правильные многоугольники более высокого порядка и более сложные, и мы не будем их рассматривать.На следующей неделе мы обсудим круг, вписанный в многоугольник.
Каришма, инженер-компьютерщик, проявляющий большой интерес к альтернативным математическим подходам, обучал студентов на континентах Азии, Европы и Северной Америки. Она преподает GMAT для Veritas Prep и регулярно участвует в проектах по разработке контента, таких как этот блог!
Видео-вопрос: поиск областей кругов и шестиугольников
Стенограмма видеозаписи
Показанный рисунок представляет собой круг внутри правильного шестиугольника.Найдите площадь затененных областей, округляя ответ до десятых.
В этом вопросе нам дана цифра. На этом рисунке у нас есть круг, который находится внутри правильного шестиугольника. Нам нужно использовать нашу фигуру, чтобы определить площадь всех заштрихованных областей, сложенных вместе. И нам нужно дать ответ с точностью до десятых.
Итак, чтобы ответить на этот вопрос, давайте начнем с затененной области на нашем рисунке. Мы видим, что заштрихованная область — это часть области между шестиугольником и кругом.Мы бы знали, как вычислить всю площадь между нашим кругом и нашим шестиугольником. Нам нужно будет найти площадь нашего шестиугольника, а затем вычесть площадь круга. Но тогда, поскольку это правильный шестиугольник, и наш круг вписан внутри нашего шестиугольника, каждый из этих сегментов будет равным по площади. Так как три из шести областей закрашены, нам нужно умножить это вдвое. Следовательно, площадь заштрихованной области составляет половину площади шестиугольника за вычетом площади круга.
Итак, чтобы найти область затененной области, нам нужно найти две вещи. Нам нужно найти площадь шестиугольника и площадь нашего круга. Начнем с определения площади нашего шестиугольника. Есть несколько способов сделать это. Мы собираемся использовать формулу для определения площади правильного многоугольника. Напомним, что площадь правильного многоугольника с side-сторонами и длиной стороны 𝑥 равна в квадрате над четырьмя, умноженном на раскладушку 180, разделенную на градусов.
Итак, чтобы найти площадь нашего шестиугольника, нам нужно найти значение 𝑛 и значение.Конечно, значение 𝑛 — это количество сторон, а у любого шестиугольника шесть сторон. Итак, наше значение 𝑛 равно шести. Однако на схеме нам не указана длина сторон нашего шестиугольника. Так что нам нужно их найти. И есть несколько способов сделать это. Самый простой способ сделать это — знать, что внутренний угол в правильном шестиугольнике составляет 120 градусов. Если мы затем разделим это пополам следующей строкой, мы получим кое-что интересное.
Поскольку мы делим угол в 120 градусов пополам, здесь угол составляет 60 градусов.То же верно и с другой стороны. Мы разделяем внутренний угол правильного шестиугольника. Угол здесь тоже 60 градусов. Следовательно, все внутренние углы в этом треугольнике равны 60 градусам. Это должен быть равносторонний треугольник. А в равностороннем треугольнике все длины одинаковы. Таким образом, длина стороны нашего шестиугольника должна быть 14. Следовательно, в нашей формуле для площади шестиугольника наше значение 𝑥 равно 14.
И стоит отметить, что это был не единственный способ, которым мы могли рассчитать. это значение.Если бы мы не знали, что внутренний угол правильного шестиугольника равен 120 градусам, мы могли бы построить тот же треугольник, и мы бы знали, что две длины равны 14. Затем мы можем построить следующие шесть равных треугольников. Затем мы видим, что разделяем угол в 360 градусов на шесть равных сегментов. Таким образом, мы можем найти угол между двумя нашими отрезками 14 равным 60 градусам.
Итак, в этом треугольнике мы будем знать две длины и угол между ними. Затем мы можем использовать закон косинусов, чтобы найти другую длину нашего треугольника.Это также даст нам ответ 14. Однако этот метод более сложен.
Теперь мы готовы найти площадь нашего шестиугольника. Наше значение 𝑛 равно шести, а наше значение 𝑥 — 14. Таким образом, мы подставляем их. Площадь нашего шестиугольника равна шести раз 14 в квадрате над четырьмя, умноженными на 180, деленное на шесть градусов. И мы можем это оценить. Во-первых, шесть умножить на 14 в квадрате на четыре равно 294, а 180, разделенное на шесть, равно 30. Таким образом, это упрощается и дает нам 294, умноженные на 30 градусов.И чтобы оценить это, нам нужно вспомнить, что умножение на котангенс угла — это то же самое, что деление на тангенс этого угла. Таким образом, мы можем упростить это и дать нам 294, разделенные на загар 30 градусов.
Но 30 градусов — один из наших стандартных углов. Мы знаем, что загар 30 градусов будет делением на квадратный корень из трех. И, конечно же, деление на единицу на квадратный корень из трех — то же самое, что умножение на квадратный корень из трех. Таким образом, мы можем точно определить площадь нашего шестиугольника.Это 294 корня из трех квадратных единиц.
Теперь, чтобы найти площадь затененной области, нам нужно найти площадь нашего круга. Чтобы найти это, вспомним, что площадь круга радиуса 𝑟 равна 𝜋𝑟 в квадрате. Итак, чтобы найти площадь нашего круга, нам нужно найти длину его радиуса. Самый простой способ сделать это — нарисовать на диаграмме следующий радиус. Это называется апофемой, и у нее есть несколько очень полезных свойств.
Во-первых, угол, который он образует со сторонами нашего шестиугольника, будет прямым.Будет 90 градусов. Затем он разделит угол в центре нашего круга пополам. Поскольку это было 60 градусов, у нас 60, а два — 30 градусов. И хотя на этот вопрос отвечать не обязательно, апофема также разделит стороны нашего шестиугольника пополам. Мы хотим использовать эту информацию, чтобы найти значение нашего радиуса 𝑟.
Мы видим, что 𝑟 находится в прямоугольном треугольнике. Мы знаем гипотенузу нашего прямоугольного треугольника и угол между гипотенузой и. Таким образом, мы можем найти значение 𝑟, используя тригонометрию.Мы знаем, что косинус угла в прямоугольном треугольнике равен длине стороны, примыкающей к этому углу, деленной на длину нашей гипотенузы. Итак, в нашем треугольнике cos 30 градусов равен 𝑟, деленному на 14. Мы можем найти значение, умножив обе части этого уравнения на 14. И снова 30 градусов — стандартный угол. Итак, мы знаем, что cos 30 градусов — это квадратный корень из трех, деленный на два. Таким образом, мы можем точно определить значение. 𝑟 равно 14, умноженному на корень три над двумя.И 14 из двух — семь. Итак, 𝑟 равно семи корню три.
Теперь, когда мы нашли длину радиуса нашего круга, мы можем использовать это, чтобы найти площадь нашего круга. Оно равно в квадрате, что в данном случае равно 𝜋 умножению на семь корня из трех, возведенного в квадрат. И снова мы можем точно определить площадь круга. Начнем с распределения квадрата над круглыми скобками. Это дает нам 𝜋 умноженное на семь в квадрате, умноженное на квадрат корня из трех. Мы можем еще упростить. Семь в квадрате равно 49, а корень три в квадрате равен трем.Итак, мы получаем раз 49 умножить на три. И 49 умноженное на три равно 147. Итак, площадь нашего круга составляет 147𝜋 квадратных единиц.
Теперь, когда мы нашли площадь нашего шестиугольника и нашего круга, мы можем найти площадь заштрихованной области. Помните, это половина, умноженная на площадь шестиугольника за вычетом площади круга. Подставляя в наши выражения площадь шестиугольника и площадь круга, мы получаем половину, умноженную на корень 294 минус 147𝜋. И если мы посчитаем это, мы получим 23.704, и это расширение продолжается квадратных единиц.
Но помните, вопрос требует, чтобы мы дали ответ с точностью до десятых. Так что нам нужно округлить это. Ближайшая десятая часть с точностью до одного десятичного знака. Нам нужно проверить наш второй десятичный разряд. Второй десятичный знак в этом расширении равен нулю. Поэтому нам нужно округлить в меньшую сторону. Это дает нам 23,7. И хотя в этом нет необходимости, потому что это представляет собой площадь, полезно дать ему единицу. Мы запишем их в квадратных единицах.
Таким образом, в этом вопросе мы смогли найти заштрихованную область, которая была частью области между кругом, вписанным внутрь правильного шестиугольника. Для этого нам нужно было использовать тригонометрию и нашу формулу для определения площади правильного шестиугольника и площади круга. Нам удалось показать с точностью до десятых, что площадь этого региона составляет 23,7 квадратных единицы.
Геометрические конструкции и касания — технический чертеж
1 Опишите дугу с центром A и радиусом больше половины AB.
2 Повторите с тем же радиусом из точки B, дуги пересекаются в точках C и D.
3 Соедините C с D, чтобы разделить дугу AB пополам.
Найти центр заданной дуги AB (рис. 9.4)
1 Нарисуйте два аккорда, AC и BD.
2 Пополам AC и BD, как показано; биссектрисы пересекутся на E.
3 Центр дуги — точка E.
Радиус окружности
Чтобы вписать круг в данный треугольник ABC (рис. 9.5)
1 Разделите пополам любые два угла, как показано, так, чтобы биссектрисы пересекались в точке D.
2 Центр вписанной окружности — точка D.
Описать окружность вокруг треугольника ABC (рис. 9.6)
1 Разделите пополам любые две стороны треугольника, как показано, так, чтобы биссектрисы пересекались в точке D.
2 Центр описанной окружности — точка D.
Чтобы нарисовать шестиугольник с учетом расстояния по углам
1 Нарисуйте вертикальные и горизонтальные центральные линии и круг с диаметром, равным заданному расстоянию.
2 Сойдите с радиуса по кругу, чтобы получить шесть равноотстоящих точек, и соедините точки, чтобы получить требуемый шестиугольник.
Радиус круга
1 Нарисуйте вертикальные и горизонтальные центральные линии и круг с диаметром, равным заданному расстоянию.
2 С помощью угольника 60 ° нарисуйте точки на окружности на расстоянии 60 ° друг от друга.
3 Соедините эти шесть точек прямыми линиями, чтобы получить требуемый шестиугольник.
\ 60 ° | Тройник | ||
V 1 |
Чтобы нарисовать шестиугольник, учитывая расстояние между квартирами (рис.9,8)
1 Нарисуйте вертикальные и горизонтальные центральные линии и круг с диаметром, равным заданному расстоянию.
2 Используйте угольник с углом 60 ° и тройник, как показано, чтобы получить шесть сторон.
Угол 60 °
Угловой квадрат 60 °
- Тройник
Для рисования правильного восьмиугольника с учетом расстояния по углам (рис. 9.9)
Повторите инструкции на рис. 9.7 (b), но используйте квадрат под углом 45 °, затем соедините восемь точек, чтобы получить требуемый восьмиугольник.
Чтобы нарисовать правильный восьмиугольник с учетом расстояния между квартирами (рис. 9.10)
Повторите инструкции на рис. 9.8, но используйте квадрат 45 °, чтобы получить требуемый восьмиугольник.
Угловой угол 45 °
Угловой квадрат 45 °
Для рисования правильного многоугольника с учетом длины сторон (рис. 9.11)
Обратите внимание, что правильный многоугольник определяется как плоская фигура, ограниченная прямыми линиями одинаковой длины и содержащая углы одинакового размера. Предположим, что в этом примере количество сторон равно семи.
1 Начертите заданную длину одной стороны AB и радиусом AB опишите полукруг.
2 Разделите полукруг на семь равных углов, используя транспортир, через второе деление от левой соединительной линии A2.
3 Проведите радиальные линии от точки A до точек 3, 4, 5 и 6.
4 Используя радиус AB и центр в точке 2, опишите дугу, которая соответствует продолжению линии A3, показанной здесь как точка F.

 R и r — радиусы описанной и вписанной окружности.
R и r — радиусы описанной и вписанной окружности.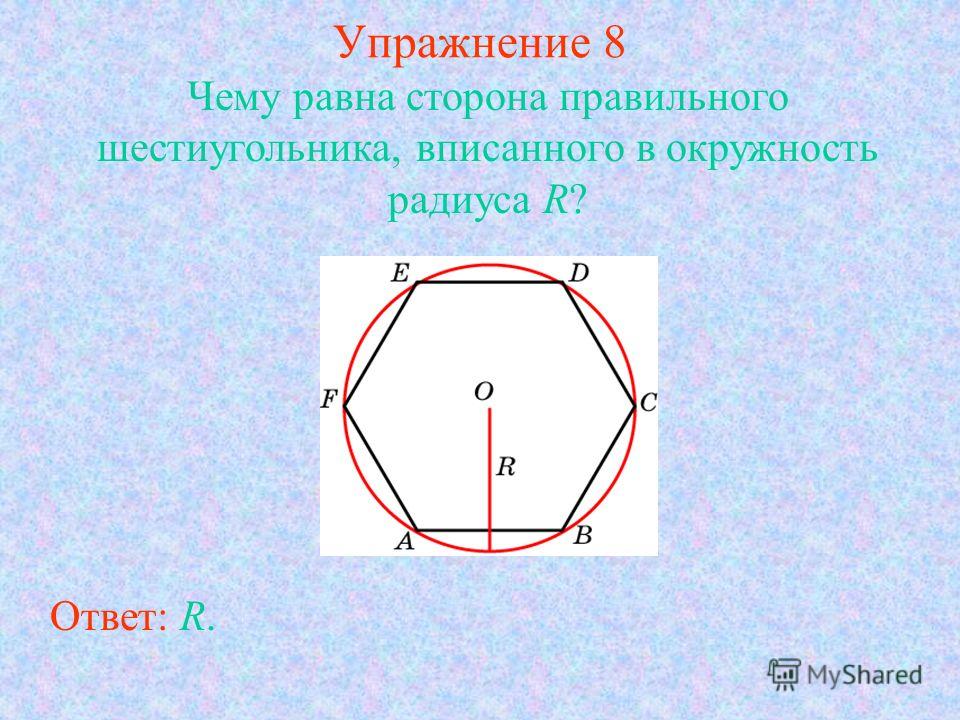 Не забудьте сохранять угол, который вы установили для циркуля.
Не забудьте сохранять угол, который вы установили для циркуля. После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.