Как в окружности нарисовать пятиугольник: Как построить пятиугольник с помощью циркуля

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A). 

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B. 

Отрезок AB будет равнозначен отрезку СD.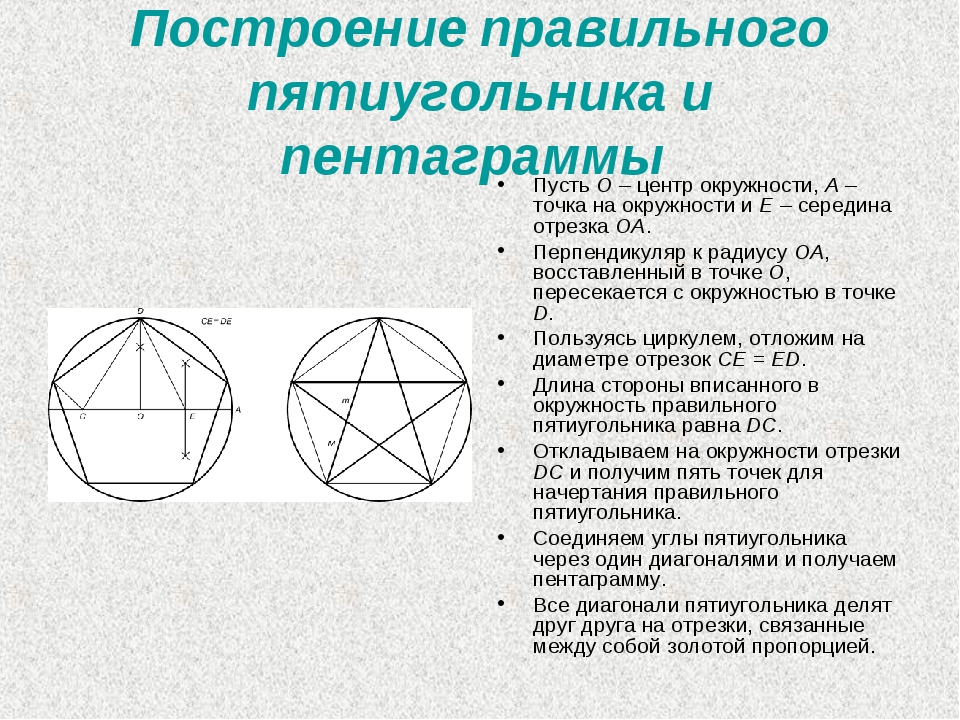

Задача решена.

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

1. Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

2. Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB.

Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников). 

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые.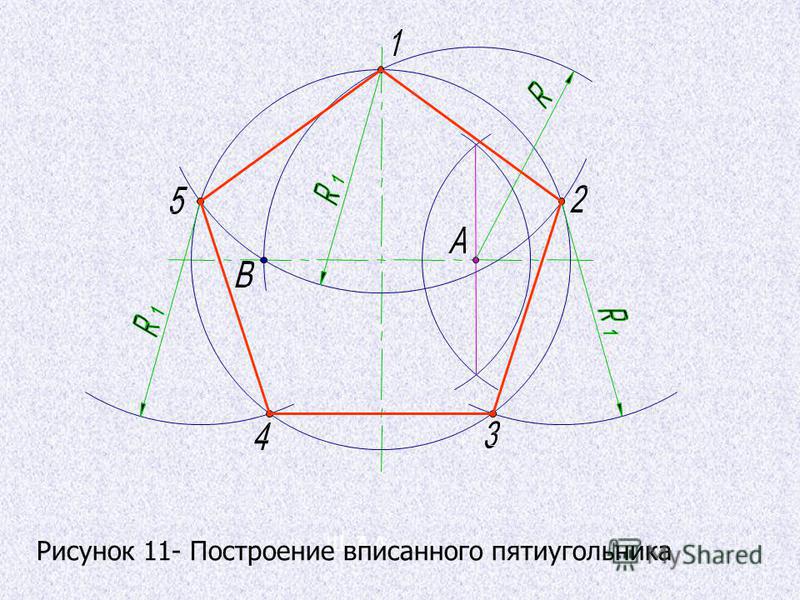 А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т.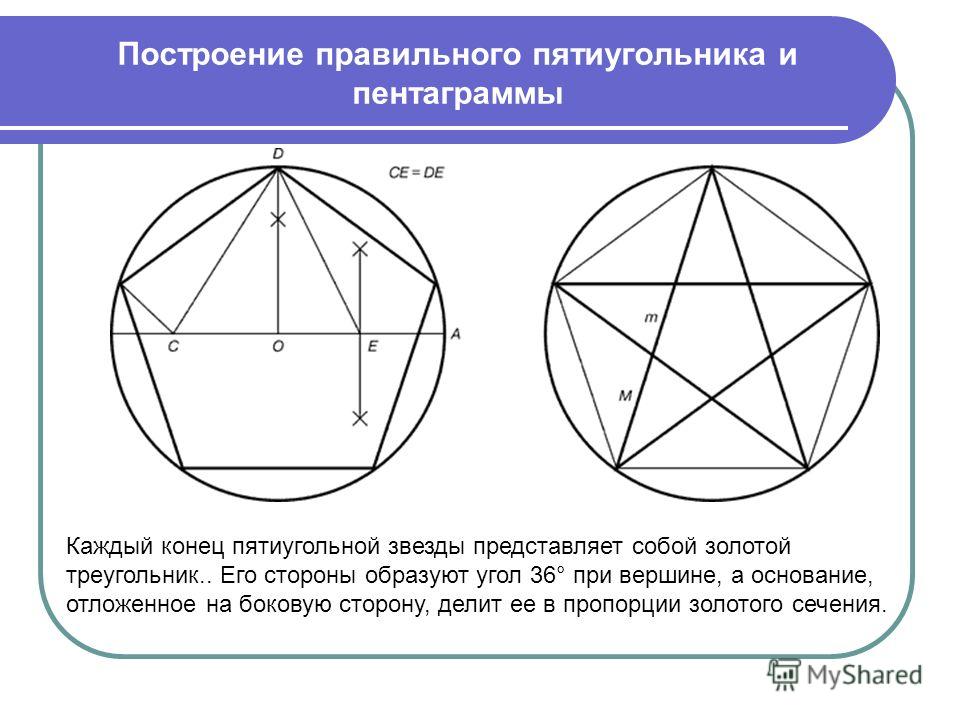 A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Задача решена.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3. 

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т.

C и рисуют дуги до их соприкосновения. 

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

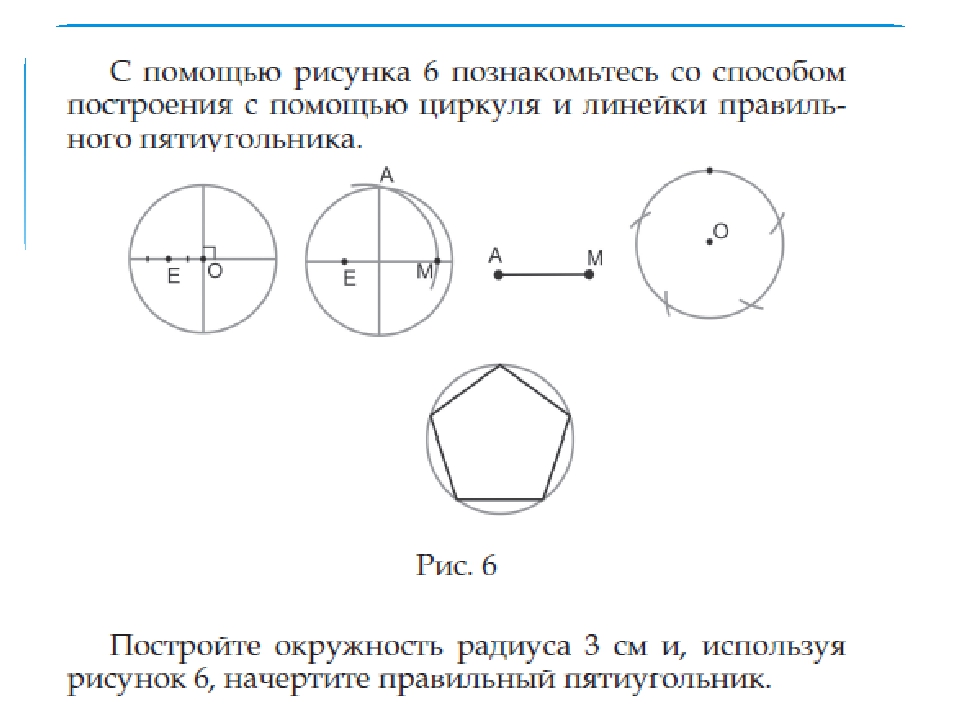
Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B. 

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника. 

Взять циркуль, величина раствора которого будет равна отрезку т. 1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Задача выполнена.

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга. 

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Правильный пятиугольник или звезда без транспортира.



Поделиться:

Правильный пятиугольник.
Давайте попробуем сделать такую форму без транспортира, при помощи складывания определённым образом листа бумаги, линейки , карандаша и ножниц.

Берём квадрат из цветного лста бумаги и складываем его пополам по намеченной линии А А1.

В полученном прямойгольнике на глаз или при помощи линейки делим короткую сторону на три части. Получаем точку В.

Поднимаем угол А и совмещаем с точкой В.
Воспользовавшись краем линейки или просто ногтём проглаживаем получившийся сгиб.

Теперь угол D отводим к центру и приминаем сгиб по линии ВС.

Приподнимаем угол F и совмещаем с отрезком ВС, проглаживаем сгиб.

Для того, чтобы более чётко видеть дальнейшую линию среза, поменяем местами угол F, он будет под углом D.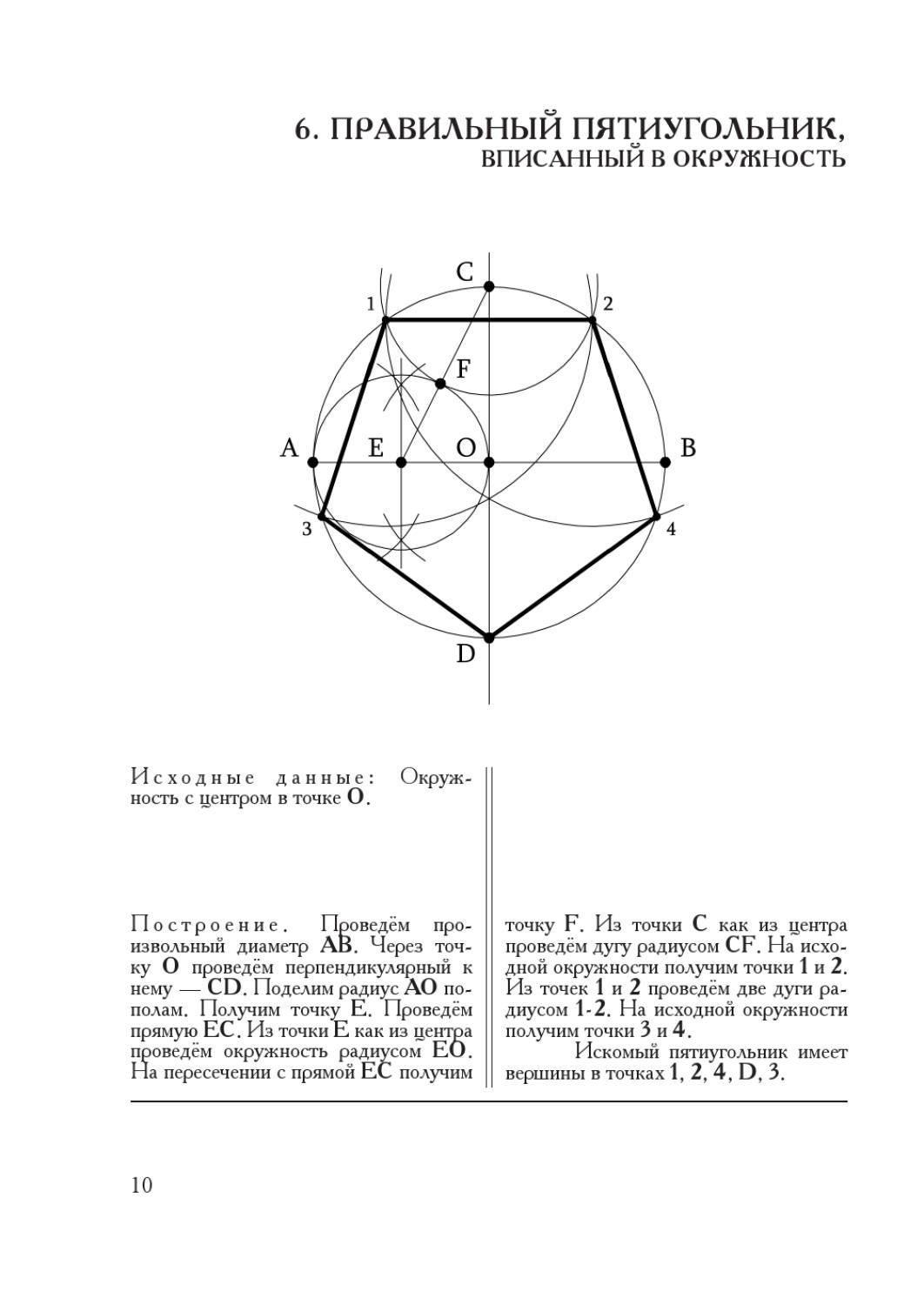

На глаз или начертив по линейке отрезок D F, отрезаем лишнее. Так мы получим правильный пятиугольник, изображённый на первом фото.
Если же вам нужна звезда, то немного изменяем угол отреза из точки D в точку Н. Получим новую линию отреза — FH.

Правильная плоская звезда готова.
Если вы хотите звезду с ещё более узкими лучами, соответственно придётся ещё немного сместиться к центру в точке С.

А если поверх исходной пятиугольной формы, подобрав округлый предмет, нарисовать полукружия, то такую форму можно тспользовать для создания быстрого шаблона при изготовлении «Шарика на все случаи жизни».
https://stranamasterov.ru/node/91485

Получается вот такая заготовка. Быстро и просто!

Всё, маленький экспресс МК готов!

Такие звёзды можно использовать при изготовлении открыток на 9-ое Мая или 23 февраля, а также, как контурная основа под торцевание на звездочке.

Такой  пятиугольный шаблон пригодится для создание шкатулочек с донышком и крышкой нетрадиционной формы, а также для изначальной формы под некоторые складушки-оригами и заполнения пятиугольной формы в технике изонити.

У Стеллы Филатовой есть вот такой способ вырезания правильного пятиугольника

https://stranamasterov.ru/node/52556?tid=451%2C560

А у Марии — похожий, но немного другой  https://stranamasterov.ru/node/72087

Как нарисовать пятиугольник с помощью окружности

Последние события

Раскраски к Хеллоуину для мальчиков

В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.

Коллекция раскрасок к Хеллоуину

Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.

На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.

Осень. Деревья и листья

Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.

Кто такие мишки Гамми?

Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.

Несколько раскрасок для самых маленьких

Совсем простенькие раскраски с крупными деталями для самых маленьких художников.

Осеннее настроение. Раскраски

В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.

Рассказы про осень. Читаем и раскрашиваем картинки

Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.

Популярное

Архив

Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.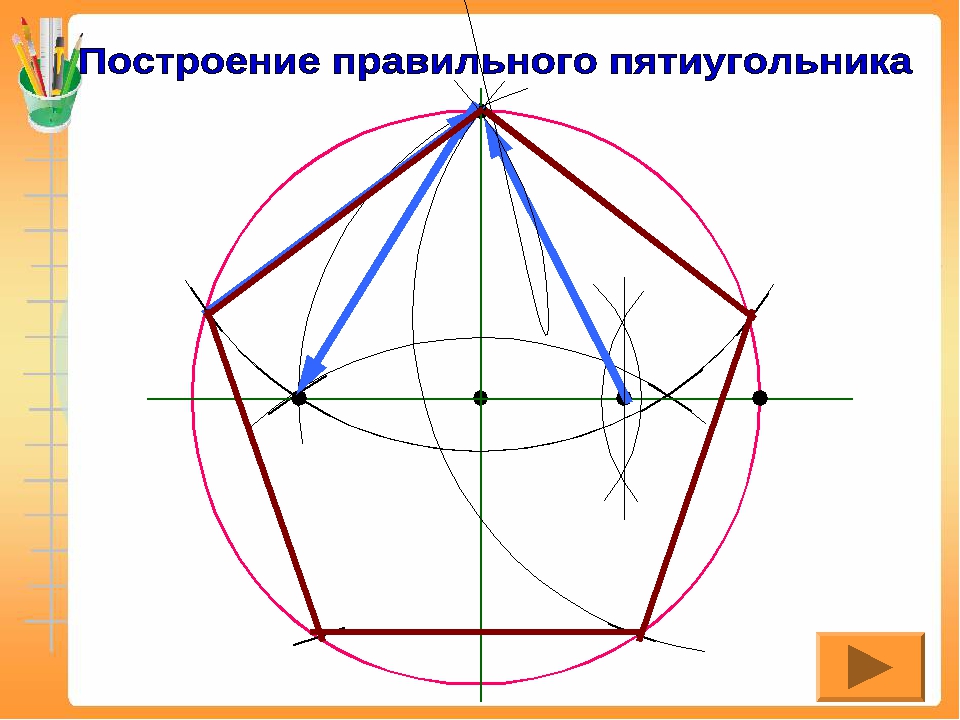

Как нарисовать правильную звездочку?

Как нарисовать правильный пятиугольник?

Как разделить круг на пять равных частей?

На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.

Конечно же, нам понадобится циркуль с карандашом и линейка.

Для начала нарисуйте циркулем круг.

Разделите его на четыре части линиями сверху вниз и справа налево.

Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.

А отрезок, соединяющий центр и точку на окружности, называется радиус.

С помощью линейки измерьте и разделите пополам один из радиусов.

У меня это отрезок слева от центра.

Серединку радиуса я обозначила

Нам понадобится точка сверху окружности.

Ее я обозначила цифрой 0.

Устанавливаем иголку циркуля

в точку 1, а карандашик в точку 0.

Рисуем дугу до пересечения с горизонтальным диаметром.

Обозначаем точку пересечения

Сейчас устанавливаем иголку циркуля

в точку 0, а карандашик в точку 2.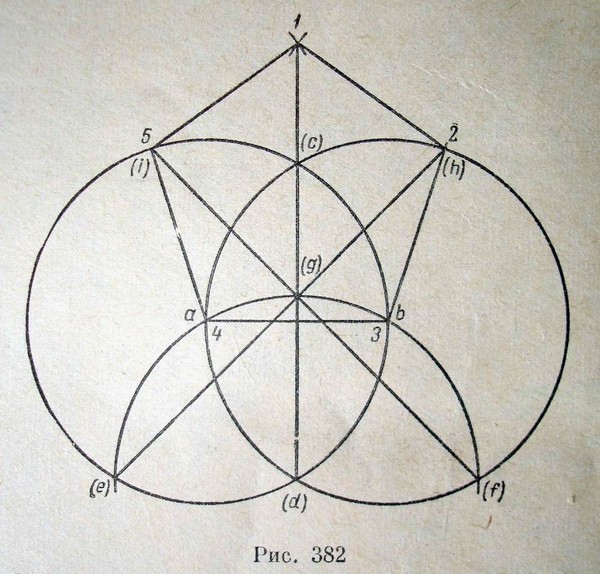

И рисуем дугу до пересечения с окружностью, причем с двух сторон.

Точки пересечения помечены

Не меняя ширину циркуля, устанавливаем иголку

в точку 3 и отмеряем кусочек окружности.

Точку 6 можно отмерить и от

точки 5 и от точки 4.

Главное, не изменять ширину (раствор) ножек циркуля.

Вот, практически и все.

Если соединим точки, получим правильный пятиугольник.

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.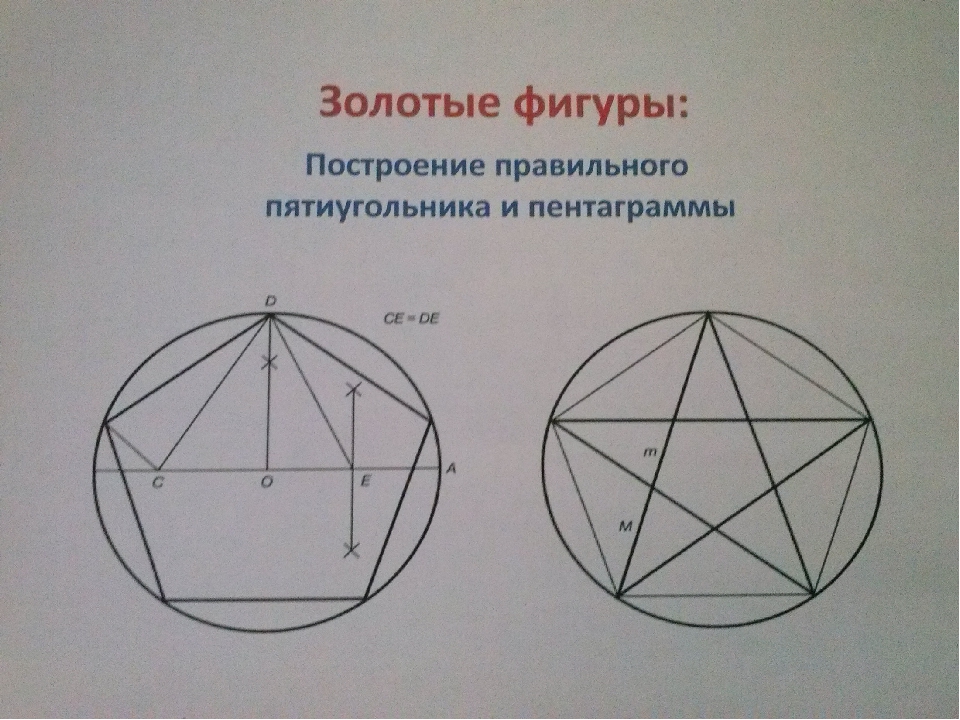

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

Как выглядит пятиугольник и звезда

Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

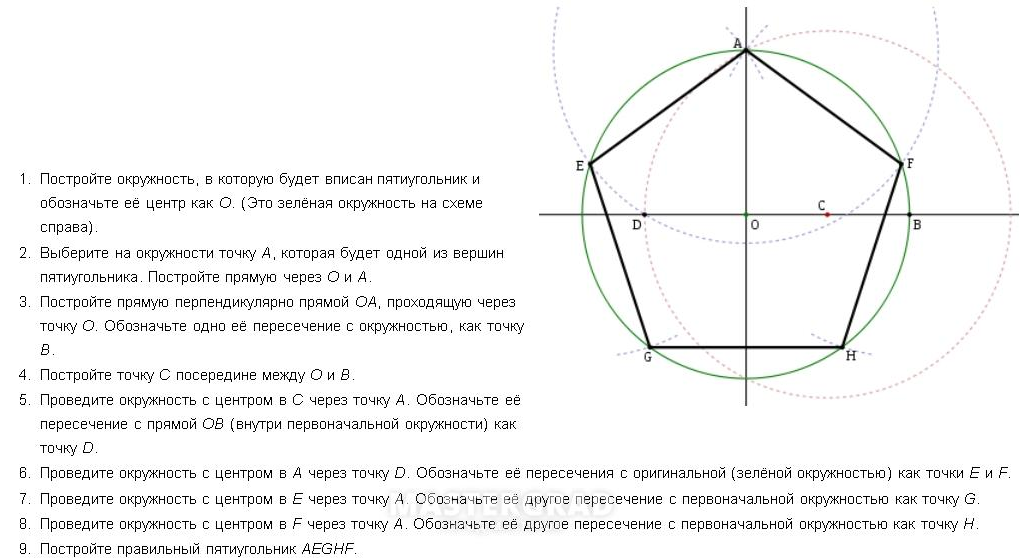
1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.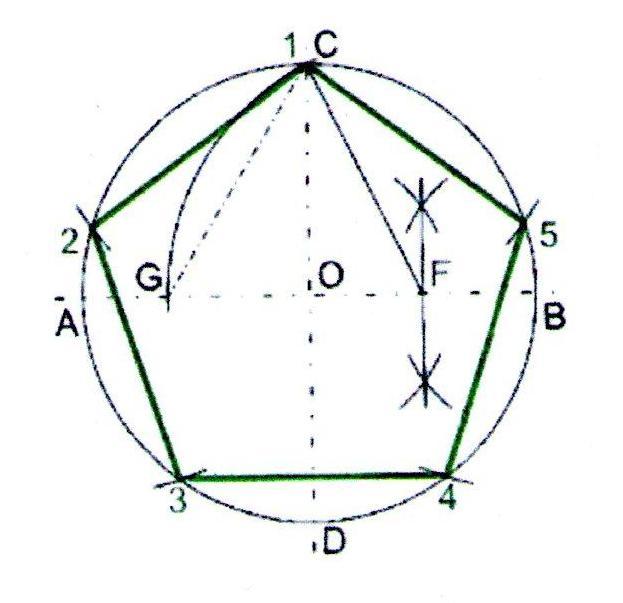

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Правильный пятиугольник | Треугольники

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

∠A₁O A₂=360º:5=72º.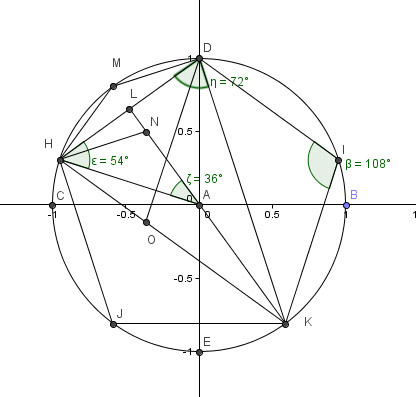

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника,  боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

В треугольнике A₁OA₅

   

   

   

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

   

   

OF — радиус вписанной в A₁A₂A₃A₄A₅ окружности: OF=r.

Рассмотрим прямоугольный треугольник A₁OF.

По определению синуса,

   

откуда

   

   

Так как

   

то

   

   

   

   

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

   

По определению котангенса,

   

   

Подставив значение котангенса 36°, получаем:

   

Итак, формула радиуса вписанной в правильный пятиугольник окружности

   

Применив формулу

   

можно найти площадь правильного пятиугольника.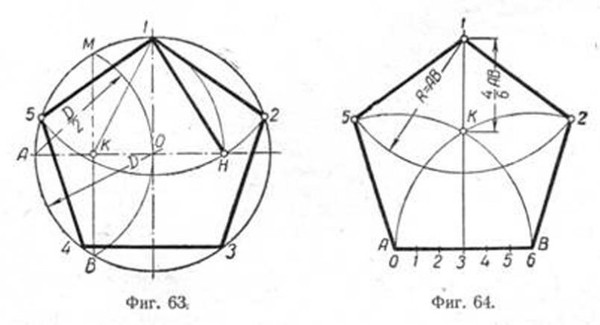 Здесь

   

следовательно, формула для нахождения площади A₁A₂A₃A₄A₅

   

Все диагонали правильного пятиугольника равны.

Длина диагонали равна

   

Как начертить пятиугольник при помощи циркуля

Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.

Вам понадобится

• – линейка
• – циркуль

Инструкция

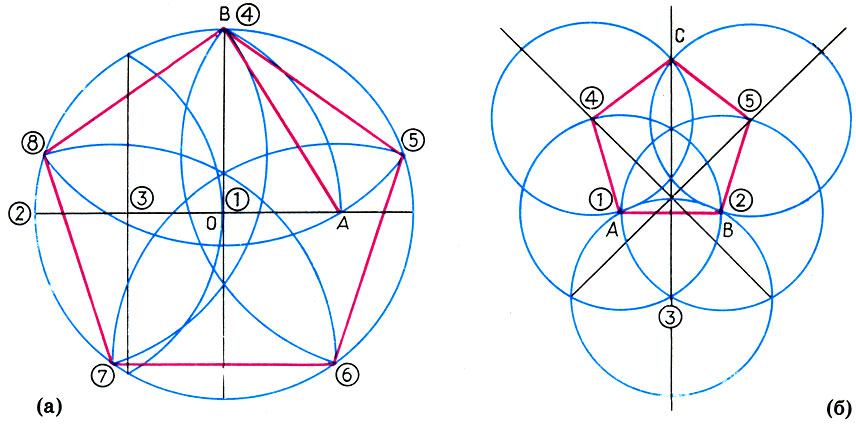
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса.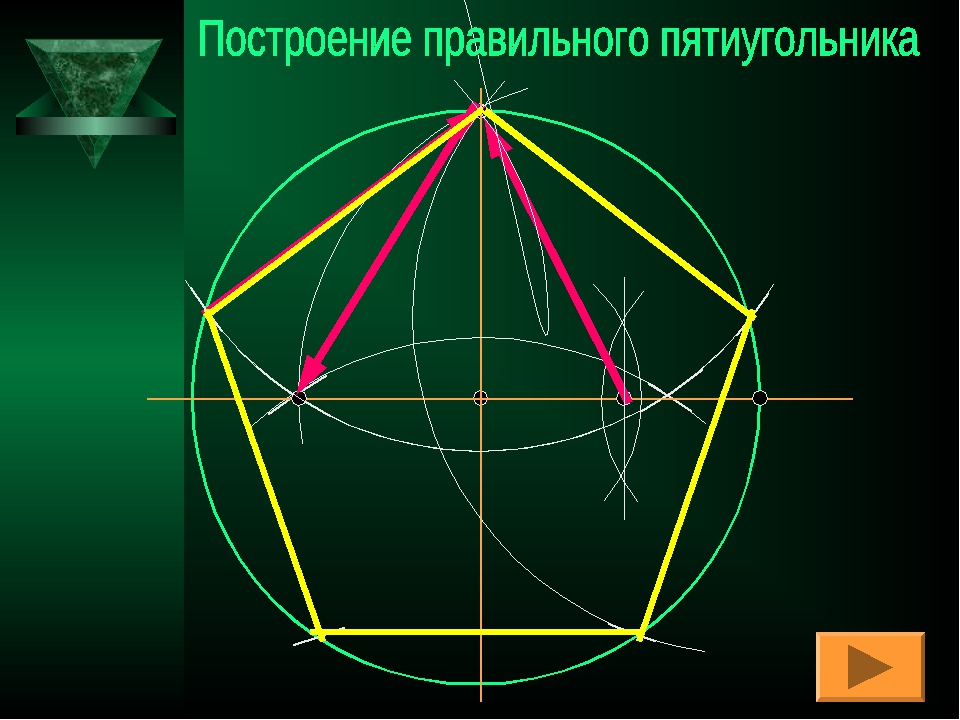 Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.

2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.

3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.

Инструкция

1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).

2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).

3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.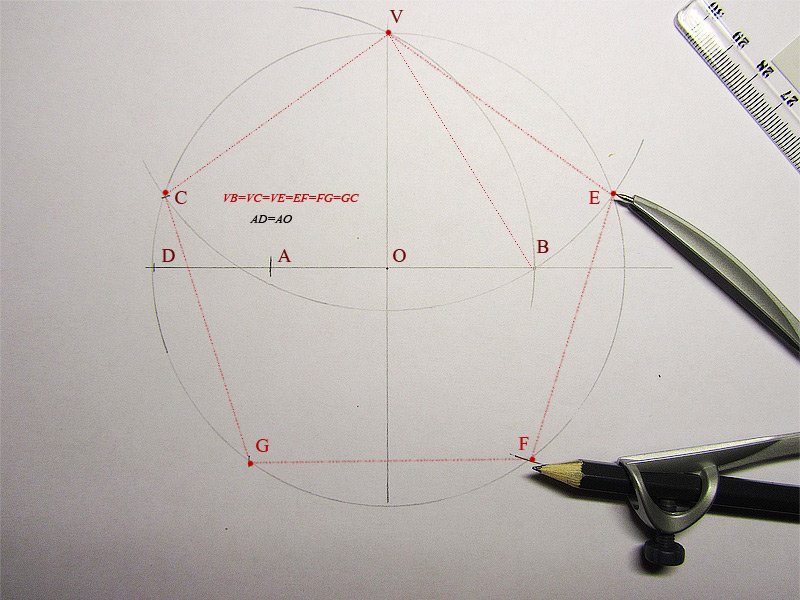 к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .

4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .

5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD : AB = 2 : n.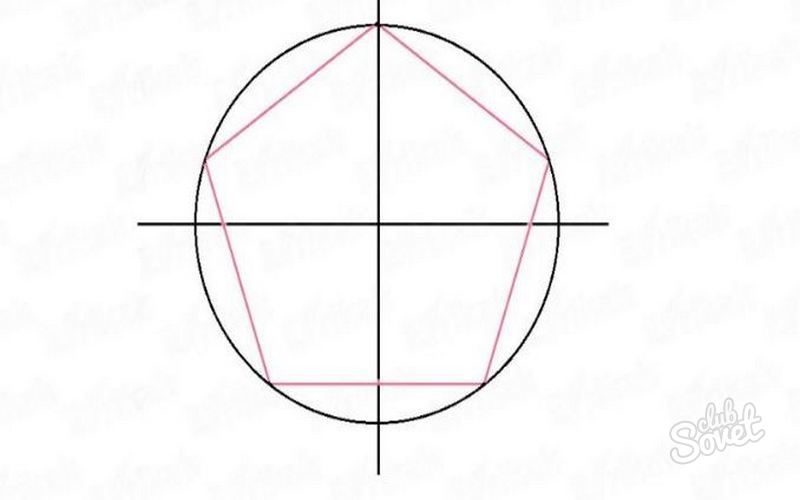 При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.

6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2 : ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).

7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.

Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.

Вам понадобится

• Циркуль, линейка, карандаш

Инструкция

1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.

2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .

3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.

4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.

5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.

Видео по теме

Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?

Вам понадобится

• Лист бумаги, карандаш и линейка.

Инструкция

1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.

2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.

3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.

4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.

5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.

6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.

Видео по теме

Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Как построить пятиугольник с помощью циркуля

Положительный пятиугольник – это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Возвести пятиугольник и поможет именно эта окружность.

Инструкция

1. В первую очередь нужно возвести циркулем окружность. Центр окружности пускай совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной грядущего пятиугольник а. В точке пересечения иной оси с окружностью расположите точку D.

2. На отрезке OD обнаружьте середину и подметьте в ней точку А. Позже этого надобно возвести циркулем окружность с центром в этой точке. Помимо того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.

3. Позже этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с изначальной обозначьте как точку F. Эта точка станет 2-й вершиной грядущего верного пятиугольник а.

4. Сейчас необходимо провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с изначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом нужно возвести еще один круг. Центр его в G. Точка пересечения его с изначальной окружностью пускай будет H. Это последняя вершина верного многоугольника.

5. У вас должно получиться пять вершин. Остается их легко объединить по линейке. В итоге всех этих операций вы получите вписанный в окружность положительный пятиугольник .

Построение положительных пятиугольников дозволено с поддержкой циркуля и линейки. Правда, процесс это довольно долгий, как, однако, и построение всякого положительного многоугльника с нечетным числом сторон. Современные компьютерные программы разрешают сделать это за несколько секунд.

Вам понадобится

• – компьютер с программой AutoCAD.

Инструкция

1. Обнаружьте в программе AutoCAD верхнее меню, а в нем — вкладку «Основная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся различные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Дозволяет рисовать самые различные правильне многоугольники. Число сторон может добиваться 1024. Дозволено применять и командную строку, в зависимости от версии набрав « _polygon» либо «мн.-угол».

2. Вне зависимости от того, пользуетесь ли вы командной строкой либо контекстными меню, на экране у вас появится окошко, в которое предлагается ввести число сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Дозволено обозначить их как (0,0), но могут быть и всякие другие данные.

3. Выберите необходимый метод построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности либо вписанным в нее, но дозволено возвести его и по заданному размеру стороны. Выберите надобный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.

4. Пятиугольник по заданной стороне вначале строится верно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” либо «сторона”. В командной строке наберите координаты исходной и финальной точек одной из сторон пятиугольника. Позже этого пятиугольник появится на экране.

5. Все операции дозволено исполнять с поддержкой командной строки. Скажем, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Дабы возвести вписанный либо описанный пятиугольник, введите позже определения числа сторон буквы «о» либо «в» (либо же английские “_с” либо “_i” )

Видео по теме

Видео по теме

Полезный совет
Таким нехитрым методом дозволено возвести не только пятиугольник. Для того дабы возвести треугольник, нужно разведите ножки циркуля на расстояние, равное радиусу окружности. После этого в всякую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины положительного треугольника.

Как нарисовать пятиугольник с помощью компаса

Пятиугольник — это пятиугольник, стороны которого равны по длине. Это может быть полезная форма при изготовлении реквизита; он также может служить основой для пятигранной звезды. Может быть сложно разметить с помощью стандартных инструментов для рисования, но с помощью метода, описанного ниже, вы можете нарисовать его только с помощью циркуля и линейки.

Начните с круга, размер которого идеально подходит для вашего пятиугольника; то есть каждый угол вашего пятиугольника будет касаться внешней стороны вашего круга.

Рисунок 1

В моем круге я нарисовал две перпендикулярные линии, проходящие через центральную точку O. Там, где они пересекают круг, я пометил A, X, Y и Z (A будет верхней точкой пятиугольника, поэтому поместите это соответственно).

Я разделил линию OY пополам, чтобы найти точку M; то есть M находится точно на полпути между O и Y.

Рисунок 2

Поместите циркуль на M и вытяните его так, чтобы карандаш касался A. Нарисуйте дугу, пересекающую линию XO; назовем это пересечение «R».

Рис. 3

Переместите точку циркуля на A и вытяните его так, чтобы карандаш касался R. Теперь радиус вашего циркуля равен длине сторон вашей пентаграммы. Когда вы рисуете дугу от R до вашего круга, вы найдете точку «B».

Рис. 4

Когда вы перемещаете компас для поворота на B и рисуете дугу, он пересекает круг в двух точках: A и в новой точке «C».

Рисунок 5

Вернув компас к точке A, нарисуйте дугу, пересекающую правую сторону круга, чтобы найти букву E.

Рис. 6

Переместите компас в положение E и нарисуйте дугу, чтобы найти «D». На картинке выше я нарисовал дугу так, чтобы она дважды пересекала круг: в точке D и снова в точке A. На самом деле этого делать не нужно.

Чтобы проверить, что у вашего пятиугольника пять равных сторон, вы можете поставить точку циркуля на D. Карандаш должен коснуться C.

Рис. 7

A, B, C, D и E — это углы вашего пятиугольника. Осталось только соединить их линейкой. Престо! Идеальные пятиугольники!

Как рисовать правильные многоугольники с помощью холста HTML — Кодирование.Академия

Учиться Рекомендуемые Курсы Дом Курсы Уроки PHP jQuery Членство Учиться Рекомендуемые Курсы Дом Курсы Уроки PHP jQuery Членство

• Фильтр
• Все
• Apache
• Bootstrap
• canvas
• Проблемы с кодированием
• Курсы
• CSS
• Google
• Хостинг
• htaccess
• HTML
• jQuery
• Mac
• MySQL
• PHP
• Python
Swift

Как нарисовать круг

Все эти круги

круга — они повсюду.

Круги позволяют нам делать все, что угодно. Они позволяют нам путешествовать быстро и эффективно. Мы используем их для обозначения обязательств на всю жизнь. Мы используем их для игр.

Без них наши самые простые машины не работали бы.

Круги предшествуют зарегистрированной истории и являются одной из самых фундаментальных и мощных существующих природных форм. На протяжении веков мы разрабатывали сложные математические формулы, чтобы узнать о них больше.

Каждая открытая планета в галактике была преобразована гравитацией в сферу — трехмерную форму круга.

Круги — часть нашей повседневной жизни, и все мы хорошо с ними знакомы.

Важность кругов при рисовании

Круги, а также прямоугольники и треугольники являются одними из самых важных основных фигур, когда дело доходит до рисования. Мы используем эти базовые формы при создании набросков объектов, собирая их вместе для создания более сложных форм.

Итак, для художников круг очень важен. И очень важно знать, как его нарисовать.

Инструменты для рисования кругов

Конечно, мы всегда можем использовать устройства или инструменты, чтобы нарисовать почти идеальный круг.

Самый очевидный инструмент — компас. Но у этого инструмента есть свои ограничения, и он непрактичен, когда дело касается создания произведений искусства.

Мы всегда можем найти круглые объекты и проследить их, чтобы создать почти идеальные круги. Но, конечно, это тоже имеет свои ограничения и не очень практично.

Тогда есть шаблоны, которые мы можем использовать.Ясно, что здесь мы тоже ограничены.

Использовать эти инструменты для рисования круга просто непрактично. Лучший подход — просто научиться рисовать круг, и это проще, чем вы думаете. Все дело в механике и в том, как использовать естественный диапазон движений вашего тела.

Почему так сложно нарисовать круг?

Когда большинство из нас пытается нарисовать круг, мы используем запястье. В результате обычно получается овал, а не круг.

Почему это?

Что ж, у вашего запястья ограниченный диапазон движений.Вы можете только сделать так, чтобы ваше запястье двигалось круговыми движениями, прежде чем ваш контроль будет принесен в жертву.

Итак, мы знаем, что почти идеальный круг не может быть достигнут только с помощью запястья.

Итак, переместимся немного выше по руке к следующему суставу — локтю.

Наш локоть обеспечивает немного больше гибкости, когда мы используем его вместе с запястьем. Но мы все еще слишком ограничены, чтобы рисовать круг.

Секрет рисования больших кругов

Мы должны полностью подняться до плеча, чтобы увидеть диапазон движения, необходимый для рисования круга.

Плечо представляет собой шар в гнезде. Этот тип соединения обеспечивает более широкий диапазон движений. Именно в этом суставе мы находим диапазон движений, необходимый для рисования неуловимого круга.

Итак, хотя это может показаться странным, мы должны рисовать круги плечом, а не запястьем или локтем.

На самом деле, мы должны попытаться зафиксировать запястье и использовать локоть минимально. Большинство движений должно исходить от нашего плеча.

И даже с задействованным плечом вам может быть трудно нарисовать большой круг с помощью всего одной отметки.

Представьте, что вы бросаете дротики в доску для дартса. Представьте, что у вас всего один дротик, и вам нужно попасть в яблочко с одной попытки. Ваши шансы на успех будут довольно низкими.

Но что, если у вас много дротиков, и только один из них должен попасть в яблочко. Ваши шансы на успех теперь намного больше.

Итак, вместо того, чтобы рисовать только одну линию для создания круга, почему бы не нарисовать несколько, а затем вытащить свой круг из коллекции линий, которые вы создаете.

Вот как это работает…

Вы можете начать с карандашом в руке, паря над поверхностью бумаги.Начните медленно двигать плечом круговыми движениями, не касаясь карандашом поверхности. Ваш локоть может немного двигаться, но постарайтесь удерживать запястье на месте.

Медленно опустите руку на поверхность, продолжая двигать плечом круговыми движениями.

Позвольте карандашу коснуться поверхности бумаги, пока ваши рука и плечо продолжают двигаться. Сделайте несколько легких круговых штрихов на бумаге для рисования. Не волнуйтесь, если они не идеальны.

Теперь у нас есть набор светлых кругов. Мы просто вытащим из этой коллекции более изящный круг.

Слегка надавив на карандаш, мы можем нарисовать круг, используя светлые линии в качестве ориентира.

Если хотите, вы можете использовать ластик, чтобы убрать лишние линии после того, как нарисовали круг.

Итак, этот подход требует некоторой практики для совершенствования. Чем больше вы будете практиковаться в рисовании кругов таким образом, тем лучше у вас это получится.Просто может потребоваться некоторое время, чтобы научить ваше плечо работать таким образом.

Но как только вы его освоите, вы можете рисовать круги в любое время и любого размера, какого хотите.

[Учебник] Как сделать идеальный круг в Paint Tool Sai от JimmuArts — Fur Affinity [точка] net

Поддержка ▼

Новости и обновления
Справка и поддержка
Реклама

ПРАВИЛА И ПОЛИТИКА

Условия использования
Конфиденциальность
Кодекс поведения
Политика загрузки

СОЦИАЛЬНЫЙ

Форумы
Twitter
Facebook

---

Просматривать Поиск

• Просмотр
• Искать
• Загрузить
• Поддержка

  Сообщество

  Новости и обновления Помощь и поддержка Реклама

  Правила и политика

  Условия использования Конфиденциальность Нормы поведения Политика загрузки

  Социальные

  Форумы Twitter Facebook
& nbsp
• Войти или Создать учетную запись Войти
  Создать учетную запись

Руководств по программированию на Python

Рисование и запись изображений OpenCV Python Tutorial

В этом руководстве по OpenCV с Python мы расскажем, как рисовать различные формы на изображениях и видео.Довольно часто возникает желание каким-либо образом пометить обнаруженные объекты, чтобы мы, люди, могли легко увидеть, работают ли наши программы так, как мы могли бы надеяться. Примером этого может быть одно из изображений, показанных ранее:

Для этого временного примера я буду использовать следующее изображение:

Вам предлагается использовать собственное изображение. Как обычно, наш начальный код может быть примерно таким:

 импортировать numpy как np
импорт cv2

img = cv2.imread ('watch.jpg', cv2.IMREAD_COLOR) 

Далее мы можем приступить к рисованию, например:

 cv2.строка (img, (0,0), (150,150), (255,255,255), 15)

cv2.imshow ('изображение', img)
cv2.waitKey (0)
cv2.destroyAllWindows () 

cv2.line () принимает следующие параметры: где, координаты начала, координаты конца, цвет (bgr), толщину линии.

Результат здесь:

Хорошо, круто, давайте добавим еще форм абсурда. Далее прямоугольник:

 cv2.rectangle (img, (15,25), (200,150), (0,0,255), 15) 

Параметры здесь: изображение, координата слева вверху, координата справа внизу, цвет и толщина линии.

Как насчет круга?

 cv2.circle (img, (100,63), 55, (0,255,0), -1) 

Параметры здесь: изображение / рамка, центр круга, радиус, цвет и толщина. Обратите внимание, что у нас есть -1 для толщины. Это означает, что объект будет фактически закрашен, поэтому мы получим закрашенный круг.

Линии, прямоугольники и круги — это круто, но что, если нам нужен пятиугольник, восьмиугольник или восьмиугольник ?! Нет проблем!

 pts = np.array ([[10,5], [20,30], [70,20], [50,10]], np.int32)
# В документации OpenCV был этот код, который преобразовывал массив в 1 x 2. Я не делал
# сочтете это необходимым, но вы можете:
#pts = pts.reshape ((- 1,1,2))
cv2.polylines (img, [pts], True, (0,255,255), 3) 

Во-первых, мы называем pts, сокращенно от points, множественным массивом координат. Затем мы используем cv2.polylines для рисования линий. Параметры следующие: где нарисован объект, координаты, должны ли мы «соединить» конечную и начальную точки, цвет и снова толщину.

Последнее, что вы можете сделать, это написать на изображении. Это можно сделать так:

 font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText (img, 'OpenCV Tuts!', (0,130), шрифт, 1, (200,255,155), 2, cv2.LINE_AA) 

Полный код до этого момента будет примерно таким:

 импортировать numpy как np
импорт cv2

img = cv2.imread ('watch.jpg', cv2.IMREAD_COLOR)
cv2.line (img, (0,0), (200,300), (255,255,255), 50)
cv2.rectangle (img, (500,250), (1000,500), (0,0,255), 15)
cv2.circle (img, (447,63), 63, (0,255,0), -1)
pts = np.массив ([[100,50], [200,300], [700,200], [500,100]], np.int32)
pts = pts.reshape ((- 1,1,2))
cv2.polylines (img, [pts], True, (0,255,255), 3)
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText (img, 'OpenCV Tuts!', (10,500), шрифт, 6, (200,255,155), 13, cv2.LINE_AA)
cv2.imshow ('изображение', img)
cv2.waitKey (0)
cv2.destroyAllWindows () 

Результат:

В следующем уроке мы рассмотрим основные операции с изображениями, которые мы можем выполнять.

Как возникла форма здания Пентагона?

Как Пентагон получил свое название? Ну это и ежу понятно.Но как образовалась гигантская штаб-квартира Министерства обороны (МО)? Это более длинная история.

Здание изначально было спроектировано таким образом, чтобы вписаться в участок земли с границами с пяти сторон. В конце концов, он был построен в другом месте, на том месте, где пятиугольная форма перестала быть необходимой. Но к тому времени, когда это место изменилось, было слишком поздно придумывать новый дизайн. Так что остался пятиугольник.

«По сути, это была случайность, которая возникла в результате … чрезвычайной ситуации военного времени», — сказал в интервью Live Стив Фогель, репортер Washington Post и автор книги «Пентагон — История» (Random House, 2007). Наука.

Летом 1941 года в Вашингтоне, округ Колумбия, было «реальное ощущение, что [] США будут втянуты во [Вторую мировую войну]», — сказал Фогель. В то время, однако, военное министерство, предшественник сегодняшнего Министерства обороны, было разбросано по многим временным зданиям в Вашингтоне. [Правительство США предлагает хакерам «взломать Пентагон»]

В ожидании войны, Бриг. Генерал Брехон Берк Сомервелл получил задание расширить штаб-квартиру департамента. Как объяснил Фогель, первоначальная идея заключалась в том, чтобы построить временные здания, но Сомервелл «в значительной степени принял эти инструкции и начал работать с ними» и решил, что лучшим решением будет одно здание для размещения всего отдела, сказал Фогель.

Фогель назвал Сомервелла «отцом Пентагона — действительно единственная фигура, которая объединила концепцию, а затем реализовала ее в удивительно короткий период времени».

Нет времени жалеть

Фогель подробно рассказал о происхождении Пентагона в отрывке из своей книги, опубликованной в The Washington Post в 2007 году.

Как объяснил Фогель в своей статье, в четверг июля 1941 года Сомервелл поручил своей команде разработчиков приехать разработали план здания, способного вместить 40 000 человек; включить паркинг на 10 000 машиномест; и быть не выше четырех этажей, чтобы сохранить сталь и не загораживать вид на Вашингтон.

Более того, Сомервелл хотел получить этот план в следующий понедельник.

Здание, площадь которого должна быть почти вдвое больше, чем Эмпайр-стейт-билдинг, не могло быть небоскребом. Он также не мог поместиться в Вашингтоне, округ Колумбия. Вместо этого команда решила разместить его через реку Потомак из округа Колумбия на территории Арлингтонской фермы, государственной экспериментальной сельскохозяйственной операции к востоку от Арлингтонского национального кладбища.

Участок земли на ферме Арлингтон, который рассматривали проектировщики здания, имел границы с пяти сторон.Команда дизайнеров попробовала несколько различных планировок, но «в конце концов они решили:« Почему бы нам не попытаться придать зданию форму земли? »», — сказал Фогель. Прежде всего, именно архитектор Джордж Эдвин Бергстром отстаивал пятистороннюю форму, отметил Фогель.

Возражения Пентагона

Однако Гилмор Д. Кларк, тогдашний председатель Комиссии изящных искусств США, возразил против этого предложения, заявив, что Пентагон закроет вид на Вашингтон с Арлингтонского национального кладбища, где находится вашингтонский дизайнер Пьер Л. Энфант был похоронен.Разве покойный архитектор больше не сможет смотреть на свое творение, пусть даже образно? Если бы Пентагон был построен на Арлингтонской ферме, ответ был бы отрицательным, и это, по словам Кларка, было бы проблемой.

Кроме того, Фредерик А. Делано, тогдашний председатель Национального парка столицы и комиссии по планированию, а также дядя тогдашнего президента Франклина Делано Рузвельта, выступил против этого плана в основном из-за беспокойства по поводу транспортного потока, который он создаст через Потомак. «Люди не хотели, чтобы это огромное здание, какой бы формы оно ни было, сидело на этом участке», — сказал Фогель.

В ответ на это давление Рузвельт написал письмо в подкомитет Сената, в котором выразил оговорки и попросил уменьшить здание. Но Конгресс не прислушался и принял первоначальный законопроект — о том, что штаб военного ведомства должен быть построен в урочище Арлингтон-Фарм и в первоначальном размере — в любом случае. Разочарованный тем, что Конгресс не прислушался к его совету, Рузвельт приказал строительной бригаде поставить новое здание к югу от фермы Арлингтон в том, что тогда было несколько захудалым районом, который назывался «Адское дно», — написал Фогель в своей книге.[На фотографиях: Музей чествует Тедди Рузвельта]

Там часть парковки Пентагона все равно будет перекрывать Арлингтонскую ферму, но не на пятистороннем участке, а на участке за пределами участка, который также был собственностью Арлингтонской фермы, сказал Фогель. Поскольку собственность Пентагона технически пересекалась с Арлингтонской фермой, она все еще соответствовала закону, принятому Конгрессом.

Преимущества формы

На новом месте пятиугольная форма больше не нужна, но руководители проекта решили придерживаться своего дизайна.Пентагон, больше не ограниченный территорией, мог быть симметричным, что с эстетической точки зрения было плюсом. А пятиугольная форма здания, изначально выбранная для размещения в пределах фермы Арлингтон, имела и другие преимущества: эта форма сокращала расстояния для передвижения внутри здания — на 30-50 процентов короче, чем они были бы в пределах прямоугольника, подсчитали архитекторы.

По сути, у него были геометрические преимущества круга, с точки зрения сокращения расстояний внутри здания, но у него были прямые стороны, что означало, что его было легче построить, чем было бы круглое здание, объяснил Фогель.

Это было хорошо, потому что строительство здания должно было произойти очень быстро; Сомервелл пообещал закончить строительство в течение года; согласно сайту Pentagon Tours Министерства обороны, такой проект обычно занимает в четыре раза больше времени.

Строители заложили землю на здании 11 сентября 1941 года. (Ровно 60 лет спустя это стало местом одного из самых печально известных нападений на территорию США). Семь месяцев спустя, еще до того, как строительство было завершено, въехали первые сотрудники.По словам Фогеля, Пентагон был построен по часовой стрелке.

«Они начали перемещать людей в секции здания, которые они закончили, а затем как бы продолжили свой путь, продолжая забивать сваи и заливать бетон, даже несмотря на то, что в здании начали работать тысячи людей», — сказал Фогель.

Итак, несмотря на его уникальную форму, строительство не было отложено Пентагоном.

Оригинальная статья о Live Science.

.