Как рисовать правильный пятиугольник с помощью циркуля. Правильный пятиугольник. Получение с помощью полоски бумаги
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона.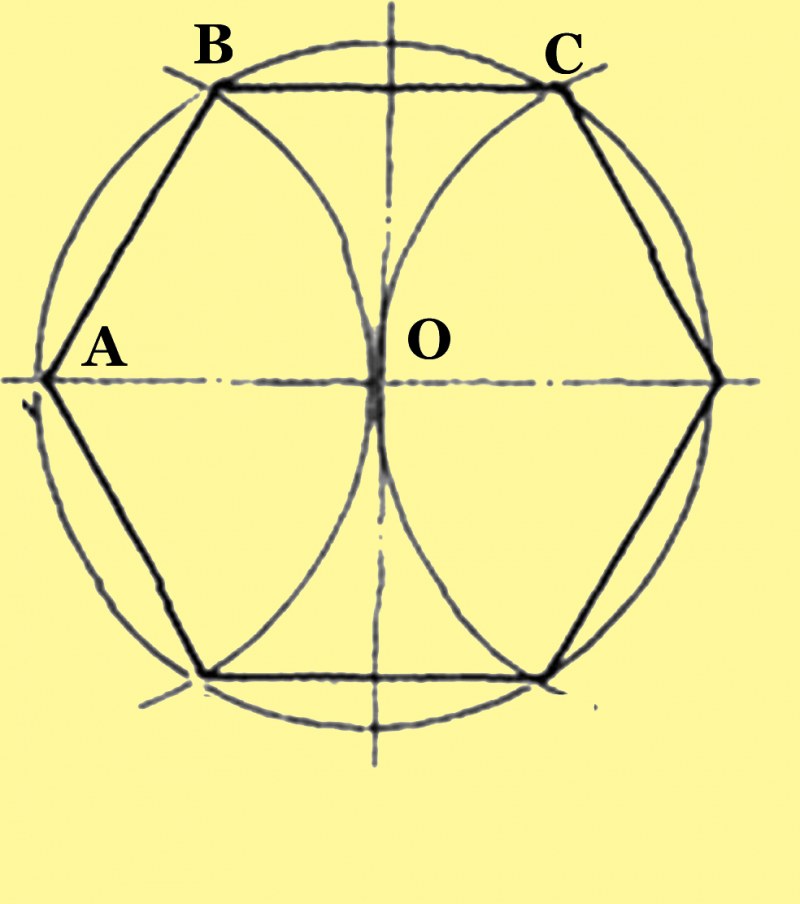
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.

- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.

- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.

- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.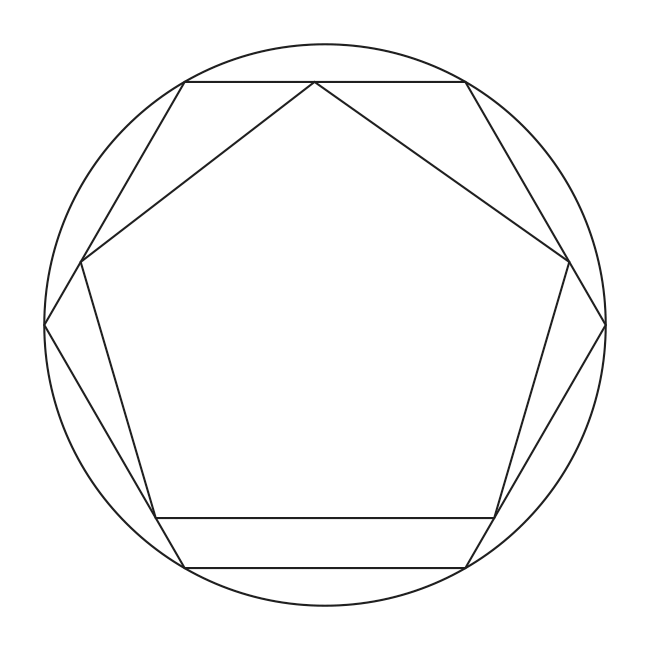
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника.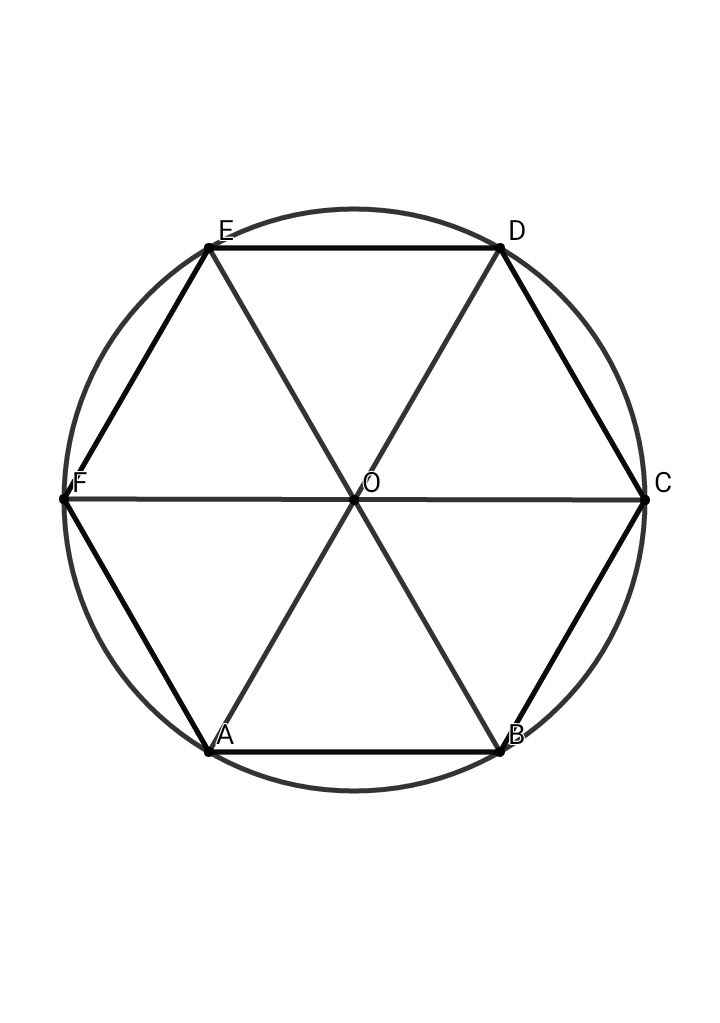 Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.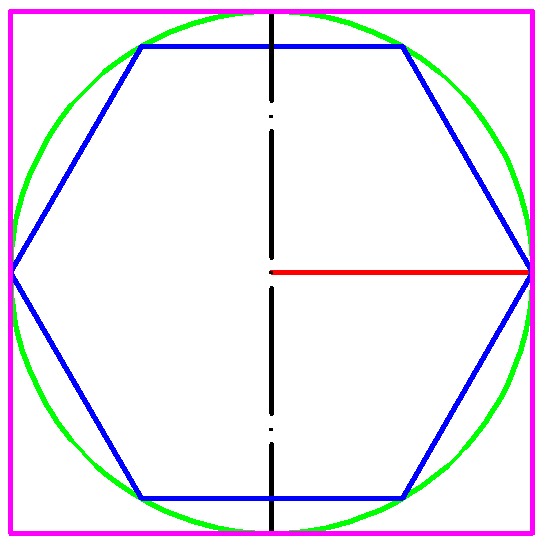 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение вписанного в окружность правильного пятиугольника. Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Построить пятиугольник и поможет именно эта окружность. В первую очередь необходимо построить циркулем окружность. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Она и представляет собой многоугольник, остается только ввести параметры. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Деление окружности на равные части и вписывание правильных многоугольников.

Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.
Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками.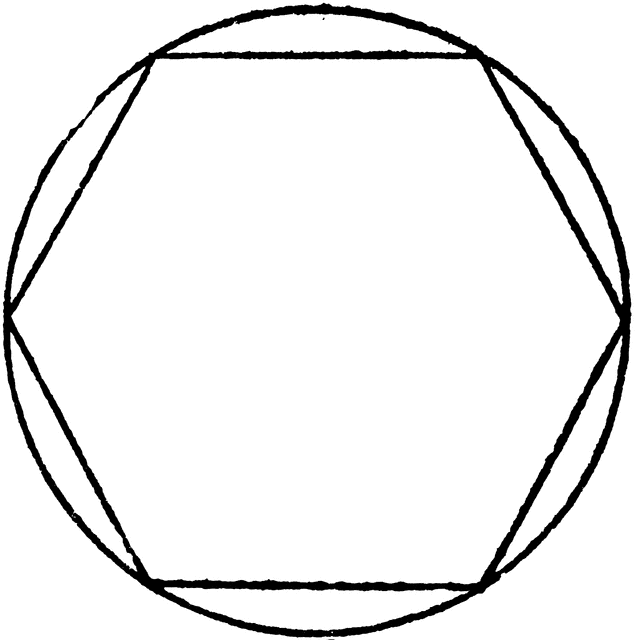 Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Окружность, дуги и многоугольники.
Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.
Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
Построение правильных многоугольников по заданной стороне
Сотрите окружности, линии и дуги, оставив только восьмиугольник. Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.
Смотреть что такое «Правильный пятиугольник» в других словарях:
Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства.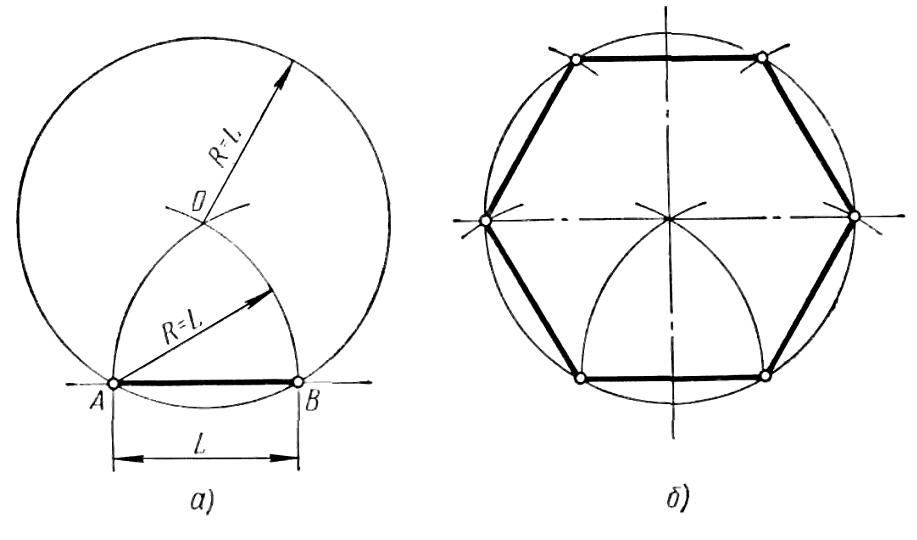 Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А.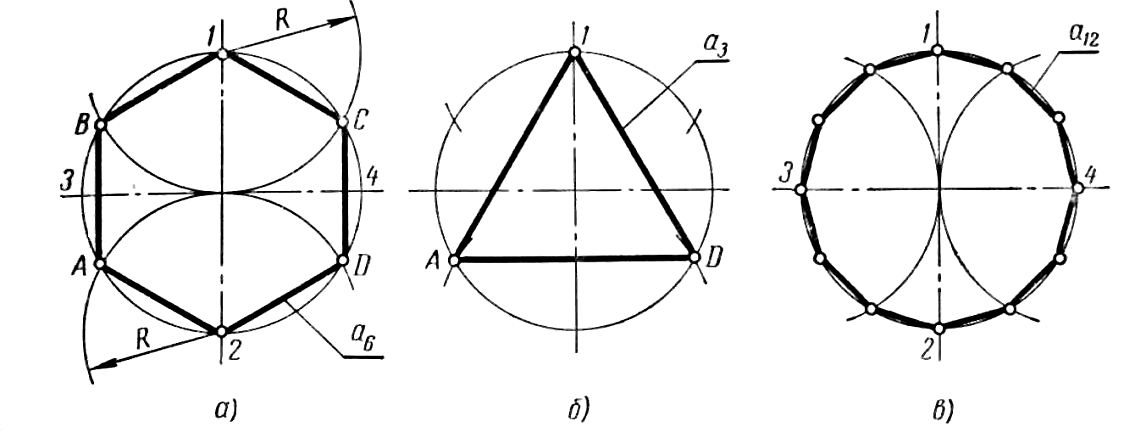 Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H. Точки G,E,B,F,H – вершины положительного пятиугольника .
Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф.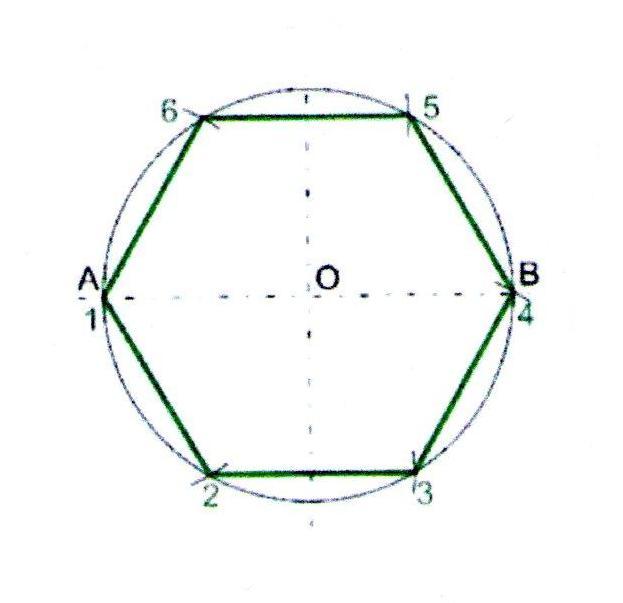 Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см.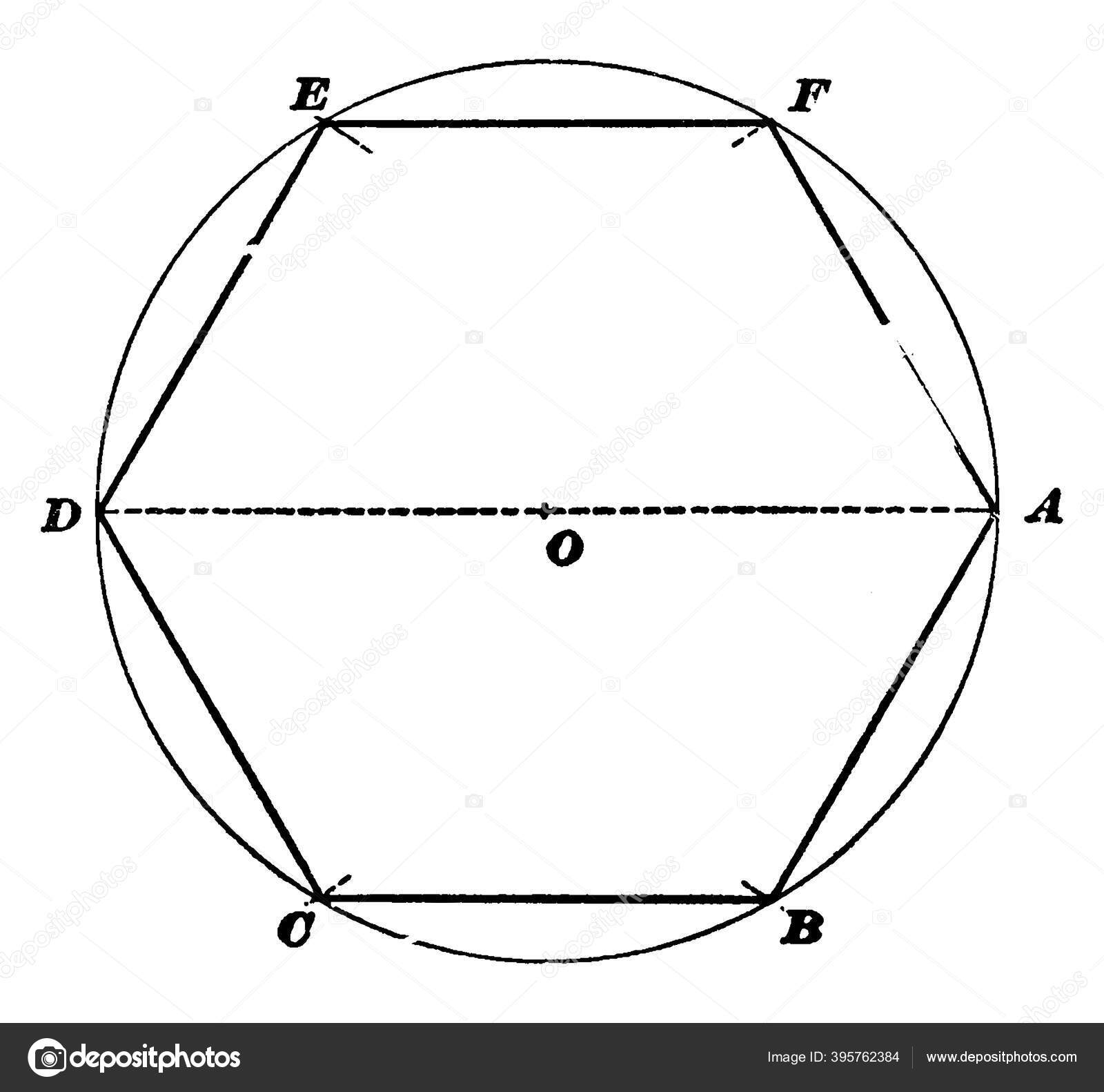 Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.
Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н.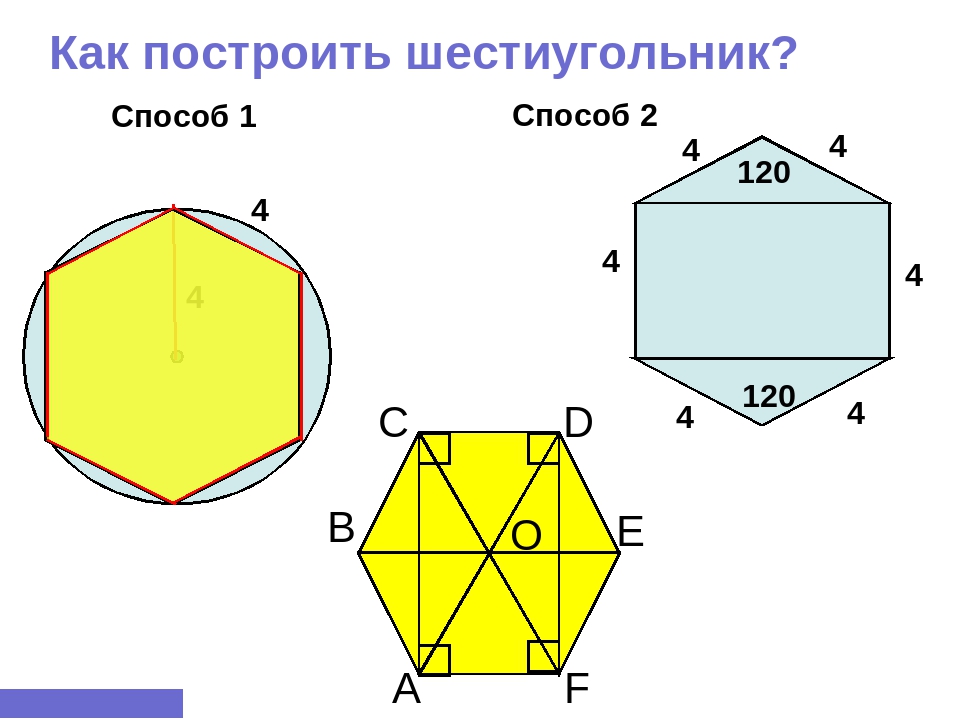 Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5.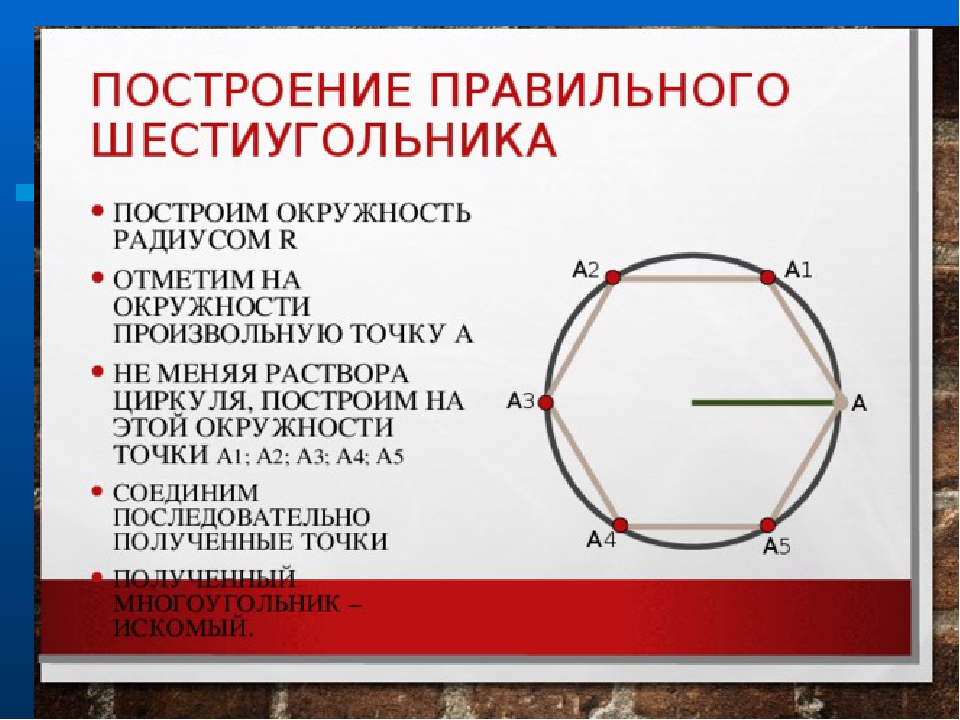 Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Как нарисовать правильный шестиугольник. Рисуем в Microsoft Word
На панели задач инструментов Рисование содержится кнопка Автофигуры . Она позволяет добавлять несколько категорий фигур: линии, соединительные линии, основные фигуры, Элементы блок-схем, звёзды и ленты, а также выноски.
Упражнение 1 .Чистая страница
1. Создайте на Рабочем столе последовательный ряд папок:
папку Рисование ;
открыв её, создайте в ней папку Word ;
открыв эту папку, создайте папку Действия с автофигурами .
1. Затем
закройте все папки и, открыв программу Microsoft
Word,
создайте в ней новый документ. Сохраните этот документ
в папке Действия с автофигурами. Это может быть файл с названием
следующего упражнения («Фигуры»), но рисовать пока ничего не
требуется: сохраните чистую страницу.
Это может быть файл с названием
следующего упражнения («Фигуры»), но рисовать пока ничего не
требуется: сохраните чистую страницу.
Упражнение 2. Фигуры
1. Откройте созданную ранее чистую страницу или создайте новую и заполните её верхнюю часть фигурами стандартного размера, используя палитру Основные фигуры. Результат должен быть приблизительно похож на рис. 2.1.
Рис.2.1. Упражнение «Фигуры». Шаг 1
2. Освободите пустое пространство в центре заполненной в упражнении страницы, как на рис. 2.2.
Рис.2.1. Упражнение «Фигуры». Шаг 2
3. Выберете одну из фигур, расположенных по краям листа, переместите её в центр страницы и измените её размер так, чтобы заполнить всё пустое пространство. При увеличении размера не изменяйте пропорции фигуры. Сравните результат с рис.2.3.
Рис.2.1. Упражнение «Фигуры». Шаг 3
4. Сохраните рисунок в своей папке под названием «Фигуры».
5. Закройте файл.
Создание автофигур
Нажмите
кнопку Автофигуры на панели инструментов Рисование, укажите
категорию Основные фигуры, а затем выберите необхадимую фигуру.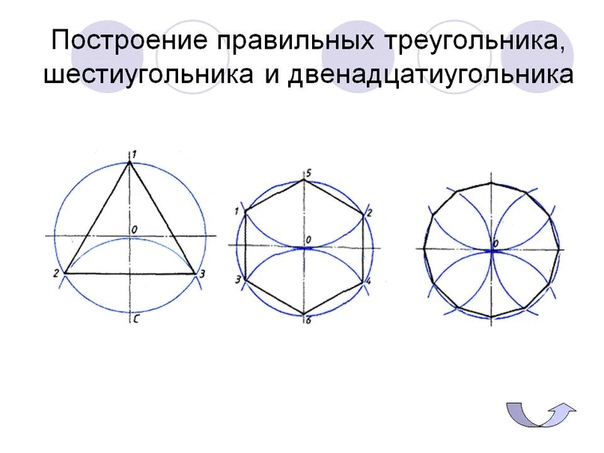
Удобнее работать, если Основные фигуры вынести за пределы панели Рисование. Для этого наведите курсор мыши на горизонтальную полосу в верхней части предварительно открытой палитры Основные фигуры. Когда полоса изменит свой цвет, нажмите левую клавишу мыши и переместите палитру на любое свободно место. Точно также вы можете выносить и перемещать по экрану большинство элементов панели Рисование, настраивая внешний вид программы для текстов или иных изобразительных задач.
Для вставки фигуры стандартного размера вначале щелкните на кнопке выбранной фигуры затем выполните резкий щелчок лево клавишей мыши в пределах белой страницы в окне программы. Если выполнить щелчок с задержкой, появится та же автофигура, но меньшего размера.
Выделение автофигур
Прежде чем
начать любые действия с автофигурами, необходимо их выделить, то
есть указать, с кокой именно фигурой или фигурами вы намеренны
выполнить действие. Выделение осуществляется щелчком левой клавиши
мыши на выбранном объекте. Вокруг выделенного объекта должны
появиться маркеры — маленькие прямоугольники белого цвета.
Вокруг выделенного объекта должны
появиться маркеры — маленькие прямоугольники белого цвета.
Удаление автофигур
Выделите автофигуру, которую хотите удалить, и нажмите на клавиатуре клавишу Delete.
Отмена действий
Любые действия, произведённые до закрытия документа, можно отменить. Для отмены последнего действия нажмите кнопку Отменить.
Чтобы возвратить результат последнего отмененного действия, нажмите кнопку Вернуть.
Перемещение
Чтобы переместить или скопировать объект, наведите на него курсор. Вид курсора-стрелки должен измениться: под стрелкой появится крестообразный символ. нажмите левой клавиши с одновременным перемещением мыши приведёт к перемещению объекта.
Нажатие правой клавиши с последующим перемещением мыши может завершить как перемещением, так и копированием объекта в зависимости от того, какая команда из появившегося списка будет выбрана: Переместить, Копировать, Отменить.
Выделенный
объект (при выделении по его периметру возникает 8 маленьких
квадратных маркеров) может быть также перемещён при помощи четырёх
клавиш со стрелками, расположенных на клавиатуре.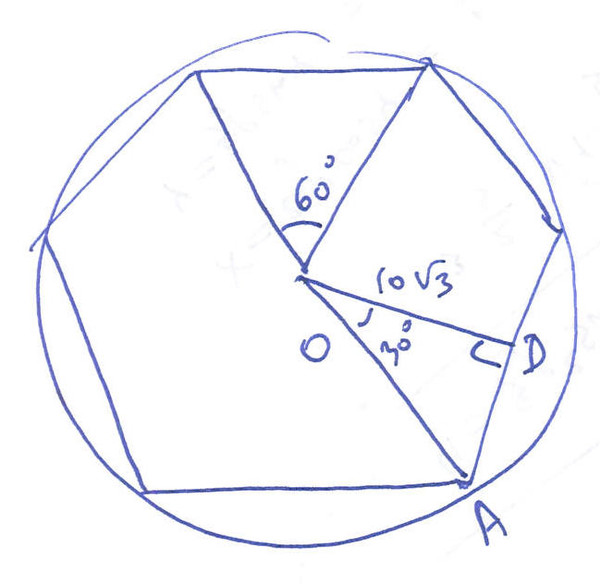
Если при нажатии клавиши со стрелками удерживать клавишу Ctrl , перемещение будет точнее.
Изменение размеров
При выделении автофигуры (щелчком левой клавиши мыши) по периметру прямоугольника выделения появляются маркеры изменения размера. Размеры объекта изменяются путём перетаскивания одного из них, при этом над маркером появляется двухсторонняя стрелка. Различают угловые и центральные маркеры.
Упражнение 3. Лестница
1. Создайте новый документ. Нарисуйте ряд из квадратов, примыкающих друг к другу, как на рис. 2.4.
Рис.2.4.Упражнение»Лестница». Шаг 1
2. Путём последовательного растяжения квадратов превратите их ряд в лестницу — рис. 2.5. Сохраните рисунок.
Рис. 2.5. Упражнение «Лестница». Шаг 2
Изменение пропорции
Чтобы изменить пропорции объекта, выделите его щелчком левой клавиши мыши, а затем перетащите по вертикали или горизонтали один из центральных маркеров.
Упражнение 4. Перспектива
Перспектива
1. Создайте ряд из пяти одинаковых автофигур.
2. Последовательно, не меняя пропорций, сократите их размеры.
3. Сравните получившийся рисунок с рис. 2.6 и сохраните файл под названием «Перспектива».
Сохранение пропорций при изменении размеров
Передвигая угловой маркер автофигуры, удерживая клавишу Shift.
Рис. 2.6. Упражнение » Перспектива»
Упражнение 5. Пирамида
1. Создайте две одинаковые автофигуры, увеличьте размер одной из них и разместите малую перед большой; если большая фигура оказалась впереди, переместите её на задний план. Составьте таким способом стопку из пяти слоёв, как на рис. 2.7.
Рис. 2.7. Упражнение «Пирамида». Шаг 1
2. Сместите вверх все фигуры, кроме самой нижней. сравните с рис. 2.8.
Рис. 2.8. Упражнение «Пирамида». Шаг 2
3. Скопируйте
и переверните пирамиду, перемещая планы. на рис. 2.9 видно, как
должна выглядеть перевёрнутая пирамида.
Рис. 2.9. Упражнение «Пирамида». Шаг 3
4. Сохраните файл под именем «Пирамида».
П еремещение планов
Чтобы изменить порядок наложения фигур, нажмите на панели Рисование кнопку Действия, выберите команду Порядок, а затем — На задний план или На передний план.
Выделение группы фигур
Способ 1 : удерживая клавишуShift , выделите последовательно выбранные объекты, щёлкая на них левой клавишей мыши.
Способ 2 : нажмите на панели Рисование кнопку Выбор объектов и, удерживая левую клавишу мыши и передвигая мышь, выделите появившимся пунктирным квадратом все объекты группировки сразу.
Копирование
Чтобы скопировать объект (или группу выделенных объектов), наведите на него курсор, нажмите правую клавишу мыши и, не пуская её, перетащите объект. В открывшимся меню выберите команду копировать.
Точное перемещение
Для точного
перемещения объектов клавишами со стрелками необходимо удерживать
клавишу Ctrl
. Кроме того, можно изменить
интервалы перемещения, заданные в окне сетка из списка команд
Действия.
Кроме того, можно изменить
интервалы перемещения, заданные в окне сетка из списка команд
Действия.
Упражнение 6. Сетка
1. Создайте четыре квадрата, как на рис. 2.10.
Рис. 2.10. Упражнение «Сетка» .Шаг 1
2. Соедините все четыре квадрата в один большой квадрат — рис. 2.11. Сгруппируйте его.
Рис. 2.11. Упражнение «Сетка». Шаг 2
3. Скопируйте полученную группу три раза, составьте из четырёх групп новый квадрат — рис. 2.12. Сгруппируйте его.
Рис. 2.12. Упражнение «Сетка». Шаг 3
4. Ещё раз повторив это действие, создайте сетку 8х8 квадратов. Сравните результат с рис. 2.13.
Рис. 2.13. Упражнение «Сетка». Шаг 4
5. Сохраните рисунок под названием «Сетка».
Группировка
Выделив группу фигур, откройте на панели Рисование меню Действия и выберите команду Группировать .
С группой
объектов можно совершать те же действия, что и с отдельными
автофигурами, то есть перемещать их, копировать, менять их
размеры, пропорции, объединять в группы.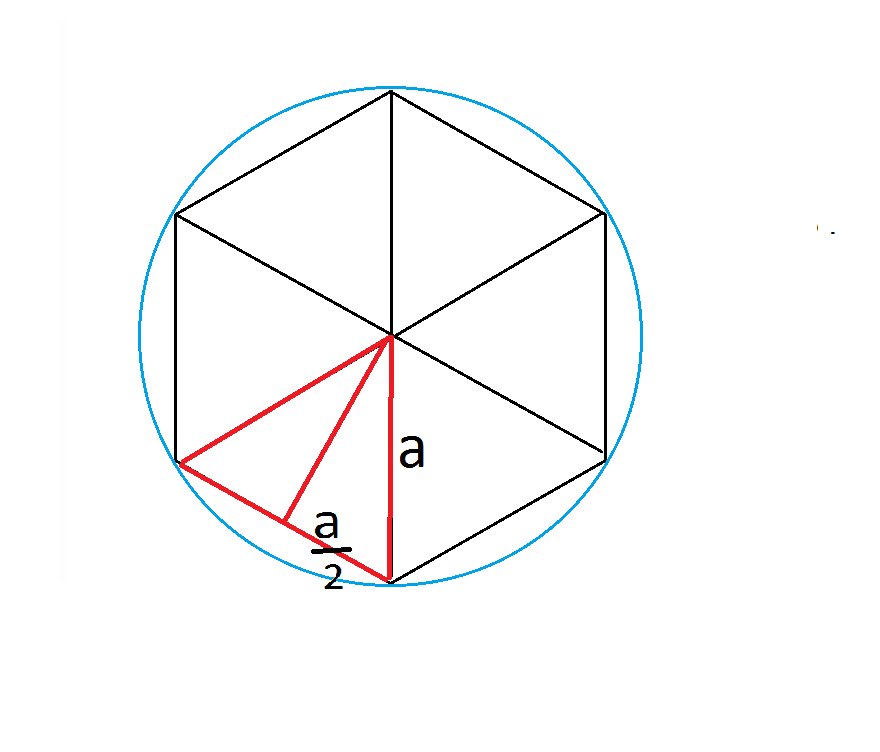
Чтобы разгруппировать объекты, в меню Действия выберите команду Разгруппировать. Чтобы сиять выделение множества объектов, щелкните левой клавишей мыши на пустом пространстве страницы.
Упражнение 7. Шестиугольник
1. Создайте три равносторонних треугольника, отразите один из них сверху вниз — рис. 2.14.
Р ис. 2.14. Упражнение «Шестиугольник». Шаг 1
2.
Соедините три полученные фигуры и сгруппируйте
их -рис. 2.15.
Рис. 2.15. Упражнение «Шестиугольник». Шаг 2.
3. Скопируйте группу, отразите копию сверху вниз рис. 2.1.6.
Рис. 2.16. Упражнение «Шестиугольник». Шаг 3
4. Соедините и сгруппируйте две симметричные части рис. 2.17.
Рис. 2.17. Упражнение «Шестиугольник». Шаг 4
5. Сохраните файл под названием «Шестиугольник ».
Отражение
В результате
действия «отражение» вид асимметричных объектов изменяется, как бы
отражаясь в зеркале.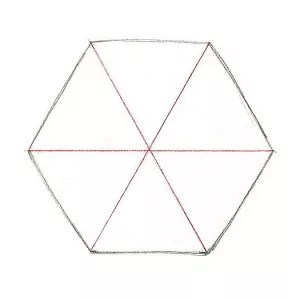 Возможны два типа отражения: по горизонтали
(слева направо) и по вертикали (сверху вниз). Чтобы отразить объект,
необходимо на панели Рисование открыть меню Действия и выбрать из
списка Повернуть /отразить нужное действие .
Возможны два типа отражения: по горизонтали
(слева направо) и по вертикали (сверху вниз). Чтобы отразить объект,
необходимо на панели Рисование открыть меню Действия и выбрать из
списка Повернуть /отразить нужное действие .
Упражнение 8. Цветок
Создайте круг стандартного размера, скопируйте его, сократите горизонтальные размеры, чтобы получился овальный лепесток -рис. 2. 18.
Сделайте копию лепестка. Разместите два лепестка на одной вертикали над и под кругом-сердцевиной, выделите и сгруппируйте лепестки — рис. 2.19.
Скопируйте группу из двух лепестков и поверните ее вправо или влево — рис. 2.2O.
Выделите, сгруппируйте, скопируйте и поверните четыре лепестка. Сравните результат с рис. 2.21.
Сохраните файл под названием «Цветок».
Рис. 2.18. Упражнение «Цветок». Шаг 1
Рис. 2.18. Упражнение «Цветок». Шаг 2
Рис. 2.18. Упражнение «Цветок». Шаг 3
Рис.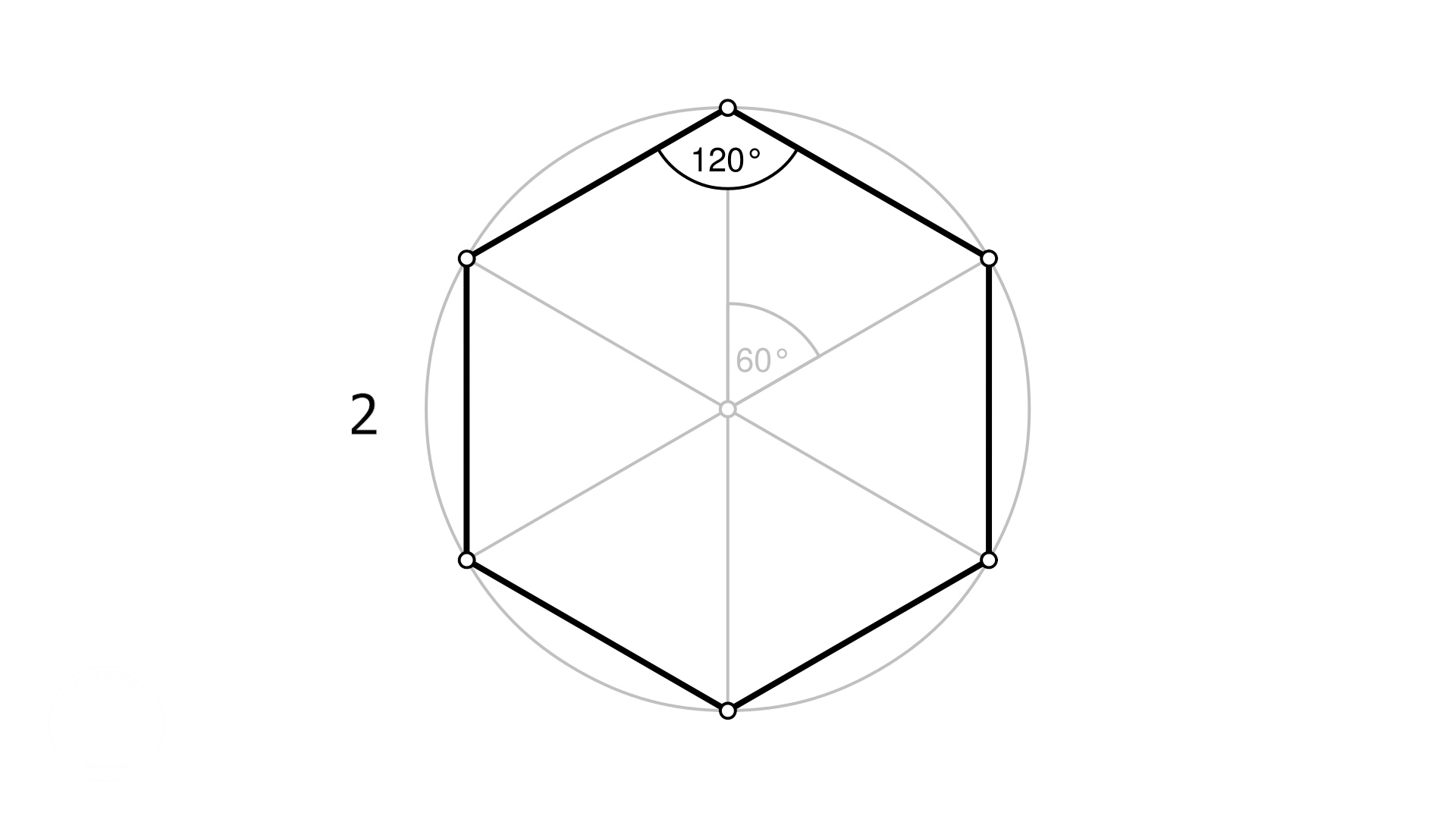 2.18. Упражнение «Цветок». Шаг 4
2.18. Упражнение «Цветок». Шаг 4
Поворот
Чтобы повернуть объект, необходимо на панели Рисование открыть меню Действия и выбрать из списка Повернуть /отразить нужное действие : Повернуть вправо, Повернуть влево или Свободное вращение.
При нажатии этой кнопки в углах выделенного объекта появляются круглые зеленые маркеры. Перемещая их при помощи мыши, можно поворачивать объект на произвольный угол.
Кнопку Свободное вращение можно установить и непосредственно на панель Рисование . Для этого в меню Сервис нажмите кнопку Настройка. В открывшемся окне выберите категорию Рисование , затем найдите команду Свободное вращение и перетащите на панель Рисование .
В последних
версиях Microsoft Word маркер поворота зеленого цвета
появляется над любой выделенной фигурой или группой, — в этом случае
нажимать на кнопку Свободное вращение нет необходимости.
Упражнение 9. Цветник
1. Нарисуйте в новом файле цветок с пятью лепестками. Стадии рисунка показаны на рис. 2.22.
Рис. 2.19. Упражнение «Цветник». Начальные стадии
2. Переместите сюда же рисунок из файла «Цветок». Скопировав исходные рисунки, создайте цветы разного размера и по-разному развернутые. В качестве фона для рисунка используйте автофигуры Прямоугольник или Овал (их кнопки находился непосредственно на панели Рисование). Чтобы выбранная фигура-фон не загораживала цветы, переместите ее на задний план. Один из возможных вариантов такой композиции показан на рис. 2.23.
3. Сохраните рисунок под названием «Цветы».
Рис. 2.23. Упражнение «Цветник». Завершенный рисунок
Перемещение рисунка в другой документ
Выделите все детали рисунка, сгруппируйте их и нажмите кнопку Копировать на стандартной панели инструментов (вверху экрана).
Затем
откройте нужный файл и нажмите кнопку Вставить .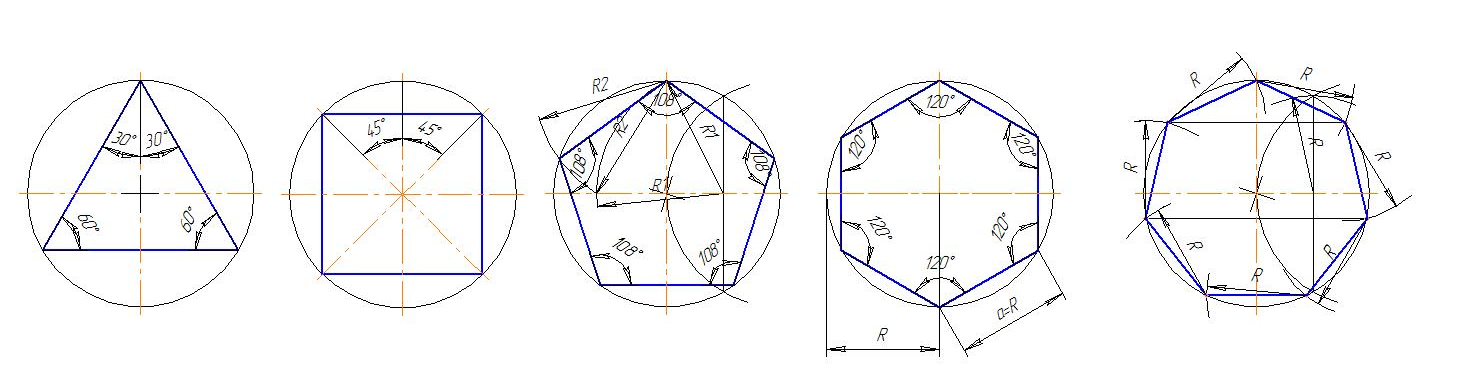 Если оба
файла уже открыты, вы можете переключаться с одного на другой с
помощью меню Окно .
Если оба
файла уже открыты, вы можете переключаться с одного на другой с
помощью меню Окно .
Если вы хотите построить на своем участке комфортное и красивое место для отдыха, то стоит присмотреться к конструкции 6-гранной беседки. В этой статье мы рассмотрим все нюансы постройки на конкретном примере, но конструкция и размер могут быть изменены в зависимости от ситуации.
Этапы постройки
Прежде чем приступить к процессу монтажа, вам потребуется наличие следующих инструментов:
- Электролобзик – для удобной резки криволинейных деталей.
- Электрорубанок – для обработки нестроганого бруса перед укладкой.
- Ручная фрезерная машинка – для создания закруглений, профилирования поверхностей.
- Электродрель – для сверления отверстий, может использоваться и как шуруповерт.
- Шуруповерт – незаменим при монтаже большого количества саморезов.
Подготовка основания
- Затем по разметке нужно снять верхний слой почвы (около 20 см).

- Установите опалубку из досок, закрепив её на вбитые колышки снаружи. Верхний её край должен быть установлен по уровню.
- Внутри делается песчаная засыпка толщиной около 10 см. Её нужно разровнять, пролить водой и тщательно утрамбовать.
- Затем насыпается и уплотняется 5-7 см щебня.
- Сверху связывается каркас из прутков арматуры 8-12 мм.
- Опалубка заливается бетоном, для увеличения прочности и удаления воздуха изнутри, после заливки его обрабатывают погружным вибратором.
- Верхний слой выравнивается с помощью правила. При необходимости вы можете сделать небольшой уклон для слива воды.
- Чтобы стяжка была гладкой и беспыльной, её нужно железнить . Это делается путем нанесения тонкого слоя сухого цемента на поверхность. Затем он затирается гладилкой до почти зеркального блеска.
- После этого нужно будет защитить бетон от быстрого высыхания . Для этого его накрывают на неделю полиэтиленовой пленкой. Полную прочность основание наберет через 28 дней.

Монтаж нижней обвязки
- Когда бетон набрал прочность, можно начинать делать нижнюю обвязку. Для этого раскладываем брус 100*100 по сторонам шестиугольника и делаем разметку для выреза пазов для их стыковки.
- Делаем ножовкой вертикальные вырезы по разметке, и удаляем ненужные части стамеской.
- Также нужно будет предусмотреть промежуточные балки, минимум 2 штуки, чтобы пол не прогибался в середине.
- Затем сверлим сквозные отверстия для крепления обвязки к фундаменту. Перьевым сверлом вырезаем верхнюю часть отверстия, чтобы утопить в него гайку.
- Вбиваем анкерные болты с резьбой в фундамент и прикручиваем к ним брус обвязки.
Сборка каркаса
- Основной каркас делается из бруса 40*100 или 50*100 мм. Предварительно он строгается с каждой стороны и на ребрах делаются скосы фрезером.
- 6 стоек одинаковой высоты прикручиваются к каждому углу деревянной обвязки. Для этого используются стальные уголки и саморезы по дереву.
 Во время установки нужно контролировать их ровность по вертикали с помощью уровня.
Во время установки нужно контролировать их ровность по вертикали с помощью уровня. - Затем из бруса такого же сечения собирается верхняя обвязка. Чтобы дерево не трескалось от саморезов, предварительно их нужно просверливать. Во время установки нужно проверять уровень столбов.
Обратите внимание! Чтобы после установки брус не потрескался и не покоробился, используйте только сушеную древесину, с влажностью менее 18%.
- Для удобства и придания дополнительной жесткости, прикручиваем по периметру перила. На этом этапе конструкция еще может быть немного хлипкой, но дальше её свяжет деревянная обшивка.
Каркас для крыши
Совет! Угол наклона кровли выбирается самостоятельно. Чем более резким он будет, тем лучше будет с крыши сходить снег зимой, и нагрузка на стропила будет ниже. Соответственно от угла ската будет зависеть и высота конструкции.
- Вначале собираем центральную деталь из двух стропил, и усиливаем их перекладиной.
 В итоге получится треугольный элемент. Оптимальным углом ската считается 45 градусов, следовательно, 2 соединенных стропила будут образовать прямой угол 90 градусов.
В итоге получится треугольный элемент. Оптимальным углом ската считается 45 градусов, следовательно, 2 соединенных стропила будут образовать прямой угол 90 градусов. - Для стропил подойдет брус 40*100 мм. Перекладины крепятся с двух сторон саморезами.
- В месте стыковки стропила и верхней обвязки делаем прямоугольный вырез для его плотной стыковки.
- Собранный треугольный элемент крепим на уголки к верхней обвязке.
- Остальные стропила крепятся по отдельности. Они прикручиваются к центральному элементу и верхней обвязке. Также от каждого из них делается перекладина к центральному стропилу.
- Затем крепятся перпендикулярные доски обрешетки толщиной 2-3 см и шириной около 10 см.
- Каркас готов, остается только обработать его в несколько слоев защитным лаком для наружных работ.
Кровля
В качестве кровельного материала можно использовать практически любой материал: профнастил, черепицу, поликарбонат, рубероид или шифер. Но нужно учитывать, что 6 гранная беседка имеет крышу сложной формы и потребует много отходов.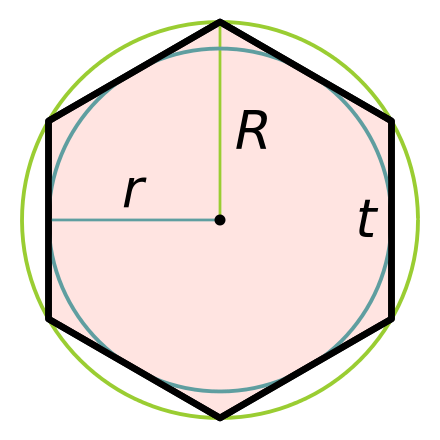 Поэтому лучшими в этом варианте считается гибкая черепица и профлист ().
Поэтому лучшими в этом варианте считается гибкая черепица и профлист ().
В данном случае была выбрана зеленая битумная черепица, она оптимальна по цене, внешнему виду и отходам.
- Гибкая черепица должна укладываться к прочному сплошному основанию с гидроизоляцией. Для этого нужно обшить обрешетку крыши листами влагостойкой фанеры 10 мм или ОСБ. Затем основание обшивается специальным гидроизоляционным ковром.
- Чтобы защитить торцы кровли от проникновения влаги, вначале по периметру нижней кромки крепится карнизная планка. Её можно купить готовую, либо сделать из оцинкованной стали самостоятельно.
- Затем можно начинать монтаж самой черепицы. Она крепится на 4 гвоздя, начиная снизу. У первого ряда нужно обрезать выступающие «усики», а каждый новый ряд укладывать внахлест предыдущего.
Устройство пола
- Пол проще всего сделать из дерева. Для этого подойдет брус 40*100. Его нужно ровно обработать с каждой стороны электрорубанком. Для плотной стыковки досок и уменьшения пригибания пола, на досках нужно вырезать шип и паз.

Совет! Также вы можете сразу купить готовую шпунтованную доску, но она обойдется вам дороже.
- Доски стыкуются шип в паз и прикручиваются к балкам со стороны паза под углом, чтобы шляпки саморезов были не видны. Только первый и последний ряд прикручивается сверху.
- В местах, где встречаются опоры, доски подрезаются по размерам электролобзиком.
- После обшивки пола, его нужно покрыть яхтным лаком в 2-3 слоя.
Обратите внимание! Если предполагается делать открытую беседку, доски нужно крепить с зазорами 3-5 мм, чтобы пол был всегда сухим и чистым. В таком случае подойдет обычная строганая доска.
Обшивка каркаса
Крыша и пол готовы – остается только обшить стены. Это защитит вас от ветра и попадания влаги внутрь. Есть множество материалов, чем обшивают 6 гранные беседки: доски, деревянные сеточки, деревянный сайдинг, блокхаус, поликарбонат, делают ветрозащитные шторы, остекляют и т. д.
д.
Тут все ограничивается лишь вашей фантазией.
- В данном примере для увеличения жесткости конструкции был выбран узкий блокхаус.
- Чаще всего делают глухую обшивку примерно до середины беседки. Если делается четырехгранная беседка своими руками, и крыша односкатная, то также под ней делают продуваемую обшивку.
- Обшивается 5 стенок, и если материал останется, короткими обрезками обшивается сторона входа.
Заключение
Чтобы подробно увидеть весь процесс строительства, посмотрите видео в этой статье.
Крепежные детали в современной технике отличаются значительным разнообразием. Это и обычные шестигранные болты и гайки, винты с плоскими и крестообразными шлицами, звездочки Torx и многие другие. Особняком здесь стоят детали с внутренним шестигранником. Отвернуть их без подходящего инструмента довольно тяжело.
Впервые внутренний шестигранный шлиц был запатентован в 1936 году немецкой фирмой Bauer & Schaurte. В зарубежной технической литературе такие винты обычно упоминаются под торговой маркой Inbus (инбус). Это сокращение немецкой фразы Innensechskantschraube Bauer und Schaurte — винт с внутренним шестигранником фирмы Bauer & Schaurte.
Это сокращение немецкой фразы Innensechskantschraube Bauer und Schaurte — винт с внутренним шестигранником фирмы Bauer & Schaurte.
Преимущества внутреннего шестигранника
Болты и винты с внутренним шестигранным шлицем имеют целый ряд преимуществ по сравнению с обычным крепежом. Во-первых, вокруг головки с таким шлицем не нужно оставлять место под крепежный инструмент. При этом можно полностью «утопить» винт в детали, что весьма удобно для всякого рода сливных пробок.
Во-вторых, передаваемый детали крутящий момент может быть почти в десять раз больше , чем у крепежа с крестообразным шлицем. Поэтому шлиц Inbus часто применяется в узлах, работающих под большой нагрузкой (металлообрабатывающие станки, дорожная техника). Это также позволяет использовать небольшие головки для винтов с большим диаметром стержня, что обеспечивает применение инструмента одного размера для обслуживания различных узлов. Это хорошо знают велосипедисты — для обслуживания велосипеда в пути достаточно одного шестигранного ключа.
В-третьих, при использовании подходящего качественного ключа сорвать насечки внутреннего шестигранника довольно сложно. Насечки почти не изнашиваются, крепеж можно использовать многократно, что важно для крепления различного рода смотровых лючков, требующих частого открывания-закрывания.
В-четвертых, ключ для внутреннего шестигранника простой и дешевый, по сравнению с рожковыми, накидными и торцевыми ключами наружных шестигранников.
И наконец, винты с внутренней шестигранной головкой значительно безопаснее , так как не имеют острых наружных граней, да и выглядят более эстетично.
Как открутить шестигранник без ключа?
Конечно, сейчас шестигранный ключ не является чем-то недоступным. В любом магазине или авторынке можно подобрать шестигранник любого размера. Но стоит ли покупать пусть и относительно дешевый ключ ради того, чтобы один-единственный раз открутить хитрый винт?
С такой проблемой часто сталкиваются автолюбители, решившие ремонтировать свой автомобиль самостоятельно .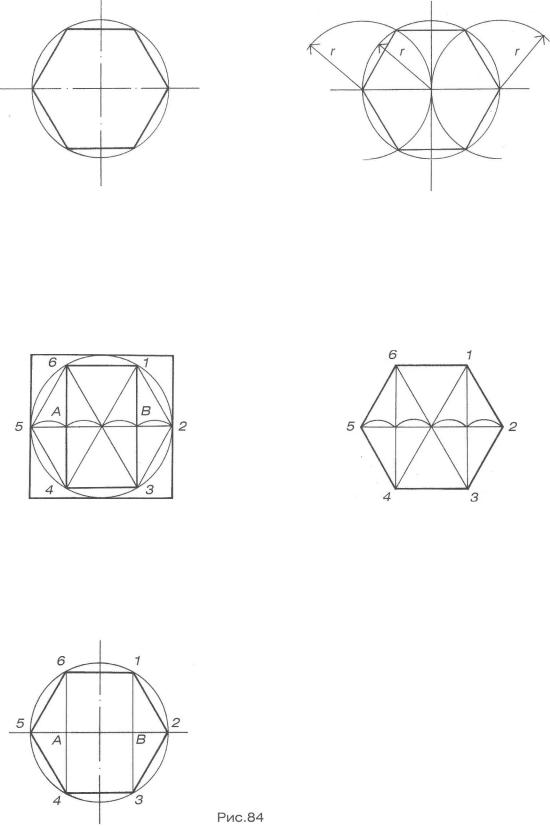 Внутренний шестигранник почти всегда имеет сливная пробка на коробке передач и часто — пробка в поддоне картера двигателя.
Внутренний шестигранник почти всегда имеет сливная пробка на коробке передач и часто — пробка в поддоне картера двигателя.
Домашний мастер может столкнуться с шестигранниками при ремонте смесителя для ванны или шарового крана — обычный крепеж там просто не умещается.
Причем во всех этих случаях размер шестигранника довольно приличный. Что делать? Поможет болт с обычной шестигранной головкой .
Головка болта вставляется в шестигранный шлиц и откручивается за стержень газовым ключом. Также можно навернуть на резьбу болта 3-4 гайки , хорошенько заклинить их друг за друга и откручивать обычным накидным ключом.
При отворачивании крутить надо за ближнюю к головке гайку, а при закручивании — наоборот, за дальнюю . Если шестигранник имеет нестандартный размер, то головку болта-ключа можно подточить напильником или на заточном станке.
Что делать, если шестигранник сорван?
Бывает, что попытки отвернуть винт с внутренним шестигранником подручными средствами или ключом немного неподходящего размера приводят к срыву граней. В этом случае тоже есть выход.
В этом случае тоже есть выход.
Если шестигранник небольшой, то в него можно забить звездочку TORX подходящего размера и выкрутить за нее. Если головка доступна, то стоит попробовать выкрутить винт пассатижами, газовым ключом или ручными тисочками.
При наличии места практически всегда помогает молоток и зубило . Зубило должно быть не очень острое, а наносить удары нужно по касательной в сторону откручивания. Кстати, проверьте , может быть, резьба на винте левая?
Для стальных болтов и винтов с внутренним шестигранником можно приварить к головке гайку, кусок арматуры или что-то похожее, за что болт можно вывернуть.
И помните, что один человек привернул — другой всегда открутить сможет.
А вот еще один способ выкручивания проблемных винтов с помощью гравера с отрезным кругом . Сделать такое можно и в большом масштабе, применив ножовку или болгарку.
Шестиугольником называют частный случай полигона — фигуры, образованной множеством точек плоскости, ограниченным замкнутой полилинией.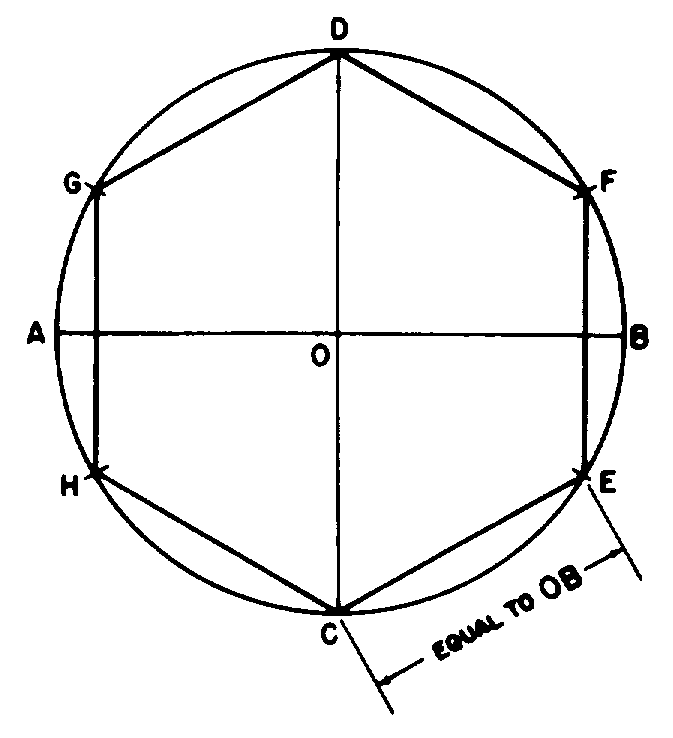 Правильный шестиугольник (гексагон), в свою очередь, также является частным случаем — это полигон с шестью равными сторонами и равными углами. Эта фигура примечательна тем, что длина каждой из ее сторон равна радиусу описанной вокруг фигуры окружности.
Правильный шестиугольник (гексагон), в свою очередь, также является частным случаем — это полигон с шестью равными сторонами и равными углами. Эта фигура примечательна тем, что длина каждой из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — лист бумаги.
Инструкция
Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на другой ножке, равным длине стороны вычерчиваемой фигуры. Для этого можно воспользоваться линейкой либо выбрать случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая возможность.
Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.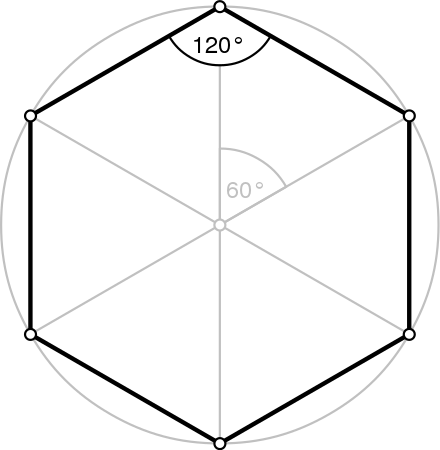
Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна точно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, чтобы она пересекла в двух точках окружность, начерченную первой.
Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с первоначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в двух точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
Подобным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении вдоль окружности (всегда по или против часовой стрелки). В результате должны быть выявлены шесть точек пересечения дуг с первоначально построенной окружностью.
Нарисуйте правильный шестиугольник. Последовательно попарно соедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки.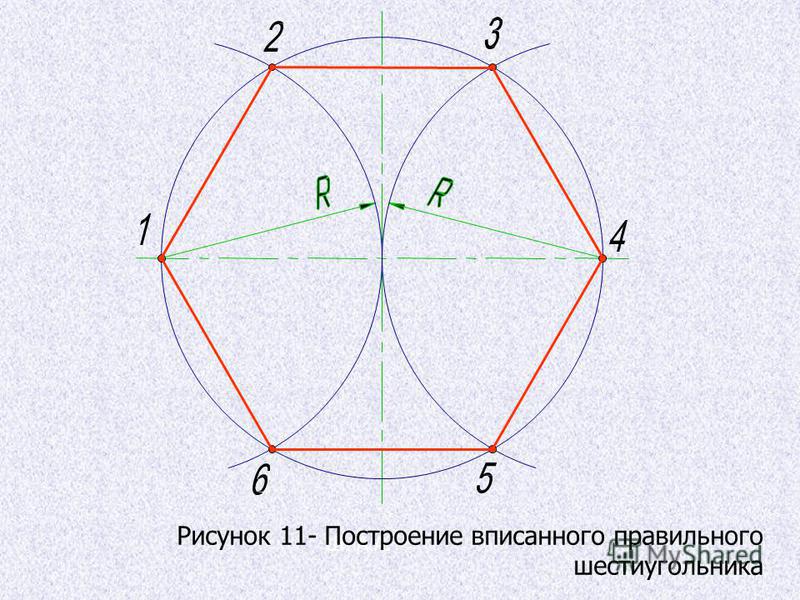 В результате будет получен правильный шестиугольник. После осуществления построения можно стереть вспомогательные элементы (дуги и окружность).
В результате будет получен правильный шестиугольник. После осуществления построения можно стереть вспомогательные элементы (дуги и окружность).
Обратите внимание
Имеет смысл выбирать такое расстояние между ножками циркуля, чтобы угол между ними был равен 15-30 градусов, иначе при осуществлении построений данное расстояние может легко сбиться.
Внимание, только СЕГОДНЯ!
Все интересное
Шестиугольник – это фигура, имеющая шесть углов. Случайный шестиугольник построить достаточно просто, но если по условиям задачи требуется построить равностороннюю фигуру, нужно будет произвести дополнительные построения с помощью циркуля. Вам…
При проведении построений различных геометрических фигур иногда требуется определить их характеристики: длину, ширину, высоту и так далее. Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой…
Десятиугольник, как и все многоугольники, можно легко построить с помощью циркуля и линейки.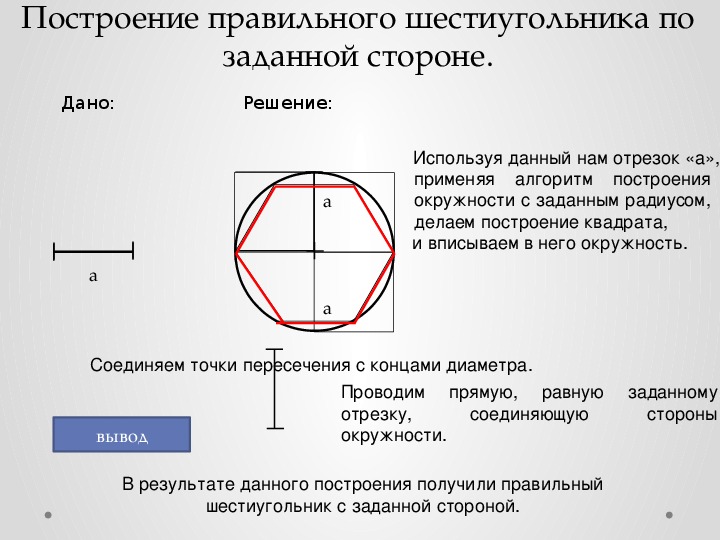 Существует два несложных способа для решения данной интересной и необычной задачи.
Существует два несложных способа для решения данной интересной и необычной задачи.
Вам понадобится- циркуль;- линейка.Инструкция 1Многоугольником…
Разделение окружностей на равные части очень удобно для построения различных равносторонних многоугольников. Построение можно выполнить без транспортира, используя только циркуль и линейку. Вам понадобитсяКарандаш, линейка, циркуль, лист…
Задача вписать в окружность многоугольник нередко может поставить взрослого человека в тупик. Ребенку-школьнику необходимо объяснить ее решение, поэтому родители отправляются в серфинг по всемирной паутине в поисках решения. Инструкция …
Задачи на осуществление построений правильных геометрических фигур тренируют пространственное восприятие и логику. Существует большое количество весьма простых задач подобного рода. Их решение сводится к модифицированию или комбинированию уже…
Являющиеся одной из неотъемлемых частей школьной программы, геометрические задачи на построение правильных многоугольников достаточно тривиальны.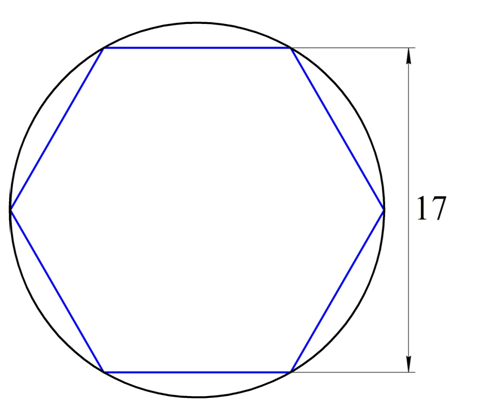 Как правило, построение ведется путем вписывания многоугольника в окружность, которая вычерчивается…
Как правило, построение ведется путем вписывания многоугольника в окружность, которая вычерчивается…
Задачи на геометрические построения весьма хорошо развивают пространственное и логическое мышление и потому являются одной из основных частей школьной программы обучения. Как и в любой предметной области, существуют типовые и нетиповые задачи. К…
Один из первых способов построения правильного шестиугольника описал древнегреческий ученый Евклид в своем известном труде «Начала». Предложенный Евклидом способ не единственно возможный. Вам понадобитсяциркуль, линейка,…
Правильный пятиугольник – это геометрическая фигура. Она имеет пять углов и равные стороны. Изображение пятиугольника широко применяют повсюду – начиная от канцтоваров и заканчивая огромными строениями, например «Пентагон» — министерство…
Как построить равносторонний пятиугольник с помощью циркуля. Правильный пятиугольник: необходимый минимум информации
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности.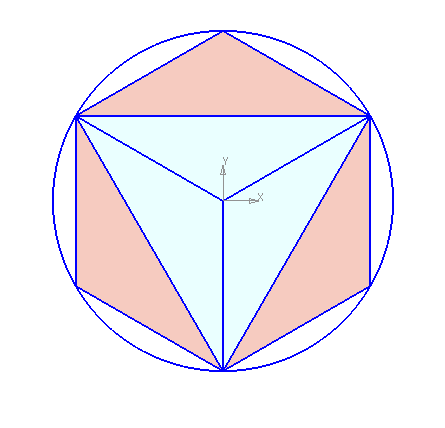 Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.

- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
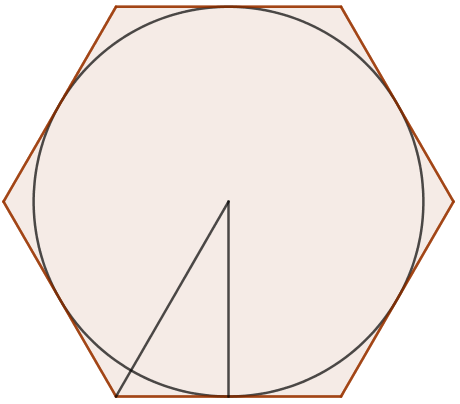
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона.
 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок. - Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи.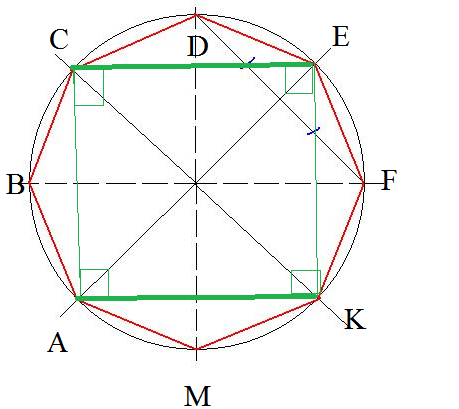 как видим на картинке ниже получается абсолютно правильный пятиугольник.
как видим на картинке ниже получается абсолютно правильный пятиугольник.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
ниже)
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.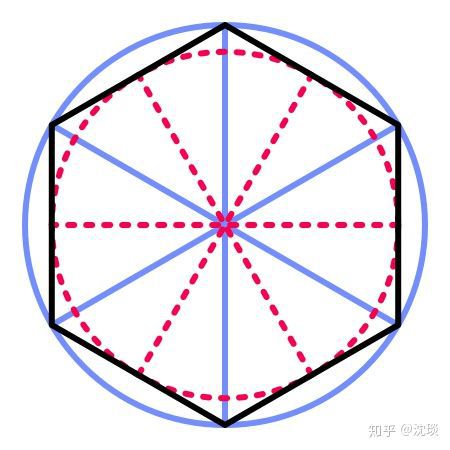
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды.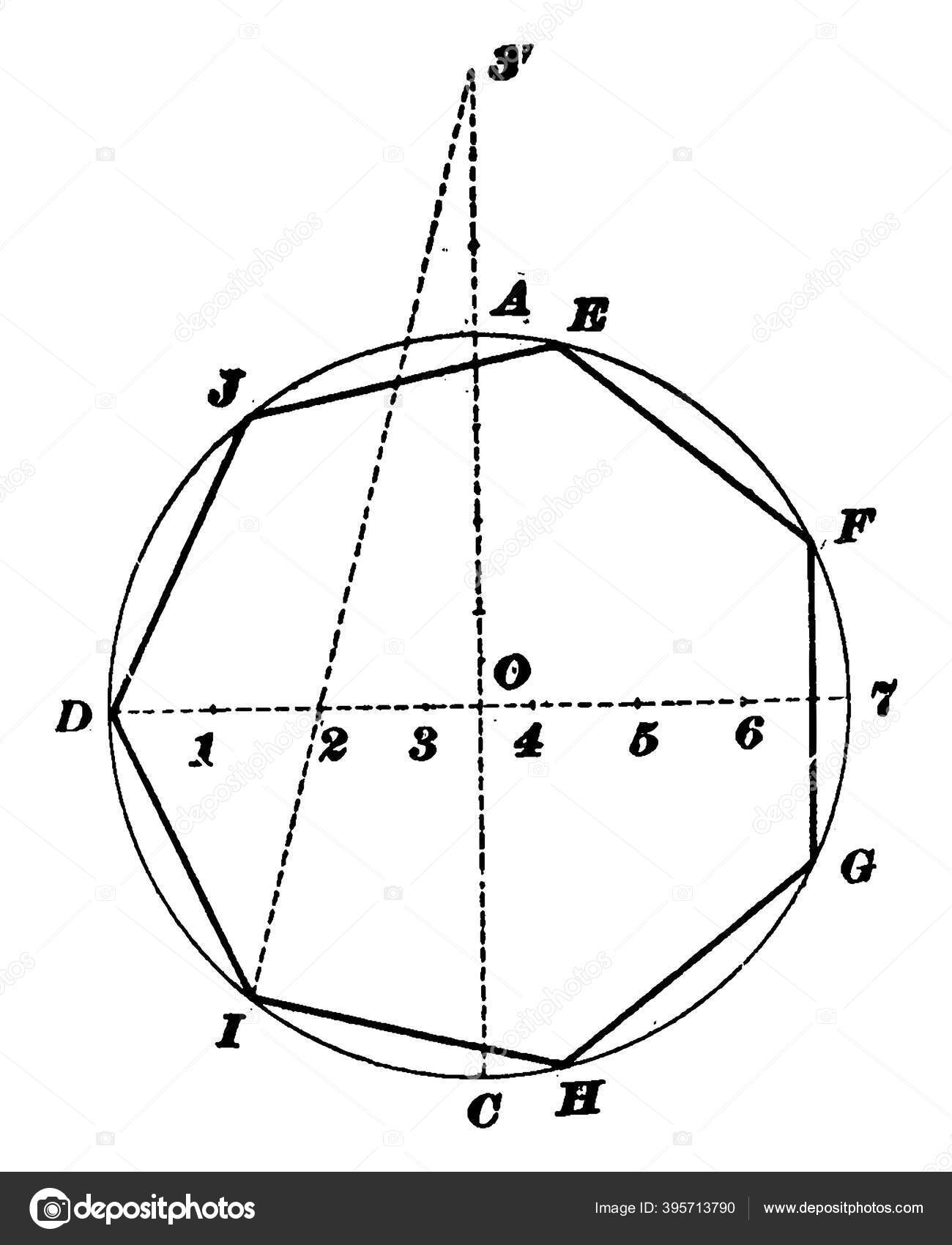 Вот так и получится пятиугольник. Вот что мы получим
Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
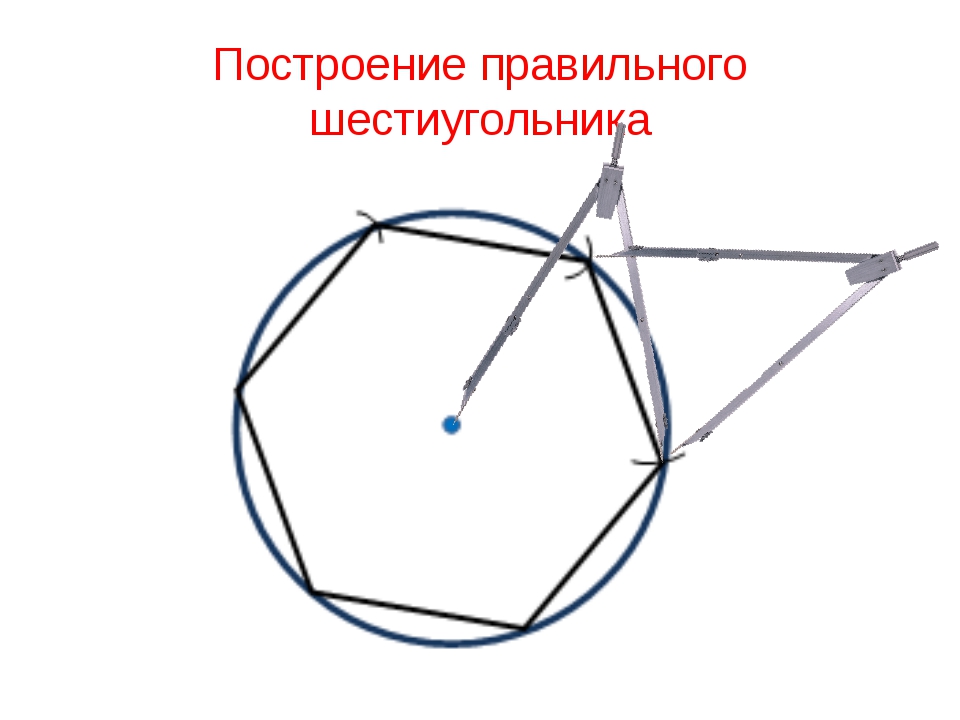
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.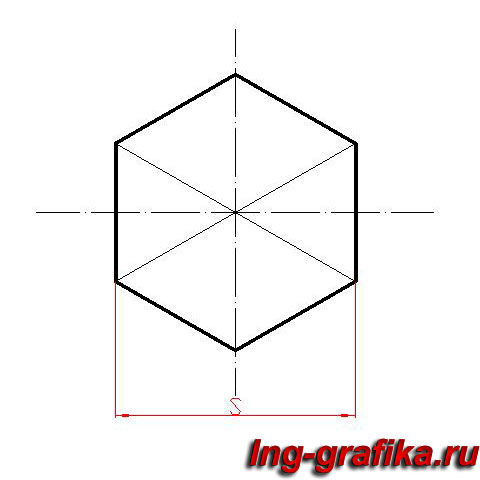
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля.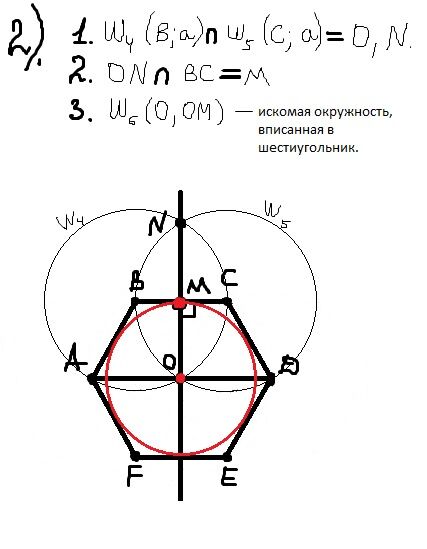 Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.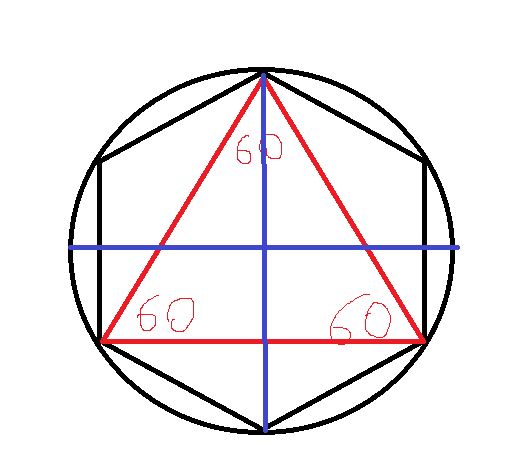
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Как нарисовать шестиугольник в AutoCAD? — Вокруг-Дом
Самый простой способ нарисовать шестиугольник в AutoCAD — это использовать инструмент многоугольника, введя шесть в качестве числа сторон. Если вы знаете радиус, который хотите использовать, то вы можете выбрать размер многоугольника от центра. Затем вы можете выбрать, хотите ли вы, чтобы шестиугольник был вписан в радиус или ограничен радиусом. В качестве альтернативы, если вы знаете длину ребра, которую хотите использовать, вы можете выбрать опцию «Край», выбрать базовую точку и затем ввести длину ребра по вашему выбору.
Если вы знаете радиус, который хотите использовать, то вы можете выбрать размер многоугольника от центра. Затем вы можете выбрать, хотите ли вы, чтобы шестиугольник был вписан в радиус или ограничен радиусом. В качестве альтернативы, если вы знаете длину ребра, которую хотите использовать, вы можете выбрать опцию «Край», выбрать базовую точку и затем ввести длину ребра по вашему выбору.
Шестиугольник, используя радиус
Начало действия Полигон. Кредит: Тим ЭшвудТип POL или же ПОЛИГОН в командной строке или щелкните значок многоугольника.
Ввод числа сторон, для шестиугольника, 6.credit: Tim AshwoodВойти 6 когда предложено для количества сторон.
Выбор, как измерить радиус. Кредит: Тим ЭшвудНажмите в области рисования, чтобы определить свой Центральная точка.
Понимание вписанного против Circumscribeed.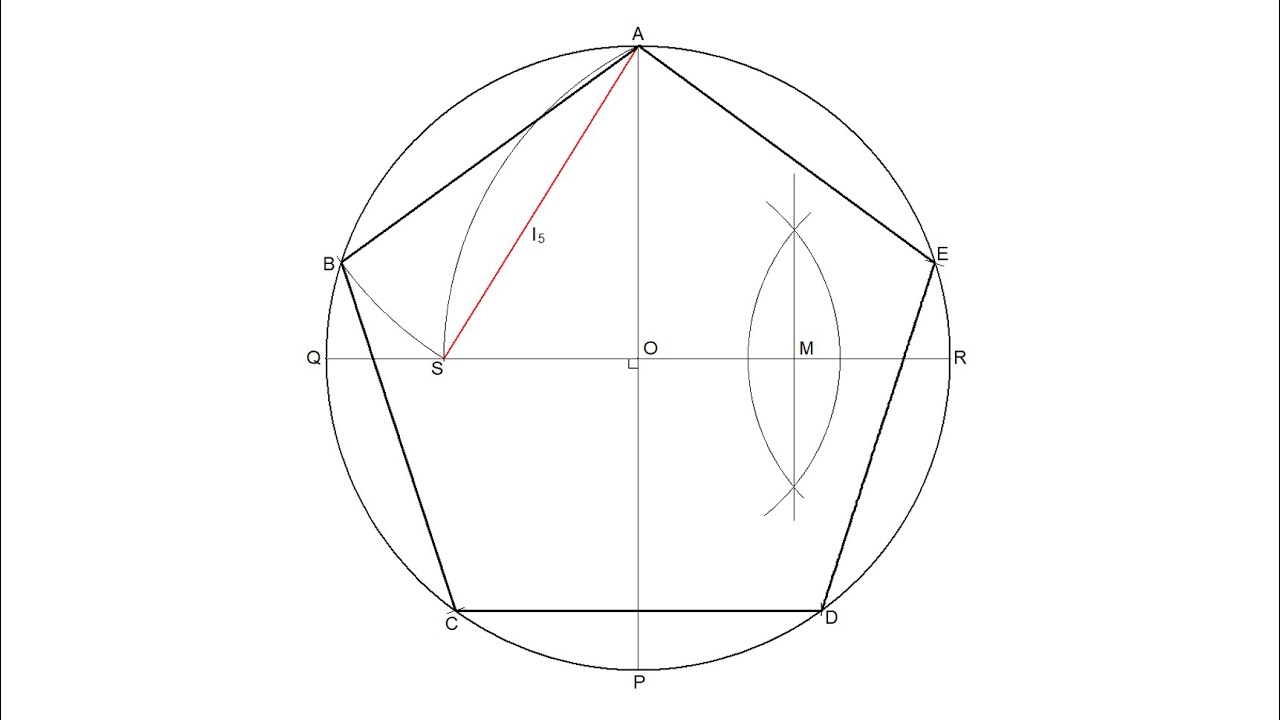 credit: Тим Эшвуд
credit: Тим ЭшвудВыберите, хотите ли вы использовать вписанный по кругу или ограниченный о круге.
Закрытие шестиугольника с помощью radius.credit: Тим ЭшвудНажмите в области рисования или введите радиус.
Шестиугольник используя длину края
Шаг 1
Тип POL или же ПОЛИГОН в командной строке или щелкните значок многоугольника.
Шаг 2
Войти 6 когда предложено для количества сторон.
Выбор варианта. Кредит: Тим Эшвуднажмите стрелка вниз на клавиатуре и нажмите Войти или введите край.
Выбор базовой точки. Кредит: Тим ЭшвудНажмите в области рисования, чтобы указать базовая точка для длины ребра.
Закрытие шестиугольника с помощью длины ребра.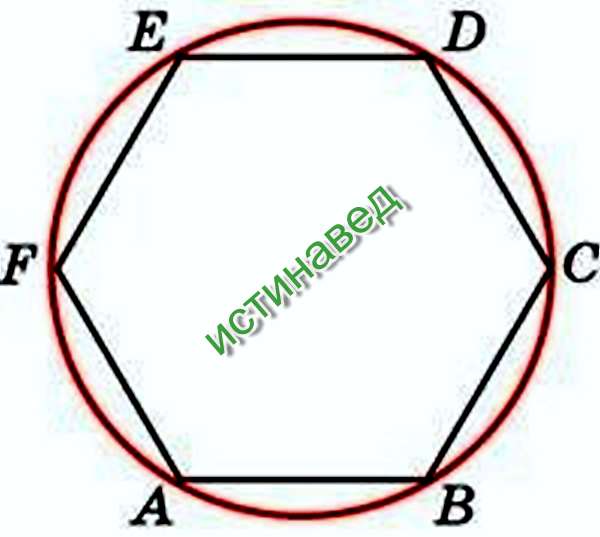 Кредит: Тим Эшвуд
Кредит: Тим ЭшвудВведите длина по вашему выбору или нажмите в области рисования снова на желаемой длине.
Как нарисовать шестиугольник с помощью линейки
Пятиугольник
Здравствуйте коллеги.Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая.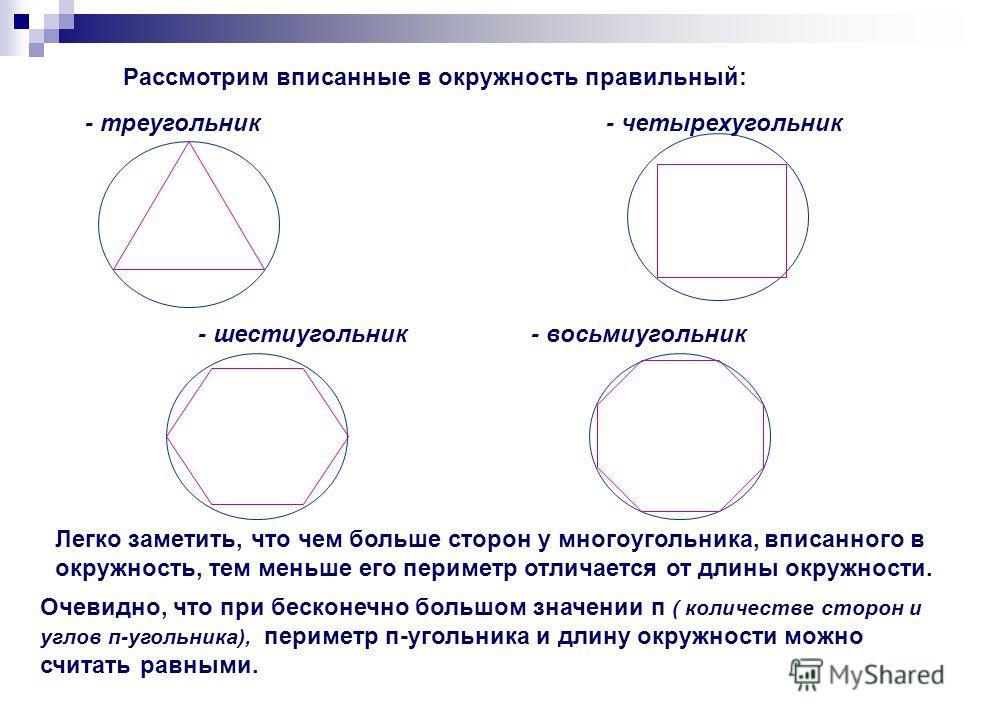 Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как построить и нарисовать правильный пятиугольник по окружности
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов.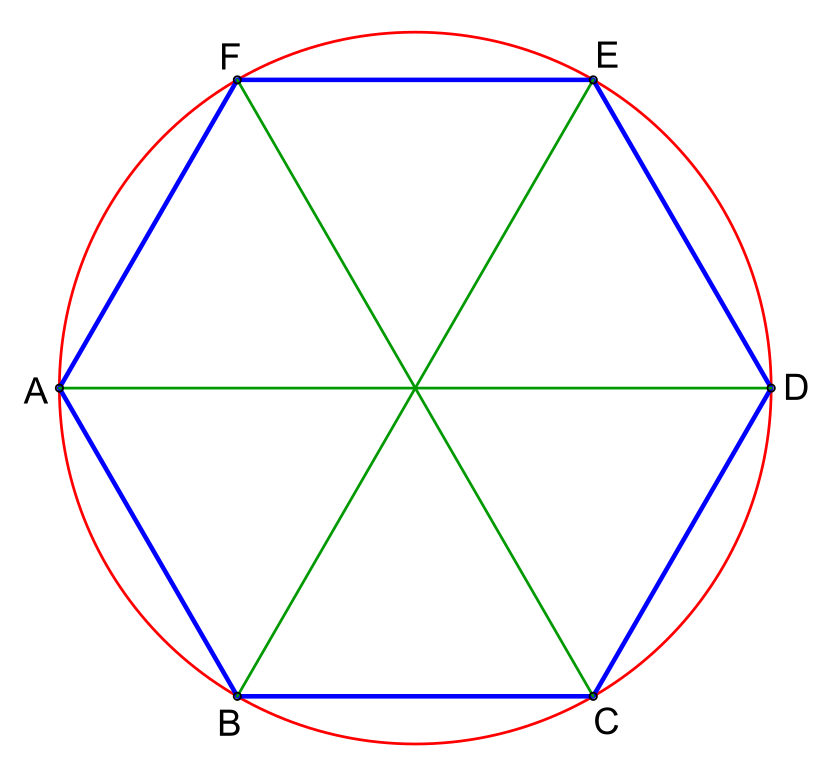 Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов.
 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.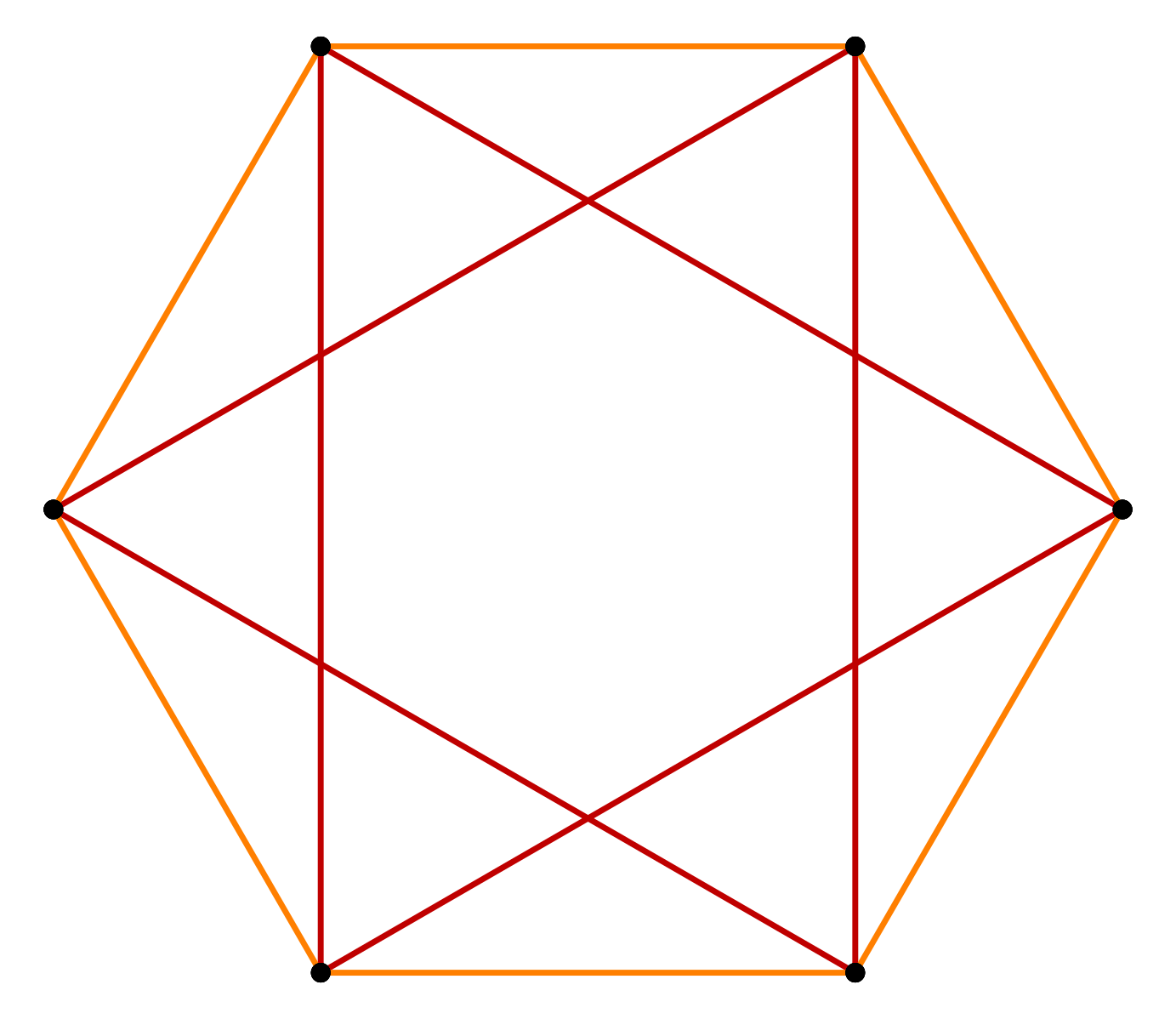
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F.
 На ее пересечении с начальной ставится точка Н.
На ее пересечении с начальной ставится точка Н. - На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е.
 Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.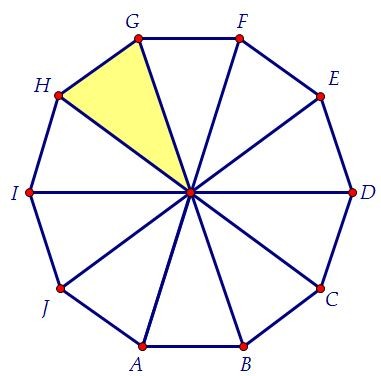
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Я РАСТУСайт для детей и их родителейПоследние события
Как из картинки сделать раскраску?
Раскраски любят и дети, и взрослые. И это неудивительно. Ведь даже не умея профессионально рисовать, можно создавать красивые рисунки, вкладывая в них своё умение и виденье .
Рисуем цыпленка
Вот такого цыпленка вы сможете нарисовать, если вы выполните все действия четко по шагам. Пробуйте и все у вас получится!
Елка-раскраска на стену
А так как скоро Новый Год, предлагаю скачать шаблон большой елки-раскраски. Этот шаблон состоит из 22 двух листов формата А4. На них нанесен и основной рисунок, и линии по которым нужно эти листочки склеить.
Дедушка Мороз и дети
Дед Мороз, Снегурочка, Снеговик, птицы и звери в лесу , дети на новогоднем празднике — вот герои этой книжки-раскраски. А создал их художник В. Жигарев.Маша и Медведь. Зимние раскраски
Мультик про шуструю озорную маленькую девочку Машу и ее приятеля медведя нравится всем — и детишкам, и их родителям.
Раскраски с дедом Морозом
Новый год наступил. Но впереди еще старый новый год, да и зима еще вся впереди. Раскрашиваем картинки с Дедом Морозом и Снегурочкой.Раскраски к новому году
Новогодние раскраски. Зима, елка, дед Мороз в санях, подарки. Скачайте забавные картинки, пусть они напоминают вам о веселом празднике.
Популярное
Архив
Как нарисовать правильную звездочку
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.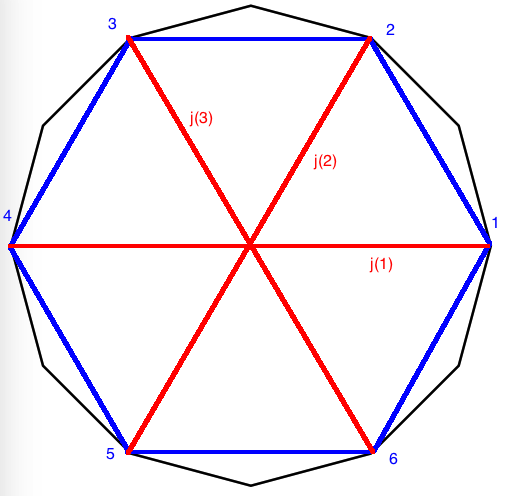
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Построение на плоскости
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.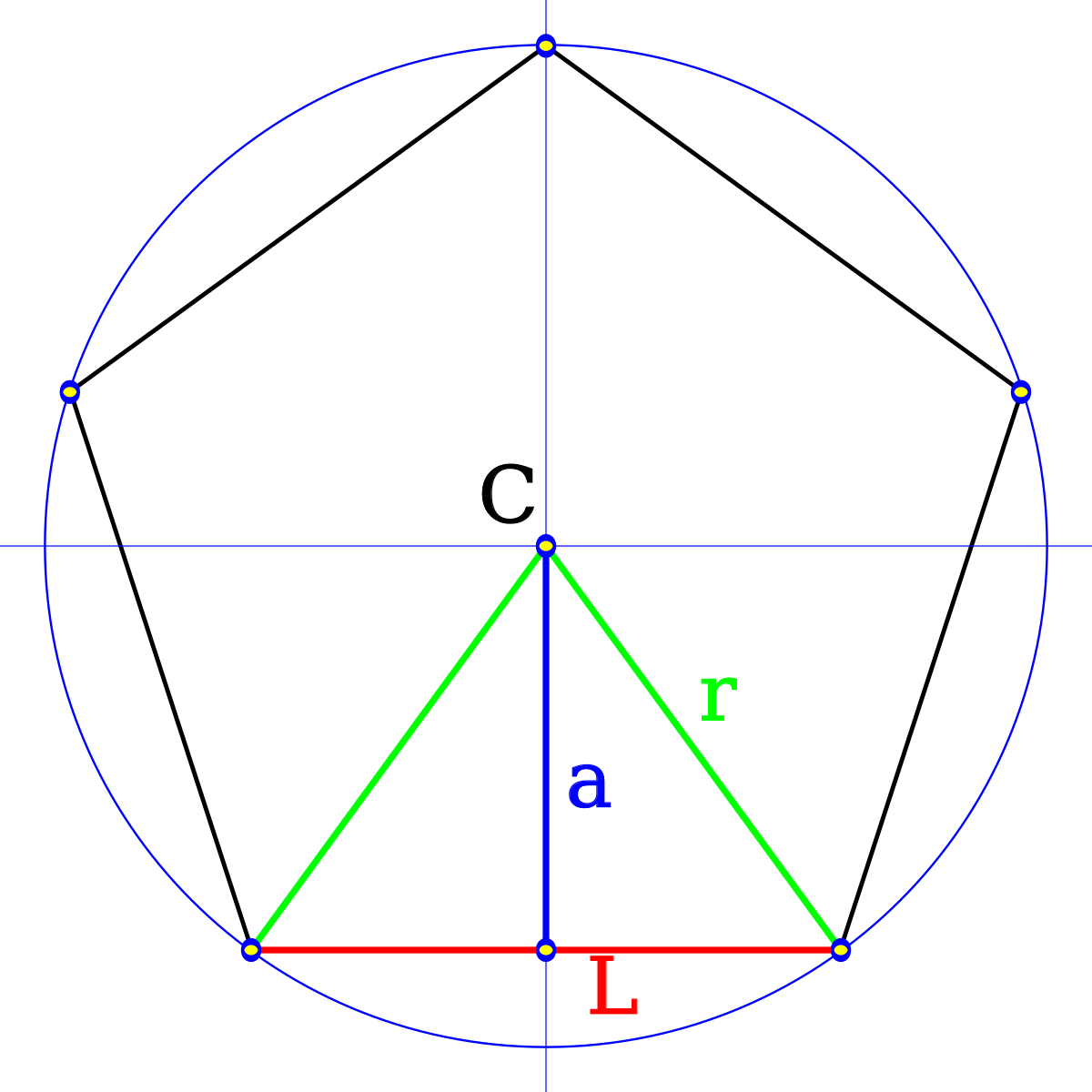
Построение угла в 45
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить.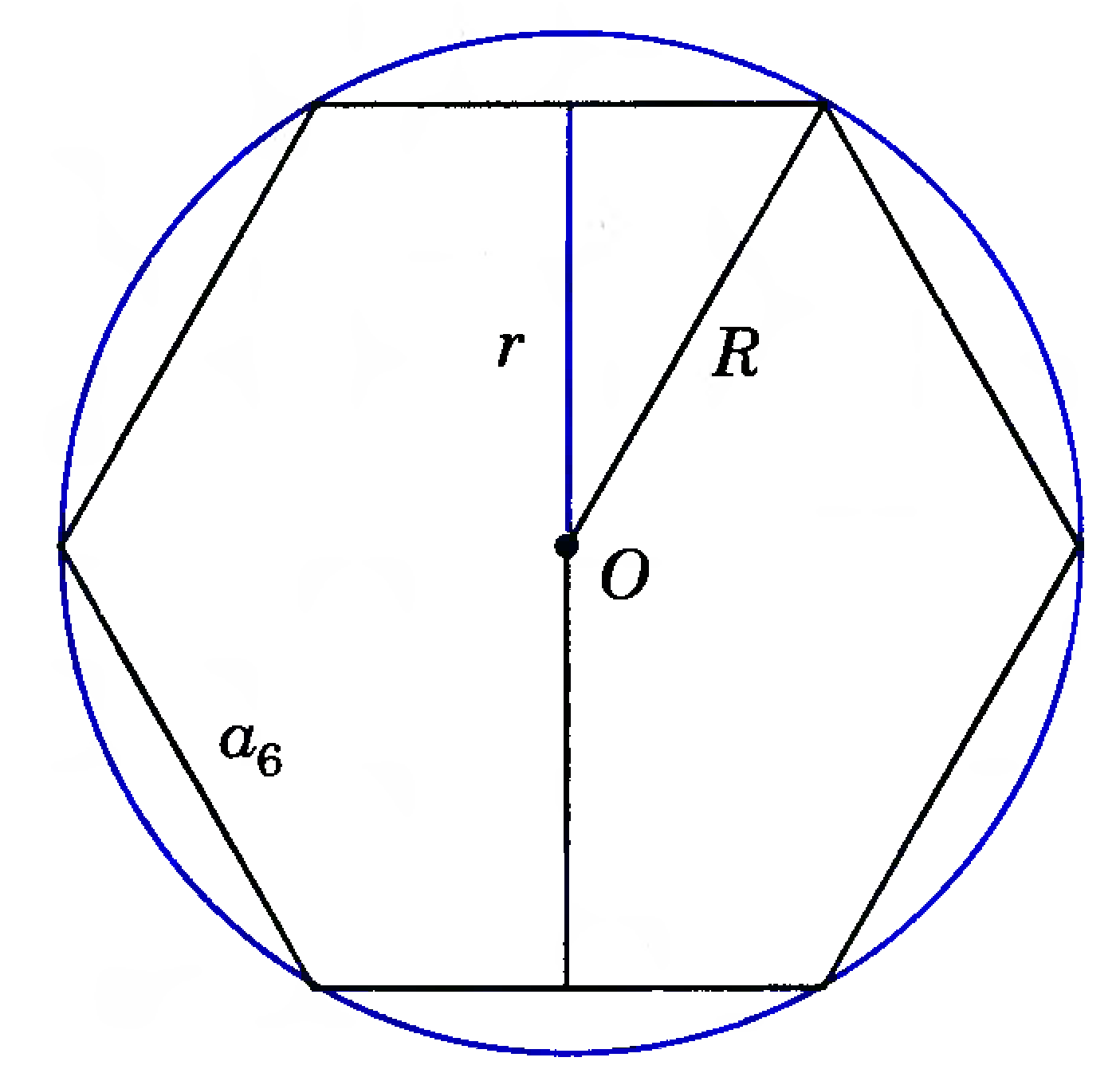 Для примера показано построение одиннадцатиугольника.
Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Линейно-конструктивный рисунок шестигранной призмы
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыГоризонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис.
Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис.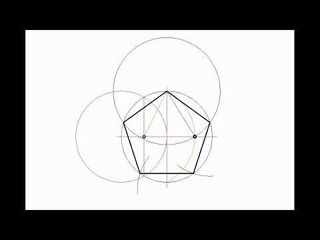 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис.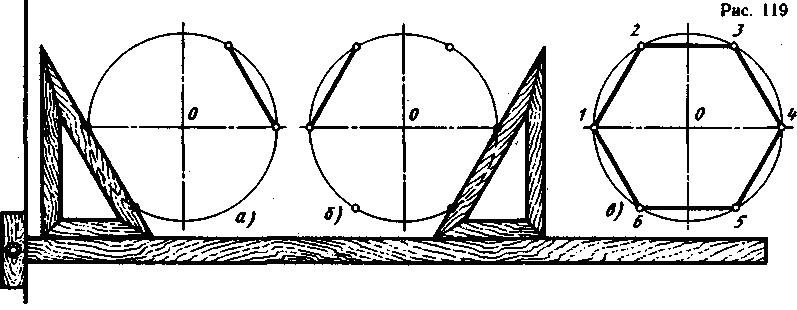 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.![]()
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКак нарисовать невозможный шестиугольник – Невозможные фигуры
Понравились мои уроки рисования? Получите больше на YouTube:
Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Что такое невозможный объект? Также называемые невозможными фигурами или неразрешимыми фигурами, эти рисунки являются разновидностью оптического обмана.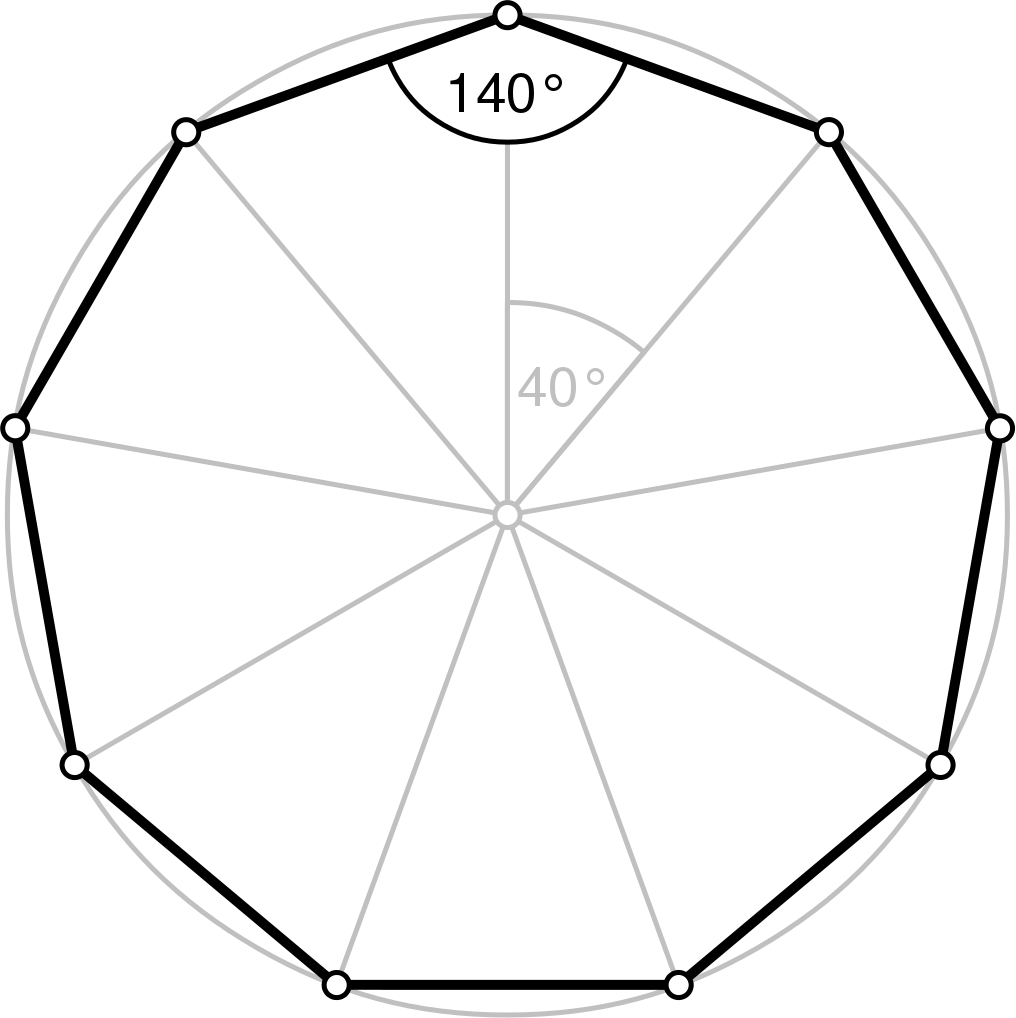 Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Полигоны Пенроуза, такие как этот шестиугольник, строятся путем добавления дополнительных сторон к треугольнику Пенроуза.
Тем не менее, оптическая иллюзия становится менее яркой, поскольку добавляется больше сторон. Таким образом, шестиугольник может казаться искривленным, заплетенным или искривленным, а не «невозможным».
Шестиугольники являются общими структурами как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрывать большое пространство как можно меньшим количеством воска.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого, пошагового руководства по рисованию фигур.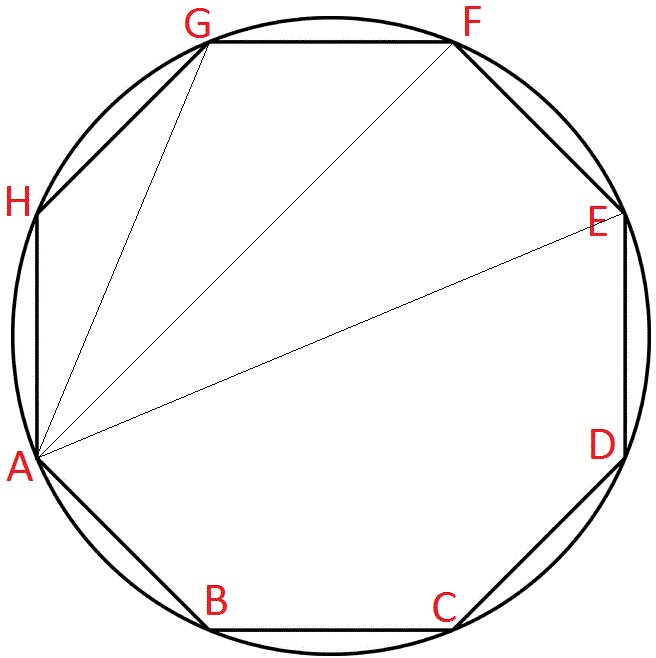 Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.
Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.
Пошаговая инструкция по рисованию – Невозможный шестиугольник
1. Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, в которой все стороны имеют одинаковую длину.
2. Нарисуйте короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую линию, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Нарисуйте короткую прямую линию, идущую от следующего угла шестиугольника. Протяните от него прямую линию, параллельную стороне шестиугольника.
4. Протяните короткую прямую линию от нижнего угла шестиугольника. Из этой линии нарисуйте прямую линию, параллельную нижней части шестиугольника. Затем продлите еще одну линию вверх, параллельно следующей стороне шестиугольника.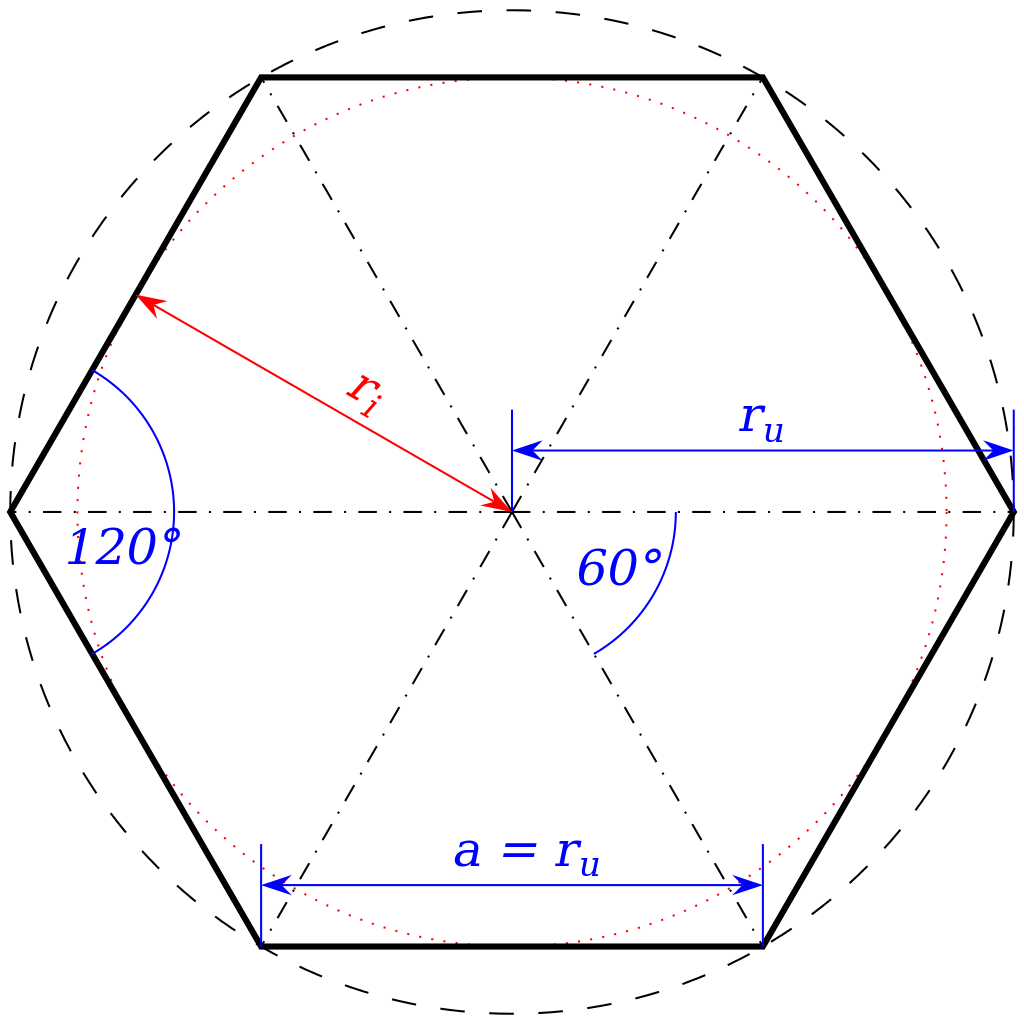
5. Проведите короткую линию от оставшегося нижнего угла шестиугольника. Отсюда нарисуйте прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию параллельно следующей стороне шестиугольника.
6. Нарисуйте короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника. Отсюда вытяните прямую линию, параллельную вершине шестиугольника.
8. Начните соединять внешние края невозможного шестиугольника. Расширьте короткие линии от верхнего угла и стороны формы. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть рисунка.
9. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все открытые линии, пока фигура не будет полностью заключена.
Цвет и тень вашего невозможного шестиугольника. Обратите внимание, как затенение в нашем примере делает трехмерную иллюзию более яркой.

геометрические построения | Справочник по математике
На отрезке ВК, равном 2а, как и на диаметре, строим (рис.1) полукруг. Этот полукруг делим на n равных частей точками C, D, E, F, G (вершинами правильного вписанного 2n-угольника; на нашем рисунке n=6). Центр А соединяем лучами со всеми полученными точками, кроме двух последних (K и G). Из точки В радиусом АВ проводим дугу ab, засекая на луче AD точку М и т.д. Точки B, L, M, N и т.д. последовательно соединяем прямыми. Многоугольник ABLMNF – искомый.
рис.1
Решить эту задачу с помощью циркуля и линейки можно не всегда; например, при n=7, n=9 этого сделать нельзя, так как полукруг с помощью циркуля и линейки на 7 или 9 точно не делится.
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник.Отметим на окружности (рис.1) вершины A, B, …, F правильного вписанного многоугольника с тем же числом сторон (см. §33 и §36). Проведем радиусы ОА, ОВ, …, OF и продолжим их. Дугу АВ разделим пополам точкой Е (см. §15). Через Е проведем JP⊥OE. Отрезок JP, заключенный между продолжениями соседних радиусов, есть сторона искомой фигуры. На продолжении остальных радиусов откладываем отрезки ОК, OL, …, ON, равные OP. Точки J, K, L, …, N, P последовательно соединяем. Многоугольник JKLM…NP – искомый.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, окружность.
Построим точку F (рис.1), как и в §33 OF есть сторона искомой фигуры. Раствором циркуля, равным OF, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, десятиугольник, круг, многоугольник, окружность.Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Разделив пополам дуги AD, DB, BC, CA точками E, F, G, H (см. §15), последовательно соединяем полученные восемь точек.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками восьмиугольник, геометрические построения, круг, многоугольник, окружность.Раствором циркуля, равным радиусу круга, делаем на окружности засечки в точках A, B, C, D, E, F (рис. 1). Соединяя точки A, B, C, D, E, F подряд, получим правильный шестиугольник. Соединяя их через одну, получим правильный (равносторонний) треугольник.
1). Соединяя точки A, B, C, D, E, F подряд, получим правильный шестиугольник. Соединяя их через одну, получим правильный (равносторонний) треугольник.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, треугольник, шестиугольник.Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Делим пополам радиус АО точкой Е. Из Е радиусом ЕС проводим дугу CF, пересекая ее диаметр АВ в точке F. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(=CF) есть одна сторона искомой фигуры. Проводим тем же радиусом дугу mn из точки П как из центра, получаем еще одну вершину H искомой фигуры и т.д.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, круг, многоугольник, окружность, пятиугольник.
Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Из их концов, как из центров, описываем четыре полуокружности радиусами, равными ОА. Точки F, G, H и E их пересечения – вершины искомого квадрата.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, круг, многоугольник, окружность.Проводим два взаимно перпендикулярных диаметра АВ и СD; ACBD – искомый квадрат (рис.1)
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, круг, многоугольник, окружность.Через середину АВ (рис.1) проводим к АВ перпендикуляр MN (см. п. §2). От точки О его пересечения с АВ откладываем на MN отрезки ОС и OD, равные ОА; соединяем точки С и D с точками А и В; ABCD – искомый квадрат.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.Поступаем как в пп. §27 и §28
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.Как начертить двенадцатиугольник
Умение строить правильные многоугольники необходимо любому специалисту, по роду своей деятельности связанному с черчением или геометрией. Построить двенадцатиугольник с помощью обычных чертежных инструментов можно как минимум тремя способами. Компьютерные же программы позволяют это сделать за несколько минут.Вам понадобитсяПервый «классический» способ заключается позволяет обойтись без циркуля. Поставьте на листе точку и проведите через нее произвольную прямую. Точку можно как-нибудь обозначить. Например, это может быть точка О.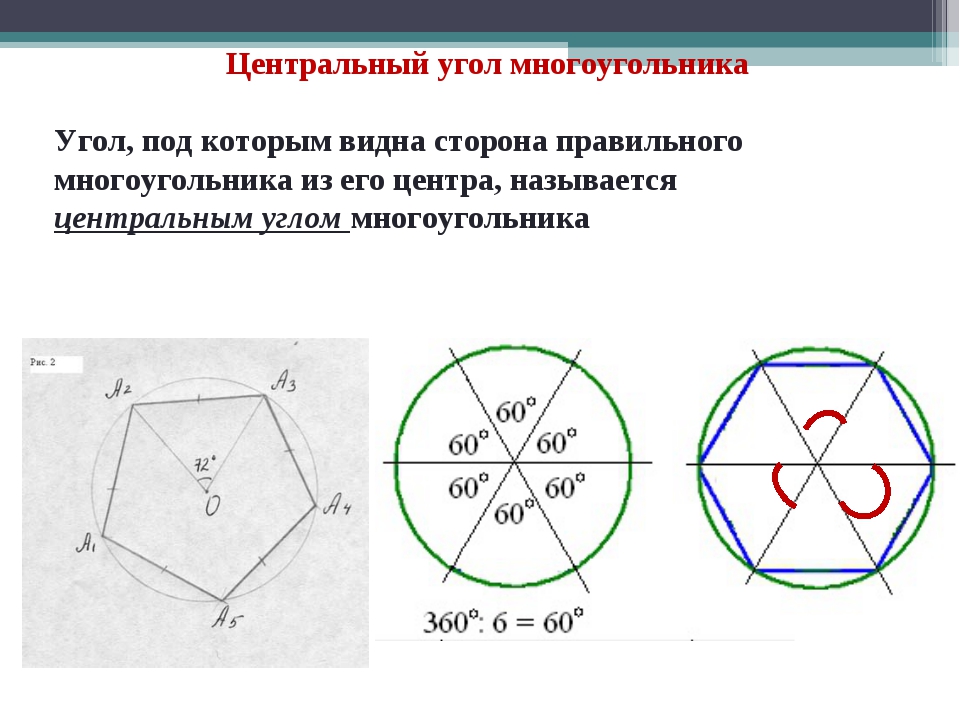 В одну из сторон отложите от нее отрезок любой длины. Обозначьте его как ОА.
В одну из сторон отложите от нее отрезок любой длины. Обозначьте его как ОА.
Разделите 360° на 12. Полученную величину в 30° отложите от отрезка ОА, совместив нулевое деление транспортира с точкой О. На полученном луче отложите размер, равный длине отрезка ОА. Таким же образом отложите угол в 30° и от этого нового отрезка. Продолжите построение, откладывая размер угла от каждой новой линии. Соедините конечные точки всех отрезков прямыми.
Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.
Разведите ножки циркуля на длину радиуса окружности. Иголку инструмента поставьте в точку А. На окружности сделайте отметку В. Переставьте циркуль в эту точку и сделайте на окружности еще одну отметку С. Повторяйте операцию до тех пор, пока не разделите окружность на 6 равных частей.
Отметки на окружности соедините отрезками.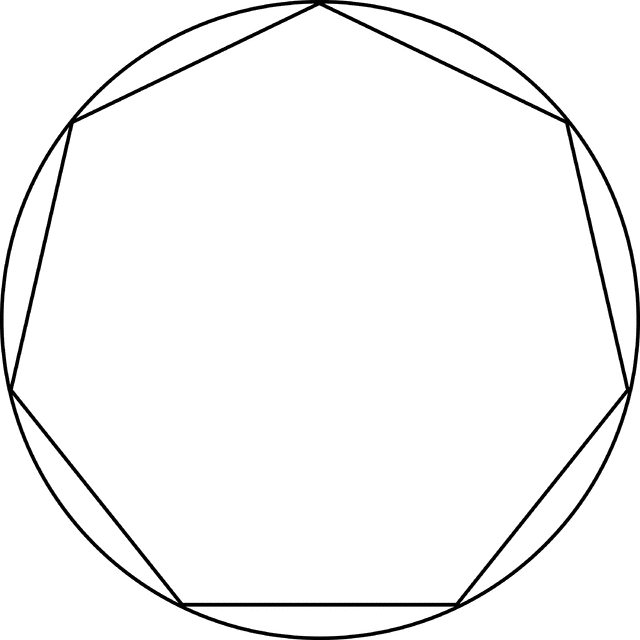 У вас получился правильный шестиугольник. Каждую его сторону разделите пополам и к полученной точке проведите перпендикуляр. Перпендикуляры необходимо продлить, чтобы они пересекли окружность. У вас получится еще 6 точек.
У вас получился правильный шестиугольник. Каждую его сторону разделите пополам и к полученной точке проведите перпендикуляр. Перпендикуляры необходимо продлить, чтобы они пересекли окружность. У вас получится еще 6 точек.
Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.
Соедините полученные точки с соседними вершинами правильного шестиугольника. У вас получился правильный двенадцатиугольнрик. Лишние линии при необходимости можно убрать.
Построить правильный двенадцатиугольник с помощью циркуля можно и иначе. Начните с построения окружности. Начертите 2 диаметра перпендикулярно друг другу. Если вы сделаете конечные точки каждого центрами новых окружностей того же радиуса, то исходная окружность разделится на 12 равных частей. Вам останется только соединить соседние вершины отрезками.
Правильный двенадцатиугольник в программе AutoCAD строится с помощью команды «Многоугольник», он же polygon. Ее можно ввести в командную строку (латиницей, причем перед командой ставится значок «_»..Перед вами появится окошко, в которое нужно просто ввести число сторон. Соответствующий инструмент можно найти также в панели инструментов на рабочем столе или через вкладку «Рисование» в главном меню.
Ее можно ввести в командную строку (латиницей, причем перед командой ставится значок «_»..Перед вами появится окошко, в которое нужно просто ввести число сторон. Соответствующий инструмент можно найти также в панели инструментов на рабочем столе или через вкладку «Рисование» в главном меню.
Программа предложит вам определить способ, по которому вы будете строить двенадцатиугольник. В AutoCAD любой многоугольник можно начертить по длине стороны, центру и радиусу вписанной или описанной окружности. Выберите нужное.
Если вы будете строить двенадцатиугольник по одному из радиусов, укажите центр фигуры. Это можно сделать, задав координаты или отметив нужную точку щелчком мыши. Укажите, радиус какой окружности вам задан, и введите нужное значение.
Обычный, Идеальный, От Квадрата
Как нарисовать шестиугольник? Как разделить круг на пять равных частей? Вы можете найти ответ на все эти вопросы, если выполните эти шаги вслед за мной. Шестиугольник — это любой многоугольник с шестью сторонами. Однако правильный шестиугольник состоит из шести равных частей и шести равных углов.
Однако правильный шестиугольник состоит из шести равных частей и шести равных углов.
Посмотрите на изображения шестиугольников, чтобы получить четкое представление о том, что вы рисуете. О том, как нарисовать шестиугольник и идеально правильную форму, и пойдет речь в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте подумайте, просто начертите доступное изображение шестиугольника.
С помощью линейки и транспортира начертите идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы указать рукой. Если точность не имеет первостепенного значения, не стесняйтесь подготовить легкий шестиугольник, используя всего лишь карандаш и свое чутье. Конечно, нам понадобится циркуль с ручкой и линейка, чтобы нарисовать красивый шестиугольник!
Чертеж идеального шестиугольника Для начала нарисуйте циркуль.
Разделите его на четыре части линиями сверху вниз и справа налево.
Сразу объясните ребенку, что отрезок, соединяющий две точки на окружности и проходящий через его центр, называется диаметром.
А отрезок, соединяющий центр и точку на окружности, называется радиусом.
Как нарисовать правильную звездочку
С помощью линейки отмерьте и разрежьте пополам один из радиоприемников.
У меня этот сегмент находится слева от центра.
Я отметил середину радиуса.
номер 1.
Нам нужна точка поверх круга.
Я отметил его цифрой 0.
Установить стрелку компаса
до точки 1 и карандашом указать 0.
Нарисуйте дугу до пересечения с горизонтальным диаметром.
Обозначим точку пересечения
номер 2.
Теперь устанавливаем стрелку компаса.
до точки 0 и карандашом указать 2.
И нарисуйте дугу до пересечения с кругом, причем с двух сторон.
Обозначены точки пересечения.
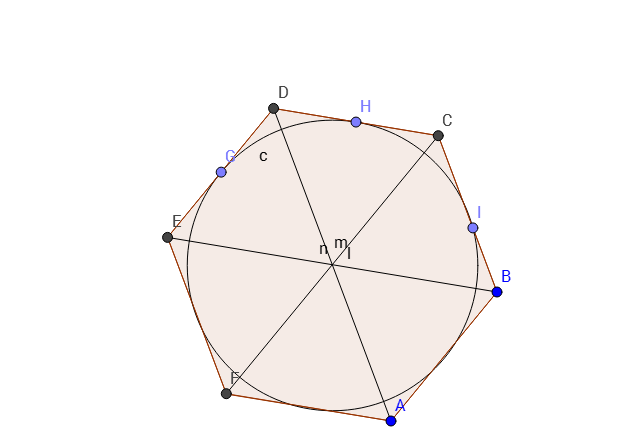
числа 3 и 4.
Не меняя ширины циркуля, установите стрелку.
в точке 3 и отмерьте кусок круга.
Ставим точку 5.
Точку 6 можно измерить от
точки 5 и из пункта 4.
Главное не менять ширину (раствор) ножек суппорта.
Здесь почти все.
Если соединить точки, получится правильный пятиугольник. Звездочку нарисовать можно, если хотите!
Вот так звездочка нарисована.
Построение равносторонних треугольников, квадратов и правильных шестиугольников, вписанных в круги — класс геометрии (видео)
Шестиугольник в круге
Нарисуйте круг. Размер вашего круга будет определять внешние края вашего шестиугольника, поэтому выберите размер, который вам нравится. Возьмите компас, воткните бумагу в нужное место в центре шестиугольника, установите радиус между ножками компаса и нарисуйте.
Когда у вас есть круг, мы можем начать забавные вещи:
- Выберите место на краю круга для одной точки вашего шестиугольника и сделайте там небольшую отметку карандашом.

- Вставьте металлический наконечник компаса в бумагу на этой отметке. Убедитесь, что ваш циркуль все еще настроен на длину радиуса, и сделайте еще одну отметку на краю круга.
- Обходите круг, делая отметки на одинаковом расстоянии друг от друга.
- Используя линейку, проведите прямую линию между каждой меткой и двумя метками по обе стороны от нее.
Вот оно! Шестиугольник вписан в , что означает, что он находится внутри круга, и все его внешние углы касаются края круга.Ладно, теперь перейдем к начертанию треугольника.
Равносторонний треугольник в круге
Теперь мы построим равносторонний треугольник, который представляет собой замкнутую трехстороннюю фигуру с прямыми сторонами. Все его стороны имеют одинаковую длину, а все его внутренние углы составляют 60 градусов.
Мы уже проделали большую работу.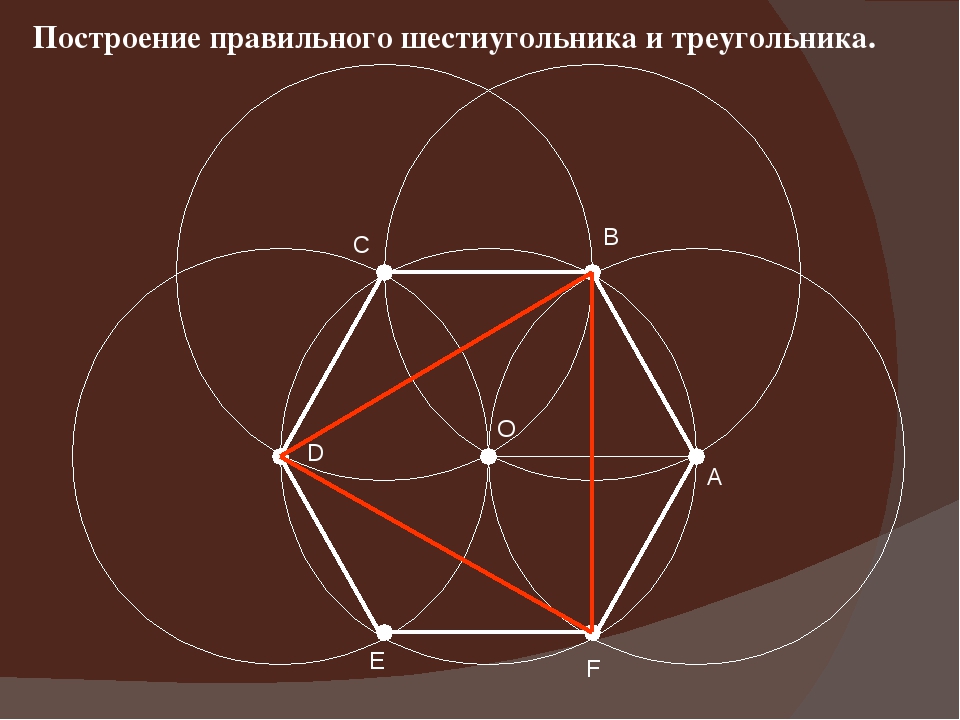 Если вы возьмете круг с шестью отметками, которые вы сделали для шестиугольника, вы можете использовать те же отметки, чтобы сделать свой треугольник. Выберите одну из меток в качестве угла, затем соедините эту метку с каждой второй меткой по кругу.Когда вы закончите, три метки будут соединены линиями, образующими треугольник, а три других не будут частью треугольника.
Если вы возьмете круг с шестью отметками, которые вы сделали для шестиугольника, вы можете использовать те же отметки, чтобы сделать свой треугольник. Выберите одну из меток в качестве угла, затем соедините эту метку с каждой второй меткой по кругу.Когда вы закончите, три метки будут соединены линиями, образующими треугольник, а три других не будут частью треугольника.
Квадрат внутри круга
Хорошо, теперь немного поменяем передачи и построим квадрат. Квадрат — это четырехгранная фигура с равными прямыми сторонами и внутренними углами 90 градусов. Чтобы построить его, нам придется использовать немного другую технику, чем мы использовали шестиугольник.Прежде всего, нарисуйте круг, чтобы вставить квадрат. Вы можете использовать последний, если хотите, но другие отметки могут немного сбивать с толку, и нам действительно не нужны они для построения квадрата. Когда у вас есть круг, нарисуйте диаметр (линия, которая проходит через центр и останавливается на внешнем крае с обеих сторон круга).
Когда у вас есть круг, нарисуйте диаметр (линия, которая проходит через центр и останавливается на внешнем крае с обеих сторон круга).
Диаметр отмечает два из четырех углов вашего квадрата.Теперь нам понадобятся два других угла. Чтобы получить их, мы построим перпендикулярную линию (пересекающуюся под углом 90 градусов), пересекающую ваш диаметр в центре круга.
- Вдавите металлический наконечник компаса в бумагу на одном из концов своего диаметра.
- Установите длину немного больше, чем расстояние от этой точки до центра.
- Нарисуйте дугу около центра диаметра, но сразу за пределами круга.
- Оставьте настройки компаса без изменений и переместите точку на другой конец диаметра.
- Нарисуйте дугу, пересекающую вашу предыдущую дугу. Если вы не можете дотянуться до конца, возможно, вам придется немного удлинить первую дугу.

- Соедините точки. Нарисуйте линию, соединяющую центр круга с местом пересечения двух ваших дуг. Это перпендикулярная линия. Убедитесь, что ваша линия достаточно длинная, чтобы обозначить весь диаметр (касается изогнутого края круга с обоих концов).
Почти готово! Теперь все, что вам нужно сделать, это соединить четыре метки, которые вы построили на краю круга.Обратите внимание, что то, где вы разместите, ваши диаметры будут определять положение вашего ящика.
Если вы разместили их в виде X, у вас будет квадрат, который кажется лежащим на поверхности. Тот, который мы здесь нарисуем, будет больше похож на ромб, но вы можете поставить квадрат в любом положении, просто поместив свой первый диаметр под другим углом.
Хорошо, нарисуем наш квадрат.
Резюме урока
Построение геометрических фигур означает их рисование с помощью только циркуля и линейки. Надписать их внутри круга означает построить их так, чтобы каждый внешний угол касался изогнутого края круга. Вы можете строить шестиугольники и треугольники, используя радиус (расстояние от центра до края круга) в качестве ориентира. Вы можете построить квадрат, используя перпендикулярные диаметры. Когда вы привыкнете делать их, вы сможете рисовать правильные правильные шестиугольники, равносторонние треугольники и квадраты в любом месте, где они вам понадобятся.
Надписать их внутри круга означает построить их так, чтобы каждый внешний угол касался изогнутого края круга. Вы можете строить шестиугольники и треугольники, используя радиус (расстояние от центра до края круга) в качестве ориентира. Вы можете построить квадрат, используя перпендикулярные диаметры. Когда вы привыкнете делать их, вы сможете рисовать правильные правильные шестиугольники, равносторонние треугольники и квадраты в любом месте, где они вам понадобятся.
Нарисуйте шестиугольник
Как нарисовать шестиугольник — youtube
Как нарисовать шестиугольник шаг за шагом для детей, Спасибо за просмотр нашего канала.Как нарисовать шестиугольник Шаг за шагом для детей, как нарисовать шестиугольник без циркуля, как нарисовать шестиугольник, как нарисовать он
как нарисовать шестиугольник., Шестиугольник | Нарисуйте шестиугольник | Инженерный рисунок. Почему люди считают, что они не умеют рисовать, и как доказать, что они умеют | Грэм Шоу | TEDxHull — Продолжительность: 15:04.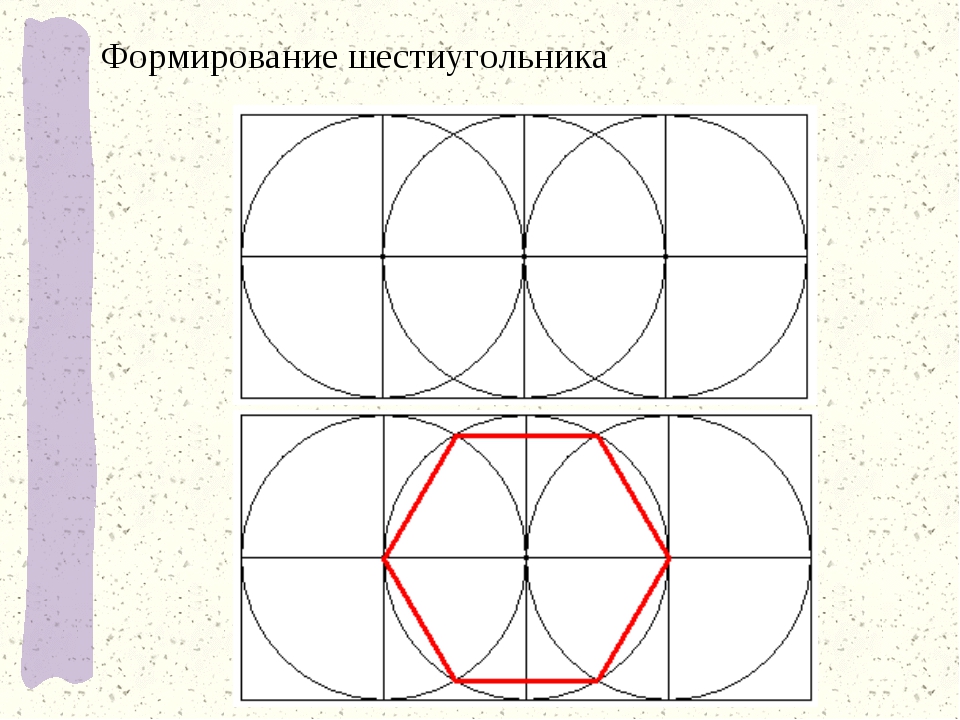 TEDx Talks Рекомендуется для вас
TEDx Talks Рекомендуется для вас
Как нарисовать идеальный шестиугольник, Здравствуйте, Gyz .. Это учебное пособие по геометрической работе с изображением с помощью MATLAB.. Итак, здесь мы узнаем о том, как нарисовать шестиугольник с помощью MATL
.Как нарисовать восьмиугольник
Как нарисовать восьмиугольник (с изображениями), прямая вертикальная линия (также разделяющая круг на равные части), центр которой будет пересекаться с центром горизонтальной линии. Несколько восьмиугольников 1. Нарисуйте квадрат в центре страницы. 2. Нарисуйте прямые линии, которые соединят один угол с его прямым противоположным углом. 3. Отметьте расстояние от центральной точки (где линии пересекаются) до одного из углов квадрата.4. Обратите внимание на точку, где находится круг и
, как нарисовать восьмиугольник с циркулем и линейкой, Шаг 3: Создайте восьмиугольник из 9 квадратов. Сделайте восьмиугольник из 9 квадратов. Нарисуйте линии так, чтобы восьмиугольник. Нарисуйте линию между двумя метками, ближайшими к каждому углу, и сотрите углы квадрата и букву «X», чтобы завершить равносторонний восьмиугольник. КАК ЭТО РАБОТАЕТ: Используя теорему Пифагора, которая составляет A² + B² = C², вычислите длину гипотенузы, или «C» на рисунке. Длина одной стороны квадрата составляет 5 дюймов, поэтому 1/2 этой длины составляет 2-1 / 2 дюйма.
Нарисуйте линию между двумя метками, ближайшими к каждому углу, и сотрите углы квадрата и букву «X», чтобы завершить равносторонний восьмиугольник. КАК ЭТО РАБОТАЕТ: Используя теорему Пифагора, которая составляет A² + B² = C², вычислите длину гипотенузы, или «C» на рисунке. Длина одной стороны квадрата составляет 5 дюймов, поэтому 1/2 этой длины составляет 2-1 / 2 дюйма.
Как нарисовать восьмиугольник в квадрате, Нарисуйте правильный восьмиугольник, используя шаблон жесткого квадрата, прямой край и карандаш или ручку. Задача, поставленная в заголовке этих инструкций, может заключаться в том, чтобы нарисовать квадрат, т.е. используется для рисования этого восьмиугольника.
Нарисуйте шестиугольник онлайн
Бесплатный онлайн-генератор шестиугольника, Используйте этот бесплатный онлайн-генератор шестиугольника для создания шаблонов шестиугольника. Рисуя шаблон прямо на листе сушилки, пришейте его прямо к ткани, используя «Нарисовать шестигранный график».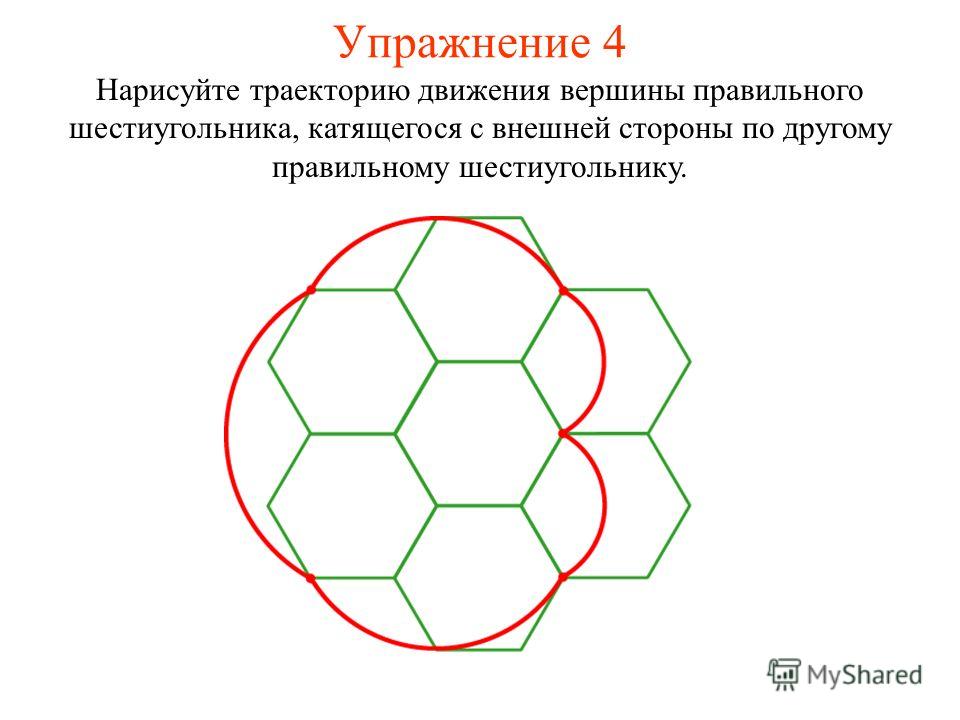 Онлайн-калькулятор для построения графиков, который позволяет вам изобразить / нарисовать фигуру шести (6) стороннего многоугольника / шестиугольника с заданным радиусом. Построение шестиугольного графика стало проще с помощью этого онлайн-калькулятора.
Онлайн-калькулятор для построения графиков, который позволяет вам изобразить / нарисовать фигуру шести (6) стороннего многоугольника / шестиугольника с заданным радиусом. Построение шестиугольного графика стало проще с помощью этого онлайн-калькулятора.
Калькулятор шестиугольника, Размер шестигранника: дюймы, см. Добавить точку: поставьте точку в середине каждого шестиугольника. Цвет: Hex # Вычисление различных бит о правильных шестиугольниках. Заданная длина. Для случайного (неправильного) шестиугольника ответ прост: нарисуйте любую 6-стороннюю фигуру так, чтобы она была замкнутым многоугольником, и все готово.Но с правильным шестиугольником все не так просто, так как мы должны убедиться, что все стороны имеют одинаковую длину. Для получения идеального результата вам понадобится циркуль для рисования. Нарисуйте круг и с тем же радиусом запустите
Бесплатная онлайн-миллиметровка / шестиугольник, Калькулятор шестиугольника. Расчеты на правильном шестиугольнике, многоугольнике с 6 вершинами.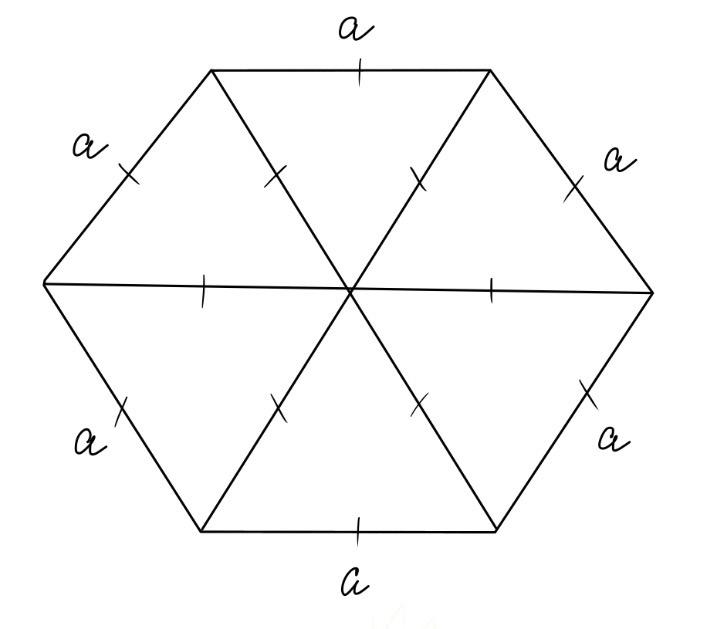 Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику. Как нарисовать шестиугольник и его идеально правильную форму, мы обсудим в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте подумайте, просто начертите доступное изображение шестиугольника.Примените линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Для более грубого шестиугольника попробуйте использовать круглую форму и линейку
Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику. Как нарисовать шестиугольник и его идеально правильную форму, мы обсудим в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте подумайте, просто начертите доступное изображение шестиугольника.Примените линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Для более грубого шестиугольника попробуйте использовать круглую форму и линейку
Как нарисовать шестиугольник на миллиметровой бумаге
Нарисовать шестиугольник намного проще, если вы рисуете его на миллиметровой бумаге внутри сетки размером четыре на четыре . Картинка стоит тысячи слов, а вот и одно: секрет здесь не в подсчете квадратов, а в пересчете миллиметровой бумаги. Как только вы это сделаете, шестиугольник будет красиво рисоваться из четных точек.
Если у вас нет циркуля, вы можете нарисовать шестиугольник другим способом, для чего потребуется миллиметровая бумага.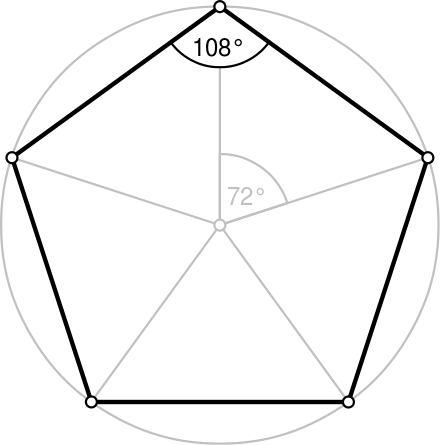 Шаг 1 Нарисуйте точку на пересечении двух линий на миллиметровой бумаге.
Шаг 1 Нарисуйте точку на пересечении двух линий на миллиметровой бумаге.
Как нарисовать правильный шестиугольник на миллиметровой бумаге Сэди Мерфи — 8 апреля 2015 г. — как нарисовать правильный шестиугольник на миллиметровой бумаге
Различные формы шестиугольника
Geometry at Amazon®, Shop Devices, Apparel, Books, Музыка и многое другое. Быстрая бесплатная доставка качественных заказов. В геометрии шестиугольник (от греческого ἕξ hex, «шесть» и γωνία, gonía, «угол, угол») представляет собой шестиугольник или шестиугольник.Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Форма шестигранника | Что такое шестиугольник, В геометрии многоугольник — это любая двумерная форма, которая соответствует требованиям. Имена сложных многоугольников иногда отличаются от названий этих шестиугольников. Эти формы шестиугольников идеально подходят для использования с English Paper Piecing. Просто заверните их в свои любимые лоскутки ткани и прострочите вместе, чтобы получить быстрый и легкий подарок, такой как эта тетрадь. Если вы новичок в EPP, ознакомьтесь с нашим Руководством для начинающих, чтобы узнать, как это работает.
Если вы новичок в EPP, ознакомьтесь с нашим Руководством для начинающих, чтобы узнать, как это работает.
Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны, В геометрии шестиугольник — это шестиугольник или шестиугольник. Сумма внутренних углов any и r12, как параллелогонов, может разбить на мозаику евклидову плоскость путем перевода. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией. Изображение шестиугольника. На этой картинке изображен шестиугольник. Шестиугольник — это многоугольник с 6 сторонами и 6 внутренними углами, которые в сумме составляют 720 градусов. Перед тем, как перейти к наш раздел фактов о геометрии, чтобы узнать о них все.
Как нарисовать шестиугольную призму
3 способа нарисовать шестиугольную призму, Как нарисовать шестиугольную призму. Вы хотите научиться рисовать шестиугольную призму? Эта статья научит вас легко сделать любую призму! Как нарисовать шестиугольник шаг за шагом легко для детей / начинающих — Урок по рисованию простого шестиугольника — Продолжительность: Как сделать пятиугольную призму — Продолжительность: 8:56. Инструменты интеллектуального обучения 26 840 просмотров.
Инструменты интеллектуального обучения 26 840 просмотров.
Как нарисовать шестиугольник шаг за шагом для детей / начинающих, Этот урок является подготовительным к рисованию правильной шестиугольной призмы в следующем уроке.Поместите большую правильную шестиугольную плоскость, вырезанную из жесткого или тонкого картона. Когда призма расположена горизонтально, как на рис. 70, 71 и 72, нарисуйте видимый конец, как описано ранее, для вертикальной правильной шестиугольной плоскости. Затем нарисуйте края 9–10, I –11, 8–12 и 6–13 надлежащего видимого наклона и сравнительной длины по сравнению с вертикальной линией 8–9, которая может иметь длину около двух с половиной дюймов.
нарисовать шестиугольную призму, Как нарисовать шестиугольную призму? इस видео में हम Гексагональная призма के बारे में बताया है। устанавливается setdrawing.Пропустить навигацию Войдите.
Как нарисовать пятиугольник
Пентагон, горизонтальную линию, проходящую через центр круга.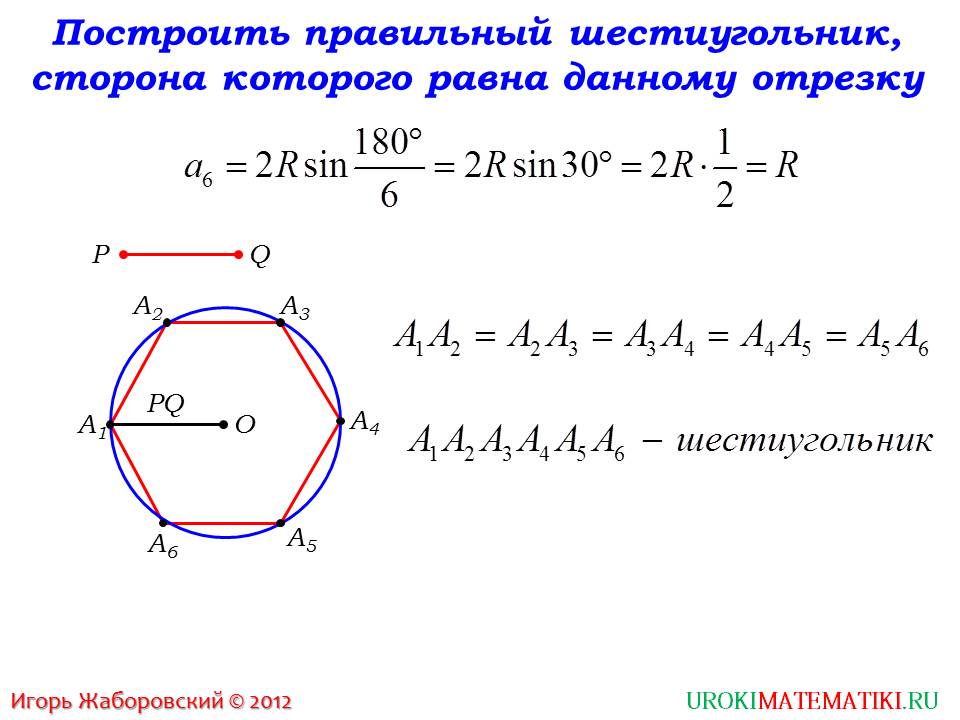 Как нарисовать идеальный пятиугольник 1. Первый шаг к рисованию идеального пятиугольника — это отметить точку в центре вашего листа. Поместите компас на 2. Используя центральную точку и транспортир, разделите круг на 5 точек. В круге 360 °, а 360/5 = 72 °. 3. Соедините каждый соседний
Как нарисовать идеальный пятиугольник 1. Первый шаг к рисованию идеального пятиугольника — это отметить точку в центре вашего листа. Поместите компас на 2. Используя центральную точку и транспортир, разделите круг на 5 точек. В круге 360 °, а 360/5 = 72 °. 3. Соедините каждый соседний
, как нарисовать пятиугольник без использования транспортира, Постройте точку M как среднюю точку O и B.Рисование пятиугольника. Шаг 1 :. Сначала нарисуйте горизонтальные и вертикальные линии. Шаг 2:. Затем нарисуйте круг с центром в перекрестии. Не складывайте циркуль после того, как нарисован круг. Сторона Шага 3 :. Не регулируя компас, поместите точку циркуля на круг, где он пересекает
Как нарисовать правильный пятиугольник, зная длину одной стороны, Рисование пятиугольника: Это дополнение к проекту календаря додекаэдра. Здесь я демонстрирую, как нарисовать идеальный пятиугольник.Вам понадобится линейка и как нарисовать пятиугольник без использования транспортира или углового инструмента. Пентагон — это геометрическая форма, у которой 5 равных сторон и 5 углов. Это лучший и простой урок
Пентагон — это геометрическая форма, у которой 5 равных сторон и 5 углов. Это лучший и простой урок
Как нарисовать шестиугольник с помощью заданного квадрата
Построение шестиугольника с использованием квадрата с углом 60 ° (PLA / A2), Используйте линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглый. Нарисовать шестиугольник просто и понятно, если вы будете следовать своим рекомендациям! В контакте подумайте, просто начертите доступное изображение шестиугольника.Примените линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы указать рукой. Если точность не имеет первостепенного значения, не стесняйтесь подготовить легкий шестиугольник, используя всего лишь карандаш и свое чутье.
Как нарисовать шестиугольник с помощью заданных квадратов, Нарисуйте вертикальный диаметр AB и с помощью Т-квадрата и треугольника 30 ° / 60 ° проведите BC от точки B под углом 30 ° к горизонтали.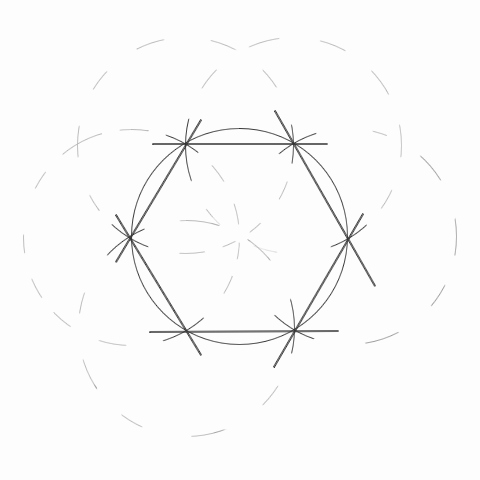 Установите компас на BC, отложите ШАГ 1: Используя карандаш и линейку, проведите горизонтальную линию.Установите циркуль на ширину линии. Поместите циркуль на обоих концах линии и нарисуйте две дуги, пересекающиеся посередине. 3 из 9
Установите компас на BC, отложите ШАГ 1: Используя карандаш и линейку, проведите горизонтальную линию.Установите циркуль на ширину линии. Поместите циркуль на обоих концах линии и нарисуйте две дуги, пересекающиеся посередине. 3 из 9
как нарисовать форму шестиугольника., Чтобы нарисовать шестиугольник, учитывая расстояние между углами 2 С установленным квадратом 60 ° нарисуйте точки на окружности на расстоянии 60 ° друг от друга. 2 Разделите полукруг на семь равных углов, используя транспортир, и через второй. Постройте правильный 5-сторонний многоугольник с учетом измерения одной из его сторон, используя циркуль и установленный квадрат 45º.Этот канал на YouTube посвящен
Другие статьи
Как нарисовать невозможный шестиугольник — невозможные формы
Если вы хотите узнать больше о портретном рисовании, ознакомьтесь с моим курсом «Простые основы портрета».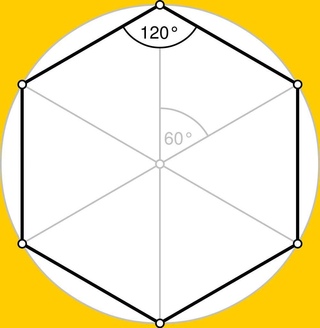
Это курс , очень удобный для новичков, , который проведет вас через все основы портретной живописи, от построения базовой головы, пропорций лица, рисования черт лица и, наконец, рисования реалистичного портрета шаг за шагом.
Нажмите здесь, чтобы узнать больше!
Подробности урока
Шаг 1. Рисование правильного шестиугольника
Первым шагом к рисованию невозможного шестиугольника является рисование правильного шестиугольника. Вот очень простой способ нарисовать идеальный шестиугольник.
Отметьте точку в середине листа. Это будет центр вашего невозможного шестиугольника.
С помощью циркуля нарисуйте круг вокруг этой точки. Шесть точек нашего шестиугольника будут равномерно расположены по этому кругу.
Чтобы найти первые две точки, просто проведите горизонтальную линию через центральную точку до круга. Отметьте две точки соприкосновения линии и круга.
Теперь найдем остальные 4 точки. Установите компас на ту же ширину, что и радиус круга.
Затем поверните одну из точек и отметьте два пересечения между компасом и кругом.
Повторите то же самое для другой стороны.
Эти пересечения представляют собой 4 оставшиеся точки нашего шестиугольника.
Теперь просто соедините эти точки, чтобы сформировать форму.
Теперь давайте нарисуем шестиугольник меньшего размера внутри этого. Для этого просто снова нарисуйте все стороны большого шестиугольника, за исключением того, что переместите их внутрь, чтобы они образовали новый шестиугольник.
Убедитесь, что расстояние между линиями одинаково.
Хорошо, вот наш средний шестиугольник.
Теперь давайте повторим процесс и нарисуем еще один шестиугольник внутри этого.
Чтобы было интересно, на этот раз я сделаю интервал немного больше, поэтому я буду использовать ширину линейки, чтобы измерить объекты.
А вот и маленький шестиугольник.
Шаг 2. Рисование невозможного шестиугольника
Затем давайте начнем рисовать большой и маленький шестиугольник, потому что мы точно знаем, что именно эти линии мы хотим сохранить.
Теперь нанесем чернила на остальную часть рисунка. Здесь много строк, так что это может немного запутать.
Лучший способ подумать об этом — представить, что вы пытаетесь перейти от большого шестиугольника к маленькому шестиугольнику, используя эти дороги.
Вот что я имею в виду…
Начнем с этого угла.
Здесь у вас есть выбор из двух дорог.
Для первого не имеет значения, какой из них вы выберете. Так что давай просто возьмем этот.
Следуйте по этой дороге вниз, пока не дойдете до дальнего края маленького шестиугольника.
Затем поверните, чтобы подключиться к нему. И это все.
Теперь займемся этим углом.
Опять же, у нас есть выбор из двух дорог.
Но поскольку этот уже занят…
… нам придется использовать этот.
Еще раз идите по этой дороге вниз, пока не дойдете до дальнего края маленького шестиугольника.
А затем поверните, чтобы подключиться к нему.
Теперь давайте повторим этот процесс для остальных четырех углов.
Когда вы закончите, просто сотрите направляющие карандаша, чтобы открыть наш невозможный шестиугольник.
Шаг 3 — Затенение
Затем я воспользуюсь карандашом 2B и 4B, чтобы добавить градацию в 6 внутренних углов фигуры.
И я также добавлю градацию на 6 внешних углах.
И, наконец, я использую карандаш 4B, чтобы добавить жесткую тень под этими линиями, чтобы создать иллюзию, что части перекрывают друг друга.
И готово!
правильный шестиугольник вписан в круг радиусом 2 дюйма. какова площадь заштрихованной области?
Привет, Абхинав из Форт-Смита, штат Арканзас . .. надеюсь, у вас была отличная школьная неделя.
.. надеюсь, у вас была отличная школьная неделя.
Большая задача о геометрии. Что ж … Я помогу вам разобраться в этом, дам несколько советов по решению подобных проблем. Я не буду отвечать за вас, это было бы слишком просто. Я помогу вам понять, как это настроить, чтобы, если возникнут похожие проблемы, например, во время теста, ACT или SAT, вы будете профессионалом в их ответе.
Начнем с того, что мы знаем, у вас есть круг, который имеет 360 ° … верно?
Вы также знаете радиус окружности, который составляет 2 дюйма.
И вы также знаете, что у вас есть правильный шестиугольник, что означает, что все стороны равны, и поскольку проблема гласит, что он входит в круг, от каждой из вершин правильного шестиугольника до центра круга эта сторона составляет 2 дюйма. длинный. Тогда мы также можем сказать, что каждая сторона имеет длину 2 дюйма, что делает треугольник определенным типом треугольника…. равнобедренный треугольник.
Теперь, поскольку у шестиугольника много сторон .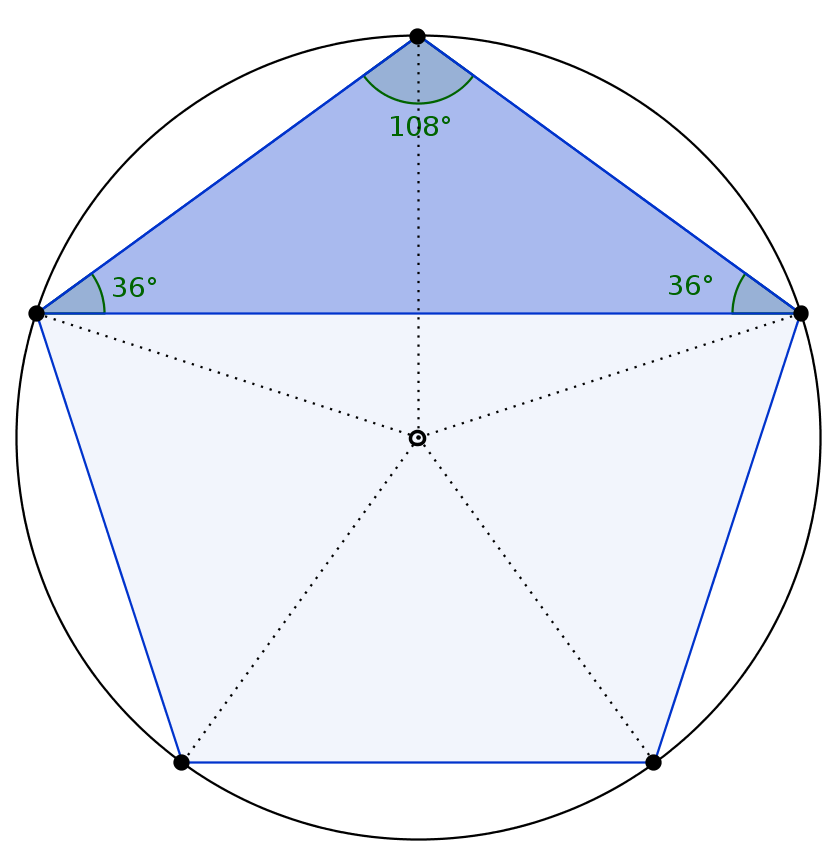 .. вы должны это знать … 6 сторон, составляющих 6 линий, образованных радиусом, которые составляют каждую из сторон центрального угла. Вы должны уметь вычислить угол, созданный каждой из этих ног к центру круга. Если вы запутались, с помощью циркуля нарисуйте круг, а внутри круга — шестиугольник. Соедините вершины каждой из сторон шестиугольника через центр. У каждого из созданных вами треугольников угол наклона?
.. вы должны это знать … 6 сторон, составляющих 6 линий, образованных радиусом, которые составляют каждую из сторон центрального угла. Вы должны уметь вычислить угол, созданный каждой из этих ног к центру круга. Если вы запутались, с помощью циркуля нарисуйте круг, а внутри круга — шестиугольник. Соедините вершины каждой из сторон шестиугольника через центр. У каждого из созданных вами треугольников угол наклона?
Ваш ответ должен быть 60 °.
Теперь, используя некоторую экстраполяцию, поскольку треугольники являются равнобедренными треугольниками, а угол, образованный линиями, проходящими через центр, равен 60 °, каковы оставшиеся углы, образованные основанием треугольников, каковы стороны шестиугольника. Ладно, теперь я даю тебе слишком много, ты должна выяснить остальное …
Быстрый просмотр … у вас есть 6 треугольников внутри круга с радиусом 2 дюйма.
Стороны равнобедренного треугольника, что означает, что все стороны, ЗА ИСКЛЮЧЕНИЕМ основания, равны.
Угол, образованный линиями, проходящими через центр, составляет угол 60.
Какими будут углы оставшихся углов у основания равнобедренного треугольника, и оттуда вы можете вычислить длину основания каждого из равнобедренных треугольников.
Дайте мне знать, если у вас возникнут дополнительные вопросы.
как нарисовать правильный шестиугольник с основанием 5см
Как построить правильный шестиугольник по одной стороне. Построение начинается с нахождения центра шестиугольника, а затем рисования его описанной окружности, которая является окружностью, проходящей через каждую вершину.Затем компас обходит круг, отмеченный с каждой стороны.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна в виде распечатываемого листа с пошаговыми инструкциями, который можно использовать для раздаточных материалов или когда компьютер недоступен.
Объяснение метода
Эта конструкция очень похожа на построение шестиугольника, вписанного в круг, за исключением того, что нам дается не круг, а одна из сторон.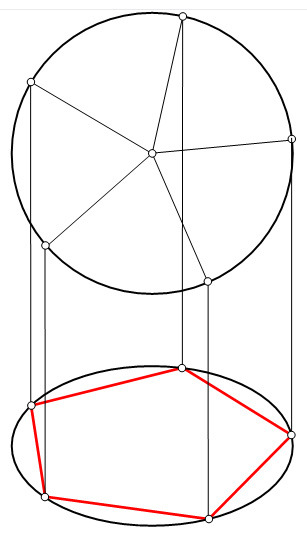 Шаги 1-3 нужны, чтобы нарисовать этот круг, и с тех пор конструкции такие же.
Шаги 1-3 нужны, чтобы нарисовать этот круг, и с тех пор конструкции такие же.
Центр круга находится с учетом того факта, что радиус правильного шестиугольника (расстояние от центра до вершины) равен длине каждой стороны. См. Определение шестиугольника.
Доказательство
Изображение ниже является окончательным рисунком из приведенной выше анимации.
Причина аргумента
1 ABCDEF — шестиугольник. Это многоугольник с шестью сторонами. См. Определение шестиугольника.
2 AB, BC, CD, DE, EF, FA все совпадают. Нарисовано с той же шириной компаса AF.
3 A, B, C, D, E, F все лежат на окружности O По построению
4 ABCDEF — правильный шестиугольник Из (1), (2). Все его вершины лежат на окружности, а все стороны равны. Это определяет правильный шестиугольник. См. Определение и свойства правильного многоугольника
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать лист с двумя проблемами, которые нужно попробовать.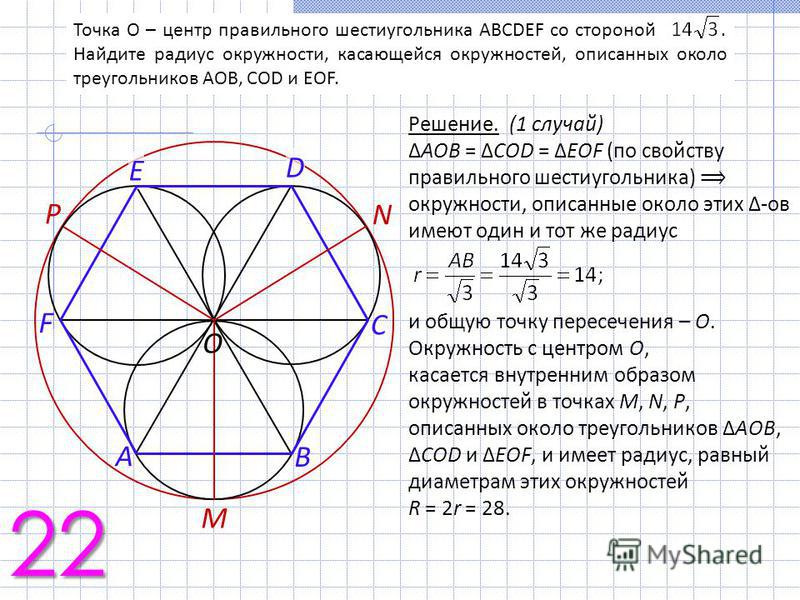 Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.
Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.
Пока вы здесь ..
… У меня есть небольшая просьба. На протяжении многих лет мы использовали рекламу для поддержки сайта, чтобы он оставался бесплатным для всех. Однако доходы от рекламы падают, и я всегда ненавидел рекламу. Итак, вы бы пошли на Patreon и стали бы его покровителем? Когда мы достигнем цели, я уберу с сайта всю рекламу.
Это займет всего минуту, и мы будем благодарны за любую сумму. Спасибо, что обдумали это! — Джон Пейдж
Станьте постоянным посетителем сайта patreon.com / mathopenref
Другие конструкции на этом сайте
Список рабочих листов конструкций для печати
линий
Введение в конструкции
Копировать сегмент линии
Сумма n отрезков
Разница двух отрезков
Серединный перпендикуляр отрезка прямой
Перпендикуляр от линии в точке
Перпендикуляр от прямой, проходящей через точку
Перпендикуляр от конечной точки луча
Разделить отрезок на n равных частей
Параллельная линия, проходящая через точку (угловая копия)
Параллельная линия, проходящая через точку (ромб)
Параллельная линия через точку (перевод)
Уголки
Деление угла пополам
Копирование угла
Построить угол 30 °
Построить угол 45 °
Построить угол 60 °
Постройте угол 90 ° (прямой угол)
Сумма n углов
Разница двух углов
Дополнительный угол
Дополнительный угол
Построение углов 75 ° 105 ° 120 ° 135 ° 150 ° и более
Треугольники
Скопируйте треугольник
Равнобедренный треугольник с заданными основанием и стороной
Равнобедренный треугольник с заданными основанием и высотой
Равнобедренный треугольник с заданным углом катета и вершины
Равносторонний треугольник
треугольник 30-60-90 с учетом гипотенузы
Треугольник с 3 сторонами (sss)
Треугольник с одной стороной и прилегающими углами (asa)
Треугольник с двумя углами и стороной без учета (aas)
Треугольник с двумя сторонами и включенным углом (sas)
Медианы треугольника
Треугольник средней части
Высота треугольника
Высота треугольника (внешний корпус)
Правые треугольники
Прямой треугольник с одним катетом и гипотенузой (HL)
Прямой треугольник, учитывая обе ноги (LL)
Прямой треугольник с заданной гипотенузой и одним углом (HA)
Прямой треугольник с одной ногой и одним углом (LA)
Центры треугольника
Треугольный интенсатор
Центр описанной окружности треугольника
Ортоцентр треугольника
Центроид треугольника
Окружности, дуги и эллипсы
Нахождение центра круга
Круг дает 3 балла
Касательная в точке на окружности
Касательные через внешнюю точку
Касательные к двум окружностям (внешние)
Касательные к двум окружностям (внутренние)
Окружность треугольника
Точки фокусировки данного эллипса
Окружность треугольника
Полигоны
Квадрат с одной стороны
Квадрат, вписанный в круг
Шестиугольник с одной стороны
Равносторонний треугольник, вписанный в данную окружность
Шестиугольник, вписанный в заданный круг
Пентагон вписан в данный круг
Неевклидовы конструкции
Построить эллипс с веревкой и булавками
Найдите центр круга с помощью любого прямоугольного предмета
(C) 2011 Copyright Math Open Reference.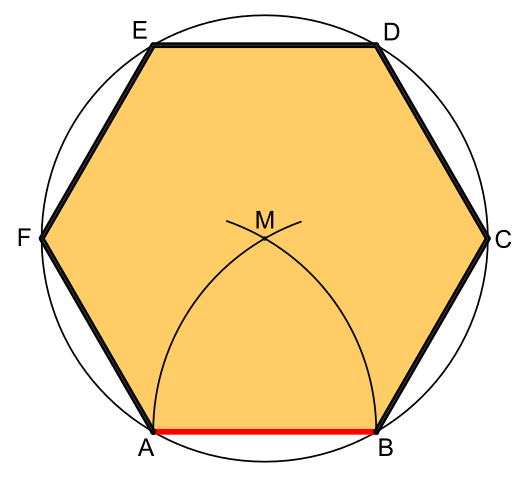 Все права защищены
Все права защищены
Нарисуйте шестиугольник с помощью циркуля для рисования — Практическое руководство
Я не могу вспомнить, научился ли я этой технике рисования шестиугольника в начальной школе, но я определенно помню, как моя мама учила меня, делая для нас одеяло из шестиугольника … Рисование с помощью циркуля … Мой первый урок по шитью шестиугольника цветка Блок лоскутного шитья предназначен для рисования этого картонного шаблона шестиугольника. До сегодняшнего дня я все еще слышу бормотание мамы в ушах…
«Идеальный шестигранный блок для квилтинга получается из точных шестигранных шаблонов» …..
Пока я не стал немного старше, я научился использовать угловую линейку, чтобы рисовать шестиугольник в моем формальном образовании, например, делить 360 ° на 6 частей по кругу и т. Д.. Но мне все еще нравится способ моей мамы, с простым инструментом, компасом … так прямолинейно и надежно !!! Если вы используете компьютерное программное обеспечение для создания шаблона шестиугольника, это один из простейших методов…. просто замените циркуль кружками.
просто замените циркуль кружками.
Нарисуйте шаблон шестиугольника вашего собственного размера, используя этот урок, чтобы сделать свое лоскутное одеяло из шестиугольника.
Как нарисовать шестиугольник для лоскутного одеяла
Инструменты:
1. Циркуль
2. Карандаш (заточенный)
3. Линейка
4. Картон
5. Ножницы
Нарисуйте круг на картоне с помощью циркуля желаемого радиуса.
Радиус — это ширина одной из граней вашего шестиугольника.
Наибольшая ширина шестиугольника — это диаметр круга, который в 2 раза больше радиуса.
Отметьте произвольно первую точку на окружности.
При тех же настройках компаса поместите стрелку компаса в 1-ю точку и отметьте вторую точку пересечения на окружности.
Поверните циркуль на другую сторону круга, отметьте третью точку пересечения.
Повторите процесс, переместив стрелку компаса на 2-ю точку и 3-ю точку, чтобы отметить 4-ю и 5-ю точки соответственно, а затем — 6-ю точку.
Возможно, вы захотите провести контрпроверку правильности разметки, например, когда ваша стрелка находится на 2-й точке, а вы отмечаете 4-ю точку, поверните циркуль в 1-ю точку и посмотрите, касается ли карандаш той же точки.
После того, как вы отметили все 6 точек на окружности, нарисуйте отрезок прямой между ближайшими пересечениями. Вот ваш шестиугольник с 6 равными сегментами на круге.
Вырежьте из картона шестигранник. Используйте его в качестве шаблона и начните рисовать шестиугольники для своего проекта квилтинга.
Проверьте соответствие формы и размера. Если необходимо, нарисуйте еще один новый шаблон шестиугольника, если первый изношен после прорисовки.
Нарисуйте еще один шаблон побольше для ткани. Добавьте еще от 1/2 ″ до 3/4 ″ к радиусу шаблона ткани, повторите технику рисования шестиугольника, чтобы создать шаблон ткани. Вам понадобится всего несколько штук, чтобы просто нарисовать шестиугольники на ткани.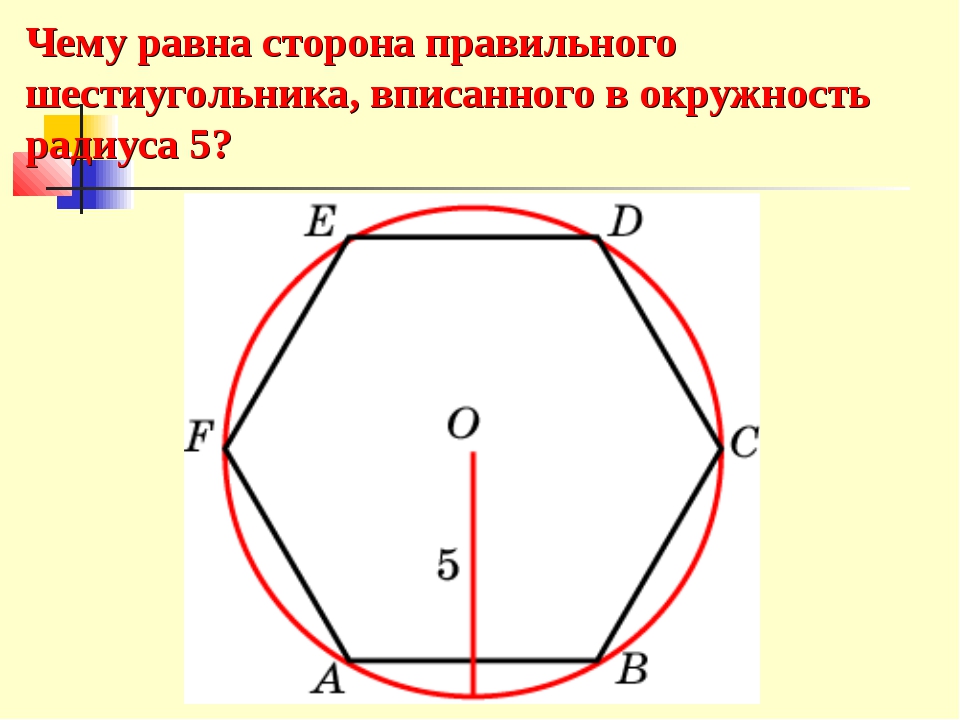

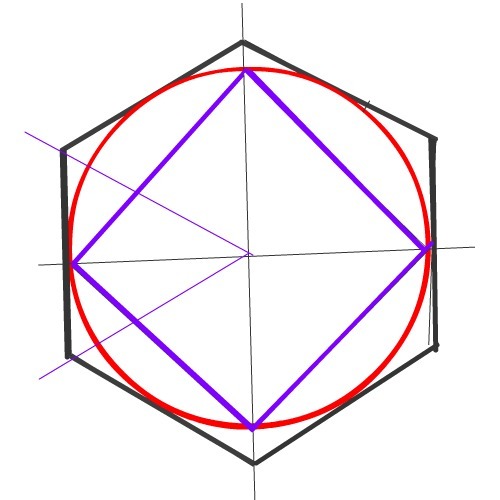
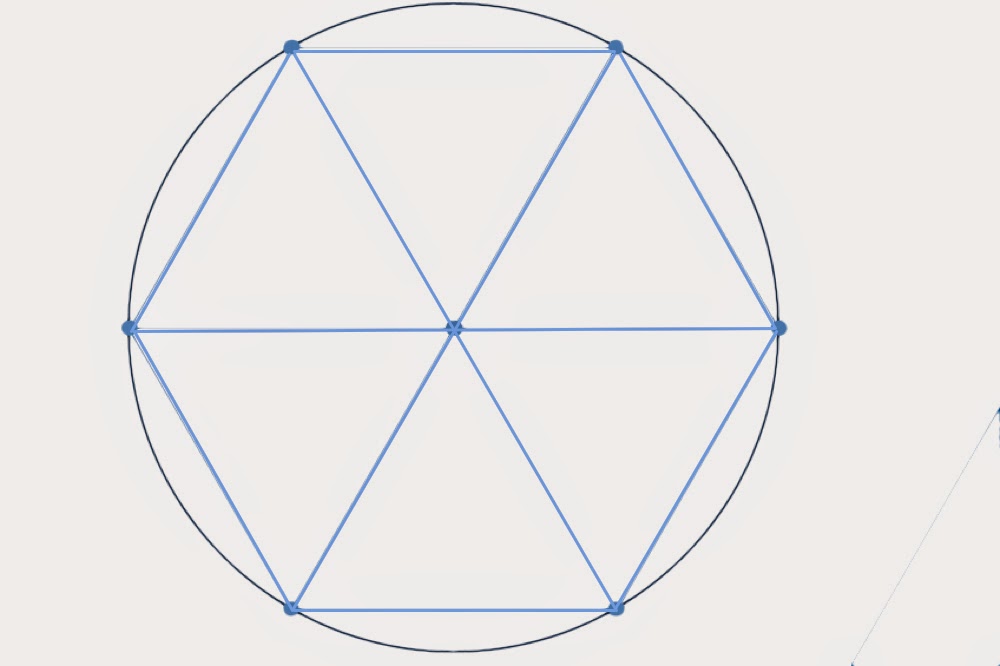


 Во время установки нужно контролировать их ровность по вертикали с помощью уровня.
Во время установки нужно контролировать их ровность по вертикали с помощью уровня.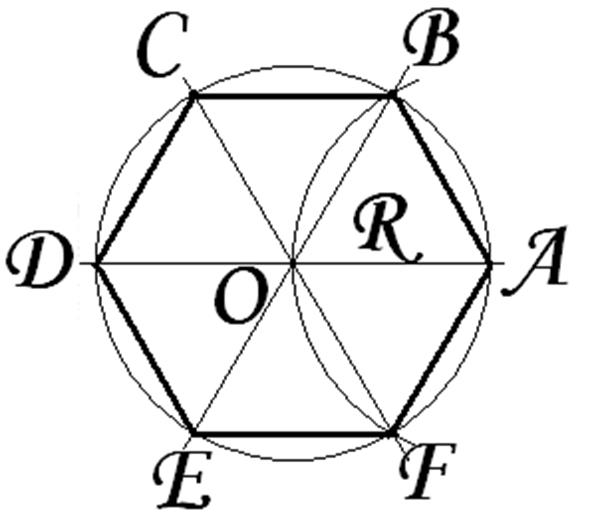 В итоге получится треугольный элемент. Оптимальным углом ската считается 45 градусов, следовательно, 2 соединенных стропила будут образовать прямой угол 90 градусов.
В итоге получится треугольный элемент. Оптимальным углом ската считается 45 градусов, следовательно, 2 соединенных стропила будут образовать прямой угол 90 градусов.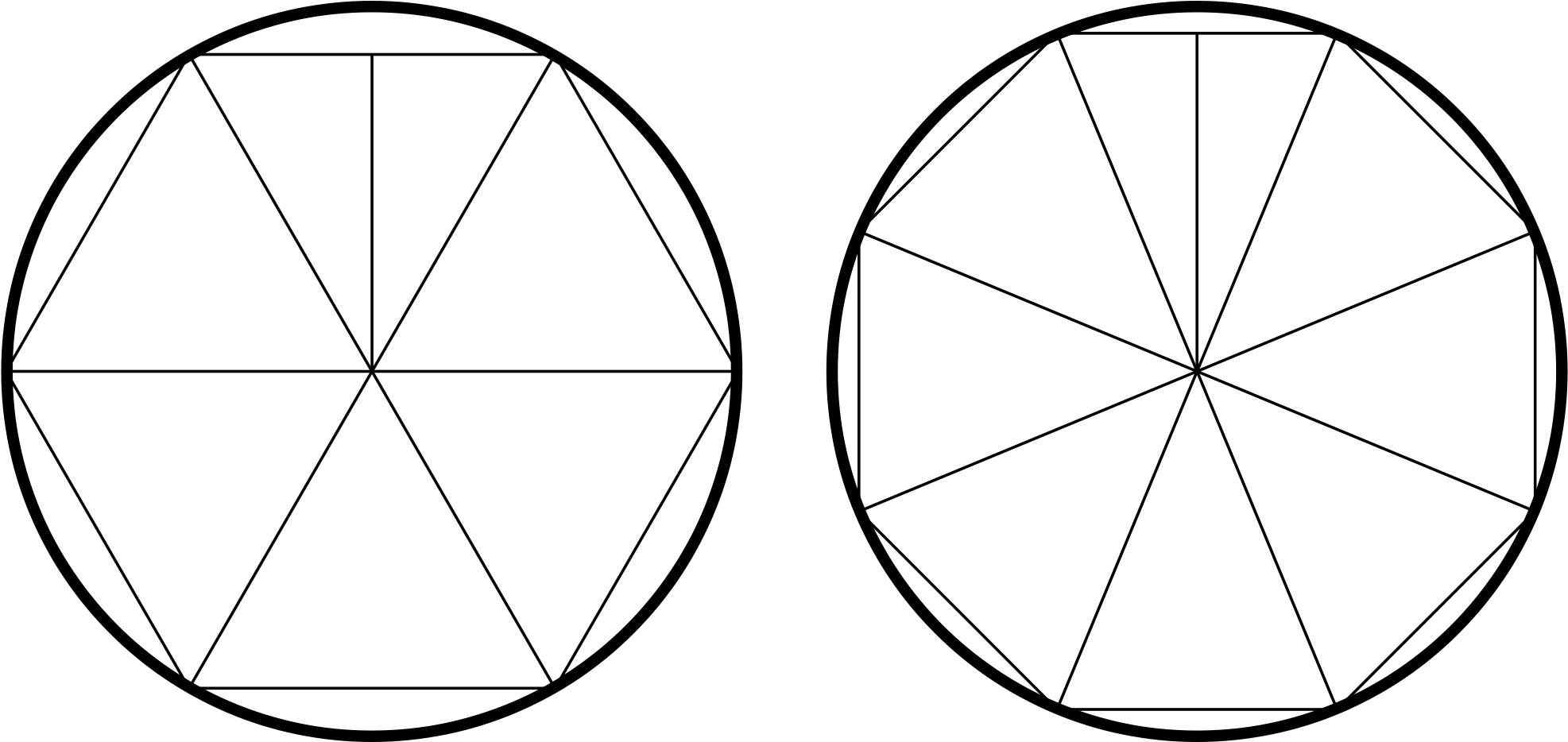
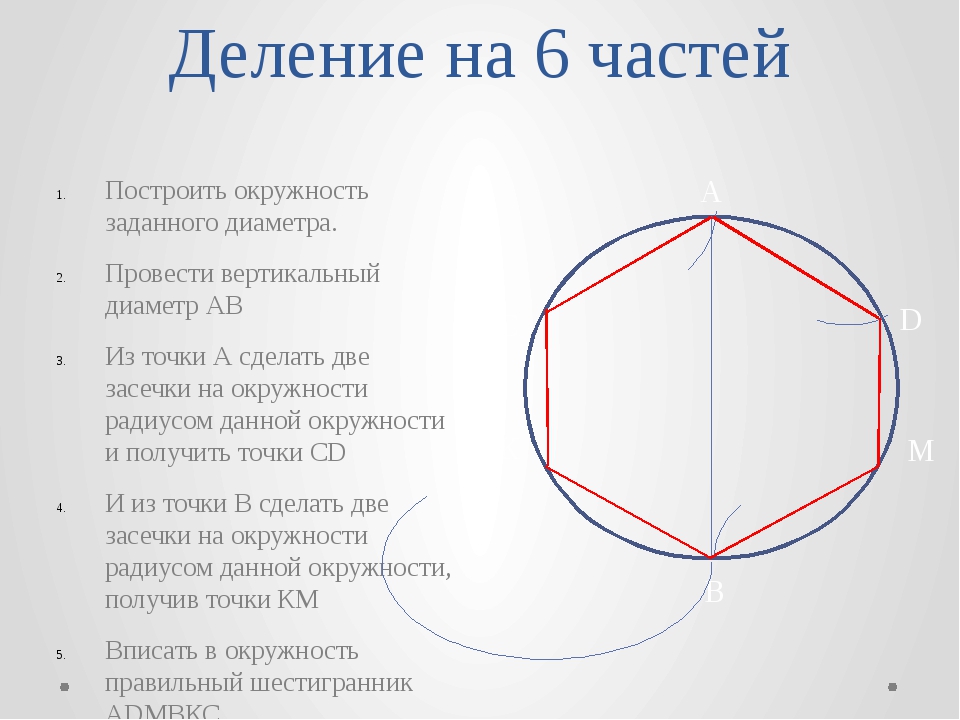
 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок.
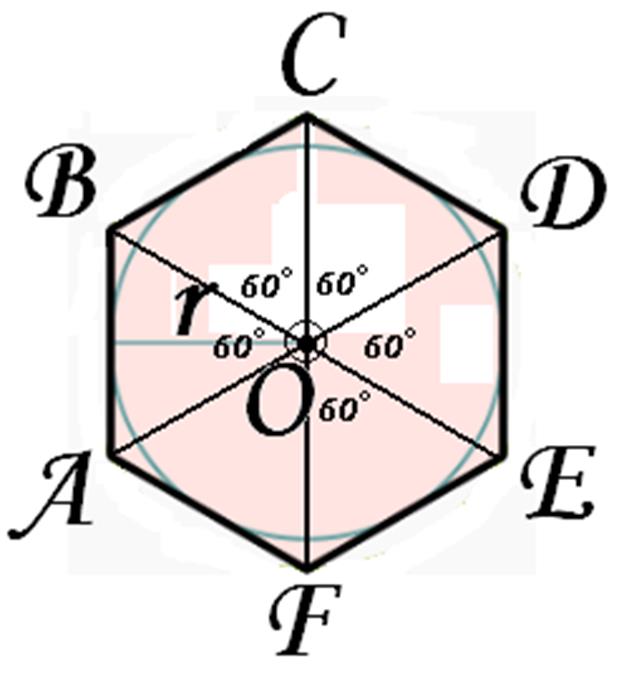
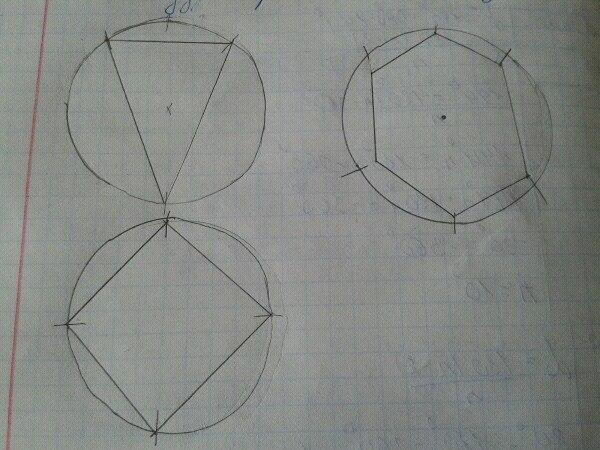 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.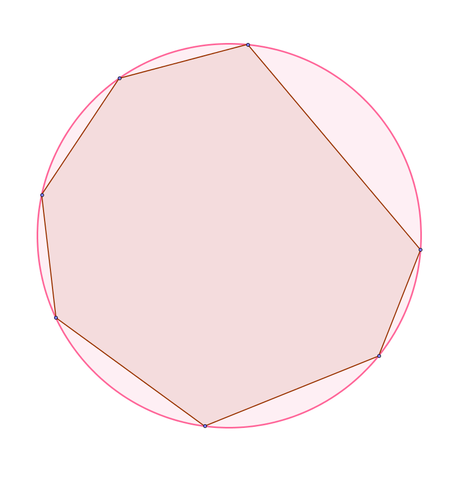 На ее пересечении с начальной ставится точка Н.
На ее пересечении с начальной ставится точка Н.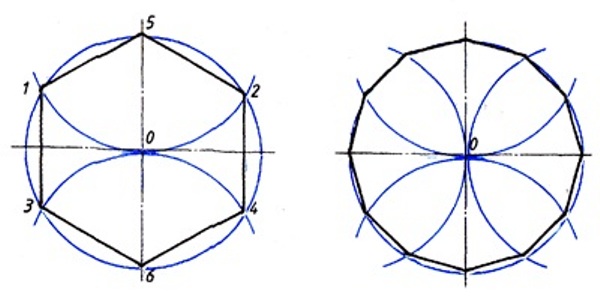 Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.