Открытый скрап-клуб: Узор из правильных шестиугольников
Добрый вам день, уважаемые читатели!
Сегодня хочется обратить ваше внимание на еще один трендовый узор — из правильных шестиугольников, который также можно назвать гексагон / Hexagon. У нас этот узор еще часто называют сотами.
Вывод о его актуальности прозвучал на страницах блога «Зроби сама» в еженедельной рубрике «Цікаве за тиждень + Новини у світі скрапу» («Интересное за неделю + Новости в скрап-мире»), и, надо сказать, я его полностью поддерживаю. А теперь предлагаю и вам убедиться в сказанном.Мастерицы, выдерживая узор, сами шестиугольники используют, как декоративные элементы на странице, выполняя их из разной бумаги,..
…или комбинируют также со штампингом
А иногда удачно дополняют узор скрап-бумаги своими гексагонами
Еще интересней, когда некоторые из шестиугольников используются в качестве носителей информации: в них вставляют фото и/или вписывают журналинг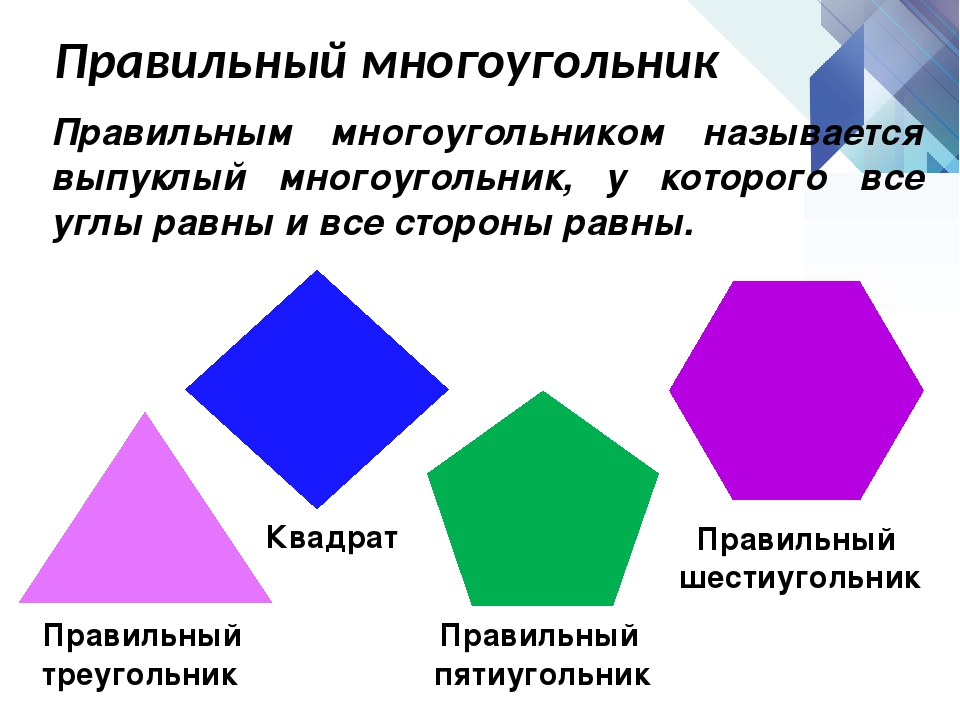 Гексагон-узор встречается в разных коллекциях бумаги от разных производителей. А если вы являетесь счастливой обладательницей вырубной машинки, то вам не составит труда сделать похожую креативную открытку
Узор из шестигранников «можно встретить практически в любой группе скрап-товаров — на бумаге, штампах, наклейках, оверлеях, трафаретах, папках для тиснения и т.д.» © «Зроби сама». А что делать тем, у кого всего этого не оказалось?! Не страшно! На помощь приходит freebies — бесплатная загрузка рисунка сот (вам нужна кнопка «Download PDF»), а имея ее — можно воспользоваться идеей со страницы, представленной ниже. Весело, живенько, разнообразно! Не правда ли?
Блуждания по интернету в поисках интересных образцов с использованием шестиугольника в узоре, вывели на статью «Значение, толкование геометрических символов». И что же гексагон? «Правильный шестиугольник — символ изобилия, красоты, гармонии,
свободы, брака, любви, милости, удовольствий, мира, симметрий, символ
числа 6, образ человека (две руки, две ноги, голова и туловище)» ©.
Гексагон-узор встречается в разных коллекциях бумаги от разных производителей. А если вы являетесь счастливой обладательницей вырубной машинки, то вам не составит труда сделать похожую креативную открытку
Узор из шестигранников «можно встретить практически в любой группе скрап-товаров — на бумаге, штампах, наклейках, оверлеях, трафаретах, папках для тиснения и т.д.» © «Зроби сама». А что делать тем, у кого всего этого не оказалось?! Не страшно! На помощь приходит freebies — бесплатная загрузка рисунка сот (вам нужна кнопка «Download PDF»), а имея ее — можно воспользоваться идеей со страницы, представленной ниже. Весело, живенько, разнообразно! Не правда ли?
Блуждания по интернету в поисках интересных образцов с использованием шестиугольника в узоре, вывели на статью «Значение, толкование геометрических символов». И что же гексагон? «Правильный шестиугольник — символ изобилия, красоты, гармонии,
свободы, брака, любви, милости, удовольствий, мира, симметрий, символ
числа 6, образ человека (две руки, две ноги, голова и туловище)» ©.
И тут для любителей объемных работ и геометрии открывается широкое поле деятельности. Уже не просто узор, а сам правильный шестиугольник ложится в основу работ. Дабы не утомлять читателя, покажу лишь несколько: вам решать — замахнуться 🙂 и сделать или только полюбоваться.
Ваш ОСК.
3
|
|
||||||||||||||||||||||||||||||||||||
Многоугольники. Правильные многоугольники. Равенство фигур.
Многоугольник — замкнутая ломаная, несмежные звенья которой не имеют
 Другими словами, периметр многоугольника — это сумма длин всех его сторон.
Другими словами, периметр многоугольника — это сумма длин всех его сторон.Любой многоугольник имеет следующие элементы: вершины, стороны и углы. Например, на рис. 1 у четырехугольника АВСD точки А, В, С, D являются его вершинами, отрезки АВ
Многоугольник с n вершинами называется n-угольником; он имеет n сторон. На рис.1 изображены четырехугольник АВСD и шестиугольник А1А2А3А4А5А6.
Соседние вершины многоугольника — вершины, принадлежащие одной стороне. На рис.1 у четырехугольника АВСD соседние вершины: А и В, В и С, С и D, А и D.
Диагональ многоугольника — отрезок, соединяющий любые две несоседние вершины
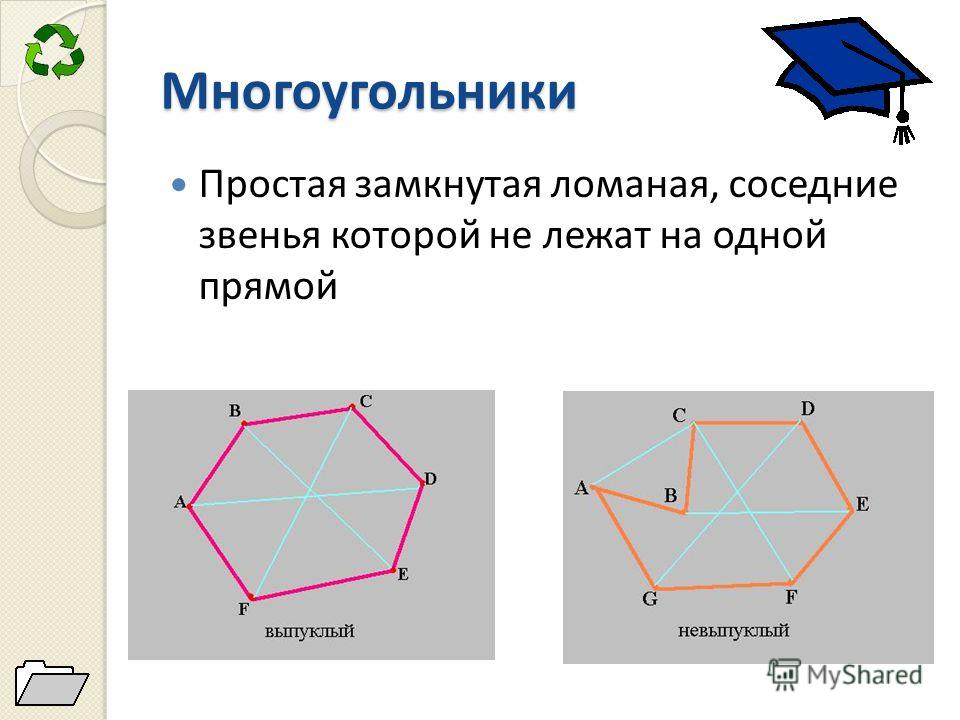
Выпуклый многоугольник — это многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. На рис.3 многоугольник М1 является выпуклым многоугольником, а многоугольник М2 —
На рис.3 многоугольник М1 является выпуклым многоугольником, а многоугольник М2 —
Правильный многоугольник — это выпуклый многоугольник, у которого все углы равны и все стороны равны. К правильным многоугольникам относятся равносторонний треугольник и квадрат. На рисунке ниже изображены правильные пятиугольник, шестиугольник, семиугольник и восьмиугольник.
Равными фигурами считаются те, которые имеют одинаковую форму и размеры. Две фигуры (в том числе и многоугольники) называются
 Например, пятиугольник ABCDF равен пятиугольнику A1B1C1D1F1:
Например, пятиугольник ABCDF равен пятиугольнику A1B1C1D1F1:Действительно данные пятиугольники равны, они совпадут при наложении, так как вершина A совместиться с вершиной А1, В — с В1, C — с C1, D
Шестигранник, его виды, выбор и основные характеристики
Шестигранник используют для работы с крепежными деталями, в шляпках которых имеется углубление в форме шестиугольника.
Это инструмент с наконечником, имеющим 6 граней, может быть сделан в виде нескольких слесарных приборов.
Наиболее часто при ремонтных и строительных работах используются ключ и отвертка.
Они выполняются в разных видах, но зачастую имеют одинаковое предназначение.
Шестигранные отвертки и ключи должны быть в каждом доме, не говоря уже о людях, занимающихся ремонтом мебели, автомобилей, техники профессионально.
Содержание статьи
Устройство и характеристики
Основой любого вида шестигранника является металлический стержень.
Он первым принимает на себя силовую нагрузку, поэтому его характеристики особенно важны.
Материал должен быть прочным, устойчивым к деформациям, способным работать долгое время.
Материал для изготовления
Обычно шестигранник любого вида изготавливают из высокопрочной легированной стали, но при производстве может использоваться другой металл, например, хромованадиевый или хромомолибденовый сплав.
При этом ГОСТ регулирует выполнение материалом технических требований, выдерживание определенных нагрузок.
Если отвертка оборудована рукояткой, материалом для нее служит мягкая, но прочная пластмасса.
Ее изготавливают с впадинами или выпуклостями, для того чтоб обеспечить плотное прилегание к руке.
Размеры и вес
Ключи и отвертки с шестью гранями изготавливаются в более чем 15 различных размерах, прописанных в метрической стандартной системе ISO и ANSI.
Сегодня на рынке можно найти варианты инструментов диаметром от 0,7 до 46 мм.
Для полноценного использования важно подбирать вид инструмента, по размеру полностью соответствующего крепежной детали.
Виды шестигранников и их назначение
Разные виды шестигранных инструментов используются для работы с разными крепежными элементами:
Имбусовый
Это самый простой вариант данного инструмента.
Его можно использовать для любых видов крепежей, имеющих внутренний профиль с шестью гранями.
Конструкция такого инструмента максимально проста: г-образный стержень производят с одинаковым по всей длине сечением.
Короткая часть ключа используется чтобы создать сильное усилие по типу рычага.
Т-образный
Шестигранный вариант используют в тех случаях, когда для крепежа требуется применить особенно большое усилие для вкручивания или откручивания крепежных элементов.
Нередко в своей работе мастера используют наборы этих ключей.
Обычно набор инструментов включает в себя основные размеры.
Приобретение целого набора позволяет подобрать ключ или отвертку, соответствующую крепежной детали.
Но еще есть и универсальный шестигранник, на котором присутствуют несколько разных размеров.
Такой ключ обычно используют в слесарном деле, но благодаря своей универсальности, пригодится он, может в любой сфере деятельности.
Что нужно знать о шестигранниках
Шестигранник имеет такую уникальную особенность, как чрезвычайно высокий крутящий момент.
Если сравнивать его характеристики с обычным видом отверток или ключей, то значение шестигранников превышает классические инструменты в 10 раз.
Некоторые путают шестигранный вид инструмента с отвертками типа Torx, выполненный в виде звезды с шестью лучами, но на деле они используются для разных видов крепежных элементов.
Для надежной фиксации и правильной работы вид инструмента должен подбираться таким образом, чтобы максимально плотно входить или обхватывать крепежную деталь.
В этом случае головка крепежа не пострадает.
Как пользоваться шестигранником
Открутить крепеж шестигранником довольно просто.
Главное соблюдать простейшую технику безопасности и не допускать нанесения ударов по ключу или отвертке, чтобы создать большую силу рычага.
Пошаговые действия включают в себя:
1. Подбор шестигранника, соответствующего виду и размеру крепежного элемента.
2. Введение во внутреннее отверстие детали одной стороны шестигранника так, чтобы он занимал всю глубину.
Г-образный вид лучше вводить короткой стороной, но при необходимости допускается использование длинной.
3. Прикладывание нагрузки на инструмент с постепенным ее усилением, пока не будет достигнут крутящий момент.
Аналогично следует действовать и при закручиваниях элементов.
Инструкция подходит как для работы с наружным болтом, так и для деталей с внутренним шлицом.
Как правильно выбрать шестигранник
Если выбрать хороший набор шестигранников, можно обеспечить себя подходящими инструментами на все случаи жизни: начиная с ремонта автомобиля и заканчивая сбором мебели дома.
Чтобы не потеряться в широком выборе разнообразных по цене и составу предложений следует помнить основные правила:
1. Для профессионального частого использования следует выбирать набор, состоящий не менее, чем из 12 видов шестигранников.
Это удобно и позволит сэкономить время на покупки.
В быту достаточно 3-5 инструментов.
Приобрести их можно по отдельности, исходя из личных потребностей, или маленьким набором по сниженной цене.
2. Наиболее прочными считаются шестигранники, выполненные из специальной инструментальной стали или хромванадия.
Они прослужат на протяжении долгих лет и не деформируются.
3. Не экономьте на выборе производителя.
Дешевые китайские инструменты с легкостью портят технику и мебель с которыми используются и ломаются сами.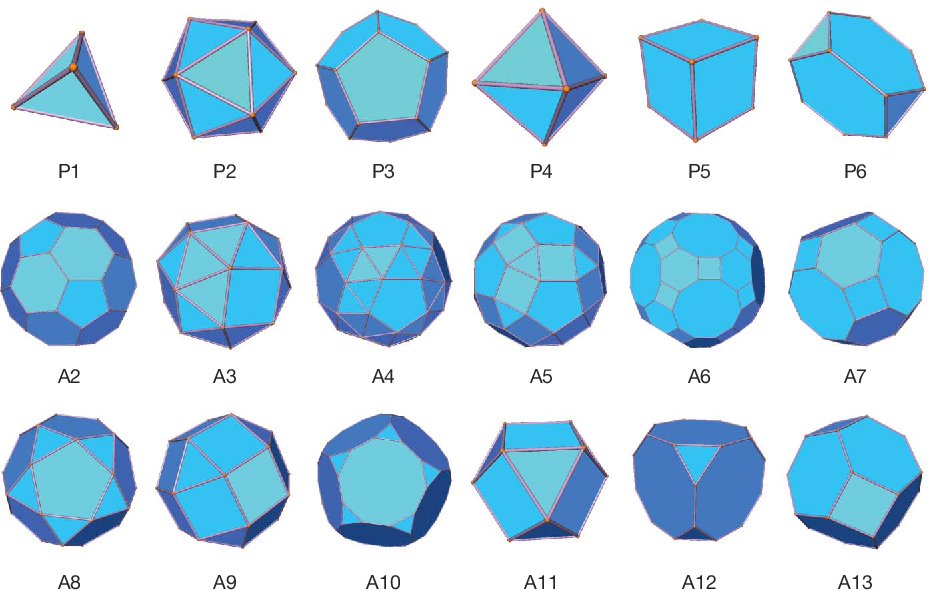
Рейтинг шестигранников
Различные модификации и виды шестигранников присутствуют в наборах ведущих производителей инструментов.
Они соответствуют ГОСТу, и в среднем состоят из 9 предметов.
Самыми популярными в последние годы являются шестигранники «ЗУБР эксперт».
Они надежны, способны выдерживать серьезные нагрузки и эксплуатируются на протяжении многих лет.
Еще одним преимуществом этого набора становится низкая цена.
Вторым по популярности считаются инструменты фирмы KRAFTOOL.
Их любят за удобный футляр, в котором можно хранить набор, не занимая места.
На третьем месте в рейтинге шестигранники фирмы STAYER.
Материалы, используемые при производстве инструментов этой компании чрезвычайно высококачественны.
Методика изучения правильных многоугольников в курсе планиметрии работа по методике преподавания математики (стр. 3 из 4)
а) равносторонний треугольник;
б) параллелограмм;
в) равнобокая трапеция;
г) прямоугольник.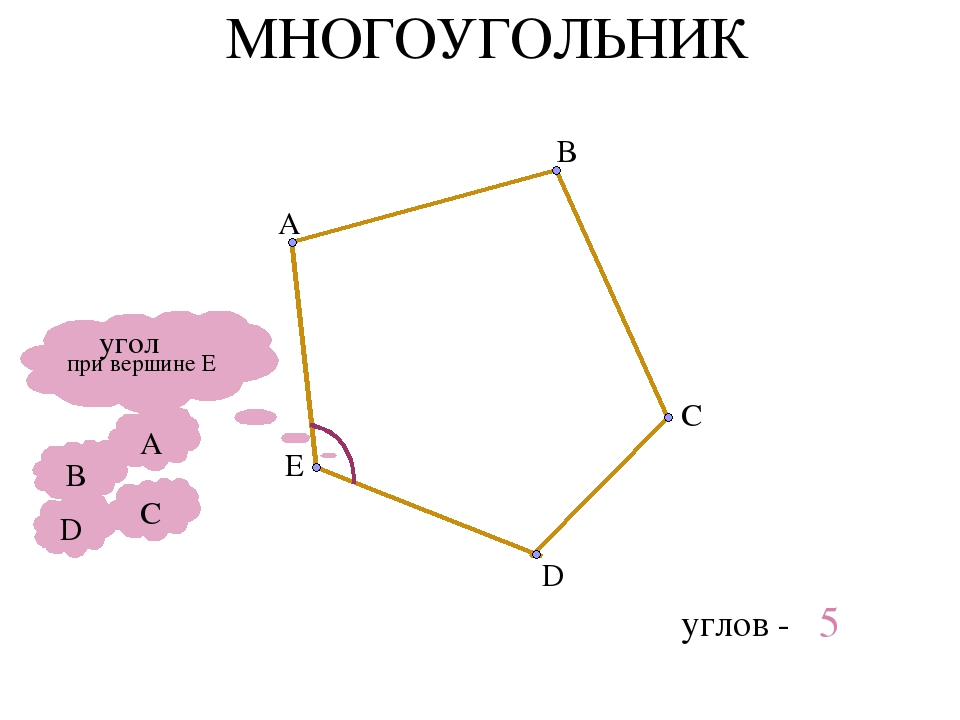
2. Закончить фразу.
Многоугольник называется описанным около окружности, если …
3. Поставить знак «+» рядом с верным утверждением.
а) Выпуклый многоугольник является вписанным в окружность и описанным около окружности.
б) Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
4. Какая из предложенных формул выражает радиус описанной окружности:
5. Треугольник DBC – правильный. Чему равна сторона треугольника, если радиус вписанной окружности равен 5 см?
а)
см;б)
см;в) 10 см;
г)
см.6. Окружность вписана в правильный шестиугольник с периметром 183 см. Найти радиус окружности.
а) 4,5 см;
б) 9 см;
в) 6 см;
г)
см.Вариант 1.
1. Закончить предложения: а) «Правильным многоугольником называется …»
б) «Угол правильного шестиугольника равен…»
2. Перечислите все известные вам формулы для сторон и площади правильного n-угольника.
3. Перечислите главные методические проблемы при изложении темы «Правильные многоугольники»
4. Отметить важные отличия при изложении материала «Выражение элементов треугольника через радиус вписанной или описанной окружностей» разными авторами.
Вариант 2.
1. Закончить предложения: а) «Выпуклый многоугольник называется правильным, если… »
б) «Угол правильного восьмиугольника равен…»
2. Перечислите все известные вам формулы для периметра и радиуса вписанной окружности правильного n-угольника.
3. Перечислите главные методические проблемы при изложении темы «Правильные многоугольники»
4. Отметить важные отличия при изложении материала «Построение правильных многоугольников» разными авторами.
Класс: 10
Учебное пособие: Н.В.Гвоздович, Т.П.Кубеко «Геометрия, 10»
Цели:
1. Знать определения правильных многоугольников, уметь строить правильный четырёхугольник, шестиугольник, 2n-угольник.
2. Воспитывать аккуратность, эстетичность, умение оценивать результаты своего труда и труда одноклассников.
Тип урока – комбинированный.
Оборудование: плакат-правильные многоугольники; чертёжные принадлежности;
Ход урока.
1. Целеполагание.
На доске изображены рисунки, получившиеся в результате комбинаций правильных многоугольников. Какой, на ваш взгляд, самый удачный рисунок? Где можно использовать на практике подобные комбинации многогранников? (Мoжно оформить таким орнаментом потолочную плитку или паркетный пол).
Возможно ли каждому из вас построить свой орнамент? Что для этого нужно уметь делать? (Уметь строить правильные многоугольники). Построение правильных многоугольников с целью создания своего орнамента – цель нашей работы сегодня.
2. Актуализация знаний.
Что называется правильным треугольником, четырёхугольником, n-угольником? (многоугольник с равными сторонами и углами – правильный).
Чему равна сумма углов в правильном треугольнике, четырёхугольнике, шестиугольнике, n-угольнике? (180º; 360º; 720º; 180º (n-2))
Чему равен каждый угол в правильном n-угольнике?
Как построить биссектрису угла, серединный перпендикуляр к отрезку с помощью циркуля и линейки? (Повторить построение, работая у доски, учащиеся – в тетрадях)
3. Изложение нового.
Изложение нового.
1) Можно около правильного треугольника описать окружность. Сделаем это. Центр окружности лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
Соединим точки пересечения серединных перпендикуляров с окружностью?
Какой получился многоугольник? (правильный шестиугольник) Докажем это.
C B DА E
∆ АВС = ∆ ЕDС (по стороне и двум прилежащим к ней углам: АС = ЕС; В треугольниках АВС и ЕDС перпендикуляры – серединные, значит они – равнобедренные и А = С, С = Е, а т. к . АВС= СDЕ (на них опираются равные углы А и С в ∆ АСЕ), то равны и половины этих дуг, а значит, ВС = СD, и А = Е.
2) Измерим сторону получившегося шестиугольника и радиус окружности. Они приблизительно равны. Позднее мы докажем, что R=а .
3) Построим окружность, проведём диаметр АС, проведём серединный перпендикуляр к нему. Соединим точки пересечения перпендикуляра и окружности. Получившаяся фигура ABCD — квадрат. Докажем это. (Углы, опирающиеся на диаметр — прямые, стороны равны в силу равенства, например, 4-х прямоугольных треугольников по двум катетам).
4)Как построить правильный восьмиугольник? (Провести серединные перпендикуляры к сторонам квадрата и соединить их точки пересечения и окружности)
4.Закрепление.
Что необходимо для создания орнамента?
— Построить правильные многоугольники, зная, что R=а ;
— Восьмиугольник строится с помощью серединных перпендикуляров к сторонам квадрата, вписанного в окружность.
Построим вначале шаблоны правильных многоугольников и начнём построение орнамента.
Пример орнамента:
5.Задание на дом.
Закончить построение орнамента.
№384(а,б).(Н.В.Гвоздович)
Анализ урока.
Данный урок является первым уроком по теме «Правильные многоугольники», на нём вводятся термины, даётся их определения (многоугольник, правильный многоугольник).
Цели урока:
1. Знать определения правильных многоугольников, уметь строить правильный четырёхугольник, шестиугольник, 2n-угольник.
2. Воспитывать аккуратность, эстетичность, умение оценивать результаты своего труда и труда одноклассников.
Структура урока – традиционна. На этапе целеполагания мотивационной основой деятельности учащихся служит её практическая направленность (научится строить правильные многоугольники, чтобы создать красивый, оригинальный орнамент).
В устной работе первой части урока запланировано решение задач, направленных на активизацию мысли ребят. Дети поставлены в условия, в которых вынуждены анализировать, сравнивать, делать выводы. Эта часть урока направлена на повторение знаний, необходимых для изучения нового материала.
На этапе изложения нового материала мотивационной основой работы учащихся служит доступный уровень сложности, а также наличие внутрипредметных связей (Построение серединного перпендикуляра к отрезку, построение треугольника) и межпредметных связей (с черчением).
На всех этапах урока учитываются психологические особенности познавательной деятельности учащихся. В связи с этим применяется наглядный материал (плакат с изображением правильных многоугольников, заготовленные орнаменты из правильных многоугольников, всё, что выполняют учащиеся в тетрадях, демонстрируется на доске с параллельными комментариями хода действий). Учащиеся применяют свой жизненный опыт, отвечая на вопрос, где используются комбинации правильных многоугольников.
Результатом работы на данном уроке явились сделанные картонные модели правильных многоугольников, необходимые для выполнения домашней работы – сделать макет, например, паркета или потолочной плитки.
Класс: 10
Учебное пособие: В.В. Шлыков
1. Проверка д/з.
2. Математический диктант (на листочках; 10 – 15 минут).
1) Могут ли стороны выпуклого шестиугольника иметь длины:
1, 2, 3, 4, 5 и 14 см [Да] | 1, 2, 3, 4, 5 и 16 см [Нет]
2) Найдите сумму углов выпуклого
32 – угольника [5400°] | 17 – угольника [2700°]
3) Найдите количество сторон выпуклого многоугольника, сумма углов которого равна: 9000° [52] | 18000° [102]
4) Укажите общий вид выпуклых многоугольников, у которых все внешние углы:
тупые [остроугольные треугольники] | прямые [прямоугольники]
5) Укажите общий вид выпуклых многоугольников, у которых сумма внутренних углов
равна сумме внешних [четырехугольники] | меньше суммы внешних [треугольники], взятых по одному при каждой вершине.
6) Существует ли выпуклый многоугольник, у которого:
три острых и один прямой угол? [Нет]| три прямых и один острый угол? [Нет]
7) Существует ли выпуклый n – угольник, у которого:
65 диагоналей? [Да, n = 13] | 27 диагоналей? [Да, n = 9]
3. Новый материал и устные упражнения.
Определение. Многоугольник называется правильным, если у него равны все стороны и равны все углы.
Обозначение углов. Многоугольник, 1-й класс
Цели:
- научить чертить, обозначать и называть углы, записывать название углов при помощи знака “? ” и букв;
- развивать математическую речь учащихся, умение устанавливать закономерности;
- совершенствовать навык использования чертежного инструмента — линейки, умение измерять и чертить отрезок заданной длины;
- воспитывать интерес к изучению математики.
Оборудование: аппликации из геометрических фигур, таблицы.
Ход урока
1. Актуализация знаний. — Посмотрите на аппликации и скажите, из каких геометрических фигур сделаны человечки? (Круг, овал, квадрат, прямоугольник, треугольник, четырехугольник.)
— На какие группы можно разделить данные фигуры? (Фигуры с углами и фигуры без углов.)
— Назовите геометрические фигуры “без углов”, т.е. фигуры, ограниченные кривыми замкнутыми линиями. (Овал и круг.)
Назовите фигуры из группы тех, что “с углами”. (Квадрат, прямоугольник, треугольник, шестиугольник.)
Как по-другому можно назвать квадрат и прямоугольник? (Четырехугольники.)
Как назвать одним термином геометрические фигуры “с углами”? (Многоугольники.)
Назовите виды многоугольников. (Четырехугольник, треугольник, пятиугольник, шестиугольник.)
От чего зависит название многоугольника? (От количества углов в нем.)
— Итак, угол — это элемент многоугольника, но все-таки нужно уточнить, какая фигура называется многоугольником. Являются ли многоугольниками фигуры, изображающие шляпы человечков?
2. Выравнивание знаний.
Незнайка приготовил задание, какие линии он начертил.’ назовите их по именам. (Прямая а, отрезок АВ, луч ОМ.)
Какая линия называется прямой, отрезком, лучом? (Прямая -это линия, не имеющая начала и конца, которую нужно чертить по линейке. Отрезок-это часть прямой, которая имеет начало и конец. Луч-это часть прямой, которая имеет начало.)
Как по-другому можно прочитать имя данного отрезка? (Отрезок ВА, имя отрезка можно читать слева направо и справа налево.)
А можно ли по-другому прочитать название данного луча? (Нельзя, называем первую букву, которая обозначает начало луча.)
Что общего между прямой, лучом, отрезком? (Луч и отрезок являются частью прямой.)
Чем они различаются? (Отрезок можно измерить, а прямую и луч измерить нельзя, они бесконечны.)
Чем отличаются прямая и луч? (Прямую можно продолжить в двух направлениях, а луч — только в одном. Ведь с другой стороны он ограничен точкой. Это начало луча.)
3. Построение углов.
Какие фигуры: прямую, луч или отрезок — нужно выбрать для построения угла? (Нужно выбрать два луча.)
Незнайка выбрал два луча.
Построил ли он угол? (Нет.)
Почему? (Незнайка не совместил начало лучей.)
— Как должны располагаться лучи? (Лучи должны выходить из одной точки.)
Как называется эта точка? (Вершина угла.)
Как называются лучи? (Сторонами угла.)
Итак, что необходимо выбрать для построения угла? (Нужно выбрать точку и провести из нее два луча.)
Сейчас каждый из вас построит угол в тетради.
Каким инструментом будете пользоваться? (Линейкой.)
Обозначьте вершину красным карандашом, стороны - синим и зеленым.
— Давайте попробуем дать формулировку углу. Что такое угол? (Угол — это геометрическая фигура, для построения которой нужно выбрать точку и провести из нее два луча.)
4. Постановка учебной задачи и ее решение.
— Я очень рада, что сегодня на уроке присутствуют все 27 учеников нашего класса. Сколько углов вы построили? (Столько же, 27.)
Как же различать такое количество углов между собой? (Нужно дать углам имена.)
Как вы думаете, как можно обозначить угол? (Можно назвать вершина.)
Назовите угол, (Угол А)
А если я начерчу несколько углов с вершиной в точке А, то как их различать? (Надо как-то “полнее обозначать углы.)
У кого есть другие варианты обозначения? (Можно обозначить лучи: луч АВ и луч АС.)
— Итак, мы обозначили угол, попробуйте назвать его, прочитайте имя. (Угол ВАС, угол CAB, угол АСВ, угол ABC, угол А.)
— Нам нужно выбрать из предложенных вами правильные названия из данных. Для этого я предлагаю выйти к доске и показать угол.
(Дети по-разному показывают углы.)
Ребята, в математике принято показывать угол от одной из сторон к вершине и от вершины к стороне. Как вы думаете, какие из названных вами имен угла будут верными? (Угол ВАС, угол CAB, угол А.)
Правильно. Нужно запомнить, что букву, которой мы обозначаем вершину угла, необходимо называть второй.
Слово “угол” в математике обозначается таким знаком “? ”.
Итак, сколько букв может быть в имени угла? (Одна буква или три.)
Запишите название начерченного вами в тетради угла. Я запишу названия того угла, что на доске, а вы мне подскажете. (Угол ВАС, угол CAB, или просто угол А.)
Как записать названия углов, когда одна точка является началом нескольких лучей? (Сначала надо обозначить лучи, расставить буквы М, К, С, Д.)
Сколько углов получилось у нас? (Два, три, даже больше.)
Чтобы показать, какие углы нужно назвать, их обозначают дугами. Назовите и запишите углы, которые я обозначаю. (Угол МАК, угол САД, угол MAC.)
Есть ли еще углы на этом чертеже? (Да, угол МАД, угол КАД, угол САМ.)
При затруднении учитель показывает угол, и дети его называют. Это задание для “сильных” учеников, для их развития. Вслед за ними учатся и остальные.
5. Обобщение. Углубление знаний о многоугольнике.
Что надо помнить, называя и записывая углы? (Букву, обозначающую вершину, называем посередине.)
Как показывать угол? (Указкой надо “пройти” по лучу — от стороны к вершине, а потом от вершины — по другой стороне.)
6. Физминутка.
— Я покажу карточки с геометрическими фигурами. Увидев многоугольник, вы должны присесть. Увидев фигуру, не являющуюся многоугольником, вы должны встать.
Раз, два, три, четыре, пять,
Все умеем мы считать,
Отдыхать умеем тоже –
Руки за спину положим
Голову поднимем выше
И легко-легко подышим.
7. Закрепление по учебнику.
Стр. 29 № 68. Запиши имена углов, используя этот знак “? ”. Данное задание выполняется комментировано.
— Сколько имен может иметь один угол? (Три имени.)
8. Закрепление нового материала в группах. (Семь групп).
Каждой группе предлагается дать три варианта названия угла.
После выполнения задания командир группы отчитывается. Например:
9. Совершенствование устных вычислительных навыков.
Игра “Расшифруй слово”. Каждому значению выражения соответствует определенная буква. 4 — Г, 5 — Л, 6 — У, 7 — О.
10-8 + 4 = 6 У 2+7-5=4 Г 8-3+2=7 О 1+9-5=5 Л
— Прочитайте слово. (Угол.)
10. Поиск углов в окружающей действительности.
— Посмотрите внимательно вокруг и назовите предметы, в которых есть углы. (Доска, тетрадь, парта, окно и т.д.)
11. Итог.
— Чему новому научились на уроке? (Научились обозначать углы.)
Сколько имен может иметь угол? (Три.)
Что обозначает буква, которая по счету называется второй? (Эта буква обозначает вершину угла.)
Все ли было понятно на уроке? Сможет ли каждый из вас назвать угол и правильно прочитать имя угла? Если да — поднимите карточку с восклицательным знаком, если нет — с вопросительным знаком.
Сегодня на уроке все активно помогали Незнайке помочь усвоить новую тему “Угол”, но еще и уточняли знания о многоугольниках. Что каждый из вас узнал нового о них? (Как удобнее чертить, какая у угла граница. Как показать угол. Чтобы показать многоугольник, его надо закрашивать.)
— Дома начертите 3 угла и дайте им названия. Еще постройте многоугольник и покажите в нем углы, дайте имя.
Плитка вытянутый шестиугольник, гексагон в интерьере — ВикиСтрой
Иногда плитку в виде вытянутого гексагона называют листиком или заборчиком. Понятно почему — по форме такие плиточки в самом деле напоминают листья деревьев и штакетины деревянной ограды. На Западе же плитку такой вытянутой шестиугольной формы часто называют crayons, то есть «мелки». Что ж, тоже обосновано.
Описывая тренды выставки Cersaie-2018 , портал Rmnt.ru упоминал, что плитки в виде сот и гексагонов было заметно меньше. Да, но это касается только обычных, классических шестиугольников! А вот вытянутые, куда более интересные, сейчас активно используются дизайнерами в своих проектах. Обычные домовладельцы тоже стали чаще обращать внимание на такой вариант плитки для пола, ванной, санузла, кухонного фартука .
В этом проекте, где вытянутые гексагоны уложены в виде микса плитки разных оттенков зелёного, хаотично, они особенно похожи на россыпь листьев. Да, такой способ укладки довольно сложный, требует предварительной раскладки, тщательного планирования и подбора. Но зато какой оригинальный кухонный фартук получился!
Укладывать вытянутые шестиугольные плитки можно как по вертикали, так и по горизонтали. Оба варианта способны визуально или поднять, или расширить пространство и по-своему очень интересны.
Красивый эффект даёт сочетание, чередование вытянутых гексагонов разного оттенка. Иногда это контрастные цвета, иногда — оттенки одного основного цвета.
Дизайнеры не боятся сочетать разные виды гексагонов в отделке, например, стен душевой кабины и пола ванной комнаты.
Стена, облицованная вытянутыми гексагонами, может стать акцентной фокусной точкой. Например, как на этой кухне, где такой плиткой обрамили широкое окно.
Вновь необычный вариант укладки и яркий синий оттенок плитки превратили кухонный фартук в очень заметную деталь дизайна интерьера.
Форма гексагонов может быть и вот такой. В результате получается очень стильная и классическая укладка, которая несколько напоминает каретную стяжку мягкой мебели.
Форма и размеры плитки в виде вытянутых гексагонов могут быть очень разными. От более широких шестиугольников размера чуть больше мозаики до узких крупных плит, использующихся на полу. Подходит плитка crayons для самых разных интерьеров — и современных, и классических, всегда выглядя необычно, элегантно и стильно.
Что означает название «шестиугольник»?
Имя
<100
в США
с 1880 г.
Фамилия
<100
в США
в 2010 г.
Какой тип имени Hexagon ?
Какое наиболее точное происхождение названия Hexagon ?
Что означает шестиугольник?
Survey: Какой из следующих списков вы найдете наиболее интересным?
Какие имена можно было бы включить в список, озаглавленный «»?
Опрос: Что за забавный / полезный / полезный различных списков имен мы можем вам показать?
Мы заметили, что у вас есть микрофон.Если вы знаете, как произносится «Hexagon», просто нажмите кнопку, чтобы записать. Мы сохраним его, рассмотрим и опубликуем, чтобы помочь другим. Запрещены записи детей младше 18 лет.
Значение и происхождение
Что означает название «Шестиугольник»? Продолжайте читать, чтобы найти значения, отправленные пользователем, словарные определения и многое другое.
Происхождение и значение шестиугольника
Происхождение отправлено пользователем
Сообщите нам происхождение и / или значение Hexagon ниже
Происхождение шестиугольникаUnknownAfricanAfrican Голландский (африкаанс) AkanAmharicArabicAramaicBantuBerberChewaEgyptianEritreaGandaGeezHausaIgboIslamic / MuslimKikuyuKurdishLesothoLuhyaLuoNdebeleNigerianPersian / IranianPortugueseShonaSwahiliTswanaUrhoboXhosaYorubaZimbabweZuluAfrican AmericanAmericanAmerican SamoaAztec (науатль) CanadianDominican RepublicEnglishGrenadianHawaiianIslamic / MuslimJamaicanJewishMexicanPortuguesePuerto RicanNative AmericanArabicAramaicArmenianBengaliCambodianChineseGeorgianGujaratiHindiHinduIndian (санскрит) IndonesianIslamic / MuslimJapaneseJewishKannadaKazakh (Казахстан) KoreanKurdishKyrgyz (Кыргызстан) MalayalamMarathiMongolianNepaliOdiaPakistaniPersian / IranianFilipino (Филиппины) PunjabiRussianSanskritSlavicTajik (Таджикистан) TamilTelugaThaiTibetanUrduUzbek (Узбекистан) VietnameseAboriginalAmerican SamoaAustralianFijianFilipino (Филиппины) ГавайскийИсламский / МусульманинМаориНовая ЗеландияПолинезийский / ГавайскийАлбанскийАнглосаксонскийАрабскийАрамейскийАрмянскийБаскскийБолгарскийКельтскийХорватскийКипрЧешскийДатскийНидерландскийАнглийскийEst онскийфинскийфранцузскийГэльскийГрузинскийНемецкийгреческийеввритвенгерскийИсландскийИрландскийИсламский / МусульманскийитальянскийеврейскийКурдскийЛатинскийЛатышскийЛитскийМакедонскийНорвежскийПерсидский / ИранскийПольскийПортугальскийРумынский Румынский
Спасибо! Мы рассмотрим вашу заявку в ближайшее время!
Полный словарь Вебстера
существительное Hex «a * gon» Плоская фигура шести углов.Этимология: L. hexagonum , Gr. — шестигранный; «x шесть (аналогично E. шесть ) + угол
шестигранник + угольник .
- (геометрия) Многоугольник с шестью сторонами и шестью углами.
Где популярно название Hexagon?
Международный интерес для Hexagon
Интерес зависит от количества людей, просмотревших это имя из каждой страны, и масштабируется на основе общего количества просмотров по каждой стране, так что большие страны не всегда проявляют наибольший интерес.Темно-синий цвет на карте означает, что люди в стране с большей вероятностью будут искать это имя.
Более длинные столбцы на гистограмме указывают на то, что люди в стране больше заинтересованы в этом имени. Не все страны, проявившие интерес к названию, перечислены на гистограмме.
Интересные факты о названии Hexagon
- Насколько уникально название Hexagon? Из 6,122,890 записей в США.S. Общедоступные данные Управления социального обеспечения, имя Hexagon не присутствовало. Возможно, имя, которое вы ищете, встречается менее пяти раз в год.
- Странные вещи в названии Hexagon: Имя, написанное задом наперед, — Nogaxeh . Случайная перестановка букв в имени (анаграмма) даст Hoaxgen . Как ты это произносишь?
Какие шестиугольники посещали эту страницу?
Прошлая жизнь для
Hexagon родился 17 мая 1930 г.Не знаю, как вы к этому относитесь, но в вашем последнем земном воплощении вы были женщиной .Вы родились где-то на территории USA South-Central примерно на 1750 . По профессии артист, музыкант, поэт и храмовый танцор .
Вы всегда любили путешествовать, расследовать дела, могли бы стать детективом или шпионом. Вы должны развить в себе любовь к себе и способность вселять надежду в сердца людей. Амбиции — это еще не все. Истинное богатство похоронено в вашей душе.
Именной плакат для Hexagon
(нажмите, чтобы сохранить качественную версию)
- Источники:
- U.S. Бюро переписи населения: часто встречающиеся фамилии из переписи 2000 года (общественное достояние).
- Пересмотренный несокращенный словарь Вебстера 1913 г. через Международный совместный словарь английского языка (лицензия)
- Другие источники словарей: WordNet 3.1 Copyright 2006 Принстонский университет (лицензия).
- Викисловарь: названия и лицензии.
Что такое пчелы и шестиугольники? : Krulwich Wonders…: NPR
Решено! Загадка 2000-летней давности, жужжащая пчелы и слизывающая мед, начинается здесь, с этого улья. Посмотрите на соты на фотографии и спросите себя: (Я знаю, что вы задавались этим вопросом всю свою жизнь, но стеснялись спрашивать вслух …) Почему каждая клетка в этой соте представляет собой шестиугольник?
В конце концов, пчелы могут строить соты из прямоугольников, квадратов или треугольников …
Но пчелы почему-то выбирают шестиугольники. Всегда шестиугольника.
И не только ваш основной шестигранный шестиугольник. Им нравятся «идеальные» шестиугольники, то есть все шесть сторон имеют равную длину . Они идут на ювелирную версию — точную, именно так. Почему?
Ну, это очень старый вопрос. Более 2000 лет назад, в 36 г. до н. Э., Римский солдат / ученый / писатель Марк Теренций Варрон предложил ответ, который с тех пор получил название «Гипотеза медоносных пчел».Варрон подумал, что у такого поведения пчел есть серьезная причина. Может быть, соты, построенные из шестиугольников, могут вместить больше меда. Может быть, шестиугольники требуют меньше строительного воска. Может быть, здесь есть скрытая логика.
Мне нравится эта идея — что ниже потока В хаосе повседневной жизни могут быть изящные причины того, что мы видим. «Гипотеза медоносной пчелы» — это пример математики, раскрывающей тайну природы, поэтому здесь с помощью физика / писателя Алана Лайтмана (который недавно писал об этом в журнале Orion) — догадка Варрона.
Соты Essential
Соты, как мы все знаем, служат для хранения меда. Очевидно, что мед представляет ценность для пчел. Кормит их детенышей. Он поддерживает улей. Это воск, скрепляющий соты. Чтобы собрать нектар с цветка за цветком за цветком, требуются тысячи и тысячи пчелиных часов, десятки тысяч перелетов через луг, поэтому разумно предположить, что в улье пчелам нужна плотная, безопасная структура хранения, которая так же прост в сборке, насколько это возможно.
Так как это построить? Что ж, предположим, что вы начинаете свои соты с такой ячейки … совершенно случайной формы, без равных сторон, просто волнистая линия …
Если вы начнете так, как будет выглядеть ваша следующая ячейка? Что ж, вам не нужны большие промежутки между ячейками. Вы хотите, чтобы структура была плотной. Поэтому следующую ячейку нужно настроить так, чтобы она цеплялась за первую, вот так …
И третья ячейка, опять же, должна быть спроектирована так, чтобы соответствовать первым двум.Каждая ячейка будет немного отличаться, и это означает, говорит Алан Лайтман …
… этот метод построения сот потребует, чтобы рабочие пчелы работали последовательно, по одной, сначала создавая одну ячейку, а затем подгонка к ней следующей ячейки и т. д.
Но это не пчелиный путь. «Посмотрите на любую версию на YouTube, где пчелы строят соты», — говорит Алан, — и вы не увидите, как много пчел бездельничают, ожидая своей очереди построить соту.Вместо этого все работают. Они делают это коллективно, одновременно и постоянно.
Таким образом, «план волнистых ячеек» создает бездействующих пчел. Это пустая трата времени. Для пчел, которые собирают соты так, как это делают пчелы, проще, чтобы каждая клетка была точно такой же. Если стороны равны — «идеально» шестиугольные — каждая ячейка плотно прилегает к любой другой ячейке. Каждый может принять участие. Таким образом, соты — это, по сути, простая головоломка. Все детали подходят.
Хорошо, это объясняет, почему сотовые ячейки одинакового размера.Но вернемся к нашему первому вопросу: почему предпочтение отдается шестиугольникам? Есть ли что-то особенное в шестигранной форме?
Некоторые формы, которые вы сразу знаете, не подходят. Соты, построенные из сфер, будут иметь небольшие промежутки между каждым блоком …
… создание зазоров, для заделки которых потребуется дополнительный воск. Итак, вы можете понять, почему соты, построенные из сфер, не были бы идеальными. Пентагоны, восьмиугольники также производят промежутки. Что лучше?
«Это математическая истина, — пишет Лайтман, — что есть только три геометрические фигуры с равными сторонами, которые могут поместиться вместе на плоской поверхности, не оставляя зазоров: равносторонние треугольники, квадраты и шестиугольники.«
Итак, что выбрать? Треугольник? Квадрат? Или шестиугольник? Какой лучше? Здесь наш римлянин Марк Теренций Варрон внес свой большой вклад. Его «гипотеза» — и это была математическая догадка — предполагала, что структура, построенная из шестиугольников, вероятно, немного компактнее, чем структура, построенная из квадратов или треугольников. Он думал, что шестиугольные соты будут иметь «наименьший общий периметр». Он не мог доказать это математически, но он так думал.
Компактность имеет значение. Чем компактнее ваша структура, тем меньше воска потребуется для создания сот. Воск стоит дорого. Пчела должна потреблять около восьми унций меда, чтобы произвести одну унцию воска. Поэтому, если вы следите за своей восковой банкнотой, вам нужен самый компактный план здания, который вы можете найти.
И знаете что?
[Соты] абсолютно идеальны с точки зрения экономии труда и воска.
Чарльз Дарвин
Через две тысячи тридцать пять лет после того, как Маркус Теренций Варрон выдвинул свою гипотезу, математик из Мичиганского университета Томас Хейлз разгадал загадку.Оказывается, Варрон был прав. Шестиугольная структура действительно на более компактна. В 1999 году Хейлз представил это математическое доказательство.
Как подозревали древние греки, как утверждал Варрон, как всегда думали любители пчел, как однажды написал сам Чарльз Дарвин, соты — это шедевр инженерной мысли. Он «абсолютно идеален с точки зрения экономии труда и воска».
Пчелы, по-видимому, пожали плечами. Как говорит Алан Лайтман: «Они всегда знали, что это правда».
Эссе Алана Лайтмана «Симметричная вселенная», , первоначально опубликованное в журнале Orion Magazine, будет включено в его новую книгу Случайная вселенная: мир, который, как вы думали, вы знали , который выйдет в начале следующего года.Я также рекомендую эссе Иварса Петерсона в Science News, The Honeycomb Conjecture.
свойств полигонов | SkillsYouNeed
На этой странице рассматриваются свойства двумерных или «плоских» многоугольников. Многоугольник — это любая форма, состоящая из прямых линий, которую можно нарисовать на плоской поверхности, например на листе бумаги. Такие формы включают квадраты, прямоугольники, треугольники и пятиугольники, но не круги или любую другую форму, которая включает кривую.
Понимание форм важно в математике.Вам, безусловно, потребуется изучать формы в школе, но понимание свойств форм имеет много практических применений в профессиональных и реальных ситуациях.
Многие профессионалы должны понимать свойства форм, включая инженеров, архитекторов, художников, агентов по недвижимости, фермеров и строителей.
Возможно, вам понадобится разбираться в формах, когда вы делаете ремонт дома и делаете самодельные работы, при работе в саду и даже при планировании вечеринки.
При работе с полигонами важны следующие основные свойства:
- Число сторон формы.
- Угол расположен под углом между сторонами фигуры.
- Длина сторон формы.
Количество сторон
Многоугольники обычно определяются количеством сторон, которые у них есть.
Трехсторонние многоугольники: треугольники
Трехсторонний многоугольник — это треугольник. Существует несколько различных типов треугольников (см. Диаграмму), в том числе:
- Равносторонний — все стороны равны по длине, а все внутренние углы равны 60 °.
- Равнобедренный — имеет две равные стороны, у третьей разной длины. Два внутренних угла равны.
- Scalene — все три стороны и все три внутренних угла разные.
Треугольники также можно описать в терминах их внутренних углов (см. Нашу страницу Углы для получения дополнительной информации об именах углов). Сумма внутренних углов треугольника всегда составляет 180 °.
Треугольник с острыми углами и внутренними углами называется острым (или остроугольным) треугольником.Один с одним тупым углом и двумя острыми углами называется тупым (тупоугольным), а другой с прямым углом известен как прямоугольный.
Каждый из них будет , а также будет либо равносторонним, равнобедренным, или разносторонним .
Четырехсторонние многоугольники — четырехугольники
Четырехсторонние многоугольники обычно называют четырехугольниками, четырехугольниками или иногда четырехугольниками. В геометрии обычно используется термин четырехугольник .Термин четырехугольник часто используется для описания прямоугольного замкнутого открытого пространства, например «новички, собранные в четырехугольнике колледжа». Термин четырехугольник соответствует многоугольнику, пятиугольнику и т. Д. Вы можете встретить его время от времени, но на практике он обычно не используется.
Семейство четырехугольников включает квадрат, прямоугольник, ромб и другие параллелограммы, трапецию / трапецию и воздушный змей.
Суммарные внутренние углы всех четырехугольников составляют 360 °.
Квадрат : четыре стороны равной длины, четыре внутренних прямых угла.
Прямоугольник : четыре внутренних прямых угла, противоположные стороны равной длины.
Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны.
Ромб : особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как квадрат, сдавленный в стороны.
Трапеция (или трапеция) : две стороны параллельны, а две другие — нет. Длина сторон и углы не равны.
Равнобедренная трапеция (или трапеция) : Две стороны параллельны, а углы основания равны, что означает, что непараллельные стороны также равны по длине.
Воздушный змей : две пары соседних сторон имеют одинаковую длину; форма имеет ось симметрии.
Неправильный четырехугольник : четырехсторонняя форма, у которой все стороны не равны по длине и внутренние углы не совпадают.Все внутренние углы по-прежнему составляют 360 °, как и у всех других правильных четырехугольников.
Более четырех сторон
Пятиугольник называется пятиугольником.
Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон…
Имена многоугольников
Имена многоугольников образованы от префиксов древнегреческих чисел. Греческий числовой префикс встречается во многих названиях повседневных предметов и понятий.Иногда они могут помочь вам вспомнить, сколько сторон имеет многоугольник. Например:
- У осьминога восемь ног — у восьмиугольника восемь сторон.
- Десятилетие — это десять лет — у десятиугольника десять сторон.
- Современное пятиборье состоит из пяти видов — пятиугольник имеет пять сторон.
- Олимпийское семиборье состоит из семи этапов, семиугольник имеет семь сторон.
Префикс «поли-» просто означает «множественный», поэтому многоугольник — это фигура с множеством сторон, точно так же, как «полигамия» означает множественность супругов.
Есть имена для многих различных типов многоугольников, и обычно количество сторон более важно, чем имя формы.
Есть два основных типа многоугольников — правильный и неправильный.
Правильный многоугольник имеет стороны равной длины с равными углами между ними. Любой другой многоугольник — это неправильный многоугольник , который по определению имеет стороны неравной длины и углы между сторонами.
Окружности и формы, включающие кривые, не являются многоугольниками. — многоугольник по определению состоит из прямых линий.Смотрите наши страницы о кругах и изогнутых формах , чтобы узнать больше.
Углы между сторонами
Углы между сторонами фигур важны при определении многоугольников и работе с ними. См. Нашу страницу об углах, чтобы узнать больше о том, как измерять углы.
Существует полезная формула для определения суммы (или суммы) внутренних углов для любого многоугольника, а именно:
(количество сторон — 2) × 180 °
Пример:
Для пятиугольника (пятиугольной формы) расчет будет:
5–2 = 3
3 × 180 = 540 °.
Сумма внутренних углов любого (несложного) пятиугольника составляет 540 °.
Кроме того, если форма представляет собой правильный многоугольник (все углы и длины сторон равны), вы можете просто разделить сумму внутренних углов на количество сторон, чтобы найти каждый внутренний угол.
540 ÷ 5 = 108 °.
Следовательно, правильный пятиугольник имеет пять углов, каждый из которых равен 108 °.
Длина сторон
Помимо количества сторон и углов между сторонами, длина каждой стороны фигур также важна.
Длина сторон плоской фигуры позволяет вычислить периметра фигуры (расстояние вокруг внешней стороны фигуры) и площадь (количество пространства внутри фигуры).
Если ваша фигура представляет собой правильный многоугольник (например, квадрат в приведенном выше примере), то необходимо измерить только одну сторону, поскольку, по определению, другие стороны правильного многоугольника имеют одинаковую длину. Обычно используются деления, чтобы показать, что все стороны имеют одинаковую длину.
В примере с прямоугольником нам нужно было измерить две стороны — две неизмеренные стороны равны двум измеренным сторонам.
Обычно некоторые размеры не отображаются для более сложных форм. В таких случаях можно рассчитать недостающие размеры.
В приведенном выше примере отсутствуют две длины.
Недостающую длину по горизонтали можно вычислить. Возьмите более короткую известную длину по горизонтали из известной длины по горизонтали.
9 м — 5,5 м = 3,5 м.
По такому же принципу можно определить недостающую длину по вертикали. То есть:
3м — 1м = 2м.
Объединение всей информации: расчет площади многоугольников
Самым простым и основным многоугольником для вычисления площади является четырехугольник. Чтобы получить площадь, просто умножьте длину на высоту по вертикали.
Для параллелограммов обратите внимание, что вертикальная высота составляет НЕ длина наклонной стороны, а расстояние по вертикали между двумя горизонтальными линиями.
Это потому, что параллелограмм представляет собой прямоугольник с треугольником, обрезанным с одного конца и наклеенным на другой:
Вы можете видеть, что если вы удалите левый синий треугольник и прикрепите его к другому концу, прямоугольник превратится в параллелограмм.
Площадь — это длина (верхняя горизонтальная линия), умноженная на высоту, расстояние по вертикали между двумя горизонтальными линиями.
Чтобы определить площадь треугольника , вы умножаете длину на высоту по вертикали (то есть высоту по вертикали от нижней линии до верхней точки) и делите ее пополам.По сути, это потому, что треугольник — это половина прямоугольника.
Чтобы вычислить площадь любого правильного многоугольника , проще всего разделить его на треугольники и использовать формулу для площади треугольника.
Итак, для шестиугольника, например:
На диаграмме видно, что имеется шесть треугольников.
Площадь:
Высота (красная линия) × длина стороны (синяя линия) × 0,5 × 6 (поскольку треугольников шесть).
Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это намного сложнее.
См. Дополнительную информацию на нашей странице Расчетная область , включая примеры.
Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это намного сложнее. См. Нашу страницу Введение в тригонометрию для получения дополнительной информации.
Как в эти выходные увидеть «Большой шестиугольник» ярких зимних звезд
Высоко на юге на этой неделе около 21:30. по местному времени мы можем увидеть «Большой шестиугольник» ярких зимних звезд; узор, который впервые был придуман автором Хансом Аугусто Рей (1898-1977) в его популярном путеводителе по небу «Звезды — новый способ увидеть их».
Главным претендентом на известность г-на Рея была его роль создателя озорной маленькой обезьянки Любопытного Джорджа. Но он также был очень усердным астрономом-любителем и обоими его звездными проводниками (второй — детской книгой «Найди то»). Созвездия ») считаются устойчивой классикой 1950-х годов и никогда не выходили из печати с тех пор, как были впервые опубликованы компанией Houghton Mifflin Co. из Бостона.
Шестиугольник — это многоугольник с шестью сторонами, а наш небесный шестиугольник состоит из шести частей. 21 ярчайшая звезда.К югу и немного восточнее находится голубоватая звезда Сириус, в Большом Пса, «Собачья звезда», самая яркая из всех звезд. Сириус примерно в два раза массивнее нашего Солнца и светит в 25 раз ярче. Но главная причина, по которой он кажется таким ослепительным, заключается в том, что он расположен относительно близко к нам; на расстоянии 8,6 световых лет от нас. Похоже, это заклепка на ошейнике Большого Пса.
Связано: Самые яркие планеты в январском ночном небе: как их увидеть
«Большой шестиугольник» зимних звезд Рея.(Изображение предоставлено приложением SkySafari)На западе находится бело-голубой Ригель в созвездии Ориона, охотника. Сверхгигантская звезда, расположенная в 860 световых годах от Земли и одна из самых ярких из всех звезд, видимых невооруженным глазом. По оценкам, его яркость примерно в 120 000 раз больше, чем у нашего Солнца.
Еще выше находится оранжевый Альдебаран в созвездии Тельца, быка, гигантской звезды на расстоянии 65 световых лет от нас, с той разницей, что планета, по оценкам, в несколько раз массивнее, чем Юпитер, вращающийся вокруг нее.Бык мчится к Ориону, и V-образный узор из звезд представляет его лицо — звездное скопление Гиады — и мы могли бы думать об Альдебаране как о разгневанном налитом кровью глазе быка,
Затем в северном конце шестиугольника мы найдем желтый Капелла в созвездии Возничего. Находясь на расстоянии 42 световых лет от нас, это на самом деле четверная звездная система, состоящая из четырех звезд. Капелла известна как «звезда козла», и если вы внимательно посмотрите ниже и вправо, вы увидите три гораздо более тусклых звезды, широко известные как «козочки» или молодые козочки.
К югу и немного восточнее мы подходим к желто-оранжевому Поллуксу, более яркой из двух звезд, отмечающих головы близнецов-Близнецов. Немного более тусклый Кастор сразу примыкает к Поллуксу.
Наконец, снова на юг к Проциону, «Маленькой собачьей звезде» в Малом Псе. Как и Сириус, он относительно близко к нам, всего в 11,5 световых годах от нас. Процион — греческое имя, означающее «перед собакой». И действительно, из средних северных широт он поднимается примерно за 25 минут до появления Сириуса над горизонтом восток-юго-восток.
Что внутри?
Внутри шестиугольника можно найти две интересные вещи. Во-первых, это очень яркая красноватая звезда, Бетельгейзе, звезда, которая довольно часто появлялась в новостях в течение 2020 года, потому что она неожиданно исчезла.
Поскольку Бетельгейзе — красная звезда-сверхгигант, а жизнь таких звезд близка к концу, было предположение, что эта звезда вскоре может закончить свою жизнь в результате взрыва сверхновой. Однако ученые в конечном итоге определили, что аномальное затухание, скорее всего, было вызвано огромным количеством горячего материала, выброшенного в космос, образуя облако пыли, которое временно заблокировало звездный свет, исходящий от поверхности Бетельгейзе.
Кроме того, внутри шестиугольника находится пересечение небесного и галактического экваторов. Небесный экватор — это просто плоскость экватора Земли, спроецированная на небо. Галактический экватор лежит в плоскости вращения Млечного Пути. Эти двое наклонены друг к другу на 62 градуса. Это значение, соответствующее угловой разнице между осью Земли и осью галактики, показывает, насколько далеко Земля наклонена с точки зрения галактики, и наоборот.
Прочие модели
С таким количеством ярких звезд, охватывающих относительно небольшую область неба, легко представить себе другие геометрические формы.Фактически, до того, как мистер Рей создал свой Великий гексагон, он использовал Сириус, Процион, Поллукс, Кастор и Капеллу, чтобы сформировать широкий полукруг, который он назвал «Великой аркой Сириуса».
И мы также можем образовать большой, почти равносторонний треугольник, образованный звездами Бетельгейзе, Сириус и Процион, иногда называемый Зимним треугольником. Как и Летний треугольник Вега-Денеб-Альтаир, он перекрывает Млечный Путь, хотя и гораздо менее заметную его часть.
А другие превратили Гексагон Рея в нечто иное: небесный «G.«Просто начните с Альдебарана и двигайтесь против часовой стрелки вниз и вокруг, пока не дойдете до Ригеля. Затем вместо того, чтобы продолжать движение к Альдебарану, поверните вместо этого к Беллатрикс, звезде, которая отмечает левое плечо Ориона; третью по яркости звезду созвездия Ориона. Затем идите вперед. прямо на восток (слева) в сторону Бетельгейзе, завершая очертание шестой буквы алфавита.
Звезды на все времена года
Орион, Телец, Близнецы и другие окружающие звёзды обычно называют зимними созвездиями, но такие сезонные обозначения довольно расплывчаты.Они просто указывают время года, когда звездный узор лучше всего виден в удобные вечерние часы.
Помимо того факта, что эти созвездия являются летними для Австралии и Бразилии, их также могут увидеть осенью те, кто в Северном полушарии может смотреть в небо между полуночью и рассветом. Например, те же звезды и созвездия, которые сейчас находятся на небе в середине вечера, можно увидеть в 5 часов утра по местному летнему времени в середине октября.
Прецессия — еще один фактор, определяющий «сезон» созвездия.Прецессия относится к колебанию оси Земли; воронкообразное движение, описывающее одно полное колебание примерно за 25 800 лет. В настоящее время звезда Полярная звезда — это Полярная звезда. Но во времена пирамид, примерно 5000 лет назад, когда звезда Тубан была Полярной звездой, Орион, Телец и Близнецы были осенними созвездиями для Северного полушария. И когда яркая звезда Вега станет Полярной звездой в 14000 году нашей эры, они станут летними группировками.
Джо Рао работает инструктором и приглашенным лектором в планетарии Хайдена в Нью-Йорке.Он пишет об астрономии для журнала Natural History, Farmers ‘Almanac и других изданий. Следуйте за нами в Twitter @Spacedotcom и на Facebook.
Как найти Зимний шестиугольник или Зимний круг | Любимые образцы звезд
Зимний шестиугольник — он же Зимний круг — через Stellarium / ConstellationGuide.com.Зимний шестиугольник — он же Зимний круг — представляет собой собрание одних из самых ярких звезд на зимнем небе Северного полушария (летнее небо Южного полушария).Зимний шестиугольник — это не созвездие, а астеризм или выдающаяся группа звезд, образующих настолько заметный узор, что у него есть отдельное название. Внутри Зимнего шестиугольника находится астеризм меньшего размера, называемый Зимним треугольником.
Зимний шестиугольник состоит из шести звезд 1-й величины из шести различных созвездий: Ригель в Орионе, Альдебаран в Тельце, Капелла Возничего, Поллукс в Близнецах, Процион в Малом Псе и Сириус в Большом Псе. Дополнительная звезда 1-й величины, Бетельгейзе в Орионе, расположена ближе к центру шестиугольника.
Посмотреть на фотографиях сообщества EarthSky. | Пратек Панди из Бхопала, Индия, сделал эту фотографию Зимнего Круга 18 апреля 2021 года. Он написал: «Луна и Марс в зимнем круге».Лунные календари EarthSky снова в наличии! Мы гарантированно продадимся. Получите, пока можете!
К зимнему солнцестоянию в Северном полушарии, примерно 21 декабря, Зимний гексагон поднимется достаточно высоко над северо-восточным горизонтом, чтобы его можно было увидеть примерно к 9 часам вечера. местное время. Если подождать до 1 а.м., Зимний шестиугольник будет высоко над южным горизонтом. А к 5 часам утра опускается к юго-западному горизонту. Западная (правая) половина Зимнего гексагона, включая Альдебаран, Ригель и Сириус, заходит на западе перед восходом солнца.
Как и все звезды, звезды в Зимнем Гексагоне каждую ночь восходят и заходят на четыре минуты раньше. К концу января Зимний шестиугольник можно найти в тех же местах, о которых говорилось выше, примерно двумя часами ранее. В конце февраля — начале марта Зимний шестиугольник находится в вашем южном небе с наступлением темноты и ранним вечером.
Гоуришанкар Лакшминараянан на Лонг-Айленде, штат Нью-Йорк, поймал луну внутри Зимнего круга в начале апреля 2017 года.Чтобы найти Зимний шестиугольник или круг, сначала найдите легко узнаваемое созвездие Ориона. Три звезды пояса выдают его. Затем посмотрите на яркую голубоватую звезду справа внизу. Эта звезда — Ригель, юго-западный угол Зимнего круга и первая из шести звезд в шестиугольнике. Ригель — самая яркая звезда Ориона и седьмая по яркости звезда на ночном небе.
Проведите линию через звезды Пояса Ориона вверх, чтобы найти Альдебаран, красный глаз в созвездии Тельца-Быка. Альдебаран — вторая звезда в Шестиугольнике и самая яркая звезда в Тельце. Альдебаран — четырнадцатая по яркости звезда на небе.
Продолжайте движение вверх против часовой стрелки, чтобы найти следующую яркую звезду, Капеллу. Капелла, третья звезда в нашем путешествии и самая северная точка Зимнего шестиугольника, является шестой по яркости звездой на небе.
Когда мы начинаем заводить циферблат наших часов, мы сталкиваемся с двумя яркими звездами, близнецами в Близнецах.Поллукс, более яркий из двух, является нашим четвертым углом в шестиугольнике, а его «близнец» Кастор лишь немного слабее. Они отмечают головы близнецов, которых также зовут Поллукс и Кастор, братья из древней мифологии. Поллукс — 17-я по яркости звезда на небе, а Кастор — 24-я.
Наша предпоследняя остановка вокруг Зимнего шестиугольника — это яркая звезда под близнецами Процион. Процион — самая яркая звезда Малого Пса и фактически одна из двух названных звезд в созвездии. Для такого «второстепенного» созвездия Процион ярко сияет как седьмая по яркости звезда на небе.
Наконец, мы подошли к самой южной звезде Зимнего Шестиугольника и самой яркой из них: Сириусу. Сириус — самый яркий не только в Зимнем гексагоне, но и во всем ночном небе. Только Луна и некоторые планеты могут затмить Сириус.
Чтобы найти Зимний треугольник, возьмите две последние звезды, Сириус в Большом Пса и Процион в Малом Псе, затем направляйтесь к центру Шестиугольника, чтобы найти красноватую Бетельгейзе, звезду на плече в Орионе, чтобы образовать третий угол треугольника.Бетельгейзе — 10-я по яркости звезда на небе и вторая по яркости звезда Ориона.
Зимний круг синим цветом и Зимний треугольник красным.Чтобы получить представление об огромных размерах астеризма, пролет от самой южной звезды в шестиугольнике, Сириус, до самой северной звезды, Капеллы, покрывает примерно 1/3 купола неба.
В качестве бонуса темной и ясной безлунной ночью вы можете поискать мягко светящуюся реку звезд, которую мы называем Млечным путем, извилистую прямо через центр Зимнего гексагона.
Юпитер был найден внутри Зимнего круга в 2014 году. Каждый месяц круг виден, и луна проходит через него. Фото сделано другом EarthSky в Facebook герцогом Маршем из Индианы.Итог: Зимний шестиугольник — это гигантская форма, созданная из одних из самых ярких звезд на небе, включая Ригель, Альдебаран, Капеллу, Поллукс, Процион и Сириус.
Нравится EarthSky? Подпишитесь на нашу бесплатную ежедневную рассылку новостей сегодня!
Брюс МакКлюр
Просмотр статейОб авторе:
Брюс МакКлюр работал ведущим автором популярных страниц журнала «Сегодня вечером» на EarthSky с 2004 года.Он страстный поклонник солнечных часов, чья любовь к небу привела его к озеру Титикака в Боливии и плаванию в Северной Атлантике, где он получил свой сертификат астрономии в Школе океанского парусного спорта и навигации. Он также пишет и ведет общественные программы по астрономии и планетарии в своем доме в северной части штата Нью-Йорк и вокруг него.
Келли Кизер Уитт
Просмотр статейОб авторе:
Келли Кизер Уитт — научный писатель, специализирующийся на астрономии более двух десятилетий.Она начала свою карьеру в журнале Astronomy Magazine, а также регулярно писала в журналах AstronomyToday и Sierra Club, а также в других изданиях. В 2012 году была опубликована ее детская книга с картинками «Прогноз солнечной системы». Она также написала роман-антиутопию для молодых взрослых под названием «Другое небо». Когда она не читает и не пишет об астрономии и не смотрит на звезды, ей нравится путешествовать по национальным паркам, разгадывать кроссворды, бегать, играть в теннис и паддлбординг. Келли живет со своей семьей в Висконсине.
Шестиугольник числовых последовательностей
Сначала посчитаем количество монет (пятен, дисков и т. Д.), Необходимых для создания контура шестиугольника
Последовательность: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66 …
n-й член равен 6n. В этом легко убедиться, если вы начнете с угла и посчитаете точки на стороне вверх до но исключая следующий угол. Таких сторон шесть. Каждое число в последовательности на 6 больше предыдущего.
Древние греки изучали «многоугольные» числа. Вот как образуются треугольные и квадратные числа:
Шестиугольные числа образуются таким образом:
Последовательность: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231 …
n-й член равен n. (2n-1)
Каждое шестиугольное число также является треугольным числом
Гексагональные числа с центрированием являются результатом подсчета количества пятен, составляющих полный шестиугольник:
Последовательность: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331…
Мы можем найти формулу для n-го члена, разделив шестиугольник на 3 параллелограмма плюс центральное пятно.
Следовательно, n-й член равен 3n. (N-1) +1.
«Звезда» с числами (названная так Мартином Гарднером в книге «Путешествие во времени и другие математические недоразумения») выглядит так:
Последовательность: 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661 …
Мы снова можем разделить их, на этот раз на 6 параллелограммов плюс центральное пятно
, что дает нам формулу для n-го члена: 6n.(п-1) +1.
Пирамидальные шестиугольные числа образуются путем создания пирамиды из последовательности шестиугольных чисел. Так, например, 4-е число — это пирамида с 28 точками на нижнем слое, 15 точками на следующем слое, 6 мест на следующем и, наконец, 1 место на вершине — всего 50 мест.
Последовательность идет 1, 7, 22, 50, 95, 161, 252, 372, 525, 715, 946 …:
n-й член последовательности равен n. (N + 1). (4n-1) / 6
Мы можем сформировать пирамидальных шестиугольных чисел с центром , составив пирамиду из последовательности центрированных шестиугольных чисел.3
Итак, первые (и вторые) члены действительно кубы, как и все остальные. QED
Обратите внимание, что отсюда сами гексагональные центрированные числа могут быть представлены как разность между двумя соседними кубами.
шестнадцатеричных слов
Мейв Мэддокс
Большинство английских слов, начинающихся с hex , являются научными терминами, используемыми математиками, химиками и практикующими врачами.Однако некоторые из них встречаются в общем использовании.
В английском языке комбинационная форма hex- означает шесть .
шестиугольник
В геометрии шестиугольник — это плоская фигура, имеющая шесть сторон и шесть углов. Прилагательное шестиугольник . Наречие по шестиугольнику .
шестигранник
В геометрии шестигранник представляет собой твердую фигуру, имеющую шесть граней, особенно «правильный шестигранник» или куб.Вы встретите это слово, если будете заниматься оригами.
hexapod
Элемент pod означает фут . Гексапод — животное ростом шесть футов. Насекомые, у которых есть три пары ног, классифицируются в подтипе Hexapoda .
гексаграмма
В геометрии гексаграмма представляет собой фигуру из шести линий. Фигура может принимать несколько форм, но наиболее знакомой является форма двух пересекающихся равносторонних треугольников, как показано на Звезде Давида.Его использование в качестве опознавательного символа иудаизма началось в средние века, но его религиозное использование началось намного раньше. Этот символ под разными названиями появляется в образах индуизма, иудаизма, ислама, мормонизма, растафарианства, теософии и масонства. Этот символ, известный как «Печать Соломона», используется в магии и колдовстве. В символике геральдики гексаграмма называется «кефаль из шести точек». Китайская «Книга перемен» (И-Цзин) основана на 64 гексаграммах, которые не являются переплетенными треугольниками.Это фигуры из шести параллельных (целых или разделенных) линий.
шестнадцатеричный
В вычислениях и математике система числового обозначения, в которой в качестве основы используется 16, а не 10, называется шестнадцатеричной .
Два шестнадцатеричных слова вне математической области:
гексархия
Гексархия — это свободная конфедерация шести государств или королевств, каждое из которых управляется своим собственным правителем.
гекзаметр
Строка стиха, состоящая из шести метрических футов, называется гекзаметром .Гекзаметр был стандартным эпическим метром в классической греческой и латинской литературе.
Наконец, есть колдовское слово шестнадцатеричный , которое не имеет ничего общего с шестью.
Глагол hex , «заниматься колдовством», пришел в американский английский от немецких поселенцев Пенсильвании.
Немецкий hexen , «в шестнадцатеричный», связано с немецким словом Hexe , «ведьма». Английское слово hag происходит от того же источника. Самая ранняя английская форма, haegtesse , была эквивалентом «женщины с пророческими и пророческими способностями».Кого-нибудь удивляет, что это слово со временем превратилось в «уродливую, вспыльчивую, злобную старуху»?
Как существительное, шестигранник — это магическое заклинание или проклятие.
Хотите улучшить свой английский за пять минут в день? Оформите подписку и начните получать наши ежедневные советы и упражнения по написанию!
Продолжайте учиться! Просмотрите категорию «Словарь», просмотрите наши популярные публикации или выберите соответствующую публикацию ниже:
Прекратите делать эти досадные ошибки! Подпишитесь на Daily Writing Tips уже сегодня!
- Вы будете улучшать свой английский всего за 5 минут в день, гарантировано!
- Подписчики получают доступ к нашим архивам с более чем 800 интерактивными упражнениями!
- Вы также получите три бонусные электронные книги совершенно бесплатно!
.

 .
.