Как называется шестиугольник с равными сторонами: Шестиугольник как называется фигура

circ>) .

Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA , OB — радиусы правильного шестиугольника.

Обозначения на рисунке для правильного шестиугольника

n=6	число сторон и вершин правильного шестиугольника,	шт
α	центральный угол правильного шестиугольника,	радианы, °
β	половина внутреннего угла правильного шестиугольника,	радианы, °
γ	внутренний угол правильного шестиугольника,	радианы, °
a	сторона правильного шестиугольника,	м
R	радиусы правильного шестиугольника,	м
p	полупериметр правильного шестиугольника,	м
L	периметр правильного шестиугольника,	м
h	апофемы правильного шестиугольника,	м

Основные формулы для правильного шестиугольника

Периметр правильного шестиугольника

Полупериметр правильного шестиугольника

Центральный угол правильного шестиугольника в радианах

Центральный угол правильного шестиугольника в градусах

Половина внутреннего угла правильного шестиугольника в радианах

Половина внутреннего угла правильного шестиугольника в градусах

Внутренний угол правильного шестиугольника в радианах

Внутренний угол правильного шестиугольника в градусах

Площадь правильного шестиугольника

Отсюда получим апофему правильного шестиугольника

Как нарисовать шестиугольник с равными сторонами

Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA , OB — радиусы правильного шестиугольника.

Обозначения на рисунке для правильного шестиугольника

n=6	число сторон и вершин правильного шестиугольника,	шт
α	центральный угол правильного шестиугольника,	радианы, °
β	половина внутреннего угла правильного шестиугольника,	радианы, °
γ	внутренний угол правильного шестиугольника,	радианы, °
a	сторона правильного шестиугольника,	м
R	радиусы правильного шестиугольника,	м
p	полупериметр правильного шестиугольника,	м
L	периметр правильного шестиугольника,	м
h	апофемы правильного шестиугольника,	м

Основные формулы для правильного шестиугольника

Периметр правильного шестиугольника

Полупериметр правильного шестиугольника

Центральный угол правильного шестиугольника в радианах

Центральный угол правильного шестиугольника в градусах

Половина внутреннего угла правильного шестиугольника в радианах

Половина внутреннего угла правильного шестиугольника в градусах

Внутренний угол правильного шестиугольника в радианах

Внутренний угол правильного шестиугольника в градусах

Площадь правильного шестиугольника

Отсюда получим апофему правильного шестиугольника

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты.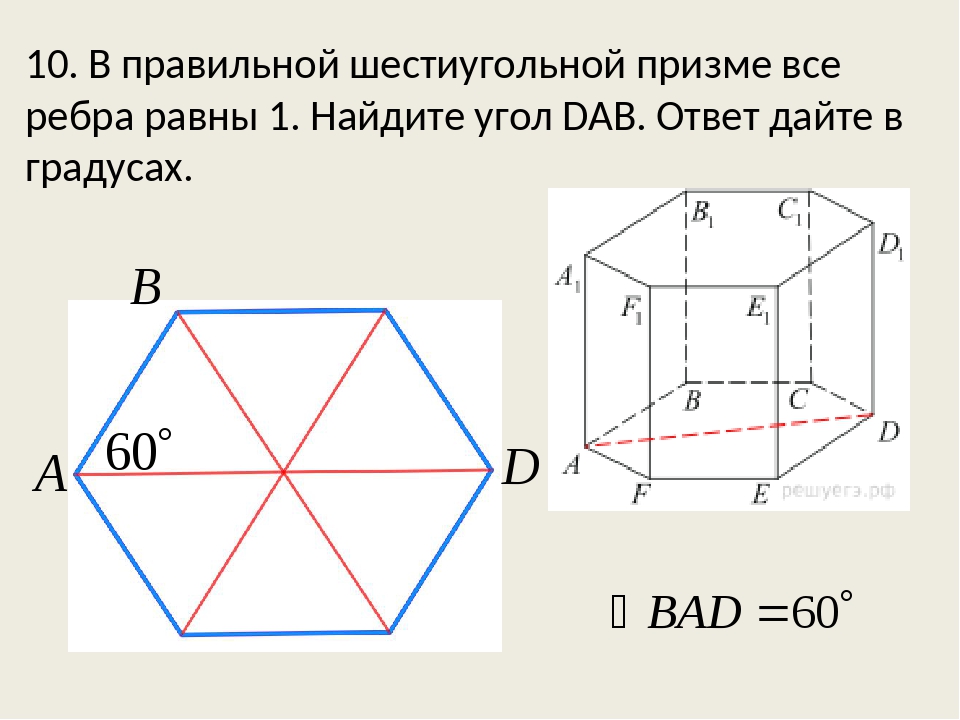

Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны

Автор Глеб Захаров На чтение 6 мин. Просмотров 1.5k. Опубликовано 25.06.2019

Двумерные правильные многоугольники везде

Немногие геометрические фигуры столь же разнообразны, как многоугольники. Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.

В геометрии многоугольник – это любая двумерная форма, которая удовлетворяет следующим условиям:

• Состоит из трех или более прямых
• Закрыто без отверстий или разрывов в форме
• Имеет пары линий, которые соединяются в углах или вершинах, где они образуют углы
• Имеет равное количество сторон и внутренних углов

Двумерный означает плоский, как лист бумаги. Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.

Специальный вид многоугольника может иметь углы, которые не все равны. В этом случае он называется неправильным многоугольником.

О полигонах

Название многоугольник происходит от двух греческих слов:

• Poly , , что означает много .
• Гон , что означает угол

Формы, которые являются полигонами

• Треугольник (треугольник): 3 стороны
• Тетрагон (квадрат): 4 стороны
• Пентагоны: 5 сторон
• Шестиугольник: 6 сторон
• Семиугольник: 7 сторон
• Восьмиугольники: 8 сторон
• Нонагон: 9 сторон
• Декагон: 10 граней
• Undecagon: 11 сторон
• Додекагоны: 12 сторон

Как называются полигоны

Названия отдельных многоугольников получаются из числа сторон или углов, которыми обладает форма. Полигоны имеют одинаковое количество сторон и углов.

Общим названием для большинства полигонов является греческий префикс «сторон», прикрепленный к греческому слову «угол» (gon).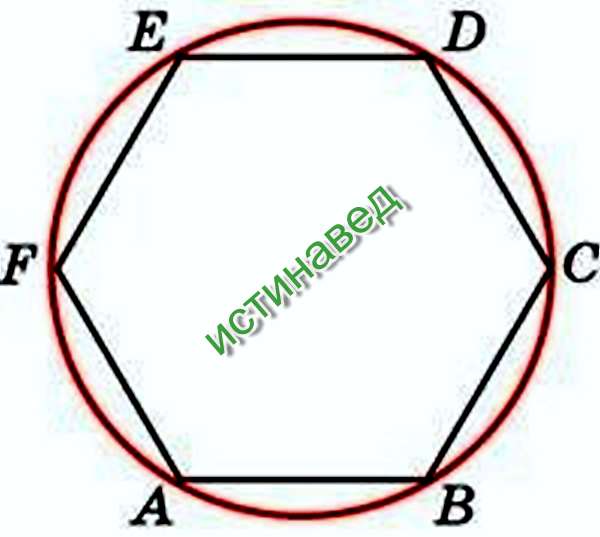

Примеры этого для пяти- и шестигранных правильных многоугольников:

• Пента (по-гречески означает пять) + гон = Пентагон
• Гекса (по-гречески означает шесть) + гон = шестиугольник

Есть исключения из этой схемы именования. В частности, со словами, которые чаще всего используются для некоторых полигонов:

• Треугольник . Использует греческий префикс Tri , но вместо греческого гона используется латинский угол . Trigon – правильное геометрическое имя, но оно используется редко.
• Четырехсторонний. Производный от латинского префикса quadri, , означающего четыре, прилагается к слову боковой, , которое является еще одним латинским словом, означающим сторона .
• Квадрат . Иногда четырехсторонний многоугольник (квадрат) называется четырехугольником или четырехугольником .

N-угольники

Полигоны с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именовании Таким образом, 100-сторонний многоугольник называется

гектогоном .

Однако в математике пятиугольники иногда удобнее называть n-гонами :

• 11-гонник: гендекагон
• 12-Гон: Додекагон
• 20-угольник: Icosagon
• 50-гонник: пятиконечный
• 1000-гон: чилиагон
• 1000000-гон: мегагон

В математике н-гоны и их греческие аналоги взаимозаменяемы.

Предел полигона

Теоретически, нет ограничения на количество сторон, которые может иметь многоугольник.

По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.

Классификация полигонов

Регулярные и неправильные полигоны

Полигоны классифицируются на основании того, равны ли все углы или стороны.

• Обычный многоугольник . Все углы имеют одинаковый размер, а все стороны равны по длине.
• Нерегулярный многоугольник . Углы или стороны одинакового размера не имеют одинаковой длины.

Выпуклые против вогнутых полигонов

Второй способ классификации полигонов – по размеру их внутренних углов.

• Выпуклые многоугольники : Внутренние углы не превышают 180 °.
• Вогнутые многоугольники . Как минимум, один внутренний угол превышает 180 °.

Простые и сложные полигоны

Еще один способ классификации полигонов – это то, как линии, образующие многоугольник, пересекаются.

• Простые полигоны : линии соединяются или пересекаются только один раз – в вершинах.
• Сложные полигоны : линии пересекаются более одного раза.

Названия сложных многоугольников иногда отличаются от названий простых многоугольников с одинаковым числом сторон.

Например:

• шестиугольник правильной формы – это шестигранный простой многоугольник.
• Звездообразная гексаграмма – это шестигранный сложный многоугольник, созданный наложением двух равносторонних треугольников.

Правило суммы внутренних углов

Как правило, каждый раз, когда сторона добавляется в многоугольник, например:

• От треугольника до четырехугольника (три-четыре стороны)
• От пятиугольника до шестиугольника (пять-шесть сторон)

еще 180 ° добавляется к сумме внутренних углов.

Это правило можно записать в виде формулы:

(n – 2) × 180 °

где n равно числу сторон многоугольника.

Таким образом, сумма внутренних углов для шестиугольника может быть найдена с помощью формулы:

(6 – 2) × 180 ° = 720 °

Сколько треугольников в этом многоугольнике?

Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:

n – 2

В этой формуле n равно числу сторон многоугольника.

Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6 – 2) и додекагон на 10 треугольников (12 – 2).

Размер угла для правильных многоугольников

Для правильных многоугольников, у которых все углы одинакового размера, а стороны одинаковой длины, размер каждого угла в многоугольнике можно рассчитать путем деления общего размера углов (в градусах) на общее количество сторон.

Для правильного шестигранного шестигранника каждый угол равен:

720 ° ÷ 6 = 120 °

Некоторые известные полигоны

Фермы

Фермы часто имеют треугольную форму. В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам, и видны в Эйфелевой башне.

Пентагон

Пентагон – штаб-квартира Министерства обороны США – берет свое название от его формы. Здание представляет собой пятисторонний, правильный пятиугольник.

Главная пластина

Другой известный пятисторонний правильный пятиугольник – домашняя тарелка на бейсбольном алмазе.

Поддельный Пентагон

Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и его иногда называют поддельным пятиугольником.

Снежинки

Каждая снежинка начинается с шестиугольника, но температура и уровень влажности добавляют ветви и усики, так что каждая из них выглядит по-разному.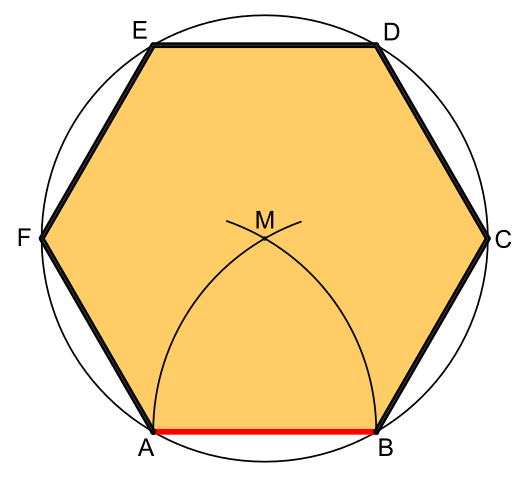

Пчелы и осы

Естественные шестиугольники также включают ульи, где каждая клетка в соте, которую пчелы строят для содержания меда, является шестиугольной. Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.

Тротуар гиганта

Шестиугольники также найдены на мощёной дорожке Гиганта, расположенной на северо-востоке Ирландии. Это естественная горная порода, состоящая из около 40000 взаимосвязанных базальтовых колонн, которые были созданы в виде лавы из-за медленно остывающего древнего вулканического извержения.

Восьмиугольник

Восьмиугольник – имя, данное кольцу или клетке, используемому в боях Ultimate Fighting Championship (UFC) – берет свое название от своей формы. Это восьмигранный правильный восьмиугольник.

Стоп Знаки

Стоп знак – один из самых знакомых дорожных знаков – еще один восьмигранный правильный восьмиугольник. Хотя цвет, формулировка или символы на знаке могут различаться, восьмиугольная форма знака остановки используется во многих странах мира.

Правильный шестиугольник

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами

.

Содержание 1 Свойства 2 Построение 3 Правильный шестиугольник в природе, технике и культуре 4 Примечания 5 Смотрите также 6 Ссылки

• Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности (), поскольку .
• Все углы равны 120°.
• Радиус вписанной окружности равен:

• Периметр правильного шестиугольника равен:

• Площадь правильного шестиугольника рассчитывается по формулам:

• Шестиугольники замещают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
• Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной (лемма Пала)^[1].

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15

.

Правильный шестиугольник в природе, технике и культуре

• Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.
• Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
• Гигантский гексагон — атмосферное явление на Сатурне.
• Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
• Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
• Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
• Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.

Слева направо: Пчелиные соты; Графен — одна из аллотропных модификаций углерода; Гигантский гексагон.

1. ↑ А. М. Райгородский Проблема Борсука. — М.: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9

• Шестиугольник
• Упаковка кругов на плоскости

• Шестиугольный мир (ЖЖ-сообщество)

;Правильные многоугольники
Основные	Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник
См. также	Многоугольник • Теорема Гаусса — Ванцеля

Футбольный мяч — Математическая составляющая

Футбольный мяч Поделиться    

Поверхность классического футбольного мяча состоит из слегка искривлённых 12 правильных пятиугольников чёрного цвета и 20 правильных белых шестиугольников. Модель мяча можно представить следующим образом.

Из 12 правильных пятиугольников и 20 правильных шестиугольников с равными сторонами можно сложить многогранник, называемый усечённым икосаэдром.

Икосаэдр — один из пяти правильных многогранников. Его название происходит от древнегреческих слов $ \varepsilon\acute\iota\kappa ο\sigma\iota $ — двадцать, $ \acute\varepsilon\delta\mkern-1mu\rho α $ — основание. У икосаэдра 12 вершин, 20 граней — правильных треугольников, 30 рёбер.

«Отрежем» (отсечём) вершины икосаэдра, отступив от вершин вдоль прямых, направленных в центр, на столько, чтобы оставшиеся части граней были правильными шестиугольниками. Срезы будут правильными пятиугольниками. Получившаяся фигура и есть усечённый икосаэдр.

Усечённый икосаэдр — один из полуправильных многогранников. Так называются многогранники, у которых все грани — правильные многоугольники нескольких разных типов (в отличие от правильных многогранников, все грани которых — одинаковые правильные многоугольники), а все вершины устроены «одинаково», т. е. многогранные углы при вершинах равны (совместимы).

При «наполнении воздухом» модели (усечённого икосаэдра) она принимает форму сферы, становится футбольным мячом. При этом вершины усечённого икосаэдра совпадут с «вершинами» мяча, рёбра перейдут в швы, а грани — в слегка искривлённые много­угольники на поверхности мяча. Таким образом получится мяч — центральная проекция усечённого икосаэдра на сферу.

Раздувание усечённого икосаэдра заставляет задуматься о степени близости к шару формы изначальной модели. Например, можно оценивать это сходство отношением радиусов концентрических сфер — описанной (проходящей через вершины; будущий мяч) и вписанной. Чем ближе это отношение к  единице, тем совершеннее модель, тем ближе она к идеально круглому мячу.

А нельзя ли придумать модель мяча, состоящую из плоских кусков (панелей), но более совершенную, чем классическая? Можно было бы взять не усечённый икосаэдр, а многогранник с большим числом вершин, но это не устраняет принципиальный недостаток — выступающие над вписанной сферой «пирамидки» (вершины), мешающие модели стать сферой. К тому же процесс изготовления существенно усложняется.

Классический пятнистый мяч появился только в 1950 году. Он был официальным мячом на чемпионатах мира с 1970 до 2002 года. Затем наступило время экспериментов, а в 2014 году на чемпионате мира в Бразилии состоялась премьера нового официального мяча, получившего название «Бразука».

Модель «Бразуки» совершеннее классической и при этом «является кубом»! Как и куб, она собирается из шести одинаковых плоских панелей, на ней выделяются восемь особых точек (вершин), в каждой из которых сходится по три панели.

На границе каждой панели есть четыре угла по $120°$. В вершинах модели встречаются три угла, сумма их величин равна $360°$, поэтому поверхность мяча вокруг вершины будет уплощённой, выступающей пирамидки не будет.

Панели можно склеивать по линиям границ между углами, поскольку длины этих линий одинаковы. Выпуклые участки границ склеиваются с вогнутыми, а линии подобраны так, что в каждой точке склейки кривизна выпуклого участка больше кривизны вогнутого. Из‐за этого плоские панели при склеивании изгибаются, образуя в результате замкнутую выпуклую поверхность. Возможность такой склейки гарантирует теорема А. Д. Александрова, академика и автора школьного учебника по геометрии.

В модели классического мяча вся кривизна сосредоточена в конечном числе «выступающих» вершин. А в модели «Бразуки» она распределена более равномерно (по длинным рёбрам), и из‐за этого модель становится более близкой к сфере.

Как построить равносторонний пятиугольник с помощью циркуля. Правильный пятиугольник: необходимый минимум информации

Уровень сложности: Несложно

1 шаг

Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.

2 шаг

Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.

3 шаг

Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.

4 шаг

Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.

• При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.

Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.

Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.

Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.

Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.

Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.

Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.

Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.

Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.

(на рисунке — завершенная, но незаполненная пентаграмма)

Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)

Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.

Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.

Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.

Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.

Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.

Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.

Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим

Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Получение с помощью полоски бумаги

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.

С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах». {\circ} = \frac{2 \sqrt{3} \sqrt{2} }{2} = \sqrt{6} $$

---

---

Что такое шестиугольник? — Определение, площадь и углы — Класс геометрии (видео)

Правильные шестиугольники

Шестиугольник — это пример многоугольника или многосторонней формы. Hex — это греческий префикс, означающий «шесть». У правильного шестиугольника шесть сторон равны или равны по размеру. Правильный шестиугольник равен выпуклому , что означает, что все точки шестиугольника направлены наружу. Все углы правильного шестиугольника равны и составляют 120 градусов.Это означает, что углы правильного шестиугольника в сумме составляют 720 градусов, или 6 умноженных на 120.

Неправильные шестиугольники

Неправильные шестиугольники могут выглядеть совершенно иначе. Неправильный шестиугольник также имеет шесть сторон, но они не одинаковой длины. Концы неправильных шестиугольников могут указывать внутрь или наружу. Когда точки шестиугольника направлены внутрь, даже если только одна точка направлена ​​внутрь, шестиугольник считается вогнутым шестиугольником .

Область поиска

Как и у всех правильных форм, есть простая формула, которую мы можем использовать для вычисления площади шестиугольника.Формула площади правильного шестиугольника выглядит так:

Где s — длина одной из сторон шестиугольника. Просто подставив длину одной из сторон в уравнение и введя ее в калькулятор, вы получите площадь шестиугольника.

Так, например, если у вас есть правильный шестиугольник, каждая сторона которого имеет длину 5 сантиметров, вы должны умножить три корня из трех на пять в квадрате и разделить ответ на два.Это даст вам 65 сантиметров в квадрате. Если вы используете другую единицу измерения длины стороны, например, метры, ответ будет в метрах в квадрате. И это все, что нужно сделать.

Краткое содержание урока

Шестиугольник — многоугольник с 6 прямыми сторонами. Это обычно встречается в природе, потому что это особенно эффективная форма. Правильный шестиугольник имеет стороны, равные , и углы, равные 120 градусам. Это означает, что углы правильного шестиугольника в сумме составляют 720 градусов.Вы можете найти площадь шестиугольника, используя измерение одной из сторон и формулу площади:

Шестигранник неправильной формы имеет стороны, размеры которых не совпадают, и точки могут быть обращены как внутрь, так и наружу. Шестиугольник даже с одной внутренней точкой считается вогнутым шестиугольником .

Hexagon — Определение, формула и примеры

В этом разделе мы познакомим вас с формулой шестиугольника.

Вы также узнаете о форме шестиугольника, примерах шестиугольника, шестиугольных формах, размерах шестиугольника, неправильном шестиугольнике, а также о площади шестиугольника на реальных примерах.

Ознакомьтесь с интерактивными симуляторами, чтобы узнать больше об уроке и попробовать свои силы в решении нескольких интересных практических вопросов о шестиугольниках в конце страницы.

Как следует из названия, шестиугольник состоит из шести сторон.

Имя разделено на шестиугольник, что означает шесть, и гония, что означает углы.

Шестиугольник — это двумерная форма, поскольку он имеет только длину и ширину.

Давайте узнаем больше об этой интересной форме.

План урока

Что такое шестиугольник?

Шестиугольная форма определяется как двухмерная геометрическая форма, состоящая из шести сторон, имеющих одинаковую или разную длину.

Давайте найдем несколько реальных примеров шестиугольника.

Наблюдали ли вы когда-нибудь за карандашом? А теперь давайте перевернем его и посмотрим, как он выглядит?

Эта форма тоже похожа на ваш карандаш? Посчитаем, сколько у него сторон.

Давайте посмотрим еще один пример:

Можете ли вы заметить фигуру выше на изображении ниже?

Да, диван похож на зеленую фигуру выше. Давайте посчитаем и количество сторон.

И в фигуре 1, и в форме 2 количество сторон равно 6, не так ли?

Следовательно, оба имеют шестиугольную форму, так как количество сторон равно 6.Обе формы шестиугольника отличаются внешним видом и размерами.

---

Типы шестиугольной формы

Подумайте немного, просто наблюдая за сторонами. Похожи ли две приведенные ниже фигуры? Давайте сравним их.

Первая форма, в которой размеры всех сторон шестиугольника одинаковы, называется правильным шестиугольником.

Вторая форма, в которой размеры каждой стороны шестиугольника различаются, называется неправильным шестиугольником.

Чтобы лучше понять концепцию правильных и неправильных шестиугольников, давайте посмотрим на моделирование ниже.

Подробнее о форме шестиугольника и его возможных размерах

Шестиугольники можно дополнительно разделить на две категории на основе измерения углов, образованных сторонами шестиугольников.

Выпуклый шестигранник	Вогнутый шестигранник
Если каждый внутренний угол в шестиугольнике меньше 180˚, он называется выпуклым шестиугольником.	Когда один или несколько внутренних углов шестиугольника составляют более 180 °, он называется вогнутым шестиугольником.

---

Свойства шестиугольника

Свойства шестиугольника следующие:

1. У шестиугольника шесть сторон.

2. Он также имеет шесть углов.

3. Имеет шесть углов.

Важные примечания

• Правильный шестиугольник также является выпуклым шестиугольником, поскольку внутренние углы меньше 180 градусов.

Уникальные свойства правильного шестиугольника

Уникальность этой шестиугольной формы объясняется нижеприведенными свойствами и уравнениями правильного шестиугольника.

1. Длина каждой стороны правильного шестиугольника равна.

2. Это симметричная форма, так как каждая сторона имеет одинаковую длину.

3. Противоположные стороны правильного шестиугольника всегда параллельны друг другу.

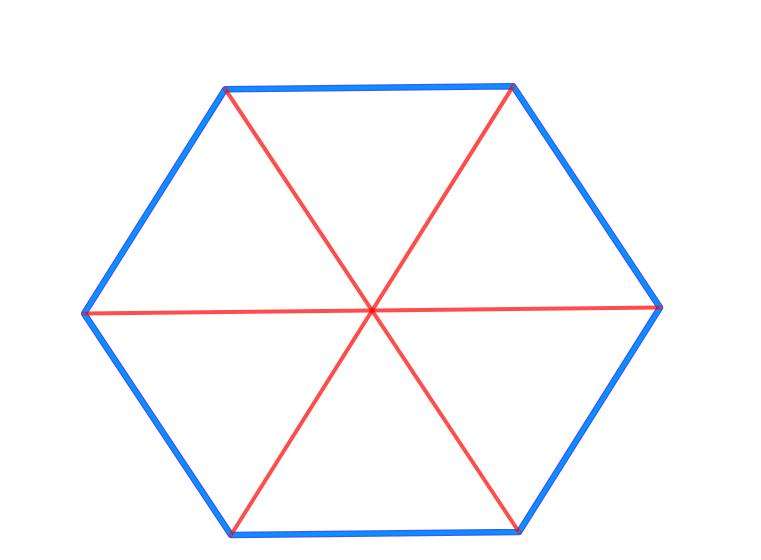
4. Правильный шестиугольник можно разделить на 6 равносторонних треугольников.

5. Каждый угол правильного шестиугольника равен 120 °.

6. Формула для числа диагоналей дается согласно уравнению ниже, где n = 6 для правильного шестиугольника.Следовательно, у него 9 диагоналей.

\ [\ begin {align} \ text {Количество диагоналей} & = \ dfrac {6 (6-3)} {2} \\ & = \ dfrac {6 \ times 3} {2} \\ & = \ dfrac {18} {2} \\ \ следовательно \ \ text {Количество диагоналей} & = 9 \ end {align} \]

7. Из этих 9 диагоналей от центральной точки проходят 6 линий. Давайте внимательно посмотрим и посчитаем количество линий, проходящих от центра.

8. Сумма внутренних углов, образованных правильным шестиугольником, равна 720˚ (потому что каждый угол равен 120˚, и имеется 6 таких углов в сумме 720˚).

   Дается формулой для правильного многоугольника, где n — количество сторон, которое имеет значение 6 для шестиугольника;

\ (\ text {Сумма внутренних углов} = \! (N-2) \ times180˚ \)

\ [\ begin {align} & \! \! = \! \! (6-2) \ times180˚ \\ & = 4 \ times180˚ \\ \ поэтому \ text {Сумма внутренних углов} & = 720˚ \ end {align} \]

Аналитический центр

• Hexagon относится к категории форм, которые могут заполнять плоскость, не теряя ее, как на рисунке ниже. Можете ли вы вспомнить две другие формы, которые подпадают под ту же категорию?

Площадь правильных шестиугольников

Скажем, каждая сторона правильного шестиугольника называется s. Чтобы найти площадь шестиугольника, мы используем следующую формулу.

Эта формула площади предназначена только для шестиугольников, которые являются правильными шестиугольниками. Размеры шестиугольника должны быть одинаковыми для его применимости.

---

Рози увидела два реальных примера шестиугольника, которые очень легко найти.Приведите два реальных примера шестиугольной формы.

Решение

\ (\ следовательно \) Гайка и соты — 2 примера

Макс нарисовал два вида шестиугольников.

A. Размеры первого шестиугольника со всех сторон 2 см

B. Второй шестиугольник имел размеры всех сторон переменной длины, как показано ниже.

• Сторона 1 = 2 см
• Сторона 2 = 3 см
• Сторона 3 = 3 см
• Сторона 4 = 2 см
• Сторона 5 = 4 см
• Сторона 6 = 4 см

Какой из двух шестиугольников, нарисованных Максом, будет правильным шестиугольником, а какой неправильным?

Решение

A — правильный шестиугольник, так как все стороны имеют одинаковую длину.

B представляет собой неправильный шестиугольник, так как все стороны имеют разную длину, что указывает на неравномерность размеров.

\ (\ следовательно \) A — правильный шестиугольник, B — неправильный шестиугольник

Рита должна найти площадь правильного шестиугольника. Если значение одной стороны составляет 3 см, какой будет площадь шестиугольника?

Решение

Применяя формулу площади правильного шестиугольника,

\ [\ text {A} = \ dfrac {(3 \ sqrt {3} \ text s ^ 2)} {2} \]

\ (\ text {Теперь, когда s = 3 см} \)

\ [\ begin {align} \ text {A} & = \ dfrac {(3 \ sqrt {3} \ times 3 ^ 2)} {2} \\ \ text {A} & = 23. 2 \\ \ text x & = 6.204 \ text {cm} \ end {align} \]

\ (\ следовательно \) Длина стороны = 6,204 см.

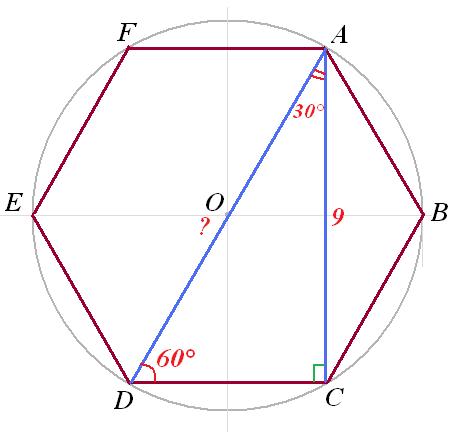
Льва попросили доказать, что правильный шестиугольник, разделенный на 6 частей, образует 6 равносторонних треугольников. Как вы думаете, как он мог это доказать?

Решение

Он привел следующие доводы, чтобы доказать свою точку зрения:

Поскольку значение каждого внутреннего угла составляет 120 °, линия, соединяющая 2 противоположные точки в шестиугольнике, разделит внутренний угол пополам, образуя 60 °.

Это произойдет одновременно со всеми сторонами, что оставит нам неизвестным только один угол шестиугольника.

Следовательно, применяя сумму трех углов треугольника, равного 180˚, мы получаем, что третий угол равен 60˚

Это доказывает, что правильный шестиугольник, когда он разделен на 6 частей, образует 6 равносторонних треугольников.

---

Интерактивные вопросы

Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

---

Подведем итоги

Надеемся, вам понравилось узнавать о шестиугольниках с помощью моделирования и интерактивных вопросов.Теперь вы сможете легко решать задачи по определению формы шестиугольника, формуле шестиугольника, примерам шестиугольника, формам шестиугольника, размерам шестиугольника, сторонам шестиугольника, свойствам шестиугольника, неправильному шестиугольнику и площади шестиугольника вместе с примерами из реальной жизни. .

О компании Cuemath

В Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.

---

Часто задаваемые вопросы (FAQ)

1. Что такое шестиугольник?

Шестиугольник определяется как двухмерная геометрическая форма с 6 сторонами.

2. Все ли шестиугольники имеют форму шестиугольника?

Да, все 6-гранные формы шестиугольники.

3. Каковы три атрибута шестиугольника?

Три атрибута шестиугольника:

• Имеет 6 сторон
• Имеет 6 углов
• Имеет 6 углов

4. Есть ли у шестиугольника равные стороны?

У шестиугольника не обязательно все стороны равны. У него также могут быть стороны переменной длины.

Шестиугольник с равными сторонами называется правильным шестиугольником, а шестиугольник с переменными сторонами — неправильным шестиугольником.

Название геометрических фигур — многоугольники, многогранники

Поиск инструмента

Название геометрических фигур

Инструмент для поиска названия геометрических фигур. Многоугольники — это геометрические фигуры в плоскости 2D, а многогранники — это геометрические фигуры в пространстве 3D

Результаты

Название геометрических фигур — dCode

Тег (ы): Geometry

Поделиться

dCode и др.

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Инструмент для поиска названия геометрических фигур.Многоугольники — это геометрические фигуры в плоскости 2D, а многогранники — это геометрические фигуры в пространстве 3D.

Ответы на вопросы (FAQ)

Как называется многоугольник с .

..?

Укажите dCode количество сторон и он найдет имя.

Пример: 6: HEXAGON
12: DODECAGON

В более общем смысле, многоугольников записываются с префиксом, указывающим их количество сторон, и суффиксом -угольник .

Вот список в виде таблицы всех различных правильных геометрических форм 2D-плоскости (таблица имен n-сторонних многоугольников ):

Как называется многогранник с…?

Укажите количество граней, и он найдет имя трехмерной геометрической фигуры.

Пример: 6: HEXAHEDRON

Пример: 12: DODECAHEDRON

Вот таблица всех правильных геометрических форм / многогранников трехмерного пространства (таблица названий n-гранных многогранников ):

Как учить геометрические фигуры?

Некоторые ресурсы для детей отлично подходят для изучения фигур и других геометрических фигур, например, здесь (ссылка)

Какие многоугольники обладают осевой симметрией?

Все правильные многоугольники имеют по крайней мере одну осевую симметрию.

Правильный многоугольник с таким количеством осей симметрии, сколько у него сторон.

Оси симметрии проходят через центр многоугольника и центр каждой стороны или каждой вершины / угла.

Какие многоугольники имеют центральную симметрию?

Все правильные многоугольников с четным номером стороны имеют центральную симметрию (центр многоугольника ). Многоугольники с нечетным числом сторон не имеют центральной симметрии.

Что такое многогранник?

Многогранник — это обобщение многоугольника / многогранника на все измерения.

Задайте новый вопрос

Исходный код

dCode сохраняет право собственности на исходный код онлайн-инструмента «Имя геометрических фигур». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) никакие данные, скрипты, копипаст или доступ к API не будут бесплатными, то же самое касается загрузки имени геометрических фигур для использования в автономном режиме на ПК, планшете, iPhone или Android!

Нужна помощь?

Пожалуйста, заходите в наше сообщество в Discord, чтобы получить помощь!

Вопросы / комментарии

Сводка

Инструменты аналогичные

Поддержка

Форум / Справка

Ключевые слова

многоугольник, многогранник, многогранник, геометрия, евклидово, форма, префикс, геометрический, сторона, грань, форма, 2d, 3d, имя, список

Ссылки

Источник: https: // www.dcode.fr/geometric-shapes

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.

геометрических фигур | Ресурсы Wyzant

В начальной школе вы узнаете несколько видов фигур; эта страница предоставит вам имена и примеры каждого из них.

Круг

Круглая форма, нарисованная так:

Треугольник

Форма с трех сторон.Иногда стороны равны, иногда — нет. Их названия иногда бывают разные в зависимости от длины сторон. Мы покажем вы обычные:

Равносторонний треугольник — у этого треугольника 3 равные стороны.

Равнобедренный треугольник — у этого треугольника 2 равные стороны.

Скаленовый треугольник — у этого треугольника нет равных сторон.

Квадрат

Форма коробки с четырьмя равными сторонами — противоположные стороны параллельны, нарисованная так:

Параллельный означает непересекающийся. Например, параллельные линии означают, что если два линии продолжались вечно, они никогда не пересекались друг с другом — они всегда быть на равном расстоянии друг от друга.

Прямоугольник

Еще одна форма коробки с двумя наборами равных сторон.Равные стороны расположены друг напротив друга. Стороны параллельны друг другу. Нарисовано это так:

Трапеция

Еще одна четырехсторонняя фигура с одним набором параллельных линий (другой набор линий не параллельно), нарисованный так:

Пентагон

Форма с пятью сторонами.Их можно нарисовать разными способами, но это самый распространенный:

Пятиугольник слева известен как правильный пятиугольник, потому что все его стороны одинаковой длины. Тот, что справа, также представляет собой общеизвестный пятиугольник в форме как дом.

Шестигранник

Фигура с шестью сторонами, нарисованная так:

Гептагон

Фигура с семью сторонами, нарисованная так:

Восьмиугольник

Фигура с восемью сторонами, нарисованная так:

Вы заметите, что восьмиугольник — это форма, которую они используют для знаков остановки.

Нонагон

Фигура с девятью сторонами, нарисованная следующим образом:

Декагон

Фигура с 10 сторонами, нарисованная следующим образом:

Додекагон

Фигура с 12 сторонами, нарисованная так:

Полигоны

Все эти формы — многоугольники.Многоугольник — это фигура, состоящая из линий, которые могут быть раскрашенным (все линии пересекаются, и у него есть «середина»).

Большая часть того, что вас попросят сделать с этими фигурами, — это распознать их и нарисовать. их, поэтому запомните, сколько у них сторон, как они выглядят и т. д. может включать вычисление площади и / или периметра этих фигур. Если вы пытаетесь чтобы узнать площадь или периметр, читайте нашу страницу на Площадь и периметр.

Полигонов — объяснения и примеры

Вы слышали о многоугольнике? Что ж, полигона нас окружают! Большинство обычных форм, которые вы видите или изучаете каждый день, — это многоугольники. Вы видите, что стена прямоугольной формы представляет собой многоугольник.

Вид спереди игральной кости, имеющей квадратную форму, представляет собой многоугольник. Кусочек пиццы имеет форму треугольника, а значит, и многоугольника.

Из этой статьи вы узнаете:

• Что такое многоугольники и как они выглядят.
• Различные типы полигонов.

Что такое многоугольник?

В математике многоугольник — это замкнутая двумерная фигура, состоящая из отрезков прямых, но не из кривых. Термин «многоугольник» происходит от греческого слова «поли -», означающего «много», и «- гон», что означает «углы».

Самыми распространенными примерами многоугольников являются треугольник, прямоугольник и квадрат. Проще говоря, многоугольники — это простые фигуры или фигуры, состоящие только из отрезков линий.

Примечание. Круги, трехмерные объекты, любые формы, включающие кривые, и любые формы, которые не замкнуты, не являются многоугольниками.

Полигоны были известны человеку с древних времен. Греки изучали невыпуклый правильный многоугольник в 7 ^-м веке до нашей эры на кратере Аристофана. Томас Брэдвардайн был первым известным человеком, изучавшим невыпуклые многоугольники в XIV ^{-х годах} века. Концепция многоугольников была обобщена в 1952 году Джеффри Колином.

Теперь, когда вы поняли, что такое многоугольник, давайте исследуем различные многоугольники и то, как они выглядят.

Типы многоугольников

В зависимости от сторон и углов, многоугольников подразделяются на различных типов, а именно:

1. Правильный многоугольник
2. Неправильный многоугольник
3. Выпуклый многоугольник
4. Вогнутый многоугольник

Правильный многоугольник Правильный многоугольник — это многоугольник, в котором все внутренние углы равны, а также все стороны равны.Есть разные типы правильных многоугольников.

Это:

• Треугольник : Равносторонний треугольник — это правильный многоугольник с тремя равными длинами сторон и тремя равными углами.

• Четырехугольник. Четырехугольник — это правильный многоугольник с четырьмя углами и четырьмя сторонами. Примеры четырехугольников:

a. Квадрат : четырехугольник, у которого четыре стороны равны, а четыре угла равны 90 градусам каждый.

б. Прямоугольник:

c. Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны

d. Воздушный змей : Две пары соседних сторон имеют одинаковую длину; форма имеет ось симметрии.

эл. Ромб : особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как квадрат, сдавленный в стороны.

• Пентагон : многоугольник с 5 равными сторонами и углом

• Шестиугольник: Правильный многоугольник с 6 равными сторонами и 6 равными углами.

• Шестиугольник: Правильный многоугольник с 7 равными длинами сторон и 7 одинаковыми углами.

• Восьмиугольник: У восьмиугольника 8 равных сторон и 8 равных углов. Лучшим примером восьмиугольника из реальной жизни является дорожный знак STOP.

• Nonagon: Имеет 9 равных сторон и 9 одинаковых углов.

• Хендекагон: Имеет 11 равных сторон и 11 равных углов.
• Додекагон: правильный многоугольник с 12 равными сторонами и 12 одинаковыми углами
• Трехугольник: Имеет 13 равных сторон и 13 одинаковых углов.
• Tetrakaidecagon : имеет 14 равных сторон и 14 одинаковых углов.
• Пентадекагон: Пятиугольник — это правильный многоугольник с 15 равными сторонами и 15 одинаковыми углами.
• Hexakaidecagon : имеет 16 сторон и углов.
• Гептадекагон : Имеет 17 сторон и углов.
• Octakaidecagon: Имеет 18 сторон и углов
• Enneadecagon: 19 сторон и 19 углов.
• Икосагон: Имеет равные стороны и 20 равных углов
• Шестиугольник: Имеет 100 равных сторон и 100 равных углов.
• Chiliagon: Имеет 1000 сторон
• Myriagon: 10000 сторон.
• Мегагон: Один миллион сторон.
• n-угольник : имеет n равных сторон.

Неправильный многоугольник

Неправильный многоугольник — это многоугольник с разными углами и длинами сторон.

Примеры неправильных многоугольников:

Выпуклый многоугольник

Это тип многоугольника, все внутренние углы которого строго меньше 180 градусов. Вершина выпуклого многоугольника всегда направлена ​​наружу от центра фигуры.

Вогнутый многоугольник

Если один или несколько внутренних углов многоугольника больше 180 градусов, он называется вогнутым многоугольником. Вогнутый многоугольник может иметь как минимум четыре стороны — вершина указывает внутрь многоугольника.

Ниже приведены несколько мнемоник, которые помогут запомнить названия некоторых многоугольников:

• У квадроцикла 4 колеса и, следовательно, четырехугольник.
• Вашингтон, округ Колумбия, в США имеет 5 сторон (Пентагон).
• Онейкомб H имеет 6 сторон ( H exagon).
• S эптагон имеет 7 сторон ( S четное).
• У осьминога 8 щупалец (восьмиугольник).
• Обе термины N onagon и N начинаются с буквы N.
• Десятиугольник имеет 10 сторон, так же как десятичная запятая D имеет 10 цифр.

Реальные приложения полигонов

Понимание форм важно в геометрии. Формы находят широкое применение в реальных приложениях.

Например:

• Плитки, по которым вы идете, имеют квадратную форму, что означает, что они являются многоугольниками.
• Ферма здания или моста, стены здания и т. Д., являются примерами многоугольников. Фермы имеют треугольную форму, а стены — прямоугольную.
• Прямоугольная часть стула, на которой вы сидите, является примером многоугольника.
• Прямоугольный экран вашего ноутбука, телевизора или мобильного телефона является примером многоугольника.
• Прямоугольное футбольное поле или игровая площадка — это пример многоугольника.
• Бермудский треугольник треугольной формы представляет собой многоугольник.
• Пирамиды Египта также являются примером многоугольника (треугольного)
• Звездообразные фигуры являются примером многоугольника.
• Дорожные знаки также являются примером многоугольников.

Пример

У Джона есть прямоугольный лист бумаги. Он хочет разрезать бумагу так, чтобы получить еще два многоугольника (кроме прямоугольника) того же размера и формы. Подскажите возможные пути.

Решение

Есть два возможных способа вырезать прямоугольный лист бумаги таким образом, чтобы он получил еще два многоугольника (кроме прямоугольника) того же размера и формы:

1. Он может вырезать прямоугольник лист бумаги ровно от центра по вертикали, чтобы получить два квадрата одинакового размера и формы.
2. Он может разрезать прямоугольный лист бумаги по диагонали, чтобы получить два треугольника одинакового размера и формы.

Практические вопросы

Угадайте многоугольник:

1. Я плоская фигура с 4 сторонами равной длины и углами 90 градусов по бокам.
2. Я — плоская фигура с 2 сторонами, каждая равной длины и углами в 90 градусов по бокам.
3. Я плоская фигура с 6 сторонами, и все внутренние углы больше 90 градусов.

Ответы

1. Квадрат
2. Прямоугольник
3. Шестиугольник

Предыдущий урок | Главная страница | Следующий урок

Геометрические фигуры

Щелкните здесь, чтобы получить бесплатные удобные для печати черно-белые рабочие листы с «фигурами».

Геометрические фигуры

Разница между 2D и 3D фигурами
Двумерные формы имеют 2 измерения, например длину и ширину, а трехмерные формы имеют дополнительное измерение, например высоту.Любая фигура, имеющая только площадь поверхности, является 2-мерной фигурой, а фигуры с объемом — 3-мерными.

Что такое многоугольник?
Многоугольник — это двумерная фигура, состоящая из прямых линий, которая является «замкнутой» (все линии соединяются). Треугольники, прямоугольники, пятиугольники, шестиугольники и т. д. являются многоугольниками.

Общие 2D-формы

Круг
Круг имеет круглую форму только с одной стороной и без углов.
Все точки круга находятся на одинаковом расстоянии от центра.

Квадрат
Имеет 4 прямых угла (90 °) и 4 равные стороны.
Это особый тип прямоугольника.

Прямоугольник
У него 4 стороны и 4 угла.
Все углы прямые (90 °).
Противоположные стороны равны и параллельны.

Треугольник
Имеет 3 стороны и 3 угла.
Три угла всегда складываются в 180 °.

Пентагон
Пятиугольник — это 5-сторонний многоугольник (плоская форма с прямыми сторонами).
Имеет 5 сторон и 5 углов.

Шестиугольник
Шестиугольник — это 6-сторонний многоугольник.
Имеет 6 сторон и 6 углов.

Heptagon
Heptagon — это 7-сторонний многоугольник.

Восьмиугольник
Восьмиугольник — это 8-сторонний многоугольник.

Нонагон
Нонагон — это 9-сторонний многоугольник.

Десятиугольник
Десятиугольник — это 10-сторонний многоугольник.

Общие 3D-фигуры

Что такое призма?
Призма — это трехмерная фигура, состоящая из двух одинаковых многоугольников. Каждый называется базой. Эти многоугольники не лежат на одной оси.
Для каждой стороны многоугольника будет параллелограмм (четырехсторонняя форма с параллельными противоположными сторонами). Все стороны плоские, а не изогнутые.
примеры: куб, прямоугольная призма, треугольная призма.

Куб
У него 6 граней.
Каждая грань имеет 4 ребра (и представляет собой квадрат).
Все стороны равны.
Имеет 12 граней.
Имеет 8 вершин (угловых точек).

Прямоугольная призма (кубоид)
Кубоид — это объект прямоугольной формы.
У него шесть плоских граней, и все углы прямые.
Все его грани прямоугольные.

Треугольная призма
Треугольная призма — это призма, состоящая из двух треугольных параллельных оснований и трех прямоугольных сторон.

Конус
Имеет плоское основание.
Имеет одну изогнутую сторону.

Квадратная пирамида
У нее 5 граней.
Четыре боковые грани представляют собой треугольники.
Основание квадратное.
Имеет 5 вершин (угловых точек).
Имеет 8 граней.

Треугольная пирамида
У нее три грани, которые являются треугольниками, и основание, которое также является треугольником.

Сфера
Совершенно симметрична.
Все точки на поверхности такое же расстояние от центра.
Не имеет кромок или вершины (углы).

Цилиндр
Имеет плоское основание и Плоская вершина.
База такая же, как верхний, а также промежуточный.
Имеет одну изогнутую сторону.

Щелкните здесь, чтобы получить бесплатные черно-белые рабочие листы «четырехугольники» для печати.

Четырехугольники

Четырехугольник — это четырехугольник с четырьмя углами. Некоторые четырехугольники имеют специальные имена из-за их сторон. У некоторых есть особые имена из-за их углы.
Некоторые типы также включены в определение других типов. Например квадрат, ромб и прямоугольник тоже параллелограммы.

Примеры:

Квадрат
4 прямых угла и 4 равные стороны.
Это также прямоугольник и параллелограмм.

Прямоугольник
4 прямых угла и противоположные стороны равны.
Это тоже параллелограмм.

Параллелограмм
2 пары параллельных сторон и противоположные стороны равны.

Ромб
2 пары параллельных сторон, все стороны равны.
Это тоже параллелограмм.

Трапеция
Только 2 стороны параллельны.
Это четырехугольник, который не является параллелограммом.

Воздушный змей
Две пары смежных сторон равны.

Треугольники

Треугольник имеет три стороны и три угла и состоит из прямых линий. Три угла всегда складываются в 180 °. Треугольник можно классифицировать по количеству его сторон имеют одинаковую длину. Или его можно классифицировать по типу углов.

Типы треугольников по длине

Равносторонний треугольник
Три равные стороны.
Три равных угла, всегда 60 °.

Равнобедренный треугольник
Две равные стороны.
Два равных угла.

Чешуйчатый треугольник
Нет равных сторон.
Нет равных углов.

Типы треугольников по углам

Острый треугольник
Все углы меньше 90 °.

Прямой треугольник
Имеет прямой угол (90 °).

Тупой треугольник
Имеет угол более 90 °.

Периметр треугольника
Периметр — это расстояние по краю треугольника.Просто сложите три стороны: p = a + b + c

Площадь треугольника
Самый распространенный способ найти площадь треугольника — это умножить основание и высоту и разделить результат на два. А = 1/2 ч

полигонов: сколько сторон?

Геометрическая фигура с тремя или более сторонами называется многоугольником или многогранником . Вот названия некоторых полигонов.

восьмиугольник 9 0028

3	треугольник, треугольник
4	четырехугольник, четырехугольник
5	пятиугольник
6	шестигранник
7	8 шестигранник		восьмиугольник
9	нонагон, эннеагон
10	десятиугольник
11	пятиугольник
12	двенадцатиугольник, двенадцатигранник
двенадцатигранник, двенадцатигранник
двенадцатиугольник, двенадцатиугольник
14	тетракаидекагон, тетрадекагон
15	пятидекагон
16	шестнадцатеричный
17	гептадекагон
18
20	icosagon

Сколько углов?

У многоугольника на столько же углов, сколько и сторон.