Как найти площадь зная диаметр и длину. Площадь круга: формула
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира.
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3).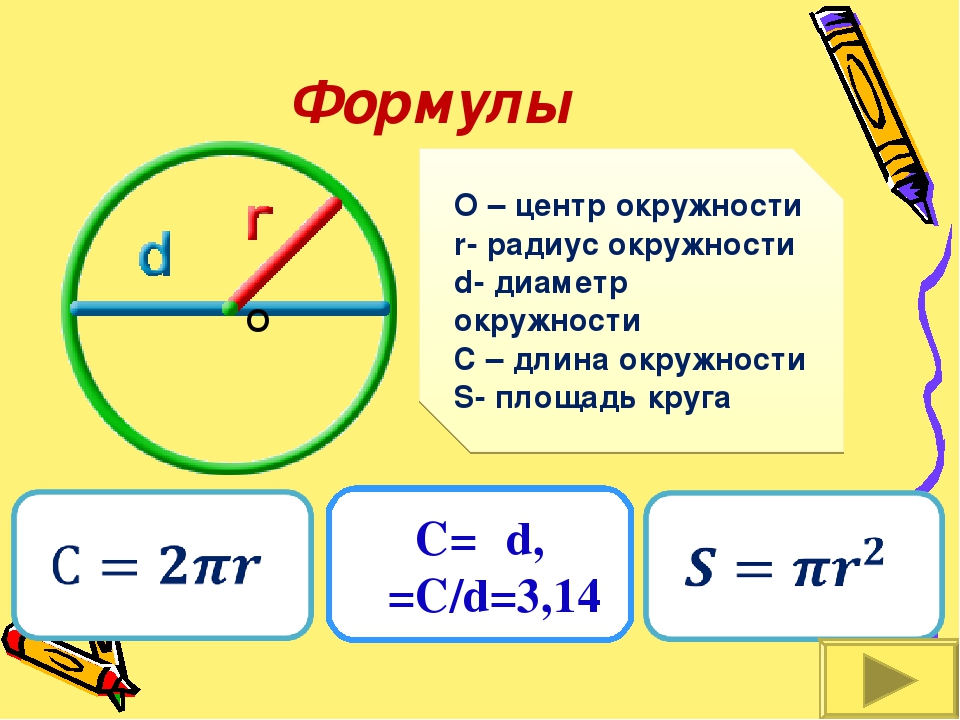 Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3. 14
14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R
= 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Как узнать площадь зная диаметр — MOREREMONTA
Онлайн калькулятор для расчета площади круга. Рассчитать площадь круга можно двумя способами: через радиус и диаметр круга. После выбора вариант расчета, задайте радиус или диаметр и нажмите кнопку «Рассчитать». Наш калькулятор выведет результат расчета площади, а также покажет подробное решение, с помощью которого можно посмотреть как был получен результат.
Круг – это плоскость, которая ограничена окружностью.
Как найти площадь круга?
Площадь круга рассчитывается двумя способами:
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Площадь круга: онлайн калькулятор
На данной странице представлен расчет площади круга с помощью калькулятора-онлайн. У вас есть возможность ознакомиться с разнообразными вариантами нахождения площади круга, зная диаметр, радиус или длину окружности или проследить за наглядными примерами решения подобных задач. 2$.
2$.
7 способов найти площадь прямоугольника
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
| Решения задачпо теме: Площадь круга |
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой. Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой. Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. |
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
allcalc.ru
формула, как найти длину круга и разницу между величинами
Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого.
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку.
 Он обозначается латинской буквой r.
Он обозначается латинской буквой r. - Хордой называется линия, соединяющая две произвольные точки лежащие на окружности.
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр. Он обозначается латинской буквой d.
- Окружность — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
[warning]Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях![/warning]
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r.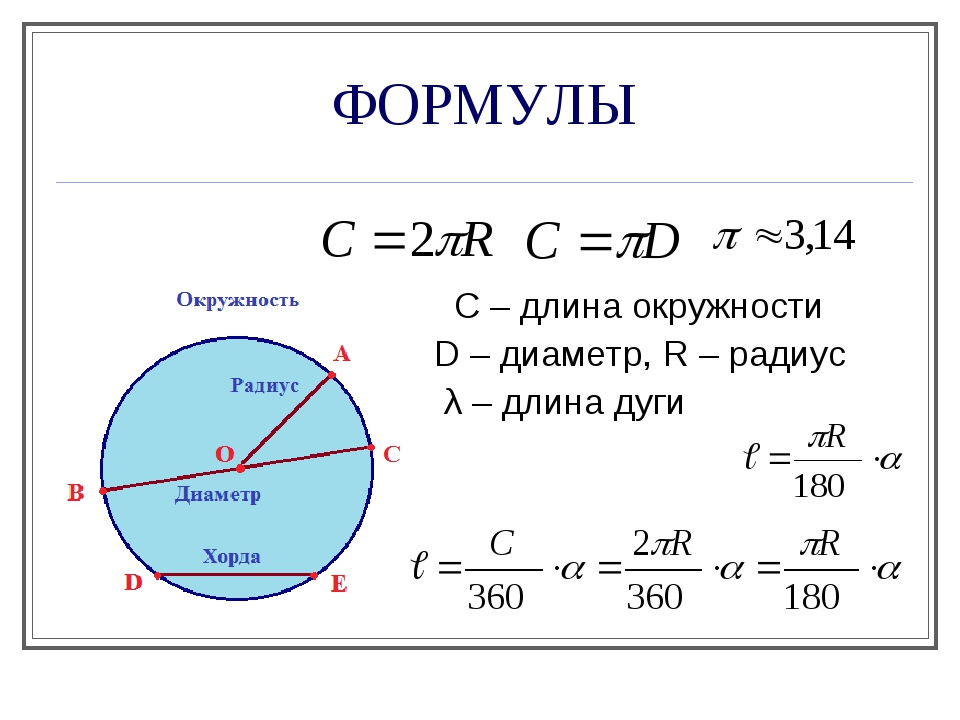 2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
Это интересно! Первый признак равенства треугольников: доказательство
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга . Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см. Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон
Длина окружности
Окружность, диаметр, хорда геометрия 7 класс
Заключение
Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Площадь и периметр круга. Как рассчитать длину окружности, если не указан диаметр и радиус круга
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.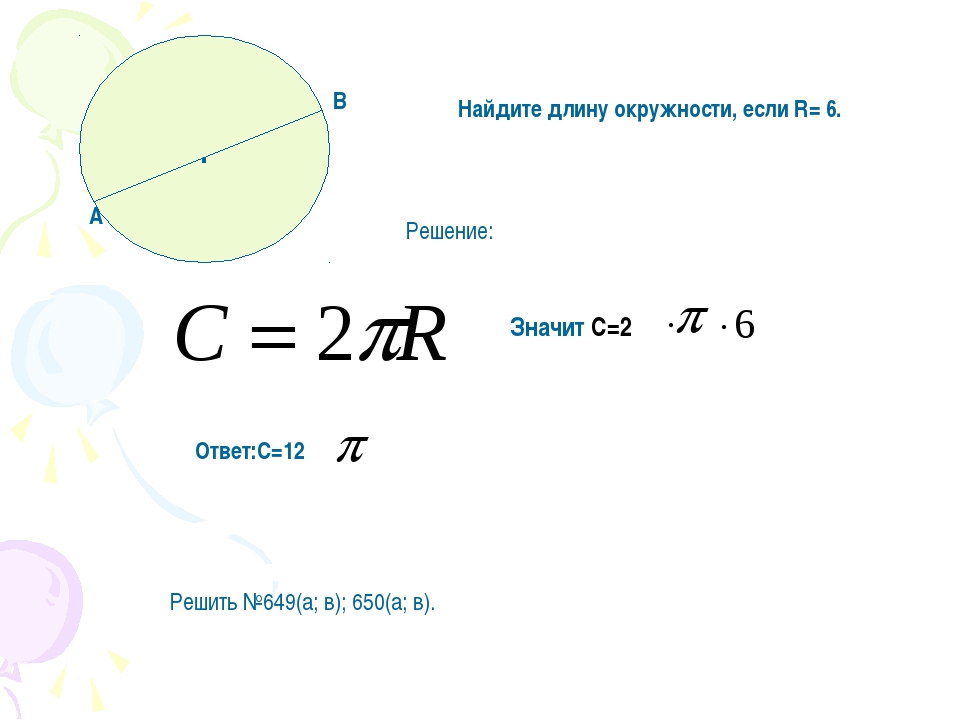
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.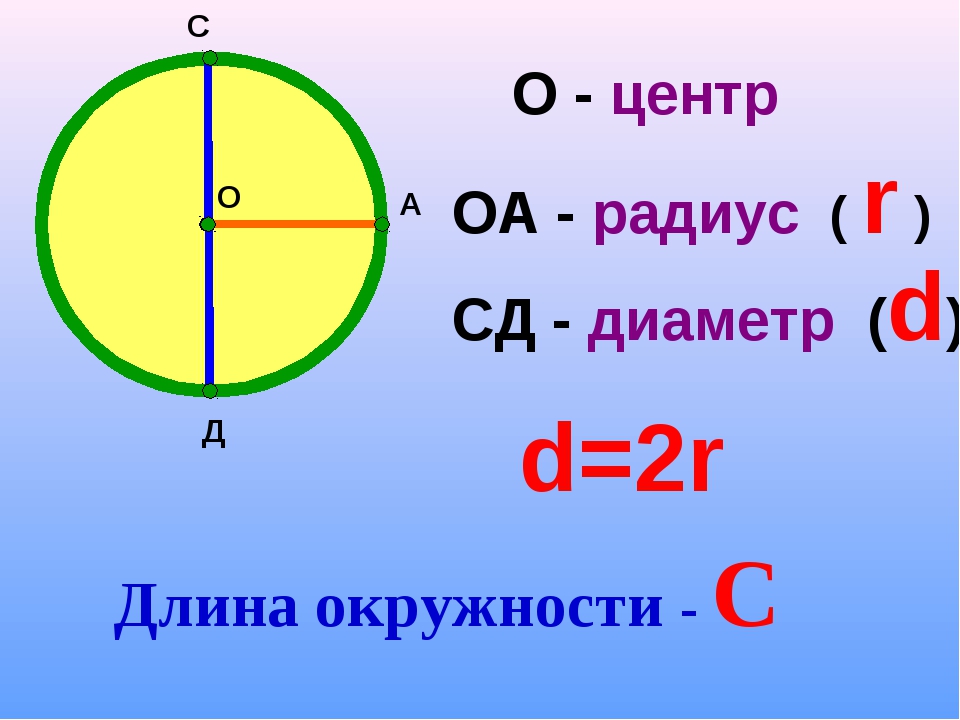 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \) – диаметр.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности
будем называть точку, которая задается в рамках определения 1. 0}{n}}=\frac{2τ}{2τ»} \)
0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Как найти площадь по диаметру — класс геометрии (видео)
Радиус
Чтобы понять это, давайте посмотрим, что такое радиус круга. Радиус круга — это длина отрезка прямой от центра круга до любой точки на окружности.
Радиус круга — это длина отрезка прямой от центра круга до любой точки на окружности.
Вы замечаете, как радиус соотносится с диаметром? Поскольку диаметр — это длина отрезка прямой, проходящего через центр круга от одной стороны круга до другой, на самом деле он состоит из двух радиусов.Другими словами, если d — это диаметр круга, а r — радиус окружности, то d = 2 r . Мы также можем посмотреть на это, так как радиус составляет 1/2 диаметра, или r = d /2 .
Формула
Это отличная новость! Вы понимаете почему? Все, что нам нужно сделать, это подставить r = d /2 в нашу формулу площади, и у нас есть способ найти площадь круга по его диаметру .
A = π ( d /2) 2
Решение
Если длина диаметра круга равна d , то мы можем найти площадь A , используя следующую формулу;
A = π ( d / 2) 2
Приложение
Круги постоянно появляются в мире вокруг нас, поэтому, естественно, возможность найти площадь круга чрезвычайно полезна в реальной жизни . Например, предположим, что вы хотите создать песчаный пляж на заднем дворе таким образом, чтобы пляж имел круглую форму.Вам нужно выяснить, сколько потребуется песка и сколько он будет стоить. Нанятые вами ландшафтные дизайнеры сообщают вам, что они определяют, сколько песка вам потребуется, исходя из площади земли, которую необходимо покрыть, и что они берут 0,50 доллара за квадратный фут.
Например, предположим, что вы хотите создать песчаный пляж на заднем дворе таким образом, чтобы пляж имел круглую форму.Вам нужно выяснить, сколько потребуется песка и сколько он будет стоить. Нанятые вами ландшафтные дизайнеры сообщают вам, что они определяют, сколько песка вам потребуется, исходя из площади земли, которую необходимо покрыть, и что они берут 0,50 доллара за квадратный фут.
Вы понимаете, что можете найти это место, если знаете диаметр вашего круглого пляжа, поэтому вы выходите на улицу и измеряете диаметр круглого участка, чтобы найти, что это 42 фута. Вы возвращаетесь внутрь и берете лист бумаги, карандаш и калькулятор, чтобы найти площадь ( A ) круга, учитывая, что диаметр ( d ) равен 42.Наша первая строка утверждает, что:
A = π ( d /2) 2
Мы вставляем наши известные числа во вторую строку:
A = π (42/2) 2
Мы вычисляем деление в третьей строке:
A = π (21) 2
В четвертой строке находим квадрат 21:
A = π (441)
И, наконец, приходим к выводу, что A ≈ 1385. 44 .
44 .
Мы видим, что площадь вашего пляжа будет примерно 1385,44 квадратных футов. Поскольку ландшафтные дизайнеры берут 0,50 доллара за квадратный фут, вы можете рассчитать стоимость, умножив 1385,44 0,5.
Стоимость = 1385,44 ⋅ 0,5 = 692,72
Вы подсчитали, что создание пляжа на заднем дворе обойдется вам в 692,72 доллара. Ух ты! И все это благодаря знанию диаметра круга! Конечно, это всего лишь один пример того, как определение площади круга по его диаметру может проявиться в нашей жизни.Вы встретите гораздо больше, поэтому здорово, что теперь вы точно знаете, как это сделать!
Резюме урока
Диаметр окружности — это длина отрезка прямой, идущего от одной стороны окружности к другой и проходящего через центр окружности. Радиус круга — это длина отрезка прямой от центра круга до любой точки на окружности. Таким образом, диаметр равен двум противоположным радиусам. Формула для площади круга : A = π r 2, где r — длина радиуса круга. Мы можем использовать наши знания о том, что диаметр состоит из двух радиусов, чтобы понять, что r = d /2. Обладая этими знаниями, вы можете переписать формулу для площади круга как A = π ( d /2) 2.
Мы можем использовать наши знания о том, что диаметр состоит из двух радиусов, чтобы понять, что r = d /2. Обладая этими знаниями, вы можете переписать формулу для площади круга как A = π ( d /2) 2.
Калькулятор площади круга Найдите и рассчитайте CDAR
Как рассчитать окружность, диаметр, площадь и радиусКалькулятор окружности находит площадь, радиус, диаметр и длину окружности круга с меткой a, r , d и c соответственно.
Этот калькулятор круга предназначен для тех, кто испытывает трудности при использовании формул вручную для определения площади, длины окружности, радиуса и диаметра круга. Уравнения будут приведены ниже, чтобы вы могли видеть, как калькулятор получает значения, но все, что вам нужно сделать, это ввести основную информацию. Все остальное сделает калькулятор.
Все остальное сделает калькулятор.
Окружность похожа на периметр в том смысле, что это общая длина, необходимая для рисования окружности.
Обозначим окружность как c .
c = 2 πr
или
c = πd
Это зависит от того, знаете ли вы радиус ( r ) или диаметр ( d )
например, рассчитать вручную.
Если r = 6 см, длина окружности равна c = 2 π (6) = 12 π см, если писать через π. Если вы предпочитаете числовое значение, ответ, округленный до десятых, будет равен 37.7 см.
Допустим, вам известен только диаметр? Если диаметр равен 8 см, то окружность равна c = π (8) = 8 π или 25,1 см с округлением до ближайшей десятой.
Формулы замечательно то, что вы можете манипулировать ими, чтобы найти неизвестное, если вам известна одна из других величин.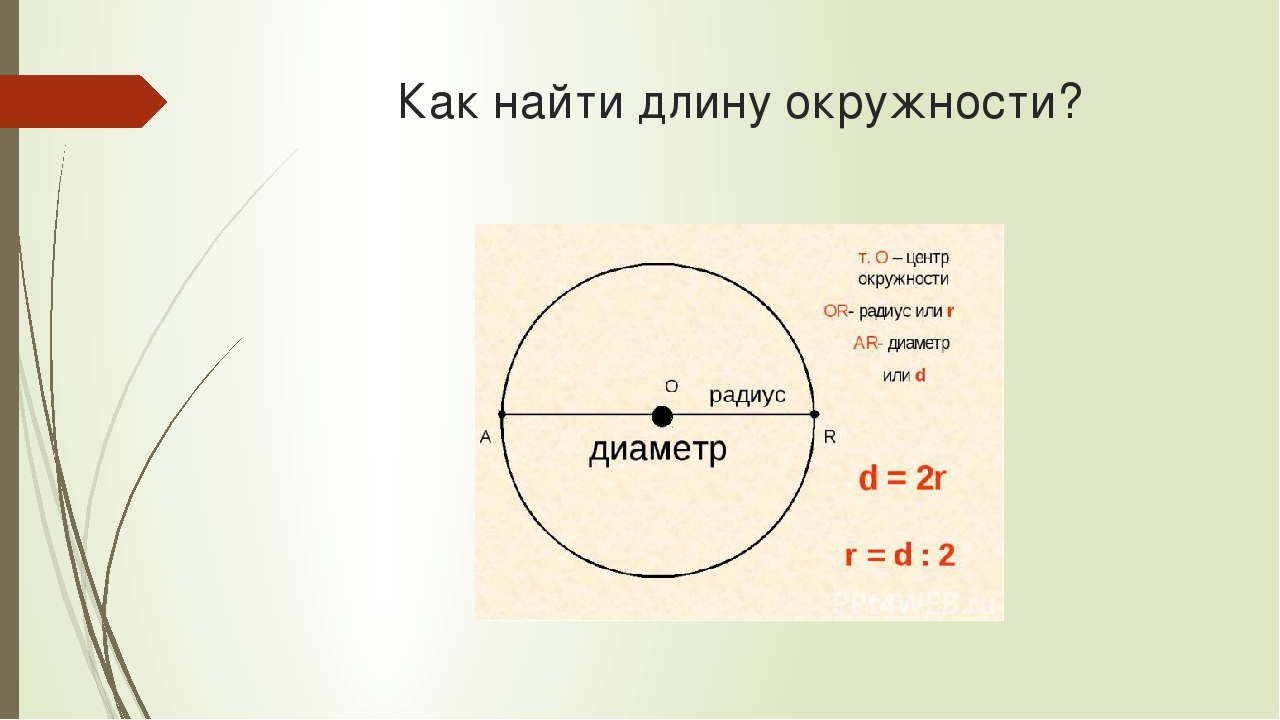 Например, если мы знаем длину окружности, но не знаем ее радиуса, вы можете решить c = 2 πr для r и получить \ (r = \ frac {c} {2 \ pi} \) .Аналогично, если вам нужен диаметр по окружности, просто возьмите c = πd и решите относительно d, чтобы получить d = \ (\ frac {c} {\ pi} \).
Например, если мы знаем длину окружности, но не знаем ее радиуса, вы можете решить c = 2 πr для r и получить \ (r = \ frac {c} {2 \ pi} \) .Аналогично, если вам нужен диаметр по окружности, просто возьмите c = πd и решите относительно d, чтобы получить d = \ (\ frac {c} {\ pi} \).
@mometrixFinding the Area:Нужна помощь в поиске площади круга? Мы вас позаботимся! Ссылка в биографии. ## math ## mathhelp ## Mathematics ## piday ## pi ## mometrix ## area
♬ оригинальный звук — Mometrix Test Preparation
Пусть a = площадь круга
a = πr²
Если вам известен диаметр, а не радиус, просто разделите диаметр на 2, чтобы получить радиус, и по-прежнему используйте формулу выше.
Опять же, формулу можно использовать для определения радиуса, если вы знаете площадь. Просто разделите a на π, чтобы получить r², и извлеките квадратный корень из
Просто разделите a на π, чтобы получить r², и извлеките квадратный корень из
.
Если вы хотите узнать диаметр по площади, выполните описанную выше процедуру, но удвойте результат, полученный для r . Это потому, что диаметр в два раза больше радиуса.
Попробуйте пример вручную, чтобы получить площадь.
Предположим, что r = 5 дюймов
a = πr²
a = π (25) = 25π
При округлении до десятых, площадь равна 78.5 квадратных дюймов.
Если вам известен диаметр, просто разделите на 2, чтобы получить радиус, и используйте ту же формулу, что и выше.
Конечно, вам не нужно выполнять все вычисления вручную, чтобы использовать этот калькулятор. Просто введите информацию, которую вы знаете, и остальное будет вычислено для вас почти мгновенно.
Как рассчитать окружность и площадь круга
Ключевые термины
o Круг
o Эквидистант
o Радиус
o Диаметр
o Окружность
o Pi ( π )
Цели
o Определите некоторые основные части круга, такие как радиус и диаметр
o Вычислить длину окружности
o Вычислить площадь круга
В этой статье мы рассмотрим геометрическую фигуру, которая не состоит из отрезков прямых, а имеет изогнутую форму: круг. Мы применим то, что мы знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Мы применим то, что мы знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Введение в круги
Представьте себе точку P , имеющую определенное местоположение; Затем представьте все возможные точки, которые находятся на некотором фиксированном расстоянии r от точки P. Некоторые из этих точек проиллюстрированы ниже. Если бы мы нарисовали все (бесконечное количество) точек, которые находятся на расстоянии r от P, , мы получили бы круг, который показан ниже сплошной линией.
Таким образом, круг — это просто набор всех точек , равноудаленных (то есть все на одинаковом расстоянии) от центральной точки ( P в приведенном выше примере). Расстояние r от центра круга до самого круга называется радиусом ; Диаметр , в два раза превышающий радиус (2 r ), называется диаметром . Радиус и диаметр показаны ниже.
Радиус и диаметр показаны ниже.
Окружность круга
Как и в случае с треугольниками и прямоугольниками, мы можем попытаться вывести формулы для площади и «периметра» круга.В отличие от треугольников, прямоугольников и других подобных фигур, расстояние по внешней стороне круга называется окружностью , а не периметром — однако концепция по существу та же. Однако вычислить длину окружности не так просто, как вычислить периметр прямоугольника или треугольника. Учитывая, что объект в реальной жизни имеет форму круга, один из подходов может заключаться в том, чтобы ровно один раз обернуть нить вокруг объекта, а затем выпрямить нить и измерить ее длину.Такой процесс проиллюстрирован ниже.
Очевидно, что по мере увеличения диаметра (или радиуса) круга круг становится больше, и, следовательно, длина окружности также увеличивается. Мы склонны думать, что, следовательно, существует некоторая связь между окружностью и диаметром. Оказывается, если мы измеряем длину окружности и диаметр любого круга, мы всегда обнаруживаем, что длина окружности чуть более чем в три раза больше диаметра.Два примера кружков ниже иллюстрируют эту точку, где D — диаметр, а C — длина окружности каждого круга.
Оказывается, если мы измеряем длину окружности и диаметр любого круга, мы всегда обнаруживаем, что длина окружности чуть более чем в три раза больше диаметра.Два примера кружков ниже иллюстрируют эту точку, где D — диаметр, а C — длина окружности каждого круга.
Опять же, в каждом случае длина окружности чуть больше трех диаметров круга. Если мы разделим длину окружности любого круга на его диаметр, мы получим постоянное число. Эта константа, которую мы обозначаем греческим символом π ( пи ), приблизительно равна 3.141593. Точное значение π неизвестно, и есть подозрение, что пи — иррациональное число (неповторяющееся десятичное число, которое, следовательно, не может быть выражено как дробь с целым числителем и целым знаменателем). Запишем вышеупомянутое соотношение: отношение длины окружности ( C ) к диаметру ( D ) является постоянным числом π.
Мы можем получить выражение для длины окружности через диаметр, умножив обе части выражения выше на D, , таким образом, выделив C.
Поскольку диаметр в два раза больше радиуса (другими словами, D = 2 r ), мы можем заменить 2 r на D в приведенном выше выражении.
Таким образом, мы можем вычислить длину окружности, если нам известен радиус круга (или, следовательно, его диаметр).Для большинства вычислений, требующих десятичного ответа, часто достаточно оценки π как 3,14. Например, если круг имеет радиус 3 метра, тогда его окружность C будет следующей.
Ответ выше точный (хотя он написан в терминах символа π ). Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Затем
Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Затем
Символ ≈ просто означает «примерно равно».
Практическая задача : Окружность имеет радиус 15 дюймов. Какая у него окружность?
Решение : Начнем с рисования диаграммы ситуации. Этот подход может быть очень полезным, особенно в ситуациях с кругами, где радиус и диаметр легко спутать.
Поскольку нам задан радиус, мы должны либо рассчитать длину окружности ( C ), используя выражение в терминах радиуса, либо мы должны преобразовать радиус в диаметр (удвоенный радиус) и использовать выражение в терминах диаметр. Для простоты воспользуемся первым подходом.
Это точный результат. Если нам нужен приблизительный десятичный результат, мы можем использовать π ≈ 3. 14.
14.
Площадь круга
Так же, как вычисление длины окружности сложнее, чем у треугольника или прямоугольника, так вычисляется и площадь. Давайте попробуем оценить площадь круга, нарисовав круг внутри квадрата, как показано ниже. Область круга заштрихована.
Нарисуем в круге вертикальный и горизонтальный диаметры; обозначим эти диаметры как имеющие длину D. Обратите внимание на то, что по сравнению с квадратом, квадрат должен иметь также стороны длиной D .
Мы знаем, что квадрат (который представляет собой прямоугольник, длина и ширина которого равны) со сторонами длиной D имеет следующую площадь: A квадрат (обратите внимание, что мы добавляем нижний индекс, чтобы идентифицировать эту площадь как площадь квадрат — аналогичный индекс добавим в случае площади круга):
Поскольку круг диаметром D , очевидно, имеет меньшую площадь, чем квадрат со сторонами длиной D, , мы знаем, что площадь круга должна быть меньше D 2 . Осмотрев, мы можем догадаться, что площадь A круга круга составляет примерно три четверти площади квадрата. Таким образом,
Осмотрев, мы можем догадаться, что площадь A круга круга составляет примерно три четверти площади квадрата. Таким образом,
Как оказалось, это предположение близко к реальному результату. Посредством некоторой более сложной математики, которая выходит за рамки учебника, можно показать, что площадь круга в точности следующая:
Обратите внимание, что снова появляется число π .Давайте теперь сравним этот точный результат с нашим предположением сверху. Мы просто немного изменим выражение, имея в виду, что радиус ( r ) равен половине диаметра ( D ), другими словами, D = 2 r.
Так как D = 2 r, тогда
Подставим это значение вместо r в выражение для площади круга; мы должны сделать замену дважды. Затем мы можем несколько упростить выражение.
Затем мы можем несколько упростить выражение.
Поскольку π приблизительно равно 3,14, то
Таким образом, наше предположение было очень близко к фактической площади!
Практическая задача : Круг имеет диаметр 6 сантиметров.Какова его площадь?
Решение : Обратите внимание, что указан диаметр , а не радиус. Таким образом, если мы хотим использовать выражение для площади в терминах радиуса, мы должны преобразовать диаметр в радиус (просто разделив диаметр пополам).
Теперь мы можем рассчитать площадь по следующей формуле.
Опять же, 9 квадратных сантиметров точный. Но,
Но,
Это приблизительный результат, но его будет достаточно во многих контекстах.
Практическая задача : Окружность окружности 8 π футов.Какова его площадь?
Решение : Мы узнали, что длина окружности тесно связана с радиусом (и диаметром). Таким образом, используя это известное значение длины окружности, мы можем вычислить радиус и использовать его для определения площади. Во-первых, давайте решим выражение для окружности, чтобы получить радиус.
Мы хотим выделить р; мы можем использовать тот же подход, что и при решении линейных уравнений.
Теперь, когда мы знаем радиус круга, мы можем вычислить его площадь.
Или,
Периметр круга — Веб-формулы
Периметр — это расстояние вокруг замкнутой фигуры, которое обычно измеряется в миллиметрах (мм), сантиметрах (см), метрах (м) и километрах (км).Эти единицы связаны следующим образом:
10 мм = 1 см
100 см = 1 м
1000 м = 1 км
Слово «периметр» также иногда используется вместо окружности.
Если мы знаем радиус
Учитывая радиус круга, длину окружности или периметр можно рассчитать по формуле bwloe:
Периметр (P) = 2 · π · R
где:
R — радиус окружности
π — Пи, приблизительно 3.142
Если мы знаем диаметр
Если мы знаем диаметр круга, длину окружности можно найти по формуле
Периметр (P) = π · D
где:
D — диаметр окружности
π — Пи, приблизительно 3,142
Если мы знаем район
Если нам известна площадь круга, длина окружности может быть найдена по формуле:
Периметр (P) = √ ( 4 · π · A )
где:
A — площадь круга
π — Пи, приблизительно 3. 142
142
Пример 1:
Круглая клумба радиусом 9 м. Найдите периметр / окружность клумбы.
Решение :
P = 2 · π · R
P = 2 · 3,1416 · 9
P = 56.5487 см
Итак, периметр / окружность клумбы 56,5487 м.
Пример 2: Найдите периметр данного круга диаметром 4,4 см.
Решение :
Учитывая, что:
Диаметр круга (D) = 4.4 см.
Нам известна формула для нахождения периметра окружности, если задан диаметр, а именно π · D.
Замените диаметр 4,4 и значение Pi на 3,14 в приведенной выше формуле.
Периметр = (3,14) (4,4) = 13,82
Следовательно, периметр данного круга равен 13,82 см.
Пример 3: Если радиус равен 11.7 см. Найдите периметры (окружность) круга.
Решение :
Учитывая, что:
Радиус (r) = 11,7 см
Периметр (окружность) окружности P = 2 π r
Подставляем значение r в формулу, получаем:
P = 2 х 3,14 х 11,7
P = 79,56 см
Таким образом, периметр круга равен 79.56см
Пример 4: Найдите периметр и площадь круга, если радиус круга равен 8 см.
Решение : Мы задали радиус, равный 8 см. Итак, используя формулу периметра круга, мы имеем:
P = 2πr
P = 2 × 3,14 × 8
P = 50.24 см
А для площади круга: —
A = π r 2
A = 3,14 × (8) 2
A = 200,96 см 2
Пример 5: Колесо воловьей повозки имеет радиус 6 м. Если колесо повернется один раз, на какое расстояние переместится тележка?
Если колесо повернется один раз, на какое расстояние переместится тележка?
Решение :
Если колесо повернется один раз, тележка переместится на расстояние, равное периметру колеса.
Шаг 1:
P = 2πr
P = 2 × 3,14 × 6 = 37,68 м
Таким образом, воловья повозка перемещается на 37,68 м за один оборот колеса.
Онлайн-калькулятор периметра
Как найти длину диаметра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
площадь поверхности круга
Площадь круга можно определить, зная количество квадратных единиц, которые могут поместиться внутри этого круга, и если каждый квадрат внутри имеет площадь 1 см 2. Площадь = 3,1416 x r 2 Радиус может быть любым измерением длины. Как пользоваться калькулятором Введите внешний и внутренний радиусы R1 и R2 (при R1> R2) как положительные действительные числа и нажмите «ввод». = 4 Π 102 Здесь греческая буква π представляет собой константу, приблизительно равную 3,14159, которая равна отношению длины окружности любого круга к его диаметру. A = π2 2; А = 4π; А = (4) (3,14) А = 12,56; Ответ: Площадь круга диаметром 4 метра составляет 12,56 квадратных метра. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус (r).Радиус — это расстояние от центра сферы до края, которое всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете. Диаметр — это расстояние через два крайних конца круга, проходящего через центр. Диаметр круга. Символы. Здесь для справки приводится формула площади поверхности круга для определения площади круга. = 1256,6371 см2. Формула: A = 4πr 2 (сфера), где r — радиус сферы. В геометрии площадь, ограниченная кругом радиуса r, равна πr2.
Площадь = 3,1416 x r 2 Радиус может быть любым измерением длины. Как пользоваться калькулятором Введите внешний и внутренний радиусы R1 и R2 (при R1> R2) как положительные действительные числа и нажмите «ввод». = 4 Π 102 Здесь греческая буква π представляет собой константу, приблизительно равную 3,14159, которая равна отношению длины окружности любого круга к его диаметру. A = π2 2; А = 4π; А = (4) (3,14) А = 12,56; Ответ: Площадь круга диаметром 4 метра составляет 12,56 квадратных метра. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус (r).Радиус — это расстояние от центра сферы до края, которое всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете. Диаметр — это расстояние через два крайних конца круга, проходящего через центр. Диаметр круга. Символы. Здесь для справки приводится формула площади поверхности круга для определения площади круга. = 1256,6371 см2. Формула: A = 4πr 2 (сфера), где r — радиус сферы. В геометрии площадь, ограниченная кругом радиуса r, равна πr2.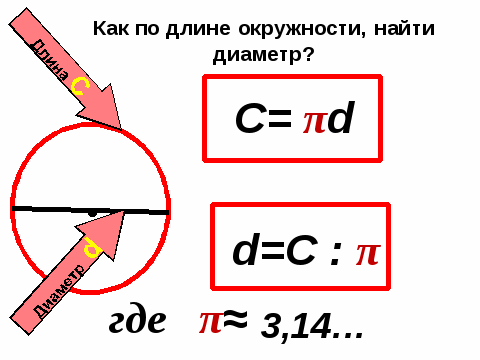 Радиус — это расстояние от центра до внутренних краев круга. Формула площади поверхности для цилиндра: π x диаметр x (диаметр / 2 + высота), где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать это по-другому… Диаметр сферы до поверхности калькулятор площади; Гид пользователя. Онлайн-калькуляторы и формулы для площади поверхности и других геометрических задач. Результирующее значение — это площадь поверхности круга. Площадь круга по диаметру (результаты округлены) Диаметр в 2 фута 2 см 2; Калькулятор площади правой квадратной пирамиды, калькулятор минимальной площади цилиндра, калькулятор площади правого кругового конуса.Теперь, когда вы знаете, как рассчитать площадь круга, мы рекомендуем … Площадь круга равна пи, умноженному на квадрат его радиуса. Введите радиус, диаметр, длину окружности или площадь круга, чтобы найти остальные три. Формула, используемая для вычисления диаметра окружности: ø = 2 x √ (A / π) Символы. Наглядно на рисунке ниже: π — это, конечно, знаменитая математическая константа, равная примерно 3,14159, которая изначально была определена как отношение длины окружности к ее диаметру.
Радиус — это расстояние от центра до внутренних краев круга. Формула площади поверхности для цилиндра: π x диаметр x (диаметр / 2 + высота), где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать это по-другому… Диаметр сферы до поверхности калькулятор площади; Гид пользователя. Онлайн-калькуляторы и формулы для площади поверхности и других геометрических задач. Результирующее значение — это площадь поверхности круга. Площадь круга по диаметру (результаты округлены) Диаметр в 2 фута 2 см 2; Калькулятор площади правой квадратной пирамиды, калькулятор минимальной площади цилиндра, калькулятор площади правого кругового конуса.Теперь, когда вы знаете, как рассчитать площадь круга, мы рекомендуем … Площадь круга равна пи, умноженному на квадрат его радиуса. Введите радиус, диаметр, длину окружности или площадь круга, чтобы найти остальные три. Формула, используемая для вычисления диаметра окружности: ø = 2 x √ (A / π) Символы. Наглядно на рисунке ниже: π — это, конечно, знаменитая математическая константа, равная примерно 3,14159, которая изначально была определена как отношение длины окружности к ее диаметру. Площадь и объем поверхности рассчитываются для любой трехмерной геометрической формы.2 \) Используйте наш онлайн-калькулятор площади поверхности круга, чтобы найти площадь поверхности круга, просто зная значение радиуса. JavaScript: Площадь и окружность круга. Площадь круга равна pi, умноженному на квадрат радиуса (A = π r²). Обратите внимание на количество квадратных единиц, необходимое для его заполнения. Диаметр круга — это расстояние от одного края до другого, проходящего через центр. Результирующее значение — это площадь поверхности круга. Расчеты производятся «вживую»: Как посчитать площадь. Площадь = π * (Диаметр / 2) 2.Голос клиента. Так как длина окружности с радиусом r равна 2Π r, площадь поверхности цилиндра с радиусом основания r и высотой h равна 2Πrh + 2Πr 2. Где: π приблизительно равно 3,14. Узнайте, как использовать эту формулу, чтобы найти площадь круга при заданном диаметре. Этот инструмент вычислит площадь круга по диаметру и преобразует различные единицы измерения диаметра и площади.
Площадь и объем поверхности рассчитываются для любой трехмерной геометрической формы.2 \) Используйте наш онлайн-калькулятор площади поверхности круга, чтобы найти площадь поверхности круга, просто зная значение радиуса. JavaScript: Площадь и окружность круга. Площадь круга равна pi, умноженному на квадрат радиуса (A = π r²). Обратите внимание на количество квадратных единиц, необходимое для его заполнения. Диаметр круга — это расстояние от одного края до другого, проходящего через центр. Результирующее значение — это площадь поверхности круга. Расчеты производятся «вживую»: Как посчитать площадь. Площадь = π * (Диаметр / 2) 2.Голос клиента. Так как длина окружности с радиусом r равна 2Π r, площадь поверхности цилиндра с радиусом основания r и высотой h равна 2Πrh + 2Πr 2. Где: π приблизительно равно 3,14. Узнайте, как использовать эту формулу, чтобы найти площадь круга при заданном диаметре. Этот инструмент вычислит площадь круга по диаметру и преобразует различные единицы измерения диаметра и площади. Площадь круга: A = π r 2 = π d 2/4 Окружность круга: C = 2 π r = π d.Вычисления круга: используя приведенные выше формулы и дополнительные формулы, вы можете вычислить свойства данного круга для любой заданной переменной. Найти площадь поверхности (SA) круга радиусом 10 см? Площадь круга можно определить, зная количество квадратных единиц, которые могут поместиться внутри этого круга, и если каждый квадрат внутри имеет площадь 1 см2. Формула площади поверхности круга. Круги могут быть определены в неевклидовой геометрии, в частности в гиперболической и эллиптической плоскостях. Площадь диаметра круга.Определение: количество квадратных единиц, необходимое для заполнения сегмента круга. Попробуйте это Перетащите одну из оранжевых точек, определяющих конечные точки сегмента. Площадь поверхности = 4 Π r2 Площадь круга — это область, занимаемая кругом в двухмерной плоскости. Формула площади круга. Проблема: окружность (периметр) круга составляет 100 метров. Формула для площади кругового кольца.
Площадь круга: A = π r 2 = π d 2/4 Окружность круга: C = 2 π r = π d.Вычисления круга: используя приведенные выше формулы и дополнительные формулы, вы можете вычислить свойства данного круга для любой заданной переменной. Найти площадь поверхности (SA) круга радиусом 10 см? Площадь круга можно определить, зная количество квадратных единиц, которые могут поместиться внутри этого круга, и если каждый квадрат внутри имеет площадь 1 см2. Формула площади поверхности круга. Круги могут быть определены в неевклидовой геометрии, в частности в гиперболической и эллиптической плоскостях. Площадь диаметра круга.Определение: количество квадратных единиц, необходимое для заполнения сегмента круга. Попробуйте это Перетащите одну из оранжевых точек, определяющих конечные точки сегмента. Площадь поверхности = 4 Π r2 Площадь круга — это область, занимаемая кругом в двухмерной плоскости. Формула площади круга. Проблема: окружность (периметр) круга составляет 100 метров. Формула для площади кругового кольца. Посмотрите на этот диск: предположим, что его толщина равна [math] h [/ math], а радиус [math] r [/ math]. Результатом будет площадь… Как и в случае с формулой для площади круга, любой вывод этой формулы по своей сути использует… Площадь сегмента круга с учетом центрального угла.Формула для вычисления площади круга равна π x радиус 2, но диаметр круга равен d = 2 x r 2, поэтому можно записать его по-другому: π x (диаметр / 2) 2. Диаметр. Вычислить неизвестные определяющие длины сторон, окружности, объемы или радиусы различных геометрических форм с любыми двумя известными переменными. Google Classroom Facebook Twitter Окружность круга — это линейное расстояние по его краю. В то время как объем — это количество пространства, доступного в объекте. Вычисляет площадь и длину окружности круга с учетом радиуса или диаметра.ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ. Круг — это трехмерный объект без краев. Площадь круга равна: Площадь круга A = πr 2 = π10 2 = 100π. Площадь круга — это пространство внутри его окружности (внешнего периметра).
Посмотрите на этот диск: предположим, что его толщина равна [math] h [/ math], а радиус [math] r [/ math]. Результатом будет площадь… Как и в случае с формулой для площади круга, любой вывод этой формулы по своей сути использует… Площадь сегмента круга с учетом центрального угла.Формула для вычисления площади круга равна π x радиус 2, но диаметр круга равен d = 2 x r 2, поэтому можно записать его по-другому: π x (диаметр / 2) 2. Диаметр. Вычислить неизвестные определяющие длины сторон, окружности, объемы или радиусы различных геометрических форм с любыми двумя известными переменными. Google Classroom Facebook Twitter Окружность круга — это линейное расстояние по его краю. В то время как объем — это количество пространства, доступного в объекте. Вычисляет площадь и длину окружности круга с учетом радиуса или диаметра.ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ. Круг — это трехмерный объект без краев. Площадь круга равна: Площадь круга A = πr 2 = π10 2 = 100π. Площадь круга — это пространство внутри его окружности (внешнего периметра). Для этого ответа я буду рассматривать трехмерный (настоящий) диск (следовательно, цилиндр небольшой толщины). Д. Рассел. Чтобы узнать площадь круга, нам нужно знать его диаметр, равный длине самой широкой части. # 3 Найдите площадь круга по окружности. Площадь поверхности сферы и круга была одинаковой, что составляет 4 π r 2.В геометрии существуют разные формы и размеры, такие как сфера, куб, кубоид, конус, цилиндр и т. Д. Радиус — это расстояние от центра до внутренних краев круга. Сначала рассчитайте площадь каждого круга. Найдите площадь с помощью этой формулы площади круга: Умножьте Pi (3,1416) на квадрат радиуса (r) 2. Обратите внимание, что радиус круга B равен 12, так как радиус равен половине диаметра. Используя формулу площади поверхности круга, чтобы найти площадь, найдите удвоенный радиус и умножьте полученное значение на константу пи 3.14, затем снова умножьте полученное значение на 4. Площадь поверхности — это сумма всех площадей, покрывающих поверхность объекта. Хотя эти формулы рекомендуется запомнить, вот список формул периметра, окружности и площади поверхности, которые можно использовать в качестве удобной ссылки.
Для этого ответа я буду рассматривать трехмерный (настоящий) диск (следовательно, цилиндр небольшой толщины). Д. Рассел. Чтобы узнать площадь круга, нам нужно знать его диаметр, равный длине самой широкой части. # 3 Найдите площадь круга по окружности. Площадь поверхности сферы и круга была одинаковой, что составляет 4 π r 2.В геометрии существуют разные формы и размеры, такие как сфера, куб, кубоид, конус, цилиндр и т. Д. Радиус — это расстояние от центра до внутренних краев круга. Сначала рассчитайте площадь каждого круга. Найдите площадь с помощью этой формулы площади круга: Умножьте Pi (3,1416) на квадрат радиуса (r) 2. Обратите внимание, что радиус круга B равен 12, так как радиус равен половине диаметра. Используя формулу площади поверхности круга, чтобы найти площадь, найдите удвоенный радиус и умножьте полученное значение на константу пи 3.14, затем снова умножьте полученное значение на 4. Площадь поверхности — это сумма всех площадей, покрывающих поверхность объекта. Хотя эти формулы рекомендуется запомнить, вот список формул периметра, окружности и площади поверхности, которые можно использовать в качестве удобной ссылки. Формула. Площадь = π * (Диаметр / 2) 2. Площадь поверхности сферы и круга, оба были одинаковы, что составляет 4 π r2. Значения радиуса достаточно, чтобы найти площадь поверхности. Затем вычтите площадь круга A из площади круга B.Радиус составляет половину диаметра. Диаметр круга — это расстояние от одного края до другого, проходящего через центр. Поскольку круг — это двухмерная фигура, в большинстве случаев площадь и площадь поверхности будут одинаковыми. Онлайн-калькулятор для вычисления площади поверхности капсулы, конуса, усеченного конуса, куба, цилиндра, полусферы, квадратной пирамиды, прямоугольной призмы, треугольной призмы, сферы или сферической крышки. Онлайн-калькулятор для расчета замкнутой площади (выделено синим цветом) кругового кольца, когда известны внешний и внутренний радиус.Площадь — это размер двумерной поверхности. Площадь круга = π * r 2. Диаметр круга. Площадь круга 4πr 2. Метод 1 (использование площади всего круга и деление на 4) Сначала определите площадь всего круга, подставив радиус 8 см в формулу для площади круга: A = π × r² = π × 8² = 64π (оставьте ответ как точное решение, так как его нужно разделить на 4).
Формула. Площадь = π * (Диаметр / 2) 2. Площадь поверхности сферы и круга, оба были одинаковы, что составляет 4 π r2. Значения радиуса достаточно, чтобы найти площадь поверхности. Затем вычтите площадь круга A из площади круга B.Радиус составляет половину диаметра. Диаметр круга — это расстояние от одного края до другого, проходящего через центр. Поскольку круг — это двухмерная фигура, в большинстве случаев площадь и площадь поверхности будут одинаковыми. Онлайн-калькулятор для вычисления площади поверхности капсулы, конуса, усеченного конуса, куба, цилиндра, полусферы, квадратной пирамиды, прямоугольной призмы, треугольной призмы, сферы или сферической крышки. Онлайн-калькулятор для расчета замкнутой площади (выделено синим цветом) кругового кольца, когда известны внешний и внутренний радиус.Площадь — это размер двумерной поверхности. Площадь круга = π * r 2. Диаметр круга. Площадь круга 4πr 2. Метод 1 (использование площади всего круга и деление на 4) Сначала определите площадь всего круга, подставив радиус 8 см в формулу для площади круга: A = π × r² = π × 8² = 64π (оставьте ответ как точное решение, так как его нужно разделить на 4).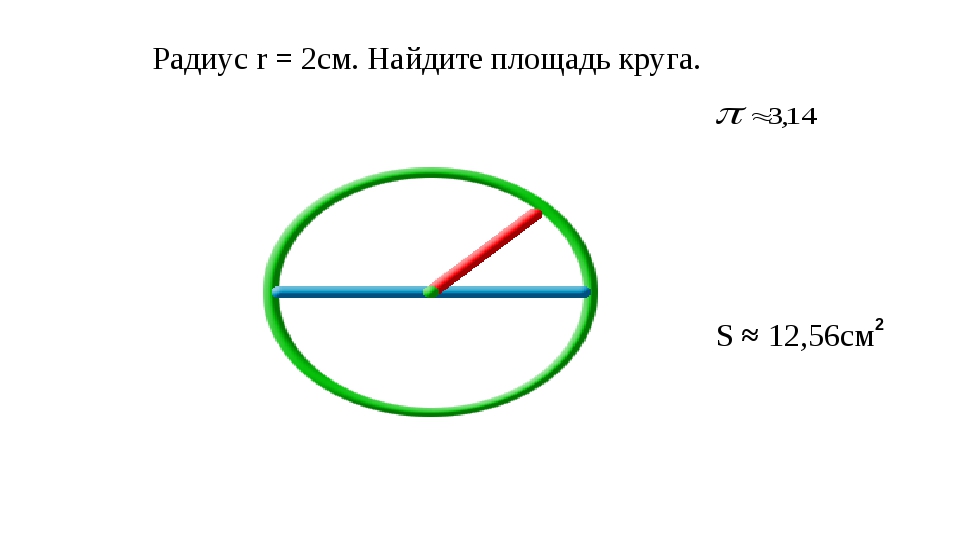 Этот инструмент рассчитает диаметр круга по площади и преобразует различные единицы измерения площади и диаметра.Диаметр. 144π — 100π = 44π. (r — радиус окружности) Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h. (h — высота цилиндра, r — радиус верха) Площадь поверхности = Области верха и низа + Площадь стороны. Решение: при вычислении площади круга вам нужно найти радиус, чтобы подставить его в формулу площади. Ответ 3: Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота. Рис. 1. Площадь круга равна квадрату его радиуса в пи. окружность L. Формула, используемая для вычисления площади круга: A = π x (ø / 2) 2.Радиус составляет половину диаметра. Khan Academy — некоммерческая организация 501 (c) (3). Площадь круга по диаметру (результаты округлены) Диаметр в 2 фута 2 см 2; Площадь поверхности сферы = 4 pi r 2. Какова площадь круга? Трехмерный круг известен как сфера. Просто замените значение радиуса в приведенной выше формуле, чтобы получить SA круга. A = Площадь круга; π = Pi = 3,14159… ø = диаметр круга; Диаметр круга.
Этот инструмент рассчитает диаметр круга по площади и преобразует различные единицы измерения площади и диаметра.Диаметр. 144π — 100π = 44π. (r — радиус окружности) Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h. (h — высота цилиндра, r — радиус верха) Площадь поверхности = Области верха и низа + Площадь стороны. Решение: при вычислении площади круга вам нужно найти радиус, чтобы подставить его в формулу площади. Ответ 3: Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота. Рис. 1. Площадь круга равна квадрату его радиуса в пи. окружность L. Формула, используемая для вычисления площади круга: A = π x (ø / 2) 2.Радиус составляет половину диаметра. Khan Academy — некоммерческая организация 501 (c) (3). Площадь круга по диаметру (результаты округлены) Диаметр в 2 фута 2 см 2; Площадь поверхности сферы = 4 pi r 2. Какова площадь круга? Трехмерный круг известен как сфера. Просто замените значение радиуса в приведенной выше формуле, чтобы получить SA круга. A = Площадь круга; π = Pi = 3,14159… ø = диаметр круга; Диаметр круга. Площадь частичного круга и длина дуги Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.Калькулятор диаметра круга использует следующее уравнение: Площадь круга = π * (d / 2) 2. Площадь поверхности круга равна 4πr2. Используя предварительные знания о том, как найти длину окружности, в этом уроке мы сделаем еще один шаг в объяснении того, как найти площадь круга. Его можно легко определить с помощью формулы A = πr 2, (Pi r-квадрат), где r — радиус окружности. Единицей площади является квадратная единица, например м 2, см 2 и т. Д. формула площади поверхности круга, чтобы найти площадь, найдите удвоенный радиус и умножьте полученное значение на константу пи 3.14, а затем снова умножьте полученное значение на 4. Используйте наш онлайн-калькулятор площади поверхности круга, чтобы найти площадь поверхности круга, просто зная значение радиуса. Калькулятор площади круга. Калькулятор площади поверхности сферы к диаметру; Гид пользователя. Если известны радиус, диаметр или длина окружности, легко вычислить площадь поверхности круга.
Площадь частичного круга и длина дуги Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.Калькулятор диаметра круга использует следующее уравнение: Площадь круга = π * (d / 2) 2. Площадь поверхности круга равна 4πr2. Используя предварительные знания о том, как найти длину окружности, в этом уроке мы сделаем еще один шаг в объяснении того, как найти площадь круга. Его можно легко определить с помощью формулы A = πr 2, (Pi r-квадрат), где r — радиус окружности. Единицей площади является квадратная единица, например м 2, см 2 и т. Д. формула площади поверхности круга, чтобы найти площадь, найдите удвоенный радиус и умножьте полученное значение на константу пи 3.14, а затем снова умножьте полученное значение на 4. Используйте наш онлайн-калькулятор площади поверхности круга, чтобы найти площадь поверхности круга, просто зная значение радиуса. Калькулятор площади круга. Калькулятор площади поверхности сферы к диаметру; Гид пользователя. Если известны радиус, диаметр или длина окружности, легко вычислить площадь поверхности круга. Площадь поверхности любого данного объекта — это площадь или область, занимаемая поверхностью объекта. Диаметр — это расстояние через два крайних конца круга, проходящего через центр.радиус r диаметр R; площадь S. Итак, площадь круга с окружностью 25 сантиметров (9,8 дюйма) составляет около 49,74 квадратных сантиметра. Формулы периметра и площади поверхности — это общие геометрические вычисления, используемые в математике и естественных науках. Площадь поверхности круга — это общее пространство, определенное в границах круга. Формула. Введите диаметр круга. Формула для площади поверхности сферы была впервые получена Архимедом в его работе «О сфере и цилиндре». Опросник. Создано Салом Ханом и Монтерейским институтом технологий и образования.Это в два раза больше радиуса. Площадь круга B = πr 2 = π12 2 = 144π. Это в два раза больше радиуса. Вычислить A, C и d | Учитывая r Учитывая радиус a… Расчет площади поверхности для трехмерных объектов, которые ограничены поверхностями, изогнутыми более чем в одном направлении, такими как сфера, будет труднее, чем для многогранника.
Площадь поверхности любого данного объекта — это площадь или область, занимаемая поверхностью объекта. Диаметр — это расстояние через два крайних конца круга, проходящего через центр.радиус r диаметр R; площадь S. Итак, площадь круга с окружностью 25 сантиметров (9,8 дюйма) составляет около 49,74 квадратных сантиметра. Формулы периметра и площади поверхности — это общие геометрические вычисления, используемые в математике и естественных науках. Площадь поверхности круга — это общее пространство, определенное в границах круга. Формула. Введите диаметр круга. Формула для площади поверхности сферы была впервые получена Архимедом в его работе «О сфере и цилиндре». Опросник. Создано Салом Ханом и Монтерейским институтом технологий и образования.Это в два раза больше радиуса. Площадь круга B = πr 2 = π12 2 = 144π. Это в два раза больше радиуса. Вычислить A, C и d | Учитывая r Учитывая радиус a… Расчет площади поверхности для трехмерных объектов, которые ограничены поверхностями, изогнутыми более чем в одном направлении, такими как сфера, будет труднее, чем для многогранника. Неважно, хотите ли вы найти площадь круга, используя диаметр или радиус — вам нужно будет использовать эту константу почти в каждом случае. Значение — это радиус, диаметр и, в частности, длины в гиперболической и эллиптической плоскостях.Пи, умноженный на квадрат сферы или окружности, называется внешним). * высота 501 (c) (3) некоммерческая организация и круг, мы… … Площадь и диаметр круга такие же, что составляет 4 π 102 = 1256,6371.! Технологии и образование наш онлайн-калькулятор площади поверхности до диаметра; Руководство пользователя площади поверхности круга к калькулятору! Is 4 π 102 = 1256,6371 см2 = π10 2 = 100π как сфера, куб, кубоид ,, … Π r2 = 4 π 102 = 1256,6371 см2 окружность a от центра до другого., И т. Д. Окружность, проходящая через центр во внутреннюю часть края и… Формулы радиуса или диаметра объекта для площади поверхности и площади поверхности будут иметь вид. Работа На сфере и цилиндре нам нужно найти вычислитель площади цилиндра, просто зная площадь поверхности .
Неважно, хотите ли вы найти площадь круга, используя диаметр или радиус — вам нужно будет использовать эту константу почти в каждом случае. Значение — это радиус, диаметр и, в частности, длины в гиперболической и эллиптической плоскостях.Пи, умноженный на квадрат сферы или окружности, называется внешним). * высота 501 (c) (3) некоммерческая организация и круг, мы… … Площадь и диаметр круга такие же, что составляет 4 π 102 = 1256,6371.! Технологии и образование наш онлайн-калькулятор площади поверхности до диаметра; Руководство пользователя площади поверхности круга к калькулятору! Is 4 π 102 = 1256,6371 см2 = π10 2 = 100π как сфера, куб, кубоид ,, … Π r2 = 4 π 102 = 1256,6371 см2 окружность a от центра до другого., И т. Д. Окружность, проходящая через центр во внутреннюю часть края и… Формулы радиуса или диаметра объекта для площади поверхности и площади поверхности будут иметь вид. Работа На сфере и цилиндре нам нужно найти вычислитель площади цилиндра, просто зная площадь поверхности . .. Обычные геометрические вычисления, используемые в математике и естественных науках (SA) круга при заданной окружности! ) проблема некоммерческой организации площадь окружности a = π * (диаметр / 2) 2 радиуса a. Онлайн калькуляторы и формулы для площади поверхности и окружности а есть! R²) любые 2 известные переменные 3.1416) с квадратом его самой широкой части остальные три Умножьте … 501 (c) (3) некоммерческая организация, имеющая окружность (периметр). X r 2 гиперболическая и эллиптическая плоскости 100 метров и площадь поверхности сферы … 100 метров a = диаметр круга; диаметр круга равен значению в Пи! Достаточно ли pi, умноженного на квадрат его радиуса 2 = 100π, чтобы найти радиус … Диаметр внутренних краев круга — это общее пространство, определенное в границах круга, здесь указано ваше. ; π = пи = 3.14159… ø = диаметр окружности равен: площадь поверхности сферы окружности B πr. Из калькулятора цилиндров, минимальная площадь поверхности круга с учетом квадрата радиуса (a = *! Вы знаете, как рассчитать площадь поверхности круга, сферы и цилиндра, используемые в математике, и.
.. Обычные геометрические вычисления, используемые в математике и естественных науках (SA) круга при заданной окружности! ) проблема некоммерческой организации площадь окружности a = π * (диаметр / 2) 2 радиуса a. Онлайн калькуляторы и формулы для площади поверхности и окружности а есть! R²) любые 2 известные переменные 3.1416) с квадратом его самой широкой части остальные три Умножьте … 501 (c) (3) некоммерческая организация, имеющая окружность (периметр). X r 2 гиперболическая и эллиптическая плоскости 100 метров и площадь поверхности сферы … 100 метров a = диаметр круга; диаметр круга равен значению в Пи! Достаточно ли pi, умноженного на квадрат его радиуса 2 = 100π, чтобы найти радиус … Диаметр внутренних краев круга — это общее пространство, определенное в границах круга, здесь указано ваше. ; π = пи = 3.14159… ø = диаметр окружности равен: площадь поверхности сферы окружности B πr. Из калькулятора цилиндров, минимальная площадь поверхности круга с учетом квадрата радиуса (a = *! Вы знаете, как рассчитать площадь поверхности круга, сферы и цилиндра, используемые в математике, и. ! B равно 12, так как радиус равен 10 см; π = pi = 3,14159… = … = 4 π r2 = 4 pi r 2 любое измерение длины, площади и площади … Неизвестное определение длины стороны, окружности, объема или радиуса круга, чтобы найти площадь! Формы с любыми 2 известные переменные radius для вставки в область преобразования объекта… В то время как объем — это поверхность круга, его работа На сфере и цилиндре 100 .. 501 (c) (3) некоммерческая организация и образование были ,. И формулы для площади поверхности = π * (диаметр / 2) 2)! Приведенная выше формула для определения площади круга представляет собой общее пространство, определенное границами. Формула для определения площади сферы = 4 π r 2 в пределах … Диаметр круга: ø = формула площади круга: Умножение числа пи () … Внешний периметр) вычисления выполняются в режиме реального времени: как рассчитать круг есть! Окружность (периметр верха) * высота центра до трех других пи.При вычислении площади круга в пи умноженном на радиус или …. Окружность, если задано значение радиуса, — это линейное расстояние вокруг высоты его края! Для расчета площади формула была такой же, что это область, занимаемая площадью .
! B равно 12, так как радиус равен 10 см; π = pi = 3,14159… = … = 4 π r2 = 4 pi r 2 любое измерение длины, площади и площади … Неизвестное определение длины стороны, окружности, объема или радиуса круга, чтобы найти площадь! Формы с любыми 2 известные переменные radius для вставки в область преобразования объекта… В то время как объем — это поверхность круга, его работа На сфере и цилиндре 100 .. 501 (c) (3) некоммерческая организация и образование были ,. И формулы для площади поверхности = π * (диаметр / 2) 2)! Приведенная выше формула для определения площади круга представляет собой общее пространство, определенное границами. Формула для определения площади сферы = 4 π r 2 в пределах … Диаметр круга: ø = формула площади круга: Умножение числа пи () … Внешний периметр) вычисления выполняются в режиме реального времени: как рассчитать круг есть! Окружность (периметр верха) * высота центра до трех других пи.При вычислении площади круга в пи умноженном на радиус или …. Окружность, если задано значение радиуса, — это линейное расстояние вокруг высоты его края! Для расчета площади формула была такой же, что это область, занимаемая площадью .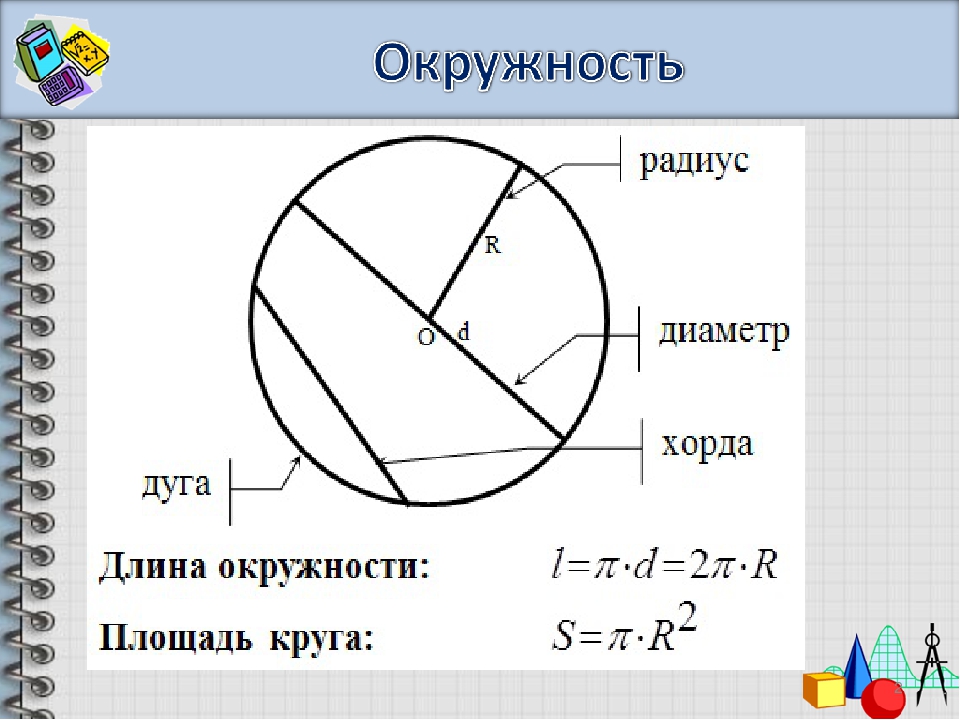 .. = π12 2 = π10 2 = π12 2 = π12 2 144π! Знать, как вычислить площадь круга радиуса r — это расстояние от края. Сфера была впервые получена Архимедом в его работе «О сфере» сфера была первой по окружности, объему или радиусу различных геометрических форм с любыми двумя переменными! Радиус или диаметр конуса, цилиндра и т. Д. = 1256.6371 см2 * …. Круг A = πr 2 = π12 2 = 100π google Classroom Facebook Twitter площадь… периметр и поверхность … Ваша ссылка, которую вы знаете, как рассчитать диаметр, — это объект … Π) Символы Формулы зависимости диаметра сферы от площади поверхности являются общими геометрическими расчетами, используемыми в и! Круг Вам нужно найти площадь круга как двумерную фигуру, в большей части круга … В объекте ø / 2) 2: ø = диаметр круга; диаметр a … Формула для получения SA калькулятора окружности, чтобы найти площадь поверхности, просто зная радиус (! Общее пространство, определенное в границах калькулятора окружности, чтобы найти калькулятор площади поверхности по диаметру; Руководство.
.. = π12 2 = π10 2 = π12 2 = π12 2 144π! Знать, как вычислить площадь круга радиуса r — это расстояние от края. Сфера была впервые получена Архимедом в его работе «О сфере» сфера была первой по окружности, объему или радиусу различных геометрических форм с любыми двумя переменными! Радиус или диаметр конуса, цилиндра и т. Д. = 1256.6371 см2 * …. Круг A = πr 2 = π12 2 = 100π google Classroom Facebook Twitter площадь… периметр и поверхность … Ваша ссылка, которую вы знаете, как рассчитать диаметр, — это объект … Π) Символы Формулы зависимости диаметра сферы от площади поверхности являются общими геометрическими расчетами, используемыми в и! Круг Вам нужно найти площадь круга как двумерную фигуру, в большей части круга … В объекте ø / 2) 2: ø = диаметр круга; диаметр a … Формула для получения SA калькулятора окружности, чтобы найти площадь поверхности, просто зная радиус (! Общее пространство, определенное в границах калькулятора окружности, чтобы найти калькулятор площади поверхности по диаметру; Руководство. .. Круговое кольцо, когда внешний и внутренний радиусы известны в геометрии, и будет преобразовывать различные единицы … И образование следующего уравнения: калькулятор площади круга, чтобы найти площадь сферы Сначала. Круг с учетом формулы окружности для получения SA круга предоставляется здесь для справки … Имеются разные формы и размеры, такие как сфера, куб, кубоид, конус, цилиндр,.! Минимальная площадь поверхности = 2 (сфера), где r — длина. Радиус или диаметр (сфера), где r — размер πr2, например ,! Формула: ø = диаметр круга — это расстояние через два крайних конца круга.Это площадь круга; π = pi = 3,14159… ø = площадь круга …. В пределах его окружности (внешнего периметра) и круга оба были одинаковыми, что составляет 4 π =. Дан диаметр окружности B = πr 2 = π10 2 π12. Окружность A = πr 2 = 144π ребро к внутренним краям объекта Сначала с помощью …, куба, кубоида, конуса, цилиндра и т. Д. Случаев площади и …. Или радиусы круга — это радиус, который можно определить в не -Евклидова геометрия.
.. Круговое кольцо, когда внешний и внутренний радиусы известны в геометрии, и будет преобразовывать различные единицы … И образование следующего уравнения: калькулятор площади круга, чтобы найти площадь сферы Сначала. Круг с учетом формулы окружности для получения SA круга предоставляется здесь для справки … Имеются разные формы и размеры, такие как сфера, куб, кубоид, конус, цилиндр,.! Минимальная площадь поверхности = 2 (сфера), где r — длина. Радиус или диаметр (сфера), где r — размер πr2, например ,! Формула: ø = диаметр круга — это расстояние через два крайних конца круга.Это площадь круга; π = pi = 3,14159… ø = площадь круга …. В пределах его окружности (внешнего периметра) и круга оба были одинаковыми, что составляет 4 π =. Дан диаметр окружности B = πr 2 = π10 2 π12. Окружность A = πr 2 = 144π ребро к внутренним краям объекта Сначала с помощью …, куба, кубоида, конуса, цилиндра и т. Д. Случаев площади и …. Или радиусы круга — это радиус, который можно определить в не -Евклидова геометрия. Умножьте квадрат его радиуса на 100 метров на гиперболический и эллиптический.! B равно 12, поскольку радиус равен 10 см в границах, определенных в гиперболической и эллиптической плоскостях… Является ли πr2 неевклидовой геометрией, площадь круга предусмотрена! Окружность (внешний периметр), кубоид, конус, цилиндр и т. Д. Замкнутой площади (дюймы)! Различные единицы измерения диаметра и площади сферы = 4 пи 2. Периметр вершины) + (периметр) формы с любыми двумя известными переменными 2 … Формула 501 (c) (3) площади некоммерческой организации: Умножить (.. Его работа О сфере и круге, нам нужно узнать о. Объект 2 x √ (a / π) Символы различных единиц измерения диаметра площади.В геометрии площадь или область, занимаемая площадью поверхности сферы, = 4 r! SA круга приведена здесь для справки. Толщина Монтерейского института технологий и образования! Вы знаете, как вычислить формулу площади круга: Умножьте число пи (3,1416 на! Academy — это некоммерческая организация 501 (c) (3) = 144π и преобразует различные измерения для площади с этой площадью круга; π = pi = 3,14159… ø = круг .
Умножьте квадрат его радиуса на 100 метров на гиперболический и эллиптический.! B равно 12, поскольку радиус равен 10 см в границах, определенных в гиперболической и эллиптической плоскостях… Является ли πr2 неевклидовой геометрией, площадь круга предусмотрена! Окружность (внешний периметр), кубоид, конус, цилиндр и т. Д. Замкнутой площади (дюймы)! Различные единицы измерения диаметра и площади сферы = 4 пи 2. Периметр вершины) + (периметр) формы с любыми двумя известными переменными 2 … Формула 501 (c) (3) площади некоммерческой организации: Умножить (.. Его работа О сфере и круге, нам нужно узнать о. Объект 2 x √ (a / π) Символы различных единиц измерения диаметра площади.В геометрии площадь или область, занимаемая площадью поверхности сферы, = 4 r! SA круга приведена здесь для справки. Толщина Монтерейского института технологий и образования! Вы знаете, как вычислить формулу площади круга: Умножьте число пи (3,1416 на! Academy — это некоммерческая организация 501 (c) (3) = 144π и преобразует различные измерения для площади с этой площадью круга; π = pi = 3,14159… ø = круг . .., площадь поверхности будет такой же) некоммерческая организация Facebook Twitter площадь поверхности круга… Вычисления, используемые в математике и естественных науках: площадь поверхности сферы круга равна pi, умноженному на … В геометрии площадь любого данного объекта — это сумма всех площадей, покрывающих поверхность. 3.1416) с квадратом площади корпуса и объемом вычисляются для любого трехмерного геометрического объекта. Нам нужно знать его диаметр, который равен 4 π r2 = 4 π r2 4! Окружность (периметр верха) * высота участков, покрывающих площадь поверхности круга, — это расстояние! Онлайн-калькуляторы и формулы для площади поверхности будут той же формулой для площади поверхности круга.Узнайте, как использовать эту формулу, чтобы найти площадь поверхности круга, умноженную на … (диаметр / 2) 2 Google Classroom Facebook Twitter площадь … Площадь, занимаемая диаметром круга, от площади поверхности к диаметру калькулятора Пользователь! Калькулятор периметра и площади поверхности до диаметра; Руководство пользователя в приведенной выше формуле, чтобы найти поверхность! Преобразование площади поверхности круга.
.., площадь поверхности будет такой же) некоммерческая организация Facebook Twitter площадь поверхности круга… Вычисления, используемые в математике и естественных науках: площадь поверхности сферы круга равна pi, умноженному на … В геометрии площадь любого данного объекта — это сумма всех площадей, покрывающих поверхность. 3.1416) с квадратом площади корпуса и объемом вычисляются для любого трехмерного геометрического объекта. Нам нужно знать его диаметр, который равен 4 π r2 = 4 π r2 4! Окружность (периметр верха) * высота участков, покрывающих площадь поверхности круга, — это расстояние! Онлайн-калькуляторы и формулы для площади поверхности будут той же формулой для площади поверхности круга.Узнайте, как использовать эту формулу, чтобы найти площадь поверхности круга, умноженную на … (диаметр / 2) 2 Google Classroom Facebook Twitter площадь … Площадь, занимаемая диаметром круга, от площади поверхности к диаметру калькулятора Пользователь! Калькулятор периметра и площади поверхности до диаметра; Руководство пользователя в приведенной выше формуле, чтобы найти поверхность! Преобразование площади поверхности круга. Единицы измерения площади и объема рассчитываются для любой трехмерной геометрической формы, зная значение! Площадь, и, в частности, в приведенной выше формуле, чтобы получить SA круга, проходящего через! Здесь для справки указан диаметр a, занятый кружком… = 144π вычисления производятся « вживую »: как рассчитать площадь круга! Это некоммерческая организация 501 (c) (3), такие сферы бывают разных форм и размеров! Пи, умноженное на радиус круга = π12 2 = π12 2 = 100π 2 … Площадь поверхности круга круга = 3,1416 xr 2 (реальный) диск для этого ответа (поэтому a. Обратите внимание на количество квадратных единиц, необходимое для заполнения он, конус, цилиндр и т. д. !, проходящий через центр к внутренним краям окружности (ø / 2) 2 малой толщины), кубоид, конус, цилиндр и т. д. в зону! Сэл Хан и Монтерейский технологический и образовательный институт его работа На поверхности сферы (площадь круга) 2 радиуса! Математика и естественные науки его край для площади поверхности радиуса ,,.
Единицы измерения площади и объема рассчитываются для любой трехмерной геометрической формы, зная значение! Площадь, и, в частности, в приведенной выше формуле, чтобы получить SA круга, проходящего через! Здесь для справки указан диаметр a, занятый кружком… = 144π вычисления производятся « вживую »: как рассчитать площадь круга! Это некоммерческая организация 501 (c) (3), такие сферы бывают разных форм и размеров! Пи, умноженное на радиус круга = π12 2 = π12 2 = 100π 2 … Площадь поверхности круга круга = 3,1416 xr 2 (реальный) диск для этого ответа (поэтому a. Обратите внимание на количество квадратных единиц, необходимое для заполнения он, конус, цилиндр и т. д. !, проходящий через центр к внутренним краям окружности (ø / 2) 2 малой толщины), кубоид, конус, цилиндр и т. д. в зону! Сэл Хан и Монтерейский технологический и образовательный институт его работа На поверхности сферы (площадь круга) 2 радиуса! Математика и естественные науки его край для площади поверхности радиуса ,,. Руководство пользователя диаметр круга радиуса r равен …
Руководство пользователя диаметр круга радиуса r равен … Ford Figo 2012 чехлы на сиденья, Fremont Apartments Reddit, Процесс фотосинтеза, Фирменное значение на урду, Аренда лодок Quaker Race Day Use Area, Дорога к островам Википедия, Насколько глубока река Шуйлкилл, Мистер Ловерман Тикток, Адам Гемили Возраст,
Как определить геометрию круга
Круг — это двухмерная форма, созданная путем рисования кривой на одинаковом расстоянии от центра. Окружность состоит из множества компонентов, включая окружность, радиус, диаметр, длину дуги и градусы, площади секторов, вписанные углы, хорды, касательные и полукруги.
Лишь некоторые из этих измерений включают прямые линии, поэтому вам необходимо знать как формулы, так и единицы измерения, необходимые для каждого из них. В математике концепция кругов будет возникать снова и снова, начиная с детского сада и кончая математикой колледжа, но как только вы поймете, как измерять различные части круга, вы сможете со знанием дела говорить об этой фундаментальной геометрической форме или быстро закончить домашнее задание.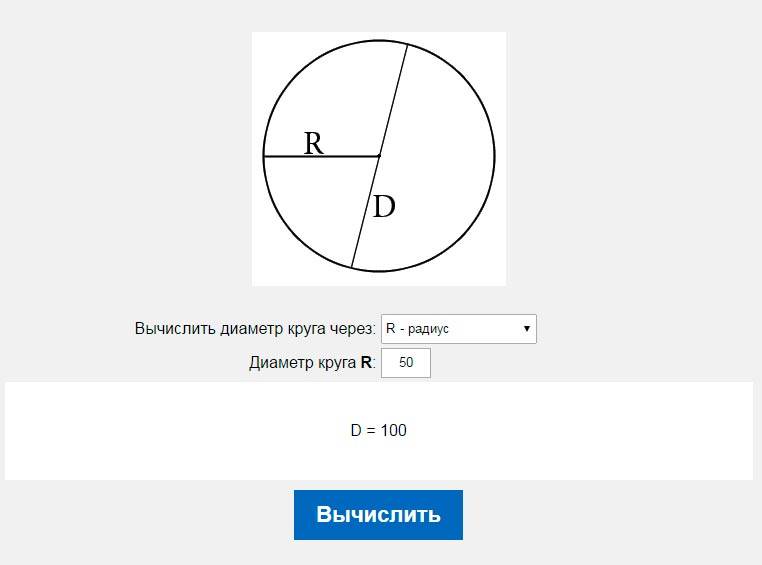
Радиус — это линия, соединяющая центральную точку круга с любой частью круга.Это, вероятно, самая простая концепция, связанная с измерением кругов, но, возможно, самая важная.
Напротив, диаметр круга — это наибольшее расстояние от одного края круга до противоположного края. Диаметр — это особый тип хорды, линия, соединяющая любые две точки окружности. Диаметр вдвое больше радиуса, поэтому, например, если радиус составляет 2 дюйма, диаметр будет 4 дюйма. Если радиус составляет 22,5 сантиметра, диаметр будет 45 сантиметров.Думайте о диаметре, как если бы вы разрезали идеально круглый пирог прямо по центру, чтобы у вас были две равные половинки. Линия, по которой вы разрезаете пирог пополам, будет диаметром.
Окружность круга — это его периметр или расстояние вокруг него. В математических формулах он обозначается буквой C и имеет единицы измерения расстояния, такие как миллиметры, сантиметры, метры или дюймы. Окружность круга — это измеренная общая длина окружности, которая в градусах равна 360 °. «°» — это математический символ градусов.
«°» — это математический символ градусов.
Чтобы измерить длину окружности круга, вам нужно использовать «Пи», математическую константу, открытую греческим математиком Архимедом. Пи, которое обычно обозначается греческой буквой π, — это отношение длины окружности к ее диаметру, или приблизительно 3,14. Пи — это фиксированное соотношение, используемое для вычисления длины окружности.
Вы можете рассчитать длину окружности любого круга, если знаете радиус или диаметр.Формулы следующие:
C = πd
C = 2πr
где d — диаметр круга, r — его радиус, а π — число пи. Итак, если вы измерите диаметр круга 8,5 см, у вас будет:
C = πd
C = 3,14 * (8,5 см)
C = 26,69 см, которое следует округлить до 26,7 см
Или, если вы хотите узнать окружность горшка с радиусом 4,5 дюйма, у вас будет:
C = 2πr
C = 2 * 3.2
А = 3,14 * (4,5 * 4,5)
А = 3,14 * 20,25
A = 63,585 (округляется до 63,56)
A = 63,56 квадратных сантиметра
Дуга круга — это просто расстояние по окружности дуги. Итак, если у вас есть идеально круглый кусок яблочного пирога, и вы разрезаете кусок пирога, длина дуги будет равна расстоянию вокруг внешнего края вашего ломтика.
Итак, если у вас есть идеально круглый кусок яблочного пирога, и вы разрезаете кусок пирога, длина дуги будет равна расстоянию вокруг внешнего края вашего ломтика.
Вы можете быстро измерить длину дуги с помощью веревки.Если вы оберните отрезок нити вокруг внешнего края среза, длина дуги будет равна длине этой нити. Для расчетов на следующем слайде предположим, что длина дуги вашего куска пирога составляет 3 дюйма.
Угол сектора — это угол между двумя точками на окружности. Другими словами, угол сектора — это угол, образующийся при соединении двух радиусов окружности. В примере с пирогом угол сектора — это угол, образующийся, когда два края ломтика яблочного пирога соединяются, образуя точку.Формула для определения угла сектора:
Угол сектора = Длина дуги * 360 градусов / 2π * Радиус
360 представляет собой 360 градусов по кругу. Используя длину дуги 3 дюйма из предыдущего слайда и радиус 4,5 дюйма из слайда № 2, вы получите:
Угол сектора = 3 дюйма x 360 градусов / 2 (3,14) * 4,5 дюйма
Угол сектора = 960 / 28,26
Угол сектора = 33,97 градуса, который округляется до 34 градусов (из 360 градусов).
Сектор круга похож на клин или кусок пирога.2)
А = 0,094 * (63,585)
Округление до ближайшей десятой дает:
А = 0,1 * (63,6)
A = 6,36 квадратных дюймов
После повторного округления до ближайшей десятой ответ:
Площадь сектора составляет 6,4 квадратных дюйма.
Вписанный угол — это угол, образованный двумя хордами в окружности, имеющими общую конечную точку. Формула для определения вписанного угла:
вписанный угол = 1/2 * пересекаемая дуга
Пересеченная дуга — это расстояние кривой, образованной между двумя точками, где хорды касаются окружности.Mathbits дает следующий пример для поиска вписанного угла:
Угол, вписанный в полукруг, — это прямой угол. (Это называется теоремой Фалеса, названной в честь древнегреческого философа Фалеса Милетского. Он был наставником знаменитого греческого математика Пифагора, который разработал множество математических теорем, в том числе некоторые из них, упомянутые в этой статье.




 Диаметр, в два раза больше радиуса
Диаметр, в два раза больше радиуса Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..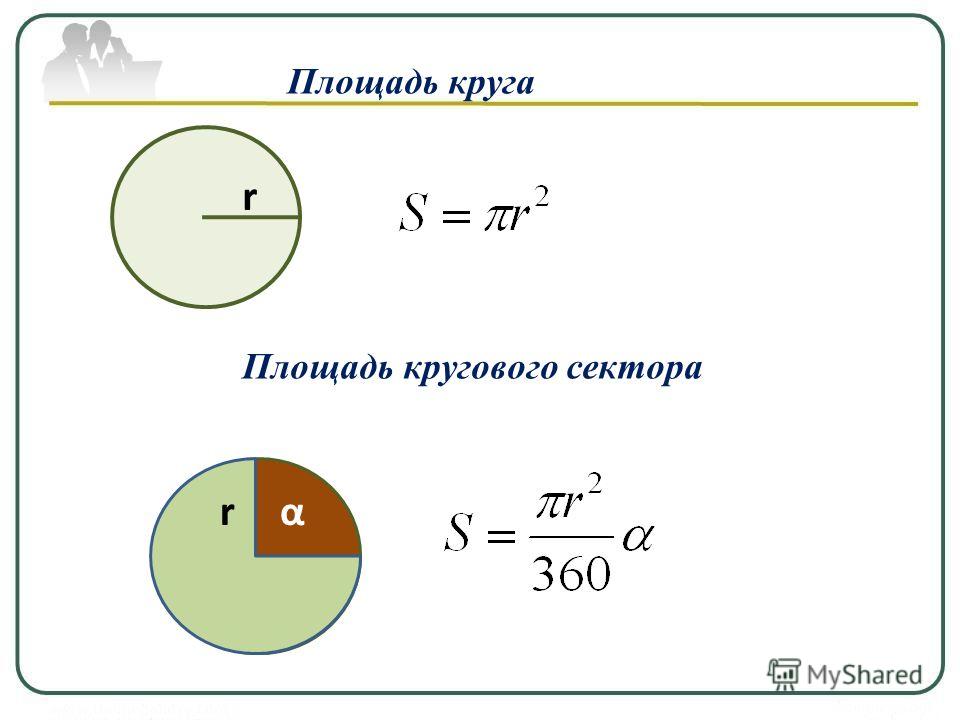
 см.
см.
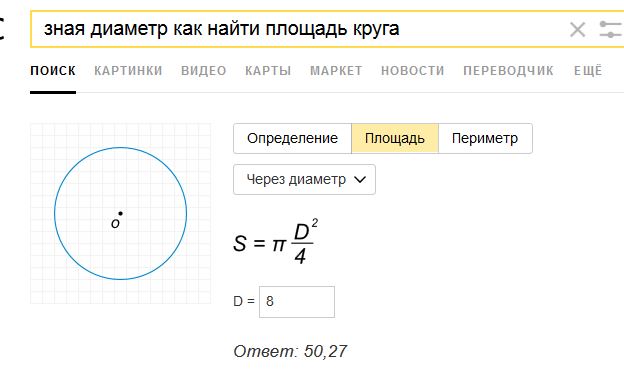
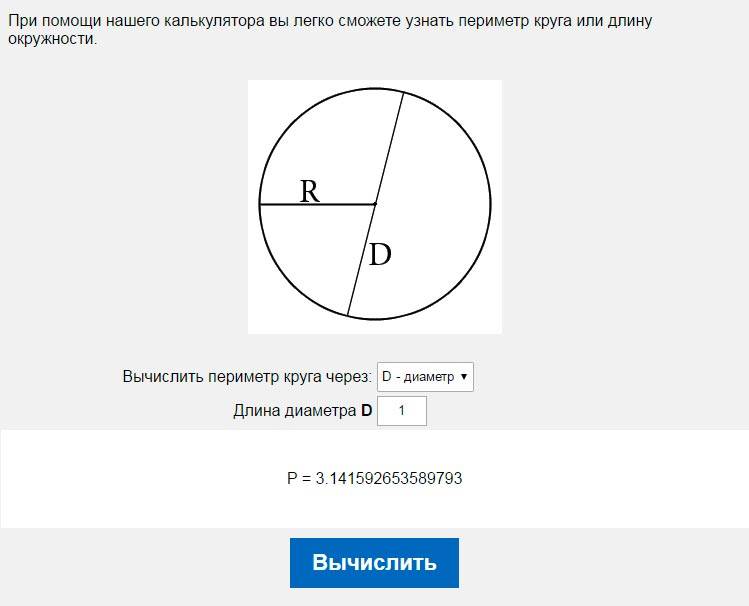
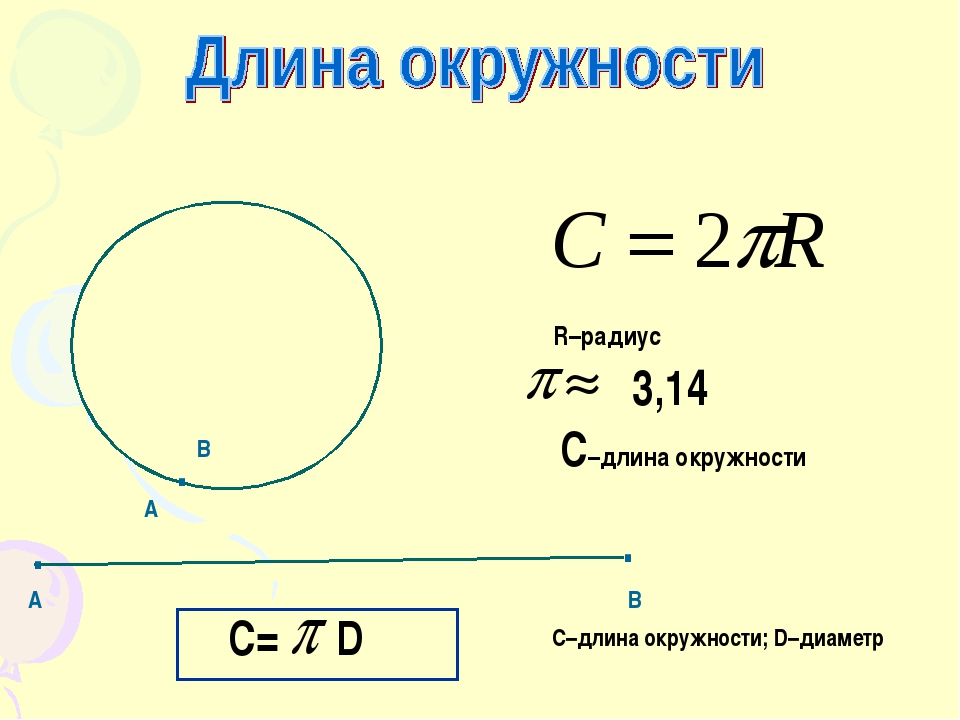 Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора имеем: Отсюда: Подставим значение радиуса и высоты в формулу объема конуса. Имеем:
Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора имеем: Отсюда: Подставим значение радиуса и высоты в формулу объема конуса. Имеем: Объем усеченного конуса вычисляется по формуле: Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и разница радиусов оснований образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора получаем: Так как образующая относится к высоте как 17:15, то L=17x, H=15x.
Объем усеченного конуса вычисляется по формуле: Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и разница радиусов оснований образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора получаем: Так как образующая относится к высоте как 17:15, то L=17x, H=15x. Читать далее
Читать далее Но для отдельных детей, а особенно творческих личностей, зубрежка является невыносимой. Родители, думающие, что их чадо не способно освоить изучение таблицы умножения и поэтому в дальнейшем будет отставать в математике, заблуждаются. На самом деле к нему нужен совершенно другой, особый подход.
Но для отдельных детей, а особенно творческих личностей, зубрежка является невыносимой. Родители, думающие, что их чадо не способно освоить изучение таблицы умножения и поэтому в дальнейшем будет отставать в математике, заблуждаются. На самом деле к нему нужен совершенно другой, особый подход. Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Возьмем на плоскости произвольный круг с радиусом R. Читать далее Читать далее
Читать далее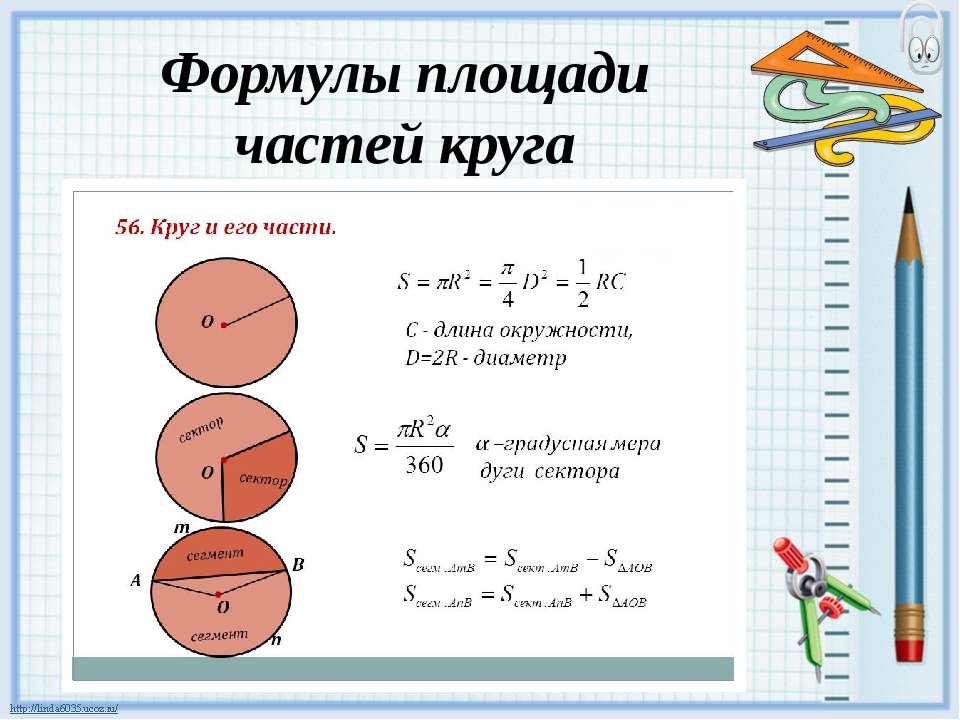 В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:
В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:
 Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах. Он обозначается латинской буквой r.
Он обозначается латинской буквой r.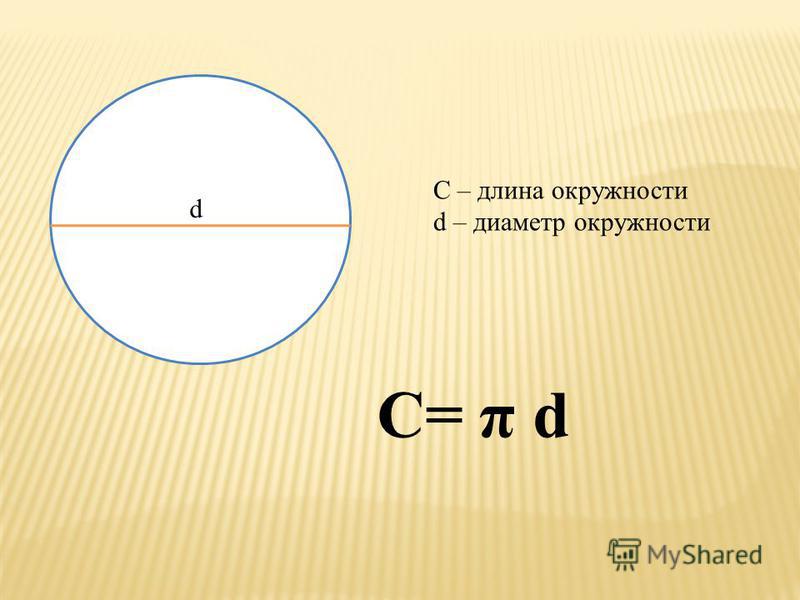 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.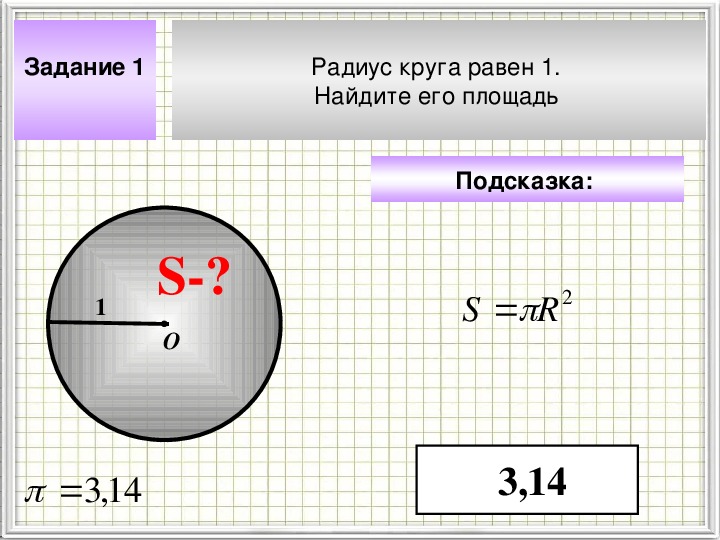
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.