КАК: Геометрия многоугольников: пятиугольники, шестиугольники и додекагоны
Немногие геометрические формы столь же разнообразны, как и многоугольники. Они включают знакомый треугольник, квадрат и пятиугольник, но это только начало.
В геометрии многоугольник представляет собой любую двумерную форму, отвечающую этим условиям:
- Состоит из трех или более прямых линий
- Закрыт без отверстий или разрывов в форме
- Имеет пары линий, которые соединяются по углам или вершинам, где они образуют углы
- Имеет равное количество сторон и внутренние углы
Двумерное означает плоское, как лист бумаги. Кубы не являются многоугольниками, потому что они трехмерны. Круги не являются многоугольниками, потому что они не содержат прямых линий.
О полигонах
Имя многоугольник происходит от двух греческих слов:
- Поли , что значитмного
- Гон , что значитугол
Формы, которые являются многоугольниками
- треугольники
- Квадраты
- Пятиугольников
- восьмиугольниками
- Додекагоны, такие как 12-сторонняя ямайская монета
Как обозначаются полигоны
Названия отдельных полигонов производятся от количества сторон или внутренних углов, которыми обладает форма. Число внутренних углов всегда равно числу сторон.
Число внутренних углов всегда равно числу сторон.
Общие имена большинства полигонов имеют греческий префикс для числа углов, прикрепленных к греческому слову для угла (gon).
Итак, префиксы и общие имена для пяти- и шестигранных правильных многоугольников:
- Penta (Греческое значение пять) + угольник
- Hexa(Греческое значение шесть) +угольник= шестиугольник
Существуют исключения из этой схемы именования. Наиболее заметно:
- Треугольникиспользует греческий префиксTri, но вместо греческого gon , латыньугол используется. треугольник редко используется.
- Четырехугольник выводится из латинского префиксаQuadri,т.е. четыре, прикрепленные к слову боковая,которое является другим латинским словом, означающимбоковая сторона .

- Иногда четырехсторонний многоугольник называютчетырехугольник или жечетырехугольник.
N-угольники
Существуют многоугольники с более чем 10 сторонами и углами, а некоторые имеют общие названия, такие как 100-сторонняяhectogon .
Они встречаются нечасто, поэтому им часто присваивается имя, которое связывает число сторон и углов с общим термином для угла, что угольник.
Таким образом, 100-сторонний многоугольник называется 100-угольник.
Несколько других п-угольникии общие имена для многоугольников с более чем 10 сторонами:
- 11-гой: Хендекагон
- 12-гой: Додекагон
- 20-гой: Икосагон
- 50-гой: Пятиконечный
- 1000-угольник: Chiliagon
- 1000000-gon: Megagon
Предел полигона
Теоретически, нет предела количеству сторон и углов для многоугольника.
Поскольку размер внутренних углов многоугольника становится меньше, а длина его сторон становится короче, полигон приближается к кругу, но он никогда не попадает туда.
Классификация полигонов
Регулярные и нерегулярные полигоны
В правильном многоугольнике все углы имеют одинаковый размер, а все стороны равны по длине.
Выпуклые и вогнутые полигоны
Второй способ классификации полигонов — размер их внутренних углов. Они либо выпуклые или вогнутой :
- выпуклость многоугольники не имеют внутренних углов, превышающих 180 °.
- вогнутый полигоны имеют по крайней мере один внутренний угол, который больше 180 °.
Простые и сложные полигоны
Другой способ классификации полигонов — это, кстати, пересечение линий, образующих полигон.
- Линии простые полигоны соединяться или пересекаться только один раз — в вершинах.
- Линии сложные полигоны пересекаются более одного раза.

Имена сложных многоугольников иногда отличаются от имен простых многоугольников с одинаковым числом сторон.
Например,
- Регулярная формашестиугольник представляет собой шестигранный простой многоугольник.
- Звездный гексаграмма представляет собой шестигранный сложный многоугольник, созданный перекрытием двух равносторонних треугольников.
Сумма правила внутренних углов
Как правило, каждый раз, когда сторона добавляется к многоугольнику, например:
- От треугольника до четырехстороннего (от трех до четырех сторон)
- От пятиугольника до шестиугольника (от пяти до шести сторон)
еще 180 ° добавляется к сумме внутренних углов.
Это правило можно записать в виде формулы:
(n — 2) × 180 °
где n равно числу сторон многоугольника.
Таким образом, сумма внутренних углов для шестиугольника может быть найдена с использованием формулы:
(6 — 2) × 180° = 720°
Сколько треугольников в этом многоугольнике?
Вышеупомянутая формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти при расчете:
n — 2
где n снова равно числу сторон многоугольника.
Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6 — 2) и додекагон на 10 треугольников (12 — 2).
Размер угла для регулярных полигонов
Для правильных многоугольников, в которых углы имеют одинаковый размер, а стороны имеют одинаковую длину, размер каждого угла в многоугольнике можно рассчитать, разделив общее число градусов на общее число сторон.
Для обычного шестигранного шестиугольника каждый угол:
720° ÷ 6 = 120°
Некоторые хорошо известные полигоны
Треугольные фермы
Кровельные фермы часто треугольные. В зависимости от ширины и высоты крыши ферма может включать равносторонние или равнобедренные треугольники.Из-за их большой силы треугольники используются при строительстве мостов и рамок велосипеда, и они видны в Эйфелевой башне.
Пентагон
Пентагон — штаб-квартира Министерства обороны США — берет свое название от своей формы. Это пятисторонний регулярный пятиугольник.
Главная пластина
Другой известный пятисторонний регулярный пятиугольник — домашняя пластина на бейсбольном алмазе.
Фальшивый Пентагон
Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме обычного пятиугольника и иногда называется фальшивым Пентагоном.
Снежинки
Каждая снежинка начинается как гексагональная пластина, но уровни температуры и влажности добавляют ветви и усики, так что каждый из них выглядит разным.
Пчелы и осы
Природные шестиугольники также включают ульи, где каждая ячейка в сотах, которую пчелы создают для хранения меда, является шестиугольной. Гнезда бумажных осы также содержат гексагональные клетки, где они выращивают своих молодых.
Тротуар гиганта
Шестиугольники также находятся в Коричневом Гиганте, расположенном в северо-восточной Ирландии. Это естественное горное образование, состоящее из около 40 000 взаимосвязанных базальтовых колонн, которые были созданы как лава из древнего вулканического извержения, медленно охлажденного.
Октагон
Octagon — название, данное кольцу или клетке, используемой в схватках Ultimate Fighting Championship (UFC), берет свое название от его формы. Это восьмигранный регулярный восьмиугольник.
Стоп-сигналы
Знак остановки — один из самых знакомых дорожных знаков — еще один восьмисторонний регулярный восьмиугольник. Хотя цвет и формулировка или символы на знаке могут различаться, восьмиугольная форма для знака остановки используется во многих странах по всему миру.
Как сделать ровный 6 угольник. Правильный шестиугольник построение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .
Рисунок 38
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Рисунок 39
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.
Рисунок 40
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:
Вот какова палитра из примера:
- Синий: C 65 M 23 Y 35 K 0
- Бежевый: C 13 M 13 Y 30 K 0
- Персиковый: C 0 M 32 Y 54 K 0
- Светло-розовый: C 0 M 64 Y 42 K 0
- Темно-розовый: C 30 M 79 Y 36 K 4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).
Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .
Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.
Геометрия
Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину.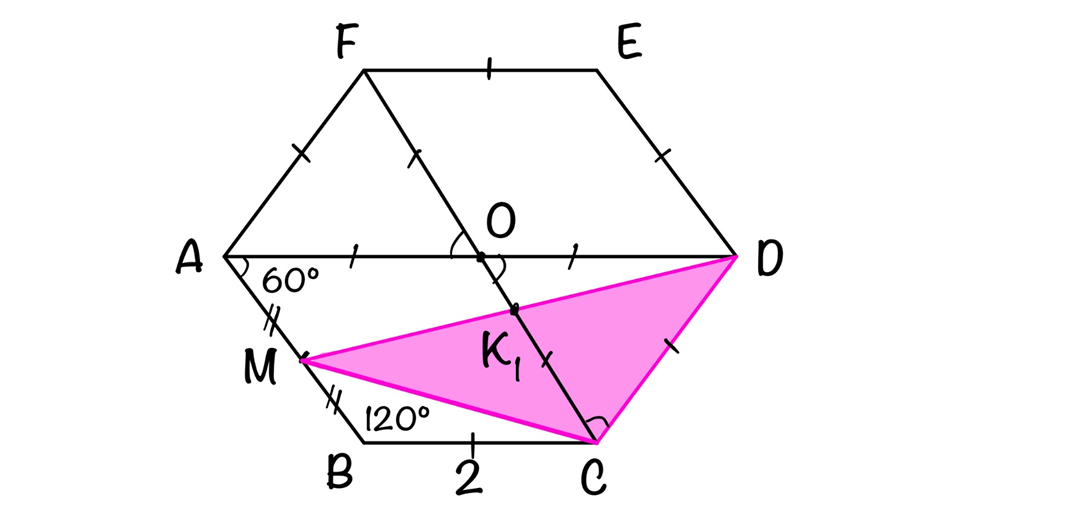 Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.
Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.
Шестиугольники с плоским (слева) и острым (справа) верхом
У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек. Каждая угловая точка общая для трёх шестиугольников. Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).
Углы
В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:Function hex_corner(center, size, i):
var angle_deg = 60 * i + 30
var angle_rad = PI / 180 * angle_deg
return Point(center.x + size * cos(angle_rad), center. y + size * sin(angle_rad))
y + size * sin(angle_rad))
Для заполнения шестиугольника нужно получить вершины многоугольника с hex_corner(…, 0) по hex_corner(…, 5) . Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в hex_corner(…, 0) .
Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.
Углы шестиугольников с плоским и острым верхом
Размер и расположение
Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника height = size * 2 . Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .Ширина шестиугольника width = sqrt(3)/2 * height . Горизонтальное расстояние между соседними шестиугольниками horiz = width .
В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.
Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.
Системы координат
Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.Координаты смещений
Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются col или q . Строки обозначаются row или r . Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.
Горизонтальное расположение «нечет-r»
Горизонтальное расположение «чёт-r»
Вертикальное расположение «нечет-q»
Вертикальное расположение «чёт-q»
Кубические координаты
Ещё один способ рассмотрения сеток шестиугольников — видеть в них три основные оси, а не две , как в сетках квадратов. В них проявляется элегантная симметрия.
В них проявляется элегантная симметрия.Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0 . Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.
Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.
Шестиугольники
Кубы
Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.
Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.
- Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z , равным 0, 1, 2, 3, чтобы увидеть связь. Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
- Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z , поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.
Существует множество различных систем координат для кубов и шестиугольников. В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.
Осевые координаты
Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие x + y + z = 0 , третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.
Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .
Оси
Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.Координаты смещения, кубические и осевые
Ось — это направление, в котором соответствующая координата увеличивается. Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.
Преобразование координат
Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:
# преобразование кубических в осевые координаты
q = x
r = z
# преобразование осевых в кубические координаты
x = q
z = r
y = -x-z
В коде эти две функции могут быть записаны следующим образом:
Function cube_to_hex(h): # осевая
var q = h.x
var r = h.z
return Hex(q, r)
function hex_to_cube(h): # кубическая
var x = h.q
var z = h.r
var y = -x-z
return Cube(x, y, z)
Координаты смещения совсем немного сложнее:
Соседние шестиугольники
Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.Кубические координаты
Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат Cube(dx, dy, dz) во время компиляции:Var directions = [
Cube(+1, -1, 0), Cube(+1, 0, -1), Cube(0, +1, -1),
Cube(-1, +1, 0), Cube(-1, 0, +1), Cube(0, -1, +1)
]
function cube_direction(direction):
return directions
function cube_neighbor(hex, direction):
return cube_add(hex, cube_direction(direction))
Осевые координаты
Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу Cube(dx, dy, dz) и преобразуем в таблицу Hex(dq, dr) :Var directions = [
Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1)
]
function hex_direction(direction):
return directions
function hex_neighbor(hex, direction):
var dir = hex_direction(direction)
return Hex(hex.q + dir.q, hex.r + dir.r)
Координаты смещения
В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row . Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2) . Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.
Нечет-r
var directions = [
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-r
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ],
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётной (EVEN) и нечётной (ODD) строк
Нечет-q
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ],
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-q
var directions = [
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётного (EVEN) и нечётного (ODD) столбцов
Диагонали
Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).Var diagonals = [
Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1),
Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1)
]
function cube_diagonal_neighbor(hex, direction):
return cube_add(hex, diagonals)
Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.
Расстояния
Кубические координаты
В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов. Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:Function cube_distance(a, b):
return (abs(a.x — b.x) + abs(a.y — b.y) + abs(a.z — b.z)) / 2
Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:
Function cube_distance(a, b):
return max(abs(a.x — b.x), abs(a.y — b.y), abs(a.z — b.z))
На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.
GIF
Осевые координаты
В осевой системе третья координата выражена неявно. Давайте преобразуем из осевой в кубическую систему для расчёта расстояния:Function hex_distance(a, b):
var ac = hex_to_cube(a)
var bc = hex_to_cube(b)
return cube_distance(ac, bc)
Если компилятор в вашем случае встраивает (inline) hex_to_cube и cube_distance , то он сгенерирует такой код:
Function hex_distance(a, b):
return (abs(a.q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе . Например, описанная «разность разностей» получается из записи a.q + a.r — b.q — b.r как a.q — b.q + a.r — b.r и с использованием формы максимального значения вместо формы деления пополам cube_distance . Все они аналогичны, если увидеть связь с кубическими координатами.
Координаты смещения
Как и в случае с осевыми координатами, мы преобразуем координаты смещения в кубические координаты, а затем используем расстояние кубической системы.Function offset_distance(a, b):
var ac = offset_to_cube(a)
var bc = offset_to_cube(b)
return cube_distance(ac, bc)
Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).
Отрисовка линий
Как нарисовать линию от одного шестиугольника до другого? Я использую линейную интерполяцию для рисования линий . Линия равномерно сэмплируется в N+1 точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.GIF
- Сначала мы вычисляем N , которое будет расстоянием в шестиугольниках между конечными точками.
- Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N , включая их, каждая точка будет A + (B — A) * 1.0/N * i . На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
- Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).
Function lerp(a, b, t): // для float
return a + (b — a) * t
function cube_lerp(a, b, t): // для шестиугольников
return Cube(lerp(a.x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
Примечания:
- Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
- Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
- Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube . Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
- Можно оптимизировать код, встроив (inline) cube_lerp , а затем рассчитав B.x-A.x , B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
- Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите .
- Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие» . Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.
Диапазон перемещения
Диапазон координат
Для заданного центра шестиугольника и диапазона N какие шестиугольники находятся в пределах N шагов от него?Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)) . Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Var results =
for each -N ≤ dx ≤ N:
for each -N ≤ dy ≤ N:
for each -N ≤ dz ≤ N:
if dx + dy + dz = 0:
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл сработает, но будет довольно неэффективным. Из всех значений dz , которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов dx + dy + dz = 0 . Вместо этого мы напрямую вычислим значение dz , удовлетворяющее условию:
Var results =
for each -N ≤ dx ≤ N:
for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N):
var dz = -dx-dy
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
GIF
Пересекающиеся диапазоны
Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N , и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0 , чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.
Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме x min ≤ x ≤ x max , и примем x min = center.x — N и x max = center.x + N . Сделаем то же самое для y и z , в результате получив общий вид кода из предыдущего раздела:
Var results =
for each xmin ≤ x ≤ xmax:
for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin):
var z = -x-y
results.append(Cube(x, y, z))
Пересечением двух диапазонов a ≤ x ≤ b и c ≤ x ≤ d является max(a, c) ≤ x ≤ min(b, d) . Поскольку область шестиугольников выражена как диапазоны над x , y , z , мы можем отдельно пересечь каждый из диапазонов x , y , z , а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении. Для одной области шестиугольников мы принимаем x min = H.x — N and x max = H.x + N , аналогично для y и z . Для пересечения двух областей шестиугольников мы принимаем x min = max(h2.x — N, h3.x — N) и x max = min(h2.x + N, h3.x + N), аналогично для y и z . Тот же шаблон работает для пересечения трёх или более областей.
GIF
Препятствия
При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде fringes[k] — это массив всех шестиугольников, которых можно достичь за k шагов. При каждом проходе по основному циклу мы расширяем уровень k-1 на уровень k .Function cube_reachable(start, movement): var visited = set() add start to visited var fringes = fringes.append() for each 1
Повороты
Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:
[ x, y, z]
to [-z, -x, -y]
Поворот на 60° влево сдвигает каждую координату на одну позицию влево:
[ x, y, z]
to [-y, -z, -x]
«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60° меняет знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.
Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:
- Преобразование положений P и C в кубические координаты.
- Вычисление вектора вычитанием центра: P_from_C = P — C = Cube(P.x — C.x, P.y — C.y, P.z — C.z) .
- Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C .
- Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z) .
- Преобразование кубического положения R обратно в нужную систему координат.
Кольца
Простое кольцо
Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса radius , нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно radius . Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.Function cube_ring(center, radius): var results = # этот код не работает для radius == 0; вы понимаете, почему? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i В этом коде cube начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла cube двигается на один шестиугольник по кольцу. Через 6 * radius шагов он завершает там, где начал.
Спиральные кольца
Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:Function cube_spiral(center, radius):
var results =
for each 1 ≤ k ≤ radius:
results = results + cube_ring(center, k)
return results
Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра. Для вычисления площади используйте эту формулу .
Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).
Область видимости
Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.
GIF
Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд. Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.
Я хочу в дальнейшем расширять это руководство. У меня есть
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- – циркуль;
- – линейка;
- – карандаш;
- – лист бумаги.
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
python — Шестиугольники из треугольников на сфере: построение гексагональной / геодезической сетки из сетки икосаэдра (только Северный полюс)
Я пытаюсь построить гексагональную / геодезическую сетку на сфере. Для моих целей я сосредоточен только на Северном полюсе. До сих пор мне удалось построить треугольную сетку на основе икосаэдра, используя пакет stripy. Пакет stripy позволяет уточнить сетку путем деления пополам: каждое ребро делится пополам или, что то же самое, каждый треугольник делится на 4 меньших треугольника.
Я хочу создать (почти) шестиугольную сетку, комбинируя 6 треугольников (5 на полюсе) следующим образом:
У меня есть следующая информация:
- широта / долгота всех вершин как
np.array - тройки индексов вершин треугольника
Ограничение состоит в том, что индексы являются скорее «случайными», то есть они не увеличиваются при движении по спирали или что-то подобное.
Можно найти средние точки каждого шестиугольника (/ пятиугольника) и сгруппировать все треугольники, которые имеют эту среднюю точку в качестве одной из трех своих вершин, но я не уверен, как это сделать алгоритмически. Каким был бы эффективный способ найти вершины, обозначающие середины каждого шестиугольника? Может ли это быть как-то связано с более грубой версией сетки (т.е. до деления пополам)?
0
falidoro 3 Окт 2019 в 01:19
2 ответа
Лучший ответ
Кроме того, можно построить диаграмму Вороного триангуляции; например, используя scipy.spatial.SphericalVoronoi(). Диаграмма Вороного икосаэдрической сетки дает геодезическую (гексагональную) сетку. Смотри, например, Wang et al. ( 2011 ) .
Аналогичным образом, вместо использования диаграммы Вороного, можно также создать новую триангуляцию, используя средние точки граней каждого треугольника, что приводит к более правильному шаблону, но менее тривиально определить, в каком шестиугольнике находится точка.
Для диаграммы Вороного это намного проще, так как по определению содержащий шестиугольник соответствует шестиугольнику, созданному ближайшей вершиной в исходной триангуляции.
Ван, Нин и Джин-Луен Ли. «Геометрические свойства икосаэдрально-гексагональной сетки на двух сферах». Журнал SIAM по научным вычислениям 33,5 (2011): 2536-2559.
0
falidoro 25 Окт 2019 в 09:55
Я думаю, что, возможно, только что подумал об ответе, но было бы здорово, если бы кто-то мог проверить, сработает ли это, и предложить оптимальные пути реализации.
- Пусть V0 — множество, содержащее все вершины, а E0 — множество, содержащее все ребра. Пусть V1 будет пустым множеством, которое мы будем использовать для хранения новых вершин шестиугольника-середины для каждого прохода. Пусть V2 будет пустым набором, который будет содержать окончательный набор середин шестиугольника. Пусть E1 будет набором ребер, которые образуют «переднюю линию» идентифицированных шестиугольников, и пусть E2 будет пустым набором, который будет содержать окончательный набор ребер шестиугольника.
- Определите вершину на Северном полюсе. Переместите его из V0 в V1
- Найдите все ребра, противоположные этой вершине. Переместите эти края в E1.
- Из E0 удалите ребра, которые связаны с вершиной (более поздние вершины) в V1.
- Из V0 удалите вершины, соединенные ребрами в E1.
- Переместите все вершины из V1 в V2.
- Каждое ребро в E1 является частью другого треугольника, для которого оно образует ребро, противоположное вершине, являющейся центром шестиугольника. Определите вершины, противоположные ребрам в E1. Переместите их в V1.
- Переместите ребра от E1 до E2.
- В E0 все ребра противоположны вершинам в V1. Переместите их на E1.
- Из E0 удалите ребра, которые связаны с вершинами в V1.
- Из V0 удалите вершины, соединенные ребрами в E1.
- Переместите все вершины из V1 в V2.
И тд и тп
0
falidoro 2 Окт 2019 в 22:46
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
Объемный шестиугольник из бумаги схема
Правильный шестиугольник из квадрата | Страна Мастеров
1. 2.Начинаем складывать с квадрата.
3.Намечаем на квадрате диагонали.
4.С помощью защипа намечаем середину правой стороны.
5.Возвращаем правый угол в исходное положение.
6.Верхнюю половину правой стороны делим пополам. Для этого закрепку совмещаем с верхним углом. Обе закрепки должны быть параллельны левой стороне.
7.Сгибаем правый угол так, что бы линия сгиба прошла из середины основания, и намеченные закрепки совпали.
8.Переворачиваем на противоположную сторону.
9.Перегибаем правый угол. Линия сгиба идет из основания. Нижняя сторона правого угла совмещается с левой боковой стороной.
10.Отгибаем треугольник.
11.Возвращаем верхний треугольник.
12.По намеченной линии отрезаем верхнюю часть.
13.Расправляем фигурку и получаем правильный шестиугольник.
Шестиугольник (гексагон) из бумаги
Просмотров 31 Обновлено
Поделки оригами собираются не только из квадратного листа, но и из правильного шестиугольника. Обычно такими поделками являются: шестиконечные звезды, сложные животные (с кучей лапок), красивые орнаменты и снежинки.
Для сборки понадобится:
- Прямоугольный или квадратный лист бумаги;
- 5-10 минут свободного времени.
Внимательно смотрим пошаговый видео урок от Сары Адамс и у вас обязательно все получиться. В первой половине правильный шестиугольник (гексагон) собирают из квадратного листа, а во второй из прямоугольного. Выбирайте сами для себя приемлемый способ.
Схема (1 вариант). Нажать для увеличенияСхема (2 вариант). Нажать для увеличения Оцените статью: Поделитесь с друзьями!
Геометрические фигуры схемы
Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают.
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно на
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Объемные фигуры из картона выкройки. Геометрические фигуры из бумаги своими руками с описанием и фото схем
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоно
Оригами: объёмная шестигранная звезда-цветок из бумаги | Лучшие самоделки
Сегодня мы будем делать объёмную шестигранную звезду из бумаги в технике оригами, хотя мне она напоминает больше цветок или снежинку. Причём в этом уроке я покажу как из одной звезды сделать ещё более красивую фигуру. Данная звезда очень хорошо подходит в качестве игрушки на ёлку или украшения интерьера на праздники, так как выглядит очень красиво, особенно если выполнить её из цветной, текстурированной бумаги, плюс когда она будет не нужна то можно её сложить до плоской формы, а потом при надобности также быстро сделать снова объёмной.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Что нам понадобится чтобы сделать объёмную звезду из бумаги:
- Квадратный листок бумаги – 17,5х17,5 см;
- Ножницы;
- Клей (не обязательно).
Делаем объёмную шестигранную звезду-цветок из бумаги, инструкция:
При использовании квадратного листа бумаги размерами – 17,5х17,5 см, звезда в итоге получиться – 7х7х3 см.
Шаг 1
Берём лист бумаги, и сворачиваем его по диагонали, придавливаем и разглаживаем место сгиба.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 2
Теперь кладём созданный треугольник как на фото, правый угол загибаем к верхнему углу и придавливаем и разглаживаем не весь изгиб, а лишь верхнюю часть где-то на два пальца.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 3
Переворачиваем треугольник на обратную сторону.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Затем разворачиваем полностью лист и правую верхнюю грань загибаем до согнутой на прошлом шаге линии изгиба и снова приглаживаем только верхушку на два пальца и разгибаем эту грань.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 4
Складываем опять лист по диагонали по старой линии изгиба.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 5
Складываем треугольник пополам и проглаживаем изгиб только снизу, примерно на палец и снова разгибаем его.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 6
Теперь согните левый нижний угол так как показано на фото, так, чтобы вверху обе линии изгибов сомкнулись вместе как можно ровнее на сколько это возможно (это место указано красным кружком). И хорошо разгладьте место изгиба полностью.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 7
Затем левый нижний угол сохните зеркально правому только загибайте с обратной стороны фигуры. Чтобы при этом с правой и с левой стороны грани совпали и фигура получилась ровной. Пригладьте линию изгиба.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 8
Теперь правый уголок загибаем немного к низу, линия загиба должна идти ровно к правому углу нижележащего слоя. Приглаживаем этот изгиб и разгибаем.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Теперь нужно отрезать по этой линии изгиба через все слои фигуры. После этого должен образоваться равносторонний треугольник.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Разворачиваем его и у нас получился шестиугольный листок бумаги. Если у Вас бумага с разными цветами на обоих сторонах то выберите на данном этапе какой цвет Вы бы хотели видеть вверху готовой звезды и поверните этим цветом к себе.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 9
Сворачиваем шестигранник пополам по одной ранее созданной линии изгиба (верхний слой должен оказаться сейчас внутри) и снова разворачиваем, так повторяем по всем линиям изгибов, нам нужно добиться чтобы все изгибы были вдавлены одинаково. Затем разворачиваем наш шестигранник.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 10
Затем загибаем нижнюю сторону шестигранника к центральной линии, приглаживаем полностью линию сгиба и разворачиваем.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Проделываем то же самое с остальными 5-ю сторонами шестиугольника.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 11
Теперь загибаем сначала одну сторону шестигранника к самой верхней линии загиба, приглаживаем полностью изгиб, чтобы образовалась складка и снова разгибаем эту сторону.
Повторяем то же самое с остальными 5-ю сторонами (на фото видно не хватает 1-й складки из этого шага, я просто не досмотрела и не сделала её сразу, ничего сделаю её позже).
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 12
Переворачиваем шестигранник на обратную сторону (у меня это более тёмный оттенок, он теперь сверху).
Загибаем нижнюю сторону до первой линии сгиба, как это видно с картинки, приглаживаем изгиб и снова разгибаем эту сторону.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Проделываем то же самое с остальными 5-ю сторонами.
Шаг 13
Пригибаем пальцами все 6 уголков, чтобы образовалась как бы корзинка.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 14
Загибаем все углы в одну сторону.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Переворачиваем шестигранник на другую сторону.
Загибаем сначала один из 6-ти углов к центру и приглаживаем только нижнюю центральную часть, та которая более тёмная.
Оригами: объёмная шестигранная звезда-цветок из бумаги
И то же самое проделываем с оставшимися 5-ю углами. Таким образом у нас получился выдавленный внутри шестигранника ещё один более маленький шестигранник.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 15
Теперь берём в руки нашу фигуру и снова сворачиваем сначала верхний угол по той же линии что мы сделали в прошлом шаге, а затем поверх этого угла сворачиваем следующий по часовой стрелке угол, как бы сворачивая лепестки цветка (всё при этом должно сгибаться по ранее созданным линиям, а не как попало).
Оригами: объёмная шестигранная звезда-цветок из бумаги
И после этого у нас должна получиться такая фигура:
Оригами: объёмная шестигранная звезда-цветок из бумаги
Шаг 16
Теперь будем делать эту фигуру объемной, для этого вдавливаем боковые (более тёмные участки) внутрь фигуры пока не образуется шестиугольная бумажная звезда.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Если фигура не держится достаточно крепко и пытается как бы рассыпаться, это всё зависит от жёсткости Вашей бумаги то можно внутренние стороны лепестков смазать клеем и склеить.
В принципе звезда из бумаги готова но дальше мы можем её ещё немного улучшить, сделав похожей на цветок или снежинку. Для этого снова сделаем фигуру плоской.
Шаг 17
Нужно выдернуть сначала один внутренний треугольный «лепесток» из под верхнего лепестка. И придать ему такую форму:
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Далее уголки этого лепестка нужно загнуть к задней стороне и хорошо пригладить, чтобы не разгибались.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Так проделываем и с остальными 5-ю лепестками. Получаем такую фигуру.
Оригами: объёмная шестигранная звезда-цветок из бумаги
Теперь возвращаем нашей фигуре объёмную форму звезды или цветка и готово!
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Оригами: объёмная шестигранная звезда-цветок из бумаги
Готовые игрушки смотрятся просто замечательно, я ещё иногда украшаю их разными камешками из бижутерии и тогда из этих цветков из бумаги получаются очень красивые украшения для интерьера.
Шестиугольник из квадрата
Некоторые модели оригами начинаются с шестиугольника вместо квадратного листа бумаги. В этом случае вам нужно сделать шестигранные формы, прежде чем начать. Эта страница покажет вам, как получить шестиугольник из квадрата. Также можно сделать шестиугольник из прямоугольника.
Шестиугольник из квадрата Инструкции
- Сложите и разверните бумагу вчетверо, как показано.
- Согните правый верхний угол листа бумаги так, чтобы угол совпадал с ближайшей складкой, сделанной на шаге 1 (соедините синие точки).Расположите сгиб таким образом, чтобы новая складка совпадала с необработанным краем бумаги в месте сгиба на половину отметки.
Повторите то же самое с тремя другими углами: соедините точки, загибая угол, чтобы он встретился с ближайшей вертикальной складкой. Раскройте полностью.
- Сложите бумагу пополам, сложив нижнюю половину вверх.
- Модель должна выглядеть так.
- Повторите описанные выше складки, но уже с загнутым краем. Согните правый нижний угол до его ближайшей линии сгиба. Повторите с левой стороны.Полностью разверните бумагу.
- Вы должны увидеть контур неправильного шестиугольника, ширина которого немного больше его высоты. Используя пересечение складок (показано точкой) в качестве ориентира, сложите бумагу, чтобы получился контур правильного шестиугольника (соедините точки вертикально).
- Разверните и разрежьте по складкам, чтобы получился шестиугольник.
.
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
.% PDF-1.4 % 121 0 объект > endobj xref 121 30 0000000016 00000 н. 0000000951 00000 п. 0000001046 00000 н. 0000001990 00000 н. 0000002148 00000 п. 0000002372 00000 н. 0000003446 00000 н. 0000004521 00000 н. 0000004743 00000 н. 0000004967 00000 н. 0000006022 00000 н. 0000009211 00000 п. 0000009435 00000 н. 0000009669 00000 н. 0000010747 00000 п. 0000011822 00000 п. 0000012025 00000 п. 0000052011 00000 п. 0000052089 00000 п. 0000092171 00000 п. 0000092248 00000 п. 0000092363 00000 п. 0000092477 00000 п. 0000107644 00000 п. 0000107758 00000 н. 0000107871 00000 п. 0000118641 00000 н. 0000120258 00000 н. 0000001197 00000 н. 0000001968 00000 н. трейлер ] >> startxref 0 %% EOF 122 0 объект > endobj 123 0 объект > / Кодировка> >> / DA (/ Helv 0 Tf 0 г) >> endobj 149 0 объект > поток H | HSQǏ {N̠hci1TTMN6 k Дв # X 6u- ̜ (Ͻ {
.9 самых распространенных форм и способы их определения
Вы, наверное, много узнали о формах, даже не задумываясь о том, что они собой представляют. Но понимание того, что такое фигура, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.
В этой статье мы рассмотрим, что такое фигура, а также множество общих фигур, как они выглядят и основные формулы, связанные с ними.
Что такое форма?
Если вас спросят, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но «форма» тоже имеет особое значение — это не просто названия кругов, квадратов и треугольников.
Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальную форму, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.
Форма может иметь любой размер и появляться где угодно; они не ограничены ничем
.Треугольник Тоннец против Шестиугольника Тоннеца
Эти две диаграммы образуют то, что математики могут назвать двойным графом , поскольку они являются своего рода зеркальным отражением друг друга. Я кратко опишу это для пользы других.
На первом изображении узлы представляют высоту тона (ну, классы основного тона), тогда как на втором изображении узлы представляют аккорды . Чтобы построить второе изображение из первого, поместите точку в центре каждого треугольника, пометьте его названием аккорда, образованного окружающими тремя шагами , и соедините его с центрами трех соседних треугольников. Чтобы создать первое изображение из второго, просто повторите этот процесс: поместите точку в центре каждого шестиугольника, пометьте его названием шага, который является общим для шести окружающих аккордов , и соедините его с центрами шести соседние шестиугольники. Например, шестиугольник (cCaFfA represents) представляет шаг C, а если вы идете на один шестиугольник над ним (gGeCcE ♭), это представляет шаг G. Линия, соединяющая эти два шестиугольника, совпадает с кромкой CG на первом изображении.
Таким образом, все интервальные отношения на первой диаграмме существуют на второй диаграмме, но в несколько менее удобной форме (линии между центрами фигур, а не ребрами). Аналогично, на второй диаграмме ребра представляют переходы между двумя аккордами, которые имеют две общие ноты. Но эту же информацию можно увидеть на первой диаграмме, пересекая ребро от одного треугольника к соседнему.
Вы можете подумать, что, поскольку вторая диаграмма больше фокусируется на аккордах (делая их узлами), она лучше подходит для анализа последовательности аккордов. Однако здесь мы видим обратную сторону второй диаграммы: на диаграмме представлены не все аккорды, только основные и второстепенные триады. Здесь нет уменьшенных или расширенных аккордов, гораздо меньше подвесок, седьмых или других комбинаций. Кроме того, если вы рассматриваете любую пару соседних узлов как последовательность аккордов, они всегда являются аккордами, которые отличаются одной нотой.
С другой стороны, первая диаграмма способна отображать любую возможную комбинацию тонов, независимо от того, является ли она большой или второстепенной триадой. Тем не менее, последовательности аккордов становятся довольно абстрактными, поскольку одна форма превращается в другую.
Подвести итоги:
треугольники
- Узлы : все классы подачи
- Края : интервалы, но только согласные (м3 / м6, м3 / м6, P4 / P5)
- Формы : Аккорды (любая возможная комбинация узлов)
Шестигранники
- Узлы : Аккорды, но только основные / второстепенные триады .
- Края : последовательности аккордов, но только если они имеют два общих тона .
- Формы : Pitch классы (общий тон окружающих аккордов).
Учитывая явные ограничения диаграммы, основанной на шестиугольниках (которые легко преодолеваются на диаграмме треугольника), я не уверен, почему кто-то выбрал бы ее вместо диаграммы треугольника, учитывая выбор (исторически, я думаю, он был разработан первым, хотя). Честно говоря, мне трудно думать о любых случаях, когда вы можете легко и ясно сделать что-то в шестнадцатеричной сетке, чего вы абсолютно не можете сделать в треугольнике.
Это согласуется с тем фактом, что более естественно думать о аккорде как о комбинации нескольких высот, а не думать о высоте как о перекрытии нескольких аккордов.
Факты о гексагональных сетках — ProGamer.Ru
В Gamelogic просто одержимы всевозможными клетками. Они создают инструментарий для их формирования, пишут про них, но на самом деле их одержимость заходит гораздо дальше (даже бывают «Пятницы футболок в клетку»).
Они поделились интересными (и непонятными) фактами на страницах Gamasutra, на которые мы наткнулись в своей миссии по изучению всего и вся про клетки и их применение в играх. В этом переводе статьи подробнее описаны принципы сеток из шестигранных клеток.
Если вы хотите приобщиться к клеточному движению, следите за твиттером @gamelogicZA или ищите хэштег #fungridfacts.
Примечание: Здесь представлены образцы некоторых занимательных фактов о шестиугольниках. В качестве более серьёзного и детального математического взгляда на шестигранные клетки авторы создали PDF-документ, освещающий множество аспектов, о которых вы больше нигде не прочтёте, с особым упором на вещи, касающиеся игровой разработки: определение формы на шестигранной сетке через простые уравнения (для треугольников это max(x, y, z) < r), скалярные и векторные произведения для упрощённой тригонометрии, матрицы переходов, шестигранный аналог дерева квадрантов, процедурная генерация (с аналогом шума Перлина) и представление сеток из треугольников, ромбов и пятигранных лепестков.
Скачать его можно здесь: https://www.gamelogic.co.za/downloads/HexMath3.pdf (англ.).
Пример изображения из файла:
Агон – старейшая из (известных нам) игр с шестигранными клетками
Использовать шестиугольники в играх стали относительно недавно. Насколько мы знаем, первой из таких игр является Агон, или «Стража королевы». Она появилась в 18 веке во Франции и стала популярной благодаря простым правилам и комплексной стратегии: у каждого игрока есть королева и шесть стражников. Игроки решают, кто ходит первым, затем ходят по очереди. Каждый ход двигается по одной фигурке. Цель – первым достичь центрального гекса (трона в центре поля) королевой и расположить всех стражей вокруг неё.
Джон Нэш (тот самый из «Игр разума») заново изобрёл игру гекс в целях подтверждения «стратегии заимствования стратегии»
Гекс – это стратегическая настольная игра на шестигранной сетке любого размера и нескольких возможных форм. Впервые была придумана датским математиком Питом Хейном в 1942.
Для победы игроку нужно первым соединить две своих противоположных стороны цепочкой фишек. Гекс не может закончиться вничью, один из игроков всегда побеждает. Единственный способ не дать оппоненту составить соединяющую цепочку – составить собственную.
Джон Нэш самостоятельно изобрёл игру в 1947. Он продемонстрировал, что первый игрок может добиться победы с помощью принципа заимствования стратегии. Любой дополнительный ход только улучшит положение любого игрока. Поэтому, если у второго игрока есть выигрышная стратегия, первый может её позаимствовать. Для этого первый ход делается как угодно, а затем копируются ходы второго игрока. Даже, если стратегия предполагает ход на уже занятую клетку, можно просто сделать произвольный ход. Это гарантированно принесёт победу первому игроку.
Для набросков алгоритмов и механик игр с шестиугольниками можно использовать кирпичную сетку
Рисование сильно помогает при разработке алгоритмов и механик, но рисовать гексы не очень удобно. Конечно, можно распечатать шестигранную сетку, но если идея приходит в голову внезапно (или вы просто много рисуете, как и я сам), приходится быстро рисовать шестиугольники. Один из вариантов – рисовать кирпичи, как на картинке ниже. Это намного проще, а вся топологическая информация сохраняется: у каждого кирпича есть шесть соседей, расположенных с тех же сторон.
Площадь любого параллелограмма с вершинами на шестиугольных клетках равна целому количеству гексов
Напомним, что площадь параллелограмма в обычном евклидовом векторном пространстве со сторонами, заданными векторами (x1, y1) и (x2, y2), равна |x1y2 — x2y1|.
Следовательно, если все элементы формулы – целые числа, то и площадь будет целым числом. При сдвиге точек, параллельных оси x, площадь параллелограмма остаётся прежней, так что, если сдвиг вызван заменой прямоугольной решётки на шестиугольную, площади параллелограммов рассчитываются так же, как и на прямоугольной решётке, а значит тоже должны быть целыми числами.
Из этого факта следует, что площадь любого треугольника с вершинами на гексах равна половине целого числа гексов (поскольку площадь треугольника равна половине площади параллелограмма). Следовательно, любой многоугольник с вершинами на клетках имеет площадь, равную половине целого числа клеток.
Свёрнутая прямоугольная сетка – это тор, как и свёрнутая шестиугольная
Поскольку дисплеи прямоугольные, идея прямоугольного сворачивания вполне естественна – что уходит в одну сторону, появляется с другой. Не так просто сразу сообразить, как аналогичным образом свернуть шестигранную сетку. На самом деле, это можно сделать несколькими способами, в зависимости от формы сетки.
Сетка в виде параллелограмма сворачивается почти так же. как и прямоугольная. Можно легко представить её топологическое соответствие тору. Для сетки в форме шестиугольника всё уже интереснее. В данном случае, уйдя за одну грань, вы появитесь с противоположной. Но, в отличие от прямоугольника, вы пересечёте шестиугольник дважды, прежде чем появиться в начале пути. Это не очень легко представить, но это тоже топологически соответствует тору. На рисунке ниже показано, как всё работает:
Существует только один магический шестиугольник, состоящий более, чем из одной клетки
Существуют магические квадраты любого порядка с числами от единицы до итогового количества клеток. Но, за исключением одноклеточного, существует лишь один такой магический шестиугольник (если не брать в расчёт отражения и вращения).
Магические фигуры с последовательностями целых чисел, начиная от единицы, называются нормальными. Аномальные магические фигуры содержат последовательности, начинающиеся с другого целого числа. Если говорить об аномальных магических шестиугольниках, то их будет больше.
Ромбододекаэдральные соты – трёхмерные родственники шестиугольной сетки среди заполняющих пространство многоугольников
Вокруг одного круга можно вплотную разместить ровно шесть кругов такого же радиуса. Можно предположить, что и сферы возможно разместить так же плотно. Однако, нет – мы может прислонить к центральной сфере 12 сфер, при этом останется довольно много места, но 13-ю поместить уже будет некуда (это называют проблемой контактных чисел).
Ромбододекаэдральные соты – это заполнители трёхмерного пространства. Это разбиение Вороного кубической гранецентрированной упаковки, считающейся самым плотным заполнением обычного пространства одинаковыми сферами. Гранецентрированная упаковка – это размещение одинаковых шаров (к примеру, пушечных ядер) при их складировании.
Квадраты и треугольники скользят, а гексы – нет
Поэтому гекс-тетрис и не особо популярен – палка из гексов не пролезает в оставленное для неё место.
Эту проблему можно обойти, уменьшив размер шестиугольников или же заменив их кругами. Круги будут соприкасаться, но в то же время скользить, что и требуется в подобных играх.
Шестигранная сетка может служить основой для треугольной
Гексы и треугольники связаны друг с другом, как показано на картинке. Фокус в том, чтобы использовать единую окраску из трёх цветов: один для направленных вверх треугольников, другой для направленных вниз и третий для вершин.
Если вы до этого не работали с треугольными сетками, вы не сразу поймёте, насколько это облегчает математику. Треугольные сетки часто скоординированы довольно нескладным образом, и у вас не получается применять векторные вычисления для решения простых геометрических задач, как в случае с квадратами и гексами. Например, при схеме, как на рисунке, не удастся получить вектор «смещения» для вычисления движений. Однако, если в схеме на заднем плане присутствуют гексы, вы можете пользоваться элегантной векторной математикой для смещений и непостоянных форм, а также выполнять вращение и отражение с помощью умножения матриц.
Lego-образные гексовые блоки бывают двух видов – обычные и боковые
Конструкционные блоки из шестиугольников открывают интересные возможности в дизайне. Ниже показаны два их вида.
При грамотном расположении выемок и шипов можно соединять блоки не только «синхронно», как в самом конструкторе Lego, но и «несинхронно».
Края можно оставлять открытыми, чтобы шипы было можно помещать и в «полувыемки».
Также можно сделать соединительные блоки, чтобы квадратные и шестиугольные блоки работали совместно.
Шестиугольные клетки могут обеспечить структурную целостность марсианских зданий
Да, жилища из шестиугольников – не прерогатива пчёл.
На картинке выше показан дом Queen B, спроектированный для защиты людей от радиации и погодных условий Марса. Список особенностей дома с официального сайта:
- Полноценная кухня, 2 спальни, 2 ванных комнаты, сад, лаборатория 3D-печати, комната отдыха, прачечная и комната декомпрессии/прихожая в качестве стандартного набора.
- Дизайн с расчётом на удержание тепла и рельефная крыша, препятствующая скоплению мусора.
- Панели из обеднённого урана, снижающие радиацию до безопасного уровня.
- Привлекательная эстетика, помогающая в продвижении миссии и поиске добровольцев.
Последний пункт особенно важен для игр: дома из гексов помогут их продвигать 🙂
Невозможно окрасить шестигранную сетку в два цвета, так чтобы соседние гексы всегда были разного цвета
Иногда это создаёт неудобства в играх, рассчитанных на двоих.
Впрочем, дополнительные цвета сразу решат проблему. Трёхцветная схема используется в шестигранных шахматах. Слон в такой схеме тоже ходит только по клеткам одного цвета, как и в обычных шахматах.
Сферу нельзя полностью покрыть одними шестиугольниками
Как минимум вам понадобится добавить 12 пятиугольников. Подобные сферические многогранники основаны на икосаэдре (правильный многогранник, состоящий из 20 треугольников), смотрите видео:
Есть множество других способов составления сфер из шести- и пятиугольников, и химия изучает их на примере фуллеренов (молекул углерода в форме сферы, цилиндра и т.п.).
Из шестиугольников можно выстраивать цилиндры, торы и даже ленты Мёбиуса.
Хоть вы и не можете выстроить сферу с помощью гексов, вы можете подделать её, сделав цилиндр или тор, с виду похожий на сферу. Один из таких приёмов работает в игре Antipod.
Другой приём использует свёрнутый шестиугольник (а значит тор), превращённый в полусферу, как сделали тут.
Полигекс – плоская фигура, состоящая из n шестиугольников, соединённых гранями, как в обычной шестигранной сетке
Фигуры в Тетрисе называют тетромино (четыре соединённых гранями квадрата в фигуре), это подвид полимино (любое число соединённых гранями квадратов в фигуре). Шестигранный эквивалент полимино называется полигекс.
Есть много головоломок на использование полигексов. В самых распространённых игроку требуется составить заданную форму из набора полигексов. Не существует формулы для вычисления количества полигексов заданного порядка.
Выбор между вертикально и горизонтально ориентированными гексами – не просто вопрос эстетики
Аргументы за и против:
- Горизонтальная ориентация схожа с раскладкой клавиатуры: для перемещения можно использовать WEADZX, также, как WASD на квадратной сетке. Однако, QWEASD прекрасно подходит для вертикальных клеток.
- Горизонтальная схема лучше подходит для 3D/изометрии, где нижний ряд ближе к игроку, а верхний дальше. Таким образом высокие спрайты не будут загораживать центр ближайших клеток, затрагивая только край. Вероятно, поэтому вертикальная ориентация лучше подойдёт для вида ровно сверху.
- Вертикально ориентированные клетки можно сделать вдвое шире, чем их высота, с точностью до пикселя. Ограниченная высота по сравнению с шириной добавляет глубины, особенно когда на гексах располагаются объекты, способные перекрывать стоящие позади клетки.
- В сетке вида NxN горизонтальная ориентация приведёт к увеличенной ширине, как у PC-мониторов. Иными словами, карта из горизонтальных клеток лучше подойдёт для широких экранов, благодаря относительно схожему соотношению строк и столбцов. В зависимости от размера и видимой области карты, это может дать игроку лучший обзор и позволит избежать лишнего скроллинга.
- С вертикальными клетками будут видны все стены. Если у вас горизонтальная ориентация и есть стены, идущие вдоль вертикальных линий, вряд ли получится обогатить их деталями (дверьми или проходами). Более того, если использовать вышеупомянутый тип перспективы, гексы будут выглядеть на порядок лучше, поскольку вы сделаете их приплюснутыми. Если сплюснуть горизонтальный гекс, уклон на вершинах получится не очень крутым (около 1/8 против 1/2 у вертикальных). Иными словами, если вы делаете вид с высоты птичьего полёта или применяете пиксель-арт, вертикальные гексы будут смотреться лучше.
Только три типа выпуклых шестиугольников могут заполнить плоскость (то есть выступать в качестве сетки)
Плоскость можно заполнить не только правильными шестиугольниками. Из выпуклых шестиугольников подходящими будут три типа, удовлетворяющих следующим условиям:
- A + B + C = 360, a = d
- A + B + D = 360, a = d, c = e
- A = C = D = 120, a = b, c = d, e = f
Поиграть с такими клетками можно здесь: https://www.geogebratube.org/student/m155779
Что касается пятиугольников, никто не знает, сколько разных типов фигур может заполнить плоскость (известно минимум о 14, но может быть и больше).
Вместо векторов в качестве координат гексов можно использовать комплексные числа
Координаты сетки можно представить в виде комплексных чисел. Для прямоугольной сетки это будут Гауссовы целые числа. Для шестигранной сетки это будут целые числа Эйзенштейна.
У этих чисел много общего с настоящими целыми. Например, у вас есть понятие о делении с остатком или без, так что можно определить простые числа, и, следовательно, выстроить полную теорию чисел.
Такие числа могут использоваться в реализации определённых алгоритмов, например, раскрашивания, формирующего составные блоки многих других алгоритмов.
Треугольная сетка – двойственная сетка шестиугольной
Это означает, что любая игра, разыгрываемая на вершинах треугольных клеток, на самом деле играется на гранях шестиугольников. Этот факт пригодится как в дизайне, так и в разработке алгоритмов (для реализации китайских шашек сама логика велит пользоваться шестигранной сеткой, а не треугольной!).
Использование треугольников вместо гексов позволяет снизить количество разных плиток в наборе
Многие плиточные игры спланированы так, чтобы их грани совпадали и таким образом выстраивались более крупные формы. Набор плиток при этом может быть очень обширным, и одним из решений проблемы является деление гексов на треугольники. Это серьёзно сократит количество необходимых плиток и будет особенно полезным в компьютерных играх, где треугольники можно сделать абсолютно невидимыми для игрока.
Шестиугольные клетки могут служить имитацией трёхмерных кубов
Изометрическая проекция куба – это шестиугольник. Разделяя каждую клетку на три ромба и используя подходящее затенение, можно добиться эффекта трёхмерных кубов (если нужно, чтобы каждая «грань» куба была отдельной ячейкой, используйте ромбическую сетку – она сама построена на основе шестиугольной).
Этот факт пригодился многим играм, первой из которых была Q*bert, в своё время (1982) расхваливаемая за использование 3D.
Если вы допускаете пересечение шестиугольников, можно добиться и более впечатляющих 3D-эффектов. Такое уже использовалось в карточных играх, как на примере ниже.
Дополнительно по теме:
шестиугольников — промежуточная геометрия
Объяснение:Есть несколько способов найти площадь шестиугольника.
- Разделите фигуру правильным шестиугольником на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы площадь можно найти, вычислив половину длины стороны, умноженную на апофему.
Правильные шестиугольники:
Правильные шестиугольники — это интересные многоугольники.Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны равны по длине, а все внутренние углы имеют одинаковую меру; следовательно, мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка находится на равном расстоянии от всех вершин.В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны: у каждого треугольника есть две стороны внутри шестиугольника, а также основная сторона, которая составляет периметр шестиугольника. Подобным образом у всех треугольников одинаковые углы. Они находятся в круге, а шестиугольник на нашем изображении разделил его на шесть равных частей; следовательно, мы можем написать следующее:
Нам также известно следующее:
Теперь давайте посмотрим на каждый из треугольников шестиугольника.Мы знаем, что у каждого треугольника две стороны равны; следовательно, каждый из углов основания каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть, и можем найти два основных угла каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен. Теперь мы знаем, что все треугольники равносторонние и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту важную информацию для определения площади шестиугольника.Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа. Если мы проведем через треугольник высоту, то получим два треугольника.
Давайте решим длину этого треугольника. Помните, что в треугольниках длина сторон треугольников находится в следующем соотношении:
Теперь мы можем проанализировать, используя заменяющую переменную для длины стороны,.
Нам известны размеры основания и высоты, и мы можем вычислить их площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы решили для площади правильного шестиугольника с длиной стороны,. Если мы знаем длину стороны правильного шестиугольника, мы можем найти площадь.
Если нам не дан правильный шестиугольник, то мы вычисляем площадь шестиугольника, используя длину стороны (т.е.е. ) И апофема (т.е.), которая представляет собой длину линии, проведенной от центра многоугольника до прямого угла любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и, то мы можем найти площадь шестиугольника по следующей формуле:
В этом уравнении площадь, периметр и апофема. Мы должны рассчитать периметр, используя длину стороны и уравнение, где — длина стороны.
Решение:
В задаче сказано, что соты два сантиметра в диаметре. Чтобы решить задачу, нам нужно разделить диаметр на два. Это потому, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в соте. Найдем длину стороны правильного шестиугольника / соты.
Заменить и решить.
Нам известна следующая информация.
В результате мы можем написать следующее:
Давайте подставим это значение в формулу площади правильного шестиугольника и решим.
Упростить.
Решить.
Округлите до ближайшей десятой доли сантиметра.
Способы создания урока для первого класса: Hexagon Edition
Время работы учащихся: Я предлагаю учащимся поработать 5 минут, а затем расскажу партнеру, как они построили шестиугольник.Основание предложения в поддержку обсуждения: как вы построили свой шестиугольник? Я построил свой шестиугольник из…
- Пока студенты работают, я специально ищу 2 шестиугольника, которые можно разделить — предпочтительно один с двумя трапециями, а другой с трапецией и комбинацией других форм. Таким образом, мы можем заметить, как другие формы были равны трапеции.
Студенческий ресурс: во время студенческого обмена я упоминаю онлайн-инструмент, который использовал. Вы можете найти инструмент блока узоров по этой ссылке «Освещение».
Давайте рассмотрим несколько способов сложения шестиугольника и сосредоточимся на том, как вы можете записать, как вы это сделали, чтобы вспомнить, как строить шестиугольники завтра.
Поделиться 1: Я покажу, как один ученик сделал шестиугольник, используя 2 трапеции, с помощью онлайн-инструмента для создания шаблонов. Прежде чем сложить трапеции вместе, я поощряю навыки визуализации студентов, задавая вопрос: как я могу взять эти две трапеции и превратить их в шестиугольник?
- Я смоделирую рисунок того, что мы сделали на диаграммной бумаге.Подумайте вслух: «Чтобы упростить задачу, я не буду рисовать всю фигуру. Я собираюсь нарисовать только то место, где я бы вырезал шестиугольник, чтобы показать формы. Я буду использовать красный маркер, чтобы показать свои трапеции. Я вижу, что линия, разделяющая шестиугольник на 2 трапеции, проходит прямо через середину. Вы видите мои две трапеции? Где они?»
Поделиться 2: Я покажу второй способ сделать шестиугольник с помощью онлайн-инструмента. Перед тем, как сделать форму, я посоветую поговорить со студентами: как я могу сделать из этой трапеции, ромба и треугольника шестиугольник?
После того, как я покажу это на прометейовой доске, я снова нарисую, как мы это делали, на диаграммной бумаге.
Поделиться Сравните: Во время этой части урока я хочу, чтобы студенты начали изучать, как мы можем использовать эквивалентность форм, чтобы помочь нам найти новые пути. Другими словами, я хочу, чтобы они увидели, что, поскольку ромб и треугольник составляют трапецию, мы можем использовать их как взаимозаменяемые с трапецией.
Руководящие вопросы:
- Как мы изменили первые формы, чтобы получился второй шестиугольник?
- Чем отличаются эти две композиции форм?
- Я буду моделировать, используя термин «эквивалент». Вынули трапецию и поставили ромб и треугольник. Ромб и треугольник эквивалентны трапеции. Мы можем заменить трапецию на ромб и треугольник.
Треугольный поднос с шестигранной головкой | Моя любовь 2 Создать
Как часть команды Power Tool Challenge, я с радостью делюсь своим проектом на этот месяц — шестиугольным треугольным лотком.
Это имя сбивает с толку? Ха-ха! Да, это шестиугольник, но я сделал его из треугольников, там — это метод к моему безумию! 😉Темой этого месяца было создание проекта с использованием вашего любимого инструмента.Выбор любимого инструмента — это что-то вроде выбора любимого члена семьи, вы просто не можете этого сделать, потому что вы их всех любите … верно!?!
Я пошел с пилой Mitre, мне очень нравится этот инструмент. Отчасти потому, что это был мой первый большой электроинструмент, а также потому, что с его помощью можно сделать так много крутых разрезов, и он прост в использовании. 🙂 Что ведет в этот лоток …
Разве это не круто!?! К тому же это легче сделать, чем вы думаете, но вы никогда не узнаете, пока не попробуете! Так что не смотрите на это и не говорите: «Я никогда не смогу этого сделать, ПОТОМУ ЧТО ВЫ МОЖЕТЕ !!!»
Позвольте мне рассказать вам немного о том, как появился этот проект.Несколько лет назад я сделал аналогичный проект с треугольниками, мой стол из поддонов, и мне он до сих пор нравится.В то время, когда я сделал это, я просто выбрал случайный угол на своей торцовочной пиле и начал вырезать треугольники. Я понятия не имел, что случайный угол, на который я установил пилу, который составлял 30 градусов, также оказался волшебным углом для создания шестиугольников. Я просто хотел забавный узор.
Перенесемся на год или около того, и я сделал свои шестигранные кашпо своими руками, для создания которых нужно вырезать древесину под углом 30 градусов. Недавно у меня возникла мысль, что если бы мои треугольники и шестиугольники были разрезаны под углом 30 градусов, вы могли бы объединить их и все ваши углы совпадали.Я попробовал, и это сработало!Как сделать поднос с шестиугольником треугольника:
Этот пост содержит партнерские ссылки, которые помогают мне бесплатно для вас! Огромное спасибо! Читать далее.Принадлежности:
- Лом доски 1×3 или 1-1 «x3» x8 «доски
- Обрезка досок 1×2 или 1-1 «x2» x8 «доски
- Лом 1/4 «ДВП или фанеры. Размер зависит от того, сколько треугольников вы используете, для 25 треугольников, вырезанных из доски 1×3, вам понадобится примерно 11» x 11 «
- Клей для дерева Gorilla
- Морилка (на ваш выбор)
- Гвозди отделочные
- Пистолет с гвоздями 1 1/4 »
- Торцовочная пила
Шаг 1: Разрежьте доску 1×3 на треугольники.
Установите торцовочную пилу под углом 30 градусов и отрежьте квадратный или прямой конец доски (вверху слева). Затем переверните доску (вверху справа). Придвиньте доску к забору и выровняйте ее с лезвием, чтобы разрезать ее на кончике доски (внизу слева). Затем вырежьте свой первый треугольник (внизу справа).
Удалите треугольник, переверните доску и вырежьте еще один треугольник. Повторяйте этот процесс, пока не получите 25 треугольников.
Шаг 2: Вырежьте заднюю часть 1/4 дюйма в форме шестиугольника.
Я нашел тонкий кусок жесткой доски, можно использовать фанеру толщиной 1/4 дюйма. Я собрал свои треугольники поверх задней доски в форме шестиугольника, затем обвел их вокруг фигур (вверху слева). Это дало мне форму, которую нужно вырезать (вверху справа). Поскольку моя пила уже была установлена на 30 градусов, я просто выровнял края доски по забору и разрезал все линии, чтобы получить заднюю часть шестигранника (внизу слева / справа).
Шаг 3: Окрашиваем треугольные части.
Если вы хотите, чтобы на ваших треугольных деталях был контрастный узор, из которого получится крутой геометрический узор, то вам нужно сначала окрасить их, прежде чем прикреплять к нижней части.Я выбираю темное пятно и светлое пятно, чередуя каждый треугольник.
Шаг 4: приклейте треугольные детали к спинке.
Поместите треугольные детали на спинку. Снимайте по одной части и приклейте ее к задней части столярным клеем. В конце концов, я поленился и начал вместо этого добавлять клей на заднюю часть, а затем прикрепил треугольники, этот метод был намного быстрее. После этого я убедился, что они находятся в правильном положении на задней части, и затем положил сверху большую книгу и банку с краской, пока клей высох.
Шаг 5: Вырежьте части рамы 1×2.
Установите пилу на 30 градусов. Поместите 1×2 на тонкую сторону, чтобы вырезать части рамы.
* Простой способ сделать разметку для точных пропилов под углом — соединить короткие концы досок вместе (верхнее правое фото), а затем разметить для второго пропила.
* СОВЕТ: Для большей точности при обрезке угловых деталей вырежьте по одной детали за раз и измеряйте ее в соответствии с вашим проектом в процессе работы (нижнее левое фото выше).Если вы сомневаетесь, ВСЕГДА лучше резать слишком долго, вы можете продолжать делать меньшие пропилы, пока не получите идеальную посадку … но вы не можете снова добавить древесину!
* Короткие стороны частей рамы должны быть той же длины, что и стороны шестиугольника в вашем проекте.
* Совет : Если я делаю МНОГО одинаковых пропилов, стоит сделать остановку на торцовочной пиле. Для этого нужно отрезать кусок лома под тем же углом, под которым вы выполняете пропил, а затем зажать его на упоре торцовочной пилы.Убедитесь, что вы зажимаете его так, чтобы кусок дерева, который вы режете, был нужного вам размера, при необходимости отрегулируйте. Использование этого метода гарантирует, что все ваши разрезы будут одинаковыми. На снимке выше показан упор, который я использовал, когда делал свои шестигранные сеялки. Это сэкономило мне массу времени, потому что мне не пришлось проводить измерения! Если я делаю только несколько разрезов, я предпочитаю использовать ранее упомянутые методы. Вы также можете разрезать большие доски под углом 30 градусов, это делается с помощью скоса, когда вы фактически наклоняете пильное полотно в одну сторону, а не просто перекручиваете его (как я делаю в этом проекте).Чтобы узнать, как это сделать, ознакомьтесь с моей публикацией о шестиугольных и треугольных полках.Шаг 6: приклейте и прибейте к деталям каркаса.
После того, как я отшлифовал и окрасил части рамы 1×2 и дал им высохнуть, я приклеил и прибил их к своему треугольному шестиугольнику с помощью пистолета Ryobi Nail Gun.Оберните все детали рамы вокруг шестиугольника, затем по очереди добавьте клей и прибейте их прибитыми гвоздями. Мне нравится держать детали на месте, чтобы я знал, что добавляю их в проект именно в нужном месте. После того, как вы прибили всю деталь рамы в треугольную форму шестиугольника.Вернитесь назад и прикрепите гвозди к углам рамы, чтобы закрепить их (внизу справа).
Шаг 7: Добавьте прозрачную отделку и ручки.
Я запечатал лоток 3 слоями пластыря, слегка отшлифуя зернистостью 400 между слоями 1 и 2. Шлифование придает ему действительно гладкую поверхность.
В качестве ручек я взял несколько ремней с письмами, оставшихся от моего ящика с кожаным поясом, и отрезал их длиннее, чем стороны подноса. Я прибил их гвоздями для ковров. Затем я добавила маленькие кружочки из фетра снизу, чтобы не поцарапать.Это идеальный размер для хранения безделушек, мыла и лосьонов, или для всего, что вам нужно!
И, честно говоря, я считаю, что это тоже искусство! Конечно, если вам это нужно для этой цели, вам не нужно добавлять ручки. 😉
Когда вы думаете об этом, возможности безграничны! Если вы хотите, чтобы он был больше, просто вырежьте доски большего размера, например, 1×4 или 1×6. Меньше? Разрежьте 1×2. Или просто добавьте больше треугольников, чтобы сделать его больше, или меньше, чтобы сделать его меньше.Если у вас их достаточно, чтобы сделать из них шестиугольник, вы можете сделать его настолько большим или маленьким, насколько захотите!
Он идеально сочетается с моим деревянным треугольным сердцем, которое также было вырезано на моей торцовочной пиле. Только вот эти треугольники я разрезал под углом 45 градусов. Посмотри, как это весело!?!Надеюсь, вы вдохновились попробовать торцовочную пилу. Я обещаю, что сначала ваши углы будут не идеальными, и это нормально !! Поверьте, мои углы НЕ всегда идеальны. Это требует практики, но, честно говоря, это не имеет особого значения для проектов такого типа! Так что наберитесь смелости и попробуйте, вы не пожалеете !!
Теперь давайте посмотрим на все проекты других членов команды Power Tool Challenge Team и посмотрим, какие инструменты они выбрали как свои любимые! Обязательно проявите к ним немного любви и нажмите, чтобы увидеть их сообщения по ссылкам ниже!
Спасибо, что зашли!
Обнимаю!
Я буду ссылаться на эти вечеринки, Savvy Southern Style.СохранитьСохранить
Shaping Up | NZ Maths
В этих трех упражнениях учащиеся исследуют области блоков шаблонов относительно друг друга. Затем они рассматривают различные способы создания шестиугольника и двенадцатиугольника из блоков шаблона. Делая это, они исследуют поведение эквивалентных дробей.
Activity One
В этом упражнении используются правильные шестиугольники. Студенты скоро обнаружат, что есть 7 способов сделать правильный шестиугольник, используя треугольник, трапецию и блоки узора 60/120 (см. Ответы), и на их основе они смогут писать различные уравнения.
Действие два
В этом упражнении ученики строят правильные двенадцатиугольники со сторонами, соответствующими краю квадратного блока. Они не нуждаются в представлении к вопросу 1. Они быстро обнаружат, что существует множество способов использования различных блоков узора для завершения формы. Задача для них будет заключаться в том, чтобы систематически записывать свои решения в виде аккуратных набросков.
В вопросе 2а ученики записывают сумму площади двенадцатиугольника как сумму трех различных форм, но, как они обнаружат в следующих частях этого вопроса, они могут выразить ее как сумму всего двух фигур.
Для этого они должны сначала показать (в вопросе 2b), что квадрат имеет такую же площадь, как 2 ромба 30/150. Возможно, им будет полезно вырезать из картона 2 ромба и квадрат, используя блоки выкройки в качестве шаблонов. Затем они могут наложить ромбы на квадрат. Если они отрежут перекрывающиеся части, они могут переместить их, чтобы заполнить пробелы на квадрате.
При выполнении вопросов 2e-f учащиеся должны использовать эквивалентности, обнаруженные в Задании 1 и в вопросе 2b.(Они обобщены на панели в ответах.) Используя эти эквиваленты, они могут заменить каждые 2 ромба 30/150 1 квадратом и каждые 6 треугольников (или их эквивалент) 1 шестиугольником.
Для первого двенадцатиугольника в вопросе 1 работа может быть изложена следующим образом:
Площадь = 4 квадрата + 4 30/150 ромба + 12 треугольников
= 4 квадрата + 2 квадрата + 12 треугольников
= 6 квадратов + 12 треугольников
= 6 квадратов + 2 шестиугольника
При выполнении вопросов 2e-f учащиеся должны увидеть, что площадь любого из додекагонов может быть выражена как сумма 6 квадратов и 2 шестиугольников.Следовательно, площадь каждого двенадцатиугольника одинакова.
Три действия
Если мы пытаемся создать сплошной квадрат (как подразумевается), ответ на вопрос 1 — «нет». Но можно создать мозаику с квадратными промежутками. Ответы объясняют, почему и как.
Когда учащиеся исследуют вопрос 1b, они обнаружат, что невозможно сделать правильный восьмиугольник или правильный десятиугольник, используя блоки образца.
Вы можете добавить к объяснению в ответах, показав вашему классу, как найти размер внутреннего угла правильного многоугольника.Один из способов — сначала разделить многоугольник на треугольники, как на схеме. Поскольку сумма трех углов в треугольнике равна 180 градусам, вы можете умножить количество треугольников на 180, чтобы получить сумму
всех внутренних углов многоугольника. (Это работает, потому что все углы треугольников вместе составляют углы многоугольника.) Многоугольник является правильным, поэтому разделите эту сумму на количество углов в многоугольнике, чтобы получить размер каждого внутреннего угла.
Еще раз, для вопроса 2 полезной стратегией является начертание и вырезание 6 квадратов и 2 шестиугольников из картона.Затем шестиугольники можно разрезать пополам, чтобы сформировать 4 трапеции. Когда трапеции накладываются на квадраты, они не закрывают их полностью. Это показывает, что площадь квадратов больше площади шестиугольников.
Ответы на занятия
1. Другие способы:
2.
1 = 1
1/2 + 1/2 = 1
1/2 + 1/3 + 1/6 = 1
1/2 + 1/6 + 1/6 + 1/6 = 1
1/3 + 1/3 + 1/3 = 1
1/3 + 1/6 + 1/6 + 1/6 + 1/6 = 1
1/6 + 1/6 + 1/6 + 1/6 + 1 / 6 + 1/6 = 1
Действие два
1.Есть много возможных способов. Вот некоторые из них:
2. а. Площадь = 4 квадрата + 12 треугольников + 4 ромба 30/150
б. Способы могут отличаться. В качестве возможного объяснения вы можете поставить 2 ромба на вершине квадрата. Затем вы можете увидеть, что «лишние» биты можно отрезать и использовать для точного заполнения промежутков внутри квадрата. Таким образом, площадь двух ромбов должна быть равна
площади 1 квадрата.
г. Площадь = 6 квадратов + 12 треугольников
d. Площадь = 6 квадратов + 2 шестиугольника
эл.- ф. Практические задания. Используйте факты, которые вы обнаружили в предыдущих частях этого вопроса (суммированных на панели ниже), чтобы показать, что площадь каждого двенадцатиугольника может быть уменьшена до 6 квадратов и 2 шестиугольников.
3. а. Хотя у него по-прежнему 12 сторон, стороны больше не одинаковой длины. На самом деле это полуправильный двенадцатигранник (полурегулярный, потому что в нем есть образец).
г. Площадь = 12 квадратов + 5 шестиугольников. (Площадь двенадцатиугольника составляла 6 квадратов и 2 шестиугольника. К ним вы добавили еще 6 квадратов и 6 трапеций [эквивалент 3 шестиугольника]).
Три активности
1. а. Нет. Чтобы получилась квадратная форма, нужны прямые углы. За исключением квадратного блока и ромба 30/150, углы всех блоков составляют 60 o или 120 o , которые сами по себе не образуют 90, o .
Однако вы можете создать узор, который оставит зазор размером и формой квадратного блока. Вы можете сделать это, сделав полуправильный восьмиугольник из 4 треугольников и 4 блоков ромба 30/150.Этот восьмиугольник можно комбинировать с другими, чтобы сформировать мозаику с квадратными промежутками
г. Для правильного восьмиугольника требуются внутренние углы 135 o (невозможно), а для десятиугольника 144 o (невозможно). Углы всех блоков рисунка кратны 30 o . 135 o и 144 o не кратны 30 o .
2. 6 квадратов имеют большую площадь, чем 2 шестиугольника.
Вот один из способов показать это:
2 шестиугольника имеют ту же площадь, что и 4 трапеции.Сделайте параллелограмм из 4 трапеций и положите его поверх сетки квадратов 3 на 2, например:
Если бы выступающий участок трапеции слева был обрезан, он точно соответствовал бы зазору справа, чтобы получился прямоугольник. Но этот прямоугольник будет меньше прямоугольника, образованного шестью квадратами. (Отличие в узкой полосе сверху.)
Видеоурок: Составление 2D-фигур
Стенограмма видео
Составление 2D-фигур
В этом видео мы узнаем, как составлять простые 2D-формы для создания более крупных фигур.Мы могли бы сделать прямоугольник, используя два треугольники. Мы сделали или составили форму, используя меньшие формы. Мы сделали этот прямоугольник с помощью квадрат и меньший прямоугольник. Мы использовали две меньшие формы, чтобы сделать более крупная форма. Мы могли бы составить квадрат из двух треугольники или четыре треугольника. Попрактикуемся в создании простых 2D фигуры для создания более крупных фигур.
Какую фигуру разглядела Виктория? треугольников?
Виктория разместила два треугольника вместе, чтобы создать новую форму.Как называется новая форма что она сделала? Это прямоугольник. Виктория использовала два треугольника, чтобы сделайте прямоугольник.
Могу ли я сделать прямоугольник, соединив эти квадраты вместе?
Если мы разместим наши три квадрата вместе мы сделали прямоугольник? Да у нас есть. Ответ на вопрос да. Если мы соединим три квадрата вместе, мы можем сделать прямоугольник.
Даниил пытается подогнать треугольники в этот шестиугольник.Сколько треугольников ему понадобится в общее?
Даниил пытается сделать шестиугольник с помощью треугольников. Нам нужно выяснить, сколько треугольники ему понадобятся. До сих пор Дэниел использовал один, два, три, четыре треугольника. Сколько еще треугольников нам нужно завершить шестиугольник? Мы добавили еще один треугольник. Если мы добавим еще один, шестиугольник будет полный. Даниэль уже разместил четыре треугольники вместе, чтобы получился шестиугольник.Нам понадобилось еще два треугольника, чтобы завершите это. Общее количество треугольников, которые Даниил использовал шесть, потому что четыре плюс два — шесть. Чтобы завершить шестиугольник Даниила, он всего понадобится шесть треугольников.
Какая форма была создана с использованием только треугольники?
Какая из трех фигур была сделано с использованием только треугольников? Первая форма — треугольник. Но было ли это сделано из трех треугольники? Нет, это не так.И наша вторая форма была сделана из двух треугольников. Но также используется прямоугольник. Наша третья форма состоит из четырех треугольники. Квадрат создан с использованием только треугольники. Это форма, которую мы ищем для. Квадрат создан с использованием только треугольники.
Что мы узнали из этого видео? Мы научились составлять 2D формы, чтобы создавать новые формы.
MathScene, Геометрия.Урок 3.
MathScene, Геометрия. Урок 3.| 2006 Rasmus ehf | Геометрия — площадь | Печать |
Урок 3
Площадь различных плоскостей (2-мерные фигуры)
Параллелограмм
Если вы знаете, как найти площадь квадрата и треугольника, вы можете использовать эти знания, чтобы найти площадь других плоских фигур.
Основные формы — треугольники, прямоугольники и круги. Большинство плоских фигур можно сделать из этих основных фигур. Другими словами, большинство плоских фигур представляют собой комбинации этих основных форм.
Для
Например, параллелограмм можно разбить на прямоугольник и 2 треугольника.
Самолеты можно разбить на основные формы
нарисовав соответствующие линии на схеме.
Это также возможно перемещать части фигуры, чтобы сформировать другие формы.Для Например, вы можете превратить параллелограмм в прямоугольник, как показано выше. диаграмма. Желтая и серая области на диаграмме образуют параллелограмм. Если серый треугольник перемещен в левую часть параллелограмма, он образует прямоугольник (зеленый треугольник плюс желтая фигура). Таким образом, вы можете рассчитать площадь параллелограмма путем вычисления площади прямоугольника.
Трапеция
Трапеция — четырехсторонняя фигура с двумя параллельные стороны.Добавленные строки показывают, что трапеция состоит из прямоугольника и 2-х треугольников. Район можно найти по сложение площади прямоугольника и двух треугольников.
Обычный Шестиугольник
Правильный шестиугольник — это шестигранная фигура, со всеми сторонами равной длины. Его можно разделить на 2 треугольника и прямоугольник. Площадь можно найти, сложив площадь прямоугольника и два треугольника.
Попрактикуйтесь в этих методах, а затем попробуйте Тест 3 на Область. Не забудьте использовать Контрольный список, чтобы отслеживать свою работу.
Цыпленок с шитьем | Учебное пособие по Hexagon Quilt
Итак, теперь у вас есть стопка шестиугольных блоков (правда, есть?), И вам нужно знать, как их собрать. Шестиугольники универсальны и могут быть расположены разными способами. Из этого туториала Вы узнаете, как добавить треугольники к шестиугольникам, чтобы создать этот дизайн.
На этой диаграмме показано, сколько блоков, полублоков и треугольников вам нужно, исходя из центра шестиугольника 5 ″ и «бревен» шириной 1,25 ″. Это одеяло, пригодное для рулонов желе. Каждую полоску желе можно разрезать пополам по длине, в результате чего получатся две полоски по 1,25 дюйма. В каждом блоке используется эквивалент только одной полосы рулона желе: (для 18 блоков требуется 18 полосок, для 32 блоков требуется 32 полосы и т. Д.) И 6-дюймового обрезка для центра.
Чтобы получить шаблон для треугольников A и B, щелкните здесь, чтобы получить PDF-файл.Из-за различий в припусках на швы эти шаблоны могут не подходить для ваших блоков. Нет проблем, вы можете сделать свои собственные шаблоны, измерив сторону вашего шестиугольного блока и добавив 3/8 ″. Это будет расстояние между сторонами треугольника A. Используйте треугольную линейку 60 градусов или линию 60 градусов на прямоугольной линейке, чтобы нарисовать шаблон. Для треугольника B используйте тот же шаблон и добавьте 1/2 дюйма в сторону.
Чтобы вырезать треугольники, вырежьте полоску 4 7/8 ″ x WOF (или высотой вашего треугольника).Воспользуйтесь шаблоном, линейкой и дисковым ножом. Чередуя треугольники вверх и вниз, из одной полоски можно вырезать 13 треугольников.
Если хотите, после того, как вы вырежете первый треугольник, вы можете вырезать остальные без шаблона. Просто совместите 60-градусную линию с краем полосы, а край линейки — с острием треугольника.
Вы заметите на диаграмме, что чередующиеся ряды имеют по полублока на каждом конце. Вы можете подумать: «А нельзя ли просто сделать блок и разрезать его пополам?» Неа.Вам понадобится половина блока плюс припуск на шов 1/4 дюйма, чтобы это не сработало. Вы могли сделать целые блоки и обрезать лишнее, но мне это показалось пустой тратой, поэтому я сделал половину блоков, отрезав один конец центра шестиугольника и добавив полосы к оставшимся 4 сторонам.
Отрежьте, как показано. Убедитесь, что в каждом ряду есть правая и левая сторона.
Добавьте полоски, как вы делали для полных блоков. Начните с вершины центрального шестиугольника и добавьте полоски по часовой стрелке.
Я рекомендую разложить блоки перед сшиванием, чтобы понять, как лоскутное одеяло будет складываться вместе, и убедиться, что вам понравился дизайн. Вы также избавитесь от головной боли позже, если обрежете все шестиугольники до одинакового размера. Припуски на швы могут отличаться, и небольшая обрезка не будет видна на готовом квилте, тогда как несовпадающие точки будут.
А теперь добавим эти треугольники.
К каждому шестиугольнику пришейте треугольник A к нижнему левому и верхнему правому краям.Загладьте швы по направлению к треугольникам. К полублокам пришейте треугольник только вверху справа (левая сторона) или внизу слева (правая сторона).
| СОВЕТ: прострочите так, чтобы треугольник внизу и кончик 1/4 дюйма выступал на каждом конце. |
Это та часть, где я бы посоветовал вам выровнять ваш блок, но это не квадрат, так что… «треугольник вверх» ваш блок ?? Только убедитесь, что стороны прямые. Опять же, линия в 60 градусов на вашей линейке очень кстати.
Затем сшейте эти части вместе, чтобы образовать ряды. Мне нравится использовать здесь много булавок, и я начинаю с того, что прикрепляю их к середине, где точки треугольника сходятся. Затем сколите каждый конец булавками, оставив на каждом конце треугольный наконечник 1/4 дюйма. Ослабьте середину и прострочите. Загладьте эти швы в одну сторону, все в одном направлении. Меняйте направление швов для каждого ряда.
| СОВЕТ: Заколите припуски на стыки швов.Затем поместите булавку с обеих сторон. |
| Приколите концы, затем посередине. |
Чтобы завершить ряд, пришейте треугольник B к верхнему левому и нижнему правому краям крайних блоков.
Треугольник B больше, чтобы добавить припуск на шов 1/4 дюйма сбоку ряда. Позже он будет урезан, сейчас не беспокойтесь об этом.
Из-за смещения краев треугольников ряды могут быть немного неровными.Края расправляем и аккуратно прижимаем. Обрежьте где нужно.
Сшейте ряды вместе. Это та часть, где вы задерживаете дыхание и надеетесь, что точки треугольника совпадают! Опять же, используйте много булавок и начните с закрепления точек треугольника.
| … и выдохните !! |
Когда все ряды сшиты вместе, обрежьте стороны лоскутного одеяла на 1/4 дюйма от кончиков конечных шестиугольников.
СОВЕТ: измеряйте поперек стеганого одеяла от точки до точки в каждом ряду.Эти измерения должны быть такими же. При необходимости вы можете обрезать немного меньше, чтобы выровнять его.
Ta Da !! Ты сделал это!!
Обложите верх тканью основы и ватином. Затем стегайте одеяло, как хотите. Думаю, я собираюсь сделать это с большим круговым дизайном.
Вы можете использовать тот же метод добавления треугольников, но не смещайте блоки из одной строки в другую для создания такого расположения.


