Расчет балки
Подробный ход решения — расчет балки, построение эпюр
Заменим распределенную нагрузку равнодействующей
Q1 = 6·2 = 12кН
Составим уравнения равновесия для определения реакций опор
Σ MA = + P · 2 + M + Q1 · 3 — RE · 6= + 12 · 2 + 8 + 12 · 3 — RE · 6=0
Σ ME = — P · 4 + M — Q1 · 3 + RA · 6= — 12 · 4 + 8 — 12 · 3 + RA · 6=0
Из этих уравнений находим реакции опор
RA = 12.67кН.
RE = 11.33кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 12.67 = 12.667 кН
M(z1) = + RA · z = + 12.67 · z
M(0) = 0 кНм
M(2) = 25.333 кНм
На участке BC: (2 ≤ z2 ≤ 4 м )
Q(z2) = + RA — P — q1·(z — 2) = + 12.
Q(2) = 0.667 кН
Q(4) = -11.333 кН
M(z2) = + RA · z — P·(z — 2) — q1·(z — 2)2/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)2/2
M(2) = 25.333 кНм
M(4) = 14.667 кНм
Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M
M(2.11) = 25.4 кНм
На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA — P — Q1 = + 12.67 — 12 — 12 = -11.333 кН
M(z3) = + RA · z — P·(z — 2) — Q1·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)
M(4) = 14.667 кНм
M(5) = 3.333 кНм
На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA — P — Q1 = + 12.67 — 12 — 12 = -11.333 кН
M(z4) = + RA · z — P·(z — 2) + M — Q1·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)
M(5) = 11. 333 кНм
333 кНм
M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 25.4 кНм. По этому значению подбираем сечение балки.
Условие прочности при изгибе σ = Mmax / W ≤ [σ]
Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
Понравились наши онлайн-расчетчики — поделитесь с друзьями
Сопромат. Решение задач. Онлайн решение
является одной из основных общетехнических дисциплин, определяющих уровень подготовки и составляющих необходимый «инженерный багаж» будущего бакалавра или специалиста.
При переходе на новые федеральные государственные образовательные стандарты, в условиях существенного сокращения числа аудиторных часов, выделенных в новых учебных планах на данную дисциплину, у студента увеличивается доля самостоятельной работы, а именно выполнение индивидуальных заданий (контрольных работ, расчетно-графических работ, расчетно-проектировочных работ).
На нашем сайте Вы найдете примеры решения задач по сопромату (сопротивлению материалов) на такие темы как:
- Плоский изгиб балки- построение эпюр изгибающих моментов и поперечных сил, подбор поперечных сечений балок при плоском изгибе, определение перемещений в балках методом Верещагина, Симпсона, используя интеграл Мора, метод начальных параметров; плоский изгиб рамы-эпюры N, Q, M.
- Центральное растяжение и сжатие стержней- построение эпюр продольных сил, напряжений, перемещений в статически определимых и статически неопределимых стержнях;
- Геометрические характеристики поперечных сечений- определение геометрических характеристик: осевые моменты инерции, полярные моменты инерции, осевые моменты сопротивления, положение центра тяжести составных несимметричных и симметричных сечении;
- Напряженное и деформированное состояние в точке- плоское напряженное состояние, величина и направление главных площадок;
- Кручение вала, расчет на прочность- условия прочности и жесткости вала, абсолютные и относительные углы закручивания, кручение валов прямоугольного сечения, распределение касательных напряжений, изгиб с кручением;
- Расчет статически неопределимых балок и рам- используя метод сил, каноническое уравнение метода сил, способ Верещагина, Симпсона;
- Косой изгиб, сложное сопротивление-расчет на прочность при косом изгибе, положение нулевой линии при косом изгибе, расчет пространственного стержня на прочность;
- Внецентренное растяжение и сжатие- положение нулевой линии, напряжения в точках сечения;
- Устойчивость сжатых стержней, стержень Эллера — допускаемая и критическая силы, гибкость стержня, минимальный радиус инерции, условие устойчивости по допускаемым напряжениям, подбор поперечного сечения сжатой стойки, коэффициенты приведения длины;
- Динамическое действие нагрузок- расчеты на удар, коэффициент динамичности, статический прогиб, круговая частота свободных колебаний;
А так же поможем с решением задач по сопромату (сопротивлению материалов), онлайн решение задач по сопротивлению материалов, строительной механике, теоретической механике
Онлайн помощь по сопромату включает в себя оперативное решение задачи (в кратчайшие сроки, время на решение от 5 минут) на такие темы:
- Построение эпюр в балке;
- Расчет рамы;
- Расчет фермы;
- Геометрические характеристики;
- Растяжение -сжатие;
- Напряжения в точках сечения;
- Кручение вала;
- Расчет на удар;
- Стержень Эллера;
- Косой изгиб;
- Метод сил;
- Статически неопределимая балка;
- Статически неопределимая рама;
- Теоретическая механика;
- Строительная механика;
Выполняли работы в большинство основных государственных университетов России, в такие города как:
Москва, Новосибирск, Волгоград, Тюмень, Липецк, Орел, Санкт-Петербург, Уфа, Пермь, Иваново, Псков, Казань, Ижевск, Тверь, Белгород, Воронеж, Курск, Архангельск, Вологда, Ростов-на-Дону, Челябинск.
[свернуть]
Построение эпюр»эпюра моментов»эпюры сил»эпюры изгибающих моментов
Заказать решение Способ оплаты
1.
Виды опорных закрепленийС технической точки зрения опорные закрепления конструкций весьма разнообразны. При решении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых
наиболее часто встречаются: шарнирно-подвижнаяопора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).
Рис. 1
В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.
Пример 1.Построить эпюру продольных сил для жестко защемленной балки (рис.2).
Порядок расчета:
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
По найденным значениям строим эпюру
рис. 2
3. Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.
Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).
Порядок расчета.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.
По найденным значениям строимэпюру Мкр (рис.3,б).
рис. 3
3
4. Правила контроля эпюр Nz и Мкр.
Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.
1. Эпюры Nz и Мкр всегда прямолинейные.
2. На участке, где нет распределенной нагрузки, эпюра Nz(Мкр) — прямая, параллельная оси, а на участке под распределенной нагрузкой — наклонная прямая.
3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.
5. Построение эпюр поперечных сил Qy и изгибающих моментов Mx в балках
Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — поперечная сила Qy и изгибающий момент Mx .
Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.
Правило знаков для Qy: условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде
Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.
Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде:
Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.
6. Консольные балки
При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
Пример 3.Построить эпюры Qy и Mx (рис.4).
рис. 4
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечную силу Qy в каждом характерном сечении.
Определяем поперечную силу Qy в каждом характерном сечении.
По вычисленным значениям строим эпюру Qy.
3. Определяем изгибающий момент Mx в каждом характерном сечении.
По вычисленным значениям строим эпюру Mx, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
7. Балки на двух опорах
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.
Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:
Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:
Пример 4. Построить эпюры Qy, Mx для балки с шарнирным опиранием (рис.5).
Порядок расчета.
1. Вычисляем реакции опор.
Проверка:
</p>
2. Намечаем характерные сечения.
В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.
3. Определяем поперечные силы в характерных сечениях.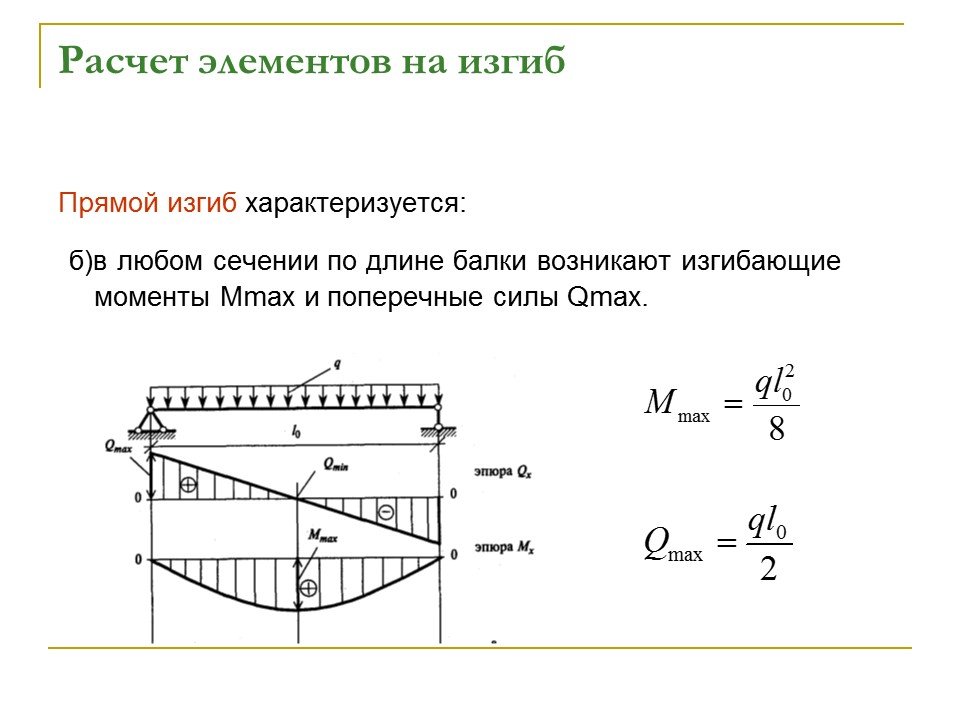
Строим эпюру Qy.
4. Определяем изгибающие моменты в характерных сечениях.
рис. 5
Строим эпюру Mx.
8. Правила контроля эпюр Qу и Mx
Дифференциальные зависимости между q, Qy, Mx определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.
Эпюра Qy является прямолинейной на всех участках; эпюра Mx — криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке q, и прямолинейная на всех остальных участках.
Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.
Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.
Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy=0), то эпюра Mx в этом сечении имеет экстремум.
На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy>0 эпюра Mx возрастает слева направо; при Qy<0 — убывает.
Порядок линии на эпюре Qy всегда на единицу меньше, чем на эпюре Mx. Например, если эпюра Mx — квадратная парабола, то эпюра Qy на этом участке — наклонная прямая; если эпюра Mx — наклонная прямая, то эпюра Qy на этом участке — прямая, параллельная оси; если Mx=const (прямая, параллельная оси), то на этом участке Qy=0.
Заказать решение Способ оплаты
Задачи на изгиб | ПроСопромат.ру
Проектный и проверочный расчеты.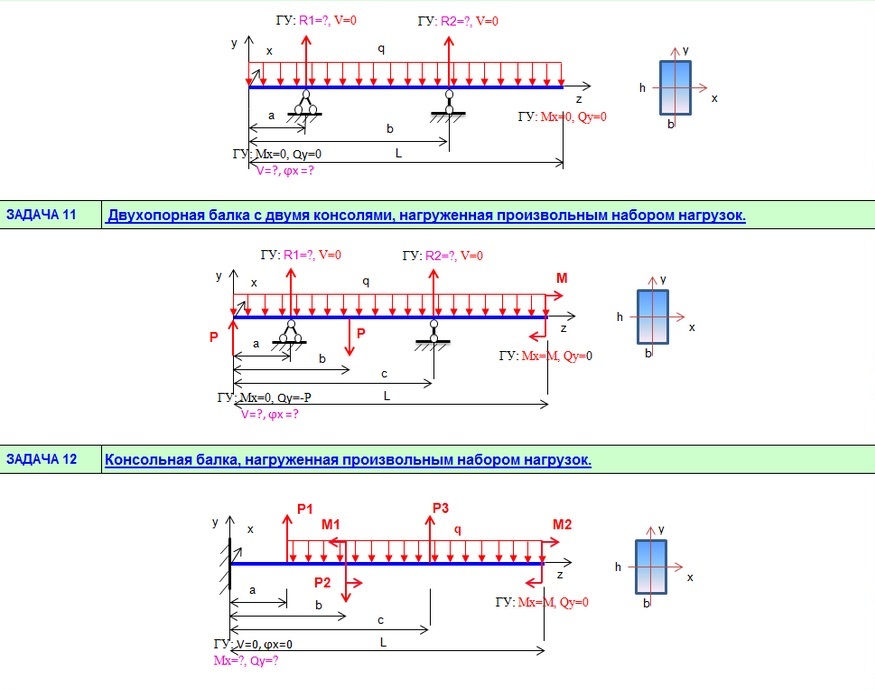 Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Покажем балку с построенными эпюрами Q и М
Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм.
Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров.
Определим необходимое расчетное значение осевого момента сопротивления сечения:
Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения:
Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:
Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Условие прочности по касательным напряжениям имеет вид:
Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h1=20 см, ширина полки b1=8 см.
Для поперечного сечения из двух швеллеров:
Sx= 2Sx1=2·95,9=191,8 см3,
Ix=2Ix1=2·1670=3340 см4,
b=2d1=2·0,52=1,04 см.
Определяем значение максимального касательного напряжения:
τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа.
Как видно, τmax <τadm (27МПа<75МПа).
Следовательно, условие прочности выполняется.
Проверяем прочность балки по энергетическому критерию.
Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН.
Проведем анализ напряженного состояния в точках сечения С
Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)
Уровень 1-1: y1-1=h1/2=20/2=10см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 2−2: y2-2=h1/2−t1=20/2−0,97=9,03см.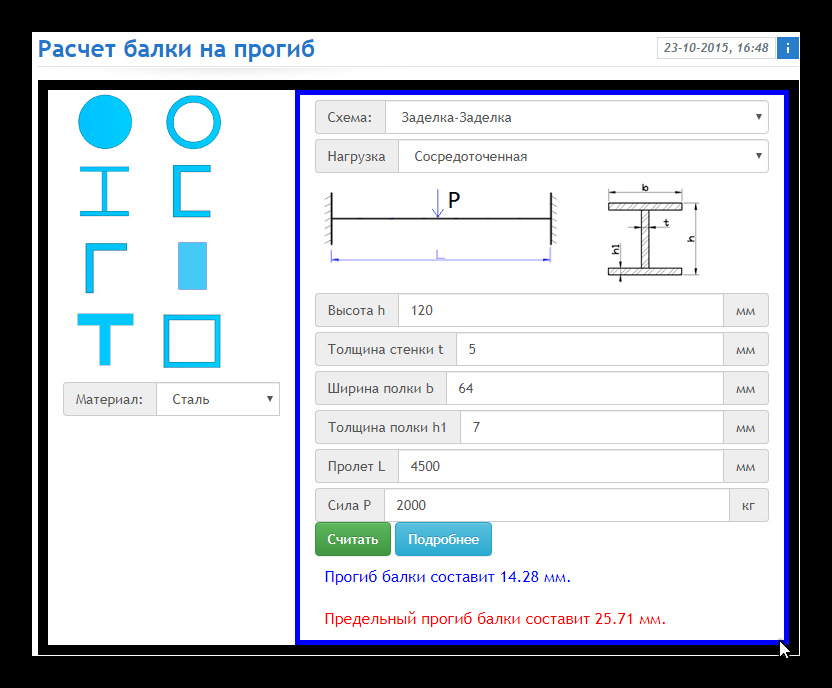
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 3−3: y3-3=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 4−4: y4-4=0.
Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 5−5:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 6−6:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 7−7:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых:
Используя энергетический критерий прочности, получим
Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется
(135,3 МПа<150 МПа).
Расчет деревянных балок перекрытия: онлайн-калькулятор и методика
Ссылка на статью успешно отправлена!
Отправим материал вам на e-mail
Расчет нагрузки на балку перекрытия – это важнейший этап в проектировании. Об этом говорит тот факт, что студентов строительных специальностей на протяжении всего периода обучения натаскивают на решение подобных задач. Допущенная ошибка может вылиться в полное обрушение здания, обвал перекрытия и абсолютную непригодность здания к дальнейшей эксплуатации.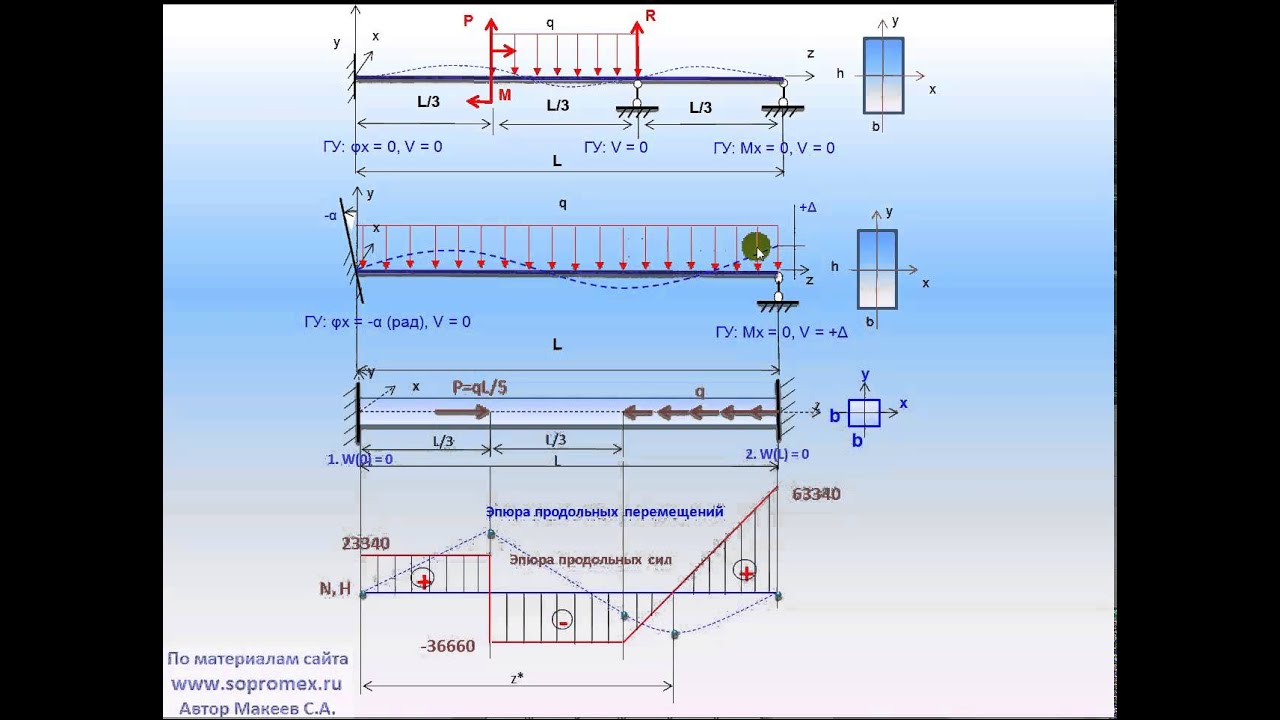 Именно поэтому расчет деревянных балок перекрытия онлайн-калькулятор выполняет с учетом всех существующих ныне норм.
Именно поэтому расчет деревянных балок перекрытия онлайн-калькулятор выполняет с учетом всех существующих ныне норм.
Балки перекрытия
Содержание статьи
Назначение калькулятораВ частном строительстве в качестве лагов перекрытия используют деревянный брус. Дерево как строительный материал имеет больше достоинств, чем недостатков. Единственное, что настораживает при выборе – это горючесть древесины. В корне неверно считать, что бетон не горит. Он начинает трескаться при температуре 250 – 300 градусов, а при температуре 550 градусов перекрытия осыпаются. Дерево, обработанное специальными составами, загорается очень медленно, и даже обугленные брусья могут служить надежной опорой еще многие годы.
Такая надежность возможна только в том случае, если брус уложен с запасом прочности. При эксплуатации деревянные брусья работают на изгиб и должны выдерживать постоянную нагрузку. К таковым относится все, что лежит над перекрытием: пол, перегородки, мебель, техника люди и так далее. Нормы требуют нагрузки брать с запасом. Расчет деревянных балок перекрытия онлайн калькулятор осуществляет для того, чтобы найти такое сочетание длины и сечения, при которых прочность будет оптимальной.
Нормы требуют нагрузки брать с запасом. Расчет деревянных балок перекрытия онлайн калькулятор осуществляет для того, чтобы найти такое сочетание длины и сечения, при которых прочность будет оптимальной.
Деревянные лаги в доме из бетонных блоков
Калькулятор расчета деревянных балок перекрытияФормулы и элементы расчетаКалькулятор при расчетах использует следующие исходные данные:
- длина балки – это параметр, который закладывается проектом и зависит от расстояния между несущими стенами;
- сечение бруса – его ширина и высота, причем высота всегда должна быть больше для лучшего сопротивления специфическим изгибающим нагрузкам;
- порода дерева – от нее зависит пластичность и глубина прогиба балки, а соответственно, и максимально возможная нагрузка;
- предполагаемая нагрузка – берется из стандартов и зависит от типа помещения и количества жильцов.
На лаги укладывается доска, формирующая перекрытие
Кроме исходных данных в калькуляторе заложена переменная – шаг бруса. Меняя его значение, можно подобрать оптимальный вариант размещения балок. В калькуляторе заложены справочные значения, характерные для каждого из выбранных параметров:
Меняя его значение, можно подобрать оптимальный вариант размещения балок. В калькуляторе заложены справочные значения, характерные для каждого из выбранных параметров:
- разрушающее усилие – это величина постоянной нагрузки на балку, при достижении которой произойдет обрушение, зависит от габаритов бруса;
- распределенное усилие – зависит от величины предполагаемой нагрузки;
- прогиб в миллиметрах – максимально допустимая величина деформации, зависит от длины балки, величина приведена для сравнения, она не должна превышать расчетный прогиб;
- расчетный прогиб в миллиметрах – зависит от породы дерева.
В итоге после введения всех данных калькулятор сообщает о том, существует ли запас по прогибу и прочности при заданных пользователем параметрам. Если запас есть, балку можно использовать, если нагрузка превышена, следует откорректировать один из параметров. Для справки в калькуляторе приведены такие величины, как крутящий момент и масса самой балки. Первый параметр интересен для общего развития, а вот вес полезно знать, так как от него зависит стоимость доставки леса на стройплощадку.
Щитовой дом с деревянным перекрытием
Допуски при расчетахРасчет несущих деревянных балок перекрытия онлайн-калькулятор производит с целью выявления допусков. Результатом подбора являются такие определения, как запас по прочности и запас по прогибу, который выражается в кратных единицах. Иными словами, чем больше у результата запас прочности, тем лучше. Однако для рационального строительства и недопущения перерасхода следует стремиться к значению коэффициентов от 1,5 до 3.
Видео: расчет деревянных балок
Экономьте время: отборные статьи каждую неделю по почте
Расчетно-графическая работа. Изгиб. Построение эпюр. Подбор поперечного сечения.
ИЗГИБ.
ПОСТРОЕНИЕ ЭПЮР. ПОДБОР ПОПЕРЕЧНОГО СЕЧЕНИЯ
Последовательность решения задачи
1. Определить опорные реакции и проверить правильность найденных реакций.
Определить опорные реакции и проверить правильность найденных реакций.
2. Балку разделить на участки по характерным сечениям.
3. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.
4. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов.
5. Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т. к. определить Wхв опасном сечении, где изгибающий момент имеет наибольшее по модулю значение.
Пример 1. Для заданной двухопорной балки (рис.1) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения в форме прямоугольника или круга, приняв для прямоугольника h/b = 1,5.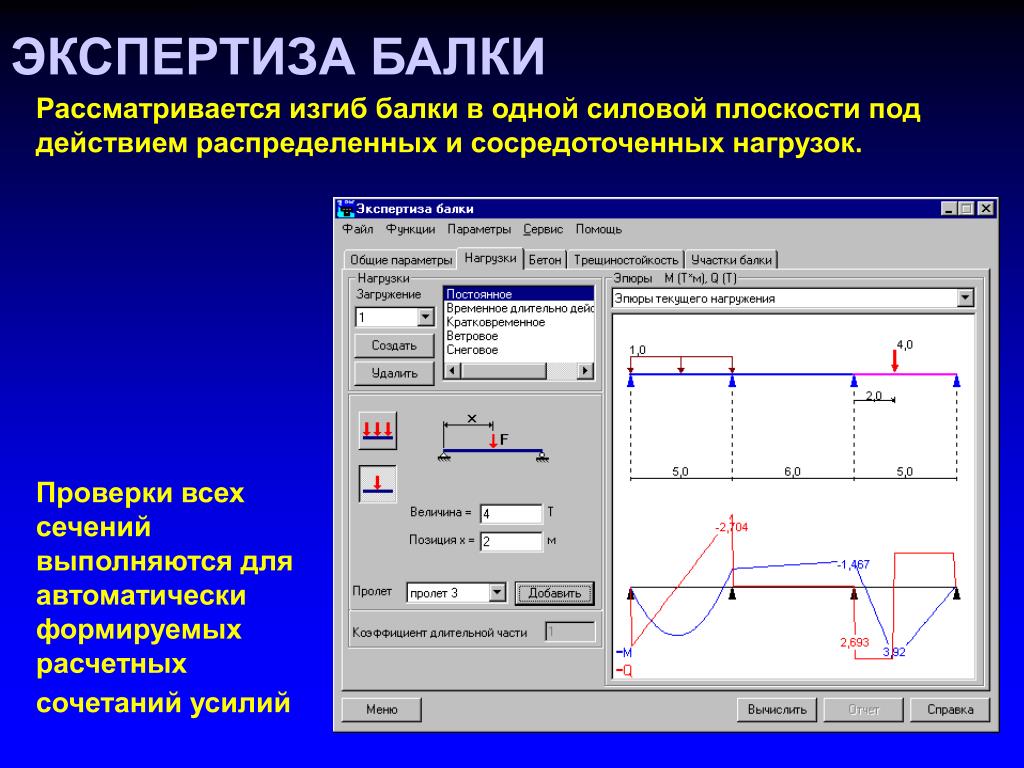 Считать [σ]= 160 МПа.
Считать [σ]= 160 МПа.
Рис. 1 — Схема задачи
Решение:
1. Определяем опорные реакции и проверяем их найденные значения:
å МD = 0; — M1 + F2 CD + M2 + RB BD — F1 OD = 0;
Σ·MB = 0; — F1 OB + M2 — F2 BC — RD BD — M1 = 0;
Проверяем правильность найденных результатов:
å Fi y = 0; — F1 + RB+ F2 +RD = -18+10+30-22 = 0
Условие равновесия å Fi y = 0 выполняется, следовательно, реакции опор найдены верно.
При построении эпюр используем только истинные направления реакций опор.
2. Делим балку на участки по характерным сечениям O,B,C,D (рис. 2).
Рис. 2 — Схема истинных реакций балки и участков
3. Определяем в характерных сечениях значения поперечной силы Qy и строим эпюру слева направо (рис. 3):
Рис. 3 — Эпюра поперечных сил
4. Вычисляем в характерных сечениях значения изгибающего момента Мх и строим эпюру (рис. 4):
Рис. 4 — Эпюра изгибающих моментов
5. Вычисляем размеры сечения данной балки из условий прочности на изгиб:
, отсюда
а) сечение – прямоугольник
Используя формулу и учитывая, что h = 1,5b, находим
h = 1,5b = 1,5 127 = 190,5 мм
б) сечение – круг
Используя формулу и учитывая, что h = 1,5b, находим
Задача 1. Для заданной двухопорной балки (рис.5) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения в форме прямоугольника или круга, приняв для прямоугольника h = 2 b. Считать [σ]= 150 МПа.
Для заданной двухопорной балки (рис.5) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения в форме прямоугольника или круга, приняв для прямоугольника h = 2 b. Считать [σ]= 150 МПа.
Таблица 1 — Исходные данные
Номер схемы на рисунке 5
F1
F2
M
1
2
3
4
5
6
7
8
9
10
Варианты
кH
кHм
1
2
3
4
5
6
7
8
9
10
5
2
6
11
12
13
14
15
16
17
18
19
20
12
3
8
21
22
23
24
25
26
27
28
29
30
8
6
2
1
6
2
7
3
8
4
9
5
10
Рис. 5 — Схема задачи
5 — Схема задачи
Задача 2. Для стальной балки, жестко защемленной одним концом и нагруженной в соответствии с рисунком 3, построить эпюры поперечных сил, изгибающих моментов и, исходя из условия прочности при [] = 160 МПа, подобрать необходимый размер поперечного сечения двутавра.
Данные своего варианта брать из таблицы 2
Указание. При решении задачи использовать справочные материалы приложения А.
Таблица 2 — Исходные данные
Номер схемы на рисунке 6
F
q
M
1
2
3
4
5
6
7
8
9
10
Варианты
кH
кH/м
кHм
1
2
3
4
5
6
7
8
9
10
40
6
50
11
12
13
14
15
16
17
18
19
20
50
4
40
21
22
23
24
25
26
27
28
29
30
30
2
28
Рис. 6 — Схема задачи
6 — Схема задачи
Приложение А
(справочное)
ГОСТ 8239- 89 Двутавры стальные горячекатанные. Сортамент
Обозначение:
H — высота двутавра;
B — ширина полки;
S — толщина стенки;
T — средняя толщина полки;
R — радиус внутреннего закругления;
R — радиус закругления полки
I — момент инерции;
W — момент сопротивления;
S — статический момент полусечения;
I — радиус инерции.
Таблица 3
Номер двутавра
Размеры
Площадь поперечного сечения, см2
Масса 1 м, кг
Справочные значения для осей
h
b
s
t
R
r
X — X
Y — Y
не более
Ix,
см4
Wx,
см3
ix,
см
Sx,
см3
Iy,
см4
Wy,
см3
iy,
см
мм
10
100
55
4,5
7,2
7,0
2,5
12,0
9,46
198
39,7
4,06
23,0
17,9
6,49
1,22
12
120
64
4,8
7,3
7,5
3,0
14,7
11,50
350
58,4
4,88
33,7
27,9
8,72
1,38
14
140
73
4,9
7,5
8,0
3,0
17,4
13,70
572
81,7
5,73
46,8
41,9
11,50
1,55
16
160
81
5,0
7,8
8,5
3,5
20,2
15,90
873
109,0
6,57
62,3
58,6
14,50
1,70
18
180
90
5,1
8,1
9,0
3,5
23,4
18,40
1290
143,0
7,42
81,4
82,6
18,40
1,88
20
200
100
5,2
8,4
9,5
4,0
26,8
21,00
1840
184,0
8,28
104,0
115,0
23,10
2,07
22
220
110
5,4
8,7
10,0
4,0
30,6
24,00
2550
232,0
9,13
131,0
157,0
28,60
2,27
24
240
115
5,6
9,5
10,5
4,0
34,8
27,30
3460
289,0
9,97
163,0
198,0
34,50
2,37
27
270
125
6,0
9,8
11,0
4,5
40,2
31,50
5010
371,0
11,20
210,0
260,0
41,50
2,54
30
300
135
6,5
10,2
12,0
5,0
46,5
36,50
7080
472,0
12,30
268,0
337,0
49,90
2,69
33
330
140
7,0
11.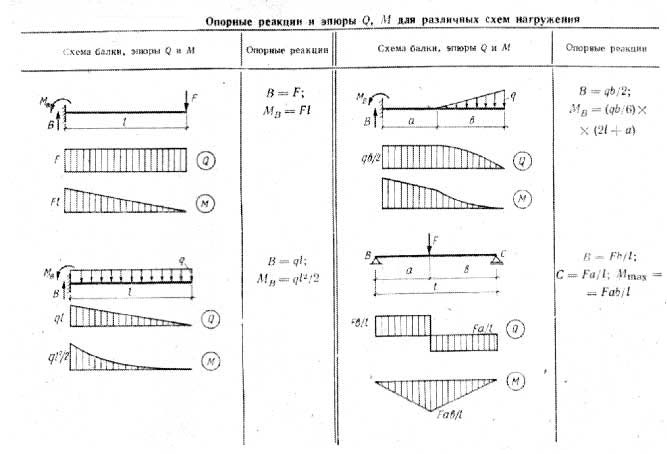 2
2
13,0
5,0
53,8
42,20
9840
597,0
13,50
339,0
419,0
59,90
2,79
36
360
145
7,5
12,3
14,0
6,0
61,9
48,60
13380
743,0
14,70
423,0
516,0
71,10
2,89
40
400
155
8,3
13,0
15,0
6,0
72,6
57,00
19062
953,0
16,20
545,0
667,0
86,10
3,03
45
450
160
9,0
14,2
16,0
7,0
84,7
66,50
27696
1231,0
18,10
708,0
808,0
101,00
3,09
50
500
170
10,0
15,2
17,0
7,0
100,0
78,50
39727
1589,0
19,90
919,0
1043,0
123,00
3,23
55
550
180
11,0
16,5
18,0
7,0
118,0
92,60
55962
2035,0
21,80
1181,0
1356,0
151,00
3,39
60
600
190
12,0
17,8
20,0
8,0
138,0
108,00
76806
2560,0
23,60
1491,0
1725,0
182,00
3,54
Двутавры от № 24 до № 60 не рекомендуется применять в новых разработках.
Расчет деревянных балок перекрытия калькулятор онлайн
Сделать надежное перекрытие можно только с правильно подобранным размером балок. Чтобы определить этот самый точный размер потребуется произвести расчет. Это можно сделать с помощью онлайн программы, которая представляет своего рода калькулятор.
Зачем надо рассчитывать?
Вся нагрузка на межэтажное перекрытие, ложится на деревянные балки, поэтому они являются несущими. От прочности балок перекрытия зависит целостность постройки и безопасность находящихся в ней людей.
Производить расчет деревянных элементов необходимо для выяснения допустимой вертикальной нагрузки, действующей на нее. Строительство новой или реконструкция старой постройки без предварительного расчета сечения несет огромный риск.
Выстроенное наугад перекрытие из слабых деревянных балок может в любой момент обрушиться, что приведет к большим финансовым затратам, а еще хуже, к травматизму людей. Взятые с запасом балки большого сечения создадут лишнюю нагрузку на стены и основание постройки.
Взятые с запасом балки большого сечения создадут лишнюю нагрузку на стены и основание постройки.
Кроме определения прочности, существует расчет прогиба деревянных элементов. Он больше определяет эстетичную сторону строения. Даже если крепкая балка перекрытия выдержит припадающий на нее вес, она может прогнуться. Кроме испорченного внешнего вида, прогнувшийся потолок создаст дискомфорт пребывания в такой комнате. По нормам прогиб не должен превышать 1/250 длины балки.
Онлайн расчет
Сделать расчет всех элементов перекрытия можно через онлайн калькулятор. Это специальная программа, позволяющая подсчитать величину прогиба деревянной балки при заданных параметрах, а также определить оптимальное сечение для определенного перекрытия. Использование онлайн расчета поможет перед началом строительства учесть все нагрузки, припадающие на несущие конструкции. Можно сделать расчет нагрузки 1 м опоры и высчитать количество деревянных элементов необходимых для возведения крыши. Работает онлайн калькулятор просто надо лишь правильно внести требуемые данные.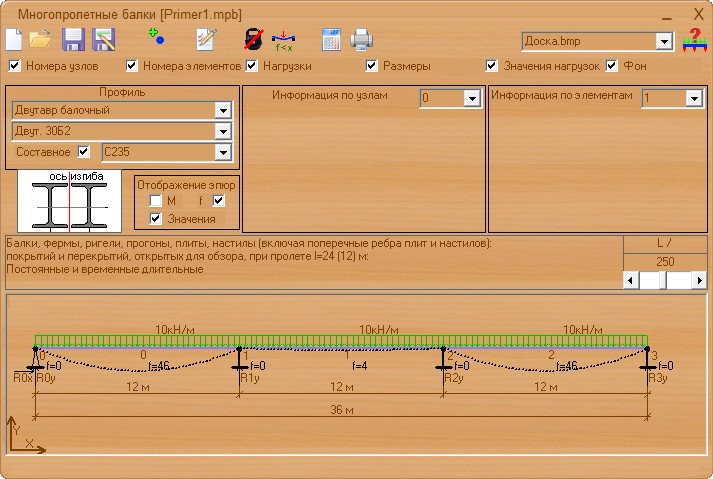
Общая инструкция проведения онлайн расчета
Интерфейс программы довольно прост и с ним может разобраться даже новичок. Калькулятор состоит из маленьких окошек, куда необходимо вводить данные. После нажатия кнопки «рассчитать», пользователь получает готовый результат расчета.
На разных сайтах оформление программы может отличаться, но принцип ее действия одинаков:
- Вначале потребуется выбрать в окошке программы конструкцию, для которой будет производиться расчет деревянных балок. Здесь надо знать ограничение некоторых показателей: максимальная длина элементов перекрытия составляет 12 м, а стропильной системы — 13 м.
- Далее, в программу вводят данные максимального размера пролета между элементами перекрытия или опорами стропильной системы.
- Указывается планируемое расстояние для монтажа балок. Надо учесть, что все десятичные значения в онлайн калькулятор вписывают с точкой, а не с запятой. Возьмем, к примеру, значение 0.9 м.
- Следующими указывают стандартные нагрузки, которые для деревянного перекрытия составляют 400 кг/м2, а для стропильной системы — 220 кг/м2.

- Последнее значение, вводимое в онлайн калькулятор, в градусах указывает наклон стропил.
Введенные в программу данные должны быть точными без погрешностей, иначе результат получится неправильным.
Выполнение расчета в ручном режиме
Многие опытные строители не доверяют подобным онлайн программам, предпочитая использовать для расчета обычный калькулятор. Производя в ручном режиме расчет по деревянным балкам, надо учесть следующие рекомендации:
- Заход деревянных балок сделанных из бруса в бетонной или кирпичной постройке должен составлять не меньше 150 мм. Если вместо бруса используется доска, ее минимальный заход равен 100 мм. По деревянным домам показатель немного другой. Минимальный заход элемента, изготовленного с бруса или доски, составляет 70 мм;
- При использовании металлических крепежей, пролет должен равняться длине конструкции перекрытия. На металлические части припадет вес перекрытия и других элементов;
- Стандартная планировка дома имеет ширину пролета 2,5–4 м.
 Его можно перекрыть шестиметровым элементом. Большие пролеты перекрывают клееным брусом или выстраивают дополнительные стены-перегородки.
Его можно перекрыть шестиметровым элементом. Большие пролеты перекрывают клееным брусом или выстраивают дополнительные стены-перегородки.
Применяя для расчета обычный калькулятор, эти рекомендации помогут сделать крепкое перекрытие.
Определение нагрузки
Перекрытие совместно с находящимися на нем предметами создает деревянным балкам определенную нагрузку. Точно ее высчитать можно только в проектных организациях. Примерный расчет делают калькулятором, пользуясь следующими рекомендациями:
- Чердаки утепленные минватой и подшитые доской отличаются минимальной нагрузкой, примерно 50 кг/м2. Расчет нагрузки выполняют по формуле: значение запаса прочности — 1,3 умножают на показатель максимальной нагрузки — 70.
- Если вместо минваты применяется более тяжелый теплоизолятор и массивная подшивная доска, нагрузка увеличивается в среднем до 150 кг/м2. Определить общую нагрузку можно следующим образом: значение запаса прочности умножается на средний показатель нагрузки и ко всему приплюсовывается размер требуемой нагрузки.

- Делая расчет для мансарды, нагрузку допускают до 350 кг/м2. Это связно с тем, что добавляется вес пола, мебели и др.
С этим определением разобрались, теперь идем далее.
Определение сечения и шага установки элементов перекрытия
Данный процесс требует придерживаться следующих правил:
- Соотношение ширины к высоте конструкции приравнивается 1,4/1. Следовательно, ширина элементов перекрытия зависит от этого показателя и может варьироваться от 40 до 200 мм. Толщина и высота деревянных элементов зависит от толщины теплоизоляции примерно 100–3000 мм;
- Расстояние между элементами, то есть их шаг, может быть от 300 до 1200 мм. Здесь надо учесть габариты теплоизоляции с подшивочным материалом. В каркасной постройке расстояние между балками приравнивают к шагу каркасных стоек;
- Деревянным балкам допускается небольшой изгиб, который для перекрытия чердака составляет — 1/200, а для межэтажного — 1/350;
- При нагрузке 400 кг/м2 соотношение шага к сечению составляет 75/100 мм.
 Вообще, чем больше сечение балок, тем больше расстояние между ними.
Вообще, чем больше сечение балок, тем больше расстояние между ними.
Применяя калькулятор для определения сечения, необходимо пользоваться справочными материалами для более точных результатов.
Кроме полученных точных результатов, прочность конструкции зависит от качества материала.
Заготовки используют из хвойных пород дерева, влажностью до 14%. Древесина не должна быть поражена грибком и насекомыми. Ну а чтобы увеличить срок эксплуатации деревянной конструкции, заготовки перед монтажом необходимо обрабатывать антисептиком.
В следующем видео можно понаблюдать пример работы в программе для расчетов перекрытий.
Что еще почитать по теме?
Автор статьи:Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.
Понравилась статья? Поделись с друзьями в социальных сетях:Вконтакте
Одноклассники
Google+
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки.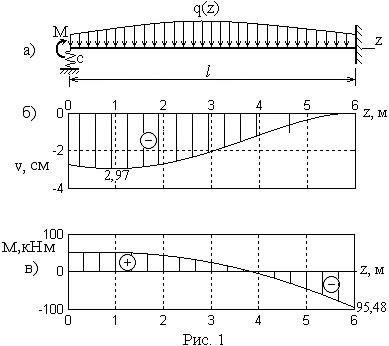 Используйте этот калькулятор пролета балки, чтобы определить реакции на опорах, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки.Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает полное программное обеспечение для структурного анализа.
Используйте этот калькулятор пролета балки, чтобы определить реакции на опорах, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки.Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента будут запущены после нажатия кнопки «Решить» и автоматически сгенерируют диаграммы сдвига и изгибающего момента.Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах. Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций для консольной балки, которая имеет реакцию изгибающего момента, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке.Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными вверх или вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это может быть использовано для наблюдения расчетного прогиба балки без опоры или консольной балки. Возможность добавления форм и материалов сечения делает его полезным в качестве калькулятора деревянных балок или калькулятора стальных балок для проектирования балок lvl или i.На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и улучшать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.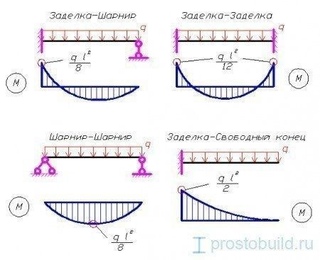
| SkyCiv
Наличие хорошего ресурса для размеров двутавровых балок очень важно при проектировании конструкций.Для нас, как для инженера-строителя, важно определить разделы, которые не только безопасны, но и экономичны. С помощью приведенной ниже таблицы размеров стальных балок SkyCiv стремится получить бесплатный ресурс, к которому можно будет получить доступ в любое время через браузер. Приведенная ниже таблица размеров стальных балок поможет инженерам-строителям найти подходящий размер и форму, которые вам нужны для вашего проекта. Эти свойства важны при проверке прочности секции, что является само определение конструкции конструкции.
Таблица размеров стальных балок — это интерактивная таблица, в которой перечислены размерные и геометрические свойства сечения. Эти свойства могут помочь инженерам найти желаемый стальной профиль, который они ищут. Просто выберите систему единиц измерения, библиотеку перед тем, как выбрать форму, чтобы отобразить размеры балки этой формы.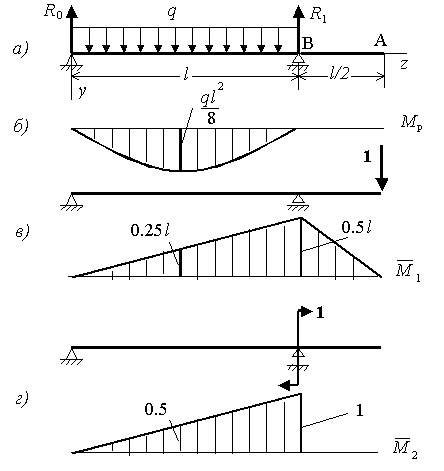 В библиотеке есть разделы из Австралии, США, Канады, Великобритании и Европы. Программное обеспечение извлекает размеры балки непосредственно из базы данных Structural 3D, которая является основным программным обеспечением для трехмерного структурного анализа платформы SkyCiv, которое также можно использовать в веб-браузере.Эта информация обычно требует, чтобы пользователь держал под рукой ручные или стальные диаграммы балок, что может быть неудобно, т. Е. Если у пользователя есть копия. Несмотря на то, что приобретение руководства по стали требует денежных затрат, мы должны еще раз подчеркнуть, что справочная таблица SkyCiv легко доступна здесь бесплатно.
В библиотеке есть разделы из Австралии, США, Канады, Великобритании и Европы. Программное обеспечение извлекает размеры балки непосредственно из базы данных Structural 3D, которая является основным программным обеспечением для трехмерного структурного анализа платформы SkyCiv, которое также можно использовать в веб-браузере.Эта информация обычно требует, чтобы пользователь держал под рукой ручные или стальные диаграммы балок, что может быть неудобно, т. Е. Если у пользователя есть копия. Несмотря на то, что приобретение руководства по стали требует денежных затрат, мы должны еще раз подчеркнуть, что справочная таблица SkyCiv легко доступна здесь бесплатно.
Некоторые из размеров, которые может отображать этот инструмент:
- Размеры двутавровой балки
- Размеры S-образной балки
- Квадрат полый / HSS Размеры
- Круглые размеры из быстрорежущей стали
- Размеры балки с широким фланцем
- Т-образная балка Размеры
- Размеры каналов
- Размеры уголков
- Имперские и метрические размеры балки
Приведенные выше размеры стальных секций должны дать пользователю возможность легко получить доступ к свойствам элементов и размерам часто используемых секций в различных библиотеках по всему миру. Мы надеемся, что инженеры найдут ссылки на эти размеры и размеры стальных балок, которые будут полезны для их рабочего процесса. Опять же, в настоящее время существуют размеры и размеры стали для профилей из Австралии, США, Великобритании, Европы и Канады. Если конкретная используемая вами библиотека недоступна, вы можете связаться с нами здесь. Мы открыты для улучшения и расширения нашей базы данных. Еще одним замечательным аспектом этого инструмента является то, что он может преобразовывать размеры балки из метрических в британские и наоборот. Это экономит время инженера при работе с единичными системами и снижает риск ошибки в расчетах.
Мы надеемся, что инженеры найдут ссылки на эти размеры и размеры стальных балок, которые будут полезны для их рабочего процесса. Опять же, в настоящее время существуют размеры и размеры стали для профилей из Австралии, США, Великобритании, Европы и Канады. Если конкретная используемая вами библиотека недоступна, вы можете связаться с нами здесь. Мы открыты для улучшения и расширения нашей базы данных. Еще одним замечательным аспектом этого инструмента является то, что он может преобразовывать размеры балки из метрических в британские и наоборот. Это экономит время инженера при работе с единичными системами и снижает риск ошибки в расчетах.
Свойства сечения, отображаемые в приведенной выше таблице, включая площадь поперечного сечения (A), полярный момент инерции (J), момент площади (Iz, Iy), модуль упругости сечения и постоянную деформации (Iw). Эти результаты чрезвычайно важны при выборе конструкционной стали для конструкций балок и колонн. Это свойства, которые контролируют количество и тип силы, которую может принять стальной элемент.
Здесь, в SkyCiv, у нас есть ряд программного обеспечения (бесплатного и платного), которое позволяет инженерам моделировать и проектировать свои конструкции.Наш калькулятор свободных балок — это простой в использовании калькулятор, помогающий анализировать консольные балки и балки с простой опорой. Вы также можете воспользоваться нашим калькулятором ферм для быстрого анализа 2D ферм. Для небольших 2D-рам вы можете использовать наш бесплатный калькулятор несущих конструкций. Для типичных форм из стали нестандартных размеров калькулятор свободного момента инерции является хорошим источником для определения их геометрических характеристик и характеристик сечения.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений.Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и улучшать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Бесплатный калькулятор многопролетных балок
О калькуляторе изгиба балки
Калькулятор отклонения балки
Этот калькулятор использует метод анализа конечных элементов для расчета перемещений, сил и реакций в многопролетные балки с множественными нагрузками.Метод конечных элементов (FEA) основан на законе Хука. найти высокоточное приближенное решение балки. Модель дискретизирована на мелкие элементы, и для каждого элемента устанавливается жесткость пружины. Применяются силы (нагрузки) к пружинам, матрица жесткости (k) создается из малых элементов, а перемещения равны находят путем инвертирования матрицы жесткости и умножения ее на вектор силы.Вспомните закон Хука для пружин:
`F = kx`
Мы расширяем это до 2-х и 3-х измерений, используя линейную алгебру:
`| F | = [k] | x | `
Калькулятор момента пучка и поперечной силы
Калькулятор многопролетных балок — отличный инструмент для быстрой проверки сил в балках с несколькими пролетами. и загрузить.Используйте его для проектирования стальных, деревянных и бетонных балок при различных условиях нагрузки.
и загрузить.Используйте его для проектирования стальных, деревянных и бетонных балок при различных условиях нагрузки.
Калькулятор стальных, деревянных и бетонных балок
Если у вас стальная, деревянная или бетонная балка со сложными граничными условиями и нагрузками это отличный инструмент для численного решения проблемы. Если вы хотите проверить этот калькулятор Воспользуйтесь нашим калькулятором закрытых балок для сравнения результатов: Калькулятор луча.Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для конструкции стальных или деревянных балок и вы хотите создать свой следующий луч за считанные минуты, вам может понравиться наш Инструмент Beam Designer.
Проектирование балок из стали и дерева по стандарту AISC по стандарту NDS
Наша цель с WebStructural — вернуть инженерное сообщество, предоставляя бесплатные, облачное программное обеспечение для расчета конструкций. Нечего устанавливать, просто перейдите к одному из наших
калькуляторы вроде этого и начинаем
проектирование! Если вам понравился инструмент и вы решили сохранить и распечатать проекты, вы можете
обновление за 19 долларов в месяц. Нет долгосрочного контракта. Отменить в любое время,
мы сохраним ваши проекты, и вы сможете повторно подписаться позже, чтобы получить к ним доступ.
Нечего устанавливать, просто перейдите к одному из наших
калькуляторы вроде этого и начинаем
проектирование! Если вам понравился инструмент и вы решили сохранить и распечатать проекты, вы можете
обновление за 19 долларов в месяц. Нет долгосрочного контракта. Отменить в любое время,
мы сохраним ваши проекты, и вы сможете повторно подписаться позже, чтобы получить к ним доступ.Другие бесплатные онлайн-калькуляторы
Мы создаем простое в использовании мощное программное обеспечение для проектирования конструкций и расчета конструкций.Попробуйте некоторые из наших другие бесплатные инструменты:
Калькулятордля балок: реакции опор, изгибающий момент, напряжения
Этот онлайн-калькулятор балки рассчитывает силы и моменты и моменты в двух подшипниках (= реакции опоры) и углы наклона статически определенных или
статически неопределимые балки.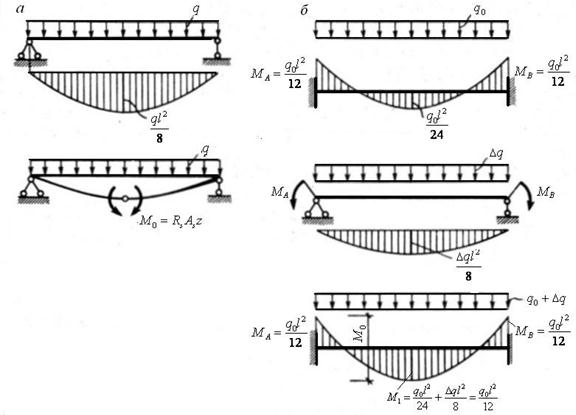 Кроме того, поперечная сила , изгибающий момент , , напряжение изгиба и Прогиб можно определить в желаемом месте.Изгибающий момент, поперечная сила и прогиб как функция длины x показаны. графически на двух диаграммах . Расчет максимального изгибающего момента , максимального напряжения изгиба , Максимальный прогиб и связанное с ним положение тоже возможно.
Кроме того, поперечная сила , изгибающий момент , , напряжение изгиба и Прогиб можно определить в желаемом месте.Изгибающий момент, поперечная сила и прогиб как функция длины x показаны. графически на двух диаграммах . Расчет максимального изгибающего момента , максимального напряжения изгиба , Максимальный прогиб и связанное с ним положение тоже возможно.
Подшипники могут быть выполнены в виде неподвижного подшипника, подвижного подшипника, фиксированного зажима или свободного конца.В качестве нагрузки, равной нагрузки или точечной нагрузки, или их комбинации, или треугольной нагрузки. (влево или вправо) можно выбрать.
* Чтобы ввести эти значения, выберите в разделе «Поперечное сечение A» -> «Другие профили» -> «Собственный профиль».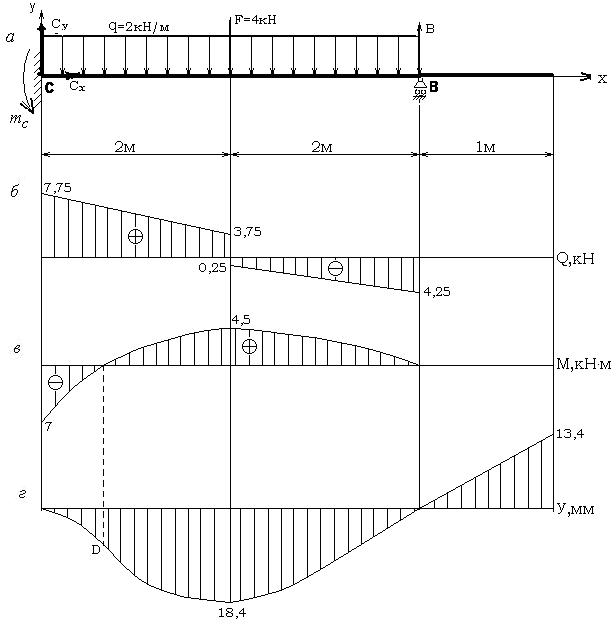
** Модуль упругости вводится автоматически при выборе материала и может быть изменен в любой момент; подходящих значений вы можете найти например в википедии.
Внимание:
Для профилей с отверстием только I, W и максимальное напряжение изгиба правильно рассчитываются с помощью дополнительных функций.Для других значений выберите профиль без отверстия!
С помощью этого калькулятора можно рассчитать опорные силы как статически определенных, так и статически неопределенных систем. Возможны следующие комбинации:
Страница создана в августе 2019 года. Последнее изменение: 24 октября 2020 года.
Онлайн-программа для проектирования конструкций | Гибка балок | Подгонка кривой | Расчет напряжений фермы, оболочки и плиты
Онлайн-программа для проектирования конструкций | Гибка балок | Подгонка кривой | Расчет напряжений фермы, оболочки и плиты | КороблениеПрограммное обеспечение для конструкций
SOFTWARE FOR STRUCTURES — компания, занимающаяся разработкой программного обеспечения, исследованиями и консультированием.Калькулятор балкиНаша цель в области программного обеспечения — создать веб-сайт, на котором инженеры-строители и аналитики, преподаватели и студенты могут найти коллекцию мощных, полезных и простых в использовании онлайн-расчетов и моделей. Наша специальность — расчет конструкций: балок, ферм, колонн, плит и оболочек. Наши программы включают дисциплины гражданского, механического, космического, авиационного, химического машиностроения и науки. Мы предлагаем решения очень распространенных проблем, таких как изгиб балок и пластин, анализ напряжений ферм, изгиб пластин и колонн, а также сложные проблемы нелинейного поведения и устойчивости тонких оболочек.В нашем онлайн-программном обеспечении для проектирования конструкций мы используем типовые методы для простых конструкций (балок и ферм), предоставляя клиентам все основные этапы решения, что особенно полезно для обучения студентов. Для решения сложных задач, например задач нелинейной теории оболочек, мы применяем наши ноу-хау подходы, основанные на наших предыдущих исследованиях.
Мы также предлагаем очень эффективный расчет аппроксимации кривой, результат которого представлен в виде графиков и простых в использовании формул.
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ СТРУКТУР находится в Торонто, Онтарио, Канада, и было создано в 2002 году.Ею владеют и управляют Алексей Евкин, кандидат структурных наук, доктор прикладных математических наук, и Глеб Евкин, бакалавр наук. в области компьютерных наук.
Помимо разработки программного обеспечения, SOFTWARE FOR STRUCTURES предоставляет консультации и исследования в областях, представленных нашим программным обеспечением. Просматривая наш сайт, вы можете заметить, что некоторые расчеты бесплатны .
— PolyBeam прост и удобен в использовании!
Простой в использовании калькулятор луча Первое, что наши пользователи связывают с PolyBeam, — это простота.PolyBeam — это очень простой и интуитивно понятный калькулятор луча, который делает его очень простым в использовании, даже если вы не знакомы с ИТ и программным обеспечением.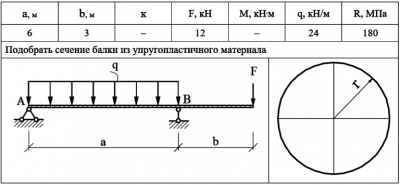 Опоры, нагрузки и свойства сечений вставляются с минимальным вмешательством пользователя. Одновременно с этим PolyBeam построит графическое представление балки с приложенными нагрузками, рассчитает поперечные силы и определит коэффициент использования балки.
Опоры, нагрузки и свойства сечений вставляются с минимальным вмешательством пользователя. Одновременно с этим PolyBeam построит графическое представление балки с приложенными нагрузками, рассчитает поперечные силы и определит коэффициент использования балки.
Критический изгибающий момент от поперечного продольного изгиба при кручении определяется на основе энергетического метода, который учитывает высоту атаки нагрузки, поперечные силы и ограничения.С помощью этого метода с высокой точностью определяется критический момент. Это часто приводит к более высокой несущей способности по сравнению с традиционными расчетами.
Упругость и пластичность Поперечные силы В отличие от традиционного программного обеспечения для проектирования, PolyBeam определяет поперечные силы как упруго, так и пластично. Это позволяет более эффективно использовать наиболее часто используемые стальные профили для статически неопределимых балок.
Можно указать комбинацию нагрузок ULS.Если это будет сделано, PolyBeam проверит поперечные силы из расчета балки с несущей способностью выбранного участка и определит коэффициент использования. Для получения дополнительных сведений о том, что входит в проверку конструкции ULS, см. Вопрос «Что включает проверка конструкции?».
Расчет предельного состояния эксплуатационной пригодности (SLS)Можно указать два различных типа комбинаций нагрузок SLS: анализ собственной частоты или анализ прогиба. Анализ собственных частот определяет первую собственную частоту балки и позволяет пользователю указать порог — это очень полезно при работе с требованиями к вибрации.аналогичным образом можно указать порог отклонения, поскольку по умолчанию используется L / 400.
Противопожарное исполнение Если указана комбинация пожарной нагрузки, PolyBeam рассчитывает температуру стали на основе продолжительности пожара и определяет несущую способность.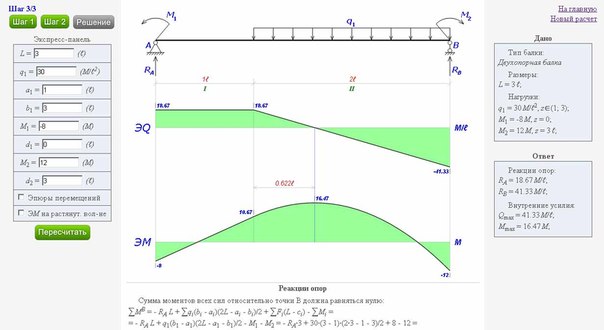 Если секция не может выдержать нагрузку, можно определить критическую температуру стали и использовать ее для определения необходимой противопожарной изоляции.
Если секция не может выдержать нагрузку, можно определить критическую температуру стали и использовать ее для определения необходимой противопожарной изоляции.
Когда вы закончите расчет балки, ее очень легко задокументировать.Просто нажмите на экспорт, выберите, какой контент вы хотите включить, и позвольте PolyBeam создать для вас короткий и элегантный документ PDF. Эта функция — одна из самых популярных среди наших пользователей. См. Пример.
Рабочий пример конструкции стальной балки [Универсальная балка]
Рабочий пример конструкции стальной балки описывает конструкцию балки с простой опорой, имеющей равномерно распределенную нагрузку. Балка считается просто поддерживаемой, и ниже приведены расчетные данные для расчета изгибающего момента и поперечных сил.
Кроме того, свойства раздела, которые необходимо учитывать, также задаются на каждом этапе проверки раздела.
Теоретические аспекты и процедуры проектирования кодов обсуждаются в проекте статьи стальной балки согласно BS 5950 .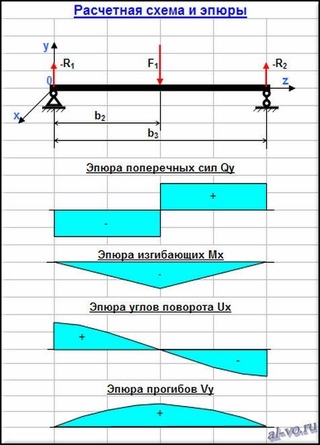
- Нагрузка UDL 20 кН / м
- Пролет балки 6 м
- Балка без опоры
- Расчетная прочность стали, Py = 275 Н / мм 2
Максимальный изгибающий момент
= wl 2 /8 = 20 x 6 2 /8 = 90 кНм
Максимальное поперечное усилие
= wl / 2 = 20 x 6/2 = 60 кН
Рассмотрим универсальную балку 500x200x89.7 кг / м (P y = 275 Н / мм 2 )
Данные профиля- D = 500 мм
- T = 16 мм
- t = 10 мм
- B = 200 мм
- b = 100 мм
- r 1 = 20 мм
- d = 500 — 16 x 2 — 2 x 20 = 428 мм
- S x = 2175 × 10 3 мм 3
- Z x = 1914 × 10 3 мм 3
- r y = 43,3 мм
Начнем расчет конструкции стальной балки.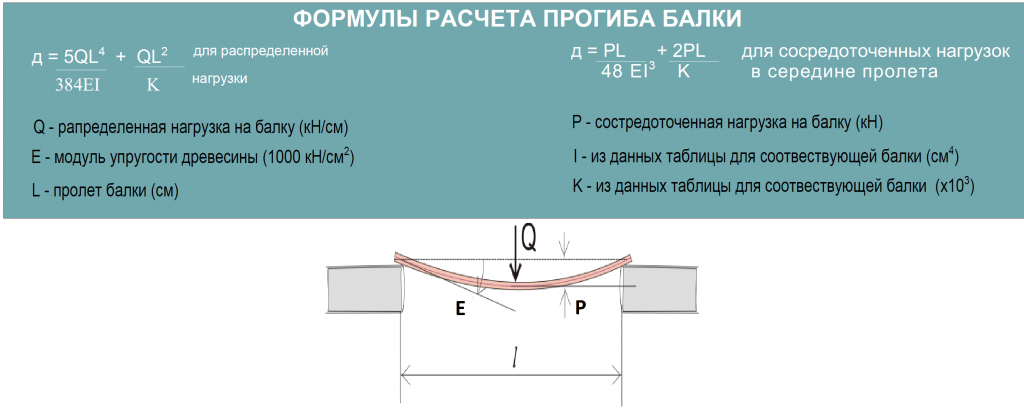 В рамках этого расчета конструкции стальной балки выполняются следующие проверки.
В рамках этого расчета конструкции стальной балки выполняются следующие проверки.
- Классификация сечения
- Расчет на сдвиг
- Расчет на изгиб
- Проверка бокового продольного изгиба
- Проверка прогиба
- Проверка подшипника перемычки
- Проверка продольного изгиба стенки
Классификация секции
Первым этапом проектирования стальной балки является классификация секции, чтобы определить, является ли она пластичной, полупластичной, компактной или тонкой.
T = 16 мм, P y = 275 Н / мм 2
ε = (275 / P y ) 0,5 = 1
Контрольный фланец
b / T = 100/16 = 6,25 <9ε = 9 - Фланец пластиковый
Проверить полотно
d / t = 428/10 = 42,8 <80ε = 80 - полотно пластиковый
Кроме того, d / t <70ε = 70 - Следовательно, нет необходимости проверять коробление при сдвиге
Следовательно, профиль пластиковый
Расчетное усилие на сдвиг
Расчетное усилие сдвига, F v = 60 кН
P v = 0.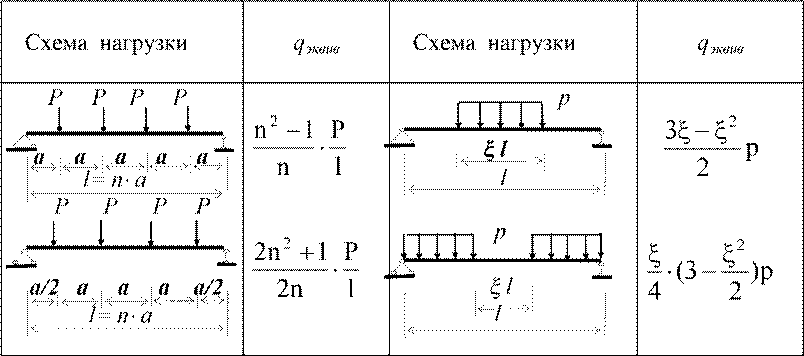 6 P y A v = 0,6 P y tD = 0,6 x 275 x 10 x 500 x 10 -3 = 825 кН
6 P y A v = 0,6 P y tD = 0,6 x 275 x 10 x 500 x 10 -3 = 825 кН
F v
v Допустимая нагрузка на сдвиг
В зависимости от силы сдвига решается, подвергается ли секция низкому или высокому сдвигу в конструкции стальной балки.
Расчет для гибки
Проверить, подвергается ли секция низкому или высокому сдвигу
60% x P v = 0,6 x 825 = 495 кН
F v <0.6 P v Секция, подверженная низкому сдвигу
M c должна быть меньше 1,2 P y Z x или P y S x согласно Cl. 4.2.5.1 и кл. 4.2.5.2
M c ≤ 1.2P y Z x = 1,2 x 275 x 1914 x10 3 x 10 -6 = 613,62 кНм
M c = P y S x = 275 x 2175 x 10 3 x 10 -6 = 598,125 кНм
Следовательно,
M c = 598.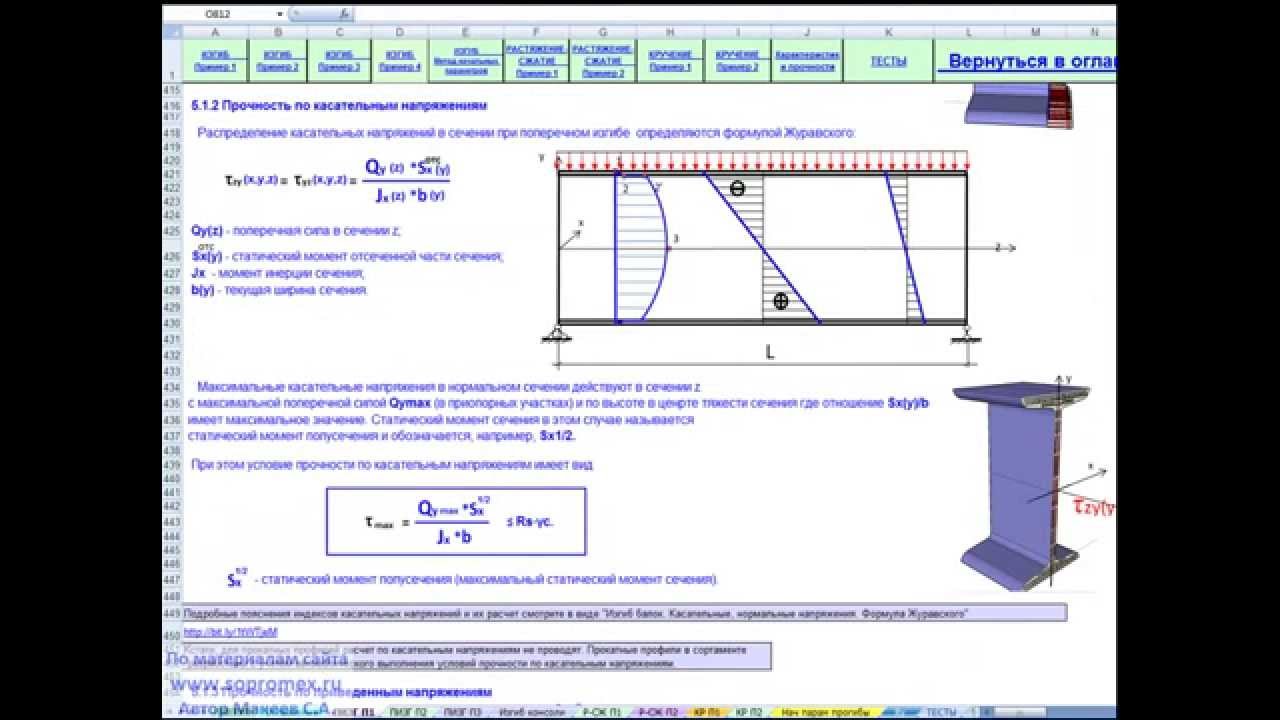 125 кНм> 90 кНм
125 кНм> 90 кНм
Изгиб в норме
Проверка бокового продольного изгиба при кручении
M x
В этом примере промежуточные ограничения не учитывались
м LT , Таблица 18, BS 5950
M b = P b S x Cl. 4.3.6.4
Существует два метода проверки продольного изгиба при кручении, как описано в статье , конструкция стальной балки в соответствии с BS 5950 .Это строгий метод и упрощенный метод.
В этом примере конструкции стальной балки мы обсудили оба метода, чтобы подробно описать процедуры, которые необходимо соблюдать при использовании любого из этих методов.
Кроме того, основное различие между этими двумя методами заключается в оценке прочности на изгиб .
Строгий метод
M b = P b S x
P b в зависимости от λ LT и P y
λ LT = uv2λ√ (β 9025 w )
λ = L E / r y
L E — следует брать из таблицы 13 согласно кл. 4.3.5.1 и рассмотрим L LT = L — пролет
4.3.5.1 и рассмотрим L LT = L — пролет
L E = 1,0 L LT = 1 x 6 = 6 м
λ = L E / r y = 6000 / 43,3 = 138,568
Для катаных двутавровых и двутавровых профилей, кл. 4.3.6.8
x = D / T используется с u = 0,9
x = D / T = 500/10 = 50
β w должно быть получено из класса 4.3.6.9
β w = 1 для пластмассовых секций класса 1 или компактных секций класса 2
v — коэффициент гибкости должен быть получен из таблицы 19 на основе λ / x и η
λ / x = 138.568/50 = 2,771
η = 0,5 для равных фланцев
v = 0,919 из таблицы 19
λ LT = uvλ√ (β w ) = 0,9 x 0,919 x 138,568 x √ (1) = 114,6
λ LO можно получить из таблицы 16 (см. Нижнюю часть таблицы)
Если λ LO ≥ λ LT ; P b = P y или в противном случае P b следует брать из таблицы 16 для сортового проката.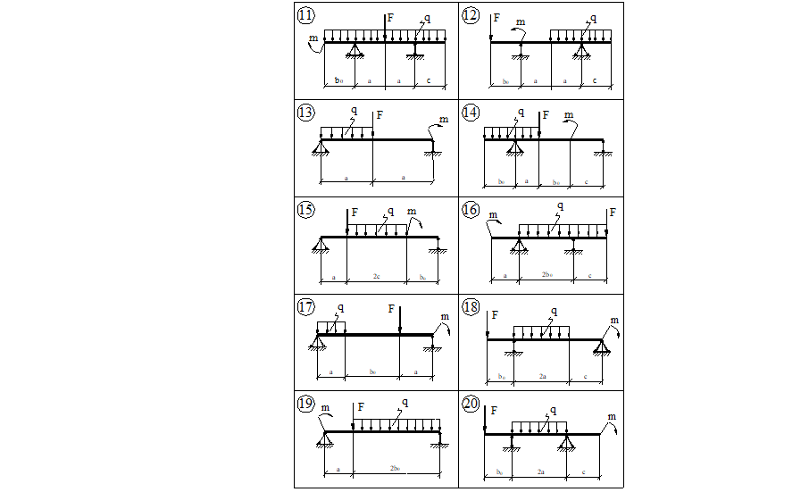
Если λ LO ≥ λ LT не нужно делать припуск на продольный изгиб при кручении, и в противном случае проверьте наличие продольного изгиба при кручении.
P y = 275 Н / мм 2 ; λ LO = 37,3
λ LO <λ LT Поэтому проверьте наличие бокового продольного изгиба при кручении
Из таблицы 16 для λ LT = 114,6; P b = 102 Н / мм 2
M b = P b S x = 102 x 2175 x 10 3 x 10 -6 = 221,85 кНм
M b / m LT = 221.85 / 0,925 = 239,838 кНм
Следовательно, M x = 90 кНм
Сечение адекватное .
Упрощенный метод
Примечание. При проектировании балки применять оба метода не требуется. Достаточно следовать упрощенному или строгому методу.
Достаточно следовать упрощенному или строгому методу.
M b = P b S x : кл. 4.3.7
В этом методе определение P b отличается по сравнению с предыдущим методом.Этот метод дает консервативные ответы. P b может быть получен из Таблицы 20 стандарта BS 5950 на основе √ (β w ) (L E / r y ) и D / T
β w = 1; предыдущий расчет
L E / r y = 138,568; предыдущий расчет
√ (β w ) (L E / r y ) = 1 0,5 x 135,568 = 138,568
D / T = 500/16 = 31,25
P b = 116 .646 Н / мм 2 Из таблицы 20
M b = P b S x = 116,646 x 2175 x 10 3 x 10 -6 = 253,705 кНм
M b / м LT = 253,705 / 0,925 = 274,3 кНм
Следовательно, M x = 90 кНм
Сечение адекватное
19 Максимальный прогиб (δ) для равномерно распределенной балки с свободно опертой опорой можно оценить по следующему уравнению.
δ = 5W e L 4 / (384EI)
Это уравнение можно упростить следующим образом.
δ = 0,104M max L 2 / (EI)
Поскольку мы оцениваем прогиб из-за приложенных нагрузок, в этом расчете принимаем приложенную нагрузку как 10 кН / м.
δ = 0,104 x 90 x 10 6 6000 2 / (205 x 10 3 x 478 x 10 6 ) = 1,7 мм
При условии использования хрупкой поверхности
Пролет / 360 = 6000 / 360 = 16.7 мм
δ Различные методы расчета отклонений обсуждаются в статье Википедии отклонение (инженерное дело) . Необходимо проверить несущую способность стенки в конструкции стальной балки. В этой категории выполняются подшипники и изгиб стенки. P bw = (b 1 + nk) tP yw t = 10 мм T = 10 мм r = 10 мм g = 5 мм b e = 5 мм b 1 = t + T + 0. k = T + r = 16 + 20 = 36 мм (для сортового проката) на конце, n = (2 + 0,6b e / k), но ≤ 5 n = (2 + 0,6 x 5/36) = 2,083 <5 P yw = 275 Н / мм 2 из таблицы 9 P bw = (b 1 + nk) tP yw = (23 +2,083 x 36) x 10 x 275 x 10 -3 = 269,5 кН Сопротивление опоры составляет 60 кН. Подшипник перемычки в порядке, ребра жесткости не требуются. Когда F x > P bw , нам необходимо предусмотреть ребра жесткости для обеспечения баланса сил (F x — P bw ). Допустимая нагрузка ребер жесткости должна быть получена из P s = A s.net P y . Где A s.net — площадь поперечного сечения жесткости. Если стенка и жесткость имеют разную прочность, меньшее значение следует использовать для расчета P s и P bw . Несущая способность стенки
 8r — g = 10 + 10 + 0,8 x 10-5 = 23 мм
8r — g = 10 + 10 + 0,8 x 10-5 = 23 мм

 Его можно перекрыть шестиметровым элементом. Большие пролеты перекрывают клееным брусом или выстраивают дополнительные стены-перегородки.
Его можно перекрыть шестиметровым элементом. Большие пролеты перекрывают клееным брусом или выстраивают дополнительные стены-перегородки.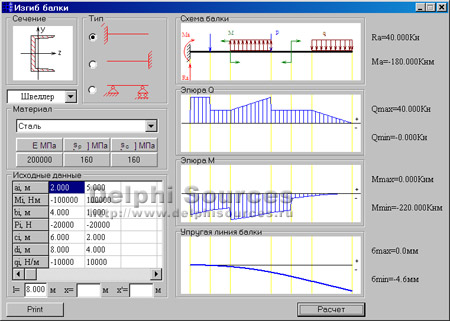
 Вообще, чем больше сечение балок, тем больше расстояние между ними.
Вообще, чем больше сечение балок, тем больше расстояние между ними. Наша цель в области программного обеспечения — создать веб-сайт, на котором инженеры-строители и аналитики, преподаватели и студенты могут найти коллекцию мощных, полезных и простых в использовании онлайн-расчетов и моделей. Наша специальность — расчет конструкций: балок, ферм, колонн, плит и оболочек. Наши программы включают дисциплины гражданского, механического, космического, авиационного, химического машиностроения и науки. Мы предлагаем решения очень распространенных проблем, таких как изгиб балок и пластин, анализ напряжений ферм, изгиб пластин и колонн, а также сложные проблемы нелинейного поведения и устойчивости тонких оболочек.В нашем онлайн-программном обеспечении для проектирования конструкций мы используем типовые методы для простых конструкций (балок и ферм), предоставляя клиентам все основные этапы решения, что особенно полезно для обучения студентов. Для решения сложных задач, например задач нелинейной теории оболочек, мы применяем наши ноу-хау подходы, основанные на наших предыдущих исследованиях.
Наша цель в области программного обеспечения — создать веб-сайт, на котором инженеры-строители и аналитики, преподаватели и студенты могут найти коллекцию мощных, полезных и простых в использовании онлайн-расчетов и моделей. Наша специальность — расчет конструкций: балок, ферм, колонн, плит и оболочек. Наши программы включают дисциплины гражданского, механического, космического, авиационного, химического машиностроения и науки. Мы предлагаем решения очень распространенных проблем, таких как изгиб балок и пластин, анализ напряжений ферм, изгиб пластин и колонн, а также сложные проблемы нелинейного поведения и устойчивости тонких оболочек.В нашем онлайн-программном обеспечении для проектирования конструкций мы используем типовые методы для простых конструкций (балок и ферм), предоставляя клиентам все основные этапы решения, что особенно полезно для обучения студентов. Для решения сложных задач, например задач нелинейной теории оболочек, мы применяем наши ноу-хау подходы, основанные на наших предыдущих исследованиях. Мы также предлагаем очень эффективный расчет аппроксимации кривой, результат которого представлен в виде графиков и простых в использовании формул.
Мы также предлагаем очень эффективный расчет аппроксимации кривой, результат которого представлен в виде графиков и простых в использовании формул.