Формула площадь сечения куба: Расчет площади сечения куба — онлайн калькулятор и формулы

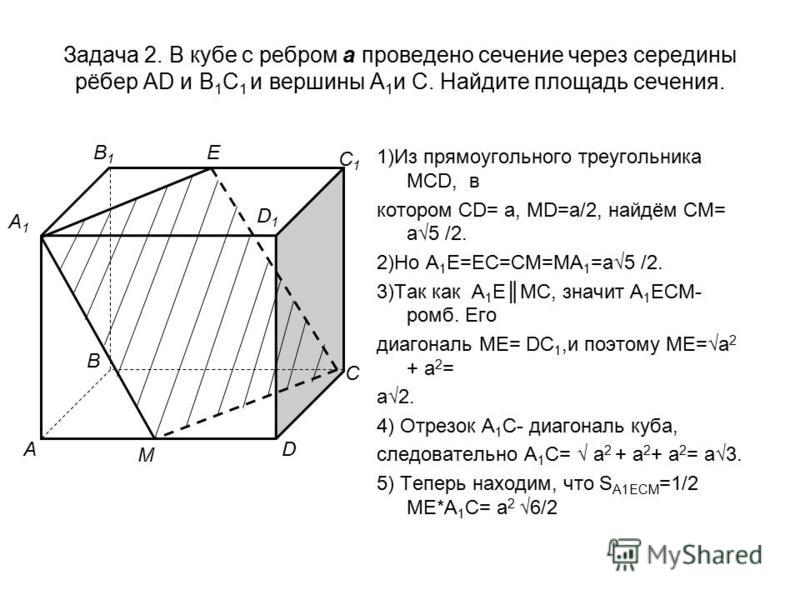
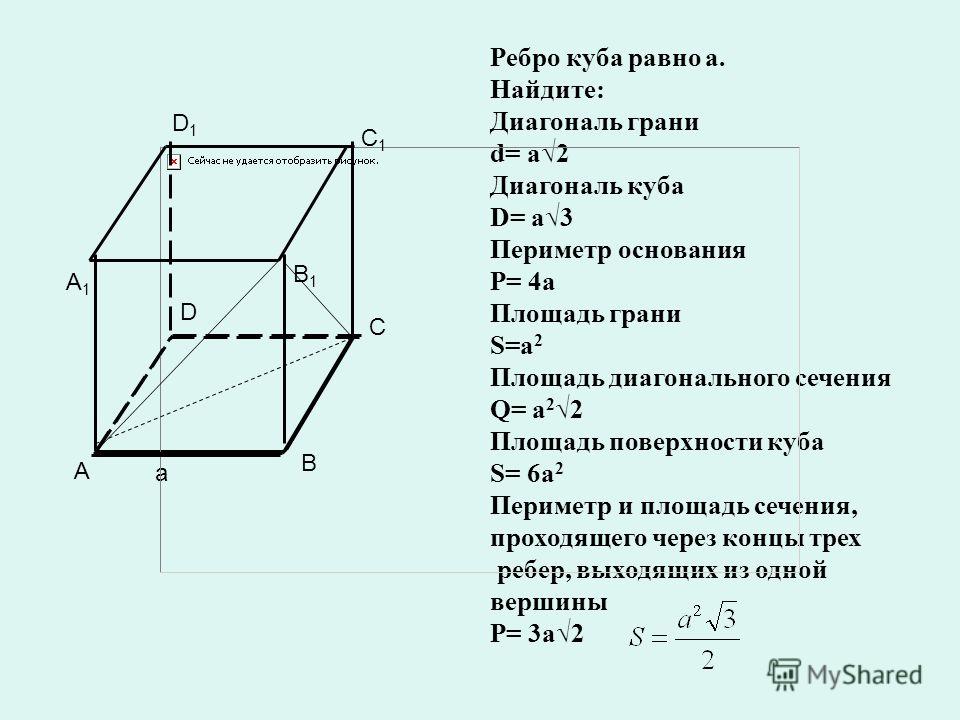
как найти его площадь, примеры, решение / Справочник :: Бингоскул

Диагональное сечение куба: как найти его площадь, примеры, решение

добавить в закладки удалить из закладок

Содержание:

Куб (правильный гексаэдр) – геометрическое тело, состоящее из шести попарно параллельных поверхностей и 12 одинаковых граней. Ещё ним называют правильный многогранник, основание коего – квадрат. Рассмотрим, как найти площадь диагонального сечения куба. После ознакомления с формулой решим пару несложных задач.

Диагональное сечение куба

Для геометрических тел с правильным многоугольником в основании можно провести диагональ последнего. Если эту линию спроецировать к вершине (для пирамиды) либо вершинам, например, для куба или параллелограмма, получим диагональное сечение объёмного тела. Если площадь куба вычисляется путём возведения длины стороны в квадрат, то с размером занимаемой сечением поверхности дело сложнее.

Секущая площадь куба имеет форму прямоугольника, где одна пара сторон представлена рёбрами кубика, вторая – диагоналями граней. Для вычисления её площади нужна только длина ребра правильного прямоугольника, ведь одна из них выполняет роль высоты. Длина диагонали для треугольников, где высота – это гипотенуза, а рёбра – катеты, определяется по формуле a*√2. Занимаемая диагональным сечением куба площадь равняется:

S = a * a * √2 = a²*√2.

Задачи

Дан куб со стороной 20 см, разделённый плоскостью сечения по диагонали на две части. Вычислить площадь поверхности получившегося геометрического тела без боковых поверхностей (треугольников).

Решение. Мы знаем, как вычислить площадь прямоугольника, который лежит в основании сечения, и двух боковых поверхностей тела.

Для боковой поверхности используем формулу: S_БП = 2a2 – умножаем длину стороны саму на себя, затем – на два – количество сторон усечённого кубика.

Для прямоугольника S_ОСН = a * a√2 = a²*√2.

S_ПОЛН = S_ОСН + S_БП = a²*√2 + 2a² = 202*√2 + 2 * 202 = 400*√2 + 800 = 1365,7 см².

Ответ: S = 1365,7 см².

Вычислить поверхность куба, если его диагональное сечение равно 8 * √2 см².

Решение.

Необходимо вычислить размер грани правильного гексаэдра, затем – возвести в квадрат – для нахождения S одной поверхности, далее – умножить на их количество – шесть штук.

Возьмём длину ребра, равную a; величины его поверхности – a²; полная поверхность – 6a².

Форма сечения гексаэдра с равными гранями – прямоугольник, где пара сторон – ребра квадрата, вторая – диагонали оснований. Из формулы они равны a√2. Подставим значения:

S = a²*√2. Длина грани рассматриваемого куба: a = √8, площадь одной грани – √8² = 8, а полная равна её произведению на количество сторон: S_П = 6 * 8 = 48 см².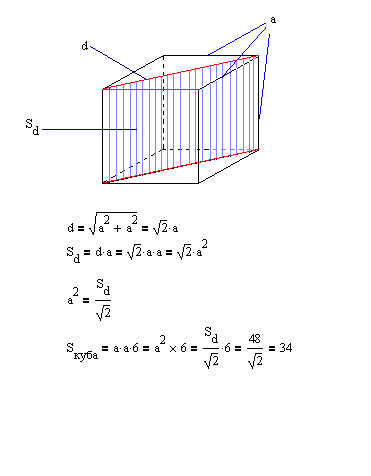

Ответ: S_П = 48 см².

Для проведения более сложных расчётов часто придётся задействовать теорему Пифагора.

Поделитесь в социальных сетях:

20 ноября 2021, 14:35

Геометрия

Could not load xLike class!

Сечения куба — квадрат и прямоугольник

Сечения куба — квадрат и прямоугольник — Mnogogranniki.ru

Вы здесь:
• Главная
• Сечения белого куба

Здесь вы найдете математические задачи, для решения которых этот куб очень удобно использовать в качестве наглядного пособия.

В разделе «Тесты» — вы можете проверить себя и самостоятельно решить задачи на сечение куба плоскостью.

 

Задача № 1

Задача № 1

Сложность 1/5

Задание:

FН – диагональ грани куба с ребром 6. Найдите ее длину.

Варианты ответов:

1) 6
2) 6√2
3) невозможно найти.

Решение:

1. Рассмотрите модель белого цвета, а именно, её среднее сечение, содержащее диагонали двух граней. Посчитайте количество диагоналей единичных квадратов. Каждая диагональ единичного квадрата равна √2. Всего их 6. Следовательно, длина диагонали 6√2.
2. Рассмотрим прямоугольный равнобедренный треугольник FGH, с катетами по 6 см, тогда по теореме Пифагора получаем, что гипотенуза

Ответ:

2) 6√2

Задача № 2

Задача № 2

Сложность 3/5

Задание:

Округлите иррациональное число 6√2 до десятых.

Варианты ответов:

1) 7
2) 8,5
3) 12,2
4) невозможно.

 

Решение:

 

1. Рассмотрите модель белого цвета, а именно, её среднее сечение, содержащее диагонали двух граней. Посчитайте количество диагоналей единичных квадратов. Каждая диагональ единичного квадрата равна √2. Всего их 6. Следовательно, длина диагонали 6√2. Измерьте эту диагональ линейкой. Полученный результат и является ответом: 8,5 см.

2. Методом подбора узнаем, что 1,414²=1,9994<2, а 1,415²=2,00223>2, таким образом, так как нас просят округлить до десятых, получаем, что √2 ≈1. 414. Тогда 6√2=8,484≈8,5

Ответ:

2) 8,5

Задача № 3

Задача № 3

Сложность 3/5

Задание:

Найдите расстояние от точки E до прямой FH.

Варианты ответов:
1) 3
2) 3√2
3) 4

Решение:

1. Рассмотрите модель белого цвета, а именно, её среднее сечение, содержащее диагонали двух граней. Проведите еще одну диагональ одной из граней. Так как грани имеют форму квадрата, а диагонали пересекаются под прямым углом, то половина диагонали и будет расстоянием от точки до прямой. Сосчитаем количество диагоналей единичных квадратов. Получим 3√2

2. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из это точки на прямую. В прямоугольном равнобедренном треугольнике FEH построим высоту EM к гипотенузе. Легко доказать, что EM=FH/2=3√2

Ответ:

2) 3√2

Задача № 4

Задача № 4

Сложность 4/5

Задание:

На сколько минут уменьшится время обхода кровельщика по периметру крыши, если сделать помост на высоте 2/3 от верхнего гребня? Если крыша покрывает здание с периметром почти в 29 м.

, а именно 12⋅(√2+1)м, а возможная скорость кровельщика не более 0,4 м/с.

Варианты ответов: 

1) 1 минута,т.е. 60 секунд
2) не изменится
3) 14 секунд.

Решение:

1. Рассмотрев белую модель куба, заметим, что большее сечение имеет периметр состоящий из 12 диагоналей единичных квадратов и 12 сторон единичных квадратов. А периметр меньшего сечения лишь из 12 сторон единичных квадратов, но лишь из 8 диагоналей. Таким образом, отметим, что разница периметров равна 4 диагоналям единичных квадратов. Диагональ единичного квадрата, по теореме Пифагора, равна √2. Это означает, что путь уменьшится на 4⋅√2≈5,66. А время, соответственно, на 4⋅√2:0,4≈14 секунд

2. Построив два прямоугольных сечения куба с ребром равным 6 единичным отрезкам, так как P=12⋅(√2+1)=12√2+12=2⋅(6√2+6), найдем периметры указанных сечений и рассчитаем по формуле T=S/V время.

Ответ:

3) 14

Задача № 5

Задача № 5

Сложность 5/5

Задание:

Муравьи смогли прогрызть кубик сахара, аналогичный белой модели куба. Благодаря чему, кубик сахара распался на 3 кусочка. Какое минимальное количество муравьев необходимо на каждый кусочек, если каждый муравей может поднять массу, превышающую массу самого муравья в 50 раз. При этом, известно, что самые легкие муравьи — фараоновы, всем известные домашние вредители, и некоторые виды тропических муравьев, такие же мелкие. Масса муравья из касты рабочих у этих видов составляет 1-2 миллиграмма (т.е 0,01 гр). А масса 1м

3 сахара равен 1600 кг.
Подсказка: попробуйте угадать ответ, основываясь на ощущениях объема данных частей. Во сколько раз каждая часть больше по объему?

Варианты ответов:

1) 250, 250 и 500
2) 112, 224 и 336
3) 154, 346, 538
4) 154, 192, 346

Решение 1:

Для подсчета количества муравьев, необходимо понять, каков объем каждой части. Обратившись к соответствующей модели, произведем следующие измерения:

Первым многогранником рассмотрим наименьший из трех. Его объем будем искать интегрированием (не стоит бояться этого слова, все очень просто). Сперва измерим площадь торцевого треугольника ELK. Имея модель в руках, ее можно просто посчитать по квадратикам (не имея данной модели, так же возможно выполнить подсчет, но необходимо воспользоваться соответствующей формулой площади треугольника). Получаем 8 единичных квадратов. Каждый квадрат при этом имеет площадь равную 1 см² или 100 мм². То есть, S=800 мм². Далее, рассмотрим, что грань EKJ имеет длину 6 единичных квадратов (KJ = 6 ед). То есть, если начать отрезать слои треугольной формы, двигаясь вдоль KJ, и толщиной в 1 миллиметр, то у нас получится 6⋅10=60 таких слоев. Осталось выполнить последнее умножение: 800 ⋅ 60 = 48000 мм ³ = 48 см³.
Теперь разберем величины массы сахара. В условии задачи указано, что вес 1 м³ сахара равен 1600 кг. 1 м³ означает, что у вас рассматривается куб с ребром 1 м. Мы же получили объем кусочка в см³. Перевод единиц не вызовет затруднений, если вспомнить, что в 1 метре содержится 100 см. Т.е. 1 м³ = 100 ³ см³ = 1 000 000 см³ . Тогда, чтобы узнать, вес 1 см³, необходимо вес 1м³ разделить на 1 000 000, то есть 1600 кг = 1 600 000 гр : 1 000 000 = 1,6 гр.
Это означает, что рассмотренный нами кусочек имеет массу 48⋅1,6=76,8 гр. И его смогут поднять: 76,8:(0,01⋅50)=153,6 муравья. Но муравьев лучше не рубить на части, поэтому лучше с запасом взять 154 муравья.
Аналогичные расчеты проведем и для большего кусочка:
1800⋅60 : 1000 = 108 см³.
Или проще: 6³ : 2 = 108 см³
Тогда для подсчета количества муравьев:
108⋅1,6 : (0,01⋅50) = 345, 6
То есть, 346 муравьев.
Чтобы найти объем средней части нашего куба, достаточного из общего объема вычесть уже найденные два объема:
6³ = 216 — 108 — 48 = 60
Тогда количество муравьев:
60 ⋅ 1,6 : (0,01 ⋅ 50) = 192
Количество муравьев, конечно же, поражает. Но и кусочек сахара в данном примере взят довольно большим. Но его модель помогает разобраться и в более реальной ситуации. В том числе становится понятно то, что наименьший кусов почти в 2 раза меньше среднего

 

Решение 2:

В основном школьном курсе стереометрии, в разделе пирамид, мы не найдем формулы для вычисления объема «крыши», объема маленького кусочка сахара. Однако, если поставить эту «крышу» на торец, то получится призма с верхним и нижним основаниями в форме треугольников. Тогда, вспомнив формулу нахождения объема треугольной призмы, мы с Вами легко поймем, что, умножив площадь треугольника на высоту этой призмы, получим ее объем: 18 ⋅ 6 = 108 см

3. Если же формула никак не вспоминается или не была пройдена, то тоже не беда. Ведь в школе прекрасно объясняется умение делить объемы. И если, общий объем куба 6³=216 см³, то его половина равна 6³ : 2 = 216 : 2 = 108 см³. Так находится объем большего многогранника их трех имеющихся. Дальше хотелось бы воспользоваться понятием коэффииента подобия.

Ведь, мы знаем с вами, что отношение периметров подобных фигур равно коэффициенту подобия (k), отношение площадей равное коэффициенту подобия в квадрате (k²), а объемы — k³. Но, к сожалению, данные кусочки не подобны (подумайте самостоятельно, почему). Поэтому для подсчета объема самого маленького кусочка, мы достроим его до параллелепипеда с ребрами 6 и 4,4. Его объем найти легко: 6 ⋅ 4 ⋅ 4 = 96 см³. И так как, наш искомый многогранник является его половиной, то 96 : 2 = 48 см³
Далее займемся вычитаем объемов. Из общего вычтем найденные части:
216 — 108 — 48 = 60
И получим, что объем средней части равен 60 см³
Теперь остается посчитать количество муравьев, как в предыдущем примере решения.

Ответ:

3) 154, 192, 346

Задача № 6

Задача № 6

Сложность 3/5

Задание:

Крыша государственного исторического музея имеет схожую форму со средней частью модели белого цвета. И если для модели нашего куба изменения не сильно повлияют на массу изделия, то изменение в пропорции крыши музея может привести к ее обрушению. Данные задачи решаются еще на этапе проектирования. Давайте и мы попробуем узнать, на какую площадь увеличится средняя часть заготовки белого цвета, если к ней приклеить первую, наименьшую часть .

*Подсчет площади применяется при подсчетах расходного материала для настила кровли. Подсказка: Чтобы узнать площадь малой части, достаточно посчитать количество квадратов. Обратите внимание, что в сумме получается целое число.

Варианты ответов: 

1) на 32 ед²
2) на 100√2 ед²
3) 64 ед²

Ответ:

3) 64 ед²

Задача № 7

Задача № 7

Сложность 3/5

Задание:

Насыпь шоссейной дороги имеет в верхней части ширину 40√2 м. Какова ширина насыпи в нижней ее части, если угол наклона откосов равен 45°, а высота 10√2 м?

Варианты ответов:

1) 60√2
2) 50√2
3) 100√2

Решение 1:

Рассмотрите белую модель. Найдите соответствующую деталь. Сосчитайте количество диагоналей единичного куба.

Решение 2:

 

Ответ:

1) 60√2

 

Автор задач: математик Соколова Александра

 

посмотреть другие сечения куба можно здесь 

Площадь поверхности куба – формула, определение, примеры

Площадь поверхности куба может быть определена как общая площадь, покрытая всеми шестью гранями куба. Полную площадь поверхности куба можно вычислить, если вычислить площадь двух оснований и площадь четырех боковых граней. Куб — объемная объемная фигура, состоящая из квадратных граней. Площадь поверхности важно знать в ситуациях, когда мы хотим обернуть куб, покрасить поверхности куба и т. д.

1.	Какова площадь поверхности куба?
2.	Площадь поверхности куба Formula
3.	Как найти площадь поверхности куба?
4.	Часто задаваемые вопросы о площади поверхности куба

Какова площадь поверхности куба?

Площадь поверхности куба будет равна сумме площадей оснований и площадей боковых поверхностей куба. Поскольку все шесть граней куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой шесть раз. Он измеряется как «количество квадратных единиц» (квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.). Площадь поверхности куба может быть двух типов,

• Площадь боковой поверхности
• Общая площадь поверхности

Общая площадь поверхности куба

Общая площадь поверхности куба относится к общей площади, покрытой всеми шестью гранями куба. Чтобы вычислить ВПС куба, находим сумму площадей этих 6 граней.

Площадь боковой поверхности куба

Площадь боковой поверхности куба относится к общей площади, покрытой боковыми или боковыми гранями куба. Для расчета LSA находим сумму площадей этих 4-х граней.

Площадь поверхности формулы куба

Площадь поверхности куба можно рассчитать по длине ребра. Разберемся с формулой боковой и полной поверхности куба.

Общая площадь поверхности куба Формула

Формула общей площади поверхности куба используется для определения площади, занимаемой шестью поверхностями. TSA куба получается путем умножения квадрата длины его стороны на 6. Таким образом, формула площади поверхности куба с длиной стороны «а» равна 9.0067 «6а ² «.

Общая площадь поверхности куба = (6 × сторона ² ) квадратных единиц

Формула площади боковой поверхности куба

четыре боковые или боковые поверхности. LSA куба получается путем умножения квадрата длины его стороны на 4. Таким образом, формула площади боковой поверхности куба с длиной стороны «а» равна «4а ² «.

Площадь боковой поверхности куба = (4 × сторона ² ) квадратных единиц

Как найти площадь поверхности куба?

Общая площадь поверхности куба равна квадрату длины его стороны, умноженному на 6. Аналогичным образом, для площади боковой поверхности мы умножаем квадрат длины стороны на 4. Следуя приведенным ниже шагам, мы можем найти поверхность площадь куба:

• Шаг 1 : Определите длину стороны куба.
• Шаг 2 : Найдите квадрат длины стороны куба.
• Шаг 3 : Для получения общей площади найдите произведение квадрата длины стороны на 6, а для площади боковой поверхности умножьте произведение квадрата длины стороны на 4.
• Шаг 4 : Запишите ответ в квадратных единицах.

Связанные статьи:

Посмотрите эти интересные статьи, связанные с концепцией площади поверхности куба.

• Площадь поверхности прямоугольного параллелепипеда
• Площадь поверхности цилиндра
• Площадь поверхности призмы
• Площадь поверхности конуса
• Площадь поверхности сферы
• Площадь поверхности пирамиды
• Разница между площадью и площадью поверхности
• Формулы площади поверхности
• Калькулятор площади поверхности куба

 

Площадь поверхности куба Примеры

1. Пример 1: Длина стороны куба 15 дюймов. Найдите общую площадь поверхности куба.

   Решение:

   Длина стороны куба, a = 15 дюймов

   Используя формулу площади куба, которая: × 15

   A = 1350

   Следовательно, площадь поверхности куба равна 1350 квадратных дюймов.

2. Пример 2: Оливке дан куб с базовой площадью 64 квадратных единицы. Найдите длину стороны куба и площадь полной поверхности куба.

   Решение:

   Площадь основания куба = 64 кв.

   Длина стороны куба ‘a’ = √64 = 8 единиц.

   Общая площадь поверхности: A = 6a ²

   A = 6 × 8 ²

   A = 384

   Следовательно, длина основания куба равна 8 единицам, а площадь куба равна 384 кв.

3. Пример 3: Чему равна площадь боковой поверхности куба со стороной 12 футов?

   Решение:

   Дано, длина стороны (а) = 12 футов.

   Площадь боковой поверхности: L = 4a ²

   L = 4 × 12 ²

   L = 576

   Следовательно, площадь боковой поверхности куба составляет 576 квадратных футов.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по площади поверхности куба

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади поверхности куба

Какова площадь поверхности куба?

Площадь поверхности куба определяется как общая площадь, покрытая гранями куба. Чтобы вычислить площадь поверхности куба, найдем сумму площадей всех граней куба.

Какая формула площади поверхности куба?

Площадь поверхности куба с длиной ребра, равной «a», может быть рассчитана по следующим формулам: LSA куба = 4a ² квадратных единиц и TSA куба = 6a ² квадратных единиц.

Какая единица используется для выражения площади поверхности куба?

Площадь поверхности куба выражается в квадратных единицах, например, с использованием таких единиц, как ² , футы ² , ярды ² , м ² , см ² и т. д.

Что такое площадь боковой поверхности куба?

Боковая площадь куба – это общая площадь, занимаемая боковыми или боковыми гранями куба. Формула для расчета площади боковой поверхности куба имеет следующий вид: Площадь боковой поверхности = 4a ² , где «a» — длина ребра куба.

Как найти полную площадь поверхности куба?

Общая площадь поверхности куба — это площадь, покрытая всеми шестью гранями куба.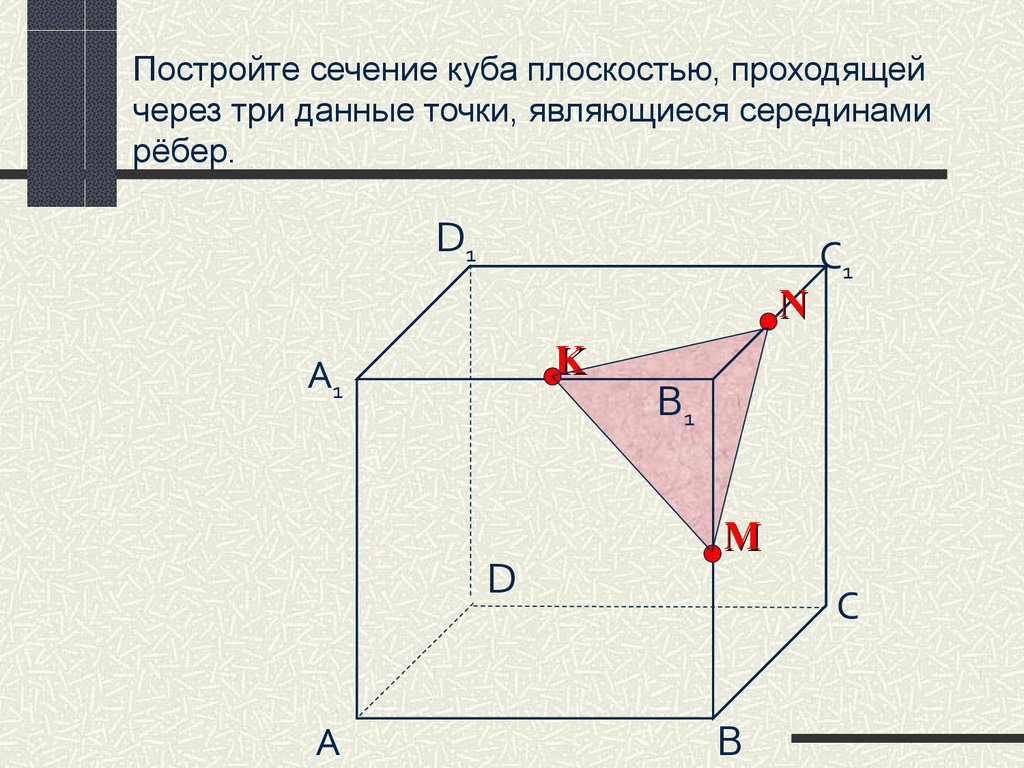 Формула для нахождения общей площади поверхности куба выглядит следующим образом: Общая площадь поверхности = 6a ² , где «a» — длина ребра куба.

Как найти площадь поверхности куба, зная объем?

Когда задан объем, мы сначала находим длину одной стороны куба, а затем применяем формулу площади поверхности куба. Объем формулы куба (сторона) ³ , который можно использовать для нахождения длины стороны. Например, если объем куба 64 кубических единицы, то длина одной стороны куба = ³ √64 = 4 единицы. Теперь, используя площадь поверхности формулы куба, то есть 6 × (сторона) ² , мы можем найти его площадь поверхности. Отсюда следует, что TSA = 6 × 4 × 4 = 96 квадратных единиц.

Как найти площадь поверхности куба с диагональю?

Формула диагонали куба: a√3 единицы, где a — длина одной стороны куба. Используя эту формулу и заданное значение диагонали, мы можем сначала найти длину стороны куба, а затем найти площадь его поверхности.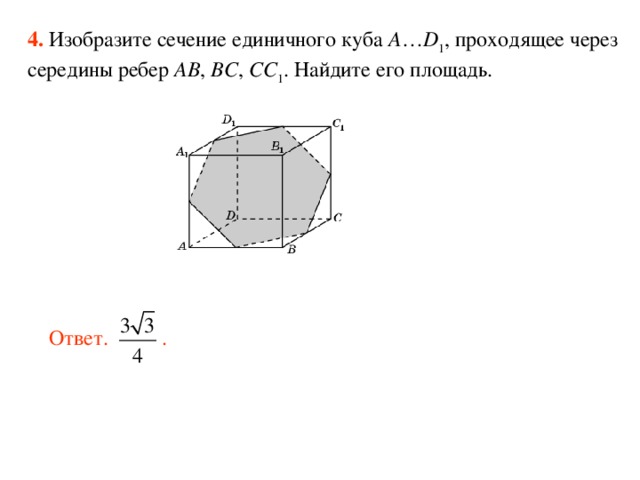

По какой формуле найти площадь основания куба?

Основание куба имеет форму квадрата. Формула для нахождения площади основания куба равна 9.0071 2 , где а — длина стороны куба.

Скачать БЕСПЛАТНЫЕ учебные материалы

Площадь поверхности куба Рабочие листы

Как найти площадь поверхности куба

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

ACT Math Help » Геометрия » Твердая геометрия » Кубики » Как найти площадь поверхности куба

Если площадь поверхности куба равна 96, какова длина одной стороны куба?

Возможные ответы:

Правильный ответ:

4

Пояснение:

Площадь поверхности куба = 6a ² , где a — длина стороны каждого ребра куба.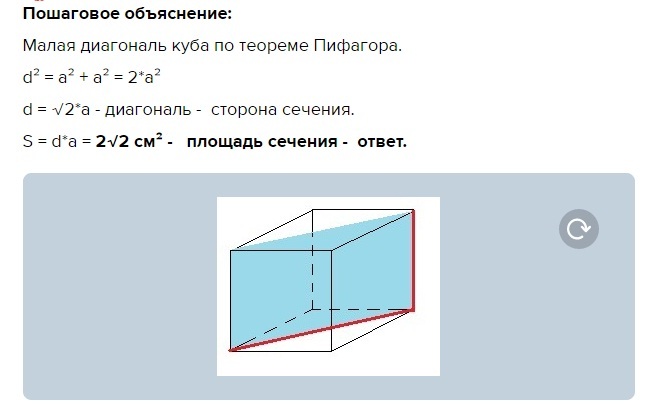 Иными словами, поскольку все стороны куба равны, а — это просто длина одной стороны куба.

Имеем 96 = 6a ²  → a ² = 16, так что это площадь одной грани куба.

Решив, мы получим √16, поэтому a = 4

Сообщить об ошибке

Сторона куба имеет длину . Какова общая площадь поверхности куба?

Возможные ответы:

Правильный ответ:

Пояснение:

Куб имеет 6 граней. Площадь каждой грани находится путем возведения в квадрат длины стороны.

Умножьте площадь одной грани на количество граней, чтобы получить общую площадь поверхности куба.

Сообщить об ошибке

Какова площадь поверхности куба, если его высота 3 см?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь одной грани равна длине стороны в квадрате.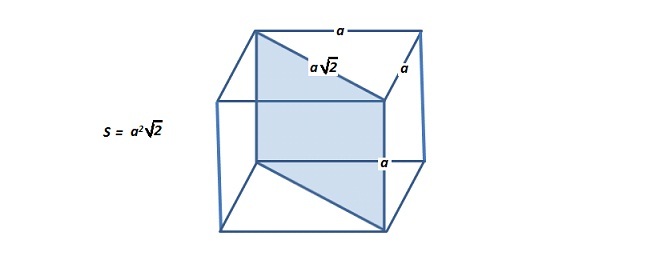

Площадь шести граней равна шестикратной площади одной грани: 54 см ² .

Сообщить об ошибке

Сфера объемом вписана в куб, как показано на диаграмме ниже.

Какова площадь поверхности куба в ?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала мы должны найти радиус сферы, чтобы решить эту задачу. Поскольку мы уже знаем объем, для этого воспользуемся формулой объема.

Имея в руках радиус сферы, мы можем применить его к кубу. Радиус сферы равен половине расстояния от вершины до низа куба (или половине расстояния от одной стороны до другой). Следовательно, радиус представляет собой половину длины стороны квадрата. Таким образом, в этом случае

Формула площади поверхности куба:

Площадь поверхности куба равна

 

Сообщить об ошибке

Какова площадь поверхности четырехдюймового куба в квадратных дюймах?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы ответить на этот вопрос, нам нужно найти площадь поверхности куба.

Для этого нужно найти площадь одной грани и умножить ее на , потому что у куба есть грани квадратной формы и одинакового размера.

Чтобы найти площадь квадрата, нужно умножить его длину на ширину. (Обратите внимание, что длина и ширина квадрата одинаковы.) Следовательно, для этих данных:

Теперь мы должны умножить площадь одной грани на 6, чтобы получить общую поверхность куба.

Следовательно, поверхность четырехдюймового куба равна .

Сообщить об ошибке

Какова площадь поверхности куба с объемом ? При необходимости округлите ответ до сотых

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала нам нужно найти длину стороны куба. Сделайте это, взяв кубический корень из объема.

 = 
Затем подставьте длину стороны в формулу площади поверхности куба:

Сообщить об ошибке

Какова площадь поверхности в квадратных дюймах куба с измеряемыми сторонами  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь поверхности куба — это мера общей площади   поверхностей всех сторон этого куба.

 

Поскольку куб содержит квадратные стороны, площадь поверхности умножается на площадь квадратной стороны.

 

Площадь одной стороны квадрата равна длине стороны длины стороны, или в данном случае. Таким образом, площадь поверхности этого куба равна квадратным дюймам.

Сообщить об ошибке

Какова длина стороны куба, площадь поверхности которого равна объему?

Возможные ответы:

Недостаточно информации для определения ответа.

Правильный ответ:

Объяснение:

Чтобы найти длину стороны куба, площадь поверхности которого равна его объему, приравняйте уравнения площади поверхности и объема куба, решите длину стороны:

Установите эти две формулы, равные друг другу и решить для s.

Сообщить об ошибке

Какова площадь поверхности куба со стороной длиной ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба с заданной длиной стороны,  используйте формулу:

Сообщить об ошибке

Найдите площадь поверхности куба, длина стороны которого равна .