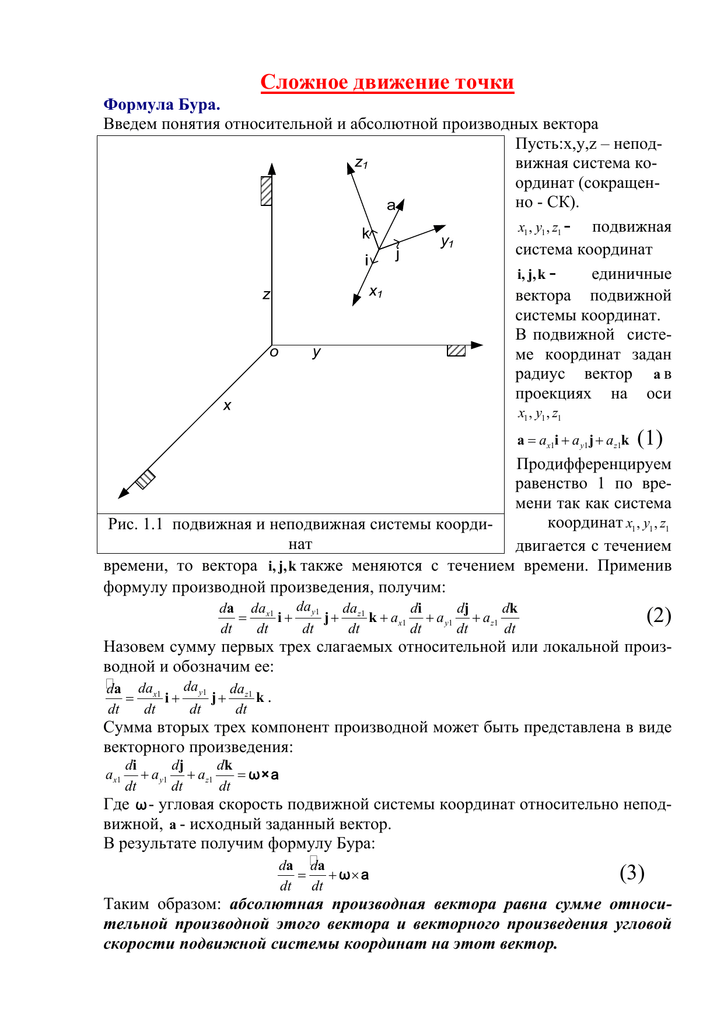
22) Полная и локальная производные вектора. Формула Бура.
Рассмотрим изменение вектора b(t) по отношению к двум системам координат — подвижной O’XYZ и неподвижной Oxyz.
Абсолютной, или полной, производной вектора b по аргументу t назьшается вектор определяющий изменение вектоpa b(t) в неподвижной системе Oxyz.
Относительная, или локальная, производная определяет измененине вектора b(t) в подвижной системе O’XYZ.
Формула Бура (получается из зависимости между полной и локальной производными): .
Рассомтрим частные случаи.
1) угловая скорость = 0, то =;
2) вектор b не меняется в подвижной системе отсчета (=0), то ;
3) ,
т.е. вектор b все время параллелен вектору
угловой скорости (),
то =.
В частности, если ,
то ,
т.е. вектор угловой скорости изменяется
одинаково для подвижной и неподвижной
систем координат.
Дополнение:
Выведение формулы Бура:
Найдем зависимость между полной и локальными производными. Если воспользоваться проекциями вектора b(t) на оси подвижной системы O’XYZ, то можно записать:, где I, J, К — орты, не изменяемые в этой системе отсчета. Поэтому локальная производная , а полная производная с учетом изменения также ортов I, J , К имеет вид: . В правой части уравнения первые три слагаемых выражают локальную производную, а производные от ортов I, J, K определяются формулами Пуассона (), т.е. . С учетом получаем: .
23) Скорости и ускорения точки при сложном движении.
ρ = r0 + r
dp/dt = d(r0+r)/dt = dr0/dt + dr/dt
dp/dt = v0 + dr/dt + ω*r = v0 + vr + ω*r
v = v0 + ω*r + vr = ve + vr
a = dv/dt = d(v0 + ω*r +vr)/dt = a0 + (dω/dt)*r + ω*(dr/dt) + dvr/dt
dr/dt = d(~)r/dt + ω*r = vr + ω*r
dvr/dt = d(~)vr/dt + ω*vr = ar + ω*vr
a = a0 + ε*r + ω*vr + ω*vr + ω*(r*ω) + ar + ω*vr = a0 + a(вр) + ω*vr + ω*vr + а(ос) + ar + ω*vr
a
= a0 + ε*r + ω*(r*ω) + ar + + 2*ω*vr, где 2*ω*vr — добавочное
(поворотное) ускорение, a0 + ε*r + ω*(r*ω) —
(ае) переносное ускорение.
24) Ускорение Кориолиса. Правило Жуковского.
Кинематическая теорема Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений — относительного, переносного и ускорения Кориолиса.
Ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки: , следовательно по модулю ускорение Кориолиса: (sin90=1).
Кориолисово ускорение обращаетсяв нуль, когда: 1) переносное движение — поступательное, т.е. омега переносное равно нулю; 2) в те моменты времени, когда в относительном движении точка останавливается, например. при изменении направления относительного движения.
Правило
Жуковского: Кориолисово
ускорение можно получить, спроецировав
вектор радиальной скорости на плоскость,
перпендикулярную вектору омега
переносное, увеличив полученную проекцию
радиальной скорости в 2*(омега переносное)
раз и повернув ее на 90 градусов в
направлении переносного вращения.
25) Сложное вращение твердого тела вокруг пресекающихся осей.
В случае вращательных относительного и переносного движений твердого тела, когда оси их вращений пересекаются в точке О (рис. 7.2), абсолютное движение будет движением твердого тела вокруг неподвижной точки О (сферическим движением) с угловой скоростью, определяемой согласно .
Нетрудно убедиться, что скорости всех точек, лежащих на линии, по которой направлен вектор угловой скорости, равны нулю. В самом деле, например, скорость находящейся на этой линии точки А тела (по свойству произведения коллинеарных векторов «омега» и r). Таким образом, прямая, на которой расположен вектор угловой скорости, является мгновенной осью вращения тела.
Скорость любой точки М тела в данном случае можно определить так: или , где .
Модули
составляющих, а также абсолютной скорости
точки М равны модулям соответствующих
векторных произведений и могут быть
вычислены по формулам: ,
где —
кратчайшие расстояния от точки М до
соответствующих осей вращения.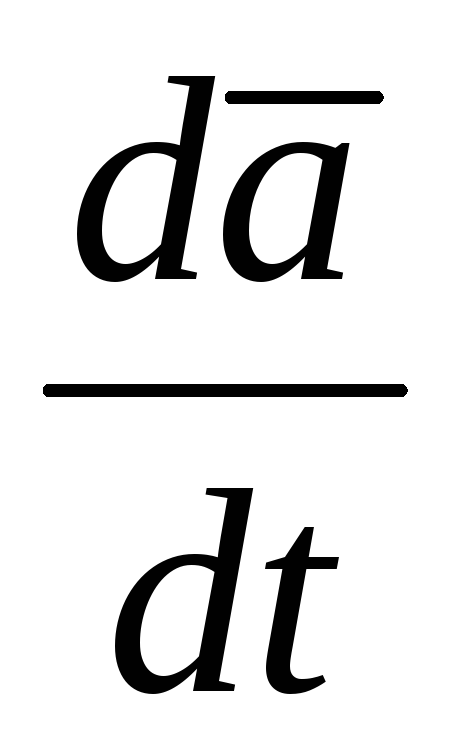
Бура — Borax — qaz.wiki
Соединение бора, соль борной кислоты
| Имена | |
|---|---|
| Название ИЮПАК Декагидрат тетрабората натрия | |
| Другие имена Октагидрат буры | |
| Идентификаторы | |
| 3D модель ( JSmol ) | |
| ЧЭБИ | |
| ЧЭМБЛ | |
| ChemSpider | |
| Номер ЕС | |
| Номер E | E285 (консерванты) |
| КЕГГ | |
| UNII | |
| |
| |
| Свойства | |
| Na 2 B 4 O 7 · 10H 2 O или Na 2 [B 4 O 5 (OH) 4 | |
| Молярная масса | 201,22 (безводный) 381,38 (декагидрат) |
| вид | белое твердое вещество |
| Плотность | 2,4 г / см 3 (безводный, твердый) 1,73 г / см 3 (декагидрат, твердый) |
| Температура плавления | 743 ° C (1369 ° F, 1016 K) (безводный) 75 ° C (декагидрат, разлагается) |
| Точка кипения | 1575 ° С (2867 ° F, 1848 К) (безводный) |
| 31,7 г / л (оба) | |
| -85,0 · 10 -6 см 3 / моль (безводный) | |
| Состав | |
| Моноклиника , МС92 , №15 | |
| C2 / c | |
| 2 / м | |
a = 1,1885 нм, b = 1,0654 нм, c = 1,2206 нм α = 90 °, β = 106,623 °, γ = 90 ° | |
| 1,4810 нм 3 | |
| 4 | |
| Фармакология | |
| S01AX07 ( ВОЗ ) | |
| Опасности | |
| Пиктограммы GHS | |
| | |
| «>P201 , P308 + 313 | |
| NFPA 704 (огненный алмаз) | |
| NIOSH (пределы воздействия на здоровье в США): | |
| никто | |
| REL (рекомендуется) | TWA 1 мг / м 3 (безводный и пентагидрат) TWA 5 мг / м 3 (декагидрат) |
| IDLH (Непосредственная опасность) | ND |
| Родственные соединения | |
| Алюминат натрия | |
| Лития тетраборат | |
Родственные соединения | Борная кислота , перборат натрия |
| N проверить ( что есть ?) YN | |
| Ссылки на инфобоксы | |
Бура , также известное как борат натрия , тетраборат натрия или динатрия тетраборат , представляет собой соединение с формулой Na
2ЧАС
4О
9• n H
2O или, точнее, [Na • (H
2O)+
м]
2 [B
4О
5(ОЙ)2-
4] .
Формулу часто неправильно записывают как Na
2B
4О
7• ( n +2) H
2О , что отражает более старое неправильное понимание молекулярной структуры аниона . Имя может относиться к любому из нескольких тесно связанных бора отработанного минеральных или химических соединений , которые отличаются по их кристаллизационной воде содержания. Наиболее часто встречающимся является октагидрат Na
2ЧАС
4B
4О
9• 8H
2O или [Na (H
2O)+
4]
2 [B
4О
5(ОЙ)2-
4] (или Na
2B
4О
7• 10H
2О , «декагидрат» в старых обозначениях). Это бесцветное кристаллическое твердое вещество, растворяющееся в воде.

Бура входит в состав многих моющих средств , косметики и эмалевых глазурей. Он используется для приготовления буферных растворов в биохимии , в качестве антипирена , в качестве противогрибкового соединения, при производстве стекловолокна , в качестве флюса в металлургии , защиты нейтронов для радиоактивных источников, текстурирующего агента в кулинарии, в качестве сшивающий агент в слизи , в качестве щелочи в проявителях фотографий, в качестве предшественника других соединений бора и полезен в качестве инсектицида (аналогично борной кислоте ).
В кустарных добыче золота , буры иногда используется в качестве части процесса ( в качестве флюса) предназначены для устранения потребности в токсичной ртути в добыче золота процесса, хотя он не может непосредственно заменить ртуть. Сообщается, что бура использовалась золотодобытчиками в некоторых частях Филиппин в 1900-х годах.
Бура была впервые обнаружена в высохших озерах Тибета и была завезена по Шелковому пути на Аравийский полуостров в 8 веке нашей эры. Боракс впервые стала широко использоваться в конце 19 века, когда компания Фрэнсиса Мариона Смита на Тихоокеанском побережье Боракс начала продавать и популяризировать большое количество разнообразных приложений под торговой маркой 20 Mule Team Borax , названной в честь метода, с помощью которого первоначально бура была извлечена. из пустыни в Калифорнии и Неваде .
Боракс впервые стала широко использоваться в конце 19 века, когда компания Фрэнсиса Мариона Смита на Тихоокеанском побережье Боракс начала продавать и популяризировать большое количество разнообразных приложений под торговой маркой 20 Mule Team Borax , названной в честь метода, с помощью которого первоначально бура была извлечена. из пустыни в Калифорнии и Неваде .
Химия
Состав
Термин бура часто используется для обозначения ряда тесно связанных минералов или химических соединений, которые различаются по содержанию кристаллической воды :
- безводный тетраборат натрия, Na 2 B 4 O 7
- пентагидрат тетрабората натрия, Na 2 B 4 O 7 · 5H 2 O
- декагидрат тетрабората натрия, Na 2 B 4 O 7 · 10H 2 O или эквивалентный октагидрат, Na 2 B 4 O 5 (OH) 4 · 8H 2 O
С химической точки зрения бура содержит ион [B 4 O 5 (OH) 4 ] 2– . В этой структуре есть два четырехкоординатных центра бора и два трехкоординатных центра бора.
В этой структуре есть два четырехкоординатных центра бора и два трехкоординатных центра бора.
Реакции
Бура также легко превращается в борную кислоту и другие бораты , которые находят множество применений. Его реакция с соляной кислотой с образованием борной кислоты:
- Na 2 B 4 O 7 · 10H 2 O + 2 HCl → 4 B (OH) 3 + 2 NaCl + 5H 2 O
«Декагидрат» достаточно стабилен, чтобы найти применение в качестве первичного стандарта для кислотно-щелочной титриметрии .
Когда бура добавляется в пламя, она приобретает желто- зеленый цвет. Бура не используется для этой цели в фейерверках из-за сильного желтого цвета натрия. Борная кислота используется для окрашивания пламени метанола в прозрачный зеленый цвет.
Бура хорошо растворяется в этиленгликоле, умеренно растворяется в диэтиленгликоле и метаноле, слабо растворяется в ацетоне. Он плохо растворяется в холодной воде, но его растворимость значительно увеличивается с температурой.
Этимология
Английское слово borax латинизировано: среднеанглийская форма была boras , от старофранцузских boras, bourras . Это могло быть от средневекового латинского baurach (другое английское написание), borac (- / um / em), borax , наряду с испанским borrax (> borraj ) и итальянским borrace , в 9 веке. Другое название буры — тинкал с санскрита .
Слово tincal ɪ ŋ к əl / «дребезжание», или tincar ɪ ŋ к ər / «ремесленник», относится к сырой буры, прежде чем он будет очищен, а добывается из озерных отложений в Тибете, Персии, и другие части Азии. Слово было принято в 17 — м веке из малайского tingkal и с урду / персидский / арабский تنکار tinkār / Танкар ; таким образом, две формы на английском языке. Все это кажется относящимся к санскритскому шанкаде .
Слово было принято в 17 — м веке из малайского tingkal и с урду / персидский / арабский تنکار tinkār / Танкар ; таким образом, две формы на английском языке. Все это кажется относящимся к санскритскому шанкаде .
Природные источники
Бура «ватный шарик»Бура встречается в естественных условиях в эвапоритовых отложениях, образовавшихся в результате многократного испарения сезонных озер . Волокнистые узелки улексита и proberite (натрий и борат кальция минералов) , известная как «cottonball» были найдены в соляных отложениях на дне долины Калифорния «s Долина смерти в 1880 годе и доставлены на рынок на 20-муле вагонов команды. К 1890-м годам железные дороги перевозили более чистые формы добытой буры, такие как колеманит, кернит, прайдит и улексит.
Наиболее коммерчески важные месторождения находятся в: Турции ; Борон, Калифорния ; и озеро Сирлс , Калифорния.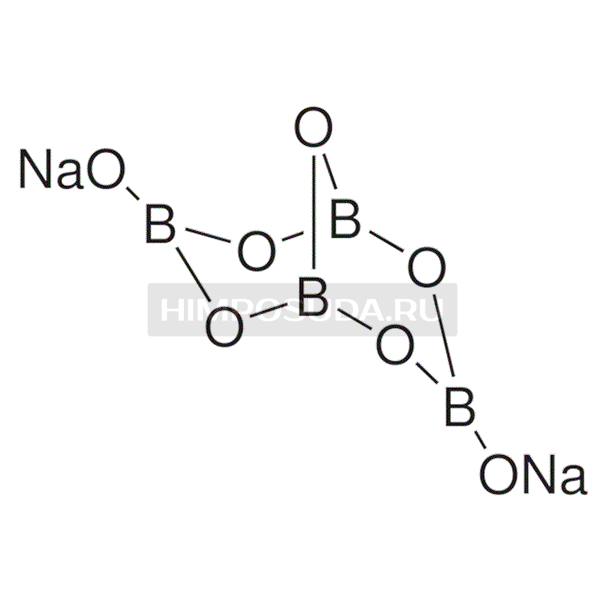 Бура была обнаружена во многих других местах на юго-западе США , в пустыне Атакама в Чили , а также в Боливии , Тибете и Румынии .
Бура была обнаружена во многих других местах на юго-западе США , в пустыне Атакама в Чили , а также в Боливии , Тибете и Румынии .
Встречающаяся в природе бура очищается путем перекристаллизации .
Бура может быть произведена синтетическим путем из других соединений бора.
Использует
Товары для дома
Borax используется в различных бытовых средствах для стирки и чистки, включая средство для стирки « 20 Mule Team Borax », порошковое мыло для рук « Boraxo » и некоторые формулы для отбеливания зубов .
буфер pH
Борат-ионы (обычно поставляемые в виде борной кислоты) используются в биохимических и химических лабораториях для создания буферов, например, для электрофореза ДНК и РНК в полиакриламидном геле , такого как буфер TBE (трис-гидроксиметиламинометоний, забуференный боратом) или новый буфер SB или буфер BBS ( забуференный боратом физиологический раствор) в процедурах нанесения покрытия. Боратные буферы (обычно с pH 8) также используются в качестве предпочтительного уравновешивающего раствора в реакциях сшивания на основе диметилпимелимидата (DMP).
Со-комплексообразующий агент
Бура как источник бората была использована для того, чтобы воспользоваться способностью бората образовывать комплекс с другими агентами в воде с образованием комплексных ионов с различными веществами. Борат и подходящий полимер кровать используются для хроматографа не- гликозилированного гемоглобина дифференцированно из гликозилированного гемоглобина (главным образом HbA1c ), который является показателем долгосрочной гипергликемии при сахарном диабете .
Средство для смягчения воды
Сама по себе бура не обладает высоким сродством к катионам жесткости , хотя ее использовали для смягчения воды. Его химическое уравнение для смягчения воды приведено ниже:
- Ca 2+ (водн.) + Na 2 B 4 O 7 (водн.) → Ca B 4 O 7 (т.) ↓ + 2 Na + (водн.)
- Mg 2+ (водн.) + Na 2 B 4 O 7 (водн.
 ) → Mg B 4 O 7 (т) ↓ + 2 Na + (водн.)
) → Mg B 4 O 7 (т) ↓ + 2 Na + (водн.)
В натриевые ионы введены не делают воду «жесткой». Этот метод подходит для удаления как временной, так и постоянной твердости.
Поток
Смесь буры и хлорида аммония используется в качестве флюса при сварке чугуна и стали . Он снижает температуру плавления нежелательного оксида железа ( окалины ), позволяя ему стекать. Бура также используется смешанным с водой в качестве флюса при пайке ювелирных металлов , таких как золото или серебро , где оно позволяет расплавленный припою , чтобы смачивать металл и поток равномерно в сустав. Бура также является хорошим флюсом для «предварительного лужения» вольфрама цинком, что делает его пригодным для мягкой пайки. Бура часто используется в качестве флюса для кузнечной сварки .
Мелкомасштабная золотодобыча
Бура заменяет рту
Бура 5-водная и 10-водная: свойства и применение — Статьи
Бура, более известная, как тетраборат натрия (борат натрия) — минеральный состав из бора, то есть натриевая соль борной кислоты. Борная кислота — это слабая неорганическая кислота, она имеет вид бесцветных кристаллов с трехклеточной решеткой. Обезвоживается, то есть теряет воду, при нагреве до 70 ° С. При нагревании она растворяет в себе оксиды металлов, и в результате образует соли. Применяется в разного рода промышленности, медицине и сельском хозяйстве.
Борная кислота — это слабая неорганическая кислота, она имеет вид бесцветных кристаллов с трехклеточной решеткой. Обезвоживается, то есть теряет воду, при нагреве до 70 ° С. При нагревании она растворяет в себе оксиды металлов, и в результате образует соли. Применяется в разного рода промышленности, медицине и сельском хозяйстве.
Бура, как термин, применяют к химическим соединениям и минералам, которые между собой отличаются содержанием кристаллической воды. Обычно, именно декагидрат и именуют называют бурой. Именно их и предлагает наша компания.
Приводим формулы
Безводная бура, в которой нет воды, имеет формулу:
Na2B4O7
Бура, в которой есть 5 молекул воды, называется пентагидрат тетрабората натрия (бура 5-водная):
Na2B4O7 • 5h3O
С декагидрат тетрабората натрия теперь все очевидно, у него 10 молекул воды. Он известен также как бура 10-водная. Его формула, как уже нетрудно догадаться:
Na2B4O7 • 10h3O
Физические свойства
На вид это просто белый порошок, который состоит из множества кристаллов, не имеющих цвета. Если поместить их в воду, они легко растворяются. Молярная масса безводной буры — 201,22, а декагидрата — 381,38. Безводный тетраборат расплавляется при температуре 743 ° C.
Если поместить их в воду, они легко растворяются. Молярная масса безводной буры — 201,22, а декагидрата — 381,38. Безводный тетраборат расплавляется при температуре 743 ° C.
Химические свойства
При реакции с соляной кислотой, бура легко преобразуется в борную кислоту. Если буру внести в пламя она начнет окрашивать его в красивый желто-зеленый цвет. Водный раствор буры имеет щелочную реакцию. Попробуйте нагреть бурю до 400 ° С, и вы получите стекло, а бура потеряет свою кристаллическую воду.
Использование
Бура используется:
— в производстве красок, лаков, поливы и алкидных эмалей,
— сварке и плавке в качестве флюса,
— производстве бумаги, фармацевтических препаратов и косметических средств,
— создании оптики и цветного стекла,
— производстве иных соединений бора.
Бура также является компонентом моющих средств, с ее помощью можно эффективно преодолеть ржавчину и налет. Она применяется в сельском хозяйстве в качестве источника бора для растений.
Где купить буру 5-водную и 10-водную?
Бура 5-водная и 10 -водная продается в нашем интернет-магазине. Чтобы купить буру водную, вам необходимо сделать заказ на сайте, или просто позвонить по номерам, указанным в контактной информации.
ЗАДАЧА № 1 — Студопедия
Вычислить массу навески натрия тетрабората, необходимую для приготовления 200 мл раствора с молярной концентрацией эквивалента 0,1 моль/л. Определить титр, молярную концентрацию эквивалента и поправочный коэффициент раствора, если для его приготовления была взята навеска натрия тктрабората массой 3,7995 г.
Мм (Na2B4O7• 10 H2O) = 381,4 г/моль
Рассуждения: Бура (натрия тетраборат) – это исходное (стандартное) вещество метода нейтрализации. Так как необходимо найти массу навески буры – то это задача на приготовление раствора исходного (стандартного) вещества. Известна масса практически взятой навески буры и необходимо провести расчеты по определению показателей концентрации практически приготовленного раствора. Исходя из этого, делаем вывод, что это задача I типа. Придерживаясь рекомендаций приведенных выше, записываем «Дано» и начинаем решать задачу.
Известна масса практически взятой навески буры и необходимо провести расчеты по определению показателей концентрации практически приготовленного раствора. Исходя из этого, делаем вывод, что это задача I типа. Придерживаясь рекомендаций приведенных выше, записываем «Дано» и начинаем решать задачу.
| Дано: | Решение: |
| С1/Z (буры) т.= 0,1 моль/л V(буры) = 200 мл m пр. (буры) = 3,7995 г Мм(Na2B4O7•10H2O)=381,4г/моль | 1) Вычислим теоретическую массу навески буры, необходимую для приготовления 200 мл растворы с молярной концентрацией эквивалента 0,1 моль/л по формуле:
m = C1/Z •M1/Z • V(л)Преобразуем формулу для нашей ситуации. Так как ищем массу навески теоретическую, то и молярную концентрацию эквивалента тоже берем теоретическую. m теор. буры = C1/Z т. буры•M1/Z буры•V(л) буры
а) Нам не известна молярная масса эквивалента буры, поэтому ее необходимо предварительно рассчитать.
m теор. буры = C1/Z т. буры•M1/Z буры•V(л) буры
а) Нам не известна молярная масса эквивалента буры, поэтому ее необходимо предварительно рассчитать.
|
| Найти: m теор. (буры) = ? Т~0,1 моль/л буры = ? С1/Z~0,1 моль/л буры = ? Кп~0,1 моль/л буры = ? |
Рассуждаем при этом следующим образом:
— натрия тетраборат (Na2B4O7) – это соль, образованная двумя атомами одновалентного металла, следовательно, число эквивалентности для него будет равно 2. Исходя из этого: M1/z= Mм/Z
M1/z буры= Mм буры/Z буры =381,4 г/моль: 2 = 190,7 г/ моль
— натрия тетраборат – это исходное вещество метода ацидиметрии и реагирует с хлористоводородной кислотой в соотношении 1:2
Na2B4O7 + 2 HCl + 5 H2O = 2 NaCl + 4 H3BO3
1 моль 2 экв.
Следовательно, fэкв. буры будет равет ½
fэкв. буры = ½M1/z буры= Mм буры•fэкв. буры =381,4 г/моль • ½ = 190,7 г/моль
б) По условию задачи объем раствора дан в мл, а в формуле он должен быть выражен в л, следовательно, его необходимо преобразовать:
V(буры) = 200 мл = 200: 1000 = 0,2 л
Подставляем в формулу эти цифры:
m теор. буры =0,1 моль/л • 190,7 г/моль • 0,2 л= 3,814 г
2) Вычислим титр практически приготовленного раствора. Так как это раствор исходного вещества (раствор с титром приготовленным) то пользуемся формулой:
m
T = —-
V(мл)
Преобразуем формулу для нашей ситуации. Так как рассчитываем титр практически приготовленного раствора, то и массу навески берем практически взятую. Объем раствора берем в мл! тоесть данный по условию задачи.
Объем раствора берем в мл! тоесть данный по условию задачи.
m пр. буры
Т~0,1 моль/л буры = —————
V(мл) буры
3,7995 г
Т~0,1 моль/л буры = ———— = 0,0189975 г/мл округляем и получаем 0,01900 г/мл
200 мл
Не забываем обосновать показатель, то есть написать, что он показывает. Так как это титр раствора исходного вещества, то это всегда содержание грамм вещества в 1 миллилитре раствора.
Таким образом, Титр показывает, что в 1 мл приготовленного раствора буры содержится 0,01900 г х.ч. (химически чистой) буры.
3) Рассчитываем поправочный коэффициент практически приготовленного раствора через массы навесок (так как это исходное вещество)
m практ.
Kп= ———
m теор.
Преобразуем эту формулу для нашего случая:
m пр. буры
Kп~0,1 моль/л буры = —————
m т. буры
Подставляем цифры в формулу:
3,7995 г
Kп~0,1 моль/л буры = ————— =0, 996198 округляем и получаем 0,9962
3,814 г
Снова не забываем обосновать показатель. Помним о том, что поправочный коэффициент в идеале равен 1,0000 , следовательно, полученный нами результат должен быть близок к этому значению (мы получили сопоставимый результат – 0,9962). Сравнивают его с 1,0000 и видим, что цифра меньше (0,9962<1,0000), следовательно, и концентрация практически приготовленного раствора слабее (меньше) требуемой, а значит, меньше будут и показатели концентрации – титр и молярная концентрация эквивалента.
Таким образом, Поправочный коэффициент показывает, что титр и молярная концентрация эквивалента практически приготовленного раствора буры меньше, чем титр и молярная концентрация эквивалента теоретического (точного) раствора буры.
4) Рассчитываем молярную концентрацию эквивалента практически приготовленного раствора буры.
а) Проще всего это сделать через поправочный коэффициент
С1/Z~
Kп = ——— следовательно, С1/Z~ = С1/Z т•Кп
С1/Z
Преобразуем формулу для нашей ситуации
С1/Z~0,1 моль/л буры = С1/Z т буры•Кп~0,1 моль/л буры
Подставляем значения и рассчитываем показатель:
С1/Z~0,1 моль/л буры=0,1 моль/л • 0,9962=0,09962 моль/л округляем и получаем 0,0996 моль/л
б) Можно рассчитать молярную массу эквивалента через массу навески:
m
С1/Z = —————
M1/Z • V(л)
Преобразуем формулу для нашей ситуации:
m пр. буры
буры
С1/Z~0,1 моль/л буры = ————————
M1/Z буры•V(л) буры
Подставляем значения и рассчитываем показатель:
3,7995 г
С1/Z~0,1 моль/л буры=———————= 0,0996198моль/л округляем и получаем 0, 0996 моль/л
190,7 г/моль • 0,2 л
в) Можно также провести расчет через титр:
T • 1000
С1/Z = —————
M1/Z
Преобразуем формулу для нашей ситуации:
T~0,1 моль/л буры• 1000
С1/Z ~0,1 моль/л буры = —————————
M1/Zбуры
Подставляем значения и рассчитываем показатель:
0,01900 г/мл • 1000
С1/Z~0,1 моль/л буры= ———————=0,099632 моль/л округляем и получаем 0, 0996 моль/л
190,7 г/моль
То есть при любом из вариантов расчетов результат идентичен и сопоставим (так как в теории молярная концентрация эквивалента должна быть равна 0,1 моль/л, а 0,0996» 0,1)
Обосновываем найденный показатель. Так как это молярная концентрация эквивалента, то и содержание будет моль-эквивалентов вещества в 1 литре раствора.
Так как это молярная концентрация эквивалента, то и содержание будет моль-эквивалентов вещества в 1 литре раствора.
Таким образом, Молярная концентрация эквивалента показывает, что в 1 л приготовленного раствора буры содержится 0,0996 моль-эквивалентов буры.
Все необходимые показатели найдены и обоснованы, поэтому далее можно записывать ответ задачи.
Ответ: m теор. буры=3,814 г Kп ~0,1 моль/л буры = 0,9962
Т~0,1 моль/л буры= 0,01900 г/мл С1/Z~0,1 моль/л буры = 0, 0996 моль/л
| Температура | гр/100,00 гр воды | гр/100,00 гр этанола | гр/100,00 гр метанола | гр/100,00 гр ацетона | гр/100,00 гр глицерина | гр/100,00 гр этилацетата | гр/100,00 гр этиленгликоля | ||
|---|---|---|---|---|---|---|---|---|---|
| (безводный) | (пентагидрат) | (декагидрат) | (декагидрат) | (декагидрат) | (декагидрат) | (декагидрат) | (декагидрат) | (декагидрат) | |
| 0°C 273,15 K | 1,11 | 2,04 | |||||||
| 10°C 283,15 K | 3,19 | ||||||||
| 15°C 288,15 K | 3,94 | 2,54 | |||||||
| 20°C 293,15 K | 4,94 | 110,97 | |||||||
| 25°C 298,15 K | 6,16 | 24,84 | 0,6 | 0,14 | 71,23 | ||||
| 30°C 303,15 K | 7,76 | ||||||||
| 40°C 313,15 K | 12,64 | ||||||||
| 50°C 323,15 K | 15,87 | 21,82 | |||||||
| 60°C 333,15 K | ~17,9 | 43,53 | |||||||
| 70°C 343,15 K | 20 | 58,58 | |||||||
| 80°C 353,15 K | 23 | 79,57 | |||||||
| 90°C 363,15 K | 28 | 113,58 | |||||||
| 100°C 373,15 K | 52,5 | 35 | 191,04 | ||||||
АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПРОИЗВОДНЫЕ ОТ ВЕКТОРА. ФОРМУЛА БУРА — Мегаобучалка
ФОРМУЛА БУРА — Мегаобучалка
При рассмотрении сложного движения точки в общем случае переносного движения приходится рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга. Одно изменение имеет векторная величина относительно подвижной системы отсчета, движущейся относительно другой, неподвижной, и другое – относительно неподвижной системы отсчета. Неподвижной системой отсчета считается система, движение которой относительно других систем отсчета не рассматривается.
Введем обозначения производных от векторных величин при рассмотрении их изменения относительно различных систем отсчета, движущихся друг относительно друга. Для любого вектора его производную по времени по отношению к неподвижной системе отсчета называют полной (или абсолютной) производной и обозначают . Производную по времени при учете изменения вектора относительно подвижной системы отсчета называют относительной (или локальной) производной и обозначают или .
Установим зависимость между полной и относительной производными по времени вектора и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной (рис. 64). Для этого разложим вектор на составляющие, параллельные осям подвижной системы координат. Имеем
. (123)
Изменение вектора относительна неподвижной системы координат в зависимости от времени состоит из изменения его проекций на подвижные оси координат и изменения единичных векторов подвижных осей вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора , используя формулу (123). Получим
. (124)
Первые три слагаемых учитывают изменение вектора при неизменных и поэтому составляют относительную производную, т. е.
. (125)
Производные по времени единичных векторов определим по формулам Пуассона
, , .
так как эти векторы не изменяются от поступательного движения со скоростью вместе с подвижной системой отсчета (рис. 64). Вектор есть угловая скорость вращательной части движения вокруг точки подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (124) и вынося за скобки, получим
64). Вектор есть угловая скорость вращательной части движения вокруг точки подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (124) и вынося за скобки, получим
,
или, учитывая (123),
. (126)
Получена формула зависимости производных векторов в двух системах отсчета, движущихся друг относительно друга. Формула (126) называется формулой Бура.
Известно, что произвольное движение системы координат как свободного твердого тела можно представить как поступательное движение вместе с полюсом, например с точкой , и вращение вокруг этой точки. Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.
Рассмотрим частные случаи.
1. Если вектор не изменяется относительно подвижной системы координат, то его относительная производная и по формуле (126) получаем
.
Это формула для производной от вектора постоянного модуля, доказанная ранее для радиуса-вектора при вращении вокруг неподвижной оси. Она справедлива для любого вектора при произвольном движении подвижной системы осей координат. В рассматриваемом случае не только угловая скорость вращения подвижной системы координат, но и угловая скорость вращения вектора , так как вектор можно при этом считать скрепленным с подвижной системой координат.
2. Если вектор не изменяется относительно основной системы координат, то полная производная и, согласно (126), его относительная производная
3. Если , т. е. вектор все время параллелен вектору угловой скорости , то и
.
В частности, если , то
.
Полная и локальная производные также равны друг другу в те моменты времени, в которые вектор параллелен вектору угловой скорости .
СЛОЖЕНИЕ СКОРОСТЕЙ
Если – неподвижная система осей координат, а – подвижная (рис. 65), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным – ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают и , переносные – и , а абсолютные – и . Другие характеристики этих движений снабжаются соответствующими значками.
65), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным – ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают и , переносные – и , а абсолютные – и . Другие характеристики этих движений снабжаются соответствующими значками.
Движение подвижной системы осей координат относительно неподвижной можно охарактеризовать скоростью ее поступательного движения , например вместе с точкой и вектором угловой скорости ее вращения вокруг . Пусть точка движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведем векторы и , характеризующие положение точки относительно неподвижной и подвижной систем осей координат, и вектор точки . Для любого момента времени
. (127)
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
е. вычислим полные производные. Получим
.
По определению, является абсолютной скоростью точки , – абсолютной скоростью точки . Для вычисления применим формулу Бура. Имеем
.
Относительная производная является относительной скоростью точки по отношению к подвижной системе отсчета, а – угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора , если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, из (127) получаем
. (128)
Скорость
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки . Из (128) получаем следующую теорему сложения скоростей для точки:
. (129)
т.е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
Эти списки в алфавитном порядке включают синонимы общепринятых названий минералов, произношение этого имени, происхождение имени и информация о местности. Посетите наш расширен выбор картинок с минералами.
Другие алфавитные списки минеральных видов в Интернете
|
Молекулярная масса буры
Молярная масса of Na2B4O7.10h3O = 381,37214 г / моль
Перевести граммы буры в моль или моль буры в граммы
Расчет молекулярной массы:
22,98977 * 2 + 10,811 * 4 + 15,9994 * 7 + 10 * (1,00794 * 2 + 15,9994)
| Элемент | Обозначение | Атомная масса | Число атомов | Массовый процент |
| Натрий | Na | 22. 989770 989770 | 2 | 12,056% |
| Водород | H | 1,00794 | 20 | 5,286% |
| Бор | В | 10,811 | 4 | 11,339% |
| Кислород | O | 15,9994 | 17 | 71,319% |
В химии вес формулы — это величина, вычисляемая путем умножения атомного веса (в единицах атомной массы) каждого элемента в химической формуле на количество атомов этого элемента, присутствующего в формуле, с последующим сложением всех этих продуктов вместе.
Используя химическую формулу соединения и периодическую таблицу элементов, мы можем сложить атомные веса и вычислить молекулярную массу вещества.
Определение молярной массы начинается с единиц граммов на моль (г / моль). При расчете молекулярной массы химического соединения он говорит нам, сколько граммов содержится в одном моль этого вещества. Вес формулы — это просто вес в атомных единицах массы всех атомов в данной формуле.
Формула веса особенно полезна при определении относительного веса реагентов и продуктов в химической реакции.Эти относительные веса, вычисленные по химическому уравнению, иногда называют весами по уравнениям.
Атомные веса, используемые на этом сайте, получены от NIST, Национального института стандартов и технологий. Мы используем самые распространенные изотопы. Вот как рассчитать молярную массу (среднюю молекулярную массу), которая основана на изотропно взвешенных средних. Это не то же самое, что молекулярная масса, которая представляет собой массу одной молекулы четко определенных изотопов. Для объемных стехиометрических расчетов мы обычно определяем молярную массу, которую также можно назвать стандартной атомной массой или средней атомной массой.
Часто на этом сайте просят перевести граммы в моль. Чтобы выполнить этот расчет, вы должны знать, какое вещество вы пытаетесь преобразовать. Причина в том, что на конверсию влияет молярная масса вещества. Этот сайт объясняет, как найти молярную массу.
Если формула, используемая при расчете молярной массы, является молекулярной формулой, вычисленная формула веса является молекулярной массой. Весовой процент любого атома или группы атомов в соединении можно вычислить, разделив общий вес атома (или группы атомов) в формуле на вес формулы и умножив на 100.
pH обычных кислот и оснований
pH обычных кислот и оснований
Расчетные значения pH обычных кислот и оснований для 1, 10 и 100 ммоль / л (действительно для стандартных условий при 25 ° C, 1 атм ; константы кислотности взяты отсюда):
pH кислот — отсортировано по pH
| Кислота | Имя | 1 мМ | 10 мМ | 100 мМ | |
|---|---|---|---|---|---|
| h3SeO4 | селеновая кислота | 2. 74 74 | 1,83 | 0,97 | |
| h3SO4 | серная кислота | 2,75 | 1,87 | 1.01 | |
| Привет | иодоводородная кислота | 3,01 | 2,04 | 1.08 | |
| HBr | бромистоводородная кислота | 3.01 | 2,04 | 1.08 | |
| HCl | соляная кислота | 3,01 | 2,04 | 1.08 | |
| HNO3 | азотная кислота | 3,01 | 2,04 | 1.08 | |
| h4PO4 | ортофосфорная кислота | 3.06 | 2,26 | 1,63 | |
| h4AsO4 | мышьяковая кислота | 3,08 | 2,31 | 1,70 | |
| ч3SeO3 | селеновая кислота | 3,15 | 2,47 | 1,90 | |
| h3CrO4 | хромовая кислота | 3. 03 03 | 2,33 | 2,06 | |
| h4 Цитрат | лимонная кислота, C6H8O7 | 3,24 | 2,62 | 2,08 | |
| ВЧ | плавиковая кислота | 3,27 | 2,65 | 2,12 | |
| HNO2 | азотистая кислота | 3.28 | 2,67 | 2,13 | |
| Гианат | изоциановая кислота, HOCN | 3,35 | 2,76 | 2,23 | |
| H Формат | муравьиная кислота, Ch3O2 (метановая кислота) | 3,47 | 2,91 | 2,38 | |
| h3Se | селенид водорода | 3.49 | 2,93 | 2,41 | |
| ч3MoO4 | молибденовая кислота | 3,46 | 2,94 | 2,43 | |
| H Лактат | молочная кислота, C3H6O3 (молочная кислота) | 3,51 | 2,96 | 2,44 | |
| H Ацетат | уксусная кислота, C2h5O2 (этановая кислота) | 3. 91 91 | 3,39 | 2,88 | |
| ч 3CO3 | угольная кислота | 4,68 | 4,18 | 3,68 | |
| h3S | сероводород | 4,97 | 4,47 | 3,97 | |
| h4AsO3 | мышьяковистая кислота | 6.07 | 5,58 | 5,09 | |
| Гианид | синильная кислота, HCN | 6,11 | 5,62 | 5,12 | |
| h4BO3 | борная кислота | 6,12 | 5,62 | 5,12 | |
| h5SiO4 | кремниевая кислота | 6.40 | 5,91 | 5,42 | |
| h5SiO4 | кремниевая кислота (с осаждением SiO2 (а)) | 6. 40 40 | 6,26 | 6,26 |
pH кислот — отсортировано по молекулярной формуле
| Кислота | Имя | 1 мМ | 10 мМ | 100 мМ | |
|---|---|---|---|---|---|
| ч3CO3 | угольная кислота | 4.68 | 4,18 | 3,68 | |
| h3CrO4 | хромовая кислота | 3,03 | 2,33 | 2,06 | |
| ч3MoO4 | молибденовая кислота | 3,46 | 2,94 | 2,43 | |
| h3S | сероводород | 4.97 | 4,47 | 3,97 | |
| h3Se | селенид водорода | 3,49 | 2,93 | 2,41 | |
| ч3SeO3 | селеновая кислота | 3,15 | 2,47 | 1,90 | |
| h3SeO4 | селеновая кислота | 2. 74 74 | 1,83 | 0,97 | |
| h3SO4 | серная кислота | 2,75 | 1,87 | 1.01 | |
| h4AsO3 | мышьяковистая кислота | 6,07 | 5,58 | 5,09 | |
| h4AsO4 | мышьяковая кислота | 3.08 | 2,31 | 1,70 | |
| h4BO3 | борная кислота | 6,12 | 5,62 | 5,12 | |
| h4 Цитрат | лимонная кислота, C6H8O7 | 3,24 | 2,62 | 2,08 | |
| h4PO4 | ортофосфорная кислота | 3.06 | 2,26 | 1,63 | |
| h5SiO4 | кремниевая кислота | 6. 40 40 | 5,91 | 5,42 | |
| h5SiO4 | кремниевая кислота (с осаждением SiO2 (а)) | 6.40 | 6,26 | 6,26 | |
| H Ацетат | уксусная кислота, C2h5O2 (этановая кислота) | 3.91 | 3,39 | 2,88 | |
| HBr | бромистоводородная кислота | 3,01 | 2,04 | 1.08 | |
| HCl | соляная кислота | 3,01 | 2,04 | 1.08 | |
| Гианат | изоциановая кислота, HOCN | 3.35 | 2,76 | 2,23 | |
| Гианид | синильная кислота, HCN | 6,11 | 5,62 | 5,12 | |
| ВЧ | плавиковая кислота | 3,27 | 2,65 | 2,12 | |
| H Формат | муравьиная кислота, Ch3O2 (метановая кислота) | 3.47 | 2,91 | 2,38 | |
| Привет | иодоводородная кислота | 3,01 | 2,04 | 1.08 | |
| H Лактат | молочная кислота, C3H6O3 (молочная кислота) | 3,51 | 2,96 | 2,44 | |
| HNO2 | азотистая кислота | 3.28 | 2,67 | 2,13 | |
| HNO3 | азотная кислота | 3,01 | 2,04 | 1.08 |
pH оснований — отсортировано по pH
Учитывается ограниченная растворимость гидроксидов (как указано в сносках в последнем столбце).
| База | Имя | 1 мМ | 10 мМ | 100 мМ | |
|---|---|---|---|---|---|
| Ba (OH) 2 | гидроксид бария | 11.27 | 12,22 | 13,08 | |
| Sr (OH) 2 | гидроксид стронция | 11,27 | 12,22 | 13,09 | |
| NaOH | натрия гидроксид | 10,98 | 11,95 | 12,88 | |
| КОН | калия гидроксид (едкий калий) | 10.98 | 11,95 | 12,88 | |
| Na2SiO3 | метасиликат натрия | 11,00 | 11,91 | 12,62 | |
| Ca (OH) 2 | гидроксид кальция (известь, CaO: h3O) | 11,27 | 12.20 | 12,46 | |
| Na3PO4 | тринатрийфосфат | 10.95 | 11,71 | 12,12 | |
| К2СО3 | карбонат калия | 10,52 | 11,00 | 11,36 | |
| Na2CO3 | натрия карбонат (кальцинированная сода) | 10,52 | 10,97 | 11,26 | |
| Nh5OH | гидроксид аммония (Nh4: h3O) | 10.09 | 10,61 | 11,12 | |
| Мг (OH) 2 | гидроксид магния (MgO: h3O) | 10,40 | 10,40 | 10,40 | |
| CaCO3 | карбонат кальция (кальцит) | 9,91 | 9,91 | 9,91 | |
| Fe (OH) 2 | гидроксид железа (II) (гидроксид железа) | 9.45 | 9,45 | 9,45 | |
| Cd (OH) 2 | кадмия гидроксид | 9,36 | 9,36 | 9,36 | |
| Na2B4O7 | борат натрия (бура) | 9,21 | 9,17 | 9,05 | |
| Co (OH) 2 | гидроксид кобальта (II) | 9.15 | 9,15 | 9,15 | |
| Zn (OH) 2 | цинка гидроксид | 8,88 | 8,88 | 8,88 | |
| Ni (OH) 2 | гидроксид никеля (II) | 8,37 | 8,37 | 8,37 | |
| КАцетат | ацетат калия (Ch4COOK) | 7.87 | 8,33 | 8,75 | |
| Na-ацетат | натрия ацетат (Ch4COONa) | 7,87 | 8,33 | 8,75 | |
| KHCO3 | гидрокарбонат калия | 8,27 | 8,25 | 8,13 | |
| NaHCO3 | натрия гидрокарбонат | 8.27 | 8,22 | 8,02 | |
| Ве (ОН) 2 | гидроксид бериллия | 7,90 | 7,90 | 7,90 | |
| Cu (OH) 2 | гидроксид меди (II) | 7,69 | 7,69 | 7,69 | |
| Pb (OH) 2 | гидроксид свинца (II) | 7.54 | 7,54 | 7,54 | |
| Cr (OH) 3 | гидроксид хрома (III) | 7,04 | 7,04 | 7,04 | |
| Hg (OH) 2 | гидроксид ртути (II) | 7,03 | 7,03 | 7,03 |
pH оснований — отсортировано по молекулярной формуле
| База | Имя | 1 мМ | 10 мМ | 100 мМ | |
|---|---|---|---|---|---|
| Ba (OH) 2 | гидроксид бария | 11.27 | 12,22 | 13,08 | |
| Ве (ОН) 2 | гидроксид бериллия | 7,90 | 7,90 | 7,90 | |
| Ca (OH) 2 | гидроксид кальция (известь, CaO: h3O) | 11,27 | 12.20 | 12,46 | |
| CaCO3 | карбонат кальция (кальцит) | 9.91 | 9,91 | 9,91 | |
| Cd (OH) 2 | кадмия гидроксид | 9,36 | 9,36 | 9,36 | |
| Co (OH) 2 | гидроксид кобальта (II) | 9,15 | 9,15 | 9,15 | |
| Cr (OH) 3 | гидроксид хрома (III) | 7.04 | 7,04 | 7,04 | |
| Cu (OH) 2 | гидроксид меди (II) | 7,69 | 7,69 | 7,69 | |
| Fe (OH) 2 | гидроксид железа (II) (гидроксид железа) | 9,45 | 9,45 | 9,45 | |
| Hg (OH) 2 | гидроксид ртути (II) | 7.03 | 7,03 | 7,03 | |
| К2СО3 | карбонат калия | 10,52 | 11,00 | 11,36 | |
| КАцетат | ацетат калия (Ch4COOK) | 7,87 | 8,33 | 8,75 | |
| KHCO3 | гидрокарбонат калия | 8.27 | 8,25 | 8,13 | |
| КОН | калия гидроксид (едкий калий) | 10,98 | 11,95 | 12,88 | |
| Мг (OH) 2 | гидроксид магния (MgO: h3O) | 10,40 | 10,40 | 10,40 | |
| Na2B4O7 | борат натрия (бура) | 9.21 | 9,17 | 9,05 | |
| Na2CO3 | натрия карбонат (кальцинированная сода) | 10,52 | 10,97 | 11,26 | |
| Na2SiO3 | метасиликат натрия | 11,00 | 11,91 | 12,62 | |
| Na3PO4 | тринатрийфосфат | 10.95 | 11,71 | 12,12 | |
| Na-ацетат | натрия ацетат (Ch4COONa) | 7,87 | 8,33 | 8,75 | |
| NaHCO3 | натрия гидрокарбонат | 8,27 | 8,22 | 8,02 | |
| NaOH | натрия гидроксид | 10.98 | 11,95 | 12,88 | |
| Nh5OH | гидроксид аммония (Nh4: h3O) | 10,09 | 10,61 | 11,12 | |
| Ni (OH) 2 | гидроксид никеля (II) | 8,37 | 8,37 | 8,37 | |
| Pb (OH) 2 | гидроксид свинца (II) | 7.54 | 7,54 | 7,54 | |
| Sr (OH) 2 | гидроксид стронция | 11,27 | 12,22 | 13,09 | |
| Zn (OH) 2 | цинка гидроксид | 8,88 | 8,88 | 8,88 |
Примечания
Гидроксиды являются сильными основаниями, но имеют низкую растворимость, что ограничивает pH верхней границей.Это достигается включением соответствующей твердой фазы в расчет равновесия.
[последнее изменение: 20 апреля 2016 г.]
.

 2Na.10h3O / c5-1-7-3-9-2 (6) 10-4 (8-1) 11-3 ;;;;;;;;;;;; / ч; ;; 10 * 1h3 / q-2; 2 * + 1 ;;;;;;;;;;;
2Na.10h3O / c5-1-7-3-9-2 (6) 10-4 (8-1) 11-3 ;;;;;;;;;;;; / ч; ;; 10 * 1h3 / q-2; 2 * + 1 ;;;;;;;;;;; ) → Mg B 4 O 7 (т) ↓ + 2 Na + (водн.)
) → Mg B 4 O 7 (т) ↓ + 2 Na + (водн.) ФОРМУЛА БУРА — Мегаобучалка
ФОРМУЛА БУРА — Мегаобучалка


