Диагонали в шестиугольнике: Правильный шестиугольник свойства диагоналей

Задачи по физике и математике с решениями и ответами

Задача по математике — 3704

На сторонах остроугольного треугольника $ABC$ во внешнюю сторону построены три подобных между собой остроугольных треугольника $AC_1B > BA_1C, CB_1A$ (при этом $\angle AB_1C = \angle ABC_1 = \angle AXBC_1 \angle BA_1C = \angle BAC_1 = \angle B_1AC$).
а) Докажите, что окружности, описанные вокруг треугольников $AC_1B, BA_1C$ и $CB_1A$, пересекаются в одной точке.
б) Докажите, что в той же точке пересекаются прямые $AA_1, BB_1$ и $CC_1$. Подробнее

Задача по математике — 3707

Дан выпуклый $n$-угольник с попарно непараллельными сторонами и точка внутри него. Докажите, что через эту точку нельзя провести больше $n$ прямых, каждая из которых делит площадь $n$-угольника пополам.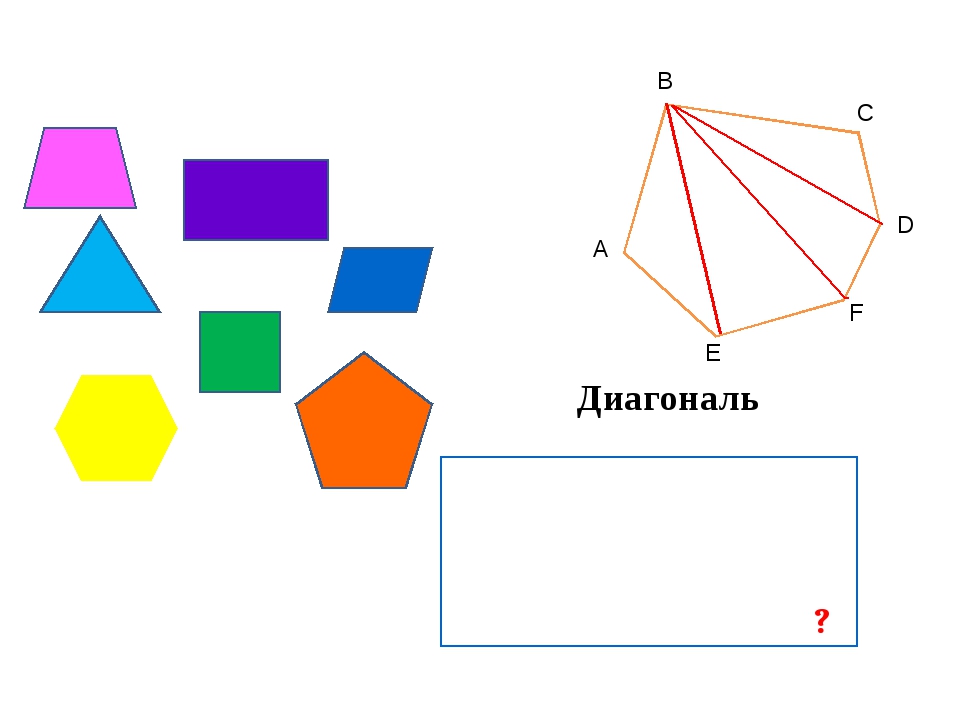 Подробнее

Задача по математике — 3709

В пространстве заданы 4 точки, не лежащие в одной плоскости. Сколько существует различных параллелепипедов, для которых эти точки служат вершинами? Подробнее

Задача по математике — 3712

а) Каждая из сторон выпуклого шестиугольника имеет длину больше 1. Всегда ли в нем найдется диагональ длины больше 2?
б) В выпуклом шестиугольнике $ABCDEF$ длины диагоналей $AD, BE$ и $CF$ больше 2. Всегда ли у него найдется сторона длины больше 1?

Подробнее

Задача по математике — 3713

Даны две окружности радиусов $R$ и $r$, касающиеся внешним образом.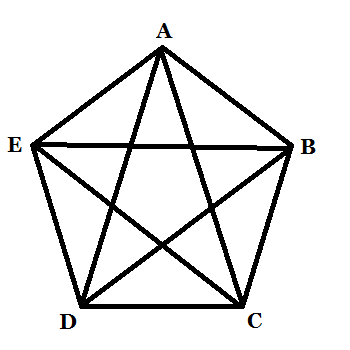 Строятся различные трапеции $ABCD$ так, чтобы каждая из окружностей касалась обеих боковых сторон и одного из оснований трапеции. Найдите наименьшую возможную длину боковой стороны $AB$. Подробнее

Задача по математике — 3714

На плоскости даны $n$ векторов, длина каждого из которых равна 1. Сумма всех $n$ векторов равна нулевому вектору. Докажите, что векторы можно занумеровать так, чтобы при всех $k = l, 2, \cdots, n$ выполнялось следующее условие: сумма первых $k$ векторов имеет длину не более 2. Подробнее

Задача по математике — 3716

Дан квадрат $ABCD$. Точки $P$ и $Q$ лежат соответственно на сторонах $AB$ и $BC$, причем $BP = BQ$. Пусть $R$ — основание перпендикуляра, опущенного из точки $B$ на отрезок $PC$.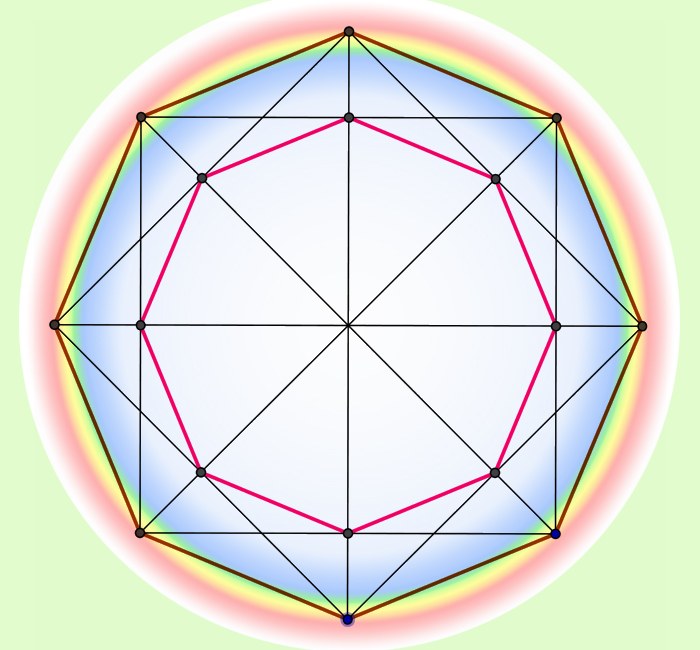 Докажите, что угол $DHQ$ прямой. Подробнее

Задача по математике — 3719

На катетах $CA$ и $CB$ равнобедренного прямоугольного треугольника $ABC$ выбраны соответственно точки $D$ и $E$ так, что $CD = CE$. Продолжения перпендикуляров, опущенных из точек $D$ и $C$ на прямую $AE$, пересекают гипотезу $AB$ соответственно в точках $K$ и $L$. Докажите, что $KL = LB$. Подробнее

Задача по математике — 3723

Дан выпуклый многоугольник, в который нельзя поместить никакой треугольник площади 1. Докажите, что этот многоугольник можно поместить в треугольник площади 4. Подробнее

Задача по математике — 3725

Дан треугольник $ABC$ площади 1. {\circ}$, получили четырехугольник $A_1B_1C_1D_1$. Докажите, что точки пересечения соответствующих друг другу при повороте прямых: $AB$ и $A_1B_1$, $BC$ и $B_1C_1, CD$ и $C_1D_1, DA$ и $D_1A_1$ служат вершинами параллелограмма. Подробнее

Задача по математике — 3727

Дан треугольник $ABC$ площади 1. Первый игрок выбирает точку $X$ на стороне $AB$, второй — $Y$ на стороне $BC$, затем первый — $Z$ на стороне $AC$. Цель первого — получить треугольник $XYZ$ наибольшей площади, второго — наименьшей. Какую наибольшую площадь может обеспечить себе первый? Подробнее

Задача по математике — 3730

В выпуклом шестиугольнике $A_1A_2A_3A_4A_5A_6$ середины диагоналей $A_6A_2$, $A_1A_3, A_2A_4, A_3A_5, A_4A_6, A_5A_1$ обозначим соответственно через $B_1, B_2, B_3, B_4, B_5, B_6$. Докажите, что если шестиугольник $B_1B_2B_3B_4B_5B_6$ выпуклый, то его площадь в четыре раза меньше площади $A_1A_2A_3A_4A_5A_6$. Подробнее

Задача по математике — 3732

В плоскости дано конечное множество многоугольников, каждые два из которых имеют общую точку. Докажите, что некоторая прямая пересекает все эти многоугольники. Подробнее

Большая диагональ основания шестиугольной призмы

Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.

О какой призме пойдет речь?

Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.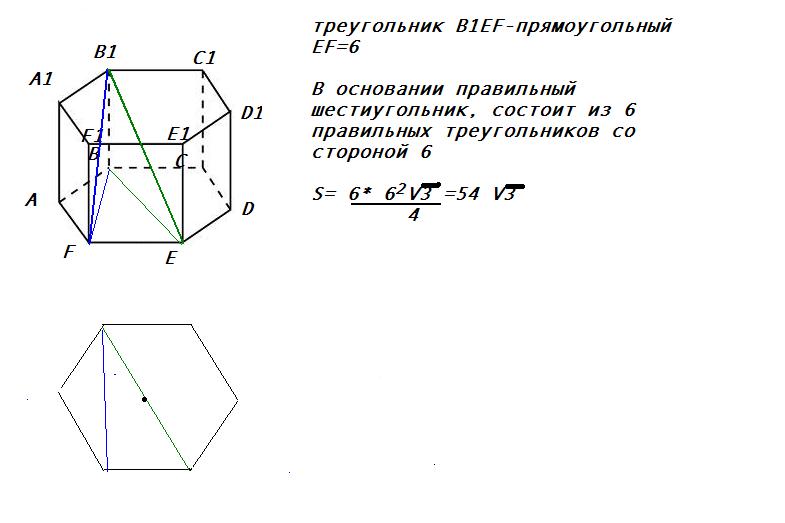

На рисунке изображен пример этой призмы.

Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.

Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.

Элементы

Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).

В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:

число ребер = число граней + число вершин — 2.

Указанные выше цифры удовлетворяют этой формуле.

Диагонали призмы

Все диагонали шестиугольной призмы можно разделить на два типа:

• те, которые лежат в плоскостях ее граней;
• те, которые принадлежат всему объему фигуры.

Рисунок ниже показывает все эти диагонали.

Видно, что D₁ — это диагональ боковой стороны, D₂ и D₃ — диагонали всей призмы, D

4 и D₅ — диагонали основания.

Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:

Диагональ D₄ также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D₄ является диаметром этой окружности, то есть получим следующую формулу:

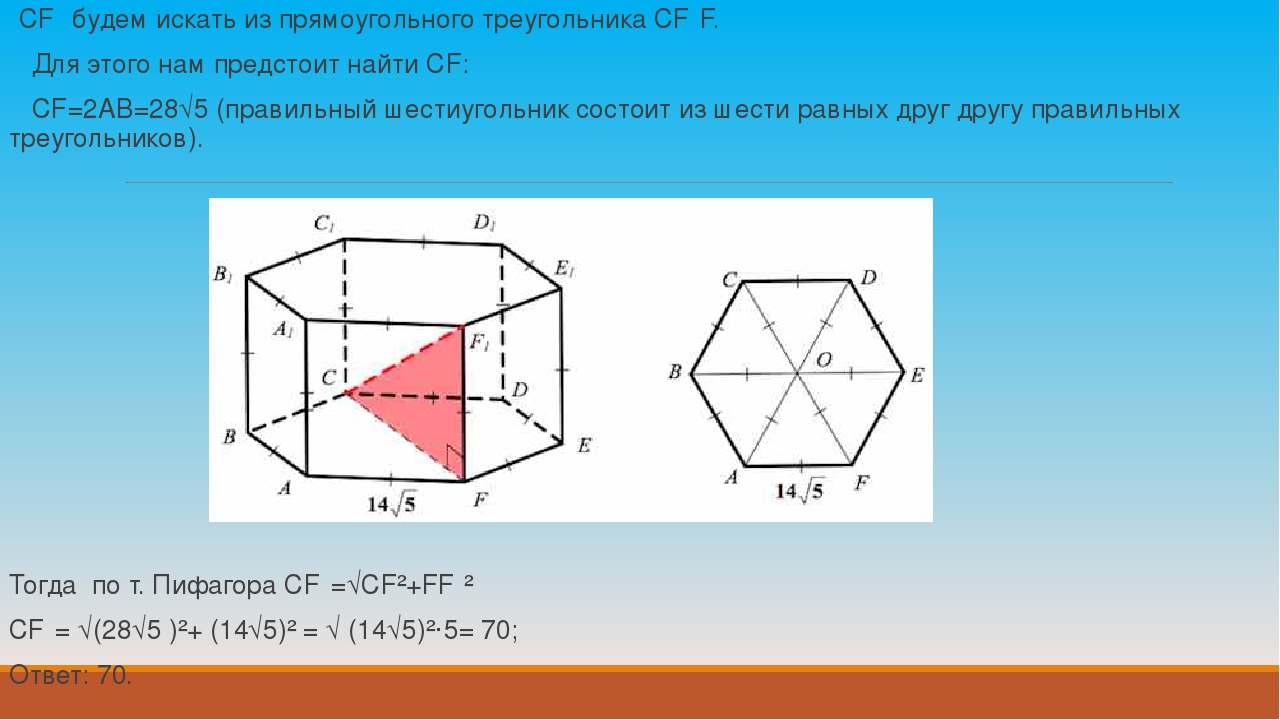
Диагональ D₅ основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:

Сторона AC является диагональю D₅, поэтому получаем:

Теперь остается найти диагонали D₂ и D₃ правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:

Таким образом, самой большой диагональю для любых значений a и b является D₂.

Площадь поверхности

Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.

Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.

Для площади прямоугольника получаем:

Тогда площадь боковой поверхности равна:

Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:

Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:

Это выражение следует умножить на два, чтобы получить площадь оснований призмы:

Остается сложить S_os и S₂, чтобы получить полную площадь поверхности фигуры:

Объем призмы

После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого.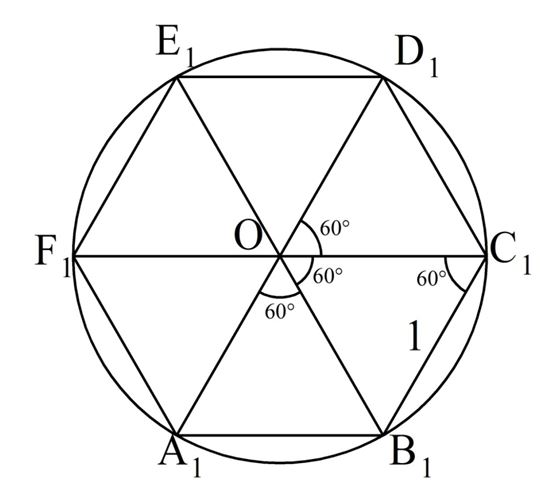 Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:

Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.

Из каждой вершины призмы, например из вершины А₁ (рис.), можно провести три диагонали (A₁E, A₁D, A₁C).

Они проектируются на плоскость ABCDEF диагоналями основания (АЕ, AD, АС). Из наклонных A₁E, A₁D, A₁C наибольшая та, у которой проекция — самая большая. Следовательно, наибольшая из трех взятых диагоналей есть A₁D (в призме есть еще диагонали, равные A₁D, но больших нет).

Площадь равностороннего треугольника АОВ равна 1 /₄• АО 2 • √ 3 .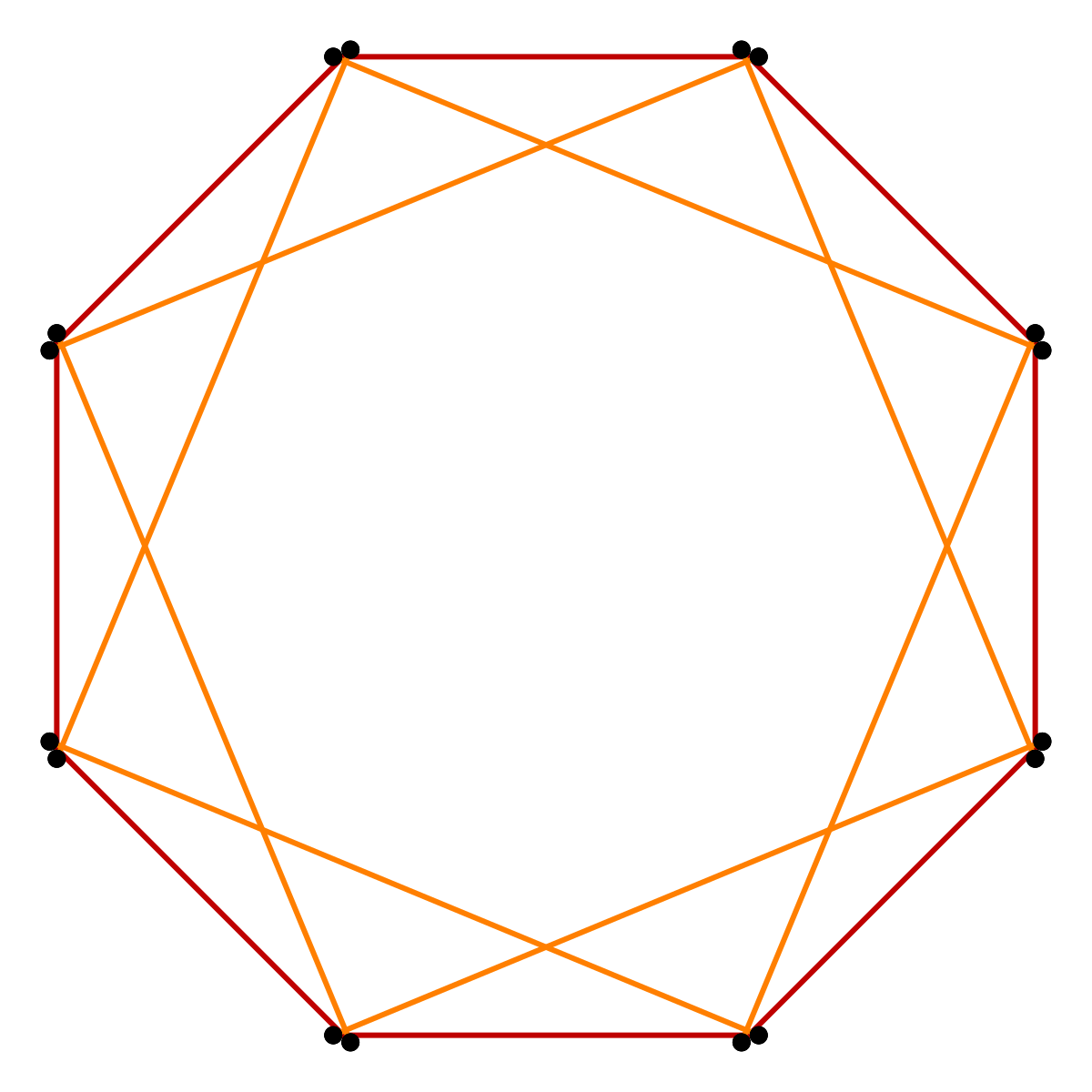 Следовательно,

Объем V = S•H = 3√ 3 /₈ • АD 2 • АA₁

Замечание. Для изображения правильного шестиугольника (основания призмы) можно построить произвольный параллелограмм BCDO. Откладывая на продолжениях прямых DO, CO, ВО отрезки OA = OD, OF= OC и ОЕ= ОВ, получаем шестиугольник ABCDEF. Точка О изображает центр.

оБЙВПМШЫБС ДЙБЗПОБМШ РТБЧЙМШОПК ЫЕУФЙХЗПМШОПК РТЙЪНЩ ТБЧОБ d Й УПУФБЧМСЕФ У ВПЛПЧЩН ТЕВТПН РТЙЪНЩ ХЗПМ 30 o . оБКДЙФЕ ПВЯЈН РТЙЪНЩ.
фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

тЕЫЕОЙЕ

рХУФШ УФПТПОБ РТБЧЙМШОПЗП ЫЕУФЙХЗПМШОЙЛБ, МЕЦБЭЕЗП Ч ПУОПЧБОЙЙ ДБООПК РТЙЪНЩ, ТБЧОБ a . фПЗДБ ОБЙВПМШЫБС ЕЗП ДЙБЗПОБМШ ТБЧОБ 2a , РТЙЮЈН ПОБ СЧМСЕФУС ПТФПЗПОБМШОПК РТПЕЛГЙЕК ОБ РМПУЛПУФШ ПУОПЧБОЙС ОБЙВПМШЫЕК ДЙБЗПОБМЙ РТЙЪНЩ. рХУФШ h – ЧЩУПФБ РТЙЪНЩ, V – ЕЈ ПВЯЈН. йЪ ХУМПЧЙС ЪБДБЮЙ УМЕДХЕФ, ЮФП
2a = d, h = d cos 30 o = .
еУМЙ S – РМПЭБДШ ПУОПЧБОЙС РТЙЪНЩ, ФП
S = 6· = = .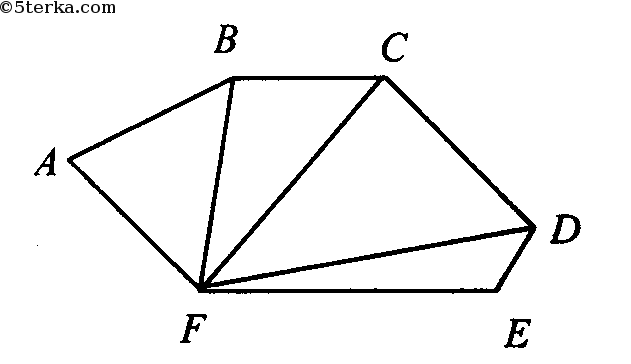
уМЕДПЧБФЕМШОП,
V = Sh = · = .

фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

пФЧЕФ

.
фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС

web-УБКФ
оБЪЧБОЙЕ	уЙУФЕНБ ЪБДБЮ РП ЗЕПНЕФТЙЙ т.л.зПТДЙОБ
URL	http://zadachi.mccme.ru
ОЕЙЪЧЕУФОП
оПНЕТ	7734

рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .

Диагональ треугольника

Диагональ треугольника

      Диагональ треугольника — это несуществующий элемент треугольника. По определению, диагональю называется элемент геометрической фигуры под названием отрезок, соединяющий две вершины, которые не лежат на одной стороне. У треугольника есть только одна вершина, не лежащая на одной стороне и соединена эта вершина отрезками под названием «стороны треугольника». В четырехугольниках и многоугольниках диагонали существуют и при помощи диагоналей эти геометрические фигуры можно разбить на треугольники или многоугольники с меньшим количеством вершин, чем в исходном многоугольнике. На рисунке ниже красным цветом показаны диагонали шестиугольника.

      При разбиении любого многоугольника на треугольники путем построения диагоналей все диагонали многоугольника превращаются в стороны составляющих его треугольников. Поэтому можно сказать, что диагональ треугольника — это его сторона. В математике и геометрии не принято давать понятие «диагональ треугольника». Ведь в этом случае треугольник будет состоять из трех диагоналей, которые одновременно являются сторонами треугольника. Геометрия и математика оперируют понятиями «сторона треугольника» а не понятием «диагональ треугольника».

      При разбиении прямоугольника на два треугольника при помощи диагонали, стороны прямоугольника превращаются в катеты прямоугольного треугольника, а диагональ прямоугольника становится гипотенузой прямоугольного треугольника. Если выполнить обратное построение — превратить прямоугольный треугольник в прямоугольник, где сторонами прямоугольника будут являться катеты прямоугольного треугольника, тогда гипотенуза прямоугольного треугольника превратится в диагональ прямоугольника.

      Поэтому можно сказать, что диагональ прямоугольного треугольника — это гипотенуза. Напомню еще раз, что понятие «диагональ треугольника» в математике и геометрии отсутствуют. Стороны прямоугольного треугольника называются катеты и гипотенуза.

      06 декабря 2010 года — 22 сентября 2019 года.

© 2006 — 2019 Николай Хижняк. Все права защишены.

В правильном шестиугольнике сторона равна 10см. Найти наибольшую диагональ этого шестиугольника.

Длина окружности (или ее периметр) вычисляется по формуле:

L = 2пR, где

п — математическая постоянная, равная п = 3,14;

R — радиус окружности.

Вычислим длину окружности, радиус которой равен R = 5 см:

L = 2 * 3,14 * 5 = 31,4 см.

Ответ: длина окружности равна 31,4 см.

Нет, так как они параллельны прямым, проходящим через одну точку, которые параллельными быть не могут.

6 месяцев назад

НУ элементарно, конечно если ваши углы образованы прямыми или векторами. Потому , что так  не пишется. На будущее — фотографируйте рисунок из учебника. НУ а собственно решение будет состоять из одного действия 150-120=30 градусов. 

7 месяцев назад

Высота в равнобедренном треугольнике-это и медиана, и биссектриса
Следовательно AH=HB=5
Т. к. треугольник ABC -равнобедренный, то AC=CB
Треугольник CHB тоже равнобедренный, тк угол HCB=углу CBH=45 градусов
Следовательно СH=CB=AC=12 
Ответ: AC=12

8 месяцев назад

Высота прямоугольного треугольника равна среднему геометрическому отрезков, на которые она разбивает гипотенузу:
h = √(n · m)        или        h² = n · m

Катет прямоугольного треугольника равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу:
a = √(c · n)          или        a² = c · n
b = √(c · m)         или        b² = c · m

6 месяцев назад

Как найти длину диагонали шестиугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Что такое диагональ, определение, примеры, факты и формула — Cuemath

Диагональ — это отрезок прямой, соединяющий один угол с другим, но не являющийся краем. Таким образом, мы получаем диагональ, когда напрямую соединяем любые два угла (вершины), которые еще не соединены ребром.В случае многоугольника это прямая линия, соединяющая противоположные углы многоугольника через его вершины.

Что такое диагональ?

Отрезок, соединяющий один угол с другим, но не являющийся ребром, называется диагональю. Итак, мы получаем диагональ, напрямую соединяя любые два угла (вершины), которые еще не соединены ребром.

Форма диагонали

Поскольку диагональ — это отрезок прямой, соединяющий несмежные вершины или углы, форма диагонали — это прямая линия.

Диагонали многоугольников

«Диагональ многоугольника — это отрезок прямой, полученный путем соединения любых двух несмежных вершин». Мы знаем, что многоугольник — это замкнутая форма, образованная соединением смежных вершин. Например, у квадрата 4 стороны, у пятиугольника — 5 сторон, у шестиугольника — 6 сторон и так далее. В зависимости от типа многоугольника, основанного на количестве ребер, количество диагоналей и их свойства будут различаться. Точно так же свойства диагоналей меняются в зависимости от типа твердого тела.

Давайте теперь разберемся с диагоналями для разных многоугольников.

• Диагональ треугольника
• Диагональ квадрата
• Диагональ прямоугольника
• Диагональ ромба
• Диагональ пятиугольника
• Диагональ шестиугольника

Диагональ треугольника

Треугольник — это замкнутая фигура или фигура, имеющая 3 стороны, 3 угла и 3 вершины. Треугольник — самый простой тип многоугольника.В треугольнике нет несмежных вершин. Это означает, что нет отрезков, которые могут образовывать диагонали.

Количество диагоналей треугольника = 0.

Диагональ квадрата

Квадрат определяется как замкнутая двумерная фигура, имеющая четыре стороны и четыре угла. Все стороны параллельны друг другу и имеют одинаковую длину. Диагональ квадрата — это отрезок прямой, соединяющий любые две его противоположные вершины. В следующем квадрате две пары несмежных вершин.Соединяя вершины каждой такой пары, мы получаем две диагонали квадрата AC и BD. Длины линий AC и BD в данном квадрате одинаковы. Диагональ любого квадрата разрезает его на два равных прямоугольных треугольника, так что диагональ образует гипотенузу прямоугольных треугольников. Количество диагоналей квадрата = 2.

Диагональ прямоугольника

Диагональ прямоугольника — это отрезок прямой, соединяющий любые две его несмежные вершины.В следующем прямоугольнике AC и BD — диагонали. Вы можете видеть, что длины AC и BD одинаковы. Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, у которых стороны равны сторонам прямоугольника и с гипотенузой. Эта гипотенуза — диагональ.

Диагональ ромба

Диагонали ромба — это отрезки прямой, соединяющие противоположные вершины и разделяющие друг друга пополам под углом 90 °, что означает, что две половины любой диагонали будут иметь одинаковую длину.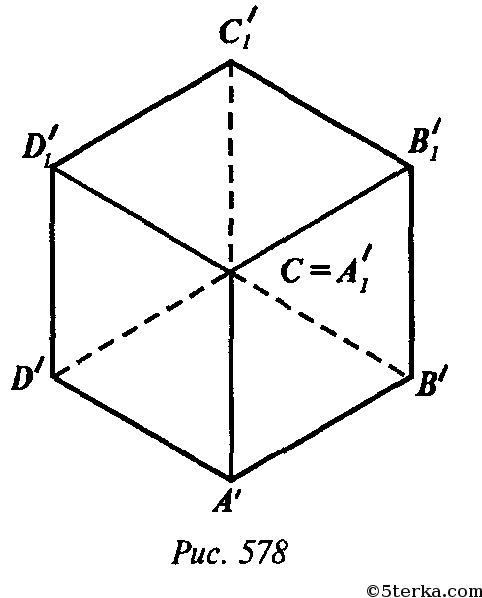 Ромб можно определить как четырехугольник в форме ромба, у которого все четыре стороны равны. Диагонали ромба будут иметь разные значения, если ромб не квадрат.

Диагональ пятиугольника

Пятиугольник — это замкнутая двумерная фигура с пятью сторонами и пятью углами. У правильного пятиугольника длина всех пяти сторон равна. У пятиугольника пять диагоналей, как показано на изображении ниже:

Диагональ шестиугольника

Шестиугольник — это замкнутая двумерная фигура с шестью сторонами и шестью углами.У правильного шестиугольника длина всех шести сторон равна. У шестиугольника девять диагоналей, как показано на изображении ниже:

Здесь все 9 красных линий внутри шестиугольника — это диагонали.

Помимо многоугольников, для разных тел, в зависимости от количества ребер, количество диагоналей и их свойства будут различаться.

• Диагональ куба
• Диагональ кубоида

Диагональ куба

Куб — это трехмерное твердое тело, также известное как квадратное твердое тело, имеющее ребра одинаковой длины.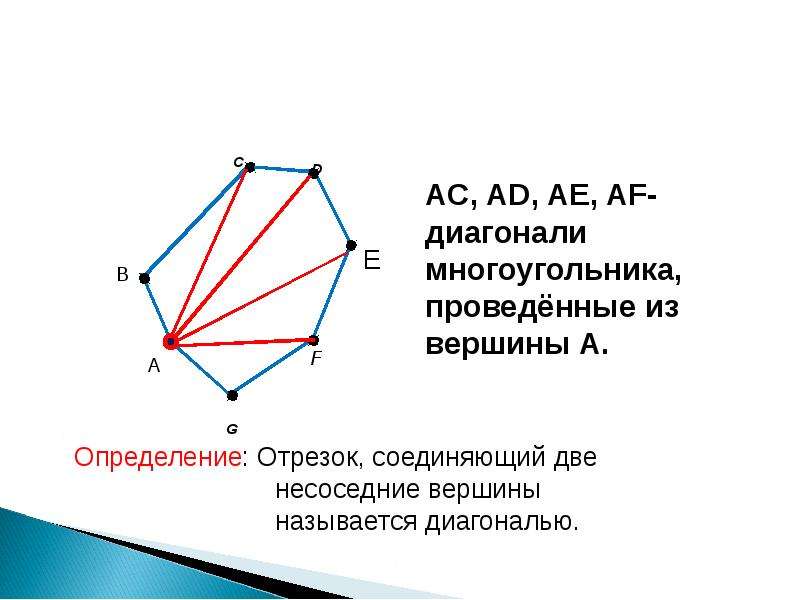 Это означает, что длина, ширина и высота равны, и каждая из его граней представляет собой квадрат. Главная диагональ куба — это отрезок прямой, пересекающий его центр и соединяющий противоположные вершины. В то время как диагональ грани куба соединяет противоположные вершины на каждой грани. Таким образом, это не главная диагональ.

Диагональ кубоида

Кубоид — трехмерный аналог прямоугольника в двух измерениях. Главная диагональ кубоида — это та, которая пересекает центр кубоида; диагональ грани кубоида не является главной диагональю.

Формула числа диагоналей

Формула количества диагоналей может использоваться для вычисления количества диагоналей в многоугольнике. Он различается в зависимости от типа многоугольника и количества сторон. Мы можем использовать эту формулу, чтобы найти количество диагоналей любого многоугольника, не рисуя их на самом деле:

Количество диагоналей многоугольника с числом сторон n = n (n-3) / 2

В следующей таблице показано количество диагоналей некоторых многоугольников, вычисленное по этой формуле.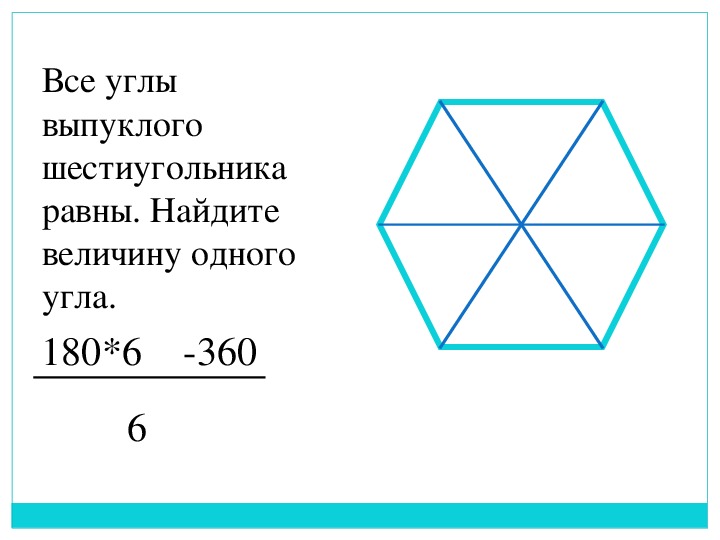

Форма	Количество сторон, н	Число диагоналей
Треугольник	3	3 (3−3) / 2 = 0
Четырехугольник	4	4 (4−3) / 2 = 2
Пентагон	5	5 (5−3) / 2 = 5
Шестигранник	6	6 (6−3) / 2 = 9
Гептагон	7	7 (7−3) / 2 = 14
Восьмиугольник	8	8 (8−3) / 2 = 20
Nonagon	9	9 (9−3) / 2 = 27
Десятиугольник	10	10 (10−3) / 2 = 35
Хендекагон	11	11 (11−3) / 2 = 44
Додекагон	12	12 (12−3) / 2 = 54

Пример: Найдите количество диагоналей десятиугольника.

Решение:

Число сторон десятиугольника равно n = 10. Число диагоналей десятиугольника рассчитывается по формуле:

п (п-3) / 2 = 10 (10-3) / 2 = 10 (7) / 2 = 70/2 = 35

Количество диагоналей десятиугольника = 35

Длина диагонали

Длина диагонали любого многоугольника зависит от типа многоугольника. Нет общей формулы для расчета длины диагонали. Скорее, исходя из размеров конкретного многоугольника, можно найти формулу для расчета длины диагонали.В этом разделе будет рассмотрена формула для расчета длины диагонали для некоторых многоугольников и твердых тел на основе их структуры и размеров.

• Длина диагонали квадрата
• Длина диагонали прямоугольника
• Длина диагонали куба
• Длина диагонали кубовида

Длина диагонали квадрата

В квадрате длина обеих диагоналей одинакова. Длина диагонали d квадрата со стороной x единиц вычисляется по теореме Пифагора.Используя теорему Пифагора, d = √ (x ² + x ² ) = √ (2x ² ) = √2x единиц.

Длина диагонали квадрата = √2x единиц

Длина диагонали прямоугольника

Подобно квадрату, длина обеих диагоналей в прямоугольнике одинакова. Длина диагонали d прямоугольника длиной l единиц и шириной b единиц вычисляется по теореме Пифагора.

Используя теорему Пифагора, d ² = l ² + b ²

Длина диагонали прямоугольника = √l ² + b ² шт.

Длина диагонали куба

Рассмотрим куб длиной x единиц.У куба 6 граней. Каждая грань куба представляет собой квадрат. Таким образом, у каждой грани две диагонали. Следовательно, длина каждой такой диагонали равна длине диагонали квадрата. Длина каждой диагонали грани куба = √2x единиц.

Помимо диагоналей на гранях, есть еще 4 диагонали (главные диагонали или диагонали тела), которые проходят через центр квадрата. Формула для длины диагонали куба выводится так же, как мы выводим длину диагонали квадрата.Длина диагонали тела куба = √3x единиц.

Длина диагонали кубоида (прямоугольная призма)

Рассмотрим кубоид длиной l, шириной w и высотой h. Предположим, что главная диагональ (или диагональ тела), проходящая через центр кубоида, равна d. Длина диагонали кубоида = √ (l ² + w ² + h ² ).

Важные примечания

• Количество диагоналей многоугольника с n сторонами равно n (n-3) / 2.
• Длина диагонали квадрата со стороной x равна 2.
• Длина диагонали прямоугольника со сторонами l и b равна √ (l ² + w ² ).
• Длина диагонали куба со стороной x равна √3x.
• Длина диагонали кубоида со сторонами l, w и h равна √ (l ² + w ² + h ² ).

---

Часто задаваемые вопросы по диагонали

Каков угол диагонали в квадрате?

Каждая диагональ квадрата делит угол в каждой вершине на две равные части.Следовательно, угол между любой стороной и любой диагональю составляет 45 градусов.

Что вы имеете в виду под диагоналями?

Диагональ многоугольника — это отрезок прямой, полученный путем соединения любых двух несмежных вершин. В случае многоугольника это прямая линия, соединяющая противоположные углы многоугольника через его вершину. Таким образом, мы получаем диагональ, когда напрямую соединяем любые два угла (вершины), которые еще не соединены ребром.

Как выглядит диагональ?

Диагональ представляет собой отрезок прямой.Он начинается и заканчивается в двух противоположных вершинах многоугольника.

Как найти количество диагоналей в многоугольнике?

Количество диагоналей для любого многоугольника различается в зависимости от типа многоугольника и количества сторон. Формула количества диагоналей может использоваться для вычисления количества диагоналей в многоугольнике. Количество диагоналей многоугольника с числом сторон «n» = n (n-3) / 2, где n — общее количество сторон многоугольника.

Как узнать количество сторон диагонали?

Сама диагональ — это отрезок прямой.Это отрезок прямой, соединяющий несмежные вершины любой формы.

Как рассчитать длину диагонали любой формы?

Длина диагонали любого многоугольника зависит от типа многоугольника. Нет общей формулы для расчета длины диагонали. Скорее, исходя из размеров конкретного многоугольника, можно найти формулу для расчета длины диагонали. Например, длина диагонали квадрата = √2x единиц.

Сколько диагоналей у треугольника?

В треугольнике нет несмежных вершин.Это означает, что нет отрезков, которые могут образовывать диагонали. Таким образом, в треугольнике 0 диагоналей.

Количество диагоналей в многоугольнике

Какова вероятность случайного выбора одной из самых коротких диагоналей из всех диагоналей правильного шестиугольника?

Неверно. [[snippet]]

Неправильно. [[snippet]]

Правильно.Это вероятностный вопрос, связанный с геометрией. Вопрос в количестве диагоналей в шестиугольнике. Сначала определите общее количество результатов. Количество диагоналей многоугольника задается формулой > $$ \ text {Diagonals} = \ frac {n (n-3)} {2} $$, где $$ n $$ — количество сторон. В случае шестиугольника $$ n = 6 $$. > $$ \ text {Diagonals} = \ frac {n (n-3)} {2} = \ frac {6 (6-3)} {2} = 9 $$. Чтобы узнать количество желаемых результатов, нарисуйте правильный шестиугольник и его диагонали и посмотрите, сколько диагоналей короче.Поскольку мы говорим здесь о шестиугольнике, нарисовать диагонали довольно просто. ! [] (Данные: изображения / SVG + XML; base64, PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0idXRmLTgiPz4NCjwhLS0gR2VuZXJhdG9yOiBBZG9iZSBJbGx1c3RyYXRvciAyNC4wLjEsIFNWRyBFeHBvcnQgUGx1Zy1JbiAuIFNWRyBWZXJzaW9uOiA2LjAwIEJ1aWxkIDApICAtLT4NCjxzdmcgdmVyc2lvbj0iMS4xIiBpZD0i0KHQu9C + 0LlfMSIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayIgeD0iMHB4IiB5PSIwcHgiDQoJIHdpZHRoPSIzNDJweCIgaGVpZ2h0PSIyOTYuN3B4IiB2aWV3Qm94PSIwIDAgMzQyIDI5Ni43IiBzdHlsZT0iZW5hYmxlLWJhY2tncm91bmQ6bmV3IDAgMCAzNDIgMjk2Ljc7IiB4bWw6c3BhY2U9InByZXNlcnZlIj4NCjxzdHlsZSB0eXBlPSJ0ZXh0L2NzcyI + DQoJLnN0MHtmaWxsOm5vbmU7c3Ryb2tlOiNDNEM0QzQ7c3Ryb2tlLW1pdGVybGltaXQ6MTA7fQ0KCS5zdDF7ZmlsbDpub25lO3N0cm9rZTojQzRDNEM0O3N0cm9rZS1taXRlcmxpbWl0OjEwO3N0cm9rZS1kYXNoYXJyYXk6OCw4O30NCgkuc3Qye2ZpbGw6bm9uZTtzdHJva2U6IzAwMDAwMDtzdHJva2Utd2lkdGg6MjtzdHJva2UtbWl0ZXJsaW1pdDoxMDt9DQo8L3N0eWxlPg0KPGc + DQoJPGxpbmUgY2xhc3M9InN0MCIgeDE9IjIuNCIgeTE9IjE0Ny43IiB4Mj0iMzM5LjgiIHkyPSIxNDcuNyIvPg0KCTxsaW5lIGNsYXNzPSJzdDAiIHgxPSIyNTUuNiIgeT E9IjEiIHgyPSI4Ni4yIiB5Mj0iMjk0LjYiLz4NCgk8bGluZSBjbGFzcz0ic3QwIiB4MT0iODUuOSIgeTE9IjEiIHgyPSIyNTUuMSIgeTI9IjI5My4yIi8 + DQoJPHBhdGggY2xhc3M9InN0MSIgZD0iTTg1LjYsMjk1LjciLz4NCgk8bGluZSBjbGFzcz0ic3QwIiB4MT0iODguMSIgeTE9IjI5MS40IiB4Mj0iODguMSIgeTI9IjI5MS40Ii8 + DQoJPGxpbmUgY2xhc3M9InN0MSIgeDE9IjI1NS42IiB5MT0iMSIgeDI9IjI1NS4xIiB5Mj0iMjkzLjIiLz4NCgk8bGluZSBjbGFzcz0ic3QxIiB4MT0iODYuNiIgeTE9IjIiIHgyPSI4Ni4xIiB5Mj0iMjk0LjgiLz4NCgk8bGluZSBjbGFzcz0ic3QxIiB4MT0iMi40IiB5MT0iMTQ3LjciIHgyPSIyNTUuNiIgeTI9IjEiLz4NCgk8bGluZSBjbGFzcz0ic3QxIiB4MT0iODYuMiIgeTE9IjI5NC42IiB4Mj0iMzM5LjgiIHkyPSIxNDcuNyIvPg0KCTxsaW5lIGNsYXNzPSJzdDEiIHgxPSI4Ni42IiB5MT0iMiIgeDI9IjMzOS44IiB5Mj0iMTQ3LjciLz4NCgk8bGluZSBjbGFzcz0ic3QxIiB4MT0iMS4yIiB5MT0iMTQ3LjciIHgyPSIyNTUuMSIgeTI9IjI5My4yIi8 + DQoJPHBvbHlnb24gY2xhc3M9InN0MiIgcG9pbnRzPSIxLjIsMTQ3LjcgODUuOSwxIDI1NS42LDEgMzQwLjksMTQ3LjcgMjU1LjYsMjk1IDg1LjYsMjk0LjcgCSIvPg0KPC9nPg0KPC9zdmc + DQo =) и видим, что 9 диагоналей разделены на две группы: 3 диагонали длиннее (главные диагонали, соединяющие противоположные вершины), а остальные 6 короче.Это $$ \ frac {6} {9} = \ frac {2} {3} $$ шанс случайным образом выбрать более короткую диагональ.

Неправильно. [[snippet]]

Неправильно. [[snippet]]

$$ \ frac {1} {4} $$

$$ \ frac {1} {3} $$

$$ \ frac {1} {2} $$

$$ \ frac {2} {3} $$

$$ \ frac {7} {9} $$

.