Правильный шестиугольник | Онлайн-школа » Прорыв»
Вам тоже становится страшно, когда вы видите в условии задачи «правильный шестиугольник»? Вам хочется сразу перейти к другой задаче? Вы не знаете, как с ним работать ?
? Страх перед задачами подобного рода возникает по простой причине — незнание свойств правильного шестиугольника. Ознакомившись с ними, вы с легкостью будете решать задачи с шестиугольниками. В них нет ничего сложного. Давайте разбираться.
! Правильный шестиугольник — многоугольник с шестью равными сторонами и углами. Правильный шестиугольник состоит из шести правильных треугольников. Правильный треугольник = равносторонний треугольник. А в равностороннем треугольнике все углы равны 60 градусам.
Площадь и периметр
1. Периметр равен сумме длин всех его сторон.
P = 6a, где a — длина стороны шестиугольника
1. Для того, чтобы найти площадь правильного шестиугольника, необходимо найти площадь равностороннего треугольника и умножить её на шесть.
S = 6 * (площадь треугольника)
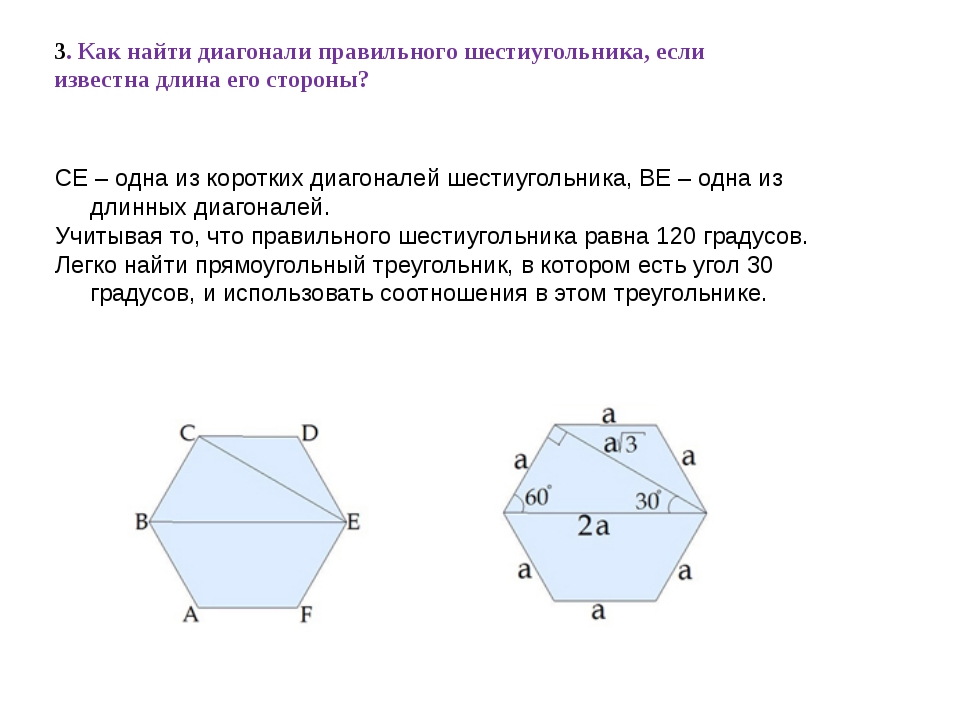
Диагональ правильного шестиугольника
Диагонали в правильном шестиугольнике бывают двух типов: малые (d) и большие (D).
Радиусы вписанной и описанной окружностей
r — радиус вписанной окружности
R — радиус описанной окружности
! Обратите внимание на то, что радиусы окружностей в 2 раза меньше, чем диагонали.
Пример
Стороны основания правильной шестиугольной пирамиды равны 12, высота равна 9. Найдите длину бокового ребра пирамиды.
Решение
1. Так как в основании лежит правильный шестиугольник, то он состоит из правильных треугольников, у которых все стороны равны —> FO = 12;
2. Рассмотрим треугольник SOF и найдём в нём по теореме Пифагора длину гипотенузы SF;
3. В правильных пирамидах все боковые рёбра равны —> SF = 15.
Ответ: 15
Ждем Вас на нашем сайте >>
Все формулы для радиуса описанной окружности
Все формулы для радиуса описанной окружности
, , — стороны треугольника
— полупериметр
— центр окружности
Формула радиуса описанной окружности треугольника ( R ) :
— сторона треугольника
— высота
— радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.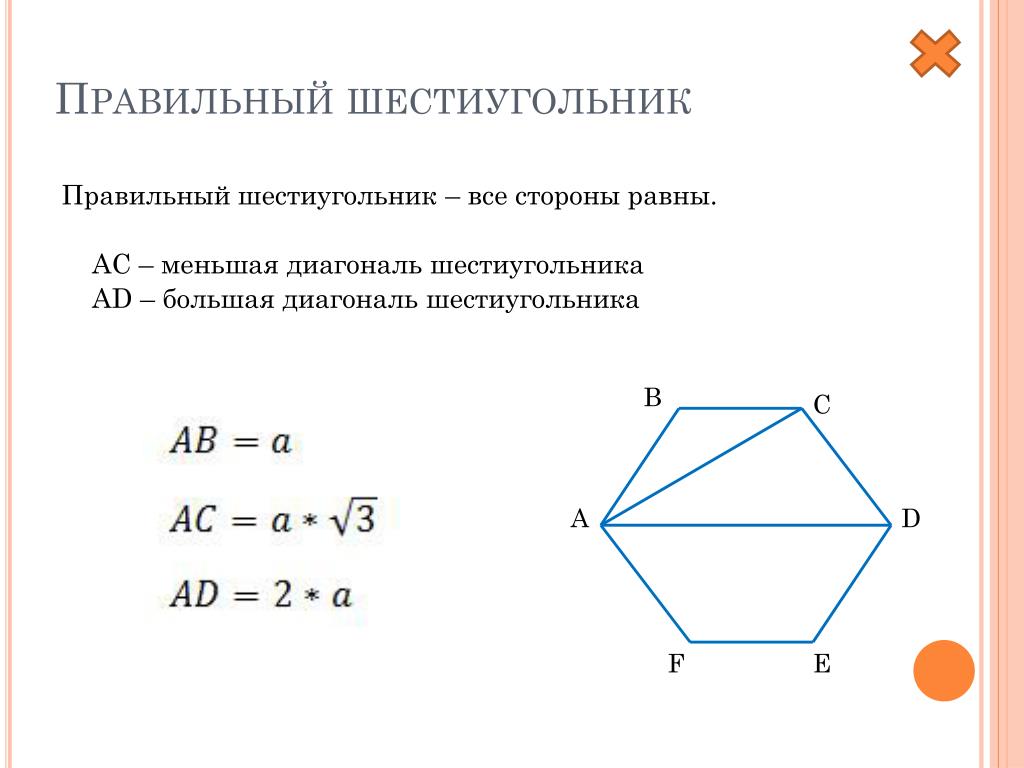
a, b — стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
p — полупериметр треугольника DBC
p = (a+d+c
Формула радиуса описанной окружности равнобокой трапеции, (R)
Радиус описанной окружности квадрата равен половине его диагонали
a — сторона квадрата
d — диагональ
Формула радиуса описанной окружности квадрата (R):
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
Формула радиуса описанной окружности прямоугольника (R):
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Радиус описанной окружности
Наверх
При использовании материалов данного сайта обязательно указывать ссылку на источник.
Все стороны шестиугольника. Смотреть что такое «Правильный шестиугольник» в других словарях
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы
, например графит, имеют гексагональную кристаллическую решётку.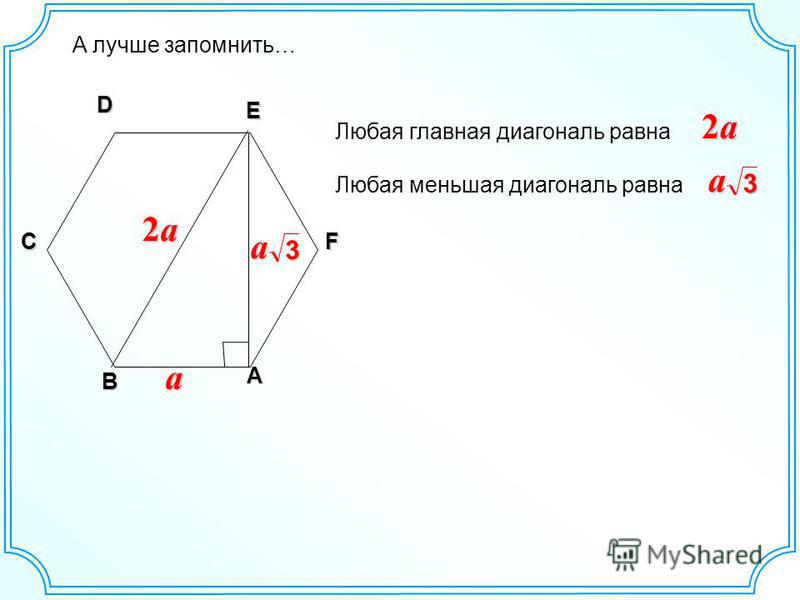
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение.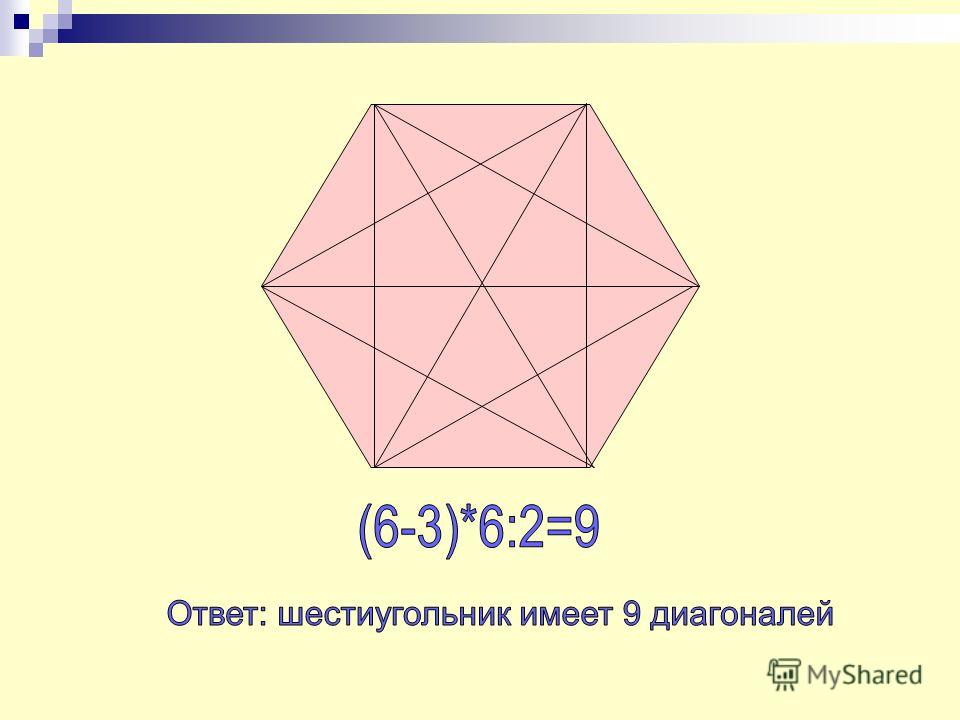 Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2.
 Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек.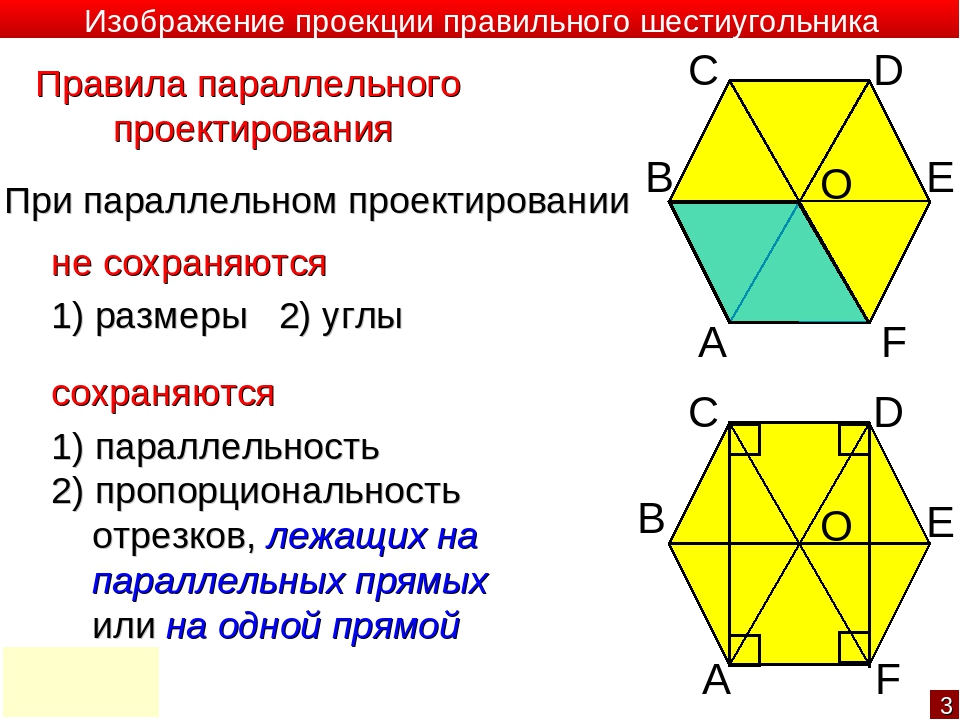 Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Шестиугольник — Hexagon — other.wiki
Форма с шестью сторонами
В геометрии , A шестиугольник (от греческой ЕЕ , ) — язык текста»> гекса , что означает «шесть», и γωνία , Gonia , что означает «угол, угол») представляет собой шестигранный многоугольник или 6-угольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Правильный шестиугольник
Регулярный шестиугольник имеет символ шлефли {6} , а также может быть выполнен в виде усеченного равностороннего треугольника , т {3}, который чередует два типа ребер.
Если задана длина стороны AB , построение дуги окружности из точки A и точки B дает пересечение M, центр описанной окружности . Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки. Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным . Он бицентрический , что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).
Общая длина сторон равна радиусу окружности или окружности , которая равна раз превышает апофемой (радиус вписанной окружности ). Все внутренние углы составляют 120 градусов . Правильный шестиугольник имеет шесть симметрий вращения ( вращательная симметрия шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляющих группу диэдра D 6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого можно видеть, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним , и что правильный шестиугольник можно разделить на шесть равносторонних треугольников. 2 3 {\ displaystyle {\ tfrac {2} {\ sqrt {3}}}}
Подобно квадратам и равносторонним треугольникам , правильные шестиугольники подходят друг к другу без каких-либо зазоров, чтобы замостить плоскость (три шестиугольника, пересекающиеся в каждой вершине), и поэтому полезны для построения мозаики .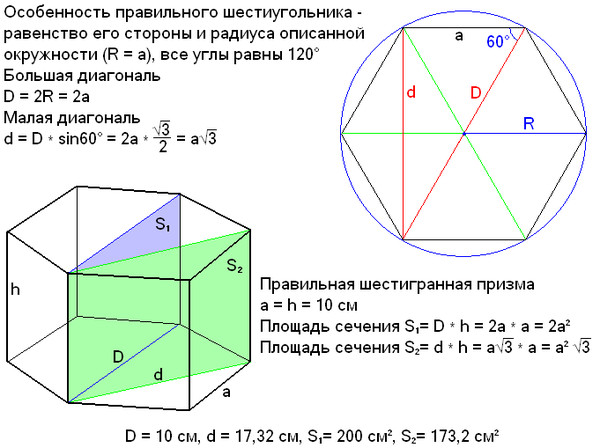 Ячейки сотового улья имеют шестиугольную форму по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного регулярной треугольной решетки является сотовая тесселяция из шестиугольников. Обычно не считается триамбусом , хотя он равносторонний.
Ячейки сотового улья имеют шестиугольную форму по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного регулярной треугольной решетки является сотовая тесселяция из шестиугольников. Обычно не считается триамбусом , хотя он равносторонний.
Параметры
Максимальный диаметр (который соответствует длинной диагонали шестиугольника), D , в два раза превышает радиус максимальной или описанной окружности , R , которая равна длине боковой, т . Минимальный диаметр или диаметр вписанной окружности (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d , в два раза больше минимального радиуса или inradius , r . Максимумы и минимумы связаны одним и тем же фактором:
- 1 2 d знак равно р знак равно потому что ( 30 ∘ ) р знак равно 3 2 р знак равно 3 2 т {\ displaystyle {\ frac {1} {2}} d = r = \ cos (30 ^ {\ circ}) R = {\ frac {\ sqrt {3}} {2}} R = {\ frac {\ sqrt {3}} {2}} t} и аналогично d знак равно 3 2 D .
 {2}. \ end {align}}}
{2}. \ end {align}}}
Правильный шестиугольник заполняет часть его окружности . 3 3 2 π ≈ 0,8270 {\ displaystyle {\ tfrac {3 {\ sqrt {3}}} {2 \ pi}} \ приблизительно 0,8270}
Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD .
Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1,0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.
Точка в плоскости
Для произвольной точки на плоскости правильного шестиугольника с описанным радиусом , расстояния до центра тяжести правильного шестиугольника и его шести вершин равны и соответственно, имеем р {\ displaystyle R} L {\ displaystyle L} d я {\ displaystyle d_ {i}}
- d 1 2 + d 4 2 знак равно d 2 2 + d 5 2 знак равно d 3 2 + d 6 2 знак равно 2 ( р 2 + L 2 ) , {\ displaystyle d_ {1} ^ {2} + d_ {4} ^ {2} = d_ {2} ^ {2} + d_ {5} ^ {2} = d_ {3} ^ {2} + d_ { 6} ^ {2} = 2 (R ^ {2} + L ^ {2}),}
- d 1 2 + d 3 2 + d 5 2 знак равно d 2 2 + d 4 2 + d 6 2 знак равно 3 ( р 2 + L 2 ) , {\ displaystyle d_ {1} ^ {2} + d_ {3} ^ {2} + d_ {5} ^ {2} = d_ {2} ^ {2} + d_ {4} ^ {2} + d_ { 6} ^ {2} = 3 (R ^ {2} + L ^ {2}),}
- d 1 4 + d 3 4 + d 5 4 знак равно d 2 4 + d 4 4 + d 6 4 знак равно 3 ( ( р 2 + L 2 ) 2 + 2 р 2 L 2 ) .
 {4 }.}
{4 }.}
Симметрия
| Пример шестиугольников по симметрии |
|---|
Правильный шестиугольник имеет DIH 6 симметрии, порядок 12. Есть три подгруппы: двугранная DIH 3 , DIH 2 и DIH 1 , и четыре циклических подгрупп: Z 6 , Z 3 , Z 2 и Z 1 .
Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. r12 — полная симметрия, а a1 — несимметрия. p6 , изогональный шестиугольник, образованный тремя зеркалами, может чередовать длинные и короткие края, и d6 , изотоксический шестиугольник, построенный с равными длинами ребер, но вершинами, чередующимися с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. В i4 формы правильные шестиугольники уплощены или растягиваются вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб , а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи . Шестиугольники g2 , противоположные стороны которых параллельны, также называются шестиугольными параллелогонами .
Джон Конвей помечает их буквой и групповым порядком. r12 — полная симметрия, а a1 — несимметрия. p6 , изогональный шестиугольник, образованный тремя зеркалами, может чередовать длинные и короткие края, и d6 , изотоксический шестиугольник, построенный с равными длинами ребер, но вершинами, чередующимися с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. В i4 формы правильные шестиугольники уплощены или растягиваются вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб , а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи . Шестиугольники g2 , противоположные стороны которых параллельны, также называются шестиугольными параллелогонами .
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм.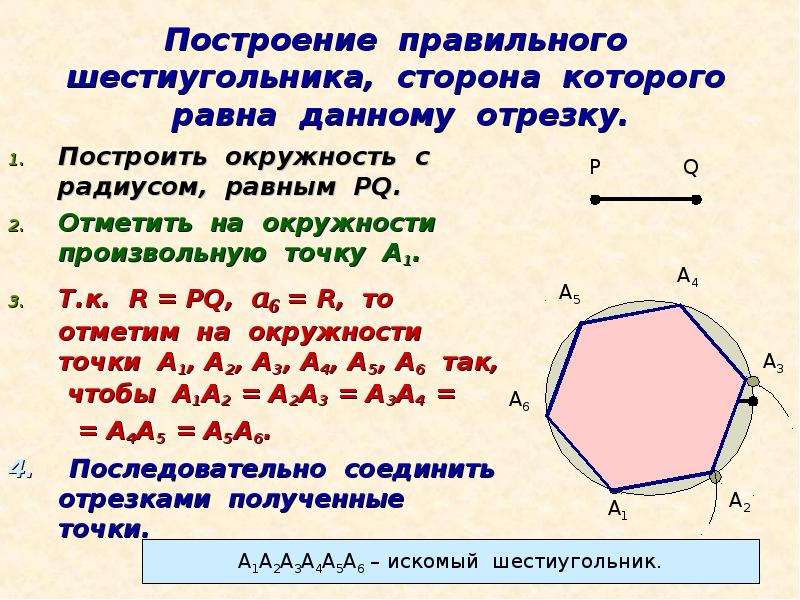 Только подгруппа g6 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Только подгруппа g6 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Шестиугольники симметрии g2 , i4 и r12 , как параллелогоны, могут разбить евклидову плоскость путем сдвига. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.
Группы A2 и G2
Шесть корней простой группы Ли A2 , представленной диаграммой Дынкина , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
12 корней исключительной группы Ли G2 , представленной диаграммой Дынкина также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
Расслоение
Кокстеровские гласит , что каждый зоногон (2 м -угольник которого противоположные стороны параллельны и равны по длине) можно разрезать на м ( м -1) / 2 параллелограммов. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими.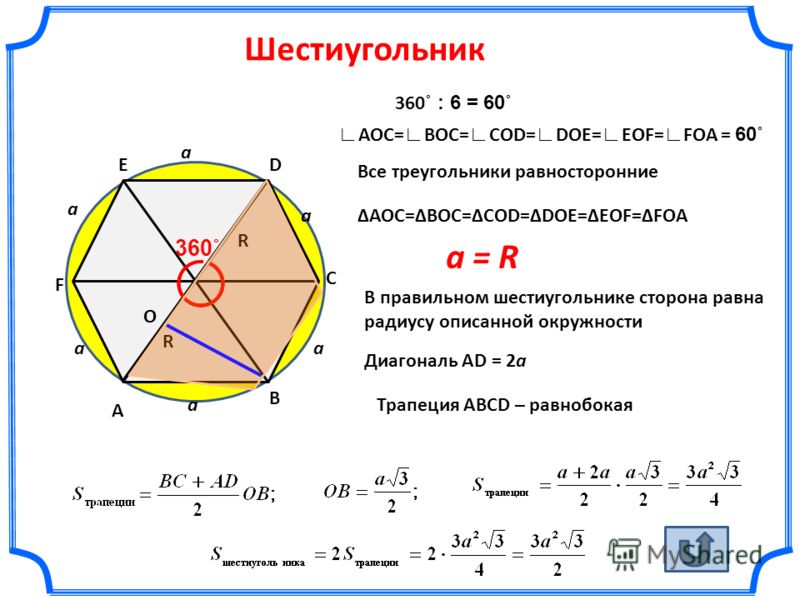 Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами .
Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами .
Связанные полигоны и мозаики
На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольными гранями вокруг каждой вершины.
Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}. Эта форма, имеющая два типа (цвета) ребер, имеет только симметрию D 3 .
Усеченный шестиугольник, т {6}, является двенадцатиугольник , {12}, чередуя два типа (цвета) ребер. Чередовались шестиугольник, ч {6}, представляет собой равносторонний треугольник , {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму .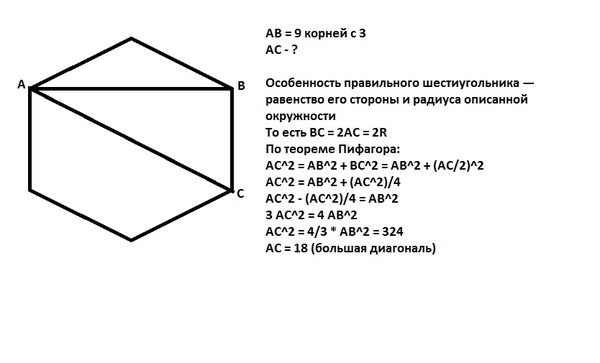 Правильный шестиугольник можно разрезать на шесть равносторонних треугольников , добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки .
Правильный шестиугольник можно разрезать на шесть равносторонних треугольников , добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки .
Правильный шестиугольник можно расширить до правильного двенадцатиугольника , добавив вокруг него чередующиеся квадраты и равносторонние треугольники . Этот узор повторяется внутри ромбогексагональной плитки .
Самопересекающиеся шестиугольники
Всего шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:
Шестиугольные конструкции
Дорога гигантов крупным планом От пчелиных сот до Дороги гигантов , гексагональные узоры широко распространены в природе из-за их эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии .
Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами и также могут перекрывать плоскость путем сдвига. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.
Месселяция шестиугольниками
В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея, будет мозаикой плоскости.
Шестиугольник, вписанный в коническое сечение
Теорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение , и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, то » Линия Паскаля »этой конфигурации.
Циклический шестиугольник
Шестигранной Лемуан является циклическим шестиугольника (один вписан в окружность) с вершинами , заданных шести пересечений ребер треугольника и трех линий, которые параллельны краям , которые проходят через его симедиана точки .
Если последовательные стороны циклического шестиугольника — это a , b , c , d , e , f , то три главных диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf .
Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то сегменты, соединяющие центры описанных окружностей противоположных треугольников, совпадают .
Если шестиугольник имеет вершины на окружности в качестве острого треугольника в шести точках ( в том числе трех вершин треугольника) , где расширенные Высоты треугольника встречается окружности, то площадь шестиугольника в два раза превышает площадь треугольника.
Шестиугольник, касательный к коническому сечению
Пусть ABCDEF — шестиугольник, образованный шестью касательными конического сечения. Тогда теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.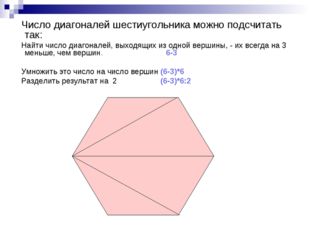
В шестиугольнике, который является касательным к окружности и имеет последовательные стороны a , b , c , d , e и f ,
- а + c + е знак равно б + d + ж . {\ displaystyle a + c + e = b + d + f.}
Равносторонние треугольники по сторонам произвольного шестиугольника
Равносторонние треугольники по сторонам произвольного шестиугольникаЕсли равносторонний треугольник построен снаружи с каждой стороны любого шестиугольника, то середины отрезков, соединяющих центроиды противоположных треугольников, образуют другой равносторонний треугольник.
Наклоненный шестиугольник
Правильный косой шестиугольник, видимый как края (черные) треугольной антипризмы , симметрия D 3d , [2 + , 6], (2 * 3), порядок 12. Перекос шестиугольник является перекос многоугольник с шестью вершинами и ребрами , но не существующие на одной и той же плоскости. Внутренняя часть такого шестиугольника обычно не определяется. Перекос зигзаг шестиугольник имеет вершины чередующихся между двумя параллельными плоскостями.
Внутренняя часть такого шестиугольника обычно не определяется. Перекос зигзаг шестиугольник имеет вершины чередующихся между двумя параллельными плоскостями.
Регулярный перекос шестиугольник является вершина-симметрический с равными длинами ребер. В трех измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых гранях треугольной антипризмы с той же симметрией D 3d , [2 + , 6], порядок 12.
Куб и октаэдр (такой же , как трехстороннее антипризма) имеют регулярные косые шестиугольники как Питрите полигоны.
Полигоны Петри
Правильный косой шестиугольник — это многоугольник Петри для этих правильных , однородных и двойственных многогранников и многогранников более высокой размерности , показанных в этих косых ортогональных проекциях :
Выпуклый равносторонний шестиугольник
Главная диагональ шестиугольника является диагональной , который делит шестиугольник в четырехугольники. В любом выпуклом равностороннем шестиугольнике (все стороны равны) с общей стороной a существует главная диагональ d 1 такая, что
В любом выпуклом равностороннем шестиугольнике (все стороны равны) с общей стороной a существует главная диагональ d 1 такая, что
- d 1 а ≤ 2 {\ displaystyle {\ frac {d_ {1}} {a}} \ leq 2}
и главную диагональ d 2 такую, что
- d 2 а > 3 . {\ displaystyle {\ frac {d_ {2}} {a}}> {\ sqrt {3}}.}
Многогранники с шестиугольниками
Не существует Платонова тела, состоящего только из правильных шестиугольников, потому что шестиугольники мозаичны , не позволяя результату «складываться». В архимедовых твердых частиц с некоторыми шестиугольными гранями являются усеченным тетраэдром , усеченный октаэдром , усеченный икосаэдром (из футбольного мяча и фуллерена известности), усеченный кубооктаэдра а усеченный икосододекаэдр . Эти шестиугольники можно рассматривать как усеченные треугольники, причем диаграммы Кокстера имеют вид а также .
Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например многогранник Гольдберга G (2,0):
Также есть 9 тел Джонсона с правильными шестиугольниками:
Галерея натуральных и искусственных шестиугольников
Смотрите также
Рекомендации
Внешние ссылки
Формула диагонали(квадрат, прямоугольник, куб и многоугольник) // Tutors.com
Формула диагонали для квадратов, прямоугольников, кубов и многоугольников
Многоугольники — это формы нашего мира. Компьютерные и телевизионные экраны, двери и листы бумаги — все это многоугольники. Также полезны диагонали многоугольников. Узнайте, как мгновенно узнать, сколько диагоналей может иметь любой многоугольник, используя эту формулу:
Количество диагоналей = n (n — 3) 2
Содержание
- Что такое простой многоугольник?
- Что такое диагональ?
Что такое простой многоугольник?
Простой многоугольник — это любая двумерная (плоская) форма, созданная только с прямыми сторонами, которые закрываются в пространстве, и со сторонами, которые не пересекаются друг с другом (если они пересекаются, это сложный многоугольник). Треугольник — это многоугольник. Дротик, воздушный змей, четырехугольник и звезда — все это многоугольники. Простые многоугольники могут быть вогнутыми или выпуклыми. Формула, которую мы будем использовать, работает для всех простых многоугольников.
Треугольник — это многоугольник. Дротик, воздушный змей, четырехугольник и звезда — все это многоугольники. Простые многоугольники могут быть вогнутыми или выпуклыми. Формула, которую мы будем использовать, работает для всех простых многоугольников.
Что такое диагональ?
Диагональ многоугольника — это линия, соединяющая вершину с несмежной вершиной. Итак, у треугольника, самого простого многоугольника, нет диагоналей. Вы не можете провести линию от одного внутреннего угла к любому другому внутреннему углу, который не является стороной треугольника. У следующего по простому четырехугольника две диагонали.Правильный или неправильный пятиугольник имеет пять диагоналей.
В выпуклых простых многоугольниках диагонали всегда будут внутри . Рассмотрим прямоугольную дверь. Вы можете провести линию от верхнего угла петли до нижнего противоположного угла. Вы также можете провести линию от нижнего угла петли до верхнего противоположного угла.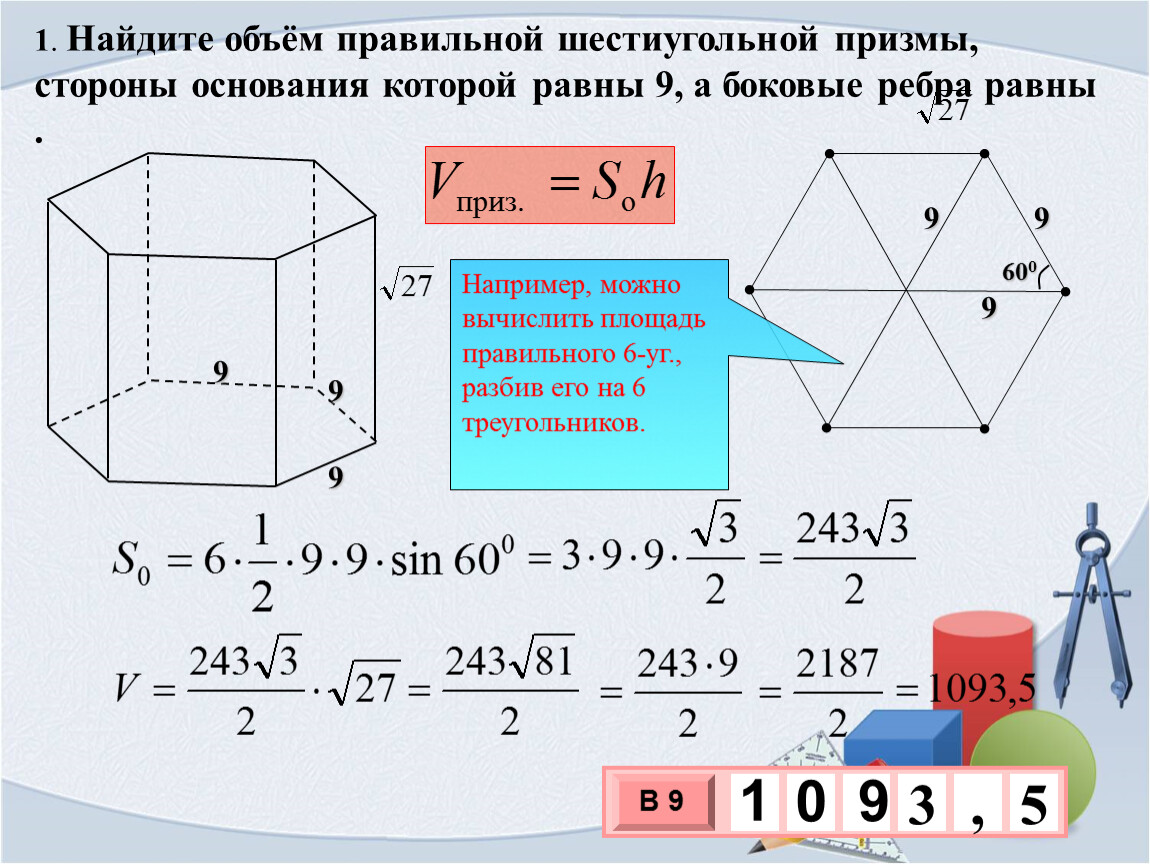 Это единственные возможные диагонали.
Это единственные возможные диагонали.
В вогнутых простых многоугольниках диагонали могут выходить на за пределы многоугольника , пересекать стороны и частично лежать на внешней стороне формы.Они по-прежнему диагонали. Дартс и звезды — типичные примеры вогнутых многоугольников, диагонали которых выходят за рамки их форм.
Не , а не попытайтесь применить эти концепции и нашу диагональную формулу к сложным многоугольникам (многоугольникам с самопересекающимися линиями).
Диагонали в реальной жизни
Квадраты и прямоугольники по диагонали добавляют прочности конструкции, будь то стена дома, мост или высокое здание. Вы можете увидеть диагональные тросы, которые используются для фиксации мостов.Когда строятся дома, ищите диагональные распорки, которые удерживают стены ровно и точно.
Книжные полки и строительные леса скреплены диагоналями. Чтобы кэтчер в софтболе или бейсболе выбросил бегуна на второй базе, кэтчер бросает по диагонали от домашней пластины до второй.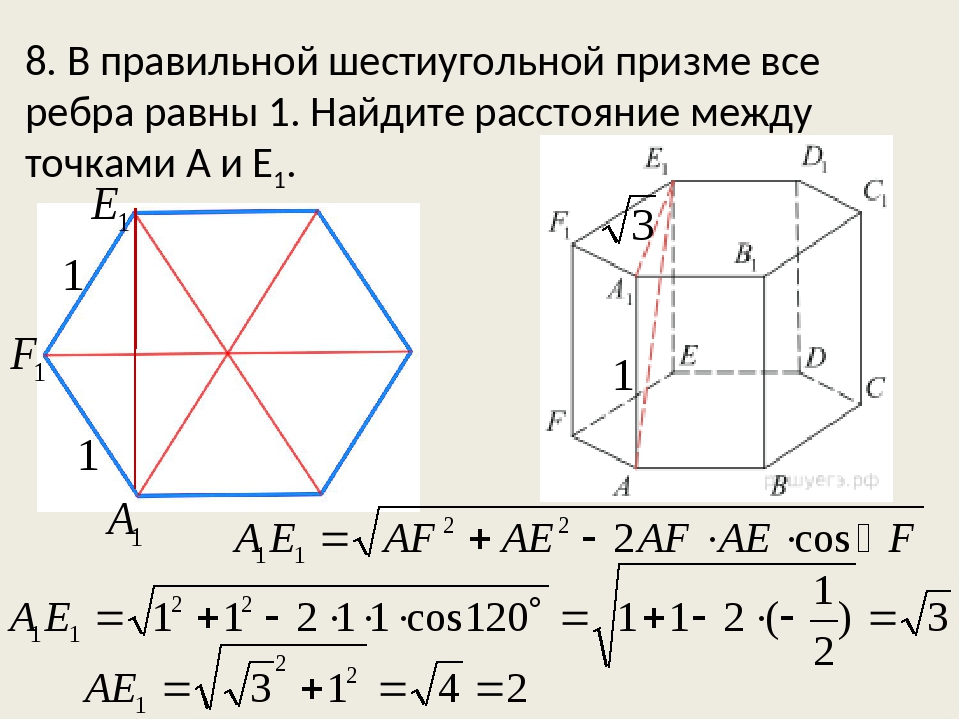
Экран телефона или компьютера, на котором вы просматриваете этот урок, измеряется по диагонали. 21-дюймовый экран никогда не сообщает вам ширину и высоту; это 21 дюйм от одного угла до противоположного.
Диагональ многоугольника формулы
Чтобы найти все возможные диагонали простого многоугольника с несколькими сторонами, вы можете легко их пересчитать. Когда многоугольник немного усложняется, их подсчет может быть очень трудным.
К счастью, существует простая формула, которая точно скажет вам, сколько диагоналей имеет многоугольник. Помните, что любая вершина (угол) соединена сторонами с двумя другими вершинами, поэтому эти соединения не могут считаться диагоналями. Эта вершина также не может соединиться с собой.Таким образом, для n сторон мы сразу уменьшим возможное количество диагоналей на три.
Мы также не хотим пересчитывать одну и ту же диагональ дважды. У нашей двери, например, всего две диагонали; Вы не учитываете переход от верхней петли к противоположной нижней и обратно. Вам придется разделить любой ответ на два.
Вам придется разделить любой ответ на два.
Диагональная формула
Это оставляет нам элегантную формулу, где n — количество сторон (или вершин):
Количество диагоналей = n (n — 3) 2
Как найти диагональ прямоугольника
Проверьте эту формулу с чем-нибудь, что мы знаем: диагоналями прямоугольника.Прямоугольник имеет четыре стороны и четыре вершины.
Количество диагоналей = n (n — 3) 2
= 4 (4–3) 2
= 4 (1) 2
= 42
= 2
Будьте скептичны! Попробуйте для пятиугольника (пять сторон):
= 5 (5–3) 2
= 5 (2) 2
= 102
= 5
У пятиугольника всего пять диагоналей; наша формула работает.
Будь действительно скептически! Попробуйте его для тетраконтакаи-гептагона, смехотворно длинного (но правильного) названия 47-угольника:
.= 47 (47 — 3) 2
= 47 (44) 2
= 2,0682
= 1,034
Доверяйте формуле. У 47-угольника 1034 диагонали. Эта формула работает каждый раз, чтобы точно сказать, сколько диагоналей можно построить внутри (или снаружи) любого простого многоугольника, независимо от того, является ли форма выпуклой или вогнутой.
У 47-угольника 1034 диагонали. Эта формула работает каждый раз, чтобы точно сказать, сколько диагоналей можно построить внутри (или снаружи) любого простого многоугольника, независимо от того, является ли форма выпуклой или вогнутой.
Диагональ прямоугольника по формуле
Для прямоугольников l — длина прямоугольника, а b — высота прямоугольника.
Диагональ прямоугольника = l2 + b2
Диагональ квадратной формулы
Теперь давайте рассмотрим несколько различных формул диагонали, чтобы найти длину диагонали.
Диагональ квадрата = a2
Где — сторона квадрата.
Диагональ куба Формула
Для куба диагональ находим, используя трехмерную версию теоремы Пифагора / формулу расстояния:
Диагональ куба = s2 + s2 + s2
Краткое содержание урока
Вы узнали много нового об особо важных частях многоугольников, их диагоналях. Теперь вы знаете, как определить диагонали любого многоугольника, какие есть примеры диагоналей из реальной жизни и как использовать формулу: # of Diagonals = n (n — 3) 2, где n — количество сторон. (или вершины) многоугольника.Кроме того, мы кратко рассмотрели диагональные форумы, чтобы найти длину диагонали в кубах, квадратах и прямоугольниках.
(или вершины) многоугольника.Кроме того, мы кратко рассмотрели диагональные форумы, чтобы найти длину диагонали в кубах, квадратах и прямоугольниках.
Следующий урок:
Как найти периметр многоугольника
Сколько диагоналей имеет каждый из следующих элементов? (B) Правильный шестиугольник
Нокаут NEET, май 2023 г. (легкая рассрочка)
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
5499 / —
купить сейчасKnockout JEE Main, апрель 2021 г.
 (один месяц)
(один месяц)Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасНокаут NEET, август 2021 г. (один месяц)
Персонализированный наставник с ИИ и адаптивное расписание,
Материал для самообучения,
Уроки выходного дня,
Наставничество от наших экспертов,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасKnockout JEE Main Май 2021 г.
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
22999 ₹ / — 9999 ₹ / —
купить сейчасНокаут NEET Август 2021
Персонализированный наставник с ИИ и адаптивное расписание,
Материал для самообучения,
Уроки выходного дня,
Наставничество от наших экспертов,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.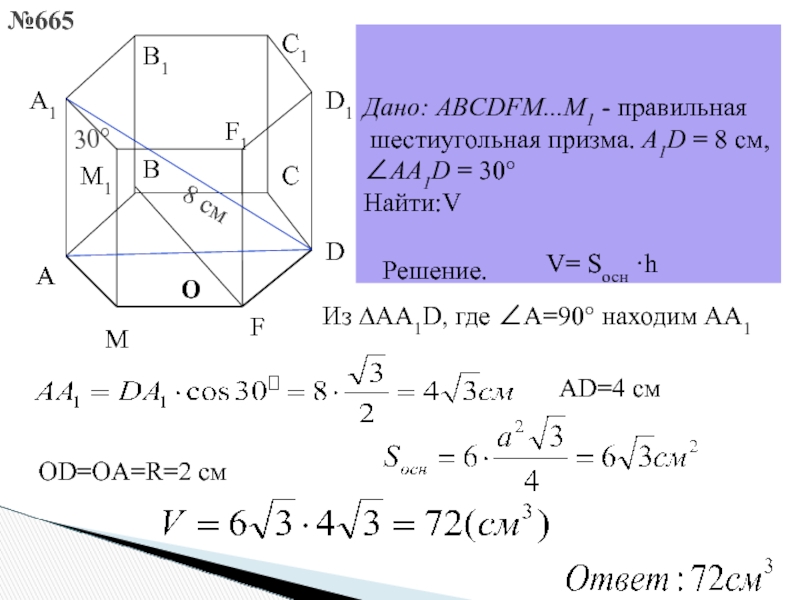
22999 ₹ / — 9999 ₹ / —
купить сейчасДано: Правильный шестиугольник ABCDEF с диагональю A ¯ C ¯ и внешней стороной ∠ 1.Докажите: m ∠ 2 + m ∠ 3 = m ∠ 1
73-75 Обсудите кривую, следуя указаниям раздела 3.5. y = exsinx, 0x2
Исчисление (список курсов MindTap)
Найдите b. 9. | а | = 7, | б | = 4, угол между a и b равен 30
Calculus: Early Transcendentals
Спрос Функция спроса на товар равна p = 14,751 + 0,01x, x0, где p — цена за единицу, а x — число …
Исчисление: прикладной подход (список курсов MindTap)
SOC Результаты 15 респондентов по четырем переменным приведены здесь. Эти оценки были взяты из общедоступного …
Эти оценки были взяты из общедоступного …
Essentials Of Statistics
Найдите значения x, для которых ряд сходится. Найдите сумму ряда для этих значений x. 60. n = 0 (…
Многопараметрическое исчисление
Полукруг диаметром PQ расположен на равнобедренном треугольнике PQR, образуя область в форме двумерного …
Исчисление с одной переменной: ранние трансцендентальные методы, том I
(a) Что не так в следующем уравнении? X2 + x6x2 = x + 3 (b) С учетом части (a) объясните, почему уравнение li…
Исчисление одной переменной
В упражнениях 1-4 используйте график функции f, чтобы найти приближения заданных значений. а. е (2) б. f (0) c …
Конечная математика и прикладное исчисление (список курсов MindTap)
Перепишите каждое выражение в упражнении 116 как единое рациональное выражение, максимально упрощенное. x21x2 …
Конечная математика
Рассмотрим систему компонентов, связанных, как показано на рисунке. Компоненты 1 и 2 подключены…
Компоненты 1 и 2 подключены…
Вероятность и статистика для инженерии и науки
Повторить упражнение 3 в движении снаряда для случая, когда бомбардировщик смотрит в сторону от стартовой площадки, так как …
Расчет: ранние трансцендентные функции
Солнце В ресторане Rise 10 столов на 6 человек каждый плюс 12 столов на 4 человека каждый. Каждый серв …
Элементарная техническая математика
В упражнениях с 53 по 62 найдите количество элементов каждого из следующих наборов.Для некоторых упражнений вам может потребоваться c …
Mathematical Excursions (MindTap Course List)
В Упражнениях 3148, (а) множить данное выражение, и (б) установить выражение, равное нулю, и решить для .. .
Прикладное исчисление
Вычисление производных Найдите следующее для данной функции f: (a) f (a), где a находится в области f, an …
Precalculus: Mathematics for Calculus (Standalone Book)
Исследователь проводит исследование с независимыми измерениями, сравнивая два лечения, и сообщает статистику t как t (2. ..
..
Статистика для поведенческих наук (список курсов MindTap)
Статистическая грамотность Марси провела исследование стоимости хлопьев для завтрака. Она записала затраты на несколько …
Основные сведения о статистике
Для задач 51-78 упростите каждое числовое выражение. Задача 3 3 3 + 4685
Intermediate Algebra
Исследования показали сильные гендерные различия в подходах подростков к решению проблем психического здоровья…
Основы статистики для поведенческих наук (список курсов MindTap)
Найдите производные функций в задачах 1-32. Упростите и выразите ответ, используя положительный показатель степени …
Математические приложения для менеджмента, жизни и социальных наук
В упражнениях 73-80 найдите указанные пределы, если они существуют. 80. limx2x21x3 + x2 + 1
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
`68.Использование двух методов Интегрируйте x4xdx (a) по частям, позволяя dv = 4xdx.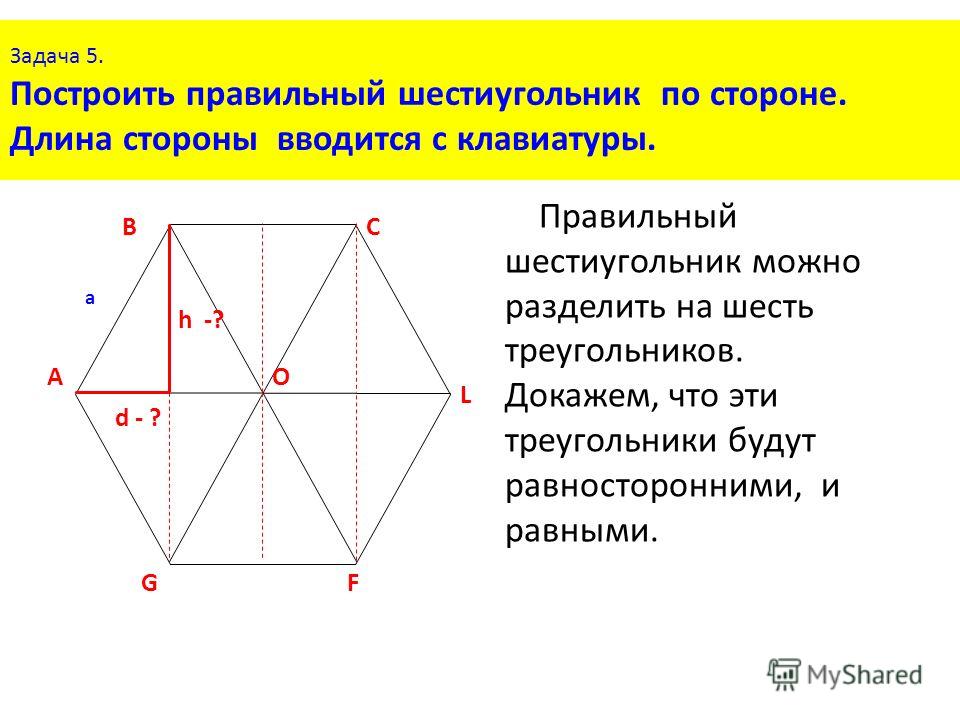 (б) заменой, положив u = 4 + x2.
(б) заменой, положив u = 4 + x2.
Исчисление одной переменной
Докажите, что сложение коммутативно в Q.
Элементы современной алгебры
Найдите объем, полученный вращением области, ограниченной кривыми вокруг данной оси. 64.y = secx, y = cosx, 0x …
Исчисление с одной переменной: ранние трансцендентальные методы
Завершите упражнения 25–30, поскольку они относятся к методу амортизации, основанному на единицах продукции.Округлить до ближайшего …
Contemporary Mathematics for Business & Consumers
Для каждого из следующих уравнений решите (a) все решения в градусах и (b), если 0360. Приближайте все ответы …
Тригонометрия (MindTap Список курсов)
Иногда, всегда или никогда: Если {an} возрастает и ограничено сверху, то {an} сходится.
Учебное пособие по многомерному исчислению Стюарта, 8-я
Расстояние между параллельными плоскостями Покажите, что расстояние между параллельными плоскостями ax + by2 + cz + d1 = 0andax + by + cz + d. ..
..
Исчисление: ранние трансцендентные функции (список курсов MindTap)
В упражнении 17-31 решите каждую задачу линейного программирования симплексным методом. Максимизируйте P = 3x + 3y + 4z при условии …
Конечная математика для управленческих, жизненных и социальных наук
For, f ′ (x) =
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные методы, 8-е
В начале этой главы (стр. 186) мы описали исследование, сравнивающее эффективность изучения материала…
Методы исследования поведенческих наук (Список курсов MindTap)
Для сборки предмета мебели деревянный колышек необходимо вставить в предварительно просверленное отверстие. Предположим, что диаметр …
Введение в статистику и анализ данных
Дивидендная доходность — это годовой дивиденд, выплачиваемый компанией, выраженный в процентах от цены акций (Di …
Статистика для бизнеса и экономики, Пересмотрено (Список курсов MindTap)
ИЗУЧЕНИЕ ПОНЯТИЙ Приближение В упражнениях 79 и 80 определите, какое значение лучше всего приближается к области th.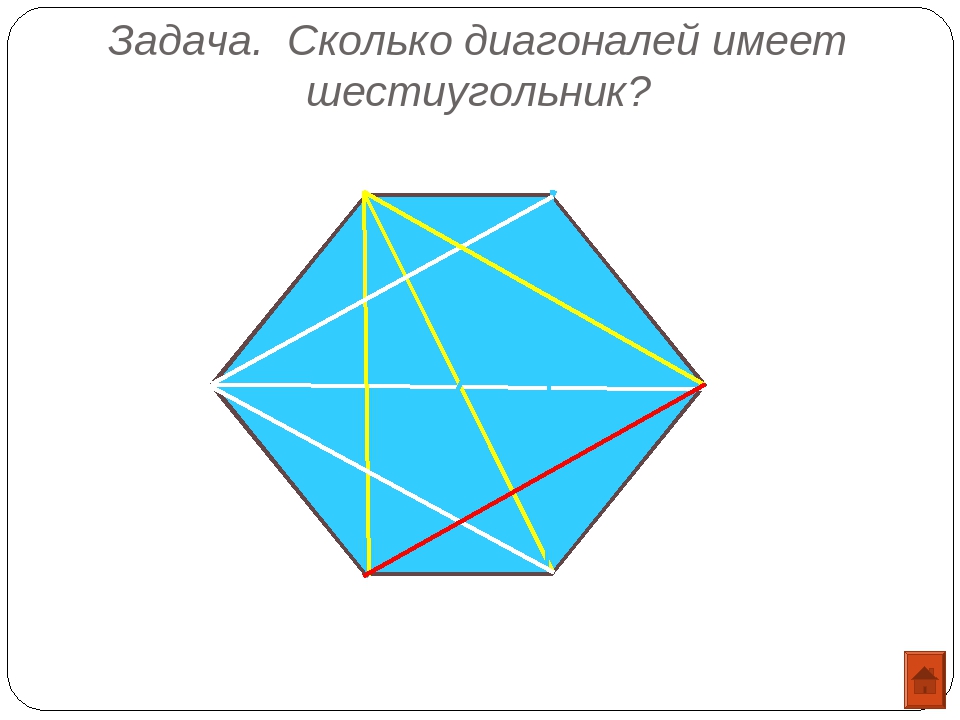 ..
..
Исчисление (список курсов MindTap)
Определите три основных метода ограничения смешения за счет индивидуальных различий между субъектами ex …
Методы исследования поведенческих наук (список курсов MindTap)
Поиск основного блока Вектор нормали В упражнениях 15-20 найдите вектор нормали главной единицы к кривой …
Многопараметрическое исчисление
Здесь показаны дни до погашения для выборки из пяти фондов денежного рынка.Суммы в долларах, вложенные в …
СТАТИСТИКА F / БИЗНЕС + ЭКОНОМИКА-ТЕКСТ
Увеличьте следующие термины до указанной степени и объедините аналогичные термины, где это возможно. [(x 2) 3 (y 3) 2] 2
Математика для машинной техники
Упражнение Используйте график для определения области и диапазона функций.
College Algebra (Список курсов MindTap)
Поиск неопределенного интеграла В упражнениях 91-108 найдите неопределенный интеграл. ex + exexexdx
Calculus
Графики степенных функций Упражнения с S-1 по S-6 имеют дело с графиками степенных функций.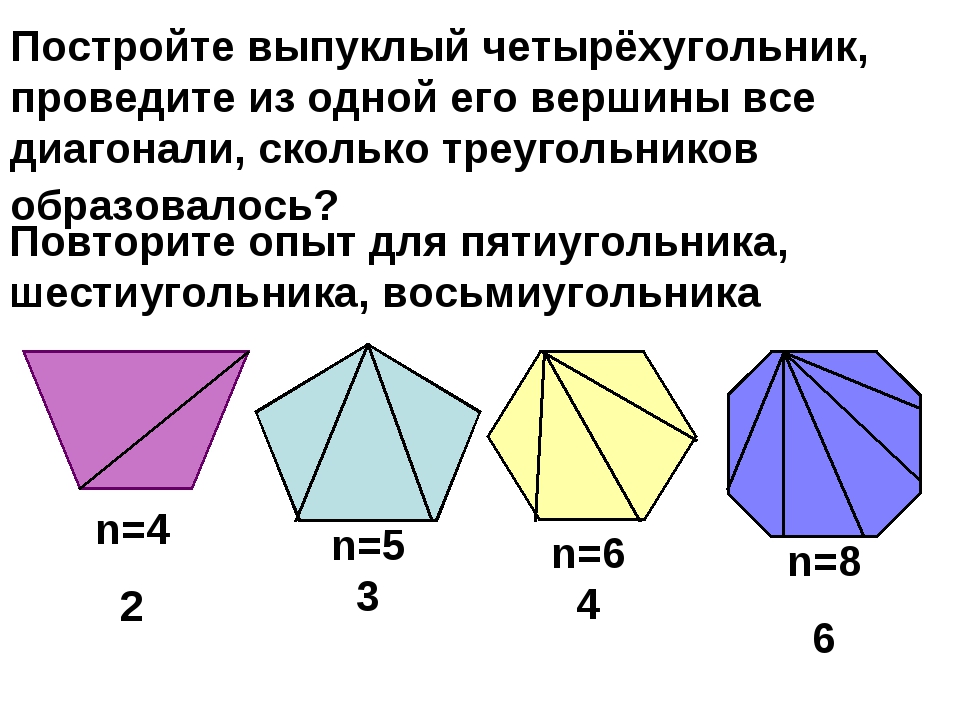 Нарисуйте график cx …
Нарисуйте график cx …
Функции и изменения: подход к моделированию алгебры колледжа (список курсов MindTap)
В Задаче 2124 убедитесь, что указанное семейство функций является решением данного дифференциального уравнения …
Первый курс по дифференциальным уравнениям с приложениями для моделирования (список курсов MindTap)
Результаты вступительных экзаменов в колледж. Предположим, что результаты вступительного испытания в колледж обычно распределяются …
Основы статистики для бизнеса и экономики
В упражнениях 1–14 найдите будущую стоимость данного аннуитета.Обычная рента, 100 ежемесячных выплат, 578 меж …
Математика: практическая одиссея
Ниже приведены результаты опроса 1364 человек, которых спросили, используют ли они социальные сети и другие веб-сайты …
Современная бизнес-статистика с Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)
In каждый из 5-13 либо рисует граф с указанными свойствами, либо объясняет, почему такого графа не существует. Simple g …
Simple g …
Дискретная математика с приложениями
В следующих упражнениях используйте теорему вычисления, чтобы выразить интеграл как функцию F (x).190. axt2dt
Calculus Volume 2
В следующих упражнениях используйте прямую замену для оценки каждого предела. 92. limx3Ine3x
Calculus Volume 1
Нахождение миноров и кофакторов матрицы: в упражнениях 29-34 найдите все (a) минорные и (b) кофакторы …
College Algebra
Определите оба типа Ошибки I и II типа для следующего сценария: предположить нулевую гипотезу H0. в котором говорится …
Вступительная статистика
Характеристика правильных n -угольников, пары диагоналей которых либо совпадают, либо несоизмеримы
Анатриелло, Дж., Лаудано, Ф., Винченци, Дж .: Sur l ’несоразмерный dans les polygones réguliers. Квадратура 115 , 1–5 (2020)
Google Scholar
Бертон, Д.: Элементарная теория чисел. Макгроу-Хилл, Нью-Йорк (2012)
Макгроу-Хилл, Нью-Йорк (2012)
Google Scholar
Barbeau, E.J .: Доказательство несоизмеримости: шаблон, который исчезает. Math Mag. 56 (2), 82–90 (1983)
MathSciNet Статья Google Scholar
Беккер, Л.К., Беккер, К.Б .: Энциклопедия этики. Рутледж, Нью-Йорк (2013)
Книга Google Scholar
Филеп, Л .: Теория пропорций в греческой математике. Acta Math. Акад. Paedaog. Нихази. (Н.С.). 19 (2), 167–174 (2003)
MathSciNet МАТЕМАТИКА Google Scholar
Фонтейн, А., Херли, С .: Доказательство изображением: произведение и обратные величины соотношений длины диагонали в правильном многоугольнике.Форум Geom. 6 , 97–101 (2006)
MathSciNet МАТЕМАТИКА Google Scholar

Хэвил, Дж .: Иррациональные. Princeton University Press, Princeton (2012)
MATH Google Scholar
Harborth, H .: Diagonalen im Regaren \ (n \) — Eck. Elem. Математика. 24 , 104–109 (1969)
MathSciNet МАТЕМАТИКА Google Scholar
Heineken, H .: Regelmässige Vielecke und ihre Diagonalen II. Ренд. Сем. Мат. Univ. Падуя 41 , 332–344 (1968)
MathSciNet МАТЕМАТИКА Google Scholar
Кеплер, Дж .: Harmonices Mundi. В: Линц Л.В. (ред.) anastatica: Брюссель, Культура и цивилизация, 1968; Болонья, Форни (1969)
Лагерлунд, Х .: Энциклопедия средневековой философии: философия между 500 и 1500 годами. Спрингер, Берлин (2010)
Google Scholar
Нивен, И .: Иррациональные числа. Математическая монография Каруса. Математическая ассоциация Америки. Вили, Хобокен (1956)
Математическая ассоциация Америки. Вили, Хобокен (1956)
Нивен И., Цукерман Х.С., Монтгомери Х.Л .: Введение в теорию чисел, 5-е изд. Уайли, Нью-Йорк (1991)
MATH Google Scholar
Ригби, Дж. Ф .: Множественные пересечения диагоналей правильных многоугольников и связанные темы. Геом. Dedicata 9 , 207–238 (1980)
MathSciNet Статья Google Scholar
Стиллвелл, Дж .: Числа и геометрия. UTM, Springer (1998)
Фон Фриц, К .: Открытие несоизмеримости гиппазом метапонта. Аня. Математика. Второй сер. 46 (2), 242–264 (1945)
MathSciNet Статья Google Scholar
Сяо, Дж .: Элементарная теория чисел. Международная пресса Бостона, Бостон (2010)
Google Scholar
Убийственная математика: самая длинная диагональная формула!
Убийственная математика: самая длинная диагональная формула! В книге ММ «Идеальная колбаса и другие основные формулы» есть две формулы для определения наибольшей диагонали правильного многоугольника.
Если у правильного многоугольника ЧЕТНОЕ количество сторон …
… тогда самая длинная диагональ равна диаметру описанной окружности, т. Е. Окружности, проходящей полностью снаружи. Это связано с тем, что самая длинная диагональ довольно удобно проходит через центр круга. Это упрощает жизнь, поскольку формула для диаметра описанной окружности хорошо известна, и вы можете найти ее на множестве других веб-сайтов.
Проблема в том, что у «Убийственной математики» есть ПРОФЕССОР ФИЕНДИШ, который создает проблемы, и он заставил нас выяснить, какая диагональ самая длинная в , если у многоугольника нечетное число сторон . Сначала у нас была действительно УЖАСНАЯ формула …
Но, к счастью, нас спасли наши друзья Мэтт Кимптон и Том Винч. (Между прочим, мама Мэтта Дайана Кимптон — наш постоянный эксперт по математике в серии MM.)
Посмотри на эту красавицу .. .!
.!
Это намного аккуратнее и проще, но дает точно такие же результаты!
Так как же Мэтт и Том с этим справились?
Для начала вам нужно немного разобраться в простой алгебре и тригонометрии, поэтому поспешите и прочтите «Призрак Икс» и «Дьявольский англетрон». Затем нарисуйте (или представьте) любой многоугольник с нечетным числом сторон. Мы показали вам пятиугольник с пятью сторонами, а также семиугольник с семью сторонами, чтобы показать, что их метод работает с любым из них.
На что следует обратить внимание на обеих диаграммах:
- сторона CD находится напротив точки A, а сторона DE — напротив точки B
- все углы, отмеченные буквой «а», равны на каждой диаграмме.
- Каждый из больших углов A и B многоугольника имеет угол «a», взятый из середины. Следовательно, по симметрии все углы, отмеченные буквой «b», на каждой диаграмме равны
- линия AB продлена до Z
- Треугольники ACD и BDE равнобедренные.

- Треугольники DYA и DYB соответствуют прямоугольным треугольникам
Ну вот, тогда …
Большое спасибо Мэтту Кимптону и Тому Винчу за то, что они разработали это для нас!1 / Пусть количество сторон многоугольника будет нечетным, и назовите это н. Пусть длина каждой стороны будет равна «L», а самая длинная диагональ будет равна «d».
2 / Поскольку сумма углов в треугольнике равна 180 °, сложение углов в треугольнике ABD дает нам
УРАВНЕНИЕ I: 3a + 2b = 1803 / Продлите линию AB через точку B и завершите ее в новой точке Z.Угол между Z и ближайшей стороной многоугольника — это внешний угол многоугольника, который составляет (360 / n) º. (Это связано с тем, что внешний угол правильного многоугольника всегда равен центральному углу, как показано здесь и объясняется в разделе «Замкнутые круги».)4 / Углы на линии в сумме составляют 180 °, поэтому исследуя углы на B на линии ABZ дает нам
УРАВНЕНИЕ II: a + 2b + 360 / n = 1805 / Переместите (II) в 2b = 180-360 / n -a, а затем подставив это значение 2b в (I), получим 3a + 180-360 / n -a = 180.180 отменяют, а остальные перемещаются, чтобы дать
УРАВНЕНИЕ III: 2a = 360 / n6 / Прямая DY делит треугольник ABD пополам, поэтому угол ADY равен a / 2, а длина AY = половина AD = L / 2. Линия DA — это d, самая длинная диагональ, которую мы пытались проработать все это время, помните?7 / Тригонометрия говорит, что в прямоугольном треугольнике sin = противоположность / гипотенуза. Итак, в треугольнике AYD мы получаем
УРАВНЕНИЕ IV: sin (a / 2) = (L / 2) / d.8 / Переставьте (IV), чтобы получить d = L / 2sin (a / 2), и используйте (III), чтобы получитьУРАВНЕНИЕ V: d = L / 2sin (90 / n)
Злые круги и другие дикие формы
Идеальная колбаса и другие основные формулы
Главная страница указателя «Убийственная математика»
Правильные многоугольники | Блестящая вики по математике и науке
Площадь правильного многоугольника может быть найдена разными способами в зависимости от заданных переменных. \ circ} {n} \ right) = \ frac {n a s} {2}. \ _ \ square na2tan (n180∘) = 4ns2 кроватка (n180∘) = 2nR2 sin (n360∘) = 2nas. □
\ circ} {n} \ right) = \ frac {n a s} {2}. \ _ \ square na2tan (n180∘) = 4ns2 кроватка (n180∘) = 2nR2 sin (n360∘) = 2nas. □
Доказательство следует из использования переменной для вычисления площади равнобедренного треугольника и последующего умножения на nnn треугольников. Вот доказательство или вывод приведенной выше формулы площади правильного многоугольника.
На рисунке ниже показан один из равнобедренных треугольников nnn, образующих правильный многоугольник.
Длина стороны обозначена как sss, радиус обозначен как RRR, а половина центрального угла обозначена как θ \ theta θ.{2} \ big). \ _\квадратный \ end {align} Ap = 45 (62) cot6180∘ = 45⋅cot30∘≈77,9 (см2). □
Апофема правильного шестиугольника имеет размер 6. Найдите площадь шестиугольника.
Пусть CCC будет центром правильного шестиугольника, а ABABAB — одной из его сторон. Нарисуйте CA, CB, CA, CB, CA, CB и апофему CDCDCD (((которая, как вы должны помнить, перпендикулярна ABABAB в точке D) .
D) .D). Тогда, поскольку CA≅CBCA \ cong CBCA≅CB, △ ABC \ треугольник ABC △ ABC равнобедренный, и, в частности, для правильного шестиугольника ABC \ треугольник ABC △ ABC равносторонний.
Длина CDCDCD (((которая в данном случае также является высотой равностороннего △ ABC) \ треугольник ABC) △ ABC) составляет 32 \ frac {\ sqrt {3}} {2} в 23 раза больше длины одной стороны (((здесь AB) .AB) .AB). Таким образом, CD = 32AB ⟹ AB = 23CD = 233 (6) = 43. CD = \ frac {\ sqrt {3}} {2} {AB} \ подразумевает AB = \ frac {2} {\ sqrt {3}} {CD } = \ frac {2 \ sqrt {3}} {3} (6) = 4 \ sqrt {3}. CD = 23 AB⟹AB = 3 2 CD = 323 (6) = 43 . Теперь, когда мы нашли длину одной стороны, приступаем к поиску площади. Для этого есть (как минимум) 3 способа:
Первый метод: Используйте формулу периметра-апофемы .2} {2} \ sqrt {3} = 72 \ sqrt {3}. \ _ \ SquareA = 4ns2 cotn180∘ = 46s2 cot6180∘ = 23s2 cot30∘ = 23s2 3 = 723. □
Отправьте свой ответ
Какова площадь красной области, если площадь синей области равна 5?
Примечание: Шестигранник правильный. 2, x2, где xxx — целое положительное число.Найдите xxx.
2, x2, где xxx — целое положительное число.Найдите xxx.
Найдите правильный ответ на диагонали многоугольника в этом вопросе GMAT
В сегодняшнем посте давайте обсудим n-сторонние многоугольники и количество их диагоналей.
Мы обсудим следующее:
1. Как определить количество диагоналей n-стороннего многоугольника?
2. Сколько диагоналей покрывает каждая вершина?
3. Что произойдет, если одна или несколько вершин не образуют диагонали?
4.Как обрабатывать случаи, когда игнорируемые вершины смежны / не смежны?
Прежде всего, давайте начнем с довольно простого вопроса:
Для n-стороннего многоугольника сколько диагоналей у него будет?
У n-стороннего многоугольника n вершин. Если мы соединим каждую отдельную пару вершин, мы получим nC2 прямых. Эти nC2 прямых включают n сторон многоугольника, а также его диагонали.
Итак, количество диагоналей определяется выражением nC2 — n.
нК2 — п = п (п-1) / 2 — п = п (п — 3) / 2
Вы также можете думать об этом так: каждая вершина образует диагональ с (n — 3) вершинами.Он не образует диагональ между собой и двумя соседними вершинами с обеих сторон (поскольку он образует стороны с этими двумя). Получается n * (n — 3) диагоналей. Но здесь каждая диагональ учитывается дважды, по одному разу для каждой из двух ее вершин. Следовательно, мы делим n * (n — 3) на 2, чтобы получить фактическое количество диагоналей. Это еще один способ получить n (n — 3) / 2
Давайте рассмотрим несколько примеров, чтобы укрепить эту концепцию:
Пример 1: Сколько диагоналей у многоугольника с 25 сторонами?
№диагоналей = nC2 — n = n (n — 3) / 2 = 25 * (25-3) / 2 = 275
Пример 2: Сколько диагоналей у многоугольника с 20 сторонами, если одна из его вершин не отправляет диагональ?
Количество диагоналей 20-гранной фигуры = 20 * (20-3) / 2 = 170
Но одна вершина не передает диагоналей.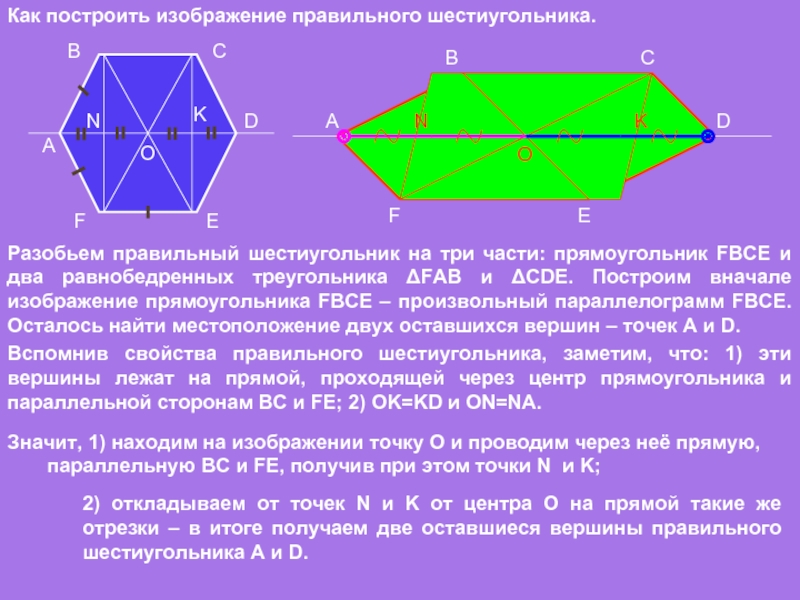 Каждая вершина образует диагональ с (n-3) другими вершинами — она не образует диагонали с 3 вершинами: сама, вершина непосредственно слева от нее и вершина непосредственно справа от нее.Со всеми остальными вершинами он образует диагональ. Итак, нам нужно убрать из общей суммы 20 — 3 = 17 диагоналей.
Каждая вершина образует диагональ с (n-3) другими вершинами — она не образует диагонали с 3 вершинами: сама, вершина непосредственно слева от нее и вершина непосредственно справа от нее.Со всеми остальными вершинами он образует диагональ. Итак, нам нужно убрать из общей суммы 20 — 3 = 17 диагоналей.
Общее количество диагоналей, если одна вершина не образует диагоналей = 170 — 17 = 153 диагонали.
Мы надеемся, что все, что было сделано до сих пор, имеет смысл, чтобы мы могли немного развить концепцию. Теперь давайте дадим нам вопрос с двумя решениями и двумя разными ответами. Мы должны найти правильный ответ и объяснить, почему другой ошибается.
Вопрос: Сколько диагоналей имеет многоугольник с 18 сторонами, если три его смежные друг с другом вершины не имеют диагоналей?
Ответ: Мы будем использовать два разных метода для решения этого вопроса:
Метод 1: Используя формулу, описанную выше
Количество диагоналей в многоугольнике из 18 сторон = 18 * (18-3) / 2 = 135 диагоналей
Каждая вершина образует диагональ с n-3 другими вершинами — как обсуждалось ранее.
Итак, каждая вершина будет составлять 15 диагоналей.
Общее количество диагоналей, если 3 вершины не отправляют диагонали = 135-15 * 3 = 135-45 = 90 диагоналей.
Метод 2:
У многоугольника 18 вершин. 3 вершины не участвуют, поэтому нам нужно сделать все диагонали с 15 вершинами.
Количество линий, которые мы можем сделать с 15 вершинами = 15C2 = 15 * 14/2 = 105
Но эта 105 включает и стороны. Многоугольник с 18 вершинами имеет 18 сторон.Поскольку 3 соседние вершины не участвуют, 4 стороны не будут сформированы. У 15 вершин будет 14 сторон, которые будут частью из 105, которые мы вычислили ранее.
Общее количество диагоналей, если 3 вершины не отправляют диагонали = 105 — 14 = 91
Обратите внимание, что два ответа не совпадают. Метод 1 дает нам 90, а метод 2 дает нам 91. Оба метода выглядят правильными, но на самом деле правильным является только один, а правильный — метод 2. Итак, в чем проблема с методом 1?
Когда мы вычитаем 45 из 135 (для каждой из 15 диагоналей, образованных тремя вершинами, которые нам нужно игнорировать), мы дважды считаем 1 диагональ на этом рисунке, равном 45. На самом деле нам нужно вычесть только 44 диагонали. По какой диагонали мы учитываем дважды? Та, которая соединяет 2 из трех игнорируемых вершин. Попробуйте создать многоугольник с несколькими вершинами. Сделайте несколько диагоналей. Удалите 3 вершины рядом друг с другом. Две из трех вершин, между которыми есть вершина, будут соединены диагональю. Когда мы удаляем 15 диагоналей для каждой вершины, мы удаляем эту диагональ дважды.
На самом деле нам нужно вычесть только 44 диагонали. По какой диагонали мы учитываем дважды? Та, которая соединяет 2 из трех игнорируемых вершин. Попробуйте создать многоугольник с несколькими вершинами. Сделайте несколько диагоналей. Удалите 3 вершины рядом друг с другом. Две из трех вершин, между которыми есть вершина, будут соединены диагональю. Когда мы удаляем 15 диагоналей для каждой вершины, мы удаляем эту диагональ дважды.
Следовательно, нам нужно 135 — 44 = 91.
Правильный ответ — 91 диагональ.
Имейте в виду, мы предположили, что удаленные вершины находятся рядом друг с другом. В противном случае ответ был бы другим, поскольку двойного счета было бы больше. Давайте рассмотрим это на примере.
Вопрос: Сколько диагоналей имеет многоугольник с 18 сторонами, если три его несмежные вершины не посылают диагоналей? (Две из трех вершин не находятся рядом друг с другом)
Количество диагоналей в многоугольнике из 18 сторон = 18 * (18-3) / 2 = 135 диагоналей
Каждая вершина образует диагональ с n-3 другими вершинами — как обсуждалось ранее.
Итак, каждая вершина будет составлять 15 диагоналей.
Поскольку 3 вершины не учитываются, они не отправят каждую из этих 15 диагоналей, то есть 45 диагоналей. Но в этой цифре 45 мы дважды посчитали 3 диагонали. Чтобы понять это, мы нумеруем вершины от 1 до 18. Скажем, мы опускаем вершины 1, 4 и 16.
Вершина 1 образует диагонали с вершинами 3, 4, 5… 16, 17 (всего 15 диагоналей)
Вершина 4 образует диагонали с вершинами 6, 7, 8,… 16, 17, 18, 1, 2 (всего 15 диагоналей)
Вершина 16 образует диагонали с вершинами 18, 1, 2, 3, 4,… 15, 16 (всего 15 диагоналей)
Из 45 вершин мы дважды посчитали диагональ вершин 1 и 4.Мы также дважды посчитали диагональ вершин 1 и 16 и дважды диагональ вершин 4 и 16. Итак, в нашем рисунке 45 мы дважды подсчитали 3 диагонали. Нам нужно вычесть только 42 диагонали из 135.
Общее количество диагоналей, если 3 вершины не отправляют диагонали = 135 — 42 = 93 диагонали.
Ответ — 93 диагонали.
Обратите внимание, что в предыдущем примере только 1 диагональ учитывалась дважды, а здесь 3 диагонали учитывались дважды. Поймите, почему — в предыдущем примере, поскольку вершины были смежными, они составляли стороны многоугольника.Итак, предполагая, что вершины 1, 2 и 3 были проигнорированы, 1 и 2 соединены, чтобы образовать сторону многоугольника, а 2 и 3 соединены, чтобы образовать сторону многоугольника. Только вершины 1 и 3 соединились в диагональ, поэтому диагональ учитывалась дважды. В нашей формуле n (n — 3) / 2 мы уже избавились от сторон, поэтому они вообще не появляются на картинке. Формула дает нам только количество диагоналей. Итак, в предыдущем примере мы уже проигнорировали две стороны, образованные смежными вершинами (когда мы использовали формулу n (n-3) / 2), и должны были позаботиться о двойном подсчете только одной диагонали.В этом примере каждая игнорируемая вершина образовывала диагональ с другой игнорируемой вершиной, и, следовательно, нам пришлось обрабатывать двойной подсчет 3 диагоналей.
Поймите, почему — в предыдущем примере, поскольку вершины были смежными, они составляли стороны многоугольника.Итак, предполагая, что вершины 1, 2 и 3 были проигнорированы, 1 и 2 соединены, чтобы образовать сторону многоугольника, а 2 и 3 соединены, чтобы образовать сторону многоугольника. Только вершины 1 и 3 соединились в диагональ, поэтому диагональ учитывалась дважды. В нашей формуле n (n — 3) / 2 мы уже избавились от сторон, поэтому они вообще не появляются на картинке. Формула дает нам только количество диагоналей. Итак, в предыдущем примере мы уже проигнорировали две стороны, образованные смежными вершинами (когда мы использовали формулу n (n-3) / 2), и должны были позаботиться о двойном подсчете только одной диагонали.В этом примере каждая игнорируемая вершина образовывала диагональ с другой игнорируемой вершиной, и, следовательно, нам пришлось обрабатывать двойной подсчет 3 диагоналей.
Мы надеемся, что все это вам понятно, и теперь вы сможете легко решить любой вопрос, касающийся диагоналей многоугольников.

 Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности. {2}. \ end {align}}}
{2}. \ end {align}}} {4 }.}
{4 }.}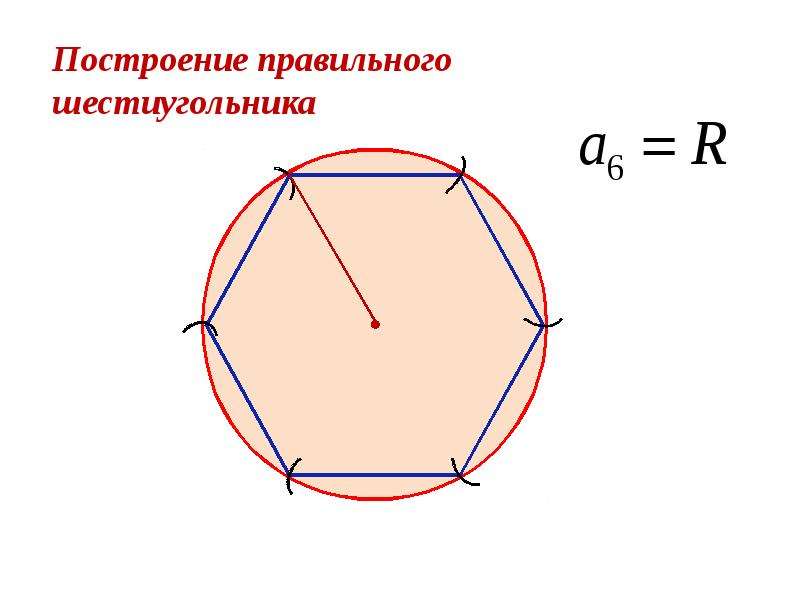
 180 отменяют, а остальные перемещаются, чтобы дать
180 отменяют, а остальные перемещаются, чтобы дать D) .D). Тогда, поскольку CA≅CBCA \ cong CBCA≅CB, △ ABC \ треугольник ABC △ ABC равнобедренный, и, в частности, для правильного шестиугольника ABC \ треугольник ABC △ ABC равносторонний.
D) .D). Тогда, поскольку CA≅CBCA \ cong CBCA≅CB, △ ABC \ треугольник ABC △ ABC равнобедренный, и, в частности, для правильного шестиугольника ABC \ треугольник ABC △ ABC равносторонний.